Test charge driven response of a dusty plasma with polarization force

Ali, S.; Masood, W.; Singh, K.; Jahangir, R.

doi:10.3389/fspas.2022.987561

ORIGINAL RESEARCH article

Front. Astron. Space Sci., 11 October 2022
Sec. Low-Temperature Plasma Physics
Volume 9 - 2022 | https://doi.org/10.3389/fspas.2022.987561

Test charge driven response of a dusty plasma with polarization force

S. Ali^1,2

W. Masood³* www.frontiersin.org

K. Singh²

R. Jahangir¹

¹National Centre for Physics at Quaid-e-Azam University Campus, CoE Physics, Islamabad, Pakistan
²Department of Mathematics, College of Arts and Sciences, Khalifa University of Science and Technology, Abu Dhabi, United Arab Emirates
³Department of Physics, COMSATS University, Islamabad Campus, Islamabad, Pakistan

By using the framework of kinetic model, the test charge driven response of a dusty plasma is evaluated in the presence of polarization force. The plasma containing electrons, singly ionized positive ions, and highly charged negative dust particulates is known as a dusty plasma, which can be perturbed by a test particle of charge q_T moving with velocity v_T along the z-axis. The polarization force purely comes from the high charging state of micron-sized dust particles, causing a deformation of shielding length due to density gradient and modifying the collective motion and particulates’ acceleration. The application of Fourier transformation technique to the set of dynamical equations may result in the shielded potential for a test charge with a modified dielectric constant. Several possibilities have been explored to evaluate the shielded potentials by imposing different conditions on the test charge speed in comparison with the thermal speeds of plasma species. It is found that the profiles of wakefield, Debye-Hückel and farfield (FF) potentials are strongly modified by the polarization force coefficient via the dust charging state and dust concentration. The present findings are useful in the study of strongly coupled dusty plasma, where micron-sized negatively charged dust grains are characterized by a high charging state.

1 Introduction

Most of the solid matter in the solar system indicates the presence of dust particles. In the gaseous form, the matter is ionized and dust particles coexist with it to give rise to the formation of dusty plasmas (Goertz, 1989). The dust particles are at least 10 to 12 orders of magnitude more massive than the ions (Goertz, 1989) and therefore, a unique situation arises that leads to the emergence of new spatio-temporal scales and hence new normal modes in the system. Dust particles are originally neutral, while the fragile and slippery electrons (whose electron thermal velocity is comparatively larger than the ion thermal velocity) stick onto the surface of dust to acquire a negative charge. However, there are instances where positively charged dust particles are also reported, for instance, on Jupiter (Horányi et al., 2004). Many new phenomena are associated with waves and instabilities in astrophysical and space environments due to the inclusion of dust components (Rao et al., 1990; Shukla, 2001). The most fundamental normal modes in a dusty plasma are the dust-acoustic (DA) (Rao et al., 1990) and dust-ion-acoustic (DIA) (Shukla and Silin, 1992) modes, which have been observed in laboratory experiments (Barkan et al., 1995; Barkan et al., 1996). Several distinct features of the linear waves have been confirmed later by analytical and experimental analyses (Shukla and Mamun, 2002) and new characteristics for nonlinear waves were explained by using various plasma compositions including the nonthermal character and magnetic field effects in dusty plasmas (Barkan et al., 1995; Barkan et al., 1996; Shukla and Mamun, 2002; Shukla and Mamun, 2003; Masood et al., 2010a; Masood et al., 2010b; Masood and Mirza, 2010; Masood et al., 2012; Sabeen et al., 2017; Nawaz et al., 2022; Shohaib et al., 2022).

The electrostatic potential in the close proximity of a free electron is the single-particle Coulomb potential (Clemmow and Dougherty, 1969; Chen, 1974). In case of plasmas, there are a number of moving charges that contribute to the field at any point and, therefore, the combined potential field at a certain location for a particular electron rapidly changes with time. It is extremely difficult to give an exact description of the fluctuating microfield in the vicinity of any given electron, however, the averaged, say over a time, value of the microfield and a volume adequate to contain a large number of particles, the fluctuating field can become sizeable and of practical interest (Clemmow and Dougherty, 1969). It is well-known that the effect of a single electron and its associated field in the presence of many other electrons is heavily shielded in the plasma. Such shielding is termed Debye shielding and it wards off the effect of an externally applied potential much quicker in the plasma (Neufeld and Ritchie, 1955; Joyce and Montgomery, 1967; Montgomery et al., 1968; Clemmow and Dougherty, 1969; Cooper, 1969; Kan, 1971; Laingal et al., 1971; Stenflo et al., 1973; Yu et al., 1973; Chen, 1974). This effect is intimately related to the effect of charged grains in dusty plasmas (Chen et al., 2001; Stoffels et al., 2001; Denysenko et al., 2005), in satellites and re-entry vehicles in space and ionosphere (Al’Pert et al., 1963; Liu, 1965; Gurevich et al., 1969).

It is to be noted that the expression for the Debye shielding due to a charged particle was obtained by considering it as static charge and infinitesimally small. In such a situation, the ambient plasma often acts as a Maxwellian plasma having the plasma species in thermal equilibrium. In a variety of physical situations, there could be a partial breakdown of Debye shielding for test charges, for instance, when the charge is moving or the plasma is inhomogeneous, anisotropic, collisional, magnetized, etc. (Neufeld and Ritchie, 1955; Joyce and Montgomery, 1967; Montgomery et al., 1968; Cooper, 1969; Kan, 1971; Laingal et al., 1971; Stenflo et al., 1973; Yu et al., 1973). Stenflo and Yu (Stenflo et al., 1973) utilized the Bhatnager-Gross-Krook (BGK) model (Bhatnagar et al., 1954) to investigate the electrostatic shielding of a slowly moving test charge in a collisional plasma and showed a parametric regime in which the Debye shielding could break down and lead to the possibility of completely unshielded charge along the direction of its motion. Such an occurrence could seriously affect the theories of charged-particle collisions that rely on the Debye cutoff in the interaction range. In other cases, the resonant interaction of the test charge with a plasma wave gives rise to an oscillatory wakefield behind the test particle. The wake potential was initially introduced by Nambu and Akama (Nambu and Akama, 1985). Since then, many investigations have been made to explain the wakefield potential distribution in different scenarios (Lemons et al., 2000; Ali, 2009; Ali, 2016). The dielectric response function and modified potential distribution around a test charge have also been studied in strongly coupled unmagnetized and magnetized dusty plasmas (Shahmansouri et al., 2017; Shahmansouri and Khodabakhshi, 2018; Shahmansouri, 2019).

The polarization force for dust particles arises on account of the deformation of the Debye sheath for density gradient. The polarization force is negligibly small for electrons and ions but becomes significant for dust species due to the higher charging state in complex plasmas. The polarization force on the dust particles can be written (Hamaguchi and Farouki, 1994a; Hamaguchi and Farouki, 1994b) as $F_{p} = - \frac{q_{d}^{2}}{2} \frac{\nabla λ_{D}}{λ_{D}^{2}}$ , where $q_{d} (= - z_{d 0} e)$ is the charge of the dust particles, $λ_{D} = λ_{D i} λ_{D e} / {(λ_{D e}^{2} + λ_{D i}^{2})}^{1 / 2}$ is the effective Debye length due to the electron and ion species with electron and ion Debye radii $λ_{D e} = {(T_{e} / 4 π e^{2} n_{e})}^{1 / 2}$ , and $λ_{D i} = {(T_{i} / 4 π e^{2} n_{i})}^{1 / 2}$ , respectively. The electron and ion temperatures are represented by T_e and T_i (in energy units), whereas n_e and n_i refer to the electron and ion densities. If there are no gradients in temperature and the plasma is assumed to be weakly nonuniform in density, then $\nabla λ_{D} = - \frac{λ_{D}}{2} (\nabla n_{i} + \frac{T_{i}}{T_{e}} \nabla n_{e}) / (n_{i} + \frac{T_{i}}{T_{e}} n_{e})$ . The latter can be simplified by considering the electron and ion species as inertialess. Hence, the polarization force becomes $F_{p} = - q_{d} R E$ with its coefficient $R = \frac{1}{4} \frac{z_{d 0} e^{2}}{λ_{D} T_{i}} \{1 - \frac{T_{i}}{T_{e}} (1 - z_{d 0} η)\},$ where $η (= n_{d 0} / n_{i 0})$ represents the dust concentration and z_d0 the dust charging state. Note that this force only accounts for high dust charging states or dust charges.

It is worth mentioning that polarization force acts on the dust particles when a low-frequency wave propagates and plasma background turns into a nonuniform plasma locally. This force always acts opposite to an electric field, regardless of the sign of charged dust particles. The polarization effect was first studied by Hamaguchi and Farouqi (Hamaguchi and Farouki, 1994a; Hamaguchi and Farouki, 1994b) and later, the idea was implemented by Kharapak et al. (Khrapak et al., 2009) to investigate the linear properties of DA waves in dusty plasmas. They showed that the phase speed of the DA waves decreases as long as the dust polarization force coefficient increases. Since then, numerous investigations have been carried out to examine the effect of polarization force on the profiles of linear and nonlinear wave propagation in polarized dusty plasmas (Mamun et al., 2010; Bandyopadhyay et al., 2012; Singh et al., 2018a). Recently, the modification of polarization force has been carried out with non-Maxwellian hybrid distribution (Singh et al., 2018b; Mehdipoor, 2022) and Tsallis statistics (Bentabet et al., 2017) for applications in dusty plasmas. Furthermore, the dispersive properties of dust acoustic waves have also been analyzed with charge-fluctuating dust grains (Shahmansouri and Mamun, 2016). In the case of degenerate plasmas, the magnitude of polarization force is shown to be enhanced and the DA wave frequency is exhibited to be reduced as compared to classical plasmas (Shahmansouri and Misra, 2019).

The layout of this manuscript is as follows: In Section 2, we adopt a kinetic approach to evaluate the electrostatic potential distribution around a test charge, moving with a constant speed in a (polarized) dusty plasma. On account of the dust polarization effect, the dielectric constant of the DA wave becomes significantly modified. Several limiting cases are derived for shielded potentials by imposing certain conditions on the test charge speed in comparison with the thermal speeds of plasma species. The profiles of the Debye–Hückel and wakefield and farfield potentials are analyzed for varying the polarization force coefficient and dust concentration. Section 3 presents numerical findings and discussion while Section 4 summarizes the main results and concludes this manuscript.

2 Kinetic model and shielded potentials

We consider a collisionless, unmagnetized multicomponent plasma containing electrons, singly ionized positive ions, and negatively charged dust particulates. On a dust timescale, an extremely low-frequency DA wave is produced due to dust motion in the presence of inertialess electrons and ions. The dusty plasma is globally a quasineutral gas of charged particles which holds an equilibrium charge-neutrality condition of the form n_i0 = n_e0 + z_d0n_d0, where n_e0, n_i0, n_d0 and z_d0 denote the equilibrium electron density, equilibrium ion density, equilibrium dust density and dust charging state, respectively. Dust particles attain a negative charge on their surface due to the impingement of ambient electrons and ions, resulting in the charge variation. However, for simplicity, the charge on the dust surface is treated as a constant (fixed) quantity in the limit when the dust charging period is much smaller than the dust plasma period.

The test charge-driven response of a (polarized) dusty plasma can be governed by the following linearized set of coupled Vlasov–Poisson equations (Krall and Trivelpiece, 1973; Nasim, 1999):

\frac{\partial f_{d 1}}{\partial t} + v \cdot \frac{\partial f_{d 1}}{\partial r} + \frac{z_{d 0} e (1 - R)}{m_{d}} \frac{\partial ϕ_{1}}{\partial r} \cdot \frac{\partial f_{d 0}}{\partial v} = 0, (1)

and

\nabla^{2} ϕ_{1} = - 4 π e (- n_{e 1} + n_{i 1} - z_{d 0} \int f_{d 1} d v) - 4 π q_{T} δ (r - v_{T} t), (2)

where

n_{e 1} ≃ n_{e 0} \frac{e ϕ_{1}}{T_{e}}, and n_{i 1} ≃ - n_{i 0} \frac{e ϕ_{1}}{T_{i}}, (3)

where m_d and e, are the customary notations for dust mass and electronic charge, respectively. The perturbed (equilibrium) dust distribution function is denoted by $f_{d 1} (≪ f_{d 0})$ and perturbed electron (ion) number density by n_e1 (n_i1). It is to be noted that electrostatic and polarization forces are added up to express the total force as $F = z_{d 0} e (1 - R) \partial ϕ_{1} / \partial r$ acting on the dust particles with induced potential ϕ₁. Dust polarization coefficient $R(< 1)$ not only modifies the Vlasov equation but also its associated force acts opposite to the electrostatic force and contributes to the dust susceptibility term for high dust charging state. For $R > 1$ , the dust polarization force dominates over the electrostatic force causing a null net restoring force on dust particles and leads to unstable oscillations. In the limit T_e ≫ T_i, the polarization force coefficient may reduce to $R= \frac{1}{4} \frac{z_{d 0} e^{2}}{λ_{D} T_{i}}$ in cgs units. In the present investigation, we shall focus our attention on the situation $R < 1$ . On the other hand, the first term in Eq. 2 indicates the plasma species density and the last term corresponds to the test charge density. A 3D Dirac delta function is denoted by the symbol δ and an observation point by r.

For the ES potential caused by a test charge, we now apply the space − time Fourier transformation to Eqs 1–3 and obtain the transformed quantities into ω − k space, as

{\tilde{f}}_{d 1} (k, ω) = \frac{z_{d 0} e (1 - R)}{m_{d} (ω - k \cdot v)} {\tilde{ϕ}}_{1} (k, ω) k \cdot \frac{\partial f_{d 0}}{\partial v}, (4)

\begin{align} k^{2} {\tilde{ϕ}}_{1} (k, ω) & = 4 π e \{{\tilde{n}}_{i 1} (k, ω) - {\tilde{n}}_{e 1} (k, ω) - z_{d 0} \int {\tilde{f}}_{d 1} (k, ω) d v\} \\ + 4 π q_{T} \int \exp [- i ({k \cdot v}_{T} - ω) t] d t, \end{align} (5)

{\tilde{n}}_{e 1} (k, ω) ≃ n_{e 0} \frac{e {\tilde{ϕ}}_{1} (k, ω)}{T_{e}}, (6)

and

{\tilde{n}}_{i 1} (k, ω) ≃ - n_{i 0} \frac{e {\tilde{ϕ}}_{1} (k, ω)}{T_{i}}, (7)

where ω and k pinpoint the wave frequency and wave number. Solving Eqs 4–7 together, we perform time integration to eventually come up with a transformed potential in this form

k^{2} D (k, ω) {\tilde{ϕ}}_{1} (k, ω) = 8 π^{2} q_{T} δ (ω - {k \cdot v}_{T}) . (8)

For instance, if q_T = 0 in Eq. 8, then we immediately get the dispersion relation for DA waves from $D (k, ω) = 0$ , because ${\tilde{ϕ}}_{1} (k, ω) \neq 0$ . See that dielectric constant $D (k, ω)$ is now modified by the dust-polarization effect, which appears in the dust-susceptibility term, can be given by:

D (k, ω) = 1 + \frac{1}{k^{2} λ_{D}^{2}} + \frac{(1 - R) ω_{p d}^{2}}{k^{2}} \int_{- \infty}^{\infty} \frac{k}{ω - k u} \frac{\partial f_{d 0} (u)}{\partial u} d u, (9)

where $f_{d 0} (u) = [1 / {(2 π)}^{1 / 2} v_{T d}] \exp (- u^{2} / 2 v_{T d}^{2})$ is the reduced 1D Maxwellian dust distribution function with dust-thermal speed $v_{T d} [= {(T_{d} / m_{d})}^{1 / 2}]$ . Eq. 9 shows the presence of inertialess electrons and ions besides the mobile dust species. Expressing the dust-susceptibility term into the well-known dust dispersion function (Fried and Conte, 1961), one obtains from Eq. 9 as

D (k, ω) = 1 + \frac{1}{k^{2} λ_{D}^{2}} + \frac{1 - R}{k^{2} λ_{D d}^{2}} W (C_{d}), (10)

where $λ_{D d} [= {(T_{d} / 4 π e^{2} z_{d 0}^{2} n_{d 0})}^{1 / 2}]$ stands for the dust Debye length and $W (C_{d}) [= {(2 π)}^{- 1 / 2} \int_{- \infty}^{\infty} q \exp (- q^{2}) / (q - C_{d}) d q]$ the dust dispersion function with its argument $C_{d} (= ω / k v_{T d})$ . The expansion of W − function for C_d > 1 exactly recovers the previous result (Bandyopadhyay et al., 2012) from (10).

To proceed further, we simplify Eq. 8 by applying the inverse Fourier transformation and integrating over ω, to eventually arrive at the standard result (Krall and Trivelpiece, 1973)

ϕ_{1} (r, t) = \frac{q_{T}}{2 π^{2}} \int \frac{\exp [i k \cdot (r - v_{T} t)]}{k^{2} D (k, k {\cdot v}_{T})} d k . (11)

This is the ES potential of a test charge, which is moving along the z-axis with a constant speed v_T in the polarized dusty plasma. The ES potential shall be solved either in spherical polar or cylindrical coordinate systems (depending upon the situation and mathematical tractability). The choice of the coordinate system may rely on the motion of the test charge; if the test charge is at rest or slowly moving, it exhibits spherically symmetric potential distribution around it. However, if the test charge moves with a finite speed in a certain direction, the potential distribution appears behind the test charge and may be appropriately solved by using cylindrical coordinates. Some limiting cases are to be discussed in the upcoming subsections by imposing certain conditions on the test charge speed in regard to the plasma thermal and phase speeds, for example (A) v_T ≃ ω/k, (B) v_T ≪ v_Td (C) v_T ≫ v_Te, (D) v_T = 0, and (E) v_Td ≪ ω/k ≪ v_Te, v_Ti.

2.1 Potential distribution around the resonating test charge

In this subsection, we shall decompose the total ES potential into two parts to investigate the Debye-Hückel and wakefield potential distributions around the test charge. Thus, we first simplify the plasma dispersion function [given in Eq. 10] in the limit C_d > 1 to immediately obtain the dielectric constant (Bandyopadhyay et al., 2012) in the form $D (k, ω) = 1 + \frac{1}{k^{2} λ_{D}^{2}} - (1 - R) \frac{ω_{p d}^{2}}{ω^{2}}$ with its reciprocal form (Ali et al., 2003)

D^{- 1} = \frac{k^{2} λ_{0}^{2}}{A + k^{2} λ_{0}^{2}} (1 + \frac{ω_{D}^{2}}{ω^{2} - ω_{D}^{2}}), (12)

and the modified DA frequency

ω_{D} = \frac{\sqrt{1 - R} ω_{p d} k λ_{0}}{{(k^{2} λ_{0}^{2} + A)}^{1 / 2}} .

Observe that effective Debye length can be expressed in the usual form of the Debye length for an electron-ion plasma, as

λ_{D} = {(λ_{D e}^{- 2} + λ_{D i}^{- 2})}^{- 1 / 2} \equiv \frac{λ_{0}}{\sqrt{A}}, (13)

where $λ_{0} = {(T_{e} / 4 π e^{2} n_{0})}^{1 / 2}$ , $A = \frac{n_{e 0}}{n_{0}} + \frac{T_{e}}{T_{i}}$ with n₀ = n_i0 ≡ n_e0 + z_d0n_d0. It is worth mentioning that dust polarization force coefficient is always taken less than unity (viz., $R < 1$ ) for micron-sized charged particulates and tends to unity for large-sized charged particulates. The variation of dust polarization force coefficient gives rise to a reduction of the phase speed of DA waves as compared to the conventional DA wave speed. Substituting Eq. 12 into (11), the Debye-Hückel (DH) and wakefield (WF) potentials can be expressed separately, as

ϕ_{D H} (r, t) = \frac{q_{T}}{2 π^{2}} \int \frac{λ_{0}^{2}}{A + k^{2} λ_{0}^{2}} \exp [i k \cdot (r - v_{T} t)] d k, (14)

and

ϕ_{W F} (r, t) = \frac{q_{T}}{2 π^{2}} \int \frac{λ_{0}^{2}}{A + k^{2} λ_{0}^{2}} \frac{ω_{D}^{2}}{ω^{2} - ω_{D}^{2}} \exp [i k \cdot (r - v_{T} t)] d k . (15)

Now solving the DH potential first, we need to express the wave, position, and velocity vectors into spherical polar coordinates (Yaqoob et al., 2002; Ali et al., 2003), respectively, as $k = (k \sin θ_{k} \cos ϕ_{k}, k \sin θ_{k} \sin ϕ_{k}, k \cos θ_{k})$ , $r = (r \sin θ_{r} \cos ϕ_{r}, r \sin θ_{r} \sin ϕ_{r}, r \cos θ_{r})$ , and $v_{T} = (0, 0, v_{T})$ . Hence one has $k \cdot (r - v_{T} t) = k X \cos ϕ_{k} + k Y \sin ϕ_{k} + k μ Z$ , where $X = ρ {(1 - μ^{2})}^{1 / 2} \cos ϕ_{r}$ , $Y = ρ {(1 - μ^{2})}^{1 / 2} \sin ϕ_{r}$ and Z = ξ ≡ z − v_Tt represent the separation of the test charge from an observation point r in a moving frame. Here μ = cos θ_k, $\sin θ_{k} = {(1 - μ^{2})}^{1 / 2}$ , ρ = r sin θ_r, and z = r cos θ_r. After some more simplifications, Eq. 14 is finally reduced to the following result (Ali et al., 2003)

ϕ_{D H} = \frac{q_{T}}{r} \exp (\frac{- r}{λ_{D}}), (16)

This is the DH potential for the test charge in a new moving frame having the radial and axial distances $ρ (= r \sin θ_{r})$ and $ξ (= z - v_{T} t)$ , respectively, and $r [= {(ρ^{2} + ξ^{2})}^{1 / 2}]$ refers to the distance of the test charge from an observer. Notice that DH potential decreases exponentially with distance r and has no influence on the dust polarization effect because (14) does not rely on the dust dynamics.

To solve Eq. 15, we utilize cylindrical coordinates and adopt the same standard procedures (Nambu et al., 1995; Vladimirov and Nambu, 1995; Salimullah and Nambu, 2000; Nambu et al., 2001), to eventually obtain the main contribution to the WF potential, as

\begin{align} ϕ_{W F} (ρ = 0, ξ) & \approx \frac{2 q_{T}}{ξ A} (1 + \frac{(1 - R) ω_{p d}^{2} λ_{0}^{2}}{A v_{T}^{2}}) {(1 - \frac{(1 - R) ω_{p d}^{2} λ_{0}^{2}}{A v_{T}^{2}})}^{- 1} \\ \times \cos (\frac{\sqrt{1 - R} ω_{p d} ξ}{v_{T} \sqrt{A}}) . \end{align} (17)

This is the WF potential of a test charge moving with a uniform speed v_T along the z-axis in the polarized dusty plasma. The WF potential also leads to the existence of an attractive oscillatory potential (Nambu et al., 1995; Vladimirov and Nambu, 1995; Salimullah and Nambu, 2000; Nambu et al., 2001) for holding the limits $v_{T} > C_{D} (\equiv \sqrt{1 - R} ω_{p d} λ_{0} / A)$ and $\cos (\sqrt{1 - R} ω_{p d} ξ / v_{T} \sqrt{A}) < 0$ , where $ξ (= r_{‖} - v_{T} t)$ is the axial distance from the test charge. It is now clear that attractive WF potential is significantly influenced by the dust polarization force coefficient $R$ and could have important consequences on the attraction forces between the same polarity charges to forming the ordered crystalline structures in (polarized) dusty plasmas (Fortov et al., 1996). The numerical analysis also confirms that attractive WF potential dominates over the repulsive DH potential as the DH potential fastly decreases beyond the shielding length or cloud.

2.2 Potential distribution around the slow test charge

Here we calculate the potential distributions around the slow test charge q_T having speed v_T in comparison with the dust thermal speed v_Td in a polarized dusty plasma. Thus, assuming that v_T ≪ v_Td, which further implies that v_T ≪ v_Te,Ti as well. Consequently, the test charge is shielded by all the plasma species and there will be no resonance and no wakefields in this case. For slow test charge, the dielectric function takes the following form:

D = 1 + \frac{1}{k^{2} λ_{D e}^{2}} + \frac{1}{k^{2} λ_{D i}^{2}} + \frac{1 - R}{k^{2} λ_{D d}^{2}} [1 + i \sqrt{\frac{π}{2}} C_{d} \exp (\frac{C_{d}^{2}}{2})] . (18)

One observes that if the test charge is static (v_T = 0), then the Landau damping term gets vanished and ultimately the DH potential (similar to Eq. 16 is obtained but with a modified shielding length as (Lakshmi et al., 1993)

λ_{Def} = {(λ_{D e}^{- 2} + λ_{D i}^{- 2} + (1 - R) λ_{D d}^{- 2})}^{- 1 / 2}

λ_{Def} = λ_{0} / {\{A + (1 - R) \frac{T_{e}}{T_{d}} z_{d 0}^{2} η\}}^{1 / 2} (19)

Moreover, it was examined (Montgomery et al., 1968) later that Landau damping term cannot be rigorously neglected, especially in the situation when test charge speed is much slower compared to the dust thermal speed. Thus, keeping the Landau damping term, we simplify Eq. 18 to obtain its reciprocal form (Ali and Eliasson, 2017), as

D^{- 1} = \frac{k^{2} λ_{Def}^{2}}{k^{2} λ_{Def}^{2} + 1} - i \sqrt{\frac{π}{2}} \frac{(1 - R) μ v_{T}}{v_{T d} λ_{D d}^{2}} \frac{k^{2} λ_{Def}^{4}}{{(k^{2} λ_{Def}^{2} + 1)}^{2}} . (20)

Here, μ is the angle between the wave number (k) and the test charge velocity v_T. On substituting Eq. 20 into (11) and decomposing the total ES potential into two parts, as ϕ₁ = ϕ_DH + ϕ_FF, where $ϕ_{D H} [= (q_{T} / r) \exp (- r / λ_{Def})]$ is the usual short-range DH potential (Debye et al., 1923) with a modified shielding length λ_Def. Recalling Eqs 13, 19, it is found that there is only a difference in the finite dust temperature and polarization coefficient. By adopting the standard technique (Ali and Eliasson, 2017), the second part of the ES potential can be solved, as

ϕ_{F F} = \frac{4 q_{T}}{\sqrt{2 π} r} \frac{(1 - R) v_{T} λ_{Def}}{v_{T d} λ_{D d}} \frac{ξ}{λ_{D d}} \frac{λ_{Def}^{3}}{r^{3}} . (21)

This is the farfield (FF) potential caused by a slow test charge, derived under the limit r ≫ λ_Def. The FF potential decays as the inverse cube of the axial and radial distances from the test charge is strongly affected by the polarization coefficient $R$ and shielding length λ_Def.

2.3 Potential distribution around the rapidly moving test charge

Here, we assume that if the test charge is moving very fast as compared to the electron thermal speed (viz., v_T ≫ v_Te) in the polarized dusty plasma. This would further imply that v_T ⋙ v_Ti and v_T ⋙ v_Td. Hence we need to consider all the plasma species (i.e., the electrons, ions, and dust particulates) as dynamical in the dielectric constant (9) for holding the large velocity limit and so it becomes as

\begin{align} D & ≃ 1 - \frac{1}{k^{2} λ_{D e}^{2} \sqrt{2 π} v_{T e}} \frac{k}{{k \cdot v}_{T}} \int_{- \infty}^{\infty} u \exp (- \frac{u^{2}}{2 v_{T e}^{2}}) d u \\ - \frac{1}{k^{2} λ_{D i}^{2} \sqrt{2 π} v_{T i}} \frac{k}{{k \cdot v}_{T}} \int_{- \infty}^{\infty} u \exp (- \frac{u^{2}}{2 v_{T i}^{2}}) d u \\ - \frac{1 - R}{k^{2} λ_{D d}^{2} \sqrt{2 π} v_{T d}} \frac{k}{{k \cdot v}_{T}} \int_{- \infty}^{\infty} u \exp (- \frac{u^{2}}{2 v_{T d}^{2}}) d u . \end{align} (22)

In Eq. 22, we have only collected up to first order terms in the expansions from (9). Using the fact $\int_{- \infty}^{\infty} u \exp (- β u^{2}) d u = 0$ in (22), the dielectric constant eventually reduces to $D (k, k \cdot v_{T}) ≃ 1$ and the corresponding potential yields the Coulomb potential

ϕ_{1} (ρ, ξ) = ϕ_{c} (ρ, ξ, t) \equiv \frac{q_{T}}{r}, (23)

with $r = {(ρ^{2} + ξ^{2})}^{1 / 2}$ . This confirms that if the test charge is moving very fast as compared to all the surrounding plasma species then it would not be screened anymore by the plasma species and hence no shielding effect in the dusty plasma.

2.4 Potential distribution around the static test charge

For a static test charge, we assume that v_T = 0 in the expression of the total ES potential (11), which turns out to be

ϕ_{1} (r, 0) = \frac{q_{T}}{2 π^{2}} \int \frac{\exp (i k \cdot r)}{k^{2} D (k, 0)} d k, (24)

with

\begin{align} D & ≃ 1 + \frac{1}{k^{2} λ_{D e}^{2} \sqrt{2 π} v_{T e}} \int_{- \infty}^{\infty} \exp (- \frac{u^{2}}{2 v_{T e}^{2}}) d u \\ + \frac{1}{k^{2} λ_{D i}^{2} \sqrt{2 π} v_{T i}} \int_{- \infty}^{\infty} \exp (- \frac{u^{2}}{2 v_{T i}^{2}}) d u \\ + \frac{1 - R}{k^{2} λ_{D d}^{2} \sqrt{2 π} v_{T d}} \int_{- \infty}^{\infty} \exp (- \frac{u^{2}}{2 v_{T d}^{2}}) d u . \end{align} (25)

In obtaining (25), we have assumed that electrons and ions are also dynamical besides dust particles in Eq. 9. After solving the above integrals using $\int_{- \infty}^{\infty} u \exp (- β u^{2}) d u = \sqrt{2 π / β}$ , we immediately come up with the result $D (k, 0) = (k^{2} λ_{Def}^{2} + 1) / k^{2} λ_{Def}^{2}$ , where the modified effective shielding length λ_Def is already defined in Eq. 19. Thus Eq. 24 finally turns out to be

ϕ_{1} (ρ, z, 0) = ϕ_{D H} \equiv \frac{Q_{t}}{r} \exp (- \frac{r}{λ_{Def}}) . (26)

This confirms that for a null test charge speed, the test particle acts as static, and is screened by all the plasma species in the polarized dusty plasma.

2.5 Potential distribution around an intermediately moving test charge

For an intermediate velocity regime, like v_Td ≪ v_T ≪ v_Te, v_Ti, the dielectric function (9) can be expressed in this form

D = 1 + \frac{1}{k^{2} λ_{D}^{2}} - \frac{1 - R}{k^{2} λ_{D d}^{2} \sqrt{2 π} v_{T d}} \frac{k}{{k \cdot v}_{T}} \int_{- \infty}^{\infty} u \exp (- \frac{u^{2}}{2 v_{T d}^{2}}) d u . (27)

Solving the above integral, we get the dielectric function, as

\begin{align} D & = 1 + \frac{1}{k^{2} λ_{D}^{2}} - \frac{1 - R}{k^{2} λ_{D d}^{2} \sqrt{2 π} v_{T d}} \frac{k}{{k \cdot v}_{T}} (0) \\ = 1 + \frac{1}{k^{2} λ_{D}^{2}}, \end{align} (28)

where λ_D is already given in (13). The dust particulates act as the inertial term, which contains dust polarization force coefficient $R$ and gets vanished because only collecting the first order term in its expansion. Therefore, the velocity-dependent contribution does not appear in Eq. 28. As a consequence, the test charge potential finally reduces to the DH potential (Debye et al., 1923)

ϕ_{1} (ρ, ξ, t) = ϕ_{D H} \equiv \frac{q_{T}}{r} \exp (- \frac{r}{λ_{D}}), (29)

where $r = {(ρ^{2} + ξ^{2})}^{1 / 2}$ . Observe that only electrons and ions take part in the shielding process when the test charge is moving slower than the electron and ion species but faster than the mobile dust species.

3 Results and discussion

For numerical analysis, we first normalize the resultant Eqs 17, 19, and 21 by using the scaling parameters such as ${\bar{λ}}_{Def} = {\bar{λ}}_{Def} / λ_{0}$ , $\bar{ρ} = ρ / λ_{0}$ , $\bar{ξ} = ξ / λ_{0}$ , ${\bar{ϕ}}_{W F} = ϕ_{W F} / (q_{T} / λ_{0})$ , ${\bar{ϕ}}_{D H} = ϕ_{D H} / (q_{T} / λ_{0})$ , ${\bar{ϕ}}_{F F} = ϕ_{F F} / (q_{T} / λ_{0})$ and ${\bar{v}}_{T} = v_{T} / C_{D}$ . We also choose some recent simulation data (Bandyopadhyay et al., 2012) that has been used in the studies of Mach cones in dusty plasmas, namely, the equilibrium ion density n_i0 ∼ 10⁸cm⁻³, the equilibrium electron density n_e0 ∼ 1.9 × 10⁷ cm⁻³, the dust charging state z_d0 = 4,007, the dust radius r_d ≃ 4.5 μm, the average inter-particle distance d ≃ 230 μm, the ion temperature T_i = 0.1eV, and the electron temperature T_e = 1.5eV. These values further help to find other physical quantities, e.g., the dust plasma frequency ω_pd ∼ 68Hz, the dust thermal speed v_Td ∼ 0.025 cm/s, the DA speed C_D = ω_pdλ₀ ≡ 1.36 cm/s with λ₀ ∼ 0.02 cm and dust polarization force coefficient $R = 0.05$ . The latter strongly depends on the dust charging state and leads to the reduction of the phase speed of DA waves in a polarized dusty plasma.

The modifications due to dust-charge fluctuations and dust-neutral collisions (Ali et al., 2003) have been ignored in the present model, just to make more simple the analytical calculations and analysis. The dust charging process is actually a complex phenomenon (Popel et al., 2005) that occurs on a very fast scale in laboratory plasmas (Hazelton and Yadlowsky, 1994; Praburam and Goree, 1996) as well as in numerical simulations (Choi and Kushner, 1994). Hence, ignoring the dust charge variation effects, the primary focus is to examine the impact of dust polarization force on the shielding and dynamical potentials by imposing certain conditions on the test charge speed in relation to the thermal speeds of plasma species. However, an effort has already been made to investigate the characteristics of the Debye shielding with dust-charge fluctuation and dust-neutral collisional effects in negatively charged dusty plasmas (Ali et al., 2003). Later, Ali (Ali, 2016) continued his investigation to study a positive-dust electron plasma and examined the influence of secondary electron and photoelectron emissions on the potential profiles.

Figure 1 displays the normalized WF potential $({\bar{ϕ}}_{W F})$ of a test charge against the normalized axial distance $(\tilde{ξ})$ as a function of (A) dust charging state 1,000 ≤ z_d0 ≤ 6,000 with η ≃ 10^–6 and (B) dust concentration 10^–4 ≤ η ≤ 8 × 10^–6 with z_d0 = 4,007 at constant speed $v_{T} (= 0.3 C_{D})$ . When the test charge resonates with a DA mode, an asymmetric wakefield is excited behind the test charge in the form of potential distribution in an axial direction. Since the dust polarization coefficient $R$ (z_d0, η) is the function of dust charging state and dust concentration, therefore, the variation in these parameters significantly mitigates (increases) the magnitude of the WF potentials, respectively. The wakefield is oscillatory in nature and appears in terms of positive and negative potential regions that damp behind the test charge particle for several Debye lengths [see Figure 1A]. The strength of the WF potential decreases because the dust polarization force coefficient effectively reduces the phase speed of the collective DA mode. It is important to note that Eq. 17 is only valid in the limit when $R < 1$ for micron-sized dust grains. However, the variation of dust concentration which appears through an equilibrium charge-neutrality condition, significantly modifies the amplitudes of wakefield [as shown by Figure 1B] and its potential regions. The increase in dust concentration essentially makes the depletion of electrons in the system and consequently, the phase speed of the DA wave increases. This effect pronounces the potential associated to the wakefield, and also has fundamental importance in attracting the same polarity dust grains and forming the ordered crystalline structures in the (polarized) dusty plasma (Fortov et al., 1996). If a test charge moves with a speed slower than the dust thermal speed (viz., v_T ≪ v_Td), then all the plasma species (viz., the electrons, ions, and negatively charged dust grains) would shield the test particle, which may lead to significant modification of the shielding length.

FIGURE 1

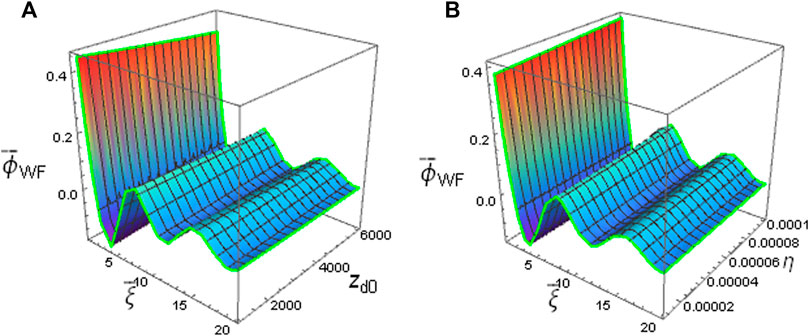
FIGURE 1. The profiles of WF potential $({\bar{ϕ}}_{W F})$ are displayed against the normalized axial distance $(\bar{ξ})$ as a function of (A) dust charging state 1000 ≤ z_d0 ≤ 6000 with η ≃ 10^–6 and (B) dust concentration 10^–4 ≤ η ≤ 8 × 10^–6 with z_d0 = 4007 at constant speed $v_{T} (= 0.3 C_{D})$ . All other parameters are the same as mentioned in Section 3.

In Figure 2, we show how effective shielding length varies as function of electron-to-dust temperature ratio for different values of dust polarization force coefficient $R = 0.057$ (black dashed curve), 0.058 (blue dashed curve), 0.059 (red solid curve). It is observed that dust polarization coefficient is effectively modified by the dust concentration parameter η(= 10^–5, 3 × 10^–5, 9 × 10^–5) at fixed charging state z_d0 = 4,007 and so the shielding effect diminishes in dusty plasmas. Moreover, the variation of dust charging states $z_{d 0} (= 2000,3000,4990)$ not only affects the dust polarization coefficient $R$ but also the effective shielding length, showing a reduction in the shielding length as long as the electron-to-dust temperature ratio varies as a function.

FIGURE 2

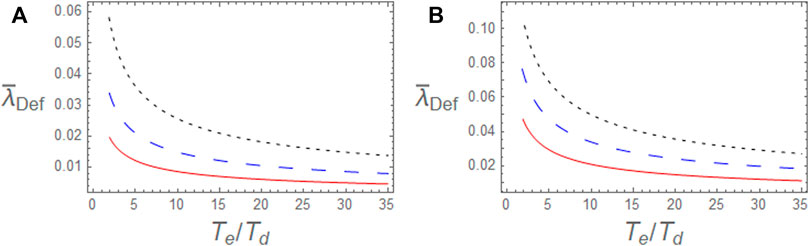
FIGURE 2. The profiles of the effective-shielding length $({\bar{λ}}_{Def})$ are shown as a function of electron-to-dust temperature ratio (T_e/T_d) for varying (A) the polarization coefficient $R = 0.057$ (black dashed curve), 0.058 (blue dashed curve), 0.059 (red solid curve) with z_d0 = 4007, and (B) the dust charging state z_d0 = 2000, 3000, 4990 at η = 10^–5. All other parameters are the same as given in Section 3.

Figure 3 depicts the effect of the dust polarization force coefficient $R$ on the profiles of normalized DH potential $({\bar{ϕ}}_{D H})$ against the normalized axial distance $\bar{ξ}$ at fixed radial distance ρ = 0.15 for (A) z_d0 = 3500 and (B) z_d0 = 5000. It may be noticed that the values of dust polarization coefficient $R$ [ = 0.05053 (black dashed curve), 0.05054 (blue dashed curve), 0.05057 (red solid curve)] are not only dependent on the dust concentration parameter η(= 10^–6, 2 × 10^–6, 4 × 10^–6) but also on the dust charging state and leading to the reduction of DH potential, as can be seen from Figure 3A. However, keeping the same dust concentrations at high dust charging state z_d0 (= 5000) would result in the modification of dust polarization coefficient R (= 0.07148, 0.07151, 0.07156) with more decreased DH potential profiles [see Figure 3B]. The DH potentials are mainly caused by the static or slow moving test charges in a polarized dusty plasma. Figure 4 represents how a normalized FF potential $({\bar{ϕ}}_{F F})$ is affected by the normalized axial distance $\bar{ξ}$ for varying (A) the dust polarization R [ = 0.05766 (black dashed curve), 0.05769 (blue dashed curve), 0.05772 (red solid curve)] at z_d0 = 4007 and (B) the dust polarization R [ = 0.06454 (black dashed curve), 0.06459 (blue dashed curve), 0.06463(red solid curve)] at z_d0 = 4500. Such type of potentials often arise from very slow motion of test charges as compared to dust thermal speed, viz., v_T = 0.02v_Td. The magnitudes of the FF potentials become lower (higher) at high (low) dust charging state in both the cases and are significantly altered by the impact of dust polarization coefficient. The FF potentials are only derived in the long-range limit when r ≫ λ_Def.

FIGURE 3

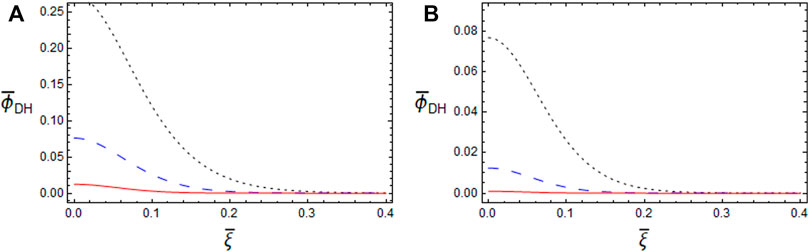
FIGURE 3. The variation of DH potential $({\bar{ϕ}}_{D H})$ is displayed against the normalized axial distance $(\bar{ξ})$ for changing dust polarization coefficient $(R)$ at low and high charging states (A) z_d0 = 3500 and (B) z_d0 = 5000 with $\bar{ρ} = 0.15$ . All other parameters are the same as given in Section 3.

FIGURE 4

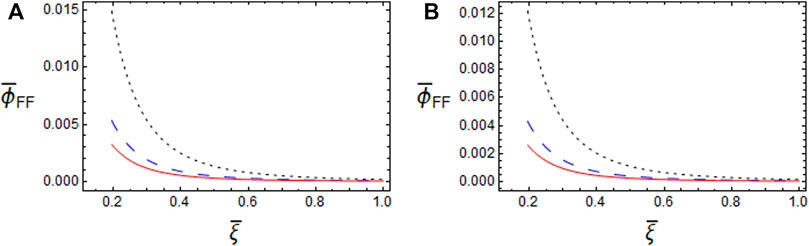
FIGURE 4. The profiles of the FF potential $({\bar{ϕ}}_{F F})$ are plotted against the normalized axial distance $(\bar{ξ})$ for varying the polarization coefficient $(R)$ at low and high charging states (A) z_d0 = 4007 and (B) z_d0 = 4500 with $\bar{ρ} = 0.1$ , ${\bar{v}}_{T} = 0.02$ and T_e/T_d = 20. All other parameters are the same as given in Section 3.

4 Summary and conclusion

To summarize, we have studied the test charge-driven response of a polarized dusty plasma, showing distinct features of interaction potentials. In this context, we have solved the coupled linearized set of Vlasov-Poisson equations by using the Fourier transformation technique and derived an expression for the total electrostatic potential with a modified dielectric constant that accounts for dust polarization force. The latter acts as an opposite force to the electrostatic force and plays a vital role in interaction potentials for micron-sized dust particulates. Imposing certain conditions on the test charge speed in comparison with thermal speeds of plasma species, the total electrostatic potential is analyzed for various limiting cases, obtaining oscillatory wakefield (WF), Debye-Hückel (DH), Farfield (FF) and Coulomb potentials. It is found that dust polarization force coefficient is essentially dependent on the dust charging state and dust concentration to modifying the profiles of DH potential, which decay exponentially with the distance, the FF potential which decays as the inverse cube of the distance and WF potential behind a test charge due to resonant interaction. Moreover, dust polarization and dust concentration do not influence the Coulomb potential because the test charge moves very fast relative to plasma species and so no shielding occurs around it in the polarized dusty plasma. Many years ago (Nambu et al., 1995; Vladimirov and Nambu, 1995; Salimullah and Nambu, 2000; Nambu et al., 2001), the concept of wakefield was proposed for making new materials with help of attractive forces between the same polarity dust grains in negative regions of the potential. The negatively charged dust grains are attracted in the similar way as that of Cooper pairing of electrons in superconductors (De Gennes-Pierre, 1966) and in turn, may lead to the possibility to have dust crystallization and dust-coagulation in dusty plasmas.

Test charge technique is one of the effective techniques, which is used as a diagnostic tool for studying interaction potentials in dusty plasmas. The present findings are important to understand the physics of the shielding phenomenon and to explore new features of dynamical potentials caused by the wave-particle interaction in the presence of dust polarization force. Various effects like dust-charge perturbations and dust-neutral collisions (Ali et al., 2003; Ali et al., 2005a; Ali et al., 2005b), external magnetic field and ion-streaming (Vladimirov and Nambu, 1995; Nambu et al., 2001), two-body correlations, etc., have been investigated with significant modifications to potential distribution both analytically and numerically. In many laboratories, the massive charged dust grains are assumed to be strongly coupled due to their high dust charge, low temperature, and small intergrain spacing. Relying on the specific simulation data (Bandyopadhyay et al., 2012), the test charge potential profiles are analyzed in a negatively charged dusty plasma, which corresponds to a strongly coupled regime owing to a large coupling parameter, i.e., Γ_c ≫ 1. However, dust temperature can play a decisive role in the transition from strongly coupled to weakly coupled dusty plasmas and vice versa. In particular, dust-charge variation and dust-neutral collisions have significantly modified the profiles of the shielding and wakefield potentials elsewhere (Ali et al., 2003), but in the present model, it is beyond the scope of our interest and would be addressed in future studies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SA: Introduced the main idea and performed both analytical and numerical calculations. WM: Involved in write-up and analysis. KS: Discussed modeling and findings. RJ: Analyzed calculations and prepared analysis.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, S., and Eliasson, B. (2017). Slow test charge response in a dusty plasma with Kappa distributed electrons and ions. Phys. Scr. 92, 084003. doi:10.1088/1402-4896/aa7c09

ORIGINAL RESEARCH article

Test charge driven response of a dusty plasma with polarization force

1 Introduction

2 Kinetic model and shielded potentials

2.1 Potential distribution around the resonating test charge

2.2 Potential distribution around the slow test charge

2.3 Potential distribution around the rapidly moving test charge

2.4 Potential distribution around the static test charge

2.5 Potential distribution around an intermediately moving test charge

3 Results and discussion

4 Summary and conclusion

Data availability statement

Author contributions

Conflict of interest

Publisher’s note

References

This article is part of the Research Topic

People also looked at