Thermal fluctuations, QNMs, and emission energy of charged ADS black hole with nonlinear electrodynamics

1 Introduction

Black holes (BHs) are considered one of the most distinctive attributes of strong gravitational fields in the present arena of research. Classically, nothing can get away (either particles or radiations) from the event horizon of a BH due to strong gravitational influence. However, it swallows everything found in the surroundings. These thermodynamic entities not only characterize some remarkable classical insights but also come up with a better perception of their quantum gravitational features. The well-known BH configurations, including Schwarzschild, Reissner–Nordstrom (RN) $\ddot{o}$, Kerr, and Kerr–Newman, have curvature singularity beyond their event horizons. The quantum mechanical consequences endorse the ejection of thermal radiations from BHs, known as Hawking radiations (Hawking, 1975). These radiations cause a gradual drop in the mass of BH, thus leading to its evaporation, but tend to increase its temperature radically. Hence, thermal radiations play an astonishing role in the thermodynamic aspects of smaller BHs due to a significant increase in temperature. The discovery of Hawking radiation reveals that BHs have a temperature. The entropy and the temperature of BHs indicate that the rules of BH and classical thermodynamics are connected. Specifically, temperature and surface gravity are interrelated, while energy is connected to the BH mass. Entropy is crucial for analyzing the thermal properties of a thermodynamic system and is connected to the field ofBH’s event horizon (Bekenstein, 1973). This similarity argues that, for the second law of thermodynamics to not be violated, the BH entropy must be higher than that of some other object with a volume similar to that of BH. Thus, it is not possible to attain thermal equilibrium between BH and thermal radiations, illustrating the requirement for logarithmic corrections derived from the thermal fluctuations in the entropy area relation provided by Bekenstein (More, 2005).

One of the primary issues with the classical Maxwell theory is the appearance of an infinite self-energy for a point-like charge at the charge position. In quantum electrodynamics, this divergence can be eliminated, but it still presents a challenge in classical electrodynamics. To resolve this issue, Born and Infeld developed a novel Lagrangian (Born and Infeld, 1934). Other nonlinear electrodynamic fields, such as the logarithmic, exponential, and power law Maxwell fields, have drawn greater attention than Born–Infeld nonlinear electrodynamics (NED) (Hendi et al., 2015; Dehghani, 2016; Dayyani et al., 2017; Dehghani and Hamidi, 2017). These theories, which can be reduced to linear Maxwell theory, are more complex than linear electrodynamics. In the existence of nonlinear electrodynamic impacts, Balart and Vagenas (2014) gave the exact solutions of a variety of regularly charged BHs and showed that the behavior of some BHs coincides asymptotically with that of RN BH. Studying the thermal properties of four regular BHs, Tharanath et al. (2015) discovered a second-order phase transition. Inferring the leading-order corrections to thermodynamic quantities of RN, Kerr, and charged anti-de-sitter (AdS) BHs, Faizal and Khalil (2015) concluded that these BHs produce remanence in all three cases. In an attempt to better understand the local thermal stability and logarithmic entropy adjustments of charged accelerating BHs, Pradhan (2019) detected second-order phase transitions in these BHs. According to the investigation of Sharif and Akhtar (2020)into the impact of thermal fluctuations on the thermodynamics of charged BHs with Weyl corrections, tiny BHs are unstable when logarithmic corrections are included. The stability and thermodynamics of asymptotically flat RN BH were examined by Sinha (2021). Additionally, he noted that BH displays a phase transition that is distinct from that of the Schwarzschild BH. Javed et al. (2023) studied thin-shell wormholes and gravastars in the background of different BH geometries.

The impact of logarithmic corrections on the thermodynamic variables such as heat capacity, Hawking temperature, and entropy of the modified Hayward BH was discussed by Pourhassan et al. (2016). In the presence of the cosmological constant, Jawad and Shahzad (2017) examined thermodynamic stability and the impact of thermal fluctuations on the non-minimal regular BHs. They concluded that normal BHs exhibit stable behavior for increasing cosmological constant values. The thermodynamic characteristics of the Hayward and the asymptotically AdS BHs under equilibrium conditions were investigated by Haldar and Biswas (2018) to an impact of thermal disturbances. Saleh et al. (2018) observed that the presence of the magnetic charge and quintessence produces the phase transition in regular BH after analyzing the behavior of thermal quantities such as heat capacity and temperature of Bardeen BH surrounded by quintessence. Javed et al. (2018) studied the thermodynamic characteristics and phase transition of regular charged BHs. They discovered that for charged BH with exponential distribution of variables, the phase transition curves diverge around critical points. Sharif and Nawaz (2020) explored the thermodynamic features of rotating regular BHs and their AdS versions and concluded that considered BHs are thermodynamically more stable and less hot than ordinary Kerr and Kerr-AdS BHs. Sharif and Ama-Tul-Mughani (2021) discussed the phase transition of the Kerr-Sen-AdS BH and concluded that BH attains the same phase transition as that of liquid–gas van der Waals fluid. They also analyzed how thermal fluctuations impact the stability of the considered BH. Sharif and Khan (2022a) studied how thermodynamic properties, thermal stability, and logarithmic correction impact on thermodynamic quantities and phase transitions of regular de Sitter BH. They demonstrated that the phase of Hawking’s temperature varies from positive to negative, whereas the phase of heat capacity varies from negative to positive for greater values of the de Sitter parameter.

The generalization of thermodynamic analogy between the van der Waals system and AdS BH is the Joule–Thomson expansion process. According to classical thermodynamics, the Joule–Thomson expansion describes how a fluid moves from an area with high pressure into a low-pressure area through a porous plug while maintaining a constant enthalpy. Ökcü and Aydýner (2017) examined the charged RN AdS BH’s Joule–Thomson expansion in the extended phase space. They discovered the inversion/isenthalpic curves and the cheating/cooling regions. This groundbreaking research has since been applied to a variety of different BHs, including the quintessence-charged AdS BH (Ghaffarnejad et al., 2018), the Kerr-AdS BH (Ökcü and Aydýner, 2018), the d-dimensional charged AdS BH (Mo et al., 2018), the holographic superfluid (D’Almeida and Yogendran, 2018), the charged AdS BH in f(R) gravity (Chabab et al., 2018), the charged AdS BH with a global monopole (Rizwan et al., 2018), the charged AdS BH in Lovelock gravity (Mo and Li, 2018), and the charged Gauss–Bonnet BH (Lan, 2018). Pacilio and Brito (2018) examined the QNMs of weakly charged Einstein–Maxwell dilaton BHs and found that gravitational modes are only weakly affected by coupling with the dilaton. The QNMs and quantization were studied for the analytical solutions in a cosmic string Born–Infeld dilaton BH geometry in Sakalli et al. (2018). Greybody factors of modified BH geometry in the background of NEDs were studied in Kanzi et al. (2020). QNMs, photon spheres, and shadows of regular BH with string cloud parameters were discussed in Singh et al. (2022). Nomura and Yoshida (2022) investigated the QNMs of charged BHs with corrections from NEDs and found that the isospectrality of QNMs under parity is generally violated due to NEDs.

Thermal stability with emission energy and Joule–Thomson expansion of regular BTZ-like BH are studied in Ditta et al. (2022) and tunneling analysis of null aether BH in Ali et al. (2022). The thermodynamics of accelerating BHs in ADS spacetime were discussed in Anabalon et al. (2018). The effects of NED on the BH shadow, deflection angle, quasinormal modes (QNMs), and graybody factors are calculated in Kuang et al. (2018) and Okyay and Övgün (2022). QNMs are observed for hairy BHs in (Yang et al., 2022a), QNMs of f(Q) BH are examined in Gogoi et al. (2023), and Kerr-like black bounce spacetime is calculated in Yang et al., (2022b); Övgün et al., (2021). The deflection angle of the photon, QNMs, the greybody factor, and shadows were discussed in Övgün (2018), Övgün and Jusufi (2018), Javed et al. (2019), and Pantig et al. (2022). Guo et al. (2020) examined the Joule–Thomson expansion for the regular AdS BH and determined the inversion temperature for Bardeen-AdS BH in the extended phase space. They analyzed the inversion and isenthalpic curves for the BH under consideration and found that their intersection points are the inversion points discriminating the cooling from the heating process. Gracia et al. (2021) studied this expansion for uncharged noncommutative BHs characterized by a parameter (present in the horizon function) and found that the uncharged BH in a noncommutative scenario acts as a charged commutative BH.

In this study, we explore the thermodynamic features and QNMs of charged ADS BH with NED. This study is devoted to exploring the effects of NED on thermodynamic quantities of charged ADS BH geometry. It is outlined as follows: Section 2 presents the charged ADS BH structure with NED and discusses the thermodynamic quantities and thermal stability through heat capacity, Section 3 discusses the rate of emission energy of the considered BH geometry, and Section 4 explains the relationship between the QNMs and Davies’s point. The consequences of thermal fluctuations on uncorrected thermodynamic physical quantities are examined in Section 5. In the last section, we present some concluding remarks.

2 Thermodynamics of charged ADS black hole with nonlinear electrodynamics

The following action is described as the minimal interaction between NED and gravity (Yu and Gao, 2020):

$S=\int \left[Y\left[\psi \right]+R\right]\frac{\sqrt{-g}}{16\pi }{d}^{4}x,(1)$

where

$F_{\gamma \beta }={\nabla }_{\gamma }{A}_{\beta }-{\nabla }_{\beta }{A}_{\gamma },\psi =F_{\gamma \beta }{F}^{\gamma \beta },\gamma ,\beta =\mathrm{0,1,2,3},$

where R is the Ricci scalar, A_γ denotes the Maxwell field, and Y[ψ] is a function of ψ. By varying the aforementioned action, the corresponding field equations result in Yu and Gao (2020):

$G_{\gamma \beta }=\frac{1}{2}{g}_{\gamma \beta }Y\left[\psi \right]-2Y\left[\psi \right]{,}_{\psi }{F}_{\gamma \mu }{F}_{\beta }^{\mu },(2)$

where $Y[\psi ]{,}_{\psi }=\frac{dY[\psi ]}{d\psi }$.The associated generalized Maxwell equations are provided as

${\nabla }_{\gamma }\left[Y\left[\psi \right]{,}_{\psi }{F}^{\gamma \beta }\right]=0.(3)$

The parameterizations of the spherically symmetric static spacetime are

$d{s}^2=-\mathcal{B}\left(r\right)d{t}^2+{\mathcal{B}}^{-1}\left(r\right)d{r}^2+r^{2}d{\theta }^2+r^2{\sin }^2\theta d{\varphi }^2.(4)$

Here, the metric function is denoted as $\mathcal{B}(r)$. The respective non-zero component of the Maxwell field tensor is A₀ = ϕ(r) and ψ = −2ϕ′².

Now, we consider a specific expression of $Y[\psi ]=-2\sqrt{2}\beta \sqrt{-\psi }+\psi +2\mathrm{\Lambda }$, where the coupling constant is denoted as β and the corresponding solution of field equations is (Yu and Gao, 2020)

$\varphi \left(r\right)=-q/r-r\beta ,(5)$

$\mathcal{B}\left(r\right)=-\frac{2M}{r}+2\beta Q+\frac{Q^2}{r^2}-\frac{{\beta }^2{r}^2}{3}+1-\frac{1}{3}\mathrm{\Lambda }{r}^2,(6)$

where Λ, Q, and m are the cosmological constant, charge, and mass of BH geometry, respectively. Here, we consider the following choices of physical parameters Q and β, and the respective manifolds become as follows:

• If β = 0 = Q, then Schwarzschild-ADS BH is recovered.

• If β = 0 and Q ≠ 0, then RN-ADS BH is recovered.

• If β ≠ 0 and Q ≠ 0, then it shows the charged ADS BH with NED (D’Ambrosio et al., 2022).

It is interesting to mention that the BH event horizon is located at a radial position for which the metric function becomes 0. In Figures 1–3, we discuss the behavior of the metric function for suitable values of physical parameters. It is noted that the position of the event horizon (dashed line $\mathcal{B}(r)=0$) in between the shaded regions depends on β, M, and Q. It is interesting to mention that BH event horizon shows symmetric behavior for different values of coupling constant. (Figure 1). The position of the event horizon becomes larger as the coupling constant approaches 0 (β ⇒ 0). As the charge of the BH geometry increases, the range of coupling parameters of the event horizon also enhances. Conversely, there is a small possibility of an event horizon of charged BH with NED for only 0 < Q < 0.2 at β = 0.4, whereas for higher values of β, the ranges of charge the existence of event horizon increase (Figure 2). The possible existence of an event horizon depends on the charge and the coupling constant. The inner and outer horizons of charged ADS BH with NED depend on the cosmological constant (Figure 3).

FIGURE 1

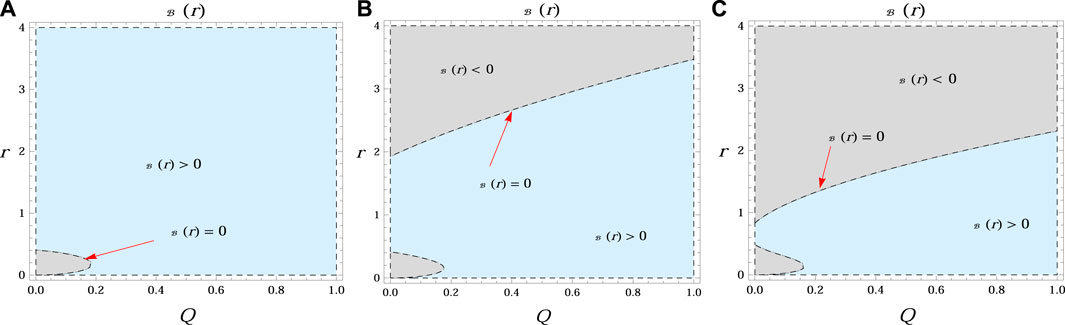
FIGURE 1. Region plots of the metric function charged with NED versus r and Q for different values of β[β = 0.4 (A), β = 0.8 (B), β = 1.5 (C)] with M = 0.2, Λ = 0. The central black dashed line $(\mathcal{B}(r)=0)$ between light gray ($(\mathcal{B}(r)<0)$) and light blue regions ($(\mathcal{B}(r)>0)$) represents the position of an event horizon.

FIGURE 2

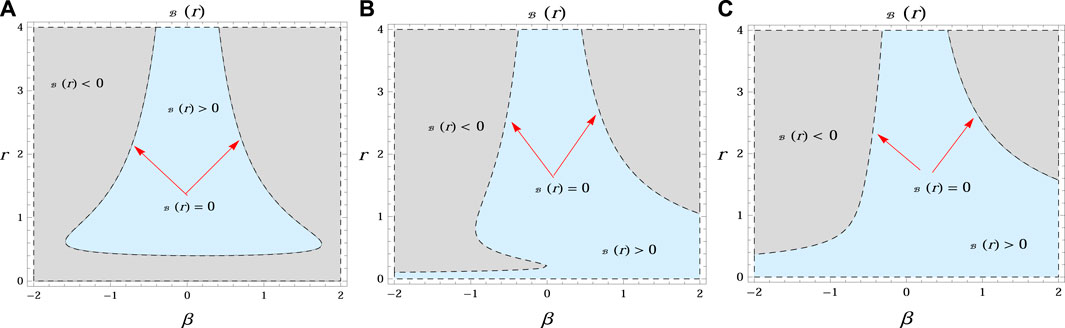
FIGURE 2. Region plots of the metric function charged with NED versus r and βfor different values of charge [Q = 0.1 (A), Q = 0.3 (B), Q = 0.6 (C)] with M = 0.2, Λ = 0.

FIGURE 3

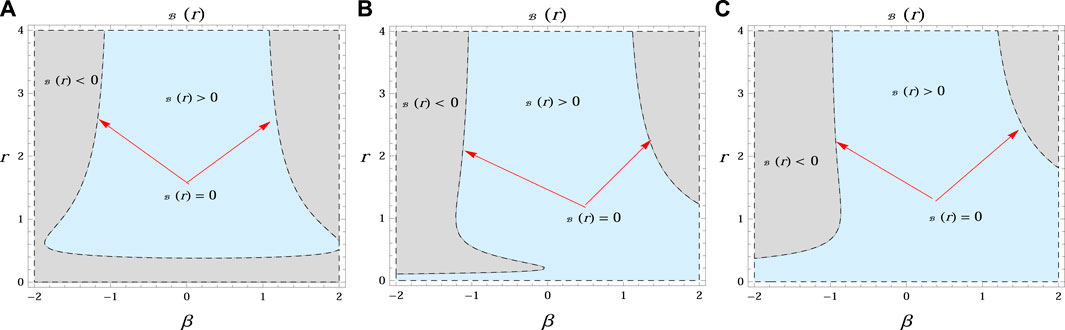
FIGURE 3. Region plots of the metric function of charged ADS with NED BH versus r and βfor different values of charge [Q = 0.1 (A), Q = 0.3 (B), Q = 0.6 (C)] with M = 0.2, Λ = −1.

Here, we are interested in evaluating the Hawking temperature heat capacity of the considered BH spacetime. Such thermodynamic entities play a crucial role in exploring the thermodynamically stable characteristics of BH. The respective mass of BH in terms of the event horizon is given as

$M=\frac{3Q^2+6\beta Q{r}_h^2+r_h^4\left(-\left({\beta }^2+\mathrm{\Lambda }\right)\right)+3r_h^2}{6r_h},(7)$

The surface gravity $\left(\kappa =\frac{1}{2}\frac{d\mathcal{B}(r_h)}{d{r}_h}\right)$ of BH has the following form:

$\kappa =\frac{M}{r_h^2}-\frac{Q^2}{r_h^3}-\frac{{\beta }^2{r}_h}{3}-\frac{\mathrm{\Lambda }{r}_h}{3}.$

Consequently, we get the Hawking temperature $\left(\mathbb{T}=\frac{\kappa }{2\pi }\right)$ as (Hawking, 1975)

$\mathbb{T}=\frac{M}{2\pi r_h^2}-\frac{Q^2}{2\pi r_h^3}-\frac{{\beta }^2{r}_h}{6\pi }-\frac{\mathrm{\Lambda }{r}_h}{6\pi }.(8)$

Figure 4 analyzes the behavior of the Hawking temperature in terms of the entropy of BH geometry. The left plot shows that the temperature of the system greatly depends on the mass of the geometry. It is noted that temperature increases initially and then decreases as the entropy of the system increases. In the background of the cosmological constant, the Hawking temperature enhances compared to the charged BH with NED in Figure 5.

FIGURE 4

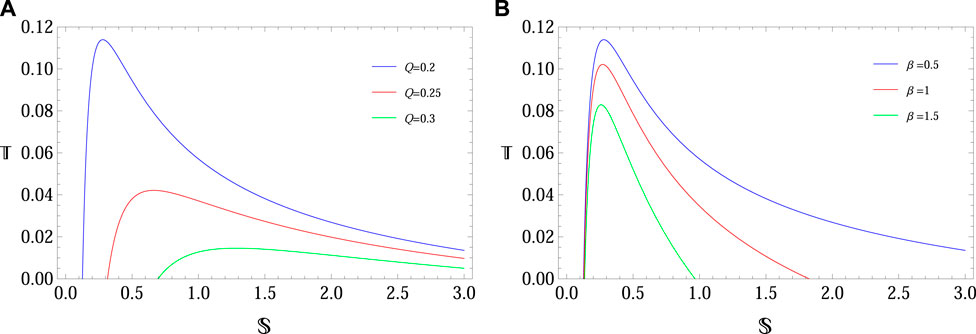
FIGURE 4. Plots of Hawking temperature of charged BH with NED BH versus entropy of the BH with different values of Q with β = 0.5 (A) and βwith Q = 0.2 (B) with M = 0.2, Λ = 0.

FIGURE 5

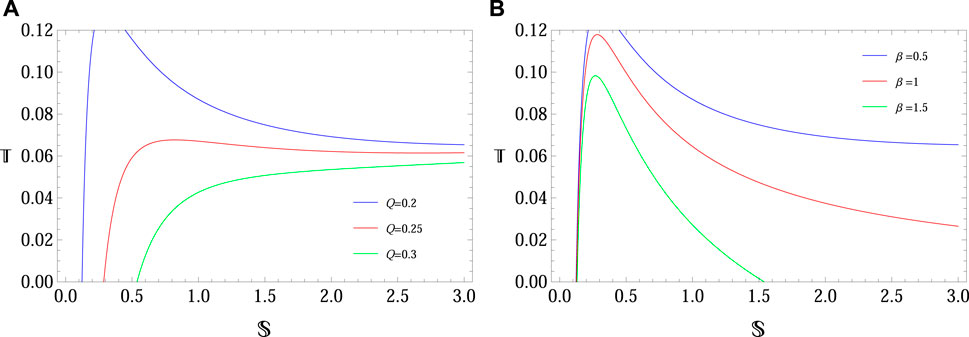
FIGURE 5. Plots of Hawking temperature of charged ADS BH with NED BH versus entropy of the BH with different values of Q with β = 0.5 (A) and βwith Q = 0.2 (B) with M = 0.2, Λ = −1.

By considering the Bekenstein area entropy relationship, the entropy of the system is given as (Das et al., 2002)

$S={\int }_0^{2\pi }{\int }_0^{\pi }\sqrt{g_{\theta \theta }{g}_{\varphi \varphi }}d\theta d\varphi =\pi r_h^2.(9)$

The heat capacity $\left(\mathbb{T}\frac{\partial S}{\partial \mathbb{T}}\right)$ of the system has the following form (Das et al., 2002; Sharif and Khan, 2022b):

$\mathbb{C}=\frac{2\pi r_h^2\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)}{6M{r}_h-9Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)}.(10)$

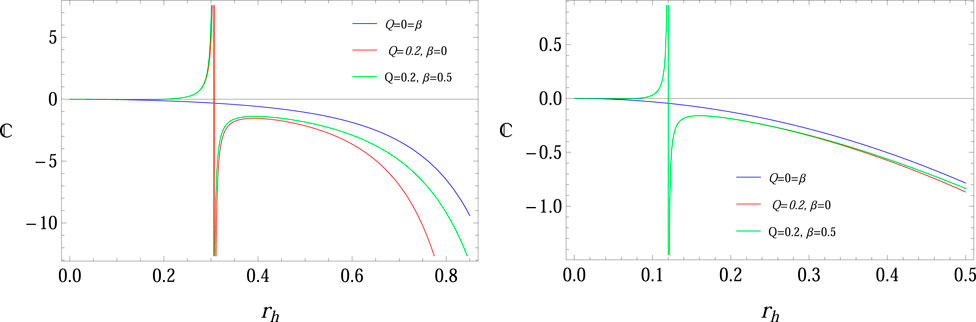
The divergence point of the heat capacity is referred to as Davies’s point, which plays an important role in discussing the thermodynamic stability of the BH structure. Davies’s point is also known as the phase change point from negative to positive or positive to negative. It is noted that the positive region before the Davies point shows a stable region, and the negative region after the Davies point represents an unstable region (Das et al., 2002; Sharif and Khan, 2022b). Hence, the radial position of BH at which it changes the phase is given where r_DP is represented by the position of Davies point.

Figure 6 is used to discuss stable and unstable configurations using the Davies point of heat capacity of BH. In the absence of β and Q (as Schwarzschild-ADS BH), the BH structure shows an unstable configuration, while for non-zero values of β and Q, the system shows a stable configuration for smaller BHs. It is also noted that the stable configuration is increased for higher values of β. Hence, the presence of NED-charged BH shows a stable configuration for smaller ADS BHs, while larger ADS BH shows unstable behavior.

FIGURE 6

FIGURE 6. Plot of heat capacity versus BH horizon radius with M = 0.2, Λ = −1.

3 Emission energy

The formation and destruction of an excessive number of particles very close to the horizon are known as emission energy, and quantum fluctuations in the interior of BHs are the source of this energy. The main reason for the BH evaporation within a certain period is due to the positive-energy particles that tunnel out of the BH in the core area where Hawking radiation occurs. Here, we are interested in exploring the energy emission rate associated with the considered BH geometry with NED. At very high energy, the absorption cross-section often oscillates around a limiting constant value σ_lim. The limiting value of σ_lim is related to the radius of the event horizon (Wei and Liu, 2013; Papnoi et al., 2014; Eslam Panah et al., 2020):

${\sigma }_{\mathit{lim}}\approx \pi r_h^2.(11)$

The respective expression of the rate of BH energy emission becomes (Wei and Liu, 2013; Papnoi et al., 2014; Eslam Panah et al., 2020)

$\frac{d^2\epsilon }{d\omega dt}=\frac{2{\pi }^2{\sigma }_{\mathit{lim}}}{{\exp }^{\frac{\omega }{\mathbb{T}}}-1}{\omega }^3,(12)$

and by considering the Hawking temperature $\mathbb{T}$ of the considered BH, we get

$\frac{d^2\epsilon }{d\omega dt}=\frac{2{\pi }^3{r}_h^2{\omega }^3}{\exp \left(-\frac{6\pi r_h^3\omega }{-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)}\right)-1}.(13)$

Figure 7 shows the behavior of the rate of emission energy along the frequency with suitable values of physical parameters. It is found that the energy rate increases as frequency gradually increases initially, approaches its peak value, and then decreases. It is concluded that the rate of emission energy decreases for higher values of charge and NED parameter.

FIGURE 7

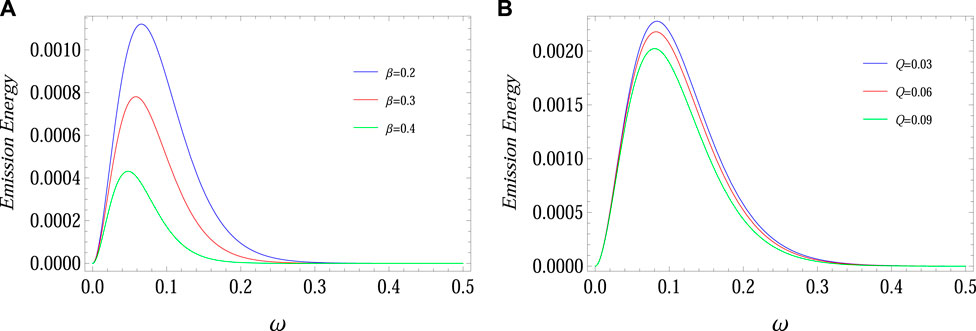
FIGURE 7. Graphical analysis of the rate of emission energy versus frequency for uncharged ADS (A) and charged ADS BHs (B) with M = 0.2, Λ = −1.

4 Null geodesics and quasinormal modes

Here, we are interested in calculating the null geodesics and radius of the photon sphere of charged ADS BH with NEW. Then, we determine the photon angular velocity and Lyapunov exponent using photon radius.

4.1 Null geodesics

The Lagrangian at the equatorial plane $\left(\theta =0,\frac{\pi }{2}\right)$ has the following form (Cardoso et al., 2009; Sharif and Khan, 2022b):

$2\mathcal{L}=\mathcal{B}\left(r\right){\dot{t}}^2-\mathcal{B}{\left(r\right)}^{-1}{\dot{r}}^2-r^2{\dot{\varphi }}^2,(14)$

where ϕ is referred to as an angular coordinate. The generalized momenta components $\left({\mathcal{P}}_u,=,g_{uv},{\dot{x}}^v,=,\frac{\partial \mathcal{L}}{\partial {\dot{x}}^u}\right)$ become

$\begin{array}{l}\hfill \begin{array}{cc}\hfill {\mathcal{P}}_{\varphi }& =-r^2\dot{\varphi }\equiv -l=constant,{\mathcal{P}}_t=\mathcal{B}\left(r\right)\dot{t}=\bar{E}=constant,\hfill \\ \hfill {\mathcal{P}}_r& =-\mathcal{B}{\left(r\right)}^{-1}\dot{r},\hfill \end{array}\end{array}(15)$

where $\bar{E}$ denotes the energy, and l is the angular momentum. Consequently, t and ϕ-motions become

$\dot{t}=\mathcal{B}{\left(r\right)}^{-1}\bar{E},\dot{\varphi }=\frac{1}{r^2}l.$

Hence, the Hamiltonian becomes the photon:

$2\mathcal{H}=-{\dot{r}}^2{\mathcal{B}\left(r\right)}^{-1}+\mathcal{B}\left(r\right){\dot{t}}^2-r^2{\dot{\varphi }}^2=\bar{E}\dot{t}-{\dot{r}}^2{\mathcal{B}\left(r\right)}^{-1}-l\dot{\varphi }=0,(16)$

which yields

$V_{\text{eff}}=-{\dot{r}}^2,$

where the respective potential function yields

$V_{\text{eff}}=\frac{\mathcal{B}\left(r\right)l^2-{\bar{E}}^2{r}^2}{r^2}.(17)$

It is noted that positive values of ${\dot{r}}^2$ indicate the negative behavior of effective potential. This shows that the photon is unable to escape from the large negative effective potential region.The photon will drive out before falling inside the BH for large l and small r, whereas the photon will fall inside the BH for large r and small l. Conversely, the photon rotates around BH with zero radial velocity (at a different region) at a distance equal to the radius of the BH horizon (Cardoso et al., 2009; Sharif and Khan, 2022b). These photon spheres are unstable circular orbits.

The photon sphere for the four-dimensional spherically symmetric geometry is determined using the following constraints:

$V_{\text{eff}}=0,\frac{\partial V_{\text{eff}}}{\partial r}=0,\frac{{\partial }^2{V}_{\text{eff}}}{\partial r^2}<0.(18)$

Now, we consider the second condition to calculate the photon radius $\left({\mathit{r}}_{\mathit{p}\mathit{s}}\right)$ and the third constraint represents the unstable configuration and association among QNMs of BH. By considering Eq. 17 in the second condition, we get

${\mathcal{B}}^{\prime }\left(r_{ps}\right)r_{ps}-2\mathcal{B}\left(r_{ps}\right)=0.(19)$

By using the metric function of BH, we get

$3M{r}_{ps}=2Q^2+2\beta Q{r}_{ps}^2+r_{ps}^2.$

The respective radius of the photon sphere yields

$r_{ps}=\frac{3M-\sqrt{9M^2-8Q^2\left(2\beta Q+1\right)}}{4\beta Q+2}.(20)$

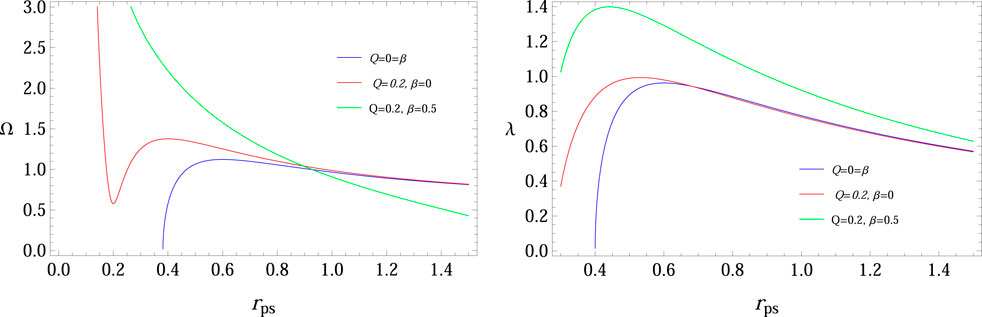
We plot this function for suitable physical parameters, and the root of this function represents the position photon radius, as shown in Figure 8. This function also represents the stability of the photon motion around the BH at the event horizon. It is interesting to mention that the case of the Schwarzschild-ADS BH system shows an unstable structure, and the position of photon radius is decreased for higher values of β and Q. It is found that the system shows a stable configuration for RN and charged ADS BH with NED.

FIGURE 8

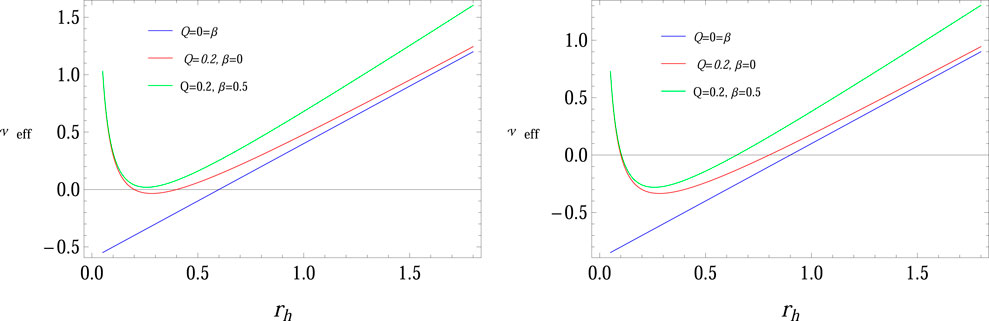
FIGURE 8. Plot of V_eff to determine the position of photon sphere for M = 0.2. It is noted that the roots of V_eff are denoted by the position of the photon’s spherical radius.

4.2 Quasinormal modes

The QNMs are determined through the property of the photon sphere in the eikonal limit (l ≫ 1) as follows (Das et al., 2002; Sharif and Khan, 2022b):

$w_Q=\mathrm{\Omega }l-i|\lambda |\left(\frac{2n+1}{2}\right),(21)$

where n represents the number of overturns of the perturbations. The Lyapunov exponent λ and angular velocity Ω are two major physical quantities of the photon sphere. Both are associated with QNMs as

$\mathrm{\Omega }={\left.\dot{\varphi }\frac{1}{\dot{t}}\right|}_{r_{ps}}=\frac{\sqrt{{\mathcal{B}}_{ps}}}{r_{ps}},\lambda ={\left.\sqrt{\frac{-V_{\text{eff}}^{\prime \prime }}{2{\dot{t}}^2}}\right|}_{r_{ps}}=\sqrt{\frac{\left(2{\mathcal{B}}_{ps}-{\mathcal{B}}_{ps}^{\prime \prime }{r}_{ps}^2\right){\mathcal{B}}_{ps}}{2r_{ps}^2}},(22)$

which yields

$\mathrm{\Omega }=\frac{1}{r_{ps}}\sqrt{-\frac{2M}{r_{ps}}+\frac{Q^2}{r_{ps}^2}+2\beta Q-\frac{{\beta }^2{r}_{ps}^2}{3}-\frac{\mathrm{\Lambda }{r}_{ps}^2}{3}+1},$

and

$\lambda =\frac{1}{\sqrt{3}{r}_{ps}^3}\sqrt{\begin{array}{c}-\left(-2Q^2+2\beta Q{r}_{ps}^2+r_{ps}^2\right)\left(r_{ps}\left(6M\right.\right.\left.\left.+r_{ps}\left(r_{ps}^2\left({\beta }^2+\mathrm{\Lambda }\right)-3\right)\right)-3Q^2-6\beta Q{r}_{ps}^2\right).\hfill \end{array}}$

Now, we explore the effects of physical parameters on the angular velocity and Lyapunov exponent. For this purpose, we plot the mathematical expressions of both angular velocity and Lyapunov exponent versus r_ps as shown in Figure 9. Initially, both physical quantities decrease for higher values of horizon radius.

FIGURE 9

FIGURE 9. Plots angular velocity and Lyapunov exponent versus r_ps for M = 0.2, Λ = −1.

5 Thermal fluctuations

Here, we discuss the effects of thermal fluctuation on the charged ADS BH with NED. For this purpose, we find the mathematical expression of the corrected entropy of the system using the partition function defined as follows (Pourhassan et al., 2018; Pradhan, 2019; Sharif and Khan, 2022b):

$R\left(\xi \right)={\int }_0^{\infty }\rho \left(E\right)\exp \left(-\xi E\right)dE,(23)$

where the density state is denoted with ρ(E) and the average energy is E. The density state is evaluated using the inverse Laplace transformation of the previously defined function given as

$\begin{array}{ll}\hfill \rho \left(E\right)& =\frac{1}{2i\pi }{\int }_{-i\infty +{\xi }_0}^{i\infty +{\xi }_0}\exp \left(\xi E\right)R\left(\xi \right)d\xi \hfill \\ \hfill & =\frac{1}{2i\pi }{\int }_{-i\infty +{\xi }_0}^{i\infty +{\xi }_0}\exp \left(\tilde{S}\left(\xi \right)\right)d\xi ,\hfill \end{array}(24)$

where the exact corrected expression of entropy is $\tilde{S}(\xi )=\beta E+\ln Z(\xi )$ with ξ > 0. By considering Taylor series expansion of ξ₀, we get

$\tilde{S}\left(\xi \right)={\left.S+\frac{1}{2}{\left(\xi -{\xi }_0\right)}^2\frac{{\partial }^2\tilde{S}\left(\xi \right)}{\partial {\xi }^2}\right|}_{\xi ={\xi }_0}+O{\left(\xi -{\xi }_o\right)}^2.(25)$

The equilibrium entropy S satisfies the relations $\frac{\partial S}{\partial \xi }=0$ and $\frac{{\partial }^{2}S}{\partial {\xi }^2}>0$. Using Eq. 25 in Eq. 24, we obtain

$\rho \left(E\right)=\frac{1}{2\pi i}\exp \left(S\right)\int d\xi \exp \left(\frac{1}{2}{\left(\xi -{\xi }_0\right)}^2\frac{{\partial }^2\tilde{S}\left(\xi \right)}{\partial {\xi }^2}\right).(26)$

Furthermore, it yields (Pourhassan et al., 2018; Pradhan, 2019; Sharif and Khan, 2022b)

$\rho \left(E\right)=\frac{1}{\sqrt{2\pi }}\exp \left(S\right){\left({\left.\left(\frac{{\partial }^2\tilde{S}\left(\xi \right)}{\partial {\xi }^2}\right)\right|}_{\xi ={\xi }_0}\right)}^{-\frac{1}{2}},(27)$

which becomes

$\tilde{S}=S-\frac{1}{2}\ln \left(S{\mathbb{T}}^2\right)+\frac{\eta }{S}.(28)$

We may use a broader parameter χ without losing generality, except for the factor $\frac{1}{2}$, which increases the influence of correction terms on the entropy of BH. The corrected entropy may be expressed in this context as follows (Sharif and Khan, 2022b):

$\tilde{S}=S-\gamma \ln \left(S{\mathbb{T}}^2\right)+\frac{\eta }{S}.(29)$

By considering alternative correction parameter values γ and η, we obtain

• Uncorrected entropy (UCE) ⇒ if η, γ → 0.

• Simple logarithmic corrections (SLCs) ⇒ if η → 0, γ → 1.

• Second-order correction terms (SOCs) ⇒ if η → 1, γ → 0.

• Higher-order correction terms (HOCs) ⇒ if η, γ → 1.

The respective expression of perturbed entropy is evaluated by considering Eqs 8, 9 in Eq. 29 as

$\begin{array}{ll}\hfill \tilde{S}& =\gamma \log \left(36\pi \right)-\gamma \log \left(\frac{{\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)}^2}{r_h^4}\right)\hfill \\ \hfill & +\frac{\eta }{\pi r_h^2}+\pi r_h^2.\hfill \end{array}(30)$

Figure 10 shows the graph of corrected entropy through four different cases as UCE, SLCs, SOCs, and HOCs for Schwarzschild-ADS (first plot), RN-ADS (second plot), and charged ADS BH with NED (third and fourth plots). It is noted that for all cases, system entropy is monotonically increasing throughout the considered domain for larger BHs. It is noted that the graph of usual entropy is increasing smoothly (left plot blue curve), but the corrected expression fluctuates for smaller BHs, increasing smoothly for larger ones. Thus, these correction terms are more effective for small BHs. The corrected entropy shows the larger behavior for the case of HOCs.

FIGURE 10

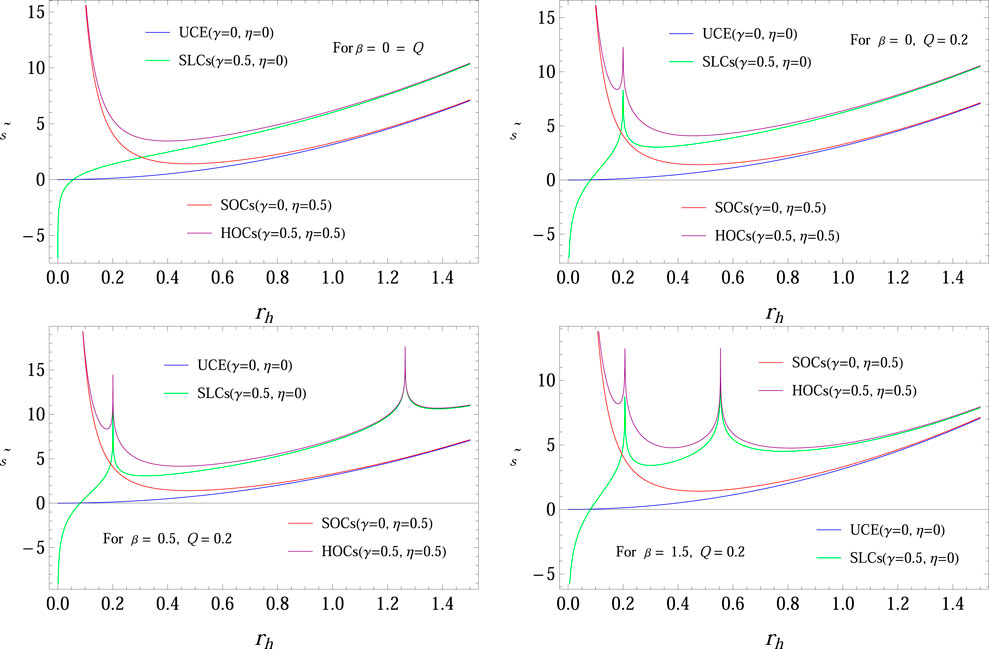
FIGURE 10. Plots of corrected entropy versus r_h for different values of χ and η with M = 0.2, Λ = −1.

Now, we consider the expression of corrected entropy to explore the corrected energies of the considered BH solution. Under thermal fluctuations, the modified first rule of BH thermodynamics may be expressed as follows (Jawad and Shahzad, 2017; Sharif and Khan, 2022b):

$dM=\mathcal{T}d\tilde{S}+VdP+\mathrm{\Phi }dQ+\mathrm{\Psi }d\beta ,(31)$

where $\mathcal{T}$ denotes the corrected Hawking temperature. In this case, Φ and Ψ are the new conjugate quantities and Q and β are new thermodynamic variables. The relations can be used to derive these potential functions:

$\begin{array}{ll}\hfill \mathcal{T}& ={\left(\frac{\partial M}{\partial \tilde{S}}\right)}_{Q,P,\beta },V={\left(\frac{\partial M}{\partial P}\right)}_{\mathbb{T},\mathbb{Q},\beta },\mathrm{\Phi }={\left(\frac{\partial M}{\partial Q}\right)}_{\mathbb{T},P,\beta },\hfill \\ \hfill \mathrm{\Psi }& ={\left(\frac{\partial M}{\partial \beta }\right)}_{\mathbb{T},Q,P}\hfill \end{array}$

which turns out to be

$\begin{array}{ll}\hfill \mathcal{T}& =\frac{\pi r_h\left({\left(Q-\beta r_h^2\right)}^2+\mathrm{\Lambda }{r}_h^4-r_h^2\right)\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)}{4\left(\eta \left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)-{\pi }^2{r}_h^4\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)+\pi \gamma r_h^2\left(3M{r}_h-6Q^2+2r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\right)},\hfill \\ \hfill \mathrm{\Phi }& =-\frac{3\sqrt{r_h\left(6M+r_h\left(r_h^2\left(4{\beta }^2+\mathrm{\Lambda }\right)-3\right)\right)}\left({\left(Q-\beta r_h^2\right)}^2+\mathrm{\Lambda }{r}_h^4-r_h^2\right)}{2r_h^2\left(-6\beta r_h\sqrt{r_h\left(6M+r_h\left(r_h^2\left(4{\beta }^2+\mathrm{\Lambda }\right)-3\right)\right)}+3\sqrt{3}M+\sqrt{3}{r}_h\left(2r_h^2\left(4{\beta }^2+\mathrm{\Lambda }\right)-3\right)\right)},\hfill \\ \hfill \mathrm{\Psi }& =-\frac{r\sqrt{3r_h^4\left(r_h\left(r_h-2M\right)+4Q^2\right)-\mathrm{\Lambda }{r}_h^8}\left({\left(Q-\beta r_h^2\right)}^2+\mathrm{\Lambda }{r}_h^4-r_h^2\right)}{6\left(-2Q\sqrt{3r_h^4\left(r_h\left(r_h-2M\right)+4Q^2\right)-\mathrm{\Lambda }{r}_h^8}+r_h^3\left(r_h-3M\right)+8Q^2{r}_h^2\right)},\hfill \\ \hfill V& =\frac{4\pi r_h^3}{3}.\hfill \end{array}$

When the foregoing expressions are substituted in Eq. 31, the modified first law of BH is verified, suggesting that the existence of thermal fluctuations enhances the reliability of the first law of BH thermodynamics.

5.1 Corrected energies of black hole

The Helmholtz free energy can be determined in this context by applying the following relation (Jawad and Shahzad, 2017; Sharif and Khan, 2022b):

$\tilde{F}=-\int \tilde{S}d\mathbb{T},(32)$

which yields

$\begin{array}{ll}\hfill \tilde{F}& =\frac{1}{6{\pi }^2}\left(-\frac{\pi \gamma }{r_h^3}\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\right.\hfill \\ \hfill & \times \log \left(\frac{{\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)}^2}{r_h^4}\right)-\frac{3\eta M}{2r_h^4}\hfill \\ \hfill & -\frac{3\pi \gamma M\left(1+\log \left(36\right)+\log \left(\pi \right)\right)}{r_h^2}+6{\pi }^{2}M\log \left(r_h\right)+\frac{9\eta Q^2}{5r_h^5}\hfill \\ \hfill & +\frac{\pi \gamma Q^2\left(4+3\log \left(36\pi \right)\right)}{r_h^3}+\frac{9{\pi }^2{Q}^2-\eta \left({\beta }^2+\mathrm{\Lambda }\right)}{r_h}+\frac{1}{3}{\pi }^2{r}_h^3\hfill \\ \hfill & \times \left.\left({\beta }^2+\mathrm{\Lambda }\right)+\pi \gamma r_h\left(4+\log \left(36\right)+\log \left(\pi \right)\right)\left({\beta }^2+\mathrm{\Lambda }\right)\right).\hfill \end{array}$

The identity that can be used to evaluate the internal energy of the system under consideration is given as $\tilde{U}=\tilde{S}\mathbb{T}+\tilde{F}$ (Pourhassan and Upadhyay, 2021; Sharif and Khan, 2022b). Hence, we have

$\begin{array}{ll}\hfill \tilde{U}& =\frac{1}{180{\pi }^2{r}_h^5}\left(10{\pi }^2{r}_h^4\left(9M{r}_h+18Q^2-2r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\right.\hfill \\ \hfill & -3\eta \left(5r_h\left(4r_h^3\left({\beta }^2+\mathrm{\Lambda }\right)-3M\right)+12Q^2\right)+30\pi \gamma r_h^2\hfill \\ \hfill & \times \left.\left(-3M{r}_h+4Q^2+4r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)+180{\pi }^{2}M{r}_h^5\log \left(r_h\right)\right).\hfill \end{array}$

The BH’s volume can be expressed as (Pourhassan and Faizal, 2015; Sharif and Khan, 2022b)

$\mathbb{V}=\frac{4}{3}\pi r_h^3.(33)$

The relationship that can be used to determine the pressure of the BH is as follows:

$\tilde{\mathbb{P}}=-\frac{d\tilde{F}}{d\mathbb{V}}=-\frac{d\tilde{F}}{d{r}_h}\frac{d{r}_h}{d\mathbb{V}},(34)$

and hence,

$\begin{array}{ll}\hfill \tilde{\mathbb{P}}& =-\frac{\left(6M{r}_h-9Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)}{24{\pi }^3{r}_h^8}\hfill \\ \hfill & \times \left(\eta -\pi \gamma r_h^2\log \left(\frac{{\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)}^2}{r_h^4}\right)\right.\hfill \\ \hfill & \left.+{\pi }^2{r}_h^4+\pi \gamma r_h^2\log \left(36\pi \right)\right).\hfill \end{array}$

The enthalpy of considered BH is determined using $(\tilde{H}=\tilde{U}+\mathbb{V}\tilde{\mathbb{P}})$ (Pourhassan and Faizal, 2015). It is given as

$\begin{array}{ll}\hfill \tilde{H}& =\frac{1}{180{\pi }^2{r}_h^5}\left(10{\pi }^2{r}_h^4\left(9M{r}_h+18Q^2-2r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\right.\hfill \\ \hfill & -3\eta \left(5r_h\left(4r_h^3\left({\beta }^2+\mathrm{\Lambda }\right)-3M\right)+12Q^2\right)-10\left(6M{r}_h\right.\hfill \\ \hfill & \left.-9Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\left(\eta -\pi \gamma r_h^2\log \right.\hfill \\ \hfill & \times \left(\frac{{\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)}^2}{r_h^4}\right)+{\pi }^2{r}_h^4+\pi \gamma r_h^2\hfill \\ \hfill & \times \left.\log \left(36\pi \right)\right)+30\pi \gamma r_h^2\left(-3M{r}_h+4Q^2+4r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\hfill \\ \hfill & \left.+180{\pi }^{2}M{r}_h^5\log \left(r_h\right)\right).\hfill \end{array}$

The Gibbs free energy $(\tilde{G}=-\tilde{S}\mathbb{T}+\tilde{H})$ can be obtained as (Pourhassan and Faizal, 2015)

$\begin{array}{ll}\hfill \tilde{G}& =\frac{1}{180{\pi }^2{r}_h^5}\left(\eta \left(144Q^2-5\left(21M{r}_h+8r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\right)-60{\pi }^2{r}_h^4\right.\hfill \\ \hfill & \times \left(M{r}_h-6Q^2\right)+10\pi \gamma r_h^2\left(-3M{r}_h\left(3+5\log \left(36\pi \right)\right)+6Q^2\right.\hfill \\ \hfill & \times \left.\left(2+3\log \left(36\pi \right)\right)+2r_h^4\left(6+\log \left(36\right)+\log \left(\pi \right)\right)\left({\beta }^2+\mathrm{\Lambda }\right)\right)\hfill \\ \hfill & -10\pi \gamma r_h^2\left(-15M{r}_h+18Q^2+2r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\hfill \\ \hfill & \times \log \left(\frac{{\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)}^2}{r_h^4}\right)\left.+180{\pi }^{2}M{r}_h^5\log \left(r_h\right),\right).\hfill \end{array}$

The graphical analysis of corrected energies of the considered BHs can be expressed as follows:

• Thermal fluctuation affects the physical quantities of BH geometry. It is noted that for the small values of radii, the graph of Helmholtz free energy gradually decreases and then increases for higher BHs (first-panel plot of Figure 11). It shows larger behavior in the presence of β and Q for larger BHs. The Helmholtz free energy is maximum for larger BHs for non-zero values of β and Q.

• The corrected internal energy of Schwarzschild-ADS BH represents the gradually increasing behavior for higher values of BH event horizons (left plot of the second panel of Figure 11). It fluctuates in the presence of NED for higher BHs (right plot of the second panel of Figure 11). The internal energy of charged ADS BH with NED fluctuates, while for RN-ADS, it increases gradually.

• The enthalpy and Gibbs free energy of RN-ADS BH increase gradually while fluctuating for charged ADS BH with NED for SLCs and HOCs (third and fourth panels of Figure 11).

FIGURE 11

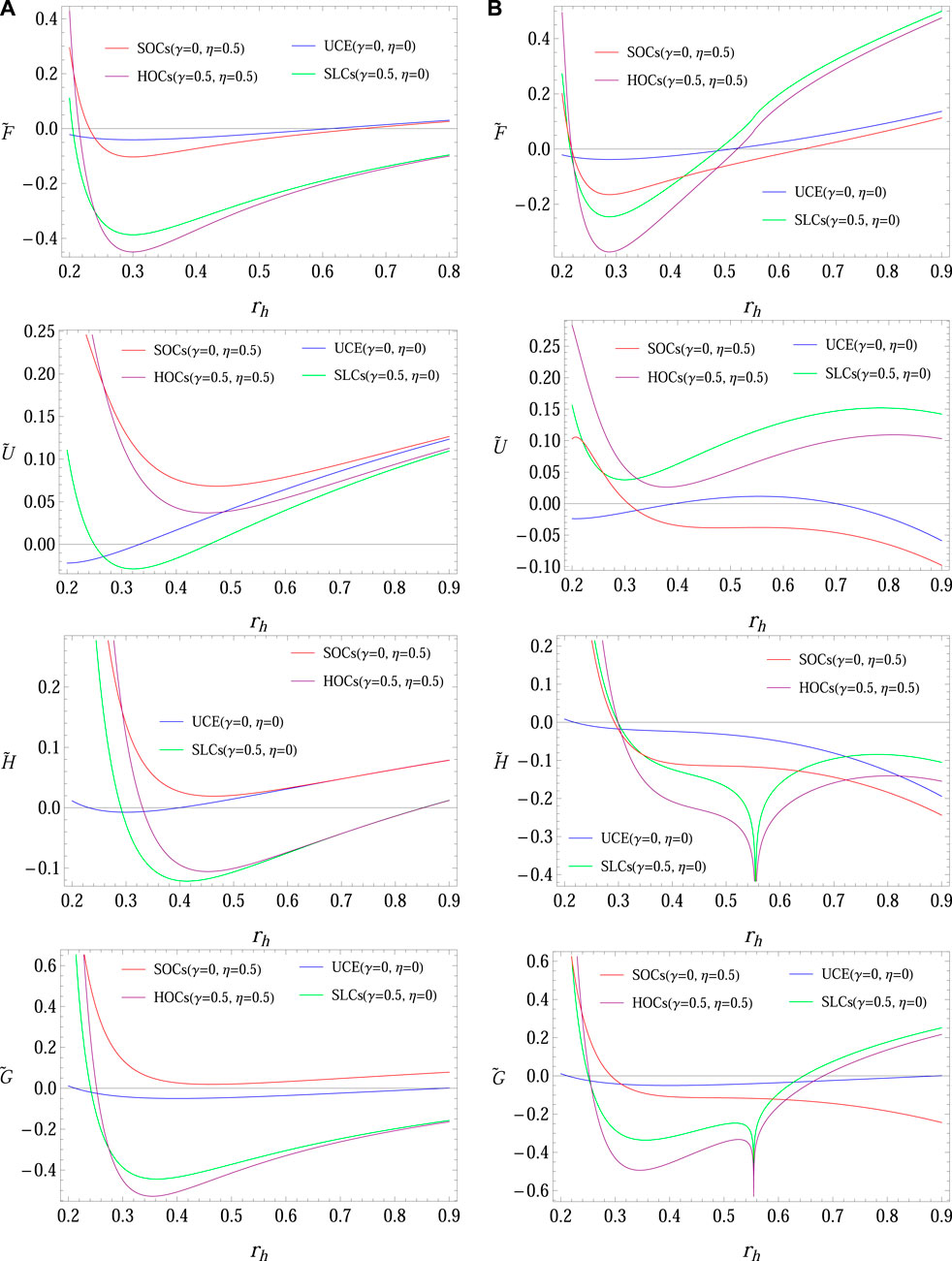
FIGURE 11. Plots of corrected energies of the BH versus horizon radius for RN BH (Q = 0.2, β = 0) (A) and charged BH with NED (Q = 0.2, β = 1.5) (B) with M = 0.2, Λ = −1.

5.2 Phase transition

Another method for locally determining the BH’s thermodynamic stability is to study the sign of the specific heat ${\mathbb{C}}_{\mathbb{S}}=\frac{d\tilde{U}}{d\mathbb{T}}$. It is noted that BH is locally unstable for ${\mathbb{C}}_{\mathbb{S}}<0$, the point of the phase transition can be found at ${\mathbb{C}}_{\mathbb{S}}=0$, and BH is locally stable if ${\mathbb{C}}_{\mathbb{S}}>0$. The mathematical expression of specific heat is given as follows (Pourhassan and Upadhyay, 2021; Sharif and Khan, 2022b):

${\mathbb{C}}_{\mathbb{S}}=\frac{2\left(\eta \left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)-{\pi }^2{r}_h^4\left(-3M{r}_h+3Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)+\pi \gamma r_h^2\left(3M{r}_h-6Q^2+2r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)\right)}{-\pi r_h^2\left(6M{r}_h-9Q^2+r_h^4\left({\beta }^2+\mathrm{\Lambda }\right)\right)},$

Now, we discuss the thermodynamic stability of the system through the graphical behavior of specific heat with four different cases of thermodynamic fluctuations as UCE, SLCs, SOCs, and HOCs (Figure 12). It shows the behavior-specific heat of RN-ADS BH using UCE, SLCs, SOCs, and HOCs with M = 0.2. It is interesting to mention that specific heat expresses a stable structure for smaller BHs and an unstable configuration for larger BHs. Hence, the second- and higher-order correction provides the possibility of a more stable structure of BHs.

FIGURE 12

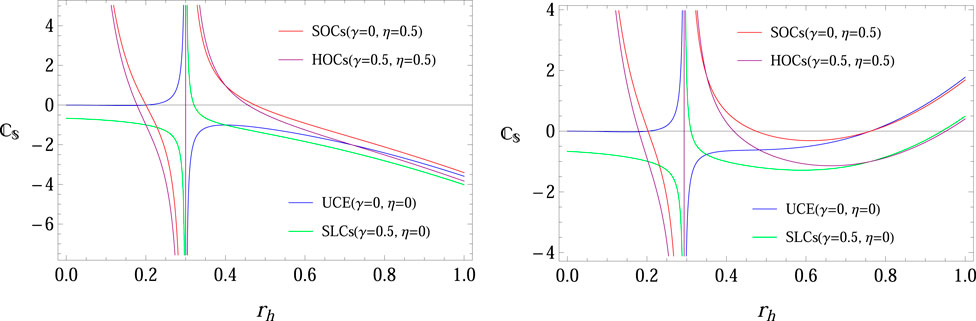
FIGURE 12. Plots of specific heat versus r_h using four different cases of thermodynamic fluctuations as UCE, SLCs, SOCs, and HOCs for RN BH Q = 0.2, β = 0, and charged BH with nonlinear electrodynamics Q = 0.2, β = 1 with M = 0.2, Λ = −1.

6 Concluding remarks

This study is devoted to exploring the thermodynamics of charged ADS BH with NED through QNMs and thermal fluctuations. We explore the effects of NED parameter β on the thermodynamic quantities of charged ADS BH. Some important features of the present study are itemized as follows:

• The graphical behavior of the lapse function under the effect of involved model parameters is provided in Figures 1, 2. The position of the event horizon depends on the charge and the coupling constant β.

• We observed the behavior of temperature versus entropy of the system in Figure 4. It is noted that temperature initially increases and then decreases as the entropy of the system increases.

• The Davies point and heat capacity are presented in Figure 6 to check the stable and unstable regions for the BH configuration. In the absence of β and Q (as Schwarzschild-ADS BH), the BH structure shows unstable configuration, while non-zero values of β and Q systems show stable configurations for smaller BHs. Hence, the presence of NED-charged ADS BH shows the stable configuration for smaller BHs, while larger BH shows unstable behavior.

• Figure 7 shows that the rate of emission energy decreases for higher values of charge and NED parameter.

• We calculated the null geodesics and radius of the photon sphere of BH geometry in the background charged ADS BH with NED. It is interesting to mention that the case of the Schwarzschild-ADS BH system shows an unstable structure, and the position of photon radius is decreased for higher values of β and Q (Figure 8). It is found that the system shows a stable configuration for RN-ADS and charged BH with NED.

• The angular velocity and Lyapunov exponent versus r_ps, as shown in Figure 9, and both physical quantities initially decrease for higher values of the horizon radius.

• The behavior of thermal fluctuations (UCE, SLCs, SOCs, and HOCs) on the entropy of the system is provided graphically in Figure 10. It is noted that for all cases, the system entropy is monotonically increasing throughout the considered domain for larger BHs.

• The corrected, uncorrected Helmholtz free energy and internal energy for the BH versus r_h are presented graphically in Figure 11. Helmholtz free energy shows larger behavior in the presence of β and Q for larger BHs. The internal energy of charged ADS BH with NED fluctuates, while for RN-ADS, it increases gradually. The enthalpy and Gibbs free energy of RN-ADS BH gradually increases while fluctuating for charged ADS BH with NED for SLCs and HOCs.

• It is interesting to mention that specific heat expresses a stable structure for smaller BHs and an unstable configuration for larger BHs. Hence, the second- and higher-order correction provides the possibility of a more stable structure of BHs (Figure 12).

Hence, to sum up, it is determined that the cosmological constant and NED greatly affect the thermodynamic properties of charged ADS BHs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.

Author contributions

FJ conceived the presented idea. FJ and AB developed the theory while FJ performed the computations. FJ, AB, and AC verified the analytical methods. All authors discussed the results and contributed to the final manuscript. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

AB was supported by startup funding from Zhejiang Normal University through Grant no. ZC304021948 and from Zhejiang Provincial Postdoctoral Science Foundation through Grant no. ZC304022995. FJ is very thankful to Prof. Lin Ji from the Department of Physics, Zhejiang Normal University, for his kind support and help during this research. Also, FJ acknowledges Grant No. YS304023917 to support his Postdoctoral Fellowship at Zhejiang Normal University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, R., Babar, R., Asgher, M., and Mustafa, G. (2022). Tunneling analysis of null aether black hole theory in the background of Newman–Janis algorithm. Int. J. Mod. Phys. A 37, 2250134. doi:10.1142/S0217751X22501342

CrossRef Full Text | Google Scholar

Anabalon, A., Appels, M., Gregory, R., Kubizňák, D., Mann, R. B., and Övgün, A. Holographic thermodynamics of accelerating black holes doi:10.1103/PhysRevD.98.104038Phys. Rev. D. 98(2018)104038. doi:10.1103/PhysRevD.98.104038

CrossRef Full Text | Google Scholar

Balart, L., and Vagenas, E. C. (2014). Regular black holes with a nonlinear electrodynamics source. Phys. Rev. D. 90, 124045. doi:10.1103/physrevd.90.124045

CrossRef Full Text | Google Scholar

Bekenstein, D. (1973). Black holes and entropy. Phys. Rev. D. 7, 2333.

CrossRef Full Text | Google Scholar

Born, M., and Infeld, L. (1934). Foundations of the new field theory. Proc. R. Soc. Lond. A 144, 425.

Google Scholar

Cardoso, V., Miranda, A. S., Berti, E., Witek, H., and Zanchin, V. T. (2009). Geodesic stability, Lyapunov exponents and quasinormal modes. Phys. Rev. D. 79, 064016. doi:10.1103/PhysRevD.79.064016

CrossRef Full Text | Google Scholar

Chabab, M., Moumni, H. E., Iraoui, S., Masmar, K., and Zhizeh, S. (2018). Joule-thomson expansion of reissner-nordstrom AdS black holes in f(R) gravity. arXiv:1804.10042.

Google Scholar

D’Almeida, R., and Yogendran, K. P. (2018). Thermodynamic properties of holographic superfluids. arXiv: 1802.05116.

Google Scholar

D’Ambrosio, F., Fell, S. D. B., Heisenberg, L., and Kuhn, S. (2022). Black holes in f(Q) gravity. Phys. Rev. D. 105, 024042. doi:10.1103/physrevd.105.024042

CrossRef Full Text | Google Scholar

Das, S., Majumdar, P., and Bhaduri, R. K. (2002). General logarithmic corrections to black hole entropy. Cl. Quantum Grav. 19, 2355. doi:10.1088/0264-9381/19/9/302

CrossRef Full Text | Google Scholar

Dayyani, Z., Sheykhi, A., and Dehghani, M. H. (2017). Counterterm method in Einstein dilaton gravity and the critical behavior of dilaton black holes with a power-Maxwell field. Phys. Rev. D. 95, 084004. doi:10.1103/PhysRevD.95.084004

CrossRef Full Text | Google Scholar

Dehghani, M. (2016). Dimensional charged black holes with power-law Maxwell field. Phys. Rev. D. 94, 104071.

CrossRef Full Text | Google Scholar

Dehghani, M., and Hamidi, S. F. (2017). Thermal stability analysis of nonlinearly charged asymptotic AdS black hole solutions. Phys. Rev. D. 96, 044025. doi:10.1103/PhysRevD.96.044025

CrossRef Full Text | Google Scholar

Ditta, A., Tiecheng, X., Mustafa, G., Muhammad, Y., and Atamurotov, F. (2022). Thermal stability with emission energy and Joule–Thomson expansion of regular BTZ-like black hole. Eur. Phys. J. C 82, 756. doi:10.1140/epjc/s10052-022-10708-z

CrossRef Full Text | Google Scholar

Eslam Panah, B., Jafarzade, K., and Hendi, S. H. (2020). Charged 4D Einstein-Gauss-Bonnet-AdS black holes: Shadow, energy emission, deflection angle and heat engine. Nucl. Phys. B 961, 115269. doi:10.1016/j.nuclphysb.2020.115269

CrossRef Full Text | Google Scholar

Faizal, M., and Khalil, M. M. (2015). GUP-corrected thermodynamics for all black objects and the existence of remnants. Int. J. Mod. Phys. A 30, 1550144. doi:10.1142/s0217751x15501444

CrossRef Full Text | Google Scholar

Ghaffarnejad, H., Yaraie, E., and Farsam, M. (2018). Quintessence reissner nordström anti de Sitter black holes and Joule thomson effect. Int. J. Theo. Phys. 57, 1671–1682. doi:10.1007/s10773-018-3693-7

CrossRef Full Text | Google Scholar

Gogoi, D. J., Övgün, A., and Koussour, M. (2023). Quasinormal Modes of Black holes in f(Q) gravity. arXiv:2303.07424.

CrossRef Full Text | Google Scholar

Gracia, J. P. M., Capossoli, E. F., and Boschi-Filho, H. (2021). Joule-Thomson expansion for noncommutative uncharged black holes. Europhys. Lett. 135, 41002. doi:10.1209/0295-5075/ac24c1

CrossRef Full Text | Google Scholar

Guo, S., Pu, J., Jiang, Q. Q., and Zu, X. T. (2020). Joule-Thomson expansion of the regular(Bardeen)-AdS black hole *. Chin. Phys. C 44, 035102. doi:10.1088/1674-1137/44/3/035102

CrossRef Full Text | Google Scholar

Haldar, A., and Biswas, R. (2018). Thermodynamic studies of different black holes with modifications of entropy. Astrophys. Space Sci. 363, 27. doi:10.1007/s10509-017-3238-1

CrossRef Full Text | Google Scholar

Hawking, S. W. (1975). Particle creation by black holes. Commun. Math. Phys. 43, 199–206. doi:10.1007/BF02345020

CrossRef Full Text | Google Scholar

Hendi, S. H., Panahiyan, S., and Panah, B. E. (2015). Geometrical method for thermal instability of nonlinearly charged BTZ black holes. Adv. High. Energy Phys. 2015, 743086. doi:10.1155/2015/743086

CrossRef Full Text | Google Scholar

Javed, F., Fatima, G., Mustafa, G., and Övgün, A. (2023). Effects of variable equations of state on the stability of nonlinear electrodynamics thin-shell wormholes. Int. J.Geo. M. Mod. Phys. 20, 2350010. doi:10.1142/S021988782350010X

CrossRef Full Text | Google Scholar

Javed, W., Abbas, J., and Övgün, A. (2019). Deflection angle of photon from magnetized black hole and effect of nonlinear electrodynamics. Eur. Phys. J. C 79, 694. doi:10.1140/epjc/s10052-019-7208-3

CrossRef Full Text | Google Scholar

Javed, W., Yousaf, Z., and Akhtar, Z. (2018). Thermodynamics and glassy phase transition of regular black holes. Mod. Phys. Lett. A 33, 1850089. doi:10.1142/s021773231850089x

CrossRef Full Text | Google Scholar

Jawad, A., and Shahzad, M. U. (2017). Effects of thermal fluctuations on non-minimal regular magnetic black hole. Eur. Phys. J. C 77, 349. doi:10.1140/epjc/s10052-017-4914-6

CrossRef Full Text | Google Scholar

Kanzi, S., Mazharimousavi, S. H., and Sakalli, I. (2020). Greybody factors of black holes in dRGT massive gravity coupled with nonlinear electrodynamics. Ann. Phys. 422, 168301. doi:10.1016/j.aop.2020.168301

CrossRef Full Text | Google Scholar

Kuang, X. M., Liu, B., and Övgün, A. (2018). Nonlinear electrodynamics AdS black hole and related phenomena in the extended thermodynamics. Eur. Phys. J. C 78, 840. doi:10.1140/epjc/s10052-018-6320-0

CrossRef Full Text | Google Scholar

Lan, S. Q. (2018). Black-hole spectroscopy by making full use of gravitational-Wave Modeling. Phys. Rev. D. 98, 084014. doi:10.1103/PhysRevD.98.084038

CrossRef Full Text | Google Scholar

Mo, J. X., and Li, G. Q. (2018). Effects of Lovelock gravity on the joule-thomson expansion. arXiv: 1805.04327.

Google Scholar

Mo, J. X., Li, G. Q., Lan, S. Q., and Xu, X. B. (2018). Joule-Thomson expansion of d-dimensional charged AdS black holes. Phys. Rev. D. 98, 124032. doi:10.1103/physrevd.98.124032

CrossRef Full Text | Google Scholar

More, S. S. (2005). Back reaction, the Hawking emission spectrum from the charged black hole. Cl. Quantum Grav. 22, 4129.

CrossRef Full Text | Google Scholar

Nomura, K., and Yoshida, D. (2022). Quasinormal modes of charged black holes with corrections from nonlinear electrodynamics. Phys. Rev. D. 105, 044006. doi:10.1103/physrevd.105.044006

CrossRef Full Text | Google Scholar

Ökcü, O., and Aydýner, E. (2017). Joule-thomson expansion of charged AdS black holes. Eur. Phys. J. C 77, 24. doi:10.1140/epjc/s10052-017-4598-y

CrossRef Full Text | Google Scholar

Ökcü, O., and Aydýner, E. (2018). Measurement of quarkonium production in proton–lead and proton–proton collisions at 5.02 TeV with the ATLAS detector. Eur. Phys. J. C 78, 123.

Google Scholar

Okyay, M., and Övgün, A. (2022). Nonlinear electrodynamics effects on the black hole shadow, deflection angle, quasinormal modes and greybody factors. J. Cosm. Astro. Phys. 01, 009. doi:10.1088/1475-7516/2022/01/009

CrossRef Full Text | Google Scholar

Övgün, A. (2018). P-V criticality of a specific black hole in f(R) gravity coupled with yang-mills field. Adv. High. Energy Phys. 2018, 8153721. doi:10.1155/2018/8153721

CrossRef Full Text | Google Scholar

Övgün, A., and Jusufi, K. (2018). Quasinormal modes and greybody factors of f(R) gravity minimally coupled to a cloud of strings in 2+1 dimensions. Ann. Phys. 395, 138. doi:10.1016/j.aop.2018.05.013

CrossRef Full Text | Google Scholar

Övgün, A., Sakalli, I., and Mutuk, H. (2021). Quasinormal modes of dS and AdS black holes: Feedforward neural network method. Int. J. Geometric Methods Mod. Phys. 18, 2150154. doi:10.1142/S0219887821501541

CrossRef Full Text | Google Scholar

Pacilio, C., and Brito, R. (2018). Quasinormal modes of weakly charged Einstein-Maxwell-dilaton black holes. Phys. Rev. D. 98, 104042. doi:10.1103/physrevd.98.104042

CrossRef Full Text | Google Scholar

Pantig, R. C., Mastrototaro, L., Lambiase, G., and Övgün, A. (2022). Shadow, lensing, quasinormal modes, greybody bounds and neutrino propagation by dyonic ModMax black holes. Eur. Phys. J. C 82, 1155. doi:10.1155/2018/8153721

CrossRef Full Text | Google Scholar

Papnoi, U., Atamurotov, F., Ghosh, S. G., and Ahmedov, B. (2014). Shadow of five-dimensional rotating Myers-Perry black hole. Phys. Rev. D. 90, 024073. doi:10.1103/physrevd.90.024073

CrossRef Full Text | Google Scholar

Pourhassan, B., Faizal, M., and Debnath, U. (2016). Effects of thermal fluctuations on the thermodynamics of modified Hayward black hole. Eur. Phys. J. C 76, 145. doi:10.1140/epjc/s10052-016-3998-8

CrossRef Full Text | Google Scholar

Pourhassan, B., Kokabi, K., and Sabery, Z. (2018). Higher order corrected thermodynamics and statistics of Kerr–Newman–Gödel black hole. Ann. Phys. 399, 181–192. doi:10.1016/j.aop.2018.10.011

CrossRef Full Text | Google Scholar

Pourhassan, B., and Upadhyay, S. (2021). Perturbed thermodynamics of charged black hole solution in Rastall theory. Eur. Phys. J. Plus 136, 311. doi:10.1140/epjp/s13360-021-01271-9

CrossRef Full Text | Google Scholar

Pourhassan, M., and Faizal, M. (2015). Thermal fluctuations in a charged AdS black hole. Eur. Phys. Lett. 111, 40006. doi:10.1209/0295-5075/111/40006

CrossRef Full Text | Google Scholar

Pradhan, P. (2019). Horizon areas and logarithmic correction to the charged accelerating black hole entropy. Universe 5, 57. doi:10.3390/universe5020057

CrossRef Full Text | Google Scholar

Rizwan, C. L. A., Kumara, A. N., Vaid, D., and Ajith, K. M. (2018). Joule–Thomson expansion in AdS black hole with a global monopole. Int. J. Mod. Phys. A 33, 1850210. doi:10.1142/s0217751x1850210x

CrossRef Full Text | Google Scholar

Sakalli, I., Jusufi, K., and Övgün, A. (2018). Analytical solutions in a cosmic string born–infeld-dilaton black hole geometry: Quasinormal modes and quantization. Gen. Relativ. Gravit. 50, 125. doi:10.1007/s10714-018-2455-4

CrossRef Full Text | Google Scholar

Saleh, M., Thomas, B. B., and Kofane, T. C. (2018). Thermodynamics and phase transition from regular bardeen black hole surrounded by quintessence. Int. J. Theor. Phys. 57, 2640–2647. doi:10.1007/s10773-018-3784-5

CrossRef Full Text | Google Scholar

Sharif, M., and Akhtar, Z. (2020). Quasi-normal modes and thermal fluctuations of charged black hole with Weyl corrections. Phys. Dark Universe 29, 100589. doi:10.1016/j.dark.2020.100589

CrossRef Full Text | Google Scholar

Sharif, M., and Ama-Tul-Mughani, Q. (2021). Gravitational decoupled solutions of axial string cosmology. Eur. Phys. J. Plus 136, 20500911. doi:10.1142/S0217732320500911

CrossRef Full Text | Google Scholar

Sharif, M., and Khan, A. (2022b). Effects of non-linear electrodynamics on thermodynamics of charged black hole. Chin. J. Phys. 77, 1130–1144. doi:10.1016/j.cjph.2021.08.026

CrossRef Full Text | Google Scholar

Sharif, M., and Khan, A. (2022a). Thermodynamics of regular black hole with de Sitter core. Mod. Phys. Lett. A 37, 2250049. doi:10.1142/S0217732322500493

CrossRef Full Text | Google Scholar

Sharif, M., and Nawaz, H. S. (2020). Thermodynamics of rotating regular black holes. Chin. J. Phys. 67, 193. doi:10.1016/j.cjph.2020.06.021

CrossRef Full Text | Google Scholar

Singh, D. V., Shukla, A., and Upadhyay, S. (2022). Quasinormal modes, shadow and thermodynamics of black holes coupled with nonlinear electrodynamics and cloud of strings. Ann. Phys. 447, 169157. doi:10.1016/j.aop.2022.169157

CrossRef Full Text | Google Scholar

Sinha, A. K. (2021). Thermodynamics of asymptotically flat Reissner–Nordstrom black hole. Mod. Phys. Lett. A 36, 2150071. doi:10.1142/s0217732321500711

CrossRef Full Text | Google Scholar

Tharanath, R., Suresh, J., and Kuriakose, V. C. (2015). Phase transitions and Geometrothermodynamics of Regular black holes. Gen. Relativ. Gravit. 46, 47. doi:10.1007/s10714-015-1884-6

CrossRef Full Text | Google Scholar

Wei, S.-W., and Liu, Y.-X. (2013). Observing the shadow of Einstein-Maxwell-Dilaton-Axion black hole. J. Cosmol. A. P. 2013, 063. doi:10.1088/1475-7516/2013/11/063

CrossRef Full Text | Google Scholar

Yang, Y., Liu, D., Övgün, A., Long, Z. W., and Xu, Z. (2022a). Probing hairy black holes caused by gravitational decoupling using quasinormal modes, and greybody bounds. arXiv:2203.11551.

Google Scholar

Yang, Y., Liu, D., Övgün, A., Long, Z. W., and Xu, Z. (2022b). Quasinormal modes of Kerr-like black bounce spacetime. arXiv:2205.07530.

Google Scholar

Yu, S., and Gao, C. (2020). Exact black hole solutions with nonlinear electrodynamic field. Int. J. Mod. Phys. D. 29, 2050032. doi:10.1142/s0218271820500327

CrossRef Full Text | Google Scholar