A review of basic results on the Bose–Einstein condensate dark matter model

We review basic results on the Bose–Einstein condensate dark matter (BECDM) model. Self-gravitating BECs experience a collisionless process of gravitational cooling and violent relaxation, leading to BECDM halos with a “core-envelope” structure. The quantum core (soliton), which is the ground state of the Gross–Pitaevskii–Poisson (GPP) equations, may solve the core–cusp problem of the cold dark matter (CDM) model. The approximately isothermal envelope, resulting from the quantum interferences of the excited states, is similar to the Navarro–Frenk–White (NFW) profile of CDM halos and accounts for the flat rotation curves of the galaxies. We derive the core mass–radius relation, the halo mass–radius relation, and the core mass–halo mass relation of BECDM halos. We show that the core mass increases with the halo mass and we discuss the possibility that it collapses above a maximum mass arising from general relativity or from the attractive self-interaction of the bosons. We discuss the secular evolution of BECDM halos induced by the formation of granules (or quasiparticles) in the envelope, and we mention the analogy with the evolution of globular clusters. We also discuss the basic elements of BECDM cosmology. Throughout this review, we emphasize the importance of the maximum mass of dilute axion stars with an attractive self-interaction [P.H. Chavanis, Phys. Rev. D 84, 043531 (2011)] and its consequences.

1 Introduction

Even after 100 years of research, the nature of dark matter (DM) remains elusive. The cold dark matter (ΛCDM) model works extremely well at large (cosmological) scales and can account for precise measurements of the cosmic microwave background (CMB) from the Wilkinson Microwave Anisotropy Probe (WMAP) (Hinshaw et al., 2009) and Planck missions (Ade et al., 2014; Ade et al., 2016). However, in addition to the lack of evidence for any CDM particle such as a weakly interacting massive particle (WIMP) with a mass in the GeV–TeV range, the CDM model faces serious problems at small (galactic) scales.

One of these problems is the “core-cusp problem” (Moore et al., 1999). Classical $N$-body numerical simulations (Navarro et al., 1996) lead to DM halos with a universal density profile called the Navarro–Frenk–White (NFW) profile. The density decreases at large distances as $r^{-3}$ and presents a $r^{-1}$ cusp at the center. On the other hand, the results of observations can be fitted by the empirical Burkert profile (Burkert, 1995). The density also decreases at large distances as $r^{-3}$ but, contrary to the NFW profile, it presents a core at the center. Therefore, the observations favor a core with an approximately constant density instead of a cusp.

Another problem is the “missing satellites problem” (Kauffmann et al., 1993; Klypin et al., 1999; Kamionkowski and Liddle, 2000). For a cold classical gas, the Jeans length vanishes or is extremely small $({\lambda }_J\simeq 0)$, implying that structures can form at all scales as a result of gravitational collapse. However, observations reveal that, contrary to the prediction of the CDM model, there are no halos below a certain scale. These ultracompact dark matter (UDM) halos correspond typically to dwarf spheroidal galaxies (dSphs) like Fornax. To be specific, we shall assume that Fornax is the smallest halo observed in the universe. We will call it the “minimum halo” and take

${\left(M_h\right)}_{\text{min}}\sim 10^8{M}_{\odot },{\left(r_h\right)}_{\text{min}}\sim 1\mathrm{k}\mathrm{p}\mathrm{c}(1)$

for its characteristic mass and characteristic radius (this corresponds to a typical density $\rho \sim 10^{-18}\mathrm{g}/{\mathrm{m}}^{\mathrm{3}}$ and a typical surface density $\mathrm{\Sigma }\sim 100M_{\odot }/{\mathrm{p}\mathrm{c}}^2$). These values can certainly be refined, but they will be sufficient (and practical) for our purposes.

The “small-scale crisis of CDM” (Bullock and Boylan-Kolchin, 2017) is somehow related to the assumption that DM is pressureless. A first possibility to solve the CDM crisis is to take into account the feedback of the baryons that can transform cusps into cores (Romano-Díaz et al., 2008; Pontzen and Governato, 2014; Oñorbe et al., 2015). Another possibility is to consider self-interacting dark matter (SIDM) (Spergel and Steinhardt, 2000) or warm dark matter (WDM) (Bode et al., 2001), where a pressure arises as a result of particle dispersion. In that case, we have to deal with a gas at nonzero temperature $(T\ne 0)$. The Jeans length is increased, possibly solving the missing satellite problem. On the other hand, SIDM and WDM halos present an isothermal core, possibly solving the core–cusp problem. The problems of the CDM model may also be solved by taking into account the quantum (or wave) nature of the DM particle. Indeed, in quantum mechanics, an effective pressure is present even at zero temperature $(T=0)$. This quantum pressure may balance the gravitational attraction at small scales and solve the CDM crisis.

Some authors have considered the case where the DM particle is a fermion, like a massive sterile neutrino. In this model, gravitational collapse is prevented by the quantum pressure arising from the Pauli exclusion principle. Other authors have considered the case where the DM particle is a boson like the QCD axion¹ or like an ultralight axion (ULA) or an axion-like particle (ALP) predicted by string theory. In this model, gravitational collapse is prevented by the quantum pressure arising from the Heisenberg uncertainty principle or by the scattering of the bosons when their self-interaction is repulsive. In these quantum (fermionic and bosonic) models, the minimum halo is interpreted as the ground state of the self-gravitating quantum gas at $T=0$. As we shall see, this constraint determines the typical characteristics of the DM particle.

We shall not review the literature on fermionic and bosonic DM in detail here because this literature is extensive, and this review has already been done in our previous contributions where we cite numerous references. A short history of fermionic DM can be found in the introductions of Chavanis (2006), Chavanis et al. (2015a), Chavanis et al. (2015b), Chavanis (2020d), Alberti and Chavanis (2020b), Chavanis (2023d), Chavanis (2022g) and a short history of bosonic DM can be found in the introductions of Chavanis (2011c), Chavanis (2016a), Chavanis (2018b), Chavanis (2019d), Chavanis (2020c), Chavanis (2023c). It is fascinating to note that the basic equations governing self-gravitating Fermi and Bose gases have been used to describe not only astrophysical objects (white dwarfs, neutron stars, fermion stars, boson stars, axion stars, and DM halos) but also extended elementary particles with an effective gravity accounting, for example, for the strong interaction (see the discussion in the introduction of Chavanis (2023c)). To some extent, the two communities working on these similar equations do not know each other.

In this paper, we focus on bosonic DM. At $T=0$, bosons form Bose–Einstein condensates (BECs), and they are described by a single wavefunction $\psi (\mathbf{r},t)$ called the condensate wavefunction.² This wavefunction can be interpreted as a scalar field (SF). Due to the very large occupation number, the SF can be treated as a classical field. The bosons may be noninteracting, or they may have a repulsive or an attractive self-interaction (for example, the QCD axion has an attractive self-interaction). On astrophysical scales, one must generally take into account gravitational interactions between the bosons. The evolution of the wave function of self-gravitating BECs is then governed by the Schrödinger–Poisson (SP) equations when the bosons are noninteracting (Ruffini and Bonazzola, 1969; Membrado et al., 1989b; Widrow and Kaiser, 1993; Sin, 1994; Ji and Sin, 1994; Hu et al., 2000; Guzmán and Ureña-López, 2004; Sikivie and Yang, 2009) or by the Gross–Pitaevskii–Poisson (GPP) equations when the bosons are self-interacting (Guzmán and Ureña-López, 2006; Böhmer and Harko, 2007; Chavanis, 2011c; Chavanis and Delfini, 2011; Chavanis, 2011a; Chavanis, 2012b; Rindler-Daller and Shapiro, 2012). In general relativity, one must use the Klein–Gordon–Einstein (KGE) equations (Kaup, 1968; Ruffini and Bonazzola, 1969; Baldeschi et al., 1983; Colpi et al., 1986; Seidel and Suen, 1994; Lee and Koh, 1996; Guzmán and Matos, 2000; Goodman, 2000; Peebles, 2000; Arbey et al., 2001; Arbey et al., 2003). DM halos made of BECs can thus be viewed as gigantic bosonic atoms where the bosonic particles are condensed in a single macroscopic quantum state. The wave properties of the SF are negligible at large (cosmological) scales where the SF behaves as CDM, but they gain importance at small (galactic) scales where they can prevent gravitational collapse, providing halo cores and suppressing small-scale structures. This can solve the CDM small-scale crisis such as the core–cusp problem and the missing satellite problem. The bosonic model is also called wave DM, fuzzy dark matter (FDM), quintessential DM, ultralight dark matter (ULDM), BECDM, $\psi$DM, SFDM, etc. In the present review, following our previous works, we shall use the name BECDM.

The evolution of a self-gravitating BEC presents three main periods:

(i) Initially, the universe (assumed to be made of bosons in the form of BECs) is spatially homogeneous. If slightly perturbed,³ it experiences a quantum Jeans instability, leading to the growth of the perturbations and the formation of condensations (clumps) (Jeans, 1902; Khlopov et al., 1985; Bianchi et al., 1990; Hu et al., 2000; Sikivie and Yang, 2009; Chavanis, 2011c; Chavanis, 2012b; Suárez and Matos, 2011; Suárez and Chavanis, 2015a; Suárez and Chavanis, 2018; Chavanis, 2020b; Chavanis, 2021a). This corresponds to the linear regime of structure formation describing the initiation of the large-scale structures of the universe.

(ii) When the density contrast reaches a sufficiently large value, the condensations (overdensities) decouple from the Hubble flow, experience free fall and virialization, and grow through collisions, merging, and accretion before being diluted by the expansion of the universe. This corresponds to the nonlinear regime of structure formation, leading to the DM halos that are observed today.⁴ BECDM halos are formed by a dissipationless (“collisionless”) relaxation process called gravitational cooling (Seidel and Suen, 1994) or violent relaxation (Lynden-Bell, 1967). By this process, BECDM halos acquire a “core-envelope” structure with a quantum core (soliton) surrounded by an extended quasi-isothermal envelope that results from the quantum interferences of the excited states. This core–envelope structure has been evidenced in numerical simulations of the SP, GPP, and KGE equations (Seidel and Suen, 1994; Schive et al., 2014a; Schive et al., 2014b; Schwabe et al., 2016; Mocz et al., 2017; Mocz et al., 2018; Veltmaat et al., 2018; Mocz et al., 2019; Mocz et al., 2020; Veltmaat et al., 2020; Glennon and Prescod-Weinstein, 2021; Mocz et al., 2023; Liu et al., 2023; Nori et al., 2023; Painter et al., 2024). The quantum core (soliton) results from the balance between the gravitational attraction and the quantum pressure arising from the Heisenberg uncertainty principle or the self-interaction of the bosons. This is the ground state of the SP, GPP, or KGE equations. The envelope results from the balance between the gravitational attraction and an effective thermal pressure. The quantum core may solve the core–cusp problem of the CDM model and the approximately isothermal envelope, which is similar to the classical NFW profile, accounts for the flat rotation curves of the galaxies at large distances (Chavanis, 2019d).⁵ The mass of the quantum core $M_c$ increases with the halo mass $M_h$. The minimum halo ${(M_h)}_{\text{min}}$ corresponds to a purely solitonic core without envelope $(M_c=M_h)$. This is the ground state of the SP, GPP, or KGE equations. One interesting problem is to determine the core mass–halo mass relation $M_c(M_h)$ of BECDM halos and see what happens when the core mass becomes sufficiently large (Chavanis, 2019d; Chavanis, 2019a; Chavanis, 2020a; Chavanis, 2021a; Chavanis, 2023c; Padilla et al., 2021).

(iii) The envelope of BECDM halos has a granular structure as a result of quantum fluctuations (Schive et al., 2014a; Schive et al., 2014b; Hui et al., 2017). These granules (or quasiparticles) induce the secular evolution of the envelope (Levkov et al., 2018; Bar-Or et al., 2019; Marsh and Niemeyer, 2019; El-Zant et al., 2020; Bar-Or et al., 2021; Chavanis, 2021b). During this “collisional” process, some particles of the envelope condense and the mass of the soliton increases, being fed by the envelope (Levkov et al., 2018; Eggemeier and Niemeyer, 2019; Chen et al., 2021; Chen et al., 2022). This scenario was originally introduced to describe the Bose–Einstein condensation and the formation of axion stars in virialized DM halos and axion miniclusters (Levkov et al., 2018). It was then applied to the formation of inflaton stars in inflaton clusters (Musoke et al., 2020; Niemeyer and Easther, 2020; Eggemeier et al., 2021; Eggemeier et al., 2022).

There have been several recent reviews on the scalar field, fuzzy, ultralight, wave, or BEC dark matter model and on axion stars (Suárez et al., 2014; Rindler-Daller et al., 2014; Chavanis, 2015d; Marsh, 2016; Lee, 2018; Braaten and Zhang, 2019; Niemeyer, 2020; Chavanis, 2023b; Ferreira, 2021; Hui, 2021; Visinelli, 2021; Khoury, 2022; Matos et al., 2024; Padilla et al., 2024). In this paper, we review the basic aspects of self-gravitating BECs. We discuss results (mainly centered on our own contributions) that have not been treated in detail in the previous reviews. We only quote the literature closely related to these topics and refer to other reviews and to the introductions in our papers (Chavanis, 2011c; Chavanis, 2016a; Chavanis, 2018b; Chavanis, 2020c; Chavanis, 2023c) for additional references on a broader context.

This review is organized as follows. Section 2 discusses the KGE and GPP equations governing self-gravitating BECs in the relativistic and nonrelativistic regimes, respectively. In the following sections, we focus on the nonrelativistic limit. Section 3 introduces the Madelung (1927) hydrodynamic representation of the GPP equations (Böhmer and Harko, 2007; Sikivie and Yang, 2009; Chavanis, 2011c; Chavanis and Delfini, 2011; Chavanis, 2011a; Chavanis, 2012b; Rindler-Daller and Shapiro, 2012). Section 4 discusses the ground state of the GPP equations, called a soliton. This ground-state solution describes either the minimum halo or the quantum core of large DM halos. The core mass–radius relation can be obtained exactly by solving the GPP equations numerically, or approximately (analytically) by using a variational approach based on a Gaussian ansatz (Chavanis, 2011c; Chavanis and Delfini, 2011). In the case of self-gravitating BECs with no self-interaction or with a repulsive self-interaction, we recall the existence of a maximum mass set by general relativity (Kaup, 1968; Ruffini and Bonazzola, 1969; Colpi et al., 1986; Chavanis and Harko, 2012). In the case of self-gravitating BECs with a strongly attractive self-interaction, we show that equilibrium states exist only below a maximum mass obtained in (Chavanis, 2011c; Chavanis and Delfini, 2011) that has a nonrelativistic origin. It corresponds to the maximum mass of dilute axion stars (Chavanis, 2023b). We introduce an interpolation formula that connects these different limiting masses (Chavanis, 2023c). We also discuss the outcomes of the collapse above the maximum mass, leading to a dense axion star, a bosenova, a black hole, axion drops, fast radio bursts, etc (Braaten et al., 2016; Chavanis, 2016a; Chavanis, 2018b; Cotner, 2016; Davidson and Schwetz, 2016; Eby et al., 2016; Helfer et al., 2017; Levkov et al., 2017; Michel and Moss, 2018; Visinelli et al., 2018). Section 5 describes the core–envelope structure of BECDM halos resulting from gravitational cooling (Seidel and Suen, 1994) and violent relaxation (Lynden-Bell, 1967). We introduce a coarse-grained Wigner equation and derive hydrodynamic equations as well as a generalized GPP equation relaxing toward an equilibrium state with a core–envelope structure (Chavanis, 2022a). In Section 6, we develop a predictive model of BECDM halos (Chavanis, 2019d). In this model, the quantum core (soliton), corresponding to the ground state of the GPP equation, can solve the core–cusp problem. It is surrounded by an isothermal envelope that accounts for the flat rotation curves of the galaxies. By using the observational fact that the surface density of DM halos is universal (Kormendy et al., 2004; Spano et al., 2008; Donato et al., 2009) we obtain the halo mass–radius relation. Then, by using a “velocity dispersion tracing” relation justified by thermodynamical arguments based on a maximum entropy principle (most probable state), we obtain a general core mass–halo mass relation valid for bosons with repulsive or attractive self-interactions (Chavanis, 2019d; Chavanis, 2019a; Chavanis, 2020a; Chavanis, 2021a; Chavanis, 2023c; Padilla et al., 2021). Previously known results (Schive et al., 2014b) are recovered in particular limits of this relation. In the case of a repulsive self-interaction, we show by a general argument that the quantum core of realistic BECDM halos can never overcome the maximum mass set by general relativity and collapse toward a black hole by this process. In the case of an attractive self-interaction, we determine the halo mass above which the soliton (“axion” star) overcomes the maximum mass of Chavanis (2011c) and collapses. Section 7 discusses the secular evolution of BECDM halos due to the granular structure of the envelope (quasiparticles) (Schive et al., 2014a; Schive et al., 2014b; Hui et al., 2017) and the resulting increase in mass of the soliton by Bose–Einstein gravitational condensation (Levkov et al., 2018; Eggemeier and Niemeyer, 2019; Chen et al., 2021; Chen et al., 2022). We show that these results can be understood in terms of a kinetic theory based on the bosonic Landau equation (Bar-Or et al., 2019; Bar-Or et al., 2021; Marsh and Niemeyer, 2019; El-Zant et al., 2020; Chavanis, 2021b) and that BECDM halos behave in a sense like globular clusters in astrophysics. We thus suggest the possibility that they experience a gravothermal catastrophe stopped by quantum mechanics (Heisenberg’s uncertainty principle) or by repulsive scattering. This provides another means to form a solitonic core (Chavanis, 2019d). This quantum core becomes unstable if the halo mass is sufficiently large, leading to a supermassive black hole (SMBH). Section 8 discusses basic results of BECDM cosmology. We determine the Jeans length and the Jeans mass of a spatially homogeneous self-gravitating BEC (Khlopov et al., 1985; Bianchi et al., 1990; Chavanis, 2011c). Then, we take into account the expansion of the universe and discuss the different stages taking place during the cosmological evolution of a spatially homogeneous BECDM universe (Li et al., 2014; Suárez and Chavanis, 2017). Finally, we consider the growth of perturbations in an expanding universe filled with BECDM and again identify different regimes of evolution (Chavanis, 2012b; Suárez and Chavanis, 2015a).

2 From the KGE equations to the GPP equations

We assume that DM is made of spinless bosons in the form of BECs at $T=0$. Basically, the wavefunction (or SF) $\phi (x^{\mu })$ of a BEC in general relativity is governed by the KGE equations (see Chavanis and Matos (2017), Chavanis (2022c), Chavanis (2023c) and references therein)

$\square \phi +\frac{m^2{c}^2}{{\hslash }^2}\phi +2\frac{dV}{d|\phi {|}^2}\phi =0,(2)$

$R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R=\frac{8\pi G}{c^4}{T}_{\mu \nu },(3)$

where $\square =D_{\mu }{D}^{\mu }$ is the d’Alembertian operator in a curved spacetime with metric $g_{\mu \nu }$ ($D_{\mu }$ is the covariant derivative), $R_{\mu \nu }$ is the Ricci tensor, $V(|\phi {|}^2)$ is the self-interaction potential of the bosons, $m$ is their mass, and

$\begin{array}{c}{T}_{\mu \nu }=\frac{1}{2}\left({\partial }_{\mu }{\phi }^{*}{\partial }_{\nu }\phi +{\partial }_{\nu }{\phi }^{*}{\partial }_{\mu }\phi \right)\hfill \\ -g_{\mu \nu }\left[\frac{1}{2}{g}^{\mu \nu }{\partial }_{\mu }{\phi }^{*}{\partial }_{\nu }\phi -\frac{m^2{c}^2}{2{\hslash }^2}|\phi {|}^2-V\left(|\phi {|}^2\right)\right]\hfill \end{array}(4)$

is the energy-momentum (stress) tensor of the SF. These equations have been introduced in the context of boson stars, first in the noninteracting case (Kaup, 1968; Ruffini and Bonazzola, 1969) and then for a self-interaction of the form Colpi et al. (1986):

$V\left(|\phi {|}^2\right)=\frac{\lambda }{4\hslash c}|\phi {|}^4,(5)$

where $\lambda$ is the dimensionless self-interaction constant. This $|\phi {|}^4$ potential is the leading term in the expansion of an arbitrary self-interaction potential $V(|\phi {|}^2)$ for small field values. In the aforementioned papers, the SF $\phi$ is complex and the conservation of the charge or the conservation of the particle number (provided that anti-bosons are counted negatively) ensures the stability of the boson stars below a maximum mass of general relativistic origin (see Section 4.5). The case of a real SF has also been considered, in particular in relation to axions. However, relativistic boson stars described by a real SF are usually unstable (see the discussion in the introduction of Chavanis (2023c) and references therein).

This review especially focuses on the nonrelativistic limit of the KGE equations, which is suitable to describe BECDM in most cases of interest. By making the Klein transformation⁶

$\phi \left(\mathbf{r},t\right)=\frac{\hslash }{m}{e}^{-im{c}^{2}t/\hslash }\psi \left(\mathbf{r},t\right),(6)$

where $\psi$ is the pseudo-wavefunction, we can first transform the KG Equation 2 into the general relativistic GP equation (Chavanis and Matos, 2017; Matos et al., 2019)

$i\hslash c{\partial }^0\psi -\frac{{\hslash }^2}{2m}\square \psi +\frac{1}{2}m{c}^2\left(g^{00}-1\right)\psi +i\frac{\hslash c^2}{2}\square t\psi -m\frac{dV}{d|\psi {|}^2}\psi =0.(7)$

Then, by taking the nonrelativistic limit $c\to +\infty$ of this wave equation and of the Einstein field equations [see Chavanis and Matos (2017), Suárez and Chavanis (2015a), Suárez and Chavanis (2015b) and Appendix B of Chavanis (2023c) for details], we obtain the GPP equations (Chavanis, 2011c; Chavanis and Delfini, 2011)

$i\hslash \frac{\partial \psi }{\partial t}=-\frac{{\hslash }^2}{2m}\mathrm{\Delta }\psi +m\frac{dV}{d|\psi {|}^2}\psi +m\mathrm{\Phi }\psi ,(8)$

$\mathrm{\Delta }\mathrm{\Phi }=4\pi G|\psi {|}^2.(9)$

These equations describe a nonrelativistic self-gravitating BEC at $T=0$ in the context of Newtonian gravity. Here $\mathrm{\Phi }(\mathbf{r},t)$ is the gravitational potential produced by the mass density of the BEC $\rho (\mathbf{r},t)=|\psi {|}^2$ through the Poisson Equation 9. For a complex SF $\phi$, the potential $V(|\psi {|}^2)$ in the GP Equation 8 coincides with the potential $V(|\phi {|}^2)$ in the KG Equation 2, provided that we substitute $|\phi |=\frac{\hslash }{m}|\psi |$ deduced from Equation 6.

For the standard BEC, we have

$V\left(|\psi {|}^2\right)=\frac{2\pi a_s{\hslash }^2}{m^3}|\psi {|}^4,(10)$

where $a_s$ is the scattering length of the bosons (it is related to the dimensionless self-interaction constant introduced above by $\lambda /8\pi =a_{s}mc/\hslash =a_s/{\lambda }_C$, where ${\lambda }_C=\hslash /mc$ is the Compton wavelength of the bosons). The interaction between the bosons is repulsive when $a_s>0$ and attractive when $a_s<0$. The GP Equation 8 with the $|\psi {|}^4$ self-interaction potential from Equation 10 can be directly obtained from the mean field Schrödinger equation valid for $N\gg 1$ bosons in interaction (Bogoliubov, 1947), by assuming that the short-range potential of interaction between the bosons can be modeled by a pair contact potential of the form $u(\mathbf{r}-{\mathbf{r}}^{\prime })=g\delta (\mathbf{r}-{\mathbf{r}}^{\prime })$ with a coupling constant $g=4\pi a_s{\hslash }^2/m^3$ (see Sec. II. A. of Chavanis (2011c) and references therein).

Remark: For a real SF, like the one describing axions, the counterpart of Equation 6 is

$\phi \left(\mathbf{r},t\right)=\frac{1}{\sqrt{2}}\frac{\hslash }{m}\left[e^{-im{c}^{2}t/\hslash }\psi \left(\mathbf{r},t\right)+e^{im{c}^{2}t/\hslash }\psi {\left(\mathbf{r},t\right)}^{*}\right].(11)$

This transformation allows us to separate the fast oscillations of the SF with proper pulsation ${\omega }_0=m{c}^2/\hslash$ caused by its rest mass from the slow evolution of $\psi (\mathbf{r},t)$. In the nonrelativistic limit $c\to +\infty$ we can neglect the oscillatory terms that average out to 0 (fast oscillation regime), and we obtain the GPP Equations 8, 9. In the present case, the potential $V(|\psi {|}^2)$ is obtained by first substituting $\phi$ from Equation 11 into the potential $V({\phi }^2)$ and then by averaging over the oscillations (see Secs. II and III of Chavanis (2018b), Appendix A of Chavanis (2020c), and Appendix C of Chavanis (2023c) for details). Therefore, $V(|\psi {|}^2)$ is different from the potential that one would naively obtain by directly substituting into $V({\phi }^2)$ the quantity $\overline{{\phi }^2}\simeq \frac{{\hslash }^2}{m^2}|\psi {|}^2$ (already averaged) obtained from Equation 11 as we can do when $\phi$ is complex. Indeed, $\overline{V({\phi }^2)}\ne V(\overline{{\phi }^2})$. For the instantonic potential of axions

$V\left(\phi \right)=\frac{m^{2}c{f}^2}{{\hslash }^3}\left[1-\cos \left(\frac{{\hslash }^{1/2}{c}^{1/2}\phi }{f}\right)\right]-\frac{m^2{c}^2}{2{\hslash }^2}{\phi }^2,(12)$

where $f$ is the axion decay constant, one obtains by this procedure a self-interaction potential of the form

$V\left(|\psi {|}^2\right)=\frac{m^{2}c{f}^2}{{\hslash }^3}\left[1-\frac{{\hslash }^{3}c}{2f^2{m}^2}|\psi {|}^2-J_0\left(\sqrt{\frac{2{\hslash }^{3}c|\psi {|}^2}{f^2{m}^2}}\right)\right],(13)$

where $J_0(x)$ is Bessel’s function. By expanding this potential for $|\psi {|}^2\ll f^2{m}^2/{\hslash }^{3}c$, we obtain the $|\psi {|}^4$ potential of Equation 10 with $a_s=-\hslash c^{3}m/(32\pi f^2)<0$. This shows that the self-interaction of axions is attractive.

3 Quantum hydrodynamics

In astrophysics, one is used to describe stars, DM, and even the universe as a whole in terms of fluid equations. At first sight, the BECDM model relies on a completely different formalism since we now have to work in terms of a complex wavefunction $\psi (\mathbf{r},t)$ whose evolution is governed by the GPP Equations 8, 9. However, by using the Madelung (1927) transformation, the GPP equations can be written in the form of quantum hydrodynamic equations for a potential flow. To that purpose, we write the wavefunction under the polar form

$\psi \left(\mathbf{r},t\right)=\sqrt{\rho \left(\mathbf{r},t\right)}{e}^{iS\left(\mathbf{r},t\right)/\hslash },(14)$

where $\rho (\mathbf{r},t)=|\psi {|}^2$ is the density of the BEC and $S(\mathbf{r},t)$ is the action from which we define the velocity field

$\mathbf{u}=\frac{\nabla S}{m}.(15)$

The velocity field is irrotational $(\nabla \times \mathbf{u}=\mathbf{0})$. It can be shown that the GPP Equations 8, 9 are equivalent⁷ to hydrodynamic equations of the form (see Chavanis (2011c), Chavanis (2017b) and references therein)

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \mathbf{u}\right)=0,(16)$

$\frac{\partial S}{\partial t}+\frac{{\left(\nabla S\right)}^2}{2m}+m\mathrm{\Phi }+m{V}^{\prime }\left(\rho \right)+Q=0,(17)$

$\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u}\cdot \nabla \right)\mathbf{u}=-\frac{1}{\rho }\nabla P-\nabla \mathrm{\Phi }-\frac{1}{m}\nabla Q,(18)$

$\mathrm{\Delta }\mathrm{\Phi }=4\pi G\rho ,(19)$

where

$Q=-\frac{{\hslash }^2}{2m}\frac{\mathrm{\Delta }\sqrt{\rho }}{\sqrt{\rho }}=-\frac{{\hslash }^2}{4m}\left[\frac{\mathrm{\Delta }\rho }{\rho }-\frac{1}{2}\frac{{\left(\nabla \rho \right)}^2}{{\rho }^2}\right](20)$

is the quantum potential taking into account the Heisenberg uncertainty principle and

$P\left(\rho \right)=\rho V^{\prime }\left(\rho \right)-V\left(\rho \right)={\rho }^2{\left[\frac{V\left(\rho \right)}{\rho }\right]}^{\prime }(21)$

is the pressure arising from the self-interaction of the bosons.⁸ For the standard BEC, using Equations 10, 21, the equation of state is

$P=\frac{2\pi a_s{\hslash }^2}{m^3}{\rho }^2,(22)$

corresponding to a polytrope of index $n=1$ (quadratic equation of state). For an attractive self-interaction between the bosons $(a_s<0)$, the pressure is negative.

Equations 16–19 have a clear physical interpretation. Equation 16 is the continuity equation, Equation 17 is the quantum Hamilton–Jacobi (or Bernoulli) equation, Equation 18 is the quantum Euler equation, and Equation 19 is the Poisson equation. We will call them the quantum Euler–Poisson equations. For $\hslash =0$ and $P=0$, we recover the classical hydrodynamic equations of the CDM model.

In the context of BECDM, the hydrodynamic representation of the GPP equations through the Madelung transformation was first considered by Böhmer and Harko (2007), Sikivie and Yang (2009), Chavanis (2011c), Chavanis and Delfini (2011), Chavanis (2011a), Chavanis (2012b), Rindler-Daller and Shapiro (2012). It is also possible to write the KGE equations in the form of quantum hydrodynamic equations by using the de Broglie transformation (de Broglie, 1927b; de Broglie, 1927c; de Broglie, 1927a). In the context of BECDM, the hydrodynamic representation of the KGE equations was first considered by Suárez and Matos (2011), Suárez and Matos (2014), Suárez and Chavanis (2015a), Suárez and Chavanis (2015b) in the weak gravity limit and by Chavanis and Harko (2012), Chavanis (2015c), Chavanis and Matos (2017), Matos et al. (2019), Chavanis (2022c), Chavanis (2023c) in a curved spacetime with an arbitrary metric (possibly including the electromagnetic field).⁹ In this review, we will essentially use the hydrodynamic representation of the GPP equations (see Chavanis (2011c), Chavanis (2017b) for the expression of the following results using the wave representation). We stress, however, that the fluid approach cannot resolve interference patterns at very small scales, in regions where the quantum pressure becomes ill-defined due to the vanishing of the wavefunction and the density. This is in general accompanied by the formation of singularities and topological defects like vortex lines.

Remark: We note that the quantum force in Equation 18 can be written as (Takabayasi, 1952)

$-\frac{1}{m}\nabla Q=-\frac{1}{\rho }{\partial }_j{P}_{ij}^Q,(23)$

where

$P_{ij}^Q=-\frac{{\hslash }^2}{4m^2}\rho {\partial }_i{\partial }_j\ln \rho =\frac{{\hslash }^2}{4m^2}\left(\frac{1}{\rho }{\partial }_i\rho {\partial }_j\rho -{\partial }_i{\partial }_j\rho \right)(24)$

is an anisotropic quantum pressure tensor. Therefore, the quantum Euler Equation 18 may be rewritten as

$\frac{\partial u_i}{\partial t}+u_j{\partial }_j{u}_i=-\frac{1}{\rho }{\partial }_{i}P-{\partial }_i\mathrm{\Phi }-\frac{1}{\rho }{\partial }_j{P}_{ij}^Q.(25)$

This shows that the quantum force is equivalent to an anisotropic pressure force. This remark will make more sense in Section 5.

4 Soliton

In this section, we consider the ground state of the GPP equations, which is usually referred to as a soliton. As explained in the introduction, this ground state solution can either describe the minimum halo of typical mass ${(M_h)}_{\text{min}}\sim 10^8{M}_{\odot }$ and typical radius ${(r_h)}_{\text{min}}\sim 1\mathrm{k}\mathrm{p}\mathrm{c}$, which is a pure soliton with no envelope, or the quantum core of larger DM halos $(M_h>{(M_h)}_{\text{min}})$ which possess an extended envelope.

4.1 Equilibrium state

In the hydrodynamic representation of the GPP equations, the equilibrium state of a BECDM halo is determined by the condition of quantum hydrostatic equilibrium

$\nabla P+\rho \nabla \mathrm{\Phi }+\frac{\rho }{m}\nabla Q=\mathbf{0}.(26)$

This equation describes the balance between the pressure due to the self-interaction of the bosons, the gravitational force, and the quantum force arising from the Heisenberg uncertainty principle. The quantum force always tends to stabilize a BECDM halo with respect to gravitational collapse. A repulsive self-interaction also stabilizes a BECDM halo similarly to the Pauli exclusion principle for fermionic DM. By contrast, an attractive self-interaction adds its effect to the gravitational attraction and destabilizes a BECDM halo above a maximum mass (see below). By combining Equation 26 with the Poisson Equation 19, we obtain the fundamental differential equation of quantum hydrostatic equilibrium (Chavanis, 2011c; Chavanis, 2017b)

$-\nabla \cdot \left(\frac{\nabla P}{\rho }\right)+\frac{{\hslash }^2}{2m^2}\mathrm{\Delta }\left(\frac{\mathrm{\Delta }\sqrt{\rho }}{\sqrt{\rho }}\right)=4\pi G\rho .(27)$

For the standard BEC, using Equation 22, it becomes

$-\frac{4\pi a_s{\hslash }^2}{m^3}\mathrm{\Delta }\rho +\frac{{\hslash }^2}{2m^2}\mathrm{\Delta }\left(\frac{\mathrm{\Delta }\sqrt{\rho }}{\sqrt{\rho }}\right)=4\pi G\rho .(28)$

The solution of this equation without node corresponds to the ground state of the GPP equations (soliton). This differential equation has been solved numerically in Chavanis and Delfini (2011) in the general case of a repulsive or an attractive self-interaction (or no self-interaction as in Membrado et al. (1989b)).¹⁰

For noninteracting self-gravitating BECs, a Gaussian density profile of the form (Chavanis, 2011c)

$\rho ={\rho }_0{e}^{-r^2/R^2}(29)$

provides a relatively good fit of the soliton up to a few halo radii. A more accurate fit of the form

$\rho =\frac{{\rho }_0}{{[1+{\left(r/R\right)}^2]}^8}(30)$

was later proposed by Schive et al. (2014a), Schive et al. (2014b). The radius $R$ and the central density ${\rho }_0$ of the soliton can be determined in each case from the exact mass–radius relation given by Equation 34 below (see Sec. III.B.1. of Chavanis (2019d) for details). We find $R=0.420R_{99}=4.18{\hslash }^2/(G{m}^{2}M)$ and ${\rho }_0=0.180M/R^3=0.00246G^3{m}^6{M}^4/{\hslash }^6=0.750{\hslash }^2/(G{m}^2{R}^4)$ with the Gaussian fit and $R=0.869R_{99}=8.64{\hslash }^2/(G{m}^{2}M)$ and ${\rho }_0=3.14M/R^3=0.00487G^3{m}^6{M}^4/{\hslash }^6=27.2{\hslash }^2/(G{m}^2{R}^4)$ with the more accurate fit. The two fits are compared, together with the exact numerical profile, in Figure 1 adapted from Chavanis (2019d).

Figure 1

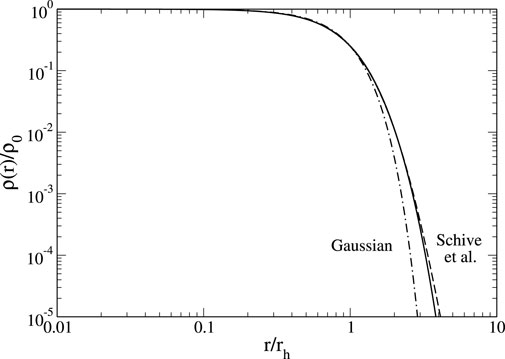
Figure 1. Normalized density profile of the soliton from Chavanis and Delfini (2011) (here ${\rho }_0$ is the central density, and $r_h$ is the radius, where the central density is divided by 4). It is compared with the Gaussian profile considered in Chavanis (2011c) and with the empirical profile proposed by Schive et al. (2014a); Schive et al. (2014b).

In the Thomas–Fermi (TF) limit where the quantum potential can be neglected (Tkachev, 1986; Membrado et al., 1989a; Lee and Koh, 1996; Goodman, 2000; Arbey et al., 2003; Böhmer and Harko, 2007; Chavanis, 2011c), the density profile has a compact support. It is analytically expressed as

$\rho \left(r\right)={\rho }_0\frac{\sin \left(\pi r/R_{\text{TF}}\right)}{\pi r/R_{\text{TF}}}.(31)$

This is the well-known density profile of a polytrope of index $n=1$ (Chandrasekhar, 1957). In that case, Equation 28 is equivalent to the Lane–Emden equation of index $n=1$. The density vanishes at a finite radius $R_{\text{TF}}$ given by Equation 35 below. The central density is ${\rho }_0=\pi M/(4R_{\text{TF}}^3)$.

Remark: In Appendix E of Chavanis (2019a), we have shown that, in the noninteracting case, the soliton resulting from the equilibrium between the gravitational attraction and the quantum repulsion (Heisenberg’s uncertainty principle) is similar to a polytrope of index $\gamma =3/2$ (i.e., $n=2$) with an effective equation of state

$P={\left(\frac{2\pi G{\hslash }^2}{9m^2}\right)}^{1/2}{\rho }^{3/2}(32)$

depending on the gravitational constant $G$. Therefore, to compute the structure of the soliton, instead of solving Equation 27 with the quantum term, we can solve Equation 27 without the quantum term but with the pressure from Equation 32. The effective $n=2$ polytropic equation of state (Equation 32) introduced in Chavanis (2019a) has been used in Schobesberger et al. (2021) to show that vortices should not arise in solitonic cores in the absence of self-interaction.

4.2 Mass–radius relation

The mass–radius relation of BECDM halos at $T=0$ (ground state) representing the minimum halo or the quantum core (soliton) of larger DM halos has been determined in Chavanis (2011c), Chavanis and Delfini (2011) for bosons with repulsive or attractive self-interactions (or no self-interaction as in Membrado et al. (1989b)). It can be obtained by solving the differential Equation 28 numerically (Chavanis and Delfini, 2011) or by minimizing the energy functional with a Gaussian ansatz for the wavefunction (Chavanis, 2011c) (see Appendices 1, 2). The variational approach gives an approximate analytical solution of the GPP equations.¹¹

Based on these works, the mass–radius relation of self-gravitating BECs can be parametrized by a function of the form

$M=\frac{a\frac{{\hslash }^2}{G{m}^{2}R}}{1-b^2\frac{a_s{\hslash }^2}{G{m}^3{R}^2}}.(33)$

The value of the coefficients $a$ and $b$ can be obtained from the Gaussian ansatz (Chavanis, 2011c) (see Appendix 2). They can also be determined so as to recover the exact mass–radius relation obtained numerically (Chavanis and Delfini, 2011) in appropriate asymptotic limits (see Chavanis (2021a); Chavanis (2023c) for details). In this section, we consider a vanishing or a repulsive self-interaction $(a_s\ge 0)$. The case of an attractive self-interaction $(a_s<0)$ is treated in the following section.

In the noninteracting case, the mass–radius relation is given by (Membrado et al., 1989b; Chavanis and Delfini 2011)

$M=9.95\frac{{\hslash }^2}{G{m}^2{R}_{99}},(34)$

where $R_{99}$ represents the radius containing $99\%$ of the mass. The scaling of Equation 34 can be obtained qualitatively by writing that the radius of the soliton is of the order of the de Broglie wavelength ${\lambda }_{\text{dB}}=h/(mv)$, where the velocity is identified with the velocity dispersion $v\sim {(GM/R)}^{1/2}$ obtained from the virial theorem.

In the TF limit where we can neglect the quantum potential, the equilibrium states have a unique radius (independent of the halo mass $M$) given by (Tkachev, 1986; Membrado et al., 1989a; Lee and Koh, 1996; Goodman, 2000; Arbey et al., 2003; Böhmer and Harko, 2007; Chavanis, 2011c)

$R_{\text{TF}}=\pi {\left(\frac{a_s{\hslash }^2}{G{m}^3}\right)}^{1/2}={\left(\frac{\pi }{8}\right)}^{1/2}\sqrt{\lambda }\frac{M_P}{m}{\lambda }_C,(35)$

where $M_P={(\hslash c/G)}^{1/2}=2.18\times 10^{-5}\mathrm{g}=1.22\times 10^{19}\mathrm{G}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ is the Planck mass.

The mass–radius relation with $a_s>0$ is represented in Figure 2. The radius decreases monotonically from $+\infty$ to $R_{\text{TF}}$ as the mass increases. Therefore, $R_{\text{TF}}$ represents the minimum radius of a BECDM halo with a repulsive self-interaction. An equilibrium state exists for any mass $M$ and is dynamically stable. There is a transition mass $M_t\sim \hslash /\sqrt{Gm{a}_s}$ corresponding to a radius $R_t\sim {(a_s{\hslash }^2/G{m}^3)}^{1/2}$ and a density ${\rho }_t\sim G{m}^4/a_s^2{\hslash }^2$ (these transition scales can be equivalently written as $M_t\sim M_P/\sqrt{\lambda }$, $R_t\sim \sqrt{\lambda }\frac{M_P}{m}{\lambda }_C$, and ${\rho }_t\sim G{m}^6{c}^2/{\lambda }^2{\hslash }^4$). The noninteracting limit is valid when $M\ll M_t$, and the TF limit is valid when $M\gg M_t$ (Chavanis, 2011c; Chavanis, 2021a).

Figure 2

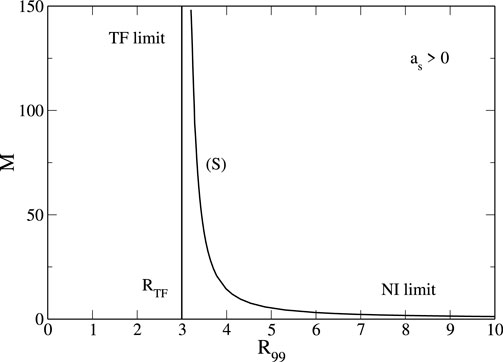
Figure 2. Mass–radius relation of self-gravitating BECs with repulsive self-interaction $(a_s>0)$ (Chavanis and Delfini, 2011). The mass is normalized by $M_a=\hslash /\sqrt{Gm{a}_s}$ and the radius by $R_a={(a_s{\hslash }^2/G{m}^3)}^{1/2}$. There is a stable equilibrium state for any mass $M$.

If we apply Equation 34 to the minimum halo of typical mass $M\sim 10^8{M}_{\odot }$ and typical radius $R\sim 1\mathrm{k}\mathrm{p}\mathrm{c}$, we get $m=2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$. This gives the typical value of the boson mass in the noninteracting limit. However, this small mass value is in tension with Lyman-$\alpha$ forest observations as it suppresses small-scale density fluctuations (Hui et al., 2017).

If we apply Equation 35 to the minimum halo of typical mass $M\sim 10^8{M}_{\odot }$ and typical radius $R\sim 1\mathrm{k}\mathrm{p}\mathrm{c}$, we get $a_s/m^3=3.28\times 10^3\mathrm{f}\mathrm{m}/{(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^3$ (or $\lambda /m^4=4.18\times 10^{-4}{(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^{-4}$). We may then use other relations to obtain the values of $m$ and $a_s$ individually, as detailed in Chavanis (2021a). For example, by using the Bullet Cluster constraint $\sigma /m\le 1.25\mathrm{c}{\mathrm{m}}^{\mathrm{2}}/\mathrm{g}$, where $\sigma =4\pi a_s^2$ is the self-interaction cross section of the bosons (Randall et al., 2008), we find that $m\le 1.10\times 10^{-3}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ and $a_s\le 4.41\times 10^{-6}\mathrm{f}\mathrm{m}$ (or $\lambda \le 6.18\times 10^{-16}$). This gives the maximum value of the boson mass and of its self-interaction.

More generally, by fixing the values of $M$ and $R$ in Equation 33 to those of the minimum halo (see Equation 1), we can obtain a relation between the mass $m$ and the scattering length $a_s$ of the DM particle (see Figure 3). This is a constraint that these two parameters must satisfy (Chavanis, 2019a; Chavanis, 2021a). There is a transition scattering length ${(a_s)}_t=3.18{({\hslash }^{2}R/G{M}^3)}^{1/2}=8.13\times 10^{-62}\mathrm{f}\mathrm{m}$ (or ${\lambda }_t=252\hslash c/G{M}^2=3.02\times 10^{-90}$ independent of $R$) corresponding to a mass $m_t=3.15{({\hslash }^2/GMR)}^{1/2}=2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$.¹² The noninteracting limit corresponds to $a_s\ll {(a_s)}_t$ (or $\lambda \ll {\lambda }_t$), and the TF limit corresponds to $a_s\gg {(a_s)}_t$ (or $\lambda \gg {\lambda }_t$). According to the above results, in the case of a repulsive self-interaction, we have the bounds $2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2\le m\le 1.10\times 10^{-3}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ and $0\le a_s\le 4.41\times 10^{-6}\mathrm{f}\mathrm{m}$ (or $0\le \lambda \le 6.18\times 10^{-16}$). We see that, depending on the strength of the self-interaction, the mass of the boson can vary by 18 orders of magnitude.¹³ Therefore, a repulsive self-interaction may solve the tensions of the noninteracting BECDM model by allowing a (much) larger mass of the bosonic particle (Chavanis, 2021a).

Figure 3

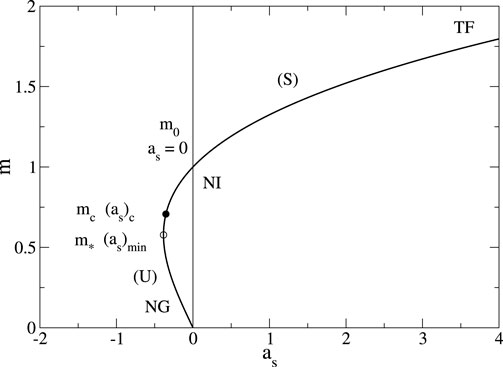
Figure 3. Mass $m$ of the DM particle as a function of the scattering length $a_s$ in order to match the characteristics of the minimum halo (Chavanis, 2019a; Chavanis, 2021a). The mass is normalized by $m_0={(a{\hslash }^2/GMR)}^{1/2}$ and the scattering length by $a_{\ast }^{\prime }=(a^{3/2}/b^2){({\hslash }^{2}R/G{M}^3)}^{1/2}$. The stable part of the curve starts at the critical minimum halo point $({(a_s)}_c,m_c)$. It differs from the minimum of the curve $a_s(m)$, as detailed in Chavanis (2019a); Chavanis (2021a).

We can also use the Gaussian ansatz to obtain the pulsation of the soliton as a function of the self-interaction parameter $a_s$ [see Chavanis (2011c), Appendix F of Chavanis (2021a), and Appendix 2]. In the noninteracting case, it is given by

${\omega }_{\text{Gauss}}=1.90{\left(\frac{GM}{R_{99}^3}\right)}^{1/2}=1.22\sqrt{G{\rho }_0},(36)$

which is in fair agreement with the numerical value $\omega =1.025\sqrt{G{\rho }_0}$ obtained in Veltmaat et al. (2018) (see their Equation 16). In the TF limit, the Gaussian ansatz yields ${\omega }_{\text{Gauss}}=1.78{(GM/R_{\text{TF}}^3)}^{1/2}=2.01\sqrt{G{\rho }_0}$. We can obtain the exact value of $\omega$ by solving the Eddington equation of pulsation, giving $\omega =1.94{(GM/R_{\text{TF}}^3)}^{1/2}=2.19\sqrt{G{\rho }_0}$. For the minimum halo, we obtain a pulsation period $T\simeq \pi {(R^3/GM)}^{1/2}\simeq 148\mathrm{M}\mathrm{y}\mathrm{r}\mathrm{s}$. It is of the order of the dynamical time $t_D\sim 1/\sqrt{G\rho }\sim {(R^3/GM)}^{1/2}=47.2\mathrm{M}\mathrm{y}\mathrm{r}\mathrm{s}$.

4.3 Maximum mass of dilute axion stars

Self-gravitating BECs with an attractive self-interaction $(a_s<0)$ can be at equilibrium only below a maximum mass given by (Chavanis, 2011c, Chavanis and Delfini, 2011)

$M_{\text{max}}^{\text{NR}}=1.012\frac{\hslash }{\sqrt{Gm|a_s|}}.(37)$

The corresponding radius is

$R_{99}^{*}=5.5{\left(\frac{|a_s|{\hslash }^2}{G{m}^3}\right)}^{1/2}.(38)$

We note that $M_{\text{max}}^{\text{NR}}=5.57{\hslash }^2/(G{m}^2{R}_{99}*)$. Since axions have an attractive self-interaction, the mass from Equation 37 represents the maximum mass of dilute axion stars.¹⁴ This maximum mass was first identified by Chavanis (2011c). It has a nonrelativistic origin, being essentially due to the attractive self-interaction of the bosons. In this sense, it is fundamentally different from the maximum mass of white dwarfs (Chandrasekhar, 1931), neutron stars (Oppenheimer and Volkoff, 1939), boson stars (Kaup, 1968; Ruffini and Bonazzola, 1969; Colpi et al., 1986; Chavanis and Harko, 2012), soliton stars (Lee, 1987a; Lee, 1987b; Friedberg et al., 1987; Lee and Pang, 1987), and oscillatons (Seidel and Suen, 1991; Alcubierre et al., 2003), which is due to special or general relativity (see Table 1).

Table 1

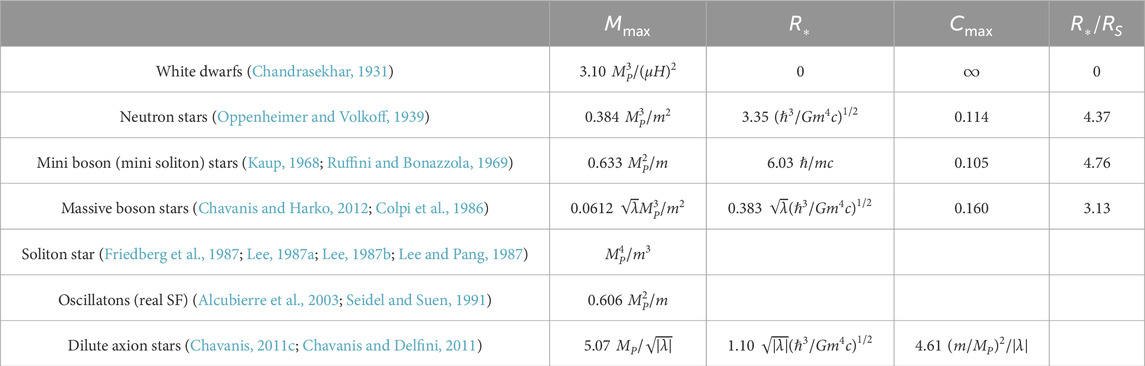
Table 1. Maximum mass $M_{\text{max}}$ of different types of fermion and boson stars. It is interesting to note that all the scalings $M_P$, $M_P^2/m$, $M_P^3/m^2$, and $M_P^4/m^3$ are represented. We have also indicated the minimum radius $R_{\ast }$ and the maximum compactness $C_{\text{max}}=G{M}_{\text{max}}/R_{\ast }{c}^2$ of the star. The compactness of a Schwarzschild black hole is $C_{\text{S}}=1/2$. The Buchdahl inequality for a barotropic relativistic star imposes $C\le 4/9=0.444$. The ratio between the star radius $R$ and the Schwarzschild radius $R_S=2GM/c^2$ is $R/R_S=R{c}^2/(2GM)=1/(2C)$. It is restricted by the Buchdahl inequality $R\ge (9/8)R_S$, so a barotropic relativistic star cannot be a black hole.

The mass–radius relation with $a_s<0$ is represented in Figure 4.

Figure 4

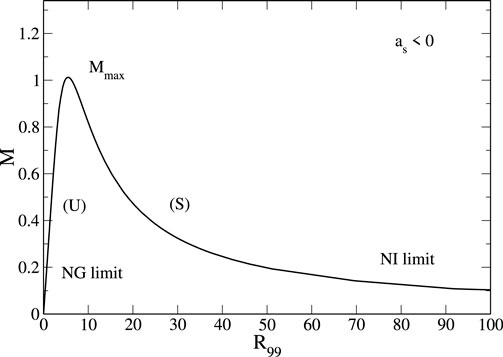
Figure 4. Mass–radius relation of self-gravitating BECs with attractive self-interaction $(a_s<0)$ (Chavanis and Delfini, 2011). The mass is normalized by $M_a=\hslash /\sqrt{Gm|a_s|}$ and the radius by $R_a={(|a_s|{\hslash }^2/G{m}^3)}^{1/2}$. There exists a maximum mass $M_{\text{max}}^{\text{NR}}$ (Chavanis, 2011c). For $M<M_{\text{max}}^{\text{NR}}$, there are two equilibrium states. On the stable branch (S), the system, when slightly perturbed, oscillates about its equilibrium state. On the unstable branch (U), different evolutions are possible depending on how the mass $M$ compares with the critical mass $M_c=(\sqrt{3}/2)M_{\text{max}}^{\text{NR}}$ (Chavanis, 2016a; Chavanis, 2020c) at which the energy of the unstable state vanishes: (i) for $M<M_c$, the unstable system can either collapse or explode and disperse away (instead of exploding, it may migrate toward the stable equilibrium state through gravitational cooling). (ii) For $M_c<M<M_{\text{max}}^{\text{NR}}$, the unstable system can either collapse or oscillate about the stable steady state (the oscillations may be damped by gravitational cooling, leading to the migration of the system toward the stable equilibrium state). There is no equilibrium state for $M>M_{\text{max}}^{\text{NR}}$. In that case, the system collapses. These different regimes (oscillations, explosion, and collapse) have been confirmed numerically in Glennon and Prescod-Weinstein (2021).

When $M<M_{\text{max}}^{\text{NR}}$, there exist equilibrium states. The equilibrium states with $R>R_{99}*$ are stable (minimum of energy at fixed mass), and the equilibrium states with $R<R_{99}*$ are unstable (maximum of energy at fixed mass) (Chavanis, 2011c; Chavanis and Delfini, 2011; Chavanis, 2018b; Chavanis, 2023c).¹⁵ Therefore, $R_{99}*$ is the minimum radius of stable equilibrium states. This stability result can be directly established from the topology of the series of equilibria by using the Poincaré turning point criterion (Poincaré, 1885),¹⁶ the Whitney theorem (Whitney, 1955), the Derrick theorem (Derrick, 1964), or the Wheeler theorem (Harrison et al., 1965), stating that the change in stability occurs at the turning point of mass $dM/dR=0$ (see Chavanis (2011c), Chavanis and Delfini (2011), Chavanis (2018b), Chavanis (2023c), and references therein). The stability of the axion star can also be obtained by computing the squared pulsation ${\omega }^2$ and investigating its sign (the squared pulsation is positive for stable configurations, negative for unstable configurations, and vanishes for marginally stable configurations). By using the Gaussian ansatz (see Chavanis (2011c), Chavanis (2016a), Chavanis (2020c), Chavanis (2017b) and Appendix 2), we can derive a relation between the squared pulsation ${\omega }^2$ and the slope of the mass–radius relation $dM/dR$. For the standard BEC $(n=1)$, it reads (see Equation A17)

$\frac{dM}{dR}=-\frac{m^{2}M{R}^3}{{\hslash }^2}{\omega }^2.(39)$

This relation shows that the equilibrium state is stable when $dM/dR<0$ and unstable when $dM/dR>0$. The pulsation vanishes at the maximum mass: $\omega =0$ at $M=M_{\text{max}}^{\text{NR}}$. We also find that the pulsation is maximum at $\tilde{M}=0.9717M_{\text{max}}^{\text{NR}}$ and ${\tilde{R}}_{99}=1.272R_{99}*$, with the value ${\omega }_{\text{max}}=0.100G{m}^2/|a_s|\hslash =1.87{(G\tilde{M}/{\tilde{R}}_{99}^3)}^{1/2}$ obtained with the Gaussian ansatz [see Chavanis (2011c), Chavanis (2016a) and Appendix F of Chavanis (2021a)]. The evolution of the pulsation as a function of the radius is represented in Figure 5. It is in good agreement with the numerical results obtained in Glennon and Prescod-Weinstein (2021).

Figure 5

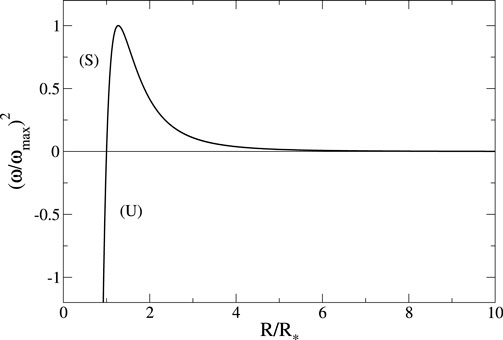
Figure 5. Squared pulsation (obtained from the Gaussian ansatz) as a function of the radius for self-gravitating BECs with $a_s<0$ (Chavanis, 2011c; Chavanis, 2016a). The squared pulsation vanishes at $R_{99}*$ and is maximum at ${\tilde{R}}_{99}$ (see the text).

There is no equilibrium state with $M>M_{\text{max}}^{\text{NR}}$. In that case, the BEC is expected to collapse (Chavanis, 2016a). The typical collapse time can be estimated with the Gaussian ansatz. Close to the maximum mass, it scales as (Chavanis, 2016a)

$\frac{t_{\text{coll}}}{t_D}\sim \frac{2.90178\dots }{{\left(M/M_{\text{max}}^{\text{NR}}-1\right)}^{1/4}}\left(M\to M_{\text{max}}^{\text{NR}+}\right),(40)$

where $t_D=3\sqrt{2}|a_s|\hslash /G{m}^2$ is the dynamical time (see Appendix 2). The collapse time for $M\to M_{\text{max}}^{\text{NR}+}$ has the same scaling as the period of oscillations about the equilibrium state for $M\to M_{\text{max}}^{\text{NR}-}$ (Chavanis, 2016a; Chavanis, 2020c):

$\frac{T}{t_D}\sim \frac{3.73600\dots }{{\left(1-M/M_{\text{max}}^{\text{NR}}\right)}^{1/4}}\left(M\to M_{\text{max}}^{\text{NR}-}\right).(41)$

We also note that dilute axion stars are metastable (local but not global minima of energy at fixed mass). Because of quantum fluctuations, they can penetrate the barrier of energy by tunnel effect and collapse. The calculation of their lifetime (Chavanis, 2020c), which is given by the WKB formula, is an interesting problem in physics. It can be performed by using the instanton theory, leading to an expression of the form (Chavanis, 2020c)

$\frac{t_{\text{life}}}{t_D}\sim \frac{0.0465}{\sqrt{N}}{\left(1-\frac{M}{M_{\text{max}}^{\text{NR}}}\right)}^{-7/8}{e}^{17.1{\left(1-\frac{M}{M_{\text{max}}^{\text{NR}}}\right)}^{5/4}N},(42)$

where the coefficients are determined by the Gaussian ansatz (see Appendix 2). We note that the detailed expression of the lifetime of dilute axion stars is unnecessary because it scales as $t_{\text{life}}\sim e^N{t}_D$. This exponential scaling is typical of systems with long-range interactions (Chavanis, 2005). Since $N$ is gigantic ($N\sim 10^{57}$ for QCD axion stars and $N\sim 10^{96}$ for axion stars made of ULAs–see below), metastable states are actually stable states.¹⁷ The metastable lifetime is reduced only extremely close to the maximum mass. Actually, because of quantum fluctuations, the critical mass of collapse (obtained when the exponential term in Equation 42 is of order 1) is $M_{\text{crit}}^{\text{NR}}\sim M_{\text{max}}^{\text{NR}}(1-0.103N^{-4/5})$ (Chavanis, 2020c). In practice, it is indistinguishable from $M_{\text{max}}^{\text{NR}}$. On the other hand, by using finite size scaling arguments, one can show that the collapse time scales like $t_{\text{coll}}\sim N^{1/5}{t}_D$ exactly at the maximum mass $M=M_{\text{max}}^{\text{NR}}$, instead of being infinite according to Equation 40. Similar results with, however, different exponents ($3/2$, $2/3$, and $1/6$ instead of $5/4$, $4/5$, and $1/5$) are obtained by investigating the effect of thermal fluctuations (Chavanis, 2020c; Chavanis, in preparation). Because of thermal fluctuations, dilute axion stars can overcome the energy barrier and collapse. In that case, the lifetime of axion stars is given by the Kramers formula, which can also be derived from the instanton theory (Chavanis, in preparation).

It is instructive to write the maximum mass and the minimum radius of dilute axion stars in different forms (Chavanis, 2011c; Chavanis, 2016a; Chavanis, 2018b)

$M_{\text{max}}^{\text{NR}}=5.073\frac{M_P}{\sqrt{|\lambda |}}=10.15\frac{f}{M_P{c}^2}\frac{M_P^2}{m},(43)$

$R_{99}^{*}=1.1\sqrt{|\lambda |}\frac{M_P}{m}{\lambda }_C=0.55\frac{M_P{c}^2}{f}{\lambda }_C,(44)$

where $f={(\hslash c^{3}m/32\pi |a_s|)}^{1/2}=m{c}^2/(2\sqrt{|\lambda |})$ is the axion decay constant. We note that the maximum mass $M_{\text{max}}^{\text{NR}}$ depends only on $|\lambda |$. Assuming naively $|\lambda |\sim 1$, Formula 43 suggests that the maximum mass of dilute axion stars is of the order of the Planck mass. Furthermore, the nonrelativistic limit is valid for $|\lambda |$ “large” (see below). Therefore, we would naively expect that the maximum mass of dilute axion stars is smaller than the Planck mass. That would make these objects relevant to particle physics $(M_{\text{max}}^{\text{NR}}\ll M_P)$ rather than astrophysics $(M_{\text{max}}^{\text{NR}}\gg M_P)$.¹⁸ However, “large” means nothing in itself. We must specify a reference value. Now, the precise criterion of validity of the nonrelativistic limit is $|\lambda |\gg {(m/M_P)}^2$, i.e., $|a_s|\gg 2Gm/c^2$ or $f\ll M_P{c}^2$ (see Equation 140 in Chavanis (2023c) and Section 4.6 below). Since the axion mass $m$ is much smaller than $M_P$, the nonrelativistic approximation is valid even when $|\lambda |$ is extremely small as compared to unity (e.g., up to $10^{-100}$!), allowing us to have a large maximum mass $M_{\text{max}}^{\text{NR}}$ of the order of the mass of astrophysical bodies (see the examples below).

For QCD axions with $m\sim 10^{-4}\mathrm{e}\mathrm{V}/c^2$ and $a_s\sim -5.8\times 10^{-53}\mathrm{m}$ (corresponding to $\lambda \sim -7.39\times 10^{-49}$ and $f\sim 5.82\times 10^{10}\mathrm{G}\mathrm{e}\mathrm{V}$), we get $M_{\text{max}}^{\text{NR}}=6.46\times 10^{-14}{M}_{\odot }$ and $R_{99}*=227\mathrm{k}\mathrm{m}$, which are of the order of the mass and size of asteroids. This leads to the notion of “axteroids.”

For ULAs, we can have a much larger maximum mass, of the order of galactic masses (or, more precisely, of their DM quantum cores). Its precise value depends on the values of $m$ and $a_s$, which are not well-known. Taking $m=2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$ and $a_s=-3.18\times 10^{-68}\mathrm{f}\mathrm{m}$ (corresponding to $\lambda =-1.18\times 10^{-96}$ and $f=1.34\times 10^{17}\mathrm{G}\mathrm{e}\mathrm{V}$) predicted in Chavanis (2019a), Chavanis (2021a) from particle physics and cosmology constraints (see Sec. VII.C of Chavanis (2019a) and Sec. IV.D of Chavanis (2021a)), we get $M_{\text{max}}^{\text{NR}}=5.10\times 10^{10}{M}_{\odot }$ and $R_{99}*=1.09\mathrm{p}\mathrm{c}$.¹⁹

In these two examples, the nonrelativistic approximation is justified because $|\lambda |\gg {(m/M_P)}^2\sim 10^{-64}$ and $10^{-100}$, respectively (the second approximation is marginally valid). The amazingly small value of $\lambda$ was first emphasized in Chavanis (2011c), Chavanis and Delfini (2011), Chavanis (2018b).

Remark: For the minimum halo of typical mass $M\sim 10^8{M}_{\odot }$ and typical radius $R\sim 1\mathrm{k}\mathrm{p}\mathrm{c}$ to be stable (see Figure 3), we must have $-1.11\times 10^{-62}\mathrm{f}\mathrm{m}\le a_s\le 0$ (corresponding to $-3.07\times 10^{-91}\le \lambda \le 0$ or $f\ge 1.97\times 10^{14}\mathrm{G}\mathrm{e}\mathrm{V}$) and $2.19\times 10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}\le m\le 2.92\times 10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ (Chavanis, 2021a). We note that $m$ does not change substantially from the noninteracting case, while $a_s$ (or $\lambda$ and $f$) can change by many orders of magnitude.

4.4 Outcome of the collapse

When $M>M_{\text{max}}^{\text{NR}}$, there is no equilibrium state, and the dilute axion star collapses (Chavanis, 2016a).²⁰ The outcome of the collapse above the maximum mass has been discussed by several authors (Braaten et al., 2016; Davidson and Schwetz, 2016; Cotner, 2016; Chavanis, 2016a; Eby et al., 2016; Levkov et al., 2017; Helfer et al., 2017; Chavanis, 2018b; Visinelli et al., 2018; Michel and Moss, 2018), and different scenarios have been developed:

(i) The first possibility is to form a dense axion star (Braaten et al., 2016). When the star becomes overdense as a consequence of the collapse, one needs to take into account higher-order terms in the expansion of the self-interaction potential. The next-order term is a $|\phi {|}^6$ term. A repulsive $|\phi {|}^6$ self-interaction (Braaten et al., 2016; Eby et al., 2016; Chavanis, 2018b) can stabilize the star against complete collapse and lead to a dense axion star. The mass–radius relation of dilute and dense axion stars has been obtained in Braaten et al. (2016) by solving the GPP equations numerically and in Chavanis (2018b) by using a Gaussian ansatz (see Figure 6).²¹ Phase transitions between dilute and dense axion stars have been studied in Chavanis (2018b). Dilute axion stars collapse above a maximum mass $M_{\text{max}}^{\text{NR}}$ and become dense axion stars. Dense axion stars explode below a minimum mass $M_{\text{min,dense}}$ and disperse away. Dense axion stars collapse above a maximum mass $M_{\text{max,dense}}^{\text{GR}}$ of general relativistic origin [see Chavanis, (2018b) and Appendix D of Chavanis (2020c) for more details]. Interestingly, the mass–radius relation of dilute and dense axion stars shares formal similarities with the mass–radius relation of compact objects going from white dwarfs to neutron stars (Harrison et al., 1965) (see Sec. XI.C of Chavanis (2018b)).

(ii) The second possibility is a bosenova phenomenon (Levkov et al., 2017) if special relativity is taken into account in the wave equation. The collapse of the axion star may be accompanied by a burst of relativistic axions when the density reaches high values. In that case, the implosion of the core is followed by an explosion of the halo, like in supernovae (Chavanis et al., 2019). This may lead to an emission of radio-photons via parametric resonance (Hertzberg et al., 2020).

(iii) The third possibility, in the case where general relativity is taken into account, is the formation of a black hole if the mass of the axion star is sufficiently large or if the self-interaction is sufficiently weak $(f\gg M_P{c}^2)$. This possibility has been demonstrated numerically in Helfer et al. (2017), Michel and Moss (2018).

(iv) The axion star may also fragment in several stable pieces (axion drops) of mass $M^{\prime }<M_{\text{max}}^{\text{NR}}$, thereby preventing its complete collapse (Davidson and Schwetz, 2016; Cotner, 2016). This result suggests that some astrophysical objects made of self-gravitating BECs with an attractive self-interaction may present several cores (solitons) instead of just one. This possibility was mentioned in Chavanis (2018b). The collapse of the soliton and the formation of multi-boson stars in miniclusters by a process of fragmentation when the bosons have an attractive self-interaction and $M_s>M_{\text{max}}^{\text{NR}}$ has been shown in the numerical simulations of Chen et al. (2021), Chen et al. (2022), Glennon and Prescod-Weinstein (2021), Mocz et al. (2023), Painter et al. (2024).

(v) Finally, it has been proposed that fast radio bursts, whose origin is one of the major mysteries of high energy astrophysics, could be caused by axion stars that have reached the maximum mass $M_{\text{max}}^{\text{NR}}$ and collapsed (see Raby (2016), Di (2024), Di et al. (2024) and references therein).

Figure 6

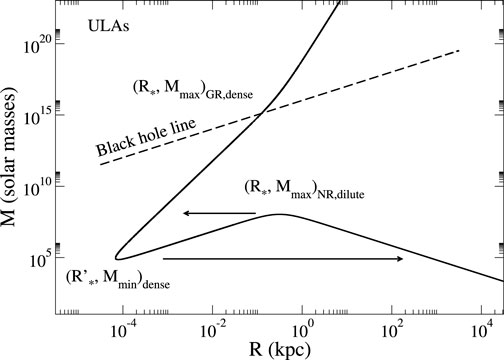
Figure 6. Mass–radius relation of self-gravitating BECs with an attractive $|\phi {|}^4$ self-interaction and a repulsive $|\phi {|}^6$ self-interaction obtained from the Gaussian ansatz (Chavanis, 2018b). Close to $M_{\text{max,dense}}^{\text{GR}}$, the actual mass–radius relation $M(R)$ should form a spiral like in Figure 7. The stability of the solutions can be determined by applying the Poincaré turning point criterion (Chavanis, 2018b). The branch of dilute axion stars is stable until the maximum mass $M_{\text{max}}^{\text{NR}}$, and then it becomes unstable until the minimum mass $M_{\text{min,dense}}$. The branch of dense axion stars is stable between the minimum mass $M_{\text{min,dense}}$ and the maximum mass $M_{\text{max,dense}}^{\text{GR}}$, and then it becomes unstable along the presumed spiral.

4.5 Maximum mass of boson stars in general relativity

We have seen that the radius of Newtonian self-gravitating BECs with a repulsive self-interaction (or no self-interaction) decreases as their mass increases. General relativity must be taken into account when the radius of the object $R$ becomes comparable to its Schwarzschild radius $R_S=2GM/c^2$. In that case, there is a maximum mass of general relativistic origin above which no equilibrium state is possible. Above that mass, the star is expected to collapse and form a black hole.

The maximum mass and the minimum radius of a noninteracting boson star at $T=0$ set by general relativity are (Kaup, 1968; Ruffini and Bonazzola, 1969)

$M_{\text{max,NI}}^{\text{GR}}=0.633\frac{\hslash c}{Gm}=0.633\frac{M_P^2}{m},(45)$

$R_{\text{min,NI}}^{\text{GR}}=6.03\frac{\hslash }{mc}=9.53\frac{G{M}_{\text{max}}}{c^2}.(46)$

The minimum radius of the boson star is of the order of the Compton wavelength ${\lambda }_C=\hslash /mc$ of the particle. The scalings of Equations 45, 46 can be obtained qualitatively by equating the mass–radius relation from Equation 34 with the Schwarzschild relation $R\sim GM/c^2$, as explained in Appendix B of Chavanis (2011c) [see also Chavanis (2023c)]. For $m\sim 1\mathrm{G}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ (nucleon mass), we get $M_{\text{max,NI}}^{\text{GR}}\sim 8.46\times 10^{-20}{M}_{\odot }$ corresponding to a miniboson star (Kaup, 1968; Ruffini and Bonazzola, 1969). The maximum mass becomes comparable to the solar mass $M_{\text{max,NI}}^{\text{GR}}\sim M_{\odot }$ for $m\sim 10^{-10}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$. For a DM boson of mass $m=2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$ (see above), one obtains $M_{\text{max,NI}}^{\text{GR}}=2.90\times 10^{11}{M}_{\odot }$ and $R_{\text{min,NI}}^{\text{GR}}=0.132\mathrm{p}\mathrm{c}$.

The maximum mass and the minimum radius of a self-interacting boson star or BEC star at $T=0$ in the TF limit set by general relativity are (Colpi et al., 1986; Chavanis and Harko, 2012)

$M_{\text{max,TF}}^{\text{GR}}=0.307\frac{\hslash c^2\sqrt{a_s}}{{\left(Gm\right)}^{3/2}}=0.0612\sqrt{\lambda }\frac{M_P^3}{m^2},(47)$

$\begin{array}{ll}\hfill R_{\text{min,TF}}^{\text{GR}}=1.92{\left(\frac{a_s{\hslash }^2}{G{m}^3}\right)}^{1/2}& =0.3836\sqrt{\lambda }\frac{M_P}{m}{\lambda }_C\hfill \\ \hfill & =6.25\frac{G{M}_{\text{max}}}{c^2}.\hfill \end{array}(48)$

The minimum radius of a boson star in the TF limit is of the same order as its radius in the nonrelativistic limit (see Equation 35). On the other hand, for $\lambda \sim 1$, the scaling $M_P^3/m^2$ of the maximum mass of a self-interacting boson star is the same as for fermion stars (see Section 6.7). The scalings of Equations 47, 48 can be obtained qualitatively by equating the radius from Equation 35 with the Schwarzschild relation $R\sim GM/c^2$, as explained in Appendix B of Chavanis (2011c) [see also Chavanis (2023c)]. For $m\sim 1\mathrm{G}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ (nucleon mass) and $\lambda \sim 1$, the maximum mass $M_{\text{max,TF}}^{\text{GR}}\sim M_{\odot }$ is of the order of the solar mass, like the Chandrasekhar mass of white dwarfs or the Oppenheimer–Volkoff mass of neutron stars. This corresponds to a massive boson star (Colpi et al., 1986; Chavanis and Harko, 2012).²² The TF approximation is justified because $\lambda \sim 1\gg {(m/M_P)}^2\sim 10^{-38}$ (see Section 4.6). For a DM boson with ratio $a_s/m^3=3.28\times 10^3\mathrm{f}\mathrm{m}/{(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^{\mathrm{3}}$ (see above), one obtains $M_{\text{max,TF}}^{\text{GR}}=2.04\times 10^{15}{M}_{\odot }$ and $R_{\text{min,TF}}^{\text{GR}}=611\mathrm{p}\mathrm{c}$.

One can show [see Appendix C of Chavanis (2020a) and Section 6.4 below] that the mass of the quantum core of a DM halo is always much smaller than the maximum mass set by general relativity. Therefore, the soliton can be treated in the nonrelativistic limit and does not collapse toward a black hole by this process.

Remark: The maximum mass (Equation 47) of self-interacting boson stars can be obtained either by solving the KGE equations (Colpi et al., 1986) or from a fluid approach (Chavanis and Harko, 2012). Indeed, in the TF regime, one can show [see Suárez and Chavanis (2017), Chavanis (2022c), Chavanis (2023b) and Appendix B.8 of Chavanis (2023c) for details] that the SF behaves as a relativistic fluid with an equation of state (Colpi et al., 1986; Chavanis and Harko, 2012)

$P=\frac{m^3{c}^4}{72\pi a_s{\hslash }^2}{\left(\sqrt{1+\frac{24\pi a_s{\hslash }^2}{m^3{c}^4}ϵ}-1\right)}^2,(49)$

where $ϵ$ is the energy density. At low densities $ϵ\sim \rho c^2\ll m^3{c}^4/a_s{\hslash }^2$, we recover the quadratic equation of state (Equation 22) of a nonrelativistic BEC (polytrope of index $n=1$). At high densities $ϵ\gg m^3{c}^4/a_s{\hslash }^2$, we get a linear equation of state $P\sim ϵ/3$ similar to the equation of state of the radiation (ultrarelativistic regime). The structure of a general relativistic BEC star can, therefore, be determined by solving the Tolman–Oppenheimer–Volkoff (TOV) equations with the equation of state from Equation 49. This has been done by Chavanis and Harko (2012). The mass–radius relation has the form of a spiral (see Figure 7), similar to the one found for neutron stars (see Figure 2 in Chavanis (2023d)) and for relativistic stars with a linear equation of state (Chavanis, 2002; Chavanis, 2008).²³ Chavanis and Harko (2012) applied this model to boson stars, condensate DM stars, BECDM halos, and neutron stars (see also Chavanis (2015c) for a related study). They proposed that neutron stars may have a superfluid core in which neutrons form Cooper pairs and behave as bosons of mass $2m_n$ (where $m_n$ is the neutron mass). In this sense, neutron stars (which are made of fermions) behave as boson stars or BEC stars. Since the maximum mass of general relativistic BEC stars depends on the self-interaction parameter, it can be larger than the Oppenheimer–Volkoff limit $M_{\text{OV}}=0.384{(\hslash c/G)}^{3/2}/m_n^2=0.710M_{\odot }$ obtained when the neutron star is modeled as an ideal Fermi gas. This could explain certain observations of neutron stars with a mass $\sim 2M_{\odot }$ (Lattimer and Prakash, 2011), which cannot be explained with the Oppenheimer–Volkoff model.

Figure 7

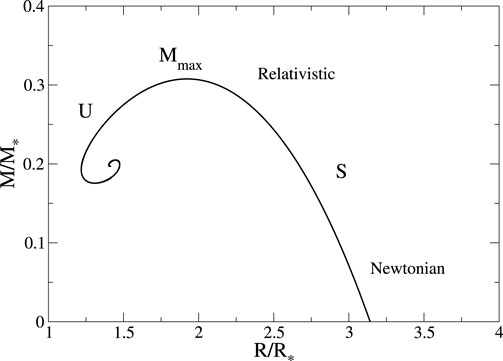
Figure 7. Mass–radius relation of general relativistic BEC stars with a repulsive $|\phi {|}^4$ self-interaction in the TF limit (Chavanis and Harko, 2012).

4.6 Interpolation formula for the maximum mass of boson stars with repulsive or attractive self-interactions

In the case of boson stars with a repulsive self-interaction $(a_s\ge 0)$, when the scattering length $a_s$ increases from 0 to infinity, there is a transition between the general relativistic maximum mass of noninteracting boson stars (see Equation 45) and the general relativistic maximum mass of self-interacting boson stars in the TF limit (see Equation 47). An interpolation formula between these two masses has been proposed under the form (Chavanis, 2023c)

$M_{\text{max}}=0.633\frac{\hslash c}{Gm}\sqrt{1+0.235\frac{a_s{c}^2}{Gm}}(50)$

with corresponding radius

$R_{*}=6.03\frac{\hslash }{mc}\sqrt{1+0.101\frac{a_s{c}^2}{Gm}}.(51)$

As expected, the maximum mass and the minimum radius increase as the self-interaction becomes more and more repulsive since the pressure due to the self-interaction opposes itself to the gravitational attraction and stabilizes the boson star.

In the case of dilute axion stars with an attractive self-interaction $(a_s\le 0)$, when $|a_s|$ increases from 0 to infinity, there is a transition between the general relativistic maximum mass of noninteracting boson stars (see Equation 45) and the nonrelativistic maximum mass of dilute axion stars due to the attractive self-interaction of the bosons (see Equation 37). This transition has been studied in detail in Chavanis (2018b). An interpolation formula between these two masses has been proposed under the form (Chavanis, 2023c)

$M_{\text{max}}=0.633\frac{\hslash c}{Gm}\frac{1}{\sqrt{1+0.391\frac{|a_s|c^2}{Gm}}}(52)$

with corresponding radius

$R_{*}=6.03\frac{\hslash }{mc}\sqrt{1+0.833\frac{|a_s|c^2}{Gm}}.(53)$

As expected, the maximum mass decreases while the minimum radius increases as the self-interaction becomes more and more attractive since the negative pressure due to the self-interaction adds itself to the gravitational attraction and destabilizes the axion star.

We see that the transition between these two regimes (weak self-interaction and strong self-interaction) occurs for a scattering length of the order of

${\left(a_s\right)}_t=\frac{2Gm}{c^2}=r_S.(54)$

The noninteracting limit corresponds to $|a_s|\ll {(a_s)}_t$, and the strongly self-interacting limit (TF limit when $a_s>0$ and nonrelativistic limit when $a_s<0$) corresponds to $|a_s|\gg {(a_s)}_t$. The abovementioned formulae can also be expressed in terms of $\lambda$ and $f$. The corresponding transition scales are

$\frac{{\lambda }_t}{16\pi }=\frac{G{m}^2}{\hslash c}={\left(\frac{m}{M_P}\right)}^2,(55)$

$f_t=\frac{M_P{c}^2}{8\sqrt{\pi }}\sim 10^{18}\mathrm{G}\mathrm{e}\mathrm{V}.(56)$

The noninteracting limit corresponds to $|\lambda |\ll {\lambda }_t$ or $f\gg f_t$, and the strongly self-interacting limit corresponds to $|\lambda |\gg {\lambda }_t$ or $f\ll f_t$. We note that ${(a_s)}_t$ is of the order of the Schwarzschild radius of the boson $r_S=2Gm/c^2$, ${\lambda }_t$ is of the order of the gravitational coupling constant ${\alpha }_g=G{m}^2/\hslash c={(m/M_P)}^2$, and $f_t$ is of the order of the Planck mass–energy $M_P{c}^2\sim 10^{19}\mathrm{G}\mathrm{e}\mathrm{V}$ (note that $f_t$ is independent of the mass $m$ of the boson) (Chavanis, 2023c).

The results of this section together with those of Section 4.4 allow us to construct the phase diagram of boson stars with a $|\phi {|}^4$ (and a $|\phi {|}^6$) self-interaction. It is represented in Figure 8 (see Chavanis (2018b), Chavanis (2023c) for details). For $a_s\ge 0$ (repulsive case) and for $|a_s|\ll {(a_s)}_t$ in the attractive case $(a_s\le 0)$, we form a boson star when $M<M_{\text{max}}^{\text{GR}}$ and a black hole when $M>M_{\text{max}}^{\text{GR}}$. For $|a_s|\gg {(a_s)}_t$ in the attractive case $(a_s\le 0)$, we form a dilute axion star when $M<M_{\text{max}}^{\text{NR}}$, a dense axion star or a bosenova when $M_{\text{max}}^{\text{NR}}<M<M_{\text{max,dense}}^{\text{GR}}$, and a black hole when $M>M_{\text{max,dense}}^{\text{GR}}$ (see Section 4.4).

Figure 8

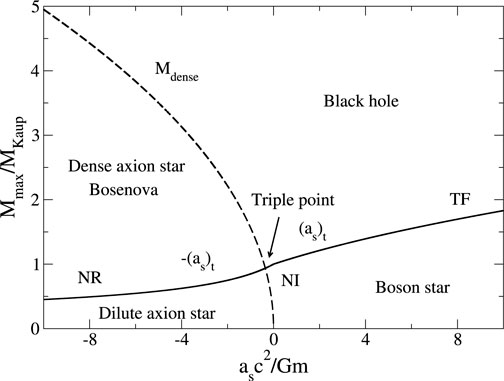
Figure 8. Phase diagram of boson stars with a $|\phi {|}^4$ self-interaction. We have represented the maximum mass $M_{\text{max}}$ above which the boson star becomes unstable as a function of the scattering length (see Equations 50, 52). This maximum mass is $M_{\text{max,NI}}^{\text{GR}}$ (Kaup, 1968; Ruffini and Bonazzola, 1969) when $a_s=0$ (noninteracting limit), $M_{\text{max,TF}}^{\text{GR}}$ (Colpi et al., 1986; Chavanis and Harko, 2012) when $a_s\gg {(a_s)}_t$ (repulsive case, TF limit), and $M_{\text{max}}^{\text{NR}}$ (Chavanis, 2011c; Chavanis and Delfini, 2011) when $|a_s|\gg {(a_s)}_t$ (attractive case, nonrelativistic limit). We have added (dashed line) the mass $M_{\text{max,dense}}^{\text{GR}}$ above which dense axion stars $(a_s<0)$ with a repulsive $|\phi {|}^6$ self-interaction become general relativistically unstable and collapse toward a black hole. This phase diagram displays a triple point at $(a_s,M)\sim [-r_S,M_{\text{Kaup}}]$ separating boson stars (or dilute axion stars), black holes, and dense axion stars (or bosenova) (Helfer et al., 2017; Chavanis, 2018b).

5 Core–envelope structure of BECDM halos

5.1 Violent relaxation and gravitational cooling

A self-gravitating BEC that is initially out-of-equilibrium undergoes a rapid relaxation toward a virialized state with a core–envelope structure. The quantum core (soliton) corresponds to the ground state of the KGE or GPP equations discussed in the previous section. It is surrounded by an extended envelope arising from the quantum interferences of excited states. This relaxation process was first identified by Seidel and Suen (1994), who numerically solved the KGE equations with spherical symmetry and showed the formation of a soliton (boson star) accompanied by an outward traveling scalar wave radiation. They called it “gravitational cooling.” They mentioned the similarity of this process with the “violent relaxation” of collisionless stellar systems discussed by Lynden-Bell (1967). In this sense, the core–envelope structure of the equilibrium (virialized) state can be interpreted as being the “most probable state” reached by the system as a result of a violent relaxation. It can be understood from a maximum entropy principle based on the Lynden–Bell entropy. The relaxation of BECDM halos governed by the SP equations was illustrated more recently by Schive et al. (2014a), Schive et al. (2014b) with use of spectacular colorful numerical simulations. They clearly showed the formation of a solitonic core surrounded by an NFW-like envelope. They also discovered that the envelope possesses a fluctuating granular structure.

5.2 Wigner–Kramers equation

In order to theoretically understand this core–envelope structure and make the link with previous works on the theory of violent relaxation, we have to introduce a phase-space description and use a set of equations similar to the Vlasov–Poisson equations governing the evolution of collisionless stellar systems. This can be accomplished in the framework of the Wigner–Poisson equations. It can be shown [see Appendix A of Chavanis (2022a)] that the Schrödinger equation is equivalent to the Wigner equation

$\begin{array}{c}\frac{\partial f}{\partial t}+\mathbf{v}\cdot \frac{\partial f}{\partial \mathbf{r}}-\frac{i{m}^4}{{\left(2\pi \hslash \right)}^3\hslash }\int e^{im\left(\mathbf{v}-{\mathbf{v}}^{\prime }\right)\cdot \mathbf{y}/\hslash }\hfill \\ \times \left[\mathrm{\Phi }\left(\mathbf{r}+\frac{\mathbf{y}}{2},t\right)-\mathrm{\Phi }\left(\mathbf{r}-\frac{\mathbf{y}}{2},t\right)\right]f\left(\mathbf{r},{\mathbf{v}}^{\prime },t\right)d\mathbf{y}d{\mathbf{v}}^{\prime }=0,\hfill \end{array}(57)$

where the Wigner distribution function is defined by

$f\left(\mathbf{r},\mathbf{v},t\right)=\frac{m^3}{{\left(2\pi \hslash \right)}^3}\int d\mathbf{y}{e}^{im\mathbf{v}\cdot \mathbf{y}/\hslash }{\psi }^{*}\left(\mathbf{r}+\frac{\mathbf{y}}{2},t\right)\psi \left(\mathbf{r}-\frac{\mathbf{y}}{2},t\right).(58)$

One can check that $\int fd\mathbf{v}=|\psi {|}^2=\rho$ and that $\frac{1}{\rho }\int f\mathbf{v}d\mathbf{v}=\nabla S/m=\mathbf{u}$, as in standard kinetic theory [see Appendix A of Chavanis (2022a)]. In the semiclassical limit $\hslash \to 0$, the Wigner equation reduces to the Vlasov equation (see Mocz et al. (2018), Chavanis (2022a), Widrow and Kaiser (1993), Uhlemann et al. (2014) for a discussion on the Schrödinger–Poisson–Vlasov–Poisson correspondence).

Like in the case of collisionless stellar systems (Lynden-Bell, 1967), we need to introduce a coarse-grained description in order to describe the relaxation of the system toward a quasiequilibrium state. By analogy with our former paper (Chavanis et al., 1996) on the kinetic theory of the violent relaxation of stellar systems, we introduced in Chavanis (2022a) a coarse-grained Wigner equation of the form

$\begin{array}{l}\hfill \frac{\partial \bar{f}}{\partial t}+\mathbf{v}\cdot \frac{\partial \bar{f}}{\partial \mathbf{r}}-\frac{i{m}^4}{{\left(2\pi \hslash \right)}^3\hslash }\int e^{im\left(\mathbf{v}-{\mathbf{v}}^{\prime }\right)\cdot \mathbf{y}/\hslash }\\ \hfill \times \left[\mathrm{\Phi }\left(\mathbf{r}+\frac{\mathbf{y}}{2},t\right)-\mathrm{\Phi }\left(\mathbf{r}-\frac{\mathbf{y}}{2},t\right)\right]\bar{f}\left(\mathbf{r},{\mathbf{v}}^{\prime },t\right)d\mathbf{y}d{\mathbf{v}}^{\prime }\\ \hfill =\frac{\partial }{\partial \mathbf{v}}\cdot \left[D\left(\frac{\partial \bar{f}}{\partial \mathbf{v}}+\beta \bar{f}\mathbf{v}\right)\right].\end{array}(59)$

The effective collision term on the right hand side of Equation 59 parameterizes the process of violent relaxation in terms of a Fokker–Planck (Kramers) operator. Therefore, Equation 59 can be called the Wigner–Kramers equation.²⁴ The friction coefficient and the diffusion coefficient are linked by a form of Einstein relation $\xi =\beta D$, where $\beta =m/k_{B}T$ is an effective inverse temperature. The Einstein relation expresses the fluctuation–dissipation theorem. At equilibrium, the diffusion and the friction balance each other, leading to a virialized state described by a Boltzmann-like distribution

${\bar{f}}_{\text{th}}=A{e}^{-\beta ϵ},(60)$

which corresponds to the dilute (nondegenerate) limit of the Lynden–Bell distribution (here $ϵ=v^2/2+\mathrm{\Phi }$ is the individual energy by unit of mass). The Boltzmann distribution from Equation 60 can be interpreted as a maximum entropy state (most probable state) in the sense of Lynden-Bell (1967).

The Wigner–Kramers Equation 59 well accounts for the core–envelope structure of BECDM halos. The advection (Wigner) term on the left-hand side characterizes the quantum core (soliton) studied in Section 4, while the collision (Kramers) term on the right-hand side characterizes the envelope. If we take into account tidal effects from other galaxies and use the fact that quantum effects are negligible in the envelope in an average sense (i.e., apart from the presence of granules considered in Section 7), we can show that the distribution function governed by the Wigner–Kramers Equation 59 relaxes, in the envelope, toward the King distribution

$\bar{f}=A\left[e^{-\beta \left(ϵ-{ϵ}_m\right)}-1\right]\left(ϵ\le {ϵ}_m\right),(61)$

$\bar{f}=0\left(ϵ\ge {ϵ}_m\right),(62)$

which is a truncated Boltzmann distribution (King, 1965). A more elaborate model would be the fermionic King model (Chavanis, 1998) taking into account the effects of degeneracy in the sense of Lynden–Bell. These degeneracy effects arising from the coarse-grained Vlasov and Wigner equations are similar to those arising from the Pauli exclusion principle in quantum mechanics, but we will not consider them here (see Chavanis (2022a)).

Remark: The connection between the wave description (in terms of $\psi$) and the kinetic description (in terms of $f$) has been discussed in Lin et al. (2018), Yavetz et al. (2022), Chavanis (2022a), Galazo García et al. (2024), Álvarez-Rios et al. (2024). Using this connection, Lin et al. (2018) have shown that the time-average distribution function in the envelope of BECDM halos obtained in numerical simulations is well-fitted by the King (or fermionic King) model (Chavanis, 1998). This gives further support to the claims made in Chavanis et al. (2015a) and Chavanis et al. (2015b) that the (fermionic) King model may be a good model for the envelope of DM halos (see below).

5.3 Hydrodynamic equations

We can derive a hierarchy of hydrodynamic equations by taking the successive moments of the Wigner–Kramers Equation 59 (Chavanis et al., 1996; Mocz et al., 2018; Chavanis, 2022a), also called the quantum damped Jeans equations. With introduction of the density $\rho =\int \bar{f}d\mathbf{v}$ and the velocity field $\mathbf{u}=\frac{1}{\rho }\int \bar{f}\mathbf{v}d\mathbf{v}$, the first moment returns the equation of continuity (Equation 16), and the second moment yields an equation of the form

$\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u}\cdot \nabla \right)\mathbf{u}=-\frac{1}{\rho }{\partial }_j{P}_{ij}-\nabla \mathrm{\Phi }-\xi \mathbf{u},(63)$

where $P_{ij}=\int \bar{f}{(\mathbf{v}-\mathbf{u})}_i{(\mathbf{v}-\mathbf{u})}_{j}d\mathbf{v}$ is the pressure (or stress) tensor.

This hierarchy of equations can be closed by making a local thermodynamic equilibrium (LTE) approximation. In Mocz et al. (2018), Chavanis (2022a), we argued heuristically that the pressure tensor $P_{ij}$ has two components: a quantum pressure component like in Equation 25 and a thermal pressure component arising from the process of violent relaxation. Therefore, we proposed to approximate the pressure tensor in Equation 63 by $P_{ij}=P_{ij}^Q+P_{\text{th}}(\rho ){\delta }_{ij}$, where $P_{ij}^Q$ is the anisotropic quantum pressure tensor from Equation 24 and $P_{\text{th}}(\rho )$ is the effective thermal pressure (in the sense of Lynden–Bell) arising from the isothermal distribution from Equation 60. It is given by

$P_{\text{th}}\left(\rho \right)=\rho \frac{k_{B}T}{m}.(64)$

Combining the previous results, and adding the pressure due to a possible self-interaction between the bosons, we deduce that the quantum hydrodynamic equations parameterizing the complex dynamics of BECDM halos in our model are

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \mathbf{u}\right)=0,(65)$

$\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u}\cdot \nabla \right)\mathbf{u}=-\frac{1}{\rho }\nabla P_{\text{th}}-\frac{1}{\rho }\nabla P_{\text{int}}-\frac{1}{m}\nabla Q-\nabla \mathrm{\Phi }-\xi \mathbf{u}.(66)$

In the quantum damped Euler Equation 66, the friction term forces the system to relax toward an equilibrium state in which the pressure balances the gravitational attraction.²⁵ The resulting DM halo has a core–envelope structure. The quantum pressure and the self-interaction pressure (in the repulsive case) stabilize the system against gravitational collapse and lead to a central density core (soliton) instead of a cusp. Quantum effects can thus solve the core–cusp problem of CDM. On the other hand, quantum effects are negligible as a first approximation in the envelope. An isothermal envelope leads to flat rotation curves like in the CDM model.²⁶

Some comments are as follows:

(i) We note that the anisotropic quantum tensor from Equation 24, which is equivalent to the quantum potential from Equation 20, can be interpreted as a stress tensor of the form $P_{ij}=\int \bar{f}{(\mathbf{v}-\mathbf{u})}_i{(\mathbf{v}-\mathbf{u})}_{j}d\mathbf{v}$, i.e., $P_{ij}=\rho (⟨v_i{v}_j⟩-⟨v_i⟩⟨v_j⟩)$ [see Appendix A of Chavanis (2022a)]. This provides a physical interpretation of the quantum potential (or quantum tensor) in terms of kinetic theory.

(ii) To obtain the simple isothermal equation of state (Equation 64), we have assumed that the distribution function in the envelope can be represented by a Boltzmann-like distribution (see Equation 60). We recall, however, that an isothermal distribution cannot be valid at infinitely large distances since it yields DM halos of infinite mass (Chandrasekhar, 1957; Binney and Tremaine, 1987). In principle, we should use the King distribution function (see Equations 61, 62), or the fermionic King distribution function (Chavanis, 1998), for which the density drops to 0 at a finite radius. This would give a more complicated (nonlinear) equation of state, generalizing Equation 64, which would account for the fact that the envelope is not exactly isothermal. Actually, depending on the degree of central concentration, the King distribution evolves from a polytrope of index $n=5/2$ to an isothermal distribution $(n\to +\infty )$. Accordingly, the density of the envelope decreases as $\rho \sim r^{-\alpha }$ with an exponent evolving between $\alpha \gtrsim 4$ (similar to Hénon’s isochrone profile Henon (1959)) and $\alpha =2$ (isothermal profile Chandrasekhar (1957), Binney and Tremaine (1987)), as shown in Figure 20 of Chavanis et al. (2015a), before abruptly falling down to 0. This degree of freedom may account for a variety of envelopes (see Figure 9).²⁷ In particular, at the critical point of instability (gravothermal catastrophe) discussed in Section 7.7, the density slope is close to $\alpha =3$ (similar to the modified Hubble profile (Binney and Tremaine, 1987)) and the marginal King distribution resembles the Burkert profile (Burkert, 1995) (see Figure 18 in Chavanis et al. (2015a) and Figure 1 in Chavanis (2022g)), which has a central core and decreases at large distances as $\rho \sim r^{-3}$, like the NFW profile (Navarro et al., 1996).

(iii) We have closed the hierarchy of hydrodynamic equations at the level of the momentum equation (second moment) by assuming a uniform temperature $T$ (isothermal model). We can also consider a more general model with a space-dependent temperature $T(\mathbf{r},t)$ and close the hierarchy of hydrodynamic equations at the level of the energy equation (third moment), as detailed in Chavanis et al. (1996) and in Appendix D.4 of Chavanis (2022a). This corresponds to a microcanonical (fixed energy) description instead of a canonical (fixed temperature) description.

Figure 9

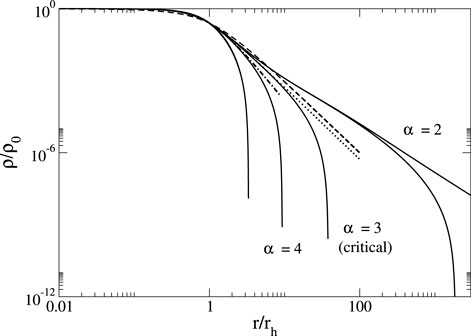
Figure 9. Normalized density profiles of the classical King model in logarithmic scales for different values of the central concentration (adapted from Chavanis et al., 2015a). Dotted line: modified Hubble profile. Dashed line: Burkert profile. Dashed–dotted line: Hénon’s isochrone profile. The critical King profile is relatively close to the Burkert profile up to $10r_h$ (Chavanis et al., 2015a).

Remark: In the strong friction limit $\xi \to +\infty$, we can neglect the inertial term (l.h.s.) in the damped quantum Euler Equation 66 and substitute the resulting equation into the continuity Equation 65, thereby obtaining the quantum Smoluchowski equation (Chavanis, 2011b; Chavanis, 2017b)

$\xi \frac{\partial \rho }{\partial t}=\nabla \cdot \left(\nabla P_{\text{int}}+\nabla P_{\text{th}}+\frac{\rho }{m}\nabla Q+\rho \nabla \mathrm{\Phi }\right).(67)$

The friction term in the damped quantum Euler equation, therefore, allows us to establish a link between quantum mechanics and Brownian theory. However, the strong friction limit is usually not relevant in astrophysics. Rather, the low friction limit is found relevant. Therefore, in the present context, the relation to Brownian theory is just formal (see Chavanis (2023a) for more details about the analogy between generalized equations in quantum mechanics and Brownian theory and for a short history of these topics).

5.4 Generalized wave equation

Based on the aforementioned results derived from the coarse-grained Wigner (or Wigner–Kramers) equation, we have introduced a generalized wave equation (Chavanis, 2017b; Chavanis, 2019d; Chavanis, 2022a)

$\begin{array}{c}i\hslash \frac{\partial \psi }{\partial t}=-\frac{{\hslash }^2}{2m}\mathrm{\Delta }\psi +m\frac{dV}{d|\psi {|}^2}\psi +m\mathrm{\Phi }\psi +k_{B}T\ln \left(|\psi {|}^2\right)\psi \hfill \\ -i\frac{\hslash }{2}\xi \left[\ln \left(\frac{\psi }{{\psi }^{*}}\right)-⟨\ln \left(\frac{\psi }{{\psi }^{*}}\right)⟩\right]\psi ,\hfill \end{array}(68)$

which is equivalent through the Madelung transformation to the damped Euler Equations 65, 66. This wave equation can be viewed as a generalized GP equation that includes a thermal term and a friction term resulting from the processes of gravitational cooling and violent relaxation. The thermal term, which is associated to the isothermal equation of state (Equation 64), is equivalent to a logarithmic potential

$V_{\text{th}}=\frac{k_{B}T}{m}|\psi {|}^2\left[\ln \left(|\psi {|}^2\right)-1\right].(69)$

The friction term also leads to a logarithmic nonlinearity but of a different nature.

Interestingly, we can derive this generalized wave equation (in the noninteracting case) from a completely different formalism based on Nottale’s theory of scale relativity (Nottale, 2011; Chavanis, 2017a; Chavanis, 2018a). We know that the Schrödinger equation can be derived from Newton’s equation by using a principle of scale covariance (Nottale, 2011). Similarly, the generalized wave Equation 68 can be derived from Newton’s equation with a linear friction by writing it under the form (Chavanis, 2017a; Chavanis, 2018a)

$\frac{D\mathbf{V}}{Dt}=-\nabla \mathrm{\Phi }-\mathrm{R}\mathrm{e}\left(\gamma \mathbf{V}\right),(70)$

where $D/Dt$ is a scale-covariant derivative, $\mathbf{V}$ is a complex velocity field, and $\gamma =\xi +2i{k}_{B}T/\hslash$ is a complex friction coefficient. The real part in Equation 70 is necessary to satisfy the conservation of the normalization condition. After simple algebraic manipulations (see Chavanis (2017a), Chavanis (2018a) for details), one can show that Equation 70 is equivalent to Equation 68, where the friction and thermal terms are related to the real and imaginary parts of the complex friction coefficient, respectively. This generalized wave equation (and its relativistic extension) can also be justified from Nelson’s stochastic quantum mechanics (Nelson, 1966; Chavanis, 2024a; Chavanis, In preparation). In these stochastic approaches, the source of the noise giving rise to quantum mechanics may have several origins. In Nottale’s theory, it is due to the structure of spacetime itself or to a chaotic dynamics that makes the trajectories of the particles nondifferentiable. In Nelson’s theory, the source of the noise is left unspecified, but some authors have suggested that it could be related to the fluctuations of the electromagnetic field (zero point energy), leading to the concept of stochastic electrodynamics (de la Peña et al., 2015). Alternatively, it may be due to the fluctuations of the gravitational field or to the fluctuations of the metric in general relativity (Calogero, 1997; Feynman et al., 1995). Therefore, quantum mechanics may have a stochastic interpretation (see Chavanis (2024a) for a more detailed discussion and for additional references). These theories have been used to determine the Planck constant in terms of cosmological quantities or, conversely, to provide an explanation for the mysterious Eddington (1931) relation²⁸

$\mathrm{\Lambda }=\frac{G^2{m}_e^6}{{\alpha }^6{\hslash }^4}=1.36\times 10^{-52}{\mathrm{m}}^{-2}(71)$

between the cosmological constant (vacuum energy) and the mass of the electron $m_e=9.11\times 10^{-28}\mathrm{g}=0.511\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$.

6 Predictive model of BECDM halos

In this section, following Chavanis (2019d), we develop a predictive model of BECDM halos with a core–envelope structure.

6.1 Equilibrium state

An equilibrium state of the generalized GPP Equations 9, 68 (equivalent to Equations 19, 65, 66) is determined, in the hydrodynamic representation, by the condition of quantum hydrostatic equilibrium from Equation 26, where the pressure $P=P_{\text{th}}+P_{\text{int}}$ contains a thermal term and a self-interaction term. For the standard BEC, we obtain an equation of state of the form (Chavanis, 2019d; Chavanis, 2022a)

$P=\rho \frac{k_{B}T}{m}+\frac{2\pi a_s{\hslash }^2}{m^3}{\rho }^2.(72)$

It has a linear part $P_{\text{th}}=\rho k_{B}T/m$ and a quadratic part $P_{\text{int}}=2\pi a_s{\hslash }^2{\rho }^2/m^3$. The linear part corresponds to an isothermal equation of state with an (effective) temperature $T$. It takes into account the process of violent relaxation. The quadratic part corresponds to a polytropic equation of state with index $n=1$. It takes into account the self-interaction of the bosons. The condition of quantum hydrostatic equilibrium describes the balance between the thermal pressure, the pressure due to the self-interaction of the bosons, the gravitational force, and the quantum force arising from the Heisenberg uncertainty principle. For the standard BEC, the fundamental differential Equation 27 of quantum hydrostatic equilibrium is

$-\frac{k_{B}T}{m}\mathrm{\Delta }\ln \rho -\frac{4\pi a_s{\hslash }^2}{m^3}\mathrm{\Delta }\rho +\frac{{\hslash }^2}{2m^2}\mathrm{\Delta }\left(\frac{\mathrm{\Delta }\sqrt{\rho }}{\sqrt{\rho }}\right)=4\pi G\rho .(73)$

It can be expressed under the form of a generalized Lane–Emden equation (Chavanis, 2019d; Chavanis, 2022a). The quadratic equation of state and the quantum potential dominate in the core where the density is high, and the isothermal (linear) equation of state dominates in the envelope where the density is low. As a result, the BECDM halo presents a quantum core (soliton) surrounded by an isothermal envelope. This composite model of BECDM halos with a core–envelope structure has been studied in detail in Chavanis (2019d).²⁹

In the quantum core, we can ignore the thermal pressure, and we recover the equations of Section 4 describing the soliton. The equilibrium of the core is due to the balance between the self-interaction pressure, the quantum pressure, and the gravitational attraction. The quantum core (soliton), which is the ground state of the GPP equations, may solve the core–cusp problem of CDM. The core mass–radius relation is given by Equation 33.

In the envelope, we can ignore quantum effects as well as the self-interaction of the bosons, and Equation 73 reduces to

$-\frac{k_{B}T}{m}\mathrm{\Delta }\ln \rho =4\pi G\rho .(74)$

This equation is equivalent to the Boltzmann–Poisson (or Emden) equation, which describes a classical self-gravitating isothermal gas (Chandrasekhar, 1957). The equilibrium of the envelope is due to the balance between the effective thermal pressure and the gravitational attraction. The Boltzmann–Poisson (or Emden) equation has no simple analytical solution and must be solved numerically. However, its asymptotic behavior is known analytically (Chandrasekhar, 1957). The density of a self-gravitating isothermal halo decreases as $\rho (r)\sim k_{B}T/(2\pi Gm{r}^2)$ for $r\to +\infty$, corresponding to an accumulated mass $M(r)\sim 2k_{B}Tr/(Gm)$ increasing linearly with $r$. This leads to flat rotation curves $v^2(r)=GM(r)/r\to v_{\infty }^2=2k_{B}T/m$ in qualitative agreement with the observations. Therefore, the approximately isothermal envelope, resulting from the quantum interferences of the excited states, is similar to the NFW envelope of classical CDM halos and accounts for the flat rotation curves of the galaxies.

The equilibrium state of a BECDM halo can also be obtained by maximizing the Lynden–Bell entropy at fixed mass and energy (Chavanis, 2022a).³⁰ This variational principle determines the most probable state of the system. It directly leads to Equation 73 and provides, in addition, a condition of thermodynamical stability: Only BECDM halos that are entropy maxima at fixed mass and energy are thermodynamically stable in the sense of Lynden–Bell. Actually, the statistical mechanics of self-gravitating systems is complicated because of incomplete relaxation, evaporation, and the gravothermal catastrophe (see Chavanis (2019d), Chavanis (2022a) and the reviews Padmanabhan (1990), Katz (2003), Chavanis (2006) for more details of these issues).³¹

The differential Equation 73 has been solved numerically in Chavanis (2019d); Chavanis (2018a). A density profile with a core–envelope structure is represented in Figure 10.

Figure 10

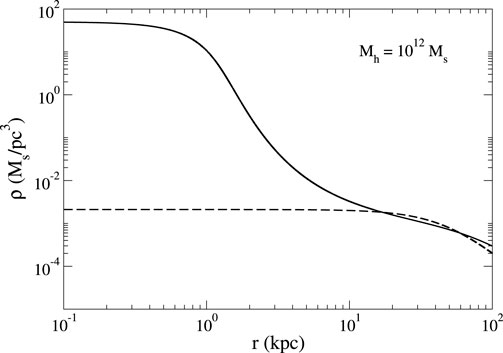
Figure 10. Density profile of a DM halo of mass $M_h=10^{12}{M}_{\odot }$ (the typical mass of the Milky Way). The full line corresponds to the core–envelope solution of the BECDM model in the TF limit with $a_s/m^3=3.28\times 10^3\mathrm{f}\mathrm{m}/{(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^3$. The dashed line corresponds to the purely isothermal solution without the quantum core. We see that the two profiles approximately match each other for $r\gtrsim 10\mathrm{k}\mathrm{p}\mathrm{c}$. As discussed in Section 5.3, the isothermal envelope should be replaced by a more general King profile.

6.2 Halo mass–radius relation

To determine the halo mass–radius relation, we use the observational evidence that the surface density of DM halos has the universal value (Kormendy et al., 2004; Spano et al., 2008; Donato et al., 2009)

${\mathrm{\Sigma }}_0^{\text{obs}}={\rho }_0{r}_h=141_{-52}^{+83}{M}_{\odot }/{\mathrm{p}\mathrm{c}}^2,(75)$

where ${\rho }_0$ is the central density and $r_h$ is the halo radius, where the central density is divided by 4, i.e., such that $\rho (r_h)={\rho }_0/4$.

In the case of BECDM halos, we must be careful to correctly define what we call the “central” density. If we were to apply the relation from Equation 75 to the quantum core (soliton) of BECDM halos with ${\rho }_0$ being the true central density at $r=0$, we would encounter a problem because the mass–radius relation of the soliton is not consistent with a universal surface density [see Appendix L of Chavanis (2019d) and Sec. IX of Chavanis (2022g)].³² Indeed, in the noninteracting case, the mass–radius relation from Equation 34 implies ${\mathrm{\Sigma }}_0\sim M/R^2\sim M^3$, and in the TF limit, the relation from Equation 35 implies ${\mathrm{\Sigma }}_0\sim M/R^2\sim M$.³³ These scalings suggest that the surface density of DM halos increases with the mass $M$ instead of being constant. This problem was first mentioned in Chavanis et al. (2015b), Chavanis (2017b), and it has also been pointed out later by other authors (Deng et al., 2018; Burkert, 2020). Following Sec. VII of Chavanis (2019d), we shall assume that the relation from Equation 75 applies to the envelope surrounding the soliton. In that case, ${\rho }_0$ is not the true central density (i.e., the central density of the soliton) but the density of the envelope at the contact with the soliton.

Assuming that the envelope is isothermal, we obtain the halo mass–radius relation (Chavanis, 2019d; Chavanis, 2022g)

$M_h=1.76{\mathrm{\Sigma }}_0{r}_h^2.(76)$

We also find that $k_{B}T/m=0.954G{\mathrm{\Sigma }}_0{r}_h=0.719G\sqrt{{\mathrm{\Sigma }}_0{M}_h}$. These scalings can be obtained qualitatively from the relations $\mathrm{\Sigma }\sim M/R^2\sim 1$ and $k_{B}T/m\sim v^2\sim GM/R$. If the envelope is not exactly isothermal (see the comment (ii) in Section 5.3), we would obtain a halo mass–radius relation similar to Equation 76 but with a slightly different prefactor.

Remark: In the isothermal envelope model, the temperature must change from halo to halo according to the law $T\propto M_h^{1/2}$ (see above) in order to yield a universal surface density. Alternatively, a universal surface density directly results from a logotropic equation of state of the form $P=A\ln (\rho /{\rho }_P)$ with an “effective temperature” $A$, which is the same for all the halos. The logotropic DM model has been introduced and studied in Chavanis (2015b), Chavanis (2016b), Chavanis and Kumar (2017), Chavanis (2019c), Chavanis (2022c), Chavanis (2022e), and Chavanis (2022f). Interestingly, this model provides a prediction of the value of the universal surface density ${\mathrm{\Sigma }}_0$ without the free parameter. Specifically, ${\mathrm{\Sigma }}_0$ can be expressed in terms of the cosmological constant as

${\mathrm{\Sigma }}_0^{\text{th}}=0.01955\frac{c^2\sqrt{\mathrm{\Lambda }}}{G}=133M_{\odot }/{\mathrm{p}\mathrm{c}}^2,(77)$

where ${\mathrm{\Sigma }}_{\mathrm{\Lambda }}=c^2\sqrt{\mathrm{\Lambda }}/G=6792M_{\odot }/{\mathrm{p}\mathrm{c}}^2$ is the surface density of the universe (Chavanis, 2024b). The prefactor in Equation 77 is predicted by the logotropic model. Remarkably, this theoretical prediction is in very good agreement with the observational value from Equation 75. Furthermore, as noted in Chavanis (2019c), Chavanis (2022f), Chavanis (2024b), the surface density of DM halos turns out to be of the same order as the surface density of the electron

${\mathrm{\Sigma }}_e=\frac{m_e}{r_e^2}=54.9M_{\odot }/{\mathrm{p}\mathrm{c}}^2,(78)$

where $m_e=9.11\times 10^{-28}\mathrm{g}=0.511\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ is the mass of the electron and $r_e=2.82\times 10^{-15}\mathrm{m}$ is the classical electron radius defined by $m_e{c}^2=e^2/r_e$. If we identify the two expressions Equations 77, 78, writing ${\mathrm{\Sigma }}_e\sim {\mathrm{\Sigma }}_{\mathrm{\Lambda }}$, we obtain the Eddington relation from Equation 71 in order of magnitude. Conversely, using the accurate Eddington relation (Equation 71) from Chavanis (2019c), Chavanis (2022f), Chavanis (2024b), and Chavanis (2024c), we find that ${\mathrm{\Sigma }}_e\simeq \alpha {\mathrm{\Sigma }}_{\mathrm{\Lambda }}\simeq 0.373{\mathrm{\Sigma }}_0$ (Chavanis, 2024c). This relation may also be interpreted in terms of the holographic principle (Chavanis, 2019c; Chavanis, 2024b).

6.3 Core mass–halo mass relation

An important challenge of the BECDM model is to predict the relation between the core mass $M_c$ and the halo mass $M_h$. In Chavanis (2019d), Chavanis (2019a), Chavanis (2020a), Chavanis (2021a), Chavanis (2023c), we have derived the core mass–halo mass relation of BECDM halos (without or with the presence of a central black hole) from a thermodynamical approach. We have obtained a general relation $M_c(M_h)$ valid for bosons with a repulsive or an attractive self-interaction (or no self-interaction), and also for fermions. To obtain this relation, we have first shown Chavanis (2019d); Chavanis (2019a) that the maximization of the Lynden–Bell entropy at fixed mass and energy (most probable state in the microcanonical ensemble) leads to the “velocity dispersion tracing relation” according to which the velocity dispersion in the core $v_c^2\sim G{M}_c/R_c$ is of the same order as the velocity dispersion in the halo $v_h^2\sim G{M}_h/r_h$. This relation can be written as³⁴

$v_c\sim v_h\Rightarrow \frac{M_c}{R_c}\sim \frac{M_h}{r_h}.(79)$

Combining the velocity dispersion tracing relation from Equation 79 with the core mass–radius relation $M_c(R_c)$ from Equation 33 and with the halo mass–radius relation $M_h(r_h)$ from Equation 76, we obtain the core mass–halo mass relation $M_c(M_h)$ under the form³⁵

$M_c=2.23\frac{\hslash {\mathrm{\Sigma }}_0^{1/4}{M}_h^{1/4}}{G^{1/2}m}{\left(1+1.06\frac{a_s}{m}{\mathrm{\Sigma }}_0^{1/2}{M}_h^{1/2}\right)}^{1/2}.(80)$

Writing $M_c=M_h$ for the minimum halo (pure soliton without envelope), we obtain the equation

${\left(M_h\right)}_{\text{min}}^{3/2}=4.99\frac{{\hslash }^2{\mathrm{\Sigma }}_0^{1/2}}{G{m}^2}\left[1+1.06\frac{a_s}{m}{\mathrm{\Sigma }}_0^{1/2}{\left(M_h\right)}_{\text{min}}^{1/2}\right].(81)$

This equation determines the mass ${(M_h)}_{\text{min}}$ of the minimum halo as a function of $m$ and $a_s$. Conversely, for a given value of ${(M_h)}_{\text{min}}$ deduced from the observations (see Equation 1), it provides a relation between $m$ and $a_s$ (Chavanis, 2019a). This leads to results qualitatively equivalent to those of Section 4.2 since the values of ${(M_h)}_{\text{min}}$ and ${(r_h)}_{\text{min}}$ adopted in Equation 1 for the minimum halo are consistent with the relation from Equation 75 (see Chavanis (2021a) for a detailed discussion).

For noninteracting bosons, the core mass–halo mass relation is

$M_c=2.23{\left(\frac{{\hslash }^4{\mathrm{\Sigma }}_0{M}_h}{G^2{m}^4}\right)}^{1/4}.(82)$

For $a_s=0$, we find from Equations 1, 81 that the mass of the boson is $m=2.25\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$. For a DM halo of mass $M_h=10^{12}{M}_{\odot }$ similar to the one that surrounds our galaxy, we obtain a core mass $M_c=10^9{M}_{\odot }$ and a core radius $R_c=63.5\mathrm{p}\mathrm{c}$.

For bosons with a repulsive self-interaction in the TF limit, the core mass–halo mass relation is

$M_c=2.30{\left(\frac{{\hslash }^2{\mathrm{\Sigma }}_0{a}_s{M}_h}{G{m}^3}\right)}^{1/2}.(83)$

Note that the core radius $R_c$ does not change with $M_h$ (see Equation 35). In the TF limit, we find from Equations 1, 81 that $a_s/m^3=4.35\times 10^3\mathrm{f}\mathrm{m}/{(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^{\mathrm{3}}$. For a DM halo of mass $M_h=10^{12}{M}_{\odot }$ similar to the one that surrounds our galaxy, we obtain a core mass $M_c=10^{10}{M}_{\odot }$ and a core radius $R_c=635\mathrm{p}\mathrm{c}$.

In these two examples, the quantum core represents a bulge or a nucleus. It cannot mimic an SMBH because it is too much extended $(R{c}^2/GM\sim 10^6\gg 1)$. A central SMBH like Sagittarius A* (see Section 6.8) has to be introduced by hand in the model (Chavanis, 2020a).

The general core mass–halo mass relation from Equation 80 is plotted in Figure 11 adapted from Chavanis (2019a) for an arbitrary (repulsive or attractive) self-interaction.

Figure 11

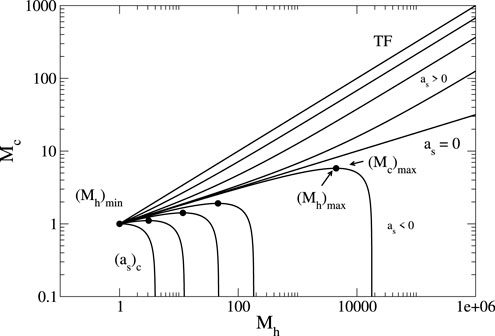
Figure 11. Core mass $M_c$ as a function of the halo mass $M_h$ for different values of $a_s$ ($m$ is determined by Equation 81). The mass is normalized by ${(M_h)}_{\text{min}}$ (typically ${(M_h)}_{\text{min}}\sim 10^8{M}_{\odot }$). We have plotted the position of the minimum halo mass ${(M_h)}_{\text{min}}$ (common origin) and the position of the maximum halo mass ${(M_h)}_{\text{max}}$ (bullets) above which the quantum core becomes unstable when $a_s<0$ (see Section 6.5). We have indicated the curve corresponding to the noninteracting case (see Equation 82) and the curve corresponding to the TF limit (see Equation 83). The transition between these two regimes occurs at a ratio ${(a_s/m)}_t\sim 1/{({\mathrm{\Sigma }}_0{M}_h)}^{1/2}$ in a given halo or at a halo mass ${(M_h)}_t\sim {(m/a_s)}^2/{\mathrm{\Sigma }}_0$ for given particle parameters.

Remark: Our results (Chavanis, 2019d; Chavanis, 2019a; Chavanis, 2020a) have been rederived and confirmed by Padilla et al. (2021) repeating the same arguments (compare Figure 2 in Padilla et al. (2021) to Fig. 19 in Chavanis (2019a)). Their scalings appear different from ours at first sight because their relations are expressed in terms of the virial mass instead of the halo mass (see Section 6.6), but the results turn out to be fully equivalent.

6.4 Collapse toward a black hole?

In the case of BECDM halos made of bosons with a repulsive self-interaction (or no self-interaction), the mass of the quantum core (soliton) increases monotonically with the halo mass (see Figure 11). Therefore, for sufficiently large halos, the core mass $M_c$ will overcome the maximum mass $M_{\text{max}}^{\text{GR}}$ set by general relativity (see Section 4.5) and collapse toward a black hole. Let us see if this scenario is possible in practice.

According to Equations 45, 47, 82, 83, the mass of the soliton would be equal to the general relativistic maximum mass $(M_c=M_{\text{max}}^{\text{GR}})$ in a DM halo of mass

${\left(M_h\right)}_{\text{max}}\sim 0.01\frac{c^4}{G^2{\mathrm{\Sigma }}_0}=3.09\times 10^{22}{M}_{\odot }.(84)$

Strikingly, this expression is independent of the characteristics of the DM particle (Chavanis, 2020a). Such a large halo mass is clearly unrealistic (the biggest DM halos observed in the universe have a mass $M_h\sim 10^{14}{M}_{\odot }$). Actually, using the relation from Equation 77, we see that the mass from Equation 84 is of the order of the mass of the universe $M_{\mathrm{\Lambda }}=c^2/(G\sqrt{\mathrm{\Lambda }})=6.43\times 10^{22}{M}_{\odot }$ (Chavanis, 2024b). Therefore, the quantum core present at the center of a BECDM halo with a repulsive self-interaction (or no self-interaction) is always much below the general relativistic maximum mass, so it can never collapse toward a black hole by this process of violent relaxation.³⁶ This conclusion was first reached in Appendix C of Chavanis (2020a) and recovered later in Padilla et al. (2021) in a less direct manner. Since $M_c\ll M_{\text{max}}^{\text{GR}}$ in all realistic DM halos, a nonrelativistic approach is justified to describe BECDM halos (see Section 7.7 for another scenario where general relativistic effects may be important).

Remark: When these arguments are applied to the context of inflaton clusters that could form in the very early universe (Musoke et al., 2020; Niemeyer and Easther, 2020; Eggemeier et al., 2021; Eggemeier et al., 2022) it is possible that the solitonic cores (inflaton stars) of sufficiently massive inflaton clusters may overcome the critical mass $M_{\text{max}}^{\text{GR}}$ set by general relativity and lead to the formation of primordial black holes (PBHs), as discussed in Padilla et al. (2022), Chavanis (2023c).

6.5 Collapse toward a dense axion star?

In the case of BECDM halos made of bosons with an attractive self-interaction (axions), the core mass–halo mass relation (see Figure 11) presents a maximum when the quantum core mass (dilute axion star) reaches the critical value from Equation 37, at which it becomes unstable and collapses (Chavanis, 2011c; Chavanis, 2016a).³⁷ According to Equations 37, 80, the collapse of the core, leading to the formation of a dense axion star, a bosenova, or a black hole (Braaten et al., 2016; Davidson and Schwetz, 2016; Cotner, 2016; Chavanis, 2016a; Eby et al., 2016; Levkov et al., 2017; Helfer et al., 2017; Chavanis, 2018b; Visinelli et al., 2018; Michel and Moss, 2018) occurs in a DM halo of mass

${\left(M_h\right)}_{\text{max}}=0.223\frac{m^2}{a_s^2{\mathrm{\Sigma }}_0}=141\frac{m^4{c}^2}{{\mathrm{\Sigma }}_0{\hslash }^2{\lambda }^2}=2255\frac{f^4}{{\hslash }^2{c}^6{\mathrm{\Sigma }}_0}.(85)$

We note that the maximum halo mass ${(M_h)}_{\text{max}}$ depends only on $f$, while the maximum core mass ${(M_c)}_{\text{max}}$ from Equation 43 depends on $f$ and $m$. On the other hand, the maximum core mass ${(M_c)}_{\text{max}}$ depends only on $\lambda$, while the maximum halo mass ${(M_h)}_{\text{max}}$ depends on $\lambda$ and $m$.

For this phase transition (collapse) to take place in practice, the critical halo mass ${(M_h)}_{\text{max}}$ must be smaller than the mass $M_h\sim 10^{14}{M}_{\odot }$ of the biggest halos observed in the universe. This requires that $f<4.22\times 10^{15}\mathrm{G}\mathrm{e}\mathrm{V}$ (corresponding to $|a_s|>1.10\times 10^{-80}\mathrm{m}$ and $|\lambda |>1.40\times 10^{-94}$ for $m\sim 10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$). The collapse of the quantum core above the maximum mass $M_{\text{max}}^{\text{NR}}$ when $f=10^{14}\mathrm{G}\mathrm{e}\mathrm{V}$ or $f=10^{15}\mathrm{G}\mathrm{e}\mathrm{V}$ has been evidenced in the numerical simulations of Mocz et al. (2023) and Painter et al. (2024) (see Chen et al. (2021), Chen et al. (2022), Glennon and Prescod-Weinstein (2021) in a different context). However, it is not quite clear if such small values of $f$ are allowed in practice (see the discussion in Chavanis (2021a)). Indeed, the constraints from particle physics and cosmology (see footnote 19) suggest that $f$ should be larger than $f=10^{16}\mathrm{G}\mathrm{e}\mathrm{V}$ (corresponding to $|a_s|<1.96\times 10^{-81}\mathrm{m}$ and $|\lambda |<2.5\times 10^{-95}$ for $m\sim 10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$), so we do not expect the collapse of the core to occur in realistic DM halos of mass $M_h<10^{14}{M}_{\odot }$. For example, taking $m=2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$ and $f=1.34\times 10^{17}\mathrm{G}\mathrm{e}\mathrm{V}$ (see above), and considering a DM halo of mass $M_h=10^{12}{M}_{\odot }$ (the typical mass of the Milky Way), we find $M_c=7.69\times 10^8{M}_{\odot }$ well below the maximum mass ${(M_c)}_{\text{max}}=5.10\times 10^{10}{M}_{\odot }$. However, even if $M_c<{(M_c)}_{\text{max}}$ initially, the core mass can increase by accretion, reach the maximum mass, and collapse (see footnote 20 and the conclusion for references on this topic). This is a point to be studied in more detail in future works.

Remark: For $m=2.19\times 10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ and $f=1.97\times 10^{14}\mathrm{G}\mathrm{e}\mathrm{V}$ (corresponding to $a_s=-1.11\times 10^{-62}\mathrm{f}\mathrm{m}$ and $\lambda =-3.07\times 10^{-91}$), we find ${(M_h)}_{\text{max}}={(M_c)}_{\text{max}}=10^8{M}_{\odot }$ and $R_{\ast }^{99}=1\mathrm{k}\mathrm{p}\mathrm{c}$. This corresponds to the condition of marginal stability of the minimum halo (see Section 4.3), implying that the quantum core of all the DM halos $(M_h\ge {(M_h)}_{\text{min}})$ would be unstable in that case. For $m=10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ and $f=1.34\times 10^{15}\mathrm{G}\mathrm{e}\mathrm{V}$ (corresponding to $a_s=-1.09\times 10^{-64}\mathrm{f}\mathrm{m}$ and $\lambda =-1.39\times 10^{-93}$), we find ${(M_h)}_{\text{max}}\sim 10^{12}{M}_{\odot }$ (the typical mass of the Milky Way), ${(M_c)}_{\text{max}}\sim 10^9{M}_{\odot }$, and $R_{\ast }^{99}\sim 300\mathrm{p}\mathrm{c}$. This corresponds to the situation where the quantum core of a DM halo similar to the one that surrounds our galaxy would become unstable.

6.6 Virial mass

In the previous sections, we have defined the halo mass $M_h$ and the halo radius $r_h$ such that $r_h$ represents the distance at which the central density is divided by 4. This corresponds to the definition given by Burkert (1995). Some authors (Schive et al., 2014b; Padilla et al., 2021; Padilla et al., 2022) use another definition of the halo mass and halo radius. They introduce the virial mass $M_v$ and the virial radius $r_v$ through the relation $M_v=\frac{4}{3}\pi {\rho }_{200}{r}_v^3$, where ${\rho }_{200}=200{\rho }_b$ is 200 times the background density ${\rho }_b$ of the universe. Using $G{M}_v/r_v\sim G{M}_h/r_h$ in consistency with Equation 79, and combining this relation with Equation 76, we obtain

$M_h\sim \frac{1}{1.76{\mathrm{\Sigma }}_0}{\left(\frac{4}{3}\pi {\rho }_{200}\right)}^{2/3}{M}_v^{4/3}.(86)$

Numerically, $M_h/M_{\odot }=6.01\times 10^{-6}{\left(M_v/M_{\odot }\right)}^{4/3}$. The relation between the halo mass $M_h$ and the virial mass $M_v$ exhibits the scaling $M_h\propto M_v^{4/3}$ (Chavanis, 2019d; Chavanis, 2019a; Chavanis, 2020a; Chavanis, 2021a; Chavanis, 2023c). We can use this relation to express the previous results in terms of $M_v$ instead of $M_h$. In particular, using Equations 82, 86, we find $M_c\propto M_v^{1/3}$ for noninteracting bosons in agreement with the original result of Schive et al. (2014b) obtained from direct numerical simulations and heuristic arguments. On the other hand, for bosons with a repulsive self-interaction in the TF limit, using Equations 83, 86, we predict that $M_c\propto M_v^{2/3}$ (Chavanis, 2019d; Chavanis, 2019a; Chavanis, 2020a; Chavanis, 2021a; Chavanis, 2023c), a result that has not yet been tested. The validity of these scalings has been criticized by some authors, and the universality or nonuniversality of the core mass–halo mass relation for BECDM halos remains an open problem (see the review in Sec. II.B of Zagorac et al. (2023) for a detailed discussion and a complete list of references). For example, some authors (Mocz et al., 2017; Bar et al., 2018) have proposed an “energy tracing relation” $G{M}_c^2/R_c\sim G{M}_h^2/r_h$ instead of the velocity tracing relation $G{M}_c/R_c\sim G{M}_h/r_h$.

6.7 Fermionic DM halos

Although this review is devoted to the case of bosonic DM, we briefly mention in this section what the previous results become in the case of fermionic DM.

For degenerate fermions, the pressure is due to the Pauli exclusion principle. The equation of state of a nonrelativistic Fermi gas at $T=0$ reads

$P=\frac{1}{20}{\left(\frac{3}{\pi }\right)}^{2/3}\frac{h^2}{m^{8/3}}{\rho }^{5/3}.(87)$

This is a polytropic equation of state of index $\gamma =5/3$ (i.e., $n=3/2$). The density profile of a fermion ball (the counterpart of the soliton) is determined by the differential equation (see Equations 27, 87)

$-\frac{1}{8}{\left(\frac{3}{\pi }\right)}^{2/3}\frac{h^2}{m^{8/3}}\mathrm{\Delta }{\rho }^{2/3}=4\pi G\rho ,(88)$

which is equivalent to the Lane–Emden equation of index $n=3/2$ (for fermionic DM halos, the TF approximation is an excellent approximation) (Chandrasekhar, 1957). The density profile has a compact support. The mass–radius relation of a fermion ball reads

$M=91.9\frac{{\hslash }^6}{G^3{m}^8{R}^3}.(89)$

The radius decreases monotonically as the mass increases. An equilibrium state exists for any mass $M$, and it is dynamically stable (using the Ledoux formula, the squared pulsation is given by $\omega =1.40\sqrt{G{\rho }_0}$). If we apply Equation 89 to the minimum halo of typical mass $M\sim 10^8{M}_{\odot }$ and typical radius $R\sim 1\mathrm{k}\mathrm{p}\mathrm{c}$, we get $m=170\mathrm{e}\mathrm{V}/c^2$ (Chavanis, 2021a). The mass of a fermionic DM particle is larger than the mass of a bosonic DM particle by a factor $\sim 10^{30}$ (Chavanis, 2024b).

The maximum mass and the minimum radius of a fermion star at $T=0$ set by general relativity are

$M_{\text{max}}^{\text{GR}}=0.384{\left(\frac{\hslash c}{G}\right)}^{3/2}\frac{1}{m^2}=0.384\frac{M_P^3}{m^2},(90)$

$R_{\text{min}}^{\text{GR}}=3.35{\left(\frac{{\hslash }^3}{G{m}^{4}c}\right)}^{1/2}=8.73\frac{G{M}_{\text{max}}}{c^2}.(91)$

These results were first obtained in the case of neutron stars (Oppenheimer and Volkoff, 1939). The scalings of Equations 90, 91 can be obtained qualitatively by equating the mass–radius relation from Equation 89 with the Schwarzschild relation $R\sim GM/c^2$, as explained in Appendix B of Chavanis (2011c). The same scalings are obtained for special relativistic white dwarf stars (Chandrasekhar, 1931). For $m\sim 1\mathrm{G}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ (nucleon mass), the maximum mass $M_{\text{max}}^{\text{GR}}\sim M_{\odot }$ is of the order of the solar mass. This is the typical mass of white dwarfs and neutron stars. For a DM fermion of mass $m=170\mathrm{e}\mathrm{V}/c^2$ (see above), one obtains $M_{\text{max}}^{\text{GR}}=2.17\times 10^{13}{M}_{\odot }$ and $R_{\text{min}}^{\text{GR}}=8.85\mathrm{p}\mathrm{c}$.

The core mass–halo mass relation is (Chavanis, 2021a)

$M_c=3.83\frac{{\hslash }^{3/2}}{m^2}{\left(\frac{{\mathrm{\Sigma }}_0{M}_h}{G^2}\right)}^{3/8}.(92)$

It terms of the virial mass we have $M_c\propto M_v^{1/2}$. For a DM halo of mass $M_h=10^{12}{M}_{\odot }$ similar to the one that surrounds our galaxy, using $m=170\mathrm{e}\mathrm{V}/c^2$ (see above), we obtain a core mass $M_c=4.47\times 10^9{M}_{\odot }$ and a core radius $R_c=284\mathrm{p}\mathrm{c}$. The quantum core represents a bulge or a nucleus. It cannot mimic an SMBH because it is too much extended $(R{c}^2/GM\sim 10^6\gg 1)$.

Like in Section 6.4, we can show that the quantum core (fermion ball) present at the center of a realistic fermionic DM halo is always below the general relativistic maximum mass from Equation 90, so it can never collapse toward a black hole by this process [see Appendix C of Chavanis (2020a)]. Since $M_c\ll M_{\text{max}}^{\text{GR}}$ in all realistic DM halos, a nonrelativistic approach is justified to describe fermionic DM halos (see Section 7.7 for another scenario where general relativistic effects may be important).

We have proposed in Chavanis (2022a); Chavanis (2022g) a generalized wave equation of the form of Equation 68 for fermionic DM with an effective potential

$V\left(|\psi {|}^2\right)=\frac{3}{40}{\left(\frac{3}{\pi }\right)}^{2/3}\frac{h^2}{m^{8/3}}|\psi {|}^{10/3}(93)$

accounting for the Pauli exclusion principle (see Equations 21, 87).

6.8 Can the quantum core mimic an SMBH?

A very massive object (Sagittarius A*) resides at the center of our galaxy of mass $\sim 10^{12}{M}_{\odot }$. This object has a mass $M=4.2\times 10^6{M}_{\odot }$ associated with a Schwarzschild radius $R_S=4.02\times 10^{-7}\mathrm{p}\mathrm{c}$. Its actual radius is not known exactly, but it must be less than $R_P=6\times 10^{-4}\mathrm{p}\mathrm{c}$, the S2 star pericenter $(R_P=1492R_S)$ (Gillessen et al., 2009). This object is believed to be an SMBH, but it could also be a compact object such as a boson star or a fermion ball.

(i) Let us first assume that this object is a noninteracting boson star (soliton).

Using the expression of the maximum mass from Equation 45 with $M=4.2\times 10^6{M}_{\odot }$, we get $m_{\text{max}}=2.01\times 10^{-17}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$. This is the maximum mass that the boson can have; otherwise, the boson star would be unstable and would collapse toward a black hole.

Using the nonrelativistic mass–radius relation from Equation 34 with $M=4.2\times 10^6{M}_{\odot }$ and $R=6\times 10^{-4}\mathrm{p}\mathrm{c}$, we find that the mass of the boson is $m_{\text{min}}=1.84\times 10^{-18}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$. This is the minimum mass that the boson can have; otherwise, the radius of the boson star would be larger than $R_P=6\times 10^{-4}\mathrm{p}\mathrm{c}$.

Using the core mass–halo mass relation from Equation 82 with $M_c=4.2\times 10^6{M}_{\odot }$ and $M_h=10^{12}{M}_{\odot }$, we find that $m=5.35\times 10^{-20}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$. This value is smaller than the minimum mass $m_{\text{min}}=1.84\times 10^{-18}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$, implying that $R_c>R_P$ (we find $R_c=0.707\mathrm{p}\mathrm{c}$).

(ii) Let us now assume that the supermassive object at the center of the galaxy is a self-interacting boson star, which can be described with the TF approximation.

Using the expression of the maximum mass from Equation 47 with $M=4.2\times 10^6{M}_{\odot }$, we get ${(a_s/m^3)}_{\text{min}}=1.39\times 10^{-14}\mathrm{f}\mathrm{m}/$${(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^3$. This is the minimum value that the ratio $a_s/m^3$ can have; otherwise, the boson star would be unstable and would collapse toward a black hole.

Using the nonrelativistic relation from Equation 35 with $R=6\times 10^{-4}\mathrm{p}\mathrm{c}$, we get ${(a_s/m^3)}_{\text{max}}=1.18\times 10^{-9}\mathrm{f}\mathrm{m}/{(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^3$. This is the maximum value that the ratio $a_s/m^3$ can have; otherwise, the radius of the boson star would be larger than $R_P=6\times 10^{-4}\mathrm{p}\mathrm{c}$.

Using the core mass–halo mass relation from Equation 83 with $M_c=4.2\times 10^6{M}_{\odot }$ and $M_h=10^{12}{M}_{\odot }$, we find that $(a_s/m^3)=7.65\times 10^{-4}\mathrm{f}\mathrm{m}/{(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^3$. This value is larger than ${(a_s/m^3)}_{\text{max}}=1.18\times 10^{-9}\mathrm{f}\mathrm{m}/{(\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}})}^3$, implying that $R_c>R_P$ (we find $R_c=0.483\mathrm{p}\mathrm{c}$).

(iii) Finally, let us assume that the supermassive object at the center of the galaxy is a fermion ball.

Using the expression of the maximum mass from Equation 90 with $M=4.2\times 10^6{M}_{\odot }$, we get $m_{\text{max}}=386\mathrm{k}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$. This is the maximum mass that the fermion can have; otherwise, the fermion ball would be unstable and would collapse toward a black hole.

Using the nonrelativistic mass–radius relation from Equation 89 with $M=4.2\times 10^6{M}_{\odot }$ and $R=6\times 10^{-4}\mathrm{p}\mathrm{c}$, we find that the mass of the fermion is $m_{\text{min}}=54.6\mathrm{k}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$. This is the minimum mass that the fermion can have; otherwise, the radius of the fermion ball would be larger than $R_P=6\times 10^{-4}\mathrm{p}\mathrm{c}$.

Using the core mass–halo mass relation from Equation 92 with $M_c=4.2\times 10^6{M}_{\odot }$ and $M_h=10^{12}{M}_{\odot }$, we find that $m=5.55\mathrm{k}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$. This value is smaller than the minimum mass $m_{\text{min}}=54.6\mathrm{k}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$, implying that $R_c>R_P$ (we find $R_c=0.266\mathrm{p}\mathrm{c}$).

In conclusion, if the core mass–halo mass relations from Equations 82, 83, 92 are valid in the present context, it is not possible to construct a quantum core which mimics an SMBH at the center of our galaxy (see Figure 12). It would be too extended $(R_c>R_P)$. A possibility to escape this conclusion could be that the core mass–halo mass relations from Equations 82, 83, 92 are not valid (see the alternative scenario of Section 7.7, leading to different results). However, there are other difficulties in assuming that the quantum core of a BECDM halo or the quantum core of a fermionic DM halo mimics an SMBH. These difficulties are discussed in detail in Chavanis (2019d), Chavanis (2022g). In particular, if we assume that the ground state of the self-gravitating Bose or Fermi gas corresponds to a minimum halo of typical mass $M\sim 10^8{M}_{\odot }$ and typical radius $R\sim 1\mathrm{k}\mathrm{p}\mathrm{c}$, we find (see Section 4.2 and Section 6.7) that the mass of the DM particle is much smaller than the one computed in the present section.³⁸ In that case, the quantum core represents a large bulge of typical size $100-1000\mathrm{p}\mathrm{c}$ (see Section 6.3) rather than mimicking an SMBH of size less than $R_P=6\times 10^{-4}\mathrm{p}\mathrm{c}$. It is possible that the difficulties pointed out in Chavanis (2019d); Chavanis (2022g) are not relevant or can be solved. In any case, the suggestion that the supermassive object at the center of our galaxy (and other galaxies) could be a boson star or a fermion ball remains attractive. It has been developed by some authors with success (see the review of Argüelles et al. (2023) on fermionic DM halos and a history of the subject in Chavanis (2023d)).

Figure 12

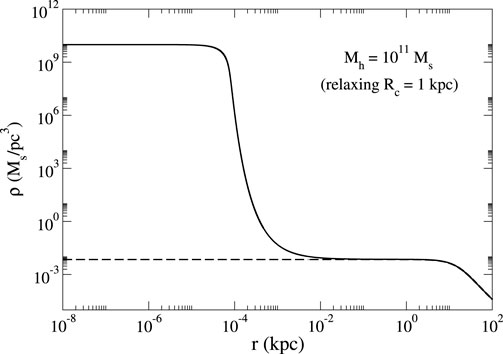
Figure 12. Core–envelope density profile of a BECDM halo with a repulsive self-interaction (TF limit) in the scenario where the quantum core mimics an SMBH of mass $M_c=4.2\times 10^6{M}_{\odot }$ like Sagittarius A*. It is compared with a purely isothermal profile (dashed line). We have considered a BECDM halo of mass $M_h=10^{11}{M}_{\odot }$. As explained in the text, the value of the core radius resulting from Equation 83 is too large to satisfy the constraint $R_c<R_P$.

7 Secular evolution of BECDM halos

7.1 Classical relaxation time

The results of the previous sections have been obtained in the “collisionless” regime where the evolution of the system is due to a process of gravitational cooling and violent relaxation. This process takes place on a few dynamical times $t_D\sim R/v\sim 1/\sqrt{G\rho }\sim 0.1\mathrm{G}\mathrm{y}\mathrm{r}\mathrm{s}$ (to make the numerical application, we have taken $R\sim 20.1\mathrm{k}\mathrm{p}\mathrm{c}$, $\rho \sim 7.02\times 10^{-3}{M}_{\odot }/{\mathrm{p}\mathrm{c}}^3$, and $v\sim 146\mathrm{k}\mathrm{m}/\mathrm{s}$ for a galaxy of mass $M\sim 10^{12}{M}_{\odot }$ like the Milky Way Chavanis (2019d)). It leads to a quasi-stationary state (or virialized state) with a core–envelope structure. On a longer timescale, the bosons in the envelope undergo a “collisional” evolution due to gravitational encounters, which operates on a slow (secular) timescale. The classical relaxation time scales as (Chandrasekhar, 1942; Binney and Tremaine, 1987)

$t_R\sim \frac{v^3}{G^2\rho m\ln \mathrm{\Lambda }}\sim \frac{N}{\ln N}{t}_D,(94)$

where $\ln \mathrm{\Lambda }\sim \ln (R/b_{90})\sim \ln N$ is the Coulomb logarithm ($b_{90}\sim Gm/v^2$ is the distance at which the particles engaged in a collision are deflected by approximately $90^{\text{o}}$, $R$ is the system’s size, and $N$ is the number of particles). For CDM made of classical particles of mass $m\sim 1\mathrm{G}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}-1\mathrm{T}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$, implying $N\sim 10^{66}-10^{69}$ for a typical DM halo of mass $M_h\sim 10^{12}{M}_{\odot }$, the relaxation time is much larger than the age of the universe by many orders of magnitude so that gravitational encounters (fluctuations, finite $N$ effects, etc.) are completely negligible. CDM halos are essentially collisionless. However, in the case of bosons, there is a huge reduction in the relaxation time because of Bose enhancement (or Bose stimulation).

7.2 Granules and quasiparticles

As shown by Schive et al. (2014a), Schive et al. (2014b), quantum wave interferences produce time-dependent small-scale density granules of the size ${\lambda }_{\text{dB}}=h/(mv)\sim 1\mathrm{k}\mathrm{p}\mathrm{c}$ of the solitonic core (we have taken $m\sim 10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$). These granules have been clearly evidenced in numerical simulations of the SP equations (Schive et al., 2014a; Schive et al., 2014b; Schwabe et al., 2016; Mocz et al., 2017; Mocz et al., 2018; Veltmaat et al., 2018; Mocz et al., 2019; Mocz et al., 2020; Veltmaat et al., 2020). They have been interpreted by Hui et al. (2017) as quasiparticles with an effective mass

$m_{\text{eff}}\sim \rho {\lambda }_{\text{dB}}^3\sim \frac{\rho h^3}{v^3{m}^3}\sim 10^7{M}_{\odot }\gg m,(95)$

which depends on the local halo density $\rho$ and velocity dispersion $v$. The effective mass $m_{\text{eff}}$ corresponds to the mass of the bosonic gas contained within the de Broglie sphere. BECDM halos therefore behave as classical self-gravitating systems (similar to globular clusters) made of quasiparticles with an effective radius ${\lambda }_{\text{dB}}\sim 1\mathrm{k}\mathrm{p}\mathrm{c}$ and an effective mass $m_{\text{eff}}\sim \rho {\lambda }_{\text{dB}}^3\sim 10^7{M}_{\odot }$ (see the justification of this effective mass from kinetic theory given in Section 7.4 below). Because of Bose enhancement, these quasiparticles are much heavier than the bosons $(m_{\text{eff}}\gg m)$. As a result, Bose enhancement strongly accelerates the collisional relaxation. For $m_{\text{eff}}\sim 10^7{M}_{\odot }$, we find that the number of quasiparticles is $N_{\text{eff}}\sim 10^5$, so that the relaxation time from Equation 94 with $m$ replaced by $m_{\text{eff}}$ and $N$ by $N_{\text{eff}}$ is considerably reduced and becomes comparable to the age of the universe or even smaller (especially in the core of the galaxy where the density is high and $t_D$ is small).

7.3 Heating and cooling

The evolution of test particles of mass $m_t$ in a BECDM halo due to “collisions” with quasiparticles of mass $m_{\text{eff}}$ has been analyzed by Bar-Or et al. (2019), Bar-Or et al. (2021). The granules can cause the diffusion (heating) of light test particles such as stars (with $m_t\ll m_{\text{eff}}$) on a secular timescale. This process can heat and expand the central regions of a stellar system embedded in the halo. On the other hand, heavy test particles such as black holes or globular clusters (with $m_t\gg m_{\text{eff}}$) experience dynamical friction (cooling). The variation of the effective mass $m_{\text{eff}}(r)$ of the quasiparticles across the system (due to the spatial variation of the density $\rho$ and velocity dispersion $v$ of the DM halo) can stall the inspiral of the massive objects toward the center of the galaxy at the distance where the effective mass of the quasiparticles $m_{\text{eff}}(r)$ becomes equal to the mass $m_t$ of the test particles. A similar description of heating and cooling in BECDM halos has been developed by Marsh and Niemeyer (2019), El-Zant et al. (2020), and Chavanis (2021b).

7.4 Kinetic theory based on the bosonic Landau equation

The granules (quasiparticles) also induce a secular evolution of the BECDM halo itself. This evolution can be described by the bosonic Landau equation Chavanis (2021b):

$\begin{array}{c}\frac{\partial f}{\partial t}=2\pi G^2\ln \mathrm{\Lambda }\frac{\partial }{\partial v_i}\int d{\mathbf{v}}^{\prime }\frac{u^2{\delta }_{ij}-u_i{u}_j}{u^3}\hfill \\ \times \left\{m{f}^{\prime }\left(1+\frac{f^{\prime }}{{\eta }_0}\right)\frac{\partial f}{\partial v_j}-mf\left(1+\frac{f}{{\eta }_0}\right)\frac{\partial f^{\prime }}{\partial v_j^{\prime }}\right\},\hfill \end{array}(96)$

where $\mathbf{u}={\mathbf{v}}^{\prime }-\mathbf{v}$ is the relative velocity of the particles engaged in an encounter, ${\eta }_0=g{m}^4/h^3$ is the phase space density, and $\ln \mathrm{\Lambda }\sim \ln (R/{\lambda }_{\text{dB}})$ is the quantum Coulomb logarithm with ${\lambda }_{\text{dB}}$ now replacing $b_{90}$. Equation 96 differs from the classical Landau equation by the presence of the factor $mf(1+f/{\eta }_0)$ instead of $mf$ that takes into account Bose enhancement. Since $f/{\eta }_0\gg 1$, the bare mass $m$ of the bosons is multiplied by a factor $\chi \sim f/{\eta }_0\sim \rho h^3/(v^3{m}^4)$ so that $m_{\text{eff}}\sim \chi m\sim \rho h^3/(v^3{m}^3)\sim \rho {\lambda }_{\text{dB}}^3$, as stated in Equation 95 above (for $m\sim 10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$, we find $\chi \sim 10^{95}$). The relaxation time is therefore given by

$t_R\sim \frac{v^3}{G^2\rho m_{\text{eff}}\ln \mathrm{\Lambda }}\sim \frac{v^3}{G^2\rho m\chi \ln \mathrm{\Lambda }}\sim \frac{v^6{m}^3}{G^2{\rho }^2{h}^3\ln \mathrm{\Lambda }}.(97)$

It corresponds to the relaxation time of a classical collisional stellar system (e.g., a globular cluster) from Equation 94 with an effective particle mass given by Equation 95. As discussed above, everything happens as if the envelope of the BECDM halo contained $N_{\text{eff}}=M/m_{\text{eff}}=N/\chi \ll N$ classical quasiparticles of mass $m_{\text{eff}}$ instead of $N$ quantum particles of mass $m$.

7.5 Growth of the soliton

This kinetic description was originally introduced by Levkov et al. (2018) who used it to investigate the condensation phenomenon and the growth of the soliton due to collisions between quasiparticles. The relaxation time $t_R$ characterizing the secular evolution of the envelope of the BECDM halo also determines the typical condensation time by gravitational encounters. This is the typical time required to form the soliton through Bose–Einstein gravitational condensation. On this secular (kinetic) timescale, a fraction of the bosons of the envelope condenses (because $T\ll T_c$) and “feeds” the soliton. As a result, the mass of the soliton increases, while the envelope of the DM halo is slowly depleted. The secular growth of the soliton has been further studied by Eggemeier and Niemeyer (2019) and Chen et al. (2021), Chen et al. (2022). They showed that the core accretes matter from the surrounding with a slow but permanent growth that goes initially as $t^{1/2}$ (Levkov et al., 2018) and then as $t^{1/8}$ (Eggemeier and Niemeyer, 2019; Chen et al., 2021) once the virial velocity of the soliton and the envelope coincide $(v_c\sim v_h)$. The corresponding saturation mass satisfies the scaling $M_c\propto M_v^{1/3}$, similar to the one found in Schive et al. (2014b) in the collisionless regime (see Section 6.6).

We stress that this mechanism of condensation, which operates on a secular timescale, is physically different from the processes of gravitational cooling and collisionless violent relaxation discussed in Section 5.1 which operate on a much shorter timescale (a few dynamical times). In the present case, the formation and growth of the soliton is due to the condensation caused by gravitational interactions (collisions). There are therefore two distinct mechanisms (collisionless vs. collisional) to form the soliton (see the introduction of Chavanis (2021b) for more details). The distinction between the phase of violent relaxation (formation of the soliton) and the phase of slow collisional relaxation (formation and/or growth of the soliton) is illustrated numerically in Seidel and Suen (1994), Schive et al. (2014a), Schive et al. (2014b), Schwabe et al. (2016), Mocz et al. (2017), Mocz et al. (2018), Veltmaat et al. (2018), Mocz et al. (2019), Mocz et al. (2020), Veltmaat et al. (2020), Glennon and Prescod-Weinstein (2021), Mocz et al. (2023), Liu et al. (2023), Nori et al. (2023), Painter et al. (2024) and in Levkov et al. (2018), Eggemeier and Niemeyer (2019), Chen et al. (2021), Chen et al. (2022), respectively.

7.6 Self-interacting dark matter

For completeness, we mention another possible scenario of evolution of BECDM halos (Chavanis, 2019d). If the bosons have a strongly repulsive self-interaction, the collisional evolution of the envelope may be driven by self-interactions instead of gravitational encounters.³⁹ This is usually referred to as self-interacting dark matter (SIDM) (Spergel and Steinhardt, 2000). The evolution of SIDM halos can be described by the ordinary Boltzmann kinetic equation. If the particles are self-interacting, with a scattering length $a_s$, they experience a relaxation due to direct “collisions” with a cross-section $\sigma =4\pi a_s^2$. As discussed previously, a relevant situation corresponds to bosons with a mass $m=1.10\times 10^{-3}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ and scattering length $a_s=4.41\times 10^{-6}\mathrm{f}\mathrm{m}$ determined by the Bullet Cluster constraint $\sigma /m=1.25\mathrm{c}{\mathrm{m}}^{\mathrm{2}}/\mathrm{g}$ (see Section 4.2). In that case, the relaxation time due to self-interaction (neglecting here Bose enhancement) is

$t_{\text{self}}\sim \frac{m}{\rho v\sigma }\sim 3.66\mathrm{G}\mathrm{y}\mathrm{r}\mathrm{s}.(98)$

Since the Bullet Cluster constraint determines $\sigma /m$, the value of the relaxation time due to self-interaction is independent of the mass of the DM particle. It is comparable to the age of the universe (especially in the core of the galaxy where the density is high). In comparison, the relaxation time due to gravitational encounters is $t_{\text{gr}}\sim 10^{81}{t}_D\sim 10^{89}\mathrm{y}\mathrm{r}\mathrm{s}$.

Remark: If we account for Bose enhancement, the relaxation time scales generically as $t_R\sim m/(\chi \rho v\sigma )\sim m^5{v}^2/({\rho }^2\sigma h^3)$. In the general case, the bosons experience a relaxation due to their self-interaction with a cross-section ${\sigma }_{\text{self}}=4\pi a_s^2$, leading to $t_{\text{self}}\sim m/(\chi \rho v{a}_s^2)\sim m^5{v}^2/({\rho }^2{a}_s^2{h}^3)$, and a relaxation due to gravitational scattering with a Rutherford cross-section ${\sigma }_{\text{gr}}\sim G^2{m}^2\ln \mathrm{\Lambda }/v^4$, leading to $t_{\text{gr}}\sim v^3/(\chi \rho G^{2}m\ln \mathrm{\Lambda })\sim m^3{v}^6/(G^2{\rho }^2{h}^3\ln \mathrm{\Lambda })$. The total cross-section is ${\sigma }_{\text{tot}}={\sigma }_{\text{gr}}+{\sigma }_{\text{self}}$, and the relaxation time is $t_R=t_{\text{gr}}{t}_{\text{self}}/(t_{\text{gr}}+t_{\text{self}})$ (Chen et al., 2022; Kirkpatrick et al., 2022). For QCD axions and ULAs, Levkov et al. (2018) showed that the collisional relaxation due to the self-coupling is slower than the collisional relaxation due to two-body gravitational encounters. Indeed, for $m=2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$ and $a_s=-3.18\times 10^{-68}\mathrm{f}\mathrm{m}$, we have $t_{\text{self}}/t_{\text{gr}}\sim {\sigma }_{\text{gr}}/{\sigma }_{\text{self}}\sim G^2{m}^2\ln \mathrm{\Lambda }/(a_s^2{v}^4)\sim 10^{10}$. However, for bosons with $m=1.10\times 10^{-3}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ and $a_s=4.41\times 10^{-6}\mathrm{f}\mathrm{m}$, we find the opposite. Self-interaction wins over gravity by $t_{\text{gr}}/t_{\text{self}}\sim {\sigma }_{\text{self}}/{\sigma }_{\text{gr}}\sim a_s^2{v}^4/(G^2{m}^2\ln \mathrm{\Lambda })\sim 10^{77}$.

7.7 Gravothermal catastrophe

Gravitational encounters between quasiparticles or collisions between bosons due to their self-interaction induce the secular evolution of a BECDM halo on a relevant timescale and establish an isothermal distribution, especially in the core of the halo where the density is high and the relaxation time is short. If we account for evaporation and tidal effects, this collisional evolution can provide another justification of the King distribution (see Equations 61, 62 without the bar on $f$). In that case, BECDM halos behave similarly to globular clusters with additional specificities due to quantum mechanics. Because of collisions and evaporation, they slowly follow a series of equilibria (the King sequence) toward configurations of higher and higher central density (see Figure 13). At some point, when the central density reaches a critical value corresponding to the minimum energy in the series of equilibria (caloric curve), the DM halo becomes thermodynamically unstable and experiences a gravothermal catastrophe (Lynden-Bell and Wood, 1968).

Figure 13

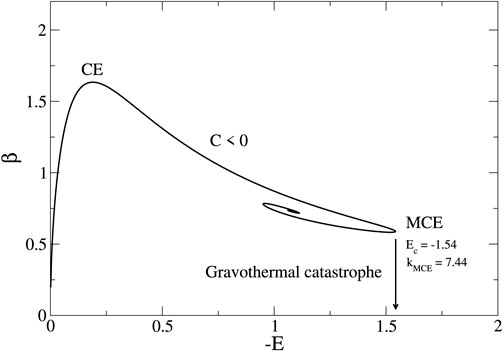
Figure 13. Series of equilibria (caloric curve) of the classical King model (Chavanis et al., 2015a; Chavanis et al., 2015b) giving the inverse temperature $\beta$ as a function of minus the energy $-E$. It has a snail-like (spiral) structure, but only the part of the curve up to MCE is stable in the microcanonical ensemble (note that between CE and MCE, the specific heat is negative). At the point of minimal energy $E_c$, the system undergoes a gravothermal catastrophe and collapses.

Most DM halos are close to the point of marginal stability. The marginal King density profile, which is flat at the center and decreases approximately as $\rho \sim r^{-3}$ at large distances (before decreasing to 0 at the tidal radius) (Chavanis et al., 2015a), is similar to the modified Hubble profile (Binney and Tremaine, 1987), which is itself relatively similar to the Burkert profile (Burkert, 1995) that gives a good fit of many DM halos (see Figure 18 of Chavanis et al. (2015a), Figure 1 of Chavanis (2022g), and Figure 9 of this paper for a comparison between these different profiles). Therefore, as suggested in Chavanis et al. (2015a), Chavanis et al. (2015b), Chavanis (2019d), and Chavanis (2022g), the marginal King profile may justify the empirical Burkert profile of DM halos.⁴⁰

If the BECDM halo is not too massive, the gravothermal catastrophe is stopped by quantum mechanics (Heisenberg’s uncertainty principle) or by the repulsive self-interaction of the bosons. This leads to BECDM halos with a core–envelope structure made of a bosonic condensate (soliton) surrounded by an approximately isothermal envelope or, more realistically, a King envelope (Chavanis, 2019d). Therefore, the soliton may result from the gravothermal catastrophe stopped by quantum mechanics or by repulsive scattering. This scenario provides another mechanism for the formation of a solitonic core (Chavanis, 2019d). Depending on the characteristics of the DM particle (mass, scattering length…), the condensed object (soliton) may mimic an SMBH at the center of a galaxy or represent a large DM bulge (see Section 6.8).⁴¹

If the BECDM halo is sufficiently massive, the gravothermal catastrophe may be followed by an instability of general relativistic origin (Balberg et al., 2002), leading to the formation of an SMBH instead of a quantum core (soliton). This soliton/SMBH transition (Chavanis, 2019d) occurs when the mass of the solitonic core overcomes the maximum mass $M_{\text{max}}^{\text{GR}}$ set by general relativity (see Section 4.5). As a result, medium-sized galaxies like the Milky Way may harbor a soliton (mimicking an SMBH or representing a bulge), while very large galaxies should harbor an SMBH of mass $M_{\text{max}}^{\text{GR}}$ (for noninteracting BECs with $m=2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$, one finds $M_{\text{max,NI}}^{\text{GR}}=2.90\times 10^{11}{M}_{\odot }$). This scenario could account for the mass of SMBHs (quasars) in active galactic nuclei (AGNs) like the one recently photographed in M87 ($M_h\sim 10^{13}{M}_{\odot }$ and $M_{\text{BH}}\sim 10^{10}{M}_{\odot }$).

Note that during the gravothermal catastrophe and the gravitational collapse, the envelope remains unaltered. Therefore, the resulting structure is a marginal King profile (with a flat core and a $\rho \sim r^{-3}$ envelope), similar to the Burkert profile, containing either a central condensed object (soliton) or an SMBH (Chavanis, 2019d). The density in the envelope may also decay more rapidly than $r^{-3}$ according to the recent results of Gaia DR3 discussed in footnote 27.

Similar results are obtained for fermionic DM where the soliton is replaced by a fermion ball (Bilic et al., 2003; Destri et al., 2013; Chavanis, 2006; Chavanis et al., 2015a; Chavanis et al., 2015b; Ruffini et al., 2015; Chavanis and Alberti, 2020; Alberti and Chavanis, 2020b; Chavanis, 2020d; Chavanis, 2020e; Argüelles et al., 2021; Chavanis, 2023d; Chavanis, 2022g; Argüelles et al., 2023).⁴² We refer to Chavanis (2019d), Chavanis (2022g), Chavanis (2023d), Argüelles et al. (2023) and references therein for more details about this scenario valid for fermionic and bosonic DM. At this stage, it is not possible to favor fermionic DM over bosonic DM or the converse. Note that fermionic and bosonic DM halos involve particles with a very different mass differing by 30 orders of magnitude (see Section 4, Section 6.7 and Chavanis, 2024b). It is also possible that DM is made of several types of fermions and bosons, as suggested in Sec. XII.E of Chavanis (2022g).

8 Basics of BECDM cosmology

The large-scale structures of the universe such as galaxies and DM halos are formed in the homogeneous background by Jeans instability (Jeans, 1902).⁴³ For a cold classical gas, the Jeans length vanishes or is extremely small $({\lambda }_J\simeq 0)$, implying that structures form at all scales. This is not what we observe (there is no DM halo with a mass smaller than ${(M_h)}_{\text{min}}\sim 10^8{M}_{\odot }$), and this leads to the small-scale problems of the CDM model such as the missing satellite problem (see the Introduction). By contrast, when quantum mechanics (or a repulsive self-interaction) is taken into account, the Jeans length is nonzero, implying the absence of structures below a minimum mass ${(M_h)}_{\text{min}}\sim 10^8{M}_{\odot }$ (for suitably chosen parameters of the DM particle), in agreement with the observations.⁴⁴

The Jeans instability of a self-gravitating BEC (or a complex SF) with repulsive or attractive self-interactions was first considered by Khlopov et al. (1985) and Bianchi et al. (1990) in a general relativistic framework based on the KGE equations. The Jeans instability of a noninteracting self-gravitating BEC in Newtonian gravity described by the SP equations was studied by Hu et al. (2000) and Sikivie and Yang (2009). The Jeans instability of a Newtonian self-gravitating BEC with repulsive or attractive self-interactions described by the GPP equations was studied by Chavanis (2011c). These results were extended in general relativity by Suárez and Chavanis (2015a), and Suárez and Chavanis (2018). In these different studies, the authors determined the Jeans length and the Jeans mass of the unstable structures and used them to obtain an estimate of the minimum size and minimum mass of BECDM halos. These studies were performed in a static universe. The Jeans instability of an infinite homogeneous self-gravitating BEC in an expanding universe was studied by Bianchi et al. (1990), Suárez and Matos (2011) and Suárez and Chavanis (2015a) in general relativity and by Sikivie and Yang (2009) (without self-interaction) and Chavanis (2012b) (with self-interaction) in Newtonian gravity. These studies are valid for a complex SF describing the wavefunction of a BEC. They rely on a hydrodynamical representation of the wave equation. We refer to Chavanis (2020b) for a review about the Jeans instability of self-gravitating BECs. The Jeans instability of a real SF in general relativity has been studied by numerous authors, and a detailed list of references is given in Chavanis (2021a).

The Jeans instability is only valid in the linear regime of structure formation. It describes the initiation of the large-scale structures of the universe. The Jeans instability leads to the increase in the perturbations and the formation of condensations (clumps). When the density contrast reaches a sufficiently large value, the condensations (overdensities) decouple from the Hubble flow and experience a free fall, followed by a complicated process of gravitational cooling (Seidel and Suen, 1994) and violent relaxation (virialization) (Lynden-Bell, 1967). They can also grow through collisions, merging, and accretion before being diluted by the expansion of the universe. This corresponds to the nonlinear regime of structure formation, leading to the DM halos that we observe today. BECDM halos result from the balance between the gravitational attraction, the quantum pressure arising from the Heisenberg uncertainty principle, the pressure due to the self-interaction of the bosons, and the effective thermal pressure. They have a core–envelope structure with a quantum core (soliton) surrounded by an approximately isothermal envelope due to quantum interferences, as discussed in the previous sections.

8.1 Gravitational instability of an infinite homogeneous BEC in a static universe

Let us apply the GPP Equations 8, 9 to the universe as a whole in order to study the initiation of structure formation. We use a hydrodynamic approach. Specifically, following Chavanis (2011c), we study the linear dynamical stability of an infinite homogeneous self-gravitating BEC with density $\rho$ and vanishing velocity $\mathbf{u}=\mathbf{0}$ described by the quantum Euler–Poisson Equations 16–19. In this section, we consider a static universe and make the Jeans swindle (Binney and Tremaine, 1987). This is the generalization of the classical Jeans problem (Jeans, 1902) to a quantum fluid.⁴⁵

Considering a small perturbation about an infinite homogeneous self-gravitating BEC, linearizing the quantum Euler–Poisson Equations 16–19, and decomposing the perturbation into plane waves, we obtain the generalized dispersion relation (Chavanis, 2011c)

${\omega }^2=\frac{{\hslash }^2{k}^4}{4m^2}+c_s^2{k}^2-4\pi G\rho ,(99)$

where $c_s^2=P^{\prime }(\rho )=\rho V^{″}(\rho )$ (see Equation 21) is the squared speed of sound in the BEC. The dispersion relation from Equation 99 is plotted in Figure 14. The medium is stable when ${\omega }^2>0$ (in that case, the perturbation oscillates with the pulsation $\omega$) and unstable when ${\omega }^2<0$ (in that case, the perturbation grows exponentially rapidly with a growth rate $\gamma =\sqrt{-{\omega }^2}$). In the TF limit $\hslash \to 0$, we recover the Jeans (1902) dispersion relation of a classical self-gravitating gas. In the absence of self-gravity $(G=0)$, we recover the Bogoliubov (1947) dispersion relation of a nonideal boson gas. The dispersion relation from Equation 99 originally derived in Chavanis (2011c) has been used in Slepian and Goodman (2012), Guth et al. (2015), Harko (2019), Berezhiani et al. (2019), Ourabah (2020), Buehler and Desjacques (2023), Berezhiani et al. (2023), and Glennon et al. (2024).

Figure 14

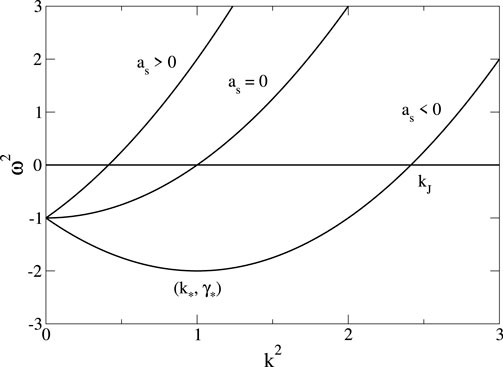
Figure 14. Dispersion relation of a self-gravitating BEC with repulsive or attractive self-interaction. The pulsation is normalized by ${\omega }_0=\sqrt{4\pi G\rho }$, the wavenumber by $k_0={(16\pi G\rho m^2/{\hslash }^2)}^{1/4}$, and the scattering length by $a_0={(G{m}^4/4\pi \rho {\hslash }^2)}^{1/2}$. For $a_s<0$, the maximum growth rate ${\gamma }_{\ast }=\sqrt{16{\pi }^2{a}_s^2{\hslash }^2{\rho }^2/m^4+4\pi G\rho }$ is reached for $k_{\ast }^2=8\pi |a_s|\rho /m$, which is independent of $G$ (Chavanis, 2011c).

The generalized Jeans wavenumber $k_J$, corresponding to the mode of marginal stability $(\omega =0)$, is given by (Chavanis, 2011c)

$k_J^2=\frac{2m^2}{{\hslash }^2}\left(-c_s^2+\sqrt{c_s^4+\frac{4\pi G\rho {\hslash }^2}{m^2}}\right).(100)$

A perturbation with wavelength $\lambda =2\pi /k$ is stable if $\lambda <{\lambda }_J$ and unstable if $\lambda >{\lambda }_J$. In the TF limit $\hslash \to 0$, we recover the classical Jeans wavenumber (Jeans, 1902)

$k_J^2=\frac{4\pi G\rho }{c_s^2}.(101)$

In the noninteracting limit $c_s^2=0$, we obtain the quantum Jeans wavenumber (Khlopov et al., 1985)

$k_J^2={\left(\frac{16\pi G\rho m^2}{{\hslash }^2}\right)}^{1/2}.(102)$

For a repulsive self-interaction $(c_s^2>0)$, the maximum growth rate of the instability ${\gamma }_{\text{max}}={(4\pi G\rho )}^{1/2}$ is obtained for $k\to 0$ (infinitely long wavelengths). For an attractive self-interaction $(c_s^2<0)$, the system can be unstable even in the absence of self-gravity $(G=0)$.⁴⁶ This is a purely hydrodynamic instability, also called tachyonic instability for an SF. The critical wavenumber of the instability is (Chavanis, 2011c)

$k_J^2=\frac{4m^2|c_s^2|}{{\hslash }^2}.(103)$

The maximum growth rate of the instability ${\gamma }_{\text{max}}=m|c_s^2|/\hslash$ is obtained for a wave number $k_m^2=k_J^2/2$. The effect of self-gravity is considered in Chavanis (2011c) (see also Figure 14).

From the Jeans length ${\lambda }_J$, one can define a Jeans mass $M_J\sim \rho {\lambda }_J^3$. The Jeans scales $M_J$ and ${\lambda }_J$ determine the typical mass and size of the clusters that are unstable in the linear regime. These unstable clusters undergo a process of violent relaxation in the nonlinear regime and evolve into BECDM halos. In Chavanis (2021a), we showed that the Jeans mass–radius relation $M_J({\lambda }_J)$ of a self-gravitating BEC parameterized by the mean density $\rho$ of the universe in the linear regime of structure formation is similar to the mass–radius relation $M(R)$ of the quantum core (soliton) of BECDM halos parameterized by the central density ${\rho }_0$ in the nonlinear regime of structure formation (compare Figures 7, 9 in Chavanis (2021a) with Figures 2, 3 in Chavanis (2011c)). Following the Jeans mass–radius relation $M_J({\lambda }_J)$ along the sequence of decreasing density $\rho$ (see Figures 7, 9 in Chavanis (2021a)) amounts to taking into account the expansion of the universe. Following the mass–radius relation $M(R)$ of BECDM halos along the sequence of increasing central density ${\rho }_0$ (see Figures 2, 3 in Chavanis (2011c)) amounts to following their “collisional” evolution in the secular regime. Similar results are obtained for self-gravitating fermions (Suárez and Chavanis, 2018).

Remark: The study of the Jeans instability for a self-gravitating BEC has been extended in general relativity in Suárez and Chavanis (2018) by using a hydrodynamic representation of the KGE equations in the weak gravity limit. The case of a dissipative self-gravitating BEC has been considered in Chavanis (2017b), Chavanis (2020b), and Ourabah (2020). The effect of a rotation and a magnetic field is discussed in Appendix 5.

8.2 Cosmological evolution of a BECDM universe

The cosmological evolution of a spatially homogeneous complex SF with a self-interaction potential $V(|\phi {|}^2)$, possibly describing a self-gravitating BEC, has been studied by Li et al. (2014) and Suárez and Chavanis (2017), by using a general relativistic treatment. In the fast oscillation regime $\omega \gg H$, where $\omega$ is the pulsation of the SF and $H$ the Hubble constant, the equation of state $P(ϵ)$ of the SF is given in parametric form by (Suárez and Chavanis, 2017)

$ϵ=\rho c^2+V\left(\rho \right)+\rho V^{\prime }\left(\rho \right),(104)$

$P=\rho V^{\prime }\left(\rho \right)-V\left(\rho \right),(105)$

where $\rho =\frac{m^2}{{\hslash }^2}|\phi {|}^2=|\psi {|}^2$ is the pseudo rest-mass density of the BEC. These equations can also be obtained in the TF approximation [see Sec. II.D of Suárez and Chavanis (2017), Section 3.3 of Chavanis (2022c), and Appendix B.3 of Chavanis (2023c)]. In that case, they apply both to a spatially homogeneous SF (cosmological background) and to a spatially inhomogeneous SF (boson star). For a $|\phi {|}^4$ self-interaction, using Equations 10, 104, 105, one obtains the equation of state from Equation 49. The pseudo rest-mass density $\rho$ is related to the scale factor $a$ by (Suárez and Chavanis, 2017)

$\rho \sqrt{1+\frac{2}{c^2}{V}^{\prime }\left(\rho \right)}={\rho }_m=\frac{Qm}{a^3},(106)$

where $Q$ is the charge of the complex SF, which is a conserved quantity (${\rho }_m=nm$ is the rest-mass density). This relation is a consequence of “spintessence” (Boyle et al., 2002). Using Equations 104–106, one can obtain the evolution of the energy density $ϵ(a)$ and pressure $P(a)$ in parametric form with parameter $\rho$. When there is no self-interaction or when the self-interaction is weakly repulsive, the SF undergoes a stiff matter era (in the slow oscillation regime of “kination”),⁴⁷ followed by a pressureless DM era. When the self-interaction is strongly repulsive, the SF undergoes a stiff matter era, followed by a radiation-like era due to its self-interaction, and then by a pressureless DM era. The transition between the weakly self-interacting regime and the strongly self-interacting regime depends on how the scattering length of the bosons $a_s$ compares with their effective Schwarzschild radius $r_S=2Gm/c^2$. The dynamical phase diagram of an SF with a repulsive quartic self-interaction is represented in Figure 15. When the self-interaction is attractive, the evolution of the SF is peculiar (Suárez and Chavanis, 2017; Carvente et al., 2021).

Figure 15

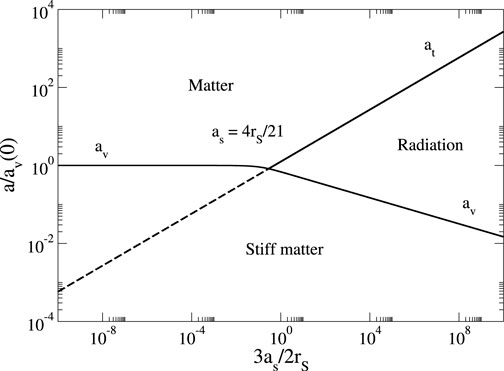
Figure 15. Phase diagram of a BEC universe showing the different eras of the SF during the evolution of the universe as a function of the scattering length of the bosons in the case of a repulsive self-interaction.

Remark: The study of the cosmological evolution of a relativistic SF with a $|\phi {|}^4$ potential (Li et al., 2014; Suárez and Chavanis, 2017) has been extended in Chavanis (2022b), Chavanis (2022e) to arbitrary power-law and logarithmic self-interaction potentials associated with isothermal, polytropic, and logotropic equations of state. As discussed in detail in Chavanis (2022c), we must distinguish between the equation of state $P(\rho )$ and the equation of state $P(ϵ)$. For example, for a power-law potential of the form $V(\rho )=\frac{K}{\gamma -1}{\rho }^{\gamma }$, corresponding to the polytropic equation of state $P(\rho )=K{\rho }^{\gamma }$, we obtain an equation of state $P(ϵ)$ given in the reversed form by (Suárez and Chavanis, 2017; Chavanis, 2022b; Chavanis, 2022c)

$ϵ={\left(\frac{P}{K}\right)}^{1/\gamma }{c}^2+\frac{\gamma +1}{\gamma -1}P.(107)$

For $\gamma =2$ and $K=2\pi a_s{\hslash }^2/m^3$, we recover Equation 49. Other examples are given in Chavanis (2022b), Chavanis (2022e), and Chavanis (2022c).

8.3 Growth of perturbations in an expanding universe filled with BECDM

The growth of perturbations in an expanding universe filled with BECDM has been studied in Chavanis (2012b). The expansion of the universe avoids the Jeans swindle (Peebles, 1980). In Chavanis (2012b), we focused on the matter era where the evolution of the universe is described by the Einstein-de Sitter (EdS) solution, and we used a nonrelativistic approach.⁴⁸ We generalized the classical Bonnor (1957) study to a BEC universe by taking into account the quantum potential arising from the Heisenberg uncertainty principle and the pressure due to the self-interaction of the bosons.

The GPP equations in an expanding universe read (Chavanis, 2012b; Suárez and Chavanis, 2015a; Chavanis, 2020b; Chavanis, 2021a)

$i\hslash \frac{\partial \mathrm{\Psi }}{\partial t}+\frac{3}{2}i\hslash H\mathrm{\Psi }=-\frac{{\hslash }^2}{2m{a}^2}\mathrm{\Delta }\mathrm{\Psi }+m\frac{dV}{d|\mathrm{\Psi }{|}^2}\mathrm{\Psi }+m\varphi \mathrm{\Psi },(108)$

$\frac{\mathrm{\Delta }\varphi }{4\pi G{a}^2}=|\mathrm{\Psi }{|}^2-\frac{3H^2}{8\pi G},(109)$

where $H=\dot{a}/a$ is the Hubble parameter, $a$ is the scale factor, and ${\rho }_b=3H^2/8\pi G$ is the background density of the universe. The associated quantum Euler–Poisson equations are given by (Chavanis, 2012b; Suárez and Chavanis, 2015a; Chavanis, 2020b; Chavanis, 2021a)

$\frac{\partial \rho }{\partial t}+3H\rho +\frac{1}{a}\nabla \cdot \left(\rho \mathbf{v}\right)=0,(110)$

$\frac{\partial \mathrm{\Sigma }}{\partial t}+\frac{{\left(\nabla \mathrm{\Sigma }\right)}^2}{2m{a}^2}+m\varphi +m{V}^{\prime }\left(\rho \right)+Q=0,(111)$

$\frac{\partial \mathbf{v}}{\partial t}+\frac{1}{a}\left(\mathbf{v}\cdot \nabla \right)\mathbf{v}+H\mathbf{v}=-\frac{1}{\rho a}\nabla P-\frac{1}{a}\nabla \varphi -\frac{1}{ma}\nabla Q,(112)$

$\mathrm{\Delta }\varphi =4\pi G{a}^2\left(\rho -{\rho }_b\right),(113)$

with the quantum potential

$Q=-\frac{{\hslash }^2}{2m{a}^2}\frac{\mathrm{\Delta }\sqrt{\rho }}{\sqrt{\rho }}=-\frac{{\hslash }^2}{4m{a}^2}\left[\frac{\mathrm{\Delta }\rho }{\rho }-\frac{1}{2}\frac{{\left(\nabla \rho \right)}^2}{{\rho }^2}\right].(114)$

The evolution of the homogeneous background ($\rho ={\rho }_b(t)$ and $\mathbf{v}=\mathbf{0}$) is determined by the EdS solution ${\rho }_b\propto a^{-3}$, $a\propto t^{2/3}$, $H=2/(3t)$, and ${\rho }_b=1/(6\pi G{t}^2)$.

In the linear regime of structure formation, we showed that the evolution of the Fourier transform of the density contrast ${\delta }_{\mathbf{k}}(t)=\delta {\rho }_{\mathbf{k}}/{\rho }_b$ is determined by (Chavanis, 2012b)

$\ddot{\delta }+2\frac{\dot{a}}{a}\dot{\delta }+\left(\frac{{\hslash }^2{k}^4}{4m^2{a}^4}+\frac{c_s^2{k}^2}{a^2}-4\pi G{\rho }_b\right)\delta =0.(115)$

This equation extends the classical Bonnor (1957) equation to a quantum (BEC) gas. It has been solved analytically in Chavanis (2012b) by considering just the effect of the quantum potential (noninteracting SF) or just the effect of a polytropic equation of state corresponding to a power-law self-interaction potential (TF limit).⁴⁹ In the noninteracting regime, the solutions of Equation 115 representing the damped mode (upper sign) and the growing mode (lower sign) are

$\delta \left(a\right)\propto \frac{1}{a^{1/4}}{J}_{\pm 5/2}\left(\sqrt{6}\frac{k^2}{{\kappa }_J^2}\frac{1}{a^{1/2}}\right)(116)$

with ${\kappa }_J={(16\pi G{\rho }_b{a}^3{m}^2/{\hslash }^2)}^{1/4}$ and $k_J={\kappa }_J{a}^{1/4}$. In the TF regime, for the standard BEC, we find

$\delta \left(a\right)\propto \frac{1}{a^{1/4}}{J}_{\pm 5/4}\left(\sqrt{\frac{3}{2}}\frac{k}{{\kappa }_J}\frac{1}{a}\right)(117)$

with ${\kappa }_J={(4\pi G{\rho }_b/c_s^2)}^{1/2}={(G{m}^3/a_s{\hslash }^2)}^{1/2}$ and $k_J={\kappa }_{J}a$. Equation 115 has also been solved numerically in Sec. VII of Suárez and Chavanis (2015a) with all the terms for the standard self-interacting BEC. All the possible regimes have been investigated depending on the strength of the self-interaction. An interesting typical evolution is shown in Figure 16. For a self-interacting SF, the density contrast first displays growing oscillations in the TF regime (they grow as $a^{1/4}\sim t^{1/6}$), then oscillates with a constant amplitude in the noninteracting regime, and finally grows as $a\sim t^{2/3}$ like pressureless DM (CDM model). The SF behaves like CDM at large scales $(\lambda \gg {\lambda }_J)$ and is stabilized by quantum mechanics or self-interaction at small scales $(\lambda \ll {\lambda }_J)$. This may solve the small-scale problems of the CDM model. The case of an attractive self-interaction has also been considered in Chavanis (2012b); Suárez and Chavanis (2015a). In that case, the density perturbation increases exponentially rapidly (instead of algebraically), and it is possible to neglect the expansion of the universe on this timescale of exponential growth, returning the results of Chavanis (2011c) in a static universe (see Section 8.1).

Figure 16

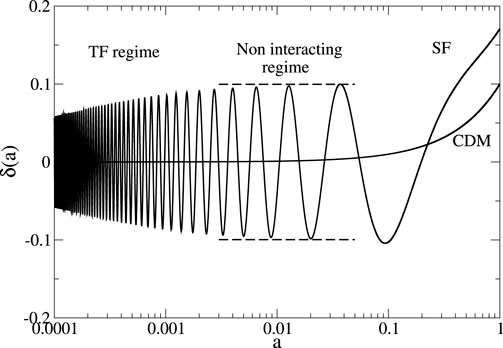
Figure 16. Evolution of the density contrast $\delta (a)$ of a self-interacting SF. The BEC is stable $(\lambda <{\lambda }_J(a))$ in the TF and noninteracting regimes and unstable $(\lambda >{\lambda }_J(a))$ in the CDM-like regime, where ${\lambda }_J(a)$ is the Jeans length.

Remark: The differential Equation 115 for the density contrast of a nonrelativistic BEC in an expanding universe originally derived in Chavanis (2012b) has been used in Marsh (2015), Marsh (2016), Fan (2016), Desjacques et al. (2018), Brax et al. (2019), Brax et al. (2020c), Mocz et al. (2023), Hwang and Noh (2022), Proukakis et al. (2024), Arakawa et al. (2024), and Guth et al. (2015). It has been extended to the context of general relativity in Suárez and Chavanis (2015a) by using the hydrodynamic representation of the KGE equations in the weak gravity regime.

9 Conclusion

In this paper, we have reviewed basic results on the BECDM model. We have discussed the core–envelope structure of BECDM halos and determined the core mass–radius relation, the halo mass–radius relation, and the core mass–halo mass relation. We have distinguished the violent (rapid) collisionless relaxation of BECDM halos through gravitational cooling and their secular (slow) collisional evolution induced by the formation of granules. We have explained how quantum mechanics may solve certain problems of the CDM model such as the core–cusp problem and the missing satellite problem. We have emphasized the importance of the maximum mass of dilute axion stars with attractive self-interactions (Chavanis, 2011c; Chavanis and Delfini, 2011) and its consequences.⁵⁰ We have also discussed basic results of BECDM cosmology.

Many interesting studies have been developed in relation to the BECDM model. Although we cannot discuss them in detail, we briefly list some of them (we apologize for the many other valuable works that we cannot mention). They include, for example, the effect of temperature on the formation of compact objects in self-gravitating BECs (Slepian and Goodman, 2012; Robles and Matos, 2013; Verma et al., 2021; Proukakis et al., 2023; Shukla et al., 2024b), models of pulsar glitches interpreted as rotating self-gravitating BECs with a crust (Verma et al., 2022; Shukla et al., 2024a), the infall of an SF onto a central black hole (Brax et al., 2020a; Brax et al., 2020b), angular momentum and vortex formation in BECDM halos (Rindler-Daller and Shapiro, 2012; Harko, 2019), the formation of scalar clumps (solitons) in the early universe (Amin and Mocz, 2019; Brax et al., 2020c), self-similar solutions for FDM (Galazo-García et al., 2022), dynamical friction in FDM (Lora et al., 2012; Berezhiani et al., 2019; Lancaster et al., 2020; Buehler and Desjacques, 2023; Glennon et al., 2024; Bar-Or et al., 2019; Chavanis, 2021b; Hui et al., 2017; Boudon et al., 2022; Boudon et al., 2023), and gravitational waves from binary black holes in a self-interacting scalar dark matter cloud (Boudon et al., 2024). Some works more specifically related to axion stars and their maximum mass (Chavanis, 2011c) include, for example, the detectability of accretion-induced bosenovae in the Milky Way (Arakawa et al., 2024; Eby et al., 2022; Maseizik et al., 2024), the detectability of axion stars via photon emission (Bai and Hamada, 2018; Hertzberg et al., 2020; Patkós, 2023) or by gravitational microlensing events (Fujikura et al., 2021; Chang et al., 2024; Yin and Visinelli, 2024), the signature in the Lyman-$\alpha$ forest (Desjacques et al., 2018), the possibility that the recently observed $2.6M_{\odot }$ compact object in the gravitational wave event GW190814 may be a bosonic DM admixed compact star (Lee et al., 2021), the possibility that planet 9 may be an axion star (Di and Shi, 2023), and the possibility that fast radio bursts may be generated by collapsing axion stars (Raby, 2016; Di, 2024; Di et al., 2024).

In this review, we have mainly focused on nonrelativistic self-gravitating BECs. There is of course a huge literature on boson stars in general relativity that we have just briefly mentioned. We refer to the introduction of our paper Chavanis (2023c) and to specific reviews on boson stars (Jetzer, 1992; Liddle and Madsen, 1992; Schunck and Mielke, 2003; Liebling and Palenzuela, 2017; Visinelli, 2021) for more details and references. It could also be interesting to further develop the analogies between BEC stars, superfluid stars, quark stars, and quark matter in neutron stars (Chavanis and Harko, 2012; Haghani and Harko, 2022; Sharma et al., 2022; Tangphati et al., 2024; Banerjee et al., 2025).

Author contributions

P-HC: writing – original draft and writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor TM declared a past co-authorship with the author.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The QCD axion is a pseudo-Nambu–Goldstone boson of the Peccei–Quinn phase transition associated with a $U(1)$ symmetry, which was proposed as a possible solution to the strong charge parity (CP) problem in quantum chromodynamics (QCD).

²The condensation occurs when the particles in the gas become correlated in a quantum mechanical manner, i.e., when the de Broglie thermal wavelength of a particle ${\lambda }_{\text{dB}}={({\hslash }^2/m{k}_{B}T)}^{1/2}$ turns out to be greater than the mean interparticle distance $l=n^{-1/3}$ (i.e., $n{\lambda }_{\text{dB}}^3>1$). In the nonrelativistic regime, the exact condensation temperature is given by $T_c=2\pi {\hslash }^2{n}^{2/3}/[m{k}_B\zeta {(3/2)}^{2/3}]$, where $\zeta (3/2)=2.612\dots$ is the value of the Riemann zeta function at $s=3/2$.

³These perturbations may come from quantum fluctuations produced during the inflation. In this sense, the universe is never exactly homogeneous. It is spatially homogeneous only in an average sense. We speak of the homogeneous background.

⁴Spherical DM halos are connected by filaments. This network pattern with a filamentary structure is similar to the initiation of a vasculature in biology (see Gamba et al. (2003), Chavanis and Sire (2007), Chavanis and Sire (2008) for the development of the analogy between gravity and chemotaxis).

⁵Fermionic DM halos have a similar core–envelope structure, except that the soliton is replaced by a “fermion ball” similar to a white dwarf or a neutron star (Chavanis, 2022g). This core–envelope structure, involving a fermion ball surrounded by an isothermal envelope, directly results from the Fermi–Dirac distribution function coupled to gravity. Because of its isothermal distribution function, fermionic DM is an example of WDM.

⁶A short history of the early development of quantum mechanics (Schrödinger, KG and Dirac wave equations) is given in the introductions of Chavanis and Matos (2017), Chavanis, In preparation.

⁷Actually, the Madelung hydrodynamic equations are not fully equivalent to the Schrödinger equation (Bialynicki-Birula and Bialynicka-Birula, 1971; Wallstrom, 1994). To achieve perfect equivalence, we must assume that $\mathbf{p}=m\mathbf{u}$ is equal to a gradient $\nabla S$. Furthermore, we must add by hand a quantization condition $\oint m\mathbf{u}\cdot d\mathbf{l}=nh$, where $n$ is an integer, as in the old Bohr–Sommerfeld quantum theory. This ensures that the wavefunction is single-valued (indeed $\psi \propto e^{iS/\hslash }$ with $S/\hslash =\theta =\mathrm{m}\mathrm{o}\mathrm{d}[2\pi ]$ implies $\oint \mathbf{p}\cdot d\mathbf{l}=\oint \nabla S\cdot d\mathbf{l}=\hslash \oint \nabla \theta \cdot d\mathbf{l}=2\pi n\hslash =nh$). Using the Stokes theorem, we obtain $\int (\nabla \times \mathbf{u})\cdot d\mathbf{S}=nh/m$. The vorticity $\nabla \times \mathbf{u}$ vanishes everywhere, except on certain singular points where it has $\delta$-type singularities. These arguments led Onsager (1949) and Feynman (1955), Feynman (1958) to conjecture that superfluids ${\text{like}}^4\mathrm{H}\mathrm{e}$ can sustain singular-point vortices with circulation quantized in units of $h/m$. The point vortices can group themselves to produce a macroscopic rotation of the BEC. These types of arguments (including the electromagnetic field) were also developed by Dirac (1931) in his theory of magnetic monopoles.

⁸This relation, which can be rewritten as $V(\rho )/\rho =-{\int }^{\rho }P({\rho }^{\prime })d(1/\rho )$, is equivalent to the first principle of thermodynamics $d(u/\rho )=-Pd(1/\rho )$ for a barotropic gas at $T=0$, where $V(\rho )$ plays the role of the density of internal energy $u$ [see Appendix H in Chavanis (2021a)].

⁹The Madelung and the de Broglie hydrodynamic equations (which aim at a causal interpretation of quantum mechanics) were much criticized by the founders of quantum mechanics, notably by Pauli, because their interpretation is not clear in the case of a single particle like an electron. However, they take more sense in the case of BECs with many bosons $(N\gg 1)$ in the same quantum state that form a quantum fluid (see Chavanis and Matos (2017), for discussions and references). They are now commonly adopted by the BEC community.

¹⁰The density profile of the soliton can also be obtained by directly solving the GPP equations for the wavefunction (Guzmán and Ureña-López, 2006).

¹¹In a recent paper, Indjin et al. (2024) have refined this variational approach by using an ansatz for the wavefunction that depends on the self-interaction parameter $g$. See also the paper by Eby et al. (2018a) who compared different ansätze. The form of the mass–radius relation can be determined from a general $f$-ansatz (Chavanis, 2021a; Chavanis, 2023c).

¹²We stress the very small value of ${\lambda }_t=252{(M_P/M)}^2=3.02\times 10^{-90}$ (Chavanis and Delfini, 2011). This shows the relevance of the TF approximation which is valid as soon as $\lambda \gg 10^{-90}$.

¹³In a very interesting paper, Delgado and Muñoz Mateo (2023) determined the core mass and core radius of several DM-dominated halos by fitting their rotation curves with the velocity profile from Equation A8 and located them on the $M(R)$ curve of Figure 2 (see their Figure 4). They found that the observational data fall either deep in the TF regime (constant core radius) or just at the transition between the TF regime and the noninteracting regime. They extracted the values $m\simeq 2.2\times 10^{-22}\mathrm{e}\mathrm{V}/{\mathrm{c}}^{\mathrm{2}}$ and $a_s\simeq 7.8\times 10^{-77}\mathrm{m}$ for the mass and scattering length of the DM particle, respectively. These values are close to the transition scales $m_t=2.92\times 10^{-22}\mathrm{e}\mathrm{V}/c^2$ and ${(a_s)}_t=8.13\times 10^{-62}\mathrm{f}\mathrm{m}$ (see above) corresponding to the BECt model of Chavanis (2021a).

¹⁴Dilute axion stars can be described by the nonrelativistic GPP equations with an attractive $|\psi {|}^4$ potential. The case of dense axion stars is discussed in Section 4.4.

¹⁵The noninteracting limit corresponds to $R\gg R_{99}*$, and the nongravitational limit corresponds to $R\ll R_{99}*$. In the nongravitational limit, a BEC with an attractive self-interaction is always unstable.

¹⁶A detailed exposition of the Poincaré theory of linear series of equilibria is given in Appendix C.2 of Alberti and Chavanis (2020b).

¹⁷The detailed expression of the lifetime of dilute axion stars could be useful in order to interpret future laboratory experiments of self-gravitating BECs with an effective gravity. In that case, the number $N$ of bosons will be relatively small, and the fluctuations will be important.

¹⁸Recall that the KGE and GPP equations have sometimes been used in the context of particle physics (independently from the context of boson stars) in order to describe classically extended particles consisting, e.g., of confined quarks with an effective gravity accounting for strong interactions (see the introduction of Chavanis (2023c)).

¹⁹The maximum mass can be smaller if $f$ is smaller. For example, taking $f\sim 10^{14}\mathrm{G}\mathrm{e}\mathrm{V}$ (Mocz et al., 2023) or $f\sim 10^{15}\mathrm{G}\mathrm{e}\mathrm{V}$ (Painter et al., 2024), one gets $M_{\text{max}}^{\text{NR}}=3.78\times 10^7{M}_{\odot }$ and $M_{\text{max}}^{\text{NR}}=3.78\times 10^8{M}_{\odot }$, respectively. However, small values of $f$ may be in tension with the constraint $10^{16}\mathrm{G}\mathrm{e}\mathrm{V}\le f\le 10^{18}\mathrm{G}\mathrm{e}\mathrm{V}$ expected in particle physics ($f$ is bounded above by the reduced Planck mass and below by the grand unified scale of particle physics) (Hui et al., 2017).

²⁰An axion star may grow overcritical $(M>M_{\text{max}}^{\text{NR}})$ through accretion or through a succession of collisions and mergers with astrophysical sources (other axion stars, ordinary stars, neutron stars…) (Raby, 2016; Eby et al., 2017; Eby et al., 2018b). We use here the word axion “star” in a loose sense. It could also refer to the quantum core of DM halos. A more general term could be “axion ball” or “boson ball.”

²¹Visinelli et al. (2018) and Eby et al. (2019b), Eby et al. (2019a) argue that relativistic effects are crucial on the branch of dense axion stars, while self-gravity is negligible. As a result, dense axion stars correspond to “pseudobreathers” or “oscillons,” which are described by the sine-Gordon equation. For a real SF, these objects are known to be unstable and to decay via emission of relativistic axions on a timescale much shorter than any cosmological timescale. This conclusion is, however, contested by Braaten and Zhang (2019). On the other hand, dense axion stars may be stable in the relativistic regime if they are made of a complex SF. In that case, they are called “axion boson stars” (Guerra et al., 2019).

²²These results were first obtained qualitatively in Tkachev (1986).

²³It is also similar to the caloric curve of self-gravitating isothermal spheres (see Figure 3 in Chavanis (2023d)).

²⁴We have neglected degenerate effects in the sense of Lynden–Bell. More general kinetic equations are the fermionic Wigner–Kramers equation and the fermionic Wigner–Landau equation (see Chavanis (2022a) for details).

²⁵The Kramers equation and the damped Euler equations satisfy a form of $H$-theorem for the Lynden–Bell entropy (Chavanis et al., 1996; Chavanis, 2022a).

²⁶The density profile of the self-gravitating isothermal sphere decreases at large distances as $\rho \sim r^{-2}$ (Chandrasekhar, 1957), leading to a constant circular velocity: $v_c(r)=\sqrt{GM(r)/r}\to \mathrm{c}\mathrm{s}\mathrm{t}$. Many authors consider that the envelope of BECDM halos is described by the NFW profile, like for CDM halos, with a density decreasing as $r^{-3}$ at large distances. However, this profile has no theoretical justification. By contrast, an isothermal distribution is justified by statistical mechanics as being the most probable equilibrium state. There are results from numerical simulations of the SP equations tending to corroborate the fact that the envelope of BECDM halos is isothermal. For example, Veltmaat et al. (2018) find that the velocity distribution in the envelope is Maxwellian. For virialized spherical halos, according to the Jeans theorem (Binney and Tremaine, 1987), this implies that the envelope is isothermal, being described by the Boltzmann distribution from Equation 60. On the other hand, Mocz et al. (2018) find that the density of BECDM halos decreases at large distances as $r^{-2}$, which is characteristic of an isothermal distribution.

²⁷The recent results of Gaia DR3 (Jiao et al., 2023) indicate that the rotation curve of the Milky Way decreases more rapidly than previously thought. In the framework of the King model (Chavanis et al., 2015a), this suggests that the halo is more “polytropic” than “isothermal” (see Figs. 21 and 27 in Chavanis et al. (2015a)) in the sense that it is strongly concentrated (see Krut et al. (2025) for fermionic DM halos). It has been suggested (Chavanis et al., 2015a; Chavanis et al., 2015b; Simon-Petit et al., 2019) that the virialized state resulting from violent relaxation could correspond to Hénon’s isochrone profile with a $r^{-4}$ density decay (Henon, 1959).

²⁸We have written here the refined Eddington relation obtained in Chavanis (2019c), Chavanis (2022f), Chavanis (2024b), and Chavanis (2024c). This relation provides a remarkable agreement with the observations and solves the cosmological constant problem.

²⁹The equation of state (Equation 72) and the corresponding generalized Lane–Emden equation introduced in Chavanis (2019d), Chavanis (2022a) have been used in Dawoodbhoy et al. (2021), Shapiro et al. (2022), Pils and Rindler-Daller (2022), and Foidl et al. (2023) to approximate their accurately simulated halo profiles (see also Korshynska et al. (2023)). Their studies confirm that an isothermal equation of state correctly describes the envelope of BECDM halos.

³⁰We call it the Lynden–Bell entropy (for the coarse-grained distribution function $\bar{f}$) instead of the Boltzmann entropy (for the fine-grained distribution function $f$) because, in the present context, the equilibrium state of a DM halo results from a process of collisionless violent relaxation, not a process of collisional relaxation (Chavanis, 2022d).

³¹A short history of the statistical mechanics of self-gravitating systems is given in the introductions of Alberti and Chavanis (2020a), Alberti and Chavanis (2020b), and Chavanis (2020e).

³²Equation 75 with ${\rho }_0=\rho (0)$ is valid only for the minimum halo (see Equation 1) which is a pure soliton without envelope.

³³Similarly, for fermionic DM halos, using the mass–radius relation from Equation 89, we find ${\mathrm{\Sigma }}_0\sim M/R^2\sim M^{5/3}$ (Chavanis, 2022g).

³⁴This relation was empirically introduced in Mocz et al. (2017), Bar et al. (2018) without rigorous justification. In Chavanis (2019d), Chavanis (2019a), we provided a thermodynamical justification. We determined the actual core mass $M_c$ of a BECDM halo by maximizing the Lynden–Bell entropy $S(M_c)$ at fixed total mass and total energy and showed that it satisfies the velocity dispersion tracing relation from Equation 79.

³⁵The numerical values in this expression rely on the Gaussian ansatz. As a result, the values of the parameters obtained below slightly differ from the “exact” values given in the previous sections.

³⁶Of course, there is always the possibility that the quantum core grows by accretion and reaches the maximum mass (see the conclusion for references on this topic).

³⁷Note that the maximum of the core mass–halo mass relation $M_c(M_h)$ differs from the critical mass $M_{\text{max}}^{\text{NR}}$ when the DM halo contains a central black hole (Chavanis, 2020a).

³⁸Conversely, the values of the DM particle mass computed in the present section lead to a minimum halo of mass ${(M_h)}_{\text{min}}\sim 1M_{\odot }$ and radius ${(r_h)}_{\text{min}}\sim 0.05\mathrm{p}\mathrm{c}$ (Chavanis, 2019d; Chavanis, 2022g) much smaller than the mass of the halos observed in the Universe (see Equation 1). Therefore, this scenario cannot apparently solve the missing satellite problem.

³⁹These comments also apply to fermionic DM (Chavanis, 2022g) for which gravitational encounters are completely negligible (Bose enhancement which increases the effective mass of the particles is replaced by Pauli blocking, which reduces the effective mass of the particles and increases the gravitational relaxation time (Chavanis, 2021b)).

⁴⁰The Burkert profile is similar to the NFW profile (Navarro et al., 1996) at large distances, but it presents a central core instead of a $r^{-1}$ cusp when $r\to 0$ in agreement with the observations.

⁴¹In the second case, we need to assume the presence of a primordial central SMBH to account for the observations.

⁴²This scenario assumes that fermionic DM is self-interacting so as to justify its secular evolution. These ideas also apply to other models of SIDM and WDM. Indeed, fermionic DM, SIDM, and WDM halos present an isothermal core and may experience a gravothermal catastrophe. For not too massive DM halos, the collapse of the core is stopped by quantum mechanics (Pauli’s exclusion principle) or by the repulsive self-interaction of the particles. For massive DM halos, core collapse leads to the formation of an SMBH as proposed in Balberg et al. (2002) and further discussed in Chavanis et al. (2015a), Chavanis et al. (2015b), Chavanis (2020e), Chavanis and Alberti (2020), Alberti and Chavanis (2020b), Chavanis (2023d), and Chavanis (2022g) (see in particular Sec. XIII.D of Chavanis (2022g)).

⁴³A short history of the Jeans instability is given in the introductions of Chavanis (2012a), Suárez and Chavanis (2018).

⁴⁴WDM also implies a nonzero Jeans length due to the velocity dispersion of the particles.

⁴⁵This is essentially a toy model, useful in a first approach, because it turns out that one can never neglect the expansion of the universe when studying the growth of structures in cosmology (see Suárez and Chavanis (2018) for details). Therefore, the study of Section 8.3 is more relevant.

⁴⁶For a repulsive self-interaction $(c_s^2>0)$, the system is always stable in the absence of self-gravity $(G=0)$.

⁴⁷A cosmology with a stiff matter era has been developed in Chavanis (2015a) at a general level (not necessarily connected to BECs). New analytical solutions of the Friedmann equations have been obtained for a Universe undergoing a stiff matter era, a DM era, and a DE era due to the cosmological constant.

⁴⁸See the introductions of (Chavanis, 2013; Chavanis, 2014) for a short history of the early development of modern cosmology.

⁴⁹These results can be applied to the standard BEC described by the quadratic equation of state from Equation 22 in the TF limit. They can also be applied to fermions described by the polytropic equation of state from Equation 87.

⁵⁰In a sense, the maximum mass of dilute axion stars (Chavanis, 2023b) is the counterpart of the Chandrasekhar mass of white dwarfs (Chandrasekhar, 1931) or the Oppenheimer–Volkoff mass of neutron stars (Oppenheimer and Volkoff, 1939), but it has a nonrelativistic origin.

⁵¹For a Gaussian density profile, the relation between the radius $R$ and the radius $R_{99}$ containing $99\%$ of the mass is $R_{99}=\mu R$ with $\mu =2.38167$ (Chavanis, 2011c).

References

Ade, P. A. R., Aghanim, N., Armitage-Caplan, C., Arnaud, M., Ashdown, M., Atrio-Barandela, F., et al. (2014). Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 571, A16. doi:10.1051/0004-6361/201321591

CrossRef Full Text | Google Scholar

Ade, P. A. R., Aghanim, N., Arnaud, M., Ashdown, M., Aumont, J., Baccigalupi, C., et al. (2016). Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594, A13. doi:10.1051/0004-6361/201525830

CrossRef Full Text | Google Scholar

Alberti, G., and Chavanis, P.-H. (2020a). Caloric curves of classical self-gravitating systems in general relativity. Phys. Rev. E 101, 052105. doi:10.1103/PhysRevE.101.052105

PubMed Abstract | CrossRef Full Text | Google Scholar

Alberti, G., and Chavanis, P.-H. (2020b). Caloric curves of self-gravitating fermions in general relativity. Eur. Phys. J. B 93, 208. doi:10.1140/epjb/e2020-100557-6

CrossRef Full Text | Google Scholar

Alcubierre, M., Becerril, R., Guzmán, F. S., Matos, T., Núñez, D., and Ureña-López, L. A. (2003). Numerical studies of Φ²-oscillatons. Class. Quantum Gravity 20, 2883–2903. doi:10.1088/0264-9381/20/13/332

CrossRef Full Text | Google Scholar

Álvarez-Rios, I., Bernal, T., Chavanis, P.-H., and Guzmán, F. S. (2024). Galactic rotation curves of low surface brightness galaxies using core-halo fuzzy dark matter configurations. Phys. Rev. D. 110, 063502. doi:10.1103/PhysRevD.110.063502

CrossRef Full Text | Google Scholar

Amin, M. A., and Mocz, P. (2019). Formation, gravitational clustering, and interactions of nonrelativistic solitons in an expanding universe. Phys. Rev. D. 100, 063507. doi:10.1103/PhysRevD.100.063507

CrossRef Full Text | Google Scholar

Arakawa, J., Eby, J., Safronova, M. S., Takhistov, V., and Zaheer, M. H. (2024). Detection of bosenovae with quantum sensors on Earth and in space. Phys. Rev. D. 110, 075007. doi:10.1103/PhysRevD.110.075007

CrossRef Full Text | Google Scholar

Arbey, A., Lesgourgues, J., and Salati, P. (2001). Quintessential halos around galaxies. Phys. Rev. D. 64, 123528. doi:10.1103/PhysRevD.64.123528

CrossRef Full Text | Google Scholar

Arbey, A., Lesgourgues, J., and Salati, P. (2003). Galactic halos of fluid dark matter. Phys. Rev. D. 68, 023511. doi:10.1103/PhysRevD.68.023511

CrossRef Full Text | Google Scholar

Argüelles, C. R., Díaz, M. I., Krut, A., and Yunis, R. (2021). On the formation and stability of fermionic dark matter haloes in a cosmological framework. Mon. Not. R. Astron. Soc. 502, 4227–4246. doi:10.1093/mnras/staa3986

CrossRef Full Text | Google Scholar

Argüelles, C. R., Becerra-Vergara, E. A., Rueda, J. A., and Ruffini, R. (2023). Fermionic dark matter: physics, astrophysics, and cosmology. Universe 9, 197. doi:10.3390/universe9040197

CrossRef Full Text | Google Scholar

Bai, Y., and Hamada, Y. (2018). Detecting axion stars with radio telescopes. Phys. Lett. B 781, 187–194. doi:10.1016/j.physletb.2018.03.070

CrossRef Full Text | Google Scholar

Balberg, S., Shapiro, S. L., and Inagaki, S. (2002). Self-interacting dark matter halos and the gravothermal catastrophe. Astrophys. J. 568, 475–487. doi:10.1086/339038

CrossRef Full Text | Google Scholar

Baldeschi, M. R., Gelmini, G. B., and Ruffini, R. (1983). On massive fermions and bosons in galactic halos. Phys. Lett. B 122, 221–224. doi:10.1016/0370-2693(83)90688-3

CrossRef Full Text | Google Scholar

Bañados, M., and Ferreira, P. G. (2010). Eddington’s theory of gravity and its progeny. Phys. Rev. Lett. 105, 011101. doi:10.1103/PhysRevLett.105.011101

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, A., Pradhan, A., Sakallı, İ., and Dixit, A. (2025). Properties of interacting quark star in light of Rastall gravity. Class. Quantum Gravity 42, 025008. doi:10.1088/1361-6382/ad9c0f

CrossRef Full Text | Google Scholar

Bar, N., Blas, D., Blum, K., and Sibiryakov, S. (2018). Galactic rotation curves versus ultralight dark matter: implications of the soliton-host halo relation. Phys. Rev. D. 98, 083027. doi:10.1103/PhysRevD.98.083027

CrossRef Full Text | Google Scholar

Bar-Or, B., Fouvry, J.-B., and Tremaine, S. (2019). Relaxation in a fuzzy dark matter halo. Astrophys. J. 871, 28. doi:10.3847/1538-4357/aaf28c

CrossRef Full Text | Google Scholar

Bar-Or, B., Fouvry, J.-B., and Tremaine, S. (2021). Relaxation in a fuzzy dark matter halo. II. Self-Consistent kinetic equations. Astrophys. J. 915, 27. doi:10.3847/1538-4357/abfb66

CrossRef Full Text | Google Scholar

Berezhiani, L., Elder, B., and Khoury, J. (2019). Dynamical friction in superfluids. J. Cosmol. Astropart. Phys. 2019, 074. doi:10.1088/1475-7516/2019/10/074

CrossRef Full Text | Google Scholar

Berezhiani, L., Cintia, G., and Khoury, J. (2023). Thermalization, fragmentation, and tidal disruption: the complex galactic dynamics of dark matter superfluidity. Phys. Rev. D. 107, 123010. doi:10.1103/PhysRevD.107.123010

CrossRef Full Text | Google Scholar

Bialynicki-Birula, I., and Bialynicka-Birula, Z. (1971). Magnetic monopoles in the hydrodynamic formulation of quantum mechanics. Phys. Rev. D. 3, 2410–2412. doi:10.1103/PhysRevD.3.2410

CrossRef Full Text | Google Scholar

Bianchi, M., Grasso, D., and Ruffini, R. (1990). Jeans mass of a cosmological coherent scalar field. Astron. Astrophys. 231, 301–308.

Google Scholar

Bilic, N., Tupper, G. B., and Viollier, R. D. (2003). “Dark matter in the galaxy,” in Particle physics in the new millennium. Editors J. Trampeti, and J. Wess, 616, 24–38. doi:10.1007/3-540-36539-7_2

CrossRef Full Text | Google Scholar

Binney, J., and Tremaine, S. (1987). Galactic dynamics.

Google Scholar

Bode, P., Ostriker, J. P., and Turok, N. (2001). Halo Formation in warm dark matter models. Astrophys. J. 556, 93–107. doi:10.1086/321541

CrossRef Full Text | Google Scholar

Bogoliubov, N. (1947). On the theory of superfluidity. J. Phys. 11, 23–32.

Google Scholar

Böhmer, C. G., and Harko, T. (2007). Can dark matter be a Bose Einstein condensate? J. Cosmol. Astropart. Phys. 2007, 025. doi:10.1088/1475-7516/2007/06/025

CrossRef Full Text | Google Scholar

Bonnor, W. B. (1957). Jeans’ formula for gravitational instability. Mon. Not. R. Astron. Soc. 117, 104–117. doi:10.1093/mnras/117.1.104

CrossRef Full Text | Google Scholar

Boudon, A., Brax, P., and Valageas, P. (2022). Subsonic accretion and dynamical friction for a black hole moving through a self-interacting scalar dark matter cloud. Phys. Rev. D. 106, 043507. doi:10.1103/PhysRevD.106.043507

CrossRef Full Text | Google Scholar

Boudon, A., Brax, P., and Valageas, P. (2023). Supersonic friction of a black hole traversing a self-interacting scalar dark matter cloud. Phys. Rev. D. 108, 103517. doi:10.1103/PhysRevD.108.103517

CrossRef Full Text | Google Scholar

Boudon, A., Brax, P., Valageas, P., and Wong, L. K. (2024). Gravitational waves from binary black holes in a self-interacting scalar dark matter cloud. Phys. Rev. D. 109, 043504. doi:10.1103/PhysRevD.109.043504

CrossRef Full Text | Google Scholar

Boyle, L. A., Caldwell, R. R., and Kamionkowski, M. (2002). Spintessence! New models for dark matter and dark energy. Phys. Lett. B 545, 17–22. doi:10.1016/S0370-2693(02)02590-X

CrossRef Full Text | Google Scholar

Braaten, E., and Zhang, H. (2019). Colloquium: the physics of axion stars. Rev. Mod. Phys. 91, 041002. doi:10.1103/RevModPhys.91.041002

CrossRef Full Text | Google Scholar

Braaten, E., Mohapatra, A., and Zhang, H. (2016). Dense axion stars. Phys. Rev. Lett. 117, 121801. doi:10.1103/PhysRevLett.117.121801

PubMed Abstract | CrossRef Full Text | Google Scholar

Brax, P., Valageas, P., and Cembranos, J. A. R. (2019). Impact of kinetic and potential self-interactions on scalar dark matter. Phys. Rev. D. 100, 023526. doi:10.1103/PhysRevD.100.023526

CrossRef Full Text | Google Scholar

Brax, P., Valageas, P., and Cembranos, J. A. R. (2020a). Fate of scalar dark matter solitons around supermassive galactic black holes. Phys. Rev. D. 101, 023521. doi:10.1103/PhysRevD.101.023521

CrossRef Full Text | Google Scholar

Brax, P., Valageas, P., and Cembranos, J. A. R. (2020b). K-essence scalar dark matter solitons around supermassive black holes. Phys. Rev. D. 101, 063510. doi:10.1103/PhysRevD.101.063510

CrossRef Full Text | Google Scholar

Brax, P., Valageas, P., and Cembranos, J. A. R. (2020c). Nonrelativistic formation of scalar clumps as a candidate for dark matter. Phys. Rev. D. 102, 083012. doi:10.1103/PhysRevD.102.083012

CrossRef Full Text | Google Scholar

Buehler, R., and Desjacques, V. (2023). Dynamical friction in fuzzy dark matter: circular orbits. Phys. Rev. D. 107, 023516. doi:10.1103/PhysRevD.107.023516

CrossRef Full Text | Google Scholar

Bullock, J. S., and Boylan-Kolchin, M. (2017). Small-scale challenges to the ΛCDM paradigm. Annu. Rev. Astron. Astrophys. 55, 343–387. doi:10.1146/annurev-astro-091916-055313

CrossRef Full Text | Google Scholar

Burkert, A. (1995). The structure of dark matter halos in dwarf galaxies. Astrophys. J. 447, L25–L28. doi:10.1086/309560

CrossRef Full Text | Google Scholar

Burkert, A. (2020). Fuzzy dark matter and dark matter halo cores. Astrophys. J. 904, 161. doi:10.3847/1538-4357/abb242

CrossRef Full Text | Google Scholar

Calogero, F. (1997). Cosmic origin of quantization. Phys. Lett. A 228, 335–346. doi:10.1016/S0375-9601(97)00107-2

CrossRef Full Text | Google Scholar

Carvente, B., Jaramillo, V., Escamilla-Rivera, C., and Núñez, D. (2021). Observational constraints on complex quintessence with attractive self-interaction. Mon. Not. R. Astron. Soc. 503, 4008–4015. doi:10.1093/mnras/stab650

CrossRef Full Text | Google Scholar

Chandrasekhar, S., and Fermi, E. (1953). Problems of gravitational stability in the presence of a magnetic field. Astrophys. J. 118, 116. doi:10.1086/145732

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1931). The maximum mass of ideal white dwarfs. Astrophys. J. 74, 81. doi:10.1086/143324

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1942). Principles of stellar dynamics.

Google Scholar

Chandrasekhar, S. (1954). The gravitational instability of an infinite homogeneous medium when Coriolis force is acting and a magnetic field is present. Astrophys. J. 119, 7. doi:10.1086/145790

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1955). The gravitational instability of an infinite homogeneous medium when a Coriolis acceleration is acting. Vistas Astronomy 1, 344–347. doi:10.1016/0083-6656(55)90045-3

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1957). An introduction to the study of stellar structure.

Google Scholar

Chang, J. H., Fox, P. J., and Xiao, H. (2024). Axion stars: mass functions and constraints. J. Cosmol. Astropart. Phys. 2024, 023. doi:10.1088/1475-7516/2024/08/023

CrossRef Full Text | Google Scholar

Chavanis, P.-H., and Alberti, G. (2020). Gravitational phase transitions and instabilities of self-gravitating fermions in general relativity. Phys. Lett. B 801, 135155. doi:10.1016/j.physletb.2019.135155

CrossRef Full Text | Google Scholar

Chavanis, P.-H., and Delfini, L. (2011). Mass-radius relation of Newtonian self-gravitating Bose-Einstein condensates with short-range interactions. II. Numerical results. Phys. Rev. D. 84, 043532. doi:10.1103/PhysRevD.84.043532

CrossRef Full Text | Google Scholar

Chavanis, P.-H., and Harko, T. (2012). Bose-Einstein condensate general relativistic stars. Phys. Rev. D. 86, 064011. doi:10.1103/PhysRevD.86.064011

CrossRef Full Text | Google Scholar

Chavanis, P.-H., and Kumar, S. (2017). Comparison between the Logotropic and ΛCDM models at the cosmological scale. J. Cosmol. Astropart. Phys. 2017, 018. doi:10.1088/1475-7516/2017/05/018

CrossRef Full Text | Google Scholar

Chavanis, P.-H., and Matos, T. (2017). Covariant theory of Bose-Einstein condensates in curved spacetimes with electromagnetic interactions: the hydrodynamic approach. Eur. Phys. J. Plus 132, 30. doi:10.1140/epjp/i2017-11292-4

CrossRef Full Text | Google Scholar

Chavanis, P.-H., and Sire, C. (2004). Anomalous diffusion and collapse of self-gravitating Langevin particles in D dimensions. Phys. Rev. E 69, 016116. doi:10.1103/PhysRevE.69.016116

PubMed Abstract | CrossRef Full Text | Google Scholar

Chavanis, P.-H., and Sire, C. (2007). Kinetic and hydrodynamic models of chemotactic aggregation. Phys. A Stat. Mech. its Appl. 384, 199–222. doi:10.1016/j.physa.2007.05.069

CrossRef Full Text | Google Scholar

Chavanis, P.-H., and Sire, C. (2008). Jeans type analysis of chemotactic collapse. Phys. A Stat. Mech. its Appl. 387, 4033–4052. doi:10.1016/j.physa.2008.02.025

CrossRef Full Text | Google Scholar

Chavanis, P. H., Sommeria, J., and Robert, R. (1996). Statistical mechanics of two-dimensional vortices and collisionless stellar systems. Astrophys. J. 471, 385–399. doi:10.1086/177977

CrossRef Full Text | Google Scholar

Chavanis, P.-H., Lemou, M., and Méhats, F. (2015a). Models of dark matter halos based on statistical mechanics: the classical King model. Phys. Rev. D. 91, 063531. doi:10.1103/PhysRevD.91.063531

CrossRef Full Text | Google Scholar

Chavanis, P.-H., Lemou, M., and Méhats, F. (2015b). Models of dark matter halos based on statistical mechanics: the fermionic King model. Phys. Rev. D. 92, 123527. doi:10.1103/PhysRevD.92.123527

CrossRef Full Text | Google Scholar

Chavanis, P.-H., Denet, B., Le Berre, M., and Pomeau, Y. (2019). Supernova implosion-explosion in the light of catastrophe theory. Eur. Phys. J. B 92, 271. doi:10.1140/epjb/e2019-100435-6

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (1998). On the “coarse-grained” evolution of collisionless stellar systems. Mon. Not. R. Astron. Soc. 300, 981–991. doi:10.1046/j.1365-8711.1998.01867.x

CrossRef Full Text | Google Scholar

Chavanis, P. H. (2002). Gravitational instability of finite isothermal spheres in general relativity. Analogy with neutron stars. Astron. Astrophys. 381, 709–730. doi:10.1051/0004-6361:20011424

CrossRef Full Text | Google Scholar

Chavanis, P. H. (2005). On the lifetime of metastable states in self-gravitating systems. Astron. Astrophys. 432, 117–138. doi:10.1051/0004-6361:20041114

CrossRef Full Text | Google Scholar

Chavanis, P. H. (2006). Phase transitions in self-gravitating systems. Int. J. Mod. Phys. B 20, 3113–3198. doi:10.1142/S0217979206035400

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2007). White dwarf stars in D dimensions. Phys. Rev. D. 76, 023004. doi:10.1103/PhysRevD.76.023004

CrossRef Full Text | Google Scholar

Chavanis, P. H. (2008). Relativistic stars with a linear equation of state: analogy with classical isothermal spheres and black holes. Astron. Astrophys. 483, 673–698. doi:10.1051/0004-6361:20078287

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2011a). BEC dark matter, Zeldovich approximation, and generalized Burgers equation. Phys. Rev. D. 84, 063518. doi:10.1103/PhysRevD.84.063518

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2011b). Instability of a uniformly collapsing cloud of classical and quantum self-gravitating Brownian particles. Phys. Rev. E 84, 031101. doi:10.1103/PhysRevE.84.031101

PubMed Abstract | CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2011c). Mass-radius relation of Newtonian self-gravitating Bose-Einstein condensates with short-range interactions. I. Analytical results. Phys. Rev. D. 84, 043531. doi:10.1103/PhysRevD.84.043531

CrossRef Full Text | Google Scholar

Chavanis, P. H. (2012a). Dynamical stability of infinite homogeneous self-gravitating systems and plasmas: application of the Nyquist method. Eur. Phys. J. B 85, 229. doi:10.1140/epjb/e2012-21012-9

CrossRef Full Text | Google Scholar

Chavanis, P. H. (2012b). Growth of perturbations in an expanding universe with Bose-Einstein condensate dark matter. Astron. Astrophys. 537, A127. doi:10.1051/0004-6361/201116905

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2013). “A simple model of universe describing the early inflation and the late accelerated expansion in a symmetric manner,” in IX Mexican school on gravitation and mathematical physics: cosmology for the XXIst century: gravitation and mathematical physics division of the Mexican physical society DGFM-SMF. Editors L. A. Ureña-López, R. Becerril-Bárcenas, and R. Linares-Romero, 75–115. doi:10.1063/1.4817032

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2014). Models of universe with a polytropic equation of state: I. The early universe. Eur. Phys. J. Plus 129, 38. doi:10.1140/epjp/i2014-14038-x

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2015a). Cosmology with a stiff matter era. Phys. Rev. D. 92, 103004. doi:10.1103/PhysRevD.92.103004

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2015b). Is the universe logotropic? Eur. Phys. J. Plus 130, 130. doi:10.1140/epjp/i2015-15130-5

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2015c). Partially relativistic self-gravitating Bose-Einstein condensates with a stiff equation of state. Eur. Phys. J. Plus 130, 181. doi:10.1140/epjp/i2015-15181-6

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2015d). “Self-gravitating Bose-Einstein condensates,” in Quantum aspects of black holes. Editor X. Calmet, 151–194. doi:10.1007/978-3-319-10852-0_6

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2016a). Collapse of a self-gravitating Bose-Einstein condensate with attractive self-interaction. Phys. Rev. D. 94, 083007. doi:10.1103/PhysRevD.94.083007

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2016b). The Logotropic Dark Fluid as a unification of dark matter and dark energy. Phys. Lett. B 758, 59–66. doi:10.1016/j.physletb.2016.04.042

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2017a). Derivation of a generalized Schrödinger equation from the theory of scale relativity. Eur. Phys. J. Plus 132, 286. doi:10.1140/epjp/i2017-11528-3

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2017b). Dissipative self-gravitating Bose-Einstein condensates with arbitrary nonlinearity as a model of dark matter halos. Eur. Phys. J. Plus 132, 248. doi:10.1140/epjp/i2017-11544-3

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2018a). Derivation of a generalized Schrödinger equation for dark matter halos from the theory of scale relativity. Phys. Dark Universe 22, 80–95. doi:10.1016/j.dark.2018.09.004

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2018b). Phase transitions between dilute and dense axion stars. Phys. Rev. D. 98, 023009. doi:10.1103/PhysRevD.98.023009

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2019a). Derivation of the core mass-halo mass relation of fermionic and bosonic dark matter halos from an effective thermodynamical model. Phys. Rev. D. 100, 123506. doi:10.1103/PhysRevD.100.123506

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2019b). Mass-radius relation of self-gravitating Bose-Einstein condensates with a central black hole. Eur. Phys. J. Plus 134, 352. doi:10.1140/epjp/i2019-12734-7

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2019c). New predictions from the logotropic model. Phys. Dark Universe 24, 100271. doi:10.1016/j.dark.2019.100271

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2019d). Predictive model of BEC dark matter halos with a solitonic core and an isothermal atmosphere. Phys. Rev. D. 100, 083022. doi:10.1103/PhysRevD.100.083022

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2020a). Core mass-halo mass relation of bosonic and fermionic dark matter halos harboring a supermassive black hole. Phys. Rev. D. 101, 063532. doi:10.1103/PhysRevD.101.063532

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2020b). Jeans instability of dissipative self-gravitating Bose–Einstein condensates with repulsive or attractive $|\phi {|}^4$ self-interaction: application to dark matter. Universe 6, 226. doi:10.3390/universe6120226

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2020c). Quantum tunneling rate of dilute axion stars close to the maximum mass. Phys. Rev. D. 102, 083531. doi:10.1103/PhysRevD.102.083531

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2020d). Statistical mechanics of self-gravitating systems in general relativity: I. The quantum Fermi gas. Eur. Phys. J. Plus 135, 290. doi:10.1140/epjp/s13360-020-00268-0

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2020e). Statistical mechanics of self-gravitating systems in general relativity: II. The classical Boltzmann gas. Eur. Phys. J. Plus 135, 310. doi:10.1140/epjp/s13360-020-00291-1

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2021a). Jeans mass-radius relation of self-gravitating Bose-Einstein condensates and typical parameters of the dark matter particle. Phys. Rev. D. 103, 123551. doi:10.1103/PhysRevD.103.123551

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2021b). Landau equation for self-gravitating classical and quantum particles: application to dark matter. Eur. Phys. J. Plus 136, 703. doi:10.1140/epjp/s13360-021-01617-3

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2022a). A heuristic wave equation parameterizing BEC dark matter halos with a quantum core and an isothermal atmosphere. Eur. Phys. J. B 95, 48. doi:10.1140/epjb/s10051-022-00299-9

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2022b). Cosmological models based on a complex scalar field with a power-law potential associated with a polytropic equation of state. Phys. Rev. D. 106, 043502. doi:10.1103/PhysRevD.106.043502

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2022c). K-essence Lagrangians of polytropic and logotropic unified dark matter and dark energy models. Astronomy 1, 126–221. doi:10.3390/astronomy1030011

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2022d). Kinetic theory of collisionless relaxation for systems with long-range interactions. Phys. A Stat. Mech. Appl. 606, 128089. doi:10.1016/j.physa.2022.128089

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2022e). New logotropic model based on a complex scalar field with a logarithmic potential. Phys. Rev. D. 106, 063525. doi:10.1103/PhysRevD.106.063525

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2022f). Predictions from the logotropic model: the universal surface density of dark matter halos and the present proportions of dark matter and dark energy. Phys. Dark Universe 37, 101098. doi:10.1016/j.dark.2022.101098

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2022g). Predictive model of fermionic dark matter halos with a quantum core and an isothermal atmosphere. Phys. Rev. D. 106, 043538. doi:10.1103/PhysRevD.106.043538

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2023a). Generalized equations in quantum mechanics and Brownian theory. Symmetry 15, 2195. doi:10.3390/sym15122195

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2023b). “The maximum mass of dilute axion stars,” in The sixteenth Marcel Grossmann meeting on recent developments in theoretical and experimental general relativity, astrophysics, and relativistic field theories. Editors R. Ruffini, and G. Vereshchagin, 2149–2173. doi:10.1142/9789811269776_0168

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2023c). Maximum mass of relativistic self-gravitating Bose-Einstein condensates with repulsive or attractive |φ| ⁴ self-interaction. Phys. Rev. D. 107, 103503. doi:10.1103/PhysRevD.107.103503

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2023d). “The self-gravitating Fermi gas in Newtonian gravity and general relativity,” in The sixteenth Marcel Grossmann meeting on recent developments in theoretical and experimental general relativity, astrophysics, and relativistic field theories. Editors R. Ruffini, and G. Vereshchagin, 2230–2251. doi:10.1142/9789811269776_0174

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2024a). On the connection between Nelson’s stochastic quantum mechanics and Nottale’s theory of scale relativity. Axioms 13, 606. doi:10.3390/axioms13090606

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2024b). A mass scale law connecting cosmophysics to microphysics. Phys. Dark Universe 44, 101420. doi:10.1016/j.dark.2024.101420

CrossRef Full Text | Google Scholar

Chavanis, P.-H. (2024c). A simple model of magnetic universe without singularity associated with a quadratic equation of state. Eur. Phys. J. Plus 139, 889. doi:10.1140/epjp/s13360-024-05617-x

CrossRef Full Text | Google Scholar

Chen, J., Du, X., Lentz, E. W., Marsh, D. J. E., and Niemeyer, J. C. (2021). New insights into the formation and growth of boson stars in dark matter halos. Phys. Rev. D. 104, 083022. doi:10.1103/PhysRevD.104.083022

CrossRef Full Text | Google Scholar

Chen, J., Du, X., Lentz, E. W., and Marsh, D. J. E. (2022). Relaxation times for Bose-Einstein condensation by self-interaction and gravity. Phys. Rev. D. 106, 023009. doi:10.1103/PhysRevD.106.023009

CrossRef Full Text | Google Scholar

Chiao, R. Y., Garmire, E., and Townes, C. H. (1964). Self-trapping of optical beams. Phys. Rev. Lett. 13, 479–482. doi:10.1103/PhysRevLett.13.479

CrossRef Full Text | Google Scholar

Colpi, M., Shapiro, S. L., and Wasserman, I. (1986). Boson stars: gravitational equilibria of self-interacting scalar fields. Phys. Rev. Lett. 57, 2485–2488. doi:10.1103/PhysRevLett.57.2485

PubMed Abstract | CrossRef Full Text | Google Scholar

Cotner, E. (2016). Collisional interactions between self-interacting nonrelativistic boson stars: effective potential analysis and numerical simulations. Phys. Rev. D. 94, 063503. doi:10.1103/PhysRevD.94.063503

CrossRef Full Text | Google Scholar

Davidson, S., and Schwetz, T. (2016). Rotating drops of axion dark matter. Phys. Rev. D. 93, 123509. doi:10.1103/PhysRevD.93.123509

CrossRef Full Text | Google Scholar

Davies, E. Y., and Mocz, P. (2020). Fuzzy dark matter soliton cores around supermassive black holes. Mon. Not. R. Astron. Soc. 492, 5721–5729. doi:10.1093/mnras/staa202

CrossRef Full Text | Google Scholar

Dawoodbhoy, T., Shapiro, P. R., and Rindler-Daller, T. (2021). Core-envelope haloes in scalar field dark matter with repulsive self-interaction: fluid dynamics beyond the de Broglie wavelength. Mon. Not. R. Astron. Soc. 506, 2418–2444. doi:10.1093/mnras/stab1859

CrossRef Full Text | Google Scholar

de Broglie, L. (1927a). Corpuscules et ondes. Compt. Rend. Acad. Sci. Paris 185, 1118.

Google Scholar

de Broglie, L. (1927b). La mécanique ondulatoire et la structure atomique de la matière et du rayonnement. J. de Physique le Radium 8, 225–241. doi:10.1051/jphysrad:0192700805022500

CrossRef Full Text | Google Scholar

de Broglie, L. (1927c). Sur le rôle des ondes continues Ψ en Mécanique ondulatoire. Compt. Rend. Acad. Sci. Paris 185, 380.

Google Scholar

de la Peña, L., Cetto, A. M., and Valdés Hernández, A. (2015). The emerging quantum: the physics behind quantum mechanics. doi:10.1007/978-3-319-07893-9

CrossRef Full Text | Google Scholar

Delgado, V., and Muñoz Mateo, A. (2023). Self-interacting superfluid dark matter droplets. Mon. Notices R. Astronomical Soc. 518, 4064–4072. doi:10.1093/mnras/stac3386

CrossRef Full Text | Google Scholar

Deng, H., Hertzberg, M. P., Namjoo, M. H., and Masoumi, A. (2018). Can light dark matter solve the core-cusp problem? Phys. Rev. D. 98, 023513. doi:10.1103/PhysRevD.98.023513

CrossRef Full Text | Google Scholar

Derrick, G. H. (1964). Comments on nonlinear wave equations as models for elementary particles. J. Math. Phys. 5, 1252–1254. doi:10.1063/1.1704233

CrossRef Full Text | Google Scholar

Desjacques, V., Kehagias, A., and Riotto, A. (2018). Impact of ultralight axion self-interactions on the large scale structure of the Universe. Phys. Rev. D. 97, 023529. doi:10.1103/PhysRevD.97.023529

CrossRef Full Text | Google Scholar

Destri, C., de Vega, H. J., and Sanchez, N. G. (2013). Fermionic warm dark matter produces galaxy cores in the observed scales because of quantum mechanics. New Astron. 22, 39–50. doi:10.1016/j.newast.2012.12.003

CrossRef Full Text | Google Scholar

Di, H., and Shi, H. (2023). Can planet 9 be an axion star? Phys. Rev. D. 108, 103038. doi:10.1103/PhysRevD.108.103038

CrossRef Full Text | Google Scholar

Di, H., Shao, L., Yi, Z., and Kong, S.-B. (2024). Novel standard candle: collapsing axion stars. Phys. Rev. D. 110, 103031. doi:10.1103/PhysRevD.110.103031

CrossRef Full Text | Google Scholar

Di, H. (2024). Stimulated decay of collapsing axion stars and fast radio bursts. Eur. Phys. J. C 84, 283. doi:10.1140/epjc/s10052-024-12654-4

CrossRef Full Text | Google Scholar

Dirac, P. A. M. (1931). Quantised singularities in the electromagnetic field. Proc. R. Soc. Lond. Ser. A 133, 60–72. doi:10.1098/rspa.1931.0130

CrossRef Full Text | Google Scholar

Donato, F., Gentile, G., Salucci, P., Frigerio Martins, C., Wilkinson, M. I., Gilmore, G., et al. (2009). A constant dark matter halo surface density in galaxies. Mon. Not. R. Astron. Soc. 397, 1169–1176. doi:10.1111/j.1365-2966.2009.15004.x

CrossRef Full Text | Google Scholar

Eby, J., Leembruggen, M., Suranyi, P., and Wijewardhana, L. C. R. (2016). Collapse of axion stars. J. High Energy Phys. 2016, 66. doi:10.1007/JHEP12(2016)066

CrossRef Full Text | Google Scholar

Eby, J., Leembruggen, M., Leeney, J., Suranyi, P., and Wijewardhana, L. C. R. (2017). Collisions of dark matter axion stars with astrophysical sources. J. High Energy Phys. 2017, 99. doi:10.1007/JHEP04(2017)099

CrossRef Full Text | Google Scholar

Eby, J., Leembruggen, M., Street, L., Suranyi, P., and Wijewardhana, L. C. R. (2018a). Approximation methods in the study of boson stars. Phys. Rev. D. 98, 123013. doi:10.1103/PhysRevD.98.123013

CrossRef Full Text | Google Scholar

Eby, J., Leembruggen, M., Suranyi, P., and Wijewardhana, L. C. R. (2018b). Stability of condensed fuzzy dark matter halos. J. Cosmol. Astropart. Phys. 2018, 058. doi:10.1088/1475-7516/2018/10/058

CrossRef Full Text | Google Scholar

Eby, J., Leembruggen, M., Street, L., Suranyi, P., and Wijewardhana, L. C. R. (2019a). Global view of QCD axion stars. Phys. Rev. D. 100, 063002. doi:10.1103/PhysRevD.100.063002

CrossRef Full Text | Google Scholar

Eby, J., Mukaida, K., Takimoto, M., Wijewardhana, L. C. R., and Yamada, M. (2019b). Classical nonrelativistic effective field theory and the role of gravitational interactions. Phys. Rev. D. 99, 123503. doi:10.1103/PhysRevD.99.123503

CrossRef Full Text | Google Scholar

Eby, J., Shirai, S., Stadnik, Y. V., and Takhistov, V. (2022). Probing relativistic axions from transient astrophysical sources. Phys. Lett. B 825, 136858. doi:10.1016/j.physletb.2021.136858

CrossRef Full Text | Google Scholar

Eddington, A. (1931). On the value of the cosmical constant. Proc. R. Soc. Lond. Ser. A 133, 605–615. doi:10.1098/rspa.1931.0170

CrossRef Full Text | Google Scholar

Eggemeier, B., and Niemeyer, J. C. (2019). Formation and mass growth of axion stars in axion miniclusters. Phys. Rev. D. 100, 063528. doi:10.1103/PhysRevD.100.063528

CrossRef Full Text | Google Scholar

Eggemeier, B., Niemeyer, J. C., and Easther, R. (2021). Formation of inflaton halos after inflation. Phys. Rev. D. 103, 063525. doi:10.1103/PhysRevD.103.063525

CrossRef Full Text | Google Scholar

Eggemeier, B., Schwabe, B., Niemeyer, J. C., and Easther, R. (2022). Gravitational collapse in the postinflationary Universe. Phys. Rev. D. 105, 023516. doi:10.1103/PhysRevD.105.023516

CrossRef Full Text | Google Scholar

El-Zant, A. A., Freundlich, J., Combes, F., and Halle, A. (2020). The effect of fluctuating fuzzy axion haloes on stellar dynamics: a stochastic model. Mon. Not. R. Astron. Soc. 492, 877–894. doi:10.1093/mnras/stz3478

CrossRef Full Text | Google Scholar

Fan, J. (2016). Ultralight repulsive dark matter and BEC. Phys. Dark Universe 14, 84–94. doi:10.1016/j.dark.2016.10.005

CrossRef Full Text | Google Scholar

Ferreira, E. G. M. (2021). Ultra-light dark matter. Astron. Astrophys. Rev. 29, 7. doi:10.1007/s00159-021-00135-6

CrossRef Full Text | Google Scholar

Feynman, R. P., Morinigo, F. B., and Wagner, W. G. (1995). Feynman lectures on gravitation.

Google Scholar

Feynman, R. (1955). Progress in low temperature physics, volume 1.

Google Scholar

Feynman, R. P. (1958). Excitations in liquid helium. Physica 24, S18–S26. doi:10.1016/S0031-8914(58)80495-4

CrossRef Full Text | Google Scholar

Foidl, H., Rindler-Daller, T., and Zeilinger, W. W. (2023). Halo formation and evolution in scalar field dark matter and cold dark matter: new insights from the fluid approach. Phys. Rev. D. 108, 043012. doi:10.1103/PhysRevD.108.043012

CrossRef Full Text | Google Scholar

Friedberg, R., Lee, T. D., and Pang, Y. (1987). Scalar soliton stars and black holes. Phys. Rev. D. 35, 3658–3677. doi:10.1103/PhysRevD.35.3658

PubMed Abstract | CrossRef Full Text | Google Scholar

Fujikura, K., Hertzberg, M. P., Schiappacasse, E. D., and Yamaguchi, M. (2021). Microlensing constraints on axion stars including finite lens and source size effects. Phys. Rev. D. 104, 123012. doi:10.1103/PhysRevD.104.123012

CrossRef Full Text | Google Scholar

Galazo García, R., Brax, P., and Valageas, P. (2024). Solitons and halos for self-interacting scalar dark matter. Phys. Rev. D. 109, 043516. doi:10.1103/PhysRevD.109.043516

CrossRef Full Text | Google Scholar

Galazo-García, R., Brax, P., and Valageas, P. (2022). Self-similar solutions for fuzzy dark matter. Phys. Rev. D. 105, 123528. doi:10.1103/PhysRevD.105.123528

CrossRef Full Text | Google Scholar

Gamba, A., Ambrosi, D., Coniglio, A., de Candia, A., di Talia, S., Giraudo, E., et al. (2003). Percolation, morphogenesis, and Burgers dynamics in blood vessels formation. Phys. Rev. Lett. 90, 118101. doi:10.1103/PhysRevLett.90.118101

PubMed Abstract | CrossRef Full Text | Google Scholar

Gan, X., Wang, L.-T., and Xiao, H. (2024). Detecting axion dark matter with black hole polarimetry. Phys. Rev. D. 110, 063039. doi:10.1103/PhysRevD.110.063039

CrossRef Full Text | Google Scholar

Gillessen, S., Eisenhauer, F., Fritz, T. K., Bartko, H., Dodds-Eden, K., Pfuhl, O., et al. (2009). The orbit of the star S2 around SGR A* from very large telescope and Keck data. Astrophys. J. 707, L114–L117. doi:10.1088/0004-637X/707/2/L114

CrossRef Full Text | Google Scholar

Glennon, N., and Prescod-Weinstein, C. (2021). Modifying PyUltraLight to model scalar dark matter with self-interactions. Phys. Rev. D. 104, 083532. doi:10.1103/PhysRevD.104.083532

CrossRef Full Text | Google Scholar

Glennon, N., Musoke, N., Nadler, E. O., Prescod-Weinstein, C., and Wechsler, R. H. (2024). Dynamical friction in self-interacting ultralight dark matter. Phys. Rev. D. 109, 063501. doi:10.1103/PhysRevD.109.063501

CrossRef Full Text | Google Scholar

Goodman, J. (2000). Repulsive dark matter. New Astron. 5, 103–107. doi:10.1016/S1384-1076(00)00015-4

CrossRef Full Text | Google Scholar

Guerra, D., Macedo, C. F. B., and Pani, P. (2019). Axion boson stars. J. Cosmol. Astropart. Phys. 2019, 061. doi:10.1088/1475-7516/2019/09/061

CrossRef Full Text | Google Scholar

Guth, A. H., Hertzberg, M. P., and Prescod-Weinstein, C. (2015). Do dark matter axions form a condensate with long-range correlation? Phys. Rev. D. 92, 103513. doi:10.1103/PhysRevD.92.103513

CrossRef Full Text | Google Scholar

Guzmán, F. S., and Matos, T. (2000). Letter to the editor: scalar fields as dark matter in spiral galaxies. Class. Quantum Gravity 17, L9–L16. doi:10.1088/0264-9381/17/1/102

CrossRef Full Text | Google Scholar

Guzmán, F. S., and Ureña-López, L. A. (2004). Evolution of the Schrödinger-Newton system for a self-gravitating scalar field. Phys. Rev. D. 69, 124033. doi:10.1103/PhysRevD.69.124033

CrossRef Full Text | Google Scholar

Guzmán, F. S., and Ureña-López, L. A. (2006). Gravitational cooling of self-gravitating Bose condensates. Astrophys. J. 645, 814–819. doi:10.1086/504508

CrossRef Full Text | Google Scholar

Haghani, Z., and Harko, T. (2022). Compact stars in the Einstein dark energy model. Phys. Rev. D. 105, 064059. doi:10.1103/PhysRevD.105.064059

CrossRef Full Text | Google Scholar

Harko, T. (2019). Jeans instability and turbulent gravitational collapse of Bose–Einstein condensate dark matter halos. Eur. Phys. J. C 79, 787. doi:10.1140/epjc/s10052-019-7285-3

CrossRef Full Text | Google Scholar

Harrison, B. K., Thorne, K. S., Wakano, M., and Wheeler, J. A. (1965). Gravitation theory and gravitational collapse.

Google Scholar

Helfer, T., Marsh, D. J. E., Clough, K., Fairbairn, M., Lim, E. A., and Becerril, R. (2017). Black hole formation from axion stars. J. Cosmol. Astropart. Phys. 2017, 055. doi:10.1088/1475-7516/2017/03/055

CrossRef Full Text | Google Scholar

Henon, M. (1959). L’ amas isochrone: I. Ann. d’Astrophys. 22, 126.

Google Scholar

Hertzberg, M. P., Li, Y., and Schiappacasse, E. D. (2020). Merger of dark matter axion clumps and resonant photon emission. J. Cosmol. Astropart. Phys. 2020, 067. doi:10.1088/1475-7516/2020/07/067

CrossRef Full Text | Google Scholar

Hinshaw, G., Weiland, J. L., Hill, R. S., Odegard, N., Larson, D., Bennett, C. L., et al. (2009). Five-year Wilkinson microwave anisotropy probe observations: data processing, sky maps, and basic results. Astrophys. J. 180, 225–245. doi:10.1088/0067-0049/180/2/225

CrossRef Full Text | Google Scholar

Hu, W., Barkana, R., and Gruzinov, A. (2000). Fuzzy cold dark matter: the wave properties of ultralight particles. Phys. Rev. Lett. 85, 1158–1161. doi:10.1103/PhysRevLett.85.1158

PubMed Abstract | CrossRef Full Text | Google Scholar

Hui, L., Ostriker, J. P., Tremaine, S., and Witten, E. (2017). Ultralight scalars as cosmological dark matter. Phys. Rev. D. 95, 043541. doi:10.1103/PhysRevD.95.043541

CrossRef Full Text | Google Scholar

Hui, L. (2021). Wave dark matter. Annu. Rev. 59, 247–289. doi:10.1146/annurev-astro-120920-010024

CrossRef Full Text | Google Scholar

Hwang, J.-c., and Noh, H. (2022). Axion as a fuzzy dark matter candidate: proofs in different gauges. J. Cosmol. Astropart. Phys. 2022, 001. doi:10.1088/1475-7516/2022/03/001

CrossRef Full Text | Google Scholar

Indjin, M., Liu, I. K., Proukakis, N. P., and Rigopoulos, G. (2024). Virialized profiles and oscillations of self-interacting fuzzy dark matter solitons. Phys. Rev. D. 109, 103518. doi:10.1103/PhysRevD.109.103518

CrossRef Full Text | Google Scholar

Jeans, J. H. (1902). The stability of a spherical nebula. Philosophical Trans. R. Soc. Lond. Ser. A 199, 1–53. doi:10.1098/rsta.1902.0012

CrossRef Full Text | Google Scholar

Jetzer, P. (1992). Boson stars. Phys. Rep. 220, 163–227. doi:10.1016/0370-1573(92)90123-H

CrossRef Full Text | Google Scholar

Ji, S. U., and Sin, S. J. (1994). Late-time phase transition and the galactic halo as a Bose liquid. II. The effect of visible matter. Phys. Rev. D. 50, 3655–3659. doi:10.1103/PhysRevD.50.3655

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, Y., Hammer, F., Wang, H., Wang, J., Amram, P., Chemin, L., et al. (2023). Detection of the Keplerian decline in the Milky Way rotation curve. Astron. Astrophys. 678, A208. doi:10.1051/0004-6361/202347513

CrossRef Full Text | Google Scholar

Kamionkowski, M., and Liddle, A. R. (2000). The dearth of halo dwarf galaxies: is there power on short scales? Phys. Rev. Lett. 84, 4525–4528. doi:10.1103/PhysRevLett.84.4525

PubMed Abstract | CrossRef Full Text | Google Scholar

Katz, J. (2003). Thermodynamics of self-gravitating systems. Found. Phys. 33, 223–269. doi:10.1023/A:1023776921610

CrossRef Full Text | Google Scholar

Kauffmann, G., White, S. D. M., and Guiderdoni, B. (1993). The formation and evolution of galaxies within merging dark matter haloes. Mon. Not. R. Astron. Soc. 264, 201–218. doi:10.1093/mnras/264.1.201

CrossRef Full Text | Google Scholar

Kaup, D. J. (1968). Klein-Gordon geon. Phys. Rev. 172, 1331–1342. doi:10.1103/PhysRev.172.1331

CrossRef Full Text | Google Scholar

Khlopov, M. I., Malomed, B. A., and Zeldovich, I. B. (1985). Gravitational instability of scalar fields and formation of primordial black holes. Mon. Not. R. Astron. Soc. 215, 575–589. doi:10.1093/mnras/215.4.575

CrossRef Full Text | Google Scholar

Khoury, J. (2022). Dark matter superfluidity. SciPost Phys. Lect. Notes 42, 42. doi:10.21468/SciPostPhysLectNotes.42

CrossRef Full Text | Google Scholar

King, I. R. (1965). The structure of star clusters. II. Steady-state velocity distributions. Astron. J. 70, 376. doi:10.1086/109750

CrossRef Full Text | Google Scholar

Kirkpatrick, K., Mirasola, A. E., and Prescod-Weinstein, C. (2022). Analysis of Bose-Einstein condensation times for self-interacting scalar dark matter. Phys. Rev. D. 106, 043512. doi:10.1103/PhysRevD.106.043512

CrossRef Full Text | Google Scholar

Klypin, A., Kravtsov, A. V., Valenzuela, O., and Prada, F. (1999). Where are the missing galactic satellites? Astrophys. J. 522, 82–92. doi:10.1086/307643

CrossRef Full Text | Google Scholar

Kormendy, J., and Freeman, K. C. (2004). “Scaling laws for dark matter halos in late-type and dwarf spheroidal galaxies,” in Dark matter in galaxies. Editors S. Ryder, D. Pisano, M. Walker, and K. Freeman doi:10.48550/arXiv.astro-ph/0407321

CrossRef Full Text | Google Scholar

Korshynska, K., Bidasyuk, Y. M., Gorbar, E. V., Jia, J., and Yakimenko, A. I. (2023). Dynamical galactic effects induced by solitonic vortex structure in bosonic dark matter. Eur. Phys. J. C 83, 451. doi:10.1140/epjc/s10052-023-11548-1

CrossRef Full Text | Google Scholar

Krut, A., Argüelles, C., and Chavanis, P.-H. (2025). Thermodynamics of self-gravitating fermions as a robust theory for dark matter halos: stability analysis applied to the Milky Way. arXiv:2503.10870.

Google Scholar

Lancaster, L., Giovanetti, C., Mocz, P., Kahn, Y., Lisanti, M., and Spergel, D. N. (2020). Dynamical friction in a fuzzy dark matter universe. J. Cosmol. Astropart. Phys. 2020, 001. doi:10.1088/1475-7516/2020/01/001

CrossRef Full Text | Google Scholar

Lattimer, J., and Prakash, M. (2011). From nuclei to stars.

Google Scholar

Lee, J.-W., and Koh, I.-G. (1996). Galactic halos as boson stars. Phys. Rev. D. 53, 2236–2239. doi:10.1103/PhysRevD.53.2236

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T. D., and Pang, Y. (1987). Fermion soliton stars and black holes. Phys. Rev. D. 35, 3678–3694. doi:10.1103/PhysRevD.35.3678

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, B. K. K., Chu, M.-C., and Lin, L.-M. (2021). Could the GW190814 secondary component be a bosonic dark matter admixed compact star? Astrophys. J. 922, 242. doi:10.3847/1538-4357/ac2735

CrossRef Full Text | Google Scholar

Lee, T. D. (1987a). Soliton stars and black holes. Phys. Rev. 17, 225.

Google Scholar

Lee, T. D. (1987b). Soliton stars and the critical masses of black holes. Phys. Rev. D. 35, 3637–3639. doi:10.1103/PhysRevD.35.3637

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J.-W. (2018). Brief history of ultra-light scalar dark matter models. Eur. Phys. J. Web Conf. 168, 06005. doi:10.1051/epjconf/201816806005

CrossRef Full Text | Google Scholar

Levkov, D. G., Panin, A. G., and Tkachev, I. I. (2017). Relativistic axions from collapsing Bose stars. Phys. Rev. Lett. 118, 011301. doi:10.1103/PhysRevLett.118.011301

PubMed Abstract | CrossRef Full Text | Google Scholar

Levkov, D. G., Panin, A. G., and Tkachev, I. I. (2018). Gravitational Bose-Einstein condensation in the kinetic regime. Phys. Rev. Lett. 121, 151301. doi:10.1103/PhysRevLett.121.151301

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, B., Rindler-Daller, T., and Shapiro, P. R. (2014). Cosmological constraints on Bose-Einstein-condensed scalar field dark matter. Phys. Rev. D. 89, 083536. doi:10.1103/PhysRevD.89.083536

CrossRef Full Text | Google Scholar

Liddle, A. R., and Madsen, M. S. (1992). The structure and formation of boson stars. Int. J. Mod. Phys. D 1, 101–143. doi:10.1142/S0218271892000057

CrossRef Full Text | Google Scholar

Liebling, S. L., and Palenzuela, C. (2017). Dynamical boson stars. Living Rev. Relativ. 20, 5. doi:10.1007/s41114-017-0007-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, S.-C., Schive, H.-Y., Wong, S.-K., and Chiueh, T. (2018). Self-consistent construction of virialized wave dark matter halos. Phys. Rev. D. 97, 103523. doi:10.1103/PhysRevD.97.103523

CrossRef Full Text | Google Scholar

Liu, I. K., Proukakis, N. P., and Rigopoulos, G. (2023). Coherent and incoherent structures in fuzzy dark matter haloes. Mon. Not. R. Astron. Soc. 521, 3625–3647. doi:10.1093/mnras/stad591

CrossRef Full Text | Google Scholar

Lora, V., Magaña, J., Bernal, A., Sánchez-Salcedo, F. J., and Grebel, E. K. (2012). On the mass of ultra-light bosonic dark matter from galactic dynamics. J. Cosmol. Astropart. Phys. 2012, 011. doi:10.1088/1475-7516/2012/02/011

CrossRef Full Text | Google Scholar

Lynden-Bell, D., and Wood, R. (1968). The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. Mon. Not. R. Astron. Soc. 138, 495–525. doi:10.1093/mnras/138.4.495

CrossRef Full Text | Google Scholar

Lynden-Bell, D. (1967). Statistical mechanics of violent relaxation in stellar systems. Mon. Not. R. Astron. Soc. 136, 101–121. doi:10.1093/mnras/136.1.101

CrossRef Full Text | Google Scholar

Madelung, E. (1927). Quantentheorie in hydrodynamischer form. Z. Fur Phys. 40, 322–326. doi:10.1007/BF01400372

CrossRef Full Text | Google Scholar

Marsh, D. J. E., and Niemeyer, J. C. (2019). Strong constraints on fuzzy dark matter from ultrafaint dwarf galaxy Eridanus II. Phys. Rev. Lett. 123, 051103. doi:10.1103/PhysRevLett.123.051103

PubMed Abstract | CrossRef Full Text | Google Scholar

Marsh, D. J. E. (2015). Nonlinear hydrodynamics of axion dark matter: relative velocity effects and quantum forces. Phys. Rev. D. 91, 123520. doi:10.1103/PhysRevD.91.123520

CrossRef Full Text | Google Scholar

Marsh, D. J. E. (2016). Axion cosmology. Phys. Rep. 643, 1–79. doi:10.1016/j.physrep.2016.06.005

CrossRef Full Text | Google Scholar

Maseizik, D., Eby, J., Seong, H., and Sigl, G. (2024). Detectability of accretion-induced bosenovae in the Milky Way. arXiv e-prints, arXiv:2410.13082. doi:10.48550/arXiv.2410.13082

CrossRef Full Text | Google Scholar

Matos, T., Avilez, A., Bernal, T., and Chavanis, P.-H. (2019). Energy balance of a Bose gas in a curved space-time. General Relativ. Gravit. 51, 159. doi:10.1007/s10714-019-2644-9

CrossRef Full Text | Google Scholar

Matos, T., Ureña-López, L. A., and Lee, J.-W. (2024). Short review of the main achievements of the scalar field, fuzzy, ultralight, wave, BEC dark matter model. Front. Astronomy Space Sci. 11, 1347518. doi:10.3389/fspas.2024.1347518

CrossRef Full Text | Google Scholar

Membrado, M., Abad, J., Pacheco, A. F., and Saudo, J. (1989a). Newtonian boson spheres. Phys. Rev. D. 40, 2736–2738. doi:10.1103/PhysRevD.40.2736

PubMed Abstract | CrossRef Full Text | Google Scholar

Membrado, M., Pacheco, A. F., and Sañudo, J. (1989b). Hartree solutions for the self-Yukawian boson sphere. Phys. Rev. A Gen. Phys. 39, 4207–4211. doi:10.1103/PhysRevA.39.4207

PubMed Abstract | CrossRef Full Text | Google Scholar

Michel, F., and Moss, I. G. (2018). Relativistic collapse of axion stars. Phys. Lett. B 785, 9–13. doi:10.1016/j.physletb.2018.07.063

CrossRef Full Text | Google Scholar

Mocz, P., Vogelsberger, M., Robles, V. H., Zavala, J., Boylan-Kolchin, M., Fialkov, A., et al. (2017). Galaxy formation with BECDM - I. Turbulence and relaxation of idealized haloes. Mon. Not. R. Astron. Soc. 471, 4559–4570. doi:10.1093/mnras/stx1887

PubMed Abstract | CrossRef Full Text | Google Scholar

Mocz, P., Lancaster, L., Fialkov, A., Becerra, F., and Chavanis, P.-H. (2018). Schrödinger-Poisson–Vlasov-Poisson correspondence. Phys. Rev. D. 97, 083519. doi:10.1103/PhysRevD.97.083519

CrossRef Full Text | Google Scholar

Mocz, P., Fialkov, A., Vogelsberger, M., Becerra, F., Amin, M. A., Bose, S., et al. (2019). First star-forming structures in fuzzy cosmic filaments. Phys. Rev. Lett. 123, 141301. doi:10.1103/PhysRevLett.123.141301

PubMed Abstract | CrossRef Full Text | Google Scholar

Mocz, P., Fialkov, A., Vogelsberger, M., Becerra, F., Shen, X., Robles, V. H., et al. (2020). Galaxy formation with BECDM - II. Cosmic filaments and first galaxies. Mon. Not. R. Astron. Soc. 494, 2027–2044. doi:10.1093/mnras/staa738

CrossRef Full Text | Google Scholar

Mocz, P., Fialkov, A., Vogelsberger, M., Boylan-Kolchin, M., Chavanis, P.-H., Amin, M. A., et al. (2023). Cosmological structure formation and soliton phase transition in fuzzy dark matter with axion self-interactions. Mon. Not. R. Astron. Soc. 521, 2608–2615. doi:10.1093/mnras/stad694

CrossRef Full Text | Google Scholar

Moore, B., Quinn, T., Governato, F., Stadel, J., and Lake, G. (1999). Cold collapse and the core catastrophe. Mon. Not. R. Astron. Soc. 310, 1147–1152. doi:10.1046/j.1365-8711.1999.03039.x

CrossRef Full Text | Google Scholar

Musoke, N., Hotchkiss, S., and Easther, R. (2020). Lighting the dark: evolution of the postinflationary universe. Phys. Rev. Lett. 124, 061301. doi:10.1103/PhysRevLett.124.061301

PubMed Abstract | CrossRef Full Text | Google Scholar

Navarro, J. F., Frenk, C. S., and White, S. D. M. (1996). The structure of cold dark matter halos. Astrophys. J. 462, 563. doi:10.1086/177173

CrossRef Full Text | Google Scholar

Nelson, E. (1966). Derivation of the Schrödinger equation from Newtonian mechanics. Phys. Rev. 150, 1079–1085. doi:10.1103/PhysRev.150.1079

CrossRef Full Text | Google Scholar

Niemeyer, J. C., and Easther, R. (2020). Inflaton clusters and inflaton stars. J. Cosmol. Astropart. Phys. 2020, 030. doi:10.1088/1475-7516/2020/07/030

CrossRef Full Text | Google Scholar

Niemeyer, J. C. (2020). Small-scale structure of fuzzy and axion-like dark matter. Prog. Part. Nucl. Phys. 113, 103787. doi:10.1016/j.ppnp.2020.103787

CrossRef Full Text | Google Scholar

Nori, M., Macciò, A. V., and Baldi, M. (2023). Fuzzy aquarius: evolution of a Milky-Way like system in the fuzzy dark matter scenario. Mon. Notices R. Astronomical Soc. 522, 1451–1463. doi:10.1093/mnras/stad1081

CrossRef Full Text | Google Scholar

Nottale, L. (2011). Scale relativity and fractal space-time: a new approach to unifying relativity and quantum mechanics. doi:10.1142/p752

CrossRef Full Text | Google Scholar

Oñorbe, J., Boylan-Kolchin, M., Bullock, J. S., Hopkins, P. F., Kereš, D., Faucher-Giguère, C.-A., et al. (2015). Forged in FIRE: cusps, cores and baryons in low-mass dwarf galaxies. Mon. Not. R. Astron. Soc. 454, 2092–2106. doi:10.1093/mnras/stv2072

CrossRef Full Text | Google Scholar

Onsager, L. (1949). Statistical hydrodynamics. Il Nuovo Cimento 6, 279–287. doi:10.1007/BF02780991

CrossRef Full Text | Google Scholar

Oppenheimer, J. R., and Volkoff, G. M. (1939). On massive neutron cores. Phys. Rev. 55, 374–381. doi:10.1103/PhysRev.55.374

CrossRef Full Text | Google Scholar

Ourabah, K. (2020). Jeans instability in dark matter halos. Phys. Scr. 95, 055005. doi:10.1088/1402-4896/ab7650

CrossRef Full Text | Google Scholar

Padilla, L. E., Rindler-Daller, T., Shapiro, P. R., Matos, T., and Vázquez, J. A. (2021). Core-halo mass relation in scalar field dark matter models and its consequences for the formation of supermassive black holes. Phys. Rev. D. 103, 063012. doi:10.1103/PhysRevD.103.063012

CrossRef Full Text | Google Scholar

Padilla, L. E., Hidalgo, J. C., and Malik, K. A. (2022). New mechanism for primordial black hole formation during reheating. Phys. Rev. D. 106, 023519. doi:10.1103/PhysRevD.106.023519

CrossRef Full Text | Google Scholar

Padilla, L. E., Hidalgo, J. C., Gomez-Aguilar, T. D., Malik, K. A., and German, G. (2024). Primordial black hole formation during slow-reheating: a review. Front. Astronomy Space Sci. 11, 1361399. doi:10.3389/fspas.2024.1361399

CrossRef Full Text | Google Scholar

Padmanabhan, T. (1990). Statistical mechanics of gravitating systems. Phys. Rep. 188, 285–362. doi:10.1016/0370-1573(90)90051-3

CrossRef Full Text | Google Scholar

Painter, C. A., Boylan-Kolchin, M., Mocz, P., and Vogelsberger, M. (2024). An attractive model: simulating fuzzy dark matter with attractive self-interactions. Mon. Not. R. Astron. Soc. 533, 2454–2472. doi:10.1093/mnras/stae1912

CrossRef Full Text | Google Scholar

Patkós, A. (2023). Electromagnetic energy loss of axion stars. Phys. Rev. D. 107, 055017. doi:10.1103/PhysRevD.107.055017

CrossRef Full Text | Google Scholar

Peebles, P. J. E. (1980). The large-scale structure of the universe.

Google Scholar

Peebles, P. J. E. (2000). Fluid dark matter. Astrophys. J. 534, L127–L129. doi:10.1086/312677

PubMed Abstract | CrossRef Full Text | Google Scholar

Pils, K., and Rindler-Daller, T. (2022). Orbits and adiabatic contraction in scalar-field dark matter halos: revisiting the cusp-core problem in dwarf galaxies. Mon. Not. R. Astron. Soc. 514, 1990–2009. doi:10.1093/mnras/stac1471

CrossRef Full Text | Google Scholar

Poincaré, H. (1885). Sur l'équilibre d'une masse fluide animée d'un mouvement de rotation. Acta Math. 7, 259–380. doi:10.1007/bf02402204

CrossRef Full Text | Google Scholar

Pontzen, A., and Governato, F. (2014). Cold dark matter heats up. Nature 506, 171–178. doi:10.1038/nature12953

PubMed Abstract | CrossRef Full Text | Google Scholar

Proukakis, N. P., Rigopoulos, G., and Soto, A. (2023). Unified description of corpuscular and fuzzy bosonic dark matter. Phys. Rev. D. 108, 083513. doi:10.1103/PhysRevD.108.083513

CrossRef Full Text | Google Scholar

Proukakis, N. P., Rigopoulos, G., and Soto, A. (2024). Hybrid model of condensate and particle dark matter: linear perturbations in the hydrodynamic limit. Phys. Rev. D. 110, 023504. doi:10.1103/PhysRevD.110.023504

CrossRef Full Text | Google Scholar

Raby, S. (2016). Axion star collisions with neutron stars and fast radio bursts. Phys. Rev. D. 94, 103004. doi:10.1103/PhysRevD.94.103004

CrossRef Full Text | Google Scholar

Randall, S. W., Markevitch, M., Clowe, D., Gonzalez, A. H., and Bradač, M. (2008). Constraints on the self-interaction cross section of dark matter from numerical simulations of the merging galaxy cluster 1E 0657-56. Astrophys. J. 679, 1173–1180. doi:10.1086/587859

CrossRef Full Text | Google Scholar

Rindler-Daller, T., and Shapiro, P. R. (2012). Angular momentum and vortex formation in Bose-Einstein-condensed cold dark matter haloes. Mon. Not. R. Astron. Soc. 422, 135–161. doi:10.1111/j.1365-2966.2012.20588.x

CrossRef Full Text | Google Scholar

Rindler-Daller, T., and Shapiro, P. R. (2014). “Finding new signature effects on galactic dynamics to constrain Bose-Einstein-condensed cold dark matter,” in Accelerated cosmic expansion. Editors C. Moreno Gonzalez, J. E. Madriz Aguilar, and L. M. Reyes Barrera, 163, 163–182. doi:10.1007/978-3-319-02063-1_12

CrossRef Full Text | Google Scholar

Robles, V. H., and Matos, T. (2013). Exact solution to finite temperature SFDM: natural cores without feedback. Astrophys. J. 763, 19. doi:10.1088/0004-637X/763/1/19

CrossRef Full Text | Google Scholar

Romano-Díaz, E., Shlosman, I., Hoffman, Y., and Heller, C. (2008). Erasing dark matter cusps in cosmological galactic halos with baryons. Astrophys. J. 685, L105–L108. doi:10.1086/592687

CrossRef Full Text | Google Scholar

Ruffini, R., and Bonazzola, S. (1969). Systems of self-gravitating particles in general relativity and the concept of an equation of state. Phys. Rev. 187, 1767–1783. doi:10.1103/PhysRev.187.1767

CrossRef Full Text | Google Scholar

Ruffini, R., Argüelles, C. R., and Rueda, J. A. (2015). On the core-halo distribution of dark matter in galaxies. Mon. Notices R. Astronomical Soc. 451, 622–628. doi:10.1093/mnras/stv1016

CrossRef Full Text | Google Scholar

Schive, H.-Y., Chiueh, T., and Broadhurst, T. (2014a). Cosmic structure as the quantum interference of a coherent dark wave. Nat. Phys. 10, 496–499. doi:10.1038/nphys2996

CrossRef Full Text | Google Scholar

Schive, H.-Y., Liao, M.-H., Woo, T.-P., Wong, S.-K., Chiueh, T., Broadhurst, T., et al. (2014b). Understanding the core-halo relation of quantum wave dark matter from 3D simulations. Phys. Rev. Lett. 113, 261302. doi:10.1103/PhysRevLett.113.261302

PubMed Abstract | CrossRef Full Text | Google Scholar

Schobesberger, S. O., Rindler-Daller, T., and Shapiro, P. R. (2021). Angular momentum and the absence of vortices in the cores of fuzzy dark matter haloes. Mon. Not. R. Astron. Soc. 505, 802–829. doi:10.1093/mnras/stab1153

CrossRef Full Text | Google Scholar

Schunck, F. E., and Mielke, E. W. (2003). General relativistic boson stars. Cl. Quantum Grav. 20, R301–R356. doi:10.1088/0264-9381/20/20/201

CrossRef Full Text | Google Scholar

Schwabe, B., Niemeyer, J. C., and Engels, J. F. (2016). Simulations of solitonic core mergers in ultralight axion dark matter cosmologies. Phys. Rev. D. 94, 043513. doi:10.1103/PhysRevD.94.043513

CrossRef Full Text | Google Scholar

Seidel, E., and Suen, W.-M. (1991). Oscillating soliton stars. Phys. Rev. Lett. 66, 1659–1662. doi:10.1103/PhysRevLett.66.1659

PubMed Abstract | CrossRef Full Text | Google Scholar

Seidel, E., and Suen, W.-M. (1994). Formation of solitonic stars through gravitational cooling. Phys. Rev. Lett. 72, 2516–2519. doi:10.1103/PhysRevLett.72.2516

PubMed Abstract | CrossRef Full Text | Google Scholar

Shapiro, P. R., Dawoodbhoy, T., and Rindler-Daller, T. (2022). Cosmological structure formation in scalar field dark matter with repulsive self-interaction: the incredible shrinking Jeans mass. Mon. Not. R. Astron. Soc. 509, 145–173. doi:10.1093/mnras/stab2884

CrossRef Full Text | Google Scholar

Sharma, A., Kartvelishvili, G., and Khoury, J. (2022). Finite temperature description of an interacting Bose gas. Phys. Rev. D. 106, 045025. doi:10.1103/PhysRevD.106.045025

CrossRef Full Text | Google Scholar

Shukla, S., Brachet, M. E., and Pandit, R. (2024a). Neutron-superfluid vortices and proton-superconductor flux tubes: development of a minimal model for pulsar glitches. Phys. Rev. D. 110, 083002. doi:10.1103/PhysRevD.110.083002

CrossRef Full Text | Google Scholar

Shukla, S., Verma, A. K., Brachet, M. E., and Pandit, R. (2024b). Gravity- and temperature-driven phase transitions in a model for collapsed axionic condensates. Phys. Rev. D. 109, 063009. doi:10.1103/PhysRevD.109.063009

CrossRef Full Text | Google Scholar

Sikivie, P., and Yang, Q. (2009). Bose-Einstein condensation of dark matter axions. Phys. Rev. Lett. 103, 111301. doi:10.1103/PhysRevLett.103.111301

PubMed Abstract | CrossRef Full Text | Google Scholar

Simon-Petit, A., Perez, J., and Plum, G. (2019). The status of isochrony in the formation and evolution of self-gravitating systems. Mon. Not. R. Astron. Soc. 484, 4963–4971. doi:10.1093/mnras/stz351

CrossRef Full Text | Google Scholar

Sin, S.-J. (1994). Late-time phase transition and the galactic halo as a Bose liquid. Phys. Rev. D. 50, 3650–3654. doi:10.1103/PhysRevD.50.3650

PubMed Abstract | CrossRef Full Text | Google Scholar

Slepian, Z., and Goodman, J. (2012). Ruling out bosonic repulsive dark matter in thermal equilibrium. Mon. Not. R. Astron. Soc. 427, 839–849. doi:10.1111/j.1365-2966.2012.21901.x

CrossRef Full Text | Google Scholar

Spano, M., Marcelin, M., Amram, P., Carignan, C., Epinat, B., and Hernandez, O. (2008). GHASP: an Hα kinematic survey of spiral and irregular galaxies - V. Dark matter distribution in 36 nearby spiral galaxies. Mon. Not. R. Astron. Soc. 383, 297–316. doi:10.1111/j.1365-2966.2007.12545.x

CrossRef Full Text | Google Scholar

Spergel, D. N., and Steinhardt, P. J. (2000). Observational evidence for self-interacting cold dark matter. Phys. Rev. Lett. 84, 3760–3763. doi:10.1103/PhysRevLett.84.3760

PubMed Abstract | CrossRef Full Text | Google Scholar

Suárez, A., and Chavanis, P.-H. (2015a). Hydrodynamic representation of the Klein-Gordon-Einstein equations in the weak field limit: general formalism and perturbations analysis. Phys. Rev. D. 92, 023510. doi:10.1103/PhysRevD.92.023510

CrossRef Full Text | Google Scholar

Suárez, A., and Chavanis, P.-H. (2015b). Hydrodynamic representation of the Klein-Gordon-Einstein equations in the weak field limit. J. Phys. Conf. Ser. (IOP) 654, 012008. doi:10.1088/1742-6596/654/1/012008

CrossRef Full Text | Google Scholar

Suárez, A., and Chavanis, P.-H. (2017). Cosmological evolution of a complex scalar field with repulsive or attractive self-interaction. Phys. Rev. D. 95, 063515. doi:10.1103/PhysRevD.95.063515

CrossRef Full Text | Google Scholar

Suárez, A., and Chavanis, P.-H. (2018). Jeans-type instability of a complex self-interacting scalar field in general relativity. Phys. Rev. D. 98, 083529. doi:10.1103/PhysRevD.98.083529

CrossRef Full Text | Google Scholar

Suárez, A., and Matos, T. (2011). Structure formation with scalar-field dark matter: the fluid approach. Mon. Notices R. Astronomical Soc. 416, 87–93. doi:10.1111/j.1365-2966.2011.19012.x

CrossRef Full Text | Google Scholar

Suárez, A., and Matos, T. (2014). Bose-Einstein condensate dark matter phase transition from finite temperature symmetry breaking of Klein-Gordon fields. Class. Quantum Gravity 31, 045015. doi:10.1088/0264-9381/31/4/045015

CrossRef Full Text | Google Scholar

Suárez, A., Robles, V. H., and Matos, T. (2014). “A review on the scalar field/Bose-Einstein condensate dark matter model,” in Accelerated cosmic expansion. Editors C. Moreno Gonzalez, J. E. Madriz Aguilar, and L. M. Reyes Barrera, 107. doi:10.1007/978-3-319-02063-1_9

CrossRef Full Text | Google Scholar

Takabayasi, T. (1952). On the formulation of quantum mechanics associated with classical pictures. Prog. Theor. Phys. 8, 143–182. doi:10.1143/ptp/8.2.143

CrossRef Full Text | Google Scholar

Tangphati, T., Sakallı, İ., Banerjee, A., and Pradhan, A. (2024). Behaviors of quark stars in the Rainbow Gravity framework. Phys. Dark Universe 46, 101610. doi:10.1016/j.dark.2024.101610

CrossRef Full Text | Google Scholar

Tkachev, I. I. (1986). Coherent scalar-field oscillations forming compact astrophysical object. Sov. Astron. Lett. 12, 305–308.

Google Scholar

Uhlemann, C., Kopp, M., and Haugg, T. (2014). Schrödinger method as N-body double and UV completion of dust. Phys. Rev. D. 90, 023517. doi:10.1103/PhysRevD.90.023517

CrossRef Full Text | Google Scholar

Veltmaat, J., Niemeyer, J. C., and Schwabe, B. (2018). Formation and structure of ultralight bosonic dark matter halos. Phys. Rev. D. 98, 043509. doi:10.1103/PhysRevD.98.043509

CrossRef Full Text | Google Scholar

Veltmaat, J., Schwabe, B., and Niemeyer, J. C. (2020). Baryon-driven growth of solitonic cores in fuzzy dark matter halos. Phys. Rev. D. 101, 083518. doi:10.1103/PhysRevD.101.083518

CrossRef Full Text | Google Scholar

Verma, A. K., Pandit, R., and Brachet, M. E. (2021). Formation of compact objects at finite temperatures in a dark-matter-candidate self-gravitating bosonic system. Phys. Rev. Res. 3, L022016. doi:10.1103/PhysRevResearch.3.L022016

CrossRef Full Text | Google Scholar

Verma, A. K., Pandit, R., and Brachet, M. E. (2022). Rotating self-gravitating Bose-Einstein condensates with a crust: a model for pulsar glitches. Phys. Rev. Res. 4, 013026. doi:10.1103/PhysRevResearch.4.013026

CrossRef Full Text | Google Scholar

Visinelli, L., Baum, S., Redondo, J., Freese, K., and Wilczek, F. (2018). Dilute and dense axion stars. Phys. Lett. B 777, 64–72. doi:10.1016/j.physletb.2017.12.010

CrossRef Full Text | Google Scholar

Visinelli, L. (2021). Boson stars and oscillatons: a review. Int. J. Mod. Phys. D 30, 2130006–2130293. doi:10.1142/S0218271821300068

CrossRef Full Text | Google Scholar

Wallstrom, T. C. (1994). Inequivalence between the Schrödinger equation and the Madelung hydrodynamic equations. Phys. Rev. A. 49, 1613–1617. doi:10.1103/PhysRevA.49.1613

PubMed Abstract | CrossRef Full Text | Google Scholar

Whitney, H. (1955). On singularities of mappings of Euclidean spaces. I. Mappings of the plane into the plane. Ann. Math. 62, 374–410. doi:10.2307/1970070

CrossRef Full Text | Google Scholar

Widrow, L. M., and Kaiser, N. (1993). Using the Schroedinger equation to simulate collisionless matter. Astrophys. J. Lett. 416, L71. doi:10.1086/187073

CrossRef Full Text | Google Scholar

Yavetz, T. D., Li, X., and Hui, L. (2022). Construction of wave dark matter halos: numerical algorithm and analytical constraints. Phys. Rev. D. 105, 023512. doi:10.1103/PhysRevD.105.023512

CrossRef Full Text | Google Scholar

Yin, Z., and Visinelli, L. (2024). Axion star condensation around primordial black holes and microlensing limits. J. Cosmol. Astropart. Phys. 2024, 013. doi:10.1088/1475-7516/2024/10/013

CrossRef Full Text | Google Scholar

Zagorac, J. L., Kendall, E., Padmanabhan, N., and Easther, R. (2023). Soliton formation and the core-halo mass relation: an eigenstate perspective. Phys. Rev. D. 107, 083513. doi:10.1103/PhysRevD.107.083513

CrossRef Full Text | Google Scholar

Appendix 1: Energy functional

The GPP Equations 8 and 9 conserve the total mass

$M=\int |\psi {|}^{2}d\mathbf{r}(\mathrm{A1})$

and the total energy

$E_{\text{tot}}=\frac{{\hslash }^2}{2m^2}\int |\nabla \psi {|}^{2}d\mathbf{r}+\int V\left(|\psi {|}^2\right)d\mathbf{r}+\frac{1}{2}\int |\psi {|}^2\mathrm{\Phi }d\mathbf{r},(\mathrm{A2})$

which is the sum of the kinetic energy $\mathrm{\Theta }$, the internal energy $U$, and the gravitational energy $W$ (Chavanis, 2011c; Chavanis, 2017b).

Using the Madelung transformation, these functionals can be written in terms of hydrodynamic variables as

$M=\int \rho d\mathbf{r},(\mathrm{A3})$

$E_{\text{tot}}=\int \rho \frac{{\mathbf{u}}^2}{2}d\mathbf{r}+\frac{1}{m}\int \rho Qd\mathbf{r}+\int V\left(\rho \right)d\mathbf{r}+\frac{1}{2}\int \rho \mathrm{\Phi }d\mathbf{r},(\mathrm{A4})$

where the first two terms in Equation A4 are the classical kinetic energy ${\mathrm{\Theta }}_c$ and the quantum kinetic energy ${\mathrm{\Theta }}_Q$ (we have $\mathrm{\Theta }={\mathrm{\Theta }}_c+{\mathrm{\Theta }}_Q$), the third term is the internal energy $U$, and the fourth term is the gravitational energy $W$ (Chavanis, 2011c; Chavanis, 2017b).

An extremum of energy at fixed mass determines a stationary solution of the GPP equations. However, only minima of energy at fixed mass are dynamically stable (maxima or saddle points of energy at fixed mass are linearly unstable). A more detailed discussion of these results is given in Section 3.3 of Chavanis (2017b) and in Appendix B of Chavanis (2021a).

Appendix 2: Gaussian ansatz

We can obtain an approximate analytical solution of the GPP Equations 8 and 9 by using a Gaussian ansatz for the wavefunction and by developing a mechanical analogy (see Chavanis (2011c) and Section 8 of Chavanis (2017b) for details). We write the wavefunction as

$\psi \left(\mathbf{r},t\right)={\left[\frac{M}{{\pi }^{3/2}R{\left(t\right)}^3}\right]}^{1/2}{e}^{-r^2/2R{\left(t\right)}^2}{e}^{imH\left(t\right)r^2/2\hslash },(\mathrm{A5})$

where $R(t)$ is the typical radius⁵¹ of the BEC and $H=\dot{R}/R$. The density $\rho =|\psi {|}^2$ and the velocity field $\mathbf{u}=\nabla S/m$ are given by

$\rho \left(\mathbf{r},t\right)=\frac{M}{{\pi }^{3/2}R{\left(t\right)}^3}{e}^{-r^2/R{\left(t\right)}^2},(\mathrm{A6})$

$\mathbf{u}\left(\mathbf{r},t\right)=H\left(t\right)\mathbf{r}.(\mathrm{A7})$

We note that $H$ is similar to the Hubble parameter in cosmology [see Section 8.8 of Chavanis (2017b) for details]. We also note that the rotation curve $v_c(r)={[GM(r)/r]}^{1/2}$ (where $M(r)={\int }_0^r\rho (r^{\prime })4\pi {r^{\prime }}^{2}d{r}^{\prime }$ is the mass contained within the sphere of radius $r$) associated with the Gaussian density profile Equation A6 reads (Chavanis, 2011c)

$v_c\left(r\right)={\left(\frac{GM}{R}\right)}^{1/2}{\left[\frac{R}{r}\mathrm{e}\mathrm{r}\mathrm{f}\left(\frac{r}{R}\right)-\frac{2}{\sqrt{\pi }}{e}^{-{\left(r/R\right)}^2}\right]}^{1/2}.(\mathrm{A8})$

With the Gaussian ansatz, we find that the energy functional (Equation A4) can be written as a function of $R$ and $\dot{R}$ (for a fixed mass $M$) as

$E_{\text{tot}}=\frac{1}{2}\alpha M{\left(\frac{dR}{dt}\right)}^2+V\left(R\right).(\mathrm{A9})$

The first term in Equation A9 is the classical kinetic energy ${\mathrm{\Theta }}_c$ while the effective potential $V(R)$ comprises the quantum kinetic energy ${\mathrm{\Theta }}_Q$, the internal energy $U$, and the gravitational energy $W$ (see below). Therefore, $E_{\text{tot}}={\mathrm{\Theta }}_c+V$. Using Equation A9 and the conservation of energy (see Appendix 1) we find that the evolution of the radius $R(t)$ of the BEC is determined by the differential equation

$\alpha M\frac{d^{2}R}{d{t}^2}=-\frac{dV}{dR}.(\mathrm{A10})$

This equation is similar to the equation of motion of a particle of mass $\alpha M$ and position $R$ moving in a one-dimensional potential $V(R)$. This equation can also be obtained from the time-dependent quantum virial theorem [see Section 8.4 of Chavanis (2017b) for details]

$\frac{1}{2}\ddot{I}=2\left({\mathrm{\Theta }}_c+{\mathrm{\Theta }}_Q\right)+3\int Pd\mathbf{r}+W,(\mathrm{A11})$

where $I=\int \rho r^{2}d\mathbf{r}$ is the moment of inertia, or from the least action principle in a Lagrangian approach [see Appendix B of Chavanis (2016a)].

In the following, we shall specifically consider a standard BEC with the self-interaction potential from Equation 10 or with the equation of state from Equation 22. In that case, $U=\int V(\rho )d\mathbf{r}=\int Pd\mathbf{r}$ and the effective potential $V(R)={\mathrm{\Theta }}_Q+U+W$ reads [see Section 8.2 of Chavanis (2017b) for details]

$V\left(R\right)=\sigma \frac{{\hslash }^{2}M}{m^2{R}^2}+\zeta \frac{2\pi a_s{\hslash }^2{M}^2}{m^3{R}^3}-\nu \frac{G{M}^2}{R}(\mathrm{A12})$

with the coefficients

$\alpha =\frac{3}{2},\sigma =\frac{3}{4},\zeta =\frac{1}{{\left(2\pi \right)}^{3/2}},\nu =\frac{1}{\sqrt{2\pi }}.(\mathrm{A13})$

The equilibrium states are determined by the condition $V^{\prime }(R)=0$. This condition yields the mass-radius relation (Chavanis, 2011c; Chavanis, 2017b)

$M=\frac{\frac{2\sigma }{\nu }\frac{{\hslash }^2}{G{m}^{2}R}}{1-\frac{6\pi \zeta }{\nu }\frac{a_s{\hslash }^2}{G{m}^3{R}^2}}.(\mathrm{A14})$

This relation can also be obtained from the static quantum virial theorem (see Section 8.3 of Chavanis, 2017b for details)

$2{\mathrm{\Theta }}_Q+3\int Pd\mathbf{r}+W=0.(\mathrm{A15})$

The mass-radius relation in the noninteracting limit, the radius in the TF limit (in the repulsive case), and the maximum mass $M_{\text{max}}$ and minimum radius $R_{\ast }$ (in the attractive case) are given by Equations 34, 35, 37, 38 with the coefficients $2\sigma \mu /\nu =8.95$, ${(6\pi \zeta /\nu )}^{1/2}\mu =4.125$, $\sigma /\sqrt{6\pi \zeta \nu }=1.085$ and ${(6\pi \zeta /\nu )}^{1/2}\mu =4.12$ instead of the exact values 9.95, $\pi$, 1.012 and 5.5. We see that the prediction of the maximum mass from the Gaussian ansatz is relatively accurate (Chavanis, 2011c).

Only minima of $V(R)$ are dynamically stable. Therefore, the condition of stability is $V^{″}(R)>0$. With the Gaussian ansatz, the squared pulsation of the BEC is ${\omega }^2=V^{″}(R)/\alpha M$. We then find that [see Section 8.6 of Chavanis (2017b) for details]

${\omega }^2=\frac{6{\mathrm{\Theta }}_Q+12U+2W}{I},(\mathrm{A16})$

where $I=\alpha M{R}^2$. In addition, for the standard BEC $(\gamma =2)$, one can obtain the relation [see Chavanis (2016a), Chavanis (2020c) and Sections. 8.6 and 8.7 of Chavanis (2017b) for details and generalizations]

$\frac{dM}{dR}=-\alpha M\frac{m^2{R}^3}{2\sigma {\hslash }^2}{\omega }^2.(\mathrm{A17})$

This relation directly connects the stability of the self-gravitating BEC to the slope of the mass-radius relation. The equilibrium state is stable when $dM/dR<0$ (implying ${\omega }^2>0$) and unstable when $dM/dR>0$ (implying ${\omega }^2<0$). The change of stability occurs at the maximum mass $M_{\text{max}}$, where $dM/dR=\omega =0$, in agreement with the Poincaré turning point criterion (Poincaré, 1885). By studying the sign of the second derivatives of $V(R)$ or by using the identity from Equation A17 one can analytically show (Chavanis, 2011c) that, in the repulsive case $(a_s\ge 0)$, the equilibrium states are always stable (see Section 4.2) and that, in the attractive case $(a_s<0)$, the equilibrium states with $R>R_{\ast }$ are stable while the equilibrium states with $R<R_{\ast }$ are unstable (see Section 4.3). Therefore, $R_{\ast }$ is the minimum radius of stable equilibrium states.

In the noninteracting case $(a_s=0)$, using Equation A16 and the virial theorem $2{\mathrm{\Theta }}_Q+W=0$, we find that

${\omega }^2=-\frac{W}{I}=\frac{\nu }{\alpha }\frac{GM}{R^3}.(\mathrm{A18})$

Recalling that $R_{99}=\mu R$ and ${\rho }_0=M/({\pi }^{3/2}{R}^3)$ we obtain Equation (36). In the TF limit $(\hslash =0)$, using Equation A16 and the virial theorem $3U+W=0$, we find that ${\omega }^2=-2W/I$, which coincides with the Ledoux formula for a polytrope of index $n=1$. With the exact values of $W$ and $I$ that can be obtained analytically, we get ${\omega }_{\text{Ledoux}}=1.96{(GM/R_{\text{TF}}^3)}^{1/2}=2.21\sqrt{G{\rho }_0}$ (Chavanis, 2011c). The squared pulsation is studied as a function of the radius of the BEC in Chavanis (2011c) for an attractive or a repulsive self-interaction.

In the case of an attractive self-interaction, expanding the effective potential from Equation A12 to third order close to the maximum mass $M_{\text{max}}$, we obtain (Chavanis, 2016a; Chavanis, 2020c)

$\begin{array}{ll}\hfill \frac{V\left(R\right)}{V_0}& =\frac{1}{3R_{\ast }^3}{\left(R-R_{\ast }\right)}^3-\frac{2}{R_{\ast }}\left(1-\frac{M}{M_{\text{max}}}\right)\left(R-R_{\ast }\right)\hfill \\ \hfill & -\frac{1}{3}+\frac{5}{3}\left(1-\frac{M}{M_{\text{max}}}\right),\hfill \end{array}(\mathrm{A19})$

where $V_0=\nu G{M}_{\text{max}}^2/R_{\ast }$ or, more explicitly, $V_0=[{\sigma }^2{\nu }^{1/2}/{(6\pi \zeta )}^{3/2}]$$(\hslash m^{1/2}{G}^{1/2}/|a_s{|}^{3/2})$. Equation A19 is the normal form of a potential $V(R)$ close to a saddle-center bifurcation [see Figure 20 in Chavanis (2016a)]. With this approximation, the equation of motion Equation A10 of the fictive particle becomes

$\alpha M\frac{d^{2}R}{d{t}^2}=-\frac{V_0}{R_{\ast }^3}{\left(R-R_{\ast }\right)}^2+\frac{2V_0}{R_{\ast }}\left(1-\frac{M}{M_{\text{max}}}\right).(\mathrm{A20})$

This equation has been studied in (Chavanis, 2016a; Chavanis, 2020c), leading to the results reported in Section 4.3. The mass-radius relation close to $M_{\text{max}}$, corresponding to $V^{\prime }(R)=0$, is given by

$R-R_{\ast }=\pm \sqrt{2}{R}_{\ast }{\left(1-\frac{M}{M_{\text{max}}}\right)}^{1/2}.(\mathrm{A21})$

The upper sign corresponds to the stable branch $R>R_{\ast }$ and the lower sign corresponds to the unstable branch $R<R_{\ast }$. The squared radial pulsation of the BEC is

${\omega }^2=\pm \frac{2\sqrt{2}}{t_D^2}{\left(1-\frac{M}{M_{\text{max}}}\right)}^{1/2}=\frac{2}{t_D^2{R}_{\ast }}\left(R-R_{\ast }\right),(\mathrm{A22})$

where we have introduced the dynamical time $t_D={(\alpha /\nu )}^{1/2}{(G{\tilde{\rho }}_0)}^{-1/2}=(6\pi \zeta /\nu ){(\alpha /\sigma )}^{1/2}|a_s|\hslash /(G{m}^2)$ constructed with the characteristic density ${\tilde{\rho }}_0=M_{\text{max}}/R_{\ast }^3=[\sigma \nu /{(6\pi \zeta )}^2]G{m}^4/(a_s^2{\hslash }^2)$ (Chavanis, 2016a; Chavanis, 2020c). From these equations, we obtain

$\frac{dM}{dR}=-\frac{{\omega }^2}{2}\frac{M_{\text{max}}{t}_D^2}{R_{\ast }},(\mathrm{A23})$

which is a special case of the general identity from Equation A17 valid close to the critical point where $M_{\text{max}}=(\sigma /\nu ){\hslash }^2/G{m}^2{R}_{\ast }$.

The Gaussian ansatz approach has been generalized in Chavanis (2018b) to the case of a self-interaction potential comprising an attractive $|\psi {|}^4$ term and a repulsive $|\psi {|}^6$ term. It has also been generalized in Chavanis (2019b) in order to take into account the presence of a central black hole creating a potential $-G{M}_{\text{BH}}/r$. In particular, we have obtained the general expression of the maximum mass of an axion star with an attractive $|\psi {|}^4$ self-interaction $(a_s<0)$ in the presence of a central black hole. In the case where the self-gravity of the axion star can be neglected, this general expression reduces to [see Section 3.7.2 of Chavanis (2019b)]

$M_{\text{max}}=\frac{{\sigma }^2}{6\pi \zeta \lambda }\frac{{\hslash }^2}{G{M}_{\text{BH}}m|a_s|}(\mathrm{A24})$

with $\lambda =2/\sqrt{\pi }$. The prefactor is equal to $3\pi /(16\sqrt{2})=0.416$. An application of our Equation A24 giving the maximum mass of a dilute axion star in the presence of a central black hole (Chavanis, 2019b) has been recently developed in Gan et al. (2024) [see also Davies and Mocz (2020), Yin and Visinelli (2024) for related studies].

It is also possible to generalize the theoretical formalism developed in (Chavanis, 2017b) to a multispecies system of self-gravitating BECs described by the coupled GPP equations

$i\hslash \frac{\partial {\psi }_a}{\partial t}=-\frac{{\hslash }^2}{2m_a}\mathrm{\Delta }{\psi }_a+\frac{{\hslash }^3{\lambda }_a}{2m_a^{3}c}|{\psi }_a{|}^2{\psi }_a+m_a\mathrm{\Phi }{\psi }_a,(\mathrm{A25})$

$\mathrm{\Delta }\mathrm{\Phi }=4\pi G{\displaystyle \sum _a}|{\psi }_a{|}^2.(\mathrm{A26})$

The mass $M_a=\int |{\psi }_a{|}^{2}d\mathbf{r}$ of each species is conserved as well as the total energy

$\begin{array}{ll}\hfill E_{\text{tot}}& ={\displaystyle \sum _a}\frac{{\hslash }^2}{2m_a^2}\int |\nabla {\psi }_a{|}^{2}d\mathbf{r}\hfill \\ \hfill & +{\displaystyle \sum _a}\int \frac{{\hslash }^3{\lambda }_a}{4m_a^{4}c}|{\psi }_a{|}^{4}d\mathbf{r}+\frac{1}{2}\int \mathrm{\Phi }{\displaystyle \sum _a}|{\psi }_a{|}^{2}d\mathbf{r}.\hfill \end{array}(\mathrm{A27})$

Making a Gaussian ansatz (for each species) and adapting the procedure described in Section 8 of Chavanis (2017b) to the present situation we readily obtain the energy function

$E_{\text{tot}}={\displaystyle \sum _a}\frac{1}{2}\alpha M_a{\left(\frac{d{R}_a}{dt}\right)}^2+V\left(\{R_a\}\right)(\mathrm{A28})$

with the effective potential

$\begin{array}{ll}\hfill V\left(\{R_a\}\right)& ={\displaystyle \sum _a}\sigma \frac{{\hslash }^2{M}_a}{m_a^2{R}_a^2}+{\displaystyle \sum _a}\zeta \frac{{\hslash }^3{\lambda }_a{M}_a^2}{4m_a^{4}c{R}_a^3}\hfill \\ \hfill & -{\displaystyle \sum _{a,b}}2\sqrt{2}\nu G{M}_a{M}_b\frac{R_a^2}{{\left(R_a^2+R_b^2\right)}^{3/2}}.\hfill \end{array}(\mathrm{A29})$

This potential displays a wealth of regimes.

Appendix 3: TF approximation

We assume that the bosons have a repulsive self-interaction $(a_s>0)$. In the TF approximation, where the quantum potential is neglected, the equilibrium state results from the balance between the gravitational attraction and the repulsion arising from the $|\psi {|}^4$ self-interaction of the bosons. The system is equivalent to a polytrope of index $n=1$ (i.e. $\gamma =2$) with an equation of state of the form

$P=K_2{\rho }^2,(\mathrm{A30})$

where the constant $K_2$ may depend on the dimension of space $d$ (we leave it unspecified for the sake of generality). The condition of hydrostatic equilibrium can be reduced to a (linear) Helmholtz equation of the form

$\mathrm{\Delta }\rho +\frac{S_{d}G}{2K_2}\rho =0,(\mathrm{A31})$

which is equivalent to the Lane-Emden equation of index $n=1$ (Chavanis and Sire, 2004).

In $d=1$ dimension, the density profile is given by

$\rho \left(r\right)={\rho }_0\cos \left(\sqrt{\frac{G}{K_2}}r\right).(\mathrm{A32})$

The density vanishes at

$R_{\text{TF}}=\frac{\pi }{2}\sqrt{\frac{K_2}{G}}.(\mathrm{A33})$

The radius is independent of the mass. The central density is related to the mass by ${\rho }_0=\pi M/(4R)$.

In $d=2$ dimensions, the density profile is given by

$\rho \left(r\right)={\rho }_0{J}_0\left(\sqrt{\frac{\pi G}{K_2}}r\right).(\mathrm{A34})$

The density vanishes at

$R_{\text{TF}}=x_1\sqrt{\frac{K_2}{\pi G}},(\mathrm{A35})$

where $x_1=2.4048\dots$ is the first zero of Bessel function $J_0(x)$. The radius is independent of the mass. The central density is related to the mass by ${\rho }_0=x_{1}M/[2\pi J_1(x_1)R^2]=0.73725M/R^2$.

In $d=3$ dimensions, the density profile is given by

$\rho \left(r\right)={\rho }_0\frac{\sin \left(\sqrt{\frac{2\pi G}{K_2}}r\right)}{\sqrt{\frac{2\pi G}{K_2}}r}.(\mathrm{A36})$

The density vanishes at

$R_{\text{TF}}=\pi \sqrt{\frac{K_2}{2\pi G}}.(\mathrm{A37})$

The radius is independent of the mass. The central density is related to the mass by ${\rho }_0=\pi M/(4R^3)$. With $K_2=2\pi a_s{\hslash }^2/m^3$ we recover the results of Section 4 [see also Chavanis (2011c)].

Remark: In $d=2$ dimensions, it is possible to take into account the effect of a solid rotation $\mathrm{\Omega }$ while remaining axisymmetric (Chavanis, In preparation). For rotating polytropic cylinders of index $n=1$ the differential equation replacing Equation A31 is

$\mathrm{\Delta }\rho +\frac{\pi G}{K_2}\rho =\frac{{\mathrm{\Omega }}^2}{K_2}(\mathrm{A38})$

and its solution is

$\rho \left(r\right)=\left({\rho }_0-\frac{{\mathrm{\Omega }}^2}{\pi G}\right)J_0\left(kr\right)+\frac{{\mathrm{\Omega }}^2}{\pi G},(\mathrm{A39})$

where $k=\sqrt{\pi G/K_2}$. The density profile vanishes at some radius $R$ provided that

${\rho }_0>\frac{{\mathrm{\Omega }}^2}{\pi G}\frac{J_0\left(x_{\ast }\right)-1}{J_0\left(x_{\ast }\right)}=1.11\frac{{\mathrm{\Omega }}^2}{G},(\mathrm{A40})$

where $x_{\ast }=3.8317\dots$ corresponds to the first minimum of $J_0(x)$. In that case, the radius $R$ is related to the central density by

${\rho }_0=\frac{{\mathrm{\Omega }}^2}{\pi G}\frac{J_0\left(kR\right)-1}{J_0\left(kR\right)}.(\mathrm{A41})$

The radius of the rotating configuration lies in the interval $x_1\le kR\le x_{\ast }$. The density profile can be rewritten as

$\rho \left(r\right)=\frac{{\mathrm{\Omega }}^2}{\pi G}\left[1-\frac{J_0\left(kr\right)}{J_0\left(kR\right)}\right].(\mathrm{A42})$

The mass and the moment of inertia are related to the radius and to the angular velocity by

$M=\frac{{\mathrm{\Omega }}^2{R}^2}{G}\left[1-\frac{2J_1\left(kR\right)}{kR{J}_0\left(kR\right)}\right],(\mathrm{A43})$

$I=\frac{{\mathrm{\Omega }}^2{R}^4}{2G}\left[1+4\frac{kR{J}_3\left(kR\right)-2J_2\left(kR\right)}{k^2{R}^2{J}_0\left(kR\right)}\right].(\mathrm{A44})$

Using the Gaussian ansatz or the Ledoux formula, the squared pulsation is given by (Chavanis, 2017b)

${\omega }^2=\frac{G{M}^2}{I}-4{\mathrm{\Omega }}^2.(\mathrm{A45})$

Using Equations A43–A45 we can show that ${\omega }^2>0$ implying that the solutions are dynamically stable for any $\mathrm{\Omega }$ (Chavanis, In preparation).

Appendix 4: Mass-radius relation in $d$ dimensions

We briefly discuss the mass-radius relation of nonrelativistic self-gravitating BECs in $d$ dimensions [see Chavanis, In preparation; Chavanis (2023b) for details and for the values of $R_{\text{TF}}$, $M_{\text{min}}$, $M_{\text{max}}$ and $R_{\ast }$ mentioned below].

4.1 Repulsive self-interaction

When $d<4$, the mass-radius relation is monotonic. There is a stable equilibrium state for any mass $M$ and it has a radius $R\ge R_{\text{TF}}$. The radius decreases from infinity to $R_{\text{TF}}$ as the mass increases. The branch of noninteracting bosons is stable.

When $d=4$, the mass-radius relation presents a minimum. There is a stable equilibrium state for $M\ge M_{\text{min}}$ and it has a radius $R\ge R_{\text{TF}}$. The radius decreases from infinity to $R_{\text{TF}}$ as the mass increases from $M_{\text{min}}$. The branch of noninteracting bosons exists at a unique mass $M_{\text{min}}$ and it is marginally stable.

When $d>4$, the mass-radius relation presents a minimum. There is a stable equilibrium state for $M\ge M_{\text{min}}$ and $R_{\text{TF}}\le R\le R_{\ast }$ (the branch $R>R_{\ast }$ is unstable). The radius decreases from $R_{\ast }$ to $R_{\text{TF}}$ as the mass increases from $M_{\text{min}}$ ($R_{\ast }\to +\infty$ when $d=4$). The branch of noninteracting bosons is unstable.

These results show that the dimension of space $d=3$ of our universe is very particular as already found in the case of fermion stars (Chavanis, 2007). In particular, noninteracting fermion and boson stars are unstable in a universe of dimension $d>4$ (they are marginally stable in $d=4$).

4.2 Attractive self-interaction

When $d<2$, the mass-radius relation is monotonic. There is a stable equilibrium state for any mass $M$. The radius decreases from infinity to 0 as the mass increases.

When $d=2$, the mass-radius relation presents a maximum. There is a stable equilibrium state for $M\le M_{\text{max}}$. The radius decreases from infinity to 0 as the mass increases up to $M_{\text{max}}$. The maximum mass corresponds to the mass of a nongravitational BEC (Townes soliton). Its exact value is $M_{\text{max}}=0.465563\dots m/|a_s|$ (Chiao et al., 1964; Chavanis, In preparation).

When $2<d<4$, the mass-radius relation presents a maximum. There is a stable equilibrium state for $M\le M_{\text{max}}$ and $R\ge R_{\ast }$ (the branch $R<R_{\ast }$ is unstable). The radius decreases from infinity to $R_{\ast }$ as the mass increases up to $M_{\text{max}}$ ($R_{\ast }\to 0$ when $d=2$).

When $d\ge 4$, there is no stable equilibrium state (when $d=4$ the branch of noninteracting bosons exists at a unique mass $M_{\text{max}}=M_{\text{min}}$ and it is marginally stable).

Appendix 5: The gravitational instability of an infinite homogeneous BEC when the Coriolis force is acting and a magnetic field is present

The effect of a uniform rotation and a constant magnetic field on the Jeans instability of an infinite homogeneous self-gravitating system has been studied by Chandrasekhar (Chandrasekhar and Fermi, 1953; Chandrasekhar, 1954; Chandrasekhar, 1955) for a classical fluid. For a quantum fluid, we just have to make the substitution

$c_s^2\to c_s^2+\frac{{\hslash }^2{k}^2}{4m^2}(\mathrm{A46})$

in the linearized hydrodynamic equations (see Section 8.1). In this manner, the results of Chandrasekhar (Chandrasekhar and Fermi, 1953; Chandrasekhar, 1954; Chandrasekhar, 1955) can be generalized straightforwardly. The dispersion relation taking into account the Coriolis force, a magnetic field and the quantum potential is given by Equation 7 of Chandrasekhar (1954) where now

${\mathrm{\Omega }}_J^2=\frac{{\hslash }^2{k}^4}{4m^2}+c_s^2{k}^2-4\pi G\rho .(\mathrm{A47})$

As shown by Chandrasekhar (1954), the medium is stable if, and only if, ${\mathrm{\Omega }}_J^2>0$, which is precisely the quantum Jeans criterion from Equation 99. Therefore the condition for gravitational instability is unaffected by Corliolis and magnetic forces. There is, however, a particular case. This is when the direction of propagation of the perturbation is both perpendicular to the angular velocity $\mathbf{\Omega }$ and the magnetic field $\mathbf{B}$. In that case, the dispersion relation reduces to

${\omega }^2=\frac{{\hslash }^2{k}^4}{4m^2}+\left(c_s^2+c_A^2\right)k^2+4{\mathrm{\Omega }}^2-4\pi G\rho ,(\mathrm{A48})$

where $c_A=B/\sqrt{4\pi \rho }$ is the Alfvén velocity. The squared Jeans wavevector, which is determined by a second degree equation corresponding to Equation A48 with $\omega =0$ is given, when it exists and is positive, by

$k_J^2=\frac{-\left(c_s^2+c_A^2\right)\pm \sqrt{{\left(c_s^2+c_A^2\right)}^2-\frac{4{\hslash }^2}{m^2}\left({\mathrm{\Omega }}^2-\pi G\rho \right)}}{\frac{{\hslash }^2}{2m^2}}.(\mathrm{A49})$

Different cases can happen depending on the signs of ${\mathrm{\Omega }}^2-\pi G\rho$ and $c_s^2$. For example, in the classical case or in the TF regime $(\hslash =0)$, when $c_s^2>0$ and ${\mathrm{\Omega }}^2>\pi G\rho$ we see that ${\omega }^2>0$ so the medium is stable with respect to this type of perturbations. Otherwise, the Jeans wavenumber below which the medium is unstable is given by

$k_J^2=\frac{4\pi G\rho -4{\mathrm{\Omega }}^2}{c_s^2+c_A^2},(\mathrm{A50})$

which is different from the usual Jeans wavenumber $k_J^2=4\pi G\rho /c_s^2$. However, the situation when the direction of propagation of the perturbation is both perpendicular to the angular velocity $\mathbf{\Omega }$ and the magnetic field $\mathbf{B}$ is very particular (except in two dimensions) and, if we allow $\mathbf{k}$ to be in any direction, the system suffers the usual (quantum) Jeans instability.

Appendix 6: Theories of modified gravity

There exist several theories of modified gravity. One of them is the so-called Eddington-inspired Born-Infeld (EiBI) theory (Bañados and Ferreira, 2010). In the Newtonian limit, the EiBI theory generates a modified Poisson equation of the form

$\mathrm{\Delta }\mathrm{\Phi }=4\pi G\rho +2\pi G\kappa \mathrm{\Delta }\rho ,(\mathrm{A51})$

where $\kappa$ is a constant with the dimension of a squared length or the inverse of a cosmological constant $(\kappa \sim R^2\sim 1/\mathrm{\Lambda })$. If we introduce the “Newtonian” potential ${\mathrm{\Phi }}_N=\mathrm{\Phi }-2\pi G\kappa \rho$, we recover the usual GPP Equations 8 and 9 with an additional self-interaction potential $V(|\psi {|}^2)=\pi G\kappa |\psi {|}^4$. This is a quartic potential similar to the quartic potential of the standard BEC from Equation 10. The corresponding equation of state is $P=\pi G\kappa {\rho }^2$. Therefore, all the results established for the standard self-gravitating BEC in the Newtonian limit can be straightforwardly applied to the EiBI theory by simply making the substitution

$a_s\to a_s+\frac{\kappa G{m}^3}{2{\hslash }^2}.(\mathrm{A52})$

The case $\kappa >0$ corresponds to an effective repulsive self-interaction and the case $\kappa <0$ corresponds to an effective attractive self-interaction. The modified potential annihilates the physical self-interaction when $\kappa ={\kappa }_c=-2{\hslash }^2{a}_s/G{m}^3$.

Another theory of modified gravity consists in replacing the Poisson equation by the screened Poisson (or Yukawa) equation. This type of equations can also describe interactions different from the gravitational one. Therefore, we write it under the generic form

$\mathrm{\Delta }\varphi -\frac{1}{L^2}\varphi =g\rho ,(\mathrm{A53})$

where $L$ is a constant with the dimension of a length and $g$ is a coupling constant (positive or negative). In the strong screening limit $L\to 0$, i.e. for a short-range interaction, we obtain

$\varphi =-g{L}^2\rho -g{L}^4\mathrm{\Delta }\rho +\cdots (\mathrm{A54})$

This is similar to the Cahn-Hilliard expansion in soft matter physics. The first term leads to a self-interaction potential $V(|\psi {|}^2)=-\frac{1}{2}g{L}^2|\psi {|}^4$ corresponding to Equation 10. The second term is new in the BEC context and was originally introduced in Appendix N of Chavanis (2017b) [see also Chavanis (2018a), Chavanis (2023a)]. It leads to a generalized GP equation of the form

$i\hslash \frac{\partial \psi }{\partial t}=-\frac{{\hslash }^2}{2m}\mathrm{\Delta }\psi +m\frac{dV}{d|\psi {|}^2}\psi +m\mathrm{\Phi }\psi +m\chi \mathrm{\Delta }|\psi {|}^2\psi (\mathrm{A55})$

with $\chi =-g{L}^4$. The Jeans instability theory of Section 8 can be generalized straightforwardly by simply replacing $\hslash$ by ${\hslash }_{\text{eff}}=\sqrt{{\hslash }^2-4m^2\chi \rho }$ (Chavanis, 2017b; Chavanis, 2023a). We see that quantum effects disappear $({\hslash }_{\text{eff}}=0)$ when $\chi ={\chi }_c\equiv {\hslash }^2/(4m^2\rho )$. Furthermore, the effective Planck constant is positive for $\chi <{\chi }_c$ and imaginary for $\chi >{\chi }_c$, leading to new instabilities (Chavanis, In preparation). It is also possible to generalize the Gaussian ansatz of Appendix 2. We just have to add in $V(R)$ the potential

$W_{\chi }=-\kappa \frac{\chi M^2}{R^5}(\mathrm{A56})$

with $\kappa =3/(4\sqrt{2}{\pi }^{3/2})$ (Chavanis, 2017b). We then find that the mass-radius relation becomes

$M=\frac{\frac{2\sigma }{\nu }\frac{{\hslash }^2}{G{m}^{2}R}}{1-\frac{6\pi \zeta }{\nu }\frac{a_s{\hslash }^2}{G{m}^3{R}^2}+\frac{5\kappa }{\nu }\frac{\chi }{G{R}^4}}.(\mathrm{A57})$

Furthermore, one can show that the identity from Equation A17 remains valid in this more general situation. Under certain conditions, there is an extremum mass $M_{\text{ext}}$ at a radius $R_{\ast }$ determined by the second degree equation

$R_{\ast }^4+\frac{6\pi \zeta }{\nu }\frac{a_s{\hslash }^2}{G{m}^3}{R}_{\ast }^2-\frac{15\kappa }{\nu }\frac{\chi }{G}=0.(\mathrm{A58})$

In the noninteracting case $(a_s=0)$, when $\chi >0$, there is a maximum mass $M_{\text{max}}$ at a radius $R_{\ast }$ given by

$R_{\ast }={\left(\frac{15\kappa }{\nu }\frac{\chi }{G}\right)}^{1/4},M_{\text{max}}=\frac{3\sigma }{2\nu }\frac{{\hslash }^2}{G{m}^2{R}_{\ast }}.(\mathrm{A59})$

Stable equilibrium states only exist for $M<M_{\text{max}}$ and $R>R_{\ast }$. When $\chi <0$, there is a minimum radius

$R_{\text{min}}={\left(-\frac{5\kappa }{\nu }\frac{\chi }{G}\right)}^{1/4}(\mathrm{A60})$

at which $M\to +\infty$. The equilibrium states of any mass are stable.

In the nongravitational case $(G=0)$, when $a_s<0$ and $\chi <0$, there is a minimum mass $M_{\text{min}}$ at a radius $R_{\ast }$ given by

$R_{\ast }={\left(\frac{15\kappa }{6\pi \zeta }\frac{\chi m^3}{a_s{\hslash }^2}\right)}^{1/2},M_{\text{min}}=\frac{3\sigma }{6\pi \zeta }\frac{m{R}_{\ast }}{|a_s|}.(\mathrm{A61})$

Stable equilibrium states only exist for $M>M_{\text{min}}$ and $R_{\ast }/\sqrt{3}<R<R_{\ast }$. There is no stable equilibrium state in the other cases.

In the TF limit $(\hslash =0)$, the equilibrium states exist at a unique radius determined by the second degree equation

$R^4-\frac{6\pi \zeta }{\nu }\frac{a_s{\hslash }^2}{G{m}^3}{R}^2+\frac{5\kappa }{\nu }\frac{\chi }{G}=0.(\mathrm{A62})$