- 1 Redwood Center for Theoretical Neuroscience, University of California, Berkeley, CA, USA
- 2 Neuroscience Graduate Program, University of Southern California, Los Angeles, CA, USA
Neuronal oscillations appear throughout the nervous system, in structures as diverse as the cerebral cortex, hippocampus, subcortical nuclei and sense organs. Whether neural rhythms contribute to normal function, are merely epiphenomena, or even interfere with physiological processing are topics of vigorous debate. Sensory pathways are ideal for investigation of oscillatory activity because their inputs can be defined. Thus, we will focus on sensory systems as we ask how neural oscillations arise and how they might encode information about the stimulus. We will highlight recent work in the early visual pathway that shows how oscillations can multiplex different types of signals to increase the amount of information that spike trains encode and transmit. Last, we will describe oscillation-based models of visual processing and explore how they might guide further research.
Neural Oscillations in Early Sensory Systems
Oscillatory neural activity has been observed in the early stages of virtually every sensory system of animals, including insects, frogs and primates. For example, periodic activity has been recorded from olfactory organs (Bressler and Freeman, 1980 ; Laurent, 2002 ) as well as somatosensory (Ahissar and Vaadia, 1990 ; Ahissar et al., 2000 ), visual (Laufer and Verzeano, 1967 ; Neuenschwander and Singer, 1996 ; Arai et al., 2004 ) and auditory pathways (Langner, 1992 ; Eguiluz et al., 2000 ; Roberts and Rutherford, 2008 ).
Detecting Neural Oscillations
The strength of neural oscillations can be assessed in the time and frequency domains. In the time domain, oscillations in spike trains are often characterized by means of periodic peaks in the autocorrelogram (Figures 1 A,B); in the frequency domain, they are defined on the basis of peaks in the power spectrum (Figures 1 C,D). However, the autocorrelograms are subject to confounds caused by the refractory period and spectral peaks often fail to reveal weak rhythms. A new method, the oscillation score (Muresan et al., 2008 ) reduces these problems. It combines analyses in the time and frequency domains to indicate the strength of oscillations as one dimensionless number. Also, oscillations shared by local groups of cells can be detected in population responses, such as the local field potential (LFP) or in patterns of synaptic input.
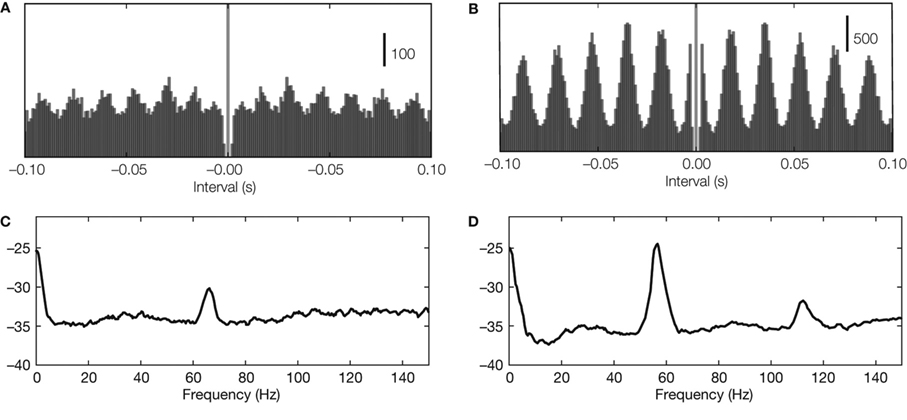
Figure 1. Detecting neural oscillations. (A,B) Oscillations in autocorrelations in two example recordings (spike trains recorded from LGN in cat) with oscillation score 10 and 29, respectively. (C,D) Oscillations in spectral power (same spike trains as used for panel A).
Sources of Oscillations
The mechanisms that generate oscillations are specific to sensory modality and brain region. Oscillations can be inherited from the temporal structure of the stimulus, as in the auditory system (Figure 2 A); originate from periodic movements of mechanical sensors, as in the rodent’s whisker system (Figure 2 B); be generated or amplified by electrical resonances of individual cells, as in auditory hair cells (Figure 2 C); or arise from intrinsic activity in recurrent neural networks, as in the olfactory system (Figure 2 D). At times, these mechanisms operate cooperatively to generate oscillations.
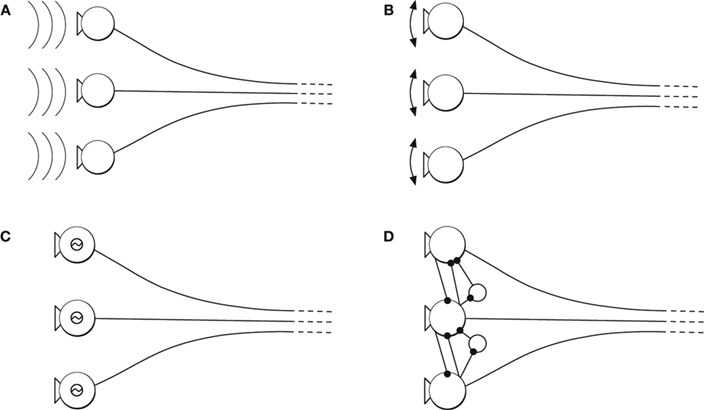
Figure 2. Origin of neural oscillations. (A) Oscillatory stimulus. (B) Oscillatory sensor movements (driven or resonance). (C) Oscillation from electrical resonance of individual cells. (D) Oscillatory intrinsic network activity due to recurrent network activity.
Functional Roles of Oscillations
Many studies have explored functional roles of neural oscillations. Work in sensory systems suggests that oscillations might improve the chance that neural activity propagates from one stage to the next. For example, oscillations might synchronize convergent inputs to a single postsynaptic cell (Usrey et al., 1998 ; Bruno and Sakmann, 2006 ) or drive downstream neurons at their preferred input frequency (Nowak et al., 1997 ; Hutcheon and Yarom, 2000 ; Fellous et al., 2001 ). Further, work in the auditory, somatosensory, olfactory and visual systems suggest that oscillations carry specific types of information about the stimulus.
Auditory system
Neural oscillations in the auditory system can be directly induced by the stimulus (Figure 2 A) and are often amplified by mechanical and electrical resonances (Figures 2 B,C). The periodicity of the spikes is phase-locked to the acoustic signal, and can be used to increase sensitivity to different features in the stimulus and sharpen tuning to specific frequencies (Eguiluz et al., 2000 ; Roberts and Rutherford, 2008 ). Information about the phase of the acoustic signal is also essential for spatial localization (Gerstner et al., 1996 ). Further, psychophysical studies suggest that the representation of acoustic phase in periodic spike trains forms the basis for the dual quality of pitch perception (Licklider, 1951 ; Langner, 1992 ; Patterson,2000 ).
Somatosensory system
Cyclical movements of the whiskers are reflected in neural oscillations in the rodent somatosensory system (Figure 2 B). The neural oscillations form a reference signal such that the spatial location of an obstacle is encoded in the phase at the time the whisker registers a contact (Ahissar et al., 2000 ; Szwed et al., 2003 ). In addition, high frequency oscillations have been proposed to encode the textures of surfaces (Brecht, 2006 ). Thus, work from the somatosensory system suggests that spatial structure in the stimulus is transformed to temporal structure in the spike train.
Olfactory system
Finally, in the olfactory system, neural oscillations are internally generated by recurrent feedback among neurons in sensory organs (Figure 2 D) (Bressler and Freeman, 1980 ). Thus, this case is different from the two previous examples, in which the neural oscillations represent external variables. Exploring the role of intrinsic versus extrinsic dynamics poses unique difficulties, but nonetheless has proven key to understanding how some forms of sensory information are analyzed (Freeman and Viana Di Prisco, 1986 ; Laurent, 2002 ). The olfactory bulb of zebra fish provides a good illustration. Information about complementary features of odors, identity and category, is encoded in the oscillating spike trains of single populations of neurons (Friedrich et al., 2004 ).
Information in Spike Trains
The discovery that the amount of force applied to the skin modulates the firing rate of peripheral nerves provided great insight into neural coding (Adrian and Zotterman, 1926 ). It led to the realization that features of sensory stimuli, like pressure, sound level or visual contrast are encoded by instantaneous spike rate. Rate coding of sensory information is, perhaps, the most successful paradigm for understanding how neurons convey information.
Techniques to estimate the amount of information transmitted by changes in spike rate (MacKay and McCulloch, 1952 ; Grüsser et al., 1962 ; Rieke et al., 1999 ; Brenner et al., 2000 ) are well established. But what if neural firing patterns are shaped not only by stimulus-evoked changes in rate, but also by intrinsic or extrinsic oscillations? How might one separate and measure the contribution of each component to the transmission of neural information? The next section discusses how to address this question.
Information in Spike Rate
The influence of a stimulus on the spike rate of a sensory neuron is usually estimated by recording neural responses to multiple repeats of the same stimulus. Firing rate during repeats of the stimulus is then averaged to obtain a peri-stimulus time histogram (PSTH). Thus, structure in the PSTH reflects temporal changes in the features of the stimulus to which the cell responded (Figure 3 A).
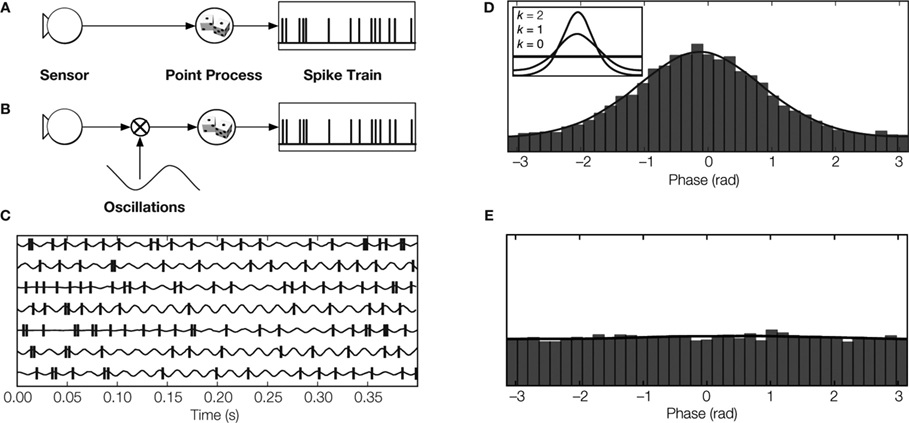
Figure 3. Modeling spike trains of sensory neurons. (A) Conventional rate coding: The spike train is modeled by a point process with an instantaneous rate that is modulated by the magnitude of the stimulus feature (Kuffler et al., 1957 ; Perkel et al., 1967 ). (B) Multiplicative model: The spike rate is modeled by a point process that is modulated by the product of the value of the sensory feature and an independent oscillatory signal. Thus, the spike train contains information about sensory stimulus and about oscillation phase (Berman, 1981 ; Koepsell and Sommer, 2008 ). (C) LGN spikes relative to oscillations detected in synaptic events originating from retinal ganglion cell spikes (Koepsell et al., 2009 ). (D Phase distribution of LGN spikes. The peak indicates phase locking. The inset depicts how the degree of phase-locking is parametrized by the so-called concentration parameter κ of the circular Von Mises distribution. (E) The phase distribution of LGN spikes relative to oscillation phase from previous trials (shift predictor) is flat, reflecting the fact that the oscillations are not locked to the stimulus.
By applying Shannon’s information theory, it is possible to quantify how much information the averaged spike rate (PSTH) conveys about the stimulus (MacKay and McCulloch, 1952 ; Grüsser et al., 1962 ; Rieke et al., 1999 ; Brenner et al., 2000 ). The result of this analysis, the information rate I (spike at t|stimulus), is usually given in bits per spike (or bits per second). In simple terms, the information rate corresponds to the mean number of yes/no questions one would have to ask in order to gather the amount of information conveyed by each action potential, or each second of the spike train.
Information in Neural Oscillations
Now consider the case of an oscillating neuron in a sensory pathway. The spike rate encodes the temporal structure of a stimulus and is also modulated by an oscillation that is not phase-locked to the onset of the stimulus (Figure 3 B). Therefore, the spikes are phase-locked rather than stimulus-locked. The PSTH, which reports averaged stimulus-evoked changes in spike timing, will not show evidence of the oscillation. This is because the phase of the oscillation varies randomly with respect to the stimulus onset; the periodic component evident during single trials of the stimulus is lost in the average. Thus, the information that the spikes carry about the oscillatory signal cannot be estimated by the standard methods.
We developed a new technique to estimate the amount of information that oscillating spike trains transmit (Koepsell and Sommer, 2008 ). It uses an oscillatory reference signal that can be extracted from various sources, for example, the simultaneously recorded LFP or presynaptic inputs. The reference signal is used to assign each spike in the train at time t a phase φ(t) (Figure 3 C). If there is a fixed relationship between the phase of the oscillation and the generation of spikes, the histogram of spike phases has a certain structure. Specifically, the histogram has a single peak if spikes are locked to a particular phase of the oscillation (Figure 3 D). Similarly, the shift-predictor of the histogram is flat (Figure 3 E) if the phase of oscillation varies relative to the onset of the stimulus.
We illustrate this technique by analyzing an oscillating spike train (Figures 3 B–E) that carries information about two messages: the stimulus feature that the spike rate encodes and the phase of the oscillation (Figures 3 C,D). Further, changes in firing rate evoked by the stimulus versus those induced by the oscillation occupy separate bands of the power spectrum of the spike train, so the two messages do not interfere with each other.
Conventional methods of estimating information in spike rates do not account for information encoded by oscillation phase, since they depend solely on the PSTH (which only reports changes in spike timing with respect to the stimulus). Our technique, the multiconditional direct method, measures both the stimulus and oscillation based information (Koepsell and Sommer, 2008 ). It uses a two-dimensional response histogram whose bins contain the average response for a given latency between the onset of the stimulus and a particular phase of the oscillation. The method yields estimates of I (spike at t|stimulus,φ(t)), the information contained in a single spike about the stimulus and the oscillation.
Because the multiconditional direct method relies on a higher dimensional response histogram than conventional PSTH-based methods, it requires substantial amounts of data. Such large datasets are difficult to acquire in the laboratory. Thus, we developed an alternative method to analyze small datasets, the phase de-jittering method (Koepsell et al., 2009 ). This method, in essence, uses the reference signal to align, or de-jitter, the oscillation phase across different repeats of the stimulus. This is done by shifting spikes in time, but with displacements so small that the structure of the spike train at low frequencies is unaltered. After de-jittering, the oscillation is retained in the PSTH and therefore it is possible to use conventional PSTH-based methods to estimate the information. Comparisons of the full multiconditional method and the de-jittering method applied to a surrogate dataset, show that both yield comparable results (Koepsell and Sommer, 2008 ).
Multiplexing with Periodic Spike Trains
In the previous section we explained how information multiplexing can occur in a single neuron, that is, the spike train conveys information about two different messages. We found that the two signals occupy separate frequency bands – a scheme called frequency division multiplexing . Spike trains that encode dual messages in this form are common in sensory pathways. Usually, information encoded by spike rate occupies the lower part of the frequency spectrum. This position reflects the temporal structure in the stimulus; the spectral power of natural signals decays with increasing temporal frequency (Ruderman and Bialek, 1994 ). By contrast, information encoded by the oscillations often resides in a separate high-frequency band, such as the gamma frequency range. For example, the frequency band of the stimulus to which auditory neurons phase-lock is usually higher than the acoustic modulation spectrum (Langner, 1992 ).
Examples for Multiplexing of Sensory Information
The transmission of oscillatory signals in spike trains can be used in various ways to convey sensory information. The frequency, phase or coherence of the oscillatory signal can convey sensory information in itself, as in the auditory system (Langner, 1992 ). The hippocampus provides an example of spike phase coding , in which the relative phases between spikes and an oscillatory signal carry sensory information. Specifically, the location of the animal can be resolved by decoding the relative phase between spikes fired by a place cell and the activity that produces the theta rhythm (OKeefe and Recce, 1993 ). Further, oscillatory signals can enable time division multiplexing within individual spike trains. Here, the idea is that different phases of the oscillation define temporal windows in which particular features of the stimulus are selectively transmitted. Thus, the rates measured in these different time windows encode different types of sensory signals. Such a coding scheme has been found in the olfactory system (Friedrich et al., 2004 ) and has also been proposed in theoretical work for other sensory systems (Masquelier et al., 2009 ; Nadasdy, 2009 ; Panzeri et al., 2010).
Multiplexing in the Visual System
Ongoing oscillations, those generated by the internal dynamics of the system, have been found at all stages of visual processing, from the retina to the cortex (Munk and Neuenschwander, 2000 ). In the cortex, oscillations reflect visual information in several different ways. Information about the stimulus is conveyed by the synchrony between two oscillating spike trains (Eckhorn et al., 1988 ; Gray and Singer, 1989 ; Samonds et al., 2006 ), in the relative phase between spikes and oscillations in the LFP (Montemurro et al., 2008 ; Kayser et al., 2009 ) and in the oscillations themselves (Kayser and Konig, 2004 ; Berens et al., 2008 ; Mazzoni et al., 2008 ). In addition to endogenous rhythms, the cortex also seems to inherit oscillations that emerge at earlier stages of the visual system (Neuenschwander and Singer, 1996 ; Castelo-Branco et al., 1998 ). The oscillations are observed in the absence (Doty et al., 1964 ; Heiss and Bornschein, 1966 ) and the presence of anesthetics [barbiturates (Heiss and Bornschein, 1965 ; Laufer and Verzeano, 1967 ), N2O and halothane (Neuenschwander and Singer, 1996 ; Castelo-Branco et al., 1998 ), propofol (Koepsell et al., 2009 )].
We recently asked how oscillations in the retina might be used by the thalamus to transmit information downstream. In particular, we asked how the spike trains of a single thalamic relay cell can transmit two separate streams of information, one encoded by firing rate and the other in oscillations (Koepsell et al., 2009 ). We used the technique of whole-cell recording in vivo, which allowed us to detect retinothalamic synaptic potentials and the action potentials they evoked from single relay cells. In other words, we were able to reconstruct the spike trains of the inputs and outputs of single relay cells. Often, we found that both spike trains had an oscillatory component. To explore whether these oscillations were able to encode information, we used the phase of the oscillation of the retinal inputs to de-jitter the timing of thalamic spikes across repeated trials of the stimulus (see Figures 1 and 3 C–E). The result of the realignment was dramatic, as illustrated in Figure 4 A. Although the oscillation was not visible in the raw PSTH, it generated a pronounced modulation in the amplitude of the PSTH made from the de-jittered signal (Figure 4 B).
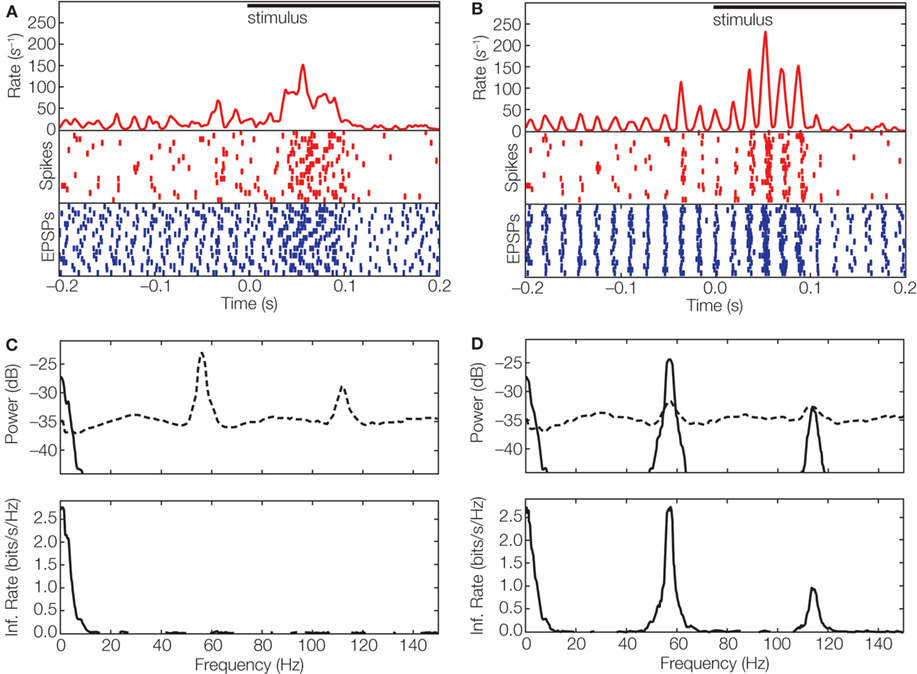
Figure 4. Multiplexed information in the visual system. (A) Event times aligned to stimulus onset displayed as averaged spike rate (red curve) and rasters for spikes (red), and EPSPs (blue) for 20 trials of a movie clip; spike rasters were smoothed with a Gaussian window (σ = 2 ms) before averaging. (B) Responses corrected for variation in latency ±10 ms by using periodicity in the ongoing activity that preceded stimulus onset; conventions as in (A). (C) Top, power spectrum of thalamic spike trains decomposed into signal (solid line) and noise (dashed line). Bottom, spectral information rate. The area under the curve corresponds to a total information rate of 12.7 bit/s; the mean spike rate 29 spikes/s yields a value of 0.4 bit/spike. (D) Power spectrum (top) of de-jittered spike train decomposed into signal (solid line) and noise (dashed line); spectral information rate (bottom). De-jittering increased the total information from 0.4 bit/spike (C) to 1.2 bit/spike (Koepsell et al., 2009 ). The movie stimulus was presented with 30 frames/s on a monitor witha high refresh rate (150 Hz). The neural response did not lock to the frame update or monitor refresh.
We then estimated the information in the de-jittered spike train. The results showed that most relay cells that received periodic synaptic inputs transmitted a significant amount of information in the gamma frequency band. For some cells, the amount of information in the oscillation-based (high frequency) channel was severalfold higher than that conveyed by rate-coded (low frequency) channel; compare Figure 4 C with Figure 4 D.
Potential New Roles for Oscillations
Gamma oscillations in retina and thalamus provide a novel channel that is able to convey information to the cortex. How might this channel contribute to visual function? In the following we outline various hypotheses about the potential roles for the new channel and how they might be tested.
One possibility we explore is the case in which the oscillatory trend of the retinal cell does not contain information about the visual stimulus. Even in this situation, the oscillations might increase the amount of information about local retinal features transmitted by the thalamic rate code. They would do so by a process akin to amplitude modulation, in which information about the retinal feature is reproduced in the frequency band of the oscillations. This redundant information could be read out and decoded in the cortex by various mechanisms, such as coincidence detection of afferent inputs or by the relative phase of the thalamic and cortical oscillations. A specific role for the second channel could be de-noising. Further, the amplitude modulation of the afferent spike train generates a signal that might enable cortical oscillations (e.g., by adjusting relative phases of the two oscillations) to route sensory information or to direct attention to a particular feature. (For discussion of potential roles of cortical oscillations in analyzing afferent input, see Buzsaki and Draguhn, 2004 ; Sejnowski and Paulsen, 2006 ; Fries et al., 2007 ).
A second possibility is that retinal oscillations are influenced by the stimulus, specifically, by displacements of the retinal image caused by eye movements. Thus, periodic activity in the retina might encode spatial information in the temporal domain, as in the whisker system (Ahissar and Arieli, 2001 ; Rucci, 2008 ). This idea is supported, at least in part, by the strong similarity between the dominant frequency bands in the LFP recorded from primary visual cortex and fixational eye movements [also note that oscillatory fixational eye movements are found in species ranging from turtle to humans (Greschner et al., 2002 ; Martinez-Conde et al., 2004 )]. Work that combines electrophysiology, measurements of eye-movements, and psychophysics should help to test this idea.
A third potential role for retinal oscillations involves computational analysis of visual stimuli. To explore this possibility, one must address two questions at the same time. First, one must determine which features of the stimulus are encoded by the oscillations. To address this question, it is helpful to recall that retinal oscillations are formed by distributed networks, and thus might be sensitive to spatially extensive features and/or context. Second, one must identify which particular attributes of the oscillations are used to encode information. Reasonable guesses include frequency, phase, relative phase, modulation of coherence among cells, or combinations of these parameters. The possible answers to these two questions are numerous, and this uncertainty precludes the design of physiological experiments. Thus, for the time being, the most promising approach to studying the computational roles of retinal oscillations in vision is to use computational models constrained by biological and psychophysical results. In fact, there are many models of oscillatory neural networks that are able to transform spatial structure of visual input into temporal structure of neural activity. These models, which were originally developed to simulate cortical computations, are built with phase-coupled oscillatory neurons (e.g., Baldi and Meir, 1990 ; Sompolinsky et al., 1991 ; Sporns et al., 1991 ; von der Malsburg and Buhmann, 1992 ; Schillen and Koenig, 1994 ; Wang and Terman, 1997 ; Ursino et al., 2006 ). It would be useful to develop such models to explore retinal and thalamic function.
Other families of models combine psychophysical results with approaches used in computer vision to determine how various image operations are able to reproduce visual perception and behavior. For example, recent work compared how well segmentation algorithms (Pal and Pal, 1993 ) matched the human ability to outline objects in images (Martin et al., 2004 ). State-of-the-art algorithms for edge detection and image segmentation approached human performance by combining local with non-local features of the image; algorithms based solely on local contrast were not successful.
Motivated by this work, we implemented the normalized cut algorithm for the computation of non-local features (Shi and Malik, 2000 ) in a network of oscillating neurons (Figure 5 ). Our preliminary results indicate that, over time, information about homogeneous image segments is encoded by different oscillation phases (Figure 5 B). Further, oscillatory spike trains are able to transmit this information as well as that about local contrast. In addition, synchronized spikes in the oscillating network provide information about edges (Figure 5 C). These results suggest that features like edge continuation, orientation, and border ownership – known to be represented by cortical firing rates – might already be available in the temporal structure of retinal activity.
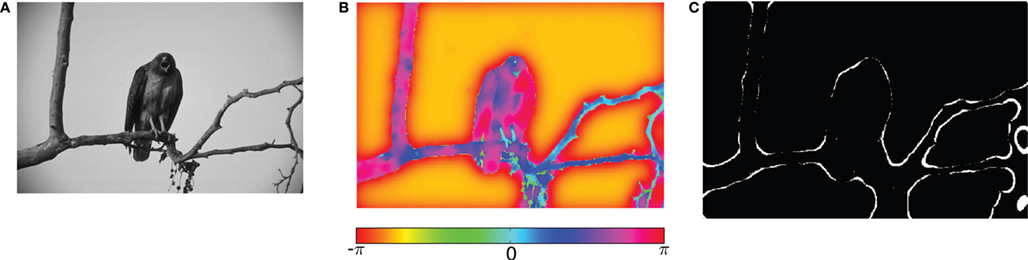
Figure 5. Visual processing using coupled oscillators. (A) Example image from the Berkeley segmentation database. (B) Phase representation in network of coupled phase oscillators ϕ(x) evolving according to the dynamic equation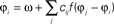 
with oscillation frequency ω, coupling function f(ϕj − ϕi) and local coupling constants cij that depend on similarity of pixel intensities. (C) Information represented by neurons spiking at a specific oscillation phase, a few cycles after the stimulus onset.
Unlike the case for mammalian vision, in which the function of oscillations remain subjects of debate, the behavioral role of gamma oscillations has been clearly established in the frog. Specifically, looming stimuli designed to simulate shadows (cast by predators) evoke synchronous oscillatory discharges in neural “dimming detectors”. By contrast, small dark spots that mimic prey fail to induce such activity (Ishikane et al., 1999 ). The consequence of the synchronous oscillations among retinal dimming detectors is important for an animal’s survival – it triggers escape behavior (Arai et al., 2004 ). Further strengthening the link between synchronous retinal activity and behavior, pharmacological suppression of gamma oscillations abolishes escape responses, but spares the slower modulation of spike rate evoked by small objects (Ishikane et al., 2005 ). Thus, in the frog, information about different types of visual signals seems to be multiplexed in different frequency bands of neural spike trains.
Summary
This review focused on research that explores the functional role of neural oscillations in the early stages of sensory pathways. We described neural oscillations that carry information about diverse sensory modalities, including olfaction, vision, audition and somatosensation. In particular, we discussed gamma oscillations in the early visual system, and showed how these form a novel channel that conveys information from the retina, via the thalamus, to the cortex. As well, we surveyed current techniques that are used to quantify the amount of information that oscillatory spike trains encode. Further, we summarized potential functions of oscillation-based channels in the periphery that are being actively explored by the community.
The work we have reviewed also bears on cortex (Eckhorn et al., 1988 ; Gray and Singer, 1989 ; Young et al., 1992 ; de Oliveira et al., 1997 ; Thiele and Stoner, 2003 ), where oscillations are generated by two sources: sensory afferents and intracortical networks. That is, we not only discussed the types of sensory information that oscillations carry downstream, but also described theoretical frameworks that can be applied to diverse cortical regions.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Tony Bell, Bruno Olshausen and the other members of the former Redwood Neuroscience Institute for helpful discussions. We thank Tim Blanche, Charles Cadieu, Jack Culpepper, and Christian Wehrhahn for valuable comments on the manuscript. Vishal Vaingankar, Yichun Wei, Qingbo Wang, Daniel Rathbun, and W. Martin Usrey contributed to the experiments we described. This work was supported by NIH grant EY09593 (Judith A. Hirsch), NSF grant IIS-0713657 (Friedrich T. Sommer), NSF grant IIS-0917342 (Kilian Koepsell), The Swartz Foundation (Kilian Koepsell), and the Redwood Neuroscience Institute (Friedrich T. Sommer, Kilian Koepsell). The data analysis, simulations and figures were produced using IPython (Pérez and Granger, 2007 ), NumPy/SciPy (Oliphant, 2007 ), and Matplotlib (Barrett et al., 2005 ).
Key Concepts
Neural oscillations: Neural oscillations are rhythmic patterns of activity. They are present in the intracellular voltage, individual spike trains and/or in local field potentials generated by populations of synchronized cells. Oscillations are usually detected by means of auto-correlations or spectrograms of the neural signal, e.g., Figure 1 .
Neural coding: Neural coding refers to the process by which one or more neurons encode information about sensory stimuli or other quantities. Typically, studies of the neural code focus on discerning which aspects of the stimulus are represented, the means by which the information is encoded in spike patterns, and how much information is conveyed, e.g., in bits per second, or bits per spike.
Rate coding: Sensory information is often encoded by changes in spike rate (the mean number of spikes in a given time interval).
Peri-stimulus time histogram: The peri-stimulus time histogram (PSTH) is a plot of spike rate during the stimulus. The PSTH is usually made by averaging responses to repeated presentations of the same stimulus.
Stimulus versus phase locking: Changes in spike rate that reliably occur with a fixed latency following the stimulus are “stimulus-locked.” If changes in firing are stimulus-locked, then the PSTH represents sensory information encoded by spike rate. When neurons are more likely to fire during one phase of an ongoing (reference) oscillation than during others, then their behavior is “phase-locked.” Phase-locking is visible in histograms of spike counts as a function of the oscillation phase (Figure 3 ).
Information multiplexing: This term refers to the case of a single signal, such as spike train, that carries different messages, each encoded in separate information channels. If different channels are displaced in the frequency or time domains, they will not interfere with each other.
Frequency division multiplexing: This is a subtype of “information multiplexing” in which the separate channels occupy different frequency bands in the spectrum of the signal, such as a spike train. Information can be encoded in the amplitude, phase or frequency modulation of a oscillatory reference signal.
Spike phase coding: In this scheme, information is encoded by the timing of spikes relative to the phase of a reference oscillation. The phase of the oscillation, at which a given spike is fired, is the “spike-phase.”
Time division multiplexing: This is a subtype of “information multiplexing” in which the separate channels occupy alternating time windows, or temporal segments, of the signal. The time windows can be defined with respect to the reference oscillation.
References
Adrian, E., and Zotterman, Y. (1926). The impulses produced by sensory nerve endings. J. Physiol. 61, 151–171.
Ahissar, E., Sosnik, R., and Haidarliu, S. (2000). Transformation from temporal to rate coding in a somatosensory thalamocortical pathway. Nature 406, 302–306.
Ahissar, E., and Vaadia, E. (1990). Oscillatory activity of single units in a somatosensory cortex of an awake monkey and their possible role in texture analysis. Proc. Natl. Acad. Sci. U.S.A. 87, 8935–8939.
Arai, I., Yamada, Y., Asaka, T., and Tachibana, M. (2004). Light-evoked oscillatory discharges in retinal ganglion cells are generated by rhythmic synaptic Inputs. J. Neurophysiol. 92, 715–725.
Baldi, P., and Meir, R. (1990). Computing with arrays of coupled oscillators: an application to preattentive texture discrimination. Neural. Comput. 2, 458–471.
Barrett, P., Hunter, J., Miller, J., Hsu, J., and Greenfield, P. (2005). matplotlib – A portable Python plotting package. In Astronomical Data Analysis Software and Systems XIV ASP Conference Series, Vol. 347, P. L. Shopbell, M. C. Britton and R. Ebert eds (San Francisco, Astronomical Society of the Pacific), pp. 91–95.
Berens, P., Keliris, G., Ecker, A., Logothetis, N., and Tolias, A. (2008). Feature selectivity of the gamma-band of the local field potential in primate primary visual cortex. Front. Neurosci. 2:199. doi:10.3389/neuro.01.037.2008.
Brecht, M. (2006). Good vibrations. Focus on texture signals in whisker vibrations. J. Neurophysiol. 95, 1307–1308.
Brenner, N., Strong, S., Koberle, R., Bialek, W., and Steveninck, R. (2000). Synergy in a neural code. Neural. Comput. 12, 1531–1552.
Bressler, S., and Freeman, W. (1980). Frequency analysis of olfactory system EEG in cat, rabbit, and rat. Electroencephalogr. Clin. Neurophysiol. 50, 19–24.
Bruno, R., and Sakmann, B. (2006). Cortex is driven by weak but synchronously active thalamocortical synapses. Science 312, 1622–1627.
Buzsaki, G., and Draguhn, A. (2004). Neuronal oscillations in cortical networks. Science 304, 1926–1929.
Castelo-Branco, M., Neuenschwander, S., and Singer, W. (1998). Synchronization of visual responses between the cortex, lateral geniculate nucleus, and retina in the anesthetized cat. J. Neurosci. 18, 6395–6410.
de Oliveira, S., Thiele, A., and Hoffmann, K. (1997). Synchronization of neuronal activity during stimulus expectation in a direction discrimination task. J. Neurosci. 17, 9248–9260.
Doty, R., Kimura, D., and Mogenson, G. (1964). Photically and electrically elicited responses in the central visual system of the squirrel monkey. Exp. Neurol. 10, 19–51.
Eckhorn, R., Bauer, R., Jordan, W., Brosch, M., Kruse, W., Munk, M., and Reitboeck, H. J. (1988). Coherent oscillations: a mechanism of feature linking in the visual cortex? Multiple electrode and correlation analyses in the cat. Biol. Cybern. 60, 121–130.
Eguiluz, V., Ospeck, M., Choe, Y., Hudspeth, A., and Magnasco, M. (2000). Essential nonlinearities in hearing. Phys. Rev. Lett. 84, 5232–5235.
Fellous, J., Houweling, A., Modi, R., Rao, R., Tiesinga, P., and Sejnowski, T. (2001). Frequency dependence of spike timing reliability in cortical pyramidal cells and interneurons. J. Neurophysiol. 85, 1782–1787.
Freeman, W., and Viana Di Prisco, G. (1986). Relation of olfactory EEG to behavior: time series analysis. Behav. Neurosci. 100, 753–763.
Friedrich, R., Habermann, C., and Laurent, G. (2004). Multiplexing using synchrony in the zebrafish olfactory bulb. Nat. Neurosci. 7, 862–871.
Gerstner, W., Kempter, R., van Hemmen, J., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–78.
Gray, C. M., and Singer, W. (1989). Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. U.S.A. 86, 1698–1702.
Greschner, M., Bongard, M., Rujan, P., and Ammermüller, J. (2002). Retinal ganglion cell synchronization by fixational eye movements improves feature estimation. Nat. Neurosci. 5, 341–347.
Grüsser, O., Hellner, K., and Grüsser-Cornehls, U. (1962). Die Informationsübertragung im afferenten visuellen System. Biol. Cybern. 1, 175–192.
Heiss, W., and Bornschein, H. (1965). Distribution of impulse of continuous activity of single optic nerve fibers. Effects of light, ischemia, strychnine and barbiturate. Pflugers. Arch. Gesamte. Physiol. Menschen. Tiere. 286, 1–18.
Heiss, W., and Bornschein, H. (1966). Multimodal interval histograms of the continuous activity of retinal cat neurons. Kybernetik. 3, 187–191.
Hutcheon, B., and Yarom, Y. (2000). Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 23, 216–222.
Ishikane, H., Gangi, M., Honda, S., and Tachibana, M. (2005). Synchronized retinal oscillations encode essential information for escape behavior in frogs. Nat. Neurosci. 8, 1087–1095.
Ishikane, H., Kawana, A., and Tachibana, M. (1999). Short-and long-range synchronous activities in dimming detectors of the frog retina. Vis. Neurosci. 16, 1001–1014.
Kayser, C., and Konig, P. (2004). Stimulus locking and feature selectivity prevail in complementary frequency ranges of V1 local field potentials. Eur. J. Neurosci. 19, 485–489.
Kayser, C., Montemurro, M., Logothetis, N., and Panzeri, S. (2009). Spike-phase coding boosts and stabilizes information carried by spatial and temporal spike patterns. Neuron 61, 597–608.
Koepsell, K., and Sommer, F. (2008). Information transmission in oscillatory neural activity. Biol. Cybern. 99, 403–416.
Koepsell, K., Wang, X., Vaingankar, V., Wei, Y., Wang, Q., Rathbun, D., Usrey, W., Hirsch, J., and Sommer, F. (2009). Retinal oscillations carry visual information to cortex. Front. Syst. Neurosci. 3:4. doi:10.3389/neuro.06.004.2009.
Kuffler, S., Fitzhugh, R., and Barlow, H. (1957). Maintained activity in the cat’s retina in light and darkness. J. Gen. Physiol. 40, 683–702.
Laufer, M., and Verzeano, M. (1967). Periodic activity in the visual system of the cat. Vis. Res. 7, 215–229.
Laurent, G. (2002). Olfactory network dynamics and the coding of multidimensional signals. Nat. Rev. Neurosci. 3, 884–895.
MacKay, D., and McCulloch, W. (1952). The limiting information capacity of a neuronal link. Bull. Math. Biol. 14, 127–135.
Martin, D., Fowlkes, C., and Malik, J. (2004). Learning to detect natural image boundaries using local brightness, color, and texture cues. IEEE Trans. Pattern Anal. Mach. Intell. 26, 530–549.
Martinez-Conde, S., Macknik, S., and Hubel, D. (2004). The role of fixational eye movements in visual perception. Nat. Rev. Neurosci. 5, 229–240.
Masquelier, T., Hugues, E., Deco, G., and Thorpe, S. (2009). Oscillations, phase-of-firing coding, and spike timing-dependent plasticity: an efficient learning scheme. J. Neurosci. 29, 13484–13493.
Mazzoni, A., Panzeri, S., Logothetis, N., and Brunel, N. (2008). Encoding of naturalistic stimuli by local field potential spectra in networks of excitatory and inhibitory neurons. PLoS Comput. Biol. 4, e1000239. doi:10.1371/journal.pcbi.1000239.
Montemurro, M., Rasch, M., Murayama, Y., Logothetis, N., and Panzeri, S. (2008). Phase-of-firing coding of natural visual stimuli in primary visual cortex. Curr. Biol. 18, 375–380.
Munk, M., and Neuenschwander, S. (2000). High-frequency oscillations (20 to 120 Hz) and their role in visual processing. J. Clin. Neurophysiol. 17, 341–360.
Muresan, R., Jurjut, O., Moca, V., Singer, W., and Nikolic, D. (2008). The oscillation score: an efficient method for estimating oscillation strength in neuronal activity. J. Neurophysiol. 99, 1333–1353.
Nadasdy, Z. (2009). Information encoding and reconstruction from the phase of action potentials. Front. Syst. Neurosci. 3:6. doi:10.3389/neuro.06.006.2009.
Neuenschwander, S., and Singer, W. (1996). Long-range synchronization of oscillatory light responses in the cat retina and lateral geniculate nucleus. Nature 379, 728–733.
Nowak, L., Sanchez-Vives, M., and McCormick, D. (1997). Influence of low and high frequency inputs on spike timing in visual cortical neurons. Cereb. Cortex 7, 487–501.
OKeefe, J., and Recce, M. (1993). Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3, 317–330.
Pal, N., and Pal, S. (1993). A review on image segmentation techniques. Pattern Recognit. 26, 1277–1294.
Panzeri, S., Brunel, N., Logothetis, N. K., and Kayser, C. (2009). Sensory neural codes using multiplexed temporal scales. Trends Neurosci. doi: 10.1016/j.tins.2009.12.001.
Patterson, R. (2000). Auditory images: How complex sounds are represented in the auditory system. Acoust. Sci. Technol. 21, 183–190.
Pérez, F., and Granger, B. (2007). IPython: a system for interactive scientific computing. Comput. Sci. Eng. 9, 21–29.
Perkel, D., Gerstein, G., and Moore, G. (1967). Neuronal spike trains and stochastic point processes: I. The single spike train. Biophys. J. 7, 391–418.
Rieke, F., Warland, D., van Steveninck, R., and Bialek, W. (1999). Spikes: Exploring the Neural Code. Cambridge, MIT Press.
Roberts, W. M., and Rutherford, M. A. (2008). Linear and nonlinear processing in hair cells. J. Exp. Biol. 211, 1775–1780.
Rucci, M. (2008). Fixational eye movements, natural image statistics, and fine spatial vision. Netw. Comput. Neural Syst. 19, 253–285.
Ruderman, D., and Bialek, W. (1994). Statistics of natural images: scaling in the woods. Phys. Rev. Lett. 73, 814–817.
Samonds, J., Zhou, Z., Bernard, M., and Bonds, A. (2006). Synchronous activity in cat visual cortex encodes collinear and cocircular contours. J. Neurophysiol. 95, 2602–2616.
Schillen, T., and Koenig, P. (1994). Binding by temporal structure in multiple feature domains of an oscillatory neuronal network. Biol. Cybern. 70, 397–405.
Sejnowski, T., and Paulsen, O. (2006). Network oscillations: emerging computational principles. J. Neurosci. 26, 1673–1676.
Shi, J., and Malik, J. (2000). Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 22, 888–905.
Sompolinsky, H., Golomb, D., and Kleinfeld, D. (1991). Cooperative dynamics in visual processing. Phys. Rev. A 43, 6990–7011.
Sporns, O., Tononi, G., and Edelman, G. (1991). Modeling perceptual grouping and figure-ground segregation by means of active reentrant connections. Proc. Natl. Acad. Sci. U.S.A. 88, 129–133.
Szwed, M., Bagdasarian, K., and Ahissar, E. (2003). Encoding of vibrissal active touch. Neuron 40, 621–630.
Thiele, A., and Stoner, G. (2003). Neuronal synchrony does not correlate with motion coherence in cortical area MT. Nature 421, 366–370.
Ursino, M., Magosso, E., La Cara, G., and Cuppini, C. (2006). Object segmentation and recovery via neural oscillators implementing the similarity and prior knowledge gestalt rules. Biosystems 85, 201–218.
Usrey, W., Reppas, J., and Reid, R. (1998). Paired-spike interactions and synaptic efficacy of retinal inputs to the thalamus. Nature 395, 384–387.
von der Malsburg, C., and Buhmann, J. (1992). Sensory segmentation with coupled neural oscillators. Biol. Cybern. 67, 233–242.
Wang, D., and Terman, D. (1997). Image segmentation based on oscillatory correlation. Neural. Comput. 9, 805–836.
Keywords: LGN, retina, visual coding, oscillations, multiplexing
Citation: Koepsell K, Wang X, Hirsch J and Sommer FT (2010) Exploring the function of neural oscillations in early sensory systems. Front. Neurosci. 4, 1: 53âÂÂ61. doi:10.3389/neuro.01.010.2010
Received: 01 October 2009;
Paper pending published: 09 November 2009;
Accepted: 10 December 2009;
Published online: 15 May 2010
Edited by:
S. Murray Sherman, University of Chicago, USAReviewed by:
Michael J. Friedlander, Baylor College of Medicine, USAJose-Manuel Alonso, Sociedad Espanola de Neurociencia, Spain; University of Connecticut, USA; State University of New York, USA
Naoum P. Issa, University of Chicago, USA
Copyright: © 2010 Koepsell, Wang, Hirsch and Sommer. This is an open-access publication subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Kilian Koepsell, Redwood Center for Theoretical Neuroscience, University of California Berkeley, 156 Stanley Hall, MC# 3220, Berkeley, CA 94720-3220, USA. e-mail: kilian@berkeley.edu; Friedrich T. Sommer, Redwood Center for Theoretical Neuroscience, University of California Berkeley, 156 Stanley Hall, MC# 3220, Berkeley, CA 94720-3220, USA. e-mail: fsommer@berkeley.edu