Multiphysics finite element investigation of galvanic transmission in dynamic human body communications

Introduction: Human body communication (HBC) utilizes the human body as a medium of communicating data. Considerable research has been done to characterize HBC channels to optimize communication techniques. However, dynamic HBC channels have been less studied.

Methods: An approach for developing dynamic models of the human body channel for galvanic communication is presented using multiphysics finite element analysis (FEA). An analytical framework is formulated that utilizes stochastic ABCD network parameters to explore and model dynamic HBC channel segments. Channel segments were subjected to mechanical forces using the finite element method (FEM) to reveal their impact on the current density and electric field.

Results: Linear regression modeling shows a strong relationship between applied force, current frequency, and channel response, with R² metrics exceeding 0.99. The dynamic nature of the channel reflects the need for stochastic modeling. This study examined candidate probability density functions (PDFs) to describe channel fading for the ABCD network parameters. Lognormal and Weibull distributions fit the magnitudes best while the generalized Pareto, generalized extreme value, and logistic distributions fit the phases best. Empirical modeling validated the accuracy of the lognormal distribution fits found using the FEM.

Discussion: The dynamic channel was characterized utilizing multiphysics FEM modeling, empirical modeling, and ABCD network parameters. This information is invaluable for EM dosimetry analysis and risk assessment in body area network (BAN) device design, as well as device optimization, because stochastic HBC parameters emulate the dynamic nature of the human body channel.

1 Introduction

Human body communication (HBC) utilizes the human body as a medium for communicating data (IEEE SA, 2008). HBC can be considered as an alternative to short-range RF communication when used for medical telemetry in body area networks (BANs) (Pereira et al., 2015). Research has shown that HBC achieves greater spectral efficiency, higher data rates, better security, and better power efficiency than radio-frequency (RF)-based BANs (Bae et al., 2012b; Cho et al., 2014; Seyedi and Lai, 2014; Ali et al., 2019; Sujaya and BhanuPrashanth, 2021). However, channel models are essential for analyzing and optimizing BAN performance. These models can be leveraged to develop application-specific physical layer (PHY) technologies (including, but not limited to, automatic gain control (AGC), channel equalization, and auto-encoders) that can be used to improve the performance of BAN transceivers to achieve better error performance, better receiver sensitivity, a higher data rate, better channel resilience, and power efficiency (Ali et al., 2019; Zhang et al., 2016b; Pereira et al., 2015). Furthermore, human body state (e.g., electrode location/state, action performed by body parts, and blood analyte concentration such as glucose) correlates with the channel response (Wang et al., 2016; Zhang et al., 2016a; Maity et al., 2018; Takamatsu et al., 2021; Roopnarine and Rocke, 2024; Tang et al., 2023; Chen et al., 2016; Ahmed et al., 2019). This type of data is crucial in medical use cases that require the monitoring of patients’ medical condition or athletes’ physical state to optimize their performance (Bouazizi et al., 2017; Smith, 2011; Dhamdhere et al., 2010). Thus, channel models are essential for BAN optimization, medical state determination, and RF safety.

Extensive research has developed channel models for the two main categories of HBC communication techniques: electric field HBC (eHBC), which involves modulating electric fields to communicate through galvanic and capacitive coupling, and magnetic HBC (mHBC), which involves modulating magneto-quasistatic fields through magnetic induction (e.g., Callejon et al., 2012a; Pereira et al., 2015; Ogasawara et al., 2014; Seyedi and Lai, 2014; Rocke and Persad, 2015; Wen et al., 2022; Ahmed et al., 2019; Chen et al., 2016; Vizziello et al., 2024; Noormohammadi et al., 2021). Each communication technique has its advantages. For example, mHBC offers channel resilience since the magnetic permeability of most materials is the same; capacitive coupling has a greater frequency range of operation that offers higher data rates; both mHBC and capacitive coupling allow for electrodes to be either on or close to the body, offering more versatility with regards to use cases; galvanic coupling offers more channel resilience against the body’s environment as it requires electrodes to be in contact with the body (Rocke and Persad, 2015; Pereira et al., 2015; Seyedi and Lai, 2014; Wen et al., 2022). This paper focuses on modeling galvanic coupling because this form of communication is standardized for HBC. However, this research can be easily extended to other HBC techniques.

Channels models can be derived from three methods.

1. Empirical measurements, which can provide channel response graphs over frequency/distance, channel response equations, statistical fitting to fading characteristics, coherence bandwidths, and coherence times (Seyedi and Lai, 2014; Zhang et al., 2016a; Maity et al., 2018; IEEE SA, 2008; Tang et al., 2023; Chen et al., 2016).

2. Analytical exploration, which can provide channel response equations and circuit models (Seyedi and Lai, 2014; Callejon et al., 2012a; Maity et al., 2018; Bae et al., 2012a).

3. Numerical simulations, which can provide channel response graphs over frequency/distance, channel response equations, and the visualization of electric fields and current distributions in the tissue (Callejon et al., 2014; Ahmed et al., 2019).

However, relatively limited emphasis has been placed on the effect of the dynamic state of the human body on the channel response. Analytical solutions typically explore the propagation of signals through the human body using Maxwell’s equations (Bae et al., 2012a). However, these solutions are closed-form and limited to standard geometries; they cannot model dynamic behavior that may cause irregular tissue deformations. In the literature surveyed, mostly empirical measurements were found to model dynamic channel behavior for HBC (Maity et al., 2018; Zhang et al., 2016b; Zhang et al., 2016a; Seyedi and Lai, 2014; Tang et al., 2023; Chen et al., 2016). Nonetheless, the fading characteristics found provide no insight into the electric field and current distribution of the body under such conditions. Furthermore, no study was found on the impact of externally applied forces to the skin on the body’s channel response in the HBC band (18.375–23.625 MHz). Maity et al. (2018) demonstrated channel loss and variability increases with decreasing pressure applied to electrodes through an empirical measurement study. However, that study was limited to the 1Hz-1 MHz frequency range and did not quantify the electrode pressures applied. HBC is standardized in the HBC band for galvanic communication (IEEE, 2012). Consequently, for standardized communication, HBC models must include the HBC band. Numerical solutions offer insight into complex structures by evaluating the foundation equations that defined the physics of a model proposed for experiments (Rocke and Persad, 2015).

Finite element method (FEM) analysis a type of numerical solution that allows the dynamic characterization of biological phenomena (Guo et al., 2011) and electro-quasistatic field visualization for defined HBC use cases (Callejon et al., 2014; Noormohammadi et al., 2021; Datta et al., 2021; Ahmed et al., 2019). This gives insight into the electrical transmission mechanism through human tissue, which is invaluable when considering radio frequency (RF) safety and transceiver optimization techniques. For example, Callejon et al. (2014) simulated current density and electric field strength across the tissue layers in the arm for different channel lengths and inter-electrode distances across 1 kHz to 1 MHz. However, for this study, the electric field visualizations of the cross-section of the arm shown did not include the HBC band. Ahmed et al. (2019) extended this work by considering different tissue thicknesses and bending angles, looking at the electric potential at the Rx for these dynamic conditions. Current density visualizations were provided at the 10 kHz frequency for some geometries where the thickness of the tissue composition was varied. Additionally, this study did not consider the HBC band. Datta et al. (2021) showed the electric field across and around an overly simplified geometry of the human body for capacitive coupling communication technique for frequencies under 1 MHz. They also investigated the variation of received voltages for different body postures and electrode configurations. However, there was no indication of the incorporation of the mechanical tissue properties which, when included, can affect the resultant bio-impedance of the body postures observed (Albulbul and Chan, 2012).

Mechanical deformations in dynamic channels lead to signal variations, commonly referred to as “fading”. This paper aims to identify and model the nature of these fading mechanisms. Consequently, to observe the electrical transmission mechanism for galvanic communication under dynamic channel conditions, this study addresses the above-mentioned research gaps through the following contributions.

• Novel framework: introduces a comprehensive framework that integrates multiphysics FEA with stochastic ABCD parameters for dynamic HBC analysis.

• Tissue deformation impact: highlights the role of tissue deformation on current distribution and EM parameters in galvanic communication.

• Linear relationship model: develops a regression model linking applied force, frequency, and channel response for improved HBC understanding.

• Stochastic characterization: identifies optimal probability distributions for ABCD parameters.

• Empirical validation: corroborates FEM model findings with empirical data, demonstrating the relevance of lognormal distribution in dynamic states.

• Broader applications: adapts the framework for various HBC communication modes and dynamic conditions, enhancing research applicability.

• Safety and design standards: insights contribute to compliance with safety standards and the optimization of wearable and implanted device designs.

This paper is organized as follows. Section 2 introduces the ABCD network parameter framework, outlines FEM model characteristics, and describes the empirical modeling approach. Section 3 presents the simulated and empirical results and analyzes them. Section 4 presents the conclusions made based on the results observed. This study extends Roopnarine et al. (2024).

2 Materials and methods

2.1 System model

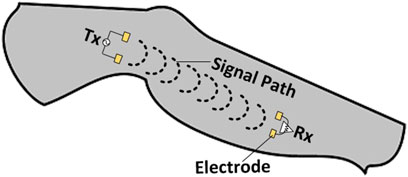
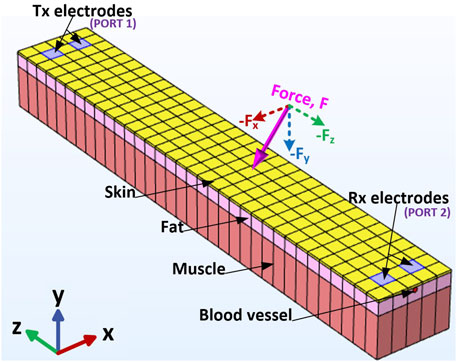
Galvanic coupling involves the application of a deferentially modulated signal through transmitter electrodes (Tx) directly in contact with the body (Figure 1). This induces galvanic currents, which are collected by receiver (Rx) electrodes also in direct contact with the body (Pereira et al., 2015).

Figure 1

Figure 1. Electrode configuration for galvanic coupling HBC.

Fading—the variation of channel gain—is related to bio-impedance since it affects the channel response. Several studies show that the electric field of the propagated signal is distributed through the different tissue layers (Callejon et al., 2012a; Callejon et al., 2012b, Callejon et al., 2014; Wang et al., 2016; Ahmed et al., 2019). Consequently, circuit-based analytical HBC channel models have been developed that incorporate the electrical parameters of the human body (Callejon et al., 2012a; Wang et al., 2016; Seyedi and Lai, 2014; Callejon et al., 2012b).

Bio-impedance, and by extension the channel response, is affected by the body’s state. Gabriel et al. (1996) demonstrated that the body’s circuit parameters depend on its electrical properties—tissue conductivity and permittivity. However, these properties are dependent on non-deterministic, time-varying factors such as channel geometry—for example, skin thickness, skin deformation (Albulbul and Chan, 2012; Maity et al., 2018), body posture (Datta et al., 2021) and presence of needle punctures (White et al., 2013)—and body chemical composition—for example, blood glucose concentration (Andersen et al., 2019). Bio-impedance is also different for different sections of the body and for subsections such as the dermis and epidermis skin layers (Tsai et al., 2019; Gabriel, 1996). The state of these sections also influences bio-impedance, such as if skin is wet or dry (Gabriel et al., 1996). The body’s biological condition (e.g., biological state of liver ischemia) influences bio-impedance (Tronstad and Strand-Amundsen, 2019).

The ABCD network parameters are essential for analyzing and optimizing human body communication (HBC) systems. The A and D parameters represent input and output voltage ratios that are vital in assessing signal gain and loss. At the same time, B and C describe the voltage–current relationship, thus revealing impedance and loading effects. Understanding these parameters enables the accurate modeling of signal propagation, efficient energy transfer, and enhanced reliability in dynamic environments. Integrating ABCD parameters into the channel model provides a robust framework for improving HBC performance and guiding design strategies.

ABCD network parameters are used in this study because of their effectiveness in modeling segmented systems as a transmission line. Callejon et al. (2012a) demonstrated that the human body can be modeled as a static transmission line consisting of a series of cascaded two-port networks to analyze signal propagation. Our research extends this by introducing ABCD parameters, leveraging the premise that two-port networks can model the channel response of individual tissue segments. This segmented approach allows for the cascading of segments to represent the entire channel as a lossy transmission line, as in transmission line theory (Notaros, 2010; Ulaby et al., 2010). Thus, any cascade can then be used to represent the entire length of the channel. The stochastic model is based upon the traditional use of deterministic ABCD parameters to model transmission lines (Callejon et al., 2012a; Ulaby et al., 2010; Notaros, 2010). Our approach involves extending this ABCD framework by introducing stochasticity to the ABCD parameters of each of these tissue segments, acknowledging the inherent randomness in tissue properties. This enables us to explore the resulting PDFs that describe the transmission parameters of the entire channel under dynamic conditions, thereby providing insights into dynamic channel fading.

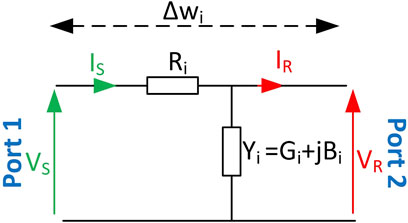
Accordingly, the human body channel is seen as non-deterministic and time-varying. This work proposes that the human body be modeled as a lossy transmission line divided into differential segments, such that the $i^{th}$ body segment, $\mathrm{\Delta }{w}_i$, is depicted in Figure 2. Hence, each differential segment of the human body channel, $\mathrm{\Delta }{w}_i$, is modeled as an ABCD 2-port network shown in Equation 1.

$\begin{array}{cc}\hfill {\mathbf{\Gamma }}_{\mathit{i}}& =\left[\begin{array}{cc}\hfill A{w}_i\hfill & \hfill B{w}_i\hfill \\ \hfill C{w}_i\hfill & \hfill D{w}_i\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill R_i{Y}_i+1\hfill & \hfill R_i\hfill \\ \hfill Y_i\hfill & \hfill 1\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}\hfill \left(R_i{G}_i+1\right)+j{B}_i\hfill & \hfill R_i\hfill \\ \hfill G_i+j{B}_i\hfill & \hfill 1\hfill \end{array}\right].\hfill \end{array}(1)$

Figure 2

Figure 2. Transmission line representation for the $i^{th}$ body segment.

The circuit parameters chosen are based on the work of Callejon et al. (2012a) where:

• $Y_i=G_i+j{B}_i$, the segment admittance consisting of the aggregate tissue conductance, $G_i$, and susceptance, $B_i$, which are responsible for coupling between the conductive pathways of the segment; and

• $R_i$, the series resistance of the segment which is responsible for signal propagation between cells.

This on-body segmented model allows for the representation of fading caused by random channel response variations that stem from bio-impedance fluctuations. ${\mathbf{\Gamma }}_{\mathit{i}}$ is a 2 × 2 matrix representing the ABCD parameters for the $i^{th}$ segment. Each element in ${\mathbf{\Gamma }}_{\mathit{i}}$ is a complex-valued random process with probability density functions (PDFs) dependent on $R_i$, $G_i$ and $B_i$ (designated as $f_{R_i}$, $f_{G_i}$ and $f_{B_i}$ respectively). Thus, ${\mathbf{\Gamma }}_{\mathit{i}}$ is a random process continuous-valued, discrete-parameter random matrix, consisting of random processes $A{w}_i$, $B{w}_i$, $C{w}_i$ and $D{w}_i$, with index set $i=\{1,\dots ,N\}$, where $N$ is the number of $\mathrm{\Delta }{w}_i$ segments that aggregate to form the channel. The channel length under observation is $L={\sum }_{i=1}^N\mathrm{\Delta }{w}_{Li}$, where $\mathrm{\Delta }{w}_{Li}$ is the length of the $i^{th}$ segment.

ABCD network modeling allows for the entire human body channel under observation to be represented as an aggregate two-port network equivalent to the cascade of the $N$ differential $\mathrm{\Delta }{w}_i$ two-port networks. This forms the resultant HBC network representation under matrix multiplication, as shown in Equation 2:

$\mathbf{\Gamma }={\displaystyle \prod _{i=1}^N}{\mathbf{\Gamma }}_{\mathit{i}}=\left[\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill C\hfill & \hfill D.\hfill \end{array}\right](2)$

Thus, $\mathbf{\Gamma }$ is the end-to-end channel ABCD matrix as a result of cascading all the ${\mathbf{\Gamma }}_{\mathit{i}}$ ‘s in the channel.

This approach can be extended to the other HBC communication modes (i.e., capacitive coupling and galvanic coupling) through modification of the $\mathrm{\Delta }{w}_i$ equivalent circuit to reflect the signal pathways in the channel.

2.2 Multiphysics finite element dynamic HBC model

The FEM model was derived using COMSOL multiphysics software through geometry design, material assignment, multiphysics selection, boundary condition assignment, mesh selection, domain configuration, and result processing configuration.

2.2.1 Geometry and model parameters

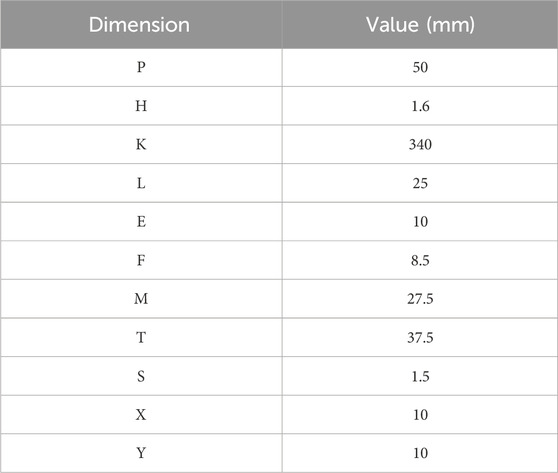
The geometry modeled is a multi-layered cuboid section of human tissue consisting of four tissue components—skin, fat, muscle, and a blood vessel—with Tx and Rx electrode pairs placed on-body (Figure 3). The model dimensions are captured in Table 1. These tissue component thicknesses are within the range of the true human anatomical dimensions, similar to Callejon et al. (2012a), Wegmueller et al. (2007), Persad and Rocke (2020), and DeSaix et al. (2013). The dielectric properties of the tissue components (i.e., permittivity, $ϵ$, and conductivity, $\sigma$) were chosen based on the Cole–Cole model by Gabriel et al. (1996) to capture their frequency response when subject to electro-quasistatic fields in the HBC band (Gabriel, 1996).

Figure 3

Figure 3. Geometry design for the proposed FEM model through (A) transverse section view and (B) plan view.

Table 1

Table 1. Geometry dimensions for the FEM model proposed.

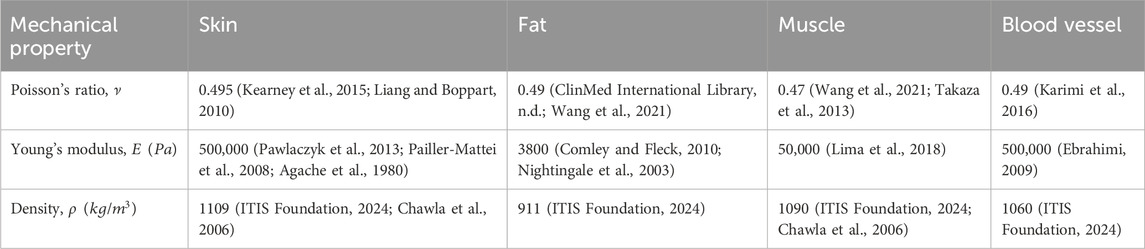
The mechanical properties of the tissue components (i.e., Young’s modulus, $E$, Poisson’s ratio, $\nu$, and density, $\rho$) were chosen based on the mechanical properties of human tissue used and derived in the literature surveyed. This is captured in Table 2.

Table 2

Table 2. Mechanical properties used for the FEM model.

2.2.2 Model equations

The FEM model proposed was derived using COMSOL Multi-physics 5.5 through the physics of electrical currents, electrical circuits, and solid mechanics. The electrical currents and circuit physics are deployed through the AC/DC module which solves the current conservation equation based on Ohm’s law—and, by extension, Kirchhoff’s conservation laws for the voltages, currents, and charges associated with the circuit elements—using the scalar electrical potential as the dependent variable, as shown in Equations 3–5.

$\nabla .\mathit{J}=Q_{j,v},(3)$

$\mathit{J}=\sigma \mathit{E}+j\omega \mathit{D}+{\mathit{J}}_e,(4)$

$\mathit{E}=-\nabla V(5)$

where $\mathit{J}$ is current density $[A/m^2]$, $Q_{j,v}$ is an external current source $[A/m^3]$, $\sigma$ is the electrical conductivity $[S/m]$, ${\mathit{J}}_e$ is an externally generated current density $[A/m^2]$, $\mathit{E}$ is the electrical field intensity $[V/m]$, $V$ is scalar electrical potential $[V]$, $\mathit{D}$ is electrical displacement $[C/m^2]$, and $\omega$ is angular frequency $[rad/s]$.

In accordance with the convention for galvanic communication, a differential signal was applied across the Tx electrodes by setting the Dirichlet boundary condition to a voltage of amplitude $V_0=1V$ of frequencies in the HBC band. $V_0$ is specified as peak voltage (COMSOL Multiphysics, 2019). The channel was surrounded by an external layer of air (a sphere surrounding the channel of radius $272mm$) configured as electric insulation by setting the Neumann condition, $\mathit{n}.\mathit{J}=0$, where $\mathit{n}$ is the surface normal. Thus, the air domain was considered an external unbounded domain. A resistor component is assigned between the Rx electrodes to read the electrical parameters necessary to derive the ABCD parameters for developing the FEM model. Separate reference nodes for the Rx and Tx pairs were configured, with Dirichlet boundary conditions of $0V$ through the relevant physics, to ensure that the Tx and Rx ports were decoupled.

The solid mechanics physics is deployed through the structural mechanics module, which solves equations of motion together with a constitutive model for a solid material to compute displacements, stresses, and strains as shown in Equation 6.

$0=\nabla .{\left(FS\right)}^T+{\mathit{F}}_V,F=I+\nabla \mathit{u},(6)$

where $F$ is the deformation gradient, $S$ is second Piola–Kirchhoff stress $[N/m^2]$, ${\mathit{F}}_V$ is the force per unit volume vector $[N/m^3]$, $I$ is the unit tensor, and $\mathit{u}$ is the displacement field $[m]$.

Each tissue component was configured to be linear elastic material to emulate the effects of applying practical, small-signal external stresses expected under normal operating conditions. The bottom surface of the FEM channel model, under the muscle tissue component, was configured to be a fixed constraint (i.e., its displacements are zero in all directions) to model the multi-layered tissue’s contact with bone. A boundary load, or force $F_{\mathit{tot}}$ in $[N]$, was applied on the upper surface of the FEM model, on the skin tissue component, to emulate pushes and pulls on the model’s surface from human activities (Lee and Jung, 2017).

2.2.3 Model computation

The simulation software discretizes the channel into finite elements using physics-controlled meshing sequences, which create meshes that consist of different element types and size features, to solve the applicable model equations defined in Section 2.2.2. When these model equations are solved, the relevant field parameters can be extracted to formulate the FEM model.

Recall that this FEM model focusing on the HBC band as galvanic communication is standardized at those frequencies (IEEE, 2012). The electrical length of the human body and signal frequency in the HBC band show that the communication scenario observed satisfies that of electro-quasistatics. However, as the signal frequency becomes larger, the quasistatic assumption may not hold, as propagation and inductive effects may become more significant. Thus, to avoid invalidating the quasistatic assumption, the frequencies are kept under 100 MHz. With galvanic communication, the electrical field is mostly localized to the human body (Callejon et al., 2014). The dimensions of the external layer of air were selected based on the extent of the electrical field observed by Callejon et al. (2014) and to accommodate the geometric deformations applied in this study.

2.2.4 Simulations

The channel was deformed with forces applied on the skin’s surface, ranging in magnitude from −30 N to 30 N in 1 N increments. These force magnitudes were selected based on research from typical activities involving the human body, such as pinching, gripping an object (Lee and Jung, 2017; Wells and Greig, 2001), tactile forces (Tang et al., 2015), indentations from micro-needles (Groves et al., 2012), and internal muscle activations (Steenbrink et al., 2009). All of these activities exert forces on the skin in various directions. In reality, the skin is subject to forces in multiple directions. Thus, this study applied mechanical forces to simulate pressing and pulling forces on the tissue.

For each of these deformations, the Tx electrodes were excited with $V_0$ of frequencies in the HBC band (18.375–23.625 MHz in 0.25 MHz increments). Each voltage was injected with two different load resistances ($1\mathrm{\Omega }$ and $1000\mathrm{\Omega }$) between the Rx electrodes to compute ABCD parameters. This data was used to determine the relationship between the $ABCD$ network parameters, force applied, $F$, and frequency of the voltage used, $f$.

The electric field, current density, and voltage field distributions were simulated on the cross-sectional plane corresponding to the Tx electrodes in the $x-y$ plane of the channel at different channel lengths ($0cm$, $5cm$, $15cm$, and $30cm$) over different frequencies ($18.375MHz,21.125MHz$ and $23.625MHz$) under different deformation forces ($-30N$,-$15N$, $0N$, $+15N$ and $+30N$). Insights into the electric field penetration of the channel were acquired by determining the average electric field magnitude and current density magnitude for each tissue component under different deformation forces ($-30N$,-$15N$, $0N$, $+15N$, and $+30N$). Negative forces represent pressing forces onto the skin while positive forces represent pulling on the skin.

The channel was divided into $\mathrm{\Delta }w$ segments, each composed of all tissue components, $1cm\times 5cm\times 3.75cm$ (Figure 4). The ABCD parameters were determined, using the currents and voltages at input and output ports recorded from the simulation for each$\mathrm{\Delta }w$ segment as well as the whole channel between the Tx and Rx electrodes; $A$ is the reverse voltage transfer ratio (or inverse channel gain), $B$ is the short circuit resistance, $C$ is the open circuit conductance, and $D$ is the reverse current transfer ratio. These values were subsequently used to perform dispersion and correlation analyses between $\mathrm{\Delta }w$ segments.

Figure 4

Figure 4. 3D view of the channel divided into $\mathrm{\Delta }w$ segments.

2.3 Empirical dynamic HBC model

The objective of this section is to empirically examine the distributions that the ABCD parameters tend toward under typical forces applied during every day dynamic activities. This analysis serves to validate the channel response distributions obtained through numerical simulations—one of the areas for further study identified by Roopnarine and Rocke (2021).

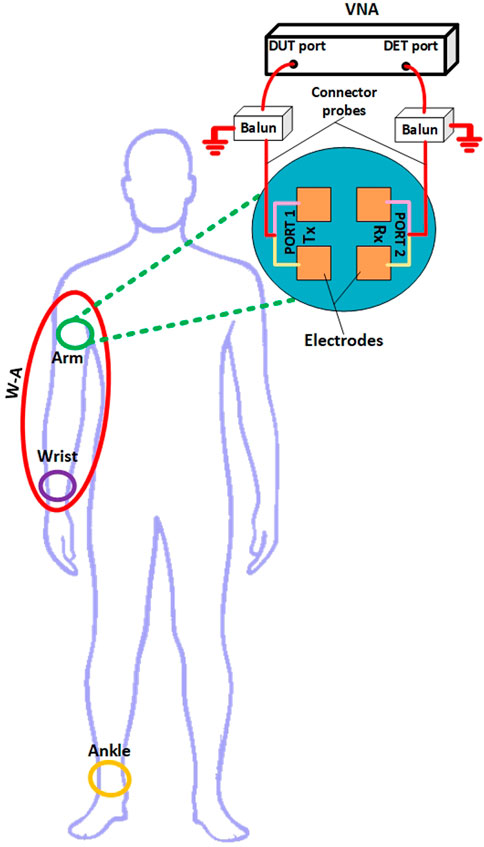
Thus, in addition to previously simulations, the candidate PDFs were examined through channel measurements of typical dynamic conditions expected in HBC use cases. The conditions studied in both simulation and empirical research were aligned to ensure consistency in the scenarios being tested. Multiple scans with averaging were used during measurements to control for experimental error, improving the reliability of the results. Transmit (Tx) and receive (Rx) electrodes, spaced 10 mm apart, were placed on a human subject in the general locations shown in Figure 5 (arm, wrist, and wrist-arm). These electrodes were connected to the Anritsu MS46122B vector network analyzer (VNA), which was used to measure the S-parameters ($S_{11}$, $S_{12}$, $S_{21}$, and $S_{22}$ through reflection and transmission mode configurations) of the channel in the general locations isolated. The Tx and Rx ports were decoupled using FTB-1-1+ Baluns. The VNA connections are also shown in Figure 5. These S-parameters were measured with a human in various states: fist clenching, writing, a bicep curl without weight, a bicep curl with weight, rotating ankle, walking, and marching. In these states, forces were naturally applied to the skin, affecting channel behavior. These S-parameters were then converted to ABCD parameters in alignment with the analytical framework outlined in Section 2.1 (Blattenberger, 2023). The VNA was calibrated to offset the effect the connector probes have on the channel response. Additionally, averaging was used to minimize measurement noise. These measurements were taken across the HBC band ($18.375MHz,21.125MHz$ and $23.625MHz$). Additionally, the output power of the VNA was set to 0dBm to comply with the ICNIRP standard for general exposure for humans (International Commission on Non-Ionizing Radiation Protection ICNIRP, 1998).

Figure 5

Figure 5. Electrode locations used for empirically deriving the stochastic, dynamic channel model.

After acquiring the data, both the empirical and simulated results were compared following simulation validation. This comparison helped identify candidate distributions for dynamic fading, capturing the stochastic nature of the dynamic HBC channel. The agreement between the simulated and measured data helped ensure that the identified PDFs could reliably represent the channel dynamics under typical HBC conditions.

3 Results and discussion

The results and analysis are broken into field-based analysis and analysis of the stochastic dynamic HBC channel model.

3.1 EM-based field analysis

Electromagnetic (EM)-based field analysis is an important aspect of electromagnetic EM dosimetry and risk assessment. In wearable and implanted system design, simulating the distribution of electric field intensity in the different tissues is essential for i) understanding the potential effects of EM radiation on human health, ii) ensuring compliance with applicable safety standards, iii) optimizing device design, and iv) facilitating personalized dosimetry analysis.

Figure 6 shows the current passing through a cross-sectional plane of the tissue components located at distances 0, 10, 20, and 30 cm (i.e., at the Rx electrodes) from the Tx electrode. These results show that the tissue current density decreases as the distance from the Tx increases, consistent across all tissue components, similar to observations made by Callejon et al. (2014) at frequencies outside of the HBC band. Additionally, the applied force significantly impacts the distribution of current density in each tissue component. Although changes in the applied pressing force cause relatively minor variations in current density, pulling force deformations notably increase the current density across all tissue components, except near the Tx electrodes. This is likely because deformation alters the geometry of the skin, increasing the cross-sectional area through which current flows, which in turn reduces resistance and impacts the current distribution.

Figure 6

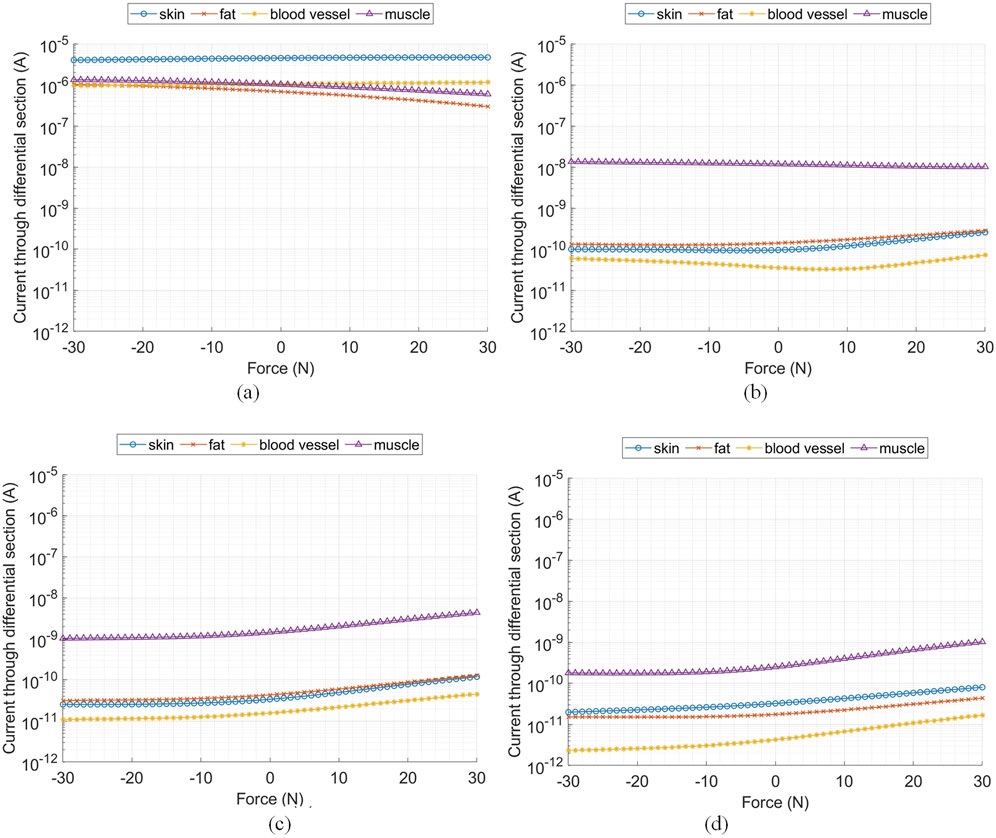
Figure 6. Current passing through various cross-sectional planes of the tissue components at 21 MHz, located at (A) Tx electrodes, (B) 10 cm from the Tx electrodes, (C) 20 cm from the Tx electrodes, and (D) 30 cm from the Tx electrodes.

Figure 7 shows the percentage of the electric field intensity, $E$, for deformed tissue components of skin, blood, fat, and muscle respectively over the entire channel length. These results show that, excepting muscle tissue, increasing a downward force on all tissues decreases the percentage of $E$ across all tissue components. In contrast, increasing the downward force in the muscle increases the percentage $E$. Furthermore, with the exception of blood, changes in the percentage $E$ remain relatively flat across frequency. Most of $E$ is concentrated in the fat, followed by muscle, skin, then blood. Knowing the E-field distribution across these different tissue layers allows for better optimization of the communication system design process as well as RF safety completeness checks (International Commission on Non-Ionizing Radiation Protection ICNIRP, 1998).

Figure 7

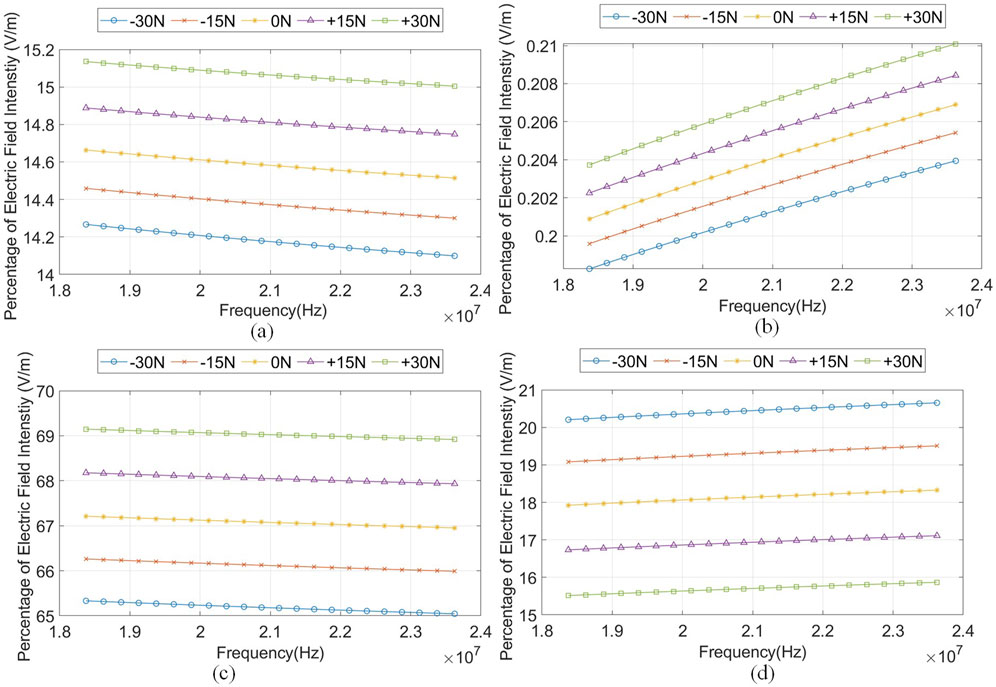
Figure 7. The percentage of electric field intensity, $E[V/m]$, when subjected to different forces. for the tissue components (A) skin, (B) blood, (C) fat, and (D) muscle.

Figure 8 shows the percentage of electric current density, $J$, for tissue components skin, blood, fat, and muscle, respectively, over the entire channel length. Similar to $E$, with the exception of muscle tissue, the percentage current density decreases with increasing downward force on all tissues. Increasing the downward force in muscle increases the percentage $J$. Furthermore, changes in the percentage $J$ remain relatively flat across frequency across all tissues. Most of $J$ is concentrated in muscle, followed by skin, fat, then blood, similar to the static study of Callejon et al. (2014).

Figure 8

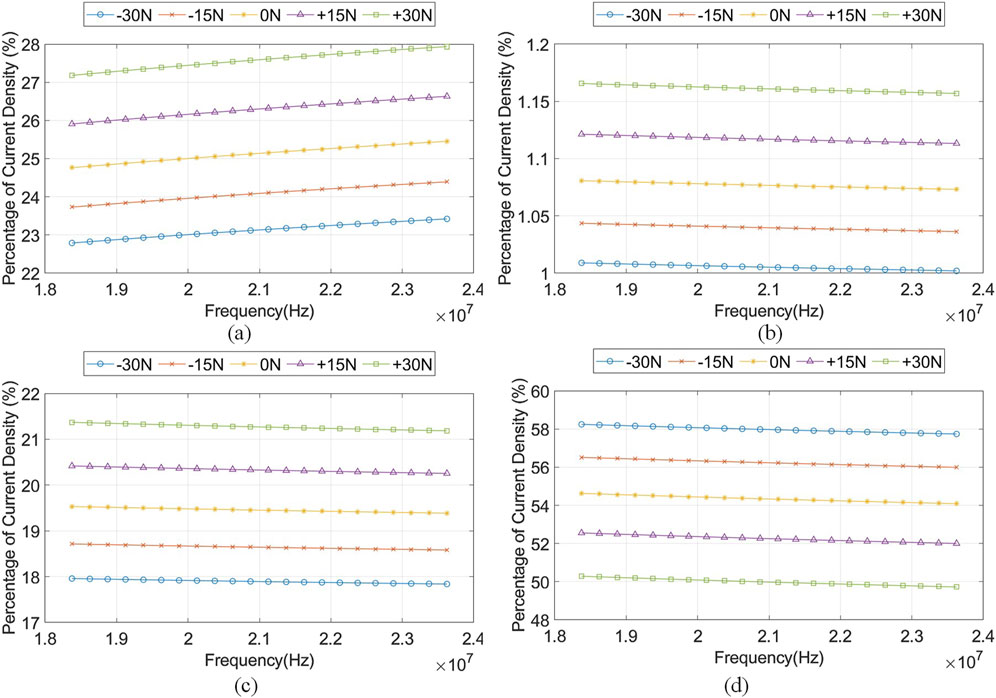
Figure 8. The percentage of current density, $J[A/m^2]$, when subject to different forces. for the tissue components (A) skin, (B) blood, (C) fat, and (D) muscle.

3.2 Stochastic ABCD model for dynamic HBC channel

Several trends were observed from analyzing the $ABCD$ network parameters for the 30 cm channel length as a whole and considering the $\mathrm{\Delta }w$ segments. The $ABCD$ network parameters, force applied, $F$, and frequency used,$f$ exhibited a linear relationship (of general form shown in Equation 7) derived in Table 3.

$\gamma =m_{A}F+m_{B}f+\alpha (7)$

Table 3

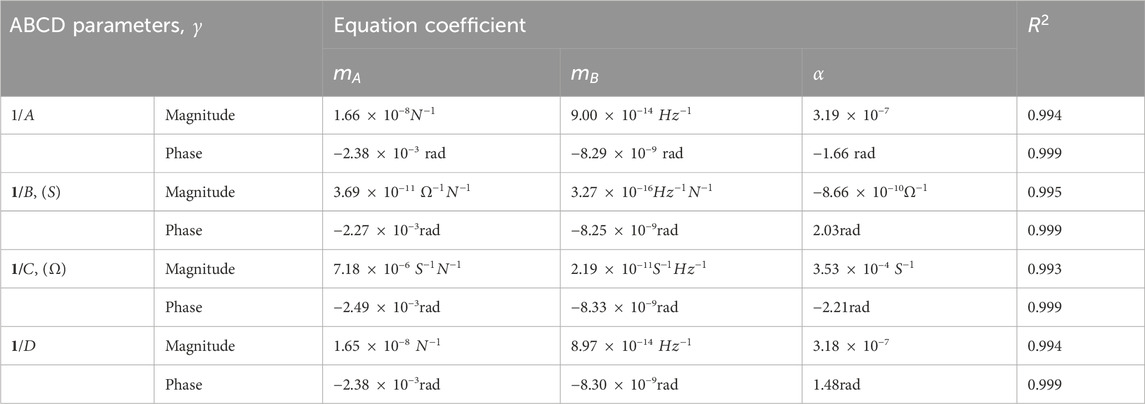
Table 3. Coefficients to regression fitting the magnitude and phase response of the inverse of the ABCD parameters with respect to force applied, $F$, and frequency, $f$, of the form $\gamma =m_{A}F+m_{B}f+C$.

The equations derived for magnitude and phase fitting for the $ABCD$ network parameters for the 30 cm channel length were fitted using linear regression to map the channel response as a function of the frequency and force applied. These fits demonstrated an impressive $R^2$ goodness of fit metric. $R^2$ is a statistical measure used to determine how well a regression model fits with the observed data (Kutner et al., 2005; Draper and Smith, 1998). Thus, the channel response and force applied demonstrated a linear relationship.

The use of $1/A$, $1/B$, $1/C$, and $1/D$ highlights how dynamic conditions impact the full range of parameters in HBC channels. $A$, the inverse channel gain, and $B$, representing impedance, help capture how movement and tissue deformation affect signal attenuation and impedance variations. Similarly, $C$, which represents the transfer of current, and $D$, the reflection coefficient, are also crucial for modeling signal behavior under dynamic conditions. Changes in $1/C$ and $1/D$ offer insights into how current transfer and signal reflection are influenced by body motion and varying tissue properties, providing a more comprehensive understanding of channel fading, signal loss, and impedance shifts in real-world HBC scenarios.

The correlation matrix for the magnitude and phases of the $ABCD$ network parameters of all the $\mathrm{\Delta }w$ segments are shown in Supplementary Figures S1 and S2 respectively (located in the Supplementary Data Sheet S1). The results intuitively show that closer $\mathrm{\Delta }w$ segment’s $ABCD$ network parameters are more correlated, with higher relative correlation coefficients, than $\mathrm{\Delta }w$ segments spaced further apart. By definition, $A$ is the inverse channel gain. From Supplementary Figure S3 (located in Supplementary Data Sheet S1), the force applied to the skin affects the correlation of the channel response between segments such that increasing the force, either in positive or negative directions, results in a stronger correlation between closer $\mathrm{\Delta }w$ segments. The general trend observed when a force of $0N$ is applied is the same when varying force. This correlation information plays a critical role in modeling the overall channel, particularly for simulations like Monte Carlo methods. The analysis of $\mathrm{\Delta }w$ segments provides essential insights into how different body segments interact with under varying conditions. This allows researchers to accurately model the relationship between adjacent segments, which can then be extended to model the full transmission path from the transmitter (Tx) to the receiver (Rx). By understanding the correlation between these segments, researchers can combine multiple segments in a correlated manner to derive a more realistic and dynamic channel model. This is essential for generating accurate received signal models, which are vital for performance analysis, design optimization, and ensuring robust communication in human body communication (HBC) scenarios.

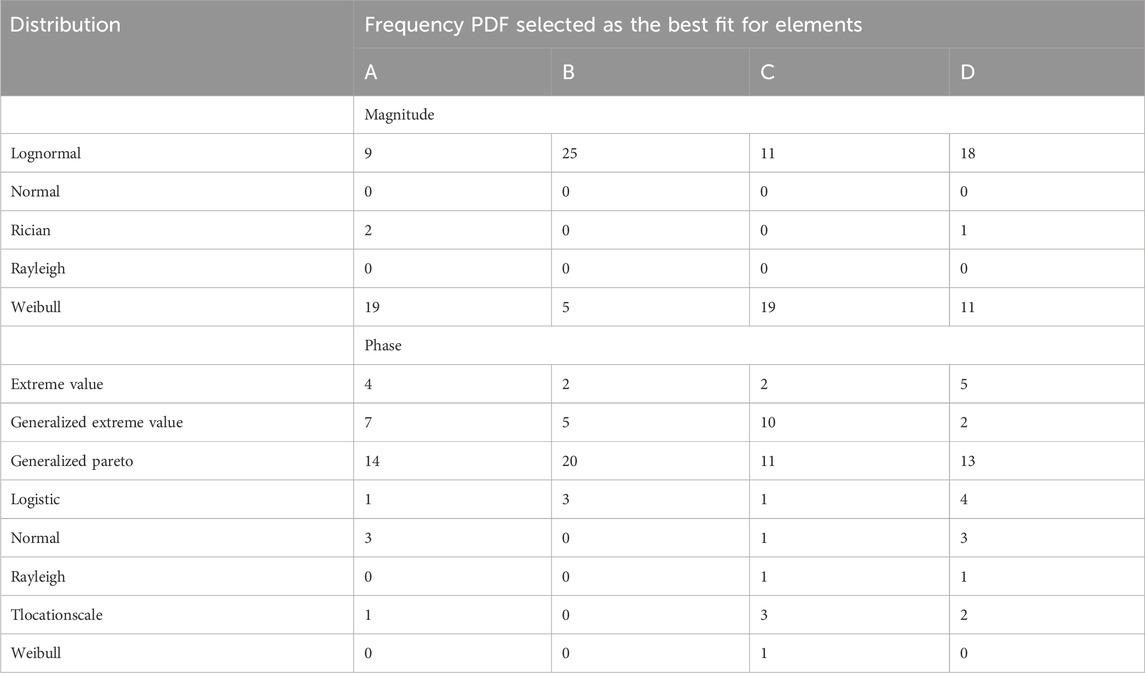
The best-fit PDFs were determined for each of the $ABCD$ parameters for each $\mathrm{\Delta }w$ segment using the Akaike information criterion (AIC), the Bayesian information criterion (BIC) and NLogL goodness of fit metrics, and the $ABCD$ parameters derived for each channel variation as a separate sample. With regards to the magnitude, the results show that the Weibull distribution fits $A$ and $C$ parameters best while the lognormal fits the $B$ and $D$ parameters best. With regards to the phase, the results show the generalized Pareto distribution fits best for all $ABCD$ parameters. Figure 9 shows a sample PDF plot of the magnitude of the $ABCD$ parameter elements for one of the $\mathrm{\Delta }w$ segments.

Figure 9

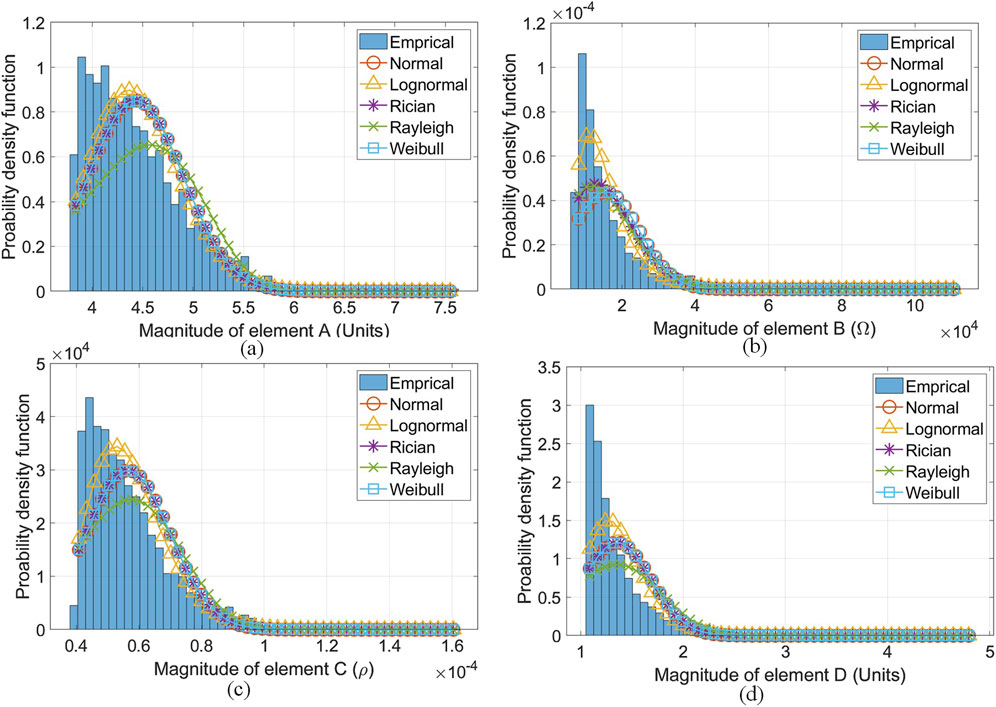
Figure 9. Best fit PDFs found for a sample $\mathrm{\Delta }w$ segment’s ABCD parameter elements in ${\mathbf{\Gamma }}_{\mathit{i}}$ (A) $A$, (B) $B$, (C) $C$, and (D) $D$.

When all the segments were cascaded to form $\mathbf{\Gamma }$, the best fit PDFs for both magnitude and phase elements were found. Regarding the magnitude, the results show that the lognormal distribution fit best for all $ABCD$ parameters. The multiphysics simulation-based approach thus provides further support for the findings of Roopnarine and Rocke (2021), in which Monte Carlo analysis of the ABCD cascade was done for assumed distributions for the $\mathrm{\Delta }w$ segments. Lognormal distributions typically model phenomena where a significant number of individual effects, not strictly independent, all act on a signal (Saunders and Aragón-Zavala, 2007). Regarding the phase, the results show that the generalized extreme value distribution fits the $A$ and $C$ parameters best, while the logistic distribution fits the $B$ and $D$ parameters best. Figure 10 illustrates the PDF plots of the magnitude of the $ABCD$ parameter elements for the cascaded elements of $\mathbf{\Gamma }$.

Figure 10

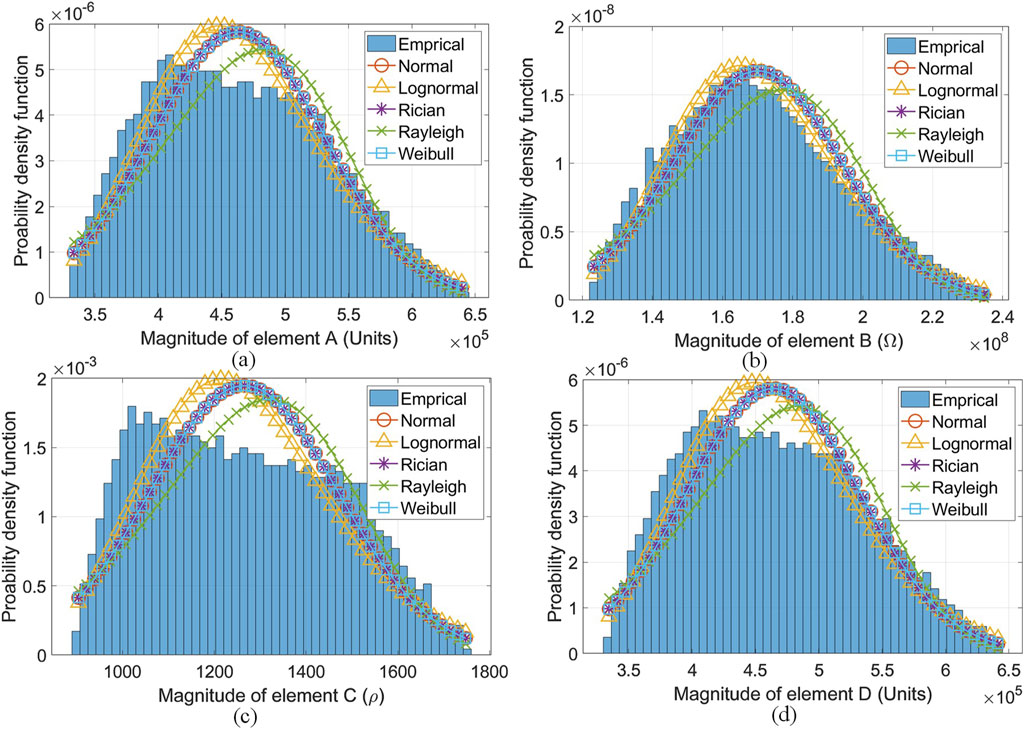
Figure 10. Best-fit PDFs found for the cascaded elements of $\mathbf{\Gamma }$ of channel length $30cm$ (A) $A$, (B) $B$, (C) $C$, and (D) $D$.

The empirically derived fading characteristics from dynamic HBC scenarios investigated for $\mathbf{\Gamma }$ can be found in Figure 11. Here, the best fit PDFs for the ABCD parameters were found by accounting for the dynamic channels investigated. Under these conditions, forces were applied to the skin through these natural positions. The results show that the lognormal distribution fits the ABCD parameters of the overall channel. This corroborates the simulated data as the top fitting distribution match.

Figure 11

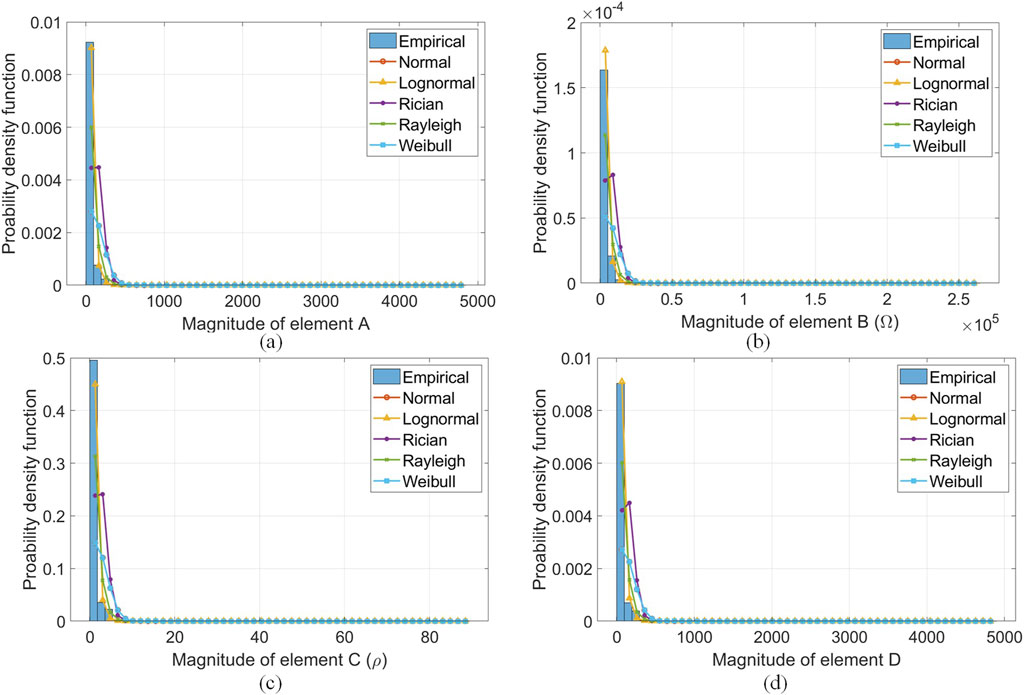
Figure 11. Best fit PDFs from empirically derived data from dynamic HBC scenarios for magnitudes of (A) $A$, (B) $B$, (C) $C$, and (D) $D$.

Consequently, there is an established relationship between applied forces and the channel response in the HBC band. This was proven using the FEM framework that incorporates the ABCD network parameters in Tables 3 and 4. This same FEM model allows the current, current density, and electric field intensity across body tissues under the dynamic conditions (i.e., channel length and applied force variations) to be observed from Figures 6–8. Channel variability (from looking at these electrical parameters in the FEM model produced) for galvanic coupling in the HBC band has been observed when the channel is subject to dynamic conditions. Further, there is a correlation between adjacent surface body segments and tissue layer under these dynamic channel conditions in the results produced from the FEM model in Supplementary Figures S1 and S2. Finally, the empirical model produced strengthens the credibility of the FEM model.

Table 4

Table 4. Best-fit PDFs found for the $\mathrm{\Delta }w$ segments for the ABCD parameter elements in ${\mathbf{\Gamma }}_{\mathit{i}}$.

4 Conclusion

A framework for multiphysics finite element analysis of dynamic HBC channels was presented, incorporating the use of stochastic ABCD network parameters. The approach was demonstrated for a galvanic communication scenario, for which tissue deformation was simulated to model the dynamic human body channel. The results showed that applied force affected the distribution of the current, current density, and electric field intensity across the different tissue layers of the channel—important elements in EM dosimetry and risk assessment studies. A linear regression model was formulated that shows the relationship between applied force, frequency of current, and the channel response. This framework can be used to consider other HBC communication modes such as capacitive and magnetic coupling as well as different dynamic conditions, such as different types of forces, environment, body posture, and activities including sitting/standing/walking states.

The dynamic nature of the channel reflected the need for stochastic modeling. Thus, the best PDFs for each of the ABCD parameters for segments and the combined channel were determined. For the segments, the results show that the Weibull distribution fits best for $A$ and $C$ magnitudes and lognormal for $B$ and $D$ magnitudes. The generalized Pareto distribution fits best for phases of all ABCD parameters. For the overall channel, the results show that the lognormal distribution fits best for the magnitudes. Generalized extreme value fits best for $A$ and $C$ phases and logistic for $B$ and $D$ phases. Based on empirical modeling, it has been observed that the lognormal distribution provides the best fit for the magnitudes $A$, $B$, $C$, and $D$ in various dynamic states experienced by the human body. This finding serves to reinforce the validity and accuracy of the FEM model used in the study. Consequently, the dynamic channel was characterized by FEM modeling, empirical analysis, and ABCD network parameters.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Ethics statement

Ethical approval was not required for the studies involving humans because we gave our own informed consent as the human in question tested was one of the co-authors. In such instances, ethics approval is not required in our current infrastructure. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

AR: conceptualization, data curation, formal analysis, investigation, methodology, project administration, software, validation, visualization, writing–original draft, and writing–review and editing. SR: conceptualization, funding acquisition, resources, supervision, writing–original draft, and writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that generative AI was used in the creation of this manuscript as a minor rephrasing tool to refine the text for review and editing.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fanpr.2025.1509439/full#supplementary-material

References

Agache, P. G., Monneur, C., Leveque, J. L., and De Rigal, J. (1980). Mechanical properties and Young’s modulus of human skin in vivo. Arch. Dermatol Res. 269, 221–232. doi:10.1007/bf00406415

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmed, D., Fischer, G., and Kirchner, J. (2019). “Simulation-based models of the galvanic coupling intra-body communication,” in 2019 IEEE sensors applications symposium (SAS), 1–6. doi:10.1109/SAS.2019.8706007

CrossRef Full Text | Google Scholar

Albulbul, A., and Chan, A. D. (2012). “Electrode-skin impedance changes due to an externally applied force,” in Medical measurements and applications proceedings (MeMeA), 2012 IEEE international symposium on IEEE, 1–4. doi:10.1109/MeMeA.2012.6226628

CrossRef Full Text | Google Scholar

Ali, A., Inoue, K., Shalaby, A., Sayed, M. S., and Ahmed, S. M. (2019). Efficient autoencoder-based human body communication transceiver for wban. IEEE Access 7, 117196–117205. doi:10.1109/ACCESS.2019.2936796

CrossRef Full Text | Google Scholar

Callejon, M. A., Naranjo-Hernandez, D., Reina-Tosina, J., and Roa, L. M. (2012a). Distributed circuit modeling of galvanic and capacitive coupling for intrabody communication. IEEE Trans. Biomed. Eng. 59, 3263–3269. doi:10.1109/tbme.2012.2205382

PubMed Abstract | CrossRef Full Text | Google Scholar

Callejon, M. A., Reina-Tosina, J., Naranjo-Hernández, D., and Roa, L. M. (2014). Galvanic coupling transmission in intrabody communication: a finite element approach. IEEE Trans. Biomed. Eng. 61, 775–783. doi:10.1109/TBME.2013.2289946

PubMed Abstract | CrossRef Full Text | Google Scholar

Andersen, J.-H., Bjerke, O., Blakaj, F., Flugsrud, V. M., Jacobsen, F. A., Jonsson, M., et al. (2019). Bioimpedance and nir for non-invasive assessment of blood glucose. J. Electr. Bioimpedance 10, 133–138. doi:10.2478/.joeb-2019-0019

PubMed Abstract | CrossRef Full Text | Google Scholar

Bae, J., Cho, H., Song, K., Lee, H., and Yoo, H.-J. (2012a). The signal transmission mechanism on the surface of human body for body channel communication. IEEE Trans. Microw. Theory Tech. 60, 582–593. doi:10.1109/TMTT.2011.2178857

CrossRef Full Text | Google Scholar

Bae, J., Song, K., Lee, H., Cho, H., and Yoo, H.-J. (2012b). A low-energy crystal-less double-fsk sensor node transceiver for wireless body-area network. IEEE J. Solid-State Circuits 47, 2678–2692. doi:10.1109/jssc.2012.2211654

CrossRef Full Text | Google Scholar

Blattenberger, K. (2023). S, h, y, z impedances - rf cafe. Available online at: https://www.rfcafe.com/references/electrical/s-h-y-z.htm.Posted: : July 25, 2023.

Google Scholar

Bouazizi, A., Zaibi, G., Samet, M., and Kachouri, A. (2017). “Wireless body area network for e-health applications: overview,” in Smart, Monitored and controlled cities (SM2C), 2017 international Conference on (IEEE), 64–68.

Google Scholar

Callejon, M. A., Roa, L. M., Reina-Tosina, J., and Naranjo-Hernandez, D. (2012b). Study of attenuation and dispersion through the skin in intrabody communications systems. IEEE Trans. Inf. Technol. Biomed. 16, 159–165. doi:10.1109/TITB.2011.2171702

PubMed Abstract | CrossRef Full Text | Google Scholar

Chawla, A., Mukherjee, S., and Karthikeyan, B. (2006). Mechanical properties of soft tissues in the human chest, abdomen and upper extremities. Mech. Eng. Available at: https://web.iitd.ac.in/∼achawla/PDF%20Files/material_properties%20of%20Soft%20Tissue.pdf (Accessed Oct 2024).

Google Scholar

Chen, X. M., Pun, S. H., Zhao, J. F., Mak, P. U., Liang, B. D., and Vai, M. I. (2016). Effects of human limb gestures on galvanic coupling intra-body communication for advanced healthcare system. Biomed. Eng. OnLine 15, 60. doi:10.1186/s12938-016-0192-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Cho, H., Lee, H., Bae, J., and Yoo, H.-J. (2014). “A 5.2mw ieee 802.15.6 hbc standard compatible transceiver with power efficient delay-locked-loop based bpsk demodulator,” in 2014 IEEE asian solid-state circuits conference (A-SSCC), 297–300. doi:10.1109/ASSCC.2014.7008919

CrossRef Full Text | Google Scholar

ClinMed International Library (1990). Young’s modulus and Poisson’s ratio for the tissues. Wilmington, DE: ClinMed International Library.

Google Scholar

Comley, K., and Fleck, N. A. (2010). A micromechanical model for the young’s modulus of adipose tissue. Int. J. Solids Struct. 47, 2982–2990. doi:10.1016/j.ijsolstr.2010.07.001

CrossRef Full Text | Google Scholar

COMSOL Multiphysics (2019). AC/DC module user’s guide.

Google Scholar

Datta, A., Nath, M., Yang, D., and Sen, S. (2021). Advanced biophysical model to capture channel variability for eqs capacitive hbc. IEEE Trans. Biomed. Eng. 68, 3435–3446. doi:10.1109/TBME.2021.3074138

PubMed Abstract | CrossRef Full Text | Google Scholar

DeSaix, P., Betts, G. J., Johnson, E., Johnson, J. E., Oksana, K., Kruse, D. H., et al. (2013). Anatomy and physiology.

Google Scholar

Dhamdhere, A., Chen, H., Kurusingal, A., Sivaraman, V., and Burdett, A. (2010). “Experiments with wireless sensor networks for real-time athlete monitoring,” in Local computer networks (LCN), 2010 IEEE 35th Conference on (IEEE), 938–945.

Google Scholar

Draper, N. R., and Smith, H. (1998). Applied regression analysis. Wiley Series in Probability and Statistics, 3rd edn. doi:10.1002/9781118625590

CrossRef Full Text | Google Scholar

Ebrahimi, A. P. (2009). Mechanical properties of normal and diseased cerebrovascular system. J. Vasc. Interv. Neurol. 2, 155–162. Available at: https://pmc.ncbi.nlm.nih.gov/articles/PMC3317338/ (Accessed Oct 2024).

PubMed Abstract | Google Scholar

Gabriel, C. (1996). Compilation of the dielectric properties of body tissues at RF and microwave frequencies. Tech. Rep. U.S. Air Force Rep. AFOSR-TR-96, U.S. Air Force. doi:10.21236/ADA303903

CrossRef Full Text | Google Scholar

Gabriel, S., Lau, R., and Gabriel, C. (1996). The dielectric properties of biological tissues: iii. parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 41, 2271–2293. doi:10.1088/0031-9155/41/11/003

PubMed Abstract | CrossRef Full Text | Google Scholar

Groves, R. B., Coulman, S. A., Birchall, J. C., and Evans, S. L. (2012). Quantifying the mechanical properties of human skin to optimise future microneedle device design. Comput. Methods Biomechanics Biomed. Eng. 15, 73–82. PMID: 21749225. doi:10.1080/10255842.2011.596481

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, L.-X., Zhang, Y.-M., and Zhang, M. (2011). Finite element modeling and modal analysis of the human spine vibration configuration. IEEE Trans. Biomed. Eng. 58, 2987–2990. doi:10.1109/TBME.2011.2160061

PubMed Abstract | CrossRef Full Text | Google Scholar

IEEE (2012). Ieee standard for local and metropolitan area networks - part 15.6: wireless body area networks. IEEE Std 802 (15.6-2012), 1–271doi. doi:10.1109/IEEESTD.2012.6161600

CrossRef Full Text | Google Scholar

IEEE, S. A. (2008). IEEE P802.15 working group for wireless personal area networks (WPANs): channel Model for body area network (BAN). Rep. IEEE P802.15-08-0033-04-0006, IEEE. Available at: https://mentor.ieee.org/802.15/file/08/15-08-0780-04-0006-tg6-channel-model.pdf (Accessed Oct 2024).

Google Scholar

International Commission on Non-Ionizing Radiation Protection ICNIRP (1998). Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to 300 GHz). International Commission on Non-Ionizing Radiation Protection. Health Phys. 74, 494–522. Available at: https://www.icnirp.org/cms/upload/publications/ICNIRPemfgdl.pdf (Accessed Oct 2024).

PubMed Abstract | Google Scholar

ITIS Foundation (2024). Tissue properties. Zurich, Switzerland: The Foundation for Research on Information Technologies in Society (IT’IS).

Google Scholar

Karimi, A., Sera, T., Kudo, S., and Navidbakhsh, M. (2016). Experimental verification of the healthy and atherosclerotic coronary arteries incompressibility via digital image correlation. Artery Res. 16, 1–7. doi:10.1016/j.artres.2016.08.002

CrossRef Full Text | Google Scholar

Kearney, S. P., Khan, A., Dai, Z., and Royston, T. J. (2015). Dynamic viscoelastic models of human skin using optical elastography. Phys. Med. Biol. 60, 6975–6990. doi:10.1088/0031-9155/60/17/6975

PubMed Abstract | CrossRef Full Text | Google Scholar

Kutner, M. H., Nachtsheim, C. J., Neter, J., and Li, W. (2005). Applied linear statistical models. 5th edn. McGraw-Hill.

Google Scholar

Lee, K.-S., and Jung, M.-C. (2017). “Total force of pinch and grasp by hand postures,” in Advances in physical ergonomics and human factors. Advances in intelligent systems and computing Springer International Publishing, 208–212. doi:10.1007/978-3-319-60825-9_23

CrossRef Full Text | Google Scholar

Liang, X., and Boppart, S. A. (2010). Biomechanical properties of in vivo human skin from dynamic optical coherence elastography. IEEE Trans. Biomed. Eng. 57, 953–959. doi:10.1109/TBME.2009.2033464

PubMed Abstract | CrossRef Full Text | Google Scholar

Lima, K. M. M. E., Costa Júnior, J. F. S., Pereira, W. C. d. A., and Oliveira, L. F. (2018). Assessment of the mechanical properties of the muscle-tendon unit by supersonic shear wave imaging elastography: a review. Ultrasonography 37, 3–15. doi:10.14366/usg.17017

PubMed Abstract | CrossRef Full Text | Google Scholar

Maity, S., Mojabe, K., and Sen, S. (2018). Characterization of human body forward path loss and variability effects in voltage-mode hbc. IEEE Microw. Wirel. Components Lett. 28, 266–268. doi:10.1109/lmwc.2018.2800529

CrossRef Full Text | Google Scholar

Nightingale, K., McAleavey, S., and Trahey, G. (2003). Shear-wave generation using acoustic radiation force: in vivo and ex vivo results. Ultrasound Med. and Biol. 29, 1715–1723. doi:10.1016/j.ultrasmedbio.2003.08.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Noormohammadi, R., Khaleghi, A., and Balasingham, I. (2021). Galvanic impulse wireless communication for biomedical implants. IEEE Access 9, 38602–38610. doi:10.1109/ACCESS.2021.3064206

CrossRef Full Text | Google Scholar

Notaros, B. M. (2010). Electromagnetics. Upper Saddle River, NJ: Pearson.

Google Scholar

Ogasawara, T., Sasaki, A.-i., Fujii, K., and Morimura, H. (2014). Human body communication based on magnetic coupling. IEEE Trans. Antennas Propag. 62, 804–813. doi:10.1109/tap.2013.2292705

CrossRef Full Text | Google Scholar

Pailler-Mattei, C., Bec, S., and Zahouani, H. (2008). In vivo measurements of the elastic mechanical properties of human skin by indentation tests. Med. Eng. and Phys. 30, 599–606. doi:10.1016/j.medengphy.2007.06.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Pawlaczyk, M., Lelonkiewicz, M., and Wieczorowski, M. (2013). Age-dependent biomechanical properties of the skin. Adv. Dermatology Allergology 5, 302–306. doi:10.5114/pdia.2013.38359

PubMed Abstract | CrossRef Full Text | Google Scholar

Pereira, M. D., Alvarez-Botero, G. A., and Rangel de Sousa, F. (2015). Characterization and modeling of the capacitive hbc channel. IEEE Trans. Instrum. Meas. 64, 2626–2635. doi:10.1109/tim.2015.2420391

CrossRef Full Text | Google Scholar

Persad, J., and Rocke, S. (2020). Investigating the impact of deformation on a 3d-printed antenna in biomedical systems. West Indian J. Eng. 42. Available at: https://sta.uwi.edu/eng/wije/vol4202_jan2020/Documents/M07-JPersadJan2020.pdf (Accessed Oct 2024).

Google Scholar

Rocke, S., and Persad, J. (2015). “Analysis of magnetically-coupled human body communications,” in 2015 COMSOL conference in Boston.

Google Scholar

Roopnarine, A., and Rocke, S. (2024). “Deep learning-based bioimpedance spectroscopy using start of frame delimiter in human body communications,” in Artificial intelligence for sustainable energy. Editors J. Mathew, L. Gopal, and F. H. Juwono (Singapore: Springer Nature Singapore), 209–219.

CrossRef Full Text | Google Scholar

Roopnarine, A., and Rocke, S. A. (2021). Stochastic bioimpedance-based channel model of the human body for galvanic coupling. J. Electr. Bioimpedance 12, 117–124. doi:10.2478/joeb-2021-0014

PubMed Abstract | CrossRef Full Text | Google Scholar

Roopnarine, A., Rocke, S. A., Mahadeo, M., and Persad, J. (2024). “Multiphysics finite element investigation of galvanic transmission for dynamic livestock-based communication,” in Proceedings of the IEEE conference on agri-food electronics (CAFE).

Google Scholar

Saunders, S., and Aragón-Zavala, A. (2007). Antennas and propagation for wireless communication systems. John Wiley and Sons.

Google Scholar

Seyedi, M. H., and Lai, D. (2014). A novel intrabody communication transceiver for biomedical applications. Melbourne, VIC: Victoria University.

Google Scholar

Smith, J. M. (2011). The doctor will see you always. iEEE Spectr. 48, 56–62. doi:10.1109/mspec.2011.6027250

CrossRef Full Text | Google Scholar

Steenbrink, F., Meskers, C. G. M., van Vliet, B., Slaman, J., Veeger, H. E. J., and De Groot, J. H. (2009). Arm load magnitude affects selective shoulder muscle activation. Med. and Biol. Eng. and Comput. 47, 565–572. doi:10.1007/s11517-009-0482-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Sujaya, B., and BhanuPrashanth, S. (2021). An efficient hardware-based human body communication transceiver architecture for wban applications. Glob. Transitions Proc. 2, 152–156. doi:10.1016/j.gltp.2021.08.070

CrossRef Full Text | Google Scholar

Takamatsu, R., Higuchi, K., and Muramatsu, D. (2021). “Measurement frequency evaluation for bioimpedance-based blood-glucose estimation,” in 2021 IEEE 3rd global conference on life sciences and technologies (LifeTech), 309–310. doi:10.1109/LifeTech52111.2021.9391845

CrossRef Full Text | Google Scholar

Takaza, M., Moerman, K. M., Gindre, J., Lyons, G., and Simms, C. K. (2013). The anisotropic mechanical behaviour of passive skeletal muscle tissue subjected to large tensile strain. J. Mech. Behav. Biomed. Mater. 17, 209–220. doi:10.1016/j.jmbbm.2012.09.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, C., Song, Y., Chen, Y., Zhou, Y., Zhang, X., and Ma, Y. (2023). “Dynamic channel modeling and characteristic analysis of wearable human body communication system,” in 2023 4th information communication technologies conference (ICTC), 49–53. doi:10.1109/ICTC57116.2023.10154827

CrossRef Full Text | Google Scholar

Tang, W., Chen, N., Zhang, J., Chen, S., Ge, S., Zhu, H., et al. (2015). Characterization of tactile perception and optimal exploration movement. Tribol. Lett. 58, 28. doi:10.1007/s11249-015-0507-4

CrossRef Full Text | Google Scholar

Tronstad, C., and Strand-Amundsen, R. (2019). Possibilities in the application of machine learning on bioimpedance time-series. J. Electr. Bioimpedance 10, 24–33. doi:10.2478/joeb-2019-0004

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, B., Xue, H., Birgersson, E., Ollmar, S., and Birgersson, U. (2019). Dielectrical properties of living epidermis and dermis in the frequency range from 1 khz to 1 mhz. J. Electr. Bioimpedance 10, 14–23. doi:10.2478/joeb-2019-0003

PubMed Abstract | CrossRef Full Text | Google Scholar

Ulaby, F. T., Michielssen, E., and Ravaioli, U. (2010). Fundamentals of applied electromagnetics. 6 edn. Upper Saddle River, NJ: Pearson.

Google Scholar

Vizziello, A., Savazzi, P., Guerra, R. R., and Dell’Acqua, F. (2024). Experimental channel characterization of human body communication based on measured impulse response. IEEE Trans. Commun. 72, 3970–3984. doi:10.1109/TCOMM.2024.3370468

CrossRef Full Text | Google Scholar

Wang, H., Tang, X., Choy, C. S., and Sobelman, G. E. (2016). Cascaded network body channel model for intrabody communication. IEEE J. Biomed. Health Inf. 20, 1044–1052. doi:10.1109/JBHI.2015.2448111

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, K., Chen, Y., Huang, S., Wang, L., and Niu, W. (2021). Subcutaneous fat thickness remarkably influences contact pressure and load distribution of buttock in seated posture. J. Healthc. Eng. 2021, 1–9. doi:10.1155/2021/4496416

PubMed Abstract | CrossRef Full Text | Google Scholar

Wegmueller, M. S., Kuhn, A., Froehlich, J., Oberle, M., Felber, N., Kuster, N., et al. (2007). An attempt to model the human body as a communication channel. IEEE Trans. Biomed. Eng. 54, 1851–1857. doi:10.1109/TBME.2007.893498

PubMed Abstract | CrossRef Full Text | Google Scholar

Wells, R., and Greig, M. (2001). Characterizing human hand prehensile strength by force and moment wrench. Ergonomics 44, 1392–1402. doi:10.1080/00140130110109702

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, E., Sievenpiper, D. F., and Mercier, P. P. (2022). Channel characterization of magnetic human body communication. IEEE Trans. Biomed. Eng. 69, 569–579. doi:10.1109/TBME.2021.3101766

PubMed Abstract | CrossRef Full Text | Google Scholar

White, E. A., Orazem, M. E., and Bunge, A. L. (2013). Characterization of damaged skin by impedance spectroscopy: mechanical damage. Pharm. Res. 30, 2036–2049. doi:10.1007/s11095-013-1052-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., He, Z., Liu, Y., Enamorado, L. A. L., and Chen, X. (2016a). “Measurement and characterization on a human body communication channel,” in 2016 IEEE 27th annual international symposium on personal, indoor, and mobile radio communications (PIMRC) IEEE, 1–6.

CrossRef Full Text | Google Scholar

Zhang, Y., Kou, B., Fan, D., Liu, Y., He, Z., and Chen, X. (2016b). “A dynamic pilot interval adjustment scheme for hbc channel estimation,” in Communications in China (ICCC workshops), 2016 IEEE/CIC international Conference on (IEEE), 1–5.

Google Scholar