Understanding the World Economy in Terms of Networks: A Survey of Data-Based Network Science Approaches on Economic Networks

The purpose of this paper is to survey studies for estimating and analyzing different types of economic networks We focus on data-based approaches that allow the direct estimation of the networks from empirical data without the need of relying on theoretical assumptions. Due to the fact that there is a large variety of different economic networks, e.g., interbank, investment, director, ownership, financial, product or trade networks, we present a systematic categorization of these by the meaning of the “nodes” within these networks. These can correspond to banks, firms, investors, products, stocks etc. Furthermore, we review practical methods for graphically exploring such networks and discuss useful databases for obtaining the empirical data for the computational construction of economic networks.

1. Introduction

In recent years, there has been more and more interest in studying economy related questions by means of network science [1–5]. A reason for this interest builds on the realization that the behavior of the economy cannot be investigated by individually studying the constituting components of it but only by considering the interplay between all relevant parts. This is in strong contrast to the standard economic theory [6–9]. Conceptually, this insight is related to general systems theory by von Bertalanffy [10, 11] having its roots in the 1940s.

From a practical point of view, the digitalization of our society, e.g., of the stock market or the availability of business records, enabled the empirical estimation and creation of different types of economic networks. This is similar to other fields like biology, chemistry or sociology [12–16]. That means, without the need of making theoretical assumptions about the structure of economic networks, data can be used for their construction. This is in contrast to, e.g., simulation-based approaches allowing to generate network topologies with certain characteristics, e.g., scale-free or smal-world networks [17–19]. In this paper, we focus on data-based network science approaches and review papers for studying economic networks based on this premise.

In general, economic networks are a special forms of social networks [20]. However, while the study of social networks has a long history dating back to the 1920's starting systematically in the 1960's [15], the history of economic networks is considerably shorter, starting in our opinion in the 1990's [21, 22], though, with an exponential growth fueled by the emergence of our digital society. In Figure 1 we list some of the first articles in this field making explicit usage of networks or graphs, which have been inferred from empirical data, by studying these structurally. This is beyond studies estimating correlations or other measures of relations that do not appreciate the resulting graph structure explicitly by means of network science, e.g., graph theory.

FIGURE 1

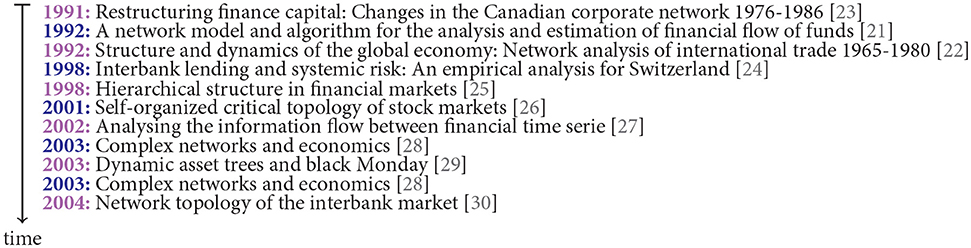
Figure 1. Historic origin of data-based approaches for studying economic networks. Listing of the first articles in this field making explicit usage of networks or graphs (shown are the title of the articles).

One of the first studies of economic networks is from Smith and White [22], where the authors investigated an international commodity trade flow network resembling the structure of the world economy to learn about the roles that particular countries play in the global system. They used information for 15 selected major types of trade commodities for import and export exchanged between 63 countries, whereas the flow was measured in U.S. dollars. As a result they obtained a general network structure spanning the countries. This is in contrast to other studied that investigated more specialized graph structures like trees. For instance, Mantegna [25] extracted the minimum spanning tree (MST) for identifying the most important connections between stocks. This solved the problem to convert a correlation matrix into a network structure in a unique way and inspired many follow up studies. Another example for a specialized graph structure is a bipartite network, e.g., studied in Souma et al. [28]. Financial networks have also been studied from a data science point of view [31]. For instance, Anand [31] investigated and inferred financial networks from partial data sets.

Due to the fact that the study of economic networks is an interdisciplinary field comprising contributions from economics, computer science, statistics, physics, management and business, the literature in this field is distributed over many different journals from the above fields. Also the focus and the perspective of these papers is heterogenous reflecting the different angels of the corresponding fields. Nevertheless, we found a commonality of all these different contributions which we use as the main structure of our review paper. This commonality refers to the basic meaning of the nodes and the edges in the economic networks and the data that have been used for constructing or inferring them. Based on this categorization, section 4 and 5 are guided and organized correspondingly. Another commonality we found is that, usually, before every quantitative analysis of a network, a visual exploration of the network is performed. For this reason, we review in section 6 practical methods for the visualization of economic networks. Our review paper starts in section 2 providing preliminaries of graph theory as needed for the subsequent sections followed by section 3 giving an overview of the different types of economic networks that have been studied. Our paper ends in section 7 by discussing extensions and future directions.

For completeness we would like to note that there exist other review papers on economic networks [32, 33], however, these have a different focus that is reflected in a more narrow presentation of the topic.

2. Basics of Graph Theory

Before we start our survey we provide relevant preliminaries from graph theory [34, 35]. The following definitions are for basic graph classes as needed for the understanding of the different economic networks, which we will discuss in later sections.

Definition 2.1. ([35]) The pair G = (V, E) where V represents a finite set of nodes or vertices and E the set of edges or links, $E\subseteq \left(\frac{V}{2}\right)$ is called a finite undirected graph or an undirected network, see [35].

Throughout the paper, we set the cardinality of the vertex set |V|: = N. The cardinality of the edge set is denoted by |E|.

Definition 2.2. ([35]) The pair G = (V, E) where V represents a finite set of vertices and E the set of edges, E⊆V×V, is called a finite directed graph or directed network.

For representing a network, the so-called adjacency matrix is often used [35].

Definition 2.3. The adjacency matrix of a finite graph G = (V, E) is defined by

$\begin{array}{ll}{A}_{ij}:=\{\begin{array}{ll}1\hfill & :(v_i,v_j)\in E\hfill \\ 0\hfill & :otherwise\hfill \end{array}& (1)\end{array}$

In the following sections we will also consider weighted networks. For this reason we need to define the weighting matrix W.

Definition 2.4. The weighting matrix of a finite graph G = (V, E) is defined by Harary [35]

$\begin{array}{ll}{W}_{ij}:=\{\begin{array}{ll}{w}_{ij}\hfill & :(v_i,v_j)\in E\hfill \\ 0\hfill & :\text{otherwise}\hfill \end{array}& (2)\end{array}$

with w_ij ∈ ℝ.

3. Overview of Economic Network Types

When speaking about economic networks there is actually not one specific meaning of these networks, but it is a complex family of different networks, each one with its own meaning. This complexity stems from the fact that there are different building block for defining the “nodes” in an economic network. In the following, we list some of the most important node types that have been used for constructing economic networks. That means nodes in economic networks can correspond to:

• Directors (management)

• Firms

• Products

• Business Groups

• Banks

• Investors

• Traders

• Cities

• Countries

It is clear that depending on the meaning of the nodes the meaning of the whole economic network is derived. For this reason, if starting from a question to be studied, e.g., providing insights into the trading of countries or the stability of banks, the nodes need to be selected correspondingly. From a different perspective, the selected meaning of nodes allows to either focus on microeconomic or macroeconomic problems. This implies that the granularity of the economic network, as explained below, can be controlled by this. In order to visualize our point, we provide in Figure 2 an example.

FIGURE 2

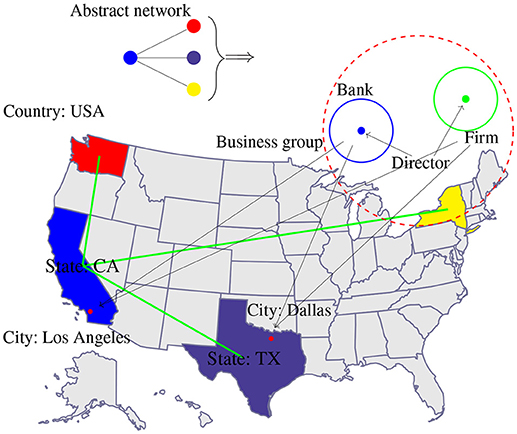
Figure 2. Visualizing the meaning of “nodes” in economic networks for an abstract four-node network (top). Each node color corresponds to a state (CA, TX, WA, and NY) and each state is a collection of its cities, whereas each city is a collection of banks and firms located therein. Furthermore, each bank or firm is directed by a board of directors. Finally, banks or firms can form business groups and the collection of states form a country.

Starting from an abstract four-node network in Figure 2 top we show a cascade of different node meanings. First, the colors of the four nodes of the small network correspond to the four states California (CA, blue), Texas (TX, purple), Washington (WA, red) and New York (NY, yellow). Each of these states consists of many cities, e.g., Los Angeles or Dallas, in which branches of banks or firms are located. Furthermore, the banks and firms are controlled by a board of directors. From this cascade, the different layers of granularity become apparent. We would like to add that this situation can become more complex in case banks or firms are forming business groups. Also, one can aggregate states to become countries. The last collection would allow to study global trade networks among countries [36, 37].

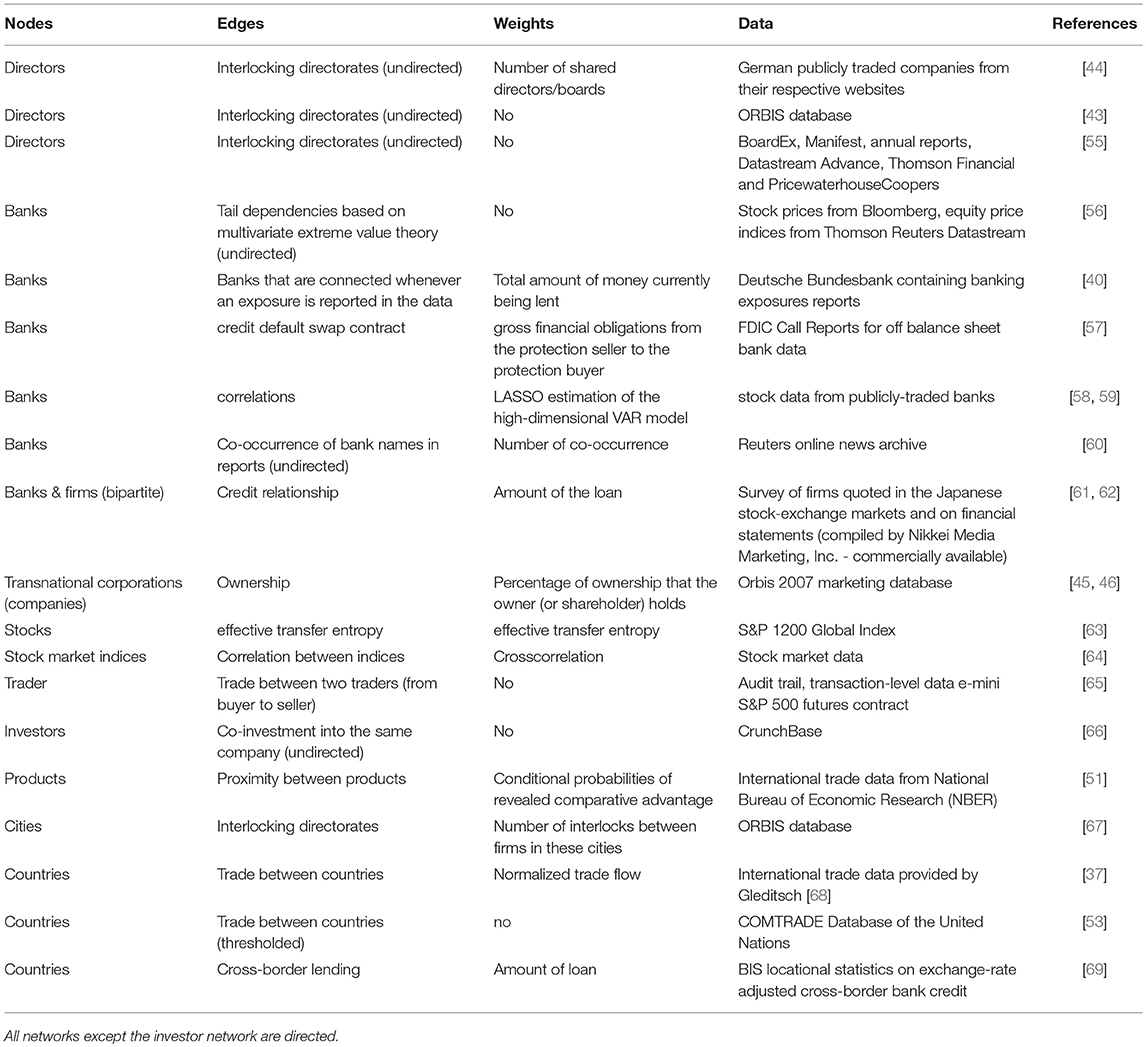
The different meaning of nodes leds to commonly used names for different types of economic networks; see Table 1. Specifically, one distinguishes interbank networks, investment networks, director networks, financial networks, product networks and trade networks. In the following, we will review important papers that studied various types of such economic networks with the above mentioned meaning of the nodes. That means, the following subsections in section 4 are categorized according to the meaning of the nodes.

TABLE 1

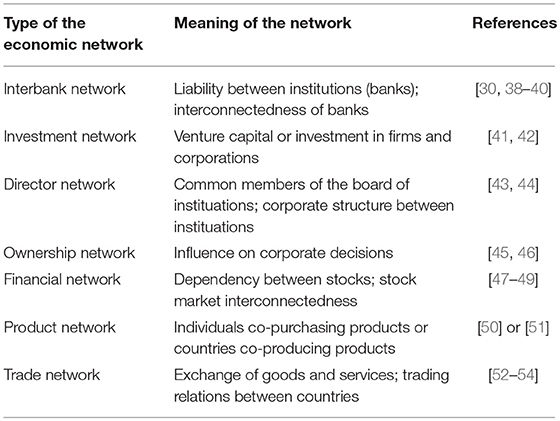
Table 1. Examples of different types of economic networks that have been frequently studied in the literature.

4. Surveying Data-Based Approaches on General Economic Networks

We begin this survey at the small scale corresponding to the corporate structure of banks or firms as represented by the board of directors and work our way up to larger units like business groups, representing a collection of firms, and countries; see Table 2 for a summary.

TABLE 2

Table 2. An overview of studies investigating different types of global economic networks.

4.1. Directors

The first type of economic networks we are discussing are director networks. Such networks are not only of interest to economists for placing them into the greater context of their influence on various aspects of the economy but also to social scientists to study sociologic aspects. In the latter context, such networks are social networks that are called affiliation networks; see [20] for a discussion.

A director network has nodes corresponding to directors serving as board members of firms, banks or other institutions. A link between two directors is established if they are a member of the same company board. This creates an undirected, unweighted network. Alternatively, an edge receives a weight corresponding to the number of boards two directors are simultaneously members of. That means a director network provides information about the interlocks of corporate boards and their directors.

Practically, such networks are indirectly constructed by means of an auxiliary bipartite network M [67, 44]. This bipartite network consists of one type of nodes corresponding to directors and a second type of nodes corresponding to institutions the directors serve as board members. A link between a director and an institution, i.e., M_ij = 1, is established if director i sits on the board of institution j. As for all bipartite networks one can extract two (weighted) networks. The first network is the desired director network, formally obtained by D = MM^t (where ^t is the transpose of the matrix), and the second is a company network, C = M^tM. The meaning of D_ij is the number of boards the directors i and j sit together, and C_ij corresponds to the number of common directors that are in board of company i and j. Usually, the diagonal elements of both matrices are set to zero.

In Milaković et al. [44] a weighted director network has been studied to identify the core of directors for publicly traded companies in Germany. For this purpose, they focused on companies which either have a market capitalization of more than 100 million Euros, or are included in one of the four major indices of the Deutsche Börse. Overall, they studied 284 companies and 3, 383 directors. A major result of their study showed that core directors are more densely connected with each other and to work for companies with a relatively large market capitalization. For this reason it seems reasonable to hypothesis that these directors have a great influence in this network, despite their small number.

In contrast, Heemskerk and Takes [43] presented an investigation of an unweighted director network. Specifically, they analyzed how the largest one million firms in the world are interconnected with each other at the level of corporate governance through interlocking directorates. They obtained their data from the ORBIS database provided by Bureau van Dijk. Overall, they studied 968, 409 companies from 208 different countries having 3, 262, 413 directors. As a result they found that on average companies share directors with 4.37 other firms. Furthermore, 60% of all firms are members of one large connected network component. This large network components consists of almost 90% of all board interlocks. Furthermore, within this large connected component the average distance between pairs of firms is 7.75. This means that the board members of these firms are tightly connected at the highest level of corporate decision-making. Further studies analyzing director networks can be found in Renneboog and Zhao [55].

4.2. Banks

Another type of economic network that has been frequently studied is the interbank network or interbank market [40, 56, 58]. For these networks banks are nodes and links between them represent interbank lending, i.e., loans or payments between banks. Due to the ongoing global financial crises [70–73] the interest in studying such networks is enormous, e.g., because of their implications on systemic risk.

In Constantin et al. [56] interbank networks have been used to study and predict bank distress. They used data for 171 listed European banks from the stock market (from Bloomberg) and the equity price index and country-level equity price indices (from Thomson Reuters Datastream) for the European banking sector in order to estimate interbank lending and exposures, because this information is not publicly available in Europe. Specifically, a multivariate extreme-value theory approach by Poon et al. [74] is used. The resulting network is combined with an early-warning model at the bank level [75]. A central finding of their study is that their combined model is better than benchmark models, which do not consider the connectivity between banks.

In Iori et al. [76], Temizsoy et al. [77], and Iori et al. [78] the e-MID market, an electronic market for interbank deposits in the USA and the Eurozone, has been studied. Interestingly, Iori et al. [78] showed that the e-MID market network structure corresponds to a random network if studied for a daily time scale, however, the structure of the market becomes non-random for longer aggregation periods. In Temizsoy et al. [77] the local and global measures of network centrality in the e-MID network have been studied for the years 2006–2009, which includes the global financial crisis in 2008. One interesting result of their study is that interbank spreads are significantly affected by measures of connectedness for local and global measures. In this context the DebtRank algorithm should be mentioned as a method for estimating the impact of shocks on financial networks [79, 80]. In simple terms, the idea of DebtRank is to estimate a value for each node (institution) in the network that quantifies the fraction of the total economic value that is affected in the case of the default of this institution [80].

In Markose et al. [57] the systemic risk of propagation of financial contagion in interbank networks has been studied for analyzing the US credit default swaps (CDS) for the years 2007–2008. A special focus was placed to gain a better understand what has been called “too interconnected to fail” (TITF). For constructing the network, data from the FDIC Call Report Data have been used providing the Gross Negative Fair Value (GNFV) for payables and Gross Positive Fair Value (GPFV) for receivables on all CDS products that a firm is involved in with all of its counterparties [57]. In total, 33 US banks have been included in the analysis. In order to model the influence of non-US banks, two auxiliary nodes have been added to the network, one representing all US firms and one non-US banks and firms. A major finding from a network analysis applying eigenvector centrality is that J.P. Morgan is the most dominant bank followed closely by the European banks. Interestingly, other well-known US banks like Goldman Sachs and Citigroup follow with a larger distance. They suggested for banks to minimize the systemic risk from their high network centrality that banks should be taxed according to a progressive tax rate which is based on the value of their eigenvector centrality.

The paper by Roukny et al. [40] is the first studying the structural evolution of two of the most important over-the-counter markets for liquidity in Germany: the market for interbank liquidity and the market for credit default swaps (CDS). They used data on individual exposures for over 2000 German banks available from the Deutsche Bundesbank. Based on these data, they constructed two networks connecting banks, one for (I) credit exposure and one for (II) derivative exposure. In the former case, the resulting network is directed and weighted with a link going from the lender to the borrower and the weight corresponds to the total amount of money lent by the lender. Similarly, a network for derivate exposures is constructed. However, due to the more complicated situation in the derivative case, these network are consider as undirected networks but with weights. An important result of their study is that the size of the connected component of the credit network decreases over time while the size of the derivative network remains constant. Interestingly, the two networks show different forms of clustering. While the credit network has a very high average clustering coefficient the derivative network has a much smaller value.

In Demirer et al. [59] a network of the world's top 150 (92 banks from developed and 14 from emerging economies) publicly-traded banks has been investigated. The interbank network is constructed by a shrinking method (applying lasso [81]) and selecting on the approximating VAR (vector autoregressive) model. This model is based on the bank stock return volatility, which needs to be estimated from daily stock price data (high, low, open and close prices) according to Garman and Klass MJ [82],

$\begin{array}{l}{\sigma }_{it}^2=-0.019\left[\left(C_{it}-O_{it}\right)\left(H_{it}+L_{it}-2O_{it}\right)-2\left(H_{it}-O_{it}\right)\left(L_{it}-O_{it}\right)\right]+\\ 0.511{\left(H_{it}-L_{it}\right)}^2-0.383{\left(C_{it}-O_{it}\right)}^2& (3)\end{array}$

Here H_it, L_it, O_it and C_it are the logarithms of daily high, low, opening and closing values for bank stock i at time t.

They showed that the connections of global banking is clearly linked to bank location, not bank assets. Overall, they found that “global banking connectedness displays both secular and cyclical variation. The secular variation corresponds to gradual increases/decreases during episodes of gradual increases/decreases in global market integration. The cyclical variation corresponds to sharp increases during crises, involving mostly cross-country, as opposed to within-country, bank linkages” [59].

A complementary approach to the investigations discussed above to study bank networks has been proposed by Rönnqvist and Sarliz [60]. In their study, a text mining approach has been introduced to convert text information to a network by detecting the co-occurrence of bank names in financial discourse, such as news, official reports and discussion forums, from 3 million articles published during 2007 and 2014 in the Reuters online news archive. The constructed network comprises 27 major consumer banks from Europe, that are classified by the European Central Bank as Large and Complex Banking Groups (LCBGs). Furthermore, 15 of these are also classified as Globally Systemically Important Banks (G-SIBs) by the Financial Stability Board.

The basic idea of their network construction algorithm is to identify co-occurrences of two bank names in the same context. As “context” they defined a 400-character sliding window in the text. In order to reduce noise they did not consider the co-occurrence of two bank if more than 5 banks are mentioned in the context window. Overall, this resulted in undirected, weighted interbank networks, each one constructed for a certain time interval. It is interesting to note that their approach is capable of reproducing know results from traditional data sources and, hence, can indeed serve as a complementary approach.

4.3. Companies

In Vitali et al. [45] and Vitali and Battiston [46] an ownership network of transnational corporations (TNC) was investigated. They used data from the Orbis marketing database which comprises about 37 million economic parties. These include physical persons and firms located in 194 countries. Overall, they have about 13 million directed and weighted ownership links (equity relations). For their analysis they used 43, 060 TNC located in 116 different countries, with 5, 675 TNC listed in various stock markets. The OECD defines a TNC as a firm that holds at least 10% of shares in companies located in more than one country. Because it is possible that a non-TNC institution holds a share in a TNC and a TNC holds a share in a non-TNC, the number of studied entities had to be enlarged by 77, 456 shareholders (SH) and 479, 992 participating companies (PC), which are not located in more than one country. Hence, in total the ownership network they studied had a size of 600, 508 nodes.

As a main result they found that the ownership network forms a “bow-tie structure” where a large portion of the control flows to a small but tightly connected core of financial institutions [45]. Interestingly, this core comprises only 295 TNC. They suggested to consider this core as an economic “superentity” and speculated about its importance for policy makers.

In a follow up study [46] of the same ownership network, its community or module structure has been analyzed [83]. They found that despite of the global and international character of the network its communities reflect the geographical location of economic players respectively the firms. Clustering according to the industrial sectors plays only a marginal role.

4.4. Business Groups

The next economic networks we are discussing uses as node types an aggregation of basic node types. Specifically, in Altomonte and Rungi [84] business groups have been studied forming a collection of individual companies and firms. More precisely, they define a Business Group as a set of at least two legally autonomous firms whose economic activity is coordinated through some form of hierarchical control, whereas a firm controls another if a firm exceeds the majority (50.01%) of voting rights on the other firm. This leads to a hierarchical graph.

For constructing this hierarchical graph two databases have been used namely the Ownership Database and Orbis, both provide by Bureau Van Dijk. The Ownership Database gives information about worldwide proprietary linkages and Orbis about financial accounts. The studied data comprised a total of 208, 181 business groups from 129 countries controlling 1, 005, 381 affiliates.

A noteworthy difference in their analysis to other studies is that the authors tried to quantify the structural complexity [85] of the hierarchical business group graph. In order to do this they extended a complexity measure of Emmert-Streib and Dehmer [86] by defining a new measure they called “Group Index of Complexity” (GIC) [84],

$\begin{array}{ll}\begin{array}{l}GIC(G)={\displaystyle \underset{L}{\overset{l}{{{\displaystyle \sum }}^{\text{}}}}}l\frac{n_l}{N}\log \left(\frac{N}{n_l}\right)\hfill \end{array}& (4)\end{array}$

Here L is the number of hierarchy levels, n_l is the number of affiliates on hierarchical level l and N is the total number of affiliates.

As a result they found a negative correlation between a vertical integration and the hierarchical complexity of business groups if conditioned on the institutional quality. Furthermore, there is a robust (non-linear) positive correlation between the hierarchical complexity of a business group and their productivity. This correlation is much stronger than the known correlation between vertical integration and productivity.

4.5. Stocks

The first financial networks that have been studied are correlation networks [25]. In order to study the hierarchical organization of such networks [25] identified the minimum spanning tree (MST) as a backbone structure to find the most important connections among all stocks in the financial network.

In Sandoval [63] a financial network between stocks of the largest 197 financial companies of the world, as measured in market volume, has been studied. Their analysis is based on companies from the S&P 1200 Global Index as in 2012. The stocks that belong to this index are involved in about 70 percent of the total world stock market capitalization. Furthermore, according to Bloomberg, 200 of them are belonging to the financial sector. Corresponding daily closing prices of stock data for the 197 financial companies have been extracted from the New York Stock Exchange (NYSE) and non-stationarity effects in the time series data have been reduced by the transformation,

$\begin{array}{ll}{R}_t=ln(P_t)-ln(P_{t-1})& (5)\end{array}$

Here R_t is the log-return of the closing price, P_t is the closing price of the stock at day t and P_t−1 is the closing price of the stock at the previous day (t−1). As a measure to identify the relations between stocks the transfer entropy (TE) [87, 88] has been used. The TE is an asymmetric measure defined by,

$\begin{array}{ll}T{E}_{Y\to X}={\displaystyle \sum _{i_{n+1},i_n,j_n}}p(i_{n+1},i_n,j_n){log}_2\frac{p(i_{n+1}|i_n,j_n)p(i_n)}{p(i_{n+1},i_n)p(i_n,j_n)}& (6)\end{array}$

Here i_n is element n of the time series of variable X and j_n is element n of the time series of variable Y. Due to the asymmetry of TE the resulting network is directed and the weighted with TE_Y→X being its weights.

As a result they found that the structure of the transfer entropy network is very different from a correlation network. This is certainly related to the asymmetry of the TE but also its capability of identifying more causal influences between the stocks. Interestingly, nodes in the network are related, first, by the country from which the stocks are issued, and then by industry and sub industry.

Furthermore, by studying the centralities of the stocks they showed that the most central ones belong to insurance companies or banks from Europe and the USA. “Since insurance and reinsurance companies are major CDS (Credit Default Securities) sellers, and banks are both major CDS buyers and sellers, some of this centrality of insurance companies, followed by banks, might be explained by the selling and buying of CDS” [63].

Additional studies investigating financial networks based on correlation measures can be found in Bonanno et al. [89], Emmert-Streib and Dehmer [48], Emmert-Streib and Dehmer [90], Tabak et al. [91], and Ulusoy et al. [92] and for extensions based on mutual information allowing to estimate non-linear effects in time series data (see e.g., [93, 94]). An aggregate analysis of stocks has been conducted in Saeedian et al. [64]. In this study 40 stock market indices, instead of individual stocks, have been investigated to estimate a correlation network of the world market. As a result, they found that the world financial market comprises three communities, each of which includes stock markets with geographical proximity.

4.6. Products

The next type of economic networks we are discussing are product networks. Specifically, in order to understand the entire economy of countries the product network has been investigated. For instance, Hidalgo et al. [51] used the measure revealed comparative advantage (RCA) by Balassa [95],

$\begin{array}{ll}\begin{array}{l}RC{A}_{ci}=\hfill \end{array}\frac{x(c,i)}{\underset{i}{{{\displaystyle \sum }}^{\text{}}}x(c,i)}/\frac{\underset{c}{{{\displaystyle \sum }}^{\text{}}}x(c,i)}{\underset{c,i}{{{\displaystyle \sum }}^{\text{}}}x(c,i)}& (7)\end{array}$

evaluated for international trade data provided by National Bureau of Economic Research (NBER), to estimate the proximity Φ_ij between product i and j,

$\begin{array}{ll}\begin{array}{l}{\Phi }_{ij}=\min \left\{P(RC{A}_{xi}|RC{A}_{xj}),P(RC{A}_{xj}|RC{A}_{xi})\right\}\hfill \end{array}& (8)\end{array}$

From Φ_ij the resulting product network is obtained by using the Φ_ij values as weights. Prioritizing and thresholding of these weights led them to the conclusion that countries are developing goods that are already close to those ones that are currently produced. Furthermore, they hypothesized that for a country to produce more remote product categories economic policies, especially of underdeveloped countries, need to take risks by allowing “long jumps” for generating subsequent structural transformation, convergence, and growth.

A follow-up study by Hidalgo et al. [96] investigated higher-order properties of a country-product bipartite network, M_{c, p}, resulting from thresholded values of the RCA (see Equation 7). These higher-order properties are extracted by recursive equations, called Methods of Reflection, which are defined by

$\begin{array}{ll}{k}_{c,N}=\frac{1}{k_{c,0}}{\displaystyle \sum _p}{M}_{c,p}{k}_{p,N-1}& (9)\end{array}$

$\begin{array}{ll}{k}_{p,N}=\frac{1}{k_{p,0}}{\displaystyle \sum _c}{M}_{c,p}{k}_{c,N-1}& (10)\end{array}$

The initial values are given by

$\begin{array}{ll}{k}_{c,0}={\displaystyle \sum _p}{M}_{c,p}& (11)\end{array}$

$\begin{array}{ll}{k}_{p,0}={\displaystyle \sum _c}{M}_{c,p}& (12)\end{array}$

They used the above measures for k_{c, i} and k_{p, i} to define a complexity measure for the economy of countries and showed that this measure correlates with the income level. Furthermore, they showed that their complexity measures are predictive of future growth and future exports of countries, making this way a strong empirical case that the level of the development of a country is indeed associated with the complexity of its economy.

4.7. Geographic Indicators

Also the last type of economic networks we are reviewing consist in an aggregation of base entities. In Heemskerk et al. [67] data from the Orbis database have been used to extract information about the board of directors. In total 8, 090, 796 senior level directors have been identified serving at 18, 211, 838 firms. This information allowed the construction of a bipartite network of firms and directors. From this bipartite network the projected firm network has been constructed in which the nodes represent firms and weighted edges represent shared senior level directors. That means the edge weights give the number of shared directors between two firms.

The resulting network consists of a number of components which are not all connected with each other. The giant connected component (GCC) of the network consists of 5, 262, 534 firms connected by over 37 million board interlocks. Using the GCC, firms located in the same city have been aggregated in a node and two city nodes are connected if there are directors serving in at least one firm of these cities. The weight of a link corresponds to the number of directors in such firms. In total, the resulting city network consisted of 24, 747 cities, connected by 874, 8104 links.

Similar to other studies they confirmed that geographic location of firms is reflected in the community structure of the network. Even more interesting, they found that this is even true if countries no longer exist as, e.g., Czechoslovakia or the original Kingdom of the Netherlands. From the city-perspective they found that London is the most central city in the network of the global corporate elite.

Another example of such an agloromative approach is given by Fagiolo et al. [37]. In their paper the network of trade relationships among world countries, also called the international trade network (ITN) or World Trade Web (WTW), has been studied. For constructing such a network, international trade data from import and export flows are used [68]. They construct a weighted ITN by defining a weight as,

$\begin{array}{ll}{w}_{ij}^t=\frac{e_{ij}^t}{{GDP}_i^t}& (13)\end{array}$

where $e_{ij}^t$ are time (deflated) exports from country i to country j, and $GD{P}_i^t$ is the real gross domestic product of country i in year t. In this way 20 networks for T = 20 years (1981–2000) are constructed for N = 159 countries [37].

As a result, they showed that the international trade network is quite symmetric. That means almost all trade relationships between two countries are equal with respect to import and export. Furthermore, the majority of countries have only a few connections to other countries, but a small number of countries have many relations. The latter connections have also higher weights. Further studies of international trade networks can be found in Bhattacharya et al. [97], Garlaschelli and Loffredo [98], Serrano and Boguná [99], and Serrano et al. [100].

5. Data

Due to the fact that the discussed economic networks of the preceding sections are not immediately available but need to be constructed from empirical data, we provide in this sections some frequently used databases containing valuable data for such a construction.

5.1. UN Comtrade

The UN Comtrade database [101, 102] is provided by the United Nations International Trade Statistics. The database contains information about trade statistics data from over 170 countries detailed by commodities and service categories. The UN COMTRADE is one of the largest public depositories of international trade data with over 3 billion data records since 1962. In order to simplify the usage of the data, all values of commodities are converted from national currency into US dollars and quantities are converted into metric units.

5.2. ORBIS

The ORBIS database [103] provided commercially by Bureau van Dijk gives information on private companies worldwide. ORBIS has information for over 220 million companies of which information about 70, 000 listed companies is more detailed. It provides information about the name of firms, geographical localization (country and city), industrial classification (NACE) and several financial data. Moreover, the database includes standardized information about corporate ownership including beneficial owners, M&A data and financial strength metrics. A helpful analysis giving detailed information about the usage of this database and potential problems and biases of the data are reported in Kalemli-Ozcan et al. [104].

5.3. OECD

The OECD (Organization for Economic Co-operation and Development) database [105] provides public economic and society related information for the 35 member countries of the OECD and additional major countries, e.g., China and Russia. It contains over 5 billion data points across 1, 800 datasets. The comprehensive list of topics covered by the database includes population and migration; production; household income, wealth and debt; globalization, trade and foreign direct investment (FDI); prices, interest rates and exchange rates; energy and transportation; labor, employment and unemployment; science and technology including research and development (R&D); environment including natural resources, water, air and climate; education resources and outcomes; government expenditures, debt, revenues, taxes, foreign aid; and, health status, risk and resources. Access to these datasets is provide via the OECDiLibrary page.

5.4. DICE

The DICE (Database for Institutional Comparisons in Europe) database [106] by the Ifo Institute at the University of Munich (Germany) provides public cross-country information on institutions, regulations and policies. DICE gives not only information on European countries but also includes information on other major countries as well as the BRIC countries (Brazil, Russia, India and China). The topic list of DICE includes banking and financial markets, business, education and ennovation, energy, resources, natural environment, infrastructure, labor market, migration, public sector, social policy, values, and country characteristics.

5.5. CEPII

CEPII is a French research center with a focus on international economics established in 1978. The data provided are from the fields Competitiveness & Growth, Economic Policy, Emerging Countries, Environment & Natural Resources, Europe, Migrations, Money & Finance, Trade & Globalization. CEPII is a collection of different data sets, one of which is BACI [107]. BACI is the World trade database at a high level of product disaggregation. It contains information for more than 200 countries since 1995.

5.6. BIS

The Bank of International Settlements (BIS) [108] provides data about cross-country bilateral exposures for domestically owned and foreign-owned banking offices in the reporting countries giving information about the balance sheet positions on other countries. For this reason the BIS is also known as “bank of central banks”. The database contains information for 230 countries since 2008.

5.7. Stock Market Data

Public historical stock market data can be obtained from many places, including Yahoo Finance, Google Finance or MSN Moneycentral. However, for downloading bulk stock market data these sites do not offer much functionality and require an individual downloading for each stock. For this reason, the R package quantmod [109] has been developed that allows to connect to Yahoo Finance or Google Finance or to get FX rates from FRED (Federal Reserve Economic Data). Other R packages available for getting such data are Quandl [110] (download from the Quandl database collecting financial and economic datasets from hundreds of publishers), pdfetch [111] (St Louis Fed's FRED system, Yahoo Finance, the US Bureau of Labor Statistics, the US Energy Information Administration, the World Bank, Eurostat, the European Central Bank, the Bank of England, the UK's Office of National Statistics, Deutsche Bundesbank, and INSEE) and WDI [112] (data from the World Development Indicators provided by the World Bank).

We would like to note the such stock market data provide usually no intra-day trading data, e.g., on the hour or even minute level, but only end-of-day information. Intra-day trading data is only available via commercial subscription.

6. Visualization of Economic Networks

The analysis of complex economic networks starts typically with the visualization of the network itself. The reason for this is that network visualization can be seen as a form of an exploratory data analysis [113], which aims to visually highlighting patterns in the data. Unfortunately, the graphical visualization of a network is not trivial at all and the problem becomes even more difficult the larger the network is. For this reason, we discuss in the next subsections some visualization approaches that can help in accomplishing this task.

For reasons of a practical realizability, we focus on software packages written in R Development Core Team [114] because these packages are free to use and provide flexibility for a problem specific fine tuning. However, for reasons of completeness we want to mention that there are also stand-alone tools for network exploration (e.g., Gephi [115], Pajek [116], or Cytoscape [117]), which do not require programming knowledge.

6.1. General Visualization of Networks

For the visualization of general networks we developed an R package called NetBioV [118, 119]. NetBioV provides many easy to use functions, layout styles and color schemes to visualize networks. Specifically, NetBioV provides three principle layout styles.

• global layouts

• modular layouts

• layered layouts

These layouts can be either used separately or combined with each other. Briefly, a global layout style treats essentially all nodes of the network in the same way and tries to find a global arrangement according to some algorithm, e.g., Fruchterman-Reingold or Kamada-Kawai. A modular layout acknowledges the fact that some nodes are more close to each other forming, e.g., a cluster, a module or a community within the network. Finally, a layered layout emphasizes the presence of a hierarchical order in the network, e.g., a tree. Depending on which property one would like to emphasize and highlight, one needs to choose the corresponding layout style. We would like to remark that for the graphical representation of networks, the package NetBioV makes use of the igraph package [120]. Igraph2 can also directly be used for the visualization of networks but it is more basic and elementary in its usage and requires for this reason more manual fine tuning in order to obtain satisfactory results.

6.2. Combining Networks, Geographic and Economic Information

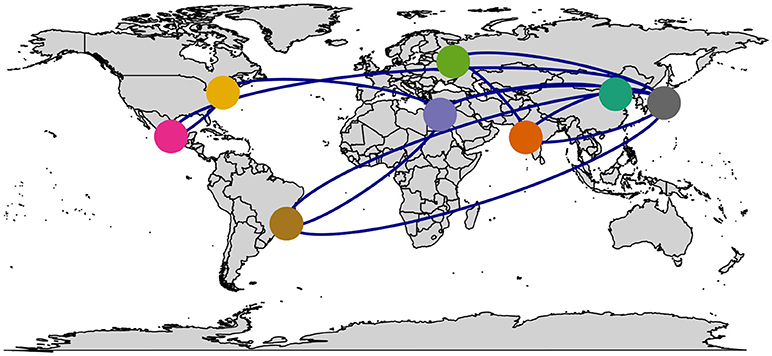
Many of the different networks discussed in the previous sections carry in addition to the economic information geographic information. For instance, banks or firms are located in certain cities which are located in certain countries. That means the nodes of such economic networks, which correspond to banks or firms, can be overlain a geographic map. In this way the interpretability of these networks is enhanced, see as an example Figure 3. This is especially beneficial if one considers the fact that “networks” or “graphs” are topological mathematical objects. A topological object does not have any geometric properties, e.g., for the location of the nodes of a network, but can be deformed arbitrarily without changing its properties. For this reason, the meaningful connection of networks with geometric information helps 2-fold. First, the visualization of the network is simplified because no algorithm is needed for finding the coordinates of the nodes for drawing them in form of a diagram but this information is directly provided by the geographic information, e.g., for the location of cities. Second, the interpretation of the networks is enhanced, e.g., because geographic clusters become immediately spottable.

FIGURE 3

Figure 3. Mapping economic networks with geographic locations by the maps R package.

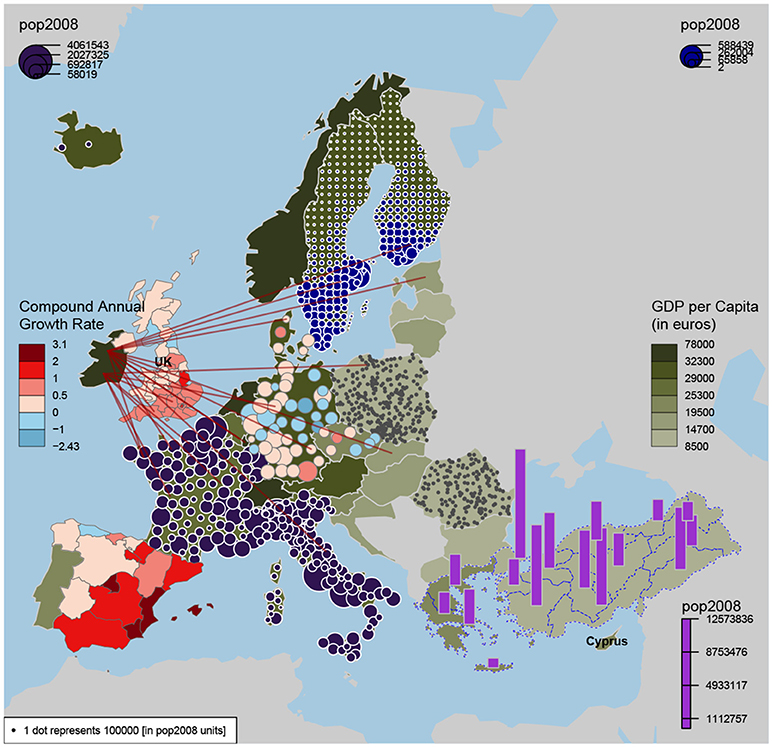
A practical solution to the above problem is given by the R package maps. This package was also used to generate the example in Figure 3 overlaying a network on the world map. Another R package that provides even more functionality is cartography [121]. In Figure 4 we show an example. This package allows in addition to the visualization of a network, the visualization of additional economic factors like GDP, population size or compound annual growth rate. These additional elements enhance even further the interpretability of the obtained economic networks. In Figure 4 we added some examples showcasing the functionality of this package. Specifically, information about the GDP per capita is visualized in the color of the country (see e.g., Island, Norway or Finland), population size is shown as bar charts (Turkey and Greece) and the compound annual growth rate is color highlighted (Spain).

FIGURE 4

Figure 4. Mapping economic networks with geographic locations by the cartography R package.

6.3. Bipartite Networks

Another network visualization that is useful for economic networks relates to bipartite networks. The R packages bipartite [122] provides such a functionality with many options to customize the resulting visualization. We would like to note that so far the direct analysis of bipartite networks has not received much attention but, usually, projected networks are extracted from bipartite networks which are then analyzed, because these projected networks are ordinary networks which can be analyzed in the conventional way with the standard methods. However, there are also direct methods available for analyzing bipartite networks [123–126] and it seems that such approaches are generating more and more interest.

7. Extensions and Future Directions

As we have seen in the previous sections, so far many different economic networks have been studied. In this section, we discuss some possible extensions that would help in advancing the field.

First of all, it is apparent from our discussions that most economic networks are constructed or inferred from one data source only. This is certainly the easiest way to create such networks but it is not necessarily the best way. It would be interesting to investigate the integration of more than one data source to see in how far the results are changed. Also it seems reasonable to assume that the amount of noise in the networks can be reduced by using multiple data sources. This is especially true for the financial networks requiring time series data for their inference which are only available for a limited duration.

Another form of data integration that could be studied relates to combining multiple “node types”; see Table 2. Instead of focusing on only one node type, e.g., banks or directors, one could study a combination of these in one network. This would require that one uses weighted networks [127], which allows different node types in the same network.

In general, the quality of economic networks is not easy to assess because these are abstract networks and its links are not immediately observable. This is in contrast to a neural network or a gene regulatory network where links connecting pairs of neurons or indicate the regulation of one gene on another [128–130]. In both cases, wet lab experiments can be performed in order to confirm such connections. For financial networks, where nodes correspond to stocks, this is obviously not possible. For this reason the assessment of the quality of the obtained networks needs to be done indirectly, e.g., by quantifying predictive or forecasting abilities of the networks. This topic relates to the difference between causal networks and association networks [131, 132].

Another problem of the current research in economic networks is that there is no database to which constructed networks could be uploaded so that other scientists can re-use them in follow-up studies, e.g., for comparative investigations with alternative approaches. This would simplify such comparative analyses considerably and also help in reducing errors when reproducing previous results. Also a data repository integrating information from various databases, as discussed in section 5, bringing them into a standardized form, would reduce the obstacles accompanying computational economics studies simplifying the time consuming preprocessing of the data considerably.

8. Conclusion

In this paper we reviewed studies for estimating and analyzing different types of economic networks. Despite the fact that economic networks are a special form of social networks which having been studied since many decades starting in the 1960s, for economic networks it took much longer to start. Maybe it is no accident that the sparking interest in economic networks in recent years coincides with the emergence of computational social science [133–135] as a general appreciation of phenomena outside the natural sciences. A further reason is certainly that one global economic crises is followed by another making us as a society realize that only a more thorough understanding of the global economy can help in preventing future meltdowns. Since it is hard to imagine how one would study an interconnected system, such as the world economy, without the usage of networks, we anticipate to see many more studies about economic networks in the years to come and hope that our contribution can help in fostering this process.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MD thanks the Austrian Science Funds for supporting this work (project P 30031).

References

1. Barabási A-L. Network science. Phil Trans R Soc A (2013) 371:20120375. doi: 10.1098/rsta.2012.0375

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Borgatti SP, Mehra A, Brass DJ, Labianca G. Network analysis in the social sciences. Science (2009) 323:892–5. doi: 10.1126/science.1165821

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Fang J-Q, Wang X-F, Zheng Z-G, Bi Q, Di Z-R, Xiang L. New interdisciplinary science: network science (1). Prog Phys Nanjing (2007) 27:239.

Google Scholar

4. Jackson MO. Social and Economic Networks. Princeton, NJ: Princeton University Press (2010).

Google Scholar

5. Schweitzer F, Fagiolo G, Sornette D, Vega-Redondo F, White DR. Economic networks: What do we know and what do we need to know? Adv Complex Syst. (2009) 12:407–22. doi: 10.1142/S0219525909002337

CrossRef Full Text | Google Scholar

6. Allen F, Babus A. Networks in Finance. Wharton Financial Institutions Center Working Paper No. 08–07 (2008). doi: 10.2139/ssrn.1094883

CrossRef Full Text

7. Kirman A. The economy as an evolving network. J Evolut Econ. (1997) 7:339–53.

Google Scholar

8. Schweitzer F, Fagiolo G, Sornette D, Vega-Redondo F, Vespignani A, White DR. Economic networks: the new challenges. Science (2009) 325:422–5. doi: 10.1126/science.1173644

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Nagurney A, Siokos S. Financial Networks: Statics and Dynamics. Berlin; Heidelberg: Springer (1997).

Google Scholar

10. von Bertalanffy L. An outline of general systems theory. Br J Phil Sci. (1950) 1:134–65.

Google Scholar

11. von Bertalanffy L. General System Theory: Foundation, Development, Application. New York, NY: George Braziller (1968).

Google Scholar

12. Bonchev D, Rouvray D. Chemical Graph Theory: Introduction and Fundamentals. Mathematical Chemistry. Boca Raton, FL: Abacus Press (1991).

Google Scholar

13. Dehmer M, Emmert-Streib F, Graber A, Salvador A. (eds.). Applied Statistics for Network Biology: Methods for Systems Biology. Weinheim: Wiley-Blackwell (2011).

Google Scholar

14. Emmert-Streib F, Dehmer M. Networks for systems biology: conceptual connection of data and function. IET Syst Biol. (2011) 5:185. doi: 10.1049/iet-syb.2010.0025

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Freeman L. The Development of Social Network Analysis. A Study in the Sociology of Science. Vancouver, BC: Empirical Press (2004).

Google Scholar

16. Newman M. Networks: An Introduction. Oxford: Oxford University Press (2010)

Google Scholar

17. Barabási A L, Albert R. (1999). Emergence of scaling in random networks. Science 206:509–12.

Google Scholar

18. Watts D, Strogatz S. Collective dynamics of “small-world” networks. Nature (1998) 393:440–2.

PubMed Abstract | Google Scholar

19. Dehmer M, Emmert-Streib F. (eds.). Analysis of Complex Networks: From Biology to Linguistics. Weinheim: Wiley-VCH (2009).

Google Scholar

20. Wasserman S, Faust K. Social Network Analysis. Cambridge; New York, NY; Cambridge University Press (1994).

Google Scholar

21. Hughes M, Nagurney A. (1992). A network model and algorithm for the analysis and estimation of financial flow of funds. Comput Econ. 5:23–39.

Google Scholar

22. Smith DA, White DR. Structure and dynamics of the global economy: network analysis of international trade 1965–1980. Soc Forces (1992) 70:857–93.

Google Scholar

23. Carroll WK, Lewis S. Restructuring finance capital: changes in the canadian corporate network 1976-1986. Sociology (1991) 25:491–510.

Google Scholar

24. Sheldon G, Maurer M. Interbank lending and systemic risk: an empirical analysis for switzerland. Revue Suisse D Econ Polit Et De Stat. (1998) 134:685–704.

Google Scholar

25. Mantegna R. Hierarchical structure in financial markets. Eur Phys J B (1999) 11:193–7.

Google Scholar

26. Vandewalle N, Brisbois F, Tordoir X. Self-organized critical topology of stock markets. arXiv[preprint] arXiv (2000).

Google Scholar

27. Marschinski R, Kantz H. Analysing the information flow between financial time series. Eur Phys J B Condens Matter Complex Syst. (2002) 30:275–81. doi: 10.1140/epjb/e2002-00379-2

CrossRef Full Text | Google Scholar

28. Souma W, Fujiwara Y, Aoyama H. Complex networks and economics. Physica A (2003) 324:396–401. doi: 10.1016/S0378-4371(02)01858-7

CrossRef Full Text | Google Scholar

29. Onnela J-P, Chakraborti A, Kaski K, Kertesz J. Dynamic asset trees and black monday. Phys A (2003) 324:247–52. doi: 10.1016/S0378-4371(02)01882-4

CrossRef Full Text | Google Scholar

30. Boss M, Elsinger H, Summer M, Thurner S. Network topology of the interbank market. Quant Finance (2004) 4:677–84. doi: 10.1080/14697680400020325

CrossRef Full Text | Google Scholar

31. Anand K, van Lelyveld I, Banai A, Friedrich S, Garratt R, Halaj G, et al. The missing links: a global study on uncovering financial network structures from partial data. J Financ Stability (2017) 35:107–19. doi: 10.1016/j.jfs.2017.05.012

CrossRef Full Text | Google Scholar

32. Battiston S, Glattfelder JB, Garlaschelli D, Lillo F, Caldarelli G. The Structure of Financial Networks. London: Springer (2010). p.131–63.

Google Scholar

33. Heemskerk E, Young K, Takes F, Cronin B, Garcia-Bernardo J, Popov V, et al. The promise and perils of using big data in the study of corporate networks: problems, diagnostics and fixes. Glob Netw J Trans Aff. (2017) 18:3–32. doi: 10.1111/glob.12183

CrossRef Full Text | Google Scholar

34. Bang-Jensen J, Gutin G. Digraphs. Theory, Algorithms and Applications. London; Berlin; Heidelberg: Springer (2002).

Google Scholar

35. Harary F. Graph Theory. Reading, MA: Addison Wesley Publishing Company (1969).

Google Scholar

36. Garratt R, Mahadeva L, Svirydzenka K. Mapping systemic risk in the international banking network. Bank of England Working Papers (2011).

Google Scholar

37. Fagiolo G, Reyes J, Schiavo S. The evolution of the world trade web: a weighted-network analysis. J Evolut Econ (2010) 20:479–514. doi: 10.1007/s00191-009-0160-x

CrossRef Full Text | Google Scholar

38. Arnold J, Bech M, Beyeler W, Glass R, Soramäki K. The Topology of Interbank Payment Flows. Federal Reserve Bank of New York, Staff Report (2006) 243.

39. Degryse H, Nguyen G. Interbank exposure: an empirical examination of systemic risk in the belgian banking system. Econstor Working Papers 62 (2004).

Google Scholar

40. Roukny T, Georg C-P, Battiston S. A Network Analysis of the Evolution of the German Interbank Market. Technical Report, Discussion Paper, Deutsche Bundesbank (2014).

41. Hochberg YV, Ljungqvist A, Lu Y. Whom you know matters: venture capital networks and investment performance. J Finance (2007) 62:251–301. doi: 10.1111/j.1540-6261.2007.01207.x

CrossRef Full Text | Google Scholar

42. Siddiqui AI, Marinova D, Hossain A. Venture capital networks in australia: emerging structure and behavioural implications. J Manag Sustainability 6. (2016). Available online at: https://heinonline.org/HOL/LandingPage?handle=hein.journals/jms6&div=21&id=&page=

Google Scholar

43. Heemskerk EM, Takes FW. The corporate elite community structure of global capitalism. New Polit Econ. (2016) 21:90–118. doi: 10.1080/13563467.2015.1041483

CrossRef Full Text | Google Scholar

44. Milaković M, Alfarano S, Lux T. The small core of the german corporate board network. Comput Math Organ Theory (2010) 16:201–15. doi: 10.1007/s10588-010-9072-4

CrossRef Full Text | Google Scholar

45. Vitali S, Glattfelder JB, Battiston S. The network of global corporate control. PLoS ONE (2011) 6:e25995.

PubMed Abstract | Google Scholar

46. Vitali S, Battiston S. The community structure of the global corporate network. PLoS ONE (2014) 9:e104655. doi: 10.1371/journal.pone.0104655

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Boginski V, Butenko S, Pardalos P. (2005). Statistical analysis of financial networks. Comput Stat Data Anal. 48:431–43. doi: 10.1016/j.csda.2004.02.004

CrossRef Full Text | Google Scholar

48. Emmert-Streib F, Dehmer M. Identifying Critical Financial Networks of the DJIA: towards a Network-based Index. Complexity (2010) 16:24–33. doi: 10.1002/cplx.20315

CrossRef Full Text | Google Scholar

49. Qiu T, Zheng B, Chen G. Financial networks with static and dynamic thresholds. New J Phys. (2010) 12:043057. doi: 10.1088/1367-2630/12/4/043057/meta

CrossRef Full Text | Google Scholar

50. Dhar V, Geva T, Oestreicher-Singer G, Sundararajan A. Prediction in economic networks. Inform Syst Res. (2014) 25:264–84.

Google Scholar

51. Hidalgo CA, Klinger B, Barabási A-L, Hausmann R. The product space conditions the development of nations. Science (2007) 317:482. doi: 10.1126/science.1144581

PubMed Abstract | CrossRef Full Text | Google Scholar

52. De Benedictis L, Nenci S, Santoni G, Tajoli L, Vicarelli C. Network Analysis of World Trade using the BACI-CEPII dataset. Glob Econ J. (2014) 14:287–343. Available online at: https://www.degruyter.com/view/j/gej.2014.14.issue-3-4/gej-2014-0032/gej-2014-0032.xml

Google Scholar

53. Kali R, Reyes J. The architecture of globalization: a network approach to international economic integration. J Int Bus Stud. (2007) 38:595–620. doi: 10.1057/palgrave.jibs.8400286

CrossRef Full Text | Google Scholar

54. Mahutga MC, Smith DA. Globalization, the structure of the world economy and economic development. Soc Sci Res. (2011) 40:257–72. doi: 10.1016/j.ssresearch.2010.08.012

CrossRef Full Text | Google Scholar

55. Renneboog L, Zhao Y. Us knows us in the uk: On director networks and ceo compensation. J Corp Finance (2011) 17:1132–57. doi: 10.1016/j.jcorpfin.2011.04.011

CrossRef Full Text | Google Scholar

56. Constantin A, Peltonen TA, Sarlin P. Network linkages to predict bank distress. J Financ Stability (2016) 35:226–24. doi: 10.1016/j.jfs.2016.10.011

CrossRef Full Text | Google Scholar

57. Markose S, Giansante S, Shaghaghi AR. ‘Too interconnected to fail’ financial network of US CDS market: Topological fragility and systemic risk. J Econ Behav Organ. (2012) 83:627–46. doi: 10.1016/j.jebo.2012.05.016

CrossRef Full Text | Google Scholar

58. Diebold FX, Yilmaz K. Trans-atlantic equity volatility connectedness: U.s. and european financial institutions, 2004–2014. J Financ Econom. (2015) 14:81–127. doi: 10.1093/jjfinec/nbv021

CrossRef Full Text | Google Scholar

59. Demirer M, Diebold FX, Liu L, Yılmaz K. Estimating Global Bank Network Connectedness. Technical Report, National Bureau of Economic Research (2017).

Google Scholar

60. Rönnqvist S, Sarliz P. Bank networks from text: interrelations, centrality and determinants. Quant Finance (2015) 15:1619–35. doi: 10.1080/14697688.2015.1071076

CrossRef Full Text | Google Scholar

61. De Masi G, Fujiwara Y, Gallegati M, Greenwald B, Stiglitz JE. An analysis of the japanese credit network. Evolut Inst Econ Rev. (2011) 7:209–32. doi: 10.14441/eier.7.209

CrossRef Full Text | Google Scholar

62. Marotta L, Micciche S, Fujiwara Y, Iyetomi H, Aoyama H, Gallegati M, et al. Bank-firm credit network in japan: an analysis of a bipartite network. PLoS ONE (2015) 10:e0123079. doi: 10.1371/journal.pone.0123079

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Sandoval L. Structure of a global network of financial companies based on transfer entropy. Entropy (2014) 16:4443–82. doi: 10.3390/e16084443

CrossRef Full Text | Google Scholar

64. Saeedian M, Jamali T, Kamali MZ, Bayani H, Yasseri T, Jafari GR. Emergence of world-stock-market network. arXiv[preprint] ArXiv e-prints (2017).

Google Scholar

65. Adamic L, Brunetti C, Harris J H, Kirilenko A. Trading networks. Econom J.(2017) 20:S126–S149 doi: 10.1111/ectj.12090

CrossRef Full Text | Google Scholar

66. Werth JC, Boeert P. Co-investment networks of business angels and the performance of their start-up investments. Int J Entrepreneurial Venturing (2013) 5:240–56. doi: 10.2139/ssrn.1977970

CrossRef Full Text | Google Scholar

67. Heemskerk E, Takes F, Garcia-Bernardo J, Huijzer M. Where is the global corporate élite? Sociologica (2016) 2016:1–31. Available online at: https://dare.uva.nl/search?identifier=7c2efec1-5024-4bf9-9ec2-cc0c4664397e

Google Scholar

68. Gleditsch KS. Expanded trade and gdp data. J Conflict Resolut. (2002) 46:712–24.

Google Scholar

69. Minoiu C, Reyes JA. A network analysis of global banking: 1978?2010. J Financ Stability (2013) 9:168–84. doi: 10.1016/j.jfs.2013.03.001

CrossRef Full Text | Google Scholar

70. Heiberger RH. Stock network stability in times of crisis. Phys A (2014) 393:376–81. doi: 10.1016/j.physa.2013.08.053

CrossRef Full Text | Google Scholar

71. Sornette D. Why Stock Markets Crash: Critical Events in Complex Financial Systems. Princeton: NJ: Princeton University Press (2003).

Google Scholar

72. Stiglitz J. What i learned at the world economic crisis. Global Poor Exploitation Equal. (2000) 195–204. Available online at: http://books.google.de/books?hl=en&lr=&id=p5nAFNVI-
tQC&oi=fnd&pg=PA195&dq=What+i+
learned+at+the+world+economic+crisis.&
ots=KfunFCSkwl&sig=G1czCCAe40iUrsvrAI7ZPoPoJrA&redir_esc=y#v=onepage&q=What%20i%20learned
%20at%20the%20world%20economic%20crisis.&f=false

Google Scholar

73. Kotz DM. The financial and economic crisis of 2008: a systemic crisis of neoliberal capitalism. Rev Radic Polit Econ. (2009) 41:305–17. doi: 10.1177/0486613409335093

CrossRef Full Text | Google Scholar

74. Poon S-H, Rockinger M, Tawn J. Extreme value dependence in financial markets: Diagnostics, models, and financial implications. Rev Financ Stud. (2003) 17:581–610. doi: 10.1093/rfs/hhg058

CrossRef Full Text | Google Scholar

75. Betz F, Oprică S, Peltonen TA, Sarlin P. Predicting distress in european banks. J Bank Financ. (2014) 45:225–41. doi: 10.1016/j.jbankfin.2013.11.041

CrossRef Full Text | Google Scholar

76. Iori G, Mantegna RN, Marotta L, Micciche S, Porter J, Tumminello M. Networked relationships in the e-mid interbank market: a trading model with memory. J Econ Dyn Control (2015) 50:98–116. doi: 10.1016/j.jedc.2014.08.016

CrossRef Full Text | Google Scholar

77. Temizsoy A, Iori G, Montes-Rojas G. Network centrality and funding rates in the e-mid interbank market. J Financ Stabil. (2016) 33:346–65. doi: 10.1016/j.jfs.2016.11.003

CrossRef Full Text | Google Scholar

78. Iori G, De Masi G, Precup OV, Gabbi G, Caldarelli G. A network analysis of the italian overnight money market. J Econ Dyn Control (2008) 32:259–78. doi: 10.1016/j.jedc.2007.01.032

CrossRef Full Text | Google Scholar

79. Bardoscia M, Battiston S, Caccioli F, Caldarelli G. (2015). Debtrank: a microscopic foundation for shock propagation. PLoS ONE 10:e0130406. doi: 10.1371/journal.pone.0130406

CrossRef Full Text | Google Scholar

80. Battiston S, Puliga M, Kaushik R, Tasca P, Caldarelli G. Debtrank: too central to fail? financial networks, the fed and systemic risk. Sci Rep (2012) 2:541. doi: 10.1038/srep00541

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc B (1994) 58:267–88.

Google Scholar

82. Garman MB, Klass MJ. On the estimation of security price volatilities from historical data. J Bus. (1980) 67–78.

Google Scholar

83. Girvan M, Newman MEJ. Community structure in social and biological networks. Proc Natl Acad Sci USA. (2002) 99:7821–6. doi: 10.1073/pnas.122653799

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Altomonte C, Rungi A. Business groups as hierarchies of firms: determinants of vertical integration and performance. European Central Bank WP Series (2013).

Google Scholar

85. Emmert-Streib F, Dehmer M. Exploring statistical and population aspects of network complexity. PLoS ONE (2012) 7:e34523. doi: 10.1371/journal.pone.0034523

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Emmert-Streib F, Dehmer M. Information theoretic measures of UHG graphs with low computational complexity. Appl Math Comput. (2007) 190:1783–94. doi: 10.1016/j.amc.2007.02.095

CrossRef Full Text | Google Scholar

87. Schreiber T. Measuring information transfer. Phys Rev Lett (2000) 85:461. doi: 10.1103/PhysRevLett.85.461

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Baek SK, Jung W-S, Kwon O, Moon H-T. (2005). Transfer entropy analysis of the stock market. arXiv [preprint]

Google Scholar

89. Bonanno G, Caldarelli G, Lillo F, Micciché S, Vandewalle N, Mantegna RN. Networks of equities in financial markets. Eur Phys J B (2004) 38:363–71. doi: 10.1140/epjb/e2004-00129-6

CrossRef Full Text | Google Scholar

90. Emmert-Streib F, Dehmer M. Influence of the time scale on the construction of financial networks. PLoS ONE (2010) 5:e12884. doi: 10.1371/journal.pone.0012884

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Tabak BM, Serra TR, Cajueiro DO. Topological properties of stock market networks: the case of brazil. Physica A (2010) 389:3240–9. doi: 10.1016/j.physa.2010.04.002

CrossRef Full Text | Google Scholar

92. Ulusoy T, Keskin M, Shirvani A, Deviren B, Kantar E, Cagri Donmez C. Complexity of major uk companies between 2006 and 2010: hierarchical structure method approach. Phys A (2012) 391:5121–31. doi: 10.1016/j.physa.2012.01.026

CrossRef Full Text | Google Scholar

93. Fiedor P. Networks in financial markets based on the mutual information rate. Phys Rev E (2014) 89:052801. doi: 10.1103/PhysRevE.89.052801

PubMed Abstract | CrossRef Full Text | Google Scholar

94. You T, Fiedor P, Hołda A. Network analysis of the shanghai stock exchange based on partial mutual information. J Risk Financ Manag (2015) 8:266–84. doi: 10.3390/jrfm8020266

CrossRef Full Text | Google Scholar

95. Balassa B. Comparative advantage in manufactured goods: a reappraisal. Rev Econ Stat. (1986) 68:315–9.

Google Scholar

96. Hidalgo CA, Blumm N, Barabási A-L, Christakis NA. A dynamic network approach for the study of human phenotypes. PLoS Comput Biol. (2009) 5:e1000353. doi: 10.1371/journal.pcbi.1000353

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Bhattacharya K, Mukherjee G, Saramäki J, Kaski K, Manna SS. The international trade network: weighted network analysis and modelling. J Stat Mech Theory Exp. (2008) 2008:P02002. doi: 10.1088/1742-5468/2008/02/P02002

CrossRef Full Text | Google Scholar

98. Garlaschelli D, Loffredo MI. Structure and evolution of the world trade network. Phys A Stat Mech Appl. (2005) 355:138–44. doi: 10.1016/j.physa.2005.02.075

CrossRef Full Text | Google Scholar

99. Serrano MA. Boguná M. Topology of the world trade web. Phys Rev E (2003) 68:015101. doi: 10.1103/PhysRevE.68.015101

CrossRef Full Text | Google Scholar

100. Serrano MÁ, Boguñá M, Vespignani A. Patterns of dominant flows in the world trade web. J Econ Interact Coord. (2007) 2:111–24. doi: 10.1007/s11403-007-0026-y

CrossRef Full Text | Google Scholar

101. Comtrade U. United Nations Commodity Trade Statistics Database. Available online at: URL: http://comtrade.un.org (2010).

102. Yearbook UC Trade Statistics [data file] (2012).

103. Van Dijk B. Orbis Database. Bureau Van Dijk Electronic Publishing (2011).

Google Scholar

104. Kalemli-Ozcan S, Sorensen B, Villegas-Sanchez C, Volosovych V, Yesiltas S. How to Construct Nationally Representative Firm Level Data From the ORBIS Global Database. Techcnical Report, National Bureau of Economic Research (2015).

Google Scholar

105. OECD. Oecd Factbook 2015-2016 (2016).

106. Hoffmann N, Rohwer A. Dice-eine datenbank von institutionellen regelungen im internationalen vergleich. Ifo Schnelldienst (2010) 63:31.

Google Scholar

107. Gaulier G, Zignago S. BACI: International Trade Database at the Product-Level (the 1994-2007 Version) (October 2010). CEPII Working Paper 2010–23. doi: 10.2139/ssrn.1994500

CrossRef Full Text

108. Caruana J, Borio C, Shin H. 87th Annual Report, 2016/17. Basel: Bank of International Settlements (2017).

Google Scholar

109. Ryan JA. quantmod: Quantitative Financial Modelling Framework. R package version 0.3-5. Available online at: https://cran.r-project.org/web/packages/quantmod/index.html (2008)

110. McTaggart R, Daroczi G. Quandl: Quandl Data Connection, 2013. Available online at: URL https://cran.r-project.org/web/packages/Quandl/index.html (2013).

111. Reinhart A. pdfetch: Fetch Economic Financial Time Series Data from Public Sources. R package version 0.2.2. Available online at: https://CRAN.R-project.org/package=pdfetch (2017).

112. Arel-Bundock V. Wdi: World development indicators (world bank), (2013). Available online at: URL https://cran.r-project.org/web/packages/WDI/index.html

113. Tukey J. Exploratory Data Analysis New York, NY: Addison-Wesley (1977).

Google Scholar

114. R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing ISBN 3-900051-07-0 (2008).

Google Scholar

115. Bastian M, Heymann S, Jacomy M. Gephi: an open source software for exploring and manipulating networks. In: Third International AAAI Conference on Weblogs and Social Media. San Jose, CA (2009). p. 361–2.

Google Scholar

116. Batagelj V, Mrvar A. Pajek-program for large network analysis. Connections (1998) 21:47–57.

Google Scholar

117. Shannon P, Markiel A, Ozier O, Baliga NS, Wang JT, Ramage D, et al. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. (2003) 13:2498–504. doi: 10.1101/gr.1239303

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Tripathi S, Dehmer M, Emmert-Streib F. NetBioV: an r package for visualizing large-scale data in network biology. Bioinformatics (2014) 30:2834–6. doi: 10.1093/bioinformatics/btu384

CrossRef Full Text | Google Scholar

119. Tripathi S, Moutari S, Dehmer M, Emmert-Streib F. Visualization of Biological Networks Using NetBioV. In: Dehmer M, Shi Y, Emmert-Streib F, editors Computational Network Analysis with R: Applications in Biology, Medicine and Chemistry. Hoboken, NJ: Wiley Backwell (2016). pp. 307–34.

Google Scholar

120. Csardi G, Nepusz T. The igraph software package for complex network research. InterJournal (2006) 1695:1–9.

Google Scholar

121. Giraud T, Lambert N. cartography: create and Integrate maps in your R Workflow. J Open Source Softw. (2016) 1:54. doi: 10.21105/joss.00054

CrossRef Full Text | Google Scholar

122. Dormann CF, Gruber B, Fruend J. Introducing the bipartite package: analysing ecological networks. R News (2008) 8:8–11.

Google Scholar

123. Caldarelli G, Cristelli M, Gabrielli A, Pietronero L, Scala A, Tacchella A. A network analysis of countries? export flows: Firm grounds for the building blocks of the economy. PLoS ONE (2012) 7:1–11. doi: 10.1371/journal.pone.0047278

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Chessa A, Crimaldi I, Riccaboni M, Trapin L. Cluster analysis of weighted bipartite networks: a new copula-based approach. PLoS ONE (2014) 9:e109507. doi: 10.1371/journal.pone.0109507

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Melamed D. Community structures in bipartite networks: a dual-projection approach. PLOS ONE (2014) 9:e97823. doi: 10.1371/journal.pone.0097823

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Tumminello M, Micciche S, Lillo F, Piilo J, Mantegna RN. Statistically validated networks in bipartite complex systems. PLoS ONE 6:e17994. (2011) doi: 10.1371/journal.pone.0017994

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Bollabás B. Modern Graph Theory. Graduate Texts in Mathematics. New York, NY: Springer (1998).

Google Scholar

128. Sporns O. Networks of the Brain. Cambridge, MA: MIT Press (2011).

Google Scholar

129. Emmert-Streib F, Dehmer M, Haibe-Kains B. Gene regulatory networks and their applications: understanding biological and medical problems in terms of networks. Front Cell Dev Biol. (2014) 2:38. doi: 10.3389/fcell.2014.00038

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Emmert-Streib F, de Matos Simoes R, Mullan P, Haibe-Kains B, Dehmer M. The gene regulatory network for breast cancer: integrated regulatory landscape of cancer hallmarks. Front Genet. (2014) 5:15. doi: 10.3389/fgene.2014.00015

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Pearl J. Probabilistic Reasoning in Intelligent Systems. Burlington, MA: Morgan-Kaufmann (1988).

Google Scholar

132. Emmert-Streib F, Glazko G, Altay G, de Matos Simoes R. Statistical inference and reverse engineering of gene regulatory networks from observational expression data. Front Genet. (2012) 3:8. doi: 10.3389/fgene.2012.00008 PMCID: PMC3271232

PubMed Abstract | CrossRef Full Text | Google Scholar

133. Lazer D, Pentland AS, Adamic L, Aral S, Barabasi AL, Brewer D, et al. Life in the network: the coming age of computational social science. Science (2009) 323:721. doi: 10.1126/science.1167742

CrossRef Full Text | Google Scholar

134. Conte R, Gilbert N, Bonelli G, Cioffi-Revilla C, Deffuant G, Kertesz J, et al. Manifesto of computational social science. Eur Phys J Spec Top. (2012) 214:325–46.

Google Scholar

135. Chang RM, Kauffman RJ, Kwon Y. Understanding the paradigm shift to computational social science in the presence of big data. Decis Support Syst. (2014) 63:67–80. doi: 10.1016/j.dss.2013.08.008

CrossRef Full Text | Google Scholar