- 1Department of Psychology, Università degli Studi di Torino, Turin, Italy
- 2Department of Humanities and Social Sciences, Università della Valle d'Aosta, Aosta, Italy
When there is an interest in tracking longitudinal trends of student educational achievement using standardized tests, the most common linking approach generally involves the inclusion of a common set of items across adjacent test administrations. However, this approach may not be feasible in the context of high-stakes testing due to undesirable exposure of administered items. In this paper, we propose an alternative design, which allows for the equating of multiple operational tests with no items in common based on the inclusion of common items in an anchor test administered in a post-test condition. We tested this approach using data from the assessment program implemented in Italy by the National Institute for the Educational Evaluation of Instruction and Training for the years 2010–2012, and from a convenience sample of 832 8th grade students. Additionally, we investigated the impact on functioning of common items of varying item position and orders across test forms. Linking of tests was performed using multiple-group Item Response Theory modeling. Results of linking indicated that operational tests showed little variation in difficulty over the years. Investigation of item position and order effects showed that changes in item position closer to the end of the test, as well as the positioning of difficult items at the beginning or in the middle section of a test lead to a significant increase in difficulty of common items. Overall, findings indicate that this approach represents a viable linking design, which can be useful when the inclusion of common items across operational tests is not possible. The impact of differential item functioning of common items on equating error and the ability to detect ability trends is discussed.
Introduction
When there is an interest in tracking longitudinal trends of student educational achievement at the population level, the most common approach employed by national and international Large-Scale Assessment Programs (LSAPs)–such as the PISA [1] and IEA Trends in Mathematical and Science Study (TIMSS, [2]) programs–is to include a common set of items across adjacent test administrations. In the absence of common examinees, the common item set provides the statistical link between administered test forms, which require equating, hereafter referred to as the operational test forms. Based on examinees' responses on the common-item set, equating procedures, such as those provided in the framework of Item Response Theory (IRT; [3–5])–can be implemented on collected data to estimate the equating parameters required to put the operational tests, and the population ability estimates, on a common metric scale. This equating approach, which is generally referred to as the Non-Equivalent groups Anchor Test (NEAT) design, is one of the most popular and flexible tools for linking examinations in educational LSAPs [6]. The implementation of longitudinal NEAT designs, however, may not be feasible in the context of high-stakes testing due to test security concerns related to the inclusion of common items across multiple operational test forms (e.g., undesired item exposure), in particular when the common items are required to contribute to test scores (i.e., internal common items). When administered more than one time, items may lose their original psychometric properties, and cause a decrease in the test's validity and fairness (e.g., only some examinees may have learned the correct response). The use of external common-item sets, that is the inclusion of common items that do not contribute to test scores but are only used for equating purposes, is a common alternative to the use of internal common items. However, use of external items can also be problematic due the differences in “stakes” and test conditions (e.g., external items are usually administered as a separately timed section) associated with the internal and external portion of the test which may introduce unwanted variations in examinees' test-taking behaviors and motivation [6, 7]. Further, alternative equating designs using sample matching of non-equivalent groups based on relevant selection variables (e.g., [8, 9]) is also not always feasible due to the by-design lack of collateral information about examinees linked with privacy regulations. In similar situations, the preferred equating approach is often the so-called “common item equating to a calibrated item pool” design ([6]; equating-to-a-pool design, for short). As in NEAT designs, the equating-to-a-pool design involves the administration of an anchor form that can provide the necessary statistical adjustment to put multiple operational test forms on a common metric scale. In the equating-to-a-pool design, the operational test forms are not required to be linked to each other by a common-item set, but instead share a set of common items with a common base form (e.g., a previously calibrated item pool), which remains undisclosed prior to the administration of the operational tests. This common base form is generally administered prior to the administration of the operational tests for item calibration purposes. Then, items are selected from this previously calibrated item pool (i.e., the base form) and included in the operational tests as anchor items. Multiple versions of this equating approach are implemented in the Netherlands in the context of the annual statewide high-stakes examinations administered at the end of both the primary and lower-secondary education cycles [10–12]. Due to security reasons, administered tests are required to not share items with each other. Instead, set of items belonging to different operational test forms are included into an anchor test forms which are administered either before the operational forms (i.e., pre-equating design), or in a post-test condition (e.g., post-equating design), to one or more non-equivalent groups of examinees, namely, the linking groups. Hence, in pre-equating, the operational test forms are administered after the data necessary for equating is collected. In post-equating, operational test forms are administered before anchor data is available, which is collected to groups of non-participating examinees. One advantage of using the post-equating approach over the pre-equating design is that its allows the security of all items to be preserved as the administration of allowing equating takes place post-hoc, and all items included in the operational test are allowed to contribute to the examinees' scores.
Furthermore, one possible drawback of using post-test anchor data is the risk that unwanted item exposure might influence the performance of examinees taking the anchor test (i.e., the linking group) and introduce bias in the linking procedure. Under this design, the anchor test serves the role of a base form providing the link between the operational tests forms. The anchor test data, then, may be combined with the data collected administering the operational test forms and calibrated to a measurement model in a single calibration run (e.g., by using multiple-group IRT modeling techniques, [13, 14]), resulting in the operational test forms being scaled on a common metric scale.
The use of anchor data collected on linking groups either prior or after the administration of operational test forms has some limitations, the most obvious being the potential presence of differences in examinees' motivation between the high-stakes condition of the operational tests and the low-stakes condition of the anchor assessment. This difference in test conditions may introduce bias in the equating results due to differential performance of examinees, especially in the final section of the tests, due to fatigue, lack of motivation, or test speededness effects [15–17]. Another limitation is linked to the inevitable presence of differences in item position across both operational and anchor test forms. Due to its negative impact on stability of item parameters [18], changes in the context and order in which items are presented are expected to be a relevant source of equating error for large-scale assessment programs using common-items equating approaches [19, 20]. Traditionally, a common recommendation for test construction has generally been to present items in ascending order of difficulty, as this is expected to mitigate test anxiety effects and lead to an improvement in test scores (easy-to-hard order; [21–23]). Arranging item using a random difficulty order has been shown to have similar effects to the easy-hard order approach (for a review, see [21]). In turn, findings indicate the arrangement of test items in descending order of difficulty (i.e., hard-easy order) as the most disruptive for students' performance, favoring both an increase in missing responses and a decrease of correct responses when compared to both easy-to-hard and random order [21, 24, 25]. Further, Meyers et al. [26] found the implementation of an item order in which the most difficult items were placed in the middle of a test while easier items were placed toward the beginning and the end of the test (i.e., easy-hard-easy order) to result in low equating error. The authors however only compared different random implementations of the easy-hard-easy approach, thus they were not able to report about the relative improvement in equating error due its use compared to the use of other order approaches. Using data from two statewide assessments of reading and mathematics, the authors also showed that changes in the location of an item across parallel test forms would have significant impact on the difficulty of the item as estimated under the Rasch model [27]. In particular, the relocation of an item closer to the end of a test would result in an overestimation of item difficulty, while the item would appear easier when relocated near the start of the test. Similar results were also reported concerning PISA reading assessments, and indicate a decrease in performance, and a concurrent increase in estimated item difficulty, as item gets closer to the end of the test [28], an effect which seems to be linked to changes in test taking effort over the course of the test [29]. The existence of significant differences in item difficulty across test forms challenges the assumption of item parameter invariance across test forms, which is a fundamental requisite of equating procedures based on the exploitation of common items [6]. The practical consequence of the presence of Differential Item Functioning (DIF) on the common-item set is a significant increase in the error associated with the equating procedure, in particular when the common items are limited in number [30].
The INVALSI Case
Introduced in Italy in 2003 by the National Institute for the Educational Evaluation of Instruction and Training (INVALSI), the INVALSI LSAP include a statewide high-stakes assessment of proficiency in mathematics which is administered annually as part of the state exam marking the end of the lower-secondary cycle of education (i.e., 8th grade). The 8th grade examination is particularly relevant since it represents the last statewide assessment of learning achievement in the framework of a common Italian national curriculum. Starting from grade 9, in fact, Italian students attend upper secondary schools with different curricula, thus rendering comparisons in terms of academic achievement more difficult. Since 2010, the math tests contribute to the score on the state exam; because of specific regulations concerning the Italian state exams, the administered tests are not allowed to share common items over the years. In fact, the test is constructed by INVALSI for the sole purpose of the annual administration: after each administration, the included items are retired from use and released to the public domain. The INVALSI test administration design, thus, does not allow the direct implementation of equating procedures based on common items (e.g., NEAT design). The implementation of other equating approaches, such as common-person equating [31], sample-matching equating [8], random groups equating designs [6], is also not feasible due to the tests being administered to different individuals and populations, and the lack of collateral information collected about examinees. Further, to our knowledge, neither pre-test data nor post-test data is regularly collected for the purpose of equating the tests1. As a result, no information is available allowing for a comparison of the average difficulty of the tests administered over the years, nor concerning student achievement trends. INVALSI has repeatedly stressed the need for the implementation of an equating design for the administered tests [33–35]. Indeed, INVALSI has recently introduced an equating design for the low-stakes examinations administered at other levels of educations (i.e., at grade 5, 6, and 9, [36]); at this time, however, an equating procedure for the 8th grade high-stakes examinations is still not available.
Aims of the Study
The main aim of the present study is to present and discuss the implementation of a linking procedure allowing for the equating of test administrations sharing no common items or persons that is based on the administration of an anchor test in a post-test condition. This approach can be useful in situations in which security concerns prevent the implementation of NEAT and pre-equating designs. For the purpose of the present study, we use data from the INVALSI 8th grade high-stakes math assessment program from 2010 to 2012 and data collected administering an anchor test to a convenience sample of examinees in a low-stakes condition. Given the potential difference in test condition and sample characteristics (e.g., examinees' motivation and math proficiency) between the INVALSI (high-stakes) and the anchor test (low-stakes) administration, we expect that significant differences in estimated ability might emerge in the examined groups. In particular, we expect that the examinees taking the test in the low-stakes condition will show lower ability when compared to examinees taking the tests in the high-stakes condition.
As a secondary aim, we investigate the impact of differences in item position and item-orders across test forms on the DIF computed on the common-item set by also controlling for the effect of time of item exposure. Based on previous findings, we expect that results will highlight a significant impact of item position and different item orders on estimated item difficulty. In particular, we expect that positioning items closer to the end of the test, might lead to a significant increase in the items' estimated difficulty.
Method
Equating Design
The equating design employed in this study consists of a variation of the equating-to-a-pool design [6] which instead uses data collected administering an anchor test in a post-test condition, i.e., a post-equating non-equivalent groups design. Figure 1 illustrates the employed design. In the example, three non-equivalent groups of examinees (Groups A, B, C) are each administered operational test forms sharing no common items (Test forms 1, 2, and 3), resulting in the lack of internal linking allowing the equating of the tests. To resolve this issue, an anchor test comprised of subsets of common items (Blue blocks in Figure 1) are extracted from each operational test form (Test forms 1, 2, 3) and administered to a new group of non-equivalent examinees in a post-test condition (i.e., the linking group, Group D). Under the assumption of measurement invariance of the selected anchor items, the data collected on group D may provide the external statistical link to equate test forms 1, 2, and 3.
The INVALSI Math Tests
The INVALSI 8th grade math assessment is intended to assess students' proficiency across multiple math content and cognitive domains; for the development of the tests, INVALSI used as reference the math assessment framework proposed for the IEA-TIMSS 2003 tests [37], with minor differences in the definition and number of the domains. Students' proficiency is evaluated across four math domains: Relations and functions (RF), Numbers (N), Geometry (GEO) (redefined in 2009 as Space and figures, SF); Measures, data and predictions (MDP) (redefined in 2011 as Data and predictions, DP; for an in-depth explanation of math domains and cognitive processes involved in the INVALSI assessment, see [38]). The booklets are presented as mixed-format tests including closed-ended, multiple-choice (MC) items and both open-ended and closed constructed-response (CR) questions. In spite of the inclusion of items with different response formats and assessing multiple math domains, the tests have shown good fit to the unidimensional Rasch model [39, 40].
Over the years, INVALSI has provided teachers with slightly different scoring instructions for the tests. Inconsistencies between the years concerned specifically the scoring rubrics of items comprising multiple questions sharing a common passage/stimulus, such as Brief Constructed-Response (B-CR) items (i.e., items requiring students to provide an answer and its demonstration/explanation) and item bundles of Short-Answer Constructed-Response (SA-CR) and Multiple-Choice (MC) items. In order to achieve congruence across years, the following dichotomous scoring rubric was implemented in this study:
• Multiple-Choice Items: A score of 1 was awarded to students indicating the correct option, otherwise a score of 0 was assigned;
• SA-CR: A score of 1 was assigned to students providing the correct answer, otherwise a score of 0 was assigned;
• Multiple true-false MC or SA-CR items: Item bundles of k items were scored 1 for a number of correct responses ≥k – 1, otherwise were scored 0;
• B-CR: A score of 1 was awarded to students providing both the correct answer and its explanation or solution steps, otherwise a score of 0 was assigned.
• We also distinguished in the scoring procedure between the following responses to items:
• Invalid responses and omitted responses were scored 0;
• As suggested by many authors (e.g., [23, 41]), unreached items (i.e., items that students were not able to complete in the time given) were scored as non-administered items.
The Anchor Test
For the construction of the anchor test, we selected 31 items from the INVALSI [33–35] operational forms and combined them together in a single test form, i.e., the anchor test. That is, from each operational test, an adequately numbered subset of items was selected for inclusion in the anchor test, i.e., to serve as common item. As suggested by many scholars ([6, 42, 43]), each set of common items was selected as to represent a mini-version of the operational tests from which they were extracted, both in terms of mean and standard deviation of the difficulty estimates, and item content/format representation. Findings indicate that the length of the common-item set is a key factor in assuring the accuracy of equating results between two test-forms [44, 45]. As a general indication, the length of the common-item set should be at least 20% of the operational test (e.g., considering a test of 40 items, [3, 6, 46], although some authors suggest that fewer items may also be adequate for IRT linking [47, 48]. Correlation between the raw scores computed on the anchor test and on the full test should be high: the common knowledge on this matter is that “higher correlation leads to better equating” [42, 46, 49].
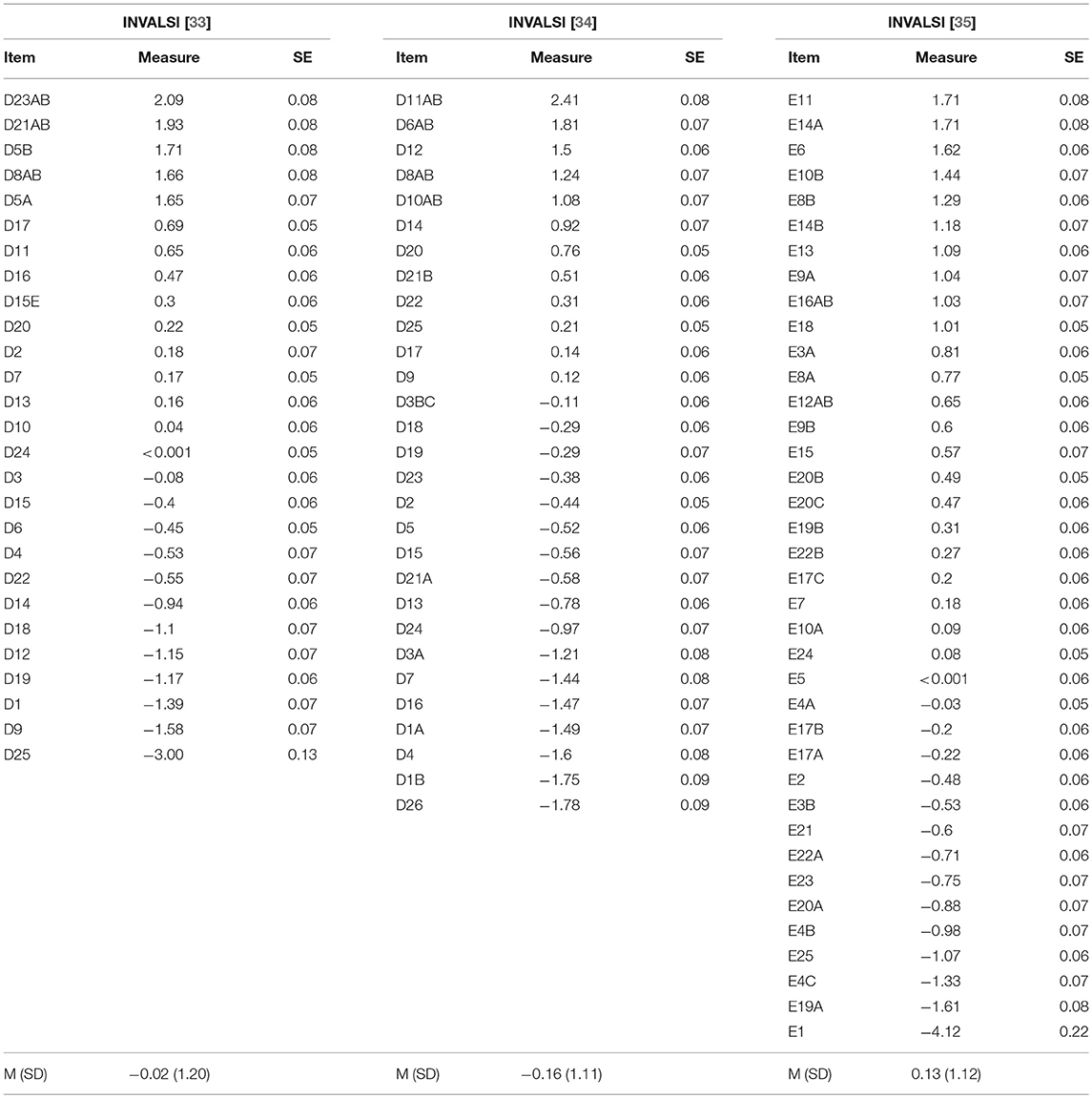
Preliminary to the selection of the anchor items, the difficulty estimates for operational tests were obtained implementing the Rasch model on INVALSI sample data for each year of administration of the tests. Due to potential issues related to the scoring procedure (i.e., potential variability between raters in applying the scoring rubric), brief constructed-response (B-CR) items were not included in the common-item sets. Table 1 provides a comparison of the characteristics of the full tests and the selected common item sets, while full information for each considered year of the test, the full test and the selected item set shows similar distribution of item format and investigated domains, as well as average difficulty. Rasch difficulty estimates for both the full tests and the common item sets selected for inclusion in the anchor test, along with information about item characteristics (Item format and domain) are reported in full in Tables A1–A3 of the Appendix. The length of the selected item sets ranged from 30 to 35 percent of each INVALSI test ([33]: 8 out of 27 items; [34]: 9 out of 29 items; [35]: 14 out of 38 items). Further, the Pearson correlation coefficients computed between the raw scores on the full tests and the common-item sets were 0.84, 0.82, and 0.87, respectively for the INVALSI [33–35] forms. Knowing that raw score reliabilities of the 2010–2012 operational tests are in the range of 0.8–0.9, and that reliabilities of the selected item sets are in the range 0.6–0.7, then the corresponding disattenuated correlations all exceed the well-known rule-of-thumb of 0.85 for lack of discriminant validity, as well as the more stringent cut-off of 0.95 for score equality between full and shortened version of tests [50]. The high value of these correlations suggests that the operational tests and the common item sets are in fact measuring the same construct.
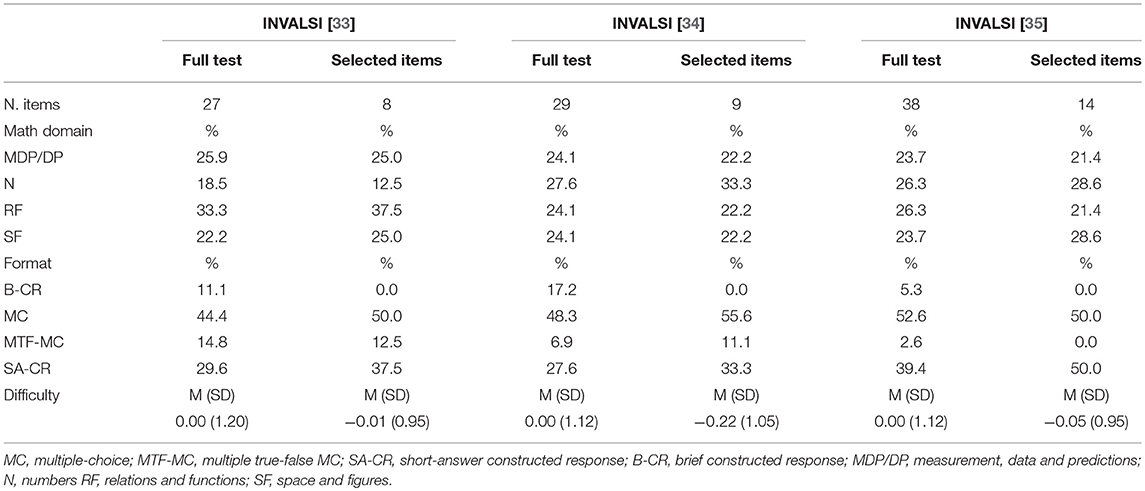
Table 1. Characteristics of INVALSI full test and selected item sets: percentage of items by item format and math domain, and mean item difficulty.
In order to ensure item parameter invariance of the common item set, a generally advised practice in equating is to administer the common items in an identical order across test forms [6, 26]. However, this may often be unfeasible when multiple test forms are linked to a common base form. In order to mitigate this issue and investigate the impact of change in item position and orders across test forms on DIF, four parallel forms of the anchor test were randomly administered to the examinees. Each parallel form was characterized by a specific item order based on the item difficulty parameters as estimated in the independent calibration of the three operational tests to the Rasch model. The following item-orders were implemented in the parallel forms of the anchor test: easy-to-hard, hard-to-easy, easy-hard-easy and random order (i.e., as in the INVALSI test forms).
Data Sources
Response data for the INVALSI operational tests were obtained by completing an online request through the INVALSI institutional site. Provided data consisted of responses for the entire 8th grade population who took the INVALSI standardized math tests for the years 2010–2012 in their basic unedited version and with no extra time added for test completion. For the purpose of the present study, analyses were performed on random samples extracted from the total 8th grade population taking the INVALSI tests in the Piedmont and Aosta Valley regions of Italy (2010: N = 1819; 2011: N = 1794; 2012: N = 1813). This choice is related to the need to maintain the highest possible comparability with the linking sample, which consisted of 832 8th grade students (49.6% females; 89.8% Italians) attending schools in urban areas of the Piedmont and Aosta Valley regions. Sample size was balanced across different order forms (easy-hard-easy: N = 204; easy-hard: N = 216; hard-easy: N = 206; random: N = 206). Test administration took place at the end of the school year as to assure students had reached the necessary level of proficiency for test completion. To mitigate the issue of possible item exposure, teachers from participating classrooms were required to not administer the items included in the anchor test prior to the anchor-test administration. To reduce the possibility of student cheating, proctors were present in the classroom during the administration of the test, and students were allowed 75 min to complete the test.
Data Analysis
Equating the Tests
In order to equate the INVALSI operational tests, a multiple-group IRT equating procedure was implemented in this study. As a first step, all available response data (i.e., INVALSI sample data for the years 2010–2012 + anchor test data; N = 6258) was combined in a single dataset by scoring the non-common items as not administered items (i.e., as missing items). The combined response data was then calibrated to the Rasch model using the concurrent calibration approach available within the multiple-group IRT modeling framework [13]. More specifically, BILOG-MG version 3 was used to implement the Rasch model for dichotomous data with marginal maximum likelihood estimation (MMLE) by distinguishing in the analysis the existence of four non-equivalent groups of examinees–the INVALSI samples for the years 2010–2012 and the post-test sample [51]. In the concurrent calibration the empirical prior ability distributions for the INVALSI samples were estimated concurrently with item parameters, while the ability distribution was fixed to the standard normal for the post-test sample (i.e., the linking group) for the purpose of model identification. By using the concurrent calibration approach, all the item difficulty estimates and the ability estimates for the four groups were placed on a common metric scale in a single analytical step. The choice of implementing the equating of the tests using a concurrent calibration approach was supported by findings indicating that this approach is more accurate than approaches based on separate calibrations when the data fit the IRT model, overall resulting in lower equating errors ([6, 44, 52]).
As a preliminary step to implementation of the equating procedure we investigate the presence of DIF between the INVALSI tests and the anchor test. When conducting equating based on common items, the presence of differences in item difficulty across test forms is evaluated visually by inspection of cross-plots of the common-item parameters across test conditions [53–55], by computing correlations between parameter estimates, and by computing DIF statistics across the test administration on the common-items. In this study, for each INVALSI test, the functioning of the common-item set across the operational and anchor test forms was evaluated based on the significance and size of DIF, and by visual inspection of the plot of the difficulty parameters of the common items across the test forms. DIF estimates were obtained by implementing a single-item anchor estimation approach, and by using the Mean test statistic threshold selection strategy to select the anchor items [56, 57]. The single-anchor method has been shown to represent a viable, valid alternative to more traditional approaches, such as the equal-mean-difficulty and all-other anchor classes, whose requirements (i.e., DIF-free or balanced-DIF tests) have been shown to be unrealistic for most practical assessment situations [56–58]. Analyses were performed with R using the psychotools package [59]. For the purpose of this study, and in accordance with the well-known Educational Testing Service DIF classification rules [60, 61], items reporting absolute DIF estimate ≥0.43 logit units and a significant item-wise Wald test statistic (z-values, p < 0.05) [62] were flagged for non-negligible DIF. As an additional diagnostic step, the cross-plot of the difficulty parameters as estimated under the two test conditions was inspected: items positioning far from the identity line were considered as problematic. Hence, flagged items were dropped from the common-item sets for the purpose of implementing the concurrent calibration. The adequacy of the equating procedure was evaluated by examining the equating error2 associated with the item difficulty and person ability estimates as obtained with the concurrent calibration. The scoring of the test was performed by computing the Expected-A-Posteriori (EAP) person ability estimates [63]. The reliability coefficients and average Standard Error of Measurement (SEM)3 for the ability scores were also computed and examined.
Examining Item Position and Item Order Effects on DIF
In order to investigate the impact of changes in item position and item orders across test forms, on the presence of common-item DIF, we performed a three-step procedure. First, DIF analyses were performed on the common-item sets data by comparing the INVALSI administration condition to the four parallel administration of the anchor test. In this way, the single-anchor DIF estimation approach described above was implemented on the data, resulting in 124 DIF estimates (i.e., 31 items × 4 orders) comparing the difficulty estimates obtained in the anchor test compared to those emerging from the INVALSI operational samples. Then, for each common item, four distinct position change values were also obtained by subtracting the position of the item in the INVALSI test to the position of the same item in each of the four parallel forms of the anchor test: a value of 0 indicate no position change across test forms, while positive and negative values would indicate, respectively an increase or decrease in position. Finally, a multilevel analysis was implemented to evaluate the impact on DIF estimates of both changes in position of the common items and different item orders while controlling for a proxy indicator of item exposure (i.e., items' year of public release). We chose to perform analyses using a multilevel approach given the presence of clustering in the data due to the inclusion in the model of four distinct DIF estimates for each item (31 items × 4 forms = 124 observations). More specifically, analyses were performed using a random intercept model [65], in which the intercept parameter was included as a random effect to control for the non-independence present among level-1 outcomes (i.e., item DIF estimates) clustered according to a level-2 grouping variable (i.e., the item). The items' year of public release, change in item position, and order form were included in the model as fixed effects, and DIF estimates served as dependent variable. Prior to the estimation of the model, in order to evaluate the amount of clustering in the data at the item level and the appropriateness of analyzing data using the chosen multilevel approach, we examined the Intra-Class Correlation (ICC, [66]) for the DIF estimates, and used the ICC value to compute the design effect for the null model. Using single level analysis on multilevel data characterized by a design effect >2 has been shown to lead to misleading results in the estimation and testing of fixed effects [67].
The random intercept model was implemented with R using the Lmer package [68]. Estimates of marginal and conditional R2 [69] were obtained using the r.squaredGLMM procedure of the MuMIn package ([70], p. 18). Marginal R2 informs about variance explained by fixed factors, while conditional R2 concerns both fixed and random factors. Effects were deemed significant if p < 0.05.
Results
Parameter Invariance
The results of the DIF analyses revealed the presence of significant violations of measurement invariance when comparing the functioning of the common items in the INVALSI operational samples and the post-test sample. The cross-plots in Figures 2–4 provide a visual representation of the results: overall, the difficulty parameters for the 2010 and 2011 items showed good stability across test conditions, the majority of the items being located near the identity line. The inspection of the cross-plot for the 2012 items showed a more varied situation, with many items sitting far from the identity line. Table 2 reports the DIF estimates for all the items. Overall, nine items showed non-negligible DIF across the two test conditions. By looking at Table 2, it's easy to note that the majority of the common items flagged for non-negligible DIF were those originally included in the INVALSI [35] test (6 items), while respectively only 1 and 2 item from the INVALSI [33] and INVALSI [34] tests were flagged for DIF. For all test, the removal of flagged items from the common-item sets resulted in an increase in correlation between the item difficulty estimates as obtained in the two test conditions. More specifically, the correlation of the difficulty estimates for the full common-item sets ranged from 0.93 to 0.97, while for all the tests the correlation computed on the reduced common-item sets was 0.98. After the removal of the flagged items, the length of the common-item sets still accounted for at least 20% of the operational test.
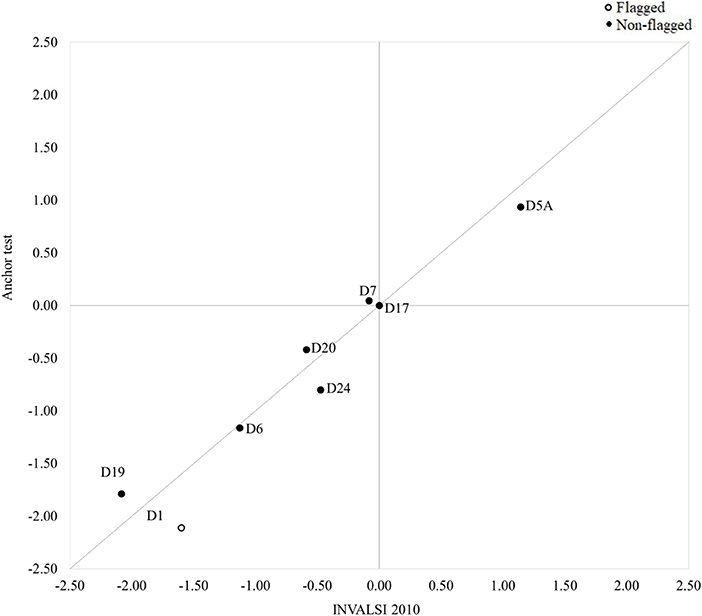
Figure 2. Cross-plot: Difficulty (logit) of common items as estimated in the INVALSI [33] and anchor test forms (full set: r = 0.96; reduced set: r = 0.98).
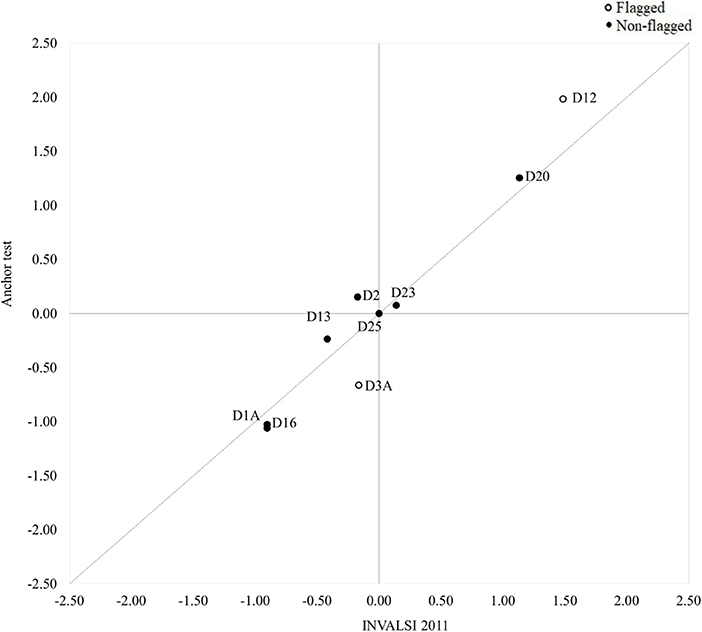
Figure 3. Cross-plot: Difficulty (logit) of common items as estimated in the INVALSI [34] and anchor test forms (full set: r = 0.97; reduced set: r = 0.98).
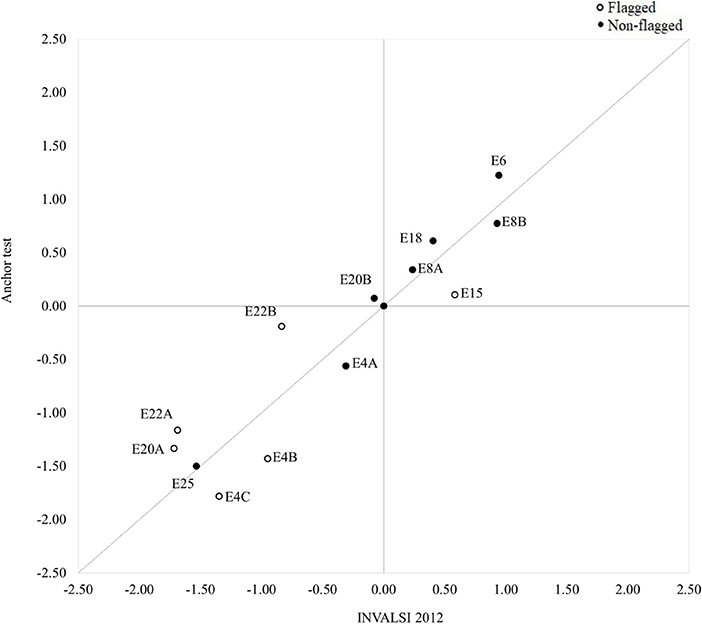
Figure 4. Cross-plot: Difficulty (logit) of common items as estimated in the INVALSI [35] and anchor test forms (full set: r = 0.93; reduced set: r = 0.98).
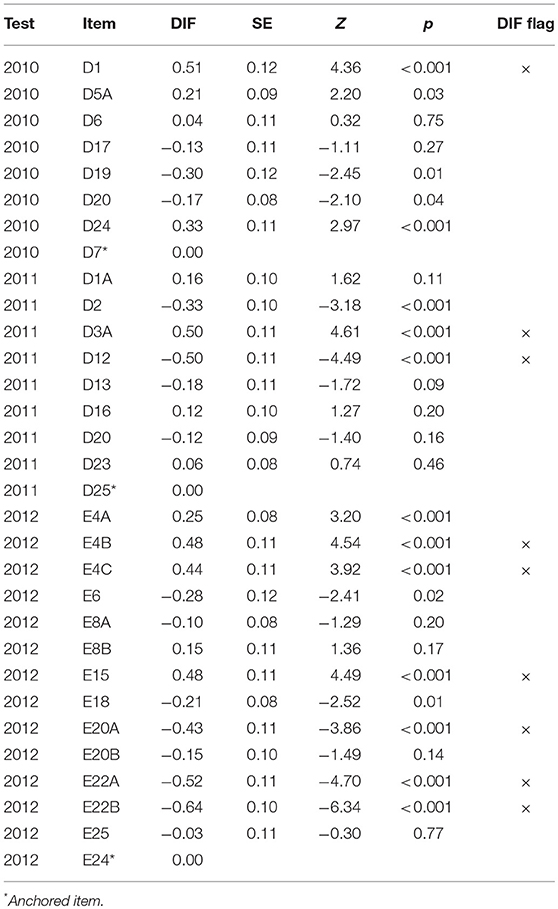
Table 2. Post-test vs. INVALSI administration: DIF estimates, z statistic, and DIF diagnosis for the common items.
Equating the Tests: Concurrent Calibration
Tables 3, 4 report the estimates of item difficulty parameters, student ability distributions and EAP ability scores for the three INVALSI examinations as obtained implementing the concurrent calibration procedure on the dataset. Overall, the results indicated the existence of only minor variations in the mean difficulty of the INVALSI math assessment over the years under focus (Range = −0.16–0.13 logit). Comparably, the mean ability of the INVALSI samples for the INVALSI [33–35] examinations also showed limited variability over the years (Range = 0.01–0.32 logit); as expected, the post-test sample reported the lowest mean ability score (−0.06 logit). For each year of administration of the INVALSI test, Table 3 also reports the equating error associated with equating procedure, as well as the Rasch person reliability and the average SEM associated with the EAP ability scores. Due to the limited number of common items used to perform the linking of the tests, the amount of error associated with the equating procedure estimates was relatively high, and ranged from 0.06 to 0.07 logit. Still, upon examination of Table 3, it is easy to note that the largest source of measurement error is the average SEM associated with the EAP ability scores, which in turn is strongly related to the relatively low reliability of the administered tests. For example, when comparing the ability scores of examinees from the 2011 and 2012 examinations, on average the standard error of the difference4 in ability due only to SEM would be as large as 0.48 logit, while the standard error of the difference due to equating error would be as low as 0.08 logit.

Table 3. Concurrent calibration equating: distribution of the ability scores and estimated equating errors.
Item Order and Position Effects on DIF Estimates
The results of the random intercept model implemented to examine the effect of both different item orders and item position changes on DIF across test forms are reported in Table 5. The inspection of the ICC for the model confirmed the existence of significant clustering in the data: the ICC was 0.54, indicating a moderate correlation among the DIF estimates computed for the same item. Based on the computed ICC, the design effect was found to be 2.63, thus supporting the use of a hierarchical model for the analysis of the data [67]. Results of multilevel analyses are reported in Table 5. Overall, the fixed component of the model accounted for 25% of the variance of DIF estimates (Marginal R2: 0.25), while the random component accounted for an additional 46% (Conditional R2 = 0.71), indicating significant clustering in DIF estimates for the same item, and thus further supporting the appropriateness of the multilevel approach. Upon examination of the parameters for the fixed effects included in the model, both item position changes [F(1,114.32) = 27.194, p = 0.00] and the presence of difference in item order [F(3,89.12) = 14.92, p = 0.00] across test forms was found to have a significant impact on the presence of DIF on the common items. In particular, the relocation of an item closer to the end of the anchor test form when compared to their original position in the INVALSI tests was associated with a significant (positive) increase in the DIF estimate, i.e., an increase in the estimated difficulty of the item. Based on the estimated effect (B = 0.01, p < 0.001), relocating an item 30 positions further in the test would result in an increase in difficulty of 0.30 logit. Concurrently, by using the random item order as a reference group, a significant increase in item difficulty was associated with the administration of the common-items using the easy-hard-easy (B = 0.24, p < 0.001) and hard-easy (B = 0.19, p < 0.001) orders, while no significant difference was observed by implementing the easy-hard order. The results of an additional descriptive analyses also indicated that, when compared with the item order in the INVALSI operational test, the easy-hard-easy order was associated with the largest bias (Average absolute DIF value = 0.32 logit). In turn, at 0.25 logit, the random order showed the lowest average absolute DIF, while both the easy-hard and hard-easy orders showed an intermediate position (Range = 0.27–0.28 logit). No significant effects [F(2,28.24) = 0.74, p = 0.49] emerged from the analysis concerning the year of release of the common items to the public.
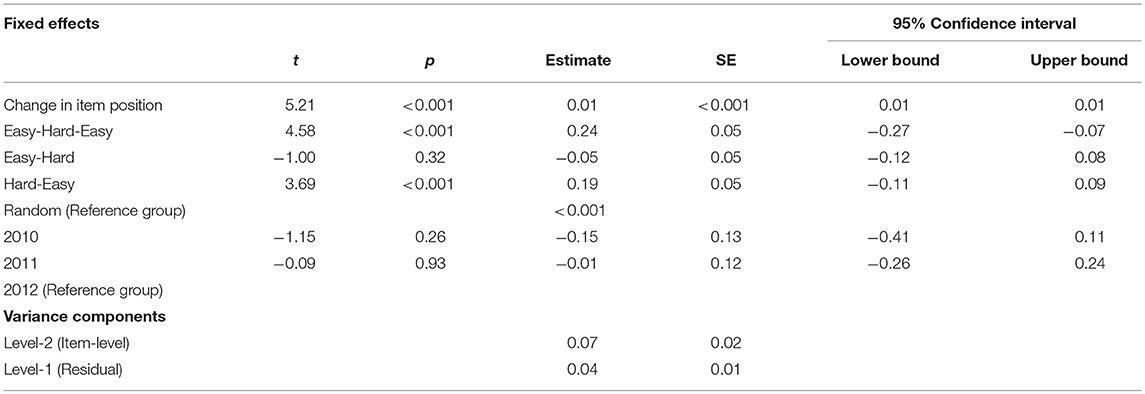
Table 5. Random intercept model: DIF estimate on item position changes and item orders controlling for year of exposure (N = 124).
Discussion
The aim of the present study was 2-fold. As a first aim, we investigated the feasibility of a tentative equating procedure aiming at providing a link for the INVALSI 8th grade assessments of mathematical proficiency for the years 2010–2012. By design, The INVALSI 8th grade examinations are not internally linked to each other–i.e., the tests do not share common items or examinees–thus requiring an external link to be equated. Further, the tests are administered yearly to non-equivalent groups, rendering the use of equivalent-group equating approaches unfeasible. For the purpose of this study, we instead employed an equating procedure based on a post-test administration of an anchor test comprised of block of items originally included in the INVALSI tests to a convenience sample of 8th grade students. The data collected in this post-test condition served as a common base form providing the external link required to equate the tests. As a preliminary diagnostic step to the equating, the existence of DIF on the items included in the anchor test when comparing the post-test administration and the INVALSI test administrations was investigated. The degree of error associated with the equating procedure was also examined.
Equating the Tests
Overall, results of linking analyses indicate that the employed design could represent a viable approach to link adjacent high-stakes test sharing no common items or persons. In spite of differences in testing conditions between the INVALSI and anchor test administrations (i.e., high-stakes vs. low-stakes), the difficulty parameters of common items showed remarkable stability, with correlations on the final common-item sets approaching 1 after removal of items showing non-negligible parameter instability across groups. At the same time, by decreasing the length of the common item sets, the identification and exclusion from the equating procedure of a few misbehaving items had a relevant impact on the amount of error associated with the ability estimates; in part compromising the possibility to detect small differences in the accuracy of the estimated person ability trend. In light of these considerations, an increase in the number of common items to be included in the anchor test would be advisable to reduce the impact of the removal of misbehaving items on the accuracy of the equating, and thus to the use of the equating results for practical purposes. Assuming only a small portion of problematic data is detected, this approach would be helpful in reducing the bias in the anchor test data when compared to operational response data, mitigating the DIF on common items and improving the accuracy of the equating.
Regarding the INVALSI tests, the results of the equating procedure suggested the existence of a relative stability in the average difficulty of the math tests administered by INVALSI as part of the 8th grade examinations for the period 2010–2012. This is a relevant finding; given the high-stakes nature of the INVALSI 8th grade math examination, it is important that the administered tests provide a stable and comparable assessment of proficiency over the years. When comparing individual ability across examinations, the standard error of measurement associated with the ability estimates emerged as the most significant source of error. This issue is mainly due to the limited number of items included in INVALSI assessments, resulting in low score reliability at the individual level. To mitigate this problem, and allow for an accurate ranking of examinees, the length of the tests should be increased.
Item Order and Position Effects
As a secondary aim of the study, we examined the impact of position changes and different item orders across test forms on the presence of DIF in the common item sets. In the present study, the variation of item position across test forms was a significant source of violation of measurement invariance for common items. As reported by other authors [26], we found the existence of changes in item position across test forms to be positively related to changes in item difficulty as estimated using the Rasch model. In particular, a shift in their position closer to the end of the anchor test when compared to the original location in the INVALSI tests was associated with an increase in the difficulty of the items, while a decrease in difficulty was observed when items where placed closer to the start of the test. Next, we found the item orders characterized by the positioning of difficult items at the beginning of the test (i.e., hard-easy order) and in the middle section of a test (i.e., easy-hard-easy order) to be both associated with a significant increase in difficulty of common items when compared with the random item order. Conversely, the random order was characterized by lower levels of absolute DIF on the common-item sets. These results are compatible with findings indicating the hard-easy order to be the most difficult for students, while the random and easy-hard orders to be the less disruptive [21]. Findings concerning the easy-hard-easy order appear to be in contradiction with what was reported by Meyers et al. [26] concerning its mitigating effect on DIF detect on common items linking two test forms. Still, in their study, the authors did not compare the performance of the easy-hard-easy order to other approaches, but only compared alternative implementations of the same order approach, i.e., the easy-hard-easy item order. Similarly, in the present study we found the lowest amount of DIF when comparing the anchor form implementing the random difficulty order approach and the INVALSI test forms, which also implement a positioning of items based on a random distribution of item difficulty. Combined, these findings seem to indicate that, when equating two test forms sharing a set of common items, a reduction of the DIF on the common item set may be observed when the items included in the two forms are positioned according to a similar item order approach. On the other hand, the amount of detected DIF may increase when different item orders approaches are implemented [6]. As for the study of Meyer and colleagues, however, findings from the present study should not be generalized to other equating situations. To achieve generalizability, future research should examine the functioning of common items in the equating of test forms characterized by implementations of the different order approaches by also ensuring randomization of item position changes both within and across item orders. Due to limitations related to the employed design (item position did vary only between orders), the interaction of these two aspects was not investigated in this study.
Strength and Limitations
This study has several strengths. First, results from this study suggest that, with only minor improvements, the employed equating could represent a viable and cost-effective approach for the linking of adjacent high-stakes examinations sharing no common items. In particular, this approach can be useful in situations in which test security concerns prevent the implementation of NEAT and pre-equating designs. Second, we provide practitioners with valuable information about potential biases in the comparability of difficulty parameters of common items due to changes in position across test forms. Nonetheless, the present study has also several limitations. First, the use of a non-random sampling approach does not allow generalization of the results to the full population of 8th graders taking the INVALSI tests for the period 2010–2012. Moreover, the anchor test was administered as a low-stake assessment having no real consequences on students, while the INVALSI tests are originally administered as high-test tests, resulting in presence of potential differences in student motivation across the two test conditions. For the purpose of this study, this issue was partially taken in account by recoding unreached items as not administered items, and thus treated as “by-design” missing data in the analyses [23]. Still, more sophisticated approaches (e.g., the implementation of mixed Rasch models allowing for the identification latent classes of examinees characterized by different test taking behaviors, [71, 72]) could be implemented to evaluate (and control for) the bias introduced in the equating procedure due to the presence of examinees with different levels of motivation. This will be the aim of a future publication based on the data presented in this study. Next, as stated in the introduction, B-CR items were not included in the common-item set, due to their subjective scoring procedure. Indeed, we expected that the variability in scoring procedure due to the differences in raters' characteristics (e.g., leniency, adherence to scoring procedure, etc.) would have led to an increase in overall linking error, worsening the linking procedure outcomes [6]. However, due to the employed linking design, we were not able to test this hypothesis empirically. Future studies should address this issue more in detail, by comparing stability of difficulty parameter (and resulting linking error) estimates obtained using linking designs characterized by the inclusion or exclusion of extended constructed response items in the common items set.
Ethics Statement
This study was carried out in accordance with the recommendations of Italian Association of Psychology, AIP with written informed consent from all subjects. All subjects gave written informed consent in accordance with the Declaration of Helsinki.
Author Contributions
DM, RM, and MS: project design; DM and RM: data analysis; DM, RM, RR, and MS: paper writing and revision; DM: participants recruitment and testing; RM and RR project supervision.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer EP and handling Editor declared their shared affiliation at time of review.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2018.00050/full#supplementary-material
Footnotes
1. ^An equating procedure aiming at linking the 8th grade reading and mathematics assessment for the years 2008-2009 was performed and documented by INVALSI personnel using a post-test approach [32]. In the study, however, no information concerning the quality of the equating results was disclosed. The equating results were also not included in the technical reports for the tests.
2. ^For the purpose of the present, the computation of equating error was performed by employing the procedure presented by Monseur and Berezner [30]. By referencing the methodology implemented by the PISA 2003 program, Monseur and Berezner [30] provide the following formula for the computation of equating error in common-items design:
where σ2 is the variance of the item parameter differences (i.e., the DIF size) across test forms on the common item set, and n is the number of common items used to link the test forms. Under this formulation, it is easy to see that the degree of equating error in liking two forms is positively related the amount of DIF on the common items and inversely related to the number of common items included in the anchor test.
3. ^Given a sample of examinees taking a test, a well-known formula [64] for the calculation of the average SEM is the following:
where Sxrepresents the standard deviation of the test scores observed in the sample, and rxx′ represent the reliability of the test. Under this formulation, it is easy to note the presence of a significant relationship linking test reliability to measurement error.
4. ^As suggested by Wu [20], the SEM associated with individual differences in ability can be computed by using the following formula:
where SEM1 and SEM2 respectively indicate the standard error of measurement for individual 1 and 2.
References
2. Mullis IV, Martin MO, Foy P, Arora A. TIMSS 2011 International Results in Mathematics. International Association for the Evaluation of Educational Achievement. Herengracht (2012). 487, Amsterdam, Netherlands.
3. Hambleton RK, Swaminathan H, Rogers HJ. Fundamentals of Item Response Theory Newbury Park, CA: Sage (1991).
4. Lord FM. Application of Item Response Theory to Practical Testing Problems Hillsdale, NJ: Erlbaum (1980).
6. Kolen MJ, Brennan RL. Test Equating, Scaling, and Linking. New York, NY: Springer (2004). p. 201–5.
7. De Ayala RJ. The Theory and Practice of Item Response Theory. New York, NY: Guilford Publications (2013).
8. Powers SJ, Kolen MJ. Using matched samples equating methods to improve equating accuracy. In: Kolen MJ, Lee W, editors. Mixed-Format Tests: Psychometric Properties With a Primary Focus on Equating, Vol. 2. (CASMA Monograph Number 2.2). Iowa, IA: The University of Iowa (2012). p. 87–114.
9. Wright NK, Dorans NJ. Using the Selection Variable for Matching or Equating (RR-93-4). Princeton, NJ: Educational Testing Service (1993).
10. Alberts RVJ. Equating exams as a prerequisite for maintaining standards: experience with dutch centralised secondary examinations. Assess. Edu. (2001) 8:353–67. doi: 10.1080/09695940120089143
11. Béguin AA. Robustness of Equating High-Stakes Tests. Ph.D. thesis, University of Twente, Enschede (2000).
12. Cito. Handleiding Eindtoets Basisonderwijs [Manual End of Primary School Test], Arnhem, Cito (2012).
13. Bock RD, Zimowski MF. Multiple group IRT. In: van der Linden W, Hambleton R, editors, Handbook of Modern Item Response Theory. New York, NY: Springer (1997). p. 433–48.
14. Hanson BA, Beguin AA. Separate Versus Concurrent Estimation of IRT Item Parameters in the Common Item Equating Design: ACT Research Report Series. Iowa City, IA: American College Testing (1999).
16. Kolen MJ, Harris DJ. Comparison of item preequating and random groups equating using IRT and equipercentile methods. J Educ Measure. (1990) 27:27–39.
17. Mittelhaëuser MA, Béguin AA, Sijtsma K. Selecting a data collection design for linking in educational measurement: taking differential motivation into account. In: Millsap RE, van der Ark LA, Bolt DM, Wang WC, editors. Quantitative Psychology Research: The 78th Annual Meeting of the Psychometric Society. New York, NY:Springer International Publishing (2015). p. 181–93.
18. Leary LF, Dorans NJ. Implications for altering the context in which test items appear: A historical perspective on an immediate concern. Rev Educ Res. (1985) 55:387–413. doi: 10.3102/00346543055003387
19. Zwick R. Effects of item order and context on estimation of NAEP reading proficiency. Educ Measure. (1991) 10:10–6.
20. Wu M. Measurement, sampling, and equating errors in large-scale assessments. Educ. Measure. (2010) 29:15–27.
21. Aamodt MG, McShane T. A meta-analytic investigation of the effect of various test item characteristics on test scores and test completion times. Public Person Manage. (1992) 21:151–60.
22. Kingston NM, Dorans NJ. Item location effects and their implications for IRT equating and adaptive testing. Appl Psychol Measure. (1984) 8:147–54.
23. Oshima TC. The effect of speededness on parameter estimation in item response theory. J. Educ. Measure. (1994) 31:200–19.
24. Leary LF, Dorans NJ. The effects of item rearrangement on test performance: a review of the literature. ETS Res Rep Series (1982) 1982:27.
25. Towle NJ, Merrill PF. Effects of anxiety type and item-difficulty sequencing on mathematics test performance. J Educ Measur. (1975) 12:241–9.
26. Meyers JL, Miller GE, Way WD. Item position and item difficulty change in an IRT-based common item equating design. Appl Measur Educ. (2008) 22:38–60. doi: 10.1080/08957340802558342
27. Rasch G. Probabilistic Models for Some Intelligence and Attainment Tests. Chicago: University of Chicago Press (1960/1980).
28. Debeer D, Buchholz J, Hartig J, Janssen R. Student, school, and country differences in sustained test-taking effort in the 2009 PISA reading assessment. J Educ Behav Statist. (2014) 39:502–23. doi: 10.3102/1076998614558485
29. Weirich S, Hecht M, Penk C, Roppelt A, Böhme K. Item position effects are moderated by changes in test-taking effort. Appl Psychol Measur. (2017) 41:115–29. doi: 10.1177/0146621616676791
30. Monseur C, Berezner A. The computation of equating errors in international surveys in education. J Appl Measure. (2007) 8:323–35.
32. Ricci R, Falzetti P. Un primo esperimento sullo studio diacronico dei risultati della prova nazionale INVALSI al termine del primo ciclo di istruzione in Italia (Anchoring the INVALSI National Examination Results at the End of Lower Secondary School in Italy). Induzioni (2011) 43:21–36.
33. INVALSI. Prova Nazionale 2010. Prime Analisi. [The National Examination 2010. Preliminary Analyses]. Rome (2010).
34. INVALSI. La Rilevazione Degli Apprendimenti A.S. 2010/2011 [The National Examination of Students' Learning Achievement, School Year 2010/2011]. Rome (2011).
35. INVALSI. Rilevazioni Nazionali Sugli Apprendimenti 2011–2012. [The National Examinations of Learning Achievement 2011–2012]. Rome (2012).
36. INVALSI Misurazione dei Progressi e Degli Apprendimenti NELLE Scuole (The Measurement of Progress and Learning in Schools) (2014). Available online at: http://www.invalsi.it/invalsi/ri/sis/misurazione.php (retrieved February 17, 2015).
37. INVALSI (National Institute for the Evaluation of the Education System). La prova Nazionale al Termine del Primo Ciclo. Aspetti Operativi E Prime Valutazioni Sugli Apprendimenti Degli Studenti [The National Examination at the End of Lower Secondary Education. Operational Aspects and Preliminary Analysis of Students' Learning Achievement]. (2008). Available online at: http://www.invalsi.it/EsamiDiStato/documenti/Rapporto_master_12_10_2008_finale.pdf
38. Gnaldi M. A multidimensional IRT approach for dimensionality assessment of standardised students' tests in mathematics. Qual Quant. (2017) 51:1167–82. doi: 10.1007/s11135-016-0323-4
39. Miceli R, Marengo D, Molinengo G, Settanni M. Emerging Problems and IRT-based operational solutions in large-scale programs of student assessment: the italian case. TPM (2015) 22:53–70. doi: 10.4473/TPM22.1.5
40. Marengo D, Miceli R, Settanni M. Do mixed item formats threaten test unidimensionality? Results from a standardized math achievement test. TPM Appl Psychol. (2016) 23:25–36. doi: 10.4473/TPM23.1.2
41. Simon M, Ercikan K, Rousseau M. Improving Large-Scale Assessment in Education: Theory, ISSUES, and Practice. New York, NY: Routledge (2012). doi: 10.4324/9780203154519
42. von Davier AA, Holland PW, Thayer DT. The kernel Method of Equating. New York, NY: Springer (2004). doi: 10.1007/b97446
43. Dorans NJ, Kubiak A, Melican GJ. Guidelines for Selection of Embedded Common Items for Score Equating (ETS SR-98-02). Princeton, NJ: ETS. (1998).
44. Petersen NS, Cook LL, Stocking ML. IRT versus conventional equating methods: a comparative study of scale stability. J Educ Behav Stat. (1983) 8:137–56. doi: 10.2307/1164922
45. Budescu D. Efficiency of linear equating as a function of the length of the anchor test. J Educ Measure. (1985) 22:13–20.
46. Angoff WH. Scales, norms, and equivalent scores. In: Thorndike RL, Editors. Educational Measurement, 2nd ed. Washington, DC: American Council of Education (1971). p. 508–600.
47. Norcini J, Shea J, Grosso L. The effect of numbers of experts and common items on cutting score equivalents based on expert judgment. Appl Psychol Measure. (1991) 15:241–6.
48. Hanick PL, Huang CY. Effects of Decreasing the Number of Common Items in Equating Link Item Sets (2002).
49. Petersen NS, Kolen MJ, Hoover HD. Scaling, norming, and equating. In: Linn RL, editors. Educational Measurement, 3rd ed. Washington, DC: American Council on Education. (1989). p. 221–62.
50. Larwin K, Harvey M. A Demonstration of a systematic item-reduction approach using structural equation modeling. Pract Assess Res Eval. (2012) 17:1–19.
51. Zimowski MF, Muraki E, Mislevy RJ, Bock RD. BILOG-MG: Multiple-group IRT Analysis and Test Maintenance for Binary Items [Computer program] Chicago, IL: Scientific Software International (1996).
52. Hanson BA, Beguin AA. Obtaining a common scale for the item response theory item parameters using separate versus concurrent estimation in the common-item equating design. Appl Psychol Meas. (2002) 26:3–24. doi: 10.1177/0146621602026001001
53. Luo G, Seow A, Chin CL. Linking and Anchoring Techniques in Test Equating Using the Rasch Model. Singapore: Nanyang Technological University (2001).
54. Michaelides MP, Haertel EH. Sampling of Common Items: An Unrecognized Source of Error in Test Equating. CSE Report 636. Center for Research on Evaluation Standards and Student Testing CRESST (2004).
55. Wells CS, Hambleton RK, Kirkpatrick R, Meng Y. An examination of two procedures for identifying consequential item parameter drift. Appl Measure Educ. (2014) 27:214–31. doi: 10.1080/08957347.2014.905786
56. Kopf J, Zeileis A, Strobl C. A framework for anchor methods and an iterative forward approach for DIF detection. Appl Psychol Measure. (2015) 39:83–103. doi: 10.1177/0146621614544195
57. Kopf J, Zeileis A, Strobl C. Anchor selection strategies for DIF analysis: review, assessment, and new approaches. Educ Psychol Measure. (2015) 75:22–56. doi: 10.1177/0013164414529792
58. Wang WC. Effects of anchor item methods on the detection of differential itemfunctioning within the family of rasch models. J Exp Educ. (2004) 72:221–61. doi: 10.3200/JEXE.72.3.221-261
59. Zeileis A, Strobl C, Wickelmaier F, Komboz B, Kopf J. Psychotools: Infrastructure for Psychometric Modeling. R package version (2016) 0.4-2.
60. Longford NT, Holland PW, Thayer DT. Stability of the MH D-DIF statistics across populations. In: Holland PW, Wainer H, editors. Differential Item Functioning. Hillsdale, NJ: Lawrence Erlbaum (1993). p. 171–96.
61. Zwick R. A review of ETS differential item functioning assessment procedures: flagging rules, minimum sample size requirements, and criterion refinement. ETS Res Rep Ser. (2012) 2012:1–30. doi: 10.1002/j.2333-8504.2012.tb02290.x
62. Zwick R, Thayer DT, Lewis C. An empirical bayes approach to mantel-haenszel DIF analysis. J Educ Measure. (1999) 36:1–28.
63. Bock RD, Mislevy RJ. Adaptive EAP estimation of ability in a microcomputer environment. Appl Psychol Measure. (1982) 6:431–44.
64. Harvill LM. Standard error of measurement: an NCME instructional module on. Educ Meas. (1991) 10:33–41. doi: 10.1111/j.1745-3992.1991.tb00195.x
66. Maas CJ, Hox JJ. Sufficient sample sizes for multilevel modeling. Methodology (2005) 1:86–92. doi: 10.1027/1614-2241.1.3.86
67. Muthén B, Satorra A. Complex sample data in structural equation modeling. In: Marsden PV, editors. Sociological Methodology. Oxford: Blackwell (1995). p. 267–316.
68. Kuznetsova A, Brockhoff PB, Christensen RHB. LmerTest: Tests for Random and Fixed Effects for Linear Mixed Effect Models (Lmer Objects of lme4 Package), 2(6) R package version (2013).
69. Nakagawa S, Schielzeth H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol Evol. (2013) 4:133e142. doi: 10.1111/j.2041-210x.2012.00261.x
71. Rost J. Rasch models in latent classes: an integration of two approaches to item analysis. Appl Psychol Measure. (1990) 14:271–82.
Keywords: educational measurement, test linking, test equating, Rasch model, differential item functioning
Citation: Marengo D, Miceli R, Rosato R and Settanni M (2018) Placing Multiple Tests on a Common Scale Using a Post-test Anchor Design: Effects of Item Position and Order on the Stability of Parameter Estimates. Front. Appl. Math. Stat. 4:50. doi: 10.3389/fams.2018.00050
Received: 12 October 2017; Accepted: 08 October 2018;
Published: 30 October 2018.
Edited by:
Pietro Cipresso, Istituto Auxologico Italiano (IRCCS), ItalyReviewed by:
Boris Forthmann, Universität Münster, GermanyElisa Pedroli, Istituto Auxologico Italiano (IRCCS), Italy
Copyright © 2018 Marengo, Miceli, Rosato and Settanni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michele Settanni, bWljaGVsZS5zZXR0YW5uaUB1bml0by5pdA==
 Davide Marengo
Davide Marengo Renato Miceli2
Renato Miceli2 Rosalba Rosato
Rosalba Rosato Michele Settanni
Michele Settanni