A Variational Model for Data Fitting on Manifolds by Minimizing the Acceleration of a Bézier Curve

We derive a variational model to fit a composite Bézier curve to a set of data points on a Riemannian manifold. The resulting curve is obtained in such a way that its mean squared acceleration is minimal in addition to remaining close the data points. We approximate the acceleration by discretizing the squared second order derivative along the curve. We derive a closed-form, numerically stable and efficient algorithm to compute the gradient of a Bézier curve on manifolds with respect to its control points, expressed as a concatenation of so-called adjoint Jacobi fields. Several examples illustrate the capabilities and validity of this approach both for interpolation and approximation. The examples also illustrate that the approach outperforms previous works tackling this problem.

AMS subject classification (2010). 65K10, 65D10, 65D25, 53C22, 49Q99.

1. Introduction

This papers addresses the problem of fitting a smooth curve to data points d₀, …, d_n lying on a Riemannian manifold ${M}$ and associated with real-valued parameters t₀, …, t_n. The curve strikes a balance between a data proximity constraint and a smoothing regularization constraint.

Several applications motivate this problem in engineering and the sciences. For instance, curve fitting is of high interest in projection-based model order reduction of one-dimensional dynamical systems [1]. In that application, the dynamical system depends on the Reynolds number and the model reduction is obtained by computing suitable projectors as points on a Grassmann manifold. Finding a projector is however a time- and memory-consuming task. Based on projectors precomputed for given parameter values, fitting is used to approximate the projector associated with a new parameter value. In Gousenbourger et al. [2], the same strategy is used to approximate wind field orientations represented as points on the manifold of positive semidefinite covariance matrices of size p and rank r. Further applications are involving rigid-body motions on SE(3), like Cosserat rods applications [3], or orientation tracking [4]. Sphere-valued data are also of interest in many applications of data analysis, for storm tracking and prediction, or the study of bird migration [5].

There exists different approaches to tackle the curve fitting problem. Among others, we name here the subdivision schemes approach [6, 7] or the Lie-algebraic methods [8]. However, the most popular approach nowadays is probably to encapsulate the two above-mentioned constraints into an optimization problem

$\begin{array}{cc}\underset{\gamma \in \Gamma }{\min }{E}_{\lambda }(\gamma ):=\underset{\gamma \in \Gamma }{\min }{{\displaystyle {\int }_{t_0}^{t_n}\Vert \frac{{\text{D}}^2\gamma (t)}{\text{d}{t}^2}\Vert }}_{\gamma (t)}^2\text{d}t+\frac{\lambda }{2}{\displaystyle \sum _{i=0}^n{d}^2}(\gamma (t_i),d_i)),& (1)\end{array}$

where Γ is an admissible space of curves $\gamma :\left[t_0,t_n\right]\to {M}$, t↦γ(t), $\frac{D^2}{\text{d}{t}^2}$ denotes the (Levi-Civita) second covariant derivative, and ∥·∥_γ(t) denotes the Riemannian metric at γ(t) from which we can define a Riemannian distance d(·, ·). Finally, λ∈ℝ is a parameter that strikes the balance between the regularizer ${\int }_{t_0}^{t_n}{\parallel \frac{D^2\gamma (t)}{\text{d}{t}^2}\parallel }_{\gamma (t)}^2\text{d}t$ and the fitting term ${\displaystyle \sum _{i=0}^n}{\text{d}}^2(\gamma (t_i),d_i))$. This approach leads to the remarkable property that, when the manifold ${M}$ reduces to the Euclidean space and Γ is the Sobolev space $H^2(t_0,t_n)$, the solution to (1) is the natural cubic spline [9].

Optimization on manifolds has gained a lot of interest this last decade, starting with the textbook [10] that summarizes several optimization methods on matrix manifolds. Recently, toolboxes have emerged, providing easy access to such optimization methods, e.g., Manopt [11] and MVIRT [12]. The former received a very positive return in many different topics of research, with applications for example in low-rank modeling in image analysis [13], dimensionality reduction [14], phase retrieval [15] or even 5G-like MIMO systems [16]. The latter stems from recent interest in manifold-valued image and data processing, phrased as variational models on the product manifold ${{M}}^N$, where N is the number of pixels. Starting with total variation (TV) regularization of phase-valued data [17, 18], different methods for TV on manifolds [19, 20] have been developed as well as second order methods [21, 22] up to infimal convolution [23] and total generalized variation [23, 24]. Furthermore, different algorithms have been generalized to manifold-valued data, besides the previous works using gradient descent or cyclic proximal point methods, a Douglas–Rachford splitting [25], iteratively reweighted least squares [26] and more general half-quadratic minimization [27] have been introduced.

The curve fitting problem (1), has been tackled differently the past few years. Samir et al. [28] considered the case where Γ is an infinite dimensional Sobolev space of curves, and used the Palais-metric to design a gradient descent algorithm for (1) (see e.g., [29] for an application of this approach). Another method consists in discretizing the curve γ in N points, and therefore considering $\Gamma ={{M}}^N$ (see e.g., [30] for a result on SO(3)). Finally, the limit case where λ → 0 is already well studied and known as the geodesic regression [31–33].

A recent topic concerns curve fitting by means of Bézier curves. In that approach, the search space Γ is reduced to as set of composite Bézier curves. Those are a very versatile tool to model smooth curves and surfaces for real- and vector-valued discrete data points (see [34] for a comprehensive textbook), but they can also be used to model smooth curves and surfaces for manifold-valued data [35, 36]. The advantage to work with such objects, compared to classical approaches, are that (i) the search space is drastically reduced to the so-called control points of the Bézier curves (and this leads to better time and memory performances) and (ii) it is very simple to impose differentiability for the optimal curve, which is appreciated in several of the above-mentioned applications. However, while obtaining such an optimal curve reduces directly to solving a linear system of equations for data given on a Euclidean space, there is up to now no known closed form of the optimal Bézier curve for manifold valued data.

In this work, we derive a gradient descent algorithm to compute a differentiable composite Bézier curve $\text{B}:\left[t_0,t_n\right]\to {M}$ that satisfies (1), i.e., such that B(t) has a minimal mean squared acceleration, and fits the set of n+1 manifold-valued data points at their associated time-parameters. We consider the manifold-valued generalization of Bézier curves [36] in the same setting as in Arnould et al. [37], or more recently in Gousenbourger et al. [38]. We employ the (squared) second order absolute difference introduced in Bačák et al. [22] to obtain a discrete approximation of the regularizer from (1). The quality of the approximation depends only on the number of sampling points. We exploit the recursive structure of the De Casteljau algorithm [36] to derive the gradient of the objective function with respect to the control points of B(t). The gradient is built as a recursion of Jacobi fields that, for numerical reasons, are implemented as a concatenation of so-called adjoint Jacobi fields. Furthermore, the corresponding variational model only depends on the number of control points of the composite Bézier curve, and not on the number of sampling points. We finally obtain an approximating model to (1) that we solve with an algorithm only based on three tools on the manifold: the exponential map, the logarithmic map, and a certain Jacobi field along geodesics.

The paper is organized as follows. We introduce the necessary preliminaries—Bézier curves, Riemannian manifolds and Riemannian second order finite differences— in section 2. In section 3 we derive the gradient of the discretized mean squared acceleration of the composite Bézier curve with respect to its control points, and thus of the regularizer of (1). In section 4, we present the corresponding gradient descent algorithm, as well as an efficient gradient evaluation method, to solve (1) for different values of λ. The limit case where λ → ∞ is studied as well. Finally, in section 5, we validate, analyze and illustrate the performance of the algorithm for several numerical examples on the sphere S² and on the special orthogonal group SO(3). We also compare our solution to existing Bézier fitting methods. A conclusion is given in section 6.

2. Preliminaries

2.1. Bézier Functions and Composite Bézier Spline

Consider the Euclidean space ℝ^m. A Bézier curve of degree K∈ℕ is a function ${\beta }_K:\left[0,1\right]\to {ℝ}^m$ parametrized by control points $b_0,\dots ,b_K\in {ℝ}^m$ and taking the form

$\begin{array}{c}{\beta }_K(t;b_0,\dots ,b_K)\text{ :=}{\displaystyle \sum _{j=0}^K{b}_j}{B}_{j,K}(t),\end{array}$

where $B_{j,K}(t)=\left(\genfrac{}{}{0.0pt}{}{K}{j}\right)t^j{(1-t)}^{K-j}$ are the Bernstein basis polynomials [34]. For example the linear Bézier curve β₁ is just the line segment (1−t)b₀+tb₁ connecting the two control points b₀ and b₁. The explicit formulae of the quadratic and cubic Bézier curves read

$\begin{array}{c}\begin{array}{l}{\beta }_2(t;b_0,b_1,b_2)=b_0{\left(1-t\right)}^2+2b_1(1-t)t+b_2{t}^2,\hfill \\ {\beta }_3(t;b_0,b_1,b_2,b_3)=b_0{\left(1-t\right)}^3+3b_1{\left(1-t\right)}^{2}t+3b_2(1-t)t^2\hfill \\ +b_3{t}^3,\hfill \end{array}\end{array}$

for given control points $b_0,b_1,b_2\in {ℝ}^m$ and an additional point $b_3\in {ℝ}^m$ for the cubic case.

A composite Bézier curve is a function B:[0, n] → ℝ^m composed of n Bézier curves and defined as

$\begin{array}{c}\text{B}(t):=\{\begin{array}{l}{\beta }_{K_0}(t;b_0^0,\dots ,b_{K_0}^0)ift\in [0,1]\hfill \\ {\beta }_{K_i}(t-i;b_0^i,\dots ,b_{K_i}^i)ift\in (i,i+1],\hfill \\ i\in \{1,\dots ,n-1\},\hfill & (2)\end{array}\end{array}$

where K_i∈ℕ denotes the degree of the ith Bézier curve β_Ki of B and $b_j^i$, j = 0, …, K_i, are its control points. Furthermore, B(t) is continuous if the last and first control points of two consecutive segments coincide [34]. We introduce p_i as the point at the junction of two consecutive Bézier segments, i.e., $p_i:=b_{K_{i-1}}^{i-1}=b_0^i$. Differentiability is obtained if the control points of two consecutive segments are aligned. We introduce further $b_{i+1}^{-}:=b_{K_i-1}^i$ and $b_{i+1}^{+}:=b_1^{i+1}$ such that the differentiability condition reads $p_{i+1}=\frac{K_i{b}_{i+1}^{-}+K_{i+1}{b}_{+}^{i+1}}{K_i+K_{i+1}}$.

Example 1 (C¹ conditions for composite cubic Bézier curves). We consider the case where the Bézier segments are all cubic, as represented in Figure 1. The composite Bézier curve B(t) is C¹ if $p_i=\frac{1}{2}(b_i^{-}+b_i^{+})$, i = 1, …, 4, with $p_i=b_3^{i-1}=b_0^i$, $b_i^{-}=b_2^{i-1}$, and $b_i^{+}=b_1^i$.

FIGURE 1

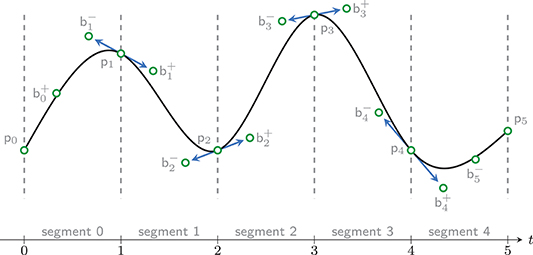
Figure 1. Schematic representation of the composite cubic Bézier curve $\text{B}:\left[0,5\right]\to {M}$, for ${M}=ℝ$ (black), and its control points (green circles). Continuous differentiability is reached at the junction of the segments (the blue arrows draw the first derivative of B).

2.2. Riemannian Manifolds

We consider a complete m-dimensional Riemannian manifold ${M}$. We refer to O'Neill [39] and do Carmo [40] for an introduction to Riemannian manifolds and to [10] for optimization thereon. We will use the following terminology and notations.

We denote by $T_a{M}$ the (Euclidean) tangent space to ${M}$ at $a\in {M}$; $T{M}:={\cup }_{a\in {M}}{T}_a{M}$ is the tangent bundle to ${M}$; 〈·, ·〉_a denotes the inner product in the tangent space $T_a{M}$ at a and from which we deduce the norm of $v\in T_a{M}$ denoted by $\parallel v{\parallel }_a=\sqrt{{\langle v,v\rangle }_a}$. For a (not necessarily unique) shortest geodesic between a and $b\in {M}$, we write $g(·;a,b):ℝ\to {M}$, t↦g(t; a, b), parametrized such that g(0;a, b) = a and g(1;a, b) = b. This choice of parametrization also means that the covariant derivative $\frac{D}{dt}$ of g with respect to time satisfies $\parallel \frac{D}{dt}g(t;a,b){\parallel }_{g(t)}=d_{{M}}(a,b)$, for all t∈[0, 1], where $d_{{M}}(a,b)$ is the geodesic distance between a and $b\in {M}$. The Riemannian exponential reads ${exp}_a:T_a{M}\to {M},v\mapsto b={exp}_a(v)$ and we denote by r_a∈ℝ the maximal radius such that the exponential map is bijective on ${{D}}_a:=\left\{b\in {M}:d_{{M}}(a,b)<r_a\right\}$. Then $\text{lo}{\text{g}}_a:{{D}}_a\to T_a{M},b\mapsto v=\text{lo}{\text{g}}_a(b)$ is called the Riemannian logarithm which is (locally) the inverse of the exponential. A Riemannian manifold is called symmetric in $x\in {M}$ if the geodesic reflection s_x at $x\in {M}$ given by the mapping γ(t)↦γ(−t) is an isometry at least locally near x, for all geodesics through γ(0) = x. If ${M}$ is symmetric in every $x\in {M}$, the manifold is called (Riemannian) symmetric space or symmetric manifold.

In the following we assume, that both the exponential and the logarithmic map are available for the manifold and that they are computationally not too expensive to evaluate. Furthermore, we assume that the manifold is symmetric.

2.3. Composite Bézier Curves on Manifolds

One well-known way to generalize Bézier curves to a Riemannian manifold ${M}$ is via the De Casteljau algorithm [36, section 2]. This algorithm only requires the Riemannian exponential and logarithm and conserves the interpolation property of the first and last control points. Some examples on interpolation and fitting with Bézier curves or Bézier surfaces, i.e., generalizations of tensor product Bézier curves, can be found in Absil et al. [35].

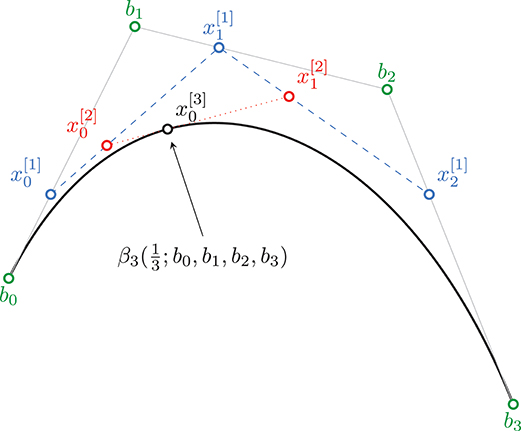
Consider ${\beta }_K:\left[0,1\right]\to {M},t\mapsto {\beta }_K(t;b_0,b_1,\dots ,b_K)$, the manifold-valued Bézier curve of order K driven by K+1 control points $b_0,\dots ,b_K\in {M}$. We introduce the points $x_i^{\left[0\right]}=b_i$ and iterate the construction of further points. For i = 0, …, K−k, k = 1, …, K, we define

$\begin{array}{cc}{x}_i^{\left[k\right]}:={\beta }_k(t;b_i,\dots ,b_{i+k})=g(t;x_i^{\left[k-1\right]},x_{i+1}^{\left[k-1\right]})& (3)\end{array}$

as the ith point of the kth step of the De Casteljau algorithm, and obtain ${\beta }_K(t;b_0,\dots ,b_K)=x_0^{\left[K\right]}$.

The De Casteljau algorithm is illustrated on Figure 2 for a Euclidean cubic Bézier curve β₃(t; b₀, b₁, b₂, b₃). The general cubic Bézier curve can be explicitly expressed on a manifold ${M}$ as

$\begin{array}{l}{\beta }_3(t;x_0^{\left[0\right]},x_1^{\left[0\right]},x_2^{\left[0\right]},x_3^{\left[0\right]})=g(t;g(t;g(t;x_0^{\left[0\right]},x_1^{\left[0\right]}),g(t;x_1^{\left[0\right]},x_2^{\left[0\right]})),\\ g(t;g(t;x_1^{\left[0\right]},x_2^{\left[0\right]}),g(t;x_2^{\left[0\right]},x_3^{\left[0\right]})))\\ =g(t;g(t;x_0^{\left[1\right]},x_1^{\left[1\right]}),g(t;x_1^{\left[1\right]},x_2^{\left[1\right]}))\\ =g(t;x_0^{\left[2\right]},x_1^{\left[2\right]})\\ =x_0^{\left[3\right]}.\end{array}$

FIGURE 2

Figure 2. Construction of a cubic Bézier curve via the De Casteljau algorithm.

The conditions of continuity and differentiability are generalized to manifolds in Popiel and Noakes [36].

Lemma 2 (Differentiability conditions [36]). Consider the composite Bézier curve $\text{B}:\left[0,2\right]\to {M}$ consisting of $f:\left[0,1\right]\to {M},t\mapsto f(t)={\beta }_K(t;b_0^0,b_1^0,\dots ,b_K^0)$ and $g:\left[1,2\right]\to {M},t\mapsto g(t)={\beta }_{\bar{K}}(t-1;b_0^1,b_1^1,\dots ,b_{\bar{K}}^1)$, i.e.,

$\begin{array}{c}B(t):=\{\begin{array}{ll}f(t)\hfill & fort\in [0,1],\hfill \\ g(t)\hfill & fort\in (1,2].\hfill \end{array}\end{array}$

The composite Bézier curve B(t) is continuous and continuously differentiable if the two following conditions hold:

$\begin{array}{cc}\begin{array}{cc}{b}_K^0=b_0^1 and b_K^0& =g(s;b_{K-1}^0,b_1^1),s=\frac{K}{K+\overline{K}}.\end{array}& (4)\end{array}$

The composite Bézier curve $\text{B}:\left[0,n\right]\to {M}$ is then defined completely analogously to the Euclidean case from Equation (2). The differentiability conditions (4) of Lemma 2 have to be satisfied at each junction point p_i, i = 1, …, n − 1.

Example 3 (Composite cubic Bézier curves). The composite cubic Bézier curve $\text{B}(t):\left[0,n\right]\to {M}$ is C¹ if $p_i=g(\frac{1}{2};b_i^{-},b_i^{+})$. See Figure 1 for an example on ${M}=ℝ$ with n = 5 segments and Figure 3 for an example on ${M}=S^2$ with n = 3 segments.

FIGURE 3

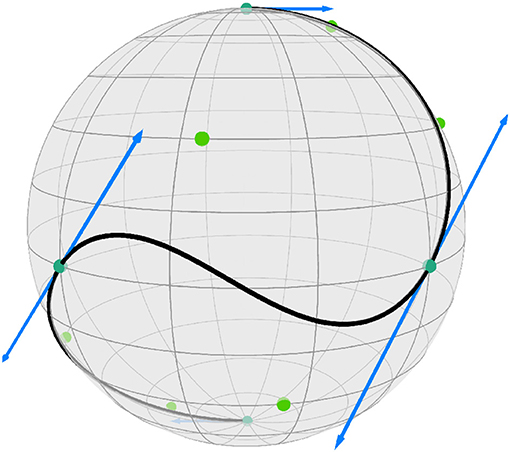
Figure 3. A composite cubic Bézier curve B:[0, 3] → S². The end points p_i, i = 0, …, 3, (cyan) and intermediate points $b_i^{\pm }$ (green) determine its shape; continuous differentiability is illustrated by the logarithmic maps ${log}_{p_i}{b}_i^{\pm }$, i∈{1, 2} (blue arrows).

2.4. Discrete Approximation of the Mean Squared Acceleration

We discretize the mean squared acceleration (MSA) of a curve $\gamma :\left[0,1\right]\to {M}$, by discretizing the corresponding integral

$\begin{array}{cc}{\displaystyle {\int }_0^1\Vert \frac{D^2\gamma (t)}{\text{d}{t}^2}{\Vert }_{\gamma (t)}^2\text{d}t,}& (5)\end{array}$

i.e., the regularizer from (1). We approximate the squared norm of the second (covariant) derivative by the second order absolute finite difference introduced by Bačák et al. [22]. Consider three points $x,y,z\in {M}$ and the set of mid-points of x and z

$\begin{array}{c}{{C}}_{x,z}:=\left\{c\right|c=g\left(\frac{1}{2};x,z\right)\},\end{array}$

for all (not necessarily shortest) geodesics g connecting x and z. The manifold-valued second order absolute finite difference is defined by

$\begin{array}{c}\begin{array}{ll}{\text{d}}_2[x,y,z]=\underset{c\in {{C}}_{x,z}}{\min }2d_{{M}}(c,y).\hfill & (6)\end{array}\end{array}$

This definition is equivalent, on the Euclidean space, to $\parallel x-2y+z\parallel =2\parallel \frac{1}{2}(x+z)-y\parallel$.

Using equispaced points t₀, …, t_N, N∈ℕ, with step size ${\Delta }_t=t_1-t_0=\frac{1}{N}$, we approximate ${\parallel \frac{D^2\gamma (t_i)}{\text{d}{t}^2}\parallel }_{\gamma (t_i)}\approx \frac{1}{{\Delta }_t^2}{d}_2\left[\gamma (t_{i-1}),\gamma (t_i),\gamma (t_{i+1})\right]$, i = 1, …, N−1, and obtain by the trapezoidal rule

$\begin{array}{c}{\displaystyle {\int }_0^1\Vert \frac{D^2\gamma (t)}{\text{d}{t}^2}{\Vert }_{\gamma (t)}^2}\text{d}t\approx {\displaystyle \underset{k=1}{\overset{N-1}{{{{\displaystyle \sum }}^{\text{}}}^{\text{}}}}}\frac{{\Delta }_t{d}_2^2[\gamma (t_{i-1}),\gamma (t_i),\gamma (t_{i+1})]}{{\Delta }_t^4}.\end{array}$

For Bézier curves γ(t) = B(t) we obtain for the regularizer in (1) the discretized MSA A(b) that depends on the control points b and reads

$\begin{array}{cc}\begin{array}{c}A(\text{b}):={\displaystyle \sum }_{i=1}^{N-1}\frac{{\text{d}}_2^2[\text{B}(t_{i-1}),\text{B}(t_i),\text{B}(t_{i+1})]}{{\Delta }_t^3}.\end{array}& (7)\end{array}$

3. The Gradient of the Discretized Mean Squared Acceleration

In order to minimize the discretized MSA A(b), we aim to employ a gradient descent algorithm on the product manifold ${{M}}^M$, where M is the number of elements in b. In the following, we derive a closed form of the gradient ∇_bA(b) of the discretized MSA (7). This gradient is obtained by means of a recursion and the chain rule. In fact, the derivative of (6) is already known [22], such that it only remains to compute the derivative of the composite Bézier curve.

We first introduce the following notation. We denote by $D_{x}f\left[\eta \right](x_0)\in T_{f(x_0){M}}$ the directional derivative of $f:{M}\to {M}$ evaluated at x₀, with respect to its argument x and in the direction $\eta \in T_x{M}$. We use the short hand D_xf[η] = D_xf[η](x) whenever this directional derivative is evaluated afterwards again at x.

We now state the two following definitions, which are crucial for the rest of this section.

Definition 4 (Gradient [10, Equation (3.31), p. 46]). Let $f:{M}\to ℝ$ be a real-valued function on a manifold ${M}$, $x\in {M}$ and $\eta \in T_x{M}$.

The gradient ${\nabla }_{{M}}f(x)\in T_x{M}$ of f at x is defined as the tangent vector that fulfills

$\begin{array}{cc}{\langle {\nabla }_{ℳ}f(x),\eta \rangle }_x=D_{x}f[\eta ]\text{ \hspace{0.05em}for all \hspace{0.05em}}\eta \in T_xℳ.& (8)\end{array}$

For multivariate functions f(x, y), we denote the gradient of f with respect to x at (x₀, y₀) by writing ${\nabla }_{{M},x}f(x_0,y_0)$. We shorten this notation as ${\nabla }_{{M},x}f={\nabla }_{{M},x}f(x,y)$ when this gradient is seen as a function of x (and y).

Definition 5 (Chain rule on manifolds [10, p. 195]). Let $f:{M}\to {M}$, $h:{M}\to {M}$ be two functions on a manifold ${M}$ and $F:{M}\to {M}$, x↦F(x) = (f ° h)(x) = f(h(x)), their composition. Let $x\in {M}$ and $\eta \in T_x{M}$. The directional derivative D_xF[η] of F with respect to x in the direction η is given by

$\begin{array}{ll}{D}_{x}F[\eta ]=D_{h(x)}f[D_{x}h[\eta ]],& (9)\end{array}$

where $D_{x}h\left[\eta \right]\in T_{h(x)}{M}$ and $D_{x}F\left[\eta \right]\in T_{F(x)}{M}$.

The remainder of this section is organized in four parts. We first recall the theory on Jacobi fields in section 3.1 and their relation to the differential of geodesics (with respect to start and end point). In section 3.2, we apply the chain rule to the composition of two geodesics, which appears within the De Casteljau algorithm. We use this result to build an algorithmic derivation of the differential of a general Bézier curve on manifolds with respect to its control points (section 3.3). We extend the result to composite Bézier curves in section 3.4, including their constraints on junction points p_i to enforce the C¹ condition (4), and finally gather these results to state the gradient ${\nabla }_{{M}}A(\text{b})$ of the discretized MSA (7) with respect to the control points.

3.1. Jacobi Fields as Derivative of a Geodesic

In the following, we introduce a closed form of the differential D_xg(t; ·, y) of a geodesic g(t; x, y), t∈[0, 1], with respect to its start point $x\in {M}$. The differential with respect to the end point $y\in {M}$ can be obtained by taking the geodesic g(t, y, x) = g(1−t; x, y).

As represented in Figure 4, we denote by γ_{x, ξ}, the geodesic starting in γ_{x, ξ}(0) = x and with direction $\frac{D}{dt}{\gamma }_{x,\xi }(0)=\xi \in T_x{M}$. We introduce ζ(s): = log_{γx, ξ(s)}y, the tangential vector in $T_{{\gamma }_{x,\xi }(s)}{M}$ pointing toward y. Then, the geodesic variation Γ_{g, ξ}(s, t) of the geodesic g(·;x, y) with respect to the tangential direction $\xi \in T_x{M}$ is given by

$\begin{array}{c}{\Gamma }_{g,\xi }(s,t):={\exp }_{{\gamma }_{x,\xi }(s)}(t\zeta (s)),s\in (-\epsilon ,\epsilon ),t\in [0,1],\end{array}$

where ε>0. The corresponding Jacobi field J_{g, ξ} along g is then given by the vector field

$\begin{array}{c}{J}_{g,\xi }(t):={\frac{D}{\partial s}{\Gamma }_{g,\xi }(s,t)|}_{s=0}\end{array}$

that represents the direction of the displacement of g if x is perturbed in a direction ξ.

FIGURE 4

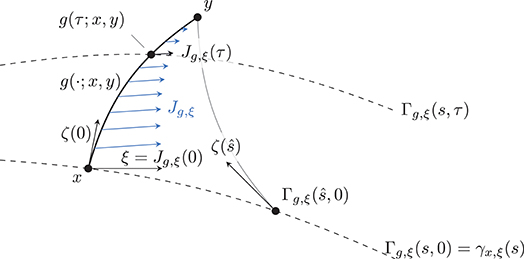
Figure 4. Schematic representation of the variation Γ_{g, ξ}(s, t) of a geodesic g w.r.t. the direction $\xi \in T_x{M}$. The corresponding Jacobi field along g and in the direction ξ is the vector field $J_{g,\xi }(t)=\frac{\partial }{\partial s}{\Gamma }_{g,\xi }(s,t){|}_{s=0}$.

We directly obtain J_{g, ξ}(0) = ξ, and J_{g, ξ}(1) = 0 as well as $J_{g,\xi }(t)\in T_{g(t;x,y)}{M}$. Since Γ_{g, ξ}(s, t) = g(t; γ_{x, ξ}(s), y) we obtain by the chain rule

$\begin{array}{cc}{D}_{x}g(t,·,y)[\xi ]={\frac{d}{ds}g(t;{\gamma }_{x,\xi }(s),y)|}_{s=0}\text{}={\frac{d}{ds}{\Gamma }_{g,\xi }(s,t)|}_{s=0}\text{}=J_{g,\xi }(t).& (10)\end{array}$

Remark. This relation between the derivative of geodesics and Jacobi fields is of high interest on symmetric spaces, where Jacobi fields can be computed in closed form, as summarized in the following Lemma.

Lemma 6. [22, Prop. 3.5] Let ${M}$ be a m-dimensional symmetric Riemannian manifold. Let g(t; x, y), t ∈ [0, 1], be a geodesic between $x,y\in {M}$, $\eta \in T_x{M}$ a tangent vector and {ξ₁, …ξ_m} be an orthonormal basis (ONB) of $T_x{M}$ that diagonalizes the curvature operator of ${M}$ with eigenvalues κ_ℓ, ℓ = 1, …, m. For details, see Ch. 4.2 and 5 (Ex. 5) of [40]. Let further denote by {Ξ₁(t), …, Ξ_m(t)} the parallel transported frame of {ξ₁, …, ξ_m} along g. Decomposing $\eta =\sum _{\ell =1}^m{\eta }_{\ell }{\xi }_{\ell }\in T_x{M}$, the derivative D_xg[η] becomes

$\begin{array}{c}{D}_{x}g(t;x,y)[\eta ]=J_{g,\eta }(t)={\displaystyle \sum _{\ell =1}^m{\eta }_{\ell }}{J}_{g,{\xi }_{\ell }}(t),\end{array}$

where the Jacobi field $J_{g,{\xi }_{\ell }}:ℝ\to T_{g(t;x,y)}{M}$ along g and in the direction ξ_ℓ is given by

$\begin{array}{cc}{J}_{g,{\xi }_{\ell }}(t)=\{\begin{array}{ll}\frac{\sinh \left(d_g(1-t)\sqrt{-{\kappa }_{\ell }}\right)}{\sinh \left(d_g\sqrt{-{\kappa }_{\ell }}\right)}{\Xi }_{\ell }(t)\hfill & \text{if }{\kappa }_{\ell }<0,\hfill \\ \frac{\sin \left(d_g\left(1-t\right)\sqrt{{\kappa }_{\ell }}\right)}{\sin \left(\sqrt{{\kappa }_{\ell }}{d}_g\right)}{\Xi }_{\ell }(t)\hfill & \text{if }{\kappa }_{\ell }>0,\hfill \\ (1-t){\Xi }_{\ell }(t)\hfill & \text{if }{\kappa }_{\ell }=0,\hfill \end{array}& (11)\end{array}$

with d_g = d(x, y) denoting the length of the geodesic g(t; x, y), t∈[0, 1].

The Jacobi field of the reversed geodesic ḡ(t): = g(t; y, x) = g(1−t; x, y) is obtained using the same orthonormal basis and transported frame but evaluated at s = 1−t. We thus obtain D_yg(t; x, y)[ξ_ℓ] = D_yg(1−t; y, x)[ξ_ℓ] = J_ḡ,ξℓ(1−t), where

$\begin{array}{c}{J}_{\overline{g},{\xi }_{\ell }}(1-t)=\{\begin{array}{ll}\frac{\sinh \left(d_{g}t\sqrt{-{\kappa }_{\ell }}\right)}{\sinh \left(d_g\sqrt{-{\kappa }_{\ell }}\right)}{\Xi }_{\ell }(t)\hfill & \text{if }{\kappa }_{\ell }<0,\hfill \\ \frac{\sin \left(d_{g}t\sqrt{{\kappa }_{\ell }}\right)}{\sin \left(d_g\sqrt{{\kappa }_{\ell }}\right)}{\Xi }_{\ell }(t)\hfill & \text{if }{\kappa }_{\ell }>0,\hfill \\ t{\Xi }_{\ell }(t)\hfill & \text{if }{\kappa }_{\ell }=0.\hfill \end{array}\end{array}$

Note that $T_{g(t)}{M}=T_{ḡ(1-t)}{M}$. Therefore ${\Xi }_{\ell }(t)\in T_{g(t)}{M}$, ℓ = 1, …, m, is an orthonormal basis for this tangent space.

3.2. Derivative of Coupled Geodesics

Let ${M}$ be a symmetric Riemannian manifold. We use the result of Lemma 6 to directly compute the derivative of coupled geodesics, i.e., a function composed of g₁(t): = g(t; x, y) and g₂(t): = g(t; g₁(t), z). By Definition 5, we have

$\begin{array}{c}{D}_x{g}_2(t)[\eta ]=D_{g_1(t)}g(t;·,z)[D_x{g}_1(t)[\eta ]]\end{array}$

and by (10), we obtain

$\begin{array}{c}{D}_x{g}_2(t)[\eta ]=J_{g_2,D_x{g}_1(t)[\eta ]}(t),\end{array}$

where the variation direction used in the Jacobi field is now the derivative of g₁(t) in direction η. Similarly, we compute the derivative of a reversed coupled geodesic g₃(t): = g(t; z, g₁(t)) as

$\begin{array}{c}{D}_x{g}_3(t)[\eta ]=D_{g_1(t)}g(t;z,·)[D_x{g}_1(t)[\eta ]]=J_{{\overline{g}}_3,D_x{g}_1(t)[\eta ]}(1-t).\end{array}$

Note that the Jacobi field is reversed here, but that its variation direction is the same as the one of the Jacobi field introduced for g₂(t). In a computational perspective, it means that we can use the same ONB for the derivatives of both g₃ and ḡ₃ Furthermore, in this case, the variation direction is also computed by a Jacobi field since D_xg₁(t)[η] = J_{g1, η}(t).

Finally the derivative of g₂ (resp. g₃) on symmetric spaces is obtained as follows. Let $\left\{{\xi }_1^{\left[1\right]},\dots ,{\xi }_m^{\left[1\right]}\right\}$ be an ONB of $T_x{M}$ for the inner Jacobi field along g₁, and $\left\{{\xi }_1^{\left[2\right]},\dots ,{\xi }_m^{\left[2\right]}\right\}$ be an ONB of $T_{g_1(t)}{M}$ for the outer Jacobi field along g₂ (resp. g₃). As $\eta =\sum _{\ell =1}^m{\eta }_{\ell }{\xi }_{\ell }^{\left[1\right]}\in T_x{M}$, and stating $J_{g_1,{\xi }_{\ell }^{\left[1\right]}}(t)=\sum _{l=1}^m{\mu }_l{\xi }_l^{\left[2\right]}\in T_{g_1(t)}{M}$, the derivative of g₂ (resp. g₃) with respect to x in the direction $\eta \in T_x{M}$ reads

$\begin{array}{cc}{D}_x{g}_2(t)[\eta ]={\displaystyle \sum _{l=1}^m{\displaystyle \sum _{\ell =1}^m{J}_{g_2,{\xi }_l^{[2]}}}}(t){\mu }_l{\eta }_{\ell },& (12)\end{array}$

and accordingly for g₃.

3.3. Derivative of a Bézier Curve

Sections 3.1 and 3.2 introduced the necessary concepts to compute the derivative of a general Bézier curve β_K(t; b₀, …, b_K), as described in Equation (3), with respect to its control points b_j. For readability of the recursive structure investigated in the following, we introduce a slightly simpler notation and the following setting.

Let K be the degree of a Bézier curve β_K(t; b₀, …, b_K) with the control points $b_0,\dots ,b_K\in {M}$. We fix k∈{1, …, K}, i∈{0, …, K−k} and t∈[0, 1]. We introduce

$\begin{array}{cc}{g}_i^{\left[k\right]}(t):=g(t;g_i^{\left[k-1\right]}(t),g_{i+1}^{\left[k-1\right]}(t))={\beta }_i^{\left[k\right]}(t;b_i,\dots ,b_{i+k}),& (13)\end{array}$

for the i^th Bézier curve of degree k in the De Casteljau algorithm, and $g_i^{\left[0\right]}(t)=b_i$.

Furthermore, given x∈{b_i, …, b_i+k}, we denote by

$\begin{array}{cc}{\eta }_i^{\left[k\right]}:=D_x{g}_i^{\left[k\right]}(t)[\eta ],& (14)\end{array}$

its derivative with respect to one of its control points x in the direction $\eta \in T_x{M}$.

Remark. Clearly any other derivative of $g_i^{\left[k\right]}$ with respect to x = b_j, j<i or j>i+k is zero. In addition we have ${\eta }_i^{\left[0\right]}=D_x{g}_i^{\left[0\right]}\left[\eta \right]=\eta$ for x = b_i and zero otherwise.

Theorem 7 (Derivative of a Bézier curve). Let k ∈ {1, …, K}and i ∈ {0, …, K−k}be given. The derivative ${\eta }_i^{\left[k\right]}=D_x{g}_i^{\left[k\right]}(t)\left[\eta \right]$ of $g_i^{\left[k\right]}$ with respect to its control point x: = b_j, i ≤ j ≤ i+k, and in the direction $\eta \in T_x{M}$ is given by

$\begin{array}{l}{\eta }_i^{\left[k\right]}:=D_x{g}_i^{\left[k\right]}(t)[\eta ]\\ =\{\begin{array}{ll}{J}_{g_i^{\left[k\right]},{\eta }_i^{\left[k-1\right]}}(t)\hfill & \text{ if }j=i,\hfill \\ J_{g_i^{\left[k\right]}k,{\eta }_i^{\left[k-1\right]}}(t)+J_{{\overline{g}}_i^{\left[k\right]},{\eta }_{i+1}^{\left[k-1\right]}}(1-t)\hfill & \text{ if }i<j<i+k,\hfill \\ J_{{\overline{g}}_i^{\left[k\right]},{\eta }_{i+1}^{\left[k-1\right]}}(1-t)\hfill & \text{ if }j=i+k.\hfill \end{array}\end{array}$

Proof. Let fix t∈[0, 1] and x = b_j, i ≤ j ≤ i+k. For readability we set $a:=g_i^{\left[k-1\right]}(t)$, $b:=g_{i+1}^{\left[k-1\right]}(t)$, and $f:=g_i^{\left[k\right]}(t)=g(t;a,b)$. Note that while f depends on the control points b_i, …, b_i+k and is a Bézier curve of degree k, both a and b are Bézier curves of degree k−1. The former does not depend on b_i+k, and the latter is independent of b_i.

We prove the claim by induction. For k = 1 the function $g_i^{\left[1\right]}$ is just a geodesic. The case i<j<i+1 does not occur and the remaining first and third cases follow by the notation introduced for k = 0 and Lemma 6.

For k>1 we apply the chain rule (9) to D_xf[η] and obtain

$\begin{array}{c}{D}_{x}f[\eta ]=D_{a}f[D_{x}a[\eta ]]+D_{b}f[D_{x}b[\eta ]].\end{array}$

Consider the first term D_af[D_xa[η]] and j<i+k. By (10) and the notation from (14), one directly has

$\begin{array}{c}{D}_{a}f[{\eta }_i^{\left[k-1\right]}]=J_{f,{\eta }_i^{\left[k-1\right]}}(t).\end{array}$

For j = i+k, clearly D_xa[η] = D_af[D_xa[η]] = 0, as a does not depend on b_i+k.

We proof the second term similarly. For j>i, by applying the chain rule and using the reversed Jacobi field formulation of Lemma 6 for the derivative of a geodesic with respect to its end point, we obtain

$\begin{array}{c}{D}_{b}f[{\eta }_{i+1}^{\left[k-1\right]}]=J_{\overline{f},{\eta }_{i+1}^{\left[k-1\right]}}(1-t).\end{array}$

Finally, as D_xb[η] = D_bf[D_xb[η]] = 0 for x = b_i, the assumption follows. □

Figure 5 represents one level of the schematic propagation tree to compute the derivative of a Bézier curve.

FIGURE 5

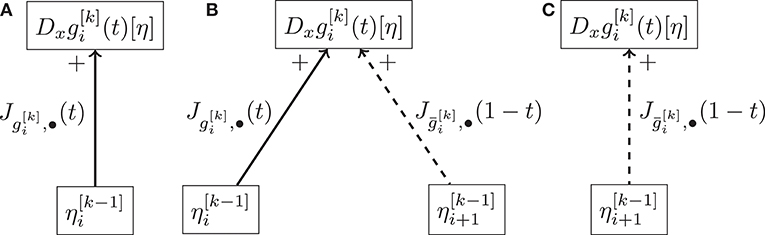
Figure 5. Schematic representation of the cases where elements compose the chained derivative of the ith Bézier curve of order k in the De Casteljau algorithm. The solid line represents a Jacobi field along $g_i^{\left[k\right]}$, while the dashed one represents a reversed Jacobi field. (A) Represents the case x = b_i, (B) represents the cases where x∈{b_i+1, …, b_i+k+1}, and (C) represents the case x = b_i+k.

Example 8 (Quadratic Bézier curve). Consider the quadratic Bézier curve ${\beta }_2:\left[0,1\right]\to {M}$ defined as

$\begin{array}{c}{\beta }_2(t;b_0,b_1,b_2)=g(t;g(t;b_0,b_1),g(t;b_1,b_2)).\end{array}$

Using the notations (13), we have

$\begin{array}{l}{g}_0^{\left[1\right]}(t):=g(t;b_0,b_1),g_1^{\left[1\right]}(t):=g(t;b_1,b_2),\\ g_0^{\left[2\right]}(t):=g(t;g_0^{\left[1\right]},g_1^{\left[1\right]}).\end{array}$

The derivative of β₂ at t with respect to b₀ in the direction $\eta \in T_{b_o}{M}$, is given by

$\begin{array}{c}{D}_{b_0}{\beta }_2[\eta ]=J_{g_0^{\left[2\right]},{\eta }_0^{\left[1\right]}}(t),\text{ with }{\eta }_0^{\left[1\right]}:=J_{g_0^{\left[1\right]}1,\eta }(t).\end{array}$

The derivative of β₂ at t with respect to b₂ in the direction $\eta \in T_{b_2}{M}$ can be seen as deriving by the first point after inverting the Bezier curve, i.e., looking at ${\bar{\beta }}_2(t)={\beta }_2(1-t)$, hence we have analogously to the first term

$\begin{array}{c}{D}_{b_2}{\beta }_2[\eta ]=J_{{\overline{g}}_0^{\left[2\right]},{\eta }_1^{\left[1\right]}}(1-t),\text{ with }{\eta }_1^{\left[1\right]}:=J_{{\overline{g}}_1^{\left[1\right]},\eta }(1-t).\end{array}$

The case D_b1β₂[η], $\eta \in T_{b_1}{M}$, involves a chain rule, where b₁ appears in both $g_0^{\left[1\right]}$ (as its end point) and $g_1^{\left[1\right]}$ (as its starting point). Using the two intermediate results (or Jacobi fields of geodesics)

$\begin{array}{c}{\eta }_0^{\left[1\right]}:=J_{{\overline{g}}_0^{\left[1\right]},\eta }(1-t)\text{ \hspace{0.05em}and \hspace{0.05em}}{\eta }_1^{\left[1\right]}:=J_{g_1^{\left[1\right]},\eta }(t),\end{array}$

we obtain

$\begin{array}{c}{D}_{b_1}{\beta }_2[\eta ]=J_{g_0^{\left[2\right]},{\eta }_0^{\left[1\right]}}(t)+J_{{\overline{g}}_0^{\left[2\right]},{\eta }_1^{\left[1\right]}}(1-t).\end{array}$

Example 9 (Cubic Bézier curve). Consider the cubic Bézier curve ${\beta }_3:\left[0,1\right]\to {M}$ defined as

$\begin{array}{c}{\beta }_3(t;b_0,b_1,b_2,b_3)=g(t;{\beta }_2(t;b_0,b_1,b_2),{\beta }_2(t;b_1,b_2,b_3)).\end{array}$

As in Example 8, we use the notations (13) and define

$\begin{array}{l}{g}_j^{\left[1\right]}(t):=g(t;b_j,b_{j+1}),j=0,1,2,\\ g_j^{\left[2\right]}(t):=g(t;g_j^{\left[1\right]},g_{j+1}^{\left[1\right]}),j=0,1,and\\ g_0^{\left[3\right]}(t):=g(t;g_0^{\left[2\right]},g_1^{\left[2\right]}).\end{array}$

The derivation of β₃ with respect to b₀ or b₃ follows the same structure as in Example 8. The case of D_b1β₃[η], however, requires two chain rules. The needed Jacobi fields follow the tree structure shown in Figure 6B: given $\eta \in T_{b_1}{M}$, we define at the first recursion step

$\begin{array}{c}{\eta }_0^{\left[1\right]}:=J_{{\overline{g}}_0^{\left[1\right]},\eta }(1-t),{\eta }_1^{\left[1\right]}:=J_{g_1^{\left[1\right]},\eta }(t),\end{array}$

and at the second recursion step

$\begin{array}{c}{\eta }_0^{\left[2\right]}:=J_{g_0^{\left[2\right]},{\eta }_0^{\left[1\right]}}(t)+J_{{\overline{g}}_0^{\left[2\right]},{\eta }_1^{\left[1\right]}}(1-t),{\eta }_1^{\left[2\right]}:=J_{g_1^{\left[2\right]},{\eta }_1^{\left[1\right]}}(t).\end{array}$

Note that both ${\eta }_0^{\left[2\right]}$ and ${\eta }_1^{\left[2\right]}$ are actually the derivative of β₂(t; b₀, b₁, b₂) and β₂(t; b₁, b₂, b₃), respectively, with respect to b₁ and direction $\eta \in T_{b_1}{M}$. Finally we have

$\begin{array}{c}{D}_{b_1}{\beta }_3[\eta ]=J_{g_0^{\left[3\right]},{\eta }_0^{\left[2\right]}}(t)+J_{{\overline{g}}_0^{\left[3\right]},{\eta }_1^{\left[2\right]}}(1-t).\end{array}$

FIGURE 6

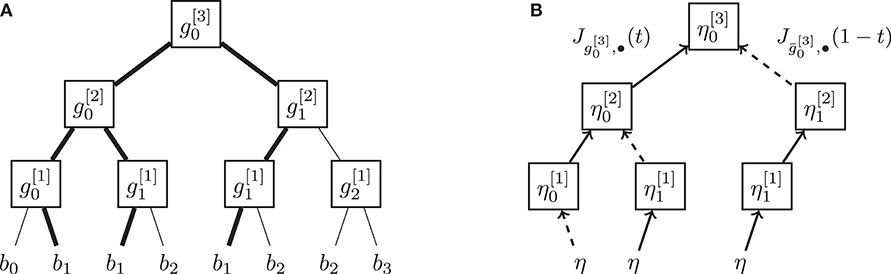
Figure 6. Construction and derivation tree of a Bézier curve β₃(t; b₀, b₁, b₂, b₃). The derivative with respect to a variable b_i is obtained by a recursion of Jacobi fields added at each leaf of the tree. (A) Tree-representation of the construction of a cubic Bezier curve. The thick line tracks the propagation of b₁ within the tree. (B) Tree-representation of the construction of ${\eta }_0^{\left[3\right]}:={\mathit{\text{D}}}_{b_1}{\beta }_3\left[\eta \right]$. The solid lines are Jacobi fields while dashed lines are reversed Jacobi fields.

The case of D_b2β₃[η] is obtained symmetrically, with arguments similar to b₁.

Note that computing the Jacobi fields involved just follows the same decomposition tree as the De Casteljau algorithm (Figure 6A).

3.4. Joining Segments and Deriving the Gradient

In this subsection we derive the differential of a composite Bézier curve B(t) consisting of n segments and take the C¹ conditions into account. We simplify the notations from section 2.1 and set the degree fixed to K_i = K for all segments, e.g., K = 3 for a cubic composite Bézier curve. Then the control points are $b_j^i$, j = 0, …, K, i = 0, …, n−1. We further denote by $p_i=b_K^{i-1}=b_0^i$, i = 1, …, n−1 the common junction point of the segments and p₀ and p_n the start and end points, respectively. For ease of notation we denote by $b_i^{-}=b_{K-1}^i$ and $b_i^{+}=b_1^i$, i = 1, …, n−1, the two points needed for differentiability (C¹) condition investigation, cf. Figure 1 for an illustration of the framework on ${M}=ℝ$, with K = 3.

One possibility to enforce the C¹ condition (4) is to include it into the composite Bézier curve by replacing $b_i^{+}$ with

$\begin{array}{cc}{b}_i^{+}=g\left(2;b_i^{-},p_i\right),i=1,\dots ,n-1.& (15)\end{array}$

This way both the directional derivatives of B(t) with respect to $b_i^{-}$ and p_i change due to a further (most inner) chain rule.

Lemma 10 (Derivative of a composite Bézier curve with C¹ condition). Let B be a composite Bézier curve and $p_i,b_i^{+},b_i^{-}$introduced as above. Replacing $b_i^{+}=g(2;b_i^{-},p_i)$ eliminates that variable from the composite Bezier curve and keeps the remaining differentials unchanged, except the following which now read

$\begin{array}{c}{D}_{b_i^{-}}B(t)[\eta ]=\{\begin{array}{ll}\begin{array}{l}{D}_{b_i^{-}}{\beta }_K(t-i+1;\hfill \\ p_{i-1},b_{i-1}^{+},\dots ,·,p_i)[\eta ]\hfill \end{array}\hfill & t\in (i-1,i],\hfill \\ \begin{array}{l}{D}_{b_i^{+}}{\beta }_K(t-i;p_i,b_i^{+},\dots ,·,p_{i+1})\hfill \\ \left[D_{b_i^{-}}g(2;·,p_i)[\eta ]\right]\hfill \end{array}\hfill & t\in (i,i+1],\hfill \end{array}\end{array}$

and

$\begin{array}{c}{D}_{p_i}B(t)[\eta ]=\{\begin{array}{ll}\begin{array}{l}{D}_{p_i}{\beta }_K(t-i+1;p_{i-1},\hfill \\ b_{i-1}^{+},\dots ,b_i^{-},·)[\eta ]\hfill \end{array}\hfill & t\in (i-1,i],\hfill \\ \begin{array}{l}{D}_{p_i}{\beta }_K(t-i;·,\hfill \\ b_i^{+},\dots ,b_{i+1}^{-},p_{i+1})[\eta ]\hfill \end{array}\hfill & \hfill \\ \begin{array}{l}+D_{b_i^{+}}{\beta }_K(t-i;p_i,·,\dots ,\hfill \\ b_{i+1}^{-},p_{i+1})\left[D_{p_i}g(2;b_i^{-},·)[\eta ]\right]\hfill \end{array}\hfill & t\in (i,i+1].\hfill \end{array}\end{array}$

In both cases, the first interval includes i−1 = 0, when i = 1.

Proof. Both first cases are from the derivation of a Bézier curve as before, for both second cases replacing $b_i^{+}=g(2;b_i^{-},p_i)$ yields one (for p_i additional) term.

We now derive the gradient of the objective function (7). We introduce the abbreviation ${\text{B}}_i=\text{B}(t_i)\in {M}$, and ${\text{d}}_{2,i}^2={\text{d}}_2^2({\text{B}}_{i-1},{\text{B}}_i,{\text{B}}_{i+1})$.

Theorem 11. Let ${M}$ be a m-dimensional manifold, x be one of the control points of a composite Bézier curve B, and {ξ₁, …, ξ_m} be a corresponding orthonormal basis (ONB) of $T_x{M}$. The gradient ${\nabla }_{{M},x}A(\text{b})$ of the discretized mean squared acceleration A(b) of B, w.r.t. x, discretized at N+1 equispaced times t₀, …, t_N is given by

$\begin{array}{c}{\nabla }_{{M},x}A(b)=\frac{1}{\Delta t^3}{\displaystyle \sum _{\ell =1}^m{\displaystyle \sum _{i=1}^{N-1}{\displaystyle \sum _{j=i-1}^{i+1}{\langle {\nabla }_{{M}}{\text{d}}_{2,i}^2,D_x{B}_j[{\xi }_{\ell }]\rangle }_{B_j}}}}{\xi }_{\ell }.\end{array}$

Proof: As ${\nabla }_{{M},x}A(\text{b})\in T_x{M}$, we seek for the coefficients a_ℓ: = a_ℓ(x) such that

$\begin{array}{cc}{\nabla }_{{M}}f(x)={\displaystyle \sum _{\ell =1}^m{a}_{\ell }}{\xi }_{\ell }.& (16)\end{array}$

Therefore, for any tangential vector $\eta :=\sum _{\ell =1}^m{\eta }_{\ell }{\xi }_{\ell }\in T_x{M}$, we have,

$\begin{array}{cc}{\langle {\nabla }_{{M},x}A(b),\eta \rangle }_x={\displaystyle \sum _{\ell =1}^m{a}_{\ell }}{\eta }_{\ell }.& (17)\end{array}$

By definition of A and Definition 4 this yields

$\begin{array}{cc}{\langle {\nabla }_{{M},x}A(b),\eta \rangle }_x=\text{ }\frac{1}{\Delta t^3}{\displaystyle \sum _{i=1}^{N-1}{\langle {\nabla }_{{M}}{d}_{2,i}^2(x),\eta \rangle }_x}=\text{ }\frac{1}{\Delta t^3}{\displaystyle \sum _{i=1}^{N-1}{D}_x}{\text{d}}_{2,i}^2[\eta ].& (18)\end{array}$

We compute $D_x{\text{d}}_{2,i}^2\left[\eta \right]$ using the chain rule (Definition 5) as

$\begin{array}{cc}{D}_x{\text{d}}_{2,i}^2[\eta ]={\displaystyle \sum _{j=i-1}^{i+1}{D}_{B_j}}{\text{d}}_{2,i}^2[D_x{B}_j[\eta ]],& (19)\end{array}$

which, by Definition 4, again becomes

$\begin{array}{c}{D}_{B_j}{\text{d}}_{2,i}^2[D_x{B}_j[\eta ]]={\langle {\nabla }_{{M}}{\text{d}}_{2,i}^2,D_x{B}_j[\eta ]\rangle }_{B_j}.\end{array}$

The term on the left of the inner product is given in Bačák et al. [22, section 3] and the right term is given in section 3.3. While the former can be computed using Jacobi fields and a logarithmic map, the latter is the iteratively coupling of Jacobi fields. Furthermore, the differential D_xB_j[η] can be written as

$\begin{array}{c}{D}_x{B}_j[\eta ]={\displaystyle \sum _{\ell =1}^m{\eta }_{\ell }}{D}_x{B}_j[{\xi }_{\ell }]\in T_{B_j}{M}.\end{array}$

Hence, we obtain

$\begin{array}{c}{D}_{B_j}{\text{d}}_{2,i}^2[D_x{B}_j[\eta ]]={\displaystyle \sum _{\ell =1}^m{\eta }_{\ell }}{\langle {\nabla }_{{M}}{\text{d}}_{2,i}^2,D_x{B}_j[{\xi }_{\ell }]\rangle }_{B_j},\end{array}$

and by (17), (18), and (19), it follows

$\begin{array}{c}{\langle {\nabla }_{{M},x}A(b),\eta \rangle }_x=\frac{1}{\Delta t^3}{\displaystyle \sum _{\ell =1}^m{\eta }_{\ell }}{\displaystyle \sum _{i=1}^{N-1}{\displaystyle \sum _{j=i-1}^{i+1}{\langle {\nabla }_{{M}}{\text{d}}_{2,i}^2,D_x{B}_j[{\xi }_{\ell }]\rangle }_{B_j}}},\end{array}$

which yields the assertion (16).

4. Application to the Fitting Problem

The fitting problem has been tackled different ways this last decades. The approach with Bézier curves is more recent, and we refer to Absil et al. [35], Arnould et al. [37], and Gousenbourger et al. [38] for a detailed overview of these methods.

In this section, we present the numerical framework we use in order to fit a composite Bézier curve B to a set of data points $d_0,\dots ,d_n\in {M}$ associated with time-parameters t₀, …, t_n, such that we meet (1). For the sake of simplicity, we limit the study to the case where t_i = i, i = 0, …, n. Therefore, the fitting problem (1) becomes

$\begin{array}{cc}\underset{b\in {\Gamma }_B}{\min }{E}_{\lambda }(\text{b}):={\min }_{\text{b}\in {\Gamma }_B}{{\displaystyle {\int }_{t_0}^{t_n}\Vert \frac{{\text{D}}^{2}B(t)}{\text{d}{t}^2}\Vert }}_{B(t)}^2\text{d}t+\frac{\lambda }{2}{\displaystyle \sum _{i=0}^n{\text{d}}^2}(p_i,d_i),& (20)\end{array}$

where ${\Gamma }_{\text{B}}\in {{M}}^M$ is the set of the M control points of B. Remark that, compared to (1), the optimization is now done on the product manifold ${{M}}^M$. Furthermore, the fitting term now implies a distance between d_i and p_i, as B(t_i) = p_i.

The section is divided in three parts: the product manifold ${{M}}^M$ is defined in section 4.1, where the contribution of the fitting term in the gradient of E is also presented. Then, we propose an efficient algorithm to compute the gradient of the discretized MSA, based on so-called adjoint Jacobi fields. We finally shortly mention the gradient descent algorithm we use as well as the involved Armijo rule.

4.1. Fitting and Interpolation

Let us clarify the set ${\Gamma }_{\text{B}}\in {{M}}^M$ from (20). We will explicitly present the vector b and state its size M. The set Γ_B is the set of the M remaining free control points to optimize, when the ${{C}}^1$ continuity constraints are imposed. We distinguish two cases: (i) the fitting case, that corresponds to formulae presented in section 3, and (ii) the interpolation case (λ → ∞) where the constraint d_i = p_i is imposed as well.

For a given composite Bézier curve $\text{B}:\left[0,n\right]\to {M}$ consisting of a Bézier curve of degree K on each segment, and given the C¹ conditions (4), the segments are determined by the points

$\begin{array}{cc}b=(p_0,b_0^{+},b_2^0,\dots ,b_{K-2}^0,b_1^{-},p_1,\dots ,b_n^{-},p_n)\in {ℳ}^M.& (21)\end{array}$

We investigate the length of M. First, $b_i^{+}$ is given by p_i and $b_i^{-}$ via (4). Second, for the segments i = 2, …, n we can further omit p_i−1 since the value also occurs in the segment i−1 as last entry. Finally, the first segment contains the additional value of $b_0^{+}$ that is not fixed by C¹ constraints. The first segment is thus composed of K+1 control points, while the n−1 remaining segments are determined by K−1 points. In total we obtain M = n(K−1)+2 control points to optimize.

Minimizing A(b) alone leads to the trivial solution, for any set of control points b = (x, …, x), $x\in {M}$, and this is why the fitting term from (20) is important.

Fitting (0 < λ < ∞). If the segment start and end points are obstructed by noise or allowed to move, we employ a fitting scheme to balance the importance given to the data points d₀, …, d_n. Equation (20) reads

$\begin{array}{cc}\underset{b\in {\Gamma }_B}{\text{argmin}}\tilde{A}(b),\tilde{A}(b):=A(b)+\frac{\lambda }{2}{\displaystyle \sum _{i=0}^n{d}_{{M}}^2}(d_i,p_i),& (22)\end{array}$

where λ∈ℝ⁺ sets the priority to either the data term (large λ) or the mean squared acceleration (small λ) within the minimization. The gradient of the data term is given in Karcher [41], and the gradient of à is given by

$\begin{array}{c}{\nabla }_{{{M}}^M,x}\tilde{A}(b)=\{\begin{array}{ll}{\nabla }_{{{M}}^M,x}A(b)-\lambda {\log }_{p_i}{d}_i\hfill & \text{ if }x=p_i,i=0,\dots ,n,\hfill \\ {\nabla }_{{{M}}^M,x}A(b)\hfill & \text{ otherwise.}\hfill \end{array}\end{array}$

Interpolation (λ → ∞). For interpolation we assume that the start point p_i−1 and end point p_i of the segments i = 1, …, n are fixed to given data d_i−1 and $d_i\in {M}$, respectively. The optimization of the discrete mean squared acceleration A(b) reads

$\begin{array}{cc}\underset{b\in {\Gamma }_B}{\text{argmin}}A(b)\text{ \hspace{0.05em}s}. \text{t}.p_{\text{i}}=d_{\text{i}},i=\text{0},\dots ,n.& (23)\end{array}$

Since the p_i are fixed by constraint, they can be omitted from the vector b. We obtain

$\begin{array}{c}b=(b_0^{+},b_2^0,\dots ,b_1^{-},b_2^1,\dots ,b_n^{-})\in {ℳ}^{M^{\prime }}\end{array}$

Since there are n+1 additional constraints, the minimization is hence performed on the product manifold ${{M}}^{M^{\prime }}$, M′ = M−(n+1) = n(K−2)+1.

4.2. Adjoint Jacobi Fields

In the Euclidean space ℝ^m, the adjoint operator T* of a linear bounded operator T:ℝ^m → ℝ^q is the operator fulfilling

$\begin{array}{c}{\langle T(x),y\rangle }_{{ℝ}^q}={\langle x,T^{*}(y)\rangle }_{{ℝ}^m},\text{ \hspace{0.05em} for all }x\in {ℝ}^m,y\in {ℝ}^q.\end{array}$

The same can be defined for a linear operator $S:T_x{M}\to T_y{M}$, $x,y\in {M}$, on a m-dimensional Riemannian manifold ${M}$. The adjoint operator $S^{*}:T_y{M}\to T_x{M}$ satisfies

$\begin{array}{c}{\langle S(\eta ),\nu \rangle }_y={\langle \eta ,S^{*}(\nu )\rangle }_x,\text{ \hspace{0.05em} for all }\eta \in T_x{M},\nu \in T_y{M}.\end{array}$

We are interested in the case where S is the differential operator D_x of a geodesic F(x) = g(t; x, y) for some fixed t∈ℝ and $y\in {M}$. The differential $D_{x}F:T_x{M}\to T_{F(x)}{M}$ can be written as

$\begin{array}{c}{D}_{x}F[\eta ]=J_{g,\eta }(t)={\displaystyle \sum _{\ell =1}^m{\langle \eta ,{\xi }_{\ell }\rangle }_x}{\alpha }_{\ell }{\Xi }_{\ell }(t),\end{array}$

where α_ℓ are the coefficients of the Jacobi field (11), and ξ_ℓ, Ξ_ℓ(t) are given as in Lemma 6. To derive the adjoint differential ${(D_{x}F)}^{*}:T_{F(x)}{M}\to T_x{M}$ we observe that for any $\nu \in T_{F(x)}{M}$ we have

$\begin{array}{c}\begin{array}{l}{\langle D_{x}F[\eta ],\nu \rangle }_{F(x)}={\displaystyle \sum _{\ell =1}^m{\langle \eta ,{\xi }_{\ell }\rangle }_x{\alpha }_{\ell }{\langle {\Xi }_{\ell }(t),\nu \rangle }_{F(x)}}\hfill \\ ={\langle \eta ,{\displaystyle \sum _{\ell =1}^m{\langle {\Xi }_{\ell }(t),\nu \rangle }_{F(x)}{\alpha }_{\ell }{\xi }_{\ell }}\rangle }_x.\hfill \end{array}\end{array}$

Hence the adjoint differential is given by

$\begin{array}{c}{(D_{x}F)}^{*}[\nu ]={\displaystyle \sum _{\ell =1}^m{\langle \nu ,{\Xi }_{\ell }(t)\rangle }_{F(x)}}{\alpha }_{\ell }{\xi }_{\ell },\nu \in T_{F(x)}{M}.\end{array}$

We introduce the adjoint Jacobi field $J_{F,\nu }^{*}:ℝ\to T_x{M}$, $\nu \in T_{F(x)}{M}$ as

$\begin{array}{c}{J}_{F,\nu }^{*}(t)={\displaystyle \sum _{\ell =1}^m{\langle \nu ,{\Xi }_{\ell }(t)\rangle }_{F(x)}}{J}_{F,{\Xi }_{\ell }(t)}^{*}(t)={\displaystyle \sum _{\ell =1}^m{\langle \nu ,{\Xi }_{\ell }(t)\rangle }_{F(x)}}{\alpha }_{\ell }{\xi }_{\ell }.\end{array}$

Note that evaluating the adjoint Jacobi field J* involves the same transported frame {Ξ₁(t), …Ξ_m(t)} and the same coefficients α_ℓ as the Jacobi field J, which means that the evaluation of the adjoint is in no way inferior to the Jacobi field itself.

The adjoint D* of the differential is useful in particular, when computing the gradient ${\nabla }_{{M}}(h°F)$ of the composition of $F:{M}\to {M}$ with $h:{M}\to ℝ$. Setting $y:=F(x)\in {M}$, we obtain for any $\eta \in T_x{M}$ that

$\begin{array}{l}{\langle {\nabla }_{{M},x}\left(h°F\right)\left(x\right),\eta \rangle }_x=D_x(h°F)[\eta ]\\ =D_{F(x)}h[D_{x}F[\eta ]]\\ ={\langle {\nabla }_{{M},y}h(y),D_{x}F[\eta ]\rangle }_y\\ ={\langle {\left(D_{x}F\right)}^{*}[{\nabla }_{{M},y}h(y)],\eta \rangle }_x.\end{array}$

Especially for the evaluation of the gradient of the composite function h°F we obtain

$\begin{array}{c}{\nabla }_{{M},x}(h\circ F)(x)={(D_{x}F)}^{*}[{\nabla }_{{M},y}h(y)]=J_{F,{\nabla }_{{M},y}h(y)}^{*}(t).\end{array}$

The main advantage of this technique appears in the case of composite functions, i.e., of the form h°F₁°F₂ (the generalization to composition with K functions is straightforward). The gradient ${\nabla }_{{M},x}(h°F_1°F_2)(x)$ now reads,

$\begin{array}{c}\begin{array}{l}{\nabla }_{{M},x}(h\circ F_1\circ F_2)(x)={\left(D_x{F}_2\right)}^{*}[{\nabla }_{{M},y_2}h\circ F_1(y_2)]\hfill \\ =J_{F_2,{\nabla }_{{M},y_2}h\circ F_1(y_2))}^{*}(t).\hfill \end{array}\end{array}$

The recursive computation of ${\eta }^{\left[3\right]}={\nabla }_{{M},x}h(x)$ is then given by the following algorithm

$\begin{array}{l}{\eta }^{\left[1\right]}={\nabla }_{{M},y_1}h(y_1),\\ {\eta }^{\left[2\right]}=J_{F_1,{\eta }^{\left[1\right]}}^{*}(t),\\ {\eta }^{\left[3\right]}=J_{F_2,{\eta }^{\left[2\right]}}^{*}(t).\end{array}$

Example 12. For $h=d_2^2:{{M}}^3\to ℝ$ we know ${\nabla }_{{{M}}^3}h$ by Lemma 3.1 and Lemma 3.2 from Bačák et al. [22]. Let t₁, t₂, t₃∈[0, 1] be time points, and $\text{b}\in {{M}}^M$ be a given (sub)set of the control points of a (composite) Bézier curve B. We define $F:{{M}}^M\to {{M}}^3,\text{b}\mapsto F(\text{b})=(\text{B}(t_1),\text{B}(t_2),\text{B}(t_3))$ as the evaluations of B at the three given time points. The composition h°F hence consists of (in order of evaluation) the geodesic evaluations of the De Casteljau algorithm, the mid point function for the first and third time point and a distance function.

The recursive evaluation of the gradient starts with the gradient of the distance function. Then, for the first and third arguments, a mid point Jacobi field is applied. The result is plugged into the last geodesic evaluated within the De Casteljau “tree” of geodesics. At each geodesic, a tangent vector at a point g(t_j; a, b) is the input for two adjoint Jacobi fields, one mapping to $T_a{M}$, the other to $T_b{M}$. This information is available throughout the recursion steps anyways. After traversing this tree backwards, one obtains the required gradient of h°F.

Note also that even the differentiability constraint (4) yields only two further (most outer) adjoint Jacobi fields, namely $J_{g(2,b_i^{-},p_i),{\nabla }_{{M},b_i^{+}}\text{B}(t_j)}^{*}(2)$ and $J_{\tilde{g}(2,b_i^{-},p_i),{\nabla }_{{M},b_i^{+}}\text{B}(t_j)}^{*}(2)$. They correspond to variation of the start point $b_i^{-}$ and the end point p_i, respectively as stated in (10).

4.3. A Gradient Descent Algorithm

To address (22) or (23), we use a gradient descent algorithm, as described in Absil et al. [10, Ch. 4]. For completeness the algorithm is given in Algorithm 1.

ALGORITHM 1

Algorithm 1. Gradient descent algorithm on a manifold ${}N={{M}}^M$

The step sizes are given by the Armijo line search condition presented in Absil et al. [10, Def. 4.2.2]. Let ${N}$ be a Riemannian manifold, $x=x^{(k)}\in {N}$ be an iterate of the gradient descent, and β, σ∈(0, 1), α>0. Let m be the smallest positive integer such that

$\begin{array}{cc}F(x)-F({\exp }_x(-{\beta }^m\alpha {\nabla }_{{N}}F(x)))\ge \sigma {\beta }^m\alpha \Vert {\nabla }_{{N}}F(x){\Vert }_x.& (24)\end{array}$

We set the step size to $s_k:={\beta }^m\alpha$ in Algorithm 1.

As a stopping criterion we use a maximal number k_max of iterations or a minimal change per iteration $d_{{N}}(x^k,x^{k+1})<\epsilon$. In practice, this last criterion is matched first.

The gradient descent algorithm converges to a critical point if the function F is convex [10, sections 4.3 and 4.4]. The mid-points model (6) posesses two advantages: (i) the complete discretized MSA (7) consists of (chained) evaluations of geodesics and a distance function, and (ii) it reduces to the classical second order differences on the Euclidean space. However, this model is not convex on general manifolds. An example is given in the arXiv preprint (version 3) of Bačák et al. [22]¹, Remark 4.6. Another possibility (also reducing to classical second order differences in Euclidean space) is the so-called Log model (see e.g., [42])

$\begin{array}{c}{d}_{2,\text{Log}}[x,y,z]={\Vert {\log }_{y}x+{\log }_{y}z\Vert }_y.\end{array}$

The (merely technical) disadvantage of the Log model is that the computation of the gradient involves further Jacobi fields than the one presented above, namely to compute the differentials of the logarithmic map both with respect to its argument D_xlog_yx as well as its base point D_ylog_yx. Still, these can be given in closed form for symmetric Riemannian manifolds [23, Th. 7.2][43, Lem. 2.3]. To the best of our knowledge, the joint convexity of the Log model in x, y and z is still an open question.

5. Examples

In this section, we provide several examples of our algorithm applied to the fitting problem (20).

We validate it first on the Euclidean space and verify that it retrieves the natural cubic smoothing spline. We then present examples on the sphere S² and the special orthogonal group SO(3). We compare our results with the fast algorithm of Arnould et al. [37], generalized to fitting, and the so-called blended cubic splines from Gousenbourger et al. [38]. The control points of the former are obtained by generalizing the optimal Euclidean conditions of (20) (in ℝ^m, this is a linear system of equations) to the manifold setting; the curve is afterwards reconstructed by a classical De Casteljau algorithm. In the latter, the curve is obtained as a blending of solutions computed on carefully chosen tangent spaces, i.e., Euclidean spaces.

We will show in this section that the proposed method performs as good as the existing methods when the data is from the Eulidean space (section 5.1). This also means that all methods work equally well whenever the data points on the manifold are local enough. However, we will show by the other examples (sections 5.2 and 5.3) that our proposed method outperforms the others whenever the data points are spread out on the manifold.

The following examples were implemented in MVIRT [12]², and the comparison implementations from Arnould et al. [37] and Gousenbourger et al. [38] use Manopt [11]³. Note that both toolboxes use a very similar matrix structure and are implemented in Matlab, such that the results can directly be compared.

5.1. Validation on the Euclidean Space

As a first example, we perform a minimization on the Euclidean space ${M}={ℝ}^3$. A classical result on ℝ^m is that the curve γ minimizing (1) is the natural (${{C}}^2$) cubic spline when Γ is a Sobolev space $H^2(t_0,t_n)$. We compare our approach to the tangential linear system approach derived in Arnould et al. [37] in order to validate our model. We use the following data points

$\begin{array}{cc}\begin{array}{l}{d}_0=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right],d_1=\left[\begin{array}{c}0\\ -1\\ 0\end{array}\right],d_2=\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right],d_3=\frac{1}{\sqrt{82}}\left[\begin{array}{c}0\\ -1\\ -9\end{array}\right],\hfill \end{array}& (25)\end{array}$

as well as the control points p_i = d_i, and

$\begin{array}{l}{b}_0^{+}={\exp }_{p_0}\frac{\pi }{8\sqrt{2}}\left[\begin{array}{c}1\\ -1\\ 0\end{array}\right],b_1^{+}={\exp }_{p_1}-\frac{\pi }{2\sqrt{2}}\left[\begin{array}{c}1\\ 0\\ 1\end{array}\right],\\ b_1^{-}=g(2;b_1^{+},p_1),\\ b_2^{+}={\exp }_{p_2}\frac{\pi }{2\sqrt{2}}\left[\begin{array}{c}0\\ 1\\ -1\end{array}\right],b_3^{-}={\exp }_{p_3}\frac{\pi }{8}\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right],\\ b_2^{-}=g(2;b_2^{+},p_2),& (26)\end{array}$

where the exponential map and geodesic on ℝ³ are actually the addition and line segments, respectively. Note that, by construction, the initial curve is continuously differentiable but (obviously) does not minimize (1). The parameter λ is set to 50. The MSA of this initial curve Ã(b) is approximately 18.8828.

The data points are given to the algorithm of Arnould et al. [37] to reconstruct the optimal Bézier curve B(t), which is the natural ${{C}}^2$ cubic spline. The result is shown in Figure 7A together with the first order differences along the curve in Figure 7B as a dotted curve.

FIGURE 7

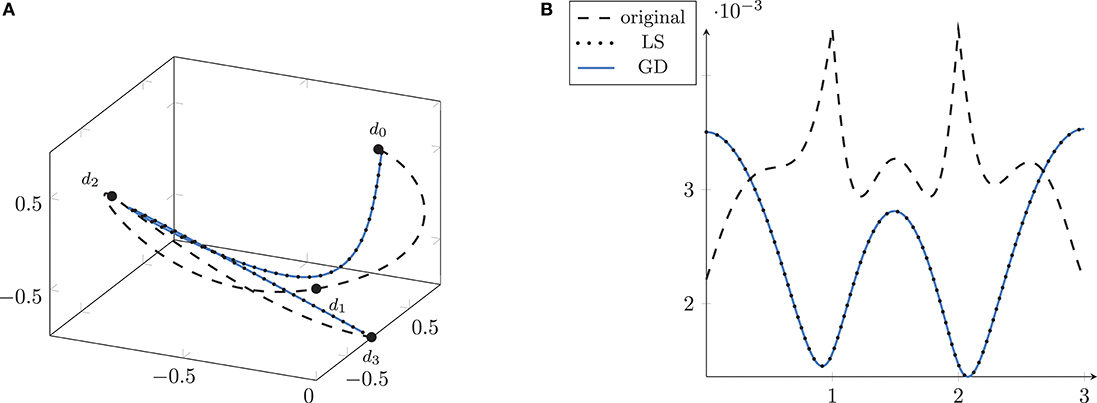
Figure 7. The initial interpolating Bézier curve in ℝ³ (dashed, A) with an MSA of 18.8828 is optimized by the linear system method (LS) from [37] (dotted) and by the proposed gradient descent (GD, solid blue). As expected, both curve coincide, with an MSA of 4.981218. The correspondance is further illustrated with their first order differences in (B).

The set of control points $(p_0,b_0^{+},\dots ,b_3^{-},p_3)$ is optimized with our proposed method. We discretize the second order difference using N = 1600 points. The resulting curve and the first order difference plots are also obtained using these sampling values and a first order forward difference. The gradient descent algorithm from Algorithm 1 employs the Armijo rule (24) setting $\beta =\frac{1}{2}$, σ = 10⁻⁴, and α = 1. The stopping criteria are $\sum _{i=1}^{1600}{d}_{{M}}(x_i^{(k)},x_i^{(k+1)})<ϵ=10^{-15}$ or $\parallel {\nabla }_{{{M}}^n}Ã{\parallel }_2<10^{-9}$, and the algorithm stops when one of the two is met. For this example, the first criterion stopped the algorithm, while the norm of the gradient was of magnitude 10⁻⁶.

Both methods improve the initial functional value of Ã(b)≈18.8828 to a value of Ã(b_min)≈4.981218. Both the linear system approach and the gradient descent perform equally. The difference of objective value is 2.4524 × 10⁻¹¹ smaller for the gradient descent, and the maximal distance of any sampling point of the resulting curves is of size 4.3 × 10⁻⁷. Hence, in the Euclidean space, the proposed gradient descent yields the natural cubic spline, as one would expect.

5.2. Examples on the Sphere S²

Validation on a geodesic. As a second example with a known minimizer, we consider the manifold ${M}=S^2$, i.e., the two-dimensional unit sphere embedded in ℝ³, where geodesics are great arcs. We use the data points

$\begin{array}{c}{d}_0=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right],d_1=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right],d_2=\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]\end{array}$

aligned on the geodesic connecting the north pole p₀ and the south pole p₂, and running through a point p₁ on the equator. We define the control points of the cubic Bézier curve as follows:

$\begin{array}{l}{x}_0=\frac{1}{\sqrt{6}}\left[\begin{array}{c}1\\ 1\\ 2\end{array}\right],b_0^{+}={\exp }_{p_0}(3{\text{log}}_{p_0}(x_0)),\\ b_1^{-}=\frac{1}{\sqrt{6}}\left[\begin{array}{c}1\\ 2\\ 1\end{array}\right],\\ x_2=\frac{1}{\sqrt{6}}\left[\begin{array}{c}-1\\ 1\\ -2\end{array}\right],b_1^{+}=\frac{1}{\sqrt{6}}\left[\begin{array}{c}-1\\ 2\\ -1\end{array}\right],\\ b_2^{-}={\exp }_{p_2}(\frac{1}{3}{\text{log}}_{p_0}(x_2)),\end{array}$

where x₀ and x₂ are temporary points and p_i = d_i. We obtain two segments smoothly connected since ${log}_{p_1}{b}_1^{-}=-{log}_{p_1}{b}_1^{+}$. The original curve is shown in Figure 8A, where especially the tangent vectors illustrate the different speed at p_i.

FIGURE 8

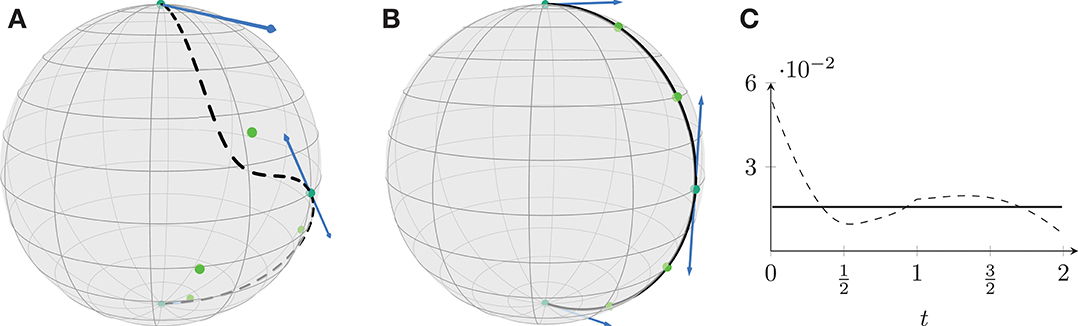
Figure 8. The initial curve (dashed, A) results in a geodesic (solid, B) when minimizing the discrete acceleration. This can also be seen on the first order differences (C).

The control points are optimized with our interpolating model, i.e., we fix the start and end points p₀, p₁, p₂ and minimize A(b).

The curve, as well as the second and first order differences, is sampled with N = 201 equispaced points. The parameters of the Armijo rule are again set to $\beta =\frac{1}{2}$, σ = 10⁻⁴, and α = 1. The stopping criteria are slightly relaxed to 10⁻⁷ for the distance and 10⁻⁵ for the gradient, because of the sines and cosines involved in the exponential map.

The result is shown in Figure 8B. Since the minimizer is the geodesic running from p₀ to p₂ through p₁, we measure the perfomance first by looking at the resulting first order difference, which is constant, as can be seen in Figure 8C. As a second validation, we observe that the maximal distance of the resulting curve to the geodesic is of 2.2357 × 10⁻⁶. These evaluations again validate the quality of the gradient descent.

Effect of the data term. As a third example we investigate the effect of λ in the fitting model. We consider the data points

$\begin{array}{l}{d}_0={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^{\text{T}},d_1={\left[\begin{array}{ccc}0& -1& 0\end{array}\right]}^{\text{T}},d_2={\left[\begin{array}{ccc}-1& 0& 0\end{array}\right]}^{\text{T}},\\ d_3={\left[\begin{array}{ccc}0& 0& -1\end{array}\right]}^T,\end{array}$

as well as the control points p_i = d_i, and

$\begin{array}{l}{b}_0^{+}={\exp }_{p_0}(\frac{\pi }{8\sqrt{2}}{\left[\begin{array}{ccc}1& -1& 0\end{array}\right]}^{\text{T}}),\text{ }{b}_1^{+}={\exp }_{p_1}(-\frac{\pi }{4\sqrt{2}}{\left[\begin{array}{ccc}-1& 0& 1\end{array}\right]}^{\text{T}}),\\ b_2^{+}={\exp }_{p_2}(\frac{\pi }{4\sqrt{2}}{\left[\begin{array}{ccc}0& 1& -1\end{array}\right]}^{\text{T}}),\text{ }{b}_3^{-}={\exp }_{p_3}(-\frac{\pi }{8\sqrt{2}}{\left[\begin{array}{ccc}-1& 1& 0\end{array}\right]}^{\text{T}}).\end{array}$

The remaining control points $b_1^{-}$ and $b_2^{-}$ are given by the ${{C}}^1$ conditions (4). The corresponding curve B(t), t∈[0, 3], is shown in Figure 9 in dashed black. When computing a minimal MSA curve that interpolates B(t) at the points p_i, i = 0, …, 3, the acceleration is not that much reduced, see the blue curve in Figure 9A.

FIGURE 9

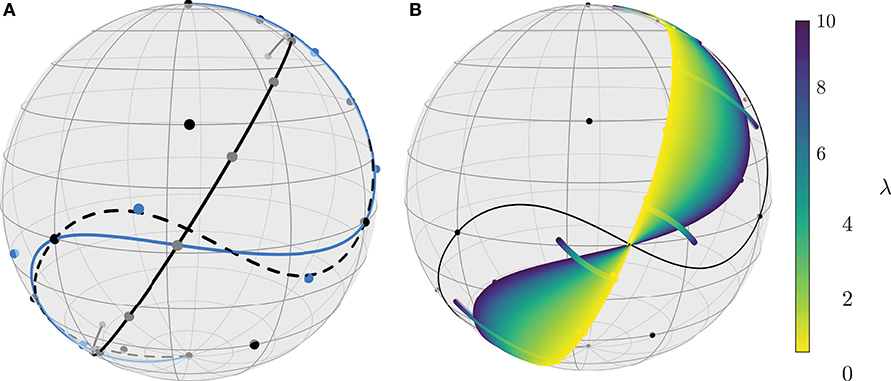
Figure 9. The composite Bézier curves are composed of three segments. The initial curve (dashed, A) is optimized with the interpolating model (solid blue, A) as well as with the fitting model for a continuum of values of λ, from λ = 10 (violet, B) to λ = 0.01 (yellow, B). The limit case where λ = 0 yields an unconstrained geodesic (solid black, A).

For fitting, we consider different values of λ and the same parameters as for the last example. The optimized curve fits the data points closer and closer as λ grows, and the limit λ → ∞ yields the interpolation case. On the other hand smaller values of λ yield less fitting, but also a smaller value of the mean squared acceleration. In the limit case, i.e., λ = 0, the curve (more precisely the control points of the Bézier curve) just follows the gradient flow to a geodesic.

The results are collected in Figure 9. In Figure 9A, the original curve (dashed) is shown together with the solution of the interpolating model (solid blue) and the gradient flow result, i.e., the solution of the fitting model (solid black) with λ = 0. Figure 9B illustrates the effect of λ even further with a continuous variation of λ from a large value of λ = 10 to a small value of λ = 0.01. The image is generated by sampling this range with 1000 equidistant values colored in the colormap viridis. Furthermore, the control points are also shown in the same color.

Several corresponding functional values, see Table 1, further illustrate that with smaller values of λ the discretized MSA also reduces more and more to a geodesic. For λ = 0 there is no coupling to the data points and hence the algorithm does not restrict the position of the geodesic. In other words, any choice for the control points that yields a geodesic, is a solution. Note that the gradient flow still chooses a reasonably near geodesic to the initial data (Figure 9A, solid black).

TABLE 1

Table 1. Functional values for the three-segment composite Bézier curve on the sphere and different values of λ.

Comparison with the tangential solution. In the Euclidean space, the method introduced in Arnould et al. [37] and Gousenbourger et al. [38] and the gradient descent proposed here yield the same curve, i.e., the natural cubic spline. On Riemannian manifolds, however, all approaches approximate the optimal solution. Indeed, their method provides a solution by working in different tangent spaces, and ours minimizes a discretization of the objective functional.

In this example we take the same data points d_i as in (25) now interpreted as points on ${M}=S^2$. Note that the control points constructed in (26) still fit to the sphere since each $b_i^{\pm }$ is built with a vector in $T_{p_i}{M}$ and using the corresponding exponential map. The result is shown in Figure 10A. The norm of the first order differences is given in Figure 10B. The initial curve (dashed black) has an objective value of 10.9103. The tangent version (dotted) reduces this value to 7.3293. The proposed method (solid blue) yields a value of 2.7908, regardless of whether the starting curve is the initial one, or the one already computed by Arnould et al. [37]. Note that, when $p_3={\left[0,0,-1\right]}^{\text{T}}$, the tangent version is even not able to compute any result, since the construction is performed in the tangent space of p₀ and since log_p0p₃ is not defined.

FIGURE 10

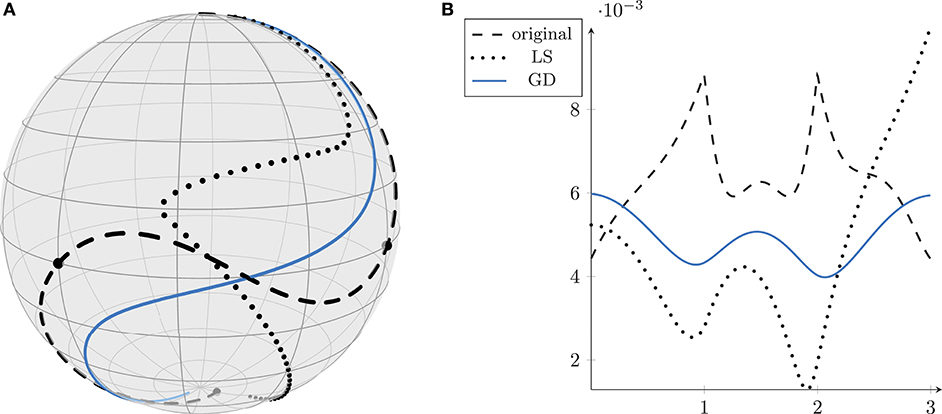
Figure 10. The initial composite Bézier curve on S² (dashed, A) has an MSA of 10.9103. The curve obtained with the linear system (LS, dotted) of [37] has an MSA of 7.3293. The solution returned by our proposed method (GD, solid blue) outperforms them all with an MSA of 2.7908. This is further illustrated by the first order derivative approximated by first order differences in (B).

5.3. An Example of Orientations

Finally we compare our method with the blended splines introduced in Gousenbourger et al. [38] for orientations, i.e., data given on SO(3). Let

$\begin{array}{l}{R}_{\text{xy}}(\alpha )=\left[\begin{array}{ccc}\cos \alpha & \sin \alpha & 0\\ -\sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right],R_{\text{xz}}(\alpha )=\left[\begin{array}{ccc}\cos \alpha & 0& \sin \alpha \\ 0& 1& 0\\ -\sin \alpha & 0& \cos \alpha \end{array}\right],\\ R_{\text{yz}}(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & \sin \alpha \\ 0& -\sin \alpha & \cos \alpha \end{array}\right]\end{array}$

denote the rotation matrices in the x−y, x−z, and y−z planes, respectively. We introduce the three data points

$\begin{array}{l}{d}_0=R_{\text{xy}}\left(\frac{4\pi }{9}\right)R_{yz}\left(-\frac{\pi }{2}\right),\\ d_1=R_{\text{xz}}\left(-\frac{\pi }{8}\right)R_{\text{xy}}\left(\frac{\pi }{18}\right)R_{yz}\left(-\frac{\pi }{2}\right),\\ d_2=R_{\text{xy}}\left(\frac{5\pi }{9}\right)R_{yz}\left(-\frac{\pi }{2}\right).\end{array}$

These data points are shown in the first line of Figure 11 in cyan.

FIGURE 11

Figure 11. From top row to bottom row: (1) the initial data points (cyan), (2) the control points computed by the blended Bézier approach from Gousenbourger et al. [38], (3) 17 points on the corresponding curve, where the height represents the absolute first order difference, and the comparing curve is the first order differences from our model, (4) 17 points along the resulting curve from gradient descent, and (5) the resulting control points of the curve in (4).

We set λ = 10 and discretize (20) with N = 401 equispaced points. This sampling is also used to generate the first order finite differences. The parameters of the gradient descent algorithm are set to the same values as for the examples on the sphere.

We perform the blended spline fitting with two segments and cubic splines. The resulting control points are shown in the second row of Figure 11, in green. The objective value is Ã(b) = 0.6464. We improve this solution with the minimization problem (22) on the product manifold SO(3)⁶. We obtain the control points shown in the last line of Figure 11 and an objective value of $Ã(\widehat{\text{b}})=0.2909$ for the resulting minimizer $\widehat{\text{b}}$.

We further compare both curves by looking at their absolute first order differences. In the third line of Figure 11, we display 17 orientations along the initial curve with its first order difference as height. The line without samples is the absolute first order differences of the minimizer $\widehat{\text{b}}$, scaled to the same magnitude. The line is straightened especially for the first Bézier segment. Nevertheless, the line is still bent a little bit and hence not a geodesic. This can be seen in the fourth line which represents 17 samples of the minimizing curve compared to its control points in the last line, which are drawn on a straight line.

6. Conclusion and Future Work

In this paper, we introduced a method to solve the curve fitting problem to data points on a manifold, using composite Bézier curves. We approximate the mean squared acceleration of the curve by a suitable second order difference and a trapezoidal rule, and derive the corresponding gradient with respect to its control points. The gradient is computed in closed form by exploiting the recursive structure of the De Casteljau algorithm. Therefore, we obtain a formula that reduces to a concatenation of adjoint Jacobi fields.

The evaluation of Jacobi fields is the only additional requirement compared to previous methods, which are solely evaluating exponential and logarithmic maps. For these, closed forms are available on symmetric manifolds.

On the Euclidean space our solution reduces to the natural smoothing spline, the unique acceleration minimizing polynomial curve. The numerical experiments further confirm that the method presented in this paper outperforms the tangent space(s)-based approaches with respect to the functional value.

It is still an open question whether there exists a second order absolute finite difference on a manifold, that is jointly convex. Then convergence would follow by standard arguments of the gradient descent. For such a model, another interesting point for future work is to find out whether only an approximate evaluation of the Jacobi fields suffices for convergence. This would mean that, on manifolds where the Jacobi field can only be evaluated approximately by solving an ODE, the presented approach would still converge.

Author Contributions

Both authors listed have contributed equally to the content of this work and approved the paper for publication.

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by the following fundings: RB gratefully acknowledges support by DFG grant BE 5888/2–1; P-YG gratefully acknowledges support by the Fonds de la Recherche Scientifique – FNRS and the Fonds Wetenschappelijk Onderzoek – Vlaanderen under EOS Project no 30468160, and Communauté française de Belgique - Actions de Recherche Concertées (contract ARC 14/19-060). Figure 9A is based on an idea of Rozan I. Rosandi.

Footnotes

1. ^See arxiv.org/abs/1506.02409v3

2. ^Open source, available at http://ronnybergmann.net/mvirt/

3. ^Open source, available at http://www.manopt.org

References

1. Pyta L, Abel D. Interpolatory Galerkin models for Navier-Stokes-equations. IFAC-PapersOnLine (2016) 49:204–9. doi: 10.1016/j.ifacol.2016.07.442

CrossRef Full Text | Google Scholar

2. Gousenbourger PY, Massart E, Musolas A, Absil PA, Jacques L, Hendrickx JM, et al. Piecewise-Bézier C1 smoothing on manifolds with application to wind field estimation. In: ESANN2017. Bruges: Springer (2017). Available online at: https://www.elen.ucl.ac.be/Proceedings/esann/esannpdf/es2017-77.pdf

Google Scholar

3. Sander O. Geodesic finite elements for cosserat rods. Int J Numer Methods Eng. (2010) 82:1645–70. doi: 10.1002/nme.2814

CrossRef Full Text | Google Scholar

4. Park J. Interpolation and tracking of rigid body orientations. In: ICCAS, Gyeonggi-do (2010). p. 668–73. doi: 10.1109/ICCAS.2010.5670237

CrossRef Full Text | Google Scholar

5. Su J, Kurtek S, Klassen E, Srivastava A. Statistical analysis of trajectories on Riemannian manifolds: bird migration, Hurricane tracking and video surveillance. Ann Appl Stat. (2014) 8:530–52. doi: 10.1214/13-AOAS701

CrossRef Full Text | Google Scholar

6. Dyn N. Linear and nonlinear subdivision schemes in geometric modeling. In: Cucker F, Pinkus A, Todd MJ, editors. FoCum. Vol. 363 of London Math. Soc. Lecture Note Ser. Hong Kong: Cambridge University Press (2009). p. 68–92. doi: 10.1017/CBO9781139107068.004

CrossRef Full Text | Google Scholar

7. Wallner J, Nava Yazdani E, Grohs P. Smoothness properties of Lie group subdivision schemes. Multiscale Model Simulat. (2007) 6:493–505. doi: 10.1137/060668353

CrossRef Full Text | Google Scholar

8. Shingel T. Interpolation in special orthogonal groups. IMA J Numer Anal. (2008) 29:731–45. doi: 10.1093/imanum/drn033

CrossRef Full Text | Google Scholar

9. Green PJ, Silverman BW. Nonparametric Regression and Generalized Linear Models: A Roughness Penalty Approach. CRC Press (1993). Available online at: https://www.crcpress.com/Nonparametric-Regression-and-Generalized-Linear-Models-A-roughness-penalty/Green-Silverman/p/book/9780412300400

Google Scholar

10. Absil PA, Mahony R, Sepulchre R. Optimization Algorithms on Matrix Manifolds. Princeton, NJ: Princeton University Press (2008). Available online at: https://press.princeton.edu/absil

Google Scholar

11. Boumal N, Mishra B, Absil PA, Sepulchre R. Manopt, a matlab toolbox for optimization on manifolds. J Mach Learn Res. (2014) 15:1455–9. Available online at: http://jmlr.org/papers/v15/boumal14a.html

Google Scholar

12. Bergmann R. MVIRT a toolbox for manifold-valued image registration. In: IEEE International Conference on Image Processing, IEEE ICIP 2017, Beijing. (2017). Available online at: https://ronnybergmann.net/mvirt/

Google Scholar

13. Zhou X, Yang C, Zhao H, Yu W. Low-rank modeling and its applications in image analysis. ACM Comput Surveys (2015) 47:36. doi: 10.1145/2674559

CrossRef Full Text | Google Scholar

14. Cunningham JP, Ghahramani Z. Linear dimensionality reduction: survey, insights, and generalizations. J Mach Learn Res. (2015) 16:2859–900. Available online at: http://jmlr.org/papers/v16/cunningham15a.html

Google Scholar

15. Sun J, Qu Q, Wright J. A geometric analysis of phase retrieval. Found Comput Math. (2017) 8:1131–98. doi: 10.1007/s10208-017-9365-9

CrossRef Full Text | Google Scholar

16. Yu X, Shen JC, Zhang J, Letaief KB. Alternating minimization algorithms for hybrid precoding in millimeter wave MIMO systems. IEEE J Selected Top Signal Process. (2016) 10:485–500. doi: 10.1109/JSTSP.2016.2523903

CrossRef Full Text | Google Scholar

17. Strekalovskiy E, Cremers D. Total variation for cyclic structures: convex relaxation and efficient minimization. In: IEEE Conference on Computer Vision and Pattern Recognition (2011). p. 1905–11.

Google Scholar

18. Strekalovskiy E, Cremers D. Total cyclic variation and generalizations. J Mat Imaging Vis. (2013) 47:258–77. doi: 10.1007/s10851-012-0396-1

CrossRef Full Text | Google Scholar

19. Lellmann J, Strekalovskiy E, Koetter S, Cremers D. Total variation regularization for functions with values in a manifold. In: IEEE International Conference on Computer Vision. Sydney, NSW (2013). p. 2944–51. doi: 10.1109/ICCV.2013.366

CrossRef Full Text | Google Scholar

20. Weinmann A, Demaret L, Storath M. Total variation regularization for manifold-valued data. SIAM J Imaging Sci. (2014) 7:2226–57. doi: 10.1137/130951075

CrossRef Full Text | Google Scholar

21. Bergmann R, Laus F, Steidl G, Weinmann A. Second order differences of cyclic data and applications in variational denoising. SIAM J Imaging Sci. (2014) 7:2916–53. doi: 10.1137/140969993

CrossRef Full Text | Google Scholar

22. Bačák M, Bergmann R, Steidl G, Weinmann A. A second order nonsmooth variational model for restoring manifold-valued images. SIAM J Comput. (2016) 38:567–97. doi: 10.1137/15M101988X

CrossRef Full Text | Google Scholar

23. Bergmann R, Fitschen JH, Persch J, Steidl G. Priors with coupled first and second order differences for manifold-valued image processing. J Math Imaging Vis. (2017) 60:1459–81. doi: 10.1007/s10851-018-0840-y

CrossRef Full Text | Google Scholar

24. Bredies K, Holler M, Storath M, Weinmann A. Total generalized variation for manifold-valued data. SIAM J Imaging Sci. (2018) 11:1785–48. doi: 10.1137/17M1147597

CrossRef Full Text | Google Scholar

25. Bergmann R, Persch J, Steidl G. A parallel Douglas–Rachford algorithm for restoring images with values in symmetric Hadamard manifolds. SIAM J Imaging Sci. (2016) 9:901–37. doi: 10.1137/15M1052858

CrossRef Full Text | Google Scholar

26. Grohs P, Sprecher M. Total variation regularization on Riemannian manifolds by iteratively reweighted minimization. Inform Inference (2016) 5:353–78. doi: 10.1093/imaiai/iaw011

CrossRef Full Text | Google Scholar

27. Bergmann R, Chan RH, Hielscher R, Persch J, Steidl G. Restoration of manifold-valued images by half-quadratic minimization. Inverse Prob Imaging (2016) 10:281–304. doi: 10.3934/ipi.2016001

CrossRef Full Text | Google Scholar

28. Samir C, Absil PA, Srivastava A, Klassen E. A gradient-descent method for curve fitting on Riemannian manifolds. Found Comput Math. (2012) 12:49–73. doi: 10.1007/s10208-011-9091-7

CrossRef Full Text | Google Scholar

29. Su J, Dryden IL, Klassen E, Le H, Srivastava A. Fitting smoothing splines to time-indexed, noisy points on nonlinear manifolds. Image Vis Comput. (2012) 30:428–42. doi: 10.1016/j.imavis.2011.09.006

CrossRef Full Text | Google Scholar

30. Boumal N, Absil PA. A discrete regression method on manifolds and its application to data on SO(n). In: IFAC Proceedings Volumes (IFAC-PapersOnline). Vol. 18. Milano (2011). p. 2284–89. doi: 10.3182/20110828-6-IT-1002.00542

CrossRef Full Text | Google Scholar

31. Kim KR, Dryden IL, Le H. Smoothing splines on Riemannian manifolds, with applications to 3D shape space. (2018). arXiv[Preprint]:1801.04978.

Google Scholar

32. Fletcher PT. Geodesic regression and the theory of least squares on Riemannian manifolds. Int J Comput Vis. (2013) 105:171–85. doi: 10.1007/s11263-012-0591-y

CrossRef Full Text | Google Scholar

33. Rentmeesters Q. A gradient method for geodesic data fitting on some symmetric Riemannian manifolds. In: Decision and Control and European Control Conference (CDC-ECC), 2011 50th IEEE Conference on. Orlando, FL (2011). p. 7141–6. doi: 10.1109/CDC.2011.6161280

CrossRef Full Text | Google Scholar

34. Farin G. Curves Surfaces for CAGD. Morgan Kaufmann (2002). Available online at: https://www.elsevier.com/books/curves-and-surfaces-for-cagd/farin/978-1-55860-737-8

35. Absil PA, Gousenbourger PY, Striewski P, Wirth B. Differentiable Piecewise-Bézier Surfaces on Riemannian Manifolds. SIAM J Imaging Sci. (2016) 9:1788–828. doi: 10.1137/16M1057978

CrossRef Full Text | Google Scholar

36. Popiel T, Noakes L. Bézier curves and ${{C}}^2$ interpolation in Riemannian manifolds. J Approx Theory (2007) 148:111–27. doi: 10.1016/j.jat.2007.03.002

CrossRef Full Text | Google Scholar

37. Arnould A, Gousenbourger PY, Samir C, Absil PA, Canis M. Fitting smooth paths on Riemannian manifolds: endometrial surface reconstruction and preoperative MRI-based navigation. In: Nielsen F, Barbaresco F, editors. GSI2015. Springer International Publishing (2015). p. 491–8.

Google Scholar

38. Gousenbourger PY, Massart E, Absil PA. Data fitting on manifolds with composite Bézier-like curves and blended cubic splines. J Math Imaging Vis. (2018). doi: 10.1007/s10851-018-0865-2

CrossRef Full Text | Google Scholar

39. O'Neill B. Elementary Differential Geometry. London: Academic Press Inc. (1966).

Google Scholar

40. do Carmo MP. Riemannian Geometry. Vol. 115. Basel: Birkhäuser; 1992. Tranl. by F. Flatherty.

Google Scholar

41. Karcher H. Riemannian center of mass and mollifier smoothing. Commun Pure Appl Math. (1977) 30:509–41. doi: 10.1002/cpa.3160300502

CrossRef Full Text | Google Scholar

42. Boumal N. Interpolation and regression of rotation matrices. In: Nielsen F, Barbaresco F, editors. Geometric Science of Information. Berlin; Heidelberg: Springer. (2013). p. 345–52.

Google Scholar

43. Persch J. Optimization Methods in Manifold-Valued Image Processing [Dissertation]. Technische Universität Kaiserslautern (2018).

Google Scholar