Performance of Some Estimators of Relative Variability

The classic coefficient of variation (CV) is the ratio of the standard deviation to the mean and can be used to compare normally distributed data with respect to their variability, this measure has been widely used in many fields. In the Social Sciences, the CV is used to evaluate demographic heterogeneity and social aggregates such as race, sex, education and others. Data of this nature are usually not normally distributed, and the distributional characteristics can vary widely. In this sense, more accurate and robust estimator variations of the classic CV are needed to give a more realistic picture of the behavior of collected data. In this work, we empirically evaluate five measures of relative variability, including the classic CV, of finite sample sizes via Monte Carlo simulations. Our purpose is to give an insight into the behavior of these estimators, as their performance has not previously been systematically investigated. To represent different behaviors of the data, we considered some statistical distributions—which are frequently used to model data across various research fields. To enable comparisons, we consider parameters of these distributions that lead to a similar range of values for the CV. Our results indicate that CV estimators based on robust statistics of scale and location are more accurate and give the highest measure of efficiency. Finally, we study the stability of a robust CV estimator in psychological and genetic data and compare the results with the traditional CV.

1. Introduction

The coefficient of variation (CV) is a standardized, dimensionless measure of dispersion relative to a data set's average [1]. It enables the comparison of several datasets [2] with different units of measurement [3, p. 84]. Karl Pearson was likely one of the first researchers to propose this measure of relative statistical dispersion [4, pp. 276–277]:

“In dealing with the comparative variation of men and women (or, indeed, very often of the two sexes of any animal), we have constantly to bear in mind that relative size influences not only the means but the deviations from the means. When dealing with absolute measurements, it is, of course, idle to compare the variation of the larger male organ directly with the variation of the smaller female organ. […] we may take as a measure of variation the ratio of standard deviation to mean, or what is more convenient, this quantity multiplied by 100. We shall, accordingly, define V, the coefficient of variation, as the percentage variation in the mean, the standard deviation being treated as the total variation in the mean. […] Of course, it does not follow because we have defined in this manner our “coefficient of variation,” that is coefficient is really a significant quantity in the comparison […]; it may be only a convenient mathematical expression, but I believe there is evidence to show that it is a more reliable test of “efficiency” […] than absolute variation.”

Based on Pearson's idea, the classic version of the CV is often expressed as a percentage. It is defined as the ratio of the standard deviation σ to the mean μ (or its absolute value, |μ|)¹. In this way, the coefficient of variation should be computed only for data measured on a ratio scale [5], as these are the measurements that can only take non-negative values. The coefficient of variation may not have any meaning for data on an interval scale [6] or in data sets with discrete scales involving a true zero point and equal intervals (count data) such as Likert data. In such situations, data do not have the property that originally motivated the use of the coefficient of variation [7, pp. 44]: “big things tend to vary much and small things little” (see also [8]). On the other hand, bounded data, such as rates and proportions often exhibit heterogeneity in variance (i.e., the variety tends to be higher for data values in the middle range than for those toward the boundaries, given the dependency between location and scale [9]), and the CV cannot be interpreted directly. The usual practice is to transform the data so that the transformed response assumes values in the real line and then apply the classic CV. This practice, however, leads to abnormal CV values.

The classic version of the CV has been used in different areas. For example, it has been used in engineering as a normalized measure of dispersion for quality control [10], in biochemistry as a threshold to select cells per well (see Figure 1C in [11]), in medical physics as an estimator of PET cardiac image noise [12], in biology as a measure to compare the robustness of different biological traits [13], and in neuroscience as a method for analysing synaptic plasticity [14] and variability in interspike intervals [15]. In psychology, specifically, the classic CV has been used in psychopathology and speech pathology as a way of distinguishing between a healthy control group and people suffering from a psychological or pathological disorder [16], and as a way of comparing age patterns of simple and four-choice reaction time (RT) tasks in older adults [17]. Yet, the CV is still under-utilized and not extensively taught in psychology [18–20], particularly in experimental psychology. In social science, Bedeian and Mossholder [21] discussed the theoretical underpinnings most commonly used to explain demographic diversity. They questioned if the CV should be used to index the relative internal variability of work groups, such as top-management teams, task groups, boards of directors, departments, and other social aggregates. Srensen et al. [22] evaluated the use of the coefficient of variation as a measure of demographic heterogeneity in the construct of organizational demography research. Empirical analyses suggested that using the coefficient of variation may lead to incorrect conclusions about the effects of heterogeneity.

Generally speaking, a sample with a standard deviation larger than the mean will produce CVs > 1 (see [23]). CVs ≈ 0 suggest that there is a high precision of the sample's central tendency; i.e., the variability of the location parameter is very low. The CV is also known as the relative standard deviation (RSD), which is the result of multiplying the absolute value of the CV by 100; its interpretation, however, is similar to that of the classic CV.

There are various methods available for estimating the CV. McKay [24] and David [25] provided a method for point estimation and construction of a confidence interval (CI) for normal coefficient of variation that was later modified by Vangel [26]. Zeigler [27] compared several estimators of a common coefficient of variation shared by k populations in large and equal sample sizes. Inference for the coefficient of variation in normal distributions was studied by Forkman [28] and Forkman and Verrill [29]. Díaz-Francés and Rubio [30] explored the CV in the estimation of the ratio of means, such that CV values smaller than a certain threshold help to justify normality assumptions of the ratio of two normal random variables. Note that this is an area where robust estimation [31] of the relative variability (of the variable in the denominator) may prove useful. Also, Mahmoudvand and Hassani [32] introduced approximate, unbiased estimators for the population coefficient of variation, in a normal distribution. Hoseini and Mohammadi [33] proposed two approaches—the central limit theorem and generalized variable—to estimate the coefficient of variation in uniform distributions. Consulin et al. [34] and Albatineh et al. [35] evaluated the performance of different parametric and nonparametric estimators for the population coefficient of variation considering ranked set sampling (RSS) under different distributional assumptions on data. Bayes estimation for the coefficient of variation in shifted exponential distributions was studied by Liang [36].

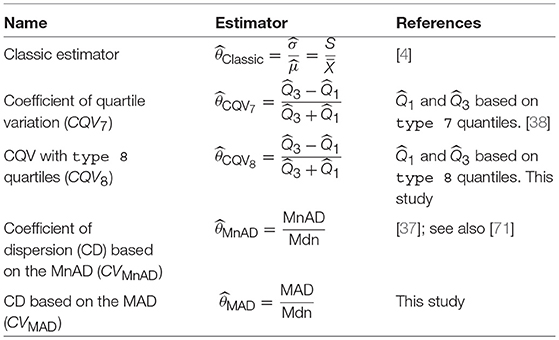
Robust estimation of location and scale [31] can be used to construct CV estimators. One proposal is to use a ratio of the mean absolute deviation from the median (MnAD) to the median (Mdn), known as the coefficient of dispersion (CD) [37, pp. 22]. Another proposal is to use a ratio of the difference between the interquartile range and the sum of the 1st and 3rd quartiles, which is known as the coefficient of quartile variation (CQV) [38]. The CQV is a robust version of the studentised range defined as q = (x_(n) − x₍₁₎)/S, where x_(i) is the ith order statistic and S is the sample standard deviation [39–41]. Incidentally, q is a related statistic used in the construction of multiple comparison methods (e.g., Tukey's honest significance test). A conceivable robust version of the CD could be the ratio of the median absolute deviation (MAD) to the Mdn, two well-known robust measures of scale and location, respectively [42]. Note that the CD and CQV estimators depend entirely on the estimation of location and the quartiles themselves, which in turn can be influenced by how the quantiles and means are estimated [43, 44], the support of the target distribution, especially for doubly-bounded supports such as [0,1] and the trade-off between efficiency and resistance of the statistics used for its construction [45, 46].

The goal of the current study is to compare the performance of some CV estimators based on the classic approach to the CV estimator. Here robust location and scale estimation are used. We investigate the estimation problem by varying distributional parameters under several statistical distributions commonly used to model data in several research fields. The rest of the paper is organized as follows: section 2 introduces the notations, definitions and the CV estimators used in the study; section 3 presents the simulation study and results; section 4 reports a discussion of empirical applications; and section 5 presents some concluding comments.

2. Definitions and Background

Let X₁, …, X_n be independently and identically distributed observations of a random variable having an unknown, cumulative distribution function (CDF) F_X(x). From the random variable X, we can obtain μ = E(X), the location parameter and $\sigma =\sqrt{V\text{ar}(X)}$, the scale parameter; i.e., the mean and the standard deviation. This work focuses on the population parameter θ = σ/μ, namely the CV. Based on the definition of population CV (θ), we note that the CV is a unit-free measure that quantifies the degree of variability relative to the mean. It can be used in comparing two distributions of different types with respect to their variability.

Let $\hat{\theta }$ be an estimator of θ the population CV. For example, a natural estimator of θ is

$\begin{array}{ll}\widehat{\theta }=\frac{\widehat{\sigma }}{\widehat{\mu }}=\frac{S}{\overline{X}}=\frac{\sqrt{{(n-1)}^{-1}{\displaystyle {\sum }_{i=1}^n{(X_i-\overline{X})}^2}}}{{\displaystyle {\sum }_{i=1}^n{X}_i/n}},& (1)\end{array}$

where $\overline{X}$ and S are the sample mean and sample deviation [4]². In order to obtain a non-zero standard deviation, we assume that at least two of the collected data points are distinct and $\overline{X}\ne 0.$ It is known that inference procedures are hypersensitive to minor violations when a population with normal distribution is assumed [44, 49]. For example, working with CVs when the expected value of the estimator $S/\overline{X}$ is infinite [50, p. 75] or when there is large asymmetry and heavy tails could hinder differences in variance [51, 52]. For example, the Cauchy distribution is clearly symmetric and heavy-tailed [53], but the moment-based definitions of skewness and kurtosis are undefined (its expected value and its variance are undefined). As the method of moment estimation fails and Bayesian estimation is very unstable, the estimation of the traditional CV becomes unfeasible,and hence it is necessary to establish robust and efficient estimators in terms of finite samples [54]. On the other hand, classic inference, such as confidence intervals for the CV, are not robust to counteract violations of the normality assumption [26]. Fortunately, some nonparametric and robust estimators are available to deal with such situations. Next, some basic results and notations are put forward.

The population quantile distribution function (QDF) Q(p) returns the value x such that F(x): = Pr(X ≤ x) = p is defined as Q(p): = F(p)⁻¹ = inf{x ∈ ℝ:p ≤ F(x)}, where 0 < p < 1. Accordingly, the empirical quantile function (EQF) is given by $\hat{Q}(p):=F_n{(p)}^{-1}=inf\left\{x\in ℝ:p\le F_n(x)\right\}$, where F_n(x) is the empirical distribution function $F_n(x)=n^{-1}{\displaystyle \sum _{i=1}^n\mathbb{I}}(X_i\le x),$ and ${\mathbb{I}}_A$ is the indicator of event A. By its definition, F_n(x) = 0 whenever x < X₍₁₎, and F_n(x) = 1 whenever x ≥ X_(n). Note that EQF is simply a stair function that places the constant value k/n for all x-values in the interval [X_(k), X_{(k + 1)}), where x₍₁₎ ≤ x₍₂₎ ≤ ⋯ ≤ x_(n−1) ≤ x_(n) are the order statistics of the sample. In this sense, an empirical estimator of the pth quantile [55, 56] can be obtained by linear interpolation of the order statistics, that is, $\hat{Q}(p)=x_{(k)}+t(x_{(k+1)}-x_{(k)})=(1-t)x_{(k)}+t{x}_{(k+1)},$ with k ∈ {1, 2, …, n}, t ∈ [0, 1) and (n−1)p + 1 = k + t. Note that the pth quantile type 7 and type 8 are obtained when k = ⌊(n−1)p + 1⌋ and k = ⌊(n + 1/3)p + 1/3⌋, respectively. Here, the function ⌊·⌋ is the integer part of the desired rank [43].

We denote Q₁ = Q(0.25), Q₂ = Q(0.5) and Q₃ = Q(0.75) the population quartiles of a distribution. In particular, Q₂ is the population median and can be estimated by the sample median, $\mathrm{\text{Mdn}}={\hat{Q}}_2=\hat{Q}(0.5)=F_n{(0.5)}^{-1}.$ Here, Mdn is the 0.5th quantile type 1 [43], which assumes the value x_{(k + 1)} if n = 2k + 1 (an odd integer) and x_(k) if n = 2k (an even integer). Also, Mdn is an estimator of location that is robust, as it has a high breakdown³. In the R software [59] type 7 is the default quantile to evaluate ${\hat{Q}}_2$ [43]. For a scale estimator, we look at the interquartile range, $IQR={\hat{Q}}_3-{\hat{Q}}_1,$ as an estimator that is less sensitive to outliers than the standard deviation [60]. In this work, ${\hat{Q}}_1$ and ${\hat{Q}}_3$ are calculated by using type 7 or type 8 quantiles [38].

In L₁-norm, the counterpart of the population standard deviation is the mean absolute deviation, denoted by δ₁ = E(|X−μ|) and by considering Q₂ instead of μ, we have the mean absolute deviation about the population median δ₂ = E(|X−Q₂|). Note that this measure is still based on expectations (or “averages”). Based on the sample median (or “middle value”), we can define the median absolute deviation as λ = Median(X−Q₂), which is a robust measure [61–63]. A scale estimator of δ₂ is the sample mean of deviations around the sample median (called the sample mean absolute deviation around the median, MnAD). It is also known as the coefficient of dispersion, CD [37, 44, p. 22], given by

$\begin{array}{ll}\text{MnAD}=\frac{1}{n}{\displaystyle \sum _{i=1}^n|}{x}_i-{\widehat{Q}}_2|.& (2)\end{array}$

This estimator also has a breakdown point of 0. A robust scale estimator of λ is the median absolute deviation about the median (MAD), given by

$\begin{array}{ll}\text{MAD}=1.4826·\text{Median}\{|x-{\hat{Q}}_2|\},& (3)\end{array}$

and its finite, sample breakdown point is approximately 0.5 [61, 64, 65].

3. The Estimators of Relative Variability

Statistical analysis of the classic estimator of the population CV given by the ratio $\hat{\theta }=S/\overline{X}$ is typically based on the assumption that sufficient moments from a random variable X of the population of interest exist [66]. Typically, for small sample sizes, the ratio of estimators, such as the estimator $\hat{\theta }$, are biased [55]. Under normally distributed data, the exact distribution of $\hat{\theta }$ is available [26, 67, 68]; however, in many practical situations, the data are non-normally distributed or the existence of moments of random variable X is not always ensured, and thus the ratio of estimators should be used with caution [69]. Based on the idea of the classic version of the CV, it is possible to construct robust ratio estimators by using robust estimators of location and scale [31]. We use the interquartile range IQR, MnAD and MAD as point estimators of scale. On the other hand, the combined quantile [70] given by $({\hat{Q}}_3+{\hat{Q}}_1)$ and the Mnd can be used as point estimators of location. Table 1 summarizes the estimators of the population parameter θ = σ/μ, considered herein.

TABLE 1

Table 1. Estimators of relative variability considered in this study.

4. Simulation Study

We carried out a Monte Carlo simulation study to analyse the efficiency and robustness of the proposed estimators and to compare them with the Classic CV estimator.

4.1. Design of Experiments

The main objective is to recommend a good estimator for a population CV via simulations in order to overcome problems of the analytical intractability under a theoretical comparison approach. We consider different distributions that represent a wide variety of probabilistic patterns of data and various degrees of non-normality obtained in different applications (i.e., uniform, normal, Binomial, Poisson, Exponential, Chi-square, Beta, Gamma, Ex-Gaussian).

In the context of the design and analysis of Monte Carlo experiments [72–74], we adopted a space-filling design composed of B = 10, 000 multidimensional input points representing sample sizes, distribution model (depending on parameters) and estimators of the population CV. To control the population CV of all distributions and make the properties of the estimators given in Table 1 comparable, we adopted a reparameterization of these distributions as a possible observed range of the population CV in the unit interval, i.e., θ ∈ (0, 1).

To select an estimator among the estimators under study, we proceeded as follows: for each simulation (Monte Carlo iteration), we randomly drew a total of n observations from the given distribution f_X in Table 2. We then used the sample values to calculate the different estimators given in Table 1. The estimates obtained were subsequently contrasted with the true population value using the mean squared error (MSE) as the scoring metric, since it is widely used in practice and is a good measure to evaluate the trade-off in terms of bias and variance of the estimator⁴. Other alternatives to the MSE metric include the relative bias, concordance coefficient, relative maximum absolute error, Pearson correlation, and mean absolute error [75–78]. Although it is outside the scope of this paper to discuss these alternatives, it is indeed a discussion needed in future work.

TABLE 2

Table 2. Probability parametric distributions considered in this study.

Let ${E}=\left\{CQ{V}_7,CQ{V}_8,C{V}_{\mathrm{\text{MAD}}},C{V}_{\mathrm{\text{MnAD}}}\right\}$ be the set of names that define the alternative estimators to the classic CV estimator given in Table 1. To assess the accuracy of ${\hat{\theta }}_j$ with respect to the classic estimator of CV, we used the ratio

$\begin{array}{ll}{\gamma }_j=\frac{{\text{MSE}}_j}{{\text{MSE}}_{\text{Classic}}},j\in {E},& (4)\end{array}$

where the estimate of MSE was given by

$\begin{array}{ll}{\text{MSE}}_j=\text{MSE}({\hat{\theta }}_j)=\frac{1}{B}{\displaystyle \sum _{i=1}^B}{({\hat{\theta }}_{ij}-\theta )}^2,& (5)\end{array}$

and where ${\hat{\theta }}_{ij}$ was the jth estimator evaluated in the ith sample for i = 1…B, and B was the size of the Monte Carlo experiment. We shall say that the jth estimator was better than an alternative to the classic estimator of the CV if γ_j < 1. In this sense, γ_j can be seen as a measure of efficiency [79]. We can rescale γ to log₁₀(γ) which represents a measure's information or weight of evidence [80] given in ban or dig (short for decimal digit). In this sense, higher values of log₁₀(γ) indicate that the content of information, in the sense used by Hartley [81], Shannon [82], and MacKay [83], of a particular CV estimator is less than that of the classic estimator of the population CV. When log₁₀(γ) = 0, it indicates that a particular CV performs like the population's CV, and small values of log₁₀(γ) suggest that a particular CV is more informative that the population's CV.

We implemented in R [59] the following procedure for the Monte Carlo simulation study:

1. Select a distribution f_X from Table 2.

2. Draw a sample of size n from f_X, where θ is the parameter of interest (population CV).

3. Calculate the estimators for the CV, as shown in Table 1.

4. Repeat steps 2 and 3, B times.

5. Evaluate the MSE, γ and rescale to log₁₀(γ).

A similar experimental design to the Monte Carlo scheme was described by Vélez and Correa [79], Marmolejo-Ramos et al. [84] and Vélez et al. [85]. The number of simulation runs B is equal to 10,000. The samples of size n = {10, 25, 50, 100, 200} were generated from each distribution in Table 2⁵.

4.2. Identification of Simulation Scenarios

We use the normal distribution denoted by ${N}(\mu ,{\sigma }^2)$ as the baseline. For this distribution, we set μ = {0.1, 0.4, 0.7, 1, 5, 15, 30} and σ = {0.1, 0.3, 0.6, 1, 3, 5} and used the sample sizes mentioned above. In this way, θ takes values in the interval (0, 1). The total number of scenarios under evaluation was 210. The values of μ and σ² were chosen to guarantee that no observations would fall outside the (μ − 2σ, μ + 2σ) limits and so the sample estimators of the CVs in Table 1 would always be positive. Let us recall that, for normally distributed data, approximately 95% of the distribution falls within two standard deviations around the mean.

To evaluate the efficiency of the estimators given in Table 1, we considered scaled-contaminated normal distributions (variance inflation), ${CN}(\mu ,\sigma ,\alpha ,\lambda ).$ More precisely, the following finite mixture model ${CN}$ was used to simulate data that contain outliers:

$\begin{array}{ll}{{CN}}_X(x)=(1-\alpha )\Phi ((x-\mu )/\sigma )+\alpha \Phi ((x-\mu )/\sqrt{\lambda }\sigma ).& (6)\end{array}$

Here, we considered the level of contamination α = {5%, 10%, 15%, 20%} and λ = 3. Note that for α = 0% in Equation (6) we obtained the Normal distribution ${N}(\mu ,{\sigma }^2).$ By using combinations of μ and σ, and keeping α and λ fixed, a total of 140 simulation scenarios were evaluated in each case.

The robustness of the estimators given in Table 1 was analyzed by considering symmetric contaminated normal distributions, ${HN}t(\mu ,\sigma ,\alpha ,\nu )$, close to the Normal(μ, σ²) but with heavier-than-normal tails [86]. The following contaminated model ${HN}t$ was used for creating outliers and modeling data sets that exhibit heavy tails:

$\begin{array}{ll}{HN}{t}_X(x)=(1-\alpha )\Phi ((x-\mu )/\sigma )+\alpha t_{\nu }(x),& (7)\end{array}$

where t_ν(·) is the Student's t-distribution with ν degrees of freedom [87]. Again, we considered the level of contamination α = {5%, 10%, 15%, 20%} and ν = 2.5. Note that for α = 0% in Equation (7) we obtained the Normal distribution ${N}(\mu ,{\sigma }^2).$ By combinations of μ, σ, α and fixed ν in the contaminated distribution with heavy tails, a total of 140 simulation scenarios were evaluated.

To evaluate the flexibility of the estimators in Table 1, we computed accuracy measures for a determinate choice of distributions from Table 2. We reparameterized the distributions in this table in terms of μ and σ of the normal distribution ${N}(\mu ,{\sigma }^2)$ so that they assumed the θ values close to the baseline distribution. This made the estimators comparable.

We generated samples for the Uniform distribution with the set parameters $a=\mu -\sigma \sqrt{3}$ and $b=\mu +\sigma \sqrt{3}$; thus the mean is μ and the variance is σ². The values of μ and σ used the same values of the baseline distribution. A total of 210 simulation scenarios were studied.

In the Binomial distribution, we impose the restriction 0 < σ²/μ < 1 to the probability of successes p = 1 − (σ²/μ). The number of trials m = ⌊μ/p⌋ make up a total of 3,950 simulation scenarios (combinations of p and m). Here, the function ⌊·⌋ is the integer part of the desired rank. The mean and standard deviation are mp and $\sqrt{mp(1-p)}$, respectively. In particular, for p = 0.5 (the value that maximizes the variance) it follows that $\theta =\sqrt{mp(1-p)}/mp=1/\sqrt{m}.$ Note that, independently of p, when m → ∞, the population CV, θ, tends to zero.

When working with the Poisson(λ) distribution, we considered λ = μ²/σ². The normal distribution can also be used to approximate the Poisson distribution for large values of λ. Because values of λ > 20 produce suitable normal approximations, we did not consider larger scenarios. Note that for large values of λ, θ converges to zero. We therefore evaluated 105 simulation scenarios obtained by combinations of μ and σ and imposed the condition 0 < λ^−1/2 < 1.

Among all the distributions considered in this study, the Exponential(λ) distribution is particularly interesting because, regardless of λ, the value of the classic CV is always equal to 1. In fact, the mean and standard deviations are 1/λ and $\sqrt{1/{\lambda }^2}$, respectively. Therefore, the mean and standard deviations are completely tied together and the interpretation of the CV as a “percentage-like” is eroded. In practice the exponential distribution is used as a baseline and, when CV < 1 (such as for an Erlang distribution), distributions are considered low-variance, while distributions with CV > 1 (such as a hyper-exponential distribution) are considered high-variance [88]. We set λ = μ/σ and used the same sample sizes mentioned above to compare the different estimators of the CV across a total of 175 simulation scenarios obtained by combinations of μ and σ with the condition 0 < σ/μ < 1.

The Shifted Exponential (β, λ) distribution, where β ∈ ℝ is the threshold parameter such that β < x, and the scale parameter λ > 0, is widely used in applied statistics; principally in reliability (see [89–91]). When β = 0 we have the Exponential distribution and in that case we can evaluate “spread” effects. The mean and standard deviations are μ = β + λ and σ = λ, respectively. We used the same sample sizes mentioned above to compare the different estimators of the CV across a total of 915 simulation scenarios obtained using combinations of μ and σ with the condition 0 < σ/μ < 1.

In order to evaluate the effect of the sample size and the parameter ν (degrees of freedom) on the estimators of the CV when the data came from a ${\chi }_{\nu }^2$ distribution, n was varied as previously described and ν = ⌊2μ²/σ²⌋. By imposing the condition 0 < σ/μ < 1, we carried out a total of 105 simulation scenarios (combinations of μ and σ).

For the Beta(α, β) distribution, we set the parameters α = μ((μ(1−μ)/σ²)−1) and β = (1−μ)((μ(1−μ)/σ²)−1). The mean and variance of the Beta(α, β) distribution were given by α/(α + β) and αβ/{(α + β)²(α + β + 1)} respectively. This showed that θ = β^1/2{α(α + β + 1)}^−1/2. Letting α = β, the expression for the mode simplifies to 1/2, showing that for α = β > 1, the mode (anti-mode when α = β < 1) is at the center of the distribution and the $\theta =1/\sqrt{2\beta +1}$ is a decreasing function of β. By reparameterization of this distribution in terms of μ and σ we have a mean μ and dispersion σ. Thus, the variance measures the dispersion relative to how far the mean is from 0 or 1 (i.e., distance from the support bounds), so the variance already contains the information in a CV measure: the CV measures the dispersion relative to the odds. Combinations of μ and σ and imposing the restrictions α > 0, β > 0 and 0 < θ < 1 resulted in 655 scenarios.

A similar approach was used for the Gamma(α, β) distribution. In this case α = μ²/σ², β = μ/σ², and the mean, variance and classic CV were given by αβ⁻¹, αβ⁻² and θ = β^−1/2 respectively. Note that θ is a function of scale parameters only. In the case of the Gamma distribution, the CV interpretation as a measure of dispersion relative to central tendency is inadequate; however, the CV can be interpreted as a precision of measurement [92] or relative risk [93]. Again, combinations of μ and σ and imposing the restriction α > 0, β > 0 and 0 < θ < 1 resulted in 4,680 scenarios.

The Ex-Gaussian distribution, also called the exponentially modified Gaussian (EMG), is defined by the parameters μ, σ, and ν. The Ex-Gaussian distribution is typically used to model reaction time (RT) data [94–96]. Its shape resembles a normal distribution [97–99] but with a heavy right tail. The Ex-Gaussian model assumes that an RT distribution can be approximated by convolution of a normal and an exponential function. The parameters μ and σ are the mean and the standard deviation of a Normal distribution, while ν is a decay rate (exponent relaxation time) and reflects extremes in performance [100, 101]. To generate observations from this distribution, we followed the strategy described by Marmolejo-Ramos et al. [84]. In the present study, μ = {0.1−ν, 0.4−ν, 0.7−ν, 1−ν, 5−ν, 15−ν, 30−ν}, σ² = {0.1²−ν², 0.3²−ν², 0.6²−ν², 1²−ν², 3²−ν², 5²−ν²}, where ν = {0.7, 7, 14} represent small, middle and highly exponent relaxation-time behaviors. Under the restriction 0 < θ < 1, a total of 315 simulated scenarios were evaluated.

The Lognormal distribution has been widely employed in sciences [102]; in particular, it is used to fit empirical reaction times (RTs) and has the status of a baseline distribution in RT research [103]. In this distribution, $\mu =exp\left(\alpha +\frac{{\beta }^2}{2}\right)\in ℝ$ and 0 < σ = [exp(β²)−1]exp(2α + β²) are the mean and standard deviation of the variable's natural logarithm. In the case of the Lognormal distribution, the CV is independent of the mean. Here, combinations of μ and σ resulted in 3,045 scenarios.

4.3. Results

In this section, we describe the simulation studies designed to compare the proposed estimators of the population CV. Figures 1–12 present scatter plots (with jitter) of the accuracy metric log₁₀(γ) vs. the true value of the population coefficient of variation θ ∈ (0, 1), by combining different sample sizes. The blue, red, green, brown, and orange points represent the sample sizes 10, 25, 50 (small sample sizes) and 100, 200 (large sample size) respectively. The red horizontal line represents the benchmark of equal accuracy between the classic estimator and an alternative estimator.

FIGURE 1

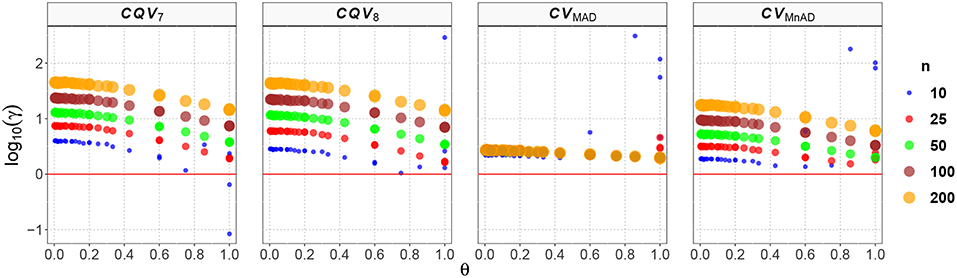
Figure 1. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the Normal(μ, σ²) distribution.

These plots of the performance of the estimators can be interpreted as follows. Higher positive values of log₁₀(γ) indicate that the MSE of a particular CV estimator distribution is higher than that of the classic estimator. This, in turn, implies that the estimator is not a good alternative to estimate the CV when the data come from those distributions. Negative values of log₁₀(γ) indicate that the proposed estimator is more efficient than the classic estimator and can be considered as an optimal estimator of the population CV. Values of log₁₀(γ) that closely approximate to zero indicate that the alternative estimator has a similar behavior to the classic estimator of the population CV.

Figure 1 shows the results of the log₁₀(γ) accuracy metric for the Normal(μ, σ²) distribution. The plots in Figure 1 indicate an increase of the estimators' MSE as the sample size increases. Also, the accuracy obtained by the CQV₇, CQV₈, CV_MnAD increases (values closer to zero) when θ tends to 1. On the other hand, the performance of the CV_MnAD is less sensitive to changes of θ and the log₁₀(γ)_CVMAD slightly increases with n. The values of log₁₀(γ) for the CQV₇ estimator increase as the sample size increases, with a minimum value of log₁₀(γ)_min = −1.07 when n = 10, μ = 0.1, and σ = 0.1, and a maximum value of log₁₀(γ)_max = 1.65 when n = 200, μ = 5.0, and σ = 0.3. In practical terms, this result implies that as n increases, the CQV₇ will produce higher MSE values than the classic CV estimator. In other words, this finding plays against using the CQV₇ estimator instead of the classic CV estimator when the data comes from a ${N}(\mu ,{\sigma }^2)$ distribution, especially when the sample size is large. A similar result was obtained for the CQV₈ estimator (log₁₀(γ)_min = 0.01 at n = 10, μ = 0.4 and σ = 0.3; log₁₀(γ)_max = 2.46 at n = 10, μ = 5.0 and σ = 5.0).

Our findings suggest that the CV_MAD estimator performs better than the CV_MnAD. In particular, our results indicate a more consistent behavior of the former estimator over the latter. Close inspection shows that log₁₀(γ)_CVMAD ∈ (0.28, 2.49) and log₁₀(γ)_CVMnAD ∈ (0.13, 2.25), from which it can be concluded that the MAD-based estimator is a better choice.

Despite the advantages of using the normal distribution in many applications, the normality assumption is too restrictive for modeling real data sets, which usually exhibit asymmetry or tails heavier than the normal tails; hence, we chose the scaled-contaminated normal given in Equation 6 to represent symmetric contaminated normal distributions, close to the normal, but with tails heavier than normal. We believe that this approach, frequently reported in the literature [104–106], is sufficient to keep track of the robustness of the estimators considered in this study.

Table 3 presents the median values of the log₁₀(γ) accuracy metric of the scaled-contaminated normal distribution for all sample sizes. An inspection of this table reveals that for non-contaminated samples (α = 0%) all estimators performed efficiently (see also Figure 1). As in the normal distribution case, each estimator improved when θ tends to the value of 1. The MSE of the CQV₇, CQV₈, CV_MnAD estimators increased as sample size increased. The performance of the CV_MnAD was more stable under changes in θ and sample sizes (see plots in Figure 2). Under contamination, the alternative estimators produced higher MSE values than the classic CV estimator; however, the values decreased when the level of contamination α increased; i.e., the performance of all estimators improved slightly. This information is presented in Figure 1 (α = 0% of contamination) and Figure 2 (with contamination). Note, for example, 16.29% = (1−(1.13/1.35)) ·100, 15.90% = (1−(1.11/1.32)) · 100, 13.68% = (1−(0.82/0.95)) · 100, and 45% = (1−(0.23/0.42)) · 100, an increase in accuracy of the CQV₇, CQV₈, CV_MnAD, and CV_MAD estimators under 10% contamination when the sample size is n = 100, respectively. We observe in Figure 2 that between the alternative estimators, the CV_MAD is the most robust and efficient estimator as the tail-weight of the underlying distribution increases. The simulation results led us to suggest the use of the CV_MAD estimator as a good alternative to the classic CV estimator.

TABLE 3

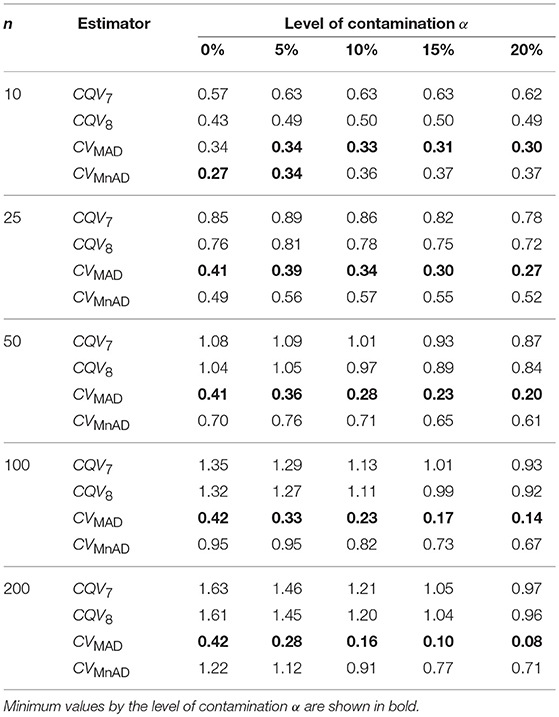
Table 3. Median values of log₁₀(γ) accuracy metric across θ produced for each estimator and sample sizes under the scaled-contaminated normal distribution ${CN}(\mu ,\sigma ,\alpha ,\lambda )$.

FIGURE 2

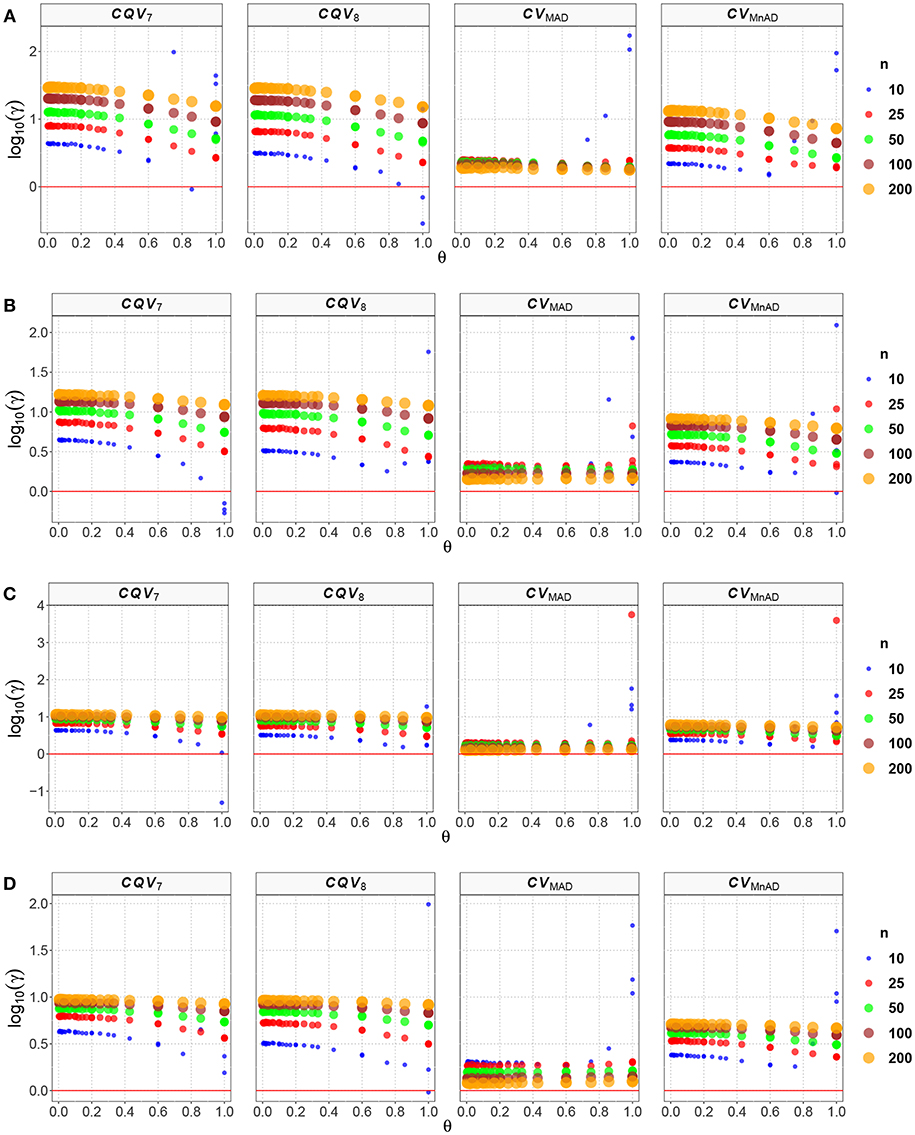
Figure 2. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the scaled-contaminated normal distribution ${CN}(\mu ,\sigma ,\alpha ,\lambda )$ distribution. Each horizontal panel represents a level of contamination, respectively: (A) α = 5%, (B) α = 10%, (C) α = 15%, and (D) α = 20%. Here, μ, σ, and λ are defined in section Identification of Simulation Scenarios.

Table 4 presents the median values of the log₁₀(γ) accuracy metric of the contaminated normal distribution with heavy tails for all sample sizes. Visual inspection of this table reveals that, for α = 0% and α = 5% of contamination with heavy tails, all estimators performed in a similar way to a scaled-contaminated normal distribution. As in the normal distribution case, each estimator improved when θ tended to the value of 1. Generally, the MSE of the CQV₇, CQV₈, CV_MAD estimators increased as sample size increased. For large values of contamination (α = 10%, 15%, and 20%) the CQV₇, CQV₈ produced the smallest MSE values; however, their behavior was rather unstable.

TABLE 4

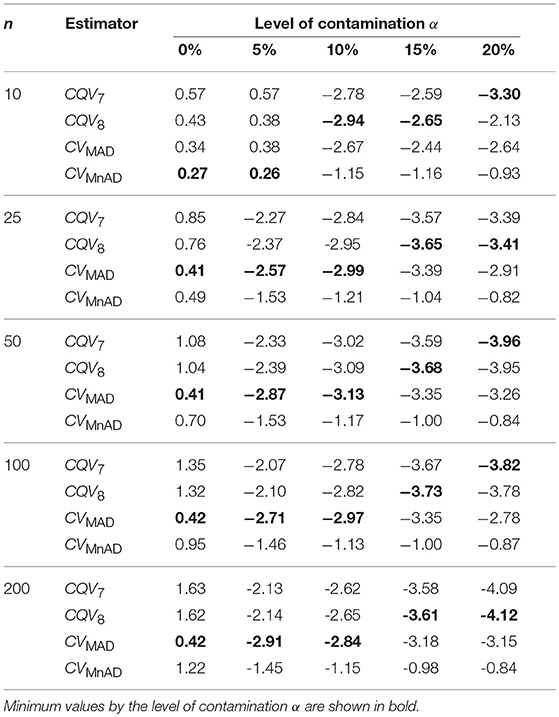
Table 4. Median values of log₁₀(γ) accuracy metric across θ produced for each estimator and sample sizes under the contaminated normal distribution ${HN}t(\mu ,\sigma ,\alpha ,\nu )$ with heavy tails.

Like the result in the scaled-contaminated normal distribution case, the performance of the CV_MAD was more stable under changes in θ and the sample sizes (see Figure 3). Under heavy-tails contamination, the alternative estimators produce smaller MSE values than the classic CV estimator; however, the values increased when the level of contamination α increased; i.e., the performance of all estimators improved slightly. This information is presented in Figure 3. That figure also indicated that between the alternative estimators, the CV_MAD is the most robust and stable estimator as the heavy-tail-weight of the underlying distribution increases. These results suggest the use of the CV_MAD estimator as a good alternative to the classic CV estimator in the presence of heavy-tail observations in the sample (Table 4 summarizes the key results).

FIGURE 3

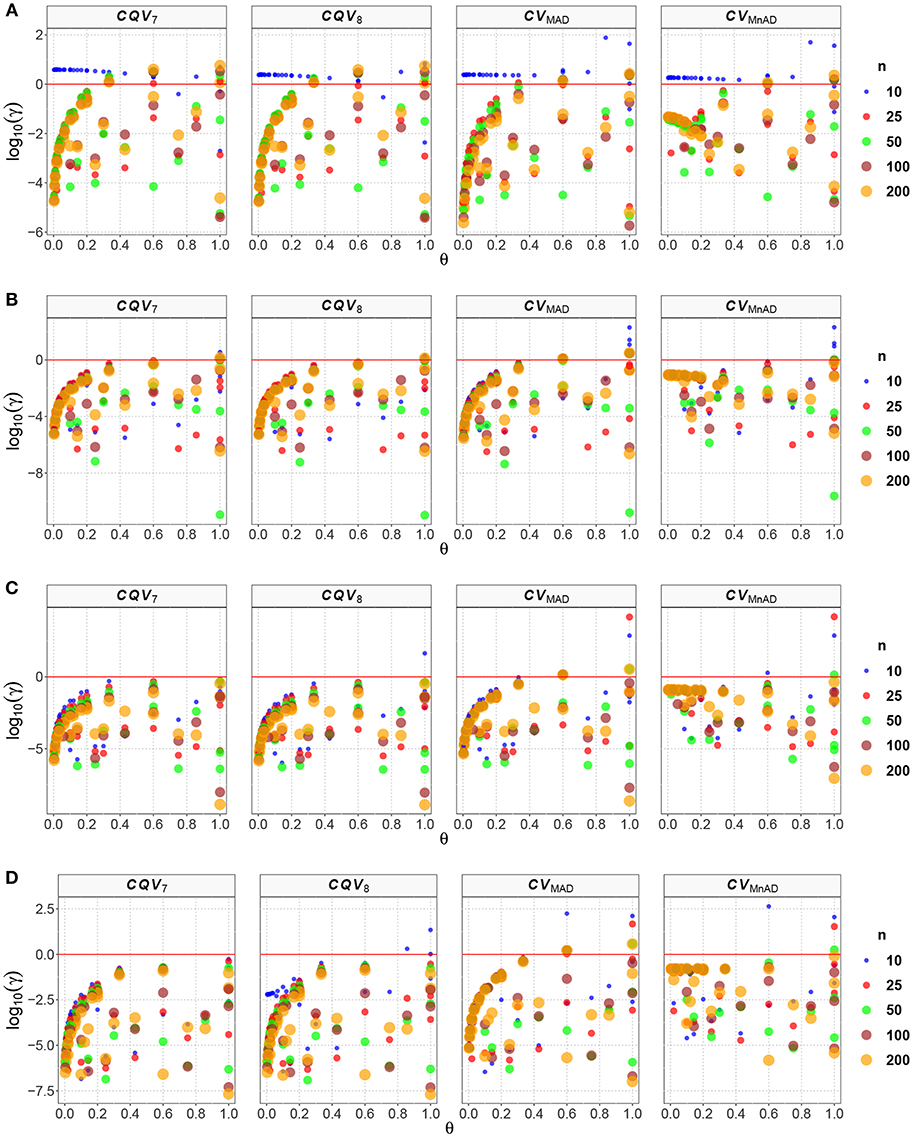
Figure 3. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the contaminated normal distribution ${HN}t(\mu ,\sigma ,\alpha ,\nu )$ with heavy tails. Each horizontal panel represents a level of contamination, respectively: (A) α = 5%, (B) α = 10%, (C) α = 15%, and (D) α = 20%. Here, μ, σ, and ν are defined in section Identification of Simulation Scenarios.

Figure 4 displays our findings for the Uniform distribution. Note that the values of the log₁₀(γ) accuracy metric decreased when θ increased, and also that the larger the sample size, the higher the MSE. Compared with the classic estimator of the CV, the CV_MnAD estimator seems to be a plausible alternative, with higher relative efficiency than the baseline, regardless of n, followed by the CQV₈, CQV₇ and CV_MAD estimators. In fact, for n = 100, the median values of the log₁₀(γ) accuracy metric of the CVs were CQV₇ = 1.122, CQV₈ = 1.071, CV_MAD = 1.565, and CV_MnAD = 1.004. Note there was a slight difference in performance between the CQV₇ and CQV₈ estimators of the CV, which highlights the importance of carefully selecting the type of quantile estimator to be used. A close inspection shows that log₁₀(γ)_CQV7 ∈ (0.14, 3.03), log₁₀(γ)_CQV8 ∈ (0.11, 1.35), log₁₀(γ)_CVMAD ∈ (0.57, 5.31), and log₁₀(γ)_CVMnAD ∈ (0.34, 5.29). From this it can be concluded that the CV_MAD estimator is not necessarily a reasonable choice.

FIGURE 4

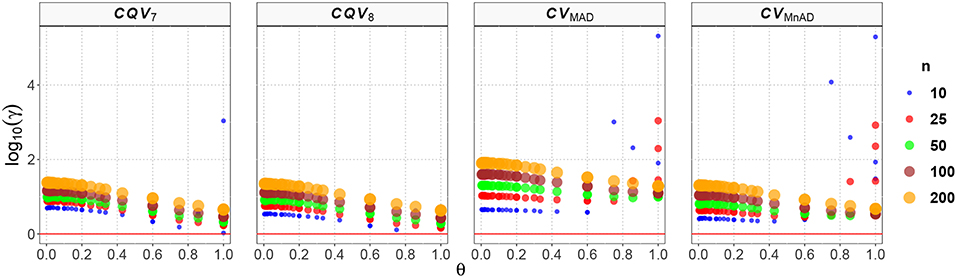
Figure 4. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the reparametrized Uniform distribution.

Table 5 presents the median values of the log₁₀(γ) accuracy metric of the Binomial distribution. This table reveals that the CQV₇ and CQV₈ estimators of the CV present the highest values among all evaluated estimators.

TABLE 5

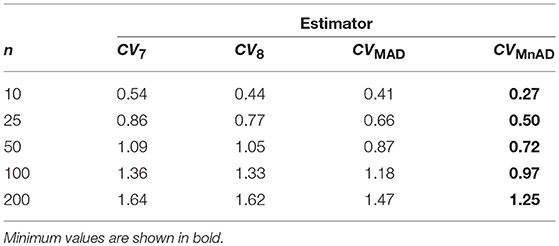
Table 5. Median values of log₁₀(γ) accuracy metric across θ produced for each estimator and sample sizes under the Binomial distribution.

Figure 5 shows that in the case of the Binomial distribution the CV_MnAD estimator was more stable and showed the lowest values of log₁₀(γ) regardless of m and p. The plots also reveal that there were some combinations of m and p for which log₁₀(γ) was negative; i.e., in some situations, the alternative estimators were more efficient than the classic estimator of the CV for this distribution. However, there is not a clear pattern for this behavior. For example, for n = 200 there were the following cases: m = 2 = 9, p = 0.1, log₁₀(γ)_CV7 = −28.27; m = 9, p = 0.1, log₁₀(γ)_CV8 = −28.27; and m = 90, p = 0.97, log₁₀(γ)_CVMAD = −1.46. For n = 10, the following estimation was observed: m = 2, p = 0.64, log₁₀(γ)_CVMnAD = −0.15.

FIGURE 5

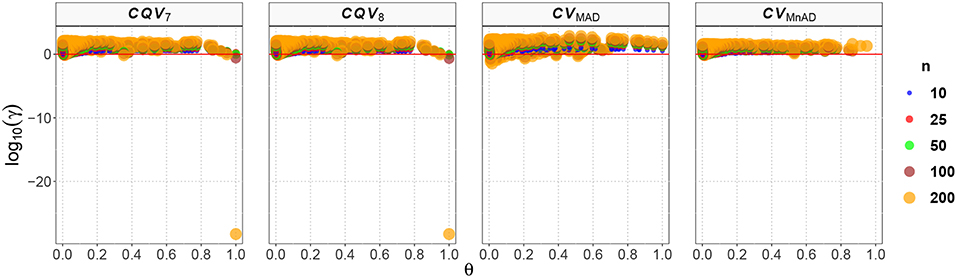
Figure 5. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the reparametrized Binomial distribution.

From Figure 6 with the Poisson distribution, note that the CQV₇ and CQV₈ estimators behaved similarly in terms of the log₁₀(γ) accuracy metric for almost all sample sizes independently of θ and showed higher values than the CV_MnAD. The CV_MAD estimator exhibited a behavior completely different from the CQV₇, CQV₈, and CV_MnAD estimators. For this estimator, we observed an association between increases in the values of θ and higher MSEs. In terms of the median values of the log₁₀(γ) accuracy metric, Table 6 reveals that the CV_MAD estimator presented the smallest accuracy metric values when the sample size became greater than 10. In practical terms, this implies that the median-based estimators evaluated herein perform better than the CQV₇ and CQV₈ estimators.

FIGURE 6

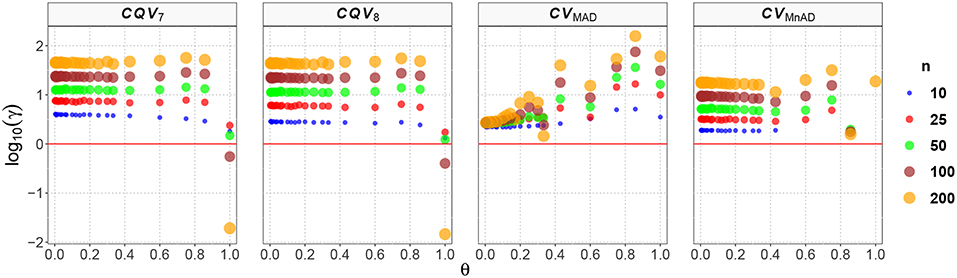
Figure 6. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the reparametrized Poisson distribution.

TABLE 6

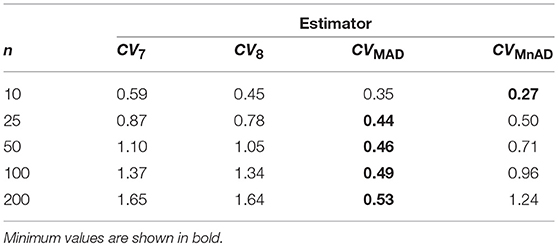
Table 6. Median values of log₁₀(γ) accuracy metric across θ produced for each estimator and sample sizes under Poisson distribution.

Figure 7 reveals our findings for the Exponential distribution. Recall that if the number of arrivals in a time interval of length T follows a Poisson process with mean rate λ, then the corresponding interarrival time follows an Exponential distribution.Values for T of the Poisson distribution were similar to those observed for the Exponential distribution. While the CQV₇ and CQV₈ estimators performed poorly, the CV_MAD and CV_MnAD estimators had a better performance. That is log₁₀(γ)_CV7 ∈ (0.52, 1.42), log₁₀(γ)_CV8 ∈ (0.39, 1.41), log₁₀(γ)_CVMAD ∈ (0.00, 0.11), and log₁₀(γ)_CVMnAD ∈ (0.33, 0.64). This result indicates that the CV_MAD estimator is a feasible alternative to the classic estimator of the CV, especially with all sample sizes. In practical terms, this implies that compared with that of the classic estimator of the CV, the MSE of the CV_MAD estimator is relatively low.

FIGURE 7

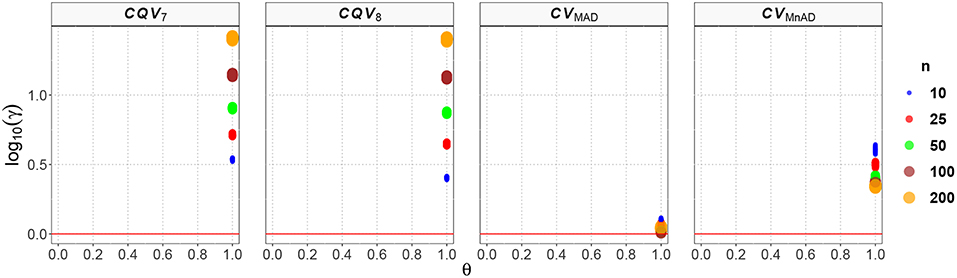
Figure 7. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the reparametrized Exponential distribution.

The behavior of the CV estimates for the Shifted-Exponential distribution is represented in Figure 8. The effect of the shift is to produce a large distortion on the MSE leading to a nonlinear form in relation to the values of θ for all estimators in the different sample sizes. We observed an inflection point when θ = 0.1. For θ < 0.1 the MSE of the estimators' decreasing and smallest values were obtained when n = 200, μ = 5.1, σ = 0.1. In fact, CQV₇ = −1.36, CQV₈ = −1.35, CV_MAD = −1.00, and CV_MnAD = −1.04. When θ > 0.1 the MSE increased in θ with the larger value for the CV_MnAD = −0.07 when n = 10, μ = 33, σ = 0.3. Note that the highest values were obtained when θ ≈ 0 or θ ≈ 1. In this situation, we obtained a degenerate distribution at 0 when λ ≈ 0 and in the Exponential distribution when β = 0.

FIGURE 8

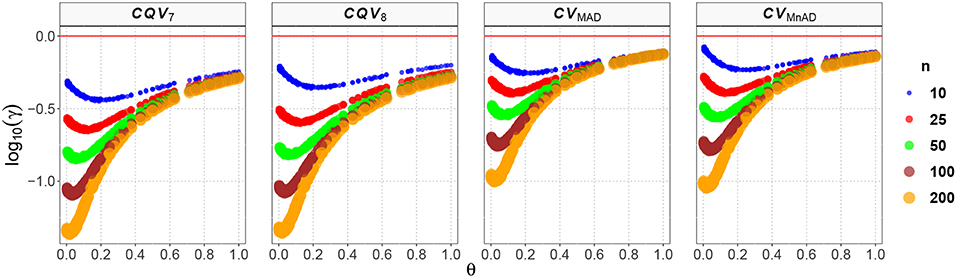
Figure 8. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the Shifted-Exponential distribution.

Figure 9 presents the behavior of the estimators when samples of size n are drawn from a ${\chi }_{\nu }^2$ distribution. From the reparameterization of this distribution in terms of μ and σ, we have an inverse relationship between θ and ν; that is, we observe that the values of the log₁₀(γ) accuracy metric decreases when θ increases (or similarly, when ν decreases) and also that a large sample size is associated with a high MSE. Here, the CQV₇ and CQV₈ estimators behave similarly but perform poorly when compared with the CV_MAD and CV_MnAD estimators. Detailed analysis of the results from estimators of the CV revealed that log₁₀(γ)_CV7 ∈ (0.54, 1.65), log₁₀(γ)_CV8 ∈ (0.40, 1.64), log₁₀(γ)_CVMAD ∈ (0.02, 0.44), and log₁₀(γ)_CVMnAD ∈ (0.26, 1.24). Overall, our findings indicate that the CV_MAD is a good alternative to the classic CV estimator for this particular distribution.

FIGURE 9

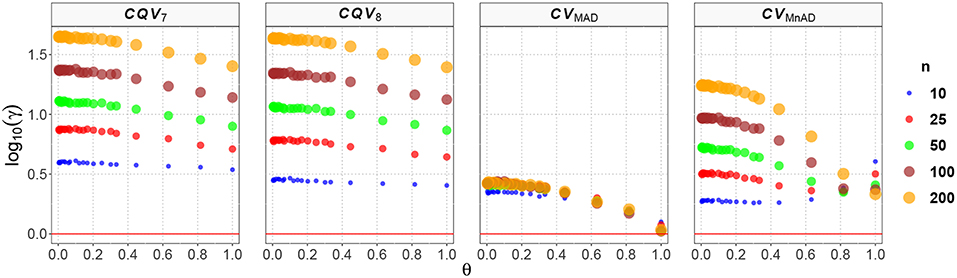
Figure 9. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the reparametrized Chi-square distribution.

Figure 10 depicts the values of the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) for the Beta distribution and the CV estimators. Three regions in each plot are clearly distinguishable, as the alternative estimators of the population CV behave differently. When 0 < θ ≤ 0.33, we have α > β; and for this case, the Beta distribution has a negative skew. We observe that in almost all cases, the values of the log₁₀(γ) accuracy metric increase when θ increases. When 0.89 ≤ θ < 1, we have α < β, and for this case, the Beta distribution has a positive skew. We observe that the values of the log₁₀(γ) accuracy metric decrease in almost all cases when θ increases. When 0.5 ≤ θ ≤ 0.54, we have α≅β; i.e., the Beta distribution is approximately symmetrical. In that case the CQV₇ and CQV₈ estimators behave similarly. On the other hand, in this region, the CV_MAD produced the highest values of MSE. Those findings suggest that the alternative estimators of the population CV are considerably affected by α and β. Table 7 presents the median values of the log₁₀(γ) accuracy metric of the Beta distribution. It reveals that the MAD- and MnAD-based estimators are the better choices.

FIGURE 10

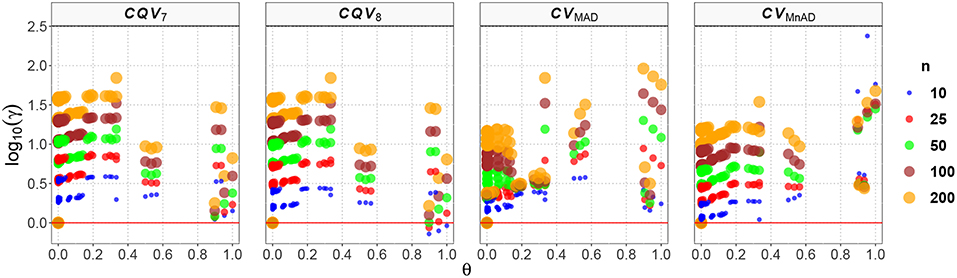
Figure 10. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the reparametrized Beta distribution.

TABLE 7

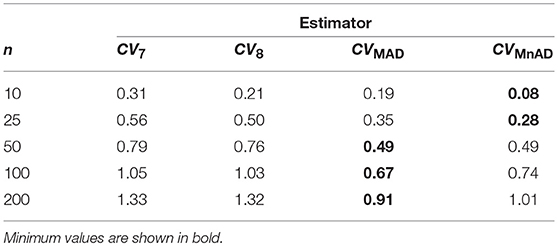
Table 7. Median values of log₁₀(γ) accuracy metric across θ produced for each estimator and sample sizes under Beta distribution.

The results for the Gamma distribution are shown in Figure 11. As expected, the results are similar to what was found in the Chi-square distribution, as that distribution is a special case of the Gamma distribution. Reparameterization of the Gamma distribution in terms of μ and σ resulted in a positive relationship between θ and the log₁₀(γ) accuracy metric; i.e., the accuracy increased when θ increased and a positive relationship existed between sample size and MSE. The CQV₇ and CQV₈ estimators performed equally poorly. This result implies that the CQV-based estimators do not perform as well as the classic estimator when n increases. Detailed analysis of the results from estimators of the CV revealed that log₁₀(γ)_CV7 ∈ (0.52, 1.66), log₁₀(γ)_CV8 ∈ (0.38, 1.65), log₁₀(γ)_CVMAD ∈ (0.00, 0.45), and log₁₀(γ)_CVMnAD ∈ (0.24, 1.25). Overall, our findings indicate that the behavior of estimators is close to the Chi-square case and that the CV_MAD can be a good alternative to the classic estimator of the CV for this particular distribution.

FIGURE 11

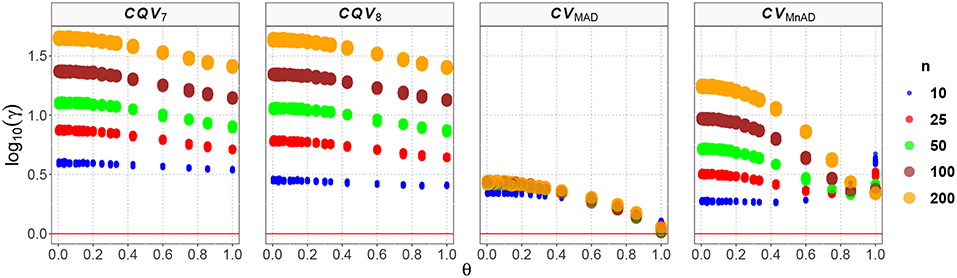
Figure 11. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the reparametrized Gamma distribution.

Figure 12 shows the values of the log₁₀(γ) accuracy metric for the Ex-Gaussian distribution. Although in almost every case none of the evaluated estimators showed an equivalent or better performance than the classic estimator of the CV, some aspects do deserve to be described. Firstly, the values of the log₁₀(γ) accuracy metric for the CQV₇ and CQV₈ estimators, as observed in the previous distributions, increase as a function of n. In general, log₁₀(γ)_CQV7 ∈ (0, 1.64) and log₁₀(γ)_CQV8 ∈ (0, 1.62). However, we found only one case where the CQV₇ and CQV₈ estimators are more efficient than the classic estimator when μ = 4.3, σ = 4.9, ν = 0.7, n = 10 such that log₁₀(γ)_CQV7 = −1.34, and log₁₀(γ)_CQV78 = −2.10 respectively. Generally, the MSE of these two estimators is higher than that of the classic estimator of the CV, making them, in practice, less feasible alternatives to the classic CV. Altogether, these results indicate how similar the performances of the CQV-based estimators are, and that they do not represent a suitable choice, to replace the classic CV estimator for this particular distribution.

FIGURE 12

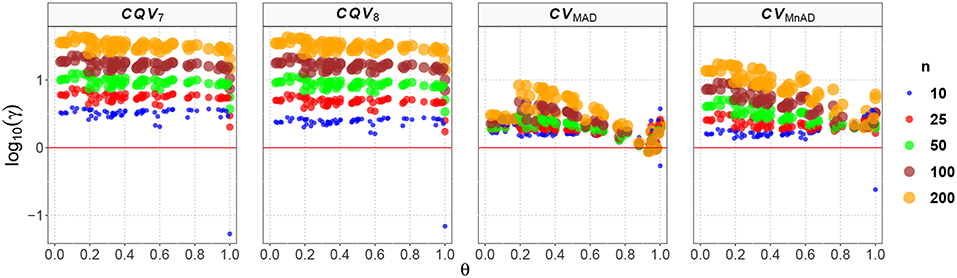
Figure 12. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the reparametrized Ex-Gaussian distribution.

Table 8 presents the median values of the log₁₀(γ) accuracy metric of the Ex-Gaussian distribution. This table reveals that the MAD estimator is the best choice. There are cases where the CV_MAD performs slightly better than the classic estimator of the CV. For example, when μ = 0.3, σ = 0.7, ν = 1, n = 200, we have log₁₀(γ)_CVMAD = −0.027, from which it can be concluded that the CV_MAD estimator is a reasonable choice.

TABLE 8

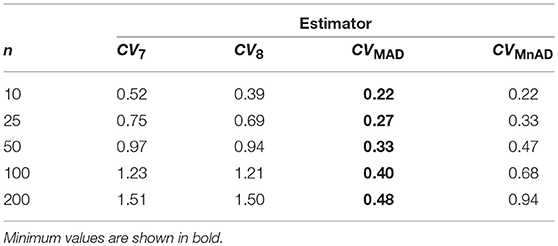
Table 8. Median values of log₁₀(γ) accuracy metric across θ produced for each estimator and sample sizes under the Ex-Gaussian distribution.

Finally, the results for the Lognormal distribution are shown in Figure 13. Although our results indicate that only the CV_MnAD estimators provided values of γ ≤ 1, there are several aspects worth highlighting. First, the CQV₇ and CQV₈ estimators have the poorest performance among the four estimators under evaluation. Second, γ rapidly increases with n for the CQV₇ and CQV₈ estimators, but the same does not seem to occur for the CV_MAD or CV_MnAD estimators. In the plot of the CV_MnAD estimator, note a behavior completely different to the CQV₇, CQV₈, and CV_MAD estimators. For this estimator, we observed a negative tendency in relation to the values of θ producing smaller MSEs than the other estimators when θ increases. On the other hand, the CV_MAD estimator present a slow positive tendency in relation to the values of θ producing higher MSEs when θ increases. Table 9 presents the median values of the log₁₀(γ) accuracy metric of the Lognormal distribution. This table reveals that the MnAD estimator is the best choice.

FIGURE 13

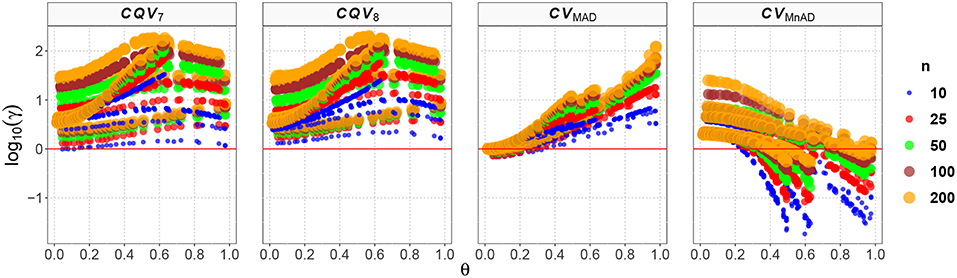
Figure 13. Scatter plots comparing the log₁₀(γ) accuracy metric as a function of θ ∈ (0, 1) produced for each estimator and sample size under the Lognormal distribution.

TABLE 9

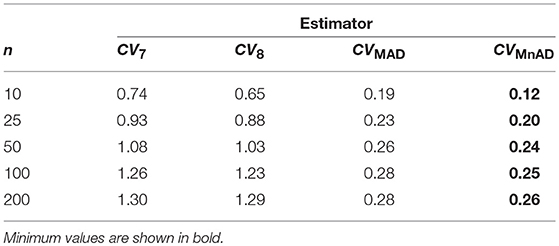
Table 9. Median values of log₁₀(γ) accuracy metric across θ produced for each estimator and sample sizes under the Lognormal distribution.

Through the simulations, we demonstrate that the proposed estimators can expand the existing methods for estimating the CV population and thus can enrich the literature. Specifically, some accepted estimators in the literature of the CV population have serious limitations and are less satisfactory in practice because they do not fully incorporate the distributional behavior of the data, and thus we conclude that our estimator CV_MAD is the most stable and robust in almost all the scenarios considered herein.

5. Examples

The simulation results in the previous section indicate that, overall, the CV_MAD gives a good performance. The applicability of this measure is examined by re-analysing two real data sets: one data set from the field of psychology and one from the field of genomics. Both examples represent cases in which data do not resemble Gaussian shapes and thus preclude the use of the classic Pearson version of the CV.

5.1. Age and Gender Differences in Reaction Time in Adulthood

Der and Deary [17] analyzed simple reaction times (SRTs) of 7,130 male and female adult participants whose ages ranged between 18 and 82 years. In the SRT task, participants underwent 20 test trials and the mean and standard deviation (SD) were estimated for each participant across trials. With that information, classic CVs were estimated for each participant. It is important to note that in the original data set [107, 108], reanalyzed by Der and Deary [17], only the mean RT and SD per participant were given (i.e., the raw results for the 20 trials each participant underwent were summarized via these sample estimators of location and scale). A more accurate reanalysis of such data could have been performed if the raw data were available. However, this is not the case, as the original data set was obtained in that way between 1984 and 1985 [17]⁶. Analyses of the CVs with respect to age showed a curvilinear trend, no gender (gender) effects, and a slowing of SRTs (y) after the age (age) of 50. Figure 14A represents the mean CV per age group originally reported in the upper left panel of Figure 3 in Der and Deary [17].

FIGURE 14

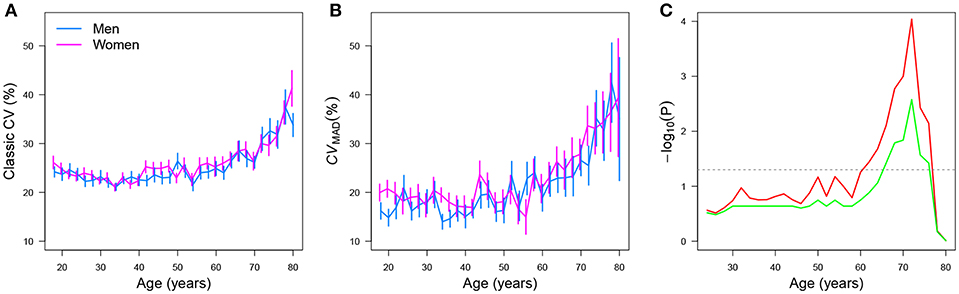
Figure 14. Mean and standard error for the simple RT classic CV, by gender, as a function of age when the (A) classic and (B) CV_MAD estimators of the CV are used. The plot (C) shows −log₁₀(P) for the structural change test as a function of age. Here, the value P indicates the p-value obtained by performing the test. Raw and FDR-corrected p-values are shown in red and green, respectively. Values above the gray horizontal line are significant at 5%.

Figure 14B shows the point estimatives of the CV by use of the CV_MAD estimator per age group. Standard errors were estimated via nonparametric bootstrap [109] using B = 1, 000 samples with replacement. (This method is used when the statistic's distribution is unknown). Using a linear regression model, a likelihood ratio test confirmed a quadratic (curvilinear) trend (F = 102.66, p = 1.3 ×10⁻¹⁴) and that females had, on average, a higher CV_MAD than males $(\hat{\beta }=0.0134,{\hat{\sigma }}_{\hat{\beta }}=0.0065,p=0.0428)$. A structural change analysis using the Chow test [110], implemented in the strucchange [111] add-on package for R, was used to further examine the data via the sctest() function:

 

  R>  sctest(y  gender  +  age, data = dataset,

                                     type = ‘‘Chow'')

 

The results indicated that the CV_MAD increased after 60 years, regardless of gender (red line, Figure 14C). We used the false discovery rate method (FDR) [112, 113] to correct our results for multiple testing using the p.adjust() function implemented in R. After FDR correction, we found that that the CV_MAD increased after the age of 66, regardless of gender (green line, Figure 14C). These analyses by no means undermine those originally reported by Der and Deary [17]; instead, they offer an extension of the original analyses by using robust CV estimators.

5.2. Age of Onset in Alzheimer's Disease

Alzheimer's disease (AD) is clinically characterized by learning disabilities, cognitive decline and memory loss that are sufficient to interfere with the everyday activities and performance of individuals [114–118]. As of 2010, more than 36 million people worldwide had AD or a related dementia [114]. Without new medicines to prevent, delay or stop the disease, this figure is projected to dramatically increase to approximately 116 million dementia cases by 2050 [119].

Recently, Vélez et al. [120] clinically and genetically characterized 93 individuals with familial AD from the world's largest pedigree in which a single-base mutation in the Presenilin 1 (PSEN1) gene causes AD, namely the E280A mutation [121–124]. One of the most intriguing characteristics of this pedigree is the high variability (strong evidence that the data are not necessarily normally distributed) in the age of onset (AOO) of the disease, which ranges from early thirties to late seventies [123]. Vélez et al. [120] found strong evidence that mutations in the apolipoprotein E (APOE) gene modify AOO in carriers of the E280A mutation. In particular, the presence of the APOE^*E2 allele in patients with PSEN1 E280A AD increases AOO by approximately 8.2 years when no other genetic variants or demographic information are controlled for.

Figure 1d reported by Vélez et al. [120] clearly indicates that the presence/absence of the APOE^*E2 allele on ADAOO data are non-normally distributed; and in this case, a robust measure of the CV for comparing those groups may be more appropriate, and thus we used the CV_MAD proposed herein. The sample-based CV_MAD is 11.04% (n = 86) when the APOE^*E2 allele is absent, and 10.4% (n = 7) when it is present. The difference between these estimates (0.636) is negligible. (This result was also confirmed via a non-parametric bootstrap using the CV_MAD as the statistic of interest [p = 0.317]). Comparison with the original findings showed that this conclusion is in line with that initially reached, where the variance of the AOO among APOE^*E2 allele groups did not differ (p = 0.453, Vélez et al. [120]).

6. Discussion

The aim of this study was to compare the performance of a selected set of CVs across several statistical distributions. Our results indicated that, overall, the CV estimated by the ratio of the median absolute deviation to the median (i.e., the CV_MAD estimator) provided a suitable performance when compared to the classic estimator. We hypothesize that this is the case, because the MAD and median are robust estimators of location and scale (for details see [37, 44, 61, 65]).

As shown in Table 10, the smallest median values of the log₁₀(γ) accuracy metric were obtained by the CV_MAD and CV_MnAD estimators under different sample sizes and each distribution in Table 2. Based on these results, we recommend the MAD-based estimators as alternative estimators of the population CV.

TABLE 10

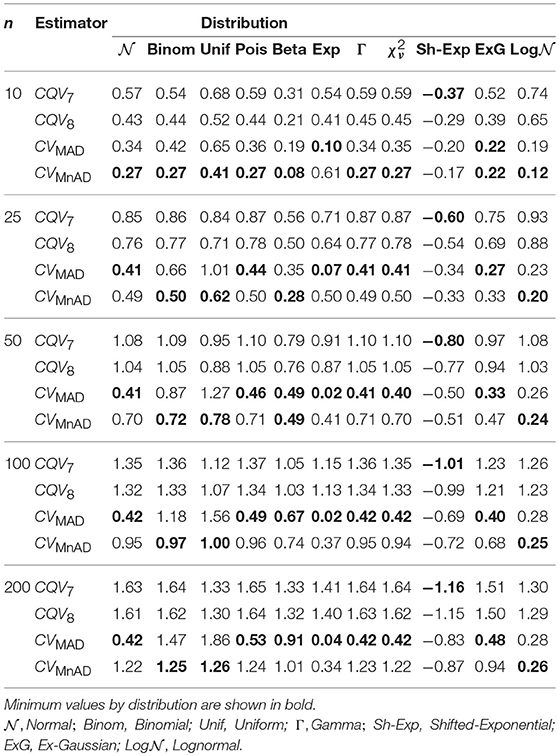
Table 10. Median values of log₁₀(γ) accuracy metric across θ produced for each estimator and sample sizes by distribution.

The methods studied here are by no means exhaustive; indeed, further variations could be conceived by using other estimators of location and scale. For example, it has been shown that the Harrell-Davis version of the median outperforms the classic median estimator [79, 125], the 20% trimmed mean tends to work well in many practical situations [126], and estimators of the mode have been shown to be highly efficient [127]. As for estimators of scale, in addition to those already in use (i.e., the SD, MAD, MnAD and IQR), estimators such as the percentage bend midvariance, the biweight midvariance or the τ measure of variation could be used [44]. For example, by using a mode estimator, say the Venter [128], another estimator of the CV could be proposed, such as MoAD/MoV, where MoAD is the (Venter) mode absolute deviation from the (Venter) mode, and MoV is the (Venter) mode⁷.

Probability distributions with positive and negative support can arise in the case of electroencephalogram (EEG) data. Such data could be modeled via the Johnson distribution [129]. This distribution is characterized by the parameter vector (μ, σ, ν, τ) where μ, σ, ν, and τ are the location, scale, skewness, and kurtosis, respectively. Preliminary results show that the median-based estimators of the CV give negative values of the log₁₀(γ) accuracy metric when random samples of size n = 50 from a negatively-skewed Johnson distribution with parameters (μ, σ, ν, τ) = (2, 2, −1, 1) were simulated. The estimation and suitable interpretations of the CV in asymmetric truncated (e.g., truncated reaction times), bounded discrete (e.g., M-point Likert ratings), contaminated, heavy-tailed and finite mixture distributions should be comprehensibly discussed and evaluated in upcoming in silico studies.

In summary, our results confirmed that (i) the type of quantile used to construct the CQV₇ and CQV₈ affects the performance of the estimators, and (ii) the MAD-based version of the CV performs better than the other estimators evaluated herein. Although Hyndman and Fan [43] provide a theoretical basis for the selection of quartile estimations, a thorough simulation study is still needed. We are working on this front. The preliminary results suggest that it is only in the case of the normal, continuous distributions that all quartiles fail to provide accurate estimates as the sample size decreases. This is, in fact, an expected result given that the smaller the sample size, the less reasonable the estimations are likely to be. Out of the quantiles' estimators for continuous distributions (i.e., type 4 to type 9; see [43], for more details), the type 6 quantile estimator seems to provide the most accurate results.

Author Contributions

FM-R and RO proposed the overall idea and contributed equally to the discussion sections. RO implemented the simulations.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

RO acknowledges financial support from CNPq/Brazil and FACEPE/Brazil. The authors thank Susan Brunner for proofreading earlier versions of this manuscript and Joan Gladwyn (https://properwords.co.nz) for professionally proofreading the published version. FM-R thanks Iryna Losyeva and Alexandra Marmolejo-Losyeva (ratoncito blanco) for their support.

Footnotes

1. ^In this paper, it is understood that the classic CV is a measure of relative variability (MRV) defined as σ/μ, which are parameters of scale and location of normally distributed data. We consider variations of this classic MRV—those cases in which the estimators in the numerator and the denominator are other than the classic sample dispersion and mean estimators. For simplicity, though, we tend to refer to the MRVs considered here merely as CVs.

2. ^Note the CV has been used in the context of pairwise comparisons and hypothesis testing [28, 47], see also [48, Form. 2, p. 326].

3. ^The breakdown value is the smallest fraction of contamination that can cause the estimator to take on values far from its value on the uncontaminated data [57, 58].

4. ^Suppose $\hat{\theta }$ is an estimator for an unknown parameter θ. Then the mean squared error (MSE) $\hat{\theta }$ is defined as $MSE(\hat{\theta })=Var(\hat{\theta })+{[B(\hat{\theta })]}^2$, where $B(\hat{\theta })=E(\hat{\theta })-\theta$ and $Var(\hat{\theta })=E[{(\hat{\theta }-\theta )}^2]$ are the bias and the variance term of the estimator, respectively. If two estimators ${\hat{\theta }}_1$ and ${\hat{\theta }}_2$ of θ are given, the estimator ${\hat{\theta }}_2$ is said to be superior to ${\hat{\theta }}_1$ with respect to the MSE criterion, if and only if $MSE({\hat{\theta }}_1)-MSE({\hat{\theta }}_2)\ge 0.$ Note that the MSE is a special case of a non-negative function called “loss function” that generally increases as the distance between $\hat{\theta }$ and θ increases. If θ is real-valued (as is the population CV), the most widely used loss function is defined as $L(\hat{\theta },\theta )={(\hat{\theta }-\theta )}^2$, which is the squared error loss.

5. ^The R code used in this simulation study is available in the following repository: https://github.com/Raydonal/Performance-CV

6. ^The distribution of RTs rarely resembles a normal distribution. Instead, positively-skewed distributions, e.g., the Ex-Gaussian, fit RT data more appropriately [99]. It is possible that estimating the mean and the SD as parameters of location and scale for RT data can lead to biased results as the mean and SD are optimal for normally-distributed data. Thus, when dealing with non-normal distributions, robust estimators of location and scale are preferred.

7. ^Various robust estimators of location and scale are already implemented in the R packages robustbase, modeest, and WRS2. The DescTools package offers some tools for winsorizing, mean trimming, robust standardization, among others (e.g., 95% CIs around the median, the Hodges-Lehmann estimator of location, the Huber M-estimator of location, etc.).

References

1. Martin JD, Gray LN. Measurement of relative variation: sociological examples. Am Sociol Rev. (1971) 36:496–502. doi: 10.2307/2093089

CrossRef Full Text | Google Scholar

2. Stevens SS. On the theory of scales of measurement. Science. (1946) 103:677–80. doi: 10.1126/science.103.2684.677

CrossRef Full Text | Google Scholar

3. Soong TT. Fundamentals of Probability and Statistics for Engineers. New York, NY: John Wiley & Sons (2004).

Google Scholar

4. Pearson K. Mathematical contributions to the theory of evolution. III. Regression, heredity, and panmixia. Philos Trans R Soc Lond Ser A. (1896) 187:253–318. doi: 10.1098/rsta.1896.0007

CrossRef Full Text | Google Scholar

5. Michell J. Measurement scales and statistics: a clash of paradigms. Psychol Bull. (1986) 100:398–407. doi: 10.1037/0033-2909.100.3.398

CrossRef Full Text | Google Scholar

6. Velleman PF, Wilkinson L. Nominal, ordinal, interval, and ratio typologies are misleading. Am Stat. (1993) 47:65–72. doi: 10.1080/00031305.1993.10475938

CrossRef Full Text | Google Scholar

7. Snedecor GW, Cochran WG. Statistical Methods, 8th Edn. Ames, IA: Iowa State university Press (1989).

8. Chattopadhyay B, Kelley K. Estimation of the coefficient of variation with minimum risk: a sequential method for minimizing sampling error and study cost. Multivar Behav Res. (2016) 51:627–48. doi: 10.1080/00273171.2016.1203279

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Kieschnick R, McCullough BD. Regression analysis of variates observed on (0, 1): percentages, proportions and fractions. Stat Model. (2003) 3:193–213. doi: 10.1191/1471082X03st053oa

CrossRef Full Text | Google Scholar

10. Castagliola P, Achouri A, Taleb H, Celano G, Psarakis S. Monitoring the coefficient of variation using a variable sampling interval control chart. Qual Reliabil Eng Int. (2013) 29:1135–49. doi: 10.1002/qre.1465

CrossRef Full Text | Google Scholar

11. Gao Y, Vogt A, Forsyth CJ, Koide K. Comparison of splicing factor 3b inhibitors in human cells. ChemBioChem. (2013) 14:49–52. doi: 10.1002/cbic.201200558

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lamare F, Le Maitre A, Dawood M, Schäfers KP, Fernandez P, Rimoldi OE, et al. Evaluation of respiratory and cardiac motion correction schemes in dual gated PET/CT cardiac imaging. Med Phys. (2014) 41:072504. doi: 10.1118/1.4881099

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Félix MA, Barkoulas M. Pervasive robustness in biological systems. Nat Rev Genet. (2015) 16:483–96. doi: 10.1038/nrg3949

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Faber DS, Korn H. Applicability of the coefficient of variation method for analyzing synaptic plasticity. Biophys J. (1991) 60:1288–94. doi: 10.1016/S0006-3495(91)82162-2

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Christodoulou C, Bugmann G. Coefficient of variation vs. mean interspike interval curves: what do they tell us about the brain? Neurocomputing. (2001) 38–40:1141–9. doi: 10.1016/S0925-2312(01)00480-5

CrossRef Full Text | Google Scholar

16. Hulstijn JH, Van Gelderen A, Schoonen R. Automatization in second language acquisition: what does the coefficient of variation tell us? Appl Psycholinguist. (2009) 30:555–82. doi: 10.1017/S0142716409990014

CrossRef Full Text | Google Scholar

17. Der G, Deary IJ. Age and sex differences in reaction time in adulthood: results from the United Kingdom health and lifestyle survey. Psychol Aging. (2006) 21:62–73. doi: 10.1037/0882-7974.21.1.62

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Sheskin DJ. Handbook of Parametric and Nonparametric Statistical Procedures. New York, NY: CRC Press (2011).

Google Scholar

19. Trafimow D. On teaching about the coefficient of variation in introductory statistics courses. Teach Stat. (2014) 36:81–2. doi: 10.1111/test.12042

CrossRef Full Text | Google Scholar

20. Trafimow D. The implication of the coefficient of centrality for assessing the meaning of the mean. Front Psychol. (2014) 5:1356. doi: 10.3389/fpsyg.2014.01356

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Bedeian AG, Mossholder KW. On the use of coefficient of variation as a measure of diversity. Organ Res Methods. (2000) 3:285–97. doi: 10.1177/109442810033005

CrossRef Full Text | Google Scholar

22. Sørensen JB, Sorensen JB, Soerensen JB. The use and misuse of the coefficient of variation in organizational demography research. Sociol Methods Res. (2002) 30:475–91. doi: 10.1177/0049124102030004001

CrossRef Full Text | Google Scholar

23. Ugarte MD, Militino AF, Arnholt AT. Probability and statistics with R. New York, NY: CRC Press (2016).

Google Scholar

24. McKay AT. Distribution of the coefficient of variation and the extended t distribution. J R Stat Soc. (1932) 95:695–8. doi: 10.2307/2342041

CrossRef Full Text | Google Scholar

25. David FN. Note on the application of Fisher's k-statistics. Biometrika. (1949) 36:383–93. doi: 10.1093/biomet/36.3-4.383

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Vangel MG. Confidence intervals for a normal coefficient of variation. Am Stat. (1996) 50:21–6. doi: 10.1080/00031305.1996.10473537

CrossRef Full Text | Google Scholar

27. Zeigler RK. Estimators of coefficient of variation using k samples. Technometrics. (1973) 15:409–14. doi: 10.1080/00401706.1973.10489053

CrossRef Full Text | Google Scholar

28. Forkman J. Estimator and tests for common coefficients of variation in normal distributions. Commun Stat Theory Methods. (2009) 38:233–51. doi: 10.1080/03610920802187448

CrossRef Full Text | Google Scholar

29. Forkman J, Verrill S. The distribution of McKay's approximation for the coefficient of variation. Stat Probabil Lett. (2008) 78:10–4. doi: 10.1016/j.spl.2007.04.018

CrossRef Full Text | Google Scholar

30. Díaz-Francés E, Rubio FJ. On the existence of a normal approximation to the distribution of the ratio of two independent normal random variables. Stat Papers. (2013) 54:309–23. doi: 10.1007/s00362-012-0429-2

CrossRef Full Text | Google Scholar

31. Huber PJ. Robust Statistics. New York, NY: Springer (2011).

Google Scholar

32. Mahmoudvand R, Hassani H. Two new confidence intervals for the coefficient of variation in a normal distribution. J Appl Stat. (2009) 36:429–42. doi: 10.1080/02664760802474249

CrossRef Full Text | Google Scholar

33. Hoseini J, Mohammadi A. Estimator and tests for coefficient of variation in uniform distribution. J Biometr Biostat. (2012) 3:1–5. doi: 10.4172/2155-6180.1000149

CrossRef Full Text | Google Scholar

34. Consulin CM, Ferreira D, de Lara IAR, Lorenzo AD, di Renzo L, Taconeli CA. Performance of coefficient of variation estimators in ranked set sampling. J Stat Comput Simulat. (2018) 88:221–34. doi: 10.1080/00949655.2017.1381959

CrossRef Full Text | Google Scholar

35. Albatineh AN, Kibria BMG, Wilcox ML, Zogheib B. Confidence interval estimation for the population coefficient of variation using ranked set sampling: a simulation study. J Appl Stat. (2014) 41:733–51. doi: 10.1080/02664763.2013.847405

CrossRef Full Text | Google Scholar

36. Liang T. Empirical Bayes estimation of coefficient of variation in shifted exponential distributions. J Nonparametr Stat. (2009) 21:365–78. doi: 10.1080/10485250802587992

CrossRef Full Text | Google Scholar

37. Gastwirth JL. Statistical Reasoning in Law and Public Policy, Vol. I. San Diego, CA: Academic Press (1988).

38. Bonett DG. Confidence interval for a coefficient of quartile variation. Comput Stat Data Anal. (2006) 50:2953–7. doi: 10.1016/j.csda.2005.05.007

CrossRef Full Text | Google Scholar

39. Brown RA. Robustness of the studentized range statistic. Biometrika. (1974) 61:171–5. doi: 10.1093/biomet/61.1.171

CrossRef Full Text | Google Scholar

40. Day RW, Quinn GP. Comparisons of treatments after an analysis of variance in ecology. Ecol Monogr. (1989) 59:433–63. doi: 10.2307/1943075

CrossRef Full Text | Google Scholar

41. Lund RE, Lund JR. Algorithm AS 190: probabilities and upper quantiles for the studentized range. J R Stat Soc. (1983) 32:204–10. doi: 10.2307/2347300

CrossRef Full Text | Google Scholar

42. Hoaglin DC, Mosteller F, Tukey JW. Understanding Robust and Exploratory Data Analysis. New York, NY: John Wiley & Sons (1983).

Google Scholar

43. Hyndman RJ, Fan Y. Sample quantiles in statistical packages. Amer Stat. (1996) 50:361–5. doi: 10.1080/00031305.1996.10473566

CrossRef Full Text | Google Scholar

44. Wilcox RR. Introduction to Robust Estimation and Hypothesis Testing. 3rd ed. San Diego, CA: Academic Press (2012) 471–532. doi: 10.1016/B978-0-12-386983-8.00010-X

CrossRef Full Text

45. Cajal B, Gervilla E, Palmer A. When the mean fails, use an M-estimator. Anales de Psicología. (2012) 28.

Google Scholar

46. Golan A, Judge GG, Miller D. Maximum Entropy Econometrics: Robust Estimation With Limited Data. New York, NY: Wiley (1996).

Google Scholar

47. Kohrding RK. A test of equality of two normal population means assuming homogeneous coefficients of variation. Ann Math Statist. (1969) 40:1374–85. doi: 10.1214/aoms/1177697509

CrossRef Full Text | Google Scholar

48. Banik S, Kibria BMG, Sharma D. Testing the population coefficient of variation. J Mod Appl Stat Methods. (2012) 11:325–35. doi: 10.22237/jmasm/1351742640

CrossRef Full Text | Google Scholar

49. Zimmerman DW. Invalidation of parametric and nonparametric statistical tests by concurrent violation of two assumptions. J Exp Educ. (1998) 67:55–68. doi: 10.1080/00220979809598344

CrossRef Full Text | Google Scholar

50. Johnson NL, Kotz S, Balakrishnan N. Continuous Univariate Distributions, 2nd Edn. New York, NY: Wiley (1994).

51. Groeneveld RA, Meeden G. Measuring skewness and kurtosis. J R Stat Soc Ser D. (1984) 33:391–9. doi: 10.2307/2987742

CrossRef Full Text | Google Scholar

52. Bonett DG, Seier E. Confidence intervals for mean absolute deviations. Am Stat. (2003) 57:233–6. doi: 10.1198/0003130032323

CrossRef Full Text | Google Scholar

53. Johnson NL, Kotz S, Balakrishnan N. Univariate Continuous Distributions. New York, NY: John Wiley & Sons (1994).

54. Zhang J. A highly efficient L-estimator for the location parameter of the Cauchy distribution. Comput Stat. (2010) 25:97–105. doi: 10.1007/s00180-009-0163-y

CrossRef Full Text | Google Scholar

55. Serfling R. Approximation Theorems of Mathematical Statistics. Wiley series in probability and mathematical statistics: probability and mathematical statistics. New York, NY: Wiley (1980).

Google Scholar

56. Parzen E. Quantile probability and statistical data modeling. Stat Sci. (2004) 19:652–62. doi: 10.1214/088342304000000387

CrossRef Full Text | Google Scholar

57. Hampel FR, Ronchetti EM, Rousseeuw PJ, Stahel WA. Robust Statistics: The Approach Based on Influence Functions. Vol. 114. New York, NY: John Wiley & Sons (2011).

58. Rousseeuw PJ, Leroy AM. Robust Regression and Outlier Detection, Vol. 589. New York, NY: John Wiley & Sons (2005).

Google Scholar

59. R Core Team D. R: A Language and Environment for Statistical Computing. Vienna: R Core Team (2010). Available online at: http://www.r-project.org

PubMed Abstract

60. Brys G, Hubert M, Struyf A. A robust measure of skewness. J Comput Graph Stat. (2004) 13:996–1017. doi: 10.1198/106186004X12632

CrossRef Full Text | Google Scholar

61. Rousseeuw PJ, Croux C. Alternatives to the median absolute deviation. J Am Stat Assoc. (1993) 88:1273–83. doi: 10.1080/01621459.1993.10476408

CrossRef Full Text | Google Scholar

62. Leys C, Ley C, Klein O, Bernard P, Licata L. Detecting outliers: do not use standard deviation around the mean, use absolute deviation around the median. J Exp Soc Psychol. (2013) 49:764–6. doi: 10.1016/j.jesp.2013.03.013

CrossRef Full Text | Google Scholar

63. Dodge Y. Statistical Data Analysis Based on the L1-Norm and Related Methods. Statistics for Industry and Technology. Basel: Birkhäuser (2012).

Google Scholar

64. Gather U, Hilker T. A note on Tyler's modification of the MAD for the Stahel-Donoho estimator. Ann Statist. (1997) 25:2024–26. doi: 10.1214/aos/1069362384

CrossRef Full Text | Google Scholar

65. Maronna RA, Martin DR, Yohai VJ. Robust Statistics: Theory and Methods. New York, NY: John Wiley and Sons (2006).

Google Scholar

66. Maesono Y. Asymptotic representation of ratio statistics and their mean squared errors. J Jpn Stat Soc. (2005) 35:73–97. doi: 10.14490/jjss.35.73

CrossRef Full Text | Google Scholar

67. Jayakumar GDS, Sulthan A. Exact sampling distribution of sample coefficient of variation. J Reliabil Stat Stud. (2015) 8:39–50.

Google Scholar

68. Hürlimann W. A uniform approximation to the sampling distribution of the coefficient of variation. Stat Probabil Lett. (1995) 24:263–8. doi: 10.1016/0167-7152(94)00182-8

CrossRef Full Text | Google Scholar

69. Albrecher H, Teugels JL. Asymptotic Analysis of Measures of Variation. Eindhoven: Eurandom (2004).

Google Scholar

70. Brown BM. Symmetric quantile averages and related estimators. Biometrika. (1981) 68:235–42. doi: 10.2307/2335824

CrossRef Full Text | Google Scholar

71. Bonett DG, Seier E. Confidence interval for a coefficient of dispersion in nonnormal distributions. Biometr J. (2006) 48:144–8. doi: 10.1002/bimj.200410148

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Paxton P, Curran PJ, Bollen KA, Kirby J, Chen F. Monte Carlo experiments: design and implementation. Struct Equat Model. (2001) 8:287–312. doi: 10.1207/S15328007SEM0802_7

CrossRef Full Text | Google Scholar

73. Pronzato L, Müller WG. Design of computer experiments: space filling and beyond. Stat Comput. (2012) 22:681–701. doi: 10.1007/s11222-011-9242-3

CrossRef Full Text | Google Scholar

74. Dupuy D, Helbert C, Franco J. DiceDesign and DiceEval: two R packages for design and analysis of computer experiments. J Stat Softw. (2015) 65:1–38. doi: 10.18637/jss.v065.i11

CrossRef Full Text | Google Scholar

75. Li R, Zhao Z. “Measures of performance for evaluation of estimators and filters,” IN Proceedings of SPIE Conference on Signal and Data Processing of Small Targets. Bellingham (2001). p. 4473–61.

Google Scholar

76. García S, Fernández A, Luengo J, Herrera F. A study of statistical techniques and performance measures for genetics-based machine learning: accuracy and interpretability. Soft Comput. (2008) 13:959. doi: 10.1007/s00500-008-0392-y

CrossRef Full Text | Google Scholar

77. Robert C, Casella G. Monte Carlo Statistical Methods. Springer Texts in Statistics. New York, NY: Springer (2005).

Google Scholar

78. Lin LIK. A concordance correlation coefficient to evaluate reproducibility. Biometrics. (1989) 45:255–68. doi: 10.2307/2532051

PubMed Abstract | CrossRef Full Text

79. Vélez JI, Correa JC. Should we think of a different Median estimator? Comunicaciones en Estadística. (2014) 7:11–7. doi: 10.15332/s2027-3355.2014.0001.01

CrossRef Full Text

80. Weed DL. Weight of evidence: a review of concept and methods. Risk Anal. (2005) 25:1545–57. doi: 10.1111/j.1539-6924.2005.00699.x

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Hartley RV. Transmission of information 1. Bell Syst Tech J. (1928) 7:535–63. doi: 10.1002/j.1538-7305.1928.tb01236.x

CrossRef Full Text | Google Scholar

82. Shannon C. A mathematical theory of communication. Bell Syst Tech J. (1948) 27:379–423, 623–656. doi: 10.1002/j.1538-7305.1948.tb00917.x

CrossRef Full Text | Google Scholar

83. MacKay DJ. Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press (2003).

Google Scholar

84. Marmolejo-Ramos F, Vélez JI, Romão X. Automatic outlier detection of discordant outliers using Ueda's method. J Stat Distribut Appl. (2015) 2:1–14. doi: 10.1186/s40488-015-0035-7

CrossRef Full Text

85. Vélez JI, Correa JC, Marmolejo-Ramos F. A new approach to the Box-Cox transformation. Front Appl Math Stat. (2015) 1:12. doi: 10.3389/fams.2015.00012

CrossRef Full Text | Google Scholar

86. Bryson MC. Heavy-tailed distributions: properties and tests. Technometrics. (1974) 16:61–8. doi: 10.1080/00401706.1974.10489150

CrossRef Full Text | Google Scholar

87. Student. The probable error of a mean. Biometrika. (1908) 6:1–25. doi: 10.1093/biomet/6.1.1

CrossRef Full Text | Google Scholar

88. Cox DR, Cox DR, Cox DR, Cox DR. Renewal Theory. Vol. 1. London: Methuen (1967).

Google Scholar

89. Thangjai W, Niwitpong SA. Confidence intervals for the weighted coefficients of variation of two-parameter exponential distributions. Cogent Math. (2017) 4:1315880. doi: 10.1080/23311835.2017.1315880

CrossRef Full Text | Google Scholar

90. Baten A, Kamil A. Inventory management systems with hazardous items of two-parameter exponential distribution. J Soc Sci. (2009) 5:183–7. doi: 10.3844/jssp.2009.183.187

CrossRef Full Text | Google Scholar

91. Grubbs FE. Approximate fiducial bounds on reliability for the two parameter negative exponential distribution. Technometrics. (1971) 13:873–6. doi: 10.1080/00401706.1971.10488858

CrossRef Full Text | Google Scholar

92. Reh W, Scheffler B. Significance tests and confidence intervals for coefficients of variation. Comput Stat Data Anal. (1996) 22:449–52. doi: 10.1016/0167-9473(96)83707-8

CrossRef Full Text | Google Scholar

93. Aalen OO, Valberg M, Grotmol T, Tretli S. Understanding variation in disease risk: the elusive concept of frailty. Int J Epidemiol. (2014) 44:1408–21. doi: 10.1093/ije/dyu192

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Brewer GA. Analyzing response time distributions. Zeitschrift Psychol. (2011) 219:117–24. doi: 10.1027/2151-2604/a000056

CrossRef Full Text | Google Scholar

95. Leth-Steensen C, Elbaz ZK, Douglas VI. Mean response times, variability, and skew in the responding of ADHD children: a response time distributional approach. Acta Psychol. (2000) 104:167–90. doi: 10.1016/S0001-6918(00)00019-6

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Gordon B, Carson K. The basis for choice reaction time slowing in Alzheimer's disease. Brain Cogn. (1990) 13:148–66. doi: 10.1016/0278-2626(90)90047-R

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Palmer EM, Horowitz TS, Torralba A, Wolfe JM. What are the shapes of response time distributions in visual search? J Exp Psychol Hum Percept Perform. (2011) 37:58–71. doi: 10.1037/a0020747

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Marmolejo-Ramos F, Cousineau D, Benites L, Maehara R. On the efficacy of procedures to normalize Ex-Gaussian distributions. Front Psychol. (2015) 5:1548. doi: 10.3389/fpsyg.2014.01548

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Marmolejo-Ramos F, González-Burgos J. A power comparison of various tests of univariate normality on ex-Gaussian distributions. Methodology. (2013) 9:137–49. doi: 10.1027/1614-2241/a000059

CrossRef Full Text | Google Scholar

100. Burbeck SL, Luce RD. Evidence from auditory simple reaction times for both change and level detectors. Percept Psychophys. (1982) 32:117–33. doi: 10.3758/BF03204271

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Dawson MRW. Fitting the ex-Gaussian equation to reaction time distributions. Behav Res Methods Instrum Comput. (1988) 20:54–7. doi: 10.3758/BF03202603

CrossRef Full Text | Google Scholar

102. Crow EL, Shimizu K. Lognormal Distributions. New York, NY: Marcel Dekker (1987).

Google Scholar

103. Limpert E, Stahel WA, Abbt M. Log-normal Distributions across the Sciences: Keys and Clues: On the charms of statistics, and how mechanical models resembling gambling machines offer a link to a handy way to characterize log-normal distributions, which can provide deeper insight into variability and probability—normal or log-normal: that is the question. AIBS Bull. (2001) 51:341–52. doi: 10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2

CrossRef Full Text | Google Scholar

104. Tukey JW. A survey of sampling from contaminated distributions. Contribut Probabil Stat. (1960) 2:448–85.

Google Scholar

105. Huber PJ. Robust estimation of a location parameter. Ann Math Stat. (1964) 35:73–101. doi: 10.1214/aoms/1177703732

CrossRef Full Text

106. Hettmansperger TP, McKean JW. Robust Nonparametric Statistical Methods. New York, NY: CRC Press (2010).

Google Scholar

107. Cox B, Blaxter M, Buckle A, Fenner N, Golding J, Gore M, et al. The Health and Lifestyle Survey. Preliminary Report of a Nationwide Survey of the Physical and Mental Health, Attitudes and Lifestyle of a Random Sample of 9,003 British Adults. London: Health Promotion Research Trust (1987).

108. Cox BD, Huppert FA, Whichelow MJ. The Health and Lifestyle Survey: Seven Years on: A Longitudinal Study of a Nationwide Sample, Measuring Changes in Physical and Mental Health, Attitudes and Lifestyle. Hanover: Dartmouth Publishing Group (1993).

Google Scholar

109. Efron B. Bootstrap methods: another look at the jacknife. Ann Stat. (1979) 1:1–26. doi: 10.1214/aos/1176344552

CrossRef Full Text | Google Scholar

110. Chow GC. Tests of equality between sets of coefficients in two linear regressions. Econometrica. (1960) 28:591–605. doi: 10.2307/1910133

CrossRef Full Text | Google Scholar

111. Zeileis A, Leisch F, Hornik K, Kleiber C. strucchange: an R package for testing for structural change in linear regression models. J Stat Softw. (2002) 7:1–38. doi: 10.18637/jss.v007.i02

CrossRef Full Text | Google Scholar

112. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Ser B. (1995) 57:289–300. doi: 10.1111/j.2517-6161.1995.tb02031.x

CrossRef Full Text | Google Scholar

113. Vélez JI, Correa JC, Arcos-Burgos M. A new method for detecting significant p-values with applications to genetic data. Rev Colomb Estadist. (2014) 37:67–76. doi: 10.15446/rce.v37n1.44358

CrossRef Full Text

114. Alzheimer's A. 2014 Alzheimer's disease facts and figures. Alzheimer's Dement. (2014) 10:e47–e92. doi: 10.1016/j.jalz.2014.02.001

CrossRef Full Text | Google Scholar

115. Alzheimer's A. About a peculiar disease of the cerebral cortex. By Alois Alzheimer, 1907 (Translated by L. Jarvik and H. Greenson). Alzheimer Dis Assoc Disord. (1987) 1:3–8.

116. Qiu C, Kivipelto M, von Strauss E. Epidemiology of Alzheimer's disease: occurrence, determinants, and strategies toward intervention. Dial Clin Neurosci. (2009) 11:111–28.

PubMed Abstract | Google Scholar

117. Reitz C, Brayne C, Mayeux R. Epidemiology of Alzheimer's disease. Nat Rev Neurol. (2011) 7:137–52. doi: 10.1038/nrneurol.2011.2

CrossRef Full Text | Google Scholar

118. Reitz C, Mayeux R. Alzheimer disease: epidemiology, diagnostic criteria, risk factors and biomarkers. Biochem Pharmacol. (2014) 88:640–51. doi: 10.1016/j.bcp.2013.12.024

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Prince M, Bryce R, Albanese E, Wimo A, Ribeiro W, Ferri CP. The global prevalence of dementia: a systematic review and meta-analysis. Alzheimer's Dement. (2013) 9:63–75. doi: 10.1016/j.jalz.2012.11.007

CrossRef Full Text | Google Scholar

120. Vélez JI, Lopera F, Sepulveda-Falla D. APOE^*E2 allele delays age of onset in PSEN1 E280A Alzheimer's disease. Mol Psychiatry. (2016) 21:916–24. doi: 10.1038/mp.2015.177

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Lopera F, Ardilla A, Martínez A, Madrigal L, Arango-Viana JC, Lemere CA, et al. Clinical features of early-onset Alzheimer disease in a large kindred with an E280A presenilin-1 mutation. JAMA. (1997) 277:793–9. doi: 10.1001/jama.277.10.793

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Arcos-Burgos M, Muenke M. Genetics of population isolates. Clin Genet. (2002) 61:233–47. doi: 10.1034/j.1399-0004.2002.610401.x

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Acosta-Baena N, et al. Pre-dementia clinical stages in presenilin 1 E280A familial early-onset Alzheimer's disease: a retrospective cohort study. Lancet Neurol. (2011) 10:213–20. doi: 10.1016/S1474-4422(10)70323-9

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Vélez JI, Chandrasekharappa SC, Henao E, Martinez AF, Harper U, Jones M, et al. Pooling/bootstrap-based GWAS (pbGWAS) identifies new loci modifying the age of onset in PSEN1 p. Glu280Ala Alzheimer's disease. Mol Psychiatry. (2013) 18:568–75. doi: 10.1038/mp.2012.81

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Harrell FE, Davis CE. A new distribution-free quantile estimator. Biometrika. (1982) 69:635–40. doi: 10.1093/biomet/69.3.635

CrossRef Full Text | Google Scholar

126. Wilcox R. Trimming and winsorization. Encycl Biostatist. (2005) 8:1–3. doi: 10.1002/0470011815.b2a15165

CrossRef Full Text | Google Scholar

127. Bickel DR. Robust and efficient estimation of the mode of continuous data: the mode as a viable measure of central tendency. J Stat Comput Simulat. (2003) 73:899–912. doi: 10.1080/0094965031000097809

CrossRef Full Text | Google Scholar

128. Venter JH. On estimation of the mode. Ann Math Stat. (1967) 38:1446–55. doi: 10.1214/aoms/1177698699

CrossRef Full Text | Google Scholar

129. Johnson NL. Systems of frequency curves derived from the first law of Laplace. Trabajos Estadística. (1955) 5:283–91. doi: 10.1007/BF03005988

CrossRef Full Text | Google Scholar