- 1Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, IL, United States
- 2Department of Mathematical Sciences, Worcester Polytechnic Institute, Worcester, MA, United States
Estimates of risk-neutral densities of future asset returns have been commonly used for pricing new financial derivatives, detecting profitable opportunities, and measuring central bank policy impacts. We develop a new nonparametric approach for estimating the risk-neutral density of asset prices and reformulate its estimation into a double-constrained optimization problem. We evaluate our approach using the S&P 500 market option prices from 1996 to 2015. A comprehensive cross-validation study shows that our approach outperforms the existing nonparametric quartic B-spline and cubic spline methods, as well as the parametric method based on the normal inverse Gaussian distribution. As an application, we use the proposed density estimator to price long-term variance swaps, and the model-implied prices match reasonably well with those of the variance future downloaded from the Chicago Board Options Exchange website.
1 Introduction
A financial derivative, such as option, swap, future, or forward contract, is an asset that is contingent on an underlying asset. Its fair price can be obtained by calculating the expected future payoff under a risk-neutral probability distribution. Therefore, the problem of pricing a derivative can be addressed via estimating the risk-neutral density (RND) of the future payoff of the underlying asset. The estimated prices, known as fair prices, may help companies and investors to avoid financial risk or detect profitable opportunities, especially on over-the-counter (OTC) securities. The estimated risk-neutral distribution can be further used by, for example, central banks to infer market belief on economic events of interest and measure impacts of monetary policies [1–3]. On the other hand, the market prices of the derivatives traded in a financial market reveal information about the RND. Breeden and Litzenberger (1978) [4] were among the first to use option prices to estimate the risk-neural probability distribution of the future payoff of the underlying asset. Among the financial products that can be used to recover the RND, European options are the most common ones, which give the investors rights to trade assets at a preagreed price (i.e., strike price) at the maturity date. Among all the underlying assets that options are written on, Standard and Poor’s 500 Index (S&P 500) is a popular one, which aggregates the values of stocks of 500 large companies traded on American stock exchanges and provides a credible view of the American stock market for investors.
There are a plethora of approaches toward recovering RND functions in the literature (see, for example, [5], for an extensive review). Parametric approaches typically specify a statistical model for the RND and the structural parameters are recovered by solving an optimization problem. For instance, a lognormal distribution was used in [6]; a mixture of lognormal distributions proposed by [7] was considered in [2]; and a three-parameter Burr distribution was employed in [8], called the Burr family, which covers a broad range of shapes, including distributions similar to gamma, lognormal, and J-shaped beta. Another commonly used probability distribution in the literature of derivative pricing is the generalized hyperbolic distribution that contains variance gamma, normal inverse Gaussian (NIG), and t distributions as special cases (see, for instance, [9, 10]).
Nonparametric procedures, by contrast, are free from distributional assumptions on the underlying asset and thus achieve more flexibility than parametric methods. For example, in [11], cubic spline functions to model the unknown RND were used. An estimated density is numerically obtained by solving a quadratic programming problem with a convex objective function and nonnegativity constraints. The authors deliberately chose more knots than option strikes for higher flexibility. Lee (2014) [12] approximated the risk-neutral cumulative distribution function using quartic B-splines with power tails and the minimum number of knots that meet zero bid-ask spread. Their estimation was based on out-of-the-money option prices.
In this article, we propose a simpler but more powerful nonparametric solution using piecewise constant (PC) functions to estimate the RND. It is easy to implement since the estimating problem is formulated as a weighted least squared (WLS) procedure. It is more powerful since our method can recover the RND more effectively with all available option market prices without screening. Furthermore, our solution provides a practical way to explore profitable investment opportunities in financial markets by comparing the estimated prices and corresponding market prices.
The rest of this article is structured as follows. In Materials and Methods, we introduce the proposed nonparametric approach after reviewing cubic splines, quartic B-splines, and the NIG parametric approaches in the literature. In Pricing European Options, we run comprehensive cross-validation studies using the S&P 500 European option data to compare different methods and provide theoretical justifications on the consistency of our estimator for fair option prices. In Pricing Variance Swap, we apply the proposed nonparametric approach to price variance swaps, which is challenging in practice [13, 14]. We conclude in Discussion. The proofs and more formulae are collected in the Supplementary Material.
2 Materials and Methods
In this section, we first provide a brief review of the cubic splines, quartic B-splines, and NIG approaches in the literature for recovering the RND. Then, we introduce the proposed PC nonparametric approach with least square (LS) and WLS procedures.
2.1 Nonnegative Cubic Spline Estimate for RND
Given the current trading date t and the expiration date T of European options, let
For the sake of nonnegativity of the estimated RNDs, in [11], the solution is much more complicated and computationally expensive than the usual cubic spline estimates. For comparison purposes, we keep only the constraints that ensure the nonnegativity of the density function on knots in their optimization procedure. By evaluating the difference between the estimated fair prices and the market prices of options, if our approach achieves higher accuracy than the cubic spline estimate with fewer constraints, then our approach is considered to be superior to that of [11].
When it comes to practical implementation [11], eliminating option prices is suggested that led to potential arbitrage opportunities according to the bid-ask interval, put-call parity, monotonicity, and strict convexity. They also generated “fake” call option prices using put-call parity to eliminate “artificial” arbitrage opportunities. Our comprehensive studies in Pricing European Options show that their screening and cleaning procedure may result in substantial information loss.
2.2 Quartic B-Spline Estimate
Lee (2014) [12] adopted a uniform quartic B-spline to estimate the risk-neutral cumulative distribution function (CDF). They used power tails to extrapolate outside the strike price range. They suggested using only the out-of-the-money (hereafter, OTM) options to estimate the CDF, including OTM call options whose strikes are higher than the underlying asset price and OTM put options whose strikes are lower than the underlying asset price. OTM options are typically cheaper than in-the-money (ITM) options and are considered to be more liquid as well. Nevertheless, our case studies in Pricing European Options show that ITM options may help recover the RND as well.
Due to fewer parameters, the quartic B-spline estimate is computationally more efficient than the nonnegative cubic spline approach. Lee (2014) [12] chose the number of knots needed as the minimum number that satisfies zero bid-ask pricing spread. They also suggested eliminating options that violate monotonicity and strict convexity constraints.
2.3 NIG Parametric Approach
For comparison purposes, we choose one parametric approach for approximating the RND, as suggested by [9, 15]. It is based on the NIG distribution, which belongs to the generalized hyperbolic class and can be characterized by its first four moments, i.e., mean, variance, skewness, and kurtosis. According to [16], these four moments can be estimated by the OTM European call and put options. One major issue with NIG density estimate is that, as shown in [10], the feasibility of NIG approach drops down as the time-to-maturity increases since more estimated skewness and kurtosis pairs fall outside the feasible domain of the NIG distribution.
2.4 The Proposed Piecewise Constant Nonparametric Approach
The PC approach that we propose in this article is nonparametric by nature. It is simpler but more efficient. Let
To be precise, suppose that we have a collection of market prices of European put and call options that are traded on date t and expire on date T. Let
Given a RND
respectively, where
To account for the RND outside the range
and zero elsewhere. Here,
due to the condition
Given the approximate RND
respectively, which are essentially linear functions of
Proposition 2.1. Given
where
The proof of Proposition 2.1 is relegated to Supplementary Material A.
The unknown parameters
subject to
From an investment point of view, because a more expensive option tends to be less liquid, an alternative approach to determining
The WLS estimate is in favor of OTM options over ITM options in that OTM options are typically less expensive and more liquid.
3 Pricing European Options
In this section, we use the S&P 500 European options to evaluate the performances of various RND estimators.
3.1 S&P 500 European Option Data
We consider European calls and puts written on the S&P 500 indices from January 2, 1996, to August 31, 2015, in the United States [10, 14]. The expiration dates are the third Saturday of the delivery month. Following [14], we keep only the options with positive bid prices and positive volumes and with expiration date of more than seven days in our analysis. Similar to [10], we categorize options into seven groups with expiration in
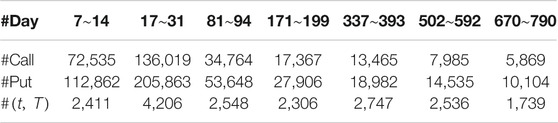
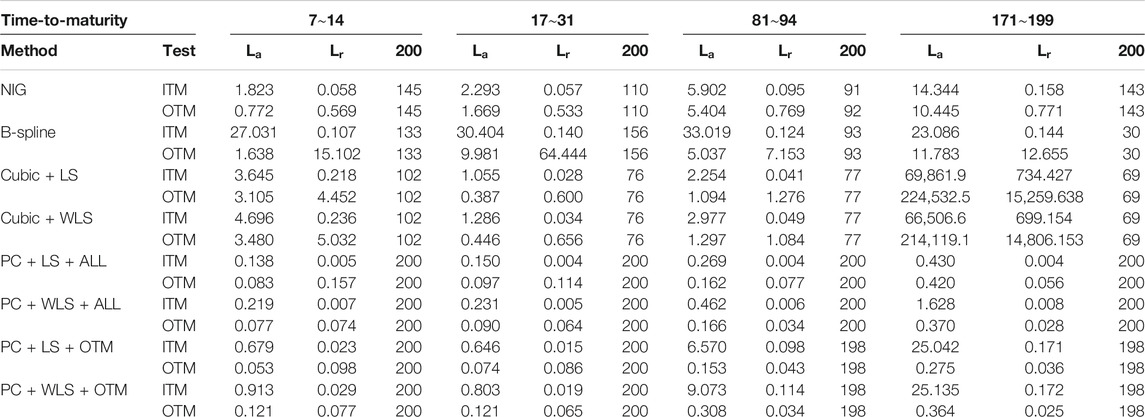
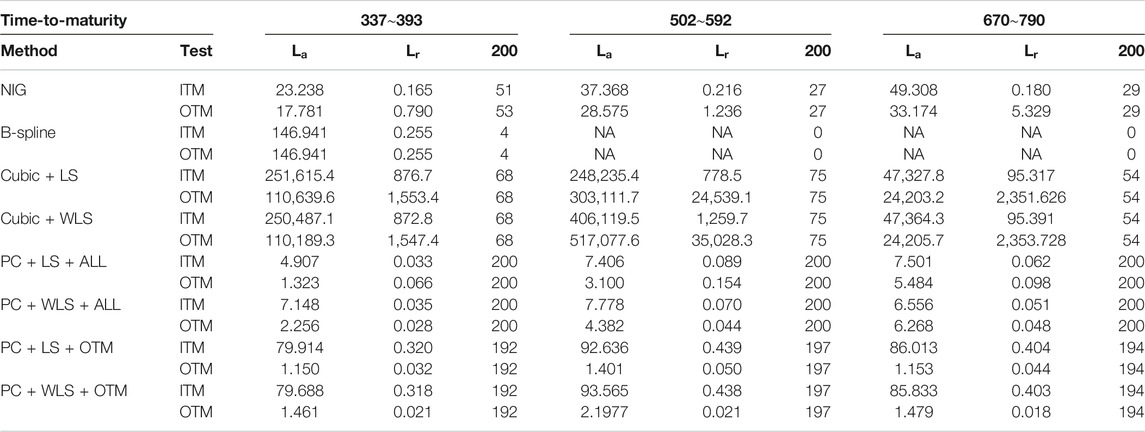
TABLE 1. Numbers of calls, puts, and
3.2 Comprehensive Comparisons With Existing Methods
We use the S&P 500 European options to evaluate the performance of the following methods: the parametric NIG estimate, the quartic B-spline (B-spline) estimate, the nonnegative cubic spline estimates with either LS criterion (cubic + LS) or WLS criterion (cubic + WLS), and the proposed PC estimate with either LS or WLS objective function using OTM options only (PC + LS + OTM or PC + WLS + OTM) or using all available options (PC + LS + ALL or PC + WLS + ALL). All the comparisons are made based on their ability to recover option market prices.
For each of the seven time-to-maturity categories listed in Table 1, we randomly selected 200 pairs of
where
In terms of the absolute error
3.3 Consistency of PC Estimates for Fair Prices
Given distinct strike prices
provided that RND
According to Eq. 1, the proposed PC approach provides the following approximation:
to the RND
Because
Theorem 3.1. Suppose there exists a continuous RND
Remark 1. Since
3.4 Detecting Profitable Opportunities
Theorem 3.1 provides analytical foundations for the consistency of the proposed PC method under the assumption of the existence of a continuous RND. Nevertheless, the PC method is still applicable even when there is an arbitrage opportunity in the market. In this case, a significant difference between the market price and its estimated fair price would be expected.
With a given set of market option prices, our nonparametric method can recover a fair option price for any strike price. From an investment point of view, we are able to detect options on the markets that are under- or overpriced. It may not be adequate to claim arbitrage opportunities due to the lack of guarantee to earn and since there is a mature market system designed to catch such kind of difference among the option prices. Nevertheless, we can still report profitable investment opportunities for investors.
In Figure 1, we provide an illustrative example using
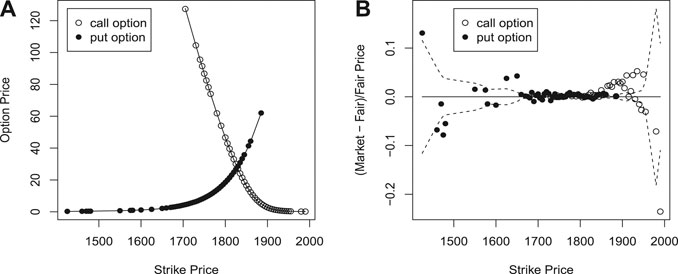
FIGURE 1. Leave-one-out cross-validation for options traded on April 14, 2014 with an expiration date of September 5, 2014 (round dot: market price; solid line: fair price based on PC; dash line: 95% confidence interval based on bootstrap).
To have a closer look at the difference between market price and fair price, we plot the relative difference, that is (market price - fair price)/fair price, against strike price in Figure 1B. The sign of the relative difference tells us whether the option is under- or overpriced. In addition, in order to check if the difference between a market price and its fair price is statistically significant, we bootstrap the rest of the market prices 50 times to obtain a 95% confidence interval of the fair price. The dash lines in Figure 1B show the upper and lower ends of the bootstrap confidence intervals. When a market price falls outside its bootstrap confidence interval, we may report to investors that the corresponding option is significantly under-/overpriced compared with the market prices of the other options.
4 Pricing Variance Swap
With an estimated RND, one can calculate the fair price of any derivative whose payoff is a function of
A variance swap is a financial product that allows investors to trade realized variance against current implied variance of log returns. More specifically, let
where the variance notional
Variance swaps provide investors with pure exposure to the variance of the underlying asset without directional risk. It is notably liquid across major equities, indices, and stock markets and is growing across other markets. Historical evidence indicates that selling variance is systematically profitable.
There are numerous methods in the literature of pricing variance swaps, both analytically and numerically (see [13] for an extensive review). Nevertheless, a pricing formula or procedure that relies on a certain stochastic process, for instance, Lévy process [14], MRG-Vasicek model [17], or Hawkes jump-diffusion model [18], may suffer from a lack of parsimony or might not fit the real data well due to the inappropriateness of model assumptions (see, for instance, [14]).
In this section, we propose a moment-based method in conjunction with our PC RND estimate to price variance swaps, which is free of model assumption.
Assuming the existence of a risk-neutral measure
where
Assumption 1. The increments of the process
Consequently, the fair price of a variance swap can be represented by a sequence of the risk-neutral moments of the underlying asset.
Proposition 4.1. Assuming the existence of a risk-neutral measure
The proof of Proposition 4.1 is relegated to Supplementary Material C.
4.1 Moments Calculation
In view of Eq. 12, pricing variance swaps requires estimating the first and second moments of
Recall that the step function
Note that there are no market prices available for options that expire on a day that is other than the third Saturday of the delivery month. We would have to interpolate the mean and standard deviation of
4.2 Replicating by Variance Futures
In order to evaluate the fair price of a variance swap, we replicate variance swap using available market prices of variance futures. Variance future is a financial contract that is traded over the counter. As stated in [20], variance swap and variance future are essentially the same since they both trade the difference of variance and one can replicate a variance swap by the corresponding variance future. As a matter of fact, if variance future and variance swap share the same expiration date, then at the start point of the observation period, there is no difference between trading a variance future and trading a variance swap with $50 variance notional. The formula for the fair price of a variance swap contract induced from variance future is given by
where M is the number of observed days to date,
4.3 Variance Future Data
Variance future data were downloaded from the Chicago Board Options Exchange (CBOE) website (http://cfe.cboe.com/). Variance future products with 12-month (with futures symbol VA) or 3-month (with futures symbol VT) expirations are traded on the CBOE Futures Exchange. We use VA in the subsequent analysis. The continuously compounded zero-coupon interest rates cover dates from January 2, 1996 to August 31, 2015. For variance futures, the trading dates are from December 10, 2012, to August 31, 2015, with start dates from December 21, 2010, to July 30, 2015, and expiration dates from January 18, 2013, to January 1, 2016. We use variance futures to replicate variance swaps, so the time spans of variance swaps are in line with those of variance futures.
4.4 Results
In order to assess the accuracy of our estimated fair prices of a variance swap, we compare three relevant quantities:
1. OP: Fair price of a variance swap based on our moment-based nonparametric approach, using option market prices till day t
2. VF: Induced market price of a variance swap from CBOE traded variance future till day t
3. True: Realized price of a variance swap at expiration day T with known
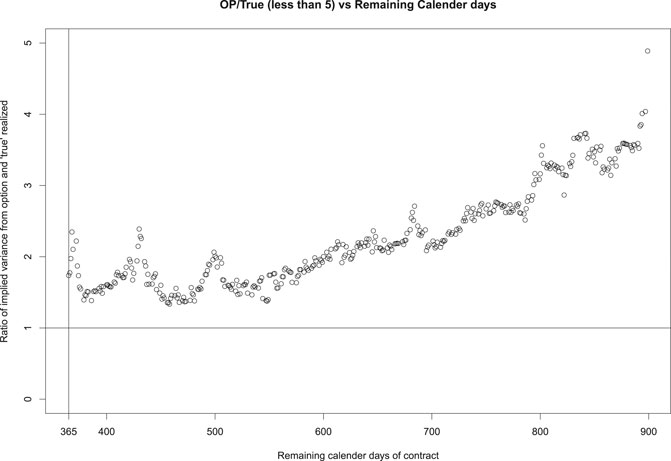
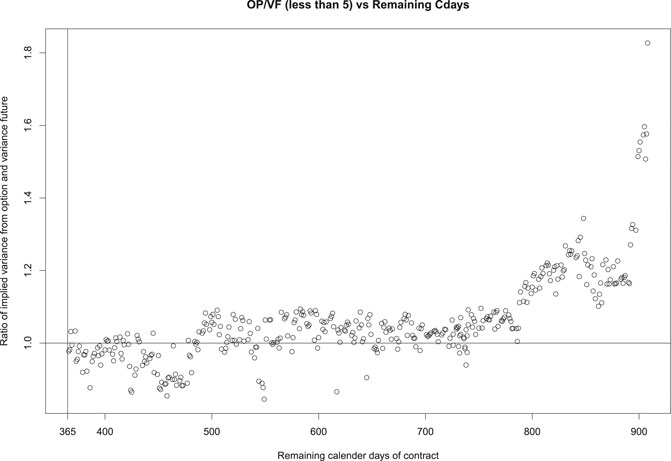
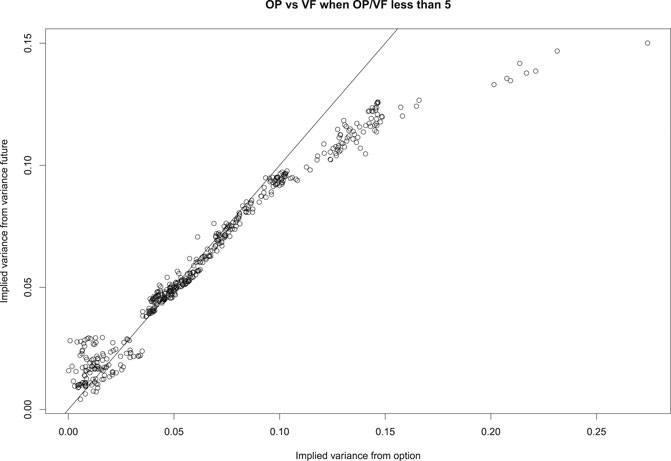
We present three ratios, OP/True, VF/True, and OP/VF, in Figures 2–4, respectively, against the remaining calendar days of variance swaps. Compared with ‘True’ prices based on realized underlying asset prices, Figure 2 and Figure 3 suggest that OP and VF have a similar increasing pattern along with the remaining calendar days. This is in part due to the uncertainty in the estimate of the variance, which increases with the number of days to expiration. On the other hand, Figure 4 and Figure 5 show that the fair price OP based on our proposed method matches the market price VF pretty well on variance swaps with expiration between 365 and 800 days. For variance swaps expiring in less than 365 days (not shown here), OP and VF do not match well. This is plausibly attributed to the fact that long-term options are more reasonable and stable, which are less likely to be affected by external factors or noises. For variance swaps longer than 800 days, the relatively low VF might indicate underpriced variance futures.
5 Discussion
In this article, we propose a new nonparametric approach for estimating the RND. It is data-driven and is not built on any model assumption about the data generating process of underlying asset prices. It only assumes the existence of an RND and the independence of increments of log return for pricing variance swaps. That is why it can capture the market price very well.
In contrast with other nonparametric methods, such as cubic spline and B-spline, our method is much simpler but fits the real data better. We choose only distinct strikes as knots and assume constant values between knots to avoid overfitting. By sacrificing the continuity of estimated RND, the nonnegativity of a density function is readily satisfied.
On the other hand, the proposed approach utilizes market prices of all options, not just OTM options. In our opinion, ITM options, despite not being as liquid as OTM options, still contain market information and should be incorporated when estimating a RND. Our comprehensive analysis shows that it recovers OTM option prices better by including ITM option prices.
One of the potential applications of our work is to price OTC securities. The comprehensive comparisons of different methods using S&P 500 European option data in Pricing European Options show the outperformance of our estimates across various time-to-maturity periods. With our estimated RNDs, financial engineers may be able to develop more sophisticated financial products to fit the needs of their customers better. A fair price of the new financial product will not only facilitate the traders but also reduce their financial risk.
Another potential application is to build up profitable portfolios for investment purposes. In Detecting Profitable Opportunities, we show how to use leave-one-out and bootstrap techniques to identify under- or overpriced options from fair-priced options. Real-time trading algorithms may be developed based on our estimates toward catching up profitable opportunities by buying underpriced options and shorting overpriced options.
Pricing variance swaps is a difficult job when dealing with real data. We display in Figures 2–5 only the cases where the ratio OP/True is less than 5. There are cases where OP and VF disagree significantly. Overall, our OP prices work better for variance futures that expire in the last four months of 2015, which are also the last four months available in our dataset.
In the literature, RND is naturally connected to the concept of statistic discount factor or pricing kernel, which can be described as the ratio of the RND and the physical density [21]. The proposed nonparametric estimate of RND could be applied to estimate pricing kernel as well.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://cfe.cboe.com/, Chicago Board Options Exchange (CBOE) website.
Author Contributions
LJ and SZ processed the experimental data and performed the analysis. LJ drafted the manuscript. JY, LJ, and KL developed the theory and performed the analytical calculations. FW and KL helped supervise the project. JY, FW, and LJ conceived the original idea. JY supervised the project. All authors discussed the results and contributed to the final manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Liming Feng from the University of Illinois at Urbana-Champaign and Yuhang Liang from Northwestern University for their enormous help during data collection.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2020.611878/full#supplementary-material.
References
1. Malz, AM. A simple and reliable way to compute option-based risk-neutral distributions. In: Staff report New York, NY: Federal Reserve Bank of New York. (2014). p 677.
2. Melick, W, and Thomas, C. Recovering an asset’s implied pdf from option prices: an application to crude oil during the gulf crisis. J Financ Quant Anal (1997). 32:91–115. doi:10.2307/2331318
3. Taboga, M. Option-implied probability distributions: how reliable? How jagged? Int Rev Econ Finance (2016). 45:453–69. doi:10.1016/j.iref.2016.07.013
4. Breeden, D, and Litzenberger, R. Prices of state-contingent claims implicit in option prices. J Bus (1978). 51:621–51.
5. Bliss, R, and Panigirtzoglou, N. Testing the stability of implied probability density functions. J Bank Finance (2002). 26:381–422. doi:10.2139/ssrn.209650
6. Jarrow, R, and Rudd, A. Approximate option valuation for arbitrary stochastic process. J Financ Econ (1982). 10:347–69. doi:10.1016/0304-405X(82)90007-1
7. Ritchey, R. Call option valuation for discrete normal mixtures. J Financ Res (1990). 13:285–96. doi:10.1111/j.1475-6803.1990.tb00633.x
8. Sherrick, B, Irwin, S, and Forster, D. Option-based evidence of the nonstationarity of expected SP 500 futures price distributions. J Futures Mark (1992). 12:275–90. doi:10.1002/fut.3990120304
9. Eriksson, A, Ghysels, E, and Wang, F. The normal inverse Gaussian distribution and the pricing of derivatives. J Deriv (2009). 16:23–37. doi:10.3905/JOD.2009.16.3.023
10. Ghysels, E, and Wang, F. Moment-implied densities: properties and applications. J Bus Econ Stat (2014). 32:88–111. doi:10.1080/07350015.2013.847842
11. Monteiro, A, Tutuncu, R, and Vicente, L. Recovering risk-neutral probability density functions from options prices using cubic splines. Eur J Oper Res (2008). 187:525–42. doi:10.1016/j.ejor.2007.02.041
12. Lee, S. Estimation of risk-neutral measures using quartic b-spline cumulative distribution functions with power tails. Quant Finance (2014). 14:1857–79. doi:10.1080/14697688.2012.742202
13. Zhu, SP, and Lian, GH. A closed-form exact solution for pricing variance swaps with stochastic volatility. Math Finance (2010). 21:233–56. doi:10.1111/j.1467-9965.2010.00436.x
14. Carr, P, Lee, R, and Wu, L. Variance swaps on time-changed Lévy processes. Finance Stochast (2012). 16:335–55. doi:10.1007/s00780-011-0157-9
15. Eriksson, A, Ghysels, E, and Forsberg, L. Approximating the probability distribution of functions of random variables: a new approach. Montreal, Canada:Cirano (2004). p 503.
16. Bakshi, G, Kapadia, N, and Madan, D. Stock return characteristics, skew laws, and the differential pricing of individual equity options. Rev Financ Stud (2003). 16:101–43. doi:10.2139/srn.282451
17. Han, Y, and Zhao, L. A closed-form pricing formula for variance swaps under MRG-Vasicek model. Comput Appl Math (2019). 38:142. doi:10.1007/s40314-019-0905-6
18. Liu, W, and Zhu, SP. Pricing variance swaps under the Hawkes jump-diffusion process. J Futures Mark (2019). 39:635–55. doi:10.1002/fut.21997
19. Rompolis, LS, and Tzavalis, E. Retrieving risk neutral moments and expected quadratic variation from option prices. Rev Quant Finance Account (2017). 48:955–1002. doi:10.2139/ssrn.936670
20. Biscamp, L, and Weithers, T. Variance swaps and cboe s and p 500 variance futures. Chicago Trading Company, LLC. (2007). p 25.
Keywords: pricing, risk-neutral density, double-constrained optimization, normal inverse Gaussian distribution, variance swap
Citation: Jiang L, Zhou S, Li K, Wang F and Yang J (2021) A New Nonparametric Estimate of the Risk-Neutral Density with Applications to Variance Swaps. Front. Appl. Math. Stat. 6:611878. doi: 10.3389/fams.2020.611878
Received: 29 September 2020; Accepted: 03 December 2020;
Published: 25 January 2021.
Edited by:
Eleftherios Ioannis Thalassinos, University of Piraeus, GreeceReviewed by:
Ramona Rupeika-Apoga, University of Latvia, LatviaInna Romānova, University of Latvia, Latvia
Copyright © 2021 Jiang, Zhou, Li, Wang and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jie Yang, anlhbmcwNkB1aWMuZWR1
 Liyuan Jiang1
Liyuan Jiang1 Keren Li
Keren Li Jie Yang
Jie Yang