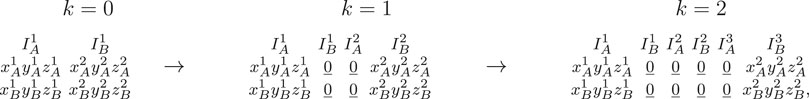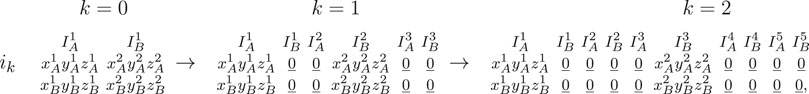- Department of Mathematics, College of Engineering, Mathematics and Physical Sciences, University of Exeter, Exeter, United Kingdom
We analyse periodic solutions in a system of four delayed differential equations forced by periodic inputs representing two competing neural populations connected with fast mutual excitation and slow delayed inhibition. The combination of mechanisms generates a rich dynamical structure that we are able to characterize using slow-fast dissection and a binary classification of states. We previously proved the existence conditions of all possible states 1:1 locked to the inputs and applied this analysis to the tracking of the rhythms perceived when listening to alternating sequences of low and high tones. Here we extend this analysis using analytical and computational tools by proving the existence a set of n:1 periodically locked states and their location in parameter space. Firstly we examine cycle skipping states and find that they accumulate in an infinite cascade of period-incrementing bifurcations with increasing periods for decreasing values of the local input strength. Secondly we analyse periodic solutions that alternate between 1:1 locked states that repeat after an integer multiple of the input period (swapping states). We show that such states accumulate in similar bifurcation cascades with decreasing values of the lateral input strength. We report a parameter-dependent scaling constant for the ratio of widths of successive regions in the cascades, which generalises across cycle skipping and swapping states. The periodic states reported here - emergent behaviours in the model - can be linked to known phenomena in auditory perception that are beyond the original scope of the model’s design.
1 Introduction
Differentiating between sound sources that overlap or are interleaved in time is a fundamental part of auditory perception (the so-called cocktail party problem) [1, 2]. The neural computations underpinning this segregation of sound sources has been the subject of dynamical systems models in various frameworks that focus on feature separation (e.g., differences in pitch) between interleaved, periodic sequences of sounds [3–5]. However, these studies failed to address neural computations where temporal mechanisms interact with inputs on the timescale of the input period. A recent study by the authors [6] addressed these computations in a framework inspired by the structure of the auditory processing pathway and by common features of neural computation in cortical brain areas (excitatory-inhibitory interactions, time-scale separation, transmission delays). Whilst our previous study focused on 1:1 locked states, here we report on more exotic dynamics that organise in cascades of bifurcations leading to solutions with increased period.
The encoding of sensory information in cortex involves subpopulations of tens of thousands to millions of neurons that are suitably represented by coarse-grained variables representing e.g., the mean firing rate of the population. The Wilson-Cowan equations [7] for localised populations of neurons describes the firing rates of neural populations, and they are widely used in small networks with excitatory and inhibitory coupling, intrinsic synaptic dynamics, neural adaptation and a nonlinear gain function [8–10].
Timescale separation is a common feature of models at the single neuron level [11, 12], and in populations of neurons [13]. Slow-fast analysis including singular perturbation theory has been instrumental in revealing the dynamical mechanisms behind spiking and bursting [12, 14] and in explaining complex dynamics in population models of neural competition [10, 15]. Extensions of these methods have been applied to systems with delays [16], in non-smooth settings [17] and in networks capable of instrinsically generating patterns of rhythmic behaviours (so-called central pattern generators, CPGs), such as locomotion, breathing, sleep [18].
Delayed inhibition modelled with slow variables in systems of ODEs representing CPG circuits with spiking units is important for the generation of patterns of activity reminiscent of those considered in this paper [19, 20]. Delays in small neural circuits modelled using DDE equations can lead to many interesting phenomena including inhibition-induced Hopf oscillations, oscillator death, multistability and switching between oscillatory solutions [21–23]. Two other key features of our study are that 1) units are not instrinsically oscillating and 2) periodic forcing of the units drives oscillations. Periodically forced systems with timescale separation have been explored in models of perceptual competition [24, 25], but not in the presence of delays. Periodic solutions in autonomous delay differential equations with Heaviside and monotonic gain functions have been studied analytically in a recent paper from the authors [26].
Periodic orbits can undergo cascades of bifurcations under parameter variation. This phenomena leads to an increase in period and/or complexity of the emerging orbits. The mostly widely studied of these is the period-doubling cascade, a typical route to chaos that can be found in simple dynamical systems such as the smooth, discrete logistic map [27], or the periodically-forced, continuous-time duffing oscillator [28]. Continuous-time dynamical systems with a separation of timescales can produce mixed-mode oscillations with a sequence of bifurcations leading to additional low-amplitude excursions via a canard-induced mechanisms [29]. Analysis of so-called spike adding bifurcations have been instrumental in understanding bursting phenomena in excitable cells [30]: additional large-amplitude excursions can appear in a smooth bifurcation sequence. Here we show analytically that a cascade of periodic solutions with discrete steps in period that exist in non-overlapping, contiguous parameter regions. As the cascade progresses (here decreasing a parameter) these regions become narrower and the period increases in discrete jumps. These features are akin to a period-incrementing bifurcation sequence as reported in non-smooth maps [31]. We note that 1) overall these solutions exist in large parameter regions that overlap with 1:1 locked states previously reported, 2) in a non-smooth setting we cannot specify the bifurcation occurring at boundaries between regions and 3) nevertheless the solution branches persist when we relax the non-smooth assumptions as confirmed numerically.
We consider a periodically-driven competition network of two localised Wilson-Cowan units with lumped excitation and inhibition, generalised to include dynamics via inhibitory synaptic variables. The units A and B are driven by stereotyped input signals representative of neural responses in early auditory areas. Whilst mutual excitation between the units is fast, inhibition activates slowly and transmission between the units is delayed. The units’ activation function is taken as a Heaviside function restricting the possible state of each unit to be active (ON), inactive (OFF) or in a fast transition between these two states. This combination of modelling assumptions (fixed delays, slow-fast timescale separation, heaviside activation function) allows for all possible model states to be conveniently represented in a binary matricial form with entries specifying the state of the system in time intervals relating to the input timecourse, delay and activation timescales. This approach allows for exact parameter-dependent existence conditions to be derived, as for all 1:1 locked states in [6] and for more exotic states as reported here.
The paper is organised as follows. In Section 2 we propose a discontinuous system of delay differential equations to encode auditory perception. In Section 3 we report some results from our previous study of this system [6] that are used here to analyse new network states of interest. Specifically, we classify the possible dynamics of states in the intervals when tones are active and propose a binary matrix representation for each state in the system. In Section 4 we define cycle skipping states with period a multiple of the input period. We also derive analytically their existence conditions and show that they accumulate in cascades of period-incrementing bifurcations for decreasing values of the local input strength. A similar analysis is carried out in Section 5 to study switching states: a class of states in which the units’ dynamics alternate between TR-periodic states (thus forming solutions with larger period). Finally, in Section 6 we construct a smooth version of the model consisting of ordinary differential equations and use numerical simulations and continuation to show that our findings are not contingent on the presence of non-smooth components.
2 Model Description
We consider a periodically forced neural network of two Wilson-Cowan populations coupled by fast direct excitation and slow delayed inhibition (Figure 1A). Inhibition from both units act on a slower time scale and its dynamics is described by synaptic variables. The forcing terms mimic stereotyped synaptic inputs in the auditory cortex [32] to alternating sequences of A and B tones and has been used to study the auditory streaming paradigm (see [6] for more details). The combination between the timescale separation, forcing and delays give rise to a rich repertoire of dynamical states.
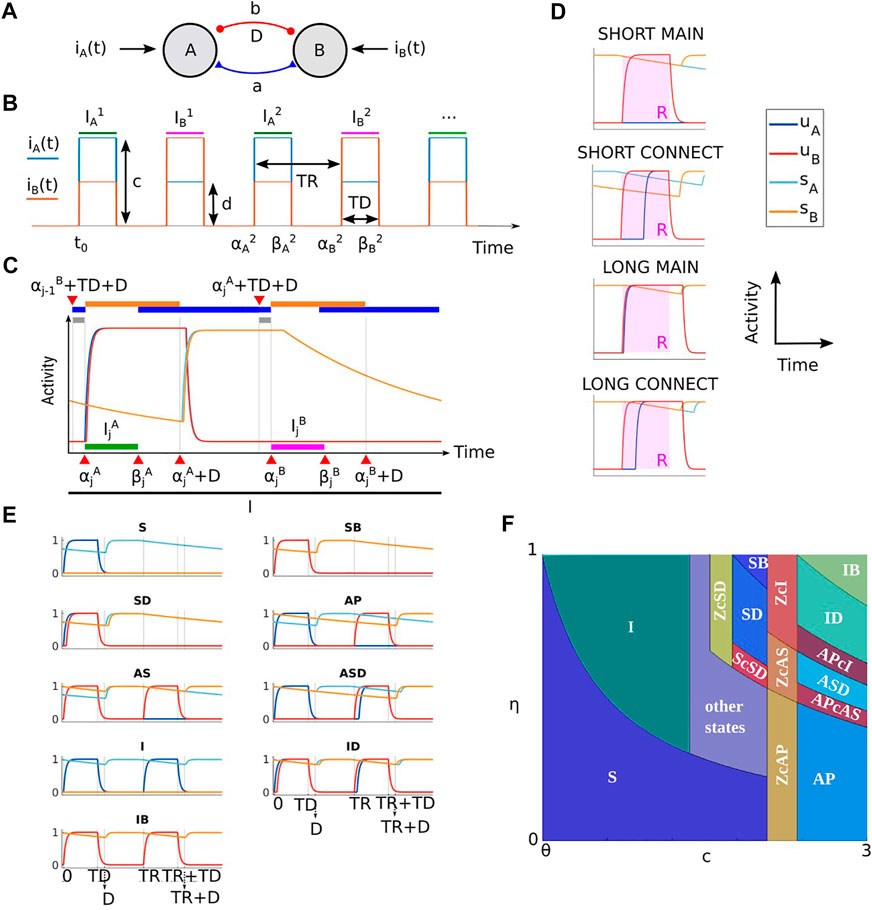
FIGURE 1. (A) Sketch of the model circuit: two neural populations (A and B) are mutually connected by excitation and inhibition with strengths a and b. Inhibition is delayed of the amount D. (B) Input to A and B populations are square-wave functions iA(t) and iB(t), respectively. These inputs mimic primary auditory cortical responses to sequences of interleaved A and B tones with duration TD and presentation rate PR (the repetition time TR is the inverse of PR). Parameters c is the local input strength from A (B) locations to unit A(B). Parameters d is the lateral input strength from B (A) locations to unit A(B). (C) Example dynamics for a solution of system (1) in a 2TR interval I (black interval) shows the subdivision into different intervals where the units’ dynamics is constrained (colored intervals, see Theorem 1). (D). Classification of states based on the dynamics during an active tone interval R ∈Φ. (E). Time histories for 2TR-periodic MAIN SHORT states. (F). Existence regions for 2TR-periodic MAIN and CONNECT states at varying (c, η). Parameters in panels E and F are TD = 0.025, D = 0.03, PR = 17, a = 0.6, b = 2, θ = 0.5.
The model is described by the following system of four DDEs representing two periodically forced neural populations (A and B populations) coupled by fast direct excitation and slow delayed inhibition
The variables uA and uB represent the activity of the A and B populations and have timescale τ, while sA and sB represent the activity of the inhibitory synaptic variables, have timescale τi and are delayed by fixed D. We will assume τi to be large and τ to be small. This condition poses system (1) in a slow-fast regime which will enable us to apply analytical tools to study model states. We consider a Heaviside gain function with threshold θ ∈ (0, 1): H(x) = 1 if x ≥θ and 0 otherwise, which is a common choice in Wilson Cowan models [10, 33]. Parameters a ≥ 0 and b ≥ 0 respectively represent the strengths of the excitatory and inhibitory coupling.
The forcing, square-waved periodic inputs (shown in Figure 1B) iA and iB, are defined by:
where c ≥ 0 and d ≥ 0 represent the local and lateral input strengths, respectively; χI is the indicator function χI(t) = 1 for t ∈ I and 0 otherwise. Throughout this work we will assume that local inputs are stronger than lateral ones, i.e., c ≥ d. We define the parameter TD representing the duration of each tone’s presentation and TR representing the time between tone onsets. The intervals when A and B tones are on (active tone intervals) are given by
for j = 1, …, ∞. Let us name the set of active tone intervals R as
In this work we assume that TD < D and TD + D < TR, which are guaranteed for moderate delays (motivated in [6]). We further assume that a − b < θ and c ≥ θ to avoid trivial saturating or resting dynamics in the system (as discussed in [6]). Throughout this paper system 1 was numerically integrated using Matlab’s built-in delay differential equation solver dde23 with fixed time step dt = 10–5.
Remark 2.1. The dynamics of the synaptic variable sA (sB) is dictated by that unit A (B). Indeed sA (sB) turns ON the fast time scale when A (B) is ON and slowly decays to zero when A (B) is OFF.
Remark 2.2 (Model symmetry). Let us consider the map swapping the A and B indexes in the variables of system (1)
and the application of the time shift TR. Since iA (t + TR) = iB(t) and iB (t + TR) = iA(t), the model is symmetrical under the composition of these two maps (
3 Background
In our previous paper [6] we split system (1) into slow and fast subsystems to characterise their quasi-equlibria. This analysis enabled us to classify all the possible 2TR-periodic states and determine their existence conditions in the parameter space. We now provide a summary of the main ideas, which are important for the new analysis presented here. The following theorem summarises three key properties characterizing the dynamics of each network state during any 2TR interval (Figure 1C), reported from Theorem 1, Lemma 1 and Lemma 2 in [6].
Theorem 1. Consider an arbitrary interval 2TRtime intervalIcontaining intervals
1. No unit can turn ON between successive active tone intervals (blue intervals)
2. The delayed synaptic variablessA (t − D) andsB (t − D) are monotonically decaying in the intervals
3. Both units are OFF in the intervals
As shown below, this theorem enabled us to split the dynamics of all network states in four different classes: the disjoint classes of MAIN and CONNECT states and the disjoint classes of SHORT and LONG states (Figure 1C).
Point 1. in Theorem 1 guarantees that the turning ON times for the units can only occur during an active tone interval. Since the A and B active tone intervals (green and purple intervals in Figure 1C) are included in intervals where the delayed synaptic variables are decaying the total inputs to the units in these active tone intervals is monotonically decaying, too. Thus if a unit turns ON at any time in an active tone interval it must remain ON at least until the offset of the interval. Given an active tone interval R ∈Φ we can therefore classify the set of states where the units may turn ON at onset of R (MAIN states) and the set of states where the units turn ON with some non-infinitesimal delay after the onset of R (CONNECT states). The following definition extends this classification for an arbitrary number of active tone intervals (see Figure 1D for examples of MAIN/CONNECT states in R).
Definition 3.1 (MAIN and CONNECT states). A state (solution) of system (1) is:
• MAIN if ∀R ∈Φ, if ∃t* ∈ R turning ON time for A or B, then t* = min(R)
• CONNECT if ∃R ∈Φ and ∃t* ∈ R, t* > min(R) turning ON time for A or B, with
Moreover, due to point 2. in Theorem 1 if both units are ON at the offset of an active tone interval R they may continue to be ON for some time after such offset time. However, due to point 3. in the same theorem, there exists a subsequent interval where both units turn OFF (i.e., before the onset of the next active tone interval). This leads to two possible classes of states: SHORT states for which both units are/turn OFF between the offset of R and the onset of its successive active tone interval, and LONG states for which the units remain ON for some time after the offset of R. We now extend this classification for an arbitrary number of active tone intervals (see Figure 1D for examples of SHORT/LONG states in R).
Definition 3.2 (LONG and SHORT states). We define any state of system (1):
• LONG if
• SHORT if both units are OFF
Moreover, in our earlier paper [6] we showed that the dynamics a unit’s jump up points during an active tone interval determine the subsequent dynamics in the same interval, as stated in the following theorem, which corresponds to Lemma 5 in [6].
Theorem 2. Given an active tone intervalR = [α, β] ∈ Φ we have:
1. A (B) turns ON at timet* ∈ R ⇔ A (B) is ON ∀t ∈ (t*, β]
2. A (B) is OFF at timet* ⇔ A (B) is OFF ∀t ∈ (α, t*]
We used this theorem to define the matrix form (a binary matrix) of each state, which describes the units’ dynamics in one active tone interval R. We extended this representation for two active tone intervals
3.1 Intuitive Construction of the Matrix Form
The matrix form for a given state in an active tone interval R = [α, β] ∈Φ is the 2 by 3 binary matrix
where the first (second) row follow the A (B) unit’s dynamics in R. Due to Theorem 2 if a unit turns ON at some time t* ∈ R if must be ON in (t*, β]. Therefore we have only four possible cases to consider for the first row of V. If unit A turns ON at time α then it is ON in all the interval R and we have xA = yA = zA = 1. If unit A is OFF at time α but turns ON after a small delay α + δ due to the excitation from unit B (δ is an infinitesimal delay on the fast time scale, δ ∼ τ) then we have xA = 0, yA = 1 and zA = 1. If unit A turns ON at some intermediate time t* ∈ (α + δ, β) then we have xA = 0, yA = 0 and zA = 1. Otherwise, if unit A is OFF in R all entries in the first row are zero. Analogous arguments lead to the construction of the second row via the dynamics of unit B.
Since the units’ dynamics dictate the dynamics of the synaptic variables (Remark 2.1) the matrix form uniquely describes the complete four dimensional dynamics of system (1) in all active tone intervals. However, the matrix form does not provide information about the dynamics between each pair of successive active tone intervals (thus establishing if the state is LONG or SHORT, see Remark 3.1 below).
The matrix form extension to 2TR-periodic states during two active tone intervals I1 = [0, TD] and I2 = [TR, TR + TD] is the 2 × 6 binary matrices of the form
where V1 and V2 are the matrix forms in the intervals I1 and I2, respectively in Eq. (3). The matrix form of these states is shown in Table 1. One can easily check that the matrix form of each state provides a visualization of the associated dynamics in the active tone intervals I1 and I2 shown in Figure 1E. In our previous work [6] we defined the matrix form Eq. (4) rigorously using analytical tools. Here we used an intuitive approach to facilitate the reading. The matrix form definition enabled us to derive the existence conditions for all viable 2TR-periodic states (and to rule out which states are impossible) and to visualise their existence regions in the space of parameters.

TABLE 1. Matrix form of all 2T R-periodic MAIN states (* asymmetrical states with coexisting conjugate). States were named following their proposed link with percepts in the auditory streaming paradigm ([6]). Specifically, names starting with S, I and AS represent segregation, integration and bistability, respectively. The ending letter B indicates states in which both units turn ON at the onset of the same active tone interval. The ending letter D indicates states in which a unit turns ON an infinitesimal delay after the other unit for at least one active tone interval.
A similar technique was used to find all CONNECT states and to define their existence conditions. Table 2 shows the matrix form of these states. We omit time histories because these can be visualised from the matrix forms of each state. Figure 1F shows the regions of existence of 2TR-periodic SHORT MAIN and CONNECT states in the (c, η) parameter plane, where η is a newly introduced parameter for scaling the lateral input as d = ηc and all other parameters are fixed.

TABLE 2. Matrix form of 2TR-periodic CONNECT states (* asymmetrical states). The existence regions of each state are located between the existence regions of specific MAIN states (Figure 1F). CONNECT states were named to indicate the branches of such MAIN states interspersed by the letter c. For example, the existence region of state APcAS is located between states AP and AS. Names containing the letter Z indicate that they connect branches of zero solutions (which cannot appear in the system for our parameter constraints).
Remark 3.1. The matrix forms shown in Tables 1, 2 do not provide information on the units’ dynamics outside the active tone intervals. Therefore, to establish if a state is SHORT or LONG we need to impose additional conditions at the offset times of the active tone intervals. As shown in [6] if both units are ON at the end of an active tone interval, they may continue to be ON after the offset of the active tone interval and turn OFF before the onset of the next active tone interval (LONG condition). The 2T R-periodic states in which at least one unit is OFF at the end of both intervals I1 and I2 are those states with matrix form given by S, AP, INT and ZcAP in Table 1 and Table 2 (these states cannot therefore be LONG). The remaining states can be LONG. The analysis of all the combinations of SHORT/LONG and MAIN/CONNECT states is given in [6].
4 Cycle Skipping States
In this section we define and study the conditions for the existence of cycle skipping states with 2TR-multiple period and show that they accumulate in cascades for decreasing values of the local input strength. For cycle skipping states we start from 2TR-periodic MAIN states with active tone intervals
where SB, SD, IB and ID are the states having matrix form given by their corresponding name (Table 1). As we shall soon prove, cycle skipping solutions of all other states do not exist.
The existence conditions for cycle skipping states of order k depend on the following quantities:
We note that for these quantities
We now proceed by defining kth-order cycle skipping segregated and integrated states and their matrix form. For simplicity in the notation of the next sections we introduce the vector
Definition 4.1. A cycle skipping segregated state sk of order
Figure 2 shows one period of the segregated cycle skipping MAIN state SD1. We notice that Definition 4.1 for k = 1 introduces two active tone intervals of silence (
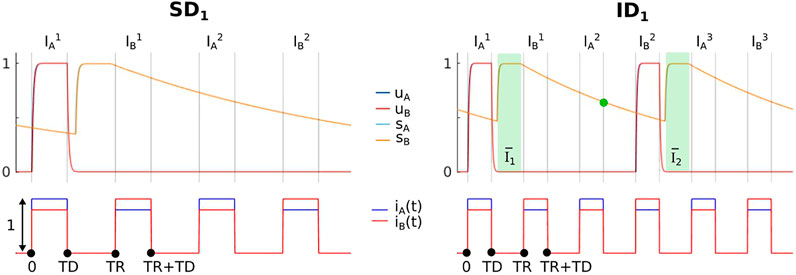
FIGURE 2. Time histories for states SD1 and ID1. Model parameters in both figures are a = 0.6, b = 2, d = 0.8, θ = 0.5, PR = 17, TD = 0.025, D = 0.03, τ = 0.001 and τi = 0.2. In addition, c = 1.4 for the left panel and c = 1.7 for the right panel.
The matrix form of each cycle skipping segregated state sk consists of 2 rows and n = 2k + 2 three dimensional row vector elements per column that describe the dynamics of the two units during the active tone intervals
where the A and B active tone intervals are indicated using the matrix form. We note that for k = 0 the cycle skipping states correspond to the original segregated state (i.e., SD0 = SD).
Theorem 3. There are no cycle skipping segregated states of the 2T R-periodic statesIB,ID,AP,ASorASD.
Proof. We assume that these states are SHORT (the proof for LONG states is analogous). All of these states have a general matrix form given by.
for some binary values x, y, z, w, p and q. Application of Definition 4.1 would give the following matrix form for the corresponding kth-order cycle skipping state:
Where
We now introduce a new class of cycle skipping states obtained from integrated states.
Definition 4.2. A cycle skipping integrated state ik of order
Figure 2 shows an example dynamics of the integrated cycle skipping MAIN state ID1. In this case the Definition 4.2 for k = 1 introduces four active tone intervals of silence (
Definition 4.2 can be applied to segregated states s ∈ S (not just to integrated states). The resulting cycle skipping state sk is equal to the segregated cycle skipping state S2k defined by 4.1. Therefore, Definition 4.1 include segregated cycle skipping states and we can omit an equivalent of Definition 4.2 for segregated states.
The matrix form of any cycle skipping integrated state ik has 2 rows and n = 4k + 2 three dimensional vector elements per column that describe the dynamics of the two units during the active tone intervals
where the A and B active tone intervals are indicated using the matrix form. Therefore corresponding cycle skipping states have period T = (4k + 2)TR. We note that for k = 0 the cycle skipping states correspond to the original integrated state (i.e., ID0 = ID).
Theorem 4. There are no cycle skipping solutions of states AP,AS,ASD,S and INT.
Proof. In Theorem 3 we showed that cycle skipping segregated states AP, AS and ASD cannot be defined by Definition 4.1. Thus, by contradiction suppose that there exist cycle skipping integrated states of AP, AS and ASD defined by Definition 4.2. The matrix forms of each of these cycles skipping states extends the matrix form of AP, AS and ASD shown in Table 1 and can written in the general form:
where
where x = y = z = 0 for state S and x = y = z = 1 for state INT. In both cases the B unit is OFF at all times. Therefore the synaptic variable sB is constant and equal to zero and the total inputs to unit A at the start of intervals
We have therefore proven that the only possible cycle skipping MAIN states are obtained from segregated states s ∈ S or integrated states i ∈ I by adding 2TR-multiple silent periods. It is possible to derive the existence conditions of cycle skipping states in dependence on the model parameters. Table 3 shows the matrix form and the existence conditions of all cycle skipping segregated and integrated MAIN states. We now prove how these existence conditions are obtained in one example: IDk (shown in Figure 2 right for k = 1). The proofs for the remaining cases are analogous.
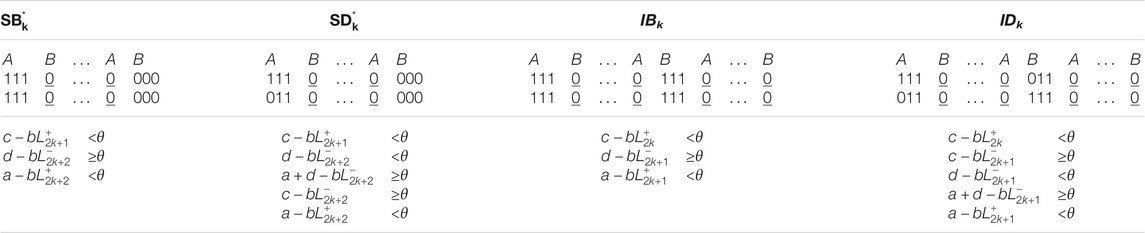
TABLE 3. Name, matrix form and existence conditions of cycle skipping MAIN states (* asymmetrical states).
Theorem 5. The existence conditions for stateIDkare
Proof. For this state the A and B unit turn and remain ON during the interval
Remark 4.1 (Analysis of SHORT CONNECT and LONG states). Cycle skipping SHORT CONNECT states can be defined using Definitions 4.1 and 4.2 by adding periods of silence multiple of 2T R after I1 and/or I2 to the states in Table 2. More precisely, Definition 4.1 can be applied to states ZcS, ScSD and Definition 4.2 can be applied to states ZcI, APcI. It can be proven that these definition cannot be applied to all remaining CONNECT states (ZcAP, ScAS, SDcAS, ZcAS and APcAS). This proof is analogous to the one of Theorem 4. In Supplementary Appendix A1 we derived the existence conditions of all possible cycle skipping SHORT CONNECT states using a similar approach to that of Theorem 5.
4.1 Analysis of the Remaining Classes of Cycle Skipping States
The analysis of LONG MAIN and CONNECT states follows analogously to the SHORT case. One caveat of this analysis is the need to extend the matrix form for short states during an active tone interval R (3) by adding one binary entry at the end of both rows in this matrix (see [6]). This additional entries are either both 0 or both 1. If they are both 1 both units are active after the offset of the interval R (LONG condition), if they are both 0 the units turn OFF at the end of the interval R. The possible LONG cycle skipping states and their existence conditions are shown in Supplementary Appendix A2 (for LONG MAIN cycle skipping states) and Supplementary Appendix A3 (for LONG CONNECT cycle skipping states). We note that these conditions depend on both quantities
Using the analysis above we can group all cycle skipping states of order k in two classes. The class Sk of all (2k + 2)TR-periodic segregated cycle skipping states having the same number of turning ON times as state sk defined by (4.1):
and the class Ik of all (4k + 2)TR-periodic integrated cycle skipping states having the same number of turning ON times as state ik defined by (4.2):
4.2 Organization in the Parameter Space
Figure 3A shows an example (for other parameters fixed) of the regions of existence for grouped states Sk and Ik when varying c and η. As c → θ cycle skipping solutions Sk and Ik accumulate in infinite cascades with period tending to infinity and are separated by exclusive transition boundaries (Figure 3B, there is no bistability between these states). The existence regions for each class Sk and Ik form a repeating pattern as k → ∞ with c decreasing. We note that at k = 0 these regions correspond to the regions of existence of 2TR-periodic MAIN and CONNECT states (compare with Figure 1F; same parameter values). Figures 3C,D show the zoom of regions in panel A highlighting the features of subdivisions of existence conditions for states in Sk and Ik. Panel C shows an example of a pattern formed by SHORT states in S1 and I1. As k increases (c decreases) this pattern continues for states in groups Sk and Ik and with decreasing (increasing) width (height). The lower borders separating ZcIk (ZcSk) and APcIDk (ScSDk) from other non cycle skipping states shifts downwards and reaches the axis η = 0. At the intersection with η = 0 existence regions for cycle skipping states change to match a pattern formed by LONG states. Figure 3D shows an example of this pattern for k = 7, a pattern that repeats as c → θ.
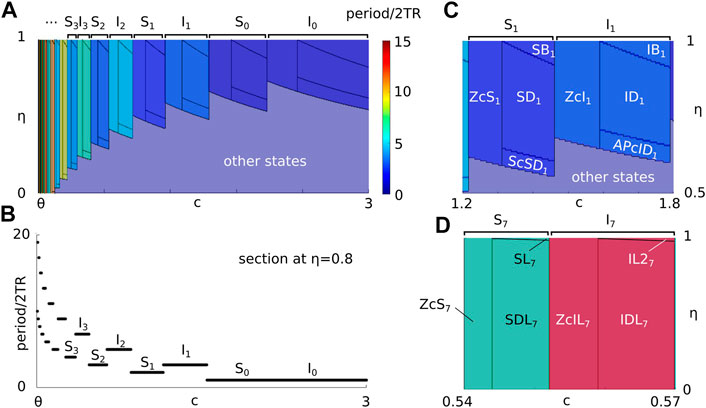
FIGURE 3. (A) Regions of existence of cycle skipping states in the space of parameters (c, η), where colors show the states’ periods (scaled by 2TR). (B) Section of panel A at fixed η = 0.8 shows the dependence of states’ period on c. (C) Zoom of panel A showing the subdivision of existence regions for states in groups S1 and I1. (D) Zoom of panel A showing the subdivision of existence regions for states in groups S7 and I7. Model parameters are the same as in Figure 1F.
4.3 Parameter Region Relationships
We now show that the width ratio of the region of existence of successive cycle skipping states in group Sk converges to a constant in the limit as k → ∞. A similar proof holds for states in Ik and is therefore omitted. The existence region of each state Sk is bounded horizontally by vertical lines (Figure 3A). The right vertical boundary
5 Switching States
The remaining two classes of states considered in our study consist of SHORT states with a period that is multiple of TR. Following the approach outlined in the previous section we define these states using their matrix form and use the matrix form to derive their existence conditions. To simplify the notation we introduce vector
Definition 5.1. Let m be even. The Q-switching state MQm,k is the periodic SHORT MAIN state with period (m + 2k)TR described by the matrix form:
We note that this state is characterised by silence in m repetitions of the half period TR (blue boxes) and k repetitions of the B unit’s turning ON at every other tone (red boxes). A time history example of one Q-switching state Q2,3 is shown in Figure 4. In the next theorem we used an similar analysis to the one in the previous section to prove the existence conditions for MQm,k states.
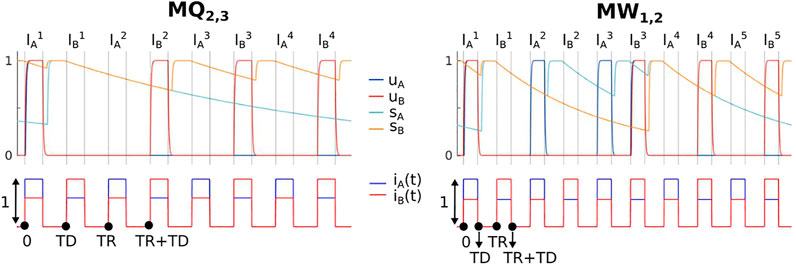
FIGURE 4. Time history examples of the Q-switching state Q2,3 and W-switching state W1,2. All parameters are the same as in Figure 2, except for the following: c = 2.076, d = 0.605 and τi = 0.4 for the left panel; c = 2, d = 0.57 and τi = 0.2 for the right panel.
Theorem 6. The existence conditions of stateMQm,kare given by:
Proof. Due to the monotonic decay of the delayed synaptic variables in the m between intervals
In Supplementary Appendix A4, 5 we provide a definition and analyses of the existence conditions for SHORT CONNECT Q-switching states of order m and k, which have the same period as MQm,k. We classify these states as: 1) simple CONNECT Q-switching states (cQm,k, dQm,k and gQm,k) for which one unit turns ON during only one interval at a delayed time from the interval’s onset, and 2) complex CONNECT Q-switching states (cdQm,k, cgQm,k, dgQm,k and cdgQm,k) with delayed turning ON of the units across multiple intervals. These classes complete CONNECT Q-switching states. For a fixed k and m, CONNECT Q-switching states preserve the number and the order of the units’ turning ON times during each active tone interval from MQm,k, except for delaying at least one unit’s turning ON time during at least one active tone interval.
Next we proceed to define the final class of states considered in this paper: the W-switching states.
Definition 5.2. Let m ≥ 0 be odd. A W-switching state MWm,k is the periodic SHORT MAIN state with period 2 (m + 2k)TR described by the matrix form:
where p(k) = k + (m + 1)/2.
Figure 4 shows the dynamics of state W1,2. We note that this state demonstrates switching between unit A being active at every other tone whilst unit B is inactive, and unit B being active at every other tone whilst unit A is active. With respect to auditory streaming this state may be interpreted as a segregated percept with periodic switching between the A tone in the foreground and the B tone in the foreground (see Discussion).
We define SHORT CONNECT W-switching states of order m and k as those states that preserve the number and the order of the units’ turning ON times during each active tone interval of state MWm,k, and that delay a unit’s turning ON time during one or more active tone intervals. The matrix form and existence conditions for all W-switching states are similar to those of Q-switching states and are presented in Supplementary Appendix A6. Also in the case of CONNECT Q-switching states we differentiate between simple CONNECT W-switching states (cWm,k, dWm,k and gWm,k) and complex CONNECT W-switching states (cdWm,k, cgWm,k, dgWm,k and cdgWm,k) based on the number of active tone intervals for which the units’ turning ON times are delayed.
From the analysis of Q- and W-switching states we may group all switching states of order m and k based on having the same number and order of the units’ turning ON times during each active tone intervals. Specifically, we have the class of SHORT Q-switching states formed by all Q-switching states of order m and k:
and the class of SHORT W-switching states formed by all W-switching states of order m and k:
Figure 5A shows example of the dependence of the regions of existence of grouped states Qm,k and Wm,k when varying parameters c and η (same parameters as Figures 1F, 3). For decreasing values of η switching groups Qm,k and Wm,k accumulate in cascades with increasing period so that k → ∞ (Figure 5B) until they reach the curve η = θ/c, which is the upper boundary of state S shown in Figure 1F. By definition d = ηc. Therefore, this accumulation occurs for decreasing values of the lateral input strength d for d → θ. We note that there is no bistability between these states (i.e., coexistence between any pair of states in Qm,k). Figures 5C,D show details from panel A. These panels show example patterns of the existence regions for states in groups Q2,4 and W1,3. These patterns repeat at different sizes as d → θ. In this limit the height of the intervals of existence of groups Qm,k and Wm,k decreases to zero.
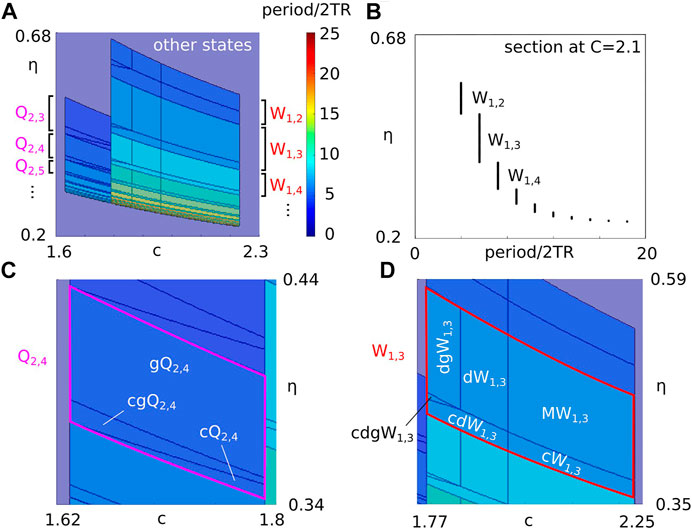
FIGURE 5. (A) Regions of existence of Q- and W-switching states in the space of parameters (c, η), where colors show the states’ period (scaled by 2T R). (B) Section of panel A at fixed c = 2.1 shows the dependence of the states’ period on η. (C) Zoom of panel A showing the subdivision of existence regions for states in group Q2,4. (D) Zoom of panel A showing the subdivision of existence regions for states in group W1,3. Model parameters are the same as in Figure 1F.
Remark 5.1. We note that the some Q- and W-switching do not exist for the selected parameter values in Figure 5 (for example states MQm,k). However, we numerically checked that these states exist in other parameter regions (see Figure 4 for state MQ2,3).
We now show that the ratio of the height between successive W-switching states converges to a constant. An analogous proof holds for Q-switching states and is therefore omitted. The transition boundary between groups Wm,k and Wm,k−1 shown in Figure 5A is marked by the upper existence boundary of states MWm,k, dWm,k and dgWm,k expressed as a function of c as
This constant is independent from c and equal to the width ratio of successive cycle skipping states Eq. (8).
6 Computational Analysis in a Smooth and Continuous System
In this section we extend the analysis of switching states Wm,k using a continuous version of model (1), described by the following system of six ordinary differential equations (ODEs):
where the gain function S is defined as a sigmoid Sσ(z) = 1/(1 + e−σ(x−θ)), which approximates a Heaviside function for large σ. The interpretations of parameters a, b, θ, τ, τi and of variables uA, uB, sA, sB are the same as the ones described in Section 2 for model (1). The new parameters αx and βx represent the rate of activation and inactivation of the variables xA and xB. The parameters σ = 180 and λ = 20 are the selected slopes of the sigmoid.
System (12) differs from the discontinuous delayed model studied in the previous sections because the delay in the synaptic variable sA (sB) is introduced by a second variable xA (xB) instead of the fixed amount D, following [19] as motivated by indirect synapses. For example, if uA turns ON then xA will activate when uA crosses the threshold θ. In this case the synaptic variable sA activates when xA crosses the threshold θ. The delays produced by the indirect synapses depend on the rates αx and βx. Preliminary simulations revealed that the variation of these two parameters allows for only small delays to be produced whilst guaranteeing the convergence to 1 when variables sA and sB turn ON (delays measured to the peak of sA and sB, in the range 0–20 ms). Since our previous analysis assumes that D > TD we consider values of αx and βx that give a delay of approximately 15 ms and fixed TD = 10 ms.
The input functions iA and iB are redefined as:
where x = sin (δt), y = cos (δt), z = sin (δ ⋅ TD)y − cos (δ ⋅ TD)x and δ = π ⋅ PR. We recall that parameter η is a scaling of the input strength c so that the lateral inputs have amplitude d = ηc. The new input function iA and iB are similar to the discontinuous inputs shown in Figure 1B but with smoothed, square waveform. To allow numerical continuation with periodical forcing in AUTO-07p [34] we append the following two ODEs to system (13), for which x = sin (δt) and y = cos (δt) is a solution:
We simulate model (12) at fixed parameters and find a set of states W1,k analogous to the ones shown in Figures 4, 5 for model (1). We numerically continue each branch of periodic orbit W1,k for k = 2, 3, 4, 5 varying the parameter η (Figure 6). We find large regions of stability that accumulate with k increasing as η decreases (in agreement with Figure 5B). These regions of stability are non overlapping (no bistability) and are separated by unidentified bifurcation points (the continuation algorithm fails to converge at these points). We suspect that these bifurcation correspond to period-incrementing bifurcations.
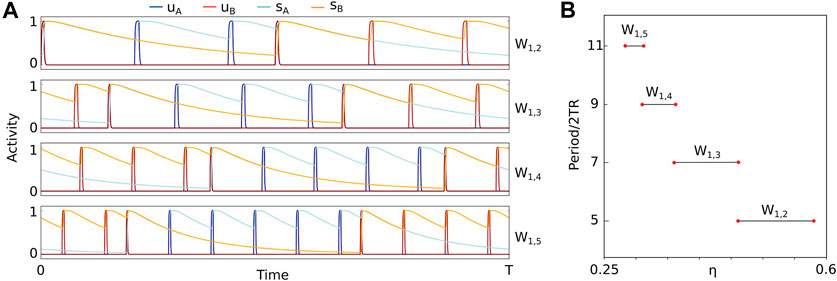
FIGURE 6. Numerical analysis of switching states. (A) Time histories of switching states W1,k for k = 2, 3, 4, 5 computed using forward numerical integration of system (12) at different values of η. (B) Codimension-1 bifurcation diagram of the stable states in panel A at varying parameter η. Red circles indicate failure of convergence of the numerical continuation. Model parameters in both panels are a = 0.6, b = 2, c = 2, PR = 10, α = 150, β = 20, θx = 0.5, τi = 0.3, τ = 0.001, θ = 0.5 and T D = 0.01.
Overall, this analysis confirms the existence and of W-switching states and their organisation in a cascade for decreasing values of η using a smooth and continuous version of the original model (1). The numerical continuation of branches of W-switching states reveals discontinuous transition points that suggest bifurcation phenomena that cannot be detected using continuation software. A similar analysis of system (12) could be applied to study cycle skipping and Q-switching states.
7 Discussion
In this paper we analysed a system of four periodically forced delay differential equation encoding rhythm perception. The system represents two neural populations mutually connected by fast excitation and slow delayed inhibition receiving square-wave sound inputs consisting of two alternating pure tones. We previously used singular perturbation techniques to classify all viable states 1:1 locked to the inputs and to define their existence conditions using a binary matrix representation [6]. Here we extended this analysis to study two classes of n:1 locked states called cycle skipping and switching states. Cycle skipping states were derived from 1:1 locked states by adding intervals of silence (i.e., without response) equal to a multiple of the input period. Switching states are defined by dynamic alternation between 1:1 locked states. We generalised the matrix form for these states to visualise their dynamics and derive their existence conditions. We then analysed the existence regions in the space of parameters (c, η), where c is the strength of the local inputs and η the scaling strength of the lateral input. We found that cycle skipping and switching states accumulate in cascades with diverging periods for decreasing values of c and η respectively, and that this accumulation derives from an infinite period-incrementing cascade of bifurcations. Lastly, we confirmed the analytical predictions using numerical integration and continuation in a smooth ODE version of the model.
7.1 Period Incrementing Cascades
Sequences of bifurcations leading to an increased period are a common features of dynamical systems, a period-doubling cascade being the most commonly observed. Other period-increasing cascades have been most widely studied in non-smooth maps: the period-adding scenario and period-incrementing scenario (see [35] for a recent review). In the period-incrementing scenario the period increments from a base value p0 by a fixed amount Δp in integer n steps: in each successive increment of the cascade the period is pn = p0 + nΔp. In the period-adding scenario, the sequence of periods observed as a parameter is varied is more complicated, with a Cantor-set like structure [35]. Either scenario can be found in 1D piecewise-linear maps [31, 36] (and their regularised, smooth counterparts [37]). Successive intervals typically exist in wedge-shaped regions converging to a point in the parameter plane (a so-called big bang bifurcation) and an infinite cascade of period-adding or period-incrementing transitions is found by following a radial path in parameter space around these organising centers in the parameter plane [31, 36]. In some cases, bands of chaotic dynamics (like periodic windows found in the period-doubling route to chaos) can be found between parameter intervals with periodic states [31]. Period-incrementing and period-adding cascades are found in a broad range of applications in settings that include 1D or nD maps (non-smooth or smooth), and include continuous time dynamical systems with delays or with non-smooth characteristics [35–37]. Our discussion here will focus on a comparison of our findings with canonical examples [31, 36] and with models from mathematical neuroscience (below).
In our model we identified several cascades characteristic of period-incrementing sequences. In each successive parameter region the period increases in steps associated with the period of the model inputs. In the case of skipping states the sequence progresses with increasing period for decreasing values of the local input strength c. The boundaries of these regions are parallel in the (c, η)-plane (and thus do not converge at a big bang bifurcation). Interestingly there are two interleaved period-incrementing sequences associated with integrated-like states (both units respond together) and segregated-like states (only one unit responds). We further found that the ratio of width in c of successive intervals to be a parameter dependent constant
7.2 Cascades in Neural Models
Models of single neurons typically feature a time-scale separation with rapid activation and inactivation dynamics that generate spikes and slower recovery dynamics leading to a refractory period between spikes [12]. Methods from singular-perturbation theory have been central to the development of our understanding of more complex spiking phenomena such as bursting [12, 13]. Successive spikes appear on the bursting plateau as a parameter is varied through a complex series of homoclinic bifurcations [30, 38, 39]. However, the period does not change much [40] in these spike-adding sequences (therefore not classified as period-adding or period-incrementing). However, there are several examples of single-neuron models with non-smooth spike resetting dynamics where such cascades have been reported. In [41], a piece-wise linear approximation of the Fitzhugh-Nagumo’s nonlinearity was taken. The periodically forced system exhibits rich dynamics that includes a period-adding sequence and chaotic dynamics. An integrate and fire model (with spike reset) also features a period-adding sequence and chaotic dynamics [42]. More recently a similar model was reported to have a period-incrementing structure [43] as revealed through a map on the model’s adaptation variable. In the present study we did not find evidence of chaotic dynamics. Indeed our analysis precludes any ‘gaps’ in the contiguous parameter intervals with cycle skipping and switching states where such dynamics are found in other models [42, 43].
In canonical models of neural competition at the population level, timescale separation leads to relaxation oscillations in models of perceptual rivalry [8, 44] (i.e., perceptual bistability, as for binocular rivalry or the necker cube). Mixed-mode oscillations can emerge in these models through a canard mechanism [15, 45, 46]. A cascade of non-local bifurcations leads to disjoint, contiguous parameter regions with branches that have increased period [46], though the period is not fixed on each segment in this smooth model. This class of models can exhibit a cascade sharing many features of a period-incrementing cascade: when periodic forcing is introduced a sequence of non-local bifurcations lead to a family of solutions, similar to the W-switching states reported here, with step-increments in the period matching the period of the forcing [46]. Periodic inputs to competition networks have been considered in several other models [5, 24, 25, 47, 48], but these typically only report 1:1 locked states or oscillatory states modulated by forcing but not locked with the forcing. A model featuring a Heaviside activation function and step-function or sinusoidal inputs exhibited cycle-skipping states [25], much like the cycle skipping states found in the present study. Our study reveals richer dynamics than these earlier studies and demonstrates a link between the regions with the switching and cycle skipping states through a single, parameter-dependent ratio for existence intervals.
7.3 Modelling Assumptions
Our model features several mechanisms that are known to lead to complex dynamics (in isolation, or in combination with each other): slow-fast timescale separation, delays, periodic inputs, a non-smooth (heaviside) activation function and non-smooth steps in the input profile. In Section 6 we explored whether the skipping and switching cascades persist when we relax the non-smooth characteristic of the activation function and the inputs. We demonstrated that a sequence of solutions selected from the skipping cascade persists and that, these non-smooth components in the model are not a requirement to find the period-incrementing cascades reported. We further explored the skipping states in a version of the model where the delays were introduced via synaptic coupling [19] in an extended ODE rather than DDE formulation. Tracking branch segments with numerical continuation allowed us to confirm that the skipping states persist in this case. Whilst it may be possible to produce switching states [46] and cycle skipping states [25] without delays, removing the delays in the present model dramatically simplified the dynamics. Indeed excitation and inhibition would instantaneously turn ON when the units turn ON. In the slow-fast limit there are only two possible states: a state where both units instantaneously turn and remain ON for each active tone interval (corresponding to IB or ID described in Section 3) or a state where unit A (B) turns ON for each A (B) active tone interval (corresponding to AP described in Section 3). In summary the rich dynamics produced by our model result from an interaction between slow-fast mechanisms with delays and periodic forcing.
The condition TD < D assumed in our study guarantees that the delayed synaptic variables of system 1 are monotonically decaying in each active tone interval. This simplifies the system under study by reducing the number of possible states and their existence conditions (see also [6]). A more detailed analysis of the case TD ≥ D leads to switching and cycle skipping states similar to those studied here (not shown). Under this condition for integrated and segregated cycle skipping states the units’ turn ON for some active tone interval and must turn OFF after the delay D, instead of TD as in the case TD < D (see Figure 2). This leads to additional existence conditions for these states. Overall, a similar organization of the parameter space with cascades of period adding bifurcations can be proven analogously under condition TD ≥ D. The latter condition may be relevant when modelling auditory perception, as the potential factors for generating delayed inhibition in brain circuits would most likely lead to short or moderate delays that could be less than TD.
7.4 Interpretation for Neural Encoding of Auditory Streams
The solutions found in the switching and skipping cascades each have a meaningful interpretation for the model. In the motivating auditory streaming paradigm, two sequences of interleaved tones can be perceived by human listeners in different configurations: integrated into a single stream, segregated with A in the foreground or segregated with B in the foreground [49]. Some experiments consider only bistable perception (integrated vs segregated [5, 50]), whilst others consider tri-stability [49] or multi-stability [51], allowing for two different segregated states (A or B in the foreground). In the present model, switching states correspond to periodic states with alternations between an equal number of A-foreground and B-foreground cycles separated by a single integrated cycle during the transition. Tri-stability in perceptual competition has been investigated elsewhere in competition models [52].
In the perception of a regular beat, we can follow along (e.g., clapping, or tapping a foot) in time with different elements in the time-structure. Musical rhythms are perceived to have a pulse or basic beat in the range 0.5–4 Hz that is further subdivided by higher beat frequencies above 4 Hz, nevertheless, we are able to follow along at the pulse frequency. The skipping states can be linked to the encoding of neural rhythms at periods that span multiple cycles of the input (say tracking every 2nd or 3rd A tone). Such cycle skipping behaviour has been studied in m: k Arnold resonance tongues in a model of beat perception [53]. By contrast we find 1: k locked states appearing in a period-incrementing cascade in our model. We further find much larger regions of parameter space (i.e., range of c-values) with skipping states when the presentation rate is large. The model therefore predicts that the tendency to skip cycles is more likely when the inputs are too fast to follow.
8 Conclusion
In this study we address the formation of exotic dynamics via several complex mechanisms (see “Modelling assumptions” above). The architecture of the proposed model is probably not unique in producing such dynamics. We expect that similar network dynamics could be obtained by modification of the connectivity (i.e., by introducing global inputs and removing the mutual excitation). Whilst the presented methods should generalise to larger populations of neurons, this would result in significantly increased in complexity for the number of possible states and their existence criteria.
The states analysed here, and in our previous study [6], do not cover all the possible dynamics the model can produce. In preliminary simulations we detected states of infinite period (quasi-periodic), which remains a topic for future study. A further topic for future analysis is to modify the inputs by considering 4TR-periodic inputs representing the repetition of the triplet ABA-consisting of A and B pure tones and by a silent gap -, which has been widely used in behavioural experiments [54].
Our approach generalises to the study of complex oscillatory dynamics in neural population models featuring delays and different architectures, such as competition models in the visual or tactile domains. A model is currently being investigated to study perceptual competition with vibrotactile stimulation [55].
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Both authors were involved with the study formulation, discussion of results and writing the manuscript. AF carried out the mathematical analysis and numerical simulations. JR coordinated the study and provided valuable insights in the analysis of the model.
Funding
The authors acknowledge support from an Engineering and Physical Sciences Research Council (EPSRC) New Investigator Award (EP/R03124X/1) and from the EPSRC Hub for Quantitative Modelling in Healthcare (EP/T017856/1).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.716288/full#supplementary-material
References
1. Cherry, EC. Some Experiments on the Recognition of Speech, With One and With Two Ears. The J Acoust Soc America (1953) 25:975–9. doi:10.1121/1.1907229
2. Bizley, JK, and Cohen, YE. The What, Where and How of Auditory-Object Perception. Nat Rev Neurosci (2013) 14:693–707. doi:10.1038/nrn3565
3. Almonte, F, Jirsa, VK, Large, EW, and Tuller, B. Integration and Segregation in Auditory Streaming. Physica D: Nonlinear Phenomena (2005) 212:137–59. doi:10.1016/j.physd.2005.09.014
4. Wang, D, and Chang, P. An Oscillatory Correlation Model of Auditory Streaming. Cogn Neurodyn (2008) 2:7–19. doi:10.1007/s11571-007-9035-8
5. Rankin, J, Sussman, E, and Rinzel, J. Neuromechanistic Model of Auditory Bistability. Plos Comput Biol (2015) 11:e1004555. doi:10.1371/journal.pcbi.1004555
6. Ferrario, A, and Rankin, J. Auditory Streaming Emerges From Fast Excitation and Slow Delayed Inhibition. J Math Neurosci (2021) 11:1–32. doi:10.1186/s13408-021-00106-2
7. Wilson, HR, and Cowan, JD. Excitatory and Inhibitory Interactions in Localized Populations of Model Neurons. Biophysical J (1972) 12:1–24. doi:10.1016/S0006-3495(72)86068-5
8. Laing, CR, and Chow, CC. A Spiking Neuron Model for Binocular Rivalry. J Comput Neurosci (2002) 12:39–53. doi:10.1023/a:1014942129705
9. Shpiro, A, Curtu, R, Rinzel, J, and Rubin, N. Dynamical Characteristics Common to Neuronal Competition Models. J Neurophysiol (2007) 97:462–73. doi:10.1152/jn.00604.2006
10. Curtu, R, Shpiro, A, Rubin, N, and Rinzel, J. Mechanisms for Frequency Control in Neuronal Competition Models. SIAM J Appl Dyn Syst (2008) 7:609–49. doi:10.1137/070705842
11. Rinzel, J, and Ermentrout, GB. Analysis of Neural Excitability and Oscillations. In: C. Koch, and I. Segeveditors Methods in Neuronal Modelling: From Ions to Networks. Cambridge: MIT press (1989):135–171.
13. Ermentrout, GB, and Terman, DH. Mathematical Foundations of Neuroscience. Berlin: Springer Science & Business Media (2010).
14. Desroches, M, Guillamon, A, Ponce, E, Prohens, R, Rodrigues, S, and Teruel, AE. Canards, Folded Nodes, and Mixed-Mode Oscillations in Piecewise-Linear Slow-Fast Systems. SIAM Rev (2016) 58:653–91. doi:10.1137/15m1014528
15. Curtu, R. Singular Hopf Bifurcations and Mixed-Mode Oscillations in a Two-Cell Inhibitory Neural Network. Physica D: Nonlinear Phenomena (2010) 239:504–14. doi:10.1016/j.physd.2009.12.010
16. Krupa, M, and Touboul, JD. Canard Explosion in Delay Differential Equations. J Dyn Diff Equat (2016) 28:471–91. doi:10.1007/s10884-015-9478-2
17. Teixeira, MA, and da Silva, PR. Regularization and Singular Perturbation Techniques for Non-smooth Systems. Physica D: Nonlinear Phenomena (2012) 241:1948–55. doi:10.1016/j.physd.2011.06.022
18. Marder, E, and Calabrese, RL. Principles of Rhythmic Motor Pattern Generation. Physiol Rev (1996) 76:687–717. doi:10.1152/physrev.1996.76.3.687
19. Rubin, J, and Terman, D. Geometric Analysis of Population Rhythms in Synaptically Coupled Neuronal Networks. Neural Comput (2000) 12:597–645. doi:10.1162/089976600300015727
20. Ferrario, A, Merrison-Hort, R, Soffe, SR, Li, W-C, and Borisyuk, R. Bifurcations of Limit Cycles in a Reduced Model of the Xenopus Tadpole Central Pattern Generator. J Math Neurosc (2018) 8:10. doi:10.1186/s13408-018-0065-9
21. Ashwin, P, Coombes, S, and Nicks, R. Mathematical Frameworks for Oscillatory Network Dynamics in Neuroscience. J Math Neurosc (2016) 6:2. doi:10.1186/s13408-015-0033-6
23. Dhamala, M, Jirsa, VK, and Ding, M. Enhancement of Neural Synchrony by Time Delay. Phys Rev Lett (2004) 92:074104. doi:10.1103/PhysRevLett.92.074104
24. Vattikuti, S, Thangaraj, P, Xie, HW, Gotts, SJ, Martin, A, and Chow, CC. Canonical Cortical Circuit Model Explains Rivalry, Intermittent Rivalry, and Rivalry Memory. Plos Comput Biol (2016) 12:e1004903. doi:10.1371/journal.pcbi.1004903
25. Jayasuriya, S, and Kilpatrick, ZP. Effects of Time-Dependent Stimuli in a Competitive Neural Network Model of Perceptual Rivalry. Bull Math Biol (2012) 74:1396–426. doi:10.1007/s11538-012-9718-0
26. Krisztin, T, Polner, M, and Vas, G. Periodic Solutions and Hydra Effect for Delay Differential Equations With Nonincreasing Feedback. Qual Theor Dyn. Syst. (2017) 16:269–92. doi:10.1007/s12346-016-0191-2
27. Fick, E, Fick, M, and Hausmann, G. Logistic Equation With Memory. Phys Rev A (1991) 44:2469–73. doi:10.1103/physreva.44.2469
28. Novak, S, and Frehlich, RG. Transition to Chaos in the Duffing Oscillator. Phys Rev A (1982) 26:3660–3. doi:10.1103/physreva.26.3660
29. Desroches, M, Guckenheimer, J, Krauskopf, B, Kuehn, C, Osinga, HM, and Wechselberger, M. Mixed-Mode Oscillations With Multiple Time Scales. SIAM Rev (2012) 54:211–88. doi:10.1137/100791233
30. Linaro, D, Champneys, A, Desroches, M, and Storace, M. Codimension-Two Homoclinic Bifurcations Underlying Spike Adding in the Hindmarsh--Rose Burster. SIAM J Appl Dyn Syst (2012) 11:939–62. doi:10.1137/110848931
31. Avrutin, V, and Schanz, M. On Multi-Parametric Bifurcations in a Scalar Piecewise-Linear Map. Nonlinearity (2006) 19:531–52. doi:10.1088/0951-7715/19/3/001
32. Fishman, YI, Arezzo, JC, and Steinschneider, M. Auditory Stream Segregation in Monkey Auditory Cortex: Effects of Frequency Separation, Presentation Rate, and Tone Duration. The J Acoust Soc America (2004) 116:1656–70. doi:10.1121/1.1778903
33. Bressloff, PC. Spatiotemporal Dynamics of Continuum Neural fields. J Phys A: Math Theor (2011) 45:033001. doi:10.1088/1751-8113/45/3/033001
34. Doedel, EJ, Champneys, AR, Dercole, F, Fairgrieve, TF, Kuznetsov, YA, Oldeman, B, et al. Auto-07P: Continuation and Bifurcation Software for Ordinary Differential Equations (2007). Available at http://indy.cs.concordia.ca/auto/.
35. Granados, A, Alsedà, L, and Krupa, M. The Period Adding and Incrementing Bifurcations: From Rotation Theory to Applications. SIAM Rev (2017) 59:225–92. doi:10.1137/140996598
36. Avrutin, V, and Schanz, M. On the Scaling Properties of the Period-Increment Scenario in Dynamical Systems. Chaos, Solitons & Fractals (2000) 11:1949–55. doi:10.1016/s0960-0779(99)00071-5
37. Pring, SR, and Budd, CJ. The Dynamics of Regularized Discontinuous Maps With Applications to Impacting Systems. SIAM J Appl Dyn Syst (2010) 9:188–219. doi:10.1137/080743123
38. Channell, P, Cymbalyuk, G, and Shilnikov, A. Origin of Bursting Through Homoclinic Spike Adding in a Neuron Model. Phys Rev Lett (2007) 98:134101. doi:10.1103/physrevlett.98.134101
39. Desroches, M, Kaper, TJ, and Krupa, M. Mixed-Mode Bursting Oscillations: Dynamics Created by a Slow Passage Through Spike-Adding Canard Explosion in a Square-Wave Burster. Chaos (2013) 23:046106. doi:10.1063/1.4827026
40. Barrio, R, Ibáñez, S, Pérez, L, and Serrano, S. Spike-Adding Structure in Fold/hom Bursters. Commun Nonlinear Sci Numer Simulation (2020) 83:105100. doi:10.1016/j.cnsns.2019.105100
41. Coombes, S, and Osbaldestin, AH. Period-Adding Bifurcations and Chaos in a Periodically Stimulated Excitable Neural Relaxation Oscillator. Phys Rev E (2000) 62:4057–66. doi:10.1103/physreve.62.4057
42. Touboul, J, and Brette, R. Spiking Dynamics of Bidimensional Integrate-And-Fire Neurons. SIAM J Appl Dyn Syst (2009) 8:1462–506. doi:10.1137/080742762
43. Rubin, JE, Signerska-Rynkowska, J, Touboul, JD, and Vidal, A. Wild Oscillations in a Nonlinear Neuron Model With Resets: (I) Bursting, Spike Adding and Chaos. Discrete Contin Dyn Syst Ser B (2017) 22:3967–4002.
44. Wilson, HR. Minimal Physiological Conditions for Binocular Rivalry and Rivalry Memory. Vis Res (2007) 47:2741–50. doi:10.1016/j.visres.2007.07.007
45. Curtu, R, and Rubin, J. Interaction of Canard and Singular Hopf Mechanisms in a Neural Model. SIAM J Appl Dyn Syst (2011) 10:1443–79. doi:10.1137/110823171
46. Darki, F, and Rankin, J. Methods to Assess Binocular Rivalry With Periodic Stimuli. J Math Neurosci (2020) 10:10. doi:10.1186/s13408-020-00087-8
47. Wilson, HR. Computational Evidence for a Rivalry Hierarchy in Vision. Proc Natl Acad Sci (2003) 100:14499–503. doi:10.1073/pnas.2333622100
48. Li, H-H, Rankin, J, Rinzel, J, Carrasco, M, and Heeger, DJ. Attention Model of Binocular Rivalry. Proc Natl Acad Sci USA (2017) 114:E6192–E6201. doi:10.1073/pnas.1620475114
49. Hupé, J-M, and Pressnitzer, D. The Initial Phase of Auditory and Visual Scene Analysis. Phil Trans R Soc B (2012) 367:942–53. doi:10.1098/rstb.2011.0368
50. Pressnitzer, D, and Hupé, J-M. Temporal Dynamics of Auditory and Visual Bistability Reveal Common Principles of Perceptual Organization. Curr Biol (2006) 16:1351–7. doi:10.1016/j.cub.2006.05.054
51. Denham, S, Bõhm, TM, Bendixen, A, Szalárdy, O, Kocsis, Z, Mill, R, et al. Stable Individual Characteristics in the Perception of Multiple Embedded Patterns in Multistable Auditory Stimuli. Front Neurosci (2014) 8:25–15. doi:10.3389/fnins.2014.00025
52. Huguet, G, Rinzel, J, and Hupé, J-M. Noise and Adaptation in Multistable Perception: Noise Drives When to Switch, Adaptation Determines Percept Choice. J Vis (2014) 14:19. doi:10.1167/14.3.19
53. Large, EW, Herrera, JA, and Velasco, MJ. Neural Networks for Beat Perception in Musical Rhythm. Front Syst Neurosci (2015) 9:159. doi:10.3389/fnsys.2015.00159
Keywords: neural circuit, fast excitation, slow inhibition, periodic forcing, period incrementing bifurcation
Citation: Ferrario A and Rankin J (2021) Cascades of Periodic Solutions in a Neural Circuit With Delays and Slow-Fast Dynamics. Front. Appl. Math. Stat. 7:716288. doi: 10.3389/fams.2021.716288
Received: 28 May 2021; Accepted: 31 August 2021;
Published: 01 October 2021.
Edited by:
Víctor F. Breña-Medina, Instituto Tecnológico Autónomo de México, MexicoReviewed by:
Ludwig Reich, University of Graz, AustriaFabiano Baroni, Autonomous University of Madrid, Spain
Copyright © 2021 Ferrario and Rankin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrea Ferrario, QS5BLkZlcnJhcmlvQGV4ZXRlci5hYy51aw==
 Andrea Ferrario
Andrea Ferrario James Rankin
James Rankin