- 1Nonlinearity and Complexity Research Group, Department of Mathematics, Aston University, Birmingham, United Kingdom
- 2School of Life Sciences, University of Lincoln, Lincoln, United Kingdom
- 3School of Computing, University of Leeds, Leeds, United Kingdom
- 4Faculty of Biological Sciences, University of Leeds, Leeds, United Kingdom
- 5Laboratory of Mechanics and Materials, Aristotle University of Thessaloniki, Thessaloniki, Greece
Model analogies and exchange of ideas between physics or chemistry with biology or epidemiology have often involved inter-sectoral mapping of techniques. Material mechanics has benefitted hugely from such interpolations from mathematical physics where dislocation patterning of platstically deformed metals and mass transport in nanocomposite materials with high diffusivity paths such as dislocation and grain boundaries, have been traditionally analyzed using the paradigmatic Walgraef-Aifantis (W-A) double-diffusivity (D-D) model. A long standing challenge in these studies has been the inherent nonlinear correlation between the diffusivity paths, making it extremely difficult to analyze their interdependence. Here, we present a novel method of approximating a closed form solution of the ensemble averaged density profiles and correlation statistics of coupled dynamical systems, drawing from a technique used in mathematical biology to calculate a quantity called the basic reproduction number R0, which is the average number of secondary infections generated from every infected. We show that the R0 formulation can be used to calculate the correlation between diffusivity paths, agreeing closely with the exact numerical solution of the D-D model. The method can be generically implemented to analyze other reaction-diffusion models.
1. Introduction
Transport of mass, heat or electricity in inhomogeneous media has been modeled [1–3] involving distinct conducting paths such as diffusion in metals containing a large number of dislocations and/or grain boundaries [4], fluid flows in fissured rocks and media with double porosity [5, 6], heat or electricity conduction in fiber reinforced composites [10] have been addressed by Aifantis through continuous models, typically based on coupled sets of linear partial differential equations (the double diffusivity or D-D model) involving 4 phenomenological constants: 2 diffusion coefficients for each one of the two paths and two mass exchange constants between the paths. The above two-state idea was also utilized later in developing the first dynamical model of dislocation patterning, commonly known as the Walgraef-Aifantis (W-A) model [1, 2] that could distinguish between two dislocation populations: slow or “immobile” dislocation and fast or “mobile” ones that brings plastic deformation about. It turns out that the linearized version of the W-A model is identical in form to the D-D model variant of the two-state reaction-diffusion (R-D) formulation used to describe transport of multiple families of species such as vacancies and interstitials in crystalline lattices, impurity, segregation in dislocation and grain boundaries or trapping and precipitation process in alloys.
Over the last two decades, the D-D and W-A models have become quite popular in both the applied mathematics [11] and the material science [12] communities due to the interesting mathematical properties of the former and robust interpretation of experimental observations of the latter groups of models. This includes implementation of D-D type models in interpreting molecular and mesoscopic transport in condensed matter and cosmological systems [13], i.e., Most of such models though overlooked the contribution of stochastic forcing or spatial randomness, e.g., surface impurities in materials, restricting the implementation of such models in explaining experimental observations. A recent series of stochastically driven D-D models [7–9] have not only addressed this issue of steering qualitative phenomenological models closer to experimental descriptions, technically these have opened up further possibilities of cross-disciplinary implementation of these models from material science to other fields and vice versa.
Anomalous diffusion involving multiple species and media has for long remained an interesting field of research. The diffusive behavior changes their characteristics depending on the choice of medium. There are many plausible reasons for this. One of them is that there exists some void grain boundary in the medium which represents an especially high diffusivity path inside the medium. Also, there are relatively narrow domains in the medium where the diffusion rate is slower. Simultaneous diffusion in multiple media has been traditionally analyzed using double-diffusion models [4–6, 10, 14] that is a coupled system of partial differential equations involving interacting variables. These D-D models considered two species of diffusive elements, one that follows the regular path, another following a high-diffusive path, with eventual dynamics determined by a dynamical equilibrium of these competing paths.
1.1. State of the Art
Elias C. Aifantis developed and introduced the concept of double diffusion step by step in Aifantis and Hill [5, 6] and Aifantis [15, 16]. A continuum basis for diffusion in regions with multiple diffusivity was introduced in Aifantis [15]. Simultaneously, in Aifantis [17], the diffusion in media with a continuous distribution of high-diffusivity paths was modeled. Finally, Aifantis provided a formulation generalizing this idea of the diffusion in solid media for wide range of applicability in different physical process, in double porosity [18], from metallurgy to soil science [14] polymer physics and geophysics, in Aifantis and Hill [5, 6]. Another explanation of this double diffusion model was provided in Hill [19] using the concept of discrete random walk model. In [5, 6]–[19], Aifantis and Hill studied the basic mathematical questions of the model. Mainly they studied uniqueness, maximum principles and basic source solutions in Aifantis [20] and Hill [19] and boundary value problems in Hill [19]. Kuttler and Aifantis studied the existence and uniqueness of the weak form of the nonclassical diffusion equation in Kuttler and Aifantis [21].
The diffusion process in a media is not deterministic. Indeed there are stochastic effects initiated and controlled by several factors. Randomness can be related to thermal fluctuations, grain size changes, impurity effects, etc. Recent studies of a type of non-equilibrium system involving multiple states of diffusion of a diffusing species, called stochastic resetting, is governed by a dynamics similar to a double-diffusion system [22]. These types of interactive features play an important role in the process and it became necessary to take into account of the stochastic agents. In nanoscales or nanopolycrystals, the diffusion near the grain boundary following two paths, regular and high diffusive, can be affected by stochastic fluctuations [7]. Deterministic internal length gradient method can not completely explain relaxation time for diffusion in nanopolycrystals. Considering boundary layer fluctuations, stochasticity was added in the modeling and first stochastic gradient nanomechanics (SGNM) model was proposed in Chattopadhyay and Aifantis [8]. Using SGNM model, relaxation time is discussed thoroughly for a specific superconductors [23] in Chattopadhyay and Aifantis [9]. Also, linear stochastic resonance has been predicted and how stochastic effects start affecting the system is explained in Chattopadhyay and Aifantis [9].
1.2. Open Questions
The present article is the first in line to provide a closed form approximate perturbative solution of the nonlinear model (close to the linearized stationary state) resulting from a combination of the D-D and W-A models. The D-D:W-A composite model leads to a coupled system of reaction-diffusion (R-D) equations where the diffusion terms are identical to those contained in both models, the linear terms as in the D-D model [7, 8] while the nonlinear terms resemble the W-A model (3rd order). In addition, the composite model contain second order cross-coupled terms that do not lend themselves to an exact analytical solution, not even in their linearized form. The underlying physical picture represents a system of multiple diffusive relaxation, including boundary layer shear (nonlinear terms), and driven by stochastic forcing as in the two models. The present model considers simultaneous diffusion in the lattice or grain interior along the grain boundaries but also allow for trapping and impurity effects. In other words, diffusing species can be trapped in both grain interiors along dislocation cores and dislocation dipoles as well as in the counterparts of the defects within the grain boundary space, as also impurity of lattice imperfection that are stochastically distributed and hence extremely difficult to account for.
While diffusion mediated interaction between multiple species is intrinsically nonlinear, traditional analyzes have relied on the dual approach of numerical modeling (nonlinear systems) and exactly solvable linear models (approximate only). Most of these studies are deterministic with occasional stochastic models strictly restricted to linear models. The present study outlines a generic approach, repurposed from the field of mathematical biology, to provide approximate closed form solutions of inherently nonlinear coupled systems irrespective of their origin. While there is no paucity of numerical estimation of nonlinear models, including those for double diffusion ([8] and references therein), from the perspective of theoretical modeling, analytical clarity had to give way to quantitative precision. More importantly, a closed form solution offers a direct methodological link between the process and its parameters that is not available from brute numerical evaluation in a multi-parameter space. The present study is thus a major breakaway from the linearity assumption, retaining closer proximity to experiments while also comparing favorably with numerical solutions, as we will later show.
Nonlinear diffusion equations, a classical example of parabolic type equations, play an important role in the modeling of diffusion equations with nonlinearity [24], in particular, for stochastically driven diffusive systems. One is for free boundary problems such as the distribution of temperature in a homogeneous material during phase-transition [25], i.e., the time evolution of the phase boundaries, the so called Stefan problem.
Another is for reaction-diffusion problems, such as the Fisher-Kolmogorov-Petrovsky-Piskunov (Fisher-KPP) model for propagation of an advantageous gene in a population [26, 27], Gray Scott Model for diffusion of chemical species [28]. Similar style of modeling can be found for dislocation profiles in a material. Walgraef and Aifantis (WA model) proposed a model of a system of Reaction-Diffusion equations considering two profiles of dislocation flows, immobile dislocation for slow moving and mobile for relatively speedy moving [1]. The W-A model has been studied extensively numerically, toward bifurcation analysis and pattern formation in Pontes et al. [11] and Spillotis et al. [12]. None of these were targeting a closed form analysis, as is the target in this study.
The article provides a generic technique, repurposed from a diverse domain (mathematical biology), to solve systems of coupled nonlinear equations. Following a general introduction and pointers to open questions in Section 1, Section 2 summarizes the model equation and provides a physical explanation of the mechanisms involved. Section 3 represents the nondimensionalized representation of the model in Section 2, the relevant non-dimensional governing equations and their linear stability analysis. Section 4 first discusses a popular method used in mathematical epidemiology in the calculation of the time varying reproduction number R0, then identifies the phenomenology as one of analyzing the covariance of two (or more) coupled variables in a dynamical system, and then uses this hypothesis to connect with the cross-coupling between D-D variables. Section 5 provides the anatomy of the time (t) evolution of the reproduction number R0(t) in the equivalent D-D model as one measuring the strength of cross-correlation between the different diffusing species. Finally, Section 6 summarizes the outcomes of this continuum (approximate) mapping that then is compared against direct numerical evaluation of this model.
2. The Model
In this work, we focus on a closed-form, albeit approximate, solution of the D-D model for nano polycrystal diffusion by considering nonlinear source terms in the original W-A model, representing additional exchange of diffusion species between the two paths. These new non-linear exchange terms represent the transfer of diffusion species through dislocation atmosphere i.e., diffusing species segregated in dislocation cores and dislocation dipoles. We study in particular how the “transmissibility” of the species affect their diffusion and corresponding trapping processes. We observe how their internal interactions can affect their behavior. We study how the transmissibility of the species affects their diffusion.
Considering and as the concentrations/densities for the two distinct D-D species along two different paths, the governing equations of diffusion are given by
where D1, D2 are diffusion coefficients, k1, k2 are the rate mass exchange between different paths. The nonlinear terms represent the interactions between different species (or dislocation paths, in case of two diffusive paths in the material body) when the density of one species influences the creation or annihilation of the other.
3. Non-Dimensionalization of the Double Diffusing Walgraef-Aifantis Model
Let , . Substituting in Equations (1a–1b), then assuming that the diffusion coefficients remain unchanged after scaling, and choosing coefficients of nonlinear product terms as unity after scaling, for σ1 = σ2 = σ, we have
Note, the variables ρ1 and ρ2, representing Equations (2a, 2b), are non-dimensional. The numerical model uses this system of a non-dimensional dynamical system.
3.1. Linear Stability Analysis
Equations (2a,2b) can be represented as the following coupled reaction-diffusion model
where , and . We analyze the system stability near the Homogeneous Equilibrium (HE) state or at the uniform steady state [1, 12], in line with the approach used in Spillotis et al. [12], i.e., where
Solving these equations we get the HE state, . Perturbing around this equilibrium state, perturbations defined as , we get .
Now near the HE states, the linearized version of the Equations (3a, 3b) are
where , and JF is the Jacobian of at the equilibrium states . We consider for real ω and get
where . As this is a system of two variables, the signatures of trace and determinant of the matrix defines the stability of the system. The determinant should be always positive and trace should be always negative for all real values of ω. We test these conditions for the HE state at (0, 0) and arrive at the following closed form expressions for the Trace (Tr) and Determinant (Det) of the model:
For , Trace is always negative and determinant is always positive. Hence, the HE state at (0, 0) is a stable state.
4. Biology to Materials' Modeling
It is usual practice in infectious disease epidemiology and modeling to measure the “speed” of the propagation of the infection. This measurement is generally called the basic reproduction number R0 that effectively equates to the number of secondary infections generated from each infected member of the population. R0 depends on the numbers of currently infected, susceptible and the rate of infection in the population. This R0 is the threshold parameter for an infectious disease, determining whether it becomes an epidemic, pandemic, or extinct in a community. The epidemiologists follow several methods to calculate R0. Two of these, referred to as the next generation method and the age-structured method [29–31] are widely used. Both are effective and popular in infection modeling studies.
In this work, we show how the concept of R0 can be made an auxiliary method in studying the diffusion process in a medium. We show how the profile of time evolution of R0 can help us to understand the diffusion-dynamics of two species, and can be used as a substitute to the enumeration of correlation functions.
Our starting point in this “reverse mapping” scheme from mathematical biology to material science relates to the origin of the concept of basic reproduction number R0. Let I(t) be a time-evolving quantity whose value at time t is dependent on its values at previous time points. This essential non-Markovian distribution ensures non-trivial values for all I(t − τ), where 0 ≤ τ ≤ t, as long as I(t) is defined. Representing I(t) as the number of infected individuals at time t in a population, non-Markovian kinetics ensures that I(t) should depend on the number of infected, present in the population, at time t − τ, since the new infections can only be generated by the previous infections. The time required for an infected individual to generate a new infection, from the onset of its infection, is called the generation time τ. Clearly, τ is a non-negative continuous random variable which has a probability density function, say g(τ). In the case of infectious diseases, g(τ) is generally taken as Gamma or a lognormal distribution.
5. “Generation Time” in Double Diffusion: Comparison With Random Walk Model
We can think of double diffusion as the continuum limit of a random walk model where the random walker diffuses along two different diffusive paths, occasionally jumping between them [19]. Here, by different diffusivity of paths we mean the probability of left jump (pi), right jump (qi), staying at same position without making any jump (ri) are different for the two paths, where i = 1, 2 for path-1 and path-2. Let us introduce a random time interval τ, having a probability density function g(τ), during which the walker diffuses along the same path before making any jump to the other path. The time τ can be thought of as the generation time for the double diffusion model, in parallel with the well defined generation time for an infectious disease. For this random walk model of double diffusion, let the probability of jumping from path-1 to path-2 be ℙ(1 → 2) = s1 and same for path-2 to path-1 be ℙ(2 → 1) = s2. Therefore, the generation time in case of our double diffusion model can be compared to the survival time of the random walker on a single path before making a jump to the other. Now, for the random walk model of double diffusion we must have pi + qi + ri + si = 1 for i = 1, 2. Therefore, the probability that the random walker continues on path i, in two consecutive jumps, is (1 − si). Hence the corresponding survival probability on path i is given by a geometric distribution. More explicitly, the probability that the walker will stay on path i for n consecutive jumps is . Motivated by the fact that the geometric distribution has memoryless property, and exponential distribution is the only continuous distribution having memoryless property, it is reasonable to assume that the generation time is exponentially distributed in the continuum limit of this random walk model of double diffusion.
5.1. The Reproduction Number R0 and Its Mapping to the D-D Model
Following the similar concept in the case of double diffusion, we can think of the density ρ(t) of certain species is dependent on its density ρ(t − τ) at earlier times (0 ≤ τ ≤ t). The time required for generating new particles of the same species from the old ones is a continuous random variable τ with some density function g(τ). Therefore, in the same token, as defined in case of infectious diseases, we can define a quantity R0 for a species in a double-diffusive process as
where g(τ) is the generation time.
Figures 1–4 compare the R0 equivalent of an equivalent epidemic rate model with that of the autocorrelation function (Equations (2a, 2b) at the quantitative level, providing interesting insights into the D-D reaction-diffusion model. It can be easily understood from the mathematical expression of R0(t) that it is a measure of the production rate of a species from the population of the same species at an earlier epoch, rather than due the conversion of other species. On the other hand, autocorrelation is a measure of the abundance of a species as a whole, aggregating the production of a species from it's own population as well as due to the conversion of other species. Therefore, the autocorrelation function together with the time-varying R0(t), gives us interesting spatio-temporal insights about the observed abundance.
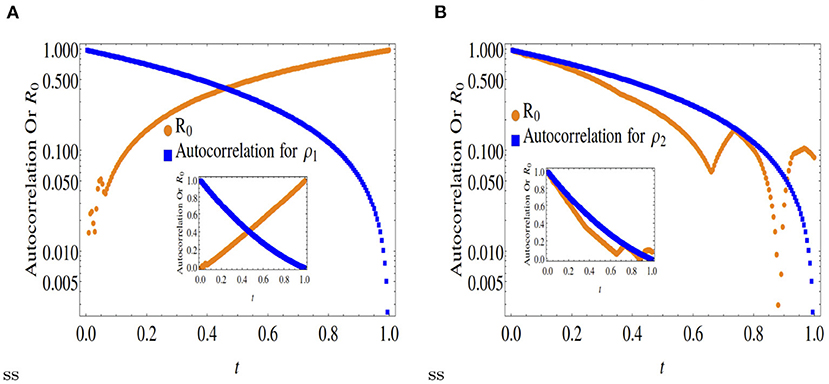
Figure 1. Comparison of normalized autocorrelation and R0 at x = 0.2. Outset is in log scale and inset is in original scale. (A) Shows that the autocorrelation (in blue) is decreasing at later times although the R0 is increasing for the species ρ1 (orange curve). This indicates that at x = 0.2 the production of ρ1 occurs from its own population at small timescales. On the other hand in (B), the simultaneous decreasing behavior of the autocorrelation and R0 indicate that at x = 0.2 the production of ρ2 also occurs at smaller timescales. However, in case of ρ2, its production occurs due to the conversion of ρ1 into ρ2, since the measure of self-creation R0 is decreasing in this case.
A comparison between Figures 1, 2 with Figure 3 clearly indicates that while asymmetric cases (x < 0.5) ensure only partial convergence between the R0 and autocorrelation profiles, i.e., only one of the two double diffusing variables match both profiles, at x = 0.5, the profiles match (approximately) for both variables.
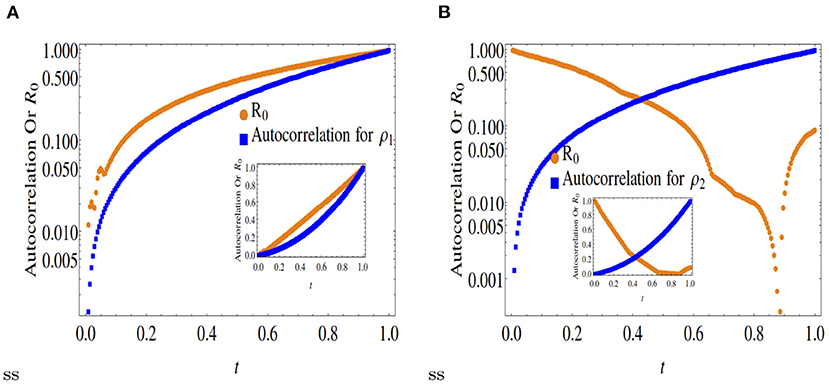
Figure 2. Comparison of normalized autocorrelation and R0 at x = 0.3. Outset is in log scale and inset is in original scale. (A) Shows that the autocorrelation function and R0 for the species ρ1 have the same increasing trend as a function of time. The understanding we get from this trend is that the species ρ1 is produced fom its own species for long time-scales. (B) Indicates that the dynamics of the species ρ2 is quite different than ρ1. The species ρ2 is produced from the conversion of ρ1 instead from its own ancestors, as the R0 for ρ2 decreases over time.
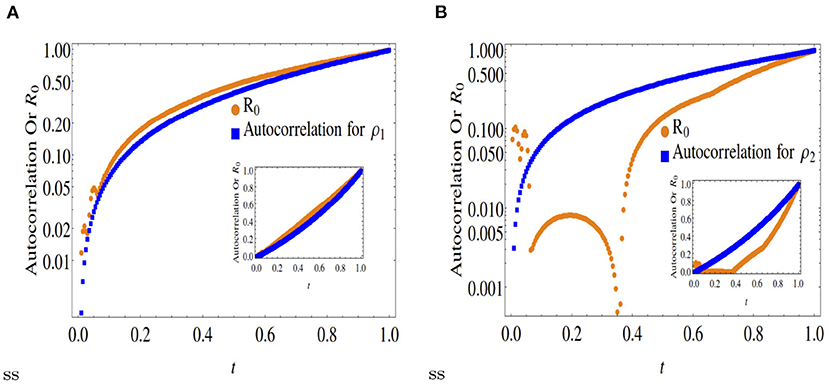
Figure 3. Comparison of normalized autocorrelation and R0 at x = 0.5. Outset is in log scale and inset is in original scale. (A) Shows similar trend for R0 and autocorrelation as in Figure 2A, which indicates that the production of ρ1 is boosted by the abundance of its ancestor. (B) Whereas, the production of ρ2 occurs both by the conversion of ρ1 for some time and due to its own population at later times.
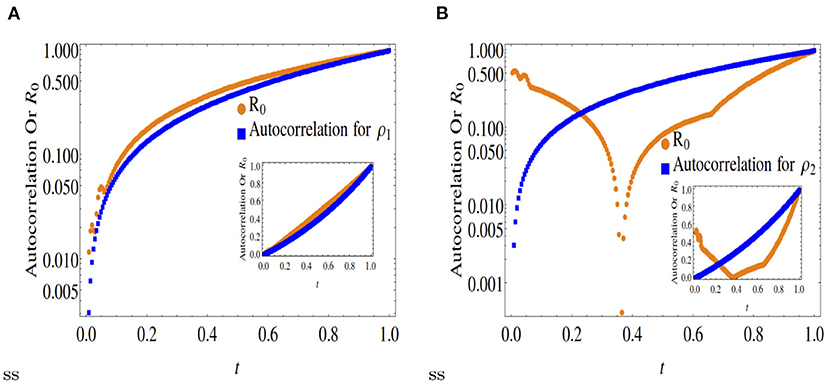
Figure 4. Comparison of normalized autocorrelation and R0 at x = 0.6. Outset is in log scale and inset is in original scale. The dynamics at x = 0.6 is almost similar to that of at x = 0.5, as shown in Figure 3. (A) Autocorrelation and R0 of ρ1 at x = 0.6. (B) Autocorrelation and R0 of ρ2 at x = 0.6.
Note, the dynamics of ρ1 as shown in Figure 5 matches those for x = 0.3, 0.5, 0.6. However, the species ρ2 is mostly created by the conversion of the species ρ1. These 5 figures clearly indicate that only for the symmetric case x = 0.5, the time dynamical evolution of the reproductive number for an epidemic model matches the average energy dissipation rate of individual variables (expressed as autocorrelation functions), not otherwise. This is not unexpected as the point x = 0.5 (spatial scale 0 < x <1) represents the point of dynamical equilibrium between two diffusing species, that also represents infection flux equilibrium between susceptible-infected-recovered species in an epidemic model. In other words, a fair quantitative comparison between the R0 vs. the D-D model is only ensured at x = 0.5.
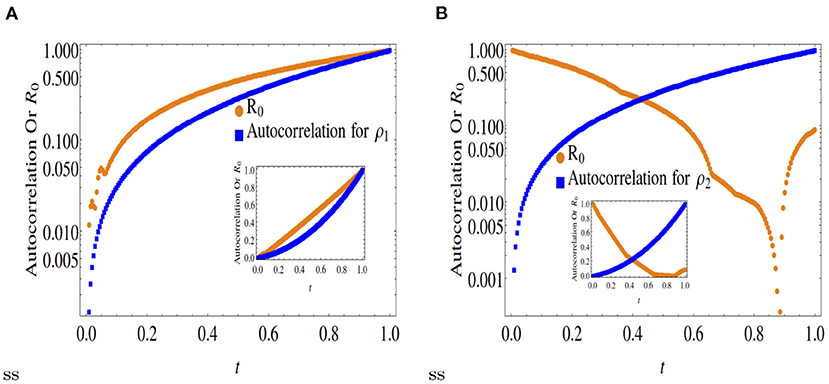
Figure 5. Comparison of normalized autocorrelation and R0 at x = 0.7. Outset is in log scale and inset is in original scale. (A) Autocorrelation and R0 of ρ1 at x = 0.7. (B) Autocorrelation and R0 of ρ2 at x = 0.7.
6. Conclusions
Clearly, a comparison of the dynamical variable R0(t), motivated by the epidemiological literature, with the autocorrelation function reveals the richness of the dynamics of a reaction-diffusion system which offers an option of interpolating the results from the epidemic model into the double-diffusion domain, in the process providing a closed form solution of the latter that has remained elusive thus far. Comparing the time evolution of R0 with the autocorrelation function gives the information of the origin of the observed abundance of different species in a reaction-diffusion system as explained in Figures 1–5. The analogy is strictly restricted to the spatially symmetric (x = 0.5) conformation though, a point of dynamical equilibrium between two (or multiple) diffusing species, an analogy with the stationary state fixed point of an epidemic model in dynamical equilibrium.
Therefore, the introduction of the epidemiologically motivated quantity R0(t) into the studies of the reaction-diffusion systems can play a crucial role in understanding such systems in more depth. Since this interpolation between two unrelated disciplines only uses the mathematical similarity between two (or multiple) reaction-diffusion species, expressed as double-diffusion in material science, as compared to infection rate growth in epidemiology, the approach is generic enough to be applied to all coupled reaction-diffusion models. At the point of symmetry (x = 0.5 in our model), both quantities (R0 and autocorrelation) will asymptotically match their values with evolving time allowing for a closed form mapped (from mathematical biology) solution of the R-D model. As a comparison with the numerical solution confirms close convergence with the approximate mapped solution (based on the R0(t) formula as a descriptor of the correlation strength of the diffusing variables), the solution provides handle to studies analyzing higher order perturbations and relevant bifurcations, also including stochastic terms. Future studies involving calculation of correlated superconducting fluxes would be presented using the same method.
Data Availability Statement
All data that support the findings of this study are included within the article (and any supplementary files).
Author Contributions
AC led the project, conceived the model, and the mapping between mathematical biology to material science. BK and SKN executed the analytical calculations, model simulations, and introduced the connection with statistical physics. EA provided the material science backbone. All authors jointly wrote the paper and contributed equally to this manuscript.
Funding
The authors gratefully acknowledge partial financial support from the H2020-MSCA-RISE-2016 program, Grant No. 734485, entitled Fracture Across Scales and Materials, Processes and Disciplines (FRAMED). BK acknowledges funding by UKRI Grant No. (MR/T046619/1), part of the NSF/CIHR/DFG/FRQ/UKRI-MRC Next Generation Networks for Neuroscience Program. SKN acknowledges the Leverhulme Trust (RPG-2018-137) for supporting his time and resources for research in the UK.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Walgraef D, Aifantis EC. Dislocation patterning in fatigued metals as a result of dynamical instabilities. J Appl Phys. (1985) 58:688. doi: 10.1063/1.336183
2. Walgraef D, Aifantis EC. Dislocation patterning in fatigued metals: labyrinth structures and rotational effects. Int J Eng Sci. (1986) 24:1789–98. doi: 10.1016/0020-7225(86)90127-8
3. Aifantis EC. On the dynamical origin of dislocation patterns. Mater Sci Eng. (1986) 81:563–74. doi: 10.1016/0025-5416(86)90293-4
4. Aifantis EC. Gradient nanomechanics: applications to deformation, fracture, and diffusion in nanopolycrystals. Metall Mater Trans A. (2011) 42:2985–98. doi: 10.1007/s11661-011-0725-9
5. Aifantis EC, Hill JM. On the theory of diffusion in media with double diffusivity I–Basic mathematical results. Q J Mech Appl Math. (1980) 33:1.
6. Aifantis EC, Hill JM. On the theory of diffusion in media with double diffusivity II–Basic mathematical results. Q J Mech Appl Math. (1980) 33:1.
7. Chattopadhyay K, Aifantis EC. Double diffusivity model under stochastic forcing. Physical Review E. (2017) 95:052134. doi: 10.1103/PhysRevE.95.052134
8. Chattopadhyay K, Aifantis EC. On stochastic resonance in a model of double diffusion. Mater Sci Technol. (2018) 34:1606–13. doi: 10.1080/02670836.2018.1507697
9. Chattopadhyay K, Aifantis EC. Stochastically forced dislocation density distribution in plastic deformation. Phys Rev E. (2016) 94:022139. doi: 10.1103/PhysRevE.94.022139
10. Vardoulakis J, Aifantis EC. A gradient flow theory of plasticity for granular materials. Acta Mech. (1991) 87:197–217. doi: 10.1007/BF01299795
11. Pontes J, Walgraef D, Aifantis EC. On dislocation patterning: multiple slip effects in the rate equation approach. Intl J Plasticity. (2006) 22:1488–505. doi: 10.1016/j.ijplas.2005.07.011
12. Spillotis KG, Russo L, Aifantis EC. Analytical and numerical bifurcation analysis of dislocation pattern formation of the Walgraef-Aifantis model. Int J Non Linear Mech. (2018) 102:41–52. doi: 10.1016/j.ijnonlinmec.2018.03.002
13. Aifantis EC. Gradient extension of classical material models: from nuclear & condensed matter scales to earth & cosmological scales. In: Ghavanloo E, Fazelzadeh SA, Marotti de Sciarra F, editor. Size-Dependent Continuum Mechanics Approaches. Springer; Cham: Springer Tracts in Mechanical Engineering.
14. Tsambali A, Konstantinidis A, Aifantis EC. Modeling double diffusion in soils and materials. J Mech Behav Mater. (2018) 27:5–6. doi: 10.1515/jmbm-2018-2003
15. Aifantis EC. A new interpretation of diffusion in high-diffusivity paths–a continuum approach. Acta Metllurgica. (1979) 27:683–91. doi: 10.1016/0001-6160(79)90019-1
16. Aifantis EC. Comments on the calculation of the formation volume of vacancies in solids. Phys Rev B. (1979) 19:6622. doi: 10.1103/PhysRevB.19.6622
17. Aifantis EC. Continuum basis for diffusion in regions with multiple diffusivity. J Appl Phys. (1979) 50:1334. doi: 10.1063/1.326167
18. Wilson RK, Aifantis EC. On the theory of consolidation with double porosity. Int J Eng Sci. (1982) 20:1009–35. doi: 10.1016/0020-7225(82)90036-2
19. Hill JM. A discrete random walk model for diffusion in media with double diffusivity. ANZIAM J. (1980) 22:58–74. doi: 10.1017/S0334270000002551
20. Aifantis EC. On the problem of diffusion in solids. Acta Mech. (1980) 37:265–96. doi: 10.1007/BF01202949
21. Kuttler K, Aifantis EC. Existence and uniqueness in nonclassical diffusion. Q Appl Math. (1987) 45:549–60. doi: 10.1090/qam/910461
22. Santra I, Das S, Nath SK. Brownian motion under intermittent harmonic potentials. J Phys A Math Theor. (2021) 54:334001. doi: 10.1088/1751-8121/ac12a0
23. Konstantinidis D, Eleftheriadis I, Aifantis EC. Application of double diffusivity model to superconductors. J MaterProcess Technol. (2001) 108:185–7. doi: 10.1016/S0924-0136(00)00750-0
24. Vázquez JL, Arturo P, Fernando Q, Ana R. Classical solutions and higher regularity for nonlinear fractional diffusion equations. J Eur Math Soc. (2017) 19:1949–75. doi: 10.4171/JEMS/710
26. El-Hachem M, McCue SW, Jin W, Du Y, Simpson MJ. Revisiting the Fisher-Kolmogorov-Petrovsky-Piskunov equation to interpret the spreading-extinction dichotomy. Proc Roy Soc A. (2019) 475:20190378. doi: 10.1098/rspa.2019.0378
28. Pearson JE. Complex patterns in a simple system. Science. (1993) 261:189–92. doi: 10.1126/science.261.5118.189
29. Nishiura H. Correcting the actual reproduction number: a simple method to estimate r0 from early epidemic growth data. Int J Environ Res Public Health. (2010) 7:291–302. doi: 10.3390/ijerph7010291
30. Cori A, Ferguson NM, Fraser C, Cauchemez S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am J Epidemiol. (2013) 178:1505–12. doi: 10.1093/aje/kwt133
Keywords: double diffusion, reproduction number, autocorrelation, spatiotemporal correlation, Fick's diffusion
Citation: Chattopadhyay AK, Kundu B, Nath SK and Aifantis EC (2022) Transmissibility in Interactive Nanocomposite Diffusion: The Nonlinear Double-Diffusion Model. Front. Appl. Math. Stat. 8:852040. doi: 10.3389/fams.2022.852040
Received: 10 January 2022; Accepted: 10 May 2022;
Published: 03 June 2022.
Edited by:
Erik Andreas Martens, Lund University, SwedenReviewed by:
Alain Miranville, University of Poitiers, FranceConstantinos Siettos, University of Naples Federico II, Italy
Copyright © 2022 Chattopadhyay, Kundu, Nath and Aifantis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amit K. Chattopadhyay, YS5rLmNoYXR0b3BhZGh5YXlAYXN0b24uYWMudWs=
 Amit K. Chattopadhyay
Amit K. Chattopadhyay Bidisha Kundu
Bidisha Kundu Sujit Kumar Nath
Sujit Kumar Nath Elias C. Aifantis
Elias C. Aifantis