Hidden dual mathematical symmetry in the genetic code

We describe the genetic code in terms of numbers that help us to find several dual symmetries. Our formulation can even be rewritten regarding the up-down and right-left dual concepts. We argue that our work may bring many topological tools to studying the DNA molecule, including the Grassmann-Plücker coordinates, which are important in mathematical and physical contexts.

1 Introduction

It is a fact that mathematics continues to play an important role in the understanding of genomes [1]. For instance, there is no doubt that the efforts to describe mathematical aspects of the DNA structure helped to have a better understanding of the dynamics of the creation of proteins [2].

A well-known example of the above comment is provided by the knowledge base of triplet codons, a DNA sequence, consisting of three nucleotides (3 -nucleotide), the basic building blocks of DNA [3], coding for a specific amino acid sequence that is translated into a polypeptide molecule called proteins, the main functional and structural molecules in most organisms. The DNA consists of two strands in the form of a double right-handed helix of repeating units called nucleotides, each consists of four bases (or 4 -nucleotide), adenine (A), thymine (T), cytosine (C), and guanine (G) which form the stair rungs and a sugar molecule (either ribose in RNA or deoxyribose in DNA) attached to a phosphate group which forms the poles of the staircase. The 4-nucleotide (in the DNA), in turn, forms the corresponding sequence of amino acids and, finally, proteins. From the chemical properties of the four bases, it is clear that adenine can only be combined with thiamine and cytosine only with guanine (see Ref. [2] and references therein). Schematically, we can consider these four options in the form;

$\begin{array}{ll}\begin{array}{c}A-T,\\ T-A,\\ C-G,\\ G-C.\end{array}& (1)\end{array}$

We observe that the bases on the two strands of a DNA structure are complementary or dual (see Refs. [4–7] and references therein). The reason for this seems to be that adenine and thymine form two hydrogen bonds, while the cytosine and guanine form three hydrogen bonds.

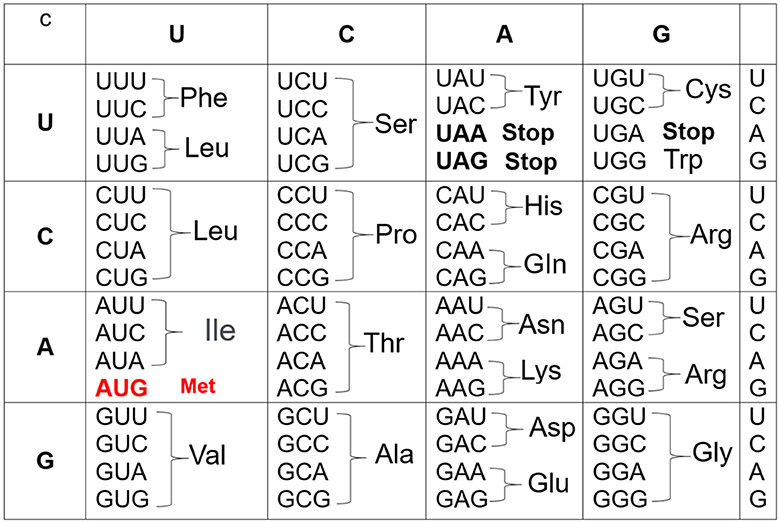
The starting point in constructing the genetic code is to consider the codons, which are triality of the 4-nucleotide. In turn, the triality of nucleotides means that there are 64 = 4 × 4 × 4 possible combinations or codons. Indeed, 61 codons specify 20 amino acids, one as starting (initiation) codon which establishes the beginning of synthesis and, at the same time, it codes the amino acid methionine; on the other hand, three are used as stop signals (see Ref. [8]). Moreover, the first problem is how to distribute the 41 = 61 − 20 codons in 20 amino acids. This is possible if some associated amino acids are specified for more than one codon. In the end, after years of hard work, a consistent and valuable genetic table was obtained (see Figure 1), where U is associated with the RNA structure but corresponds to T in the DNA. Surprisingly and interestingly, this genetic table applies to most genes in animals, plants, and microorganisms.

Figure 1

Figure 1. Genetic Code regarding the set {U, C, A, G}.

On the other hand, it is known that in nature, there are visible and hidden symmetries. A very good explanation of this phenomenon can be found in a book by Moshinsky: Simetría en la Naturaleza (symmetry in Nature) [9]. This author put an example of such a phenomenon by presenting a picture of a mural called “La Nueva Democracia” (“The New Democracy”) by Siqueiros (a famous muralist in Mexico). In such a mural, one can find a natural symmetry as bilateral of two sides of the central figure. However, if we look at the original sketched structure of the mural, we find a series of hidden symmetries such as circles, triangles, and squares, which were important for the development of the final mural. In analogy to this Siquerios mural, the question arises whether the genetic code associated with the DNA also contains hidden symmetries.

With the above purpose, in this study, we have as a main goal to rewrite the genetic code in more mathematical terms. We show that our strategy helps us find hidden duality symmetry, which allows us to reduce the 64 = 4 × 4 × 4 possible codons to only 32. Moreover, we also present an even more abstract notion of the genetic code in terms of duality concepts up-down and left-right. We believe that our approach may help not only to have a better understanding of symmetry in the genetic code but also to establish a bridge between different mathematical tools in both mathematics and physics. We think that it will improve our understanding of the nature of coding activity and the evolution of the genetic code.

2 Genetic code in terms of the set {1, 2, 3, 4}

Assume we consider the following identifications.

$\begin{array}{ll}\begin{array}{c}T\leftrightarrow 1,\\ C\leftrightarrow 2,\\ A\leftrightarrow 3,\\ G\leftrightarrow 4.\end{array}& (2)\end{array}$

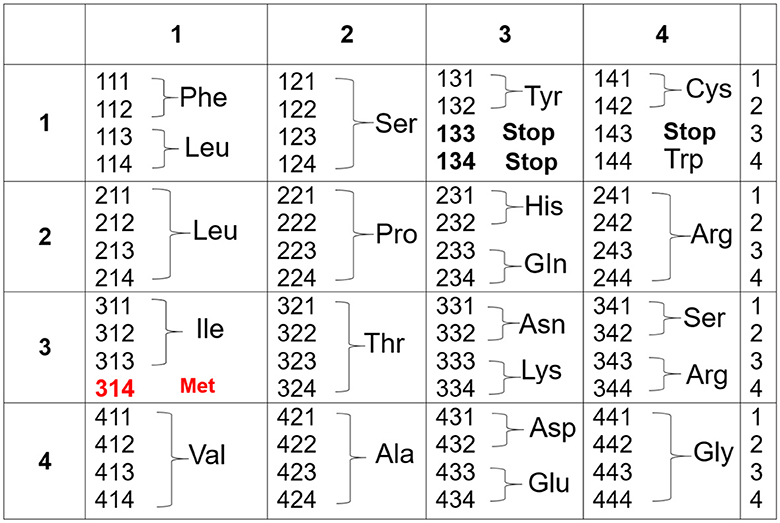
The genetic code in Figure 1 now becomes Figure 2:

Figure 2

Figure 2. Genetic code in terms of the set {1 ,2, 3, 4}.

At first sight, there does not seem to be any new advantage of the genetic code according to Figure 2 over the one presented in Figure 1. But considering Figure 3, we would like to present a very good example that this is not the case. In Figure 3, we do not include the corresponding amino acids at this stage because we would like to discover hidden relations. Let us assume that the codons (ijk), with i, j, k = 1, 2, 3, 4, are symmetric in any permutation of the indices i, j, k. If we use the formula

$\begin{array}{ll}N=\frac{(n+d-1)!}{(d-1)!n!},& (3)\end{array}$

which applies to any symmetric permutation, we observe that N = 20. This is because, in our case, d = 4 and n = 3. This number coincides with the number of amino acids. Moreover, this coincidence may motivate us to associate only one codon with each value of the symmetric permutation of (ijk). First, we notice that when i = j = k, we have the four results {(111), (222), (333), (444)}. Therefore, in this case, the other degenerated values in Figure 3 are eliminated; for instance, we have

$\begin{array}{ll}Gly=\left\{(444)\right\}.& (4)\end{array}$

But

$\begin{array}{ll}Gly\ne \left\{(144),(344),(244)\right\}.& (5)\end{array}$

Now consider

$\begin{array}{ll}Glu=\left\{(224),(244)\right\}.& (6)\end{array}$

Since

$\begin{array}{ll}Arg=\left\{(134),(334),(234),(344),(224),(244)\right\},& (7)\end{array}$

we observe that if we choose (244) for Glu, Arg must be (224). Similarly if we choose (224) for Glu, Arg must be (244). This is because for any two repeated index values of (ijk), there are only three possibilities. Thus, we have that

$\begin{array}{ll}\begin{array}{c}\hspace{1em}ifGlu=(244)thenArg(224),\\ \hspace{1em}and\hfill \\ \hspace{1em}ifGlu=(244)thenArg(224).\end{array}& (8)\end{array}$

This shows that we must choose

$\begin{array}{ll}Arg\ne \left\{(134),(334),(234),(344)\right\},& (9)\end{array}$

Thus, since

$\begin{array}{ll}Pro=\left\{(333)\right\},& (10)\end{array}$

$\begin{array}{ll}Pro\ne \left\{(133),(233),(334)\right\}& (11)\end{array}$

and

$\begin{array}{ll}Ala=\left\{(134),(334),(234),(344)\right\},& (12)\end{array}$

we must choose

$\begin{array}{ll}Ala=\left\{(334)\right\}.& (13)\end{array}$

However, by Arg and Gly, we observe that we must have

$\begin{array}{ll}Ala=\left\{(344)\right\}.& (14)\end{array}$

Therefore, Ala has inevitably two assigned codons. This contradicts the fact that each codon must have only one associated codon. Therefore, with the help of Figure 3, we have proven that the codon structure (ijk) can not be a totally symmetric quantity.

Figure 3

Figure 3. Genetic code in terms of the set {1, 2, 3, 4} without the associated amino acids.

3 Genetic code in terms of the sets {1, 2} and {1^*, 2^*}

Now that we have the genetic code according to Figure 3, we wonder if we can go a step further in a more abstract mathematical structure. For this purpose, let us make the new correspondences

$\begin{array}{ll}\begin{array}{c}1\leftrightarrow 1,\\ 2\leftrightarrow 2,\\ 3\leftrightarrow 1^{*},\\ 4\leftrightarrow 2^{*}.\end{array}& (15)\end{array}$

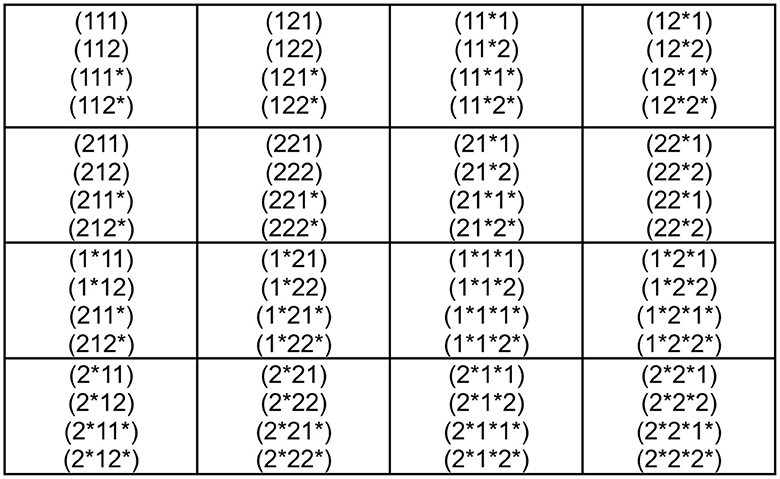
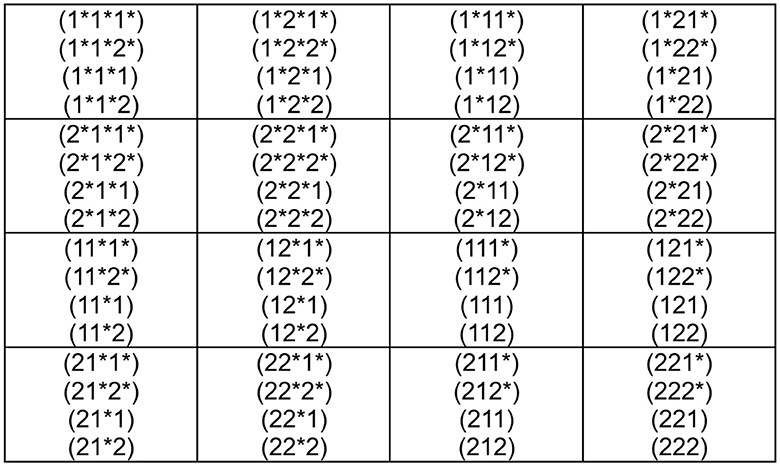
With this identification Figure 3, we can construct the genetic code of Figure 4. The reason for this proposal is that thiamine T = 1 can only be combined adenine A = 3 and cytosine C = 2 with guanine G = 4. This additional requirement must lead us to consider the relations 1↔1^* and 2↔2^*, which start to look as a type of duality relations. The anti-code associated with each codon of Figure 4 is established in Figure 5.

Figure 4

Figure 4. Genetic code in terms of the set {1, 2, 1*, 2*}.

Figure 5

Figure 5. Genetic code in terms of the anticodons.

Let us make the following index identification:

$\begin{array}{ll}\begin{array}{c}a=(1,2),\\ a^{*}=(1^{*},2^{*}).\end{array}& (16)\end{array}$

Inspired by tensor analysis [10], we also may rewrite the expression

$\begin{array}{ll}{C}_{ijk}=(ijk),& (17)\end{array}$

with the indices i, j, k, ...etc running from 1 to 4. Moreover, combining Equations (16) and (17), we shall get

$\begin{array}{ll}{C}_{ijk}=\left(\begin{array}{cc}{C}_{abc}& C_{a{b}^{\ast }c}\\ C_{ab{c}^{\ast }}& C_{a{b}^{\ast }{c}^{\ast }}\\ C_{a^{\ast }bc}& C_{a^{\ast }{b}^{\ast }c}\\ C_{a^{\ast }b{c}^{\ast }}& C_{a^{\ast }{b}^{\ast }{c}^{\ast }}\end{array}\right)& (18)\end{array}$

Using Equation (17), it is possible to verify that this is consistent with the structure of Figure 3. As we mentioned, we have the duality relations 1↔1^* and 2↔2^*. From Equation (16), this means that

$\begin{array}{ll}a\leftrightarrow a^{*}.& (19)\end{array}$

Duality has always the property (^A*)^* = A for any quantity A . From Equation (19), we observe that this is the case because (^a*)^* = a. Hence, the expression (18) leads us to establish the following connections:

$\begin{array}{ll}\begin{array}{cc}{C}_{abc}\leftrightarrow C_{a^{*}{b}^{*}{c}^{*}}& C_{a{b}^{*}c}\leftrightarrow C_{a^{*}b{c}^{*}}\\ C_{ab{c}^{*}}\leftrightarrow C_{a^{*}{b}^{*}c}& C_{a{b}^{*}{c}^{*}}\leftrightarrow C_{a^{*}bc}\end{array}.& (20)\end{array}$

This result means that from the four quantities

$\begin{array}{ll}\begin{array}{cc}{C}_{abc}& C_{a{b}^{*}c}\\ C_{ab{c}^{*}}& C_{a{b}^{*}{c}^{*}}\end{array},& (21)\end{array}$

we can obtain via duality the other four quantities

$\begin{array}{ll}\begin{array}{cc}{C}_{a^{*}bc}& C_{a^{*}{b}^{*}c}\\ C_{a^{*}b{c}^{*}}& C_{a^{*}{b}^{*}{c}^{*}}\end{array}.& (22)\end{array}$

One of the consequences of this development is that if duality is used, out of the 64 possible codons, only 32 are necessary.

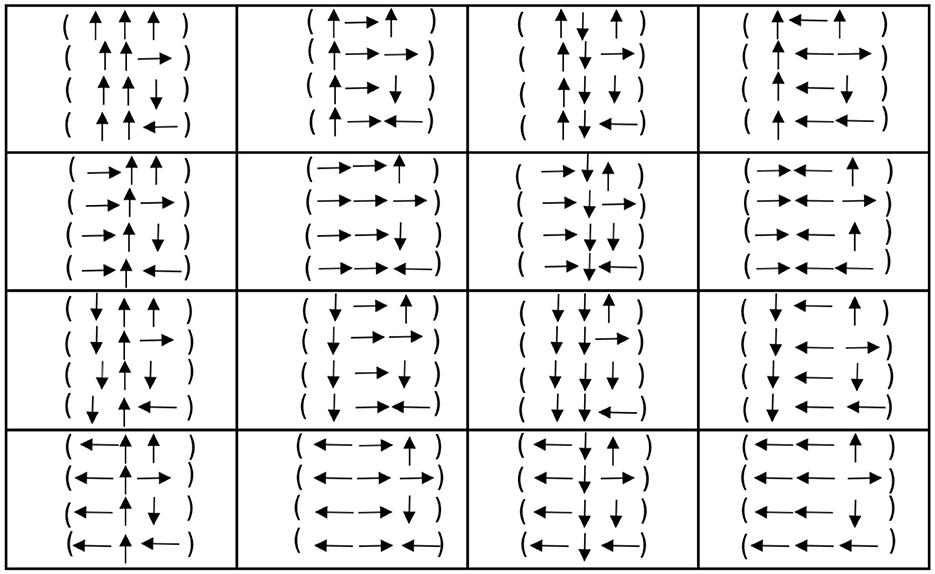
4 Genetic code in terms of the sets {↑, ↓} and { → , ←}

Motivated by the duality prescription of the previous section, we propose an even clearer construction for duality in this section. The idea is to write 1 as ↑, 1^* as ↓, while 2 as → and 2^* as ←. We call ↑ up, ↓ down, while we call → right and ← left. With this new notation, we may construct Figure 6. Of course, it is evident that up/down are dual concepts, while right/left are also dual concepts. This means that all the codons and, consequently, all the genetic code are written in terms of two dual concepts: up/down and right/left.

Figure 6

Figure 6. Genetic code regarding the dual concepts up/down and right/left.

An interesting thing from the present perspective is that with the sets

$\begin{array}{ll}\{\uparrow ,\downarrow \}\text{and}\{\to ,\leftarrow \}& (23)\end{array}$

we may consider options of the form;

or

which are well-known mathematical structures in topology [11] and differential geometry [12].

5 Final remarks

The prescription of Section 4 recalls the dual concepts of the spin associated with particles in higher energy theory. For instance, it is known that the electron spin can have only two possible states: spin up or down. This is because the electron is a fermion with half-integer spin. Conversely, the neutrino spin is classified as left-handed or right-handed. Moreover, although the scenarios of the genetic code and particle theory describe different scenarios, there could be, at the fundamental level, some dual principles in both cases.

The two options {↑, ↓} and { → , ←} can be considered that describe a 2 -dimensional structure. Our world, however, at our scales is 3 -dimensional. Moreover, we wonder whether there is a 3-dimensional genetic code structure.

Recently, we became aware of Reference [13], where there are several reflections on the origin and early evolution of the genetic code. An important issue raised in this reference is why the codons are composed of three nucleotides; in our language, why the codons are described by the quantity C_ijk, why not C_ij or C_ijkl. Of course, C_ij gives only 16 different codons, which are not enough to code the 20 amino acids. While C_ijkl, we shall have 254 codons, which is too big number for the code of the 20 amino acids. However, if C_ijkl is a totally symmetric object, C_ijkl describes only 35 codons. Another possibility is that C_ijkl has the symmetries

$\begin{array}{ll}{C}_{ijkl}=-C_{ijlk}=-C_{jikl},& (27)\end{array}$

and

$\begin{array}{ll}{C}_{k\left[lij\right]}=0& (28)\end{array}$

(as the Riemann tensor in general relativity theory; see page 326 of Reference [14]). Let us assume that i, j, k and l run from 1 to p then the first condition (27) leads to

$\begin{array}{ll}\frac{p(p-1)}{2}& (29)\end{array}$

and from the last condition in Equation (27), we obtain the same result. Moreover, the conditions in Equation (27) determine a square matrix of $\frac{p(p-1)}{2}\times \frac{p(p-1)}{2}$. This means that, in principle, there are

$\begin{array}{ll}\frac{p^2{(p-1)}^2}{4}& (30)\end{array}$

components in C_ijkl. However, due to Equation (28), no all of these conditions are independent; we must subtract from Equation (30) all the combinations obtained from Equation (28), namely

$\begin{array}{ll}p\frac{p!}{3!(p-3)!}& (31)\end{array}$

or

$\begin{array}{ll}\frac{p(p-1)(p-2)}{6}& (32)\end{array}$

components. Thus, the total number of independent components in C_ijkl satisfying (27) and (28) can be obtained from the expression

$\begin{array}{ll}\frac{p^2{(p-1)}^2}{4}-\frac{p(p-1)(p-2)}{6}.& (33)\end{array}$

We obtain

$\begin{array}{ll}\frac{p^2(p^2-1)}{12},& (34)\end{array}$

which is the formula that determines the number of independent components of the quantity C_ijkl (see page 326 of Reference [14]). In particular, in our case p = 4 and therefore, surprisingly from Equation (34), we obtain that the several possible codons for C_ijkl is 20, the same number of amino acids!

In Reference [4], a link was established between the DNA molecule and the Grassmann–Plücker coordinates, which, in both mathematics and physics, are of great importance and are connected with oriented matroid theory (see [5, 6] references therein). It is worth mentioning that recently, it has been shown [15] how the matroid concept can be used to determine the existence of mutations in DNA and RNA. Moreover, in Reference [16], the importance of mathematical modeling methods in analyzing complex signal systems is raised. It is tempting to assume that the dynamics of mutations in DNA and RNA can be studied using a dynamical-oriented matroid theory. Thus, further study may be very interesting to establish a link between the present study with these mathematical developments.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

NN-M: Writing – original draft, Writing – review & editing. CN-M: Writing – review & editing. IN-M: Writing – original draft, Writing – review & editing. JN: Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors want to thank P. A. Nieto-Marín for the helpful comments. JN would like to thank the mathematical department of the Arizona State University, where a part of this study was developed.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Benham CJ, Harvey S, Olson WK, Sumners DWL, Swigon D. Mathematics of DNA Structure, Function and Interactions. London: Springer Dordrecht Heidelberg (2000). doi: 10.1007/978-1-4419-0670-0

Crossref Full Text | Google Scholar

2. Karp G. Cell and Molecular Biology. New York, NY: John Wiley and Sons (2009).

Google Scholar

3. Watson JD, Berry A. DNA: The Secret of Life. Kindle of Knopf edition. New York, NY: Knopf (2009).

Google Scholar

4. Nieto JA, Nieto-Marín CC, Nieto-Marín N, Nieto-Marín I. New mathematical tools for the study of the DNA structure. J App Math Phys. (2021) 9:1896–903. doi: 10.4236/jamp.2021.98123

Crossref Full Text | Google Scholar

5. Bokowski J, Sturmfels B. Computational Synthetic Geometry. New York, NY: Springer-Verlag (1980).

Google Scholar

6. Björner A, Las Vergnas M, Sturmfels B, White N, Ziegler GM. Oriented Matroids. Cambridge, MA: Cambridge University Press (1993).

Google Scholar

7. Nieto JA. Oriented matroid theory as a mathematical framework for M-theory. Adv Theor Math Phys. (2006) 10:747–57. doi: 10.4310/ATMP.2006.v10.n5.a5

Crossref Full Text | Google Scholar

8. Křížek M, Křížek P. Why has nature invented three stop codons of DNA and only one start codon? J Theor Biol. (2012) 304:183–7. doi: 10.1016/j.jtbi.2012.03.026

PubMed Abstract | Crossref Full Text | Google Scholar

9. Moshinsky M. Simetría en la Naturaleza. Mexico: El Colegio Nacional (2013) (in Spanish). Available online at: https://colnal.mx/wp-content/uploads/2019/11/Discurso-Marcos-Moshinsky.pdf

PubMed Abstract | Google Scholar

10. Sokolnikoff S. Tensor Analysis: Theory and Applications. New York, NY: John Wiley & Sons (1956).

Google Scholar

11. Nash C, Sen S. Topology and Geometry for Physicists. Garden City, NY: Dover Publications (2013).

PubMed Abstract | Google Scholar

12. Göckeler M, Schücker T. Differential Geometry, Gauge Theories, and Gravity. Cambridge, MA: Cambridge University Press (1987).

Google Scholar

13. Fontecilla-Camps C. Reflections on the origin and early evolution of the genetic code. ChemBioChem. (2023) 24:e202300048. doi: 10.1002/cbic.202300048

PubMed Abstract | Crossref Full Text | Google Scholar

14. Misner CW, Thorne KS, Wheeler JA. Gravitation. New York, NY: W. H. Freeman (1973).

Google Scholar

15. Badr M, Abu-Gdairi R, Nasef AA. Mutations of nucleic acids via matroidal structures. Symmetry. (2023) 15:1741. doi: 10.3390/sym15091741

Crossref Full Text | Google Scholar

16. Li Y. Mathematical modeling methods and their application in the analysis of complex signal systems. Adv Math Phys. (2022) 2022:1816814. doi: 10.1155/2022/1816814

Crossref Full Text | Google Scholar