Sensitivity analysis for a delay mathematical model: the glucose-insulin model

We investigate glucose-insulin regulation through a delay differential equation model formulated in Sobolev spaces. A physiologically motivated time delay is incorporated into an advanced modeling framework that builds upon the classical ordinary differential equation based model proposed by Bergman and Cobelli. The resulting system is formulated within a semigroup-theoretical setting that ensures well-posedness. Sensitivity analysis based on Fréchet derivatives is employed to quantify parameter influence, while optimal design criteria derived from the Fisher Information Matrix are used to improve parameter estimation. The findings highlight the effectiveness of Sobolev-space and semigroup techniques in providing a rigorous and adaptable foundation for modeling delayed physiological processes.

1 Introduction

Over the past half-century, a substantial amount of data on glucose and insulin levels has been collected, and mathematical modeling has been extensively applied in diabetes research. Numerous studies have explored various aspects of the disease, including glucose–insulin dynamics; the pharmacokinetics of insulin injections, as presented in Lauritzen et al. [1], Binder et al. [2], and Heinemann [3]; and the signaling pathways involved in insulin production and glucose uptake, as described in Bergman [4], Edgerton et al. [5], Norton et al. [6], and Rosenstock et al. [7]. The study of these dynamics often reveals feedback loops and regulatory mechanisms governing the glucose-insulin system. For instance, the balance between insulin secretion and glucose absorption plays a crucial role in maintaining homeostasis in healthy individuals.

This paper addresses a significant gap in the mathematical modeling of diabetes by providing a rigorous framework for parameter estimation and sensitivity analysis in glucose insulin dynamics, formulated within infinite-dimensional abstract spaces using semigroup theory. Although numerous models have been proposed since the development of the classical minimal model [8–11], the challenges of ill-posedness and sensitivity in parameter estimation, particularly in models incorporating physiological time delays, have not been systematically studied. These issues are especially critical when fitting models to clinical data, as highlighted in recent simulation-based studies [12, 13], which often overlook the underlying instability of the inverse problem.

The novelty of this work lies in its dual contribution: (i) the integration of sensitivity analysis based on Fréchet derivatives and semigroup methods as a diagnostic tool for guiding parameter estimation in delay differential models; and (ii) the explicit treatment of the ill-conditioned nature of the associated inverse problems, which remains largely unexamined even in advanced semigroup-based formulations [14, 15]. By revisiting the minimal model and extending the analysis to delayed systems within a Sobolev-space framework, we offer a new perspective that unifies biological relevance with mathematical rigor and provides a foundation for more robust estimation strategies in diabetes modeling.

A mathematical model in diabetes or other biological fields is a simplified representation of complex phenomena, capturing only the most essential aspects of the underlying system. Given the inherent complexity and variability found in biological processes, these models necessarily provide highly abstracted views of reality. Typically, the process of developing a physiological mathematical model begins by formulating key research questions based on physiological insights. Researchers then construct mathematical equations that reflect the biological processes involved, explicitly stating all assumptions. Subsequently, they solve these equations and thoroughly analyze the model's behavior. This is followed by estimating model parameters based on available data or empirical observations. Finally, results are interpreted, the model is validated, and its accuracy is rigorously assessed.

Mathematical modeling follows an iterative process, beginning with encoding a real-world phenomenon into mathematical equations, followed by a decoding phase where the model's accuracy is evaluated. Assumptions made during the encoding phase simplify the complexity of the system, while the decoding phase ensures the model remains a reliable representation of reality. Some diabetes models gain widespread acceptance due to their simplicity and ease of use. However, it is crucial to acknowledge their limitations, particularly when important factors, such as exercise or stress are excluded [16–18].

Mathematical modeling plays a critical role in understanding complex biological systems, particularly in glucose-insulin dynamics. The regulation of blood glucose levels is a fundamental physiological process, and its disruption can lead to serious metabolic disorders such as diabetes. Delay differential equations (DDEs) have been widely used to model this system, as they effectively capture the inherent time delays in glucose metabolism and insulin response. While classical models provide valuable insights, they often rely on simplifications that overlook important dynamical properties.

This work aims to advance the mathematical analysis of glucose-insulin interaction by employing semigroup theory and Fréchet derivatives in abstract functional spaces. Unlike previous studies that primarily focus on numerical simulations or empirical parameter estimation, we establish a rigorous theoretical framework that enables a deeper understanding of the systems sensitivity to parameter variations. The novelty of our approach lies in the integration of semigroup theory with sensitivity analysis, providing a systematic way to assess the stability and robustness of delay models. Moreover, by leveraging optimization techniques such as the Fisher Information Matrix, we improve parameter estimation strategies, refining the accuracy and reliability of these models.

By bridging abstract mathematical theory with real-life physiological processes, this study offers a new perspective on the mathematical foundations of insulin-glucose regulation. The results contribute not only to the theoretical development of delay models but also to practical applications in improving model-based predictions for medical and biological studies. With this foundation, we can gain deeper insights into the complexities of mathematical modeling in diabetes research.

2 Overview of diabetes mellitus

Diabetes mellitus encompasses a group of disorders characterized by elevated blood glucose levels. Chronic high blood glucose, if left unmanaged, can lead to complications affecting both large blood vessels, known as macroangiopathy, which can result in conditions such as coronary artery disease, peripheral artery disease, and cerebrovascular disease, and small blood vessels, known as microangiopathy, which can lead to diabetic retinopathy, nephropathy, and neuropathy. These complications can result in serious health issues such as blindness, cardiovascular and cerebrovascular diseases, kidney failure, sensory and autonomic neuropathy, and an increased susceptibility to infections [19].

Glucose is the primary energy source for the body, serving as essential fuel for cellular functions. Carbohydrates from food are broken down by enzymes in the intestinal mucosa into simpler sugars, such as glucose and galactose, which are then absorbed into the bloodstream. The blood from the intestines is transported to the liver via the portal vein. After processing in the liver, the blood re-enters the general circulation through the hepatic veins and the inferior vena cava [20].

In the microcirculation, glucose diffuses into the interstitial fluid, where it is available for uptake by cells. Insulin, a hormone produced by the pancreas, facilitates the uptake of glucose from the interstitial fluid into insulin-sensitive tissues, such as muscle and adipose tissue. In the absence of adequate insulin, or if the body's cells become resistant to insulin's effects, blood glucose levels can rise above the normal fasting level of 6.4mmol/L, leading to hyperglycemia [21, 22].

Diabetes mellitus affects millions worldwide, and its incidence is steadily increasing. According to the International Diabetes Federations 11th Edition Diabetes Atlas (2024), approximately 589 million adults aged 20–79 were living with diabetes about 1 in 9 of the global adult population. This number is projected to rise to 853 million by 2050 approximately 1 in 8 [23]. Over 90% of these cases are type 2 diabetes, driven by socio-economic, demographic, environmental, and genetic factors [23]. The growing prevalence of diabetes imposes a significant burden on public health systems and economies worldwide, making it one of the top ten causes of death and disability [17, 24].

Efforts to improve diabetes management and outcomes are critical. These include preventive measures for type 2 diabetes, early diagnosis, and proper care for all types of diabetes. These efforts are supported by mathematical modeling and system-based approaches [12, 25, 26], emphasizing the need for continuous research in diabetes care. In 2022, the WHO launched global targets for diabetes coverage as part of its Global Diabetes Compact, aiming for 80% glycemic control among diagnosed individuals by 2030 [27].

Improved therapies and interventions are essential to enhance the quality of life for diabetics and reduce the long-term burden of the disease. These statistics underscore the urgent need for effective strategies to combat the global diabetes epidemic, emphasizing the importance of continuous research and innovation in diabetes care, as demonstrated by novel approaches to treatment adherence in type 1 diabetes [28].

Insulin secretion is primarily regulated by the feedback effect of blood glucose levels on pancreatic beta cells. Glucose enters the islets at a rate dependent on plasma glucose concentration, unaffected by insulin. Elevated blood glucose levels increase insulin secretion into pancreatic venous blood. Autonomic influences also contribute to insulin regulation: vagal stimulation increases insulin secretion, while sympathetic stimulation inhibits it. Gastric inhibitory peptide (GLP-1) from the gastrointestinal mucosa stimulates insulin secretion, explaining why orally administered glucose has a greater insulin-stimulating effect than intravenous glucose [16, 29].

There are several diagnostic methods for diabetes. Historically, physicians diagnosed diabetes by tasting the patient's urine for sweetness. Modern diagnostics rely on biochemical criteria, including fasting plasma glucose, the oral glucose tolerance test (OGTT), and glycated hemoglobin (HbA1c). According to Harreiter and Roden [30], the World Health Organization defines type 2 diabetes as fasting plasma glucose levels ≥126mg/dL (7.0mmol/L), 2-hour plasma glucose levels ≥200mg/dL (11.1mmol/L) after a 75 g OGTT, or HbA1c values ≥6.5% (48mmol/mol), each confirmed on at least two occasions in the absence of classical hyperglycemic symptoms. These thresholds are established to reflect the increased risk for complications such as diabetic retinopathy. When test results are borderline or discordant, confirmation using a different method or a repeated test is recommended. For further details and clinical guidance, see Table 2 and the associated discussion in Harreiter and Roden [30], with references therein.

The glucose-insulin regulatory mechanism operates as a closed-loop feedback system. When plasma glucose levels rise, such as after food intake, a sequence of physiological responses occurs to reduce blood glucose levels. Initially, beta cells in the pancreas detect elevated glucose and respond by producing insulin. Although some glucose uptake into cells occurs independently of insulin, the majority is facilitated after insulin is distributed from the bloodstream into a distal compartment, becoming interstitial insulin. This interstitial insulin interacts with cell membranes, facilitating glucose uptake, particularly in skeletal muscles and peripheral tissues. Consequently, cells utilize this glucose for energy production, while insulin simultaneously promotes the storage of glucose in the liver [5, 10, 31].

Conversely, when blood glucose levels fall below an acceptable threshold, the body initiates mechanisms to restore glucose to homeostasis. In this scenario, alpha cells in the pancreas respond by secreting glucagon, which travels via the circulation to the liver. There, glucagon binds to hepatocyte receptors and stimulates the breakdown of glycogen stores (glycogenolysis) and promotes gluconeogenesis, releasing glucose into the bloodstream and thus raising blood glucose levels [32, 33].

Importantly, these physiological processes inherently involve delays, such as the time between an increase in blood glucose and insulin secretion by pancreatic beta cells, or between a drop in blood glucose and the subsequent release of glucose from glycogen stores. Furthermore, tissue glucose uptake involves intricate signaling pathways. Insulin production itself is pulsatile, characterized by rapid oscillations every 5–15 min and broader ultradian oscillations occurring approximately every 50–150 min [34–36].

One of the earliest attempts to measure insulin effectiveness was in 1932 by Himsworth [37], termed insulin sensitivity [38, 39]. Insulin sensitivity refers to insulin's ability to reduce blood glucose by promoting uptake by muscle and fat cells and increasing hepatic glycogen storage. Insulin resistance [40–42], a key feature of diabetes mellitus, occurs when insulin sensitivity is reduced. Tests such as the euglycemic hyperinsulinemic clamp (EHC), frequently sampled intravenous glucose tolerance test (FSIGT), and intravenous glucose tolerance test (IVGTT) help quantify insulin sensitivity [43, 44].

The minimal model, developed by Bergman and colleagues, leverages intravenous glucose tolerance test (IVGTT) data and insights into postprandial insulin and glucose dynamics to provide a comprehensive framework for understanding glucose-insulin interactions. This model is particularly valuable because it offers a method to independently assess insulin production and insulin sensitivity, which is often challenging due to the complex interplay between these two factors. Mathematical modeling, in this context, plays a crucial role in elucidating the dynamics of glucose and insulin in both diabetic and non-diabetic populations.

The minimal model's ability to quantify insulin sensitivity and pancreatic responsivity has made it a cornerstone in diabetes research. By simulating how insulin and glucose interact within the body, researchers can better understand the underlying mechanisms of diabetes and the effectiveness of various treatment strategies. This approach is not only useful for identifying the degree of insulin resistance but also for determining how different interventions may improve insulin sensitivity.

Furthermore, the development and application of mathematical models extend beyond just the minimal model. These models incorporate various physiological parameters and simulate different scenarios, providing insights into the progression of diabetes and the potential impact of lifestyle changes, medications, and other therapeutic interventions. By predicting outcomes and optimizing treatment plans, these models are indispensable tools in diabetes research, helping to unravel the complexities of the disease and leading to more effective treatments. With this foundation, we can deeply understand the complexity of the mathematical modeling of diabetes.

3 Hormonal regulation of glucose metabolism

The hormones insulin and glucagon are secreted by beta cells and alpha cells, respectively, in the islets of Langerhans in the pancreas. These hormones play a crucial role in regulating the metabolism of carbohydrates, proteins, and fats. Insulin promotes anabolic processes, increasing the storage of glucose, fatty acids, and amino acids, while glucagon promotes catabolic processes, mobilizing these substances from storage into the bloodstream. Specifically, glucagon stimulates the liver to release glucose, thereby raising blood sugar levels. The antagonistic actions of these hormones are typically reciprocally regulated [6, 22, 36].

Research indicates that an excess of insulin can cause hypoglycemia, whereas insulin deficiency, whether absolute or relative, leads to diabetes mellitus. Conversely, glucagon deficiency can also result in hypoglycemia, while an excess of glucagon raises blood glucose levels. Glucagon primarily acts on the liver, stimulating glycogen breakdown and the formation of glucose from non-carbohydrate sources, and also stimulates insulin secretion by the beta cells [32, 33, 36, 40].

Insulin exerts its effects on glucose uptake primarily at the cell membrane and liver. Binding of insulin to specific receptors on the cell membrane is necessary for efficient glucose transport into the cell. The number and affinity of insulin receptors are influenced by factors such as hormone levels, physical activity, and diet. Increased insulin levels lead to down-regulation of receptor concentration, while decreased insulin levels increase receptor affinity. Conditions such as obesity and acromegaly decrease the number of insulin receptors per cell, while excess glucocorticoids reduce receptor affinity [5]. Insulin has a half-life of about 5 minutes in the human circulation, with the liver and kidneys metabolizing over 80% of secreted insulin [5].

Without insulin, glucose uptake by skeletal, cardiac, and smooth muscle, as well as by the liver, is significantly diminished, although intestinal and renal glucose absorption remain unaffected. Notably, glucose uptake by most brain cells and red blood cells occurs independently of insulin. The liver has a dual function: storing glucose as glycogen under insulin stimulation and releasing glucose into the bloodstream when glucagon levels rise during hypoglycemia. Elevated blood glucose levels stimulate insulin secretion, thereby reducing hepatic gluconeogenesis. The liver, exposed to higher concentrations of naturally secreted insulin via the portal vein, captures approximately half of the administered insulin dose [5, 25, 38].

Exercise notably increases glucose uptake in skeletal muscle cells, primarily due to anaerobic metabolic conditions and enhanced affinity of insulin receptors in muscle tissue during physical activity. However, it is essential to acknowledge the limitations of these physiological models, especially when significant factors such as exercise or stress are omitted [16–18].

4 The minimal model and its limitations

One of the first modeling attempts in the literature was provided by Bolie [45]. The model assumes a single compartment for insulin and glucose, i.e., insulin/glucose associated with the liver, pancreas, and peripheral tissues are not separated. The equations are of the following form in this model, which has been sometimes referred to as the minimal model as in Bergman et al. [10, 11]

$\begin{array}{ll}\frac{dI(t)}{dt}=p-aI+bG,& (1)\end{array}$

$\begin{array}{ll}\frac{dG(t)}{dt}=q-cI-dG.& (2)\end{array}$

Here I and G are deviations of insulin and glucose values from their physiological mean values. The main purpose of the Bergman model was to use control systems theory to determine optimal values of the parameters a, b, c, and d. in Bergman et al. [8, 9], methods for determining these parameter values of the above equations are given.

The start of mathematical modeling for the insulin-glucose dynamics can really be attributed to Bergman et al. [9, 31]. The Model given in Bergman [46] is now typically referred to in the literature as the minimal model. Their starting point was measurements in dogs of plasma glucose and insulin after an IVGTT type test. The goal in Bergman model to mathematically model the resulting insulin-glucose dynamics, with the specific aim of arriving at insulin sensitivity and glucose effectiveness. In Bergman [46], we see the time evolution of plasma glucose and insulin at one-minute intervals, after glucose injection in a dog. The glucose data exhibits an exponential decay, while the insulin data shows a peak at first followed by a slower decline and secondary peaks.

It is tempting to model plasma glucose simply as an exponential decay. Since we know that there is a lower threshold (baseline glucose level G_b) in plasma, we could propose the following equation, where G(t) denotes plasma glucose

$\begin{array}{ll}\frac{dG(t)}{dt}=-p_1(G(t)-G_b),& (3)\end{array}$

where G(t) is measured in mg/dL or in mmol/L (1 mg/dL = 18 mmol/L). This model can be fit to the available IVGTT data for an individual to obtain values of p₁, which represents glucose effectiveness. In Bergman et al. [9], this model is presented as an initial attempt. The authors also modify the exponential term to a Michaelis-Menten type function and subsequently explore glucose uptake within a two-compartment model. However, without accounting for insulin-dependent behavior, these models lack realism. When the influence of insulin on glucose uptake in peripheral tissues is introduced through a mass action term, the dynamic equations in Bergman et al. [9] are updated accordingly to reflect this interaction in this form

$\begin{array}{llll}\frac{dG(t)}{dt}& =& -p_1(G(t)-G_b)-X(t)G(t),G(0)=p_0,& (4)\end{array}$

$\begin{array}{llll}\frac{dX(t)}{dt}& =& -p_{2}X(t)+p_3(I(t)-I_b),X(0)=0.& (5)\end{array}$

The assumptions in this model are that glucose exists in a single compartment, which is essentially the blood plasma. Since this is a model for dynamics after a glucose injection in an IVGTT, the rate of change of glucose corresponds only to glucose uptake, as it can be assumed that the liver will not release any glucose under these circumstances. The rate of change of blood glucose uptake is assumed to depend linearly on the level of glucose in the blood, independent of insulin. The uptake also depends on insulin in a distal compartment corresponding to interstitial insulin, X(t). This remote insulin is responsible for glucose disappearance in a mass action form. The rate of change of interstitial insulin in turn depends linearly on both the existing levels of interstitial insulin and on the insulin in blood plasma, I(t).

Note that the role of glucose in insulin production is not accounted for in this model. When Bergman et al. [9] first formulated this model, they partitioned the glucose kinetics from the insulin kinetics. Thus, in the above equations, I(t) is considered to be an input. The baseline glucose value of G_b determines the sign of the first term in Equation 4. If glucose falls below this value, the first term becomes positive, effectively increasing blood glucose plasma, which would correspond to the release of glucose stored in the form of glycogen from the liver. This action is not explicitly modeled. A glucose injection at time t = 0 is the starting point of the model. We can also assume that X(t) has a rate parameter embedded in it. That is, $X(t)=\alpha \frac{dI(t)}{dt}$ where $\frac{dI(t)}{dt}$ is remote insulin.

The equation for I(t) dynamics in the presence of glucose is considered separately as follows. Here G(t) is considered as an input

$\begin{array}{ll}\begin{array}{l}\frac{dI(t)}{dt}=p_4{(G(t)-p_5)}^{+}t-p_6(I(t)-I_b),\hfill \\ I(0)=p_7+I_b.\hfill \end{array}& (6)\end{array}$

Using the notation $(G(t)-p_5{)}^{+}$, the mathematical expression can be written as

$\begin{array}{l}(G(t)-p_5{)}^{+}=max(G(t)-p_5,0).\end{array}$

In Equation 6, the authors [43] use the notation $(G(t)-p_5{)}^{+}$ to represent that only the positive part of G(t)−p₅ is taken, meaning the value is G(t)−p₅ when G(t)>p₅, and 0 otherwise. This term plays a crucial role in influencing insulin production by the pancreas as long as the glucose level exceeds a certain target glycemia rate, p₅. The term $(G(t)-p_5{)}^{+}$ dominates the initial growth of the insulin response due to its exponential decay, causing an initial increase for small t values. Over time, this effect reaches a peak before decreasing. Simultaneously, the term I(t)−I_b serves to reduce blood insulin after an initial peak. Although Bergman et al. [10] did not originally intend for this to be a coupled model, simulating it over a finite time period reveals dynamics that closely match physiological observations. Decoupling the equations would overlook the critical feedback mechanisms in insulin-glucose dynamics, which are thoroughly discussed in Toffolo et al. [47] and De Gaetano et al. [43].

Several critical limitations have been identified in the minimal model of the glucose-insulin system, particularly when attempting to describe the system comprehensively [43]. The minimal model often fails to admit an equilibrium when its two compartments are coupled, resulting in unrealistic predictions such as unbounded insulin concentrations. It also exhibits pathological behavior under certain conditions, notably when baseline glycemia exceeds the pancreatic target glycemia. Additionally, the model incorporates non-autonomous elements and unrealistic assumptions about linear insulin secretion over time, which do not accurately reflect physiological processes. Furthermore, the delay in insulin action is oversimplified, failing to capture the biphasic nature of insulin responses. The model's two-step parameter fitting process can also produce inconsistencies, and its sensitivity to parameter variations further undermines its reliability. Collectively, these limitations highlight the need for a more integrated and stable model capable of accurately representing glucose-insulin dynamics.

The role of parameters in a model is crucial. Without parameters, a model only provides information about the functional form that approximates the physical phenomenon being modeled. The use of parameters allows the model to be trained on sample data, determine the ranges of valid behavior, and quantify meaningful physiological information. In the case of the minimal model, determining parameters by fitting to patient data enables us to model the IVGTT dynamics at an individual level, specifically by determining insulin sensitivity and glucose effectiveness.

A crucial question in the coupled system is the relationship between the target glycemia p₅ and the baseline glucose level G_b, a measured quantity. According to Pacini [39], parameter estimates often show G_b>p₅. However, De Gaetano et al. [43] demonstrated that if G_b>p₅, the system of equations does not exhibit an equilibrium point. Even if G_b = p₅, the solution G(t) does not converge to G_b. This highlights an important modeling consideration: models that appear to behave reasonably may not be mathematically sound. Therefore, it is more meaningful to have an equilibrium point in the system that corresponds to baseline values for glucose and insulin.

5 Advanced modeling approaches: delay models and limitations

In recent decades, numerous models have been developed to describe the insulin-glucose regulatory system. Among these, Bergmans minimal model [38, 46] is one of the simplest and most widely employed, appreciated for its practicality and ease of use. However, this model and its variants often oversimplify the physiological complexity by combining two distinct insulin functions, namely the promotion of glucose uptake and the suppression of hepatic glucose production, into a single parameter called insulin sensitivity. To overcome these limitations, several extended models have been proposed [21, 22, 24, 26, 43, 48], incorporating more detailed representations of patient-specific dynamics, particularly with respect to insulin sensitivity. Comprehensive reviews of mathematical models of the glucose-insulin system, including surveys of available computational tools and parameter values, are provided in Polonsky et al. [49], Radziuk [50], Bonner-Weir et al. [51], and Weir [52]; these sources serve as benchmarks for the parameter estimation methods employed in this study. Additionally, models accounting for oscillatory insulin secretion, described by delay differential equations, are based on foundational studies by Sturis [34] and Tolić et al. [35].

The delay model proposed in Wang et al. [53] ensures that all solutions to the model equations

$\begin{array}{l}\frac{dG(t)}{dt}=G_{\text{in}}-f_2(G(t))-f_3(G(t))f_4(I(t-{\tau }_2))\\ +f_5(I(t-{\tau }_1)),t\ge 0,& (7)\end{array}$

$\begin{array}{llll}\frac{dI(t)}{dt}& =& I_{\text{in}}(t)-d_{i}I(t),t\ge 0,& (8)\end{array}$

exist for all t≥0, and remain positive and bounded, as demonstrated in Lemma 3.1 and Figure 4.5 of Wang et al. [53]. The authors also provide a comprehensive qualitative analysis of the system, where the parameters employed in the model, along with their respective units, are detailed explicitly in Wang et al. [53]. The initial conditions are given by G(0) = G₀ and I(θ) = I₀ for θ∈[−max(τ₁, τ₂), 0], with delay parameters τ₁, τ₂>0. Where G(0) = G₀ and I(θ) = I₀, θ∈[−max(τ₁, τ₂), 0], τ₁, τ₂>0.

In this delay model, the non-linear function f₂(G) represents the insulin-independent component of glucose utilization, primarily capturing glucose uptake by tissues that do not require insulin, such as the brain and nerve cells. This function is defined as

$\begin{array}{l}{f}_2(G)=U_b\left(1-exp(\frac{-G}{C_2{V}_g})\right),\end{array}$

with parameters (U_b, C₂, V_g). It describes how glucose uptake increases with concentration but eventually levels off as the concentration continues to rise.

The function f₃(G), a linear expression, represents the insulin-dependent component of plasma glucose uptake and is given by

$\begin{array}{l}{f}_3(G)=\frac{G}{C_3{V}_g},\end{array}$

with parameters (C₃, V_g). This function suggests that glucose uptake by insulin-sensitive tissues, such as muscle and fat, is directly proportional to the glucose concentration in the bloodstream.

Next, f₄(I) represents the insulin-dependent component of glucose uptake, modeled as

$\begin{array}{l}{f}_4(I)=U_0+\frac{U_m-U_0}{1+exp\left(-\beta ln\left(\frac{I}{C_4(\frac{1}{V_i}+\frac{1}{0.2t_i})}\right)\right)},\end{array}$

with parameters (U₀, U_m, β, C₄, V_i, t_i). This function captures how insulin stimulates glucose uptake, with the uptake rate increasing rapidly once insulin levels exceed a certain threshold, which is a critical aspect of blood glucose regulation during insulin therapy.

Finally, f₅(I) characterizes the effect of insulin on glucose production by the liver

$\begin{array}{l}{f}_5(I)=\frac{R_g}{1+exp\left(\widehat{\alpha }\left(\frac{I}{V_p}-C_5\right)\right)},\end{array}$

with parameters $(R_g,\widehat{\alpha },V_p,C_5)$. This function illustrates how insulin suppresses hepatic glucose production, an essential mechanism for maintaining glucose homeostasis. The delay terms τ₁ and τ₂ introduce a symmetry in the time-delayed responses of glucose uptake that is both dependent and independent of insulin. As insulin levels rise, the rate of glucose production by the liver decreases, aiding in the stabilization of blood glucose levels. The corresponding parameter values are detailed extensively in Stur [34] and Wang et al. [53]. In their analysis [53], they use the following step functions for glucose intake G_in and insulin infusion I_in

$\begin{array}{ll}{G}_{in}(t)=\{\begin{array}{ll}0.05+\frac{5t}{15},\hfill & \text{if }0\le t<15,\hfill \\ 0.05+5\frac{45-t}{30},\hfill & \text{if }15\le t<45,\hfill \\ 0.05,\hfill & \text{if }45\le t<240.\hfill \end{array}& (9)\end{array}$

Similarly, the insulin infusion rate is defined as

$\begin{array}{ll}{I}_{in}(t)=\{\begin{array}{ll}0.25,\hfill & \text{if }0\le t<5,\hfill \\ 0.25+\left(1+\frac{t-30}{25}\right),\hfill & \text{if }5\le t<30,\hfill \\ 0.25+\left(1-\frac{t-30}{90}\right),\hfill & \text{if }30\le t<120,\hfill \\ 0.25,\hfill & \text{if }120\le t<240.\hfill \end{array}& (10)\end{array}$

6 Solutions and approximations

We begin by summarizing key well-posedness and abstract computational results that have been recently established in the literature, particularly in the works of Banks [14, 15, 54]. Our focus is on nonlinear, non-autonomous dynamical systems with delays, represented by general forms of delay differential equations. Specifically, we address the well-posedness and computational aspects of the solutions for these systems using semigroup theory, drawing on the abstract formulation provided by the glucose-insulin delay model Equations 7, 8. These systems can be described by the following differential equation

$\begin{array}{llll}\frac{d\text{x}(t)}{dt}& =& 𝔉(t,\text{x}(t),\text{x}(t-{\tau }_1),\text{x}(t-{\tau }_2),\text{p}),0\le t\le t_{max},& (11)\end{array}$

where $\text{x}(t)=(\begin{array}{c}G(t)\\ I(t)\end{array})\in {ℝ}^2$ and $\text{p}={(U_b,C_2,V_g,C_3,U_0,U_m,\beta ,C_4,V_i,t_i,R_g,\widehat{\alpha },V_p,C_5)}^T$. The function 𝔉(x(t), x(t−τ₁), x(t−τ₂), p) is defined as

$\begin{array}{l}F(t,x(t),x(t-{\tau }_1),x(t-{\tau }_2),p)=\\ \left(\begin{array}{c}-f_2(G(t))-f_3(G(t))f_4(I(t-{\tau }_2))+f_5(I(t-{\tau }_1))+G_{in}(t)\\ -d_{i}I(t)+I_{in}(t)\end{array}\right),& (12)\end{array}$

where the non-linear function 𝔉 is formally defined as

$𝔉=𝔉(t,\eta ,{\text{x}}_1,{\text{x}}_2,\text{p}):\left[0,T\right]\times {ℝ}^2\times {ℝ}^4\times {ℝ}^{15}\to {ℝ}^2,$

and the initial condition x(θ) = ϕ(θ) for −τ = max(τ₁, τ₂) ≤ θ ≤ 0, where θ represents the past state of the system, and the time-dependent perturbations or control inputs described by Equations 9, 10. Throughout this work, we adopt the standard notation for delay systems, where x_t(θ) = x(t+θ) for −τ ≤ θ ≤ 0. We denote by H¹(a, b; ℝ²) the Sobolev space W^{1, 2}((a, b);ℝ²), which consists of function x:(a, b) → ℝ² such that both x and its derivative $\stackrel{•}{\text{x}}$ belong to L²((a, b);ℝ²) where $\stackrel{•}{\text{x}}(t)=\frac{d\text{x}(t)}{dt}$. Additionally, we define the spaces

$H={ℝ}^2\times L^2(-\tau ,0;{ℝ}^2),$

$X=\left\{(\varphi (0),\varphi )\mid \varphi \in C(-\tau ,0;{ℝ}^2)\right\},$

and

$W=\left\{(\varphi (0),\varphi )\mid \varphi \text{satisfies a Lipschitz condition on}\left[-\tau ,0\right]\right\}.$

The norms on H, X and W are defined as follows

$||(\eta ,\varphi )|{|}_H=||\eta |{|}_2^2+||\varphi |{|}_{L^2(-\tau ,0;{ℝ}^2)},$

$||(\varphi (0),\varphi )|{|}_X=||\varphi |{|}_{C(-\tau ,0;{ℝ}^2)},$

$||(\varphi (0),\varphi )|{|}_W=max(||\varphi (0)|{|}_{{ℝ}^2},||\stackrel{°}{\varphi }|{|}_{L^{\infty }(-\tau ,0;{ℝ}^2)}).$

Where ||·||₂ is the Euclidean norm on ℝ², $\left|\right|\stackrel{•}{\varphi }|{|}_{L^{\infty }(-\tau ,0;{ℝ}^2)}$ is the L^∞ (essential supremum) norm on L^∞(−τ, 0;ℝ²) of $\stackrel{•}{\varphi }(\theta )=\frac{d\varphi (\theta )}{d\theta }$, $\left|\right|\varphi |{|}_{L^2(-\tau ,0;{ℝ}^2)}$ is the L² (Lebesgue) norm on L²(−τ, 0;ℝ²), and $\left|\right|\varphi |{|}_{C(-\tau ,0;{ℝ}^2)}$ is the supremum (uniform) norm on C(−τ, 0;ℝ²). The initial condition is given by $\varphi ={(G_0,I_0)}^T$, and its clear that ϕ satisfies a Lipschitz condition on [−τ, 0] and belongs to ϕ∈C(−τ, 0;ℝ²) and L²(−τ, 0;ℝ²). Furthermore, we observe that the embeddings W↪X↪H are dense and continuous. We can now define the function 𝔉, where the pair of functions (ϕ(0), ϕ) is defined in either W, X, or H as follows

$\begin{array}{l}F(t,\varphi ,p)=F(t,\varphi (0),\varphi (-{\tau }_1),\varphi (-{\tau }_2),p),\\ \varphi \in X,0\le t\le t_{\max }.& (13)\end{array}$

We now turn to the mathematical framework underlying these nonlinear delay functional differential systems and provide an overview of the essential foundations. We begin by describing the transformation of the nonlinear delay functional differential equations into an abstract evolution equation, along with the corresponding existence and uniqueness results. Building upon concepts from the linear semigroup theory, originally developed for approximating linear delay systems, this approach serves as a foundation for addressing a broader class of nonlinear delay functional differential systems. The semigroup approach not only ensures the well-posedness of the system but also reveals inherent symmetries in the behavior of the solution over time, particularly in the invariance of specific solution structures under parameter transformations. Further details and advancements on these methods are provided in recent works [14, 15, 54–59].

Following the discussion by Kappel [60, 61] and Hale [62, 63], the choice of working in H versus X has significant implications. Kappel highlights that in H, certain growth restrictions can be imposed, providing a more structured and systematic approach to solving delay differential equations. By contrast, working within the space X requires the use of the pointwise variation of parameters formula, which is both tedious and technically demanding. This makes the analysis more complex and less convenient, as emphasized in the discussion of the decomposition of the nonhomogeneous equation [see [63] for more details]. In X, the solution must be expressed in terms of two components that depend on both t and θ. If 𝔉 = 0, neither component can be written as a function of t+θ for θ∈[−r, 0], meaning that neither satisfies the delay differential equations independently. Only their sum, representing the entire solution, satisfies the delay differential equations. This limitation underscores the challenges of working in X, where the individual components cannot easily be interpreted in terms of the delayed variable t+θ. In contrast, working in H allows for a more straightforward and practical formulation, avoiding these complications. Next, we have to choose the appropriate C₀-semigroup T(·) on H, where Equation 11 corresponds to the Cauchy problem

$\begin{array}{ll}\dot{u}(t)={\mathcal{A}}_{0}u(t)+ℬu(t),0\le t\le t_{\max }.& (14)\end{array}$

where 𝒜₀ is the infinitesimal generator of the C₀-semigroup T corresponding to the delay equation $\stackrel{•}{u}(t)=0,$ given by

$\begin{array}{llll}\text{dom }{\mathcal{A}}_0& =& \left\{(\varphi (0),\varphi )\mid \varphi \in H^1(-\tau ,0;{ℝ}^2)\right\},& (15)\end{array}$

$\begin{array}{llll}{\mathcal{A}}_0(\varphi (0),\varphi )& =& (0,\dot{\varphi }),& (16)\end{array}$

$\begin{array}{llll}T(t)(\eta ,\varphi )& =& (\eta ,g_t),& (17)\end{array}$

where the function g:[−τ, ∞) → ℝ² is defined by

$g(s)=\{\begin{array}{ll}\varphi (s),\hfill & s\in [-\tau ,0],\hfill \\ \eta ,\hfill & s>0.\hfill \end{array}$

and

$\begin{array}{llll}\mathcal{B}(\eta ,\varphi )& =& (𝔉(t,\varphi ,\text{p}),0).& (18)\end{array}$

Now, we can investigate the integrated form of the delay differential equations using the following equivalent form

$\begin{array}{llll}u(t)& =& T(t)\varphi +{\displaystyle {\int }_0^t}T(t-s)\mathcal{B}u(s)ds,0\le t\le t_{max},\varphi \in H.& (19)\end{array}$

Now, we are ready to apply Proposition 11.7 [64], where we establish the connection between the solutions of the delay differential Equation 11 and the corresponding abstract problem (Equation 14) defined by Equations 15–18. For now its clear that:

(a) If u(·) = (v(·)(0), v(·)) is a solution of Equation 19, for some t_max>0, then $\text{x}(·)=(\begin{array}{c}G(·)\\ I(·)\end{array})$ defined by

$\begin{array}{ll}x(t)=\{\begin{array}{ll}v(t)(0)\hfill & \text{for }0\le t\le t_{\max },\hfill \\ \varphi (t)\hfill & \text{for }-\tau \le \theta \le 0,\hfill \end{array}& (20)\end{array}$

is a Lipschitz-continuous function on [−τ, t_max] and satisfies

$\begin{array}{l}x(t)=\varphi (0)+{\displaystyle {\int }_0^{t}F}(s,x(s),x(s-{\tau }_1),x(s-{\tau }_2),p)ds,\\ 0\le t\le t_{\max },& (21)\end{array}$

and v(t) = x_t, t>0, where

$\begin{array}{l}F(t,x(t),x(t-{\tau }_1),x(t-{\tau }_2),p)=\\ \left(\begin{array}{c}-f_2(G(t))-f_3(G(t))f_4(I(t-{\tau }_2))+f_5(I(t-{\tau }_1))+G_{in}(t)\\ -d_{i}I(t)+I_{in}(t)\end{array}\right),& (22)\end{array}$

(b) Conversely, if $\text{x}=(\begin{array}{c}G\\ I\end{array})$ is a Lipschitz-continuous function on [−τ, t_max] and solves (Equation 21), then

$u(t)=(\text{x}(t),{\text{x}}_t),t\in \left[0,t_{max}\right],$

defines a solution of Equation 19.

To approximate the solutions of these systems, the dynamical system is reformulated as an abstract evolution equation, which is then solved using a Galerkin approach. This method, analogous to the linear finite element approximation for partial differential equations, enables the numerical computation of generalized Fourier coefficients for approximate solutions using splines. Through this process, an approximation of the original system's solutions is reconstructed, and the theoretical results are computationally validated. The mathematical foundations for this approach were developed extensively between the 1970s and 1990s, as documented in key works such as [61, 65–74].

Based on the theory developed in this section, we construct a concrete approximation scheme for delay systems of the form (Equation 11) as considered in Ito and Kappel [61, 64]. For N = 1, 2, … , let

$X_N={ℝ}^{(N+1)2}\text{and }{U}_N={ℝ}^2.$

We choose the mesh points t_j = −jτ/N, j = 0, …, N, N = 1, 2, … . Corresponding to $\xi ={({\xi }_0,{\xi }_1,\dots ,{\xi }_N)}^T\in X_N$, where ${\xi }_j\in {ℝ}^n$, j = 0, …, N, we define the injective operator E_N:X_N→X such that

$E_N\xi =({\varphi }_N(0),{\varphi }_N),$

with ${\varphi }_N=\sum _{j=0}^N{B}_j{\xi }_j$, where B_j denotes the first-order spline with B_j(t_i) = δ_ij, i, j = 0, …, N (where δ_ij is the Kronecker-delta). In other words, φ_N is the first-order spline with φ_N(t_j) = ξ_j, j = 0, …, N. The projections P_N:X→X_N are defined by

$P_N(\varphi (0),\varphi )={(\varphi (t_0),\varphi (t_1),\dots ,\varphi (t_N))}^T,\varphi \in C(-\tau ,0;{ℝ}^2).$

The norms ||ξ||_XN = ||E_Nξ||_X and ||ξ||_WN = ||E_Nξ||_W on X_N, are given by

$||\xi |{|}_{X_N}={\displaystyle \underset{j=0,\dots ,N}{max}}||{\xi }_j|{|}_2,$

$||\xi |{|}_{W_N}=max\left(||{\xi }_0|{|}_2,{\displaystyle \underset{j=0,\dots ,N-1}{max}}\frac{||{\xi }_{j+1}-{\xi }_j|{|}_n}{\tau /N}\right),\xi \in X_N.$

In the following, X_N always denotes the space (X_N, ||·||_XN), whereas W_N denotes the space (W_N, ||·||_WN). The simplest choice for B_N is

${\mathcal{B}}_{N}u={(u,0,\dots ,0)}^T\in {ℝ}^{(N+1)2},u\in {ℝ}^2,$

i.e.,

${\mathcal{B}}_N=\left(\begin{array}{c}{I}_2\\ 0\\ ⋮\\ 0\end{array}\right)\in {ℝ}^{(N+1)2\times 2},$

where I_n is the n×n identity matrix. The motivation for the definition of 𝒜_N is as follows: In view of (11.25), 𝒜E_Nξ, ξ∈X_N, is given by $(0,\sum _{j=1}^N{𝔉}_j({\xi }_{j-1}-{\xi }_j){\mathcal{B}}_j)$, which is not generally in X. Therefore, we cannot take the projection P_N𝒜E_Nξ. But it turns out to be reasonable to take left-hand limits at the mesh points t₁, …, t_N instead of the non-existent values at these points. This leads to the definition

${\mathcal{A}}_N\xi ={\left(0,\frac{{\xi }_1-{\xi }_0}{\tau },\dots ,\frac{{\xi }_N-{\xi }_{N-1}}{\tau }\right)}^T,\xi \in X_N,$

which gives

${\mathcal{A}}_N=\frac{1}{h_0}\left(\begin{array}{ccccc}0& 0& 0& \dots & 0\\ I_2& 0& 0& \dots & 0\\ 0& I_2& 0& \dots & 0\\ ⋮& ⋮& \ddots & \ddots & 0\\ 0& 0& \dots & I_2& 0\end{array}\right)\in {ℝ}^{(N+1)2\times (N+1)2}.$

Following the steps in Ito and Kappel [61, 64], consider the approximating equations in X_N, we have $u_N(t)={(u_0^N(t),\dots ,u_N^N(t))}^T$ is the solution of

$\begin{array}{llll}\frac{d}{dt}{u}_N(t)& =& {\mathcal{A}}_N{u}_N(t)+{\mathcal{B}}_N𝔉(t,u_0(t),(E_N{u}_N(t))(-\tau )),& (23)\end{array}$

$\begin{array}{llll}{u}_N(0)& =& P_N(\varphi (0),\varphi ),\varphi \in W^{1,\infty }(-\tau ,0;{ℝ}^2).& (24)\end{array}$

Its clear that the condition (B1)−(B3) in Ito and Kappel [64] are satisfied on any interval [0, t_max]. As a consequence of we have

${\displaystyle \underset{N\to \infty }{lim}}||E_N{u}_N(t)-u(t)|{|}_X=0$

uniformly for t∈[0, t_max], where ϕ∈W^{1, ∞}(−τ, 0;ℝ²).

The convergence established in Theorem 3 enables state approximation techniques for nonlinear delay differential systems, incorporating both spline methods and a variant of the Trotter-Kato theorem, as outlined in Kato [75] and Ito and Kappel [76]. These results are directly applicable to control and identification challenges, as examined in Banks [14, 15, 55, 57, 65, 66, 69, 74]. For special classes of these systems, similar results can be derived from the arguments for nonautonomous nonlinear delay systems in Banks [71]. In this approach, discrete delays appear in the linear part of the system dynamics, while continuous delays are in the nonlinear part. The system is then expressed as a linear semigroup generated by the autonomous linear part, plus a nonlinear perturbation. The Trotter-Kato theorem and Gronwall inequalities are used in conjunction with Picard iterates to establish the existence of solutions for the nonlinear system.

7 Sensitivity analysis

In parameter estimation, error functions quantify the discrepancy between experimentally measured and model-predicted response data. Classical sensitivity analysis (CSA) evaluates how each model output (which could be model states but need not be) changes with respect to small changes in each of the model parameters. This analysis helps track the influence of each parameter on output variables that can be compared with measured data, such as interstitial subcutaneous glucose concentration or insulin levels. If an output is highly sensitive to a parameter, that parameter can be estimated from corresponding data, provided there are no functional dependencies with other parameters. The results of CSA can be used to rank model parameters from most to least influential. Parameters are then categorized into “sensitive” and “insensitive” groups. Sensitive parameters undergo parameter identification using available data and chosen estimation techniques, while insensitive parameters are estimated based on subject-specific characteristics such as age, height, body mass index, and literature values. This approach reduces the dimensionality of the parameter identification problem significantly. Despite its widespread application in structural optimization [e.g., [77–79]], sensitivity analysis has yet to make a significant impact on modeling biological systems or adapting models of the insulin-glucose system in humans.

To calculate the various sensitivities, assume a model is given as a system of differential equations

$\begin{array}{ll}\frac{dx(t}{dt}=f(t,x(t),p),x(0)=x_0,& (25)\end{array}$

with state variables x = (x₁, x₂, …, x_n) and parameters p = (p₁, p₂, …, p_m). We assume for simplicity that the states are model outputs for which data can be acquired. To compute the sensitivities of the state variables with respect to the parameters, we calculate the derivatives ∂x_i(t)/∂p_j, for i = 1, …, n and j = 1, …, m, at baseline values p₀ = (p_{1, 0}, …, p_{m, 0}). Let S(t) =∂_{xi(t)/∂pji = 1, …, n, j = 1, …, m}. These derivatives indicate how small changes in a model parameter induce changes in a specific model output, providing a measure of the sensitivities of model states to the model parameters at fixed time points t. The term “sensitivity” usually refers to normalized derivatives (relative to the baseline state and parameter values). To calculate S(·), we solve the following augmented system of equations

$\begin{array}{llll}\frac{dx(t)}{dt}& =& f(t,x(t),\text{p}),& (26)\end{array}$

$\begin{array}{llll}\frac{dS(t)}{dt}& =& \frac{\partial f}{\partial x}(t,x(t),\text{p})S(t)+\frac{\partial f}{\partial \lambda }f(t,x(t),\text{p}),& (27)\end{array}$

$\begin{array}{llll}x(0)& =& x_0,& (28)\end{array}$

$\begin{array}{llll}S(0)& =& \frac{\partial x_0}{\partial \text{p}}.& (29)\end{array}$

This set of equations includes the model equations. Taking partial derivatives of the model equations with respect to the parameters and changing the order of differentiation leads to the differential equations for the sensitivities (Equation 29). The feasibility of this strategy for sensitivity analysis will be tested using the minimal model (Equations 4–6) and the delay model (Equations 7, 8).

In Figures 1, 2, we present the sensitivities of G and I with respect to the parameters of the Bergman model system (Equations 4–6). We observe two groups of parameters: G is less sensitive with respect to p₄, p₅, and p₇ than with respect to p₁, p₂, p₃, and p₆. Similarly, I is less sensitive with respect to p₁, p₂, p₃, p₅, and p₇ than with respect to p₄ and p₆. Note that as the system approaches the steady state, all parameters become insensitive, as there is minimal change in the model output. Therefore, data near the steady state in this model will make it difficult to use sensitivity analysis to reduce the number of parameters.

Figure 1

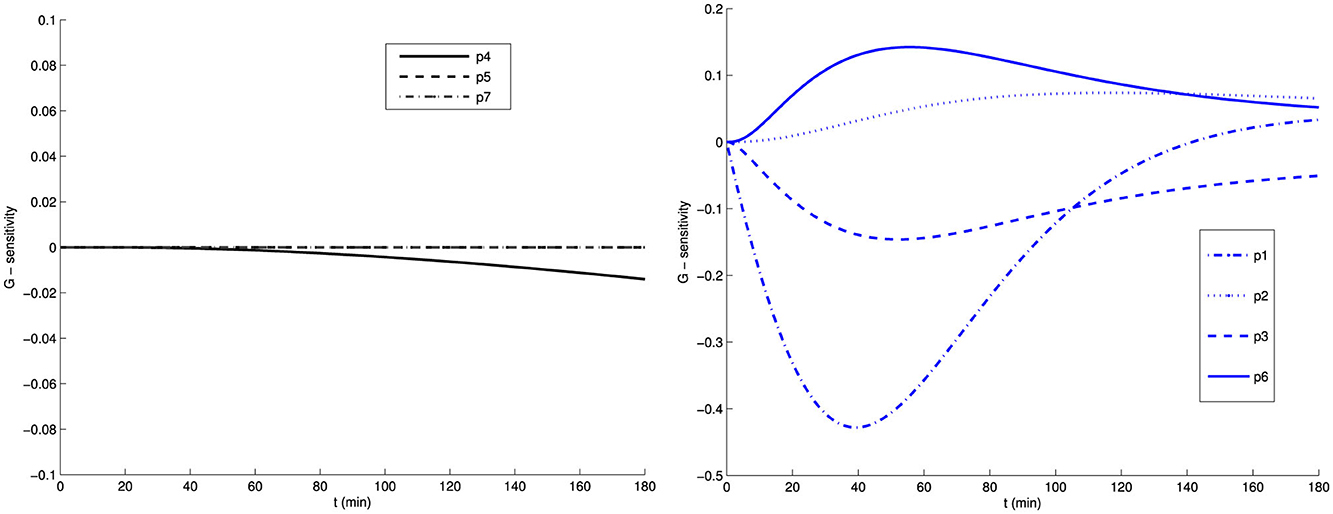
Figure 1. Sensitivity of glucose G with respect to the model parameters of the Bergman model (Equations 4–6).

Figure 2

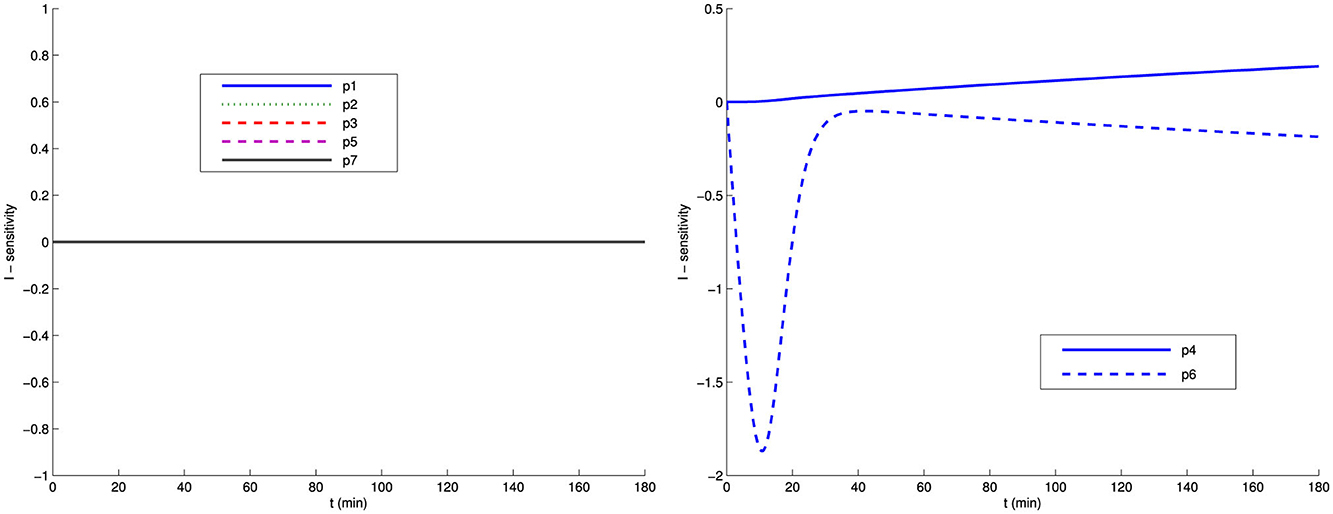
Figure 2. Sensitivity of insulin I with respect to the Bergman model parameters (Equations 4–6).

To study the sensitivity of delay differential equations, we will follow the theory developed by Brewer [80], which is thoroughly described by Robbins in his dissertation [14, 15, 81]. Brewers work on Fréchet derivatives in the context of linear abstract Cauchy problems is foundational for sensitivity analysis. He developed a theory for the differentiability of solutions with respect to parameters, particularly for linear autonomous systems where the operator may be unbounded [80]. Brewer extended earlier results by Gibson and Clark [82], which focused on parameter-dependent bounded operators, by incorporating unbounded operators into the analysis. Using semigroup theory, he proved the existence of Fréchet derivatives with respect to parameters, including delays, and applied this to linear discrete delay systems. This theory is framed within Banach spaces but can be extended to Hilbert spaces.

Later, Brewer, Burns, and Cliff applied this theory to parameter identification problems using quasilinearization [83]. Their goal was to establish the convergence of gradient-based parameter estimation algorithms for problems defined by an unbounded, parameter-dependent evolution operator. This work further emphasizes the importance of Fréchet derivatives for sensitivity analysis and parameter identification.

However, Brewers methods are primarily suited to linear autonomous systems and face limitations when applied to more complex, non-autonomous, or nonlinear cases. In such scenarios, alternative approaches, such as those introduced by Banks [72, 74], are more appropriate. Banks work, which utilizes spline methods and other analytical tools, addresses the sensitivity to delay parameters in nonlinear systems. While Brewers results [80, 83] offer valuable insights, Banks methods rely on different mathematical frameworks, such as fixed-point theory and classical tools from differential equations, to manage more complex dynamics.

In the case of delay differential equations, we demonstrate the sensitivity analysis method for the Wang model (Equations 7, 8). This model can also be formally written as

$\begin{array}{llll}\frac{d\text{x}(t)}{dt}& =& 𝔉(t,\text{x}(t),\text{x}(t-{\tau }_1),\text{x}(t-{\tau }_2),\text{p}),0\le t\le T,& (30)\end{array}$

$\begin{array}{l}x(s)=\varphi (s)\in C(-r,0,{ℝ}^2),-\tau \le s\le 0,\\ \tau =\max ({\tau }_1,{\tau }_2),& (31)\end{array}$

where x(t) = (G(t), I(t))^T∈ℝ² is the solution of the Wang model (Equations 7, 8). To compute the sensitivities of the delay differential model (Equations 7, 8), we utilize the properties of the nonlinear function 𝔉(t, x(t), x(t−τ₁), x(t−τ₂), p) given in Equation 12. This function is composed of standard functions that have continuous Fréchet derivatives with respect to the state x and the parameter p, and are uniformly bounded over bounded intervals; see Wang et al. [53] for more details. Furthermore, 𝔉(t, η, x₁, x₂, p) possesses continuous Fréchet derivatives with respect to its arguments, specifically 𝔉_η, 𝔉_x1, 𝔉_x2, and 𝔉_p, subject to the following bounds

$\left|{𝔉}_{\eta }\right|\le M_0,\left|{𝔉}_{{\text{x}}_1}\right|\le M_1,\left|{𝔉}_{{\text{x}}_2}\right|\le M_2,\left|{𝔉}_{\text{p}}\right|\le M_3,$

where M_j are constants for j = 0, 1, 2, 3. By applying Theorem 5 from [84], we establish that the Fréchet derivative $S(t)=\frac{\partial \text{x}(t)}{\partial \text{p}}\in {ℝ}^{n\times m}$ exists and is the unique solution to the following system of equations

$\begin{array}{l}\frac{dS(t)}{dt}=F_x(t,x(t),x(t-{\tau }_1),x(t-{\tau }_2),p)S(t)\\ +F_{x_1}(t,x(t),x(t-{\tau }_1),x(t-{\tau }_2),p)S(t-{\tau }_1)\\ +F_{x_2}(t,x(t),x(t-{\tau }_1),x(t-{\tau }_2),p)S(t-{\tau }_2)\\ +F_p(t,x(t),x(t-{\tau }_1),x(t-{\tau }_2),p),0\le t\le T,& (32)\end{array}$

with the initial condition

$\begin{array}{llll}S(\xi )& =& 0,-\tau \le \xi \le 0.& (33)\end{array}$

We apply sensitivity analysis to the Wang model. If certain parameters of the model show insensitivity to the available data, these parameters may be fixed based on general considerations, or the model can be simplified by eliminating them. For the sensitive parameters, we apply the singular value decomposition method to the Fisher information matrix S^TS to refine the set of parameters for estimation. We rank the eigenvalues of the Fisher Information Matrix (FIM) to assess parameter sensitivity. The availability of derivatives of the state variables with respect to parameters also improves the performance of optimization algorithms that utilize gradient information [85, 86]. Sensitivities of the states to parameters for the Wang model are illustrated in Figure 3.

Figure 3

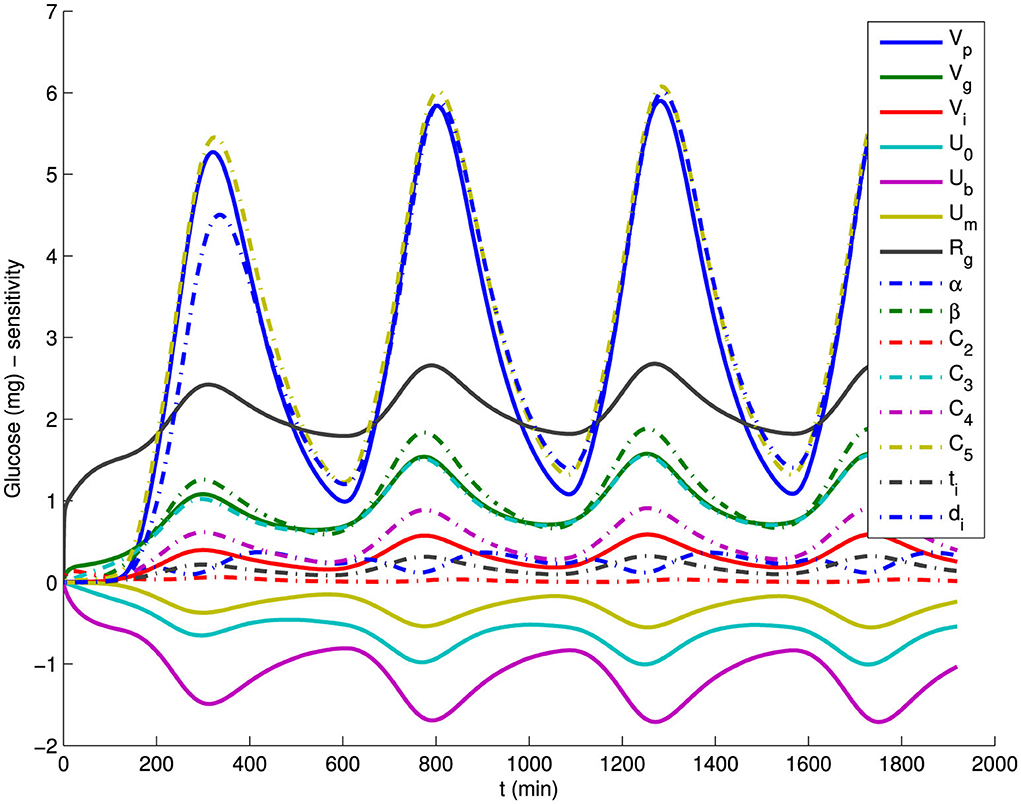
Figure 3. Sensitivities of all model parameters for the model output glucose G of the Wang et al. model (Equations 8, 9).

A Standard approach to estimate the unknown parameters is in terms of the least-square error criterion

$\begin{array}{lll}J(\text{p})& ={\displaystyle {\int }_{t_0}^T}{(G(t,\text{p})-\hat{G}(t))}^{2}dt& (34)\end{array}$

where $\hat{G}(t)$ is the data fitted by model output G(t, p) by optimum choice of p. We proposed to use Gauss-Newton method for optimization,

To rank the sensitivities (normalized derivatives) of the various states with respect to parameters we define a global time-invariant normalized sensitivity measure (GTIS) using a weighted 2-norm

$\begin{array}{llll}{z}_{ij}& =& \frac{p_j}{(t_{end}-t_0){\displaystyle {max}_{t_0\le t\le t_0}}\left|x_i(t,\text{p})\right|}{({\displaystyle {\int }_{t_0}^{t_{end}}}|\frac{\partial x_i}{\partial p_j}{|}^{2}dt)}^{1/2};& (35)\end{array}$

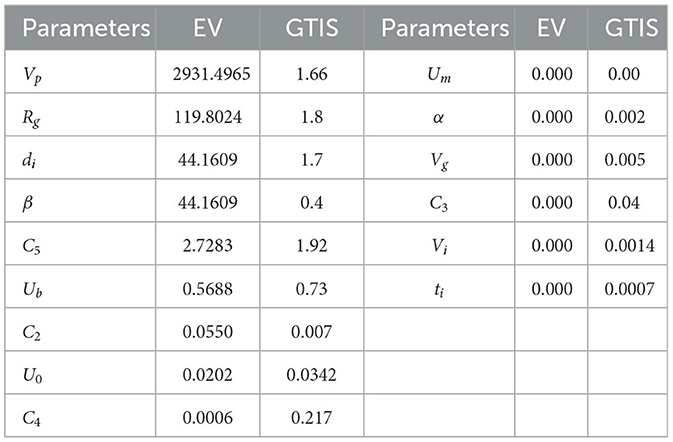
Table 1 provides the GTIS sensitivity measure of the model Equation 7 and the eigenvalues of the FIM for glucose data while Figure 3 illustrates the sensitivities of glucose with respect to all parameters for the Wang model.

Table 1

Table 1. Eigenvlaues (EV) and GTIS sensitivity norms for the Wang et al. model.

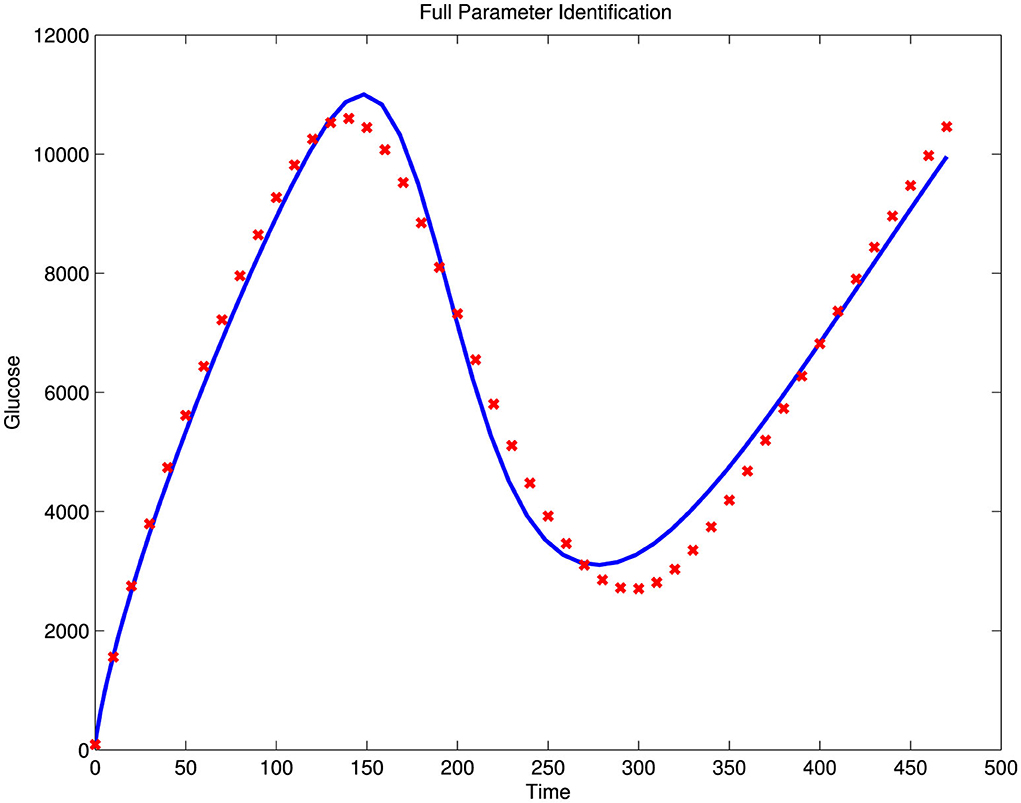
Illustrated in Figure 4 is an attempt to perform a full parameter estimation using simulated data generated with the model's chosen parameter values, with 30% noise superimposed on the simulated glucose output. This estimation was not successful, as the norm of the error was too high, with Norm(Error) = 2.8877e+003. However, by estimating only the sensitive parameters, we achieved a better fit, with a significantly smaller error, Norm(Error) = 7.6993e−003, as shown in the left panel of Figure 5. In this case, we selected the nine parameters with the largest eigenvalues, as presented in Table 1, which also generally correspond to higher GTIS sensitivities. Moreover, when we applied this method to noisy data using the same set of parameters, we were able to produce a good fit to the data, as illustrated in the right panel of Figure 5.

Figure 4

Figure 4. Estimation attempt using all parameters and glucose data.

Figure 5

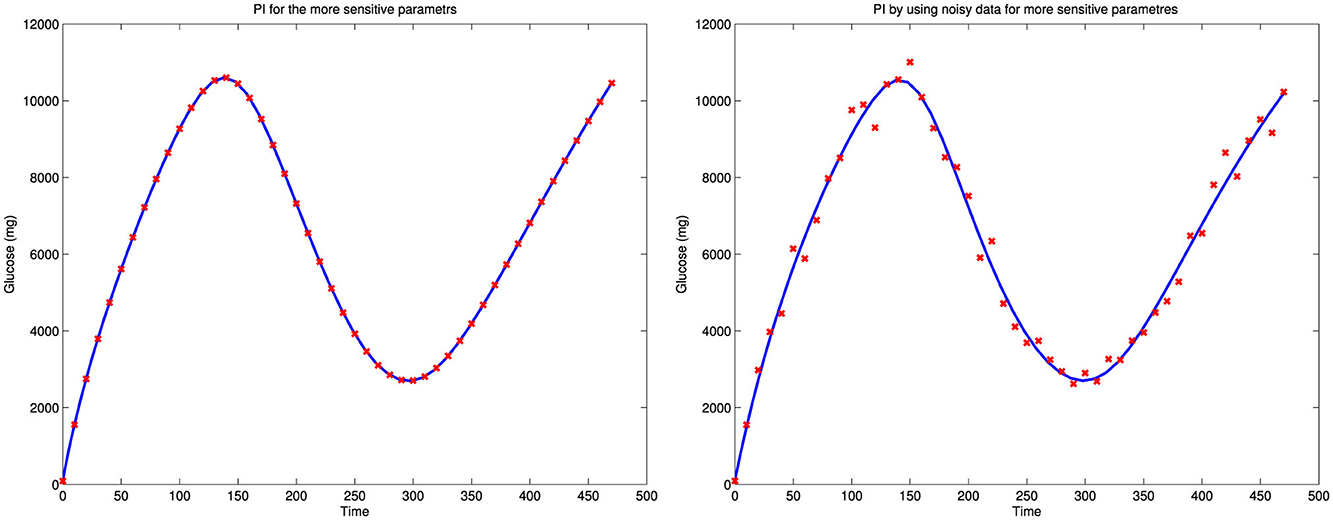
Figure 5. A parameters estimation of sensitive parameters $\hat{p}=(V_p,R_g,\beta ,d_i,C_5,C_2,C_4,U_b,U_0)$ and also the parameter estimation of the more sensitive parameters using noisy data.

8 Conclusion

Mathematical models are indispensable tools for understanding the complex dynamics of biological systems such as insulin glucose regulation. However, their effectiveness depends on integration with high-quality experimental data. A major challenge in this integration is the presence of measurement noise, which can obscure accurate predictions of system behavior. Therefore, detailed sensitivity analyses are essential for enhancing model validation and ensuring reliability.

This study addresses a fundamental gap in diabetes modeling by presenting a rigorous framework for parameter estimation and sensitivity analysis within the context of glucose insulin dynamics, formulated in infinite-dimensional Sobolev spaces using semigroup theory. We identified key parameters that significantly influence system dynamics, particularly during transient phases, under the assumption of parameter independence. Our analysis revealed the ill-posedness and sensitivity challenges inherent in parameter estimation for models that include time delays. These difficulties become especially evident when applying such models to clinical data, a point that is often underemphasized in simulation-based studies such as [12, 13], which do not fully consider the instability of the underlying inverse problems.

For parameters with low sensitivity, rough estimates from existing literature [9, 43, 53] are generally sufficient, since their influence on model outputs is minimal outside critical periods. This finding is consistent with previous results in Banks [14, 15, 84, 85, 87], where accurate estimation was shown to depend strongly on the timing and structure of the data used.

Although several previous studies have examined to some extent the sensitivity analysis in insulin glucose models [25, 88, 89], they have not systematically addressed the mathematical challenges posed by models with time delays. In particular, the impact of transient dynamics on parameter identifiability has not been comprehensively investigated. Our study extends this body of work by introducing a structured sensitivity analysis framework based on Fréchet derivatives and semigroup theory, allowing for a more detailed assessment of parameter influence in delayed systems.

We also emphasized the issue of parameter interdependence, such as when parameters appear as ratios, which further complicates estimation during periods of high variability. To address this, we adapted subset selection techniques based on variations of the Fisher information matrix, building on earlier work in the sensitivity analysis literature [54, 66, 80, 83]. Unlike previous studies, our analysis applies these tools specifically to delay differential models in the context of diabetes, filling an important methodological gap.

In conclusion, this study contributes a mathematically rigorous and practically relevant framework that enhances the modeling of glucose–insulin dynamics. Compared to earlier works, our approach provides a deeper treatment of sensitivity, ill-posedness, and parameter interaction in models with delays. These developments support more accurate parameter identification and model calibration. Future research should focus on developing optimal experimental designs tailored to transient dynamics, strengthening the link between theoretical modeling and real-world applications in diabetes research.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

MB: Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the Ongoing Research Funding program (ORF-2025-963), King Saud University, Riyadh, Saudi Arabia. The author declares that no external funding was received beyond this support.

Acknowledgments

M. Bachar, with full address: ‘Department of Mathematics, College of Science, King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia; bWJhY2hhckBrc3UuZWR1LnNh', would like to extend his appreciation to the Ongoing Research Funding program (ORF-2025-963), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lauritzen T, Pramming S, Deckert T, Binder C. Pharmacokinetics of continuous subcutaneous insulin infusion. Diabetologia. (1983) 24:326–9. doi: 10.1007/BF00251817

PubMed Abstract | Crossref Full Text | Google Scholar

2. Binder C, Lauritzen T, Faber O, Pramming S. Insulin pharmacokinetics. Diab Care. (1984) 7:188–199. doi: 10.2337/diacare.7.2.188

PubMed Abstract | Crossref Full Text | Google Scholar

3. Heinemann L. Variability of insulin absorption and insulin action. Diab Technol Therapeut. (2002) 4:673–82. doi: 10.1089/152091502320798312

PubMed Abstract | Crossref Full Text | Google Scholar

4. Bergman RN. New concepts in extracellular signaling for insulin action: the single gateway hypothesis. Recent Prog Horm Res. (1997) 52:359–85.

PubMed Abstract | Google Scholar

5. Edgerton DS, Kraft G, Smith M, Farmer B, Williams PE, Coate KC, et al. Insulin's direct hepatic effect explains the inhibition of glucose production caused by insulin secretion. JCI Insight. (2017) 2:e91863. doi: 10.1172/jci.insight.91863

PubMed Abstract | Crossref Full Text | Google Scholar

6. Norton L, Shannon C, Gastaldelli A, DeFronzo RA. Insulin: the master regulator of glucose metabolism. Metabolism. (2022) 129:155142. doi: 10.1016/j.metabol.2022.155142

PubMed Abstract | Crossref Full Text | Google Scholar

7. Rosenstock J, Juneja R, Beals JM, Moyers JS, Ilag L, McCrimmon RJ. The basis for weekly insulin therapy: evolving evidence with insulin Icodec and insulin Efsitora Alfa. Endocrine Rev. (2024) 45:379–413. doi: 10.1210/endrev/bnad037

PubMed Abstract | Crossref Full Text | Google Scholar

8. Bergman R, Kalaba R, Springarn K. Optimizing inputs for diagnosis of diabetes I. fitting minimal model to data. J Optim Theory Applic. (1976) 20:47–63. doi: 10.1007/BF00933347

Crossref Full Text | Google Scholar

9. Bergman R, Kalaba R. Optimal inputs for blood glucose regulation parameter estimation. In: IEEE Circuits, Systems and Computers, 1977. Conference Record. 1977 11th Asilomar Conference. (1977). p. 405–409. doi: 10.1109/ACSSC.1977.748954

Crossref Full Text | Google Scholar

10. Bergman R, Ider Y, Bosden C, Cobelli C. Quantitative estimation of insulin sensitivity. Physiol. (1979) 236:E667–77. doi: 10.1152/ajpendo.1979.236.6.E667

PubMed Abstract | Crossref Full Text | Google Scholar

11. Bergman R, Phillips LS, Cobelli C. Physiologic evaluation of factors controlling glucose tolerance in man. J Chin Invest. (1981) 68:1456–67. doi: 10.1172/JCI110398

Crossref Full Text | Google Scholar

12. López-Palau NE, Olais-Govea JM. Mathematical model of blood glucose dynamics by emulating the pathophysiology of glucose metabolism in type 2 diabetes mellitus. Sci Rep. (2020) 10:12697. doi: 10.1038/s41598-020-69629-0

PubMed Abstract | Crossref Full Text | Google Scholar

13. Jin J, Li J, Xu R, Yu L, Jin Z. A novel IVGTT model including interstitial insulin. Mathem Appl Sci Eng. (2023) 4:1–78. doi: 10.5206/mase/15505

Crossref Full Text | Google Scholar

14. Banks HT, Cintrón-Arias A, Kappel F. Parameter selection methods in inverse problem formulation. In: Mathematical modeling and validation in physiology. vol. 2064 of Lecture Notes in Math. Heidelberg: Springer (2013). p. 43–73. doi: 10.1007/978-3-642-32882-4_3

Crossref Full Text | Google Scholar

15. Banks HT, Robbins D, Sutton KL. Generalized sensitivity analysis for delay differential equations. In:Bredies K, Clason C, Kunisch K, , editors. Control and Optimization with PDE Constraints. Basel: Springer (2013). p. 19–44. doi: 10.1007/978-3-0348-0631-2_2

Crossref Full Text | Google Scholar

16. Derouich M, Boutayeb A. The effect of physical exercise on the dynamics of glucose and insulin. J Biomech. (2002) 35:911–7. doi: 10.1016/S0021-9290(02)00055-6

Crossref Full Text | Google Scholar

17. Boutayeb A, Chetouani A. A critical review of mathematical models and data used in diabetology. Biomed Eng Online. (2006) 5:43. doi: 10.1186/1475-925X-5-43

PubMed Abstract | Crossref Full Text | Google Scholar

18. Wake AD. Protective effects of physical activity against health risks associated with type 1 diabetes: “Health benefits outweigh the risks”. World J Diabetes. (2022) 13:161–84. doi: 10.4239/wjd.v13.i3.161

PubMed Abstract | Crossref Full Text | Google Scholar

19. American Diabetes Association Professional Practice Committee. Improving Care and Promoting Health in Populations: Standards of Medical Care in Diabetes 2022. Diab Care. (2021) 45:S8–S16. doi: 10.2337/dc22-S001

PubMed Abstract | Crossref Full Text | Google Scholar

20. Hall JE, Hall ME. Guyton and Hall Textbook of Medical Physiology. 15th ed Philadelphia, PA: Elsevier/Urban & Fischer. (2025).

Google Scholar

21. Li J, Kuang Y, Li B. Analysis of IVGTT glucose-insulin interaction models with time delay. Discrete Contin Dyn Syst Ser B. (2001) 1:103–24. doi: 10.3934/dcdsb.2001.1.103

Crossref Full Text | Google Scholar

22. Li J, Kuang Y, Mason CC. Modeling the glucose-insulin regulatory system and ultradian insulin secretory oscillations with two explicit time delays. J Theoret Biol. (2006) 242:722–35. doi: 10.1016/j.jtbi.2006.04.002

PubMed Abstract | Crossref Full Text | Google Scholar

23. International Diabetes Federation editor. IDF Diabetes Atlas, 11th Edition. 11th ed. Brussels, Belgium: International Diabetes Federation (2025).

Google Scholar

24. Rathee S, Nilam. ODE models for the management of diabetes: a review. Int J Diab Dev Countr. (2017) 37:4–15. doi: 10.1007/s13410-016-0475-8

Crossref Full Text | Google Scholar

25. Makroglou A, Li J, Kuang Y. Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: an overview. Appl Numer Mathem. (2006) 56:559–73. doi: 10.1016/j.apnum.2005.04.023

Crossref Full Text | Google Scholar

26. Topp B, Promislow K, de Vries G, Miura RM, Finegood DT. A model of beta-cell mass, insulin, and glucose kinetics: pathways to diabetes. J Theor Biol. (2000) 206:605–19. doi: 10.1006/jtbi.2000.2150

PubMed Abstract | Crossref Full Text | Google Scholar

27. World Health Organization. Global Diabetes Compact and 2022 Coverage Targets. World Health Organization (2022).

Google Scholar

28. Kitzler TM, Bachar M, Skrabal F, Kotanko P. Evaluation of treatment adherence in type 1 diabetes: a novel approach. Eur J Clin Invest. (2007) 37:207–13. doi: 10.1111/j.1365-2362.2007.01771.x

PubMed Abstract | Crossref Full Text | Google Scholar

29. Nauck MA, Homberger E, Siegel EG, Allen RC, Eaton RP, Ebert R, et al. Incretin effects of increasing glucose loads in man calculated from venous insulin and C-peptide responses. J Clin Endocrinol Metabol. (1986) 63:492–8. doi: 10.1210/jcem-63-2-492

PubMed Abstract | Crossref Full Text | Google Scholar

30. Harreiter J, Roden M. Diabetes mellitus-definition, klassifikation, diagnose, screening und prävention (Update 2023). Wien Klin Wochenschr. (2023) 135:7–17. doi: 10.1007/s00508-022-02122-y

PubMed Abstract | Crossref Full Text | Google Scholar

31. Bergman R. Pathogenesis and prediction of diabetes mellitus: Lessons from integrative physiology. Mount Sinai J Med. (2002) 69:280–90.

PubMed Abstract | Google Scholar

32. Rix I, Nexe-Larsen C, Bergmann NC, Lund A, Knop FK. Glucagon physiology. In:Feingold KR, Anawalt B, Boyce A, et al., , editors Endotext. South Dartmouth, MA: MDTextcom, Inc. (2019).

Google Scholar

33. MacDonald PE, De Marinis YZ, Ramracheya R, Salehi A, Ma X, Johnson PRV, et al. A K_ATP channel dependent pathway within α-cells regulates glucagon release from both rodent and human islets of langerhans. PLoS Biol. (2007) 5:e143. doi: 10.1371/journal.pbio.0050143

PubMed Abstract | Crossref Full Text | Google Scholar

34. Sturis J, Polonsky KS, Moseklide E, Van Cauter E. Computer model for mechanisms underlying ultradian oscillations of insulin and glucose. Am J Physiol-Endocrinol Metab. (1991) 260:E801–9. doi: 10.1152/ajpendo.1991.260.5.E801

PubMed Abstract | Crossref Full Text | Google Scholar

35. Tolić IM, Mosekilde E, Sturis J. Modeling the insulin-glucose feedback system: the significance of pulsatile insulin secretion. J Theor Biol. (2000) 207:361–75. doi: 10.1006/jtbi.2000.2180

PubMed Abstract | Crossref Full Text | Google Scholar

36. Keener J. Diffusion induced oscillatory insulin secretion. Bull Math Biol. (2001) 63:625–41. doi: 10.1006/bulm.2001.0235

PubMed Abstract | Crossref Full Text | Google Scholar

37. Himsworth HP. Diabetes mellitus: its differentiation into insulin-sensitive and insulin-insensitive types. Int J Epidemiol. (2013) 42:1594–8. doi: 10.1093/ije/dyt203

PubMed Abstract | Crossref Full Text | Google Scholar

38. Cobelli C, Federspil G, Pacini G, Salvan A, Scandellari C. An integrated mathematical model of the dynamics of blood glucose and its hormonal control. Math Biosci. (1982) 58:27–60. doi: 10.1016/0025-5564(82)90050-5

Crossref Full Text | Google Scholar

39. Pacini G, Bergman RN. MINMOD: a computer program to calculate insulin sensitivity and pancreatic responsivity from the frequently sampled intravenous glucose tolerance test. Comput Methods Programs Biomed. (1986) 23:113–22. doi: 10.1016/0169-2607(86)90106-9

PubMed Abstract | Crossref Full Text | Google Scholar

40. Wilcox G. Insulin and insulin resistance. Clin Biochem Rev. (2005) 26:19–39.

Google Scholar

41. Schiavon M, Dalla Man C, Kudva YC, Basu A, Cobelli C. Quantitative estimation of insulin sensitivity in type 1 diabetic subjects wearing a sensor-augmented insulin pump. Diabetes Care. (2014) 37:1216–23. doi: 10.2337/dc13-1120

PubMed Abstract | Crossref Full Text | Google Scholar

42. Hampton GS, Bartlette K, Nadeau KJ, Cree-Green M, Diniz Behn C. Mathematical modeling reveals differential dynamics of insulin action models on glycerol and glucose in adolescent girls with obesity. Front Physiol. (2022) 13:895118. doi: 10.3389/fphys.2022.895118

PubMed Abstract | Crossref Full Text | Google Scholar

43. De Gaetano A, Arino O. Mathematical modelling of the intravenous glucose tolerance test. J Math Biol. (2000) 40:136–68. doi: 10.1007/s002850050007

PubMed Abstract | Crossref Full Text | Google Scholar

44. Erlandsen M, Martinussen C, Gravholt CH. Integrated model of insulin and glucose kinetics describing both hepatic glucose and pancreatic insulin regulation. Comput Methods Programs Biomed. (2018) 156:121–31. doi: 10.1016/j.cmpb.2017.12.009

PubMed Abstract | Crossref Full Text | Google Scholar

45. Bolie V. Coefficients of normal blood glucose regulation. J Appl Physiol. (1961) 16:783–8. doi: 10.1152/jappl.1961.16.5.783

PubMed Abstract | Crossref Full Text | Google Scholar

46. Bergman RN. Origins and history of the minimal model of glucose regulation. Front Endocrinol. (2021) 11:583016. doi: 10.3389/fendo.2020.583016

PubMed Abstract | Crossref Full Text | Google Scholar

47. Toffolo G, Bergman RN, Finegood DT, Bowden CR, Cobelli C. Quantitative estimation of beta cell sensitivity to glucose in the intact organism: a minimal model of insulin kinetics in the dog. Diabetes. (1980) 29:979–90. doi: 10.2337/diab.29.12.979

PubMed Abstract | Crossref Full Text | Google Scholar

48. Fernandez J, Aguilar N, Fernandez de Canete R, Ramos-Diaz JC. Causal modeling of the glucose-insulin system in type-1 diabetic patients. World Acad Sci Eng Technol Int J Bioeng Life Sci. (2017) 11.

Google Scholar

49. Polonsky KS, Given BD, Hirsch LJ, Shapiro ET, Tillil H, Beebe C. Profiles of pancreatic beta cell secretion during meal-related glycemic excursions in normal and obese subjects. J Clin Invest. (1996) 81:442–8.

Google Scholar

50. Radziuk J. Measurement of glucose turnover in diabetic subjects using a new model. Diabetes. (2000) 29:9–20.

Google Scholar

51. Bonner-Weir S, Deery D, Leahy JL, Weir GC. Compensatory growth of pancreatic beta-cells in adult rats after short-term glucose infusion. Diabetes. (1989) 38:49–53. doi: 10.2337/diab.38.1.49

PubMed Abstract | Crossref Full Text | Google Scholar

52. Weir GC, Laybutt DR, Kaneto H, Bonner-Weir S, Sharma A. Beta-cell adaptation and decompensation during the progression of diabetes. Diabetes. (2001) 50: S154–9. doi: 10.2337/diabetes.50.2007.S154

Crossref Full Text | Google Scholar

53. Wang H, Li J, Kuang Y. Mathematical modeling and qualitative analysis of insulin therapies. Mathem Biosci. (2007) 210:17–33. doi: 10.1016/j.mbs.2007.05.008

PubMed Abstract | Crossref Full Text | Google Scholar

54. Banks HT. A Functional Analysis Framework for Modeling, Estimation and Control in science and Engineering. Boca Raton, FL: CRC Press. (2012). doi: 10.1201/b12209

Crossref Full Text | Google Scholar

55. Banks HT, Bortz DM. A parameter sensitivity methodology in the context of HIV delay equation models. J Math Biol. (2005) 50:607–25. doi: 10.1007/s00285-004-0299-x

PubMed Abstract | Crossref Full Text | Google Scholar

56. Kappel F. Generalized sensitivity analysis in a delay system. Proc Appl Math Mech. (2007) 7:1061001–2. doi: 10.1002/pamm.200700458

Crossref Full Text | Google Scholar

57. Banks HT, Rehm K, Sutton K. Inverse problems for nonlinear delay systems. Methods Applic Anal. (2010) 17:331–56. doi: 10.4310/MAA.2010.v17.n4.a2

Crossref Full Text | Google Scholar

58. Lenz SM, Schlöder JP, Bock HG. Numerical computation of derivatives in systems of delay differential equations. Math Comput Simul. (2014) 96:124–56. doi: 10.1016/j.matcom.2013.08.003

Crossref Full Text | Google Scholar

59. Ingalls B, Mincheva M, Roussel MR. Parametric sensitivity analysis of oscillatory delay systems with an application to gene regulation. Bull Math Biol. (2017) 79:1539–63. doi: 10.1007/s11538-017-0298-x

PubMed Abstract | Crossref Full Text | Google Scholar

60. Kappel F, Schappacher W. Nonlinear functional-differential equations and abstract integral equations. Proc Roy Soc Edinburgh Sect A. (1979) 84:71–91. doi: 10.1017/S0308210500016966

Crossref Full Text | Google Scholar

61. Ito K, Kappel F. Approximation of semilinear cauchy problems. Nonl Anal. (1995) 24:51–80. doi: 10.1016/0362-546X(94)E0022-9

Crossref Full Text | Google Scholar

62. Hale J. Theory of Functional Differential Equations. Vol 3 of Applied Mathematical Sciences 2nd ed New York-Heidelberg: Springer-Verlag. (1977). doi: 10.1007/978-1-4612-9892-2

Crossref Full Text | Google Scholar

63. Hale JK. History of delay equations. In: Delay Differential Equations and Applications. vol. 205 of NATO Sci. Ser. II Math. Phys. Chem. Dordrecht: Springer (2006). p. 1–28. doi: 10.1007/1-4020-3647-7_1

Crossref Full Text | Google Scholar

64. Ito K, Kappel F. Evolution Equations and Approximations. River Edge, NJ: World Scientific Publishing Co, Inc. (2002). doi: 10.1142/9789812777294

Crossref Full Text | Google Scholar

65. Banks HT, Burns JA. An abstract framework for approximate solutions to optimal control problems governed by hereditary systems. In:Antosiewicz H, , editor. International Conference on Differential Equations. San Diego: Academic Press (1975). p. 10–25. doi: 10.1016/B978-0-12-059650-8.50009-0

Crossref Full Text | Google Scholar

66. Banks HT, Burns JA. Hereditary control problems: numerical methods based on averaging approximations. SIAM J Control Optim. (1978) 16:169–208. doi: 10.1137/0316013

Crossref Full Text | Google Scholar

67. Kappel F, Schappacher W. Autonomous nonlinear functional differential equations and averaging approximations. Nonl Anal. (1978) 2:391–422. doi: 10.1016/0362-546X(78)90048-2

Crossref Full Text | Google Scholar

68. Reddien GW, Webb GF. Numerical approximation of nonlinear functional differential equations with L² initial functions. SIAM J Mathem Anal. (1978) 9:1017–31. doi: 10.1137/0509093

Crossref Full Text | Google Scholar

69. Banks HT, Kappel F. Spline approximations for functional differential equations. J Differ Equ. (1979) 34:496–522. doi: 10.1016/0022-0396(79)90033-0

Crossref Full Text | Google Scholar

70. Banks HT. Identification of nonlinear delay systems using spline methods. In:Lakshmikantham V, , editor. Nonlinear Phenomena in Mathematical Sciences. Academic Press (1982). p. 47–55.

Google Scholar

71. Banks HT. Approximation of nonlinear functional differential equation control systems. J Optim Theory Appl. (1979) 29:383–408. doi: 10.1007/BF00933142

Crossref Full Text | Google Scholar

72. Banks HT. Identification of nonlinear delay systems using spline methods. In:Lakshmikantham V, , editor. Nonlinear Phenomena in Mathematical Sciences. New York: Academic Press (1982). p. 47–55.

Google Scholar

73. Kappel F. An approximation scheme for delay equations. In:Lakshmikantham V, , editor. Nonlinear Phenomena in Mathematical Sciences. New York: Academic Press (1982). p. 585–595. doi: 10.1016/B978-0-12-434170-8.50074-1

Crossref Full Text | Google Scholar

74. Banks HT, Lamm PKD. Estimation of delays and other parameters in nonlinear functional differential equations. SIAM J Control Optim. (1983) 21:895–915. doi: 10.1137/0321054

Crossref Full Text | Google Scholar

75. Kato T. Perturbation Theory for Linear Operators. New York: Springer (1976).

Google Scholar

76. Ito K, Kappel F, Salamon D. A variational approach to approximation of delay systems. Differ Integr Equat. (1991) 4:51–72. doi: 10.57262/die/1371569634

Crossref Full Text | Google Scholar

77. Banichuk NE. Optimization of Structures: With Applications to Mechanics of Solids and Fluids. Berlin, Heidelberg: Springer-Verlag (1990).

Google Scholar

78. Haftka RT, Gürdal Z. Elements of Structural Optimization. Kluwer: Academic Publishers (1993). p. 1–486.

Google Scholar

79. Haftka RT, Gürdal Z. Structural optimization: a study of optimal design with various types of objectives and constraints. J Optim Theory Applic. (1992) 73:55–75.

Google Scholar

80. Brewer D. The differentiability with respect to a parameter of the solution of a linear abstract Cauchy problem. SIAM J Math Anal. (1982) 13:607–20. doi: 10.1137/0513039

Crossref Full Text | Google Scholar

81. Robbins D. Sensitivity Functions for Delay Differential Equation Models [Ph.D. Dissertation]. North Carolina State University, Raleigh, North Carolina (2011).

Google Scholar

82. Gibson JS, Clark JD. Sensitivity analysis for a class of evolution equations. J Math Anal Appl. (1977) 58:22–31. doi: 10.1016/0022-247X(77)90224-4

Crossref Full Text | Google Scholar

83. Brewer D, Burns JA, Cliff EM. Parameter Identification for an Abstract Cauchy Problem by Quasilinearization. ICASE Rep No 89-75, NASA Langley Res Center. (1989).

Google Scholar

84. Banks HT, Robbins D, Sutton KL. Theoretical foundations for traditional and generalized sensitivity functions for nonlinear delay differential equations. Mathem Biosci Eng. (2013) 10:1301–33. doi: 10.3934/mbe.2013.10.1301

PubMed Abstract | Crossref Full Text | Google Scholar

85. Banks HT, Dediu S, Ernstberger SL, Kappel F. Generalized sensitivities and optimal experimental design. J Inverse Ill-Posed Probl. (2010) 18:25–83. doi: 10.1515/jiip.2010.002

Crossref Full Text | Google Scholar

86. Banks HT, Holm K, Kappel F. Comparison of optimal design methods in inverse problems. Inverse Probl. (2011) 27:075002. doi: 10.1088/0266-5611/27/7/075002

PubMed Abstract | Crossref Full Text | Google Scholar

87. Batzel JJ, Bachar M, Kappel F. Mathematical Modeling and Validation in Physiology. vol. 2064 of Lecture Notes in Mathematics. Heidelberg: Springer (2013). doi: 10.1007/978-3-642-32882-4

Crossref Full Text | Google Scholar

88. Li J, Bao Y, Chen X, Tian L. Decision models in type 2 diabetes mellitus: a systematic review. Acta Diabetol. (2021) 58:1451–69. doi: 10.1007/s00592-021-01742-6

PubMed Abstract | Crossref Full Text | Google Scholar

89. Saini P, Ahuja R. A review for predicting diabetes mellitus using different techniques and methods. In:Saraswat M, Roy S, Chowdhury C, Gandomi AH, , editors. Proceedings of the International Conference on Data Science and Applications. Singapore: Springer (2022). p. 425–40. doi: 10.1007/978-981-16-5120-5_32

Crossref Full Text | Google Scholar