A diffusion-based HIV model with inflammatory cytokines and adaptive immune impairment

HIV continues to pose a critical threat to global public health, contributing to a high number of deaths worldwide. The virus predominantly attacks CD4⁺T lymphocytes, which are essential for coordinating immune responses. A progressive decline in these cells is a hallmark of HIV pathogenesis. Recent research has underscored the role of inflammatory cytokines in promoting viral spread and exacerbating immune dysfunction. This study presents a spatially structured model of HIV infection incorporating the role of inflammatory cytokines. The model consists of six interacting components: healthy CD4⁺ T cells, HIV-infected cells, inflammatory cytokines, free viral particles, cytotoxic T lymphocytes (CTLs), and antibodies. It accounts for both cell-free (virus-to-cell) and direct (cell-to-cell) modes of transmission. The model also captures the suppression of adaptive immune responses involving CTLs and B cells. Motivated by recent findings that immune and infected cells, as well as viruses, may migrate from high to low concentration areas, we introduce diffusion terms to represent spatial movement, resulting in a system of nonlinear partial differential equations. We first establish the model's mathematical well-posedness by proving the existence and boundedness of global solutions. A basic reproduction number ${\mathcal{R}}_0$ is derived, serving as a threshold parameter that governs the stability of two equilibria: the HIV-free equilibrium ($\mathcal{F}\mathcal{E}$) and the HIV-persistent equilibrium ($\mathcal{PE}$). By constructing suitable Lyapunov functions and applying LaSalle's invariance principle, we demonstrate that $\mathcal{F}\mathcal{E}$ is globally asymptotically stable when ${\mathcal{R}}_0\le 1$, while $\mathcal{PE}$ becomes globally stable if ${\mathcal{R}}_0>1$. Numerical simulations are performed to validate the analytical results, and a sensitivity analysis of ${\mathcal{R}}_0$ is carried out to evaluate the impact of critical model parameters.

1 Introduction

The human immunodeficiency virus (HIV), a fast-replicating retrovirus within the lentivirus genus, specifically targets and disrupts the functionality of critical immune cells, with a strong preference for CD4⁺T cells. These immune cells play a vital role in regulating and coordinating immune defense mechanisms. Once HIV enters the body, it integrates its genetic material into the host genome, gradually depleting the number of CD4⁺T cells. In a healthy individual, the CD4⁺T cell count is typically around 1,000 cells per mm³ of blood. As the infection progresses, these levels decline steadily, often without immediate symptoms. When the count falls below 200 cells/mm³, the individual is considered to have developed acquired immunodeficiency syndrome (AIDS), a condition characterized by increased susceptibility to opportunistic infections and certain types of cancer [1, 2]. In the absence of appropriate antiretroviral therapy, the continuous weakening of the immune system can lead to severe complications and, ultimately, death. The adaptive immune response is vital in managing viral infections and operates primarily through two pathways: antibodies produced by B cells that neutralize HIV particles, and cytotoxic T lymphocytes (CTLs) that identify and destroy infected host cells. These coordinated responses work to inhibit viral replication and reduce the rate of disease advancement.

Mathematical modeling serves as an essential approach for exploring the complex interactions between viral infections and the host's immune defenses. By representing biological processes through mathematical equations, these models enable a deeper investigation into the factors that influence infection dynamics, the strength and limitations of immune responses, and the potential outcomes of various scenarios. This approach has greatly enhanced our comprehension of virus-immune system relationships and has become instrumental in guiding the design of effective treatments and shaping public health policies. A basic model for analyzing HIV dynamics was proposed by Nowak and Bangham [3], capturing the interactions between healthy CD4⁺T cells, infected cells, and free virus particles. Since its introduction, this foundational framework has been extended in various directions to incorporate the CTL response [4–9], the antibody-mediated immune response [10, 11], and more comprehensive formulations that include both CTL and antibody responses simultaneously [12–16].

Pyroptosis, unlike the controlled and non-inflammatory nature of apoptosis, is a pro-inflammatory programmed cell death mechanism closely linked to immune system activation and inflammatory responses. In HIV-infected individuals, Doitsh et al. [17] demonstrated that caspase-1, a cysteine-dependent protease, becomes activated and promotes the secretion of inflammatory mediators such as interleukin-1β (IL-1β). These cytokines sustain a chronic inflammatory environment that draws in uninfected CD4⁺T cells, rendering them vulnerable to death. As a result, a destructive feedback loop is created in which infected CD4⁺T cells undergoing pyroptosis release inflammatory factors that drive the death of surrounding uninfected CD4⁺T cells, accelerating the decline of immune function [17]. Studies indicate that merely about 5% of CD4⁺T cell death is attributed to apoptosis triggered by caspase-3, whereas the majority are lost through pyroptosis, driven by caspase-1 activation [18].

Wang et al. [19] developed a mathematical model of HIV infection that incorporates the contribution of pyroptosis to CD4⁺T cell depletion. The model is given by a system of ordinary differential equations (ODEs) which describes the interaction of healthy CD4⁺T cells, productively infected cells, abortively infected cells, inflammatory cytokines, and free HIV particles. In this framework, the impact of inflammatory cytokines on the basic reproduction number is not considered. As a result, the model overlooks the potential rise in infection rates driven by cytokine-induced recruitment of CD4⁺T cells to inflamed areas, which could lead to an underestimation of the basic reproduction number.

Recent research has highlighted the role of cytokine-driven mechanisms in the accumulation of infected CD4⁺T cells and their impact on HIV dynamics [20]. Failing to account for the rise in viral infection caused by the higher concentration of CD4⁺T cells, which are attracted to inflamed regions by cytokines, could lead to an underestimation of the basic reproduction number [21]. Cytokine-induced viral infections can disturb the balance between cell renewal and viral replication, particularly through mechanisms such as pyroptosis [18]. The growth of the infected CD4⁺T cell population is shaped by two main pathways: (i) direct infection of healthy CD4⁺T cells through viral contact, and (ii) an increase in infection rates linked to the elevated presence of CD4⁺T cells in inflamed tissues, where cytokines actively recruit them (a process known as cytokine-enhanced viral infection). To capture the combined effects of these mechanisms, the following system of equations models the dynamics of HIV infection under cytokine influence [20]:

$\begin{array}{ll}\{\begin{array}{l}\frac{dN(t)}{dt}=\delta -{\phi }_{N}N(t)-{\omega }_{1}N(t)B(t)-{\omega }_{2}N(t)S(t),\\ \frac{dU(t)}{dt}={\omega }_{1}N(t)B(t)+{\omega }_{2}N(t)S(t)-({\beta }_1+{\phi }_U)U(t),\\ \frac{dS(t)}{dt}={\beta }_{2}U(t)-{\phi }_{S}S(t),\\ \frac{dB(t)}{dt}=\mu U(t)-{\phi }_{B}B(t).\end{array}& (1)\end{array}$

Here, N(t), U(t), S(t) and B(t) represent the time-dependent concentrations of healthy CD4⁺T cells, CD4⁺T cells infected with HIV, inflammatory cytokines, and free HIV virions, respectively. The parameter δ represents the production rate of uninfected CD4⁺T cells. The term ω₁NB corresponds to the rate at which CD4⁺T cells become infected through direct interaction with the virus, while ω₂NS captures the cytokine-induced enhancement of infection. Cytokine and viral particle release from infected cells are modeled by the terms β₂U and μU, respectively. The expression φ_ηη denotes the natural death rate of a given compartment η, and β₁U specifically accounts for the loss of infected CD4⁺T cells through pyroptotic cell death. Various versions of this model have been developed to incorporate key biological aspects, including (i) time delays [8, 20, 22], (ii) cell-to-cell transmission [23–25], (iii) CTL response [26, 27], (iv) antibody response [28, 29], and (v) the combined effects of CTL and antibody responses [25, 30].

Model (Equation 1) and its aforementioned extension presume a homogeneous distribution of both cells and viruses, thereby ignoring their spatial movement and localized interactions. While this assumption simplifies analysis, it fails to account for the critical influence of spatial organization on viral behavior. In actual biological systems, the uneven distribution of infected and healthy cells, along with constraints on viral mobility, often creates spatial variability. This heterogeneity can significantly shape how infections emerge, spread, and are contained, influencing immune response and treatment outcomes. Phenomena such as clustering of infections, formation of infection hotspots, and restricted viral spread are examples of effects that uniform mixing models cannot represent. Therefore, integrating spatial dynamics into modeling frameworks offers a more realistic and nuanced understanding of viral infections and their progression. Brainard et al. [31] and Tattermusch and Bangham [32] highlighted that T cells are capable of moving along concentration gradients, typically from regions of higher density to lower density. More recent research has extended this idea, proposing that immune cells, infected cells, and viral particles may also undergo migration from areas of abundance to those with lower presence [see, for example, [33–41]].

Wang and Zhang [42] proposed a nonlocal partial differential equations (PDEs) model incorporating time delays to analyze the role of pyroptosis in infection dynamics. Their framework includes both latent and actively infected cell populations. The infection process between healthy cells and the virus is modeled using a saturating function. Similarly, the influence of inflammatory cytokines on healthy CD4⁺T cells via pyroptosis is described by saturating function. In Wang et al. [43], the authors formulated a reaction-diffusion model that includes time-periodic parameters, spatial heterogeneity, and a latent infection stage to explore the role of pyroptosis in CD4⁺T cell loss during HIV infection. The model employs a Beddington-DeAngelis type functional response to characterize the formation rate of newly infected cells. The analysis focuses on threshold behavior governed by the basic reproduction number, providing insights into conditions for disease persistence or clearance. Wang et al. [44] introduced a partial differential equation model to investigate the effects of gasdermin D inhibition on pyroptosis in settings characterized by spatial and temporal heterogeneity. The framework includes both productively and abortively infected cell populations and accounts for the role of CTL response. The interaction between the virus and host cells is described using a general incidence function. Wang et al. [45] developed a periodic partial differential equation model to explore the dynamics of infected cell production, incorporating the heightened infection risk caused by cytokine-driven T cell migration to inflamed tissues. Their model also included the effect of necrosulfonamide, a pharmacological agent that inhibits pyroptosis. Wang and Feng [21] developed a partial differential equation model that incorporates spatial heterogeneity by introducing general functional forms to represent the dynamics of healthy CD4⁺T cell regeneration, virus-cell interactions, and cytokine-enhanced viral infection. However, in Wang and Feng [21], while the spatial dynamics of inflammatory cytokines and the virus are included, the movement of both healthy and infected CD4⁺T cells is omitted. Additionally, the immune response is not taken into account. In Chen et al. [46], the authors introduced a reaction-diffusion framework to study HIV dynamics, employing a general incidence function while accounting for cytokine-mediated enhancement of infection, CTL response, and the influence of time delay.

The models developed in Chen et al. [25] and Dahy et al. [30] assume that the presence of HIV and infected cells solely triggers CTL and antibody responses, overlooking the potential for immune suppression, commonly referred to as immune impairment. As noted in Lydyard et al. [47], HIV can weaken the immune system's functionality. Several studies have incorporated immune impairment into viral dynamics, focusing either on CTL dysfunction [e.g., [48–54]] or B-cell impairment [e.g., [54–57]]. More recently, AlShamrani et al. [58, 59] examined HIV dynamics by considering the impairment of both CTL and antibody responses. However, these studies did not consider the role of inflammatory cytokines. Although Song et al. [60] introduced CTL impairment alongside cytokine effects, it did not account for target cell population dynamics or the spatial mobility of viruses, infected cells and immune cells.

Accordingly, the objective of this work is to construct a comprehensive HIV infection model that captures several critical aspects of within-host viral dynamics. Specifically, the model aims to incorporate:

• the modulatory effects of pro-inflammatory cytokines, which play a key role in immune activation and disease progression;

• the functional impairment or exhaustion of both cytotoxic T lymphocyte (CTL) responses and antibody-mediated immunity, which are commonly observed in chronic HIV infection;

• the spatial mobility of viruses, infected cells, and various immune cell populations, allowing for a more realistic representation of cellular interactions and viral dissemination;

• and dual transmission mechanisms, encompassing both classical virus-to-cell infection and direct cell-to-cell viral spread.

By integrating these features, the proposed model seeks to provide deeper insights into HIV pathogenesis and to support the development of more effective therapeutic strategies.

We establish the well-posedness of the model by proving the existence and boundedness of global solutions, identify the equilibria and derive the basic reproduction number, and analyze the global asymptotic stability of the equilibria using appropriate Lyapunov functions and LaSalle's invariance principle. The theoretical findings are supported by detailed numerical simulations, and a sensitivity analysis of the basic reproduction number is conducted to assess the influence of key parameters.

2 Model construction

We formulate a reaction-diffusion model based on partial differential equations to describe the variation of the concentrations of six compartments with respect to spatial location ϰ and time t; healthy CD4⁺T cells N(ϰ, t), HIV-infected CD4⁺T cells U(ϰ, t), inflammatory cytokines S(ϰ, t), free HIV particles B(ϰ, t), Cytotoxic T Lymphocytes (CTLs) M(ϰ, t), and antibodies H(ϰ, t).

$\begin{array}{ll}\{\begin{array}{l}\frac{\partial N(\varkappa ,t)}{\partial t}=D_N\Delta N(\varkappa ,t)+\delta -{\phi }_{N}N(\varkappa ,t)-{\omega }_{1}N(\varkappa ,t)B(\varkappa ,t)\\ -{\omega }_{2}N(\varkappa ,t)S(\varkappa ,t)-{\omega }_{3}N(\varkappa ,t)U(\varkappa ,t),\\ \frac{\partial U(\varkappa ,t)}{\partial t}=D_U\Delta U(\varkappa ,t)+{\omega }_{1}N(\varkappa ,t)B(\varkappa ,t)+{\omega }_{2}N(\varkappa ,t)S(\varkappa ,t)\\ +{\omega }_{3}N(\varkappa ,t)U(\varkappa ,t)-({\beta }_1+{\phi }_U)U(\varkappa ,t)-{\varrho }_{1}U(\varkappa ,t)\\ M(\varkappa ,t),\\ \frac{\partial S(\varkappa ,t)}{\partial t}=D_S\Delta S(\varkappa ,t)+{\beta }_{2}U(\varkappa ,t)-{\phi }_{S}S(\varkappa ,t),\\ \frac{\partial B(\varkappa ,t)}{\partial t}=D_B\Delta B(\varkappa ,t)+\mu U(\varkappa ,t)-{\phi }_{B}B(\varkappa ,t)-{\varrho }_{2}B(\varkappa ,t)\\ H(\varkappa ,t),\\ \frac{\partial M(\varkappa ,t)}{\partial t}=D_M\Delta M(\varkappa ,t)+\xi U(\varkappa ,t)-{\phi }_{M}M(\varkappa ,t)-{\lambda }_{1}U(\varkappa ,t)\\ M(\varkappa ,t),\\ \frac{\partial H(\varkappa ,t)}{\partial t}=D_H\Delta H(\varkappa ,t)+\psi B(\varkappa ,t)-{\phi }_{H}H(\varkappa ,t)-{\lambda }_{2}B(\varkappa ,t)\\ H(\varkappa ,t),\end{array}& (2)\end{array}$

where ϰ = (ϰ₁, ϰ₂, ..., ϰ_ℓ) ∈ Λ, and t > 0. The spatial region Λ ⊂ ℝ^ℓ, is a connected, bounded domain, and has a smooth boundary ∂Λ, where ℓ is an integer such that ℓ ≥ 1. The diffusion coefficient $D_{\mathcal{G}}$ is positive for each $\mathcal{G}$ in the set {N, U, S, B, M, H}. The Laplace operator, represented by Δ, is defined as $\frac{{\partial }^2}{\partial {\varkappa }^2}$. The infection rate resulting from cellular infection is ω₃NU. The terms ξU and ψB represent the rates at which CTLs and antibodies proliferate, respectively, from infected cells and free HIV particles. The rate at which infected cells are killed by CTLs is denoted as ϱ₁UM, whereas free HIV particles are neutralized by antibodies at rate ϱ₂BH. The rates at which CTL and antibody immunities are impaired are labeled as λ₁UM and λ₂BH, respectively. The natural death rates associated with CTLs and antibodies are represented by φ_M and φ_H, respectively. As previously outlined in Section 1, all other parameters share an identical biological interpretation.

In the following, the initial conditions, as well as the homogeneous Neumann boundary conditions adopted for system (Equation 2), are given as:

$\begin{array}{ll}\{\begin{array}{l}N(\varkappa ,0)={\mathcal{I}}_1(\varkappa ),U(\varkappa ,0)={\mathcal{I}}_2(\varkappa ),S(\varkappa ,0)={\mathcal{I}}_3(\varkappa ),\\ B(\varkappa ,0)={\mathcal{I}}_4(\varkappa ),M(\varkappa ,0)={\mathcal{I}}_5(\varkappa ),H(\varkappa ,0)={\mathcal{I}}_6(\varkappa ),\varkappa \in \bar{\Lambda }.\end{array}& (3)\end{array}$

$\begin{array}{ll}\{\frac{\partial N}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial U}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial S}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial B}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial M}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial H}{\partial \overrightarrow{\sout{Z}}}=0,t>0,\varkappa \in \partial \Lambda .& (4)\end{array}$

Here, the functions ${\mathcal{I}}_j(\varkappa )$, for j = 1, ..., 6, are both continuous and non-negative. Meanwhile, $\frac{\partial }{\partial \overrightarrow{\sout{Z}}}$ represents the outward normal derivative on the boundary ∂Λ. The boundary conditions (Equation 4) ensure that all populations are prohibited from traversing the isolated boundary ∂Λ [61].

Remark 1. The mathematical model developed in Hattaf [6] incorporates CTL immune responses and considers the spatial mobility of both immune cells and viruses. However, it omits several key immunological factors, such as the contribution of antibody-mediated immunity, the regulatory role of pro-inflammatory cytokines, and the potential dysfunction or exhaustion of CTL response that may occur during chronic infection. Conversely, the study by Hajhouji et al. [62] focuses on the antibody response in the context of HIV dynamics but does not include CTL-mediated immunity, cytokine-driven inflammation, or the spatial migration of immune cells and viral particles. Together, these limitations highlight the need for more comprehensive models that integrate multiple layers of the immune system and spatial effects to better capture the complexity of HIV pathogenesis. These limitations have been addressed in the present model, which incorporates both CTL and antibody-mediated immune responses, accounts for the effects of pro-inflammatory cytokines, and includes the mobility of immune cells and viruses. By integrating these critical biological factors, our model offers a more comprehensive framework for analyzing HIV infection dynamics and immune system interactions.

3 Characteristics of solutions

The following result addresses the existence, uniqueness, non-negativity, and boundedness of solutions for model (Equation 2), which describe the densities of healthy CD4⁺T cells, HIV-infected CD4⁺T cells, inflammatory cytokines, free HIV particles, CTLs, and antibodies.

Lemma 1. Let the assumption $D_N=D_U=D_S=D_B=D_M=D_H=\widehat{D}$ hold true. For any initial function $\mathcal{I}={({\mathcal{I}}_1,{\mathcal{I}}_2,{\mathcal{I}}_3,{\mathcal{I}}_4,{\mathcal{I}}_5,{\mathcal{I}}_6)}^T\in {\mathcal{Y}}_{+}$ satisfying the initial conditions (Equation 3), model (Equation 2) has a unique, non-negative and bounded solution (N(ϰ, t), U(ϰ, t), S(ϰ, t), B(ϰ, t), M(ϰ, t), H(ϰ, t)) defined on $\bar{\Lambda }\times [0,+\infty )$.

Proof. Let $\mathcal{Y}=BUC(\bar{\Lambda },{ℝ}^6)$ be defined as the set of all functions from $\bar{\Lambda }$ to ℝ⁶ that are both bounded and uniformly continuous, with the norm $\parallel \varphi {\parallel }_{\mathcal{Y}}=\underset{\varkappa \in \bar{\Lambda }}{sup}\left|\varphi (\varkappa )\right|$. We denote the positive cone ${\mathcal{Y}}_{+}=BUC(\bar{\Lambda },{ℝ}_{+}^6)\subset \mathcal{Y}$ which establishes a partial order on $\mathcal{Y}$. This characterization demonstrates that the space $(\mathcal{Y},\parallel ·{\parallel }_{\mathcal{Y}})$ forms a Banach lattice [63, 64].

Concerning every initial data $\mathcal{I}={({\mathcal{I}}_1,{\mathcal{I}}_2,{\mathcal{I}}_3,{\mathcal{I}}_4,{\mathcal{I}}_5,{\mathcal{I}}_6)}^T\in {\mathcal{Y}}_{+}$, we define $K={(K_1,K_2,K_3,K_4,K_5,K_6)}^T:{\mathcal{Y}}_{+}\to \mathcal{Y}$ as follows:

$\begin{array}{l}\{\begin{array}{l}{K}_1(\mathcal{I})(\varkappa )=\delta -{\phi }_N{\mathcal{I}}_1(\varkappa )-{\omega }_1{\mathcal{I}}_1(\varkappa ){\mathcal{I}}_4(\varkappa )-{\omega }_2{\mathcal{I}}_1(\varkappa ){\mathcal{I}}_3(\varkappa )\\ -{\omega }_3{\mathcal{I}}_1(\varkappa ){\mathcal{I}}_2(\varkappa ),\\ K_2(\mathcal{I})(\varkappa )={\omega }_1{\mathcal{I}}_1(\varkappa ){\mathcal{I}}_4(\varkappa )+{\omega }_2{\mathcal{I}}_1(\varkappa ){\mathcal{I}}_3(\varkappa )+{\omega }_3{\mathcal{I}}_1(\varkappa ){\mathcal{I}}_2(\varkappa )-\\ ({\beta }_1+{\phi }_U+{\varrho }_1{\mathcal{I}}_5(\varkappa )){\mathcal{I}}_2(\varkappa ),\\ K_3(\mathcal{I})(\varkappa )={\beta }_2{\mathcal{I}}_2(\varkappa )-{\phi }_S{\mathcal{I}}_3(\varkappa ),\\ K_4(\mathcal{I})(\varkappa )=\mu {\mathcal{I}}_2(\varkappa )-{\phi }_B{\mathcal{I}}_4(\varkappa )-{\varrho }_2{\mathcal{I}}_4(\varkappa ){\mathcal{I}}_6(\varkappa ),\\ K_5(\mathcal{I})(\varkappa )=\xi {\mathcal{I}}_2(\varkappa )-{\phi }_M{\mathcal{I}}_5(\varkappa )-{\lambda }_1{\mathcal{I}}_2(\varkappa ){\mathcal{I}}_5(\varkappa ),\\ K_6(\mathcal{I})(\varkappa )=\psi {\mathcal{I}}_4(\varkappa )-{\phi }_H{\mathcal{I}}_6(\varkappa )-{\lambda }_2{\mathcal{I}}_4(\varkappa ){\mathcal{I}}_6(\varkappa ).\end{array}\end{array}$

We observe that K is locally Lipschitz on ${\mathcal{Y}}_{+}$, which is a fact straightforward to verify (see Corollary 4 in Martin and Smith [65]). System (Equation 2) subject to initial conditions (Equation 3) and boundary conditions (Equation 4) can be reformulated as the following abstract functional differential equation:

$\begin{array}{l}\{\begin{array}{l}\frac{d\mathcal{L}}{dt}=\Gamma \mathcal{L}+H(\mathcal{L}),t>0,\\ \mathcal{L}(0)=\mathcal{I}\in {\mathcal{Y}}_{+},\end{array}\end{array}$

where $\mathcal{L}={(N,U,S,B,M,H)}^T$ and $\Gamma \mathcal{L}={(D_N\Delta N,D_U\Delta U,D_S\Delta S,D_B\Delta B,D_M\Delta M,D_H\Delta H)}^T$. One can prove that

$\begin{array}{l}{\displaystyle \underset{\upsilon \to 0^{+}}{lim}}\frac{1}{\upsilon }\text{dist}\left(\mathcal{I}(0)+\upsilon K(\mathcal{I}),{\mathcal{Y}}_{+}\right)=0,\text{for every }\mathcal{I}\in {\mathcal{Y}}_{+}.\end{array}$

Follows the work of Xu and Xu [63], Zhang and Xu [64], and Smith [66], we deduce that for any $\mathcal{I}\in {\mathcal{Y}}_{+}$, system (Equation 2) subject to (Equations 3, 4) possesses a unique non-negative mild solution (N(ϰ, t), U(ϰ, t), S(ϰ, t), B(ϰ, t), M(ϰ, t), H(ϰ, t)). This solution is defined on $\bar{\Lambda }\times [0,{\mathcal{T}}_M)$, where $[0,{\mathcal{T}}_M)$ is the maximal time interval over which the solution remains in existence. Furthermore, this solution constitutes a classical solution to the problem at hand.

To confirm that the solutions have a bounded nature, we introduce

$\begin{array}{l}\mathcal{P}(\varkappa ,t)=N(\varkappa ,t)+U(\varkappa ,t)+\frac{{\beta }_1+{\phi }_U}{2{\beta }_2}S(\varkappa ,t)\\ +\frac{{\beta }_1+{\phi }_U}{4\mu }B(\varkappa ,t)+\frac{{\beta }_1+{\phi }_U}{8\xi }M(\varkappa ,t)+\frac{{\phi }_B({\beta }_1+{\phi }_U)}{8\mu \psi }H(\varkappa ,t).\end{array}$

Based on the fact that $D_N=D_U=D_S=D_B=D_M=D_H=\widehat{D}$, using system (Equation 2) we derive

$\begin{array}{l}\frac{\partial \mathcal{P}\left(\varkappa ,t\right)}{\partial t}-\widehat{D}\Delta \mathcal{P}\left(\varkappa ,t\right)=\delta -{\phi }_{N}N(\varkappa ,t)-\frac{{\beta }_1+{\phi }_U}{8}U(\varkappa ,t)\\ -\frac{{\phi }_S\left({\beta }_1+{\phi }_U\right)}{2{\beta }_2}S(\varkappa ,t)\\ -\frac{{\phi }_B\left({\beta }_1+{\phi }_U\right)}{8\mu }B(\varkappa ,t)-\frac{{\phi }_M\left({\beta }_1+{\phi }_U\right)}{8\xi }M(\varkappa ,t)\\ -\frac{{\phi }_B{\phi }_H\left({\beta }_1+{\phi }_U\right)}{8\mu \psi }H(\varkappa ,t)-\left({\varrho }_1+\frac{{\lambda }_1\left({\beta }_1+{\phi }_U\right)}{8\xi }\right)U(\varkappa ,t)M(\varkappa ,t)\\ -\frac{{\beta }_1+{\phi }_U}{4\mu }\left({\varrho }_2+\frac{{\phi }_B{\lambda }_2}{2\psi }\right)B(\varkappa ,t)H(\varkappa ,t)\\ <\delta -{\phi }_{N}N(\varkappa ,t)-\frac{{\beta }_1+{\phi }_U}{8}U(\varkappa ,t)-\frac{{\phi }_S\left({\beta }_1+{\phi }_U\right)}{2{\beta }_2}S(\varkappa ,t)\\ -\frac{{\phi }_B\left({\beta }_1+{\phi }_U\right)}{8\mu }B(\varkappa ,t)-\frac{{\phi }_M\left({\beta }_1+{\phi }_U\right)}{8\xi }M(\varkappa ,t)\\ -\frac{{\phi }_B{\phi }_H\left({\beta }_1+{\phi }_U\right)}{8\mu \psi }H(\varkappa ,t)\\ \le \delta -\varpi (N(\varkappa ,t)+U(\varkappa ,t)+\frac{{\beta }_1+{\phi }_U}{2{\beta }_2}S(\varkappa ,t)+\frac{{\beta }_1+{\phi }_U}{4\mu }B(\varkappa ,t)\\ +\frac{{\beta }_1+{\phi }_U}{8\xi }M(\varkappa ,t)+\frac{{\phi }_B\left({\beta }_1+{\phi }_U\right)}{8\mu \psi }H(\varkappa ,t))=\delta -\varpi \mathcal{P}\left(\varkappa ,t\right),\end{array}$

where $\varpi =min\{{\phi }_N,\frac{{\beta }_1+{\phi }_U}{8},{\phi }_S,\frac{{\phi }_B}{2},{\phi }_M,{\phi }_H\}$. Consequently, $\mathcal{P}(\varkappa ,t)$ fulfills the subsequent system

$\begin{array}{l}\{\begin{array}{l}\frac{\partial \mathcal{P}(\varkappa ,t)}{\partial t}-\widehat{D}\Delta \mathcal{P}(\varkappa ,t)\le \delta -\varpi \mathcal{P}(\varkappa ,t),\\ \mathcal{P}(\varkappa ,0)={\mathcal{I}}_1(\varkappa )+{\mathcal{I}}_2(\varkappa )+\frac{{\beta }_1+{\phi }_U}{2{\beta }_2}{\mathcal{I}}_3(\varkappa )+\frac{{\beta }_1+{\phi }_U}{4\mu }{\mathcal{I}}_4(\varkappa )\\ +\frac{{\beta }_1+{\phi }_U}{8\xi }{\mathcal{I}}_5(\varkappa )+\frac{{\phi }_B({\beta }_1+{\phi }_U)}{8\mu \psi }{\mathcal{I}}_6(\varkappa )\ge 0,\\ \frac{\partial \mathcal{P}}{\partial \overrightarrow{\sout{Z}}}=0.\end{array}\end{array}$

Consider a solution, $\tilde{\mathcal{P}}(t)$, for the following ordinary differential equation:

$\begin{array}{l}\{\begin{array}{l}\frac{d\tilde{\mathcal{P}}(t)}{dt}=\delta -\varpi \tilde{\mathcal{P}}(t),\\ \tilde{\mathcal{P}}(0)={\displaystyle \underset{\varkappa \in \bar{\Lambda }}{max}}\mathcal{P}(\varkappa ,0).\end{array}\end{array}$

This results in $\tilde{\mathcal{P}}(t)\le max\left\{\frac{\delta }{\varpi },\underset{\varkappa \in \bar{\Lambda }}{max}\mathcal{P}(\varkappa ,0)\right\}$. With reference to the comparison principle (refer to Protter and Weinberger [67]), we find that $\mathcal{P}(\varkappa ,t)\le \tilde{\mathcal{P}}(t)$. From this, we derive

$\begin{array}{l}\mathcal{P}(\varkappa ,t)\le max\left\{\frac{\delta }{\varpi },{\displaystyle \underset{\varkappa \in \bar{\Lambda }}{max}}\mathcal{P}(\varkappa ,0)\right\},\end{array}$

which demonstrates that N(ϰ, t), U(ϰ, t), S(ϰ, t), B(ϰ, t), M(ϰ, t), and H(ϰ, t) are bounded on $\bar{\Lambda }\times [0,{\mathcal{T}}_M)$. According to the standard theory for semi-linear parabolic systems, we infer that ${\mathcal{T}}_M=+\infty$ [68]. The solution (N(ϰ, t), U(ϰ, t), S(ϰ, t), B(ϰ, t), M(ϰ, t), H(ϰ, t)) exists and is uniquely determined and non-negative for all ϰ ∈ Λ, t > 0.

4 Equilibria and basic reproduction number

In this section, we assess the equilibria and identify the threshold parameter necessary to confirm their existence. The results are outlined in the subsequent lemma:

Lemma 2. Considering system (Equation 2), a basic reproduction number

$\begin{array}{l}{\mathcal{R}}_0=\frac{\delta (\mu {\phi }_S{\omega }_1+{\phi }_B({\beta }_2{\omega }_2+{\phi }_S{\omega }_3))}{{\phi }_N{\phi }_S{\phi }_B({\beta }_1+{\phi }_U)}>0\end{array}$

can be identified, which fulfills the following statements:

1. The system ensures that it consistently achieves an HIV-free equilibrium, labeled as $\mathcal{F}\mathcal{E}=(N_0,0,0,0,0,0)$, N₀ = δ/φ_N.

2. The system also maintains an HIV-persistent equilibrium, labeled as $\mathcal{PE}=(\bar{N},\bar{U},\bar{S},\bar{B},\bar{M},\bar{H})$, in the case of ${\mathcal{R}}_0>1.$

Proof. The basic reproduction number, ${\mathcal{R}}_0$, is computed through the next-generation matrix technique described in van den Driessche and Watmough [69]. To accomplish this, we can represent the right-hand side of system (Equation 2) as ${\mathcal{J}}_1-{\mathcal{J}}_2$ with

$\begin{array}{c}\begin{array}{c}{\mathcal{J}}_1=\left(\begin{array}{c}{\omega }_{1}NB+{\omega }_{2}NS+{\omega }_{3}NU\\ 0\\ 0\end{array}\right),\\ {\mathcal{J}}_2=\left(\begin{array}{c}({\beta }_1+{\phi }_U)U+{\varrho }_{1}UM\\ -{\beta }_{2}U+{\phi }_{S}S\\ -\mu U+{\phi }_{B}B+{\varrho }_{2}BH\end{array}\right).\end{array}\end{array}$

System (Equation 2) consistently exhibits an HIV-free equilibrium $\mathcal{F}\mathcal{E}=(N_0,0,0,0,0,0)$, where $N_0=\frac{\delta }{{\phi }_N}$.

Upon computing the Jacobian matrices, ${\mathcal{J}}_1$ and ${\mathcal{J}}_2$, at the equilibrium $\mathcal{F}\mathcal{E}$, we find

$\begin{array}{c}\begin{array}{cc}{J}_1=\left(\begin{array}{ccc}{\omega }_3{N}_0& {\omega }_2{N}_0& {\omega }_1{N}_0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),& J_2=\left(\begin{array}{ccc}{\beta }_1+{\phi }_U& 0& 0\\ -{\beta }_2& {\phi }_S& 0\\ -\mu & 0& {\phi }_B\end{array}\right).\end{array}\end{array}$

Note that, the next generation matrix is in the following form:

$\begin{array}{l}{J}_1{J}_2^{-1}=\left(\begin{array}{ccc}\frac{N_0(\mu {\phi }_S{\omega }_1+{\phi }_B({\beta }_2{\omega }_2+{\phi }_S{\omega }_3))}{{\phi }_S{\phi }_B({\beta }_1+{\phi }_U)}& \frac{N_0{\omega }_2}{{\phi }_S}& \frac{N_0{\omega }_1}{{\phi }_B}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right).\end{array}$

The basic reproduction number ${\mathcal{R}}_0$is determined by the spectral radius of the matrix product $J_1{J}_2^{-1}$, expressed as:

$\begin{array}{ll}{\mathcal{R}}_0=\frac{N_0(\mu {\phi }_S{\omega }_1+{\phi }_B({\beta }_2{\omega }_2+{\phi }_S{\omega }_3))}{{\phi }_S{\phi }_B({\beta }_1+{\phi }_U)}={\mathcal{R}}_{0B}+{\mathcal{R}}_{0S}+{\mathcal{R}}_{0U},& (5)\end{array}$

where

$\begin{array}{l}{\mathcal{R}}_{0B}=\frac{N_0\mu {\omega }_1}{{\phi }_B({\beta }_1+{\phi }_U)},{\mathcal{R}}_{0S}=\frac{N_0{\beta }_2{\omega }_2}{{\phi }_S({\beta }_1+{\phi }_U)},{\mathcal{R}}_{0U}=\frac{N_0{\omega }_3}{{\beta }_1+{\phi }_U}.\end{array}$

To clarify, the contributions of viral and cellular infections are represented, respectively, by ${\mathcal{R}}_{0B}$ and ${\mathcal{R}}_{0U}$, whereas ${\mathcal{R}}_{0S}$ denotes the influence of inflammatory cytokines.

To identify the additional equilibrium beyond $\mathcal{F}\mathcal{E}$, we assume (N, U, S, B, M, H) represents any equilibrium that fulfills the following equations:

$\begin{array}{ll}0=\delta -{\phi }_{N}N-{\omega }_{1}NB-{\omega }_{2}NS-{\omega }_{3}NU,& (6)\end{array}$

$\begin{array}{ll}0={\omega }_{1}NB+{\omega }_{2}NS+{\omega }_{3}NU-({\beta }_1+{\phi }_U)U-{\varrho }_{1}UM,& (7)\end{array}$

$\begin{array}{ll}0={\beta }_{2}U-{\phi }_{S}S,& (8)\end{array}$

$\begin{array}{ll}0=\mu U-{\phi }_{B}B-{\varrho }_{2}BH,& (9)\end{array}$

$\begin{array}{ll}0=\xi U-{\phi }_{M}M-{\lambda }_{1}UM,& (10)\end{array}$

$\begin{array}{ll}0=\psi B-{\phi }_{H}H-{\lambda }_{2}BH.& (11)\end{array}$

Referring to Equations 10, 11, we derive

$\begin{array}{ll}M=\frac{\xi U}{{\phi }_M+{\lambda }_{1}U},H=\frac{\psi B}{{\phi }_H+{\lambda }_{2}B}.& (12)\end{array}$

Replacing the values from Equation 12 in Equation 9, we obtain

$\begin{array}{ll}U=\frac{{\phi }_H{\phi }_{B}B+({\lambda }_2{\phi }_B+{\varrho }_2\psi )B^2}{\mu ({\phi }_H+{\lambda }_{2}B)}.& (13)\end{array}$

By substituting the expression from Equation 13 into Equation 12, we yield

$\begin{array}{ll}M=\frac{\xi \left({\phi }_H{\phi }_{B}B+({\lambda }_2{\phi }_B+{\varrho }_2\psi )B^2\right)}{{\phi }_M\mu ({\phi }_H+{\lambda }_{2}B)+{\lambda }_1\left({\phi }_H{\phi }_{B}B+({\lambda }_2{\phi }_B+{\varrho }_2\psi )B^2\right)}.& (14)\end{array}$

Replacing the values from Equation 13 in Equation 8 gives

$\begin{array}{ll}S=\frac{{\beta }_2\left({\phi }_H{\phi }_{B}B+({\lambda }_2{\phi }_B+{\varrho }_2\psi )B^2\right)}{\mu {\phi }_S({\phi }_H+{\lambda }_{2}B)}.& (15)\end{array}$

From Equations 6, 7, we get

$\begin{array}{ll}\delta -{\phi }_{N}N=({\beta }_1+{\phi }_U)U+{\varrho }_{1}UM.& (16)\end{array}$

Substituting from Equations 13, 14 into Equation 16, we get

$\begin{array}{l}N=\frac{1}{{\phi }_N}(\delta -\frac{({\beta }_1+{\phi }_U)(\psi {\varrho }_{2}B+{\phi }_B({\phi }_H+{\lambda }_{2}B))B}{\mu ({\phi }_H+{\lambda }_{2}B)}\\ +\frac{\xi {\varrho }_1{(\psi {\varrho }_{2}B+{\phi }_B({\phi }_H+{\lambda }_{2}B))}^2{B}^2}{\mu ({\phi }_H+{\lambda }_{2}B)(\mu {\phi }_M({\phi }_H+{\lambda }_{2}B)+{\lambda }_1(\psi {\varrho }_{2}B+{\phi }_B({\phi }_H+{\lambda }_{2}B))B)}).& (17)\end{array}$

Substituting from Equations 13–15, 17 into Equation 7, we get

$\begin{array}{c}\frac{B\left(A_5{B}^5+A_4{B}^4+A_3{B}^3+A_2{B}^2+A_{1}B+A_0\right)}{{\phi }_N{\phi }_S{\mu }^2(\mu {\phi }_M{\phi }_H+({\lambda }_2\mu {\phi }_M+{\lambda }_1{\phi }_B{\phi }_H)B+{\lambda }_1({\lambda }_2{\phi }_B+\psi {\varrho }_2)B^2){({\phi }_H+{\lambda }_{2}B)}^2}\\ =0,& (18)\end{array}$

where

$\begin{array}{l}{A}_5=({\lambda }_1({\beta }_1+{\phi }_U)-\xi {\varrho }_1){({\lambda }_2{\phi }_B+\psi {\varrho }_2)}^2({\lambda }_2({\beta }_2{\phi }_B{\omega }_2\\ +{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3)+\psi {\varrho }_2({\beta }_2{\omega }_2+{\phi }_S{\omega }_3)),\end{array}$

$\begin{array}{l}{A}_4=({\lambda }_2{\phi }_B+\psi {\varrho }_2)(-{\phi }_H\psi {\varrho }_2(\xi {\varrho }_1-{\lambda }_1{\phi }_U)(3{\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+\\ 3{\phi }_B{\omega }_3))\\ +\mu {\lambda }_2^2(\xi {\phi }_N{\phi }_S{\phi }_B{\varrho }_1+{\phi }_U{\phi }_M({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))\\ +{\lambda }_1({\phi }_N{\phi }_U{\phi }_S{\phi }_B\\ -\delta ({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))))+{\lambda }_2(\mu {\phi }_U{\phi }_M\psi {\varrho }_2({\beta }_2{\omega }_2\\ +{\phi }_S{\omega }_3)+\xi {\varrho }_1(\mu {\phi }_N{\phi }_S\psi {\varrho }_2\\ -3{\phi }_B{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3)))+{\lambda }_1(\mu \psi {\varrho }_2({\phi }_S\\ ({\phi }_N{\phi }_U-\delta {\omega }_3)-{\beta }_2\delta {\omega }_2)\\ +3{\phi }_U{\phi }_B{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))))+{\beta }_1({\lambda }_2\mu {\phi }_M\\ (\psi {\varrho }_2({\beta }_2{\omega }_2+{\phi }_S{\omega }_3)\\ +{\lambda }_2({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3)))+{\lambda }_1({\phi }_H\psi {\varrho }_2(3{\beta }_2{\phi }_B{\omega }_2\\ +{\phi }_S(\mu {\omega }_1+3{\phi }_B{\omega }_3))\\ +{\lambda }_2^2\mu {\phi }_N{\phi }_S{\phi }_B+{\lambda }_2(3{\phi }_B{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))\\ +\mu {\phi }_N{\phi }_S\psi {\varrho }_2)))),\end{array}$

$\begin{array}{l}{A}_3=-{\lambda }_2^3{\mu }^2{\phi }_M({\beta }_2\delta {\phi }_B{\omega }_2+\delta {\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3)-{\phi }_N{\phi }_U{\phi }_S{\phi }_B)\\ +{\lambda }_2{\phi }_H(2\mu {\phi }_U{\phi }_M\psi {\varrho }_2(2{\beta }_2{\phi }_B{\omega }_2\\ +{\phi }_S(\mu {\omega }_1+2{\phi }_B{\omega }_3))-\xi {\phi }_B{\varrho }_1(3{\phi }_B{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1\\ +{\phi }_B{\omega }_3))-4\mu {\phi }_N{\phi }_S\psi {\varrho }_2)\\ +{\lambda }_1(3{\phi }_U{\phi }_B^2{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))-2\mu \psi {\varrho }_2\\ (2{\beta }_2\delta {\phi }_B{\omega }_2+\delta {\phi }_S(\mu {\omega }_1+2{\phi }_B{\omega }_3)\\ -2{\phi }_N{\phi }_U{\phi }_S{\phi }_B)))+{\phi }_H\psi {\varrho }_2(\mu {\phi }_U{\phi }_M\psi {\varrho }_2({\beta }_2{\omega }_2+{\phi }_S{\omega }_3)\\ +\xi {\varrho }_1(\mu {\phi }_N{\phi }_S\psi {\varrho }_2\\ -{\phi }_B{\phi }_H(3{\beta }_2{\phi }_B{\omega }_2+{\phi }_S(2\mu {\omega }_1+3{\phi }_B{\omega }_3)))+\\ {\lambda }_1(\mu \psi {\varrho }_2({\phi }_S({\phi }_N{\phi }_U-\delta {\omega }_3)-{\beta }_2\delta {\omega }_2)\\ +{\phi }_U{\phi }_B{\phi }_H(3{\beta }_2{\phi }_B{\omega }_2+{\phi }_S(2\mu {\omega }_1+3{\phi }_B{\omega }_3))))\\ +\mu {\lambda }_2^2(\mu {\phi }_M\psi {\varrho }_2({\phi }_N{\phi }_U{\phi }_S-\delta ({\beta }_2{\omega }_2+{\phi }_S{\omega }_3))\\ +3{\phi }_B{\phi }_H({\phi }_U{\phi }_M({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))\\ +\xi {\phi }_N{\phi }_S{\phi }_B{\varrho }_1+{\lambda }_1({\phi }_N{\phi }_U{\phi }_S{\phi }_B\\ -\delta ({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3)))))+{\beta }_1({\lambda }_2^3{\mu }^2{\phi }_N{\phi }_S{\phi }_B{\phi }_M+\\ \mu {\lambda }_2^2(\mu {\phi }_N{\phi }_S{\phi }_M\psi {\varrho }_2\\ +3{\phi }_B{\phi }_H({\phi }_M({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))+{\lambda }_1{\phi }_N{\phi }_S{\phi }_B))\\ +{\lambda }_2{\phi }_H(2\mu {\phi }_M\psi {\varrho }_2(2{\beta }_2{\phi }_B{\omega }_2\\ +{\phi }_S(\mu {\omega }_1+2{\phi }_B{\omega }_3))+{\lambda }_1{\phi }_B(3{\phi }_B{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1\\ +{\phi }_B{\omega }_3))+4\mu {\phi }_N{\phi }_S\psi {\varrho }_2))\\ +\psi {\varrho }_2{\phi }_H(\mu {\phi }_M\psi {\varrho }_2({\beta }_2{\omega }_2+{\phi }_S{\omega }_3)+{\lambda }_1({\phi }_B{\phi }_H(3{\beta }_2{\phi }_B{\omega }_2\\ +{\phi }_S(2\mu {\omega }_1+3{\phi }_B{\omega }_3))+\mu {\phi }_N{\phi }_S\psi {\varrho }_2))),\end{array}$

$\begin{array}{l}{A}_2={\phi }_H({\lambda }_2\mu (2\mu {\phi }_M\psi {\varrho }_2({\phi }_N{\phi }_U{\phi }_S-\delta ({\beta }_2{\omega }_2+{\phi }_S{\omega }_3))\\ +3{\phi }_B{\phi }_H(\xi {\phi }_N{\phi }_S{\phi }_B{\varrho }_1\\ +{\phi }_U{\phi }_M({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))+{\lambda }_1({\phi }_N{\phi }_U{\phi }_S{\phi }_B\\ -\delta ({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3)))))\\ +{\phi }_H(\mu {\phi }_U{\phi }_M\psi {\varrho }_2(2{\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+2{\phi }_B{\omega }_3))-\\ \xi {\phi }_B{\varrho }_1({\phi }_B{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))\\ -2\mu {\phi }_N{\phi }_S\psi {\varrho }_2)+{\lambda }_1({\phi }_U{\phi }_B^2{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))\\ -\mu \psi {\varrho }_2(2{\beta }_2\delta {\phi }_B{\omega }_2+\delta {\phi }_S(\mu {\omega }_1+2{\phi }_B{\omega }_3)-2{\phi }_N{\phi }_U{\phi }_S{\phi }_B)))\\ +{\beta }_1({\lambda }_2\mu (3{\phi }_B{\phi }_H({\phi }_M({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))\\ +{\lambda }_1{\phi }_N{\phi }_S{\phi }_B)+2\mu {\phi }_N{\phi }_S{\phi }_M\psi {\varrho }_2)\\ +{\phi }_H({\lambda }_1{\phi }_B({\phi }_B{\phi }_H({\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3))\\ +2\mu {\phi }_N{\phi }_S\psi {\varrho }_2)\\ +\mu {\phi }_M\psi {\varrho }_2(2{\beta }_2{\phi }_B{\omega }_2+{\phi }_S(\mu {\omega }_1+2{\phi }_B{\omega }_3)))\\ +3{\lambda }_2^2{\mu }^2{\phi }_N{\phi }_S{\phi }_B{\phi }_M)\\ -3{\lambda }_2^2{\mu }^2{\phi }_M({\beta }_2\delta {\phi }_B{\omega }_2+\delta {\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3)-{\phi }_N{\phi }_U{\phi }_S{\phi }_B)),\end{array}$

$\begin{array}{l}{A}_1=\mu {\phi }_H^2(\xi {\phi }_N{\phi }_S{\phi }_H{\phi }_B^2{\varrho }_1+\mu {\phi }_S{\phi }_M{\phi }_H{\phi }_B{\omega }_1({\beta }_1+{\phi }_U)\\ +\mu {\phi }_N{\phi }_S{\phi }_M\psi {\varrho }_2({\beta }_1+{\phi }_U)\\ -(3{\lambda }_2\mu {\phi }_M+{\lambda }_1{\phi }_B{\phi }_H)({\beta }_2\delta {\phi }_B{\omega }_2-{\beta }_1{\phi }_N{\phi }_S{\phi }_B\\ +\delta {\phi }_S(\mu {\omega }_1+{\phi }_B{\omega }_3)-{\phi }_N{\phi }_U{\phi }_S{\phi }_B)\\ -{\beta }_2{\phi }_M{\omega }_2(\delta \mu \psi {\varrho }_2-{\phi }_B^2{\phi }_H({\beta }_1+{\phi }_U))-{\phi }_S{\phi }_M{\omega }_3(\delta \mu \psi {\varrho }_2\\ -{\phi }_B^2{\phi }_H({\beta }_1+{\phi }_U))),\end{array}$

$\begin{array}{l}{A}_0={\phi }_N{\phi }_S{\phi }_B{\phi }_M{\mu }^2{\phi }_H^3({\beta }_1+{\phi }_U)(1-{\mathcal{R}}_0),\end{array}$

where ${\mathcal{R}}_0$ is outlined in Equation 5. According to Equation 18, it follows that

1. If B = 0, then based on Equations 12–15, 17 we deduce the HIV-free equilibrium, $\mathcal{F}\mathcal{E}=(N_0,0,0,0,0,0)$, with N₀ = δ/φ_N.

2. If B ≠ 0, the equation $A_5{B}^5+A_4{B}^4+A_3{B}^3+A_2{B}^2+A_{1}B+A_0=0$ holds. In this context, we introduce a function Ω(B) on [0, ∞) as:

$\begin{array}{l}\Omega (B)=A_5{B}^5+A_4{B}^4+A_3{B}^3+A_2{B}^2+A_{1}B+A_0.\end{array}$

We have $\Omega (0)={\phi }_N{\phi }_S{\phi }_B{\phi }_M{\mu }^2{\phi }_H^3({\beta }_1+{\phi }_U)(1-{\mathcal{R}}_0)<0$ when ${\mathcal{R}}_0>1$, and $\underset{B\to \infty }{lim}\Omega (B)=\infty$, which indicates that Ω possesses a positive real root, $\bar{B}$. By substituting the expressions from Equations 13, 15 into Equation 6, we get

$\begin{array}{l}\bar{N}=\frac{\delta }{{\phi }_N+{\omega }_1\bar{B}+{\omega }_2\bar{S}+{\omega }_3\bar{U}},\end{array}$

where

$\begin{array}{l}\bar{U}=\frac{{\phi }_H{\phi }_B\bar{B}+\left({\lambda }_2{\phi }_B+{\varrho }_2\psi \right){\bar{B}}^2}{\mu \left({\phi }_H+{\lambda }_2\bar{B}\right)},\\ \bar{S}=\frac{{\beta }_2\left({\phi }_H{\phi }_B\bar{B}+\left({\lambda }_2{\phi }_B+{\varrho }_2\psi \right){\bar{B}}^2\right)}{\mu {\phi }_S\left({\phi }_H+{\lambda }_2\bar{B}\right)},\\ \bar{M}=\frac{\xi \left({\phi }_H{\phi }_B\bar{B}+\left({\lambda }_2{\phi }_B+{\varrho }_2\psi \right){\bar{B}}^2\right)}{{\phi }_M\mu \left({\phi }_H+{\lambda }_2\bar{B}\right)+{\lambda }_1\left({\phi }_H{\phi }_B\bar{B}+\left({\lambda }_2{\phi }_B+{\varrho }_2\psi \right){\bar{B}}^2\right)},\\ \bar{H}=\frac{\psi \bar{B}}{{\phi }_H+{\lambda }_2\bar{B}}.\end{array}$

It is evident that the existence of the HIV-persistent equilibrium, $\mathcal{PE}=(\bar{N},\bar{U},\bar{S},\bar{B},\bar{M},\bar{H})$, is confirmed when ${\mathcal{R}}_0>1$.

5 Global stability investigation

This section focuses on exploring the global asymptotic stability of all equilibria through the technique of the Lyapunov method. Take the function ϒ_j(N, U, S, B, M, H) into consideration, and let ${\widehat{{\rm Y}}}_j(t)$ be defined as follows:

$\begin{array}{l}{\widehat{{\rm Y}}}_j(t)={\displaystyle {\int }_{\Lambda }}{{\rm Y}}_j(\varkappa ,t)\text{d}\varkappa ,j=0,1.\end{array}$

Assume that ${\Theta }_j^{\prime }$ is the largest invariant subset of Θ_j, where

$\begin{array}{l}{\Theta }_j=\left\{(N,U,S,B,M,H):\frac{d{\widehat{{\rm Y}}}_j}{dt}=0\right\}\text{, }j=0,1.\end{array}$

The inequality relating the arithmetic and geometric means will be employed in the analysis as follows:

$\begin{array}{ll}\frac{{\mathcal{G}}_1+{\mathcal{G}}_2+...+{\mathcal{G}}_n}{n}\ge \sqrt[n]{({\mathcal{G}}_1)({\mathcal{G}}_2)...({\mathcal{G}}_n)}\text{.}& (19)\end{array}$

We introduce a function $\text{Ψ}(\mathcal{\upsilon })$ as follows:

$\begin{array}{l}\text{Ψ}(\mathcal{\upsilon })=\mathcal{\upsilon }-1-ln\mathcal{\upsilon }.\end{array}$

According to the Numann boundary conditions (Equation 4), along with the Divergence Theorem, they lead to the conclusion that

$\begin{array}{l}0={\displaystyle {\int }_{\partial \Lambda }}\nabla \mathcal{G}·\overrightarrow{\sout{Z}}\text{ d}\varkappa ={\displaystyle {\int }_{\Lambda }}\text{div}(\nabla \mathcal{G})\text{ d}\varkappa ={\displaystyle {\int }_{\Lambda }}\Delta \mathcal{G}\text{ d}\varkappa ,\\ 0={\displaystyle {\int }_{\partial \Lambda }}\frac{1}{\mathcal{G}}\nabla \mathcal{G}·\overrightarrow{\sout{Z}}\text{ d}\varkappa ={\displaystyle {\int }_{\Lambda }}\text{div}(\frac{1}{\mathcal{G}}\nabla \mathcal{G})\text{ d}\varkappa =\\ {\displaystyle {\int }_{\Lambda }}\left(\frac{\Delta \mathcal{G}}{\mathcal{G}}-\frac{\parallel \nabla \mathcal{G}{\parallel }^2}{{\mathcal{G}}^2}\right)\text{ d}\varkappa ,\\ {\displaystyle {\int }_{\Lambda }}\mathcal{G}\Delta \mathcal{G}\text{ d}\varkappa =-{\displaystyle {\int }_{\Lambda }}\parallel \nabla \mathcal{G}{\parallel }^2\text{ d}\varkappa +{\displaystyle {\int }_{\partial \Lambda }}\mathcal{G}\frac{\partial \mathcal{G}}{\partial \overrightarrow{\sout{Z}}}\text{ d}\varkappa ,\end{array}$

for $\mathcal{G}\in \left\{N,U,S,B,M,H\right\}.$ As a consequence, we arrive at

$\begin{array}{l}{\displaystyle {\int }_{\Lambda }}\Delta \mathcal{G}\text{ d}\varkappa =0,\\ {\displaystyle {\int }_{\Lambda }}\frac{\Delta \mathcal{G}}{\mathcal{G}}\text{ d}\varkappa ={\displaystyle {\int }_{\Lambda }}\frac{\parallel \nabla \mathcal{G}{\parallel }^2}{{\mathcal{G}}^2}\text{ d}\varkappa ,\\ {\displaystyle {\int }_{\Lambda }}\mathcal{G}\Delta \mathcal{G}\text{ d}\varkappa =-{\displaystyle {\int }_{\Lambda }}\parallel \nabla \mathcal{G}{\parallel }^2\text{ d}\varkappa .& (20)\end{array}$

The input notation is omitted for the purpose of simplicity, i.e., (N, U, S, B, M, H) = (N(ϰ, t), U(ϰ, t), S(ϰ, t), B(ϰ, t), M(ϰ, t), H(ϰ, t)).

Theorem 1. The HIV-free equilibrium $\mathcal{F}\mathcal{E}$ exhibits global asymptotic stability when ${\mathcal{R}}_0\le 1$.

Proof. Introduce a Lyapunov function ϒ₀(ϰ, t) as follows:

$\begin{array}{l}{{\rm Y}}_0(\varkappa ,t)=N_0\text{Ψ}\left(\frac{N}{N_0}\right)+U+\frac{{\omega }_2{N}_0}{{\phi }_S}S+\frac{{\omega }_1{N}_0}{{\phi }_B}B+\frac{{\varrho }_1}{2\xi }{M}^2+\frac{{\varrho }_2{\omega }_1{N}_0}{2\psi {\phi }_B}{H}^2.\end{array}$

It is evident that ${\widehat{{\rm Y}}}_0(N,U,S,B,M,H)>0$ for all positive values of N, U, S, B, M, H, and ${\widehat{{\rm Y}}}_0(N_0,0,0,0,0,0)=0$. The derivative $\frac{\partial {{\rm Y}}_0}{\partial t}$ is computed along the solutions of model (Equation 2) as:

$\begin{array}{l}\frac{\partial {{\rm Y}}_0}{\partial t}=\left(1-\frac{N_0}{N}\right)(D_N\Delta N+\delta -{\phi }_{N}N-{\omega }_{1}NB-{\omega }_{2}NS-{\omega }_{3}NU)\\ +D_U\Delta U+{\omega }_{1}NB+{\omega }_{2}NS+{\omega }_{3}NU-({\beta }_1+{\phi }_U)U-{\varrho }_{1}UM\\ +\frac{{\omega }_2{N}_0}{{\phi }_S}(D_S\Delta S+{\beta }_{2}U-{\phi }_{S}S)+\frac{{\omega }_1{N}_0}{{\phi }_B}(D_B\Delta B+\mu U\\ -{\phi }_{B}B-{\varrho }_{2}BH)+\frac{{\varrho }_{1}M}{\xi }\\ (D_M\Delta M+\xi U-{\phi }_{M}M-{\lambda }_{1}UM)\\ +\frac{{\varrho }_2{\omega }_1{N}_{0}H}{\psi {\phi }_B}(D_H\Delta H+\psi B-{\phi }_{H}H-{\lambda }_{2}BH)\\ =(\delta -{\phi }_{N}N)\left(1-\frac{N_0}{N}\right)+{\omega }_3{N}_{0}U-({\beta }_1+{\phi }_U)U\\ +\frac{{\omega }_2{\beta }_2{N}_0}{{\phi }_S}U\\ +\frac{{\omega }_1\mu N_0}{{\phi }_B}U-\frac{{\varrho }_1{\phi }_M}{\xi }{M}^2-\frac{{\varrho }_1{\lambda }_1}{\xi }U{M}^2-\frac{{\varrho }_2{\omega }_1{\phi }_H{N}_0}{\psi {\phi }_B}{H}^2\\ -\frac{{\varrho }_2{\omega }_1{\lambda }_2{N}_0}{\psi {\phi }_B}B{H}^2+D_N\left(1-\frac{N_0}{N}\right)\Delta N+D_U\Delta U\\ +\frac{{\omega }_2{N}_0{D}_S}{{\phi }_S}\Delta S\\ +\frac{{\omega }_1{N}_0{D}_B}{{\phi }_B}\Delta B+\frac{{\varrho }_{1}M{D}_M}{\xi }\Delta M+\frac{{\varrho }_2{\omega }_1{N}_{0}H{D}_H}{\psi {\phi }_B}\Delta H.\end{array}$

By setting N₀ = δ/φ_N, we deduce that

$\begin{array}{l}\frac{\partial {{\rm Y}}_0}{\partial t}=-\frac{{\phi }_N{(N-N_0)}^2}{N}+({\beta }_1+{\phi }_U)({\mathcal{R}}_0-1)U-\\ \frac{{\varrho }_1}{\xi }({\phi }_M+{\lambda }_{1}U)M^2\\ -\frac{{\varrho }_2{\omega }_1{N}_0}{\psi {\phi }_B}({\phi }_H+{\lambda }_{2}B)H^2+D_N\left(1-\frac{N_0}{N}\right)\Delta N\\ +D_U\Delta U\\ +\frac{{\omega }_2{N}_0{D}_S}{{\phi }_S}\Delta S+\frac{{\omega }_1{N}_0{D}_B}{{\phi }_B}\Delta B+\frac{{\varrho }_1{D}_M}{\xi }M\Delta M+\\ \frac{{\varrho }_2{\omega }_1{N}_0{D}_H}{\psi {\phi }_B}H\Delta H.\end{array}$

As a result, we evaluate $\frac{d{\widehat{{\rm Y}}}_0}{dt}$ as follows:

$\begin{array}{l}\frac{d{\widehat{{\rm Y}}}_0}{dt}=-{\phi }_N{\displaystyle {\int }_{\Lambda }}\frac{{(N-N_0)}^2}{N}\text{ d}\varkappa +({\beta }_1+{\phi }_U)({\mathcal{R}}_0-1)\\ {\displaystyle {\int }_{\Lambda }}U\text{ d}\varkappa -\frac{{\varrho }_1{\phi }_M}{\xi }{\displaystyle {\int }_{\Lambda }}{M}^2\text{ d}\varkappa \\ -\frac{{\varrho }_1{\lambda }_1}{\xi }{\displaystyle {\int }_{\Lambda }}U{M}^2\text{ d}\varkappa -\frac{{\varrho }_2{\omega }_1{\phi }_H{N}_0}{\psi {\phi }_B}{\displaystyle {\int }_{\Lambda }}{H}^2\text{ d}\varkappa -\frac{{\varrho }_2{\omega }_1{\lambda }_2{N}_0}{\psi {\phi }_B}\\ {\displaystyle {\int }_{\Lambda }}B{H}^2\text{ d}\varkappa \\ +D_N{\displaystyle {\int }_{\Lambda }}\left(1-\frac{N_0}{N}\right)\Delta N\text{ d}\varkappa +D_U{\displaystyle {\int }_{\Lambda }}\Delta U\text{ d}\varkappa +\frac{{\omega }_2{N}_0{D}_S}{{\phi }_S}\\ {\displaystyle {\int }_{\Lambda }}\Delta S\text{ d}\varkappa \\ +\frac{{\omega }_1{N}_0{D}_B}{{\phi }_B}{\displaystyle {\int }_{\Lambda }}\Delta B\text{ d}\varkappa +\frac{{\varrho }_1{D}_M}{\xi }{\displaystyle {\int }_{\Lambda }}M\Delta M\text{ d}\varkappa +\frac{{\varrho }_2{\omega }_1{N}_0{D}_H}{}\\ {\displaystyle {\int }_{\Lambda }}H\Delta H\text{ d}\varkappa .& (21)\end{array}$

Through the use of equality (Equation 20), Equation 21 takes the following form:

$\begin{array}{l}\frac{d{\widehat{{\rm Y}}}_0}{dt}=-{\phi }_N{\displaystyle {\int }_{\Lambda }}\frac{{(N-N_0)}^2}{N}\text{ d}\varkappa +({\beta }_1+{\phi }_U)({\mathcal{R}}_0-1){\displaystyle {\int }_{\Lambda }}U\text{ d}\varkappa \\ -\frac{{\varrho }_1{\phi }_M}{\xi }{\displaystyle {\int }_{\Lambda }}{M}^2\text{ d}\varkappa \\ -\frac{{\varrho }_1{\lambda }_1}{\xi }{\displaystyle {\int }_{\Lambda }}U{M}^2\text{ d}\varkappa -\frac{{\varrho }_2{\omega }_1{\phi }_H{N}_0}{\psi {\phi }_B}{\displaystyle {\int }_{\Lambda }}{H}^2\text{ d}\varkappa -\frac{{\varrho }_2{\omega }_1{\lambda }_2{N}_0}{\psi {\phi }_B}\\ {\displaystyle {\int }_{\Lambda }}B{H}^2\text{ d}\varkappa \\ -D_N{N}_0{\displaystyle {\int }_{\Lambda }}\frac{\parallel \nabla N{\parallel }^2}{N^2}\text{ d}\varkappa -\frac{{\varrho }_1{D}_M}{\xi }{\displaystyle {\int }_{\Lambda }}\parallel \nabla M{\parallel }^2\text{ d}\varkappa \\ -\frac{{\varrho }_2{\omega }_1{N}_0{D}_H}{\psi {\phi }_B}{\displaystyle {\int }_{\Lambda }}\parallel \nabla H{\parallel }^2\text{ d}\varkappa .\end{array}$

Therefore, $\frac{d{\widehat{{\rm Y}}}_0}{dt}\le 0$ for all N, U, M, H, B > 0 under the condition that ${\mathcal{R}}_0\le 1$. Equality $\frac{d{\widehat{{\rm Y}}}_0}{dt}=0$ is achieved in the case when (N, U, B, M, H) = (N₀, 0, 0, 0, 0). The solutions of system (Equation 2) converge to ${\Theta }_0^{\prime }$. The elements of ${\Theta }_0^{\prime }$ satisfy (N, U, B, M, H) = (N₀, 0, 0, 0, 0). At this point, $\frac{\partial S}{\partial t}=\frac{\partial Y}{\partial t}=\Delta S=\Delta Y=0$. The first equation of system (Equation 2) simplifies to

$\begin{array}{l}0=\frac{\partial N}{\partial t}=\delta -{\phi }_N{N}_0-{\omega }_2{N}_{0}S.\end{array}$

From this S = 0, leading to ${\Theta }_0^{\prime }=\{\mathcal{F}\mathcal{E}\}$. By applying the Lyapunov-LaSalle asymptotic stability theorem [70], it is concluded that the equilibrium $\mathcal{F}\mathcal{E}$ is globally asymptotically stable.

Theorem 2. The HIV-persistent equilibrium $\mathcal{PE}$ achieves global asymptotic stability when ${\mathcal{R}}_0>1$.

Proof. Define a function ϒ₁(ϰ, t) as:

$\begin{array}{l}{{\rm Y}}_1\left(\varkappa ,t\right)=\bar{N}\text{Ψ}\left(\frac{N}{\bar{N}}\right)+\bar{U}\text{Ψ}\left(\frac{U}{\bar{U}}\right)+\frac{{\omega }_2\bar{N}}{{\phi }_S}\bar{S}\text{Ψ}\left(\frac{S}{\bar{S}}\right)+\frac{{\omega }_1\bar{N}}{{\phi }_B+{\varrho }_2\bar{H}}\\ \bar{B}\text{Ψ}\left(\frac{B}{\bar{B}}\right)\\ +\frac{{\varrho }_1}{2\left(\xi -{\lambda }_1\bar{M}\right)}{\left(M-\bar{M}\right)}^2+\frac{{\varrho }_2{\omega }_1\bar{N}}{2\left(\psi -{\lambda }_2\bar{H}\right)\left({\phi }_B+{\varrho }_2\bar{H}\right)}\\ {\left(H-\bar{H}\right)}^2.\end{array}$

Equations 10, 11 indicate that $\xi -{\lambda }_1\bar{M}=\frac{{\phi }_M\bar{M}}{\bar{U}}>0$ and $\psi -{\lambda }_2\bar{H}=\frac{{\phi }_H\bar{H}}{\bar{B}}>0.$ The computation of $\frac{\partial {{\rm Y}}_1}{\partial t}$ yields

$\begin{array}{l}\frac{\partial {{\rm Y}}_1}{\partial t}=\left(1-\frac{\overline{N}}{N}\right)(D_N\Delta N+\delta -{\phi }_{N}N-{\omega }_{1}NB-{\omega }_{2}NS-{\omega }_{3}NU)\\ +\left(1-\frac{\overline{U}}{U}\right)(D_U\Delta U+{\omega }_{1}NB+{\omega }_{2}NS+{\omega }_{3}NU-({\beta }_1+{\phi }_U)\\ U-{\varrho }_{1}UM)\\ +\frac{{\omega }_2\overline{N}}{{\phi }_S}\left(1-\frac{\overline{S}}{S}\right)(D_S\Delta S+{\beta }_{2}U-{\phi }_{S}S)\\ +\frac{{\omega }_1\overline{N}}{{\phi }_B+{\varrho }_2\overline{H}}\left(1-\frac{\overline{B}}{B}\right)(D_B\Delta B+\mu U-{\phi }_{B}B-{\varrho }_{2}BH)\\ +\frac{{\varrho }_1}{\xi -{\lambda }_1\overline{M}}(M-\overline{M})(D_M\Delta M+\xi U-{\phi }_{M}M-{\lambda }_{1}UM)\\ +\frac{{\varrho }_2{\omega }_1\overline{N}}{(\psi -{\lambda }_2\overline{H})({\phi }_B+{\varrho }_2\overline{H})}(H-\overline{H})(D_H\Delta H+\psi B-{\phi }_{H}H\\ -{\lambda }_{2}BH)\\ =(\delta -{\phi }_{N}N)\left(1-\frac{\overline{N}}{N}\right)+{\omega }_1\overline{N}B+{\omega }_3\overline{N}U-({\beta }_1+{\phi }_U)\\ (U-\overline{U})\\ -{\varrho }_{1}M(U-\overline{U})-{\omega }_1\frac{NB\overline{U}}{U}-{\omega }_2\frac{NS\overline{U}}{U}-{\omega }_{3}N\overline{U}+\frac{{\omega }_2{\beta }_2\overline{N}}{{\phi }_S}U\\ -\frac{{\omega }_2{\beta }_2\overline{N}}{{\phi }_S}\frac{U\overline{S}}{S}+{\omega }_2\overline{N}\overline{S}+\frac{{\omega }_1\mu \overline{N}}{{\phi }_B+{\varrho }_2\overline{H}}U-\frac{{\omega }_1{\phi }_B\overline{N}}{{\phi }_B+{\varrho }_2\overline{H}}(B-\overline{B})\\ -\frac{{\varrho }_2{\omega }_1\overline{N}}{{\phi }_B+{\varrho }_2\overline{H}}H(B-\overline{B})-\frac{{\omega }_1\mu \overline{N}}{{\phi }_B+{\varrho }_2\overline{H}}\frac{\overline{B}U}{B}\\ +\frac{{\varrho }_1}{\xi -{\lambda }_1\overline{M}}(M-\overline{M})(\xi U-{\phi }_{M}M-{\lambda }_{1}UM)\\ +\frac{{\varrho }_2{\omega }_1\overline{N}}{(\psi -{\lambda }_2\overline{H})({\phi }_B+{\varrho }_2\overline{H})}(H-\overline{H})(\psi B-{\phi }_{H}H-{\lambda }_{2}BH)\\ +D_N\Delta N\left(1-\frac{\overline{N}}{N}\right)+D_U\left(1-\frac{\overline{U}}{U}\right)\Delta U+\frac{{\omega }_2\overline{N}{D}_S}{{\phi }_S}\\ \left(1-\frac{\overline{S}}{S}\right)\Delta S\\ +\frac{{\omega }_1\overline{N}{D}_B}{{\phi }_B+{\varrho }_2\overline{H}}\left(1-\frac{\overline{B}}{B}\right)\Delta B+\frac{{\varrho }_1{D}_M}{\xi -{\lambda }_1\overline{M}}(M-\overline{M})\Delta M\\ +\frac{{\varrho }_2{\omega }_1\overline{N}{D}_H}{(\psi -{\lambda }_2\overline{H})({\phi }_B+{\varrho }_2\overline{H})}(H-\overline{H})\Delta H.\end{array}$

The equilibrium conditions associated with $\mathcal{PE}$ indicate that

$\begin{array}{l}\delta ={\phi }_N\bar{N}+{\omega }_1\bar{N}\bar{B}+{\omega }_2\bar{N}\bar{S}+{\omega }_3\bar{N}\bar{U},\\ {\omega }_1\bar{N}\bar{B}+{\omega }_2\bar{N}\bar{S}+{\omega }_3\bar{N}\bar{U}=({\beta }_1+{\phi }_U+{\varrho }_1\bar{M})\bar{U},\\ \bar{S}=\frac{{\beta }_2\bar{U}}{{\phi }_S},\bar{B}=\frac{\mu \bar{U}}{{\phi }_B+{\varrho }_2\bar{H}},\\ \xi \bar{U}={\phi }_M\bar{M}+{\lambda }_1\bar{U}\bar{M},\psi \bar{B}={\phi }_H\bar{H}+{\lambda }_2\bar{B}\bar{H}.\end{array}$

From this, we find

$\begin{array}{l}\frac{\partial {{\rm Y}}_1}{\partial t}=({\phi }_N\overline{N}-{\phi }_{N}N)\left(1-\frac{\overline{N}}{N}\right)+({\omega }_1\overline{N}\overline{B}+{\omega }_2\overline{N}\overline{S}\\ +{\omega }_3\overline{N}\overline{U})\left(1-\frac{\overline{N}}{N}\right)\\ +{\omega }_1\overline{N}B+{\omega }_3\overline{N}U-({\beta }_1+{\phi }_U)(U-\overline{U})\\ -{\varrho }_{1}M(U-\overline{U})-{\omega }_1\overline{N}\overline{B}\frac{NB\overline{U}}{\overline{N}\overline{B}U}\\ -{\omega }_2\overline{N}\overline{S}\frac{NS\overline{U}}{\overline{N}\overline{S}U}-{\omega }_3\overline{N}\overline{U}\frac{N}{\overline{N}}+\frac{{\omega }_2{\beta }_2\overline{N}}{{\phi }_S}U-{\omega }_2\overline{N}\overline{S}\frac{U\overline{S}}{\overline{U}S}\\ +{\omega }_2\overline{N}\overline{S}\\ +\frac{{\omega }_1\mu \overline{N}}{{\phi }_B+{\varrho }_2\overline{H}}U-\frac{{\omega }_1{\phi }_B\overline{N}}{{\phi }_B+{\varrho }_2\overline{H}}(B-\overline{B})-\frac{{\varrho }_2{\omega }_1\overline{N}}{{\phi }_B+{\varrho }_2\overline{H}}\\ H(B-\overline{B})-{\omega }_1\overline{N}\overline{B}\frac{\overline{B}U}{B\overline{U}}\\ +\frac{{\varrho }_1(M-\overline{M})}{\xi -{\lambda }_1\overline{M}}(\xi U-{\phi }_{M}M-{\lambda }_{1}UM-\xi \overline{U}+{\phi }_M\overline{M}\\ +{\lambda }_1\overline{U}\overline{M}-{\lambda }_{1}U\overline{M}+{\lambda }_{1}U\overline{M})\\ +\frac{{\varrho }_2{\omega }_1\overline{N}(H-\overline{H})}{(\psi -{\lambda }_2\overline{H})({\phi }_B+{\varrho }_2\overline{H})}(\psi B-{\phi }_{H}H-{\lambda }_{2}BH-\psi \overline{B}\\ +{\phi }_H\overline{H}+{\lambda }_2\overline{B}\overline{H}-{\lambda }_{2}B\overline{H}+{\lambda }_{2}B\overline{H})\\ +D_N\Delta N\left(1-\frac{\overline{N}}{N}\right)+D_U\left(1-\frac{\overline{U}}{U}\right)\Delta U+\frac{{\omega }_2\overline{N}{D}_S}{{\phi }_S}\\ \left(1-\frac{\overline{S}}{S}\right)\Delta S+\frac{{\omega }_1\overline{N}{D}_B}{{\phi }_B+{\varrho }_2\overline{H}}\\ \times \left(1-\frac{\overline{B}}{B}\right)\Delta B+\frac{{\varrho }_1{D}_M}{\xi -{\lambda }_1\overline{M}}(M-\overline{M})\Delta M\\ +\frac{{\varrho }_2{\omega }_1\overline{N}{D}_H}{(\psi -{\lambda }_2\overline{H})({\phi }_B+{\varrho }_2\overline{H})}(H-\overline{H})\Delta H.\end{array}$

Simplifying, we arrive at

$\begin{array}{l}\frac{\partial {{\rm Y}}_1}{\partial t}=-\frac{{\phi }_N{(N-\bar{N})}^2}{N}+({\omega }_1\bar{N}\bar{B}+{\omega }_2\bar{N}\bar{S}+{\omega }_3\bar{N}\bar{U})\left(1-\frac{\bar{N}}{N}\right)\\ +{\omega }_1\bar{N}B+{\omega }_3\bar{N}U\\ -({\beta }_1+{\phi }_U)(U-\bar{U})-{\varrho }_{1}M(U-\bar{U})+{\varrho }_1\bar{M}(U-\bar{U})\\ -{\varrho }_1\bar{M}(U-\bar{U})\\ -{\omega }_1\bar{N}\bar{B}\frac{NB\bar{U}}{\bar{N}\bar{B}U}-{\omega }_2\bar{N}\bar{S}\frac{NS\bar{U}}{\bar{N}\bar{S}U}-{\omega }_3\bar{N}\bar{U}\frac{N}{\bar{N}}+\frac{{\omega }_2{\beta }_2\bar{N}}{{\phi }_S}U\\ -{\omega }_2\bar{N}\bar{S}\frac{U\bar{S}}{\bar{U}S}\\ +{\omega }_2\bar{N}\bar{S}+\frac{{\omega }_1\mu \bar{N}}{{\phi }_B+{\varrho }_2\bar{H}}U-\frac{{\omega }_1{\phi }_B\bar{N}}{{\phi }_B+{\varrho }_2\bar{H}}(B-\bar{B})-\frac{{\varrho }_2{\omega }_1\bar{N}}{{\phi }_B+{\varrho }_2\bar{H}}\\ H(B-\bar{B})\\ +\frac{{\varrho }_2{\omega }_1\bar{N}}{{\phi }_B+{\varrho }_2\bar{H}}\bar{H}(B-\bar{B})-\frac{{\varrho }_2{\omega }_1\bar{N}}{{\phi }_B+{\varrho }_2\bar{H}}\bar{H}(B-\bar{B})-{\omega }_1\bar{N}\bar{B}\frac{\bar{B}U}{B\bar{U}}\\ +{\varrho }_1(M-\bar{M})(U-\bar{U})-\frac{{\varrho }_1({\phi }_M+{\lambda }_{1}U)}{\xi -{\lambda }_1\bar{M}}{(M-\bar{M})}^2\\ +\frac{{\varrho }_2{\omega }_1\bar{N}(H-\bar{H})}{{\phi }_B+{\varrho }_2\bar{H}}(B-\bar{B})\\ -\frac{{\varrho }_2{\omega }_1\bar{N}({\phi }_H+{\lambda }_{2}B)}{(\psi -{\lambda }_2\bar{H})({\phi }_B+{\varrho }_2\bar{H})}{(H-\bar{H})}^2+D_N\Delta N\left(1-\frac{\bar{N}}{N}\right)\\ +D_U\left(1-\frac{\bar{U}}{U}\right)\Delta U+\frac{{\omega }_2\bar{N}{D}_S}{{\phi }_S}\left(1-\frac{\bar{S}}{S}\right)\Delta S+\frac{{\omega }_1\bar{N}{D}_B}{{\phi }_B+{\varrho }_2\bar{H}}\\ \left(1-\frac{\bar{B}}{B}\right)\Delta B\\ +\frac{{\varrho }_1{D}_M}{\xi -{\lambda }_1\bar{M}}(M-\bar{M})\Delta M+\frac{{\varrho }_2{\omega }_1\bar{N}{D}_H}{(\psi -{\lambda }_2\bar{H})({\phi }_B+{\varrho }_2\bar{H})}\\ (H-\bar{H})\Delta H.& (22)\end{array}$

In this way, Equation 22 is rewritten in the form

$\begin{array}{l}\frac{\partial {{\rm Y}}_1}{\partial t}=-\frac{{\phi }_N{(N-\bar{N})}^2}{N}+({\omega }_1\bar{N}\bar{B}+{\omega }_2\bar{N}\bar{S}+{\omega }_3\bar{N}\bar{U})\left(1-\frac{\bar{N}}{N}\right)\\ +{\omega }_3\bar{N}U-({\beta }_1+{\phi }_U+{\varrho }_1\bar{M})(U-\bar{U})-{\omega }_1\bar{N}\bar{B}\frac{NB\bar{U}}{\bar{N}\bar{B}U}\\ -{\omega }_2\bar{N}\bar{S}\frac{NS\bar{U}}{\bar{N}\bar{S}U}\\ -{\omega }_3\bar{N}\bar{U}\frac{N}{\bar{N}}+\frac{{\omega }_2{\beta }_2\bar{N}}{{\phi }_S}U-{\omega }_2\bar{N}\bar{S}\frac{U\bar{S}}{\bar{U}S}+{\omega }_2\bar{N}\bar{S}+\frac{{\omega }_1\mu \bar{N}}{{\phi }_B+{\varrho }_2\bar{H}}U\\ +{\omega }_1\bar{N}\bar{B}\\ -{\omega }_1\bar{N}\bar{B}\frac{\bar{B}U}{B\bar{U}}-\frac{{\varrho }_1({\phi }_M+{\lambda }_{1}U){(M-\bar{M})}^2}{\xi -{\lambda }_1\bar{M}}-\\ \frac{{\varrho }_2{\omega }_1\bar{N}({\phi }_H+{\lambda }_{2}B){(H-\bar{H})}^2}{(\psi -{\lambda }_2\bar{H})({\phi }_B+{\varrho }_2\bar{H})}\\ +D_N\Delta N\left(1-\frac{\bar{N}}{N}\right)+D_U\left(1-\frac{\bar{U}}{U}\right)\Delta U+\frac{{\omega }_2\bar{N}{D}_S}{{\phi }_S}\\ \left(1-\frac{\bar{S}}{S}\right)\Delta S\\ +\frac{{\omega }_1\bar{N}{D}_B}{{\phi }_B+{\varrho }_2\bar{H}}\left(1-\frac{\bar{B}}{B}\right)\Delta B+\frac{{\varrho }_1{D}_M}{\xi -{\lambda }_1\bar{M}}(M-\bar{M})\Delta M\\ +\frac{{\varrho }_2{\omega }_1\bar{N}{D}_H}{(\psi -{\lambda }_2\bar{H})({\phi }_B+{\varrho }_2\bar{H})}(H-\bar{H})\Delta H.\end{array}$

Since we have

$\begin{array}{l}\left(\frac{{\omega }_1\mu \bar{N}}{{\phi }_B+{\varrho }_2\bar{H}}\bar{U}+\frac{{\omega }_2{\beta }_2\bar{N}}{{\phi }_S}\bar{U}+{\omega }_3\bar{N}\bar{U}-({\beta }_1+{\phi }_U+{\varrho }_1\bar{M})\bar{U}\right)\\ \frac{U}{\bar{U}}=0.\end{array}$

This results in the following form

$\begin{array}{l}\frac{\partial {{\rm Y}}_1}{\partial t}=-\frac{{\phi }_N{\left(N-\bar{N}\right)}^2}{N}+\left({\omega }_1\bar{N}\bar{B}+{\omega }_2\bar{N}\bar{S}+{\omega }_3\bar{N}\bar{U}\right)\left(2-\frac{\bar{N}}{N}\right)\\ -{\omega }_1\bar{N}\bar{B}\frac{NB\bar{U}}{\bar{N}\bar{B}U}\\ -{\omega }_2\bar{N}\bar{S}\frac{NS\bar{U}}{\bar{N}\bar{S}U}-{\omega }_3\bar{N}\bar{U}\frac{N}{\bar{N}}-{\omega }_2\bar{N}\bar{S}\frac{U\bar{S}}{\bar{U}S}+{\omega }_2\bar{N}\bar{S}+{\omega }_1\bar{N}\bar{B}\\ -{\omega }_1\bar{N}\bar{B}\frac{\bar{B}U}{B\bar{U}}\\ -\frac{{\varrho }_1\left({\phi }_M+{\lambda }_{1}U\right){\left(M-\bar{M}\right)}^2}{\xi -{\lambda }_1\bar{M}}-\\ \frac{{\varrho }_2{\omega }_1\bar{N}\left({\phi }_H+{\lambda }_{2}B\right){\left(H-\bar{H}\right)}^2}{\left(\psi -{\lambda }_2\bar{H}\right)\left({\phi }_B+{\varrho }_2\bar{H}\right)}\\ +D_N\Delta N\left(1-\frac{\bar{N}}{N}\right)+D_U\left(1-\frac{\bar{U}}{U}\right)\Delta U+\frac{{\omega }_2\bar{N}{D}_S}{{\phi }_S}\\ \left(1-\frac{\bar{S}}{S}\right)\Delta S\\ +\frac{{\omega }_1\bar{N}{D}_B}{{\phi }_B+{\varrho }_2\bar{H}}\left(1-\frac{\bar{B}}{B}\right)\Delta B+\frac{{\varrho }_1{D}_M}{\xi -{\lambda }_1\bar{M}}\left(M-\bar{M}\right)\Delta M\\ +\frac{{\varrho }_2{\omega }_1\bar{N}{D}_H}{\left(\psi -{\lambda }_2\bar{H}\right)\left({\phi }_B+{\varrho }_2\bar{H}\right)}\left(H-\bar{H}\right)\Delta H\\ =-\frac{\left({\phi }_N+{\omega }_3\bar{U}\right){\left(N-\bar{N}\right)}^2}{N}\\ +{\omega }_1\bar{N}\bar{B}\left(3-\frac{\bar{N}}{N}-\frac{NB\bar{U}}{\bar{N}\bar{B}U}-\frac{\bar{B}U}{B\bar{U}}\right)\\ +{\omega }_2\bar{N}\bar{S}\left(3-\frac{\bar{N}}{N}-\frac{NS\bar{U}}{\bar{N}\bar{S}U}-\frac{U\bar{S}}{\bar{U}S}\right)\\ -\frac{{\varrho }_1\left({\phi }_M+{\lambda }_{1}U\right){\left(M-\bar{M}\right)}^2}{\xi -{\lambda }_1\bar{M}}\\ -\frac{{\varrho }_2{\omega }_1\bar{N}\left({\phi }_H+{\lambda }_{2}B\right){\left(H-\bar{H}\right)}^2}{\left(\psi -{\lambda }_2\bar{H}\right)\left({\phi }_B+{\varrho }_2\bar{H}\right)}+D_N\Delta N\left(1-\frac{\bar{N}}{N}\right)\\ +D_U\left(1-\frac{\bar{U}}{U}\right)\Delta U\\ +\frac{{\omega }_2\bar{N}{D}_S}{{\phi }_S}\left(1-\frac{\bar{S}}{S}\right)\Delta S+\frac{{\omega }_1\bar{N}{D}_B}{{\phi }_B+{\varrho }_2\bar{H}}\left(1-\frac{\bar{B}}{B}\right)\Delta B\\ +\frac{{\varrho }_1{D}_M}{\xi -{\lambda }_1\bar{M}}\left(M-\bar{M}\right)\Delta M+\frac{{\varrho }_2{\omega }_1\bar{N}{D}_H}{\left(\psi -{\lambda }_2\bar{H}\right)\left({\phi }_B+{\varrho }_2\bar{H}\right)}\\ \left(H-\bar{H}\right)\Delta H.\end{array}$

Differentiating with respect to time ${\widehat{{\rm Y}}}_1\left(t\right)$ and utilizing equality (Equation 20) gives

$\begin{array}{l}\frac{d{\widehat{{\rm Y}}}_1}{dt}=-\left({\phi }_N+{\omega }_3\bar{U}\right){\displaystyle {\int }_{\Lambda }}\frac{{\left(N-\bar{N}\right)}^2}{N}\text{ d}\varkappa +{\omega }_1\bar{N}\bar{B}\\ {\displaystyle {\int }_{\Lambda }}\left(3-\frac{\bar{N}}{N}-\frac{NB\bar{U}}{\bar{N}\bar{B}U}-\frac{\bar{B}U}{B\bar{U}}\right)\text{ d}\varkappa \\ +{\omega }_2\bar{N}\bar{S}{\displaystyle {\int }_{\Lambda }}\left(3-\frac{\bar{N}}{N}-\frac{NS\bar{U}}{\bar{N}\bar{S}U}-\frac{U\bar{S}}{\bar{U}S}\right)\text{ d}\varkappa -\frac{{\varrho }_1}{\xi -{\lambda }_1\bar{M}}\\ {\displaystyle {\int }_{\Lambda }}\left({\phi }_M+{\lambda }_{1}U\right){\left(M-\bar{M}\right)}^2\text{ d}\varkappa \\ -\frac{{\varrho }_2{\omega }_1\bar{N}}{\left(\psi -{\lambda }_2\bar{H}\right)\left({\phi }_B+{\varrho }_2\bar{H}\right)}{\displaystyle {\int }_{\Lambda }}\left({\phi }_H+{\lambda }_{2}B\right){\left(H-\bar{H}\right)}^2\text{ d}\varkappa \\ -D_N\bar{N}{\displaystyle {\int }_{\Lambda }}\frac{\parallel \nabla N{\parallel }^2}{N^2}\text{ d}\varkappa \\ -D_U\bar{U}{\displaystyle {\int }_{\Lambda }}\frac{\parallel \nabla U{\parallel }^2}{U^2}\text{ d}\varkappa -\frac{{\omega }_2\bar{N}{D}_S\bar{S}}{{\phi }_S}{\displaystyle {\int }_{\Lambda }}\frac{\parallel \nabla S{\parallel }^2}{S^2}\text{ d}\varkappa \\ -\frac{{\omega }_1\bar{N}{D}_B\bar{B}}{{\phi }_B+{\varrho }_2\bar{H}}{\displaystyle {\int }_{\Lambda }}\frac{\parallel \nabla B{\parallel }^2}{B^2}\text{ d}\varkappa \\ -\frac{{\varrho }_1{D}_M}{\xi -{\lambda }_1\bar{M}}{\displaystyle {\int }_{\Lambda }}\parallel \nabla M{\parallel }^2\text{ d}\varkappa -\frac{{\varrho }_2{\omega }_1\bar{N}{D}_H}{\left(\psi -{\lambda }_2\bar{H}\right)\left({\phi }_B+{\varrho }_2\bar{H}\right)}\\ {\displaystyle {\int }_{\Lambda }}\parallel \nabla H{\parallel }^2\text{ d}\varkappa .\end{array}$

Employing the inequality between the arithmetic and geometric means, as presented in Equation 19, we obtain

$\begin{array}{l}3\le \frac{\bar{N}}{N}+\frac{NB\bar{U}}{\bar{N}\bar{B}U}+\frac{\bar{B}U}{B\bar{U}},3\le \frac{\bar{N}}{N}+\frac{NS\bar{U}}{\bar{N}\bar{S}U}+\frac{U\bar{S}}{\bar{U}S}.\end{array}$

At this stage, we guarantee that $\frac{d{\widehat{{\rm Y}}}_1}{dt}\le 0$ for all positive values of N, U, S, B, M, H when ${\mathcal{R}}_0>1$. Meanwhile, $\frac{d{\widehat{{\rm Y}}}_1}{dt}=0$ when $\left(N,U,S,B,M,H\right)=\left(\bar{N},\bar{U},\bar{S},\bar{B},\bar{M},\bar{H}\right)$. The solutions of model (Equation 2) approach ${\Theta }_1^{\prime }=\left\{\mathcal{PE}\right\}$. By applying Lyapunov-LaSalle asymptotic stability theorem, we conclude that $\mathcal{PE}$ attains global asymptotic stability.

Remark 2. Exploring memory effects within our model through the use of fractional differential equations (FDEs) represents a valuable avenue for future investigation [71, 72]. FDEs are particularly well-suited for capturing systems characterized by memory and non-local interactions–features that are highly relevant in both biological [73] and epidemiological contexts. Recent studies have demonstrated that the Lyapunov method is an effective analytical tool for evaluating the global stability of fractional-order systems [73, 74]. The Lyapunov functions constructed in this section lay the groundwork for future analysis of the stability properties in a fractional-order HIV-1 model.

6 Numerical simulations

This section focuses on performing numerical simulations to explore the theoretical findings of our study. Furthermore, a detailed sensitivity analysis will be conducted for each parameter. To solve the system of PDEs, we employed MATLAB's built-in PDEPE solver, which is designed for one-dimensional parabolic and elliptic PDEs. The PDEPE solver utilizes a spatial discretization based on the Galerkin or Petrov–Galerkin method, converting the PDE system into a set of ODEs. These ODEs are then solved using the ode15s solver, a variable-order, implicit numerical integrator well-suited for stiff problems. This method offers a robust and efficient approach for numerically approximating the dynamics of the model over time and space.

6.1 Stability of equilibrium points

Here, we undertake a numerical investigation into the global stability of all equilibria. To achieve this, a time step size of 0.1 is applied for t > 0, and the domain Λ, defined as Λ = [0, 2], is used with a step size of 0.02. Based on Theorems 1 and 2 which ensure the global stability of both equilibria, convergence is guaranteed irrespective of the initial values. Therefore, the initial conditions for system (Equation 2) are chosen randomly as follows:

$\begin{array}{l}N\left(\varkappa ,0\right)=500\left[1+0.1{cos}^2\left(\pi \varkappa \right)\right],\\ U\left(\varkappa ,0\right)=3\left[1+0.2{cos}^2\left(\pi \varkappa \right)\right],\\ S\left(\varkappa ,0\right)=3\left[1+0.2{cos}^2\left(\pi \varkappa \right)\right],B\left(\varkappa ,0\right)=2\left[1+0.2{cos}^2\left(\pi \varkappa \right)\right],\\ M\left(\varkappa ,0\right)=8\left[1+0.2{cos}^2\left(\pi \varkappa \right)\right],\\ H\left(\varkappa ,0\right)=30\left[1+0.2{cos}^2\left(\pi \varkappa \right)\right],\varkappa \in \left[0,2\right].& (23)\end{array}$

Additionally, we apply the homogeneous Neumann boundary conditions:

$\begin{array}{ll}\frac{\partial N}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial U}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial S}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial B}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial M}{\partial \overrightarrow{\sout{Z}}}=\frac{\partial H}{\partial \overrightarrow{\sout{Z}}}=0,t>0,\varkappa =0,2.& (24)\end{array}$

For numerical calculations, ω₁, ω₂, and ω₃ are varied, whereas the other parameters are kept constant as specified in Table 1. Those parameters are sourced from existing literature, except for the diffusion coefficients, which are predetermined.

Table 1

Table 1. The values of the model's parameters.

Therefore, the following cases arise:

Case 1. Assigning ω₁ = ω₂ = ω₃ = 0.0001, the basic reproduction number ${\mathcal{R}}_0$ is calculated to be 0.59, which is less than unity. In accordance with Theorem 1, the equilibrium point $\mathcal{F}\mathcal{E}=\left(1000,0,0,0,0,0\right)$ demonstrates global asymptotic stability, as depicted in Figure 1. This finding indicates the successful clearance of HIV infection from the human body, highlighting the conditions under which the virus cannot persist.

Figure 1

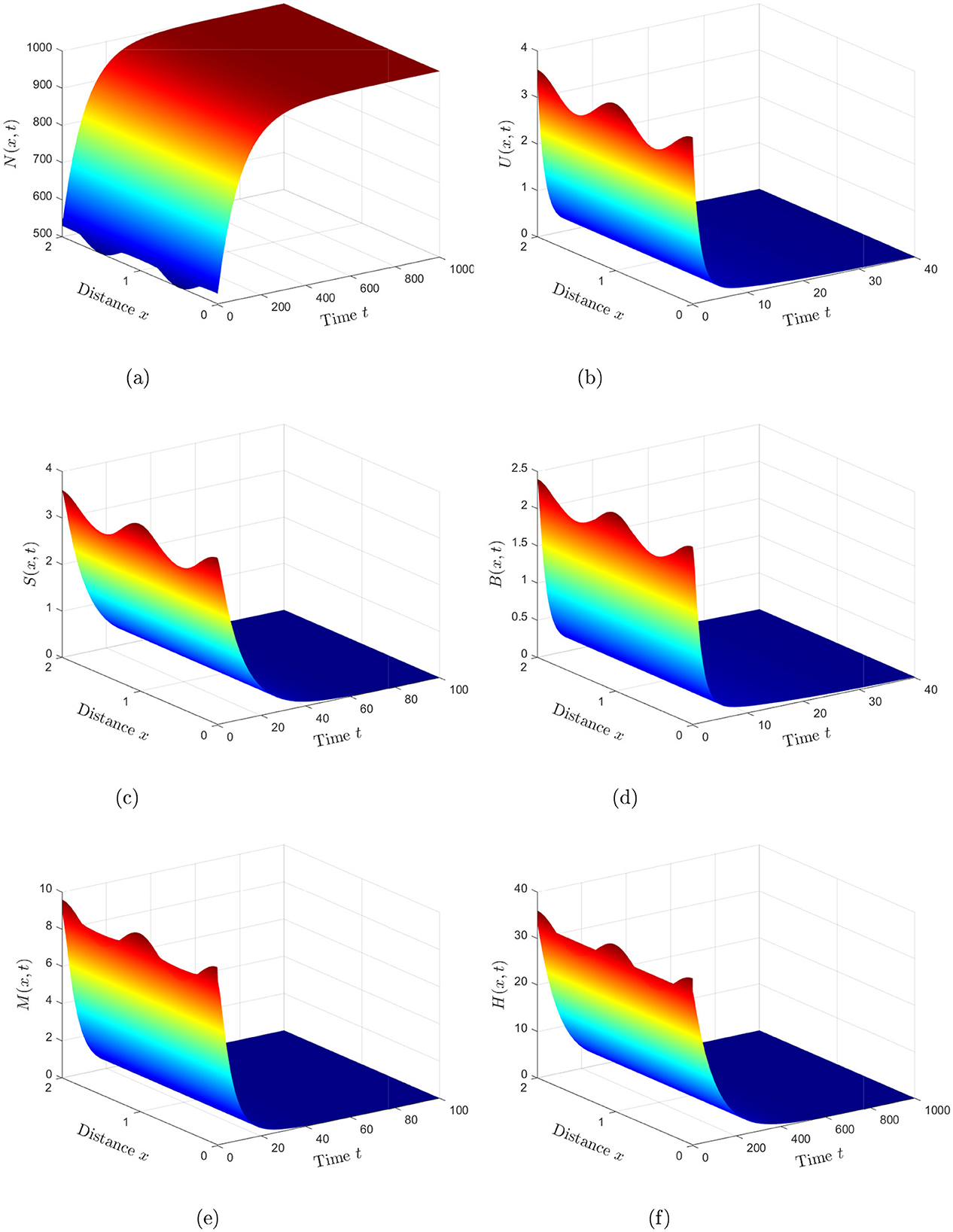
Figure 1. Numerical simulations reveal that the solution of system (Equation 2) stabilizes at the HIV-free equilibrium $\mathcal{F}\mathcal{E}=\left(1000,0,0,0,0,0\right)$ when ${\mathcal{R}}_0\le 1$ (Case 1). (a) Healthy CD4⁺T cells. (b) HIV-infected CD4⁺T cells. (c) Inflammatory cytokines. (d) Free HIV particles. (e) CTLs. (f) Antibodies.

Case 2. The values ω₁ = 0.0004, ω₂ = 0.0006, and ω₃ = 0.0005 are assigned. With these parameters, the basic reproduction number, ${\mathcal{R}}_0$, is determined to be 2.7, exceeding unity. Theorem 2 confirms that the equilibrium point $\mathcal{PE}=\left(641.9,4.16,4.16,2.5,10.2,39.98\right)$ exhibits global asymptotic stability, as depicted in Figure 2. This analysis reflects the ability of the virus to maintain a stable presence in the human body under this condition and cause chronic infection, highlighting the persistence of HIV infection.

Figure 2

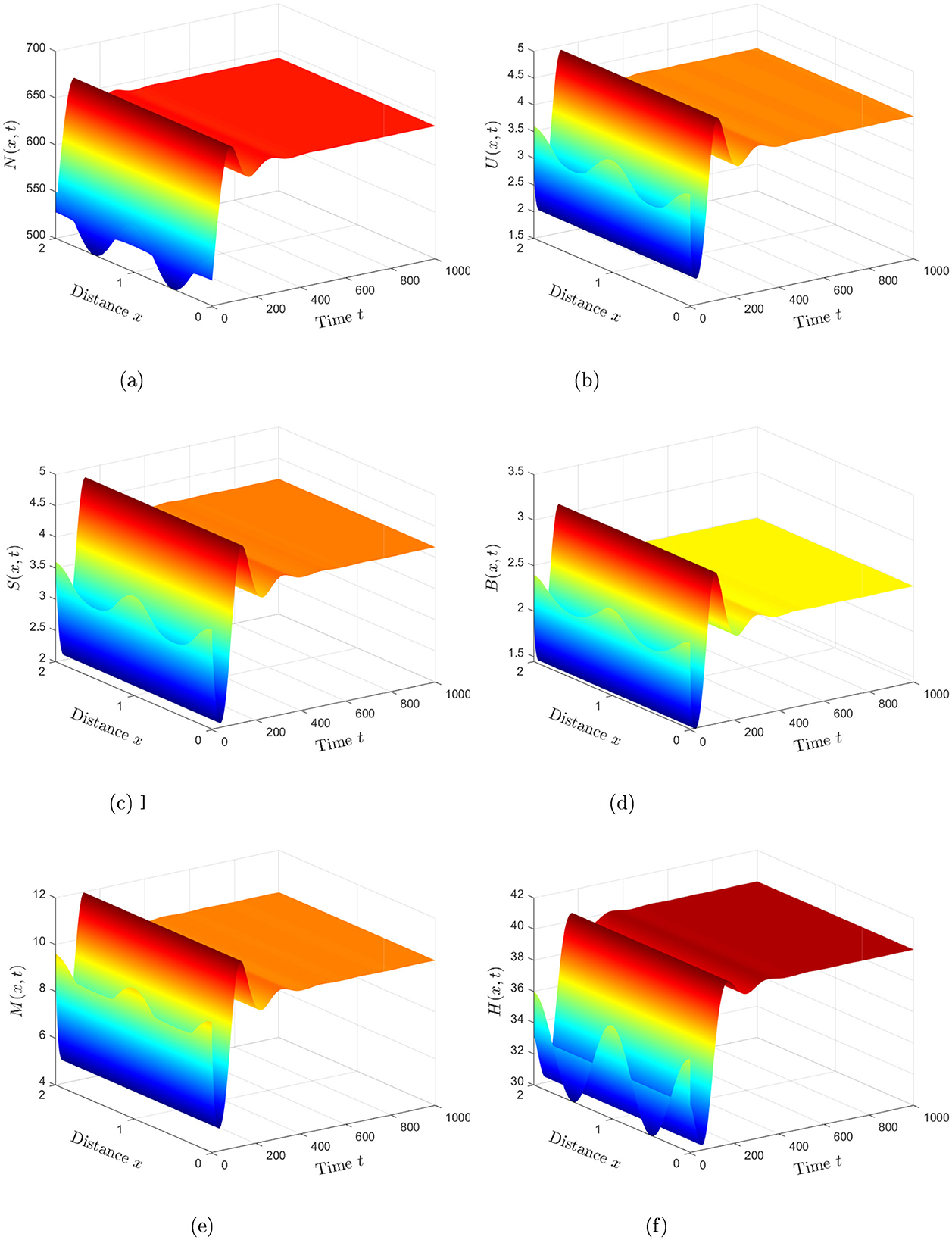
Figure 2. Numerical simulations reveal that the solution of system (Equation 2) stabilizes at the HIV-persistent equilibrium $\mathcal{PE}=\left(641.9,4.16,4.16,2.5,10.2,39.98\right)$ when ${\mathcal{R}}_0>1$ (Case 2). (a) Healthy CD4⁺T cells. (b) HIV-infected CD4⁺T cells. (c) Inflammatory cytokines. (d) Free HIV particles. (e) CTLs. (f) Antibodies.

6.2 Sensitivity analysis

The main objective of this subsection is to discuss the sensitivity analysis of model (Equation 2). Specifically, the analysis aims to assess the impact of various parameters on the advancement of HIV infection in a host, offering insights that can be useful for the development of novel antiviral therapies. The sensitivity index will be determined by employing partial derivatives to examine how variables fluctuate in accordance to parameter changes. The following formula represents the normalized forward sensitivity index of ${\mathcal{R}}_0$ in relation to the parameter:

$\begin{array}{ll}{Q}_{\tau }=\frac{\tau }{{\mathcal{R}}_0}\times \frac{\partial {\mathcal{R}}_0}{\partial \tau }.& (25)\end{array}$

Here, τ accounts for a specified parameter. The values of Q_τ range from −1 to 1, with a positive Q_τ indicating a positive correlation and a negative value reflecting a negative correlation. The absolute value of Q_τ signifies the level of sensitivity: values close to zero imply a minimal effect, whereas values near one point to a strong impact[75]. The sensitivity indices for ${\mathcal{R}}_0$ were computed using Equation 25 by applying the parameter values provided in Table 1, including ω₁ = 0.0004, ω₂ = 0.0006, and ω₃ = 0.0005. The calculated sensitivity indices, derived from these values, are summarized in Table 2. The sensitivity indices of ${\mathcal{R}}_0$, as demonstrated in Table 2 and Figure 3, shed light on the varying influences of each parameter. From these, it is apparent that parameters δ, ω₁, ω₂, ω₃, μ, and β₂ exhibit positive index values. This indicates that an increase in the values of these parameters is linked to a higher ${\mathcal{R}}_0$ value, leading to a greater level of HIV endemicity. In contrast, the parameters φ_N, β₁, φ_U, φ_S, and φ_B show negative sensitivity indices, meaning that as their values rise, ${\mathcal{R}}_0$ decreases. Among all the parameters, the most influential are δ, ω₁, and μ, while ω₂, ω₃, and β₂ have relatively minor impacts. Moreover, the parameters related to CTL and antibody responsiveness, ξ and ψ, seem to have no impact on ${\mathcal{R}}_0$.

Table 2

Table 2. Quantifying parameters' influence on ${\mathcal{R}}_0$ in model (Equation 2): sensitivity index.

Figure 3

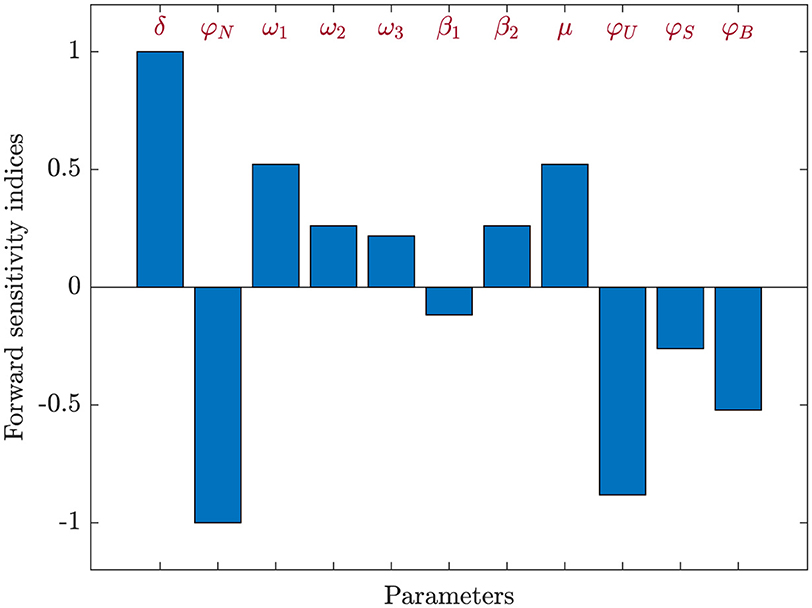
Figure 3. Assessment of parameter influence on ${\mathcal{R}}_0$ in system (Equation 2) using forward sensitivity analysis.

7 Conclusion and discussion

This study proposed and investigated a within-host HIV infection model that integrates both the influence of inflammatory cytokines and the weakening of adaptive immune responses (CTL and antibody). The framework comprises six biologically relevant compartments and incorporates two modes of viral transmission: traditional virus-to-cell spread and direct cell-to-cell contact. By introducing diffusion terms, the model also captures spatial movement of immune and infected cells, as well as free viral particles—a feature supported by recent biological findings. We conducted a thorough mathematical analysis, establishing the existence and boundedness of global solutions, ensuring the model's well-posedness. A key threshold parameter, the basic reproduction number ${\mathcal{R}}_0$, was derived and found to dictate the system's long-term behavior. Specifically, the model predicts global stability of the HIV-free equilibrium when ${\mathcal{R}}_0\le 1$ and global stability of HIV-persistent equilibrium when ${\mathcal{R}}_0>1$. These analytical results were supported by numerical simulations that also revealed how variations in key parameters affect disease progression. Further, sensitivity analysis of ${\mathcal{R}}_0$ helped identify the most influential factors in viral persistence and immune control.

An important challenge in controlling HIV infection lies in reducing the basic reproduction number ${\mathcal{R}}_0$ to a value less than or equal to one, thereby preventing sustained transmission. One effective strategy involves the use of antiviral therapies aimed at interrupting different modes of viral spread. To capture this therapeutically induced suppression, we introduce parameters 0 ≤ ϵ_i ≤ 1, for i = 1, 2, where ϵ₁ represents the efficacy of treatment in inhibiting cell-free virus transmission, and ϵ₂ accounts for the suppression of cell-to-cell viral transfer. In addition to standard antiretroviral therapies, we also consider the role of Necrosulfonamide (NSA), a selective inhibitor of pyroptosis, a highly inflammatory form of programmed cell death that exacerbates immune depletion in HIV-positive individuals [76]. The parameter ϵ₃∈[0, 1] is used to denote the therapeutic effectiveness of NSA in curbing inflammation-driven cell death. Under these assumptions, the modified expression for the basic reproduction number becomes:

$\begin{array}{l}{\mathcal{R}}_0=\frac{\delta \left(\mu {\phi }_S\left(1-{ϵ}_1\right){\omega }_1+{\phi }_B\left({\beta }_2\left(1-{ϵ}_2\right){\omega }_2+{\phi }_S\left(1-{ϵ}_3\right){\omega }_3\right)\right)}{{\phi }_N{\phi }_S{\phi }_B\left({\beta }_1+{\phi }_U\right)}.\end{array}$

It is evident from this formulation that ${\mathcal{R}}_0$ is a monotonically decreasing function of the drug efficacy parameters ϵ₁, ϵ₂, ϵ₃. Hence, by appropriately increasing the effectiveness of these interventions, through optimal drug combinations or dosing strategies, it is theoretically possible to drive ${\mathcal{R}}_0\le 1$, thereby achieving infection control or even eradication within the modeled population.

Future extensions of this model could involve incorporating more detailed biological mechanisms, such as latent viral reservoirs, time delays, and stochastic variations in immune responses, as well as clinical interventions including antiretroviral therapy (ART) and anti-inflammatory treatments targeting cytokine activity. Formulating the model as a nonlinear control system, with antiviral drug efficacy treated as a control input, also presents a promising avenue for optimizing treatment strategies-balancing therapeutic effectiveness with minimized drug costs and side effects. Moreover, integrating fractional differential equations may offer a more realistic representation of immunological memory. The inclusion of individual-level data could further enhance model accuracy and support more personalized predictions of treatment outcomes. Clinically, a better understanding of cytokine-induced inflammation and the spatial distribution of immune and infected cells may aid in developing novel therapeutic strategies aimed at preserving immune function and reducing chronic immune activation in HIV-positive individuals.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

NA: Conceptualization, Formal analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer KH declared a past co-authorship with the author NA to the handling editor.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wodarz D, Levy DN. Human immunodeficiency virus evolution towards reduced replicative fitness in vivo and the development of AIDS. Proc R Soc B Biol Sci. (2007) 274:2481–91. doi: 10.1098/rspb.2007.0413

PubMed Abstract | Crossref Full Text | Google Scholar

2. Guo T, Qiu Z, Shen M, Rong L. Dynamics of a new HIV model with the activation status of infected cells. J Math Biol. (2021) 82:51. doi: 10.1007/s00285-021-01604-3

PubMed Abstract | Crossref Full Text | Google Scholar

3. Nowak MA, Bangham CRM. Population dynamics of immune responses to persistent viruses. Science. (1996) 272:74–9. doi: 10.1126/science.272.5258.74

PubMed Abstract | Crossref Full Text | Google Scholar

4. Deng J, Shu H, Wang L, Wang XS. Viral dynamics with immune responses: Effects of distributed delays and Filippov antiretroviral therapy. J Math Biol. (2023) 86:37. doi: 10.1007/s00285-023-01869-w

PubMed Abstract | Crossref Full Text | Google Scholar

5. Chen C, Zhou Y. Dynamic analysis of HIV model with a general incidence, CTLs immune response and intracellular delays. Math Comput Simul. (2023) 212:159–81. doi: 10.1016/j.matcom.2023.04.029

Crossref Full Text | Google Scholar

6. Hattaf K. Spatiotemporal dynamics of a generalized viral infection model with distributed delays and CTL immune response. Computation. (2019) 7:21. doi: 10.3390/computation7020021

Crossref Full Text | Google Scholar

7. Tan M, Lan G, Wei C. Dynamic analysis of HIV infection model with CTL immune response and cell-to-cell transmission. Appl Math Lett. (2024) 156:109140. doi: 10.1016/j.aml.2024.109140

Crossref Full Text | Google Scholar

8. Lv L, Yang J, Hu Z, Fan D. Dynamics analysis of a delayed HIV model with latent reservoir and both viral and cellular infections. Math Methods Appl Sci. (2025) 48:6063–80. doi: 10.1002/mma.10655

Crossref Full Text | Google Scholar

9. Hmarrass H, Qesmi R. Global stability and Hopf bifurcation of a delayed HIV model with macrophages, CD4+ T cells with latent reservoirs and immune response. Eur Phys J Plus. (2025) 140:335. doi: 10.1140/epjp/s13360-025-06001-z

Crossref Full Text | Google Scholar

10. Lin J, Xu R, Tian X. Threshold dynamics of an HIV-1 virus model with both virus-to-cell and cell-to-cell transmissions, intracellular delay humoral immunity. Appl Math Comput. (2017) 315:516–30. doi: 10.1016/j.amc.2017.08.004

Crossref Full Text | Google Scholar

11. Xie Z, Liu X. Global dynamics in an age-structured HIV model with humoral immunity. Int J Biomathem. (2021) 14:2150047. doi: 10.1142/S1793524521500479

Crossref Full Text | Google Scholar

12. Lin J, Xu R, Tian X. Threshold dynamics of an HIV-1 model with both viral and cellular infections, cell-mediated and humoral immune responses. Mathem Biosci Eng. (2018) 16:292–319. doi: 10.3934/mbe.2019015

PubMed Abstract | Crossref Full Text | Google Scholar

13. Guo T, Qiu Z, Rong L. Analysis of an HIV model with immune responses and cell-to-cell transmission. Bull Malaysian Mathem Sci Soc. (2018) 43:581–607. doi: 10.1007/s40840-018-0699-5

Crossref Full Text | Google Scholar

14. Alshamrani NH. Stability of a general adaptive immunity HIV infection model with silent infected cell-to-cell spread. Chaos, Solitons Fract. (2021) 150:110422. doi: 10.1016/j.chaos.2020.110422

PubMed Abstract | Crossref Full Text | Google Scholar

15. Zhang Z, Chen Y, Wang X, Rong L. Dynamic analysis of a latent HIV infection model with CTL immune and antibody responses. Int J Biomathem. (2024) 17:2350079. doi: 10.1142/S1793524523500791

Crossref Full Text | Google Scholar

16. Guo T, Deng Q, Gao S, Qiu Z, Rong L, HIV. infection dynamics with broadly neutralizing antibodies and CTL immune response. Discr Cont Dyn Syst-S. (2024) 2024:2024151. doi: 10.3934/dcdss.2024151

Crossref Full Text | Google Scholar

17. Doitsh G, Cavrois M, Lassen K, Zepeda O, Yang Z, Santiago M, et al. Abortive HIV infection mediates CD4 T cell depletion and inflammation in human lymphoid tissue. Cell. (2010) 143:789–801. doi: 10.1016/j.cell.2010.11.001

PubMed Abstract | Crossref Full Text | Google Scholar

18. Doitsh G, Galloway NL, Geng X, Yang Z, Monroe KM, Zepeda O, et al. Cell death by Pyroptosis drives CD4 T-cell depletion in HIV-1 infection. Nature. (2014) 505:509–514. doi: 10.1038/nature12940

PubMed Abstract | Crossref Full Text | Google Scholar

19. Wang S, Hottz P, Schechter M, Rong L. Modeling the slow CD4⁺T cell decline in HIV-infected individuals. PLoS Comput Biol. (2015) 11:e1004665. doi: 10.1371/journal.pcbi.1004665

PubMed Abstract | Crossref Full Text | Google Scholar

20. Jiang Y, Zhang T. Global stability of a cytokine-enhanced viral infection model with nonlinear incidence rate and time delays. Appl Math Lett. (2022) 132:108110. doi: 10.1016/j.aml.2022.108110

Crossref Full Text | Google Scholar

21. Wang W, Feng Z. Global dynamics of a diffusive viral infection model with spatial heterogeneity. Nonl Analy. (2023) 72:103763. doi: 10.1016/j.nonrwa.2022.103763

Crossref Full Text | Google Scholar

22. Xu J, Huang G, Zhang S, Hao M, Wang A. Global dynamical behavior of a delayed cytokine-enhanced viral infection model with nonlinear incidence. Int J Biomathem. (2024) 35:2450072. doi: 10.1142/S1793524524500724

Crossref Full Text | Google Scholar

23. Hong L, Li J, Rong L, Wang X. Global dynamics of a delayed model with cytokine-enhanced viral infection and cell-to-cell transmission. AIMS Mathem. (2024) 9:16280–96. doi: 10.3934/math.2024788

Crossref Full Text | Google Scholar

24. Xu J. Dynamic analysis of a cytokine-enhanced viral infection model with infection age. Mathem Biosci Eng. (2023) 20:8666–84. doi: 10.3934/mbe.2023380

PubMed Abstract | Crossref Full Text | Google Scholar

25. Chen C, Zhou Y, Ye Z. Stability and optimal control of a cytokine-enhanced general HIV infection model with antibody immune response and CTLs immune response. Comput Methods Biomech Biomed Engin. (2023) 27:2199–230. doi: 10.1080/10255842.2023.2275248

PubMed Abstract | Crossref Full Text | Google Scholar

26. Zhang T, Xu X, Wang X. Dynamic analysis of a cytokine-enhanced viral infection model with time delays and CTL immune response. Chaos, Solitons Fractals. (2023) 170:113357. doi: 10.1016/j.chaos.2023.113357

PubMed Abstract | Crossref Full Text | Google Scholar

27. Cao X, Hou S, Kong X. A cytokine-enhanced viral infection model with CTL immune response, distributed delay and saturation incidence. arXiv preprint arXiv:2409.10223. (2024).

Google Scholar

28. Chen C, Ye Z, Zhou Y. Stability and Hopf bifurcation of a cytokine-enhanced HIV infection model with saturation incidence and three delays. Int J Bifurcat Chaos. (2024) 34:2450133. doi: 10.1142/S0218127424501335

Crossref Full Text | Google Scholar

29. Ye Z, Zhou Y, Zheng Z, Chen C. Stability and Hopf bifurcation of a cytokine-enhanced HIV infection model with antibody immune response delay. Int J Biomathem. (2024) 2450037. doi: 10.1142/S1793524524500372

Crossref Full Text | Google Scholar

30. Dahy E, Elaiw AM, Raezah AA, Zidan HZ, Abdellatif AA. Global properties of cytokine-enhanced HIV-1 dynamics model with adaptive immunity and distributed delays. Computation. (2023) 11:217. doi: 10.3390/computation11110217

Crossref Full Text | Google Scholar

31. Brainard DM, Tager AM, Misdraji J, Frahm N, Lichterfeld M, Draenert R, et al. Decreased CXCR3+ CD8 T cells in advanced human immunodeficiency virus infection suggest that a homing defect contributes to cytotoxic T-lymphocyte dysfunction. J Virol. (2007) 81:8439–50. doi: 10.1128/JVI.00199-07

PubMed Abstract | Crossref Full Text | Google Scholar

32. Tattermusch S, Bangham CRM. HTLV-1 infection: what determines the risk of inflammatory disease? Trends Microbiol. (2012) 20:494–500. doi: 10.1016/j.tim.2012.07.004

PubMed Abstract | Crossref Full Text | Google Scholar

33. Bellomo N, Painter KJ, Tao Y, Winkler M. Occurrence vs. Absence of taxis-driven instabilities in a May-Nowak model for virus infection. SIAM J Appl Mathem. (2019) 79:1990–2010. doi: 10.1137/19M1250261

Crossref Full Text | Google Scholar

34. Gao Y, Wang J. Threshold dynamics of a delayed nonlocal reaction-diffusion HIV infection model with both cell-free and cell-to-cell transmissions. J Math Anal Appl. (2020) 488:124047. doi: 10.1016/j.jmaa.2020.124047

Crossref Full Text | Google Scholar

35. Wang W, Wang X, Guo K, Ma W. Global analysis of a diffusive viral model with cell-to-cell infection and incubation period. Math Methods Appl Sci. (2020) 43:5963–78. doi: 10.1002/mma.6339

Crossref Full Text | Google Scholar

36. Ren X, Tian Y, Liu L, Liu X. A reaction-diffusion within-host HIV model with cell-to-cell transmission. J Math Biol. (2018) 76:1831–72. doi: 10.1007/s00285-017-1202-x

PubMed Abstract | Crossref Full Text | Google Scholar

37. Liu Z, Wang L, Tan R. Spatiotemporal dynamics for a diffusive HIV-1 infection model with distributed delays and CTL immune response. Discr Contin Dyn Syst-B. (2022) 27:2767–90. doi: 10.3934/dcdsb.2021159

Crossref Full Text | Google Scholar

38. Han R, Dai B, Chen Y. Chemotaxis-driven stationary and oscillatory patterns in a diffusive HIV-1 model with CTL immune response and general sensitivity. Chaos. (2023) 33:073142. doi: 10.1063/5.0150072

PubMed Abstract | Crossref Full Text | Google Scholar

39. Shu H, Jin HY, Wang XS, Wu J. Viral infection dynamics with immune chemokines and CTL mobility modulated by the infected cell density. J Math Biol. (2024) 88:43. doi: 10.1007/s00285-024-02065-0

PubMed Abstract | Crossref Full Text | Google Scholar

40. Lyu G, Wang J, Zhang R. Threshold dynamics of a diffusive HIV infection model with infection-age, latency and cell-cell transmission. Commun Nonl Sci Numer Simulat. (2024) 138:108248. doi: 10.1016/j.cnsns.2024.108248

Crossref Full Text | Google Scholar

41. Chen Z, Dai C, Shi L, Chen G, Wu P, Wang L. Reaction-diffusion model of HIV infection of two target cells under optimal control strategy. Electr Res Archive. (2024) 32:4129–63. doi: 10.3934/era.2024186

Crossref Full Text | Google Scholar

42. Wang W, Zhang T. Caspase-1-mediated pyroptosis of the predominance for driving CD4⁺T cells death: a nonlocal spatial mathematical model. Bull Math Biol. (2018) 80:540–82. doi: 10.1007/s11538-017-0389-8

PubMed Abstract | Crossref Full Text | Google Scholar

43. Wang W, Ma W, Feng Z. Complex dynamics of a time periodic nonlocal and time-delayed model of reaction-diffusion equations for modelling CD4⁺T cells decline. J Comput Appl Math. (2020) 367:112430. doi: 10.1016/j.cam.2019.112430

Crossref Full Text | Google Scholar

44. Wang W, Ren X, Ma W, Lai X. New insights into pharmacologic inhibition of pyroptotic cell death by necrosulfonamide: A PDE model. Nonl Analy. (2020) 56:103173. doi: 10.1016/j.nonrwa.2020.103173

Crossref Full Text | Google Scholar

45. Wang W, Ren X, Wang X. Spatial-temporal dynamics of a novel PDE model: Applications to pharmacologic inhibition of pyroptosis by necrosulfonamide. Commun Nonl Sci Numer Simul. (2021) 103:106025. doi: 10.1016/j.cnsns.2021.106025

Crossref Full Text | Google Scholar

46. Chen C, Ye Z, Zhou Y, Zheng Z. Dynamics of a delayed cytokine-enhanced diffusive HIV model with a general incidence and CTL immune response. Eur Phys J Plus. (2023) 138:1083. doi: 10.1140/epjp/s13360-023-04734-3

Crossref Full Text | Google Scholar

47. Lydyard P, Whelan A, Fanger M. BIOS Instant Notes in Immunology. New York: Taylor & Francis e-Library (2005). doi: 10.4324/9780203488287

Crossref Full Text | Google Scholar

48. Regoes R, Wodarz D, Nowak MA. Virus dynamics: the effect to target cell limitation and immune responses on virus evolution. J Theor Biol. (1998) 191:451–462. doi: 10.1006/jtbi.1997.0617

PubMed Abstract | Crossref Full Text | Google Scholar

49. Wang ZP, Liu XN. A chronic viral infection model with immune impairment. J Theor Biol. (2007) 249:532–42. doi: 10.1016/j.jtbi.2007.08.017

PubMed Abstract | Crossref Full Text | Google Scholar

50. Hu Z, Zhang J, Wang H, Ma W, Liao F. Dynamics analysis of a delayed viral infection model with logistic growth and immune impairment. Appl Math Model. (2014) 38:524–34.

PubMed Abstract | Google Scholar

51. Krishnapriya P, Pitchaimani M. Analysis of time delay in viral infection model with immune impairment. J Appl Mathem Comput. (2017) 55:421–53. doi: 10.1007/s12190-016-1044-5

Crossref Full Text | Google Scholar

52. Zhang L, Xu R. Dynamics analysis of an HIV infection modelwith latent reservoir, delayed CTL immune response and immune impairment. Nonl Anal. (2023) 28:1–19. doi: 10.15388/namc.2023.28.29615

PubMed Abstract | Crossref Full Text | Google Scholar

53. Hou S, Tian X. Stability and Hopf bifurcation analysis of an HIV infection model with latent reservoir, immune impairment and delayed CTL immune response. arXiv preprint arXiv:2503.21143. (2025). doi: 10.1142/S1793524525500846

Crossref Full Text | Google Scholar

54. Miao H, Abdurahman X, Teng Z, Zhang L. Dynamical analysis of a delayed reaction-diffusion virus infection model with logistic growth and humoral immune impairment. Chaos, Solitons Fract. (2018) 110:280–291. doi: 10.1016/j.chaos.2018.03.006

Crossref Full Text | Google Scholar

55. AlShamrani NH, Halawani RH, Shammakh W, Elaiw AM. Stability of impaired humoral immunity HIV-1 models with active and latent cellular infections. Computation. (2023) 11:207. doi: 10.3390/computation11100207

Crossref Full Text | Google Scholar

56. Elaiw AM, Alshehaiween SF. Global stability of delay-distributed viral infection model with two modes of viral transmission and B-cell impairment. Math Methods Appl Sci. (2020) 43:6677–701. doi: 10.1002/mma.6408

Crossref Full Text | Google Scholar

57. Elaiw AM, Alshehaiween SF, Hobiny AD. Impact of B-cell impairment on virus dynamics with time delay and two modes of transmission. Chaos, Solitons Fract. (2020) 130:109455. doi: 10.1016/j.chaos.2019.109455

Crossref Full Text | Google Scholar

58. AlShamrani NH, Halawani RH, Elaiw AM. Effect of impaired B-cell and CTL functions on HIV-1 dynamics. Mathematics. (2023) 11:4385. doi: 10.3390/math11204385

Crossref Full Text | Google Scholar

59. AlShamrani NH, Halawani RH, Elaiw AM. Analysis of general HIV-1 infection models with weakened adaptive immunity and three transmission modalities. Alexandria Eng J. (2024) 106:101–46. doi: 10.1016/j.aej.2024.06.033

Crossref Full Text | Google Scholar

60. Song Q, Wang S, Xu F. Robustness and bistability in a cytokine-enhanced viral infection model. Appl Math Lett. (2024) 158:109215. doi: 10.1016/j.aml.2024.109215

Crossref Full Text | Google Scholar

61. Wang Z, Guo Z, Peng H. Dynamical behavior of a new oncolytic virotherapy model based on gene variation. Discrete Cont Dyn Syst Series S. (2017) 10:1079–93. doi: 10.3934/dcdss.2017058

Crossref Full Text | Google Scholar

62. Hajhouji Z, Hattaf K, Yousfi N. A generalized fractional HIV-1 infection model with humoral immunity and highly active antiretroviral therapy. J Math Comput Sci. (2024) 32:160–74. doi: 10.22436/jmcs.032.02.06

Crossref Full Text | Google Scholar

63. Xu Z, Xu Y. Stability of a CD4⁺T cell viral infection model with diffusion. Int J Biomathem. (2018) 11:1850071. doi: 10.1142/S1793524518500717

Crossref Full Text | Google Scholar

64. Zhang Y, Xu Z. Dynamics of a diffusive HBV model with delayed Beddington-DeAngelis response. Nonl Analy. (2014) 15:118–39. doi: 10.1016/j.nonrwa.2013.06.005

Crossref Full Text | Google Scholar

65. Martin RH, Smith HL. Abstract functional differential equations and reaction-diffusion systems. Trans Am Mathem Soc. (1990) 321:1–44. doi: 10.1090/S0002-9947-1990-0967316-X

PubMed Abstract | Crossref Full Text | Google Scholar

66. Smith HL. Monotone dynamical systems: an introduction to the theory of competitive and cooperative systems. In: Mathematical Surveys and Monographs, Vol. 41. American Mathematical Society (1995).

Google Scholar

67. Protter MH, Weinberger HF. Maximum Principles in Differential Equations. Englewood Cliffs: Prentic Hall. (1967).

Google Scholar

68. Henry D. Geometric Theory of Semilinear Parabolic Equations. New York: Springer-Verlag (1993).

Google Scholar

69. van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. (2002) 180:29–48. doi: 10.1016/S0025-5564(02)00108-6

PubMed Abstract | Crossref Full Text | Google Scholar

70. Khalil HK. Nonlinear Systems. 3rd Edition, Upper Saddle River: Prentice Hall. (2002).

Google Scholar

71. Hattaf K, A. new class of generalized fractal and fractal-fractional derivatives with non-singular kernels. Fractal Fract. (2023) 7:395. doi: 10.3390/fractalfract7050395

Crossref Full Text | Google Scholar

72. Hattaf K. A new mixed fractional derivative with applications in computational biology. Computation. (2024) 12:7. doi: 10.3390/computation12010007

PubMed Abstract | Crossref Full Text | Google Scholar

73. Sardar P, Biswas S, Das KP, Sahani SK, Gupta V. Stability, sensitivity, and bifurcation analysis of a fractional-order HIV model of CD4⁺T cells with memory and external virus transmission from macrophages. Eur Phys J Plus. (2025) 140:160. doi: 10.1140/epjp/s13360-025-06081-x

Crossref Full Text | Google Scholar

74. Yaagoub Z. Fractional two-strain SVLIR epidemic model with vaccination and quarantine strategies. Int J Dyn Control. (2025) 13:55. doi: 10.1007/s40435-024-01561-x

Crossref Full Text | Google Scholar

75. Elaiw AM, Almohaimeed EA, Hobiny AD. Stability analysis of a diffusive HTLV-2 and HIV-1 co-infection model. Alexandria Eng J. (2025) 116:232–70. doi: 10.1016/j.aej.2024.11.074

Crossref Full Text | Google Scholar

76. Rathkey JK, Zhao J, Liu Z, Chen Y, Yang J, Kondolf HC, et al. Chemical disruption of the pyroptotic pore-forming protein gasdermin D inhibits inflammatory cell death and sepsis. Sci Immunol. (2018) 3:eaat2738. doi: 10.1126/sciimmunol.aat2738

PubMed Abstract | Crossref Full Text | Google Scholar

77. Sahani SK, Yashi. Effects of eclipse phase and delay on the dynamics of HIV infection. J Biol Syst. (2018) 26:421–454. doi: 10.1142/S0218339018500195

Crossref Full Text | Google Scholar

78. Elaiw AM, Raezah AA, Alofi BS. Dynamics of delayed pathogen infection models with pathogenic and cellular infections and immune impairment. AIP Adv. (2018) 8:025323. doi: 10.1063/1.5023752

Crossref Full Text | Google Scholar

79. Wang S, Song X, Ge Z. Dynamics analysis of a delayed viral infection model with immune impairment. Appl Math Model. (2011) 35:4877–85. doi: 10.1016/j.apm.2011.03.043

Crossref Full Text | Google Scholar