A deep learning forecasting of downside risk: application of a combined ESRNN-VAE

Introduction: Traditional time-series models such as the ARIMA and the Generalized Autoregressive Conditional Heteroscedasticity depend nonlinear dynamics and stationarity, limiting their ability to model nonlinear relationships and sudden regime changes.

Methods: This research introduces a combined forecasting model that uses the clear structure of an Exponential Smoothing Recurrent Neural Network and the creative features of a Variational Autoencoder to predict the risk of falling stock prices for Sasol Limited from 2010 to 2025. The model seeks to find long-term trends and short-term changes in the value of stocks linked to commodities, which can face big losses due to political events, changes in oil prices, and shifts in climate policies.

Results: A weighted combination of the deterministic ESRNN, which gets 60% of the weight, and the stochastic VAE, which gets 40%, shows strong accuracy in predicting stock prices over short, medium, and long periods. Shapley value analysis identifies 24-day lags, investor sentiment, oil prices, the 2015/2016 Shanghai Stock Exchange crash, the Russia-Ukraine war, and South African monetary policy news as the primary predictors of downside risk. The model effectively quantifies essential tail risk metrics, such as Maximum Drawdown, Sortino Ratio, and Marginal Expected Shortfall. A 99% prediction interval width (PIW) of 3.4398 indicates the model's reliability in capturing extreme events and uncertainty during turbulent periods.

Discussion: The results indicate the model's robustness and practical utility as a decision-support tool for risk-aware forecasting in resource-dependent financial markets.

1 Introduction

Commodity markets are experiencing unprecedented volatility driven by a triad of exogenous shocks: geopolitical fragmentation, supply chain disruptions, and climate-induced instabilities [1–3]. These factors highlight the critical need for improved methods to quantify downside risk, particularly for commodity-linked equities that are structurally exposed to such external pressures. Firms with integrated commodity exposure face asymmetric risks, where adverse developments can rapidly erode shareholder value. A pertinent case is Sasol Limited (JSE: SOL), a South African energy and chemical conglomerate, which has suffered 17 notable declines—each exceeding 10%—between 2010 and 2025, often triggered by falling oil prices or abrupt shifts in climate regulation [4, 5]. These episodes illustrate the sector's heightened vulnerability to tail-risk events and the inherent difficulty in forecasting their occurrence and magnitude.

Classical time-series models, such as ARIMA (herein referenced Autoregressive Integrated Moving Average) proposed by Box and Jenkins [6] and the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) proposed by Bollerslev [7], offer essential resources for modeling volatility. Nevertheless, their dependence on linear dynamics and stationary assumptions limits their ability to capture nonlinear relationships and sudden regime changes typical in commodity-linked equities [8]; hence, novel hybrid models, such as Transformer-Convolutional Neural Networks (Transformer-CNNs) proposed by Li et al. [9] and long short term memory-GARCH (LSTM-GARCH) by Xiong et al. [10], have improved forecasting accuracy, particularly for volatility estimation. These techniques, however, are typically designed for smooth volatility patterns and frequently maintain parametric assumptions, which limit their capacity for capturing fat-tailed, asymmetric risks that predominate during periods of systemic stress [11], while Sasol's 54% drop in March 2020 during the COVID-19 pandemic highlighted this limitation.

A distinct gap remains in the financial time series literature despite the growing interest in deep learning. Sezer et al. [12] found that only 12% of deep learning applications explicitly target downside risk, with most focusing narrowly on return or volatility forecasting. To our knowledge, no prior work combines the structural interpretability of exponential smoothing with a deep generative model to jointly capture trend, seasonality, and tail-dependent volatility. This limitation is particularly problematic for commodity-linked equities such as Sasol, which experience extended earnings cycles (e.g., 5-year commodity super-cycles) that interact nonlinearly with short-term volatility clustering—evident in a correlation of ρ = 0.82^*** with Brent crude oil and are further disrupted by regime-shifting events like South Africa's electricity crises and carbon tax implementation [13, 14]. The research by Li and Law [15] highlights the lack of attention devoted to downside risk in deep learning applications, supporting the argument made by Sezer et al. [12]. The objectives of Li and Law [15] were to introduce and review methodologies for modeling time series data, outline the commonly used time series forecasting datasets and different evaluation metrics. These authors delved into the essential architectures for trending an input dataset and offered a comprehensive assessment of the recently developed deep learning prediction models. While Novyko et al. [16], on the other hand, provides a systematic literature review of deep learning applications for portfolio management, Huang et al. [17] presented a novel approach to portfolio optimisation that addresses tail risks. The approach begins with the prediction of Conditional Value-at-Risk (CVaR) using a deep neural network. The predicted CVaR was then incorporated into a tail risk-adjusted utility function to calculate the portfolio weights. Specifically, their paper predicts CVaR using a Long Short-Term Memory neural network, but in this study, we use maximum drawdown, Sortino, and marginal expected shortfall.

Forecasting financial series presents challenges, including structural seasonality, nonlinear volatility regimes, and exogenous shocks. Econometric models possess inherent limitations. Autoregressive Integrated Moving Average models are predicated on linearity and difference-stationarity, rendering them inadequate for regime-switching behaviors. In contrast, GARCH models, while adept at managing conditional volatility, do not effectively account for leverage effects, display residual kurtosis, and operate under the assumption of fixed distributions [8]. During the 2020 pandemic, ARIMA's forecasting error rose by 28%, while GARCH underestimated tail risk by more than 35% amid oil price shocks [13]. Recent hybrid deep learning architectures enhance the management of these nonlinearities. The LSTM-GARCH models integrate memory and conditional variance; however, they frequently neglect seasonality, leading to an underestimation of volatility [18]. Transformer-CNN architectures, on the other hand, effectively detect cross-asset spillovers; however, they exhibit limitations in interpretability. Dynamically weighted ensembles decrease root mean square error (RMSE) [19], yet their application to modeling volatility clustering in resource-driven equities remains limited. The ESRNN, however, effectively captures structural components such as trend and seasonality, yet it does not account for latent volatility clustering. In contrast, VAEs generatively model hidden volatility regimes but lack structural interpretability [20].

We propose the ESRNN-VAE hybrid to address these trade-offs, integrating ESRNN's decomposition with the VAE's latent regime learning. This approach provides (i) enhanced economic interpretability via decomposable components, (ii) the capacity to identify unobservable volatility regimes influenced by exogenous factors, and (iii) adaptability to regime shifts, thereby achieving a robust bias–variance trade-off as indicated by Zhang and Lin [19]. The model, applied to Sasol's 15-year dataset (2010–2025), effectively captures long-term cycles and short-term volatility within a cohesive and adaptable charter. The non-parametric, data-driven methodology effectively models heavy-tailed, asymmetric returns, therefore, enhancing the accuracy of Sortino Ratio and Marginal Expected Shortfall estimates in the context of volatile geopolitical, supply chain, and market disruptions. In contrast to Chen [21] and Yin and Barucca [22], which employ Generative Adversarial Networks (GANs) or VAEs and RNNs independently without a unified approach to modeling trend, seasonality, and tail risk in commodities, our combined architecture cohesively integrates these elements. While this study does not include direct benchmarking against LSTM-GARCH or Transformer-based models, these alternatives often face challenges such as restrictive assumptions, interpretability issues, or computational complexity. The ESRNN-VAE offers a flexible and interpretable solution that effectively addresses complex financial dynamics without rigid distributional constraints. Future research could extend this work by including comparative analyses.

1.1 Contribution and research highlights

The main contribution of this study is building a combined ESRNN-VAE model for forecasting Sasol's stock prices and estimating downside risk. By combining long-range trend extracting (ESRNN) and short-range volatility modeling (VAE) features, the model performs better in different horizons, identifies primary risk drivers (oil prices, geopolitics, etc.), and foresees downside measures (drawdown, Sortino ratio, tail risk) correctly. The research highlights are summarized as follows:

• Individual models are surpassed by hybrid ESRNN-VAE stock price prediction in multi-horizon.

• Sasol stock prices have left-skewed, non-normal distributions with persistent tail risks.

• Long-term ESRNN forecasts reduce MSE by 96% from horizons of 5 days to 60 days.

• VAE outperforms short-term, achieving 92.73% forecast efficiency on predictions of 5-days.

• SHAP analysis finds oil prices, geopolitical incidents, and investor sentiment driving the model.

• Downside risk metrics (drawdown, Sortino ratio, and tail loss) are accurately predicted.

2 Theoretical and empirical literature review

Financial time series forecasting has moved from ARIMA and GARCH to machine learning models that can capture nonlinear trends, regime transitions, and severe occurrences. Even though these econometrics models provide theoretical foundations, they struggle to forecast downside risk, especially in volatile, commodity-linked markets. Recurrent Neural Networks, Long Short-Term Memory models, and Variational Autoencoders are now popular deep learning techniques for recognizing complicated patterns and hidden fluctuations in data. However, few studies directly address tail-risk indicators like Maximum Drawdown, Sortino Ratio, and Marginal Expected Shortfall. This study examines volatility and risk forecasting theory and practice, focusing on downside risk modeling in resource-sensitive financial markets. In this section, we present mathematical representations, theoretical structures, and empirical evidence from recent studies with regard to market risk and volatility.

2.1 Mathematical representation

Let y_t denote the observed time series. The ESRNN decomposes this series into a level component l_t, trend level b_t and seasonality s_t, with an additive residual term ε_t given in Equation 1 as

$\begin{array}{ll}{y}_t=l_t+b_t+s_t+{\epsilon }_t.& (1)\end{array}$

The residual ε_t in Equation 1 is passed to the VAE, which approximates the posterior distribution of latent variables z given by Equation 2 as

$\begin{array}{ll}q(z|{\epsilon }_t)=\aleph (z;{\mu }_{{\epsilon }_t},{\sigma }_{{\epsilon }_t}^2).& (2)\end{array}$

From here, the decoder reconstructs volatility-adjusted residuals as given by

$\begin{array}{ll}{\widehat{\epsilon }}_t=f_{\theta }(z).& (3)\end{array}$

The VAE's optimisation is guided by the maximization of the Evidence Lower Bound (ELBO), which balances two components: the reconstruction loss, encouraging fidelity in the generation of ${\widehat{\epsilon }}_t$ and the Kullback-Leibler (KL) divergence, regularizing the learned latent distribution to remain close to a prior, typically standard normal given by

$\begin{array}{ll}L(\theta ,\Phi ;{\epsilon }_t)=E_{q_{\Phi }(z|{\epsilon }_t}[(\log p_{\theta }|z)]-DKL[q_{\Phi }(z|{\epsilon }_t)\parallel p(z)].& (4)\end{array}$

This dual objective ensures the model captures the volatility patterns embedded in residuals and maintains a smooth and structured latent representation, enhancing generalizability, and robustness in downstream forecasting.

2.1.1 Implication for downside risk modeling

The assimilation of the VAE into the ESRNN architecture significantly enhances downside risk modeling for volatile stocks like Sasol Ltd. By encoding the residual volatility into a latent Gaussian space; the model captures hidden, nonlinear, and regime-switching dynamics often associated with sharp equity drawdowns—such as those triggered by oil price shocks or macroeconomic instability. This probabilistic latent representation allows for estimating tail-risk measures like Conditional Value-at-Risk (CVaR), offering superior sensitivity to asymmetries in Sasol's return distribution. The hybrid approach balances the interpretability of time series decomposition with the adaptability of deep generative models, delivering a robust, explainable, and forward-looking tool for financial risk forecasting in complex market environments.

2.2 Theoretical frameworks in time series risk forecasting

Time series models such as ARIMA effectively capture linear dependencies but are inadequate for nonlinear patterns and volatility clustering. The GARCH-type models [7], including Exponential-GARCH and GJR-GARCH, incorporate time-varying variance but rely on restrictive assumptions that break down during regime shifts and market discontinuities. Moreover, they cannot model heavy tails, volatility persistence, and asymmetries [8].

Hybrid methods offer a robust alternative. The Exponentially Smoothed Recurrent Neural Network integrates exponential smoothing with recurrent neural networks, consistent with adaptive learning theory. Variational AutoEncoders, rooted in Bayesian inference, can extract latent volatility regimes and model their stochastic behavior. The ESRNN-VAE hybrid is underpinned by bias-variance decomposition theory [23], enabling it to balance interpretability with the flexibility needed for modeling extreme market dynamics. This approach bridges the gap between deterministic forecasting and generative probabilistic modeling, addressing a critical lacuna in the literature.

2.3 Empirical evidence from recent studies

Empirical studies highlight the superiority of hybrid deep learning models over classical or individual models. The LSTM-GARCH models have better performance in forecasting commodity volatility, outpacing standalone GARCH models [10]. Transformer-based models have achieved enhanced prediction accuracy in highly volatile areas such as cryptocurrency markets [9]. South African studies provide further validation, classical models, such as historical, Monte Carlo, and variance-covariance, etc, are reported to underestimate Value-at-Risk by 22% for Sasol Ltd during crisis periods. According to Hemraj [24], the Carbon Tax Act is one of several structural headwinds weighing on Sasol—and it is factored heavily into its depressed share price. The stock may struggle if carbon pricing alarms grow louder and allowances shrink. However, should Sasol succeed in its decarbonisation roadmap and operational improvements, there is room for a meaningful rebound. Similarly, Xaba et al. [25] demonstrated that EGARCH forecasts were 34% less accurate during episodes of sharp ZAR depreciation. Moreover, dynamic ensemble methods such as those evaluated by Li et al. [9] reduced RMSE by 18% through data-adaptive weighting. In contrast, Smyl [26] in their study indicated that the ESRNN model ranked among the top performers in the M4 forecasting competition, highlighting the efficacy of combining structural decomposition with neural networks. Despite these advancements, a dual challenge remains unaddressed: the simultaneous modeling of structural periodicity and volatility asymmetry in commodity-linked equities.

Although several new general-purpose machine learning methodologies have surfaced, they are still poorly understood and incompatible with conventional statistical modeling techniques. Dixon [27] presents a new type of exponentially smoothed recurrent neural networks that work well for modeling changing systems found in industries. The author looked closely at how well these networks can describe the complex patterns in time series data and clearly show the effects of changes over time, like seasonal variations and trends. Using exponentially smoothed recurrent neural networks to forecast power demand, weather data, and stock market prices shows how well exponential smoothing works for making predictions over multiple time steps. In their study, Xie [28] looks at three common ways to estimate value-at-risk: historical simulation, the variance-covariance method, and Monte Carlo simulation, using ten years of data from the NASDAQ Composite Index. The results demonstrate that, at the 95% confidence level, VaR estimates from the three methods show a high degree of consistency. At the 99% confidence level, the Monte Carlo and variance-covariance methods usually produce slightly higher Value at Risk (VaR) values compared to historical simulation. Historical simulation, while not based on specific assumptions and providing fairly dependable results, is not as strong as the ESRNN-VAE model presented in this study. However, our proposed ESRNN-VAE is different from the method of Xie [28] because it can predict stock prices in real-time and better understands complex patterns and hidden changes in volatility, making it more effective for modeling risks in unstable, commodity-related stocks. No published study has integrated ESRNN and VAE for downside risk forecasting in resource equities within emerging market contexts. This study fills that gap by proposing a regime-sensitive hybrid model specifically tailored to the volatility dynamics of resource-dependent equities in volatile economies.

3 Methodology

This section outlines the comprehensive methodological framework employed to forecast downside risk in Sasol Ltd.'s stock using a hybrid deep learning model that synergises the Ensemble of Seasonal Recurrent Neural Networks with the Variational Autoencoder. The methodology is based on quantitative time series forecasting and is tailored to consider latent volatility and deterministic structures. It integrates structural decomposition with generative volatility modeling to address nonlinear dynamics, regime shifts, and tail-risk sensitivity inherent in Sasol Ltd.'s commodity-linked equity (JSE: SOL). This chapter offers comprehensive insights into the training strategy, model architecture, data preprocessing, study design, and assessment metrics to guarantee methodological transparency and repeatability.

3.1 Research design

The modeling structure proposed in this study combines interpretable time-series decomposition via ESRNN with probabilistic residual modeling in a rolling-horizon design [26, 29]. Its key innovation is the joint modeling of structural components (trend and seasonality) alongside latent volatility regimes through variational inference. To enhance sensitivity to shocks, the model incorporates several exogenous drivers in the post hock analysis via explainable AI (that is SHAP for feature impotance): COVID-19 daily cases (South Africa): Sourced from Our World in Data, capturing the health shock intensity over time. 2015–2016 Shanghai stock market crash: Included as a shock dummy based on event timing identified through financial archives and public resources such as Investopedia. Data extraction involved web scraping and text mining, specifically topic modeling via Latent Dirichlet Allocation (LDA) (see https://www.investopedia.com/articles/investing/022716/4-consequences-government-intervention-chinas-markets.asp). Russia–Ukraine war indicator: A binary variable marking the conflict's onset and persistence, derived from web-scraped reports and processed using LDA-based topic modeling for the period from 24 February 2022 to 27 July 2025 (https://www.russiamatters.org/news/russia-ukraine-war-report-card/russia-ukraine-war-report-card-july-30-2025). Oil prices: Benchmarked Brent crude prices obtained via the Python yfinance package. Monetary policy news (South Africa): Incorporated as a qualitative driver, extracted via automated web scraping and text mining techniques analogous to those used for the Shanghai crash and Russia-Ukraine war data. Investor sentiment: Weekly data from the American Association of Individual Investors (AAII) Sentiment Survey, quantifying bullish, bearish, and neutral market outlooks. These data were collected through automated web scraping of the AAII website (https://www.aaii.com/sentimentsurvey) to align sentiment shifts with exchange rate dynamics into the VAE's latent space, amplifying tail-risk capture during structural breaks (e.g., the implementation of the Carbon Tax Act) [30, 31]. Validation is conducted through 5-fold time-series cross-validation with chronological blocking to prevent look-ahead bias as demonstrated by Bergmeir et al. [32].

3.2 Data description and pre-processing

The dataset comprises daily adjusted closing prices of Sasol Ltd., listed on the Johannesburg Stock Exchange (JSE), spanning from January 2010 to May 2025, denominated in South African Rand (ZAR) to avoid exchange-rate distortion. This extended 15-year horizon captures a wide range of market regimes, including macroeconomic shocks, periods of economic contraction, and episodes of heightened volatility—conditions critical for robust downside risk modeling. The target variable is specified as the natural logarithm of prices to stabilize variance and linearize exponential growth trends given in Equation 5 as

$\begin{array}{ll}{y}_t=\text{ln}(P_t),& (5)\end{array}$

where P_t denotes the adjusted closing price at time t. This transformation stabilizes the variance and ensures additive time series behavior [33]. To ensure data quality and statistical validity, the preprocessing pipeline consists of the following sequential steps:

• Handling of missing values: Gaps of three trading days or fewer were addressed using linear interpolation to preserve temporal continuity without introducing systematic bias. This approach ensures that short-term gaps—often caused by market holidays or brief data outages—do not distort the time series' statistical properties. In contrast, Ndlovu and Chikobvu [34] filled missing values with zeros, reasoning that since stock markets are closed on weekends and holidays, no profits or losses could occur during these periods. While their justification aligns with market closure logic, zero imputation may underestimate volatility and suppress the magnitude of extreme events in tail-risk modeling, particularly when applied to high-frequency financial data.

• Stationarity testing: The Augmented Dickey-Fuller (ADF) test is applied to the log-transformed series:

$\begin{array}{ll}\Delta y_t=\alpha +{\beta }_t+\gamma y_{t-1}+{\displaystyle \sum _{i=1}^p}{\Phi }_i\Delta y_{i-1}+{\epsilon }_i,& (6)\end{array}$

To make it stationary, we differentiate the data for p-values greater than 0.05. This is a requirement for many deep learning models, such as RNNs [33]. Nevertheless, Bature et al. [40] argues that testing stationarity helps in deciding if the dynamic model should be implemented or a static model and this is based on the results of the ADF test.

• Calculation of log returns: For components of the model which are sensitive to volatility (e.g., VAE latent variables), we calculate the log returns as follows:

Normalization: We normalize all continuous inputs, including log prices and returns, shown in 7 as

$\begin{array}{ll}{Z}_t=\frac{R_t-\mu }{\sigma },& (7)\end{array}$

where σ is the standard deviation of the log returns and μ is the sample mean.

• Data splitting: The time series is split into three sets: training set, 70% validation set, 15% and test set, 15%. This is done to maintain temporal consistency and to avoid data leakage.

3.2.1 External variables: definitions and data sources

This study implemented a Bottom-Up Hierarchical Time Series (BUHTS) framework to improve predictive accuracy and account for the multiscale characteristics of financial time series. This structure facilitates the integration of internally derived components from the BWP/USD exchange rate series with externally sourced macroeconomic and geopolitical indicators. Each component is analyzed as a disaggregated series at the lower hierarchical level and later aggregated to create the final forecasting input. Based on a bottom-up disaggregated time hierarchy, the BWP/USD exchange rate is broken down into a number of interpretable time series components for the internal structure. Daily trends, weekend impacts, and more general seasonalities, including monthly, quarterly, semi-annual, and yearly cycles, are some examples of these elements. These components are extracted using classical decomposition, which captures a variety of temporal characteristics within the series. The forecasting model can identify and use significant signals across a variety of time scales thanks to this hierarchical decomposition, which also maintains the integrity of the time series.

3.3 ESRNN-VAE hybrid integration: architecture and computation

The hybrid Exponential Smoothing Recurrent Neural Networks–Variational Autoencoder architecture, which is used for modeling Sasol's equity, is presented in this section. The model architecture jointly captures the latent volatility (via VAE) and the deterministic patterns (via ESRNN). This enables modeling both the stochastic and structured elements of the financial time series.

3.3.1 ESRNN component

The Exponential Smoothing Recurrent Neural Network (ESRNN) is a hybrid forecasting architecture that combines the strengths of exponential smoothing and recurrent neural networks to produce accurate and interpretable time series forecasts.

3.3.2 Purpose

The ESRNN sub-model is designed to extract the structural components of the time series—specifically, the level l_t, trend b_t, and seasonality s_t—while maintaining temporal consistency and interpretability. It handles deterministic decomposition for improved forecasting accuracy. In Figure 1, we present the 24 business day closing stock prices daily closing stock prices for November 2017 (i.e., a month). The time series for this month exhibits a trend with weekly, monthly variabilities, and random fluctuations. For 5 and 60 business days, see Appendix Figures 5, 6.

Figure 1

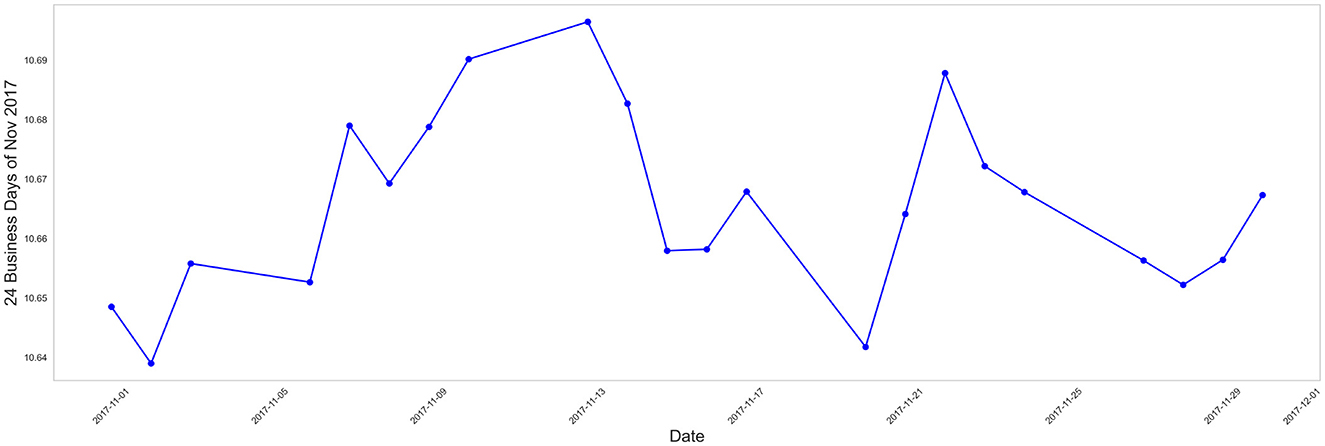
Figure 1. Time series plot for the 24 business day closing stock prices daily closing stock prices for November 2017.

3.3.3 Mathematical formulation of the ESRNN

The Exponential Smoothing Recurrent Neural Network, introduced by Smyl [26], combines classical exponential smoothing with recurrent neural networks to produce interpretable and accurate forecasts for time series exhibiting trend and seasonality. In this study, the ESRNN is implemented using an additive decomposition structure owing to the variance reduction achieved by the logarithmic transformation of the time series. The final forecast is computed as

$\begin{array}{ll}{\widehat{y}}_t^{ESRNN}=l_t+b_t·h+s_{t-m+h}& (8)\end{array}$

where l_t is the estimated level component at time t, b_t is the estimated local trend, and s_t−m+h is the seasonal component extrapolated h steps ahead and h is the forecasting horizon. Finally, m∈{5, 24, 60} represents the seasonal lag in trading days.

3.4 Model inputs and smoothing

The model first removes trend and seasonality from the input series using exponential smoothing, estimating the components recursively as

$\begin{array}{l}{l}_t=\alpha ·(y_t-s_{t-m})+(1-\alpha )(l_{t-1}+b_{t-1})\\ b_t=\beta ·(l_t-l_{t-1})+(1-\beta )b_{t-1}\\ s_t=\gamma ·(y_t-l_t)+(1-\gamma )s_{t-m}& (9)\end{array}$

where α, β, γ∈(0, 1) are smoothing parameters learned during training. The residual (i.e., seasonally adjusted) series is computed as

$\begin{array}{ll}{z}_t=y_t-l_t-s_{t-m}& (10)\end{array}$

3.5 Recurrent neural network component

The residual component z_t in Equation 10 is passed to a recurrent neural network (typically LSTM) by

$\begin{array}{ll}{h}_t=\text{RNN}(z_t,h_{t-1}).& (11)\end{array}$

The RNN learns nonlinear temporal dynamics in the adjusted signal and forecasts the deseasonalized component ẑ_t+h, which can be reintegrated with the trend and seasonal parts for the final prediction in Equation 9. To enhance memory detection over multiple temporal horizons, the model incorporates 5-day and 24-day lagged log prices as input features. Hence, our training setup consists of Adm as an optimiser, 500 epochs, the pinball loss (quantile regression), which is robust to outliers and effective in modeling asymmetric downside risk.

3.5.1 VAE component

Purpose: The VAE sub-model is tasked with modeling the stochastic residuals defined as:

$\begin{array}{ll}{\epsilon }_t=y_t-{\widehat{y}}_t^{ESRNN}& (12)\end{array}$

This residual modeling captures latent volatility regimes, especially during tail-risk episodes, regime shifts, or structural breaks (e.g., implementation of the Carbon Tax Act). The architecture consists of: (1) the Endcoder that maps residuals to a latent space using a parameterised Gaussian distribution given by

$\begin{array}{ll}{q}_{\Phi }(z|{\epsilon }_t)=\aleph (z;{\mu }_z,{\sigma }_z^2)& (13)\end{array}$

(2) Reparameterization Trick that enables backpropagation through stochastic nodes given by

$\begin{array}{ll}z={\mu }_z+{\sigma }_z\odot \epsilon ,\epsilon ~\aleph (0,1)& (14)\end{array}$

(3) The decoder, which reconstructs the residual sequence using the learned latent variable by

$\begin{array}{ll}{\widehat{\epsilon }}_t~p\theta ({\epsilon }_t|z)=\aleph ({\mu }_{\epsilon },{\sigma }_{\epsilon }^2).& (15)\end{array}$

and finally, the loss Function (Evidence Lower Bound)—ELBO which is given by

$\begin{array}{ll}L=E_{q\Phi }\left[log{p}_{\theta }({\epsilon }_t|z)\right]-D_{KL}(q_{\Phi }(z|{\epsilon }_t)\parallel p(z)).& (16)\end{array}$

Residual sequences are passed as input through a 24-day rolling window to detect local volatility anomalies [26, 35], and this joint ESRNN-VAE configuration combines deterministic structure extraction with variational inference of volatility, providing a robust hybrid model designed for nonlinearities and tail-risk behavior in commodity-linked equities such as Sasol Ltd.

3.6 Weighted hybrid integration

The final forecast combines outputs from both sub-models using a weighted ensemble strategy to balance deterministic accuracy and stochastic responsiveness which is now given as

$\begin{array}{ll}{\widehat{y}}_t^{hybrid}=w_1·{\widehat{y}}_t^{ESRNN}+w_2·({\widehat{y}}_t^{ESRNN}+{\widehat{ϵ}}_t^{VAE})& (17)\end{array}$

where w₁ = 0.6 is the base weight assigned to the ESRNN forecast, w₂ = 0.4 is the VAE-corrected forecast, w₁+w₂ = 1, ensuring convex weight. Equation 17 means that the combined forecast is an ensemble of ESRNN and ESRNN-VAE corrected outputs. This enables the model to ensure predictability of ${ŷ}_t^{ESRNN}$ and adapt to volatility spikes via $({\widehat{ϵ}}_t^{VAE})$.

3.6.1 Dynamic weighting option

During elevated volatility or structural breaks, w₂ can be increased adaptively to reflect greater reliance on the stochastic correction. For example, if volatility is detected via a GARCH-based volatility filter or realized variance threshold, the system dynamically adjusts as

$\begin{array}{ll}{w}_2=min(0.4+\alpha ·{\sigma }_t,0.7),w_1=1-w_2,& (18)\end{array}$

where α is a sensitivity hyperparameter and σ_t is the detected conditional volatility. This ensures the ensemble model reallocates trust to the VAE during turbulent market regimes.

The ESRNN-VAE hybrid, however, is a multi-resolution architecture that captures both deterministic structure and uncertainty-driven dynamics. Its layered integration enables the model to generalize across market conditions, performing accurately during stable trends and remaining robust during crashes or regime shifts. This makes it particularly well-suited for forecasting downside risk in highly sensitive stocks such as Sasol Ltd., which are exposed to commodity and regulatory shocks.

3.7 Final forecasting formulation and training protocol

The final ESRNN-VAE hybrid forecast combines the ESRNN's structural output with VAE-modeled residuals to account for latent volatility as

$\begin{array}{ll}{\widehat{y}}_t={\widehat{y}}_t^{ESRNN}+{\widehat{\epsilon }}_t^{VAE}.& (19)\end{array}$

This allows the model to preserve trend, seasonality, and level components while correcting for nonlinear shocks and tail risks. We first train the ESRNN on the full dataset using the quantile pinball loss. Once converged, its parameters are frozen. The VAE is trained on the ESRNN residuals using the Evidence of Lower Bound (ELBO) loss. Finally, ensemble weights w₁ and w₂ are tuned based on validation metrics such as Quantile Loss and VaR exceedance ratios. Lastly, the k step ahead forecasts are given by

$\begin{array}{ll}{\widehat{y}}_{t+h}=w_1·{\widehat{y}}_{t+h}^{ESRNN}+w_2·({\widehat{y}}_{t+h}^{ESRNN}+{\widehat{\epsilon }}_{t+h}^{VAE})& (20)\end{array}$

subject to w₁+w₂ = 1 where these weights are optimized using validation metrics, including: (1) Quantile Loss (for downside risk) and (2) Value-at-Risk exceedance ratios (for tail-event calibration). Last but not least, we dynamically adjust the weights based on realized volatility. When volatility spikes, w₂ increases, amplifying the VAE's influence as Zhang and Lin [19] has recommended. And this follows

$\begin{array}{ll}{w}_2=min(w_2^{base}+\alpha ·\sigma ,w_2^{max}),& (21)\end{array}$

where σ_t is realized volatility or GARCH-estimated conditional variance, α being a sensitivity parameter and $w_2^{base}=0.4,w_2^{max}=0.7$. This formulation ensures that the model increases reliance on the VAE correction during extreme market turbulence (e.g., oil price collapses, political shocks) while maintaining ESRNN dominance during stable regimes.

3.8 Evaluation metrics

To rigorously assess the predictive performance and risk sensitivity of the hybrid ESRNN-VAE model, this study employs a suite of both point forecast accuracy and risk-based evaluation metrics. These metrics ensure that the model is statistically sound and aligned with financial risk management standards. They facilitate the robust evaluation of the model's ability to capture extreme events, volatility clustering, and distributional asymmetries that typify financial time series, such as Sasol Ltd.'s stock returns.

3.8.1 Quantile loss (pinball loss)

The model's performance is assessed over several quantiles of the prediction distribution using quantile loss, sometimes called the pinball loss function. Because it directly assesses the precision of Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR) calculations, this metric is especially suitable for risk forecasting, and it is given by

$\begin{array}{ll}QL(\tau )=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left[\left(\tau -I_{y_i<{\widehat{y}}_i}\right)\left(y_i-{\widehat{y}}_i\right)\right]}.& (22)\end{array}$

This quantile level of interest (e.g., 0.05 for the 5% VaR) is represented by τε(0, 1) and I_{·} is the indicator function that captures whether the realized value y_i falls below the predicted quantile ŷ_i. The quantile loss is essential for downside risk modeling since it asymmetrically penalizes both overestimation and underestimation of quantiles [36].

3.8.2 Root mean squared error

Captures the average magnitude of forecast error:

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{n}{(y_t-{\widehat{y}}_t)}^2}& (23)\end{array}$

RMSE captures the average magnitude of forecast errors without regard to direction. While not specifically tailored for tail risk, RMSE provides a general-purpose evaluation of the model's ability to capture the central tendency of Sasol's stock returns. It offers a baseline comparison for assessing improvements introduced by the probabilistic latent representations of the VAE component.

In summary, these evaluation metrics collectively offer a comprehensive validation charter. They assess not only central forecast accuracy (via RMSE) but also distributional tail behavior (via QL and QLIKE) and statistical reliability of risk forecasts (via Kupiec and Christoffersen tests). Their combined application ensures that the ESRNN-VAE model is empirically accurate, theoretically sound, and practically relevant for financial risk management and investment decision-making under uncertainty.

4 Empirical results and discussion

The empirical analysis employs time series data to implement combined forecasting for stock prices, specifically by utilizing Sasol's adjusted closing stock prices from January 2010 to May 2025. The architectures are implemented in TensorFlow version 2.15, developed by Ramchandani et al. [37]. We do time series cross-validation on the training and test sets. Each set covers a continuous sample period to avoid look-ahead bias, and the test set has the most recent data. Figure 2a presents the stock's closing price trends, revealing significant fluctuations, including a notable crash around 2020, followed by a recovery and a more recent decline. The kernel density plot in Figure 2b indicates a non-normal, multimodal distribution with a primary peak around a closing price of 10.5 and other clusters at lower values, a characteristic further supported by the Q-Q plot in Figure 2c, which shows deviations from a theoretical normal distribution, particularly in the lower tails. While the Box Plot in Figure 2d visualizes a median closing price slightly above 10.0 and an interquartile range largely between 9.5 and 10.7, it highlights numerous lower-priced occurrences identified as outliers, emphasizing the complex and volatile nature of the closing price behavior over the observed period.

Figure 2

Figure 2. Time series plot for the Sasol adjusted closing price: Time series plot (a), Kernel density plot (b), QQ Plot (c), and Box plot (d).

The summary data in Table 1 indicate that the distribution of the closing prices deviates significantly from a normal distribution. The skewness of –1.49 shows a strong left tail, which means that the Sasol closing stock has had a few large losses that have happened very seldom. Most of the observations are to the right of the mean. A kurtosis of about 56.2926 (greater than the typical value of 3) indicates that the tails are more pronounced than a price of 10.33, and the low volatility, with a standard deviation of 0.50, helps to establish the scale. The very high Jarque–Bera statistic (2,375) reveals that the joint skew/kurtosis severely violates normality; hence, the calculated probability value is less than 5% level of significance. This led to the rejection of normality in the Sasol closing stock prices.

Table 1

Table 1. Descriptive statistics for closing prices.

To sum up, Sasol's closing price distribution is not symmetrical. Most days, there are small gains or losses, but the occasional large losses create a long left tail and strong non-normal impacts. Moreover, the left-skewed and leptokurtic profile suggests a downside risk that may undermine investor confidence. In practice, investors anticipate ‘frequent small gains and a few large losses', indicating that the observed asymmetry reveals high tail events. Sasol's profitability is associated with fluctuating oil and chemical prices, which means that abrupt changes in commodity values (such as a drop in oil or petrol prices) have led to significant negative returns observed in the data [38]. In the context of South Africa, the connection between foreign investment and growth is intricately linked to commodity cycles, making such volatility particularly significant. In Sub-Saharan Africa, a downturn in commodity prices often aligns with a decrease in inward investment, highlighting that Sasol's volatility reflects wider risks associated with resource dependence [39].

4.1 Short-, medium-, and long-term forecasts of closing stock prices

This section employs exponentially smoothed recurrent neural networks and Variational Autoencoders to generate short- to long-term forecasts of closing stock prices. Before training and testing these architectures, we perform the Augmented Dickey-Fuller (ADF) test to assess stationarity. The test results indicate that the null hypothesis of a unit root cannot be rejected at the 5% significance level. Consequently, these findings support the use of a dynamic modeling approach rather than a static model for the time series data because the data are non-stationary; hence, a dynamic model that accounts for temporal changes is more appropriate and effective than a static one.

4.1.1 Exponentially smoothed recurrent neural network

The ESRNN architecture is designed to predict stock prices in the next five, 24, and 60 business days. To achieve this, the data is first divided into training and test sets, with the final five, 24, and 60 observations set aside for testing and validation. The model 5-day and 24-day lag values, to provide contextual insight into recent, medium and long-term market trends. These features effectively help the model interpret short- and medium-term momentum and seasonality. To enhance sensitivity to shocks, several exogenous drivers discussed previously are incorporated in the post-hoc analysis via explainable AI (SHAP for feature importance). We configure our ESRNN to detect a seasonality pattern of five, 24, and 60 business days, reflecting a typical weekly, monthly and 3-month trading cycle. The model bases its predictions on the last 5, 24, and 60 business days, which correspond roughly to one week, a month and 3 months of data. It is trained on the historical data for up to 500 iterations or epochs. This design allows ESRNN to capture regular seasonal behaviors and complex, nonlinear market dynamics that frequently arise in financial time series.

Table 2 shows how well the exponential smoothing recurrent neural network performs for short-term (5-step), medium-term (24-step), and long-term (60-step) forecasts. Forecast accuracy is enhanced with an increasing prediction horizon, as evidenced by a decrease in mean squared error from 0.1399 in the short term to 0.0053 in the long term and a reduction in mean absolute error from 0.3087 to 0.0674. The forecast error percentage exhibits a notable decline, indicating a reduction in substantial forecast errors over extended horizons. Theil's inequality coefficient decreases from 0.0216 to 0.0041, suggesting that ESRNN's forecasts significantly surpass naĩve benchmarks at extended horizons. The trends indicate that the ESRNN model effectively captures long-term dependencies and smoother patterns in the data, rendering it highly suitable for extended forecast intervals.

Table 2

Table 2. Short, medium, and long term rolling forecasts for ESRNN.

Regarding training performance, the model stays efficient; training time rises slightly from 0.40 seconds (short-term) to 2.17 seconds (long-term), and training loss is quite low throughout all horizons. This efficiency supports the viability of the ESRNN for real-world applications in which both speed and accuracy are critical. Long-term projections are often the most accurate and reliable tool for macro-level studies and investment planning. Appropriate for operational or policy planning, the medium-term predictions provide a solid mix of accuracy and computing cost. However, short-term predictions have bigger errors because it is harder to predict unpredictable market changes, which indicates that using more specialized methods or faster data might be helpful for these tasks.

4.1.2 Variational autoencoder

We use a variational autoencoder (VAE) to find hidden patterns in the time series data and forecast future prices. The VAE design has an encoder that reduces the lag features (5-day and 24-day lags) into a simpler form and a decoder that rebuilds the expected price from this simpler form. VAE facilitates uncertainty-aware predictions by modeling the distribution over latent variables. The reparameterization trick facilitates model training through backpropagation, while the overall loss function maintains a balance between reconstruction accuracy and the regularization enforced by the Kullback–Leibler (KL) divergence. The model was trained for 100 epochs using the Adam optimiser, which facilitated stable convergence. The VAE demonstrates robust generalization across various market conditions, making it an appropriate option for probabilistic forecasting. The system accurately identifies patterns based on current market behavior, providing a flexible, nonlinear model that captures its inherent volatility. This feature is important in financial settings where visible trends and underlying factors influence price fluctuations. We constructed datasets for short-term (H = 5), medium-term (H = 24), and long-term (H = 60) horizons using rolling windows to assess forecasting performance. We made predictions using past data with the trained VAE and then compared these predictions to the real values. The results are reported in Table 3.

Table 3

Table 3. Short, medium, and long term rolling forecasts for VEA.

Table 3 shows the performance of the Variational Autoencoder model on short-term (5-day), medium-term (24-day), and long-term (60-day) rolling forecast horizons. Short-term forecasts are the most accurate, with the lowest Mean Squared Error (0.0184), lowest Mean Absolute Error (0.0845), and highest Forecast Efficiency Percentage (92.73%). Furthermore, exhibiting excellent short-term prediction performance is Theil's Inequality Coefficient (0.0065). Minimum training duration and resultant loss in the short-term environment indicate that the VAE fits short-term market dynamics with less complexity and quicker convergence. In contrast to medium- and long-term predictions, which undergo a gradual decrease in performance, medium- and long-term projections do not suffer from such significant loss. With the Forecast Efficiency Percentage being 73.65%, MSE and MAE go up to 0.0671 and 0.1803, respectively, over the 24-day horizon; the final training loss increases to 8.2762. Forecast accuracy is also reduced (MSE of 0.0818, FEP of 68.16%), and loss is at its highest point at 13.5488 for the 60-day horizon. Training times continue to be very stable across all horizons despite diminishing accuracy with longer horizons, further bringing out the scalability of the VAE paradigm. The VAE provides a computationally lightweight, uncertainty-aware architecture that is computationally tractable with increasing prediction horizons and exhibits overall good short-term predictability. Large economic and financial effects depend on how well the Variational Autoencoder (VAE) model works over different times for making predictions. The high short-term accuracy (MSE = 0.0184, FEP = 92.73%) shows that recent trends affect current price changes, which are well caught by features that look back in time. Such performance supports the idea that short-term market behaviors may follow structured patterns, which aligns with the idea that prices quickly reflect new public information while allowing for clever trade strategies. The bigger estimate errors for the medium forecast (MSE = 0.0671, FEP = 73.65%) and long-term (MSE = 0.0818, FEP = 68.16%) ranges, on the other hand, show that longer rolling windows come with more doubt and volatility. It is harder to figure out how these things affect prices in the future just by looking at price lags. These trends show how macroeconomic forces, market mood, and policy changes affect prices over time. This makes the VAE model especially helpful for high-frequency or short-term forecasting techniques, including day trading or short-horizon portfolio rebalancing, where fast and precise forecasts are crucial for stock price prediction. However, its declining performance over longer timeframes indicates little independent relevance for long-term planning or strategic investment guidance. Still, its latent variable model and uncertainty-aware design make it useful for applications such as stress testing and Value-at-Risk relating to volatility forecasting and risk management. The VAE's probabilistic modeling of transient price fluctuations enhances deterministic models such as ESRNN to provide a more complex understanding of market dynamics over periods.

4.1.3 Combined ESRNN-VAE and feature importance for forecasting downside risk

To enhance the reliability of our forecasting system, we adopt a model combination strategy that merges predictions from the ESRNN and the VAE using a weighted average—60% ESRNN and 40% VAE. This weighting is informed by empirical findings: the ESRNN provides superior accuracy in long-term forecasting, while the VAE performs better in the short term but is less consistent over extended horizons. By amalgamating the strengths of both architectures, the model achieves improved generalizability across diverse forecast periods. In this model, investor sentiments, oil prices, 24 lags (i.e., month), COVID-19, the Russia and Ukraine war, 5 lags (i.e., a week), the 2015/2016 Shanghai stock crash and SA monetary policy news are included. The aim is to enhance the prediction and interpretability of the model for downside risk.

As shown in Table 4, the combined model performs well across all horizons, with particularly strong long-term results. In the short term (H = 5), the model yields low error metrics (MSE = 0.000412, MAE = 0.00161), though it requires the longest training time and incurs the highest training loss, reflecting the complexity of short-term dynamics. In the medium term (H = 24), it maintains balanced accuracy (MSE = 0.00052, MAE = 0.00057) with improved training efficiency, demonstrating the effective interplay between the ESRNN and VAE. For long-term forecasts (H = 60), the model achieves its lowest MSE (0.000224), lowest forecast error percentage (0.09%), and fastest training, although a higher MAE (0.09716) suggests the presence of a few larger deviations. Overall, the results validate the effectiveness of the weighted combination, delivering reliable and generalisable forecasts across varying time horizons.

Table 4

Table 4. Forecasting performance of the combined ESRNN-VAE model.

The empirical application of the ESRNN-VAE model on SASOL stock prices demonstrates its ability to generate robust, horizon-sensitive forecasts that enhance downside risk management. By combining the ESRNN's strength in capturing long-term dependencies with the VAE's ability to model short-term volatility, the model improves return prediction accuracy. These forecasts enable forward-looking risk assessments, including Maximum Drawdown (MDD), Marginal Expected Shortfall (MES), and the Sortino Ratio—key metrics for evaluating downside exposure. Given the sensitivity of SASOL's performance to oil prices, market conditions, and geopolitical events, this approach supports the anticipation of large losses, portfolio stress testing, and systemic risk evaluation. Additionally, it informs trading decisions by identifying periods of heightened risk or favorable risk-adjusted returns and supports dynamic asset allocation across varying market regimes. The model's adaptability makes it suitable for broader financial applications, including equities, commodities, and multi-asset portfolios.

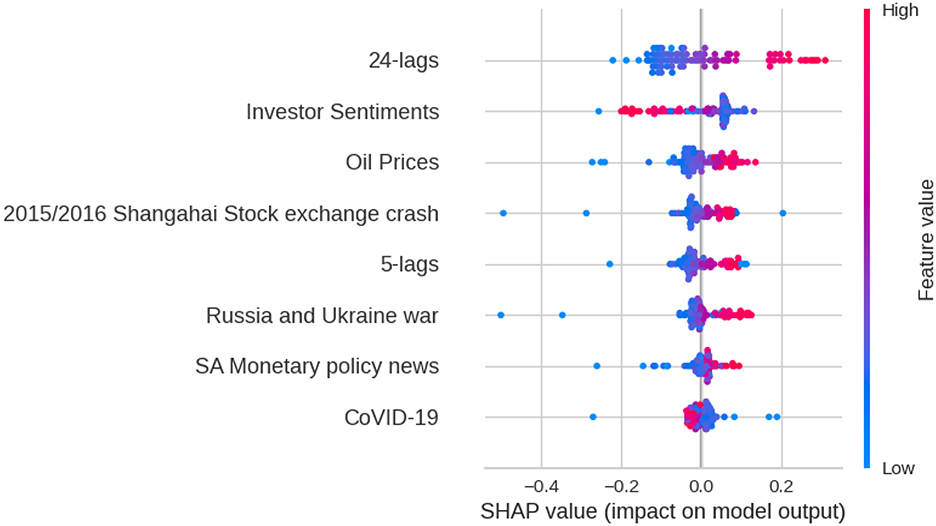
The model integrates economic and stock market features pertinent to the Johannesburg Stock Exchange (JSE) to improve predictive performance. The factors encompass “SA Monetary Policy News,” “Oil Prices,” “Investor Sentiments,” “COVID-19,” the “2015/2016 Shanghai Stock Exchange Crash,” and the “Russia and Ukraine War,” along with autoregressive components like “5-lags” and “24-lags.” By employing Shapley Additive exPlanations (SHAP), we are able to quantify the contribution of individual features to the predictions of our combined model; therefore, Figure 3 illustrates that the most influential features include oil prices, investor sentiment, and time-dependent behavior (24 lags), which are equivalent to monthly seasonal variation, which are essential for understanding the real-world dynamics of Sasol's returns. The results suggest that downside risk in Sasol stock market is primarily influenced by significant uncertainty and changes in sentiment, followed by oil prices, particularly during crisis events such as the COVID-19 pandemic or geopolitical tensions.

Figure 3

Figure 3. SHAP values for feature importance.

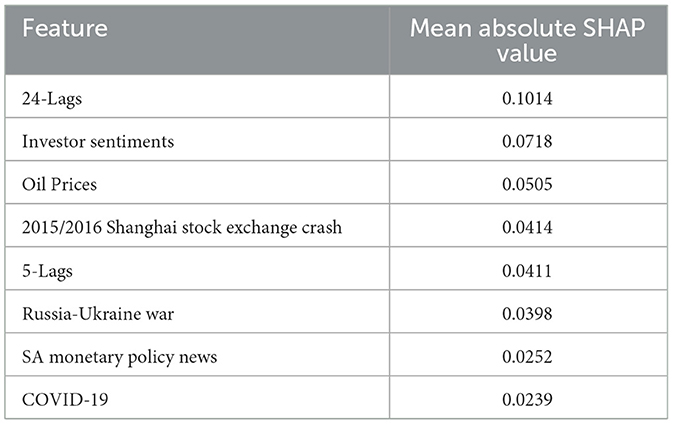
By integrating behavioral, macroeconomic, geopolitical, and autoregressive signals, the ESRNN-VAE model—supported by SHAP analysis—provides interpretable and actionable insights into downside risk. The model not only identifies key risk contributors but also quantifies their effects, enhancing its utility in proactive risk management and adaptive portfolio construction. This reinforces its value as a practical tool for understanding and responding to complex financial environments. The global SHAP analysis is conducted to quantify the contribution of each feature, indicating that the 24-day lag is the most influential in predicting Sasol's returns, with a mean absolute SHAP value of 0.1014. This finding underscores the significance of long-term autoregressive dynamics and possibly monthly seasonality in influencing return behavior. Investor sentiments represent the second most significant feature (0.0718), underscoring the influence of behavioral factors and market psychology on asset prices, especially the propensity for heightened sentiments to precede corrections. Oil prices (0.0505) demonstrate a significant impact, which is expected due to Sasol's involvement in global energy markets; variations in oil prices directly influence profitability and investor expectations. The 5-day lag (0.0411) and SA Monetary Policy News (0.0252) significantly contribute, suggesting that the model effectively incorporates both short-term memory effects and localized macroeconomic policy signals. These findings demonstrate the model's capacity to integrate internal time series patterns with pertinent external drivers. Refer to Table 5.

Table 5

Table 5. Global feature importance based on mean absolute SHAP values.

Geopolitical and systemic events also feature prominently. The 2015/2016 Shanghai Stock Exchange Crash (0.0414), the Russia-Ukraine War (0.0398), and COVID-19 (0.0239) all significantly influence the model's forecasts, validating its sensitivity to exogenous shocks, but have less impact as compared to investor sentiments and oil prices among others. These events typically increase uncertainty and risk premiums, leading investors to re-price assets, which the ESRNN-VAE effectively captures. The contribution of such rare but impactful events demonstrates the model's strength in recognizing downside risk triggers. Overall, the SHAP values provide a transparent and interpretable breakdown of how macroeconomic, behavioral, and autoregressive factors shape forecasted returns. This enhances the model's practical utility in informing risk-aware decision-making and highlights its robustness in environments characterized by both persistent patterns and sudden shocks.

4.2 Forecasting downside risk

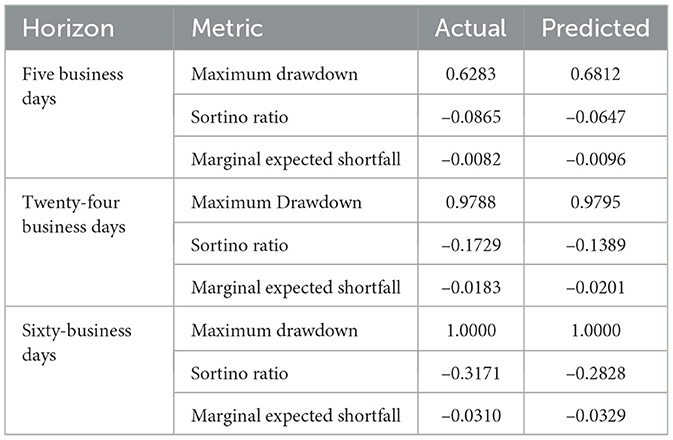
We use maximum drawdown, Sortino ratio, and marginal expected shortfall metrics to model downside risk. Table 6 indicates that the integrated ESRNN-VAE model successfully predicts downside risk metrics for all investment horizons. The predicted values for Maximum Drawdown align closely with actual values across all horizons, exhibiting only minor discrepancies, such as 0.6812 predicted vs. 0.6283 actual over five business days, demonstrating the model's effectiveness in capturing potential peak-to-trough losses. The Sortino Ratio, emphasizing downside volatility, shows a marginal improvement in predictions across all horizons (e.g., from –0.0865 actual to –0.0647 predicted in the short term), suggesting the model forecasts slightly enhanced risk-adjusted returns. In contrast, marginally expected shortfall predictions exhibit a more conservative approach, indicating slightly greater losses than the actual values, with a prediction of –0.0096 compared to an actual value of –0.0082 over five days. This indicates that the model prioritizes caution in estimating tail risk, which may be advantageous for risk-averse decision-making. The horizon extending to 60 business days shows that all three predicted metrics remain closely aligned with actual values, reinforcing the model's ability to generalize over extended forecasting periods. These results indicate that the ESRNN-VAE model delivers reliable and realistic forecasts of downside risk, which can facilitate informed investment and risk management strategies.

Table 6

Table 6. Performance metrics for actual and predicted returns.

The practical use of the combined ESRNN-VAE model on SASOL stock prices and the wider financial markets shows that it effectively predicts downside risk over different investment time frames. Table 6 shows that the model reliably estimates the real values of Maximum Drawdown, Sortino Ratio, and Marginal Expected Shortfall (MES), which are important for evaluating different parts of downside risk. Over short (5-day), medium (24-day), and long-term (60-day) periods, the predicted values match the actual risk measurements, showing that the model works well in both unstable and stable situations. The predicted Sortino Ratios consistently exhibit lower negative values than the actuals, indicating that the model forecasts reduced downside volatility. In contrast, the MES values maintain a realistic and forward-looking perspective regarding tail risk. For SASOL, which is affected by changes in oil prices and market issues, these predictions can help make smarter and safer adjustments to investment strategies, protection methods, and ways to keep capital safe. This integrated forecasting approach can be applied to various financial assets, enabling investors and risk managers to more effectively anticipate drawdowns, evaluate tail losses, and maximize risk-adjusted performance across diverse market conditions.

4.3 Testing the stability of ESRNN-VAE

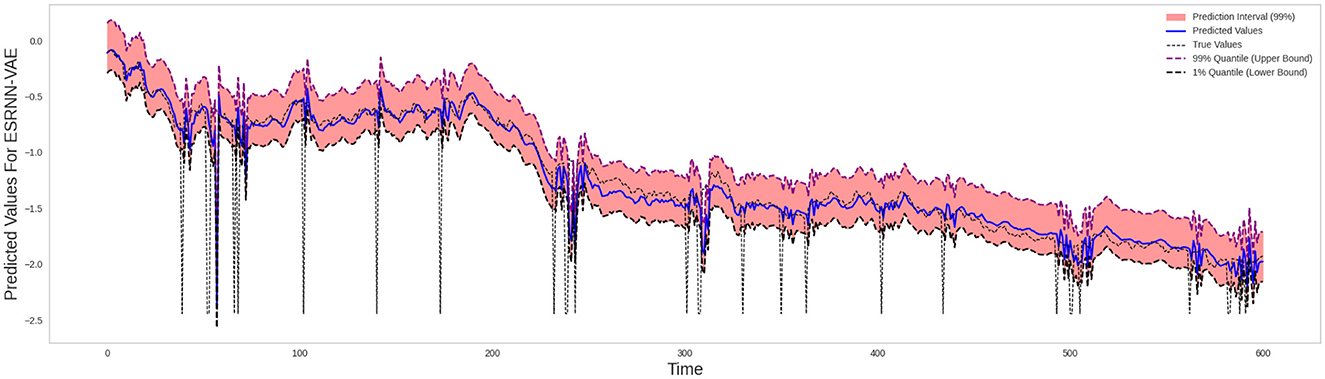
Evaluating the stability of the model is necessary to determine whether the model accurately predicts extreme market fluctuations and whether potential losses are underestimated. The average prediction interval width (PIW) of 3.4398 at the 99% confidence level shows that the model expects future values to vary widely, covering 99% of the predicted results. This large period greatly benefits from forecasting downside risk, enabling the model to incorporate infrequent yet severe events that significantly impact financial performance. The larger prediction interval ensures that risks of extreme losses and tail risks are properly considered in risk metrics like Maximum Drawdown, Sortino Ratio, and Marginal Expected Shortfall (MES). For example, this cautious projection range helps Maximum Drawdown discover possible peak-to-trough losses. In a similar vein, a larger interval that captures more downward dispersion improves the Sortino ratio, which emphasizes negative volatility. Additionally, combining the 99% PIW with MES enhances the model's ability to show systemic risk in very challenging situations. Generally, the 99% PIW of 3.4398 enables a more accurate and careful appraisal of downside risk, which is crucial for educated financial decision-making and risk-reducing techniques. These results are also reported in Figure 4.

Figure 4

Figure 4. Assessment of model stability.

5 Conclusion and recommendations

This study demonstrates the effectiveness of a hybrid ESRNN-VAE model in forecasting the stock prices of Sasol Limited, a commodity-linked equity characterized by non-normal, left-skewed return distributions driven by geopolitical shocks and commodity super-cycles. The ESRNN component excels in capturing long-term structural patterns such as trend and seasonality, while the VAE proves particularly adept at modeling short-term volatility and tail-risk regimes. When combined in a weighted ensemble (60% ESRNN, 40% VAE), the model yields robust forecasts across various time horizons, with the long-term mean squared error reaching as low as 0.000224. Importantly, Shapley value analysis confirms that oil prices, investor sentiment, and monetary policy announcements are critical drivers of downside risk, reinforcing the model's economic relevance. The ESRNN-VAE accurately estimates risk measures such as Maximum Drawdown and Marginal Expected Shortfall, with the 99% prediction interval (PIW: 3.4398) demonstrating the model's reliability under extreme market conditions.

The results provide compelling evidence that this combined approach offers a practical and scalable solution for downside risk forecasting in resource-sensitive markets. Its capacity to account for structural seasonality, nonlinear volatility regimes, and exogenous shocks renders it highly applicable to real-world financial decision-making. As such, the model offers valuable insights for institutional investors, risk managers, and policymakers operating in commodity-dependent economies. Future research could expand the model's application to other emerging market equities with similar exposure profiles, while also incorporating real-time macroeconomic indicators for adaptive learning. Furthermore, integrating attention-based architectures or transformer models may enhance the model's capacity to capture long-range dependencies and improve interpretability in multivariate settings.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.moneyweb.co.za/tools-and-data/click-a-company/SOL/.

Author contributions

CSi: Conceptualization, Writing – original draft. NM: Conceptualization, Methodology, Writing – review & editing. KM: Formal analysis, Writing – original draft. CSh: Methodology, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors are grateful to the numerous people who have provided helpful comments on this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Corbet S, Larkin C, Lucey B. The contagion effects of the 2014 Ebola crisis. J Econ Behav Organ. (2020) 174:1–17.

Google Scholar

2. Ivanov D. Supply chain viability and the COVID-19 pandemic. Int J Prod Res. (2021) 59:3535–52. doi: 10.1080/00207543.2021.1890852

Crossref Full Text | Google Scholar

3. Batten J. Climate risk and energy commodities: a review. Energy Econ. (2023) 118:106499. doi: 10.1016/j.eneco.2022.106499

Crossref Full Text | Google Scholar

4. Ding R. Climate risk and commodity dependencies. J Bank Fin. (2021) 133:106248.

Google Scholar

5. Sasol IR. Investor Relations Reports: Price Sensitivity Analysis. Sandton: Sasol Limited. (2025).

Google Scholar

6. Box GEP, Jenkins GM. Time Series Analysis: Forecasting and Control. New York: John Wiley & Sons. (1976).

Google Scholar

7. Bollerslev T. Generalized autoregressive conditional heteroskedasticity. J Econom. (1986) 31:307–27. doi: 10.1016/0304-4076(86)90063-1

Crossref Full Text | Google Scholar

8. Cont R. Empirical properties of asset returns: stylized facts and statistical issues. Quant Finance. (2001) 1:223–36. doi: 10.1080/713665670

Crossref Full Text | Google Scholar

9. Li Y, Zheng W, Zheng Z. Deep robust transformer for stock prediction. Expert Syst Appl. (2023) 213:119209.

Google Scholar

10. Xiong Y, Li Q, Zhang J. LSTM-GARCH fusion models for commodity volatility prediction. J Risk. (2023) 25:33–58.

Google Scholar

11. Taleb NN. Statistical Consequences of Fat Tails. Cape Town: STEM Academic Press. (2020).

Google Scholar

12. Sezer OB, Gudelek MU, Ozbayoglu AM. Financial time series forecasting with deep learning: a systematic literature review: 2005–2019. Appl Soft Comput. (2020) 90:106181. doi: 10.1016/j.asoc.2020.106181

Crossref Full Text | Google Scholar

13. Ready M. Volatility asymmetry and GARCH models. J Finan Econometr. (2018) 16:20–45.

Google Scholar

14. Eskom. South African Electricity Supply and Demand Report. Eskom Holdings SOC Ltd. (2025).

Google Scholar

15. Li W, Law KLE. Deep learning models for time series forecasting: a review. IN IEEE Access. (2024) 12:92306–27. doi: 10.1109/ACCESS.2024.3422528

Crossref Full Text | Google Scholar

16. Novyko V, Bison C, Gepp A, Harris, Vanstone BJ. Deep learning applications in investment portfolio management: a systematic literature review. J Account Literat. (2025) 47:245–76. doi: 10.1108/JAL-07-2023-0119

Crossref Full Text | Google Scholar

17. Huang X, Tan L, Su H, Cheah JET. Using deep learning conditional value-at-risk-based utility function in cryptocurrency portfolio optimization. Int J Finan Econ. (2025) 2025:e70012. doi: 10.1002/ijfe.70012

Crossref Full Text | Google Scholar

18. Eliasson E. Long Horizon Volatility Forecasting Using GARCH-LSTM Hybrid Models: A Comparison Between Volatility Forecasting Methods on the Swedish Stock Market. Master's thesis, KTH Royal Institute of Technology, Stockholm, Sweden. (2023). Available online at https://kth.diva-portal.org/smash/record.jsf?pid=diva2%3A1849031anddswid=7416 (Accessed June 29, 2025).

Google Scholar

19. Zhang J, Lin W. Weighted ensemble methods in deep financial forecasting. Quantit Finan. (2022) 22:2089–106.

Google Scholar

20. Feugang NB, Azemtsa DH, Wafo SC. Variational autoencoders for completing the volatility surfaces. J Risk Finan Manag. (2025) 18:239. doi: 10.3390/jrfm18050239

Crossref Full Text | Google Scholar

21. Chen L. Risk management with feature-enriched generative adversarial networks (FE-GAN). arXiv preprint arXiv:2411.15519 (2024).

Google Scholar

22. Yin Z, Barucca P. Variational heteroscedastic volatility model. arXiv preprint arXiv:2204.05806 (2022).

Google Scholar

23. Geman H. Portfolio insurance and synthetic securities. Appl Stochast Models Data Analy. (1992) 8:209–20. doi: 10.1002/asm.3150080307

Crossref Full Text | Google Scholar

24. Hemraj S. 2019 Carbon Tax Act—South Africa: Workshop on Carbon Taxation. Presented at the Swedish Ministry of Finance workshop, Jacobsgatan 24, Stockholm. National Treasury, South Africa. (2019). Available online at https://www.financeministersforclimate.org/sites/cape/files/inline-files/South%20Africa%20Carbon%20Tax.pdf (Accessed June 14, 2025).

Google Scholar

25. Xaba LD, Moroke ND, Metsileng LD. Performance of MS-GARCH models: Bayesian MCMC-based Estimation. In:Adıgüzel Mercangöz, B., , editor Handbook of Research on Emerging Theories, Models, and Applications of Financial Econometrics. Cham: Springer (2021). doi: 10.1007/978-3-030-54108-8_14

Crossref Full Text | Google Scholar

26. Smyl S. A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. Int J Forecast. (2020) 36, 75–85. doi: 10.1016/j.ijforecast.2019.03.017

Crossref Full Text | Google Scholar

27. Dixon M. Industrial forecasting with exponentially smoothed recurrent neural networks. Technometrics. (2022) 64:114–24. doi: 10.1080/00401706.2021.1921035

Crossref Full Text | Google Scholar

28. Xie Y. Historical simulation, variance-covariance and monte carlo simulation methods for market risk assessment: from NASDAQ index 2015–2024. In: Proceedings of the 3rd International Conference on Management Research and Economic Development (2025). doi: 10.54254/2754-1169/2025.21835

Crossref Full Text | Google Scholar

29. Kingma DP, Welling M. Auto-encoding variational Bayes. arXiv preprint arXiv:1312.6114 (2014).

Google Scholar

30. Brownlees C, Mesters G. Detecting granular time series in large panels. J Econom. (2021) 220:544–61. doi: 10.1016/j.jeconom.2020.04.013

Crossref Full Text | Google Scholar

31. Salinas D, Flunkert V, Gasthaus J, Januschowski T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int J Forecast. (2020) 36:1181–91. doi: 10.1016/j.ijforecast.2019.07.001

Crossref Full Text | Google Scholar

32. Bergmeir C, Hyndman RJ, Koo B. A note on the validity of cross-validation for evaluating autoregressive time series prediction. Comput Stat Data Anal. (2018) 120:70–83. doi: 10.1016/j.csda.2017.11.003

Crossref Full Text | Google Scholar

33. Tsay RS. Analysis of Financial Time Series (3rd ed.). New York, NY: Wiley and Sons (2010). doi: 10.1002/9780470644560

Crossref Full Text | Google Scholar

34. Ndlovu T, Chikobvu D. The generalised Pareto distribution model approach to comparing extreme risk in the exchange rate risk of Bitcoin/US Dollar and South African Rand/US Dollar returns. Risks. (2023) 11:100. doi: 10.3390/risks11060100

Crossref Full Text | Google Scholar

35. Cleveland RB, Cleveland WS, McRae JE, Terpenning I. STL: a seasonal-trend decomposition procedure based on loess. J Off Stat. (1990) 6:3–73.

Google Scholar

36. Taylor JW. Forecasting value at risk and expected shortfall using a semiparametric approach based on the asymmetric laplace distribution. J Busin Econ Statist. (2019) 37:121–33. doi: 10.1080/07350015.2017.1281815

Crossref Full Text | Google Scholar

37. Ramchandani M, Khandare H, Singh P, Rajak P, Suryawanshi N, Jangde AS, et al. Survey: tensorflow in machine learning. In: Journal of Physics: Conference Series. IOP Publishing (2022). doi: 10.1088/1742-6596/2273/1/012008

Crossref Full Text | Google Scholar

38. Moneyweb. Is Sasol a screaming buy? (2025). Available online at: https://www.moneyweb.co.za/news/companies-and-deals/is-sasol-a-screaming-buy/#::text=Additionally%2C%20the%20company%20has%20experienced,years%2C%20Sasol%20has%20faced%20financial (Accessed May 19, 2025).

Google Scholar

39. Papadavid P. The unfolding commodity price correction: Africa's resource risks and investment resilience. (2025). Available online at: https://odi.org/en/insights/the-unfolding-commodity-price-correction-africas-resource-risks-and-investment-resilience/#::text=continents.%20For%20Sub,driven%20by%20a%20key%20mega (Accessed May 19, 2025).

Google Scholar

40. Bature TA, Lasisi KE, Abdulkadir A, Adenomon MO, Usman M. Testing for stationarity on selected linear and non-linear time series models of different orders. FUDMA J Renewable Atomic Energy. (2024) 1:90–102. doi: 10.33003/fjorae.2024.0101.08

Crossref Full Text | Google Scholar

Appendix

Figure 5

Figure 5. Five business day trend.

Figure 6

Figure 6. Sixty business day trend.