Quantum adaptive search: a hybrid quantum-classical algorithm for global optimization of multivariate functions

Introduction: We present Quantum Adaptive Search (QAGS), a hybrid quantum-classical algorithm for global optimization of multivariate functions. The method employs an adaptive mechanism that dynamically narrows the search space based on a quantum-estimated probability distribution of the objective function.

Methods: A quantum state encodes information about solution quality through a complex-amplitude mapping, enabling identification of promising regions and progressive tightening of the search bounds; a classical optimizer then performs local refinement. The analysis shows contraction of the search space toward global optima with controlled computational complexity.

Results: In simulation on standard benchmarks (Rastrigin, Styblinski-Tang, Rosenbrock), QAGS attains solutions at or near the true minima with very small absolute errors. Against an Adaptive Grid Search on the Sphere function, QAGS achieves comparable accuracy and shows increasing efficiency with dimensionality.

Discussion: These results indicate that amplitude-encoded region selection combined with classical refinement effectively contracts the search space and can reduce time and space requirements, especially at higher dimensions, while practical hardware implementations of amplitude encoding remain challenging.

1 Introduction

Quantum optimization algorithms aim to utilize quantum mechanical principles to solve problems that are classically hard due to their exponential scaling in the number of variables. Variational methods such as the Variational Quantum Eigensolver (VQE) and the Quantum Approximate Optimization Algorithm (QAOA) have gained popularity. QAOA, through the alternating application of cost and mixing Hamiltonians, explores the solution space in a non-classical manner, while a classical optimizer iteratively refines the parameters to maximize the expectation value of the target Hamiltonian. As demonstrated in the original work [1], this approach can offer theoretical advantages for problems like MaxCut, where quantum superposition allows sampling states that would be difficult to explore classically. Despite promising theoretical speedups, real-world implementations of quantum algorithms have so far failed to demonstrate significant advantages over classical methods, except in highly specialized scenarios and with massive resource overhead. Indeed, it has been shown that quantum advantage for Max-Cut requires hundreds of qubits [2], and even when QAOA exhibits accelerations, these are often negated by the overhead of error correction and the need for repeated measurements. Benchmarks [3] show QAOA's NISQ implementations achieve only marginal improvements, with performance highly sensitive to parameters and problem structure, limiting its current scalability. Further background on hybrid methods and QAOA/VQE variants appears in [4–15]; see also advances in quantum simulation [16] and high-dimensional ML optimization context [17].

In this work, we introduce a non-variational approach to the problem of optimizing a continuous n-variable function. Specifically, we propose a hybrid non-variational method that leverages amplitude encoding, serving as an alternative to the aforementioned quantum optimization algorithms. This approach may offer computational advantages over current classical algorithms, particularly for large-scale problems and the search for minima of complex functions in high-dimensional domains. The QAGS algorithm effectively combines the advantages of quantum computing with classical optimization techniques, and its implementation enables overcoming the curse of dimensionality.

2 Method implementation

We consider the problem of finding the global minimum of a function f:Ω → ℝ defined on a d-dimensional domain.

$\begin{array}{l}{\text{x}}^{*}=arg{\displaystyle \underset{\text{x}\in \text{Ω}}{min}}f(\text{x})\text{ Ω}={\displaystyle \prod _{i=1}^d}\left[l_i,u_i\right]\end{array}$

where [l_i, u_i] are the initial bounds for each variable x_i.

The algorithm start defining a gird on the initial space. For each dimension i, we discretize the interval [l_i, u_i] in 2ⁿ points, where n is the number of qubits for each dimension:

$\begin{array}{l}{x}_{ij}=l_i+j\frac{u_i-l_i}{2^n-1},j=0,\dots ,2^n-1.\end{array}$

This discretization creates a uniform grid that maps classical points to quantum states. We construct a quantum state whose amplitudes encode the value of the objective function.

$\begin{array}{l}\psi (\text{x})=\frac{1}{Z}exp\left(-\frac{f(\text{x})-f_{min}}{\sigma }\right)\end{array}$

where:

- f_min is the current minimum

- σ is the standard deviation

- Z normalize the state.

The algorithm evaluates f at all points in the grid $\mathbf{\text{x}}\in \mathcal{G}$ and constructs a quantum state:

$|\psi \rangle ={\displaystyle \sum _{x\in \mathcal{G}}\sqrt{d(x)}}|x\rangle$

where the probability amplitudes are derived from the function values:

$\begin{array}{l}d(\text{x})\propto \frac{exp\left(-\frac{f(\text{x})-f_{\text{min}}}{\sigma }\right)}{Z}\end{array}$

The amplitude encoding follows the Boltzmann distribution that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system.:

$\begin{array}{l}p(\text{x})\propto exp\left(-\frac{f(\text{x})}{k{T}_{\text{eff}}}\right)\end{array}$

where kT_eff = σ and the ground state energy is shifted by f_min.

The quantum circuit measures the state |ψ〉, yielding probabilities:

$\begin{array}{l}P(\text{x})=|\langle \text{x}|\psi \rangle {|}^2\end{array}$

These probabilities form a discrete probability distribution over the search space, with higher probabilities corresponding to more promising regions. Our amplitude-encoded sampling and measurement steps follow standard gate-model concepts and amplitude amplification/estimation ideas [14, 15, 18, 19].

We identify the most promising regions as those comprising the top 25% probability mass:

$\begin{array}{l}{\text{Ω}}_h^{(k)}=\left\{\text{x}|P(\text{x})\ge P_{75}\right\}\end{array}$

where the 75-th percentile P₇₅ is used as threshold to concentrate the search on regions most likely to contain the global minimum. The new bounds for each dimension are computed by restricting to the projection of ${\text{Ω}}_h^{(k)}$, where the points represent the decimal encoding of quantum states corresponding to the selected probability amplitudes. This yields the refined search domain:

$\begin{array}{l}\left[l_i^{(k+1)},u_i^{(k+1)}\right]={\left[max(l_i,min{x}_i),min(u_i,max{x}_i)\right]}_{\text{x}\in {\text{Ω}}_h^{(k)}}\end{array}$

This contracts the search space to the hyperrectangle enclosing the high-probability region.

A classical optimization routine is then applied within the refined bounds to determine the solution.

$\begin{array}{l}{\text{x}}_l^{(k+1)}=arg{\displaystyle \underset{\text{x}\in \left[{\text{l}}^{(k+1)},{\text{u}}^{(k+1)}\right]}{min}}f(\text{x})\end{array}$

The algorithm terminates when:

- The search space contraction becomes insignificant (|u^(k+1) − l^(k+1)| < δ)

- The maximum iteration count is reached (k = K_max)

- The quantum distribution becomes overly concentrated

The progressive contraction of the search space ensures:

$\begin{array}{l}{\displaystyle \underset{k\to \infty }{lim}}\text{Vol}({\text{Ω}}^{(k)})=0\end{array}$

with probability density concentrating around global minima.

Exemple 1. We consider a 2D function optimization with:

- Global bounds: x₁ ∈ [−5, 5], x₂ ∈ [−10, 10]

- Current promising region ${\text{Ω}}_h^{(k)}$: x₁ ∈ [−2.1, 1.8], x₂∈[3.5, 7.2]

The updated bounds become:

- For x₁: [max(−5, −2.1), min(5, 1.8)] = [−2.1, 1.8]

- For x₂: [max(−10, 3.5), min(10, 7.2)] = [3.5, 7.2]

This strategy ensures:

- Progressive contraction of the search space

- Bounds never exceed the original limits.

3 Experimental analysis

The proposed quantum-classical hybrid approach demonstrates compelling theoretical advantages, although its practical implementation requires careful consideration of several key factors. The simulation results are obtained using Python 3.10, NumPy 1.24, and Qiskit 1.0.0. For simulation frameworks and GPU-accelerated backends, see [20–22]. However, implementing amplitude encoding on real hardware remains challenging, particularly when using a large number of qubits, as implementing numerous gates becomes impractical. Consequently, the results presented here utilize a limited number of qubits for each dimension, especially as the problem dimension increases. Nevertheless, our method's design explicitly accounts for this constraint, offering a distinct advantage over:

- Quantum approaches requiring many qubits on dense grids (e.g., VQE)

- Classical methods needing extensive sampling for higher accuracy

Although a low qubit count may pose challenges only for very large domains, the method remains highly promising in most scenarios.

To visualize the behavior of the search process, we consider the 2D Sphere function: Figure 1 illustrates the progressive refinement of the search space on three Sphere minima, with nested bounding boxes converging to the global optimum.

$\begin{array}{l}f(x,y)={(x-x^{*})}^2+{(y-y^{*})}^2\end{array}$

Figure 1

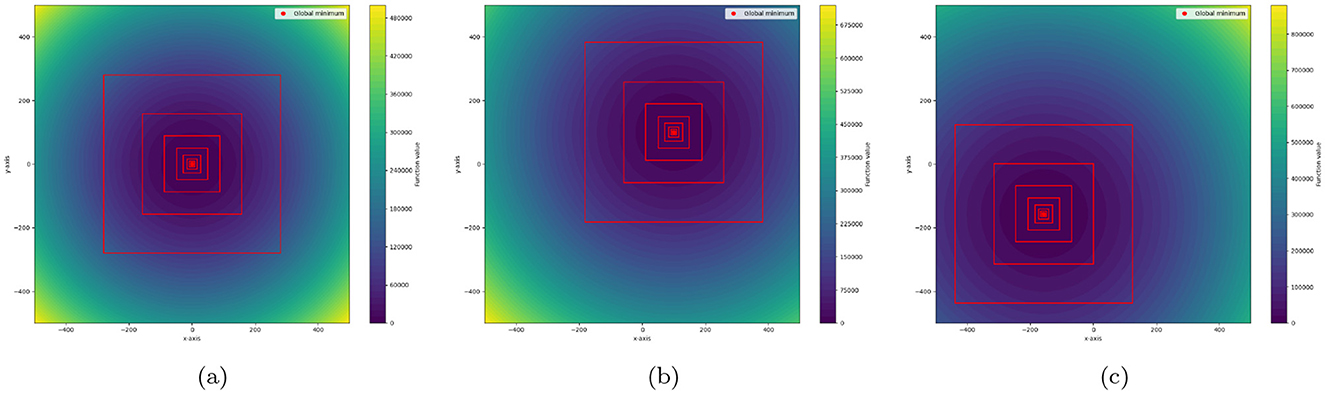
Figure 1. Progressive refinement of the search space on the 2D Sphere function for three different global minima: (a) minimum at (0, 0), (b) minimum at (100, 100), and (c) minimum at (−50π, −50π)≈(−157.08, −157.08). In each plot, the red dot marks the true global minimum (x^*, y^*), while the red rectangles represent the bounding boxes at successive iterations of the quantum search algorithm.

We display three different sequences of rectangular bounding boxes that simulate the iterative contraction of the search domain. In each figure, the red rectangles represent the bounds at successive iterations, and the red dot marks the true minimum. As the iterations proceed, the bounds become increasingly narrow and concentrate around the global optimum.

Tests on result accuracy were performed on standard optimization benchmark functions, detailed below along with the algorithm's performance results. The classical optimizer used is scipy.optimize.minimize with the default L-BFGS-B method (a quasi-Newton bounded optimization algorithm). For classical numerical background and statistical methodology we refer to [23–25].

3.1 Rastrigin function

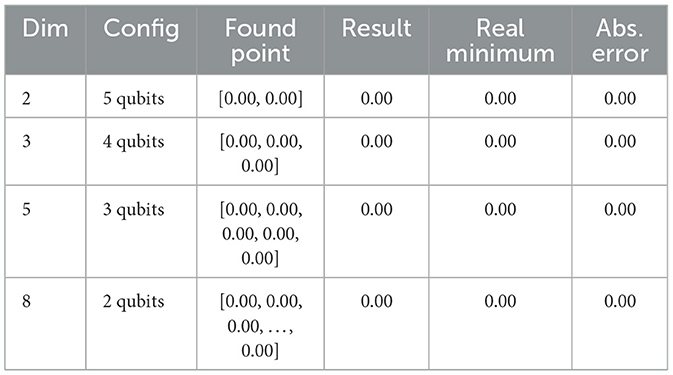
The Rastrigin function (Figure 2a) is defined as follows:

$\begin{array}{l}f(\text{x})=10n+{\displaystyle \sum _{i=1}^n}\left[x_i^2-10cos(2\pi x_i)\right],\end{array}$

where the domain is [−5.12, 5.12]ⁿ and the global minimum is in x = 0, with f(0) = 0.

Figure 2

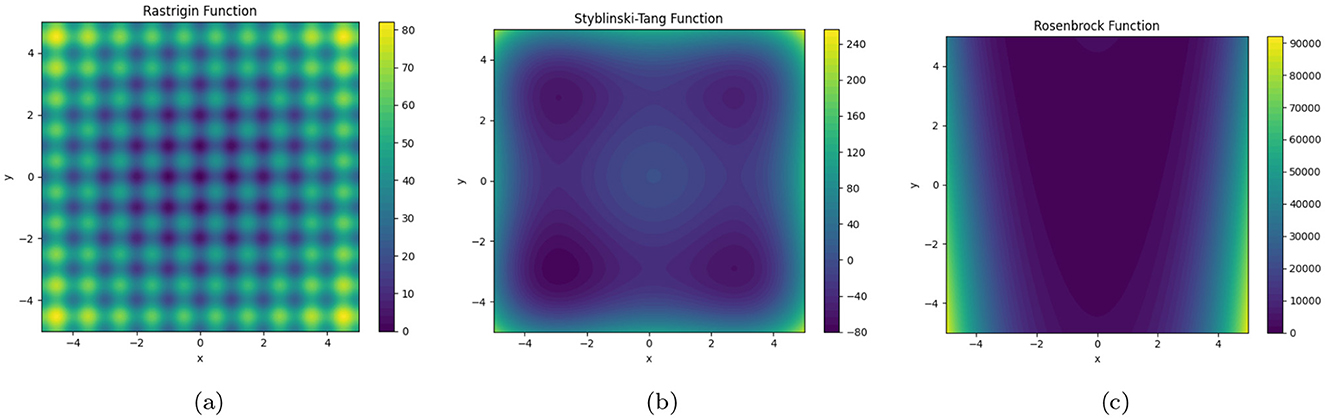
Figure 2. Testing optimization algorithms on benchmark functions: (a) Rastrigin; (b) Styblinski-Tang; (c) Rosenbrock. Experimental results highlight performance and robustness.

As shown in Table 1, the algorithm produces virtually exact results when applied to the Rastrigin function in simulation.

Table 1

Table 1. Rastrigin function results.

3.2 Styblinski-Tang function

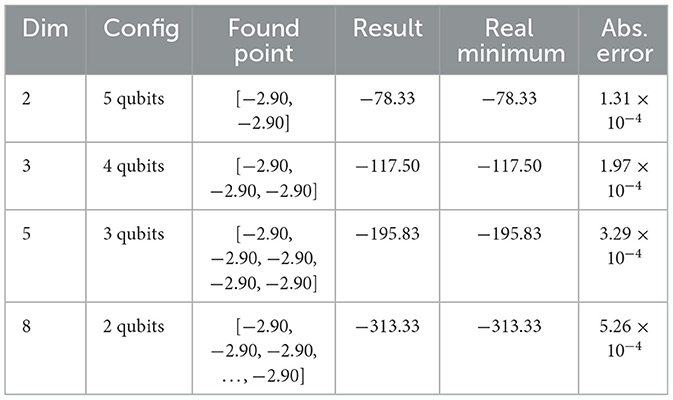
The Styblinski-Tang function (Figure 2b) is defined as follows:

$\begin{array}{l}f(\text{x})=\frac{1}{2}{\displaystyle \sum _{i=1}^n}(x_i^4-16x_i^2+5x_i),\end{array}$

where the domain is [−5, 5]ⁿ and the global minimum is x_i≈−2.903534, with f(x)≈−39.166n. The numerical results and absolute errors obtained by QAGS on different dimensions are summarized in Table 2.

Table 2

Table 2. Styblinski-Tang function results.

3.3 Rosenbrock function

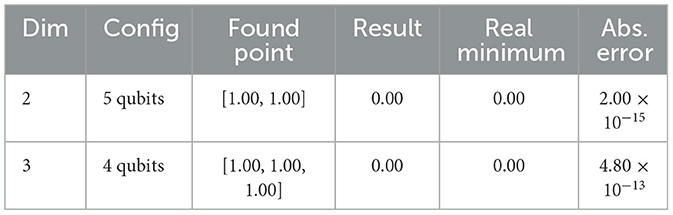
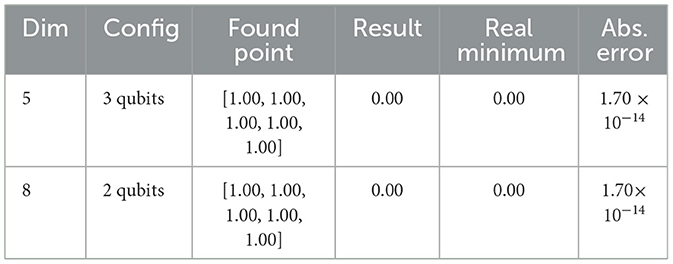
The Rosenbrock function (Figure 2c) is

$\begin{array}{l}f(\text{x})={\displaystyle \sum _{i=1}^{n-1}}\left[100{(x_{i+1}-x_i^2)}^2+{(1-x_i)}^2\right],\end{array}$

where the domain is ℝⁿ. The global minimum in x = (1, …, 1), with f(x) = 0.

Table 3 shows highly accurate results in an extensive domain ([−500, 500]ⁿ), demonstrating a significant advantage over classical methods. However, increasing the dimensionality without proportionally increasing the number of qubits may compromise both the solution accuracy and convergence, potentially leading the search toward suboptimal regions. To maintain performance without additional qubits in higher dimensions, domain restriction becomes essential, as evidenced by the results presented in Table 4.

Table 3

Table 3. Rosenbrock function results ([−500, 500]ⁿ domain).

Table 4

Table 4. Rosenbrock function results ([−10, 10]ⁿ domain domain).

3.4 Classical vs. quantum comparison

This section presents a performance comparison between the QAGS algorithm and an Adaptive Grid Search. The results highlight significant advantages, particularly in memory efficiency, of the quantum-classical hybrid approach. All tests were conducted on the sphere function. As an alternative baseline, adaptive grid search procedures are discussed in [26].

$\begin{array}{l}f(\text{x})={\displaystyle \sum _{i=1}^d}{x}_i^2,\end{array}$

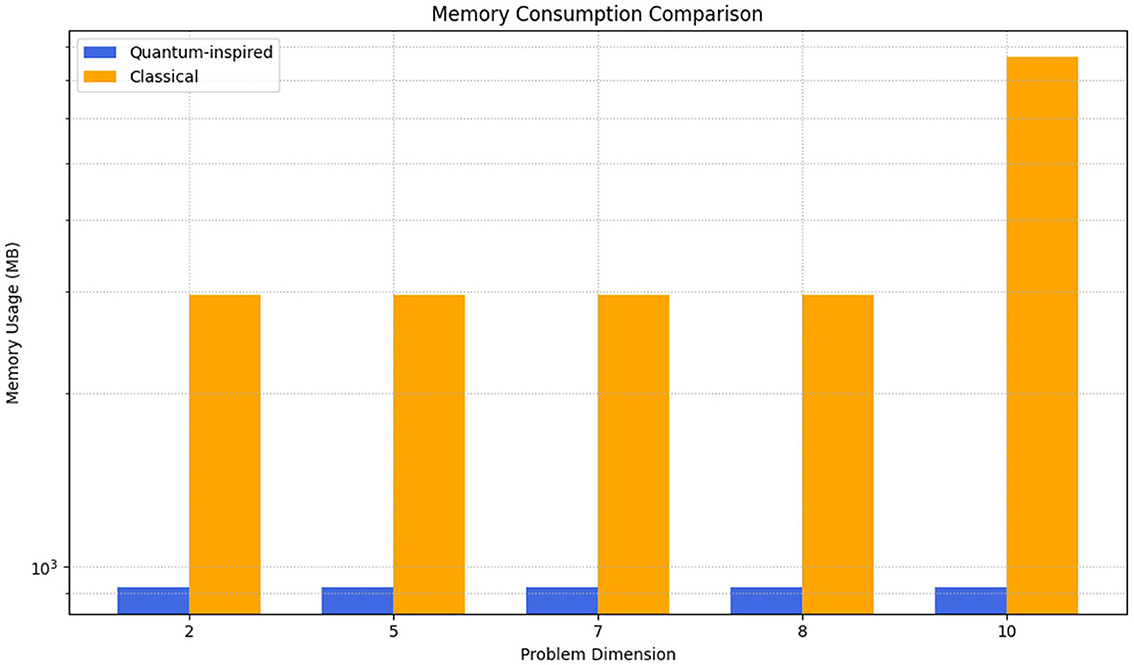
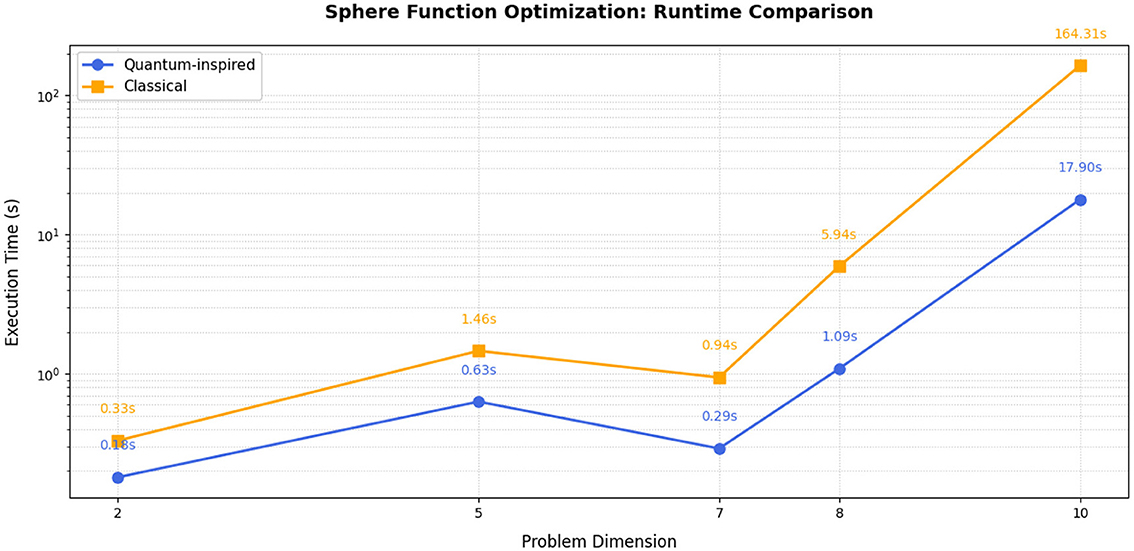
Table 5 shows that when both classical and quantum approaches achieve convergence, the quantum method shows significantly reduced execution times and memory usage. These results were obtained for a restricted domain of [−5, 5]^d.

Table 5

Table 5. Comparative optimization results for [−5, 5]^d.

Figure 3 shows the comparative memory usage both methods. Figure 4 shows that the quantum approach demonstrates variable performance scaling with dimensionality, while classical methods exhibit more consistent behavior in lower dimensions but progressively worse scaling in higher-dimensional spaces.

Figure 3

Figure 3. Memory usage distribution in hybrid-quantum computation (domain [−5, 5]^d).

Figure 4

Figure 4. Comparative performance analysis for Sphere function optimization (domain [−5, 5]^d).

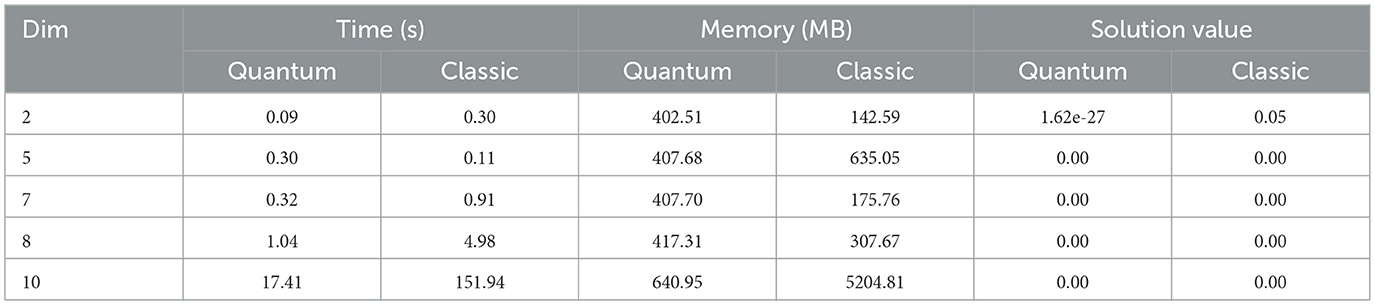
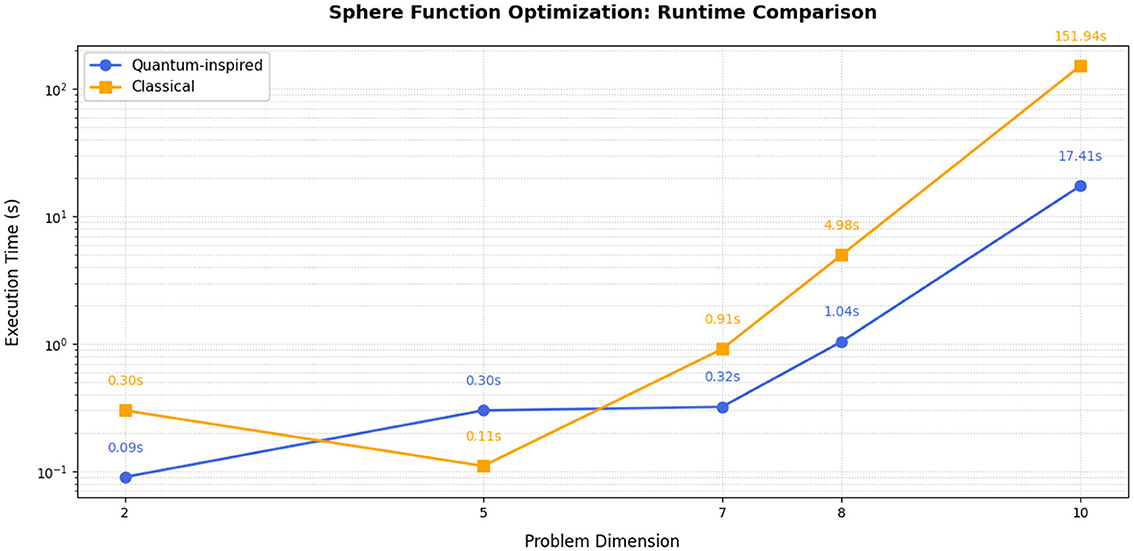
We now examine whether this performance trend persists when expanding the domain range. Table 6 presents the classical versus quantum benchmark results for the Sphere function evaluated in the extended domain [−500, 500]^d. Figure 5 reports the comparative memory usage and Figure 6 reports the runtime for the extended domain [−500, 500]^d.

Table 6

Table 6. Comparative optimization results for sphere function (domain [-500,500]^d).

Figure 5

Figure 5. Memory usage distribution in hybrid-quantum computation (domain [−500, 500]^d).

Figure 6

Figure 6. Comparative performance analysis for Sphere function optimization (domain [−500, 500]^d).

Our analysis first examines the classical memory behavior, which remains approximately constant across domain variations. This stability arises from the adaptive grid point selection strategy implemented to address computational constraints. Specifically, the classical approach was modified to reduce grid density while maintaining convergence guarantees, as excessive grid points (constrained by the curse of dimensionality) previously caused runtime failures. This optimization creates an apparent memory advantage over the quantum approach in lower dimensions.

However, the fundamental quantum advantage becomes evident at higher dimensionality. With dimension d = 10 comparative measurements show that the quantum approach requires 87.7% less memory than the classical implementation.

The same behavior is observed in runtime performance, as the reduction of grid points in certain dimensions may skew the results. However, the data clearly show that for dimension 10, the quantum approach achieves a 88.54% reduction in computation time compared to the classical method.

4 Conclusion

This study introduces a novel methodology for continuous multivariate function optimization, designed to address inherent limitations in classical optimization techniques and could have practical quantum hardware implementations. Although the results presented demonstrate significant promise, they do not incorporate potential errors and noise arising from real-world quantum gate operations. Nevertheless, our primary objective has been to establish that emerging quantum scientific computing approaches can surpass classical methods, particularly in mitigating the curse of dimensionality that plagues high-dimensional optimization problems.

The proposed approach makes substantive contributions to the field of mathematical optimization by providing a robust theoretical foundation capable of addressing complex problems while enabling new interdisciplinary applications. The methodology demonstrates particular effectiveness in scenarios where traditional methods face computational bottlenecks due to dimensional scaling. Notably, our results reveal consistent quantum advantages in both memory efficiency (up to 87.7% reduction) and computational speed (88.54% faster convergence) for problems beyond ten dimensions, even when accounting for domain expansion effects.

Future research should prioritize testing polynomial-guided initialization within the computational frameworks established in [27], where the distinctive properties of U-type polynomials could offer new insights into quantum state preparation. A systematic comparison of encoding efficiency across different polynomial bases, from the q-deformed structures in [28] to the discrete Appell systems in [29], would help identify optimal function representations for high-dimensional problems. Crucially, these theoretical advances must translate into hardware-aware implementations that retain QAGS' demonstrated advantages in memory efficiency and convergence speed. Such efforts would not only bridge abstract polynomial theory with practical quantum optimization but also clarify which mathematical features yield tangible algorithmic benefits.

Future work will apply this hybrid method to additional classical optimizers such as CMA-ES [30] and its limited-memory variant [32], as well as BOBYQA [31].

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GI: Conceptualization, Investigation, Writing – review & editing, Methodology, Visualization, Software, Formal analysis, Writing – original draft. SC: Validation, Supervision, Methodology, Writing – review & editing, Investigation, Visualization. UC: Writing – review & editing, Validation, Visualization. GP: Visualization, Investigation, Writing – review & editing, Validation, Supervision. VS: Visualization, Writing – review & editing, Validation.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

UC, VS, and SC are co-founders of Quantum2pi S.r.l. The company provided no funding and had no role in study design, data collection and analysis, decision to publish, or manuscript preparation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Farhi E, Goldstone J, Gutmann S. A quantum approximate optimization algorithm. arXiv [preprint] arXiv:1411.4028. (2014). doi: 10.48550/arXiv.1411.4028

Crossref Full Text | Google Scholar

2. Guerreschi GG, Matsuura A. QAOA for Max-Cut requires hundreds of qubits for quantum speed-up. Sci Rep. (2019) 05:9. doi: 10.1038/s41598-019-43176-9

PubMed Abstract | Crossref Full Text | Google Scholar

3. Shaydulin R, Alexeev Y. Evaluating quantum approximate optimization algorithm: a case study. In: 2019 Tenth International Green and Sustainable Computing Conference (IGSC). Alexandria, VA: IEEE (2019). p. 1–6.

Google Scholar

4. Lloyd S. Hybrid quantum computing. In: Quantum Information with Continuous Variables. Cham: Springer (2003). p. 37–45.

Google Scholar

5. Choi J, Kim J. A tutorial on quantum approximate optimization algorithm (QAOA): Fundamentals and applications. In: 2019 International Conference on Information and Communication Technology Convergence (ICTC). Jeju: IEEE (2019). p. 138–142.

Google Scholar

6. Kitaev AY, Shen A, Vyalyi MN. Classical and quantum computation. In: Graduate Studies in Mathematics. Rhode: American Mathematical Society (2002). p. 151–175.

Google Scholar

7. Zhang Z, Paredes R, Sundar B, Quiroga D, Kyrillidis A, Dueñas-Osorio L, et al. Grover-QAOA for 3-SAT: quadratic speedup, fair-sampling, and parameter clustering. Quant Sci Technol. (2024) 11:10. doi: 10.1088/2058-9565/ad895c

Crossref Full Text | Google Scholar

8. Endo S, Cai Z, Benjamin SC, Yuan X. Hybrid quantum-classical algorithms and quantum error mitigation. J Phys Soc Japan. (2021) 90:032001. doi: 10.7566/JPSJ.90.032001

PubMed Abstract | Crossref Full Text | Google Scholar

9. Zhang DB, Yuan ZH, Yin T. Variational quantum eigensolvers by variance minimization. arXiv [preprint] arXiv:2006.15781. (2020). doi: 10.48550/arXiv.2006.15781

Crossref Full Text | Google Scholar

10. Montanaro A, Zhou L. Quantum Speedups in Solving Near-Symmetric Optimization Problems by Low-Depth QAOA. (2024).

Google Scholar

11. Golden J, Bärtschi A, O'Malley D, Eidenbenz S. Numerical Evidence for Exponential Speed-Up of QAOA over Unstructured Search for Approximate Constrained Optimization (2023). p. 496–505.

Google Scholar

12. Truger F, Barzen J, Leymann F, Obst J. Warm-starting the VQE with approximate complex amplitude encoding. arXiv [preprint] arXiv:2402.17378 (2024). doi: 10.48550/arXiv.2402.17378

Crossref Full Text | Google Scholar

13. Bechtold M, Barzen J, Leymann F, Mandl A, Obst J, Truger F, et al. Investigating the effect of circuit cutting in QAOA for the MaxCut problem on NISQ devices. Quant Sci Technol. (2023) 8:045022. doi: 10.1088/2058-9565/acf59c

Crossref Full Text | Google Scholar

14. Steane A. Quantum computing. Rep Prog Phys. (1998) 61:117. doi: 10.1088/0034-4885/61/2/002

Crossref Full Text | Google Scholar

15. Scherer W. Mathematics of Quantum Computing. Cham: Springer. (2019).

Google Scholar

16. Daley AJ, Bloch I, Kokail C, Flannigan S, Pearson N, Troyer M, et al. Practical quantum advantage in quantum simulation. Nature. (2022) 607:667–76. doi: 10.1038/s41586-022-04940-6

PubMed Abstract | Crossref Full Text | Google Scholar

17. Mathematical Aspects of Deep Learning. Cambridge: Cambridge University Press (2022).

Google Scholar

18. Brassard G, Hoyer P, Mosca M, Tapp A. Quantum amplitude amplification and estimation. AMS Contemp Mathem Series. Providence, RI: American Mathematical Society (AMS) (2000) 06:305. doi: 10.1090/conm/305/05215

Crossref Full Text | Google Scholar

19. Williams CP. Quantum Gates. London: Springer London (2011). p. 51–122.

Google Scholar

20. Faj J, Peng I, Wahlgren J, Markidis S. Quantum computer simulations at warp speed: assessing the impact of GPU acceleration: a case study with IBM Qiskit Aer, Nvidia Thrust & cuQuantum. In: 2023 IEEE 19th International Conference on e-Science (Limassol). Piscataway, NJ: IEEE (2023). p. 1–10.

Google Scholar

21. Pasquale A, Papaluca A, Farias RMS, Robbiati M, Pedicillo E, Carrazza S. Beyond full statevector simulation with Qibo. arXiv [preprint] arXiv:2408.00384 (2024). doi: 10.48550/arXiv.2408.00384

Crossref Full Text | Google Scholar

22. Javadi-Abhari A, Treinish M, Krsulich K, Wood CJ, Lishman J, Gacon J, et al. Quantum computing with Qiskit. arXiv [preprint] arXiv:2405.08810 (2024). doi: 10.48550/arXiv.2405.08810

Crossref Full Text | Google Scholar

23. Press WH Teukolsky SA Vetterling WT Flannery BP. Numerical Recipes The Art of Scientific Computing. Cambridge: Cambridge University Press. (2007).

Google Scholar

24. Freund RJ, Wilson WJ. Statistical Methods. London: Elsevier. (2003).

Google Scholar

25. Gautschi W. Numerical Analysis. Boston, MA: Springer Science+Business Media (2011).

Google Scholar

26. Poštuvan T, You J, Banaei M, Lebret R, Leskovec J. AdaGrid: adaptive grid search for link prediction training objective. arXiv [preprint] arXiv:2203.16162 (2022). doi: 10.48550/arXiv.2203.16162

Crossref Full Text | Google Scholar

27. Díaz S, Ramírez W, Wani S, Cesarano C, Urieles A. Δ_h-Appell versions of U-Bernoulli and U-Euler polynomials: properties, zero distribution patterns, and the monomiality principle. Afrika Matematika. (2025) 03:36. doi: 10.1007/s13370-025-01286-w

Crossref Full Text | Google Scholar

28. Heredia-Moyano MF, Hernandez WAK, Ramirez SAW. On discrete Appell polynomials of Apostol-Bernoulli-type polynomials and their patterns of distribution of zeros. J Math Comput Sci. (2025) 39:280–91. doi: 10.22436/jmcs.039.02.07

Crossref Full Text | Google Scholar

29. Zayed M, Alqurashi T, Wani S, Ryoo C, Ramírez W. Several characterizations of bivariate quantum-Hermite-Appell Polynomials and the structure of their zeros. AIMS Mathem. (2025) 10:11184–207. doi: 10.3934/math.2025507

Crossref Full Text | Google Scholar

30. Hansen N. The CMA Evolution Strategy: A Tutorial Ithaca, NY: Cornell University Library (2023).

Google Scholar

31. Powell M. The BOBYQA algorithm for bound constrained optimization without derivatives. In: Technical Report, Department of Applied Mathematics and Theoretical Physics. Cambridge: University of Cambridge (2009).

Google Scholar

32. Loshchilov I. A Computationally Efficient Limited Memory CMA-ES for Large Scale Optimization. (2014). p. 397–404.

Google Scholar