- 1Department of Mathematics, Physics and Electrical Engineering, Northumbria University, Newcastle, United Kingdom
- 2Culham Centre for Fusion Energy, Abingdo, United Kingdom
In this article we aim to investigate the kinetic turbulence in a reconnecting current sheet (RCS) with X- and O-nullpoints and to explore its link to the features of accelerated particles. We carry out simulations of magnetic reconnection in a thin current sheet with 3D magnetic field topology affected by tearing instability until the formation of two large magnetic islands using particle-in-cell (PIC) approach. The model utilizes a strong guiding field that leads to the separation of the particles of opposite charges, the generation of a strong polarization electric field across the RCS, and suppression of kink instability in the “out-of-plane” direction. The accelerated particles of the same charge entering an RCS from the opposite edges are shown accelerated to different energies forming the “bump-in-tail” velocity distributions that, in turn, can generate plasma turbulence in different locations. The turbulence-generated waves produced by either electron or proton beams can be identified from the energy spectra of electromagnetic field fluctuations in the phase and frequency domains. From the phase space analysis we gather that the kinetic turbulence may be generated by accelerated particle beams, which are later found to evolve into a phase-space hole indicating the beam breakage. This happens at some distance from the particle entrance into an RCS, e.g. about 7di (ion inertial depth) for the electron beam and 12di for the proton beam. In a wavenumber space the spectral index of the power spectrum of the turbulent magnetic field near the ion inertial length is found to be −2.7 that is consistent with other estimations. The collective turbulence power spectra are consistent with the high-frequency fluctuations of perpendicular electric field, or upper hybrid waves, to occur in a vicinity of X-nullpoints, where the Langmuir (LW) can be generated by accelerated electrons with high growth rates, while further from X-nullponts or on the edges of magnetic islands, where electrons become ejected and start moving across the magnetic field lines, Bernstein waves can be generated. The frequency spectra of high- and low-frequency waves are explored in the kinetic turbulence in the parallel and perpendicular directions to the local magnetic field, showing noticeable lower hybrid turbulence occurring between the electron’s gyro- and plasma frequencies seen also in the wavelet spectra. Fluctuation of the perpendicular electric field component of turbulence can be consistent with the oblique whistler waves generated on the ambient density fluctuations by intense electron beams. This study brings attention to a key role of particle acceleration in generation kinetic turbulence inside current sheets.
1 Introduction
The processes of magnetic reconnection are often observed during eruptive events in the Sun (flares and coronal mass ejections (CMEs)) (Antiochos et al., 1994; Antiochos, 1998; Vilmer et al., 2011; Zharkova et al., 2011; Benz, 2017), heliospheric current sheet (Zharkova & Khabarova, 2012; Zank et al., 2014; Khabarova et al., 2015, 2017), and Earth magnetosphere (Øieroset et al., 2002; Angelopoulos et al., 2008; Chen et al., 2008). The energetic particles generated by magnetic reconnection processes can be detected via hard X-ray (Holman et al., 2011; Zharkova et al., 2011) and γ-ray (Vilmer et al., 2011) emission in solar flares, which are often obscured by various transport effects of particles or radiations. More details can be obtained via in-situ observations of the heliospheric structures by WIND or ACE spacecraft, or the observations in magnetosphere current sheets (CSs) by Clusters mission (Cattell et al., 2005) or by the multi-spacecraft Magnetospheric Multiscale Mission (MMS) (Øieroset et al., 2001; Burch et al., 2016), which can measure particle distributions inside RCSs, while a spacecraft passes through.
The recent space observations of current sheets in the magnetosphere and heliosphere (Fujimoto & Sydora, 2008; Zhou et al., 2009; Huang et al., 2016; Pucci et al., 2017; Eastwood et al., 2018; Phan et al., 2020) and 2D/3D full kinetic and Hall-MHD simulations (Daughton et al., 2004; Matthaeus & Velli, 2011; Roytershteyn et al., 2012; Boldyrev et al., 2013; Franci et al., 2017; Loureiro & Boldyrev, 2017; Papini et al., 2019; Pezzi et al., 2021) had already pointed to a link between reconnection and turbulence. Current sheets contain a sufficient amount of free energy that is released by instabilities in collisionless plasmas at the smallest, kinetic scales often revealing in both hybrid-kinetic and Hall-MHD turbulence simulations the onset of energy transfer at the smallest scales as soon as reconnection is triggered (see for details Matthaeus and Velli, 2011; Papini et al., 2019; Pezzi et al., 2021, and references therein). The small-scale turbulence in a vicinity of those CSs was usually associated with spectral breaks in the magnetic fluctuation spectra near the ion cyclotron frequency Ωci. At larger scales (low frequencies), there is the characteristic inertial range of the turbulent cascade, while below ion scales the turbulent spectra show a clear power law with spectral indices close to −2.7–2.8 (Boldyrev et al., 2013; Franci et al., 2017; Loureiro & Boldyrev, 2017; Pucci et al., 2017; Muñoz & Büchner, 2018). Moreover, the power laws and spectral breaks near CSs are very similar to those measured in homogeneous turbulent solar wind plasmas (Chen et al., 2008; Zhou et al., 2009; Huang et al., 2016; Eastwood et al., 2018; Phan et al., 2020).
Also one of the longest-known instabilities connected with reconnection is the lower hybrid drift instability (LHDI) long suspected to play a role in reconnection (process as observed in space (Cattell et al., 2005; Chen et al., 2008; Divin et al., 2015; Artemyev et al., 2016) and in the laboratory (Carter et al., 2001). Such LHDI occurs near the lower hybrid frequency
The kinetic turbulence in reconnecting current sheets has been extensively investigated (see, for example, Drake et al., 2003; Fujimoto & Machida, 2006; Fujimoto, 2014; Muñoz & Büchner, 2018; Lapenta et al., 2020, and references therein). Cattell et al. (2005) observed the electron holes in the separatrix regions similar to the prediction of 3D PIC simulations (Drake et al., 2003) that are considered to be the nonlinear evolution of the bump-in-tail instability, or Buneman instability (Omura et al., 1996). Lapenta et al. (2020) identified the two regimes of turbulent fluctuations in current sheets: one in the outflow leading to a turbulent regime where the fluctuations involve both fields and particles and the other in the inflow and separatrix region, which involves only the electromagnetic fields, without significantly affecting the particles. The two regimes differ much in practical consequences. The outflow regime is capable of inducing a strong and turbulent energy exchange as well as strong anomalous momentum exchange dominated primarily by the electrostatic term in Ohm’s law. The inflow regime, in contrast, does not lead to substantial fluctuations in the field–particle energy exchange nor significant anomalous viscosity or resistivity limiting turbulence to the electromagnetic fields only. However, the authors presented a more intuitive interpretation of the detected turbulence obtained from PIC simulations without linking it to the regimes of particle acceleration during magnetic reconnection in the presence of magnetic islands.
To understand these kinetic instabilities generated in reconnecting current sheets one needs to explore acceleration of particles dragged into the reconnection region and to investigate the turbulence generated by them. For this reason, we need to refresh our views about the properties of accelerated particles gained during their passage through a reconnecting current sheet with a single and multiple X-nullpoints and to explore which of them, if any, can lead to the formation of turbulence and in what locations. Since the plasma turbulence introduced by beam instabilities is, in general, inherently a 3D problem in PIC simulations (Goldreich & Sridhar, 1995; Siversky & Zharkova, 2009; Muñoz & Büchner, 2018), it requires the simulation domain for acceleration of particles in current sheets to be a 3-dimensional one. The theoretical and numerical studies of magnetic reconnection are typically performed using a simplified system of 2D antiparallel reconnecting magnetic fields with an additional out-of-plane guiding magnetic field (Bg) in the third dimension. Such RCSs with a finite Bg are observed in Earth magnetopause (Silin & Büchner, 2006) and at the impulsive phases of flares and CME eruptions (Fletcher et al., 2011). Owing to large magnetic field gradients and curvatures surrounding the reconnection sites, combined with strong gradients of the plasma temperature and density, the electromagnetic fields vary dramatically inside reconnecting current sheets (RCSs) (Shay et al., 2016; Xia & Zharkova, 2020).
Furthermore, thin elongated RCSs formed in the diffusion region between the reversed magnetic field lines are often broken down by tearing instability into multiple islands, or O-type nullpoints separated by X-nullpoints (Furth et al., 1963; Loureiro et al., 2007; Bhattacharjee et al., 2009). The presence of magnetic islands in reconnecting current sheets was demonstrated by magnetohydrodynamic (Biskamp, 1986; Loureiro et al., 2005; Drake et al., 2006; Lapenta, 2008; Bárta et al., 2011) and kinetic simulations (Huang & Bhattacharjee, 2010; Karimabadi et al., 2011; Markidis et al., 2012). Such chains of magnetic islands have been identified in many solar flares Lin et al. (2005); Oka et al. (2010); Bárta et al. (2011); Takasao et al. (2012); Nishizuka et al. (2015) and CMEs (Song et al., 2012), in the in-situ observations in the heliosphere (Zharkova & Khabarova, 2012; Khabarova et al., 2015, 2021) and Earth magnetotail (Zong et al., 2004; Chen et al., 2008; Wang et al., 2016).
In the case of full 3D RCSs, the guiding field is accepted varying in time and space. In some configurations of 3D RCSs, the out-of-plane variations of the helical magnetic structures become pretty significant, due to the kink instability, obscuring current sheet structures and making it hard to define clear X-nullpoints (Daughton et al., 2011; Egedal et al., 2012). A strong guiding field Bg can suppress the out-of-plane kink instability while leaving the concept of magnetic islands still applicable (Lapenta & Brackbill, 1997; Daughton, 1999; Cerutti et al., 2014; Sironi & Spitkovsky, 2014). Nevertheless, further studies have shown that both the cases do not significantly change the scenarios of energy conversion and particle acceleration in 3D RCSs, because the dominant mechanisms of particle energization remain the same as in the 2.5D scenario (Hesse et al., 2001; Zharkova et al., 2011; Guo et al., 2014; Dahlin et al., 2017).
Depending on magnetic field topologies, the presence of a guiding field in an RCS would cause partial or full charge separation between electrons and ions (Pritchett & Coroniti, 2004; Zharkova & Gordovskyy, 2004) because they gyrate in the opposite directions in a magnetic field. This, in turn, can lead to the preferential ejection of the oppositely charged particles into the opposite semiplanes of CSs, or opposite footpoints of reconnecting loops. It makes the hard X-ray sources spatially separated from the γ − ray sources in the opposite footpoints of reconnecting magnetic loops (Lin et al., 2003; Hurford et al., 2003, 2006). This charge-separation phenomenon is also confirmed in the laboratory experiments (Zhong et al., 2016).
Furthermore, there is a polarization electric field in RCSs confirmed by 3D PIC simulations (Fujimoto, 2006; Zenitani & Hoshino, 2008; Cerutti et al., 2013; Fujimoto, 2014) but its nature was not clear and sometimes mixed with the parallel electric field of accelerated electrons. Then it was shown that the polarization electric field is induced across the reconnection current sheet midplane by the separation of particles of opposite charges (electrons and protons) during their acceleration in current sheets with a strong out-of-plane guiding field; and its magnitude is much larger (by two orders of magnitude) than a reconnecting electric field itself (Siversky & Zharkova, 2009; Zharkova & Agapitov, 2009). Furthermore, the spatial profiles of a polarization electric field were found dependent on magnetic field topologies because this electric field is induced by the separated electrons and protons (Siversky & Zharkova, 2009; Zharkova & Agapitov, 2009; Zharkova & Khabarova, 2012). The presence of polarization electric field is shown to explain the in-situ observations of ion velocity profiles during spacecraft crossings of the heliospheric current sheet, which are found to follow closely the profiles of polarization electric field (Zharkova & Khabarova, 2012, 2015). Therefore, the ambient plasma feedback to a presence of accelerated particles during their passage through reconnecting current sheets is very important for the particles of opposite charges.
However, the particles of the same charge entering the 3D RCS from the opposite edges would also lead to different energy gains by the particles with the same charge (Siversky & Zharkova, 2009; Zharkova & Khabarova, 2012; Khabarova et al., 2020). The particles that enter the RCS from the side opposite to that, to which they are to be ejected, are classified as “transit” particles, while the particles entering the RCS from the same side where they are to be ejected to, are classified as “bounced” particles. The transit particles gain significantly more energy because they become accelerated on their way to the midplane where the main acceleration occurs, while bounced particles lose their energy while they approach the midplane, thus, gaining much less energy in the current sheet (Zharkova & Gordovskyy, 2005; Siversky & Zharkova, 2009; Zharkova & Agapitov, 2009; Zharkova & Khabarova, 2012).
The energy difference between the transit and bounced particles creates the particle beams with “bump-in-tail” velocity (energy) distributions, which could trigger different two beam instabilities (Buneman, 1958) and naturally generate plasma turbulence. Although, strong turbulence very often appears in the off-plane guiding field direction at the very early stages of 3D PIC simulations of magnetic reconnection (Daughton et al., 2011; Egedal et al., 2012) that obscures any other types of turbulence present in the simulations at later times. And, of course, the kinetic turbulence generated in current sheets can also contribute to particle acceleration by modifying the parameters of accelerated particles (Zharkova & Agapitov, 2009; Drake et al., 2010; Matthaeus & Velli, 2011; Fujimoto, 2014; Muñoz & Büchner, 2016; Huang et al., 2017; Trotta et al., 2020).
The goal of the current research is to explore kinetic turbulence generated by accelerated particles in reconnecting current sheets with multiple X-an O-nullpoints based on the specifics of particle acceleration on 3D magnetic field topologies. As one can note, the accelerated particles definitely gain non-Maxwellian (power-law) distributions during their acceleration in current sheets. Hence, we will attempt to explore the conditions in the phase and frequency domains for energetic particle beams to maintain the pressure anisotropy (Le et al., 2013) and their effects on instabilities generated due to asymmetric acceleration by a reconnection electric field. In addition, we wish to explore anisotropy of the electric and magnetic field fluctuations in turbulence along and perpendicular to the local mean magnetic field Bm0 (Howes et al., 2008; Boldyrev et al., 2013) for different locations inside a reconnection region.
The simulation model and magnetic field topology are described in Section 2, the results of simulations of energetic particles and generate turbulence for a current sheet with single and multiple X-nullpoints are presented in section 3 and the general discussion and conclusions are drawn in section 4.
2 Simulation Model
2.1 Magnetic Field Topology
In the current article, unlike our previous simulation (Siversky & Zharkova, 2009; Xia & Zharkova, 2020), we do not separate the original and induced electromagnetic fields, and adopt the self-consistent 3D PIC simulation to investigate particle acceleration in magnetic islands generated by a magnetic reconnection. However, we will use the previous results (Xia & Zharkova, 2020) about particle acceleration in the similar reconnection scenarios to evaluate possible mechanisms of the recorded kinetic turbulence. We extend the 3D simulation region to a larger domain compared to the previous 2.5D studies (Siversky & Zharkova, 2009; Muñoz & Büchner, 2016).
The simulations start with a Harris-type current sheet in the x − z plane:
where dcs is the half thickness of RCS. The B0 is the initial guiding field, which is perpendicular to the reconnection plane. In the presented simulation bg = B0y/B0z = 1.0. The initial density variation across the CS is:
where n0 is the ambient density in a current sheet, nb is the density of an accelerated particle beam, and dcs is a current sheet thickness.
2.2 Particle Motion Equations
The motion of a charged particle in an electromagnetic field
where
2.3 The Plasma Feedback
Similarly to the early article (Xia & Zharkova, 2020), in the initial PIC approach we split the electromagnetic field E and B into two components, the background Estatic and Bstatic, and the local self-consistent
where je and jp are the current densities of electrons and protons updated by the particle solver. The Maxwell’s equations are solved by standard finite-difference time-domain method (FDTD) numerically. This approach can help us to identify the effect of the ambient particles that are drifted into a current sheet and accelerated. Then we rerun the 3D PIC simulations by relaxing all the electromagnetic fields and following the reconnection process until the certain time when maximal turbulence is formed.
2.4 Numeric Method
After clarifying the accelerated particle dynamics by splitting the electro-magnetic fields as above, we rerun the PIC simulations with VPIC code by relaxing electromagnetic fields of particles and allowing them to interact together with the initial electromagnetic field to reflect a reconnection process initiated by some perturbation. PIC simulations were carried out using the fully relativistic 3D VPIC code (Bowers et al., 2008). Our setup is somehow similar to the one employed in Muñoz & Büchner (2018) with some essential differences. The RCS thickness was dcs = 0.5di (versus 0.25 di by Muñoz & Büchner, 2018), where di is the ion inertial length. We chose a mass ratio mi/me = 100, a temperature ratio Ti/Te = 5, a background plasma density nb/n0 = 0.2 versus nb/n0 = 1.0 accepted by Muñoz & Büchner (2018), and a frequency ratio ωpe/Ωce = 1.5, where ωpe is the electron plasma frequency and Ωce is the electron gyro-frequency. Plasma beta is estimated as
Following the approach discussed by Siversky & Zharkova (2009), for the current sheet thickness equal to the ion inertial length, di, we select the number of cells across the current sheet in a PIC simulation to be
The simulation box size is Lx × Ly × Lz = 12.8di × 1.6di × 51.2di with grid number 512 × 64 × 2048 using 100 particles per cell. To avoid the problem with the small Debye length λD, only a small fraction of the plasma particles (with a density of 1012 m−3 = 106 cm−3) is included in the current PIC simulation. This makes the ratio
Along the direction x, the conducting boundary condition for the electromagnetic field and open boundary condition for particles are used. The periodic boundary conditions are applied along the z- and y- directions (in the current sheet midplane X = 0) to the electromagnetic field and particles. We use a real speed of light without scaling it to Alfven speed, while using a reduced mass ratio between protons and electrons, like Siversky & Zharkova (2009) did. This approach is valid for the coronal magnetic fields only while the density would need to be modified if applied to current sheets in the magnetosphere or heliosphere as the applied setting can lead to larger than real Alfven velocities in the Earth magnetosphere.
To trigger a magnetic reconnection in the plane with magnetic islands, we introduce a small perturbation at the beginning of the simulation, which is written in terms of
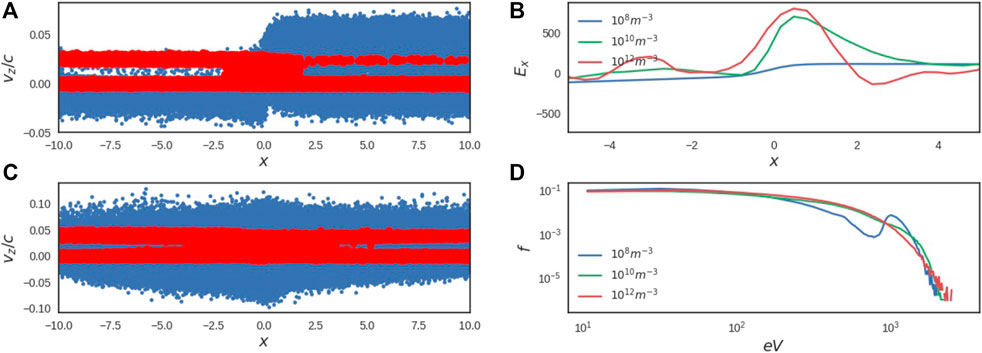
FIGURE 1. Density (left column) and energy (right column) distributions of electrons on the x − z plane at y =0 at different times (A, B)
We will gather the kinetic turbulence in the whole simulation region at the particular moment when turbulence is stabilized (experiment 1). Also we will collect the kinetic turbulence data by a hypothetical spacecraft sampling the simulation domains at a few particular points with respect to the local mean magnetic field Bm0 (experiment 2). Because the streaming instabilities are often observed in the separatrices (current sheet midplanes) and at the exhaust regions (Cattell et al., 2005; Lapenta et al., 2011; Markidis et al., 2012; Zhang et al., 2019; Lapenta et al., 2020), the positions of the virtual spacecraft are to be simultaneously located in the three points close to the separatrices at different distances away from the X-nullpoints inside the current sheet structure that forms a magnetic island.
Given the relativistic velocities of accelerated particles, which generate the turbulence within a very short timescale after the acceleration start, we can safely assume that any Doppler shifts in the frequencies of turbulence induced by accelerated particles caused by the motion of the ambient plasma particles inside a current sheet are negligible, because the motion of charged particles in an RCS strictly follows rigidly the magnetic field topology completely forgetting its initial velocity at the entry (Zharkova & Gordovskyy, 2004, 2005; Dalla & Browning, 2005; Wood & Neukirch, 2005; Siversky & Zharkova, 2009; Xia & Zharkova, 2018; 2020).
3 Simulation Results
3.1 Single X-Nullpoints
To understand the physical nature of the turbulence generated inside RCSs with magnetic islands, let us use the models described in our previous papers (Xia & Zharkova, 2018; 2020), which compared particle acceleration in a single X-nullpoint and in coalescent and squashed magnetic islands. The current sheet with a single X-nullpoint was described by the set of equations with the following magnetic field components: Bz = −
In the PIC approach, there is also a feedback of the ambient plasma considered to the presence of accelerated particles by calculating the electric and magnetic fields induced by accelerated particles as described by Eqs. 5, 6 in Section 2.4. Similarly to Siversky & Zharkova (2009), in the PIC code the authors (Xia & Zharkova, 2020) introduced the initial (static) background electric and magnetic fields (Verboncoeur et al., 1995; Bowers et al., 2008) and then followed particle acceleration as well as their induced electric and magnetic fields in the current sheets with the single or multiple X-nullpoints (with magnetic islands).
This approach can help us to separate the original magnetic field configuration of the magnetic reconnection from that induced by the plasma feedback due to the presence of accelerated particles. This separation helps to discover potential triggers of plasma turbulence inside these complex magnetic configurations.
3.1.1 Polarization Electric Field
The trajectories of electron and protons calculated in the RCS near a single X-nullpoint for a strong guiding field By reveal a significant difference between the acceleration paths of the particles with opposite charges. The particles with different charges are shown separated into the opposite sides from the RCS midplane and then ejected to the opposite semi-planes (Siversky & Zharkova, 2009; Xia & Zharkova, 2018; 2020). For a given magnetic topology, energetic electrons can primarily be ejected to the x > 0 semi-plane, while protons to the x < 0 semi-plane.
One important outcome of this separation is the polarization electric fields induced by the separated particles with opposite charges across the current sheets. This polarization electric field δEx shown in Figure 2 is perpendicular to the RCS midplane, and it is much larger than the reconnecting electric field Ey0 induced by the magnetic reconnection process. A polarization electric field was first reported in the 2D PIC simulations by Arzner & Scholer (2001); Fujimoto (2006) and was assigned to particle’s inertia motion. However, the particles passing through 2D current sheets do not gain much energy (Litvinenko & Somov, 1993; Litvinenko, 1996) and, as a result, the polarization electric field induced by these accelerated particles owing to separation by inertia would have low magnitudes, in comparison with the reconnection electric field magnitude accelerating particles. Only later by considering acceleration of particles in 3D current sheets with a strong guiding field (Pritchett & Coroniti, 2004; Zharkova & Gordovskyy, 2004; Pritchett, 2005; Zharkova & Gordovskyy, 2005), this polarization electric field was shown to be enforced by significant energy gains by all particles and the separation of electrons from protons/ions across the current sheet midplane. This separation of very energetic electrons and protons generates a significant polarization electric field exceeding by up to two orders the reconnection electric field magnitude (Siversky & Zharkova, 2009; Zharkova & Agapitov, 2009; Zharkova & Khabarova, 2012).
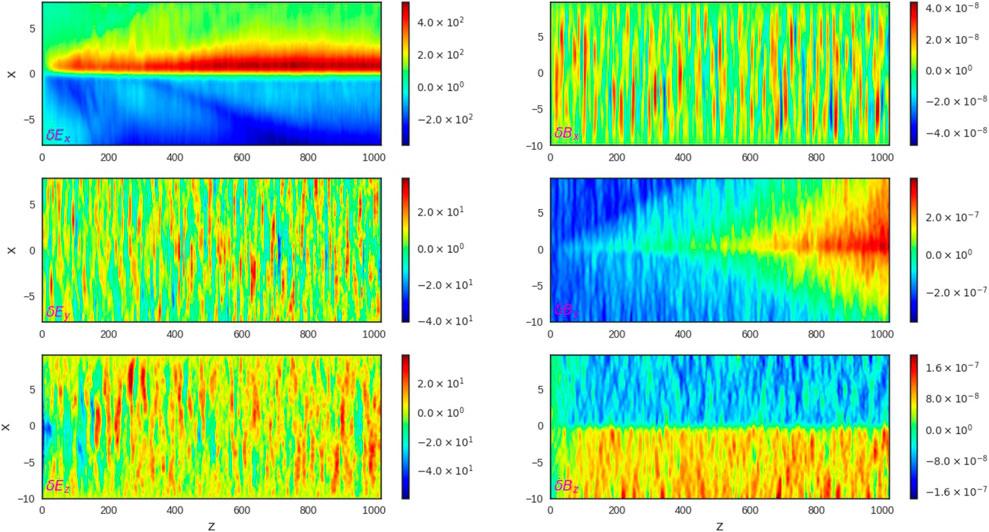
FIGURE 2. The 3D simulations at t = 8×10–3 s: (A) the polarization electric field Ex (V/m) across the current sheet midplane; the densities of electrons (B) and (C) protons in the x − z plane normalized to the initial density (n0); (D) the pitch-angle distribution of accelerated electrons about the midplane with the color bar showing particle density in units of n0; (d) the energy (eV, shown by color bar) of the accelerated electrons (E) and protons (F). The distances X (from the midplane) and Z (from X-nullpoint) are measured in the units of an ion inertial depth di). The magnetic field B0 = 10–3 T, By/B0 = 0.1, Bx/B0 = 0.02, and the reconnection electric field E0 = 250 V/m.
In our further simulations, the plasma density is accepted to vary as 108 m−3 and 1012 m−3. The polarization electric field distributions are found sensitive to the ambient plasma density as shown in Figure 3B If the density is low, the particle separation is more distinguishable in the phase space as shown in Figure 3A. However, the polarization electric field induced in the more rarified ambient plasma is lower than in the dense plasma. This happens, we believe, because the gradient of magnetic field (the first term in Eq. (5)) remains the same while being much smaller than the currents of accelerated electrons and protons, which are increased for more dense plasma, thus making higher the resulting electric field Ex induced by these accelerated particles in denser plasma.
Besides, there is a bump-in-tail at high-energy electrons in the spectrum of Figure 3D which is clearly seen for lower density plasma. When the polarization electric field, Ex, becomes larger with a larger density (the charged particle density should also increase) as shown in Figure 3B, the preferential ejection becomes less clear, and the bump-in tail in the particle energy spectrum is smoothed out. Although, this does not change the maximum energy gains by particles as shown by the spectra in Figure 3D, which still remain of the same order of magnitude for all the simulations with different plasma densities.
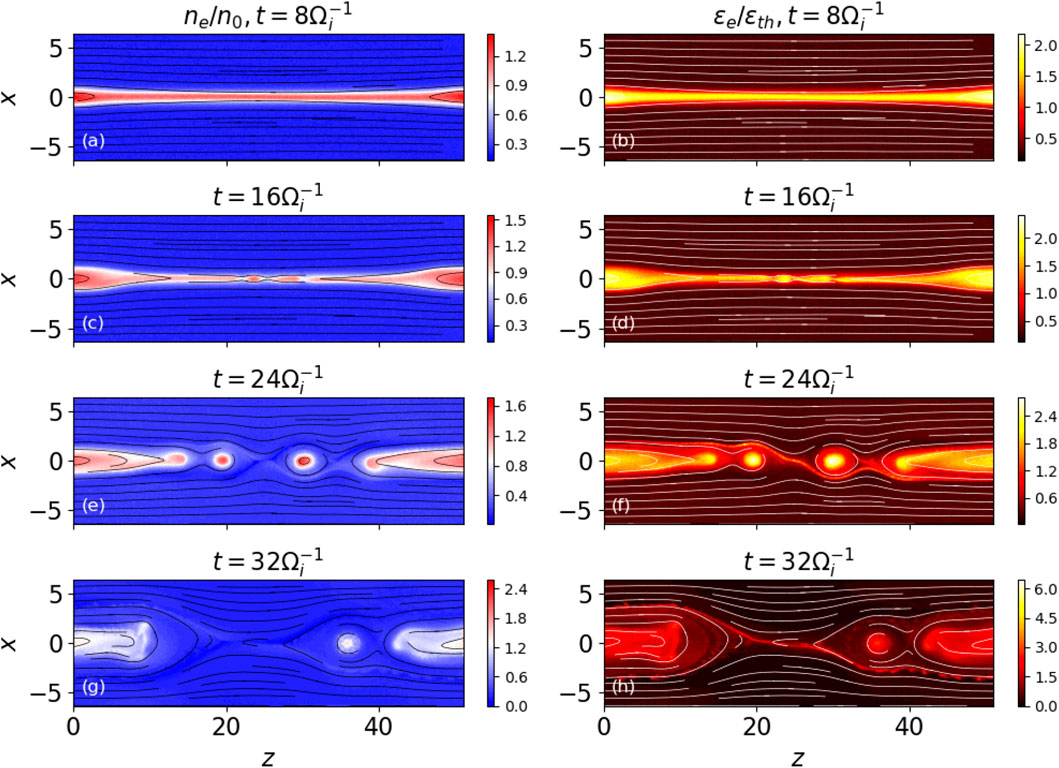
FIGURE 3. The Vz distributions in the phase space for electrons (blue dots) and protons (red dots) versus a distance X from the midplane (in the units of the ion inertial x depth di) for the current sheets with the same magnetic field topology as in Figure 2 (A) n0 = 108 m−3 and (C) n0 = 1012 m−3. The polarization electric fields (in V/m) and the energy spectra for different ambient densities are compared in (B) and (D), respectively.
3.1.2 Plasma Turbulence Generated by Two Beams
Because of the bump-on tail distribution of the energy spectra of accelerated particles shown of Figures 3A,C, there is turbulence formed by Buneman instability (Buneman, 1958), or the electron two stream instability, which, in addition to the background electro-magnetic fields, leads to fluctuations of electric δEx, δEy, δEz and magnetic field vectors |δBx/Bx,0|, |δBy/By,0|, |δBz/Bz,0| < 1.0 × 10–4 in the diffusion region.
The fluctuations of magnetic field are rather small as shown in Figure 4 (right column), while the electric field shows very strong fluctuations (see the left column in Figure 4). Moreover, the fluctuations of δEx are found to be larger than δEy, δEz by an order of the magnitude. The small fluctuations of magnetic field can be understood in terms of the gradient of Ex to occur along the x-axis, which shows from Faraday’s law, ∂B/∂t = −∇×E that Ex would not change the magnetic field, as demonstrated by δB pictures in Figure 4.
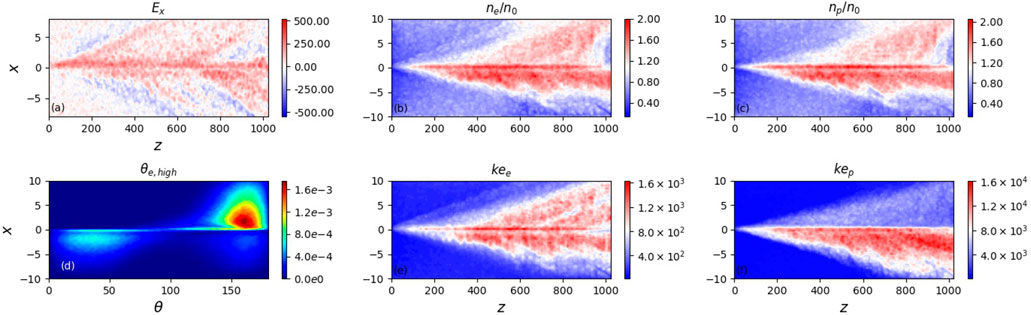
FIGURE 4. The changes of three components (x,y,z) of the electric vector δE (in V/m, shown by color bars) (left column) and magnetic δB vector (in T, shown by color bars) (right column) in a reconnecting current sheet simulated at t = 5 × 10–4 s (
As shown in Figure 4, the electric field fluctuations propagate along the z- and y-directions rather than along the x-direction following the trajectories of accelerated particles. The Ez component represents Langmuir waves oscillating at ω−1 ≈ 1.3 × 10–7 s, which is close to the electron plasma frequency ωpe for the plasma density of 1012 m3 accepted in this simulation (Siversky & Zharkova, 2009).
3.2 Turbulence in the Vicinity of Multiple X-Nullpoints
3.2.1 Reconnection With Multiple Magnetic Islands
As a result of the simulation setting described in section 2, we present simulations for four different times up to 32
Owing to the periodic boundary conditions at both the ends of the z-axis, the simulation domain represents the RCSs with a chain of magnetic islands, rather than a single X-nullpoint geometry with open exhausts. The energy distributions of electrons at
It has to be noted that our model thickness of the 3D current sheet is twice the thickness used by Muñoz & Büchner (2018), but it has a much smaller beam density nb, or the plasma β, inside the diffusion region. This explains the occurrence of kinetic turbulence in our simulations while it does not appear for the current sheet with the thickness used for the simulations by Muñoz & Büchner (2018).
3.2.2 Suppression of Kink Instability
The reconnection process is shown to be weakly affected by the kink instability at a later time, as evidenced in the isosurface of the electron energy distribution in Figure 5. The distributions are similar in the different x − z planes along the y − direction.
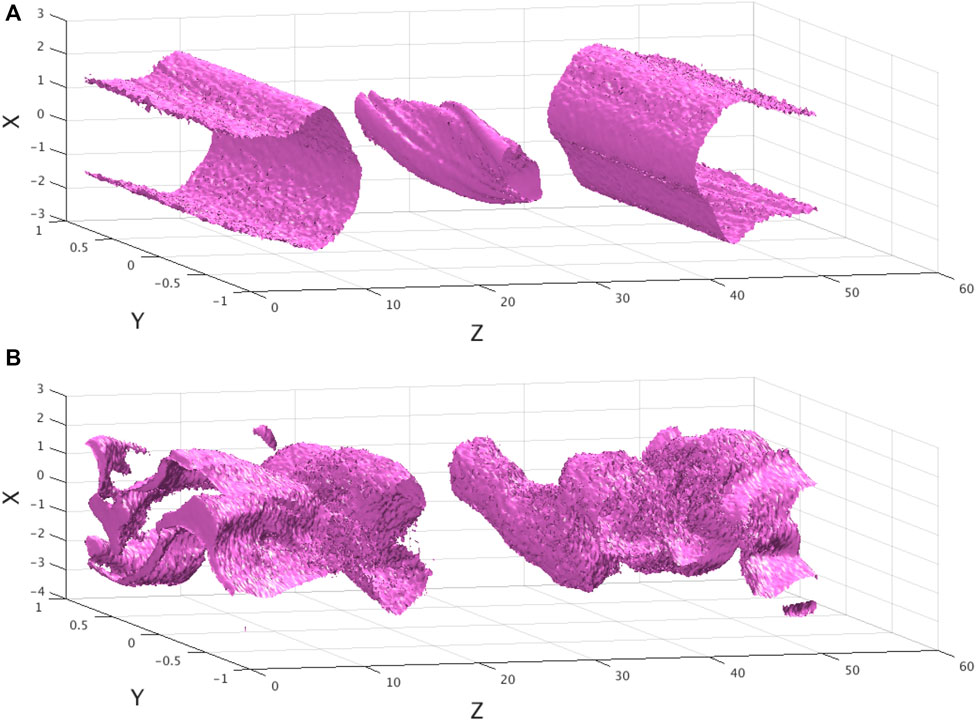
FIGURE 5. Upper plot: Isosurface of the electron energy distribution (the 35% contour of the max energy) for a strong guiding field (bg = 1) in the simulation box of Figure 1 at
If the guiding field is weak and polarization electric field is weak as well, the reconnecting magnetic fields would be strongly perturbed by turbulence as reported previously (Daughton et al., 2011; Egedal et al., 2012). For example, in the Bg = 0 case, we observed a twist of the magnetic flux ropes in the simulation box caused by kink instability after the same running time shown in Figure 5B. However, with the increase of the guiding field and the polarization electric field induced by separated electrons and ions, the twists are suppressed shown in Figure 5A.
Thus, the locations and the sizes of magnetic islands in different x − z planes would change, which makes it hard to make statistical analysis depending on the distance from the X-nullpoint on different x − z planes along the y − direction. Therefore, to concentrate on the turbulence other than kink instability, we should stick to the cases with a strong guiding field (bg = 1), to avoid this complication.
3.2.3 Evaluation of Generated Turbulence
In our simulation, the ion-scale magnetic islands were formed during magnetic reconnection events as shown in Figures 4A–H. The size of the largest magnetic island reached ∼ 36di after
It allows us to get statistical results of turbulence power spectrum collected in the full 3D simulation box including 64 grid points along the y-direction. The isotropized 1D power spectra, similar to the one proposed by Franci et al. (2017), are calculated in the 2D Fourier x − z-plane and averaged/summed over the y-direction. The power spectra of electric (magnetic) fields of the whole box are measured at
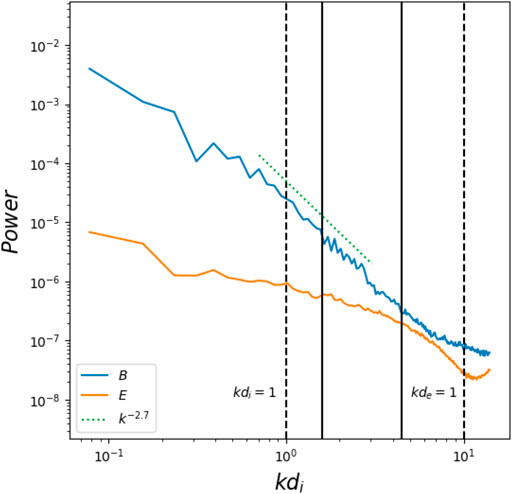
FIGURE 6. Power spectra of the electric (normalized by
In this model, the wave-number spectrum of the magnetic field formed a quasi-stable range from kdi = 1 down to above kde = 1. A least-square fitting of |B|2(k) ∝ kα over this range indicates the slope α ≈ − 2.7 suggesting that at this moment there is quasi-stable turbulence built up. Hence, in this large 3D simulation box, the turbulent magnetic field power spectrum in the RCS formed a steady spectral slope ∝ k−2.7 near the ion inertial length, and a steeper cascade at electron scales at
The power spectrum of the electric field drops significantly at the spatial scale close to the electron inertial scale (the solid line,
Also, in the simulations obtained by Muñoz & Büchner (2018) the 1D turbulence about the X-nullpoint obtained along the z-direction has spectral indices varying in time, which can be explained by stochastic acceleration of particles near X-nullpoint (Zharkova & Gordovskyy, 2004; Dalla & Browning, 2005; Wood & Neukirch, 2005). We understand this shifting index can be caused by the fact that the “bump-it-tail” positions in the velocity spectra of accelerated transit particles near X-nullpoint are constantly changing (Xia & Zharkova, 2020) and so does the turbulence, which this beam produces. In contrast at the time of maximum reconnection rate in Muñoz & Büchner (2018) the accelerated particles of the same charge (transit and bounced) gain the maximal energy close to the critical one that causes quasi-stable turbulence with noticeable power-law distribution in the wavenumber domain.
3.2.4 Phase Space Distributions
Now let us consider the final reconnection configuration with the two large magnetic islands separated by the X-nullpoint and explore with instant virtual spacecrafts the turbulence generated in the three locations A, B, C within the magnetic island (A), close to its edge (B), and close to X-nullpoint (C) in the current sheet x − z plane shown in the upper plot of Figure 7.
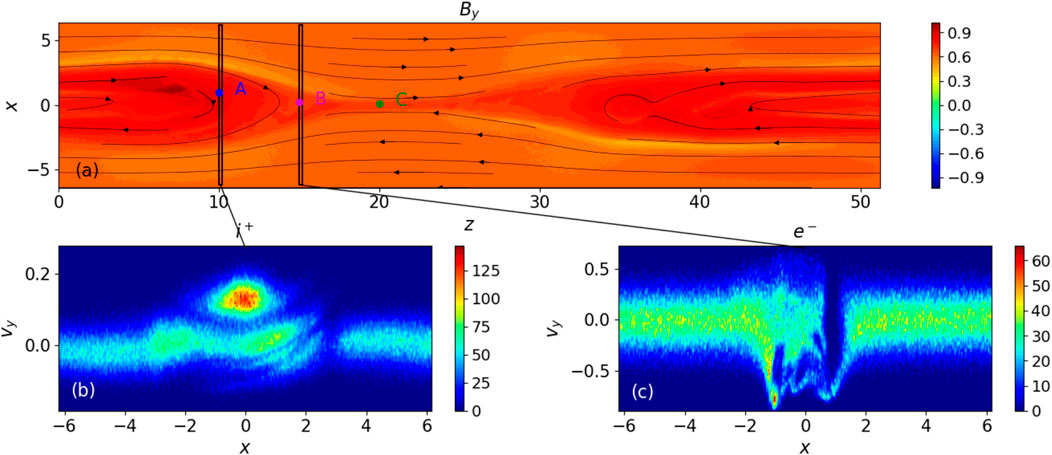
FIGURE 7. The reconnection plane (x − z magnetic field topology (black solid lines) with the out-of-plane magnetic field component By at y = 0 colored (in units of Bz) in panel (A). The simulation started with a strong guiding field (bg = 1). The main X-nullpoint is located at z = 22, x = 0. The phase-space distribution functions of velocities (in the units of speed of light c) of accelerated ions (panel (B)) and electrons (panel (C)) at difference locations at
To establish a link between the turbulence and accelerated particles in the locations of these points, let us examine the changes of accelerated particle characteristics in the associated plane x − y perpendicular to the current sheet plane shown by the vertical lines in the upper plot of Figure 7 in the locations of points A and B. This gives a complete 3D presentation of the current sheet, and shows that the accelerated particles have very specific trajectories in the magnetic topology of a current sheet. In the bottom row of Figure 7 we present the particle velocity distributions in the x − y plane, e.g. the x − vy phase space for both ions (bottom left) and electrons (bottom right) along the direction perpendicular to the reconnection midplane at points A and B far away from the X-nullpoint.
From the phase space analysis we can speculate that the kinetic turbulence is mainly generated by accelerated particle beams, which are later found to evolve into a phase-space hole indicating their breakage: this happens at the distance from the particle entrance in an RCS of about 7di for electron beams and at the distances about 12di for proton beams, where di is an ion inertial depth. This was consistent with the previous numerical findings for simulations in different reconnecting regimes (Drake et al., 2003; Muñoz & Büchner, 2016) and the observations in the Earth’s magnetotail (Khotyaintsev et al., 2010).
The particle distributions demonstrate clear non-Maxwellian features in electron beam distribution shown in location B in Figure 7C: at z = 15di (or Δz ∼ 7di away from the main X-nullpoint). There are clearly seen two beams at the distance x ≈ 3.5di: one with lower velocities and another one moving with much higher velocities while revealing a clear fragmented structure. In addition, there are electron holes formed in the phase space between x = − 1.5di to 1.5di, which can be triggered by the beam-driven lower hybrid instability discussed in section 3.3.
As the inspecting spacecraft moves deeper into the magnetic island to location A, there is also the perturbation in the ion phase space found at z = 10di (or Δz ∼ 12di away from the X-nullpoint) in Figure 7B, with the three quasi-parallel arcs located in the region between x = 0 to 2di and a very bright blob of very energetic protons located at x = 0 representing the different groups of the ion beams formed during acceleration. At this instance there were no electron beams at location A, because the electron beams dissipated at the distance 7di closer to location B (Figure 7C), so there should be only the proton ones present at the point A and any turbulence generated in this location has to be produced by proton beams and their interaction with the ambient plasma (Kucharek et al., 2000; Gomberoff et al., 2002).
There are no any clear ion holes in the phase space, but these few arcs are found to quickly disappear further in the downstream of the beam that suggests the ion beams become scattered by the plasma turbulence generated by them that is discussed in section 3.3. Therefore, the particle velocity distributions suggest that accelerated electron or ion beams move away from the X-nullpoint until gaining the critical energy to break from this current sheet. The accelerated ions and electrons form different types of two-beam velocity distributions at different regions of the current sheet, thus producing different types of instabilities (Buneman, 1958; Kucharek et al., 2000; Gomberoff et al., 2002; Siversky & Zharkova, 2009; Muñoz & Büchner, 2018).
3.3 Frequency Analysis
Now let us study the plasma turbulence introduced by the beam instabilities using electric and magnetic fluctuations in the frequency domain.
3.3.1 Wavelet Analysis
After we identified the instability signals in the particle phase space, let us utilize the discrete wavelet transform, which is a powerful tool to analyze time-series data collected by a pinpoint in the domain (Farge, 1992). The signals at different grids along the y-direction were transformed to the wavelet power spectra using Morlet wavelet for the simulation domain and time up to 80 Ωci. The turbulent fields were approximated by a short-time Fourier transform using a sliding Tukey window with an appropriate overlap. Then the results were averaged along the direction of the out-of-plane y-axis and presented at the instances in the positions of virtual spacecrafts located on the grid points along the y-direction at some given (x, z) coordinates (measured in the units of a proton inertial length di).
Then we record the fluctuations of electric and magnetic fields in the hypothetical locations of probes A, B, and C during the acceleration of particles in the RCS. The signals from different probes are separately transformed to the wavelet power spectra using Morlet wavelet. Then the results are averaged over all the probes with the same (x, z) coordinates.
The wavelet power spectra of both the electric and magnetic field components shared the similar features at the electron plasma frequency as expected from the results presented in section 3.1.2 and Figure 4. For example, Figure 8 shows the results using the data of the Bx component recorded at point B (z = 15di, x = 0.25di), where the electron holes were observed in the phase space in Figure 7C for a period of
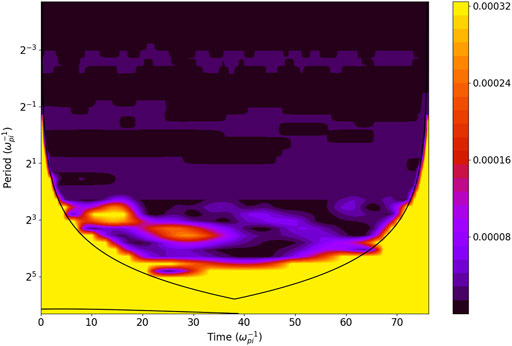
FIGURE 8. Local wavelet power spectrum of Bx (the purple point B in Figure 7) at z = 15, x = 0.25 (in the units of the ion inertial depth di) of the time series of Bx components, using Morlet wavelet. Note that X and Z as in other plots are measured. The solid dark curve encloses the regions of >95% confidence. By using as a base the X-axis of the frequency spectra shown in Figure 9, the lower-hybrid frequency ωlh can be roughly drawn just above the period of 23 (in the units of
Furthermore, the wavelet transform revealed wide purple features in the high-frequency region. Figure 8 depicts several high-frequency signals represented by a wide purple strip 3 below and wide purple strip four above the electron plasma frequency ωce). Thus, the electromagnetic fields spectra, presented via the wavenumbers and via the wavelet transform, both indicate the important role of electrons in plasma turbulence developed in the given location B of the current sheet between its X and O-nullpoints.
3.3.2 Frequency Spectra of Electromagnetic Fields
We assume that the virtual spacecraft was placed simultaneously at the three different locations: A, B, and C in Figure 7 with the selected points C → A being further away from the X-nullpoint. The selected turbulent magnetic fields are collected in the surveyed boxes of the size of ΔLx(= 0.2di) × Ly × ΔLz(= 0.2di) surrounding the selected points in Figure 7. The values of turbulent fields were averaged in space and time over
Now let us explore the resulting turbulent components of electro-magnetic fields, B and E, in every grid point of the selected locations (A, B, C) by projecting them onto the background field Bm0. This will allow us to get the parallel and perpendicular components of the turbulent field and to evaluate more accurately the turbulence nature in these locations. Note that the distributions presented in Figure 7 are taken from the left-hand side of the X-nullpoint. They are the same as those found at the similar distances on the right-hand side because the model is symmetric with respect to the X-nullpoint. The results are presented in Figure 9 for the parallel (left column) and perpendicular (right column) components of the turbulent electric and magnetic fields.
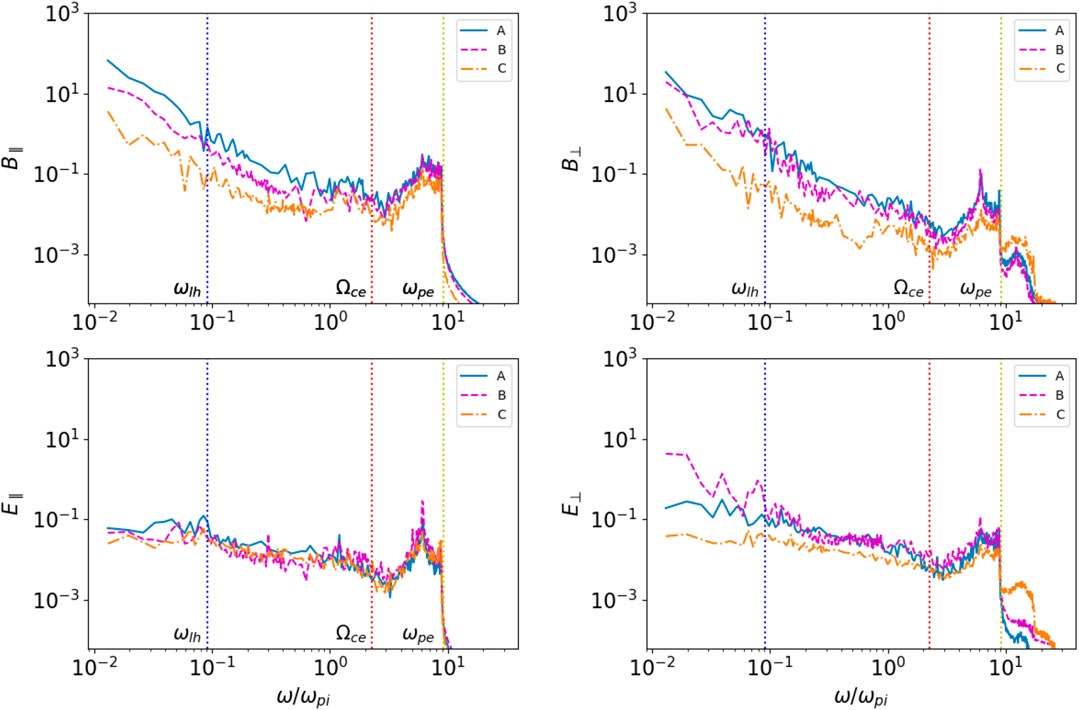
FIGURE 9. The spectra of different E and B components at selected points (marked in the corresponding colors in Figure 7) as functions of the frequency (normalized to ωpi): B∥, E∥, B⊥, E⊥ with respect to the local mean magnetic field in 3D. The characteristic lower-hybrid frequency ωlh, electron gyro frequency Ωce, and electron plasma frequency ωpe are labeled as vertical dotted lines.
In the sub-high-frequency region, Ωce < ω < ωpe, we found several distinct spikes in all the turbulent fields at three locations marked by blue, purple, and yellow curves. In fact, there are the two small peaks occurring at higher amplitude turbulence at the frequencies below the lower-hybrid frequency, which are specifically well seen in E⊥, and the another two stronger peaks appearing at lower amplitude turbulence in parallel and perpendicular electric and magnetic fields at the frequencies between Ωce and ωpe. Considering that the periodic boundary condition along the z-axis stands for simulating a chain of magnetic islands, it suggests that the magnetic island pool is fulfilled with these electromagnetic fluctuations above Ωce. Furthermore, both high-frequency fluctuations of δE and δB are mainly perpendicular to Bm0. In the very high-frequency part (≥ωpe), we first noticed that the perpendicular electric field E⊥ at f > ωpe is damped significantly as it moves away from the X-nullpoint. In the other words, these high-frequency waves represented by E⊥ are only observable near X-nullpoints (points B and C), which are also clearly seen in the wide purple patterns (strips 3 and 4) shown in the wavelet plot at these frequencies (see Figure 8).
This high-frequency turbulence is likely to be generated by two-beam instability of electron beams with “bump-in-tail” distributions in the vicinity of X-nullpoint producing Langmuir waves with the wavelength of 2 m (or 2di in the current setting) and a speed of propagation of (1.7–2.0)⋅107 m/s (or about 0.07c) with the period of 1.5⋅10–7 s (close to
The most puzzling features in the current evaluation are in the low-frequency part: right below Ωce, we found a large enhancement in the amplitude of B⊥ (and a spike in E∥) in the point A. Further down in the lower frequency region, the amplitudes of B∥, B⊥, and E⊥ are much larger over a wider range. The small bump near ωlh (especially in the parallel electric fields) near point A at z = 10, x = 1, measured in the units of di, where ωlh is the lower hybrid frequency represents the lower hybrid waves. Since in this location A we recorded only a very intense proton beam shown in Figure 7B while electron beams in the vicinity of point B were broken and formed an electron hole as shown in Figure 7C; it is safe to assume that at this instance the turbulence in point A is generated by ion/proton beams (Kucharek et al., 2000; Gomberoff et al., 2002). There is a noticeable increase of the turbulence close to the lower-hybrid frequency in the parallel components at point A and in the perpendicular components in points A and B (see Figure 9) in the parallel B in the left top plot and perpendicular electric field E in the right bottom plot).
The lower-frequency turbulence is also seen in point B shown in the wavelet plot in Figure 8 as very bright strips 1 and 2 that could be driven the field-aligned drifts of highly accelerated electrons (Drake et al., 2003). This turbulence is seen in locations B and C revealing initially a growth of parallel turbulence and strong levels of oblique lower hybrid (LH) waves at later times (for which we recorded the turbulence) coinciding with a substantial parallel electron acceleration. In low-β plasmas with intense parallel currents and both with or without parallel E fields, LH waves are shown to grow even for electron distributions stable to the parallel Buneman instability, or the electron two-stream instability, and to accelerate electrons parallel to B very rapidly (McMillan & Cairns, 2006; Fujimoto & Sydora, 2008). This instability may be seen as the oblique limit of the ion acoustic and Buneman two-stream instabilities at the location where electrons beam eventually fully dissipates (Figure 7A, point B).
Moreover, Fujimoto (2014) has shown that the intense electron beams can trigger the electron two-stream instability (ETSI) and the beam-driven whistler instability (WI). The ETSI generates the Langmuir waves, while the WI gives lower hybrid waves. This is, we believe, what is observed in the perpendicular components of turbulence in locations A and B as shown in Figure 9, right column, where strong intense accelerated beams propagate (see Figures 7B,C).
As shown in the b and c plots of Figure 7, the particle densities in these points A and B have well recorded inhomogeneities of particle densities clearly seen in Figures 7B,C, which could attribute to the generation of whistler waves in the region near these points as suggested by Zudin et al. (2019). This suggestion is also confirmed by studies of McMillan & Cairns (2007) showing that in plasmas with low beta (as we use in our model) the most unstable mode is not occurring at parallel propagation, but may be at intermediate and very oblique angles. The simulations (McMillan & Cairns, 2007) demonstrate that the very oblique lower hybrid (LH) waves can also arise. The oblique whistler waves are sometimes observed at the lower hybrid frequency in thin current sheets in the heliosphere (Zhou et al., 2009; Artemyev et al., 2016).
Also for point A one can also add generation of the right-polarized resonant instability by very intense proton beams (Kucharek et al., 2000; Gomberoff et al., 2002). In addition, a kinetic branch of Kelvin-Helmholtz instability can be also enhancing the plasma turbulence near the lower-hybrid frequency since we clearly detected in locations B and A shown in Figure 7 the flows of protons traveling from the X-nullpoint to the O-nullpoint.
These turbulent electro-magnetic field enhancements near lower-hybrid frequency f ≈ ωlh, f < Ωce, and at higher frequencies Ωce < f < ωpe are also consistent with the dark horizontal stripes in the wavelet power spectrum shown in section 3.3.1. Evidently, by splitting the electromagnetic fluctuations into the parallel and perpendicular directions, we managed to identify the differences between these striped signals in the frequency analysis, which also appeared in the wavelet analysis reported in section 3.3.1. This allows us to assume that the detected turbulence signals could be the real features.
4 Discussion and Conclusion
In this article we investigate kinetic turbulence generated by accelerated particles in a reconnecting current sheet (RCS) with X- and O-nullpoints and explore the kinetic turbulence spectra in the wavenumber and frequency domains. We consider reconnection in a thin current sheet with 3D magnetic field topology using 3D particle-in-cell (PIC) approach and carry out the simulations or magnetic reconnection affected by tearing instability. In this simulation we set a larger 3D simulation domain, in which the magnetic reconnection generates two large magnetic islands each ∼ 32di long. A strong guiding field Bg is implemented to suppress the out-of-plane kink instability and to keep the geometry quasi-similar on each x − z plane. It allows us to get statistical results by averaging the data collected from the 64 grid points along the y-direction.
We reiterated our previous findings (Siversky & Zharkova, 2009; Xia & Zharkova, 2020) that during a magnetic reconnection in the presence of a guiding magnetic field, the particles of the same charge drifting into the RCSs from the opposite boundaries would gain different energies, higher for the transit particles and lower for the bounced particles. As a result, the high-energy accelerated particles of the same charge form non-Maxwellian distributions with the “bump-in-tail,” which leads to Buneman instability (Buneman, 1958) or the electron two-stream instability, and generates the observed turbulence (Jaroschek et al., 2004; Siversky & Zharkova, 2009; Drake et al., 2010; Muñoz & Büchner, 2016, 2018). The turbulent magnetic and electric fields generated in the RCS gathered in the large 3D simulation box at the time of
The characteristic waves produced by either electron or proton beams can be identified from the energy spectra of electromagnetic field fluctuations in the phase and frequency domains and compared with the particle energy gains. We selected the specific point inside the simulated 3D current sheet close to X and O-nullpoints to explore the frequencies of generated turbulence in these particular locations. We inspected the phase space of accelerated particles at this selected time, and identified the two regions with clear non-Maxwellian distributions: close to the X-nullpoints related to drift instabilities produced by accelerated electrons and away from X-nullpoints related either to drift instabilities produced by ions.
From the phase space analysis we gather the kinetic turbulence and speculate that it can be generated by accelerated particle beams seen in these locations. These beams are later found to evolve into the phase-space hole indicating their breakage: this happens at the distance of about 7di from the particle entrance in an RCS for electron beams and at the distances of about 12di for proton beams, where di is the ion inertial depth. This demonstrated that in some locations of current sheet the turbulence can be generated by accelerated electron beams, while in others by proton beams. In addition, there is electron-ion hybrid instability, the kinetic branch of Kelvin-Helmholtz instability, which can also enhance the plasma turbulence near the lower-hybrid frequency since there are clearly detected flows of proton/ions traveling from the X-nullpoint to the O-nullpoint, This was consistent with the previous numerical findings for simulations in different reconnecting regimes (Drake et al., 2003; Muñoz & Büchner, 2016) and the observations in the Earth’s magnetotail (Khotyaintsev et al., 2010).
To explore the kinetic turbulence in more detail, we distinguish the parallel and perpendicular components of the electric and magnetic turbulent fields (Boldyrev et al., 2013; Loureiro & Boldyrev, 2017) that reveals different levels of turbulence in the presence of a strong magnetic field. By analyzing the changes in the electric and magnetic fields in the frequency domain at different locations, we can connect non-Maxwellian features in the particle phase space with distinct fluctuations of turbulence. This frequency analysis of the generated turbulence was carried out inside the simulated current sheets: close to X-nullpoint (point C), far away from X-nullpoint (point B) and inside O-nullpoint (point A). The frequency analysis was also supported by Morlet wavelet analysis carried out in point B over the timescale of 80
The particle distributions in points A-C clearly demonstrate non-Maxwellian features in particle distributions, e.g. the electron beam distribution in location B in Figure 7C at z = 15di (or Δz ∼ 7di away from the main X-nullpoint) reveals two beams at the distance x 1.5: one with lower velocities and another one moving with much higher velocities while revealing a clear fragmented structure. In addition, there are electron holes formed in the phase space between x = −1.5di to 1.5di, which can be triggered by the beam-driven lower hybrid instability. Also we show that in point A inside the magnetic island there are a few proton beams observed with arc-type structure and a break in the flow that can also produce a well-defined turbulence.
The electron beams introduced high-frequency electromagnetic fluctuations above Ωce, which were observed in Figure 9 in the frequency spectra of the turbulence generated by beams in the surveyed points (B-C) shown in Figure 7 and also confirmed by the two wide purple strips below and above the electron plasma frequency seen clearly in the wavelet spectra in Figure 8 calculated in point B.
These rapid signals appear as distinct spikes near the high-frequency tail of the power spectra of electric and magnetic fields in Figure 9. These fluctuations are spread from the electron gyro frequency to the electron plasma frequency. This high-frequency turbulence is likely to be generated by two-beam (Buneman), or two-beam instability, of electron beams with “bump-in-tail” distributions in the vicinity of X-nullpoint as indicated by some other simulations (Siversky & Zharkova, 2009; Muñoz & Büchner, 2018) producing Langmuir waves. Although, as one can observe from Figure 7C, in some locations electron beams start moving across the magnetic field lines producing the enhanced ultra-high frequency fluctuations in the E⊥ component, or Bernstein waves (Bernstein, 1958; Gusakov & Surkov, 2007). The similar signals were found in the inflow region close to the X-nullpoint by Lapenta et al. (2020).
Such high-frequency harmonics above Ωce have been recently discovered by the MMS satellites near the electron diffusion region in the magnetopause (Dokgo et al., 2019). On the other hand, Li et al. (2020) reported the signals in E⊥ and B⊥ power spectra peaks at the harmonics of nΩce, where n = 1, 2, 3, … near an electron diffusion region in the magnetotail and they were attributed to the electron Bernstein waves. One difference in the observation is that ωpe/Ωce ≈ 27 in the magnetosphere, which keeps those two signals well separated. But this ratio is much lower in most PIC simulations including ours (ωpe/Ωce = 15), so we could not distinguish them clearly.
While in location A deeper into the magnetic island there is seen perturbation in the ion phase space at z = 10di (or Δz ∼ 12di away from the X-nullpoint) in Figure 7B, with the three quasi-parallel arcs located in the region between x = 0 to 2di and a very bright blob of very energetic protons located at x = 0 representing the different groups of the ion beams formed during acceleration. These few arcs are found to disappear quickly further in the downstream of the beam that suggest the ion beams become scattered by the plasma turbulence. Thus, the ion beams would also be quickly suppressed by two-stream instabilities. The difference between the electron and ion phase space suggests that to understand the full picture of plasma turbulence due to magnetic reconnection, it requires the simulation size to be much bigger than the diffusion region (Eastwood et al., 2018; Zhang et al., 2019).
Although, there is a noticeable increase of the turbulence close to the lower-hybrid frequency in the parallel components at point A and in the perpendicular components in points A and B (see Figure 9, parallel B in the left top plot and the perpendicular electric field E in the right bottom plot). As shown in the lower plots of Figure 7, the particle densities in these points A and B have well-recorded inhomogeneities of particle densities clearly seen in Figures 7B,C. The lower-hybrid waves can be generated by two-stream instabilities as shown in the energy distribution of Figure 7B (Papadopoulos & Palmadesso, 1976; Fujimoto & Sydora, 2008; Zhou et al., 2014; Xia & Zharkova, 2020), or due to the strong density gradient near the separatrices and in the outflow (Drake et al., 2003; Scholer et al., 2003; Divin et al., 2015; Zudin et al., 2019).
In the current simulation the lower-hybrid waves are clearly seen in both the frequency and wavelet analysis applied to the gathered kinetic turbulence. The wavelet power spectrum showed that the low-frequency fluctuations at the lower-hybrid frequency have largest amplitudes and, thus, dominate in the region. These turbulent electro-magnetic field enhancements near f ≈ ωlh, f < Ωce, and Ωce < f < ωpe are well consistent with the bright yellow and red stripes in the wavelet power spectrum shown in section 3.3.1.
The field-aligned drifts often drive instabilities (Drake et al., 2003) revealing a growth of parallel propagating turbulence initially and strong levels of oblique lower hybrid waves at later times coinciding with substantial parallel electron acceleration (Fujimoto & Sydora, 2008). In low-β plasmas with intense parallel currents and both with or without parallel E fields, LH waves are shown to grow even for electron distributions stable to the parallel Buneman instability and to accelerate electrons parallel to B very rapidly (McMillan & Cairns, 2006). This instability may be seen as the oblique limit of the ion acoustic and Buneman instabilities (McMillan & Cairns, 2007). The low-frequency waves in the current model dominate the turbulence in the regions located further away from the X-nullpont (points A and B) since accelerated particle beams become more intense (Fujimoto & Sydora, 2008) and amplitudes of the fluctuations are increased near the lower-hybrid frequency (Rogers et al., 2000).
This suggestion is also consistent with the other study (McMillan & Cairns, 2007) showing that in plasmas with low beta the most unstable mode is not occurring at parallel propagation, but may be at intermediate and very oblique angles that are observed in the perpendicular components of turbulence in locations A and B shown in Figure 9. Evidently, by splitting the electromagnetic fluctuations into the parallel and perpendicular directions, we managed to identify the differences between these striped signals, confirming them to be the real features since the oblique whistler waves are sometimes observed in thin current sheets (Zhou et al., 2009; Artemyev et al., 2016).
Also, further investigation is required of the kinetic turbulence generated in reconnecting current sheets with different magnetic field topologies and scenarios of reconnections and their links to the specific acceleration paths of the ambient particles dragged into a current sheet with a given magnetic field topology. This dual approach to investigation of kinetic turbulence combining investigation of accelerated particle paths and distributions with the turbulence they can generate can help to uncover more accurately the mechanisms for the generation of kinetic turbulence during magnetic reconnections and its effect on accelerated particles and the whole reconnection process.
In summary, we have identified the plasma turbulence in the RCS with magnetic islands and linked the characteristic fluctuations to the non-Maxwellian distributions of particles in the phase and frequency spaces. The observed waves are found to vary as a function of the distance away from the X-nullpoint. The high-frequency perpendicular fluctuations damp quickly out of the electron diffusion region, while the lower-frequency lower-hybrid (possibly whistler) waves are developing because of the streaming instabilities generated by two electron or two proton beams.
Identifying these characteristic signals in the observation could indicate the existing scenarios of local particle acceleration during their passage through magnetic reconnection regions in the solar wind. These results can be potentially beneficial for the in-situ observations of RCSs near the Sun obtained with the Parker Solar Probe, which has already detected some reconnection sites during its first encounter (Phan et al., 2020).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
The authors contribute equally to the paper. VZ formulated the problem and suggested the simulation scheme. QX carried the simulations, produced the plots. The both authors contributed to the data presentation, analysis and interpretation.
Funding
The authors acknowledge the funding for this research provided by the U.S. Air Force grant PRJ02156. This research used the DiRAC Complexity system, operated by the University of Leicester IT Services, which forms part of the STFC DiRAC HPC Facility (www.dirac.ac.uk). This equipment is funded by BIS National E-Infrastructure capital grant ST/K000373/1 and STFC DiRAC Operations grant ST/K0003259/1. DiRAC is part of the National e-Infrastructure.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors with to express their gratitude to the reviewers for their useful and constructive comments from which the paper strongly benefited.
References
Angelopoulos, V., McFadden, J. P., Larson, D., Carlson, C. W., Mende, S. B., Frey, H., et al. (2008). Tail Reconnection Triggering Substorm Onset. Science 321, 931–935. doi:10.1126/science.1160495
Antiochos, S. K., Dahlburg, R. B., and Klimchuk, J. A. (1994). The Magnetic Field of Solar Prominences. ApJ 420, L41. doi:10.1086/187158
Antiochos, S. K. (1998). The Magnetic Topology of Solar Eruptions. Astrophysical J. Lett. 502, L181–L184. doi:10.1086/311507
Artemyev, A., Agapitov, O., Mourenas, D., Krasnoselskikh, V., Shastun, V., and Mozer, F. (2016). Oblique Whistler-Mode Waves in the Earth's Inner Magnetosphere: Energy Distribution, Origins, and Role in Radiation Belt Dynamics. Space Sci. Rev. 200, 261–355. doi:10.1007/s11214-016-0252-5
Arzner, K., and Scholer, M. (2001). Kinetic Structure of the post Plasmoid Plasma Sheet during Magnetotail Reconnection. J. Geophys. Res. 106, 3827–3844. doi:10.1029/2000ja000179
Bárta, M., Büchner, J., Karlický, M., and Skála, J. (2011). Spontaneous Current-Layer Fragmentation and Cascading Reconnection in Solar Flares. I. Model and Analysis. Astrophysical J. 737, 24. doi:10.1088/0004-637X/737/1/24
Bernstein, I. B. (1958). Waves in a Plasma in a Magnetic Field. Phys. Rev. 109, 10–21. doi:10.1103/physrev.109.10
Bhattacharjee, A., Huang, Y.-M., Yang, H., and Rogers, B. (2009). Fast Reconnection in High-Lundquist-Number Plasmas Due to the Plasmoid Instability. Phys. Plasmas 16, 112102. doi:10.1063/1.3264103
Birdsall, C. K., and Langdon, A. B. (1991). Plasma Physics via Computer Simulation. Bristol, England: CRC Press, Adam Hilger.
Biskamp, D. (1986). “Magnetic Reconnection via Current Sheets,” in Magnetic Reconnection and Turbulence. Editors M. A. Dubois, D. Grésellon, and M. N. Bussac, 19.
Boldyrev, S., Horaites, K., Xia, Q., and Perez, J. C. (2013). Toward a Theory of Astrophysical Plasma Turbulence at Subproton Scales. ApJ 777, 41. doi:10.1088/0004-637x/777/1/41
Bowers, K. J., Albright, B. J., Yin, L., Bergen, B., and Kwan, T. J. T. (2008). Ultrahigh Performance Three-Dimensional Electromagnetic Relativistic Kinetic Plasma Simulation. Phys. Plasmas 15, 055703. doi:10.1063/1.2840133
Buneman, O. (1958). Instability, Turbulence, and Conductivity in Current-Carrying Plasma. Phys. Rev. Lett. 1, 8–9. doi:10.1103/physrevlett.1.8
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9
Carter, T. A., Ji, H., Trintchouk, F., Yamada, M., and Kulsrud, R. M. (2001). Measurement of Lower-Hybrid Drift Turbulence in a Reconnecting Current Sheet. Phys. Rev. Lett. 88, 015001. doi:10.1103/PhysRevLett.88.015001
Cattell, C., Dombeck, J., Wygant, J., Drake, J. F., Swisdak, M., Goldstein, M. L., et al. (2005). Cluster Observations of Electron Holes in Association with Magnetotail Reconnection and Comparison to Simulations. J. Geophys. Res. Space Phys. 110, 1. doi:10.1029/2004JA010519
Cerutti, B., Werner, G. R., Uzdensky, D. A., and Begelman, M. C. (2013). Simulations of Particle Acceleration beyond the Classical Synchrotron Burnoff Limit in Magnetic Reconnection: an Explanation of the Crab Flares. ApJ 770, 147. doi:10.1088/0004-637x/770/2/147
Cerutti, B., Werner, G. R., Uzdensky, D. A., and Begelman, M. C. (2014). Three-dimensional Relativistic Pair Plasma Reconnection with Radiative Feedback in the Crab Nebula. ApJ 782, 104. doi:10.1088/0004-637x/782/2/104
Chen, L.-J., Bhattacharjee, A., Puhl-Quinn, P. A., Yang, H., Bessho, N., Imada, S., et al. (2008). Observation of Energetic Electrons within Magnetic Islands. Nat. Phys 4, 19–23. doi:10.1038/nphys777
Dahlin, J. T., Drake, J. F., and Swisdak, M. (2017). The Role of Three-Dimensional Transport in Driving Enhanced Electron Acceleration during Magnetic Reconnection. Phys. Plasmas 24, 092110. doi:10.1063/1.4986211
Dalla, S., and Browning, P. K. (2005). Particle Acceleration at a Three-Dimensional Reconnection Site in the Solar corona. A&A 436, 1103–1111. doi:10.1051/0004-6361:20042589
Daughton, W., Lapenta, G., and Ricci, P. (2004). Nonlinear Evolution of the Lower-Hybrid Drift Instability in a Current Sheet. Phys. Rev. Lett. 93, 105004. doi:10.1103/physrevlett.93.105004
Daughton, W., Roytershteyn, V., Karimabadi, H., Yin, L., Albright, B. J., Bergen, B., et al. (2011). Role of Electron Physics in the Development of Turbulent Magnetic Reconnection in Collisionless Plasmas. Nat. Phys 7, 539–542. doi:10.1038/nphys1965
Daughton, W. (1999). The Unstable Eigenmodes of a Neutral Sheet. Phys. Plasmas 6, 1329–1343. doi:10.1063/1.873374
Divin, A., Khotyaintsev, Y. V., Vaivads, A., André, M., Markidis, S., and Lapenta, G. (2015). Evolution of the Lower Hybrid Drift Instability at Reconnection Jet Front. J. Geophys. Res. Space Phys. 120, 2675–2690. doi:10.1002/2014ja020503
Dokgo, K., Hwang, K. J., Burch, J. L., Choi, E., Yoon, P. H., Sibeck, D. G., et al. (2019). High‐Frequency Wave Generation in Magnetotail Reconnection: Nonlinear Harmonics of Upper Hybrid Waves. Geophys. Res. Lett. 46, 7873–7882. doi:10.1029/2019gl083361
Drake, J. F., Opher, M., Swisdak, M., and Chamoun, J. N. (2010). A Magnetic Reconnection Mechanism for the Generation of Anomalous Cosmic Rays. ApJ 709, 963–974. doi:10.1088/0004-637x/709/2/963
Drake, J. F., Swisdak, M., Cattell, C., Shay, M. A., Rogers, B. N., and Zeiler, A. (2003). Formation of Electron Holes and Particle Energization during Magnetic Reconnection. Science 299, 873–877. doi:10.1126/science.1080333
Drake, J. F., Swisdak, M., Che, H., and Shay, M. A. (2006). Electron Acceleration from Contracting Magnetic Islands during Reconnection. Nature 443, 553–556. doi:10.1038/nature05116
Eastwood, J. P., Mistry, R., Phan, T. D., Schwartz, S. J., Ergun, R. E., Drake, J. F., et al. (2018). Guide Field Reconnection: Exhaust Structure and Heating. Geophys. Res. Lett. 45, 4569–4577. doi:10.1029/2018gl077670
Egedal, J., Daughton, W., and Le, A. (2012). Large-scale Electron Acceleration by Parallel Electric fields during Magnetic Reconnection. Nat. Phys 8, 321–324. doi:10.1038/nphys2249
Farge, M. (1992). Wavelet Transforms and Their Applications to Turbulence. Annu. Rev. Fluid Mech. 24, 395–458. doi:10.1146/annurev.fl.24.010192.002143
Fletcher, L., Dennis, B. R., Hudson, H. S., Krucker, S., Phillips, K., Veronig, A., et al. (2011). An Observational Overview of Solar Flares. Space Sci. Rev. 159, 19–106. doi:10.1007/s11214-010-9701-8
Franci, L., Cerri, S. S., Califano, F., Landi, S., Papini, E., Verdini, A., et al. (2017). Magnetic Reconnection as a Driver for a Sub-ion-scale Cascade in Plasma Turbulence. ApJ 850, L16. doi:10.3847/2041-8213/aa93fb
Fujimoto, K., and Machida, S. (2006). A Generation Mechanism of Electrostatic Waves and Subsequent Electron Heating in the Plasma Sheet-Lobe Boundary Region during Magnetic Reconnection. J. Geophys. Res. 111, A09216. doi:10.1029/2005ja011542
Fujimoto, K., and Sydora, R. D. (2008). Whistler Waves Associated with Magnetic Reconnection. Geophys. Res. Lett. 35, L19112. doi:10.1029/2008gl035201
Fujimoto, K. (2006). Time Evolution of the Electron Diffusion Region and the Reconnection Rate in Fully Kinetic and Large System. Phys. Plasmas 13, 072904. doi:10.1063/1.2220534
Fujimoto, K. (2014). Wave Activities in Separatrix Regions of Magnetic Reconnection. Geophys. Res. Lett. 41, 2721–2728. doi:10.1002/2014gl059893
Furth, H. P., Killeen, J., and Rosenbluth, M. N. (1963). Finite-Resistivity Instabilities of a Sheet Pinch. Phys. Fluids 6, 459. doi:10.1063/1.1706761
Goldreich, P., and Sridhar, S. (1995). Toward a Theory of Interstellar Turbulence. 2: Strong Alfvenic Turbulence. ApJ 438, 763. doi:10.1086/175121
Gomberoff, L., Gomberoff, K., and Brinca, A. L. (2002). New Parametric Decays of Proton Beam-Plasma Electromagnetic Waves. J. Geophys. Res. 107, 1123. doi:10.1029/2001ja000265
Guo, F., Li, H., Daughton, W., and Liu, Y.-H. (2014). Formation of Hard Power Laws in the Energetic Particle Spectra Resulting from Relativistic Magnetic Reconnection. Phys. Rev. Lett. 113, 155005. doi:10.1103/physrevlett.113.155005
Gusakov, E. Z., and Surkov, A. V. (2007). Induced Backscattering in an Inhomogeneous Plasma at the Upper Hybrid Resonance. Plasma Phys. Control Fusion 49, 631–639. doi:10.1088/0741-3335/49/5/005
Hesse, M., Kuznetsova, M., and Birn, J. (2001). Particle-in-cell Simulations of Three-Dimensional Collisionless Magnetic Reconnection. J. Geophys. Res. 106, 29831–29841. doi:10.1029/2001ja000075
Holman, G. D., Aschwanden, M. J., Aurass, H., Battaglia, M., Grigis, P. C., Kontar, E. P., et al. (2011). Implications of X-ray Observations for Electron Acceleration and Propagation in Solar Flares. Space Sci. Rev. 159, 107–166. doi:10.1007/s11214-010-9680-9
Howes, G. G., Dorland, W., Cowley, S. C., Hammett, G. W., Quataert, E., Schekochihin, A. A., et al. (2008). Kinetic Simulations of Magnetized Turbulence in Astrophysical Plasmas. Phys. Rev. Lett. 100, 065004. doi:10.1103/physrevlett.100.065004
Huang, C., Lu, Q., Wang, R., Guo, F., Wu, M., Lu, S., et al. (2017). Development of Turbulent Magnetic Reconnection in a Magnetic Island. ApJ 835, 245. doi:10.3847/1538-4357/835/2/245
Huang, S. Y., Sahraoui, F., Retino, A., Le Contel, O., Yuan, Z. G., Chasapis, A., et al. (2016). MMS Observations of Ion-Scale Magnetic Island in the Magneto Sheath Turbulent Plasma. Geophys. Res. Lett. 43, 7850. doi:10.1002/2016GL070033
Huang, Y.-M., and Bhattacharjee, A. (2010). Scaling Laws of Resistive Magnetohydrodynamic Reconnection in the High-Lundquist-Number, Plasmoid-Unstable Regime. Phys. Plasmas 17, 062104. doi:10.1063/1.3420208
Hurford, G. J., Krucker, S., Lin, R. P., Schwartz, R. A., Share, G. H., and Smith, D. M. (2006). Gamma-Ray Imaging of the 2003 October/November Solar Flares. ApJ 644, L93–L96. doi:10.1086/505329
Hurford, G. J., Schwartz, R. A., Krucker, S., Lin, R. P., Smith, D. M., and Vilmer, N. (2003). First Gamma-Ray Images of a Solar Flare. ApJ 595, L77–L80. doi:10.1086/378179
Jaroschek, C. H., Treumann, R. A., Lesch, H., and Scholer, M. (2004). Fast Reconnection in Relativistic Pair Plasmas: Analysis of Particle Acceleration in Self-Consistent Full Particle Simulations. Phys. Plasmas 11, 1151–1163. doi:10.1063/1.1644814
Karimabadi, H., Dorelli, J., Roytershteyn, V., Daughton, W., and Chacón, L. (2011). Study of Magnetic Reconnection in Large-Scale Magnetic Island Coalescence via Spatially Coupled MHD and PIC Simulations. Phys. Rev. Lett. 107, 025002. doi:10.1103/physrevlett.107.025002
Karlický, M. (2008). Separation of Accelerated Electrons and Positrons in the Relativistic Reconnection. ApJ 674, 1211–1216. doi:10.1086/522926
Khabarova, O., Malandraki, O., Malova, H., Kislov, R., Greco, A., Bruno, R., et al. (2021). Current Sheets, Plasmoids and Flux Ropes in the Heliosphere. Space Sci. Rev. 217, 38. doi:10.1007/s11214-021-00814-x
Khabarova, O. V., Zank, G. P., Malandraki, O. E., Li, G., Le Roux, J., Webb, G. M., et al. (2017). Re-Acceleration of Energetic Particles in Large-Scale Heliospheric Magnetic Cavities. Sun and Geosphere 12, 23.
Khabarova, O., Zank, G. P., Li, G., Roux, J. A. l., Webb, G. M., Dosch, A., et al. (2015). Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. I. Dynamics of Magnetic Islands Near the Heliospheric Current Sheet. ApJ 808, 181. doi:10.1088/0004-637x/808/2/181
Khabarova, O., Zharkova, V., Xia, Q., and Malandraki, O. E. (2020). Counterstreaming Strahls and Heat Flux Dropouts as Possible Signatures of Local Particle Acceleration in the Solar Wind. ApJ 894, L12. doi:10.3847/2041-8213/ab8cb8
Khotyaintsev, Y. V., Vaivads, A., André, M., Fujimoto, M., Retinò, A., and Owen, C. J. (2010). Observations of Slow Electron Holes at a Magnetic Reconnection Site. Phys. Rev. Lett. 105, 165002. doi:10.1103/physrevlett.105.165002
Kucharek, H., Scholder, M., and Matthews, A. P. (2000). Three-dimensional Simulation of the Electromagnetic Ion/ion Beam Instability: Cross Field Diffusion. Nonlin. Process. Geophys. 7, 167–172. doi:10.5194/npg-7-167-2000
Lapenta, G., and Brackbill, J. U. (1997). A Kinetic Theory for the Drift-Kink Instability. J. Geophys. Res. 102, 27099–27108. doi:10.1029/97ja02140
Lapenta, G., Markidis, S., Divin, A., Goldman, M. V., and Newman, D. L. (2011). Bipolar Electric Field Signatures of Reconnection Separatrices for a Hydrogen Plasma at Realistic Guide Fields. Geophys. Res. Lett. 38, L17104. doi:10.1029/2011gl048572
Lapenta, G., Pucci, F., Goldman, M. V., and Newman, D. L. (2020). Local Regimes of Turbulence in 3D Magnetic Reconnection. ApJ 888, 104. doi:10.3847/1538-4357/ab5a86
Lapenta, G. (2008). Self-Feeding Turbulent Magnetic Reconnection on Macroscopic Scales. Phys. Rev. Lett. 100, 235001. doi:10.1103/physrevlett.100.235001
Le, A., Egedal, J., Ohia, O., Daughton, W., Karimabadi, H., and Lukin, V. S. (2013). Regimes of the Electron Diffusion Region in Magnetic Reconnection. Phys. Rev. Lett. 110, 135004. doi:10.1103/physrevlett.110.135004
Li, W. Y., Graham, D. B., Khotyaintsev, Y. V., Vaivads, A., André, M., Min, K., et al. (2020). Electron Bernstein Waves Driven by Electron Crescents Near the Electron Diffusion Region. Nat. Commun. 11, 141. doi:10.1038/s41467-019-13920-w
Li, X., Guo, F., Li, H., Stanier, A., and Kilian, P. (2019). Formation of Power-Law Electron Energy Spectra in Three-Dimensional Low-β Magnetic Reconnection. ApJ 884, 118. doi:10.3847/1538-4357/ab4268
Lin, J., Ko, Y. K., Sui, L., Raymond, J. C., Stenborg, G. A., Jiang, Y., et al. (2005). Direct Observations of the Magnetic Reconnection Site of an Eruption on 2003 November 18. ApJ 622, 1251–1264. doi:10.1086/428110
Lin, R. P., Krucker, S., Hurford, G. J., Smith, D. M., Hudson, H. S., Holman, G. D., et al. (2003). RHESSI Observations of Particle Acceleration and Energy Release in an Intense Solar Gamma-Ray Line Flare. ApJ 595, L69–L76. doi:10.1086/378932
Litvinenko, Y. E. (1996). Particle Acceleration in Reconnecting Current Sheets with a Nonzero Magnetic Field. ApJ 462, 997. doi:10.1086/177213
Litvinenko, Y. E., and Somov, B. V. (1993). Particle Acceleration in Reconnecting Current Sheets. Sol. Phys. 146, 127–133. doi:10.1007/bf00662174
Loureiro, N. F., and Boldyrev, S. (2017). Collisionless Reconnection in Magnetohydrodynamic and Kinetic Turbulence. ApJ 850, 182. doi:10.3847/1538-4357/aa9754
Loureiro, N. F., Cowley, S. C., Dorland, W. D., Haines, M. G., and Schekochihin, A. A. (2005). X-Point Collapse and Saturation in the Nonlinear Tearing Mode Reconnection. Phys. Rev. Lett. 95, 235003. doi:10.1103/physrevlett.95.235003
Loureiro, N. F., Schekochihin, A. A., and Cowley, S. C. (2007). Instability of Current Sheets and Formation of Plasmoid Chains. Phys. Plasmas 14, 100703. doi:10.1063/1.2783986
Markidis, S., Lapenta, G., Divin, A., Goldman, M., Newman, D., and Andersson, L. (2012). Three Dimensional Density Cavities in Guide Field Collisionless Magnetic Reconnection. Phys. Plasmas 19, 032119. doi:10.1063/1.3697976
Matthaeus, W. H., and Velli, M. (2011). Who Needs Turbulence? Space Sci. Rev. 160, 145–168. doi:10.1007/s11214-011-9793-9
McMillan, B. F., and Cairns, I. H. (2006). Lower Hybrid Turbulence Driven by Parallel Currents and Associated Electron Energization. Phys. Plasmas 13, 052104. doi:10.1063/1.2198212
McMillan, B. F., and Cairns, I. H. (2007). Parallel and Lower Hybrid Turbulence in Low β Plasmas Driven by strong Parallel Currents and the Resulting Parallel Electron and Perpendicular Ion Energization. Phys. Plasmas 14, 012103. doi:10.1063/1.2409764
Muñoz, P. A., and Büchner, J. (2018). Kinetic Turbulence in Fast 3D Collisionless Guide-Field Magnetic Reconnection. Phys. Rev. E 98, 043205. doi:10.1103/PhysRevE.98.043205
Muñoz, P. A., and Büchner, J. (2016). Non-Maxwellian Electron Distribution Functions Due to Self-Generated Turbulence in Collisionless Guide-Field Reconnection. Phys. Plasmas 23, 102103. doi:10.1063/1.4963773
Nishizuka, N., Karlický, M., Janvier, M., and Bárta, M. (2015). Particle Acceleration in Plasmoid Ejections Derived from Radio Drifting Pulsating Structures. ApJ 799, 126. doi:10.1088/0004-637x/799/2/126
Øieroset, M., Lin, R. P., Phan, T. D., Larson, D. E., and Bale, S. D. (2002). Evidence for Electron Acceleration up To∼300 keVin the Magnetic Reconnection Diffusion Region of Earth's Magnetotail. Phys. Rev. Lett. 89, 195001. doi:10.1103/physrevlett.89.195001
Øieroset, M., Phan, T. D., Fujimoto, M., Lin, R. P., and Lepping, R. P. (2001). In Situ detection of Collisionless Reconnection in the Earth's Magnetotail. Nature 412, 414–417. doi:10.1038/35086520
Oka, M., Phan, T.-D., Krucker, S., Fujimoto, M., and Shinohara, I. (2010). Electron Acceleration by Multi-Island Coalescence. ApJ 714, 915–926. doi:10.1088/0004-637x/714/1/915
Omura, Y., Matsumoto, H., Miyake, T., and Kojima, H. (1996). Electron Beam Instabilities as Generation Mechanism of Electrostatic Solitary Waves in the Magnetotail. J. Geophys. Res. 101, 2685–2697. doi:10.1029/95ja03145
Papadopoulos, K., and Palmadesso, P. (1976). Excitation of Lower Hybrid Waves in a Plasma by Electron Beams. Phys. Fluids 19, 605. doi:10.1063/1.861501
Papini, E., Franci, L., Landi, S., Verdini, A., Matteini, L., and Hellinger, P. (2019). Can Hall Magnetohydrodynamics Explain Plasma Turbulence at Sub-ion Scales? ApJ 870, 52. doi:10.3847/1538-4357/aaf003
Pezzi, O., Liang, H., Juno, J. L., Cassak, P. A., V´asconez, C. L., Sorriso-Valvo, L., et al. (2021). Dissipation Measures in Weakly Collisional Plasmas. Monthly Notices R. Astronomical Soc. 505 (4), 4857–4873. doi:10.1093/mnras/stab1516
Phan, T. D., Bale, S. D., Eastwood, J. P., Lavraud, B., Drake, J. F., Oieroset, M., et al. (2020). Parker Solar Probe In Situ Observations of Magnetic Reconnection Exhausts during Encounter 1. Astrophysical J. Suppl. 246, 34. doi:10.3847/1538-4365/ab55ee
Pritchett, P. L., and Coroniti, F. V. (2004). Three-dimensional Collisionless Magnetic Reconnection in the Presence of a Guide Field. J. Geophys. Res. (Space Physics) 109, A01220. doi:10.1029/2003JA009999
Pritchett, P. L. (2005). Onset and Saturation of Guide-Field Magnetic Reconnection. Phys. Plasmas 12, 062301. doi:10.1063/1.1914309
Pucci, F., Servidio, S., Sorriso-Valvo, L., Olshevsky, V., Matthaeus, W. H., Malara, F., et al. (2017). Properties of Turbulence in the Reconnection Exhaust: Numerical Simulations Compared with Observations. ApJ 841, 60. doi:10.3847/1538-4357/aa704f
Rogers, B. N., Drake, J. F., and Shay, M. A. (2000). The Onset of Turbulence in Collisionless Magnetic Reconnection. Geophys. Res. Lett. 27, 3157–3160. doi:10.1029/2000gl000038
Roytershteyn, V., Daughton, W., Karimabadi, H., and Mozer, F. S. (2012). Influence of the Lower-Hybrid Drift Instability on Magnetic Reconnection in Asymmetric Configurations. Phys. Rev. Lett. 108, 185001. doi:10.1103/physrevlett.108.185001
Scholer, M., Sidorenko, I., Jaroschek, C. H., Treumann, R. A., and Zeiler, A. (2003). Onset of Collisionless Magnetic Reconnection in Thin Current Sheets: Three-Dimensional Particle Simulations. Phys. Plasmas 10, 3521–3527. doi:10.1063/1.1597494
Shay, M. A., Phan, T. D., Haggerty, C. C., Fujimoto, M., Drake, J. F., Malakit, K., et al. (2016). Kinetic Signatures of the Region Surrounding the X Line in Asymmetric (Magnetopause) Reconnection. Geophys. Res. Lett. 43, 4145–4154. doi:10.1002/2016gl069034
Silin, I., and Büchner, J. (2006). Three-dimensional Vlasov-Code Simulations of Magnetopause-like Current Sheets. Adv. Space Res. 37, 1354–1362. doi:10.1016/j.asr.2005.05.025
Sironi, L., and Spitkovsky, A. (2014). Relativistic Reconnection: an Efficient Source of Non-thermal Particles. ApJ 783, L21. doi:10.1088/2041-8205/783/1/l21
Siversky, T. V., and Zharkova, V. V. (2009). Particle Acceleration in a Reconnecting Current Sheet: PIC Simulation. J. Plasma Phys. 75, 619–636. doi:10.1017/s0022377809008009
Song, H.-Q., Chen, Y., Li, G., Kong, X.-L., and Feng, S.-W. (2012). Coalescence of Macroscopic Magnetic Islands and Electron Acceleration from STEREO Observation. Phys. Rev. X 2, 021015. doi:10.1103/physrevx.2.021015
Takasao, S., Asai, A., Isobe, H., and Shibata, K. (2012). Simultaneous Observation of Reconnection Inflow and Outflow Associated with the 2010 August 18 Solar Flare. ApJ 745, L6. doi:10.1088/2041-8205/745/1/l6
Trotta, D., Franci, L., Burgess, D., and Hellinger, P. (2020). Fast Acceleration of Transrelativistic Electrons in Astrophysical Turbulence. ApJ 894, 136. doi:10.3847/1538-4357/ab873c
Verboncoeur, J. P., Langdon, A. B., and Gladd, N. T. (1995). An Object-Oriented Electromagnetic PIC Code. Comp. Phys. Commun. 87, 199–211. doi:10.1016/0010-4655(94)00173-y
Vilmer, N., MacKinnon, A. L., and Hurford, G. J. (2011). Properties of Energetic Ions in the Solar Atmosphere from γ-Ray and Neutron Observations. Space Sci. Rev. 159, 167–224. doi:10.1007/s11214-010-9728-x
Wang, R., Lu, Q., Nakamura, R., Huang, C., Du, A., Guo, F., et al. (2016). Coalescence of Magnetic Flux Ropes in the Ion Diffusion Region of Magnetic Reconnection. Nat. Phys 12, 263–267. doi:10.1038/nphys3578
Wood, P., and Neukirch, T. (2005). Electron Acceleration in Reconnecting Current Sheets. Sol. Phys. 226, 73–95. doi:10.1007/s11207-005-5686-y
Xia, Q., and Zharkova, V. (2018). Particle Acceleration in Coalescent and Squashed Magnetic Islands. A&A 620, A121. doi:10.1051/0004-6361/201833599
Xia, Q., and Zharkova, V. (2020). Particle Acceleration in Coalescent and Squashed Magnetic Islands. A&A 635, A116. doi:10.1051/0004-6361/201936420
Zank, G. P., le Roux, J. A., Webb, G. M., Dosch, A., and Khabarova, O. (2014). Particle Acceleration via Reconnection Processes in the Supersonic Solar Wind. ApJ 797, 28. doi:10.1088/0004-637x/797/1/28
Zenitani, S., and Hoshino, M. (2008). The Role of the Guide Field in Relativistic Pair Plasma Reconnection. ApJ 677, 530–544. doi:10.1086/528708
Zhang, Q., Drake, J. F., and Swisdak, M. (2019). Instabilities and Turbulence in Low-β Guide Field Reconnection Exhausts with Kinetic Riemann Simulations. Phys. Plasmas 26, 102115. doi:10.1063/1.5121782
Zharkova, V., and Khabarova, O. (2015). Additional Acceleration of Solar-Wind Particles in Current Sheets of the Heliosphere. Ann. Geophys. 33, 457–470. doi:10.5194/angeo-33-457-2015
Zharkova, V. V., and Agapitov, O. V. (2009). The Effect of Magnetic Topology on Particle Acceleration in a Three-Dimensional Reconnecting Current Sheet: a Test-Particle Approach. J. Plasma Phys. 75, 159–181. doi:10.1017/s002237780800771x
Zharkova, V. V., Arzner, K., Benz, A. O., Browning, P., Dauphin, C., Emslie, A. G., et al. (2011). Recent Advances in Understanding Particle Acceleration Processes in Solar Flares. Space Sci. Rev. 159, 357–420. doi:10.1007/s11214-011-9803-y
Zharkova, V. V., and Gordovskyy, M. (2005). Energy Spectra of Particles Accelerated in a Reconnecting Current Sheet with the Guiding Magnetic Field. JMNRAS 356, 1107–1116. doi:10.1111/j.1365-2966.2004.08532.x
Zharkova, V. V., and Gordovskyy, M. (2004). Particle Acceleration Asymmetry in a Reconnecting Nonneutral Current Sheet. ApJ 604, 884–891. doi:10.1086/381966
Zharkova, V. V., and Khabarova, O. V. (2012). Particle Dynamics in the Reconnecting Heliospheric Current Sheet: Solar Wind Data versus Three-Dimensional Particle-In-Cell Simulations. ApJ 752, 35. doi:10.1088/0004-637x/752/1/35
Zhong, J. Y., Lin, J., Li, Y. T., and Wang, X. (2016). Relativistic Electrons Produced by Reconnecting Electric fields in a Laser-Driven Bench-Top Solar Flare. Astrophysical J. Suppl. Ser. 225, 30. doi:10.3847/0067-0049/225/2/30
Zhou, M., Deng, X. H., Li, S. Y., Pang, Y., Vaivads, A., Rème, H., et al. (2009). Observation of Waves Near Lower Hybrid Frequency in the Reconnection Region with Thin Current Sheet. J. Geophys. Res. 114, A02216. doi:10.1029/2008JA013427
Zhou, M., Li, H., Deng, X., Huang, S., Pang, Y., Yuan, Z., et al. (2014). Characteristic Distribution and Possible Roles of Waves Around the Lower Hybrid Frequency in the Magnetotail Reconnection Region. J. Geophys. Res. Space Phys. 119, 8228–8242. doi:10.1002/2014ja019978
Zong, Q.-G., Fritz, T. A., Pu, Z. Y., Fu, S. Y., Baker, D. N., Zhang, H., et al. (2004). Cluster Observations of Earthward Flowing Plasmoid in the Tail. Geophys. Res. Lett. 31, L18803. doi:10.1029/2004gl020692
Zudin, I. Y., Zaboronkova, T. M., Gushchin, M. E., Aidakina, N. A., Korobkov, S. V., and Krafft, C. (2019). Whistler Waves' Propagation in Plasmas with Systems of Small‐Scale Density Irregularities: Numerical Simulations and Theory. J. Geophys. Res. Space Phys. 124, 4739–4760. doi:10.1029/2019ja026637
Keywords: particle acceleration, magnetic reconnection, plasma, methods: numerical, beam instability, kinetic turbulence
Citation: Zharkova V and Xia Q (2021) Kinetic Plasma Turbulence Generated in a 3D Current Sheet With Magnetic Islands. Front. Astron. Space Sci. 8:665998. doi: 10.3389/fspas.2021.665998
Received: 09 February 2021; Accepted: 22 September 2021;
Published: 26 November 2021.
Edited by:
Luca Sorriso-Valvo, Institute for Space Physics, SwedenReviewed by:
Narges Ahmadi, University of Colorado Boulder, United StatesKeizo Fujimoto, Beihang University, China
Copyright © 2021 Zharkova and Xia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Valentina Zharkova, dmFsZW50aW5hLnpoYXJrb3ZhQG5vcnRodW1icmlhLmFjLnVr, dmFsamE0NkBnbWFpbC5jb20=
 Valentina Zharkova
Valentina Zharkova Qian Xia1,2
Qian Xia1,2