- 1Inter-University Centre for Astronomy and Astrophysics, Pune University Campus, Pune, India
- 2Institut für Theoretische Physik, Goethe Universität, Frankfurt, Germany
The appearance of strangeness in the form of hyperons within the inner core of neutron stars is expected to affect its detectable properties, such as its global structure or gravitational wave emission. This work explores the parameter space of hyperonic stars within the framework of the Relativistic Mean Field model allowed by the present uncertainties in the state-of-the-art nuclear and hypernuclear experimental data. We impose multi-physics constraints at different density regimes to restrict the parameter space: Chiral effective field theory, heavy-ion collision data, and multi-messenger astrophysical observations of neutron stars. We investigate possible correlations between empirical nuclear and hypernuclear parameters, particularly the symmetry energy and its slope, with observable properties of neutron stars. We do not find a correlation for the hyperon parameters and the astrophysical data. However, the inclusion of hyperons generates a tension between the astrophysical and heavy-ion data constraining considerably the available parameter space.
1 Introduction
Understanding strong interaction among hadrons is one of the most intriguing topics in nuclear physics. Despite the recent progress in understanding the phase diagram of Quantum Chromodynamics (QCD), the theory of strong interactions (Baym et al., 2018; David et al., 2020), we are still far from achieving a unified description of nuclear matter under extreme conditions of density and temperature. While terrestrial nuclear experiments probe densities close to nuclear saturation density (n0 ∼ 0.16 fm−3) (Gandolfi et al., 2015; Lattimer, 2015), heavy-ion collision (HIC) experiments (Le Fèvre et al., 2016; Russotto et al., 2016) provides information about the hot and dense matter at several times n0. Recent progress in Lattice QCD (Inoue, 2016; Inoue, 2019; Fabbietti et al., 2021) also provides new constraints on the properties of matter at high temperature and low densities. Neutron stars, on the contrary, are astrophysical laboratories that provide us an opportunity to investigate ultra-high density (up to 10 times n0) and low-temperature regime of the QCD phase diagram, given the conditions that exist only in its interior (Lattimer and Prakash, 2004; Glendenning, 2012).
Strangeness adds a new dimension to the description of nuclear matter. The presence of strangeness has already been established in heavy-ion collisions (appearance of hyperons and kaons) or in finite nuclear systems (hypernuclei). It is also conjectured that strangeness-containing matter, in the form of hyperons, kaons, or even deconfined quark matter, can appear at the ultra-high densities that exist in the core of a neutron star (NS). The appearance of strangeness can have a significant impact on NS composition, structure, and observable astrophysical properties, such as its mass, radius, cooling, or gravitational wave (GW) emission (Oertel et al., 2017).
In order to connect the NS internal composition with its global properties, one requires an equation of state (EoS) (Lattimer, 2012; Lattimer, 2015; Baym et al., 2018). The theoretical description of NS matter, therefore, requires the construction of models of hadron–hadron interaction, using non-relativistic (such as Skyrme or Gogny interactions) (Vautherin and Brink, 1972; Stone and Reinhard, 2007; Dutra et al., 2012) or relativistic (Relativistic Mean Field or Dirac-Brueckner-Hartree-Fock methods) (Serot and Walecka, 1992; Serot and Walecka, 1997) techniques. In the case of microscopic models (such as the Brueckner-Hartree-Fock method), the interactions are rigorously calculated from lowest order term to increasing order. Nevertheless, the poor knowledge of three-nucleon forces limits their applicability to reproduce real astrophysical data. Phenomenological models are more successful, with the model parameters usually constrained at densities close to n0 and low isospin values (neutron-proton ratio), but the uncertainty increases at larger densities and asymmetries. The nuclear symmetry energy (the difference between the binding energies of symmetric nuclear matter and neutron matter) is a key quantity that governs the difference in the behavior of infinite symmetric nuclear matter and neutron star matter.
Neutron stars are particularly interesting, as they can be observed via electromagnetic (X-ray, γ-ray, radio waves) and gravitational waves, opening up a new era of multi-messenger astronomy. Electromagnetic multi-wavelength observations of NSs reveal a wealth of details about its global structure (Demorest et al., 2010; Antoniadis et al., 2013). NS masses can be determined to high precision using post-Keplerian effects in NSs in binary (Thorsett and Chakrabarty, 1999). Traditionally radius measurements from thermal emission suffered from large uncertainties (Özel et al., 2010; Guillot et al., 2013; Steiner et al., 2013), but the recently launched NICER (Neutron Star Interior Composition Explorer) (Arzoumanian et al., 2014; Miller et al., 2019a; Riley et al., 2019; Miller et al., 2021; Riley et al., 2021) mission has improved NS estimates by exploiting a novel scheme of modulation profiles of pulses. Finally, with the recent detection of GWs for the first time from NS-NS (GW170817) (Abbott et al., 2017), NS-BH (GW200105 and GW200115) (Abbott et al., 2021), and GW190425 (Abbott et al., 2020) systems by LIGO (Aasi et al., 2015) and Virgo (Acernese et al., 2014), GW astronomy is allowing us to probe the interior of NSs directly. The tidal deformation of NSs in the strong gravitational field of its binary companion measured during the inspiral phase of the merger depends on the EoS and, therefore, reveals information about its radius and interior composition (Abbott et al., 2018; Annala et al., 2018; Most et al., 2018; Abbott et al., 2019).
In the recent past, there have been several attempts to impose constraints on the NS EoS using data from NS multi-messenger astrophysical observations within a statistical Bayesian scheme (Coughlin et al., 2019; Dietrich et al., 2020; O’Boyle et al., 2020; Biswas, 2021a; Biswas, 2021b; Biswas et al., 2021; Pang et al., 2021). In such a scheme, the low-density EOS constrained by theoretical and experimental nuclear physics is matched with parametrized high-density EOSs satisfying gravitational wave and electromagnetic data (Tews et al., 2018; Tews et al., 2019a; Tews et al., 2019b; Gandolfi et al., 2019; Capano et al., 2020). Usually, the EoSs are based on different parametrization schemes such as piecewise polytropes (Read et al., 2009; Hebeler et al., 2013; Annala et al., 2018; Gamba et al., 2019), spectral representation (Lindblom, 2018; Fasano et al., 2019), speed-of-sound parametrization (Tews et al., 2018; Greif et al., 2019; Landry et al., 2020), or nuclear meta-modeling technique (Güven et al., 2020). Only a few recent works used the RMF model (Traversi et al., 2020) or hybrid (nuclear + piecewise polytope) parametrizations (Biswas et al., 2021) to obtain posterior distributions of empirical parameters. Correlations among empirical nuclear parameters and some chosen NS observables have only recently been explored (Carson et al., 2019; Xie and Li, 2019; Zhang and Li, 2019; Zimmerman et al., 2020). Although several of these works suggested probing the effect of the presence of hyperons, none of them consistently included hyperons within such a scheme. It, therefore, remains to be investigated whether one can restrict the parameter space of uncertainties associated with hyperons (hypernuclear potentials or hyperon couplings) or if they show any physical correlations with measurable properties such as nuclear saturation parameters or NS astrophysical observables.
In recent work (Ghosh et al., 2022), multi-physics constraints were imposed at different density regimes on the nuclear EoS using a “cut-off scheme,” and correlations of nuclear saturation parameters with astrophysical observables were investigated. Motivated by the Bayesian approach, the parameters of the realistic nuclear model were varied within their allowed uncertainties, compatible with the state-of-the-art nuclear experimental data and the parameter space, constrained using a combination of current best-known physical constraints at different density regimes: theoretical (chiral effective field theory) at low densities, multi-messenger (multi-wavelength electromagnetic as well as GW) astrophysical data at high densities, and experimental (nuclear and heavy-ion collision) at intermediate densities (Tsang et al., 2018; Dexheimer et al., 2021) to restrict the parameter space of the nuclear model. Furthermore, nuclear and heavy-ion collision experiments are isospin symmetric (same number of neutrons and protons), so studying NS matter provides information about the unknown nuclear symmetry energy.
This article extends the above investigation to neutron star matter including strangeness, particularly hyperons. Within the framework of the RMF model and allowing for a parameter space spanning current uncertainties in nuclear and hypernuclear physics, we impose multi-physics constraints in different density regimes from terrestrial nuclear/hypernuclear and multi-messenger astrophysical data. This study aims to investigate possible correlations between empirical nuclear and hypernuclear parameters (particularly the symmetry energy and its slope) with NS astrophysical observables.
The structure of the article is as follows: in Section 2, we describe the methods used to determine the composition of NS matter including hyperons in the framework of the RMF model. In Section 3, we impose constraints at different densities on the hyperonic EoS. In Section 4, we discuss the results of this investigation, and in Section 5 we discuss the implications of these findings.
2 Methods
As discussed in Section 1, we calculate the beta equilibrated, charge-neutral NS EoS within the RMF framework. For our investigation, we consider the standard baryon octet, as well as electrons and muons. The interaction Lagrangian density
where
In Eq. 1, B stands for the baryon octet (p, n, Λ, Σ−, Σ0, Σ+, Ξ−, Ξ0) whereas Y stands for hyperons (Λ, Σ−, Σ0, Σ+, Ξ−, Ξ0). One can solve the equation of motion governing constituent particle fields (Ψ) as well as those of the following mesons (Hornick et al., 2018; Pradhan and Chatterjee, 2021). Replacing the meson fields with their mean values in RMF framework, the energy density (ϵ) corresponding to the Lagrangian given in Eq. 1 can be expressed as
where gsi and kFi represent the spin degeneracy and Fermi momentum of the ith species, respectively. The baryon effective mass
with ni being the number density of ith constituent. The chemical potentials for baryon (μB) and lepton (μℓ) are given by
2.1 Nucleonic Matter
The isoscalar nucleon-meson coupling parameters (gσN, gωN, b, and c) are determined by fixing the nuclear saturation parameters: nuclear saturation density (n0), binding energy per nucleon at saturation (Esat), incompressibility (Ksat), and the effective nucleon mass (m*) at saturation. On the other contrary, the isovector couplings gρN and Λω are fixed to the symmetry energy (Esym) and slope of symmetry energy (Lsym) at saturation (Chen and Piekarewicz, 2014; Hornick et al., 2018; Ghosh et al., 2022). The range of empirical parameters considered in this work are consistent with the state-of-the-art nuclear experimental data (Ghosh et al., 2022) and are summarized in Table 1.

TABLE 1. Range (minimum and maximum values) of nuclear and hypernuclear parameters at saturation density used in this work. Masses of mesons and the nucleon are fixed as mσ = 550 MeV, mω = 783 MeV, mρ = 770 MeV, mϕ = 1020 MeV and mN = 939 MeV.
2.2 Hyperonic Matter
In the Lagrangian Eq. 1, the attractive interaction among hyperons is mediated by the exchange of strange scalar (σ*) meson, and the repulsive interaction is mediated by the exchange of strange vector (ϕ) meson. However, it has been concluded that models with attractive hyperon–hyperon interaction show incompatibility with observations of the maximum NS mass (Weissenborn et al., 2012). Hence, we set the strange scalar couplings to 0, i.e., gσY = 0, and the remaining non-strange hyperon meson coupling constants (gσY) are fitted to the hyperon-nucleon potential (UY) at saturation using Eq. 5 (Weissenborn et al., 2012). Among the nucleon-hyperon potentials, the best-known potential is that of the hyperon Λ, having a value of UΛ = −30 MeV (Millener et al., 1988; Schaffner et al., 1992). Although the potential depths for hyperons Σ and Ξ are not known precisely, it has been concluded that the Σ-nucleon potential is repulsive (Mareš et al., 1995; Schaffner-Bielich and Gal, 2000; Friedman and Gal, 2007) whereas UΞ is attractive in nature (Fukuda et al., 1998; Khaustov et al., 2000; Schaffner-Bielich and Gal, 2000). Hence, for this investigation, we vary UΣ in the range of 0 to +30 MeV and UΞ from −30MeV to 0. The vector hyperon couplings (gωY, gϕY) are fixed to their SU(6) values (see Eq. 6) (Schaffner et al., 1993; Weissenborn et al., 2012):
Recent lattice QCD calculations by the HALQCD group extracted hyperon potentials at almost physical quark masses and used it to estimate the hyperon potentials in pure neutron matter and the nuclear matter using the Brueckner-Hartree-Fock approximation (Inoue, 2016; Inoue, 2019). They find that the hyperon potentials in nuclear matter are UΛ = −28 MeV, UΣ = +15MeVand UΞ = −4 MeV. From Figure 4 in Inoue (2019), one can read off the hyperon potentials for Σ− and Σ+, as well as for Ξ0 and Ξ− in pure neutron matter. The relevant potentials for neutron star matter are the ones for the Σ− and the Ξ− with the potentials of +25 MeV and +6 MeV, respectively. However, these results suggest that the isovector hyperon coupling (gρY) differs from its SU(6) quark model values, where the isospin potential for the Ξ would be as large as the one for nucleons, and the one for the Σ is even twice as large. For a typical nucleon isospin potential of about 32 MeV, one arrives at hyperon isospin potentials, which are more than a factor two larger than those from the HALQCD analysis. We, therefore, introduce a scaling parameter y, which ranges from 0 to 1 (0 to SU(6) coupling strength) to span the uncertainty in the hyperon-isovector coupling. In that case, gρY can be expressed as
The effect of the variation in the y-parameter (isovector hyperon coupling) on the particle fractions can be understood from Figure 1. For a chosen parameter set from Table 1, Ξ− starts to appear at 2.27, 2.34, and 2.45 n0 for y values 0, 0.5, and 1, respectively. However, Ξ0 starts to appear at 6.977, 6.943, and 6.850 n0 for y changing from 0 to 1 in steps of 0.5. One must note that the threshold of appearance of the hyperons will depend upon the hyperon potentials and the nuclear saturation parameters chosen for the EoS.

FIGURE 1. Particle fractions for varying y parameter (isovector hyperon coupling). The nuclear and hyper nuclear parameters are fixed to m* = 0.65 mN, Esat = −16 MeV, Ksat = 240 MeV, Jsym = 32 MeV, Lsym = 60 MeV, UΛ = −30 MeV, UΣ = +30 MeV, UΞ = −28 MeV. (A) Particle fractions with y = 0. (B) Particle fractions with y = 0.5. (C) Particle fractions with y given by SU(6) symmetry.
2.3 Global Structure
The equilibrium structure of a non-rotating, relativistic NS is obtained by solving the coupled equations of hydrostatic equilibrium known as the Tolman-Oppenheimer-Volkof (TOV) equations (Glendenning, 2012; Schaffner-Bielich, 2020):
with the given equation of state, which gives a relation between the energy density (ɛ) and pressure (p). These TOV in Eq. 8 are integrated from the center of the star to the surface with the boundary conditions of vanishing mass, m|r=0 = 0, at the center of the star, and a vanishing pressure, p|r=R = 0, at the surface. By varying the central density for a given EoS, we can get a sequence of NSs with different mass and radii, thus giving the M-R curves.
The tidal deformability parameter quantifies the degree of the tidal deformation effects due to the companion in coalescing binary NS systems during the early stages of an inspiral. It is defined as
where Qij is the induced mass quadrupole moment of the NS and ɛij is the gravitational tidal field of the companion. The tidal deformability λ is related to the dimensionless l = 2 tidal Love number k2 as follows (Flanagan and Hinderer, 2008; Hinderer, 2008):
The tidal Love number (k2) can be obtained by solving a set of differential equations coupled with the TOV equations (Yagi and Yunes, 2013). The total tidal effect of two neutron stars in an inspiraling binary system is given by the mass-weighted (dimensionless) tidal deformability
where Λ1 = Λ1(M1) and Λ2 = Λ2(M2) are the (dimensionless) tidal deformabilities and M1, M2 are the masses of the individual binary components, respectively.
3 Multi-Density Constraints
In this work, we constrain the parameter space of the nucleonic and hyperonic matter as described in Section 2 using a “cut-off filter” scheme where we impose strict limits from nuclear and astrophysical observation to obtain the posteriors. In the language of Bayesian analysis, the priors are obtained by varying the nuclear empirical parameters, hyperon potentials, and isovector couplings uniformly within their uncertainty range in Table 1, and the likelihood functions are appropriately chosen physical conditions as the Filter functions described in Section 3.1.
Miller et al. (2019b) pointed out the statistical uncertainties in constraining EoS by putting strict limits from multi-messenger observations of neutron stars like we have used here. With many priors, this cut-off scheme gives a correct estimate of the nuclear parameter ranges consistent with the observations. Recent works (Annala et al., 2018; Most et al., 2018; Annala et al., 2020; Wei et al., 2020; Annala et al., 2021) also used similar cut-off schemes for constraining the EoS of ultra-dense matter. In the recent work by Ghosh et al. (2022), it was explicitly shown that including the statistical re-weighting using χ-squared statistics might change the posterior probability distribution slightly, but it does not significantly alter the physical correlation between nuclear empirical parameters and astrophysical observables. So, we adopt this “cut-off filter” scheme for this work.
3.1 Filter Functions
The following physical constraints at different densities from multi-disciplinary physics are applied in this work:
• At Low Densities: χEFT
Chiral EFT is an effective theory of QCD that describes strong many-body interactions among nucleons using order by order expansions in terms of contact interactions and long-range pion exchange interactions. In particular, the χ EFT expansion gives estimates of theoretical uncertainties depending on local chiral two and three-nucleon interactions using quantum Monte Carlo methods, which are one of the most precise many-body methods for nuclear physics (Drischler et al., 2016; Drischler et al., 2020). The EoS of pure neutron matter (PNM) can be well constrained at low baryon densities nb in the range of ∼ 0.5–1.4 n0 (Drischler et al., 2019).
• At High Densities: NS Astrophysical Data
The constraints on the EoS at high density come from multi-messenger astrophysical observations, such as high mass NS observations, GW measurement of tidal deformability from binary neutron star mergers as follows:
(1) From the recent observations of the heaviest known pulsar PSR J0740+6620, the maximum mass of the neutron stars should be equal to or exceed
(2) The recent analyses of the GW170817 event (Abbott et al., 2019) apply a constraint on the upper bound of the effective tidal deformability
• At Intermediate Densities: Heavy-Ion Collision Experiments
Heavy-ion collision experiments can provide additional information about the behavior of hot dense matter at intermediate densities
(1) KaoS experiment: subthreshold K+ meson production in Au+Au & C+C nuclear collisions at the Kaon Spectrometer (KaoS) experiment at GSI, Darmstadt (Hartnack et al., 2006) yield kaon multiplicity, which is an indicator of the compressibility of dense matter at densities
(2) FOPI experiment: elliptic flow data in Au+Au collisions between 0.4 and 1.5A GeV by the FOPI collaboration (Le Fèvre et al., 2016) provide constraints for the EoS of compressed symmetric nuclear matter (SNM). By analyzing the FOPI data using IQMD transport codes, one can obtain a constraint for the binding energy of SNM in the density region of nb/n0 ∼ 1.4–2.0 (Le Fèvre et al., 2016). In order to impose this constraint, the binding energy for SNM is calculated for the input parameters and only permitted if they lie inside the band allowed by the FOPI data in this density range.
(3) ASY-EOS experiment: information about the symmetry energy for ANM at supra-saturation densities can be obtained from directed and elliptic flows of neutrons and light charged particles measured for the reaction 197Au+197Au at 400 MeV/nucleon incident energy within the ASY-EOS experimental campaign at the GSI, Germany (Russotto et al., 2016). In order to impose the ASY-EOS filter, the symmetry energy of ANM EoS is calculated for the input parameters and allowed only if the symmetry energy lies inside the band allowed by the data in the range of
3.2 Correlations
Using the posterior obtained from the analysis, we look for any physical correlation of the nuclear parameters, hyperon potentials, and isovector coupling among themselves and also with the astrophysical observables such as the mass and radius of the canonical 1.4M⊙ and the massive 2M⊙ NS. For this study, we use Pearson’s linear correlation coefficient defined as (Kirch, 2008)
where Cov(X, Y) is the co-variance between two variables X and Y defined as
where N is the number of sample points and M(X) is the mean of the variable X defined as
4 Results
4.1 Effect of χEFT + Astro Filters
By randomly varying the parameter space of the nuclear parameters and hyperon potentials from Table 1, we generate the uniformly distributed prior set. After generating the random EoSs, we use the χEFT and astrophysical filters described in Section 3.1 to obtain filtered sets for the parameters and NS observables. For χEFT, we evaluate the binding energies in the density range of nb/n0 ∼ 0.5–1.4 corresponding to the χEFT data and allow only those parameter sets that lie within the band allowed by χEFT calculations (Figure 2).
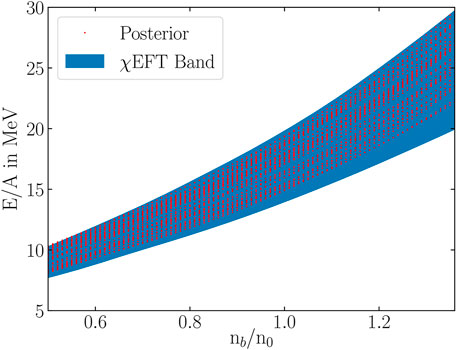
FIGURE 2. Binding energy E/A of posterior pure neutron matter EoSs as a function of normalized density nb/n0 allowed by chiral effective field theory (χEFT) data (Drischler et al., 2019).
After obtaining the posterior χEFT, we use the same parameter set to obtain the hyperonic EoS using hyperon potentials and couplings given in Section 2.2. We then solve the coupled TOV Equations 8 and 10 to obtain the mass, radius, and tidal deformability of the NSs. Using the multi-messenger astrophysical and GW observation of NSs given in Section 3.1, we rule out further combinations of parameter sets and allow only the combinations that simultaneously satisfy all constraints on NS observables. In Figure 3, we plot the mass-radius relations and the dimensionless tidal deformability as a function of NS mass corresponding to the filtered hyperonic EoSs. We can see that NS radii span a wide range from 11 to 14 km.
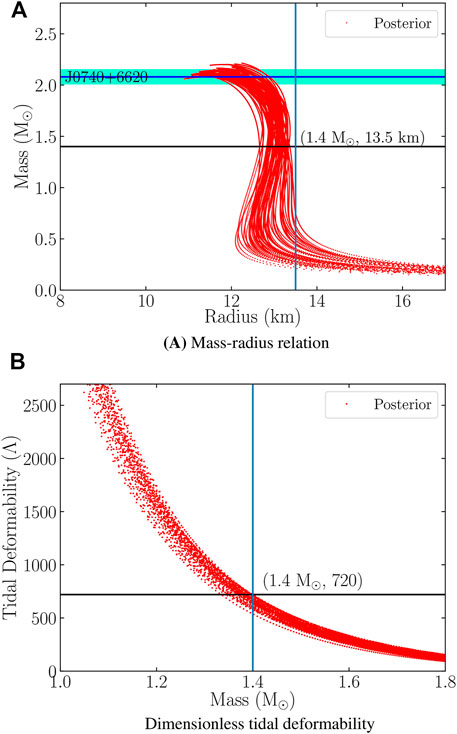
FIGURE 3. NS observables for the posterior hyperon EoSs after passing through χEFT and NS observations filters. The light green band indicates the uncertainty in the measurement of the maximum mass of PSR J0740 + 6620 (Fonseca et al., 2021) (A) Mass-radius relation. (B) Dimensionless tidal deformability.
4.2 Correlations
After obtaining the posterior parameter space, we look for any physical correlation among the parameters and the NS observables as well as within themselves. In Figure 4, we display the correlation matrix of the following quantities: nuclear empirical parameters (n0, Esat, Ksat, Esym, Lsym), the effective mass m*/m, hyperon potentials (UΣ, UΞ), hyperon-isovector coupling parameter y, and the NS observables (
• n0 and m*/m show a high correlation (0.71).
• n0 has a moderate correlation with the NS observables. The correlation is noticeable (0.54) for the constraints for 1.4M⊙ NS but is negligible for the constraints for 2 M⊙.
• Symmetry energy Esym and its slope Lsym display a strong correlation (0.79) which only appears when we apply the χEFT filter. This correlation only comes from the χEFT filter around saturation density, which is in agreement with previous literature (Hornick et al., 2018; Ghosh et al., 2022).
• We see a moderate correlation (0.44) between Lsym and effective mass m*/m after applying the χEFT filter.
• The correlation of m*/m with the NS observables is pretty low (
• The correlation between slope of symmetry energy Lsym and radius of 1.4M⊙ NS is also lower (around 0.4). A correlation between Lsym and
• All the NS observables (radius and dimensionless tidal deformability for 1.4 M⊙ and 2 M⊙ NS), as expected, show a strong correlation with each other (according to Eq. 9), although we find a moderate correlation with the observables between 1.4 M⊙ and 2 M⊙ NSs.
• We did not find any correlation between the hyperon potentials and the isovector coupling parameter y with other nuclear parameters and the astrophysical observables.
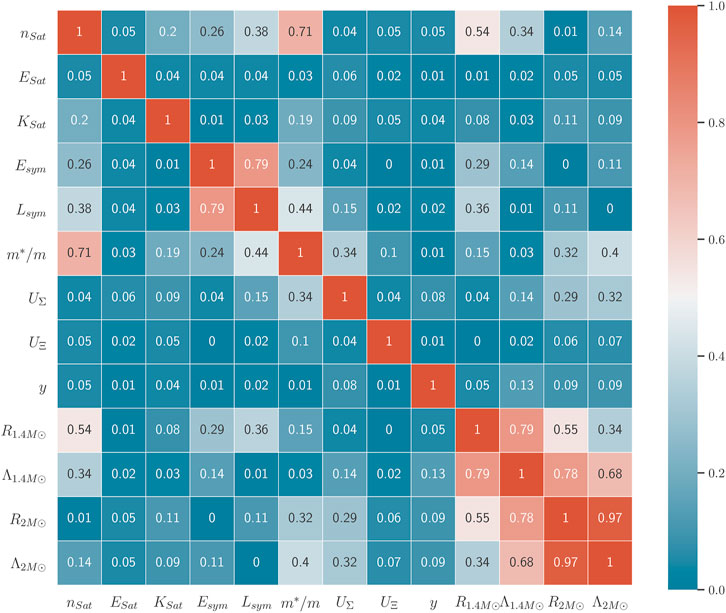
FIGURE 4. Posterior correlation matrix for variation of nuclear empirical parameters and NS observables, after application of the χEFT and NS observations filter.
To understand the correlations better, in Figure 5, we plot the posterior distribution of the nuclear parameters (n0, Esym, Lsym, and m*/m), which show significant correlations and the astrophysical observables (
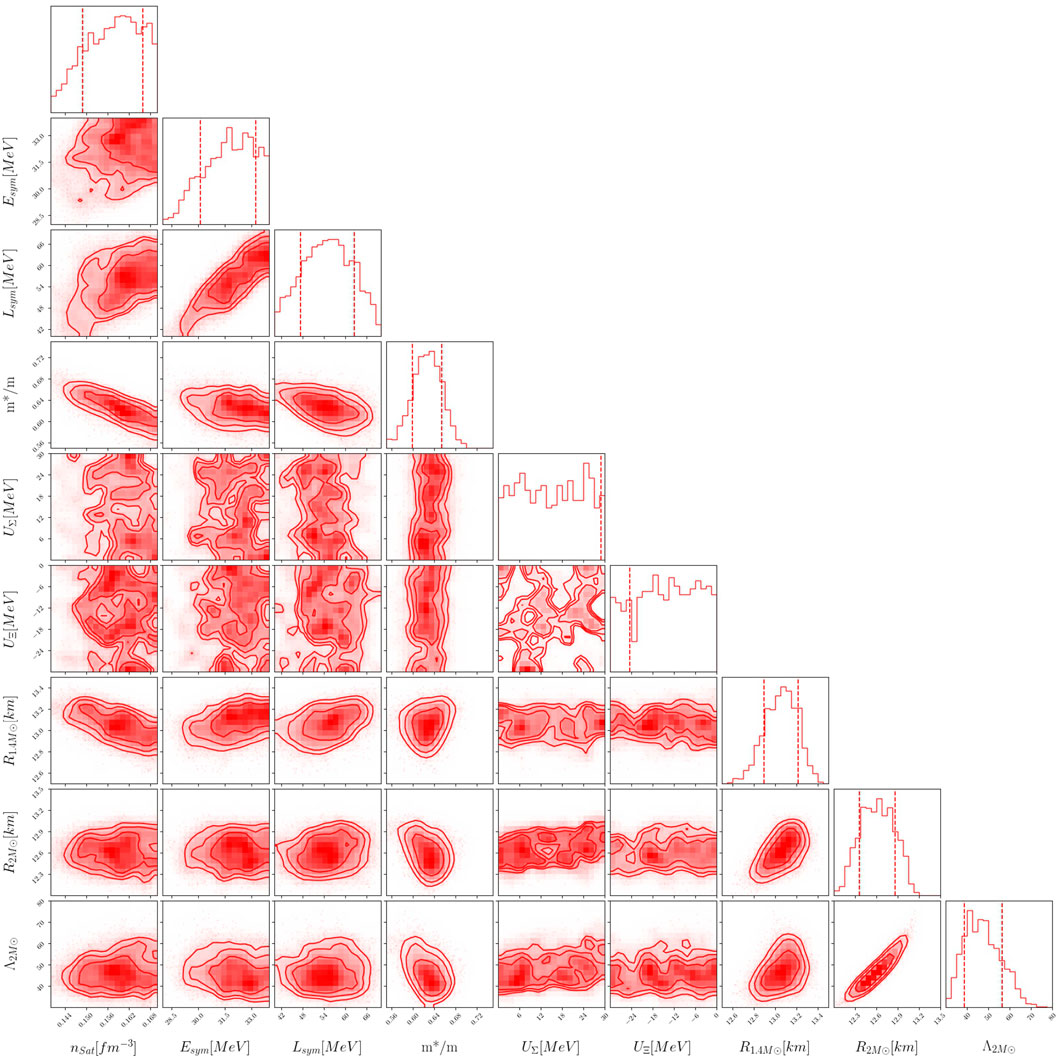
FIGURE 5. Posterior distributions of nuclear parameters and astrophysical observables after applying the χEFT and the astrophysical constraints.
From the corner plots, we see that after applying the χEFT filter, both the median values of symmetry energy and its slope Lsym shift toward a higher value compared to their prior range in Table 1, which leads to their strong correlation. For the effective mass, we see that the peak is around 0.63, which is lower than what we observed for purely nucleonic matter (Hornick et al., 2018; Ghosh et al., 2022) because when we include hyperon, the EoSs become softer (Pradhan and Chatterjee, 2021). Therefore, in order to satisfy the astrophysical constraint of maximum mass above 2M⊙ and tidal deformability, the posterior of m*/m shifts toward a lower value. Also, from Figure 5 in Ghosh et al. (2022), we know that the χEFT filter removes parameter sets with low effective mass and slope of symmetry energy, which gives rise to a moderate correlation between Lsym and m*/m observed here. For this reason, for the hyperonic case along with the χEFT filter, the range of effective mass becomes narrow and peaks toward a lower value (around 0.63), which indeed restricts the radius of 1.4M⊙ star to 12.6–13.4 km. That is why we observe a very low correlation between m*/m and the astrophysical observables. We also conclude that there is no correlation between the hyperon potentials (UΣ, UΞ) and the NS astrophysical observables.
4.3 Effect of all Filters: χEFT + Astro + HIC (KaoS + FOPI + ASY-EOS)
We first generated 50,000 prior sets, and applying all filters (χEFT, astrophysical data, HIC) obtained almost no posterior sets. In order to understand the effect of the HIC filters, we then passed the prior sets only through the KaOS, FOPI, and ASY-EOS filters and plotted the posterior of each nuclear parameter (see Figure 6). From the figures, we observe that, in the Ksat distribution, the values are restricted below 240 MeV after HIC filters, which is the effect of the KaoS filter. In the Lsym distribution, the values are restricted to
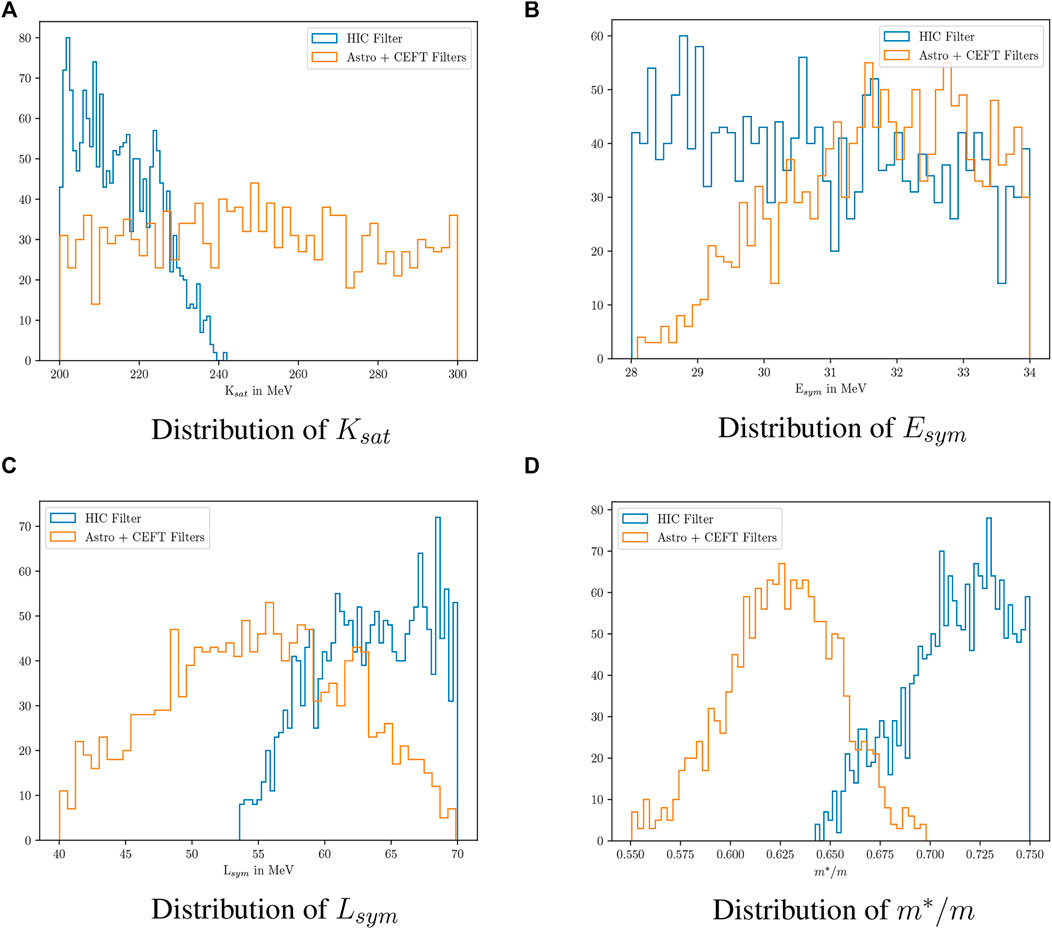
FIGURE 6. Distribution of some nuclear saturation parameters after application of the HIC filters (KaoS, FOPI, ASY-EOS). (A) Distribution of Ksat. (B) Distribution of Esym. (C) Distribution of Lsym. (C) Distribution of m*/m
In order to obtain a correlation plot after applying all filters, we generated a very large number (2 million) of priors after restricting the prior range to m*/m to 0.64–0.7 and managed to obtain 200 posterior sets. The resulting correlation plot with this set is given in Figure 7. We see that the effects of the HIC filters on correlations are the same as in the nucleonic case (Ghosh et al., 2022): decrease in Lsym − Esym correlation, increase in n0 correlation with NS astrophysical observables, and increase in Ksat − m*/m correlation. We checked that allowing for hyperons means that hyperons appear in all the cases investigated; Λ hyperons always appear close to 2n0, while the threshold for the appearance of Σ and Ξ hyperons depends on the value of the corresponding hyperon potentials. One may also note that, for 1.4M⊙ stars, the fraction of hyperons in the core is lower than in more massive 2M⊙ stars.
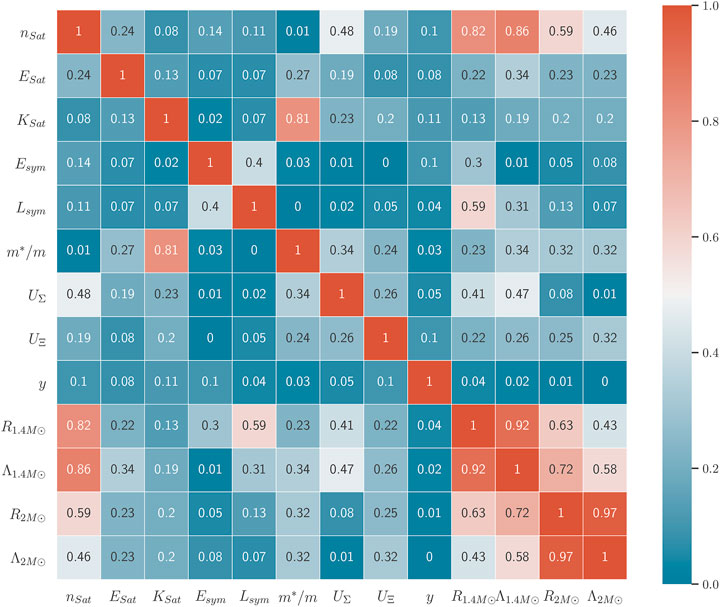
FIGURE 7. Posterior correlation matrix for variation of nuclear empirical parameters and NS observables, after application of the χEFT, HIC, and NS observations filters.
5 Discussion
5.1 Summary of Present Results
The motivation of this study is to investigate any existing correlations between empirical nuclear and hypernuclear parameters (particularly the symmetry energy and its slope) and with NS multi-messenger astrophysical observables such as its mass, radius, and tidal deformability. To this aim, we extended our previous investigation (Ghosh et al., 2022) from nucleonic to hyperonic matter in NSs. In other words, within the framework of the RMF model, we constrained the parameter space allowed by current uncertainties in nuclear and hypernuclear physics by imposing multi-physics constraints at different density regimes: chiral effective field theory at low densities, astrophysical constraints at high densities, and heavy-ion collision data at intermediate energies.
First, using the filtered EoSs satisfying constraints from both χEFT and astrophysical data, we searched for any physical correlation among the parameters and the NS observables, as well as among themselves. We found that the effective nucleon mass m*/m and saturation nuclear density n0 show a strong correlation. We found n0 to be moderately correlated with radius and tidal deformability of 1.4M⊙ NSs, but weakly correlated with those of 2M⊙ stars. The correlation of m*/m with the NS observables was low, contrary to the purely nucleonic case. Interestingly, the symmetry energy Esym and its slope Lsym showed a significant correlation after imposing the χEFT filter. There is a non-negligible correlation of m*/m with Lsym.
On applying all filters from χEFT, astrophysical and heavy-ion data, we found that very few nuclear parameter sets can satisfy all constraints simultaneously. By monitoring the individual posterior distributions of the nuclear saturation parameters, we confirmed the existence of a “tension” between the constraints from the first two filters with those of heavy-ion data. The values of Ksat are restricted to below 240 MeV due to the KaoS constraint and Lsym to values larger than 55 MeV, drastically reducing the available parameter space. Further, low values of m*/m are allowed by astrophysical filters, while heavy-ion data allow large values. The overall effect of applying the heavy-ion filters was the same as in the nucleonic case (Ghosh et al., 2022): a decreased Lsym − Esym correlation, increased n0 correlation with NS astrophysical observables, and enhanced Ksat − m*/m correlation.
5.2 Comparison With Prior Research
There are several contrasting results in the hyperonic case compared with the nucleonic case (Ghosh et al., 2022). Mainly, we found a decreased correlation of m*/m with the NS observables and an increased correlation of n0 with m*/m and NS observables for 1.4M⊙ NS. Radii and dimensionless tidal deformability (for 1.4M⊙ and 2M⊙) show a strong correlation with each other, as expected. However, we find a moderate correlation with observables of 1.4M⊙ with 2M⊙ stars because of the reduced range of radii for hyperonic stars. We checked that the distribution of m*/m shifts to lower values (peak around 0.63) in posteriors for hyperons compared to nucleons, which peak around 0.7, restricting values of
In another recent work (Traversi et al., 2020), Bayesian inference of the NS EoS was performed within the RMF model using astrophysical and nuclear saturation data. Using a selected class of nucleonic models with five empirical parameters and exploring different types of priors, they reported that the EoSs with the largest evidence were the ones featuring a strong reduction of the nucleon effective mass. However, the major drawback of this model was the omission of interaction terms (Λω in our work) in the Lagrangian, due to which other saturation parameters, such as symmetry energy or its slope, were not included. A preliminary investigation of the effect of hyperons was also performed by switching on only the Λ hyperon, with a fixed potential depth and coupling constants. However, the effect of the other baryons of the octet and variation of the couplings and their correlations with other nuclear saturation parameters or NS observables were unexplored.
Another recent study (Güven et al., 2020) used Bayesian statistics to combine low-density nuclear physics data, such as the ab initio χEFT predictions and the isoscalar giant monopole resonance, with astrophysical NS data, within the “meta-model” approach for the dense matter EoS. The posterior probability distribution functions were marginalized over several higher-order nuclear empirical parameters (Lsym, Ksym, Qsat, Qsym) and observational quantities such as a radius of 1.4M⊙ NS. This study also explored correlations among Lsym − Ksym and Ksat − Qsym parameters and reported marked tension between astrophysical and nuclear physics constraints. Biswas (2021b) combined laboratory experiments and NS astrophysical observation using Bayesian statistics along with the LIGO/Virgo and NICER observations within a hybrid nuclear + piecewise polytrope (PP) EoS parameterization. This work reported a very weak correlation between Lsym and
5.3 Limitations and Future Directions
In this work, the correlations between nuclear and hypernuclear parameters and NS astrophysical observables have been explored within the framework of the Relativistic Mean Field model. Although the advantage of this realistic phenomenological model is that, unlike polytropic or parametrized EoSs, the results provide important understanding of the underlying nuclear physics, it, however, remains to be established whether such physical correlations are also found in other realistic EoS models in order to generalize the results of this investigation. It would be interesting, for example, to see whether the conclusions would still hold for a Lagrangian with density-dependent couplings. Such possibilities will be addressed in a forthcoming publication. We recall here that the constraints from heavy-ion data are model-dependent and should therefore be treated on a different footing from astrophysical constraints and their implications on the results discussed with a word of caution.
In the future, improved measurements of hyperon potentials in hypernuclear experiments, such as GSI in Germany, JLAB in the United States, and J-PARC in Japan (Chatterjee and Vidaña, 2016), will reduce the uncertainties in the hyperon-nucleon and hyperon-hyperon coupling strengths. With the advent of multi-messenger astronomy, new upcoming observations of NS properties will also help provide more stringent constraints on the dense matter EoS in NSs.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
SG and BP contributed equally to this work and shared first authorship. DC and JS-B shared senior authorship and contributed to the conception of the study. DC was the corresponding author of this article. Both SG and BP performed the theoretical, numerical, and statistical analysis. DC wrote the first draft. SG and BP wrote sections of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.
Funding
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the CRC-TR 211 “Strong-Interaction Matter Under Extreme Conditions”– project number 315477589—TRR 211.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
DC is grateful to the hospitality of the Institut für Theoretische Physik, J. W. Goethe Universität Frankfurt, Germany, where this work was carried out within the collaborative project “Astrophysical Constraints for Hyperons in Neutron Stars.” SG, BP, and DC acknowledge the usage of the IUCAA HPC computing facility for numerical calculations.
References
Aasi, J., Abbott, B. P., Abbott, R., Abbott, T., Abernathy, M. R., Ackley, K., et al. (2015). Advanced LIGO. Classical Quan. Gravity 32, 074001. doi:10.1088/0264-9381/32/7/074001
Abbott, B. P., et al. (2017). Gw170817: Observation of Gravitational Waves from a Binary Neutron star Inspiral. Phys. Rev. Lett. 119, 161101. doi:10.1103/PhysRevLett.119.161101
Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2018). Gw170817: Measurements of Neutron star Radii and Equation of State. Phys. Rev. Lett. 121, 161101. doi:10.1103/PhysRevLett.121.161101
Abbott, B., Abbott, R., Abbott, T., Acernese, F., Ackley, K., Adams, C., et al. (2019). Properties of the Binary Neutron star Merger Gw170817. Phys. Rev. X 9, 011001. doi:10.1103/PhysRevX.9.011001
Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2020). GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M. Astrophys. J. Lett. 892, L3. doi:10.3847/2041-8213/ab75f5
Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., Adams, A., et al. (2021). Observation of Gravitational Waves from Two Neutron star–black Hole Coalescences. Astrophys. J. Lett. 915, L5. doi:10.3847/2041-8213/ac082e
Acernese, F., Agathos, M., Agatsuma, K., Aisa, D., Allemandou, N., Allocca, A., et al. (2014). Advanced Virgo: a Second-Generation Interferometric Gravitational Wave Detector. Classical Quan. Gravity 32, 024001. doi:10.1088/0264-9381/32/2/024001
Alam, N., Agrawal, B. K., Fortin, M., Pais, H., Providência, C., Raduta, A. R., et al. (2016). Strong Correlations of Neutron star Radii with the Slopes of Nuclear Matter Incompressibility and Symmetry Energy at Saturation. Phys. Rev. C 94, 052801. doi:10.1103/PhysRevC.94.052801
Annala, E., Gorda, T., Kurkela, A., and Vuorinen, A. (2018). Gravitational-wave Constraints on the neutron-star-matter Equation of State. Phys. Rev. Lett. 120, 172703. doi:10.1103/PhysRevLett.120.172703
Annala, E., Gorda, T., Kurkela, A., Nättilä, J., and Vuorinen, A. (2020). Evidence for Quark-Matter Cores in Massive Neutron Stars. Nat. Phys. 16, 907–910. doi:10.1038/s41567-020-0914-9
Annala, E., Gorda, T., Katerini, E., Kurkela, A., Nättilä, J., Paschalidis, V., et al. (2021). Multimessenger Constraints for Ultra-dense Matter. arXiv e-prints. arXiv:2105.05132.
Antoniadis, J., Freire, P. C. C., Wex, N., Tauris, T. M., Lynch, R. S., van Kerkwijk, M. H., et al. (2013). A Massive Pulsar in a Compact Relativistic Binary. Science 340, 1233232. doi:10.1126/science.1233232
Arzoumanian, Z., Gendreau, K. C., Baker, C. L., Cazeau, T., Hestnes, P., Kellogg, J. W., et al. (2014). “The Neutron star interior Composition Explorer (NICER): mission Definition,” in Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray. Editors T. Takahashi, J. W. A. den Herder, and M. Bautz (Montréal, QC, Canada: SPIE), 9144, 914420. doi:10.1117/12.2056811
Baym, G., Hatsuda, T., Kojo, T., Powell, P. D., Song, Y., and Takatsuka, T. (2018). From Hadrons to Quarks in Neutron Stars: a Review. Rep. Prog. Phys. 81, 056902. doi:10.1088/1361-6633/aaae14
Biswas, B., Char, P., Nandi, R., and Bose, S. (2021). Towards Mitigation of Apparent Tension between Nuclear Physics and Astrophysical Observations by Improved Modeling of Neutron star Matter. Phys. Rev. D 103, 103015. doi:10.1103/physrevd.103.103015
Biswas, B. (2021). Impact of PREX-II and Combined Radio/NICER/XMM-Newton’s Mass–Radius Measurement of PSR J0740+6620 on the Dense-Matter Equation of State. Astrophys. J. 921, 63. doi:10.3847/1538-4357/ac1c72
Biswas, B. (2021). Bayesian Model-Selection of Neutron star Equation of State Using Multi-Messenger Observations. arXiv e-prints. arXiv:2106.02644.
Capano, C. D., Tews, I., Brown, S. M., Margalit, B., De, S., Kumar, S., et al. (2020). Stringent Constraints on Neutron-star Radii from Multimessenger Observations and Nuclear Theory. Nat. Astron. 4, 625–632. doi:10.1038/s41550-020-1014-6
Carson, Z., Steiner, A. W., and Yagi, K. (2019). Constraining Nuclear Matter Parameters with Gw170817. Phys. Rev. D 99, 043010. doi:10.1103/PhysRevD.99.043010
Chatterjee, D., and Vidaña, I. (2016). Do hyperons Exist in the interior of Neutron Stars? Eur. Phys. J. A52, 29. doi:10.1140/epja/i2016-16029-x
Chen, W. C., and Piekarewicz, J. (2014). Building Relativistic Mean Field Models for Finite Nuclei and Neutron Stars. Phys. Rev. C 90, 044305. doi:10.1103/PhysRevC.90.044305
Coughlin, M. W., Dietrich, T., Margalit, B., and Metzger, B. D. (2019). Multimessenger Bayesian Parameter Inference of a Binary Neutron star Merger. Monthly Notices R. Astronom. Soc. Lett. 489, L91–L96. doi:10.1093/mnrasl/slz133
Danielewicz, P., Lacey, R., and Lynch, W. G. (2002). Determination of the Equation of State of Dense Matter. Science 298, 1592–1596. doi:10.1126/science.1078070
David, B., Alexander, A., Alexandra, F., and Hovik, G. (2020). Compact Stars in the QCD Phase Diagram. Basel, Switzerland: Universe. doi:10.3390/books978-3-03921-959-9
Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., and Hessels, J. W. T. (2010). A Two-Solar-Mass Neutron star Measured Using Shapiro Delay. Nature 467, 1081–1083. doi:10.1038/nature09466
Dexheimer, V., Noronha, J., Noronha-Hostler, J., Yunes, N., and Ratti, C. (2021). Future Physics Perspectives on the Equation of State from Heavy Ion Collisions to Neutron Stars. J. Phys. G: Nucl. Part. Phys. 48, 073001. doi:10.1088/1361-6471/abe104
Dietrich, T., Coughlin, M. W., Pang, P. T. H., Bulla, M., Heinzel, J., Issa, L., et al. (2020). Multimessenger Constraints on the Neutron-star Equation of State and the Hubble Constant. Science 370, 1450–1453. doi:10.1126/science.abb4317
Drischler, C., Carbone, A., Hebeler, K., and Schwenk, A. (2016). Neutron Matter from Chiral Two- and Three-Nucleon Calculations up to N3LO. Phys. Rev. C 94, 054307. doi:10.1103/PhysRevC.94.054307
Drischler, C., Hebeler, K., and Schwenk, A. (2019). Chiral Interactions up to Next-To-Next-To-Next-To-Leading Order and Nuclear Saturation. Phys. Rev. Lett. 122, 042501. doi:10.1103/PhysRevLett.122.042501
Drischler, C., Furnstahl, R. J., Melendez, J. A., and Phillips, D. R. (2020). How Well Do We Know the Neutron-Matter Equation of State at the Densities inside Neutron Stars? a Bayesian Approach with Correlated Uncertainties. Phys. Rev. Lett. 125, 202702. doi:10.1103/PhysRevLett.125.202702
Dutra, M., Lourenço, O., Sá Martins, J. S., Delfino, A., Stone, J. R., and Stevenson, P. D. (2012). Skyrme Interaction and Nuclear Matter Constraints. Phys. Rev. C 85, 035201. doi:10.1103/PhysRevC.85.035201
Fabbietti, L., Sarti, V. M., and Doce, O. V. (2021). Study of the strong Interaction Among Hadrons with Correlations at the LHC. Ann. Rev. Nucl. Part. Sci. 71, 377–402. doi:10.1146/annurev-nucl-102419-034438
Fasano, M., Abdelsalhin, T., Maselli, A., and Ferrari, V. (2019). Constraining the Neutron star Equation of State Using Multiband Independent Measurements of Radii and Tidal Deformabilities. Phys. Rev. Lett. 123, 141101. doi:10.1103/physrevlett.123.141101
Fattoyev, F. J., Carvajal, J., Newton, W. G., and Li, B. A. (2013). Constraining the High-Density Behavior of the Nuclear Symmetry Energy with the Tidal Polarizability of Neutron Stars. Phys. Rev. C 87, 015806. doi:10.1103/PhysRevC.87.015806
Flanagan, E. E., and Hinderer, T. (2008). Constraining Neutron-star Tidal Love Numbers with Gravitational-Wave Detectors. Phys. Rev. D 77, 021502. doi:10.1103/PhysRevD.77.021502
Fonseca, E., Cromartie, H. T., Pennucci, T. T., Ray, P. S., Kirichenko, A. Y., Ransom, S. M., et al. (2021). Refined Mass and Geometric Measurements of the High-Mass PSR J0740+6620. Astrophys. J. Lett. 915, L12. doi:10.3847/2041-8213/ac03b8
Friedman, E., and Gal, A. (2007). In-medium Nuclear Interactions of Low-Energy Hadrons. Phys. Rep. 452, 89–153. doi:10.1016/j.physrep.2007.08.002
Fuchs, C., Faessler, A., Zabrodin, E., and Zheng, Y. M. (2001). Probing the Nuclear Equation of State by K+ Production in Heavy-Ion Collisions. Phys. Rev. Lett. 86, 1974–1977. doi:10.1103/PhysRevLett.86.1974
Fukuda, T., Higashi, A., Matsuyama, Y., Nagoshi, C., Nakano, J., Sekimoto, M., et al. (1998). Cascade Hypernuclei in the (K−,K+) Reaction on 12C. Phy. Rev. C 58, 1306–1309. doi:10.1103/physrevc.58.1306
Gamba, R., Read, J. S., and Wade, L. E. (2019). The Impact of the Crust Equation of State on the Analysis of GW170817. Classical Quan. Gravity 37, 025008. doi:10.1088/1361-6382/ab5ba4
Gandolfi, S., Gezerlis, A., and Carlson, J. (2015). Neutron Matter from Low to High Density. Annu. Rev. Nucl. Part. Sci. 65, 303–328. doi:10.1146/annurev-nucl-102014-021957
Gandolfi, S., Lippuner, J., Steiner, A. W., Tews, I., Du, X., and Al-Mamun, M. (2019). From the Microscopic to the Macroscopic World: from Nucleons to Neutron Stars. J. Phys. G: Nucl. Part. Phys. 46, 103001. doi:10.1088/1361-6471/ab29b3
Ghosh, S., Chatterjee, D., and Schaffner-Bielich, J. (2022). Imposing Multi-Physics Constraints at Different Densities on the Neutron Star Equation of State. Eur. Phys. J. A 58, 37.
Glendenning, N. (2012). Compact Stars: Nuclear Physics, Particle Physics and General Relativity. Astronomy and Astrophysics Library. New York: Springer.
Greif, S. K., Raaijmakers, G., Hebeler, K., Schwenk, A., and Watts, A. L. (2019). Equation of State Sensitivities when Inferring Neutron star and Dense Matter Properties. Monthly Notices R. Astronom. Soc. 485, 5363–5376. doi:10.1093/mnras/stz654
Guillot, S., Servillat, M., Webb, N. A., and Rutledge, R. E. (2013). Measurement of the Radius of Neutron Stars with High Signal-To-Noise Quiescent Low-Mass X-ray Binaries in Globular Clusters. Astrophys. J. 772, 7. doi:10.1088/0004-637x/772/1/7
Güven, H., Bozkurt, K., Khan, E., and Margueron, J. (2020). Multimessenger and Multiphysics Bayesian Inference for the Gw170817 Binary Neutron star Merger. Phys. Rev. C 102, 015805. doi:10.1103/PhysRevC.102.015805
Hartnack, C., Oeschler, H., and Aichelin, J. (2006). Hadronic Matter Is Soft. Phys. Rev. Lett. 96, 012302. doi:10.1103/PhysRevLett.96.012302
Hebeler, K., Lattimer, J. M., Pethick, C. J., and Schwenk, A. (2013). Equation of State and Neutron star Properties Constrained by Nuclear Physics and Observation. Astrophys. J. 773, 11. doi:10.1088/0004-637x/773/1/11
Hinderer, T., Lackey, B. D., Lang, R. N., and Read, J. S. (2010). Tidal Deformability of Neutron Stars with Realistic Equations of State and Their Gravitational Wave Signatures in Binary Inspiral. Phys. Rev. D 81, 123016. doi:10.1103/PhysRevD.81.123016
Hinderer, T. (2008). Tidal Love Numbers of Neutron Stars. Astrophys. J. 677, 1216–1220. doi:10.1086/533487
Hornick, N., Tolos, L., Zacchi, A., Christian, J. E., and Schaffner-Bielich, J. (2018). Relativistic Parameterizations of Neutron Matter and Implications for Neutron Stars. Phys. Rev. C 98, 065804. doi:10.1103/PhysRevC.98.065804
Huth, S., Pang, P. T. H., Tews, I., Dietrich, T., Le Fèvre, A., Schwenk, A., et al. (2021). Constraining Neutron-Star Matter with Microscopic and Macroscopic Collisions. arXiv e-prints. arXiv:2107.06229.
Inoue, T. (2016). “Hyperon Single-Particle Potentials from QCD on Lattice,” in PoS INPC, 2016, Adelaide, SA, Australia, September 11–16, 2016, 277. doi:10.22323/1.281.0277
Inoue, T. (2019). Hyperon Forces from QCD and Their Applications. JPS Conf. Proc. 26, 023018. doi:10.7566/jpscp.26.023018
Khaustov, P., Alburger, D. E., Barnes, P. D., Bassalleck, B., Berdoz, A. R., Biglan, A., et al. (2000). Evidence of Ξ Hypernuclear Production in the 12C(K-,K+)12Ξ Be Reaction. Phys. Rev. C 61, 054603. doi:10.1103/physrevc.61.027601
Kirch, W. (2008). Pearson’s Correlation Coefficient. Dordrecht: Springer Netherlands, 1090–1091. doi:10.1007/978-1-4020-5614-7_2569
Landry, P., Essick, R., and Chatziioannou, K. (2020). Nonparametric Constraints on Neutron star Matter with Existing and Upcoming Gravitational Wave and Pulsar Observations. Phys. Rev. D 101, 123007. doi:10.1103/PhysRevD.101.123007
Lattimer, J. M., and Prakash, M. (2004). The Physics of Neutron Stars. Science 304, 536–542. doi:10.1126/science.1090720
Lattimer, J. M. (2012). The Nuclear Equation of State and Neutron star Masses. Annu. Rev. Nucl. Part. Sci. 62, 485–515. doi:10.1146/annurev-nucl-102711-095018
Lattimer, J. M. (2015). Introduction to Neutron Stars. AIP Conf. Proc. 1645, 61–78. doi:10.1063/1.4909560
Le Fèvre, A., Leifels, Y., Reisdorf, W., Aichelin, J., and Hartnack, C. (2016). Constraining the Nuclear Matter Equation of State Around Twice Saturation Density. Nucl. Phys. A 945, 112–133. doi:10.1016/j.nuclphysa.2015.09.015
Lim, Y., and Holt, J. W. (2018). Neutron star Tidal Deformabilities Constrained by Nuclear Theory and experiment. Phys. Rev. Lett. 121, 062701. doi:10.1103/PhysRevLett.121.062701
Lindblom, L. (2018). Causal Representations of Neutron-star Equations of State. Phys. Rev. D 97, 123019. doi:10.1103/physrevd.97.123019
Mareš, J., Friedman, E., Gal, A., and Jenning, B. (1995). Constraints on σ-nucleus Dynamics from Dirac Phenomenology of σ− Atoms. Nucl. Phys. A 594, 311–324. doi:10.1016/0375-9474(95)00358-8
Millener, D. J., Dover, C. B., and Gal, A. (1988). Λ-Nucleus Single-Particle Potentials. Phys. Rev. C 38, 2700–2708. doi:10.1103/PhysRevC.38.2700
Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2019). Psr J0030+0451 Mass and Radius from Nicer Data and Implications for the Properties of Neutron star Matter. Astrophys. J. 887, L24. doi:10.3847/2041-8213/ab50c5
Miller, M. C., Chirenti, C., and Lamb, F. K. (2019). Constraining the Equation of State of High-Density Cold Matter Using Nuclear and Astronomical Measurements. Astrophys. J. 888, 12. doi:10.3847/1538-4357/ab4ef9
Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2021). The Radius of Psr J0740+6620 from Nicer and Xmm-newton Data. Astrophys. J. Lett. 918, L28. doi:10.3847/2041-8213/ac089b
Most, E. R., Weih, L. R., Rezzolla, L., and Schaffner-Bielich, J. (2018). New Constraints on Radii and Tidal Deformabilities of Neutron Stars from Gw170817. Phys. Rev. Lett. 120, 261103. doi:10.1103/PhysRevLett.120.261103
O’Boyle, M. F., Markakis, C., Stergioulas, N., and Read, J. S. (2020). Parametrized Equation of State for Neutron star Matter with Continuous Sound Speed. Phys. Rev. D 102, 083027. doi:10.1103/PhysRevD.102.083027
Oertel, M., Hempel, M., Klähn, T., and Typel, S. (2017). Equations of State for Supernovae and Compact Stars. Rev. Mod. Phys. 89, 015007. doi:10.1103/RevModPhys.89.015007
Özel, F., Baym, G., and Güver, T. (2010). Astrophysical Measurement of the Equation of State of Neutron star Matter. Phys. Rev. D 82, 101301. doi:10.1103/PhysRevD.82.101301
Pang, P. T. H., Tews, I., Coughlin, M. W., Bulla, M., Van Den Broeck, C., and Dietrich, T. (2021). Nuclear Physics Multimessenger Astrophysics Constraints on the Neutron Star Equation of State: Adding NICER’s PSR J0740+6620 Measurement. Astro. Phys. J. 922, 14. doi:10.3847/1538-4357/ac19ab
Pradhan, B. K., and Chatterjee, D. (2021). Effect of Hyperons on F-Mode Oscillations in Neutron Stars. Phys. Rev. C 103, 035810. doi:10.1103/PhysRevC.103.035810
Read, J. S., Lackey, B. D., Owen, B. J., and Friedman, J. L. (2009). Constraints on a Phenomenologically Parametrized Neutron-star Equation of State. Phys. Rev. D 79, 124032. doi:10.1103/physrevd.79.124032
Riley, T. E., Watts, A. L., Bogdanov, S., Ray, P. S., Ludlam, R. M., Guillot, S., et al. (2019). A Nicer View of Psr J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. 887, L21. doi:10.3847/2041-8213/ab481c
Riley, T. E., Watts, A. L., Ray, P. S., Bogdanov, S., Guillot, S., Morsink, S. M., et al. (2021). A Nicer View of the Massive Pulsar Psr J0740+6620 Informed by Radio Timing and Xmm-newton Spectroscopy. Astrophys. J. Lett. 918, L27. doi:10.3847/2041-8213/ac0a81
Russotto, P., Gannon, S., Kupny, S., Lasko, P., Acosta, L., Adamczyk, M., et al. (2016). Results of the Asy-Eos experiment at Gsi: The Symmetry Energy at Suprasaturation Density. Phys. Rev. C 94. doi:10.1103/physrevc.94.034608
Schaffner, J., Greiner, C., and Stöcker, H. (1992). Metastable Exotic Multihypernuclear Objects. Phys. Rev. C 46, 322–329. doi:10.1103/PhysRevC.46.322
Schaffner, J., Dover, C. B., Gal, A., Greiner, C., and Stöcker, H. (1993). Strange Hadronic Matter. Phys. Rev. Lett. 71, 1328–1331. doi:10.1103/PhysRevLett.71.1328
Schaffner-Bielich, J., and Gal, A. (2000). Properties of Strange Hadronic Matter in Bulk and in Finite Systems. Phys. Rev. C 62, 034311. doi:10.1103/PhysRevC.62.034311
Schaffner-Bielich, J. (2020). Compact Star Physics. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/9781316848357
Serot, B. D., and Walecka, J. D. (1992). Relativistic Nuclear many Body Theory. Rec. Prog. Many Body Theor. 3, 49–92. doi:10.1007/978-1-4615-3466-2_5
Serot, B. D., and Walecka, J. D. (1997). Recent Progress in Quantum Hadrodynamics. Int. J. Mod. Phys. E 06, 515–631. doi:10.1142/s0218301397000299
Steiner, A. W., Lattimer, J. M., and Brown, E. F. (2013). The Neutron star Mass-Radius Relation and the Equation of State of Dense Matter. Astrophys. J. 765, L5. doi:10.1088/2041-8205/765/1/l5
Stone, J., and Reinhard, P. G. (2007). The Skyrme Interaction in Finite Nuclei and Nuclear Matter. Prog. Part. Nucl. Phys. 58, 587–657. doi:10.1016/j.ppnp.2006.07.001
Tews, I., Margueron, J., and Reddy, S. (2018). Critical Examination of Constraints on the Equation of State of Dense Matter Obtained from Gw170817. Phys. Rev. C 98, 045804. doi:10.1103/PhysRevC.98.045804
Tews, I., Margueron, J., and Reddy, S. (2019). Constraining the Properties of Dense Matter and Neutron Stars by Combining Nuclear Physics and Gravitational Waves from Gw170817. AIP Conf. Proc. 2127, 020009. doi:10.1063/1.5117799
Tews, I., Margueron, J., and Reddy, S. (2019). Confronting Gravitational-Wave Observations with Modern Nuclear Physics Constraints. Eur. Phys. J. A 55, 97. doi:10.1140/epja/i2019-12774-6
Thorsett, S. E., and Chakrabarty, D. (1999). Neutron star Mass Measurements. I. Radio Pulsars. Astrophys. J. 512, 288–299. doi:10.1086/306742
Tong, H., Zhao, P., and Meng, J. (2020). Symmetry Energy at Supra-saturation Densities via the Gravitational Waves from Gw170817. Phys. Rev. C 101, 035802. doi:10.1103/PhysRevC.101.035802
Traversi, S., Char, P., and Pagliara, G. (2020). Bayesian Inference of Dense Matter Equation of State within Relativistic Mean Field Models Using Astrophysical Measurements. Astrophys. J. 897, 165. doi:10.3847/1538-4357/ab99c1
Tsang, C. Y., Tsang, M. B., Danielewicz, P., Lynch, W. G., and Fattoyev, F. J. (2018). Constraining Neutron-star Equation of State Using Heavy-Ion Collisions. arXiv e-prints. arXiv:1807.06571.
Vautherin, D., and Brink, D. M. (1972). Hartree-fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 5, 626–647. doi:10.1103/PhysRevC.5.626
Wei, J. B., Lu, J. J., Burgio, G. F., Li, Z. H., and Schulze, H. J. (2020). Are Nuclear Matter Properties Correlated to Neutron star Observables? Eur. Phys. J. A. 56, 63. doi:10.1140/epja/s10050-020-00058-3
Weissenborn, S., Chatterjee, D., and Schaffner-Bielich, J. (2012). Hyperons and Massive Neutron Stars: The Role of Hyperon Potentials. Nucl. Phys. A 881, 62–77. doi:10.1016/j.nuclphysa.2012.02.012
Xie, W. J., and Li, B. A. (2019). Bayesian Inference of High-Density Nuclear Symmetry Energy from Radii of Canonical Neutron Stars. Astrophys. J. 883, 174. doi:10.3847/1538-4357/ab3f37
Yagi, K., and Yunes, N. (2013). I-love-q Relations in Neutron Stars and Their Applications to Astrophysics, Gravitational Waves, and Fundamental Physics. Phys. Rev. D 88, 023009. doi:10.1103/PhysRevD.88.023009
Zhang, N. B., and Li, B. A. (2019). Implications of the Mass M = 2.17 +0.11 −0.10 M ⊙ of Psr J0740+6620 on the Equation of State of Super-dense Neutron-Rich Nuclear Matter. Astrophys. J. 879, 99. doi:10.3847/1538-4357/ab24cb
Zhu, Z. Y., Zhou, E. P., and Li, A. (2018). Neutron star Equation of State from the Quark Level in Light of Gw170817. Astrophys. J. 862, 98. doi:10.3847/1538-4357/aacc28
Keywords: symmetry energy, hyperons, neutron stars, equation of state, nuclear, hypernuclear, heavy-ion, multi-messenger
Citation: Ghosh S, Pradhan BK, Chatterjee D and Schaffner-Bielich J (2022) Multi-Physics Constraints at Different Densities to Probe Nuclear Symmetry Energy in Hyperonic Neutron Stars. Front. Astron. Space Sci. 9:864294. doi: 10.3389/fspas.2022.864294
Received: 31 January 2022; Accepted: 28 February 2022;
Published: 28 March 2022.
Edited by:
Helena Pais, University of Coimbra, PortugalReviewed by:
Isaac Vidana, Universities and Research, ItalyAdriana Rodica Raduta, Horia Hulubei National Institute for Research and Development in Physics and Nuclear Engineering (IFIN-HH), Romania
Copyright © 2022 Ghosh, Pradhan, Chatterjee and Schaffner-Bielich. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jürgen Schaffner-Bielich, c2NoYWZmbmVyQGFzdHJvLnVuaS1mcmFua2Z1cnQuZGU=
 Suprovo Ghosh
Suprovo Ghosh Bikram Keshari Pradhan1
Bikram Keshari Pradhan1 Debarati Chatterjee
Debarati Chatterjee Jürgen Schaffner-Bielich
Jürgen Schaffner-Bielich