- 1Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT, Australia
- 2Australian Research Council Centre of Excellence in All Sky Astrophysics (ASTRO3D), Canberra, ACT, Australia
The interstellar medium (ISM) of star-forming galaxies is magnetized and turbulent. Cosmic rays (CRs) propagate through it, and those with energies from ∼ GeV − TeV are likely subject to the streaming instability, whereby the wave damping processes balances excitation of resonant ionic Alfvén waves by the CRs, reaching an equilibrium in which the propagation speed of the CRs is very close to the local ion Alfvén velocity. The transport of streaming CRs is therefore sensitive to ionic Alfvén velocity fluctuations. In this paper we systematically study these fluctuations using a large ensemble of compressible MHD turbulence simulations. We show that for sub-Alfvénic turbulence, as applies for a strongly magnetized ISM, the ionic Alfvén velocity probability density function (PDF) is determined solely by the density fluctuations from shocked gas forming parallel to the magnetic field, and we develop analytical models for the ionic Alfvén velocity PDF up to second moments. For super-Alfvénic turbulence, magnetic and density fluctuations are correlated in complex ways, and these correlations as well as contributions from the magnetic fluctuations sets the ionic Alfvén velocity PDF. We discuss the implications of these findings for underlying “macroscopic” diffusion mechanisms in CRs undergoing the streaming instability, including modeling the macroscopic diffusion coefficient for the parallel transport in sub-Alfvénic plasmas. We also describe how, for highly-magnetized turbulent gas, the gas density PDF, and hence column density PDF, can be used to access information about ionic Alfvén velocity structure from observations of the magnetized ISM.
1 Introduction
Magnetized turbulence is the rule and not the exception for the dynamics of the interstellar medium (ISM) in star-forming galaxies. Turbulence is a high-Reynolds-number (Re > 103) fluid state, where the Reynolds number is defined as Re = (σVL)/ν, and σV is the velocity dispersion on length scale L with kinematic viscosity ν. Most astrophysical systems are vastly larger than the scales that are important for viscosity, and hence, turbulence has spread across most scales in the galaxies, with typical star-forming, cold molecular clouds boasting Re ∼ 109 (Krumholz, 2015). Due to the turbulent dynamo (e.g., Schekochihin et al., 2004; Federrath, 2016; Xu and Lazarian, 2016; McKee et al., 2020; Seta and Federrath, 2021a; Xu and Lazarian, 2021b), the energy in magnetic fields of the ISM is roughly at equipartition with the turbulent kinetic energy (Boulares and Cox, 1990; Zweibel and McKee, 1995; Beck and Wielebinski, 2013; Seta and Beck, 2019). Magnetic fields play a dynamical role in the ISM, acting as a scaffold for the gas density through large-scale flux-freezing, facilitating some of the rich structure that we observe, e.g., in ISM observations (Li and Henning, 2011; Li et al., 2013; Soler et al., 2013; Ade et al., 2016; Aghanim et al., 2016; Cox et al., 2016; Federrath et al., 2016; Malinen et al., 2016; Tritsis and Tassis, 2016; Soler et al., 2017; Tritsis et al., 2018; Heyer et al., 2020; Pillai et al., 2020), and simulations of ISM turbulence (Soler and Hennebelle, 2017; Tritsis et al., 2018; Beattie and Federrath, 2020; Körtgen and Soler, 2020; Seifried et al., 2020; Barreto-Mota et al., 2021). The ISM is also energy dense in relativistic, charged particles–cosmic rays.
1.1 Cosmic Rays and the Streaming Instability
Cosmic rays (CRs) are high-energy (non-thermal), charged particles, that spiral around magnetic field lines at a radius set by the balance between Lorentz and centrifugal forces. Averaged over the ISM in star-forming galaxies, the energy densities of CRs, turbulent motions, and magnetic fields are roughly in equipartition (Boulares and Cox, 1990; Beck and Wielebinski, 2013; Seta and Beck, 2019). CRs are important for understanding the ionization (hence chemistry) and thus heating of interstellar gas (Field et al., 1969; Xu and Yan, 2013; Krumholz et al., 2020), and in turn influence the evolution of galaxies. For example, CR pressure gradients can significantly impact the morphology of simulated, ideal galaxies (Salem et al., 2014) and can drive and sustain galactic winds (and more general outflows) with mass-loading factors of order unity, which in turn can excite turbulent gas motions (Uhlig et al., 2012; Booth et al., 2013; Girichidis et al., 2016; Crocker et al., 2021a; b). Because these processes depend upon CR pressure gradients, transport of CRs through the ISM is important to understand.
If magnetic fields in the ISM were static and structureless on scales of the CR gyroradius, CR transport would be trivial–CRs would simply spiral along field lines, moving down them at the speed of light times the cosine of the pitch angle between the CR velocity vector the local magnetic field. However, Alfvén waves with frequencies comparable to the frequency of CR gyration can resonantly scatter CRs, randomly changing their pitch angle. Moreover, when a population of CRs is numerous enough, they themselves can excite such scattering waves via the streaming instability (Lerche, 1967; Kulsrud and Pearce, 1969; Wentzel, 1969; Skilling, 1971). CRs that have an energy range between ∼ GeV − TeV, which dominate the CR pressure budget (Evoli, 2018), are likely to excite waves so efficiently that to zeroth order the CRs are scattered isotropically in pitch angle around field lines, still traveling at relativistic velocities. However, to first order, a slight asymmetry in the scattering distribution develops such that there is a bulk velocity along the field, vstream, that approaches the ion Alfvén speed,
As we have described, the streaming instability is an advective process, e.g., the small asymmetry in the scattering angle distribution leads to the population of SCRs being advected down pressure gradients, along field lines. However, consider now multiple populations of SCRs distributed across a plasma and that we are “observing” on length scales larger than the correlation length scale 1 of the magnetic field embedded in the medium,
However, it is not only tangling of magnetic field lines above the correlation length that may be responsible for creating spatial dispersion between populations of SCRs. Because SCRs become self-confined to travel at
1.2 On the Ionization State of Turbulent Density Fluctuations
We first consider the ionization fraction χ, for the purposes of demonstrating why we need not account for its fluctuations separately. In equilibrium in a region with a constant ionization rate per neutral particle ζ, the condition for equilibrium is simply balance between the ionization and recombination rates per unit volume,
where nn, ne, and nion are the number densities of neutral species, electrons, and ions, respectively and αrec is the recombination rate coefficient for free electrons with ions. For simplicity consider a region of weakly ionized plasma, χ ≪ 1, where all ions are singly ionized. In this case we have nion = ne = χρ/μionmH, where μion is the mean atomic mass of ions and mH is the hydrogen mass. Similarly, we have nn = ρ/μmH, where μ is the mean atomic mass of neutrals, and therefore
Thus in equilibrium we should expect χ ∝ ρ−1/2.
However, since we are interested in fluctuations, we must next ask whether equilibrium is an appropriate assumption. The timescale required for a given parcel of gas to reach ionization equilibrium is the ion density divided by the rate at which the ion density changes,
Significantly, this does not depend on the density, except indirectly through χ. We can therefore immediately determine characteristic values of tion for different phases of the ISM. In the atomic ISM, we generally expect to have χ ∼ 10–3 − 10–1, μ = 1.4 (for the standard cosmic mix of H and He), μion = 1 (H is the dominant ionized species), and ζ ∼ 10–16 s−1 (Wolfire et al., 2003), and therefore tion ∼ 0.4–40 Myr; in the interior of a molecular cloud, the equilibrium ionization fraction is lower, χ ∼ 10–6, and we have μ = 2.33 (H2 + He composition), μi = 29 (HCO+ is the dominant charge carrier–Krumholz et al., 2020), and ζ ∼ 10–16 − 10–17 s−1, and tion ∼ 30–300 y.
This should be compared to the characteristic timescale over which the density changes which, for a turbulent medium, Scannapieco and Safarzadeh (2018) show is given approximately by
where τ is the flow crossing time, s = ln (ρ/ρ0) is the logarithmic over-density in a region with mean density ρ0, and s∗ is a constant of order unity that depends on the Mach number and Alfvén Mach number of the flow. This timescale varies from τ/3 to zero slowly as a function of s.
The above allows a few immediate conclusions. In the molecular ISM, we can safely assume instantaneous equilibrium: molecular clouds have flow crossing times of
1.3 Lognormal Density Fluctuation Theory
One of the key differences between incompressible and compressible turbulence is the dynamical role of density fluctuations and shocked gas in the turbulent plasma. Lognormal models for the PDF of turbulent ρ/ρ0 fluctuations first originate from Vazquez-Semadeni (1994). Vazquez-Semadeni considers a linear density fluctuation in a self-similar (scale-free), isothermal plasma, where thermal pressure,
where ρ(t0)/ρ0 = ρ0/ρ0 = 1 is the initial density, before the turbulent interactions, in units of the mean. Under the log-transformation, the density fluctuations become additive,
turning the problem into one that involves the sum of random variables. If each ρ(tn)/ρ0 ∀n, is generated by the same underlying distribution and is statistically independent from each of the other fluctuations,
Where
Because lognormal models of the s-PDF are solely parameterised by the
is a function of the sonic Mach number (Vazquez-Semadeni, 1994; Padoan et al., 1997; Passot and Vázquez-Semadeni, 1998; Price et al., 2011; Konstandin et al., 2012b), the Alfvén Mach number and the strength of the large-scale field (Padoan and Nordlund, 2011; Molina et al., 2012; Beattie et al., 2021a,b), the turbulent driving parameter b (the mixture of solendoial and compressive modes in the driving source) (Federrath et al., 2008; Federrath et al., 2010), and the thermodynamics, including the adiabatic index γ (Nolan et al., 2015) and the polytropic index Γ (Federrath and Banerjee, 2015). We will find that
1.4 The Fluctuating and Large-Scale Magnetic Field in Compressible Plasmas
Next consider the statistics of the magnetic field. Due to the small-scale dynamo action, magnetic field fluctuations that are roughly at equipartition (e.g., Xu and Lazarian, 2016; McKee et al., 2020; Seta and Federrath, 2021b) with the turbulent fluctuations are ubiquitous in both incompressible and compressible MHD turbulence across the Universe (Beck and Wielebinski, 2013; Subramanian, 2016, 2019). Once saturation has occurred, based on a balance between the magnetic and kinetic energies, in an isothermal supersonic plasma,
In contrast to Alfvénic turbulence, which is determined by weak Alfvén and slow wave interactions or strong nonlinear critically balanced cascades (Goldreich and Sridhar, 1995; Lithwick and Goldreich, 2001; Schekochihin and Cowley, 2007), magnetic fluctuations parallel to B0 seem to play an important role in compressible sub-Alfvénic large-scale field turbulence (Beattie et al., 2020; Skalidis and Tassis, 2020; Skalidis et al., 2021a; Beattie et al., 2021b, 2022), which, as we have discussed in Section 1, is relevant to cold molecular gas in the ISM (Li et al., 2013; Federrath et al., 2016; Hu et al., 2019; Heyer et al., 2020; Skalidis et al., 2021b; Hoang et al., 2021; Hwang et al., 2021). In Alfvénic turbulence, the parallel fluctuations passively trace slow modes that form along the magnetic field (Goldreich and Sridhar, 1995; Lithwick and Goldreich, 2001; Schekochihin et al., 2009), but in supersonic turbulence the parallel fluctuations are excited around sites of strong shocks along the large-scale field (see Figure 10 in Beattie et al., 2021b). They also play a vital role in the formation of large-scale, non-turbulent structures in the plasma (which may be related to the formation of 2D condensates previously observed in incompressible plasmas, e.g., Boldyrev and Perez 2009; Wang et al., 2011). By decomposing the turbulence into linear modes and phases, Yang et al. (2019) found that ≈77% of the total energy was in non-propagating structures (those that do not follow a theoretical wave dispersion relation from linear theory) 4. These are system-scale (k‖ = 0) rigid body vortices that, to become stationary, require parallel magnetic field pressure gradients (and hence strong parallel fluctuations that oppose B0) to balance the centrifugal force of the rotating fluid (Beattie et al., 2020; 2021b). Because of this coupling between the vortex motions perpendicular to B0 and the shocked gas parallel to B0, they contain roughly an order of magnitude more energy than their perpendicular (Alfvénic) counterparts when the plasma is very sub-Alfvénic (but the same energy when the turbulence is super-Alfvénic) and in a quasi-stationary turbulence state act to balance the kinetic energy in these highly-compressible and sub-Alfvénic plasmas (see Figure B1 in Beattie et al., 2022). (Beattie et al., 2022). We leave a detailed analysis of these vortices to a future study. With that, we have the required background to construct magnetic field variance relations based on energy balance, and we leave further discussion of the magnetic field fluctuations until we compare theory directly with our simulation results in Section 3.2.
1.5 Outline
This study is organized as follows: In Section 2 we introduce the isothermal, compressible ideal MHD models and simulation setup that we use to understand the Alfvén velocity fluctuations over a broad range of plasma parameters. In Section 3 we begin our construction of the vA-PDF and variance by studying the density and magnetic field fluctuations, including the covariance between the two quantities. We include comparisons between compressible MHD turbulence theory discussed in this section, and the simulation data from our turbulence experiments. Then we develop a variance and 1-point volume-weighted PDF theory for the Alfvén velocity fluctuations for sub-Alfvénic MHD turbulence, where the fluctuations are dominated by the effects of compressibility. In Section 4 we discuss the implications of Alfvén velocity fluctuations for column density observations of molecular clouds and macroscopic diffusion of cosmic rays undergoing the streaming instability in sub-Alfvénic regions of the ISM. Finally, in Section 5 we summarise and itemize the key results of the study. We list the unique mathematical notation and symbols that we use in this study in Table 1.
2 Turbulence Simulations
2.1 Stochastically Driven Isothermal magnetohydrodynamic (MHD) Fluid Model
To understand the nature of Alfvén velocity fluctuations in MHD turbulence, we use a modified (see Methods section in Federrath et al., 2021) version of the flash code (Fryxell et al., 2000; Dubey et al., 2008), utilizing a second-order conservative MUSCL-Hancock 5-wave approximate Riemann scheme (Bouchut et al., 2010; Waagan et al., 2011; Federrath et al., 2021) to solve the dimensionless 3D, ideal, isothermal, compressible MHD equations with a stochastic acceleration field acting to drive the turbulence with finite temporal correlation.
Where v is the fluid velocity, ρ is the gas density,

FIGURE 1. Two-dimensional slices through the logarithmic gas density, ln (ρ/ρ0) (first column), logarithmic magnetic field, ln (B/B0) (center column) and logarithmic Alfvén velocity magnitude, ln (vA/vA0) (third column) for
2.2 Turbulent Driving and Sonic Mach Numbers
The forcing term f follows an Ornstein-Uhlenbeck process that satisfies the stochastic differential equation,
where
where δij is the Kronecker delta tensor. We control the contribution from each of the driving modes, indicated with the annotations for the two terms in the projection tensor, through the η parameter. For η = 1 we obtain purely solenoidal driving (∇ ⋅ f = 0), and η = 0 produces purely compressive driving (∇ × f = 0) (see Federrath et al., 2008; Federrath et al., 2009; 2010; Federrath et al., 2022, for a detailed discussion of the driving). We choose to inject an equal amount of energy in both compressive and solenoidal modes, a “natural mix”, by setting η = 0.5 (see Federrath et al., 2008; Federrath et al., 2009; 2010, for turbulence driving details). A natural mixture of modes is most appropriate for simulating ISM turbulence because driving mechanisms5 are diverse, for example, supernova shocks (compressive), internal instabilities in the gas (solenoidal), gravity (compressive), galactic shear (solenoidal), ambient pressure from the galactic environment (compressive) or stellar feedback (compressive or solenoidal) (Brunt et al., 2009; Elmegreen, 2009; Federrath, 2015; Krumholz and Burkhart, 2016; Federrath et al., 2017; Grisdale et al., 2017; Jin et al., 2017; Körtgen et al., 2017; Colling et al., 2018; Schruba et al., 2019; Lu et al., 2020)6.
2.3 Initial Conditions, Magnetic Field and Critical Balance
Classifying the turbulence as weak or strong is beneficial for understanding the underlying turbulence phenomenology and statistics (Sridhar and Goldreich, 1994; Goldreich and Sridhar, 1995; Perez and Boldyrev, 2008; Boldyrev and Perez, 2009; Oughton and Matthaeus, 2020; Schekochihin, 2020). The critical balance parameter on the driving scale is
2.4 Stationarity and Collecting Statistics
We run the simulations for 10τ, and report statistics from quantiles for the 50th, 16th and 84th percentiles of the time distributions over the last 5τ. This 1 ensures that the sub-Alfvénic, large-scale field simulations are statistically stationary, i.e.,
3 Ionic Alfvén Velocity Fluctuations
Consider the dimensionless magnitude of the ionic Alfvén velocities in a magnetized, compressible plasma,
The correlation between the gas density and the ionization fraction is,
where χ0 is the mass ionization fraction at density ρ0. When p → ∞ ⇒ χ = χ0, the equilibrium time between ionizing the plasma tion and a typical density fluctuation
where
We make this change of variables to bring out the symmetry in the log transform of vA,ion,
where s = ln (ρ/ρ0),
where
Thus, if we want to model the PDF and variance of
3.1 Density Fluctuations
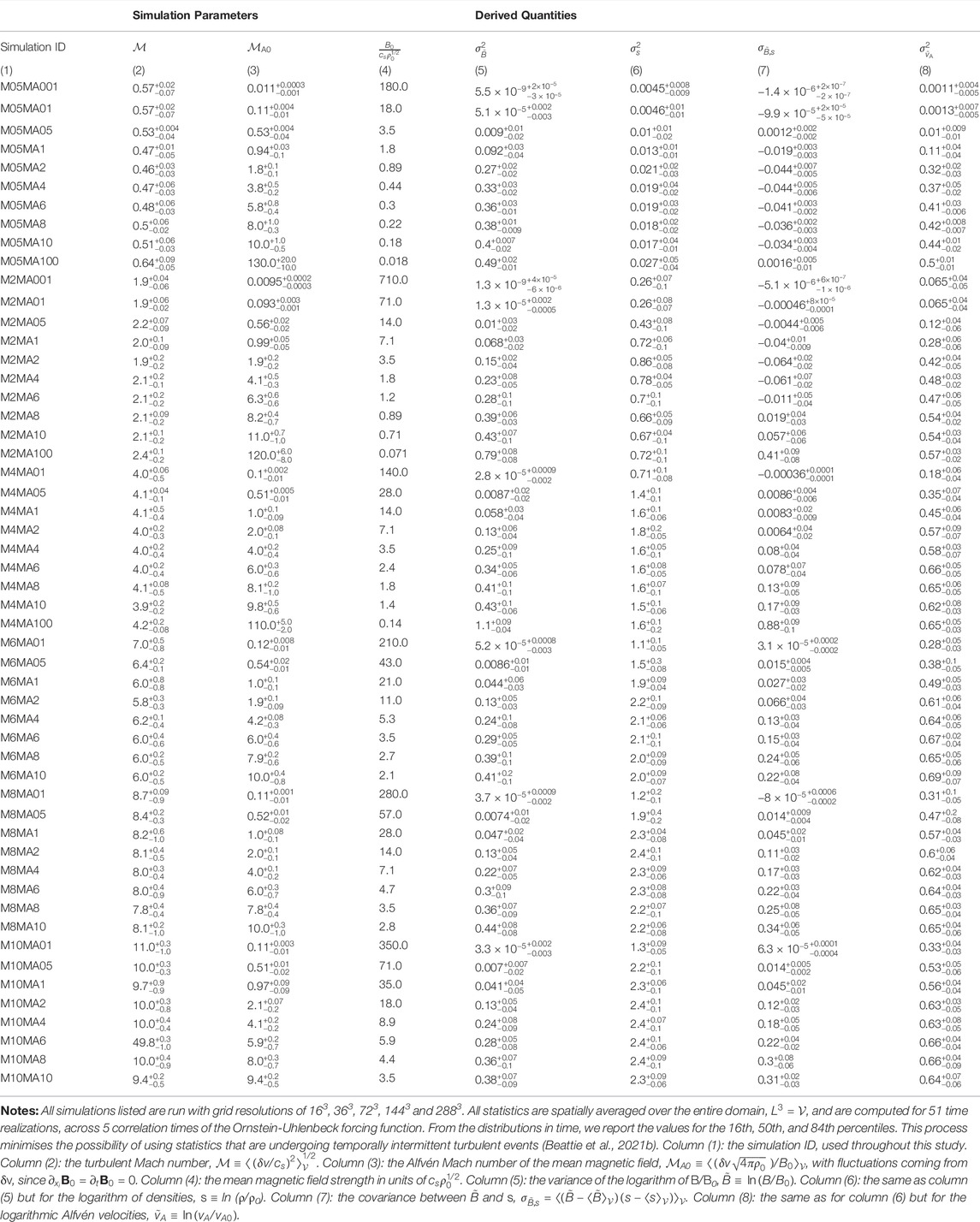
In Figure 2 we show the s-PDFs from the
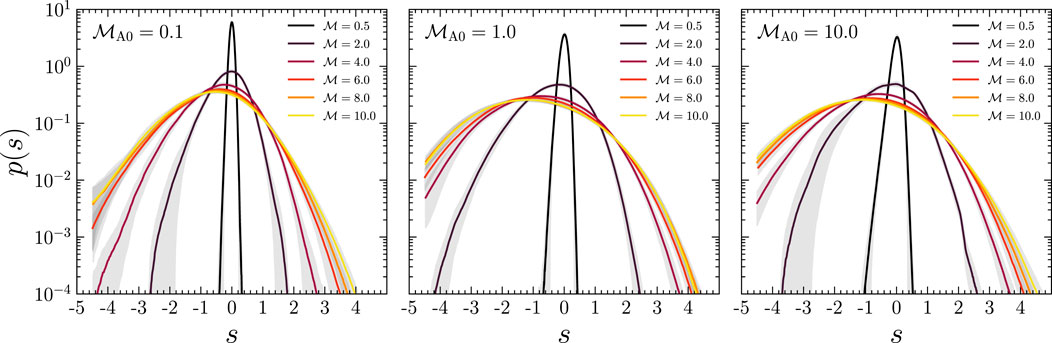
FIGURE 2. The logarithmic density PDFs for the sub-Alfvénic,
In Figure 3 we show
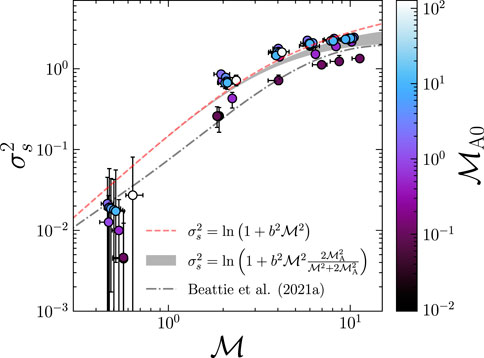
FIGURE 3. The logarithmic density variance,
(Federrath et al., 2008; Federrath et al., 2010), super-Alfvénic MHD turbulence theory (gray band),
assuming ρ ∝ B1/2 (Molina et al., 2012) evaluated between
Where,
The key point is that, regardless of
3.2 Magnetic Field Fluctuations
In a similar treatment as the last section, we plot a representative sample of the logarithmic magnetic magnitude PDFs in Figure 4 on the same scale as the PDFs shown in Figure 2. Unlike the s-PDFs, the
FIGURE 4. The same as Figure 2, but for the logarithmic magnetic field magnitudes. For
Not only are the higher-order moments of the PDFs growing with
We plot the variance of both the linear, large-scale field normalized magnetic field B/B0 (left panel) and logarithmic magnetic field (right panel) of Figure 5. Both plots show a systematic power law increase with
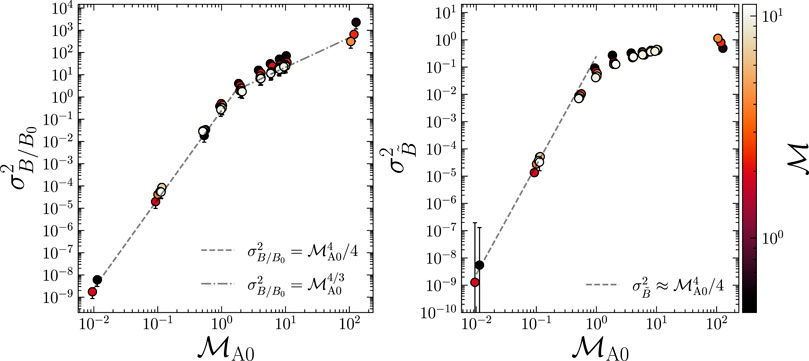
FIGURE 5. The variance of B/B0 (left) and ln (B/B0) (right) as a function of
relations between the rms magnetic field, including the effects of the large-scale field via the δB ⋅B0 term in the above equation, can be derived without any use of fitting parameters. For the variance of B/B0, this results in,
which show excellent agreement with the simulation data, across all
3.3 Covariance Between the Magnetic and Density Fluctuations
In the last two sections we developed an understanding of the global fluctuations (the variance) of the logarithmic density and magnetic field fluctuations. It may already be apparent that in the sub-Alfvénic regime the magnetic field fluctuations are completely negligible, and for
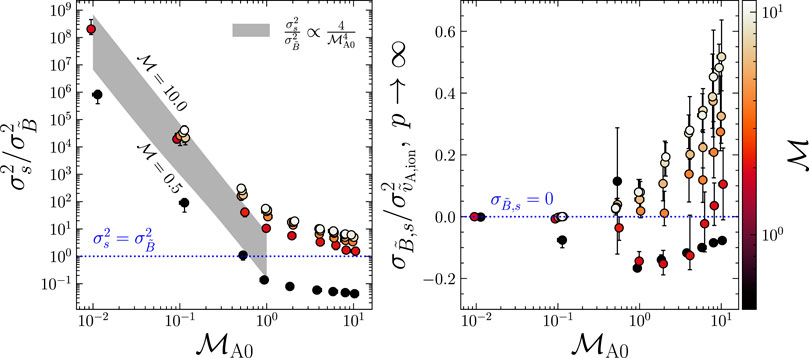
FIGURE 6. Left: The logarithmic density and magnetic field variance ratio as a function of
Using the Beattie et al. (2021a) model for the s variance, Eq. 27, which we plotted in Figure 3, and the
where the proportionality factor is Eq. 27, and for when the delta method for approximating
Of course comparing the first two terms in Eq. 21 is important to determine which is leading order, but if the covariance between the fields is large, then this will still complicate the modeling of
In contrast, the sub (to-trans)sonic, super-Alfvénic experiments give rise to a negative covariance. This could mean either the magnetic field is strong in under-densities, or the field is weak in over-densities, or both. If one carefully analyses the s-PDF and the
To understand these correlations (or lack thereof) further, we plot the time-averaged joint distributions of − [(p − 1)/2p]s and
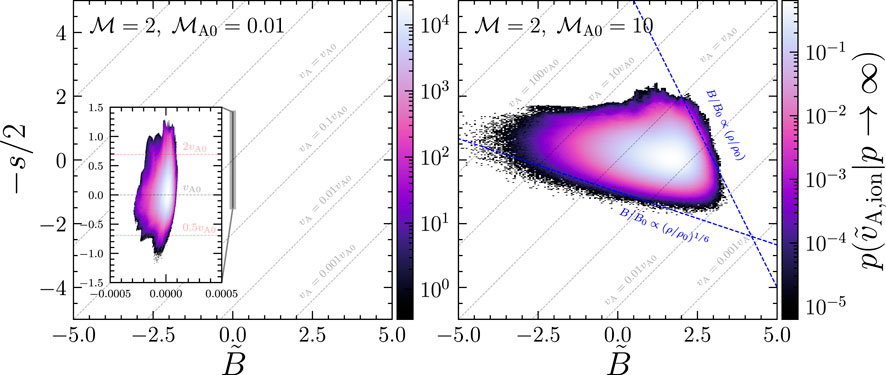
FIGURE 7. The joint
to compare directly with our simulation data. The benefit of making this joint PDF, as opposed to B versus ρ, or B2 versus ρ, is that lines in this space have constant Alfvén velocity magnitudes, as shown in Eq. 21, and the probability density is then exactly the probability density of
To be able to visualize the structure in the sub-Alfvénic data, we require a zoom-in to see the variation in
The super-Alfvénic data shows a wide spread in
3.4 Constructing an Ionic Alfvén Velocity Fluctuation Model
Throughout the last two sections we have learned that the magnetic field fluctuations are extremely weak in sub-Alfvénic large-scale field turbulence and in fact negligible compared to the total power in the density fluctuations, as shown in the left panel of Figure 6. Furthermore, in this regime channel flows along B0 are the only way to significantly shock the gas, which makes
when it is completely determined by logarithmic density fluctuations.
We plot
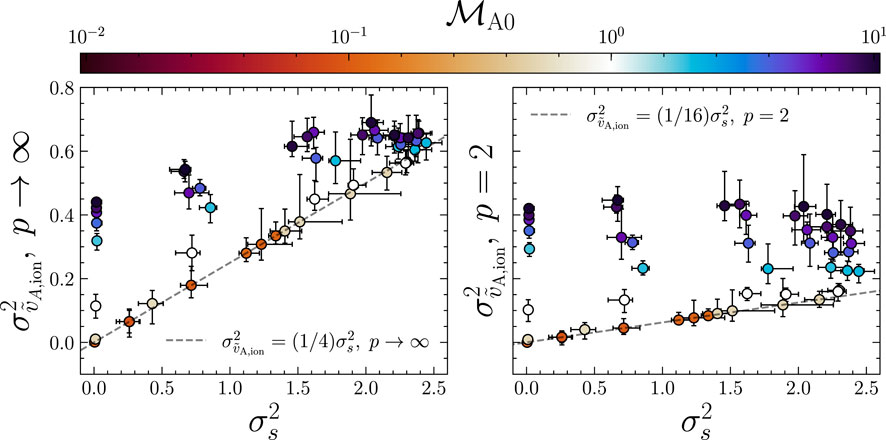
FIGURE 8. The logarithmic ion Alfvén velocity variance,
and
which we plot with the dashed-gray lines in each panel of Figure 8. For both ionization states, as expected from our analysis in Section 3.2 and above, the sub-to-trans-Alfvénic simulations closely match the relation, showing that indeed the variances of the ion Alfvén speeds are being controlled by the density fluctuations11. In the p → ∞ state, the super-Alfvénic experiments at higher
Now that we have a variance model we move on to constructing the full
which, for a lognormal s-PDF (a reasonable approximation, as discussed in Section 3.1)
and under the lognormal formalism, is solely dependent upon the s variance, and ionization-density correlation χ ∝ ρ−1/p. The strength of the 1/p correlation contracts (by a factor of [2p/(p − 1)]2) and shifts (by a factor of − [2p/(p − 1)]2/2, because
To compare with our data we take the limit in which p → ∞. This reduces Eqs. 36, 37 to
In Figure 9 we show fits of Eq. 38 for a representative sample of
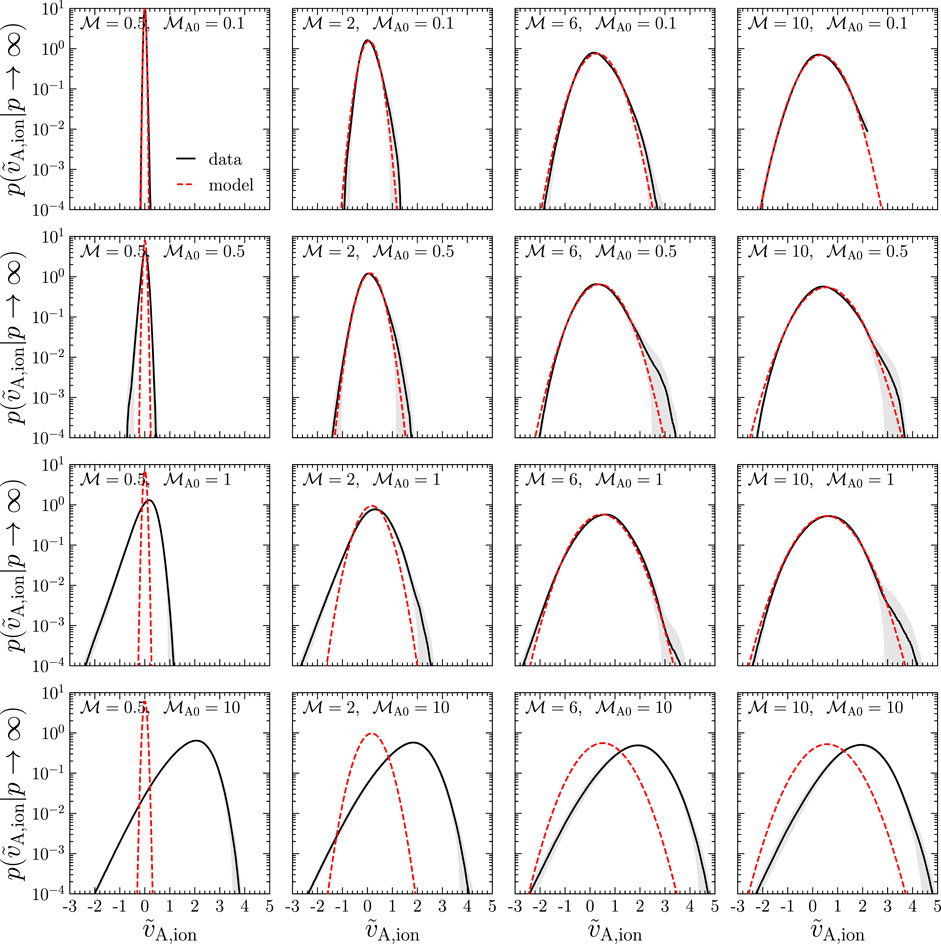
FIGURE 9. The volume-weighted logarithmic ion Alfvén velocity distribution for a selection of subsonic (left), supersonic (right) and sub-to-trans-Alfvénic (first three rows) simulations, shown in black, with 1σ fluctuations shown with the gray band. Our model, Eq. 38, is shown with the red dashed line, evaluated in the χ = χ0 = 1 limit, corresponding to p → ∞ in Eq. 36.
In the sub-to-trans-Alfvénic regime, the most significant deviation is at small
We also include
We have now created a model for the PDF and variance of the logarithm of the Alfvén velocities that works over a broad range of
4 Discussion and Implications
4.1 Measuring the
Understanding the
1) choose a trans-to-sub-Alfvénic region of the ISM (Li et al., 2013; Federrath et al., 2016; Hu et al., 2019; Heyer et al., 2020; Skalidis et al., 2021b; Hoang et al., 2021; Hwang et al., 2021),
2) obtain the column density and measure Σ/Σ0 and compute
3) apply the Brunt et al. (2010b) correction factor to derive
4) use
5) and finally, use Eq. 39,
As discussed in Section 1.2, the choice of p depends on the phase being observed. In the cold ISM, p = 2 because ionization equilibrium is reached quickly, while for diffuse atomic gas p → ∞ because ionization equilibrium is not attained before density fluctuations dissipate. We now turn to the physical process that our analysis of the vA,ion variance itself will help better understand–the macroscopic diffusion of cosmic rays undergoing the streaming instability in the highly-magnetized regions of the ISM.
4.2 Modeling the Parallel Macroscopic streaming cosmic ray (SCR) Diffusion
For the sub-Alfvénic regime, where the magnetic field lines are dominated by the large-scale, non-turbulent component (see discussion in Section 1.4), channel flows form along the field lines and give rise to the density fluctuations (see Figure 7), which in turn control the vA,ion fluctuations. In this regime we expect much faster transport (both streaming and macroscopic diffusion) along field lines than across them, and we expect the amount of parallel macroscopic diffusion to be much more sensitive to the vA,ion fluctuations than the turbulent velocities because vA,ion ≫ v. In Section 3, we found that vA,ion follows a lognormal distribution. This means that the diffusive process that the SCRs take along magnetic field lines cannot possibly be regular Gaussian diffusion (where step-sizes are drawn from a Gaussian distribution), with
The regular explanation for superdiffusion in turbulent fluids is associated with Richardson (1926) diffusion: turbulent advection of field lines causes them to separate at a rate
We leave a full exploration of the nature of parallel superdiffusion in these highly-magnetized plasmas for future work. However, to get at least an understanding of the magnitudes involved in how the density inhomogeneities enhance the along-field diffusion we can approximate the lognormal vA,ion distribution as a Gaussian process. Assuming,
which captures how the SCR populations are advected at the streaming speed, vA0,ion with some amount of macroscopic, Gaussian diffusion, or stochasticity through the Wiener process,
utilizing that
We directly compute the ρ/ρ0 correlation scale using the textbook definition,
where
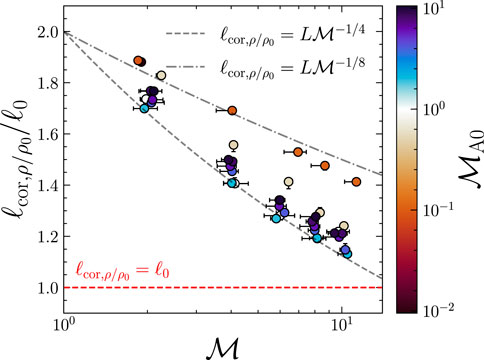
FIGURE 10. The correlation scale of ρ/ρ0 for the supersonic experiments, relevant to our κ‖ model, Eq. 41, as computed with Eq. 42, as a function of
Now we have all of the ingredients for estimating κ‖ in a relevant astrophysical system. Because our model works in a
Based on measurements of
Finally, we perform an estimate of what might be considered a galactic average for the parallel diffusion coefficient that comes from the density inhomomgeneities in a Milky Way-like galaxy. Like our toy molecular cloud model, we assume
4.3 Caveats in Our Study
This work has been done in the context of an isothermal equation of state, and it is well known that the ISM is a multiphase plasma (Ferrière, 2001; Hennebelle and Falgarone, 2012; Seta and Federrath, 2022). However, any one of the stable phases is approximately isothermal (Wolfire et al., 1995; Omukai et al., 2005). This means the results in our study are only applicable to cosmic ray transport within any single phase of the ISM. In our study we use a mixture (50:50 in energy) of isotropic compressible and solenoidal modes to establish and maintain the turbulence. As highlighted in Yoon et al. (2016), the driving prescription changes the nature of density and magnetic field correlations in the turbulence and more compressive driving will give rise to stronger density fluctuations (changing the b parameter in Eq. 27) and intermittent events, whereas solenoidal driving will have the opposite effect (Federrath et al., 2008; Federrath et al., 2009, 2010; Konstandin et al., 2012a). However, in the sub-Alfvénic regime, we do not believe that the correlations (or lack thereof) that we established in Section 3.3 will change nor the overall conclusion we make in this study. This is because it is the strong B0 that restricts the magnetic field fluctuations from ever becoming dominant, and with isotropic driving shocked gas will form along B0, inevitably facilitating the same uncorrelated joint PDF that we find in the left panel of Figure 7. This means that the density fluctuations, even if they change in magnitude for different turbulent driving, will always control
In this work we utilize ideal MHD models, free of an explicit form for the strain rate tensor in the momentum equation, or resistivity in the induction equation. Hence, the dissipation in our turbulence is purely numerical. Because the ion Alfvén velocity fluctuations are dominated by the low-k modes (see Supplementary Figure S2, which shows that the rms statistics converge quickly as the number of grid elements in the simulations increase) the macroscopic diffusion of SCRs ought to be also controlled by the low-k modes (low in the case of observations may either correspond to modes comparable to the scale of the driving source, or the largest modes in the observational region that is being examined, see e.g., Federrath et al., 2016; Stewart and Federrath 2022). This means the exact prescription for dissipation ought not to matter for the ion Alfvén velocity statistics that we describe in this study. Relevant to observations, as long as we are able to analyze approximately isothermal regions of the ISM that are not dominated by dissipation (e.g. turbulent regions), our results ought to provide some insight into the rms statistics and 1-point statistics on those scales.
The turbulence damping processes are important for the microphysics of the streaming instability. Throughout Section 4.2 we have assumed that the growth of the resonant hydromagnetic modes are balanced by the ion neutral damping rate (Kulsrud and Pearce 1969; and shown recently in PIC simulations, Bai 2022), giving rise to vstream ∼ vA,ion. However, the balance is sensitive to the physics of the damping process. For example, Plotnikov et al. (2021) showed that when the ion neutral damping rate is fast compared to the growth rate of the hydromagnetic modes, streaming velocities can reach up to
In our MHD models, we also omit self-gravity. Collapsing regions excite turbulent modes (Federrath et al., 2011; Higashi et al., 2021), create power law structure (one or two separate power laws) in the high-density tails of the s-PDF (e.g., Federrath and Klessen, 2012; Federrath and Klessen, 2013; Burkhart, 2018; Jaupart and Chabrier, 2020; Khullar et al., 2021), make the correlation scale of the density move to much smaller scales (Federrath and Klessen, 2013), and correlate the magnetic field and density based on the geometry of the collapse (e.g., Tritsis et al., 2015; Mocz and Burkhart, 2018). The analysis in this study thus corresponds to “subcritical” regions of the ISM, where the turbulent kinetic energy is greater than the gravitational potential energy, which may correspond to a large fraction of the MCs in the Milky Way (and simulated analogues Dobbs et al., 2011; Tress et al., 2020).
Our macroscopic diffusion coefficient modeling in Section 4.2 paints a simple picture for the diffusion of SCRs in a sub-Alfvénic turbulent medium: cosmic rays stream through correlation lengths of the gas density at a streaming velocity set by the large-scale magnetic field strength, modulated by the variance of the density field, which is a function of the turbulence and the large-scale magnetic field. This process results in dispersion of the displacements for the SCRs increasing by a variance every correlation scale. Clearly, this simple picture does not take into account some important processes, such as the contribution from the microphysical diffusion, magnetic field fluctuations (which we show are sub-dominant), and the turbulent fluctuations in the velocity field. Regardless, our model provides a measure of the impact of the density fluctuations alone on the diffusion process, which we know from Section 3 is the dominant mechanism for controlling the dispersion in Alfvén velocities in the low
5 Conclusion and Summary
Cosmic rays undergoing the streaming instability (streaming cosmic rays; SCRs) travel along magnetic field lines at the ionic Alfvén velocity, and hence the dispersion, or fluctuations in the Alfvén velocities act to effectively diffuse populations of SCRs. We explore the nature of these fluctuations using a large ensemble of three-dimensional isothermal magnetized, compressible (mostly supersonic) turbulence simulations, capturing a wide set of plasma parameters relevant to the interstellar medium of galaxies. The key result in this study is that when the large-scale field is sub-to-trans-Alfvénic, the magnetic field fluctuations are sub-dominant to the density fluctuations. This means the Alfvén velocity fluctuations, and likewise for the ionic Alfvén velocity fluctuations, are controlled by changes in the density, highlighting not only the role of compressibility in dispersing populations of SCRs, but also in determining the Alfvén velocity statistics in compressible MHD turbulence. We list further key results of the study below.
• In Section 1.2 we estimate the ionization equilibrium times and compare them to the typical timescales for density fluctuations in a turbulent medium. We show that the assumption of (instantaneous) ionization equilibrium, which leads to χ ∝ ρ−1/2, Eq. 2, is relevant for understanding ion Alfvén fluctuations in molecular gas (χ ∼ 10–5), e.g., star-forming regions in the ISM. However, for diffuse atomic gas (χ ∼ 10–3 − 10–1), the equilibrium and gas density fluctuation timescales become comparable, and hence we can treat χ as approximately spatially constant.
• In Section 3 we show that the logarithmic Alfvén velocity magnitudes can be written as a sum of the logarithmic magnetic field and density magnitudes, Eq. 21, and hence we study the variance and volume-weighted PDFs for the logarithmic gas density, s (Section 3.1) and the logarithmic magnetic field amplitude,
• We measure and discuss the covariance between s and
• Because the trans-to-sub-Alfvénic turbulence vA,ion fluctuations are controlled by the density, which are approximately distributed lognormally, as discussed in Section 1.3 and Section 3.1, we are able to construct a lognormal vA,ion theory, which we show in Section 3. In Figure 9 we show the PDF models, highlighting how they fit very well for the
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
JB lead this study, performed the numerical simulations, produced the figures and wrote a majority of this manuscript. MK wrote Section 1.2. JB, MK, CF, MS and RC contributed significantly to the development of the ideas presented in this study, and the detailed editing of the manuscript.
Funding
JB acknowledges financial support from the Australian National University, via the Deakin PhD and Dean’s Higher Degree Research (theoretical physics) Scholarships and the Australian Government via the Australian Government Research Training Program Fee-Offset Scholarship. CF and JB acknowledge high-performance computing resources provided by the Leibniz Rechenzentrum and the Gauss Centre for Supercomputing (grants pr32lo, pn73fi, and GCS Large-scale project 22,542), and MK, CF, and JB acknowledge high-performance computing resources provided by the Australian National Computational Infrastructure (grants jh2 and ek9) in the framework of the National Computational Merit Allocation Scheme and the ANU Merit Allocation Scheme. MK acknowledges support from the Australian Research Council’s Discovery Projects and Future Fellowship schemes, awards DP190101258 and FT180100375. CF acknowledges funding provided by the Australian Research Council (Future Fellowship FT180100495), and the Australia-Germany Joint Research Cooperation Scheme (UA-DAAD). MS acknowledges financial support from the Australian Government via the Australian Government Research Training Program Stipend and Fee-Offset Scholarship. RC acknowledges support from the Australian Research Council’s Discovery Project, award DP190101258.
Acknowledgments
JB thanks CF’s and Mark Krumholz’s research groups and Philip Mocz for many productive discussions. We thank the reviewers for their suggestions that helped enhance the clarity of this study. The fluid simulation software, flash, was in part developed by the Flash Centre for Computational Science at the Department of Physics and Astronomy of the University of Rochester. The turbulence driving module can be accessed from Federrath et al. (2022). Data analysis and visualisation software used in this study: C++ (Stroustrup, 2013), numpy (Oliphant, 2006; Harris et al., 2020), matplotlib (Hunter, 2007), scipy (Virtanen et al., 2020) and emcee (Foreman-Mackey et al., 2013).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor SX declared a past collaboration with the author(s) CF, MK, RC.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2022.900900/full#supplementary-material
Footnotes
1Here we provide a rough estimate of the correlation scale of the magnetic field, as pertaining to our estimate in this paragraph. Consider an Alfvén wave traveling along a magnetic field line, over some time, tnl that sets the timescale for the Alfvén wave to decorrelate. Clearly, by causation, this is proportional to the parallel spatial correlation length of the magnetic field, ℓcor ∼ vAtnl(ℓcor/ℓ0). tnl is the nonlinear timescale for a turbulent fluctuation to decorrelate in the plasma,
2Note that this cannot be strictly true, as discussed in detail in Hopkins (2013), Squire and Hopkins (2017), and Beattie et al. (2021b), since the PDF on each scale is constructed from convolutions of PDFs from scales below it, and convolutions of lognormal PDFs do not result in lognormal PDFs. For this reason, assuming that PDFs on all scales are lognormal violates mass conservation, and recent extremely high resolution turbulence simulations with
3Note that even though we are focusing strictly on ISM turbulence, recent works have developed density variance relations for compressible, subsonic, stratified turbulence, with applications for understanding the nature of fluctuations in the intracluster medium (Mohapatra et al., 2020a; b).
4Note that this means that even though the turbulence is driven in the weak regime, it is not clear if the turbulence could faithfully be classified as weak if over 70% of the energy budget in the fluid is from k‖ = 0 structures that are not waves (Boldyrev and Perez, 2009; Yang et al., 2019).
5Note that we are referring to driving and not momentum, i.e., gravitational collapse is a compressive source, but vorticity and compressible modes both are generated in the momentum field (Higashi et al., 2021).
6See Figure 2 in Sharda et al. (2021) for a catalog of sources that have been classified by different values of “turbulent driving parameter”, which is, in principle, an indirect measurement of η (see Federrath et al., 2009 for an empirical fit that maps one to the other). What is clear is that different turbulence driving mechanisms excite different modes, which may also depend on the galactic environment and/or time.
7We note that super-Alfvénic turbulence takes roughly 2τ to approach a statistically stationary state, similar to purely hydrodynamic turbulence (Price and Federrath, 2010).
8Note that we have naturally introduced an orientation for the density fluctuations. This is probably the most significant effect that the magnetic field has on the density variance. The overall magnitude does not change significantly, but through flux-freezing, the magnetic field acts as a scaffold for the fluctuations, making them highly anisotropic along and across B0 (see Figure 2 in Beattie and Federrath, 2020).
9Strictly speaking, the lower bound of the magnetic energy, Emin and the minimum number of crossings for any topologically equivalent magnetic fields, Cmin, respectively, such that
10Note that there are still weak compressions perpendicular to field lines, which, in the framework of linear MHD theory, are from compressible fast magnetosonic modes. These form striations of weakly compressed gas running parallel to the magnetic field (Tritsis and Tassis, 2018; Beattie et al., 2020; Beattie and Federrath, 2020).
11Note that this means that the energy spectrum of Alfvén velocities must therefore also be controlled by the density. This is a very interesting repercussion of this result, and clearly demonstrates a stark difference between incompressible MHD turbulence, which always has Alfvén velocities being determined by magnetic field fluctuations, and compressible MHD turbulence. We leave the in-depth study of the two-point statistics, such as the structure functions and power spectra for future works.
12Note
13
14Note that even though we are not reporting upon microscopic diffusion coefficients, there is no lack of measuring them in the literature (e.g., Bai, 2022, for some recent measurements utilizing 1D, local MHD-PIC simulations see).
References
Abe, D., Inoue, T., Inutsuka, S.-i., and Matsumoto, T. (2020). Classification of Filament Formation Mechanisms in Magnetized Molecular Clouds. arXiv e-printsarXiv:2012.02205.
Ade, P. A. R., Aghanim, N., Alves, M. I. R., Arnaud, M., Arzoumanian, D., et al. (2016a). Planck Intermediate Results. XXXV. Probing the Role of the Magnetic Field in the Formation of Structure in Molecular Clouds. Astron. Astrophys. 586, A138. doi:10.1051/0004-6361/201525896
Aghanim, N., Alves, M. I. R., Arnaud, M., Arzoumanian, D., Aumont, J., et al. (2016b). Planck Intermediate Results. XXXIV. The Magnetic Field Structure in the Rosette Nebula. Astron. Astrophys. 586, A137. doi:10.1051/0004-6361/201525616
Armstrong, J. W., Rickett, B. J., and Spangler, S. R. (1995). Electron Density Power Spectrum in the Local Interstellar Medium. Astrophys. J. 443, 209. doi:10.1086/175515
Bai, X.-N. (2022). Toward First-Principles Characterization of Cosmic-Ray Transport Coefficients from Multiscale Kinetic Simulations. Astrophys. J. 928, 112. doi:10.3847/1538-4357/ac56e1
Barreto-Mota, L., de Gouveia Dal Pino, E. M., Burkhart, B., Melioli, C., Santos-Lima, R., and Kadowaki, L. H. S. (2021). Magnetic Field Orientation in Self-Gravitating Turbulent Molecular Clouds. arXiv e-printsarXiv:2101.03246.
Beattie, J. R., and Federrath, C. (2020). Filaments and Striations: Anisotropies in Observed, Supersonic, Highly Magnetized Turbulent Clouds. Mon. Not. R. Astron. Soc. 492, 668–685. doi:10.1093/mnras/stz3377
Beattie, J. R., Federrath, C., Klessen, R. S., and Schneider, N. (2019). The Relation Between the Turbulent Mach Number and Observed Fractal Dimensions of Turbulent Clouds. Mon. Not. R. Astron. Soc. 488, 2493–2502. doi:10.1093/mnras/stz1853
Beattie, J. R., Federrath, C., and Seta, A. (2020). Magnetic Field Fluctuations in Anisotropic, Supersonic Turbulence. Mon. Not. R. Astron. Soc. 498, 1593–1608. doi:10.1093/mnras/staa2257
Beattie, J. R., Krumholz, M. R., Skalidis, R., Federrath, C., Seta, A., Crocker, R. M., et al. (2022). Energy Balance and Alfv∖’En Mach Numbers in Compressible Magnetohydrodynamic Turbulence with a Large-Scale Magnetic Field. arXiv e-printsarXiv:2202.13020.
Beattie, J. R., Mocz, P., Federrath, C., and Klessen, R. S. (2021a). A Multishock Model for the Density Variance of Anisotropic, Highly Magnetized, Supersonic Turbulence. Mon. Not. R. Astron. Soc. 504, 4354–4368. doi:10.1093/mnras/stab1037
Beattie, J. R., Mocz, P., Federrath, C., and Klessen, R. S. (2021b). The Density Distribution and the Physical Origins of Density Intermittency in Sub- to Trans-Alfvenic Supersonic Turbulence. arXiv e-printsarXiv:2109.10470.
Beck, R., and Wielebinski, R. (2013). Magnetic Fields Galaxies 5641. doi:10.1007/978-94-007-5612-0∖_13
Bell, A. (2013). Cosmic Ray Acceleration. Astropart. PhysicsSeeing High-Energy Universe Cherenkov Telesc. Array - Sci. Explor. CTA 43, 56–70. doi:10.1016/j.astropartphys.2012.05.022
Boldyrev, S., and Perez, J. C. (2009). Spectrum of Weak Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 103, 225001. doi:10.1103/PhysRevLett.103.225001
Boldyrev, S. (2006). Spectrum of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 96, 115002. doi:10.1103/PhysRevLett.96.115002
Bonne, L., Schneider, N., Bontemps, S., Clarke, S. D., Gusdorf, A., Lehmann, A., et al. (2020). Dense Gas Formation in the Musca Filament Due to the Dissipation of a Supersonic Converging Flow. Astron. Astrophys. 641, A17. doi:10.1051/0004-6361/201937104
Booth, C. M., Agertz, O., Kravtsov, A. V., and Gnedin, N. Y. (2013). Simulations of Disk Galaxies with Cosmic Ray Driven Galactic Winds. Astrophys. J. 777, L16. doi:10.1088/2041-8205/777/1/L16
Bouchut, F., Klingenberg, C., and Waagan, K. (2010). A Multiwave Approximate Riemann Solver for Ideal Mhd Based on Relaxation Ii: Numerical Implementation with 3 and 5 waves. Numer. Math. (Heidelb). 115, 647–679. doi:10.1007/s00211-010-0289-4
Boulares, A., and Cox, D. P. (1990). Galactic Hydrostatic Equilibrium with Magnetic Tension and Cosmic-Ray Diffusion. Astrophys. J. 365, 544. doi:10.1086/169509
Brunt, C. M., Federrath, C., and Price, D. J. (2010a). A Method for Reconstructing the PDF of a 3D Turbulent Density Field from 2D Observations. MNRAS 405, L56–L60. doi:10.1111/j.1745-3933.2010.00858.x
Brunt, C. M., Federrath, C., and Price, D. J. (2010b). A Method for Reconstructing the Variance of a 3d Physical Field from 2d Observations: Application to Turbulence in the Interstellar Medium. Mon. Not. R. Astron. Soc. 403, 1507–1515. doi:10.1111/j.1365-2966.2009.16215.x
Brunt, C. M., Heyer, M. H., and Mac Low, M. M. (2009). Turbulent Driving Scales in Molecular Clouds. Astron. Astrophys. 504, 883–890. doi:10.1051/0004-6361/200911797
Burgers, J. (1948). A Mathematical Model Illustrating the Theory of Turbulence. Adv. Appl. Mech. 1, 171–199. doi:10.1016/S0065-2156(08)70100-5
Burkhart, B., Falceta-Gonçalves, D., Kowal, G., and Lazarian, A. (2009). Density Studies of MHD Interstellar Turbulence: Statistical Moments, Correlations and Bispectrum. Astrophys. J. 693, 250–266. doi:10.1088/0004-637x/693/1/250
Burkhart, B. (2018). The Star Formation Rate in the Gravoturbulent Interstellar Medium. Astrophys. J. 863, 118. doi:10.3847/1538-4357/aad002
Bustard, C., and Zweibel, E. G. (2021). Cosmic-Ray Transport, Energy Loss, and Influence in the Multiphase Interstellar Medium. Astrophys. J. 913, 106. doi:10.3847/1538-4357/abf64c
Caprioli, D., Blasi, P., Amato, E., and Vietri, M. (2009). Dynamical Feedback of Self-Generated Magnetic Fields in Cosmic Ray Modified Shocks. Mon. Not. R. Astron. Soc. 395, 895–906. doi:10.1111/j.1365-2966.2009.14570.x
Chandrasekhar, S., and Fermi, E. (1953). Magnetic Fields In Spiral Arms. Astrophys. J. 118, 113. doi:10.1086/145731
Chen, C.-Y., and Ostriker, E. C. (2014). Formation of Magnetized Prestellar Cores with Ambipolar Diffusion and Turbulence. Astrophys. J. 785, 69. doi:10.1088/0004-637X/785/1/69
Chen, M. C.-Y., Francesco, J. D., Rosolowsky, E., Keown, J., Pineda, J. E., Friesen, R. K., et al. (2020). Velocity-Coherent Filaments in NGC 1333: Evidence for Accretion Flow? Astrophys. J. 891, 84. doi:10.3847/1538-4357/ab7378
Colling, C., Hennebelle, P., Geen, S., Iffrig, O., and Bournaud, F. (2018). Impact of Galactic Shear and Stellar Feedback on Star Formation. Astron. Astrophys. 620, A21. doi:10.1051/0004-6361/201833161
Cox, N. L. J., Arzoumanian, D., André, P., Rygl, K. L. J., Prusti, T., Men’shchikov, A., et al. (2016). Filamentary Structure and Magnetic Field Orientation in Musca. Astron. Astrophys. 590, A110. doi:10.1051/0004-6361/201527068
Crocker, R. M., Krumholz, M. R., and Thompson, T. A. (2021a). Cosmic Rays Across the Star-Forming Galaxy Sequence - I. Cosmic Ray Pressures and Calorimetry. Mon. Not. R. Astron. Soc. 502, 1312–1333. doi:10.1093/mnras/stab148
Crocker, R. M., Krumholz, M. R., and Thompson, T. A. (2021b). Cosmic Rays Across the Star-Forming Galaxy Sequence - II. Stability Limits and the Onset of Cosmic Ray-Driven Outflows. Mon. Not. R. Astron. Soc. 503, 2651–2664. doi:10.1093/mnras/stab502
Davis, L. (1951). The Strength of Interstellar Magnetic Fields. Phys. Rev. 81, 890–891. doi:10.1103/PhysRev.81.890.2
Dobbs, C. L., Burkert, A., and Pringle, J. E. (2011). Why are Most Molecular Clouds not Gravitationally Bound? Mon. Not. R. Astron. Soc. 413, 2935–2942. doi:10.1111/j.1365-2966.2011.18371.x
Dubey, A., Fisher, R., Graziani, C., Jordan, G. C., IVLamb, D. Q., Reid, L. B., et al. (2008). “Challenges of Extreme Computing Using the FLASH Code,”Numer. Model. Space Plasma Flows of. Editors N. V. Pogorelov, E. Audit, and G. P. Zank (San Franciso, CA, United States: Astronomical Society of the Pacific Conference Series), 385, 145.
Elmegreen, B. G. (2009). “Star Formation in Disks: Spiral Arms, Turbulence, and Triggering Mechanisms,”. Galaxy Disk Cosmol. Context of. Editors J. Andersen, B. m. Nordströara, and J. Bland -Hawthorn (Cambridge, United Kingdom: IAU Symposium), 254, 289–300. doi:10.1017/S1743921308027713
Falceta-Gonçalves, D., Kowal, G., Falgarone, E., and Chian, A. C.-L. (2014). Turbulence in the Interstellar Medium. Nonlinear process. geophys. 21, 587–604. doi:10.5194/npg-21-587-2014
Federrath, C., and Banerjee, S. (2015). The Density Structure and Star Formation Rate of Non-Isothermal Polytropic Turbulence. Mon. Not. R. Astron. Soc. 448, 3297–3313. doi:10.1093/mnras/stv180
Federrath, C. (2015). Inefficient Star Formation Through Turbulence, Magnetic Fields and Feedback. Mon. Not. R. Astron. Soc. 450, 4035–4042. doi:10.1093/mnras/stv941
Federrath, C., Klessen, R. S., Iapichino, L., and Beattie, J. R. (2021). The Sonic Scale of Interstellar Turbulence. Nat. Astron. 5, 365–371. doi:10.1038/s41550-020-01282-z
Federrath, C., and Klessen, R. S. (2013). On the Star Formation Efficiency of Turbulent Magnetized Clouds. Astrophys. J. 763, 51. doi:10.1088/0004-637X/763/1/51
Federrath, C., Klessen, R. S., and Schmidt, W. (2008). The Density Probability Distribution in Compressible Isothermal Turbulence: Solenoidal Versus Compressive Forcing. Astrophys. J. 688, L79–L82. doi:10.1086/595280
Federrath, C., Klessen, R. S., and Schmidt, W. (2009). The Fractal Density Structure in Supersonic Isothermal Turbulence: Solenoidal Versus Compressive Energy Injection. Astrophys. J. 692, 364–374. doi:10.1088/0004-637x/692/1/364
Federrath, C., and Klessen, R. S. (2012). The Star Formation Rate of Turbulent Magnetized Clouds: Comparing Theory, Simulations, and Observations. Astrophys. J., 156. doi:10.1088/0004-637X/761/2/156
Federrath, C. (2016). Magnetic Field Amplification in Turbulent Astrophysical Plasmas. J. Plasma Phys. 82, 535820601. doi:10.1017/S0022377816001069
Federrath, C., Rathborne, J. M., Longmore, S. N., Kruijssen, J. M. D., Bally, J., Contreras, Y., et al. (2017). “The Link Between Solenoidal Turbulence and Slow Star Formation in G0.253+0.016,”. Multi-Messenger Astrophysics Galactic Centre of. Editors R. M. Crocker, S. N. Longmore, and G. V. Bicknell (Cambridge, United Kingdom: IAU Symposium), 322, 123–128. doi:10.1017/S1743921316012357
Federrath, C., Rathborne, J. M., Longmore, S. N., Kruijssen, J. M. D., Bally, J., Contreras, Y., et al. (2016). The Link Between Turbulence, Magnetic Fields, Filaments, And Star Formation in the Central Molecular Zone Cloud G0.253+0.016. Astrophys. J. 832, 143. doi:10.3847/0004-637X/832/2/143
Federrath, C., Roman-Duval, J., Klessen, R., Schmidt, W., and Mac Low, M. M. (2010). Comparing the Statistics of Interstellar Turbulence in Simulations And Observations: Solenoidal Versus Compressive Turbulence Forcing. Astron. Astrophys. 512, A81. doi:10.1051/0004-6361/200912437
Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., and Mac Low, M. M. (2022). TG: Turbulence Generator. Houghton, Michigan, United States: Astrophysics Source Code Library record ascl:2204.001.
Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., and Klessen, R. S. (2011). A New Jeans Resolution Criterion for (M)HD Simulations of Self-Gravitating Gas: Application to Magnetic Field Amplification by Gravity-Driven Turbulence. Astrophys. J. 731, 62. doi:10.1088/0004-637X/731/1/62
Ferrière, K. M. (2001). The Interstellar Environment of Our Galaxy. Rev. Mod. Phys. 73, 1031–1066. doi:10.1103/revmodphys.73.1031
Field, G. B., Goldsmith, D. W., and Habing, H. J. (1969). Cosmic-Ray Heating of the Interstellar Gas. Astrophys. J. 155, L149. doi:10.1086/180324
Foreman-Mackey, D., Hogg, D. W., Lang, D., and Goodman, J. (2013). Emcee: The Mcmc Hammer, 125. San Francisco, CA, United States: Publications of the Astronomical Society of the Pacific, 306.
Freedman, M. H., and He, Z.-X. (1991). Divergence-Free Fields: Energy and Asymptotic Crossing Number. Ann. Math. 134, 189–229. doi:10.2307/2944336
Fryxell, B., Olson, K., Ricker, P., Timmes, F. X., Zingale, M., Lamb, D. Q., et al. (2000). Flash: An Adaptive Mesh Hydrodynamics Code for Modeling Astrophysical Thermonuclear Flashes. Astrophys. J. Suppl. Ser. 131, 273–334. doi:10.1086/317361
Gaensler, B. M., Haverkorn, M., Burkhart, B., Newton-McGee, K. J., Ekers, R. D., Lazarian, A., et al. (2011). Low-Mach-Number Turbulence in Interstellar Gas Revealed by Radio Polarization Gradients. Nature 478, 214–217. doi:10.1038/nature10446
Girichidis, P., Naab, T., Walch, S., Hanasz, M., Mac Low, M.-M., Ostriker, J. P., et al. (2016). Launching Cosmic-Ray-Driven Outflows from the Magnetized Interstellar Medium. Astrophys. J. 816, L19. doi:10.3847/2041-8205/816/2/L19
Goldreich, P., and Sridhar, S. (1995). Toward a Theory of Interstellar Turbulence. 2: Strong Alfvenic Turbulence. Astrophys. J. 438, 763–775. doi:10.1086/175121
Grisdale, K., Agertz, O., Romeo, A. B., Renaud, F., and Read, J. I. (2017). The Impact oif Stellar Feedback on the Density and Velocity Structure of the Interstellar Medium. Mon. Not. R. Astron. Soc. 466, 1093–1110. doi:10.1093/mnras/stw3133
Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R., Virtanen, P., Cournapeau, D., et al. (2020). Array Programming with Numpy. Nature 585, 357–362. doi:10.1038/s41586-020-2649-2
Hennebelle, P., and Falgarone, E. (2012). Turbulent Molecular Clouds. Astron. Astrophys. Rev. 20, 55. doi:10.1007/s00159-012-0055-y
Heyer, M., Soler, J. D., and Burkhart, B. (2020). The Relative Orientation Between the Magnetic Field and Gradients of Surface Brightness Within Thin Velocity Slices of 12CO And 13CO Emission from the Taurus Molecular Cloud. Mon. Not. R. Astron. Soc. 496, 4546–4564. doi:10.1093/mnras/staa1760
Higashi, S., Susa, H., and Chiaki, G. (2021). Amplification of Turbulence in Contracting Prestellar Cores in Primordial Minihalos. Astrophys. J. 915, 107. doi:10.3847/1538-4357/ac01c7
Hoang, T. D., Bich Ngoc, N., Diep, P. N., Tram, L. N., Hoang, T., Lim, W., et al. (2021). Studying Magnetic Fields and Dust in M17 using Polarized Thermal Dust Emission Observed by SOFIA/HAWC+. arXiv:2108.10045.
Hoef, J. M. V. (2012). Who Invented the Delta Method? Am. Statistician 66, 124–127. doi:10.1080/00031305.2012.687494
Hopkins, P. F. (2013). A Model for (non-lognormal) Density Distributions in Isothermal Turbulence. Mon. Not. R. Astron. Soc. 430, 1880–1891. doi:10.1093/mnras/stt010
Hopkins, P. F., Chan, T. K., Squire, J., Quataert, E., Ji, S., Kereš, D., et al. (2021). Effects of Different Cosmic Ray Transport Models on Galaxy Formation. Mon. Not. R. Astron. Soc. 501, 3663–3669. doi:10.1093/mnras/staa3692
Hu, Y., Lazarian, A., and Xu, S. (2022). Superdiffusion of cosmic Rays in Compressible Magnetized Turbulence. Mon. Not. R. Astron. Soc. 512, 2111–2124. doi:10.1093/mnras/stac319
Hu, Y., Yuen, K. H., Lazarian, V., Ho, K. W., Benjamin, R. A., Hill, A. S., et al. (2019). Magnetic Field Morphology in Interstellar Clouds with the Velocity Gradient Technique. Nat. Astron. 3, 776–782. doi:10.1038/s41550-019-0769-0
Hunter, J. D. (2007). Matplotlib: A 2d Graphics Environment. Comput. Sci. Eng. 9, 90–95. doi:10.1109/MCSE.2007.55
Hwang, J., Kim, J., Pattle, K., Kwon, W., Sadavoy, S., Koch, P. M., et al. (2021). The JCMT BISTRO Survey: The Distribution of Magnetic Field Strengths Toward the OMC-1 Region. Astrophys. J. 913, 85. doi:10.3847/1538-4357/abf3c4
Iroshnikov, P. S. (1964). Turbulence of a Conducting Fluid in a Strong Magnetic Field. Sov. Ast 7, 566.
Jaupart, E., and Chabrier, G. (2020). Evolution of the Density PDF in Star-Forming Clouds: The Role of Gravity. Astrophys. J. 903, L2. doi:10.3847/2041-8213/abbda8
Jin, K., Salim, D. M., Federrath, C., Tasker, E. J., Habe, A., and Kainulainen, J. T. (2017). On the Effective Turbulence Driving Mode of Molecular Clouds Formed in Disc Galaxies. Mon. Not. R. Astron. Soc. 469, 383–393. doi:10.1093/mnras/stx737
Karlsson, T., Bromm, V., and Bland-Hawthorn, J. (2013). Pregalactic Metal Enrichment: The Chemical Signatures of the First Stars. Rev. Mod. Phys. 85, 809–848. doi:10.1103/RevModPhys.85.809
Khullar, S., Federrath, C., Krumholz, M. R., and Matzner, C. D. (2021). The Density Structure of Supersonic Self-Gravitating Turbulence. arXiv e-printsarXiv:2107.00725.
Kim, J., and Ryu, D. (2005). Density Power Spectrum of Compressible Hydrodynamic Turbulent Flows. Astrophys. J. 630, L45–L48. doi:10.1086/491600
Kitsionas, S., Federrath, C., Klessen, R. S., Schmidt, W., Price, D. J., Dursi, L. J., et al. (2009). Algorithmic Comparisons of Decaying, Isothermal, Supersonic Turbulence. Astron. Astrophys. 508, 541–560. doi:10.1051/0004-6361/200811170
Kolmogorov, A. N. (1941). The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. Dokl. Akad. Nauk. Sssr 30, 301–305. doi:10.1098/rspa.1991.0075
Konstandin, L., Federrath, C., Klessen, R. S., and Schmidt, W. (2012a). Statistical Properties of Supersonic Turbulence in the Lagrangian and Eulerian Frameworks. J. Fluid Mech. 692, 183–206. doi:10.1017/jfm.2011.503
Konstandin, L., Girichidis, P., Federrath, C., and Klessen, R. S. (2012b). A New Density Variance-Mach Number Relation for Subsonic and Supersonic Isothermal Turbulence. Astrophys. J. 761, 149. doi:10.1088/0004-637X/761/2/149
Körtgen, B., Federrath, C., and Banerjee, R. (2017). The Driving Of Turbulence in Simulations of Molecular Cloud Formation and Evolution. Mon. Not. R. Astron. Soc. 472, 2496–2503. doi:10.1093/mnras/stx2208
Körtgen, B., and Soler, J. D. (2020). The Relative Orientation Between the Magnetic Field and Gas Density Structures in Non-Gravitating Turbulent Media. Mon. Not. R. Astron. Soc. 499, 4785–4792. doi:10.1093/mnras/staa3078
Kraichnan, R. H. (1965). Inertial-Range Spectrum of Hydromagnetic Turbulence. Phys. Fluids (1994). 8, 1385–1387. doi:10.1063/1.1761412
Kritsuk, A. G., Ustyugov, S. D., and Norman, M. L. (2017). The Structure and Statistics of Interstellar Turbulence. New J. Phys. 19, 065003. doi:10.1088/1367-2630/aa7156
Krumholz, M. R., and Burkhart, B. (2016). Is Turbulence in the Interstellar Medium Driven by Feedback or Gravity? an Observational Test. Mon. Not. R. Astron. Soc. 458, 1671–1677. doi:10.1093/mnras/stw434
Krumholz, M. R., Crocker, R. M., Xu, S., Lazarian, A., Rosevear, M. T., and Bedwell-Wilson, J. (2020). Cosmic Ray Transport in Starburst Galaxies. Mon. Not. R. Astron. Soc. 493, 2817–2833. doi:10.1093/mnras/staa493
Krumholz, M. R., and Ting, Y.-S. (2018). Metallicity Fluctuation Statistics in the Interstellar Medium and Young Stars - I. Variance and Correlation. Mon. Not. R. Astron. Soc. 475, 2236–2252. doi:10.1093/mnras/stx3286
Kulsrud, R., and Pearce, W. P. (1969). The Effect of Wave-Particle Interactions on the Propagation of Cosmic Rays. Astrophys. J. 156, 445. doi:10.1086/149981
Lazarian, A., and Yan, H. (2014). Superdiffusion of Cosmic Rays: Implications for Cosmic Ray Acceleration. Astrophys. J. 784, 38. doi:10.1088/0004-637X/784/1/38
Lerche, I. (1967). Unstable Magnetosonic Waves in a Relativistic Plasma. Astrophys. J. 147, 689. doi:10.1086/149045
Li, H.-b., Fang, M., Henning, T., and Kainulainen, J. (2013). The Link Between Magnetic Fields and Filamentary Clouds: Bimodal Cloud Orientations in the Gould Belt. Mon. Not. R. Astron. Soc. 436, 3707–3719. doi:10.1093/mnras/stt1849
Li, H.-B., and Henning, T. (2011). The Alignment of Molecular Cloud Magnetic Fields with the Spiral Arms in M33. Nature 479, 499–501. doi:10.1038/nature10551
Li, H. B., Goodman, A., Sridharan, T. K., Houde, M., Li, Z. Y., Novak, G., et al. (2014). “The Link Between Magnetic Fields and Cloud/Star Formation,” in Protostars and planets VI. Editors H. Beuther, R. S. Klessen, C. P. Dullemond, and T. Henning., 101. doi:10.2458/azu_uapress_9780816531240-ch005
Lithwick, Y., and Goldreich, P. (2001). Compressible Magnetohydrodynamic Turbulence in Interstellar Plasmas. Astrophys. J. 562, 279–296. doi:10.1086/323470
Litvinenko, Y. E., and Effenberger, F. (2014). Analytical Solutions of a Fractional Diffusion-Advection Equation for Solar Cosmic-Ray Transport. Astrophys. J. 796, 125. doi:10.1088/0004-637X/796/2/125
Liu, J., Qiu, K., and Zhang, Q. (2021). Magnetic Fields in Star Formation: A Complete Compilation of All the DCF Estimations. arXiv e-printsarXiv:2111.05836.
Lu, Z.-J., Pelkonen, V.-M., Padoan, P., Pan, L., Haugbølle, T., and Nordlund, Å. (2020). The Effect of Supernovae on the Turbulence and Dispersal of Molecular Clouds. arXiv e-printsarXiv:2007.09518.
Malinen, J., Montier, L., Montillaud, J., Juvela, M., Ristorcelli, I., Clark, S. E., et al. (2016). Matching Dust Emission Structures and Magnetic Field in High-Latitude Cloud L1642: Comparing Herschel and Planck Maps. Mon. Not. R. Astron. Soc. 460, 1934–1945. doi:10.1093/mnras/stw1061
Marchal, A., and Miville-Deschênes, M.-A. (2021). Thermal and Turbulent Properties of the Warm Neutral Medium in the Solar Neighborhood. Astrophys. J. 908, 186. doi:10.3847/1538-4357/abd108
Marder, B. (1987). A Method for Incorporating Gauss’ Law into Electromagnetic Pic Codes. J. Comput. Phys. 68, 48–55. doi:10.1016/0021-9991(87)90043-X
McKee, C. F., Stacy, A., and Li, P. S. (2020). Magnetic Fields in the Formation of the First Stars - I. Theory Versus Simulation. Mon. Not. R. Astron. Soc. 496, 5528–5551. doi:10.1093/mnras/staa1903
Menon, S. H., Federrath, C., and Kuiper, R. (2020). On the Turbulence Driving Mode of Expanding H II Regions. Mon. Not. R. Astron. Soc. 493, 4643–4656. doi:10.1093/mnras/staa580
Mocz, P., and Burkhart, B. (2019). A Markov Model for Non-Lognormal Density Distributions in Compressive Isothermal Turbulence. Astrophys. J. 884, L35. doi:10.3847/2041-8213/ab48f6
Mocz, P., and Burkhart, B. (2018). Star Formation from Dense Shocked Regions in Supersonic Isothermal Magnetoturbulence. Mon. Not. R. Astron. Soc. 480, 3916–3927. doi:10.1093/mnras/sty1976
Mohapatra, R., Federrath, C., and Sharma, P. (2020a). Turbulence in Stratified Atmospheres: Implications for the Intracluster Medium. Mon. Not. R. Astron. Soc. 493, 5838–5853. doi:10.1093/mnras/staa711
Mohapatra, R., Federrath, C., and Sharma, P. (2020b). Turbulent Density and Pressure Fluctuations in the Stratified Intracluster Medium. arXiv e-printsarXiv:2010.12602.
Molina, F. Z., Glover, S. C. O., Federrath, C., and Klessen, R. S. (2012). The Density Variance–Mach Number Relation in Supersonic Turbulence – I. Isothermal, Magnetized Gas. Mon. Not. R. Astron. Soc. 423, 2680–2689. doi:10.1111/j.1365-2966.2012.21075.x
Nolan, C. A., Federrath, C., and Sutherland, R. S. (2015). The Density Variance-Mach Number Relation in Isothermal and Non-Isothermal Adiabatic Turbulence. Mon. Not. R. Astron. Soc. 451, 1380–1389. doi:10.1093/mnras/stv1030
Omukai, K., Tsuribe, T., Schneider, R., and Ferrara, A. (2005). Thermal and Fragmentation Properties of Star-Forming Clouds in Low-Metallicity Environments. Astrophys. J. 626, 627–643. doi:10.1086/429955
Orkisz, J. H., Pety, J., Gerin, M., Bron, E., Guzmán, V. V., Bardeau, S., et al. (2017). Turbulence and Star Formation Efficiency in Molecular Clouds: Solenoidal Versus Compressive Motions in Orion B. Astron. Astrophys. 599, A99. doi:10.1051/0004-6361/201629220
Oughton, S., and Matthaeus, W. H. (2020). Critical Balance and the Physics of Magnetohydrodynamic Turbulence. Astrophys. J. 897, 37. doi:10.3847/1538-4357/ab8f2a
Oughton, S., Priest, E. R., and Matthaeus, W. H. (1994). The Influence of a Mean Magnetic Field on Three-Dimensional Magnetohydrodynamic Turbulence. J. Fluid Mech. 280, 95–117. doi:10.1017/S0022112094002867
Owen, E. R., On, A. Y. L., Lai, S.-P., and Wu, K. (2021). Observational Signatures of Cosmic-Ray Interactions in Molecular Clouds. Astrophys. J. 913, 52. doi:10.3847/1538-4357/abee1a
Padoan, P., Nordlund, P., and Jones, B. J. T. (1997). Universality of the Stellar Initial Mass Function. Commmunications Konkoly Observatory Hung. 100, 341–362.
Padoan, P., and Nordlund, Å. (1999). A Super-Alfvénic Model of Dark Clouds. Astrophys. J. 526, 279–294. doi:10.1086/307956
Padoan, P., and Nordlund, Å. (2011). The Star Formation Rate of Supersonic Magnetohydrodynamic Turbulence. Astrophys. J. 730, 40. doi:10.1088/0004-637X/730/1/40
Passot, T., and Vázquez-Semadeni, E. (1998). Density Probability Distribution in One-Dimensional Polytropic Gas Dynamics. Phys. Rev. E 58, 4501–4510. doi:10.1103/PhysRevE.58.4501
Pedaletti, G., Torres, D. F., Gabici, S., de Oña Wilhelmi, E., Mazin, D., and Stamatescu, V. (2013). On the Potential of the Cherenkov Telescope Array for the Study of Cosmic-Ray Diffusion in Molecular Clouds. Astron. Astrophys. 550, A123. doi:10.1051/0004-6361/201220583
Perez, J. C., and Boldyrev, S. (2008). On Weak and Strong Magnetohydrodynamic Turbulence. Astrophys. J. 672, L61–L64. doi:10.1086/526342
Pillai, T. G. S., Clemens, D. P., Reissl, S., Myers, P. C., Kauffmann, J., Lopez-Rodriguez, E., et al. (2020). Magnetized Filamentary Gas Flows Feeding the Young Embedded Cluster in Serpens South. Nat. Astron. 4, 1195–1201. doi:10.1038/s41550-020-1172-6
Plotnikov, I., Ostriker, E. C., and Bai, X.-N. (2021). Influence of Ion-Neutral Damping on the Cosmic-Ray Streaming Instability: Magnetohydrodynamic Particle-in-Cell Simulations. Astrophys. J. 914, 3. doi:10.3847/1538-4357/abf7b3
Price, D. J., and Federrath, C. (2010). A Comparison Between Grid And Particle Methods on the Statistics of Driven, Supersonic, Isothermal Turbulence. Mon. Not. R. Astron. Soc. 406, 1659–1674. doi:10.1111/j.1365-2966.2010.16810.x
Price, D. J., Federrath, C., and Brunt, C. M. (2011). The Density Variance-Mach Number Relation in Supersonic, Isothermal Turbulence. Astrophys. J. 727, L21–L1389. doi:10.1088/2041-8205/727/1/L21
Rathborne, J. M., Longmore, S. N., Jackson, J. M., Alves, J. F., Bally, J., Bastian, N., et al. (2015). A Cluster in the Making: ALMA Reveals the Initial Conditions for High-Mass Cluster Formation. Astrophys. J. 802, 125. doi:10.1088/0004-637X/802/2/125
Richardson, L. F. (1926). Atmospheric Diffusion Shown on a Distance-Neighbour Graph. Proc. R. Soc. Lond. Ser. A 110, 709–737. doi:10.1098/rspa.1926.0043
Robertson, B., and Goldreich, P. (2018). Dense Regions in Supersonic Isothermal Turbulence. Astrophys. J. 854, 88. doi:10.3847/1538-4357/aaa89e
Salem, M., Bryan, G. L., and Hummels, C. (2014). Cosmological Simulations of Galaxy Formation with Cosmic Rays. Astrophys. J. 797, L18. doi:10.1088/2041-8205/797/2/L18
Sampson, M. L., Beattie, J. R., Krumholz, M. R., Crocker, R. M., Federrath, C., and Seta, A. (2022). Turbulent Diffusion of Streaming Cosmic Rays in Compressible, Partially Ionised Plasma. arXiv e-printsarXiv:2205.08174.
Scannapieco, E., and Safarzadeh, M. (2018). Modeling Star Formation as a Markov Process in a Supersonic Gravoturbulent Medium. Astrophys. J. 865, L14. doi:10.3847/2041-8213/aae1f9
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E., et al. (2009). Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas. Astrophys. J. Suppl. Ser. 182, 310–377. doi:10.1088/0067-0049/182/1/310
Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L., and McWilliams, J. C. (2004). Simulations of the Small-Scale Turbulent Dynamo. Astrophys. J. 612, 276–307. doi:10.1086/422547
Schekochihin, A. A., and Cowley, S. C. (2007). “Turbulence and Magnetic Fields in Astrophysical Plasmas,” in Magnetohydrodynamics: Historical evolution and Trends. Editors S. Molokov, R. Moreau, and H. K. Moffatt, 85.
Schneider, N., André, P., Könyves, V., Bontemps, S., Motte, F., Federrath, C., et al. (2013). What Determines the Density Structure of Molecular Clouds? A Case Study of Orion B with Herschel. Astrophys. J. 766, L17. doi:10.1088/2041-8205/766/2/L17
Schruba, A., Kruijssen, J. M. D., and Leroy, A. K. (2019). How Galactic Environment Affects the Dynamical State of Molecular Clouds and their Star Formation Efficiency. Astrophys. J. 883, 2. doi:10.3847/1538-4357/ab3a43
Seifried, D., Walch, S., Weis, M., Reissl, S., Soler, J. D., Klessen, R. S., et al. (2020). From Parallel to Perpendicular – on the Orientation of Magnetic Fields in Molecular Clouds. arXiv e-printsarXiv:2003.00017.
Seligman, D. Z., Rogers, L. A., Feinstein, A. D., Krumholz, M. R., Beattie, J. R., Federrath, C., et al. (2022). Theoretical and Observational Evidence for Coriolis Effects in Coronal Magnetic Fields Via Direct Current Driven Flaring Events. arXiv e-printsarXiv:2201.03697.
Seta, A., and Beck, R. (2019). Revisiting the Equipartition Assumption in Star-Forming Galaxies. Galaxies 7, 45. doi:10.3390/galaxies7020045
Seta, A., and Federrath, C. (2021a). Magnetic Fields in the Milky Way from Pulsar Observations: Effect of the Correlation Between Thermal Electrons and Magnetic Fields. Mon. Not. R. Astron. Soc. 502, 2220–2237. doi:10.1093/mnras/stab128
Seta, A., and Federrath, C. (2021b). Saturation Mechanism of the Fluctuation Dynamo in Supersonic Turbulent Plasmas. Phys. Rev. Fluids 6, 103701. doi:10.1103/physrevfluids.6.103701
Seta, A., and Federrath, C. (2022). Turbulent Dynamo in the Two-Phase Interstellar Medium. arXiv e-printsarXiv:2202.08324.
Sharda, P., Menon, S. H., Federrath, C., Krumholz, M. R., Beattie, J. R., Jameson, K. E., et al. (2021). First Extragalactic Measurement of the Turbulence Driving Parameter: ALMA Observations of the Star-Forming Region N159E in the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. doi:10.1093/mnras/stab3048
Skalidis, R., Sternberg, J., Beattie, J. R., Pavlidou, V., and Tassis, K. (2021a). Why Take the Square Root? an Assessment of Interstellar Magnetic Field Strength Estimation Methods. arXiv e-printsarXiv:2109.10925.
Skalidis, R., and Tassis, K. (2020). High-Accuracy Estimation of Magnetic Field Strength in the Interstellar Medium from Dust Polarization. arXiv e-printsarXiv:2010.15141.
Skalidis, R., Tassis, K., Panopoulou, G. V., Pineda, J. L., Gong, Y., Mandarakas, N., et al. (2021b). HI-H2 Transition: Exploring the Role of the Magnetic Field. arXiv e-printsarXiv:2110.11878.
Skilling, J. (1971). Cosmic Rays in the Galaxy: Convection or Diffusion? Astrophys. J. 170, 265. doi:10.1086/151210
Soler, J. D., Ade, P. A. R., Angilè, F. E., Ashton, P., Benton, S. J., Devlin, M. J., et al. (2017). The Relation Between the Column Density Structures and the Magnetic Field Orientation in the Vela C Molecular Complex. Astron. Astrophys. 603, A64. doi:10.1051/0004-6361/201730608
Soler, J. D., Hennebelle, P., Martin, P. G., Miville-Deschênes, M. A., Netterfield, C. B., and Fissel, L. M. (2013). An Imprint of Molecular Cloud Magnetization in the Morphology of the Dust Polarized Emission. Astrophys. J. 774, 128. doi:10.1088/0004-637X/774/2/128
Soler, J. D., and Hennebelle, P. (2017). What are we Learning from the Relative Orientation Between Density Structures and the Magnetic Field in Molecular Clouds? Astron. Astrophys. 607, A2. doi:10.1051/0004-6361/201731049
Squire, J., and Hopkins, P. F. (2017). The Distribution of Density in Supersonic Turbulence. Mon. Not. R. Astron. Soc. 471, 3753–3767. doi:10.1093/mnras/stx1817
Sridhar, S., and Goldreich, P. (1994). Toward a theory of Interstellar Turbulence. 1: Weak Alfvenic Turbulence. Astrophys. J. 432, 612. doi:10.1086/174600
Stewart, M., and Federrath, C. (2022). A New Method for Measuring the 3D Turbulent Velocity Dispersion of Molecular Clouds. Mon. Not. R. Astron. Soc. 509, 5237–5252. doi:10.1093/mnras/stab3313
Subramanian, K. (2019). From Primordial Seed Magnetic Fields to the Galactic Dynamo. Galaxies 7, 47. doi:10.3390/galaxies7020047
Subramanian, K. (2016). The Origin, Evolution and Signatures of Primordial Magnetic Fields. Rep. Prog. Phys. 79, 076901. doi:10.1088/0034-4885/79/7/076901
Tress, R. G., Smith, R. J., Sormani, M. C., Glover, S. C. O., Klessen, R. S., Mac Low, M.-M., et al. (2020). Simulations of the Star-Forming Molecular Gas in an Interacting M51-Like Galaxy. Mon. Not. R. Astron. Soc. 492, 2973–2995. doi:10.1093/mnras/stz3600
Tritsis, A., Federrath, C., Schneider, N., and Tassis, K. (2018). A New Method for Probing Magnetic Field Strengths from Striations in the Interstellar Medium. Mon. Not. R. Astron. Soc. 481, 5275–5285. doi:10.1093/mnras/sty2677
Tritsis, A., Panopoulou, G. V., Mouschovias, T. C., Tassis, K., and Pavlidou, V. (2015). Magnetic Field-Gas Density Relation and Observational Implications Revisited. Mon. Not. R. Astron. Soc. 451, 4384–4396. doi:10.1093/mnras/stv1133
Tritsis, A., and Tassis, K. (2018). Magnetic Seismology of Interstellar Gas Clouds: Unveiling a Hidden Dimension. Science 360, 635–638. doi:10.1126/science.aao1185
Tritsis, A., and Tassis, K. (2016). Striations in Molecular Clouds: Streamers or MHD Waves? Mon. Not. R. Astron. Soc. 462, 3602–3615. doi:10.1093/mnras/stw1881
Uhlig, M., Pfrommer, C., Sharma, M., Nath, B. B., Enßlin, T. A., and Springel, V. (2012). Galactic Winds Driven by Cosmic Ray Streaming. Mon. Not. R. Astron. Soc. 423, 2374–2396. doi:10.1111/j.1365-2966.2012.21045.x
Vazquez-Semadeni, E. (1994). Hierarchical Structure in Nearly Pressureless Flows as a Consequence of Self-Similar Statistics. Astrophys. J. 423, 681. doi:10.1086/173847
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., et al. (2020). SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 17, 261–272. doi:10.1038/s41592-019-0686-2
Waagan, K., Federrath, C., and Klingenberg, C. (2011). A Robust Numerical Scheme for Highly Compressible Magnetohydrodynamics: Nonlinear Stability, Implementation and Tests. J. Comput. Phys. 230, 3331–3351. doi:10.1016/j.jcp.2011.01.026
Wang, Y., Boldyrev, S., and Perez, J. C. (2011). Residual Energy in Magnetohydrodynamic Turbulence. Astrophys. J. 740, L36. doi:10.1088/2041-8205/740/2/L36
Wentzel, D. G. (1969). The Propagation and Anisotropy of Cosmic Rays. I. Theory for Steady Streaming. Astrophys. J. 156, 303. doi:10.1086/149965
Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., and Bakes, E. L. O. (1995). The Neutral Atomic Phases of the Interstellar Medium. Astrophys. J. 443, 152. doi:10.1086/175510
Wolfire, M. G., McKee, C. F., Hollenbach, D., and Tielens, A. G. G. M. (2003). Neutral Atomic Phases of the Interstellar Medium in the Galaxy. Astrophys. J. 587, 278–311. doi:10.1086/368016
Xu, S., and Lazarian, A. (2021a). Cosmic Ray Streaming in the Turbulent Interstellar Medium. arXiv e-printsarXiv:2112.06941.
Xu, S., and Lazarian, A. (2022). Cosmic Ray Streaming in the Turbulent Interstellar Medium. Astrophys. J. 927, 94. doi:10.3847/1538-4357/ac4dfd
Xu, S., and Lazarian, A. (2021b). Small-Scale Turbulent Dynamo in Astrophysical Environments: Nonlinear Dynamo and Dynamo in a Partially Ionized Plasma. arXiv e-printsarXiv:2106.12598.
Xu, S., and Lazarian, A. (2016). Turbulent Dynamo in a Conducting Fluid and a Partially Ionized Gas. Astrophys. J. 833, 215. doi:10.3847/1538-4357/833/2/215
Xu, S., and Yan, H. (2013). Cosmic-Ray Parallel and Perpendicular Transport in Turbulent Magnetic Fields. Astrophys. J. 779, 140. doi:10.1088/0004-637X/779/2/140
Yang, L. P., Li, H., Li, S. T., Zhang, L., He, J. S., and Feng, X. S. (2019). Energy Occupationo of Waves and Structures in 3D Compressive MHD Turbulence. Mon. Not. R. Astron. Soc. 488, 859–867. doi:10.1093/mnras/stz1747
Yoon, H., Cho, J., and Kim, J. (2016). Density-Magnetic Field Correlation in Magnetohydrodynamic Turbulence Driven by Different Driving Schemes with Different Correlation Times. Astrophys. J. 831, 85. doi:10.3847/0004-637X/831/1/85
Keywords: magnetic fields, multi-phase interstellar medium, galaxies, cosmic rays, magnetohydrodynamic turbulence
Citation: Beattie JR, Krumholz MR, Federrath C, Sampson ML and Crocker RM (2022) Ion alfvén velocity fluctuations and implications for the diffusion of streaming cosmic rays. Front. Astron. Space Sci. 9:900900. doi: 10.3389/fspas.2022.900900
Received: 21 March 2022; Accepted: 06 June 2022;
Published: 06 October 2022.
Edited by:
Siyao Xu, Institute for Advanced Study, United StatesReviewed by:
Jonathan Squire, University of Otago, New ZealandXuening Bai, Tsinghua University, China
Copyright © 2022 Beattie, Krumholz, Federrath, Sampson and Crocker. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: James R. Beattie, amFtZXMuYmVhdHRpZUBhbnUuZWR1LmF1
 James R. Beattie
James R. Beattie Mark R. Krumholz
Mark R. Krumholz Christoph Federrath
Christoph Federrath Matt L. Sampson
Matt L. Sampson Roland M. Crocker1
Roland M. Crocker1