General features of the stellar matter equation of state from microscopic theory, new maximum-mass constraints, and causality

The profile of a neutron star probes a very large range of densities, from the density of iron up to several times the density of saturated nuclear matter, and thus no theory of hadrons can be considered reliable if extended to those regions. We emphasize the importance of taking contemporary ab initio theories of nuclear and neutron matter as the baseline for any extension method, which will unavoidably involve some degree of phenomenology. We discuss how microscopic theory, on the one end, with causality and maximum-mass constraints, on the other, set strong boundaries to the high-density equation of state. We present our latest neutron star predictions where we combine polytropic extensions and parametrizations guided by speed of sound considerations. The predictions we show include our baseline neutron star cooling curves.

1 Introduction

A fully microscopic equation of state (EoS) up to central densities of the most massive stars–potentially involving phase transitions and non-nucleonic degrees of freedom–is not within reach. Nevertheless, neutron stars are powerful natural laboratories for constraining theories of the EoS (Abbott et al., 2017a; Abbott et al., 2017b; Abbott et al., 2018; Abbott et al., 2019; Miller et al., 2019; Miller et al., 2021). One must be mindful of the theory’s limitations and the best ways to extract and interpret information from observational constraints. Recently, detection of gravitational waves from merging of binary neutron star systems provided constraints on both their radius and tidal deformability.

Large Bayesian interference analyses have become popular as a tool to constrain the properties of neutron-rich matter. An example is Huth et al., (2022), where the authors sample 15,000 EoSs, together with observational constraints and heavy ion collision (HIC) data. These analyses are important, but one must be careful about interpretation–relating HIC observables to parametrizations of the EoS is not a model-independent process. It is therefore not surprising that the authors of Huth et al. (2022). find that the HIC constraints tend to prefer stiffer EOSs than those favored by astrophysical observations, and, we add, stiffer than those generated by ab initio theory. The reasons can be found in the phenomenological density functionals inspired by Quantum Hydrodynamics (QHD), often used to relate HIC observables to the EoS parameters. This point will be discussed in sect. III. Recent empirical determinations of the stellar matter EoS from data and observations have been reported (Tsang et al., 2024; Davis et al., 2024a). A Bayesian inference study aimed at assessing the performance of the Skyrme energy density functionals can be found in Klausner et al. (2025).

When using sophisticated statistical techniques, it’s important not to lose sight of basic physics arguments, such as the importance of a realistic description of few-body data. An extensive discussion on this point can be found in Sammarruca (2024).

In this paper, keeping a firm foot in the microscopic theory–that is, with no adjustments of nuclear forces in the medium–we wish to illustrate general features of the EoS in different density regions, based only on theory (for normal to moderately-above-normal densities), and a few robust constraints, such as causality and the most recent maximum-mass constraints (Romani et al., 2022) (for high and superhigh densities).

The cooling properties of neutron stars, observationally accessible in terms of temperature (or luminosity) vs. age relations, are also an important tool to obtain a glimpse on the internal structure and composition of these exotic systems. Ages and thermal luminosities of neutron stars, inferred from observations, can be interpreted with the aid of the neutron star cooling theory to gain information on the properties of superdense matter in the interior of the star. We present our first results of cooling simulations, and compare with available observational estimates of thermally emitting isolated neutron stars (INS) (Potekhin et al., 2020). We recall that rapid cooling signals large proton fractions, which render the direct Urca (DU) process possible at lower densities in comparison with softer models. Thus, rapid cooling signals a steep symmetry energy.

This paper is organized as follows. In sect. II, we review our theoretical ingredients, omitting details that have been published elsewhere. In sect. III, we discuss continuations of the EoS above the microscopic predictions. In sect. IV, we show preliminary predictions of cooling curves. A robust analysis of neutron star cooling, including superfluid gaps and more, will appear in a later work.

2 The equation of state at normal to moderately high density

2.1 Theoretical framework

The theoretical framework we use to obtain the ab initio part of the equation of state has been published in detail elsewhere (Sammarruca and Millerson, 2021a; Sammarruca and Millerson, 2021b; Sammarruca and Millerson, 2022), and thus we will not repeat a lengthy presentation here. We will, however, briefly recall the spirit of chiral effective field theory (EFT), on which our nuclear forces are based. A comprehensive and detailed review of our theoretical tools can be found in Machleidt and Sammarruca (2024).

Given an energy scale and degrees of freedom appropriate at that scale, an EFT comprises all interactions consistent with the symmetries that govern those degrees of freedom. For the nuclear problem, relevant degrees of freedom are pions (Goldstone bosons), nucleons, and $\mathrm{\Delta }(1232)$ isobars. We use the delta-less chiral EFT. To begin with, one writes the most general Lagrangians describing all interactions between pions, nucleons, and pions with nucleons. Because pion interactions must vanish at zero momentum transfer and in the chiral limit, where the pion mass, $m_{\pi }$, goes to zero, the corresponding Lagrangian is expanded in powers of spatial derivatives or pion masses. From these Lagrangians, an infinite number of Feynman diagrams can be generated, which seems to make the theory unmanageable. The strategy is then to design a scheme for ordering the diagrams according to their importance–the essence of Chiral Perturbation Theory (ChPT). Nuclear potentials are defined by the irreducible types among these graphs. (By definition, an irreducible graph is a diagram that cannot be separated into two by cutting only nucleon lines.) These graphs are then analyzed in terms of powers of $Q$, with $Q=p/{\mathrm{\Lambda }}_b$, where $p$ is generic for a momentum, (nucleon three-momentum or pion four-momentum), or the pion mass, and ${\mathrm{\Lambda }}_b\sim m_{\rho }\sim$ 0.7 GeV (with $m_{\rho }$ the mass of the $\rho$ meson) is the breakdown scale (Furnstahl et al., 2015). Determining the power $\nu$ has become known as power counting. For a recent review of nuclear forces based on chiral EFT and their applications in nuclear and neutron matter, the reader is referred to Machleidt and Sammarruca (2024).

The neutron star crust is composed of metals in crystalline structure and cannot be described as a homogeneous fluid of nucleons, which is an appropriate system for our microscopic approach. Instead, a realistic crustal EoS (Negele and Vautherin, 1973) is joined to our previously described EoS via cubic spline interpolation. The crust is a Coulomb lattice of bound neutrons and protons clusters surrounded by a dilute neutron gas. We are aware of recently developed tools to construct unified core-crust EoS (Davis et al., 2024b; Davis et al., 2025). Given a $\beta$-equilibrated EoS and its isoscalar nuclear matter parameters, this tool derives the isovector parameters and reconstructs the crustal EoS using a model for inhomogeneous matter. The relative error for the $M(R)$ relation is very small–less than 0.1% for $M>0.5M_{\odot }$ – compared with using the original EoS matched to a realistic crust (Davis et al., 2024b).

2.1.1 Quantifying errors in chiral EFT

A reliable determination of the truncation error is a crucial aspect of chiral EFT. If observable $X$ has been calculated at order $\nu$ and at order $\nu +1$, a simple estimate of the truncation error at order $\nu$ is

$\mathrm{\Delta }{X}_{\nu }=|X_{\nu +1}-X_{\nu }|,(1)$

which is a measure for what is neglected at order $\nu$. A suitable prescription is needed, in addition to Equation 1, to estimate the uncertainty at the highest (included) order. For that purpose, we follow the prescription of (Epelbaum et al., 2015). If $p$ is of the order of the typical momentum involved in the system, the dimensionless parameter $Q$ is defined as the largest between $\frac{p}{{\mathrm{\Lambda }}_b}$ and $\frac{m_{\pi }}{{\mathrm{\Lambda }}_b}$, where ${\mathrm{\Lambda }}_b$ is the breakdown scale, taken to be about 600 MeV. Before proceeding, some comments are in place to avoid confusion. In the pion-nucleon sector, it’s natural to set the scale to the chiral symmetry breaking scale, ${\mathrm{\Lambda }}_{\chi }$, about 4$\pi F_{\pi }\approx$ 1 GeV, where $F_{\pi }$ is the pion decay constant, equal to 92 MeV [see Davis et al. (2025)] of Epelbaum et al. (2015). However, in the nucleon sector, it is common practice to apply a so-called breakdown scale, ${\mathrm{\Lambda }}_b$, chosen around 600 MeV. This scale is smaller than ${\mathrm{\Lambda }}_{\chi }$ because the non-perturbative resummation, necessary for nucleons, fails for momenta larger than approximately 600 MeV.

Throughout the paper, we will show results at the (fully consistent) third order (${\text{N}}^2$LO), and at the highest order which we have considered (fourth order, or ${\text{N}}^3$LO). In Figure 1, we show the pressure as a function of density in $\beta$-stable matter at ${\text{N}}^2$LO (red) and at ${\text{N}}^3$LO (blue), with the respective truncation errors. In both cases, the predictions are based on the high-quality nucleon-nucleon $(NN)$ potential of Entem et al. (2017) and include all three-nucleon forces (3NF) required at that order. For details on how our EoS are built, see, for instance, Sammarruca and Millerson (2021a); Sammarruca and Millerson (2022). They are available upon request from the corresponding author.

Figure 1

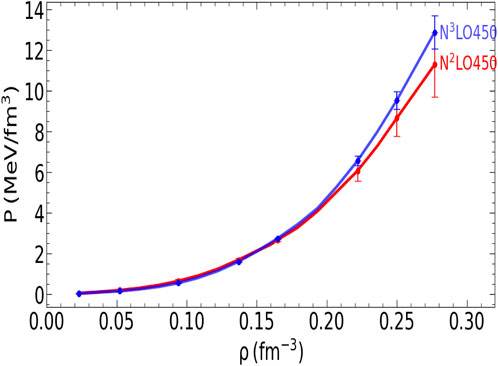
Figure 1. Pressure as a function of density in $\beta$-stable matter at ${\text{N}}^2$LO (red) and at ${\text{N}}^3$LO (blue), with the respective truncation errors. In both cases, the predictions are based on the high-quality $NN$ potential of Entem et al. (2017) and include all 3NFs required at the respective order.

The uncertainty in the value of observable $X$ at ${\text{N}}^3$LO as derived in Epelbaum et al. (2015). can be understood with the following arguments. If ${\text{N}}^3$LO ($\nu$ = 4) is the highest included order, the expression

$\mathrm{\Delta }{X}_4=|X_4-X_3|Q=\left(\mathrm{\Delta }{X}_3\right)Q,(2)$

is a reasonable estimate for $\mathrm{\Delta }{X}_4$ in absence of the value $X_5$, because $Q$ to the power of one takes the error up by one order, the desired fourth order. To avoid accidental underestimations, a more robust prescription, instead of Equation 2, is to proceed in the same way for all the lower orders ($\nu$ = 0, 2, 3) and define, at ${\text{N}}^3$LO (Epelbaum et al., 2015):

$\mathrm{\Delta }X=\max \left\{Q^5|X_{LO}|,Q^3|X_{LO}-X_{\mathit{NLO}}|,Q^2|X_{\mathit{NLO}}-X_{N^{2}LO}|\right.,$

$\left.Q|X_{N^{2}LO}-X_{N^{3}LO}|\right\}.(3)$

In infinite matter, $p$ can be identified with the Fermi momentum at the density being considered.

Cutoff variations have sometimes been used to estimate contributions beyond truncation. However, they do not allow to estimate the impact of neglected long-range contributions. Also, due to the intrinsic limitations of the EFT, a meaningful cutoff range is hard to estimate precisely, and often very limited. The method of Equation 3 allows to determine truncation errors from predictions at all lower orders, without the need to use cutoff variations.

2.1.2 Chiral orders and three-nucleon forces: unresolved issues

While the predictions at ${\text{N}}^2$LO are fully ab initio, a warning is in place for current ${\text{N}}^3$LO calculations. As pointed out in Epelbaum et al. (2020), there is a problem with the regularized 3NF at ${\text{N}}^3$LO (and higher orders) in all present nuclear structure calculations. The ${\text{N}}^3$LO 3NFs currently in use are regularized by a multiplicative regulator applied to the 3NF expressions derived from dimensional regularization. This approach leads to violation of chiral symmetry at ${\text{N}}^3$LO and destroys the consistency between two- and three-nucleon forces (Epelbaum et al., 2020; Epelbaum et al., 2023). Consequently, none of the current calculations that include 3NFs at ${\text{N}}^3$LO (and beyond) can be considered truly ab initio. An appropriate symmetry-preserving regulator (Epelbaum et al., 2020) should be applied to the 3NF at ${\text{N}}^3$LO from Bernard et al. (2008); Bernard et al. (2011). At the present time, reliable predictions exist only at N²LO, NLO, and LO. However, for the few fully ab initio calculations, the precision at ${\text{N}}^2$LO is unsatisfactory. A first step towards deriving consistently regularized nuclear interactions in chiral EFT has been proposed in Krebs and Epelbaum (2023a); Krebs and Epelbaum (2023b). It requires the cutoff to be introduced already at the level of the effective Lagrangian. A path integral approach (Krebs and Epelbaum, 2023a) can then be applied to the regularized chiral Lagrangian to derive nuclear forces through the standard power counting of chiral EFT.

Throughout the paper, we will show results at the (fully consistent) third order (${\text{N}}^2$LO), and at the highest order which we have considered (fourth order, or ${\text{N}}^3$LO). In Figure 1, we show the pressure as a function of density in $\beta$-stable matter at ${\text{N}}^2$LO (red) and at ${\text{N}}^3$LO (blue), with the respective truncation errors. In both cases, the predictions are based on the high-quality nucleon-nucleon $(NN)$ potential of Entem et al. (2017) and include all 3NFs required at that order. For details on how our EoS are built, see, for instance, Sammarruca and Millerson (2021a); Sammarruca and Millerson (2022). They are available upon request from the corresponding author.

3 The equation of state at high density

It is important to emphasize that high-density EoS continuations are not meant to be a replacement for microscopic theories which, at this time, are not feasible in those regimes. Nevertheless, causality and maximum-mass constraints do pose considerable restrictions on the general features of the high-density EoS.

Up to this point, we have used piecewise polytropes, which have the form:

$P\left(\rho \right)=\alpha {\left(\frac{\rho }{{\rho }_0}\right)}^{\gamma }.(4)$

where ${\rho }_0$ is the density of saturated nuclear matter and $\gamma$ is the adiabatic index. The corresponding energy density can be obtained from the basic relation between internal pressure and energy density,

$P\left(\rho \right)={\rho }^2\frac{d}{d\rho }\left(\frac{ϵ}{\rho }\right),(5)$

or,

$ϵ\left(\rho \right)=\frac{\alpha }{\gamma -1}{\left(\frac{\rho }{{\rho }_0}\right)}^{\gamma }+c\rho .(6)$

For a range of $\gamma$ values, the parameters $\alpha$ and $c$ are determined by matching the values of $P$ and $ϵ$ from Equations 5, 6 boundaries. In the past, we accepted polytropes which can support a maximum mass of at least 2.01 $M_{\odot }$, to be consistent with the lower limit of the (2.08 $\pm$ 0.07) $M_{\odot }$ observation reported in Miller et al. (2021). for the J0740 + 6620 pulsar, along with a radius estimate of (12.35 $\pm$ 0.75) km. Figure 2 displays results of the procedure we used in the recent past. The M(R) relations are obtained with piecewise combinations of two polytropes with different adiabatic index. Equations of state that cannot support a maximum mass of at least 2.01 $M_{\odot }$ (see above), are discarded, and solutions are cut at the central density where causality is violated (Sammarruca and Millerson, 2022). The initial range we considered for the adiabatic index, $\gamma$, was approximately between 2.5 and 4.0, based on guidance from the literature, such as Read et al. (2009), where most of the EoS available from theory or phenomenology were fitted with polytropes.

Figure 2

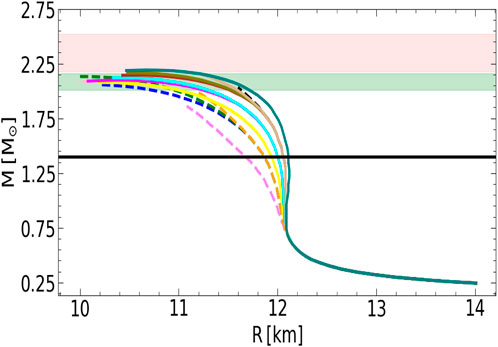
Figure 2. M(R) relations obtained with piecewise polytropes (Sammarruca and Millerson, 2022). Equations of state that cannot support a maximum mass of at least 2.01 $M_{\odot }$ (see text) are discarded. The dashed curves are cut at the central density where causality is violated, whether or not they have reached the maximum mass. The black horizontal line marks the mass of the canonical neutron star, for reference. The green and pink shaded areas are constraints from J0740 + 6620 (Fonseca et al., 2021) and J0952–0.607 (Romani et al., 2022), respectively.

Currently, the maximum-mass constraint must account for the record-setting PSR J0952-0,607, the heaviest neutron star found to date, at 2.35 $\pm$ 0.17 $M_{\odot }$ (Romani et al., 2022). We point out that this measurement was based on optical lightcurve modeling and may not be as accurate as those based on radio observations. For instance, for PSR J2215 + 5,135, the optical lightcurve modeling suggests a mass of 2.27$\pm$ 0.17 $M_{\odot }$ (Linares et al., 2018), while recent radio observations yield a significantly smaller value of 1.98 $\pm$ 0.08$M_{\odot }$ (Sullivan and Romani, 2024). The analysis in Fan et al. (2024). found a maximum mass of 2.25 $\pm$ 0.07 $M_{\odot }$ for a non-rotating neutron star.

We explored different piecewise parametrizations of the high-density EoS that preserve causality, while supporting masses at least as high as 2.2 $M_{\odot }$. We emphasize that ab initio predictions and most of the terrestrial constraints point to a soft symmetry energy at normal density, while the maximum mass constraint has moved to larger values. These considerations provide important guidance when building the phenomenological part of the EoS.

While checking different polytropic combinations, we made the observation that the “best” combination (with regard to preserving causality while satisfying maximum-mass constraints) consists of a relatively stiff polytrope attached to the microscopic piece of the EoS, followed by a second, softer polytrope.

Although polytropic extension, see Equation 4, is a very general and popular method, alternative parametrizations of the high-density EoS offer desirable features (Kanakis-Pegios et al., 2021; Tews et al., 2018), such as those in terms of the speed of sound. In Figure 3, the colorful curves are from selected EoS that generate maximum masses of about 2.1–2.2 solar masses and are consistent with causality. Table 1 provides more information about these cases. We note that chiral uncertainties as those in Figure 1 are not shown in the figures for the $M(R)$ relations. This is because chiral errors are meaningful only at the densities where the microscopic calculation is applied, which reach up to the central densities of the lighter stars (right-most side of the $M(R)$ figures). The black curve is obtained with a single parametrization in terms of the speed of sound, constructed as follows (Kanakis-Pegios et al., 2021; Tews et al., 2018). Assigning $i=0$ to values at threshold (the density at which the EoS parametrization has to be attached to the previous piece), we write

${\rho }_i={\rho }_{i-1}+\mathrm{\Delta }\rho ,(7)$

${ϵ}_i={ϵ}_{i-1}+\mathrm{\Delta }ϵ,(8)$

and

$\mathrm{\Delta }ϵ=\mathrm{\Delta }\rho \frac{{ϵ}_{i-1}+P_{i-1}}{{\rho }_{i-1}},(9)$

where we have used Equation 5.

Figure 3

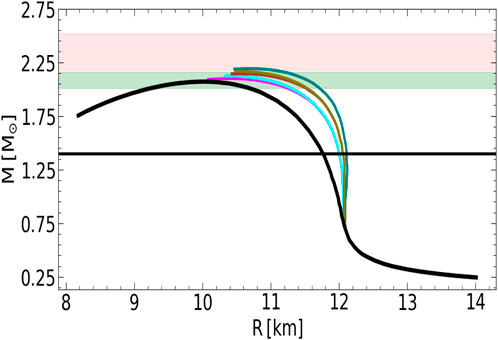
Figure 3. Several M(R) relations. The curves in color are obtained from a sequence of two polytropes with adiabatic indices given in Table 1. The black curve is obtained with a single parametrization in terms of the speed of sound, as in Equation 11.

Table 1

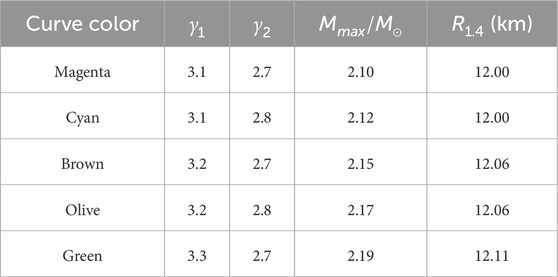
Table 1. Description of the M(R) relations in Figure 3.

The speed of sound is parametrized as

${\left(\frac{v_s}{c}\right)}_i^2=1-c_{1}exp\left[-\frac{{\left({\rho }_i-c_2\right)}^2}{w^2}\right],(10)$

where $w$ is the width of the Gaussian curve, and the constants $c_1$ and $c_2$ are determined from continuity of the speed of sound and its derivative at the threshold density. We note that the conformal limit, ${\left(\frac{v_s}{c}\right)}^2\le 1/3$, is not imposed in Equation 10. Clearly, a larger value of ${\left(\frac{v_s}{c}\right)}^2$ signifies increased pressure gradient to counterbalance the stronger gravitational force, and thus, larger masses. Therefore, observations of very massive stars require large values of the speed of sound at densities comparable to the central densities of the most massive stars.

The pressure above the threshold is

$P_i={\left(\frac{v_s}{c}\right)}_{i-1}^2\mathrm{\Delta }ϵ+P_{i-1}.(11)$

This EoS continuation is manifestly causal at any density and reaches a maximum mass of 2.07 $M_{\odot }$.

From the considerations above, we find that, for the purpose of achieving high maximum masses while respecting causality at any density, a better solution is to combine a relatively steep (on the scale of Table 1) polytrope followed by a parametrization obtained from Equations 7–11, which will maintain causality by construction. The matching densities are ${\rho }_1=0.277f{m}^{-3}$ and ${\rho }_2=0.563f{m}^{-3}$. The rationale for the first matching density is as follows. The neutron Fermi momentum in neutron matter, $k_F^n$, at ${\rho }_1$ is equal to 2.02 $f{m}^{-1}$. Of course, this is larger than the momentum in beta-stable matter at the same density due to the presence of a proton fraction,

$k_F^{\mathit{snm}}<k_F^{\beta }<k_F^n,(12)$

where $k_F^{\mathit{snm}}$ and $k_F^{\beta }$ are the Fermi momentum in symmetric nuclear matter and in beta-stable matter, respectively. Recalling that the average momentum is given by Equation 13:

$P_{av}=\sqrt{\frac{3}{5}}{k}_F^n,(13)$

we take Equation 13 as the typical momentum of the system, $p$, in defining the chiral expansion parameter, $Q=\frac{p}{{\mathrm{\Lambda }}_b}$, where ${\mathrm{\Lambda }}_b$ was previously defined. We obtain $Q=51\%$, which is well below 1, and actually a pessimistic estimate, see Equation 12. For these reasons, we are comfortable applying the EFT up to this density. The density ${\rho }_2$ is about two units of ${\rho }_0$ from the first matching point, a choice guided by Read et al. (2009), see section VB of that citation. We have tested the sensitivity of the M(R) results to moving this point out by one-half of saturation density, and found it to be negligible. Moving that point toward lower densities brings down the maximum masses, which is not desirable.

The resulting M(R) curves are shown on the LHS of Figure 4 for both ${\text{N}}^3$LO (blue) and ${\text{N}}^2$LO (red). For the dashed curves, the first extension is done with a polytrope with $\gamma$ = 3.3, followed by pressure values given by Equation 11 with the speed of sound (SoS) as in Equation 10. The solid curves (same color convention) have been obtained with $\gamma$ = 3.8, a value beyond which the EoS begins to violate causality. On the RHS, we show the dimensionless speed of sound squared corresponding to the curves on the left. The parametrization given in Equation 10 seems robust with respect to both changes in the matched EoS and in the chiral order. Table 2 displays the maximum mass, its radius, the central density, and the radius of the canonical mass neutron star, for the curves in Figure 4. We recall that the radius of a 1.4 $M_{\odot }$ is sensitive to the pressure at normal densities and thus it can pose constraints on microscopic theories of the EoS at those densities where such theories are applicable.

Figure 4

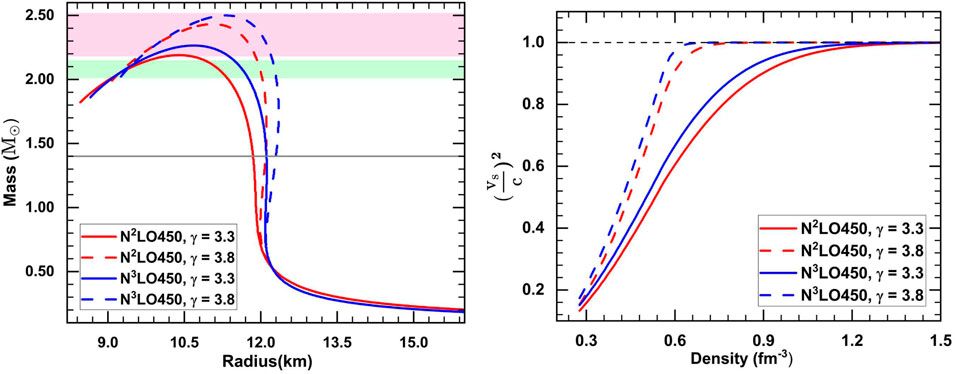
Figure 4. Left: M(R) curves at fourth order (${\text{N}}^3$LO, blue) and at third order (${\text{N}}^2$LO, red) of ChPT. Dashed curves: the first extension is done using a polytrope with $\gamma$ = 3.3, followed by pressure values given by Equation 11 together with Equation 10; Solid curves: obtained with $\gamma$ = 3.8, a value beyond which the EoS begins to violate causality. Right: Dimensionless speed of sound squared corresponding to the curves on the left. Same color and pattern conventions.

Table 2

Table 2. Some neutron star properties corresponding to the red and the blue M(R) relations shown in Figure 4.

We conclude that a polytrope which bridges the chiral EFT predictions with a causality-maintaining parametrization, has a limited range of powers. We underline that this scenario is inherently related to the softness of the chiral predictions. In other words, the nature of the predictions at normal density have a far-reaching impact, which extends to densities up to a few times normal density.

In the QCD limit of deconfined quarks in the presence of asymptotic freedom, quarks should behave like free fermions. Some perturbative QCD calculations (Brandes et al., 2023) support the conformal limit, ${(v_s/c)}^2=1/3$. We are in the process of implementing the conformal limit in our EoS. We observed that an EoS that’s subconformal at all densities (that is, Equation 10 with the asymptotic limit replaced by 1/3), cannot generate sufficiently large masses. On the other hand, the speed of sound can be asymptotically conformal and non-monotone. A scenario where the speed of sound peaks around few to several times nuclear density and then falls back to approach the QCD limit for deconfined quark matter would signify some sort of phase transition with the conformal limit reached well beyond central densities of the heaviest observed neutron stars. The superconformality condition satisfied on the average in neutron stars, $<{\left(\frac{v_s}{c}\right)}^2>1/3$, may have fundamental implications on the trace of the energy-momentum tensor at the center of rotating neutron stars (Mendes et al., 2024).

Of course, what we have presented is not the only option for building EoS that are consistent with current astronomical obervations. We maintain, though, that an EoS must be “bounded from below” by free-space few-nucleon data (which, in turn, have a strong impact on the symmetry energy and the pressure in neutron-rich matter at normal densities). Typical examples of the other end of the spectrum are phenomenological EoS, such as those from Relativistic Mean Field (RMF) models. With no constraints from microscopic few-nucleon forces, new parametrizations can be constructed using different nonlinear, self- and inter-couplings among meson and nucleon Dirac fields (Kumar et al., 2023). Isovector mesons carry isospin dependence, with the main contribution to the symmetry energy coming from the pion (Sammarruca, 2011). In the RMF (pionless) framework, the interplay between the isovector $\rho$ and $\delta$ mesons is described as the equivalent, in the isovector channel, of the $\sigma -\omega$ meson interplay in the isoscalar channel. This approach, and the resulting couplings, have little to do with free-space $NN$ interactions (Sammarruca, 2011). Not surprisingly, parametrizations can be found to cover a huge range of EoS “stiffness,” most recently incorporating CREX and/or PREX-II constraints (Kumar et al., 2023). Findings from RMF models concerning, especially, isovector quantities, such as the symmetry energy, must be interpreted with caution.

Before closing this section, we like to offer a few comments on EFT-inspired energy-density functionals (EDFs) that have been proposed in recent years. Traditional EDFs are based on the mean-field (MF) approximation and built on empirical ingredients, which clearly prevent them from having truly predictive power. Furthermore, they do not follow a power-counting scheme, which prevents a reliable estimation of theoretical uncertainties. Attempts have been made to render EDFs less empirical, trying to directly link them to microscopic ingredients so as to reduce their intrinsic uncertainties (Grasso, 2019; Burrello et al., 2020). While this is potentially an improvement over traditional EDFs, it is our understanding that these schemes are perturbative in diluted matter. In fact, the YGLO (Yang-Grasso-Lacroix-Orsay) (Yang et al., 2016) functionals are suitable at very low densities. Were they not perturbative at all, a connection with power counting would not be possible.

4 Cooling of neutron stars

4.1 General considerations

To create context, we review here some basic facts about INS cooling.

Accurate modelling of neutron star cooling with account of all possible effects is a complex problem. Cooling can be affected, for instance, by the presence of free hyperons or deconfined quarks (see Wei et al. (2020) and references therein), and pion or kaon condensation (see Yakovlev et al. (2001)) and references therein).

The internal structure of the neutron star can be taken, to a good approximation, to be spherically symmetric, except for fast rotating INS or strong magnetic fields. It is also reasonable to expect that the temperature distribution is spherically symmetric at sufficiently high densities. Under these assumptions, the mechanical structure and temperature distribution are determined by a set of differential equations (Richardson et al., 1982) which involve only one spatial coordinate, the radial coordinate $r$.

Neutron stars cool down mainly via neutrino emission from their cores and photon emission from their atmospheres. They are relativistic objects, and thus one needs to be careful about the coordinate system. The local temperature at some distance $r$ from the center is related to the temperature, $T^{\infty }$, measured by a distant observer, via the gravitational redshift between the coordinate systems:

$T^{\infty }=e^{\varphi \left(r\right)}T\left(r\right),(14)$

where $\varphi$ is the metric function.

The outermost layer of a neutron star is the atmosphere, consisting of gas elements which emit thermal photons that can be observed on the Earth. Surface luminosity and temperature can be inferred by fitting this photon flux, and is a major source of cooling for older neutron stars. Below the atmosphere, there is a thin region called envelope, whose chemical composition is uncertain.

Although the distribution of the surface temperature over the surface can be non-uniform, it is customary to approximate the surface photon emission as the blackbody radiation from the entire surface. To that end, one introduces the overall surface effective temperature of the star, $T_{s,eff}$, related to the photon luminosity, $L_{\gamma }$, by

$L_{\gamma }=4\pi {\sigma }_{SB}{R}^2{T}_{s,eff}^4,(15)$

where ${\sigma }_{SB}$ is the Stefan-Boltzmann constant. The quantities in the above equation refer to a local reference frame at the neutron-star surface. Those detected by a distant observer are redshifted,

$L_{\gamma }^{\infty }=L_{\gamma }\left(1-r_g/R\right)=4\pi {\sigma }_{SB}{R}_{\infty }^2{\left(T_{s,eff}^{\infty }\right)}^4,(16)$

$T_{s,eff}^{\infty }=T_{s,eff}\sqrt{1-r_g/R},R_{\infty }=R/\sqrt{1-r_g/R},(17)$

where $r_g$ is the Schwarzschild radius, $r_g=\frac{2GM}{c^2}$, with $G$ the gravitational constant.

Either surface temperatures or photon luminosities can be used to compare neutron-star observations with the cooling theory. Both can be obtained with spectral analysis, but accurate determination is usually a challenge. One of the problems with obtaining accurate data suitable for testing the theory of cooling is that the vast majority of neutron stars, including INS, emit intense radiation of non-thermal origin. Neutron star binary systems are usually surrounded by an accretion disk, whose emission is orders of magnitude more powerful than the thermal emission from the neutron star surface (Das et al., 2024). Non-thermal emission of INS can also be produced by other processes, and thus a careful analysis is required to extract the thermal component of the observed spectrum. Another problem is that obtaining the ages of neutron stars from observation is difficult, and thus ages are only estimates. Neutron stars that are estimated to be old have lost their initial heat, and therefore their thermal luminosity is very low, and could have been produced by reheating (Gonzalez-Jimenez et al., 2015; Gonzalez-Caniulef et al., 2019).

In summary, the “standard” cooling theory, which neglects reheating, can only be tested against observations of a small fraction of INS, using estimated ages.

4.2 Proof of concept results

In this section, we perform cooling simulations employing the two EoS used to generate the red and blue $M(R)$ dashed curves in Figure 4. Our beta-stable EoS include protons, electrons, and muons. We emphasize that these are preliminary curves, to have a first look at the mass dependence in relation to the available data. In other words, these are proof of concept calculations, to build upon.

From Figures 5, 6, one can see the mass dependence of the effective temperature and the closely related luminosity, see Equations 14–17. The more massive INS correspond to faster cooling, suggesting that enhanced neutrino emission due to DU reactions operates in those stars, where the proton fraction in the interior reaches values sufficient to enable the process. Pairing, not included here, could suppress DU processes. The data are from Potekhin et al. (2020).

Figure 5

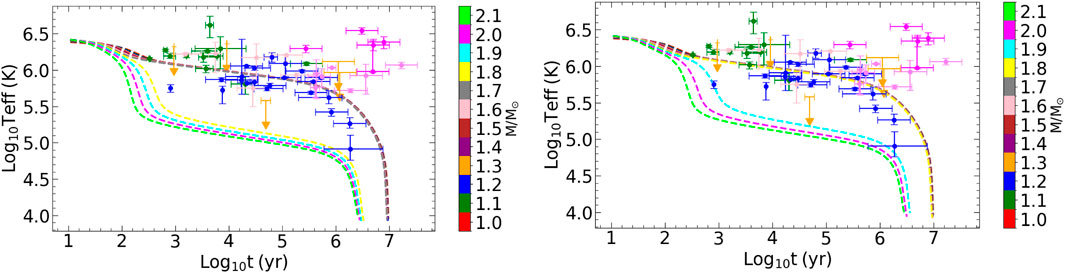
Figure 5. Effective temperature as a function of time, for different masses (colors). Left: ${\text{N}}^2$LO; Right: ${\text{N}}^3$LO. The envelope from Potekhin et al. (1997). is applied.

Figure 6

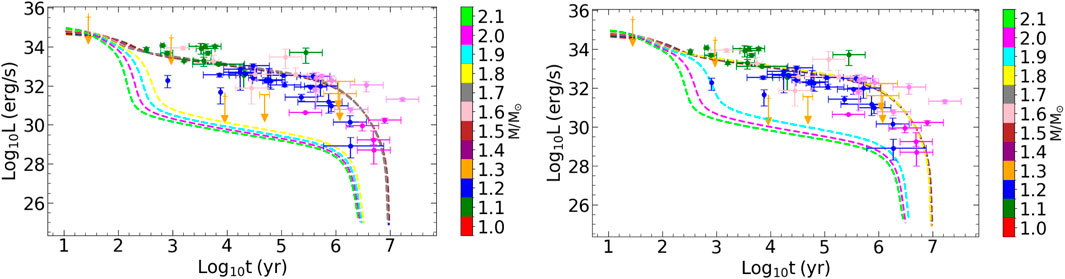
Figure 6. Photon luminosity as a function of time, for different masses (colors). Left: ${\text{N}}^2$LO; Right: ${\text{N}}^3$LO. All conditions as in Figure 5.

The difference between Figures 5, 7 is the model for the envelope. In Figure 5, the envelope contains light elements up to densities where they can still be present, and heavier elements, including iron, at the higher densities (Potekhin et al., 1997). More precisely, blanketing envelopes are composed, from surface to bottom, of hydrogen, helium, carbon, and iron shells, in a stratified structure. In Figure 7, older iron models for the envelope (Nomoto and Tsuruta, 1987) are employed to gauge the sensitivity to the chemical composition of the envelope. We find the latter to have a significant impact on the cooling curves, especially for low to medium mass neutron stars. The envelope acts as a thermal insulator between the surface and the hot interior, thus relating interior temperature to the star’s effective surface temperature. There is a large temperature gradient between the top and bottom layers of the envelope, determined by the amount of light elements such as Hydrogen or Helium. Therefore, the composition of the envelope impacts its photon cooling.

Figure 7

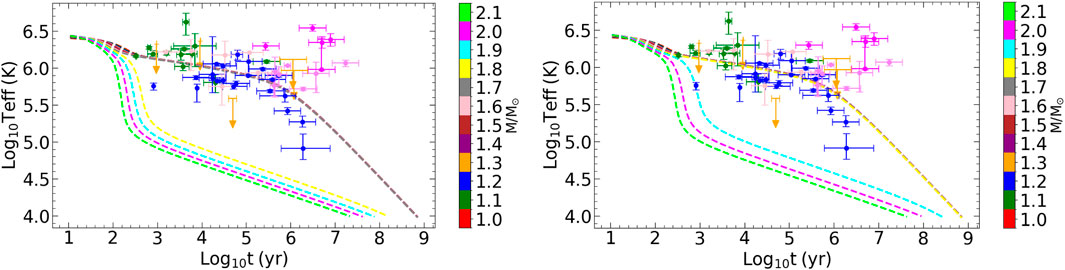
Figure 7. As in Figure 5, but with envelope model from Nomoto and Tsuruta (1987).

Some investigations (Das et al., 2024) have concluded that an EoS allowing DU cooling for a wide enough mass range of neutron stars, combined with some quenching by the ${\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{t}\mathrm{o}\mathrm{n}}^1{S}_0$ BCS gap, agrees best with the cooling data, while the neutron pairing gap in the triplet $P$-wave seems to generate overly rapid cooling. Others (Krotscheck et al., 2024) find that pairing in the triplet $P$-states prevail in neutron matter, but essentially disappear if the spin-orbit interaction is turned off. Overall, the contribution from pairing is reported to be quite sensitive to the characteristics of the model. In fact, the sensitivity of the gap to the input interaction and medium effects can be dramatic, which calls for further investigations. We will introduce short-range correlations (SRC) by replacing in the gap equation the bare potential with the G-matrix. The latter will be calculated self-consistently with the single-particle potential, which we will use in the single-particle spectrum. Typically, one would expect SRC to reduce the gap by introducing more high-momentum components and thus removing strength around the Fermi level and depleting the gap (Rios et al., 2017). As SRC are the most model-dependent part of an interaction, they certainly contribute to the gap’s model dependence. At the same time, availability of more and more accurate data from INS is crucial to constrain all important aspects of the theoretical input.

5 Conclusions and work in progress

The intrinsic and strong relation between the EoS and the maximum mass of a neutron star sequence is a remarkable feature. In fact, knowledge of one is essential to access the other. In our observations, the maximum-mass constraint moving to higher values, together with the causality requirement at any central density, poses significant restrictions on the high-density EoS. The softness of the microscopic predictions at normal density brings up the need for a (first) steeper extension. A scenario such as the one we have described, where the first part of a piecewise extension needs to become stiffer in order to support current maximum mass constraints, while the next piece must soften to maintain causality, is consistent with evolving maximum-mass constraints.

A monotone behavior of the speed of sound approaching the conformal limit seems to be excluded by mass constraints, which require a rapid growth to allow masses of 2 $M_{\odot }$ or above. We are currently investigating various scenarios where the speed of sound is not a monotone function of density.

In closing, we reiterate that a microscopic theory of the nuclear many-body problem must start from quantitative descriptions of few-nucleon interactions. Those constraints have implications at normal density and well beyond it.

We also took the opportunity to display cooling curves as the foundation of a forthcoming comprehensive analysis, including gaps and medium effects. Based on the available literature, one may conclude that the impact of including 3NFs or other medium effects in calculations of the triplet pairing gap in neutron matter vary wildly, both quantitatively and qualitatively, depending on the specifics of the input. Systematic studies with robust two- and three-nucleon forces are called for.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FS: Writing – original draft. TA: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-FG02-03ER41270.

Acknowledgments

The authors are grateful to Dany Page for help with the NSCool cooling simulation package.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbott, B. P., Abbott, R., Abbott, T., Abraham, S., Acernese, F., Ackley, K., et al. (2019). GWTC-1: a gravitational-wave transient catalog of compact binary mergers observed by LIGO and virgo during the first and second observing runs. Phys. Rev. X 9, 031040. doi:10.1103/physrevx.9.031040

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T., Acernese, F., Ackley, K., Adams, C., et al. (2017a). GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119 (16), 161101. doi:10.1103/physrevlett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T., Acernese, F., Ackley, K., Adams, C., et al. (2018). GW170817: measurements of neutron star radii and equation of state. Phys. Rev. Lett. 121 (16), 161101. doi:10.1103/physrevlett.121.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017b). Multi-messenger observations of a binary neutron star merger. Astrophys. J. Lett. 848 (2), L12. doi:10.3847/2041-8213/aa91c9

CrossRef Full Text | Google Scholar

Bernard, V., Epelbaum, E., Krebs, H., and Meissner, U.-G. (2008). Subleading contributions to the chiral three-nucleon force: long-range terms. Phys. Rev. C 77, 064004. doi:10.1103/physrevc.77.064004

CrossRef Full Text | Google Scholar

Bernard, V., Epelbaum, E., Krebs, H., and Meissner, U. G. (2011). Subleading contributions to the chiral three-nucleon force II: short-range terms and relativistic corrections. Phys. Rev. C 84, 054001. doi:10.1103/physrevc.84.054001

CrossRef Full Text | Google Scholar

Brandes, L., Weisei, W., and Kaiseri, N. (2023). Inference of the sound speed and related properties of neutron stars. Phys. Rev. D. 107, 014011. doi:10.1103/physrevd.107.014011

CrossRef Full Text | Google Scholar

Burrello, S., Grasso, M., and Yang, C. J. (2020). Towards a power counting in nuclear energy-density-functional theories through a perturbative analysis. Phys. Lett. B 811, 135938. doi:10.1016/j.physletb.2020.135938

CrossRef Full Text | Google Scholar

Das, H., Wei, J.-B., Burgio, G., and Schulze, H.-J. (2024). Neutron star cooling and mass distributions. Phys. Rev. D. 109, 123018. doi:10.1103/physrevd.109.123018

CrossRef Full Text | Google Scholar

Davis, P. J., Dinh Thi, H., Fantina, A. F., Gulminelli, F., Oertel, M., and Suleiman, L. (2024a). Inference of neutron star properties with unified crust-core equations of state for parameter estimation. Astronomy & Astrophysics 687, A44. doi:10.1051/0004-6361/202348402

CrossRef Full Text | Google Scholar

Davis, P. J., Thi, H. D., Fantina, A. F., and Gulminelly, F. (2024b). Inference of neutron-star properties with unified crust-core equations of state for parameter estimation. Astron. Astrophys. 687, 44. doi:10.48550/arXiv.2406.14906

CrossRef Full Text | Google Scholar

Davis, P. J., Thi, H. D., Fantina, A. F., and Gulminelly, F., Crust (unified) tool for equation-of-state reconstruction (cuter). (2025). 08658.

Google Scholar

Entem, D. R., Machleidt, R., and Nosyk, Y. (2017). High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys. Rev. C 96 (2), 024004. doi:10.1103/physrevc.96.024004

CrossRef Full Text | Google Scholar

Epelbaum, E., Krebs, H., and Meißner, U. G. (2015). Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order, Eur. Phys. J. A 51 (5), 53. doi:10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

Epelbaum, E., Krebs, H., and Reinart, P. (2023). “Semi-local nuclear forces from chiral EFT: state-of-the-art and challenges,” in Handbook of nuclear physics. Editors I. Tanihata, H. Toki, and T. Kajino (Singapore: Springer).

Google Scholar

Epelbaum, E., Krebs, H., and Reinert, P. (2020). High-precision nuclear forces from chiral EFT: State-of-the-art, challenges and outlook. Front. Phys. 8, 98. doi:10.3389/fphy.2020.00098

CrossRef Full Text | Google Scholar

Fan, Y.-Z., Han, M.-Z., Jiang, J.-L., Shao, D.-S., and Tang, S.-P., Maximum gravitational mass M_TOV = ${2.25}_{-0.07}^{+0.08}{M}_{\odot }$ inferred at about 3% precision with multimessanger data of neutron stars (2024). \path{arXiv:2309.12644v2}.

Google Scholar

Fonseca, E., Cromartie, H., Pennucci, T., Ray, P., Kirichenko, A. Y., Ransom, S. M., et al. (2021). Refined mass and geometric measurements of the high-mass psr j0740 + 6620. Astrophys. J. Lett. 915, L12. doi:10.3847/2041-8213/ac03b8

CrossRef Full Text | Google Scholar

Furnstahl, R. J., Klco, N., Phillips, D. R., and Wesolowski, S. (2015). Quantifying truncation errors in effective field theory. Phys. Rev. C 92 (2), 024005. doi:10.1103/physrevc.92.024005

CrossRef Full Text | Google Scholar

Gonzalez-Caniulef, D., Guillot, S., and Reisenegger, A. (2019). Neutron star radius measurement from the ultraviolet and soft x-ray thermal emission of psr j0437-4715. MNRAS 490, 5848–5859. doi:10.1093/mnras/stz2941

CrossRef Full Text | Google Scholar

Gonzalez-Jimenez, N., Petrovich, C., and Reisenegger, A. (2015). Rotochemical heating of millisecond and classical pulsars with anisotropic and density-dependent superfluid gap models. MNRAS 447, 2073–2084. doi:10.1093/mnras/stu2558

CrossRef Full Text | Google Scholar

Grasso, M. (2019). Effective density functionals beyond mean field. PPNP 106, 256–311. doi:10.1016/j.ppnp.2019.02.002

CrossRef Full Text | Google Scholar

Huth, S., Pang, P. T. H., Tews, I., Dietrich, T., Le Fèvre, A., Schwenk, A., et al. (2022). Constraining neutron-star matter with microscopic and macroscopic collisions. Nature 606, 276–280. doi:10.1038/s41586-022-04750-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanakis-Pegios, A., Koliogiannis, P. S., and Moustakidis, C. C. (2021). Probing the nuclear equation of state from the existence of a ≈ 2.6 M_⊙ neutron star: the GW190814 puzzle. Symmetry 13, 183. doi:10.3390/sym13020183

CrossRef Full Text | Google Scholar

Klausner, P., Coló, G., Roca-Maza, X., and Vigezzi, E. (2025). Impact of ground-state properties and collective excitations on the skyrme ansatz: a bayesian study. Phys. Rev. C 111, 014311. doi:10.1103/physrevc.111.014311

CrossRef Full Text | Google Scholar

Krebs, H., and Epelbaum, E. (2023a). Towards consistent nuclear interactions from chiral lagrangians I: the path integral approach. arXiv:2311.10893. [nucl-th]. doi:10.1103/PhysRevC.110.044003

CrossRef Full Text | Google Scholar

Krebs, H., and Epelbaum, E. (2023b). Towards consistent nuclear interactions from chiral lagrangians II: symmetry preserving regularization. arXiv:2312.13932. [nucl-th]. doi:10.48550/arXiv.2311.10893

CrossRef Full Text | Google Scholar

Krotscheck, E., Papaconstantinou, P., and Wang, J. (2024). Variational and parquet-diagram calculations for neutron matter. V. Triplet pairing. Phys. Rev. C 109, 015803. doi:10.1103/physrevc.109.015803

CrossRef Full Text | Google Scholar

Kumar, M., Kumar, S., Thakur, V., Kumar, R., Agrawal, B. K., and Dhiman, S. K. (2023). Crex- and prex-ii-motivated relativistic interactions and their implications for the bulk properties of nuclear matter and neutron stars. Phys. Rev. C 107, 055801. doi:10.1103/physrevc.107.055801

CrossRef Full Text | Google Scholar

Linares, M., T, S., and Casares, J. (2018). Peering into the dark side: magnesium lines establish a massive neutron star in PSR J2215+5135. ApJ 859, 54. doi:10.3847/1538-4357/aabde6

CrossRef Full Text | Google Scholar

Machleidt, R., and Sammarruca, F. (2024). Recent advances in chiral eft based nuclear forces and their applications. J. Prog. Part. Nucl. Phys. 137, 104117. doi:10.1016/j.ppnp.2024.104117

CrossRef Full Text | Google Scholar

Mendes, R. F. P., Sodré, C. F., and Falciano, F. T. (2024). Exceeding the conformal limit inside rotating neutron stars: implication to modified theories of gravity. Phys. Rev. D. 110, 104027. doi:10.1103/PhysRevD.110.104027

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2019). PSR J0030+0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys. J. Lett. 887, L24. doi:10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2021). The radius of PSR J0740+6620 from NICER and XMM-newton data. Astrophys. J. Lett. 918 (2), L28. doi:10.3847/2041-8213/ac089b

CrossRef Full Text | Google Scholar

Negele, J. W., and Vautherin, D. (1973). Neutron star matter at subnuclear densities. Nucl. Phys. A 207, 298–320. doi:10.1016/0375-9474(73)90349-7

CrossRef Full Text | Google Scholar

Nomoto, K., and Tsuruta, S. (1987). Cooling of neutron stars: effects of the finite time scale of thermal conduction. ApJ 312, 711. doi:10.1086/164914

CrossRef Full Text | Google Scholar

Potekhin, A., Chabrier, G., and Yakovlev, D. (1997). Internal temperatures and cooling of neutron stars with accreted envelopes. A&A 323, 415. doi:10.48550/arXiv.astro-ph/9706148

CrossRef Full Text | Google Scholar

Potekhin, A., Zyuzin, D., Yakovlev, D., Beznogov, M., and Shibanov, Y. (2020). Thermal luminosities of cooling neutron stars. Mon. Notices R. Astronomical Soc. 496, 5052–5071. doi:10.1093/mnras/staa1871

CrossRef Full Text | Google Scholar

Read, J. S., Lackey, B. D., Owen, B. J., and Friedman, J. L. (2009). Constraints on a phenomenologically parametrized neutron-star equation of state. Phys. Rev. D. 79, 124032. doi:10.1103/physrevd.79.124032

CrossRef Full Text | Google Scholar

Richardson, M. B., van Horn, H. M., Ratcliff, K. F., and Malone, R. C. (1982). Neutron star evolutionary sequences. ApJ 255, 624R. doi:10.1086/159865

CrossRef Full Text | Google Scholar

Rios, A., Polls, A., and Dickhoff, W. H. (2017). Pairing and short-range correlations in nuclear systems. J. Low. Temp. Phys. 189 (5-6), 234–249. doi:10.1007/s10909-017-1818-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Romani, R. W., Kandel, D., Filippenko, A. V., Brink, T. G., and Zheng, W. (2022). PSR J0952-0607: the fastest and heaviest known galactic neutron star. Astrophys. J. Lett. 934, L17. doi:10.3847/2041-8213/ac8007

CrossRef Full Text | Google Scholar

Sammarruca, F. (2011). Contribution of isovector mesons to the symmetry energy in a microscopic model. Phys. Rev. C 84, 044307. doi:10.1103/physrevc.84.044307

CrossRef Full Text | Google Scholar

Sammarruca, F. (2024). The neutron skin of ⁴⁸Ca and ²⁰⁸Pb: a critical analysis. Symmetry 16, 34. doi:10.3390/sym16010034

CrossRef Full Text | Google Scholar

Sammarruca, F., and Millerson, R. (2021a). Analysis of the neutron matter equation of state and the symmetry energy up to fourth order of chiral effective field theory. Phys. Rev. C 104 (3), 034308. doi:10.1103/physrevc.104.034308

CrossRef Full Text | Google Scholar

Sammarruca, F., and Millerson, R. (2021b). Overview of symmetric nuclear matter properties from chiral interactions up to fourth order of the chiral expansion. Phys. Rev. C 104 (6), 064312. doi:10.1103/physrevc.104.064312

CrossRef Full Text | Google Scholar

Sammarruca, F., and Millerson, R. (2022). The equation of state of neutron-rich matter at fourth order of chiral effective field theory and the radius of a medium-mass neutron star. Universe 8 (2), 133. doi:10.3390/universe8020133

CrossRef Full Text | Google Scholar

Sullivan, A. G., and Romani, R. W. (2024). The intrabinary shock and companion star of redback pulsar J2215+5135. \path{arXiv:2405.13889}.

Google Scholar

Tews, I., Carlson, J., Gandolfi, S., and Reddy, S. (2018). Constraining the speed of sound inside neutron stars with chiral effective field theory interactions and observations. Astrophys. J. 860 (2), 149. doi:10.3847/1538-4357/aac267

CrossRef Full Text | Google Scholar

Tsang, C. Y., Tsang, M. B., Lynch, W. G., Kumar, R., and Horowitz, C. J. (2024). Determination of the equation of state from nuclear experiments and neutron star observations. Nat. Astron 8, 328–336. doi:10.1038/s41550-023-02161-z

CrossRef Full Text | Google Scholar

Wei, J. B., Burgio, G. F., Schulze, H.-J., and Zappalá, D. (2020). Cooling of hybrid neutron stars with microscopic equations of state. Mon. Not. R. Astron. Soc. 498, 344–354. doi:10.1093/mnras/staa1879

CrossRef Full Text | Google Scholar

Yakovlev, D. G., Kaminker, A. D., Gnedin, O. Y., and Haensel, P. (2001). Neutrino emission from neutron stars. Phys. Rept. 354, 1. doi:10.48550/arXiv.astro-ph/0012122

CrossRef Full Text | Google Scholar

Yang, C. J., Grasso, M., and Lacroix, D. (2016). From dilute matter to the equilibrium point in the energy-density-functional theory. Phys. Rev. C 94, 031301. (R). doi:10.1103/physrevc.94.031301

CrossRef Full Text | Google Scholar