- 1Laboratory for Atmospheric and Space Physics, University of Colorado at Boulder, Boulder, CO, United States
- 2T-5 Applied Mathematics and Plasma Physics, Los Alamos National Laboratory, Los Alamos, NM, United States
Cold plasma originating from the ionosphere is a highly influential component of the magnetosphere, dominating its mass. It is typically treated as a passive background represented as an empirical density in models of the ring current, outer radiation belt, and wave propagation. While it is well established that cold plasma density plays a critical role in controlling wave properties - such as amplitude and wave vector - increasing theoretical and observational evidence suggests that cold plasma populations may actively couple with waves, exchanging energy through processes that are not yet fully understood. Importantly, these processes can energize cold plasma, gradually transforming it into warm and eventually hot plasma. This mini-review explores the role of wave-particle interactions in cold and warm plasma heating, highlighting their significance in facilitating coupling between different plasma populations in Earth’s magnetosphere.
Introduction
Cold (∼eV) plasma from the ionosphere is a key player in geospace dynamics, especially during magnetic storms, serving as a primary magnetospheric plasma source (Chappell et al., 1987; Kistler et al., 2023) and engaging in energy exchange with other populations. Simulations of the ring current (Jordanova et al., 2022), outer radiation belt (Shprits et al., 2015), and wave propagation (Walker, 1976; Usanova et al., 2022) often treat cold plasma as a density-based, passive medium. However, growing evidence highlights the need to account for energy exchange processes that modify cold plasma properties and link it to higher-energy populations, integrating it more dynamically into the geospace system (Delzanno et al., 2021).
The energy exchange between different plasma populations can be mediated by wave-particle interactions, which play an important role in heating cold plasma within the Earth’s magnetosphere. Wave-particle interactions allow for a gradual energy build-up, altering the local plasma environment and contributing to magnetospheric dynamics. These interactions can occur at various locations along magnetic field lines, including the equatorial plane and higher magnetic latitudes, influencing different magnetospheric particle populations. They can enhance ionospheric plasma outflow into the magnetosphere (Chaston et al., 2006; Liemohn et al., 2024), lead to particle acceleration in the auroral zone (André, 1997), and contribute to the formation of the warm plasma cloak (Chappell et al., 2021) and the ring current (Daglis et al., 1999; Keika et al., 2013).
Wave-particle interactions
Resonant interactions serve as an efficient mechanism for energy transfer between particles and waves, primarily through cyclotron and Landau resonances. Cyclotron resonance takes place when the Doppler-shifted wave frequency matches the particle’s cyclotron frequency:
Landau resonance occurs when charged particles with velocities close to the wave’s phase velocity exchange energy with the wave (Lifshitz and Pitaevski, 1981). The condition for this resonance is satisfied when
Other resonance interactions, such as bounce and drift-bounce resonances, have also been identified (Southwood et al., 1969; Schulz and Lanzerotti, 1974). Drift-bounce resonance arises from a particle’s combined drift and bounce motion, occurring when the wave frequency matches the drift-bounce frequency:
Cyclotron and Landau resonance interactions primarily involve particles with energies ∼100 eV, typically classified as warm plasma. In contrast, non-resonant mechanisms can heat plasma considered cold in the context of resonant wave-particle interactions, where particle thermal velocities are much lower than the phase velocities of propagating waves.
Quasilinear diffusion theory is a fundamental framework for describing energy and momentum exchange in both resonant and non-resonant wave-particle interactions. It applies to systems where wave amplitudes are small and the waves are broadband and randomly phased, allowing for a statistical treatment of diffusion in velocity space (Kennel and Engelmann, 1966). Most applications of quasilinear diffusion theory in space plasmas focus on resonant interactions, as these effects typically dominate (Albert et al., 2009). Non-resonant interactions become significant when wave packets are short, leading to a spread in wavenumber space (An et al., 2022).
For large-amplitude waves, nonlinear effects such as phase trapping and phase bunching become important. They are described by nonlinear theory (Artemyev et al., 2021 and references therein) and simulated using test-particle, particle-in-cell, and Vlasov codes (da Silva et al., 2018; Omidi et al., 2010; Nunn, 2021). Nonlinear interactions can also influence cold plasma populations, as discussed in the sections below.
Key wave modes contributing to plasma heating include whistler-mode waves (chorus and hiss), electromagnetic ion cyclotron (EMIC) waves, ultra-low-frequency (ULF) waves, and kinetic Alfvén waves (KAWs). Their typical locations within the inner magnetosphere are schematically illustrated in Figure 1. The following sections examine the role of these wave modes in cold plasma energization.
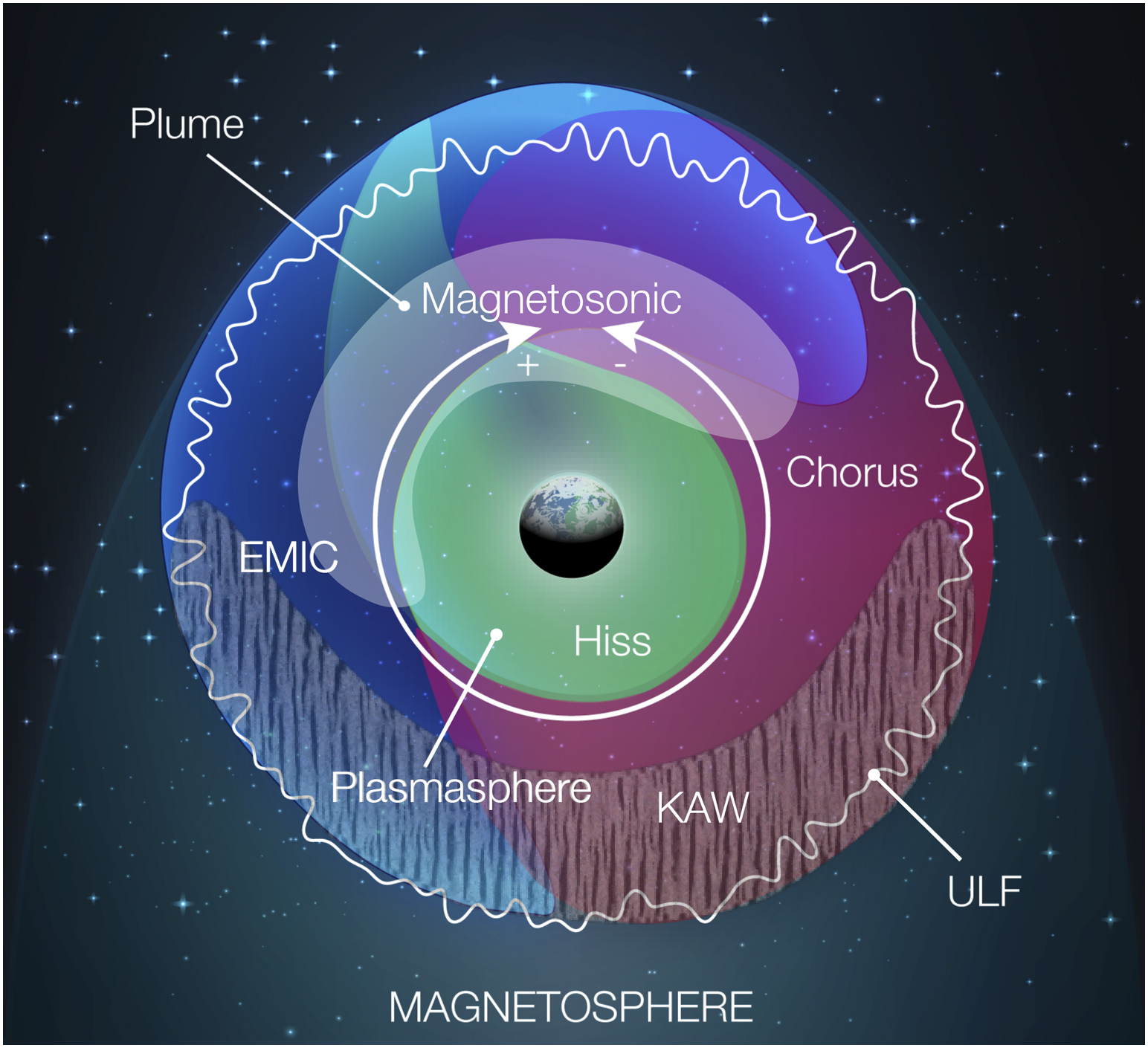
Figure 1. Schematic localization of waves critical to inner magnetosphere dynamics (adapted from Thorne, 2010): ULF (white curve), chorus (purple), hiss (green), magnetosonic (white), EMIC (blue), KAW (textured). The azimuthal drift directions for energetic electrons and ions are indicated by the “+” and “–” signs, respectively. The distribution of EMIC waves is illustrated based on a THEMIS survey (Usanova et al., 2012), while the distribution of kinetic Alfvén waves is depicted using Van Allen Probes measurements (Chaston et al., 2015a).
Ultra-low-frequency waves
ULF waves are the longest-period waves in the magnetospheric system, with frequencies ranging from 1 mHz to 5 Hz (Jacobs et al., 1964; Hartinger et al., 2022). This frequency range also includes electromagnetic ion cyclotron waves, discussed separately in a later section. ULF waves can be driven by various mechanisms and are observed across different regions of the magnetosphere. Drivers include solar wind impulses (McPherron, 2005; Shen et al., 2015), ion foreshock instabilities on the dayside (Eastwood et al., 2011; Hartinger et al., 2013), the Kelvin-Helmholtz instability on the flanks (Southwood, 1974; Mann et al., 1999; Claudepierre et al., 2008), and plasma instabilities in fast flows on the nightside (Zolotukhina et al., 2008; Yeoman et al., 2010). Additionally, ULF waves can result from resonance interactions with energetic ions in the inner magnetosphere (Ozeke and Mann, 2008).
ULF waves play a crucial role in energizing plasmaspheric and ionospheric populations, as well as modulating their fluxes. The ion E × B drift driven by the wave’s electric and magnetic fields has been proposed as a key mechanism behind the observed enhancements in ion flux at energies of tens of eV (Zong et al., 2012; Zhang et al., 2019). Additionally, Zong et al. (2012) suggested that ULF waves can interact with the oxygen torus (Chappell, 1982; Fraser et al., 2005), enhancing its density by a factor of two to three.
Betatron acceleration caused by ULF wave magnetic fields has been identified as an alternative mechanism for the acceleration of hydrogen and helium ions with energies below 100 eV, particularly in cases where E × B drift alone cannot fully account for the observed flux enhancements (Yue et al., 2016).
Ren et al. (2017), Ren et al. (2019) explored the connection between ULF waves and electrons with energies below 200 eV. Their findings show that ULF waves can accelerate electrons in the ∼eV to tens of eV range along the parallel direction, consistent with the drift-bounce resonance mechanism.
Whistler-mode waves: chorus and hiss
Chorus and hiss waves are right-hand circularly polarized electromagnetic waves that propagate predominantly along magnetic field lines in the magnetosphere. Chorus waves typically range in frequency from a few hundred Hz to several kHz, below the electron cyclotron frequency (fce). They are observed at frequencies 0.1–0.8 fce, with a gap near 0.5 fce splitting the emissions into two bands: lower-band and upper-band chorus (Tsurutani and Smith, 1977). These waves are generated by anisotropic electron distributions (∼tens of keV) with Tperp > Tpara (perpendicular temperature exceeding parallel temperature) (Omura et al., 2008). Chorus waves are primarily observed outside the plasmapause and are most common in the dawn sector of the magnetosphere, at distances between 4 and 9 Earth radii (Li et al., 2011).
Resonant interactions with oblique waves can mediate energy exchange between different particle populations (e.g., Shklyar, 2017). For example, cyclotron interactions with higher-energy particles drive chorus wave growth, while lower-energy particles can gain energy through other resonances. Chorus waves can accelerate warm (>100 eV) electrons via Landau resonance (Bortnik et al., 2007; Chen et al., 2013).
Recent studies have shown that quasi-field-aligned whistler waves can generate parametric nonlinear instabilities due to transverse currents as they propagate through cold plasma (Roytershteyn and Delzanno, 2021; Roytershteyn et al., 2024). This process leads to the damping of quasi-field-aligned waves, the excitation of oblique electrostatic modes, including electron Bernstein and oblique electrostatic whistler modes and parallel heating of cold plasma. This mechanism provides a potential pathway for transferring energy from chorus waves to cold electrons. Notably, the instability that generates oblique electrostatic waves is sensitive to the shape of the low-energy electron distribution, which highlights the importance of cold plasma distribution measurements in future missions.
Hiss waves, a subset of whistler-mode electromagnetic waves, are characterized by a broad and incoherent frequency spectrum, typically ranging from about 20 Hz to several kHz. Plasmaspheric hiss waves are observed primarily inside the plasmapause, within the plasmasphere and plasmaspheric plumes (Hayakawa and Sazhin, 1992).
Two distinct populations of hiss waves have been identified: low-frequency hiss (f < 100 Hz) and high-frequency hiss (f > 100 Hz) (Malaspina et al., 2017, and references therein). In addition, more recently, Meredith et al. (2021) distinguished a medium frequency range (200 < f < 2,000 Hz) population. These populations exhibit unique spatial distributions and amplitude characteristics, suggesting that different generation mechanisms are at play. Despite extensive research, the exact origins of hiss waves remain an active topic of investigation.
Several mechanisms have been proposed for the generation of plasmaspheric hiss waves. Lightning-generated whistlers (Meredith et al., 2006), mode conversion of chorus waves (Bortnik et al., 2008), and local generation by substorm injections (Li et al., 2023) are among the leading hypotheses. Specifically, Li et al. (2023) suggested that low-frequency hiss waves might result from in situ cyclotron wave growth driven by freshly injected electrons at low L shells. Chen et al. (2014) demonstrated that repeated wave amplification, supported by guided propagation along the plasmapause, can lead to a significant wave gain over multiple reflections between conjugate hemispheres.
Hiss waves play a crucial role in magnetospheric dynamics. For instance, quasilinear calculations by Li et al. (2019) confirmed that hiss waves can rapidly accelerate suprathermal electrons parallel to the magnetic field via Landau resonance, with acceleration occurring on timescales as short as 10 min. Similarly, Wang et al. (2019) showed that hiss waves can significantly enhance field-aligned electron fluxes in the 50–300 eV range. Through Landau damping, these fluxes can increase by a factor of 10 within approximately 1 hour.
Although Landau resonance does not directly heat the core cold plasma population - since the resonance energy is higher - the acceleration of suprathermal electrons by chorus and hiss waves, followed by their Coulomb collisions with core magnetospheric and ionospheric electrons, can contribute to energy transfer to the cold electron population (Khazanov et al., 2022).
Magnetosonic waves (also known as equatorial noise)
Magnetosonic waves are longitudinal electromagnetic plasma waves that propagate nearly perpendicular to the background magnetic field. They were first identified as emissions near the geomagnetic equator (hence their name) by Russell et al. (1970). These waves are typically observed at frequencies between the proton gyrofrequency (fcp) and the lower hybrid resonance frequency (fLHR), generally in the range of a few Hz to 100 Hz (Chen and Bortnik, 2020). Near the proton gyrofrequency, magnetosonic waves often exhibit a harmonic structure (Gurnett, 1976). The primary source of free energy for these waves is ∼10 keV protons with positive gradients in their perpendicular velocity distribution (Perraut et al., 1982).
Enhanced fluxes of electrons and ions with energies from tens to hundreds of eV have been observed in association with magnetosonic waves (Gurnett, 1976; Olsen, 1981). To explain these observations, Horne et al. (2000) performed a ray-tracing analysis and demonstrated that magnetosonic waves can resonantly interact with both electrons and ions and increase their perpendicular energy, although the nature of these interactions differs. Electrons interact with magnetosonic waves via Landau resonance, with resonance energy around 1 keV for perpendicular wave propagation, decreasing to a few eV at smaller propagation angles. Cold protons, conversely, can undergo cyclotron resonance with magnetosonic waves, resulting in heating transverse to the ambient magnetic field. This transverse proton heating becomes more significant outside the plasmasphere, where thermal proton temperatures increase up to ∼100 eV. The resonance energy decreases into the eV range but only at frequencies near the proton cyclotron frequency harmonics. These findings are consistent with the suprathermal particle distributions reported in the region (Olsen, 1981). More recently, the formation of suprathermal proton fluxes due to magnetosonic waves has been identified as an energy source for EMIC waves (see section below), highlighting a complex interplay between various wave modes and particle populations (Asamura et al., 2021).
In addition to protons, magnetosonic waves can resonantly heat 10–100 eV He+ ions (Yuan et al., 2018) and O+ ions (Hill et al., 2020). As demonstrated by Ma et al. (2019), magnetosonic waves can interact with thermal minor ion species at pitch angles up to ∼80°, mediated by multiple harmonic cyclotron resonances.
Electromagnetic ion cyclotron waves
Electromagnetic ion cyclotron (EMIC) waves are plasma waves that typically propagate along, or at a slight oblique angle to, the ambient magnetic field. They are generated by the ion cyclotron instability, driven by 10–100 keV protons with anisotropic temperatures (T⊥ > T∥) (Kennel and Petschek, 1966). EMIC waves can form in multiple bands corresponding to the ion cyclotron frequencies of H+, He+, and O+ ions. Additional ion bands, such as He++ (Anderson and Fuselier, 1993; Engebretson et al., 2018), N+ (Bashir and Ilie, 2021; Usanova et al., 2024), and O++ (Yu et al., 2021; Usanova et al., 2024), have also been reported. In this section, we highlight key aspects of EMIC wave interactions with cold plasma, which are explored more extensively in Usanova (2021).
Cold electron heating by oblique EMIC waves (Zhou et al., 2013; Yuan et al., 2014) may contribute to the formation of stable auroral red arcs (Cornwall et al., 1971; Thorne and Horne, 1992; Kozyra et al., 1997). EMIC waves can also heat He+ ions, raising their energies from ∼eV to ∼100 eV (Young et al., 1981; Roux et al., 1982; Kim et al., 2023). Quasilinear theory shows that EMIC waves can similarly heat thermal O+ ions at energies and pitch angles up to ∼80° through multiple harmonic cyclotron resonances (Ma et al., 2019). EMIC waves have been suggested as a potential source of the warm plasma cloak (Gamayunov et al., 2024).
Nonlinear processes can generate secondary electrostatic waves, resulting in parallel heating of cold He+ and H+ ions (Omidi et al., 2010; Bortnik et al., 2010). Additionally, phase bunching effects can cause nonlinear energization of cold H+ and He+ ions (Kitamura et al., 2018; Abid et al., 2021; Li et al., 2023). Notably, the presence of cold ion populations can facilitate the nonlinear coupling of different wave modes, for example, the formation of lower hybrid waves through polarization drifts induced by EMIC waves (Khazanov et al., 2017). Gamayunov et al. (2014) emphasized the need to incorporate a nonlinear energy cascade from the ULF to EMIC range, along with a dynamic model of plasmaspheric ion composition, into a global EMIC wave model.
Kinetic Alfvén waves
Kinetic Alfvén waves are a small-scale extension of shear Alfvén waves that include the kinetic behavior of ions and electrons. These waves travel along magnetic field lines, facilitating energy transfer throughout the magnetosphere. The theory of KAWs incorporates kinetic effects that become significant at spatial scales comparable to either the ion acoustic gyroradius or the electron inertial length, whichever is larger (Lysak, 2023). At these scales, the waves become dispersive and develop a parallel electric field. In spectrograms, KAWs appear as broadband electromagnetic emissions spanning frequencies from ∼0 to kHz. They are known to be accelerators of electrons parallel to the geomagnetic field (Chen and Hasegawa, 1974) and of ions in the perpendicular direction (Johnson and Cheng, 2001).
KAWs have been observed in various magnetospheric environments, including the magnetopause (Lee et al., 1994), plasma sheet (Chaston et al., 2012), auroral regions (Goertz, 1984; Tian et al., 2022), and inner magnetosphere (Chaston et al., 2015a; b). In the inner magnetosphere, KAWs are most frequently observed during disturbed geomagnetic conditions, predominantly in the nightside local time sector down to L ∼3 (Chaston et al., 2015a). Electromagnetic waves with similar characteristics have been detected in fast earthward flows in the plasma sheet at distances as far as L ∼12, covering a large portion of the nightside magnetosphere (Ergun et al., 2015). These waves are often accompanied by enhancements in electron and ion temperatures (Ergun et al., 2022; Usanova and Ergun, 2022; Usanova et al., 2023a). Chaston et al. (2014) demonstrated that broadband electromagnetic waves can drive significant ion heating perpendicular to the background magnetic field at a rate of ∼1 eV/s. Chaston et al. (2015b) reported measurements of energized outflowing ionospheric ions (ranging from tens of eV to >50 keV) and electrons heated to ∼1 keV in the inner magnetosphere by KAWs. Suprathermal electron trapping has been suggested as a mechanism for electron acceleration to several keV (Artemyev et al., 2015).
KAWs likely play a critical role in controlling O+ outflows along magnetic field lines into the equatorial inner magnetosphere through enhanced electron precipitation into the topside ionosphere, combined with subsequent transverse energization along magnetic field lines. The energized ionospheric O+ ions can ultimately contribute to ring current enhancements (Chaston et al., 2016; Breneman et al., 2022).
Discussion: challenges and prospects in cold plasma research
Future efforts should address technological and scientific limitations in cold plasma research. Spacecraft charging presents a significant challenge for measuring cold plasma populations, often preventing low-energy particles from reaching detectors. Moreover, spacecraft-generated photoelectrons and secondary electrons frequently obscure low-energy electron fluxes in the magnetosphere. Addressing these challenges requires the development of advanced instruments capable of reliably measuring cold plasma across the magnetosphere (Delzanno et al., 2023; Maldonado et al., 2023a; Maldonado et al., 2023b). These state-of-the-art instruments must also resolve the broadening of cold plasma energy distributions on timescales relevant to energization processes, with high temporal, angular, and energy resolution (Usanova et al., 2023b). Such plasma measurements are essential for characterizing, quantifying, and understanding the diverse impacts of cold particle populations on the magnetosphere. Additionally, they are crucial for improving physics-based magnetospheric plasma models, including cold electron density models (Ripoll et al., 2023). At a minimum, the development of models for cold electron and ion temperatures, which are currently lacking, is necessary. Advancing these models requires a detailed understanding of heating sources, their relative importance and spatial and temporal distributions.
Future research should prioritize the understanding and quantification of energy-exchange processes. This requires advancements in cold plasma measurement techniques to enable the simultaneous study of wave and cold plasma properties. Physics-based space weather models should incorporate wave-particle interactions to account for cold and warm plasma energization processes. Integrating machine learning techniques can further improve physics-based models' accuracy and predictive capabilities. Such integrated models can pave the way for a deeper understanding of cold and warm plasma dynamics and its impact.
Author contributions
MEU: Writing – original draft. GLD: Writing – original draft. NM: Writing – original draft.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. MEU acknowledges funding from NASA (awards 80NSSC23K0405 and 80NSSC21K518) and NSF (award S03463-01). GLD was supported by the LDRD Program of LANL under project number 20250577ER. The Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (Contract No. 89233218CNA000001). NM received support from NASA and NSF under awards 80NSSC22K1023, 80NSSC23M0192, 80GSFC23CA004, and AGS 2412296.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abid, A. A., Lu, Q., Gao, X. L., Alotaibi, B. M., Ali, S., Qureshi, M. N. S., et al. (2021). Energization of cold ions by electromagnetic ion cyclotron waves: magnetospheric multiscale (MMS) observations. Phys. Plasmas 28, 072901. doi:10.1063/5.0046764
Albert, J. M., Meredith, N. P., and Horne, R. B. (2009). Three-dimensional diffusion simulation of outer radiation belt electrons during the 9 October 1990 magnetic storm. J. Geophys. Res. 114, A09214. doi:10.1029/2009JA014336
An, X., Artemyev, A., Angelopoulos, V., Zhang, X., Mourenas, D., and Bortnik, J. (2022). Nonresonant scattering of relativistic electrons by electromagnetic ion cyclotron waves in Earth's radiation belts. Phys. Rev. Lett. 129, 135101. doi:10.1103/PhysRevLett.129.135101
Anderson, B. J., and Fuselier, S. A. (1993). Magnetic pulsations from 0.1 to 4.0 Hz and associated plasma properties in the Earth's subsolar magnetosheath and plasma depletion layer. J. Geophys. Res. 98 (A2), 1461–1479. doi:10.1029/92JA02197
André, M. (1997). Wave and wave-particle interactions in the auroral region. J. Atmos. Sol. Terr. Phys. 5914, 1687. doi:10.1016/S1364-6826(96)00173-3
Artemyev, A. V., Neishtadt, A. I., Vasiliev, A. A., Zhang, X.-J., Mourenas, D., and Vainchtein, D. (2021). Long-term dynamics driven by resonant wave–particle interactions: from Hamiltonian resonance theory to phase space mapping. J. Plasma Phys. 87 (2), 835870201. doi:10.1017/S0022377821000246
Artemyev, A. V., Rankin, R., and Blanco, M. (2015). Electron trapping and acceleration by kinetic Alfven waves in the inner magneto-sphere. J. Geophys. Res. Space Phys. 120 (10), 305–310. doi:10.1002/2015JA021781
Asamura, K., Shoji, M., Miyoshi, Y., Kasahara, Y., Kasaba, Y., Kumamoto, A., et al. (2021). Cross-energy couplings from magnetosonic waves to electromagnetic ion cyclotron waves through cold ion heating inside the plasmasphere. Phys. Rev. Lett. 127 (24), 245101. doi:10.1103/PhysRevLett.127.245101
Bashir, M. F., and Ilie, R. (2021). The first observation of N+ electromagnetic ion cyclotron waves. J. Geophys. Res. Space Phys. 126, e2020JA028716. doi:10.1029/2020JA028716
Bortnik, J., Thorne, R. M., and Meredith, N. P. (2007). Modeling the propagation characteristics of chorus using CRRES suprathermal electron fluxes. J. Geophys. Res. 112, 8204. doi:10.1029/2006JA012237
Bortnik, J., Thorne, R. M., and Meredith, N. P. (2008). The unexpected origin of plasmaspheric hiss from discrete chorus emissions. Nature 452, 62–66. doi:10.1038/nature06741
Bortnik, J., Thorne, R. M., and Omidi, N. (2010). Nonlinear evolution of EMIC waves in a uniform magnetic field: 2. Test-particle scattering. J. Geophys. Res. 115, A12242. doi:10.1029/2010JA015603
Breneman, A. W., Wygant, J. R., Tian, S., Cattell, C. A., Thaller, S. A., Goetz, K., et al. (2022). The van allen Probes electric field and waves instrument: science results, measurements, and access to data. Space Sci. Rev. 218, 69. doi:10.1007/s11214-022-00934-y
Chappell, C. R. (1982). Initial observations of thermal plasma composition and energetics from Dynamics Explorer-1. Geophys. Res. Lett. 9 (9), 929–932. doi:10.1029/GL009i009p00929
Chappell, C. R., Glocer, A., Giles, B. L., Moore, T. E., Huddleston, M. M., and Gallagher, D. L. (2021). The key role of cold ionospheric ions as a source of hot magnetospheric plasma and as a driver of the dynamics of substorms and storms. Front. Astron. Space Sci. 8, 746283. doi:10.3389/fspas.2021.746283
Chappell, C. R., Moore, T. E., and Waite, J. H. (1987). The ionosphere as a fully adequate source of plasma for the Earth’s magnetosphere. J. Geophys. Res. 92, 5896–5910. doi:10.1029/ja092ia06p05896
Chaston, C. C., Bonnell, J. W., Clausen, L., and Angelopoulos, V. (2012). Energy transport by kinetic-scale electromagnetic waves in fast plasma sheet flows. J. Geophys. Res. 117, A09202. doi:10.1029/2012JA017863
Chaston, C. C., Bonnell, J. W., Kletzing, C. A., Hospodarsky, G. B., Wygant, J. R., and Smith, C. W. (2015a). Broadband low-frequency electromagnetic waves in the inner magnetosphere. J. Geophys. Res. Space Phys. 120, 8603–8615. doi:10.1002/2015JA021690
Chaston, C. C., Bonnell, J. W., Reeves, G. D., and Skoug, R. M. (2016). Driving ionospheric outflows and magnetospheric O+ energy density with Alfvén waves. Geophys. Res. Lett. 43, 4825–4833. doi:10.1002/2016GL069008
Chaston, C. C., Bonnell, J. W., and Salem, C. (2014). Heating of the plasma sheet by broadband electromagnetic waves. Geophys. Res. Lett. 41, 8185–8192. doi:10.1002/2014GL062116
Chaston, C. C., Bonnell, J. W., Wygant, J. R., Kletzing, C. A., Reeves, G. D., Gerrard, A., et al. (2015b). Extreme ionospheric ion energization and electron heating in Alfvén waves in the storm time inner magnetosphere. Geophys. Res. Lett. 42 (10), 531–610. doi:10.1002/2015GL066674
Chaston, C. C., Genot, V., Bonnell, J. W., Carlson, C. W., McFadden, J. P., Ergun, R. E., et al. (2006). Ionospheric erosion by Alfvén waves. J. Geophys. Res. 111, A03206. doi:10.1029/2005JA011367
Chen, L., and Bortnik, J. (2020). “Chapter 4-Wave-particle interactions with coherent magnetosonic waves,” in The dynamic loss of Earth's radiation belts. Editors A. N. Jaynes, and M. E. Usanova (Elsevier), 99–120. doi:10.1016/B978-0-12-813371-2.00004-4
Chen, L., and Hasegawa, A. (1974). Plasma heating by spatial resonance of Alfvén wave. Phys. Fluids 17, 1399–1403. doi:10.1063/1.1694904
Chen, L., Thorne, R. M., Bortnik, J., Li, W., Horne, R. B., Reeves, G. D., et al. (2014). Generation of unusually low frequency plasmaspheric hiss. Geophys. Res. Lett. 41, 5702–5709. doi:10.1002/2014GL060628
Chen, L., Thorne, R. M., Li, W., and Bortnik, J. (2013). Modeling the wave normal distribution of chorus waves. J. Geophys. Res. Space Phys. 118, 1074–1088. doi:10.1029/2012JA018343
Claudepierre, S. G., Elkington, S. R., and Wiltberger, M. (2008). Solar wind driving of magnetospheric ULF waves: pulsations driven by velocity shear at the magnetopause. J. Geophys. Res. 113, A05218. doi:10.1029/2007JA012890
Cornwall, J. M., Coroniti, F. V., and Thorne, R. M. (1971). Unified theory of SAR arc formation at the plasmapause. J. Geophys. Res. 76 (19), 4428–4445. doi:10.1029/JA076i019p04428
Daglis, I. A., Thorne, R. M., Baumjohann, W., and Orsini, S. (1999). The terrestrial ring current: origin, formation, and decay. Rev. Geophys. 37 (4), 407–438. doi:10.1029/1999RG900009
da Silva, C. L., Denton, R. E., Hudson, M. K., Millan, R. M., Liu, K., and Bortnik, J. (2018). Test-particle simulations of linear and nonlinear interactions between a 2-D whistler-mode wave packet and radiation belt electrons. Geophys. Res. Lett. 45, 5234–5245. doi:10.1029/2018GL077877
Delzanno, G. L., Borovsky, J., Bortnik, J., Chappell, C., Donovan, E., Fernandes, P., et al. (2023). The need to understand the cold ion and cold electron populations of the Earth’s magnetosphere. Bull. AAS 55 (3). doi:10.3847/25c2cfeb.d3917969
Delzanno, G. L., Borovsky, J. E., Henderson, M. G., Resendiz Lira, P. A., Roytershteyn, V., and Welling, D. T. (2021). The impact of cold electrons and cold ions in magnetospheric physics. JASTP 220, 105599. doi:10.1016/j.jastp.2021.105599
Eastwood, J. P., Schwartz, S. J., Horbury, T. S., Carr, C. M., Glassmeier, K.-H., Richter, I., et al. (2011). Transient Pc3 wave activity generated by a hot flow anomaly: cluster, Rosetta, and ground-based observations. J. Geophys. Res. 116, A08224. doi:10.1029/2011JA016467
Engebretson, M. J., Posch, J. L., Capman, N. S. S., Campuzano, N. G., Bělik, P., Allen, R. C., et al. (2018). MMS, Van Allen Probes, GOES 13, and ground-based magnetometer observations of EMIC wave events before, during, and after a modest interplanetary shock. J. Geophys. Res. Space Phys. 123, 8331–8357. doi:10.1029/2018JA025984
Ergun, R. E., Goodrich, K. A., Stawarz, J. E., Andersson, L., and Angelopoulos, V. (2015). Large-amplitude electric fields associated with bursty bulk flow braking in the Earth's plasma sheet. J. Geophys. Res. Space Phys. 120 (3), 1832–1844. doi:10.1002/2014JA020165
Ergun, R. E., Usanova, M. E., Turner, D. L., and Stawarz, J. E. (2022). Bursty bulk flow turbulence as a source of energetic particles to the outer radiation belt. Geophys. Res. Lett. 49, e2022GL098113. doi:10.1029/2022GL098113
Fraser, B. J., Horwitz, J. L., Slavin, J. A., Dent, Z. C., and Mann, I. R. (2005). Heavy ion mass loading of the geomagnetic field near the plasmapause and ULF wave implications. Geophys. Res. Lett. 32, L04102. doi:10.1029/2004GL021315
Gamayunov, K. V., Engebretson, M. J., Zhang, M., and Rassoul, H. K. (2014). Model of electromagnetic ion cyclotron waves in the inner magnetosphere. J. Geophys. Res. Space Phys. 119, 7541–7565. doi:10.1002/2014JA020032
Gamayunov, K. V., Kim, H., and Shin, Y. (2024). EMIC wave energy dissipation as a source of O+ conics and warm plasma cloak in the Earth's inner magnetosphere. J. Geophys. Res. Space Phys. 129, e2023JA032399. doi:10.1029/2023JA032399
Goertz, C. K. (1984). Kinetic Alfvén waves on auroral field lines. Planet. Space Sci. 32, 1387–1392. doi:10.1016/0032-0633(84)90081-3
Gurnett, D. A. (1976). Plasma wave interactions with energetic ions near the magnetic equator. J. Geophys. Res. 81 (16), 2765–2770. doi:10.1029/JA081i016p02765
Hartinger, M. D., Takahashi, K., Drozdov, A. Y., Shi, X., Usanova, M. E., and Kress, B. (2022). ULF wave modeling, effects, and applications: accomplishments, recent advances, and future. Front. Astron. Space Sci. 9, 867394. doi:10.3389/fspas.2022.867394
Hartinger, M. D., Turner, D. L., Plaschke, F., Angelopoulos, V., and Singer, H. (2013). The role of transient ion foreshock phenomena in driving Pc5 ULF wave activity. J. Geophys. Res. Space Phys. 118, 299–312. doi:10.1029/2012JA018349
Hayakawa, M., and Sazhin, S. S. (1992). Mid-latitude and plasmaspheric hiss: a review. Planet. Space Sci. 40, 1325–1338. doi:10.1016/0032-0633(92)90089-7
Hill, S., Buzulukova, N., Boardsen, S., and Fok, M.-C. (2020). Local heating of oxygen ions in the presence of magnetosonic waves: possible source for the warm plasma cloak? J. Geophys. Res. Space Phys. 125, e2019JA027210. doi:10.1029/2019JA027210
Horne, R. B., Wheeler, G. V., and Alleyne, H. S. C. K. (2000). Proton and electron heating by radially propagating fast magnetosonic waves. J. Geophys. Res. 105 (A12), 27597–27610. doi:10.1029/2000JA000018
Jacobs, J. A., Kato, Y., Matsushita, S., and Troitskaya, V. A. (1964). Classification of geomagnetic micropulsations. J. Geophys. Res. 69, 180–181. doi:10.1029/JZ069i001p00180
Johnson, J. R., and Cheng, C. Z. (2001). Stochastic ion heating at the magnetopause due to kinetic Alfvén waves. Geophys. Res. Lett. 28, 4421–4424. doi:10.1029/2001GL013509
Jordanova, V., Morley, S., Engel, M. A., Godinez, H., Yakymenko, K., Henderson, M., et al. (2022). The RAM-SCB model and its applications to advance space weather forecasting. Adv. Space Res. 72, 5596–5606. doi:10.1016/j.asr.2022.08.077
Keika, K., Kistler, L. M., and Brandt, P. C. (2013). Energization of O+ ions in the Earth's inner magnetosphere and the effects on ring current buildup: a review of previous observations and possible mechanisms. J. Geophys. Res. Space Phys. 118, 4441–4464. doi:10.1002/jgra.50371
Kennel, C. F., and Engelmann, F. (1966). Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids 9 (12), 2377–2388. doi:10.1063/1.1761629
Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71 (1), 1–28. doi:10.1029/JZ071i001p00001
Khazanov, G. V., Boardsen, S., Krivorutsky, E. N., Engebretson, M. J., Sibeck, D., Chen, S., et al. (2017). Lower hybrid frequency range waves generated by ion polarization drift due to electromagnetic ion cyclotron waves: analysis of an event observed by the Van Allen Probe B. J. Geophys. Res. Space Phys. 122, 449–463. doi:10.1002/2016JA022814
Khazanov, G. V., Ma, Q., and Chu, M. (2022). Electron heat fluxes generated by intense whistler waves at the upper ionospheric altitudes. J. Geophys. Res. Space Phys. 127, e2022JA030753. doi:10.1029/2022JA030753
Kim, M. J., Goldstein, J., Fuselier, S. A., Vines, S. K., Usanova, M. E., Gonzalez, C. A., et al. (2023). MMS observations of warm-ion (E 100 eV) heating inside plasmaspheric plumes. J. Geophys. Res. Space Phys. 128, e2023JA031771. doi:10.1029/2023JA031771
Kistler, L. M., Asamura, K., Kasahara, S., Miyoshi, Y., Mouikis, C. G., Keika, K., et al. (2023). The variable source of the plasma sheet during a geomagnetic storm. Nat. Commun. 14, 6143. doi:10.1038/s41467-023-41735-3
Kitamura, N., Kitahara, M., Shoji, M., Miyoshi, Y., Hasegawa, H., Nakamura, S., et al. (2018). Direct measurements of two-way wave-particle energy transfer in a collisionless space plasma. Science 361, 1000–1003. doi:10.1126/science.aap8730
Kozyra, J. U., Nagy, A. F., and Slater, D. W. (1997). High-altitude energy source(s) for stable auroral red arcs. Rev. Geophys. 35 (2), 155–190. doi:10.1029/96RG03194
Lee, L. C., Johnson, J. R., and Ma, Z. W. (1994). Kinetic Alfvén waves as a source of plasma transport at the dayside magnetopause. J. Geophys. Res. 99 (A9), 17405–17411. doi:10.1029/94JA01095
Li, J., Ma, Q., Bortnik, J., Li, W., An, X., Reeves, G. D., et al. (2019). Parallel acceleration of suprathermal electrons caused by whistler-mode hiss waves. Geophys. Res. Lett. 46, 12675–12684. doi:10.1029/2019GL085562
Li, W., Bortnik, J., Thorne, R. M., and Angelopoulos, V. (2011). Global distribution of wave amplitudes and wave normal angles of chorus waves using THEMIS wave observations. J. Geophys. Res. 116, A12205. doi:10.1029/2011JA017035
Li, X., Wang, R., Gao, X., Lu, Q., Chen, H., and Ma, J. (2023). Observation of non-resonance interactions between cold protons and EMIC waves of different polarizations in the inner magnetosphere. Geophys. Res. Lett. 50, e2023GL104431. doi:10.1029/2023GL104431
Liemohn, M. W., Jahn, J.-M., Ilie, R., Ganushkina, N. Y., Welling, D. T., Elliott, H. A., et al. (2024). Reconstruction analysis of global ionospheric outflow patterns. J. Geophys. Res. Space Phys. 129, e2023JA032238. doi:10.1029/2023JA032238
Lifshitz, E. M., and Pitaevski, L. P. (1981). “Chapter III - collisionless plasmas,”. Course of theoretical physics, physical kinetics (Pergamon), 10, 115–167. doi:10.1016/B978-0-08-026480-6.50008-4
Lysak, R. L. (2023). Kinetic Alfvén waves and auroral particle acceleration: a review. Rev. Mod. Plasma Phys. 7, 6. doi:10.1007/s41614-022-00111-2
Ma, Q., Li, W., Yue, C., Thorne, R. M., Bortnik, J., Kletzing, C. A., et al. (2019). Ion heating by electromagnetic ion cyclotron waves and magnetosonic waves in the Earth's inner magnetosphere. Geophys. Res. Lett. 46, 6258–6267. doi:10.1029/2019GL083513
Malaspina, D. M., Jaynes, A. N., Hospodarsky, G., Bortnik, J., Ergun, R. E., and Wygant, J. (2017). Statistical properties of low-frequency plasmaspheric hiss. J. Geophys. Res. Space Phys. 122, 8340–8352. doi:10.1002/2017JA024328
Maldonado, C., Delzanno, G. L., Lira, P. R., Lee, J., Larsen, B., Wilson, G., et al. (2023a). The critical need for innovations in instruments and techniques to enable in-situ cold ion and cold electron measurements within the magnetosphere. Bull. AAS 55 (3). doi:10.3847/25c2cfeb.74de952f
Maldonado, C. A., Resendiz Lira, P. A., Delzanno, G. L., Larsen, B. A., Reisenfeld, D. B., and Coffey, V. (2023b). A review of instrument techniques to measure magnetospheric cold electrons and ions. Front. Astron. Space Sci. 9, 1005845. doi:10.3389/fspas.2022.1005845
Mann, I. R., Wright, A. N., Mills, K. J., and Nakariakov, V. M. (1999). Excitation of magnetospheric waveguide modes by magnetosheath flows. J. Geophys. Res. 104 (A1), 333–353. doi:10.1029/1998JA900026
McPherron, R. L. (2005). Magnetic pulsations: their sources and relation to solar wind and geomagnetic activity. Surv. Geophys. 26 (5), 545–592. doi:10.1007/s10712-005-1758-7
Meredith, N. P., Bortnik, J., Horne, R. B., Li, W., and Shen, X.-C. (2021). Statistical investigation of the frequency dependence of the chorus source mechanism of plasmaspheric hiss. Geophys. Res. Lett. 48, e2021GL092725. doi:10.1029/2021GL092725
Meredith, N. P., Horne, R. B., Clilverd, M. A., Horsfall, D., Thorne, R. M., and Anderson, R. R. (2006). Origins of plasmaspheric hiss. J. Geophys. Res. 111, A09217. doi:10.1029/2006JA011707
Nunn, D. (2021). The numerical simulation of the generation of lower-band VLF chorus using a quasi-broadband Vlasov Hybrid Simulation code. Earth Planets Space 73, 222. doi:10.1186/s40623-021-01549-3
Olsen, R. C. (1981). Equatorially trapped plasma populations. J. Geophys. Res. 86 (A13), 11235–11245. doi:10.1029/JA086iA13p11235
Omidi, N., Thorne, R. M., and Bortnik, J. (2010). Nonlinear evolution of EMIC waves in a uniform magnetic field: 1. Hybrid simulations. J. Geophys. Res. 115, A12241. doi:10.1029/2010JA015607
Omura, Y., Katoh, Y., and Summers, D. (2008). Theory and simulation of the generation of whistler-mode chorus. J. Geophys. Res. 113 (A4), 223. doi:10.1029/2007JA012622
Ozeke, L. G., and Mann, I. R. (2008). Energization of radiation belt electrons by ring current ion driven ULF waves. J. Geophys. Res. 113, A02201. doi:10.1029/2007JA012468
Perraut, S., Roux, A., Robert, P., Gendrin, R., Sauvaud, J.-A., Bosqued, J.-M., et al. (1982). A systematic study of ULF Waves above FH+ from GEOS 1 and 2 Measurements and Their Relationships with proton ring distributions. J. Geophys. Res. 87 (A8), 6219–6236. doi:10.1029/JA087iA08p06219
Ren, J., Zong, Q.-G., Miyoshi, Y., Zhou, X. Z., Wang, Y. F., Rankin, R., et al. (2017). Low-energy (<200 eV) electron acceleration by ULF waves in the plasmaspheric boundary layer: Van Allen Probes observation. J. Geophys. Res. Space Phys. 122, 9969–9982. doi:10.1002/2017JA024316
Ren, J., Zong, Q. G., Zhou, X. Z., Spence, H. E., Funsten, H. O., Wygant, J. R., et al. (2019). Cold plasmaspheric electrons affected by ULF waves in the inner magnetosphere: a Van Allen Probes statistical study. J. Geophys. Res. Space Phys. 124, 7954–7965. doi:10.1029/2019JA027009
Ripoll, J.-F., Pierrard, V., Cunningham, G. S., Chu, X., Sorathia, K. A., Hartley, D. P., et al. (2023). Modeling of the cold electron plasma density for radiation belt physics. Front. Astron. Space Sci. 10, 1096595. doi:10.3389/fspas.2023.1096595
Roux, A., Perraut, S., Rauch, J. L., de Villedary, C., Kremser, G., Korth, A., et al. (1982). Wave-particle interactions near ΩHe+ observed on board GEOS 1 and 2: 2. Generation of ion cyclotron waves and heating of He+ ions. J. Geophys. Res. 87 (A10), 8174–8190. doi:10.1029/JA087iA10p08174
Roytershteyn, V., and Delzanno, G. L. (2021). Nonlinear coupling of whistler waves to oblique electrostatic turbulence enabled by cold plasma. Phys. Plasmas 28 (4), 042903. doi:10.1063/5.0041838
Roytershteyn, V., Delzanno, G. L., and Holmes, J. C. (2024). Oblique instability of quasi-parallel whistler waves in the presence of cold and warm electron populations. Front. Astron. Space Sci. 11, 1359112. doi:10.3389/fspas.2024.1359112
Russell, C. T., Holzer, R. E., and Smith, E. J. (1970). OGO 3 observations of ELF noise in the magnetosphere: 2. The nature of the equatorial noise. J. Geophys. Res. 75 (4), 755–768. doi:10.1029/JA075i004p00755
Schulz, M., and Lanzerotti, L. J. (1974). Particle diffusion in the radiation belts. New York: Springer.
Shen, X. C., Zong, Q.-G., Shi, Q. Q., Tian, A. M., Sun, W. J., Wang, Y. F., et al. (2015). Magnetospheric ULF waves with increasing amplitude related to solar wind dynamic pressure changes: the Time History of Events and Macroscale Interactions during Substorms (THEMIS) observations. J. Geophys. Res. Space Phys. 120, 7179–7190. doi:10.1002/2014JA020913
Shklyar, D. R. (2017). Energy transfer from lower energy to higher-energy electrons mediated by whistler waves in the radiation belts. J. Geophys. Res. Space Phys. 122, 640–655. doi:10.1002/2016JA023263
Shprits, Y. Y., Kellerman, A. C., Drozdov, A. Y., Spence, H. E., Reeves, G. D., and Baker, D. N. (2015). Combined convective and diffusive simulations: VERB-4D comparison with 17 March 2013 Van Allen Probes observations. Geophys. Res. Lett. 42, 9600–9608. doi:10.1002/2015GL065230
Southwood, D. J. (1974). Some features of field line resonances in the magnetosphere. Planet. Space Sci. 22, 483–491. doi:10.1016/0032-0633(74)90078-6
Southwood, D. J., Dungey, J. W., and Etherington, R. J. (1969). Bounce resonant interaction between pulsations and trapped particles, Planet. Space Sci., 17(3), 349–361. doi:10.1016/0032-0633(69)90068-3
Thorne, R. M. (2010). Radiation belt dynamics: the importance of wave-particle interactions. Geophys. Res. Lett. 37, L22107. doi:10.1029/2010GL044990
Thorne, R. M., and Horne, R. B. (1992). The contribution of ion-cyclotron waves to electron heating and SAR-arc excitation near the storm-time plasmapause. Geophys. Res. Lett. 19, 417–420. doi:10.1029/92GL00089
Tian, S., Lyons, L. R., Nishimura, Y., Wygant, J. R., Lysak, R. L., Ferradas, C. P., et al. (2022). Auroral beads in conjunction with kinetic Alfvén waves in the equatorial inner-magnetosphere. Geophys. Res. Lett. 49, e2022GL098457. doi:10.1029/2022GL098457
Tsurutani, B. T., and Smith, E. J. (1977). Two types of magnetospheric ELF chorus and their substorm dependences. J. Geophys. Res. 82, 5112–5128. doi:10.1029/JA082i032p05112
Usanova, M., Delzanno, G. L., Chu, X., Gallagher, D., Lee, J., Lund, E., et al. (2023b). Cold ion heating in Earth’s magnetosphere. Bull. AAS 55 (3). doi:10.3847/25c2cfeb.339841dc
Usanova, M. E. (2021). Energy exchange between electromagnetic ion cyclotron (EMIC) waves and thermal plasma: from theory to observations. Front. Astron. Space Sci. 8, 744344. doi:10.3389/fspas.2021.744344
Usanova, M. E., and Ergun, R. E. (2022). Electron energization by high-amplitude turbulent electric fields: a possible source of the outer radiation belt. J. Geophys. Res. Space Phys. 127, e2022JA030336. doi:10.1029/2022JA030336
Usanova, M. E., Ergun, R. E., and Stawarz, J. E. (2023a). Ion energization by turbulent electric fields in fast earthward flows and its implications for the dynamics of the inner magnetosphere. J. Geophys. Res. Space Phys. 128, e2023JA031704. doi:10.1029/2023JA031704
Usanova, M. E., Mann, I. R., Bortnik, J., Shao, L., and Angelopoulos, V. (2012). THEMIS observations of electromagnetic ion cyclotron wave occurrence: dependence on AE, SYMH, and solar wind dynamic pressure. J. Geophys. Res. 117, A10218. doi:10.1029/2012JA018049
Usanova, M. E., Reid, R. A., Xu, W., Marshall, R. A., Starks, M. J., and Wilson, G. R. (2022). Using VLF transmitter signals at LEO for plasmasphere model validation. J. Geophys. Res. Space Phys. 127, e2022JA030345. doi:10.1029/2022JA030345
Usanova, M. E., Woodger, L. A., Blum, L. W., Ergun, R. E., Girard, C., Gallagher, D. L., et al. (2024). H+, He+, He++, O++, N+ EMIC wave occurrence and its dependence on geomagnetic conditions: results from 7 years of Van Allen Probes observations. J. Geophys. Res. Space Phys. 129, e2024JA032627. doi:10.1029/2024JA032627
Walker, A. D. M. (1976). The theory of whistler propagation. Rev. Geophys. 14 (4), 629–638. doi:10.1029/RG014i004p00629
Wang, B., Li, P., Huang, J., and Zhang, B. (2019). Nonlinear Landau resonance between EMIC waves and cold electrons in the inner magnetosphere. Phys. Plasmas 26, 042903. doi:10.1063/1.5088374
Yeoman, T. K., Klimushkin, D. Y., and Mager, P. N. (2010). Intermediate-m ULF waves generated by substorm injection: a case study. Ann. Geophys. 28, 1499–1509. doi:10.5194/angeo-28-1499-2010
Young, D. T., Perraut, S., Roux, A., deVilledary, C., Gendrin, R., Korth, A., et al. (1981). Wave-particle interactions near ΩHe+ observed on GEOS 1 and 2 1. Propagation of ion cyclotron waves in He+-rich plasma. J. Geophys. Res. 86 (A8), 6755–6772. doi:10.1029/JA086iA08p06755
Yu, X., Yuan, Z., and Ouyang, Z. (2021). First observations of O2+ band EMIC waves in the terrestrial magnetosphere. Geophys. Res. Lett. 48, e2021GL094681. doi:10.1029/2021GL094681
Yuan, Z., Xiong, Y., Huang, S., Deng, X., Pang, Y., Zhou, M., et al. (2014). Cold electron heating by EMIC waves in the plasmaspheric plume with observations of the Cluster satellite. Geophys. Res. Lett. 41, 1830–1837. doi:10.1002/2014GL059241
Yuan, Z., Yu, X., Huang, S., Qiao, Z., Yao, F., and Funsten, H. O. (2018). Cold ion heating by magnetosonic waves in a density cavity of the plasmasphere. J. Geophys. Res. Space Phys. 123, 1242–1250. doi:10.1002/2017JA024919
Yue, C., Li, W., Nishimura, Y., Zong, Q., Ma, Q., Bortnik, J., et al. (2016). Rapid enhancement of low-energy (<100 eV) ion flux in response to interplanetary shocks based on two Van Allen Probes case studies: implications for source regions and heating mechanisms. J. Geophys. Res. Space Phys. 121, 6430–6443. doi:10.1002/2016JA022808
Zhang, S., Tian, A., Degeling, A. W., Shi, Q., Wang, M., Hao, Y., et al. (2019). Pc4-5 poloidal ULF wave observed in the dawnside plasmaspheric plume. J. Geophys. Res. Space Phys. 124, 9986–9998. doi:10.1029/2019JA027319
Zhou, Q., Xiao, F., Yang, C., He, Y., and Tang, L. (2013). Observation and modeling of magnetospheric cold electron heating by electromagnetic ion cyclotron waves. J. Geophys. Res. Space Phys. 118, 6907–6914. doi:10.1002/2013JA019263
Zolotukhina, N. A., Mager, P. N., and Klimushkin, D.Yu. (2008). Pc5 waves generated by substorm injection: a case study. Ann. Geophys. 26, 2053–2059. doi:10.5194/angeo-26-2053-2008
Keywords: wave-particle interactions, warm plasma, cold plasma, plasmasphere, warm plasma cloak, plasma heating
Citation: Usanova ME, Delzanno GL and Maruyama N (2025) The role of wave-particle interactions in cold and warm plasma heating. Front. Astron. Space Sci. 12:1573386. doi: 10.3389/fspas.2025.1573386
Received: 09 February 2025; Accepted: 14 April 2025;
Published: 13 May 2025.
Edited by:
Kazue Takahashi, Johns Hopkins University, United StatesReviewed by:
Ilya Kuzichev, New Jersey Institute of Technology, United StatesCopyright © 2025 Usanova, Delzanno and Maruyama. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. E. Usanova, bWFyaWEudXNhbm92YUBsYXNwLmNvbG9yYWRvLmVkdQ==
 M. E. Usanova
M. E. Usanova G. L. Delzanno
G. L. Delzanno N. Maruyama
N. Maruyama