Sunward flows in the magnetosheath associated with the magnetic pressure gradient and magnetosheath expansion

A density structure within the magnetic cloud of an interplanetary coronal mass ejection impacted Earth and caused significant perturbations in plasma boundaries. Using spacecraft data, we describe the effects of this structure on the magnetosheath plasma downstream of the bow shock. During this event, the bow shock breathing motion is evident due to changes in the upstream dynamic pressure. A magnetic enhancement forms in the inner magnetosheath and ahead of a plasma compression region. The structure exhibits characteristics of a fast magnetosonic shock wave, propagating earthward and perpendicular to the background magnetic field and further accelerating the already heated magnetosheath plasma. Following these events, a sunward motion of the magnetosheath plasma is observed. Ion distributions show that both the high-density core population and the high-energy tail of the distribution of the distribution propagate sunward, indicating that the sunward flows are caused by magnetic field line expansion in the very low $\beta$ magnetosheath plasma. Rarefaction effects and enhancement of the magnetic pressure in the magnetosheath result in magnetic pressure gradient forcing, which drives the expansion of magnetosheath magnetic field lines. This picture is supported by a reasonable agreement between the estimated plasma accelerations and the magnetic pressure gradient force.

1 Introduction

The magnetosheath region at Earth and other planetary systems lies between the upstream solar wind and the downstream magnetic obstacle (e.g., the magnetosphere or the magnetic pileup boundary). The magnetosheath region contains heated and compressed solar wind plasma that has been scattered and slowed down to subsonic speeds. Solar wind heating involves a variety of microphysical processes that are largely dependent on upstream plasma and shock parameters (Krasnoselskikh et al., 2013; Burgess et al., 2016). These include the bow shock inclination angle $({\theta }_{Bn})$ with respect to the interplanetary magnetic field (IMF) and the upstream Mach number. The magnetosheath plasma downstream of quasi-parallel shocks, where ${\theta }_{Bn}<\sim 45°$ is more turbulent than that in the quasi-perpendicular side of the bow shock. Such asymmetries can continue through the magnetosheath and be imposed on the magnetopause (Madanian et al., 2022; Gurchumelia et al., 2022). At supercritical shocks, heating and energy dissipation occur partly through ion reflection (Schwartz et al., 2022), the rate of which is dependent on the magnetic amplification at the shock and the magnetization (Madanian et al., 2024b). Hot upstream ion populations with larger pitch angles are reflected more easily upon encountering a magnetic boundary (Burgess, 1989). Heavy ions, such as alpha particles and singly charged helium ions in proton-dominated solar wind plasma, interact differently with the bow shock, resulting in an unstable shock layer (Broll et al., 2018; Madanian et al., 2024a).

In addition to upstream effects, the magnetosheath plasma is driven by factors including the deflection pattern around Earth at the point of measurement and transient effects generated locally or transported from downstream, such as surface waves (Plaschke et al., 2013; Burkholder et al., 2023). The energy density of the magnetosheath plasma drives the magnetopause boundary stand-off distance, an important parameter in space physics that determines the state of the magnetosphere and the magnetosphere–solar wind coupling rate. Empirical models relate the location of the magnetopause boundary to the dynamic pressure in the solar wind using the hydrodynamic theory and assuming that flow pressure is entirely converted to thermal pressure in the magnetosheath (Chapman and Ferraro, 1931). Other models also include the IMF $B_z$ component as a proxy to consider the reconnection effects (Shue et al., 1998). The bow shock boundary distance in these models is simply scaled from the magnetopause based on the upstream Mach number in the solar wind (Farris and Russell, 1994).

Magnetosheath plasma jets are periods of high dynamic pressure caused by either increases in density or earthward flow velocity of the magnetosheath plasma (Krämer et al., 2025). Magnetosheath jets are typically localized, constrained in size (Fatemi et al., 2024), and are formed due to a variety of processes, including foreshock effects, upstream discontinuities, and microphysical effects at the bow shock (Plaschke et al., 2018). Discontinuities in the solar wind can also rattle the boundaries. The interaction of a tangential discontinuity (e.g., a density structure) with the bow shock and magnetosphere launches a fast-mode magnetosonic shock wave through the magnetosheath (Maynard et al., 2008; Wu et al., 1993). Another form of magnetic enhancement in the magnetosheath, known as paramagnetic plasmoids, can also form during the passage of upstream discontinuities (Karlsson et al., 2015). Both the fast shocks and paramagnetic plasmoids are compressive structures. Upon encountering the magnetopause, the magnetosheath plasma is typically either deflected around the magnetosphere or enters the magnetosphere through reconnection. The ion plasma $\beta$ difference and the magnetic shear angle between the magnetosphere and magnetosheath plasmas influence the reconnection rate at the magnetopause (Phan et al., 2010).

Sunward flows in the magnetosheath are rare. Some observational studies associate sunward flows with the magnetopause boundary motion in response to either a change in the upstream dynamic pressure or due to indentation of the magnetopause boundary (Siscoe et al., 1980; Shue et al., 2009; Archer et al., 2014; Zhou et al., 2024; Farrugia et al., 2018). As the magnetopause moves outward, it drives the magnetosheath plasma with different $\beta$ and magnetic Reynolds numbers, creating sunward flows. In spacecraft observations, this process is followed by a full or partial magnetopause crossing or the presence of the boundary layer plasma. The specific properties of the magnetosheath plasma have direct consequences on the reconnection rate and the amount of energy transfer at the magnetopause. As such, characterizing the properties and dynamics of the magnetosheath is important in understanding the connected Sun–Earth system. In this paper, we investigate the properties and the underlying cause of sunward flows observed in the Earth’s magnetosheath during a period of very low $\beta$ solar wind flow. The remainder of this paper is organized as follows: analysis of in situ observations of the solitary magnetic enhancement and sunward flows are described in Section 3, discussion and interpretation of results are provided in Section 4, and conclusions are provided in Section 5. Links to data sources are also provided in Section 5.

2 Data and methods

In this study, we use data from the Time History of Events and Macroscale Interactions during Substorms (THEMIS) (Angelopoulos, 2008), Cluster (Escoubet et al., 2001), Magnetospheric Multiscale (MMS) (Burch et al., 2016), and Wind (Harten and Clark, 1995) missions. The fortuitous configuration of these spacecraft on the dayside geospace allows for a multi-point study of this event. The magnetic field data are obtained from the fluxgate magnetometer (FGM) instruments onboard the spacecraft. For THEMIS and MMS, we use 16 Hz magnetic field data products, while for Cluster, the data cadence is 5 Hz. The THEMIS ion data are taken from the reduced distributions of the electrostatic analyzer (ESA). All plasma moments from the THEMIS spacecraft are recalculated from the returned distributions. The solar wind dynamic pressure is calculated from measurements by the Wind Three-Dimension Plasma (3DP) instrument (Lin et al., 1995).

3 Observations and analysis results

In this section, we describe the impact of a density structure in the solar wind on the magnetosheath. The density structure is observed within the magnetic cloud of an interplanetary coronal mass ejection (ICME) observed on 24 April 2023. The upstream solar wind plasma conditions and the interaction of the structure with the Earth’s bow shock have been characterized in earlier studies (Madanian et al., 2024a), and it has been shown that high abundances of protons, alpha particles, and singly charged helium ions exist within the density enhancement. This event caused significant geomagnetic activity and displacement of the bow shock and magnetopause from their nominal positions (Liu et al., 2024). Prior to the onset of the density peak, the solar wind plasma is dominated by the high magnetic pressure in the strong magnetic fields of the magnetic cloud (very low $\beta$ plasma). Figure 1 shows different pressure terms in the solar wind as measured by the solar wind monitor at Lagrange point 1 and shifted to the Earth’s bow shock by a 42-min lag time. The second panel in this figure shows that in the density structure, high dynamic pressures ($P_{\mathit{Dyn.}}=\rho \cdot |V_{SW}{|}^2$, where $\rho$ is the mass density and $|V_{SW}|$ is the solar wind speed) are superimposed on top of the relatively high magnetic pressure solar wind flow.

Figure 1

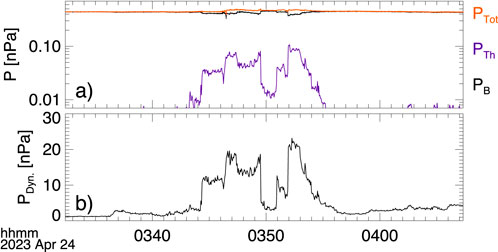
Figure 1. Pressure terms associated with the density structure in the solar wind, as observed by the solar wind monitor. The data have been time-shifted to account for the travel time to Earth’s bow shock. (a) Thermal pressure (blue), magnetic pressure (black), and the total pressure (red). (b) Dynamic pressure.

We analyze data from three constellations of spacecraft, namely, THEMIS, Cluster, and MMS, positioned across the dayside magnetosheath during this event. Figure 2 shows the spacecraft positions with respect to the nominal bow shock and magnetopause boundaries. The conic section parameters are selected to match the MMS1 and THEMIS-E (TH-E) crossings of the bow shock and magnetopause, respectively. The MMS spacecraft are initially inside the magnetosheath and close to the bow shock. We only show data from MMS1 since the four MMS spacecraft are in a close tetrahedron formation and make similar observations. TH-D, TH-A, and TH-E spacecraft are inside the magnetosheath and closer to the nose of the magnetopause, while Cluster 2 (CL2) and CL4 spacecraft are in the magnetosheath, with CL2 positioned above the ecliptic plane and separated from CL4 by 4.3 R_E.

Figure 2

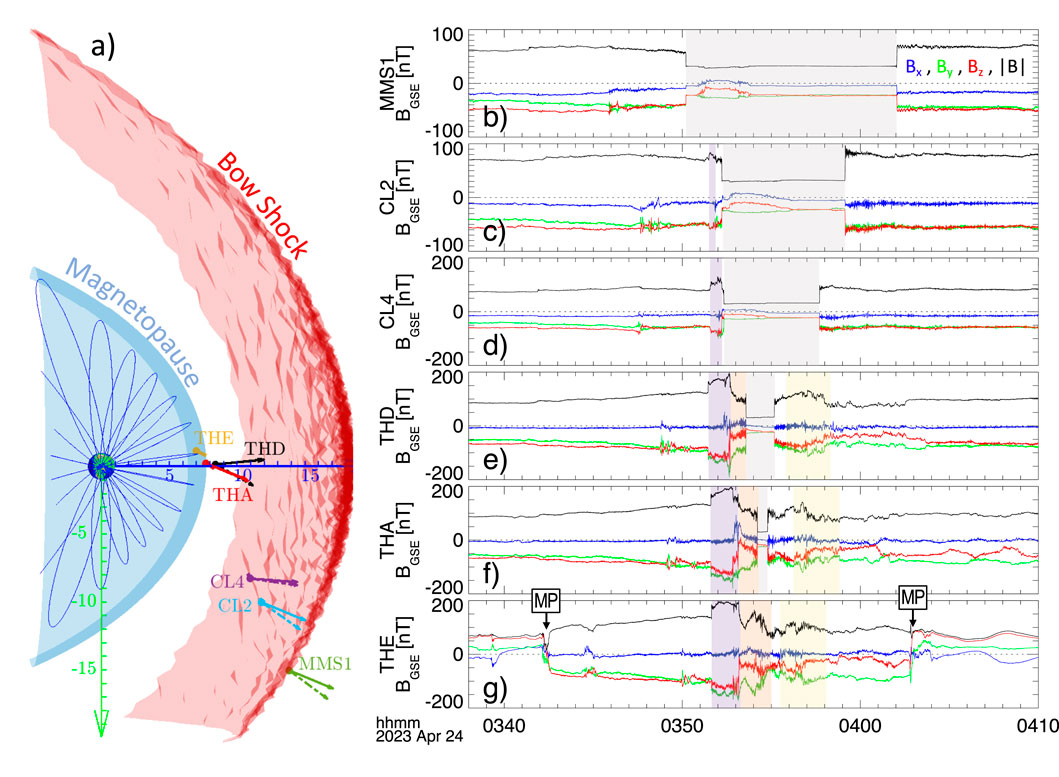
Figure 2. Spacecraft positions and magnetic field measurements. The schematic on the left (panel (a)) shows the projection of spacecraft positions on the $xy$ plane. The axes are in units of Earth radii (R_E). Vector quantities in this figure and throughout the text are given in the geocentric solar ecliptic (GSE) coordinates, where $+x$ points toward the sun, $+y$ is opposite to the planetary orbital motion, and $+z$ completes the right-hand triple. The solid and dashed vectors originating from each spacecraft show the normal vector to the bow shock during its receding and expanding motion, respectively. Panels (b) through (g) show the magnetic field components and magnitude measured by MMS1, CL2, CL4, TH-D, TH-A, and TH-E spacecraft. Shaded areas highlight the following: gray for the solar wind, purple for the fast magnetosonic shock, pink for the density pileup, and yellow for the sunward flow periods. Instances of magnetopause crossing by the TH-E spacecraft are marked by “MP” on the last panel.

The magnetic field measurements by each spacecraft are shown on the right panels in Figure 2. The Earth’s bow shock recedes inward upon encountering the high dynamic pressure structure in the solar wind, placing different spacecraft in the solar wind until it bounces back out. The durations of solar wind segments (the gray shaded areas) are consistent with the spacecraft distances to the bow shock and the bow shock breathing motion. In the solar wind, a rotation in the magnetic field is evident in MMS and CL2 data where the $B_z$ component approaches 0. This magnetic perturbation also coincides with the second density peak of the double-peak density structure. The inward motion of the bow shock stops below the TH-A spacecraft as TH-E never crosses the bow shock or encounters the solar wind. Before the end of the period, the TH-E magnetic field data in Figure 2g show a magnetopause crossing at $\sim$ 04:03:00 UT where $B_z$ changes sign from negative in the magnetosheath to positive in the magnetosphere. The magnetic field strength, however, remains roughly similar or slightly decreases from the magnetosheath to the magnetosphere. With the exception of the beginning and ending intervals when TH-E is in the magnetosphere, the spacecraft is in the magnetosheath region. Other spacecraft (MMS, CL2, CL4, TH-D, and TH-A) also observe the magnetosheath plasma, except when excursions into the solar wind occur.

We determine the normal vector direction during contraction and expansion motions (each side of the gray shaded areas in Figure 2) using the minimum variance analysis (MVA) (Sonnerup and Cahill, 1967). The solid vectors at each spacecraft in Figure 2a show the normal vectors during the inward motion, while the dashed vectors are determined for the expanding bow shock. Based on the orientation of the normal vectors, it appears that the bow shock is more curved during the expansion motion than during the receding motion. The sequence of bow shock crossings also indicates that the bow shock contraction occurs faster than its expansion at Cluster and MMS orbits, while it expands faster near the nose region where the THEMIS spacecraft are positioned. We compared MVA estimates of the normal vector with estimates from the mixed coplanarity method. For several crossings, the two estimates are consistent and within a few degrees ($<10°$), while a few other estimates, particularly during the contraction phase, show larger discrepancies. Details of the MVA and mixed coplanarity analyses and spacecraft positions are listed in Supplementary Table S1. Normal vectors in Figure 2 are from the MVA analysis.

3.1 Magnetic enhancement in the magnetosheath

An interesting feature observed inside the magnetosheath and ahead of the receding bow shock is the magnetic enhancement observed by all THEMIS and Cluster spacecraft in Figure 2. This structure is marked with purple boxes in the magnetic field time series data. The sequence of observations in the time series data begins with TH-D at 03:51:26 UT. The CL2 spacecraft observes the enhancement 4 s after TH-D, and TH-A and TH-E observe the onset of the enhancement within 9 and 12 s, respectively, after TH-D. The initial magnetic jump ratio (enhancement from the ambient magnetosheath field) is $\sim 1.3$ in all spacecraft that observe the enhancement. The magnetic field continues to grow, and the ratio increases to 1.4 and 1.5 at TH-E and TH-A, respectively, and $\sim 1.6$ at CL4. The MMS spacecraft does not show any increase in $|\mathbf{B}|$ other than the jump associated with the bow shock crossing.

Figure 3 shows the plasma and field measurements by TH-E around the magnetic peak identified by vertical dashed lines. The magnetic field components in panel (b) indicate that the field increases along the background magnetic field, while the normal vector to the shock front is mostly along the Sun–Earth line. The ion energy flux spectrogram within the magnetic enhancement in panel (c) shows higher ion energy fluxes across all energies. The flow velocity downstream of the shock is also more anti-sunward. Plasma densities in panel (e) during the magnetic enhancement also increase (both electrons and ions) by roughly similar ratios as those observed for the magnetic field enhancements. Such a correlation in density and magnetic field variations is indicative of the compressional nature of the structure. Using the mixed coplanarity method, we obtain the shock normal vector $n=[-0.90,0.09,0.43]$ at TH-E and $n=[-0.86,-0.27,0.43]$ at TH-D. The shock normal is almost exactly perpendicular to the upstream magnetic field at TH-D, while it becomes less oblique at TH-E. The propagation direction, flow velocity pattern, and compressional feature indicate that the magnetic enhancement is consistent with an FMSW propagating in the magnetosheath.

Figure 3

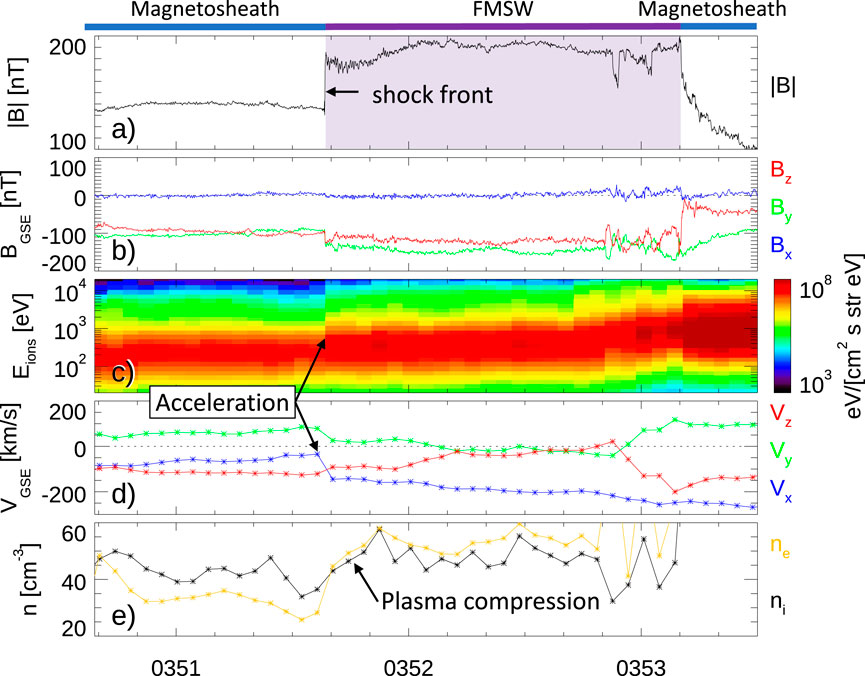
Figure 3. Magnetic field and plasma measurements around the magnetic enhancement structure measured by the TH-E spacecraft. (a,b) Magnetic field magnitude and components, (c) ion energy flux spectrogram, and (d,e) plasma velocity and density, respectively. The fast magnetosonic shock wave (FMSW) and signatures of acceleration and compression by the shock are annotated in the figure.

The magnetic enhancement ends with a sudden decrease in the absolute value of the $|B_z|$ component of the magnetic field. High ion-flux intensities at approximately 800 eV in panel (c) after the second vertical dashed line are reminiscent of the density peak in the solar wind downstream of the bow shock. A significant plasma pileup in the magnetosheath between the magnetic structure and the receding bow shock is evident in plasma densities in the last panel of Figure 3. The density pileup is associated with the compressed solar wind during the density peak and likely includes protons, alpha particles, and He⁺ ions. The ion energy spectra upstream of the receding bow shock in the solar wind (approximately 03:54:30 UT) show the cold proton beam and additional populations of alpha particles and He⁺ at higher energies within the density structure. It is also worth noting that prior to the arrival of the fast magnetosonic shock wave, the magnetic field strength in the magnetosheath exhibits a gradual increase, which is most noticeably visible in TH-E data in Figure 2g. This magnetic field enhancement could be associated with the precursor particles from the upstream density structure entering the magnetosheath before the main density enhancement occurs. However, the sharp jump in the magnetic field corresponding to the fast shock is clearly noticeable in all THEMIS spacecraft. Such a structure not only pushes the magnetopause to move further inward but also increases and adds to the magnetic energy density of the magnetosheath plasma near the magnetopause.

3.2 Sunward flows

The passage of the density structure through the magnetosheath and the breathing motion of the bow shock are followed by sunward plasma flows in the magnetosheath. These flows are observed by TH-D, TH-A, and TH-E spacecraft and are shown in Figure 4. Measurements of the proton plasma from CL4 (not shown) do not indicate any signs of sunward flows, while the MMS spacecraft near the bow shock measures anti-sunward flows (Madanian et al., 2024a). Therefore, the extent of sunward flows is limited to the inner magnetosheath. The periods of sunward flows $(+V_x)$ are highlighted with yellow in the velocity panels (b), (e), and (h) in Figure 4. TH-D and TH-A measurements are also interrupted by an excursion into the solar wind.

Figure 4

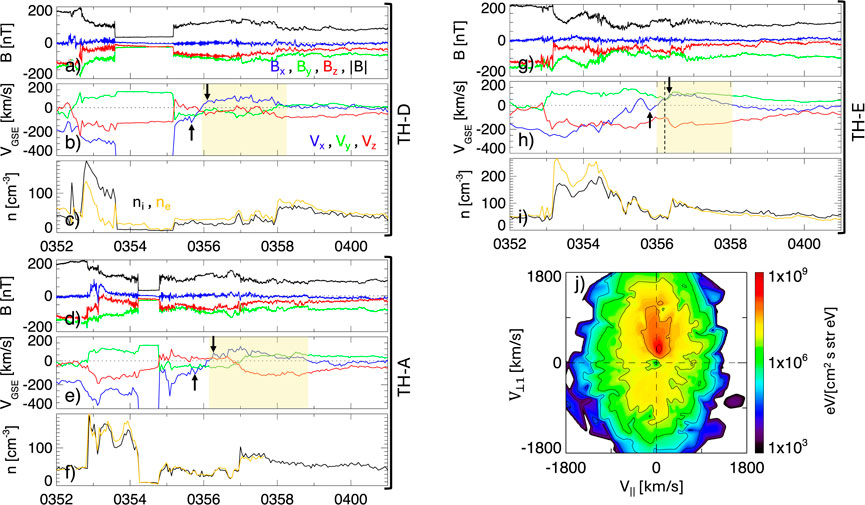
Figure 4. Sunward flows in the magnetosheath plasma. Magnetic field, the plasma velocity, and ion (black) and electron (gold) densities are shown from TH-D in panels (a–c), TH-A in panels (d–f), and TH-E in panels (g–i). Panel j shows a cut-through ion distributions in the $V_{\Vert }-V_{\perp 1}$ plane at the time of the vertical dashed line in TH-E data. $V_{\Vert }$ is parallel to the magnetic field, and $V_{\perp 1}$ is perpendicular to the field and along the flow velocity. The yellow shaded areas highlight the periods of sunward flows. The black arrows on the velocity panels indicate data points used in linear fits to estimate the expansion rates.

The flow reversal from anti-sunward to sunward directions begins with flow becoming less anti-sunward, and the initial part of the flow reversal can be due to the reduction in flux or slow-down of the anti-sunward flow (i.e., transition to the fully heated solar wind plasma). As the magnetosheath plasma flow becomes sunward, the plasma densities decrease to values comparable to those observed during the fast magnetosonic shock structure (i.e., at the beginning of each interval in panels (c), (f), and (i)). The maximum sunward plasma speed $(V_x)$ at TH-E, TH-A, and TH-D reaches as high as 94, 113, and 107 km/s, respectively. We estimate the plasma expansion acceleration rate along the Sun–Earth line in time-series data using the $V_x$ component changes, between the black arrows, and obtain sunward plasma accelerations of $d{v}_x/dt=6.7$, 5.8, and 4.2 km/s² for TH-D, TH-A and TH-E, respectively.

The distribution cut in Figure 4j in the $BV$ plane is produced from TH-E ion distribution data (at the vertical dashed line in panel h) and shows ions at different energies in both sunward and anti-sunward directions and both parallel and anti-parallel to the magnetic field. Higher-energy ions are more abundant in the perpendicular direction to the magnetic field. Determining which segment of the ion distribution constitutes the sunward flow helps in identifying the source and the underlying plasma mechanism(s). In Figure 5, we calculate partial moments of ions at different energy ranges from TH-D ion distributions. Panels (a) and (b) show the magnetic field and energy spectra downstream of the bow shock and when sunward flows are observed. The bow shock is quasi-perpendicular. In the next two panels, the plasma velocity and density of all ions are shown (similar to Figures 4b,c). The flow reversal period is evident at approximately 03:55:50 UT. In panels (e) and (f), we show the velocity vectors and densities of 3 keV–10 keV ions. These ions include mostly alpha particles and singly charged helium ions that are present during this event, in addition to the high-energy tail of the proton distributions. Abundances of heavy, helium group ions and protons in the solar wind decrease near the end of the density structure (see panels f and h). Typically, in the downstream region of a quasi-perpendicular shock, ions begin to gyrate and have a velocity component perpendicular to the background magnetic field, and their guiding center is pointed downstream. However, after the initial earthward motion at the beginning of the interval, high-energy ions begin to propagate sunward. Similar behavior is observed at lower energy ranges. Thus, the plasma as a whole moves sunward, while ions gyrate around the background magnetic field.

Figure 5

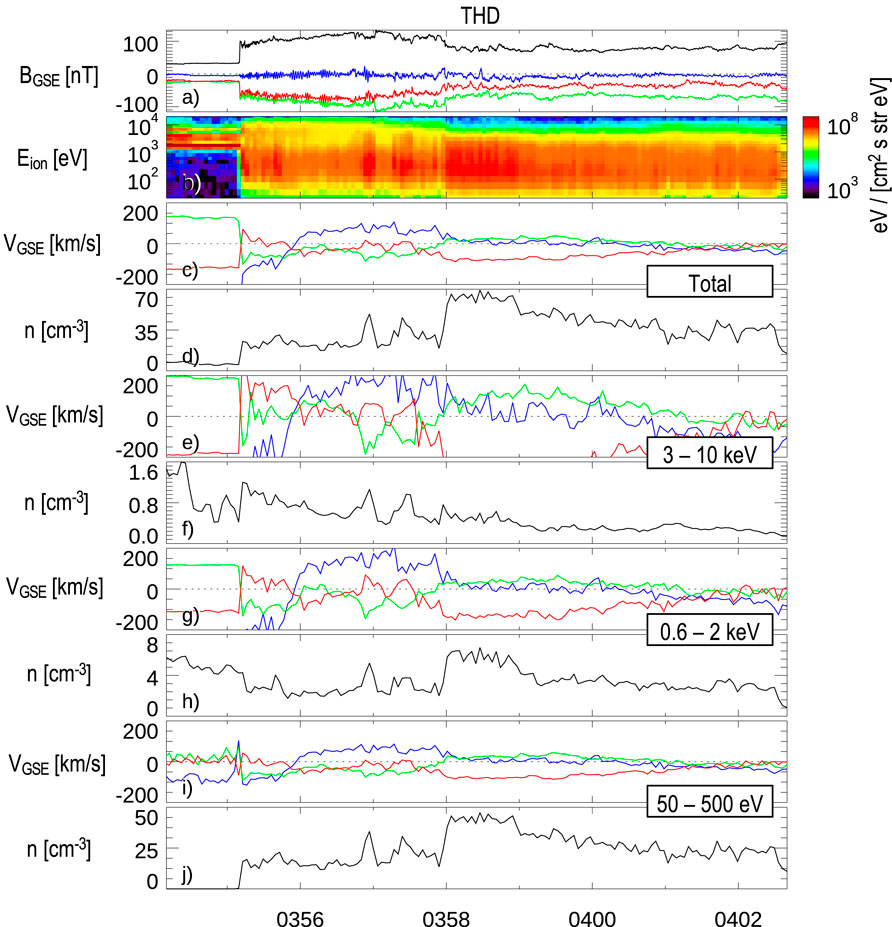
Figure 5. Partial moment analysis of sunward flows observed by the THD spacecraft. (a) Magnetic field data, (b) ion energy flux spectrogram, and (c,d) ion velocity and density, respectively, for all ions (of all measured energies); (e,f) 3–10 keV ions, (g,h) 0.6–2 keV ions, and (i,j) 50 eV–500 eV ions. The flow velocity and magnetic field components along $x$, $y$, and $z$ are shown in blue, green, and red colors, respectively.

4 Discussion

4.1 Solitary magnetic structure in the magnetosheath

Unlike the observation sequence of the receding bow shock that follows the spacecraft distances from the bow shock, the first observation of the magnetosonic shock wave in the magnetosheath is by the TH-D probe, which is downstream of the Cluster spacecraft. The MMS spacecraft positioned immediately downstream of the bow shock does not show such a magnetic enhancement. Therefore, it appears that certain conditions in the magnetosheath must be present for the fast magnetosonic shock to form, rather than being launched immediately at the bow shock. The high abundances of alpha particles and singly charged helium ions during this event result in these ion populations (and also protons, but to a lesser degree) traveling at super-Alfvénic speeds in the magnetosheath upon crossing the bow shock (Madanian et al., 2024a). If a fraction of ions crossing the bow shock remain super-Alfvénic, they can cause perturbations in the magnetosheath to generate additional heating. Alpha particles and He⁺ ions can change the accuracy of the reported plasma moments. These ions can also modify the underlying assumptions used for the fluid approximation of a planar shock (Lin et al., 2006).

While the magnetic field enhancement across the fast shock wave is along the background magnetic field, the wavefront propagates perpendicular or at highly oblique angles to the background magnetic field. The timing analysis of the shock front observations indicates that the shock wave traveled the 0.7 R_E distance along the Sun–Earth line between TH-D and TH-A spacecraft at a speed of $\sim 440$ km/s, which is comparable to the fast mode wave speed in the magnetosheath ($V_f=453$ km/s). $V_f$ increases to $\sim 550$ km/s downstream of the shock. The conservation of mass flux $([\rho v_n]=0)$ across the shock at TH-D results in a shock speed of $v_n=241$ km/s. If we assume that the difference in density between the upstream and downstream of the shock is due to helium group ions, $v_n$ increases to $\sim 413$ km/s. However, doing so increases the divergence in the tangent component of the electric field across the shock. It is also worth noting that the TH-D spacecraft observes the magnetosheath shock before the spacecraft upstream and downstream of it (e.g., TH-A and CL2), indicating that the Earthward propagating shock structure does not necessarily originate at the bow shock. Instead, it develops inside the magnetosheath when certain conditions are met. The shock front remains fairly unperturbed as it propagates through the inner magnetosheath, which is rare for any plasma structure in the typically turbulent magnetosheath plasma. The unperturbed nonlinear propagation pattern is suggestive of a soliton-like shock formation process. Regardless of the formation mechanism, such a magnetic enhancement increases the magnetic energy density near the magnetopause.

4.2 Cause of sunward flows

Observations of sunward flows thus far have been associated with the sunward motion of the magnetopause boundary and pressure gradient forces driving the plasma (Archer et al., 2015; Shue et al., 2009). During the event discussed in this study, due to strong magnetic fields within the magnetic cloud flux rope, the ion $\beta$ in the solar wind is extremely low $(\beta \ll 1)$, and it remains low even inside the magnetosheath (e.g., $\beta$ is $\sim 0.2$ at TH-D during the sunward flows). Thus, the plasma dynamics in the magnetosheath are dominated by the magnetic field, and a thermal plasma pressure gradient cannot drive the sunward flows in the magnetosheath. Instead, the enhanced magnetic field pressure in the inner magnetosheath responds to the upstream pressure changes by creating a magnetic pressure gradient force perpendicular to the background magnetic field. Given that the magnetic fields in the inner magnetosheath are dominated by $B_y$ and $B_z$ components, such a gradient force would drive the magnetosheath magnetic field lines along $x$ to expand toward rarefied upstream regions. This picture is consistent with the observations in Figures 4a,d,g, where higher magnetic field strengths emerge with sunward flows. In addition, the higher expansion rate observed at TH-D than at TH-A and TH-E is in agreement with a magnetosheath expansion in response to an upstream pressure decrease. During the magnetosheath sunward flows shown in Figure 4, the magnetic field lines in the magnetosheath are almost entirely perpendicular to the Sun–Earth line $(B_x\sim 0)$. As such, ions cannot stream along the magnetic field line to travel sunward. In addition, Figure 5 shows that ions in all energies have a net sunward flow, including high-energy ions in the 3–10 keV energy range. In strong magnetic fields of $\sim$ 120 nT, these ions are bound to the field lines with rather small gyroradii of $\sim 65-120$ km, and their dynamics (e.g., through reflection) cannot explain the observed sunward plasma flows in the magnetosheath (Fuselier et al., 1991; Farrugia et al., 2018). It seems, however, that the sunward plasma flows are the result of the sunward motion of the magnetic flux tubes and field lines.

As discussed in Section 3.1, the earthward propagating shock causes enhancement of the magnetic pressure in the magnetosheath. Figure 6a shows magnetic pressure terms from TH-A and TH-D spacecraft. In panel (b), we estimate instantaneous acceleration rates projected along the Sun–Earth line using $a_x=\frac{1}{\rho }{\nabla }_x{P}_B$, where $\rho$ is the proton mass density at TH-D. The average of instantaneous acceleration rates between vertical dashed lines results in an average acceleration rate of 2.9 km/s², which is comparable to the acceleration rate of 6.7 km/s² obtained from plasma velocities in panel (c) in the same period. This agreement between plasma acceleration and pressure gradient forcing indicates that magnetosheath sunward flows are caused by magnetosheath expansion. Data in Figure 6 also indicate that after 03:58:00 UT, magnetic pressure variations in both spacecraft decrease, and the estimated acceleration rates reduce to very small values. At this time, MMS is still in the solar wind (Figure 2b), and the magnetic pressure gradient effects have already subsided due to a short temporal scale before MMS returns to the magnetosheath, which could explain why it did not measure sunward plasma flows.

Figure 6

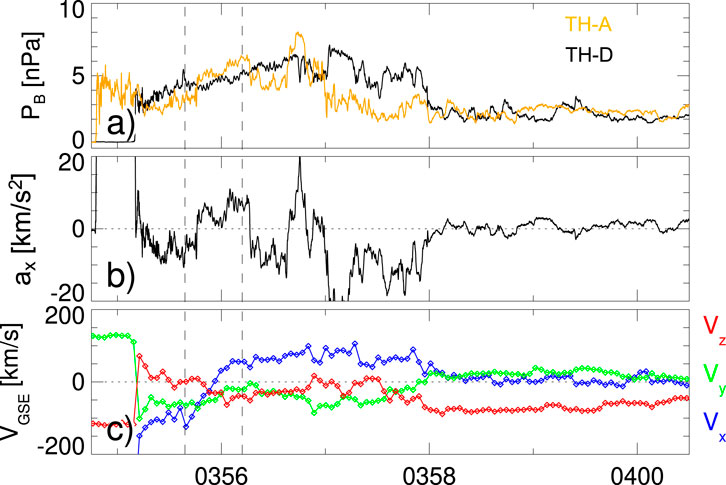
Figure 6. Magnetic pressure gradient observed by the THEMIS spacecraft. (a) Magnetic pressures from TH-D and TH-A, (b) plasma acceleration along the Sun–Earth line, and (c) ion velocities at TH-D.

Our observations further indicate that the sunward flows are unrelated to the magnetopause boundary motion. Magnetic field measurements during the magnetopause boundary crossing at 04:03:00 UT by the TH-E spacecraft in Figure 2g indicate that the magnetic pressure in the magnetosheath is slightly higher than the magnetospheric magnetic pressure. Thus, the magnetopause motion is limited by the high magnetic pressure in the magnetosheath, and the magnetopause is controlled by the strong magnetic fields within the magnetosheath. In addition, a sunward magnetopause boundary motion leads to a more consistent flow pattern across different THEMIS spacecraft. In Figure 4, when the sunward flows at TH-E begin to slow down at $\sim$ 03:57:00 UT, sunward flows at TH-D continue at the same rate and even increase at times. The observed sunward plasma flows are rather smooth and even plateau at certain velocities and are unlikely to originate at a distant reconnection zone as we see no signs of the boundary layer plasma.

5 Conclusion

In this study, we characterize a series of events in the magnetosheath caused by the interaction of an upstream density structure embedded within a strong flux rope of an ICME. Strong magnetic fields within the magnetic cloud of the ICME dominate the plasma interactions within the magnetosheath and magnetopause. We show evidence for the formation of a magnetic enhancement in the inner magnetosheath associated with a fast magnetosonic shock wave caused by the sudden surge of upstream charged particles and the associated dynamic pressure pulse. We find that the sunward flows are formed due to magnetosheath expansion and the sunward motion of the flux tubes driven by the magnetic pressure gradient force in the inner magnetosheath, with sunward expansion rates as high as 6.7 km/s². The rarefaction effects following the density structure cause sunward flows in the magnetosheath, which responds to the upstream dynamic pressure decrease caused by expanding sunward. These events cause significant geomagnetic activity and are significant in space weather.

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found at https://cdaweb.gsfc.nasa.gov/.

Author contributions

HM: Conceptualization, Methodology, Formal analysis, Investigation, Validation, Writing – original draft, Writing – review and editing. YP: Validation, Visualization, Writing – review and editing. RR: Investigation, Writing – review and editing. TL: Investigation, Writing – review and editing. TK: Investigation, Visualization, Writing – review and editing. SR: Investigation, Data curation, Writing – review and editing. DT: Validation, Visualization, Writing – review and editing. JB: Investigation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the NASA MMS project through the Partnership for Heliophysics and Space Environment Research (PHaSER) cooperative agreement. YP-K acknowledges the Research Council of Finland grant number 339756. SR acknowledges funding from the MMS Early Career Award 80NSSC25K7353. RR was supported by the MMS Early Career Grant 80NSSC23K1601.

Acknowledgments

The authors thank the THEMIS, MMS, and Cluster operation teams for making the data available. They acknowledge the THEMIS magnetometer team at the Technical University of Braunschweig for the use of FGM data, provided with the financial support of the German Federal Ministry for Economic Affairs and Climate Action (BMWK) and the German Aerospace Center (DLR) under contract 50 OC 2201.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2025.1574577/full#supplementary-material

References

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141, 5–34. doi:10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Archer, M., Turner, D., Eastwood, J., Schwartz, S., and Horbury, T. (2015). Global impacts of a Foreshock Bubble: magnetosheath, magnetopause and ground-based observations. Planet. Space Sci. 106, 56–66. doi:10.1016/j.pss.2014.11.026

CrossRef Full Text | Google Scholar

Archer, M. O., Turner, D. L., Eastwood, J. P., Horbury, T. S., and Schwartz, S. J. (2014). The role of pressure gradients in driving sunward magnetosheath flows and magnetopause motion. J. Geophys. Res. Space Phys. 119, 8117–8125. doi:10.1002/2014JA020342

CrossRef Full Text | Google Scholar

Broll, J. M., Fuselier, S. A., Trattner, K. J., Schwartz, S. J., Burch, J. L., Giles, B. L., et al. (2018). MMS observation of shock-reflected He ⁺⁺ at Earth’s quasi-perpendicular bow shock. Geophys. Res. Lett. 45, 49–55. doi:10.1002/2017GL075411

CrossRef Full Text | Google Scholar

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric Multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Burgess, D. (1989). Alpha particles in field-aligned beams upstream of the bow shock: simulations. Geophys. Res. Lett. 16, 163–166. doi:10.1029/GL016i002p00163

CrossRef Full Text | Google Scholar

Burgess, D., Hellinger, P., Gingell, I., and Trávníček, P. M. (2016). Microstructure in two- and three-dimensional hybrid simulations of perpendicular collisionless shocks. J. Plasma Phys. 82, 905820401. doi:10.1017/S0022377816000660

CrossRef Full Text | Google Scholar

Burkholder, B. L., Chen, L.-J., Sorathia, K., Sciola, A., Merkin, S., Trattner, K. J., et al. (2023). The complexity of the day-side X-line during southward interplanetary magnetic field. Front. Astronomy Space Sci. 10, 1175697. doi:10.3389/fspas.2023.1175697

CrossRef Full Text | Google Scholar

Chapman, S., and Ferraro, V. C. A. (1931). A new theory of magnetic storms. Terr. Magnetism Atmos. Electr. 36, 77–97. doi:10.1029/TE036i002p00077

CrossRef Full Text | Google Scholar

Escoubet, C. P., Fehringer, M., and Goldstein, M. (2001). IntroductionThe cluster mission. Ann. Geophys. 19, 1197–1200. doi:10.5194/angeo-19-1197-2001

CrossRef Full Text | Google Scholar

Farris, M. H., and Russell, C. T. (1994). Determining the standoff distance of the bow shock: Mach number dependence and use of models. J. Geophys. Res. 99, 17681–17689. doi:10.1029/94JA01020

CrossRef Full Text | Google Scholar

Farrugia, C. J., Cohen, I. J., Vasquez, B. J., Lugaz, N., Alm, L., Torbert, R. B., et al. (2018). Effects in the near-magnetopause magnetosheath elicited by large-amplitude alfvénic fluctuations terminating in a field and flow discontinuity. J. Geophys. Res. Space Phys. 123, 8983–9004. doi:10.1029/2018JA025724

CrossRef Full Text | Google Scholar

Fatemi, S., Hamrin, M., Krämer, E., Gunell, H., Nordin, G., Karlsson, T., et al. (2024). Unveiling the 3D structure of magnetosheath jets. Mon. Notices R. Astronomical Soc. 531, 4692–4713. doi:10.1093/mnras/stae1456

CrossRef Full Text | Google Scholar

Fuselier, S. A., Klumpar, D. M., and Shelley, E. G. (1991). Ion Reflection and transmission during reconnection at the Earth’s subsolar magnetopause. Geophys. Res. Lett. 18, 139–142. doi:10.1029/90GL02676

CrossRef Full Text | Google Scholar

Gurchumelia, A., Sorriso-Valvo, L., Burgess, D., Yordanova, E., Elbakidze, K., Kharshiladze, O., et al. (2022). Comparing quasi-parallel and quasi-perpendicular configuration in the terrestrial magnetosheath: multifractal analysis. Front. Phys. 10, 903632. doi:10.3389/fphy.2022.903632

CrossRef Full Text | Google Scholar

Harten, R., and Clark, K. (1995). The design features of the GGS wind and polar spacecraft. Space Sci. Rev. 71, 23–40. doi:10.1007/BF00751324

CrossRef Full Text | Google Scholar

Karlsson, T., Kullen, A., Liljeblad, E., Brenning, N., Nilsson, H., Gunell, H., et al. (2015). On the origin of magnetosheath plasmoids and their relation to magnetosheath jets: on the origin of magnetosheath plasmoids. J. Geophys. Res. Space Phys. 120, 7390–7403. doi:10.1002/2015JA021487

CrossRef Full Text | Google Scholar

Krämer, E., Koller, F., Suni, J., LaMoury, A. T., Pöppelwerth, A., Glebe, G., et al. (2025). Jets downstream of collisionless shocks: recent discoveries and challenges. Space Sci. Rev. 221, 4. doi:10.1007/s11214-024-01129-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Krasnoselskikh, V., Balikhin, M., Walker, S. N., Schwartz, S., Sundkvist, D., Lobzin, V., et al. (2013). The dynamic quasiperpendicular shock: Cluster discoveries. Space Sci. Rev. 178, 535–598. doi:10.1007/s11214-013-9972-y

CrossRef Full Text | Google Scholar

Lin, C. C., Chao, J. K., Lee, L. C., Lyu, L. H., and Wu, D. J. (2006). A new shock fitting procedure for the MHD Rankine-Hugoniot relations for the case of small He²⁺ slippage. J. Geophys. Res. Space Phys. 111, 2005JA011449. doi:10.1029/2005JA011449

CrossRef Full Text | Google Scholar

Lin, R. P., Anderson, K. A., Ashford, S., Carlson, C., Curtis, D., Ergun, R., et al. (1995). A three-dimensional plasma and energetic particle investigation for the wind spacecraft. Space Sci. Rev. 71, 125–153. doi:10.1007/BF00751328

CrossRef Full Text | Google Scholar

Liu, T. Z., Shi, X., Hartinger, M. D., Angelopoulos, V., Rodger, C. J., Viljanen, A., et al. (2024). Global observations of geomagnetically induced currents caused by an extremely intense density pulse during a coronal mass ejection. Space weather. 22, e2024SW003993. doi:10.1029/2024SW003993

CrossRef Full Text | Google Scholar

Madanian, H., Chen, L.-J., Ng, J., Starkey, M. J., Fuselier, S. A., Bessho, N., et al. (2024a). Interaction of the prominence plasma within the magnetic cloud of an interplanetary coronal mass ejection with the Earth’s bow shock. Astrophysical J. 976, 219. doi:10.3847/1538-4357/ad8579

CrossRef Full Text | Google Scholar

Madanian, H., Gingell, I., Chen, L.-J., and Monyek, E. (2024b). Drivers of magnetic field amplification at oblique shocks: in situ observations. Astrophysical J. Lett. 965, L12. doi:10.3847/2041-8213/ad3073

CrossRef Full Text | Google Scholar

Madanian, H., Liu, T. Z., Phan, T. D., Trattner, K. J., Karlsson, T., and Liemohn, M. W. (2022). Asymmetric interaction of a solar wind reconnecting current sheet and its magnetic hole with Earth’s bow shock and magnetopause. J. Geophys. Res. Space Phys. 127. doi:10.1029/2021JA030079

CrossRef Full Text | Google Scholar

Maynard, N. C., Farrugia, C. J., Ober, D. M., Burke, W. J., Dunlop, M., Mozer, F. S., et al. (2008). Cluster observations of fast shocks in the magnetosheath launched as a tangential discontinuity with a pressure increase crossed the bow shock: fast shocks in the magnetosheath. J. Geophys. Res. Space Phys. 113. doi:10.1029/2008JA013121

CrossRef Full Text | Google Scholar

Phan, T. D., Gosling, J. T., Paschmann, G., Pasma, C., Drake, J. F., Øieroset, M., et al. (2010). The dependence of magnetic reconnection on plasma β and magnetic shear: evidence from solar wind observations. Astrophysical J. 719, L199–L203. doi:10.1088/2041-8205/719/2/L199

CrossRef Full Text | Google Scholar

Plaschke, F., Angelopoulos, V., and Glassmeier, K. (2013). Magnetopause surface waves: THEMIS observations compared to MHD theory. J. Geophys. Res. Space Phys. 118, 1483–1499. doi:10.1002/jgra.50147

CrossRef Full Text | Google Scholar

Plaschke, F., Hietala, H., Archer, M., Blanco-Cano, X., Kajdič, P., Karlsson, T., et al. (2018). Jets downstream of collisionless shocks. Space Sci. Rev. 214, 81. doi:10.1007/s11214-018-0516-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwartz, S. J., Goodrich, K. A., Wilson, L. B., Turner, D. L., Trattner, K. J., Kucharek, H., et al. (2022). Energy partition at collisionless supercritical quasi-perpendicular shocks. J. Geophys. Res. Space Phys. 127, e2022JA030637. doi:10.1029/2022JA030637

CrossRef Full Text | Google Scholar

Shue, J., Chao, J., Song, P., McFadden, J. P., Suvorova, A., Angelopoulos, V., et al. (2009). Anomalous magnetosheath flows and distorted subsolar magnetopause for radial interplanetary magnetic fields. Geophys. Res. Lett. 36, 2009GL039842. doi:10.1029/2009GL039842

CrossRef Full Text | Google Scholar

Shue, J.-H., Song, P., Russell, C. T., Steinberg, J. T., Chao, J. K., Zastenker, G., et al. (1998). Magnetopause location under extreme solar wind conditions. J. Geophys. Res. Space Phys. 103, 17691–17700. doi:10.1029/98JA01103

CrossRef Full Text | Google Scholar

Siscoe, G. L., Crooker, N. U., and Belcher, J. W. (1980). Sunward flow in Jupiter’s magnetosheath. Geophys. Res. Lett. 7, 25–28. doi:10.1029/GL007i001p00025

CrossRef Full Text | Google Scholar

Sonnerup, B. U., and Cahill, L. J. (1967). Magnetopause structure and attitude from Explorer 12 observations. J. Geophys. Res. 72, 171. doi:10.1029/JZ072i001p00171

CrossRef Full Text | Google Scholar

Wu, B. H., Mandt, M. E., Lee, L. C., and Chao, J. K. (1993). Magnetospheric response to solar wind dynamic pressure variations: interaction of interplanetary tangential discontinuities with the bow shock. J. Geophys. Res. 98, 21297–21311. doi:10.1029/93JA01013

CrossRef Full Text | Google Scholar

Zhou, Y., Raptis, S., Wang, S., Shen, C., Ren, N., and Ma, L. (2024). Magnetosheath jets at Jupiter and across the solar system. Nat. Commun. 15, 4. doi:10.1038/s41467-023-43942-4

PubMed Abstract | CrossRef Full Text | Google Scholar