- Swiss Federal Institute of Intellectual Property, Bern, Switzerland
Introduction: Traditionally, the condensation sequence of circumstellar dust is predicted based on the thermodynamic stabilities of specific condensates in the macroscopic bulk phase. However, at the (sub-) nanometer scale clusters with non-crystalline structures and significantly different properties are energetically favoured.
Methods: For this reason, we study the thermodynamic stabilities of metal oxide clusters with generic stoichiometries of M2O3 and M3O4, where M represents a metal atom. With an upper size limit of 50 atoms, we consider clusters with sizes n = 1–10 for (M2O3)n, and n = 1–7 for (M3O4)n. The M2O3 clusters comprise alumina (Al2O3), Mg-rich pyroxene (MgSiO3) and a size-limited sample of titanates (CaTiO3), whereas the M3O4 clusters include spinel (MgAl2O4), Mg-rich olivine (Mg2SiO4) and calcium aluminates (CaAl2O4).
Results: We find that, apart from the alumina monomer, the aluminum-bearing clusters (Al2O3)n, n = 1–10, and (MgAl2O4)n, n = 1–7, are favoured over their silicate counterparts (MgSiO3)n, n = 1–10 and (Mg2SiO4)n, n = 1–7. Also, we find that calcium aluminate clusters, CaAl2O4, are energetically more favourable than magnesium aluminate clusters, MgAl2O4. Furthermore, for a limited data set of (CaTiO3)n, n = 1–2, clusters we find significantly larger stabilities than for the other considered (M2O3)n clusters, namely Al2O3 and MgSiO3.
Discussion: Future investigations, in particular on titanates and on Ca-rich silicates, are required to draw a more thorough and complete picture of the condensation sequence at the (sub-)nanoscale.
1 Introduction
Asymptotic Giant Branch (AGB) stars with their highly dynamical atmospheres and circumstellar envelopes are unique astrochemical laboratories (Höfner and Olofsson, 2018). Shell burning and mixing processes inside of AGB stars lead to a changing elemental composition at the atmosphere over time (Herwig, 2005). In AGB circumstellar envelopes the presence of large-amplitude stellar pulsations, active dust formation from the gas-phase, and maser emission indicate departures from thermodynamic equilibrium conditions, which require non-equilibrium modelling (Gobrecht et al., 2016).
In equilibrium, the chemistry is controlled by the C/O ratio, which is a consequence of the triple bonded CO molecule corresponding to the diatomic species with the highest bond energy (11.3 eV) known. As a result, an oxygen-rich chemistry with C/O < 1 and carbon-rich environments with C/O > 1 are expected, as the CO molecule locks the lesser abundant element (C or O). The observationally confirmed presence of HCN and CS in oxygen-dominated atmospheres (Schöier et al., 2013; Decin et al., 2010), as well as the detection of H2O vapour and SiO in Carbon-rich envelopes challenge this traditional dichotomy (Neufeld et al., 2013; Fonfria et al., 2014). With regard to the dust populations the situation is different. To the best of our knowledge there is no confirmed active carbonaceous dust formation in oxygen-dominated AGB stellar atmospheres and no oxide dust synthesis in carbon-rich AGB envelopes.
Circumstellar dust species in oxygen-rich conditions comprise minerals and amorphous solids that are made of metal oxides with the stoichiometric formula M2O3 including corundum (Al2O3), enstatite (MgSiO3), perovskite (CaTiO3). This is also true for metal oxides with the generic formula M3O4 that includes MgAl2O4 (spinel), CaAl2O4 (krotite), Mg2SiO4 (forsterite). Evidence for the presence of alumina and spinel is found in spectral features observed at around 13 microns (Sloan et al., 2003; Posch et al., 1999), whereas the silicates, here enstatite and forsterite, show Si-O stretching modes at 10 micron and O-Si-O bending modes at around 18 microns (Woolf and Ney, 1969).
Iron-bearing solid oxides like hematite (Fe2O3), ferrosilit (FeSiO3) or fayalite (Fe2SiO4) fall also in the M2O3 and M3O4 stoichiometric families, but are not expected to act as seed particles for dust formation, owing to the too large opacities of the Fe-bearing seeds (Woitke, 2006).
Traditionally, the thermodynamic stabilities of condensates are assessed based on a top-down approach starting with the macroscopic crystalline structure of a specific mineral. In classical nucleation theories (CNTs) the cohesive energy of a microscopic particle like a cluster is determined by an attractive volume term and a repulsive surface term resulting in a spherical particle as lowest-energy geometry. Depending on the material in question, top-down approaches like CNTs can predict reliable particle energies down to typically tens of nanometers, in rare cases even down to a few nanometers.
However, at the nanoscale and below, the lowest energy structures are significantly different from top-down derived geometries. Owing to finite size and quantum effects the properties of the small clusters including atomic coordination, bond lengths, formal charges, dipole moments are notably different from the macroscopic bulk phase. Notably, the most favourable cluster structures are non-crystalline. Therefore, the drawbacks of CNTs at the (sub-)nanoscale comprise the spherical cluster structures, fully coordinated atoms in the homogeneous interior of the cluster, growth by monomeric additions, bimolecular association reactions, and most prominently, unrealistic potential energies.
In this study we will focus on the thermochemistry of bottom-up generated, (sub-)nanometer sized clusters as precursors of dust grains in oxygen-rich circumstellar atmospheres and envelopes. Apart from Al2O3 the clusters presented in this study are ternary oxides comprising two different metal elements. In contrast, binary oxides contain just one type of metal and are therefore chemically and structurally less complex. Still, it is a challenging task to find the lowest-energy isomers referred to as global minima (GM) structures in the case of binary oxide clusters.
Smaller gas phase dust precursors in oxygen-rich environments include simple diatomic and triatomic molecules with well-defined spectroscopic constants, rotational and vibrational transitions. In the case of silicates, a very likely molecular precursor is SiO (Nuth and Donn, 1981), whereas the aluminates including alumina are preceded by AlO and AlOH (Kamiński et al., 2016; Decin et al., 2017; Danilovich et al., 2020). Titanantes originate from TiO and TiO2 molecules showing relatively strong Ti-O bonds (Kamiński et al., 2017; Danilovich et al., 2020). Moreover, the hydroxyl radical, OH, and water vapour, H2O, are considered to act as the most efficient oxidizer of the metal oxide molecules and clusters (Baudry et al., 2023).
In this study we will focus on the thermochemistry of (sub-)nanometersized clusters with M2O3 and M3O4 stoichiometries as precursors of dust grains in oxygen-rich circumstellar atmospheres and envelopes. Moreover, this study aims at overcoming the drawbacks of classical nucleation theories by employing a bottom-up approach using lowest-energy cluster configuration with the most accurate yet affordable quantum calculations, instead of using top-down generated spherical particle structures.
This paper is organized as follows. In Section 2, we describe the methods used to compute the most favourable (M2O3)n and (M3O4)n cluster structures. The results are presented in Section 3. Section 4 discusses our results in the light of previous studies and summarizes our findings.
2 Methods
The energetically most favourable cluster isomers, or GM candidates, of the considered dust precursors of alumina, spinel, Ca aluminates, Mg-rich silicates and calcium titanates were recently investigated. For our purposes we consult the GM candidates for (Al2O3)n, n = 1–10 (Gobrecht et al., 2022), MgAl2O4, CaAl2O4 (Gobrecht et al., 2023), (MgSiO3)n, n = 1–10, (Mg2SiO4)n, n = 1–7 (Macià Escatllar et al., 2019), and (CaTiO3)n, n = 1,2 (Plane, 2013).
A comparison among the trioxides Al2O3, MgSiO3, and CaTiO3 is straightforward as these cluster contain the same number of atoms, metal atoms and oxygen atoms, respectively, per formula unit or cluster size n. The same reasoning is true for a comparison among clusters of MgAl2O4, CaAl2O4 and Mg2SiO4, showing seven atoms per formula unit of which three are metals and four are oxygens. For consistency we apply the B3LYP density functional in combination with a cc-pVTZ basis set including a vibrational frequency analysis for all calculations presented in this study (Becke, 1993). This density functional basis set combination was chosen as a sensible compromise between computational cost and desired accuracy. Moreover, this combination has shown a reasonable agreement with experimental results for transition metal oxides such as titania and vanadia (Sindel et al., 2022; Lecoq-Molinos et al., 2024).
We use the RRHO (Rigid Rotor Harmonic Oscillator) approximation to compute the partition functions of the cluster leading the thermodynamic potential of interest, namely the enthalpy of formation, entropy and Gibbs Free energy of formation. For consistency, all presented quantum-chemical density functional calculations were computed with the Gaussian16 programme suite (Frisch et al., 2016).
3 Results
In Figure 1 the thermodynamic stabilities represented by the normalized Gibbs free energy Δf G(T) of formation of the (M2O3)n clusters are shown as a function of the cluster size n. The energies of CaTiO3 clusters are colour-coded in orange, those of Al2O3 clusters in purple and those of MgSiO3 clusters in green, respectively. Solid lines correspond to a temperature of T = 0 K, dash-dotted lines to a temperature of T = 1000 K, and dashed lines to a temperature of T = 2000 K.
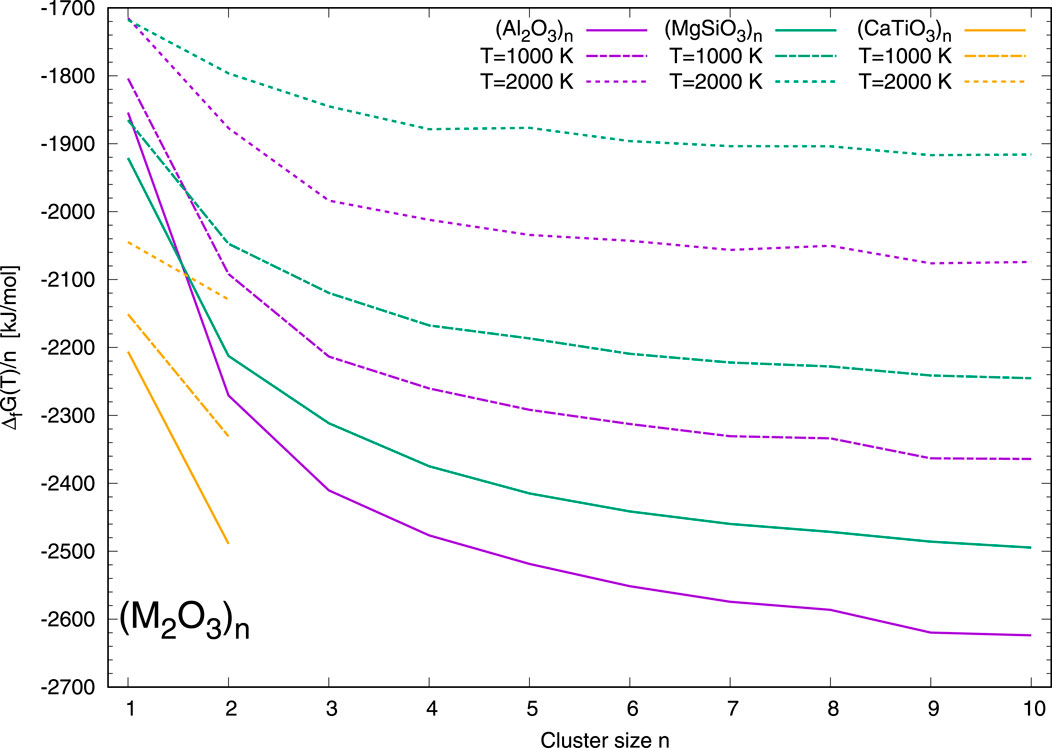
Figure 1. Gibbs free energies of formation Δf G(T) normalized to the cluster size n of the (M2O3)n clusters as a function of the cluster size n. CaTiO3 clusters are shown in orange, (Al2O3)n clusters in purple, and (MgSiO3)n clusters in green, respectively. Solid lines represent Δf G (0 K), dash-dotted lines Δf G (1000 K), and dashed lines Δf G (2000 K), respectively.
Clearly, the (CaTiO3)n family is most favourable with regard to the studied M2O3 clusters for all considered temperatures. Alumina clusters have stabilities that are more than 200 kJ/mol less per formula unit than the calcium titanates, but are more favourable than the Mg-rich pyroxene clusters by about 100–150 kJ/mol, except for the monomer. The monomers Al2O3 and MgSiO3 show almost identical Gibbs free energies at a temperature of 2000 K. Moreover, we note a comparatively lower stability for (Al2O3)n clusters at sizes n = 8 and 10 and for (MgSiO3)n at size n = 5.
In Figure 2 the normalised Gibbs free energies Δf G(T) of formation of the (M3O4)n clusters are shown as a function of the cluster size n. The energies of CaAl2O4 clusters are colour-coded in red, those of MgAl2O4 clusters in purple and those of Mg2SiO4 clusters in green, respectively. As in Figure 1, solid lines correspond to a temperature of T = 0 K, dash-dotted lines to a temperature of T = 1000 K, and dashed lines to a temperature of T = 2000 K. The calcium aluminate clusters constitute the most favourable clusters among the M3O4 set for all selected temperatures. The energy difference to their Mg-rich counterpart clusters, (MgAl2O4)n, is in the range of ∼150–200 kJ/mol. This energy difference is larger than the difference of ∼100–150 kJ/mol between the spinel clusters, (MgAl2O4)n, to the less favourable Mg-rich olivine silicate clusters. For cluster size n = 5 we find a comparatively low stability of the aluminate clusters (MgAl2O4)5 and (CaAl2O4)5.
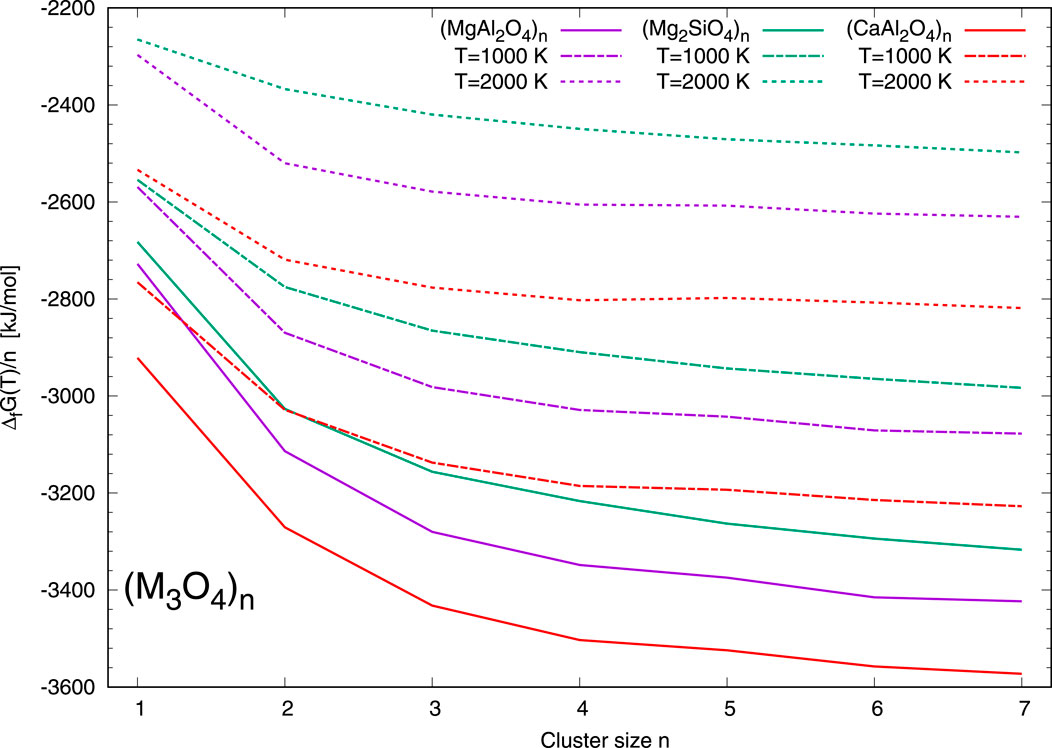
Figure 2. Gibbs free energies of formation Δf G(T) normalized to the cluster size n of the (M3O4)n clusters as a function of the cluster size n. CaAl2O4 clusters are shown in red, (MgAl2O4)n clusters in purple, and (Mg2SiO4)n clusters in green, respectively. Solid lines represent Δf G (0 K), dash-dotted lines Δf G (1000 K), and dashed lines Δf G (2000 K), respectively.
Note that the Gibbs free energies of formation in Figures 1, 2 are not scaled to the atomic heats of formation as in the JANAF tables (Chase, 1998). In this way, the enthalpy of formation Δf H (0 K) and Gibbs free energy of formation Δf H (0 K) correspond to the unscaled total binding energy of the cluster at 0 K. The corresponding thermochemical tables in the standard JANAF format can be found in the Supplementary Appendix A1. Note that the thermochemical tables of the cluster families (MgAl2O4)n and (CaAl2O4)n can be found in the supporting information of Gobrecht et al (2023).
An illustration of the applicability of the calculated Gibbs free energies of formation is shown in the form of chemical equilibrium abundances in the Supplementary Appendix A3. The corresponding computations are performed using the software GGchem (Woitke et al 2018) at a pressure of 1 bar using a solar elemental composition (Asplund et al 2009). The clusters of the M2O3 and M3O4 stoichiometries were treated separately in order to avoid interference between these families. In the M2O3 family, clusters larger than the monomer (n > 1) are present in the form of (CaTiO3)2 for temperatures of T ≤ 1500 K, (Al2O3)10 for T ≤ 1300 K, and (MgSiO3)10 for T ≤ 1200 K. The M3O4 family shows no significant amount of (MgAl2O4)n clusters, which can be explained by the presence of the thermodynamically favoured, Al-bearing (CaAl2O4)n clusters at T ≤ 1400 K and the Mg-bearing silicate clusters (Mg2SiO4)n at T ≤ 1200 K. These equilibrium abundances reflect the results presented in Figures 1 and 2 weighted by elemental abundances and indicate trends in a potential sequence of condensation.
However, we emphasize that the equilibrium abundances shown here are not representative for the actual existence or presence of the corresponding clusters in stellar atmospheres, since chemical equilibrium cannot trace the complex chemical kinetics of cluster formation. For example, formation routes that are prohibited by energy barriers or spin cannot be identified or predicted in chemical equilibrium considerations.
4 Discussion and summary
Alumina and ternary aluminium-bearing oxides are thermodynamically favoured over their silicate counterparts. Furthermore, calculations constrained to small cluster sizes indicate that titanium-bearing ternary oxides are even more favourable compared with aluminates and silicates.
The thermodynamic stabilities of the cluster families seem to follow an opposite trend with respect to the elemental abundances of their constituent metals, where Ti is about an order less abundant than Al and about two orders of magnitude less abundant than Si, according to solar abundances (Asplund et al., 2009) and AGB stellar evolution models (Cristallo et al., 2015). This trend is also seen, when comparing Mg-containing clusters with the corresponding Ca-bearing counterparts, which are more favourable and Ca is about an order of magnitude less abundant than Mg.
Apart from alumina (Al2O3) the investigated M2O3 and M3O4 clusters are ternary metal oxides comprising two different metals. A comparison with binary oxide clusters such as titania (TiO2), silica (SiO2), and magnesia (MgO) is not included in our study, since their metal-to-oxygen ratio does not agree with a M2O3 or a M3O4 stoichiometry, respectively, making such comparisons not straight-forward. Moreover, the listed binary oxide clusters can be regarded as an integral part of the presented M2O3 and M3O4 clusters. TiO2 is contained in CaTiO3, whereas SiO2 and MgO represent formal constituents of MgSiO3 and Mg2SiO4. So, albeit clusters of TiO2, SiO and MgO are tightly linked to the ternary oxide clusters of the presented study, they are not explicitly part of this study. However, we briefly discus their energetic and kinetic viabilities as well as limitations in AGB circumstellar envelopes with respect to homogeneous nucleation.
SiO is an abundant molecule in all chemical types of AGB stars (see e.g. Ramstedt et al., 2009). However, the SiO nucleation via (SiO)n clusters was found to be inefficient and negligible under circumstellar conditions (Bromley et al., 2016). Moreover, with increasing size the most favourable (SiO)n cluster exhibit segregated Si islands, further impeding the cluster growth by monomeric SiO additions. It should also be noted here that macroscopic solid SiO quickly segregates into islands of amorphous silica (SiO2) and silicon (Friede and Jansen, 1996). Therefore, SiO cannot be regarded as a stable condensate. However, at the (sub-)nanoscale (SiO)n clusters can exist. SiO is a key molecule for the formation of silicates. Goumans and Bromley (2012) explored a mechanism, where the SiO molecule is dimerized to Si2O2, which subsequently oxidized and enriched with Mg atoms in an alternating manner to form Mg4Si2O8, the dimer of Mg-rich olivine. The dimerisation of SiO represents the energetic bottleneck in their scheme at 1000 K, whereas the formation of the trimer, Si3O3, could proceed via SiO2 and Si2O3 in terms of energy. However, the oxidation of SiO to SiO2 is kinetically hampered and also the dimerization of SiO2 to Si2O4 represents a bottleneck reaction in circumstellar envelopes as has been confirmed by Andersson et al. (2023).
To our knowledge MgO does not exist in AGB circumstellar atmospheres, and Mg is predominantly expected to be in atomic form. Even if the MgO monomers were present in circumstellar envelopes, its homogeneous nucleation is hampered by particularly favourable “magic” cluster sizes that act as bottlenecks for cluster growth (Köhler et al., 1997; Bhatt and Ford, 2007). For Mg-bearing titanates and aluminates the inclusion of magnesium constitutes a kinetic bottleneck (Plane, 2013; Gobrecht et al., 2023). In these studies, it was also found that reactions with calcium atoms are significantly more efficient than those with Mg atoms and can, under certain cirumstances, lead to the formation of condensation seeds.
TiO2 exists as a strongly bond gas phase molecule, i.e. as a monomer, but also in a macroscopic crystalline phase as anatase or rutile making it a prime candidate for nucleation. Its nucleation path via stoichiometric (TiO2)n clusters follows indeed an energetically downhill process (Lamiel-Garcia et al., 2017; Sindel et al., 2022). However, a chemical-kinetic assessment of the dimerization of TiO2 to (TiO2)2, representing the first reaction in this scenario, shows a slow and ineffective reaction rate with a negative temperature-dependence (Plane, 2013). It implies that the rate is very slow at high temperatures and requires a third body to proceed. Moreover, homogeneous TiO2 nucleation is limited by the availability of Ti having a low abundance.
Formation routes towards the alumina monomer, Al2O3, are thermodynamically and kinetically hampered. The synthesis of the triplet Al2O3 monomer synthesis is prohibited by an unfavourable, i.e. an endothermic oxidation of Al2O2 (Gobrecht et al., 2022). Instead, a viable pathway leading to the formation of the alumina dimer, (Al2O3)2, was identified. Alternative solutions to form (Al2O3)n clusters might involve Al(OH)3 as suggested by Firth et al. (2025).
In summary, SiO nucleation is hampered by increasing atomic segregation and slow growth rates, MgO nucleation is hindered by the absence of the MgO monomer and energy bottlenecks at magic cluster sizes, and homogeneous TiO2 nucleation is viable, but constrained by the overall low Ti abundance. Given the chemical wealth of oxygen-rich AGB circumstellar envelopes, it is likely that ternary oxide clusters form. In particular, the above mentionned drawbacks of homogeneous nucleation of SiO, MgO and TiO2, respectively, indicate that the formation of a ternary oxide involving an additional metal is required for subsequent cluster growth.
For a comparison between the binary oxide clusters of SiO, TiO2, MgO and Al2O3 we refer to the study of Boulangier et al. (2019). Although a (chemical-)kinetic treatment of the studied clusters would be desirable, an investigation of the presented clusters is computationally very expensive or even prohibitive for cluster sizes n > 3. The reaction rates involving larger sized clusters are very expensive to compute at high level rate theories like statistical Ramsperger-Kassel-Marcus (RRKM) and transition state theories. For this reason, reaction systems comprising more than ∼12 atoms the rates are typically assessed with theories of approximative nature including classical and kinetic nucleation, collisional rates, capture rates and detailed balance.
Spectral identification of the presented clusters is challenging. Owing to their large number of degrees of freedom the presented clusters exhibit many, partly overlapping and blurred spectral features in contrast to small, di- and tri-atomic molecules with sharp, discrete and well-defined transitions. In addition, the nucleating clusters might not have a longevity to be observed. However, recent studies have attempted to identify the spectral signatures of different cluster families in theoretical frameworks (Lecoq-Molinos et al., 2024; Mariñoso Guiu et al., 2021; Plane and Robertson, 2022; Sindel et al., 2023; Lecoq-Molinos et al., 2024) as well as observationally (Decin et al., 2017; Baeyens et al., 2024).
Calcium silicate clusters, in particular the pyroxenes and olivines (CaSiO3)n and (Ca2SiO4)n, are entirely missing for both stoichiometries, M2O3 and M3O4, which constitutes one of the major limitations of the present study. Moreover, with the exception of the monomer and the dimer of perovskite (CaTiO3), the calcium titanates clusters are not part of this study. We aim to investigate the cluster families of calcium silicates and titanates in a forthcoming study.
Therefore, no final conclusion can be drawn. However, our results indicate the following trends:
(i) alumina and aluminate clusters are energetically more favourable than their silicate counterparts
(ii) Owing to their thermodynamic stability calcium titanates are promising candidates as primary condensation seeds
(iii) Clusters comprising calcium are significantly more stable than their magnesium-containing counterparts
Other stoichiometric clusters of minerals like geikielite (MgTiO3) and quandilite (Mg2TiO4) were not considered in this study. These condensates are rare and were, to the best of our knowledge, not found in meteorites. For consistency and completeness, however, these clusters as well as the aforementioned calcium silicates CaSiO3 and Ca2SiO4 should be investigated in detail to draw firmer conclusions on the cluster condensation sequence among titanates, aluminates and silicates.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
DG: Writing – review and editing, Writing – original draft, Formal Analysis, Conceptualization, Validation, Data curation, Investigation.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. The computations involved the Swedish National Infrastructure for Computing (SNIC) at Chalmers Centre for Computational Science and Engineering (C3SE) partially funded by the Swedish Research Council through grant no. 2018-05973. The computations were partially enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) partially funded by the Swedish Research Council through grant agreement no. 2022-06725.
Acknowledgments
I am deeply indebted to Tom Millar and Mauro Pirarba for enabling a publication in frontiers.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with one of the authors DG.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2025.1632593/full#supplementary-material
References
Andersson, S., Gobrecht, D., and Valero, R. (2023). Mechanisms of SiO oxidation: implications for dust formation. Front. Astron. Space Sci. 10, 1135156. doi:10.3389/fspas.2023.1135156
Asplund, M., Grevesse, N., Sauval, A. J., and Scott, P. (2009). The chemical composition of the sun. ARA&A 47, 481–522. doi:10.1146/annurev.astro.46.060407.145222
Baeyens, R., Barat, S., Decin, L., Desert, J. M., Gobrecht, D., Helling, Ch., et al. (2024). JWST proposal. Cycle 3, ID. #6045. Available online at: https://ui.adsabs.harvard.edu/abs/2024jwst.prop.6045B/abstract.
Baudry, A., Wong, K. T., Etoka, S., Richards, A. M. S., Müller, H. S. P., Herpin, F., et al. (2023). ATOMIUM: probing the inner wind of evolved O-rich stars with new, highly excited H2O and OH lines. A&A 674, A125. doi:10.1051/0004-6361/202245193
Bhatt, J. S., and Ford, J. (2007). Investigation of MgO as a candidate for the primary nucleating dust species around M stars. MNRAS 382 (1), 291–298. doi:10.1111/j.1365-2966.2007.12358.x
Boulangier, J., Gobrecht, D., Decin, L., de Koter, A., and Yates, J. (2019). Developing a self-consistent AGB wind model – II. Non-classical, non-equilibrium polymer nucleation in a chemical mixture. MNRAS 489, 4890–4911. doi:10.1093/mnras/stz2358
Bromley, S. T., Gómez Martín, J. C., and Plane, J. M. C. (2016). Phys. Chem. Chem. Phys. 18, 26913–26922. doi:10.1039/C6CP03629E
Chase, M. (1998). NIST-JANAF thermochemical tables. 4th Edition. American Institute of Physics. Available online at: https://www.nist.gov/publications/nist-janaf-thermochemical-tables-4th-edition.
Cristallo, S., Straniero, O., Piersanti, L., and Gobrecht, D. (2015). Evolution, nucleosynthesis, and yields of agb stars at different metallicities. iii. intermediate-mass models, revised low-mass models, and the ph-fruity interface. ApJS 219, 40. doi:10.1088/0067-0049/219/2/40
Danilovich, T., Gottlieb, C. A., Decin, L., Richards, A. M. S., Lee, K. L. K., Kamiński, T., et al. (2020). Rotational spectra of vibrationally excited AlO and TiO in oxygen-rich stars. ApJ 904, 110. doi:10.3847/1538-4357/abc079
Decin, L., De Beck, E., Brünken, S., Müller, H. S. P., Menten, K. M., Kim, H., et al. (2010). A&A 516, A69. doi:10.1051/0004-6361/201014136
Decin, L., Richards, A. M. S., Waters, L. B. F. M., Danilovich, T., Gobrecht, D., Khouri, T., et al. (2017). Study of the aluminium content in AGB winds using ALMA: indications for the presence of gas-phase (Al2O3)nclusters. A&A 608, A55. doi:10.1051/0004-6361/201730782
Firth, R. A., Bell, K. M., and Fortenberry, R. C. (2025). Formation of AlO, AlOH, and Al(OH)3 in the interstellar medium and circumstellar envelopes of AGB stars. ACS Earth Space Chem. 8 (5), 974–982. doi:10.1021/acsearthspacechem.3c00335
Fonfria, J. P., Fernandez-Lopez, M., Agundez, M., Sánchez-Contreras, C., Curiel, S., and Cernicharo, J. (2014). The complex dust formation zone of the AGB star IRC+10216 probed with CARMA 0.25 arcsec angular resolution molecular observations. Mon. Not. R. Astron. Soc. 445, 3289–3308. doi:10.1093/mnras/stu1968
Friede, B., and Jansen, M. (1996). Some comments on so-called ‘silicon monoxide’. J. Non-Crystalline Solids 204 (2), 202–203. doi:10.1016/S0022-3093(96)00555-8
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian’16 revision C.01. Wallingford, CT: Gaussian Inc. Available online at: https://gaussian.com/citation/.
Gobrecht, D., Cherchneff, I., Sarangi, A., Plane, J. M. C., and Bromley, S. T. (2016). Dust formation in the oxygen-rich AGB star IK tauri. A&A 585, A6. doi:10.1051/0004-6361/201425363
Gobrecht, D., Plane, J. M. C., Bromley, S. T., Decin, L., Cristallo, S., and Sekaran, S. (2022). Bottom-up dust nucleation theory in oxygen-rich evolved stars: I. Aluminium oxide clusters. A&A 658, A167. doi:10.1051/0004-6361/202141976
Gobrecht, D., Hashemi, S. R., Plane, J. M. C., Bromley, S. T., Nyman, G., and Decin, L. (2023). Bottom-up dust nucleation theory in oxygen-rich evolved stars: II. Magnesium and calcium aluminate clusters. A&A 680, A18. doi:10.1051/0004-6361/202347546
Herwig, F. (2005). Evolution of asymptotic giant branch stars. ARA&A 43, 435–479. doi:10.1146/annurev.astro.43.072103.150600
Kamiński, T., Wong, K. T., Schmidt, M. R., Müller, H. S. P., Gottlieb, C. A., Cherchneff, I., et al. (2016). An observational study of dust nucleation in mira (O Ceti): I. Vaciable features of AlO and other Al-bearing species⋆. A&A 592, A42. doi:10.1051/0004-6361/201628664
Kamiński, T., Müller, H. S. P., and Schmidt, M. R. (2017). A&A 599, A59. doi:10.1051/0004-6361/201629838
Köhler, T. M., Gail, H. P., and Sedlmayr, E. (1997). A&A 320, 553. Available online at: https://adsabs.harvard.edu/full/1997A%26A.320.553K.
Lamiel-Garcia, O., Ko, K. C., Lee, J. Y., Bromley, S. T., and Illas, F. (2017). J. Chem. Theory Comput. 13, 4. doi:10.1021/acs.jctc.7b00085
Lecoq-Molinos, H., Gobrecht, D., Sindel, J. P., and Decin, L. (2024). Vanadium oxide clusters in substellar atmospheres: a quantum chemical study. A&A 690, A34. doi:10.1051/0004-6361/202347693
Macià-Escatllar, A., Lazaukas, T., Woodley, S. M., and Bromley, S. T. (2019). Structure and properties of nanosilicates with olivine (Mg2SiO4)N and pyroxene (MgSiO3)N compositions. ACS Earth Space Chem. 3, 2390–2403. doi:10.1021/acsearthspacechem.9b00139
Mariñoso Guiu, J., Macià-Escatllar, A., and Bromley, S. T. (2021). ACS Earth and. Space Chem. 5, 4. doi:10.1021/acsearthspacechem.0c00341
Neufeld, D. A., Tolls, V., Agúndez, M., González-Alfonso, E., Decin, L., Daniel, F., et al. (2013). ApJL 767, 1–5. doi:10.1088/2041-8205/767/1/L3
Nuth, J. A., and Donn, B. (1981). Vibrational disequilibrium in low pressure clouds. ApJ 247, 925. doi:10.1086/159101
Plane, J. M. C. (2013). Philos. Trans. Roy. Soc. A: math. Phys. Eng. Sci. 371, 20120335. doi:10.1098/rsta.2012.0335
Plane, J. M. C., and Robertson, S. (2022). Master equation modelling of non-equilibrium chemistry in stellar outflows. Faraday Discuss. 238, 461–474. doi:10.1039/D2FD00025C
Posch, T., Kerschbaum, F., Mutschke, H., Fabian, D., Dorschner, J., and Hron, J. (1999). A&A 352, 609. Available online at: https://ui.adsabs.harvard.edu/abs/1999A%26A.352.609P/abstract.
Ramstedt, S., Schöier, F. L., and Olofsson, H. (2009). A&A 499, 2–515. doi:10.1051/0004-6361/200911730
Schöier, F. L., Ramstedt, S., Olofsson, H., Lindqvist, M., Bieging, J. H., and Marvel, K. B. (2013). The abundance of HCN in circumstellar envelopes of AGB stars of different chemical type. A&A 550, A78. doi:10.1051/0004-6361/201220400
Sindel, J. P., Gobrecht, D., Helling, C., and Decin, L. (2022). Revisiting fundamental properties of TiO2 nanoclusters as condensation seeds in astrophysical environments. A&A 668, A35. doi:10.1051/0004-6361/202243306
Sindel, J. P., Helling, C., Gobrecht, D., Chubb, K. L., and Decin, L. (2023). Infrared spectra of TiO2 clusters for hot Jupiter atmospheres. A&A 680, A65. doi:10.1051/0004-6361/202346347
Sloan, G. C., Kraemer, K. E., Goebel, J. H., and Price, S. D. (2003). Guilt by association: the 13 micron dust emission feature and its correlation to other gas and dust features. ApJ 594, 483–495. doi:10.1086/376857
Woitke, P. (2006). Too little radiation pressure on dust in the winds of oxygen-rich AGB stars. A&A 460, L9–L12. doi:10.1051/0004-6361:20066322
Woitke, P., Helling, C., Hunter, G. H., Millard, J. D., Turner, G. E., Worters, M., et al. (2018). Equilibrium chemistry Down to 100 K: impact of silicates and phyllosilicates on the carbon to oxygen ratio. A&A 614, A1–A28. doi:10.1051/0004-6361/201732193
Keywords: nucleation, clusters, dust, circumstellar, metal oxides, silicates, alumina
Citation: Gobrecht D (2025) Condensation sequence of circumstellar cluster seeds (CSCCS). Front. Astron. Space Sci. 12:1632593. doi: 10.3389/fspas.2025.1632593
Received: 21 May 2025; Accepted: 15 September 2025;
Published: 10 October 2025.
Edited by:
Xiaohu Li, Chinese Academy of Sciences, ChinaReviewed by:
Yong Zhang, Sun Yat-sen University, ChinaHans-Peter Gail, Heidelberg University, Germany
Copyright © 2025 Gobrecht. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Gobrecht, ZGF2aWQuZ29icmVjaHRAaXBpLmNo
 David Gobrecht
David Gobrecht