Bulk viscosity of two-flavor color superconducting quark matter in neutron star mergers

This work investigates the bulk viscosity of warm, dense, neutrino-transparent, color-superconducting quark matter, where damping of density oscillations in the kHz frequency range arises from weak-interaction-driven direct Urca processes involving quarks. We study the two-flavor red-green paired color-superconducting (2SC) phase, while allowing for the presence of unpaired strange quarks and blue color light quarks of all flavors. Our calculations are based on the SU(3) Nambu–Jona–Lasinio model, extended to include both vector interactions and the ‘t Hooft determinant term. The primary focus is on how variations in the NJL Lagrangian parameters—specifically, the diquark and vector coupling strengths—affect both the static properties of quark matter, such as its equation of state and composition, and its dynamical behavior, including bulk viscosity and associated damping timescales. We find that the bulk viscosity and corresponding damping timescale can change by more than an order of magnitude upon varying the vector coupling by a factor of two at high densities and by a lesser degree at lower densities. This sensitivity primarily arises from the susceptibility of 2SC matter, with a smaller contribution from modifications to the weak interaction rates. In comparison, changes in the diquark coupling have a more limited impact. The damping of density oscillations in 2SC matter is similar quantitatively to nucleonic matter and can be a leading mechanism of dissipation in merging hybrid stars containing color superconducting cores.

1 Introduction

The exploration of matter within the extreme environments of neutron star mergers presents a fascinating way to understand the fundamental properties of nuclear and quark matter at densities substantially exceeding the nuclear saturation density. Although recent gravitational wave observations, such as the GW170817 event (The LIGO Scientific Collaboration et al., 2017), which was accompanied by electromagnetic counterparts, have only captured the inspiral phase of the merger, it is anticipated that the post-merger phase could become observable with the next-generation of gravitational wave detectors. Nevertheless, numerical simulations of mergers offer clues into the dynamics of the merger process and the spectrum of gravitational waves that are emitted (Faber and Rasio, 2012; Baiotti and Rezzolla, 2017; Baiotti, 2019; Bauswein et al., 2019; Radice and Bernuzzi, 2023; Radice and Hawke, 2024). The gravitational waves, emitted within the first tens to hundreds of milliseconds after the merger, carry unique information about the state of matter under extreme conditions. In particular, the post-merger matter is extremely hot, produces a large number of neutrinos, and, unlike a supernova, is highly neutron-rich.

The accuracy of the predictions of simulations of binary neutron star (BNS) mergers depends on a number of factors, among which we would like to address the need for including dissipation in the typically nondissipative general-relativistic hydrodynamics. Dissipation may control the oscillations that source the gravitational waves. The possible influence of various transport phenomena has been addressed in recent years, including the electrical and thermal conductivities (Alford et al., 2018; Harutyunyan and Sedrakian, 2016; Schmitt and Shternin, 2018; Harutyunyan et al., 2018; Harutyunyan and Sedrakian, 2024; Harutyunyan et al., 2024), bulk and shear viscosities (Alford et al., 2018), etc. In recent years, much of the attention has been focused on the bulk viscosity-driven weak $\beta$-decay processes on nucleons (Alford and Harris, 2019; Alford et al., 2020; Alford et al., 2021a; Alford et al., 2021b; Alford et al., 2023), hyperons (Alford and Haber, 2021) and quarks (Cruz Rojas et al., 2024; Hernández et al., 2024; Alford et al., 2024). The microscopic computation of rates allows one to estimate the damping timescales using local snapshots of matter conditions provided by simulations (Alford et al., 2019; Alford et al., 2020; Alford et al., 2021b; Alford et al., 2023).

The explicit inclusion of bulk viscosity in numerical simulations is still an area under active development (Most et al., 2022; Celora et al., 2022; Chabanov and Rezzolla, 2025a; Chabanov and Rezzolla, 2025b). See also Hammond et al. (2021), Radice et al. (2022), Camelio et al. (2023a), Camelio et al. (2023b) for related studies that provide a more qualitative assessment of bulk viscous effects based on simulations. Some works, such as (Most et al., 2022; Celora et al., 2022), account for the bulk viscosity within frameworks that evolve the system using ideal hydrodynamics, thus neglecting the back-reaction of the bulk viscosity on the fluid motion. Other studies incorporate bulk viscosity dynamically, but assume it to be constant throughout the evolution (Chabanov and Rezzolla, 2025a; Chabanov and Rezzolla, 2025b). Although many details, such as the dependence of bulk viscosity on temperature, density, and the composition of matter at supranuclear densities, remain uncertain, it is generally expected that bulk viscosity can significantly affect the gravitational wave emission during inspiral (Ripley et al., 2023; Ghosh et al., 2025) and merger. In particular, it may damp the oscillations of the remnant stellar core more rapidly, potentially leading to a faster decay of the gravitational wave signal.

Within this context, the potential presence and behavior of quark matter remains largely unexplored. Studies of cold quark matter in hybrid and strange stars, particularly concerning the damping of $r$-mode oscillations in cold stellar configurations have spanned several decades (Madsen, 1992; Drago et al., 2005; Alford and Schmitt, 2007; Blaschke et al., 2007; Sa’d et al., 2007a; Sa’d et al., 2007b; Huang et al., 2010; Wang et al., 2010; Wang and Shovkovy, 2010). Notably, Alford and Schmitt (2007) examined 2SC quark matter at finite temperatures using a model parameterized by the 2SC gap and chemical potentials, though without enforcing electric charge neutrality. That study focused primarily on non-leptonic processes. Importantly, Alford and Schmitt (2007) also derived the bulk viscosity resulting from coupled non-leptonic and leptonic reactions—an approach similar in spirit to the one used us recently (Alford et al., 2024) and expanded further here.

The investigation of bulk viscosity in quark matter within the context of BNS mergers remains in its early stages (Cruz Rojas et al., 2024; Hernández et al., 2024; Alford et al., 2024). Cruz Rojas et al. (2024), Hernández et al. (2024) focused on bulk viscosity in unpaired quark matter arising from non-leptonic and semi-leptonic weak processes. Cruz Rojas et al. (2024) employed both perturbative QCD and holographic methods to obtain improved weak- and strong-coupling estimates of the bulk viscosity. Hernández et al. (2024) computed the bulk viscosity using the MIT bag model and perturbative QCD. Our previous work (Alford et al., 2024) presented the first calculation of bulk viscosity that incorporates the effects of color superconductivity at intermediate densities and finite temperatures in the BNS context. In doing so, the conditions specific to BNS mergers, such as the charge and color neutrality, the density and temperature dependence of pairing gaps and chemical potentials, were treated self-consistently within the vector-interaction-enhanced NJL model. We assume that, in the temperature range $T\le 10$ MeV and for densities relevant to the quark cores of neutron stars, the matter remains transparent to neutrinos. This assumption does not contradict the existing studies of the neutrino mean free path in quark matter, although the precise condition for trapping depends on the specific model employed—such as the quark matter equation of state (EoS), composition, and possible pairing patterns (see Carter and Reddy (2000), Steiner et al. (2001), Colvero and Lugones (2014)). We also expect that the bulk viscosity will be significantly suppressed once neutrinos become trapped on microscopic scales and reach equilibrium with the surrounding quark matter, consistent with our findings in the neutrino-trapped regime of nucleonic matter (Alford et al., 2020; Alford et al., 2021b; Alford et al., 2019).

Cruz Rojas et al. (2024), Hernández et al. (2024) found a peak in the bulk viscosity at temperatures $T\le 0.5$ MeV, which is due to non-leptonic processes, in agreement with earlier studies of cold quark matter (Alford and Schmitt, 2007). Furthermore, Hernández et al. (2024) identified a potential second peak at higher temperatures, around $T\sim 2$ MeV, which emerges for sufficiently large strange quark masses and is driven by semi-leptonic processes. In contrast, Alford et al. (2024) focuses on the high-temperature regime, $1\le T\le 10$ MeV, and investigates semi-leptonic processes after verifying that non-leptonic ones equilibrate too rapidly to contribute significantly at these temperatures. Their analysis shows a peak within this range, driven by semi-leptonic Urca processes. Collectively, these studies indicate the presence of two distinct peaks in the bulk viscosity: the first at low temperatures ($T\le 0.5$ MeV) driven by non-leptonic processes, and the second at higher temperatures (on the order of a few MeV) associated with semi-leptonic interactions.

This work aims to build upon our previous study (Alford et al., 2024), preserving the essential modeling framework while focusing on variations of the Lagrangian parameters within the vector-interaction-enhanced NJL model (Bonanno and Sedrakian, 2012). First, we investigate how the static composition and EoS of 2SC quark matter with strange quarks depend on the strengths of the vector and diquark couplings. Second, we examine dynamical properties, such as the bulk viscosity and corresponding damping time scales. In this context, we also analyze how Urca process rates are modified by variations in pairing strength and the repulsive vector interaction.

Before proceeding, we point out that the 2SC phase studied in this work competes with alternatives, which we briefly mention here. One example is the quarkyonic phase which features elements of the baryon spectrum for large momenta and quark spectrum at small momenta (McLerran and Reddy, 2019; Han et al., 2019; Kovensky and Schmitt, 2020; Kojo, 2024; Fujimoto et al., 2024; Bluhm et al., 2025). The quarkyonic phase is expected to occupy the finite-temperature, moderate density segment of the QCD phase diagram and its competition with the 2SC phase depends on several factors that are hard to pin down. Furthermore, it has been realized that the chiral phase transition at low temperatures and moderate densities may proceed via an inhomogeneous phase, instead of the first-order homogeneous transition line (Buballa and Carignano, 2016). This phase may have various realizations such as plane-wave sinusoidal modulation or amplitude-modulated “kink crystal” condensate, with periodically alternating positive and negative values of (real-valued) solitonic profile (Karasawa et al., 2016; Abuki, 2018; Ferrer and de la Incera, 2021; Tabatabaee, 2023; Motta et al., 2025).

Although lattice QCD at finite density is hindered by the sign problem, existing results at zero density (Bazavov et al., 2012; Aoki et al., 2024) allow one to speculate that if the $U{(1)}_A$ anomaly remains strong, it could suppress the emergence of certain exotic phases through modifications of meson masses (Kono et al., 2021). Conversely, if the anomaly becomes weaker at finite chemical potential, this may favor the appearance or extension of inhomogeneous chiral phases mentioned above. In particular, the axial anomaly contributes to the effective potential governing chiral condensate modulations. For spatially inhomogeneous phases that rely on chiral spirals or solitonic structures, any change in the strength of $U{(1)}_A$ breaking could alter the relative stability of competing condensate configurations (Carignano and Buballa, 2020; Gao et al., 2022). Below we include the ’t Hooft interaction which breaks the $U{(1)}_A$ symmetry and effectively resembles the axial anomaly.

The present paper is organized as follows. In Section 2 we discuss the equilibrium state of the 2SC phase, including the key thermodynamic parameters that are required for computing the bulk viscosity of quark matter. In Section 3 we discuss the computations of the semi-leptonic Urca rates in the 2SC phase. Section 4 presents the general formalism for computing the bulk viscosity in quark matter based on Urca processes. Our numerical results are presented in Section 5. We conclude and summarize in Section 6. Our calculations use natural units where $\hslash =c=k_B=1$.

2 Finite temperature 2SC phase

To describe the properties of 2SC quark matter, we adopt a local vector-interaction-enhanced NJL Lagrangian, which is given by (ignoring electromagnetism)

$\begin{array}{ll}\hfill {\mathcal{L}}_{\mathit{NJL}}& =\bar{\psi }(i{\gamma }^{\mu }{\partial }_{\mu }-\widehat{m})\psi +G_S{\displaystyle \sum _{a=0}^8}[{(\bar{\psi }{\lambda }_a\psi )}^2+{(\bar{\psi }i{\gamma }_5{\lambda }_a\psi )}^2]\hfill \\ \hfill & +G_V{(\bar{\psi }i{\gamma }^{\mu }\psi )}^2+G_D{\displaystyle \sum _{\gamma ,c}}[{\bar{\psi }}_{\alpha }^{a}i{\gamma }_5{ϵ}^{\alpha \beta \gamma }{ϵ}_{\mathit{abc}}{({\psi }_C)}_{\beta }^b][{({\bar{\psi }}_C)}_{\rho }^{r}i{\gamma }_5{ϵ}^{\rho \sigma \gamma }{ϵ}_{\mathit{rsc}}{\psi }_{\sigma }^s]\hfill \\ \hfill & -K\left\{{\text{det}}_f[\bar{\psi }(1+{\gamma }_5)\psi ]+{\text{det}}_f[\bar{\psi }(1-{\gamma }_5)\psi ]\right\},\hfill \end{array}(1)$

where the quark spinor fields ${\psi }_{\alpha }^a$ carry color $a=r,g,b$ and flavor ($\alpha =u,d,s$) indices, the matrix of quark current masses is given by $\widehat{m}={\text{diag}}_f(m_u,m_d,m_s)$, ${\lambda }_a$ where $a=1,\dots ,8$ are the Gell-Mann matrices in the color space, and ${\lambda }_0=(2/3){\mathbf{1}}_{\mathbf{f}}$, where ${\mathbf{1}}_{\mathbf{f}}$ is the unit matrix in the flavor space. The charge conjugate spinors are defined as ${\psi }_C=C{\bar{\psi }}^T$ and ${\bar{\psi }}_C={\psi }^{T}C$, where $C=i{\gamma }^2{\gamma }^0$ is the charge conjugation matrix. The form of Equation 1 differs from the original NJL Lagrangian (which contains only the kinetic energy terms and terms proportional to $G_S$). It has been extended by three additional terms: (i) the vector interaction with coupling $G_V$, which is assumed to be repulsive, (ii) the pairing interaction with coupling $G_D$, and (iii) the ’t Hooft interaction with coupling $K$, which breaks the $U_A(1)$ symmetry. The numerical values of the parameters of the Lagrangian are $m_{u,d}=5.5$ MeV, $m_s=140.7$ MeV, $\mathrm{\Lambda }=602.3$ MeV, $G_S{\mathrm{\Lambda }}^2=1.835$, $K{\mathrm{\Lambda }}^5=12.36$ (Rehberg et al., 1996). These parameters of the SU(3) NJL model were determined by fitting to empirical data, ensuring that the model accurately reproduces known properties of mesons and quarks. The specific physical observables that are reproduced by the model are the vacuum masses and decay constants of the pion, kaon, eta-meson, and the mass of the eta prime meson, which is particularly sensitive to the $U_A(1)$ anomaly modeled by the ’t Hooft determinant term. We note that the temperature range where the matter is neutrino transparent is limited to $T\lesssim 10$ MeV, which implies that the condition $T/\mu \ll 1$ is always fulfilled for chemical potentials of quarks of all flavors. We have checked that at the low temperatures considered in this work, there are no cutoff artifacts, as the quantities of interest are dominated by unpaired quarks near their thermally smeared Fermi surfaces. In the temperature regime of interest, the corresponding Fermi energies—approximately 300 MeV for light quarks and 500 MeV for strange quarks—remain well below the ultraviolet cutoff, placing our analysis in a regime where such effects are safely suppressed. Nevertheless, should the cutoff approach the Fermi surface, a renormalization group–based framework could be employed to systematically account for and remove any emerging artifacts (Gholami et al., 2025).

At intermediate densities, the 2SC phase is expected to be the dominant pairing channel. More intricate pairing patterns, such as crystalline and gapless color superconducting states, emerge at the low temperatures typical of cold neutron stars. However, the 2SC phase remains a robust feature at finite temperatures. In the 2SC phase, pairing occurs in a color- and flavor-antisymmetric manner between up ($u$) and down ($d$) quarks, while strange ($s$) quarks remain unpaired. The pairing gap in the quasiparticle spectrum is

${\mathrm{\Delta }}_c\propto G_D⟨{({\bar{\psi }}_C)}_{\alpha }^{a}i{\gamma }_5{ϵ}^{\alpha \beta c}{ϵ}_{\mathit{abc}}{\psi }_{\beta }^b⟩.(2)$

The overall quark pair wave function must be antisymmetric under exchange of quarks, according to the Pauli exclusion principle. It is seen that the color part of the wave function is antisymmetric, specifically in the anti-triplet configuration $(\bar{3})$ of the SU(3) color; the flavor part is anti-symmetric as well and involves light up and down quarks; finally, the spin part is anti-symmetric, implying spin-0 pairing, that is, the Cooper pairs form a spin-singlet state.

The quark-antiquark condensates are defined as

${\sigma }_{\alpha }\propto G_S⟨{\bar{\psi }}_{\alpha }{\psi }_{\alpha }⟩,(3)$

and the constituent mass of each quark flavor is given by

$M_{\alpha }=m_{\alpha }-4G_S{\sigma }_{\alpha }+2K{\sigma }_{\beta }{\sigma }_{\gamma }.(4)$

The quark dispersion relations include energy shifts arising from the quark interaction with the vector mean fields ${\omega }_0$ and ${\varphi }_0$ which are defined as ${\omega }_0=G_V⟨({\psi }_u^{†}{\psi }_u+{\psi }_d^{†}{\psi }_d)⟩$ and ${\varphi }_0=2G_V⟨{\psi }_s^{†}{\psi }_s⟩$ and are the mean field expectation values of the vector mesons $\omega$ and $\varphi$ in quark matter. The quark (thermodynamic) chemical potentials are given by

${\mu }_{f,c}=\frac{1}{3}{\mu }_B+{\mu }_Q{Q}_f+{\mu }_3{T}_3^c+{\mu }_8{T}_8^c,(5)$

with ${\mu }_B$ and ${\mu }_Q$ being the baryon and charge chemical potential, and

$Q_f={\mathrm{diag}}_f\left(\frac{2}{3},-\frac{1}{3},-\frac{1}{3}\right)(6)$

being the quark charge matrix in flavor space and

$T_3^c=\frac{1}{2}{\mathrm{diag}}_c(1,-\mathrm{1,0}),T_8^c=\frac{1}{2\sqrt{3}}{\mathrm{diag}}_c(\mathrm{1,1},-2)(7)$

the diagonal generators of the SU(3) color gauge group related to the third and eighth gluons. The values of ${\mu }_Q$, ${\mu }_3$, and ${\mu }_8$ are determined by the requirement of electrical and color neutrality. For some purposes, such as calculating Fermi-Dirac factors, these can be absorbed into “effective” quark chemical potentials

${\mu }^{*}={\mathrm{diag}}_f\left({\mu }_u-{\omega }_0,{\mu }_d-{\omega }_0,{\mu }_s-{\varphi }_0\right).(8)$

Starting from the Lagrangian (Equation 1) the partition function and the thermodynamic potential $\mathrm{\Omega }$ of the 2SC phase can be computed in the mean-field approximation; see, for example, Alford et al. (2008), Rüster et al. (2005), Blaschke et al. (2005), Gómez Dumm et al. (2006), Bonanno and Sedrakian (2012). We find the values of the chemical potentials ${\mu }_Q$, ${\mu }_3$, ${\mu }_8$ by requiring neutrality, i.e., setting $\partial \mathrm{\Omega }/\partial {\mu }_i=0$. The mean fields, including the pairing gaps, are also obtained by stationarizing $\mathrm{\Omega }$ with respect to their values. For the computation of the incompressibility of quark matter, we will need the expression for the pressure which is given by

$\begin{array}{ccc}\hfill P& =\hfill & \frac{1}{2{\pi }^2}{\displaystyle \sum _{i=1}^{18}}{\int }_0^{\mathrm{\Lambda }}dk{k}^2\left[\left|{ϵ}_i\right|+2T\ln \left(1+{\mathrm{e}}^{-\frac{\left|{ϵ}_i\right|}{T}}\right)\right]+4K{\sigma }_u{\sigma }_d{\sigma }_s-\frac{1}{4G_D}{\displaystyle \sum _{c=1}^3}{\left|{\mathrm{\Delta }}_c\right|}^2\hfill \\ \hfill & -\hfill & 2G_S{\displaystyle \sum _{\alpha =1}^3}{\sigma }_{\alpha }^2+\frac{1}{4G_V}\left(2{\omega }_0^2+{\varphi }_0^2\right)+{\displaystyle \sum _{l=e^{-},{\mu }^{-}}}{P}_l-P_0-B^{*},\hfill \end{array}(9)$

where ${ϵ}_i$ are the quasiparticle energies of quarks in quark matter, $P_l$ is lepton pressure (which is approximated as corresponding to an ideal relativistic gas), $P_0$ is the vacuum pressure, and $B^{*}$ is an effective bag constant, which controls to deconfinement phase transition density.

In the following, we will explore how the Urca rates and resultant bulk viscosity depend on key parameters in the Lagrangian. In doing so, we will vary the temperature in the range $1\le T\le 10$ MeV, in which we assume the neutrinos are free-streaming. As a main point of this work, we will vary the two additional couplings in the Lagrangian that enhance the ordinary NJL model. Specifically, to understand the role of pairing interaction strength, we consider two values of diquark coupling $G_D/G_S=1$ and 1.25. Similarly, we vary the vector interaction in the range $0.6\le G_V/G_S\le 1.2$ to highlight its role in the physics of the bulk viscosity of 2SC matter.

Figure 1 shows the density dependence of the gap for fixed temperature $T=1$ MeV and several values of $G_D/G_S$ and $G_V/G_S$ in the range indicated above. The gaps predicted by the model are much larger than the characteristic temperatures relevant for untrapped neutrinos, i.e., we are working essentially in the limit $T\ll \mathrm{\Delta }$. Therefore, the excitations are exponentially suppressed, and the variations of the gap with temperature are insignificant. The enhancement of the gap with increasing density may be associated with the increase of the density of states at the Fermi surfaces of quarks, while coupling being fixed. Further, it is seen that the increase of the attractive pairing strength $G_D/G_S$ from 1 to 1.25 increases the gap by $\ge 10\%$. Finally, the repulsive vector interaction acts oppositely by reducing the pairing gap by at most a few percent when going from $G_V/G_S=0.6$ to $G_V/G_S=1.2$. The energy gap indicates how effectively the phase space of green and red light quarks is suppressed in weak reactions, thereby limiting their contribution to bulk viscosity. The gap variations across model parameters seen in Figure 1 consistently maintain the effective shutdown of these quark color-flavor channels.

Figure 1

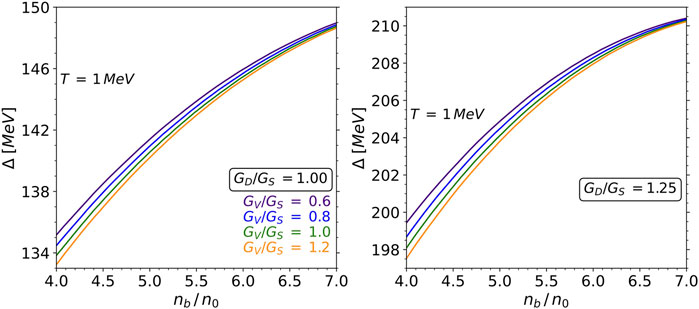
Figure 1. 2SC gap as a function of number density for temperature $T=1$ MeV and varying values of vector and diquark couplings. The temperature dependence of the gap is weak in the regime of interest, where $T\ll \mathrm{\Delta }$.

Figure 2 shows the pressure of the NJL model for fixed temperature $T=1$ MeV and several values of $G_D/G_S$ and $G_V/G_S$. As expected, the pressure increases as both the diquark and vector couplings are increased. The significance of the pressure in the present context is that its derivative with respect to baryon density enters the computation of compressibility of matter, which enters the expression for damping timescale via the bulk viscosity, see Equation 76 below. Note that we use in Equation 9 the value $B^{*}=0$ as we are interested only in the pressure derivative.

Figure 2

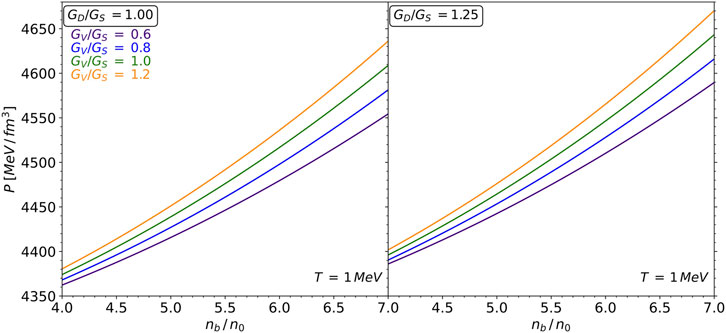
Figure 2. Pressure as a function of number density for temperature $T=1$ MeV and various fixed values of vector and diquark couplings.

Figure 3 displays the composition of the 2SC phase in $\beta$-equilibrium for varying diquark and vector couplings. It focuses on the populations of unpaired (blue-colored) up and down quarks, along with blue strange quarks, which are relevant for the computation of the bulk viscosity. Note that blue strange quarks have slightly different densities compared to their red-green counterparts, with chemical potential differences of approximately $2\%$ (roughly 10 MeV). The substantial strange quark population rapidly equilibrates with the light flavor sector through non-leptonic processes. Additionally, strange quarks are shown to reduce the lepton fraction in matter, a phenomenon that was identified decades ago (Duncan et al., 1983; Duncan et al., 1984). Examining the variations in coupling constants, we observe that increasing the attractive pairing strength $G_D/G_S$ from 1 to 1.25 slightly raises the $d$-quark population while reducing the $u$-quark population, accompanied by increased electron and muon populations. Additionally, strengthening the repulsive vector interaction increases the strange and $u$-quark populations while reducing the $d$-blue quark populations. Through $\beta$-equilibrium, electron and muon populations are suppressed as the vector coupling increases.

Figure 3

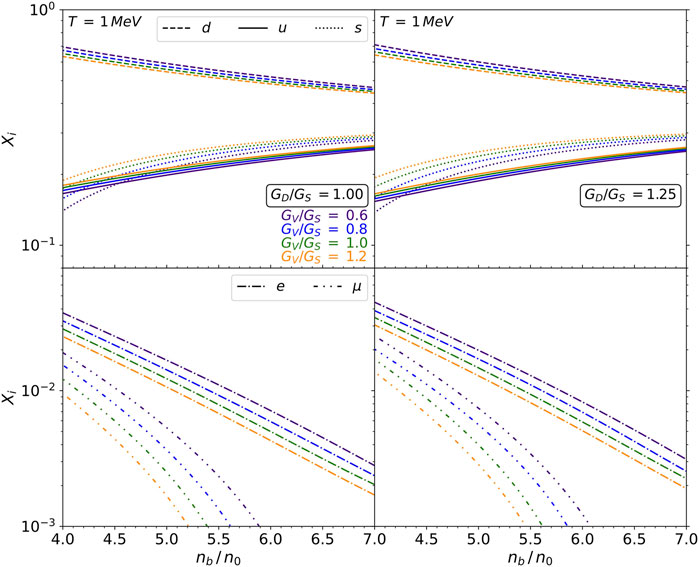
Figure 3. Composition of 2SC matter as a function of number density for $T=1$ MeV and varying vector and diquark couplings, where $X_i=n_i/n_b$ with $n_i$ being the density of any given species. Top row: unpaired (blue) quark fractions. Bottom row: charged lepton ($e^{-}$ and ${\mu }^{-}$) fractions.

Before discussing the reaction rates, we first examine the (effective) chemical potentials and masses of quarks and leptons shown in Figures 4, 5. For quarks, the masses are modified by medium effects through the chiral condensate, which generally depends on both density and temperature. This comparison reveals to what degree the different particles are relativistic. Nevertheless, the formalism applied in the following sections is fully relativistic. Figure 4 shows the effective chemical potentials defined by (Equation 8) as functions of density for fixed values of temperatures as well as coupling constants $G_D/G_S$ and $G_V/G_S$. We show only the chemical potentials of blue quarks, which are relevant for the computation of the bulk viscosity. The temperature dependence of the chemical potentials is weak in the shown density range. In addition, the lower panels show the chemical potentials of electrons and muons, which are connected through $\beta$-equilibrium conditions to the chemical potentials of quarks. The general trend is that the quark chemical potentials rise with density, as one would expect, and the lepton chemical potentials drop, as the rising fraction of strange quarks means that fewer charged leptons are needed to establish electrical neutrality. Rapid non-leptonic processes enforce down-strange flavor equilibrium, ensuring ${\mu }_d={\mu }_s$. Therefore, the observed differences between the effective chemical potentials of $d$ and $s$ quarks in Figure 4 arise from their respective couplings to $\omega$ and $\varphi$ mesons. Increasing the pairing interaction increases the chemical potentials of strange and down quarks while reducing that of up quarks. Simultaneously, the chemical potentials of electrons and muons (which are equal) also increase. Finally, increasing the repulsive vector interaction increases $s$-quark and $u$-quark chemical potentials and decreases the $d$-quark chemical potential. In parallel, through $\beta$-equilibrium, the electron and muon chemical potentials decrease.

Figure 4

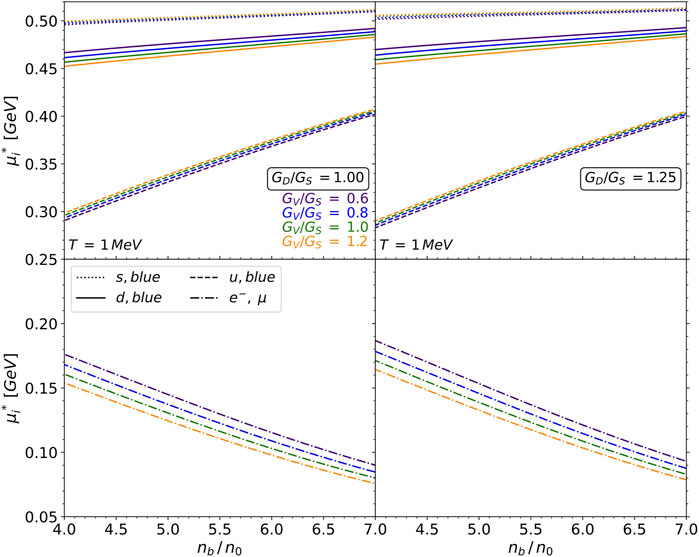
Figure 4. Effective chemical potentials as functions of number density for $T=1$ MeV and various fixed values of the vector and diquark couplings. The variations of chemical potentials with temperature are insignificant in the range of interest and are not shown.

Figure 5

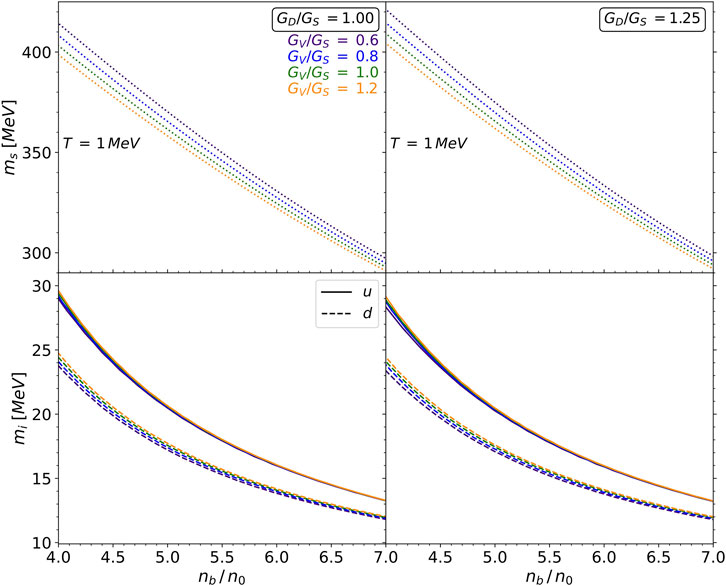
Figure 5. Quark masses as functions of number density for $T=1$ MeV and various fixed values of vector and diquark couplings. The variations of masses with temperature are insignificant in the range of interest and are not shown.

Figure 5 shows the masses of blue quarks as functions of density. An increase in the diquark coupling leads to a rise in the mass of the $s$ and a decrease in the dynamically generated masses of $d$- and $u$-quarks. Additionally, an increase in the vector coupling reduces the $s$-quark mass and raises the $u$- and $d$-quark masses. The temperature dependence of the quark masses is observed to be very weak. Comparing effective quark chemical potentials shown in Figure 4 to the respective masses of quarks, we conclude that the light quarks are ultrarelativistic in the entire density range considered. The strange quarks are mildly relativistic in the low-density limit $n_b\simeq n_0$, where $n_0$ is the saturation density, but become strongly relativistic as the density increases.

3 Urca reaction rates for ude and udse compositions

We examine neutrino-transparent $ude$ and $udse$ matter, i.e., matter consisting of $u,d$ or $u,d,s$ quarks and electrons. Muons are also included in the composition whenever they become energetically favorable. Muonic contribution to the reaction rates is subdominant and will be neglected below; the case of nuclear matter has been studied in Alford et al. (2023). The fundamental (semi-leptonic) $\beta$-equilibration processes in this system include $d$ and $s$-quark decay along with the electron capture processes of the direct Urca type

$d\to u+e^{-}+{\bar{\nu }}_e,(10)$

$u+e^{-}\to d+{\nu }_e,(11)$

$s\to u+e^{-}+{\bar{\nu }}_e,(12)$

$u+e^{-}\to s+{\nu }_e,(13)$

where ${\nu }_e$ and ${\bar{\nu }}_e$ are the electron neutrino and antineutrino, respectively. The processes (Equations 10–13) proceed exclusively from left to right because in neutrino-transparent matter, neutrinos/antineutrinos can only appear in final states. The rates of the Urca processes (Equations 10–13) can be written as

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{d/s\to ue\bar{\nu }}& =\hfill & \int \frac{d^{3}p}{{(2\pi )}^{3}2p_0}\int \frac{d^3{p}^{\prime }}{{(2\pi )}^{3}2p_0^{\prime }}\int \frac{d^{3}k}{{(2\pi )}^{3}2k_0}\int \frac{d^3{k}^{\prime }}{{(2\pi )}^{3}2k_0^{\prime }}\sum |{\mathcal{M}}_{\text{Urca}}{|}^2\hfill \\ \hfill & \times \hfill & \bar{f}(k)\bar{f}(p)f(p^{\prime }){(2\pi )}^4{\delta }^{(4)}(k+p+k^{\prime }-p^{\prime }),\hfill \end{array}(14)$

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{ue\to (d/s)\nu }& =\hfill & \int \frac{d^{3}p}{{(2\pi )}^{3}2p_0}\int \frac{d^3{p}^{\prime }}{{(2\pi )}^{3}2p_0^{\prime }}\int \frac{d^{3}k}{{(2\pi )}^{3}2k_0}\int \frac{d^3{k}^{\prime }}{{(2\pi )}^{3}2k_0^{\prime }}\sum |{\mathcal{M}}_{\text{Urca}}{|}^2\hfill \\ \hfill & \times \hfill & f(k)f(p)\bar{f}(p^{\prime }){(2\pi )}^4\delta (k+p-k^{\prime }-p^{\prime }).\hfill \end{array}(15)$

where $f(p)={\{\exp (E_p-{\mu }^{*})/T+1\}}^{-1}$ etc., are the Fermi distribution functions of fermions (quarks and leptons) with $E_p=\sqrt{p^2+m^2}$ being the single-particle spectrum of particles with mass $m$, and $\bar{f}(p)=1-f(p)$. The effective chemical potentials for quarks are given by Equation 8, and for leptons we have simply ${\mu }_l^{*}={\mu }_l$. The mapping between the particle labeling and their momenta is as follows: $(e)\to k$, $(\nu /\bar{\nu })\to k^{\prime }$, $(u)\to p$, and $(d/s)\to p^{\prime }$.

The spin-averaged relativistic matrix element of the Urca processes reads

$\sum |{\mathcal{M}}_{\text{Urca}}{|}^2=128G_F^2{\cos }^2{\theta }_c(k\cdot p)(k^{\prime }\cdot p^{\prime }),(16)$

where $G_F=1.166\cdot 10^{-5}$ ${\mathrm{G}\mathrm{e}\mathrm{V}}^{-2}$ is the Fermi coupling constant and ${\theta }_c$ is the Cabibbo angle with $\cos {\theta }_c=0.974$. For the matrix element of the Urca processes including $s$-quark, one simply needs to replace $\cos {\theta }_c$ with $\sin {\theta }_c$. The twelve-dimensional phase-space integrals in Equations 14, 15 can then be reduced to four-dimensional integrals. We follow the method of Alford et al. (2021b).

Before doing so, we note that, as has previously been noted (Alford and Schmitt, 2007; Cruz Rojas et al., 2024; Hernández et al., 2024), the non-leptonic processes

$u+d\leftrightarrow u+s(17)$

equilibrate much faster than the other Urca processes. As a result, in the regime where the semi-leptonic Urca process contributes to the bulk viscosity significantly, the non-leptonic equilibration is already completed and one can assume ${\mu }_s={\mu }_d$ at all times [see (Alford and Schmitt, 2007)]. Under this condition, we have only a single equilibrating quantity ${\mu }_{\mathrm{\Delta }}\equiv {\mu }_d-{\mu }_u-{\mu }_e$, which is the relevant measure of how much the system is driven out of $\beta$-equilibrium state by a cycle of compression and rarefaction.

Returning to Equations 14, 15, we carry out part of the integrations, as described in Alford et al. (2021b), and obtain

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{d/s\to ue\bar{\nu }}({\mu }_{\mathrm{\Delta }})& =\hfill & -\frac{G^2{T}^4}{8{\pi }^5}{\int }_{-\infty }^{\infty }dy{\int }_0^{\infty }dx\left[{({\mu }_{d/s}^{*}+yT)}^2-m_{d/s}^2-x^2{T}^2\right]\hfill \\ \hfill & \hfill & \times \left[{({\mu }_l+{\mu }_u^{*}+\bar{y}T)}^2-m_e^2-m_u^2-x^2{T}^2\right]\hfill \\ \hfill & \hfill & \times {\int }_{m_e/T-{\alpha }_e}^{{\alpha }_u+\bar{y}}dz\bar{f}(z)f(z-\bar{y}){\theta }_x{\int }_0^{\infty }d{z}^{\prime }f(z^{\prime }+y){\theta }_y,\hfill \end{array}(18)$

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{ue\to (d/s)\nu }({\mu }_{\mathrm{\Delta }})& =\hfill & \frac{G^2{T}^4}{8{\pi }^5}{\int }_{-\infty }^{\infty }dy{\int }_0^{\infty }dx\left[{({\mu }_{d/s}^{*}+yT)}^2-m_{d/s}^2-x^2{T}^2\right]\hfill \\ \hfill & \hfill & \times \left[{({\mu }_e+{\mu }_u^{*}+\bar{y}T)}^2-m_e^2-m_u^2-x^2{T}^2\right]\hfill \\ \hfill & \hfill & \times {\int }_{m_e/T-{\alpha }_e}^{{\alpha }_u+\bar{y}}dzf(z)f(\bar{y}-z){\theta }_x{\int }_0^{{\alpha }_d+y}d{z}^{\prime }f(z^{\prime }-y){\theta }_z,\hfill \end{array}(19)$

where $G=G_F\cos {\theta }_c$, $m_e$ is the electron mass, ${\alpha }_i={\mu }_i^{*}/T={\mu }_i/T-u_i$, with $u_d=u_u={\omega }_0/T$, $u_s={\varphi }_0/T$ and $u_e=u_{\nu }=0$; $\bar{y}=y+{\mu }_{\mathrm{\Delta }}/T$ with ${\mu }_{\mathrm{\Delta }}={\mu }_d-{\mu }_u-{\mu }_e$, and $f(x)={(e^x+1)}^{-1}$ is the Fermi distribution function of the dimensionless variable $x$. The $\theta$-functions in Equations 18, 19 imply

${\theta }_x : {(z_k-x)}^2\le {\left(z-{\alpha }_u-\bar{y}\right)}^2-m_u^2/T^2\le {(z_k+x)}^2,(20)$

${\theta }_y : {(z^{\prime }-x)}^2\le {\left(z^{\prime }+{\alpha }_{d/s}+y\right)}^2-m_{d/s}^2/T^2\le {(z^{\prime }+x)}^2,(21)$

${\theta }_z : {(z^{\prime }-x)}^2\le {\left(z^{\prime }-{\alpha }_{d/s}-y\right)}^2-m_{d/s}^2/T^2\le {(z^{\prime }+x)}^2.(22)$

The integration variables $y$ and $x$ are normalized-by-temperature transferred energy and momentum, respectively; the variable $z$ is the normalized-by-temperature electron energy, computed from its chemical potential, $z_k=\sqrt{{(z+{\alpha }_l)}^2-m_l^2/T^2}$ is the normalized lepton momentum, and $z^{\prime }$ is the normalized neutrino/antineutrino energy.

Alternative forms of Equations 18, 19 can be obtained by exploiting the relation $f(x)f(y)=g(x+y)[1-f(x)-f(y)]$ after which the inner two integrals can be done analytically. We find then

$\begin{array}{ll}\hfill & {\mathrm{\Gamma }}_{d/s\to ue\bar{\nu }}({\mu }_{\mathrm{\Delta }})=\frac{G^2{T}^8}{8{\pi }^5}{\int }_{-\infty }^{\infty }dy[1+g(\bar{y})]{\int }_0^{\infty }dx\hfill \\ \hfill & \left[{({\alpha }_e+{\alpha }_u+\bar{y})}^2-x^2-(m_e^2+m_u^2)/T^2\right]\left[{({\alpha }_{d/s}+y)}^2-x^2-m_{d/s}^2/T^2\right]\ln \hfill \\ \hfill & \left|\frac{1+\exp \left(-z_{2\mathrm{m}\mathrm{a}\mathrm{x}}-y\right)}{1+\exp \left(-z_{2\mathrm{m}\mathrm{i}\mathrm{n}}-y\right)}\right|\ln \left|\frac{1+\exp \left(-z_{1\mathrm{m}\mathrm{i}\mathrm{n}}\right)}{1+\exp \left(-z_{1\mathrm{m}\mathrm{i}\mathrm{n}}+\bar{y}\right)}\frac{1+\exp \left(-z_{1\mathrm{m}\mathrm{a}\mathrm{x}}+\bar{y}\right)}{1+\exp \left(-z_{1\mathrm{m}\mathrm{a}\mathrm{x}}\right)}\right|,\hfill \end{array}(23)$

$\begin{array}{ll}\hfill & {\mathrm{\Gamma }}_{ue\to (d/s)\nu }({\mu }_{\mathrm{\Delta }})=\frac{G^2{T}^8}{8{\pi }^5}{\int }_{-\infty }^{\infty }dyg(\bar{y}){\int }_0^{\infty }dx\hfill \\ \hfill & \left[{({\alpha }_e+{\alpha }_u+\bar{y})}^2-x^2-(m_e^2+m_u^2)/T^2\right]\left[{({\alpha }_{d/s}+y)}^2-x^2-m_{d/s}^2/T^2\right]\ln \hfill \\ \hfill & \left|\frac{1+\exp \left(-z_{3\mathrm{m}\mathrm{a}\mathrm{x}}+y\right)}{1+\exp \left(-z_{3\mathrm{m}\mathrm{i}\mathrm{n}}+y\right)}\right|\ln \left|\frac{1+\exp \left(-z_{1\mathrm{m}\mathrm{i}\mathrm{n}}\right)}{1+\exp \left(-z_{1\mathrm{m}\mathrm{i}\mathrm{n}}+\bar{y}\right)}\frac{1+\exp \left(-z_{1\mathrm{m}\mathrm{a}\mathrm{x}}+\bar{y}\right)}{1+\exp \left(-z_{1\mathrm{m}\mathrm{a}\mathrm{x}}\right)}\right|.\hfill \end{array}(24)$

The energy integration limits $z_{i\max }$ and $z_{i\min }$ are determined by solving Equations 20–22 and then comparing the results to the initial energy integration bounds specified in Equations 18, 19.

As discussed above, the light-flavor quarks are ultrarelativistic under the considered conditions, therefore, we take this limit in Equations 20–22, after which they simplify to (note that $z,z^{\prime },y\sim 1\ll x,{\alpha }_i$).

${\theta }_x :-z-{\alpha }_e+x\le -z+{\alpha }_u+\bar{y}\le z+{\alpha }_e+x\Rightarrow -2{\alpha }_e\le -{\alpha }_e+{\alpha }_u+\bar{y}-x\le 2z,(25)$

${\theta }_y :-z^{\prime }+x\le z^{\prime }+{\alpha }_d+y\le z^{\prime }+x\Rightarrow 0\le x-{\alpha }_d-y\le 2z^{\prime },(26)$

${\theta }_z :-z^{\prime }+x\le -z^{\prime }+{\alpha }_d+y\le z^{\prime }+x\Rightarrow 0\le {\alpha }_d+y-x\le 2z^{\prime },(27)$

which, together with the limits of integration in Equations 18, 19, imply

${\theta }_x : \theta ({\alpha }_e+{\alpha }_u+\bar{y}-x),z_{1\mathrm{m}\mathrm{i}\mathrm{n}}=\frac{-{\alpha }_e+{\alpha }_u+\bar{y}-x}{2},z_{1\mathrm{m}\mathrm{a}\mathrm{x}}={\alpha }_u+\bar{y},(28)$

${\theta }_y : \theta (x-{\alpha }_d-y),z_{2\mathrm{m}\mathrm{i}\mathrm{n}}=\frac{x-{\alpha }_d-y}{2},z_{2\mathrm{m}\mathrm{a}\mathrm{x}}=\infty ,(29)$

${\theta }_z : \theta ({\alpha }_d+y-x),z_{3\mathrm{m}\mathrm{i}\mathrm{n}}=\frac{{\alpha }_d+y-x}{2},z_{3\mathrm{m}\mathrm{a}\mathrm{x}}={\alpha }_d+y.(30)$

Further simplifications of Equations 23, 24 can be achieved in the low temperature limit, which corresponds to ${\alpha }_i\gg 1$. In this case $z_{1\mathrm{m}\mathrm{i}\mathrm{n}}\to -\infty$, $z_{\mathrm{1,2,3}\mathrm{m}\mathrm{a}\mathrm{x}}\to +\infty$, but $z_{\mathrm{2,3}\mathrm{m}\mathrm{i}\mathrm{n}}\sim y\sim 1$ because $x\simeq {\alpha }_d$. Using the limiting formula

$\underset{|z|\to \infty }{\lim }L(z,y)\equiv \underset{|z|\to \infty }{\lim }\ln \left|\frac{1+\exp \left(-z\right)}{1+\exp \left(-z-y\right)}\right|=y\theta (-z),(31)$

we can approximate the logarithms in Equations 23, 24 as

$\underset{|z|\to \infty }{\lim }{L}_1=\underset{|z|\to \infty }{\lim }[L(z_{1\mathrm{m}\mathrm{i}\mathrm{n}},-\bar{y})-L(z_{1\mathrm{m}\mathrm{a}\mathrm{x}},-\bar{y})]\simeq -\bar{y}\theta (-z_{1\mathrm{m}\mathrm{i}\mathrm{n}})=-\bar{y},(32)$

$\underset{|z|\to \infty }{\lim }{L}_2=\underset{|z|\to \infty }{\lim }\ln \left|\frac{1+\exp \left(-z_{2\mathrm{m}\mathrm{a}\mathrm{x}}-y\right)}{1+\exp \left(-z_{2\mathrm{m}\mathrm{i}\mathrm{n}}-y\right)}\right|\simeq -\ln |1+\exp \left(-z_{2\mathrm{m}\mathrm{i}\mathrm{n}}-y\right)|,(33)$

$\underset{|z|\to \infty }{\lim }\underset{3}{L}={\lim }_{|z|\to \infty }\ln \left|\frac{1+\exp \left(-z_{3\mathrm{m}\mathrm{a}\mathrm{x}}+y\right)}{1+\exp \left(-z_{3\mathrm{m}\mathrm{i}\mathrm{n}}+y\right)}\right|\simeq -\ln |1+\exp \left(-z_{3\mathrm{m}\mathrm{i}\mathrm{n}}+y\right)|,(34)$

after which we obtain

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{d\to ue\bar{\nu }}({\mu }_{\mathrm{\Delta }})& =\hfill & \frac{G^2{T}^8}{8{\pi }^5}{\int }_{-\infty }^{\infty }dy \bar{y}[1+g(\bar{y})]{\int }_{{\alpha }_d+y}^{{\alpha }_e+{\alpha }_u+\bar{y}}dx\left[{({\alpha }_e+{\alpha }_u+\bar{y})}^2-x^2\right]\hfill \\ \hfill & \hfill & \times \left[{({\alpha }_d+y)}^2-x^2\right]\ln \left|1+\exp \left(-\frac{x+y-{\alpha }_d}{2}\right)\right|\hfill \\ \hfill & \hfill & \times \theta ({\alpha }_e+{\alpha }_u+\bar{y}-{\alpha }_d-y),\hfill \end{array}(35)$

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{ue\to d\nu }({\mu }_{\mathrm{\Delta }})& =\hfill & \frac{G^2{T}^8}{8{\pi }^5}{\int }_{-\infty }^{\infty }dy \bar{y}g(\bar{y}){\int }_0^{\text{min}\{{\alpha }_d+y;{\alpha }_e+{\alpha }_u+\bar{y}\}}dx\hfill \\ \hfill & \hfill & \times \left[{({\alpha }_e+{\alpha }_u+\bar{y})}^2-x^2\right]\hfill \\ \hfill & \hfill & \times \left[{({\alpha }_d+y)}^2-x^2\right]\ln \left|1+\exp \left(\frac{x+y-{\alpha }_d}{2}\right)\right|.\hfill \end{array}(36)$

It is interesting to note that these expressions can be rewritten in terms of the shift between the chemical potentials of $u$- and $d$-quarks $\mathrm{\Delta }u=u_d-u_u$ (this shift vanishes in the case discussed here as $u$ and $d$ quarks are coupled to the $\omega$-meson due to Equation 8, but it might be nonzero if isovector channel of interaction is included in analogy to the $\rho$-meson in the case of nucleonic matter discussed in Alford et al. (2021b)). Indeed, using the relation

${\alpha }_e+{\alpha }_u+\bar{y}={\alpha }_d+y+\mathrm{\Delta }u,(37)$

we obtain

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{d\to ue\bar{\nu }}({\mu }_{\mathrm{\Delta }})& =\hfill & \frac{G^2{T}^8}{8{\pi }^5}\theta (\mathrm{\Delta }u){\int }_{-\infty }^{\infty }dy \bar{y}[1+g(\bar{y})]{\int }_{{\alpha }_d+y}^{{\alpha }_d+y+\mathrm{\Delta }u}dx\hfill \\ \hfill & \hfill & \times \left[{({\alpha }_d+y+\mathrm{\Delta }u)}^2-x^2\right]\hfill \\ \hfill & \hfill & \times \left[{({\alpha }_d+y)}^2-x^2\right]\ln \left|1+\exp \left(-\frac{x+y-{\alpha }_d}{2}\right)\right|,\hfill \end{array}(38)$

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{ue\to d\nu }({\mu }_{\mathrm{\Delta }})& =\hfill & \frac{G^2{T}^8}{8{\pi }^5}{\int }_{-\infty }^{\infty }dy \bar{y}g(\bar{y}){\int }_0^{\text{min}\{{\alpha }_d+y;{\alpha }_d+y+\mathrm{\Delta }u\}}dx\hfill \\ \hfill & \hfill & \times \left[{({\alpha }_d+y+\mathrm{\Delta }u)}^2-x^2\right]\hfill \\ \hfill & \hfill & \times \left[{({\alpha }_d+y)}^2-x^2\right]\ln \left|1+\exp \left(\frac{x+y-{\alpha }_d}{2}\right)\right|,\hfill \end{array}(39)$

which demonstrates that for $u_d=u_u$ the $d$-quark decay rate vanishes in the ultrarelativistic limit according to (Equation 38). For the $e$-capture rate, we find

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{ue\to d\nu }({\mu }_{\mathrm{\Delta }})& =\hfill & \frac{G^2{T}^8}{8{\pi }^5}{\int }_{-\infty }^{\infty }dy\bar{y}g(\bar{y}){\int }_{-{\alpha }_d-y}^{0}d{x}^{\prime }\hfill \\ \hfill & \hfill & \times \left[{({\alpha }_d+y+\mathrm{\Delta }u)}^2-{(x^{\prime }+{\alpha }_d+y)}^2\right]\hfill \\ \hfill & \hfill & \times \left[-x^{\prime }(2{\alpha }_d+2y+x^{\prime })\right]\ln \left|1+\exp \left(x^{\prime }/2+y\right)\right|,\hfill \end{array}(40)$

where we made a variable change $x=x^{\prime }+{\alpha }_d+y$ and made sure that $\mathrm{\Delta }u\ne 0$ in order to compute the derivative with respect to ${\mu }_{\mathrm{\Delta }}(\mathrm{\Delta }u)$. If we now assume that $\beta$-equilibrium is established with $\bar{y}=y$, and also $\mathrm{\Delta }u=0$ we obtain from Equation 40

$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{ue\to d\nu }& =\hfill & \frac{G^2{T}^8}{8{\pi }^5}{\int }_{-\infty }^{\infty }dyyg(y){\int }_{-{\alpha }_d-y}^{0}dx\hfill \\ \hfill & \hfill & \times \hspace{0.17em}{x}^2{(2{\alpha }_d+2y+x)}^2\ln \left|1+\exp \left(x/2+y\right)\right|\hfill \\ \hfill & \simeq \hfill & \frac{G^2{T}^8{\alpha }_d^2}{2{\pi }^5}{\int }_{-\infty }^{\infty }dyyg(y){\int }_{-\infty }^{0}dx x^2\ln \left[1+\exp \left(x/2+y\right)\right],\hfill \end{array}(41)$

where we dropped the smaller than ${\alpha }_d$ terms, and replaced the lower boundary of integration by $-\infty$ (as the logarithm is suppressed at small values of $x$).

To compute the bulk viscosity, consider next small departures from $\beta$-equilibrium ${\mu }_{\mathrm{\Delta }}\ll T$. Then, the net $u$-quark production rate can be approximated as ${\mathrm{\Gamma }}_{d\to ue\bar{\nu }}-{\mathrm{\Gamma }}_{ue\to d\nu }={\lambda }_d{\mu }_{\mathrm{\Delta }}$, where ${\lambda }_d$ is the equilibration coefficient defined as

$\begin{array}{ll}\hfill {\lambda }_d=-\frac{\partial {\mathrm{\Gamma }}_{ue\to d\nu }}{\partial {\mu }_{\mathrm{\Delta }}}{|}_{{\mu }_{\mathrm{\Delta }}=0}& =-\frac{G^2{T}^7{\alpha }_d^2}{2{\pi }^5}\left\{{\int }_{-\infty }^{\infty }dyg(y)[1-y(1+g(y))]\right.\hfill \\ \hfill & {\int }_{-\infty }^{0}dx{x}^2\ln \times \left[1+\exp \left(x/2+y\right)\right]\hfill \\ \hfill & -\left.{\int }_{-\infty }^{\infty }dyyg(y){\int }_{-\infty }^{0}dxx\ln \left[1+\exp \left(x/2+y\right)\right]\right\}.\hfill \end{array}(42)$

Note that when computing ${\lambda }_d$, we also take the derivative of the terms containing $\mathrm{\Delta }u$.

The integrals in Equations 41, 42 can be computed numerically, after which we obtain

${\mathrm{\Gamma }}_{ue\to d\nu }\simeq 0.38G^2{p}_{Fd}^2{T}^6,{\lambda }_d\simeq 0.2G^2{p}_{Fd}^2{T}^5.(43)$

We observe that, as has been noted in other treatments of Urca processes in quark matter (Burrows, 1980; Duncan et al., 1984), the $u{e}^{-}\to d$ rate contains an additional power of $T$ as compared to the low-$T$ Urca reaction rates of nonrelativistic baryons. This is because the $u$, $d$, and $e$ are all ultrarelativistic, so their Fermi momenta are on the borderline between the Urca process being allowed and being forbidden: the $u$ and $e^{-}$ momenta have to be collinear in order to create a $d$. It is only the thermal blurring of the Fermi surfaces that creates phase space for the process to occur. Consequently, the product $(k\cdot p)$ in Equation 16 contributes an additional power of $T$ beyond the $T^5$ scaling that emerges when the phase space includes a range of angles even in the low temperature limit. It is worth noting that the product $\left(k^{\prime }\cdot p^{\prime }\right)$ does not introduce an additional power of $T$ because the angle between the $d$-quark and neutrino momenta can be arbitrary, since the neutrino is thermal.

Thus, the low-temperature direct Urca rates for light quarks (when the isospin chemical shift is absent) differ qualitatively from those of massive particles. For example, Urca reactions involving the $s$ quark instead of the $d$ quark will have low-temperature rates similar to the nucleonic Urca rates (Alford et al., 2023)

${\mathrm{\Gamma }}_{s\to ue\bar{\nu }}={\mathrm{\Gamma }}_{eu\to s\nu }=0.0336G^2{T}^5{\mu }_s^{*}\left[{(p_{Fu}+p_{Fe})}^2-p_{Fs}^2\right]\theta (p_{Fe}+p_{Fu}-p_{Fs}).(44)$

The relevant coefficient ${\lambda }_s$ in the low-$T$ limit is given by

${\lambda }_s=\frac{17}{120\pi }{G}^2{T}^4{\mu }_s^{*}\left[{(p_{Fu}+p_{Fe})}^2-p_{Fs}^2\right].(45)$

In this limit we have also the relations $p_{Fe}={\mu }_e$, $p_{Fu}\simeq {\mu }_u^{*}={\mu }_u-{\omega }_0$, ${\mu }_s^{*}={\mu }_s-{\varphi }_0=\sqrt{p_{Fs}^2+m_s^2}$, therefore for the square brackets in Equation 45 we can write ${(p_{Fu}+p_{Fe})}^2-p_{Fs}^2\simeq {({\mu }_u-{\omega }_0+{\mu }_e)}^2-{({\mu }_s-{\varphi }_0)}^2+m_s^{*2}=(2{\mu }_s-{\omega }_0-{\varphi }_0)({\varphi }_0-{\omega }_0)+m_s^{*2}$, where we used the chemical equilibrium condition ${\mu }_u+{\mu }_e={\mu }_s$. Numerically, we find that ${\omega }_0,{\varphi }_0\ll m_s^{*}\simeq {\mu }_s^{*}$, therefore, the square brackets in Equation 45 can be approximated as $m_s^{*2}$, which leads to the simple expressions

${\mathrm{\Gamma }}_{s\to ue\bar{\nu }}={\mathrm{\Gamma }}_{eu\to s\nu }=0.0336G^2{\mu }_s^{*}{m}_s^{*2}{T}^5,{\lambda }_s\simeq 0.03G_F^2{\sin }^2{\theta }_c{\mu }_s^{*}{m}_s^{*2}{T}^4.(46)$

To estimate the rate of non-leptonic processes (Equation 17) we will use below the low-temperature expression (Madsen, 1993).

${\lambda }_{\text{non}-\text{lep}}=\frac{64}{5{\pi }^3}{G}_F^2{\sin }^2{\theta }_c{\cos }^2{\theta }_c{\mu }_d^{*5}{T}^2.(47)$

4 Bulk viscosity of $udse$ matter

In this section, we will derive the bulk viscosity that arises from processes (Equations 10–13) in $udse$ matter, i.e., matter consisting of $u,d,s$ quarks and electrons, with paired red-green light quarks; the unpaired excitations are blue light quarks, strange quarks of all colors, and leptons (electrons, and muons if energetically favored). Consider small-amplitude density oscillations with a frequency $\omega$. Separating the oscillating parts from the static equilibrium values of particle densities, we can write $n_j(t)=n_{j0}+\delta n_j(t)$, where $\delta n_j(t)\sim e^{i\omega t}$, and $j=\{d,u,e,s\}$ labels the particles.

Oscillations drive the system out of chemical equilibrium, leading to nonzero chemical imbalance ${\mu }_{\mathrm{\Delta }}=\delta {\mu }_d-\delta {\mu }_u-\delta {\mu }_e$ in the case of $ude$ matter. To include strange quarks, note that the non-leptonic reaction $d+u\leftrightarrow s+u$ proceeds much faster than the Urca processes; therefore, the relation ${\mu }_d={\mu }_s$ always holds, and the shift in chemical potentials is given by ${\mu }_{\mathrm{\Delta }}=\delta {\mu }_d-\delta {\mu }_u-\delta {\mu }_e=\delta {\mu }_s-\delta {\mu }_u-\delta {\mu }_e$, which can be written as

${\mu }_{\mathrm{\Delta }}=A_d\delta n_d+A_s\delta n_s-A_u\delta n_u-A_e\delta n_e,(48)$

where the susceptibilities $A_j$ and are given as

$A_d=A_{dd}-A_{ud},A_u=A_{uu}-A_{du},A_s=A_{ds}-A_{us},A_e=A_{ee},(49)$

where $A_{ij}=\partial {\mu }_i/\partial n_j$, and the derivatives are computed in the beta-equilibrium state. Note that off-diagonal elements $i\ne j$ do not vanish because of strong interactions between quarks.

If the weak processes were switched off, then the number of all particle species would be conserved separately, which implies

$\frac{\partial }{\partial t}\delta n_j^0(t)+\theta n_{j0}=0,\delta n_j^0(t)=-\frac{\theta }{i\omega }{n}_{j0},(50)$

where $\theta ={\partial }_i{v}^i$ is the fluid velocity divergence. Once the weak reactions are switched on, there is a net production of particles that should be the neutrino production rates by quarks, given by

${\mathrm{\Gamma }}_{d\to ue\bar{\nu }}-{\mathrm{\Gamma }}_{ue\to d\nu }={\lambda }_d{\mu }_{\mathrm{\Delta }},(51)$

${\mathrm{\Gamma }}_{s\to ue\bar{\nu }}-{\mathrm{\Gamma }}_{ue\to s\nu }={\lambda }_s{\mu }_{\mathrm{\Delta }},(52)$

which define the equilibration coefficients ${\lambda }_d$ and ${\lambda }_s$. Therefore, the rate equations for each fermion species can be written in this case as

$\frac{\partial }{\partial t}\delta n_d=-\theta n_{d0}-{\lambda }_d{\mu }_{\mathrm{\Delta }}-I_{ud\to us},(53)$

$\frac{\partial }{\partial t}\delta n_s=-\theta n_{s0}-{\lambda }_s{\mu }_{\mathrm{\Delta }}+I_{ud\to us},(54)$

$\frac{\partial }{\partial t}\delta n_u=-\theta n_{u0}+({\lambda }_d+{\lambda }_s){\mu }_{\mathrm{\Delta }},(55)$

$\frac{\partial }{\partial t}\delta n_e=-\theta n_{e0}+({\lambda }_d+{\lambda }_s){\mu }_{\mathrm{\Delta }}.(56)$

where $I_{ud\to us}$ denotes the rate of the non-leptonic reaction $d+u\to s+u$, which is driven by a nearly vanishing chemical potential difference, $\delta {\mu }_d-\delta {\mu }_s\ll {\mu }_{\mathrm{\Delta }}$. Despite its small magnitude, this shift cannot be neglected because the corresponding $\lambda$-coefficient may be very large; see Jones (2001) for a discussion of this point.

Among the resulting balance equations, only one is independent due to the presence of three constraints: charge neutrality (both color and electric) and baryon number conservation. These constraints can be expressed in the form

${\tilde{n}}_u+{\tilde{n}}_d+{\tilde{n}}_s=2(n_u+n_d+n_s)=2n_b,(57)$

$\frac{2}{3}(n_u+{\tilde{n}}_u)-\frac{1}{3}(n_d+n_s+{\tilde{n}}_d+{\tilde{n}}_s)=n_e+n_{\mu }=n_u+{\tilde{n}}_u-n_b,(58)$

where we denote with $n_i$ the densities of only blue quarks, and with ${\tilde{n}}_i$ – the summed densities of red and green quarks, and $n_b$ is the baryon density. Then we find

$\delta n_d+\delta n_s=\delta n_b-\delta n_u,\delta {\tilde{n}}_d+\delta {\tilde{n}}_s=2\delta n_b-\delta {\tilde{n}}_u,(59)$

$\delta n_e+\delta n_{\mu }=\delta n_u+\delta {\tilde{n}}_u-\delta n_b=\delta {\tilde{n}}_u-\delta n_d-\delta n_s,(60)$

${\mu }_{\mathrm{\Delta }}=\left(A_d+A_e\right)\delta n_b-A_1\delta n_u-A_e(\delta {\tilde{n}}_u-\delta n_{\mu })+(A_s-A_d)\delta n_s,(61)$

where $A_1=A_u+A_d+A_e$.

Substituting Equation 61 into Equation 55, assuming $\delta n_j\sim e^{i\omega t}$ and using Equation 50 for $n_b$, ${\tilde{n}}_u$, and $n_{\mu }$ (the paired quarks and muons do not participate in reactions), we obtain

$i\omega \delta n_u=-\theta n_{u0}+\lambda (A_d+A_e)\delta n_b-\lambda A_1\delta n_u-\lambda A_e(\delta {\tilde{n}}_u-\delta n_{\mu })+\lambda (A_s-A_d)\delta n_s,(62)$

where $\lambda ={\lambda }_d+{\lambda }_s$ is the summed rate of the $u$-quark production by Equations 10–13. To eliminate $\delta n_s$ from this equation, we use the condition of chemical equilibrium with respect to non-leptonic reaction

$\begin{array}{ccc}\hfill 0& =\hfill & \delta {\mu }_d-\delta {\mu }_s=(A_{dd}-A_{sd})\delta n_d+(A_{du}-A_{su})\delta n_u+(A_{ds}-A_{ss})\delta n_s\hfill \\ \hfill & =\hfill & A_B\delta n_b+A_U\delta n_u+A_S\delta n_s,\hfill \end{array}(63)$

which can be solved for $\delta n_s$, and where we introduced shorthand notations

$\begin{array}{ll}\hfill A_B& =A_{dd}-A_{sd},A_U=A_{du}-A_{su}-A_{dd}+A_{sd},\hfill \\ \hfill & A_S=A_{ds}-A_{ss}-A_{dd}+A_{sd}.\hfill \end{array}(64)$

Substituting $\delta n_s$ from Equation 63 back into Equation 62 and using Equation 50 gives

$\delta n_u=-\frac{i\omega n_{u0}+\lambda (B+A_e)n_{B0}-\lambda A_e({\tilde{n}}_{u0}-n_{\mu 0})}{i\omega +\lambda A}\frac{\theta }{i\omega }.(65)$

Subtracting from this expression $\delta n_u^0=-\theta n_{u0}/i\omega$ we obtain the nonequilibrium shift.

$\delta n_u^{\prime }=\delta n_u-\delta n_u^0=-\frac{C}{i\omega +\lambda A}\frac{\theta \lambda }{i\omega },(66)$

$C\equiv B(n_{d0}+n_{s0})-(A-B-A_e)n_{u0}-A_e{n}_{e0},(67)$

$A\equiv A_1+\frac{(A_s-A_d)A_U}{A_S},B\equiv A_d-\frac{A_U{A}_B}{A_S}.(68)$

Solving Equation 63 for $\delta n_s^{\prime }$ (recall that the non-equilibrium shifts of $n_b$, $n_{\mu }$ and the paired quarks are zero) we find

$\delta n_s^{\prime }=-\frac{A_U}{A_S}\delta n_u^{\prime }.(69)$

Then the bulk viscous pressure will be given by (using short-hand notation $c_j=\partial p/\partial n_j$)

$\mathrm{\Pi }={\displaystyle \sum _j}\frac{\partial p}{\partial n_j}\delta n_j^{\prime }=\left[(c_u-c_d+c_e)+(c_d-c_s)\frac{A_U}{A_S}\right]\delta n_u^{\prime },(70)$

where we used Equations 59, 60. Assuming isothermal perturbations to compute the pressure derivatives, and further using Equation 66 and the symmetry relation $A_{ij}=A_{ji}$ we find

$\mathrm{\Pi }=-C\delta n_u^{\prime }=\frac{C^2\lambda }{i\omega +\lambda A}\frac{\theta }{i\omega }.(71)$

The bulk viscosity is the real part of $-\mathrm{\Pi }/\theta$ and is thus defined as

$\zeta =\frac{C^2}{A}\frac{\gamma }{{\omega }^2+{\gamma }^2},(72)$

which has the classic resonant form depending on two quantities: the susceptibility prefactor $C^2/A$, which depends only on the EoS, and the relaxation rate $\gamma =\lambda A$, which depends on the EoS and the microscopic interaction rates. In the case where the non-diagonal susceptibilities can be neglected, the quantities $A$ and $C$ are given by

$A=\frac{A_d{A}_s}{A_d+A_s}+A_u+A_e=-\frac{1}{n_b}{\left.\frac{\partial {\mu }_{\mathrm{\Delta }}}{\partial x_u}\right|}_{n_b},(73)$

$C=\frac{A_d{A}_s}{A_s+A_d}(n_{d0}+n_{s0})-A_u{n}_{u0}-A_e{n}_{e0}=n_b{\left.\frac{\partial {\mu }_{\mathrm{\Delta }}}{\partial n_b}\right|}_{x_u},(74)$

where we redefined $A_i=\partial {\mu }_i/\partial n_i$ which are computed in chemical equilibrium. If we neglect the contribution from $s$-quarks, then $n_{s0}\to 0$, $A_s\to \infty$, and we find the appropriate quantities for the $ude$ quark matter

$A=A_u+A_d+A_e,C=n_{d0}{A}_d-n_{u0}{A}_u-n_{e0}{A}_e.(75)$

We note that $A$ can be interpreted as the beta-disequilibrium–$u$-quark-fraction susceptibility: it quantifies how the out-of-beta-equilibrium chemical potential responds to a change in the $u$-quark fraction. Similarly, $C$ is the beta-disequilibrium–baryon-density susceptibility: it characterizes the response of the out-of-beta-equilibrium chemical potential to a change in the baryon density, while keeping the particle fractions fixed.

5 Numerical results

5.1 Equilibration coefficients and Urca rates

As expected, the non-leptonic processes described by Equation 17 occur at significantly higher rates than the Urca processes. This is evident in Figure 6, which shows the equilibration coefficients for both the Urca processes (Equations 10–13) and the non-leptonic processes (Equation 17). Notably, in the temperature range $1\le T\le 10$ MeV the rates of the $d$-Urca and $s$-Urca processes are comparable for the matter composition predicted by the vector-enhanced NJL model. As a result, the bulk viscosity associated with the nonleptonic channels is expected to peak at much lower temperatures, well below the relevant range for BNS mergers, whose oscillation frequencies lie in the kHz regime. This observation supports our assumption that, in the temperature range $1\le T\le 10$ MeV, the bulk viscosity can be reliably calculated from the Urca processes alone, under the additional condition ${\mu }_d={\mu }_s$. The effects of diquark and vector couplings enter the equilibration coefficients through the composition (chemical potentials, pairing gap, etc.) of the participating particles. It is seen that the combined effect on the equilibration coefficients is to decrease both non-leptonic and Urca processes with increasing vector coupling. The changes associated with variations of the diquark coupling are insignificant.

Figure 6

Figure 6. The equilibration coefficients $\lambda$ of Urca and non-leptonic processes as functions of temperature for fixed values of number density and various fixed values of vector and diquark couplings.

Analytical expressions for ${\lambda }_d$ and ${\lambda }_s$ coefficients were derived in the low-temperature limit, see Equations 43, 46 under the assumptions that $T\ll {\mu }_i$, $m_d,m_s\to 0$ and ${\omega }_0-{\varphi }_0\ll m_s$. They are accurate to within a few percent when compared to numerical results that do not rely on these approximations and provide insight into the scaling of these coefficients with various parameters. In particular, it is seen that ${\lambda }_s(T)$ is suppressed by a factor of ${\sin }^2{\theta }_c=0.05$ compared to ${\lambda }_d(T)$ which has ${\cos }^2{\theta }_c=0.95$; it also has a smaller numerical prefactor from the phase space integration. Due to the influence of interactions on the chemical potentials of light quarks mediated by the isoscalar $\omega$-field, the $\beta$-equilibrium for massless particles requires that $p_{Fd}=p_{Fu}+p_{Fe}$. This condition implies that the direct Urca process is only thermally allowed. In contrast, the $s$-Urca channels are kinematically open, with a substantial available energy range given by $p_{Fu}+p_{Fe}-p_{Fs}\ge 70\mathrm{M}\mathrm{e}\mathrm{V}$, primarily due to the large mass of the strange quark (Duncan et al., 1983; Duncan et al., 1984). We previously discussed the additional power of $T$ arising from the matrix element involving the four-product of the $u$-quark and electron momenta, which are massless. In contrast, the phase-space contributes the standard $T^5$ scaling, which would be the only temperature-dependent component if all particles were massive (implicit weak dependence of masses and other thermodynamic parameters is understood). As a consequence, the difference in temperature scaling leads to the intersection of the ${\lambda }_d(T)$ and ${\lambda }_s(T)$ functions at a temperature in the MeV range, as seen in Figure 6.

We show in Figure 7 the temperature dependence of the total $\beta$-relaxation rate $\gamma$ due to the Urca processes (Equations 10–13) as a function of temperature for different fixed values of density, diquark, and vector couplings. It follows a power law scaling $\gamma \propto T^{4.5}$ in the temperature range $1\le T\le 10$ MeV. A larger vector coupling enhances the rate $\gamma$ slightly, this enhancement being more pronounced at higher density. There are no significant changes with the diquark coupling in the limit $T\ll \mathrm{\Delta }$. Due to the Lorentzian structure of bulk viscosity in the frequency domain, see Equation 72, its maximum is located at the “resonance” temperature determined by equating $\gamma$ to the characteristic angular frequency $\omega =2\pi f$. For illustration, we consider two representative frequencies. At $f=1$ kHz, the intersection occurs near $T\simeq 3-4$ MeV, while for $f=10$ kHz, it shifts to approximately $T\simeq 5-6$ MeV.

Figure 7

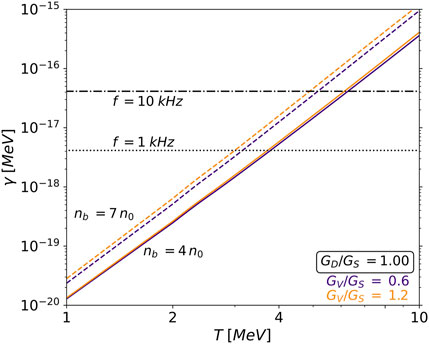
Figure 7. The $\gamma$ parameter as a function of temperature for two values of number density and various fixed values of vector and diquark couplings.

5.2 Bulk viscosity and damping timescales

Next, we turn to the main quantity of interest of this study - the bulk viscosity of neutrino-transparent quark matter in the 2SC phase. Figure 8 shows the temperature dependence of bulk viscosity for density oscillations at two frequencies $f=1$ kHz and $f=10$ kHz and at two baryon densities $n_b=4n_0$ and $n_b=7n_0$. As a key feature, the figure also shows the influence of the variation of the vector coupling $G_V/G_S$. The diquark coupling is set to $G_D/G_S=1$; results for $G_D/G_S=1.25$ were also calculated but are not shown because they are almost identical to those for $G_D/G_S=1$. This is understandable, since for either of these values of $G_D$, the gap in the spectrum of the paired quarks is much greater than the temperature, so they are frozen out.

Figure 8

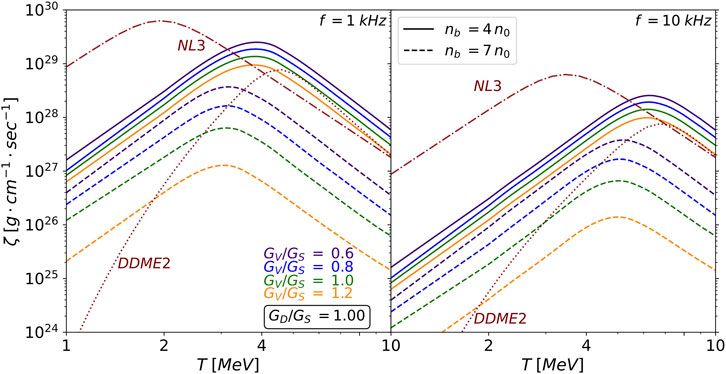
Figure 8. Bulk viscosity as a function of temperature for $n_b=4n_0$ (solid lines) and $n_b=7n_0$ (dashed lines) and various fixed values of vector and diquark couplings; here $n_0$ is the nuclear saturation density. For comparison, we also show the bulk viscosity of neutrino-transparent nucleonic matter, as was computed in Alford et al. (2023) for models DDME2 (dotted line) and NL3 (dash-dotted line) for $n_b/n_0=4$.

The curves of bulk viscosity as a function of temperature have the Lorentzian shape expected from (72). For density oscillations of angular frequency $\omega$, the maximum is reached when $\gamma (T)=\omega$, so its location along the $T$ axis is determined by the temperature dependence of the relaxation rate $\gamma$.

As density increases, the maximum slowly moves to lower temperatures because the relaxation rate $\gamma$ rises with density (as the increase in phase space near the Fermi surfaces leads to faster Urca rates), so $\gamma (T)=\omega$ is achieved at lower temperatures. The leftward shift in the curve is small because $\gamma$ rises quickly, roughly as $T^{4.5}$, so it only takes a small reduction in $T$ to compensate for the effect of rising density. This temperature dependence differs from the $T^4$ scaling seen in Hernández et al. (2024) because it is a combination of ${\lambda }_s\sim T^4$ scaling for the $u\to s{e}^{-}{\bar{\nu }}_e$ channel (Equation 44) and ${\lambda }_d\sim T^5$ for the $u\to d{e}^{-}{\bar{\nu }}_e$ Urca channel (Equation 43). The position of the maximum is even less affected by changes in the vector coupling $G_V$, since it has only a small effect on the Urca rates, see Figure 6. We also find that the effect of changing $G_D$ is quite small, therefore, we do not show this case explicitly.

The overall scale of the bulk viscosity curve (e.g., the value attained at the maximum) is controlled by the prefactor $C^2/A$ in Equation 72. The susceptibilities $C$ and $A$ are affected by the density and the couplings. As density increases, the overall scale decreases considerably, mainly due to a decrease in the $C$ susceptibility of 2SC matter. We also see a noticeable effect of the couplings. At lower density $n_b/n_0=4$, doubling the vector coupling reduces the bulk viscosity at all temperatures by a factor of 3. At higher density $n_b/n_0=7$, doubling the vector coupling reduces the bulk viscosity by more than an order of magnitude. Without explicitly showing in the figure, let us point out that increasing the magnitude of the diquark coupling $G_D/G_S$ leads to a further decrease in the bulk viscosity, which is more pronounced for a larger density $n_b/n_0=7$. The magnitude of the decrease is about a factor of two. The temperature dependence of the bulk viscosity $\zeta (T)$ is seen to be self-similar for the curves shown. From Equation 72 the rate goes as $\gamma$ well below the maximum and as $1/\gamma$ well above the maximum, so from the scaling given in the previous paragraph one would expect $\zeta \propto T^{4.5}$ and $\zeta \propto T^{-4.5}$ respectively. However, there is also a small temperature dependence from the susceptibilities, so the scaling is closer to $\zeta (T)\propto T^{-4.2}$ on the descending side.

We also reiterate that, as noticed in Alford et al. (2024), including/excluding the strange quarks increases/decreases the total relaxation rate by a factor of 1–2, resulting in only a slight shift of the viscosity peak toward lower/higher temperatures.

For comparison, we also show the bulk viscosity of neutrino-transparent nucleonic matter, as calculated in Alford et al. (2023), using the DDME2 (dotted line) and NL3 (dash-dotted line) models at a baryon density of $n_b/n_0=4$. The key difference between these two models lies in the behavior of the direct Urca process at low temperatures: it is allowed for the NL3 model but remains blocked for DDME2 at this density. Consequently, the bulk viscosities predicted by the two models differ markedly at temperatures $T\le 4$ MeV, but are rather similar at $T\ge 4$ MeV. In this temperature range, the bulk viscosity of 2SC quark matter is similar to that of nucleonic matter, and variations in the vector or diquark couplings do not significantly affect this outcome.

At lower temperatures, the bulk viscosity of 2SC quark matter falls between the values predicted by the two nucleonic models, regardless of the specific values of the vector and diquark couplings. This behavior can be attributed to the $u$-quark fraction being slightly below, but very close to the threshold for the direct Urca processes described in Equations 10, 11. Specifically, the difference in Fermi momenta between initial-state and final-state particles, $p_{Fd}-p_{Fu}-p_{Fe}$, is less than 1 MeV for densities in the range $4\le n_b/n_0\le 7$. As a result, thermal smearing at temperatures as low as $T\ge 1$ MeV is sufficient to provide the phase space required for light-quark Urca processes to occur.

Since the bulk viscosity arises from semi-leptonic weak interactions involving the unpaired blue quarks, one would expect similar behavior in unpaired quark matter, specifically a peak in the bulk viscosity at MeV-scale temperatures. This feature is indeed observed in Alford and Schmitt (2007) (Figure 8), Sa’d et al. (2007b) (Figure 3) and in Hernández et al. (2024) (Figure 4), although the maximum viscosity reported in those studies is smaller due to their assumption of a lighter strange quark.

In the aftermath of a BNS merger, the resulting remnant undergoes rapid and large-amplitude density oscillations, driven by strong differential rotation, internal thermal gradients, and potentially turbulent motion. The remnant’s temperature is highly variable over its density range, and some regions may pass through or remain within the temperature window where the bulk viscous damping is especially efficient. If so, the bulk viscosity can significantly damp oscillation modes, converting mechanical energy into heat (or radiated neutrinos) and altering the thermal evolution of the remnant. The characteristic time scale of damping of local oscillations (on the hydrodynamic scales characterized by fixed density, temperature, entropy, etc.) is given by (Alford et al., 2018; Alford and Harris, 2019; Alford et al., 2020)

$\tau =\frac{1}{9}\frac{K{n}_b}{{\omega }^2\zeta },K=9\frac{\partial P}{\partial n_b},(76)$

where $K$ is the incompressibility and $P$ is the pressure. Using our results for the bulk viscosity, we have estimated the damping timescale from Equation 76. The results are shown in Figure 9. As $\tau \propto {\zeta }^{-1}$, we see an inversion in the temperature dependence in the damping time scale, which implies that it is shortest at the resonant maximum of the bulk viscosity. We have verified that the compressibility $K$ in (Equation 76) is insensitive to the temperature within the relevant range $1\le T\le 10$ MeV. Turning to the dependence of the damping timescale $\tau$ on the diquark and vector couplings, we find that its behavior is determined by that of the bulk viscosity $\zeta$. At lower density $(n_b/n_0=4)$, varying the vector coupling by a factor of two changes the maximum value of $\tau$ by roughly a factor of 3, with the shortest damping times corresponding to the smallest values of the vector and diquark couplings. At higher density ($n_b/n_0=7$), the damping timescale becomes even more sensitive to the vector coupling: varying the coupling by a factor of two changes $\tau$ by more than an order of magnitude. While a smaller diquark coupling $G_D/G_S$ also leads to shorter damping times for a fixed vector coupling, the variation it introduces is, in comparison, not large.

Figure 9

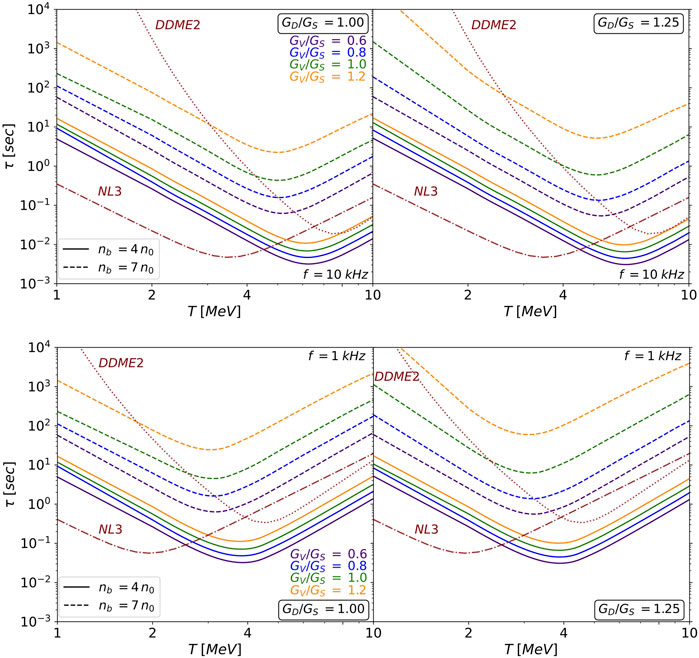
Figure 9. Dependence of bulk viscous damping timescales on temperature for two values of number density and various fixed values of vector and diquark couplings. For comparison, we also show the damping timescales of neutrino-transparent nucleonic matter as was computed in Alford et al. (2023) for models DDME2 (dotted line) and NL3 (dashed line) for $n_b/n_0=4$.

Overall, we find that the damping timescales range from a few milliseconds up to several hundred milliseconds, which are comparable to the characteristic timescales of the short-term evolution of the post-merger remnant. For longer-lived remnants, which can survive for several seconds or more, bulk viscous dissipation may play an even more significant role in their dynamical evolution.

Furthermore, a comparison with the results obtained for nucleonic matter reveals that the damping timescales in 2SC quark matter are remarkably similar. This suggests that, within the framework of our NJL model, it would be challenging to distinguish 2SC quark matter from nuclear matter based solely on their bulk viscous dissipation properties in the temperature range of 1–10 MeV.

6 Conclusion

Expanding on our previous work (Alford et al., 2024), we have studied the effects of variations in diquark and vector couplings–specifically $G_D/G_S=\mathrm{1,1.25}$ and $G_V/G_S=0.6,0.8,1.0,1.2$ – on the input parameters used to compute the weak interaction rates and the bulk viscosity of the 2SC phase of finite-temperature quark matter within the vector-enhanced NJL model. We focus on the low temperature range $1\le T\le 10\mathrm{M}\mathrm{e}\mathrm{V}$ and the baryon density range $4n_0\le n_b\le 7n_0$, within which neutrinos are expected to be free-streaming.

The primary effect of varying the vector coupling is a shift in the quark chemical potentials, which affects material properties such as bulk viscosity in two ways. Firstly, it changes the relevant static susceptibilities in the EoS; secondly, it changes flavor-changing Urca rates by altering the available phase space. In contrast, changing the diquark coupling mainly affects the degree of suppression of red-green quark contributions by changing the pairing gap. However, because red-green quarks are indirectly coupled to the unpaired blue-quark sector through $\beta$-equilibrium and charge neutrality conditions, their influence on the overall thermodynamics is nontrivial and cannot simply be neglected.

Quantitatively, we find that varying the vector coupling by a factor of two changes the bulk viscosity and corresponding damping timescale by a factor of 3–20 at densities from $4n_0$ to $7n_0$ This sensitivity primarily arises from the $C$ susceptibility of 2SC matter, see Equation 74, with a smaller contribution from modifications to the weak interaction rates. In comparison, changes in the diquark coupling have a more limited impact. The bulk viscosity and damping time for 2SC quark matter closely resemble those of nucleonic matter (Alford et al., 2023), making it difficult to distinguish these states via their bulk viscous behavior.

It is worth noting that at temperatures below the range studied here, $T\lesssim 0.1$ $\mathrm{M}\mathrm{e}\mathrm{V}$, one can no longer rely on our assumption that the nonleptonic flavor equilibration process can be treated as instantaneous. When its finite rate is taken into account, the bulk viscosity shows a second peak at $T\sim 0.05$ MeV (Alford and Schmitt, 2007; Cruz Rojas et al., 2024; Hernández et al., 2024). This peak is absent in nuclear matter. The peak we observe at temperatures in the MeV range, arising from semi-leptonic processes, is also seen in Hernández et al. (2024) (Figure 4) for their heaviest strange quark, $m_s\ge 200$ MeV. In our model the strange quark is even heavier, $300\le m_s\le 400$ MeV so the semileptonic peak can be treated as a separate feature. Note that the picture may be quantitatively different in other partly-paired phases. For example, Urca rates in the gapless 2SC phase, as computed in Jaikumar et al. (2006), may allow the red-green quarks to contribute to the Urca rates at levels comparable to blue quarks. Furthermore, as in our setup, blue quarks are unpaired, one could anticipate that semi-leptonic rates for unpaired quark matter may be similar to those for 2SC matter studied here. By extrapolation, this suggests that the unpaired quark matter at $T\approx 1$ to 10 MeV may also be difficult to distinguish from nuclear matter, as was found for the 2SC phase.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MA: Conceptualization, Investigation, Software, Writing – original draft, Writing – review and editing. AH: Conceptualization, Investigation, Software, Writing – original draft, Writing – review and editing. AS: Conceptualization, Investigation, Software, Writing – original draft, Writing – review and editing. ST: Conceptualization, Investigation, Software, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was partly supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics under Award No. DE-FG02-05ER41375 (MA), the Higher Education and Science Committee (HESC) of the Republic of Armenia through “Remote Laboratory” program, Grant No. 24RL-1C010 (AH and AS), the Polish National Science Centre (NCN) Grant 2023/51/B/ST9/02798 (AS and ST) and the Deutsche For\-schungs\-gemeinschaft (DFG) Grant No. SE 1836/6-1 (AS). ST is a member of the IMPRS for “Quantum Dynamics and Control” at the Max Planck Institute for the Physics of Complex Systems, Dresden, Germany, and acknowledges its partial support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abuki, H. (2018). Chiral crystallization in an external magnetic background: chiral spiral versus real kink crystal. Phys. Rev. D. 98, 054006. doi:10.1103/PhysRevD.98.054006

CrossRef Full Text | Google Scholar

Alford, M., Harutyunyan, A., and Sedrakian, A. (2019). Bulk viscosity of baryonic matter with trapped neutrinos. Phys. Rev. D. 100, 103021. doi:10.1103/PhysRevD.100.103021

CrossRef Full Text | Google Scholar

Alford, M., Harutyunyan, A., and Sedrakian, A. (2020). Bulk viscous damping of density oscillations in neutron star mergers. Particles 3, 500–517. doi:10.3390/particles3020034

CrossRef Full Text | Google Scholar

Alford, M., Harutyunyan, A., and Sedrakian, A. (2021b). Bulk viscosity from urca processes: npeμ matter in the neutrino-trapped regime. Phys. Rev. D. 104, 103027. doi:10.1103/PhysRevD.104.103027

CrossRef Full Text | Google Scholar

Alford, M., Harutyunyan, A., and Sedrakian, A. (2023). Bulk viscosity from Urca processes: n p e μ matter in the neutrino-transparent regime. Phys. Rev. D. 108, 083019. doi:10.1103/PhysRevD.108.083019

CrossRef Full Text | Google Scholar

Alford, M., Harutyunyan, A., Sedrakian, A., and Tsiopelas, S. (2024). Bulk viscosity of two-color superconducting quark matter in neutron star mergers. Phys. Rev. D. 110, L061303. doi:10.1103/PhysRevD.110.L061303

CrossRef Full Text | Google Scholar

Alford, M. G., Bovard, L., Hanauske, M., Rezzolla, L., and Schwenzer, K. (2018). Viscous dissipation and heat conduction in binary neutron-star mergers. Phys. Rev. Lett. 120, 041101. doi:10.1103/PhysRevLett.120.041101

PubMed Abstract | CrossRef Full Text | Google Scholar

Alford, M. G., and Haber, A. (2021). Strangeness-changing rates and hyperonic bulk viscosity in neutron star mergers. Phys. Rev. C 103, 045810. doi:10.1103/PhysRevC.103.045810

CrossRef Full Text | Google Scholar

Alford, M. G., Haber, A., Harris, S. P., and Zhang, Z. (2021a). Beta equilibrium under neutron star merger conditions. Universe 7, 399. doi:10.3390/universe7110399

CrossRef Full Text | Google Scholar

Alford, M. G., and Harris, S. P. (2019). Damping of density oscillations in neutrino-transparent nuclear matter. Phys. Rev. C 100, 035803. doi:10.1103/PhysRevC.100.035803

CrossRef Full Text | Google Scholar

Alford, M. G., and Schmitt, A. (2007). Bulk viscosity in 2SC quark matter. J. Phys. G34, 67–101. doi:10.1088/0954-3899/34/1/005

CrossRef Full Text | Google Scholar

Alford, M. G., Schmitt, A., Rajagopal, K., and Schäfer, T. (2008). Color superconductivity in dense quark matter. Rev. Mod. Phys. 80, 1455–1515. doi:10.1103/RevModPhys.80.1455

CrossRef Full Text | Google Scholar

Aoki, S., Aoki, Y., Fukaya, H., Hashimoto, S., Kanamori, I., Kaneko, T., et al. (2024). Axial U(1) symmetry near the pseudocritical temperature in N_f = 2 + 1 lattice QCD with chiral fermions. PoS, 185. doi:10.22323/1.453.0185

CrossRef Full Text | Google Scholar

Baiotti, L. (2019). Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 109, 103714. doi:10.1016/j.ppnp.2019.103714

CrossRef Full Text | Google Scholar

Baiotti, L., and Rezzolla, L. (2017). Binary neutron-star mergers: a review of Einstein’s richest laboratory. Rept. Prog. Phys. 80, 096901. doi:10.1088/1361-6633/aa67bb

PubMed Abstract | CrossRef Full Text | Google Scholar

Bauswein, A., Bastian, N. U. F., Blaschke, D. B., Chatziioannou, K., Clark, J. A., Fischer, T., et al. (2019). Identifying a first-order phase transition in neutron-star mergers through gravitational waves. Phys. Rev. Lett. 122, 061102. doi:10.1103/PhysRevLett.122.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

Bazavov, A., Bhattacharya, T., Buchoff, M. I., Cheng, M., Christ, N. H., Ding, H. T., et al. (2012). Chiral transition and U(1)_A symmetry restoration from lattice QCD using domain wall fermions. Phys. Rev. D. 86, 094503. doi:10.1103/PhysRevD.86.094503

CrossRef Full Text | Google Scholar

Blaschke, D., Fredriksson, S., Grigorian, H., Öztaş, A. M., and Sandin, F. (2005). Phase diagram of three-flavor quark matter under compact star constraints. Phys. Rev. D. 72, 065020. doi:10.1103/PhysRevD.72.065020

CrossRef Full Text | Google Scholar

Blaschke, D. B., Berdermann, J., Colangelo, P., Creanza, D., De Fazio, F., Fini, R. A., et al. (2007). Neutrino emissivity and bulk viscosity of iso-CSL quark matter in neutron stars. Am. Inst. Phys. Conf. Ser. 964, 290–295. doi:10.1063/1.2823866

CrossRef Full Text | Google Scholar

Bluhm, M., Fujimoto, Y., McLerran, L., and Nahrgang, M. (2025). Quark saturation in the qcd phase diagram. Phys. Rev. C 111, 044914. doi:10.1103/PhysRevC.111.044914

CrossRef Full Text | Google Scholar

Bonanno, L., and Sedrakian, A. (2012). Composition and stability of hybrid stars with hyperons and quark color-superconductivity. A&A 539, A16. doi:10.1051/0004-6361/201117832

CrossRef Full Text | Google Scholar

Buballa, M., and Carignano, S. (2016). Inhomogeneous chiral symmetry breaking in dense neutron-star matter. Eur. Phys. J. A 52, 57. doi:10.1140/epja/i2016-16057-6

CrossRef Full Text | Google Scholar

Burrows, A. (1980). Beta decay in quark stars. Phys. Rev. Lett. 44, 1640–1643. doi:10.1103/PhysRevLett.44.1640

CrossRef Full Text | Google Scholar

Camelio, G., Gavassino, L., Antonelli, M., Bernuzzi, S., and Haskell, B. (2023a). Simulating bulk viscosity in neutron stars. I. Formalism. Phys. Rev. D. 107, 103031. doi:10.1103/PhysRevD.107.103031

CrossRef Full Text | Google Scholar

Camelio, G., Gavassino, L., Antonelli, M., Bernuzzi, S., and Haskell, B. (2023b). Simulating bulk viscosity in neutron stars. II. Evolution in spherical symmetry. Phys. Rev. D. 107, 103032. doi:10.1103/PhysRevD.107.103032

CrossRef Full Text | Google Scholar

Carignano, S., and Buballa, M. (2020). Inhomogeneous chiral condensates in three-flavor quark matter. Phys. Rev. D. 101, 014026. doi:10.1103/PhysRevD.101.014026

CrossRef Full Text | Google Scholar

Carter, G. W., and Reddy, S. (2000). Neutrino propagation in color superconducting quark matter. Phys. Rev. D. 62, 103002. doi:10.1103/PhysRevD.62.103002

CrossRef Full Text | Google Scholar

Celora, T., Hawke, I., Hammond, P. C., Andersson, N., and Comer, G. L. (2022). Formulating bulk viscosity for neutron star simulations. Phys. Rev. D. 105, 103016. doi:10.1103/PhysRevD.105.103016

CrossRef Full Text | Google Scholar

Chabanov, M., and Rezzolla, L. (2025a). Impact of bulk viscosity on the postmerger gravitational-wave signal from merging neutron stars. Phys. Rev. Lett. 134, 071402. doi:10.1103/PhysRevLett.134.071402

PubMed Abstract | CrossRef Full Text | Google Scholar

Chabanov, M., and Rezzolla, L. (2025b). Numerical modeling of bulk viscosity in neutron stars. Phys. Rev. D. 111, 044074. doi:10.1103/PhysRevD.111.044074

CrossRef Full Text | Google Scholar

Colvero, G. C., and Lugones, G. (2014). Neutrino diffusive transport in hot quark matter: a detailed analysis. Phys. Rev. C 89, 055803. doi:10.1103/PhysRevC.89.055803

CrossRef Full Text | Google Scholar

Cruz Rojas, J., Gorda, T., Hoyos, C., Jokela, N., Järvinen, M., Kurkela, A., et al. (2024). Estimate for the bulk viscosity of strongly coupled quark matter using perturbative QCD and holography. Phys. Rev. Lett. 133, 071901. doi:10.1103/PhysRevLett.133.071901

PubMed Abstract | CrossRef Full Text | Google Scholar

Drago, A., Lavagno, A., and Pagliara, G. (2005). Bulk viscosity in hybrid stars. Phys. Rev. D. 71, 103004. doi:10.1103/PhysRevD.71.103004

CrossRef Full Text | Google Scholar

Duncan, R. C., Shapiro, S. L., and Wasserman, I. (1983). Equilibrium composition and neutrino emissivity of interacting quark matter in neutron stars. ApJ 267, 358–370. doi:10.1086/160875

CrossRef Full Text | Google Scholar

Duncan, R. C., Wasserman, I., and Shapiro, S. L. (1984). Neutrino emissivity of interacting quark matter in neutron stars. II - finite neutrino momentum effects. ApJ 278, 806–812. doi:10.1086/161850

CrossRef Full Text | Google Scholar

Faber, J. A., and Rasio, F. A. (2012). Binary neutron star mergers. Living Rev. rel. 15, 8. doi:10.12942/lrr-2012-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferrer, E. J., and de la Incera, V. (2021). Magnetic dual chiral density wave: a candidate quark matter phase for the interior of neutron stars. Universe 7, 458. doi:10.3390/universe7120458

CrossRef Full Text | Google Scholar

Fujimoto, Y., Kojo, T., and McLerran, L. D. (2024). Momentum shell in quarkyonic matter from explicit duality: a dual model for cold, dense qcd. Phys. Rev. Lett. 132, 112701. doi:10.1103/PhysRevLett.132.112701

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, B., Minamikawa, T., Kojo, T., and Harada, M. (2022). Impacts of the U (1_)A anomaly on nuclear and neutron star equation of state based on a parity doublet model. Phys. Rev. C 106, 065205. doi:10.1103/PhysRevC.106.065205

CrossRef Full Text | Google Scholar

Gholami, H., Hofmann, M., and Buballa, M. (2025). Renormalization-group consistent treatment of color superconductivity in the NJL model. Phys. Rev. D. 111, 014006. doi:10.1103/PhysRevD.111.014006

CrossRef Full Text | Google Scholar

Ghosh, S., Hernández, J. L., Keshari Pradhan, B., Manuel, C., Chatterjee, D., and Tolos, L. (2025). Tidal heating in binary inspiral of strange quark stars. arXiv e-prints arXiv:2504.07659. doi:10.48550/arXiv.2504.07659

CrossRef Full Text | Google Scholar

Gómez Dumm, D., Blaschke, D. B., Grunfeld, A. G., and Scoccola, N. N. (2006). Phase diagram of neutral quark matter in nonlocal chiral quark models. Phys. Rev. D. 73, 114019. doi:10.1103/PhysRevD.73.114019

CrossRef Full Text | Google Scholar

Hammond, P., Hawke, I., and Andersson, N. (2021). Thermal aspects of neutron star mergers. Phys. Rev. D. 104, 103006. doi:10.1103/PhysRevD.104.103006

CrossRef Full Text | Google Scholar

Han, S., Mamun, M. A. A., Lalit, S., Constantinou, C., and Prakash, M. (2019). Treating quarks within neutron stars. Phys. Rev. D. 100, 103022. doi:10.1103/PhysRevD.100.103022

CrossRef Full Text | Google Scholar

Harutyunyan, A., Nathanail, A., Rezzolla, L., and Sedrakian, A. (2018). Electrical resistivity and hall effect in binary neutron star mergers. Eur. Phys. J. A 54, 191. doi:10.1140/epja/i2018-12624-1

CrossRef Full Text | Google Scholar

Harutyunyan, A., and Sedrakian, A. (2016). Electrical conductivity of a warm neutron star crust in magnetic fields. Phys. Rev. C 94, 025805. doi:10.1103/PhysRevC.94.025805

CrossRef Full Text | Google Scholar

Harutyunyan, A., and Sedrakian, A. (2024). Thermal conductivity and thermal hall effect in dense electron-ion plasma. Particles 7, 967–983. doi:10.3390/particles7040059

CrossRef Full Text | Google Scholar

Harutyunyan, A., Sedrakian, A., Gevorgyan, N. T., and Hayrapetyan, M. V. (2024). Electrical conductivity of a warm neutron star crust in magnetic fields: neutron-Drip regime. Phys. Rev. C 109, 055804. doi:10.1103/PhysRevC.109.055804

CrossRef Full Text | Google Scholar

Hernández, J. L., Manuel, C., and Tolos, L. (2024). Damping of density oscillations from bulk viscosity in quark matter. Phys. Rev. D. 109, 123022. doi:10.1103/PhysRevD.109.123022

CrossRef Full Text | Google Scholar

Huang, X. G., Huang, M., Rischke, D. H., and Sedrakian, A. (2010). Anisotropic hydrodynamics, bulk viscosities, and r-modes of strange quark stars with strong magnetic fields. Phys. Rev. D. 81, 045015. doi:10.1103/PhysRevD.81.045015

CrossRef Full Text | Google Scholar

Jaikumar, P., Roberts, C. D., and Sedrakian, A. (2006). Direct urca neutrino rate in color superconducting quark matter. Phys. Rev. C 73, 042801. doi:10.1103/PhysRevC.73.042801

CrossRef Full Text | Google Scholar

Jones, P. B. (2001). Bulk viscosity of neutron-star matter. Phys. Rev. D. 64, 084003. doi:10.1103/PhysRevD.64.084003

CrossRef Full Text | Google Scholar

Karasawa, S., Lee, T. G., and Tatsumi, T. (2016). Brazovskii–dyugaev effect on the inhomogeneous chiral transition in quark matter. Prog. Theor. Exp. Phys. 2016, 043D02. doi:10.1093/ptep/ptw025

CrossRef Full Text | Google Scholar

Kojo, T. (2024). Stiffening of matter in quark-hadron continuity: a mini-review. arXiv e-prints arXiv:2412.20442. doi:10.48550/arXiv.2412.20442

CrossRef Full Text | Google Scholar

Kono, S., Jido, D., Kuroda, Y., and Harada, M. (2021). The role of the ua(1) breaking term in dynamical chiral symmetry breaking of chiral effective theories. Prog. Theor. Exp. Phys. 2021, 093D02. doi:10.1093/ptep/ptab084

CrossRef Full Text | Google Scholar

Kovensky, N., and Schmitt, A. (2020). Holographic quarkyonic matter. J. High Energy Phys. 2020, 112. doi:10.1007/JHEP09(2020)112

CrossRef Full Text | Google Scholar

Madsen, J. (1992). Bulk viscosity of strange quark matter, damping of quark star vibration, and the maximum rotation rate of pulsars. Phys. Rev. D. 46, 3290–3295. doi:10.1103/PhysRevD.46.3290

PubMed Abstract | CrossRef Full Text | Google Scholar

Madsen, J. (1993). Rate of the weak reaction s + u → u + d in quark matter. Phys. Rev. D. 47, 325–330. doi:10.1103/PhysRevD.47.325

PubMed Abstract | CrossRef Full Text | Google Scholar

McLerran, L., and Reddy, S. (2019). Quarkyonic matter and neutron stars. Phys. Rev. Lett. 122, 122701. doi:10.1103/PhysRevLett.122.122701

PubMed Abstract | CrossRef Full Text | Google Scholar

Most, E. R., Harris, S. P., Plumberg, C., Alford, M. G., Noronha, J., Noronha-Hostler, J., et al. (2022). Projecting the likely importance of weak-interaction-driven bulk viscosity in neutron s tar mergers. Mon. Not. Ras. 509, 1096–1108. doi:10.1093/mnras/stab2793

CrossRef Full Text | Google Scholar

Motta, T. F., Bernhardt, J., Buballa, M., and Fischer, C. S. (2025). New tool to detect inhomogeneous chiral-symmetry breaking. Phys. Rev. D. 111, 074030. doi:10.1103/PhysRevD.111.074030

CrossRef Full Text | Google Scholar

Radice, D., and Bernuzzi, S. (2023). Ab-initio general-relativistic neutrino-radiation hydrodynamics simulations of long-lived neutron star merger remnants to neutrino cooling timescales. Astrophys. J. 959, 46. doi:10.3847/1538-4357/ad0235

CrossRef Full Text | Google Scholar

Radice, D., Bernuzzi, S., Perego, A., and Haas, R. (2022). A new moment-based general-relativistic neutrino-radiation transport code: methods and first applications to neutron star mergers. Mon. Not. Ras. 512, 1499–1521. doi:10.1093/mnras/stac589

CrossRef Full Text | Google Scholar

Radice, D., and Hawke, I. (2024). Turbulence modelling in neutron star merger simulations. Liv. Rev. Comput. Astrophys. 10, 1. doi:10.1007/s41115-023-00019-9

CrossRef Full Text | Google Scholar

Rehberg, P., Klevansky, S. P., and Hüfner, J. (1996). Hadronization in the su(3) nambu–jona-lasinio model. Phys. Rev. C 53, 410–429. doi:10.1103/PhysRevC.53.410

PubMed Abstract | CrossRef Full Text | Google Scholar

Ripley, J. L., Hegade, K. R. A., and Yunes, N. (2023). Probing internal dissipative processes of neutron stars with gravitational waves during the inspiral of neutron star binaries. Phys. Rev. D. 108, 103037. doi:10.1103/PhysRevD.108.103037

CrossRef Full Text | Google Scholar

Rüster, S. B., Werth, V., Buballa, M., Shovkovy, I. A., and Rischke, D. H. (2005). Phase diagram of neutral quark matter: self-Consistent treatment of quark masses. Phys. Rev. D. 72, 034004. doi:10.1103/PhysRevD.72.034004

CrossRef Full Text | Google Scholar

Sa’d, B. A., Shovkovy, I. A., and Rischke, D. H. (2007a). Bulk viscosity of spin-one color superconductors with two quark flavors. Phys. Rev. D. 75, 065016. doi:10.1103/PhysRevD.75.065016

CrossRef Full Text | Google Scholar

Sa’d, B. A., Shovkovy, I. A., and Rischke, D. H. (2007b). Bulk viscosity of strange quark matter: urca versus nonleptonic processes. Phys. Rev. D. 75, 125004. doi:10.1103/PhysRevD.75.125004

CrossRef Full Text | Google Scholar

Schmitt, A., and Shternin, P. (2018). Reaction rates and transport in neutron stars. Astrophys. Space Sci. Libr. 457, 455–574. doi:10.1007/978-3-319-97616-7_9

CrossRef Full Text | Google Scholar

Steiner, A. W., Prakash, M., and Lattimer, J. M. (2001). Diffusion of neutrinos in proto-neutron star matter with quarks. Phys. Lett. B 509, 10–18. doi:10.1016/S0370-2693(01)00434-8

CrossRef Full Text | Google Scholar

Tabatabaee, M. (2023). Chiral symmetry breaking and phase diagram of dual chiral density wave in a rotating quark matter. Phys. Rev. D. 108, 094042. doi:10.1103/PhysRevD.108.094042

CrossRef Full Text | Google Scholar

The LIGO Scientific Collaboration, The Virgo Collaboration Abbott, R., Abbott, T., Acernese, F., Ackley, K., Adams, C., et al. (2017). Gw170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101. doi:10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Malekzadeh, H., and Shovkovy, I. A. (2010). Nonleptonic weak processes in spin-one color superconducting quark matter. Phys. Rev. D. 81, 045021. doi:10.1103/PhysRevD.81.045021

CrossRef Full Text | Google Scholar

Wang, X., and Shovkovy, I. A. (2010). Bulk viscosity of spin-one color superconducting strange quark matter. Phys. Rev. D. 82, 085007. doi:10.1103/PhysRevD.82.085007

CrossRef Full Text | Google Scholar