Occurrence of magnetic reconnection in the heliospheric current sheet

We have analyzed the solar wind properties associated with a comparable number of the heliospheric current sheet (HCS) crossing events by Parker Solar Probe (PSP) ranging from 0.07 to 0.3 au and Advanced Composition Explorer (ACE) at 0.99 au. Nearly all PSP events (7 out of 8) show signatures of magnetic reconnection, which are more frequent than the ACE events (5 out of 8) that show reconnection. Because the HCS reconnection events have occurred in a variety of wind speeds and plasma conditions, for each event, we propose to define an approximate aspect ratio (width/length) of HCS as the ratio between the absolute HCS width (derived from observations) and the distance traveled by Alfvén waves over the propagation time of the solar wind. We find that the aspect ratio defined in such a way tends to be smaller than 0.01 for most reconnecting events, and becomes much larger than 0.01 for non-reconnecting events. This analysis also explains the different occurrence rates of reconnection observed by PSP and ACE. Potential consequences of magnetic reconnection at the HCS are discussed.

1 Introduction

Magnetic reconnection is a process that occurs at thin current sheets with anti-parallel magnetic field components. It is characterized by the rapid reconfiguration of magnetic field lines and is an important process for plasma heating and particle acceleration (e.g., Birn et al., 2012; Li et al., 2021; Du et al., 2022). Spacecraft observations in the solar wind are able to identify magnetic reconnection events as characterized by an Alfvénic exhaust jet and reversal of magnetic field direction across it (Gosling et al., 2005b).

In the heliosphere, the most well-defined current sheet is the heliospheric current sheet (HCS), which is a global-scale structure created by the solar dipole magnetic field and the expanding solar wind (Smith, 2001). It is also known as sector boundaries in solar wind data as it separates inward and outward magnetic field sectors. The HCS extends throughout the heliosphere, from the inner heliosphere (Villante and Bruno, 1982) to the distant heliosheath (Burlaga et al., 2006). Although global-scale magnetic reconnection has been observed at the HCS (Gosling et al., 2005c; Gosling et al., 2006), these events are believed to be relatively rare near 1 au.

Parker Solar Probe (PSP) (Fox et al., 2016) was launched in 2018 and has entered a previously unexplored region within 0.3 astronomical unit (au) from the Sun. PSP has observed abundant HCS crossing events, where reconnection exhausts are also observed (Szabo et al., 2020; Lavraud et al., 2020; Phan et al., 2020). An interesting finding is that magnetic reconnection at HCS appears to be much more common near the Sun. Phan et al. (2021) show that reconnection signatures are detected in five out of the six complete HCS crossings during the first five orbits of PSP. However, the reason for the prevalence of HCS reconnection is unclear. For example, PSP does not find exceedingly low plasma beta close to the Sun, so diamagnetic drift may not be the major factor as some previous work suggested (Phan et al., 2010; Gosling, 2012; Swisdak et al., 2003; Swisdak et al., 2010). A salient feature of the reconnection events at the HCS, both near 1 au and closer to the Sun, is that the observed reconnection exhaust is very wide compared to kinetic scales (e.g., ion inertial length $d_i$), suggesting that the onset is not fully due to kinetic physics. A typical HCS crossing event takes a few minutes, which correspond to thousands of $d_i$ in the solar wind. A large statistical analysis of reconnecting current sheet (not just HCS) with Wind data near 1 au shows that the current sheets are found to possess a wide range of widths, from $<25d_i$ to thousands of $d_i$ (Eriksson et al., 2022). The analysis concludes that large-scale reconnecting current sheets are likely associated with the HCS because they tend to exhibit a strong alignment with the large-scale interplanetary magnetic field. The weaker alignment for smaller-scale reconnecting current sheets may suggest that they are produced by fractured HCS reconnection cascading to small scales (“HCS Avalanche”), though it is also possible that they are produced by turbulence independent of the HCS. Statistical studies are also reported using Solar Orbiter data (Fargette et al., 2023).

In this paper, we present observational analyses of several HCS crossing events observed by PSP and Advanced Composition Explorer (ACE). In contrast to most previous work, we consider both reconnecting events and non-reconnecting events. We find that most PSP HCS crossing events show reconnection whereas about only half of ACE crossing events show reconnection. We propose a model to explain this distinctively different HCS reconnection behavior near the Sun versus 1 au. Section 2 describes the spacecraft data and the analysis results. Our physical interpretation of the observational results is presented in Section 3. In addition, we discuss the implications of magnetic reconnection in the solar wind for heating and particle acceleration near the Sun as well as in the outer heliosphere.

2 Observational data analysis and results

2.1 Description of data

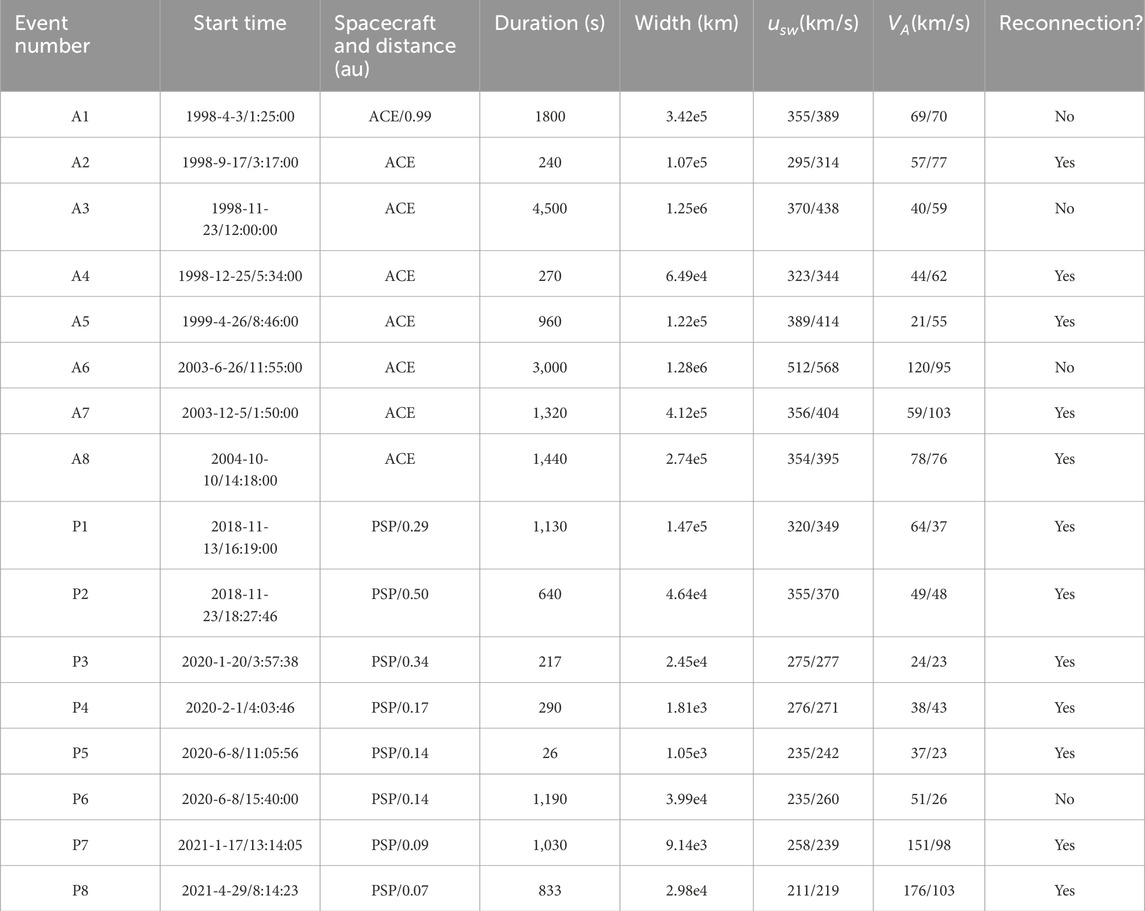
We consider a total of 16 HCS crossing events, including 8 observed by PSP and 8 by ACE, as listed in Table 1. All PSP events were reported previously (Phan et al., 2020; Phan et al., 2021; Phan et al., 2022), including 7 with signatures of reconnection exhaust and 1 without. Two ACE events (A1 and A3) with reconnection signatures were reported previously (Gosling et al., 2005c; Gosling et al., 2006). Additional ACE HCS crossing events are identified mainly based on the signature of electron strahl reversal on the two sides of HCS. The suprathermal electron pitch angle data and plots in the solar wind frame can be found at https://izw1.caltech.edu/ACE/ASC/DATA/level3/swepam/index.html. We then visually verify that three of these events show signatures of reconnection exhaust and three do not. We also find several ACE events with less pronounced signatures of reconnection exhaust, and they are excluded from our analysis. A more thorough statistical analysis is planned for the future.

Table 1

Table 1. Summary of HCS crossing events.

For each HCS event, we determine its duration $\mathrm{\Delta }t$ by visual inspection of magnetic field and plasma data. Magnetic field data are measured by ACE/MFI and PSP/FIELDS/MAG; and plasma data are measured by ACE/SWEPAM (A1, A3–A8), ACE/SWICS (A2, A7), PSP/SWEAP/SPC (P1–P6), and PSP/SWEAP/SPAN-i (P7, P8). Following Phan et al. (2021), we perform the minimum variance analysis (MVA) of magnetic field to determine the orientation of the observed current sheets (Sonnerup and Cahill, 1967), and the width of a current sheet is calculated by $w=u_n\mathrm{\Delta }t$, where $u_n$ is the spacecraft-frame flow velocity in the minimum variance direction. It has been noted by several previous studies (Knetter et al., 2004; Wang et al., 2024; Eriksson et al., 2024) that MVA sometimes produces highly questionable estimates of the current sheet normal. A more accurate normal direction can be calculated by the cross product between magnetic field before and after the current sheet, i.e., $\widehat{\mathit{n}}={\mathit{B}}_1\times {\mathit{B}}_2/|{\mathit{B}}_1\times {\mathit{B}}_2|$. A hybrid MVA coordinates are then completed by $\widehat{\mathit{m}}=\widehat{\mathit{n}}\times {\widehat{\mathit{l}}}_{\mathit{MV\; A}}/|\widehat{\mathit{n}}\times {\widehat{\mathit{l}}}_{\mathit{MV\; A}}|$, and $\widehat{\mathit{l}}=\widehat{\mathit{m}}\times \widehat{\mathit{n}}$. We use the hybrid coordinates for all but four events with large magnetic shear angles (A7, P3, P4, and P7), since the cross product normal becomes less reliable in such cases. The standard LMN coordinates with MVA are used for these four events. The solar wind speed $u_{sw}$ and Alfvén speed $V_A$ are calculated separately for periods before and after HCS crossings, giving two numbers for each event in Table 1.

Magnetic reconnection is identified by the signature of outflow jets in the maximum variance direction, i.e., $l$-direction in the LMN coordinate (e.g., Phan et al., 2010). Figure 1 shows the time series plots for Events A1 and P2 as examples of nonreconnection and reconnection events. The magnetic field and velocity are plotted in the hybrid MVA coordinates. The vertical dashed lines bound the approximate extent of HCS crossing, which is used for the calculation of current sheet width. An outflow jet in the $l$-direction is seen in the reconnection event P2 but not in the nonreconnection event A2.

Figure 1

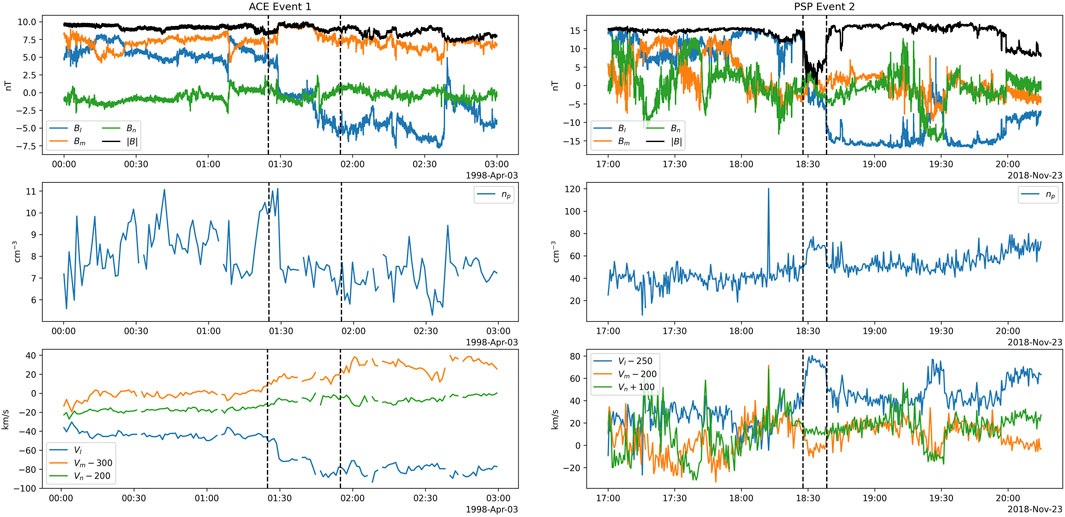
Figure 1. Time series plots for the nonreconnection event A1 (left panel) and reconnection event P2 (right panel).

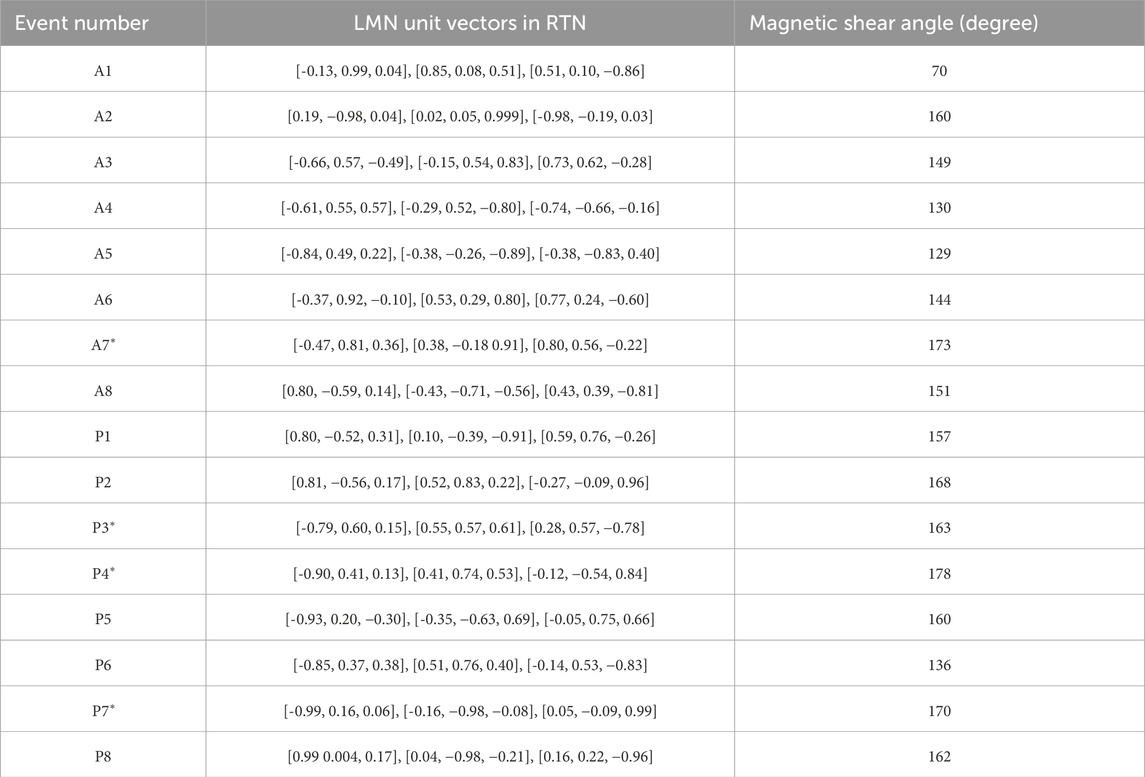
For completeness, the LMN unit vectors and magnetic shear angle for all HCS events are listed in Table 2. The LMN coordinates calculated with standard MVA are listed for four events (labeled with an asterisk in the table), three of them having a shear angle 170$°$ or larger (A7, P4, and P7). Event P3 has a shear angle of 163$°$, but the hybrid coordinates exhibits more pronounced variations in $B_n$ than $B_m$ for this event (not shown here). Nevertheless, the difference in the estimated current sheet width due to the two coordinate systems is about 25%, which is not significant. For all other events, the hybrid LMN coordinates with cross product normal are listed.

Table 2

Table 2. LMN coordinates and magnetic shear angle for all HCS events.

2.2 Aspect ratio of HCS crossing events

We have identified the reconnection and nonreconnection events and listed them in Table 1. For most of PSP crossing events, 7 of 8 analyzed events show reconnection whereas only 5 out of 8 ACE crossing events show reconnection. To further understand this result, we propose an approach to analyze the “normalized” thickness of these HCS events, which is usually characterized by the aspect ratio between its width $(w)$ and length $(L)$. Thin current sheets with a sufficiently small aspect ratio are subject to MHD tearing instabilities that trigger the onset of magnetic reconnection (e.g., Furth et al., 1963; Uzdensky and Loureiro, 2016; Comisso et al., 2016; Comisso et al., 2017; Huang et al., 2017). Inspired by this scenario, we interpret the observational results in Section 2 as a manifestation of the onset process due to tearing. We now examine the current sheet width and the length scale associated with the propagation of Alfvén waves as key parameters.

The observed width $w$ of HCS can be obtained from observations and is plotted in the top panel of Figure 2 for each event. For PSP events, the width is plotted as a function of the spacecraft location at the time of the observation. ACE events are simply ordered horizontally by the event number in Table 1. The HCS width spans several orders of magnitude and tends to increase with radial distance due to the expansion of the solar wind, consistent with the expectation from previous work (Smith, 2001). Reconnection events are represented by blue colored dots, while non-reconnection events are represented by orange colored crosses.

Figure 2

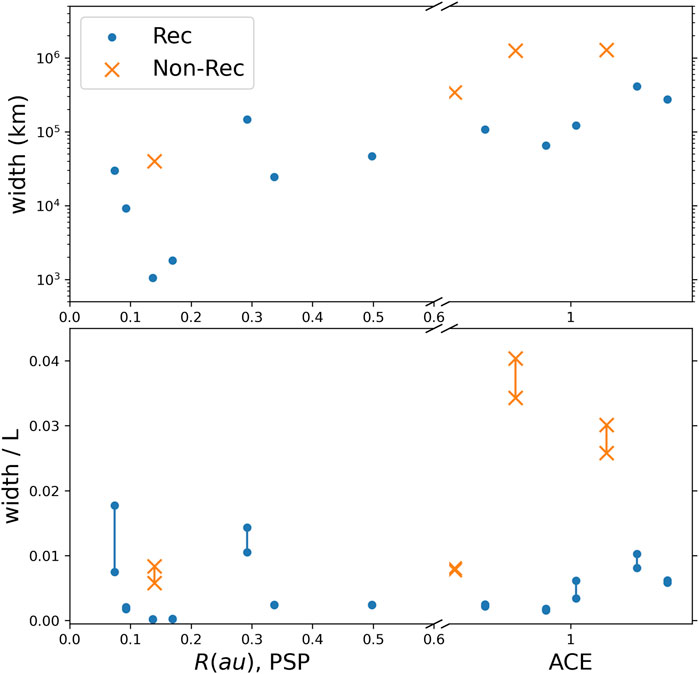
Figure 2. Estimated HCS width $w$ (top panel) and the ratio $w/L$ (bottom panel) for all PSP and ACE events. Blue dots and orange crosses represent the reconnection and non-reconnection events, respectively.

The relevant lengthscale $L$ of HCS for possible reconnection is defined by the distance traveled by Alfvén waves during the time for the solar wind to propagate from some inner boundary $r_s$ to the observer’s location $r$. This can be calculated by the formula,

$L={\int }_{r_s}^r{V}_A\left(r^{\prime }\right)\frac{d{r}^{\prime }}{u_{sw}}.(1)$

We consider the super-Alfvénic solar wind, so $L$ is typically much shorter than $r$. This Alfvén length scale may be regarded as an estimate of the length of the reconnection region within HCS if the onset takes one Alfvén crossing time. This is a reasonable assumption as perturbations to the current sheet is communicated by Alfvén waves in MHD.

For the radial evolution of the Alfvén speed $V_A(r)$, we assume Parker’s spiral interplanetary magnetic field (Parker, 1958; Weber and Davis Jr, 1967) and a constant solar wind speed $u_{sw}$ (which implies an $r^{-2}$ scaling for the solar wind density),

$V_A=V_{As}{\left(\frac{r}{r_s}\right)}^{-1}{\left[1+\frac{{\mathrm{\Omega }}^2{\left(r-r_s^2/r\right)}^2}{u_{sw}^2}\right]}^{1/2},(2)$

where $\mathrm{\Omega }\simeq 2.8\times 10^{-6}{\mathrm{s}}^{-1}$ is the angular velocity of solar rotation; and $V_{As}$ is the Alfvén speed at the solar wind source surface $r=r_s$, where the magnetic field is radial. The lower limit in Equation 1 is taken to be at $r_s$, and we approximate it as the Alfvén critical radius so that it can be determined numerically by the root of the equation $V_A(r)=u_{sw}$. The actual location of the source surface is likely to be within the Alfvén critical radius based on observations and models (Wilcox et al., 1980; Burlaga et al., 1981; Kasper et al., 2021; Verscharen et al., 2021; Chhiber et al., 2022), but magnetic field is still predominantly radial at the Alfvén radius, justifying the approximation.

With the observed width $w$ and length $L$ calculated by Equation 1, we define an aspect ratio as $w/L$ and plot it in the bottom panel of Figure 2 for the PSP and ACE events from Table 1. For each event, two values are computed based on parameters measured on two sides of the current sheet, yielding a range for the ratio $w/L$; this may be taken as the uncertainty. Most of the uncertainty is quite small so the points from two sides of the current sheets essential overlap.

Figure 2 suggests that reconnection events tend to have a smaller ratio $w/L$. A threshold ratio may be present around 0.01, as most reconnection events have ratio smaller that (with the exception of PSP events P1 and P8). The feature appears applicable to both PSP and ACE events. Our results suggest that the ratio between these two length scales, which characterize the thickness of HCS, is important in determining whether magnetic reconnection occurs at the HCS. These results are physically sensible because a small current sheet thickness is expected to favor reconnection based on MHD tearing instabilities. And a longer Alfvén length scale means that given a current sheet width, the tearing instability has more time to grow.

2.3 Notes on uncertainties

Some outstanding uncertainties should be noted regarding our width and length estimates. First, several of the events contain clear signatures of partial HCS crossings: the $B_r$ component of magnetic field switches up and down within the identified HCS boundaries, suggesting that the spacecraft likely moves back and forth within the HCS. The partial crossings are most prominent in Events P1, but are also seen in P3, P8, A6, and A8, and will likely lead to overestimating the width. Second, assuming a constant solar wind speed outside the Alfvén surface will underestimate the length $L$ since the solar wind is accelerating. We expect this effect to be strongest for events closest to the Sun (e.g., P7 and P8). For events far away from the Sun, the solar wind speed has likely stabilized throughout most of the propagation time. Incidentally, the two “outliers” in Figure 2 (Events P1 and P8) with higher $w/L$ ratios than other reconnecting events may be explained by the uncertainties. The time series data for these two events are shown in Figure 3. Event P1 is the most impacted event by partial crossings, while P8 is affected by both partial crossings and solar wind acceleration. Both uncertainties are expected to lead to an overestimation of the $w/L$ ratio. The time series plots for these two events are included in the appendix. Third, both MVA and the cross product methods for determining the current sheet normal are subject to errors in certain situations, causing uncertainties in the width estimates. Finally, the visual identification of HCS boundaries is a somewhat subjective matter. More systematic analysis of HCS, possibly with automatic detection algorithm, is beyond the scope of the present work and is deferred for a future study.

Figure 3

Figure 3. Time series similar to Figure 1, but for P1 (left) and P8 (right).

3 Discussions

3.1 Mechanism for reconnection onset at HCS

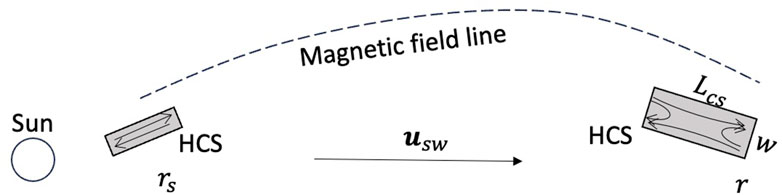
In general, our analysis confirms previous results (Gosling et al., 2005a; Phan et al., 2021, etc.) suggesting that the occurrence of reconnection at HCS appears more frequent closer to the Sun. Here, we propose a scenario to explain this observation. Because the solar wind is super-Alfvénic and supersonic for these crossing events, we consider how causality will influence the possible onset of reconnection. Considering a segment of the HCS that may eventually undergo reconnection, as illustrated in Figure 4. The length of the current sheet region is $L_{cs}$. We can define two timescales, one for the solar wind to propagate to $r$ as ${\tau }_{sw}$, and the other for Alfvén waves to communicate over $L_{cs}$ as ${\tau }_A$. Both timescales will evolve as the solar wind expands. We suggest that, for a given initial perturbation, the longer the solar wind propagation time is with respect to the Alfvén time, the more likely that the HCS will become unstable and undergo reconnection.

Figure 4

Figure 4. An illustration of the processes and parameters considered in our model.

Based on the above argument, a crucial number is the ratio between ${\tau }_{sw}$ and ${\tau }_A$, defined as

$R_A\left(r\right)\equiv \frac{{\tau }_{sw}}{{\tau }_A}={\int }_{r_s}^r\frac{V_A\left(r^{\prime }\right)d{r}^{\prime }}{L_{cs}\left(r\right)u_{sw}\left(r^{\prime }\right)}.(3)$

Using the radial profile of Alfvén speed (Equation 2), a constant solar wind speed $u_{sw}$, and an expanding box size $L_{cs}=L_s(r/r_s)$, which corresponds to a linear increase of HCS width with distance suggested by Smith (2001), we can calculate the ratio given by Equation 3,

$R_A={\int }_{r_s}^r\frac{V_{As}}{u_{sw}}{\left(\frac{r^{\prime }}{r_s}\right)}^{-1}{\left[1+\frac{{\mathrm{\Omega }}^2{\left(r^{\prime }-r_s^2/r^{\prime }\right)}^2}{u_{sw}^2}\right]}^{1/2}\frac{1}{L_s}{\left(\frac{r}{r_s}\right)}^{-1}d{r}^{\prime }.(4)$

The integration can be carried out numerically. Similar to the previous section, we assume that the source surface is located at the Alfvén critical point where $u_{sw}=V_A$. Within the critical radius, the acceleration of solar wind bulk flow cannot be neglected. The effect of such acceleration is that the current sheet is stretched in length, which then leads to the increase of the aspect ratio. Indeed, reconnection at HCS within the critical radius is commonly seen at the tip of the streamer belt (e.g., Lavraud et al., 2020; Réville et al., 2020) and this is a separate subject from our discussions.

As a demonstration, Figure 5 plots the radial profiles of Alfvén speed $V_A$ (blue curve) and the ratio $R_A$ (orange curve) with nominal solar wind parameters $r_s=0.04$ au and $u_{sw}=V_{As}=2.7\times 10^7$ cm/s. The box size at the inner boundary is set as $L_s=1.3\times 10^{11}$ cm, which is about 1,000 times the width at $r_s$ as indicated by Figure 2. The Alfvén speed decreases with increasing distance as $\sim r^{-1}$ near the Sun and approaches a constant asymptotically in the outer heliosphere. Very close to the Sun, $R_A$ is small because the short solar wind propagation time ${\tau }_{sw}$; far away from the Sun, $R_A$ becomes small again because the expansion of box size $L$ and the decreasing Alfvén speed. As a result, the ratio attains a maximum value at some radial distance within 0.3 au. At 1 au, the time available for growth has been reduced in half compared to 0.2 au. This provides a natural explanation to why HCS reconnection is more common at smaller radial distances. At $r\gg 1$ au, the ratio $R_A$ approaches a finite positive number asymptotically.

Figure 5

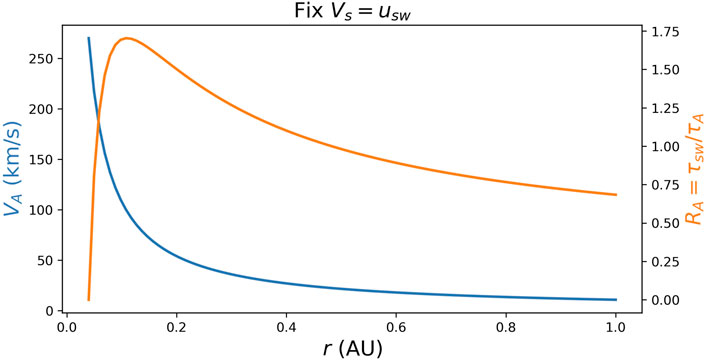
Figure 5. Radial profiles of the Alfvén speed $V_A$ (blue, left axis) and the ratio $R_A$ (orange, right axis), defined in Equation 4. Parameters for the calculation are listed in the text.

These results can be affected by the parameters. For example, a larger $r_s$ or $V_{As}$ would lead to a larger $V_A$ at all distances, and thus increases the ratio $R_A$ overall; and a larger $L_s$ would increase ${\tau }_A$ and thus decreases the ratio $R_A$. However, the general behavior of the curves in Figure 5 is independent of the choice of these parameters. Meanwhile, the behavior of $R_A$ can be affected by the assumption of $L_{cs}\propto r$. If a different scaling is adopted, i.e., $L_{cs}\propto r^{\alpha }$, the ratio $R_A$ will decrease at large $r$ only if $\alpha >0.5$. A larger index $\alpha$ would lead to a more rapid decrease of the $R_A$ at large distances. It does appear from Figure 2 that the width increases with $r$ at least as fast as linearly, but the statistics is limited by the small number of events considered. More realistic models of the solar wind speed and Alfvén speed may be used in the future, which will improve the estimate of $r_s$.

We note that the threshold ratio of $\sim$ 0.01 from our observational analysis is reminiscent of the critical aspect ratio of plasmoid instability (Loureiro et al., 2007; Bhattacharjee et al., 2009; Huang and Bhattacharjee, 2010). However, this seems to be a coincidence because an aspect ratio of 0.01 would correspond to a very thick current sheet compared to the thickness suggested by the Sweet-Parker or ideal tearing model when the Lundquist number $S=V_A{L}_{cs}/\eta \gg 10^6$ ($\eta$ is the coefficient of resistivity) (Parker, 1957; Sweet, 1958; Pucci and Velli, 2014; Huang et al., 2017). (The Lundquist number of the weakly collisional solar wind is $S\gtrsim 10^{12}$.) This means that the triggering of magnetic reconnection at HCS is likely not due to tearing instability alone, which is slow in this situation. Although plasmoid instability and kinetic processes can explain fast reconnection rates, the problem of reconnection onset remains an open question. Reconnection exhausts observed at HCS can be as wide as thousands of ion inertial lengths, suggesting that kinetic processes may not be the main triggering mechanism. We speculate that solar wind turbulence may play an important role in reconnection onset at thick current sheets. Numerical simulations may be helpful in illuminating the onset process, though 3D MHD simulations of magnetic reconnection with realistic turbulence injection in the very high-$S$ regime are still challenging.

Next, we briefly discuss the potential consequences of magnetic reconnection at HCS for the solar wind dynamics and particle energization.

3.2 Heating and particle acceleration

A major consequence of magnetic reconnection is plasma heating and particle acceleration (Li et al., 2021). If magnetic reconnection is indeed universally occurring at HCS, it could make a considerable contribution to the heating and acceleration of solar wind, especially in the inner heliosphere. While Gosling et al. (2005a) find an absence of particle acceleration due to magnetic reconnection in the solar wind, more recent observations have reported evidence of energetic particles associated with the HCS (e.g., Khabarova and Zank, 2017; Zhao et al., 2019; Desai et al., 2022; Phan et al., 2022).

The magnetic energy conversion rate per unit area of the current sheet can be estimated as

${\epsilon }_m=\frac{B^2}{4\pi }{V}_{\mathit{rec}},$

where $V_{\mathit{rec}}\simeq (w/L_{cs})V_A$ is the reconnection rate defined as the inflow velocity. Here, we assume a constant reconnection rate $V_{\mathit{rec}}=0.01V_A$ according to the results from data analysis, assuming $L_{cs}\simeq L$. The average energy gain per electron-proton pair $\mathrm{\Delta }{E}_{p1}$ due to magnetic reconnection at HCS as a function of the radial distance is

$\mathrm{\Delta }{E}_{p1}\left(r\right)=\frac{1}{2r\mathrm{\Delta }\mu n\left(r\right)4\pi r{L}_{cs}}{\int }_{r_s}^{r}4\pi r^{\prime }{L}_{cs}\frac{B^2\left(r^{\prime }\right)}{4\pi }{V}_{\mathit{rec}}\left(r^{\prime }\right)\frac{d{r}^{\prime }}{u_{sw}}.$

Here, $\mathrm{\Delta }\mu$ determines the volume filling factor of the deposited energy. If the converted magnetic energy is deposited to the entire heliosphere, i.e., $\mathrm{\Delta }\mu =1$, it would yield a lower limit for $\mathrm{\Delta }{E}_{p1}$. The upper limit is attained when all the converted energy is deposited into the narrow region corresponding to the current sheet thickness, so that $\mathrm{\Delta }\mu \sim \cos (\pi /2-w_s/r_s)\simeq 0.002$. The upper and lower limits of $\mathrm{\Delta }{E}_{p1}$ are plotted in Figure 6. The same typical parameters as in Figure 5 are used. Additionally, the magnetic field at the inner boundary is chosen as $B(r_s)\simeq 1.9\times 10^{-2}$ G according to the nominal value observed by PSP (Badman et al., 2021). This figure shows that a pair of particles may gain $\sim$ 1 eV–0.6 keV energy on average for our chosen parameters. This is significant compared to the typical solar wind thermal energy ($\sim$ 20 eV) or even kinetic energy ($\sim$ 1 keV). Indeed, keV-energy proton beams are observed near the reconnecting HCS (Phan et al., 2022). The black dashed line shows the typical thermal energy per electron-proton pair as a comparison, assuming the thermal energy per particle is 10 eV at 1 AU and the thermal energy follows an $r^{-1}$ profile based on empirical evidence (Marsch et al., 1982).

Figure 6

Figure 6. Upper and lower limits of the energy gain per electron-proton pair due to reconnection at HCS. The typical thermal energy is shown by the dashed line as a comparison.

The estimated energy release is based on continued magnetic reconnection throughout the entire range of radial distance. In reality, magnetic reconnection may only occurs at a small range of radial distance as suggested by our analysis, which will inevitably decrease the total released magnetic energy. In addition, fast reconnection is known to be bursty, which may also limit the fraction of HCS undergoing reconnection at a time. Therefore, the calculation shown here is likely an overestimation for the conversion of magnetic energy.

3.3 Reconnection in the heliosheath

Another potential application of reconnection at the HCS is for the outer heliosphere, namely, the heliosheath, which is the region between the heliospheric termination shock and the heliopause. While Figure 5 shows that the solar wind expansion makes reconnection less likely in the distant heliosphere further away from the Sun, it is possible that reconnection switches on again due to the compression at the termination shock. This possibility was discussed previously as an explanation of the increasing intensity of anomalous cosmic rays downstream of the termination shock (e.g., Drake et al., 2010; Zank et al., 2015; Le Roux et al., 2016; Zank et al., 2021). Since the number $R_A$ does not fall off to zero but tends to a constant asymptotically at $r\to \infty$ (Figure 5), a compression by a factor of 2.5 at the termination shock as observed by the Voyagers and a deceleration of the solar wind flow could elevate the $R_A$ ratio to a level comparable to that of the inner heliosphere, and thus significantly enhance the likelihood of reconnection. It should be noted that the heliosheath is a high-beta subsonic environment that is thermally dominated by interstellar pickup ions, unlike the inner heliosphere where there is significant free magnetic energy. Therefore, if reconnection does occur in the heliosheath, its impact on the solar wind dynamics may be weak.

4 Summary and conclusions

We have analyzed 8 crossing events of HCS by PSP and another 8 events by ACE near one au. We found that most PSP events contain reconnection whereas only about half of the ACE events have reconnection. These results are consistent with the surprising discovery of PSP that magnetic reconnection frequently occurs at the HCS close to the Sun while the current sheet remains thick like at 1 au (Phan et al., 2021). The idea of magnetic reconnection triggered at the thick HCS is also supported by statistical analysis by Wind (Eriksson et al., 2022). We present observational analysis of both reconnecting and non-reconnecting HCS crossing events using PSP and ACE data.

Inspired by MHD tearing instabilities and causality, we calculate ratio between HCS width and the Alfvén length scale $w/L$, which we interpret as a representation of the HCS thickness. It is found that reconnecting HCS events tend to be associated with a smaller ratio. Based on the results, we propose that whether magnetic reconnection is triggered is a result of the competition between the evolution time and the Alfvén crossing time. To grow the instability (resistive or ideal tearing) to the nonlinear stage, the evolution time needs to be long enough relative to the Alfvén time so that the initial perturbation is amplified to a significant level. Using some typical solar wind parameters, our calculation shows that the peak growth occurs around 0.1–0.3 au from the Sun, where magnetic reconnection is most likely to be triggered at the HCS. The analysis is quite general and does not rely on detailed kinetic physics. Finally, some potential consequences of magnetic reconnection at the HCS are discussed, including plamsa heating and energization, and the heliosheath.

Our data analysis relies on visual inspection of a small number of HCS events. It is somewhat surprising to us that several additional reconnecting events are identified at HCS near 1 au, given that they are expected to be rare (Gosling et al., 2006), though the events generally support our main conclusion on the width/length ratio criterion. A more systematic study of magnetic reconnection at HCS is needed in the future for more statistically significant results. Effects such as solar activities and current sheet tilt can also be studied with more events covering multiple solar cycles. Other factors that may affect reconnection onset, such as plasma beta, flow and magnetic shear (e.g., Swisdak et al., 2010; Phan et al., 2013; Doss et al., 2016), should also be considered simultaneously.

Data availability statement

Jupyter Notebooks for data analysis are available in a Zenodo Repository at https://doi.org/10.5281/zenodo.17041601 .

Author contributions

SD: Conceptualization, Formal Analysis, Methodology, Software, Visualization, Writing – original draft, Writing – review and editing. HL: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing – review and editing. RS: Data curation, Methodology, Writing – review and editing. JS: Data curation, Funding acquisition, Methodology, Project administration, Writing – review and editing. FG: Funding acquisition, Methodology, Project administration, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. We acknowledge the support from NASA awards 80HQTR20T0027, 80HQTR21T0117, and 80HQTR21T0087, the DOE OFES program, and LANL/LDRD program.

Acknowledgments

We thank B. Lavraud for a careful reading of a prior draft of the manuscript and his extensive feedback. Useful discussions with X. Fu are gratefully acknowledged. Parker Solar Probe was designed, built, and is now operated by the Johns Hopkins Applied Physics Laboratory as part of NASA’s Living with a Star (LWS) program (contract NNN06AA01C). Support from the LWS management and technical team has played a critical role in the success of the Parker Solar Probe mission.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Badman, S. T., Bale, S. D., Rouillard, A. P., Bowen, T. A., Bonnell, J. W., Goetz, K., et al. (2021). Measurement of the open magnetic flux in the inner heliosphere down to 0.13 au. Astronomy and Astrophysics 650, A18. doi:10.1051/0004-6361/202039407

CrossRef Full Text | Google Scholar

Bhattacharjee, A., Huang, Y.-M., Yang, H., and Rogers, B. (2009). Fast reconnection in high-lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16, 112102. doi:10.1063/1.3264103

CrossRef Full Text | Google Scholar

Birn, J., Borovsky, J., and Hesse, M. (2012). The role of compressibility in energy release by magnetic reconnection. Phys. Plasmas 19, 082109. doi:10.1063/1.4742314

CrossRef Full Text | Google Scholar

Burlaga, L. F., Hundhausen, A. J., and Zhao, X. P. (1981). The coronal and interplanetary current sheet in early 1976. J. Geophys. Res. Space Phys. 86, 8893–8898. doi:10.1029/JA086iA11p08893

CrossRef Full Text | Google Scholar

Burlaga, L. F., Ness, N. F., and Acuña, M. H. (2006). Magnetic fields in the heliosheath: voyager 1 observations. Astrophysical J. 642, 584–592. doi:10.1086/500826

CrossRef Full Text | Google Scholar

Chhiber, R., Matthaeus, W. H., Usmanov, A. V., Bandyopadhyay, R., and Goldstein, M. L. (2022). An extended and fragmented Alfvén zone in the young solar wind. Mon. Notices R. Astronomical Soc. 513, 159–167. doi:10.1093/mnras/stac779

CrossRef Full Text | Google Scholar

Comisso, L., Lingam, M., Huang, Y. M., and Bhattacharjee, A. (2016). General theory of the plasmoid instability. Phys. Plasmas 23, 100702. doi:10.1063/1.4964481

CrossRef Full Text | Google Scholar

Comisso, L., Lingam, M., Huang, Y. M., and Bhattacharjee, A. (2017). Plasmoid instability in forming current sheets. Astrophysical J. 850, 142. doi:10.3847/1538-4357/aa9789

CrossRef Full Text | Google Scholar

Desai, M., Mitchell, D., McComas, D., Drake, J., Phan, T., Szalay, J., et al. (2022). Suprathermal ion energy spectra and anisotropies near the heliospheric current sheet crossing observed by the parker solar probe during encounter 7. Astrophysical J. 927, 62. doi:10.3847/1538-4357/ac4961

CrossRef Full Text | Google Scholar

Doss, C., Cassak, P., and Swisdak, M. (2016). Particle-in-cell simulation study of the scaling of asymmetric magnetic reconnection with in-plane flow shear. Phys. plasmas 23, 082107. doi:10.1063/1.4960324

CrossRef Full Text | Google Scholar

Drake, J., Opher, M., Swisdak, M., and Chamoun, J. (2010). A magnetic reconnection mechanism for the generation of anomalous cosmic rays. Astrophysical J. 709, 963–974. doi:10.1088/0004-637x/709/2/963

CrossRef Full Text | Google Scholar

Du, S., Li, H., Fu, X., Gan, Z., and Li, S. (2022). Magnetic energy conversion in magnetohydrodynamics: curvature relaxation and perpendicular expansion of magnetic fields. Astrophysical J. 925, 128. doi:10.3847/1538-4357/ac3de1

CrossRef Full Text | Google Scholar

Eriksson, S., Swisdak, M., Weygand, J. M., Mallet, A., Newman, D. L., Lapenta, G., et al. (2022). Characteristics of multi-scale current sheets in the solar wind at 1 au associated with magnetic reconnection and the case for a heliospheric current sheet avalanche. Astrophysical J. 933, 181. doi:10.3847/1538-4357/ac73f6

CrossRef Full Text | Google Scholar

Eriksson, S., Swisdak, M., Mallet, A., Kruparova, O., Livi, R., Romeo, O., et al. (2024). Parker solar probe observations of magnetic reconnection exhausts in quiescent plasmas near the sun. Astrophysical J. 965, 76. doi:10.3847/1538-4357/ad25f0

CrossRef Full Text | Google Scholar

Fargette, N., Lavraud, B., Rouillard, A. P., Houdayer, P. S., Phan, T. D., Øieroset, M., et al. (2023). Clustering of magnetic reconnection exhausts in the solar wind: an automated detection study. Astronomy and Astrophysics 674, A98. doi:10.1051/0004-6361/202346043

CrossRef Full Text | Google Scholar

Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The solar probe plus mission: humanity’s first visit to our star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6

CrossRef Full Text | Google Scholar

Furth, H. P., Killeen, J., and Rosenbluth, M. N. (1963). Finite-resistivity instabilities of a sheet pinch. Phys. Fluids 6, 459–484. doi:10.1063/1.1706761

CrossRef Full Text | Google Scholar

Gosling, J. (2012). Magnetic reconnection in the solar wind. Space Sci. Rev. 172, 187–200. doi:10.1007/s11214-011-9747-2

CrossRef Full Text | Google Scholar

Gosling, J., Skoug, R., Haggerty, D., and McComas, D. (2005a). Absence of energetic particle effects associated with magnetic reconnection exhausts in the solar wind. Geophys. Res. Lett. 32. doi:10.1029/2005gl023357

CrossRef Full Text | Google Scholar

Gosling, J., Skoug, R., McComas, D., and Smith, C. (2005b). Direct evidence for magnetic reconnection in the solar wind near 1 au. J. Geophys. Res. Space Phys. 110. doi:10.1029/2004ja010809

CrossRef Full Text | Google Scholar

Gosling, J., Skoug, R., McComas, D., and Smith, C. (2005c). Magnetic disconnection from the sun: observations of a reconnection exhaust in the solar wind at the heliospheric current sheet. Geophys. Res. Lett. 32. doi:10.1029/2005gl022406

CrossRef Full Text | Google Scholar

Gosling, J., McComas, D., Skoug, R., and Smith, C. (2006). Magnetic reconnection at the heliospheric current sheet and the formation of closed magnetic field lines in the solar wind. Geophys. Res. Lett. 33. doi:10.1029/2006gl027188

CrossRef Full Text | Google Scholar

Huang, Y.-M., and Bhattacharjee, A. (2010). Scaling laws of resistive magnetohydrodynamic reconnection in the high-lundquist-number, plasmoid-unstable regime. Phys. Plasmas 17, 062104. doi:10.1063/1.3420208

CrossRef Full Text | Google Scholar

Huang, Y.-M., Comisso, L., and Bhattacharjee, A. (2017). Plasmoid instability in evolving current sheets and onset of fast reconnection. Astrophysical J. 849, 75. doi:10.3847/1538-4357/aa906d

CrossRef Full Text | Google Scholar

Kasper, J. C., Klein, K., Lichko, E., Huang, J., Chen, C., Badman, S., et al. (2021). Parker solar probe enters the magnetically dominated solar corona. Phys. Rev. Lett. 127, 255101. doi:10.1103/physrevlett.127.255101

PubMed Abstract | CrossRef Full Text | Google Scholar

Khabarova, O. V., and Zank, G. P. (2017). Energetic particles of kev–mev energies observed near reconnecting current sheets at 1 au. Astrophysical J. 843 (4), 4. doi:10.3847/1538-4357/aa7686

CrossRef Full Text | Google Scholar

Knetter, T., Neubauer, F. M., Horbury, T., and Balogh, A. (2004). Four-point discontinuity observations using Cluster magnetic field data: a statistical survey. J. Geophys. Res. Space Phys. 109, A06102. doi:10.1029/2003JA010099

CrossRef Full Text | Google Scholar

Lavraud, B., Fargette, N., Réville, V., Szabo, A., Huang, J., Rouillard, A. P., et al. (2020). The heliospheric current sheet and plasma sheet during parker solar probe’s first orbit. Astrophysical J. Lett. 894, L19. doi:10.3847/2041-8213/ab8d2d

CrossRef Full Text | Google Scholar

Le Roux, J., Zank, G., Webb, G., and Khabarova, O. (2016). Combining diffusive shock acceleration with acceleration by contracting and reconnecting small-scale flux ropes at heliospheric shocks. Astrophysical J. 827, 47. doi:10.3847/0004-637x/827/1/47

CrossRef Full Text | Google Scholar

Li, X., Guo, F., and Liu, Y.-H. (2021). The acceleration of charged particles and formation of power-law energy spectra in nonrelativistic magnetic reconnection. Phys. Plasmas 28, 052905. doi:10.1063/5.0047644

CrossRef Full Text | Google Scholar

Loureiro, N. F., Schekochihin, A. A., and Cowley, S. C. (2007). Instability of current sheets and formation of plasmoid chains. Phys. Plasmas 14, 100703. doi:10.1063/1.2783986

CrossRef Full Text | Google Scholar

Marsch, E., Mühlhäuser, K.-H., Schwenn, R., Rosenbauer, H., Pilipp, W., and Neubauer, F. (1982). Solar wind protons: Three-dimensional velocity distributions and derived plasma parameters measured between 0.3 and 1 au. J. Geophys. Res. Space Phys. 87, 52–72. doi:10.1029/ja087ia01p00052

CrossRef Full Text | Google Scholar

Parker, E. N. (1957). Sweet’s mechanism for merging magnetic fields in conducting fluids. J. Geophys. Res. 62, 509–520. doi:10.1029/JZ062i004p00509

CrossRef Full Text | Google Scholar

Parker, E. N. (1958). Dynamics of the interplanetary gas and magnetic fields. Astrophysical J. 128, 664. doi:10.1086/146579

CrossRef Full Text | Google Scholar

Phan, T. D., Gosling, J. T., Paschmann, G., Pasma, C., Drake, J. F., Øieroset, M., et al. (2010). The dependence of magnetic reconnection on plasma β and magnetic shear: evidence from solar wind observations. Astrophysical J. Lett. 719, L199–L203. doi:10.1088/2041-8205/719/2/L199

CrossRef Full Text | Google Scholar

Phan, T., Shay, M., Gosling, J., Fujimoto, M., Drake, J., Paschmann, G., et al. (2013). Electron bulk heating in magnetic reconnection at Earth's magnetopause: dependence on the inflow Alfvén speed and magnetic shear. Geophys. Res. Lett. 40, 4475–4480. doi:10.1002/grl.50917

CrossRef Full Text | Google Scholar

Phan, T. D., Bale, S. D., Eastwood, J. P., Lavraud, B., Drake, J. F., Oieroset, M., et al. (2020). Parker solar probe in situ observations of magnetic reconnection exhausts during encounter 1. Astrophysical J. Suppl. Ser. 246, 34. doi:10.3847/1538-4365/ab55ee

CrossRef Full Text | Google Scholar

Phan, T. D., Lavraud, B., Halekas, J. S., Øieroset, M., Drake, J. F., Eastwood, J. P., et al. (2021). Prevalence of magnetic reconnection in the near-Sun heliospheric current sheet. Astronomy and Astrophysics 650, A13. doi:10.1051/0004-6361/202039863

CrossRef Full Text | Google Scholar

Phan, T.-D., Verniero, J., Larson, D., Lavraud, B., Drake, J., Øieroset, M., et al. (2022). Parker solar probe observations of solar wind energetic proton beams produced by magnetic reconnection in the near-sun heliospheric current sheet. Geophys. Res. Lett. 49, e2021GL096986. doi:10.1029/2021gl096986

PubMed Abstract | CrossRef Full Text | Google Scholar

Pucci, F., and Velli, M. (2014). Reconnection of quasi-singular current sheets: the “ideal” tearing mode. Astrophysical J. Lett. 780, L19. doi:10.1088/2041-8205/780/2/L19

CrossRef Full Text | Google Scholar

Réville, V., Velli, M., Rouillard, A. P., Lavraud, B., Tenerani, A., Shi, C., et al. (2020). Tearing instability and periodic density perturbations in the slow solar wind. Astrophysical J. Lett. 895, L20. doi:10.3847/2041-8213/ab911d

CrossRef Full Text | Google Scholar

Smith, E. J. (2001). The heliospheric current sheet. J. Geophys. Res. Space Phys. 106, 15819–15831. doi:10.1029/2000ja000120

CrossRef Full Text | Google Scholar

Sonnerup, B. Ö., and Cahill, J. , L. (1967). Magnetopause structure and attitude from explorer 12 observations. J. Geophys. Res. 72, 171–183. doi:10.1029/jz072i001p00171

CrossRef Full Text | Google Scholar

Sweet, P. A. (1958). “14. the neutral point theory of solar flares.”Symposium-International Astron. Union 6, 123–134. doi:10.1017/s0074180900237704

CrossRef Full Text | Google Scholar

Swisdak, M., Rogers, B. N., Drake, J. F., and Shay, M. A. (2003). Diamagnetic suppression of component magnetic reconnection at the magnetopause. J. Geophys. Res. Space Phys. 108, 2002JA009726. doi:10.1029/2002JA009726

CrossRef Full Text | Google Scholar

Swisdak, M., Opher, M., Drake, J. F., and Alouani Bibi, F. (2010). The vector direction of the interstellar magnetic field outside the heliosphere. Astrophysical J. 710, 1769–1775. doi:10.1088/0004-637X/710/2/1769

CrossRef Full Text | Google Scholar

Szabo, A., Larson, D., Whittlesey, P., Stevens, M. L., Lavraud, B., Phan, T., et al. (2020). The heliospheric current sheet in the inner heliosphere observed by the parker solar probe. Astrophysical J. Suppl. Ser. 246, 47. doi:10.3847/1538-4365/ab5dac

CrossRef Full Text | Google Scholar

Uzdensky, D. A., and Loureiro, N. F. (2016). Magnetic reconnection onset via disruption of a forming current sheet by the tearing instability. Phys. Rev. Lett. 116, 105003. doi:10.1103/PhysRevLett.116.105003

PubMed Abstract | CrossRef Full Text | Google Scholar

Verscharen, D., Bale, S. D., and Velli, M. (2021). Flux conservation, radial scalings, mach numbers, and critical distances in the solar wind: magnetohydrodynamics and ulysses observations. Mon. Notices R. Astronomical Soc. 506, 4993–5004. doi:10.1093/mnras/stab2051

CrossRef Full Text | Google Scholar

Villante, U., and Bruno, R. (1982). Structure of current sheets in the sector boundaries: helios 2 observations during early 1976. J. Geophys. Res. Space Phys. 87, 607–612. doi:10.1029/JA087iA02p00607

CrossRef Full Text | Google Scholar

Wang, R., Vasko, I. Y., Phan, T. D., and Mozer, F. S. (2024). Solar wind current sheets: MVA inaccuracy and recommended single-spacecraft methodology. J. Geophys. Res. Space Phys. 129, e2023JA032215. doi:10.1029/2023JA032215

CrossRef Full Text | Google Scholar

Weber, E. J., and Davis, J. , L. (1967). The angular momentum of the solar wind. Astrophysical J. 148, 217–227. doi:10.1086/149138

CrossRef Full Text | Google Scholar

Wilcox, J. M., Hoeksema, J. T., and Scherrer, P. H. (1980). Origin of the warped heliospheric current sheet. Science 209, 603–605. doi:10.1126/science.209.4456.603

PubMed Abstract | CrossRef Full Text | Google Scholar

Zank, G. P., Hunana, P., Mostafavi, P., Le Roux, J., Li, G., Webb, G., et al. (2015). Diffusive shock acceleration and reconnection acceleration processes. Astrophysical J. 814, 137. doi:10.1088/0004-637x/814/2/137

CrossRef Full Text | Google Scholar

Zank, G. P., Nakanotani, M., Zhao, L., Du, S., Adhikari, L., Che, H., et al. (2021). Flux ropes, turbulence, and collisionless perpendicular shock waves: high plasma beta case. Astrophysical J. 913, 127. doi:10.3847/1538-4357/abf7c8

CrossRef Full Text | Google Scholar

Zhao, L.-L., Zank, G., Chen, Y., Hu, Q., le Roux, J., Du, S., et al. (2019). Particle acceleration at 5 au associated with turbulence and small-scale magnetic flux ropes. Astrophysical J. 872 (4), 4. doi:10.3847/1538-4357/aafcb2

CrossRef Full Text | Google Scholar