Relativistic ab initio calculations for static and rotating neutron stars

Neutron stars are extraordinary astrophysical objects with densities close to and even very far above these in atomic nuclei. Their structure and dynamic observables are governed by the equation of state (EoS). Due to difficulties in both theory and experiments, there exist still big uncertainties on the EoS for neutron stars. From the realistic nucleon–nucleon $(NN)$ interactions fitted to the experimental $NN$ scattering data, the ab initio calculations based on exact many-body theory are expected to provide a reliable EoS for neutron stars. In this mini review, the relativistic Brueckner–Hartree–Fock theory within the full Dirac space will be introduced, the technical for relieving the angle-averaging approximations will be addressed, and its description for neutron star properties will be introduced.

1 Introduction

Neutron stars serve as natural laboratories for investigating the properties of matter under extreme densities and strong gravitational fields (Lattimer and Prakash, 2004). Understanding the properties of dense nuclear matter is essential for describing the structure and evolution of neutron stars (Burgio et al., 2021; Sedrakian et al., 2023). At the core of this pursuit lies the nuclear equation of state (EoS), which connects microscopic nuclear interactions to macroscopic observables such as neutron star masses and radii (Lattimer and Prakash, 2000; Lattimer and Prakash, 2007; Oertel et al., 2017; Huth et al., 2022). The EoS essentially encapsulates the relationship between pressure and density in nuclear matter, determining how matter behaves under the extreme conditions found in neutron star interiors. In particular, the recent detection of neutron stars with masses exceeding 2 solar masses and the advent of multi-messenger astronomy have placed stringent constraints on the EoS, highlighting the necessity of developing and refining theoretical models that are not only consistent with laboratory nuclear physics data but also aligned with the latest astrophysical observations (Demorest et al., 2010; Antoniadis et al., 2013; Fonseca et al., 2016; Arzoumanian et al., 2018; Cromartie et al., 2020; Fonseca et al., 2021; Abbott et al., 2017; Abbott et al., 2018; Tong et al., 2020; Han et al., 2023).

Over the years, considerable theoretical efforts have been devoted to determining the EoS of neutron star matter using various nuclear many-body approaches. In general, these approaches can be categorized into two classes: density functional theories (DFTs) employing effective nucleon-nucleon $(NN)$ interactions, and ab initio methods based on realistic interactions. The effective $NN$ interactions in DFTs, either non-relativistic or relativistic, are tuned to reproduce the properties of finite nuclei and nuclear matter around saturation density, as in the Skyrme (1956), Dechargé and Gogny (1980), and relativistic mean-field (RMF) models (Ring, 1996; Meng et al., 2006; Meng, 2016). However, due to weak constraints on the isovector channels, their predictions for nuclear matter properties, such as the nuclear symmetry energy at higher densities, remain uncertain (Li et al., 2008). In contrast, ab initio methods based on realistic $NN$ interactions stand out for their predictive power, free from uncertainties associated with adjustable parameters. In recent years, a growing variety of ab initio methods have been developed for nuclear many-body studies, including quantum Monte Carlo (Carlson et al., 2015), coupled-cluster (Hagen et al., 2014), no-core shell model (Barrett et al., 2013), self-consistent Green’s function (Dickhoff and Barbieri, 2004), lattice effective field theory (Lee, 2009; Lähde and Meißner, 2019; Tong et al., 2025a; Tong et al., 2025b; Tong et al., 2025c), in-medium similarity renormalization group (Hergert et al., 2016), Monte Carlo shell model (Otsuka et al., 2001; Liu et al., 2012), and Brueckner-Hartree-Fock (BHF) theory (Shang et al., 2021). Among these, the relativistic Brueckner-Hartree-Fock (RBHF) theory stands out as one of the most successful ab initio methods based solely on bare two-body forces. Benefiting from the relativistic framework–which is essential at high densities due to the crucial role of Lorentz covariance, the RBHF theory has been successfully applied to both finite nuclei (Shen et al., 2016; Shen et al., 2019; Wang et al., 2019) and dense matter systems such as nuclear matter and neutron stars (Brockmann and Machleidt, 1990; Sehn et al., 1997; de Jong and Lenske, 1998; van Dalen et al., 2005; Katayama and Saito, 2013; Tong et al., 2018; Wang et al., 2020).

The RBHF theory provides a self-consistent framework to study the nuclear many-body problem by combining Dirac phenomenology with the in-medium scattering equation. In this approach, the interaction between two nucleons in the nuclear medium is described by the in-medium scattering matrix $G$, obtained by summing ladder diagrams with a realistic $NN$ potential. The effective single-particle potential is derived from $G$ matrix, which in turn modifies the nucleon spinors via the Dirac equation, thereby closing the self-consistent loop. To simplify RBHF calculations, earlier studies adopted the average center of mass (c. m.) momentum approximation for computing the binding energy (Brueckner et al., 1968; Alonso and Sammarruca, 2003; Sammarruca et al., 2012; Sammarruca, 2014). With modern computational capabilities, this approximation can be avoided. Recent work derived exact analytic expressions for the angular integration over the c. m. momentum, with a focus on asymmetric nuclear matter (Tong et al., 2018). A significant contribution to the saturation properties was found when treating the total momentum exactly, underscoring its impact on higher-order quantities in both the energy of symmetric matter and the symmetry energy. Another key challenge in RBHF theory is the self-consistent extraction of the nucleon single-particle potential from the in-medium $G$ matrix, where symmetry arguments dictate its decomposition into scalar and vector components (Serot and Walecka, 1986). Traditional approaches include the momentum-independence approximation (Brockmann and Machleidt, 1990), which neglects momentum dependence and fails to capture the correct isospin dependence of the single-particle potential in asymmetric nuclear matter (Ulrych and Müther, 1997; Schiller and Müther, 2001), and the projection method (Horowitz and Serot, 1987; Nuppenau et al., 1989; Gross-Boelting et al., 1999), which retains momentum dependence but is limited to positive-energy states (PESs). Notably, these methods yield contradictory predictions for the isospin dependence of the single-particle potential (Ulrych and Müther, 1997). Recently, a fully self-consistent RBHF framework in the full Dirac space has been developed (Wang et al., 2021), where the Lorentz structure and momentum dependence are determined without approximations. This advance resolves the long-standing discrepancy and provides a unique description of isospin effects in nuclear matter. As a result, the RBHF theory in the full Dirac space has been successfully and systematically applied to diverse nuclear systems, including the nuclear matter (Wang et al., 2022a; Wang et al., 2022b; Qu et al., 2023; Wang et al., 2023; Wang et al., 2024; Qin et al., 2025; Huang et al., 2025), the properties of ²⁰⁸Pb with a liquid droplet model (Tong et al., 2023), neutron star properties (Tong et al., 2022; Wang et al., 2022c; Qu et al., 2025; Laskos-Patkos et al., 2025), optical potential for proton-nucleus scattering (Qin et al., 2024), and in-medium nucleon-nucleon cross sections (Wang et al., 2025).

In this review, we summarize these recent advances in RBHF theory formulated in the full Dirac space and their implications for the physics of dense matter and neutron stars.

2 Relativistic Brueckner–Hartree–Fock theory and neutron stars

In the RBHF theory, nucleons within the nuclear medium are treated as dressed particles due to their interactions with surrounding nucleons. The single-particle motion of these nucleons is described by the Dirac equation

$\left[\mathit{\alpha }\cdot \mathit{p}+\beta \left(M+\mathcal{U}\right)\right]u\left(\mathit{p},s\right)=E_{\mathit{p}}u\left(\mathit{p},s\right),(1)$

where $\mathit{\alpha }$ and $\beta$ are the Dirac matrices, $M$ is the nucleon mass, $\mathit{p}$ and $E_{\mathit{p}}$ are the momentum and the single-particle energy, and $s$ denotes the spin. According to the translational and rotational invariance, time-reversal invariance, hermiticity, and parity conservation, the single-particle potential $\mathcal{U}$ can be decomposed in its Lorentz form (Serot and Walecka, 1986)

$\mathcal{U}\left(\mathit{p}\right)=U_{\text{S}}\left(p\right)+{\gamma }^0{U}_0\left(p\right)+\mathit{\gamma }\cdot \widehat{\mathit{p}}{U}_{\text{V}}\left(p\right).(2)$

The quantities $U_{\text{S}}(p)$, $U_0(p)$, and $U_{\text{V}}(p)$ are the scalar potential, timelike, and spacelike parts of the vector potential respectively with $p=|\mathit{p}|$ the magnitude of nucleon momentum. $\widehat{\mathit{p}}=\mathit{p}/|\mathit{p}|$ is the unit vector. By using the following effective quantities in Equations 3a–3c:

${\mathit{p}}^{*}=\mathit{p}+\widehat{\mathit{p}}{U}_{\text{V}}\left(p\right),(\mathrm{3a})$

$M_{\mathit{p}}^{*}=M+U_{\text{S}}\left(p\right),(\mathrm{3b})$

$E_{\mathit{p}}^{*}=E_{\mathit{p}}-U_0\left(p\right),(\mathrm{3c})$

the solution of Equation 1 leads to the in-medium positive-energy spinor $u(\mathit{p},s)$ and negative-energy spinor $v(\mathit{p},s)$

$u\left(\mathit{p},s\right)=\sqrt{\frac{E_{\mathit{p}}^{*}+M_{\mathit{p}}^{*}}{2M_{\mathit{p}}^{*}}}\left[\begin{array}{c}\hfill 1\hfill \\ \hfill \frac{\mathit{\sigma }\cdot {\mathit{p}}^{*}}{E_{\mathit{p}}^{*}+M_{\mathit{p}}^{*}}\hfill \end{array}\right]{\chi }_s,(\mathrm{4a})$

$v\left(\mathit{p},s\right)={\gamma }^{5}u\left(\mathit{p},s\right)=\sqrt{\frac{E_{\mathit{p}}^{*}+M_{\mathit{p}}^{*}}{2M_{\mathit{p}}^{*}}}\left[\begin{array}{c}\hfill \frac{\mathit{\sigma }\cdot {\mathit{p}}^{*}}{E_{\mathit{p}}^{*}+M_{\mathit{p}}^{*}}\hfill \\ \hfill 1\hfill \end{array}\right]{\chi }_s,(\mathrm{4b})$

where ${\chi }_s$ is the spin wave function.

The Dirac equation can be solved exactly once the single-particle potentials are determined. To this end, three matrix elements of $\mathcal{U}(\mathit{p})$ in the full Dirac space are introduced,

${\mathrm{\Sigma }}^{++}\left(p\right)=\bar{u}\left(\mathit{p},1/2\right)\mathcal{U}\left(\mathit{p}\right)u\left(\mathit{p},1/2\right)=U_{\text{S}}\left(p\right)+\frac{E_{\mathit{p}}^{*}}{M_{\mathit{p}}^{*}}{U}_0\left(p\right)+\frac{p^{*}}{M_{\mathit{p}}^{*}}{U}_{\text{V}}\left(p\right),(\mathrm{5a})$

${\mathrm{\Sigma }}^{-+}\left(p\right)=\bar{v}\left(\mathit{p},1/2\right)\mathcal{U}\left(\mathit{p}\right)u\left(\mathit{p},1/2\right)=\frac{p^{*}}{M_{\mathit{p}}^{*}}{U}_0\left(p\right)+\frac{E_{\mathit{p}}^{*}}{M_{\mathit{p}}^{*}}{U}_{\text{V}}\left(p\right),(\mathrm{5b})$

${\mathrm{\Sigma }}^{--}\left(p\right)=\bar{v}\left(\mathit{p},1/2\right)\mathcal{U}\left(\mathit{p}\right)v\left(\mathit{p},1/2\right)=-U_{\text{S}}\left(p\right)+\frac{E_{\mathit{p}}^{*}}{M_{\mathit{p}}^{*}}{U}_0\left(p\right)+\frac{p^{*}}{M_{\mathit{p}}^{*}}{U}_{\text{V}}\left(p\right).(\mathrm{5c})$

After obtaining ${\mathrm{\Sigma }}^{++}(p)$, ${\mathrm{\Sigma }}^{-+}(p)$, and ${\mathrm{\Sigma }}^{--}(p)$, single-particle potentials in Equation 2 can be determined uniquely through

$U_{\text{S}}\left(p\right)=\frac{{\mathrm{\Sigma }}^{++}\left(p\right)-{\mathrm{\Sigma }}^{--}\left(p\right)}{2},(\mathrm{6a})$

$U_0\left(p\right)=\frac{E_{\mathit{p}}^{*}}{M_{\mathit{p}}^{*}}\frac{{\mathrm{\Sigma }}^{++}\left(p\right)+{\mathrm{\Sigma }}^{--}\left(p\right)}{2}-\frac{p^{*}}{M_{\mathit{p}}^{*}}{\mathrm{\Sigma }}^{-+}\left(p\right),(\mathrm{6b})$

$U_{\text{V}}\left(p\right)=-\frac{p^{*}}{M_{\mathit{p}}^{*}}\frac{{\mathrm{\Sigma }}^{++}\left(p\right)+{\mathrm{\Sigma }}^{--}\left(p\right)}{2}+\frac{E_{\mathit{p}}^{*}}{M_{\mathit{p}}^{*}}{\mathrm{\Sigma }}^{-+}\left(p\right).(\mathrm{6c})$

This approach avoids approximations in the Dirac space with PESs only. The matrix elements ${\mathrm{\Sigma }}^{++}(p)$, ${\mathrm{\Sigma }}^{-+}(p)$, and ${\mathrm{\Sigma }}^{--}(p)$ can be calculated alternatively by summing up the effective two-body interaction $G$ matrix with all the nucleons inside the Fermi sea in the Hartree-Fock approximation

${\mathrm{\Sigma }}^{++}\left(p\right)={\displaystyle \sum _{s^{\prime }}}{\int }_0^{k_{\text{F}}}\frac{d^3{p}^{\prime }}{{\left(2\pi \right)}^3}\frac{M_{{\mathit{p}}^{\prime }}^{*}}{E_{{\mathit{p}}^{\prime }}^{*}}⟨\bar{u}\left(\mathit{p},1/2\right)\bar{u}\left({\mathit{p}}^{\prime },s^{\prime }\right)|{\bar{G}}^{++++}\left(W\right)|u\left(\mathit{p},1/2\right)u\left({\mathit{p}}^{\prime },s^{\prime }\right)⟩,(\mathrm{7a})$

${\mathrm{\Sigma }}^{-+}\left(p\right)={\displaystyle \sum _{s^{\prime }}}{\int }_0^{k_{\text{F}}}\frac{d^3{p}^{\prime }}{{\left(2\pi \right)}^3}\frac{M_{{\mathit{p}}^{\prime }}^{*}}{E_{{\mathit{p}}^{\prime }}^{*}}⟨\bar{v}\left(\mathit{p},1/2\right)\bar{u}\left({\mathit{p}}^{\prime },s^{\prime }\right)|{\bar{G}}^{-+++}\left(W\right)|u\left(\mathit{p},1/2\right)u\left({\mathit{p}}^{\prime },s^{\prime }\right)⟩,(\mathrm{7b})$

${\mathrm{\Sigma }}^{--}\left(p\right)={\displaystyle \sum _{s^{\prime }}}{\int }_0^{k_{\text{F}}}\frac{d^3{p}^{\prime }}{{\left(2\pi \right)}^3}\frac{M_{{\mathit{p}}^{\prime }}^{*}}{E_{{\mathit{p}}^{\prime }}^{*}}⟨\bar{v}\left(\mathit{p},1/2\right)\bar{u}\left({\mathit{p}}^{\prime },s^{\prime }\right)|{\bar{G}}^{-+-+}\left(W\right)|v\left(\mathit{p},1/2\right)u\left({\mathit{p}}^{\prime },s^{\prime }\right)⟩.(\mathrm{7c})$

In Equations 7a–7c, the anti-symmetrized $G$ matrix is expressed with $\bar{G}$, where the $\pm$-signs in the superscript denote the positive- or negative-energy states. $W$ is the starting energy which equals to the total single-particle energies in the initial states.

The $G$ matrix is obtained by solving the in-medium Thompson equation (Brockmann and Machleidt, 1990)

$\begin{array}{cc}\hfill G\left({\mathit{q}}^{\prime },\mathit{q}|\mathit{P},W\right)=& V\left({\mathit{q}}^{\prime },\mathit{q}|\mathit{P}\right)+\int \frac{d^{3}k}{{\left(2\pi \right)}^3}V\left({\mathit{q}}^{\prime },\mathit{k}|\mathit{P}\right)\hfill \\ \hfill & \times \frac{M_{\mathit{P}+\mathit{k}}^{*}{M}_{\mathit{P}-\mathit{k}}^{*}}{E_{\mathit{P}+\mathit{k}}^{*}{E}_{\mathit{P}-\mathit{k}}^{*}}\frac{Q\left(\mathit{k},\mathit{P}\right)}{W-E_{\mathit{P}+\mathit{k}}-E_{\mathit{P}-\mathit{k}}+iϵ}G\left(\mathit{k},\mathit{q}|\mathit{P},W\right),\hfill \end{array}(8)$

where $\mathit{P}=\frac{1}{2}({\mathit{k}}_1+{\mathit{k}}_2)$ is half the total momentum and $\mathit{k}=\frac{1}{2}({\mathit{k}}_1-{\mathit{k}}_2)$ is the relative momentum of the two interacting nucleons with momenta ${\mathit{k}}_1$ and ${\mathit{k}}_2$. The initial, intermediate, and final relative momenta of the two nucleons scattering in nuclear matter are denoted by $\mathit{q},\mathit{k}$, and ${\mathit{q}}^{\prime }$, respectively. $V$ is derived from a realistic $NN$ interaction. Here we introduced the one-boson-exchange potential (OBEP) as an example (Machleidt, 1989), which has been well constrained by experimental data on both $NN$ bound states and scattering observables. The $NN$ scattering in the nuclear medium is restricted with the Pauli operator in Equation 9:

$Q\left(\mathit{k},\mathit{P}\right)=\left\{\begin{array}{cc}1,\hfill & |\mathit{P}+\mathit{k}|,|\mathit{P}-\mathit{k}|>k_{\text{F}},\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\right.(9)$

The inclusion of an infinitesimal $iϵ$ term in the denominator is necessary when the starting energy $W=E_{\mathit{P}+\mathit{k}}+E_{\mathit{P}-\mathit{k}}$ approaches a pole within the continuous choice. The RBHF equations were solved self-consistently for symmetric nuclear matter in the full Dirac space within the continuous choice for the single-particle potential (Wang et al., 2022a). The resulting single-particle energy and Dirac mass exhibit smooth continuity across the Fermi surface. Equation 1, Equations 6a–6c, Equations 7a–7c, Equation 8 constitute a coupled system that has to be solved in a self-consistent way.

After the solution of $G$ matrix and the calculation of single-particle potentials converge, the binding energy per nucleon in nuclear matter can be calculated using

$\begin{array}{cc}\hfill E/A=& \frac{1}{\rho }{\displaystyle \sum _s}{\int }_0^{k_F}\frac{d^{3}p}{{\left(2\pi \right)}^3}\frac{M_{\mathit{p}}^{*}}{E_{\mathit{p}}^{*}}⟨\bar{u}\left(\mathit{p},s\right)|\mathit{\gamma }\cdot \mathit{p}+M|u\left(\mathit{p},s\right)⟩-M\hfill \\ \hfill & +\frac{1}{2\rho }{\displaystyle \sum _{s,s^{\prime }}}{\int }_0^{k_F}\frac{d^{3}p}{{\left(2\pi \right)}^3}{\int }_0^{k_F^{\prime }}\frac{d^3{p}^{\prime }}{{\left(2\pi \right)}^3}\frac{M_{\mathit{p}}^{*}}{E_{\mathit{p}}^{*}}\frac{M_{{\mathit{p}}^{\prime }}^{*}}{E_{{\mathit{p}}^{\prime }}^{*}}\hfill \\ \hfill & \times ⟨\bar{u}\left(\mathit{p},s\right)\bar{u}\left({\mathit{p}}^{\prime },s^{\prime }\right)|\bar{G}\left(W\right)|u\left(\mathit{p},s\right)u\left({\mathit{p}}^{\prime },s^{\prime }\right)⟩,\hfill \end{array}(10)$

where $\rho$ denotes the total density of nucleons.

It should also be noted that the calculation of the binding energy yields a three dimension integrals over the c. m. momentum $\mathit{P}$ and relative momentum $\mathit{q}$. The three-dimensional integrals over the c. m. momentum $\mathit{P}$ are numerically challenging. Normally, the widely used averaged c. m. momentum approximation in Equation 11 is adopted (Brueckner et al., 1968; Alonso and Sammarruca, 2003),

$P_{\text{av}}^2=\frac{{\int }_0^{k_F}{d}^3{k}_1{\int }_0^{k_F}{d}^3{k}_2{P}^2\delta \left(q-\frac{1}{2}|{\mathit{k}}_1-{\mathit{k}}_2|\right)}{{\int }_0^{k_F}{d}^3{k}_1{\int }_0^{k_F}{d}^3{k}_2\delta \left(q-\frac{1}{2}|{\mathit{k}}_1-{\mathit{k}}_2|\right)}.(11)$

It does not depend on the direction and this value is usually applied in the $G$-matrix in Equation 10. By relieving this approximation and deriving the exact expressions of the angular integrations of the momentum $\mathit{P}$ within RBHF theory, the exact results has been calculated in Ref. Tong et al. (2018), especially for the case of asymmetric nuclear matter. For the calculations in the full Dirac space, the exact evaluation of $\mathit{P}$ and its integral during the iteration are also performed.

One of the motivations for developing a microscopic and fully relativistic theory of dense nuclear matter is its application to neutron star. The neutron star matter here is assumed to be composed of nucleons and leptons (mainly electrons and muons), while neglecting possible phase transitions or the appearance of exotic degrees of freedom at densities above nuclear saturation. The matter is considered to be in beta equilibrium and charge neutrality, leading to the following equilibrium conditions for the chemical potentials of the nucleons and leptons in Equation 12:

${\mu }_p={\mu }_n-{\mu }_e,{\mu }_{\mu }={\mu }_e,(12)$

where ${\mu }_e$, ${\mu }_{\mu }$, ${\mu }_p$, and ${\mu }_n$ denote the chemical potentials of electrons, muons, protons, and neutrons, respectively. Charge neutrality is maintained in Equation 13:

${\rho }_p={\rho }_e+{\rho }_{\mu },(13)$

where ${\rho }_p,{\rho }_e$, and ${\rho }_{\mu }$ are the number densities of protons, electrons, and muons, respectively. The energy density of the beta equilibrium nuclear matter is then obtained as

$\epsilon =\rho \left[E\left(\rho ,\alpha \right)/A+Y_p{M}_p+\left(1-Y_p\right)M_n\right]+{\epsilon }_e+{\epsilon }_{\mu },(14)$

where $Y_i={\rho }_i/\rho (i=e,\mu ,p,n)$ are the equilibrium particle fractions. The chemical potential for each particle $i$ is given in Equation 15:

${\mu }_i=\frac{\partial \epsilon /\rho }{\partial Y_i}.(15)$

For a given density $\rho$, the particle fractions $Y_i$ are determined by solving the equilibrium conditions and charge neutrality, allowing the calculation of the energy density $\epsilon$ using Equation 14. The pressure $P$ is then derived from Equation 16:

$P=-\frac{\partial \left(\epsilon /\rho \right)}{\partial \left(1/\rho \right)}=\rho \frac{\partial \epsilon }{\partial \rho }-\epsilon .(16)$

This yields the EoS of beta equilibrium nuclear matter in the form of $P(\epsilon )$.

Once the EoS in the form $P(\epsilon )$ is obtained, the mass and radius of a cold, spherically symmetric, static, and relativistic star can be described by the Tolman-Oppenheimer-Volkov (TOV) equations (Oppenheimer and Volkoff, 1939; Tolman, 1939),

$\frac{dP\left(r\right)}{dr}=-\frac{\left[P\left(r\right)+\epsilon \left(r\right)\right]\left[M\left(r\right)+4\pi r^{3}P\left(r\right)\right]}{r\left[r-2M\left(r\right)\right]},(\mathrm{17a})$

$\frac{dM\left(r\right)}{dr}=4\pi r^2\epsilon \left(r\right),(\mathrm{17b})$

where $P(r)$ is the pressure at neutron star radius $r$, $M(r)$ is the total neutron star mass inside a sphere of radius $r$. Besides the masses and radii, another key property of neutron stars is their dimensionless tidal deformability (Damour et al., 1992; Hinderer, 2008; Flanagan and Hinderer, 2008), denoted by $\mathrm{\Lambda }$. This quantity characterizes the star’s response to an external tidal field and is defined in Equation 18:

$\mathrm{\Lambda }=\frac{2}{3}{k}_2{C}^{-5}.(18)$

$C=M/R$ is the compactness parameter, where $M$ is the neutron star mass and $R$ is the radius and they are determined from the following two conditions: $P(R)=0$ and $M=M(R)$. $k_2$ is the second love number quantifying the tidal response of the star in Equation 19,

$\begin{array}{cc}\hfill k_2=& \frac{8C^5}{5}{\left(1-2C\right)}^2\left[2-y_R+2C\left(y_R-1\right)\right]\times \left\{6C\left[2-y_R+C\left(5y_R-8\right)\right]\right.\hfill \\ \hfill & +4C^3\left[13-11y_R+C\left(3y_R-2\right)+2C^2\left(1+y_R\right)\right]\hfill \\ \hfill & {\left.+3{\left(1-2C\right)}^2\left[2-y_R+2C\left(y_R-1\right)\right]\ln \left(1-2C\right)\right\}}^{-1},\hfill \end{array}(19)$

where $y_R=y(R)$ characterizes the response of the metric perturbation to the external tidal field at the stellar surface, and it can be calculated by solving the following differential equation,

$r\frac{dy\left(r\right)}{dr}+y^2\left(r\right)+y\left(r\right)F\left(r\right)+r^{2}Q\left(r\right)=0,(20)$

with

$F\left(r\right)={\left[1-\frac{2M\left(r\right)}{r}\right]}^{-1}\left\{1-4\pi r^2\left[\epsilon \left(r\right)-P\left(r\right)\right]\right\},(\mathrm{21a})$

$Q\left(r\right)=\left\{4\pi \left[5\epsilon \left(r\right)+9P\left(r\right)+\frac{\epsilon \left(r\right)+P\left(r\right)}{\frac{\partial P}{\partial \epsilon }\left(r\right)}\right]-\frac{6}{r^2}\right\}\times {\left[1-\frac{2M\left(r\right)}{r}\right]}^{-1}$

$-{\left[\frac{2M\left(r\right)}{r^2}+2\times 4\pi rP\left(r\right)\right]}^2\times {\left[1-\frac{2M\left(r\right)}{r}\right]}^{-2}.(\mathrm{21b})$

The differential Equation 20 can be integrated together with the TOV equations with the boundary condition $y(0)=2$. In addition to tidal deformability, the rotational properties of neutron stars also provide crucial insights into their internal structure. The moment of inertia is calculated within the slow-rotation approximation (Hartle, 1967; Hartle and Thorne, 1968), where the frequency $\mathrm{\Omega }$ of a uniformly rotating neutron star is significantly lower than the Kepler frequency at the equator. In this approximation, the moment of inertia $I$ of a uniformly rotating, axially symmetric neutron star is given in Equation 22; Fattoyev and Piekarewicz (2010).

$I=\frac{8\pi }{3}{\int }_0^R{r}^4{e}^{-\nu \left(r\right)}\frac{\bar{\omega }\left(r\right)}{\mathrm{\Omega }}\frac{ϵ\left(r\right)+P\left(r\right)}{\sqrt{1-2M\left(r\right)/r}}dr.(22)$

Here, $\nu (r)$ is a radially-dependent metric function defined in Equation 23:

$\nu \left(r\right)=\frac{1}{2}\ln \left(1-\frac{2M}{R}\right)-{\int }_r^R\frac{M\left(x\right)+4\pi x^{3}P\left(x\right)}{x^2\left[1-2M\left(x\right)/x\right]}dx.(23)$

The frame-dragging angular velocity $\bar{\omega }$ represents the angular velocity of the fluid as measured in a local inertial reference frame, which is usually expressed through the dimensionless relative frequency $\tilde{\omega }\equiv \bar{\omega }/\mathrm{\Omega }$, which satisfies the following second-order differential equation in Equation 24:

$\frac{d}{dr}\left[r^{4}j\left(r\right)\frac{d\tilde{\omega }\left(r\right)}{dr}\right]+4r^3\frac{dj\left(r\right)}{dr}\tilde{\omega }\left(r\right)=0,(24)$

where $j(r)=e^{-\nu (r)}\sqrt{1-2M(r)/r}$ for $r\le R$. The relative frequency $\tilde{\omega }(r)$ is subject to the boundary conditions

${\tilde{\omega }}^{\prime }\left(0\right)=0,\tilde{\omega }\left(R\right)+\frac{R}{3}{\tilde{\omega }}^{\prime }\left(R\right)=1.(25)$

It should be noted that, under the slow-rotation approximation, the moment of inertia is independent of the stellar frequency $\mathrm{\Omega }$.

The quadrupole moment characterizes the degree of rotational deformation of the neutron star away from spherical symmetry (Yagi and Yunes, 2013). It can be computed by numerically solving for the interior and exterior gravitational field of a neutron star in a slow-rotation (Hartle, 1967; Hartle and Thorne, 1968) and a small-tidal-deformation approximation (Hinderer, 2008; Hinderer et al., 2010). To explore the universal dimensionless moment of inertia-tidal deformability-quadrupole moment ($I$–Love–$Q$) relations, which are nearly independent of the EoS, we introduce the following quantities in Equation 26:

$\bar{I}\equiv \frac{I}{M^3},\bar{Q}\equiv -\frac{QM}{{\left(I\mathrm{\Omega }\right)}^2}.(26)$

In addition, to describe the rapidly rotating and axisymmetric neutron star configurations in general relativity, the stellar matter is treated as a perfect fluid, characterized by the energy-momentum tensor in Equation 27:

$T^{\mu \nu }=\left(\epsilon +P\right)u^{\mu }{u}^{\nu }-g^{\mu \nu }P,(27)$

where $\epsilon$, $P$, and $u^{\mu }$ are the energy density, pressure, and fluid’s four-velocity, respectively. The Einstein field equations are solved assuming an axisymmetric and stationary spacetime with the metric in Equation 28:

$\begin{array}{c}\hfill d{s}^2=-e^{\gamma +\rho }d{t}^2+e^{2\alpha }\left(d{r}^2+r^{2}d{\theta }^2\right)+e^{\gamma -\rho }{r}^2{\sin }^2\theta {\left(d\varphi -\omega dt\right)}^2,\end{array}(28)$

where the metric potentials $\gamma ,\rho ,\alpha$, and $\omega$ are functions of the radial coordinates $r$ and the polar angle $\theta$. For numerical calculations, we utilize the RNS code (Stergioulas and Friedman, 1995; Paschalidis and Stergioulas, 2017) for rapidly rotating neutron stars.

3 Neutron star mass and radius

In this review, we have focused on recent advances in the study of neutron star properties based on RBHF theory formulated in the full Dirac space.

Figure 1 from Ref. Qu et al. (2025) illustrates the gravitational mass of both static and rotating neutron stars as a function of their equatorial radius. The left panel presents results for fixed spin ratios, $\chi \equiv f/f_K=0.0$, 0.2, 0.4, 0.6, 0.8, and 1.0, while the right panel displays cases with fixed spin frequencies, $f=0$, 400, 600, 800, 1,000 Hz, and the Keplerian limit $f=f_K$. For a given spin ratio or frequency, the gravitational mass decreases with increasing equatorial radius, but rises as the rotation rate increases, reflecting the additional centrifugal support provided by rotation. These results highlight the capability of RBHF theory to consistently describe both static and rapidly rotating neutron stars within the same microscopic framework. For the Bonn A potential, the static case yields a radius of 10.93 km at the maximum mass. In contrast, at the Keplerian frequency, the radius expands to 13.84 km, representing a 26.2% increase. In addition to the EoS obtained with the Bonn A potential, results based on the Bonn B and C potentials (Brockmann and Machleidt, 1990) are also presented. Overall, the mass–radius relations derived from these three parameterizations of realistic $NN$ interactions exhibit very similar patterns, regardless of whether the stars are static or rotating. This robust consistency across different rotation rates suggests that the influence of rotational dynamics on the mass–radius relation is relatively insensitive to the specific details of the underlying interactions governing the EoS. Specifically, the maximum masses for $\chi =0.0,0.2,0.4,0.6$, and 0.8 are 2.43, 2.46, 2.52, 2.63, and 2.80$M_{\odot }$, and the corresponding central energy densities are ${\epsilon }_c=2.26,2.25,2.21,2.12$, and $2.00\times 10^{15}$ g$/{\mathrm{c}\mathrm{m}}^3$, respectively. In particular, the maximum mass for rotating configurations $M_{\text{max}}$, can reach up to $2.93M_{\odot }$, which is 20.6% higher than the static result $M_{\text{TOV}}=2.43M_{\odot }$.

Figure 1

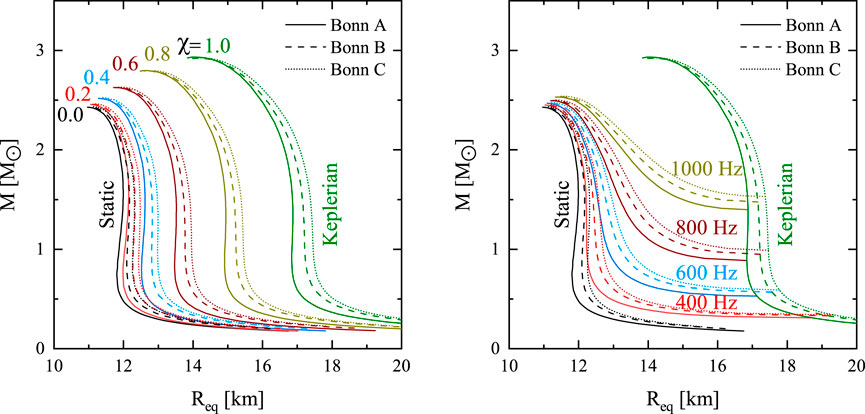
Figure 1. The gravitational mass $M$ as a function of the equatorial radii $R_{\text{eq}}$. Six cases are presented for (left panel) fixed spin ratios, $\chi =0$ (static), 0.2, 0.4, 0.6, 0.8, and 1.0 (Keplerian sequence), and (right panel) fixed spin frequencies, $f=\mathrm{0,400,600,800,1000}$ Hz, as well as $f=f_K$. The results are obtained using EoSs from RBHF calculations in the full Dirac space, based on the Bonn A (solid lines), B (dashed lines), and C (dotted lines) potentials. Figures taken from Qu et al. (2025).

Specifically, the radii of a canonical neutron star with mass $1.4M_{\odot }$ in the static case are calculated to be $R_{1.4}=11.98$, 12.17, and 12.32 km for the Bonn A, B, and C potential, respectively. The smallest radius predicted by the Bonn A potential implies that the RBHF calculations with this potential yields the softest EoS. This softness is attributed to the weakest tensor force in the Bonn A potential, which leads to the strongest attraction between nucleons. These differences underscore the sensitivity of neutron star properties to the underlying $NN$ interactions and emphasize the importance of accurately modeling these interactions to predict astrophysical observables. Further discussions on the tensor force effects in nuclear matter, derived from realistic $NN$ interactions, can be found in Ref. Wang et al. (2024). Moreover, the other results for neutron star radii shown in Ref. Tong et al. (2022) are also consistent with various empirical and observational constraints.

4 Universal relations

In the multimessenger era, the tidal deformability $\mathrm{\Lambda }$ of neutron stars has emerged as a crucial astrophysical constraint. The neutron star tidal deformabilties at 1.4$M_{\odot }$ from the RBHF theory in full Dirac space are given as ${\mathrm{\Lambda }}_{1.4M_{\odot }}=\mathrm{376,405,433}$ for Bonn A, B, C, respectively (Tong et al., 2022). Notably, the Bonn A potential predicts smaller ${\mathrm{\Lambda }}_{1.4M_{\odot }}$ values compared to Bonn B and C. This trend can be understood through the stiffness of the EoS: for a given neutron star mass, a softer symmetry energy results in more compact stellar configurations, leading to both smaller radii and reduced tidal deformabilities. These theoretical predictions can be contextualized with current observational constraints. The initial estimation for tidal deformability ${\mathrm{\Lambda }}_{1.4M_{\odot }}$ has an upper bound ${\mathrm{\Lambda }}_{1.4M_{\odot }}<800$ (Abbott et al., 2017) from the observation of binary neutron star (BNS) merger event GW170817. Subsequent revised analysis from LIGO and Virgo collaborations narrowed this to ${\mathrm{\Lambda }}_{1.4M_{\odot }}=190_{-120}^{+390}$ (Abbott et al., 2018). Importantly, the results from three potentials fall within these observational bounds, with the Bonn A results exhibiting the closest agreement with the central values inferred from GW170817.

Beyond tidal deformability, universal relations among neutron star observables offer an additional, largely EoS-independent avenue for cross-checking theoretical models against observations. Figure 2 examines the EoSs derived from RBHF theory in the full Dirac space, with the projection method, and the momentum-independence approximation with Bonn potentials–in light of the universal $I$-Love-$Q$ relations (Wang et al., 2022c). The $I$-Love and $Q$-Love are illustrated in the top panels of Figure 2. The $I$-$Q$ relations can also be found in Ref. Wang et al. (2022c). Along each curve, the mass or compactness serves as the single varying parameter, increasing towards the left in the plots. The universal relations are found to hold with high accuracy across different EoSs. Owing to their weak dependence on the specific EoS, a single empirical fit (black solid curves) can be applied, given by the functional form (Yagi and Yunes, 2017):

$\ln y_i=a_i+b_i\ln x_i+c_i{\left(\ln x_i\right)}^2+d_i{\left(\ln x_i\right)}^3+e_i{\left(\ln x_i\right)}^4,(29)$

where the fitting coefficients are summarized in Table 4 of Wang et al. (2022c). These coefficients closely agree with those obtained in Ref. Yagi and Yunes (2017), based on a broad ensemble of EoSs. The bottom panels of Figure 2 present the absolute fractional deviations between the data and the fit, which remain below 1% over the entire mass range examined. The universal relation between $\bar{I}$ and the tidal deformability $\mathrm{\Lambda }$ enables the inference of the moment of inertia for a $1.4M_{\odot }$ neutron star, ${\bar{I}}_{1.4M\odot }$, from the tidal deformability ${\mathrm{\Lambda }}_{1.4M_{\odot }}$ measured in the GW170817 event. The updated analysis from the LIGO and Virgo Collaborations reports ${\mathrm{\Lambda }}_{1.4M_{\odot }}=190_{-120}^{+390}$ (Abbott et al., 2018), corresponding to ${\bar{I}}_{1.4M_{\odot }}=10.30_{-2.10}^{+3.39}$, as shown in the left panel of Figure 2. Using the relation $\bar{I}=I/M^3$, this yields $I_{1.4M_{\odot }}=1.22_{-0.25}^{+0.40}\times 10^{45}\mathrm{g}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$.

Figure 2

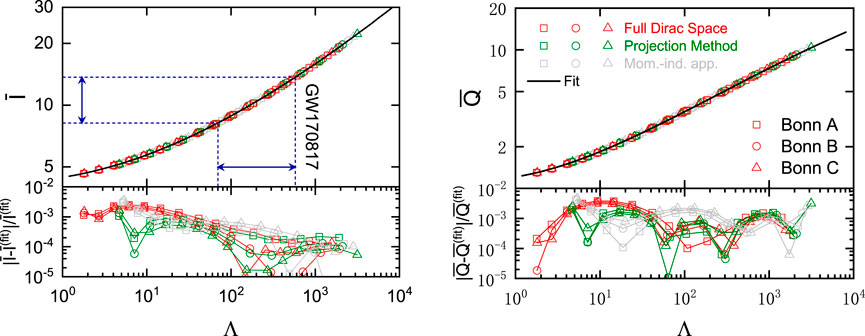
Figure 2. (Top panel) The universal $I$-Love (left) and $Q$-Love (right) relations for slowly-rotating neutron stars, calculated using EoSs derived from the RBHF theory. Different theoretical approaches are distinguished by colors: full Dirac space (red), projection method (green), and momentum-independence approximation (gray). The Bonn potentials are represented by symbols: A (squares), B (circles), and C (triangles). Each data set corresponds to a specific combination of method (color) and potential (symbol). The solid curves show the fitted results by using Equation 29. (Bottom) Corresponding absolute fractional differences between the numerical results and the fits. Figures taken from (Wang et al., 2022c).

5 Summary and perspectives

We have reviewed recent developments in RBHF theory within the full Dirac space, with particular emphasis on their implications for the properties of dense nuclear matter and neutron stars. This relativistic ab initio calculations enhance the internal consistency of relativistic many-body calculations and represent a significant advancement in the microscopic description of dense matter under extreme conditions. Further progress in the RBHF theory is anticipated through the inclusion of higher-order many-body correlations, in particular by extending beyond the two-hole-line expansion currently employed in standard RBHF theory. The incorporation of three-hole-line contributions and other higher-order terms is essential for achieving a more complete and quantitatively accurate description of in-medium nuclear interactions at supranuclear densities. In parallel, while a leading order and next-to-leading order covariant chiral nuclear forces have recently been applied within RBHF calculations under the momentum-independence approximation (Zou et al., 2024; Zou et al., 2025b; Zou et al., 2025a; Zheng et al., 2025; Shen et al., 2025), a natural next step is to implement the high-fidelity chiral nuclear forces (Ren et al., 2018; Lu et al., 2022) in the full Dirac space. Such an extension would enable a more consistent and comprehensive treatment of relativistic effects, thereby improving the predictive power of relativistic ab initio calculations for the EoS and neutron star properties.

Author contributions

HT: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. SW: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. JM: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. HT acknowledge funding by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (AdG EXOTIC, grant agreement No. 101018170), and by the MKW NRW under the funding code NW21-024-A. SW is supported in part by the National Natural Science Foundation of China (NSFC) under Grants No. 12205030. JM is supported in part by the National Natural Science Foundation of China under Grants No. 12435006, and the National Key Laboratory of Neutron Science and Technology NST202401016, and by the High performance Computing Platform of Peking University.

Acknowledgments

The authors would like to thank Xiaoying Qu for reading of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbott, B. P., Abbott, R., Abbott, T., Acernese, F., Ackley, K., Adams, C., et al. (2017). GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101. doi:10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T., Acernese, F., Ackley, K., Adams, C., et al. (2018). GW170817: measurements of neutron star radii and equation of state. Phys. Rev. Lett. 121, 161101. doi:10.1103/PhysRevLett.121.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Alonso, D., and Sammarruca, F. (2003). Microscopic calculations in asymmetric nuclear matter. Phys. Rev. C 67, 054301. doi:10.1103/PhysRevC.67.054301

CrossRef Full Text | Google Scholar

Antoniadis, J., Freire, P. C. C., Wex, N., Tauris, T. M., Lynch, R. S., van Kerkwijk, M. H., et al. (2013). A massive pulsar in a compact relativistic binary. Science 340, 1233232. doi:10.1126/science.1233232

PubMed Abstract | CrossRef Full Text | Google Scholar

Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., Chamberlin, S., Chatterjee, S., Christy, B., et al. (2018). The NANOGrav 11-year data set: high-precision timing of 45 millisecond pulsars. Astrophys. J. Suppl. 235, 37. doi:10.3847/1538-4365/aab5b0

CrossRef Full Text | Google Scholar

Barrett, B. R., Navràtil, P., and Vary, J. P. (2013). Ab initio no core shell model. Prog. Part. Nucl. Phys. 69, 131–181. doi:10.1016/j.ppnp.2012.10.003

CrossRef Full Text | Google Scholar

Brockmann, R., and Machleidt, R. (1990). Relativistic nuclear structure. I. nuclear matter. Phys. Rev. C 42, 1965–1980. doi:10.1103/PhysRevC.42.1965

PubMed Abstract | CrossRef Full Text | Google Scholar

Brueckner, K. A., Coon, S. A., and Dabrowski, J. (1968). Nuclear symmetry energy. Phys. Rev. 168, 1184–1188. doi:10.1103/PhysRev.168.1184

CrossRef Full Text | Google Scholar

Burgio, G. F., Schulze, H. J., Vidana, I., and Wei, J. B. (2021). Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 120, 103879. doi:10.1016/j.ppnp.2021.103879

CrossRef Full Text | Google Scholar

Carlson, J., Gandolfi, S., Pederiva, F., Pieper, S. C., Schiavilla, R., Schmidt, K. E., et al. (2015). Quantum monte carlo methods for nuclear physics. Rev. Mod. Phys. 87, 1067–1118. doi:10.1103/RevModPhys.87.1067

CrossRef Full Text | Google Scholar

Cromartie, H. T., Fonseca, E., Ransom, S. M., Demorest, P. B., Arzoumanian, Z., Blumer, H., et al. (2020). Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 4, 72–76. doi:10.1038/s41550-019-0880-2

CrossRef Full Text | Google Scholar

Damour, T., Soffel, M., and Xu, C. (1992). General-relativistic celestial mechanics ii. translational equations of motion. Phys. Rev. D. 45, 1017–1044. doi:10.1103/PhysRevD.45.1017

PubMed Abstract | CrossRef Full Text | Google Scholar

de Jong, F., and Lenske, H. (1998). Asymmetric nuclear matter in the relativistic Brueckner-Hartree-Fock approach. Phys. Rev. C 57, 3099–3107. doi:10.1103/PhysRevC.57.3099

CrossRef Full Text | Google Scholar

Dechargé, J., and Gogny, D. (1980). Hartree-Fock-Bogolyubov calculations with the d1 effective interaction on spherical nuclei. Phys. Rev. C 21, 1568–1593. doi:10.1103/PhysRevC.21.1568

CrossRef Full Text | Google Scholar

Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., and Hessels, J. W. T. (2010). A two-solar-mass neutron star measured using shapiro delay. Nature 467, 1081–1083. doi:10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

Dickhoff, W., and Barbieri, C. (2004). Self-consistent green’s function method for nuclei and nuclear matter. Prog. Part. Nucl. Phys. 52, 377–496. doi:10.1016/j.ppnp.2004.02.038

CrossRef Full Text | Google Scholar

Fattoyev, F. J., and Piekarewicz, J. (2010). Sensitivity of the moment of inertia of neutron stars to the equation of state of neutron-rich matter. Phys. Rev. C 82, 025810. doi:10.1103/PhysRevC.82.025810

CrossRef Full Text | Google Scholar

Flanagan, E. E., and Hinderer, T. (2008). Constraining neutron-star tidal love numbers with gravitational-wave detectors. Phys. Rev. D. 77, 021502. doi:10.1103/PhysRevD.77.021502

CrossRef Full Text | Google Scholar

Fonseca, E., Pennucci, T. T., Ellis, J. A., Stairs, I. H., Nice, D. J., Ransom, S. M., et al. (2016). The NANOGrav nine-year data set: mass and geometric measurements of binary millisecond pulsars. Astrophys. J. 832, 167. doi:10.3847/0004-637X/832/2/167

CrossRef Full Text | Google Scholar

Fonseca, E., Cromartie, H. T., Pennucci, T. T., Ray, P. S., Kirichenko, A. Y., Ransom, S. M., et al. (2021). Refined mass and geometric measurements of the high-mass psr j0740+6620. Astrophys. J. Lett. 915, L12. doi:10.3847/2041-8213/ac03b8

CrossRef Full Text | Google Scholar

Gross-Boelting, T., Fuchs, C., and Faessler, A. (1999). Covariant representations of the relativistic brueckner t-matrix and the nuclear matter problem. Nucl. Phys. A 648, 105–137. doi:10.1016/S0375-9474(99)00022-6

CrossRef Full Text | Google Scholar

Hagen, G., Papenbrock, T., Hjorth-Jensen, M., and Dean, D. J. (2014). Coupled-cluster computations of atomic nuclei. Rep. Prog. Phys. 77, 096302. doi:10.1088/0034-4885/77/9/096302

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, M.-Z., Huang, Y.-J., Tang, S.-P., and Fan, Y.-Z. (2023). Plausible presence of new state in neutron stars with masses above 0.98MTOV. Sci. Bull. 68, 913–919. doi:10.1016/j.scib.2023.04.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartle, J. B. (1967). Slowly rotating relativistic stars. I. Equations of structure. Astrophys. J. 150, 1005–1029. doi:10.1086/149400

CrossRef Full Text | Google Scholar

Hartle, J. B., and Thorne, K. S. (1968). Slowly rotating relativistic stars. II. Models for neutron stars and supermassive stars. Astrophys. J. 153, 807. doi:10.1086/149707

CrossRef Full Text | Google Scholar

Hergert, H., Bogner, S., Morris, T., Schwenk, A., and Tsukiyama, K. (2016). The in-medium similarity renormalization group: a novel ab initio method for nuclei. Phys. Rept. 621, 165–222. doi:10.1016/j.physrep.2015.12.007

CrossRef Full Text | Google Scholar

Hinderer, T. (2008). Tidal love numbers of neutron stars. Astrophys. J. 677, 1216–1220. doi:10.1086/533487

CrossRef Full Text | Google Scholar

Hinderer, T., Lackey, B. D., Lang, R. N., and Read, J. S. (2010). Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D. 81, 123016. doi:10.1103/PhysRevD.81.123016

CrossRef Full Text | Google Scholar

Horowitz, C., and Serot, B. D. (1987). The relativistic two-nucleon problem in nuclear matter. Nucl. Phys. A 464, 613–699. doi:10.1016/0375-9474(87)90370-8

CrossRef Full Text | Google Scholar

Huang, T., Yang, Y., Meng, J., Ring, P., and Zhao, P. (2025). Relativistic low-momentum interactions from renormalization group. Phys. Lett. B 866, 139502. doi:10.1016/j.physletb.2025.139502

CrossRef Full Text | Google Scholar

Huth, S., Pang, P. T. H., Tews, I., Dietrich, T., Le Fèvre, A., Schwenk, A., et al. (2022). Constraining neutron-star matter with microscopic and macroscopic collisions. Nature 606, 276–280. doi:10.1038/s41586-022-04750-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Katayama, T., and Saito, K. (2013). Properties of dense, asymmetric nuclear matter in dirac-brueckner-hartree-fock approach. Phys. Rev. C 88, 035805. doi:10.1103/PhysRevC.88.035805

CrossRef Full Text | Google Scholar

Lähde, T. A., and Meißner, U.-G. (2019). Nuclear lattice effective field theory: an introduction, volume 957. Springer. doi:10.1007/978-3-030-14189-9

CrossRef Full Text | Google Scholar

Laskos-Patkos, P., Lalazissis, G. A., Wang, S., Meng, J., Ring, P., and Moustakidis, C. C. (2025). Speed of sound bounds and first-order phase transitions in compact stars. Phys. Rev. C 111, 025801. doi:10.1103/PhysRevC.111.025801

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Prakash, M. (2000). Nuclear matter and its role in supernovae, neutron stars and compact object binary mergers. Phys. Rept. 333, 121–146. doi:10.1016/S0370-1573(00)00019-3

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Prakash, M. (2004). The physics of neutron stars. Science 304, 536–542. doi:10.1126/science.1090720

PubMed Abstract | CrossRef Full Text | Google Scholar

Lattimer, J. M., and Prakash, M. (2007). Neutron star observations: prognosis for equation of state constraints. Phys. Rept. 442, 109–165. doi:10.1016/j.physrep.2007.02.003

CrossRef Full Text | Google Scholar

Lee, D. (2009). Lattice simulations for few- and many-body systems. Prog. Part. Nucl. Phys. 63, 117–154. doi:10.1016/j.ppnp.2008.12.001

CrossRef Full Text | Google Scholar

Li, B.-A., Chen, L.-W., and Ko, C. M. (2008). Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rept. 464, 113–281. doi:10.1016/j.physrep.2008.04.005

CrossRef Full Text | Google Scholar

Liu, L., Otsuka, T., Shimizu, N., Utsuno, Y., and Roth, R. (2012). No-core monte carlo shell-model calculation for ¹⁰be and ¹²be low-lying spectra. Phys. Rev. C 86, 014302. doi:10.1103/PhysRevC.86.014302

CrossRef Full Text | Google Scholar

Lu, J.-X., Wang, C.-X., Xiao, Y., Geng, L.-S., Meng, J., and Ring, P. (2022). Accurate relativistic chiral nucleon-nucleon interaction up to next-to-next-to-leading order. Phys. Rev. Lett. 128, 142002. doi:10.1103/PhysRevLett.128.142002

PubMed Abstract | CrossRef Full Text | Google Scholar

Machleidt, R. (1989). The meson theory of nuclear forces and nuclear structure. Adv. Nucl. Phys. 19, 189–376. doi:10.1007/978-1-4613-9907-0_2

CrossRef Full Text | Google Scholar

Meng, J. (2016). Relativistic density functional for nuclear structure. World Scientific.

CrossRef Full Text | Google Scholar

Meng, J., Toki, H., Zhou, S., Zhang, S., Long, W., and Geng, L. (2006). Relativistic continuum hartree bogoliubov theory for ground-state properties of exotic nuclei. Prog. Part. Nucl. Phys. 57, 470–563. doi:10.1016/j.ppnp.2005.06.001

CrossRef Full Text | Google Scholar

Nuppenau, C., Lee, Y., and MacKellar, A. (1989). Ambiguities in the Dirac-Brueckner approach. Nucl. Phys. A 504, 839–844. doi:10.1016/0375-9474(89)90011-0

CrossRef Full Text | Google Scholar

Oertel, M., Hempel, M., Klähn, T., and Typel, S. (2017). Equations of state for supernovae and compact stars. Rev. Mod. Phys. 89, 015007. doi:10.1103/RevModPhys.89.015007

CrossRef Full Text | Google Scholar

Oppenheimer, J. R., and Volkoff, G. M. (1939). On massive neutron cores. Phys. Rev. 55, 374–381. doi:10.1103/PhysRev.55.374

CrossRef Full Text | Google Scholar

Otsuka, T., Honma, M., Mizusaki, T., Shimizu, N., and Utsuno, Y. (2001). Monte Carlo shell model for atomic nuclei. Prog. Part. Nucl. Phys. 47, 319–400. doi:10.1016/S0146-6410(01)00157-0

CrossRef Full Text | Google Scholar

Paschalidis, V., and Stergioulas, N. (2017). Rotating stars in relativity. Living Rev. Relativ. 20, 7. doi:10.1007/s41114-017-0008-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin, P., Wang, S., Tong, H., Zhao, Q., Wang, C., Li, Z. P., et al. (2024). Microscopic optical potential from the relativistic Brueckner-Hartree-Fock theory: proton-nucleus scattering. Phys. Rev. C 109, 064603. doi:10.1103/PhysRevC.109.064603

CrossRef Full Text | Google Scholar

Qin, P., Zhao, Q., Tong, H., Wang, C., and Wang, S. (2025). Isospin splitting of the dirac mass probed using the relativistic Brueckner–Hartree–Fock theory. Nucl. Sci. Tech. 36, 29. doi:10.1007/s41365-024-01609-9

CrossRef Full Text | Google Scholar

Qu, X., Tong, H., Wang, C., and Wang, S. (2023). Neutron matter properties from relativistic Brueckner-Hartree-Fock theory in the full Dirac space. Sci. China Phys. Mech. Astron. 66, 242011. doi:10.1007/s11433-022-2048-3

CrossRef Full Text | Google Scholar

Qu, X., Wang, S., and Tong, H. (2025). Rotating neutron stars with relativistic ab initio calculations. Astrophys. J. 980, 3. doi:10.3847/1538-4357/ada76b

CrossRef Full Text | Google Scholar

Ren, X.-L., Li, K.-W., Geng, L.-S., Long, B., Ring, P., and Meng, J. (2018). Leading order relativistic chiral nucleon-nucleon interaction. Chin. Phys. C 42, 014103. doi:10.1088/1674-1137/42/1/014103

CrossRef Full Text | Google Scholar

Ring, P. (1996). Relativistic mean field theory in finite nuclei. Prog. Part. Nucl. Phys. 37, 193–263. doi:10.1016/0146-6410(96)00054-3

CrossRef Full Text | Google Scholar

Sammarruca, F. (2014). Microscopic approach to the nucleon-nucleon effective interaction and nucleon-nucleon scattering in symmetric and isospin-asymmetric nuclear matter. Eur. Phys. J. 50, 22. doi:10.1140/epja/i2014-14022-1

CrossRef Full Text | Google Scholar

Sammarruca, F., Chen, B., Coraggio, L., Itaco, N., and Machleidt, R. (2012). Dirac-Brueckner-Hartree-Fock versus chiral effective field theory. Phys. Rev. C 86, 054317. doi:10.1103/PhysRevC.86.054317

CrossRef Full Text | Google Scholar

Schiller, E., and Müther, H. (2001). Correlations and the Dirac structure of the nucleon selfenergy. Eur. Phys. J. A 11, 15–24. doi:10.1007/s100500170092

CrossRef Full Text | Google Scholar

Sedrakian, A., Li, J.-J., and Weber, F. (2023). Heavy baryons in compact stars. Prog. Part. Nucl. Phys. 131, 104041. doi:10.1016/j.ppnp.2023.104041

CrossRef Full Text | Google Scholar

Sehn, L., Fuchs, C., and Faessler, A. (1997). Nucleon self-energy in the relativistic Brueckner approach. Phys. Rev. C 56, 216–227. doi:10.1103/PhysRevC.56.216

CrossRef Full Text | Google Scholar

Serot, B. D., and Walecka, J. D. (1986). The relativistic nuclear many-body problem. Adv. Nucl. Phys. 16, 1–327.

Google Scholar

Shang, X.-L., Dong, J.-M., Zuo, W., Yin, P., and Lombardo, U. (2021). Exact solution of the Brueckner-Bethe-Goldstone equation with three-body forces in nuclear matter. Phys. Rev. C 103, 034316. doi:10.1103/PhysRevC.103.034316

CrossRef Full Text | Google Scholar

Shen, S.-H., Hu, J.-N., Liang, H.-Z., Meng, J., Ring, P., and Zhang, S.-Q. (2016). Relativistic Brueckner-Hartree-Fock theory for finite nuclei. Chin. Phys. Lett. 33, 102103. doi:10.1088/0256-307X/33/10/102103

CrossRef Full Text | Google Scholar

Shen, S., Liang, H., Long, W. H., Meng, J., and Ring, P. (2019). Towards an ab initio covariant density functional theory for nuclear structure. Prog. Part. Nucl. Phys. 109, 103713. doi:10.1016/j.ppnp.2019.103713

CrossRef Full Text | Google Scholar

Shen, S., Lu, J.-X., Geng, L.-S., Meng, J., and Zou, W.-J. (2025). From bare two-nucleon interaction to nuclear matter and finite nuclei in a relativistic framework. arXiv.

Google Scholar

Skyrme, T. H. R. (1956). Cvii. the nuclear surface. Phil. Mag. 1, 1043–1054. doi:10.1080/14786435608238186

CrossRef Full Text | Google Scholar

Stergioulas, N., and Friedman, J. L. (1995). Comparing models of rapidly rotating relativistic stars constructed by two numerical methods. Astrophys. J. 444, 306. doi:10.1086/175605

CrossRef Full Text | Google Scholar

Tolman, R. C. (1939). Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 55, 364–373. doi:10.1103/PhysRev.55.364

CrossRef Full Text | Google Scholar

Tong, H., Ren, X.-L., Ring, P., Shen, S.-H., Wang, S.-B., and Meng, J. (2018). Relativistic Brueckner-Hartree-Fock theory in nuclear matter without the average momentum approximation. Phys. Rev. C 98, 054302. doi:10.1103/PhysRevC.98.054302

CrossRef Full Text | Google Scholar

Tong, H., Zhao, P.-W., and Meng, J. (2020). Symmetry energy at supra-saturation densities via the gravitational waves from GW170817. Phys. Rev. C 101, 035802. doi:10.1103/PhysRevC.101.035802

CrossRef Full Text | Google Scholar

Tong, H., Wang, C., and Wang, S. (2022). Nuclear matter and neutron stars from relativistic Brueckner–Hartree–Fock theory. Astrophys. J. 930, 137. doi:10.3847/1538-4357/ac65fc

CrossRef Full Text | Google Scholar

Tong, H., Gao, J., Wang, C., and Wang, S. (2023). Properties of Pb208 predicted from the relativistic equation of state in the full Dirac space. Phys. Rev. C 107, 034302. doi:10.1103/PhysRevC.107.034302

CrossRef Full Text | Google Scholar

Tong, H., Elhatisari, S., and Meißner, U.-G. (2025a). Ab initio calculation of hyper-neutron matter. Sci. Bull. 70, 825–828. doi:10.1016/j.scib.2025.01.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Tong, H., Elhatisari, S., and Meißner, U.-G. (2025b). Hyperneutron stars from an ab initio calculation. Astrophys. J. 982, 164. doi:10.3847/1538-4357/adba47

CrossRef Full Text | Google Scholar

Tong, H., Elhatisari, S., Meißner, U.-G., and Ren, Z. (2025c). Multi-strangeness matter from ab initio calculations. arXiv.

Google Scholar

Ulrych, S., and Müther, H. (1997). Relativistic structure of the nucleon self-energy in asymmetric nuclei. Phys. Rev. C 56, 1788–1794. doi:10.1103/PhysRevC.56.1788

CrossRef Full Text | Google Scholar

van Dalen, E. N. E., Fuchs, C., and Faessler, A. (2005). Effective nucleon masses in symmetric and asymmetric nuclear matter. Phys. Rev. Lett. 95, 022302. doi:10.1103/PhysRevLett.95.022302

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Tong, H., Zhao, P., and Meng, J. (2019). Strength of tensor forces from neutron drops in ab initio relativistic brueckner-hartree-fock theory. Phys. Rev. C 100, 064319. doi:10.1103/PhysRevC.100.064319

CrossRef Full Text | Google Scholar

Wang, C., Hu, J., Zhang, Y., and Shen, H. (2020). Properties of neutron stars described by a relativistic ab initio model. Astrophys. J. 897, 96. doi:10.3847/1538-4357/ab994b

CrossRef Full Text | Google Scholar

Wang, S., Zhao, Q., Ring, P., and Meng, J. (2021). Nuclear matter in relativistic brueckner-hartree-fock theory with bonn potential in the full dirac space. Phys. Rev. C 103, 054319. doi:10.1103/PhysRevC.103.054319

CrossRef Full Text | Google Scholar

Wang, S., Tong, H., and Wang, C. (2022a). Nuclear matter within the continuous choice in the full Dirac space. Phys. Rev. C 105, 054309. doi:10.1103/PhysRevC.105.054309

CrossRef Full Text | Google Scholar

Wang, S., Tong, H., Zhao, Q., Wang, C., Ring, P., and Meng, J. (2022b). Asymmetric nuclear matter and neutron star properties in relativistic ab initio theory in the full dirac space. Phys. Rev. C 106, L021305. doi:10.1103/PhysRevC.106.L021305

CrossRef Full Text | Google Scholar

Wang, S., Wang, C., and Tong, H. (2022c). Exploring universal characteristics of neutron star matter with relativistic ab initio equations of state. Phys. Rev. C 106, 045804. doi:10.1103/PhysRevC.106.045804

CrossRef Full Text | Google Scholar

Wang, S., Tong, H., Zhao, Q., Wang, C., Ring, P., and Meng, J. (2023). Neutron-proton effective mass splitting in neutron-rich matter. Phys. Rev. C 108, L031303. doi:10.1103/PhysRevC.108.L031303

CrossRef Full Text | Google Scholar

Wang, S., Tong, H., Wang, C., Zhao, Q., Ring, P., and Meng, J. (2024). Tensor-force effects on nuclear matter in relativistic ab initio theory. Sci. Bull. 69, 2166–2169. doi:10.1016/j.scib.2024.05.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, T., Tong, H., Wang, C., Qu, X., and Wang, S. (2025). In-medium nucleon-nucleon cross sections from relativistic ab initio calculations. arXiv.

Google Scholar

Yagi, K., and Yunes, N. (2013). I-Love-Q relations in neutron stars and their applications to astrophysics, gravitational waves and fundamental physics. Phys. Rev. D. 88, 023009. doi:10.1103/PhysRevD.88.023009

CrossRef Full Text | Google Scholar

Yagi, K., and Yunes, N. (2017). Approximate universal relations for neutron stars and quark stars. Phys. Rept. 681, 1–72. doi:10.1016/j.physrep.2017.03.002

CrossRef Full Text | Google Scholar

Zheng, R.-Y., Liu, Z.-W., Geng, L.-S., Hu, J.-N., and Wang, S. (2025). In-medium ΛN interactions with leading order covariant chiral hyperon/nucleon-nucleon forces. Phys. Lett. B 864, 139416. doi:10.1016/j.physletb.2025.139416

CrossRef Full Text | Google Scholar

Zou, W.-J., Lu, J.-X., Zhao, P.-W., Geng, L.-S., and Meng, J. (2024). Saturation of nuclear matter in the relativistic brueckner-hatree-fock approach with a leading order covariant chiral nuclear force. Phys. Lett. B 854, 138732. doi:10.1016/j.physletb.2024.138732

CrossRef Full Text | Google Scholar

Zou, W.-J., Yang, Y.-L., Lu, J.-X., Zhao, P.-W., Geng, L.-S., and Meng, J. (2025a). Nuclear and neutron matter in the relativistic Brueckner-Hartree-Fock theory with next-to-leading order covariant chiral nuclear force. arXiv.

Google Scholar

Zou, W.-J., Yang, Y.-L., Shen, S., and Meng, J. (2025b). Nuclear matter in relativistic Brueckner–Hartree–Fock theory using the leading order covariant chiral interactions with local and nonlocal regulators. Chin. Phys. Lett. 42, 080101. doi:10.1088/0256-307X/42/8/080101

CrossRef Full Text | Google Scholar