Regular Bardeen-like black holes in higher-dimensional pure Lovelock gravity with nonlinear Yang–Mills fields

Introduction: We construct spherically symmetric, static, and regular Bardeen-like black hole solutions in the framework of higher-dimensional pure Lovelock gravity coupled to nonlinear Yang–Mills (YM) fields. The aim is to generalize the notion of regular black holes to higher-curvature gravity theories while preserving regularity and asymptotic flatness.

Methods: The gauge fields are modeled using a higher-dimensional Wu–Yang ansatz, and the nonlinear YM Lagrangian is designed to reproduce Bardeen-type configurations known from Einstein gravity. The field equations are solved analytically to obtain exact metric functions, and curvature invariants are computed to verify the regularity of the spacetime.

Results: The resulting solutions are asymptotically flat and regular at the origin, with all curvature invariants remaining finite throughout the spacetime. In dimensions $N=2p+1$, the configurations describe particle-like solutions without horizons. For $N>2p+1$, depending on the model parameters, the solutions can represent either regular black holes or particle-like spacetimes. Analytic conditions determining the existence and number of horizons are derived, allowing for a full classification of the spacetime structure.

Discussion: A detailed thermodynamic analysis is performed by computing the Hawking temperature and heat capacity. The phase structure reveals regions of thermal stability and the occurrence of first- and second-order phase transitions. These findings extend the concept of regular black holes to pure Lovelock gravity and emphasize the rich interplay between nonlinearity, dimensionality, and gauge dynamics.

1 Introduction

One of the most remarkable discoveries in the history of science is the existence of black holes. The concept originated from Einstein’s theory of general relativity and was first revealed through the mathematical ingenuity of Karl Schwarzschild, who, in 1916, became the first to solve Einstein’s field equations in vacuum. The solution he obtained—now famously known as the Schwarzschild black hole—was named in his honor. The Schwarzschild black hole describes a static, spherically symmetric spacetime characterized by a single parameter: the mass of the black hole. It features a central singularity hidden behind an event horizon. At the time, both the singularity and the event horizon were entirely new and unexpected features of modern cosmology, revealed through the exact solution of Einstein’s equations. Now, more than a century since Schwarzschild introduced his solution, physicists are still grappling with the physical interpretation of the spacetime singularity. It is widely believed that, at the singularity, the mass of the black hole collapses under its own gravitational pull into a region of infinite curvature. Under such extreme conditions, classical physics breaks down, and known physical laws become inapplicable. This description is so speculative and counterintuitive that some physicists question whether singularities truly exist. The leading candidate for resolving this classical problem is quantum gravity. In other words, in such high-energy and small-scale regimes, it becomes necessary to quantize the gravitational field, thereby potentially eliminating the need to introduce singularities altogether. Unfortunately, a complete and consistent formulation of quantum gravity has not yet been achieved, although several promising frameworks are under active development, most notably string theory and loop quantum gravity (Bojowald, 2001; Blanchette et al., 2021). In a different but related direction, within classical general relativity coupled to nonlinear electrodynamics (NED), there have been attempts to construct regular black holes, i.e., black holes whose central regions are nonsingular. One of the earliest such solutions is the well-known Bardeen black hole (Ba and rdeen, 1968). The original Bardeen metric, introduced in Bardeen (1968), is described by the line element:

$d{s}^2=-\left(1-\frac{2M{r}^2}{{\left(r^2+q^2\right)}^{3/2}}\right)d{t}^2+\frac{d{r}^2}{\left(1-\frac{2M{r}^2}{{\left(r^2+q^2\right)}^{3/2}}\right)}+r^{2}d{\mathrm{\Omega }}^2,(1)$

where $M$ and $q$ are constants. Initially, the matter source for this solution was unspecified. Later, Ayón-Beato and García (2000) proposed a nonlinear electrodynamics Lagrangian to generate the Bardeen solution within Einstein gravity (Equation 2)

$\mathcal{L}=\frac{1}{2s{q}^2}{\left(\frac{\sqrt{2q^2\mathcal{F}}}{1+\sqrt{2q^2\mathcal{F}}}\right)}^{\frac{5}{2}},(2)$

with a magnetic field given by Equation 3

$\mathbf{F}=P\sin \theta d\theta \wedge d\varphi .(3)$

Solving the field equations reveals that $M=\frac{\left|q\right|}{2s}$ plays the role of the ADM mass, particularly due to the asymptotic expansion of the metric function in Equation 1

$\begin{array}{ll}\hfill & \hfill d{s}^2\to -\left(1-\frac{2M}{r}+\frac{3M{q}^2}{r^3}+\mathcal{O}\left(r^{-5}\right)\right)d{t}^2\\ \hfill & +\frac{d{r}^2}{1-\frac{2M}{r}+\frac{3M{q}^2}{r^3}+\mathcal{O}\left(r^{-5}\right)}+r^{2}d{\mathrm{\Omega }}^2,\text{as\hspace{0.17em}}r\to \infty .\hfill \end{array}(4)$

The absence of a $1/r^2$ term in the asymptotic expansion in Equation 4 implies that the NED model does not reduce to Maxwell’s linear theory in the weak-field limit. Nonetheless, the parameter $q$ still represents a magnetic monopole, consistent with Gauss’s law $q=\frac{1}{4\pi }{\int }_{S^{\infty }}\mathbf{F}.$ It is worth noting that the ADM mass $M=\frac{\left|q\right|}{2s}$ arises entirely from the nonlinear self-interaction of the electromagnetic field and that there is no separate gravitational mass as in the Schwarzschild or Reissner–Nordström black holes. Using the Newman–Janis algorithm, Bambi and Modesto extended the Bardeen solution to include rotation (Bambi and Modesto, 2013). Bardeen black holes in higher dimensions were also studied by Ali and Ghosh (2018), where the extended NED Lagrangian takes the form

$\mathcal{L}=\frac{N-2}{4s{q}^2}{\left(\frac{\sqrt{2q^2\mathcal{F}}}{1+\sqrt{2q^2\mathcal{F}}}\right)}^{\frac{2N-3}{N-2}}.(5)$

The associated magnetic field is given by (Equation 6)

$\mathbf{F}=\left(q^{N-3}\sin {\theta }_{N-3}{\displaystyle \prod _{j=1}^{N-4}}{\sin }^2{\theta }_j\right)d{\theta }_{N-3}\wedge d{\theta }_{N-2},(6)$

and the corresponding line element is provided in Equation 23.

Although the Bardeen regular black hole has been extensively studied in various contexts, these works are not directly relevant to our present investigation, aside from the general consideration of the Bardeen-type solution reviewed above. We, therefore, limit our citations to studies that directly inform our current research.

In a separate context, higher-derivative gravity theories, particularly the Lovelock theory (Lovelock, 1971), have attracted significant attention in the study of higher-dimensional black holes. The key features of Lovelock gravity are as follows (Kastor and Mann, 2006; Cai and Ohta, 2006; Cai et al., 2008) (and the references cited in): i) it is the natural extension of general relativity. This is because the Lovelock action is built from dimensionally extended Euler densities, which generalize the Einstein–Hilbert action in higher dimensions. ii) Unlike most higher-derivative gravity theories, Lovelock gravity yields equations of motion containing no more than second derivatives of the metric, avoiding the pathologies usually associated with higher-derivative theories. iii) When expanded around flat spacetime, Lovelock gravity is free of ghosts, which means it preserves unitarity and avoids instabilities. iv) The Lovelock terms (such as the Gauss–Bonnet term) arise naturally with positive coefficients as higher-order corrections in superstring theory, giving the framework strong theoretical motivation. v) Higher curvature terms in Lovelock gravity play a key role in the AdS/CFT correspondence and in brane-world physics, where TeV-scale black holes may be relevant. vi) Lovelock gravity admits black hole, black string, and black brane solutions with thermodynamic properties that can differ significantly from Einstein gravity, making it a fertile ground for exploring quantum gravity effects.

The Lovelock Lagrangian is constructed as a linear combination of dimensionally extended Euler densities

${\mathcal{L}}_{\mathit{Lov}}={\displaystyle \sum _{k=0}^{\left[\frac{N-1}{2}\right]}}{\alpha }_k{\mathcal{L}}_k,(7)$

where ${\alpha }_k\ge 0$ are the Lovelock coupling constants, ${\kappa }_N=8\pi G_N$ is the gravitational constant in $N$ dimensions, and $\left[\frac{N-1}{2}\right]$ denotes the integer part of $\frac{N-1}{2}$. The Lovelock Lagrangian densities ${\mathcal{L}}_k$ are given by

${\mathcal{L}}_k=\frac{1}{2^k}{\delta }_{{\mu }_1{\nu }_1\dots {\mu }_k{\nu }_k}^{{\alpha }_1{\beta }_1\dots {\alpha }_k{\beta }_k}{\displaystyle \prod _{i=1}^k}{R}_{{\alpha }_i{\beta }_i}^{{\mu }_i{\nu }_i},(8)$

which corresponds to the Euler densities of a $2k$-dimensional manifold. Here, in Equation 8, ${\delta }_{{\mu }_1{\nu }_1\dots {\mu }_k{\nu }_k}^{{\alpha }_1{\beta }_1\dots {\alpha }_k{\beta }_k}$ is the generalized (antisymmetric) Kronecker delta, defined as (Equation 9)

${\delta }_{{\mu }_1{\nu }_1\dots {\mu }_k{\nu }_k}^{{\alpha }_1{\beta }_1\dots {\alpha }_k{\beta }_k}=k!{\delta }_{{\mu }_1}^{\left[{\alpha }_1\right.}{\delta }_{{\nu }_1}^{{\beta }_1}\dots {\delta }_{{\mu }_k}^{{\alpha }_k}{\delta }_{{\nu }_k}^{\left.{\beta }_k\right]}.(9)$

In Equation 7, the case $k=0$ corresponds to ${\mathcal{L}}_0=1$, with ${\alpha }_0=-2\mathrm{\Lambda }$ representing the cosmological constant. For $k=1$, we recover ${\mathcal{L}}_1=R$ with ${\alpha }_1=1$, which is the standard Einstein–Hilbert Lagrangian. When $k=2$, we obtain in Equation 10

${\mathcal{L}}_2={\mathcal{L}}_{GB}=R^{\alpha \beta \gamma \delta }{R}_{\alpha \beta \gamma \delta }-4R^{\gamma \delta }{R}_{\gamma \delta }+R^2,(10)$

which is the Gauss–Bonnet (GB) Lagrangian, with ${\alpha }_2={\alpha }_{GB}$ denoting the GB coupling constant. For $k>2$, ${\mathcal{L}}_k$ is the higher-order Lovelock Lagrangian with corresponding coupling constants ${\alpha }_k$. Lovelock theory is the unique higher-order curvature theory that preserves second-order field equations, avoiding ghost instabilities (Boulware and Deser, 1985; Zwiebach, 1985). For a given order $p$, Lovelock gravity is nontrivial in dimensions $N\ge 2p+1$, and all coefficients ${\alpha }_k$ with $k\le p$ may be nonzero in general. In a special case, pure Lovelock gravity, introduced by Kastor and Mann (2006) [see also (Giribet et al., 2006)], involves only one nonzero term ${\alpha }_k$ ($1<k\le p$) corresponding to a fixed-order $k$, with or without a cosmological constant. Black holes in pure Lovelock gravity were constructed by Cai and Ohta (2006), and generalized Vaidya spacetimes were explored by Cai et al. (2008). This subclass of Lovelock gravity has attracted considerable attention (Chakraborty and Dadhich, 2018; Dadhich and Pons, 2013; Dadhich et al., 2013; Gannouji and Dadhich, 2014). In this work, we aim to construct regular black hole solutions in pure Lovelock gravity powered by a nonlinear Yang–Mills (YM) field. To this end, we propose a specific nonlinear YM model and use the standard higher-dimensional Wu–Yang ansatz (Wu et al., 1969; Yasskin, 1975; Mazharimousavi and Halilsoy, 2008) for the YM potential, leading to a Bardeen-like regular black hole configuration. Let us add that the Lovelock action uses Euler densities, which inherently maintain an Einstein-like structure in field equations and consequently the structure of regular black holes.

2 Pure Gauss–Bonnet nonlinear YM theory

We begin with the action

$I=\frac{1}{2{\kappa }_N}\int d^{N}x\sqrt{-g}\left({\mathcal{L}}_{\mathit{Lov}}+\mathcal{L}\right),(11)$

where ${\mathcal{L}}_{\mathit{Lov}}$ is the Lovelock Lagrangian given in Equation 7 and $\mathcal{L}$ is the nonlinear YM Lagrangian, given by

$\mathcal{L}=-\frac{1}{{\omega }_{N-2}}\frac{\alpha {\mathcal{F}}^{\frac{2N-3}{4}}}{{\left(1+\beta {\mathcal{F}}^{\frac{N-2}{4}}\right)}^{\frac{2N-3}{N-2}}},(12)$

where $\alpha >0$ and $\beta >0$ are real positive constants, ${\omega }_{N-2}=\frac{2{\pi }^{\frac{N-1}{2}}}{\mathrm{\Gamma }\left(\frac{N-1}{2}\right)}$, and

$\mathcal{F}={\gamma }_{pq}{F}_{\mu \nu }^p{F}^{q\mu \nu },(13)$

is the Yang–Mills field strength invariant. We add that the Yang–Mills field possesses energy and momentum, quantified by its stress–energy tensor. This tensor serves as the source term in Einstein’s equations, meaning that the field itself generates gravitational curvature. Consequently, Yang–Mills fields can produce structures like black holes, wormholes, and shape the evolution of the cosmos.

The nonlinear YM Lagrangian Equation 12 is the YM analog of the higher-dimensional Bardeen-type nonlinear electrodynamics (NED) model proposed by Ali and Ghosh (2018) (see Equation 5). Except for $N=4$, where both Lagrangians coincide, they differ in other dimensions. It is worth noting that both Lagrangians partially satisfy the conditions imposed by Shabad and Usov (2011), which arise from the requirements of causality and unitarity principles. These conditions are listed in Equation 14

${\mathcal{L}}_{\mathcal{F}}<0,{\mathcal{L}}_{\mathcal{F}\mathcal{F}}\ge 0\text{,\hspace{0.17em}and\hspace{0.17em}}{\mathcal{L}}_{\mathcal{F}}+2{\mathcal{F}\mathcal{L}}_{\mathcal{F}\mathcal{F}}\le 0.(14)$

The Yang–Mills field two-form strength is given by

${\mathbf{F}}^p=d{\mathbf{A}}^p+\frac{1}{2\sigma }{c}_{qr}^p{\mathbf{A}}^q\wedge {\mathbf{A}}^r,(15)$

where in Equation 15 ${\mathbf{A}}^p$ denotes the non-Abelian Yang–Mills one-form potential, $c_{qr}^p$ is the structure constant of the gauge group $\mathcal{G,}$ which has $\frac{\left(N-1\right)\left(N-2\right)}{2}$ generators, and $\sigma$ is the coupling constant. The gauge potential can be written as ${\mathbf{A}}^p=A_{\mu }^{p}d{x}^{\mu }$, and we choose the gauge group $\mathcal{G}=SO\left(N-1\right)$. Variation of the action (in Equation 11) with respect to $A_{\mu }^p$ yields the Yang–Mills field equations

$d\left(\star {\mathbf{F}}^p{\mathcal{L}}_{\mathcal{F}}\right)+\frac{1}{\sigma }{c}_{qr}^p{\mathcal{L}}_{\mathcal{F}}{\mathbf{A}}^p\wedge \star {\mathbf{F}}^q=0,(16)$

where $\star {\mathbf{F}}^p$ is the Hodge dual of ${\mathbf{F}}^p$, and ${\mathcal{L}}_{\mathcal{F}}=\partial \mathcal{L}/\partial \mathcal{F}$. Varying the action in Equation 11 with respect to the metric $g_{\mu \nu }$ leads to the Einstein–Lovelock–Yang–Mills field equations:

${\displaystyle \sum _{k=0}^{\left[\frac{N-1}{2}\right]}}{\alpha }_k{G}_{\mu }^{\nu \left(k\right)}={\kappa }_N{T}_{\mu }^{\nu },(17)$

where the energy–momentum tensor of the Yang–Mills field is given by Equation 18

$T_{\mu }^{\nu }=\frac{1}{2}\left(\mathcal{L}{\delta }_{\mu }^{\nu }-4{\mathcal{L}}_{\mathcal{F}}{\gamma }_{pq}{F}_{\mu \lambda }^p{F}^{q\nu \lambda }\right)(18)$

and the Lovelock tensors are (Equations 19, 20)

$G_{\mu }^{\nu \left(k\right)}={\displaystyle \sum _{i=0}^k}\frac{1}{2^{i+1}}{\delta }_{{\mu }_1{\nu }_1\dots {\mu }_i{\nu }_i}^{{\alpha }_1{\beta }_1\dots {\alpha }_i{\beta }_i}{\displaystyle \prod _{s=1}^i}{R}_{{\alpha }_s{\beta }_s}^{{\mu }_s{\nu }_s},k\ge 1(19)$

and

$G_{\mu }^{\nu \left(0\right)}=\frac{\left(N-1\right)\left(N-2\right)}{6}\mathrm{\Lambda }{\delta }_{\mu }^{\nu }.(20)$

The non-Abelian gauge potential ${\mathbf{A}}^{\left(m\right)}$ follows the generalized Wu–Yang ansatz (Mazharimousavi and Halilsoy, 2008)

${\mathbf{A}}^p=\frac{Q}{r^2}{c}_{ij}^p{x}^{i}d{x}^j,2\le j+1\le i\le N-1,1\le p\le \frac{\left(N-1\right)\left(N-2\right)}{2}(21)$

where, in Equation 21 $Q$ is the gauge charge and

$r^2={\delta }_{ij}{x}^i{x}^j,(22)$

with $i$ and $j$ running over spatial coordinates in Equation 22. The metric of the static, spherically symmetric $N$-dimensional spacetime is taken to be

$d{s}^2=-f\left(r\right)d{t}^2+\frac{d{r}^2}{f\left(r\right)}+r^{2}d{\mathrm{\Omega }}_{N-2}^2,(23)$

where

$d{\mathrm{\Omega }}_{N-2}^2=d{\theta }_1^2+{\displaystyle \sum _{i=2}^{N-2}}\left({\displaystyle \prod _{j=1}^{i-1}}{\sin }^2{\theta }_j\right)d{\theta }_i^2,(24)$

is the metric on the unit $\left(N-2\right)$-sphere, with $0<{\theta }_{N-2}\le 2\pi$ and $0<{\theta }_i\le \pi$ for $1\le i\le N-3$ in Equation 24. The generalized Wu–Yang ansatz satisfies the Yang–Mills Equation 16 provided that $\sigma =Q$. A detailed calculation yields (Equations 25, 26)

$\mathcal{F}=\frac{\left(N-3\right)\left(N-2\right)Q^2}{r^4},(25)$

and

${\gamma }_{pq}\left(F_{{\theta }_i\lambda }^p{F}^{q{\theta }_i\lambda }\right)=\frac{1}{\left(N-2\right)}\mathcal{F},\text{for}1\le i\le N-3.(26)$

Accordingly, the energy–momentum tensor simplifies to

$T_{\mu }^{\nu }=\frac{\mathcal{L}}{2}diag\left[\mathrm{1,1,1}-\frac{4}{N-2}\frac{{\mathcal{F}\mathcal{L}}_{\mathcal{F}}}{\mathcal{L}},\dots ,1-\frac{4}{N-2}\frac{{\mathcal{FL}}_{\mathcal{F}}}{\mathcal{L}}\right],(27)$

where in Equation 27 we introduced Equation 28

$\frac{\mathcal{F}{\mathcal{L}}_{\mathcal{F}}}{\mathcal{L}}=\frac{2N-3}{4}\frac{1}{1+\beta {\mathcal{F}}^{\frac{N-2}{4}}}.(28)$

To proceed, we introduce the function $\psi \left(r\right)$ via the ansatz (Equation 29)

$f\left(r\right)=1-r^2\psi \left(r\right),(29)$

which transforms the $tt$-component of the Einstein–Lovelock–Yang–Mills field Equation 17 into (Equation 30)

${\displaystyle \sum _{k=0}^{\left[\frac{N-1}{2}\right]}}{\tilde{\alpha }}_k{\psi }^k=\frac{2{\kappa }_{N}M\left(r\right)}{\left(N-2\right){\omega }_{N-2}{r}^{N-1}},(30)$

where the rescaled Lovelock coefficients are defined as ${\tilde{\alpha }}_k={\displaystyle \prod _{i=3}^{2k}}\left(N-i\right){\alpha }_k$ for $k\ge 2$, ${\tilde{\alpha }}_1=1$, and ${\tilde{\alpha }}_0=\frac{{\alpha }_0}{\left(N-1\right)\left(N-2\right)}$. The mass function $M\left(r\right)$ is given by

$M\left(r\right)={\omega }_{N-2}{\int }_0^r{\left(r^{\prime }\right)}^{N-2}\rho \left(r^{\prime }\right)d{r}^{\prime },(31)$

where in Equation 31

$\rho \left(r\right)=-T_t^t,(32)$

is the energy density (Equation 32). The explicit form of $M\left(r\right)$ is given by

$M\left(r\right)=\frac{\alpha {\left(N-2\right)}^{\frac{N-1}{4}}{\left(N-3\right)}^{\frac{N-1}{4}}{Q}^{\frac{N-1}{2}}}{2\beta \left(N-1\right){\left(1+\frac{\beta Q^{\frac{N-2}{2}}{\left(N-2\right)}^{\frac{N-2}{4}}{\left(N-3\right)}^{\frac{N-2}{4}}}{r^{N-2}}\right)}^{\frac{N-1}{N-2}}}.(33)$

Assuming that the ADM energy/mass arises purely from the Yang–Mills interaction, the total energy/mass is defined by (from Equation 33)

$\mathcal{M}=\underset{r\to \infty }{\lim }M\left(r\right),(34)$

which Equation 34 yields (Equation 35)

$\mathcal{M}=\frac{\alpha {\left(N-2\right)}^{\frac{N-1}{4}}{\left(N-3\right)}^{\frac{N-1}{4}}{Q}^{\frac{N-1}{2}}}{2\beta \left(N-1\right)}.(35)$

Finally, from Equation 30, the function $\psi \left(r\right)$ satisfies the algebraic equation

${\displaystyle \sum _{k=0}^{\left[\frac{N-1}{2}\right]}}{\tilde{\alpha }}_k{\psi }^k=\frac{2{\kappa }_N\mathcal{M}}{\left(N-2\right){\omega }_{N-2}{r}^{N-1}{\left(1+\beta \frac{Q^{\frac{N-2}{2}}{\left(\left(N-2\right)\left(N-3\right)\right)}^{\frac{N-2}{4}}}{r^{N-2}}\right)}^{\frac{N-1}{N-2}}}.(36)$

3 Pure lovelock theory

Although Equation 36 is valid in the general Lovelock framework, we now focus on the pure Lovelock theory of order $p$, in which all coupling constants vanish, except for ${\tilde{\alpha }}_p$, i.e., ${\tilde{\alpha }}_{k\ne p}=0$. In this case, the equation simplifies to (Equation 37)

${\tilde{\alpha }}_p{\psi }^p=\frac{2{\kappa }_N\mathcal{M}}{\left(N-2\right){\omega }_{N-2}{r}^{N-1}{\left(1+\frac{\beta Q^{\frac{N-2}{2}}{\left(\left(N-2\right)\left(N-3\right)\right)}^{\frac{N-2}{4}}}{r^{N-2}}\right)}^{\frac{N-1}{N-2}}},(37)$

whose solution is given by (Equation 38)

$\psi \left(r\right)=\left\{\begin{array}{c}\pm \frac{\mu }{r^{\frac{N-1-2p}{p}}{\left(1+\frac{\zeta }{r^{N-2}}\right)}^{\frac{N-1}{\left(N-2\right)p}}},\text{for}p\text{even,}\hfill \\ \frac{\mu }{r^{\frac{N-1-2p}{p}}{\left(1+\frac{\zeta }{r^{N-2}}\right)}^{\frac{N-1}{\left(N-2\right)p}}},\text{for}p\text{odd,}\hfill \end{array}\right.(38)$

and consequently the metric function becomes

$f\left(r\right)=\left\{\begin{array}{c}1\mp \frac{\mu }{r^{\frac{N-1-2p}{p}}{\left(1+\frac{\zeta }{r^{N-2}}\right)}^{\frac{N-1}{\left(N-2\right)p}}},\text{for}p\text{even,}\hfill \\ 1-\frac{\mu }{r^{\frac{N-1-2p}{p}}{\left(1+\frac{\zeta }{r^{N-2}}\right)}^{\frac{N-1}{\left(N-2\right)p}}},\text{for}p\text{odd,}\hfill \end{array}\right.(39)$

where in Equation 39 the new parameters are defined as (Equations 40, 41)

$\mu ={\left(\frac{2{\kappa }_N\mathcal{M}}{\left(N-2\right){\tilde{\alpha }}_p{\omega }_{N-2}}\right)}^{\frac{1}{p}},(40)$

$\zeta =\beta Q^{\frac{N-2}{2}}{\left(N-2\right)}^{\frac{N-2}{4}}{\left(N-3\right)}^{\frac{N-2}{4}},(41)$

and the expression is valid for $p\le \left[\frac{N-1}{2}\right]$. In the asymptotic region $(r\to \infty )$, the metric function behaves as Equation 42

$\underset{r\to \infty }{\lim }f\left(r\right)\to \left\{\begin{array}{c}1\mp \frac{\mu }{r^{\frac{N-1-2p}{p}}},\text{for}p\text{even,}\hfill \\ 1-\frac{\mu }{r^{\frac{N-1-2p}{p}}},\text{for}p\text{odd,}\hfill \end{array}\right.(42)$

while near the origin $(r\to 0)$ it yields (Equation 43)

$\underset{r\to 0}{\lim }f\left(r\right)\to \left\{\begin{array}{c}1\mp \frac{r^2}{{\ell }^2},\text{for}p\text{even,}\hfill \\ 1-\frac{r^2}{{\ell }^2},\text{for}p\text{odd,}\hfill \end{array}\right.(43)$

with the effective cosmological constant defined as Equation 44

$\frac{1}{{\ell }^2}=\frac{\mu }{{\zeta }^{\frac{N-1}{\left(N-2\right)p}}}.(44)$

Therefore, the solution is asymptotically flat and regular at the origin. An explicit calculation of the curvature invariants confirms that all spacetime scalars remain finite and regular everywhere, indicating that the spacetime is indeed regular throughout.

3.1 $N=2p+1$ represents only a particle model

As previously discussed, for a given Lovelock order $p$, the spacetime dimension $N$ must exceed a critical value defined by $N_p=2p+1$, which ensures $\left[\frac{N_p-1}{2}\right]=p$. Explicitly, this yields the following: $p=1$ requires $N\ge 3$; $p=2$ requires $N\ge 5$; $p=3$ requires $N\ge 7$, and in general, for any $p$, we require $N\ge 2p+1$. From Equation 39, it follows that for $N=N_p=2p+1$, the metric function simplifies to

$f\left(r\right)=\left\{\begin{array}{c}1\mp \frac{\mu }{{\left(1+\frac{\zeta }{r^{2p-1}}\right)}^{\frac{2}{2p-1}}},\text{for}p\text{even,}\hfill \\ 1-\frac{\mu }{{\left(1+\frac{\zeta }{r^{2p-1}}\right)}^{\frac{2}{2p-1}}},\text{for}p\text{odd,}\hfill \end{array}\right.(45)$

where the parameters $\zeta$ and $\mu$ are given by Equations 46, 47

$\xi =\beta Q^{\frac{2p-1}{2}}{\left(2p-1\right)}^{\frac{2p-1}{4}}{\left(2p-2\right)}^{\frac{2p-1}{4}},(46)$

and

$\mu ={\left(\frac{{\kappa }_N\alpha }{2\beta \left(2p-1\right){\tilde{\alpha }}_p{\omega }_{2p-1}}\right)}^{\frac{1}{p}}\sqrt{\left(2p-1\right)\left(2p-2\right)}Q.(47)$

From Equation 45, it is evident that, for even $p$, ${\lim }_{r\to \infty }f\left(r\right)\to 1\mp \mu$, for odd $p$, ${\lim }_{r\to \infty }f\left(r\right)\to 1-\mu$, and for both cases, ${\lim }_{r\to 0}f\left(r\right)\to 1$. Now consider the derivative of the metric function (Equation 48)

$\frac{df\left(r\right)}{dr}=\left\{\begin{array}{c}\mp \frac{2\mu \zeta }{r^{2p}{\left(1+\frac{\zeta }{r^{2p-1}}\right)}^{\frac{2p+1}{2p-1}}},\text{for}p\text{even,}\hfill \\ -\frac{2\mu \zeta }{r^{2p}{\left(1+\frac{\zeta }{r^{2p-1}}\right)}^{\frac{2p+1}{2p-1}}},\text{for}p\text{odd,}\hfill \end{array}\right.(48)$

which has no zeros for $r>0$. This implies that the spacetime described by Equation 45 does not admit horizons and therefore corresponds to a regular particle-like model. This interpretation is valid for the negative branch of even $p$, and for odd $p$, provided that $\mu <1\mathcal{,}$ ensuring $f\left(r\right)>0$ everywhere. In Figure 1, we plot the metric function $f\left(r\right)$ versus $r$ for representative values of the parameters. In the left panel, the negative branch is shown for $p=\mathrm{2,3,4,5,6}$, and 7. In the right panel, the positive branch is plotted for even $p=\mathrm{2,4,6}$, and 8. The results illustrate that the gravitational influence of the particle is significant only in the vicinity of the origin and quickly saturates, becoming constant at large distances.

Figure 1

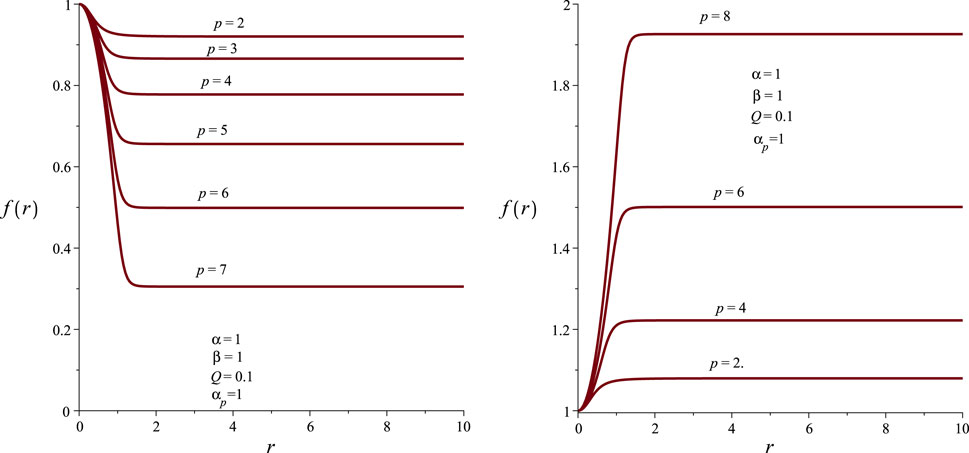
Figure 1. The left panel shows the negative branch of the metric function $f\left(r\right)$ in Equation 45 as a function of $r$ for $N=2p+1$ with $p=\mathrm{2,3},\dots ,7$. The right panel displays the positive branch of the metric function Equation 45 for $p=\mathrm{2,4,6,8}$.

3.2 $N>2p+1$ represents both black hole and particle models

Unlike the case $N=2p+1$, where the solutions represent only particle-like configurations for all $p$, Equation 39 with $N>2p+1$ can describe either black holes or particle-like models. In both the positive and negative branches, the spacetime is asymptotically flat, and the metric function satisfies $f\left(0\right)=1$. The derivative of the metric function is given by Equation 49

$\frac{df\left(r\right)}{dr}=\left\{\begin{array}{c}\pm \frac{\mu \left(\left(N-1-2p\right)r^{N-2}-2p\zeta \right)}{p{r}^{\frac{\left(N-3\right)p+N-1}{p}}{\left(1+\frac{\zeta }{r^{2p-1}}\right)}^{\frac{\left(N-2\right)p+N-1}{\left(N-2\right)p}}},\text{for}p\text{even,}\hfill \\ \frac{\mu \left(\left(N-1-2p\right)r^{N-2}-2p\zeta \right)}{p{r}^{\frac{\left(N-3\right)p+N-1}{p}}{\left(1+\frac{\zeta }{r^{2p-1}}\right)}^{\frac{\left(N-2\right)p+N-1}{\left(N-2\right)p}}},\text{for}p\text{odd,}\hfill \end{array}\right..(49)$

This derivative admits a critical point, defined by $\frac{df\left(r\right)}{dr}=0$, which occurs at

$r_c={\left(\frac{2p\zeta }{N-1-2p}\right)}^{\frac{1}{N-2}}.(50)$

At this radius (Equation 50), the positive branch reaches a maximum, and the negative branch reaches a minimum. For the negative branch, the solution represents a regular particle model if $f\left(r_c\right)>0$, an extremal black hole if $f\left(r_c\right)=0$, with a double horizon at $r_{+}=r_c$, and a black hole with two distinct horizons if $f\left(r_c\right)<0$. Explicit evaluation of $f\left(r\right)$ at the critical point yields

$f\left(r_c\right)=1-\mu {\left(\frac{N-1-2p}{2p\zeta }\right)}^{\frac{N-1-2p}{p\left(N-2\right)}}{\left(\frac{2p}{N-1}\right)}^{\frac{N-1}{\left(N-2\right)p}}.(51)$

This provides an analytical criterion for distinguishing between black hole and particle-like solutions. Substituting the definitions of $\mu$ and $\zeta$ in terms of the original parameters, we obtain Equation 52

$f\left(r_c\right)=1-{\left(\frac{{\kappa }_N\alpha }{{\alpha }_p{\omega }_{N-2}}\right)}^{\frac{1}{p}}\frac{{\left(N-2\right)}^{\frac{p-2}{2p}}\sqrt{N-3}}{{\beta }^{\frac{2N-3-2p}{p\left(N-2\right)}}{\left(N-1\right)}^{\frac{2N-3}{\left(N-2\right)p}}}{\left(N-1-2p\right)}^{\frac{N-1-2p}{p\left(N-2\right)}}{\left(2p\right)}^{\frac{2}{N-2}}Q.(52)$

Depending on the sign of this expression, if i) $f\left(r_c\right)<0$, the solution describes a black hole with two horizons, ii) $f\left(r_c\right)=0$, an extremal black hole with a double horizon, and iii) $f\left(r_c\right)>0$, a regular particle-like spacetime. For the positive branch, which is only valid for even $p$, no such restriction applies, and the solution always corresponds to a regular particle model.

4 Thermal stability of the black hole solution

In standard GR, spherically symmetric black holes (such as the Schwarzschild black hole) exhibit negative heat capacity. This implies that they are thermodynamically unstable. This is because they lose their mass through Hawking radiation that results in an increasing temperature, leading to faster evaporation. As discussed by D’Agostino et al. (2024), although modified gravity theories can partially alleviate the negative heat capacity problem for specific black hole masses and parameter choices, they do not provide a universal solution. The thermodynamic instability of spherically symmetric black holes remains a robust feature of GR, and its resolution likely requires more radical changes to gravity or the inclusion of quantum effects. In this section, we investigate the thermal stability of the black hole solution described by Equation 53

$f\left(r\right)=1-\frac{\mu }{r^{\frac{N-1-2p}{p}}{\left(1+\frac{\zeta }{r^{N-2}}\right)}^{\frac{N-1}{\left(N-2\right)p}}},(53)$

where $f\left(r_c\right)$ satisfies $f\left(r_c\right)\le 0$, as given in Equation 51. This should be noted that the thermodynamics of regular and singular black holes are the same because black hole thermodynamics depends only on the event horizon geometry, not on whether the interior contains a singularity. The differences between them show up in stability and detailed phase transitions, but not in the universal laws. Without loss of generality, we express our analysis in terms of the parameters $\mu$, $\zeta$, $N$, and $p$. For the black hole scenario, the event horizon $f\left(r_{+}\right)=0$. As previously discussed, this equation admits two horizons if $f\left(r_c\right)<0$ and a degenerate (double) horizon if $f\left(r_c\right)=0$, where $f\left(r_c\right)$ is defined in Equation 51. Solving $f\left(r\right)=0$ for $\mu$ at the horizon gives

$\mu =r_{+}^{\frac{N-1-2p}{p}}{\left(1+\frac{\zeta }{r_{+}^{N-2}}\right)}^{\frac{N-1}{\left(N-2\right)p}}.(54)$

Using Equation 54, the Hawking temperature associated with the black hole is calculated to be

$T_H=\frac{f^{\prime }\left(r_{+}\right)}{4\pi }=\frac{\left(N-1-2p\right)r_{+}^{N-2}-2p\zeta }{4\pi p{r}_{+}^{N-1}\left(1+\frac{\zeta }{r_{+}^{N-2}}\right)}.(55)$

Moreover, using the Wald entropy for the black holes in Lovelock (Jacobson and Myers, 1993; Myers and Simon, 1988; Camanho and Edelstein, 2013; Wang et al., 2016)

$S=\frac{A}{4}p{\tilde{\alpha }}_p\frac{N-2}{N-2p}\frac{1}{r_{+}^{2\left(p-1\right)}},(56)$

where in Equation 56 $A=r_{+}^{N-2}{\omega }_{N-2}$ is the black hole area, we find Equation 57

$S=\frac{\left(N-2\right)p{\tilde{\alpha }}_p{\omega }_{N-2}}{4\left(N-2p\right)}{r}_{+}^{N-2p}.(57)$

Finally, the heat capacity of the black hole is defined by

$C=T_H\frac{\partial S}{\partial T_H}=\frac{-p{\tilde{\alpha }}_p{\omega }_{N-2}{r}_{+}^{2N-2p-2}\left[N-1-2p-\frac{2p\zeta }{r_{+}^{N-2}}\right]\left(1+\frac{\zeta }{r_{+}^{N-2}}\right)}{4\left[1-\frac{\zeta \left(N-3\right)}{r_{+}^{N-2}}\right]\left(N-1-2p\right)r_{+}^{N-2}+8p\zeta \left[N-1+\frac{\zeta }{r_{+}^{N-2}}\right]}.(58)$

By introducing the rescaled variables $r=r_{0}x$ and $\mu ={\mu }_0{r}_0^{\frac{N-1-2p}{p}}$ with $\zeta =r_0^{N-2}$ the metric function becomes

$f\left(x\right)=1-\frac{{\mu }_0}{x^{\frac{N-1-2p}{p}}{\left(1+\frac{1}{x^{N-2}}\right)}^{\frac{N-1}{\left(N-2\right)p}}}.(59)$

Accordingly, the Hawking temperature (Equation 55) and heat capacity (Equation 58) are given by

$T_H=\frac{\left(N-1-2p\right)-\frac{2p}{x_{+}^{N-2}}}{4\pi p{r}_0{x}_{+}\left(1+\frac{1}{x_{+}^{N-2}}\right)}(60)$

and

$C=\frac{-p{\tilde{\alpha }}_p{\omega }_{N-2}{r}_0^{N-2p}{x}_{+}^{2N-2p-2}\left[N-1-2p-\frac{2p}{x_{+}^{N-2}}\right]\left(1+\frac{1}{x_{+}^{N-2}}\right)}{4\left[1-\frac{N-3}{x_{+}^{N-2}}\right]\left(N-1-2p\right)x_{+}^{N-2}+8p\left[N-1+\frac{1}{x_{+}^{N-2}}\right]}.(61)$

In Figure 2, we plot $f\left(x\right)$ as a function of $x$ for $N=10$ and $p=2$, using different values of ${\mu }_0$. This behavior is generic and holds for other values of $N>2p+1$ and $p$. Furthermore, Figure 3 displays the scaled Hawking temperature $4\pi r_0{T}_H$ (Equation 60) as a function of $x_{+}$ for $p=2$ and $N=\mathrm{6,7},\dots ,11$. Negative values of the temperature indicate non-black-hole configurations and must be discarded. A zero temperature corresponds to an extremal black hole. In all considered dimensions, the temperature initially increases with $x_{+}$, reaches a maximum at the Type-II transition point, and then decreases to zero as $x_{+}$ increases further. This implies that, as the black hole grows from its extremal size, its temperature increases to a peak before cooling as it becomes large. The Type-II transition also marks the point at which the heat capacity diverges, as shown in Figure 4 (Equation 61). In the left panel of Figure 4, we plot the scaled heat capacity $\frac{4}{r_0^{N-2p}{\tilde{\alpha }}_p{\omega }_{N-2}}C$ versus $x_{+}$ for $N=6$ and $p=2$. The vertical line indicates the Type-II transition radius, where the heat capacity increases significantly from $+\infty$ to $-\infty$. The right panel presents a zoomed-in view of both $\frac{4}{r_0^{N-2p}{\tilde{\alpha }}_p{\omega }_{N-2}}C$ and $4\pi r_0{T}_H$ as functions of $x_{+}$, highlighting the Type-I transition point (where both $C$ and $T_H$ vanish) and the Type-II transition point (where $C$ diverges and $T_H$ is maximized). A black hole is thermally stable if it has positive heat capacity and a well-defined (i.e., positive) Hawking temperature. Therefore, the black hole is stable only when its size lies between the Type-I and Type-II transition points.

Figure 2

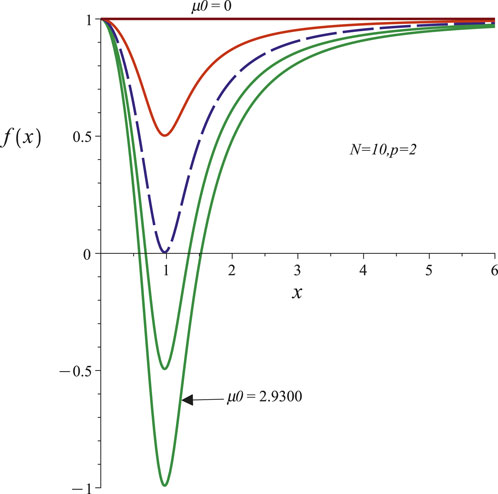
Figure 2. The metric function $f\left(x\right)$, given in Equation 59, is plotted as a function of $x$ for $p=2$ and $N=10$, and various values of ${\mu }_0$ incremented in equal steps. The extremal black hole solution serves as the boundary separating particle-like configurations from black hole solutions.

Figure 3

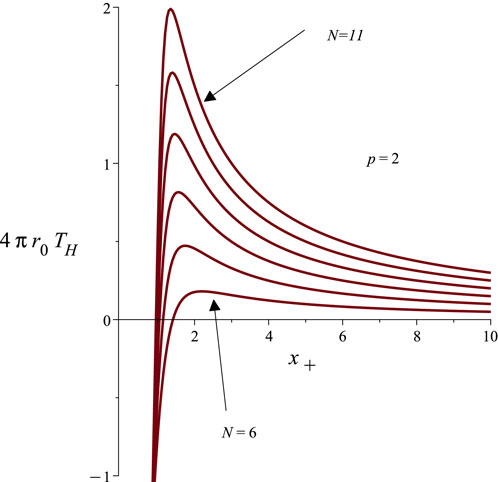
Figure 3. The scaled Hawking temperature is plotted as a function of $x_{+}$ for $p=2$, with various values of $N$ ranging from 6 to 11. The temperature vanishes for the extremal black hole and is positive for black holes with two distinct horizons. Negative values of the temperature are unphysical, indicating that no black hole exists with an event horizon smaller than that of the extremal case.

Figure 4

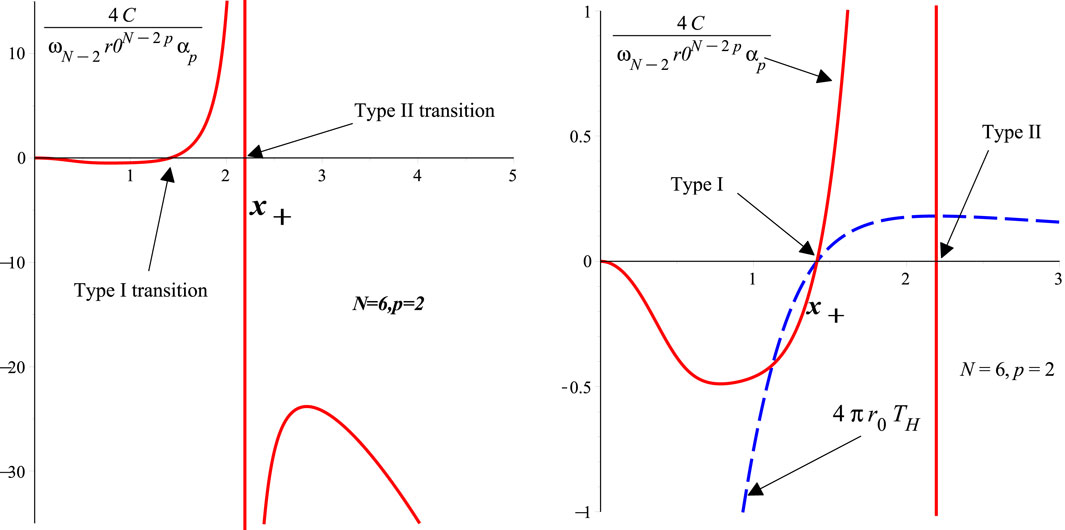
Figure 4. In the left panel, the scaled heat capacity is plotted as a function of $x_{+}$ for $p=2$ and $N=6$. The right panel presents a zoomed-in view, showing both the scaled heat capacity and the scaled Hawking temperature. The Type-I and Type-II transition points are clearly indicated on the plots.

5 Conclusion

In this work, we have derived a new class of regular black hole solutions in higher-dimensional pure Lovelock gravity, sourced by a nonlinear Yang–Mills field. The solutions generalize the Bardeen black hole in four dimensions and exhibit rich physical behavior depending on the dimension $N$ and Lovelock order $p$. Specifically, in the critical dimension $N=2p+1$, the solutions describe horizonless, particle-like spacetimes. For $N>2p+1$, both black hole and particle-like configurations emerge, depending on whether the metric function admits horizons. We obtained analytic criteria that distinguish between these possibilities. We further investigated the thermodynamic properties of the black holes, including their Hawking temperature and heat capacity. The analysis revealed the existence of two critical points: a lower (Type-I) transition point associated with extremal black holes and an upper (Type-II) transition point where the heat capacity diverges. Between these points, the black hole is thermally stable. Our results not only contribute to the understanding of regular black holes in higher-curvature gravity theories but also demonstrate the compatibility of nonlinear gauge fields with horizon-regular solutions. These findings offer a useful framework for exploring singularity resolution in classical gravity and may serve as a foundation for further investigations in quantum gravity models.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

SM: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, M. S., and Ghosh, S. G. (2018). Exact d-dimensional Bardeen-de sitter black holes and thermodynamics. Phys. Rev. D. 98, 084025. doi:10.1103/PhysRevD.98.084025

CrossRef Full Text | Google Scholar

Ayón-Beato, E., and García, A. (2000). The bardeen model as a nonlinear magnetic monopole. Phys. Lett. B 493, 149–152. doi:10.1016/S0370-2693(00)01125-4

CrossRef Full Text | Google Scholar

Bardeen, J. M. (1968). in Conference proceedings of GR5 (Tiflis: USSR), 174.

Google Scholar

Bambi, C., and Modesto, L. (2013). Rotating regular black holes. Phys. Lett. B 721, 329–334. doi:10.1016/j.physletb.2013.03.025

CrossRef Full Text | Google Scholar

Blanchette, K., Das, S., Hergott, S., and Rastgoo, S. (2021). Black hole singularity resolution via the modified raychaudhuri equation in loop quantum gravity. Phys. Rev. D. 103, 084038. doi:10.1103/PhysRevD.103.084038

CrossRef Full Text | Google Scholar

Bojowald, M. (2001). Absence of a singularity in loop quantum cosmology. Phys. Rev. Lett. 86, 5227–5230. doi:10.1103/PhysRevLett.86.5227

PubMed Abstract | CrossRef Full Text | Google Scholar

Boulware, D. G., and Deser, S. (1985). String-generated gravity models. Phys. Rev. Lett. 55, 2656–2660. doi:10.1103/PhysRevLett.55.2656

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, R.-G., and Ohta, N. (2006). Black holes in pure lovelock gravities. Phys. Rev. D. 74, 064001. doi:10.1103/PhysRevD.74.064001

CrossRef Full Text | Google Scholar

Cai, R.-G., Cao, L.-M., Hu, Y.-P., and Kim, S. P. (2008). Generalized vaidya spacetime in lovelock gravity and thermodynamics on the apparent horizon. Phys. Rev. D. 78, 124012. doi:10.1103/PhysRevD.78.124012

CrossRef Full Text | Google Scholar

Camanho, X. O., and Edelstein, J. D. (2013). A lovelock Black hole bestiary. Quant. Grav. 30, 035009. doi:10.1088/0264-9381/30/3/035009

CrossRef Full Text | Google Scholar

Chakraborty, S., and Dadhich, N. (2018). 1/r potential in higher dimensions. Eur. Phys. J. C 78, 81. doi:10.1140/epjc/s10052-018-5546-1

CrossRef Full Text | Google Scholar

Dadhich, N., and Pons, J. M. (2013). Probing pure lovelock gravity by nariai and bertotti-robinson solutions. J. Math. Phys. 54, 102501. doi:10.1063/1.4825115

CrossRef Full Text | Google Scholar

Dadhich, N., Ghosh, S. G., and Jhingan, S. (2013). Gravitational collapse in pure lovelock gravity in higher dimensions. Phys. Rev. D. 88, 084024. doi:10.1103/PhysRevD.88.084024

CrossRef Full Text | Google Scholar

D’Agostino, R., Luongo, O., and Mancini, S. (2024). Geometric and topological corrections to schwarzschild black hole. Eur. Phys. J. C 84, 1060. doi:10.1140/epjc/s10052-024-13440-y

CrossRef Full Text | Google Scholar

Gannouji, R., and Dadhich, N. (2014). Stability and existence analysis of static black holes in pure lovelock theories. Quant. Grav. 31, 165016. doi:10.1088/0264-9381/31/16/165016

CrossRef Full Text | Google Scholar

Giribet, G., Oliva, J., and Troncoso, R. (2006). Simple compactifications and black p-branes in gauss-bonnet and lovelock theories. JHEP 05 2006, 007. doi:10.1088/1126-6708/2006/05/007

CrossRef Full Text | Google Scholar

Jacobson, T., and Myers, R. C. (1993). Black hole entropy and higher curvature interactions. Phys. Rev. Lett. 70, 3684–3687. doi:10.1103/PhysRevLett.70.3684

PubMed Abstract | CrossRef Full Text | Google Scholar

Kastor, D., and Mann, R. (2006). On black strings and branes in lovelock gravity. JHEP 04, 048. doi:10.1088/1126-6708/2006/04/048

CrossRef Full Text | Google Scholar

Lovelock, D. (1971). The einstein tensor and its generalizations. J. Math. Phys. (N.Y.) 12, 498–501. doi:10.1063/1.1665613

CrossRef Full Text | Google Scholar

Mazharimousavi, S. H., and Halilsoy, M. (2008). Einstein-yang-mills black hole solution in higher dimensions by the Wu-Yang ansatz. Phys. Lett. B 659, 471. doi:10.1016/j.physletb.2007.11.006

CrossRef Full Text | Google Scholar

Myers, R. C., and Simon, J. Z. (1988). Black hole thermodynamics in lovelock gravity. Phys. Rev. D. 38, 2434–2444. doi:10.1103/PhysRevD.38.2434

PubMed Abstract | CrossRef Full Text | Google Scholar

Shabad, A. E., and Usov, V. V. (2011). Effective lagrangian in nonlinear electrodynamics and its properties of causality and unitarity. Phys. Rev. D. 83, 105006. doi:10.1103/PhysRevD.83.105006

CrossRef Full Text | Google Scholar

Wang, J.-B., Huang, C.-G., and Li, L. (2016). Entropy of nonrotating isolated horizons in lovelock theory from loop quantum gravity. Chin. Phys. C 40, 083102. doi:10.1088/1674-1137/40/8/083102

CrossRef Full Text | Google Scholar

T. T. Wu, C. N. Yang, H. Mark, and S. Fernbach (1969). Properties of matter under unusual conditions (New York: Interscience), 349.

Google Scholar

Yasskin, P. B. (1975). Solutions for gravity coupled to massless gauge fields. Phys. Rev. D. 12, 2212–2217. doi:10.1103/PhysRevD.12.2212

CrossRef Full Text | Google Scholar

Zwiebach, B. (1985). Curvature squared terms and string theories. Phys. Lett. B 156, 315–317. doi:10.1016/0370-2693(85)91616-8

CrossRef Full Text | Google Scholar