- 1Department of Language Science, University of California, Irvine, Irvine, CA, United States
- 2Department of Linguistics, Stanford University, Stanford, CA, United States
Formal and functional theories of language seem disparate, because formal theories answer the question of what a language is, while functional theories answer the question of what functions it serves. We argue that information theory provides a bridge between these two approaches, via a principle of minimization of complexity under constraints. Synthesizing recent work, we show how information-theoretic characterizations of functional complexity lead directly to mathematical descriptions of the forms of possible languages, in terms of solutions to constrained optimization problems. We show how certain linguistic descriptive formalisms can be recovered as solutions to such problems. Furthermore, we argue that information theory lets us define complexity in a way which has minimal dependence on the choice of theory or descriptive formalism. We illustrate this principle using recently-obtained results on universals of word and morpheme order.
1. Introduction
Information theory is the mathematical theory of communication and the origin of the modern sense of the word “information” (Shannon, 1948; Gleick, 2011). It proceeds from the premise (Shannon, 1948, p. 379):
The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.
In information theory, a code is any function which maps between a message (the content that is to be communicated) and a signal (any object or event that can be transmitted through a medium from a sender to a receiver). The signal is considered to contain information about the message when the message can be reconstructed from the signal. An optimal code conveys maximal information about the message in some potentially noisy medium, while minimizing the complexity of encoding, sending, receiving, and decoding the signal.
Our goal in this paper is to advance an information-theoretic characterization of human language in terms of an optimal code which maximizes communication subject to constraints on complexity. Optimality in this sense is relative: it requires specifying specific mathematical functions for communication and complexity and the ways they trade off. Once these constraints are specified, the form of the optimal code can be derived. Within this framework, the most important question becomes: what set of constraints yields optimal codes with the characteristics of human language?
The efficiency-based research program advocated here has a long scientific pedigree (Gabelentz, 1891; Zipf, 1935; Mandelbrot, 1953), and recent years have seen major advances based on ideas from information theory (for example, Ferrer i Cancho and Solé, 2003; Zaslavsky et al., 2018; Mollica et al., 2021) (see Gibson et al., 2019, for a recent review). The main contributions of the present paper are (1) to show how information theory provides a notion of complexity which is relatively neutral with respect to descriptive formalism and to discuss the consequences of this fact for linguistic theory, where differences between formalisms often play an important role, and (2) to demonstrate the utility of this framework by deriving existing linguistic formalisms from it, and by providing an example where it gives a natural explanation of a core property of human language. In the example, using previously-published results, we argue that, by minimizing the information-theoretic complexity of incremental encoding and decoding in a unified model, it is possible to derive a fully formal version of Behaghel's Principle (Behaghel, 1932): that elements of an utterance which ‘belong together mentally’ will be placed close to each other, the same intuition underlying the Proximity Principle (Givón, 1985, 1991), the Relevance Principle (Bybee, 1985), dependency locality (Gibson, 1998, 2000; Futrell et al., 2020c), and domain minimization (Hawkins, 1994, 2004, 2014).
We conclude by arguing that characterizing linguistic complexity need not be an end in itself, nor a secondary task for linguistics. Rather, a specification of complexity can yield a mathematical description of properties of possible human languages, via a variational principle that says that languages optimize a function that describes communication subject to constraints.
The remainder of the paper is structured as follows. In Section 2, we describe how information theory describes both communication and complexity, arguing that it does so in ways that are independent of questions about mental representations or descriptive formalisms. In Section 3, we show how functional information-theoretic descriptions of communication and complexity can be used to derive descriptions of optimal codes, showing that certain existing linguistic formalisms comprise solutions to information-theoretic optimization problems. In Section 4, we show how an information-theoretic notion of complexity in incremental production and comprehension yields Behaghel's Principle. Section 5 concludes.
2. Information-Theoretic Concepts of Communication and Complexity
Imagine Alice and Bob want to establish a code that will enable them to communicate about some set of messages M. For example, maybe M is the set of movies playing in theaters currently, and Alice wants to transmit a signal to Bob so that he knows which movie she wants to see. Then they need to establish a code: a mapping from messages (movies) to signals, such that when Bob receives Alice's signal, he can reconstruct her choice of message (movie). We say communication is successful if Bob can reconstruct Alice's message based on his receipt of her signal.
More formally, a code L is a function L from messages m ∈ M to observable signals s drawn from some set of possible signals S:
In general, the function L can be stochastic (meaning that it returns a probability distribution over signals, rather than a single signal). Canonically, we suppose that the set of possible signals is the set of possible strings of characters drawn from some alphabet Σ. Then codes are functions from messages to strings:
Note that these definitions are extremely general. A code is any (stochastic) function from messages to signals: we have not yet imposed any restrictions whatsoever on that function.
2.1. Definition of Information
Given this setting, we can now formulate the mathematical definition of information. Information is defined in terms of the simplest possible notion of the effort involved in communication: the length of signals that have to be sent and received. The amount of information in any object x will be identified with the length of the signal for x in the code which minimizes the average length of signals; the problem of finding such a code is called source coding.
Below, we will give an intuitive derivation showing that the information content for some object x is given by the negative log probability of x. For a more comprehensive introduction to information content and related ideas (see Cover and Thomas, 2006). This derivation of the concept of information content serves two purposes: (1) it gives some intuition for what a “bit” of information really is, and (2) it allows us to contrast the minimal-length source code against human language (which we will argue results from minimization of a very different and more interesting notion of complexity).
Consider again the case where the set of messages M is a set of movies currently playing, and suppose Alice and Bob want to find a code L which will enable perfect communication about M with signals of minimal length. That is, before Bob receives Alice's signal, he thinks the set of movies Alice might want to see is the set M, with size |M|. If the code is effective, then after Bob receives Alice's signal, he should have reduced the set of movies down to a set of size 1, {m} for the target m. The goal of the code is therefore to reduce the possible messages from a set of size |M| to a set of size 1.
Canonically we suppose that the alphabet Σ has two symbols in it, resulting in a binary code. We will define the information content of a particular movie m as the length of the signal for m in the binary code that minimizes average signal length. If Alice wants her signals to be as short as possible, then she wants each symbol to reduce the set of possible movies as much as possible. We suppose that Alice and Bob decide on the code in advance, before they know which movie will be selected, so the code should not be biased toward any movie rather than another. Therefore, the best that can be done with each symbol transmitted is to reduce the set of possible messages by half.
The problem of communication therefore reduces to the problem of transmitting symbols that each divide the set of possible message M in half, until we are left with a set of size 1. With this formulation, we can ask how many symbols n must be sent to communicate about a set of size |M|:
This equation expresses that the set M is divided in half n times until it has size 1. The length of the code is given by solving for n. Applying some algebra, we get
Taking the logarithm of both sides to solve for n, we have
Therefore, the amount of information in any object m drawn from a set M is given by log2|M|. For example, suppose that there are 16 movies currently playing, and Alice and Bob want to design a minimal-length code to communicate about the movies. Then the length of the signal for each movie is log2 16 = 4. We say that the amount of information contained in Alice's selection of any individual movie is 4 bits, the standard unit of information content. If Alice successfully communicates her selection of a movie to Bob—no matter what code she is actually using—then we say that she has transferred four bits of information to Bob.
The derivation above assumed that all the possible messages m ∈ M had equal probability. If they do not, then it might be possible to shorten the average length of signals by assigning short codes to highly probable messages, and longer codes to less probable messages. If we know the probability distribution on messages P(m), then we can follow the derivation above, calculating how many times we have to divide the total probability mass on M in half in order to specify m. This procedure yields the length of the signal for meaning m in the code which minimizes average signal length. We call this the information content of m:
The quantity in Equation (3) is also called surprisal and self-information1. The information content is high for low-probability messages and low for high-probability messages, corresponding to the assignment of longer codes to lower-probability events.
A few remarks are in order about the definition of information content.
2.1.1. Meaning of “Bit of Information”
Although the bit of information is defined in terms of a discrete binary code, it represents a fundamental notion of information which is general to all codes. A bit of information corresponds to a distinction that allows a set to be divided in half (or, more generally, which allows a probability distribution to be divided into two parts with equal probability mass).
A naïve way to define the amount of information in some object x would be to ask for the length of the description of x in some language. For example, we could identify the amount of information in an event with the length of the description of that event in English, measured in phonemes. This would not be satisfying, since our measurement of information would depend on the description language chosen. If descriptions were translated into languages other than English, then their relative lengths would change.
Information theory solves this problem by using the minimal-length code as a distinguished reference language. By measuring information content as the length of a signal under this code, we get a description-length measure that is irreducible, in the sense that there is no description language that can give shorter codes to a certain set of objects with a certain probability distribution.
For this reason, the bit is not only a unit of information communicated, but also a fundamental unit of complexity. The complexity of a particular grammar, for example, could be identified as the number of bits required to encode that grammar among the set of all possible grammars. This measure of information content would, in turn, depend on the choice of probability distribution over grammars. Choices of grammatical formalism would only matter inasmuch as they (explicitly or implicitly) define a probability distribution over grammars.
2.1.2. Representation Invariance
Surprisingly, the information content of an object x does not really depend on the object x itself. Rather, it only depends on the probability of x. This property gives information theory a very powerful general character, because it means that information content does not depend on the choice of representation for the object x—it depends only on the probability of the object. We will call this property of information theory representation invariance.
While representation invariance makes information theory very general, it also means that information theory can feel unusual compared to the usual methods deployed in linguistic theory. Traditional linguistic theory pays careful attention to the formal representation of linguistic data, with explanations for linguistic patterns often coming in the form of constraints on what can be described in the formalism (Haspelmath, 2008). In information theory, on the other hand, any two representations are equivalent as long as they can be losslessly translated one to the other—regardless of any difficulty or complexity involved in that translation. This property is what Shannon (1948, p. 379) is referring to when he writes:
Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the communication problem. The significant aspect is that the actual message is one selected from a set of possible messages.
That is, if the goal is simply to communicate messages while minimizing code length, all that matters is the set that the message is selected from, and the probability of that message in that set—the meaning of the message does not matter, nor any other aspect of the message.
Representation invariance is the source of the great generality of information theory, and also of its limits (James and Crutchfield, 2017; Pimentel et al., 2020). This property of information theory has led some to question its relevance for human language (and for human cognition more generally, e.g. Luce, 2003), where the structure of meaning clearly plays a large role in determining the form of languages, via principles of compositionality, isomorphism, and iconicity (Givón, 1991; Culbertson and Adger, 2014).
However, it is more accurate to see this property of information theory as an extreme form of the arbitrariness of the sign (Saussure, 1916) which holds in certain kinds of ideal codes. In human language, at least at the level of morphemes, there is no relationship between a form and the structure of its meaning, or only a weak relationship (Bergen, 2004; Monaghan et al., 2014; Pimentel et al., 2019); the mapping between the form and meaning of a morpheme is best described, to a first approximation, as an arbitrary lookup table which a learner of a language must memorize. A minimal-length source code yields an extreme version of this idea: in such a code, there is no consistent relationship between a form and the structure of its meaning at any level. The idea that a signal contains information about a message is totally disentangled from the idea that there is some systematic relationship between the structure of the message and the structure of the signal.
2.1.3. Natural Language Is Not a Minimal-Length Source Code
The last point above brings us to the question of what similarities and differences exist between the code described above, which minimizes average signal length, and human language, when we view it as a code. Although the lexicon of words seems to share some basic properties of minimal-length codes—for example, assigning short forms to more predictable meanings (Zipf, 1949; Piantadosi et al., 2011; Pate, 2017; Kanwal, 2018; Pimentel et al., 2021)—when we view language at the level of phrases, sentences, and discourses, it has important properties which such codes lack. Most vitally, there is a notion of systematicity or compositionality in morphology and larger levels of analysis: a word or a sentence can be segmented (at least approximately) into units that collectively convey some information as a systematic function of the meanings of the individual units. Furthermore, these units are combined together in a process that usually resembles concatenation: they are placed end to end in the signal, with phonological rules often applying at their boundaries. Although non-concatenative morphology and discontinuous syntax do exist (e.g., scrambling), they are relatively rare and limited in scope.
The minimal-length code has nothing at all corresponding to systematicity, compositionality, or concatenation of morphemes. In such a code, if two different messages have some commonality in terms of their meaning, then there is nothing to guarantee any commonality in the signals for those two messages. Even if it is (by chance) possible to identify some symbols in a minimal-length code as corresponding jointly and systematically to some aspect of meaning, then there is no guarantee that those symbols will be adjacent to each other in the signal. After some reflection, this is not surprising: minimal-length codes result only from the minimization of average signal length, subject to the constraint of enabling lossless communication. Such codes are under no pressure to have any isomorphism between messages and signals. Conversely, we can conclude that if we wish to characterize human language as an optimal code, then it must operate under some constraint which forces systematicity, compositionality, and a tendency toward concatenation as a means of combination at the level of form, as well as the other properties of human language. Minimization of average signal length alone does not suffice to derive these properties.
2.2. Further Information Quantities: Entropy, Conditional Entropy, Mutual Information
Information theory is built on top of the definition of information content given in Equation (3). Based on this definition, we can define a set of further information quantities that are useful for discussing and constraining the properties of codes. This section is not exhaustive; it covers only those quantities that will be used in this paper.
2.2.1. Entropy
The most central such quantity is entropy: the average information content of some random variable. Given a random variable X (consisting of a set of possible outcomes and a probability distribution P(x) on those outcomes), the entropy of X is
Entropy is best thought of as a measure of uncertainty: it tells the amount of uncertainty about the outcome of the random variable X.
2.2.2. Conditional Entropy
Suppose we have a code—a mapping L : M → S from messages to signals—and we want to quantify how much uncertainty remains about the underlying message M after we have received a signal S. This question is most naturally answered by the conditional entropy: the entropy of some random variable such as M that remains after conditioning on some other random variable such as S. Conditional entropy for any two random variables M and S is defined as
For example, suppose that a code L : M → S is a perfect code for M, meaning that there is no remaining uncertainty about the value of M after observing S. This corresponds to the condition
An ambiguous code would have H[M ∣ S] > 0.
2.2.3. Mutual Information
Mutual information quantifies the amount of information in one random variable S about some other random variable M:
It is best understood as a difference of entropies:
In this case, if we interpret S as signal and M as message, then I[S : M] indicates the amount of information contained in S about M, which is to say, the amount of uncertainty in M which is reduced after observing S.
2.3. Information-Theoretic Notions of Complexity
As discussed in Section 2.1, information theory gives us a notion of complexity that does not depend on the descriptive formalism used. However, the complexity of an object still depends on the probability distribution it is drawn from. The problem of choosing a probability distribution is substituted for the problem of choosing a descriptive formalism2. For this reason, information-theoretic notions of complexity are most easy and useful to apply in scenarios where the relevant probability distribution is already known3. In other scenarios, it is still useful, but loses some of its strong theory-neutrality.
When the relevant probability distributions are known, information theory gives us a complexity metric that generalizes over representations and algorithms, indicating an irreducible part of the resources required to store or compute a value. Any particular representation or algorithm might require more resources, but certainly cannot use less than the information-theoretic lower bound.
2.3.1. Example 1: Sorting
As an example of the relationship between information measures and computational complexity, consider the computations that would be required to sort an array of numbers which are initially in a random order. Information theory can provide a lower bound on the complexity of this computation in terms of the number of operations required to sort the array (Ford and Johnson, 1959). Let the array have n elements; then sorting the array logically requires determining which of the n! possible configurations it is currently in, so that they can be transformed into the desired order. Assuming all orders are equally probable and that all elements of an array are distinct, the information content of the order of the array is log(n!). Any sorting algorithm must therefore perform a series of computations on the array which effectively extract a total of log(n!) bits of information. If each operation has the effect of extracting one bit of information, then log(n!) operations will be required. Therefore the information-theoretic complexity of the computation is log(n!), which is indeed a lower bound on time complexity of the fastest known sorting algorithms, which require on the order of n log n operations on average (Cormen et al., 2009, p. 91).
This kind of thinking more generally underlies the decision tree model of computational complexity, in which the complexity of a computation is lower bounded using the minimal number of yes-or-no queries which must be asked about the input in order to specify the computation of the output. This quantity is nothing but the number of bits of information which must be extracted from the input to specify the computation of the output, yielding a lower bound on resources required to compute any function. In general, there is unavoidable cost associated with computational operations that reduce uncertainty (Ortega and Braun, 2013; Gottwald and Braun, 2019).
In this sense, information theory gives a notion of complexity which is irreducible and theory-neutral. The true complexity of computing a function using any concrete algorithm may be larger than the information-theoretic bound, but the information-theoretic bound always represents at least a component of the full complexity. In the case of information processing in the human brain, the information-theoretic bounds give good fits to data: the mutual information between input and output has been found to be a strong predictor of processing times in the human brain in a number of cognitively challenging tasks (see Zénon et al., 2019, for a review).
2.3.2. Example 2: Incremental Language Comprehension
In a more linguistic example, consider the computations required for online language comprehension. A comprehender is receiving a sequence of inputs w1, …, wT, where wt could indicate a unit such as a word. Consider the computations required in order to understand the word wt given the context of previous words w<t. Whatever information is going to be ultimately extracted from the word wt, the comprehender must identify which word it is. The comprehender can do so by performing any number of computations on sensory input; each computation will have the effect of eliminating some possible words from consideration. The minimal number of such computations required will be proportional to the information content of the correct word in its context, which is
following the definition of information content in Equation (3). Therefore, the number of computations required to recognize a word wt given preceding context w<t will be proportional to the surprisal of the word, given by Equation (4).
This insight underlies the surprisal theory of online language comprehension difficulty (Hale, 2001; Levy, 2008), in which processing time is held to be a function of surprisal. Levy (2013) outlines several distinct converging theoretical justifications for surprisal theory, all based on different assumptions about human language processing mechanisms. The reason these disparate mechanisms all give rise to the same prediction, namely surprisal theory, is that surprisal theory is based on fundamental information-theoretic limits of information processing. Furthermore, empirically, surprisal theory has the capacity to correctly model reading times across a wide variety of phenomena in psycholinguistics, including modeling the effects of syntactic construction frequency, lexical frequency, syntactic garden paths, and antilocality (Levy, 2008). Surprisal is, furthermore, a strong linear predictor of average reading times in large reading time corpora (Boston et al., 2011; Smith and Levy, 2013; Shain, 2019; Wilcox et al., 2020) (cf. Meister et al., 2021), as well as ERP magnitudes (Frank et al., 2015; Aurnhammer and Frank, 2019).
While surprisal has strong success as a predictor of reading times, it does not seem to account for all of the difficulty associated with online language processing. However, the information-theoretic argument suggests that processing difficulty will always be lower-bounded by surprisal: there will always be some component of processing difficulty that can be attributed to the surprisal of the word in context. In this connection, a recent critical evaluation of surprisal theory found that, although it makes correct predictions about the existence of garden path effects in reading times, it systematically under-predicts the magnitude of those effects (van Schijndel and Linzen, 2018, 2021). The results suggest that reading time is determined by surprisal plus other effects on top of it, which is consistent with the interpretation of surprisal as an information-theoretic lower bound on processing complexity.
2.3.3. Example 3: Effects of Memory on Language Processing
Relatedly, Futrell et al. (2020b) advance an extension of surprisal theory intended to capture the effects of memory limitations in sentence processing. In this theory, called lossy-context surprisal, processing difficulty is held to be proportional not to the information content of a word given its context as in Equation (4), but rather the information content of a word given a memory trace of its context:
where mt is a potentially noisy or lossy memory representation of the preceding words w<t. Because the memory representation mt does not contain complete information about the true context w<t, predictions based on the memory representation mt will be different from the predictions based on the true context w<t4. Memory representations may become lossy as more and more words are processed, or simply as a function of time, affecting the temporal dynamics of language processing.
This modified notion of surprisal can account for some of the interactions between probabilistic expectation and memory constraints in language processing, such as the complex patterns of structural forgetting across languages (Gibson and Thomas, 1999; Vasishth et al., 2010; Frank et al., 2016; Frank and Ernst, 2019; Hahn et al., 2020a), as well as providing a potential explanation for the comprehension difficulty associated with long dependencies (Gibson, 1998, 2000; Demberg and Keller, 2008; Futrell, 2019). Notably, lossy-context surprisal is provably larger than the plain surprisal in Equation (4) on average. The purely information-theoretic notion of complexity given by surprisal theory provides a lower bound on resource usage in language processing, and the enhanced theory of lossy-context surprisal adds memory effects on top of it.
3. Modeling Communication Under Constraints
Here we take up the question of what an information-theoretic characterization of human language as a code would look like. We show that an optimal code is defined by a set of constraints that the code operates under. So an information-theoretic characterization of human language would consist of a set of constraints which yields optimal codes that have the properties of human language.
An optimal code is defined by the constraints that it operates under. For example, a minimal-length source code operates under the constraints of (1) achieving lossless information transfer for a given source distribution, while (2) minimizing average code length, subject to (3) a constraint of self-delimitation, meaning that the end of each signal can be identified unambiguously from the signal itself. Using the concepts from Section 2.2, we can now make this notion more precise. The optimization problem that yields the minimal-length source code is a minimization over the space of all possible probability distributions on signals given messages q(s|m):
where the function l(s) gives the length of a signal, and the notation 〈·〉 indicates an average. The expression (6) specifies the minimization problem: over all possible codes q(s∣m), find the one that minimizes the average length of a signal l(s), subject to the condition that the conditional entropy of messages M given signals S must be zero, and an inequality constraint that enforces that the code must be self-delimiting5.
We argue that an information-theoretic characterization of human language should take the form of a constrained optimization problem, such that the solutions correspond to possible human languages. The set of constraints serve as a “universal grammar,” defining a space of possible languages corresponding to the optima. However, unlike typical attempts at formulating universal grammar, this approach does not consist of a declarative description of possible languages, nor a constrained formalism in which a language can be described by setting parameters. Rather, the goal is to specify the functional constraints that language operates under. These constraints might have to do with communication, and they might have to do with the computations involved in using and learning language. Optimally, each constraint can be justified independently based on experimental grounds, using empirical results from fields such as psycholinguistics and language acquisition.
In order to show the utility of this approach, here we will show how influential formalisms from linguistic theory can be recovered as solutions to suitably specified optimization problems.
A very simple objective function, generalizing the objective for minimal-length source codes, would be one which minimizes some more general notion of cost per signal. Let C(s) denote a cost associated with a signal s. Then we can write an optimization problem to find a code which minimizes ambiguity while also achieving a certain low level k of average cost:
In many cases, such a constrained optimization problem can be rewritten as an unconstrained optimization problem using the method of Lagrange multipliers6. In that case, we can find the solutions by finding minima of an objective function
where the scalar parameter β indicates how much cost should be weighed against ambiguity when finding the optimal code.
We are not aware of a simple general form for solutions of the objective (7). But a closely related objective does have general solutions which turn out to recapitulate influential constraint-based formalisms:
Equation (8) adds a maximum entropy constraint to Equation (7) (Jaynes, 2003): with weight α, it favors solutions with relatively high entropy over signals s given messages m. Note that Equation (8) reduces to Equation (7) as α → 0. The solutions of Equation (8) have the form of self-consistent equations7:
We see that the solutions of Equation (8) have the form of Maximum Entropy (MaxEnt) grammars. In MaxEnt grammars, the probability of a form is held to be proportional to an exponential function of its negative cost, which is a sum of penalties for constraints violated. These penalties encode markedness constraints on forms, which have been identified with articulatory effort (Kirchner, 1998; Cohen Priva, 2012), thus providing independent motivation for the cost terms in the objective. MaxEnt grammars are used primarily in phonology as a probabilistic alternative to Optimality Theory (OT); they differ from OT in that constraints have real-valued weights rather than being ranked (Johnson, 2002; Goldwater and Johnson, 2003; Jäger, 2007; Hayes and Wilson, 2008). Equation (9) differs from a typical MaxEnt grammar in one major respect: an additional term log q(m|s) enforces that the message m can be recovered from the signal s—this term can, in fact, be interpreted as generating faithfulness constraints (Cohen Priva, 2012, Ch. 3). Thus we have a picture of MaxEnt grammars where markedness constraints come from the term C(s) reflecting articulatory cost, and faithfulness constraints come from the term log q(m∣s) reflecting a pressure against ambiguity.
Equation (9) is also identical in form to the “speaker function” in the Rational Speech Acts (RSA) formalism for pragmatics (Frank and Goodman, 2012; Goodman and Stuhlmüller, 2013; Goodman and Frank, 2016). In that formalism, the speaker function gives the probability that a pragmatically-informed speaker will produce a signal s in order to convey a message m. A derivation of the RSA framework on these grounds can be found in Zaslavsky et al. (2020).
We therefore see that key aspects of different widely-used formalisms (MaxEnt grammars and Rational Speech Acts pragmatics models) emerge as solutions to an information-theoretic objective function. The objective function describes functional pressures—reducing ambiguity and cost—and then the solutions to that objective function are formal descriptions of possible languages. Functional and formal descriptions are thus linked by a variational principle8.
A number of objective functions for language have been proposed in the literature, which can be seen as variants of Equation (7) for some choice of cost function. For example, in the Information Bottleneck framework, which originated in information theory and physics (Tishby et al., 1999), as it has been applied to language, the complexity of a language is characterized in terms of the mutual information between words and cognitive representations of meanings. The Information Bottleneck has recently been applied successfully to explain and describe the semantic structure of the lexicon in natural language, in the semantic fields of color names (Zaslavsky et al., 2018) and animal and artefact categories (Zaslavsky et al., 2019). The same framework has been applied to explain variation in morphological marking of tense (Mollica et al., 2021).
Another objective function in the literature proposes to add a constraint favoring deterministic mappings from messages to signals. Setting C(s) = −log q(s) in Equation (7), we get an objective
which penalizes the entropy of signals, thus creating a pressure for one-to-one mappings between message and signal (Ferrer i Cancho and Díaz-Guilera, 2007) and, for carefully-chosen values of the scalar trade-off parameter β, a power-law distribution of word frequencies (Ferrer i Cancho and Solé, 2003) (but see Piantadosi, 2014, for a critique). Recently, Hahn et al. (2020b) have shown that choosing word orders to minimize Equation (10), subject to an additional constraint that word orders must be consistent with respect to grammatical functions, can explain certain universals of word order across languages. The latter work interprets the cost C(s) = −log q(s) as the surprisal of the signal, in which case minimizing Equation (10) amounts to maximizing informativity while minimizing comprehension difficulty as measured by surprisal, as discussed in Section 2.3.2.
What are the advantages to specifying a space of codes in terms of an information-theoretic objective function? We posit three:
1. The objective function can provide a true explanation for the forms of languages, as long as each term in the objective can be independently and empirically motivated. Each term in the objective corresponds to a notion of cost, which should cash out as real difficulty experienced by a speaker, listener, or learner. This difficulty can, in principle, be measured using experimental methods. When constraints are independently verified in this way, then we can really answer the question of why language is the way it is—because it satisfies independently-existing constraints inherent to human beings and their environment.
2. It is natural to model both soft and hard constraints within the framework (Bresnan et al., 2001). Constraints in the objective are weighted by some scalar, corresponding to a Lagrange multiplier, naturally yielding soft constraints whose strength depends on that scalar. Hard constraints can be modeled by taking limits where these scalars go to infinity9. More generally, all the tools from optimization theory are available for specifying and solving objective functions to capture various properties of language.
3. Objective functions and information theory are the mathematical language of several fields adjacent to linguistics, including modern machine learning and natural language processing (Goldberg, 2017). Many modern machine learning algorithms amount to minimizing some information-theoretic objective function over a space of probability distributions parameterized using large neural networks. Despite enormous advances in machine learning and natural language processing, there has been little interplay between formal linguistics and those fields, in large part because of a mismatch of mathematical languages: linguistics typically uses discrete symbolic structures with hard constraints on representation, while machine learning uses information theory and optimization over the space of all distributions. In neuroscience also, neural codes are characterized using information-theoretic objectives, most prominently in the “Infomax” framework (Linsker, 1988; Kay and Phillips, 2011; Chalk et al., 2018). If we can formulate a theory of language in this way, then we can open a direct channel of communication between these fields and linguistics.
Above, we argued that when we consider codes that maximize communication to a cost function, we recover certain linguistic formalisms and ideas. Shannon (1948) had the initial insight that there is a connection between minimal average code length and informational optimization problems. Our proposal is to extend this insight, using appropriately constrained informational optimization problems to characterize more interesting properties of human languages, not merely code length.
Within this paradigm, the main task is to characterize the cost function for human language, which represents the complexity of using, learning, and mentally representing a code. In some cases, the cost function may reflect factors such as articulatory difficulty which are not information-theoretic. But in other cases, it is possible to define the cost function itself information-theoretically, in which case we reap the benefits described in Section 2.3: we get a notion of complexity which is maximally theory-neutral. In the next section, we describe the application of such an information-theoretic cost function to describe incremental memory usage in language production and comprehension. We show that this cost function ends up predicting important universal properties of how languages structure information in time.
4. Case Study: Locality
Here we discuss a particular set of information-theoretic constraints on incremental language processing and how they can explain some core properties of human language. The properties of language we would like to explain are what we dub locality properties: the fact that elements of an utterance which jointly correspond to some shared aspect of meaning typically occur close together in the linear order of the utterance. Locality properties encompass the tendency toward contiguity in morphemes, the particular order of morphemes within words, and the tendency toward dependency locality in syntax. We will show that these properties follow from memory constraints in incremental language processing, characterized information-theoretically.
4.1. Locality Properties of Natural Language
In English utterances such as “I saw a cat” and “The cat ate the food,” there is a repeating element 〈cat〉 which systematically refers to an aspect of meaning which is shared among the two utterances: they both have to do with feline animals. The fact that natural language has this kind of isomorphism between meaning and form is what is often called systematicity—the phonemes /kæt/ jointly refer to a certain aspect of meaning in a way which is consistent across contexts, forming a morpheme. Systematicity is one of the deepest core properties of language, setting it apart from minimal-length codes and from most codes studied in information theory, as discussed in Section 2.1.
Here, we do not take up the question of what constraint on a code would force it to have the systematicity property; a large literature exists on this topic in the field of language evolution (e.g., Smith et al., 2003; Kirby et al., 2015; Nölle et al., 2018; Barrett et al., 2020), much of which suggests that systematicity emerges from a balance of pressures for communication and for compressibility of the grammar. Rather, we wish to draw attention to an aspect of linguistic systematicity which often goes unremarked-upon: the fact that, when parts of an utterance jointly correspond to some aspect of meaning in this way, those parts of an utterance are usually localized near each other in time. That is, the phonemes comprising the morpheme /kæt/ are all adjacent to each other, rather than interleaved and spread throughout the utterance, mingling with phonemes from other morphemes.
This locality property is non-trivial when we consider the space of all possible codes where signals have length >1, even if these codes are systematic. It is perfectly easy to conceive of codes which are systematic but which do not have the locality property: for example, a code which has systematic morphemes which are interleaved with each other, or broken into pieces and scattered randomly throughout the utterance, or perhaps even morphemes are simultaneously co-articulated in a way that remains systematic. Such phenomena can be found in language games such as Pig-Latin, for example.
Furthermore, these “spread out” codes are actually optimal in an environment with certain kinds of noise. If a code must operate in an environment where contiguous segments of an utterance are unavailable due to noise—imagine an environment where cars are going by, so that contiguous parts of utterances will be missed by the listener—then it would actually be best for all morphemes to be distributed as widely as possible in time, so that the meanings of all the morphemes can be recovered in the presence of the noise. Many error-correcting codes studied in coding theory work exactly this way: the information that was originally localized in one part of a signal is spread out redundantly in order to ensure robustness to noise (Moser and Chen, 2012).
Natural language is clearly not an error-correcting code of this type. Although it does have some tendencies toward spreading out information, for example using gender marking to redundantly indicate about 1 bit of information about nouns (Futrell, 2010; Dye et al., 2017), and using optional complementizers and syllable length to promote a uniform distribution of information in time (Aylett and Turk, 2004; Levy and Jaeger, 2007; Jaeger, 2010), we will argue below that the overwhelming tendency is toward localization. Therefore, constraints based on robustness, which favor spreading information out in time, exert only a relatively weak influence on natural language10.
The most striking locality property in language is the strong tendency toward contiguity in morphemes and morphology more generally. Although non-contiguous morphology such as circumfixes and Semitic-style non-concatenative morphology do exist, these are relatively rare. Most morphology is concatenative, up to phonological processes. Even non-concatenative morphology does not create large amounts of non-locality; for example, in Semitic consonantal-root morphology, the morphemes indicating plurality, aspect, etc. are spread throughout a word, but they do not extend beyond the word. Beyond the level of individual morphemes, words are usually concatenated together as contiguous units; Jackendoff (2002, p. 263) describes the concatenation of words as the “absolutely universal bare minimum” of human language.
Even within words, a kind of locality property is present in the ordering of morphemes. Morphemes are generally ordered according to a principle of relevance (Bybee, 1985): morphemes are placed in order of “relevance” to the root, with morphemes that are more relevant going closer to the root and those less relevant going farther. Mirror-image orders are observed for prefixes and suffixes. For example, in verb morphology, markers of transitivity go close to a verbal root, while markers of object agreement go farther. As we will see, the information-theoretic account yields a mathematical operationalization of this notion of “relevance” which can be calculated straightforwardly from corpora.
Beyond the level of morphology, locality properties are also present in syntax, in patterns of word order. Dependency locality refers to the tendency for words in direct syntactic relationships to be close to each other in linear order (Futrell et al., 2020c), potentially explaining a number of typological universals of word order, including Greenberg's harmonic word order correlations (Greenberg, 1963; Dryer, 1992). Dependency locality has appeared in the functionalist typological literature as the principles of Domain Minimization (Hawkins, 1994, 2004, 2014) and Head Proximity (Rijkhoff, 1986, 1990), and has been operationalized in the corpus literature as dependency length minimization (Ferrer i Cancho, 2004; Liu, 2008; Gildea and Temperley, 2010; Futrell et al., 2015; Liu et al., 2017; Temperley and Gildea, 2018). We argue here that it is an extension of the same locality property that determines the order and contiguity of morphemes.
4.2. Memory, Surprisal, and Information Locality
We propose that the locality properties of natural language can be explained by assuming that natural language operates under constraints on incremental language processing. Applying the information-theoretic model of processing difficulty from Section 2.3.3 and considering also the complexity of encoding, decoding, and storing information in memory, we get a picture of processing difficulty in terms of a trade-off of surprisal (predictability of words) and memory (the bits of information that must be encoded, decoded, and stored in incremental memory). It can be shown mathematically under this processing model that when codes do not have locality, then they will create unavoidable processing difficulty. This section summarizes theory and empirical results that are presented in full detail by Hahn et al. (2021).
The information-theoretic model of the incremental comprehension difficulty associated with a word (or any other unit) wt given a sequence of previous words w<t is given by lossy-context surprisal (Futrell et al., 2020b):
where mt is a potentially lossy memory representation of the context w<t. Since our goal is to characterize languages as a whole, we should consider the average processing difficulty experienced by someone using the language. The average of Equation (5) is the conditional entropy of words given memory representations:
where Wt and Mt are the distributions on words and memory representations given by the language and by the comprehender's memory architecture. Equation (11) represents the average processing difficulty per word under the lossy-context surprisal model11.
In addition to experiencing processing difficulty per word, a comprehender must also use memory resources in order to form the memory representations Mt that encode information about context. We can quantify the resources required to keep information in memory in terms of the entropy of the memory states:
which counts the bits of information stored in memory on average. These two quantities (average surprisal in Equation 11 and memory entropy in Equation 12) trade off with each other. If a listener stores more information in memory, then a lower average surprisal per word can be achieved. If a listener stores less information in memory, then the listener will experience higher average surprisal per word. The particular form of the trade-off will depend on the language, as summarized in Figure 1. This trade-off curve is called the memory–surprisal trade-off.
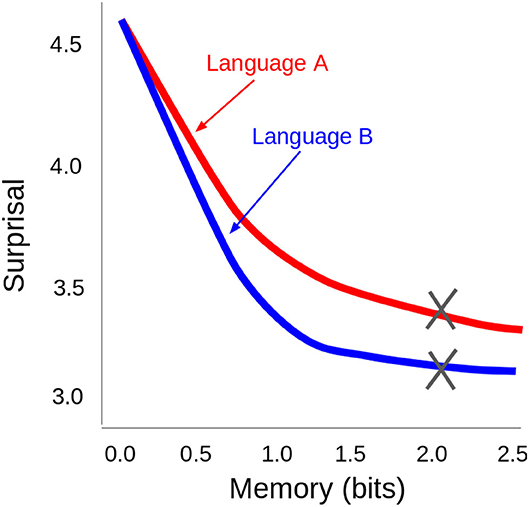
Figure 1. Example memory–surprisal trade-off curves for two possible languages, A and B. While storing 2.0 bits in memory in language A, it is possible to achieve an average surprisal of around 3.5 bits; but in language B, a lower average surprisal can be achieved at the same level of memory usage. Language B has a steeper memory–surprisal trade-off than Language A, so it requires less memory resources to achieve the same level of surprisal. Figure from Hahn et al. (2021).
In Hahn et al. (2021), it is shown that languages allow for more favorable memory–surprisal trade-offs when they have a statistical property called information locality: that is, when parts of an utterance which predict each other strongly are close to each other in time. More formally, we can define a quantity IT which is the average mutual information between words separated by a distance of T words, conditional on the intervening words:
Thus I1 indicates the mutual information between adjacent words, i.e., the amount of information in a word that can be predicted based on the immediately preceding word. Similarly, the quantity I2 indicates the mutual information between two words with one word intervening between them, etc. The curve of IT as a function of T is a statistical property of a language. Information locality means that IT falls off relatively rapidly, thus concentrating information in time12. Such languages allow words to be predicted based on only small amounts of information stored about past contexts, thus optimizing the memory–surprisal trade-off. The complete argument for this connection, as given in Hahn et al. (2021), is fully information-theoretic and independent of assumptions about memory architecture.
Information locality implies that parts of an utterance that have high mutual information with each other should be close together in time. There is one remaining logical step required to link the idea with the locality properties discussed above: it must be shown that contiguity of morphemes, morpheme order, and dependency locality correspond to placing utterance elements with high mutual information close to each other. Below, we will take these in turn, starting with dependency locality.
4.2.1. Dependency Locality
Dependency locality reduces to a special case of information locality under the assumption that syntactic dependencies identify word pairs with especially high mutual information. This is a reasonable assumption a priori: syntactically dependent words are those pairs of words whose covariance is constrained by grammar, which means information-theoretically that they predict one another. The connection between mutual information and syntactic dependency is, in fact, implicit in almost all work on unsupervised grammar induction and on probabilistic models of syntax (Eisner, 1996; Klein and Manning, 2004; Clark and Fijalkow, 2020). Empirical evidence for this connection, dubbed the HDMI Hypothesis, is given by Futrell and Levy (2017) and Futrell et al. (2019).
Information locality goes further than dependency locality, predicting that words will be under a stronger pressure to be close when they have higher mutual information. That is, dependency locality effects should be modulated by the actual mutual information of the words in the relevant dependencies. Futrell (2019) confirms that this is the case by finding a negative correlation of pointwise mutual information and dependency length across Universal Dependencies corpora of 54 languages. Futrell et al. (2020a) demonstrate that information locality in this sense provides a strong predictor of adjective order in English, and Sharma et al. (2020) show that it can predict the order of preverbal dependents in Hindi. The modulation of dependency locality by mutual information might explain why, although there exists a consistent overall tendency toward dependency length minimization across languages, the effect seems to vary based on the particular constructions involved (Gulordava et al., 2015; Liu, 2020).
4.2.2. Morpheme Order
The memory–surprisal trade-off and information locality apply at all timescales, not only to words. We should therefore be able to predict the order of morphemes within words by optimization of the memory–surprisal trade-off. Indeed, Hahn et al. (2021) find that morpheme order in Japanese and Sesotho can be predicted with high accuracy by optimization of the memory–surprisal trade-off. The ideas of “relevance” and “mental closeness” which have been used in the functional linguistics literature (Behaghel, 1932; Bybee, 1985; Givón, 1985) are cashed out as mutual information.
4.2.3. Morpheme and Word Contiguity
If we want to explain the tendency toward contiguity of morphemes using information locality, then we need to establish that morphemes have more internal mutual information among their parts than external mutual information with other morphemes. In fact, it is exactly this statistical property of morphemes that underlies segmentation algorithms that identify morphemes and words in a speech stream. In both human infants and computers, the speech stream (a sequence of sounds) is segmented into morphemes by looking for low-probability sound transitions (Saffran et al., 1996; Frank et al., 2010). Within a morpheme, the next sound is typically highly predictable from the previous sounds—meaning that there is high mutual information among the sounds within a morpheme. At a morpheme boundary, on the other hand, the transition from one sound to the next is less predictable, indicating lower mutual information. This connection between morpheme segmentation, transitional probabilities, and mutual information goes back at least to Harris (1955). Since morphemes have high internal mutual information among their sounds, the principle of information locality predicts that those sounds will be under a pressure to be close to each other, and this is best accomplished if they are contiguous.
At the level of words, we note that words have more internal mutual information among their parts than phrases (Mansfield, 2021). Thus, information locality can explain the fact that words are typically more contiguous than phrases.
4.3. Objective Function
The memory–surprisal trade-off synthesizes two notions of complexity in language processing: surprisal and memory usage. Surprisal is quantified as the conditional entropy H[Wt|Mt] of words given memory states, while memory usage is quantified using the entropy of memory states H[Mt]. These two quantities can be combined into a single expression for processing complexity by taking a weighted sum:
where α and β are non-negative scalars that indicate how much a bit of memory entropy should be weighted relative to a bit of surprisal in the calculation of complexity. The values of α and β are a property of the human language processing system, possibly varying from person to person, indicating how much memory usage a person is willing to tolerate per bit of surprisal reduced per word. When languages have information locality, then they enable lower values of Equation (14) to be achieved across all values of α and β. Therefore, languages that optimize the memory–surprisal trade-off described above can be seen as minimizing Equation (14).
The memory–surprisal trade-off as described by Equation (14) has been seen before in the literature on general complexity, although its application to language is recent. It is fundamentally a form of the Predictive Information Bottleneck (PIB) described by Still (2014), which has been applied directly to natural language based on text data by Hahn and Futrell (2019).
We have argued that when we consider codes which are constrained to be simple in the sense of the PIB, then those codes have properties such as information locality. It is therefore possible that some of the most basic properties of human language result from the fact that human language is constrained to have low complexity in a fundamental statistical sense, which also corresponds to empirically strong theories of online processing difficulty from the field of psycholinguistics.
In Section 3, we considered minimal-length codes as codes which maximize information transfer while minimizing average code length. Our proposal is that human language is a code which maximizes information transfer while minimizing not code length, but rather the notion of complexity in Equation (14). Thus, we have motivated an objective function for natural language of the form
with α and β positive scalar parameters determined by the human language processing system. This derives from using the memory–surprisal trade-off as the cost function in Equation (7). We have shown that codes which minimize the objective (15) have locality properties like natural language, via the notion of information locality.
There are still many well-documented core design features of language which have not yet been explained within this framework. Most notably, the core property of systematicity has not been shown to follow from Equation (14): what has been argued is that if a code is systematic, and it follows Equation (14), then that code will follow Behaghel's Principle, with contiguity of morphemes, relevance-based morpheme ordering, and dependency locality. A key outstanding question is whether systematicity itself also follows from this objective, or whether other terms must be added, for example terms enforcing intrinsic simplicity of the grammar.
In general, our hope is that it is possible to explain the properties of human language by defining an objective of the general form of Equation (15), in which each term is motivated functionally based on either a priori or experimental grounds, such that the solutions of the objective correspond to descriptions of possible human languages. We believe we have motivated at least the terms in Equation (15), but it is almost certain that further terms would be required in a full theory of language. The result would be a fully formal and also functional theory of human language, capable of handling both hard and soft constraints.
5. Conclusion
We conclude with some points about the motivation for the study of complexity and the role of information theory in such endeavors.
1. The study of complexity need not be an end unto itself. As we have shown, once a notion of complexity is defined, then it is possible to study the properties of codes which minimize that notion of complexity. In Section 3, we showed that MaxEnt grammars and the Rational Speech Acts model of pragmatics can be derived by minimizing generic complexity functions. In Section 4, we defined complexity in terms of a trade-off of memory and surprisal, and found that codes which minimize that notion of complexity have a property called information locality. The functional description of complexity (memory–surprisal trade-off) led to a formal description of a key property of language (information locality).
2. Information theory can provide notions of complexity that are objective and theory-neutral by quantifying intrinsic lower bounds on resource requirements for transforming or storing information. For example, surprisal measures an intrinsic lower bound on resource usage by a mechanism which extracts information from the linguistic signal.
3. The theory-neutral nature of information theory comes with two major costs: (1) by quantifying only a lower bound on complexity, it misses possible components of complexity that might exist on top of those bounds, and (2) information-theoretic measures are only truly theory-neutral when the relevant probability distributions are known or can be estimated independently. For example, in the case of predicting online comprehension difficulty, the relevant probability distribution is the probability distribution on words given contexts, which can be estimated from corpora or Cloze studies (e.g., as in Wilcox et al., 2020). On the other hand, if the relevant probability distribution is not independently known, then the choice of probability distribution is not theory-neutral. For example, the complexity of a grammar, as selected from a probability distribution on possible grammars, will depend on how precisely that probability distribution on grammars is defined—hardly a theory-neutral question.
With these points in mind, the great promise of information theory is that it can open a theoretical nexus between linguistics and other fields. Across fields with relevance to human language, information theory has been used to study fundamental notions of complexity and efficiency, including cognitive science and neuroscience (e.g., Friston, 2010; Fan, 2014; Sims, 2018; Zénon et al., 2019), statistical learning (e.g., MacKay, 2003), and biology (e.g., Adami, 2004, 2011; Frank, 2012). When a theory of human language is developed in the mathematical language of information theory, as in the examples above, then all the results from these other fields will become legible to linguistics, and the results of linguistics and language science can become immediately useful in these other fields as well.
Author Contributions
RF and MH wrote the manuscript. Both authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^Information content in bits is given using logarithms taken to base 2. Henceforward, all logarithms in this paper will be assumed to be taken to base 2.
2. ^In fact, there are conditions under which these problems are exactly equivalent. This observation forms the basis of the principle of Minimum Description Length (Grünwald, 2007).
3. ^There have been attempts to develop a version of information theory that does not depend on probabilities, where the complexity of an object is a function only of the intrinsic properties of the object and not the probability distribution it is drawn from. This is the field of Algorithmic Information Theory, and the relevant notion of complexity is Kolmogorov complexity (Li and Vitányi, 2008). The Kolmogorov complexity of an object x, denoted K(x), is the description length of x in the so-called “universal” language. Given any particular Turing-complete description language L, the description length of x in L differs from the Kolmogorov complexity K(x) only at most by a constant factor KL which is a function of L, not of x. While Kolmogorov complexity is well-defined and can be used productively in mathematical arguments about language (see for example Chater and Vitányi, 2007; Piantadosi and Fedorenko, 2017), the actual number K(x) is uncomputable in general.
4. ^In keeping with representation invariance, the actual representational format of the memory trace mt does not matter in this theory—it could be a structured symbolic object, or a point in high dimensional space, or the state of an associative store, etc. All that matters is what information it contains.
5. ^This is the Kraft Inequality; when the Kraft Inequality holds for a given set of signal lengths, then a self-delimiting code with those signal lengths exists (Cover and Thomas, 2006, Theorem 5.2.1).
6. ^We note that the optimization problem (6) cannot be solved in this way, due to the constraint of self-delimitation.
7. ^For a derivation, see Zaslavsky et al. (2020), Proposition 1. More generally, any probability distribution of the form
can be derived as a minimum of the objective
i.e., maximizing entropy subject to a constraint on the average value of C(x). This insight forms the basis of the Maximum Entropy approach to statistical inference (Jaynes, 2003)—probability distributions are derived by maximizing uncertainty (i.e., entropy) subject to constraints [i.e., C(x)]. For example, a Gaussian distribution is the result of maximizing entropy subject to fixed values of mean and variance.
8. ^The idea that possible languages should correspond to solutions of an objective function is still somewhat imprecise, because a number of different solution concepts are possible. Languages might correspond to local minima of the function, or to stationary points, or stable recurrent states, etc. The right solution concept will depend on the ultimate form of the objective function.
9. ^See for example, Strouse and Schwab (2017) who study codes that are constrained to be deterministic by adding an effectively infinitely-weighted constraint against nondeterminism in the distribution P(s|m).
10. ^Spreading information out in time in this way is only one aspect of robustness, corresponding to one particular kind of noise that might affect a signal. Language users may also implement ‘information management’ strategies such as placing high-information parts of an utterance at regular rhythmic intervals in time, lowering the information rate for faster speech (Cohen Priva, 2017), or using special focusing constructions to signal upcoming areas of high information density (Futrell, 2012; Rohde et al., 2021). The distribution of information may also be aligned with neural oscillations to facilitate language processing (Ghitza and Greenberg, 2009; Giraud and Poeppel, 2012).
11. ^In the field of natural language processing, language models are derived by finding distributions on Wt and Mt to minimize Equation (11), called “language modeling loss” in that field. The quality of language models is measured using the quantity perplexity, which is simply . The current state-of-the-art models achieve perplexity of around 20 on Penn Treebank data, corresponding to a conditional entropy of around 4.3 bits per word (Brown et al., 2020). These models are capable of generating connected paragraphs of grammatical text, having been trained solely by minimization of the objective function in Equation (11) as applied to large amounts of text data.
12. ^We can estimate values of IT for increasing T from corpora, and we find that IT generally decreases as T increases: that is, words that are close to each other contain more predictive information about each other, moreso in real natural language than in random baseline grammars (Hahn et al., 2021). Relatedly, the results of Takahira et al. (2016) imply that IT falls off as a power law, a manifestation of the Relaxed Hilberg Conjecture (Dębowski, 2011, 2018).
References
Adami, C. (2004). Information theory in molecular biology. Phys. Life Rev. 1, 3–22. doi: 10.1016/j.plrev.2004.01.002
Adami, C. (2011). The use of information theory in evolutionary biology. arXiv [Preprint] arXiv: 1112.3867. doi: 10.1111/j.1749-6632.2011.06422.x
Aurnhammer, C., and Frank, S. L. (2019). Evaluating information-theoretic measures of word prediction in naturalistic sentence reading. Neuropsychologia 134:107198. doi: 10.1016/j.neuropsychologia.2019.107198
Aylett, M., and Turk, A. (2004). The smooth signal redundancy hypothesis: a functional explanation for relationships between redundancy, prosodic prominence, and duration in spontaneous speech. Lang. Speech 47, 31–56. doi: 10.1177/00238309040470010201
Barrett, J. A., Cochran, C., and Skyrms, B. (2020). On the evolution of compositional language. Philos. Sci. 87, 910–920. doi: 10.1086/710367
Behaghel, O. (1932). Deutsche Syntax: Eine Geschichtliche Darstellung. Band IV: Wortstellung. Heidelberg: Carl Winter.
Bergen, B. K. (2004). The psychological reality of phonaesthemes. Language 80, 290–311. doi: 10.1353/lan.2004.0056
Boston, M. F., Hale, J. T., Vasishth, S., and Kliegl, R. (2011). Parallel processing and sentence comprehension difficulty. Lang. Cogn. Process. 26, 301–349. doi: 10.1080/01690965.2010.492228
Bresnan, J., Dingare, S., and Manning, C. D. (2001). “Soft constraints mirror hard constraints: voice and person in English and Lummi,” in Proceedings of the LFG 01 Conference (CSLI Publications), 13–32.
Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., et al. (2020). Language models are few-shot learners. arXiv [Preprint] arXiv:2005.14165.
Bybee, J. L. (1985). Morphology: A Study of the Relation Between Meaning and Form. Amsterdam: John Benjamins. doi: 10.1075/tsl.9
Chalk, M., Marre, O., and Tkačik, G. (2018). Toward a unified theory of efficient, predictive, and sparse coding. Proc. Natl. Acad. Sci. U.S.A. 115, 186–191. doi: 10.1073/pnas.1711114115
Chater, N., and Vitányi, P. (2007). 'Ideal learning' of natural language: positive results about learning from positive evidence. J. Math. Psychol. 51, 135–163. doi: 10.1016/j.jmp.2006.10.002
Clark, A., and Fijalkow, N. (2020). Consistent unsupervised estimators for anchored PCFGs. Trans. Assoc. Comput. Linguist. 8, 409–422. doi: 10.1162/tacl_a_00323
Cohen Priva, U. (2012). Sign and signal: deriving linguistic generalizations from information utility (Ph.D. thesis). Stanford University, Stanford, CA, United States.
Cohen Priva, U. (2017). Not so fast: fast speech correlates with lower lexical and structural information. Cognition 160, 27–34. doi: 10.1016/j.cognition.2016.12.002
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C. (2009). Introduction to Algorithms. Cambridge, MA: MIT Press.
Cover, T. M., and Thomas, J. A. (2006). Elements of Information Theory. Hoboken, NJ: John Wiley & Sons.
Culbertson, J., and Adger, D. (2014). Language learners privilege structured meaning over surface frequency. Proc. Natl. Acad. Sci. U.S.A. 111, 5842–5847. doi: 10.1073/pnas.1320525111
Dębowski, Ł. (2011). Excess entropy in natural language: present state and perspectives. Chaos 21:037105. doi: 10.1063/1.3630929
Dębowski, Ł. (2018). Is natural language a perigraphic process? The theorem about facts and words revisited. Entropy 20, 85–111. doi: 10.3390/e20020085
Demberg, V., and Keller, F. (2008). Data from eye-tracking corpora as evidence for theories of syntactic processing complexity. Cognition 109, 193–210. doi: 10.1016/j.cognition.2008.07.008
Dryer, M. S. (1992). The Greenbergian word order correlations. Language 68, 81–138. doi: 10.1353/lan.1992.0028
Dye, M., Milin, P., Futrell, R., and Ramscar, M. (2017). “A functional theory of gender paradigms,” in Morphological Paradigms and Functions, eds F. Kiefer, J. P. Blevins, and H. Bartos (Leiden: Brill), 212–239. doi: 10.1163/9789004342934_011
Eisner, J. M. (1996). “Three new probabilistic models for dependency parsing: an exploration,” in Proceedings of the 16th Conference on Computational Linguistics and Speech Processing (Taipei), 340–345. doi: 10.3115/992628.992688
Fan, J. (2014). An information theory account of cognitive control. Front. Hum. Neurosci. 8:680. doi: 10.3389/fnhum.2014.00680
Ferrer i Cancho, R. (2004). Euclidean distance between syntactically linked words. Phys. Rev. E 70:056135. doi: 10.1103/PhysRevE.70.056135
Ferrer i Cancho, R., and Díaz-Guilera, A. (2007). The global minima of the communicative energy of natural communication systems. J. Stat. Mech. 2007:P06009. doi: 10.1088/1742-5468/2007/06/P06009
Ferrer i Cancho, R., and Solé, R. V. (2003). Least effort and the origins of scaling in human language. Proc. Natl. Acad. Sci. U.S.A. 100:788. doi: 10.1073/pnas.0335980100
Ford, L. R. Jr, and Johnson, S. M. (1959). A tournament problem. Am. Math. Month. 66, 387–389. doi: 10.1080/00029890.1959.11989306
Frank, M. C., Goldwater, S., Griffiths, T., and Tenenbaum, J. (2010). Modeling human performance in statistical word segmentation. Cognition 117, 107–125. doi: 10.1016/j.cognition.2010.07.005
Frank, M. C., and Goodman, N. D. (2012). Quantifying pragmatic inference in language games. Science 336:1218633. doi: 10.1126/science.1218633
Frank, S. A. (2012). Natural selection. V. How to read the fundamental equations of evolutionary change in terms of information theory. J. Evol. Biol. 25, 2377–2396. doi: 10.1111/jeb.12010
Frank, S. L., and Ernst, P. (2019). Judgements about double-embedded relative clauses differ between languages. Psychol. Res. 83, 1581–1593. doi: 10.1007/s00426-018-1014-7
Frank, S. L., Otten, L. J., Galli, G., and Vigliocco, G. (2015). The ERP response to the amount of information conveyed by words in sentences. Brain Lang. 140, 1–11. doi: 10.1016/j.bandl.2014.10.006
Frank, S. L., Trompenaars, T., Lewis, R. L., and Vasishth, S. (2016). Cross-linguistic differences in processing double-embedded relative clauses: working-memory constraints or language statistics? Cogn. Sci. 40, 554–578. doi: 10.1111/cogs.12247
Friston, K. (2010). The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11:127. doi: 10.1038/nrn2787
Futrell, R. (2010). German noun class as a nominal protection device (Senior thesis). Stanford University, Stanford, CA, United States.
Futrell, R. (2012). Processing effects of the expectation of informativity (Master's thesis). Stanford University, Stanford, CA, United States.
Futrell, R. (2019). “Information-theoretic locality properties of natural language,” in Proceedings of the First Workshop on Quantitative Syntax (Quasy, SyntaxFest 2019) (Paris: Association for Computational Linguistics), 2–15. doi: 10.18653/v1/W19-7902
Futrell, R., Dyer, W., and Scontras, G. (2020a). “What determines the order of adjectives in English? Comparing efficiency-based theories using dependency treebanks,” in Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (Association for Computational Linguistics), 2003–2012. doi: 10.18653/v1/2020.acl-main.181
Futrell, R., Gibson, E., and Levy, R. P. (2020b). Lossy-context surprisal: an information-theoretic model of memory effects in sentence processing. Cogn. Sci. 44:e12814. doi: 10.1111/cogs.12814
Futrell, R., and Levy, R. (2017). “Noisy-context surprisal as a human sentence processing cost model,” in Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics: Volume 1, Long Papers (Valencia: Association for Computational Linguistics), 688–698. doi: 10.18653/v1/E17-1065
Futrell, R., Levy, R. P., and Gibson, E. (2020c). Dependency locality as an explanatory principle for word order. Language 96, 371–413. doi: 10.1353/lan.2020.0024
Futrell, R., Mahowald, K., and Gibson, E. (2015). Large-scale evidence of dependency length minimization in 37 languages. Proc. Natl. Acad. Sci. U.S.A. 112, 10336–10341. doi: 10.1073/pnas.1502134112
Futrell, R., Qian, P., Gibson, E., Fedorenko, E., and Blank, I. (2019). “Syntactic dependencies correspond to word pairs with high mutual information,” in Proceedings of the Fifth International Conference on Dependency Linguistics (Depling, SyntaxFest 2019) (Paris: Association for Computational Linguistics), 3–13. doi: 10.18653/v1/W19-7703
Gabelentz, G. v. d. (1901 [1891]). Die Sprachwissenschaft, ihre Aufgaben, Methoden, und bisherigen Ergebnisse, 2nd Edn. Leipzig: C. H. Tauchnitz.
Ghitza, O., and Greenberg, S. (2009). On the possible role of brain rhythms in speech perception: intelligibility of time-compressed speech with periodic and aperiodic insertions of silence. Phonetica 66, 113–126. doi: 10.1159/000208934
Gibson, E. (1998). Linguistic complexity: locality of syntactic dependencies. Cognition 68, 1–76. doi: 10.1016/S0010-0277(98)00034-1
Gibson, E. (2000). “The dependency locality theory: a distance-based theory of linguistic complexity,” in Image, Language, Brain: Papers from the First Mind Articulation Project Symposium, eds A. Marantz, Y. Miyashita, and W. O'Neil (Cambridge, MA: MIT Press), 95–126.
Gibson, E., Futrell, R., Piantadosi, S. T., Dautriche, I., Mahowald, K., Bergen, L., et al. (2019). How efficiency shapes human language. Trends Cogn. Sci. 23, 389–407. doi: 10.1016/j.tics.2019.02.003
Gibson, E., and Thomas, J. (1999). Memory limitations and structural forgetting: the perception of complex ungrammatical sentences as grammatical. Lang. Cogn. Process. 14, 225–248. doi: 10.1080/016909699386293
Gildea, D., and Temperley, D. (2010). Do grammars minimize dependency length? Cogn. Sci. 34, 286–310. doi: 10.1111/j.1551-6709.2009.01073.x
Giraud, A.-L., and Poeppel, D. (2012). Cortical oscillations and speech processing: emerging computational principles and operations. Nat. Neurosci. 15, 511–517. doi: 10.1038/nn.3063
Givón, T. (1985). “Iconicity, isomorphism and non-arbitrary coding in syntax,” in Iconicity in Syntax, ed J. Haiman (Amsterdam: John Benjamins), 187–220. doi: 10.1075/tsl.6.10giv
Givón, T. (1991). Isomorphism in the grammatical code: cognitive and biological considerations. Stud. Lang. 15, 85–114. doi: 10.1075/sl.15.1.04giv
Goldberg, Y. (2017). Neural Network Methods for Natural Language Processing, Vol. 37 of Synthesis Lectures on Human Language Technologies. San Rafael, CA: Morgan & Claypool. doi: 10.2200/S00762ED1V01Y201703HLT037
Goldwater, S., and Johnson, M. (2003). “Learning OT constraint rankings using a maximum entropy model,” in Proceedings of the Stockholm Workshop on Variation Within Optimality Theory (Stockholm), 111–120.
Goodman, N. D., and Frank, M. C. (2016). Pragmatic language interpretation as probabilistic inference. Trends Cogn. Sci. 20, 818–829. doi: 10.1016/j.tics.2016.08.005
Goodman, N. D., and Stuhlmüller, A. (2013). Knowledge and implicature: modeling language understanding as social cognition. Top. Cogn. Sci. 5, 173–184. doi: 10.1111/tops.12007
Gottwald, S., and Braun, D. A. (2019). Bounded rational decision-making from elementary computations that reduce uncertainty. Entropy 21:375. doi: 10.3390/e21040375
Greenberg, J. H. (1963). “Some universals of grammar with particular reference to the order of meaningful elements,” in Universals of Language, ed J. H. Greenberg (Cambridge, MA: MIT Press), 73–113.
Grünwald, P. D. (2007). The Minimum Description Length Principle. Cambridge, MA: MIT Press. doi: 10.7551/mitpress/4643.001.0001
Gulordava, K., Merlo, P., and Crabbé, B. (2015). “Dependency length minimisation effects in short spans: a large-scale analysis of adjective placement in complex noun phrases,” in Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 2: Short Papers) (Uppsala), 477–482. doi: 10.3115/v1/P15-2078
Hahn, M., Degen, J., and Futrell, R. (2021). Modeling word and morpheme order in natural language as an efficient tradeoff of memory and surprisal. Psychol. Rev. 128, 726–756. doi: 10.1037/rev0000269
Hahn, M., and Futrell, R. (2019). Estimating predictive rate-distortion curves using neural variational inference. Entropy 21:640. doi: 10.3390/e21070640
Hahn, M., Futrell, R., and Gibson, E. (2020a). “Lexical effects in structural forgetting: evidence for experience-based accounts and a neural network model,” in Talk Presented at the 33rd Annual CUNY Human Sentence Processing Conference.
Hahn, M., Jurafsky, D., and Futrell, R. (2020b). Universals of word order reflect optimization of grammars for efficient communication. Proc. Natl. Acad. Sci. U.S.A. 117, 2347–2353. doi: 10.1073/pnas.1910923117
Hale, J. T. (2001). “A probabilistic Earley parser as a psycholinguistic model,” in Proceedings of the Second Meeting of the North American Chapter of the Association for Computational Linguistics and Language Technologies (Pittsburgh, PA), 1–8. doi: 10.3115/1073336.1073357
Haspelmath, M. (2008). “Parametric versus functional explanations of syntactic universals,” in The Limits of Syntactic Variation, ed T. Biberauer (Amsterdam: John Benjamins), 75–107. doi: 10.1075/la.132.04has
Hawkins, J. A. (1994). A Performance Theory of Order and Constituency. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511554285
Hawkins, J. A. (2004). Efficiency and Complexity in Grammars. Oxford: Oxford University Press. doi: 10.1093/acprof:oso/9780199252695.001.0001
Hawkins, J. A. (2014). Cross-linguistic variation and efficiency. Oxford: Oxford University Press. doi: 10.1093/acprof:oso/9780199664993.001.0001
Hayes, B., and Wilson, C. (2008). A maximum entropy model of phonotactics and phonotactic learning. Linguist. Inq. 39, 379–440. doi: 10.1162/ling.2008.39.3.379
Jackendoff, R. (2002). Foundations of Language: Brain, Meaning, Grammar, Evolution. Oxford: Oxford University Press.
Jaeger, T. F. (2010). Redundancy and reduction: speakers manage syntactic information density. Cogn. Psychol. 61, 23–62. doi: 10.1016/j.cogpsych.2010.02.002
Jäger, G. (2007). “Maximum entropy models and stochastic optimality theory,” in Architectures, Rules, and Preferences: A Festschrift for Joan Bresnan eds A. Zaenen, J. Simpson, T. H. King, J. Grimshaw, J. Making, and C. Manning (Stanford, CA: CSLI), 467–479.
James, R. G., and Crutchfield, J. P. (2017). Multivariate dependence beyond Shannon information. Entropy 19:531. doi: 10.3390/e19100531
Jaynes, E. (2003). Probability Theory: The Logic of Science. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511790423
Johnson, M. (2002). “Optimality-theoretic lexical functional grammar,” in The Lexical Basis of Sentence Processing: Formal, Computational and Experimental Issues, eds P. Merlo and S. Stevenson (Amsterdam: John Benjamins), 59–74. doi: 10.1075/nlp.4.04joh
Kanwal, J. K. (2018). Word length and the principle of least effort: language as an evolving, efficient code for information transfer (Ph.D. thesis). The University of Edinburgh, Edinburgh, United Kingdom.
Kay, J. W., and Phillips, W. (2011). Coherent infomax as a computational goal for neural systems. Bull. Math. Biol. 73, 344–372. doi: 10.1007/s11538-010-9564-x
Kirby, S., Tamariz, M., Cornish, H., and Smith, K. (2015). Compression and communication in the cultural evolution of linguistic structure. Cognition 141, 87–102. doi: 10.1016/j.cognition.2015.03.016
Kirchner, R. M. (1998). An effort-based approach to consonant lenition (Ph.D. thesis). University of California, Los Angeles, CA, United States.
Klein, D., and Manning, C. D. (2004). “Corpus-based induction of syntactic structure: Models of dependency and constituency,” in Proceedings of the 42nd Annual Meeting of the Association for Computational Linguistics (ACL-04) (Barcelona: Association for Computational Linguistics), 478–486. doi: 10.3115/1218955.1219016
Levy, R, and Jaeger, T. F. (2007). Speakers optimize information density through syntactic reduction. Adv. Neural Inform. Process. Syst. 19, 849–856.
Levy, R. (2008). Expectation-based syntactic comprehension. Cognition 106, 1126–1177. doi: 10.1016/j.cognition.2007.05.006
Levy, R. (2013). “Memory and surprisal in human sentence comprehension,” in Sentence Processing, ed R. P. G. van Gompel (Hove: Psychology Press), 78–114.
Li, M., and Vitányi, P. (2008). An Introduction to Kolmogorov Complexity and Its Applications. New York, NY: Springer-Verlag. doi: 10.1007/978-0-387-49820-1
Linsker, R. (1988). Self-organization in a perceptual network. IEEE Comput. 21, 105–117. doi: 10.1109/2.36
Liu, H. (2008). Dependency distance as a metric of language comprehension difficulty. J. Cogn. Sci. 9, 159–191. doi: 10.17791/jcs.2008.9.2.159
Liu, H., Xu, C., and Liang, J. (2017). Dependency distance: a new perspective on syntactic patterns in natural languages. Phys. Life Rev. 21, 171–193. doi: 10.1016/j.plrev.2017.03.002
Liu, Z. (2020). Mixed evidence for crosslinguistic dependency length minimization. STUF-Lang. Typol. Univ. 73, 605–633. doi: 10.1515/stuf-2020-1020
Luce, R. D. (2003). Whatever happened to information theory in psychology? Rev. Gen. Psychol. 7, 183–188. doi: 10.1037/1089-2680.7.2.183
MacKay, D. J. C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge: Cambridge University Press.
Mandelbrot, B. (1953). An informational theory of the statistical structure of language. Commun. Theory 84, 486–502.
Mansfield, J. (2021). The word as a unit of internal predictability. Linguistics 59, 1427–1472. doi: 10.1515/ling-2020-0118
Meister, C., Pimentel, T., Haller, P., JÃČÂd'ger, L., Cotterell, R., and Levy, R. P. (2021). “Revisiting the uniform information density hypothesis,” in Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing (Punta Cana), 963–980. doi: 10.18653/v1/2021.emnlp-main.74
Mollica, F., Bacon, G., Zaslavsky, N., Xu, Y., Regier, T., and Kemp, C. (2021). The forms and meanings of grammatical markers support efficient communication. Proc. Natl. Acad. Sci. U.S.A. 118:e2025993118. doi: 10.1073/pnas.2025993118
Monaghan, P., Shillcock, R. C., Christiansen, M. H., and Kirby, S. (2014). How arbitrary is language? Philos. Trans. R. Soc. B Biol. Sci. 369:20130299. doi: 10.1098/rstb.2013.0299
Moser, S. M., and Chen, P.-N. (2012). A Student's Guide to Coding and Information Theory. Cambridge: Cambridge University Press.
Nölle, J., Staib, M., Fusaroli, R., and Tylén, K. (2018). The emergence of systematicity: how environmental and communicative factors shape a novel communication system. Cognition 181, 93–104. doi: 10.1016/j.cognition.2018.08.014
Ortega, P. A., and Braun, D. A. (2013). Thermodynamics as a theory of decision-making with information-processing costs. Proc. R. Soc. A Math. Phys. Eng. Sci. 469:20120683. doi: 10.1098/rspa.2012.0683
Pate, J. (2017). “Optimization of American English, Spanish, and Mandarin Chinese over time for efficient communication,” in Proceedings of the 39th Annual Meeting of the Cognitive Science Society (London), 901–906.
Piantadosi, S. T. (2014). Zipf's word frequency law in natural language: a critical review and future directions. Psychon. Bull. Rev. 21, 1112–1130. doi: 10.3758/s13423-014-0585-6
Piantadosi, S. T., and Fedorenko, E. (2017). Infinitely productive language can arise from chance under communicative pressure. J. Lang. Evol. 2, 141–147. doi: 10.1093/jole/lzw013
Piantadosi, S. T., Tily, H., and Gibson, E. (2011). Word lengths are optimized for efficient communication. Proc. Natl. Acad. Sci. U.S.A. 108, 3526–3529. doi: 10.1073/pnas.1012551108
Pimentel, T., McCarthy, A. D., Blasi, D., Roark, B., and Cotterell, R. (2019). “Meaning to form: measuring systematicity as information,” in Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics (Florence: Association for Computational Linguistics), 1751–1764. doi: 10.18653/v1/P19-1171
Pimentel, T., Nikkarinen, I., Mahowald, K., Cotterell, R., and Blasi, D. (2021). “How (non-)optimal is the lexicon?,” in Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (Mexico City: Association for Computational Linguistics). doi: 10.18653/v1/2021.naacl-main.350
Pimentel, T., Valvoda, J., Hall Maudslay, R., Zmigrod, R., Williams, A., and Cotterell, R. (2020). “Information-theoretic probing for linguistic structure,” in Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (Association for Computational Linguistics), 4609–4622. doi: 10.18653/v1/2020.acl-main.420
Rijkhoff, J. (1986). Word order universals revisited: the principle of head proximity. Belgian J. Linguist. 1, 95–125. doi: 10.1075/bjl.1.05rij
Rijkhoff, J. (1990). Explaining word order in the noun phrase. Linguistics 28, 5–42. doi: 10.1515/ling.1990.28.1.5
Rohde, H., Futrell, R., and Lucas, C. G. (2021). What's new? A comprehension bias in favor of informativity. Cognition 209:104491. doi: 10.1016/j.cognition.2020.104491
Saffran, J. R., Aslin, R. N., and Newport, E. L. (1996). Statistical learning by 8-month-old infants. Science 274, 1926–1928. doi: 10.1126/science.274.5294.1926
Shain, C. (2019). “A large-scale study of the effects of word frequency and predictability in naturalistic reading,” in Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers) (Minneapolis, MN: Association for Computational Linguistics), 4086–4094.
Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27, 623–656. doi: 10.1002/j.1538-7305.1948.tb00917.x
Sharma, K., Futrell, R., and Husain, S. (2020). “What determines the order of verbal dependents in Hindi? Effects of efficiency in comprehension and production,” in Proceedings of the Workshop on Cognitive Modeling and Computational Linguistics (Association for Computational Linguistics), 1–10. doi: 10.18653/v1/2020.cmcl-1.1
Sims, C. R. (2018). Efficient coding explains the universal law of generalization in human perception. Science 360, 652–656. doi: 10.1126/science.aaq1118
Smith, K., Brighton, H., and Kirby, S. (2003). Complex systems in language evolution: the cultural emergence of compositional structure. Adv. Complex Syst. 6, 537–558. doi: 10.1142/S0219525903001055
Smith, N. J., and Levy, R. (2013). The effect of word predictability on reading time is logarithmic. Cognition 128, 302–319. doi: 10.1016/j.cognition.2013.02.013
Still, S. (2014). Information bottleneck approach to predictive inference. Entropy 16, 968–989. doi: 10.3390/e16020968
Strouse, D., and Schwab, D. J. (2017). The deterministic information bottleneck. Neural Comput. 29, 1611–1630. doi: 10.1162/NECO_a_00961
Takahira, R., Tanaka-Ishii, K., and Dȩbowski, Ł. (2016). Entropy rate estimates for natural language—a new extrapolation of compressed large-scale corpora. Entropy 18:364. doi: 10.3390/e18100364
Temperley, D., and Gildea, D. (2018). Minimizing syntactic dependency lengths: typological/cognitive universal? Annu. Rev. Linguist. 4, 1–15. doi: 10.1146/annurev-linguistics-011817-045617
Tishby, N., Pereira, F. C., and Bialek, W. (1999). “The information bottleneck method,” in Proceedings of the 37th Annual Allerton Conference on Communication, Control, and Computing, 368–377.
van Schijndel, M., and Linzen, T. (2018). “Modeling garden path effects without explicit hierarchical syntax,” in Proceedings of the 40th Annual Meeting of the Cognitive Science Society (Madison, WI), 2603–2608.
van Schijndel, M., and Linzen, T. (2021). Single-stage prediction models do not explain the magnitude of syntactic disambiguation difficulty. Cogn. Sci. 45:e12988. doi: 10.1111/cogs.12988
Vasishth, S., Suckow, K., Lewis, R. L., and Kern, S. (2010). Short-term forgetting in sentence comprehension: crosslinguistic evidence from verb-final structures. Lang. Cogn. Process. 25, 533–567. doi: 10.1080/01690960903310587
Wilcox, E. G., Gauthier, J., Hu, J., Qian, P., and Levy, R. (2020). “On the predictive power of neural language models for human real-time comprehension behavior,” in Proceedings for the 42nd Annual Meeting of the Cognitive Science Society, 1707–1713.
Zaslavsky, N., Hu, J., and Levy, R. P. (2020). A Rat-Distortion view of human pragmatic reasoning. arXiv [Preprint] arXiv:2005.06641.
Zaslavsky, N., Kemp, C., Regier, T., and Tishby, N. (2018). Efficient compression in color naming and its evolution. Proc. Natl. Acad. Sci. U.S.A. 115, 7937–7942. doi: 10.1073/pnas.1800521115
Zaslavsky, N., Regier, T., Tishby, N., and Kemp, C. (2019). “Semantic categories of artifacts and animals reflect efficient coding,” in 41st Annual Conference of the Cognitive Science Society (Montreal), 1254–1260.
Zénon, A., Solopchuk, O., and Pezzulo, G. (2019). An information-theoretic perspective on the costs of cognition. Neuropsychologia 123, 5–18. doi: 10.1016/j.neuropsychologia.2018.09.013
Zipf, G. K. (1935). The Psycho-Biology of Language: An Introduction to Dynamic Philology. Boston, MA: Houghton-Mifflin.
Keywords: information theory, language, psycholinguistics, linguistic theory, complexity
Citation: Futrell R and Hahn M (2022) Information Theory as a Bridge Between Language Function and Language Form. Front. Commun. 7:657725. doi: 10.3389/fcomm.2022.657725
Received: 23 January 2021; Accepted: 21 February 2022;
Published: 11 May 2022.
Edited by:
Marcin Maria Kilarski, Adam Mickiewicz University, PolandReviewed by:
Vera Demberg, Saarland University, GermanyFrançois Pellegrino, Université de Lyon, France
Copyright © 2022 Futrell and Hahn. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Richard Futrell, cmZ1dHJlbGxAdWNpLmVkdQ==
 Richard Futrell
Richard Futrell Michael Hahn
Michael Hahn