Multimodality and disciplinary learning: the case of purposeful transformation in the sciences

Introduction: In this paper we discuss disciplinary learning and the roles that different modalities can play in the process. We first describe the extant research in the field of social semiotics with an emphasis on the functions of affordance and transduction in university science, before presenting the comparatively sparse research on transformation. Our goal is to identify whether the process of transformation, besides its previously described procedural functions, can have important meaning making functions as well.

Methods: Taking the discipline of cosmology as our point of reference, our data consist of four different forms of the mathematical rearrangement of the Friedmann equation, as observed in university lectures. We analyzed these forms for their meaning making functions using abductive reasoning and the framework of symbolic forms.

Results: We identify an important, hitherto undescribed type of meaning-making —purposeful transformation. We describe its key characteristics (narrowing down meaning potential, foreground-background movement and purposeful direction) and we provide a first definition.

Discussion: First, we discuss the implications of our findings on social semiotics theory, focusing on the notions of disciplinary and pedagogical affordance and the possibility of identifying purposeful transformations in other semiotic systems. Finally, we demonstrate its importance in the teaching and learning of natural sciences.

1 Introduction

This paper is framed within the field of social semiotics. We draw on Airey and Linder (2017: 95) who define social semiotics as “… the study of the development and reproduction of specialized systems of meaning making in particular sections of society.”¹ The particular section of society we are interested in are those involved in university science. Our aim is to better understand the roles of the specialized meaning-making systems developed by scientists in order to generate recommendations for teaching and learning science disciplines. Following the US National Research Council’s description of discipline-based education research, our ultimate goal is to “…understand the nature of expertise in a discipline” (2012: 9).

The transition from novice to expert has been variously framed in terms of the development of: disciplinary literacy (e.g., Moje, 2007; Shanahan and Shanahan, 2012; Airey and Larsson, 2018), representational competence (e.g., Kozma and Russell, 2005; De Cock, 2012; Volkwyn et al., 2020), professional vision (e.g., Goodwin, 1994), or disciplinary discernment (e.g., Eriksson et al. 2014). A common denominator in each of these descriptions of acquiring disciplinary expertise is learning to interpret and use the specialized meaning-making resources of the discipline in order to either: see new things, or see old things in new ways. Thus, one important way of fostering disciplinary expertise is to help students to first experience new ideas/phenomena and then to encourage them to describe these using the paradigmatic resources of the discipline. It is here that variation theory can be gainfully leveraged.

The variation theory of learning claims that the human mind is hard-wired to notice change (Marton and Booth, 1997). In this respect, it has been shown that carefully changing aspects of an object of learning can help students notice pertinent features of that object (Ling Lo, 2012; Fredlund et al., 2015). Semiotically, it has been pointed out that there are two types of change that are possible: transformation and transduction (Bezemer and Kress, 2008). Transformation involves changes to the object of learning within the same semiotic system (mode), while transduction entails moving the object of learning to a new semiotic system. Of the two, transduction has been seen as the most useful for learning, due to the particular demands placed on an object of learning when moving between semiotic systems (Volkwyn et al., 2019). Consequently, there is much less research with transformation as its focus.

Particularly within mathematics and physics education, mathematical transformation (i.e., mathematical manipulation) has often been framed as a rule-based, mechanical process employed to reach a particular result, with little, if any meaning-making function (Duval, 2006; Tuminaro and Redish, 2007). In this paper we set out to demonstrate the value of transformation in science education, not simply as a method for numerical problem solving, but rather as a central aspect of the day-to-day reasoning of science professionals. We introduce the term purposeful transformation to describe a type of transformation that we have identified that is regularly used in meaning-making situations in the natural sciences. Using Sherin’s (2001) notion of symbolic forms, we analyze a chain of mathematical transformations, revealing the underlying mechanism of this reasoning process.

Finally, in the last sections of our paper, we explore what the notion of purposeful transformation might suggest for social semiotic theory and how it reframes several ideas around multimodal and monomodal approaches in physics education.

2 Multimodality and social semiotics

Science disciplines utilize a wide range of semiotic resources (graphs, language, diagrams, mathematics, etc.) when creating and communicating scientific knowledge (Kress et al., 2001b). Building on this central observation, Airey and Linder (2009) posited that there is always a critical constellation of semiotic resources or modes that is necessary for holistic representation of any given science concept (Figure 1). Their idea is that from an educational perspective it is necessary to orchestrate a specific set of resources belonging to different semiotic systems (modes) in a very specific way, in order to provide access to the various aspects of disciplinary knowledge that make up a given disciplinary concept. It follows then, that for someone to gain such holistic access to a particular disciplinary concept, it is crucial that they acquire some measure of “fluency” (Airey and Linder, 2017: 102) in each of the meaning-making systems that together constitute the critical constellation for that concept. By the same token, this also suggests that it is often impossible to holistically experience disciplinary knowledge by becoming fluent in one semiotic system alone (Airey and Linder, 2009).

Figure 1

Figure 1. A critical constellation of semiotic resources: a specific set of semiotic resources, coordinated in a particular manner is needed to gain holistic access to disciplinary knowledge [adapted from Airey and Linder (2009)]. The question mark illustrates the fact that we usually do not know what the full set of resources needed are.

Different disciplines place different emphases on semiotic systems. Thus, while a student of history could potentially gain a great deal of disciplinary knowledge by developing fluency in written language, it is impossible for a physicist to become an expert in their field through written language alone. Typically, a physics student needs to be fluent in disciplinary language, mathematics, graphs, diagrams and hands-on work with apparatus at the very least (Airey, 2009).

Within a scientific discipline, a variety of semiotic resources are used for different purposes. These could be for conducting scientific work and communication among disciplinary experts or for teaching relevant disciplinary concepts to students. It is important to note here, that the semiotic resources needed for students to learn often differ from the ones that are used by experts within the discipline. For example, for pragmatic reasons, experts tend to use resources that omit certain information. For educational purposes however, much of the omitted information needs to be present for a student to access disciplinary knowledge for the first time. Two main concepts have been used to describe this phenomenon: disciplinary and pedagogical affordance (Airey, 2015). Disciplinary affordance is used to indicate “the agreed meaning-making functions that a semiotic resource fulfils for a particular disciplinary community,” whereas pedagogical affordance is defined as “the aptness of a semiotic resource for the teaching and learning of some particular educational content” (Airey, 2015).

Evidently, from what we have described so far, the educational task of getting students to be able to “read” disciplinary representations in an expert manner becomes important. Disciplinary representations need to be unpacked so that students can access the full meaning that they entail (see for example, Airey and Eriksson, 2019; Patron et al., 2021). Unpacking can be also seen as increasing the pedagogical affordance of a semiotic resource, and that will almost certainly result in decreasing the disciplinary affordance (Airey and Linder, 2017) (see Figure 2). Along with unpacking, repacking semiotic resources is important for the teaching and learning of a discipline (Patron, 2022). Repacking in this sense does not just mean to once again present the students with the disciplinary semiotic resource after it has been unpacked. More so, it means that students need to be guided to “translate between unpacked representations and disciplinary representations that they need to […] understand and communicate in an […] appropriate disciplinary way” (Patron, 2022, p. 89). Note that the repacked resource regains its disciplinary affordance, but of necessity loses the pedagogical affordance that the unpacked resource had.

Figure 2

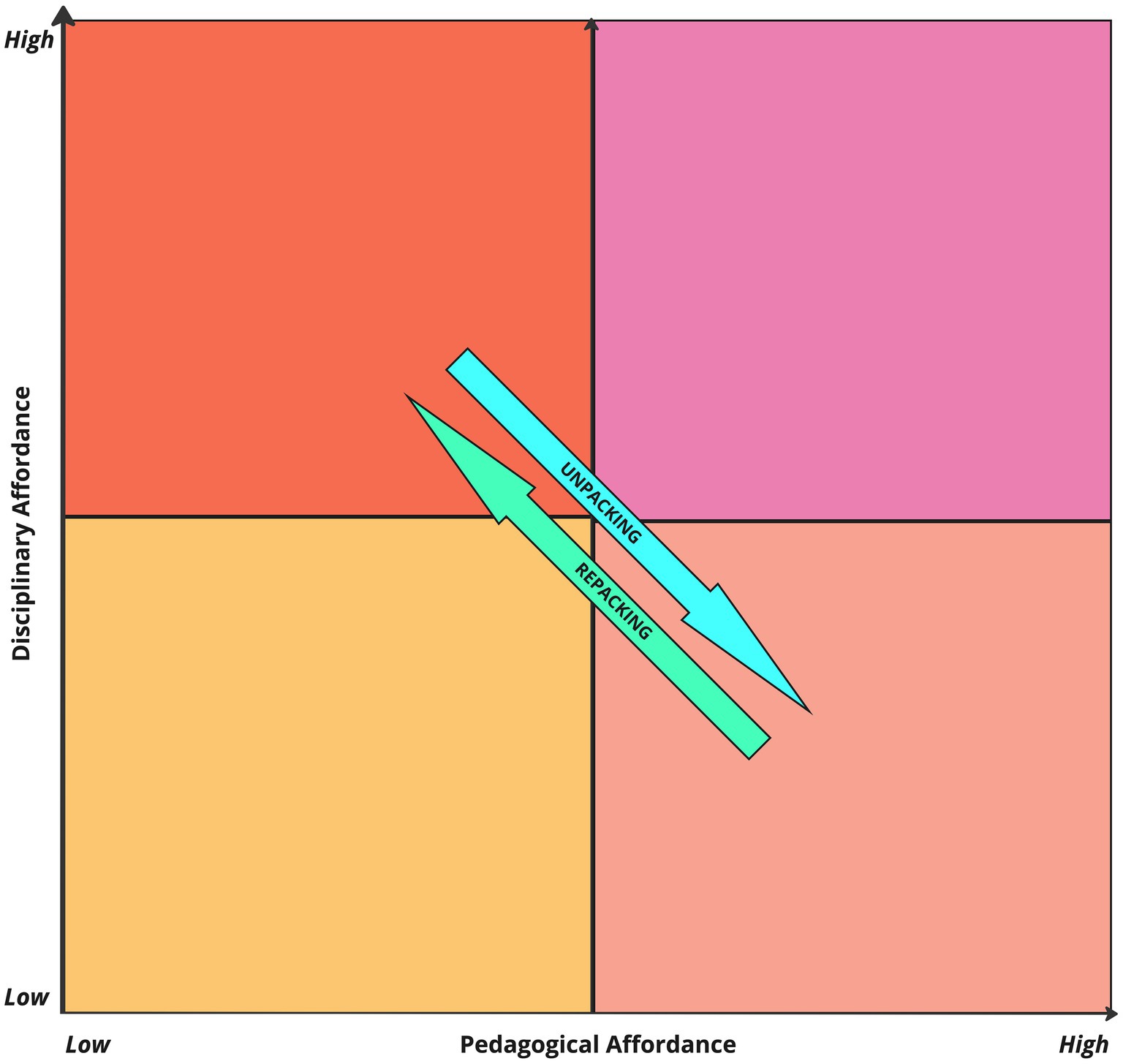
Figure 2. Disciplinary vs. pedagogical affordance (Airey and Eriksson, 2019): unpacking a semiotic resource means to raise its pedagogical but lower its disciplinary affordance. Repacking a semiotic resource leads to gaining back its disciplinary affordance, but simultaneously losing its pedagogical affordance.

2.1 Transduction as the key to multimodal learning

Based on these observations, the concept of transduction—the movement of the object of learning across different semiotic systems—has been claimed to be of the utmost importance for teaching and learning (Bezemer and Kress, 2008). This is because the differences in the affordances of the original and new semiotic systems necessitate that some aspects of the object of learning become “hidden” after transduction, whilst other aspects become foregrounded. Kress et al. (2001a,b) have further explored the idea that different semiotic systems have different affordances, or different ways of representing disciplinary knowledge. According to them, each semiotic system has its own potentials and limitations for representation. For example, language might be best at providing definitions or categorical distinctions. Images are better at contrasting and highlighting elements and identifying regions—something that language could prove to be limited in achieving.

Hence, a lot of attention has been focused on the act of moving meaning across semiotic systems (transduction). This comes with inevitable changes to the meaning being made, due to the different affordances of the semiotic systems used. A good illustration of this can be seen by considering a simple everyday phrase such as “The man moved out of the way” (Volkwyn et al., 2019). Using language as a semiotic system, this phrase allows ambiguity regarding the direction of the movement. However, if we transduce the meaning of this sentence to a sketch, then we would have to inevitably illustrate the direction of this movement, depicting whether the man moved forwards, backwards, left, right, etc.

Thus, it has been shown that carefully planned transduction can lead to students noticing new aspects of an object of learning (Volkwyn et al., 2020; Airey and Linder, 2017). Consequently, several researchers have highlighted the importance of transduction from a meaning-making perspective in teaching and learning contexts (Pantaleo, 2024; Svensson et al., 2022; Svensson and Eriksson, 2020; Tytler and Prain, 2022; Volkwyn et al., 2019, 2020).

In mathematics, for example, Duval (2006: 7) claims that “passing from one register to another [makes] explicit other properties or aspects of the same object.” For Duval, this means that when moving the object of learning across the different modes of representation (word problems, graphs, equations, etc.), different aspects of (mathematical) knowledge are made explicit, or, in meaning-making terms, different meaning potential becomes unlocked (Airey and Linder, 2017). Similarly, Volkwyn et al. (2019) highlighted the important role of transduction across semiotic systems in science teaching and learning. The authors showed how different meaning-making possibilities become available when students transduce disciplinary knowledge across different semiotic systems in a science classroom. A fundamental observation here was an end point, where students began performing spontaneous transductions of their own volition—this was seen as a sign of learning taking place (Volkwyn et al., 2019). In an even broader sense, the ability to transduce knowledge across semiotic systems is considered to be key for the goal of achieving representational competence (Volkwyn et al., 2020). This means that within a scientific discipline, representational competence is achieved in a twofold way. It can be seen as made up of the ability to fluently use and interpret resources that belong in different systems (i.e., graphs, diagrams, mathematics) accompanied by the ability to move meaning across different resources that highlight the same concepts (Volkwyn et al., 2020).

2.2 Transformation the poor relation of transduction?

In comparison to transduction, the process of transformation—manipulating a resource within the same semiotic system—has generally been viewed as having lesser importance for teaching and learning. For example, in work done in physics and mathematics, mathematical transformation has often been framed as a second order, rule-based system that should only be employed after one has reasoned conceptually about a problem, as a means to arrive at a numerical result (Duval, 2006; Tuminaro and Redish, 2007). This is because of the inherent differences between transduction and transformation (for a summary, see Table 1 below). While transduction of necessity always entails changes in an object of learning, similar changes through transformation are far from guaranteed. Educationally, this means that any change in an object of learning through transformation will probably need to be specifically engineered by the teacher in order to be effective.

Table 1

Table 1. Comparison between the processes of transduction and transformation.

Unsurprisingly, then, there is little work in the literature specifically dedicated to transformation and its functions. In mathematics, Duval (2006) has suggested that transformation (or treatment, as he calls it) fills an important disciplinary function when solving equations to arrive at numerical answers, although he suggests the process is not involved in meaning-making per-se. Duval claims that meaning is made during the two processes of transduction necessary for mathematical problem solving: firstly, when a mathematical word problem is transduced into the system of mathematics, and finally when a numerical answer has been found and its meaning is reinterpreted in the terms of the original word-based system. For Duval, then, the process of transformation—i.e. the mathematical manipulation necessary to achieve the final answer—is seen as a rule-based process that occurs quite separately from meaning-making. Similar ideas can be found in the physics education literature, in work that explores student use of mathematics in physics. For example, Tuminaro and Redish (2007) argued that physics students often resort to “plug and chug” when dealing with equations. The term “plug” refers to inserting numerical values into equations and “chug” refers to performing algorithmic transformations in order to get a numerical result. According to Tuminaro and Redish (2007), when students resort to “plug and chug,” they do not attempt to conceptually understand a physics concept or an equation—instead, they simply identify its symbol and the equation that relates that symbol to other known quantities, substitute in values and produce a numerical answer, often without an understanding of what that answer means. Airey and Linder (2017) also report instances where students suggest that although they can perform mathematical operations to calculate a specific concept (the curl of the electric field), they do not know what it actually means. Writing for physics teachers, de Winter suggests that it is important to stress for students that a number without units is meaningless. It is the process of adding units to a numerical answer that gives meaning to a number generated by the mathematics (de Winter and Airey, 2022).

To summarize, we believe that these authors all point towards the same idea: transformation is viewed as important when it comes to its technical disciplinary function (numerical computations, in this case), but it is not seen as particularly important when it comes to meaning-making functions for physics teaching and learning. Following this idea, we could argue that, since (as mentioned above) it is regarded as impossible to fully experience disciplinary knowledge in one semiotic system alone (Airey and Linder, 2009), then transformation should logically be seen as inherently less important than transduction in mathematics and physics education. This is also supported by the fact that while transduction has been quite well explored in a number of studies that analyze physics education with a social semiotics framework (Svensson et al., 2022; Svensson and Eriksson, 2020; Volkwyn et al., 2019, 2020), the concept of transformation remains underexplored.

2.3 Using mathematics in physics: the role of transformation

We believe that viewing transformation as less useful than transduction semiotically overlooks a number of specific functions that transformation plays in the creation and communication of disciplinary knowledge. Drawing from the same field of study (the use of mathematics in physics), we identify several works that highlight that the use of mathematics in physics fills other functions than simply calculating values—mathematics also plays a role in building physics intuition and engaging in meaning making (Redish, 2006, 2021). Redish (2006) points out that while we often consider mathematics to be the language of physics, there is a fundamental difference when using mathematics in mathematics and mathematics in physics; in physics, we want to not only calculate, but also to describe and understand physical systems. In other words, mathematics in physics is loaded with physical meaning, and that distinguishes the ways in which physicists engage with equations for the purposes of their scientific work. Building on this aspect, a number of researchers have explored the ways in which these two aspects of mathematics (computation and meaning making) coexist in physics, proposing models to describe how mathematics is used in physics to fulfill both of these functions (Redish, 2006; Uhden et al., 2012; Van Den Eynde et al., 2020). In this area, the seminal contribution comes from Sherin and his framework of symbolic forms (Sherin, 2001). According to Sherin, symbolic forms consist of a conceptual schema (idea or conceptual meaning) that is assigned to a mathematical symbol template, an arrangement of mathematical symbols that students identify when engaging with an equation and assign meaning to. Sherin proposed a semi-exhaustive list of symbolic forms that give insight into how students understand physics equations. In his own words, this is like “adding semantics to an equation” (Sherin, 2001, p. 504). Some examples from Sherin’s semi-exhaustive list of symbolic forms can be found in Table 2 above.

Table 2

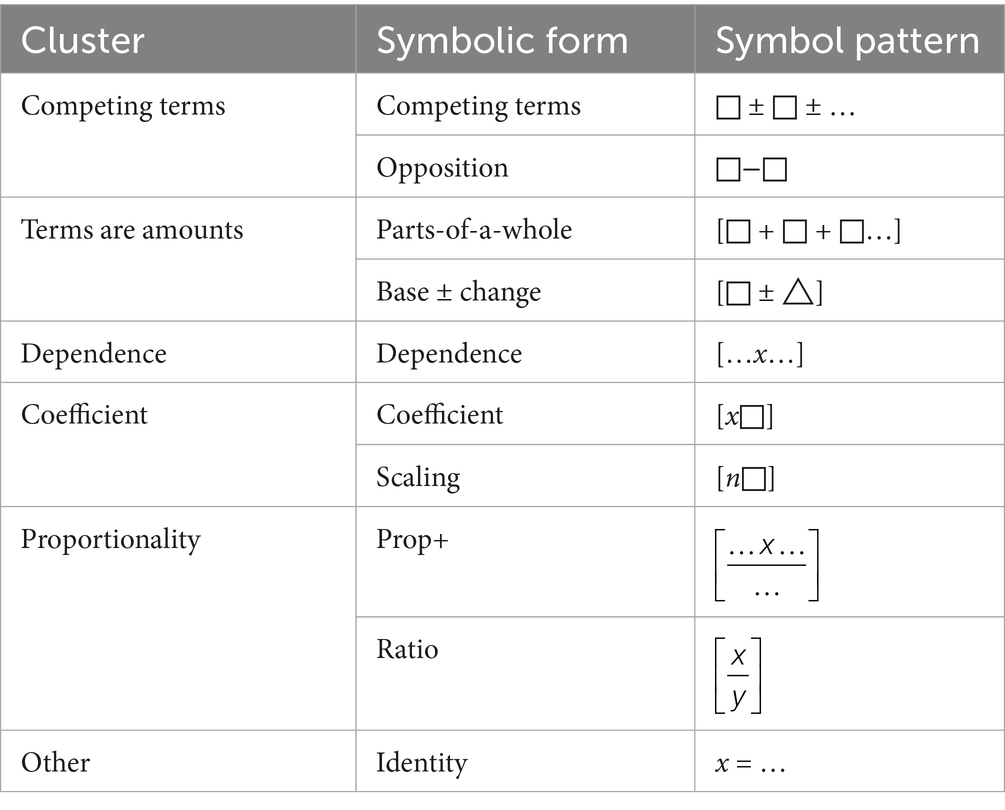
Table 2. Sherin’s semi-exhaustive list of symbolic forms (Sherin, 2001).

In our opinion, the above raises a particular question: if physics assigns meaning to mathematics, then is it possible that mathematical transformations can have important meaning making functions even though they do not change the semiotic system of representation? Performing transformations in the semiotic system of mathematics involves rearranging equations. Even though, as mentioned above, the process of rearranging has been regarded as almost exclusively serving computational functions in physics, there are some traces in the literature that suggest that rearranging an equation can also have meaning making aspects. One convincing example can be found in Eichenlaub and Redish (2019), where the authors describe how a student taking part in their study performed a rearrangement of a “formal” equation not in standardized and procedural terms, but in a way that blended physical meaning and mathematical reasoning to arrive at a logical solution. However, this topic remains underexplored.

3 Aim and research questions

For our part, our aim with this paper is to describe a certain type of transformation of a semiotic resource, which we term purposeful transformation, that we believe showcases important meaning-making functions with clear teaching and learning implications. Drawing from the ideas described in the introduction, we turned our interest to the semiotic system of mathematics in physics education, focusing on one specific equation and its rearrangement as a case study—the Friedmann equation in Cosmology. This equation gives physicists insight into both the geometry and evolution of the universe. The transformation of the Friedmann equation is popular in the physics community, as it serves a number of disciplinary functions, and is seen as a fundamental part of a novice cosmologist’s and astronomer’s education.

Our research questions are as follows:

• What are the characteristics of purposeful transformation, that make it important from a meaning making perspective?

• What are the theoretical implications of purposeful transformation in the context of social semiotics and multimodality?

In addition, in the discussion of our results, we aim to demonstrate how the concept of purposeful transformation can affect the teaching and learning of physics and astronomy.

4 Data and methodology

4.1 Data collection

Our data are collated from lecture notes for three separate university courses in Cosmology at two large research-based universities in Sweden:

i) Nuclear and particle physics, astrophysics and cosmology (undergraduate level).

ii) Cosmology (open to both undergraduate and graduate students).

iii) Cosmology and Multi-messenger Astrophysics (graduate level).

Data from these courses were collected as part of a larger semiotic audit, documenting and categorizing the various semiotic systems and individual semiotic resources used in undergraduate astronomy education (Kapodistrias and Airey, in review). For this article we focus on the semiotic system of Mathematics. Specifically, our data consist of different forms of a fundamental cosmological equation—the Friedmann Equation. This equation affords cosmologists insights regarding the dynamics and the geometry of the Universe. In all three courses, lecturers performed a specific rearrangement of this equation and subsequently gave it to their students to perform as a problem-solving activity. Despite differences in the way the rearrangement was performed, which can be associated with the individual choices of each lecturer and the different goals of each course, in all three courses we could identify a common underlying logic. The original, complex equation was transformed into a form that could be used to answer specific questions about the contents and the geometry of the Universe.

By combining data from all three courses, we chose the following transformations between different forms of the equation, which we believe to be representative of the transformations performed by all three lecturers.

The initial (well-known) form of the Friedmann equation describes how the universe expands over time, depending on what it contains. This is particularly important in cosmology because the equation is then essentially saying where the universe came from, how it developed and its future fate. By substituting in the speed of expansion of the universe that we can see today through observation and making some assumptions about the total contents of the universe, cosmologists can determine three possible scenarios for the geometry of the universe: closed, flat, or open. These three options essentially determine whether the universe will continue expanding forever, or eventually contract to a so-called “big crunch.”

In what follows, we present each of the forms of the equation in the chain of transformations along with a brief explanation of the symbols involved. Important note to the reader: it is not necessary to be able to follow the mathematics here in order to understand our later findings.

• Line 1: Initial Form

${\left(\frac{\dot{a}\left(t\right)}{a\left(t\right)}\right)}^2=\frac{8\mathit{\pi G}}{3c^2}\epsilon \left(t\right)-\frac{\kappa c^2}{R_0^2}\frac{1}{a{\left(t\right)}^2}$

Without going into too much detail, the $a\left(t\right)$ symbol indicates how much the universe has expanded at any given time, the $\epsilon \left(t\right)$ symbol indicates the amount of different components (matter, radiation, and dark energy) that make up the universe as a whole and $\kappa$ indicates the three possible types of shape of the universe:

Closed ( $\kappa =-1$ ), flat ( $\kappa =0$ ), or open ( $\kappa =+1$ ). We need not worry about the meaning of the other symbols.

In order to move to the second form of the equation, the so-called Hubble parameter is introduced:

$H\left(t\right)=\left(\frac{\dot{a}\left(t\right)}{a\left(t\right)}\right)$

The Hubble Parameter indicates how fast the universe is expanding and was first introduced by the astronomer Edwin Hubble in 1929. Estimating the current value of the Hubble Parameter is an open problem in Cosmology. Substituting this parameter into the original equation is the first transformation performed and leads to the second form of the equation:

• Line 2: Second Form

$H{\left(t\right)}^2=\frac{8\mathit{\pi G}}{3c^2}\epsilon \left(t\right)-\frac{\kappa c^2}{R_0^2}\frac{1}{a{\left(t\right)}^2}$

In order to make the next transformation, students are introduced to the concept of critical density, the energy density needed for the universe to be flat:

${\epsilon }_c\left(t\right)=\frac{3c^{2}H{\left(t\right)}^2}{8\mathit{\pi G}}$

Dividing both sides of the equation by this critical density, the previous line becomes:

$\frac{8\mathit{\pi G}}{3c^2}=\frac{8\mathit{\pi G}}{3c^2}\frac{\epsilon \left(t\right)}{{\epsilon }_c\left(t\right)}-\frac{\kappa c^2}{R_0^2}\frac{1}{a{\left(t\right)}^2}\frac{8\mathit{\pi G}}{3c^{2}H{\left(t\right)}^2}\Rightarrow$

$\text{Then},\text{dividing by}\frac{8\mathit{\pi G}}{3c^2}$

$\text{gives}:1=\frac{\epsilon \left(t\right)}{{\epsilon }_c\left(t\right)}-\frac{\kappa c^2}{R_0^{2}a{\left(t\right)}^{2}H{\left(t\right)}^2}$

Cosmologists then introduce the density parameter Ω which they define as the ratio of the energy density of the universe at any given time, over the critical energy density:

$\Omega \left(t\right)=\frac{\epsilon \left(t\right)}{{\epsilon }_c\left(t\right)}$

This means that the new term Ω indicates how “far away” the universe is from being totally flat.

$1=\Omega \left(t\right)-\frac{\kappa c^2}{R_0^{2}a{\left(t\right)}^{2}H{\left(t\right)}^2}$

A simple rearrangement leads to the third form:

• Line 3: Third Form

$1-\Omega \left(t\right)=-\frac{\kappa c^2}{R_0^{2}a{\left(t\right)}^{2}H{\left(t\right)}^2}$

By comparing the left and right side of this form of the equation, it becomes possible to make the following statements:

• If Ω = 1, then κ = 0 (flat universe).

• If Ω < 1, then κ > 0 (open universe).

• If Ω > 1, then κ < 0 (closed universe).

In the final form, the Ω parameter is broken down into the sum of all the energy densities associated with the different components of the universe (matter, radiation, dark energy) ( $\Sigma {\Omega }_i={\Omega }_m+{\Omega }_r+{\Omega }_{\Lambda }$ ). Moreover, a new density parameter is also introduced, associated with the curvature of the universe:

${\Omega }_{\kappa }=-\frac{\kappa c^2}{R_0^{2}a{\left(t\right)}^{2}H{\left(t\right)}^2}$

This leads us to the final form of the equation:

• Line 4: Fourth Form

$\Sigma {\Omega }_i+{\Omega }_{\kappa }=1$

This form of the equation clearly highlights a very important relationship for cosmologists: the density parameters of each component of the universe, plus the curvature density parameter, add up to a constant number (1). This means that depending on the shape of the universe (open, flat or closed) we would expect to find different values for the density parameters. In simpler terms, that means that the shape of the universe “tells” us how much “stuff” (energy, radiation, dark energy) we should expect to find in it (see Table 3).

Table 3

Table 3. Transformation of the initial form of the Friedmann equation.

4.2 Methodology

Our analysis is primarily inspired by Sherin’s framework of symbolic forms (Sherin, 2001). In his work, Sherin examined undergraduate physics students attempting to construct equations when dealing with physics problems. Students were faced with several physics problems with the final goal of constructing an equation that would describe the physical system at hand. By recording and analyzing their discussions during the equation construction, Sherin provided detailed descriptions about several ways in which students assign meaning to mathematical symbolism in an attempt to describe a “real world” physics situation. These descriptions were subsequently formulated into the semi-exhaustive list of symbolic forms that we described above. This semi-exhaustive list can work in two ways: it not only indicates how students make meaning when constructing equations, but also how they attempt to interpret and assign meaning to mathematical symbolism, when they are faced with a physics equation.

For our data analysis, we followed methods from the framework of abductive reasoning (Upmeier zu Belzen et al., 2021). In abductive reasoning, data are first collected in an exploratory way and in a second stage are fitted into a pre-existing theoretical framework. For us, this framework was Sherin’s semi-exhaustive list of symbolic forms. However, the subsequent steps of abductive reasoning methodology, such as collection of new data, discrimination of plausible explanations, or checking for consistency were not implemented. This is because rather than attempting to expand the already existing theoretical framework of symbolic forms, we were simply interested in applying it to our data in our attempt to better understand the transformation of the equation. Since Sherin claims that symbolic forms add semantics to an equation, we intuitively felt that this could be a useful framework for our endeavor.

We adopted the following approach: Each line in the transformation has the possibility to be associated with several of Sherin’s symbol templates. We therefore separately examined each line of the transformation of the Friedmann equation identifying all the symbolic forms that could potentially be assigned to that line. Since each of these possible symbol templates is associated with a different conceptual schema, we then essentially have a list of the possible mathematical meanings that can be made with that line of the transformation. This approach therefore gives us the opportunity to “map out” the potential conceptual meanings that can be associated with each line of the transformation. Our argument is that when students are presented with these equation forms for the first time, they will automatically attempt to interpret them using one or more of these potential templates.

Let us illustrate our methodology with a simple example of how we applied it to a specific line of the equation. For simplicity, we can choose the fourth form of the equation:

$\Sigma {\Omega }_i+{\Omega }_{\kappa }=1$

The symbolic forms framework states that this symbol template can potentially be associated with just two different conceptual schemas, resulting in two different symbolic forms: competing terms and parts of a whole. In terms of meaning making, this means that students can potentially conceptualize this line of the transformation in two different ways: Either they activate the competing terms symbolic form to make sense of the different density parameters as competing influences that “battle” each other (if one increases, the other will need to decrease), or they activate the parts of a whole symbolic form and think of them as two different “ingredients” that make a whole. In this way, we believe we have mapped out the disciplinary meaning potential of this specific line in the transformation. For reference, we have included a detailed description of all the symbolic forms used in our analysis in the Appendix.

5 Data analysis

5.1 Reduction in the number of potential symbolic forms

Our first finding from applying the methodology described above is that as we move from line to line in the rearrangement, the number of potential symbolic forms decreases. This is evident from the fact that while the initial form of the equation has very many potential symbol templates, that can be associated with it, each subsequent line is transformed so that fewer and fewer potential symbol templates are possible. Finally, what emerges as the final form of the equation can be associated with only two different schema: competing terms or parts of a whole. A summary of this analysis can be found in Table 4.

Table 4

Table 4. Reduction in the number of symbolic forms in the line-by-line rearrangement of the Friedmann equation.

5.2 Research question Ι: purposeful transformation

In this section, we would like to discuss the implications of our previous analysis, regarding the possible meaning making functions that transformation of a semiotic resource can have. Based on our analysis, we identify a certain type of transformation of semiotic resources that displays three characteristics (narrowing down meaning potential, moving meaning from the foreground to the background and a purposeful direction) and we attempt to give a first definition of this type of transformation process. These three characteristics, in our opinion showcase how transformation can play an important role in meaning making, contrary to what has been suggested in earlier research, as described in section 1.

5.2.1 Narrowing down the meaning potential

The first characteristic that stems out of our analysis is the narrowing down of the meaning potential of the initial semiotic resource. According to Airey and Linder (2017), the notion of meaning potential is one of the key reasons why the social semiotics framework can produce useful insights in the context of university physics’ teaching and learning. Meaning potential refers to the idea that each semiotic resource does not possess a single fixed meaning; rather, depending on the task at hand or a student’s prior knowledge and experience, each resource comes with a range of meaning potentials. Consequently, identifying which meaning potentials become activated by a particular semiotic resource in an educational setting becomes important. Building on this idea, it has also been suggested that for a better understanding of physics teaching and learning, we need not only to examine how meaning is transferred across semiotic systems but also to focus on individual semiotic resources and their range of meaning potentials (Airey and Linder, 2017).

Drawing on this idea of meaning potential in our analysis, we can see that each symbolic form represents a different meaning potential of the equation form that it is associated with. For example, in Line 4 of the transformation of the Friedmann equation (final form), the two different associated symbolic forms represent two different possible meanings that students may assign to it: the universe consisting of different influences in competition (competing terms) or the universe as a whole consisting of different “ingredients” (parts of a whole). Following on from that, the reduction in the number of symbolic forms as we move from line to line in the transformation, means that the initial range of meaning potentials becomes narrower. Examining the initial form of the equation, we can clearly see many different symbolic forms that can potentially be associated with it—this accounts for a wide range of meaning potentials. Whilst this is a true reflection of the many possible uses of the equation, this also makes it difficult to use the equation as is for meaning-making purposes. The final form of the equation, however, only offers the potential to make meaning in two ways and is therefore more useful (Figure 3).

Figure 3

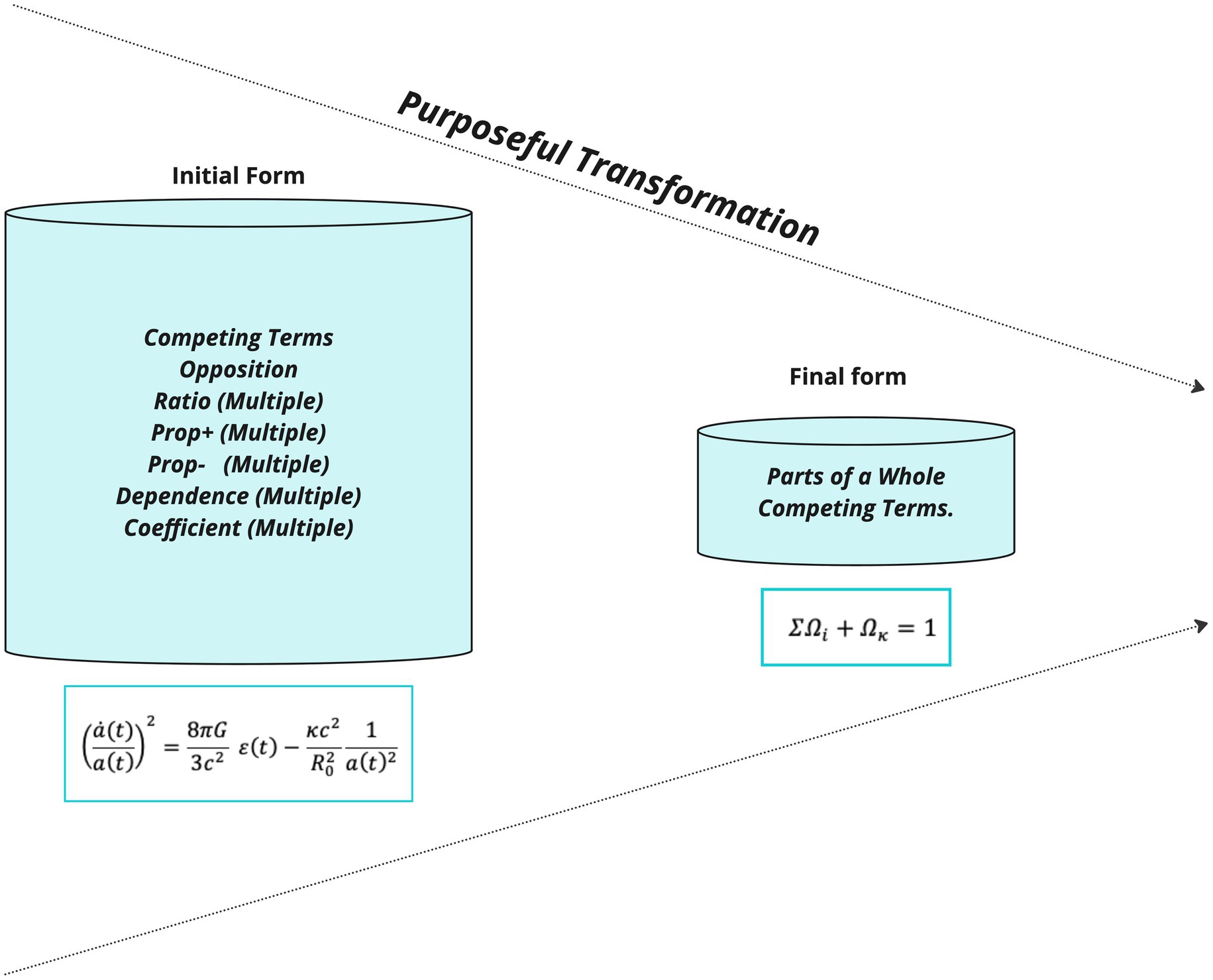
Figure 3. The reduction in the number of symbolic forms indicates a narrowing down of the meaning potential of the initial semiotic resource. Each symbolic form represents a different way of assigning meaning to the equation—a different meaning potential. Hence, when fewer symbolic forms are associated with the equation, its meaning potential has been narrowed down.

Hence, one of the meaning-making functions that we identify for this type of transformation is that it narrows down the meaning potential of the initial semiotic resource.

5.2.2 Moving meaning between the foreground and the background

The second characteristic that we identify for this type of transformation stems primarily from the introduction of new terms in each subsequent equation form. At first glance, looking at the first and the final form of the equation, it is almost impossible to recognize that they are the same equation. A lot of aspects that are present in the initial form (for example, symbols like c or a(t)) are absent from the final form, whilst new ones have emerged (e.g., the Ω symbol). It is as if the cosmologists performing this rearrangement carefully chose which aspects of the initial equation they wanted to “hide” and which others they wanted to highlight in the final form. This procedure, in the semiotic system we are examining (mathematics), occurred by grouping terms together and “hiding” them under a new, single label (in our case the Ω parameter). We identify this procedure as a movement of meaning between the foreground and the background of the semiotic resource and we believe it to have important meaning-making functions.

According to Marton and Booth (1997), in order to assign meaning to something it is crucial to be able to discern it from its environment. This is: assigning meaning to something refers to distinguishing it from the whole that it belongs to and simultaneously discerning its parts and how they relate to each other (Marton and Booth, 1997). Let us examine this particular transformation from this perspective. In the final form of the equation the mathematics leads us to the following insight:

• If Ω = 1, the universe is flat.

• If Ω < 1, the universe is open.

• If Ω > 1, the universe is closed.

In order to achieve that meaning-making capacity, the initial semiotic resource was transformed in a way that is in line with the part-whole relationship described by Marton and Booth. The parts that had to be discerned from the whole were identified (the terms that had to do with the different contents of the universe and its geometry) and they were distinguished from the whole by “hiding” the rest of the terms under newly introduced labels. Consequently, in the final form of the equation a relationship between the highlighted parts could be established and a particular meaning-making potential emerged. Therefore, we identify this foreground-background interplay as the second characteristic of our examined transformation, that gives it important meaning-making functions.

5.2.3 Purposeful direction

The previous two characteristics we described, generally provide insight as to how the initial equation is transformed into a form that is easier to reason with. The third characteristic that we observed has to do with the directionality of this process. We suggest that in order to fully describe the observed transformation, we need an element of purposefulness. The transformations made are not random, rather they are purposefully moving towards a certain end point.

If one were to look at this transformation from a purely algebraic point of view, then the procedure might be considered random and pointless. Mathematically, this grouping up of specific terms under a different label has no clear value. In addition, algebraically speaking, there are a great number of possible transformations that could have been carried out without breaking mathematical rules. However, for cosmologists, the majority of those transformations are not valued; instead, the discipline of cosmology finds clear value in the particular transformation we describe that brought very specific concepts to the fore. These concepts had to do with the distribution between the different contents of the universe and its curvature and are highlighted by the Ω parameters in the last form of the equation.

Why did cosmologists choose, via this transformation, to highlight these specific aspects instead of other ones? We believe that this is where our argument about purposefulness comes into the picture. Cosmology, as a discipline, has long-standing questions regarding the geometry of the universe (is the universe open, closed, or flat?), the distribution between its different ingredients (how much matter, radiation and dark energy are there in the universe?) and the relationship between them (how does the distribution of these different ingredients affect the geometry?). The purposefulness of the transformation lies in the fact that cosmologists took a well understood equation and introduced new mathematical terms loaded with physical meaning in a way that was directed by their discipline’s questions of interest and meaning-making agenda.

5.2.4 Purposeful transformation: a definition

To answer our first research question, we will attempt to define purposeful transformation. Drawing from the characteristics described above, we define purposeful transformation as a shift in the meaning of a semiotic resource, without changing semiotic system. This shift in meaning does not occur randomly but is dictated by disciplinary questions of interests and overall agenda. The outcome of a purposeful transformation is a transformed resource that is more useful for creating and communicating knowledge than its initial form. A comparison of the differences between transduction, transformation and purposeful transformation can be found in Table 5 below.

Table 5

Table 5. Comparison between transduction, transformation and purposeful transformation.

5.3 Research question II: implications on social semiotics

5.3.1 Disciplinary and pedagogical affordance

As mentioned earlier, the work of Fredlund et al. (2012) and Airey (2015) suggests that the disciplinary-specific semiotic resources used in science disciplines (such as Physics or Astronomy) have two different aspects of their affordances: disciplinary and pedagogical. Disciplinary affordance is described as the agreed meaning making function of a semiotic resource between the members of a disciplinary community (in this case physicists or astronomers), whereas pedagogical affordance is defined as the aptness of a semiotic resource to be used in an educational setting. Airey and Eriksson (2019) have described how these two terms generally tend to be in functional opposition; the higher the disciplinary affordance—i.e. the more disciplinary-specific the resource is—the lower the pedagogical affordance tends to be. This is mainly because disciplinary practice and discourse is based upon the creation of semiotically dense resources, that leave out information that can be taken for granted by disciplinary experts. This practice has been described as creating a disciplinary shorthand (Airey and Linder, 2017). On the other hand, when these disciplinary semiotic resources are used in teaching, they are often as impenetrable to an outsider as shorthand. As a result, raising the pedagogical affordance of disciplinary resources by unpacking becomes an important task (Patron et al., 2021). This necessarily involves lowering their disciplinary affordance—their parsimonious role as disciplinary building-blocks becomes unwieldy when everything is spelled out longhand. This is summarized in Figure 2, adapted from Airey and Eriksson (2019). However, our findings on the characteristics of purposeful transformation, give us new insight regarding the relationship between the concepts of disciplinary and pedagogical affordance. Our analysis indicates that when a semiotic resource is purposefully transformed, both its pedagogical and disciplinary affordances are raised (Figure 4, yellow arrow).

Figure 4

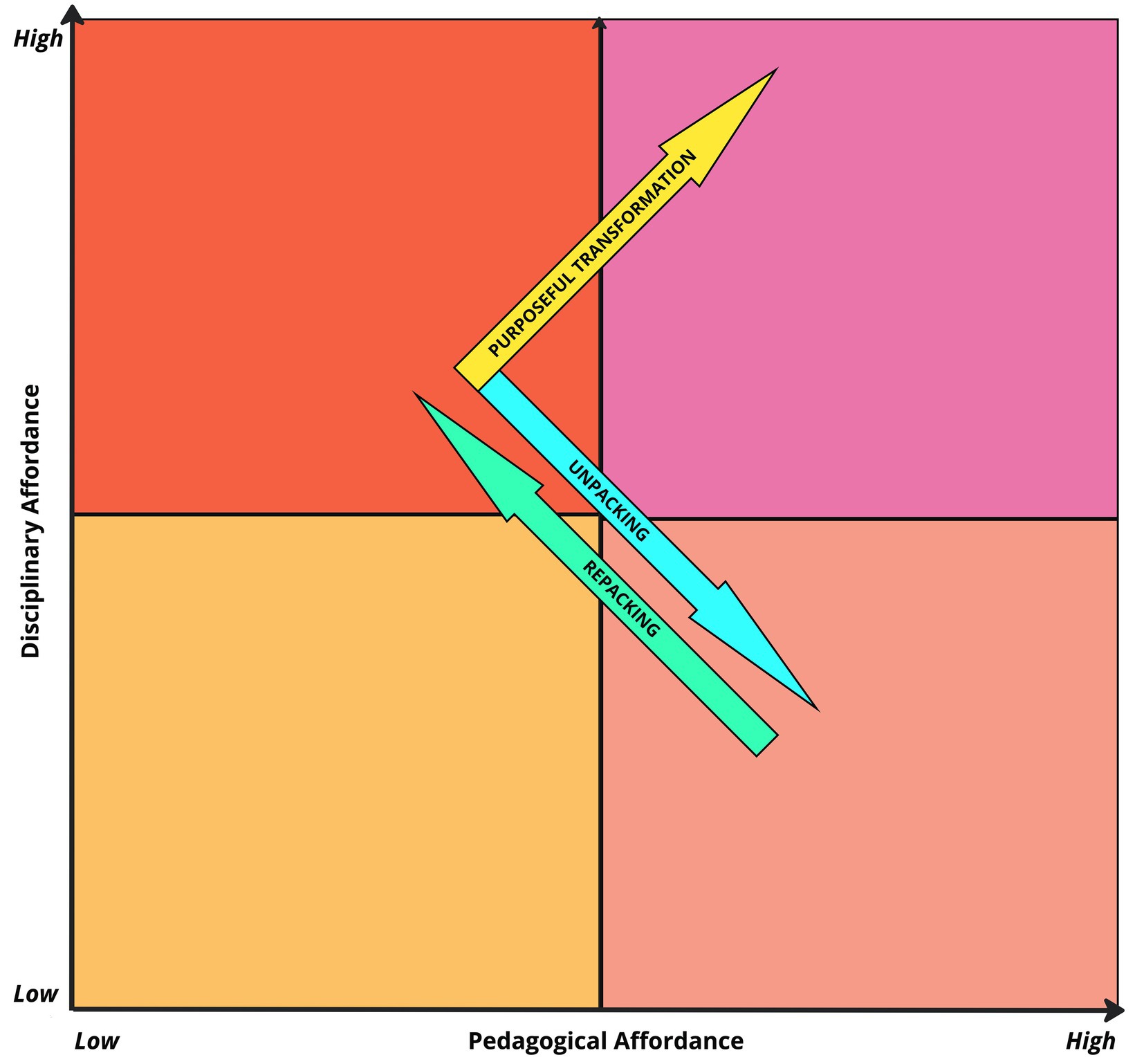
Figure 4. Disciplinary vs. pedagogical affordance. Purposeful transformation (yellow arrow) raises the disciplinary affordance and the pedagogical affordance of a semiotic resource simultaneously.

Firstly, from a disciplinary perspective, the purposeful transformation of the Friedmann equation led to a form that is widely useful for the discipline of Cosmology. As described before, the newly introduced Ω parameters are used by cosmologists to answer important questions for their discipline about the geometry of the universe, to calculate and compare with other observables and also to create new disciplinary semiotic resources (such as diagrams of model universes) with even further meaning making possibilities within the discipline. From all the above, it is evident that this purposeful transformation led to raising the disciplinary affordance of the initial equation form.

Second, from a pedagogical perspective, we believe that the first two characteristics of this purposeful transformation can lead to raising the pedagogical affordance as well. Narrowing down the meaning potential by reducing the number of associated symbolic forms with each line, brought the equation to a form where it became easier to conceptualize and reason with. From an equation with a wide range of meaning potentials, that was difficult to make sense of holistically, we transformed to an equation with just two possible meaning potentials. Introducing new terms and bringing certain aspects to the foreground of the semiotic resource, while simultaneously hiding others in the background, made it possible to transform the equation to a form where very specific physical arguments can be made with a simple, logical form (if Ω > … then the universe is…). Thus, in our opinion, purposeful transformation raises both the pedagogical affordance and the disciplinary affordance of the semiotic resource.

In summary, we have shown that the pedagogical and disciplinary affordances of a semiotic resource are not always in functional opposition. With our notion of purposeful transformation, we have demonstrated how it becomes possible to simultaneously raise both affordances. This also demonstrates that unpacking a semiotic resource is not the only method for raising pedagogical affordance.

5.3.2 Transformation just as useful as transduction: monomodal vs. multimodal

As described in our introduction section, researchers in social semiotics and multimodality generally agree that moving semiotic material across semiotic systems (transduction) is an important and challenging meaning-making task. That, along with the notion that in order to gain holistic access to disciplinary knowledge one has to become fluent in making meaning within several semiotic systems across a constellation of modes, has led to transduction being considered the primary meaning-making process. Performing transductions and their implications on the teaching and learning of science disciplines has been extensively explored in recent years, whereas transformations have not received the same attention in the literature.

We believe that with our characterization of purposeful transformation, we have demonstrated that certain types of transformation can have important meaning making functions that can also be leveraged in science teaching and learning. All of the three characteristics of purposeful transformation that we described are valuable in a teaching scenario. Narrowing down the meaning potential can help with conceptualizing and mental modeling. The interplay between foreground and background increased the meaning-making capacity of the initial semiotic resource by allowing us to discern the important disciplinary aspects of the equation from the more complex whole. Finally, the purposefulness allows us to connect the whole procedure with the questions and interests of a scientific discipline, this is in stark contrast to the empty, algorithmic process that has been frequently reported.

Fredlund et al. (2012) have shown that different semiotic resources within the same semiotic system can have very different affordances for the teaching and learning of physics. This is why, Airey and Linder (2017) have argued that when trying to understand physics teaching and learning, we need to focus not only on how we move across semiotic systems, but also on the individual semiotic resources and their particular affordances. Our work in this article builds on these arguments; we have demonstrated that individual semiotic resources can be transformed in a way that facilitates meaning making and can be leveraged in educational settings. In multimodal terms, we believe that our work shows how monomodal processes can work within multimodal ensembles of semiotic resources in order to facilitate meaning making within a scientific discipline such as Cosmology. What we have demonstrated is how, without moving meaning potential across semiotic systems in a multimodal ensemble, we can remain within the same semiotic mode (in our case, mathematics), and still narrow down the meaning potential before we transduce it to other modes. This is an example of how transformation and transduction can work together in monomodal and multimodal settings, to further advance meaning making possibilities.

Drawing from our discipline of interest (cosmology), we can see practical examples of how purposeful transformation and transduction are implemented together by cosmologists, to create multimodal ensembles and facilitate meaning making. For example, after performing the purposeful transformation we examined in section 4.1, cosmologists use the final version of the transformed equation ( $\Sigma {\Omega }_i+{\Omega }_{\kappa }=1$ ), to then plot the Ω parameters against each other and create graphs for cosmological models (Figure 5). These graphs help reveal how different combinations of cosmological parameters result in different “end of the universe” scenarios.

Figure 5

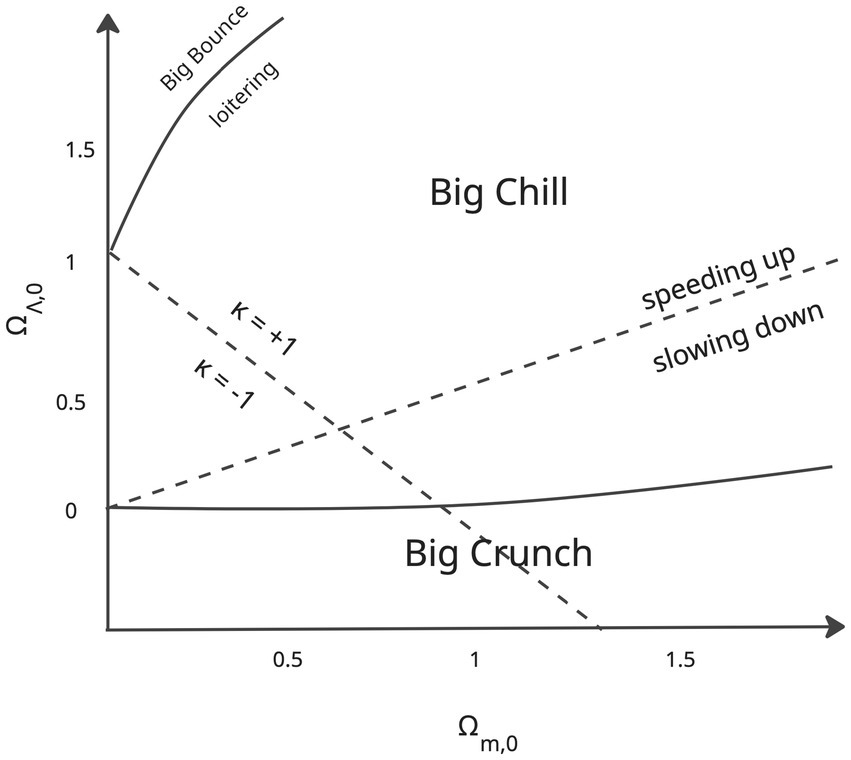
Figure 5. Example of a graph of cosmological models, that forms a multimodal ensemble with the transformed version of the Friedmann equation.

6 Discussion

6.1 Implications for future research

In this section we would like to suggest some implications of our work that can also lead to further explorations in the future. Firstly, our notion of purposeful transformation and what it means for multimodal teaching and learning can now be a topic of discussion. Exploring purposeful transformation can give us further insight into how to leverage the affordances of individual semiotic resources within a multimodal ensemble, and how to use this in coordination with transductions in order to facilitate meaning making.

Additionally, we would like to stress the fact that while our case study in this article belongs to the semiotic system of mathematics, we believe that it should be possible to identify purposeful transformations and its three characteristics in other semiotic systems. The framework of symbolic forms that we used to analyze meaning making for this particle, has already been expanded to the semiotic system of graphs (Rodriguez et al., 2020) with the introduction of the concept of graphical forms. This framework can be helpful for performing a similar analysis to the one we present in this paper in the semiotic system of graphs and further advance what we articulated as the characteristics of purposeful transformation in this article.

For example, a future question would be how the three characteristics we described for the purposeful transformation examined in this article, can occur within transformations in other semiotic systems. How might the narrowing down of meaning potential, movement between the foreground and background and the purposeful direction be instantiated in other semiotic systems, such as graphs, diagrams or images? Specifically for graphs, the framework of graphical forms should be able to help us identify similar characteristics in this semiotic system. However, it is also of interest to investigate semiotic systems where such frameworks have not yet been formulated, such as images. In the social semiotics literature, research has suggested that different systems posit different meaning making functions (Kress et al., 2001a; Lemke, 2005). Therefore, identifying how purposeful transformation may alter the meaning making functions of resources belonging in different semiotic systems appears to be a potential area of interest for further research.

An illustrative example of purposeful transformation in another semiotic system can be found in the process of fitting a theoretical curve between observational data points in a graph. When only the data points are plotted, it is impossible for disciplinary experts to infer which particular theoretical model fits the best. When theoretical lines are added to the curve (Figure 6), it becomes possible to reason that the data points correspond to a specific model better than other ones. Therefore, in this process, by transforming the initial semiotic resource without changing modes, new meanings were created by narrowing down the meaning potential of the initial form (plot of observational data points without theoretical lines).

Figure 6

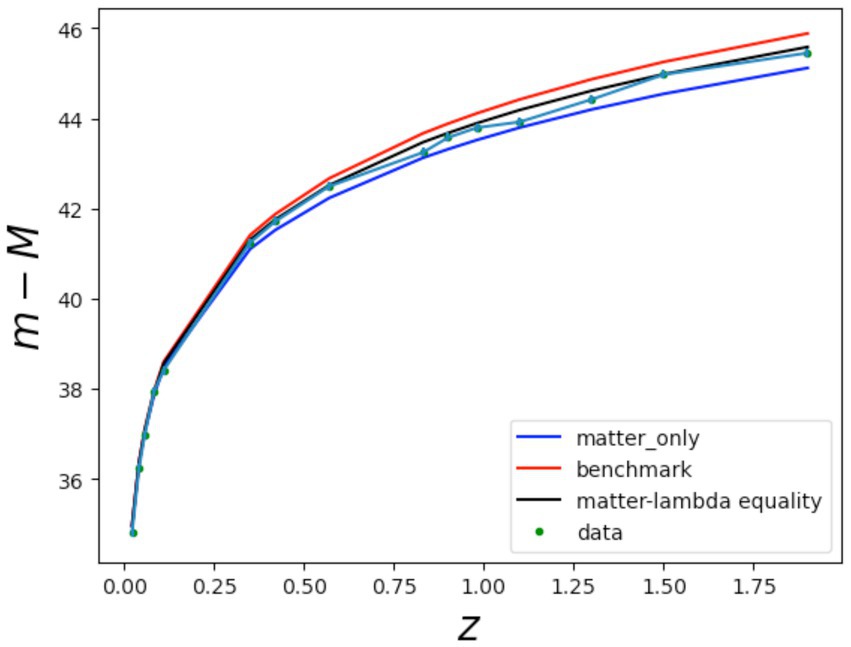
Figure 6. A plot of observational data points with the addition of three theoretical lines, used to determine which of the three theoretical models the data points best correspond to.

7 Conclusion

Finally, in this paper we have highlighted how purposeful transformation can result in a unique meaning making function that has not been described before—simultaneously raising both the pedagogical and disciplinary affordance of a semiotic resource. We believe that for future research in social semiotics, it would be also interesting to look at whether this process is possible within other semiotic systems. Our analysis demonstrates that, at least in the system of mathematics, it is possible to transform a resource in such a way. Extrapolating that idea, it is interesting to consider how could we simultaneously raise the disciplinary and pedagogical affordances of semiotic resources in other systems such as graphs, images, etc. Identifying such processes in other semiotic systems has the distinct potential for furthering our understanding of the teaching and learning of science in higher education. It is important to remember that this process of purposeful transformation is not something that we simply invented—it is something that has been going on unnoticed for a long time in higher education science that we simply identified. However, now that we have identified this process it is easier for teachers think about how to intentionally create purposeful transformations in their teaching. As discussed in our introduction, creating more accessible semiotic resources for students is crucial for developing their representational competence. Thus, we believe that our notion of purposeful transformation and its possibility for development to include other semiotic systems can potentially add one more tool to the science teacher’s “toolbox.” For disciplinary outsiders, such as communication professionals, however, we suggest that while it is useful to know about purposeful transformation, it would be difficult to leverage the process in teaching without disciplinary guidance. This is because it is important to understand the discipline’s topics of interest and how these can be realized through purposeful transformation. Rather, for this group we suggest that it is the end products of purposeful transformations that should be the focus of interest. Here, encouraging student transductions has the distinct possibility to help foster disciplinary literacy. In the example we presented here, that could entail something as simple as asking students to describe in words the disciplinary meanings represented by the final equation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AK: Conceptualization, Data curation, Investigation, Methodology, Writing – original draft, Writing – review & editing. JA: Conceptualization, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Joint funding from the Faculty of Humanities and the Faculty of Science, Stockholm University (project number: 30002527) is gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^Note that the Airey and Linder (2017) definition of social semiotics is broader than some contemporary interpretations where, for many, the field has come to be viewed as synonymous with the analysis of socially constructed power relations. This issue is discussed in Volkwyn et al. (2020), where the authors point out the limiting nature of such a narrow interpretation of social semiotics—particularly for those interested in developing more effective teaching methods through multimodal analysis of disciplinary meaning-making. For such researchers, the issue is less about unveiling and challenging hegemonic discourse patterns, but much more about understanding how a discipline multimodally constructs its knowledge claims. Following Butler (1997), the authors note that for science students, the paradox of achieving agency lies in submitting to a discourse they themselves had no part in creating.

References

Airey, J. (2009). Science, language, and literacy: case studies of learning in swedish university physics (PhD dissertation, Acta Universitatis Upsaliensis). Retrieved from https://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-9547

Google Scholar

Airey, J. (2015). Social semiotics in higher education: examples from teaching and learning in undergraduate physics. Available online at: http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-266049

Google Scholar

Airey, J., and Eriksson, U. (2019). Unpacking the Hertzsprung-Russell diagram: a social semiotic analysis of the disciplinary and pedagogical affordances of a central resource in astronomy. Des. Learn. 11, 99–107. doi: 10.16993/dfl.137

Crossref Full Text | Google Scholar

Airey, J., and Larsson, J. (2018). “Developing students’ disciplinary literacy? The case of university physics,” in Global developments in literacy research for science education. eds. K. S. Tang and K. Danielsson (Cham: Springer). doi: 10.1007/978-3-319-69197-8_21

Crossref Full Text | Google Scholar

Airey, J., and Linder, C. (2009). A disciplinary discourse perspective on university science learning: achieving fluency in a critical constellation of modes. J. Res. Sci. Teach. 46, 27–49. doi: 10.1002/tea.20265

Crossref Full Text | Google Scholar

Airey, J., and Linder, C. (2017). “Social semiotics in university physics education,” in Multiple representations in physics education. Models and modeling in science education, vol 10. eds. D. Treagust, R. Duit, and H. Fischer (Cham: Springer). doi: 10.1007/978-3-319-58914-5_5

Crossref Full Text | Google Scholar

Bezemer, J., and Kress, G. (2008). Writing in multimodal texts: a social semiotic account of designs for learning. Written Commun. 25, 166–195. doi: 10.1177/0741088307313177

Crossref Full Text | Google Scholar

Butler, J. (1997). Excitable speech: A politics of the performative. London: Routledge. doi: 10.4324/9781003146759

Crossref Full Text | Google Scholar

De Cock, M. (2012). Representation use and strategy choice in physics problem solving. Phys. Rev. Spec. Top. Phys. Educ. Res. 8:020117. doi: 10.1103/PhysRevSTPER.8.020117

Crossref Full Text | Google Scholar

de Winter, J., and Airey, J. (2022). Pre-service physics teachers’ developing views on the role of mathematics in the teaching and learning of physics. Phys. Educ. 57:065007. doi: 10.1088/1361-6552/ac8138

Crossref Full Text | Google Scholar

Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educ. Stud. Math. 61, 103–131. doi: 10.1007/s10649-006-0400-z

Crossref Full Text | Google Scholar

Eichenlaub, M., and Redish, E. F. (2019). “Blending physical knowledge with mathematical form in physics problem solving,” in Mathematics in physics education. eds. G. Pospiech, M. Michelini, and B.-S. Eylon (Cham: Springer), 127–151. doi: 10.1007/978-3-030-04627-9_6

Crossref Full Text | Google Scholar

Eriksson, U., Linder, C., Airey, J., and Redfors, A. (2014). Introducing the anatomy of disciplinary discernment: An example from astronomy. Eur. J. Sci. Math. Educ. 2, 167–182. doi: 10.30935/scimath/9409

Crossref Full Text | Google Scholar

Fredlund, T., Airey, J., and Linder, C. (2012). Exploring the role of physics representations: an illustrative example from students sharing knowledge about refraction. Eur. J. Phys. 33, 657–666. doi: 10.1088/0143-0807/33/3/657

Crossref Full Text | Google Scholar

Fredlund, T., Airey, J., and Linder, C. (2015). Enhancing the possibilities for learning: Variation of disciplinary-relevant aspects in physics representations. Eur. J. Phys. 36:055001. doi: 10.1088/0143-0807/36/5/055001

Crossref Full Text | Google Scholar

Goodwin, C. (1994). Professional Vision. Am. Anthropol. 96, 606–633.

Google Scholar

Kapodistrias, A., and Airey, J. (in review). Astronomy at university level: a social semiotic perspective. Astron. Educ. J.

Google Scholar

Kozma, R., and Russell, J. (2005). “Students becoming chemists: developing representationl competence,” in Visualization in science education (vol 1). ed. J. K. Gilbert (Springer, Dordrecht: Models and Modeling in Science Education). doi: 10.1007/1-4020-3613-2_8

Crossref Full Text | Google Scholar

Kress, G., Jewitt, C., Ogborn, J., and Tsatsarelis, C. (2001a). Multimodal teaching and learning: the Rhetorics of the science classroom. London, UK: Continuum.

Google Scholar

Kress, G., Tsatsarelis, C., Jewitt, C., and Orgon, J. (2001b). Multimodal teaching and learning. London, UK: Continuum. Available online at: https://www.bloomsbury.com/uk/multimodal-teaching-and-learning-9781441109965/

Google Scholar

Lemke, J. L. (2005). “Multiplying meaning visual and verbal semiotics in scientific text” in Reading science: Critical and functional perspectives on discourses of science. ed. J. R. Martin. 1st ed (London, UK: Routledge), 87–114.

Google Scholar

Ling Lo, M. (2012). Variation theory and the improvement of teaching and learning. Göteborg: Acta Universitatis Gothoburgensis. Available at: https://gupea.ub.gu.se/handle/2077/29645

Google Scholar

Marton, F., and Booth, S. (1997). Learning and awareness. Taylor & Francis Group. Available online at: http://ebookcentral.proquest.com/lib/sub/detail.action?docID=1123033

Google Scholar

Moje, E. B. (2007). Chapter 1 developing socially just subject-matter instruction: a review of the literature on disciplinary literacy teaching. Rev. Res. Educ. 31, 1–44. doi: 10.3102/0091732X07300046001

Crossref Full Text | Google Scholar

Pantaleo, S. (2024). Elementary students’ engagement in transduction and creative and critical thinking. Literacy 58, 58–71. doi: 10.1111/lit.12350

Crossref Full Text | Google Scholar

Patron, E. (2022). Exploring the role that visual representations play when teaching and learning chemical bonding: an approach built on social semiotics and phenomenography. Linnaeus, Sweden: Linnaeus University Press.

Google Scholar

Patron, E., Linder, C., and Wikman, S. (2021). Qualitatively different ways of unpacking visual representations when teaching intermolecular forces in upper secondary school. Sci. Educ. 105, 1173–1201. doi: 10.1002/sce.21662

Crossref Full Text | Google Scholar

Redish, E. F. (2006). Problem solving and the use of math in physics courses. arXiv. doi: 10.48550/arXiv.physics/0608268

Crossref Full Text | Google Scholar

Redish, E. F. (2021). Using math in physics: overview. Phys. Teach. 59, 314–318. doi: 10.1119/5.0021129

Crossref Full Text | Google Scholar

Rodriguez, J.-M. G., Bain, K., and Towns, M. H. (2020). Graphical forms: the adaptation of Sherin’s symbolic forms for the analysis of graphical reasoning across disciplines. Int. J. Sci. Math. Educ. 18, 1547–1563. doi: 10.1007/s10763-019-10025-0

Crossref Full Text | Google Scholar

Shanahan, T., and Shanahan, C. (2012). What is disciplinary literacy and why does it matter? Top. Lang. Disord. 32, 7–18. doi: 10.1097/TLD.0b013e318244557a

Crossref Full Text | Google Scholar

Sherin, B. L. (2001). How students understand physics equations. Cogn. Instr. 19, 479–541. doi: 10.1207/S1532690XCI1904_3

Crossref Full Text | Google Scholar

Svensson, K., and Eriksson, U. (2020). Concept of a transductive link. Phys. Rev. Phys. Educ. Res. 16:026101. doi: 10.1103/PhysRevPhysEducRes.16.026101

Crossref Full Text | Google Scholar

Svensson, K., Lundqvist, J., Campos, E., and Eriksson, U. (2022). Active and passive transductions—definitions and implications for learning. Eur. J. Phys. 43:025705. doi: 10.1088/1361-6404/ac3493

Crossref Full Text | Google Scholar

Tuminaro, J., and Redish, E. F. (2007). Elements of a cognitive model of physics problem solving: epistemic games. Phys. Rev. Spec. Top. – Phys. Educ. Res. 3:020101. doi: 10.1103/PhysRevSTPER.3.020101

Crossref Full Text | Google Scholar

Tytler, R., and Prain, V. (2022). Supporting student transduction of meanings across modes in primary school astronomy. Front. Commun. 7:863591. doi: 10.3389/fcomm.2022.863591

Crossref Full Text | Google Scholar

Uhden, O., Karam, R., Pietrocola, M., and Pospiech, G. (2012). Modelling mathematical reasoning in physics education. Sci. & Educ. 21, 485–506. doi: 10.1007/s11191-011-9396-6

Crossref Full Text | Google Scholar

Upmeier zu Belzen, A., Engelschalt, P., and Krüger, D. (2021). Modeling as scientific reasoning—the role of abductive reasoning for modeling competence. Educ. Sci. 11:Article 9. doi: 10.3390/educsci11090495

Crossref Full Text | Google Scholar

Van Den Eynde, S., Schermerhorn, B. P., Deprez, J., Goedhart, M., Thompson, J. R., and De Cock, M. (2020). Dynamic conceptual blending analysis to model student reasoning processes while integrating mathematics and physics: a case study in the context of the heat equation. Phys. Rev. Phys. Educ. Res. 16:010114. doi: 10.1103/PhysRevPhysEducRes.16.010114

Crossref Full Text | Google Scholar

Volkwyn, T. S., Airey, J., Gregorcic, B., and Heijkenskjöld, F. (2019). Transduction and science learning: multimodality in the physics laboratory. Des. Learn. 11, 16–29. doi: 10.16993/dfl.118

Crossref Full Text | Google Scholar

Volkwyn, T. S., Airey, J., Gregorcic, B., and Linder, C. (2020). Developing representational competence: linking real-world motion to physics concepts through graphs. Learn.: Res. Pract. 6, 88–107. doi: 10.1080/23735082.2020.1750670

Crossref Full Text | Google Scholar

Appendix: Symbolic forms used in our data analysis

Competing Terms

Description: Influences in competition.

Symbol pattern: □ ± □ ± □…

Identification: Frequently forces but also other directed quantities such as momentum or acceleration. Often used in tandem with free-body diagrams with influences indicated as arrows. The signs of terms are often explicitly associated with directions on the diagram. Utterances often enumerate the influences acting in a circumstance and match to terms in the expression.

Opposition

Description: Two terms, separated by a minus sign, associated with influences that work against each other.

Symbol Pattern: □ − □

Identification: Similar to competing terms but limited to the special case of two influences that oppose. Common words: “oppose” and “opposing.”

Prop+

Description: Directly proportional to a quantity, x, which appears as an individual symbol in the numerator.

Symbol pattern: $\left[\frac{\dots x\dots }{\dots }\right]$

Identification: One entity under discussion corresponds to an individual symbol that appears in the expression. Often spoken: “As X increases, then Y also increases.” Often includes the phrase proportional to.

Prop-

Description: Indirectly proportional to a quantity, x, which appears as an individual symbol in the denominator.

Symbol pattern: $\left[\frac{\dots }{\dots x\dots }\right]$

Identification: Often spoken: “As X increases, then Y decreases.”

Ratio

Description: Comparison of a quantity in the numerator and denominator.

Symbol pattern: $\left[\frac{x}{y}\right]$

Identification: In most cases, the quantities x and y have the same units. Utterances involve whether x or y is greater and whether the ratio is greater than, equal to, or less than one.

Parts-of-a-whole

Description: Amounts of generic substance, associated with terms, that contributes to a whole.

Symbol pattern: [□ + □ + □…]

Identification: Unlike competing terms, these entities are not influences. Utterances enumerate the parts that contribute to a whole, sometimes in correspondence with a diagram. Also indicated by inferences, such as the observation that if one part increases and the others are held fixed, then the whole increases.

Dependence

Description: A whole depends on a quantity associated with an individual symbol.

Symbol pattern: […x…]

Identification: The observation that a particular symbol appears in the expression. Common phrases: depends on, is a function of. Also indicated by inferences, such as if x varies, then the whole must vary.

Coefficient

Description: A product of factors is broken into two parts and one part is identified with an individual symbol, the coefficient.

Symbol pattern: [x□]

Identification: The symbol treated as the coefficient appears on the left. Utterances include that this symbol is “just a number,” “just a factor,” or “a constant.” Coefficients tune the size of an effect.

Identity

Description: A single symbol that appears alone on one side of an equation has the same properties as the expression on the other side.

Symbol pattern: x = …

Identification: Extremely common but rarely reflected in utterances. The individual symbol x is usually written on the left side of the equation. Allows very quick inferences that anything true of the expression on the right is true of the individual symbol on the left.