Secure dynamic event-triggering control for consensus under asynchronous denial of service

Introduction: This article proposes a secure implementation for consensus using a dynamic event-triggered control (DETC) scheme for general autonomous multi-agent systems (MAS) under asynchronous (distributed) denial of service (DoS) attacks. The asynchronous DoS attacks can block each communication channel independently in an unknown pattern. Depending on the impact of DoS on the communication topology, the attacks are categorized into (i): connectivity-preserved DoS (CP-DoS), and (ii): connectivity-broken DoS (CB-DoS). In CP-DoS, the operating communication topology remains connected. On the other hand, in CB-DoS the adversary breaks the communication graph into isolated sub-graphs.

Methods: The DETC scheme is employed to reduce the control updates for each agent. To guarantee consensus under both the CP-DoS and CB-DoS, a linear matrix inequality (LMI) based optimization approach is proposed, which simultaneously designs all the unknown DETC parameters as well as the state feedback control gain.

Results: The proposed optimization method prioritizes the minimum inter-event interval (MIET) between consecutive control updates. The trade-off between relevant features of the MAS, namely the consensus convergence rate, intensity of control updates, and level of resilience to DoS can be handled by the proposed optimization.

Discussion: Simulation results quantify the effectiveness of the proposed approach, showcasing its ability to maintain secure consensus in MAS under varying DoS attack scenarios.

1 Introduction

Over the past decade, cooperative control in autonomous multi-agent systems (MASs) has been a topic of extensive research in different communities. These cooperative tasks mainly include formation control, leader-following, containment, and consensus. Consensus has attracted overwhelming attention due to its vast applications in many areas such as estimation in sensor networks (Meng and Chen, 2014), attitude alignment for spacecrafts (Ren, 2007), and control of microgrids (Zhang et al., 2019; Amini et al., 2022a), to name a few. This article studies the consensus problem for general linear MASs under a class of distributed cyber attacks, namely denial of service, and an advanced class of event-based control scheme referred to as the dynamic event-triggering control.

1.1 Literature review

An important subject in cooperative control of autonomous MASs is to design suitable control schemes which utilize a reasonable amount of energy and computation resources. Conventional consensus frameworks are based on continuous-time update of the control protocol which is energy consuming and difficult to implement from the actuator point of view. Recently, event-triggered control (ETC) strategies are employed which enable the control protocol to be updated only if a pre-designed condition is satisfied. Several ETC strategies have been proposed for consensus in MAS (Peng and Li, 2018; Ge et al., 2019). More recently, dynamic event-triggering control (DETC) schemes (Hu et al., 2018; Deng et al., 2020; Zhao and Hua, 2021; Yang R. et al., 2022) have been recognized as one of the most efficient ETC schemes. Unlike conventional ETC schemes, in DETC an auxiliary dynamic variable is designed which helps in reducing the amount of control updates. The advantage of DETC scheme in reducing the amount of events over other simplified schemes is proved in Girard (2014). Recently, there has been a surge of considerable interest on DETC methodologies in different applications as surveyed in Ge et al. (2019). For instance, Meng et al. (2023) focused on DETC fault interval estimation for aeroengine sensors, where to reconstruct sensor fault a DET-based robust augmented state observer is designed. In (Cao et al., 2023) effects of time-varying delay on observer-based DETC mechanisms for MASs have been investigated. Furthermore, design of DETC mechanisms for distributed bipartite consensus in MASs has been considered in Du X. et al. (2023). He et al. (2022) surveys different secure control problems associated with MASs. The intuition behind this survey is the increased attack surface of MASs due to network-enabled information sharing as a consequence of expanded connectivity in practical scenarios. Along a similar path, Wang et al. (2023) targets surveying recent literature on resilient consensus control for MASs. Please refer to this work for a complete treatment of state-of-the-art concerning DoS attacks, spoofing attacks and Byzantine attacks in MASs, where attack model and mechanisms are introduced together with associated resilient consensus control structure. As a final note, when it comes to secure consensus of MASs, Shang (2022) proposed a median-based consensus strategy for resilient consensus control of MAS considering a time-varying directed random network. The proposed approach is superior to Weighted-Mean-Subsequence-Reduced techniques eliminating the need for the number of malicious agents in vicinity of each cooperating agent. In Shang (2021), the problem of resilient coordinated control in MASs is considered in presence o malicious agents, where agents' dynamics can be continuous-time or discrete-time. Furthermore, this work introduces the intriguing concept of heterogeneous robustness, which facilitates convergence analysis, and aims at capturing topological structure of the underlying network. Finally, Shang (2023) focused on resilient tracking consensus with a single leader considering a time-varying random directed graph, where in addition to cooperative agents, Byzantine agents are present.

Generally speaking, the DETC schemes often depend on multiple unknown parameters which should be designed based on the stability of the closed-loop MAS. The capability of the event-triggering schemes in reducing the number of control updates highly depends on the operating values of the design parameters. Regarding the DETC schemes, it is often the case that some feasible regions are derived for the design parameters (Hu et al., 2018; Yi et al., 2018; He et al., 2019; He and Mo, 2022). However, even when the feasible regions are known, selecting proper operating values that efficiently reduces the control updates is still inexplicable and requires trial and error. It is, therefore, desirable to develop a systematic design framework that computes the exact values of the unknown parameters and guarantee a substantial reduction for the control updates. Motivated by Peng and Yang (2013); Abdelrahim et al. (2014); Amini et al. (2022), where the convex optimization techniques are utilized to include some performance objectives (such as H_∞ optimization and inter-event interval maximization), in this article we develop a convex optimized design framework with a focus on reducing the control updates as much as possible.

Cyber security against malicious attacks is another important issue, which poses new challenges in performance and stability guarantees of the MASs. Generally, there exist three types of attacks targeted at cyber-physical systems, namely replay attacks, false data injection (FDI), and denial of service (DoS). In DoS (De Persis and Tesi, 2015; Zhang et al., 2018; Zhang and Feng, 2019; Liu et al., 2020), the adversary blocks the communication channels, hence the neighboring agents do not receive the transmitted signals. It is clear that DoS can significantly impact the behavior of the agents and, in extreme cases, can destabilize the MAS. In literature, the occurrence of DoS is often modeled either in a periodic (Hu et al., 2019; Xu Y. et al., 2019) or unknown pattern (Xu et al., 2018; Feng and Hu, 2019; Liu et al., 2020). In practice, the periodic scenario may not be able to fully model the pattern of DoS, as the adversary can launch the attacks in non-periodic patterns. A common assumption considered in many related works such as Xu et al. (2018); Feng and Hu (2019); Xu Y. et al. (2019); Zha et al. (2019); Amini et al. (2022); Deng and Wen (2020); Zhang and Ye (2021) is that DoS simultaneously paralyzes all communication channels. In this scenario, the MAS undergoes a binary situation based on the DoS being active or inactive. If DoS is inactive, the MAS operates normally based on the initially designated network. If DoS is active, the communication network is fully paralyzed and all agents are open-loop. In a more complex and more general DoS, which is referred to as the asynchronous (distributed) DoS (Lu and Yang, 2018; Xu W. et al., 2019; Yang Y. et al., 2020; Liu and Wang, 2021; Yang and Ye, 2022), the adversary attacks any arbitrary channel at different instants. Dealing with the asynchronous DoS is more challenging as the MAS may confront numerous connected or disconnected topologies depending on the status of each individual channel being healthy or under attack. Secure event-triggered consensus under asynchronous DoS is an important and challenging topic which, to date, has not been studied proportionately. It should be noted that the asynchronous DoS works (Lu and Yang, 2018; Xu W. et al., 2019; Yang Y. et al., 2020; Liu and Wang, 2021; Yang and Ye, 2022) have practical shortcomings which require further improvement. In particular, Lu and Yang (2018); Yang and Ye (2022); Liu and Wang (2021) are based on time-triggered or sampled-data control protocols, not event-triggered. Additionally, the ETC schemes used in Xu W. et al. (2019); Yang Y. et al. (2020) has lower inter-event interval compared to the more advanced schemes such as DETC. This motivates us to develop a DETC method for consensus under asynchronous DoS attack.

1.2 Contributions

Motivated by the above discussion and following our previous work (Amini et al., 2022), this article studies the dynamic event-triggered control for consensus in general linear MASs under unknown and asynchronous DoS attacks. The main contributions of the article are as follows:

• Unlike many existing works (Xu et al., 2018; Feng and Hu, 2019; Xu Y. et al., 2019; Zha et al., 2019; Deng and Wen, 2020; Zhang and Ye, 2021; Amini et al., 2022), where the DoS attack simply blocks all the communication channels at the same time (referred to as synchronous DoS), we consider a more general and realistic scenario where the adversary attacks any arbitrary channel at different time instants (hence called asynchronous DoS). The problem formulation for asynchronous DoS is fundamentally different from that of the synchronous DoS. In addition, we should point out that by stating asynchronous (distributed) attack in the context of this work, we eliminate imposition of any patterns on the DOS. In other words, each of the distributed agents can face a different DoS pattern.

• To the best of our knowledge, this is the first instance where a DETC protocol is formulated for consensus under unknown and asynchronous DoS attacks. Compared to Lu and Yang (2018); Xu W. et al. (2019); Yang Y. et al. (2020); Yang and Ye (2022); Liu and Wang (2021), the implementation of the DETC protocol under asynchronous DoS is novel and significantly reduces the burden of control updates.

• Unlike existing works related to DETC schemes (He et al., 2019; He and Mo, 2022), the design procedure in this article is based on a co-design optimization and simultaneously computes all required event-triggering parameters as well as the control gain. The optimization increases the minimum inter-event interval for a guaranteed level of resilience to asynchronous DoS attacks.

The remaining article is organized as follows. Section 2 introduces notation and discusses the problem to be studied. Section 3 formulates the consensus problem under DoS. Section 4 presents the main results and sufficient conditions to guarantee consensus. Simulation examples are included in Section 5. Finally, Section 6 concludes the paper.

2 Preliminaries and problem statement

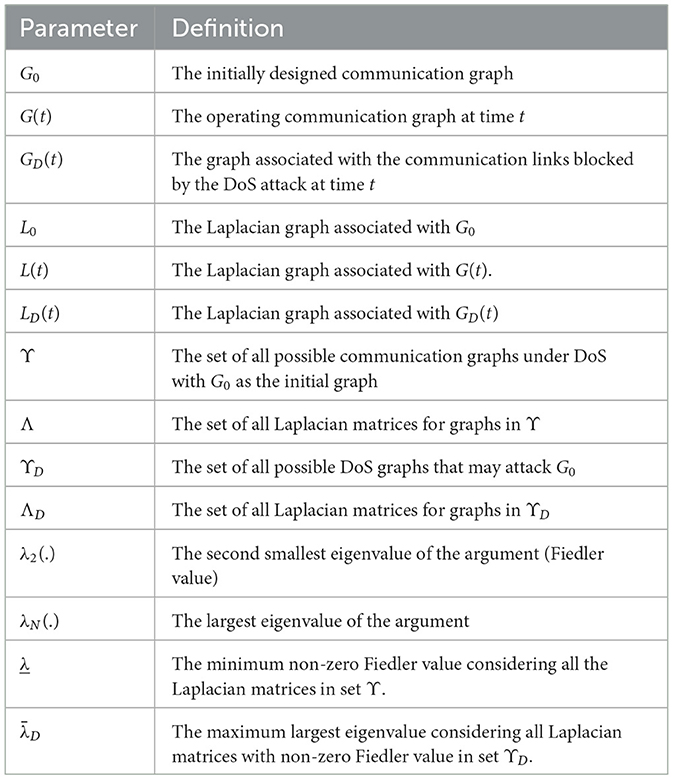
Throughout the article, vectors are denoted in bold font while matrices and scalars are represented by normal font. The following notation is used. ℕ: set of natural numbers; ℕ₀ = ℕ ∪ 0; ℝ: set of real numbers; ∥.∥: L₂ norm; M > 0: symmetric positive definite matrix M; M⁻¹: inverse of matrix M; ⊗: Kronecker product; (.)^T: transpose of a matrix or vector argument. For two sets A and B, notation A\B returns the elements which belong to set A but not to set B. The asterisk * in the lower triangle of symmetric matrices represents the transpose of the corresponding block from the upper triangle. The communication network of a MAS at time t is modeled by graph $G(t)=(\mathcal{V},\mathcal{E}(t),\mathcal{A}(t))$, where $\mathcal{V}=\left\{1,2,...,N\right\}$ is the set of agents. The pair (i, j), (1 ≤ j, i ≤ N), is included in the edge set $\mathcal{E}(t)$ iff agent j is connected to agent i at time t. Matrix $\mathcal{A}(t)=\left\{a_{i,j}\right\}\in {ℝ}^{N\times N}$ is the weighted adjacency matrix at time t, where a_i,i = 0, a_i,j ≠ 0 if $(i,j)\in \mathcal{E}(t)$, and a_i,j = 0 if $(i,j)\notin \mathcal{E}(t)$. The neighboring set for agent i at time t is defined by ${\mathcal{N}}_i(t)$. Laplacian matrices are defined by letter L with different subscripts (depending on the associated graph). We refer to the second smallest eigenvalue of L, denoted by λ₂(L), as the Fiedler value. The largest eigenvalue is denoted by λ_N(L). It is worth noting that, in our derivations, we need a symmetric Laplacian matrix where all its eigenvalues are real-valued. This is quite common practice in the LMI context. The main challenge here is that when Laplacian matrix is not symmetric, eigenvalues will be complex numbers rendering application of LMI infeasible.

Proposition 1. For a undirected graph G and λ₂(L) as its Fiedler value, it holds that λ₂(L) = 0 if and only if G is disconnected. The number of connected components of G is equal to the multiplicity of 0 in the eigenvalues of Laplacian (Newman, 2001, Thm. 1.3.4).

Consider the following general linear MAS

$\begin{array}{ll}{\dot{x}}_i(t)=A{x}_i(t)+B{u}_i(t),\forall i\in \mathcal{V},& (1)\end{array}$

where $x_i(t)\in {ℝ}^n$ and $u_i(t)\in {ℝ}^m$ are, respectively, the state and control input for agent i. Matrices A and B are constant and known. The pair (A, B) is controllable.

Definition 1. MAS Equation (1) is said to achieve state consensus if for any initial condition $x_i(0)\in {ℝ}^n$, $\forall i\in \mathcal{V}$, it holds that ${lim}_{t\to \infty }\parallel x_i(t)-x_j(t)\parallel =0$, $\forall i,j\in \mathcal{V}$.

2.1 Control protocol and dynamic even-triggering scheme

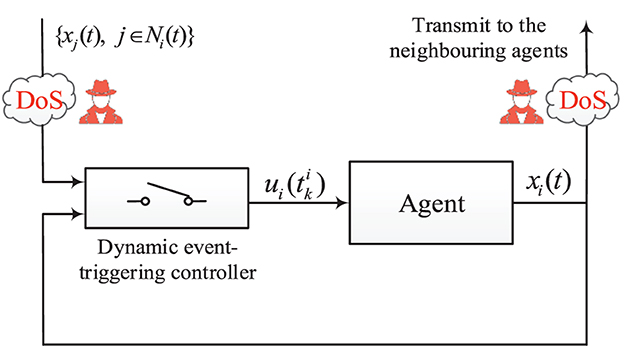
Each agent measures and transmits its state value x_i(t) to its neighbors through an undirected network. As shown in Figure 1, a DETC scheme (which will be presented later) is employed to reduce the amount of control input updates. Only if the DETC condition is fulfilled an event is triggered and u_i(t) is updated. We denote the sequence ${\left\{t_k^i\right\}}_{k\in {\mathbb{N}}_0}$ as the triggering times for agent i, where u_i(t) is being updated. Using this notation, $x_i(t_k^i)$ is the state value at the k-th event for agent i. The inter-event interval for agent i is given by ${\left\{t_{k+1}^i-t_k^i\right\}}_{k\in {\mathbb{N}}_0}$ which shows the time interval between two events in a row. We denote the following disagreement vector for agent i

$\begin{array}{ll}{q}_i(t)={\displaystyle \sum _{j\in {\mathcal{N}}_i(t)}}{a}_{i,j}(x_i(t)-x_j(t)),\forall i\in \mathcal{V}.& (2)\end{array}$

Note that the neighboring set ${\mathcal{N}}_i(t)$ is time-varying since the DoS attack, as will be discussed later, can block the communication channel between agent i and any of its neighbors. The following control protocol is used for agent i to achieve consensus

$\begin{array}{ll}{u}_i(t)=-K{q}_i(t_k^i),t\in [t_k^i,t_{k+1}^i),\forall i\in \mathcal{V},& (3)\end{array}$

where K ∈ ℝ^m×n is the control gain to be designed. Let $e_i(t)=x_i(t_k^i)-x_i(t)$, $\forall i\in \mathcal{V}$, denote the event-triggering error. Initialized by $t_0^i=0$, $\forall i\in \mathcal{V}$, the next event instant is triggered by the following DETC condition (Yi et al., 2018)

$\begin{array}{ll}{t}_{k+1}^i=inf\left\{t>{\displaystyle t_k^i}|e_i^T(t){\Phi }_1{e}_i(t)\ge q_i^T(t){\Phi }_2{q}_i(t)+{\varphi }_3{\eta }_i^2(t)\right\},& (4)\end{array}$

where matrices Φ₁ ≥ 0, Φ₂ ≥ 0 and scalar ϕ₃ ≥ 0 are design parameters. The auxiliary state η_i(t) follows

$\begin{array}{ll}{\dot{\eta }}_i(t)=-{\varphi }_4{\eta }_i^2(t)+q_i^T(t){\Phi }_5{q}_i(t),\forall i\in \mathcal{V},& (5)\end{array}$

where η_i(0) > 0. Scalar ϕ₄ ≥ 0 and matrix Φ₅ ≥ 0 are the other unknown parameters to be designed.

Remark 1. As observed in Equation (5), the updating protocol for η_i(t) is based on the disagreement vector q_i(t) and a negative quadratic self-feedback. Intuitively, η_i(t) can be regarded as a linear first-order filtered value of q_i(t). Compared to the conventional ETC strategy ||e_i(t)|| ≤ α_i∥q_i(t)∥ used in Hu et al. (2015), the utilization of the auxiliary variable η_i(t) helps in regulating the threshold (Equation 4) in a dynamic manner and in a better relationship with disagreement q_i(t). It is also proved in Girard (2014) that the inter-event interval using DETC (Equation 4) is larger than the conventional ETC strategy ||e_i(t)|| ≤ α_i∥q_i(t)∥, meaning less event triggering is proved. It is straightforward to show that the ETC schemes proposed in Qian et al. (2018); Wu et al. (2018); Xu W. et al. (2019); Yi et al. (2019) are all special cases of the DETC (Equation 4).

Figure 1

Figure 1. Block representation of the dynamic event-triggered consensus under DoS attack at node i.

Next, we show that parameter η_i(t) remains positive over time.

Proposition 2. If Φ₅ > Φ₂ and η_i(0) > 0, $\forall i\in \mathcal{V}$, parameter η_i(t) remains positive over time. In particular the following condition holds

$\begin{array}{ll}{\eta }_i(t)\ge \frac{1}{({\varphi }_3+{\varphi }_4)t+\frac{1}{{\eta }_i(0)}},\forall i\in \mathcal{V}.& (6)\end{array}$

Proof: Based on Equation (4), it holds that $e_i^T(t){\Phi }_1{e}_i(t)-{\varphi }_3{\eta }_i^2(t)\le q_i^T(t){\Phi }_2{q}_i(t)$ for $t\in [t_k^i,t_{k+1}^i)$. If Φ₅ > Φ₂, we get that ${\dot{\eta }}_i(t)\ge -({\varphi }_3+{\varphi }_4){\eta }_i^2(t)+e_i^T(t){\Phi }_1{e}_i(t)$. Since $e_i^T(t){\Phi }_1{e}_i(t)$ is non-negative, it then follows that

$\begin{array}{ll}{\dot{\eta }}_i(t)\ge -({\varphi }_3+{\varphi }_4){\eta }_i^2(t),t\in [t_k^i,t).& (7)\end{array}$

By solving differential inequality (Equation 7) for $t\in [t_k^i,t)$, we obtain $\frac{1}{{\eta }_i(t)}\le ({\varphi }_3+{\varphi }_4)(t-t_k^i)+\frac{1}{\eta (t_k^i)}.$ Considering one event-triggering interval back, i.e., $t\in [t_{k-1}^i,t_k^i)$, one obtains $\frac{1}{{\eta }_i(t_k^i)}\le ({\varphi }_3+{\varphi }_4)(t_k^i-t_{k-1}^i)+\frac{1}{\eta (t_{k-1}^i)}$. By successively moving backward through intervals $[t_k^i,t)$, $[t_{k-1}^i,t_k^i)$, …, $[0,t_1^i)$ and comparing the associated inequalities the following is obtained

$\begin{array}{ll}\frac{1}{{\eta }_i(t)}\le ({\varphi }_3+{\varphi }_4)(t-0)+\frac{1}{\eta (0)}.& (8)\end{array}$

The proof is complete, noting that Equation (8) is equivalent to Equation (6). □

From the implementation point of view, in an event-triggering scheme the time interval between two arbitrary event instants must be strictly positive. Otherwise, the event-detector scheme would potentially detect an infinite number of events in a finite interval (He et al., 2019). This undesirable phenomenon is known as the Zeno-behavior in the context of event-triggering control schemes. Therefore, it is necessary to exclude the possibility of Zeno-behavior in the proposed scheme. The exclusion of the Zeno-behavior is usually accomplished by obtaining a strictly positive lower-bound between two potential event instants. In other words, if we guarantee that the minimum inter-event time (MIET) between two successive event instants in Equation (4) is strictly positive, then the possibility of detecting infinite number of events in a finite period is ruled out. To exclude Zeno-behavior in Equation (4), in what follows we prove that the minimum inter-event interval (MIET) between any two events is strictly positive.

Proposition 3. The minimum inter-event time (MIET) for agent i, $(\forall i\in \mathcal{V})$, is strictly positive and lower-bounded by

$\begin{array}{ll}{t}_{k+1}^i-t_k^i\ge \frac{1}{\parallel A\parallel }\text{ln}\left(1+\frac{\parallel A\parallel }{{\Phi }_1^{\frac{1}{2}}{F}_i(t)}\sqrt{H_i(t_{k+1}^i)}\right),& (9)\end{array}$

where

$\begin{array}{l}{F}_i(t)={\displaystyle \underset{t\in [t_k^i,t_{k+1}^i)}{max}}\left\{\parallel BK\parallel \parallel q_i(t)\parallel +\parallel A{x}_i(t_k^i)\parallel \right\},\\ H_i(t)=q_i^T(t){\Phi }_2{q}_i(t)+\frac{{\varphi }_3}{{(({\varphi }_3+{\varphi }_4)t+\frac{1}{{\eta }_i(0)})}^2}.& (10)\end{array}$

Proof: Consider two consecutive event instants ($t_k^i$ and $t_{k+1}^i$) for agent i. Based on Equation (4), at $t=t_k^i$ it holds that $\parallel e_i(t_k^i)\parallel =0$. For $t\ge t_k^i$, the event-triggering error e_i(t) evolves from zero until Equation 4 is satisfied and the next event is detected. From $e_i(t)=x_i(t_k^i)-x_i(t)$ we obtain that ${\dot{e}}_i(t)=-{\dot{x}}_i(t)$. From Equations (3) and (1), it holds that ${\dot{x}}_i(t)=A{x}_i(t)-BK{q}_i(t)$. Combining the last three equations leads to ${\dot{e}}_i(t)=A{e}_i(t)-A{x}_i(t_k^i)+BK{q}_i(t)$, or $\parallel {\dot{e}}_i(t)\parallel \le \parallel A\parallel \parallel e_i(t)\parallel +\parallel A{x}_i(t_k^i)\parallel +\parallel BK\parallel \parallel q_i(t)\parallel$, $t\in [t_k^i,t_{k+1}^i)$. It, then, follows that $\Vert e_i(t)\Vert \le \Vert A^{-1}\Vert F_i(t)(e^{\Vert A\Vert (t-t_k^i)}-1)$ or equivalently

$\begin{array}{ll}\Vert e_i(t){\Phi }_1^{\frac{1}{2}}{\Vert }^2\le \frac{{\Phi }_1{F}_i^2(t)}{\Vert A{\Vert }^2}(e^{\Vert A\Vert (t-t_k^i)}-1)& (11)\end{array}$

where F_i(t) is defined in Equation (10). The next event is detected by Equation (4) at $t=t_{k+1}^i$ where $||e_i^T(t_{k+1}^i){\Phi }_1^{\frac{1}{2}}||{}^2=q_i^T(t_{k+1}^i){\Phi }_2{q}_i(t_{k+1}^i)+{\varphi }_3{\eta }_i^2(t_{k+1}^i)$. Then, from Equation (6), it follows that $||e_i^T(t_{k+1}^i){\Phi }_1^{\frac{1}{2}}||{}^2\ge q_i^T(t_{k+1}^i){\Phi }_2{q}_i(t_{k+1}^i)+\frac{{\varphi }_3}{{(({\varphi }_3+{\varphi }_4)t_{k+1}^i+\frac{1}{{\eta }_i(0)})}^2}$. By combining the latter inequality with Equation (11), expression (9) is obtained. The lower-bound derived in Equation (9) is strictly positive which implies that $t_{k+1}^i$ is strictly greater than $t_k^i$, i.e., $t_{k+1}^i>t_k^i$. Conceptually speaking, it is guaranteed that the next event instant is always greater than the current one. Therefore, the possibility of infinite event-triggering in finite time is ruled out and DETC (Equation 4) does not exhibit Zeno behavior.

Remark 2. In addition to excluding the possibility of the Zeno-behavior, another important observation can be made from expression (9). Based on the MIET, i.e., the right hand side of Equation (9), it can be shown that smaller values for ∥K∥, ∥Φ₁∥, and ϕ₄ increase the value of the MIET (i.e., the intensity of control updates is reduced). On the other hand, higher values for ||Φ₂||, ||Φ₃|| increase the MIET and help in reducing the control updates. Note that the impact of DETC parameters ||Φ₁||, ||Φ₂|| and ||Φ₃|| on the intensity of events is intuitive from Equation (4) and also confirmed by Equation (9). We use this observation in the proposed objective function considered in Theorems 1 and 2.

2.2 Denial of service

As shown in Figure 1, the DoS attacks, when active, target the communication channels and block the state transmission between the neighboring agents. Unlike many existing works (Xu et al., 2018; Feng and Hu, 2019; Xu Y. et al., 2019; Zha et al., 2019; Deng and Wen, 2020; Zhang and Ye, 2021; Amini et al., 2022), where it is assumed that the DoS attacks simultaneously block all communication channels, in this article we consider a more general and realistic scenario where the adversary attacks any arbitrary link.

Let $G_0=(\mathcal{V},{\mathcal{E}}_0,{\mathcal{A}}_0)$ denote the initially designed communication topology. When the adversary is completely inactive (i.e., none of the communication links are blocked) the MAS operates based on G₀. The associated Laplacian matrix to G₀ is defined by L₀. Let

$\begin{array}{ll}{D}_c^{ij}=[d_c^{ij},d_c^{ij}+{\tau }_c^{ij}),c\in {\mathbb{N}}_0,i<j,(i,j)\in {\mathcal{E}}_0,& (12)\end{array}$

denote the c-th DoS interval on channel (i, j). Parameter $d_c^{ij}$ is the time instant when the adversary begins the c-th attack on channel (i, j) and ${\tau }_c^{ij}$ is the duration of attack. Since DoS on channel (i, j) also implies DoS on channel (j, i), condition i < j is mentioned in Equation (12). Note that the first DoS can occur at t = 0, i.e., $d_0^{ij}=0$. Therefore, $d_0^{ij}$ does not need to be strictly positive.

For channels (i, j) and (j, i), the state of “being under DoS" or “being healthy" is a binary variable. Hence, there exist $2^{\frac{\left|{\mathcal{E}}_0\right|}{2}}$ possible communication topologies labeled by G₀, G₁, …, G_f, where $f=2^{\frac{\left|{\mathcal{E}}_0\right|}{2}}-1$. Let Υ and Λ, respectively, denote the set of all possible graphs under DoS attack and their corresponding Laplacian matrices, i.e.,

$\begin{array}{ll}{\rm Y}=\left\{G_0,G_1,\dots ,G_f\right\},\Lambda =\left\{L_0,L_1,\dots ,L_f\right\}.& (13)\end{array}$

During consensus iterations, the operating communication topology at time instant t is denoted by $G(t)=(\mathcal{V},\mathcal{E}(t),\mathcal{A}(t))$. It is clear that G(t) ∈ Υ, ∀t ≥ 0. We refer to $\mathcal{E}(t)$ as the set of healthy edges (i.e., not under attack) at instant t.

The DoS graph is defined by the edges that are blocked by DoS. The DoS graph at instant t is denoted by $G_D(t)=(\mathcal{V},{\mathcal{E}}_D(t),{\mathcal{A}}_D(t))$, where $(i,j)\in {\mathcal{E}}_D(t)$ if and only if the (i, j) communication channel is blocked by DoS at time t. In other words

$(i,j)\in {\mathcal{E}}_D(t)\iff \exists c\in {\mathbb{N}}_0,t\in D_c^{ij}.$

It is straightforward to verify that the “healthy edges $\mathcal{E}(t)$" and “blocked edges ${\mathcal{E}}_D(t)$" satisfy

$\begin{array}{l}{\mathcal{E}}_0=\mathcal{E}(t)\cup {\mathcal{E}}_D(t),\forall t\ge 0.\end{array}$

In a similar fashion to Equation (13), we define the following sets which include all possible DoS graphs and their corresponding Laplacian matrices

$\begin{array}{l}{{\rm Y}}_D=\left\{G_{D_0},G_{D_1},\dots ,G_{D_f}\right\},{\Lambda }_D=\left\{L_{D_0},L_{D_1},\dots ,L_{D_f}\right\}.\end{array}$

Now, we classify the DoS attack modes based on their impact on the initial communication graph G₀.

Mode I. Connectivity-preserved DoS (CP-DoS): In this type of attack, a subset of the initial transmission links are attacked by DoS. However, the resultant communication topology remains connected.

Mode II. Connectivity-broken DoS (CB-DoS): In this scenario, a subset of the initial links are blocked and the resultant communication topology is disconnected. In the extreme case, all communication channels between the agents can be blocked which is referred to as the “full DoS".

Example: Consider a MAS with five nodes as shown in Figure 2. The initially designed communication topology is labeled with G₀ which consists of 6 bidirectional edges. At t = 1, two of the edges are blocked by DoS. The corresponding DoS graphs are shown above each rightward arrows. The attack at t = 1 is a CP-DoS as the resulting graph is still connected. Then, a CB-DoS occurs at t = 2 which isolates node 4. Note that the DoS graph is always constructed based on G₀, not the previously operating communication topology. Afterwards, the adversary is inactive at t = 3, so the MAS can operate based on G₀. Finally, a full DoS is observed at t = 4 which isolates all the nodes. Note that the cardinality of Υ is 2⁶ = 64 which implies that there exist 63 different topologies under DoS for graph G₀. For ease of reference, Table 1 lists important parameters used to model the communication topology of the MAS and DoS attacks.

Figure 2

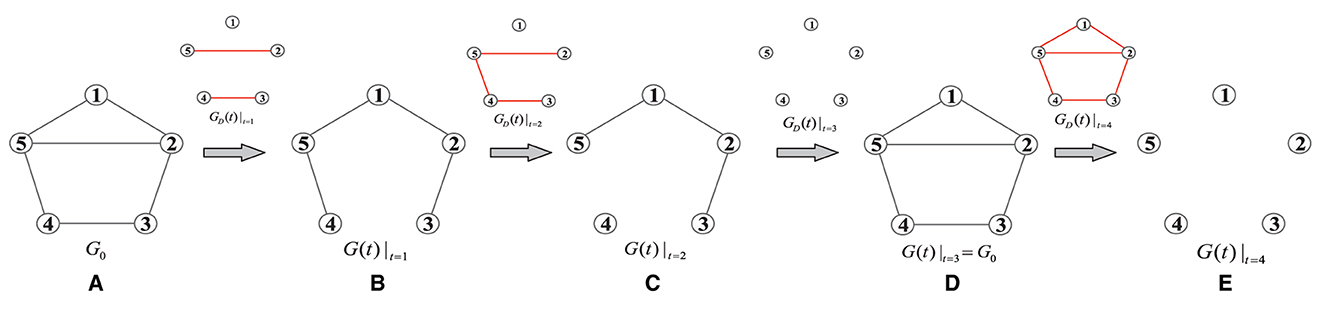
Figure 2. An illustrative example for different classes of DoS attacks. (A) The initially designed communication topology G₀, (B) a connectivity-preserved DoS, (C) a connectivity-broken DoS, (D) an inactive cycle for DoS, (E) a full DoS.

Table 1

Table 1. List of important parameters related to the communication topology under DoS.

2.3 Control objectives

The article addresses the following problems:

Problem 1. As observed earlier, the DETC protocol (Equation 4) and the auxiliary variable η_i(t) which follows Equation (5) depend on the knowledge of multiple unknown gains. These gains can significantly impact the consensus features such as the convergence rate, intensity of the events, and the amount of resilience to DoS. How to efficiently design these gains in a systematic way is a challenging matter. Many references such as Hu et al. (2018); Yi et al. (2018); He et al. (2019) derive some feasible regions for the DETC gains. However, even when the feasible regions are known, selecting the actual operating values that efficiently avoid unnecessary events remains an issue and requires some trial and error. As a more systematic approach, we propose a convex optimization to design the exact values of the unknown control and DETC gains based on an objective function which increases the minimum inter-event time (MIET). Increasing the MIET avoids unnecessary control updates.

Problem 2. In the presence of attack, it is important to develop a secure implementation under all the DoS modes and their different resulting topologies. While some of the $2^{\frac{\left|{\mathcal{E}}_0\right|}{2}}$ variations may be homomorphic graphs, the exponential growth of the situations as per the number of edges makes dealing with all the possible scenarios difficult, especially for large networks. How to design proper control and DETC gains in response to CP-DoS and CB-DoS will be investigated. It is clear that if the MAS is subject to DoS attacks with unlimited duration, the control protocol cannot receive sufficient amount of information and consensus may not be achieved. Therefore, it is reasonable to consider an assumption regarding the finiteness of the attack duration and explicitly obtain the tolerable amount of resilience to DoS.

3 Problem formulation

In this section, we analyze the closed-loop MAS (Equation 12) under asynchronous DoS attacks.

3.1 Formulation of asynchronous DoS

The asynchronous DoS given in Equation (12) can lead to both the CP-DoS and CB-DoS attacks. According to Proposition (1), if the operating graph G(t) becomes disconnected under DoS, it holds that λ₂(L(t)) = 0.

We define the c-th CB-DoS interval as follows

$\begin{array}{ll}{R}_m=[r_m,r_m+v_m),m\in {\mathbb{N}}_0,& (14)\end{array}$

where

$\begin{array}{l}{r}_m={\displaystyle \underset{\begin{array}{c}(i,j)\in {\mathcal{E}}_0,\\ c\in {\mathbb{N}}_0\end{array}}{inf}}\left\{d_c^{ij}|d_c^{ij}>r_{m-1}+v_{m-1},{\lambda }_2(L(d_c^{ij}))=0\right\},\\ v_m=inf\left\{t|t>r_m,{\lambda }_2(L(t))>0\right\}.& (15)\end{array}$

with r₋₁+v₋₁ = −1. Conceptually speaking, r_m is the earliest time when DoS on a link (i, j) leads to a disconnected graph [i.e., λ₂(L(t)) = 0]. Also, v_m is the duration of R_m, i.e., the earliest time after r_m when the graph becomes connected again [i.e., λ₂(L(t)) > 0]. Expression r₋₁+v₋₁ = −1 is selected for the initialization of r₀ as the first instance where connectivity of the network is broken. The union of all CB-DoS intervals for t ∈ [t₁, t₂) is

$\begin{array}{ll}R(t_1,t_2)={\displaystyle \bigcup _{m\in {\mathbb{N}}_0}}{R}_m\cap \left[t_1,t_2\right].& (16)\end{array}$

The complement of R_m is W_m, which represents either healthy or CP-DoS intervals. More precisely,

$\begin{array}{ll}{W}_m=[r_m+v_m,r_{m+1}),m\in {\mathbb{N}}_0.& (17)\end{array}$

The union of all healthy or CP-DoS intervals for t ∈ [t₁, t₂) is given by

$\begin{array}{ll}W(t_1,t_2)={\displaystyle \bigcup _{m\in {\mathbb{N}}_0}}{W}_m\cap \left[t_1,t_2\right].& (18)\end{array}$

Based on Equations (14)–(19), let |R(t₁, t₂)| and |W(t₁, t₂)|, respectively, denote the accumulative length of corresponding intervals for t ∈ [t₁, t₂). Since W(t₁, t₂) and R(t₁, t₂) are complements of each other, one concludes that

$\begin{array}{ll}\left|W(t_1,t_2)\right|=t_2-t_1-\left|R(t_1,t_2)\right|,t_1\le t_2.& (19)\end{array}$

The following assumption holds for the duration of the DoS attacks.

Assumption 1. There exist positive constants T₀, and T₁ such that the following upper-bounds hold (De Persis and Tesi, 2015)

$\begin{array}{ll}\left|R(t_1,t_2)\right|\le T_0+\frac{t_2-t_1}{T_1},\forall t_1,t_2\in {ℝ}_{\ge 0},t_1\le t_2.& (20)\end{array}$

The DoS attacks considered in Hu et al. (2019); Xu Y. et al. (2019) are assumed to follow a periodic pattern. Considering a periodic pattern for DoS may not fully represent the unknown and malicious nature of the adversary. Our considered asynchronous attack is more general, where the DoS is assumed to occur with an unknown pattern. Such a DoS model with unknown pattern can be characterized only by the energy constraints of the adversary. Assumption 1, which is widely used for formulation of unknown DoS attacks, constrains DoS in terms of its average duration. In other words, the strength of the DoS attacks (in terms of duration) is scalable with time. Inequality (Equation 21) expresses property that the DoS intervals satisfy a slow-on-the-average type condition. It implies that the total duration for DoS, on average, should not exceed a certain fraction of time, which is scaled by 1/T₁. Parameter T₀ is included to allow for consideration of DoS at the start time.

3.2 Closed-loop system

Let $x={\left[x_1^T(t),\dots ,x_N^T(t)\right]}^T$, $e=[e_1^T(t),\dots ,e_N^T(t){]}^T$, $\tilde{x}={\left[x_1^T(t_k^1),\dots ,x_N^T(t_k^N)\right]}^T$, $\eta ={\left[{\eta }_1(t),\dots ,{\eta }_N(t)\right]}^T$. From Equations (1) and (3), the closed-loop MAS under DoS is given below

$\begin{array}{ll}\dot{x}(t)=(I_N\otimes A-(L_0-L_D(t))\otimes BK)x(t)-(L_0-L_D(t))\otimes BKe(t).& (21)\end{array}$

Next, we transform system (21) through the eigenvalue decomposition of L₀. It is straightforward to show that

$L_0={\bar{V}}_0{\bar{J}}_0{\bar{V}}_0^T,\parallel {\bar{V}}_0\parallel =1,$

where ${\bar{J}}_0=\mathrm{\text{diag}}(0,{\lambda }_2(L_0),\dots ,{\lambda }_N(L_0))$ is a diagonal matrix consisting the eigenvalues of L₀ and matrix $\bar{V}=\left[{\bar{v}}_{i,j}\right]\in {ℝ}^{N\times N}$ includes the normalized eigenvectors of L₀. We construct the (N−1) × N dimensional matrix V₀ which includes rows 2 to N of matrix ${\bar{V}}_0^T$. In other words, matrix V₀ is obtained by removing the first row of matrix ${\bar{V}}_0^T$ (the corresponding eigenvector to eigenvalue zero). With this definition, it holds that $L_0=V_0^T{J}_0{V}_0$. Now, consider the following transformation

$\begin{array}{ll}z(t)=(V_0\otimes I_n)x(t).& (22)\end{array}$

It is proved in Ge and Han (2017) that consensus is achieved in Equation (21) iff ${lim}_{t\to \infty }z(t)=0$. Using Equation 22, system (21) is converted to

$\begin{array}{l}\dot{z}(t)=(I_{N-1}\otimes A-(J_0-J_D(t))\otimes BK)z(t)-(J_0{V}_0-W(t)V_0)\otimes \\ BKe(t),& (23)\end{array}$

where $W(t)=V_0{V}_D^T(t)J_D(t)V_D(t)V_0^T$ and J_D(t) = diag(λ₂(L_D(t)), …, λ_N(L_D(t))). Matrix V_D(t) with unity norm includes the eigenvectors of L_D(t).

4 Stability analysis and parameter design

In this section, we propose a co-design approach to compute the control and DETC parameters under asynchronous DoS attacks. For ease of comprehension, the results are presented in two theorems.

• In Theorem 1, we assume that only CP-DoS occurs. Considering this situation, we propose an optimization framework that co-designs all the unknown control and DETC parameters with a given desired rate for exponential consensus convergence.

• Theorem 2 extends Theorem 1 by considering both the CB-DoS and CP-DoS. A desired level of tolerance to asynchronous DoS can be selected a priori. The trade-offs between the rate of consensus convergence, intensity of control updates, and the amount of resilience to DoS can be controlled by Theorem 2.

4.1 Parameter design under connectivity-preserved DoS

In this section, we propose a theorem that guarantees consensus under the situation where MAS (Equation 23) is only subjected to CP-DoS. Section 4.2 extends the framework to both the DoS cases.

Theorem 1. Consider MAS (Equation 23) with the initially designed communication topology $G_0=(\mathcal{V},{\mathcal{E}}_0,{\mathcal{A}}_0)$ under CP-DoS attacks. Given a desired consensus convergence rate ω₁, if there exist positive definite matrices P_n×n > 0, M_1n×n > 0, M_2n×n > 0, M_5n×n > 0, free matrix Ω_m×n, positive scalars m₃ > 0, m₄ > 0, ϵ₁ > 0, and θ_c > 0, (1 ≤ c ≤ 7), such that the following convex minimization problem is feasible

$\begin{array}{ll}min𝔽={\theta }_1+{\theta }_2+\cdots +{\theta }_7,& (24)\end{array}$

subject to:

${\Psi }_1\left[\begin{array}{cccc}{\psi }_1& -J_0{V}_0\otimes B\Omega & 0& 0\\ \ast & -I_N\otimes M_1& 0& {\overline{\lambda }}_D{I}_N\otimes B\Omega \\ \ast & \ast & ({\varphi }_3-{\varphi }_4+\frac{{\omega }_1}{2})I_N& 0\\ \ast & \ast & \ast & -{ϵ}_{1}I\end{array}\right]<0,(25)$

$\begin{array}{ll}\Pi ={\Omega }^T{B}^T+B\Omega >0,& (26)\end{array}$

$\begin{array}{l}{C}_1=\left[\begin{array}{cc}-{\theta }_{1}I& M_1\\ \ast & -I\end{array}\right]<0,C_2=\left[\begin{array}{cc}{\theta }_{2}I& I\\ \ast & M_2\end{array}\right]>0,\\ C_3=\left[\begin{array}{cc}{\theta }_3& 1\\ \ast & m_3\end{array}\right]>0,C_4=\left[\begin{array}{cc}-{\theta }_4& m_4\\ \ast & -1\end{array}\right]<0,\\ C_5=\left[\begin{array}{cc}{\theta }_{5}I& I\\ \ast & M_5\end{array}\right]>0,C_6=\left[\begin{array}{cc}-{\theta }_{6}I& \Omega \\ \ast & -I\end{array}\right]<0,\\ C_7=\left[\begin{array}{cc}{\theta }_{7}I& I\\ \ast & P\end{array}\right]>0,\end{array}(27)$

where

$\begin{array}{l}{\psi }_1=I_{N-1}\otimes (P{A}^T+AP+{\omega }_{1}P)-\underset{\_}{\lambda }{I}_{N-1}\otimes (B\Omega +{\Omega }^T{B}^T)\\ +J_0^2\otimes (M_2+M_5)+{ϵ}_{1}I,& (28)\end{array}$

$\begin{array}{ll}\underset{\_}{\lambda }={\displaystyle \underset{i=0,\dots ,|\Lambda |-1}{min}}\left\{{\lambda }_2(L_i)|L_i\in \Lambda ,{\lambda }_2(L_i)>0\right\},& (29)\end{array}$

$\begin{array}{ll}{\bar{\lambda }}_D={\displaystyle \underset{i=0,\dots ,\left|{\Lambda }_D\right|-1}{max}}\left\{{\lambda }_N(L_{D_i})|L_{D_i}\in {\Lambda }_D,{\lambda }_2(L_{D_i})>0\right\},& (30)\end{array}$

then the unknown parameters for control protocol (Equation 2) and DETC scheme (Equation 4) are designed as follows

$\begin{array}{l}K=\Omega P^{-1},{\Phi }_1=P^{-1}{M}_1{P}^{-1},{\Phi }_2=P^{-1}{M}_2{P}^{-1},\\ {\varphi }_3=m_3,{\varphi }_4=m_4,{\Phi }_5=P^{-1}{M}_5{P}^{-1}.& (31)\end{array}$

The following bounds are guaranteed for the designed parameters associated with the convex minimization problem defined through Equations (24)–(30)

$\begin{array}{l}\parallel K\parallel \le {\theta }_7\sqrt{{\theta }_6},\parallel {\Phi }_1\parallel \le \sqrt{{\theta }_1}{\theta }_7^2,\parallel {\Phi }_2\parallel \ge \frac{1}{{\theta }_2{\theta }_7^2},{\varphi }_3\ge \frac{1}{{\theta }_3},\\ {\varphi }_4\le \sqrt{{\theta }_4},\parallel {\Phi }_5\parallel \ge \frac{1}{{\theta }_5{\theta }_7^2}.& (32)\end{array}$

Using Equation (31), the convergence rate of z(t) satisfies

$\begin{array}{ll}{\lambda }_{min}(P^{-1})z^T(t)z(t)+\eta (t)\le \mu e^{-{\omega }_{1}t}+{\omega }_1^2/2,& (33)\end{array}$

where $\mu ={\lambda }_{max}(P^{-1})z^T(0)z(0)+\eta (0)$.

Proof: For the sake of readability, we remove the time argument t in the proof. Consider the following expression

$\begin{array}{ll}\dot{V}+{\omega }_{1}V<{\omega }_1^2/2,& (34)\end{array}$

where V = V₁+V₂ and

$\begin{array}{ll}{V}_1=z^T(I_{N-1}\otimes P^{-1})z,V_2=\eta .& (35)\end{array}$

If (34) is guaranteed, condition (33) is satisfied and ω₁ determines the exponential consensus convergence rate. We compute the time derivative for V₁ as follows

$\begin{array}{ll}{\dot{V}}_1=z^T\Xi z-2z^T((J_0{V}_0-W{V}_0)\otimes P^{-1}BK)e,& (36)\end{array}$

where $\Xi =I_{N-1}\otimes (A^T{P}^{-1}+P^{-1}A)-2(J_0-J_D)\otimes P^{-1}BK.$ Remind that in this theorem we assume that the MAS is either in healthy intervals or under CP-DoS. In this situation, all the diagonal elements of J₀−J_D are non-zero. Under condition (P⁻¹BK)^T + P⁻¹BK > 0, the following holds

$\begin{array}{ll}\Xi \le I_{N-1}\otimes (A^T{P}^{-1}+P^{-1}A)-2\underset{\_}{\lambda }{I}_{N-1}\otimes P^{-1}BK.& (37)\end{array}$

We expand ${\dot{V}}_2+{\omega }_1{V}_2$ based on Equation (5)

$\begin{array}{l}{\dot{V}}_2+{\omega }_1{V}_2=-{\varphi }_4{\eta }^2+q^T{I}_N\otimes {\Phi }_{5}q+{\omega }_1\eta \\ =-{\varphi }_4{\eta }^2+x^T{(L_0-L_D)}^2\otimes {\Phi }_{5}x+{\omega }_1\eta ,& (38)\end{array}$

Since L_D ≥ 0, it holds that $x^T{(L_0-L_D)}^2\otimes {\Phi }_{5}x\le x^T{L}_0^2\otimes {\Phi }_{5}x$. Recalling that $L_0=V_0^T{J}_0{V}_0$, $V_0{V}_0^T=I$, and using transformation (22), it is straightforward to show

$\begin{array}{ll}{x}^T{(L_0-L_D)}^2\otimes {\Phi }_{5}x\le x^T{L}_0^2\otimes {\Phi }_{5}x=z^T(J_0^2\otimes {\Phi }_5)z.& (39)\end{array}$

Considering Equations (38, 39), and inequality ${\omega }_1\eta \le \frac{{\omega }_1}{2}{\eta }^2+\frac{{\omega }_1^2}{2}$, we conclude that

$\begin{array}{ll}{\dot{V}}_2+{\omega }_1{V}_2\le (-{\varphi }_4+\frac{{\omega }_1}{2}){\eta }^2+z^T(J_0^2\otimes {\Phi }_5)z+\frac{{\omega }_1^2}{2}& (40)\end{array}$

As for the DETC (Equation 4), it holds that $e_i^T(t){\Phi }_1{e}_i(t)\le q_i^T(t){\Phi }_2{q}_i(t)+{\varphi }_3{\eta }_i^2(t)$, $t\in [t_k^i,t_{k+1}^i)$. In a collective sense, we obtain $e^T(I_N\otimes {\Phi }_1)e\le q^T(I_N\otimes {\Phi }_2)q+{\varphi }_3{\eta }^T\eta$. Similar to Equation (39), we can derive that $q^T(I_N\otimes {\Phi }_2)q\le z^T(J_0^2\otimes {\Phi }_2)z$. Therefore, the following condition is obtained

$\begin{array}{ll}{e}^T(I_N\otimes {\Phi }_1)e\le z^T(J_0^2\otimes {\Phi }_2)z+{\varphi }_3{\eta }^T\eta .& (41)\end{array}$

Let ν = [z^T, e^T, η^T]T. Based on Equations (36, 37, 40), and (41), we re-arrange Equation (34) as follows

$\begin{array}{ll}\dot{V}+{\omega }_{1}V\le {\nu }^T{\overline{\text{Ψ}}}_1\nu +{\omega }_1^2/2,& (42)\end{array}$

$\begin{array}{l}{\overline{\text{Ψ}}}_1=\left[\begin{array}{l}{\bar{\psi }}_1(W{V}_0-J_0{V}_0)\otimes P^{-1}BK0\\ *-I_N\otimes {\Phi }_{1}0\\ **({\varphi }_3-{\varphi }_4+\frac{{\omega }_1}{2})I_N\end{array}\right],\\ {\bar{\psi }}_1=I_{N-1}\otimes (A^T{P}^{-1}+P^{-1}A)-2\underset{\_}{\lambda }{I}_{N-1}\otimes P^{-1}BK\\ +{\omega }_1{I}_{N-1}\otimes P^{-1}+J_0^2\otimes ({\Phi }_2+{\Phi }_5).\end{array}$

Inequality (Equation 34) is guaranteed if ${\overline{\text{Ψ}}}_1<0$. We pre- and post multiply ${\overline{\text{Ψ}}}_1$ by ℙ = diag(I_N−1⊗P, I_N⊗P, I_N), which results in $\mathbb{P}{\overline{\text{Ψ}}}_1\mathbb{P}$. Denote the following alternative variables

$\begin{array}{l}\Omega =KP,M_1=P{\Phi }_{1}P,M_2=P{\Phi }_{2}P,\\ m_3={\varphi }_3,m_4={\varphi }_4,M_5=P{\Phi }_{5}P.& (43)\end{array}$

Now, re-arrange $\mathbb{P}{\overline{\text{Ψ}}}_1\mathbb{P}$ as follows

$\begin{array}{ll}\mathbb{P}{\overline{\text{Ψ}}}_1\mathbb{P}={\overline{\text{Ψ}}}_2+S^{T}Y+Y^{T}S<0,& (44)\end{array}$

where

$\begin{array}{l}{\overline{\text{Ψ}}}_2=\left[\begin{array}{l}{\bar{\psi }}_2-J_0{V}_0\otimes B\Omega 0\\ *-I_N\otimes M_{1}0\\ **({\varphi }_3-{\varphi }_4+{\omega }_1)I_N\end{array}\right],\\ S=\left[I00\right],Y=\left[0(W{V}_0\otimes I_n)(I_N\otimes B\Omega )0\right],\\ {\bar{\psi }}_2=I_{N-1}\otimes (P{A}^T+AP+{\omega }_{1}P)-\underset{\_}{\lambda }{I}_{N-1}\otimes (B\Omega +{\Omega }^T{B}^T)\\ +J_0^2\otimes (M_2+M_5).\end{array}$

According to Young's inequality, condition (44) is guaranteed if there exists a positive scalar ϵ₁ such that

$\begin{array}{ll}{\overline{\text{Ψ}}}_2+{ϵ}_1{S}^{T}S+{ϵ}_1^{-1}{Y}^{T}Y<0,& (45)\end{array}$

The only non-zero element of Y^TY is ${(I_N\otimes B\Omega )}^T(V_0^T{W}^{T}W{V}_0\otimes I_n)(I_N\otimes B\Omega )$. Now, we consider the following upper-bound

$\begin{array}{ll}{V}_0^T{W}^{T}W{V}_0\otimes I_n\le {\bar{\lambda }}_D^2{I}_{Nn}.& (46)\end{array}$

Considering the upper-bound in Equation (46) and using the Schur complement Lemma with respect to the term ${ϵ}_1^{-1}{Y}^{T}Y$, inequality (Equation 45) turns into Ψ₁ < 0 given in Equation (25). The condition above (Equation 37) is pre- and post-multiplied by P and that results in LMI Π < 0 given in Equation (26).

Formulation of the objective function: Similar to Amini et al. (2022), a weighted-sum approach is employed to decrease/increase the control gain and DETC parameters according to their impact on MIET (Equation 9). For decision variables θ_c > 0, (1 ≤ c ≤ 7), we consider the following constraints

$\begin{array}{l}{M}_1^T{M}_1<{\theta }_{1}I,M_2^{-1}<{\theta }_{2}I,m_3^{-1}<{\theta }_3,m_4^2<{\theta }_4,\\ M_5^{-1}<{\theta }_{5}I,{\Omega }^T\Omega <{\theta }_{6}I,P^{-1}<{\theta }_{7}I.& (47)\end{array}$

Note that from Equations (43) and (47) one can obtain the bounds given in Equation (32). According to Equation (32), if one decreases the values of θ_c > 0 (1 ≤ c ≤ 7), parameters {∥K∥, ∥Φ₁∥, ϕ₄} are decreased and {∥Φ₂∥, ϕ₃, ∥Φ₅∥} are increased. This increases MIET (Equation 9). The objective function F (given in Equation 9) is constructed based on minimizing the sum of θ_c, (1 ≤ c ≤ 7). The constraints given in Equation (24) are not in the form of LMIs. To make convex constraints, we employ the Schur complement and LMIs C_i, (1 ≤ i ≤ 7), are obtained from Equation (47). Once the convex problem (Equation 24) is solved the control gain and DETC parameters are computed from Equation (31). □

Remark 3. In fact, Theorem 1 guarantees consensus based on the smallest possible Fiedler value (λ) and the maximum largest eigenvalue for the DoS graph (${\bar{\lambda }}_D$). These eigenvalues correspond to the strongest possible CP-DoS attacks on G₀. As for the performance trade-offs, a faster desired convergence rate (i.e., a larger value for ω₁) leads to a faster consensus convergence according to Equation (33). However, as ω₁ is increased the intensity of the events is increased and less saving in control updates is expected.

4.2 Extension to connectivity-broken DoS

In the following theorem, we extend Theorem 1 for the situation where both the CB-DoS and CP-DoS may occur.

Theorem 2. Consider MAS (Equation 23) with the initially designed communication topology G₀ under both the CP-DoS and CB-DoS attacks. Let ω₁ be the desired consensus convergence rate under only CP-DoS and α < 1 be the desired resilience level to CB-DoS attacks. If there exist positive definite matrices P_n×n > 0, M_1n×n > 0, M_2n×n > 0, M_5n×n > 0, free matrix Ω_m×n, positive scalars m₃ > 0, m₄ > 0, ϵ₁ > 0, ϵ₂ > 0, and θ_c > 0, (1 ≤ c ≤ 7), such that the following convex minimization problem is feasible

$\begin{array}{ll}min𝔽={\theta }_1+{\theta }_2+\cdots +{\theta }_7,& (48)\end{array}$

subject to:

$\begin{array}{ll}{\text{Ψ}}_1<0,& (49)\end{array}$

$\begin{array}{ll}{\text{Ψ}}_2=\left[\begin{array}{l}{\psi }_2-J_0{V}_0\otimes B\Omega 00\\ *-I_N\otimes M_{1}0\bar{\lambda }{I}_N\otimes B\Omega \\ **({\varphi }_3-{\varphi }_4)I_{N}0\\ ***-{ϵ}_{2}I\end{array}\right]<0,& (50)\end{array}$

$\begin{array}{l}{\text{Ψ}}_3=AP+P{A}^T-{\omega }_{2}P<0,\\ \Pi <0,C_1>0,C_2>0,C_3>0,C_4<0,\\ C_5>0,C_6<0,C_7>0,& (51)\end{array}$

where Ψ₁, Π, and C_i, (1 ≤ i ≤ 7), are previously defined in Theorem 1 and

$\begin{array}{l}{\psi }_2=I_{N-1}\otimes (P{A}^T+AP-{\omega }_{2}P)-\underset{\_}{\lambda }{I}_{N-1}\otimes (B\Omega +{\Omega }^T{B}^T)\\ +J_0^2\otimes (M_2+M_5)+{ϵ}_{2}I,\\ {\omega }_2=\frac{{\omega }_1(1-\alpha )}{\alpha },\bar{\lambda }={\displaystyle \underset{i=0,\dots ,|\Lambda |-1}{max}}\left\{{\lambda }_N(L_i)|L_i\in \Lambda \right\},& (52)\end{array}$

then the unknown parameters for control protocol (Equation 2) and DETC (Equation 4) are designed from the same expressions given in Equation (31). These parameters guarantee resilient to CB-DoS attacks satisfying

$\begin{array}{l}\frac{1}{T_1}<\alpha .\end{array}$

Additionally, the system trajectories satisfy the following exponentially bounded stability

$\begin{array}{ll}{\lambda }_{min}(P^{-1})z^T(t)z(t)+\eta (t)\le {\rho }_1\mu e^{-\zeta t}+{\rho }_2,& (53)\end{array}$

where

$\begin{array}{ll}\zeta ={\omega }_1-\frac{{\omega }_1+{\omega }_2}{T_1},\mu ={\lambda }_{max}(P^{-1})z^T(0)z(0)+\eta (0).& (54)\end{array}$

Proof: The proof considers three possible situations that the MAS may undergo: (i) Healthy or CP-DoS, (ii) CB-DoS where there exists at least one healthy channel, (iii) CB-DoS where all channels are blocked (full DoS).

(i) Healthy or CP-DoS: From Theorem 1, for healthy or CP-DoS intervals (t ∈ W_m) it is guaranteed that $\dot{V}(t)<-{\omega }_{1}V(t)+{\omega }_1^2/2$ if Ψ₁ < 0 and Π < 0. This leads to the following expression

$\begin{array}{ll}V(t)\le e^{-{\omega }_1(t-r_m-v_m)}V(r_m+v_m)+{\omega }_1/2,t\in W_m.& (55)\end{array}$

(ii) CB-DoS where there exists at least one healthy channel: In the presence of CB-DoS (t ∈ R_m), MAS (Equation 23) is disconnected and the agents may diverge. There exists a positive scalar ω₂ that the divergence rate satisfies

$\begin{array}{ll}\dot{V}(t)<{\omega }_{2}V(t),t\in R_m,& (56)\end{array}$

where V = V₁+V₂ is given in Equation (35). We expand Equation (56) as

$\begin{array}{ll}\dot{V}-{\omega }_{2}V=({\dot{V}}_1+{\dot{V}}_2)-{\omega }_2(V_1+V_2)<0.& (57)\end{array}$

Since V₂ > 0, if condition

$\begin{array}{ll}({\dot{V}}_1+{\dot{V}}_2)-{\omega }_2{V}_1<0,t\in R_m,& (58)\end{array}$

is guaranteed, then Equation (57) is also guaranteed. The time derivatives for V₁ and V₂ are given in the proof of Theorem 1 and are re-produced below for ease of reference

$\begin{array}{l}{\dot{V}}_1=z^T\Xi z-2z^T((J_0{V}_0-W{V}_0)\otimes P^{-1}BK)e,\\ {\dot{V}}_2=-{\varphi }_4{\eta }^2+x^T{(L_0-L_D)}^2\otimes {\Phi }_{5}x,\end{array}$

with Ξ given below Equation (36). When CB-DoS occurs, there exists at least one zero diagonal entry in J₀−J_D. Hence

$\begin{array}{l}\Xi \le I_{N-1}\otimes (A^T{P}^{-1}+P^{-1}A).\end{array}$

For CB-DoS with at least one healthy channel it still holds that $x^T{(L_0-L_D)}^{2}x\le x^T{L}_0^{2}x$ Therefore, the proof follows similar steps given in expressions (39) to (46). This results in Ψ₂ < 0 given in Equation (50).

(iii) CB-DoS where all channels are blocked: In the situation that all communication links are blocked we have L_D(t) = L₀ and q_i(t) = 0, $\forall i\in \mathcal{V}$. Expanding Equation (58) for this situation results in

$\begin{array}{c}{\dot{V}}_1+{\dot{V}}_2-{\omega }_2{V}_1=z^T{I}_{N-1}\otimes (A^T{P}^{-1}+P^{-1}A-{\omega }_2{P}^{-1})z-{\varphi }_4\\ {\eta }^2<0,t\in R_m.& (59)\end{array}$

Condition (59) is guaranteed if $A^T{P}^{-1}+P^{-1}A-{\omega }_2{P}^{-1}<0$. Pre- and post multiplying this condition by P results in Ψ₃ < 0 given in Equation (51).

Now, we merge the Lyapunov conditions derived for the W_m and R_m intervals from expressions (55) and (56). Let us first expand Equation (56):

$\begin{array}{ll}V(t)\le e^{{\omega }_2(t-r_m)}V(r_m),t\in R_m.& (60)\end{array}$

Consecutively using Equations (55) and (60), and assuming t ∈ R_m, we obtain that

$\begin{array}{l}V(t)\le e^{{\omega }_2(t-r_m)}V(r_m)\\ \le e^{{\omega }_2(t-r_m)}(e^{-{\omega }_1(r_m-r_{m-1}-{\nu }_{m-1})}V(r_{m-1}+{\nu }_{m-1})+\frac{{\omega }_1}{2})\\ \le e^{{\omega }_2(t-r_m)}{e}^{-{\omega }_1(r_m-r_{m-1}-{\nu }_{m-1})}{e}^{{\omega }_2{\nu }_{m-1}}V(r_{m-1})+\frac{{\omega }_1}{2}{e}^{{\omega }_2(t-r_m)}\\ \le \dots \\ \le e^{-{\omega }_1\left|H(0,t)\right|}{e}^{{\omega }_2\left|R(0,t)\right|}V(0)+\frac{{\omega }_1^2}{2}+{\omega }_1{\displaystyle \sum _{\begin{array}{c}m\in {\mathbb{N}}_0\\ r_m\le t\end{array}}}{e}^{-{\omega }_1\left|H(r_m+v_m,t)\right|}{e}^{{\omega }_2\left|R(r_m,t)\right|}.& (61)\end{array}$

From Equations (20) and (21), the first term in the right hand side of Equation (61) is upper-bounded as follows

$\begin{array}{ll}{e}^{-{\omega }_1\left|H(0,t)\right|}{e}^{{\omega }_2\left|R(0,t)\right|}\le {\rho }_1{e}^{-\zeta t},& (62)\end{array}$

$\begin{array}{ll}{\rho }_1=e^{T_0({\omega }_1+{\omega }_2)},{\rho }_2=\frac{{\omega }_1^2}{2}+{\omega }_1{e}^{T_0({\omega }_1+{\omega }_2)}{\displaystyle \sum _{\begin{array}{c}m\in {\mathbb{N}}_0\\ r_m\le t\end{array}}}{e}^{-\zeta (t-r_m)}& (63)\end{array}$

where ρ₁ and ζ are defined in Equations (54) and (63).¹ From De Persis and Tesi (2015) (Lemma 4) the summation term in Equation (61) lies within the following upper-bound

$\begin{array}{ll}{\displaystyle \sum _{\begin{array}{c}m\in {\mathbb{N}}_0\\ r_m\le t\end{array}}}{e}^{-{\omega }_1\left|H(r_m+v_m,t)\right|}{e}^{{\omega }_2\left|R(r_m,t)\right|}\le e^{T_0({\omega }_1+{\omega }_2)}{\displaystyle \sum _{\begin{array}{c}m\in {\mathbb{N}}_0\\ r_m\le t\end{array}}}{e}^{-\zeta (t-r_m)}& (64)\end{array}$

Expressions (62) and (64) lead to exponential bounded consensus given in Equation (53).

Let α = ω₁/(ω₁+ω₂). If the CB-DoS attacks satisfy $\frac{1}{T_1}<\alpha$, parameter ζ remains positive and system (Equation 1) is exponentially stable according to Equation (53). Parameter α represents the level of resilience to CB-DoS attacks. This completes the proof. □

Remark 4. In simple terms, Theorem 2 computes the control gain and DETC parameters by considering three situations: (i) All channels are healthy or the MAS is under CP-DoS. LMI Ψ₁ < 0 given in Equation (49) represents this situation. (ii) The MAS is under CB-DoS, however, at least one channel is healthy in the communication topology. This situation is represented by LMI Ψ₂ < 0 given in Equation (50). (iii) The MAS is under full CB-DoS and all communication channels are blocked. LMI Ψ₃ < 0 given in Equation (51) represents this situation. With ω₁ as the rate of consensus convergence for situation (i), ω₂ as the rate of divergence for situations (ii) and (iii), and T₁ as the time ratio of CB-DoS attacks, the condition $\zeta ={\omega }_1-\frac{{\omega }_1+{\omega }_2}{T_1}>0$ decides whether consensus is guaranteed or not.

Remark 5. Increasing the desired resilience level to CB-DoS α, by construction, would make the MAS more resilient to CB-DoS, i.e., higher overall duration for DoS is tolerable. However, higher values for α lead to lower values for ω₂ which makes LMI Ψ₃ < 0 (given in Equation 51) unlikelier to be satisfied; especially if A is inherently unstable. Additionally, a performance drop is expected in the event savings and consensus convergence when α is increased for the sake of higher tolerance to DoS. This is the trade-off between the system performance and its amount of security to DoS.

Remark 6. As observed in Theorem 2, the knowledge of parameters T₀ and T₁ is only useful for the consensus convergence rate (Equation 53). In other words, the implementation of optimization (Equation 48) does not depend on T₀ or T₁. However, for selecting a reasonable value for α and run optimization (Equation 48), it is helpful if the designer has a priori estimation of parameter T₁ (which roughly represents the average ratio of CB-DoS duration to total time).

Remark 7. The computational complexities of solving Theorems 1 and 2 grow at the $O(\sqrt{N_p\left|log{ϵ}_g\right|})$, where the problem size N_p = max{d_m, n_v}, the duality gap denoted by ϵ_g, d_m is “the highest dimension of the LMIs associated with the optimization problem", and n_v is the “total number of decision variables” involved (Amini, 2020, Remark 3.11). Both d_m and n_v are sensitive to addition of the DETC state η, and will be increased compared to the scenario without dynamic event-triggering. Consequently, the computational complexity of solving LMIs in Theorems 1 and 2 slightly grows.

Remark 8. We remind that Theorem 2 guarantees consensus in the bounded sense with system trajectories satisfying inequality (Equation 53). The reason that an asymptotic or exponential rate without a residual cannot be guaranteed comes from inequality ${\omega }_1\eta \le \frac{{\omega }_1}{2}{\eta }^2+\frac{{\omega }_1^2}{2}$ which is used to make condition 38 quadratic. Intuitively, parameter η may not converge to zero which creates a bounded consensus error in the system.

Remark 9. Recently there has been an increasing interest in the fully distributed consensus control where no global knowledge of multi-agent system is required. While our proposed implementation in this article requires the knowledge of the minimum non-zero Laplacian eigenvalue which is a global information, we have identified important simplifying assumptions and practical shortcomings in existing references on fully distributed consensus approaches compared to our work. For example, in a vast majority of the proposed approaches such as Cheng and Li (2019); Li et al. (2020); Xu et al. (2022) an ideal scenario where no attack is targeted on the network is considered. Therefore, consensus in these references are not guaranteed in the presence of DoS attacks. In Wang et al. (2022); Du S. et al. (2023) a fully distributed event-triggered consensus under DoS is formulated. However, the DoS considered in Wang et al. (2022); Du S. et al. (2023) is synchronous which significantly simplifies the formulation compared to asynchronous DoS considered in our work. A fully distributed consensus under DoS attacks represented by Markov process (which can be regarded as asynchronous DoS) is proposed in Wang et al. (2022). However, the communication and control schemes in Wang et al. (2022) is not event-triggered.

Remark 10. This article considers a continuous-time model for the agents. Additionally, the dynamic event-triggering scheme (4) needs continuous-time monitoring of the condition to detect possible events. We note that it is not challenging to extend the proposed implementation in this work to a sampled-data dynamic event-triggering scheme where continuous-time measurement and event monitoring are relaxed. In fact, without compromising other novelties of the work one can adopt the well-known family of LMI-based Lyapunov-Krasovskii functionals (LKFs) stability method developed in our prior works [Amini et al., 2021, Equation (26)] and [Amini et al., 2022b, Equation (45)]. However, in order not to overshadow the main ideas of this work (i.e, incorporation of dynamic event triggering control under asynchronous DoS attacks) under overwhelmed formulation caused by the LKF approach we have opted to consider the continuous time formulation in this article.

4.3 Special case: DoS-free situation

The DoS-free situation (where no CP-DoS and no CB-DoS occur) is a special case of Theorems 1 and 2. The following corollary shows how the results in Theorem 1 can be reduced to the DoS-free situation

Corollary 1 (DoS-free situation). Consider MAS (Equation 23) with communication topology $G_0=(\mathcal{V},{\mathcal{E}}_0,{\mathcal{A}}_0)$. Given a desired consensus convergence rate ω₁, if there exist positive definite matrices P_n×n > 0, M_1n×n > 0, M_2n×n > 0, M_5n×n > 0, free matrix Ω_m×n, positive scalars m₃ > 0, m₄ > 0, and θ_c > 0, (1 ≤ c ≤ 7), such that the following convex minimization problem is feasible

$\begin{array}{ll}min𝔽={\theta }_1+{\theta }_2+\cdots +{\theta }_7,& (65)\end{array}$

subject to:

$\begin{array}{ll}\text{Ψ}=\left[\begin{array}{l}\psi -J_0{V}_0\otimes B\Omega 0\\ *-I_N\otimes M_{1}0\\ **({\varphi }_3-{\varphi }_4+\frac{{\omega }_1}{2})I_N\end{array}\right]<0,& (66)\end{array}$

$\begin{array}{l}{C}_1>0,C_2>0,C_3>0,C_4<0,\\ C_5>0,C_6<0,C_7>0,& (67)\end{array}$

where C_i, (1 ≤ i ≤ 7), are defined in Theorem 1 and

$\begin{array}{l}\psi =I_{N-1}\otimes (P{A}^T+AP+{\omega }_{1}P)-J_0\otimes B\Omega -J_0\otimes {(B\Omega )}^T\\ +J_0^2\otimes (M_2+M_5),& (68)\end{array}$

then the unknown parameters for control protocol (Equation 2) and DETC (Equation 4) are designed from the same expressions given in Equation (31). The bounds given in Equation (32) are also guaranteed

Proof: The proof of feasibility of the convex minimization problem defined through Equations (65)–(68) can be followed from proof of Theorem 1 with L_D = 0.

5 Simulation

To evaluate the performance of the proposed theorems, we conduct two different experiments as detailed below.

Example 1: Consider a MAS comprising of five agents with the following dynamics (Xu Y. et al., 2019)

$\begin{array}{l}A=\left[\begin{array}{cccc}0.001& 0.001& 0& 0\\ 0& -0.01& 0.001& 0\\ 0& 0& -0.01& 0.001\\ 0.001& 0& 0& 0\end{array}\right],B=2I_4.\hfill \end{array}(69)$

The initially designed network topology for Equation (69) is defined by the following Laplacian matrix

$\begin{array}{l}{L}_0=\left[\begin{array}{ccccc}2& -1& 0& 0& -1\\ -1& 3& -1& 0& -1\\ 0& -1& 2& -1& 0\\ 0& 0& -1& 2& -1\\ -1& -1& 0& -1& 3\end{array}\right].\hfill \end{array}(70)$

For illustration, we consider an example of a sequence of distributed attacks with 4 CP-DoS and 4 CB-DoS given below:

$\begin{array}{ll}\text{CB-DoS }1:\hfill & D_1^{15}{=D}_1^{12}{=D}_1^{25}=[0.4,0.7),\hfill \\ \text{CP-DoS }1:\hfill & D_0^{12}{=D}_0^{25}=[1,1.2),\hfill \\ \text{CB-DoS }2:\hfill & D_1^{34}{=D}_1^{45}=[2.8,3.3),\hfill \\ \text{CP-DoS }2:\hfill & D_0^{15}{=D}_0^{34}=[3.4,4),\hfill \\ \text{CP-DoS }3:\hfill & D_2^{12}{=D}_0^{45}=[5,5.4),\hfill \\ \text{CB-DoS }3:\hfill & D_0^{23}{=D}_2^{34}=[7,7.2),\hfill \\ \text{CP-DoS }4:\hfill & D_3^{12}{=D}_2^{45}=[7.5,8),\hfill \\ \text{CB-DoS }4:\hfill & D_1^{23}=D_3^{45}=[11,11.3).\hfill \end{array}(71)$

We remind that the definition of $D_c^{ij}$ is given in Equation (12). For better visualization, the attack sequence (Equation 71) is shown in Figure 3 where the highlighted areas in “orange” are CP-DoS attack intervals and in “red" are CB-DoS ones.

Figure 3

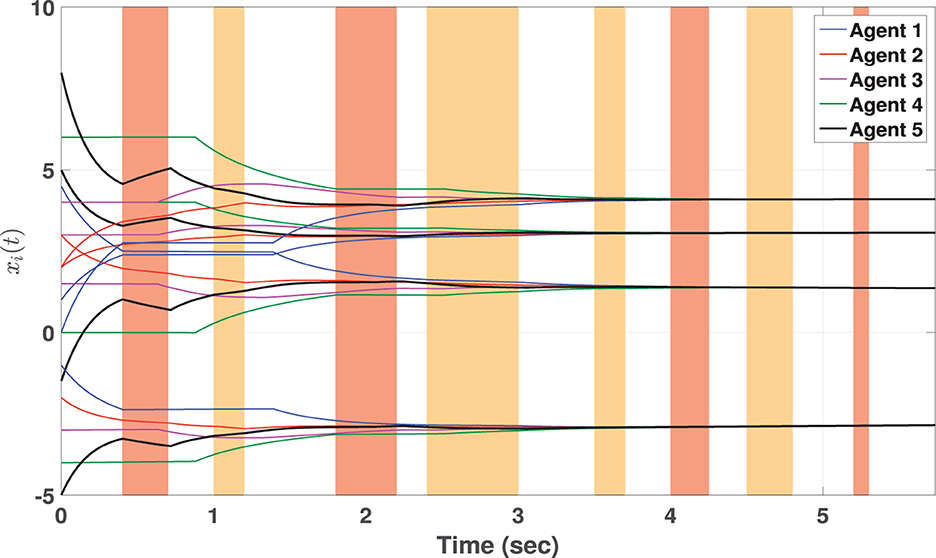
Figure 3. State consensus in MAS (Equation 69). Highlighted areas in “orange” are CP-DoS and in “red” are CB-DoS attack intervals (Equation 71).

It is easy to verify that the above DoS satisfies Assumption 1 with T₀ = 0.3 and T₁ = 7. The eigenvalues required in Equations (29), (30), and (52) are computed as λ = 0.38, $\bar{\lambda }=4.62$, and ${\bar{\lambda }}_D=2$. To compute necessary control and DETC design parameters from Theorem 2, we select ω₁ = 0.2 and α = 0.15. With T₁ = 7, it holds that $\frac{1}{T_1}=0.1429<\alpha =0.15$. The following parameters are obtained by solving optimization (Equation 48) through the MOSEK solver

$\begin{array}{l}K\text{ =}\left[\begin{array}{cccc}0.6475& 0.0022& -0.0005& 0.0026\\ 0.0022& 0.5858& 0.0166& 0.0014\\ -0.0005& 0.0165& 0.6197& 0.0006\\ 0.0026& 0.0014& 0.0006& 0.6419\end{array}\right],\hfill \\ {\Phi }_1\text{ =}\left[\begin{array}{cccc}1467.39& 9.64& -2.51& 12.89\\ 9.64& 1202.90& 77.31& 7.70\\ -2.51& 77.31& 1363.58& 1.02\\ 12.89& 7.70& 1.02& 1437.09\end{array}\right],\\ {\Phi }_2\text{ =}\left[\begin{array}{cccc}0.0713& 0.0004& -0.0001& 0.0006\\ 0.0004& 0.0587& 0.0041& 0.0004\\ -0.0001& 0.0041& 0.0673& 0\\ 0.0006& 0.0004& 0& 0.0699\end{array}\right],\\ {\varphi }_3=0.7617,{\varphi }_4=0.8617,\\ {\Phi }_5\text{ =}\left[\begin{array}{cccc}0.0714& 0.0004& -0.0001& 0.0006\\ 0.0004& 0.0590& 0.0045& 0.0004\\ -0.0001& 0.0045& 0.0687& -0.0001\\ 0.0006& 0.0004& -0.0001& 0.0699\end{array}\right].\end{array}$

Let $x_i(0)={\left[i,-1.5i+6,-i,2i-2\right]}^T$ and η_i(0) = 1, (1 ≤ i ≤ 5). The sampling period T_s for simulation is selected as T_s = 0.001s.

Consensus iteration is run until the settling time t^⋆ defined below

$\begin{array}{l}{t}^{\star }=inf\left\{t|\parallel z(t)\parallel \le 5\times 10^{-4}\parallel z(0)\parallel \right\}.\end{array}$

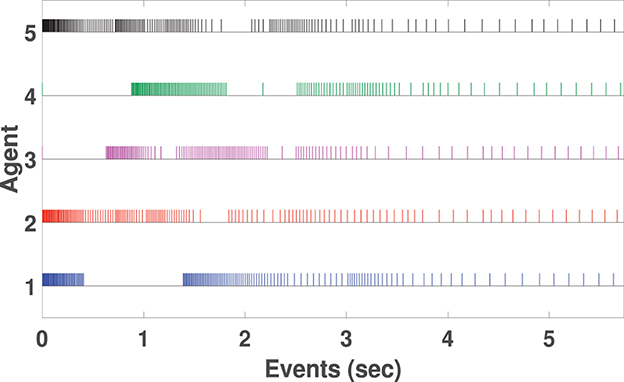
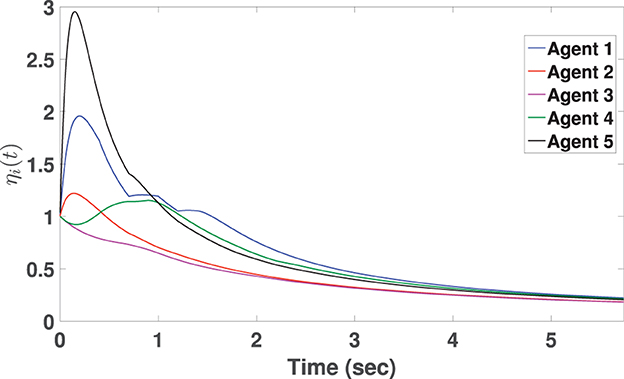
Conceptually speaking, time t^⋆ determines the consensus settling time within the 0.05% of the initial disagreement z(0). Therefore, a higher value of t^⋆ shows a slower rate of convergence and vice versa. We introduce t^⋆ as an index to compare the settling time (convergence rate) for consensus. In this example, t^⋆ = 5.73s. The states of MAS (Equation 69) are shown in Figure 3, where the agents reach consensus on respective states, despite the CB-DoS and CP-DoS given in Equation (71). In Figure 3, the highlighted areas in orange color show the CP-DoS and those in red represent intervals where CB-DoS is activated based on Equation (71). Controllers for agent 1 to agent 5 are, respectively, updated on 159, 151, 130, 138, and 176 occasions shown in Figure 4. For the sake of comparison, we introduce two parameters related to the amount of controller updates: (i) The average number of events (denoted by AE), and (ii) The average inter-event time (denoted by AIET). Parameter AE is computed by AE = (total events of all agents)/(number of agents). Additionally, AIET = t^⋆/AE. In fact, parameter AIET is an index to measure the intensity of events. For this example, we have AE=150.8 and AIET= 0.038. Figure 5 depicts the trajectories of the dynamic threshold η_i(t), (1 ≤ i ≤ 5). As observed in Figure 5, variable η_i(t) rises from its initial condition η_i(0) = 1 and greatly contributes to reducing the number of events.

Figure 4

Figure 4. Event instants (control updates) for the five agents.

Figure 5

Figure 5. Trajectories of η_i(t).

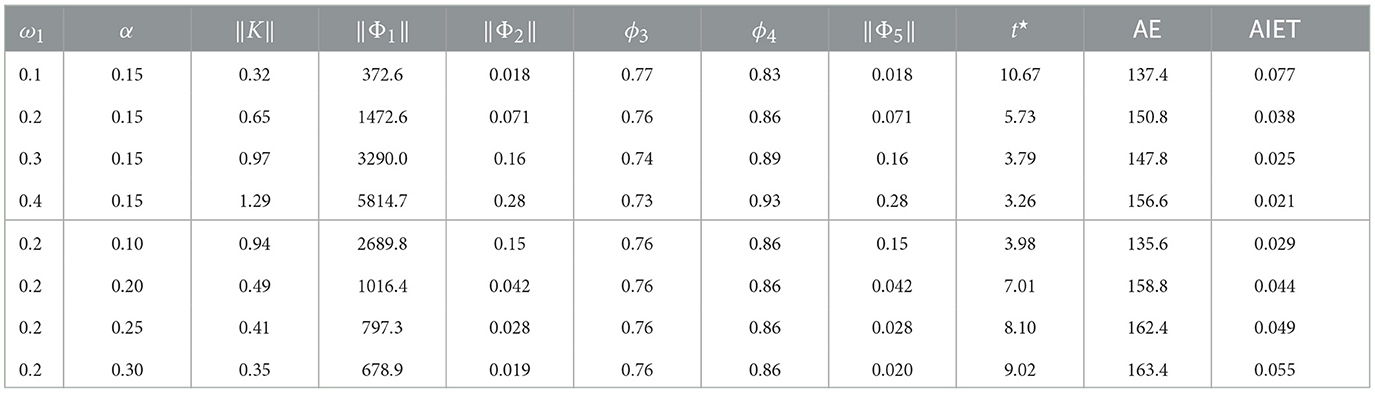
Next, we investigate how different values for convergence rate ω₁ and resilience level to CB-DoS α influence the designed parameters and consensus features. To this end, we consider two simulation scenarios. In the first scenario, α is fixed at 0.15 and ω₁ is incrementally increased in set {0.1, 0.2, 0.3, 0.4}. The purpose of this scenario is to observe the impact of ω₁ while α is fixed. In the second scenario, ω₁ is fixed at 0.2 and α is increased in set {0.1, 0.2, 0.25, 0.3}. Optimization (Equation 48) is solved for given values of ω₁ and α listed in Table 2. Using the obtained parameters, a separate consensus is run for Equation (69) with similar L₀, DoS attacks (Equation 71), and the initial conditions mentioned earlier. According to Table 2, the following design trade-offs are observed:

• When α is fixed and ω₁ is increased, we demand a faster rate of consensus. As expected, the settling time t^⋆ is reduced with higher values for ω₁ and fixed α. This scenario is useful for applications where a fast rate of convergence is important.

• However, the higher rate of consensus is achieved at the expense of more intense control updates. Looking at Table 2, this observation is verified from the reduced values of AIET with larger ω₁. This implies that the average inter-event time gets smaller and more frequent control update is demanded.

• As another observation, a higher value for α (i.e., demanding a higher resilience to CB-DoS attacks) a more conservative solution in terms of the consensus rate is obtained. In other words, consensus is achieved slower (i.e., higher t^⋆) when α is increased.

Table 2

Table 2. Impact of ω₁ and α on design parameters and consensus features.

These results verify the efficiency of the proposed method for a structured design based on the trade-off between consensus convergence rate, intensity of events, and resilience to DoS.

Example 2: In this section, we compare our work with He and Mo (2022) where another DETC scheme is formulated for consensus. The goals of this comparison are twofold: (i) Compare the essence of the parameter design approaches, and (ii) Compare the amount of savings in control updates. He and Mo (2022) studies consensus under a type of adversary known as the scaling attack. In order to focus only on the efficiency of the two event-triggering schemes and the basics of the design stages, we consider an attack-free situation. Consider the following MAS (Guo et al., 2014) with give agents and Laplacian (Equation 70)

$\begin{array}{ll}A=\left[\begin{array}{l}\mathrm{0 1}\\ 0-0.4\end{array}\right],B=\left[\begin{array}{l}0.8\\ 0.5\end{array}\right].& (72)\end{array}$

The attack-free situation in He and Mo (2022) requires setting μ = 1. The control gain K = B^TP is obtained by solving the generalized eigenvalue problem given in He and Mo (2022) (Equation 13). Except for Γ = PBB^TP, the required parameters for DETC [He and Mo, 2022, Equation (34)] (namely ξ, ζ, θ, σ) should satisfy some feasibility regions specified by conditions (38) and (39) in He and Mo (2022). With $\alpha =\tilde{\alpha }={\alpha }_1$, we have tested several different values satisfying the feasible regions and run consensus for Equation (72). These parameters are selected in such a way that conditions (38) and (39) in He and Mo (2022) are “just" satisfied so that we get the full advantage of the DETC. Three of the selected set of parameters are reported in Table 3. As for our proposed framework, we use Corollary 1 (DoS-free situation) with ω₁ ∈ {0.9, 1.0, 1.2} to compute necessary parameters for MAS (Equation 72) and run consensus. Comparing the results with He and Mo (2022), the following matters worth mentioning:

• The employed objective function 𝔽 in our design stage helps in reducing the intensity of events as compared to He and Mo (2022). This is concluded by comparing the values of AIET for the rows with almost the same range of t^⋆.

• Our proposed co-design framework computes the exact values of the necessary DETC parameters and there is no need for the process of trial and error to find efficient parameters within a region.

• Although the design stage in He and Mo (2022) has reduced complexity compared to our approach, since the extreme eigenvalues of the Laplacian matrix are used to derive the feasible regions for the DETC parameters, it inherently introduces some conservation in the DETC performance (i.e., more events are triggered than our work).

Table 3

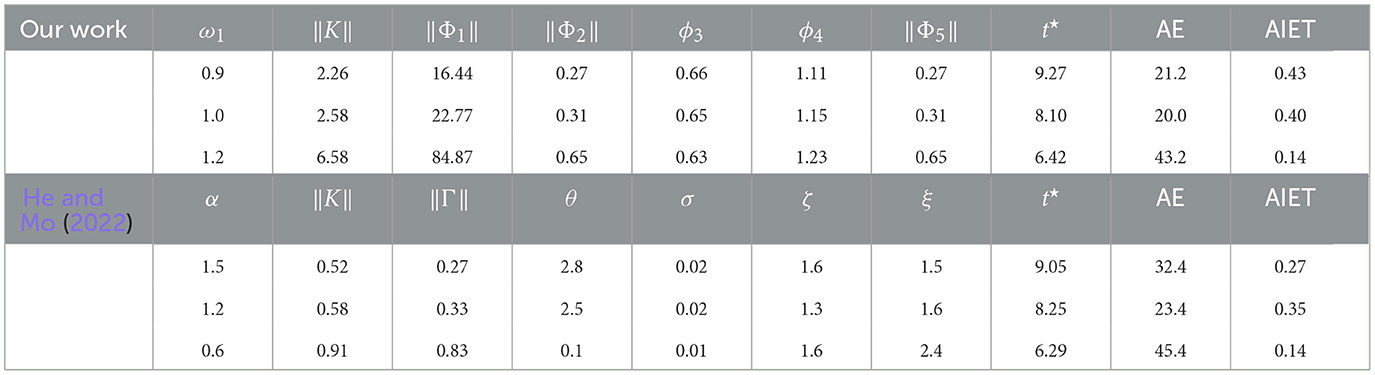
Table 3. Comparison between our work and He and Mo (2022).

6 Conclusion

This article proposes a resilient framework for consensus in multi-agent systems (MAS) using a distributed dynamic event-triggering control (DETC) protocol which reduces the burden of control updates. The MAS is under denial of service (DoS) attacks. In a general scenario, it is assumed that the DoS attack may target any arbitrary communication link between two agents in an asynchronous manner. The DoS attacks are thus categorized into connectivity-preserved DoS (CP-DoS) which does not impair the connectivity of the network, and connectivity-broken DoS (CB-DoS) which breaks the network into isolated sub-graphs. The implementation is based on the knowledge of the control gain and several DETC parameters. These parameters are co-designed through a unified distributed convex optimization. Numerical simulations are conducted to illustrate the capability of the proposed method. In future, we will study the sampled-data dynamic event-triggered control scheme for secondary control in microgrids under communication delay and asynchronous DoS attacks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AAm performed theoretical derivations with AM, MH, and AAs. AAm wrote the paper together with AM. AM and AAs supervised the study. All authors reviewed and revised the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This project was partially supported by the Department of National Defence's Innovation for Defence Excellence and Security (IDEaS) program, Canada.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^It is straightforward to show that Equation (61) also holds if t ∈ W_m.

References

Abdelrahim, M., Postoyan, R., Daafouz, J., and Nešić, D. (2014). “Co-design of output feedback laws and event-triggering conditions for linear systems,” in 53rd IEEE Conference on Decision and Control (Los Angeles, CA), 3560–3565. doi: 10.1109/CDC.2014.7039942

Crossref Full Text | Google Scholar

Amini, A., Asif, A., and Mohammadi, A. (2022). A unified optimization for resilient dynamic event-triggering consensus under denial of service. IEEE Trans. Cybernet. 52, 2872–2884. doi: 10.1109/TCYB.2020.3022568

PubMed Abstract | Crossref Full Text | Google Scholar

Amini, A., Asif, A., Mohammadi, A., and Azarbahram, A. (2021). Sampled-data dynamic event-triggering control for networked systems subject to dos attacks. IEEE Transact. Netw. Sci. Eng. 8, 1978–1990. doi: 10.1109/TNSE.2021.3070804

Crossref Full Text | Google Scholar

Amini, A., Ghafouri, M., Mohammadi, A., Hou, M., Asif, A., and Plataniotis, K. (2022a). Secure sampled-data observer-based control for wind turbine oscillation under cyber attacks. IEEE Trans. Smart Grid 13, 3188–3202. doi: 10.1109/TSG.2022.3159582

Crossref Full Text | Google Scholar

Amini, A., Mohammadi, A., Asif, A., Hou, M., and Plataniotis, K. N. (2022b). Fault-tolerant periodic event-triggered consensus under communication delay and multiple attacks. IEEE Syst. J. 16, 6338–6349. doi: 10.1109/JSYST.2022.3183863

Crossref Full Text | Google Scholar

Amini, A. (2020). Event-Triggered Consensus Frameworks for Multi-agent Systems (PhD thesis), Concordia University, Montreal, QC, Canada.

Google Scholar

Cao, L., Pan, Y., Liang, H., and Huang, T. (2023). Observer-based dynamic event-triggered control for multiagent systems with time-varying delay. IEEE Trans. Cybern. 53, 3376–3387. doi: 10.1109/TCYB.2022.3226873

PubMed Abstract | Crossref Full Text | Google Scholar

Cheng, B., and Li, Z. (2019). Coordinated tracking control with asynchronous edge-based event-triggered communications. IEEE Trans. Automat. Contr. 64, 4321–4328. doi: 10.1109/TAC.2019.2895927

Crossref Full Text | Google Scholar

De Persis, C., and Tesi, P. (2015). Input-to-state stabilizing control under denial-of-service. IEEE Trans. Automat. Contr. 60, 2930–2944. doi: 10.1109/TAC.2015.2416924

Crossref Full Text | Google Scholar

Deng, C., Che, W.-W., and Wu, Z.-G. (2020). A dynamic periodic event-triggered approach to consensus of heterogeneous linear multiagent systems with time-varying communication delays. IEEE Trans. Cybern. 51, 1812–1821. doi: 10.1109/TCYB.2020.3015746

PubMed Abstract | Crossref Full Text | Google Scholar

Deng, C., and Wen, C. (2020). Distributed resilient observer-based fault-tolerant control for heterogeneous multiagent systems under actuator faults and DoS attacks. IEEE Trans. Control. Netw. Syst. 7, 1308–1318. doi: 10.1109/TCNS.2020.2972601

Crossref Full Text | Google Scholar

Du, S., Sheng, H., Ho, D. W. C., and Qiao, J. (2023). Secure consensus of multiagent systems with DoS attacks via fully distributed dynamic event-triggered control. IEEE Trans. Systems Man Cybernet. 53, 6588–6597. doi: 10.1109/TSMC.2023.3283969

Crossref Full Text | Google Scholar

Du, X., Qu, S., Zhang, H., Xu, W., and Tang, Q. (2023). Distributed bipartite consensus for multi-agent systems with dynamic event-triggered mechanism. J. Franklin Inst. 360, 8877–8897. doi: 10.1016/j.jfranklin.2022.05.022

Crossref Full Text | Google Scholar

Feng, Z., and Hu, G. (2019). Secure cooperative event-triggered control of linear multiagent systems under DoS attacks. IEEE Trans. Control Syst. Technol. 28, 741–752. doi: 10.1109/TCST.2019.2892032

Crossref Full Text | Google Scholar

Ge, X., and Han, Q.-L. (2017). Distributed formation control of networked multi-agent systems using a dynamic event-triggered communication mechanism. IEEE Trans. Ind. Electron. 64, 8118–8127. doi: 10.1109/TIE.2017.2701778

Crossref Full Text | Google Scholar

Ge, X., Han, Q.-L., Zhang, X.-M., Ding, L., and Yang, F. (2019). Distributed event-triggered estimation over sensor networks: a survey. IEEE Trans. Cybern. 50, 1306–1320. doi: 10.1109/TCYB.2019.2917179

PubMed Abstract | Crossref Full Text | Google Scholar

Girard, A. (2014). Dynamic triggering mechanisms for event-triggered control. IEEE Trans. Automat. Contr. 60, 1992–1997. doi: 10.1109/TAC.2014.2366855

Crossref Full Text | Google Scholar

Guo, G., Ding, L., and Han, Q.-L. (2014). A distributed event-triggered transmission strategy for sampled-data consensus of multi-agent systems. Automatica 50, 1489–1496. doi: 10.1016/j.automatica.2014.03.017

Crossref Full Text | Google Scholar

He, W., and Mo, Z. (2022). Secure event-triggered consensus control of linear multiagent systems subject to sequential scaling attacks. IEEE Trans. Cybernet. 52, 10314–10327. doi: 10.1109/TCYB.2021.3070356

PubMed Abstract | Crossref Full Text | Google Scholar

He, W., Xu, B., Han, Q.-L., and Qian, F. (2019). Adaptive consensus control of linear multiagent systems with dynamic event-triggered strategies. IEEE Trans. Cybern. 50, 2996–3008. doi: 10.1109/TCYB.2019.2920093

PubMed Abstract | Crossref Full Text | Google Scholar

He, W., Xu, W., Ge, X., Han, Q.-L., Du, W., and Qian, F. (2022). Secure control of multiagent systems against malicious attacks: a brief survey. IEEE Transact. Ind. Inform. 18, 3595–3608. doi: 10.1109/TII.2021.3126644

Crossref Full Text | Google Scholar

Hu, S., Yue, D., Xie, X., Chen, X., and Yin, X. (2019). Resilient event-triggered controller synthesis of networked control systems under periodic DoS jamming attacks. IEEE Trans. Cybern. 49, 4271–4281. doi: 10.1109/TCYB.2018.2861834

PubMed Abstract | Crossref Full Text | Google Scholar

Hu, W., Liu, L., and Feng, G. (2015). Consensus of linear multi-agent systems by distributed event-triggered strategy. IEEE Trans. Cybern. 46, 148–157. doi: 10.1109/TCYB.2015.2398892

PubMed Abstract | Crossref Full Text | Google Scholar

Hu, W., Yang, C., Huang, T., and Gui, W. (2018). A distributed dynamic event-triggered control approach to consensus of linear multiagent systems with directed networks. IEEE Trans. Cybern. 50, 869–874. doi: 10.1109/TCYB.2018.2868778

PubMed Abstract | Crossref Full Text | Google Scholar

Li, X., Tang, Y., and Karimi, H. R. (2020). Consensus of multi-agent systems via fully distributed event-triggered control. Automatica 116, 108898. doi: 10.1016/j.automatica.2020.108898

Crossref Full Text | Google Scholar

Liu, H., and Wang, Z. (2021). Sampled-data-based consensus of multi-agent systems under asynchronous denial-of-service attacks. Nonlinear Anal. Hybr. 39, 100969. doi: 10.1016/j.nahs.2020.100969

Crossref Full Text | Google Scholar

Liu, J., Yin, T., Yue, D., Karimi, H. R., and Cao, J. (2020). Event-based secure leader-following consensus control for multiagent systems with multiple cyber attacks. IEEE Trans. Cybern. 51, 162–173. doi: 10.1109/TCYB.2020.2970556

PubMed Abstract | Crossref Full Text | Google Scholar

Lu, A.-Y., and Yang, G.-H. (2018). Distributed consensus control for multi-agent systems under denial-of-service. Inf. Sci. 439, 95–107. doi: 10.1016/j.ins.2018.02.008

Crossref Full Text | Google Scholar

Meng, R., Hua, C., Li, K., and Ning, P. (2023). Dynamic event-triggered control for nonlinear stochastic systems with unknown measurement sensitivity. IEEE Transact. Circ. Syst. I Regular Pap. 70, 1710–1719. doi: 10.1109/TCSI.2022.3232915

Crossref Full Text | Google Scholar

Meng, X., and Chen, T. (2014). “Optimality and stability of event triggered consensus state estimation for wireless sensor networks,” in 2014 American Control Conference (Portland, OR), 3565–3570. doi: 10.1109/ACC.2014.6859035

Crossref Full Text | Google Scholar

Newman, M. W. (2001). The Laplacian Spectrum of Graphs. Winnipeg City, MB: University of Manitoba.

Google Scholar

Peng, C., and Li, F. (2018). A survey on recent advances in event-triggered communication and control. Inf. Sci. 457, 113–125. doi: 10.1016/j.ins.2018.04.055

Crossref Full Text | Google Scholar

Peng, C., and Yang, T. C. (2013). Event-triggered communication and H_∞ control co-design for networked control systems. Automatica 49, 1326–1332. doi: 10.1016/j.automatica.2013.01.038

Crossref Full Text | Google Scholar

Qian, Y.-Y., Liu, L., and Feng, G. (2018). Distributed event-triggered adaptive control for consensus of linear multi-agent systems with external disturbances. IEEE Trans. Cybern. 50, 2197–2208. doi: 10.1109/TCYB.2018.2881484

PubMed Abstract | Crossref Full Text | Google Scholar

Ren, W. (2007). Formation keeping and attitude alignment for multiple spacecraft through local interactions. J. Guid. Control Dynam. 30, 633–638. doi: 10.2514/1.25629

Crossref Full Text | Google Scholar

Shang, Y. (2021). Resilient group consensus in heterogeneously robust networks with hybrid dynamics. Math. Methods Appl. Sci. 44, 1456–1469. doi: 10.1002/mma.6844

Crossref Full Text | Google Scholar

Shang, Y. (2022). Median-based resilient consensus over time-varying random networks. IEEE Transact. Circ. Syst. II Exp. Briefs 69, 1203–1207. doi: 10.1109/TCSII.2021.3093466

Crossref Full Text | Google Scholar

Shang, Y. (2023). Resilient tracking consensus over dynamic random graphs: a linear system approach. Eur. J. Appl. Math. 34, 408–423. doi: 10.1017/S0956792522000225

Crossref Full Text | Google Scholar

Wang, J., Deng, X., Guo, J., and Zeng, Z. (2023). Resilient consensus control for multi-agent systems: a comparative survey. Sensors 23, 2904. doi: 10.3390/s23062904

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, J., Li, Y., Duan, Z., and Zeng, J. (2022). A fully distributed robust secure consensus protocol for linear multi-agent systems. IEEE Transact. Circ. Syst. II Exp. Briefs 69, 3264–3268. doi: 10.1109/TCSII.2022.3153698

Crossref Full Text | Google Scholar

Wu, Z.-G., Xu, Y., Pan, Y.-J., Su, H., and Tang, Y. (2018). Event-triggered control for consensus problem in multi-agent systems with quantized relative state measurements and external disturbance. IEEE Trans. Circuits Syst. I Reg. Pap. 65, 2232–2242. doi: 10.1109/TCSI.2017.2777504

Crossref Full Text | Google Scholar

Xu, W., He, W., Ho, D. W., and Kurths, J. (2022). Fully distributed observer-based consensus protocol: adaptive dynamic event-triggered schemes. Automatica 139, 110188. doi: 10.1016/j.automatica.2022.110188

Crossref Full Text | Google Scholar

Xu, W., Ho, D. W., Zhong, J., and Chen, B. (2019). Event/self-triggered control for leader-following consensus over unreliable network with DoS attacks. IEEE. T. Neur. Net. Lear. 30, 3137–3149. doi: 10.1109/TNNLS.2018.2890119

PubMed Abstract | Crossref Full Text | Google Scholar

Xu, Y., Fang, M., Shi, P., and Wu, Z.-G. (2019). Event-based secure consensus of mutiagent systems against DoS attacks. IEEE Trans. Cybern. 50, 3468–3476. doi: 10.1109/TCYB.2019.2918402

PubMed Abstract | Crossref Full Text | Google Scholar

Xu, Y., Fang, M., Wu, Z.-G., Pan, Y.-J., Chadli, M., and Huang, T. (2018). Input-based event-triggering consensus of multiagent systems under denial-of-service attacks. IEEE Trans. Syst., Man, Cybern. 50, 1455–1464. doi: 10.1109/TSMC.2018.2875250

Crossref Full Text | Google Scholar

Yang, H., and Ye, D. (2022). Observer-based fixed-time secure tracking consensus for networked high-order multiagent systems against DoS attacks. IEEE Trans. Cybernet. 52, 2018–2031. doi: 10.1109/TCYB.2020.3005354

PubMed Abstract | Crossref Full Text | Google Scholar

Yang, R., Liu, L., and Feng, G. (2022). Leader-following output consensus of heterogeneous uncertain linear multiagent systems with dynamic event-triggered strategy. IEEE Trans. Syst. Man Cybernet. 52, 1626–1637. doi: 10.1109/TSMC.2020.3034352

Crossref Full Text | Google Scholar

Yang, Y., Li, Y., and Yue, D. (2020). Event-trigger-based consensus secure control of linear multi-agent systems under DoS attacks over multiple transmission channels. Sci. China Inf. Sci. 63, 1–14. doi: 10.1007/s11432-019-2687-7

Crossref Full Text | Google Scholar

Yi, X., Liu, K., Dimarogonas, D. V., and Johansson, K. H. (2018). Dynamic event-triggered and self-triggered control for multi-agent systems. IEEE Trans. Autom. Control 64, 3300–3307. doi: 10.1109/TAC.2018.2874703

Crossref Full Text | Google Scholar

Yi, X., Yang, T., Wu, J., and Johansson, K. H. (2019). Distributed event-triggered control for global consensus of multi-agent systems with input saturation. Automatica 100, 1–9. doi: 10.1016/j.automatica.2018.10.032

Crossref Full Text | Google Scholar

Zha, L., Liu, J., and Cao, J. (2019). Resilient event-triggered consensus control for nonlinear muti-agent systems with DoS attacks. J. Franklin Inst. 356, 7071–7090. doi: 10.1016/j.jfranklin.2019.06.014

Crossref Full Text | Google Scholar

Zhang, B., Dou, C., Yue, D., Zhang, Z., and Zhang, T. (2019). A packet loss-dependent event-triggered cyber-physical cooperative control strategy for islanded microgrid. IEEE Trans. Cybern. 51, 267–282. doi: 10.1109/TCYB.2019.2954181

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, D., and Feng, G. (2019). A new switched system approach to leader-follower consensus of heterogeneous linear multiagent systems with dos attack. IEEE Trans. Syst. Man Cybern. Syst. 51, 1258–1266. doi: 10.1109/TSMC.2019.2895097

Crossref Full Text | Google Scholar

Zhang, D., Liu, L., and Feng, G. (2018). Consensus of heterogeneous linear multiagent systems subject to aperiodic sampled-data and DoS attack. IEEE Trans. Cybern. 49, 1501–1511. doi: 10.1109/TCYB.2018.2806387

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, T.-Y., and Ye, D. (2021). Distributed event-triggered control for multi-agent systems under intermittently random denial-of-service attacks. Inf. Sci. 542, 380–390. doi: 10.1016/j.ins.2020.06.070

Crossref Full Text | Google Scholar

Zhao, G., and Hua, C. (2021). A hybrid dynamic event-triggered approach to consensus of multiagent systems with external disturbances. IEEE Trans. Autom. Control 66, 3213–3220. doi: 10.1109/TAC.2020.3018437

Crossref Full Text | Google Scholar