Concurrent compression and meaningful encryption of images using chaotic compressive sensing

The presented research introduces a new approach to simultaneously compressing and encrypting images using chaotic compressive sensing. This technique involves transforming the image into sparser data using the discrete cosine transform basis, which is then compressed through projection onto a lower dimensional space using a measurement matrix designed based on a new chaotic map. The proposed chaotic map produced a Lyapunov exponent value of 2.675 proving its chaotic behavior. The proposed map is also highly sensitive to initial values, making it a secure basis for encryption. The compressed data with the proposed map is then embedded onto a colorful image for transmission. This approach achieves both compression and visually meaningful encryption of images. Quantitative and Qualitative results on the proposed compression-encryption algorithm shows the effectiveness of the methodology against chosen plaintext attacks and cipher-only attacks.

1 Introduction

The transmission of images over the internet has grown exponentially in recent years, raising concerns about communication bandwidth and image security over public channels. To address these issues, various image compression and encryption algorithms have been proposed. Inspired by the idea of sparse signal approximation, compressive sensing (CS) (Candès, 2006; Donoho, 2006) has emerged as a new approach to image compression. Unlike traditional compression algorithms, CS-based compression algorithms acquire data in a compressed way, reducing the need to store all the sensed samples before compression. CS techniques have also enabled simultaneous compression and encryption of images, using measurement matrices to securely transmit the data. Chaotic compressive sensing approaches have been developed to reduce the burden of redesigning the measurement matrix on the receiver side.

However, the compression-encryption schemes discussed thus far typically generate noise-like or texture-like cipher images that provide no underlying data. To address this issue, a new methodology known as meaningful encryption has emerged. This approach embeds encrypted data onto high-frequency bands of a carrier image, usually of larger size than the original image. The insensitivity of the human vision system to changes in high-frequency content makes it difficult for intruders to detect that cipher images have been implanted onto the carrier images.

Motivated by this idea, we propose a new algorithm that achieves concurrent compression and meaningful encryption of images using compressive sensing. Our method compresses images using a CS scheme, with a measurement matrix designed based on a new chaotic map that is highly random and sensitive to its initial parameters. The compressed image is then embedded onto a high-frequency band of the carrier image, without affecting its appearance. We use a single chaotic map with different keys for compression, encryption, and embedding. The main contributions of this paper are as follows

(i) proposing a new chaotic map,

(ii) developing a compression-encryption scheme using the proposed chaotic map,

(iii) designing a chaotic map-based embedding scheme to generate visually meaningful encrypted images,

(iv) presenting simulation results to quantify the efficiency of our approach.

The rest of the paper is arranged as follows: Section 2 details some of the notable related works in recent times. Section 3 briefs the preliminaries on compressive sensing. Section 4 discusses the proposed chaotic map and its validations. Section 5 explains the proposed methodology of compression and meaningful encryption of images. The results and discussion are presented in Section 6, and finally, conclusions are drawn in Section 7.

2 Related works

Numerous compression and encryption schemes utilizing the concept of compressive sensing have been proposed in recent years (Mathivanan and Maran, 2023; Mathivanan and Balaji Ganesh, 2023; Ashwini and Amutha, 2021). Most methods demonstrate simultaneous compression and encryption using the CS methodology. In Zhang et al. (2020) proposed an image compression and encryption algorithm using compressive sensing and Fourier transform. They employed chaos and fractional Fourier transform in their proposed method, which produced good compression and reconstruction robustness. In Wang et al. (2018), the authors proposed a combination of compressive sensing and a detour cylindrical diffraction-based encoding scheme. Through various experimental analyses, they proved that their proposed work is free from plaintext and ciphertext-only attacks. An encryption algorithm based on a hyper chaotic system was proposed in Xu et al. (2020), where the authors used a 2D - SLIM hyperchaotic map for measurement matrix design. They used the GF 257 multiplication algorithm along with the hyperchaotic system for permutation and diffusion.

Musanna and Kumar (2020) proposed the use of nonlinear exponential functions and chaotic maps for CS-based image encryption. They designed the measurement matrix to be a circulant matrix obtained from a logistic map. Their proposed work obtained cipher images using a dynamic invertible exponential function.

CS-based encryption techniques have become popular to address specific applications as well. Unde and Deepthi (2019) proposed a lightweight encryption scheme for Multimedia IOTs. Their work aimed to improve the energy efficiency of CS-based cryptographic systems. The authors validated the ability of their algorithm to resist chosen plain text attack and statistical attacks. In Xue et al. (2020), the authors proposed a lightweight encryption scheme named Kryptein for cloud-enabled IoT systems, especially to secure the interaction between IoT devices and the cloud. Their algorithm requires significantly less energy and computation consumption compared to other state-of-the-art algorithms. Also multiple image encryption schemes are becoming popular in recent years (Dai et al., 2021; Chen et al., 2021). Zhou et al. (2023) proposed multi image encryption scheme using quaternion discrete transform and cross coupling operations. Zhang and Hu (2021) utilized 3D scrambling model and DNA coding for the multiple image cryptosystem. Watermarking scheme based image encryption with geometric corrections was proposed in Gong and Luo (2023).

To prevent the curiosity of intruders in knowing the underlying data, a new form of image encryption scheme known as a visually meaningful encryption scheme has evolved. Yang et al. (2021) proposed a visually meaningful image encryption algorithm using M-ary decomposition schemes. Their nonstandard preencryption algorithm passed all security analyses. They used virtual bits to embed into the host image in their embedding algorithm. In Ping et al. (2019), the authors proposed a reversible color transform-based visually secure meaningful encryption scheme. They used different measurement matrices to compress and encrypt the same secret image in different orders. Then, they obtained a meaningful encrypted image with a carrier image that is small compared to the secret image. Zhu et al. (2020) proposed a meaningful encryption scheme using block compressive sensing. They divided the plain image into blocks and compressed and preencrypted it using block compressive sensing. The authors embedded the cipher image onto the carrier image using the singular value decomposition embedding method. They claimed that their method provides a balanced performance on security, compression, and running efficiency. Ye et al. (2020) used a combination of DWT and SVD to hide the intermediate encrypted image into a cover image. They used logistic tent map and tent sine map for confusing the data and designing the measurement matrix for compression. They inserted random numbers into the preencrypted images to enhance the recovery quality at the receiver side. Gong and Luo (2023) have proposed watermarking scheme that utilizes a novel 3D chaotic system. Huang et al. (2023) proposed a meaningful encryption scheme using integer wavelet transform and RSE algorithm. Through experimental results they have proved that their algorithm can successfully resist known plain text attacks and chosen plain text attacks. An encryption algorithm using bit level extension algorithm was proposed in Zhou et al. (2024). Authors have generated secret keys using the SHA-512 hash function in order to strengthen the resistance of their encryption and decryption system against the selected plaintext and differential attacks. Hu et al. (2023) have combined matrix transform and semi-tensor product operation to generate an asymmetric compressive sensing model. Authors have used wavelet packet transform and Haar transform in their approach.

This paper proposes a new chaotic map and a new visually meaningful encryption scheme. The images are initially compressed using compressive sensing theory and meaningfully encrypted using discrete wavelet transforms of the carrier image. The rest of the paper provides a detailed explanation of the preliminaries, proposed map, and methodology, along with the necessary results.

3 Preliminaries

3.1 Compressive sensing (CS)

CS is an innovative and effective signal transform technology that can reduce the number of sampling points associated with the volume of data obtained, ensuring that the sensors never acquire redundant data. The basic idea of compressive sensing is to combine both sampling and compression in a single step. Consider a 1D signal $x\in {\Re }^{M_1}$ of length M1. Let α be the sparse representation of the signal x given by

$\begin{array}{ll}\alpha ={\text{Ψ}}^{T}x& (1)\end{array}$

where Ψ is the basis matrix over which the signal is sparsely represented. Let k be the number of nonzero elements in the sparse signal α. This sparse signal is compressively sensed using a measurement matrix Θ to obtain the reduced measurements y as given in (2).

$\begin{array}{ll}y=\Theta x=\Theta \Psi \alpha =\Phi \alpha & (2)\end{array}$

The matrices Θ and Ψ must necessarily be incoherent. The matrix Φ is called the sensing matrix. It is proven that the matrices Θ and Ψ must satisfy the restricted isometry constraint to properly reconstruct x from y (Candes, 2008). Recovery of the original signal x from their reduced measurements y is performed by solving the optimization problem:

$\begin{array}{ll}mi{n}_{\alpha }\parallel \alpha {\parallel }_{0}s.t\Theta \Psi \alpha =y& (3)\end{array}$

Solving l₀ norm minimization is an NP-hard problem and is not convex. Thus, the l₀ norm can be converted into the convex l₁−norm as

$\begin{array}{ll}mi{n}_{\alpha }\parallel \alpha {\parallel }_{1}s.t\Theta \Psi \alpha =y& (4)\end{array}$

4 Chaotic maps

Randomness generated by a deterministic system is mathematically defined as chaos. The behavior of the chaotic system is predictable if, and only if, there is knowledge about its initial parameters; otherwise, the system appears to be random. Chaotic maps are generally constructed based on chaos theory. They are classified as 1D and high-dimensional maps. A 1D map produces a simple 1D sequence with two control parameters. Examples of 1D maps include the logistic map (Phatak and Rao, 1995) and sine map (Feng et al., 2017). Higher dimension maps such as the 2D logistic sine map (Hua et al., 2014) produce a much more complex sequence with two or more control parameters. Physical implementation of a chaotic map via an electric circuit is quite easy since only two or three initial parameters have to be memorized by the circuit elements.

4.1 Proposed chaotic map

A chaotic map that has a wider chaotic range and extreme sensitivity to its initial parameters is proposed. The proposed equation is as follows:

$\begin{array}{ll}{Z}_{n+1}=mod(sin(\mu \pi (1+Z_n^2)),1)& (5)\end{array}$

The proposed map is created from the basic sine map. Bifurcation of the sine map shows that the map values are chaotic in periodic intervals. For the basic sine map, replacing Z_n with $Z_n^2$ and taking the mod 1 value results in a new map that is highly chaotic and extremely sensitive to its initial values. The proposed map has shown chaos in entire range of considered μ value. Modulus value is mainly taken to restrict the range of the map sequence between 0 and 1.

Many compressive sensing techniques are available in literature. Each technique uses different methods to obtain sparser data and also uses different measurement matrix to compress. Of many approaches available, chaotic maps are used in the proposed approach to design the measurement matrix. Since the chaotic map produces a pseudorandom sequence, a structured matrix is constructed from them to be used as a measurement matrix for compressing the images. With the exemplary properties of unpredictability, pseudo randomness, ergodicity and sensitivity to their initial parameters, chaotic maps are widely used in security applications to induce confusion and diffusion in the data, enabling secure transmission for the data owner over an insecure communication channel. Hence, using the chaotic sequence generated with the proposed chaotic map and along with the designed measurement matrix, CS-based encryption algorithms for signal recovery are devised in this paper. Various simulation results validating the chaotic property of the proposed map are presented in the subsequent sections.

4.2 Simulation results validating the proposed chaotic map

4.2.1 Bifurcation analysis

For precise representation of the nonlinear behavior of any system, bifurcation plots are used. Bifurcation analysis is one of the most important parameters for evaluating the chaotic behavior of a chaotic map. Bifurcation is usually made with the control parameter against its system values. Figure 1 compares the bifurcation plot of the proposed chaotic map along with some of the existing 1D maps for an initial random value of 0.543. From the plots, it is quite evident that the bifurcation plot of the proposed map (Figure 1E) is very chaotic throughout the whole range of μ values investigated, while other existing maps are chaotic only for small ranges of μ values. It can be seen that there are no empty spaces in the bifurcation plot of the proposed map, and that means for each μ value, the sequence values of the map are completely different. The chaotic behavior of the proposed map is thus clearly superior to that of existing 1D maps, as evidenced by these plots.

Figure 1

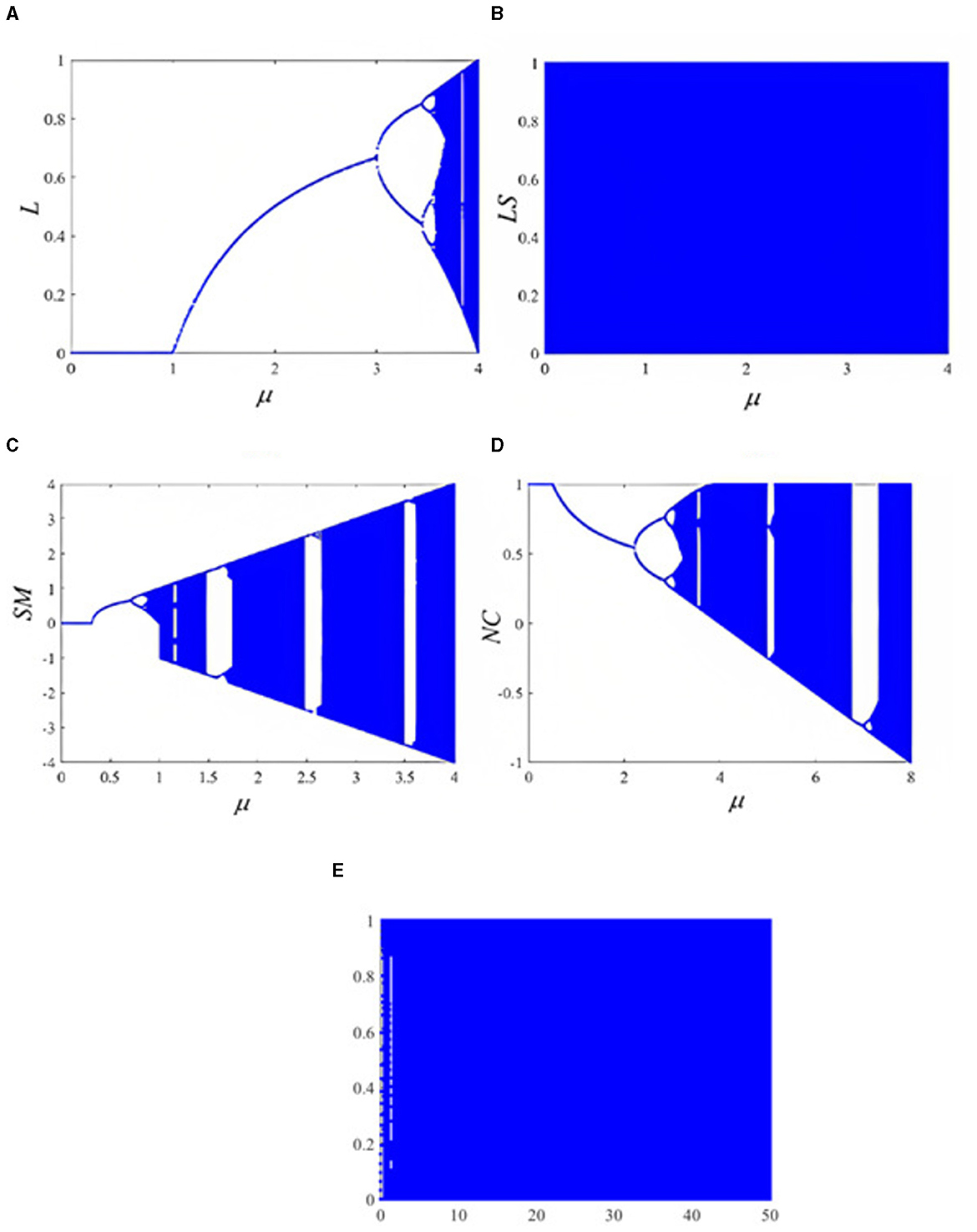
Figure 1. Comparison of the bifurcation diagram of the proposed map with existing maps: (A) logistic map, (B) logistic sine map, (C) sine map, (D) new chaotic map, and (E) proposed map.

4.2.2 Comparison of Lyapunov exponent and approximate entropy of proposed map with existing map

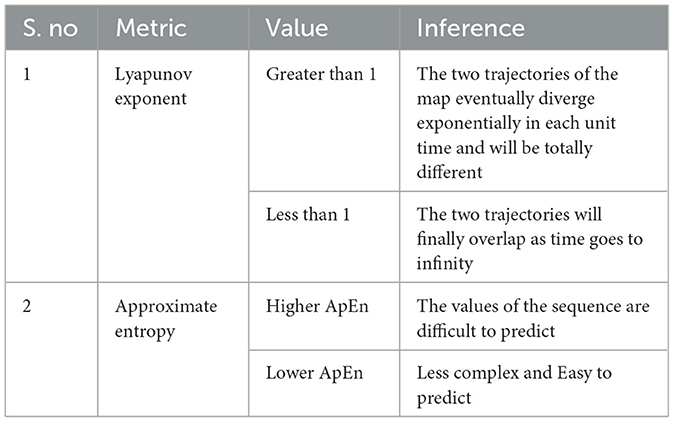
The most frequently accepted markers for assessing chaos in a map are the Lyapunov exponent (LE) (Wolf et al., 1985) and approximate entropy (ApEn) (Pincus, 1995). LE calculates the average divergence of two map trajectories with two different initial values that are closer to each other. The degree of complexity in the maps is calculated using approximate entropy.

The significance of LE and ApEn values is briefly described in Table 1. Table 2 compares the computed metrics for the proposed map along with other existing maps in the literature. It can be inferred from the tabulated values that the LE and ApEn values are almost 30 to 70% higher than the values obtained for the existing method. This is because of the chaotic nature of the proposed map for a wider range of μ values. Thus, the proposed map behaves in the same manner or even superior to the existing maps and thus can be used in compression, encryption or any other application.

Table 1

Table 1. Significance of LE and ApEn values.

Table 2

Table 2. Comparison of LE and ApEn between existing and proposed chaotic maps.

4.2.3 Sensitivity to initial parameters

A good chaotic map must be extremely sensitive to its initial values. Trajectory plots are used to validate the chaotic maps in terms of their sensitivity to their initial values. When the map sequences obtained considering different initial values and μ values are disparate, the map is considered to be highly sensitive to its parameters. In order to prove this, trajectory plots are used. Figures 2A, B shows the trajectory plot made with two different initial values and two different μ values. The deviation between two different initial values is considered to be in the range of 10–14. Similarly, the difference between two different μ values is considered to be 10–15. The plots show the value of the chaotic sequence obtained with the proposed chaotic map considering these two different initial μ values. It is quite apparent from these plots that with extremely minimal changes in the chaotic value and μ value, the chaotic sequence obtained is completely different. Hence, the suggested map being particularly sensitive to its initial values makes it ideal for use in encryption processes where the initial values of the map are secret keys.

Figure 2

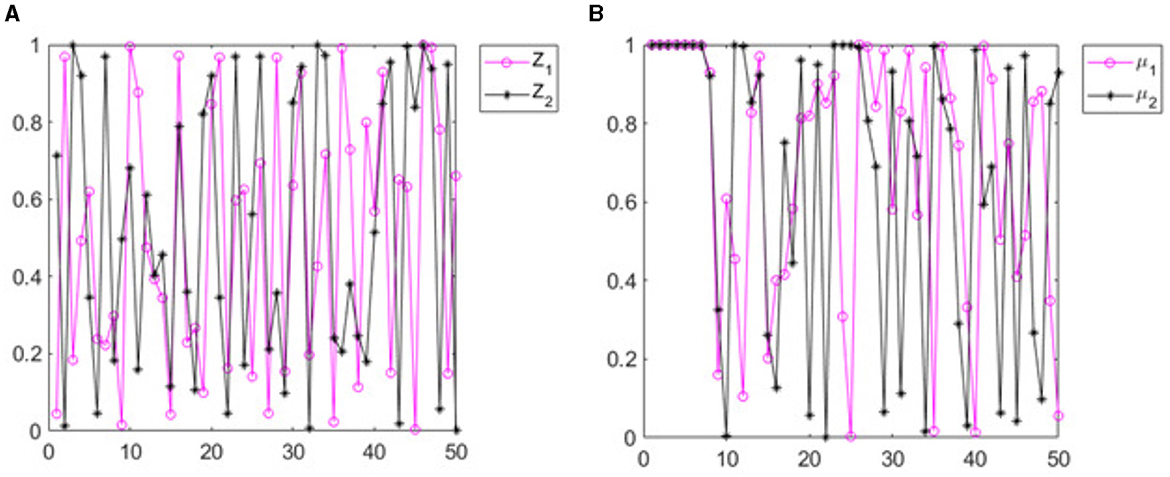
Figure 2. Trajectories of the proposed map (A) with different initial Z values and (B) with different μ values.

5 Proposed compression encryption scheme

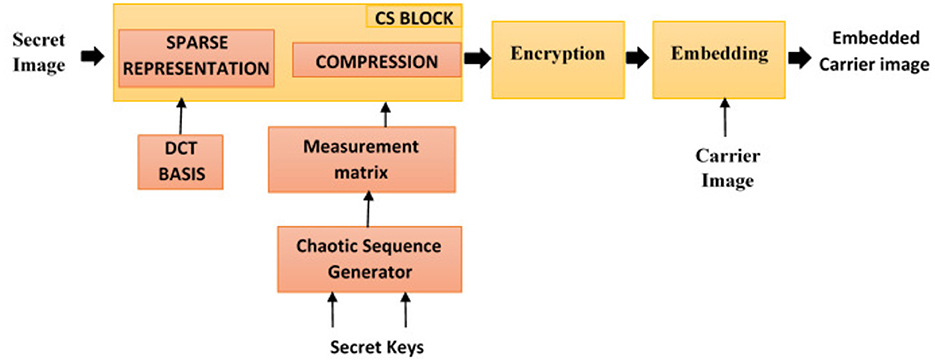
The block diagram of the proposed compression encryption scheme is shown in Figure 3. The secret image to be securely transmitted is initially converted into sparser data. The transformed data are compressed with the aid of the measurement matrix. The compressed data is pre-encrypted with chaotic sequences. Embedding of preencrypted data in a color image is carried out using the discrete wavelet transform. The following subsections provide a detailed explanation of each of the processes outlined above.

Figure 3

Figure 3. Block diagram of the proposed compression encryption scheme.

5.1 Compression and pre-encryption of image

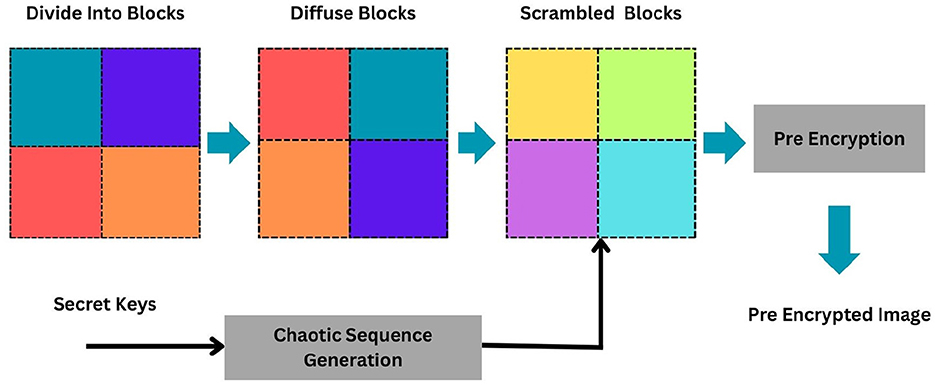
The image to be encrypted is initially compressed using the CS scheme. The image is sparsely represented using the Ψ matrix (DCT). The sparser data are then projected onto a lower dimensional space using the measurement matrix M, thus achieving compression. A pseudo random measurement matrix constructed from the chaotic sequences obtained from the proposed chaotic map is used as the measurement matrix in our work. The design of the measurement matrix is detailed in our previous work (Ashwini and Amutha, 2018). Initial parameters l₁ and μ₁ are used as key values K1 in generating the sequence to be used in MM design. Compressed data are then encrypted using the same chaotic map that is used for matrix design. Details of the encryption algorithm is explained in Algorithm 1 and the block block diagram of the same is given in Figure 4.

Algorithm 1

Algorithm 1. Diffusion of measurements.

Figure 4

Figure 4. Proposed encryption process.

5.2 Embedding pre-encrypted images

Preencrypted images are then embedded onto the carrier image to obtain the meaningful encrypted image. To produce a visually pleasing embedded image, the encrypted measurements are implanted onto the high-frequency content of the carrier image. The discrete wavelet transform is employed for this purpose. Embedding procedure is detailed in Algorithm 2.

Algorithm 2

Algorithm 2. Embedding pre encrypted measurements into carrier image.

The embedded carrier image thus contains the secret image engrafted in it in encrypted form. Data invaders will not have any idea about the underlying cipher data that the carrier image is transporting in the public channel.

5.3 De-embedding and decryption of secret image

The embedded carrier image that has been received by the intended data user must be processed to recover the secret image. As a first step, the encrypted measurements that were embedded in the carrier image are recovered. The measurements obtained are then given to the CS-based reconstruction algorithm along with the measurement matrix that was used at the sender side to recover the sparser data. With the aid of the same basis matrix, the sparser data are converted back to the secret image by taking the inverse transform. The chaotic sequence generated at the sender side must be regenerated at the receiver side so that the same measurement matrix and the embedding locations that were used at the sender side can be regenerated at the receiver side as well.

6 Experimental results and discussion

The proposed compression encryption scheme is tested on five different cover images and nine secret images downloaded from the SIPI image database https://sipi.usc.edu/database. The cover images are shown in Figure 5 and the secret images are shown in Figure 6. As mentioned earlier, cover images in Figure 5 are the carrier images that act as host and will house the secret image within it (Figure 6). Both color images and secret images are considered to be RGB images. Various simulation experiments are performed to analyse the efficiency of the proposed method in effectively compressing and encrypting the images. All the simulations are performed with MATLAB R2018 software, using an INTEL i3, 2.2 GHz processor with 6GB RAM.

Figure 5

Figure 5. Cover images. C1 4.2.05 “Airplane”. (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=11#top, licensed under CC BY 4.0) C2 4.2.07 “Peppers”. (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=13#top, licensed under CC BY 4.0) C3 “Lena”. (Reproduced from SIPI Image Database, University of Southern California, licensed under CC BY 4.0) C4 4.2.03 “Mandrill (a.k.a Baboon)”. (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=10#top, licensed under CC BY 4.0) C5 4.2.06 “Sailboat on lake”. (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=12#top, licensed under CC BY 4.0).

Figure 6

Figure 6. Secret images. S1 4.1.05 “House” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=5#top, licensed under CC BY 4.0) S2 4.1.02 “Couple (NTSC test image)” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=2#top, licensed under CC BY 4.0) S3 4.1.01 “Female (NTSC test image)” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=1#top, licensed under CC BY 4.0) S4 5.1.14 “Chemical plant” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=19#top, licensed under CC BY 4.0) S5 5.1.13 “Resolution chart” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=18#top, licensed under CC BY 4.0) S6 5.1.12 “Clock” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=17#top, licensed under CC BY 4.0) S7 5.1.11 “Airplane” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=16#top, licensed under CC BY 4.0) S8 5.1.09 “Moon surface” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=14#top, licensed under CC BY 4.0) S9 4.1.06 “Tree” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=6#top, licensed under CC BY 4.0).

6.1 Qualitative results of the proposed compression—encryption scheme

Figure 7 shows a series of sample images that have undergone compression and encryption using the proposed scheme. The result is shown for a sampling ratio of 0.5. In the example shown, the secret image moon is encrypted and embedded into the cover image Baboon. It is evident from the figure that the recovered secret image Moon from the embedded cover image (Figure 7E) is almost similar to the actual secret image (Figure 7B). The process of compression, encryption and embedding of the secret image has not degraded the visual perception of the image. The proposed method can thus be thought of as a good compression encryption scheme.

Figure 7

Figure 7. Qualitative analysis of the proposed scheme for SR = 0.5. (A) Cover image. 4.2.03 “Mandrill (a.k.a Baboon)”. (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=10#top, licensed under CC BY 4.0). (B) Secret image. 5.1.09 “Moon surface” (Reproduced from SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=14#top, licensed under CC BY 4.0). (C) Encrypted secret image. (D) Embedded cover image. (E) Recovered secret image.

6.2 Compression performance analysis

6.2.1 PSNR and SSIM

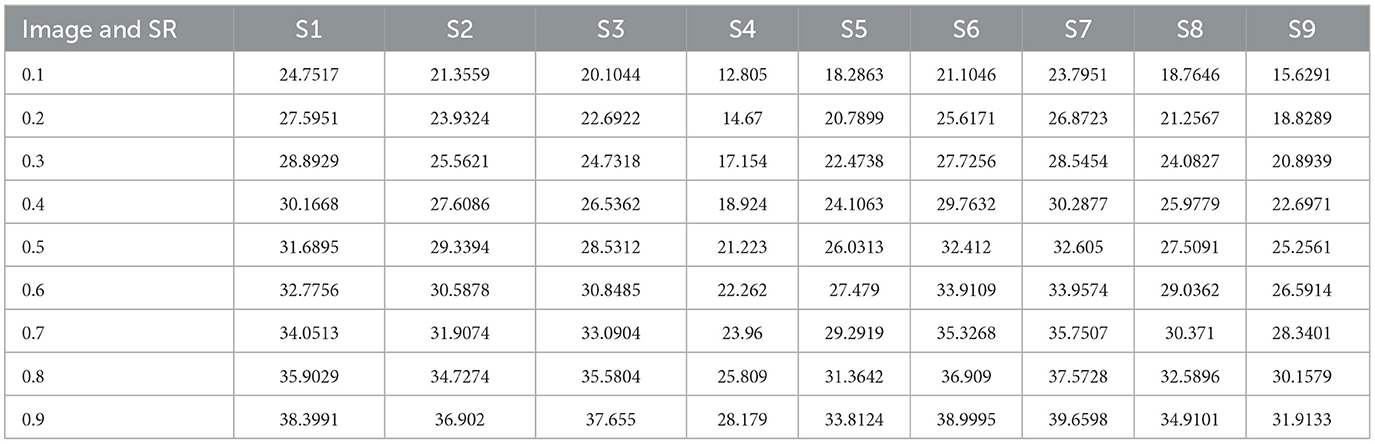
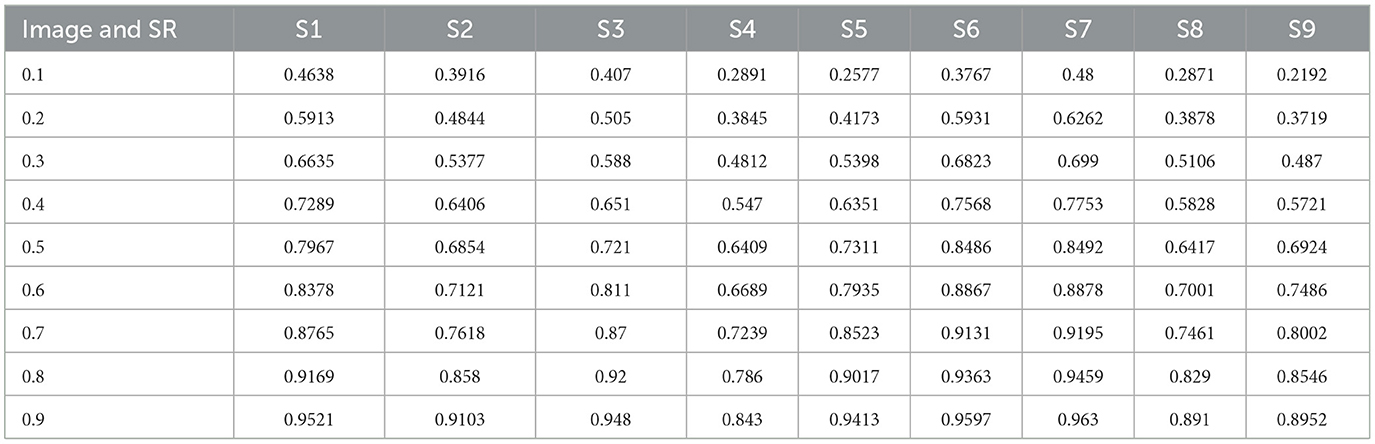
Degradation in the characteristic property of perceived images is measured by Image Quality Assessment. The assessment is performed both quantitatively and qualitatively by comparing the images with ideal or reference images. There are several techniques and metrics available for image quality assessment. Particularly, image quality metrics focus on measuring specific types of degradation, such as blurring, blocking, ringing, or all possible distortions of signals. Two main metrics, namely, the PSNR and SSIM, can be mathematically implemented in the optimization context. The PSNR computes the peak signal-to-noise ratio, in decibels, between two images. This ratio is used as a quality measurement between the original and a compressed image. Higher the PSNR, better the quality of the compressed or reconstructed image. The metric PSNR, however, is sometimes mismatched to perceive visual quality and is not normalized in representation. Hence, another famous quality metric, namely, the Structural Similarity Indexing Metric, SSIM, is also computed. The Structural Similarity Index (SSIM) measures the deterioration of image quality brought on by processing operations like data compression or transmission losses. It is a technique for estimating the perceived quality of images. The SSIM index is a complete reference metric, meaning that an original, uncompressed, or distortion-free image serves as the basis for measuring or predicting image quality. An SSIM value closer to 1 signifies better image quality. Tables 3, 4 list the PNSR and SSIM values computed between the original secret image before compression and the recovered secret image from the compressed image for SR ranging from 0.1 to 0.9. The following inferences can be drawn from Tables 3, 4.

(i) The values of PSNR between secret images remain high for higher sampling ratios, irrespective of the type of secret image.

(ii) The first highest value is observed in secret image S7, which features more primary colors. It was followed by secret image S6 with more primary colors.

(iii) The lowest value is observed for secret image S4, which features grayscale properties.

(iv) The above data inferred that the recovering property of the images depends on the color and contrast of the original secret images.

(v) The values of SSIM between secret image remain high for higher sampling ratios, irrespective of the secret images.

Table 3

Table 3. PSNR between the original secret image and recovered secret image.

Table 4

Table 4. SSIM between the original secret image and recovered secret image.

The above data inferred that the recovering property of the images depends on the color and contrast of the original secret images.

6.2.2 Comparison of PSNR and SSIM values with existing methods

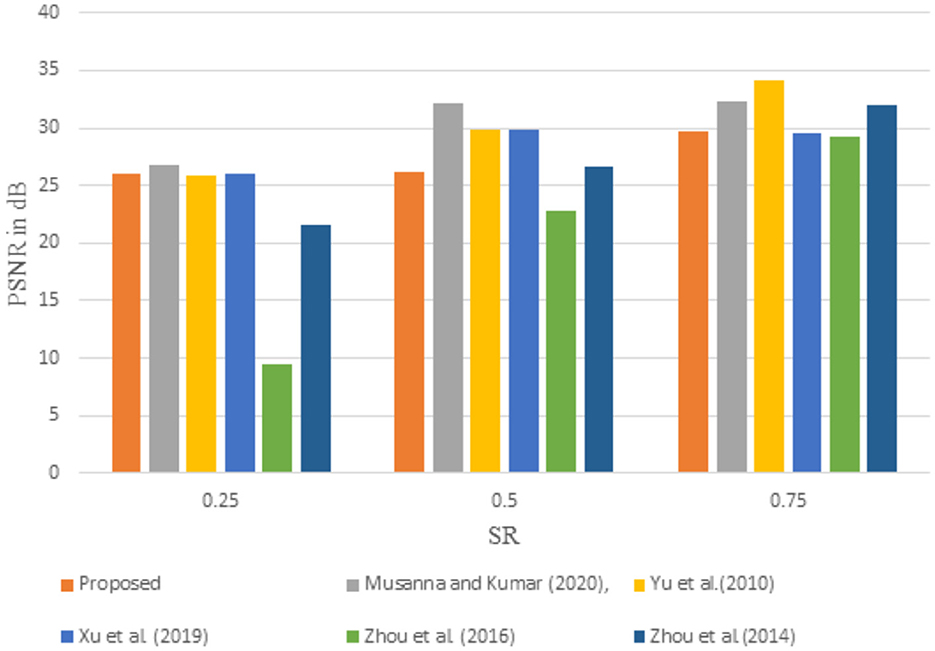
To prove the effectiveness of the proposed algorithm in compressing the secret image, the PSNR values obtained from the proposed method are compared with some of the existing methods in the literature. The comparison results are presented as bar plots in Figure 8. A Lena image of size 256 X 256 is taken as the test image. From the plot, it is evident that the PSNR value obtained with the proposed method for an SR of 0.25 is almost 5-10 dB higher than the values presented in methods (Zhou et al., 2016, 2014). The value is almost closer to the values presented by methods (Musanna and Kumar, 2020; Yu et al., 2010; Xu et al., 2019). A similar kind of pattern is observed for other SRs as well. It is thus obvious that the proposed method is capable of successfully decompressing the image data without much loss.

Figure 8

Figure 8. Comparison of the PSNR of the proposed method with existing methods.

6.3 Encryption performance analysis

6.3.1 Correlation coefficient

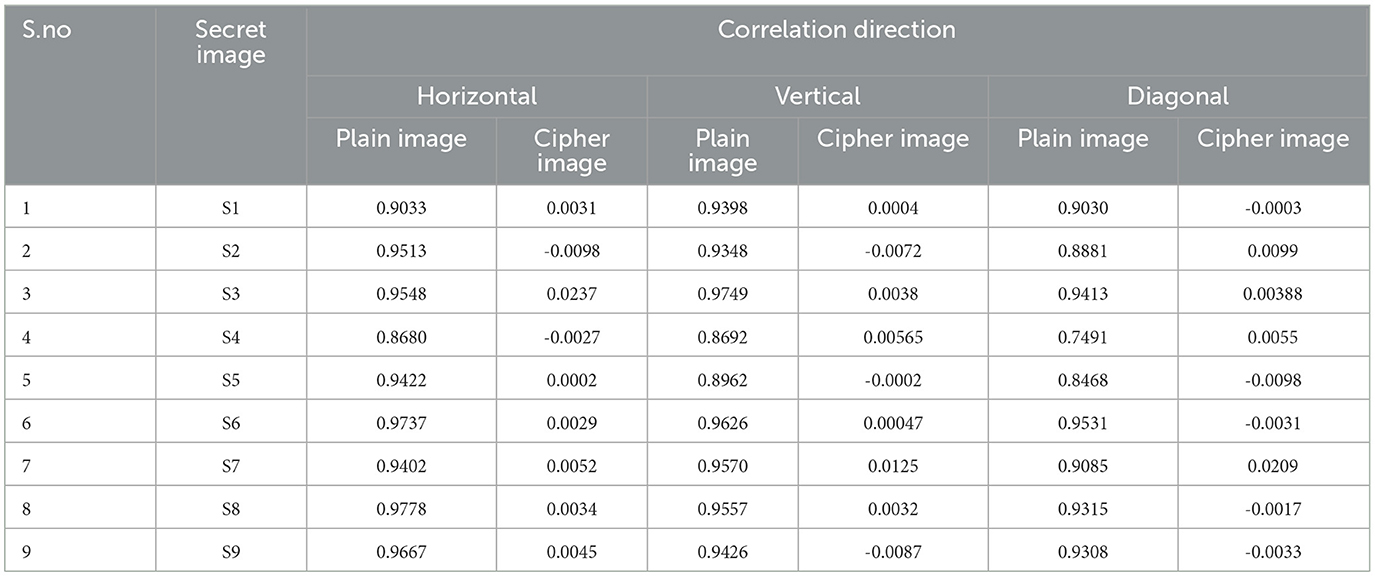
The strength of the linear relationship between any two variables is investigated with the help of correlation analysis. The correlation coefficient gives the measure of the association among any two variables and is expressed as values between -1 and +1. An effective encryption scheme should have a smaller correlation coefficient value for its encrypted image compared to the original image. The values of the correlation coefficient between neighboring pixels in the horizontal, vertical, and diagonal directions, of both the original image data and its corresponding encrypted data are shown in Table 5. The values are computed by selecting 5000 random pairs of adjacent pixels in each direction. From the tabulated values, it is clear that the correlation coefficient value of the plain image is closer to 1 in all three directions considered. For cipher images, the correlation value is almost equal to zero irrespective of the type of image. A pictorial representation of the correlation among pixels is presented with the aid of a scatter plot in Figure 9. It is evident from the plot that a kind of linear relationship among the pixels of the original image is visible, while the data points are well scattered in the case of cipher images. Thus, both the tabulated values and the scatter plot prove that, with the suggested encryption approach, the tight linear link between neighboring pixels of the original image is significantly reduced in their corresponding encrypted image, making it difficult for attackers to recover any valuable information.

Table 5

Table 5. Correlation of plain image and cipher image.

Figure 9

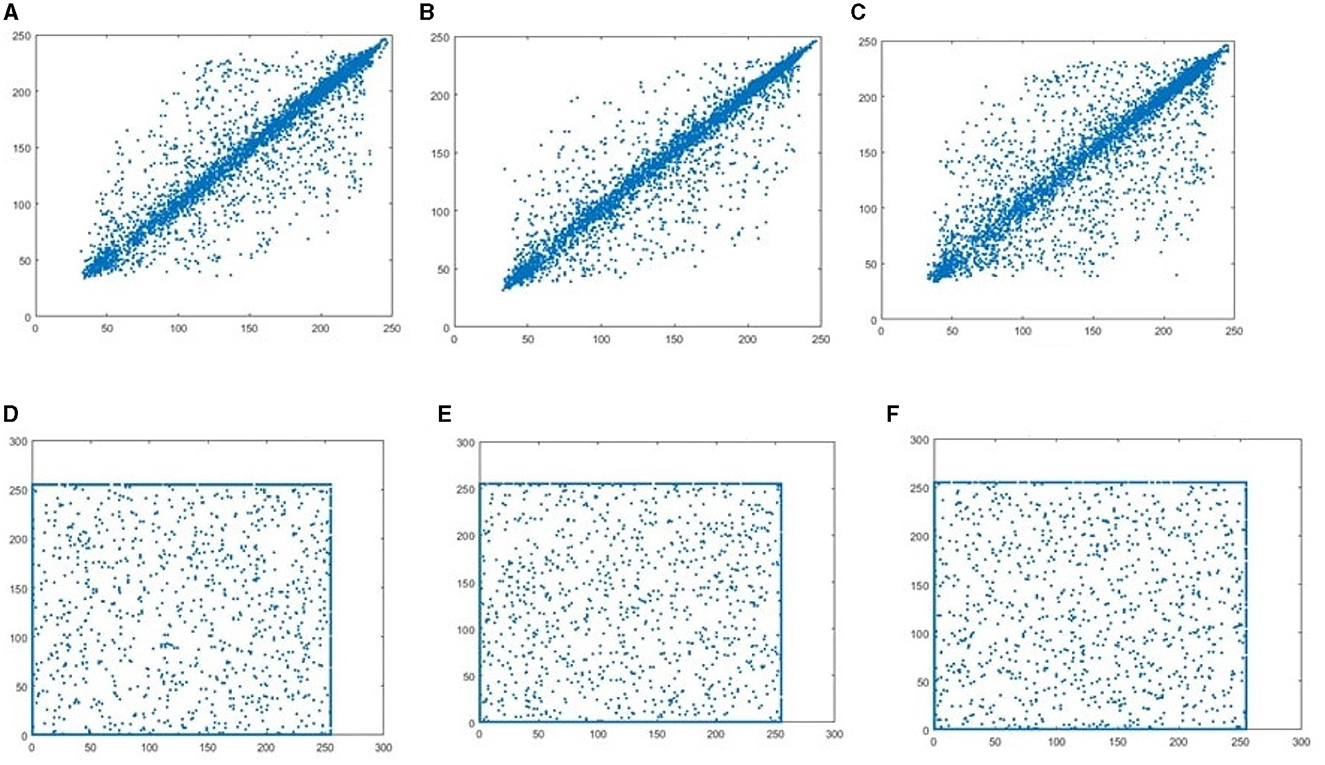
Figure 9. Plain image correlation: (A) horizontal, (B) vertical, and (C) diagonal. Cipher image correlation, (D) horizontal, (E) vertical, and (F) diagonal.

6.3.2 Histogram analysis

Image histogram serves as a graphical depiction of the tonal distribution of a digital image. Histogram analysis is commonly carried out to demonstrate the system's invulnerability to statistical attacks. Since each image has a unique histogram distribution, they are more liable to statistical attacks. Histogram plots are used to examine the encryption algorithm's ability to disrupt the regularity in the pixel distributions of the images. Figure 10 shows the histogram plots of the plain secret image, encrypted secret image, plain carrier image and embedded carrier image.

Figure 10

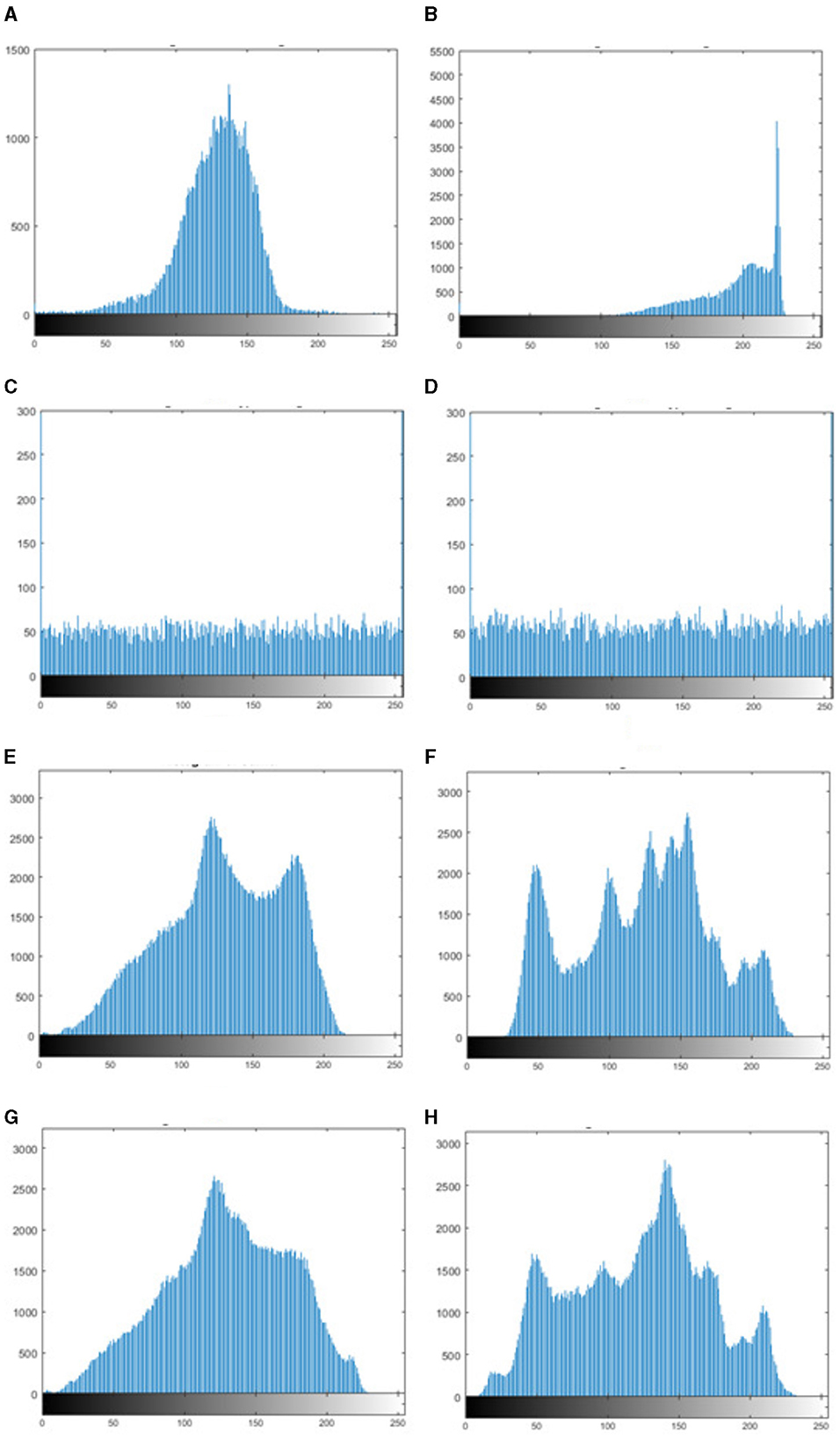
Figure 10. Histogram of (A, B) secret image, (C, D) encrypted secret image, (E, F) carrier image, and (G, H) embedded carrier image.

It can be observed from the plots that the histograms of two plain secret images are radically distinct, while their cipher images have similar histograms. Thus, when attackers examine the histograms of the encrypted images, they gain no understanding of the underlying data.

One of the main requirements of a meaningful encryption scheme, is that the attackers should not have any knowledge that the carrier image is carrying the secret image. Thus, it is necessary for the histograms of embedded carrier images to be almost similar to those of the carrier images before embedding. Figures 10G, H demonstrates the same, and thus, the proposed embedding process protects the system against statistical attacks.

6.3.3 Noise analysis

It is quite obvious for any data transmitted over a long distance to be corrupted by noise. A good encryption - decryption scheme should not be vulnerable to such corruptions. The recovery performance of the proposed encryption scheme with data distorted by noise, is examined to verify the system's immunity to such noise attacks. Noise signals of different intensity levels, varying from 5 to 30, are initially added to the carrier image, and the ability of the proposed scheme to recover back the cipher image is analyzed. Figure 11 shows the recovered cipher images after adding noise of intensities 5, 10, 15 and 30. It is noticeable from these figures that irrespective of the noise intensities added to the secret image, the proposed scheme is still able to recover the actual image with low loss of data.

Figure 11

Figure 11. Recovered secret image with noise intensities of (A) 5, (B) 10, (C) 15, and (D) 30. (Adapted from 5.1.11 “Airplane”, SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=16#top, licensed under CC BY 4.0).

6.3.4 Occlusion analysis

Occlusion in an image occurs when some part of image is obscured. Figure 12 shows the recovered secret image when some parts of the cover image are lost. Lena and plane images are taken as the cover image and secret image for this analysis. Similar to some unwanted noise being added to the images when transmitted over a channel, there is a greater chance of some part of the image data being lost during transmission. Additionally, some hackers may destroy specific data chunks to deceive the data owners/users. Any encryption scheme must be capable of retrieving images even if some parts of the images are obscured. It is clear from the qualitative results that, irrespective of the area of loss of data, our proposed scheme is able to recover the secret image with the same quality as that of one that is recovered when there is no loss of data.

Figure 12

Figure 12. Occlusion analysis. (A, C, E, G, I) Images occluded on left corner, right corner, left bottom, right bottom and center. (Adapted from “Lena”, SIPI Image Database, University of Southern California, licensed under CC BY 4.0). (B, D, F, H, J) Corresponding recovered secret image. (Adapted from 5.1.11 “Airplane”, SIPI Image Database, University of Southern California, https://sipi.usc.edu/database/database.php?volume=misc&image=16#top, licensed under CC BY 4.0).

6.4 Computational complexity analysis

6.4.1 Execution time

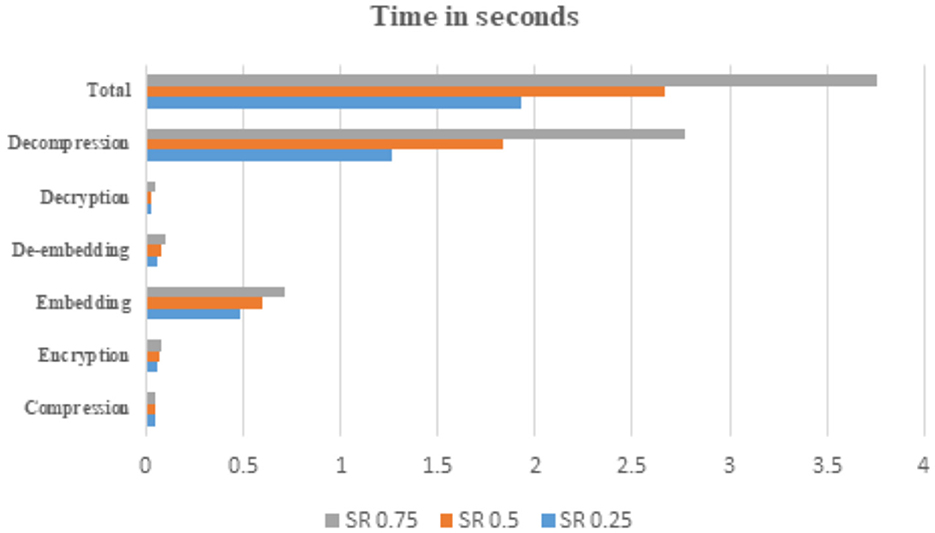
The computational complexity of the proposed scheme is calculated by measuring the amount of time required for each of the processes to execute. Figure 13 shows the execution time of different processes in the proposed scheme for different sampling ratios. From the figure, it is clear that the total time taken for the entire process of compression, encryption, embedding and recovery is 1.932468 seconds for an SR of 0.25, 2.664704 seconds for an SR of 0.5 and 3.761648 seconds for an SR of 0.75. Of all the processes, decompression of images takes more time because of the use of greedy algorithms for recovering compressed images. The embedding process takes less than 1 second, and the time for de-embedding is much less than the embedding process.

Figure 13

Figure 13. Execution time of different processes of the proposed scheme.

7 Conclusion

In this research, a novel compression-encryption technique utilizing the compressive sensing paradigm was described. A novel chaotic map with superior properties over the current maps is suggested. Both the encryption and compression operations uses the sequence that is produced by the suggested chaotic map. Meaningful encrypted images are then obtained by embedding the compressed image on a carrier image. Validation of the embedding and encryption procedure was achieved through a variety of experimental outcomes and it has been proved that the suggested technique outperforms several other existing algorithms. Furthermore, it has been demonstrated that the embedding process takes very less time than the compression method. However, the major limitation of the proposed work is the usage of Discrete Wavelet transform (DWT) onto the carrier image. Since, one level of DWT splits the carrier image into bands of reduced dimension, the secret images have to be compressed before embedding. Also, no images can be embedded onto lower band (LL) of the transformed image, since it retains most of the information of the carrier image that is required for its reconstruction.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KA: Writing – original draft. SSu: Writing – review & editing. SoS: Writing – original draft. DB: Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ashwini, K., and Amutha, R. (2018). Fast and secured cloud assisted recovery scheme for compressively sensed signals using new chaotic system. Multimed. Tools Appl. 77, 31581–31606. doi: 10.1007/s11042-018-6112-4

Crossref Full Text | Google Scholar

Ashwini, K., and Amutha, R. (2021). Compressive sensing based recognition of human upper limb motions with kinect skeletal data. Multimed. Tools Appl. 80, 10839–10857. doi: 10.1007/s11042-020-10327-4

Crossref Full Text | Google Scholar

Candès, E. J. (2006). “Compressive sampling,” in Proceedings of the International Congress of Mathematicians (Madrid: European Mathematical Society), 1433–1452.

Google Scholar

Candes, E. J. (2008). The restricted isometry property and its implications for compressed sensing. Comptes Rendus Mathematique 346, 589–592. doi: 10.1016/j.crma.2008.03.014

PubMed Abstract | Crossref Full Text | Google Scholar

Chen, H., Liu, Z., Tanougast, C., Liu, F., and Blondel, W. (2021). A novel chaos based optical cryptosystem for multiple images using dna-blend and gyrator transform. Opt. Lasers Eng. 138:106448. doi: 10.1016/j.optlaseng.2020.106448

Crossref Full Text | Google Scholar

Dai, J.-Y., Ma, Y., and Zhou, N.-R. (2021). Quantum multi-image compression-encryption scheme based on quantum discrete cosine transform and 4d hyper-chaotic henon map. Quantum Inform. Proc. 20, 1–24. doi: 10.1007/s11128-021-03187-w

Crossref Full Text | Google Scholar

Donoho, D. L. (2006). Compressed sensing. IEEE Trans. Informat. Theory 52, 1289–1306. doi: 10.1109/TIT.2006.871582

Crossref Full Text | Google Scholar

Feng, J., Zhang, J., Zhu, X., and Lian, W. (2017). A novel chaos optimization algorithm. Multimed. Tools Appl. 76, 17405–17436. doi: 10.1007/s11042-016-3907-z

Crossref Full Text | Google Scholar

Gong, L.-H., and Luo, H.-X. (2023). Dual color images watermarking scheme with geometric correction based on quaternion froofmms and LS-SVR. Optics &Laser Technology 167:109665. doi: 10.1016/j.optlastec.2023.109665

Crossref Full Text | Google Scholar

Hu, X., Jiang, D., Ahmad, M., Tsafack, N., Zhu, L., and Zheng, M. (2023). Novel 3-d hyperchaotic map with hidden attractor and its application in meaningful image encryption. Nonlinear Dyn. 111, 19487–19512. doi: 10.1007/s11071-023-08545-0

Crossref Full Text | Google Scholar

Hua, Z., Zhou, Y., Pun, C.-M., and Chen, C. P. (2014). “Image encryption using 2d logistic-sine chaotic map,” in 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC) (San Diego CA: IEEE), 3229–3234.

Google Scholar

Huang, X., Dong, Y., Ye, G., and Shi, Y. (2023). Meaningful image encryption algorithm based on compressive sensing and integer wavelet transform. Front. Comp. Sci. 17:173804. doi: 10.1007/s11704-022-1419-8

Crossref Full Text | Google Scholar

Mathivanan, P., and Balaji Ganesh, A. (2023). Ecg steganography using base64 encoding and pixel swapping technique. Multimed. Tools Appl. 82, 14945–14962. doi: 10.1007/s11042-022-14072-8

Crossref Full Text | Google Scholar

Mathivanan, P., and Maran, P. (2023). A color image encryption scheme using customized map. Imag. Sci. J. 71, 343–361. doi: 10.1080/13682199.2023.2182547

Crossref Full Text | Google Scholar

Musanna, F., and Kumar, S. (2020). A novel image encryption algorithm using chaotic compressive sensing and nonlinear exponential function. J. Inform. Security Appl. 54:102560. doi: 10.1016/j.jisa.2020.102560

Crossref Full Text | Google Scholar

Phatak, S., and Rao, S. S. (1995). Logistic map: a possible random-number generator. Phys. Rev. E 51:3670. doi: 10.1103/PhysRevE.51.3670

PubMed Abstract | Crossref Full Text | Google Scholar

Pincus, S. (1995). Approximate entropy (apen) as a complexity measure. Chaos: Interdisc. J. Nonlinear Sci. 5, 110–117. doi: 10.1063/1.166092

PubMed Abstract | Crossref Full Text | Google Scholar

Ping, P., Fu, J., Mao, Y., Xu, F., and Gao, J. (2019). Meaningful encryption: generating visually meaningful encrypted images by compressive sensing and reversible color transformation. IEEE Access 7, 170168–170184. doi: 10.1109/ACCESS.2019.2955570

Crossref Full Text | Google Scholar

Unde, A. S., and Deepthi, P. (2019). Design and analysis of compressive sensing-based lightweight encryption scheme for multimedia iot. IEEE Trans. Circuits Syst. II: Express Briefs 67, 167–171. doi: 10.1109/TCSII.2019.2897839

Crossref Full Text | Google Scholar

Wang, J., Wang, Q.-H., and Hu, Y. (2018). Image encryption using compressive sensing and detour cylindrical diffraction. IEEE Photonics J. 10, 1–14. doi: 10.1109/JPHOT.2018.2831252

Crossref Full Text | Google Scholar

Wolf, A., Swift, J. B., Swinney, H. L., and Vastano, J. A. (1985). Determining lyapunov exponents from a time series. Physica D: Nonlin. Phenom. 16, 285–317. doi: 10.1016/0167-2789(85)90011-9

Crossref Full Text | Google Scholar

Xu, Q., Sun, K., Cao, C., and Zhu, C. (2019). A fast image encryption algorithm based on compressive sensing and hyperchaotic map. Opt. Lasers Eng. 121, 203–214. doi: 10.1016/j.optlaseng.2019.04.011

Crossref Full Text | Google Scholar

Xu, Q., Sun, K., He, S., and Zhu, C. (2020). An effective image encryption algorithm based on compressive sensing and 2D-SLIM. Opt. Lasers Eng. 134:106178. doi: 10.1016/j.optlaseng.2020.106178

Crossref Full Text | Google Scholar

Xue, W., Luo, C., Shen, Y., Rana, R., Lan, G., Jha, S., et al. (2020). Towards a compressive-sensing-based lightweight encryption scheme for the internet of things. IEEE Trans. Mobile Comp. 20, 3049–3065. doi: 10.1109/TMC.2020.2992737

Crossref Full Text | Google Scholar

Yang, Y.-G., Wang, B.-P., Pei, S.-K., Zhou, Y.-H., Shi, W.-M., and Liao, X. (2021). Using m-ary decomposition and virtual bits for visually meaningful image encryption. Inf. Sci. 580:174–201. doi: 10.1016/j.ins.2021.08.073

Crossref Full Text | Google Scholar

Ye, G., Pan, C., Dong, Y., Shi, Y., and Huang, X. (2020). Image encryption and hiding algorithm based on compressive sensing and random numbers insertion. Signal Proc. 172:107563. doi: 10.1016/j.sigpro.2020.107563

Crossref Full Text | Google Scholar

Yu, L., Barbot, J. P., Zheng, G., and Sun, H. (2010). Compressive sensing with chaotic sequence. IEEE Signal Process. Lett. 17, 731–734. doi: 10.1109/LSP.2010.2052243

Crossref Full Text | Google Scholar

Zhang, M., Tong, X.-J., Liu, J., Wang, Z., Liu, J., Liu, B., et al. (2020). Image compression and encryption scheme based on compressive sensing and fourier transform. IEEE Access 8, 40838–40849. doi: 10.1109/ACCESS.2020.2976798

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, X., and Hu, Y. (2021). Multiple-image encryption algorithm based on the 3d scrambling model and dynamic dna coding. Opt. Laser Technol. 141:107073. doi: 10.1016/j.optlastec.2021.107073

Crossref Full Text | Google Scholar

Zhou, N., Pan, S., Cheng, S., and Zhou, Z. (2016). Image compression-encryption scheme based on hyper-chaotic system and 2d compressive sensing. Optics Laser Technol. 82, 121–133. doi: 10.1016/j.optlastec.2016.02.018

Crossref Full Text | Google Scholar

Zhou, N., Zhang, A., Zheng, F., and Gong, L. (2014). Novel image compression-encryption hybrid algorithm based on key-controlled measurement matrix in compressive sensing. Optics Laser Technol. 62, 152–160. doi: 10.1016/j.optlastec.2014.02.015

Crossref Full Text | Google Scholar

Zhou, N.-R., Hu, L.-L., Huang, Z.-W., Wang, M.-M., and Luo, G.-S. (2024). Novel multiple color images encryption and decryption scheme based on a bit-level extension algorithm. Expert Syst. Appl. 238:122052. doi: 10.1016/j.eswa.2023.122052

Crossref Full Text | Google Scholar

Zhou, N.-R., Tong, L.-J., and Zou, W.-P. (2023). Multi-image encryption scheme with quaternion discrete fractional tchebyshev moment transform and cross-coupling operation. Signal Proc. 211:109107. doi: 10.1016/j.sigpro.2023.109107

Crossref Full Text | Google Scholar

Zhu, L., Song, H., Zhang, X., Yan, M., Zhang, T., Wang, X., et al. (2020). A robust meaningful image encryption scheme based on block compressive sensing and svd embedding. Signal Proc. 175:107629. doi: 10.1016/j.sigpro.2020.107629

Crossref Full Text | Google Scholar