Shallow implementation of quantum fingerprinting with application to quantum finite automata

Quantum fingerprinting is a technique that maps a classical input word to a quantum state. The obtained quantum state is much shorter than the original word, and its processing uses fewer resources, making it useful in quantum algorithms, communication, and cryptography. One of the examples of quantum fingerprinting is the quantum automata algorithm for $MO{D}_p=\left\{a^{i·p}\mid i\ge 0\right\}$ languages, where p is a prime number. However, implementing such an automaton on current quantum hardware is not efficient. Quantum fingerprinting maps a word x∈{0, 1}ⁿ of length n to a state |ψ(x)〉 of O(logn) qubits, and uses O(n) unitary operations. Computing quantum fingerprint using all available qubits of the current quantum computers is infeasible due to many quantum operations. To make quantum fingerprinting practical, we should optimize the circuit for depth instead of width, in contrast to the previous works. We propose explicit methods of quantum fingerprinting based on tools from additive combinatorics, such as generalized arithmetic progressions (GAPs), and prove that these methods provide circuit depth comparable to a probabilistic method. We also compare our method to prior work on explicit quantum fingerprinting methods. We provide a series of numerical experiments with implementation of the quantum automata for MOD₁₇ language on noisy simulators of IBMQ quantum devices. We show that shallow implementation based on GAPs produces results with much smaller computational error compared to standard deep circuit implementation. Despite the fact that on the ideal quantum computational device, the opposite situation arises. We show that the shallow circuit for the quantum automaton is better for near-future quantum computational devices.

1 Introduction

A quantum finite state automaton (QFA) is a generalization of a classical finite automaton (Say and Yakaryılmaz, 2014; Ambainis and Yakaryılmaz, 2021). Here we use the simplest QFA model (Moore and Crutchfield, 2000). Formally, a QFA is 5-tuple $M=(Q,A\cup \{¢,\$\},|{\psi }_0\rangle ,\mathcal{U},{\mathscr{H}}_{acc})$, where Q = {q₁, …, q_D} is a finite set of states, A is the finite input alphabet, ¢, $ are the left and right end-markers, respectively. The state of M is represented as a vector $|\psi \rangle \in \mathscr{H}$, where $\mathcal{H}$ is the D-dimensional Hilbert space spanned by {|q₁〉, …, |q_D〉} (here |q_j〉 is a zero column vector except its j-th entry that is 1). The automaton M starts in the initial $|{\psi }_0\rangle \in \mathscr{H}$, and makes transitions according to the operators $\mathcal{U}=\left\{U_a\mid a\in A\right\}$ of unitary matrices. After reading the whole input word, the final state is observed with respect to the accepting subspace ${\mathcal{H}}_{acc}\subseteq \mathcal{H}$.

Quantum fingerprinting provides a method of constructing automata for certain problems. It maps an input word w∈{0, 1}ⁿ to much shorter quantum state, its fingerprint $|\psi \rangle (w)=U_w|0^m\rangle$, where U_w is the single transition matrix representing the multiplication of all transition matrices while reading w and $|0^m\rangle =\underset{m \text{times}}{\underbrace{|0\rangle \otimes \cdots \otimes |0\rangle }}$. The number of qubits in a fingerprint m can be exponentially less than the length of the word n. An example of such an automaton was first presented in the study by Ambainis and Freivalds (1998) and then improved as provided in the study by Ambainis and Nahimovs (2009). This result is discussed in this section. Quantum fingerprint captures essential properties of the input word that can be useful for computation.

One example of quantum fingerprinting applications is the QFA algorithms for the MOD_p language (Ambainis and Nahimovs, 2009). For a given prime number p, the language MOD_p is defined as $MO{D}_p=\left\{a^i\mid i\mathrm{\text{is divisible by}}p\right\}$. Let us briefly describe the construction of the QFA algorithms for MOD_p.

We start with a 2-state QFA M_k, where k∈{1, …, p−1}. The automaton M_k has two base states Q = {q₀, q₁}, it starts in the state |ψ₀〉 = |q₀〉, and it has the accepting subspace spanned by |q₀〉. At each step (for each letter), we perform the rotation

$U_a=\left(\begin{array}{cc}cos\frac{2\pi k}{p}& sin\frac{2\pi k}{p}\\ \\ -sin\frac{2\pi k}{p}& cos\frac{2\pi k}{p}\\ \end{array}\right).$

If w∈MOD_p, then the rotation U_a is applied i = r·p times, for some integer r. In that case, i is a multiple of p. Therefore, the total rotation angle is $\frac{2\pi k}{p}·r·p=2\pi k·r$, which is a multiple of 2π for any k. It means, the automaton is in the state |q₀〉 for any k, and it accepts the word with probability 1. It is the correct answer.

However, if w∉MOD_p, the probability of correct answer can be close to 0 rather than 1 (i.e., bounded below by 1 − cos²(π/p)). To boost the success probability we use d copies of this automaton, namely, M_k1, …, M_kd, as described below.

The QFA M for MOD_p has 2d states: Q = {q_{1, 0}, q_{1, 1}, …, q_{d, 0}, d_{d, 1}}, and it starts in the state $|{\psi }_0\rangle =\frac{1}{\sqrt{d}}{\displaystyle {\sum }_{i=1}^d|q_{i,0}\rangle }$. In each step, it applies the transformation defined as follows:

$\begin{array}{ll}|q_{i,0}\rangle \mapsto \cos \frac{2\pi k_i}{p}|q_{i,0}\rangle +\sin \frac{2\pi k_i}{p}|q_{i,1}\rangle & (1)\end{array}$

$\begin{array}{ll}|q_{i,1}\rangle \mapsto -\sin \frac{2\pi k_i}{p}|q_{i,0}\rangle +\cos \frac{2\pi k_i}{p}|q_{i,1}\rangle & (2)\end{array}$

Indeed, M enters into equal superposition of d sub-QFAs, and each sub-QFA applies its rotation. Thus, quantum fingerprinting technique associates the input word w = a^j with its fingerprint

$|\psi \rangle =\frac{1}{\sqrt{d}}{\displaystyle \sum _{i=1}^d\cos }\frac{2\pi k_{i}j}{p}|q_{i,0}\rangle +\sin \frac{2\pi k_{i}j}{p}|q_{i,1}\rangle .$

Ambainis and Nahimovs (2009) proved that this QFA accepts the language MOD_p with error probability that depends on the choice of the coefficients k_i's. They also showed that for d = 2log(2p)/ε there is at least one choice of coefficients k_i's such that the error probability is less than ε. The proof uses a probabilistic method, so these coefficients are not explicit. They also suggest two explicit sequences of coefficients: cyclic sequence $k_i=g^i(modp)$ for primitive root g modulo p and more complex AIKPS (Ajtai, Iwaniec, Komlós, Pintz, Szemerédi) sequences based on the results presented in the study by Ajtai et al. (1990).

Quantum fingerprinting is versatile and has several applications. Buhrman et al. (2001) in their study provided an explicit definition of quantum fingerprinting for constructing an efficient quantum communication protocol for equality checking. The technique was applied to branching programs in the studies by Ablayev and Vasiliev (2009, 2011, 2013b); this computational model can be considered as a non-uniform automata. They show examples of Boolean functions that can be computed by a quantum branching program with exponentially smaller complexity (width or states in terms of automata) than the deterministic ones. Based on this research, they developed the concept of cryptographic quantum hashing (Ablayev and Vasiliev, 2013a, 2014; Ablayev et al., 2014; Ablayev and Ablayev, 2015). Later, they generalized the technique and suggested a family of quantum hashes that allow us to see a trade-off between one-way resistance and collision resistance of the hash function (Ablayev et al., 2016a; Vasiliev, 2016a; Vasiliev et al., 2017; Ablayev et al., 2020). The question of computing cryptographic quantum hashes with a restricted size of memory was discussed in the study by Ablayev et al. (2018b). Connection of the approach with Quantum Fourier transom where presented in the study by Ablayev and Vasiliev (2020); Khadieva (2024). A survey on cryptographic quantum hashes can be found in the study by Ablayev et al. (2016b, 2018a). The experimental implementation on real devices was considered in the study by Vasiliev et al. (2019); Turaykhanov et al. (2021), and optimization for emulators of quantum computers was explored in the study by Zinnatullin et al. (2023). Different versions of hash functions were applied that are hash functions in the case of finite Abelian groups (Vasiliev, 2016c) and arbitrary groups (Ziatdinov, 2016b); functions based on graphs (Ziatdinov, 2016a; Zinnatullin, 2023). The technique was extended to qudits (Ablayev and Vasiliev, 2022; Vasiliev, 2023). This approach has been widely used in various areas such as

• stream processing algorithms (Le Gall, 2009, 2006). Here, the technique allows authors to obtain an advantage in memory size for a quantum version of the model.

• Query model algorithms (Ablayev et al., 2022, 2024). Here, the quantum fingerprinting algorithm is applied as a base for the quantum algorithm for the string-matching problem. The algorithm uses less memory compared to existing quantum algorithms (Ramesh and Vinay, 2003; Montanaro, 2017; Khadiev and Serov, 2025).

• Online algorithms (Khadiev and Khadieva, 2021, 2022). Here, authors present a problem that can be solved by quantum online algorithms with restricted memory size (Khadiev et al., 2018, 2022b, 2023), but cannot be solved by randomized or deterministic counterparts in the case of logarithmic memory size.

• branching programs (Khadiev and Khadieva, 2017; Khadiev et al., 2022a; Ablayev et al., 2016c, 2018a). In these studies, authors present a specially constructed Boolean function that allows them to show a hierarchy of complexity classes for quantum read-k-times branching programs. The upper bound was proven using the quantum fingerprinting technique. For read-1-times branching programs, researchers (Gainutdinova, 2002; Ablayev et al., 2005; Ablayev and Vasiliev, 2009, 2013b) presented a Boolean function that can be computed by a quantum model with smaller complexity than by classical models.

• Development of quantum devices (Vasiliev, 2016b).

• Automata. The technique was introduced for automata model (Ambainis and Freivalds, 1998) and later improved in a study by Ambainis and Nahimovs (2009). At the same time, the same technique for the constant number of qubits was used for two-way automata with classical and quantum states (Ambainis et al., 2002; Ambainis and Watrous, 2002; Yakaryilmaz, 2013; Yakaryılmaz and Say, 2009). It allows authors to show a language that can be recognized by the model but cannot be recognized by the probabilistic two-way automata.

      Later, the same idea was used for one-way automata and promise problems (Ambainis and Yakaryılmaz, 2021; Gainutdinova and Yakaryılmaz, 2017; Yakaryılmaz and Say, 2010; Gainutdinova and Yakaryılmaz, 2018, 2015; Hu et al., 2020; Nakanishi and Yakaryılmaz, 2015).

At the same time, the technique is not practical for the currently available real quantum computers. The main obstacle is that quantum fingerprinting uses an exponential (in the number m of qubits) circuit depth (e.g., see Khadieva and Ziatdinov, 2023; Birkan et al., 2021; Salehi and Yakaryılmaz, 2021; Zinnatullin et al., 2023 for some implementations of the aforementioned automaton M). Therefore, the required quantum volume¹ V_Q is roughly 2^|w|·^2m. For example, IBM reports (IBM, 2022) that its Falcon r5 quantum computer has 27 qubits with a quantum volume of 128. It means that we can use only 7 of the 27 qubits for the fingerprint technique.

This study investigates how to obtain better circuit depth by optimizing the coefficients used by M: k₁, …, k_d. We use generalized arithmetic progressions to generate a set of coefficients and show that such sets have a circuit depth comparable to the set obtained by the probabilistic method.

Additionally, we implement the circuit for the noisy emulator of the IBMQ quantum machine (IBM, 2025). The emulator emulates the behavior of real IBMQ quantum machines and allows us to see the results closely compared to the results we can obtain on real machines. Note that IBMQ is a device that allows to invoke of a quantum circuit with universal basic gates. Therefore, we can implement any unitary transformation on this machine that gives us universality (Möttönen et al., 2004). At the same time, the current quantum devices are in the Noisy Intermediate-Scale Quantum (NISQ) era (Preskill, 2018), which is why the noise and other effects do not allow for the implementation of any quantum algorithm. Our shallow circuit will enable us to obtain useful results for the quantum fingerprinting algorithm for MOD₁₇ language on 4 qubits. At the same time, it is known that we cannot recognize this language using classical automata with 4 qubits of memory (Ambainis and Freivalds, 1998). Moreover, the standard circuit for the quantum fingerprinting algorithm (not the shallow one) does not give us any useful results, even if it gives a smaller error probability in “ideal” (not noisy) devices.

We summarize the previous and our results in the following list.

• The cyclic method, for some constant c>0:

- the width is p^c/loglogp

- the depth is p^c/loglogp

- explored in the study by Ambainis and Nahimovs (2009).

• The AIKPS method:

- the width is log^2+3ϵp

- the depth is (1+2ϵ)log^1+ϵploglogp

- explored in the study by Razborov et al. (1993).

• The probabilistic method:

- the width is 4log(2p)/ε

- the depth is 2log(2p)/ε

- explored in Ambainis and Nahimovs (2009).

• The GAPs method (this study):

- the width is p/ε²

- the depth is ⌈logp−2logε⌉+2

- developed in this study.

Note that p is exponential in the number of qubits m. The depth of the circuits is discussed in Section 3.

The study is an extended version of the Ziiatdinov et al. (2023) conference paper presented at the AFL2023 conference.

In addition, we perform computational experiments for computing parameters K that minimize the error probability for our circuit and the standard circuit. We show that in the case of an “ideal” non-noisy quantum device, the error probability for the proposed circuit is at most twice as large as that of the standard circuit. At the same time, in the case of noisy quantum devices (current and near-future ones), the error probability is much less than that of the standard circuit, and allows us to implement QFA for MOD₁₇ language using 4 qubits.

The rest of the article is organized as follows. In Section 2, we give the necessary definitions and results on quantum computation and additive combinatorics to follow the rest of the article. Section 3 contains the construction of the shallow fingerprinting function and the proof of its correctness. Then, we present several numerical simulations in Section 4. We conclude the article with Section 5 by presenting some open questions and discussions for further research.

2 Preliminaries

Let us denote by ${\mathcal{H}}^2$ two-dimensional Hilbert space, and by ${({\mathcal{H}}^2)}^{\otimes m}$ 2^m-dimensional Hilbert space (i.e., the space of m qubits). We use bra- and ket-notations for vectors in Hilbert space. For any natural number N, we use ℤ_N to denote the cyclic group of order N.

Let us describe in detail how the automaton M works. As we outlined in the introduction, the automaton M has 2d states: Q = {q_{1, 0}, q_{1, 1}, …, q_{d, 0}, d_{d, 1}}, and it starts in the state $|{\psi }_0\rangle =\frac{1}{\sqrt{d}}{\displaystyle {\sum }_{i=1}^d|q_{i,0}\rangle }$. After reading a symbol a, it applies the transformation U_a defined by Equations 1, 2:

$\begin{array}{l}|q_{i,0}\rangle \mapsto \cos \frac{2\pi k_i}{p}|q_{i,0}\rangle +\sin \frac{2\pi k_i}{p}|q_{i,1}\rangle \\ |q_{i,1}\rangle \mapsto -\sin \frac{2\pi k_i}{p}|q_{i,0}\rangle +\cos \frac{2\pi k_i}{p}|q_{i,1}\rangle \end{array}$

After reading the right endmarker $, it applies the transformation U_$ defined in such way that U_$|ψ₀〉 = |q_{1, 0}〉. The automaton measures the final state and accepts the word if the result is q_{1, 0}.

So, the quantum state after reading the input word w = a^j is

$|\psi \rangle =\frac{1}{\sqrt{d}}{\displaystyle \sum _{i=1}^d\cos }\frac{2\pi k_{i}j}{p}|q_{i,0}\rangle +\sin \frac{2\pi k_{i}j}{p}|q_{i,1}\rangle .$

If j≡0 (mod p), then |ψ〉 = |ψ₀〉, and U_$ transforms it into accepting state |q_{1, 0}〉, therefore, in this case, the automaton always accepts. If the input word w∉MOD_p, then the quantum state after reading the right endmarker $ is

$|{\psi }^{\prime }\rangle =\frac{1}{d}({\displaystyle \sum _{i=1}^d\cos }\frac{2\pi k_{i}j}{p})|q_{1,0}\rangle +\dots ,$

and the error probability is

$P_e=\frac{1}{d^2}{({\displaystyle \sum _{i=1}^d\cos }\frac{2\pi k_{i}x}{p})}^2.$

In simpler terms, the automaton maintains d angles in different subspaces. After encountering the symbol a, the automaton performs d rotations: it rotates by 2πk_i/p in the i-th subspace. Since rotating p times would have the same result as not rotating at all, the automaton counts the number of a symbols modulo p. The coefficients k_i ensure that the small error probability: even if some of angles are close to 0, other subspaces are far from 0, so the whole state is far from the state q_{1, 0}.

In the rest of the article, we denote by m the number of qubits in the quantum fingerprint, by d = 2^m the number of parameters in the set K, by p the size of domain of the quantum fingerprinting function, and by U_a(K) the transformation defined above, which depends on the set K.

Let us also define a function $\epsilon :{\mathbb{Z}}_p^d\to ℝ$ as follows:

$\epsilon (K)={\max }_{x\in {\mathbb{Z}}_p}(\frac{1}{d^2}|{\displaystyle \sum _{j=1}^d\exp }\frac{2\pi i{k}_{j}x}{p}{|}^2).$

Note that P_e ≤ ε(K).

We also use some tools from additive combinatorics. We refer the reader to the textbook by Tao and Vu (2006) for a deeper introduction to additive combinatorics.

An additive set A⊆Z is a finite non-empty subset of Z, an abelian group with group operation +. We refer to Z as the ambient group.

If A, B are additive sets in Z, we define the sum set A+B = {a+b∣a∈A, b∈B}. We define additive energy E(A, B) between A, B to be

$E(A,B)=\left|\right\{(a,b,a^{\prime },b^{\prime })\in A\times B\times A\times B\mid a+b=a^{\prime }+b^{\prime }\left\}\right|.$

Let us denote by e(θ) = e^2πiθ, and by ξ·x = ξx/p bilinear form from ℤ_p×ℤ_p into ℝ/ℤ. Fourier transform of f:ℤ_p → ℤ_p is $\widehat{f}(\xi )=E_{x\in Z}f(x)\overline{e(\xi ·x)}$.

We also denote the characteristic function of the set A as 1_A, and we define $P_Z(A)=\widehat{1_A}(0)=\left|A\right|/\left|Z\right|$.

Definition 1 (Tao and Vu, 2006). Let Z be a finite additive group. If A⊆Z, we define Fourier bias $\left|\right|A|{|}_{\mathcal{U}}$ of the set A to be

$\Vert A{\Vert }_{\mathcal{U}}=\underset{\xi \in Z\backslash \left\{0\right\}}{\sup }|\widehat{1_A}(\xi )|$

Basically, the additive energy E(A, A) and the Fourier bias $\left|\right|A|{|}_{\mathcal{U}}$ tell how “structured” the set A is with respect to addition. The additive energy E(A, A) measures how many pairwise sums a+a′ of elements a, a′∈A coincide; for a random set we expect many different pairwise sums, and for an arithmetic progression the pairwise sums mostly coincide.

There is a connection between the Fourier bias and the additive energy.

Theorem 1 (Tao and Vu, 2006). Let A be an additive set in a finite additive group Z. Then

$\Vert A{\Vert }_{\mathcal{U}}^4\le \frac{1}{|Z{|}^3}E(A,A)-{\text{P}}_Z{(A)}^4\le \Vert A{\Vert }_{\mathcal{U}}^2{\text{P}}_Z(A)$

Definition 2 (Tao and Vu, 2006). A generalized arithmetic progression (GAP) of dimension d is a set

$A=\left\{x_0+n_1{x}_1+\dots +n_d{x}_d\mid 0\le n_1\le N_1,\cdots ,0\le n_d\le N_d\right\},$

where x₀, x₁, …, x_d, N₁, …, N_d∈Z. The size of GAP is a product N₁⋯N_d. If the size of set A, |A|, equals to N₁⋯N_d, we say that GAP is proper.

The GAPs generalize the usual notion of arithmetic progressions by allowing multiple differences x₁, …, x_d instead of just one x₁. The proper GAP has differences such that its elements are all distinct, i.e., its elements cannot be represented as a sum of differences in two ways.

3 Shallow fingerprinting

Quantum fingerprint can be computed using the quantum circuit shown in Figure 1. The last qubit is rotated by a different angle 2πk_jx/q in different subspaces enumerated by |j〉. The circuit rotates the qubit for all possible angles. The j-th rotation is controlled by first m qubits and applied if the values of these qubits are j. Therefore, the circuit depth is |K| = t = 2^m. As the set K is random, the depth is unlikely to be less than |K|.

Figure 1

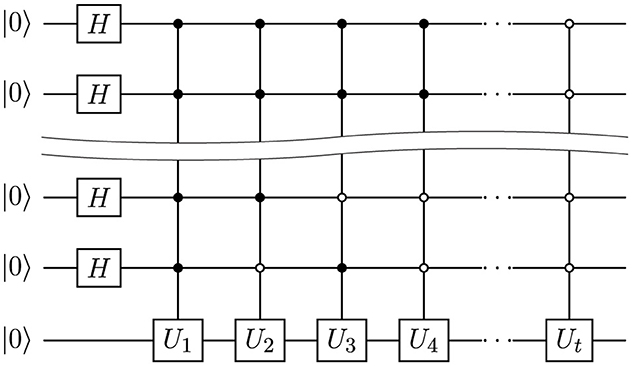
Figure 1. Deep fingerprinting circuit example. Gate U_j is a rotation R_y(4πk_jx/p) for j∈{0, …2^m−1}. Here, we have m control qubits. All possible values from 0 to 2^m−1 are encoded by all binary strings of length m. These values are presented as control values for control rotation gates U_j such that U_j is applied if the value of control qubits is j.

Let us note that fingerprinting is similar to the quantum Fourier transform. Quantum Fourier transform computes the following transformation:

$\begin{array}{ll}|x\rangle \mapsto \frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}{\omega }_N^{xk}}|k\rangle ,& (3)\end{array}$

where ω_N = e(1/N). Here is the quantum fingerprinting transform:

$|x\rangle \mapsto \frac{1}{t}{\displaystyle \sum _{j=1}^t{\omega }_N^{k_{j}x}}|k\rangle ,$

The depth of the circuit that computes quantum Fourier transform is O((logN)²), and it heavily relies on the fact that in Equation 3 the sum runs over all k = 0, …, N−1. Therefore, to construct a shallow fingerprinting circuit, we desire to find a set K with a special structure.

Suppose that we construct a coefficient set K⊂ℤ_p in the following way. We start with a set T = {t₁, …, t_m} and construct the set of coefficients as a set of sums of all possible subsets:

$K=\{{\displaystyle \sum _{t\in S}t}\mid S\subseteq T\},$

where we sum modulo p.

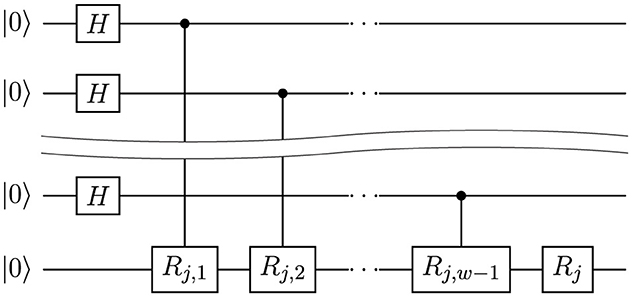
The quantum fingerprinting function with these coefficients can be computed by a circuit of depth O(m) (Kālis, 2018) (see Figure 2).

Figure 2

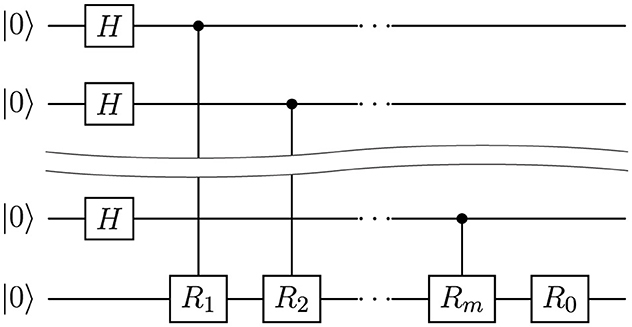
Figure 2. Shallow fingerprinting circuit example. Gate R_j is a rotation R_y(4πt_jx/p) for j∈{0, …m}. Here, we have m control qubits.

Finally, let us prove why the construction of the set K⊂ℤ_p works.

Theorem 2. Let ε>0, let m = ⌈logp−2logε⌉ and d = 2^m.

Suppose that the number t₀∈ℤ_p and the set T = {t₁, …, t_m}⊂ℤ_p are such that

$B=\left\{2t_0+n_1{t}_1+\cdots +n_m{t}_m\mid 0\le n_1<3,\dots ,0\le n_m<3\right\}$

is a proper GAP.

Then the set A defined as

$A=\left\{t_0+{\displaystyle \sum _{t\in S}}t\mid S\subseteq T\right\}$

has ε(A) ≤ ε.

Let us outline the proof of this theorem. First, we estimate the number of solutions to a+b = n. Second, we use it to bound the additive energy E(A, A) of the set A. Third, we bound the Fourier bias $\left|\right|A|{|}_{\mathcal{U}}$. Finally, we get a bound on ε(A) in terms of p and m.

Proof. Let us denote a set R_n(A) of solutions to a+b = n, where a, b∈A and n∈ℤ_p:

$R_n(A)=\left\{(a,b)\mid a+b=n;a,b\in A\right\}.$

Note that we have $E(A,A)=\sum _{n\in Z}{R_n(A)}^2$.

Suppose that n is represented as $n=2t_0+\sum _{i=1}^m{\gamma }_i{t}_i$, γ_i∈{0, 1, 2}. It is unique if such a representation exists because B is a proper GAP. Let us denote c₀: = {i∣γ_i = 0}, c₁: = {i∣γ_i = 1}, c₂: = {i∣γ_i = 2}. It is clear that c₀⊎c₁⊎c₂ = [m].

Suppose that n = a+b for some a, b∈A. But $a=t_0+\sum _i{\alpha }_i{t}_i$ and $b=t_0+\sum _i{\beta }_i{t}_i$, α_i, β_i∈{0, 1}. We get that if i∈c₀ or i∈c₂ then the corresponding coefficients α_i and β_i are uniquely determined. Consider i∈c₁. Then we have two choices: either α_i = 1;β_i = 0, or α_i = 0;β_i = 1. Therefore, we have $R_n(A)=2^{\left|c_1(n,A)\right|}$.

We have that

$E(A,A)={\displaystyle \sum _{n\in Z}}{R_n(A)}^2={\displaystyle \sum _{n\in Z}}{2}^{2\left|c_1(n,A)\right|}.$

Using the fact that |c₀(n, A)|+|c₁(n, A)|+|c₂(n, A)| = m, we see that

$E(A,A)={\displaystyle \sum _{n\in Z}{2}^{2|c_1(n,A)|}}={\displaystyle \sum _{j=0}^m\left(\begin{array}{c}m\\ j\end{array}\right)}{2}^{m-j}{2}^{2j}={\displaystyle \sum _{j=0}^m\left(\begin{array}{c}m\\ j\end{array}\right)}{2}^{m+j}\le 2^{3m}$

We can bound the Fourier bias by Theorem 1:

$\begin{array}{l}\Vert A{\Vert }_{\mathcal{U}}^4\le \frac{1}{|Z{|}^3}E(A,A)-P_Z(A{)}^4\le \Vert A{\Vert }_{\mathcal{U}}^2{P}_Z(A)\\ \Vert A{\Vert }_{\mathcal{U}}^4\le \frac{2^{3m}}{2^{3·2^m}}-\frac{2^{4m}}{2^{4·2^m}}=\frac{d^3}{2^{3d}}-\frac{d^4}{2^{4d}}\\ \Vert A{\Vert }_{\mathcal{U}}\le \frac{d^{3/4}}{p^{3/4}}\end{array}$

Finally, we have

$\epsilon (A)={(\frac{p}{d}\Vert A{\Vert }_U)}^2\le \frac{p^{1/2}}{d^{1/2}}.$

We prove the theorem by substituting the definitions of d and m.                     ⎕

Corollary 1. The depth of the circuit that computes U_a(A) is ⌈logp−2logϵ⌉.

Theorem 3 (Circuit depth for AIKPS sequences). For given ε>0, let

$\begin{array}{ll}R& =\left\{r\mid r\text{is prime},{(logp)}^{1+\epsilon }/2<r<{(logp)}^{1+\epsilon }\right\},\\ S& =\left\{1,2,\dots ,{(logp)}^{1+2\epsilon }\right\},\\ T& =\left\{s·r^{-1}\mid r\in R,s\in S\right\},\end{array}$

where r⁻¹ is the inverse of r modulo p.

Then the depth of the circuit that computes U_a(T) is less than (1+2ϵ)log^1+ϵploglogp.

Proof. Let us denote the elements of R by r₁, r₂, …. Let S·{r⁻¹} be a set {s·r⁻¹∣s∈S}.

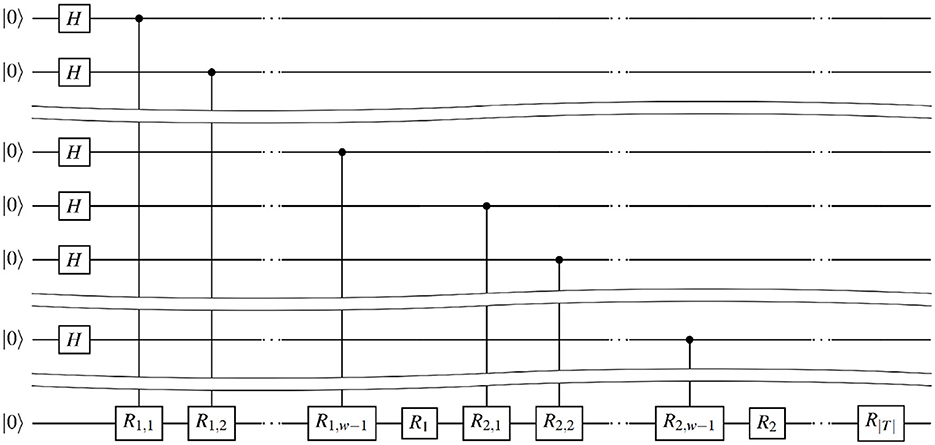
Consider the following circuit ${\mathcal{C}}_j$ (see Figure 3) with w = ⌈(1+2ε)loglogp⌉+1 wires.

Figure 3

Figure 3. Circuit ${\mathcal{C}}_j$ for AIKPS subsequence. Gate R_j is a rotation $R_y(4\pi (r_j^{-1})/p)$. Gate R_{j, k} is a rotation $R_y(2^{k-1}·4\pi (r_j^{-1})/p)$.

The circuit ${\mathcal{C}}_j$ has depth ⌈(1+2ε)loglogp⌉+1 and computes the transformation $U_a(S·\left\{r_j^{-1}\right\})$. By repeating the same circuit for all r_j∈R we get the required circuit for U_a(T) (see Figure 4).

Figure 4

Figure 4. Circuit for U_a(T). Gate R_j is a rotation $R_y(4\pi (r_j^{-1})/p)$. Gate R_{j, k} is a rotation $R_y(2^{k-1}·4\pi (r_j^{-1})/p)$.

Since |R| < (logp)^1+ε, we obtain that the depth of the circuit U_a(T) is less than

$(1+2ϵ){log}^{1+ϵ}ploglogp.$

                                                                       ⎕

4 Numerical experiments

We conduct the following numerical experiments. We compute sets of coefficients K for the automaton for the language MOD_p with minimal computational error.

Finding an optimal set of coefficients is an optimization problem with many parameters, and the running time of a brute force algorithm is large, especially with an increasing number m of control qubits and large values of parameter p. Then, the original automaton has 2d states, where d = 2^m. We observe circuits for several m values and use a heuristic method for finding the optimal sets K with respect to an error minimization. For this purpose, the coordinate descent method (Wright, 2015) is used.

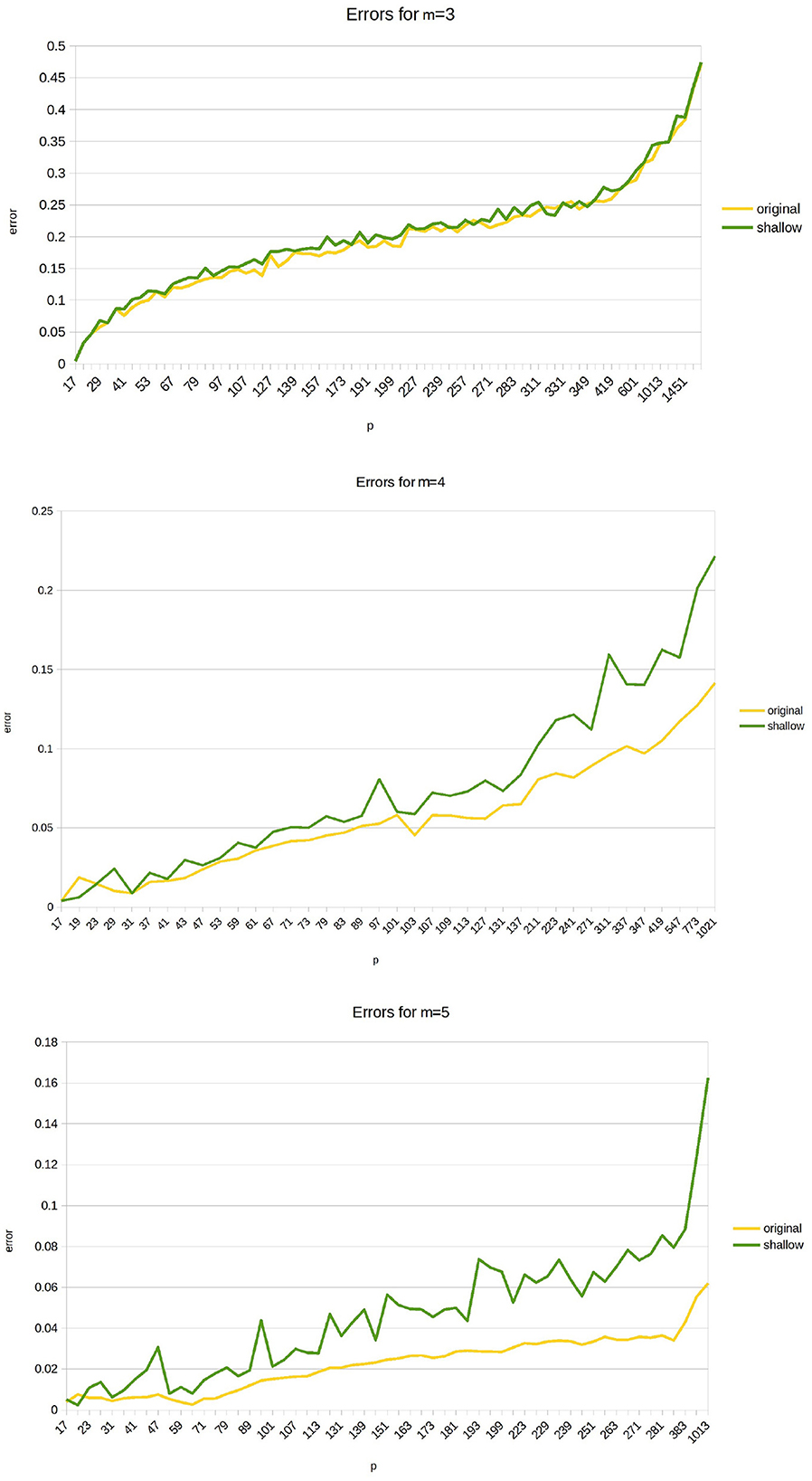
We find an optimal set of coefficients for different values of p and m and compare computational errors of original and shallow fingerprinting algorithms for the automaton (see Figure 5). Namely, we set m = 3, 4, 5 and find sets using the coordinate descent method for each case that minimizes ε(K). Even heuristic computing, for s>5, takes exponentially more computational time andis hard to implement on our devices.

Figure 5

Figure 5. Computational errors for m = 3, 4, 5 of original and shallow automata.

One can note that the difference between errors increases with increasing m, especially for higher values of p. The program code and numerical data are presented in a git repository (Khadieva, 2023).

The graphics in Figure 6 show a proportion of the errors of the original automaton over the errors of the shallow automaton for m = 3, 4, 5 and the prime numbers until 1013.

Figure 6

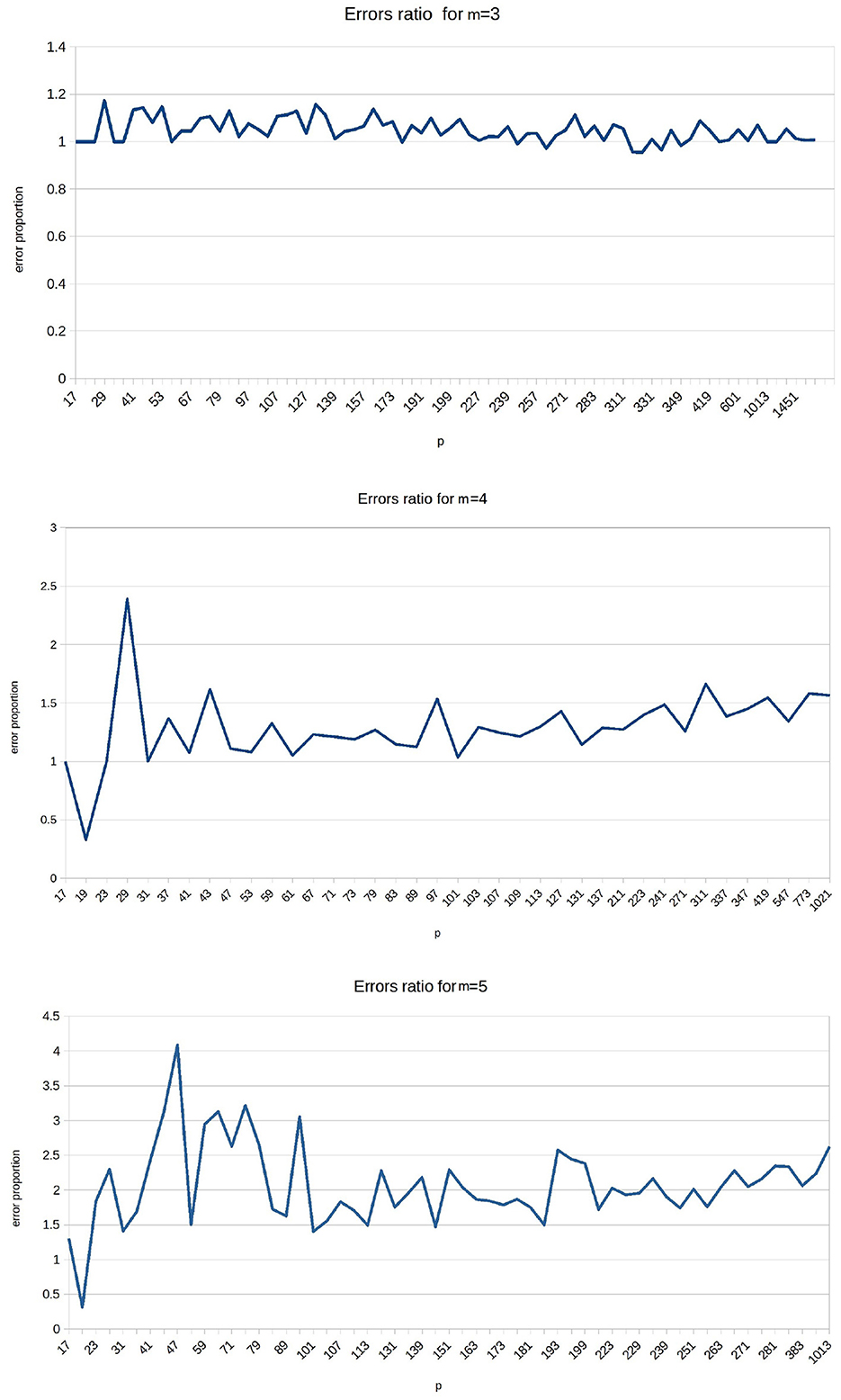
Figure 6. Proportions of the shallow automaton errors over the original automaton errors for m = 3, 4, 5 and different values of p.

As we see, for a number of control qubits m = 3, the difference between the original and shallow automata errors is approximately constant. The ratio of values fluctuates between 1 and 1.2. In the case m = 4, this ratio is approximately 1.5 for almost all observed values p. The ratio of errors is nearly between 1.5 and 3, for m = 5.

According to the results of our experiments, the circuit depth m+1 is enough for valid computations, while the original circuit uses O(2^m) gates. Since the shallow circuit is much simpler than the original one, its implementation on real quantum machines is much easier. For instance, in such machines as IBMQ Manila or Baidu quantum computer, a “quantum computer” is represented by a linearly connected sequence of qubits. CX-gates can be applied only to the neighbor qubits. For such a linear structure of qubits, the shallow circuit can be implemented using 3m+3 CX-gates. Whereas a nearest-neighbor decomposition (Bergholm et al., 2005) of the original circuit requires O(dlogd) = O(m2^m) CX-gates.

4.1 Numerical experiments for a noisy device

The numerical experiments presented above were performed on an abstract machine with no noise, that is, all operators and measurements are always correct. In contrast, current real quantum devices are the NISQ era machines (Preskill, 2018), which means that each operator is noisy. Therefore, we invoke a new series of computational experiments to find a set of coefficients K for the automaton that recognizes the language MOD_p, so that we can separate members and non-members of the language when implementing the automaton on a noisy simulator of the IBMQ quantum machine. As an example, we set the p = 17 and m = 3 control qubits. So, our device uses 4 qubits. At the same time, it is known that any deterministic device needs at least 5 classical bits to recognize the MOD₁₇ language (Ambainis and Freivalds, 1998).

For these parameters, we invoke a brute-force algorithm to find the set K that satisfies two conditions:

1. The probability of accepting member words should be as high as possible.

2. The probability of accepting non-member words should be as small as possible.

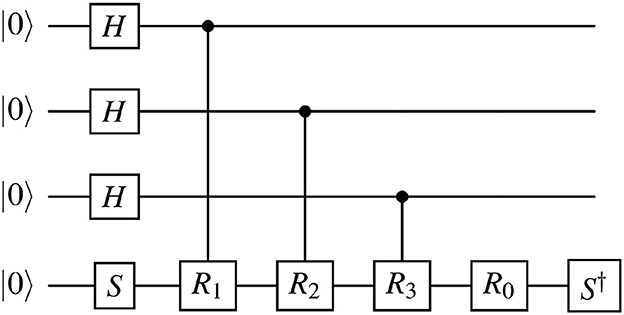
For this reason, we minimize a value diff = P(6·p)−max{P(r):r mod p≠0, 1 ≤ r ≤ 6·p+9}, where P(i) is the acceptance probability for a word of length i. The resulting set is K = {4, 8, 12, 6}. After that, we execute the circuit for this automaton on input words of length at most 7·p+9 = 128. We use an optimization of the circuit from a study by Khadieva et al. (2024) that allows us to use the Rz operator instead of the Ry operator. It is presented in Figure 7.

Figure 7

Figure 7. Shallow circuit that uses Rz operators.

It is important to use this optimization because the emulator of a real IBMQ device allows us to use only a limited set of possible gates. For instance, we cannot use the Ry operator, although the Rz gate is available.

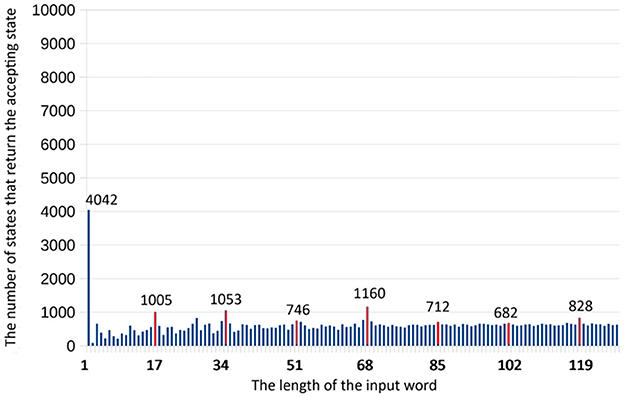
We run the program 10,000 times and calculate the number of shots that return the state |0〉 (accepting state). We use the notation $\tilde{P}(i)$ for this number, where i is the length of the word. These numbers $\tilde{P}(i)$ for each length i for 1 ≤ i ≤ 129 are presented in Section 6 and Figure 8. We can say that it is a statistical representation of probability P(i).

Figure 8

Figure 8. Computational errors for m = 3 of shallow automata for noisy device.

Normally, for the bounded error QFA (Say and Yakaryılmaz, 2014), an input of length i is accepted if the probability of observing an accepting state is P(i)>0.5+ε for some ε>0 and is rejected if P(i) < 0.5−ε. In terms of the number of shots that return the accepting state in our experiment, we can say that the word is accepted if $\tilde{P}(i)\ge 5001$, and rejected if $\tilde{P}(i)\le 4,999$. In that case, we can execute an algorithm once, return its answer, and the result will be correct with probability more than one half. In that case, we can recognize only the word of length i = p because only $\tilde{P}(p)\ge 5,001$, and $\tilde{P}(i)\le 4,999$ for any i≠p due to the results of our numerical experiments. So, the automaton rejects all other words, including members and non-members.

Another type of QFA in terms of acceptance criteria is a QFA with an isolated cut-point (Chadha et al., 2013; Bertoni, 1975; Bertoni et al., 1977; Gimbert and Oualhadj, 2010; Rabin, 1963). In that case, we choose two constants 0 < λ < 1 and 0 < ε < min{λ, 1−λ}. A word of length i is accepted if P(i)>λ+ε, and rejected if P(i) < λ−ε. For our numerical experiments, we can set a threshold (or a cut-point) $1\le \tilde{\lambda }\le 9,999$ and accept a word of length i if $\tilde{P}(i)\ge \tilde{\lambda }+1$; and reject a word of length i if $\tilde{P}(i)\le \tilde{\lambda }-1$.

Analyzing the results of the experiments, we can say that each member i of MOD_p has $\tilde{P}(i)\ge 1,021$. At the same time, each non-member i has $\tilde{P}(i)\le 925$.

So, we can choose any threshold $926\le \tilde{\lambda }\le 1,020$. Here we choose the middle of the interval $\tilde{\lambda }=973$ for more statistical safety. Finally, we can say that our algorithm accepts a word of length i if $\tilde{P}(i)\ge 974$, and rejects it if $\tilde{P}(i)\le 972$.

The criteria based on isolated cut-point are not as good as in the bounded error automata, but are also useful. For practical implementation, we should invoke our algorithm at least O(1/λ) times to have a reasonable statistic that approximates P(i).

We perform similar experiments for the standard circuit for the automaton for the MOD_p language. Since m = 3, we need to calculate 2^m = 8 integer parameters as coefficients for the rotation angles. For this case, using the brute force algorithm for parameter finding is unrealistic because the standard circuit execution on the IBMQ simulator takes much more time than in the case of the shallow circuit execution. We use three approaches:

• The coordinate descent method (Wright, 2015) for finding the first six parameters and the brute force approach for calculating the last two parameters.

• Simulated annealing algorithm (Press, 1992) for finding all parameters.

• Genetic algorithm (Mitchell, 1998) for finding all parameters.

The objective function for minimization is $dif{f}^{\prime }=\tilde{P}(p)-\{\tilde{P}(r):r$ mod p≠0, 1 ≤ r ≤ 2·p+10}. We compute $\tilde{P}(i)$, which is the number of shots that return the state |0〉 (accepting state).

We use these three algorithms, obtain the results, and choose the best result among them. The target parameters are K = {14, 9, 6, 7, 10, 4, 2, 16}.

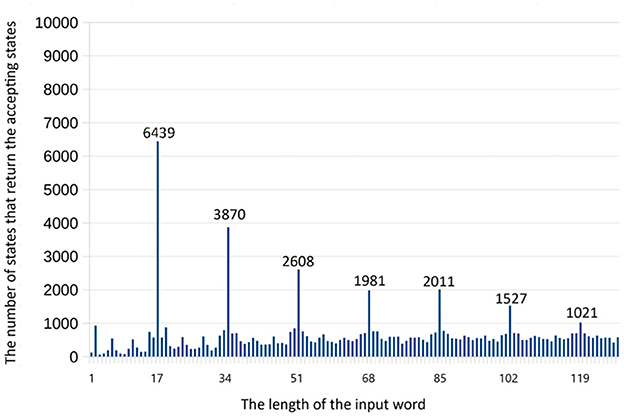
Then we invoke the circuit for the automaton using these parameters on input words of length at most 7·p+9 = 128. The program is executed 10,000 times, and we calculate $\tilde{P}(i)$. These numbers are presented in Section 6 and Figure 9.

Figure 9

Figure 9. Computational errors for m = 3 of original automata with deep circuit for noisy device.

When analyzing the data, we can see that no member word i has $\tilde{P}(i)>5,000$, which means that the probability P(i) < 0.5 for any input i. Therefore, if the automaton is the QFA with bounded error, we cannot separate members from non-members using this acceptance criterion.

However, if the automaton is the QFA with an isolated cut-point, then we can see that several members of the language, for instance, i = p, i = 2p, i = 4p, and i = 7p, can be separated from non-members. Nevertheless, other members of MOD_p are not separable from non-members, for example, i = 3p, i = 5p, and i = 6p. In addition, we can note that the number $\tilde{P}(1)>\tilde{P}(p)$. Our algorithm cannot find a set K that violates this condition. At the same time, we can ignore the case i = 1 because it can be processed separately. Even if we fix the issue with i = 1, the algorithm still detects only some members. For the members i = p, i = 2p, i = 4p, and i = 7p, the minimal value of $\tilde{P}(i)$ is 828. For the non-members except i = 1, the maximum value of $\tilde{P}(i)$ is 823. As a threshold $\tilde{\lambda }$, we can choose 824 or 825. Nevertheless, we cannot separate the members i = 3p, i = 5p, and i = 6p from non-members for any threshold.

Note that in the case of the shallow circuit, $\tilde{P}(p)$ is much higher than in the case of the standard circuit. For instance, $\tilde{P}(p)>5,100$ for the shallow circuit, which corresponds to P(p)>0.51; while for the standard circuit, the corresponding probability would be much smaller than 0.5 (approximately 0.1).

Finally, we can see that the shallow circuit is more efficient on noisy devices (emulators) than the standard circuit. However, in the case of an “ideal” noise-free device, we have an opposite situation.

5 Conclusion

We show that generalized arithmetic progressions generate some sets of coefficients k_i for the quantum fingerprinting technique with provable properties. These sets have large sizes, but their depth is small and comparable to that of the sets obtained by the probabilistic method. These sets can be used to implement quantum finite automata on current quantum hardware.

We perform numerical simulations. In the case of “ideal” (noise-free) devices, the experiments show that the error probability for the shallow circuit is close to the error probability for the standard circuit. At the same time, we show that the shallow circuit is much more efficient than the standard circuit when implemented on IBMQ noisy device simulators.

The depth optimization of quantum finite automata is also an open question. The lower bound on the size of K with respect to p and ε is already known (Ablayev et al., 2016b). Therefore, for given p and ε, quantum finite automata cannot have less than O(logp/ε) states. However, to our knowledge, a lower bound on the circuit depth of the transition function implementation is unknown. Thus, we pose an open question: Is it possible to implement a transition function with a depth less than O(logp)? What is the lower bound?

6 Numerical experiments for noisy devices

The data for the shallow circuit for fingerprinting are tabulated in Table 1.

Table 1

Table 1. The number of shots that return accepting state for different lengths of the word for the shallow automaton of MOD₁₇ on a noisy device.

The data for the standard circuit for fingerprinting are tabulated in Table 2.

Table 2

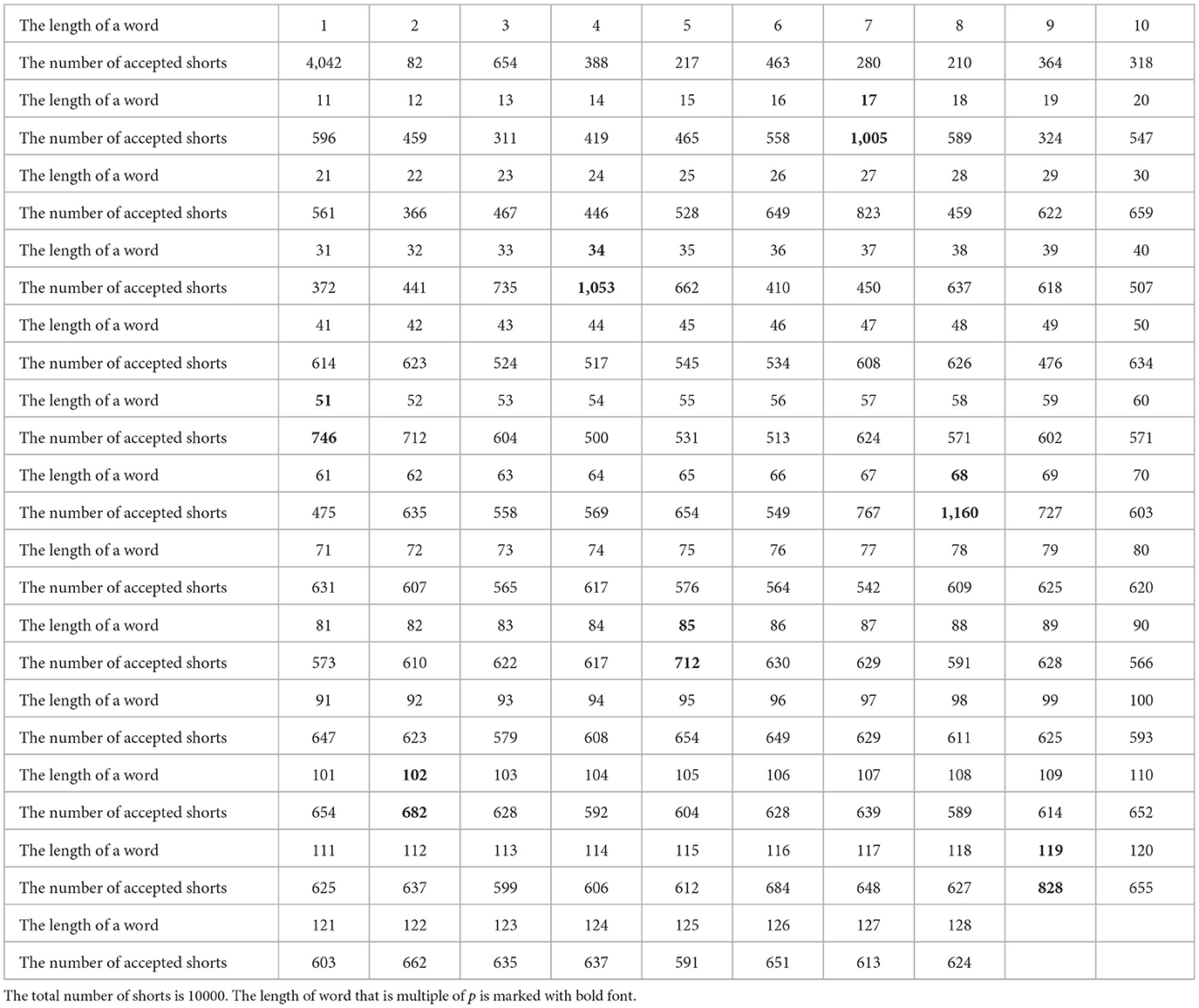
Table 2. The number of shots that return accepting state for different lengths of the word for the original automaton of MOD₁₇ on a noisy device.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

MZ: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Writing – original draft. AK: Data curation, Formal analysis, Investigation, Methodology, Validation, Writing – original draft. KK: Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The study was funded by the subsidy allocated to Kazan Federal University for the state assignment in the sphere of scientific activities (Project No. FZSM-2024-0013). The research in Section 4.1 is supported by Russian Science Foundation Grant 24-21-00406, https://rscf.ru/en/project/24-21-00406/. MZ acknowledges financial support under the National Recovery and Resilience Plan (PNRR), Mission 4, Component 2, Investment 1.4, Call for tender No. 1031 published on 17/06/2022 by the Italian Ministry of University and Research (MUR), funded by the European Union-NextGenerationEU, Project Title “National Centre for HPC, Big Data and Quantum Computing (HPC)”-Code National Center CN00000013-CUP D43C22001240001.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^Quantum volume is an exponent of the maximal square circuit size that can be implemented on the quantum computer (Cross et al., 2019; Wack et al., 2021).

References

Ablayev, F., and Ablayev, M. (2015). On the concept of cryptographic quantum hashing. Laser Phys. Lett. 12:125204. doi: 10.1088/1612-2011/12/12/125204

Crossref Full Text | Google Scholar

Ablayev, F., Ablayev, M., Khadiev, K., Salihova, N., and Vasiliev, A. (2022). “Quantum algorithms for string processing,” in Mesh Methods for Boundary-Value Problems and Applications, Vol. 141 (Lecture Notes in Computational Science and Engineering), 1–14. doi: 10.1007/978-3-030-87809-2_1

Crossref Full Text | Google Scholar

Ablayev, F., Ablayev, M., Khadiev, K., and Vasiliev, A. (2018a). Classical and quantum computations with restricted memory. LNCS 11011, 129–155. doi: 10.1007/978-3-319-98355-4_9

Crossref Full Text | Google Scholar

Ablayev, F., Ablayev, M., and Vasiliev, A. (2016a). On the balanced quantum hashing,” in J. Physics: Conference Series (IOP Publishing), 012019. doi: 10.1088/1742-6596/681/1/012019

Crossref Full Text | Google Scholar

Ablayev, F., Ablayev, M., and Vasiliev, A. (2018b). “Computing quantum hashing in the model of quantum branching programs,” in AIP Conference Proceedings (AIP Publishing LLC), 020020. doi: 10.1063/1.5025458

Crossref Full Text | Google Scholar

Ablayev, F., Ablayev, M., and Vasiliev, A. (2020). “Quantum hashing and fingerprinting for quantum cryptography and computations,” in International Computer Science Symposium in Russia (Springer), 1–15. doi: 10.1007/978-3-030-50026-9_1

Crossref Full Text | Google Scholar

Ablayev, F., Ablayev, M., Vasiliev, A., and Ziatdinov, M. (2016b). Quantum fingerprinting and quantum hashing. Computational and cryptographical aspects. Baltic J. Modern Comput. 4, 860–875. doi: 10.22364/bjmc.2016.4.4.17

Crossref Full Text | Google Scholar

Ablayev, F., Gainutdinova, A., Karpinski, M., Moore, C., and Pollett, C. (2005). On the computational power of probabilistic and quantum branching program. Inf. Comput. 203, 145–162. doi: 10.1016/j.ic.2005.04.003

Crossref Full Text | Google Scholar

Ablayev, F., Gainutdinova, A., Khadiev, K., and Yakaryılmaz, A. (2016c). Very narrow quantum OBDDs and width hierarchies for classical OBDDs. Lobachevskii J. Mathem. 37, 670–682. doi: 10.1134/S199508021606007X

Crossref Full Text | Google Scholar

Ablayev, F., Salikhova, N., and Ablayev, M. (2024). Hybrid classical-quantum text search based on hashing. Mathematics 12:1858. doi: 10.3390/math12121858

Crossref Full Text | Google Scholar

Ablayev, F., and Vasiliev, A. (2009). On quantum realisation of boolean functions by the fingerprinting technique. Discrete Mathem. Applic. 19, 555–572. doi: 10.1515/DMA.2009.037

Crossref Full Text | Google Scholar

Ablayev, F., and Vasiliev, A. (2011). “Classical and quantum parallelism in the quantum fingerprinting method,” in International Conference on Parallel Computing Technologies (Springer), 1–12. doi: 10.1007/978-3-642-23178-0_1

Crossref Full Text | Google Scholar

Ablayev, F., and Vasiliev, A. (2013a). Cryptographic quantum hashing. Laser Phys. Lett. 11:025202. doi: 10.1088/1612-2011/11/2/025202

Crossref Full Text | Google Scholar

Ablayev, F., and Vasiliev, A. (2014). “Computing boolean functions via quantum hashing,” in Computing with New Resources: Essays Dedicated to Jozef Gruska on the Occasion of His 80th Birthday, 149–160. doi: 10.1007/978-3-319-13350-8_11

Crossref Full Text | Google Scholar

Ablayev, F., and Vasiliev, A. (2020). “Quantum hashing and fourier transform,” in Journal of Physics: Conference Series (IOP Publishing), 012001. doi: 10.1088/1742-6596/1680/1/012001

Crossref Full Text | Google Scholar

Ablayev, F., and Vasiliev, A. (2022). “Quantum hashing on the high-dimensional states,” in International Conference on Micro-and Nano-Electronics 2021 (SPIE), 565–570. doi: 10.1117/12.2624628

Crossref Full Text | Google Scholar

Ablayev, F. M., Ablayev, M. F., and Vasilev, A. V. (2014). Universal quantum hashing. Uchenye Zapiski Kazanskogo Universiteta. Seriya Fiziko-Matematicheskie Nauki 156, 7–18. Available online at: https://www.mathnet.ru/eng/uzku1261

Google Scholar

Ablayev, F. M., and Vasiliev, A. (2013b). Algorithms for quantum branching programs based on fingerprinting. Int. J. Softw. Inform. 7, 485–500. Available online at: https://openurl.ebsco.com/EPDB%3Agcd%3A12%3A22738220/detailv2?sid=ebsco%3Aplink%3Ascholar&id=ebsco%3Agcd%3A95709941&crl=c&link_origin=scholar.google.com

Google Scholar

Ajtai, M., Iwaniec, H., Komlós, J., Pintz, J., and Szemerédi, E. (1990). Construction of a thin set with small fourier coefficients. Bull. London Mathem. Soc. 22, 583–590. doi: 10.1112/blms/22.6.583

Crossref Full Text | Google Scholar

Ambainis, A., and Freivalds, R. (1998). “1-way quantum finite automata: strengths, weaknesses and generalizations,” in FOCS'98 (IEEE), 332–341. doi: 10.1109/SFCS.1998.743469

Crossref Full Text | Google Scholar

Ambainis, A., and Nahimovs, N. (2009). Improved constructions of quantum automata. Theor. Comput. Sci. 410, 1916–1922. doi: 10.1016/j.tcs.2009.01.027

Crossref Full Text | Google Scholar

Ambainis, A., Nayak, A., Ta-Shma, A., and Vazirani, U. (2002). Dense quantum coding and quantum finite automata. J. ACM 49, 496–511. doi: 10.1145/581771.581773

Crossref Full Text | Google Scholar

Ambainis, A., and Watrous, J. (2002). Two-way finite automata with quantum and classical states. Theor. Comput. Sci. 287, 299–311. doi: 10.1016/S0304-3975(02)00138-X

Crossref Full Text | Google Scholar

Ambainis, A., and Yakaryılmaz, A. (2021). “Automata and quantum computing,” in Handbook of Automata Theory, ed. J. Éric Pin (European Mathematical Society Publishing House), 1457–1493. doi: 10.4171/automata-2/17

Crossref Full Text | Google Scholar

Bergholm, V., Vartiainen, J. J., Möttönen, M., and Salomaa, M. M. (2005). Quantum circuits with uniformly controlled one-qubit gates. Phys. Rev. A 71:052330. doi: 10.1103/PhysRevA.71.052330

Crossref Full Text | Google Scholar

Bertoni, A. (1975). The Solution of Problems Relative to Probabilistic Automata in the Frame of the Formal Languages Theory. GI-4. Jahrestagung: Berlin, 107–112. doi: 10.1007/978-3-662-40087-6_6

Crossref Full Text | Google Scholar

Bertoni, A., Mauri, G., and Torelli, M. (1977). “Some recursively unsolvable problems relating to isolated cutpoints in probabilistic automata,” in Automata, Languages and Programming: Fourth Colloquium, University of Turku, Finland (Springer), 87–94. doi: 10.1007/3-540-08342-1_7

Crossref Full Text | Google Scholar

Birkan, U., Salehi, Ö., Olejar, V., Nurlu, C., and Yakaryılmaz, A. (2021). “Implementing quantum finite automata algorithms on noisy devices,” in International Conference on Computational Science (Springer), 3–16. doi: 10.1007/978-3-030-77980-1_1

Crossref Full Text | Google Scholar

Buhrman, H., Cleve, R., Watrous, J., and de Wolf, R. (2001). Quantum fingerprinting. Phys. Rev. Lett. 87:167902. doi: 10.1103/PhysRevLett.87.167902

PubMed Abstract | Crossref Full Text | Google Scholar

Chadha, R., Sistla, A. P., and Viswanathan, M. (2013). “Probabilistic automata with isolated cut-points,” in International Symposium on Mathematical Foundations of Computer Science (Springer), 254–265. doi: 10.1007/978-3-642-40313-2_24

Crossref Full Text | Google Scholar

Cross, A. W., Bishop, L. S., Sheldon, S., Nation, P. D., and Gambetta, J. M. (2019). Validating quantum computers using randomized model circuits. Phys. Rev. A 100:032328. doi: 10.1103/PhysRevA.100.032328

Crossref Full Text | Google Scholar

Gainutdinova, A. (2002). On relative complexity of quantum and classical branching programs. Discrete Mathem. Applic. 12, 515–526. doi: 10.1515/dma-2002-0510

Crossref Full Text | Google Scholar

Gainutdinova, A., and Yakaryılmaz, A. (2015). “Unary probabilistic and quantum automata on promise problems,” in Developments in Language Theory (Springer), 252–263. doi: 10.1007/978-3-319-21500-6_20

Crossref Full Text | Google Scholar

Gainutdinova, A., and Yakaryılmaz, A. (2017). “Nondeterministic unitary obdds,” in Computer Science - Theory and Applications- 12th International Computer Science Symposium in Russia, CSR 2017, Kazan, Russia, June 8–12, 2017, Proceedings, volume 10304 of Lecture Notes in Computer Science (Springer), 126–140. doi: 10.1007/978-3-319-58747-9_13

Crossref Full Text | Google Scholar

Gainutdinova, A., and Yakaryılmaz, A. (2018). Unary probabilistic and quantum automata on promise problems. Quant. Inf. Proc. 17:28. doi: 10.1007/s11128-017-1799-0

Crossref Full Text | Google Scholar

Gimbert, H., and Oualhadj, Y. (2010). “Probabilistic automata on finite words: decidable and undecidable problems,” in Automata, Languages and Programming: 37th International Colloquium, ICALP 2010, Bordeaux, France, July 6–10, 2010, Proceedings, Part II 37 (Springer), 527–538. doi: 10.1007/978-3-642-14162-1_44

Crossref Full Text | Google Scholar

Hu, Y., Melnyk, D., Wang, Y., and Wattenhofer, R. (2020). “Space complexity of streaming algorithms on universal quantum computers,” in Theory and Applications of Models of Computation: 16th International Conference, TAMC 2020, Changsha, China, October 18–20, 2020, Proceedings 16 (Springer), 275–286. doi: 10.1007/978-3-030-59267-7_24

Crossref Full Text | Google Scholar

IBM (2022). Eagle's quantum performance progress. Available online at: https://www.ibm.com/quantum/blog/eagle-quantum-processor-performance (accessed April 30, 2024).

Google Scholar

IBM (2025). Qiskit SDK v2.0.0. GenericBackendV2. https://docs.quantum.ibm.com/api/qiskit/qiskit.providers.fake_provider.GenericBackendV2 (accessed March 23, 2025).

Google Scholar

Kālis, M. (2018). Kvantu algoritmu realizācija fiziskā kvantu datorā (quantum algorithm implementation on a physical quantum computer). Master's thesis, University of Latvia.

Google Scholar

Khadiev, K., and Khadieva, A. (2017). “Reordering method and hierarchies for quantum and classical ordered binary decision diagrams,” in CSR 2017 (Springer), 162–175. doi: 10.1007/978-3-319-58747-9_16

Crossref Full Text | Google Scholar

Khadiev, K., and Khadieva, A. (2021). Quantum online streaming algorithms with logarithmic memory. Int. J. Theor. Phys. 60, 608–616. doi: 10.1007/s10773-019-04209-1

Crossref Full Text | Google Scholar

Khadiev, K., and Khadieva, A. (2022). Quantum and classical log-bounded automata for the online disjointness problem. Mathematics 10:143. doi: 10.3390/math10010143

Crossref Full Text | Google Scholar

Khadiev, K., Khadieva, A., and Knop, A. (2022a). Exponential separation between quantum and classical ordered binary decision diagrams, reordering method and hierarchies. Nat. Comput. 22, 723–736. doi: 10.1007/s11047-022-09904-3

Crossref Full Text | Google Scholar

Khadiev, K., Khadieva, A., and Mannapov, I. (2018). Quantum online algorithms with respect to space and advice complexity. Lobachevskii J. Mathem. 39, 1210–1220. doi: 10.1134/S1995080218090421

Crossref Full Text | Google Scholar

Khadiev, K., Khadieva, A., Ziatdinov, M., Mannapov, I., Kravchenko, D., Rivosh, A., et al. (2022b). Two-way and one-way quantum and classical automata with advice for online minimization problems. Theor. Comput. Sci. 920, 76–94. doi: 10.1016/j.tcs.2022.02.026

Crossref Full Text | Google Scholar

Khadiev, K., and Serov, D. (2025). “Quantum algorithm for the multiple string matching problem,” in International Conference on Current Trends in Theory and Practice of Computer Science (Springer), 58–69. doi: 10.1007/978-3-031-82697-9_5

Crossref Full Text | Google Scholar

Khadiev K. and Khadieva A. Kravchenko D. Mannapov I. Rivosh A. Yamilov R. (2023). Quantum versus classical online streaming algorithms with logarithmic size of memory. Lobachevskii J. Mathem. 44, 687–698. doi: 10.1134/S1995080223020208

Crossref Full Text | Google Scholar

Khadieva, A. (2023). Optimal parameters computing code. Available online at: https://github.com/aliyakhadi/Parameters_counting (accessed April 30, 2025).

Google Scholar

Khadieva, A. (2024). Quantum hashing algorithm implementation. Technical report. arXiv:quant-ph/2024.

Google Scholar

Khadieva, A., Salehi, O., and Yakaryılmaz, A. (2024). “A representative framework for implementing quantum finite automata on real devices,” in Proceedings of UCNC 2024. doi: 10.1007/978-3-031-63742-1_12

Crossref Full Text | Google Scholar

Khadieva, A., and Ziatdinov, M. (2023). Deterministic construction of qfas based on the quantum fingerprinting technique. Lobachevskii J. Mathem. 44, 713–723. doi: 10.1134/S199508022302021X

Crossref Full Text | Google Scholar

Le Gall, F. (2006). “Exponential separation of quantum and classical online space complexity,” in SPAA '06: Proceedings of the Eighteenth Annual ACM Symposium on Parallelism in Algorithms and Architectures (ACM), 67–73. doi: 10.1145/1148109.1148119

Crossref Full Text | Google Scholar

Le Gall, F. (2009). Exponential separation of quantum and classical online space complexity. Theory Comput. Syst. 45, 188–202. doi: 10.1007/s00224-007-9097-3

Crossref Full Text | Google Scholar

Mitchell, M. (1998). An Introduction to Genetic Algorithms. London: MIT press.

Google Scholar

Montanaro, A. (2017). Quantum pattern matching fast on average. Algorithmica 77, 16–39. doi: 10.1007/s00453-015-0060-4

Crossref Full Text | Google Scholar

Moore, C., and Crutchfield, J. P. (2000). Quantum automata and quantum grammars. Theor. Comput. Sci. 237, 275–306. doi: 10.1016/S0304-3975(98)00191-1

Crossref Full Text | Google Scholar

Möttönen, M., Vartiainen, J. J., Bergholm, V., and Salomaa, M. M. (2004). Quantum circuits for general multiqubit gates. Phys. Rev. Lett. 93:130502. doi: 10.1103/PhysRevLett.93.130502

PubMed Abstract | Crossref Full Text | Google Scholar

Nakanishi, M., and Yakaryılmaz, A. (2015). “Classical and quantum counter automata on promise problems,” in International Conference on Implementation and Application of Automata (Springer), 224–237. doi: 10.1007/978-3-319-22360-5_19

Crossref Full Text | Google Scholar

Preskill, J. (2018). Quantum computing in the nisq era and beyond. Quantum 2:79. doi: 10.22331/q-2018-08-06-79

Crossref Full Text | Google Scholar

Press W. H.. (1992). The Art of Scientific Computing. Cambridge: Cambridge University Press.

Google Scholar

Rabin, M. O. (1963). Probabilistic automata. Inf. Control 6, 230–245. doi: 10.1016/S0019-9958(63)90290-0

Crossref Full Text | Google Scholar

Ramesh, H., and Vinay, V. (2003). String matching in $O(\sqrt{n}+\sqrt{m})$ quantum time. J. Discr. Algor. 1, 103–110. doi: 10.1016/S1570-8667(03)00010-8

Crossref Full Text | Google Scholar

Razborov, A., Szemerédi, E., and Wigderson, A. (1993). Constructing small sets that are uniform in arithmetic progressions. Combinat. Probab. Comput. 2, 513–518. doi: 10.1017/S0963548300000870

Crossref Full Text | Google Scholar

Salehi, Ö., and Yakaryılmaz, A. (2021). Cost-efficient QFA algorithm for quantum computers. arXiv:2107.02262.

Google Scholar

Say, A. C. C., and Yakaryılmaz, A. (2014). “Quantum finite automata: a modern introduction,” in Computing with New Resources (Springer), 208–222. doi: 10.1007/978-3-319-13350-8_16

Crossref Full Text | Google Scholar

Tao, T., and Vu, V. (2006). Additive Combinatorics, volume 105 of Cambridge Studies in Advanced Mathematics. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511755149

Crossref Full Text | Google Scholar

Turaykhanov, D., Akat'ev, D., Vasiliev, A., Ablayev, F., and Kalachev, A. (2021). Quantum hashing via single-photon states with orbital angular momentum. Phys. Rev. A 104:052606. doi: 10.1103/PhysRevA.104.052606

Crossref Full Text | Google Scholar

Vasiliev, A. (2016a). Binary quantum hashing. Russian Mathem. 60, 61–65. doi: 10.3103/S1066369X16090073

Crossref Full Text | Google Scholar

Vasiliev, A. (2016b). “A model of quantum communication device for quantum hashing,” in Journal of Physics: Conference Series (IOP Publishing), 012020. doi: 10.1088/1742-6596/681/1/012020

Crossref Full Text | Google Scholar

Vasiliev, A. (2016c). Quantum hashing for finite abelian groups. Lobachevskii J. Mathem. 37, 753–757. doi: 10.1134/S1995080216060184

Crossref Full Text | Google Scholar

Vasiliev, A. (2023). Constant-depth algorithm for quantum hashing. Russian Microelectr. 52, S399–S402. doi: 10.1134/S106373972360067X

Crossref Full Text | Google Scholar

Vasiliev, A., Latypov, M., and Ziatdinov, M. (2017). Minimizing collisions for quantum hashing. J. Eng. Appl. Sci. 12, 877–880. doi: 10.3923/jeasci.2017.877.880

Crossref Full Text | Google Scholar

Vasiliev, A., Vasilov, A., and Latypov, M. (2019). Analysis of properties of quantum hashing. J. Mathem. Sci. 241, 117–124. doi: 10.1007/s10958-019-04412-9

Crossref Full Text | Google Scholar

Wack, A., Paik, H., Javadi-Abhari, A., Jurcevic, P., Faro, I., Gambetta, J. M., et al. (2021). Quality, speed, and scale: three key attributes to measure the performance of near-term quantum computers. arXiv:2110.14108.

Google Scholar

Wright, S. J. (2015). Coordinate descent algorithms. Mathem. Program. 151, 3–34. doi: 10.1007/s10107-015-0892-3

Crossref Full Text | Google Scholar

Yakaryılmaz, A. (2013). Log-space counter is useful for unary languages by help of a constant-size quantum register. arXiv preprint arXiv:1309.4767.

Google Scholar

Yakaryılmaz, A., and Say, A. C. (2009). Efficient probability amplification in two-way quantum finite automata. Theor. Comput. Sci. 410, 1932–1941. doi: 10.1016/j.tcs.2009.01.029

Crossref Full Text | Google Scholar

Yakaryılmaz, A., and Say, A. C. C. (2010). Languages recognized by nondeterministic quantum finite automata. Quantum Inf. Comput. 10, 747–770. doi: 10.26421/QIC10.9-10-3

Crossref Full Text | Google Scholar

Ziatdinov, M. (2016a). From graphs to keyed quantum hash functions. Lobachevskii J. Mathem. 37, 705–712. doi: 10.1134/S1995080216060202

Crossref Full Text | Google Scholar

Ziatdinov, M. (2016b). Quantum hashing group approach. Lobachevskii J. Mathem. 37, 222–226. doi: 10.1134/S1995080216020165

Crossref Full Text | Google Scholar

Ziiatdinov, M., Khadieva, A., and Yakaryılmaz, A. (2023). “Gaps for shallow implementation of quantum finite automata,” in Proceedings of the 16th International Conference on Automata and Formal Languages (AFL 2023), Eger, Hungary, eds. S. I. Zsolt Gazdag and G. Kovasznai (Open Publishing Association), 269–280. doi: 10.4204/EPTCS.386.21

Crossref Full Text | Google Scholar

Zinnatullin, I. (2023). Cryptographic properties of the quantum hashing based on expander graphs. Lobachevskii J. Mathem. 44, 776–787. doi: 10.1134/S1995080223020397

Crossref Full Text | Google Scholar

Zinnatullin, I., Khadiev, K., and Khadieva, A. (2023). Efficient implementation of amplitude form of quantum hashing using state-of-the-art quantum processors. Russian Microelectr. 52, S390–S394. doi: 10.1134/S1063739723600620

Crossref Full Text | Google Scholar