Model checking deep neural networks: opportunities and challenges

Deep neural networks (DNNs) are extensively used in both current and future manufacturing, transportation, and healthcare sectors. The widespread use of neural networks in highly safety-critical applications has made it necessary to prevent catastrophic issues from arising during prediction processes. In fact, misreading a traffic sign by an autonomous car or performing an incorrect analysis of medical records could put human lives in danger. With this awareness, the number of studies related to deep neural network verification has increased dramatically in recent years. In particular, formal guarantees regarding the behavior of a DNN under particular settings are provided by model checking, which is crucial in safety-critical applications where network output errors could have disastrous effects. Model checking is an effective approach for confirming that neural networks perform as planned by comparing them to clearly stated qualities. This paper aims to highlight the critical need for and present challenges associated with using model-checking verification techniques to verify deep neural networks before relying on them in real-world applications. It examines state-of-the-art research and draws the most prominent future directions in the model checking of neural networks.

1 Introduction

Deep learning powers several artificial intelligence products and programs that promote automation by carrying out both physical and computational operations without requiring any intervention from humans. Essentially, it's a three or more-layer neural network that is able to learn from massive information sets in order to predict some results by imitating the activity of the human brain. The current widespread use of neural networks in daily life activities has made clear the seriousness of their deployment in highly safety-critical applications (Amodei et al., 2016). Eykholt et al. (2018) documented an issue with self-driving cars when a vehicle ran through a stop sign due to slight sign fading, resulting in an accident. This increases awareness of the necessity to prevent catastrophic issues from arising during prediction processes.

In order to raise awareness among contemporary businesses and organizations regarding the grave consequences of implementing deep neural networks without first confirming their functionality, readers are directed to Huang et al. (2017, 2020) for an extensive analysis of neural network safety and reliability, along with a detailed description of the problems that could arise in the most sophisticated deep neural network applications within safety-critical domains.

Given these conditions and prior reports of DNN errors [e.g., those reported in Eykholt et al. (2018) and Makino et al. (2022)], it is imperative to guarantee the proper behavior of deep neural networks prior to their exploration, particularly in safety-critical applications where human lives are involved. It has been underlined by safety-focused organizations, such as NASA (Dutta et al., 2018), how important it is to validate and confirm neural network models before using them in safety-sensitive applications.

Formal methods (Woodcock et al., 2009) offer a feasible approach to ensure system correctness, particularly in critical applications. They use mathematical tools to examine the correctness and other characteristics of systems. In a logical and comprehensive manner, formal methods can be used to evaluate and analyze models against formal specifications, refine high-level requirements, and create test scenarios. Formal verification, the foundation of formal methods, is a methodical checking process that can detect extreme case problems and design inconsistencies while considering all inputs.

Two strategies exist for formal verification: model checking (Clarke, 1997a) and theorem proving (Cook, 2023). The former reduces the problem to a finite state space and tests exhaustively. The latter consists of creating a formal axiomatic proof of correctness. In theorem proving, most tools necessitate human interaction and thus require time and expertise. However, model checkers use a brute force approach to solve a problem, and the process is fully automatic. Moreover, in the model checking process, if a property is not satisfied, a counterexample is available for possible use in fixing the fault. This explains why model-checking research has drawn significant attention from a variety of scientific communities. That is why we choose, in this paper, to rely on model checking to explore the verification of neural networks.

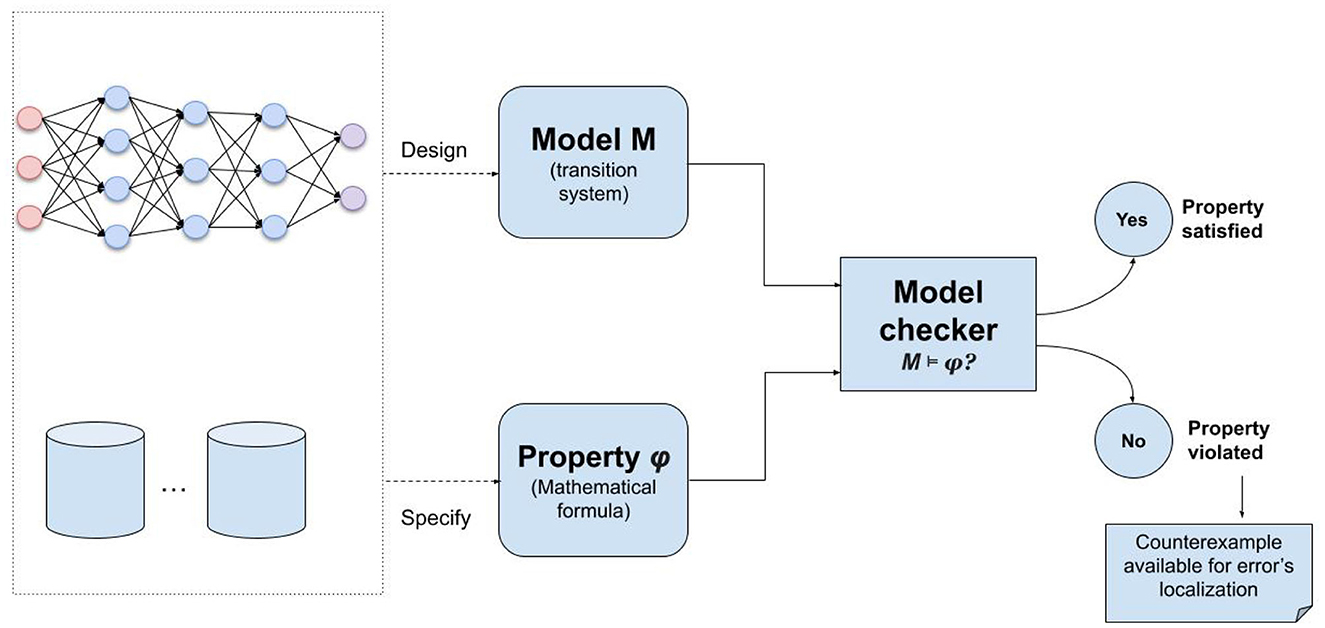
To apply model checking, a system is formally described by a model on which the correctness is evaluated. A mathematical representation of a system, called a transition system, is usually used as the model. The model's compliance with a set of properties is checked as part of the verification process. The correctness qualities in question are generally related to safety or liveness. Safety refers to the fact that something negative will never occur, and liveness states that something positive will eventually occur. In a neural network setting, model checking can be used to explicitly verify its correctness properties by creating a formal model of the network and comparing it to specific formal specifications that provide the necessary criteria.

One example of how model checking may be used with deep neural networks is the application of Counter-Example Guided Abstraction Refinement (CEGAR) (Hajdu and Micskei, 2020). Using counterexamples, CEGAR is a model-checking technique that iteratively refines the network's representation until a claim appears valid or invalid. By evaluating the degree to which deep neural networks meet specific requirements, this method can be used to assess how robust they are.

Even though model checking has a vast and useful body of literature at its disposal, there have not been many studies or advancements in its application to deep neural network-based technologies until recently. In this respect, the current work attempts to review the various approaches to model checking deep neural networks and consequently discuss the potential challenges and future research directions necessary to advance the topic toward maturity.

It is important to note that correctness, as it relates to neural networks, is the degree to which the network generates outcomes correctly given a certain input. All it takes to determine whether a neural network is correct is for it to produce the expected result for a given input. Neural networks are becoming increasingly complex and require more training data, making it harder to ensure their correctness. In general, researchers are not investigating the proof of the functional correctness of neural networks. Instead, they focus on characterizing one of the three main classes of correctness properties: robustness, safety, and consistency, which will be categorized later.

1.1 Paper contributions

The present study aims to achieve the following objectives by conducting a comprehensive assessment of the literature on deep neural networks' model checking:

• Summarize the current proposals for neural network model checking, aiming to provide a guide for researchers investigating this subject.

• Analyze the weaknesses of the current approaches and tools available to check the robustness, safety, and consistency of neural networks.

• Explore the challenges faced and the possible applications of existing techniques to tackle these challenges.

• Examine the potential avenues for future research to support the use of model checking in ensuring the secure implementation of neural networks in practical applications.

1.2 Related work

While focusing on formal specifications, the authors of Seshia et al. (2018) listed various properties that may attract researchers interested in deep neural networks. They demonstrated that formal specification is used not only for verifying DNNs but also for their retraining. The methods for testing, adversarial attacks, verifiability, and interpretability of neural networks that emerged between 2017 and 2020 are examined in Huang et al. (2020). In Liu et al. (2021), the authors mathematically defined the neural network verification problem and described various algorithms from the perspective of current neural network verifiers. Although the paper covered different existing procedures published before 2021, ranging from testing to constraint fulfillment to search and optimization, it does not present works addressing the formal models and specifications of neural networks, nor the algorithms for model checking. Urban and Miné (2021) discussed the applications of formal methods to machine learning in general and gave a glimpse on model checking application to verify neural networks used in the context of embedded critical software. The work in Meng et al. (2022) examined various adversarial robustness verification methods from a formal basis. It provided insightful explanations of the mathematical modeling of property reduction and formalization methods. A recent review of abstraction methods for verifying neural networks is published in Boudardara et al. (2023). The present study differs from existing review papers on neural network verification, making it the first to focus on model checking approaches by examining their findings, detailing their limitations, and considering their possible integration with various approaches.

1.3 Paper outline

Section 2 presents an overview of the application of model checking to deep neural networks while providing some preliminaries about DNNs and the model-checking process. Sections 3 and 4 explore, respectively, the different specification formalisms and models applied in the existing works. A categorization of the various approaches investigated according to the model-checking algorithm is given in Section 5. A discussion of the main findings of this study is presented in Section 6, and a statement of the main challenges that neural networks' model checking is currently facing is presented in Section 7. The work is concluded, and some potential research directions are listed in Section 8.

2 Model checking DNNs: an overview

To check the correctness of a neural network, it is beneficial to refer to formal verification as a rigorous process for confirming the properties of software and hardware by utilizing logical and mathematical tools to construct statements in precise mathematical terms. Formal verification strategies for neural networks seek to mathematically verify their correctness by ensuring that their behavior satisfies certain requirements. Belonging to formal methods tools, model checkers use a brute force approach to solve a question in a fully automatic process. Moreover, in the model checking process, if a property is not satisfied, a counterexample is available for possible use in fixing the fault. The application of model checking in deep learning in general has numerous advantages. Verifying the correctness of algorithms in a brute-force manner is one of its primary advantages. This can be crucial in making sure the prediction process is carried out as planned and does not lead to undesirable outcomes. Moreover, tests for safety and liveness qualities, naturally conducted by model checking, are in direct conformance with correctness properties of neural networks.

2.1 Preliminaries on DNNs

Inspired by the human brain, a neural network (Aggarwal, 2018), also known as an artificial neural network, is an interconnected network of nodes or artificial neurons, where each node performs an operation based on the inputs resulting from the previous nodes in order to perform a global complex operation. This way, neural networks can solve complex problems such as object recognition or medical diagnosis. As illustrated in Figure 1a, a neural network is a chain of relationships between a set of inputs (input layer) and a set of outputs (output layer). There are layers of units in between (hidden layers), where each one is computing a weighted sum sigmoided from the layer before it.

Figure 1

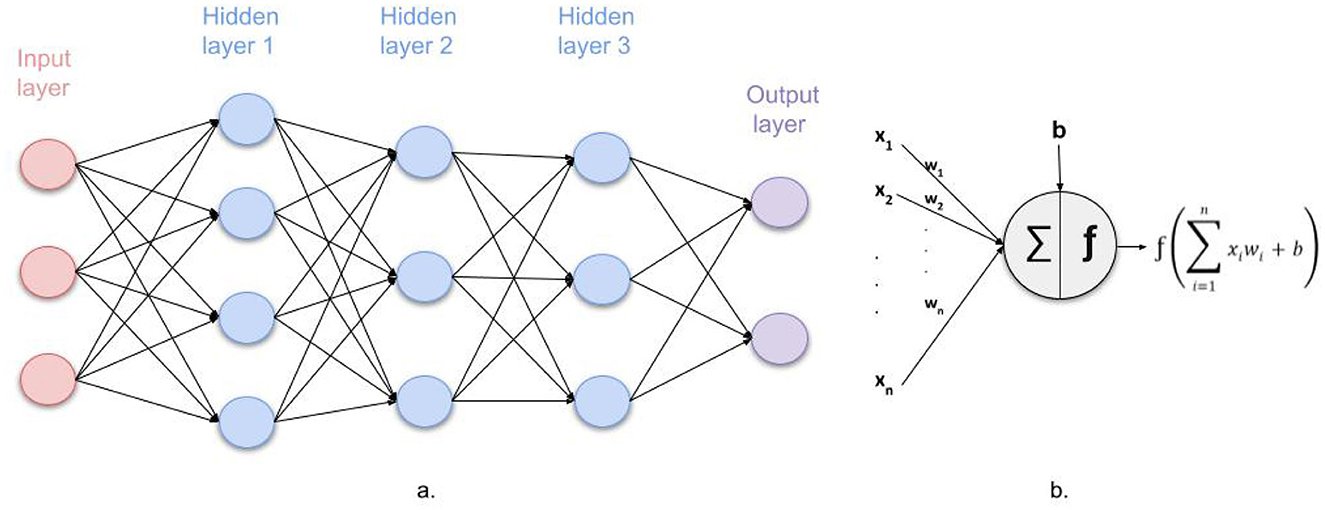
Figure 1. (a) Structure of a multilayer neural network; (b) One neuron's output calculation with x_i and w_i (1 ≤ i ≤ n) the outputs and weights respectively of the previous n neurons, b the bias and f the activation function.

The simple idea behind computing the outputs is that each neuron receives values from its preceding nodes x₁, .., x_n, where each node x_i has a weight w_i. This weight value may be seen as a score of the importance of this node for computing the corresponding output. The inputs x_i are multiplied by their weights w_i and then summed. The resulting sum, added to a certain bias b (or threshold), is then passed to an activation function f, which determines the output in a predictable form (see Figure 1b). The most popular activation function is the rectified linear activation function, or ReLU: f(x) = max(0, x). This output will be passed to the next layer and will serve as input for the specified neurons. This method of data propagation between layers characterizes the neural network as “a feedforward neural network” (Yalçın, 2021).

Formally, a feedforward neural network can be defined as follows: The network contains an input layer L₀ with n₀ nodes, m − 1 hidden layers L₁, ..., L_m−1 with n₁, ..., n_m−1 nodes respectively, and an output layer L_m containing n_m nodes. The values of the nodes in the input layer are given by the input to the neural network (denoted V₁, ..., V_n0), and the values of the nodes in the other layers are computed as follows:

$\forall j\in 1..m,\forall p\in 1..n_j,V_p^j=f({\displaystyle \sum _{i=1}^{n_{j-1}}}(W_i^{pj}{V}_i^{j-1})+b_p^j),$

where $V_a^j$ denotes the value of the neuron number a on the layer number j, f is the activation function, $b_a^j$ denotes the bias of the node a on the layer j, and $W_a^{bj}$ denotes the weight of the connection from neuron a of layer j − 1 to neuron b of layer j.

Neural networks can enhance the quality of outputs thanks to backpropagation algorithms. Backpropagation executes a reversal run across the network after each forward run while revising the weights and biases. A neural network with multiple hidden layers that processes and learns from a large amount of data by capturing complex patterns is called a deep neural network. Deep neural networks may be classified according to their structure and function. The architectures studied in papers dealing with model checking of neural networks are FNNs, RNNs, and LSTMs.

FNNs (feedforward neural networks) (Yalçın, 2021) are a type of neural network in which data flow in one direction, from the input layer through the hidden layers to the output layer. Neurons within the same layer are not interconnected, and information does not return from any node to previous layers. The network is fully connected, meaning each neuron in the input and hidden layers is connected to all neurons in the next layer.

Deep neural networks that use sequential data are called recurrent neural networks (RNNs) (Sherstinsky, 2020). They seek to retain information from previous inputs to affect present input and output. Thus, recurrent neural networks rely on the previous elements in the chain to determine their output, in contrast to typical deep neural networks, which expect inputs and outputs to be unrelated. RNNs are further differentiated by the fact that their settings are shared across all network layers. They carry one identical weight parameter throughout the network layers, compared to feedforward networks, which rely on distinct weights.

Long Short Term Memory networks (LSTM) (Sherstinsky, 2020) are RNNs that introduce a new unit known as a memory cell, enabling the network to store and retrieve data for a longer duration. An LSTM's memory cell consists of an input gate, an output gate, and a forget gate. These gates control what information is recalled and what is forgotten by governing the flow of information inside the cell that holds data. As a result, LSTMs can remember extended sequences of significant information while ignoring irrelevant details.

Modern DNNs frequently contain a large number of parameters, and deploying them on embedded devices with limited resources can, therefore, be difficult. Quantization appears to be a potential method to lessen resource requirements in order to address this problem. Quantization transforms 32/64-bit floating points to tiny bit-width numbers with low accuracy loss. Specifically, utilizing the bipolar binaries ± 1, binarized neural networks (BNNs) reflect the case of 1-bit quantization. By using bit-wise operations, BNNs may substantially decrease storage capacity requirements and processing periods, which significantly increases both energy and time efficiency.

2.2 Model checking process

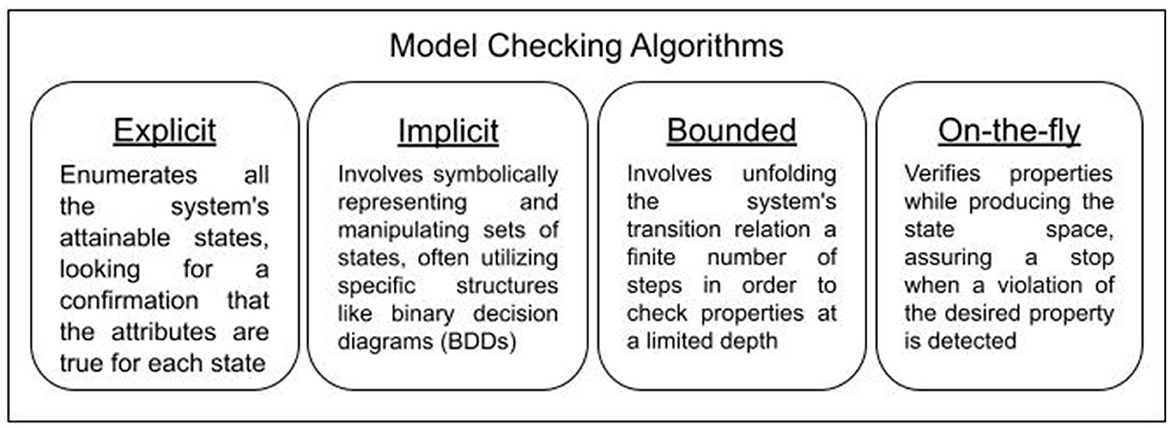
Verifying certain properties of a system by model checking (Clarke, 1997b) generally involves checking if the property is ensured by the system model. As shown in Figure 2, a mathematical illustration of the system, such as a transition system, could serve as the model in this case. Typically, the property to be verified is stated in a particular language, commonly a temporal logic. In a transition system T, all accepted system runs are stated. The system progresses by taking steps that move it from one state to another. All the states reachable from the system's original state by taking legitimate actions define the state space. The algorithm ensuring model checking takes as input the system model (commonly a transition diagram) and the specification of the property (commonly a formula written in temporal logic) and checks if the model satisfies the specification, i.e., the property is satisfied in all the possible executions of the system. In general, this satisfaction relation is formulated as M⊧φ, stating that the model M satisfies the property φ. Now, depending on how to describe all the possible system executions, the model checking algorithm may be explicit (Holzmann, 2018) or implicit (also known as symbolic) (Burch et al., 1992). Other variations exist, such as bounded and on-the-fly model checking, aiming to optimize the process and save computational costs. These model checking algorithms and their application to DNN will be sketched in Section 5.

Figure 2

Figure 2. Model checking of neural networks.

Since applying model checking requires defining a model and a specification (Figure 2), we propose in the next sections to study the various models and specifications defined in the literature to ensure the model checking of deep neural networks. However, before this, we provide a general overview of the existing applications of model checking to DNNs to give the reader insight into the comparative study we are presenting.

2.3 Applications of model checking to DNNs

Verifying a neural network poses the challenge of clearly demonstrating that the neural network meets a characteristic corresponding to its semantic function. Checking adversarial robustness, for example, involves showing that a neural network is resilient to minor perturbations of its inputs, meaning that the output remains unaffected by minor modifications of an input. Inputs that influence the outputs are referred to as adversarial examples, and finding these adversarial examples is crucial because they highlight safety issues regarding DNNs if they exist. To ensure safety in property, it suffices to show that the output of a neural network remains unaffected by specific features such as gender. Consistency checking may refer to confirming that the outputs for any two inputs that are close to one another are also similarly close.

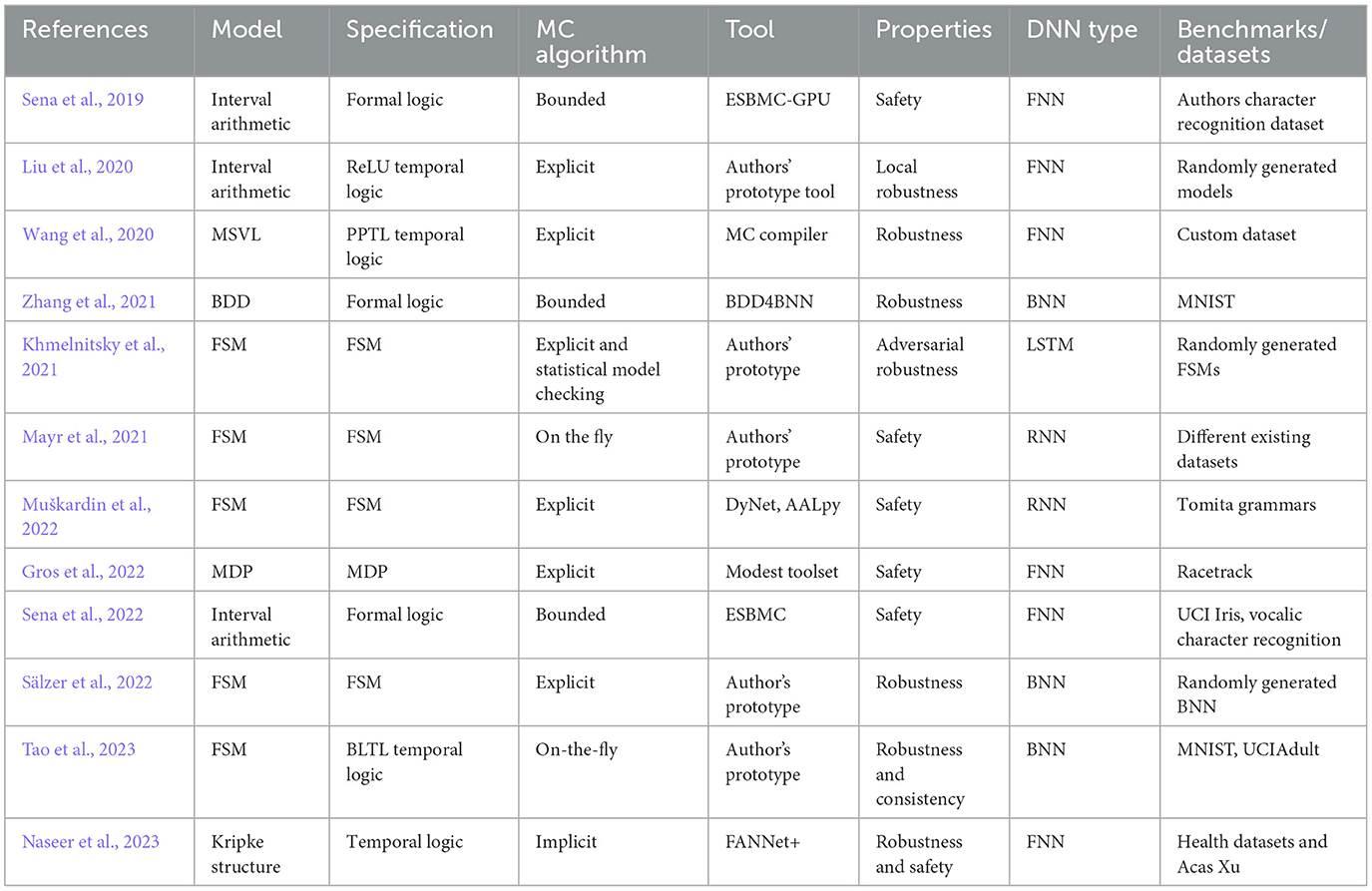
As we aim to analyze the existing approaches to model checking neural networks against all correctness properties, we provide a general synopsis in Table 1 to give the reader a glance at the studied approaches and the criteria for their distinction in this survey. In particular, for each proposal, we are looking for the following details:

• The language used or proposed to model the neural network (Model)

• The formal language proposed for properties specification (Specification)

• The class of model checking algorithm (MC algorithm)

• The tool applied or implemented to evaluate the approach

• The properties of interest: robustness, consistency, or safety

• The architecture of neural networks studied (DNN type)

• The benchmarks/datasets used for experimental evaluation if any.

Table 1

Table 1. Analysis of the works on model checking deep neural networks.

3 Formal models of DNNs

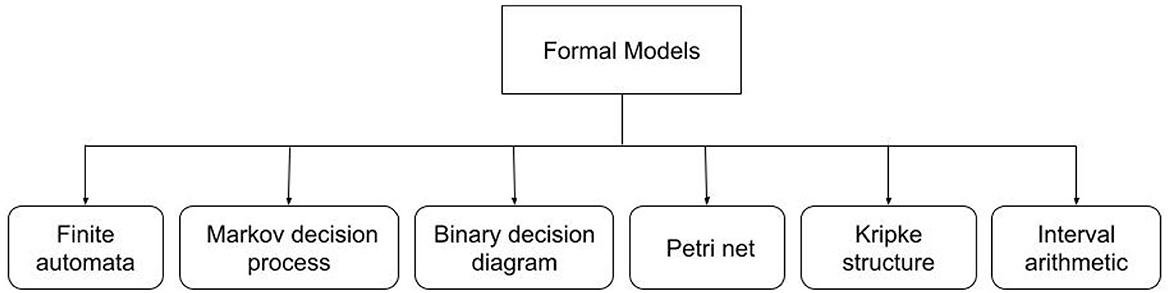
Formal models are conceptual depictions of the neural network examined in model checking. Through the use of straightforward and understandable language, these models encapsulate the fundamental behavior of the network, facilitating automated property verification. A model is keen to represent either explicitly or implicitly the transition system to be checked by a model checker against a formal specification of the desired property. In the following subsections, we categorize the different models used in the papers dealing with DNNs model checking, which are summarized in Figure 3.

Figure 3

Figure 3. Formal models applied to DNNs.

3.1 Finite automata

Numerous studies (Khmelnitsky et al., 2021; Mayr et al., 2021; Sälzer et al., 2022; Muškardin et al., 2022; Tao et al., 2023) propose modeling a deep neural network using a finite automaton. Finite automata provide a strong and effective method for capturing the dynamic behavior of DNNs. Although they might not be able to handle every type of property, their interpretability, simplicity of use, and effective verification techniques make them invaluable tools in the model-checking process. We detail some of these approaches in the following sections.

In Sälzer et al. (2022), the authors demonstrate how to transform a deep neural network into a finite automaton that can recognize words as pairs between inputs and outputs based on theoretically promising results. More specifically, they convert the network into an eventually-always weak nondeterministic Büchi automaton (WNBA_FG) (Sistla et al., 1987), which is used to recognize patterns in infinite sequences, thus allowing for the verification of complex properties, for which minimization and determinization are easy. The transformation of a DNN to a WNBA_FG is carried out by capturing the input/output behavior. Based on a white-box technique, the authors show that a WNBA_FG is defined for each computation performed on a node of the network (as defined in Figure 1b). This automaton can be obtained by combining three WNBA_FG derived from the three operations depicted in a neuron's computation, namely addition, multiplication, and the activation function (ReLU in their work). Figure 4 illustrates a WNBA_FG that recognizes the binary equality relation.

Figure 4

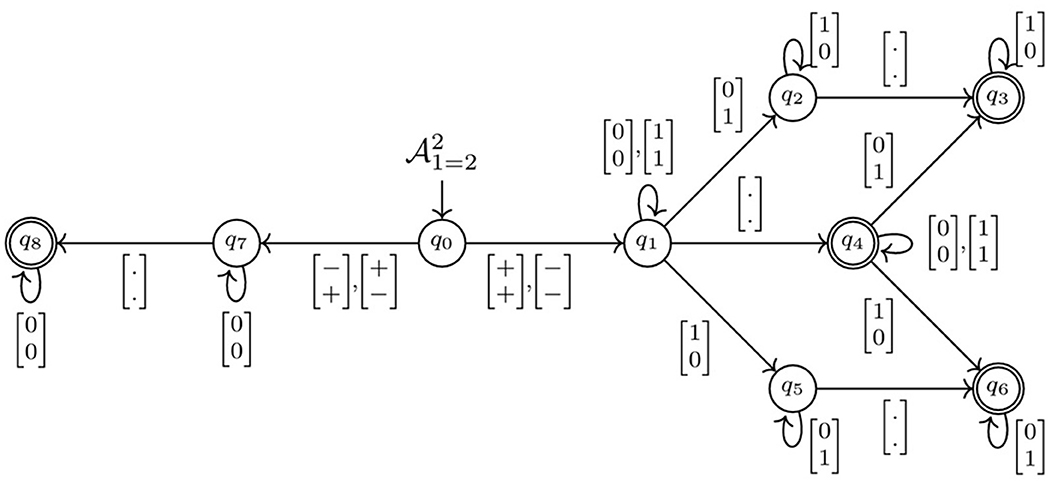
Figure 4. WNBA_FG that recognizes the binary equality relation [figure from Sälzer et al. (2022)].

Muškardin et al. (2022) proposes a formal description of the behavior of recurrent neural network classifiers based on deterministic finite automaton (DFA) extraction. Their method is applied independently of the RNN inner workings (black-box technique) and is based on active automata learning along with conformance testing guided by the model. To capture the input-output behavior of the RNN, they describe how equivalence oracles may be used in active automata learning. They examine learning within the probably approximately correct (PAC) framework, utilizing the refinement-based oracle suggested in Weiss et al. (2018), along with coverage-guided validity checking. Through several steps, they apply an input word component to the RNN and subsequently examine the results on the output layer. Since the automata learning may not halt because of the RNN modeling non-regular languages, the authors introduce a stopping condition for continuous learning, thereby achieving automata that accept a regular approximation of a non-regular language simulated by the RNN. An example of DFA extraction is illustrated in Figure 5, which shows the learning procedure of an RNN trained on a dataset generated for Tomita grammars on the right, with the extracted DFA from the trained RNN depicted on the left.

Figure 5

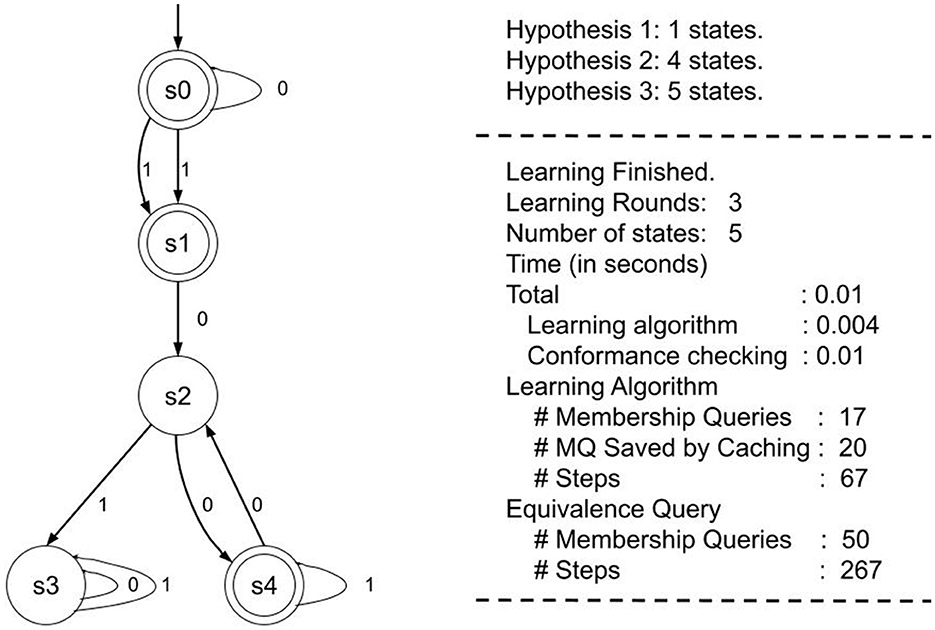
Figure 5. Example of DFA extracted from a RNN trained on Tomita 3 grammar [figure from Muškardin et al. (2022)].

3.2 Markov decision process

By expanding the capabilities of ordinary finite-state models, Markov Decision Processes (MDPs) prove useful in probabilistic model checking. Models with probability incorporated into state transitions are known as MDPs. There exists a specific probability associated with every state transition. This makes it possible to simulate systems that have inherent uncertainty or unpredictability, which is common in real-world situations. This fact helps to produce more reliable and insightful verification findings. Equally, in the domain of machine learning and neural networks, MDPs are gaining popularity, and recent developments have concentrated on resolving issues and investigating novel methods for MDP-based modeling of deep neural networks (DNN). Neural network safety features (e.g., the network's inability to produce control actions that result in collisions) can be explicitly verified using MDP models. Furthermore, it is possible to interpret how the neural network makes decisions by examining the learned probability of transitions within the MDP.

Simplified models of stochastic transitions, known as Markov chains, are represented by a collection of states S and a transition probability matrix P, which expresses the probabilities of changing states. By allowing an agent to make decisions that affect the results, MDPs expand upon the basic structure of Markov chains. In addition to S and P, they define a set of potential actions A that the agent may perform in each condition, a reward function R describing the instant reward the agent receives for acting in a particular situation, and a discount factor regulating the significance of future rewards. This explains how promising it is to use MDPs in specifying the setting and arrangement of rewards in reinforcement learning, which is used to train neural networks.

MDP can abstract that during neural network training, the weights are updated based on the gradients calculated from the loss function. This abstraction allows for modeling the configurations of the neural network (weights, activations, and so on) as states and the operations related to weight updates as actions. The rewards can be determined by the network's performance on the training data (the smaller the loss, the larger the reward). Transition probabilities depend on the optimization technique. Finally, the neural network, referred to as the agent in MDP, optimizes its predicted cumulative reward by examining various weight updates.

In the context of neural network model checking based on MDP modeling, the authors of Gros et al. (2022) consider Racetrack (Gardner, 1970) as an expandable, discrete, and basic representation of real-world stochastic events that is used as a benchmark in various verification methods (Baier et al., 2021). The authors show how to obtain the automaton from a deterministic version of the game. With an edge for each of the nine distinct acceleration vectors, the vehicle automaton begins at a certain point. Every edge provides the collision test machine with the start and end locations after updating the velocity appropriately. Three response options are possible from the collision test: “valid,” “crash,” or “reached goal.” The vehicle automaton returns to its starting position if the trajectory is “valid.” If not, it moves into a final state from which it cannot move afterward. Subsequently, the authors define the actions necessary to deal with collisions and compute the trajectory. They explain the trajectory discretization used to determine if the vehicle succeeded in passing the goal or crashed into a wall and outline all the computational work necessary for them to use the JANI framework (Budde et al., 2017). However, two possible downsides appear: reaching high confidence could require a significant number of experiment runs, and the computational cost of calling the neural network could significantly reduce its usefulness in real-time situations.

In the literature, it has been proven that there is a relation between MDP and neural networks regarding reinforcement learning. MDP specifies the environment in which a neural network functions as an agent. The states, actions, transitions, and rewards that the agent experiences are all described in the MDP. Within the MDP structure, the neural network is able to learn via trials and mistakes. It acts, then monitors the states and rewards that follow, and then modifies its actions to maximize rewards.

3.3 Binary decision diagram

In model checking, states of the transition diagram can be compactly expressed as a directed acyclic graph using binary decision diagrams (BDDs). In this graph, the nodes denote the variables, and the edges show the possible values of the variables. In relation to neural networks, BDDs can be used to represent the logic of a single neuron or a layer. BDD models are able to capture the decision-making process inside that particular unit by effectively capturing the connections between the inputs, the weights, and the activation functions.

It is possible to convert the intricate network behavior into a more readable and understandable BDD representation. In Shih et al. (2019), the authors use the BDD to run queries that perform different analyses after encoding a binarized neural network (BNN) and an input region as a BDD.

To efficiently build BDDs from BNNs, Zhang et al. (2021) directly converts a BNN and its corresponding input area into BDDs. A BNN is an ordered structure comprising several inner blocks and one output block. Each inner block consists of three layers: the batch normalization layer (BN), the binarization layer (BIN), and the linear layer (LIN). The output block contains two layers: one linear and the other argmax. The function f:{+1, −1}ⁿ → {+1, −1}^m is captured by each block, which consists of three layers (where n represents the number of inputs in a block and m the number of outputs). Given that the i^th output y_i of the block may be represented by a cardinality constraint of the form $\sum _{j=1}^n{l}_j\ge k$ (where k is a constant and l_j is either x_j or ¬x_j for input x_j), this cardinality constraint is encoded as a BDD with O((n-k)·k) nodes. This way, they encode the input-output relation of each block as a BDD, the composition of which results in the BDD for the whole BNN. Such composition allows for the support of incremental encoding and the reusability of constructed BDDs for blocks. An example illustrating their approach is shown in Figure 6.

Figure 6

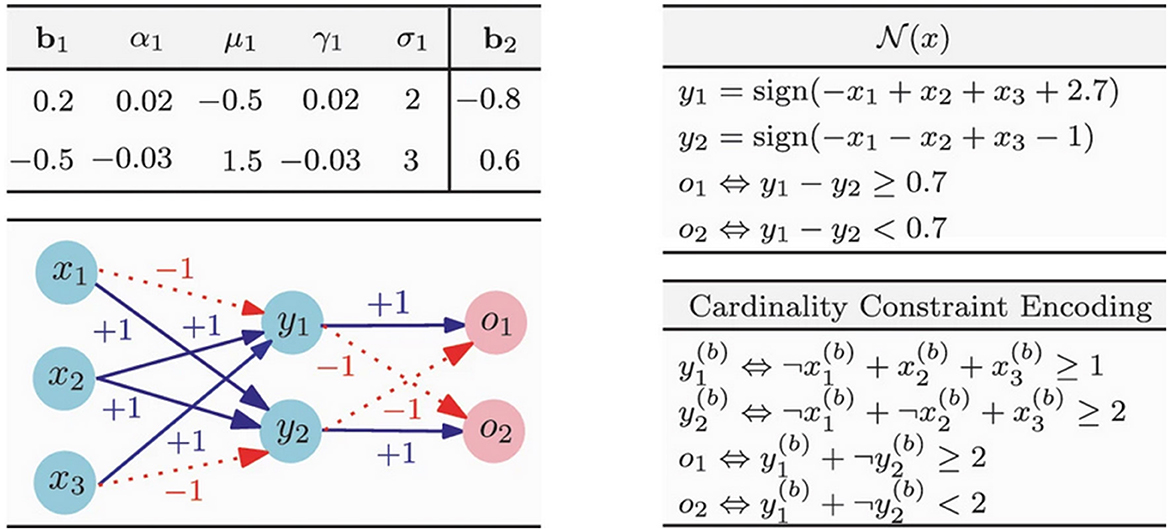
Figure 6. Example of BNN encoding in DBB (Zhang et al., 2021). Bottom-left shows the BNN which has one inner block t₁ and one outgoing block t₂. The components of the Weight matrix are connected to the edges, and the additional variables are listed in the up-left table. The bottom-right section lists the cardinality restrictions for the conversion operations on blocks t₁ and t₂, whereas the up-right table includes the transformation methods for those pieces.

Although an exact translation may not be possible, BDDs may be utilized to roughly represent the logic of particular network layers or more compact networks.

3.4 Petri net

Petri nets are graphical modeling tools that are primarily used for distributed systems, manufacturing processes, and the analysis and modeling of other concurrent systems. They are a powerful tool for modeling concurrent behavior, which allows for the simultaneous occurrence of several events. This feature is helpful in simulating specific aspects of neural networks, particularly concerning neuron activation or parallel computation. The parallelism present in neural network structures can be assessed using Petri nets. One can examine the simultaneous interactions and influences between various neural network components (neuron, layer, computing unit, and so on) by modeling them as Petri net fragments.

For the verification of neural networks, Petri net analysis approaches can be used to assess qualities such as liveness (will certain neurons constantly be activated?) and reachability (can a given output be reached?). This aids in locating possible problems with the operation of the network. Additionally, for recurrent neural networks, Petri net analysis may be able to detect deadlocks (stuck in a vicious cycle in which data circulates but does not advance).

The authors of Albuquerque et al. (2023) present a model named HTCPN-MLP, which consists of four subnets modeled in transitions named “Load dataset,” “Training,” “Validation,” and “Test.” In the first transition, the dataset is loaded and transferred to the place dataset as tokens, initiating the second stage, which is “Training.” Tokens with the input attributes and intended outputs are provided to the HTCPN-MLP during the training phase of the network. In the third step, the weights and thresholds are passed to the subnet that models the network validation by modifying the training process. Lastly, the transition “Test” initiates network testing. The four subnets are then explained in the paper, demonstrating the power of Petri nets to model the processes of training the neural network, as well as validation and testing. Different benchmarking datasets are used to evaluate the performance of the proposed model.

3.5 Kripke structure

A Kripke structure is a mathematical model used to depict how a system behaves over time. It is a basic concept in model checking and formal verification, as it effectively represents the state transition system. A Kripke structure is defined by a tuple (S, T, L) where S is a collection of states and T is a transition function defined from S to S. Each state is given a collection of atomic propositions by the labeling function L, which defines the attributes that hold in that state. A subset of S defines the possible input states.

In Naseer et al. (2023), examining the networks tolerance to adversarial attacks, the authors define the Kripke structure of the trained neural network with reference to the number of these adversarial options, denoted as n. They need one initial state representing the initial atomic propositions plus x nodes, where x is the number of possible adversarial options multiplied by the number of output classes, also containing the necessary atomic propositions. They suggest a Kripke structure with 1 + nC nodes, where C is the number of outputs. According to the authors, the hidden nodes will not appear in the Kripke structure because of the use of jump transitions that allow for regrouping the states with the same collection of atomic propositions. As for the transitions between these nodes, there will be nC(1+nC) transitions. The general issue when using a Kripke structure is that the number of states may grow exponentially, especially when working with a wide input domain. To cope with this problem, the authors of Naseer et al. (2023) propose some reduction techniques.

3.6 Interval arithmetic

To investigate how a model behaves when its input remains uncertain, one approach is to employ interval arithmetic, even though it does not fully represent the entire neural network structure or its operations. Given that real-world data tends to include some noise or uncertainty, interval arithmetic enables interval expression rather than describing these inputs as distinct values. The input intervals are processed through the layers of the network until an output interval is attained. The latter represents a spectrum of values that the network could generate as outputs while taking input uncertainty into account and will be utilized in the verification process. The output intervals allow us to assess if, for any particular input range, the result of the network stays within acceptable boundaries (safety requirements). An easy way of checking the robustness of neural networks is to compare the bounds of their outputs. Given the NP-hardness of finding exact bounds of the outputs (Katz et al., 2017), various approaches, such as those in Bunel et al. (2020); Lan et al. (2022) and Fatnassi et al. (2023), have been developed to propose tight over-approximations of the network's outputs.

Using interval arithmetic, the authors of Wang et al. (2018) calculate accurate boundaries on the neural network outputs. They also implemented a number of adjustments in ReluVal to reduce the output range overestimates while propagating the bounds through the layers of the network. Mainly, they apply symbolic intervals to allow accurate handling of input connections, which helps lower the errors of range estimation. Additionally, they apply “iterative interval refinement” when the output domain is too wide to be definitive; namely, ReluVal performs bounds spreading on the shorter input values after repeatedly splitting the source range. For greater efficiency, they propose other optimizations to examine how the network outputs are affected by the input parameters by calculating the gradients of each layer with respect to the value of the input.

A useful technique for neural network model checking is interval arithmetic, which is especially useful for examining the network's behavior when input uncertainty is present. However, it's important to take into account its limitations, which include conservative estimates, scaling issues, and restricted reasoning capabilities.

4 Formal specification

It is crucial to ensure that safety-critical systems function properly, as any malfunction could have disastrous effects. The term correctness of a function generally refers to verifying that the function's result is the expected one; in other words, it truly performs its intended task. This problem was first addressed by Alan Turing when he attempted to prove that the factorial function works correctly by creating a proof of correctness based on logic, which shows that the function's implementation corresponds to its mathematical definition.

Given that neural networks are becoming increasingly complex and require more training datasets, ensuring their functional correctness is a difficult, if not impossible, task. However, to ensure the reliability and trustworthiness of neural networks, it is sufficient if we can verify that bad outputs are not encountered or good outputs are obtained. Researchers, in particular, have looked into various aspects of the correctness of neural networks and offered different methods for validating a variety of interesting properties. The main categories of these properties are robustness, safety, and consistency.

• Robustness properties. The term robustness (Li et al., 2022; Lin R. et al., 2022) describes a neural network's capacity to retain accuracy in the face of opposing instances. Let's take an example where we wish to confirm that a neural network can withstand slight changes in the input data (the input being in a certain domain D). An epsilon ball surrounding the input data (denoted by region R) can be used to represent the robustness property, which states that the neural network's output should not vary noticeably for any input that falls inside the ball. We can formulate this as follows:

$\begin{array}{c}\forall x\in D,\exists \text{ a region }R\text{ around it such that }\forall y\in R,f(y)=f(x)\end{array}$

Adversarial robustness (Meng et al., 2022; Yu et al., 2023) is a stricter form of robustness that necessitates the network to retain accuracy in the face of deliberately designed inputs intended to trick it. When we examine a neural network's ability to withstand minor disruptions within a given range of inputs, we are addressing local robustness. However, when we consider a network's capacity to continue functioning as planned under a wide range of circumstances or inputs, we are addressing global robustness.

• Safety properties. First mentioned in Kurd and Kelly (2003), the safety of neural networks describes their capacity to generate accurate and credible outcomes when carrying out a specific activity. In other words, a neural network is safe if it does not exhibit unanticipated actions or other outcomes that could endanger its surroundings, including its users. In theory, a neural network is safe if it can forecast the outputs accurately for all potential inputs. Locating adversarial instances generally ensures that these properties are checked. Safety properties, also known as pointwise robustness (Huang et al., 2017), can be expressed for a point x in the input domain D over a certain region R by the following:

$\begin{array}{c}\nexists y\in R\text{ such that }f(y)\ne f(x)\end{array}$

• Consistency properties. Neural networks are said to be consistent (Ye et al., 2017; Lin S.-B. et al., 2022) when they can generate equivalent results for inputs that are alike. In other words, two inputs should have matching outputs that are close to each other if they are similar in any way. For neural networks, consistency is a crucial characteristic since it guarantees their durability and dependability in a range of scenarios, including autonomous vehicles, natural language processing, and image categorization. If x is an input and y is its corresponding output, R_i is an input region, and R_o is an output region, the consistency can be formalized as follows:

$\begin{array}{c}x\in R_i\to y\in R_o\end{array}$

The region around a point x comprises all the points within a certain distance from x. This distance may be measured using either Manhattan or Euclidean distance, and it may be defined according to various norms, such as infinity norms.

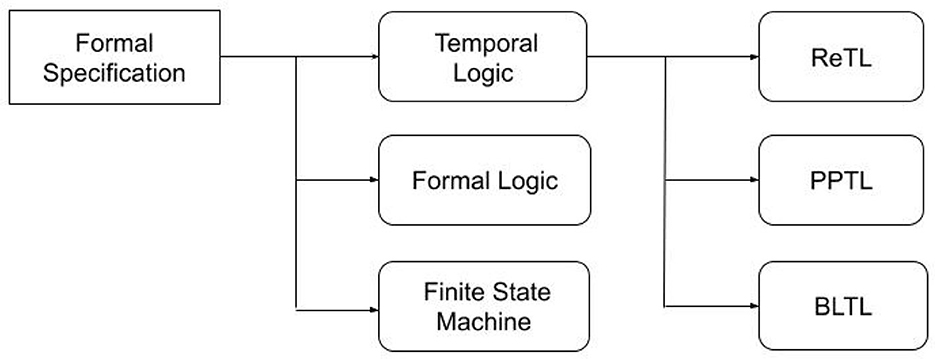
To make the verification of these properties most relevant and viable, formal specification of deep neural networks is tremendous Formal specification provides a rigorous mathematical framework for accurately defining the behavior of DNNs. It serves not only for verification but also for retraining, utilizing counterexamples, for instance. While various properties need to be tackled when verifying DNNs, we focus in this paper on exploring the techniques and languages used in the literature to formally specify these properties. In particular, we explain in the following subsections how formal specification is applied to check the properties tacked in state-of-the-art papers, namely robustness, safety, and consistency. The formal languages used in the literature to formally specify one or more of the aforementioned properties are summarized in Figure 7.

Figure 7

Figure 7. Formal specifications applied to DNNs.

4.1 Formal logic

A key tool in formal specification is formal logic, which provides a clear and concise language for describing the behavior of systems. It enables precise expression of the characteristics and connections between system elements. Numerous varieties of formal logic exist, each with distinct syntax, meaning, and uses. Propositional Logic, First-Order Logic, Temporal Logic, and Fuzzy Logic are some of the types of formal logic that can be used depending on the problem being solved. In the context of model checking, temporal logic is the first that comes to mind, prompting us to devote the next subsection to demonstrating how temporal logic is used to specify neural networks. In the remainder of this subsection, we provide a brief overview of the use of first-order logic in the formal specification of neural networks.

In Sena et al. (2022), the safety property is specified using first-order logic. To each input variable, a non-deterministic float is assigned as prescribed by the SMT-based model checker ESBMC (Monteiro et al., 2017). Then, pre-conditions and post-conditions regarding these variables are specified via the two operators, assume and assert, supported by ESBMC.

An example of two input variables is as follows:

$\begin{array}{c}float x_1=nondet\_float()\\ float x_2=nondet\_float()\end{array}$

Then, the authors define the preconditions they assume for the domains of the input variables:

$\begin{array}{c}assume(x_1>=0 \&\& x_1=<2)\\ assume(x_2>=-0.5 \&\& x_2=<0.5)\end{array}$

Finally, they specify the property with the following post-condition, which verifies whether the classifier consistently predicts the second output class; for example, in the case of binary classification with two possible outputs, y₁ and y₂:

$\begin{array}{c}assert(y_2>y_1)\end{array}$

To ensure sufficient validation for safety-critical software, covering methods use a set of logical statements that utilize an improved Condition/Decision approach. In the context of neural networks, the preceding layer's neurons represent conditions, while the subsequent layer's neurons represent decisions. In Sena et al. (2019), the adversarial nature of two images with respect to the network neurons is measured using covering methods. There are four covering methods, each treated as a property. All of the properties specifically state that an image collection must result in the method covering every neuron in the network. Utilizing every covering method, their approach assesses whether the adversarial behavior of a group of pairs of images reaches a specific percentage of all neurons. The covering methods are described via logical expressions, which will be used in the two operators, assume and assert, supported by ESBMC. The authors demonstrate that they can search for an adversarial example in an image classifier by checking the following formula:

$\begin{array}{c}{l}_{image\_misclassified}\leftrightarrow (n_{3,C}<V)\wedge (n_{3,i}>V)\end{array}$

Where l_{image_misclassified} serves as evidence for the correctness of the initial classification of the image. The parameter V indicates the reference value, while the variable C denotes the expected classification, representing the neuron's position in the output. Finally, i reflects any additional neuron locations besides C. The notations n_p,q refer to the value of the neuron at position q in layer p.

4.2 Temporal logic

In situations that require sequential information or when temporal restrictions are significant, neural network behavior can be specified and verified using temporal logic. Application-specific tasks may include ensuring the network adheres to temporal limitations set by the system, performs adequately across sequences, or interacts appropriately with time-dependent components. In general, when reasoning about the dynamic features of systems that evolve over time, temporal logic is employed. This is accomplished through the use of temporal connectors (eventually, always, and so on) to express the concept of time in the desired properties. An example of a safety property in image classification can be expressed in temporal logic as: “G ¬(output = dangerous),” which states that “always” (or globally G), a dangerous output is not reached.

Verifying that a neural network satisfies its intended requirements and is safe and dependable can be done by utilizing temporal logic. Important uses, such as self-driving cars and medical diagnosis, may benefit greatly from this. Linear Temporal Logic (LTL; Hustiu et al., 2023) and Computation Tree Logic (CTL; Nayak et al., 2024) are two popular temporal logics that are frequently applied and extended in numerous variants to enlarge their application scope. LTL is a framework for defining the characteristics of linear state sequences. To represent temporal features, it makes use of operators such as “always” (G), “eventually” (F), “until” (U), and “next” (X). For CTL, it is used to characterize features of branching-time systems, where different future routes are feasible. To express temporal features, it makes use of LTL operators as well as the path quantifiers “for all” (A) and “exists” (E).

For a variety of reasons, traditional temporal logics such as LTL and CTL are not necessarily adequate to describe the behavior of neural networks. First, due to random initialization and the intrinsic difficulty of learning, neural networks can behave in non-deterministic ways. Second, it can be difficult to describe the intricate relationships between neurons and layers in neural networks using traditional temporal logics. Third, neural networks are able to learn and adapt over time, altering their behavior in response to the data they receive. Therefore, it may be challenging to define their behavior using static temporal logics because of their dynamic nature. To overcome these limitations, extensions of traditional temporal logics have been created, offering a more appropriate framework for describing the behavior of neural networks (Liu et al., 2020; Wang et al., 2020; Tao et al., 2023).

4.2.1 ReTL

Rectified Linear Temporal Logic (ReTL) (Liu et al., 2020) is a variation of LTL that incorporates the semantics of rectified linear units (ReLU). This approach can provide continuous-valued attributes, making it suitable for modeling and validating systems with continuous dynamics, such as neural networks. Its syntax closely resembles LTL, incorporating terms that represent ReLU activation functions and continuous values. The basic syntax defines atomic propositions (p,q,..), which represent Boolean-valued properties, continuous variables (x, y, ..), which represent continuous-valued signals, and the ReLU function [relu(x)], which represents the rectified linear unit activation function. It also defines Boolean operators (¬, ∧, ∨, →), and (negation, conjunction, disjunction, implication, equivalence) temporal operators (G: always, F: eventually, U: until, X: next known also as □, ♢, U, and ∘ respectively). The comparison operators (<, ≤, >, ≥) and arithmetic operators (+, −, *, /) are used for continuous values. For ReLU activation, relu(x) represents the rectified linear unit activation function, defined as: relu(x) = max(0, x). In a simple example, the ReTL formula Grelu(output) ≥ 0 indicates that the output of a neural network will always be positive. However, the ReLU function does not appear in the formulas used because of the proposed ReLU elimination.

The ReTL formulas are defined using the following syntax:

$\phi ::=T|\perp |\neg \phi |\phi \wedge \phi |\phi \vee \phi |\phi \to \phi |\exists x\in ℝ.\phi$

$|Ax\in ℝ.\phi |X\phi \left|G\phi \right|F\phi \left|\phi U\phi \right|t~t,$

where t is an expression and ~ ∈ {>, ≥, =, ≠, <, ≤}

The expressions used in ReTL formulas are defined by the following:

$t::=v\left|x\right|{◯}^{k}t\left|t\left[i\right]\right|Mt|t+t,$

where i, k ∈ ℕ, and M is some constant matrix compatible with t. ◯^k abstracts the result of ReLU activations over the layers.

Adversarial robustness, for example, is formulated in ReTL as follows:

$\exists x\in {ℝ}^2.(x\left[1\right]<5)\wedge ({◯}^{2}x\left[1\right]={◯}^{2}x\left[2\right])$

This specification shows that there exists an adversarial example for which the first feature does not reach 5.

4.2.2 PPTL

In Wang et al. (2020), the authors propose specifying the neural network's robustness and the samples' correctness in Propositional Projection Temporal Logic (PPTL) (Duan et al., 2008). This is a variant of PTL that abstracts predicates, variables, and quantifiers in the formulas. PTL is originally applied to make decisions regarding the functioning of systems projected onto a simpler, lower-dimensional domain. The syntax of PPTL formulas is defined as follows:

$P::=p|\circ P|\neg P|P_1\vee P_2|(P_1,..,P_m)prjP,$

where p is an atomic proposition, P₁, .., P_m as well as P are PPTL formulas, ∘ (next) and prj(projection) are basic temporal operators.

For example, the PPTL formula for the robustness property (Wang et al., 2020) is as follows:

$p\wedge q\wedge r,$

where, for example, p states that the number of iterative attacks is fewer than 1,000, q suggests that the initial forecast error exceeds the average error, and r shows that when the program runs, the prediction error is greater than the average one.

4.2.3 BLTL

In Tao et al. (2023), the authors define a temporal logic known as BLTL, which serves as a specification language for binarized neural network features. BLTL results from applying LTL to BNNs.

The following grammar outlines the syntax of BLTL formulas:

$\psi ::=T|t~t|\neg \psi |\psi \vee \psi |X\psi |\psi \cup \psi ,$

where ~ ∈ {≤, ≥, <, >, = }, X and U are Next and Until operators. The Boolean and temporal operators ∧, →, F, and G, as well as the quantifiers ∀ and ∃, can be derived from the defined operators similarly to LTL temporal logic.

According to Tao et al. (2023), the local robustness can be specified by the following BLTL formula:

$\forall x\in {𝔹}^n,{\displaystyle \sum _{i=1}^{\left|u\right|}}(x\left[i\right]\oplus u\left[i\right])\le ϵ\to \mathcal{N}(x)=\mathcal{N}(u)$

This formula states that the neural network $\mathcal{N}$ is robust for an input u with width n if all the inputs in the region 𝔹(u, ϵ) yield the same result of classification for u. The region 𝔹(u, ϵ) regroups the set of vectors that differ from u in at most ϵ positions.

4.3 Finite state machine

Neural network features can be precisely specified using deterministic finite automata, also known as Finite State Machines (FSMs). By abstracting the ongoing values and intricate dynamics of the network through a limited collection of states and transitions, FSMs can be employed in neural networks. They can model how information transits across a neural network, where states represent various neuronal activation patterns and transitions model updates to these activations. Reachability (can a particular output state be reached?) and liveness (will a particular neuron always fire?) are two examples of properties of the neural network that may be verified using FSMs. By using transitions to represent changes to weights and biases, FSMs can also mimic the learning process of a neural network. Finite automata can be created by compiling several abstracted specification languages, including regular expressions and temporal logics.

In Khmelnitsky et al. (2021), the authors consider an RNN R for binary classification over a limited alphabet Σ. R classifies a given string w as positive if w ∈ Σ^*. The set of all positive strings is denoted by L(R)⊆Σ^* and is said to be the language of R. In order to validate the adversarial robustness of recurrent neural networks, they check if a small modification in a word of L does not change the classification result. They employ Angluin's L^* learning algorithm (Berg et al., 2005) to extract a finite automaton (denoted H) and then check if L(H)⊆L(A) using traditional model checking procedures. Moreover, in Mayr et al. (2021) and Muškardin et al. (2022), the authors extract a finite automaton during RNN classification to be used to check the intended property with the help of Angluin's L^* algorithm.

FSMs might be a helpful tool for formally defining specific features of neural networks, but they may not be appropriate for representing every facet of intricate contemporary networks. With numerous layers and neurons, and since neural networks frequently work with continuous values, it can be challenging to express them with FSMs. Although discretizing continuous numbers is feasible, doing so may limit the model's accuracy and introduce approximations. Other formalisms, such as temporal logic or Petri nets, might be more suitable for networks with a higher level of complexity.

5 Algorithms to check models against specifications

This section is dedicated to exploring existing approaches to the formal verification of neural networks based on model checking. Model checking is a method that examines a system's behavior in response to a set of formal specifications to confirm its correctness. It can be used to ensure that deep neural networks meet certain specifications, including robustness, consistency, and safety. This process involves thoroughly examining the network's state space to determine if it fulfills the requirements that should be formally stated.

Model-checking algorithms fall into two main categories: explicit and implicit model checking. Additional variations exist within these two main categories: bounded, on-the-fly, and probabilistic model checking. Hybrid model checking is also possible when integrating explicit and symbolic techniques. The system's size, the properties that need to be confirmed, and the availability of tools are some of the variables that influence the category selection.

The works studied in this article align with the direct application of the model-checking process and are classified in the following subsections according to the class of model-checking algorithm used. Figure 8 illustrates the model-checking algorithms applied to neural networks.

Figure 8

Figure 8. Model checking algorithms applied to DNNs.

5.1 Explicit model checking

In the case of explicit model checking, the algorithm looks for a desirable (or undesirable) state that relates to the checked property when traversing all the runs of the transition system. A suitable language for formulating such behaviors is temporal logic, as it provides tools to express a formula P through propositional variables, Boolean operators, universal quantifiers, and specifically temporal operators. Given a transition system T and a formula P, the model checking procedure determines if T ⊧ P (where ⊧ is known to be the satisfaction relation). Technically, the problem is reduced to determining if the language of an automaton A is empty, given that A results from the Cartesian product of the automaton modeling the system and the automaton resulting from the negation of the property. If the language is empty, meaning that there is no run of the system for which the property is invalid, then the algorithm returns yes (property satisfied). If not, meaning there is an intersection between the runs of the system and the negation of the property, the algorithm returns no (property unsatisfied), and the example found in the intersection may be used as a counterexample.

Liu et al. (2020) presents a thorough application of model checking in neural network verification. The authors of this research introduce ReLU Temporal Logic (ReTL), which is based on ReLU neural networks and applies LTL (Hustiu et al., 2023) enhanced with data properties. They explicitly define the ReTL logic and design a procedure for model checking a portion of this logic. By converting a formula from ReLU into a system of equalities and inequalities and then searching for solutions to the system primarily using the Moore-Penrose inverse (Courrieu, 2008), they demonstrate the decidability of ReTL model checking. They use the parameter emptiness approach and the suggested ReLU-elimination technique to achieve this. Since the study addresses only a small portion of ReTL, not all desired properties may be expressed. Furthermore, scalability for very large networks may be limited by the EXPSPACE complexity. Based on their approach, the authors developed a prototype tool and tested it on a range of ReLU networks. Although the outcomes demonstrate how feasible and promising their strategy is, future studies could explore expanding the expressive capabilities of ReTL, enhancing the effectiveness of model-checking methods, and utilizing the technique to different kinds of neural networks.

In Wang et al. (2020), the Message Compiler (MC) Yang et al. (2017) is used to interactively verify the DNN accuracy and robustness properties. Initially, the MSVL programming language is used to generate the neural network (Zhang et al., 2016). This construction can be done directly or indirectly by using the C2MSVL translation tool to translate a C-language model into an MSVL model [which is also used for CNN in (Zhao L. et al., 2022)]. Next, the neural network's robustness and accuracy attributes are described in PPTL (Duan et al., 2008). Specifically, each detail can be represented by an atomic proposition, and a PPTL formula can be obtained by combining the atomic propositions that are derived. Lastly, the MSVL model and the PPTL formula are passed to MC for satisfiability checking. If this satisfiability is not guaranteed, MC will produce a counterexample demonstrating the anomaly that occurred when the model was running. The paper discusses the approach by studying an example of a linear model fitting procedure with data automatically generated by a Python script. However, the work lacks a general demonstration of the applicability of the approach to different neural networks and an evaluation of its performance.

In Khmelnitsky et al. (2021), the authors consider an RNN, R, as a binary classifier over a limited alphabet Σ in order to validate the robustness of recurrent neural networks. This means that R represents the set of strings that fall into the acceptable category. They denote this set by L(R) (L(R)⊆Σ^*) and call it the language of R. The aim of their research is to determine whether two specifications, A and R, are compatible, where A is a finite state machine (FSM). Therefore, they want to know if L(R)⊆L(A). They employ black-box checking, which is based on Angluin's L^* learning algorithm (Berg et al., 2005), to accomplish this. L^* generates a set of hypothesis automata (denoted H) by utilizing R's queries. Assessing whether L(H)⊆L(A) using traditional model checking procedures now solves the original problem. Statistical model checking (Legay et al., 2019) is used by the authors to verify if L(R)⊆L(H) in order to confirm the outcome if the response is yes. In case it is not, a counterexample will be utilized to enhance H; even better, a group of counterexamples may be located. Based on statistical model checking, this approach may be employed in the analysis of complex systems' behavior, especially those with extensive and complicated state spaces. However, the paper is limited to binary classifiers and, in general, to LSTMs with less expressive languages. Additionally, the paper's findings are not compared to state-of-the-art approaches, and scalability to large networks is not demonstrated.

In Sälzer et al. (2022), the authors demonstrate how to transform a neural network into a finite automaton that can recognize words as pairs of inputs and outputs based on theoretically promising results. More specifically, they convert the network to an eventually-always weak nondeterministic Büchi automaton (WNBA_FG) (Sistla et al., 1987), for which minimization and determinization are straightforward. This results in improved algorithmic features. Subsequently, the neural network verification procedure is converted into an emptiness check of a decidable automaton. The practicality of the approach is shown through several use cases involving the abstract interpretation of real numbers and symbolic optimizations using a nondeterministic finite automaton. Further development is needed to prove the efficacy of the proposal and its adaptability to other deep neural networks.

Muškardin et al. (2022) presents a recent black-box technique for RNN verification based on FSM extraction. The method successfully proposes a formal description of the behavior of the RNN classifier without regard to its inner workings. The authors uncover counterexamples that refute false premises about arguments that were picked up from earlier methods. This means that testing based on learned automata can be a useful method for detecting inputs that are misclassified due to incorrect generalization or that are irrelevant. They describe how equivalence oracles may be used in active automata learning. They examine learning within the PAC framework, learning using the refinement-based oracle suggested in Weiss et al. (2018), and coverage-guided validity checking in their studies. The strategy yielding the model that most closely resembles the actual model, which captures the input-output behavior of the RNN, is determined by measuring the size of the learned models. The reason for this is that each counterexample discovered by an equivalence query alters the size of the premise. By contrasting their approach with existing black-box and white-box techniques, the authors demonstrate the potential of their methodology in identifying counterexamples. However, a rigorous application of formal methods and concrete automata learning is postponed to future investigations.

The authors of Gros et al. (2022) present a scalable verification method called Deep Statistical Model Checking (DSMC), which is a simple variation of statistical model checking based on Markov decision processes (Garcia and Rachelson, 2013) and neural networks. The method aims to address decisions in the context of a bigger picture with uncertainty. Thus, they have used DSMC to confirm the efficacy of a trained neural network. The authors use the Modest Toolset to implement the neural network examination, demonstrate its scalability, and provide case studies from Racetrack to prove its practicality. Even though the DSMC approach is open-ended, generic, and scalable for the examined case studies, scaling becomes more difficult when dealing with systems that have larger state spaces.

A recent theoretical study presented in Tao et al. (2023) defines a temporal logic known as BLTL as a specification language for binarized neural network (BNN) features. After characterizing the data attributes of BNNs, a BLTL specification is transformed into an automaton to ensure verification by tracing a path from the starting state to the end state. The authors employ a tableau-based technique to quickly determine whether a path leads to a final state, thus preventing the state explosion problem. If a path does not lead to a final state, they carefully reverse it to avoid backtracking on failed attempts. The solver's solution provides the BNN's hyperparameters, including the network's length and significant block input-output relations. A suitable BNN can then be produced by performing block-wise learning. The authors employ a prototype combining tool and test their approach on local robustness and consistency. The MNIST and UCI Adult (Frank, 2010) datasets are used to assess the prototype's performance.

Although explicit model checking has achieved considerable success and offers many benefits for verifying software, its primary issue is the state explosion problem, which results in significant demands on memory and computational complexity.

5.2 Implicit model checking

Symbolic or implicit model checking aims to address the issue of state space explosion by regrouping states and succinctly describing formulas and relationships. Suitable rigorous representations for these formulas include Binary Decision Diagrams (BDDs) (Burch et al., 1992). BDDs are data structures that represent implicit, compact arrangements of sets or connections, which can be utilized to express Boolean expressions. The use of BDDs significantly reduces the set of states, leading to a more manageable model-checking process. However, for complex software, even in the symbolic case, a very large transition system is generated, and the number of symbolic states can become enormous, making it challenging for the verification algorithm, which requires a thorough examination of all these states.

To improve robustness testing and network interpretability, the authors of Zhang et al. (2021) offer the prototype BDD4BNN to ensure the quantitative verification of binarized neural networks by encoding them in binary decision diagrams. They present a method to gradually calculate the maximum Hamming distance (Ruan et al., 2019) to ensure that the network satisfies the necessary robustness requirements. To address network interpretability, the authors investigate the characteristics that all samples categorized in a given class have in common, as well as the reasons certain inputs are misclassified. The method is tested using BNNs that are larger than those considered in Shih et al. (2019), demonstrating a faster qualitative analysis. In Zhang et al. (2022), the authors further explore new parallelization techniques designed to accelerate BDD encoding.

The difficulty of large-scale verification of deep neural networks is addressed in Naseer et al. (2023), where the authors present FANNet+, an enhanced framework that expands on FANNet (Naseer et al., 2019), an earlier DNN model-checking tool. To increase scalability, FANNet+ uses input segmentation and state-space reduction. The former technique seeks to control the size of the model representation utilized in the verification process. The latter makes it possible to verify smaller subproblems instead of the complete input space by segmenting the input space into smaller parts. Due to these enhancements, FANNet+ can verify networks with up to 80 times more parameters than FANNet and can check them in up to 8,000 times less time. Furthermore, FANNet+ broadens the analysis range by allowing the validation of safety attributes in addition to current functions such as input sensitivity, noise tolerance, and robustness analysis. The study demonstrates the potential of FANNet+ for large-scale DNN verification by showing its effectiveness on multiple DNNs, including the well-known ACAS Xu benchmark.

5.3 Bounded model checking

Bounded Model Checking can save computing costs by avoiding the exploration of unneeded states, only going as far as a bounded level in the state space. A bounded model is produced by unrolling the transition system to a fixed length. The behavior of the system is represented by this limited model through a given depth. A satisfiability modulo theories (SMT) solver is used to encapsulate the bounded model and the falsification of the attributes that need to be proved as a Boolean formula. It then checks if the formula is satisfiable (SAT) or unsatisfiable (UNSAT). SAT means that the property is infringed, and thus a counterexample can be retrieved. If the formula is UNSAT, this indicates that the property holds for the model up to the fixed depth; in this case, the bound is raised, and the procedure is repeated until the formula becomes SAT or a prefixed limit is reached. SMT-based model checking may be superior to other types because it can be fully automated and performs well for large models.

A method for assessing safety qualities based on this type of verification is presented in Sena et al. (2019), involving the investigation of adversarial scenarios with various inputs. They suggest leveraging CUDA (Luebke, 2008) to create neural networks and utilize SMT solvers to accomplish incremental bounded model checking. Their experimental results demonstrate that the methodology successfully evaluates safety characteristics and produces adversarial instances in neural networks when used with the SMT-based Context Bounded Model Checker for Graphical Processing Units (ESBMC-GPU) (Monteiro et al., 2017). The authors expand their approach in Sena et al. (2021) by offering the possibility to validate networks that go beyond the function known as ReLU by decoding fixed-point computations and efficiently treating non-linear activation functions. Although more case studies, benchmarks, and comparisons are discussed in their new paper, the authors claim uncertainty regarding which combination of methods performs best when scaling to large networks and that subsequent work will compare their verification strategy to existing methods as well as improve verification efficacy.

The authors of Sena et al. (2022) propose a method based on model checking and SMT for artificial neural network (ANN) verification. Instead of viewing the ANN as an abstract mathematical model, it is considered a real piece of software that performs various fixed- or floating-point arithmetic operations. From this vantage point, they can easily translate numerous software verification techniques to ANN verification. Their verification process is based on Software Model Checking, and they show through experiments the effectiveness of techniques such as interval analysis, constant folding, tree balancing, and slicing in reducing the overall verification time. Moreover, they propose a specific discretization strategy for non-linear activation functions, enabling them to verify ANNs beyond the piecewise-linear assumptions that underlie many existing techniques.

5.4 On-the-fly model checking

For large or sophisticated systems with parallel or real-time aspects, on-the-fly verification of models is a powerful tool for confirming their correctness. This method relies on assessing the property while the state space is being computed, allowing for the early detection of potential violations of the property. In other words, on-the-fly checking (Holzmann, 1996) is based on the concept that an automaton can be built concurrently alongside the model's creation, enabling results to be obtained before all reachable states are created in the event that the property is violated.

In Mayr et al. (2021), on-the-fly checking through learning is suggested. During an RNN classification task, an automaton is extracted and then used to verify the intended property. The authors evaluate language membership and any assessing challenges that can be reduced to proving emptiness, in order to avoid state explosion issues during model checking and to prevent false counterexamples. The authors technically address potential limitations of the L* algorithm by constraining the state space of hypotheses and the length of membership queries. Additionally, they introduce a novel on-the-fly property-checking approach that utilizes an automaton approximation of the intersection between the RNN language and the complement of the property to be verified. By applying their algorithms to various use cases, they demonstrate significant outcomes.

6 Discussion

According to Table 1, despite the limited number of approaches addressing model-checking neural networks, the proposed methods greatly differ in the techniques used for model-checking. Indeed, the system model and property specifications vary across all the proposed works. If we focus on FNNs, for example, different formalisms are used for specifications: formal logic, MDP, PPTL, and ReTL. For BNNs, the three papers that propose the model-checking of these networks adopt three distinct specification languages. The same diversity is evident in the models applied as well as the benchmarks and datasets used to evaluate the various approaches. These observations highlight the difficulty of comparing the existing approaches, and clearly, this diversity hinders the progress of model-checking deep neural networks.

According to the previous sections, there is a set of clear difficulties with the current specifications. (1) They are informal and ambiguous: Many definitions of neural networks are imprecise and informal, lacking the precision and coherence required for trustworthy validation. This uncertainty could lead to errors and inconsistencies in interpretation during the verification process. (2) They lack standardization: The lack of a common language to describe neural network behavior makes it difficult to compare and communicate verification results across different frameworks and research projects. (3) They have limited expressiveness: It is plausible that current specification languages are unable to fully capture the details and intricacies of neural network behavior, which may result in the absence of important information required for verification.

Every verification technique currently in use provides an abstraction of the neural network models that are presented. Instead of investigating novel specifications, a concentration on precisely characterizing fewer specification languages would encourage more researchers to focus on improving the current verification techniques. Since temporal logics have always been efficient in specifying properties to be verified by model checkers, it is promising to look for extensions of the existing temporal logics to specify the intrinsic attributes to be considered during neural network training. Another opportunity to study states that, by incorporating logical reasoning ability and accounting for domain experience, it is intriguing to expand on the limited work on DNN formal specifications. One way is to build on the existing works on mining specifications (Fan and Wang, 2024; Bensalem et al., 2024).

Apart from the specification concerns, it should be noted that many papers consider neural networks as black boxes. Black-box models can be easier to depict and may simplify the verification process by concentrating solely on the input-output behavior of the network, thus lowering the complexity of the verification process and possibly simplifying the analysis. In certain instances, black-box models may require less computing power to validate than techniques that necessitate an in-depth understanding of the internal workings and decision-making procedures. However, using a black-box method makes validating complicated attributes that rely on the internal behavior of the network difficult or perhaps impossible. Additionally, it is challenging to troubleshoot issues and enhance the network's performance due to the lack of interpretability. In general, black-box models may pose difficulties in guaranteeing that the network operates consistently and reliably in real-world situations, particularly when it comes to figuring out and clarifying the justification behind the network's choices.

7 Open challenges

The purpose of the ongoing research on model-checking techniques for neural networks is to develop techniques that are more complex, efficient, and varied. However, these approaches often come with their own set of challenges, such as scaling to large networks and managing the non-linear properties of neural networks. Even though the number of papers in this field has significantly increased, particularly over the last three years, the community still faces significant obstacles to moving the field of study closer to maturity. Some of the challenges are related to complexity and scalability, interpretability, and verification completeness.

7.1 Complexity and scalability

Neural networks comprise millions or even billions of variables, making them incredibly complex systems. Due to the high dimensionality and non-linear nature of these systems, formal verification, in general, poses significant challenges. Creating formal models that accurately capture the behavior of such intricate networks is a difficult task. To detect complex patterns, neural networks are often trained on large datasets. As a result, the verification process must be scalable to accommodate increasing computational demands and network sizes. Significant obstacles arise when using these techniques on real-world networks.

On the one hand, the exploding state space is always the first obstacle. With increasing network size and depth, a neural network can occupy an exponential number of states. Even with moderate network dimensions, exhaustively searching all these states becomes computationally difficult. Although symbolic execution provides a streamlined method for illustrating state spaces, it continues to encounter difficulties with scaling when applied to massive networks. Its symbolic capacity for reasoning may be easily overwhelmed by complicated activation mechanisms and elaborate network structures.

On the other hand, simplifying networks through abstraction methods such as abstract interpretation enhances scalability. However, this reduction may introduce errors that lead to over-approximations or the omission of important details, potentially affecting the accuracy of the verification findings (Eramo et al., 2022). One can also consider applying compositional checking, which is the process of breaking down large networks into smaller, verifiable pieces. However, this requires careful design of modules and efficient property decomposition.

Additional difficulties may arise in cases of uncertain treatment, which involve unreliable activation functions combined with inherent uncertainty resulting from unpredictability in training data and weights. For verification procedures to provide significant assurance, these uncertainties must be taken into consideration (Xiao et al., 2023). Statistical model checking may be applied to estimate the probability that certain properties will hold for a neural network.

Although numerous approaches to explore scalability challenges in neural network verification are being developed, the real-world networks utilized in safety-critical applications are frequently too complex for existing verification techniques to manage. Indeed, constraints on scalability may lead to a focus on confirming immediate characteristics or discrete network elements, thereby overlooking the examination of long-term and overall behavior. Furthermore, analyzing violations in a large state space can be challenging, making improvements and efficient debugging more difficult for networks.

To address scalability issues in the development of model checking algorithms for neural networks, it is promising to explore the formal technique of compressing neural networks while preserving their semantics, as introduced in Ressi et al. (2024). The presented method is supported by solid mathematical proofs and has been shown to be applicable to two neural network architectures: CNN and Autoencoder. Thus, its extension and adaptation for use in the context of model checking for neural networks is advantageous.

It is also recommended to leverage hardware innovations so that rapidly verifying processes can be achieved by employing GPUs and other parallel computing architectures. Additionally, it is conceivable to formalize uncertainty while establishing probabilistic promises by integrating uncertainty quantification methods into testing tools. Finally, for rigorous work on scalability and precision, combining several verification techniques, such as compositional verification or symbolic execution with abstraction, may be significant.

7.2 Interpretability

Given that neural networks are considered black-box models, comprehending their workings may be challenging. Their lack of interpretability makes it difficult to grasp their functions and verify the reasoning behind their predictions. Creating formal verification techniques that can reason about and interpret the operation of these black-box models remains a constant challenge. Numerous methods such as LRP and LIME have been created to improve the interpretability (Samek et al., 2021; Camacho and McIlraith, 2019) in the DNN verification and their integration within the model checking techniques of DNN may be promising. By assigning significant scores to provided features, the Layer-wise Relevance Propagation (LRP) approach (Montavon et al., 2019) seeks to explain the guesses made by neural networks. The method determines which input properties have the most influence on the network's output by propagating relevance backward over the network.

To provide integrated support for analyzing verification results, LRP can be integrated into current model-checking tools. Scientists and developers can improve their understanding of neural network activity and ensure the accuracy and reliability of neural networks in safety-critical applications by incorporating LRP alongside model-checking methods. In summary, LRP can be scaled to enhance DNN model checking by providing neuron-level explanations through relevance scores assigned to individual neurons. This approach offers insights into their roles in the final output or any property violation detected by model checking. Additionally, it facilitates error analysis, as examining variations in LRP scores for different inputs can reveal characteristics essential for preventing violations, thereby aiding in debugging and improvement. Finally, it may be used in various model-checking contexts due to its compatibility with different networks.

On the other hand, Local Interpretable Model-agnostic Explanations (LIME) (Zafar and Khan, 2021) can be used to offer justifications for each unique prediction made by machine learning models, such as neural networks. For every prediction, it creates models that can be understood locally to describe how the input features affect the prediction. To offer built-in assistance for interpreting verification findings, LIME can be incorporated into currently used model-checking frameworks. Researchers and practitioners can achieve important insights into neural network activity and guarantee the accuracy and dependability of neural networks in safety-critical applications by integrating LIME with model-checking approaches. In particular, since LIME is intended to help explain why a certain forecast came true rather than provide thorough verification, it can be integrated with the model-checking process to explain why a certain violation occurred and to track the routes that lead to violations, emphasizing the particular neurons or activation processes that are engaged.

While combining formal verification with interpretability techniques, Explainable Model Checking (XMC) tools (Abeywickrama and Ramchurn, 2024) can assist users in comprehending the behavior of the network and developing confidence in its safety and dependability by offering concise explanations for violations. This may be applied to a self-driving car network, for example, where an XMC tool could point out a particular set of sensor readings that result in a safety lapse. The behavior of the network might then be improved by considering erroneous explanations, which could propose different sensor readings that would not cause the violation. Another example of when a natural language processing model fails on a particular text is that attention analysis may highlight words or phrases that are misclassified. With the help of more varied instances, the model might be retrained, or its attention mechanism may be modified.

7.3 Verification entirety

The aim of neural network formal verification is to assess behavioral properties, such as safety and accuracy. However, due to the complexity and flexibility of neural networks, it is often challenging to achieve complete verification (Xu et al., 2021).

Neural networks' high dimensionality greatly affects how comprehensively formal verification can be completed. In fact, as dimensionality increases, traditional verification methods that primarily rely on analytical reasoning or thorough exploration become less successful. The intricate relationships between high-dimensional characteristics and network outputs are difficult for these methods to grasp. Due to resource constraints, the formal verification techniques that are currently in use may not scale well to high-dimensional issues, becoming computationally costly or producing results that are insufficient. To address this difficulty, verification methods that incorporate interpretability techniques can help identify any infractions and provide information for additional network investigation or improvement. Furthermore, complex networks have inherent uncertainty (Gawlikowski et al., 2023), which may be more effectively addressed by probabilistic verification methods that provide promises with trust intervals rather than absolutes.

Another crucial factor that affects verification completeness is the non-linearity of neural networks (Kulathunga et al., 2021). Non-linearity in neural networks describes how information moves and changes throughout the network. Non-linear networks exhibit more intricate interactions than linear systems, which demonstrate that changes in input cause changes in output to be proportional. Although this complexity is essential for their strong learning capabilities, it also makes it difficult to comprehend and validate their behavior. To minimize the effect of non-linearity on verification completeness, researchers in the field are encouraged to further explore relaxation techniques (Lan et al., 2022), probabilistic verification (Fazlyab et al., 2019), XMC (Abeywickrama and Ramchurn, 2024), as well as the use of hardware (Dlugosz and Dlugosz, 2018). Another promising approach is to investigate the results achieved in deep reinforcement learning and formal verification (Boudi et al., 2023).

To achieve verification completeness, an important number of works (Pulina and Tacchella, 2010; Katz et al., 2017; Ehlers, 2017; Dethise et al., 2021; Song et al., 2021) utilize satisfiability solvers to verify the existence of an execution that does not satisfy the specification. The applicability of these solvers is limited because they require specialized techniques to convert the neural networks into a specification and provide white-box access to the networks. Furthermore, the use of non-linear constraints significantly deteriorates the performance of the primary practicality solver, resulting in evaluations that cannot adapt to larger structures.

To mitigate these issues and others, a number of approaches based on abstract interpretation have been proposed (Singh et al., 2018, 2019c; Li et al., 2019; Gehr et al., 2018; Sotoudeh and Thakur, 2020; Baader et al., 2020; Wang et al., 2022; Zhao Z. et al., 2022; Müller et al., 2022). Generally, abstract interpretation places too much emphasis on the network's potential outputs, which might lead to false positives (over-approximation), or it might be overly conservative, resulting in overlooked potential errors or false negatives (under-approximation) (Gehr et al., 2018; Singh et al., 2019b; Eliyahu et al., 2021; Ryou et al., 2021; Henriksen and Lomuscio, 2021; Bonaert et al., 2021; Liu et al., 2022; Mao et al., 2023). Additionally, these works suffer from incompleteness and challenges in handling non-linearity.

8 Conclusion and future outlook

The application of model checking to the verification of deep neural networks has been thoroughly researched recently. Model checking is a method used to verify the properties of deep neural networks, such as their ability to withstand adversarial attacks and to maintain specific input qualities.

This study presents a comprehensive survey that is valuable for researchers interested in model checking of neural networks. It explores various state-of-the-art contributions to the field and reviews the challenges that may arise in the process of verifying neural networks. Improvements in formal methods, computational approaches, and interpretability tools are required to increase the resilience, scalability, and reliability of neural networks' model checking. There is a promising amount of research being done in this area to tackle these issues and develop more effective techniques for formal verification of neural networks. But there still important not answered questions and challenges about scalability and complexity of the proposed approaches.

To advance the state of the art in neural network formal verification, it is wise to focus on strengthening the formal specification of the networks (Seshia et al., 2018), which will help guarantee the neural networks correctness, dependability, and explainability (Samek et al., 2021; Biecek and Samek, 2024). Formal specification, especially in critical scenarios, can contribute to the development of trust in DNN integration within complex systems by offering a rigorous mathematical framework. One idea would be the formalization of activation functions, as in Aleksandrov and Völlinger (2023), that can be rigorously reasoned about in relation to their influence on network behavior during verification by providing a mathematical definition with exact attributes. Another direction is to clearly describe the intended input and output ranges of the network (Dutta et al., 2018; Xu et al., 2023) to ensure that verification stays focused on pertinent situations and steers clear of unforeseen edge cases. Moreover, verification techniques that address the inherent noise and ambiguity in real-world data (Anderson and Sojoudi, 2023) may be made possible by incorporating uncertainty quantification into the specification (Abdar et al., 2021). It would be possible to take advantage of the emergence and ongoing use of the ONNX format (Shridhar et al., 2020) to propose a formal specification language that is standardized and portable across the different DNN verification frameworks.

Moreover, while being well-known as very effective automatic verification techniques that have been shown to be reliable in safety-critical systems, successful model checkers are relatively underutilized in DNN verification because of the nature of neural networks. It is worthwhile to explore applying more complex findings to model checking. Using complex outcomes in model checking, such as probabilistic model checking (Jawaddi et al., 2022), is a direction that is valuable to pursue.

Moreover, it is important to focus on the standardization of benchmarks and to insist on continuing the efforts that are being made for this purpose (Brix et al., 2023). Standardized metrics and benchmarks are vital for tackling certain major issues in the model checking of neural networks. In fact, developing realistic benchmarks that accurately reflect the intricacies of various real-world settings will lead to greater confidence in the reliability of certified networks.

In conclusion, developing ideas for neural network verification using model-checking tools focuses on scalability and hybrid approaches. Researchers are encouraged to investigate neuro-symbolic methods, which combine learning with symbolic reasoning, to bridge the gap between formal guarantees and data-driven models (Baheri and Alm, 2025). There is an urgent need for more effective abstraction approaches that take advantage of network structure and sparsity when tackling larger, more intricate networks.

Author contributions

ZS: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The author extends her appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2024/01/29842).

Acknowledgments

The author expresses gratitude to Prince Sattam bin Abdulaziz University for funding this research work.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdar, M., Pourpanah, F., Hussain, S., Rezazadegan, D., Liu, L., Ghavamzadeh, M., et al. (2021). A review of uncertainty quantification in deep learning: techniques, applications and challenges. Inform. Fusion 76, 243–297. doi: 10.1016/j.inffus.2021.05.008

Crossref Full Text | Google Scholar

Abeywickrama, D. B., and Ramchurn, S. D. (2024). Engineering responsible and explainable models in human-agent collectives. Appl. Artif. Intellig. 38:2282834. doi: 10.1080/08839514.2023.2282834

PubMed Abstract | Crossref Full Text | Google Scholar

Aggarwal, C. C. (2018). Neural Networks and Deep Learning. Cham: Springer.

Google Scholar

Albuquerque, R., Júnior, C., Barroso, G., and Barreto, G. (2023). A novel fully adaptive neural network modeling and implementation using colored petri nets. Discrete Event Dynam. Syst. 33, 129–160. doi: 10.1007/s10626-023-00377-9

Crossref Full Text | Google Scholar

Aleksandrov, A., and Völlinger, K. (2023). “Formalizing piecewise affine activation functions of neural networks in COQ,” in NASA Formal Methods, K. Y. Rozier, and S. Chaudhuri (Cham: Springer Nature Switzerland), 62–78.

Google Scholar

Amodei, D., Olah, C., Steinhardt, J., Christiano, P. F., Schulman, J., and Mané, D. (2016). Concrete problems in AI safety. arXiv [preprint] arXiv:1606.06565. doi: 10.48550/arXiv.1606.06565

Crossref Full Text | Google Scholar

Anderson, B. G., and Sojoudi, S. (2023). Certifying Neural Network Robustness to Random Input Noise from Samples.

Google Scholar

Baader, M., Mirman, M., and Vechev, M. T. (2020). “Universal approximation with certified networks,” in 8th International Conference on Learning Representations, ICLR 2020 (Addis Ababa: OpenReview.net).

Google Scholar

Baheri, A., and Alm, C. O. (2025). Hierarchical Neuro-Symbolic Decision Transformer. arXiv preprint arXiv:2503.07148.

Google Scholar

Baier, C., Christakis, M., Gros, T. P., Groß, D., Gumhold, S., Hermanns, H., et al. (2021). “Lab conditions for research on explainable automated decisions,” in Trustworthy AI - Integrating Learning, Optimization and Reasoning, F. Heintz, M. Milano, and B. O'Sullivan (Cham. Springer International Publishing), 83–90.

Google Scholar

Bensalem, S., Huang, X., Ruan, W., Tang, Q., Wu, C., and Zhao, X. (2024). Bridging formal methods and machine learning with model checking and global optimisation. J. Logical Algeb. Methods Program. 137:100941. doi: 10.1016/j.jlamp.2023.100941

Crossref Full Text | Google Scholar

Berg, T., Jonsson, B., Leucker, M., and Saksena, M. (2005). Insights to angluin's learning. Electron. Notes Theor. Comput. Sci. 118, 3–18. doi: 10.1016/j.entcs.2004.12.015

Crossref Full Text | Google Scholar

Biecek, P., and Samek, W. (2024). Explain to Question not to Justify.

Google Scholar

Bonaert, G., Dimitrov, D. I., Baader, M., and Vechev, M. (2021). Fast and Precise Certification of Transformers, in Proceedings of the 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation (PLDI '21) (New York, NY: ACM), 18. doi: 10.1145/3453483.3454056

Crossref Full Text | Google Scholar

Boudardara, F., Boussif, A., Meyer, P.-J., and Ghazel, M. (2023). A review of abstraction methods towards verifying neural networks. ACM Trans. Embedded Comp. Syst. 23, 1–19. doi: 10.1145/3617508

Crossref Full Text | Google Scholar

Boudi, Z., Wakrime, A. A., Toub, M., and Haloua, M. (2023). A deep reinforcement learning framework with formal verification. Formal Aspects of Comp. 35, 1–17. doi: 10.1145/3577204

Crossref Full Text | Google Scholar

Brix, C., Müller, M. N., Bak, S., Johnson, T. T., and Liu, C. (2023). First three years of the international verification of neural networks competition (VNN-COMP). Int. J. Softw. Tools for Technol. Transfer 25, 329–339. doi: 10.1007/s10009-023-00703-4

Crossref Full Text | Google Scholar

Budde, C. E., Dehnert, C., Hahn, E. M., Hartmanns, A., Junges, S., and Turrini, A. (2017). “Jani: quantitative model and tool interaction,” in Tools and Algorithms for the Construction and Analysis of Systems: 23rd International Conference, TACAS 2017, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2017 9 (Uppsala: Springer), 151–168.

PubMed Abstract | Google Scholar

Bunel, R., Turkaslan, I., Torr, P. H. S., Kumar, M. P., Lu, J., and Kohli, P. (2020). Branch and bound for piecewise linear neural network verification. J. Mach. Learn. Res. 21:1. doi: 10.48550/arXiv.1909.06588

Crossref Full Text | Google Scholar

Burch, J., Clarke, E., McMillan, K., Dill, D., and Hwang, L. (1992). Symbolic model checking: 1020 states and beyond. Inform. Comp. 98, 142–170. doi: 10.1016/0890-5401(92)90017-A

Crossref Full Text | Google Scholar

Camacho, A., and McIlraith, S. A. (2019). “Learning interpretable models expressed in linear temporal logic,” in Proceedings of the International Conference on Automated Planning and Scheduling, 29, 621–630. doi: 10.1609/icaps.v29i1.3529

Crossref Full Text | Google Scholar

Clarke, E. M. (1997a). “Model checking,” in Foundations of Software Technology and Theoretical Computer Science: 17th Conference Kharagpur, India (Kharagpur: Springer), 54–56.

Google Scholar

Clarke, E. M. (1997b). “Model checking,” in Foundations of Software Technology and Theoretical Computer Science, eds. S. Ramesh, and G. Sivakumar (Berlin, Heidelberg: Springer Berlin Heidelberg), 54–56.

Google Scholar

Cook, S. A. (2023). “The complexity of theorem-proving procedures,” in Logic, Automata, and Computational Complexity: The Works of Stephen A. Cook, 143–152.

Google Scholar

Courrieu, P. (2008). Fast computation of Moore-Penrose inverse matrices. arXiv [preprint] arXiv:0804.4809. doi: 10.48550/arXiv.0804.4809

Crossref Full Text | Google Scholar

Dethise, A., Canini, M., and Narodytska, N. (2021). “Analyzing learning-based networked systems with formal verification,” in IEEE INFOCOM 2021 - IEEE Conference on Computer Communications (Vancouver, BC: IEEE), 1–10.

Google Scholar

Dlugosz, Z., and Dlugosz, R. (2018). “Nonlinear activation functions for artificial neural networks realized in hardware,” in 2018 25th International Conference “Mixed Design of Integrated Circuits and System” (MIXDES) (Gdynia: IEEE), 381–384.

Google Scholar

Duan, Z., Tian, C., and Zhang, L. (2008). A decision procedure for propositional projection temporal logic with infinite models. Acta Inform. 45, 43–78. doi: 10.1007/s00236-007-0062-z

Crossref Full Text | Google Scholar

Dutta, S., Jha, S., Sankaranarayanan, S., and Tiwari, A. (2018). “Output range analysis for deep feedforward neural networks,” in NASA Formal Methods Symposium (Cham: Springer), 121–138.

Google Scholar

Ehlers, R. (2017). “Formal verification of piece-wise linear feed-forward neural networks,” in Automated Technology for Verification and Analysis - 15th International Symposium, ATVA 2017, eds. D. D'Souza, and K. N. Kumar (Pune: Springer), 269–286.

Google Scholar

Eliyahu, T., Kazak, Y., Katz, G., Schapira, M., Kuipers, F., and Caesar, M. (2021). “Verifying learning-augmented systems,” in Proceedings of the 2021 ACM SIGCOMM 2021 Conference (New York, NY: ACM), 305–318. doi: 10.1145/3452296.3472936

Crossref Full Text | Google Scholar

Eramo, R., Fanni, T., Guidotti, D., Pandolfo, L., Pulina, L., and Zedda, K. (2022). “Verification of Neural Networks: Challenges and Perspectives in the AIDOART Project,” in Proceedings of RiCeRcA, 3345.

PubMed Abstract | Google Scholar

Eykholt, K., Evtimov, I., Fernandes, E., Li, B., Rahmati, A., Xiao, C., et al. (2018). “Robust physical-world attacks on deep learning visual classification,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT: IEEE), 1625–1634.

Google Scholar

Fan, Y., and Wang, M. (2024). Specification mining based on the ordering points to identify the clustering structure clustering algorithm and model checking. Algorithms 17:28. doi: 10.3390/a17010028

Crossref Full Text | Google Scholar

Fatnassi, W., Khedr, H., Yamamoto, V., and Shoukry, Y. (2023). “BERN-NN: tight bound propagation for neural networks using bernstein polynomial interval arithmetic,” in Proceedings of the 26th ACM International Conference on Hybrid Systems: Computation and Control (ACM), 1–11.

Google Scholar

Fazlyab, M., Morari, M., and Pappas, G. J. (2019). Probabilistic Verification and Reachability Analysis of Neural Networks via Semidefinite Programming, in 2019 IEEE 58th Conference on Decision and Control (CDC) (IEEE), 2726–2731.

Google Scholar

Frank, A. (2010). UCI Machine Learning Repository. Available online at: http://archive.ics.uci.edu/ml (accessed December 30, 2024).

Google Scholar

Garcia, F., and Rachelson, E. (2013). “Markov decision processes,” in Markov Decision Processes in Artificial Intelligence (John Wiley & Sons, Ltd.), 1–38. doi: 10.1002/9781118557426.ch1

Crossref Full Text | Google Scholar

Gardner, M. (1970). Mathematical games. Sci. Am. 222, 132–140. doi: 10.1038/scientificamerican0670-132

Crossref Full Text | Google Scholar

Gawlikowski, J., Tassi, C. R. N., Ali, M., Lee, J., Humt, M., Feng, J., et al. (2023). A survey of uncertainty in deep neural networks. Artif. Intell. Rev. 56, 1513–1589. doi: 10.48550/ARXIV.2107.03342

Crossref Full Text | Google Scholar

Gehr, T., Mirman, M., Drachsler-Cohen, D., Tsankov, P., Chaudhuri, S., and Vechev, M. (2018). “AI2: Safety and robustness certification of neural networks with abstract interpretation,” in 2018 IEEE Symposium on Security and Privacy (SP) (San Francisco, CA: IEEE), 3–18.

Google Scholar

Gros, T. P., Hermanns, H., Hoffmann, J., Klauck, M., and Steinmetz, M. (2022). Analyzing neural network behavior through deep statistical model checking. Int. J. Softw. Tools Technol. Transfer. 25, 407–426. doi: 10.1007/s10009-022-00685-9

PubMed Abstract | Crossref Full Text | Google Scholar

Hajdu, Á., and Micskei, Z. (2020). Efficient strategies for cegar-based model checking. J. Automat. Reason. 64, 1051–1091. doi: 10.1007/s10817-019-09535-x

Crossref Full Text | Google Scholar

Henriksen, P., and Lomuscio, A. (2021). “Deepsplit: an efficient splitting method for neural network verification via indirect effect analysis,” in Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI-21, eds. Z. H. Zhou (Jeju: International Joint Conferences on Artificial Intelligence Organization), 2549–2555.

Google Scholar

Holzmann, G. (1996). On-the-fly model checking. ACM Comput. Surv. 28:120. doi: 10.1145/242224.242379

Crossref Full Text | Google Scholar

Holzmann, G. J. (2018). “Explicit-state model checking,” in Handbook of Model Checking, 153–171.

Google Scholar

Huang, X., Kroening, D., Ruan, W., Sharp, J., Sun, Y., Thamo, E., et al. (2020). A survey of safety and trustworthiness of deep neural networks: Verification, testing, adversarial attack and defence, and interpretability. Comput. Sci. Rev. 37:100270. doi: 10.1016/j.cosrev.2020.100270

Crossref Full Text | Google Scholar

Huang, X., Kwiatkowska, M., Wang, S., and Wu, M. (2017). “Safety verification of deep neural networks,” in Computer Aided Verification, eds. R. Majumdar, and V. Kunčak (Cham: Springer International Publishing), 3–29.

Google Scholar

Hustiu, I., Mahulea, C., and Kloetzer, M. (2023). “Software tool for distribution of linear temporal logic specifications,” in 2023 The 22nd World Congress of the International Federation of Automatic Control (IFAC). Available online at: https://drive.google.com/file/d/1svTaotOoPE-2VmSoEXgCRXpzDa7jyjvf/view?usp=sharing

Google Scholar

Jawaddi, S. N. A., Johari, M. H., and Ismail, A. (2022). A review of microservices autoscaling with formal verification perspective. Software: Pract. Exp. 52, 2476–2495. doi: 10.1002/spe.3135

Crossref Full Text | Google Scholar

Katz, G., Barrett, C., Dill, D. L., Julian, K., and Kochenderfer, M. J. (2017). “Reluplex: an efficient SMT solver for verifying deep neural networks,” in Computer Aided Verification, eds. R. Majumdar, and V. Kunčak (Cham: Springer International Publishing), 97–117.

Google Scholar

Khmelnitsky, I., Neider, D., Roy, R., Xie, X., Barbot, B., Bollig, B., et al. (2021). “Property-directed verification and robustness certification of recurrent neural networks,” in Automated Technology for Verification and Analysis: 19th International Symposium, ATVA 2021 (Gold Coast, QLD: Springer), 364–380.

Google Scholar

Kulathunga, N., Ranasinghe, N. R., Vrinceanu, D., Kinsman, Z., Huang, L., and Wang, Y. (2021). Effects of nonlinearity and network architecture on the performance of supervised neural networks. Algorithms 14:51. doi: 10.3390/a14020051

Crossref Full Text | Google Scholar

Kurd, Z., and Kelly, T. (2003). “Establishing Safety Criteria for Artificial Neural Networks,” in International Conference on Knowledge-Based and Intelligent Information and Engineering Systems (Berlin, Heidelberg: Springer), 163–169.

Google Scholar

Lan, J., Zheng, Y., and Lomuscio, A. (2022). “Tight neural network verification via semidefinite relaxations and linear reformulations,” in Proceedings of the AAAI Conference on Artificial Intelligence, 36, 7272–7280. doi: 10.1609/aaai.v36i7.20689

Crossref Full Text | Google Scholar

Legay, A., Lukina, A., Traonouez, L. M., Yang, J., Smolka, S. A., and Grosu, R. (2019). “Statistical model checking,” in Computing and Software Science: State of the Art and Perspectives (Cham: Springer), 478–504.

Google Scholar

Li, J., Liu, J., Yang, P., Chen, L., Huang, X., and Zhang, L. (2019). “Analyzing deep neural networks with symbolic propagation: towards higher precision and faster verification,” in Static Analysis (Cham: Springer International Publishing), 296–319.

Google Scholar

Li, R., Yang, P., Huang, C.-C., Sun, Y., Xue, B., and Zhang, L. (2022). “Towards practical robustness analysis for dnns based on pac-model learning,” in Proceedings of the 44th International Conference on Software Engineering, ICSE '22 (New York, NY: Association for Computing Machinery), 2189–2201.

Google Scholar

Lin, R., Zhou, Q., Wu, B., and Nan, X. (2022). Robustness evaluation for deep neural networks via mutation decision boundaries analysis. Inf. Sci. 601, 147–161. doi: 10.1016/j.ins.2022.04.020

Crossref Full Text | Google Scholar

Lin, S.-B., Wang, K., Wang, Y., and Zhou, D.-X. (2022). Universal consistency of deep convolutional neural networks. IEEE Trans. Inform. Theory 68, 4610–4617. doi: 10.1109/TIT.2022.3151753

Crossref Full Text | Google Scholar

Liu, C., Arnon, T., Lazarus, C., Strong, C., Barrett, C., and Kochenderfer, M. J. (2021). Algorithms for verifying deep neural networks. Found. Trends Optim. 4, 244–404. doi: 10.1561/2400000035

Crossref Full Text | Google Scholar

Liu, J., Xing, Y., Shi, X., Song, F., Xu, Z., and Ming, Z. (2022). Abstraction and Refinement: Towards Scalable and Exact Verification of Neural Networks.

Google Scholar

Liu, W., Song, F., Zhang, T., and Wang, J. (2020). Verifying relu neural networks from a model checking perspective. J. Comput. Sci. Technol. 35, 1365–1381. doi: 10.1007/s11390-020-0546-7

Crossref Full Text | Google Scholar

Luebke, D. (2008). “CUDA: Scalable parallel programming for high-performance scientific computing,” in 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro (Paris: IEEE), 836–838.

PubMed Abstract | Google Scholar

Makino, T., Jastrzebski, S., Oleszkiewicz, W., Chacko, C., Ehrenpreis, R., Samreen, N., et al. (2022). Differences between human and machine perception in medical diagnosis. Sci. Rep. 12:6877. doi: 10.1038/s41598-022-10526-z

PubMed Abstract | Crossref Full Text | Google Scholar

Mao, Y., Muller, M. N., Fischer, M., and Vechev, M. T. (2023). Understanding certified training with interval bound propagation. arXiv [preprint] arXiv:2306.10426. doi: 10.48550/arXiv.2306.10426

Crossref Full Text | Google Scholar

Mayr, F., Yovine, S., and Visca, R. (2021). Property checking with interpretable error characterization for recurrent neural networks. Machine Learn. Knowl. Extract. 3, 205–227. doi: 10.3390/make3010010

Crossref Full Text | Google Scholar

Meng, M. H., Bai, G., Teo, S. G., Hou, Z., Xiao, Y., Lin, Y., et al. (2022). Adversarial robustness of deep neural networks: A survey from a formal verification perspective. IEEE Trans. Depend. Secure Comp. 1:1. doi: 10.1109/TDSC.2022.3179131

Crossref Full Text | Google Scholar

Montavon, G., Binder, A., Lapuschkin, S., Samek, W., and Müller, K.-R. (2019). “Layer-wise relevance propagation: an overview,” in Explainable AI: Interpreting, Explaining and Visualizing Deep Learning, eds. W. Samek, W. Montavon, A. Vedaldi, L. Hansen, K. R. Müller (Cham: Springer), 11700. doi: 10.1007/978-3-030-28954-6_10

Crossref Full Text | Google Scholar

Monteiro, R. F., Alves, E., Silva, I., Ismail, H., Cordeiro, L., and Filho, E. (2017). ESBMC-GPU a context-bounded model checking tool to verify cuda programs. Sci. Comp. Program. 152:5. doi: 10.1016/j.scico.2017.09.005

Crossref Full Text | Google Scholar

Müller, M. N., Makarchuk, G., Singh, G., Püschel, M., and Vechev, M. (2022). PRIMA: general and precise neural network certification via scalable convex hull approximations. Proc. ACM Program. Lang. 6:3462308. doi: 10.1145/3462308

Crossref Full Text | Google Scholar

Muškardin, E., Aichernig, B. K., Pill, I., and Tappler, M. (2022). “Learning finite state models from recurrent neural networks,” in Integrated Formal Methods, eds. M. H. ter Beek, and R. Monahan (Cham: Springer International Publishing), 229–248.

Google Scholar

Naseer, M., Hasan, O., and Shafique, M. (2023). Scaling model checking for dnn analysis via state-space reduction and input segmentation (extended version). arXiv [preprint] arXiv:2306.17323. doi: 10.48550/arXiv.2306.17323

Crossref Full Text | Google Scholar

Naseer, M., Minhas, M. F., Khalid, F., Hanif, M. A., Hasan, O., and Shafique, M. A. (2019). “FANNet: formal analysis of noise tolerance, training bias and input sensitivity in neural networks,” in 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE) (Grenoble: IEEE), 666–669.

Google Scholar

Nayak, S. P., Neider, D., Roy, R., and Zimmermann, M. (2024). “Robust computation tree logic,” in Innovations in Systems and Software Engineering, 1–23.

Google Scholar

Pulina, L., and Tacchella, A. (2010). “An abstraction-refinement approach to verification of artificial neural networks,” in Computer Aided Verification, eds. T. Touili, B. Cook, and P. Jackson (Berlin, Heidelberg: Springer Berlin Heidelberg), 243–257.

Google Scholar

Ressi, D., Romanello, R., Rossi, S., and Piazza, C. (2024). Compressing neural networks via formal methods. Neural Netw. 178:106411. doi: 10.1016/j.neunet.2024.106411

PubMed Abstract | Crossref Full Text | Google Scholar

Ruan, W., Wu, M., Sun, Y., Huang, X., Kroening, D., and Kwiatkowska, M. (2019). Global Robustness Evaluation of Deep Neural Networks with Provable Guarantees for the Hamming Distance. Montreal: IJCAI-19.

Google Scholar

Ryou, W., Chen, J., Balunovic, M., Singh, G., Dan, A., and Vechev, M. (2021). “Scalable polyhedral verification of recurrent neural networks,” in Computer Aided Verification: 33rd International Conference, CAV 2021, Virtual Event, July 20-23, 2021, Proceedings, Part I 33 (Springer International Publishing), 225–248.

Google Scholar

Sälzer, M., Alsmann, E., Bruse, F., and Lange, M. (2022). Verifying and interpreting neural networks using finite automata. arXiv [preprint] arXiv:2211.01022. doi: 10.48550/arXiv.2211.01022

Crossref Full Text | Google Scholar

Samek, W., Montavon, G., Lapuschkin, S., Anders, C. J., and Muller, K.-R. (2021). Explaining deep neural networks and beyond: a review of methods and applications. Proc. IEEE 109, 247–278. doi: 10.1109/JPROC.2021.3060483

Crossref Full Text | Google Scholar

Sena, L., Song, X., Alves, E., Bessa, I., Manino, E., Cordeiro, L., et al. (2021). Verifying quantized neural networks using smt-based model checking. arXiv [preprint] arXiv:2106.05997. doi: 10.48550/arXiv.2106.05997

Crossref Full Text | Google Scholar

Sena, L. H., Bessa, I. V., Gadelha, M. R., Cordeiro, L. C., and Mota, E. (2019). “Incremental bounded model checking of artificial neural networks in CUDA,” in 2019 IX Brazilian Symposium on Computing Systems Engineering (SBESC) (Natal: IEEE), 1–8.

Google Scholar

Sena, L. H. C. (2022). Automated Verification and Refutation of Quantized Neural Networks.

Google Scholar

Seshia, S., Desai, A., Dreossi, T., Fremont, D., Ghosh, S., Kim, E., et al. (2018). Formal Specification for Deep Neural Networks: 16th International Symposium, ATVA 2018. Los Angeles, CA: ATVA, 20–34.

Google Scholar

Sherstinsky, A. (2020). Fundamentals of recurrent neural network (RNN) and long short-term memory (lstm) network. Physica D: Nonlinear Phenomena 404:132306. doi: 10.1016/j.physd.2019.132306

Crossref Full Text | Google Scholar

Shih, A., Darwiche, A., and Choi, A. (2019). “Verifying binarized neural networks by angluin-style learning,” in Theory and Applications of Satisfiability Testing-SAT 2019, eds. M. Janota, and I. Lynce (Cham: Springer International Publishing), 354–370.

Google Scholar

Shridhar, A., Tomson, P., and Innes, M. (2020). “Interoperating deep learning models with ONNX.ji,” in Proceedings of the JuliaCon Conferences, 59.

Google Scholar

Singh, G., Gehr, T., Mirman, M., Püschel, M., and Vechev, M. (2018). “Fast and effective robustness certification,” in Advances in Neural Information Processing Systems, eds. S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (New York: Curran Associates, Inc).

Google Scholar

Singh, G., Gehr, T., Püschel, M., and Vechev, M. (2019b). An abstract domain for certifying neural networks. Proc. ACM Program. Lang. 3, 1–30. doi: 10.1145/3290354

PubMed Abstract | Crossref Full Text | Google Scholar

Singh, G., Gehr, T., Püschel, M., and Vechev, M. (2019c). “Boosting robustness certification of neural networks,” in 7th International Conference on Learning Representations, ICLR 2019 (New Orleans).

Google Scholar

Sistla, A. P., Vardi, M. Y., and Wolper, P. (1987). The complementation problem for büchi automata with applications to temporal logic. Theor. Comput. Sci. 49, 217–237. doi: 10.1016/0304-3975(87)90008-9

Crossref Full Text | Google Scholar

Song, X., Manino, E., Sena, L., Alves, E., Bessa, I., Lujan, M., et al. (2021). QNNVerifier: a tool for verifying neural networks using smt-based model checking. arXiv [preprint] arXiv:2111.13110. doi: 10.48550/arXiv.2111.13110

Crossref Full Text | Google Scholar

Sotoudeh, M., and Thakur, A. V. (2020). “Abstract neural networks,” in Static Analysis, eds. D. Pichardie, and M. Sighireanu (Cham: Springer International Publishing), 65–88.

Google Scholar

Tao, Y., Liu, W., Song, F., Liang, Z., Wang, J., and Zhu, H. (2023). An automata-theoretic approach to synthesizing binarized neural networks. arXiv [preprint] arXiv:2307.15907. doi: 10.1007/978-3-031-45329-8_18

Crossref Full Text | Google Scholar

Urban, C., and Miné, A. (2021). A review of formal methods applied to machine learning. arXiv [preprint] arXiv:2104.02466. doi: 10.48550/arXiv.2104.02466

Crossref Full Text | Google Scholar

Wang, S., Pei, K., Whitehouse, J., Yang, J., and Jana, S. (2018). “Formal security analysis of neural networks using symbolic intervals,” in 27th USENIX Security Symposium (USENIX Security 18) (Baltimore, MD: USENIX Association), 1599–1614.

Google Scholar

Wang, X., Yang, K., Wang, Y., Zhao, L., and Shu, X. (2020). “Towards formal verification of neural networks: A temporal logic based framework,” in Structured Object-Oriented Formal Language and Method, eds. H. Miao, C. Tian, S. Liu, and Z. Duan (Cham: Springer International Publishing), 73–87.

Google Scholar

Wang, Z., Albarghouthi, A., Prakriya, G., and Jha, S. (2022). Interval universal approximation for neural networks. Proc. ACM Program. Lang. 6, 1–29. doi: 10.1145/3498675

Crossref Full Text | Google Scholar

Weiss, G., Goldberg, Y., and Yahav, E. (2018). “Extracting automata from recurrent neural networks using queries and counterexamples,” in International Conference on Machine Learning (New York: PMLR), 5247–5256.

Google Scholar

Woodcock, J., Larsen, P. G., Bicarregui, J., and Fitzgerald, J. (2009). Formal methods: Practice and experience. ACM comp. Surveys 41, 1–36. doi: 10.1145/1592434.1592436

Crossref Full Text | Google Scholar

Xiao, J., Sun, R., and Luo, Z.-Q. (2023). “PAC-Bayesian Spectrally-Normalized Bounds for Adversarially Robust Generalization,” in Proceedings of the 37th International Conference on Neural Information Processing Systems (NIPS '23) (ACM), 36305–36323.

Google Scholar

Xu, K., Zhang, H., Wang, S., Wang, Y., Jana, S., Lin, X., et al. (2021). Fast and Complete: Enabling Complete Neural Network Verification with Rapid and Massively Parallel Incomplete Verifiers.

Google Scholar

Xu, Z., Liu, Y., Qin, S., and Ming, Z. (2023). Output range analysis for feed-forward deep neural networks via linear programming. IEEE Trans. Reliabil. 72, 1191–1205. doi: 10.1109/TR.2022.3209081

Crossref Full Text | Google Scholar

Yalçın, O. G. (2021). Feedforward Neural Networks (Berkeley, CA: Apress), 121–143.

Google Scholar

Yang, K., Duan, Z., Tian, C., and Zhang, N. (2017). A compiler for msvl and its applications. Theor. Comput. Sci. 749:32. doi: 10.1016/j.tcs.2017.07.032

Crossref Full Text | Google Scholar

Ye, C., Yang, Y., Fermuller, C., and Aloimonos, Y. (2017). On the importance of consistency in training deep neural networks. arXiv preprint arXiv:1708.00631. doi: 10.48550/arXiv.1708.00631

Crossref Full Text | Google Scholar

Yu, X., Smedemark-Margulies, N., Aeron, S., Koike-Akino, T., Moulin, P., Brand, M., et al. (2023). Improving adversarial robustness by learning shared information. Pattern Recognit. 134:109054. doi: 10.1016/j.patcog.2022.109054

Crossref Full Text | Google Scholar

Zafar, M. R., and Khan, N. (2021). Deterministic local interpretable model-agnostic explanations for stable explainability. Mach. Learn. Knowl. Extract. 3, 525–541. doi: 10.3390/make3030027

Crossref Full Text | Google Scholar

Zhang, N., Duan, Z., and Tian, C. (2016). Model checking concurrent systems with msvl. Sci. China Inform. Sci. 59, 1–3. doi: 10.1007/s11432-015-0882-6

Crossref Full Text | Google Scholar

Zhang, Y., Zhao, Z., Chen, G., Song, F., and Chen, T. (2021). “BDD4BNN: a bdd-based quantitative analysis framework for binarized neural networks,” in Computer Aided Verification, eds. A. Silva, and K. R. Leino (Cham: Springer International Publishing), 175–200.

Google Scholar

Zhang, Y., Zhao, Z., Chen, G., Song, F., and Chen, T. (2022). Precise quantitative analysis of binarized neural networks: a BDD-based approach. ACM Trans. Softw. Eng. Methodol. 32:3563212. doi: 10.1145/3563212

Crossref Full Text | Google Scholar

Zhao, L., Wu, L., Gao, Y., Wang, X., and Yu, B. (2022). “Formal modeling and verification of convolutional neural networks based on MSVL,” in 2022 9th International Conference on Dependable Systems and Their Applications (DSA) (Wulumuqi), 280–289. doi: 10.1109/DSA56465.2022.00046

Crossref Full Text | Google Scholar

Zhao, Z., Zhang, Y., Chen, G., Song, F., Chen, T., and Liu, J. (2022). “CLEVEREST: Accelerating CEGAR-based neural network verification via adversarial attacks,” in Static Analysis, eds. G. Singh, and C. Urban (Cham: Springer Nature Switzerland), 449–473.

Google Scholar