- 1School of Information Engineering and Robot Technology Used for Special Environment Key Laboratory of Sichuan Province, Southwest University of Science and Technology, Mianyang, China
- 2Department of Energy Technology, Aalborg University, Aalborg, Denmark
- 3School of Pharmacy and Life Sciences, Robert Gordon University, Aberdeen, United Kingdom
Lithium-ion batteries play an important role in our daily lives. The prediction of the remaining service life of lithium-ion batteries has become an important issue. This article reviews the methods for predicting the remaining service life of lithium-ion batteries from three aspects: machine learning, adaptive filtering, and random processes. The purpose of this study is to review, classify and compare different methods proposed in the literature to predict the remaining service life of lithium-ion batteries. This article first summarizes and classifies various methods for predicting the remaining service life of lithium-ion batteries that have been proposed in recent years. On this basis, by selecting specific criteria to evaluate and compare the accuracy of different models, find the most suitable method. Finally, summarize the development of various methods. According to the research in this article, the average accuracy of machine learning is 32.02% higher than the average of the other two methods, and the prediction cycle is 9.87% shorter than the average of the other two methods.
Introduction
Among various energy storage solutions, Lithium-ion (Li-ion) batteries are widely regarded as promising candidates for various applications due to their advantages of high energy density and low self-discharge (Peng et al., 2019; Gao et al., 2020). However, the life span of Li-ion batteries is not unlimited, and the cost and aging of Li-ion batteries are the two main factors hindering their development (She et al., 2020; Zhang et al., 2021; Ren et al., 2021). The performance of Li-ion batteries will decrease with time (calendar aging) and use (cycle aging), which is called the aging phenomenon (Jinlei et al., 2019; Liu et al., 2019a). The aging of the battery will increase operating costs, reduce the service life of the equipment, and affect the safe operation of the equipment (Qi et al., 2019; Xu et al., 2018; Zhang et al., 2019a). Moreover, there is no ideal solution for the recycling of Li-ion batteries, and premature failures will lead to a large number of second-hand Li-ion batteries that cannot be properly handled. Generally, when the capacity drops to more than 80% of the initial value, the battery has reached the end of its service life (Liu et al., 2020a; White et al., 2021). The remaining useful lifetime (RUL) is defined as the time at which equipment performance first or first arrival time drops to the failure threshold. It represents the period from the observation to the end of life (EOL) (Corno and Pozzato, 2020; Ma et al., 2020a; Liu et al., 2020b). EOL refers to the time and the number of charge-discharge cycles when the battery characteristic parameters reach the replacement threshold.
Battery degradation is a complex process controlled by electrochemical reactions. The battery degradation process is highly non-linear and is affected by many factors, such as temperature, charge, and discharge rate; many electrochemical side reactions and operating conditions of the anode, electrolyte, and cathode will severely affect performance, thereby affecting the battery life. This complicates battery capacity prediction (Liu et al., 2020a; Shi et al., 2019). Therefore, how to accurately predict the RUL under various working conditions is a crucial and challenging problem in a battery management system. From an economic point of view, RUL predicts that it will help reduce the return on investment of the system and increase the profitability of the system (El Mejdoubi et al., 2019; Wu et al., 2019). If the RUL can be accurately predicted, the equipment can be maintained predictively, and battery life can be extended (Xue et al., 2020; Xiong et al., 2018). Therefore, this article will conduct a timely and comprehensive review of battery life pre-diction technology, focusing on the latest developments based on models, data-driven, and hybrid methods (Hu et al., 2020a).
Methods include model-based methods (such as physical models, electrochemical models, etc.) or data-driven methods (Guha and Patra, 2018a; Khodadadi Sadabadi et al., 2021; Lyu et al., 2021). Different types of aging models have been proposed in the literature. The electrochemical model can represent the internal variables of the battery well, so it can achieve high accuracy (Wang et al., 2020a). However, this detailed mathematical representation means an increase in complexity and computational cost. The development of electrochemical models assumes a challenging modeling stage that usually requires the disassembly of cells (Chen et al., 2019; Tian et al., 2020). Data-driven is a method of building a rough model and then using a large amount of data to refine the data to make the model consistent with the data. For the complex electrochemical dynamics system in LIB, model-based methods are usually complicated to implement, but the data-driven method does not consider the electrochemical reactions and failure mechanisms inside LIB (Hui et al., 2021; Lin et al., 2020; Lipu et al., 2018).
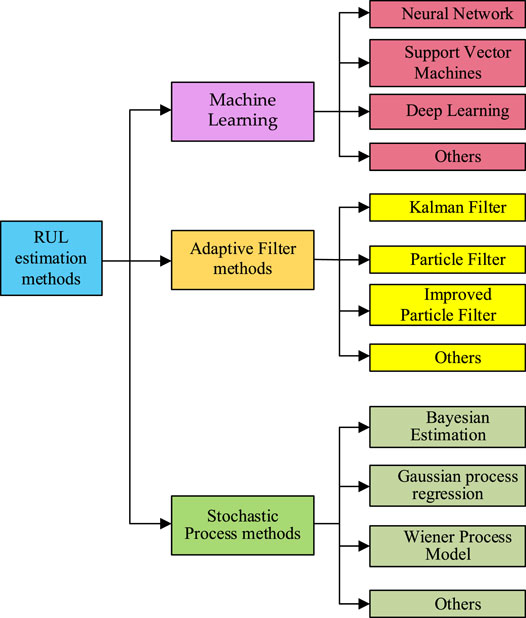
Therefore, data-driven forecasting methods have become a research hotspot (Liu et al., 2021; Ren et al., 2021). According to the principles and applicable conditions of the methods used, this section refers to the methods used in many documents and divides the data-driven RUL prediction methods into artificial intelligence-based methods Ji et al. (2021), filtering-based methods Xu et al. (2021), and statistical data-driven methods. These methods can describe relationships and trends related to degradation based on data. RUL prediction methods can be divided into three categories. Figure 1 shows the main RUL prognosis methods for Li-ion batteries (Motaqi and Mosavi, 2020; Xiong et al., 2019; Lucu et al., 2018).
This article aims to guide the search for the most suitable method to develop an adaptive Li-ion battery aging model and puts forward specific evaluation criteria based on method classification. The three methods are compared in terms of input and output complexity, percentage of the training period, and prediction accuracy. The intuitive and accurate comparison results are given based on the calculation and emphasize the main advantages and disadvantages of each adaptive model in the special case of Li-ion aging prediction.
Machine Learning
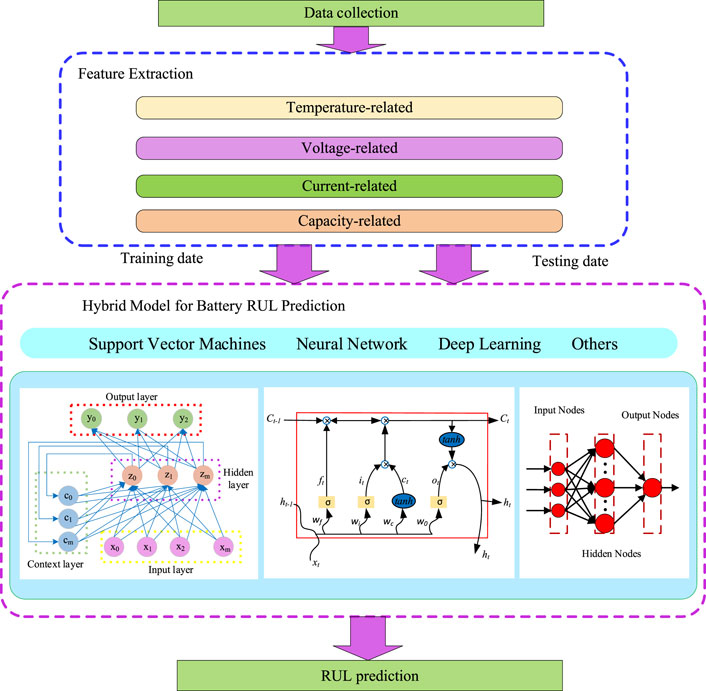
The artificial neural network has been widely used for self-organization and self-learning, and it does not rely on the electrochemical principles inside the battery. Machine learning algorithms can learn and recognize more complex patterns of system data in many applications based on experience (Khumprom and Yodo, 2019). Machine learning is the preferred method for forecasting by collecting historical data in the life cycle (Liu et al., 2017). Moreover, they are suitable for strongly nonlinear systems and approximate the real state of the system by adaptively optimizing network parameters. But these methods still have inevitable limitations. They rely to a large extent on a large amount of historical data to fully train the model, which may be time-consuming and computationally intensive in the actual system, and it is also easy to cause data overfitting (Xiong and Lu, 2018). Figure 2 shows the main flow of machine learning.
There are three basic methods of machine learning, neural network, support vector machine, and deep learning. This article will start with these three basic methods and summarize the progress of using machine learning to predict RUL in recent years.
Neural Network
The neural network can contain many layers, and each layer can also contain multiple neurons. Each neuron in the current layer can be regarded as a node, and the value is obtained by logistic regression calculation of all neurons in the previous layer. She et al. (2020) used a combination of incremental capacity analysis (ICA) and a radial basis function neural network (RBFNN) model to assess battery aging. Validation based on the electric city bus operation data set shows that the average prediction error of this method reaches 4.00%, the confidence interval of the derived model is 92%, and the prediction accuracy is 90%. Wu et al. (2019) proposed a neural network (NN) degradation model + bat particle filter (Bat-PF) prediction method to recursively update model parameters and intelligently estimate RUL. The RUL prediction error in 500 prediction periods is 2 periods. The width of the probability density function is 35 cycles. In Ref. Wu et al. (2016) proposed a method for online estimation of Li-ion battery RUL using fast Fourier transform the neural network, using importance sampling (IS) to select the feedforward neural network (FFNN) input to realize the charging curve The accurate reconstruction of, and the number of hidden layer neurons is set to 40, the prediction error of the actual RUL in actual operation is less than 5%.
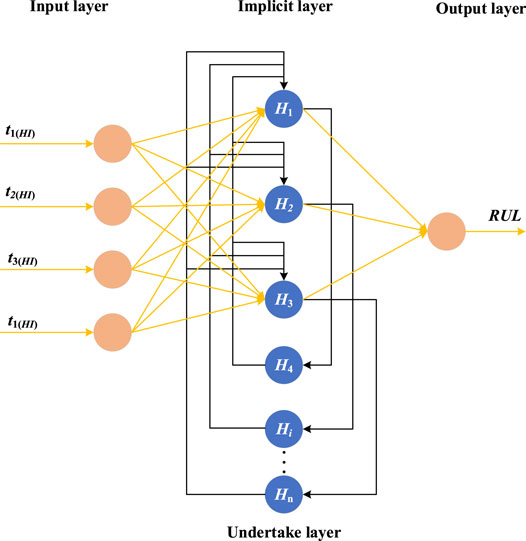
Li et al. (2019a) used grey relational analysis to indirectly estimate battery capacity and established an indirect prediction method based on the Ellman neural network to estimate the feasibility of the application in RUL prediction of Li-ion batteries under vibration stress. The average error (MAE) of the estimation results is 0.0243, and the mean square error (MSE) is 0.0278. The flowchart is shown in Figure 3. Zhou et al. (2020a) proposed a time convolutional network (TCN)-based Li-ion battery SOH monitoring and RUL prediction model framework. For the RUL prediction task, the offline data is denoised through empirical mode decomposition (EMD), and then some online data is combined to locally adjust the model to achieve high-precision prediction of RUL. The average RMSE accuracy of the TCN model is 5% higher than that of the traditional network with different starting points. Compared with commonly used models, the average error of RUL prediction is nearly 8 cycles higher. In Ref. Tang et al. (2020) proposed a new method of feedforward migration neural network to predict RUL trajectory. The model is constructed by the input-output slope and bias correction (SBC) method, and further integrated into a four-layer feedforward migration NN and trained via the gradient correlation algorithm. When only the first 30% of the aging trajectory is used for neural network training, the root means square error (RMSE) of prediction under high-noise conditions is within 2.5%.
Zhang et al. (2019b) proposed an online estimation of battery SOH and RUL by combining partial incremental capacity with an artificial neural network (ANN) under constant current discharge. By constructing two neural network models, Spearman correlation analysis is used to extract the training set and validation set of the model. The model estimates that the MAE and RMSE of RUL are less than 4 cycles and 6 cycles, respectively, and the relative error rate of SOH is not higher than 3%. It has good generalization ability and high prediction accuracy.
In Ref. Ma et al. (2019a) used the pseudo-nearest neighbor (FNN) method with a hybrid neural network (HNN) combining long and short-term memory and convolutional neural networks to predict battery RUL. The accuracy of the proposed method can reach 98.21%.Qiao et al. (2020) proposed an RUL prediction method based on empirical mode decomposition, deep neural network (DNN), and long‐short‐term memory model. Compared with empirical mode decomposition and autoregressive integrated moving average mixed model, the average error and root mean square error of this algorithm are reduced by 75 and 90.8%, respectively. The standard deviation of the predicted RUL is 1.36626. It can accurately and effectively predict the SOH and RUL of the battery.
Support Vector Machines
The Support vector machine is a linear classifier with the largest interval defined in the feature space of the basic model. The learning strategy of SVM is to maximize the interval, which can be formalized as a problem of solving convex quadratic programming. Zhao et al. (2018) extrapolated the battery capacity through equal charge voltage difference time interval (TIECVD) and equal discharge voltage difference time interval (TIEDVD), and combined feature vector selection (FVS) and SVR to form the FVS-SVR algorithm. Realize online prediction of battery SOH and RUL. The maximum prediction root means the square error of this method is less than 1%. Du et al. (2018) proposed an SVR-based ternary Li-ion battery coupling stress modeling and prediction RUL method, using 6 sets of coupling stress experimental data to establish an RUL prediction model. The relative error of 600 cycles is within 5%. Wang and Mamo (2018) used the differential evolution (DE) algorithm to obtain the support vector regression (SVR) kernel parameters, and fuse and predict the RUL of Li-ion batteries. This method has an error of about 1/99 at the starting point of 80 cycles, which has higher prediction accuracy. Patil et al. (2015) extracted key features from the voltage and temperature curves and based on the key features, established an RUL classification and regression model using support vector machines (SVM). The RMSE of the model is 0.357%, and the estimated upper and lower errors are 95%, 7.87%, which are 7.87%, and 10.75%, respectively. The accurate RUL prediction of multiple batteries is realized.
Wei et al. (2018) established a battery SOH state-space model based on support vector regression to simulate the dynamic characteristics of battery aging. The particle filter method is used to estimate the impedance attenuation parameters and deal with the measurement noise of current and voltage. Ben Ali et al. (2020) proposed a combined method based on Quantum Behavioral Particle Swarm Optimization (QBPSO) and Incremental Support Vector Regression (ISVR). The RMSE of this method is 0.0202 ah, and the MAPE is 0.0255%, which is more robust. Wang et al. (2019a) proposed a method to predict RUL by using an artificial bee colony (ABC) based on SVR. The ABC algorithm is used to optimize the SVR core parameters. The RMSE of the ABC-SVR method is less than 0.05, and the average value of all units is less than 27%.
Deep Learning
Deep learning is derived from artificial neural networks, and a multi-layer perceptron with multiple hidden layers is a deep learning structure. Deep learning forms a more abstract high-level by combining low-level features to represent attribute categories or features. Liu et al. (2021) used the empirical mode decomposition (EMD) method to decompose the data, then used the long-short-term memory (LSTM) sub-model to estimate the residuals, and the Gaussian process regression (GPR) sub-model was fitted to IMFs. Compared with different models, the LSTM + GPR combined model can obtain accurate one-step and multi-step prediction results. It has good adaptability and reliable uncertainty quantification. Qu et al. (2019) based on the neural network method, fused particle swarm optimization, and attention mechanism to optimize the long‐short‐term memory (LSTM) network to predict battery RUL and monitor SOH. Using the CEEMDAN method to denoise the original data, the average error and RMSE values of PA-LSTM are −3 and 0.0362, respectively. It can accurately monitor the status of Li-ion batteries and predict RUL. Li et al. (2019b) combined the empirical mode decomposition algorithm with long‐short‐term memory (LSTM) and Elman neural network and proposed a new hybrid Kalman-LSTM hybrid model to predict battery RUL. Using the LSTM model and the EMDLSTM model for comprehensive testing, the relative prediction errors are 3.3 and 3.21%, respectively.
Cui and Hu (2020) used machine learning and model filtering techniques to estimate the SOH and RUL of lithium batteries. The Unscented Kalman (UKF) algorithm is combined with the LSTM network and the NN model to form a data model fusion method to filter out the network output noise. The comparison with other traditional methods through 4 cell cycle experiments verifies its superior estimation ability. Zhu et al. (2019) proposed the DGWO-ELM algorithm to predict the RUL of lithium-ion batteries, combining ELM, Gray Wolf Optimization (GWO), and Differential Evolution (DE) to improve input weights and bias. The algorithm uses the GWO algorithm to optimize the weights and thresholds of ELM and improves the three defects of the GWO algorithm. The minimum root means the square error of this algorithm is 0.43%.
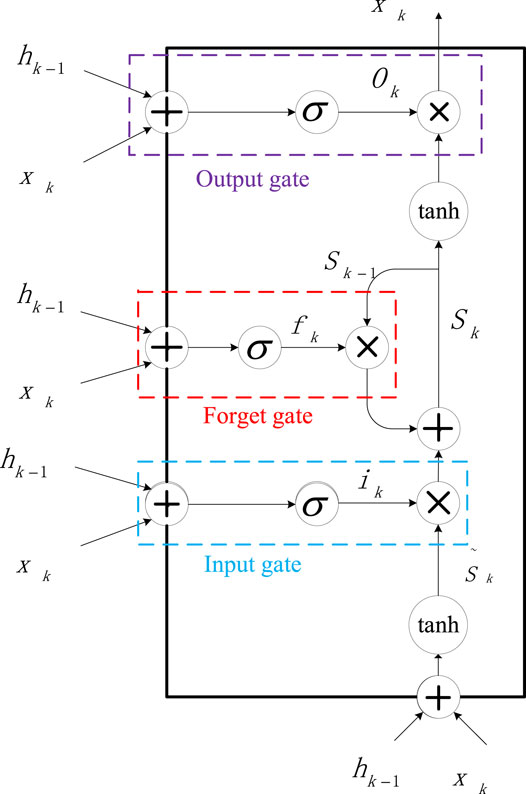
Hong et al. (2020) proposed an end-to-end deep learning framework to predict the remaining service life of Li-ion batteries. This framework solves the challenge of predicting the remaining battery life through short-term measurements. The average absolute error rate of the proposed framework’s remaining service life prediction reaches 10.6%. Li et al. (2020a) designed a variant of long and short memory neural network, called AST-LSTM NN, to perform multiple battery sharing predictions. The AST-LSTM neural network has a many-to-one and one-to-one mapping structure to predict battery SOH and RUL. This method estimates that the ARMSE of SOH is 0.0216, and the CE of RUL is 0.0831. Yang et al. (2020a) proposed a hybrid neural network to predict the RUL of Li-ion capacitors (LIC), which combines convolutional neural networks and bidirectional long-short-term memory networks (Bi-LSTM) and removes periodic data. Noise pro-cessing. The minimum error of this method can reach 1.04%. The RNN structure based on LSTM is shown in Figure 4.
Zhang et al. (2018a) proposed a battery RUL prediction method using long-short-term memory recurrent neural network (LSTM-RNN). Use elastic mean square back-propagation (RMSprop) technology to adaptively optimize LSTM-RNN, and a dropout technique is used to address the overfitting problem. Park et al. (2020) proposed a new LSTM-based RUL prediction technology. Use a many-to-one structure instead of a one-to-one structure to accurately predict RUL. The mean absolute percentage error (MAPE) of the single-channel LSTM model is 39.2% higher than that of the baseline LSTM model. At the same time, the MAPE of the multi-channel LSTM model is improved by 63.7% compared to the baseline. Chinomona et al. (2020) proposed a recurrent neural network-long‐short‐term memory (RNN-LSTM) model to select the best subset, and use a partial charge/discharge data set to predict battery RUL performance. The RMSE is 0.00286 and the MAE is 0.00222. Sun et al. (Sun et al., 2019) proposed a method for hybrid prediction of battery RUL based on a particle filter (PF)-based extreme learning machine (ELM) model. The absolute error of RUL predicted by the PFELM algorithm from the 50th cycle is 0, which has a good prediction effect. Gou et al. (2020) proposed a hybrid integrated data-driven battery SOH estimation and RUL prediction method based on ELM and RVFL networks, using a nonlinear autoregressive structure to reduce RUL prediction errors, and designing an uncertainty management method based on bootstrap To quantitatively evaluate the RUL prediction interval. Compared with the latest learning algorithms, this method has smaller prediction errors and better performance.
Others
Fan et al. (2019) used the Forgotten Online Sequential Extreme Learning Machine (FOS-ELM) to construct an algorithm and combined the Hybrid Gray Wolf Optimizer (HGWO) algorithm and attention mechanism to detect SOC and predict RUL. Use Variant Mode Decomposition (VMD) to denoise the original data. The RMSE of this method can reach 0.0121. Ma et al. (2020b) combined the transfer learning method of an example with a deep learning method called stacked denoising autoencoder (SDA). The transferability measurement method based on average Euclidean distance-based (AED) selects the battery most similar to the target battery from the historical test database as the reference battery. Then, its data is used to train a prediction model based on SDA to estimate the RUL of the target battery. The proposed optimization method can shorten nearly more than 30% of the test cycles on average. Yang et al. (2020b) proposed a gradient boosting regression tree (GBRT), which is used to model complex nonlinear battery dynamics and predict battery lifetime by extracting various battery characteristics. The absolute average percentage error is about 7%. Wang and Mamo (2020) proposed the gradient enhancement regression (GBR) model of the ABC algorithm to analyze the degradation behavior of prismatic elements. For the four invisible data sets, the MAPE of this model is 0.70, 0.62, 0.87, and 0.46%, respectively. The prediction errors are 0.18, 0.21, 0.21, and 0.17%, respectively, which can reliably predict prism cells by RUL.
Wang et al. (2020b) proposed an LRD-based FBM model-based Li-ion battery RUL pre-diction method and optimized the H of the prediction model through the Fruit-fly Optimization Algorithm (FOA). The parameters of the Fractional Brownian Motion (FBM) model are estimated by maximum likelihood estimation (MLE). And use an FOA to optimize the Hurst exponent (H). Xu et al. (2021) extracted health indicators based on the partial charge voltage curve of cells. And based on the capacity data in the moving window, a linear aging model is constructed to predict battery remaining useful life, combined with Monte Carlo simulation to generate prediction uncertainties. Li et al. (2020b) predicted the RUL of the engineering system by developing the most suitable meta-learner for both accuracy and diversity as two conflicting goals. The selection of meta-learners follows a multi-objective evolutionary algorithm called non-dominated sorting genetic algorithm-II to balance two conflicting goals in terms of accuracy and diversity. Before inputting, select sensor signals, normalize them in two data sets and process them through the long-term and short-term feature extraction strategy in the C-MAPSS data set. The RMSE of the C-MAPSS dataset increased by 2.215, and the average score increased by 1,617.6. The RMSE of the Li-ion battery data set increased by 5.45 on average.
Summary
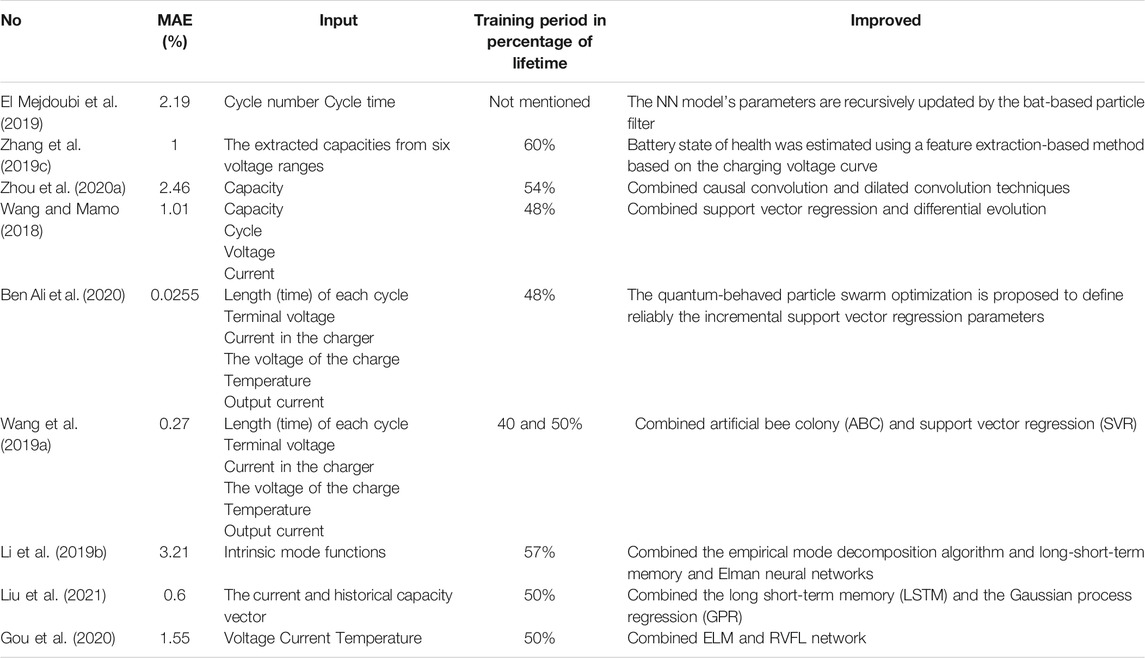
The comparison of machine learning methods parameters is shown in Table 1.
As shown in Table 1, each method in the table is improved and fused in different degrees based on the traditional algorithm. In addition, the proportion of training data is less than 60% of the total life cycle. The maximum prediction error is 3.21%. The average training period is 52.43%. The average error is 1.3684%. The input feature vector of machine learning is clear and accurate, and the amount of training period data required is relatively small.
Adaptive Filter Methods
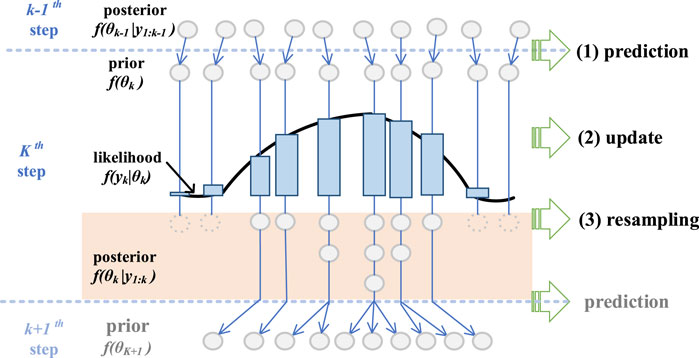
The adaptive filter is a digital filter, and its coefficient changes with the target to make the filter converge to the best state (Ahwiadi and Wang, 2019). The optimization criterion is the cost function, and the most common is the root mean square of the error signal between the output of the adaptive filter and the desired signal (Zhang et al., 2018b). When you change the characteristics of the input data, the filter adapts to the new environment by generating a new set of coefficients for the new data (Cadini et al., 2019; Liu et al., 2020c). The adaptive filter can make an early prediction of the system state based on the confidence interval. For PF-based methods, the pdf of these states ap-proximates a large number of particles (Pugalenthi and Raghavan, 2018). However, for PF-based methods, particle degeneracy is a common phenomenon, and most particles have negligible weights after several iterations (Guha and Patra, 2018b; Kim et al., 2021).
Improved Kalman Filtering Algorithms
The Kalman filter algorithm is essentially a data fusion algorithm, which fuses data with the same measurement purpose, from different sensors, and with different units to obtain a more accurate target measurement value. The biggest advantage of the Kalman filter is that the amount of calculation is small, and the state at the previous moment and possible measurement values can be used to obtain the optimal estimation of the state at the current moment. Various optimized Kalman filter methods improve the traditional methods in algorithms or parameters to enhance performance. Li et al. (2019c) proposed an integrated hybrid model to predict the RUL of Li-ion batteries through outlier identification. Based on the UKF model and improved by the isolation forest algorithm to obtain the final prediction result. The RMSE of this method can reach 0.0064499. Song et al. (2018) proposed an iterative update method to improve the long-term prediction performance of battery RUL prediction. First, when RVM outputs a new estimator, it will use the KF to optimize the estimator through a physical degradation model. Then, this optimized estimator is added to the training set as an online sample, and the RVM model is retrained, and then the coefficient matrix and correlation vector can be dynamically adjusted for the next iteration prediction.
Xue et al. (2020) established a double exponential state-space model to describe the degradation of lithium batteries, and introduced the adaptive unscented Kalman filter (AUKF) algorithm to adaptively update the process noise covariance and the observed noise covariance, and then use genetic algorithms to optimize the key parameters of SVR to achieve multiple Step prediction, and introduce the AUKF algorithm to adaptively update the process noise covariance and the observed noise covariance. An integrated algorithm combining AUKF and genetic algorithm optimized support vector regression (GA-SVR) is formed. The accuracy of the algorithm can reach at least 0.933. Park et al. (2020) proposed a hybrid prediction method based on the combination of the kernel adaptive filter (KAF) -based prediction model and the DGM-based UKF algorithm. Based on the double Gaussian mixture (DGM) cost function, a robust KAF algorithm was derived. Understand the mechanism of capacity reduction and establish a long-term prediction model. Secondly, a robust UKF algorithm based on the DGM cost function was developed and then combined with the KAF-based prediction model. Under the hybrid prediction framework, the proposed UKF algorithm was used to filter noisy observations. In Ref. Duong and Raghavan (2018), Duong and Raghavan (2018) introduced the heuristic Kalman algorithm, a meta-heuristic optimization method, combined with particle filtering to solve the problem of sample degradation and poverty. The maximum RMSE should be 3.9246e-4. Qiu et al. (2020) proposed the Backward Smoothing Square Root Colony Kalman Filter (BS-SRCKF). Then the multi-scale hybrid Kalman filter (MHKF) composed of BS-SRCKF and extended Kalman filter (EKF) is used for the joint estimation of SOC and SOH. By transferring the particles in the prior distribution area to the maximum likelihood area, the improved cuckoo search (ICS) algorithm is embedded in the standard PF to improve its performance. Dong et al. (2020a) proposed a new data-driven Brownian motion model, which uses an adaptive extended Kalman filter (AEKF) parameter identification method. The proposed model can update model parameters online and adapt to uncertain degradation operations. Drift parameters, system noise covariance matrix, and EKF parameters can be estimated online adaptively using this method. With the help of the sliding window adaptive law, the model parameters can be adjusted online to different degradation speeds (acceleration and deceleration).
Particle Filtering Prediction Strategies
Particle filtering uses particle sets to represent probability and can be used in any form of the state-space model. The core idea is to express the distribution of random state particles drawn from the posterior probability. Sun et al. (2018) used a combination of capacitance, resistance, and constant current charging time to predict the remaining service life with the help of the beta distribution function. A third-order polynomial model is used to fit the battery life degradation process, the PF algorithm is used to predict the remaining service life, and then the probability density function of the remaining battery life is provided. By comparing the prediction error of RUL and STD, it can be found that the RUL prediction of the 500th cycle is more accurate than the 400th cycle. Chang and Fang (2019) combined a PF and a relevance vector machine (RVM) to propose a hybrid prediction scheme with uncertainty evaluation capabilities. This hybrid method can obtain prediction uncertainty while predicting the degradation process.
Pugalenthi et al. (2020) proposed a piecewise model to capture the two-phase degradation trend including linear and exponential models. The proposed model is incorporated into the particle filter framework to predict the degradation trajectory of the battery. The proposed framework may be suitable for online prediction of slowly degrading systems and can explicitly and automatically estimate the moment of turning from one mechanism to another. Yang et al. (2019) proposed a semi-empirical model based on the relationship between CE and battery degradation. The proposed model effectively captures the convexity of the degradation curve and shows better goodness of fit than the commonly used square root time model. The PF-based method effectively tracks the model parameters, and the estimation error quickly converges to within 0.5%.
Khodadadi Sadabadi et al. (2021) developed a technique based on an electrochemical model that can estimate the SOH of LMO-NMC batteries using simulated in-situ vehicle data. The composite SOH metric derived from the estimated enhanced single particle model (eSPM) parameters is used to design the RUL predictor based on the PF. Based on the features extracted from the charging process by the dynamic Bayesian network (DBN), Dong et al, (2020b) used a PF inference algorithm to perform battery SOH estimation and RUL prediction. The extension of the DBN-PF method with incomplete battery operating characteristic information applies to various practical situations. Song et al. (2017) proposed a hybrid method of the IND-AR model and the PF algorithm. Non-linear degradation factors and iterative parameter update methods can improve long-term prediction performance. The capacity prediction result is used as the measurement function of the PF algorithm. The nonlinear degradation factor can make the linear AR model suitable for nonlinear degradation estimation. The predictor will continue to iterate until the capacity reaches the failure threshold to calculate the RUL value.
Zhang et al. (2019d) developed a fusion technology composed of a correlation vector machine and a PF. Based on the fusion technology, the training data can be reduced to 30% of the entire degraded data. The Monte Carlo (MC) method is used as a benchmark to verify the predictive performance of the PF to calibrate the particle number of the PF and the model noise level. Within the predicted range of 560 cycles, the calibrated PF is 18 cycles ahead of the actual value to predict the failure time. Chen et al. (2020a) proposed an improved RUL prediction method by combining line-ar optimization resampling particle filter (LORPF) with sliding window gray model (SGM). The relative error of SGM-LORPF under constant current discharge conditions is within 7.20%, and the relative error under dynamic current discharge conditions is within 2.75%, both of which can achieve accurate RUL prediction. The PF program diagram is shown in Figure 5.
Sun et al. (2021) proposed a hybrid method using UPF and an optimized multiple kernel relevance vector machine (OMKRVM). After initial estimation and CEEMD reconstruction through the UPF model, the OMKRVM algorithm is used to provide predictive information for the future trend of residual evolution. According to the OMKRVM model, the initial estimate is corrected by the prediction trend of residual evolution. Zhang et al. (2018c) proposed a UPF algorithm based on linear optimized combined resampling (U-LOCR-PF) (i.e., U-LOCR-PF algorithm). By using discarded particles and creating new particles, the U-LOCR-PF algorithm can increase the diversity of particles. Dong et al. (2018) based on Brownian motion (BM) degradation model and PF online short-term SOH estimation and long-term RUL prediction. The long-term RUL prognosis has a smaller RMSE rather than 25% of all cells. Compared with GPR, this method has better performance, simpler topology, and more stable prediction results.
Improved Particle Filtering Algorithms
Many methods optimize the algorithm based on the traditional particle filter method so that its performance is greatly improved. In Ref. Wu et al. (2019), El Mejdoubi et al. (2019) based on the model of Rao-Blackwellization particle filter, a prognostic model of Li-ion battery considering battery aging conditions is proposed. The filter can estimate the posterior value of the aging index and predict RUL. The RUL pre-diction using the proposed prediction model shows a maximum relative error of 6.64%, which is relatively low compared to 14.3% when using the simple particle filter prediction model. Yang et al. (2019) proposed a method for predicting the RUL of non-linear and non-Gaussian systems of Li-ion batteries based on Gauss-Hermit particle filter (PDF). Based on the multi-scale extended Kalman filter method to jointly estimate the SOC and SOH on a dual time scale, GHPF was developed to update the parameters of the capacity reduction model in real-time and predict the RUL of Li-ion batteries.
Zhang et al. (2020a) proposed an innovative F-distribution PF and Kernel Smoothing (FPFKS). The weight of the particles is dynamically updated by the F kernel, and a first-order independent Markov capacity degradation model is established. Also, the kernel smoothing algorithm is integrated into the PF, so that the parameter variance of the capacity reduction model remains unchanged. The proposed method has low computational complexity and is suitable for online pre-diction.
Chu et al. (2020) used the NMC-LMO chemical method to develop a random prediction model for the capacity loss and remaining service life of Li-ion batteries. The estimator uses particle filters to develop an equivalent circuit battery model, establishes a random prognostic model, and validates it on 11 experimental data units and 250,000 comprehensive data points. The random model can predict a capacity loss with an RMSE of less than 1% and an RUL with an RMSE of 1.6 kAh.
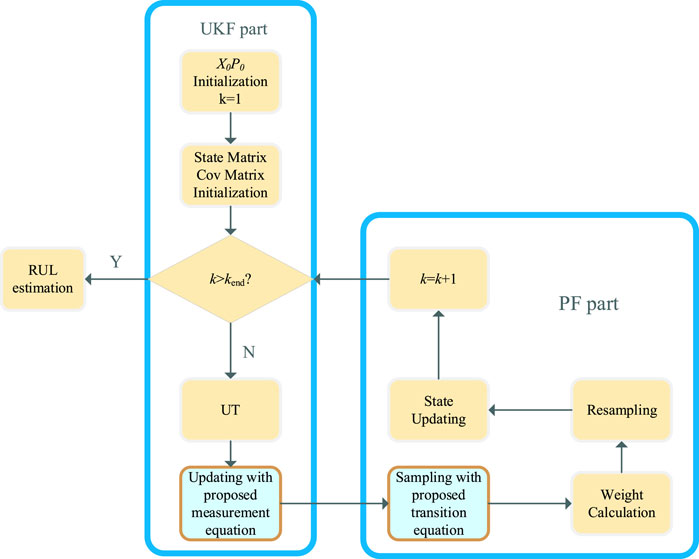
Chen et al. (2020b) proposed a second-order central difference particle filter (SCDPF). By optimizing the importance of the probability density function, the particle phenomenon of particle degeneracy can be solved. The maximum error and the RMSE of the SCDPF fitting method are very small, and the minimum values are 0.006102 Ah and 0.001599. Cong et al. (2020a) proposed an improved method for predicting the RUL of Li-ion batteries using an im-proved UPF Li(NiMnCo)O 2 cathode, to deal with the problem of capacity decay curve capacity diving in the future. The model includes a segmented processing technique that uses inflection point inspection and system noise sampling in the Gamma distribution. The improved UPF flowchart is shown in Figure 6.
Chen et al. (2020c) used a novel FRGM to update the state transition equation in UPF and used UPF to infer the indicator trend and realize RUL prediction. Developed an innovative Fractional Gray Model (FRGM) UPF framework. The absolute error of the FRGM-UPF frame does not exceed ten cycles. Zhang et al. (2018c) proposed an improved PF algorithm based on the UPF of linear optimization combined resampling (U-LOCR-PF). On the one hand, the UKF is used to generate the proposal distribution as an important function of particle filtering. On the other hand, the linear optimization combined resampling (LOCR) algorithm is used to overcome the lack of particle diversity. In Ref. Wang et al. (2016) first constructed a state-space model of Li-ion battery capacity to evaluate the capacity decline. Then, the spherical petri dish particle filter (SCPF) was introduced to solve the state-space model. A predictive method was formed to predict the RUL of Li-ion batteries. The main idea of SCPF is to use a Kalman filter based on spherical culture integration to provide the important function of a standard PF. Once the state-space model is determined, the state-space model is extrapolated to the specified failure threshold to infer the RUL of the Li-ion battery.
Others
Yan et al. (2017) proposed an online model parameter adaptation scheme, which is implemented by the recursive least square method with a forgetting factor. The uncertainty of the RUL prediction can be managed by adjusting the model noise through short-term prediction and correction loops. Long et al. (2020) proposed a Li-ion battery RUL estimation method based on improved particle swarm optimization (PSO) and the technique for order preference by similarity to ideal solution (TOPSIS). Use the moving average filter (MAF) to perform battery raw data filtering to obtain a smooth battery life decline curve. Jiao et al. (2020) proposed a new PF framework based on conditional variational autoencoder (CVAE) and reweighting strategy to alleviate degeneracy problems. Cong et al. (2020b) proposed a hybrid method considering error correction to predict the RUL of Li-ion batteries with reduced capacity. The improved empirical capacity attenuation model is combined with the improved UPF tracking to obtain the prediction results. Based on the error sequence prediction of the Gaussian Process Regression (GPR) algorithm, the error sequence of the fully integrated empirical mode decomposition (CEEMD) algorithm is decomposed into the data-driven part. The average absolute percentage error of predicting battery capacity degradation does not exceed 0.4%. Based on the electrochemical mechanism of capacity decay, Liu et al. (2019b) proposed an improved degradation model for Li-ion batteries, which takes into account the influence of circulating current. A genetic algorithm is applied to identify the inaitial values of model parameters. A data-driven framework based on particle filters is also designed to track changes in model parameters and states during the cycle. For RUL predictions, RMSE results are less than 40 cycles, and MAE results are less than 35 cycles, which is less than 8% of its cycle life.
Summary
The comparison of adaptive filter method parameters is shown in Table 2.
As shown in Table 2, the adaptive filtering method combines with other methods to improve the accuracy based on the traditional method. The maximum proportion of training data is 80% of the total life cycle. The maximum prediction error is 5%. The average training period is 57.71%. The average error is 2.6121%. The training period is relatively long. The input signal of the entire prediction algorithm is more complicated.
Stochastic Process Methods
Stochastic process methods are based on statistical theory and combined with other mathematical principles (Sierra et al., 2019). Statistics-driven methods are generally divided into three categories: bayesian estimation, GPR, and wiener process (WP). GPR is a data-driven method proposed by Williams and Rasmussen (Wang et al., 2020c). It is a new type of machine learning method based on Bayesian theory and statistical learning theory (Wen et al., 2018).
A battery model based on the Thevenin model is used, taking into account its advantages of low error, long-term testing, and accounting for polarization effects and transient analysis for power battery charging and discharging. The Kalman filter algorithm effectively reduces the influence of nonlinear equations and successfully realizes the SOC estimation of the lithium battery at the hole. The experimental results are more accurate, the experimental steps are simple and convenient, and the algorithm complexity is moderate. It has a certain reference value for the rational use and distribution of current power lithium batteries. However, in this method: the use of EKF will inevitably introduce linearization errors if the linearization of the battery is not established. Using this algorithm will cause the filter performance to drop so that the result will diverge, so if you want to improve the accuracy and avoid linearization errors, you need to consider other algorithms. Moreover, the charge-discharge efficiency η itself is advanced by the charge-discharge experiment, but the current of the power lithium battery is irregular when it is applied actually, which may exceed the set data and the estimated range in the experiment and bring errors.
Bayesian estimation requires the use of posterior prediction distributions for predictive inference, predicting the distribution of new, unobserved data points (Zhang et al., 2020b; Karimi Pour et al., 2021). Instead of a fixed point as a prediction, return the distribution of possible points (Wang et al., 2020d; Downey et al., 2019). GPR is suitable for dealing with complex regression problems, such as high dimensions, small samples, and nonlinearity (Johnen et al., 2020). WP is a typical random process, which belongs to the so-called independent incremental process. It starts with the theory and application of random processes (Eleftheroglou et al., 2019; Pang et al., 2021). WP can describe not only the monotonic degradation of equipment performance but also the non-monotonic degradation of equipment (Changhao et al., 2020; Hu et al., 2018; Xiaowei et al., 2019). The RUL prediction framework of the random process method is shown in Figure 7.
Bayesian Estimation
The Bayesian estimation uses the Bayes theorem to combine new evidence and previous prior probabilities to obtain new probabilities. It provides a method for calculating the probability of a hypothesis, based on the prior probability of the hypothesis, the probability of observing different data under a given hypothesis, and the observed data. Mosallam et al. (2016) proposed a two-stage data-driven RUL prediction method. The data-driven prediction method based on the Bayesian method can directly predict the remaining service life. In the offline phase, the unsupervised variable selection method is used to find variables that contain information about degradation behavior. In the online stage, the method uses the k-nearest neighbor classifier as the RUL predictor variable. Zhang et al. (2018d) proposed a novel Bayesian reliability analysis framework, which combines binary degradation data and life data. Combining the Bayesian method and Markov chain Monte Carlo (MCMC) simulation, the limited bivariate degradation data is integrated with the life data of other similar RLBs. Then perform reliability assessment and RUL prediction for PHM. The Bayesian nonparametric method of Richardson et al.
Tang et al. (2019a) produced technical novelty by appropriately using model migration technology to solve the battery problem. In the presence of noise measurement and modeling errors, the Bayesian Monte Carlo algorithm is applied to health prediction tasks. Based on 30 cycles of training data, the RMSE of the proposed algorithm is within 2.5%, while using only five cycles of data, it is within 5%. Liu et al. (2019c) proposed a deep learning integrated prediction method with uncertainty management based on Bayesian model averaging and long short-term memory network. The proposed BMA-LSTMN method en-sembled LSTMN sub-models trained from different sub-datasets and its accuracy is 0.923.
Tang et al. (2019b) proposed a migration-based framework for battery modeling, in which the effects of temperature and aging are regarded as uncertain factors. An accurate model of the new battery was established and migrated to the degraded battery through the Bayesian Monte Carlo method. For temperature changes as high as 40°C and capacity degradation as high as 20%, the typical voltage prediction error can be limited to 20 mV. Based on the accelerated aging model, Tang et al. (2019c) established a normal speed aging model through the migration process, and the migration factor was determined by the Bayesian Monte Carlo method and hierarchical resampling technology. The RMSE limit of the predicted aging trajectory is 1%, while the cyclic aging data is only 25%. Zhao et al. (2020) proposed an update method for the Li-ion battery RUL prediction model based on Bayesian simulator evaluation theory. Developed some uncertainty quantification methods, used a simulator to evaluate the statistical structure of the theory, and incorporated the bias function and the measurement error into the Bayesian model update in the form of GP. The modular Markov chain Monte Carlo method is used to update the model with multiple uncertain parameters. Because uncertainty is systematically considered in the inference process, reliable RUL predictions can be provided.
Gaussian Process Regression
Gaussian process regression is suitable for dealing with complex regression problems such as high dimensionality, small samples, and nonlinearity. Compared with neural networks and support vector machines, this method has the advantages of easy implementation, adaptive acquisition of hyperparameters, and probabilistic output. Yu et al. (2018) proposed a Li-ion battery RUL prediction method combining the wavelet denoising (WD) method and mixed Gaussian process function regression (HGPFR) model. Remove the original data noise. For the data repository, the relative error of most predictions is less than 7%. Compared with the same value of 6.7% of the HGPFR model, the confidence interval of the hybrid method for predicting RUL is 95%, and an accuracy of 2.2% can be obtained. Li et al. (2020c) proposed a new multi-time scale framework to calculate short-term SOH and predict long-term RUL. By analyzing part of the incremental capacity, four important features are extracted and input into Gaussian process regression. The nuclear modified Gaussian process is used to establish a short-term battery aging model, which is combined with nonlinear regression to predict the battery SOH. The long-term RUL predicted MAE and RMSE are less than 26 cycles. The error frequency of battery RUL is mainly concentrated in the range of 5–20 cycles. Tagade et al. (2020) proposed a matrix-variate Gaussian process algorithm to monitor the SOH and EOL predictions of Li-ion batteries. The Gaussian process is used to model the mapping between layers, and the matrix variable Gaussian distribution is used to model the correlation between nodes in a given layer. The algorithm predicts that the coefficient of determination for capacity and service life is greater than 0.9, and the average absolute error is less than 0.1 Richardson et al. (2019) using Gaussian process regression can predict the capacity attenuation under various usage conditions. In the best case, the standardized root means the square error is 4.3%.
Hu et al. (2020b) proposed a double Gaussian process regression model to predict the SOH during the entire life cycle of the battery pack and the RUL at the end of the life cycle. For RUL prediction, MaAE, MeAE, and RMSE are 2 cycles, 1 cycle, and 1 cycle respectively. The calculation time required is less than 5 s. Li et al. (2019e) proposed a new method of synergy between partial incremental capacity and Gaussian process regression to predict the health of the battery based on the double Gaussian process regression model. Using four different cycles of testing, the short-term SOH estimates that both MAEs and RMSEs are not more than 1%, and the long-term RUL predicts that both MAEs and RMSEs are within 23 cycles. Liu et al. (2019a), Liu and Chen (2019) proposed an RUL prediction method combining indirect health indicators (HIs) and multiple GPR models to achieve single-point, different-period RUL prediction. On the one hand, the three HIs extracted from the CC and CV charging process can effectively characterize the battery SOH. On the other hand, the fusion of the kernel function and multi-dimensional input is used to optimize the ground-penetrating radar model. For the long-term RUL prediction of the battery, the RMSE and MAE are no more than 10 cycles and 6 cycles, respectively.
Kang et al. (2020) proposed an RUL prediction method based on Fuzzy Evaluation Gaussian Process Regression (FE-GPR). Combined with the characteristics of the GPR method, the observation data is preprocessed through fuzzy evaluation. Use the Gravity Search Algorithm (GSA) and historical data to effectively combine to optimize the classification node. The GSA-AS method has strong data extraction capabilities and can more accurately realize RUL prediction. Moreover, GPR and finite element methods have effectively improved the accuracy of high-level small sample data prediction, and the small sample regression analysis value reached 0.739. Yu (2018) proposed a prediction method based on the combination of multi-scale logistic regression (LR) and GPR. Empirical model decomposition is used to extract the global degradation of battery SOH, local regeneration effects, and battery capacity time series fluctuations. An LR model with a variable moving window is provided to capture the overall degradation trend. A ground-penetrating radar with a lag vector can recursively estimate local regeneration and fluctuations. This design captures the degradation behavior of Li-ion batteries over time and reduces the impact of local regeneration phenomena.
Wiener Process Model
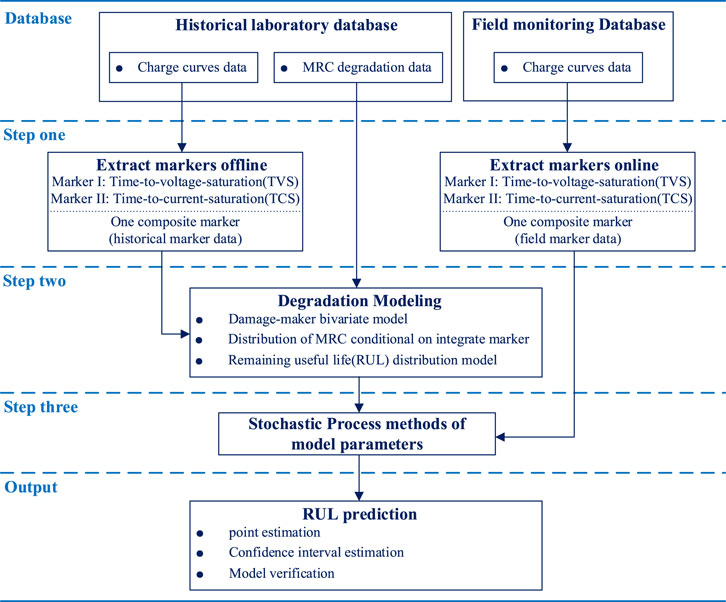
The Wiener process is a typical random process belonging to an independent incremental process. In any finite time, the change of the Wiener process obeys a normal distribution, and its variance increases linearly with the length of the time interval. Liao et al. (2021) established a multiphase degradation model with jumps based on the Wiener process to describe the multiphase degradation model. Under the Bayesian framework, prediction includes two stages, the offline stage, and the online stage. Feng et al. (2016) proposed a method that can use online tag data (TCS and TVS)to predict the RUL of Li-ion battery packs online without the need for additional capacity measurement. Based on the two-dimensional Wiener process, damage marking model and an RUL prediction model is established. Li et al. (2020d) proposed a sequential Bayesian method to update the random drift parameters in the Wiener process model. The historical degradation measurement is used to determine the initial model parameters based on the maximum likelihood estimation (MLE) method. Finally, the analytical expression of RUL distribution is derived based on the concept of the first passage time (FPT).
Wang et al. (2019b) established a general degradation model based on the nonlinear Wiener process to simultaneously characterize the inter-unit change, time change, measurement change, and nonlinearity in RUL estimation and derived the relevant RUL distribution in an explicit form. Shen et al. (2021) established a new state-space model and then introduced the UPF algorithm to post-update the model parameters and RUL distribution. The two-stage Wiener process model can well describe the degradation behavior of Li-ion batteries in different degradation stages and has high prediction accuracy and robustness. An odor-less particle filter algorithm is introduced to use the latest online measurements to adaptively update all the parameters in the model and the remaining service life allocation of Li-ion batteries. Zhai and Ye (2017) proposed a new adaptive Wiener process model, which uses Brownian motion for adaptive drift. A model estimation method based on maximum likelihood estimation is proposed, and RUL prediction is made based on this model. Based on KF technology, the update formula of implicit adaptive drift is derived, and the explicit distribution function of RUL is obtained.
Others
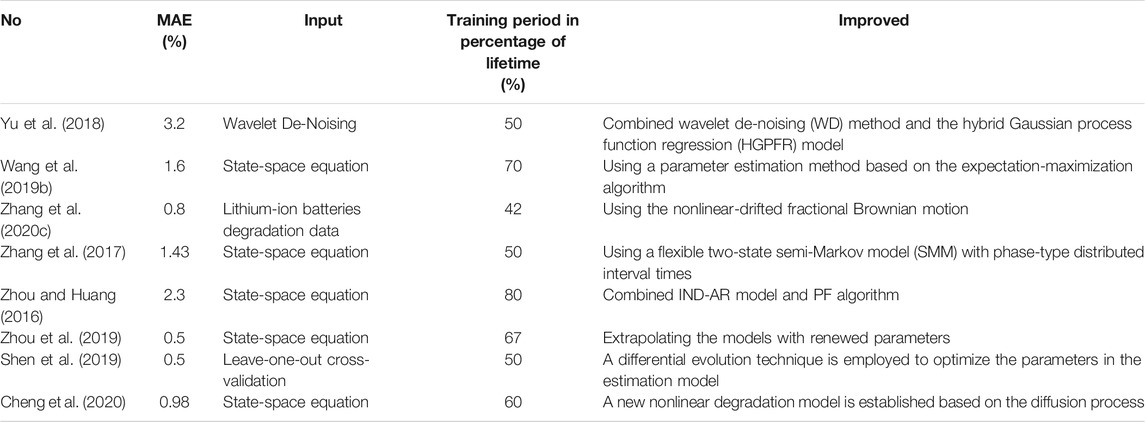
Zhang et al. (2020c)c proposed a prediction framework based on nonlinear drift score Brownian motion and multiple hidden state variables. All the parameters of the nonlinear function are defined as the specific hidden state variables of the Li-ion battery degradation model, and all the state measurement values are used to estimate the distribution of multiple hidden state variables after the fact through the tasteless particle filter algorithm. Zhang et al. (2019c) used a method based on feature extraction to estimate the state of health of the battery based on the charging voltage curve. The RLS method with variable forgetting factor can predict accurate RUL in the early stages of life, and the calculation time for each RUL prediction is about 0.3 s. After 300 cycles, the prediction error of most cycles is less than 10, and the 95% confidence interval of each prediction covers about 20 cycles. Zhang et al. (2020c) proposed an SLE model based on historical CM data and operating data, which is used for the MLE framework and the SMM model of the operating process with elastic degraded model parameter estimation. Consider the recovery time and the time dependence of the recovery time and random properties. The two-state semi-Markov model (SMM) with PHT distribution interval time has been used to model the random operation process. Zhang et al. (2019e) developed an RUL prediction method based on the Box-Cox transformation (BCT) and Monte Carlo (MC) simulation. This method can be implemented independently of offline training data. This method can reduce the acceleration time of the tested cells by 70–85%. Compared with the particle filtration method, it can save one to 3 months of acceleration time.
Zhou et al. (2016a), Zhou and Huang (2016) proposed a new method combining empirical mode decomposition (EMD) and autoregressive integrated moving average (ARIMA) models. EMD is used to decouple the global deterioration trend and capacity regeneration from the SOH time series and use it in the ARIMA model to predict the global deterioration trend and capacity regeneration respectively. Next, all the individual prediction results are added to obtain the comprehensive SOH prediction from which RUL is obtained. Ma et al. (2021) proposed a test optimization method based on prediction. The hybrid transfer learning method can best select the trained predictive model of historical test data and other formulas to help build a model of the target battery. With different formulations and test stop thresholds, it can reach an average accuracy of 89.18% and save 0.7–5.5 months.
Zhou et al. (2020b) developed a remaining service life estimation model based on k-nearest neighbor regression. The differential evolution technique is used to optimize the parameters in the estimation model. The average error of the remaining service life estimation result obtained by the developed method is 9 cycles, while the error of the best estimation is only 2 cycles, and the relative error is 0.5%. All these estimates are completed within 10 ms. Compared with particle filtering and support vector regression, the developed method reduces the estimated average error by 83.14 and 89.79%, respectively.
Zhou et al. (2019) proposed a new error correction gray prediction model. The proposed method uses the error correction factor ψ to eliminate the inherent error of the original grayscale model (GM) while retaining the original simplicity and rapid prototyping capabilities. Compared with the traditional GM, the accuracy can be improved by at least 11.7%, and for the optimized GM, the accuracy can reach 9.2%. Shen et al. (2019) proposed a method for predicting the remaining service life of Li-ion batteries based on a stochastic model. A new nonlinear degradation model was established based on the diffusion process to characterize the degradation process of Li-ion batteries. Use the maximum likelihood estimation method and historical battery degradation data to estimate the unknown parameters of the model. Beganovic and Söffker (2019) proposed a method to estimate LIB aging indicators using acoustic emission measurements. Features selected from acoustic emission (AE) measurements are considered as model input. The proposed method provides the possibility of obtaining reliable information about the current RUL/SOH without needing to understand the basic physical processes that occur in LIB. Cheng et al. (2020) proposed an inductive ordered weighted average (iowa) operator based on verification data, which realized the weight distribution that changes over time, that is, the V-IOWA operator. By summing the weighted prediction results of each member prediction algorithm, the overall prediction result is finally obtained. In terms of root mean square error, average absolute error, and average absolute percentage error, it reduced the prognostic error by 5.08, 6.38, and 4.42%, respectively.
Summary
The comparison of stochastic process methods parameters is shown in Table 3.
As shown in Table 3, the stochastic process method also improves the original method to a certain extent. The maximum proportion of training data is 80% of the total life cycle. The maximum prediction error is 3.2%. The average training period is 58.63%. The average error is 1.4138%. The input signal is complex and the training period is relatively long.
Comparison
Through the above description, we comprehensively compare the accuracy of the three methods, the complexity of the input feature quantity, and the length of the prediction period. According to the calculation of the average training period and average prediction error of the three methods, the average accuracy of machine learning is 32.02% higher than the average of the other two methods, and the prediction period is 9.87% shorter than the average of the other two methods. The advantages and disadvantages of each method are summarized in Table 4.
It can be seen from the above comparison that the application of machine learning to predict RUL has the advantages of high accuracy, simple input, and a relatively short training period. In short, the advantages of the artificial intelligence methods are that it does not require a data model, the algorithm is simple and feasible, and the algorithm is the best solution for nonlinear systems. The advantage of the filtering technique method is that it can be used in any form of the state-space model. The disadvantage is that it requires a data model (state-space model). The advantage of the stochastic process method is that it considers the time dependence of the degradation process and describes the uncertainty of predictable results. The disadvantage is high computational complexity and many uncertain factors.
Conclusion
This paper classifies several adaptive Li-ion battery aging models proposed in the literature. Specific criteria are defined to evaluate the accuracy and computational cost of such models. According to the analysis of the results in the research literature and publications according to these standards, machine learning is considered to be the most suitable algorithm, with relatively robust and computationally acceptable predictive ability. The average accuracy of machine learning is 32.02% higher than the average of the other two methods, and the prediction period is 9.87% shorter than the average of the other two methods.
Driven by machine learning algorithms and artificial intelligence technology, data-driven modeling has made encouraging progress. However, machine learning algorithms rely on large amounts of data, and improving the accuracy and performance of predictions will increase computing time. The continuous changes in the internal and external environmental conditions of the battery and the generalization problem of the prediction method itself are still difficult to accurately predict the remaining life in practical applications. In the future, prediction accuracy can be improved by integrating cloud computing platforms and machine learning technology. At the same time, this technology can make predictions without prior knowledge of the system, reducing the data dependence of prediction methods. Data-driven machine learning based on big data and cloud computing platforms seems to be the most promising method for advanced battery modeling in the future.
Author Contributions
Conceptualization, SW; SJ; methodology, SW; SJ; software, SW; SJ; DD and CF; formal analysis, SW; SJ; investigation, SWang; SJ; resources, SW; data curation, SW; SJ; writing―original draft preparation, SJ; writing―review and editing, SW; SJ; DD and CF; visualization, SW; SJ; supervision, SW; project administration, SW; funding acquisition, SW. All authors have read and agreed to the published version of the manuscript.
Funding
The article was supported by National Natural Science Foundation of China (No. 61801407), China Scholarship Council (No. 201908515099), Fund of Robot Technology Used for Special Environment Key Laboratory of Sichuan Province (No. 18kftk03) and Natural Science Foundation of Southwest University of Science and Technology (No.17zx7110, 18zx7145). Thanks to the sponsors.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahwiadi, M., and Wang, W. (2019). An Enhanced Mutated Particle Filter Technique for System State Estimation and Battery Life Prediction. IEEE Trans. Instrum. Meas. 68 (3), 923–935. doi:10.1109/TIM.2018.2853900
Beganovic, N., and Söffker, D. (2019). Estimation of Remaining Useful Lifetime of Lithium-Ion Battery Based on Acoustic Emission Measurements. J. Energ. Resour. Technol. Trans. ASME 141 (4), 1–10. doi:10.1115/1.4042234
Ben Ali, J., Azizi, C., Saidi, L., Bechhoefer, E., and Benbouzid, M. (2020). Reliable State of Health Condition Monitoring of Li-Ion Batteries Based on Incremental Support Vector Regression with Parameters Optimization. Proc. Inst. Mech. Eng. J. Syst. Control. Eng., 8 (1), 1–12. doi:10.1177/0959651820950849
Cadini, F., Sbarufatti, C., Cancelliere, F., and Giglio, M. (2019). State-of-life Prognosis and Diagnosis of Lithium-Ion Batteries by Data-Driven Particle Filters. Appl. Energ. 235, 661–672. doi:10.1016/j.apenergy.2018.10.095
Chang, Y., and Fang, H. (2019). A Hybrid Prognostic Method for System Degradation Based on Particle Filter and Relevance Vector Machine. Reliability Eng. Syst. Saf. 186, 51–63. doi:10.1016/j.ress.2019.02.011
Changhao, W., Zhiguo, L., Tang, S., Sun, X., and Si, X. (2020). Remaining Useful Life Prediction Under Imperfect Prior Degradation Information. IEEE Access 8, 189262–189275. doi:10.1109/access.2020.3030632
Chen, L., An, J., Wang, H., Zhang, M., and Pan, H. (2020). Remaining Useful Life Prediction for Lithium-Ion Battery by Combining an Improved Particle Filter with Sliding-Window gray Model. Energ. Rep. 6, 2086–2093. doi:10.1016/j.egyr.2020.07.026
Chen, L., Chen, J., Wang, H., Wang, Y., An, J., Yang, R., et al. (2020). Remaining Useful Life Prediction of Battery Using a Novel Indicator and Framework with Fractional Grey Model and Unscented Particle Filter. IEEE Trans. Power Electron. 35, 5850–5859. doi:10.1109/TPEL.2019.2952620
Chen, W., Liang, J., Yang, Z., and Li, G. (2019). A Review of Lithium-Ion Battery for Electric Vehicle Applications and beyond. Energ. Proced. 158, 4363–4368. doi:10.1016/j.egypro.2019.01.783
Chen, Y., He, Y., Li, Z., Chen, L., and Zhang, C. (2020). Remaining Useful Life Prediction and State of Health Diagnosis of Lithium-Ion Battery Based on Second-Order central Difference Particle Filter. IEEE Access 8, 37305–37313. doi:10.1109/ACCESS.2020.2974401
Cheng, Y., Song, D., Wang, Z., Lu, C., and Zerhouni, N. (2020). An Ensemble Prognostic Method for Lithium-Ion Battery Capacity Estimation Based on Time-Varying Weight Allocation. Appl. Energ. 266, 114817. doi:10.1016/j.apenergy.2020.114817
Chinomona, B., Chung, C., Chang, L.-K., Su, W.-C., and Tsai, M.-C. (2020). Long Short-Term Memory Approach to Estimate Battery Remaining Useful Life Using Partial Data. IEEE Access 8, 165419–165431. doi:10.1109/access.2020.3022505
Chu, A., Allam, A., Cordoba Arenas, A., Rizzoni, G., and Onori, S. (2020). Stochastic Capacity Loss and Remaining Useful Life Models for Lithium-Ion Batteries in Plug-In Hybrid Electric Vehicles. J. Power Sourc. 478 (April), 228991. doi:10.1016/j.jpowsour.2020.228991
Cong, X., Zhang, C., Jiang, J., Zhang, W., and Jiang, Y. (2020). A Hybrid Method for the Prediction of the Remaining Useful Life of Lithium-Ion Batteries with Accelerated Capacity Degradation. IEEE Trans. Veh. Technol. 69 (11), 12775–12785. doi:10.1109/TVT.2020.3024019
Cong, X., Zhang, C., Jiang, J., Zhang, W., Jiang, Y., and Jia, X. (2020). An Improved Unscented Particle Filter Method for Remaining Useful Life Prognostic of Lithium-Ion Batteries with Li(NiMnCo)O2 Cathode with Capacity Diving. IEEE Access 8, 58717–58729. doi:10.1109/ACCESS.2020.2978245
Corno, M., and Pozzato, G. (2020). Active Adaptive Battery Aging Management for Electric Vehicles. IEEE Trans. Veh. Technol. 69, 258–269. doi:10.1109/TVT.2019.2940033
Cui, X., and Hu, T. (2020). State of Health Diagnosis and Remaining Useful Life Prediction for Lithium-Ion Battery Based on Data Model Fusion Method. IEEE Access 8, 207298–207307. doi:10.1109/access.2020.3038182
Dong, G., Chen, Z., Wei, J., and Ling, Q. (2018). Battery Health Prognosis Using Brownian Motion Modeling and Particle Filtering. IEEE Trans. Ind. Electron. 65, 8646–8655. doi:10.1109/TIE.2018.2813964
Dong, G., Han, W., and Wang, Y. (2020). Dynamic Bayesian Network Based Lithium-Ion Battery Health Prognosis for Electric Vehicles. IEEE Trans. Ind. Electron. 68 (11), 10949–10958. doi:10.1109/TIE.2020.3034855
Dong, G., Yang, F., Wei, Z., Wei, J., and Tsui, K.-L. (2020). Data-Driven Battery Health Prognosis Using Adaptive Brownian Motion Model. IEEE Trans. Ind. Inf. 16 (7), 4736–4746. doi:10.1109/TII.2019.2948018
Downey, A., Lui, Y.-H., Hu, C., Laflamme, S., and Hu, S. (2019). Physics-based Prognostics of Lithium-Ion Battery Using Non-linear Least Squares with Dynamic Bounds. Reliability Eng. Syst. Saf. 182, 1–12. doi:10.1016/j.ress.2018.09.018–12
Du, J., Zhang, W., Zhang, C., and Zhou, X. (2018). Battery Remaining Useful Life Prediction under Coupling Stress Based on Support Vector Regression. Energ. Proced. 152, 538–543. doi:10.1016/j.egypro.2018.09.207
Duong, P. L. T., and Raghavan, N. (2018). Heuristic Kalman Optimized Particle Filter for Remaining Useful Life Prediction of Lithium-Ion Battery. Microelectron. Reliab. 81, 232–243. doi:10.1016/j.microrel.2017.12.028
El Mejdoubi, A., Chaoui, H., Gualous, H., Van Den Bossche, P., Omar, N., and Van Mierlo, J. (2019). Lithium-ion Batteries Health Prognosis Considering Aging Conditions. IEEE Trans. Power Electron. 34, 6834–6844. doi:10.1109/TPEL.2018.2873247
Eleftheroglou, N., Mansouri, S. S., Loutas, T., Karvelis, P., Georgoulas, G., Nikolakopoulos, G., et al. (2019). Intelligent Data-Driven Prognostic Methodologies for the Real-Time Remaining Useful Life until the End-Of-Discharge Estimation of the Lithium-Polymer Batteries of Unmanned Aerial Vehicles with Uncertainty Quantification. Appl. Energ. 254, 113677. doi:10.1016/j.apenergy.2019.113677
Fan, J., Fan, J., Liu, F., Qu, J., and Li, R. (2019). A Novel Machine Learning Method Based Approach for Li-Ion Battery Prognostic and Health Management. IEEE Access 7, 160043–160061. doi:10.1109/ACCESS.2019.2947843
Feng, J., Kvam, P., and Tang, Y. (2016). Remaining Useful Lifetime Prediction Based on the Damage-Marker Bivariate Degradation Model: A Case Study on Lithium-Ion Batteries Used in Electric Vehicles. Eng. Fail. Anal. 70, 323–342. doi:10.1016/j.engfailanal.2016.04.014
Gao, Y., Zhang, X., Guo, B., Zhu, C., Wiedemann, J., Wang, L., et al. (2020). Health-Aware Multiobjective Optimal Charging Strategy with Coupled Electrochemical-Thermal-Aging Model for Lithium-Ion Battery. IEEE Trans. Ind. Inf. 16, 3417–3429. doi:10.1109/TII.2019.2935326
Gou, B., Xu, Y., and Feng, X. (2020). State-of-Health Estimation and Remaining-Useful-Life Prediction for Lithium-Ion Battery Using a Hybrid Data-Driven Method. IEEE Trans. Veh. Technol. 69 (10), 10854–10867. doi:10.1109/TVT.2020.3014932
Guha, A., and Patra, A. (2018). Online Estimation of the Electrochemical Impedance Spectrum and Remaining Useful Life of Lithium-Ion Batteries. IEEE Trans. Instrum. Meas. 67 (8), 1836–1849. doi:10.1109/TIM.2018.2809138
Guha, A., and Patra, A. (2018). State of Health Estimation of Lithium-Ion Batteries Using Capacity Fade and Internal Resistance Growth Models. IEEE Trans. Transp. Electrific. 4 (1), 135–146. doi:10.1109/TTE.2017.2776558
Hong, J., Lee, D., Jeong, E.-R., and Yi, Y. (2020). Towards the swift Prediction of the Remaining Useful Life of Lithium-Ion Batteries with End-To-End Deep Learning. Appl. Energ. 278, 115646. doi:10.1016/j.apenergy.2020.115646
Hu, C., Ye, H., Jain, G., and Schmidt, C. (2018). Remaining Useful Life Assessment of Lithium-Ion Batteries in Implantable Medical Devices. J. Power Sourc. 375, 118–130. doi:10.1016/j.jpowsour.2017.11.056
Hu, X., Che, Y., Lin, X., and Deng, Z. (2020). Health Prognosis for Electric Vehicle Battery Packs: A Data-Driven Approach. IEEE ASME Trans. Mechatron. 25 (6), 2622–2632. doi:10.1109/TMECH.2020.2986364
Hu, X., Xu, L., Lin, X., and Pecht, M. (2020). Battery Lifetime Prognostics. Joule 4, 310–346. doi:10.1016/j.joule.2019.11.018
Hui, Y., Li, M., Downey, A., Shen, S., Nemani, V. P., and Ye, H. (2021). Physics-based Prognostics of Implantable-Grade Lithium-Ion Battery for Remaining Useful Life Prediction. J. Power Sourc. 485, 229327. doi:10.1016/j.jpowsour.2020.229327
Ji, Y., Chen, Z., Shen, Y., Yang, K., Wang, Y., and Cui, J. (2021). An RUL Prediction Approach for Lithium-Ion Battery Based on SADE-MESN. Appl. Soft Comput. 104, 107195. doi:10.1016/j.asoc.2021.107195
Jiao, R., Peng, K., and Dong, J. (2020). Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Conditional Variational Autoencoders-Particle Filter. IEEE Trans. Instrum. Meas. 69 (11), 8831–8843. doi:10.1109/TIM.2020.2996004
Jinlei, S., Lei, P., Ruihang, L., Qian, M., Chuanyu, T., and Tianru, W. (2019). Economic Operation Optimization for 2nd Use Batteries in Battery Energy Storage Systems. IEEE Access 7, 41852–41859. doi:10.1109/ACCESS.2019.2902402
Johnen, M., Schmitz, C., Kateri, M., and Kamps, U. (2020). Fitting Lifetime Distributions to Interval Censored Cyclic-Aging Data of Lithium-Ion Batteries. Comput. Ind. Eng. 143, 106418. doi:10.1016/j.cie.2020.106418
Kang, W., Xiao, J., Xiao, M., Hu, Y., Zhu, H., and Li, J. (2020). Research on Remaining Useful Life Prognostics Based on Fuzzy Evaluation-Gaussian Process Regression Method. IEEE Access 8, 71965–71973. doi:10.1109/ACCESS.2020.2982223
Karimi Pour, F., Theilliol, D., Puig, V., and Cembrano, G. (2021). Health-aware Control Design Based on Remaining Useful Life Estimation for Autonomous Racing Vehicle. ISA Trans. 113, 196–209. doi:10.1016/j.isatra.2020.03.032
Khodadadi Sadabadi, K., Jin, X., and Rizzoni, G. (2021). Prediction of Remaining Useful Life for a Composite Electrode Lithium Ion Battery Cell Using an Electrochemical Model to Estimate the State of Health. J. Power Sourc. 481, 228861. doi:10.1016/j.jpowsour.2020.228861
Khumprom, P., and Yodo, N. (2019). A Data-Driven Predictive Prognostic Model for Lithium-Ion Batteries Based on a Deep Learning Algorithm. Energies 12, 660. doi:10.3390/en12040660
Kim, S., Park, H. J., Choi, J.-H., and Kwon, D. (2021). A Novel Prognostics Approach Using Shifting Kernel Particle Filter of Li-Ion Batteries under State Changes. IEEE Trans. Ind. Electron. 68, 3485–3493. doi:10.1109/tie.2020.2978688
Li, F., Zhang, L., Chen, B., Gao, D., Cheng, Y., Zhang, X., et al. (2020). An Optimal Stacking Ensemble for Remaining Useful Life Estimation of Systems under Multi-Operating Conditions. IEEE Access 8, 31854–31868. doi:10.1109/ACCESS.2020.2973500
Li, P., Zhang, Z., Xiong, Q., Ding, B., Hou, J., Luo, D., et al. (2020). State-of-health Estimation and Remaining Useful Life Prediction for the Lithium-Ion Battery Based on a Variant Long Short Term Memory Neural Network. J. Power Sourc. 459, 228069. doi:10.1016/j.jpowsour.2020.228069
Li, T., Pei, H., Pang, Z., Si, X., and Zheng, J. (2020). A Sequential Bayesian Updated Wiener Process Model for Remaining Useful Life Prediction. IEEE Access 8, 5471–5480. doi:10.1109/ACCESS.2019.2962502
Li, W., Jiao, Z., Du, L., Fan, W., and Zhu, Y. (2019). An Indirect RUL Prognosis for Lithium-Ion Battery under Vibration Stress Using Elman Neural Network. Int. J. Hydrogen Energ. 44 (23), 12270–12276. doi:10.1016/j.ijhydene.2019.03.101
Li, X., Wang, Z., and Yan, J. (2019). Prognostic Health Condition for Lithium Battery Using the Partial Incremental Capacity and Gaussian Process Regression. J. Power Sourc. 421, 56–67. doi:10.1016/j.jpowsour.2019.03.008
Li, X., Yuan, C., and Wang, Z. (2020). Multi-time-scale Framework for Prognostic Health Condition of Lithium Battery Using Modified Gaussian Process Regression and Nonlinear Regression. J. Power Sourc. 467 (April), 228358. doi:10.1016/j.jpowsour.2020.228358
Li, X., Zhang, L., Wang, Z., and Dong, P. (2019). Remaining Useful Life Prediction for Lithium-Ion Batteries Based on a Hybrid Model Combining the Long Short-Term Memory and Elman Neural Networks. J. Energ. Storage 21, 510–518. doi:10.1016/j.est.2018.12.011
Li, Z., Fang, H., and Yan, Y. (2019). “An Ensemble Hybrid Model with Outlier Detection for Prediction of Lithium-Ion Battery Remaining Useful Life,” in Chinese Control And Decision Conference (CCDC), 2630–2635. doi:10.1109/CCDC.2019.8832623
Liao, G., Yin, H., Chen, M., and Lin, Z. (2021). Remaining Useful Life Prediction for Multi-phase Deteriorating Process Based on Wiener Process. Reliability Eng. Syst. Saf. 207, 107361. doi:10.1016/j.ress.2020.107361
Lin, C.-P., Cabrera, J., Yang, F., Ling, M.-H., Tsui, K.-L., and Bae, S.-J. (2020). Battery State of Health Modeling and Remaining Useful Life Prediction through Time Series Model. Appl. Energ. 275, 115338. doi:10.1016/j.apenergy.2020.115338
Lipu, M. S. H., Hannan, M. A., Hussain, A., Hoque, M. M., Ker, P. J., Saad, M. H. M., et al. (2018). A Review of State of Health and Remaining Useful Life Estimation Methods for Lithium-Ion Battery in Electric Vehicles: Challenges and Recommendations. J. Clean. Prod. 205, 115–133. doi:10.1016/j.jclepro.2018.09.065
Liu, C., Wang, Y., and Chen, Z. (2019). Degradation Model and Cycle Life Prediction for Lithium-Ion Battery Used in Hybrid Energy Storage System. Energy 166, 796–806. doi:10.1016/j.energy.2018.10.131
Liu, H., Chen, F., Tong, Y., Wang, Z., Yu, X., and Huang, R. (2020). Impacts of Driving Conditions on EV Battery Pack Life Cycle. World Electr. Veh. J. 11, 17. doi:10.3390/wevj11010017
Liu, J., and Chen, Z. (2019). Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Health Indicator and Gaussian Process Regression Model. IEEE Access 7, 39474–39484. doi:10.1109/ACCESS.2019.2905740
Liu, K., Hu, X., Wei, Z., Li, Y., and Jiang, Y. (2019). Modified Gaussian Process Regression Models for Cyclic Capacity Prediction of Lithium-Ion Batteries. IEEE Trans. Transp. Electrific. 5, 1225–1236. doi:10.1109/TTE.2019.2944802
Liu, K., Li, Y., Hu, X., Lucu, M., and Widanage, W. D. (2020). Gaussian Process Regression with Automatic Relevance Determination Kernel for Calendar Aging Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Inf. 16, 3767–3777. doi:10.1109/TII.2019.2941747
Liu, K., Shang, Y., Ouyang, Q., and Widanage, W. D. (2021). A Data-Driven Approach with Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-Ion Battery. IEEE Trans. Ind. Electron. 68 (4), 3170–3180. doi:10.1109/TIE.2020.2973876
Liu, Q., Zhang, J., Li, K., and Lv, C. (2020). The Remaining Useful Life Prediction by Using Electrochemical Model in the Particle Filter Framework for Lithium-Ion Batteries. IEEE Access 8, 126661–126670. doi:10.1109/ACCESS.2020.3006157
Liu, Y., Zhao, G., and Peng, X. (2019). Deep Learning Prognostics for Lithium-Ion Battery Based on Ensembled Long Short-Term Memory Networks. IEEE Access 7, 155130–155142. doi:10.1109/ACCESS.2019.2937798
Liu, Z., Sun, G., Bu, S., Han, J., Tang, X., and Pecht, M. (2017). Particle Learning Framework for Estimating the Remaining Useful Life of Lithium-Ion Batteries. IEEE Trans. Instrum. Meas. 66 (2), 280–293. doi:10.1109/TIM.2016.2622838
Long, B., Gao, X., Li, P., and Liu, Z. (2020). Multi-Parameter Optimization Method for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Access 8, 142557–142570. doi:10.1109/ACCESS.2020.3011625
Lucu, M., Martinez-Laserna, E., Gandiaga, I., and Camblong, H. (2018). A Critical Review on Self-Adaptive Li-Ion Battery Ageing Models. J. Power Sourc. 401, 85–101. doi:10.1016/j.jpowsour.2018.08.064
Lyu, Z., Gao, R., and Chen, L. (2021). Li-Ion Battery State of Health Estimation and Remaining Useful Life Prediction through a Model-Data-Fusion Method. IEEE Trans. Power Electron. 36 (6), 6228–6240. doi:10.1109/TPEL.2020.3033297
Ma, G., Zhang, Y., Cheng, C., Zhou, B., Hu, P., and Yuan, Y. (2019). Remaining Useful Life Prediction of Lithium-Ion Batteries Based on False Nearest Neighbors and a Hybrid Neural Network. Appl. Energ. 253, 113626. doi:10.1016/j.apenergy.2019.113626
Ma, J., Shang, P., Zou, X., Ma, N., Ding, Y., Su, Y., et al. (2020). Remaining Useful Life Transfer Prediction and Cycle Life Test Optimization for Different Formula Li-Ion Power Batteries Using a Robust Deep Learning Method. IFAC-PapersOnLine 53 (3), 54–59. doi:10.1016/j.ifacol.2020.11.064
Ma, J., Shang, P., Zou, X., Ma, N., Ding, Y., Sun, J., et al. (2021). A Hybrid Transfer Learning Scheme for Remaining Useful Life Prediction and Cycle Life Test Optimization of Different Formulation Li-Ion Power Batteries. Appl. Energ. 282, 116167. doi:10.1016/j.apenergy.2020.116167
Ma, J., Xu, S., Shang, P., ding, Y., Qin, W., Cheng, Y., et al. (2020). Cycle Life Test Optimization for Different Li-Ion Power Battery Formulations Using a Hybrid Remaining-Useful-Life Prediction Method. Appl. Energ. 262, 114490. doi:10.1016/j.apenergy.2020.114490
Ma, Y., Chen, Y., Zhou, X., and Chen, H. (2019). Remaining Useful Life Prediction of Lithium-Ion Battery Based on Gauss-Hermite Particle Filter. IEEE Trans. Contr. Syst. Technol. 27, 1788–1795. doi:10.1109/TCST.2018.2819965
Mosallam, A., Medjaher, K., and Zerhouni, N. (2016). Data-driven Prognostic Method Based on Bayesian Approaches for Direct Remaining Useful Life Prediction. J. Intell. Manuf. 27, 1037–1048. doi:10.1007/s10845-014-0933-4
Motaqi, A., and Mosavi, M. R. (2020). Blind and Task-ware Multi-Cell Battery Management System. Eng. Sci. Technol. Int. J. 23 (3), 544–554. doi:10.1016/j.jestch.2019.07.005
Pang, Z., Si, X., Hu, C., Du, D., and Pei, H. (2021). A Bayesian Inference for Remaining Useful Life Estimation by Fusing Accelerated Degradation Data and Condition Monitoring Data. Reliability Eng. Syst. Saf. 208, 107341. doi:10.1016/j.ress.2020.107341
Park, K., Choi, Y., Choi, W. J., Ryu, H.-Y., and Kim, H. (2020). LSTM-Based Battery Remaining Useful Life Prediction with Multi-Channel Charging Profiles. IEEE Access 8, 20786–20798. doi:10.1109/ACCESS.2020.2968939
Patil, M. A., Tagade, P., Hariharan, K. S., Kolake, S. M., Song, T., Yeo, T., et al. (2015). A Novel Multistage Support Vector Machine Based Approach for Li Ion Battery Remaining Useful Life Estimation. Appl. Energ. 159, 285–297. doi:10.1016/j.apenergy.2015.08.119
Peng, J., Zhou, Z., Wang, J., Wu, D., and Guo, Y. (2019). Residual Remaining Useful Life Prediction Method for Lithium-Ion Batteries in Satellite with Incomplete Healthy Historical Data. IEEE Access 7, 127788–127799. doi:10.1109/ACCESS.2019.2938060
Pugalenthi, K., Park, H., and Raghavan, N. (2020). Piecewise Model-Based Online Prognosis of Lithium-Ion Batteries Using Particle Filters. IEEE Access 8, 153508–153516. doi:10.1109/ACCESS.2020.3017810
Pugalenthi, K., and Raghavan, N. (2018). A Holistic Comparison of the Different Resampling Algorithms for Particle Filter Based Prognosis Using Lithium Ion Batteries as a Case Study. Microelectron. Reliab. 91, 160–169. doi:10.1016/j.microrel.2018.08.007
Qi, N., Dai, K., Yi, F., Wang, X., You, Z., and Zhao, J. (2019). An Adaptive Energy Management Strategy to Extend Battery Lifetime of Solar Powered Wireless Sensor Nodes. IEEE Access 7, 88289–88300. doi:10.1109/ACCESS.2019.2919986
Qiao, J., Liu, X., and Chen, Z. (2020). Prediction of the Remaining Useful Life of Lithium-Ion Batteries Based on Empirical Mode Decomposition and Deep Neural Networks. IEEE Access 8, 42760–42767. doi:10.1109/ACCESS.2020.2977429
Qiu, X., Wu, W., and Wang, S. (2020). Remaining Useful Life Prediction of Lithium-Ion Battery Based on Improved Cuckoo Search Particle Filter and a Novel State of Charge Estimation Method. J. Power Sourc. 450, 227700. doi:10.1016/j.jpowsour.2020.227700
Qu, J., Liu, F., Ma, Y., and Fan, J. (2019). A Neural-Network-Based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 7, 87178–87191. doi:10.1109/ACCESS.2019.2925468
Ren, L., Dong, J., Wang, X., Meng, Z., Zhao, L., and Deen, M. J. (2021). A Data-Driven Auto-CNN-LSTM Prediction Model for Lithium-Ion Battery Remaining Useful Life. IEEE Trans. Ind. Inf. 17 (5), 3478–3487. doi:10.1109/tii.2020.3008223
Richardson, R. R., Osborne, M. A., and Howey, D. A. (2019). Battery Health Prediction under Generalized Conditions Using a Gaussian Process Transition Model. J. Energ. Storage 23, 320–328. doi:10.1016/j.est.2019.03.022
She, C., Wang, Z., Sun, F., Liu, P., and Zhang, L. (2020). Battery Aging Assessment for Real-World Electric Buses Based on Incremental Capacity Analysis and Radial Basis Function Neural Network. IEEE Trans. Ind. Inf. 16, 3345–3354. doi:10.1109/TII.2019.2951843
Shen, D., Wu, L., Kang, G., Guan, Y., and Peng, Z. (2021). A Novel Online Method for Predicting the Remaining Useful Life of Lithium-Ion Batteries Considering Random Variable Discharge Current. Energy 218, 119490. doi:10.1016/j.energy.2020.119490
Shen, D., Xu, T., Wu, L., and Guan, Y. (2019). Research on Degradation Modeling and Life Prediction Method of Lithium-Ion Battery in Dynamic Environment. IEEE Access 7, 130638–130649. doi:10.1109/ACCESS.2019.2929177
Shi, Y., Xu, B., Tan, Y., Kirschen, D., and Zhang, B. (2019). Optimal Battery Control under Cycle Aging Mechanisms in Pay for Performance Settings. IEEE Trans. Automat. Contr. 64, 2324–2339. doi:10.1109/TAC.2018.2867507
Sierra, G., Orchard, M., Goebel, K., and Kulkarni, C. (2019). Battery Health Management for Small-Size Rotary-wing Electric Unmanned Aerial Vehicles: An Efficient Approach for Constrained Computing Platforms. Reliability Eng. Syst. Saf. 182, 166–178. doi:10.1016/j.ress.2018.04.030
Song, Y., Liu, D., Hou, Y., Yu, J., and Peng, Y. (2018). Satellite Lithium-Ion Battery Remaining Useful Life Estimation with an Iterative Updated RVM Fused with the KF Algorithm. Chin. J. Aeronautics 31, 31–40. doi:10.1016/j.cja.2017.11.010
Song, Y., Liu, D., Yang, C., and Peng, Y. (2017). Data-driven Hybrid Remaining Useful Life Estimation Approach for Spacecraft Lithium-Ion Battery. Microelectron. Reliab. 75, 1. doi:10.1016/j.microrel.2017.06.045
Sun, T., Xia, B., Liu, Y., Lai, Y., Zheng, W., Wang, H., et al. (2019). A Novel Hybrid Prognostic Approach for Remaining Useful Life Estimation of Lithium-Ion Batteries. Energies 12, 3678. doi:10.3390/en12193678
Sun, X., Zhong, K., and Han, M. (2021). A Hybrid Prognostic Strategy with Unscented Particle Filter and Optimized Multiple Kernel Relevance Vector Machine for Lithium-Ion Battery. Measurement 170, 108679. doi:10.1016/j.measurement.2020.108679
Sun, Y., Hao, X., Pecht, M., and Zhou, Y. (2018). Remaining Useful Life Prediction for Lithium-Ion Batteries Based on an Integrated Health Indicator. Microelectron. Reliab. 88-90, 1189–1194. doi:10.1016/j.microrel.2018.07.047
Tagade, P., Hariharan, K. S., Ramachandran, S., Khandelwal, A., Naha, A., Kolake, S. M., et al. (2020). Deep Gaussian Process Regression for Lithium-Ion Battery Health Prognosis and Degradation Mode Diagnosis. J. Power Sourc. 445, 227281. doi:10.1016/j.jpowsour.2019.227281
Tang, X., Liu, K., Wang, X., Gao, F., MacRo, J., and Widanage, W. D. (2020). Model Migration Neural Network for Predicting Battery Aging Trajectories. IEEE Trans. Transp. Electrific. 6, 363–374. doi:10.1109/TTE.2020.2979547
Tang, X., Wang, Y., Zou, C., Yao, K., Xia, Y., and Gao, F. (2019). A Novel Framework for Lithium-Ion Battery Modeling Considering Uncertainties of Temperature and Aging. Energ. Convers. Manage. 180, 162–170. doi:10.1016/j.enconman.2018.10.082
Tang, X., Yao, K., Zou, C., Liu, B., and Gao, F. (2019). Predicting Battery Aging Trajectory via a Migrated Aging Model and Bayesian Monte Carlo Method. Energ. Proced. 158, 2456–2461. doi:10.1016/j.egypro.2019.01.320
Tang, X., Zou, C., Yao, K., Lu, J., Xia, Y., and Gao, F. (2019). Aging Trajectory Prediction for Lithium-Ion Batteries via Model Migration and Bayesian Monte Carlo Method. Appl. Energ. 254, 113591. doi:10.1016/j.apenergy.2019.113591
Tian, H., Qin, P., Li, K., and Zhao, Z. (2020). A Review of the State of Health for Lithium-Ion Batteries: Research Status and Suggestions. J. Clean. Prod. 261, 120813. doi:10.1016/j.jclepro.2020.120813
Wang, D., Kong, J.-z., Yang, F., Zhao, Y., and Tsui, K.-L. (2020). Battery Prognostics at Different Operating Conditions. Measurement 151, 107182. doi:10.1016/j.measurement.2019.107182
Wang, D., Yang, F., Tsui, K.-L., Zhou, Q., and Bae, S. J. (2016). Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Spherical Cubature Particle Filter. IEEE Trans. Instrum. Meas. 65, 1282–1291. doi:10.1109/TIM.2016.2534258
Wang, F.-K., and Mamo, T. (2018). A Hybrid Model Based on Support Vector Regression and Differential Evolution for Remaining Useful Lifetime Prediction of Lithium-Ion Batteries. J. Power Sourc. 401, 49–54. doi:10.1016/j.jpowsour.2018.08.073
Wang, F.-K., and Mamo, T. (2020). Gradient Boosted Regression Model for the Degradation Analysis of Prismatic Cells. Comput. Ind. Eng. 144, 106494. doi:10.1016/j.cie.2020.106494
Wang, H., Ma, X., and Zhao, Y. (2020). A Mixed-Effects Model of Two-phase Degradation Process for Reliability Assessment and RUL Prediction. Microelectron. Reliab. 107, 113622. doi:10.1016/j.microrel.2020.113622
Wang, H., Song, W., Zio, E., Kudreyko, A., and Zhang, Y. (2020). Remaining Useful Life Prediction for Lithium-Ion Batteries Using Fractional Brownian Motion and Fruit-Fly Optimization Algorithm. Measurement 161, 107904. doi:10.1016/j.measurement.2020.107904
Wang, X., Hu, C., Si, X., Pang, Z., and Ren, Z. (2019). An Adaptive Remaining Useful Life Estimation Approach for Newly Developed System Based on Nonlinear Degradation Model. IEEE Access 7, 82162–82173. doi:10.1109/ACCESS.2019.2924148
Wang, Y., Ni, Y., Lu, S., Wang, J., and Zhang, X. (2019). Remaining Useful Life Prediction of Lithium-Ion Batteries Using Support Vector Regression Optimized by Artificial Bee Colony. IEEE Trans. Veh. Technol. 68 (10), 9543–9553. doi:10.1109/TVT.2019.2932605
Wang, Y., Tian, J., Sun, Z., Wang, L., Xu, R., Li, M., et al. (2020). A Comprehensive Review of Battery Modeling and State Estimation Approaches for Advanced Battery Management Systems. Renew. Sustain. Energ. Rev. 131, 110015. doi:10.1016/j.rser.2020.110015
Wei, J., Dong, G., and Chen, Z. (2018). Remaining Useful Life Prediction and State of Health Diagnosis for Lithium-Ion Batteries Using Particle Filter and Support Vector Regression. IEEE Trans. Ind. Electron. 65, 5634–5643. doi:10.1109/TIE.2017.2782224
Wen, Y., Wu, J., Das, D., and Tseng, T.-L. (2018). Degradation Modeling and RUL Prediction Using Wiener Process Subject to Multiple Change Points and Unit Heterogeneity. Reliability Eng. Syst. Saf. 176, 113–124. doi:10.1016/j.ress.2018.04.005
White, C., Thompson, B., and Swan, L. G. (2021). Comparative Performance Study of Electric Vehicle Batteries Repurposed for Electricity Grid Energy Arbitrage. Appl. Energ. 288, 116637. doi:10.1016/j.apenergy.2021.116637
Wu, J., Zhang, C., and Chen, Z. (2016). An Online Method for Lithium-Ion Battery Remaining Useful Life Estimation Using Importance Sampling and Neural Networks. Appl. Energ. 173, 134–140. doi:10.1016/j.apenergy.2016.04.057
Wu, Y., Li, W., Wang, Y., and Zhang, K. (2019). Remaining Useful Life Prediction of Lithium-Ion Batteries Using Neural Network and Bat-Based Particle Filter. IEEE Access 7, 54843–54854. doi:10.1109/ACCESS.2019.2913163
Xiaowei, D., Guoning, X., Zhaojie, L., Ying, M., Shuai, Z., and Hao, D. (2019). Remaining Useful Life Prediction of Lithium-Ion Batteries of Stratospheric Airship by Model-Based Method. Microelectron. Reliab. 100-101, 113400. doi:10.1016/j.microrel.2019.113400
Xiong, R., Li, L., and Tian, J. (2018). Towards a Smarter Battery Management System: A Critical Review on Battery State of Health Monitoring Methods. J. Power Sourc. 405, 18–29. doi:10.1016/j.jpowsour.2018.10.019
Xiong, R., and Lu, J. (2018). Preparation of Papers for IFAC Conferences & Symposia: A Comparative Study of Remaining Useful Life Predictions for Lithium-Ion Battery. IFAC-PapersOnLine 51 (31), 268–273. doi:10.1016/j.ifacol.2018.10.048
Xiong, R., Zhang, Y., Wang, J., He, H., Peng, S., and Pecht, M. (2019). Lithium-Ion Battery Health Prognosis Based on a Real Battery Management System Used in Electric Vehicles. IEEE Trans. Veh. Technol. 68, 4110–4121. doi:10.1109/TVT.2018.2864688
Xu, B., Zhao, J., Zheng, T., Litvinov, E., and Kirschen, D. S. (2018). Factoring the Cycle Aging Cost of Batteries Participating in Electricity Markets. IEEE Trans. Power Syst. 33, 2248–2259. doi:10.1109/TPWRS.2017.2733339
Xu, W., Wang, S., Jiang, C., Fernandez, C., Yu, C., Fan, Y., et al. (2021). A Novel Adaptive Dual Extended Kalman Filtering Algorithm for the Li‐ion Battery State of Charge and State of Health Co‐estimation. Int. J. Energ. Res 45, 14592–14602. doi:10.1002/er.6719
Xue, Z., Zhang, Y., Cheng, C., and Ma, G. (2020). Remaining Useful Life Prediction of Lithium-Ion Batteries with Adaptive Unscented Kalman Filter and Optimized Support Vector Regression. Neurocomputing 376, 95–102. doi:10.1016/j.neucom.2019.09.074
Yan, W., Zhang, B., Zhao, G., Weddington, J., and Niu, G. (2017). Uncertainty Management in Lebesgue-Sampling-Based Diagnosis and Prognosis for Lithium-Ion Battery. IEEE Trans. Ind. Electron. 64 (10), 8158–8166. doi:10.1109/TIE.2017.2701790
Yang, F., Song, X., Dong, G., and Tsui, K.-L. (2019). A Coulombic Efficiency-Based Model for Prognostics and Health Estimation of Lithium-Ion Batteries. Energy 171, 1173–1182. doi:10.1016/j.energy.2019.01.083
Yang, F., Wang, D., Xu, F., Huang, Z., and Tsui, K.-L. (2020). Lifespan Prediction of Lithium-Ion Batteries Based on Various Extracted Features and Gradient Boosting Regression Tree Model. J. Power Sourc. 476, 228654. doi:10.1016/j.jpowsour.2020.228654
Yang, H., Wang, P., An, Y., Shi, C., Sun, X., Wang, K., et al. (2020). Remaining Useful Life Prediction Based on Denoising Technique and Deep Neural Network for Lithium-Ion Capacitors. eTransportation 5, 100078. doi:10.1016/j.etran.2020.100078
Yu, J. (2018). State of Health Prediction of Lithium-Ion Batteries: Multiscale Logic Regression and Gaussian Process Regression Ensemble. Reliability Eng. Syst. Saf. 174, 82–95. doi:10.1016/j.ress.2018.02.022
Yu, P., Hou, Y., Song, Y., Pang, J., and Liu, D. (2018). Lithium-Ion Battery Prognostics with Hybrid Gaussian Process Function Regression. Energies. 11 (6), 1–20. doi:10.3390/en11061420
Zhai, Q., and Ye, Z.-S. (2017). RUL Prediction of Deteriorating Products Using an Adaptive Wiener Process Model. IEEE Trans. Ind. Inf. 13 (6), 2911–2921. doi:10.1109/TII.2017.2684821
Zhang, C., Wang, Y., Gao, Y., Wang, F., Mu, B., and Zhang, W. (2019). Accelerated Fading Recognition for Lithium-Ion Batteries with Nickel-Cobalt-Manganese Cathode Using Quantile Regression Method. Appl. Energ. 256, 113841. doi:10.1016/j.apenergy.2019.113841
Zhang, H., Miao, Q., Zhang, X., and Liu, Z. (2018). An Improved Unscented Particle Filter Approach for Lithium-Ion Battery Remaining Useful Life Prediction. Microelectron. Reliab. 81 (24), 288–298. doi:10.1016/j.microrel.2017.12.036
Zhang, H., Mo, Z., Wang, J., and Miao, Q. (2020). Nonlinear-drifted Fractional Brownian Motion with Multiple Hidden State Variables for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Rel. 69 (2), 768–780. doi:10.1109/TR.2019.2896230
Zhang, K., Zhao, P., Sun, C., Wang, Y., and Chen, Z. (2020). Remaining Useful Life Prediction of Aircraft Lithium-Ion Batteries Based on F-Distribution Particle Filter and Kernel Smoothing Algorithm. Chin. J. Aeronaut. 33 (5), 1517–1531. doi:10.1016/j.cja.2020.01.007
Zhang, L., Mu, Z., and Sun, C. (2018). Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Exponential Model and Particle Filter. IEEE Access 6, 17729–17740. doi:10.1109/ACCESS.2018.2816684
Zhang, S., Guo, X., and Zhang, X. (2020). Multi-objective Decision Analysis for Data-Driven Based Estimation of Battery States: A Case Study of Remaining Useful Life Estimation. Int. J. Hydrogen Energ. 45 (27), 14156–14173. doi:10.1016/j.ijhydene.2020.03.100
Zhang, S., Zhai, B., Guo, X., Wang, K., Peng, N., and Zhang, X. (2019). Synchronous Estimation of State of Health and Remaining Useful Lifetime for Lithium-Ion Battery Using the Incremental Capacity and Artificial Neural Networks. J. Energ. Storage 26, 100951. doi:10.1016/j.est.2019.100951
Zhang, Y., Jia, X., and Guo, B. (2018). Bayesian Framework for Satellite Rechargeable Lithium Battery Synthesizing Bivariate Degradation and Lifetime Data. J. Cent. South. Univ. 25 (2), 418–431. doi:10.1007/s11771-018-3747-2
Zhang, Y., Xiong, R., He, H., and Pecht, M. G. (2019). Lithium-Ion Battery Remaining Useful Life Prediction with Box-Cox Transformation and Monte Carlo Simulation. IEEE Trans. Ind. Electron. 66 (2), 1585–1597. doi:10.1109/TIE.2018.2808918
Zhang, Y., Xiong, R., He, H., and Pecht, M. G. (2018). Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 67 (7), 5695–5705. doi:10.1109/TVT.2018.2805189
Zhang, Y., Xiong, R., He, H., and Pecht, M. (2019). Validation and Verification of a Hybrid Method for Remaining Useful Life Prediction of Lithium-Ion Batteries. J. Clean. Prod. 212, 240–249. doi:10.1016/j.jclepro.2018.12.041
Zhang, Y., Xiong, R., He, H., Qu, X., and Pecht, M. (2019). Aging Characteristics-Based Health Diagnosis and Remaining Useful Life Prognostics for Lithium-Ion Batteries. eTransportation 1, 100004. doi:10.1016/j.etran.2019.100004
Zhang, Y., Yang, Y., Xiu, X., Li, H., and Liu, R. (2021). A Remaining Useful Life Prediction Method in the Early Stage of Stochastic Degradation Process. IEEE Trans. Circuits Syst. 68 (6), 2027–2031. doi:10.1109/tcsii.2020.3034393
Zhang, Z.-X., Si, X.-S., Hu, C.-H., and Pecht, M. G. (2017). A Prognostic Model for Stochastic Degrading Systems with State Recovery: Application to Li-Ion Batteries. IEEE Trans. Rel. 66 (4), 1293–1308. doi:10.1109/TR.2017.2742298
Zhao, L., Li, Q., and Suo, B. (2020). Simulator Assessment Theory for Remaining Useful Life Prediction of Lithium-Ion Battery under Multiple Uncertainties. IEEE Access 8, 71447–71459. doi:10.1109/ACCESS.2020.2987426
Zhao, Q., Qin, X., Zhao, H., and Feng, W. (2018). A Novel Prediction Method Based on the Support Vector Regression for the Remaining Useful Life of Lithium-Ion Batteries. Microelectron. Reliab. 85 (37), 99–108. doi:10.1016/j.microrel.2018.04.007
Zhou, D., Al-Durra, A., Zhang, K., Ravey, A., and Gao, F. (2019). A Robust Prognostic Indicator for Renewable Energy Technologies: A Novel Error Correction Grey Prediction Model. IEEE Trans. Ind. Electron. 66 (12), 9312–9325. doi:10.1109/TIE.2019.2893867
Zhou, D., Li, Z., Zhu, J., Zhang, H., and Hou, L. (2020). State of Health Monitoring and Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Temporal Convolutional Network. IEEE Access 8, 53307–53320. doi:10.1109/ACCESS.2020.2981261
Zhou, Y., and Huang, M. (2016). Lithium-ion Batteries Remaining Useful Life Prediction Based on a Mixture of Empirical Mode Decomposition and ARIMA Model. Microelectron. Reliab. 65, 265–273. doi:10.1016/j.microrel.2016.07.151
Zhou, Y., Huang, M., and Pecht, M. (2020). Remaining Useful Life Estimation of Lithium-Ion Cells Based on K-Nearest Neighbor Regression with Differential Evolution Optimization. J. Clean. Prod. 249, 119409. doi:10.1016/j.jclepro.2019.119409
Keywords: lithium-ion batteries, remaining useful lifetime, machine learning, adaptive filtering, stochastic process methods
Citation: Wang S, Jin S, Deng D and Fernandez C (2021) A Critical Review of Online Battery Remaining Useful Lifetime Prediction Methods. Front. Mech. Eng 7:719718. doi: 10.3389/fmech.2021.719718
Received: 02 June 2021; Accepted: 16 July 2021;
Published: 03 August 2021.
Edited by:
Kailong Liu, University of Warwick, United KingdomReviewed by:
Jinhao Meng, Sichuan University, ChinaZhongbao Wei, Beijing Institute of Technology, China
Qian Xiao, Tianjin University, China
Copyright © 2021 Wang, Jin, Deng and Fernandez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shunli Wang, d2FuZ3NodW5saUBzd3VzdC5lZHUuY24=; Siyu Jin, c2ppQGV0LmFhdS5kaw==
 Shunli Wang
Shunli Wang Siyu Jin
Siyu Jin Dan Deng1
Dan Deng1 Carlos Fernandez
Carlos Fernandez