- 1Mechanical Engineering Department, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
- 2Electrical Engineering Department, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
- 3Interdisciplinary Research Center for Intelligent Manufacturing and Robotics, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
Dynamic vibration absorbers (DVAs) have been widely employed in vibration suppression applications for decades. While DVAs offer an effective solution, they are limited by the need for a high mass ratio between the DVA and the primary system to achieve significant vibration attenuation. To overcome this, researchers have introduced lever mechanisms, allowing for enhanced vibration suppression without increasing the mass ratio. However, levers, commonly used as amplification mechanisms, suffer from high inertia and limited amplification, particularly in larger applications. Another limitation is when DVAs are employed for energy harvesting as a secondary objective, they exhibit high sensitivity to system parameter variations, requiring extensive optimization. Various optimization techniques have been applied to DVAs for multi-objective optimization, including fixed-point theory, which is complex and requires intensive mathematical derivation, and simple metaheuristic techniques such as genetic algorithms (GA). This study proposes four novel DVAs using a hydraulic amplifier (HA) to address the limitations of traditional lever mechanisms and a mechanical inerter to improve the vibration damping. Also, multi-objective optimization was performed using particle swarm optimization (PSO) which is considered innovative in this application and compared with commonly used genetic algorithms (GA). The governing equations were derived using Newton’s second law and solved numerically with the Runge-Kutta method. An AI-based approach was utilized for HA design. The results show that integrating HA and mechanical inerters significantly enhances vibration attenuation and broadens the frequency response. Additionally, the location of the mechanical inerter is critical in reducing vibration amplitude. Also, the multi-objective PSO outperforms GA in solution diversity and quality. The proposed integration of HA in DVAs offers potential applications across various engineering fields.
Introduction
Vibration control mechanisms are typically employed to adjust and attenuate vibrations within a system, utilizing both passive and active control methodologies (Balaji and Karthik SelvaKumar, 2020). One such innovative approach is the DVA. The DVA design incorporates an additional mass that interacts with the primary system. The resultant system will exhibit two resonance frequencies instead of one. However, at the primary system’s resonance frequency, the excitation will be minimized. This differs from conventional damping methods, which seek to dissipate vibration energy by using dampers that convert it into heat through fluid friction. DVAs have been the subject of extensive research in the last decades (Martins et al., 2020a; Auleley et al., 2021; Sun et al., 2023). Initially, DVA is primarily employed to attenuate vibrations at the resonance frequency of the primary system. Then, several proposed designs aim to expand the frequency range of DVA absorption, such as the system introduced in (Wang et al., 2019). However, the effectiveness of DVA at non-resonance frequencies is inherently constrained by the mass ratio between the primary and secondary systems. Engineers often seek to overcome these limitations by utilizing amplification techniques to adjust the mass and natural frequency ratios. Su et al. (2023) proposed an innovative inerter-lever type DVA that offers superior control characteristics, making it a more efficient and feasible solution. Shen et al. (2019) introduced a model that integrates ground stiffness and amplification mechanisms, successfully reducing the maximum amplitude and broadening the effective frequency range. Similarly, Shi et al. (2022) investigated a novel DVA design featuring a lever, ground stiffness, and an inerter, achieving significant amplitude reduction and an expanded frequency range. Li et al. (2023) proposed an optimized novel Maxwell DVA, which demonstrates superior absorption performance.
In mechanical engineering, leverage systems and Hydraulic systems serve as the most common amplification mechanisms. Leverage systems encounter challenges with high inertia in systems with significant masses or large arm ratios, leading to inefficient response and control difficulties. Conversely, hydraulic systems demonstrate superior control and generate substantial force outputs in heavy systems. HA, operating on Pascal’s principle of confined fluid, finds widespread application in various fields for amplifying displacement or force (Bartnicki and Klimek, 2019; Xu et al., 2021). Energy loss in HA primarily arises from friction between the fluid and pipe walls, as well as between the piston ring and the inner wall of the pipe (Qin et al., 2023). Traditionally, a mass, spring element, and damping mechanism constitute the mass-spring-damper system, forming the core of a vibration absorber. Recently, engineers have uncovered the mechanical inerter as one of the damping mechanisms. A mechanical inerter, designed to produce force proportional to the relative acceleration between its terminals, enhances system damping with minimal added mass (Jangid, 2021) Numerous studies have been dedicated to enhancing the capabilities of mechanical inerters (Zhang et al., 2020), finding applications in various DVAs to improve overall system performance. These inerter devices have found applications within various DVAs with the intent of enhancing the overall system performance. In another study, Li et al. (2022) introduced a novel DVA incorporating an inerter mass, broadening the frequency range while mitigating peak excitation levels. Alotta and Failla (2021) proposed an inerter-based DVA integrated into a rhombus truss structure, which offers mechanical amplification and facilitates frequency adjustment through geometric configuration alterations. Additionally, Barredo et al. (2020) developed an inerter-based DVA specifically designed for civil engineering structures, effectively attenuating stochastic vibrations. In addition to that the application of hydraulic systems in dynamic vibration absorbers (DVAs) has attracted significant interest among researchers. For instance, Rong et al. (2024) have developed a nonlinear gas-spring dynamic vibration absorber (NGSDVA), which exhibits broad-spectrum vibration suppression capabilities across different excitation amplitudes. Additionally, through experimental studies, Brötz et al. (2024) have designed a fluid-based dynamic vibration absorber (FDVA) specifically for automotive suspension systems, achieving a 3.5% improvement in ride comfort and a 4.3% reduction in wheel load fluctuations.
Vibrational energy harvesting involves capturing vibrational energy and converting it into usable energy (Zhou et al., 2022). This method overcomes many limitations of renewable energy sources, which often rely on specific weather or environmental conditions (Muscat et al., 2022). The primary methods of energy harvesting include piezoelectric, electrostatic, and electromagnetic (Ahmad and Khan, 2021). Piezoelectric materials, with their mechanical-electric coupling characteristics, can convert strain into voltage. Due to their ability to both dampen vibrations and harness energy, DVAs have garnered attention from numerous researchers in the context of energy harvesting. Wang et al. (2023) introduced a quasi-zero-stiffness DVA for energy harvesting and low-frequency vibration mitigation. Their model effectively dampened vibrations within the ultra-low frequency range. By optimizing DVA parameters, they observed an increase in peak power output. In a similar study, Wang et al. (2020) utilized a non-linear spring element to broaden the effective bandwidth in a dual-function vibrational apparatus (DVA), serving both energy harvesting and vibration damping purposes. Zoka and Afsharfard (2019) proposed a double-stiffness DVA for energy harvesting and vibration suppression. The proposed DVA exhibited a higher Perfection Rate (PR) parameter compared to traditional DVAs, enhancing its energy harvesting capabilities while effectively dampening vibrations.
Numerous techniques have been employed in optimizing DVAs, with two prominent methodologies taking the lead: fixed-point theory, described in (Shen et al., 2019; Baduidana and Kenfack-Jiotsa, 2022) and more recently the adoption of meta-heuristic algorithmic techniques (Kassem et al., 2021; Wang et al., 2022; Xu et al., 2024). Meta-heuristic techniques, such as GA, DE, and PSO, are stochastic methods that navigate the solution space in search of the optimal solution. These approaches prove invaluable when tackling problems characterized by immense complexity or lacking a well-defined mathematical structure, a common scenario in vibrational system optimization. Among the meta-heuristic techniques, GA, DE, and PSO are the most prevalent. DE functions as a population-based meta-heuristic method that evaluates differences among candidate solutions (Bilal et al., 2020). Renowned for its efficiency and resilience (Ahmad et al., 2022), DE generates vast volumes of optimized datasets for training purposes and finds extensive application in engineering systems optimization, as evidenced in (Kim et al., 2019; Arthur et al., 2020). The PSO technique represents a meta-heuristic optimization approach inspired by the collective behavior of birds (Gad, 2022). In this approach, each solution dynamically adjusts its position by integrating its historical performance and the collective experiences of other solution particles (Wang et al., 2017). This mechanism allows PSO to have a distinctive capacity for enhancing both global and local exploration. PSO offers several key advantages, such as its ease of execution and minimal requirement for controlling parameters (Shami et al., 2022).
Despite the various amplification mechanisms employed in the design of DVAs, the implementation of a HA offers distinct advantages. Traditional methods, such as lever mechanisms, often necessitate high lever arm ratios for large vibration suppression, leading to larger, less efficient systems with challenges related to rigidity and high inertia. In contrast, amplification in DVAs equipped with HAs relies only on the diameter’s ratio. It provides the capability to absorb vibrations at alternative locations, thereby enhancing design flexibility and efficiency. In addition to that, the inertia in HA-based systems can be readily adjusted by modifying the hydraulic fluid, further improving their adaptability. These characteristics position HA-equipped DVAs as superior to those utilizing traditional amplification mechanisms.
The integration of AI into vibration applications has significantly advanced the field, particularly in optimization and data training. Although existing optimization methods have shown effectiveness, they are often limited by complexity and a lack of adaptability. PSO is recognized for its efficiency and often outperforms GA in various applications. However, many researchers, such as Martins et al. (2020), have employed GA for multi-objective optimization of DVAs, while the application of PSO, as seen in the works of Song et al. (2022) and Zhe-Ming et al. (2019), has primarily focused on single-objective optimizations. However, multi-objective optimization, which aims to maximize output voltage while minimizing the maximum amplitude of the main system within a designated operating frequency range, remains underexplored. In this research, PSO and GA are used as the multi-objective optimization methods for the proposed. Then, Artificial Neural Networks (ANNs) are utilized to predict the parameters of the HA.
This research makes significant contributions by introducing the novel application of HAs in DVAs to overcome the limitations of traditional lever mechanisms. Additionally, it utilizes AI in structural dynamic systems, focusing on the multi-objective optimization of DVAs using PSO and GA, and includes a comparative analysis between the two methods. Together, these innovations offer a more adaptive and efficient approach to vibration absorption and energy harvesting. Click or tap here to enter text. Click or tap here to enter text. Click or tap here to enter text. The structure of the paper is outlined as follows: Section 2 1 presents the mathematical model of the proposed systems and describes the HA modeling and optimization using the DE algorithm to minimize friction loss and reduce pipe weight. It also includes the training process of ANN for predicting the optimal HA design based on input parameters. Sectio 2 2 presents the derivation of the governing equation of the integrated DVA with piezoelectric components. Additionally, it investigates the utilization of a multi-objective weighted sum approach using PSO and GA to determine the optimal parameters of the DVA, with the dual objective of minimizing vibration amplitude and maximizing output voltage. Finally, Section 3 and Section 4 discuss the results and conclusions, respectively.
Methodology
DVA proposed systems
Mathematical modeling
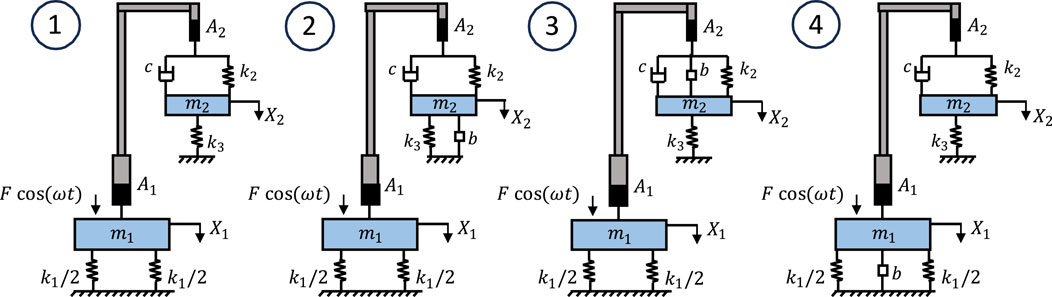
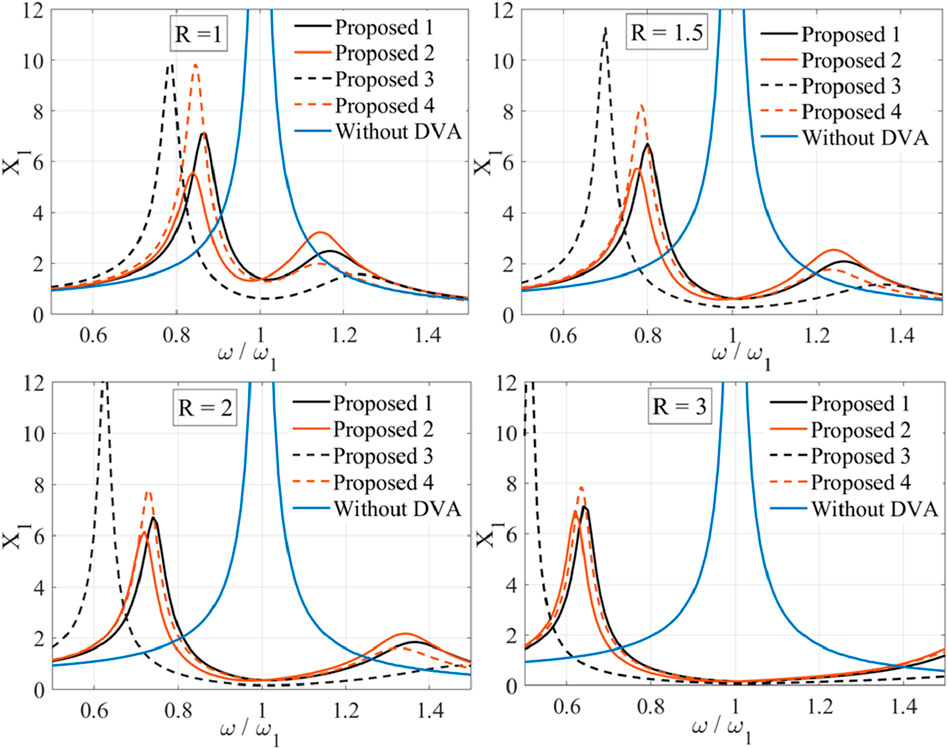
Four DVAs have been proposed with the implementation of the HA and the mechanical inerter to improve the performance of the DVA as illustrated in Figure 1. Only the HA was introduced to the system at the beginning. Then mechanical inerter has been introduced in different configurations to find the best locations. The equation of motion of the four proposed systems is generated.
Propose 1:
Propose 2:
Propose 3:
Propose 4:
In Equations 1–8
HA analysis
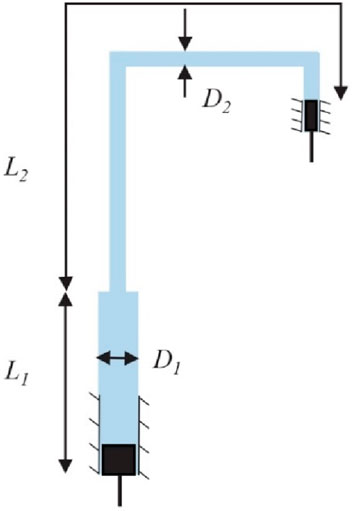
HA is modeled with a circular cross-section tube, and the total loss within the HA is constrained to be less than 10% of the applied force. This constraint was established following a parametric study in the second part of the analysis, which revealed that an increase in the damping coefficient
where
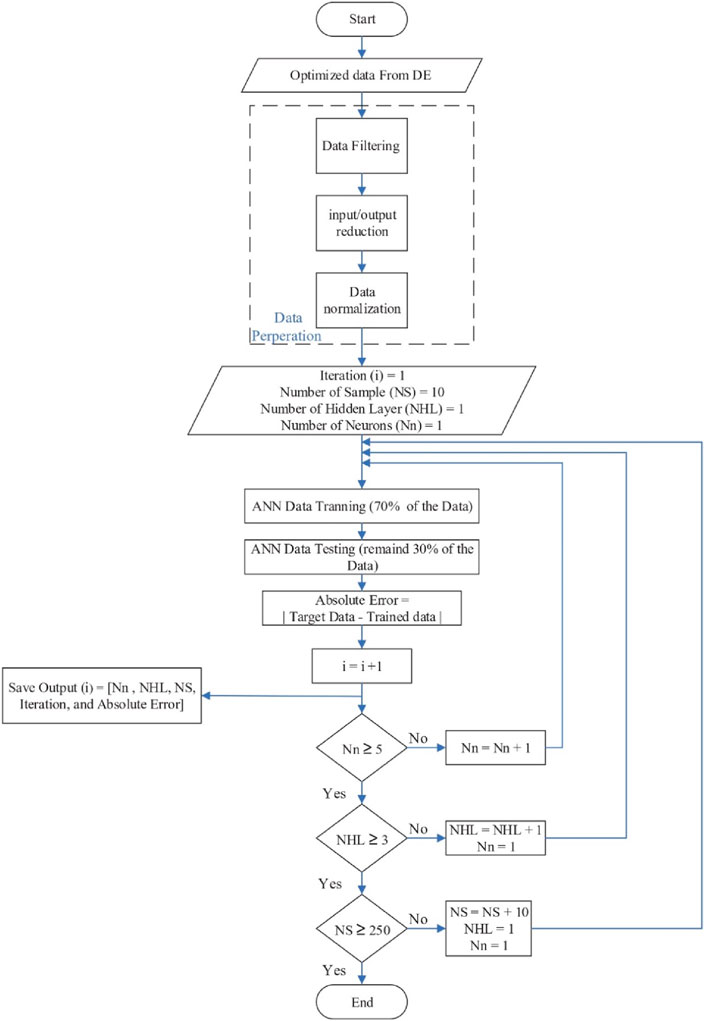
Following the flowchart in Figure 3, the optimized dataset is filtered to exclude penalty results. Initially, a reduction in inputs and outputs is initiated, where vibration forces are multiplied by the velocity to derive a single input (power). Additionally, a ratio is computed between
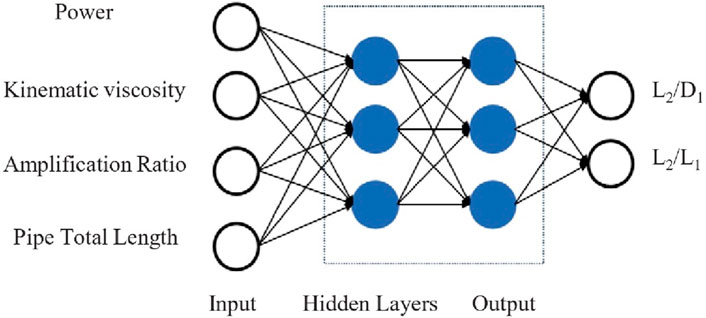
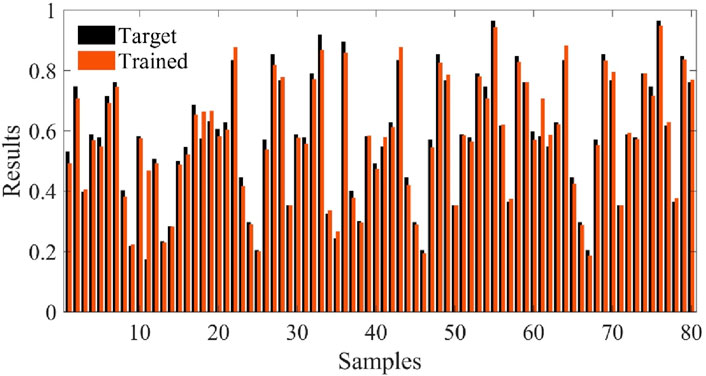
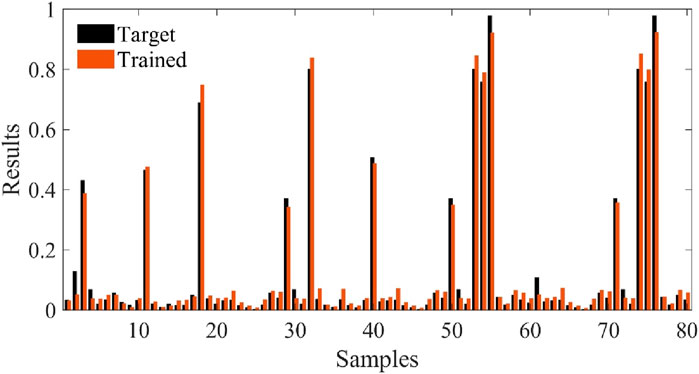
The chosen ANN configuration consisted of 560 patterns, featuring 2 hidden layers with 3 hidden neurons each, as delineated in Figure 5.
DVA multi-objective optimization
The second proposed system was used for the analysis. Then, the piezoelectric material is attached to the secondary mass for energy harvesting. The equation of motion of DVA after attaching the piezoelectric material are:
where
where
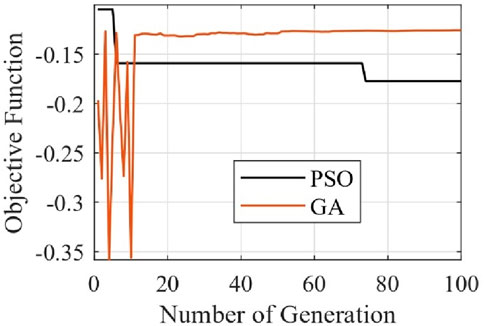
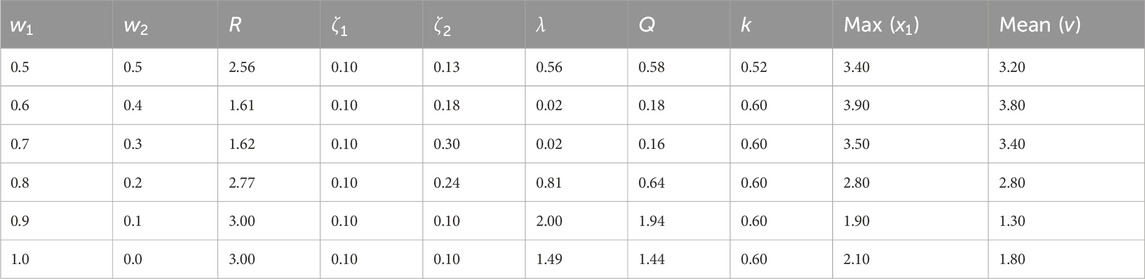
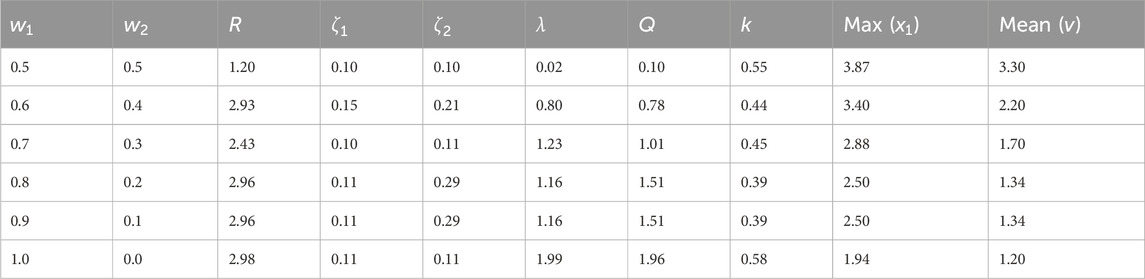
The dimensionless parameters have been optimized using PSO and GA, the number of populations was set to 20, and the stopping criteria were defined as reaching the maximum number of generations (equal to 100 generations). The study integrates two objective functions: minimizing the maximum vibration amplitude and maximizing the output voltage. The output voltage is calculated as the average value over the study dimensionless frequency range (0.5–1.5). The weight sum optimization method is employed for the multi-objective optimization process. This approach converts the multiple objectives into a single objective, thereby transforming the problem into a minimization or maximization scenario. In this study, energy harvesting is considered a secondary objective, while vibration reduction serves as the primary objective. Consequently, the minimum weight for the primary objective is set at 0.5. The weight sum method is utilized with varying weights assigned to the primary objective (
where
Results and discussion
DVA analysis results
The four proposed systems are compared with different
ANN results
The ANN model depicted in Figure 5 serves as a predictive tool for determining the design parameters of the HA (
Multi-objective PSO and GA optimization
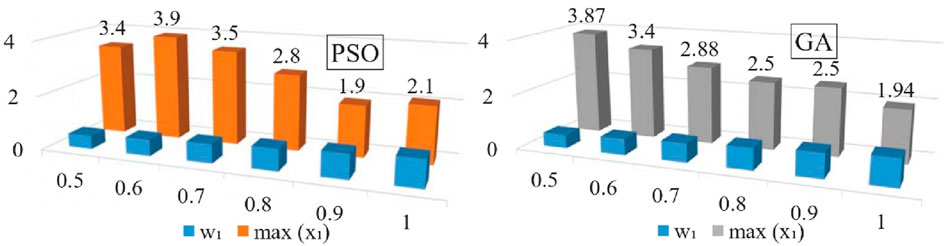
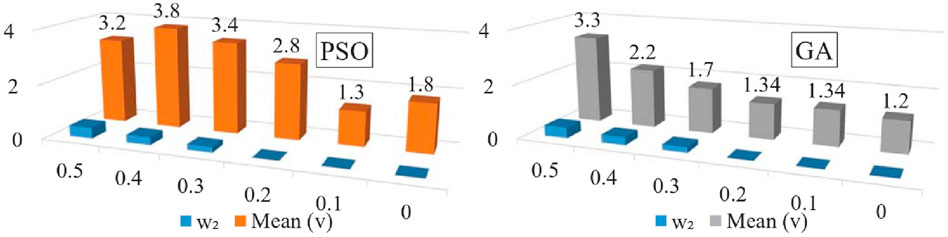
The proposed system in Equation 14–16 is optimized to minimize the maximum vibration amplitude and maximize the average output voltage. The weight sum method with different weights using PSO and GA is used for the optimization. The vibration amplitude of the primary system and the output voltage of the optimized system with different weights are illustrated in Figure 10. The black circles and the red stars represent the optimization points of PSO and GA respectively. Since the step value of
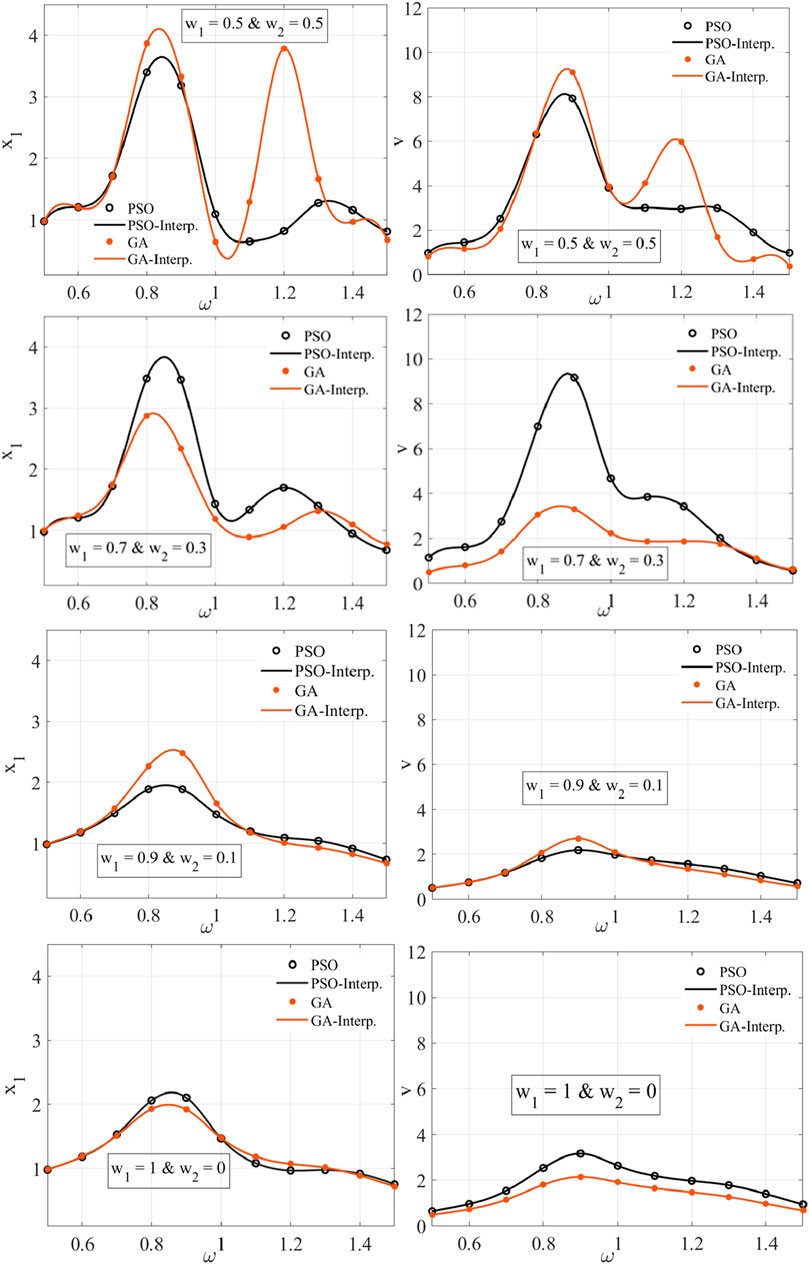
Figure 10. PSO and GA frequency-response results of
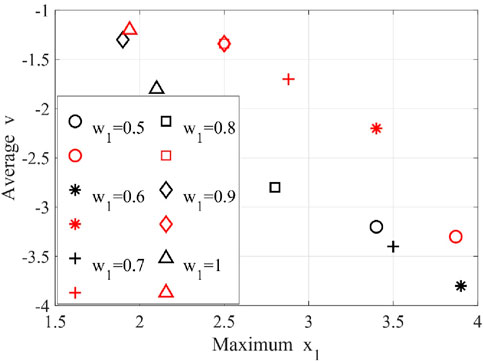
To compare PSO and GA in this multi-objective problem, the Pareto front is conducted for the two techniques. The Pareto front which contains the best solutions is illustrated in Figure 11. The results show that the multi-objective optimization using PSO gives a better solution than GA in general. The results manifest as nondominated between PSO and GA with the same weights.
Notably, an additional observation emerges regarding the stability of PSO solutions with weight trends, revealing fluctuations in PSO compared to GA solutions under corresponding weight settings as illustrated in Figures 12, 13. Moreover, a general trend surfaces where PSO yields more diverse solutions relative to GA, exemplified by the presence of two repeated solutions at
Additionally, the existence of resonance constraints within the problem and intricacies in the simulation steps contribute to the observed nuances in the optimization analyses.
Conclusion
The proposed model of the DVA incorporating an HA and a mechanical inerter effectively mitigates the limitation imposed by the mass ratio necessary to enhance attenuation. Additionally, it broadens the operational frequency range of the DVA. Also, it has been found that the location of the mechanical inerter is critical in reducing vibration amplitude. The proposed HA design systematically addresses the issue of power loss, and the training data from the ANN successfully facilitates the selection of optimal HA dimensions for various input parameters, achieving a maximum friction loss of less than 10% of the vibration force. In terms of optimization, the multi-objective PSO generally surpasses Genetic Algorithms GA in both diversity and quality of solutions. However, fluctuations in stability have been observed in the PSO weighted sum due to the system’s complexity. Therefore, PSO is recommended for future optimization processes in multi-objective vibration system applications.
The characteristics of the DVA with the HA and mechanical inerter proposed in this study make it suitable for a wide range of vibration suppression applications in structural engineering, automotive engineering, and industrial equipment. However, certain limitations of the proposed system must be considered during selection. These include the higher cost compared to lever mechanisms, the need for regularly scheduled maintenance, and the time response limitation, which must be factored into the design. This system is typically better suited for applications involving low-frequency vibrations.
This study demonstrates the effectiveness of meta-heuristic optimization techniques in optimizing complex systems. Future research should include experimental analyses of DVA with HA in vibrating machines and explore the design of an integrated system that connects a single DVA with vibrating equipment.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
AS: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Validation, Writing–original draft, Writing–review and editing. MA: Conceptualization, Methodology, Project administration, Supervision, Writing–review and editing. AA: Conceptualization, Methodology, Supervision, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors would like to acknowledge the support provided by the Interdisciplinary Research Center for Sustainable Energy Systems, (IRC-SES), Research Institute, KFUPM, through project #INRE2328. MA also acknowledges the support received from the Saudi Data and AI Authority (SDAIA) and KFUPM under SDAIA-KFUPM Joint Research Center for Artificial Intelligence Grant no. JRC-AI-RFP-09.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2024.1464692/full#supplementary-material
References
Ahmad, M. F., Isa, N. A. M., Lim, W. H., and Ang, K. M. (2022). Differential evolution: a recent review based on state-of-the-art works. Alexandria Eng. J. 61, 3831–3872. doi:10.1016/J.AEJ.2021.09.013
Ahmad, M. M., and Khan, F. U. (2021). Review of vibration-based electromagnetic–piezoelectric hybrid energy harvesters. Int. J. Energy Res. 45, 5058–5097. doi:10.1002/ER.6253
Alotta, G., and Failla, G. (2021). Improved inerter-based vibration absorbers. Int. J. Mech. Sci. 192, 106087. doi:10.1016/J.IJMECSCI.2020.106087
Arthur, C. K., Temeng, V. A., and Ziggah, Y. Y. (2020). A Self-adaptive differential evolutionary extreme learning machine (SaDE-ELM): a novel approach to blast-induced ground vibration prediction. SN Appl. Sci. 2, 1845–1923. doi:10.1007/s42452-020-03611-3
Auleley, M., Thomas, O., Giraud-Audine, C., and Mahé, H. (2021). Enhancement of a dynamic vibration absorber by means of an electromagnetic shunt. J. Intell. Mater Syst. Struct. 32, 331–354. doi:10.1177/1045389X20957097/
Baduidana, M., and Kenfack-Jiotsa, A. (2022). Parameters optimization and performance evaluation for the novel tuned inertial damper. Eng. Struct. 250, 113396. doi:10.1016/J.ENGSTRUCT.2021.113396
Balaji, P. S., and Karthik SelvaKumar, K. (2020). Applications of nonlinearity in passive vibration control: a review. J. Vib. Eng. Technol. 2020 9, 183–213. doi:10.1007/S42417-020-00216-3
Barredo, E., Mendoza Larios, J. G., Colín, J., Mayén, J., Flores-Hernández, A. A., and Arias-Montiel, M. (2020). A novel high-performance passive non-traditional inerter-based dynamic vibration absorber. J. Sound. Vib. 485, 115583. doi:10.1016/J.JSV.2020.115583
Bartnicki, A., and Klimek, A. (2019). The research of hydraulic pressure intensifier for use in electric drive system. IEEE Access 7, 20172–20177. doi:10.1109/ACCESS.2019.2897148
Bilal, , Pant, M., Zaheer, H., Garcia-Hernandez, L., and Abraham, A. (2020). Differential Evolution: a review of more than two decades of research. Eng. Appl. Artif. Intell. 90, 103479. doi:10.1016/J.ENGAPPAI.2020.103479
Brötz, N., Rexer, M., Puff, N., and Pelz, P. F. (2024). Fluid dynamic vibration absorber for vehicle suspension system. Veh. Syst. Dyn. 62, 1122–1141. doi:10.1080/00423114.2023.2223325
Friction Loss In Hydraulic Cylinder, (2017). Available at: https://iphco.in/learn/learn/learn/friction-loss-in-hydraulic-cylinder/ (Accessed August 14, 2024).
Gad, A. G. (2022). Particle swarm optimization algorithm and its applications: a systematic review. Archives Comput. Methods Eng. 2022 29, 2531–2561. doi:10.1007/S11831-021-09694-4
Jangid, R. S. (2021). Optimum tuned inerter damper for base-isolated structures. J. Vib. Eng. Technol. 9, 1483–1497. doi:10.1007/s42417-021-00309-7
Kassem, M., Yang, Z., Gu, Y., and Wang, W. (2021). Modeling and control design for flutter suppression using active dynamic vibration absorber. J. Vib. Eng. Technol. 9, 845–860. doi:10.1007/s42417-020-00267-6
Kim, N., Kim, S., and Lee, J. (2019). Vibration-based damage detection of planar and space trusses using differential evolution algorithm. Appl. Acoust. 148, 308–321. doi:10.1016/J.APACOUST.2018.08.032
Li, J., Gao, T., Zhu, S., and Yang, X. (2023). H∞ optimization of a novel Maxwell dynamic vibration absorber with lever, inerter, and grounded stiffness. Appl. Sci. 13, 3697. doi:10.3390/APP13063697
Li, J., Gu, X., Zhu, S., Yu, C., and Yang, X. (2022). Parameter optimization for a novel inerter-based dynamic vibration absorber with negative stiffness. J. Nonlinear Math. Phys. 29, 280–295. doi:10.1007/s44198-022-00042-z
Martins, L. A., Lara-Molina, F. A., Koroishi, E. H., and Cavalini, A. A. (2020). Optimal design of a dynamic vibration absorber with uncertainties. J. Vib. Eng. Technol. 8, 133–140. doi:10.1007/s42417-019-00084-6
Muscat, A., Bhattacharya, S., and Zhu, Y. (2022). Electromagnetic vibrational energy harvesters: a review. Sensors (Basel) 22, 5555. doi:10.3390/S22155555
Qin, Z., Wu, Y. T., He, L., Gao, X., and Lyu, S. K. (2023). Empirical research on the friction behavior of O-rings in hydraulic cylinders. PLoS One 18, e0280815. doi:10.1371/JOURNAL.PONE.0280815
Rong, K., Yang, M., Lu, Z., Zhang, J., Tian, L., and Wu, S. (2024). Energy analysis of a nonlinear gas-spring dynamic vibration absorber subjected to seismic excitations. J. Build. Eng. 89, 109253. doi:10.1016/J.JOBE.2024.109253
Shami, T. M., El-Saleh, A. A., Alswaitti, M., Al-Tashi, Q., Summakieh, M. A., and Mirjalili, S. (2022). Particle swarm optimization: a comprehensive survey. IEEE Access 10, 10031–10061. doi:10.1109/ACCESS.2022.3142859
Shen, Y., Xing, Z., Yang, S., and Sun, J. (2019). Parameters optimization for a novel dynamic vibration absorber. Mech. Syst. Signal Process 133, 106282. doi:10.1016/J.YMSSP.2019.106282
Shi, A., Shen, Y., and Wang, J. (2022). Parameter optimization of a grounded dynamic vibration absorber with lever and inerter. J. Low Freq. Noise Vib. Act. Control 41, 784–798. doi:10.1177/14613484211068250
Song, Q. H., Xiao, L. J., Song, Q. J., Jiang, H. Y., and Liu, X. J. (2022). Adaptive multiswarm particle swarm optimization for tuning the parameter optimization of a three-element dynamic vibration absorber. Mech. Sci. 13, 505–517. doi:10.5194/MS-13-505-2022
Su, N., Bian, J., Chen, Z., and Xia, Y. (2023). A novel lever-type inerter-based vibration absorber. Int. J. Mech. Sci. 254, 108440. doi:10.1016/J.IJMECSCI.2023.108440
Sun, R., Zhou, S., and Cheng, L. (2023). Ultra-low frequency vibration energy harvesting: mechanisms, enhancement techniques, and scaling laws. Energy Convers. Manag. 276, 116585. doi:10.1016/J.ENCONMAN.2022.116585
Wang, D., Tan, D., and Liu, L. (2017). Particle swarm optimization algorithm: an overview. Soft Comput. 22 (2), 387–408. doi:10.1007/S00500-016-2474-6
Wang, M., Xu, H., He, D., Wang, T., and Zhang, J. (2022). Design of a damped vibration absorber to control the resonant vibration of roll. Mech. Syst. Signal Process 178, 109262. doi:10.1016/J.YMSSP.2022.109262
Wang, Q., Zhou, J., Wang, K., Gao, J., Lin, Q., Chang, Y., et al. (2023). Dual-function quasi-zero-stiffness dynamic vibration absorber: low-frequency vibration mitigation and energy harvesting. Appl. Math. Model 116, 636–654. doi:10.1016/J.APM.2022.12.007
Wang, X., He, T., Shen, Y., Shan, Y., and Liu, X. (2019). Parameters optimization and performance evaluation for the novel inerter-based dynamic vibration absorbers with negative stiffness. J. Sound. Vib. 463, 114941. doi:10.1016/J.JSV.2019.114941
Wang, X., Wu, H., and Yang, B. (2020). Nonlinear multi-modal energy harvester and vibration absorber using magnetic softening spring. J. Sound. Vib. 476, 115332. doi:10.1016/J.JSV.2020.115332
Xu, H., Ren, C., He, D., Zhou, B., Wang, Q., Gao, H., et al. (2024). Coupling vibration characteristics and vibration suppression of rolling mill rolls with dynamic vibration absorber. J. Manuf. Process 120, 1157–1179. doi:10.1016/J.JMAPRO.2024.04.066
Xu, Y., Zhou, H., Zhu, S., and Pan, G. (2021). Research on a hydraulic displacement amplifier for a piezoactuator. J. Phys. Conf. Ser. 1985, 012043. doi:10.1088/1742-6596/1985/1/012043
Zhang, R., Zhao, Z., Pan, C., Ikago, K., and Xue, S. (2020). Damping enhancement principle of inerter system. Struct. Control Health Monit. 27, e2523. doi:10.1002/STC.2523
Zhe-Ming, C., Peng, W., Jiang-Hua, F., and Bao, C. (2019). Application of SA-PSO algorithm in parameter optimization of dynamic vibration absorber. IOP Conf. Ser. Earth Environ. Sci. 267, 042174. doi:10.1088/1755-1315/267/4/042174
Zhou, S., Lallart, M., and Erturk, A. (2022). Multistable vibration energy harvesters: principle, progress, and perspectives. J. Sound. Vib. 528, 116886. doi:10.1016/J.JSV.2022.116886
Keywords: dynamic vibration absorber, energy harvesting, particle swarm optimization, artificial neural networks, mechanical inerter, hydraulic amplifier
Citation: Shamseldin A, Abido MA and Alofi A (2024) AI-driven optimization of dynamic vibration absorbers with hydraulic amplifier and mechanical inerter integration. Front. Mech. Eng. 10:1464692. doi: 10.3389/fmech.2024.1464692
Received: 14 July 2024; Accepted: 16 September 2024;
Published: 30 September 2024.
Edited by:
Kai Wang, Hunan University, ChinaReviewed by:
Yaopeng Chang, Changsha University of Science and Technology, ChinaQiang Wang, Hunan University, China
Xia Shuyan, Guangzhou University, China
Copyright © 2024 Shamseldin, Abido and Alofi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohammad A. Abido, bWFiaWRvQGtmdXBtLmVkdS5zYQ==
 Ahmed Shamseldin
Ahmed Shamseldin Mohammad A. Abido2*
Mohammad A. Abido2* Abdulrahman Alofi
Abdulrahman Alofi