Controlling windscreen wiper vibration through yaw angle adjustments: a study of dynamic contact behavior using fluorescence observation

Friction-induced vibration in the wiper system of passenger cars not only causes impaired visibility as a result of uneven water film distribution on the windscreen surface, but also leads to noise problems by transmitting vibrations as sound to the passengers. In this study, a novel experimental apparatus was developed to simulate the wiper system, enabling the change in normal support stiffness and the precise adjustment of the yaw angles of a shortened rubber blade and its flexible base relative to the drive direction of a glass plate. The use of fluorescence observation provided a significant advantage, enabling precise measurements of the position of the rubber blade tip and the water film thickness in the contact area of the rubber blade and the glass plate during operation. In conjunction with this, an accelerometer and a gap sensor were employed to measure the normal and tangential motions of the support structures, respectively. This comprehensive setup allows for precise control of blade support conditions, and provides accurate measurement for motions of rubber blade and support structures, making it a powerful tool for investigating friction-induced vibration in the wiper system. The experimental results clearly demonstrated the effectiveness of applying large yaw angles to both the rubber blade and the flexible base in suppressing friction-induced vibration, resulting in smooth motion at any drive speed. These findings have the potential to improve wiper performances under actual operating conditions.

1 Introduction

The wiper system of vehicles is designed to maintain clear visibility for drivers by moving a rubber blade pressed against a windshield with a wiper arm in reciprocating motions. During these wiping motions, the friction between the rubber blade and the windshield can cause a self-excited vibration known as friction-induced vibration. If the rubber blade forms an uneven water sheet failing to sweep water drops, the refraction of light hinders clear view (Kitayama et al., 2012). Friction-induced vibraion can also result in noise problems if the sound of the vibration is transmitted to passengers (Wang et al., 2023). This problem is particularly pronounced in electric vehicles, where the lower levels of interior sound and vibration compared to those in internal combustion engine vehicles make friction-induced vibration and noise more noticeable (Farfan-Cabrera, 2019; Li and Xu, 2023). Therefore, research on suppressing friction-induced vibration contributes not only to traffic safety by maintaining clear visibility but also to user comfort by reducing noise.

To suppress the friction-induced vibration in the wiper system, it is crucial to understand the vibration mechanism in detail. The types of vibration in the wiper system can be categorized as follows (Goto et al., 2001; Reddyhoff et al., 2015): (1) high-frequency vibration, called squeal noise, around 1 kHz, generated at the rubber blade (Goto et al., 2001; Reddyhoff et al., 2015; Le Rouzic et al., 2013; Min et al., 2014; Unno et al., 2017). (2) low-frequency vibration, referred to as chattering, less than 100 Hz, generated in the wiper system including support parts of the rubber blade such as the wiper arm (Suzuki and Yasuda, 1998; Lancioni et al., 2016). (3) impact sound and vibration, called reversal noise, caused by the tip of the rubber blade hitting the glass surface when the wiper changes direction. Regarding (1) and (2), the velocity-weakening friction, which appears in the mixed lubrication regime of the Stribeck curve, is known to cause friction-induced vibration (Reddyhoff et al., 2015; Le Rouzic et al., 2013; Suzuki and Yasuda, 1998). Specifically for squeal noise, the mechanism has been demonstrated theoretically (Goto et al., 2001), experimentally (Reddyhoff et al., 2015; Le Rouzic et al., 2013; Min et al., 2014), and numerically (Unno et al., 2017), showing that the vibrational modes of the rubber blade are excited by the instability caused by the velocity-weakening friction. This phenomenon is independent of the characteristics of the support structure in the wiper system. Several studies have investigated the relationship between friction behavior and noise in terms of the surface roughness, coating treatment, blade material, and wear status (Wang et al., 2023). On the other hand, for chattering, the behavior of the rubber blade tip in friction-induced vibration and the influence of the support structure of the rubber blade are not sufficiently understood to design the wiper system without any vibration and noise problems in advance. In an actual wiper system, not only the velocity conditions but also the yaw support angles of the rubber blade and the deformation direction and stiffness of the wiper arm depend on the position along the rubber blade, complicating the understanding of the phenomenon. It has been demonstrated that the application of a leaf spring support with a yaw angle misalignment between the support deformation direction and the drive velocity can suppress the friction-induced vibration of a tribometer, which is considered a single-degree-of-freedom vibrating system (Kado et al., 2013). In addition, direct observations of water-lubricated elastomer/glass contacts are effective in understanding the mechanism of the velocity-weakening friction (Deleau et al., 2009; Dalzin et al., 2016). Fluorescence observation can be applied to examine the motion of objects with rough surfaces like rubber (Fowell et al., 2014; Vlădescu et al., 2019).

In this study, to understand the influence of the adjustments on yaw angles and support stiffness of the rubber blade on chattering vibration in the wiper system, a custom-made apparatus simulating a wiper system was developed. This apparatus included yaw angle adjustments and support structures in the tangential and normal directions for a short piece of a commercial rubber blade. In addition, to examine the relationship between the motions of the support structure and the rubber blade tip, the in-plane behavior of the rubber blade tip and the distance between the rubber blade tip and glass surface under water lubrication were measured using fluorescence observation. The findings of this study are expected to contribute not only to advancing the fundamental understanding of vibration mechanisms but also to provide insights for the design of quieter and more effective wiper systems.

2 Experimental details

2.1 Apparatus

The experimental apparatus was designed to simulate the interaction between the rubber blade and glass surface of a wiper system, reproducing the dynamic conditions and frictional behavior observed in practical use. The experimental apparatus allows for precise control of normal load, drive velocity, and yaw angles, enabling detailed study of friction-induced vibration. Figures 1, 2 show a photograph and a schematic diagram of the experimental apparatus, which consists of drive and driven parts that simulate the wiper system, along with an optical setup for monitoring the motion of the rubber blade. A glass plate (material: borosilicate glass, diameter: 50 mm, thickness: 5 mm, and arithmetic average roughness: 4 nm) and a short piece of a commercial rubber blade (made by DENSO WIPER SYSTEMS, INC., model number: AS70GN, width: 10 mm, and arithmetic average roughness: 1 µm) were placed in the drive and driven parts respectively, forming a line contact. In the drive part, the glass plate was mounted on a motorized linear stage (KS101-30R, SURUGA SEIKI, JAPAN) via a holder and a loading mechanism to drive at a constant drive speed V. The loading mechanism employed a lever mechanism with a coil spring, including a load cell (stiffness: 2.4 kN/mm, LMB-A-50N, Kyowa Electronic Instruments, JAPAN) above the coil spring to monitor the normal load. The normal load was applied to the contact by the restoring force generated by deforming the coil spring. The coil spring could be replaced with one of three coil springs with different stiffness values (K = 4, 10, and 60 N/mm). This change would adjust the natural frequency of the loading mechanism to f_L = 18, 26, and 40 Hz, respectively. To monitor the Z-axis motion of the loading mechanism including the glass plate during the sliding test with the rubber blade, an accelerometer (frequency range: 1 Hz–10 kHz, NP-3211, Ono Sokki, JAPAN) was placed on the opposite surface of the glass plate from the contact. In the driven part, the rubber blade was mounted on a base plate supported by parallel leaf springs (stiffness k: 4 N/mm), where the natural frequency of the base structure of the rubber blade was f_B = 29 Hz. The displacement x_base of the base plate was measured by a gap sensor (resolution: 0.4 µm, EX-614V, KEYENCE, JAPAN). A manual Z-axis stage was placed right under the parallel leaf springs to adjust the height position of the rubber blade tip. A manual rotational stage was placed under the parallel leaf springs to adjust the yaw angle φ₁ between the direction of drive velocity V and the direction of the deformation x_base of the parallel leaf springs. Another manual rotational stage was placed between the rubber blade and the base plate to adjust the yaw angle φ₂ between the direction of drive velocity V and the direction of the deformation of the rubber blade.

Figure 1

Figure 1. Photograph of experimental apparatus; red words: components in drive part; blue words: components in driven part.

Figure 2

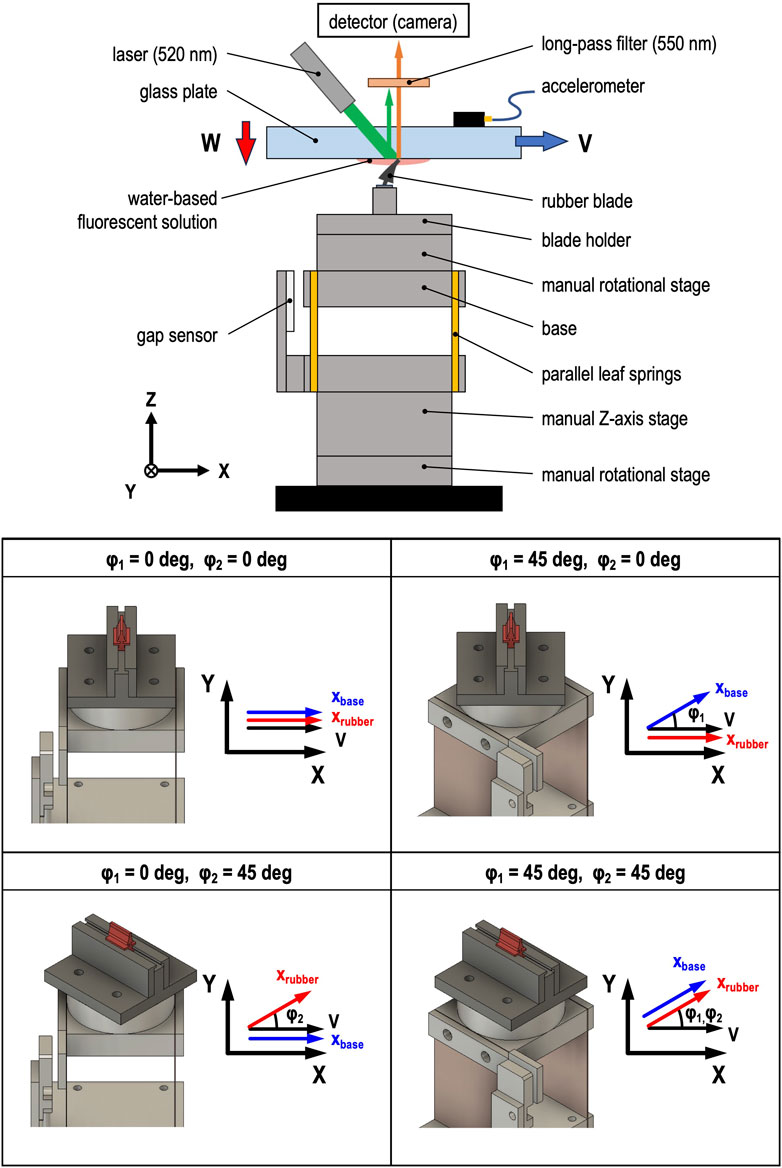
Figure 2. Schematic diagram of experimental apparatus; upper diagram: side view of experimental apparatus; lower diagram: configurations of driven part with different yaw angles (φ₁ and φ₂).

Fluorescence observation of the contact between the glass plate and rubber blade was performed to measure the water film thickness and the position of the rubber blade tip using the optical setup consisting of a laser (wavelength: 520 nm), microscope, and an intensified CMOS camera (ORCA-Flash4.0 V3, HAMAMATSU PHOTONICS, JAPAN). A fluorescent solution was prepared by adding Rhodamine-B (concentration: 0.3 mol/m³) to pure water, and this solution was used as a lubricant in the contact. The laser beam was directed at the contact area lubricated with the water-based fluorescent solution. The emitted light (wavelength: 570–590 nm) was captured using the camera at a frame rate of 200 fps (exposure time: 1/frame rate) through the microscope equipped with a 5x objective lens and long-pass filter (cut-off wavelength: 550 nm) in the optical path. The resolution of the captured images was 500 × 500 px; the pixel size was 1.28 µm/px; the gradation was 65,536 levels of gray. A manual XY-axis linear stage was mounted at the bottom of the microscope to adjust the camera’s view to the contact area.

2.2 Procedure

The glass plate was cleaned with acetone and hexane for 5 min each using an ultrasonic cleaner, dried with hot air from a blower, and installed into the holder of the drive part. The accelerometer was fixed to the glass plate with solid glue. The rubber blade was wiped by an ethanol-moistened paper towel and then installed onto the base plate via the blade holder. Each yaw angle (φ₁ and φ₂) was adjusted to be 0, 15, 30, or 45 degrees using the manual rotational stages, as shown in Figure 2. The contact between the glass plate and rubber blade was made while keeping the glass plate horizontal using the loading mechanism in the drive part and the manual Z-axis stage in the driven part. The water-based fluorescent solution of 100 mm³ was injected around the contact. After driving the glass 10 mm at V = 20 mm/s, the normal load W was adjusted to be 0.17 N while maintaining the glass plate horizontal and the rubber blade bent with static friction. The microscope position was adjusted using the manual XY-axis linear stage to observe the contact with the camera. The laser beam was then directed at the contact. When the glass was moved 20 mm at V = 5, 10, 15, and 20 mm/s, the displacement x_base of the base plate and the acceleration a_z of the glass plate were measured at sampling frequencies of 1,000 Hz and 51.2 kHz, respectively. A signal of 1 V for 0.05 s was used as a trigger to synchronize the start timing of recording x_base and a_z and capturing the fluorescence intensity images. The ambient temperature and relative humidity during the experiments were 25°C and 20%–40%, respectively.

3 Results and discussion

3.1 Calibration of water film thickness under contact between glass plate and rubber blade

Figure 3 illustrates the calibration of film thickness measurements for the water-based fluorescent solution using the images captured by the camera. To calibrate the intensity of the captured images to the water film thickness, a shim film (material: stainless steel) with known thickness h_s of 5, 10, and 15 µm was placed between the glass plate and rubber blade, creating three distinct contact situations: contact via the shim film, contact via the fluorescent water, and direct contact of the glass plate and rubber blade, as shown in Figure 3A. In Figure 3B, green, red, and blue plots represent the fluorescence intensity values measured with shim films of different thicknesses (5, 10, and 15 μm, respectively). Each color plot showed that the fluorescence intensity was maximum at the end of the shim film (position: 0 µm) and decreased with increasing distance from the shim film. The water film thickness at the position where the fluorescence intensity was the maximum was assumed to be equal to the thickness of the shim film. The minimum value of the fluorescence intensity was assumed to indicate the water film thickness of zero. The relationship between the water film thickness and the fluorescence intensity measured at the position of zero using each shim is shown in Figure 3C. The solid back line represents a fitting line with the equation: h = a (I–b), where h is the water film thickness, I is the intensity measured by fluorescence observation, and a and b are fitting parameters. The fitting line shown in Figure 3C has parameters a = 1.15 and b = 102.5 (determined by the least squares method, R²: 0.95).

Figure 3

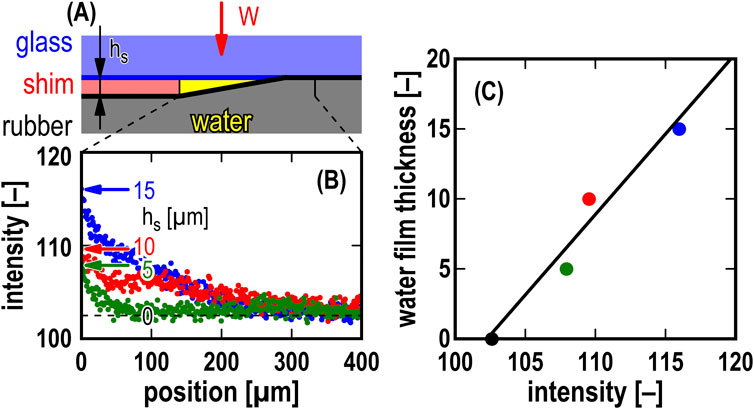
Figure 3. Calibration of film thickness measurement; (A) schematic of the contact of glass plate and rubber blade with constant-thickness shim (h_s = 5, 10, 15 µm) and water-based fluorescent solution; (B) fluorescence intensity measured under the contact; (C) water film thickness versus fluorescence intensity measured at position of zero.

3.2 Typical vibration observed in simulated wiper system

Figure 4 illustrates a typical result of fluorescence observation for the sliding contact of the glass and rubber blade at K = 10 N/mm, φ₁ = φ₂ = 0 deg, and V = 5 mm/s, where t = 0.065 s in Figure 5. In the fluorescence intensity image with a grayscale range of 0–500 shown in Figure 4A, the intensity decreased as it approached X = 2.04 mm but did not change significantly along the Y-axis direction. The black line in Figure 4B represents the mean values of the film thickness h of water, calculated from the intensity averaged from Y = −0.32 to 0.32 mm. The red and blue lines represent the mean values of h plus and minus standard deviation (STD), respectively, also calculated from Y = −0.32 to 0.32 mm. The variation of h with X shows the tip-corner shape of the rubber blade and the minimum value h_min of the water film thickness, which is 2.3 μm at X = 2.04 mm. The position where the minimum film thickness h_min was observed is defined as x_rubber. Considering the STD value shown by the blue line, the value of h at X = 2.04 mm was almost zero, implying that the lubrication regime in the experiment was mixed lubrication.

Figure 4

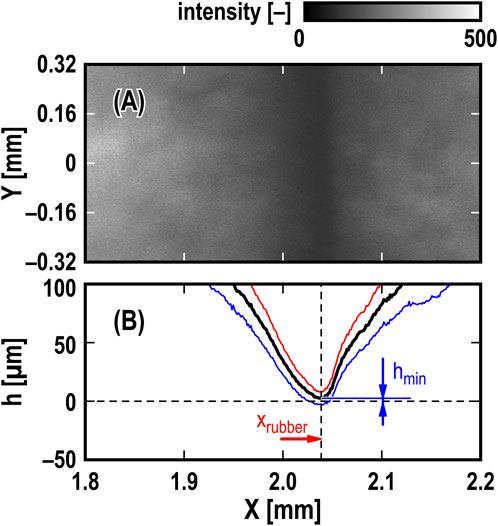
Figure 4. Typical result of fluorescence observation for sliding contact of glass plate and rubber blade; (A) snapshot of fluorescence observation; (B) cross-section of h versus X; bold black line: h converted from average intensity of snapshot from Y = −0.32 to 0.32 mm, red line: h + STD, blue line: h – STD; K = 10 N/mm, φ₁ = φ₂ = 0 deg, and V = 5 mm/s; t = 0.065 s in Figure 5.

Figure 5

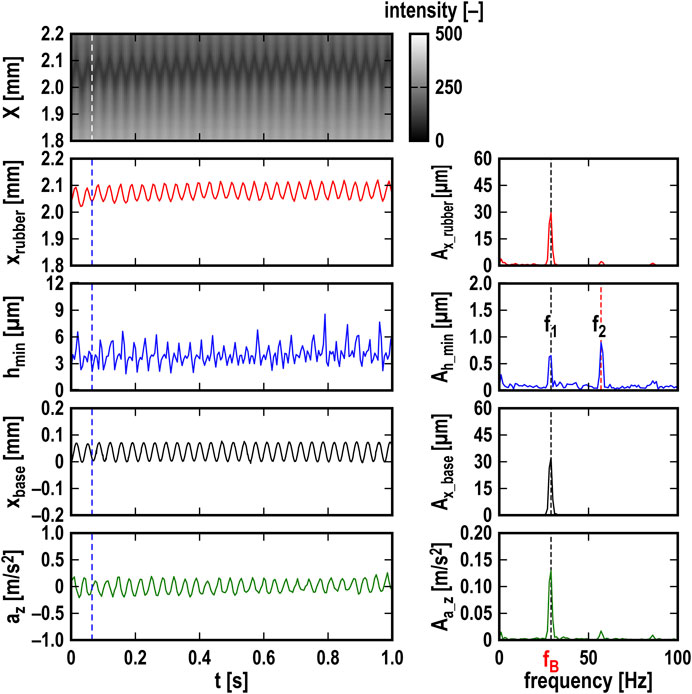
Figure 5. Temporal changes and FFT analyses of fluorescence intensity, h_min, x_rubber, x_base, and a_z; K = 10 N/mm, φ₁ = φ₂ = 0 deg, and V = 5 mm/s; white and blue dashed lines indicate t = 0.065 s (snapshot in Figure 4); f_B = 29 Hz.

Figure 5 illustrates temporal changes in fluorescence intensity, x_rubber, h_min, x_base, and a_z as a typical experimental result at K = 10 N/mm, φ₁ = φ₂ = 0 deg, and V = 5 mm/s, where the values from the last one second of the four-second sliding time in the test were extracted. A low-pass filter (cut-off frequency: 200 Hz) was applied to the temporal change in a_z. In addition, the spectra shown in the right-hand side column of Figure 5 were obtained using the fast Fourier transform (FFT) method applied to the temporal changes in x_rubber, h_min, x_base, and a_z shown in the left-hand side column of Figure 5. The values of x_rubber and h_min were obtained from the fluorescence image at the top of the left-hand side column in Figure 5, which was made by combining the intensity profiles averaged in the Y-axis direction from each snapshot. x_base is the displacement of the base, which was connected to parallel leaf springs. a_z is the acceleration of the glass plate with the lever in the loading mechanism. x_rubber, x_base, and a_z showed steady waveforms of 29 Hz, which matched the natural frequency of the base (f_B = 29 Hz), as shown in the spectra, where their amplitudes were 30 μm, 32 μm, 0.13 m/s², respectively. On the other hand, the waveform of h_min contained two components of f₁ = 29 Hz and f₂ = 57 Hz. The first-order frequency f₁ was the same as f_B = 29 Hz, and the second-order frequency f₂ was approximately twice f_B. The amplitude A_{h_min} at f₁ was 0.63 µm and that at f₂ was 0.88 µm.

Figure 6 shows the cross-sections of h_min, x_base, and z versus x_rubber at K = 10 N/mm, φ₁ = φ₂ = 0 deg, and V = 5 mm/s, where the values were extracted at t = 0.065–0.100 s as shown in Figure 5. z is the Z-axis displacement of the glass plate, calculated by dividing a_z by – (2πf)², assuming a_z to be a harmonic vibration, where f = 29 Hz as shown in Figure 5. The open plot represents the start point of the period (t = 0.065 s). Regarding the cross-section of h_min versus x_rubber in Figure 6A, the values of h_min at the top and bottom end points of x_rubber were the minima of 2 µm in one stroke. The value of h_min at the center of the backward stroke of x_rubber was 6 μm, larger than that at the center of the forward stroke, which was 4 µm. This result suggests that the in-plane motion of the rubber blade tip generated a hydrodynamic effect, such as the wedge effect, increasing the film thickness of water in the middle of the forward and backward strokes where the velocity of the rubber blade tip reached two local maxima in one stroke, causing the 2f_B component in h_min. On the other hand, the cross-section of x_base versus x_rubber shown in Figure 6B displayed a positively inclined elliptical orbit. As the value of x_rubber increased, the value of x_base also increased, but with a lag relative to the change in x_rubber. This result suggests that the motion of the rubber blade tip is the origin of the vibration. In addition, the cross-sections of z versus x_rubber in Figure 6C showed a horizontal elliptical orbit. The difference between the cross-sections of z versus x_rubber and h_min versus x_rubber indicates that the change in h_min was in the Z-axis direction but did not affect the Z-axis motion of the lever in the loading system.

Figure 6

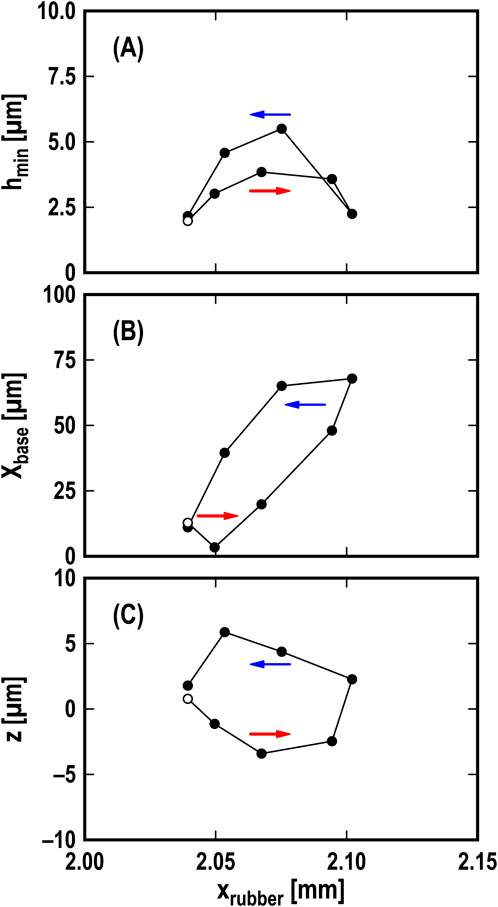
Figure 6. Cross-sections of (A) h_min versus x_rubber, (B) x_base versus x_rubber, and (C) z versus x_rubber; K = 10 N/mm, φ₁ = φ₂ = 0 deg, and V = 5 mm/s; open plot: start point of period (t = 0.065 s); arrows: direction of time progress.

3.3 Influence of drive speed on friction-induced vibration

Figure 7 illustrates the effect of drive speed on the amplitude and frequency of x_rubber, h_min, x_base, and a_z at K = 10 N/mm and φ₁ = φ₂ = 0 deg. The amplitude and frequency were extracted at a predominant frequency in each spectrum, calculated using the FFT method for the temporal change in x_rubber, h_min, x_base, and a_z for 1.0 s, as shown in Figure 5. A_{x_rubber}, A_{h_min}, A_{x_base}, and A_{a_z} represent the amplitude of x_rubber, h_min, x_base, and a_z, respectively. The diameter of circles in Figure 7 represents the amplitude. The thresholds for extracting the predominant components in the spectrum were A_{x_rubber} = 5 μm, A_{h_min} = 0.25 µm, A_{x_base} = 5 μm, and A_{a_z} = 0.025 m/s². For x_rubber, x_base, and a_z, the frequency of the vibration was consistent with f_B = 29 Hz, as shown in Figure 5, and did not change with increasing drive speed V. On the other hand, the values of A_{x_rubber}, A_{x_base}, and A_{a_z} increased with increasing V. The tendencies for the vibration frequency to correspond to the natural frequency derived from the supporting structure, rather than the natural frequency of the rubber blade alone, and for the amplitude to increase with drive speed are consistent with the results of Suzuki et al.‘s research (Suzuki and Yasuda, 1998). Regarding h_min, there are three predominant frequencies: f₁, f₂, and f₃. The first-order frequency f₁ = 29 Hz was the same as f_B = 29 Hz, the second-order frequency f₂ = 57 Hz, as also shown in Figure 5, was approximately 2 × f_B, and the third-order frequency f₃ = 85 Hz was close to 3 × f_B. The values of f₁, f₂, and f₃ did not change with increasing V. In contrast, the values of A_{h_min} at f₂ = 57 Hz increased with increasing V, but those at f₁ = 29 Hz and f₃ = 85 Hz did not increase significantly with increasing V. Note that the second-order frequency was not the natural frequency of the system’s second mode, but could have been caused by the speed-dependent hydrodynamic effect.

Figure 7

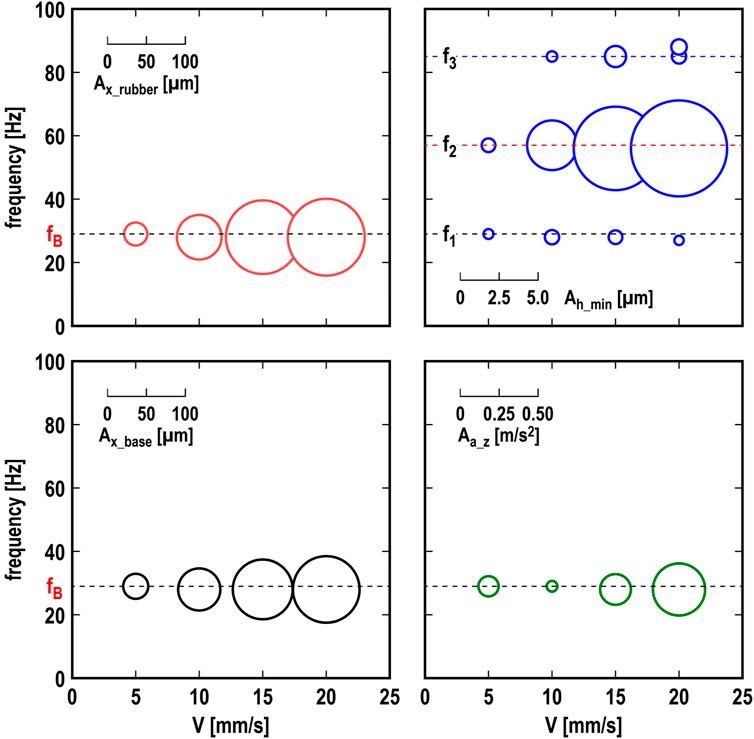
Figure 7. Effect of drive speed V on amplitude and frequency of x_rubber, h_min, x_base, and a_z; K = 10 N/mm; φ₁ = φ₂ = 0 deg.

Figure 8 illustrates the comparison between the maximum speed of the rubber blade tip and the drive speed. The maximum speed of the rubber blade tip was calculated with A_{x_rubber} · ω, where ω was obtained from 2π f₁. The plot of A_{x_rubber} · ω at each V was along the dashed line, which shows A_{x_rubber} · ω = V. This result implies that the amplitude A_{x_rubber} of vibration was saturated when the maximum speed A_{x_rubber} · ω of the rubber blade tip reached the drive speed V.

Figure 8

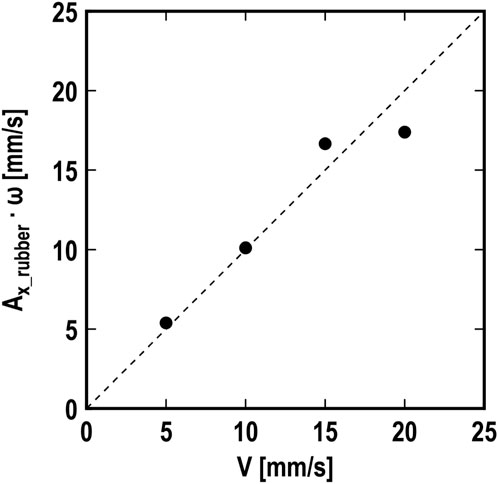
Figure 8. Maximum speed A_{x_rubber ·} ω of rubber blade tip versus drive speed V; K = 10 N/mm; φ₁ = φ₂ = 0 deg; dashed line: A_{x_rubber ·} ω = V.

3.4 Effect of yaw support angles and system stiffness on friction-induced vibration

Figure 9 illustrates the effect of the yaw support angles (φ₁ and/or φ₂) and stiffness K of the loading system at V = 5 mm/s on the amplitude and frequency of the rubber blade’s vibration x_rubber, which were extracted with thresholds of A_{x_rubber} = 5 µm. The diameter of circles in Figure 9 represents the amplitude. Figures 9B, E, H show the effect of the yaw support angles (φ₁ and/or φ₂) at K = 10 N/mm, where the value of A_{x_rubber} at φ₁ = φ₂ = 0 was extracted from that shown at V = 5 mm/s in Figure 7. Increasing only φ₁ (φ₂ = 0) or φ₂ (φ₁ = 0) at K = 10 N/mm as shown in Figures 9B, E, the values of A_{x_rubber} around 29 Hz did not significantly change. On the other hand, increasing the value of φ₁ = φ₂ at K = 10 N/mm as shown in Figure 9H, the value of A_{x_rubber} decreased and at φ₁ = φ₂ = 45 deg was lower than the threshold of A_{x_rubber} = 5 µm. When the stiffness K of the loading system was 4 N/mm, which made the situation f_B > f_L, the frequency of the vibration shifted from f_B to around f_L with increasing only φ₁ (Figure 9A) or both φ₁ and φ₂ (Figure 9G). When K = 60 N/mm, which made the situation of f_B < f_L in Figures 9C, F, I, the frequency of the vibration did not change with increasing φ₁ and/or φ₂. A_{x_rubber} decreased with increasing the value of only φ₁ (Figure 9C) or both φ₁ and φ₂ (Figure 9I), and disappeared at φ₁ = φ₂ > 30 deg.

Figure 9

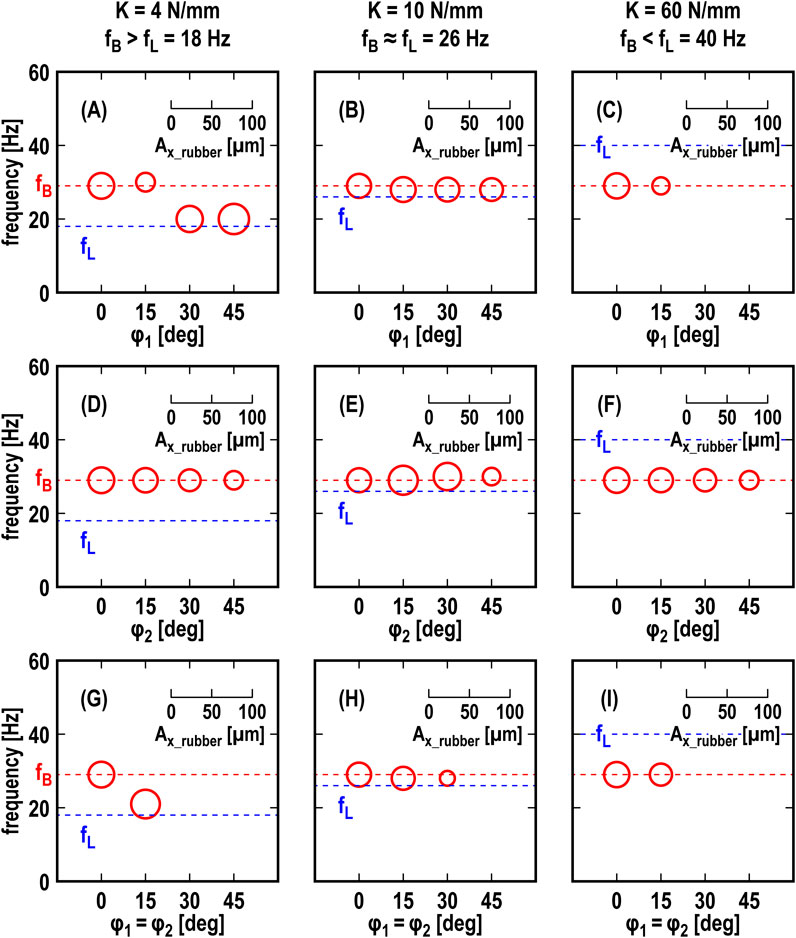
Figure 9. Effect of φ₁ and/or φ₂ on amplitude A_{x_rubber} and frequency F of rubber blade tip V = 5 mm/s; top row (A–C): effect of φ₁ (φ₂ = 0), middle row (D–F): effect of φ₂ (φ₁ = 0), bottom row (G–I): effect of φ₁ = φ₂; left column (A,D,G) : K = 4 N/mm (f_B = 29 Hz > f_L = 18 Hz), center column (B,E,H): K = 10 N/mm (f_B ≈ f_L = 26 Hz), right column (C,F,I) : K = 60 N/mm (f_B < f_L = 40 Hz).

Figure 10 illustrates the effect of the yaw support angles (φ₁ and/or φ₂), the stiffness K of the loading system, and the drive speed V on the maximum amplitude A_{x_r_max} of the rubber blade’s vibration x_rubber, which included the maximum amplitude at a different frequency as shown in Figures 9A, G. Increasing the value of φ₁ = φ₂ in Figures 10G–I, the value of A_{x_r_max} decreased under any drive speed and stiffness conditions. When the stiffness of the loading system was relatively high (K = 60 N/mm), the value of A_{x_r_max} decreased with increasing only φ₁ (φ₂ = 0) in Figure 10C. These results suggest that the yaw support angles in a wiper system could work as the yaw angular misalignment effect (Kado et al., 2013; Nakano et al., 2013-01; Tadokoro et al., 2021), which provides a positive damping effect generated by rotating the friction force vector and suppress the friction-induced vibration. For an actual wiper system in which the wiping motion is in an arc, a parallel misalignment between the drive rotational axis and the driven torsional axis (Tadokoro et al., 2018) could be effective in adding the yaw angular misalignment effect.

Figure 10

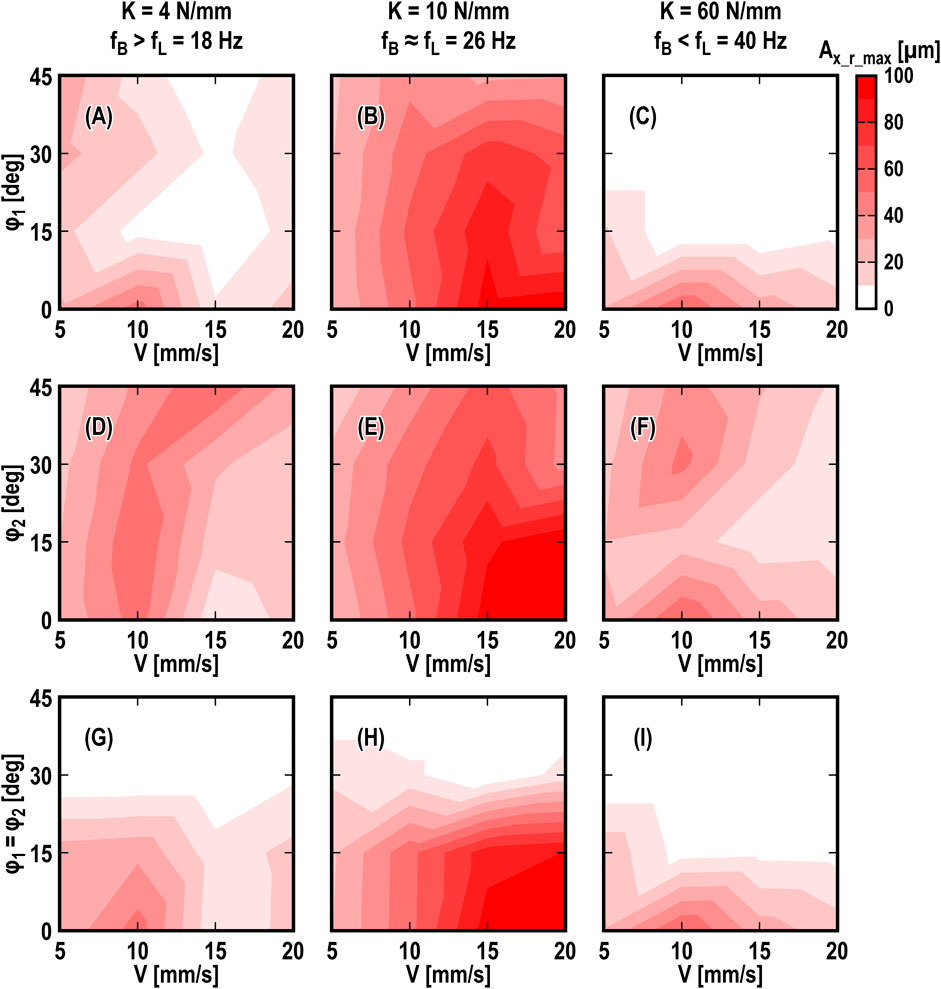
Figure 10. Effect of φ₁, φ₂, and V on A_{x_r_max}; top row (A–C) : effect of φ₁ (φ₂ = 0), middle row (D–F) : effect of φ₂ (φ₁ = 0), bottom row (G–I): effect of φ₁ = φ₂; left column (A,D,G) : K = 4 N/mm (f_B = 29 Hz > f_L = 18 Hz), center column (B,E,H): K = 10 N/mm (f_B ≈ f_L = 26 Hz), right column (C,F,I): K = 60 N/mm (f_B < f_L = 40 Hz).

3.5 Effect of drive speed and yaw support angles on water film thickness and friction coefficient

Figure 11 illustrates the effect of drive speed V on the friction coefficient µ and average value h_{min_mean} of h_min. Black and red plots represent the values at φ₁ = φ₂ = 0 and 45 deg, respectively. The friction coefficient in Figure 11A was calculated using the following Equation 1 (Kado et al., 2013):

$\mu =\frac{k{x}_{\text{base}\_\text{mean}}}{W\cos {\phi }_1}(1)$

where x_{base_mean} is the time-averaged value of x_base. The friction coefficient at φ₁ = φ₂ = 0 and 45 deg showed the velocity-weakening property, with black and red lines representing the fitting lines with the following Equation 2:

$\mu ={\alpha }_{\mu }V+{\beta }_{\mu }(2)$

Figure 11

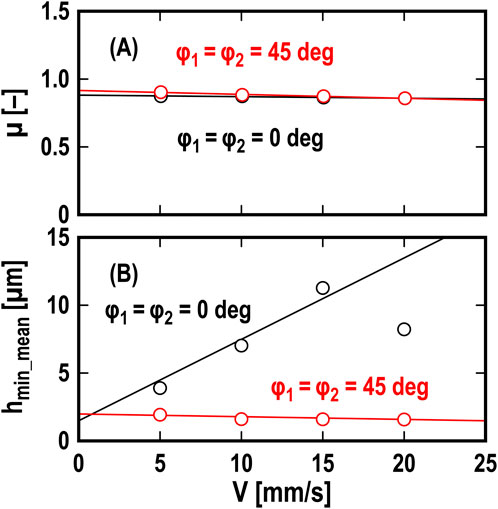
Figure 11. Effect of drive speed V on (A) µ and (B) h_{min_mean}; black plots: φ₁ = φ₂ = 0 deg and red plots: φ₁ = φ₂ = 45 deg.

The black line corresponds to α_µ = −0.001 and β_µ = 0.88 (R²: 0.92), and the red line corresponds to α_µ = −0.003 and β_µ = 0.92 (R²: 0.99). The slope of the fitting lines at φ₁ = φ₂ = 0 deg was slightly lower than that at φ₁ = φ₂ = 45 deg. In Figure 11B, h_{min_mean} is the time-averaged value of h_min. At φ₁ = φ₂ = 0 deg, h_{min_mean} increased with increasing the drive speed V, where the fitting line was adjusted with the following Equation 3:

$h_{\min \_\text{mean}}={\alpha }_{h}V+{\beta }_h(3)$

The black line corresponds to α_h = 0.6 and β_h = 1.5 (R²: 0.42). On the other hand, at φ₁ = φ₂ = 45 deg, h_{min_mean} slightly decreased with increasing V; the red line corresponds to α_h = −0.02 and β_h = 2.0 (R²: 0.58). These results show that the time-averaging value of h_min did not significantly affect the change in the friction coefficient. Also, note that friction-induced vibration causes measurement errors in the friction coefficient (Kado et al., 2013). Therefore, to fully understand the details of the friction-induced vibration in the wiper system, further verifications through numerical approaches are also needed.

4 Conclusions

To examine the effects of the yaw support angles and support stiffness in the wiper system on the friction-induced vibration, concurrent measurements were conducted on the tangential displacement of the translational support base and the normal acceleration of the loading mechanism, as well as fluorescence observation to measure the water film thickness and the rubber blade tip position. The main conclusions derived from the results are summarized as follows:

(1) Friction-induced vibration appears as both in-plane vibration at the natural frequency f_B of the base translationally supporting the wiper blade and out-of-plane vibration at 2 × f_B of the wiper blade tip, which is attributed to fluctuations in the water film thickness.

(2) Higher drive speeds lead to increased vibration amplitude, particularly when the natural frequency f_L of the loading mechanism is close to f_B.

(3) Friction-induced vibration is suppressed by applying large yaw angles to both the rubber blade and tangential support structure at any drive speed.

(4) At sufficiently high stiffness of the loading mechanism, suppressing friction-induced vibration requires only the addition of the yaw angle of the tangential support structure.

These findings provide valuable insights for improving wiper performances under practical operating conditions. However, further research is necessary to investigate the behavior of different wiper materials under varying environmental conditions, such as temperature, humidity, and wear over extended periods. Further studies should also incorporate numerical simulations and physical models to predict wiper behavior across diverse practical applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

CT: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. HK: Data curation, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. MS: Formal Analysis, Methodology, Validation, Writing–review and editing, Writing–original draft. TN: Conceptualization, Formal Analysis, Methodology, Resources, Supervision, Writing–review and editing, Writing–original draft. S-CV: Conceptualization, Methodology, Supervision, Visualization, Writing–review and editing, Writing–original draft. TR: Conceptualization, Methodology, Supervision, Writing–review and editing, Writing–original draft. KN: Conceptualization, Resources, Supervision, Writing–review and editing, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially supported by JSPS KAKENHI Grant Number JP 22KK0236.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Dalzin, F., Le Bot, A., Perret-Liaudet, J., and Mazuyer, D. (2016). Tribological origin of squeal noise in lubricated elastomer-glass contact. J. Sound Vib. 372, 211–222. doi:10.1016/j.jsv.2016.01.019

CrossRef Full Text | Google Scholar

Deleau, F., Mazuyer, D., and Koenen, A. (2009). Sliding friction at elastomer/glass contact: influence of the wetting conditions and instability analysis. Tribol. Int. 42, 149–159. doi:10.1016/j.triboint.2008.04.012

CrossRef Full Text | Google Scholar

Farfan-Cabrera, L. I. (2019). Tribology of electric vehicles: a review of critical components, current state and future improvement trends. Tribol. Int. 138, 473–486. doi:10.1016/j.triboint.2019.06.029

CrossRef Full Text | Google Scholar

Fowell, M. T., Myant, C., Spikes, H. A., and Kadiric, A. (2014). A study of lubricant film thickness in compliant contacts of elastomeric seal materials using a laser induced fluorescence technique. Tribol. Int. 80, 76–89. doi:10.1016/j.triboint.2014.05.028

CrossRef Full Text | Google Scholar

Goto, S., Takahashi, H., and Oya, T. (2001). Clarification of the mechanism of wiper blade rubber squeal noise generation. JSAE Rev. 22, 57–62. doi:10.1016/s0389-4304(00)00095-3

CrossRef Full Text | Google Scholar

Kado, N., Tadokoro, C., and Nakano, K. (2013). Measurement error of kinetic friction coefficient generated by frictional vibration. Trans. Jpn. Soc. Mech. Eng. Ser. C 79, 2635–2643. doi:10.1299/kikaic.79.2635

CrossRef Full Text | Google Scholar

Kitayama, T., Kawasumi, M., Yamasaki, H., Nakano, T., Yamamoto, S., Yamada, M., et al. (2012). Method for evaluating performance of wipers based on visibility. IEICE Trans. Electron. 95, 1716–1723. doi:10.1587/transele.e95.c.1716

CrossRef Full Text | Google Scholar

Lancioni, G., Lenci, S., and Galvanetto, U. (2016). Dynamics of windscreen wiper blades: squeal noise, reversal noise and chattering. J. Non-Linear Mech. 80, 132–143. doi:10.1016/j.ijnonlinmec.2015.10.003

CrossRef Full Text | Google Scholar

Le Rouzic, J., Le Bot, A., Perret-Liaudet, J., Guibert, M., Rusanov, A., Douminge, L., et al. (2013). Friction-induced vibration by stribeck’s law: application to wiper blade squeal noise. Tribol. Lett. 49, 563–572. doi:10.1007/s11249-012-0100-z

CrossRef Full Text | Google Scholar

Li, Y., and Xu, J. (2023). Dynamic characteristics and generation mechanism of windscreen frameless wiper blade oscillations. Nonlinear Dyn. 111, 3053–3079. doi:10.1007/s11071-022-08030-0

CrossRef Full Text | Google Scholar

Min, D., Jeong, S., Yoo, H. H., Kang, H., and Park, J. (2014). Experimental investigation of vehicle wiper blade’s squeal noise generation due to windscreen waviness. Tribol. Int. 80, 191–197. doi:10.1016/j.triboint.2014.06.024

CrossRef Full Text | Google Scholar

Nakano, K., Tadokoro, C., and Kado, N. (2013-01-2069), (2013). Yawing angular misalignment provides positive damping to suppress frictional vibration: basic applicability to disc brake systems. SAE Int. J. Passeng. Cars-Mechanical Syst. 6, 1493–1498. doi:10.4271/2013-01-2069

CrossRef Full Text | Google Scholar

Reddyhoff, T., Dobre, O., Le Rouzic, J., Gotzen, N. A., Parton, H., and Dini, D. (2015). Friction induced vibration in windscreen wiper contacts. J. Vib. Acoust. 137, 041009. doi:10.1115/1.4029987

CrossRef Full Text | Google Scholar

Suzuki, R., and Yasuda, K. (1998). Analysis of chatter vibration in an automotive wiper assembly. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 41, 616–620. doi:10.1299/jsmec.41.616

CrossRef Full Text | Google Scholar

Tadokoro, C., Aso, Y., Nagamine, T., and Nakano, K. (2021). Anti-vibration and traction control of rotary sliding systems by orthogonal rotation providing transverse sliding. Tribol. Int. 159, 106992. doi:10.1016/j.triboint.2021.106992

CrossRef Full Text | Google Scholar

Tadokoro, C., Nagamine, T., and Nakano, K. (2018). Stabilizing effect arising from parallel misalignment in circular sliding contact. Tribol. Int. 120, 16–22. doi:10.1016/j.triboint.2017.12.003

CrossRef Full Text | Google Scholar

Unno, M., Shibata, A., Yabuno, H., Yanagisawa, D., and Nakano, T. (2017). Analysis of the behavior of a wiper blade around the reversal in consideration of dynamic and static friction. J. Sound Vib. 393, 76–91. doi:10.1016/j.jsv.2017.01.018

CrossRef Full Text | Google Scholar

Vlădescu, S. C., Putignano, C., Marx, N., Keppens, T., Reddyhoff, T., and Dini, D. (2019). The percolation of liquid through a compliant seal– an experimental and theoretical study. J. Fluids Eng. 141, 031101. doi:10.1115/1.4041120

CrossRef Full Text | Google Scholar

Wang, Y. S., Guo, H., Yuan, T., Ma, L. F., Liu, N. N., and Sun, P. (2023). Friction-induced noise of vehicle wiper-windshield system: a review. Results Eng. 20, 101557. doi:10.1016/j.rineng.2023.101557

CrossRef Full Text | Google Scholar