Numerical investigation of Dean vortex evolution in turbulent flow through 90° pipe bends

The current study focuses on numerically simulating turbulent flow in a 90° pipe bend using the k-ε turbulence model. Following validation of present numerical approach against prior experimental findings, extensive research was conducted to elucidate the development of Dean vortices and the secondary flow within the pipe bend. This study illustrated the distribution of mean axial velocity, secondary flow phenomena, and the occurrence of Dean vortices in various sections. Velocity vector distributions vividly depict the secondary motion induced by fluid transitioning from the inner to the outer wall of the bend, leading to flow separation. The interplay between the centrifugal force from the bend and adverse pressure gradient results in the formation of two counter-rotating vortices in the streamwise direction. This study presents numerical results aimed at providing insights into the behaviour of Dean vortices and the formation of secondary flow in a 90° pipe bend.

1 Introduction

Turbulent flows in 90-degree pipe bends are frequently encountered in various industrial settings. Curved pipes are widely used in engineering applications across mechanical equipment, including in chemical processing, manufacturing, agriculture, and minerals processing. They play crucial roles in fluid transport, heat exchange, petrochemical systems, gas transmission, thermal and nuclear power plants. These pipes serve specific functions such as providing pathways for centrifugal compressors, configuring passages for pumps, and directing fluid flow in pipelines. The combination of turbulent flow and particle presence in these scenarios leads to complex flow conditions. The curvature of the pipe induces centrifugal forces and unstable pressure gradients, resulting in pronounced secondary flows, increased pressure drops, and occurrences of flow separation and reattachment. Given the intricacies involved, the investigation of such systems has garnered significant attention in recent times.

Over the past 20 years, there has been substantial research, both experimental and simulated, on turbulent flows in curved pipes. Kalpakli Vester et al. (2016) provided comprehensive reviews in this field. Experimental studies consistently reveal certain key findings, including the observation that mean streamwise velocity increases along the inner wall of 30-degree pipe bends, coinciding with the formation of Dean vortices. These vortices, resulting from adverse pressure gradients induced by curvature, cause high-velocity fluid to deflect outward, forming counter-rotating vortices. The mean flow deviates from fully developed turbulent profiles at distances approximately one pipe diameter upstream. Sudo et al. (1998) conducted detailed measurements using hot-wire anemometry in a 90-degree pipe bend, widely referenced by subsequent researchers. Sattarzadeh Shirvan (2011) experiments showed greater axial velocity fluctuations along the inner wall of such bends. Takamura et al. (2012) visualized flow fields in a single elbow pipe at high Reynolds numbers, finding slight changes in flow separation and reattachment points with increased Reynolds numbers, leading to expanded separation regions and increased velocity fluctuations. Some researchers (Takamura et al., 2012; Hellstrom et al., 2011; Di Piazza and Ciofalo, 2011; Noorani et al., 2013; El Khoury et al., 2013; Di Liberto et al., 2013) utilized proper orthogonal decomposition of experimental data, though results were inconclusive. As highlighted by Kalpakli Vester et al. (2016), Vester et al. (2016) capturing the spatial evolution of turbulent flow within 90-degree bends experimentally is challenging, suggesting numerical simulations as a valuable alternative for gaining insights into such flows.

A considerable body of research has focused on numerical simulations of flow in curved pipes, predominantly employing Reynolds-averaged Navier-Stokes (RANS) simulations. These studies, often from an engineering perspective, typically aim to simulate high Reynolds number conditions, emphasizing parameters like pressure drop, friction, and average statistics. Duarte et al. (2017) and Dutta et al. (2022a) utilized an unsteady RANS approach to investigate particle wear in 90-degree pipe bends, a significant industrial concern. Kim et al. (2014) employed various RANS models available in Open FOAM to simulate turbulent flow in such bends, with results suggesting that the renormalization group k-ε turbulence model outperforms others, particularly in modeming primary stream wise velocity and secondary swirling velocity profiles. While RANS models offer computational efficiency and reasonable accuracy for mean turbulence statistics, they struggle to capture flow field fluctuations accurately. Centrifugal forces resulting from streamline curvature exert their influence not only on the bulk flow in the vicinity of the pipe’s central axis but also on areas adjacent to the walls, thereby posing challenges to conventional turbulence modelling assumptions (Wallin and Johansson, 2002). Direct numerical simulation (DNS) and large eddy simulation (LES) can resolve turbulent fluctuations by directly simulating the instantaneous turbulent flow field, but they become computationally demanding, especially at high Reynolds numbers. DNS is often impractical for engineering applications due to computational costs, whereas LES is more feasible. DNS and LES are typically employed for low Reynolds number flows in simple geometries, with periodic boundary conditions helping reduce computational costs for statistically steady, fully developed turbulent flows. Hüttl and Friedrich (2001) conducted DNS studies on low curvature bends, while Noorani et al. (2013) used periodic boundary conditions to study the impact of curvature on turbulence, finding that in comparison to straight pipes, curved pipes typically exhibit a higher critical Reynolds number for turbulence transition, often leading to partial laminarization along the highly curved surfaces of the pipe. Despite recent availability, there is still a scarcity of DNS and LES studies on spatially developing turbulence in practical curved pipes. Some researchers (Wang et al., 2018; Hufnagel et al., 2018; Dutta et al., 2016; Dutta and Nandi, 2019; Dutta and Nandi, 2021) investigated unsteady fluid motions downstream of bends, analysing swirl-switching phenomena affecting Dean vortices, highlighting the complexity of bend flow and the need for detailed three-dimensional characterization of these phenomena.

Over the past decade, many researchers have employed soft-computing methodologies to address technical issues, particularly turbulent flow in curved sections. Among these methodologies, artificial neural networks (ANN) have become the most widely used metamodeling tool for tackling highly nonlinear fluid flow problems. For example, Ganesh et al. (2020) recently developed a metamodel using genetic programming to accurately detect fluid flow velocity in a 90-degree curved conduit. Similarly, Narayanan et al. (2020) designed a particle swarm optimization (PSO) tuned support vector machine metamodel to analyze the turbulent flow field at an elbow. They also applied this metamodel to perform a parameter inquiry on a computational fluid dynamics (CFD) simulation dataset, aiming to better understand the impact of various parameters on turbulent fluid behavior at the elbow. Jain et al. (2021) propose a computationally efficient method using machine learning, specifically, random forest regression (RFR) model. They found, RFR models significantly reduce computational costs compared to CFD models, with only a minor loss in accuracy. While the magnitude of complex flow features like additional vortices is accurately predicted, there is some error in their location. Additionally, Gamahara and Hattori (2017) utilized ANN to develop a subgrid model for subgrid-scale stress in large-eddy simulations. Gholami et al. (2016a) combined ANN with decision trees to predict fluid velocity in a severe 90-degree bend. In another study, Gholami et al. (2016b) employed a multilayer perceptron ANN to estimate the velocity and pressure of fluid moving in a channel bed with a 90-degree acute bend.

Recently, researchers in the nuclear sector have shown interest in the fatigue induced by the fluctuating motion of vortices (Takamura et al., 2012; Ono et al., 2011; Sakakibara and Machida, 2012; Tanaka and Ohshima, 2012). On the other hand, the dielectric barrier discharge (DBD) plasma actuator has emerged as an active flow control device in the last decade (Abdolahipour et al., 2022a; Abdolahipour et al., 2022b; Abdolahipour et al., 2021; Mirzaei et al., 2012; Taleghani et al., 2018; Abdolahipour, 2023). In general, studies on vortex dynamics (Al-Rashed et al., 2017; Marmorino et al., 2018; Ghanbari et al., 2022; Gul et al., 2024; Abbasi et al., 2024) and flow accelerated corrosion rate (Rani et al., 2014; Hari Ponnamma et al., 2014; Madasamy et al., 2021) in pipes are attending interest of researchers nowadays in many engineering applications. A comprehensive understanding of the fundamental aspects of this phenomenon remains elusive. The literature presents divergent findings: some studies suggest the dominance of a single pair of Dean vortices, while others propose the existence of a single vortex spanning the entire pipe. This research aims to numerically simulate turbulent flow within a 90-degree pipe bend with a bend curvature ratio of 1.25, focusing on the development and behavior of Dean vortices and secondary flow structures. Employing the k−ε turbulence model, the study seeks to validate the numerical approach against experimental data and provide an in-depth analysis of the mean axial velocity distribution, secondary flow phenomena, and Dean vortex formation at various sections of the pipe bend.

2 Governing equations and numerical methodology

The segregated implicit solver is utilized in order to discover solutions to the Reynolds Averaged Navier–Stokes (RANS) equations in three dimensions. It is well known that dealing with an issue involving turbulent flow in an industrial setting, selecting the appropriate turbulence model is of the utmost importance. This is especially true when the problem involves flow phenomena that occur in three dimensions, which requires precise modelling.

The equations that regulate the flow of an incompressible fluid characterised by constant characteristics are as follows:

$\frac{\partial \overline{u_i}}{\partial \overline{x_i}}=0(1)$

$\frac{\partial \overline{u_i}}{\partial t}\left(\overline{u_j}\frac{\partial \overline{u_i}}{\partial x_j}\right)=-\frac{1}{\rho }\frac{\partial \overline{p}}{\partial x_i}+\frac{\partial }{\partial x_i}\left[\left(\mu +{\mu }_t\right)\frac{{\partial }^2\overline{u_i}}{\partial x_j\partial x_j}\right](2)$

To complete the equations mentioned above, an expression for turbulent viscosity (${\mu }_t$) is required. In this study, we use the k−ε model, a member of the two-equation RANS family, to determine the value of ${\mu }_t$ as follows:

${\mu }_t=C_{\mu }\frac{k^2}{\mathrm{\epsilon }}(3)$

2.1 Turbulence model

For this particular investigation, the k-ε model is utilized. This model has been utilized by a number of researchers (Kim et al., 2014; Homicz, 2004; Dutta et al., 2022b; Röhrig et al., 2015; Yang et al., 2023; Han et al., 2021; Carloni et al., 2022; Ekat et al., 2023) to analyse single-phase flows in pipe bends. For the purpose of determining the coefficient of turbulent viscosity (µ_t), the kinetic energy of the turbulence (k) and the rate at which the turbulence dissipates (ε) are taken into consideration and solved in this model.

Transport equation for k-epsilon

$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho k\overline{u_i}\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]P_k-\rho \epsilon (4)$

$\frac{\partial \left(p\epsilon \right)}{\partial t}+\frac{\partial \left(p\epsilon \overline{u_i}\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial k}{\partial x_j}\right]+C_{1\epsilon }\frac{\epsilon }{k}{P}_k-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}(5)$

In this context, the variable $\overline{{\mu }_i}$ denotes the time averaged velocity in the fitting direction, ${\mu }_t$ characterizes the eddy viscosity variable and $P_k$ signifies the production of turbulence kinetic energy. Additionally, the equation numbers (4) and (5) include a number of coefficients that may be adjusted (Tu et al., 2018), and the constants are:

$C_{\mu }=0.09,{\sigma }_{\kappa }=1.00,{\sigma }_{\epsilon }=1.30,C_{1\epsilon }=1.44,C_{2\epsilon }=1.92$

The current computations make use of the second order upwind technique, and the SIMPLE algorithm is utilized in order to produce a pressure velocity coupling to solve the governing Equations 1–8. All of the models were constructed with the default relaxation factors used in order to facilitate convergence. In ANSYS Fluent 18.0, a three-dimensional solver is used to resolve the discretized equations iteratively through an implicit technique. In simulation, all variables had a convergence requirement of 10^–5 absolute residual values.

2.2 Boundary conditions

In the present model, a time averaged velocity profile (U = U_in, V = 0, W = 0) is applied as the Dirichlet condition at the inlet. The no-slip condition (U = 0, V = 0, W = 0) is assumed at the pipe wall, while a zero-stress outflow condition is assumed at the outlet of the straight pipe section downstream. This zero-stress condition implies that all flow variables have a zero-diffusion flux, maintaining an overall mass balance correction.

3 Problem definition

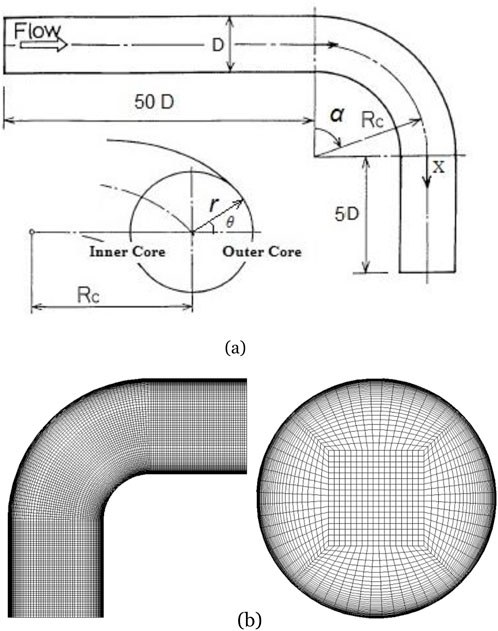
For the purpose of analysing the growth of Dean vortices and the secondary flow motion within the pipe bend, the current work is computational research that employs the k-ε model. The problem that is being studied in this context is the stream of fluid through pipe bend that is 90° in angle and have a diameter of ($D$). The ratio of the bend curvature ($\raisebox{1ex}{$R_c$}\!\left/ \!\raisebox{-1ex}{$D$}\right.$) is equal to 1.25 (where $R_c$ is the bend curvature ratio) for a Reynolds number ($Re=\raisebox{1ex}{$\rho D{U}_{in}$}\!\left/ \!\raisebox{-1ex}{$\mu $}\right.$) of 1 × 10⁵ and Dean number ($D_n=Re\sqrt{\frac{D}{2Rc}}$) of 63,245 based on inlet velocity ($U_{in}$) and bend diameter ($D$). In order to reduce the amount of time spent on computations, the entrance length of the straight pipe was adjusted to 50D in the calculations. For the purpose of this study, the fluid medium that is being investigated is water. A grid-independence analysis was utilized to improve the utilization of a three-dimensional structured mesh that contained hexahedron parts. Figures 1A, B respectively depict the geometry of the bend and the mesh that exists within it. The axial direction downstream of the bend is designated as the x-coordinate, while the path from the inner core wall to the outer core wall of the bend is labelled as the y-coordinate. The z-coordinate denotes the direction perpendicular to both x and y axes.

Figure 1

Figure 1. Representation figure of the (A) flow geometry and (B) current mesh configuration.

3.1 Grid test and validation

At the very beginning of the research project, grid test was carried out for different size ranges from 1.2 million to 2.6 million at $Re=1\times {10}^5$ at same location (bend inlet i.e., $\alpha =0°$. As illustrated in Figure 2A, the final grid (Grid C) employed in this study is as precise as a considerably finer grid (Grid D), with a compromise between computing time and percentage inaccuracy. For validation purposes, present model and simulation setup are tested by comparing them to the data that has already been collected through experiments. This intention is reflected in the use of the same geometrical arrangement. In the experiment detailed by Kalpakli and Örlü (2013), the researchers employed a 90° bend with a circular cross-section and a curvature ratio (Rc/D) of 1.5. Velocity measurements were conducted at a Reynolds number of 24,000, while the swirl number (S) was set to 0. To validate current model, simulations are performed on a computational mesh comprising a total of 2.14 million hexahedral components. In the downstream direction, the mean axial velocity profile, which has been normalized with the input velocity at the symmetry line at X/D = 0.67, demonstrates a very excellent agreement with the experimental findings (Figure 2B). To reinforce confidence in our findings, we have conducted an error analysis as part of the grid independence study and validation. Our results indicate that the maximum error is 12%, with an average error of 7%. These error margins are within acceptable limits and are considered reasonable for conducting further analysis in the context of this study. As a consequence of the validation process, it has been determined that the model follows the published findings with a high degree of precision; hence, the technique of mesh creation and simulation setup has been utilized for the purpose of conducting additional study.

Figure 2

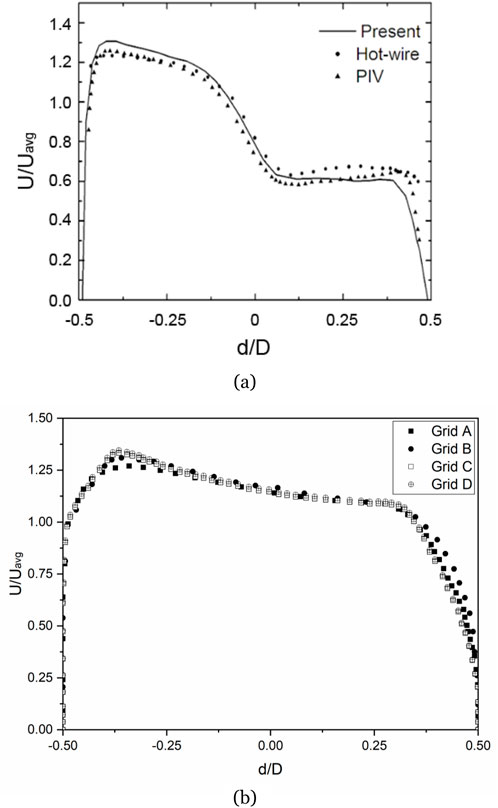
Figure 2. (A) Grid test and (B) Validation of present model against available experimental data (Kalpakli and Örlü, 2013).

4 Results and discussions

Through the use of numerical simulation, the purpose of this work is to investigate the formation of Dean vortices as well as the secondary turbulent flow that occurs by means of a pipe bend that is 90°. This part presents the findings of the mean axial velocity profile, secondary flow, and the creation of Dean vortices. These findings are brought to light in this section.

Figure 3A illustrates the normalized mean axial velocity magnitude within the pipe bend, normalized with the average input velocity, as derived from the present simulation. This presentation aims to provide an insight into the qualitative behaviour of flow within the curved pipe. Figure 3B displays plots showing the distributions of the normalized mean axial velocity at various points (α = 0°, 30°, 60°, and 90°, where α = 0° denotes the bend inlet, α = 90° denotes the bend outlet and X/D denotes positions from bend outlet towards the downstream straight pipe such as X/D = 0 is the bend outlet) along the bend’s central symmetry plane. Negative values on the y-axis indicate positions on the inner wall of the bend. Due to centrifugal force effects, flow is redirected from the bend’s centre towards the outer wall of the curve. Upstream, flow remains unaffected by the pipe’s curvature, retaining its turbulent velocity profile. Between 0 and 60°, acceleration of fluid occurs near the inner core of the bend, with deceleration noted on the outer core. Beyond sixty degrees, the inner wall’s boundary layer thickens while the outer wall’s thins due to centrifugal force influence. Secondary flow emerges after sixty degrees, leading to boundary layer separation from the inner wall as centrifugal force persists. At approximately 90°, the axial velocity reaches its nadir near the inner wall, distinctly revealing the secondary flow pattern in this segment.

Figure 3

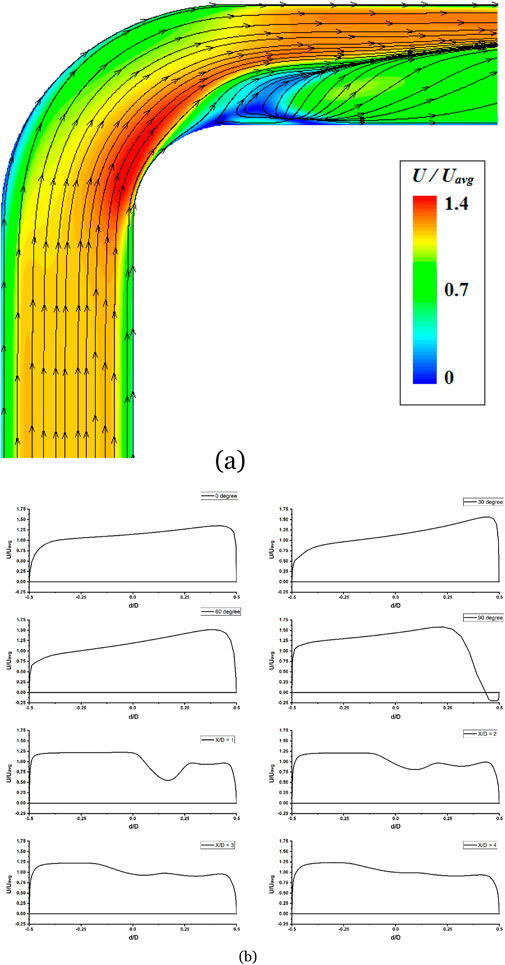
Figure 3. Couture plot of normalized mean axial velocity magnitude (A) and Velocity profiles (normalized) at various positions within the bend along the central symmetry plane (B) for D_n = 63245.

Not only does the existence of a centrifugal force brought about by the bend curvature have an effect on the main flow around the pipe centre, but it also has an effect on the portions that are close to the wall. The contour of the normalized mean axial velocity is displayed in the left portion of each picture in Figure 4, while the vector plot of the mean secondary flow is displayed in the right section of the figure. This is a clear demonstration of the issue. Alternatively, the inner wall is located at the bottom of each figure, while the outside wall is located at the top of each structure. A low velocity zone emerged near the inner wall, which can be readily noticed in the sectional view due to the centrifugal force. As was said before, the velocity moved towards the top wall after sixty degrees, and this region can be seen well. Due to the disproportion between the centrifugal force and the axial pressure gradient, it is reasonable to anticipate that the cross-sectional motion will be of this intensity. By looking at the vector plots of the mean secondary flow, which are displayed in the right-hand section of Figure 4, it is possible to observe this impact quite clearly. Within this context, every instance generates a unique cross-flow boundary layer at the side walls. This secondary motion results in the formation of a vertical velocity component, which in turn accelerates the flow in the direction of the bend centre in the radial direction.

Figure 4

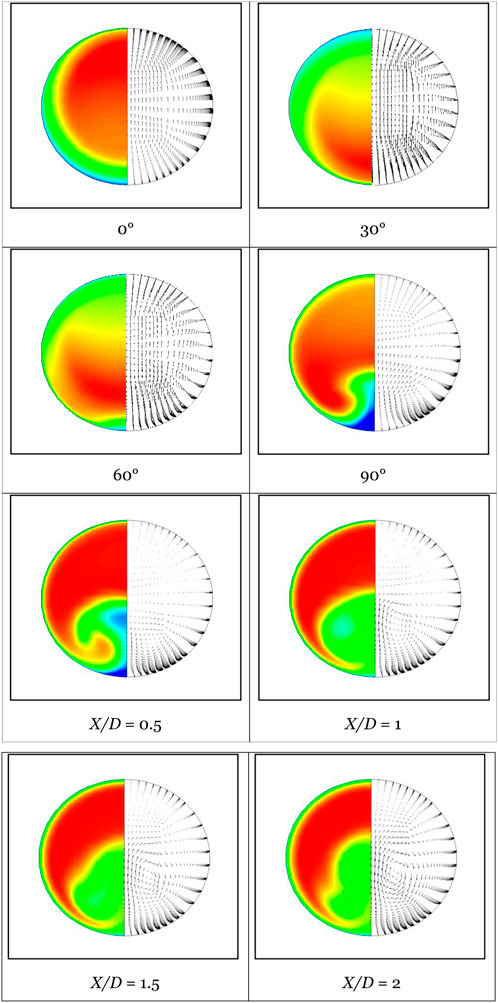
Figure 4. Contour plot (left section) of normalized axial velocity and vector plot (right section) of mean secondary flow in different section plane as indicated in each figure for D_n = 63245. Colour legends are same as Figure 3A.

Figure 5 clearly illustrates the flow direction towards the inner wall at 0°, while between 30 and 60°, a secondary flow gradually develops, leading to the creation of two vortices within the cross-section. This phenomenon arises due to the combined effects of centrifugal and viscous forces. Positioned near the pipe wall on the middle plane between the inner and outer walls, these opposing vortices rotate in opposite directions. As the angle approaches sixty degrees, the boundary layer starts detaching from the inner wall, forming a gap between the boundary layer and the wall. Concurrently, the main flow begins to recirculate, causing the vortices to tilt towards the inner wall. Near the inner wall region, a distinct pair of vortices becomes apparent at the bend outlet (90°). Beyond the bend outlet, located downstream of the curve, there is a noticeable tendency for the vortices to migrate towards the pipe centre as the distance from the bend increases.

Figure 5

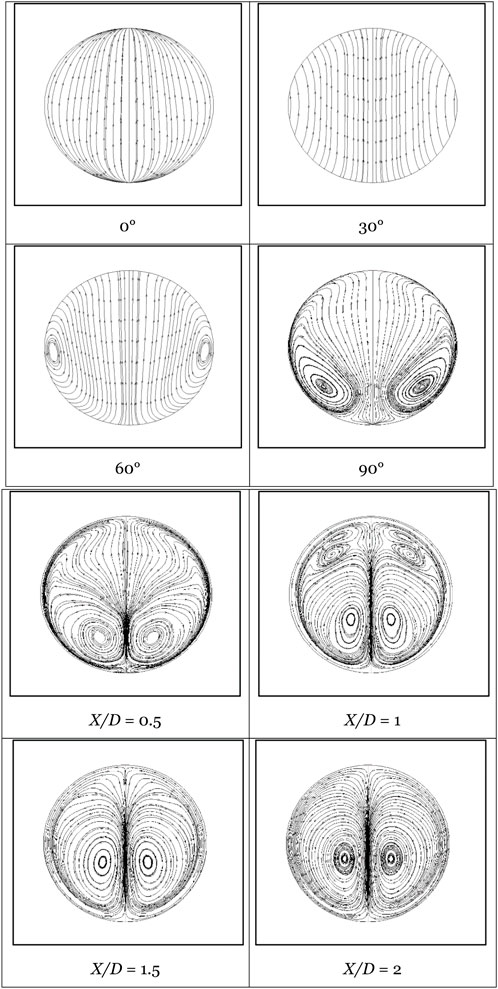
Figure 5. Secondary motion are shown as sectional streamlines in different section plane as indicated in each figure for D_n = 63245.

Figures 6A, B shows contour plots of pressure, normalized by reference pressure ($P_{ref}$) at x’/D = −17.6 [as suggested by (Sudo et al., 1998)], at the wall of the pipe bend and the contour plots pressure coefficient {$C_p=2\left(P-P_{ref}\right)/\rho U_{avg}^2$}. In the straight section upstream of the bend inlet pressure is found uniform. As the flow enters the bend, pressure rises on the outer wall and drops on the inner wall due to curvature. From the bend inlet (α = 0°) to the bend outlet (α = 90°), pressure on the outer wall increases rapidly while it drops sharply on the inner wall due to centrifugal force. Between α = 90° and α = 90°, high pressure is observed on the outer wall and low pressure on the inner wall influenced by centrifugal forces and boundary-layer separation. After this point, pressure on the outer wall decreases due to fluid reflection from the outer to inner wall. As the flow exits the bend and stabilizes, pressure in the downstream straight section (x/D = 5) is lower on the outer wall and higher on the inner wall compared to the bend outlet (α = 90°), The Q-criterion is an effective tool for visualizing vortex structures in fluid flow. Figure 7 illustrates the three-dimensional flow structures using the iso-surfaces of the Q-criterion to analyse the flow development in the current study.

Figure 6

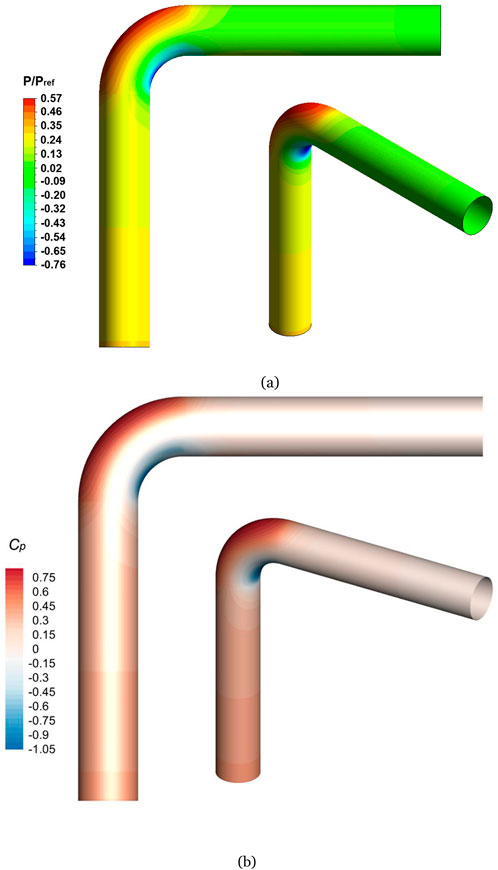
Figure 6. Pressure distribution in pipe wall; Contour plots of (A) normalized pressure and (B) pressure coefficient (C_p).

Figure 7

Figure 7. Iso-surfaces of Q-criterion (Q = 0.01, colour based on velocity) for D_n = 63245.

The Q-criterion is defined as follows:

$Q=\frac{1}{2}\left({\mathrm{\Omega }}_{ij}^2-S_{ij}^2\right)(6)$

where vorticity (function of rotation) and shear strain (rate of shear) $\mathrm{\Omega }$ and S, can be calculated as:

$\mathrm{\Omega }=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}-\frac{\partial u_j}{\partial x_i}\right)(7)$

$S_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)(8)$

As can be seen from Figure 7, upstream of the bend, flow remains unaffected by the bend’s curvature. The fluid released from the bend inlet ($\alpha =0°$) accelerate instantaneously near the bend inner part, causing the shear layer to develop. Higher velocity region is observed near the bend inner part. Two separate zones of vortices are observed in between ($\alpha =45°-90°$) due to development of centrifugal force inside of the bend regarding the bend curvature. At the bend outlet ($\alpha =90°$), two counter-rotating vortices, previously observed in Figure 5, are located near the bend wall as the flow progresses downstream. Additionally, a strong recirculation zone is identified near the center of the pipe.

5 Conclusion

In this study, a numerical simulation utilizing the k-ε turbulent model was conducted to meticulously investigate the turbulent flow of a single-phase, incompressible fluid as it navigates through a 90-degree pipe bend. Detailed insights into the fluid dynamics within the bend were provided by the simulation. Upstream of the bend, the flow was found to be largely unaffected by the curvature of the pipe, maintaining a steady state. As the fluid progressed through the bend, specifically from 0 to 60°, a distinct pattern was observed: the flow accelerated at the inner core and decelerated at the outer core. This behaviour was driven by centrifugal forces that pushed the fluid away from the bend’s centre towards the outer wall, thereby generating secondary flow. Around the 60-degree mark, it was noted that the boundary layer began to detach from the inner wall, indicating a significant shift in flow characteristics. Furthermore, between 30 and 60°, the gradual formation of two vortices near the pipe wall at the mid-plane between the inner and outer walls was revealed by the simulation. These vortices were inclined towards the inner wall, reflecting complex flow interactions. By the time the fluid reached the bend outlet at 90°, a pronounced pair of vortices became evident near the inner wall region. As the flow moved further downstream from the bend, these vortices progressively migrated towards the centre of the pipe. This comprehensive analysis highlighted the intricate nature of turbulent flow in pipe bends and underscored the importance of understanding centrifugal forces and vortex dynamics for optimizing fluid transport systems.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PD: Writing–original draft, Writing–review and editing. NR: Conceptualization, Writing–original draft. RC: Formal Analysis, Funding acquisition, Writing–review and editing. RK: Data curation, Formal Analysis, Writing–review and editing. HK: Investigation, Methodology, Supervision, Writing–review and editing. YN: Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This article was co-funded by the European Union under the REFRESH – Research Excellence For REgion Sustainability and High-tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Programme Just Transition and has been done in connection with project Students Grant Competition SP2025/062 “Specific research on progressive and sustainable production technologies” financed by the Ministry of Education, Youth and Sports and Faculty of Mechanical Engineering VŠB-TUO.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbasi, W. S., Ehsan, M., Rahman, H., Uddin, Z., Hassan, M. M., and Saleem, K. (2024). Analysis of the wake mechanism in external flow around tandem bluff bodies with different aspect ratios. Front. Mech. Eng. 10. doi:10.3389/fmech.2024.1341618

CrossRef Full Text | Google Scholar

Abdolahipour, S. (2023). Effects of low and high frequency actuation on aerodynamic performance of a supercritical airfoil. Front. Mech. Eng. 9. doi:10.3389/fmech.2023.1290074

CrossRef Full Text | Google Scholar

Abdolahipour, S., Mani, M., and Shams Taleghani, A. (2021). Parametric study of a frequency-modulated pulse jet by measurements of flow characteristics. Phys. Scr. 96, 125012. doi:10.1088/1402-4896/ac2bdf

CrossRef Full Text | Google Scholar

Abdolahipour, S., Mani, M., and Shams Taleghani, A. (2022a). Experimental investigation of flow control on a high-lift wing using modulated pulse jet vortex generator. J. Aerosp. Eng. 35. doi:10.1061/(ASCE)AS.1943-5525.0001463

CrossRef Full Text | Google Scholar

Abdolahipour, S., Mani, M., and Shams Taleghani, A. (2022b). Pressure improvement on a supercritical high-lift wing using simple and modulated pulse jet vortex generator. Flow. Turbul. Combust. 109, 65–100. doi:10.1007/s10494-022-00327-9

CrossRef Full Text | Google Scholar

Al-Rashed, A. A. A. A., Roy, N. C., and Hossain, M. A. (2017). Effects of viscous dissipation on unsteady mixed convection heat transfer from a circular cylinder for parallel and contra flows. Front. Mech. Eng. 3. doi:10.3389/fmech.2017.00002

CrossRef Full Text | Google Scholar

Carloni, A. C. N., de Conde, K. E., Pantaleão, A. V., de Azevedo, J. L. F., and Rade, D. A. (2022). Validation and analysis of turbulence modeling in pipe elbow under secondary flow conditions. J. Braz. Soc. Mech. Sci. Eng. 44, 595. doi:10.1007/s40430-022-03899-9

CrossRef Full Text | Google Scholar

Di Liberto, M., Di Piazza, I., and Ciofalo, M. (2013). Turbulence structure and budgets in curved pipes. Comput. Fluids 88, 452–472. doi:10.1016/j.compfluid.2013.09.028

CrossRef Full Text | Google Scholar

Di Piazza, I., and Ciofalo, M. (2011). Transition to turbulence in toroidal pipes. J. Fluid Mech. 687, 72–117. doi:10.1017/jfm.2011.321

CrossRef Full Text | Google Scholar

Duarte, C. A. R., de Souza, F. J., Salvo, R. de V., and dos Santos, V. F. (2017). The role of inter-particle collisions on elbow erosion. Int. J. Multiph. Flow. 89, 1–22. doi:10.1016/j.ijmultiphaseflow.2016.10.001

CrossRef Full Text | Google Scholar

Dutta, P., Chattopadhyay, H., and Nandi, N. (2022a). Numerical studies on turbulent flow field in a 90 deg pipe bend. J. Fluids Eng. 144. doi:10.1115/1.4053547

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutta, P., Chattopadhyay, H., and Nandi, N. (2022b). Numerical studies on turbulent flow field in a 90 deg pipe bend. J. Fluids Eng. 144. doi:10.1115/1.4053547

CrossRef Full Text | Google Scholar

Dutta, P., and Nandi, N. (2019). Numerical study on turbulent separation reattachment flow in pipe bends with different small curvature ratio. J. Inst. Eng. Ser. C 100, 995–1004. doi:10.1007/s40032-018-0488-9

CrossRef Full Text | Google Scholar

Dutta, P., and Nandi, N. (2021). Numerical analysis on the development of vortex structure in 90° pipe bend. Prog. Comput. Fluid Dyn. An Int. J. 21, 261. doi:10.1504/pcfd.2021.10039615

CrossRef Full Text | Google Scholar

Dutta, P., Saha, S. K., Nandi, N., and Pal, N. (2016). Numerical study on flow separation in 90° pipe bend under high Reynolds number by k-ε modelling. Eng. Sci. Technol. Int. J. 19, 904–910. doi:10.1016/j.jestch.2015.12.005

CrossRef Full Text | Google Scholar

Ekat, A.-K., Weissenbrunner, A., Straka, M., Eichler, T., and Oberleithner, K. (2023). Hybrid LES/RANS simulations of a 90° pipe bend using different CFD solvers. OpenFOAM® J. 3, 49–65. doi:10.51560/ofj.v3.36

CrossRef Full Text | Google Scholar

El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G., and V Johansson, A. (2013). Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Turbul. Combust. 91, 475–495. doi:10.1007/s10494-013-9482-8

CrossRef Full Text | Google Scholar

Gamahara, M., and Hattori, Y. (2017). Searching for turbulence models by artificial neural network. Phys. Rev. Fluids 2, 054604. doi:10.1103/physrevfluids.2.054604

CrossRef Full Text | Google Scholar

Ganesh, N., Dutta, P., Ramachandran, M., Bhoi, A. K., and Kalita, K. (2020). Robust metamodels for accurate quantitative estimation of turbulent flow in pipe bends. Eng. Comput. 36, 1041–1058. doi:10.1007/s00366-019-00748-7

CrossRef Full Text | Google Scholar

Ghanbari, J., Dehparvar, A., and Zakeri, A. (2022). Design and analysis of prosthetic heart valves and assessing the effects of leaflet design on the mechanical attributes of the valves. Front. Mech. Eng. 8. doi:10.3389/fmech.2022.764034

PubMed Abstract | CrossRef Full Text | Google Scholar

Gholami, A., Bonakdari, H., Fenjan, S. A., and Akhtari, A. A. (2016b). Flow variables prediction using experimental, computational fluid dynamic and artificial neural network models in a sharp bend. Int. J. Eng. 29, 14–22.

Google Scholar

Gholami, A., Bonakdari, H., Zaji, A. H., Michelson, D. G., and Akhtari, A. A. (2016a). Improving the performance of multi-layer perceptron and radial basis function models with a decision tree model to predict flow variables in a sharp 90° bend. Appl. Soft Comput. 48, 563–583. doi:10.1016/j.asoc.2016.07.035

CrossRef Full Text | Google Scholar

Gul, F., Nazeer, G., Sana, M., Shigri, S. H., and Islam, S. U. (2024). Extensive study of flow characters for two vertical rectangular polygons in a two-dimensional cross flow. Front. Mech. Eng. 9. doi:10.3389/fmech.2023.1334830

CrossRef Full Text | Google Scholar

Han, Y., Zhou, L., Bai, L., Shi, W., and Agarwal, R. (2021). Comparison and validation of various turbulence models for U-bend flow with a magnetic resonance velocimetry experiment. Phys. Fluids. 33. doi:10.1063/5.0073910

CrossRef Full Text | Google Scholar

Hari Ponnamma, R., Teegala, D., Ravi Ranjan, S., Kain, V., and Dipak Kumar, B. (2014). Numerical simulation of turbulent flow in carbon steel pipes leading to flow accelerated corrosion. Arab. J. Sci. Eng. 39, 6435–6451. doi:10.1007/s13369-014-1262-9

CrossRef Full Text | Google Scholar

Hellstrom, L. H. O., Zlatinov, M. B., Smits, A. J., and Cao, G. (2011). “Turbulent pipe flow through a 90 bend,” in Seventh int. Symp. Turbul. Shear flow phenom. (Danbury, Connecticut, USA: Begel House Inc.).

Google Scholar

Homicz, G. F. (2004). Computational Fluid Dynamic simulations of pipe elbow flow. New Mexico, California: Sandia National Laboratories.

Google Scholar

Hufnagel, L., Canton, J., Örlü, R., Marin, O., Merzari, E., and Schlatter, P. (2018). The three-dimensional structure of swirl-switching in bent pipe flow. J. Fluid Mech. 835, 86–101. doi:10.1017/jfm.2017.749

CrossRef Full Text | Google Scholar

Hüttl, T. J., and Friedrich, R. (2001). Direct numerical simulation of turbulent flows in curved and helically coiled pipes. Comput. Fluids 30, 591–605. doi:10.1016/S0045-7930(01)00008-1

CrossRef Full Text | Google Scholar

Jain, P., Choudhury, A., Dutta, P., Kalita, K., and Barsocchi, P. (2021). Random forest regression-based machine learning model for accurate estimation of fluid flow in curved pipes. Processes 9, 2095. doi:10.3390/pr9112095

CrossRef Full Text | Google Scholar

Kalpakli, A., and Örlü, R. (2013). Turbulent pipe flow downstream a 90° pipe bend with and without superimposed swirl. Int. J. Heat. Fluid Flow. 41, 103–111. doi:10.1016/j.ijheatfluidflow.2013.01.003

CrossRef Full Text | Google Scholar

Kalpakli Vester, A., Örlü, R., and Alfredsson, P. H. (2016). Turbulent flows in curved pipes: recent advances in experiments and simulations. Appl. Mech. Rev. 68. doi:10.1115/1.4034135

CrossRef Full Text | Google Scholar

Kim, J., Yadav, M., and Kim, S. (2014). Characteristics of secondary flow induced by 90-degree elbow in turbulent pipe flow. Eng. Appl. Comput. Fluid Mech. 8, 229–239. doi:10.1080/19942060.2014.11015509

CrossRef Full Text | Google Scholar

Madasamy, P., Chandramohan, P., Mukunthan, M., Krishna Mohan, T. V., Rangarajan, S., Uttam, N., et al. (2021). Flow accelerated corrosion rate on carbon steel pipe bend by thin layer activation technique and computational modeling: under PHWR operating conditions. Eng. Fail. Anal. 121, 105125. doi:10.1016/j.engfailanal.2020.105125

CrossRef Full Text | Google Scholar

Marmorino, G. O., Smith, G. B., North, R. P., and Baschek, B. (2018). Application of airborne infrared remote sensing to the study of ocean submesoscale eddies. Front. Mech. Eng. 4. doi:10.3389/fmech.2018.00010

CrossRef Full Text | Google Scholar

Mirzaei, M., Taleghani, A. S., and Shadaram, A. (2012). Experimental study of vortex shedding control using plasma actuator. Appl. Mech. Mater. 186, 75–86. doi:10.4028/www.scientific.net/AMM.186.75

CrossRef Full Text | Google Scholar

Narayanan, G., Joshi, M., Dutta, P., and Kalita, K. (2020). PSO-tuned support vector machine metamodels for assessment of turbulent flows in pipe bends. Eng. Comput. 37, 981–1001. doi:10.1108/ec-05-2019-0244

CrossRef Full Text | Google Scholar

Noorani, A., El Khoury, G. K. K., and Schlatter, P. (2013). Evolution of turbulence characteristics from straight to curved pipes. Int. J. Heat. Fluid Flow. 41, 16–26. doi:10.1016/j.ijheatfluidflow.2013.03.005

CrossRef Full Text | Google Scholar

Ono, A., Kimura, N., Kamide, H., and Tobita, A. (2011). Influence of elbow curvature on flow structure at elbow outlet under high Reynolds number condition. Nucl. Eng. Des. 241, 4409–4419. doi:10.1016/j.nucengdes.2010.09.026

CrossRef Full Text | Google Scholar

Rani, H. P., Divya, T., Sahaya, R. R., Kain, V., and Barua, D. K. (2014). CFD study of flow accelerated corrosion in 3D elbows. Ann. Nucl. Energy. 69, 344–351. doi:10.1016/j.anucene.2014.01.031

CrossRef Full Text | Google Scholar

Röhrig, R., Jakirlić, S., and Tropea, C. (2015). Comparative computational study of turbulent flow in a 90° pipe elbow. Int. J. Heat. Fluid Flow. 55, 120–131. doi:10.1016/j.ijheatfluidflow.2015.07.011

CrossRef Full Text | Google Scholar

Sakakibara, J., and Machida, N. (2012). Measurement of turbulent flow upstream and downstream of a circular pipe bend. Phys. Fluids. 24, 41702. doi:10.1063/1.4704196

CrossRef Full Text | Google Scholar

Sattarzadeh Shirvan, S., Experimental study of complex pipe flow, (2011).

Google Scholar

Sudo, K., Sumida, M., and Hibara, H. (1998). Experimental investigation on turbulent flow in a circular-sectioned 90-degree bend. Exp. Fluids. 25, 42–49. doi:10.1007/s003480050206

CrossRef Full Text | Google Scholar

Takamura, H., Ebara, S., Hashizume, H., Aizawa, K., and Yamano, H. (2012). Flow visualization and frequency characteristics of velocity fluctuations of complex turbulent flow in a short elbow piping under high Reynolds number condition. J. Fluids Eng. 134. doi:10.1115/1.4007436

CrossRef Full Text | Google Scholar

Taleghani, A. S., Shadaram, A., Mirzaei, M., and Abdolahipour, S. (2018). Parametric study of a plasma actuator at unsteady actuation by measurements of the induced flow velocity for flow control. J. Braz. Soc. Mech. Sci. Eng. 40, 173. doi:10.1007/s40430-018-1120-x

CrossRef Full Text | Google Scholar

Tanaka, M., and Ohshima, H. (2012). Numerical investigation on large scale eddy structure in unsteady pipe elbow flow at high Reynolds number conditions with large eddy simulation approach. J. Power Energy Syst. 6, 210–228. doi:10.1299/jpes.6.210

CrossRef Full Text | Google Scholar

Tu, J., Yeoh, G. H., and Liu, C. (2018). Computational fluid dynamics: a practical approach. Butterworth-Heinemann.

Google Scholar

Vester, A. K., Sattarzadeh, S. S., and Örlü, R. (2016). Combined hot-wire and PIV measurements of a swirling turbulent flow at the exit of a 90° pipe bend. J. Vis. 19, 261–273. doi:10.1007/s12650-015-0310-1

CrossRef Full Text | Google Scholar

Wallin, S., and Johansson, A. V. (2002). Modelling streamline curvature effects in explicit algebraic Reynolds stress turbulence models. Int. J. Heat. Fluid Flow. 23, 721–730. doi:10.1016/S0142-727X(02)00168-6

CrossRef Full Text | Google Scholar

Wang, Z., Örlü, R., Schlatter, P., and Chung, Y. M. (2018). Direct numerical simulation of a turbulent 90° bend pipe flow. Int. J. Heat. Fluid Flow. 73, 199–208. doi:10.1016/j.ijheatfluidflow.2018.08.003

CrossRef Full Text | Google Scholar

Yang, Q., Dong, J., Xing, T., Zhang, Y., Guan, Y., Liu, X., et al. (2023). RANS-based modelling of turbulent flow in submarine pipe bends: effect of computational mesh and turbulence modelling. J. Mar. Sci. Eng. 11, 336. doi:10.3390/jmse11020336

CrossRef Full Text | Google Scholar