Experimental study on hydrodynamic characteristics of a taut moored floating box

To investigate the hydrodynamic capabilities of the floating breakwater with a taut mooring system, a two-dimensional physical modelling experiment was performed to investigate the hydrodynamic characteristics of the hydrodynamic pressure on the front surface of the floating box, mooring line tension and transmission coefficient under regular waves, considering factors such as mooring angle, mooring line pre-tension and relative width. The results show that, with the increase of the mooring angle, the hydrodynamic pressure on the floating box first increases and then decreases, the mooring line tension first increases and then decreases slightly, and the transmission coefficient obviously decreases. As the mooring line pre-tension increases, the hydrodynamic pressure and the mooring line tension increase, and the transmission coefficient first decreases and then increases. As the relative width increases, the hydrodynamic pressure, mooring line tension and transmission coefficient all show a decreasing trend. The results can provide a reference for the design and safety assessment of taut moored single pontoon floating breakwater.

1 Introduction

In the past few decades, an increasing number of floating marine structures have been designed to address the growing need for enhanced exploration and utilization of marine resources (Du Kim and Jang, 2016; Xiang et al., 2022; Wei et al., 2024). The use of floating breakwaters has become increasingly prevalent in recent years, due to their efficacy in protecting fragile coastlines, as well as their versatility in applications such as floating structures, marinas and ports. These structures offer a high wave attenuation capacity, coupled with economic benefits, making them a valuable asset in coastal protection.

As a result of this positive effect, a number of novel types of floating breakwaters with intricate configurations were put forth with the objective of enhancing the wave attenuation efficiency, for instance, F-type (Duan et al., 2017, the‘⊥’-type) (Christensen et al., 2018), water ballast type (Yang et al., 2021), airbag-type (Cheng et al., 2021), kelp-box type (Sun et al., 2022), the π-type (Ji et al., 2023), the winglet-type (Yuan et al., 2024). Their mooring systems could be divided into two types-taut mooring type and catenary mooring type. Currently, the predominant focus of researches lies in the floating breakwaters with catenary mooring system type (Tang et al., 2023; Sujantoko et al., 2023; Fouladi et al., 2023). The studies primarily focused on the transmission coefficient of the floating breakwaters, and subsequently directed attention towards parameters such as mooring line tension and motion response (Li et al., 2023; Wei and Yin, 2022; Rajabi and Ghassemi, 2021). Recent studies have focus on the machine learning method for the prediction of wave transmission coefficients, for example, Saghi and Hirdaris (Saghi et al., 2021) utilized the CS–LSSVM to assess the hydrodynamic performance of moored rectangular and trapezoidal floating breakwaters.

These studies offer valuable insights into the hydrodynamic performance of new geometry designs of floating breakwaters with catenary mooring systems. Nevertheless, the box-type represents the most prevalent type (Masoudi and Marshall, 2024), connected and moored by catenary chains or taut cables to the seabed, and the influence of the mooring system still needs systematic experimental investigations (Liu et al., 2020a; Liang et al., 2022). In recent years, the integrated systems of box-type breakwaters and wave energy converters (WEC) have also attracted the attention of many scholars (Zhao and Ning, 2018; Zhao et al., 2019; Jalani et al., 2022). They indicated that the integrated breakwater-WEC systems improved the wave attenuation performance of breakwaters and could convert wave energy into electric energy.

The taut mooring system exhibits a relatively small mooring radius, which can effectively reduce the occupation of the sea area (Xiong, 2017; Guo et al., 2020). Consequently, it finds extensive application in marine floating structures (Qiao et al., 2020; Liu et al., 2020b), particularly for floating bridges, tension leg platforms, and floating submarine tunnels. The wave-induced motion of the floating breakwater generates radiated waves, which superimpose onto the transmitted waves in the shelter area. Therefore, a tight mooring restraint is generally beneficial to the wave dissipation performance, as it diminishes the radiated waves by inhibiting the floating breakwater motion. In this regard, the floating breakwater with taut moorings is optimal. Yoon et al. (2018) carried out a series of laboratory experiments for a floating breakwater to compare the mooring performance of the taut and catenary mooring system, and concluded that taut mooring system can improve the wave control performance of the floating breakwaters. Liu (2020) conducted physical model tests to compare the mooring line tension of the offshore platform between taut and catenary mooring type, demonstrating that taut mooring exhibited better stability and effectively prevented the structures from sinking. It is therefore necessary to study the hydrodynamic characteristics of floating breakwaters with a taut mooring system.

Given that there are many coastal regions where the tidal ranges are large, Guo et al. (2022) proposed a hybrid mooring system composed of seaward taut ropes and leeward slack chains to meet the requirements of wave attenuation at all tide levels. They compared the hydrodynamic characteristics of a floating breakwater with taut, slack, and hybrid mooring systems via numerical simulations. They concluded that at low tide or in the shorter-wave regime at high tide, a tautly moored floating breakwater has the best wave attenuation performance, while in the longer-wave regime, a hybrid mooring system becomes the best. As the real seabed is not flat due to the existence of reefs, Cui et al. (2020) performed experimental and numerical studies on the hydrodynamic performance of a box-floating breakwater in different terrains under regular and irregular wave actions and found that terrain plays an important role in the mooring forces. Considering the effects of the varying seabed on the motion responses, Wang et al. (2019) numerically studied the motion responses of catenary–taut–tendon hybrid moored single module of a semisubmersible-type VLFS and found that mooring lines with larger tendon and taut stiffness could reduce motion responses in severe environmental condition. However, risk of breaking the mooring lines is amplified as the axial stiffness increases. Studies have revealed that the force on taut mooring lines of a floating breakwater was relatively more complex than that of the catenary mooring type (Jin et al., 2021).

The above researches show that, the floating breakwater with a taut mooring system demonstrates superior wave dissipating performance in sea areas with large tidal range but shorter-wave regime, suitable for installations in very deep water. Yet, there is a paucity of studies on the floating breakwaters with taut mooring lines. The investigation of taut moored floating breakwaters remains an area of significant scope for further research. The predominant emphasis has thus far been on the structural motion response and mooring tension. In the case of a taut mooring system intended to serve as a floating breakwater, it is of the utmost importance to pay close attention to both its wave dissipating performance and mooring line tension. Peng et al. (2013) compared the motion response and mooring tension of rectangular and circular floating breakwater through physical and numerical studies. However, their research primarily focused on the submerged taut moored floating breakwater. Sujantoko et al. (2022) carried out a series of experiments on irregular waves to study the influence of mooring angles and configurations of floating breakwater widths on the stability of floating breakwaters with concrete blocks as anchors. Rossell et al. (2021) explored that the effect of the angle and pretension of mooring lines on wave transmission coefficients. Elchahal et al. (2009) conducted the effects of the stiffness and angle of mooring lines on the transmission coefficient and motions of the floating breakwater. Based on experiments and 2-D CFD numerical analysis of a box-type floating breakwater with restrained piles, Yin et al. (2023) utilized the least squares and dimensional analysis methods to obtain the prediction formulas of wave dissipation parameters. Yet a comprehensive analysis of hydrodynamic characteristics (such as hydrodynamic water pressure) encompassing the influence of draft conditions, mooring angles, and mooring line pretensions has not been thoroughly conducted. The gradual implementation of marine tourism, ocean power generation, marine ranching, and deep-water port development has presented new requirements for breakwaters’ performance. Due to its small anchorage radius, the taut mooring floating breakwater effectively minimizes the sea area occupation and exhibits relatively stable structural behavior during normal operation, thereby garnering increasing attention in terms of research and application.

In order to gain a deeper understanding of the hydrodynamic characteristics of the taut mooring floating breakwater, a series of physical experiments have been conducted in a wave flume. The influences of mooring angle, mooring line pre-tension, relative width and wave height on the hydrodynamic characteristics of the floating breakwater have been investigated. The wave pressure, mooring line tension and transmission coefficient under regular wave conditions are measured and calculated in order to express the hydrodynamic characteristics. The results of this study can serve as a valuable reference for the engineering application of taut mooring floating breakwaters.

2 Physical model test

2.1 Test equipment

The hydrodynamic characteristics of the floating breakwaters are simulated using a two-dimensional (2D) model test, given the significantly greater longitudinal length compared to the transverse width. The experiments were conducted in the two-dimensional wave flume at the Engineering Hydrodynamics Laboratory of Ocean University of China (OUC). The flume has a length of 30 m, a width of 1 m, and a depth of 1.2 m. The motorized wave-generation system located at one end of the flume is capable of producing waves with heights ranging from 3 to 30 cm and periods ranging from 0.5 to 3 s. At the opposite end, an energy dissipation net effectively mitigates any interference caused by reflected waves within the flume. The experiment utilized a 2008-type data acquisition system, comprising of the BG08-40 wave height meter, a 32-channel data acquisition instrument, the Smart Sensor4.10 pressure testing system, and an associated computer data processing module. This configuration facilitates the real-time acquisition and examination of data pertaining to wave height and hydrodynamic water pressure. The mooring line tension was quantified through the utilization of the DHDAS dynamic signal acquisition and analysis system, which is equipped with a DYMH-103 type tension sensor. The sensor has a range of 0–30 kg and an output sensitivity of 20 mV/V, meeting the requirements for acquiring tension data in the experiment.

2.2 Design of experiment

The scale design of the experiment was conducted in accordance with the criterion of gravity similarity. Considering the offshore conditions of the Yellow Sea in China, wherein the target water depth range from 10 to 20 m, wave height varies between 1.0 and 3.0 m, and wave periods ranges from 3.0 to 8.0 s, a model scale of λ = 1:30 was selected by taking into account the size limitations of the test flume and the capabilities of the wave generator. Accordingly, the water depths for the model experiment were established at d = 0.5, 0.6, and 0.7 m, respectively. Three groups of wave heights (H = 0.05, 0.07, and 0.1 m) were designated to examine the hydrodynamic characteristics of the floating breakwater. Furthermore, four periods (T = 0.80, 1.10, 1.25 and 1.40 s) were designated for each group of wave heights to examine the impact of the floating breakwater’s relative width on its wave dissipating performance.

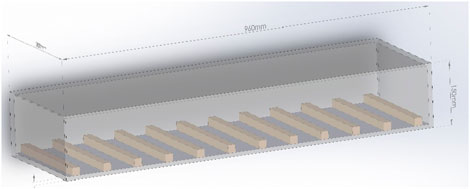
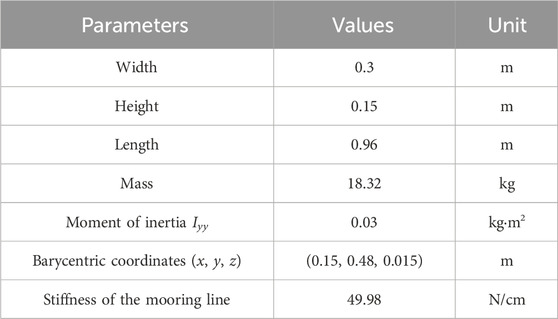
The box is constructed using Plexiglass material with a thickness of 8 mm. The scaled model dimension is 0.96 m long, 0.30 m wide, and 0.15 m high, as depicted in Figure 1. In order to maintain the desired draft during the experiment, a row of lead bars with appropriate weight are affixed at the bottom of the floating box. The total mass of the box is 18.32 kg and its mass center is 0.015 m away from the bottom surface. Its moment of inertia in y-axis (the length direction) is approximately calculated by using an integral method with a value of 0.03 kg·m². The tension sensor and mooring line connected through hooks positioned at each corner. The mooring line consists of two parts: a spring and a ring-buckle chain. A 2 mm diameter ring buckle chain is used to simulate the length of the mooring line. The stiffness of this chain is high enough to be negligible, so its tensile deformation is ignored. A spring at the lower end connection of the mooring line is utilized to simulate the realistic stiffness of the mooring system because of the difficulties to the model to satisfy both gravity similarity criterion and elastic similarity criterion. The other end of the spring is fastened to a hook fixed on the base at the anchor point located beneath the wave tank floor surface. Considering typical properties of flexible mooring lines in engineering applications, a prototype stiffness range of 100–200 MN has been determined, which corresponds to a model stiffness value (k) of 49.98 N/cm for the spring after proportional conversion.

Figure 1

Figure 1. Design of the floating box model.

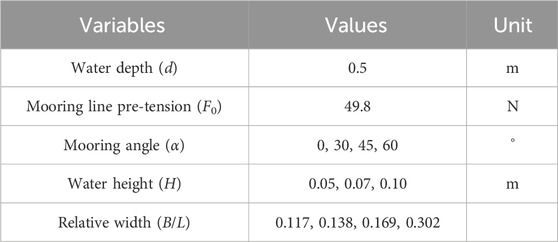
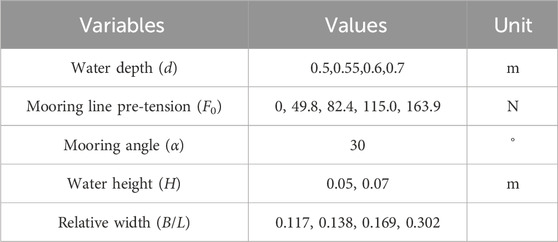
The experiment primarily investigates the influence of three factors, namely, mooring angle, relative width, and mooring line pre-tension on the hydrodynamic characteristics of a floating breakwater. In examining the influence of mooring angle, the water depth was fixed at d = 0.5 m, the mooring line pre-tension was set to F₀ = 49.8 N, and four distinct mooring angles were considered: α = 0°, 30°, 45°, and 60°. A summary of the experimental conditions is provided in Table 1. In examining the impact of mooring line pre-tension, a fixed mooring angle of α = 30° was utilized. In considering the impact of pre-tension on the hydrodynamic characteristics of a floating breakwater, it is essential to acknowledge the influence of the weight of the floating breakwater as a key variable. To ensure the comparability of the results across different cases, the floating box is designed as a constant quantity. Accordingly, the variations in mooring line pre-tension were achieved by adjusting the water depth and the draft of the floating breakwater. Specifically, three distinct water depths (d = 0.5, 0.07 and 0.1 m) were examined, with five corresponding groups for each depth: F₀ = 0 N (representing catenary mooring), 49.8, 82.4, 115, and 163.9 N. The experimental conditions are presented in Table 2. The four distinct periods (T = 0.80, 1.10, 1.25 and 1.40 s) were selected in the two kinds of experimental conditions to investigate the influence of relative width (B/L) of the floating breakwater, in which B is the width of the floating breakwater and L is the incident wave length.

Table 1

Table 1. Experimental conditions for the influence of the mooring angle.

Table 2

Table 2. Experimental conditions for the influence of the mooring line pre-tension.

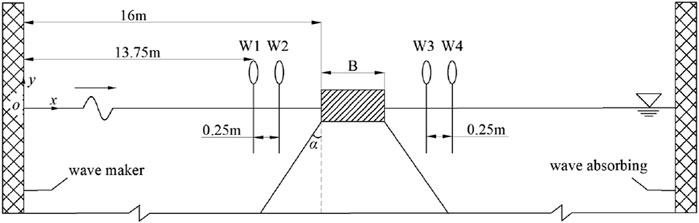
The model was situated in the central leeward zone of the wave flume to guarantee uninterrupted wave propagation over an appropriate distance and to minimize the influence of secondary reflection waves between the box and the wave generator. The particular configuration is depicted in Figure 2. Two wave height gauges are positioned on either side of the floating box. The distance between 2 # and 3 # from the box is 200 cm, while the separation between 1 # and 2 # measures 25 cm, which equal to the distance between 3 # and 4 #. The Goda’s two-point method was utilized to effectively separate incident and reflected data.

Figure 2

Figure 2. Layout diagram of the model.

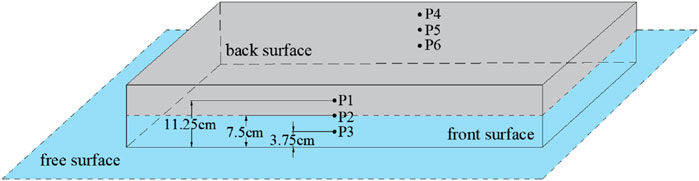
There are six pressure measurement points positioned along the center line of the box’s surface, as depicted in Figure 3. The distance between two adjacent measurement points on the same surface is 3.75 cm. Measurement points 1 # and 4 # are situated above the free surface, while 2 # and 5 # are located near it, and measurement points 3 # and 6 # lie below it. We selected 1 #, 2 # and 3 # for detailed analysis.

Figure 3

Figure 3. Distribution of pressure measurement points on the surface of the floating box.

2.3 Data acquisition and processing

Prior to conducting the experiment, it is of the utmost importance to perform a calibration of the wave generation process under the specified water depth. This is necessary to guarantee that the generated waves will satisfy the prescribed test requirements. It is essential to gather data on the mooring tension prior to the initiation of wave generation and to retain this data following the conclusion of the process. The average peak hydrodynamic pressure is determined by calculating the mean of 10 dynamic pressure peaks obtained during 10 smooth periods. To mitigate potential errors arising from accidental factors during the experimental process, each experimental case was conducted three times, and the resulting data were averaged across the three trials.

The transmission coefficient C_t is a measure of the wave dissipation performance of the floating breakwaters. The calculation formula is Equation 1:

${\mathit{C}}_{\mathbf{t}}=\frac{{\mathit{H}}_{\mathbf{1}}}{{\mathit{H}}_{\mathbf{2}}}(1)$

in which, C_t means the transmission coefficient, while H₁ is the average wave height of 3 # and 4 # wave gauges, and H₂ is the incident wave height calculated by Goda method.

The side view of the box during the experiment for a condition with H = 0.07 m and T = 1.40 s is showed in Figure 4. The temporal evolution of mooring tension on the mooring line of the front surface under the same wave condition is depicted in Figure 5. In Figure 5, the time history of mooring tension exhibits a high-frequency oscillation phenomenon in which the peak value undergoes slight variations across each period. The upward zero-crossing method was utilized for the analysis of the measured tension data, wherein the tension amplitude was determined by averaging the first 1/3 of the peak tension values in the sequenced data. The mooring line tension was then calculated as the average of the tension amplitudes observed over 10 consecutive steady periods. Furthermore, the mooring line tension represents the sum of both individual mooring line tensions on each side.

Figure 4

Figure 4. Side view of the floating breakwater during experimental run.

Figure 5

Figure 5. Time record of the tension of the mooring line in the experiment.

3 Results

3.1 Hydrodynamic pressure on front surface of the floating box

According to the design conditions specified in Table 3, an experimental investigation was conducted to examine the impact of mooring angle (α) on the hydrodynamic water pressure (P). The experiment results are presented in Figure 6.

Table 3

Table 3. Design parameters of the floating box.

Figure 6

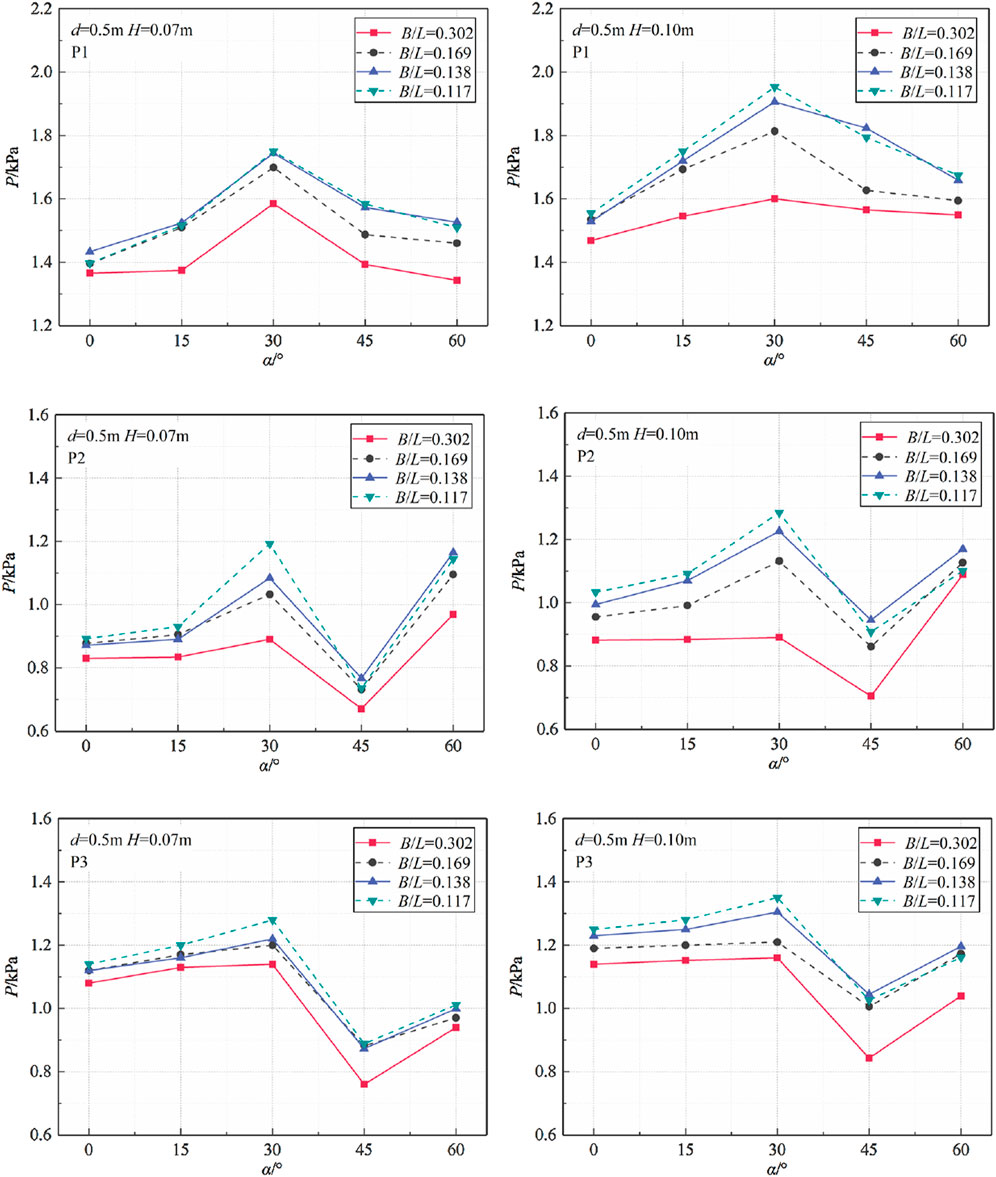
Figure 6. Influence of mooring angle on hydrodynamic pressure on the front surface of the floating breakwater.

3.1.1 Effect of mooring angle

From Figure 6, we can see that the variations of hydrodynamic water pressure measured at points 2 and 3, situated near and below the free surface, exhibit similar trends, whereas those recorded at point 1, located above the free surface, display a slightly divergent pattern.

The hydrodynamic water pressure at point 1 demonstrates an initial increase followed by a subsequent decrease with the elevation of the mooring angle, attaining its maximum value at α = 30°. This observation indicates that the wave interacts more strongly with the box in this condition, resulting in an intense slamming effect on the front surface of the floating breakwater. The hydrodynamic water pressures at points 2 and 3 demonstrate a pattern of increasing, then decreasing, followed by another increase. A minimum value is observed at α = 45°, while a maximum value occurs at α = 30°. This phenomenon can be explained by the fact that at a larger mooring angle, the mooring imposes greater restrictions on the movement response of the box, which results in that this condition is similarity to the interaction between waves and stationary floating boxes where only a small portion of wave energy is converted into kinetic energy of the floating box, while the majority of the wave energy impacts the box directly. Consequently, this results in higher peak values in hydrodynamic water pressure.

In summary, in the perspective of the hydrodynamic water pressure, there exists an optimal mooring angle as α = 45°, that makes the hydrodynamic water pressure at each point remains relatively low, thereby beneficial to the wall safety of the floating structure. Conversely, a worst mooring angle is found as α = 30°, in which condition the pressure at each point is significantly higher, which poses a risk to structural stability. Therefore, it is advisable to avoid using 30° mooring angle in design.

3.1.2 Effect of mooring line pre-tension

The influence of mooring line pre-tension on the hydrodynamic water pressure was investigated based on the specified conditions outlined in Table 1. The corresponding experimental findings are presented in Figure 7. The catenary mooring system (F₀ = 0) is situated at the same water depth as the case of F₀ = 49.8 N. However, there exist differences in both the length of the mooring line and the draught depth of the box. For the cases of F₀ = 49.8, 82.4, 115.0, and 163.9 N, the mooring line length is held constant, while there are variations in both the water depth and the draught of the pontoon. It is noteworthy that an increase in mooring line pre-tension is accompanied by a corresponding increase in water depth and draught of the box.

Figure 7

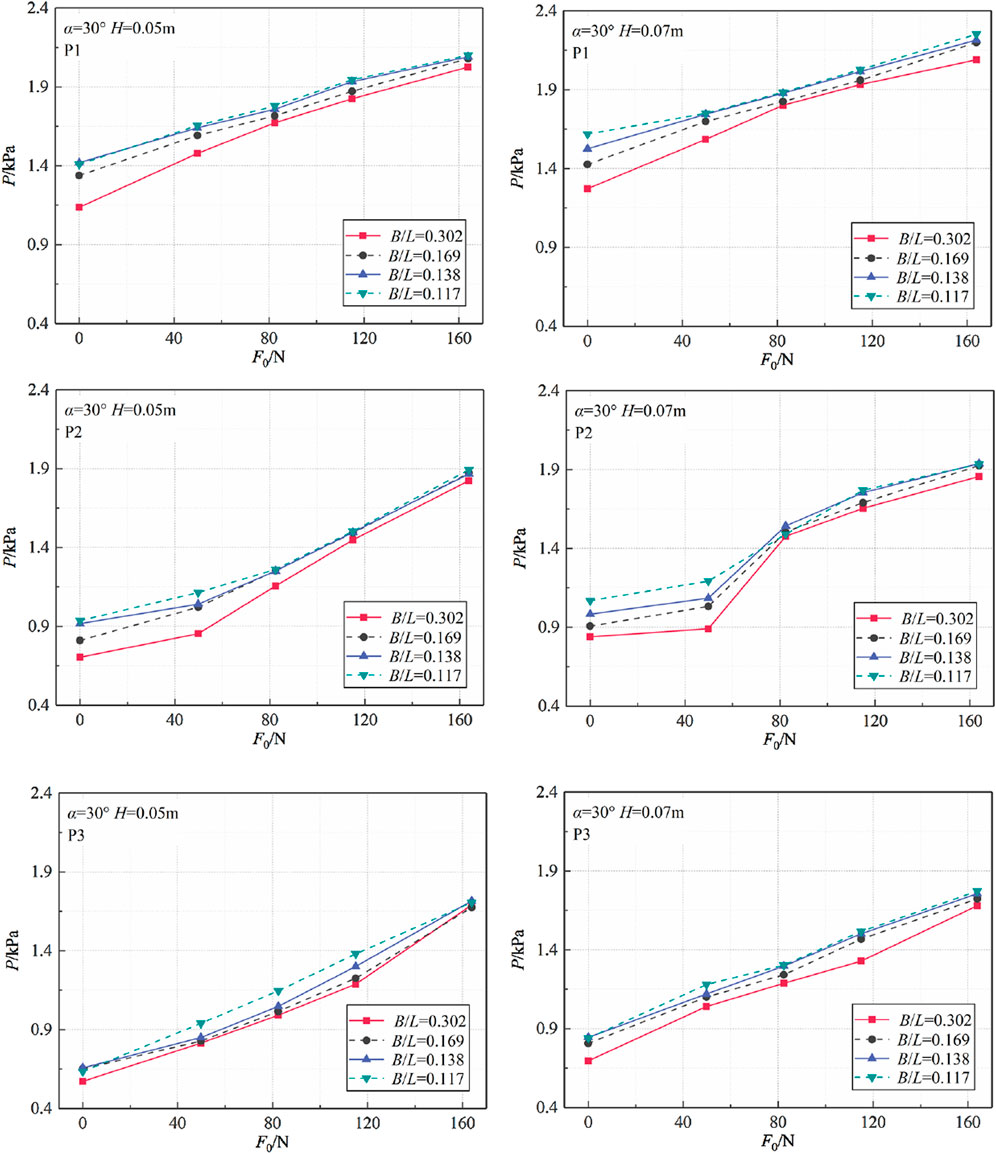
Figure 7. Influence of mooring line pre-tension on hydrodynamic pressure on the front surface of the floating breakwater.

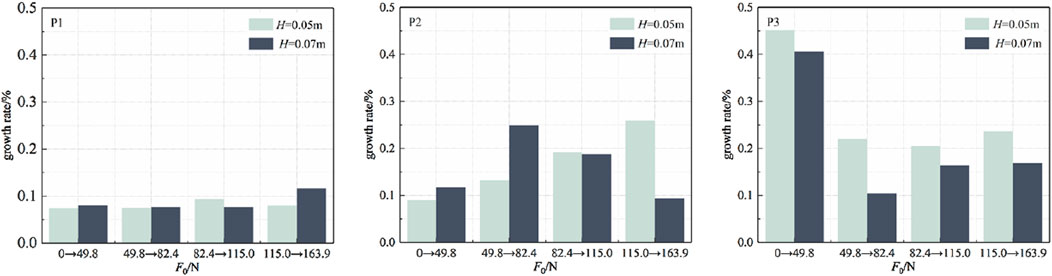
The hydrodynamic water pressure at each point demonstrates a comparable pattern in response to changes in mooring line pre-tension, as depicted in Figure 7. In particular, the hydrodynamic water pressure rises in conjunction with mooring line pre-tension. However, the degree of increase different slightly among different points. Notably, when the mooring line pre-tension is low, there are considerable differences in the peak values of hydrodynamic water pressure at the three points. Nevertheless, these discrepancies tend to diminish as the mooring line pre-tension increases. Furthermore, as the mooring line pre-tension increases, the impact of relative width on hydrodynamic water pressure diminishes. This phenomenon can be attributed to the increased rigidity of the system resulting from elevated mooring line pre-tension, which constrains the motion response of the floating body and consequently gives rise to an intense wave impact effect. The growth rate of hydrodynamic water pressure is influenced by an increase in pre-tension, as depicted in Figure 8. Point 1 exhibits the highest amplitude of pressure, albeit with the slowest growth rate. Conversely, point 3 displays the smallest amplitude but with the fastest growth rate. With the increase in mooring line pre-tension, the draft of the box increases, resulting in a gradual reduction in the distance between point 1 and the still water surface. Simultaneously, point 2 changes from a free surface position to a submerged state, while there is a progressive increase in the distance between point 3 and the still water surface.

Figure 8

Figure 8. Influence of mooring line pre-tension on the hydrodynamic pressure growth rate.

3.1.3 Effect of relative width of the floating breakwater

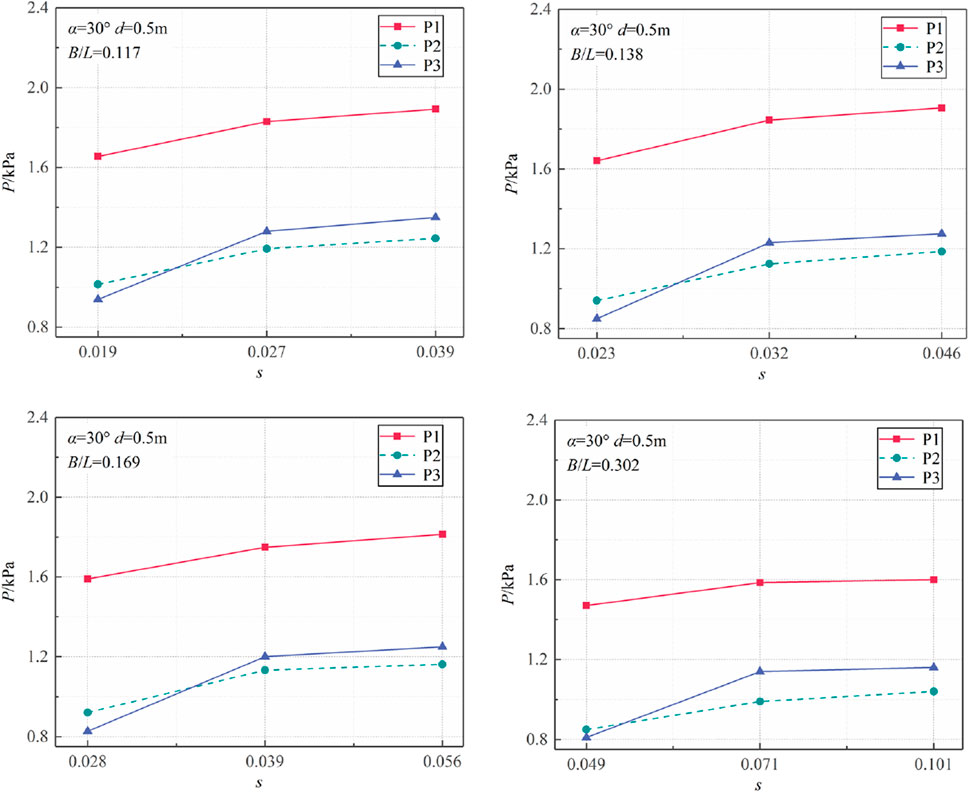
With the decrease of relative width, defined as B/L, the influence of relative width on the hydrodynamic water pressure varies under different wave heights and mooring angle. When mooring angles are within the range of α = 20°∼40°, the influence of B/L on the pressure is pronounced, whereas the influence is less discernible under other angles. Two cases, H = 0.05 m and H = 0.10 m, were selected for analysis to investigate the influence of B/L on the pressure under the conditions of d = 0.5 m and α = 30° (Figure 9). As can be observed, an increase in B/L results in a reduction in pressure, reaching a minimum value at B/L = 0.302. The rationale for this is that as B/L increases, the wavelength decreases while the width of the floating box remains constant. The shorter waves with the same wave height carry less wave energy and induce less intense motion of the floating box, thus reducing the impact force.

Figure 9

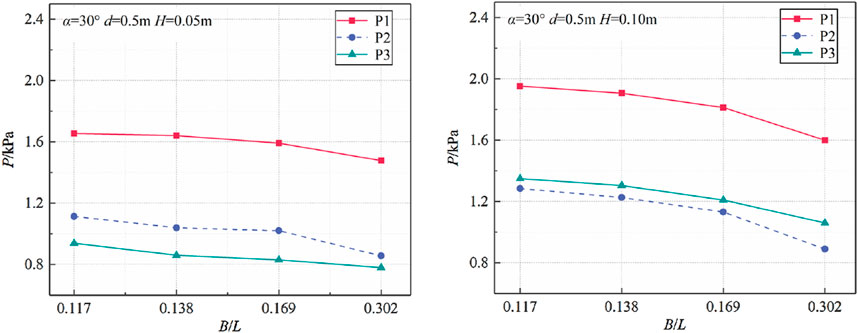
Figure 9. Influence of relative width on hydrodynamic pressure on the front surface of the floating breakwater.

3.1.4 Effect of wave height

The hydrodynamic water pressure is influenced by a number of factors, including the mooring angle, mooring line pre-tension, relative width, and, most significantly affected by wave height. To investigate the impact of different wave heights on the pressure, three conditions were selected for comparative analysis: α = 30°, d = 0.5, 0.10 m, T = 0.80, 1.10, 1.25 and 1.40 s; and H = 0.05, 0.07 and 0.10 m respectively. The x-axis is represented by the non-dimensional parameter wave steepness (s = H/L), as shown in Figure 10.

Figure 10

Figure 10. Influence of wave height on hydrodynamic pressure on the leeward surface.

The hydrodynamic water pressure increases with the increase of wave height for all points, as depicted in Figure 10. Nevertheless, the degree of influence tends to diminish with the growth of wave height. This phenomenon can be attributed to the fact that larger wave heights result in greater kinetic energy of the waves, which in turn leads to a more intense interaction between the waves and the floating box. Consequently, this intensifies the impact of the waves on the box, thereby further elevating the pressure. It is noteworthy that the wave steepness (s) has a significant impact on the hydrodynamic water pressure, with a notable weakening in the growth rate of pressure observed when s is between 0.039 and 0.056. Conversely, when s is between 0.028 and 0.039, the wave steepness has a significant effect on the hydrodynamic water pressure. For waves with a fixed period, an increase in wave height results in a higher movement speed of water particles, accompanied by a gradual intensification of eddy current intensity and viscous dissipation effects which subsequently decelerate the growth rate of pressure.

3.2 Mooring line tension

According to the design conditions delineated in Tables 1, 3, a comprehensive investigation was undertaken to ascertain the impact of mooring angle and mooring line pre-tension on the mooring line tension. The experimental findings were shown in Figures 11, 12.

Figure 11

Figure 11. Influence of mooring angle on mooring line tension.

Figure 12

Figure 12. Influence of mooring line pre-tension on mooring line tension.

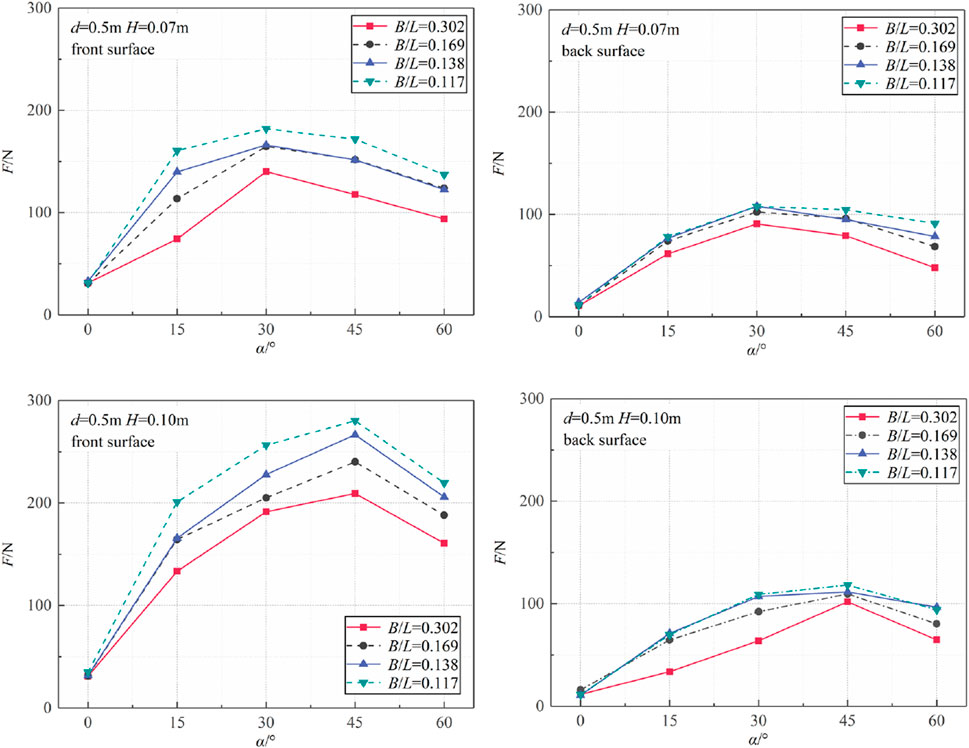
3.2.1 Effect of mooring angle

Apparently, it is observed that the amplitude of mooring line tension on the fore side is about 1.5 times greater than that on the leeward side. This phenomenon can be attributed to the partial dissipation of the incident wave energy by the floating breakwater, leading to a reduction in the interaction forces of the mooring line on the leeward side.

The mooring line tension initially increases and then decreases as the mooring angle increases, as shown in Figure 11. Moreover, there exists a mooring angle leading to the maximum mooring tension, which increases with a rise in wave height. Specifically, the mooring line tension, which varies with different wave heights, reaches its maximum value when α = 30° under H = 0.07 m and when α = 45° under H = 0.10 m, followed by a gradual decrease in tension. This phenomenon can be attributed to the increasing restriction of box movement as the mooring angle increases, causing a transition of the mooring line tension from the vertical to the horizontal direction, where the heave movement has little effect on the horizontal mooring tension. Therefore, it can be inferred that there is a decrease in mooring line tension within the angle range of 30°–45°. The observed phenomenon is consistent with the characteristics of the maximum hydrodynamic pressure in 3.1.1. It can be suggested that, to minimize the mooring tension for optimal design, it is necessary to avoid the mooring angles between 30° and 45° as much as possible.

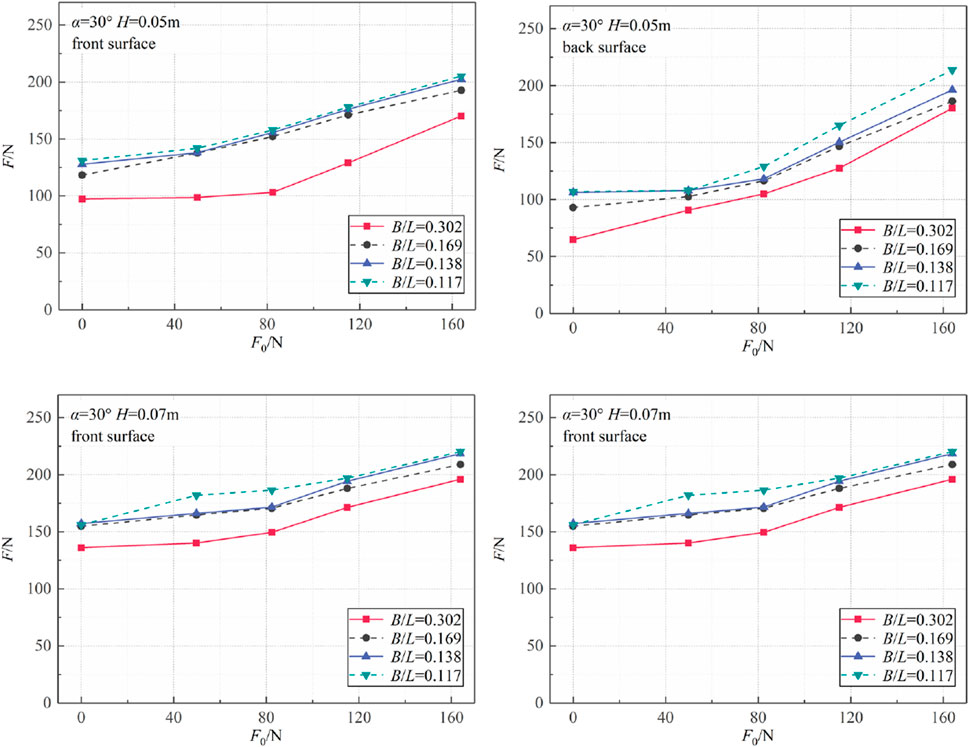
3.2.2 Effect of mooring line pre-tension

The variation of mooring line tension with the pre-tension F₀ for different relative widths (Figure 12) is illustrated in Figure 2. As the mooring line pre-tension F₀ increases, the growth rate of the mooring line tension on the front surface slows down, while it accelerates on the front surface of the floating box it accelerates, resulting in a gradual reduction of the disparity between these tensions on two sides. At an initial pre-tension value of F₀ = 163.9 N, the mooring line tension on the front surface reaches approximately 90% of that on the front surface of the floating box.

This can be explained that as the mooring line pre-tension increases, resulting in an enhancement of the structural rigidity, box movement response is reduced, and thus the mooring angle difference between the front surface and leeward surface of floating box is reduced. When the mooring line pre-tension is small, the box’s significant motion response gives rise to a notable alteration in mooring angle on the front surface, resulting in a markedly elevated horizontal component of mooring line tension in comparison to that on the leeward surface. Consequently, there is a larger disparity between the mooring line tensions on these two sides. Conversely, when the mooring line pre-tension is large, an opposite trend can be observed. Thus it can be seen that excessive mooring line pre-tension may result in more tension in the mooring line, heightened tension during swell or long wave attack, and potential line failure; therefore, it is not advisable to opt for excessively high mooring line pre-tension.

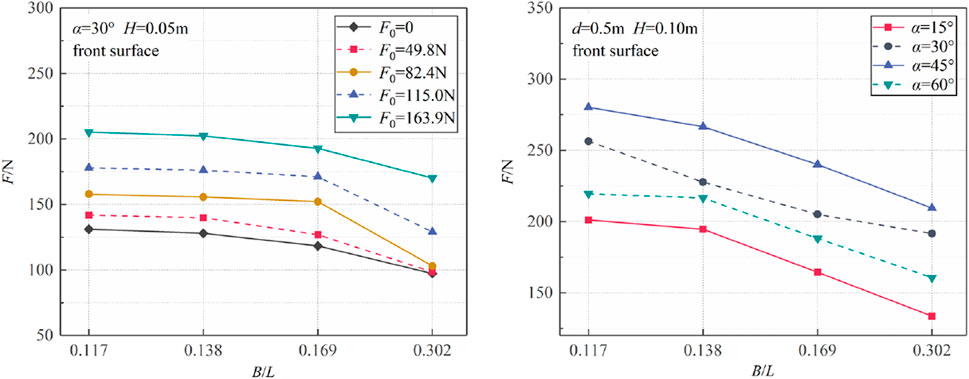
3.2.3 Effect of relative width

In order to analyze the influence of relative width of the floating breakwater on mooring line tension, Figure 13 illustrates the effect of relative width on mooring line tension under different mooring angle conditions (d = 0.5 m, H = 0.10 m) and various mooring line pre-tension conditions (α = 30°, H = 0.05 m). Given that the mooring line tension is negligible when α = 0°, it is not included in the subsequent analysis. As depicted in the figure, an increase in relative width leads to a gradual decrease in mooring line tension until it reaches a minimum at B/L = 0.302. This observation aligns with the dynamic wave pressure exerted on the front surface as it varies with relative width. The reduction in mooring line tension can be attributed to a number of factors, including a reduction in the relative wave period due to an increase in relative width, a decrease in the horizontal impact of waves on the structure, a reduction in the motion response, and a decline in the horizontal component of mooring line tension.

Figure 13

Figure 13. Influence of relative width on mooring line tension.

3.3 Transmission coefficient

The transmission coefficient is a pivotal parameter for evaluating the efficacy of breakwaters. A diminished transmission coefficient signifies enhanced energy dissipation of the incident waves by the breakwaters, thereby enhancing the wave-protection capabilities of the water area situated the breakwaters. Figures 14–16 illustrate how the transmission coefficient varies with mooring angle, relative width, and mooring line pre-tension.

Figure 14

Figure 14. Influence of mooring angle on transmission coefficient.

Figure 15

Figure 15. Influence of mooring line pre-tension on transmission coefficient.

Figure 16

Figure 16. Influence of relative width on transmission coefficient.

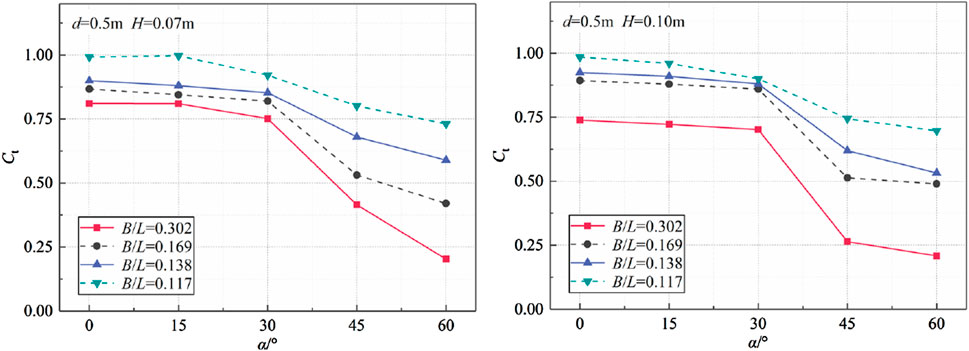
3.3.1 Effect of mooring angle

The transmission coefficient, as shown in Figure 14, exhibits a decreasing trend with increasing mooring angle at different relative widths. For mooring angles less than 30°, there is no significant change in the transmission coefficient, resulting in a value that is considerably higher than that required for wave prevention. However, for mooring angles ranging from 30° to 60°, a more pronounced decrease in the transmission coefficient is observed, which can be attributed to the transition of the dominant motion mode of the floating breakwater from heave to sway. This transition allows for effective dissipation of incident wave energy, which consequently reduces the transmission coefficient.

3.3.2 Effect of mooring line pre-tension

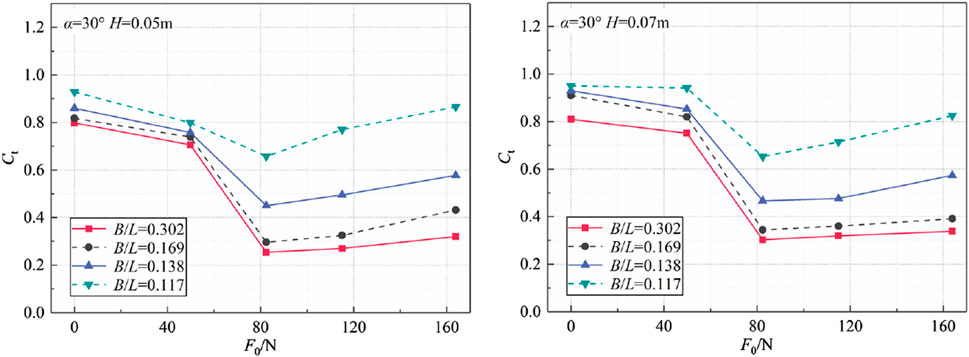
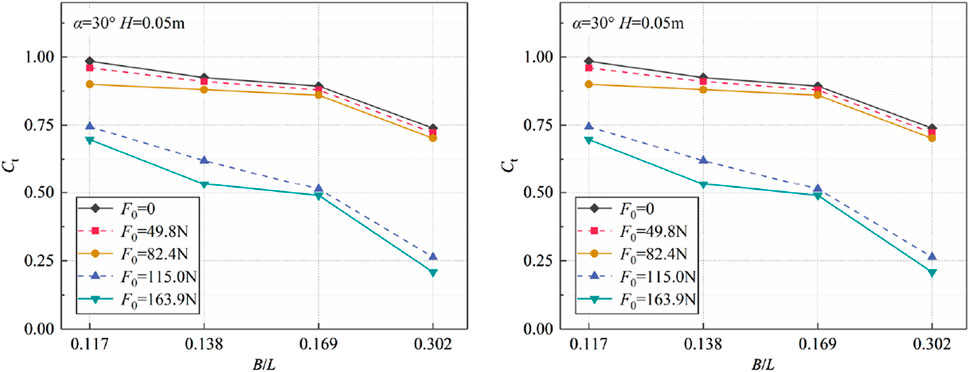
When the relative width varies, refer to Figure 15 for the transmission coefficient as it changes with mooring line pre-tension. As the mooring line pre-tension increases, there is initially a decrease in the transmission coefficient, followed by an increase. At F₀ = 82.4 N, the transmission coefficient attains its minimum value. This is attributed to a greater force exerted on the floating box by the mooring line, which restricts its movement and leads to increased wave reflection and dissipation of incident wave energy, consequently reducing the transmission coefficient. As the mooring line pre-tension is increased further, the non-linear effects between the waves and the floating box become more pronounced, resulting in complex motion due to wave breaking and slamming. Consequently, there is a slight elevation in wave height behind the floating box. It is evident that higher mooring line pre-tension does not necessarily yield better results; instead, there exists an optimal pre-tension level that minimizes the transmission coefficient of the floating box and maximizes other performance metrics.

3.3.3 Effect of relative width

Under different conditions of mooring angle and mooring line pre-tension, the transmission coefficient exhibits a dependence on the relative width, as depicted in Figure 16. As the relative width increases, there is a decreasing trend observed in the transmission coefficients. This indicates that this floating breakwater is more effective for the shorter waves. However, for the cases of α ≤ 15° and F₀≤49.8 N, the transmission coefficients exceed 0.5, failing to meet practical engineering requirements. Under both wave heights, when B/L = 0.117, the transmission coefficients are significantly higher, indicating poor wave dissipation performance. Conversely, in the range of B/L ≥ 0.169, for the cases of small wave heights (H = 0.05 m) with large mooring line pre-tensions (F₀ = 100–180 N), or large wave heights (H = 0.10 m) with mooring angles (α = 30°–60°), all transmission coefficients fall below 0.5, satisfying wave-protection requirements.

4 Conclusion

The hydrodynamic characteristics of a taut floating breakwater were investigated through physical model experiments in this study. Furthermore, the effects of mooring line angle, mooring line pre-tension, and relative width on hydrodynamic wave pressure, mooring line tension, and transmission coefficient were thoroughly discussed. The conclusions are as follows:

As the mooring angle increases, the dynamic wave pressure and mooring line tension both undergo a first rise and subsequent decline, while the transmission coefficient exhibits a decreasing trend. For P1 above the free surface, the hydrodynamic water pressure attains its maximum value at α = 30°, whereas for P2 and P3 around and below the free surface, it reaches its minimum at α = 45°. The mooring line tension reaches its maximum at α = 30°–45°.

As the mooring line pre-tension increases, both the hydrodynamic water pressure and the mooring line tension increase. However, the transmission coefficient initially decreases and then increases, reaching its minimum at F₀ = 82.4 N. Hence, a larger mooring line pre-tension does not necessarily yield superior results, potentially leading to mooring line fracture during extreme sea states.

The effect of the relative width of the floating box on hydrodynamic water pressure, mooring line tension, and transmission coefficient remains consistent, exhibiting an inverse proportion relationship. At B/L = 0.302, the hydrodynamic water pressure and mooring line tension reach their minimum values. For mooring angles greater than 30°and mooring line pre-tensions exceeding 100N, the transmission coefficient demonstrates a notable decline, reaching a value below 0.5 at B/L ≥ 0.169. This outcome aligns with the criteria for wave protection in sheltered water areas.

In the present study, the box-floating breakwater with a taut mooring system is demonstrated to have a superb wave dissipation performance. Nevertheless, it must be acknowledged that this experiment was conducted in regular wave sea states, its validity should be compared against theoretical results in the future investigations. Moreover, further experiments and numerical simulations in irregular waves are necessary to perform a detailed study for engineering applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

QJ: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Writing–original draft, Writing–review and editing. XJ: Data curation, Formal Analysis, Visualization, Writing–original draft. YX: Data curation, Formal Analysis, Investigation, Visualization, Writing–original draft. YC: Funding acquisition, Writing–review and editing. GZ: Formal analysis, Validation, Funding acquisition, Visualization, Writing–review and editing. ZL: Visualization, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Author GZ was employed by Offshore Oil Engineering Co.(Qingdao), LTD.

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cheng, X. F., Liu, C., Zhang, Q. L., He, M., and Gao, X. (2021). Numerical study on the hydrodynamic characteristics of a double-row floating breakwater composed of a pontoon and an airbag. J. Mar. Sci. Eng. 9, 983. doi:10.3390/jmse9090983

CrossRef Full Text | Google Scholar

Christensen, E. D., Bingham, H. B., Friis, A. P. S., Larsen, A. K., and Jensen, K. L. (2018). An experimental and numerical study of floating breakwaters. Coast. Eng. 137, 43–58. doi:10.1016/j.coastaleng.2018.03.002

CrossRef Full Text | Google Scholar

Cui, J., Liu, H., Deng, X., Tao, S., and Li, Q. (2020). An experimental study on hydrodynamic performance of a box-floating breakwater in different terrains. J. Mar. Sci. Technol. 25, 991–1009. doi:10.1007/s00773-019-00695-4

CrossRef Full Text | Google Scholar

Duan, W., Xu, S., Xu, Q., Ertekin, R. C., and Ma, S. (2017). Performance of an F-type floating breakwater: a numerical and experimental study. Proc. Institution Mech. Eng. Part M J. Eng. Marit. Environ. 231, 583–599. doi:10.1177/1475090216673461

CrossRef Full Text | Google Scholar

Du Kim, J., and Jang, B. S. (2016). Application of multi-objective optimization for TLP considering hull-form and tendon system. Ocean. Eng. 116, 142–156. doi:10.1016/j.oceaneng.2016.02.033

CrossRef Full Text | Google Scholar

Elchahal, G., Younes, R., and Lafon, P. (2009). Parametrical and motion analysis of a moored rectangular floating breakwater. J. Offshore Mech. Arct. Eng. 131, 031303. doi:10.1115/1.3124125

CrossRef Full Text | Google Scholar

Fouladi, M. Q., Farhad, B., Shiva, R., Kollolemad, F., Mashayekhi, M., and Viccione, G. (2023). Investigating the sidewall's effects on π-shaped floating breakwaters interacting with water waves by the scaled boundary FEM. Ocean. Eng. 284, 115200. doi:10.1016/j.oceaneng.2023.115200

CrossRef Full Text | Google Scholar

Guo, W. J., Zou, J. B., He, M., Mao, H., and Liu, Y. (2022). Comparison of hydrodynamic performance of floating breakwater with taut, slack, and hybrid mooring systems: an SPH-based preliminary investigation. Ocean. Eng. 258, 111818. doi:10.1016/j.oceaneng.2022.111818

CrossRef Full Text | Google Scholar

Guo, Y. C., Mohapatra, S. C., and Guedes Soares, C. (2020). Review of developments in porous membranes and net-type structures for breakwaters and fish cages. Ocean. Eng. 200, 107027. doi:10.1016/j.oceaneng.2020.107027

CrossRef Full Text | Google Scholar

Jalani, M. A., Ismail, N. I., Saad, M. R., Samion, M. K. H., Imai, Y., Nagata, S., et al. (2022). Experimental study on a bottom corner of the floating WEC. Ocean. Eng. 243, 110237. doi:10.1016/j.oceaneng.2021.110237

CrossRef Full Text | Google Scholar

Ji, C. Y., Bian, X. Q., Xu, S., Guo, J., and Huo, F. (2023). Numerical study on the hydrodynamic performance of floating breakwaters with complex configurations. Ocean. Eng. 273, 114032. doi:10.1016/j.oceaneng.2023.114032

CrossRef Full Text | Google Scholar

Jin, Z. F., Zhang, J. F., and Zhang, Q. H. (2021). Study on numerical model of hydrodynamics of mooring line floating breakwater under wave actions. Ocean Eng. 39, 21–31. doi:10.16483/j.issn.1005-9865.2021.01.003

CrossRef Full Text | Google Scholar

Li, H., Xie, W. H., and lv, B. C. (2023). Study on the motion response and wave slamming of floating breakwater under focused wave action. J. Waterw. Harb. 2, 183–189.

Google Scholar

Liang, J.-ming1, Liu, Y. 1, and Chen, Y.-kun. (2022). Experimental study on hydrodynamic characteristics of the box-type floating breakwater with different mooring configurations. Ocean. Eng. 254, 111296. doi:10.1016/j.oceaneng.2022.111296

CrossRef Full Text | Google Scholar

Liu, H. (2020). Study on shallow water mooring design and hydrodynamic analysis method of floating marine structures. Jiangsu, China: Jiangsu University of Science and Technology.

Google Scholar

Liu, Q. K., Ji, Q. L., and Wang, Y. (2020a). Experimental study on hydrodynamic characteristics of chain moored single pontoon floating breakwater. Port and Waterw. Eng. 01, 23–28. doi:10.16233/j.cnki.issn1002-4972.20191227.020

CrossRef Full Text | Google Scholar

Liu, Q. K., Ji, Q. L., and Wang, Y. (2020b). Experimental study on hydrodynamic characteristics of chain moored single pontoon floating breakwater. Port and Waterw. Eng. 01, 23–28. doi:10.16233/j.cnki.issn1002-4972.20191227.020

CrossRef Full Text | Google Scholar

Masoudi, E., and Marshall, A. (2024). Diffraction of waves by multi-pontoon rectangular floating breakwaters. Ocean. Eng. 310, 118789. doi:10.1016/j.oceaneng.2024.118789

CrossRef Full Text | Google Scholar

Peng, W., Lee, K. H., Shin, S. H., and Mizutani, N. (2013). Numerical simulation of interactions between water waves and inclined-moored submerged floating breakwaters. Coast. Eng. 82, 76–87. doi:10.1016/j.coastaleng.2013.07.002

CrossRef Full Text | Google Scholar

Qiao, D. S., Qi, X. L., and Yan, J. (2020). Analysis of snap loading of a taut mooring system in the slack-taut process. J. Harbin Eng. Univ. 196, 206–211. doi:10.11990/jheu.201904061

CrossRef Full Text | Google Scholar

Rajabi, M., and Ghassemi, H. (2021). Hydrodynamic performance improvement of double-row floating breakwaters by changing the cross-sectional geometry. Math. Problems Eng. 2021, 1–21. doi:10.1155/2021/2944466

CrossRef Full Text | Google Scholar

Rossell, W., Ozeren, Y., and Wren, D. (2021). Experimental investigation of a moored, circular pipe breakwater. J. Waterw. Port, Coast. Ocean Eng. 147, 04021019. doi:10.1061/(asce)ww.1943-5460.0000657

CrossRef Full Text | Google Scholar

Saghi, H., Mikkola, T., and Hirdaris, S. (2021). A machine learning method for the evaluation of hydrodynamic performance of floating breakwaters in waves. Ships Offshore Struct. 17, 1447–1461. doi:10.1080/17445302.2021.1927358

CrossRef Full Text | Google Scholar

Sujantoko, E., Armono, H. D., Djatmiko, E. B., and Putra, R. D. (2022). Stability analysis of concrete block anchor on steep-slope floating breakwater. Fluids 7, 259. doi:10.3390/fluids7080259

CrossRef Full Text | Google Scholar

Sujantoko, E., Djatmiko, E. B., Wardhana, W., and Gemilang Firmasyah, I. N. (2023). Numerical modeling of hydrodynamic performance on porous slope type floating breakwater. Nase More 70, 77–87. doi:10.17818/nm/2023/2.1

CrossRef Full Text | Google Scholar

Sun, B., Li, C., Yang, S. L., Zhang, H., and Song, Z. (2022). Experimental and numerical study on the wave attenuation performance and dynamic response of kelp-box type floating breakwater. Ocean. Eng. 263, 112374. doi:10.1016/j.oceaneng.2022.112374

CrossRef Full Text | Google Scholar

Tang, Z. S., Wu, W. W., and Zhao, S. H. (2023). Experimental and numerical study on hydrodynamic characteristics of a new type of floating breakwater. Shipbuild. China 5, 98–106.

Google Scholar

Wang, Y., Xu, S., and Wang, L. (2019). Motion responses of a catenary-taut-tendon hybrid moored single module of a semisubmersible-type VLFS over uneven seabed. J. Mar. Sci. Technol. 24, 780–798. doi:10.1007/s00773-018-0587-6

CrossRef Full Text | Google Scholar

Wei, K., and Yin, X. S. (2022). Numerical study into configuration of horizontal flanges on hydrodynamic performance of moored box-type floating breakwater. Ocean. Eng. 266, 112991. doi:10.1016/j.oceaneng.2022.112991

CrossRef Full Text | Google Scholar

Wei, Y. J., Yu, S. R., Li, X., Zhang, C., Ning, D., and Huang, L. (2024). Hydrodynamic analysis of a heave-hinge wave energy converter combined with a floating breakwater. Ocean. Eng. 293, 116618. doi:10.1016/j.oceaneng.2023.116618

CrossRef Full Text | Google Scholar

Xiang, G., Xiang, X. B., and Yu, X. C. (2022). Dynamic response of a SPAR-type floating wind turbine foundation with taut mooring system. J. Mar. Sci. Eng. 10, 1907. doi:10.3390/jmse10121907

CrossRef Full Text | Google Scholar

Xiong, L. Z. (2017). “Taut mooring system and its interaction with offshore foundations,” in Doctoral dissertation. Shanghai, China: Shanghai Jiao Tong University.

Google Scholar

Yang, Z., Ji, X., Xie, M., Li, J., Zhang, H., and Wang, D. (2021). Experimental study on the dynamic response of a water ballast type floating breakwater. Ocean. Eng. 233, 109012. doi:10.1016/j.oceaneng.2021.109012

CrossRef Full Text | Google Scholar

Yin, Z. G., Ni, Z. H., Luan, Y. N., Zhang, X., Li, J., and Li, Y. (2023). Hydrodynamic characteristics of a box-type floating breakwater with restrained piles under regular waves. Ocean. Eng. 280, 114408. doi:10.1016/j.oceaneng.2023.114408

CrossRef Full Text | Google Scholar

Yoon, J. S., Ha, T., Jung, J., and Jung, J. (2018). Laboratory experiments on characteristics of perforated-type floating breakwaters. J. Coast. Res. 85, 1051–1055. doi:10.2112/si85-211.1

CrossRef Full Text | Google Scholar

Yuan, H. S., Zhang, H. Z., Wang, G. Y., and Tu, J. (2024). A numerical study on a winglet floating breakwater: enhancing wave dissipation performance. Ocean. Eng. 309, 118532. doi:10.1016/j.oceaneng.2024.118532

CrossRef Full Text | Google Scholar

Zhao, X., and Ning, D. (2018). Experimental investigation of breakwater-type WEC composed of both stationary and floating pontoons. Energy 155, 226–233. doi:10.1016/j.energy.2018.04.189

CrossRef Full Text | Google Scholar

Zhao, X., Ning, D., and Liang, D. (2019). Experimental investigation on hydrodynamic performance of a breakwater-integrated WEC system. Ocean. Eng. 171, 25–32. doi:10.1016/j.oceaneng.2018.10.036

CrossRef Full Text | Google Scholar