Role of curvature in controlling SWBLI behavior in a hypersonic double ramp flow

Hypersonic flows generate intense unsteady pressure and thermal loads, posing significant challenges for high-speed aerospace applications such as re-entry vehicles and hypersonic cruise systems. These extreme conditions necessitate effective flow control strategies to enhance aerodynamic performance and structural integrity. This study examines the influence of surface curvature on these loads in a double-wedge geometry, aiming to optimize flow control approaches. Unsteady Mach 7 flow simulations are conducted using a high-fidelity, time-accurate solver with third-order MUSCL as well as seventh-order WENO schemes, ensuring precise resolution of shock interactions and flow structures. A standard double-ramp configuration is analyzed alongside two smooth ramp configurations, where the faceted intersection of the front and aft wedges is replaced with different curvature levels. The computational results are validated against experimental heat-flux data to confirm the accuracy of the numerical approach. The findings reveal that the high-curvature geometry (curvature, $\kappa =1.01$) introduces only marginal variations in mean pressure and thermal loads. However, transient flow characteristics are notably altered. In contrast, the low-curvature configuration $(\kappa =0.49)$ significantly reduces both pressure and thermal loads by 43% and 58%, respectively, while also minimizing the separation region. The reduced separation leads to a smoother and more stable flowfield, contributing to improved aerodynamic efficiency. Long-term analysis further indicates that the low-curvature configuration accelerates the decay of large-amplitude unsteady signals, suggesting enhanced flow stability over extended durations. These results underscore the potential benefits of surface curvature in mitigating aerodynamic heating and structural stresses in hypersonic flows, and therefore provide insights for the development of more efficient hypersonic vehicles with improved thermal management, enhanced vehicle survivability, and better overall performance in extreme flight conditions.

1 Introduction

Hypersonic flows are typically characterized by complex Shock-wave/Boundary-layer interactions (SWBLI) and Shock-Shock interactions. These interactions generate high unsteady pressure and thermal loads, which can lead to structural fatigue, material degradation, and even failure of aerospace vehicles, particularly those constructed with composite materials (Fame et al., 2021; 2023). The intense aerodynamic heating associated with hypersonic speeds can severely impact thermal protection systems (Agarwal, 2024).

The intake, particularly, plays a critical role in managing the conditions of the incoming freestream flow in a scramjet engine. It gradually decelerates the hypersonic flow to supersonic speeds, ensuring conditions suitable for stable combustion. As the flow enters the scramjet intake, a series of oblique shocks and expansion fans form and reflect along the internal flow path. The intake design must achieve an optimal balance between air compression, temperature management, and minimizing drag and total pressure losses.

The high pressure and temperature gradients generated by shocks impose substantial structural and thermal loads on the scramjet engine geometry. Consequently, significant efforts have been made to develop novel flow control techniques to reduce localized heat flux and prevent overheating. Some recent advancements in active and passive flow control approaches include: plasma actuators for aerodynamic and propulsion applications (Mirzaei et al., 2012), pulse jet actuation for flow modulation (Abdolahipour et al., 2021) and placement of subcavities to alter frequencies (Bhaduri et al., 2024).

A relatively simple but commonly found configuration in most hypersonic vehicles is a double wedge or double ramp (see Figure 1a). This geometry is present at the intake of a scramjet engine, the nose of a fuselage, and the corners between the fuselage and control surfaces, among many others.

Figure 1

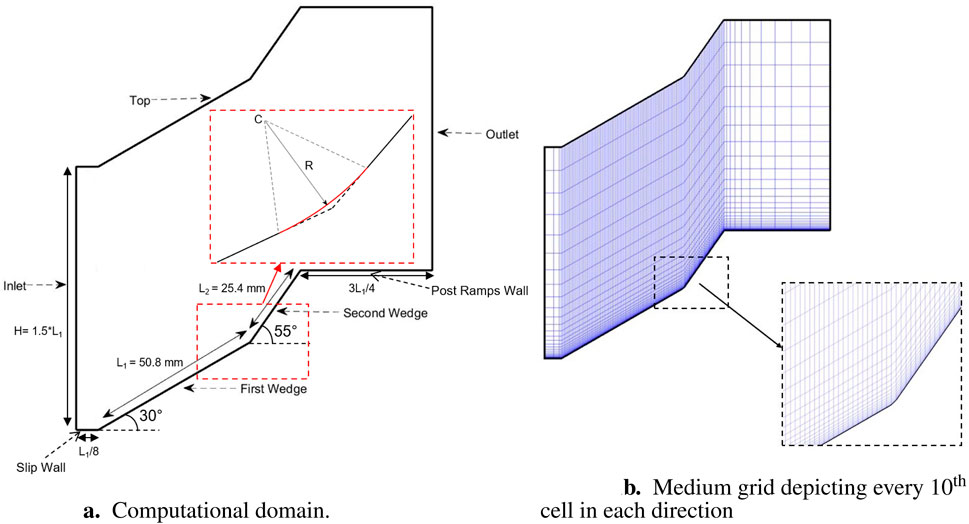
Figure 1. Computational domain and grid. The inset in (a) shows a representative curvature geometry with radius R. (a) Computational domain. (b) Medium grid depicting every 10th cell in each direction.

When a double ramp is subjected to hypersonic inflow conditions in a viscous environment, complicated flow physics consisting of multiple shock-shock interactions, large separation regions, SWBLI, and shock-shear layer interactions can be seen. Additionally, very high heat flux and pressures are observed at the reattachment location. Therefore, understanding flow in this configuration offers the opportunity to improve the designs of hypersonic vehicles.

Swantek and Austin (2012), Swantek and Austin (2015) performed experiments on a $30^0-55^0$ double-ramp configuration with an intention to create a dataset suitable for the validation of computational codes. Experiments were performed with air and nitrogen for different freestream Mach numbers and stagnation enthalpies. Although they only reported the flow evolution for a very limited flow time, this study has subsequently been used in several numerical campaigns for benchmarking as well as flow control studies.

Multiple groups have performed simulations for this flow as a part of NATO STO AVT Task Group 205 activity. Badr and Knight (2014) simulated low and high enthalpy cases using commercial solver GASPex with a two-dimensional setup by taking perfect gas assumptions and achieved a steady state for low enthalpy cases after 3.3 ms. While their results exhibit a good match for the low-enthalpy case (2.1 MJ/kg), the agreement with the high-enthalpy case (8 MJ/kg) was poor. Komives et al. (2014) also simulated the low enthalpy case with perfect gas assumption using the implicit finite volume hypersonic solver US3D. They found a reasonable agreement of wall heating with the experiment (Swantek and Austin, 2012) when simulated till the experimental run time; however, appreciable differences between the computed and measured flowfield structures were found. Further, as the simulation continued, inconsistencies in heating predictions were also observed. The authors emphasized the need for high-fidelity solvers to capture small-scale physical structures and pointed out that the results using lower-order schemes could be spurious.

Due to the significance of double ramp configuration in hypersonic configurations, several attempts have been made to study the change in SWBLI behavior due to various geometrical alterations. Hashimoto (2009) experimentally investigated the effect of different aft wedge angles. They observed minimal flow unsteadiness for $40^0$ and $50^0$, but a significant increase at $68^0$. Durna et al. (2016); Durna and Celik (2019) performed several computational studies using the open-source density-based solver rhoCentralFoam distributed by OpenFOAM and studied the effects of changing the angle of the second wedge. They observed the presence of time-periodicity as the aft angle reaches a threshold value of $47^0$. Kumar and De (2021a), Kumar and De (2021b) also employed OpenFOAM but with slightly modified schemes to examine different modes of unsteadiness in this flow when wedge-length ratios and aft angles are altered. Recently, Ray and De (2024) performed a study of double wedge flow for turbulent conditions at various aft-wedge angles between $45^0$ and $60^0$. Adityanarayan Ray and De (2023) studied the effect of leading-edge bluntness in a double ramp flow and observed that the bubble size first increases and then decreases as the bluntness is increased.

It is clear from the above discussion that a lot of work has been done studying the double ramp configuration with changing wedge length ratios as well as aft angles; however, literature studying the effect of change in curvature at the ramp intersection of a double ramp is relatively scarce. In the context of the compression ramp, some studies are done to study this important aspect. Cao et al. (2023) studied the effect of curvature at the compression corner and found that the size of the separation bubble reduces with curvature and the bubble disappears at a critical value. Some other work on curved compression corners (Tong et al., 2017; Hu et al., 2020; Tang et al., 2021) indicates the presence of bistable states of separation/attachment.

In the current work, we aim to examine the impact of curvature at the ramp intersection in hypersonic double-wedge geometries on unsteady pressure and thermal loads. This is motivated by the need to mitigate structural fatigue and material degradation, particularly in regions like the scramjet engine intake, where such loads are most pronounced. The double ramp flow $(30^0-55^0)$ is evaluated at a high Mach number of 7.1 and low stagnation enthalpy of 2.1 MJ/kg using a high-order compressible flow solver. Simulations are performed using an in-house curvilinear finite difference CFD code with seventh-order WENO as well as third-order MUSCL reconstruction schemes based on the Roe approximation solver. The evolution of the flowfield is discussed based on Edney’s interactions (Edney, 1968), and individual shock movements are tracked. Flow are simulated much longer than experiments to establish the presence or absence of the steady state.

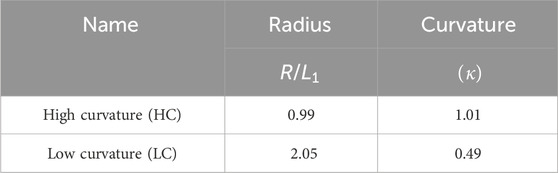
Subsequently, for studying the effect of curvature, smooth ramps of two different curvatures, $\kappa =0.49$ and $\kappa =1.01$, are created by shaving the faceted region at the intersection of the front and aft wedges while keeping other configurations unaltered. The numerical results are compared with the baseline (blunt intersection) case for instantaneous flow features, average heat flux and pressure, as well as long-time behavior. The comparison in the flowfields is done at multiple time instants in the developmental stage of the flow. Lastly, flows are simulated for sufficiently long durations for all the cases to observe steady states if any, and changes in dynamics are reported.

2 Solution methodology

2.1 Governing equations

Two-dimensional compressible Navier-Stokes equations are solved in the non-dimensional form on a curvilinear $(\xi ,\eta )$-coordinate system:

$\frac{\partial }{\partial t}\left(\frac{\mathit{Q}}{J}\right)=-\left[\left(\frac{\partial {\mathit{F}}_{\mathit{i}}}{\partial \xi }+\frac{\partial {\mathit{G}}_{\mathit{i}}}{\partial \eta }\right)+\frac{1}{Re}\left(\frac{\partial {\mathit{F}}_{\mathit{v}}}{\partial \xi }+\frac{\partial {\mathit{G}}_{\mathit{v}}}{\partial \eta }\right)\right](1)$

where, $\mathit{Q}={[\rho ,\rho u,\rho v,\rho E]}^{\prime }$ denotes the solution vector defined in terms of the fluid density $\rho$, Cartesian velocity components, $(u,v)$ and total specific internal energy $E=\mathrm{\Theta }/(\gamma -1)M^2+(u^2+v^2)/2$. Here $M$ is the reference Mach number, $\gamma$ is the ratio of the specific heats, and $\mathrm{\Theta }$ is the fluid temperature. Additionally, the ideal gas law has been used to connect pressure $p$ to $\rho$ and $\mathrm{\Theta }$ as $p=\rho \mathrm{\Theta }/\gamma M^2$. Sutherland’s law is used to express fluid viscosity $\mu$ as a function of temperature $\mathrm{\Theta }$. $J=\partial (\xi ,\eta )/\partial (x,y)$ is the Jacobian of the transformation from the Cartesian $(x,y)$ to the curvilinear $(\xi ,\eta )$-coordinate system. The inviscid and viscous fluxes in $(\xi ,\eta )$-directions are represented in Equation 1 by $({\mathit{F}}_{\mathit{i}},{\mathit{G}}_{\mathit{i}})$ and $({\mathit{F}}_{\mathit{v}},{\mathit{G}}_{\mathit{v}})$, respectively. The expression for the inviscid flux $F_i$ is given as

${\mathit{F}}_{\mathit{i}}=\left[\begin{array}{c}\hfill \rho \mathit{U}\hfill \\ \hfill \rho u\mathit{U}+{\widehat{\xi }}_{x}p\hfill \\ \hfill \rho v\mathit{U}+{\widehat{\xi }}_{y}p\hfill \\ \hfill \left(\rho E+p\right)\mathit{U}\hfill \end{array}\right](2)$

where $\mathit{U}=({\widehat{\xi }}_{x}u+{\widehat{\xi }}_{y}v)$, ${\widehat{\xi }}_x=J^{-1}\partial \xi /\partial x$, and ${\widehat{\xi }}_y=J^{-1}\partial \xi /\partial y$. The expressions for other inviscid flux $G_i$ can also be similarly defined by replacing $\xi$ in Equation 2 by $\eta$. The viscous flux ${\mathit{F}}_{\mathit{v}}$ is given as:

${\mathit{F}}_{\mathit{v}}=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill {\widehat{\xi }}_{x_i}{\tau }_{i1}\hfill \\ \hfill {\widehat{\xi }}_{x_i}{\tau }_{i2}\hfill \\ \hfill {\widehat{\xi }}_{x_i}\left(u_j,{\tau }_{ij},+,\frac{1}{\left(\gamma -1\right)M^2},\frac{1}{Pr},q_i\right)\hfill \end{array}\right](3)$

where Einstein summation convention over tensor notations is used.

Here $Pr$ denotes the Prandtl number of the fluid. The expressions for stress tensor ${\tau }_{ij}$ and heat flux $q_i$ appearing in Equation 3 are given below by Equations 4, 5 respectively where λ denotes thermal conductivity.

${\tau }_{ij}=\mu \left(\frac{\partial {\xi }_k}{\partial x_j}\frac{\partial u_i}{\partial {\xi }_k}+\frac{\partial {\xi }_k}{\partial x_i}\frac{\partial u_j}{\partial {\xi }_k}-\frac{2}{3}{\delta }_{ij}\frac{\partial {\xi }_l}{\partial x_k}\frac{\partial u_k}{\partial {\xi }_l}\right)(4)$

$q_i=\lambda \frac{\partial {\xi }_j}{\partial x_i}\frac{\partial \mathrm{\Theta }}{\partial {\xi }_j}(5)$

Expressions for other viscous fluxes namely, ${\mathit{G}}_{\mathit{v}}$, can also, be similarly defined by replacing $\xi$ in Equation 3 by $\eta$.

2.2 Numerical approach

The in-house compressible flow solver PRAVAH has been used to carry out 2D laminar unsteady simulations of Navier-Stokes equations in a finite-difference curvilinear framework. This code implements higher-order compact schemes as well as Roe shock-capturing scheme in a finite-difference curvilinear setup. For the current simulations, the Roe scheme has been employed for inviscid flux computations with $3^{rd}$ order MUSCL reconstruction as well as a hybrid-WENO reconstruction. The latter is a combination of $7^{th}$ order WENO and MUSCL reconstruction, with WENO being applied everywhere except near the shock, where MUSCL takes over (see Unnikrishnan and Gaitonde, 2020). Viscous terms are computed using a second-order central differencing scheme. Time-stepping is performed using the total variation diminishing third-order Runge-Kutta scheme as proposed by Shu and Osher (1988). PRAVAH has been successfully ported to GPUs, achieving a speedup of over 300x (Phirke and Ranjan, 2024). The validation of this code is presented for a supersonic backwards-facing step flow in Appendix 1.

The solver is used in a non-dimensional form, with scales given by free-stream flow velocity $(U_{\infty })$, density and temperature, and the length of the first ramp $(L_1)$. One flowtime, $T$, is defined by $L_1$/$U_{\infty }$ ($\approx$ 25.76 $\mu$s). Due to the relatively cold hypersonic nature of the flow, thermochemistry was not considered, and the working gas is assumed to be perfect. Ninni et al. (2022) performed simulations for this flow including thermochemistry effects. However, they concluded that “thermochemical non-equilibrium does not influence the flow features” as the maximum value of the temperature does not exceed 2000 K. Similar observations were found in other computational studies at low enthalpy (Komives et al., 2014; Badr and Knight, 2014). Simulations are performed using air as the working gas, but experiments suggest that there is no significant difference between air and nitrogen in the low-enthalpy case (Swantek and Austin, 2012).

2.3 Flow domain and boundary conditions

The double-wedge configuration has been adopted with $L_1=50.8$ mm and $L_2=25.4$ mm, front wedge-aft wedge angle configuration of $(30^0-55^0)$ as given in the experiments (Swantek and Austin, 2012) for the baseline geometry. The height of the computational domain is taken to be $1.5L_1$ everywhere, which is sufficient to capture the desired physics. A schematic of the domain and names of the boundaries can be seen in Figure 1a.

For the effect of curvature study, two curved geometries are made by adding tangent arcs to both wedges at distances of 0.22$L_1$ and 0.45$L_1$ on either side of the junction between the two wedges. The details of such arcs fulfilling the tangency criteria can be seen in Table 1 and a depiction of a representative arc showing R as the radius can be seen in the inset of Figure 1a.

Table 1

Table 1. Details of curved configurations.

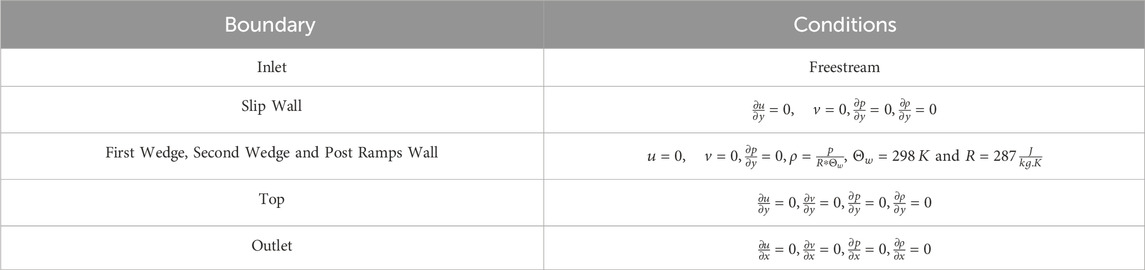
The boundary conditions employed are given in Table 2. A slip wall is given before the first wedge to provide developmental length for the flow before the first wedge. The wall temperature $({\mathrm{\Theta }}_w)$ is taken to be $298K$ as mentioned in the experiment Knight et al. (2017).

Table 2

Table 2. Boundary conditions.

Freestream conditions for the flow are tabulated in Table 3 as per the Mach 7 flow experiment in low-enthalpy conditions (2.1 $MJ/kg$) (Swantek and Austin, 2012). Initial conditions throughout the domain are taken as the freestream conditions, as done in the numerical studies in the literature (Knight et al., 2017).

Table 3

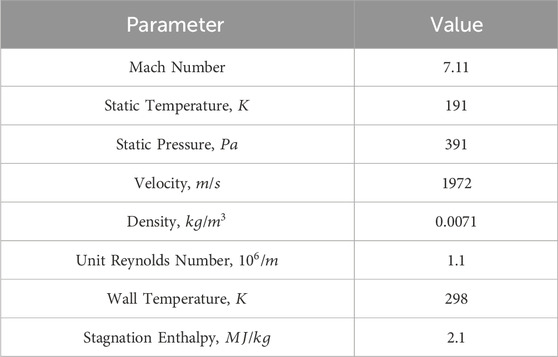
Table 3. Free-stream conditions for the low-enthalpy double ramp flow (Swantek and Austin, 2012).

2.4 Computational grid and numerical convergence

Three non-uniform cartesian grids of 0.1 million, 0.38 million and 0.69 million cells have been constructed. Details for all the grids can be seen in Table 4. For all the grids, in the vertical direction, there is one-sided stretching from wall to top and in the horizontal direction, there is uniform spacing on both wedges, while grid stretching is used on the slip wall and post ramps wall. Since, the topology is same for all the grids, the medium one is depicted in Figure 1b.

Table 4

Table 4. Details of computational grids.

For brevity, the results of grid convergence using the Roe-MUSCL scheme are shown in Figure 2a. Wall pressure profiles are used for the comparison between the different grids. A very good agreement in the medium and fine grids demonstrate grid convergence. Similar convergence was also achieved in a hybrid WENO case between the two grids. For future analysis, the numerical data from the medium grid has been used.

Figure 2

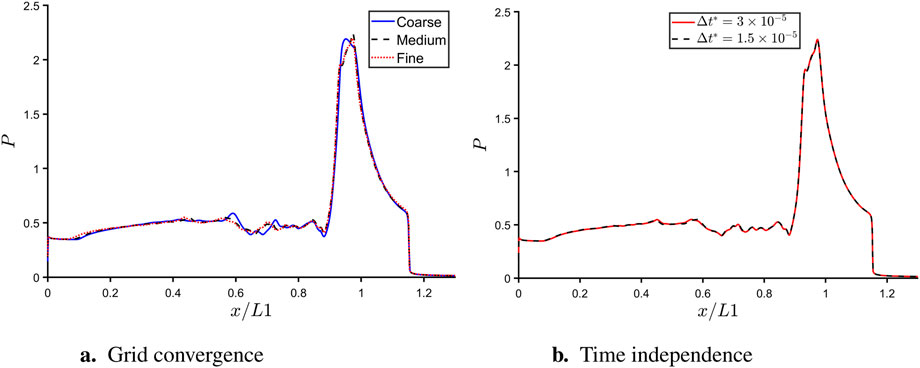
Figure 2. Grid convergence and time independence studies. (a) Grid convergence. (b) Time independence.

The time-step size for simulations is determined using the Courant–Friedrichs–Lewy (CFL) criterion to ensure numerical stability by keeping the CFL number below 1. For the calculations on the medium grid, the non-dimensional timestep $(\mathrm{\Delta }{t}^{\star }=\frac{\mathrm{\Delta }t\times U_{\infty }}{L_1})$ is of the order of $3\ast 10^{-5}$, which in dimensional unit $(\mathrm{\Delta }t)$ is about 0.773 ns. To verify time independence, additional simulations are performed with a reduced time-step size $(\mathrm{\Delta }{t}^{\star }=1.5\times 10^{-5})$. Figure 2b compares the average wall pressure obtained using both time steps. The overlapping curves indicate that the results remain unchanged, justifying the use of $\mathrm{\Delta }{t}^{\star }=3\times 10^{-5}$ for further simulations with this mesh. Although the chosen time step is significantly smaller than those typically used in implicit time schemes, the current approach accurately captures transient flow behavior.

3 Baseline simulations

3.1 Flowfield description

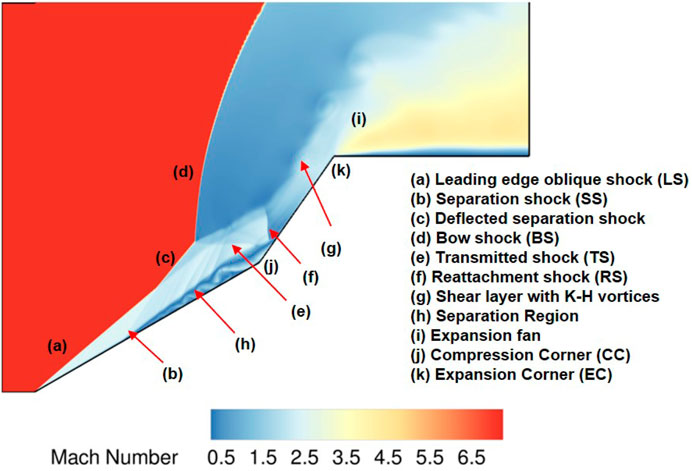
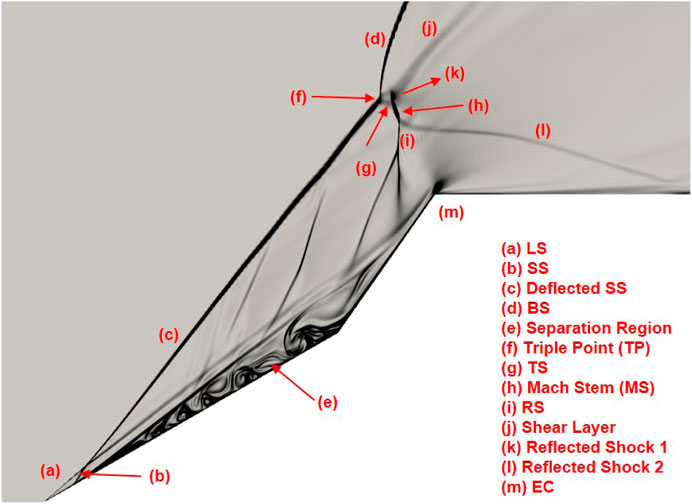
Figure 3 shows a representative flowfield at 185 $\mu$s from the start of the simulation through Mach number contours. The key flow features are marked. All the shock interactions observed in the experimental schlieren (Swantek and Austin, 2012) can be seen here. The contours clearly depict the leading edge oblique shock (LS), bow shock (BS), separation shock (SS), transmitted shock (TS), and reattachment shock (RS). Unsteady separation regions with vortical structures, shear layers with Kelvin-Helmholtz (K-H) vortices, and compression waves originating from the separation region are also captured.

Figure 3

Figure 3. Instantaneous Mach contour at 185 $\mu$s ($\approx$ 7.2 $T$).

The mechanism behind the formation of flow features is briefly described. The LS is formed due to the first ramp, and the BS is observed due to the high angle of the aft wedge. The difference between the angles of two wedges makes the adverse pressure gradient at the compression corner (CC) high enough to induce a separation region, primary separation, along with the separation and reattachment shocks, termed as SS₁ and RS₁, respectively. At early $T$, this separation region is not large enough, which allows the LS to interact with the BS to impinge a high-strength shock on the aft wedge, where peak aerothermal loads are observed in the flow, and also causing a shock-induced separation, termed secondary separation (along with separation and reattachment shocks, SS₂ and RS₂). However, at this instant, the compression waves originating from CC have reached sufficiently upstream so that the LS does not directly interact with the BS, instead, the LS interacts with the SS, and the resultant shock further interacts with the BS to create the TS marked by (e) in Figure 3. Furthermore, the secondary separation has already merged with the primary separation, resulting in a single large separation region. Reattachment occurs downstream of the transmitted shock (TS) with the formation of the reattachment shock (RS). The long-time evolution of this rich flowfield with the type of Edney interactions is discussed in detail in Section 3.2.

Now, for quantitative validation, the wall heat flux, $q_w=\lambda \frac{d\mathrm{\Theta }}{dn}$ variations across the ramp are computed, where $\lambda$ is thermal conductivity, and $n$ is the wall-normal direction. Heat flux averaging is done from 128.8 $\mu$s to 304.6 $\mu$s. In the experiments (Swantek and Austin, 2012; 2015), the averaging window is decided based on the useful test time, which is the difference of total available test time, 327$\mu$s, and the maximum of viscous establishment times at each thermocouple location. Viscous establishment time in experiments is defined as the time when the heat flux value at a specific location first attains the mean heat flux throughout the total available test time at the same location. For the M7_2 air case, the averaging window came to be about 175.8 $\mu$s. Despite the difference in the initial conditions, which could affect the initial dynamics of the flow, for this study, the times in simulation when the heat flux values at the given thermocouple locations first reach the experimental mean values were found and termed as numerical establishment times, and finally, the maximum of those was taken. Using this approach, averaging was started at 128.8 $\mu$s and the experimental averaging window was added to it to get the averaging end time of 304.6 $\mu$s. Other authors compare the instantaneous heat flux with experiments (Komives et al., 2014) or calculate the averaging window by mapping the experimental flowfield at t = 0 with their numerical schlieren (Durna et al., 2016).

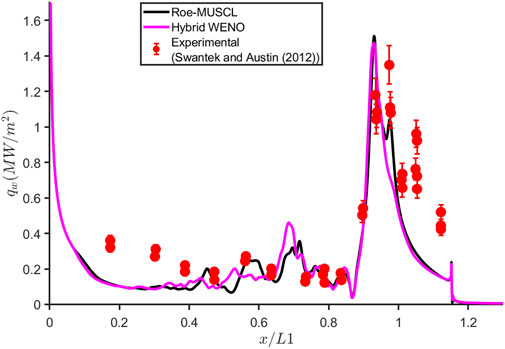
Figure 4 shows the average heat flux as obtained with third-order MUSCL and hybrid MUSCL-WENO schemes along with the experimental data. Overall, both schemes provide nearly similar predictions in terms of prediction of separation (where fluctuations begin) and reattachment region of peak heat flux. On the aft wedge, the experiment predicts a peak heat load of about 1.35 $MW/m^2$, while both MUSCL and Hybrid-WENO schemes predict a peak of about 1.53 $MW/m^2$ at $x/L_1$ = 0.93, which is close to the error bar of the peak experimental heat flux. The MUSCL scheme shows another peak at around $x/L_1\approx 0.97$, which is absent in the hybrid-WENO simulation. A similar second peak was also found in the second-order simulations of Kumar and De (2021b). These differences suggest the high sensitivity of these flows to adopted numerical schemes at the granular level (Komives et al., 2014). Fluctuations in the heat flux in the separation region are captured as present in the experiments.

Figure 4

Figure 4. Comparison with experiments.

Slight differences in the predictions of heat load may be due to the alteration of initial dynamics caused by the uncertainty in initial conditions or the averaging window (Komives et al., 2014; Durna et al., 2016; Durna and Celik, 2019; Kumar and De, 2021a; Adityanarayan Ray and De, 2023). However, in an overall sense, the averaged heat flux is in good agreement with the experiments to study the dynamics of the flow.

3.2 Temporal evolution of flowfield

Now, the temporal evolution of the flowfield is discussed that provides key insights into the development of shocks, separation regions, and shear layers in the hypersonic environment. The primary features are marked in Figure 3 using the flow while development. Table 5 lists the major events in the flowfield evolution, and Figure 5 shows these events using density gradient contours.

Table 5

Table 5. Major events in the flowfield evolution.

Figure 5

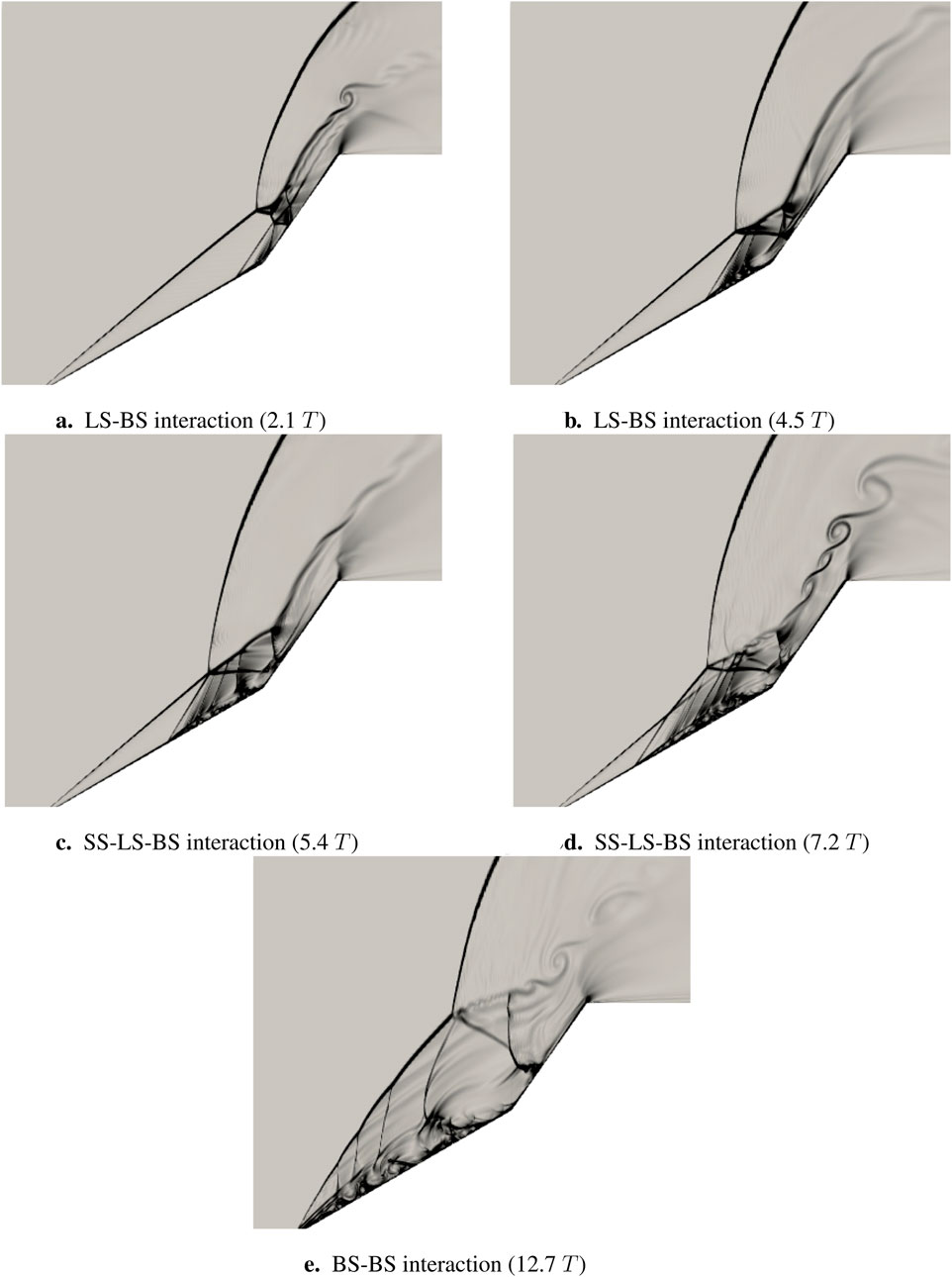
Figure 5. Evolution of flowfield shown using density gradient contours. (a): LS-BS interaction (2.1 $T$). (b): LS-BS interaction (4.5 $T$). (c): SS-LS-BS interaction (5.4 $T$). (d): Deflected SS-BS interaction (7.2 $T$). (e): BS-BS interaction (12.7 $T$).

Since the simulation was started from free-stream conditions, it took around $t=2.1T$ (54 $\mu$s) for the LS to get established, the established LS can be seen in Figure 5a. From this instant, LS interaction with BS is observed, which leads to the formation of TS and shear layer (or contact discontinuity (CD)). Subsequently, as the TS interacts with the boundary layer, shock-induced separation takes place on the second wedge, which is termed as secondary separation. Edney (1968) studied these shock-shock interferences in detail and categorized them into different types. At 2.1 $T$, shock-shock interaction is similar to Edney type V interaction.

As time progresses, the first and second separation regions come closer to each other and finally merge to make one big separation region, as shown in Figure 5b at $t=4.5T$ (116 $\mu$s). At this instant, shock-shock interaction similar to Edney type III is observed. The separation shock of the second separation (SS₂) overlaps with the reattachment shock of the first separation (RS₁), which further coalesces with the reattachment shock of the second separation (RS₂) region and interacts with the shear layer to turn it. The vortical structures inside the separation zone are due to the transient nature of the flowfield and also the reason for fluctuations in heat flux (see Figure 2b). These vortical structures are also responsible for strong compression waves emerging from the separation region, which interact with the contact discontinuity and are reflected as expansion waves.

The separation region size continues to grow with time, SS moves upstream, and at about 5.4 $T$ (140 $\mu$s), SS intersects the LS and the BS, which can be seen in Figure 5c. The compression waves emerging from the separation region increase in number with size and continue to reflect as expansion waves on interacting with CD. The RS also interacts with the thickened shear layer and reflects as an expansion fan. Some vortical activity can also be seen in the shear layer.

After this, LS intersects with SS, and the resultant deflected SS interacts with BS to form a triple point. Figure 5d (also Figure 3 shown earlier) at 7.2 $T$ (185 $\mu$s) shows this type of interaction; the vortical structures observed in the shear layer are K-H vortices, and again the shear layer is turned by interaction with reattachment shock. Edney type III interaction is observed at this instant as well. Further, the interactions between compression waves and shear layers, as observed earlier, are also present in this case.

At the end of experimental test time, 327$\mu$s ($\approx$12.7 $T$), Figure 5e, the separation region has reached near the leading edge of the double wedge. This makes the effective angle of the first wedge, as seen by freestream flow, more than the maximum deflection angle for oblique shock to be present at this Mach number, and hence a bow shock is now observed on the first wedge. The interaction of the compression waves with the leading bow shock bends its structure. A bow shock-bow shock (BS-BS) interaction is observed here, which leads to the formation of a transmitted shock as well as a contact discontinuity. The resultant shock from the interaction of transmitted shock and reattachment shock strikes the shear layer.

To understand the long-term behaviour of double ramp flow, the simulations were performed for a much longer time as compared to the experimental test time. Figure 6a shows the variation of wall pressure with time using a probe point kept at the intersection of the two wedges, which lies in the separation region. It can be seen that even after 12.7 $T$, the flow shows significant unsteadiness. This unsteadiness was not observed in the experiments due to low runtime but was observed in several numerical studies (Reinert et al., 2017). It is observed that after a duration of 55 $T$, the amplitude of pressure and its fluctuations begin to dampen significantly. Concurrently, the flowfield reveals the establishment of outer shock structures and interactions, as shown in Figure 7. At this time, the LS interacts with the SS, and the deflected SS, further interacts with bow shock to form a TS and shear layer, similar to that shown in Figure 5d. The separation region is quite long, with the inception of separation very close to the leading edge. Furthermore, multiple vortices are trapped within the separation zone. They appear much more organized with their size gradually increasing with the ramp distance. The size, number, and strength of these vortices depend on the aft angle as mentioned in (Durna and Celik, 2019). The RS and TS interact to form a Mach stem and two reflection shocks (see locations $h$, $k$, and $l$ in Figure 7). The reflected shock 1 interacts with the shear layer to turn it, and the reflected shock 2 results in strong SWBLI on the horizontal surface, which leads to the formation of a new separation bubble, separation shock, and reattachment shock on the horizontal surface. Edney type-V interactions are observed from this instant. Vortical structures inside the separation region seem to be unsteady even after 55 $T$, although the unsteadiness is much decreased.

Figure 6

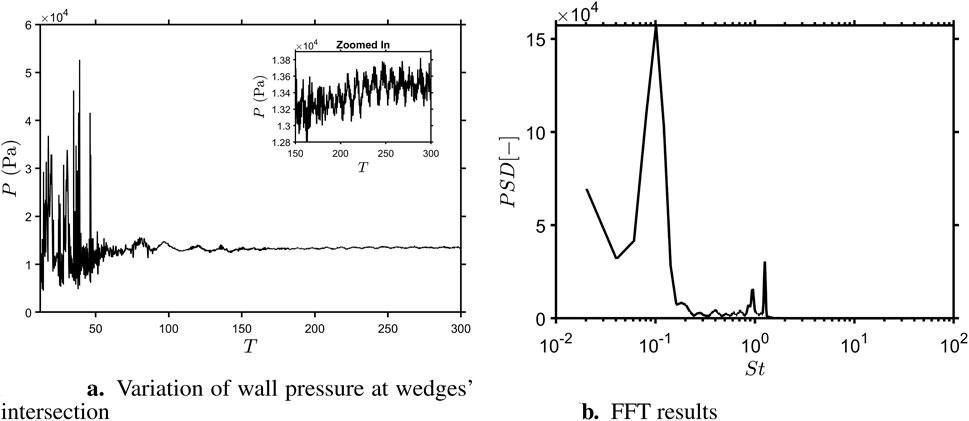
Figure 6. Unsteady pressure signatures for the Sharp geometry along with frequency data. (a) Variation of wall pressure at wedges’ intersection. (b) FFT results.

Figure 7

Figure 7. Long-time behavior of double ramp flow. Flow structure at 55 $T$.

Despite the damping of high-amplitude pressure fluctuations and the establishment of outer shock interactions after 55 $T$, low-amplitude fluctuations are observed at the wall as shown in Figure 6a. After about $T=150$, these fluctuations become significantly small (see inset for variation) and a ‘quasi-steady state’ is observed (Reinert et al., 2017). To capture the frequency of this state, Fast Fourier Transform (FFT) analysis is performed on the time-series of pressure data (Figure 6a), starting from 200 $T$. Figure 6b shows the power spectral density (PSD) of the signal. Peaks are observed at Strouhal Number $(St=\frac{f{L}_1}{U_{\infty }})$ of 0.0203, or equivalently $f=0.79$ kHz, and its superharmonics. For the same low enthalpy case, Reinert et al. (2017) observe a similar low-frequency $(St=0.034)$ using three-dimensional simulations associated with the dynamics of the separation bubble. The highest PSD was observed for $St=0.1017$. A high-frequency signal at $St\simeq 1.26$ was also found.

4 Effects of curvature

4.1 Mean flow behavior

Now the effect of introducing the curvature at the compression corner is discussed. This effect is first studied using the variation of averaged physical quantities in the streamwise direction. Since high loads are observed due to the initial dynamics of the flow, averaging has been done from the start of the simulation to 12 $T$ for all the cases. Figure 8 shows the mean flowfield using the velocity magnitude for all three cases. The baseline configuration (no curvature) is termed ‘sharp’, while the two curved configurations are termed as ‘Low curvature’ (LC; $\kappa =0.49$) and “High curvature” (HC; $\kappa =1.01$). Note that the HC configuration has a smaller radius of curvature $(R/L_1)$ at the interaction and hence is closer to “sharp” configuration.

Figure 8

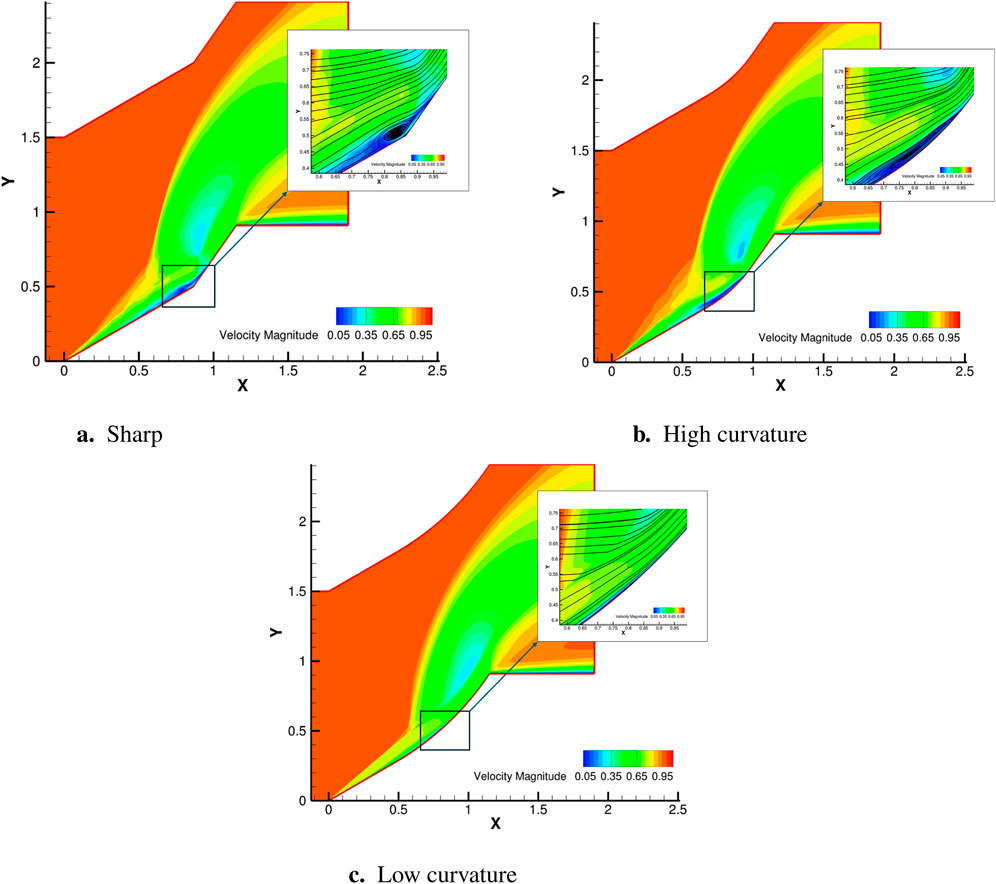
Figure 8. Non-dimensional velocity contours of mean flow for curved and sharp cases. (a) Sharp. (b) High curvature. (c) Low curvature.

Broadly all three configurations show similar flow structures in the outer region; however, there are large changes close to the ramp. The sharp configuration, Figure 8a, shows a large mean separation bubble at the compression corner. In the HC configuration, Figure 8b, the bubble becomes slightly elongated, but there is not much change in the overall dimension. However, in the LC case, Figure 8c, the mean separation bubble is reduced to a large extent. Note that there is no geometry-induced separation for any of the curved cases, hence, separation is only induced by the impinging shock.

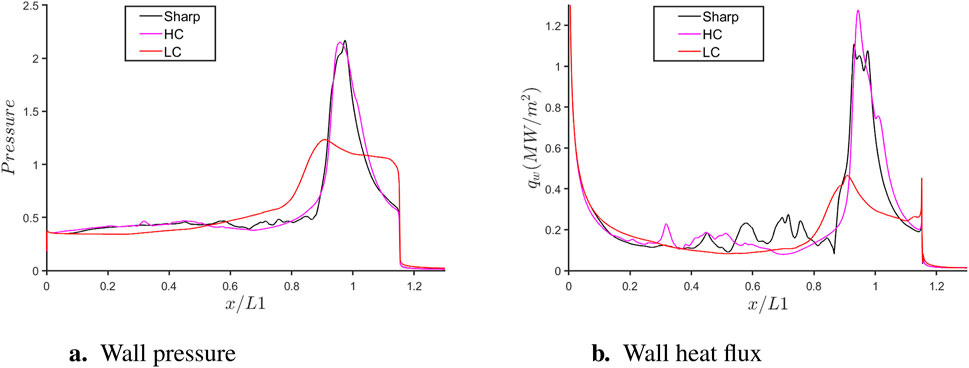
These changes influence the pressure load and heat-transfer on the ramps. Figures 9a,b respectively, show the streamwise variations of wall pressure and wall heat flux. For the HC case, the wall pressure distribution is similar to the curved case, albeit the fluctuations have decreased. Further, the peak pressure load is almost the same magnitude as the baseline case. Similar patterns are noted for the heat-flux distribution for the HC case. There is a slight increase in the peak heat flux compared to the sharp case, but a single peak is observed due to smooth geometry.

Figure 9

Figure 9. Effect of curvature on averaged flow quantities. (a) Wall pressure. (b) Wall heat flux.

Now the LC case is discussed, for which large changes were observed in the mean separation region. For this case, both pressure and heat-flux distributions are very different from sharp and HC configurations. Both the pressure and heat flux peaks are reduced significantly and are shifted upstream. The peak heat-flux in this case is about $0.47MW/m^2$ compared to about $1.11MW/m^2$ for the baseline case, which translates to about 58% reduction. Also, the peak pressure is reduced by 43% The fluctuations upstream of the peak region have also been dampened significantly as expected. These reductions in thermal and pressure loads are particularly beneficial for hypersonic vehicles, where thermal protection systems (TPS) play a critical role in managing extreme heat fluxes, especially in regions like the scramjet engine intake. By optimizing surface geometry to reduce thermal loads, the design and maintenance of TPS can be simplified, potentially enhancing the overall efficiency and reliability of hypersonic systems. To delve more into the origins of such mean data, the differences in the evolution of flowfield for all the cases are investigated. This is discussed in the next section.

4.2 Changes in transient behavior

To analyze the changes in the transient behavior, the instantaneous flowfields are visualized at four progressive instants (3, 6, 9, and 12 $T$). Further, at each time instant, flowfields have been mapped with the streamwise pressure variation. Finally, to see the effect of curvature on the long-term behavior of the flow, both curvature cases are simulated for a sufficiently longer duration, and unsteady data are analysed.

4.3 Short-term behavior

Three flowtimes $(3T)$: The flowfields at 3 $T$ are shown in Figures 10a–c with ramp shock impingement regions marked for subsequent discussions. Figure 10d compares pressure loads at this instant with regions identified corresponding to the flowfields.

Figure 10

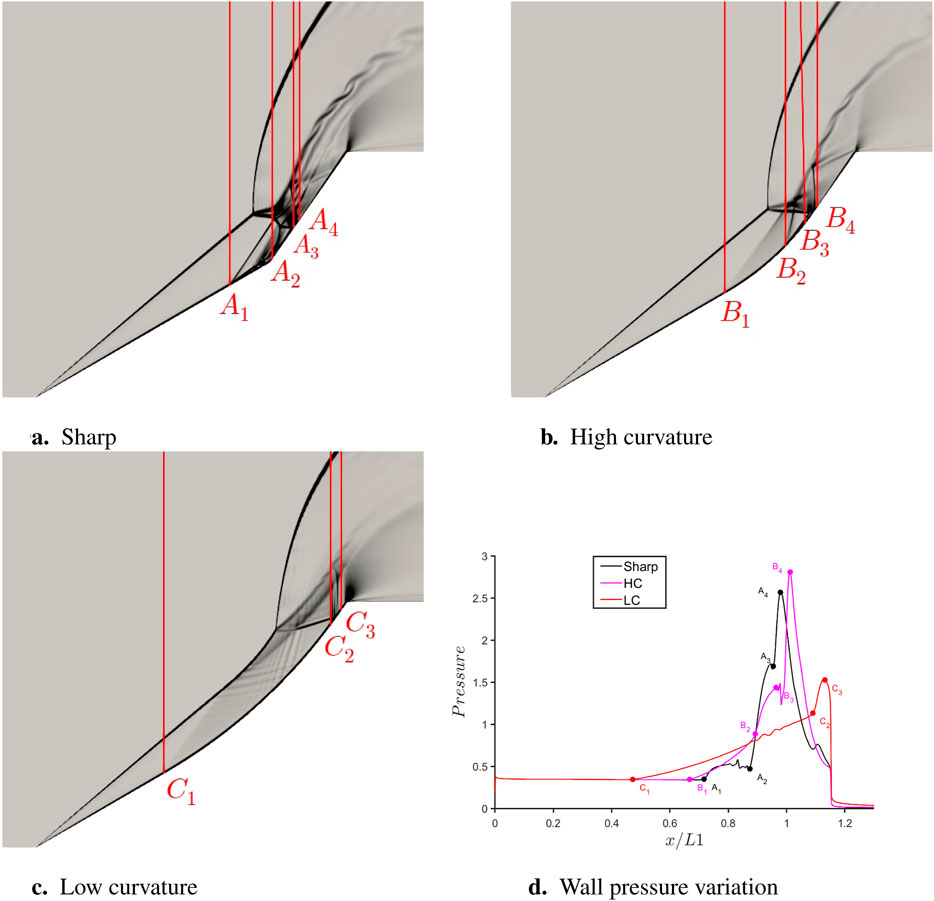
Figure 10. Comparison of different curvatures at 3 $T$. (a–c) Density gradient contours for three different geometries, (d) Streamwise wall pressure variation.

For the sharp case, Figure 10a, two strong SWBLIs are observed: (1) between $A_1$ and $A_3$, and (2) between $A_2$ and $A_4$, which leads to the formation of primary and secondary separation regions as discussed in detail in Section 3. $A_1$ marks the beginning of the primary separation region with the SS₁. Reattachment compression waves for this separation region coalesce to form RS₁ at $A_2$. The ending of the primary separation region, between $A_2$ and $A_3$ is not very transparent, as the compression waves from the second SWBLI are also present in the same region, and hence a rise in pressure throughout $A_2$ to $A_3$, Figure 10d, is seen. The shock that induces the secondary separation, formed by the interaction of TS (caused by LS-BS interaction) and the reattachment shock, impinges at $A_3$, and the flow finally reattaches with the RS₂ at $A_4$. The highest pressure load is observed at $A_4$, which depicts the role of impingement shock in high aerothermal loads.

For both the curvature cases, no primary separation is observed, as there is no steep change in angle at any location. However, one strong SWBLI, between $B_2$ and $B_4$, is observed for the HC case, and a weak SWBLI, between $C_2$ and $C_3$ for the LC geometry. For the HC geometry, the shock impinges upstream than LC and thus causes strong SWBLI, as seen from the pressure plot between $B_2$ and $B_4$. The pressure plot has an inflection point at $B_2$, as before $B_2$, the pressure was slowly rising from $B_1$ due to the curvature, but $B_2$ marks the separation shock formed by SWBLI, and pressure rises much more quickly. As expected, the peak pressure is observed at $B_4$, where the flow finally reattaches after impingement.

For the LC geometry, the flowfield looks much more simple at this instant. The leading shock and compression waves between $C_1$ and $C_3$ are seen, owing to the curvature. The waves turn the oblique shock, which finally interacts with the BS to impinge a shock between $C_2$ and $C_3$. The pressure variation confirms this flowfield and the highest pressure is achieved at $C_3$ after the shock reflection. As observed for the mean case, the highest pressure peak is observed for the HC case but is close to sharp. The LC case has quite low peak pressure compared to the other two cases. Note that the difference between the streamwise locations of separation shock for the sharp and HC configurations ($A_1$ and $B_2$) at this instant is about 0.146 units.

Six flowtimes $(6T)$: At 6 $T$ (Figure 11), for sharp case, primary and secondary separation have already been merged as discussed in the representative flowfield in Section 3.1. For both sharp case (between $A_1$ and $A_4$) and HC case (between $B_1$ and $B_2$), the extent of strong SWBLI is increased. For LC case also, strong SWBLI is seen now from $C_2$ to $C_4$. An inflection point in the pressure variation is observed at $C_2$, as was observed at $B_2$ for HC at 3 $T$. One more weak SWBLI was observed for the LC case at $C_5$. The reattachment shock, starting from $C_4$, on hitting the shear layer, forms an expansion wave and a shock that impinges at $C_5$. However, the high pressure at $C_4$ was already reduced by the expansion fans between $C_4$ and $C_5$, and hence the peak pressure is observed at $C_4$.

Figure 11

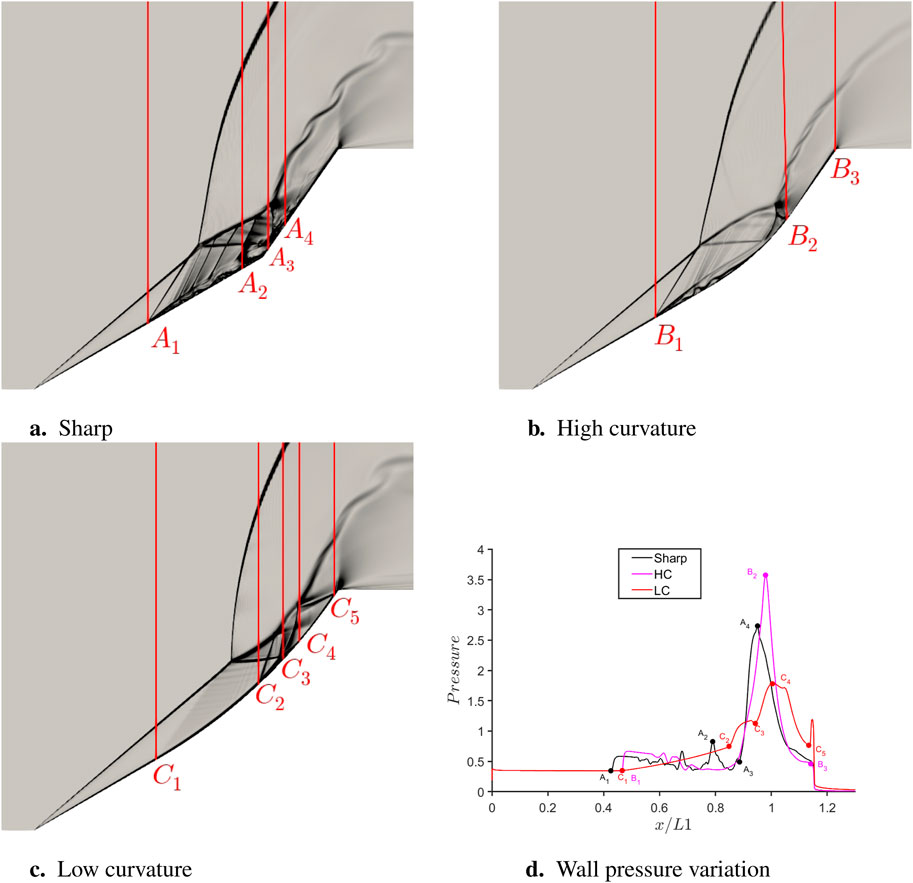
Figure 11. Comparison of different curvatures at 6 $T$. (a–c) Density gradient contours for three different geometries, (d) Streamwise wall pressure variation.

The highest peak pressure is observed for the HC geometry here as well, though the difference between the peak values has increased with respect to the sharp configuration. The LC geometry still has quite low peak pressure compared to the other two cases. The difference between the streamwise locations of separation shock for the sharp and HC configurations ($A_1$ and $B_1$) at this instant is now reduced to 0.04 units.

Nine flowtimes $(9T)$: At 9 $T$ (Figure 12), the extent of strong SWBLI increases for all the cases. For the sharp and HC cases, the highest pressure is still observed at the reattachment locations, i.e., $A_4$ and $B_3$ respectively. Interestingly, for the LC case, the weak shock interaction observed at 6 $T$ is now converting to the strong interaction, and the peak pressure is observed at $C_4$.

Figure 12

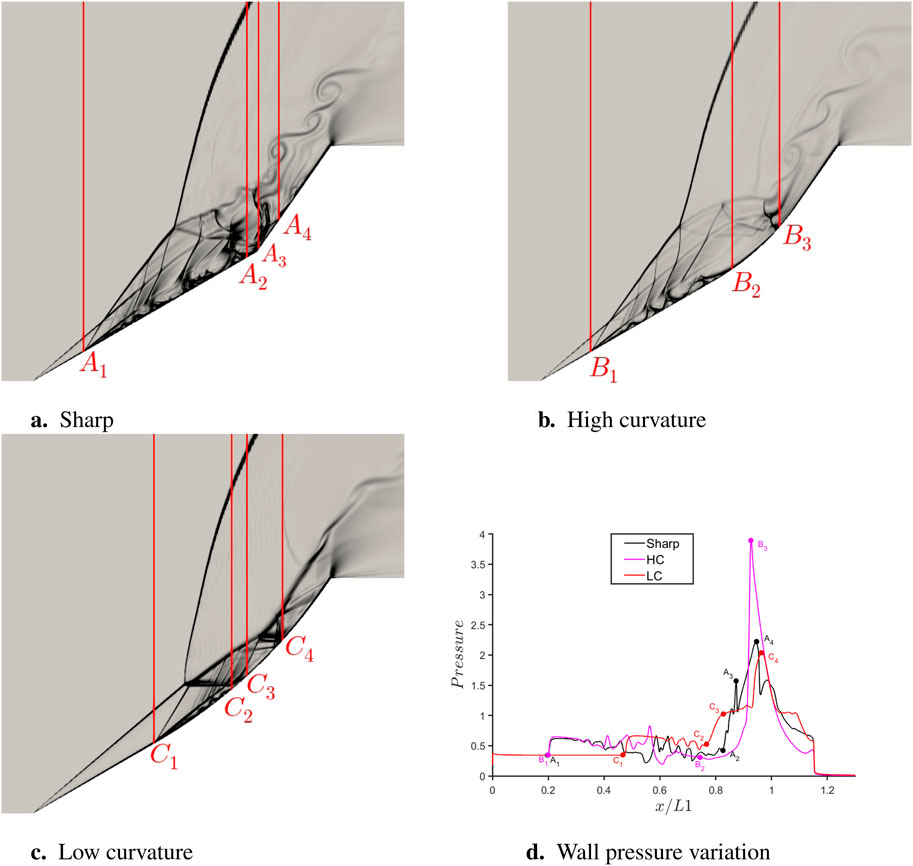
Figure 12. Comparison of different curvatures at 9 $T$. (a–c) Density gradient contours for three different geometries, (d) Streamwise wall pressure variation.

The highest pressure load is for the HC geometry, though there is not much difference between the pressure peaks for the sharp and LC cases. The separation shock locations for the sharp and HC configurations ($A_1$ and $B_1$) now coincide with each other.

12 flowtimes $(12T)$: Finally, at 12 $T$ (Figure 13), a large extent of strong SWBLI is observed for all the cases. For the HC case, the separation point has almost reached the leading edge, causing a very large separation region. For the LC case, separation shock is observed that resembles a lambda shock intersecting the wedge at $C_1$ and $C_2$. The peak pressures are observed at the reattachment locations for all the cases.

Figure 13

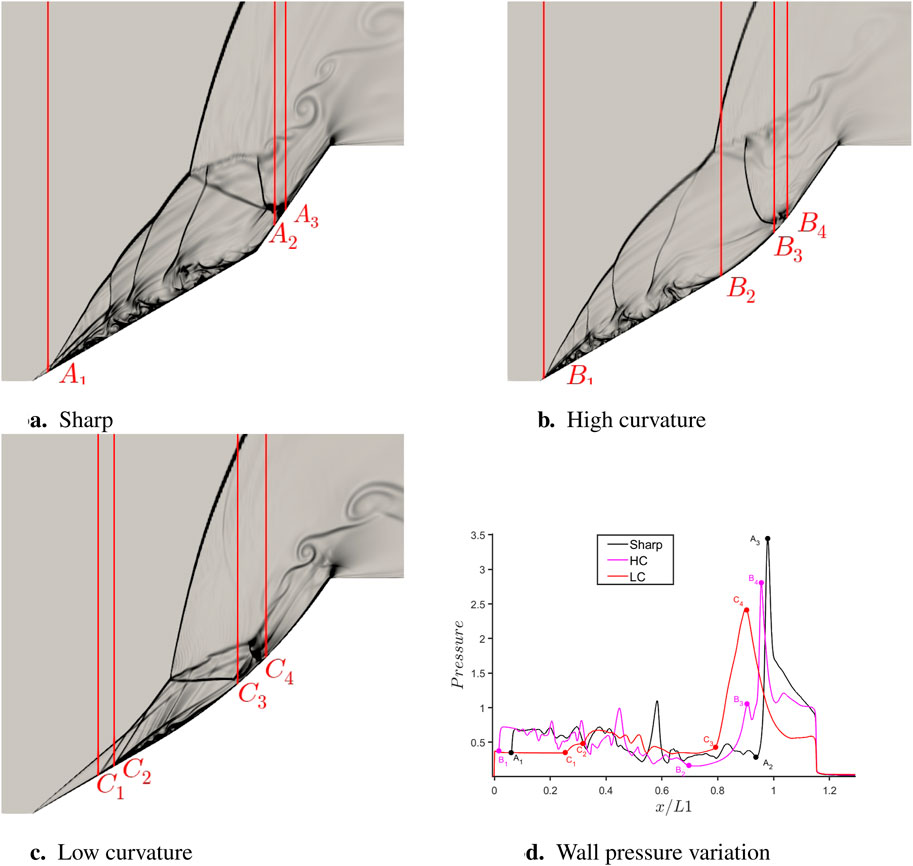
Figure 13. Comparison of different curvatures at 12 $T$. (a–c) Density gradient contours for three different geometries, (d) Streamwise wall pressure variation.

Looking at the wall pressure variation, similar features are noted for all three configurations: pressure rise at the separation shock, fluctuating pressure in the separation region, a large increase of pressure at the reattachment location, and a decrease in pressure due to the presence of the expansion fan. The highest pressure load is observed for the sharp case at this instant. Note that the separation shock location for the HC configuration at the final time has surpassed the sharp case and is closer to the leading edge than the latter. For the LC case, pressure loads were quite low for a significant amount of averaging window, which resulted in lower averaged loads. This was caused by the delay in the establishment of a strong SWBLI due to the smoother geometry.

4.4 Long-term behavior

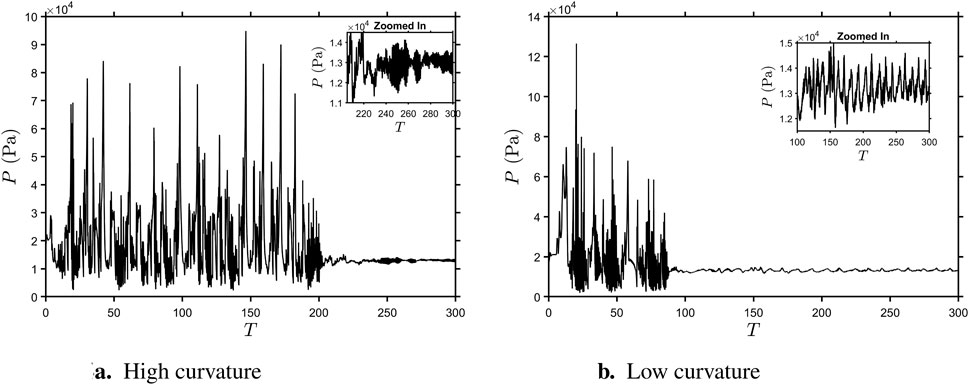
Now, the long-term behavior of curved cases is studied briefly. Simulations were performed for long durations for both curved cases until there were no more high-amplitude oscillations. Figure 14 illustrates the pressure variation over time as measured by probes positioned at the midpoint of the curved outline. Earlier, the long-term behavior of the sharp case, utilizing a probe at a comparable location (the junction of both ramps), was presented in Figure 6a. In this case, quasi-steady conditions were achieved after approximately 150 $T$. In contrast, for the HC case, as shown in Figure 14a, it takes significantly longer, around 205$T$, for the flow to reach the quasi-steady state. For the LC case (see Figure 14b), this state is attained at about 100 $T$, much earlier than the sharp case.

Figure 14

Figure 14. Variation of pressure with time. (a) High curvature. (b) Low curvature.

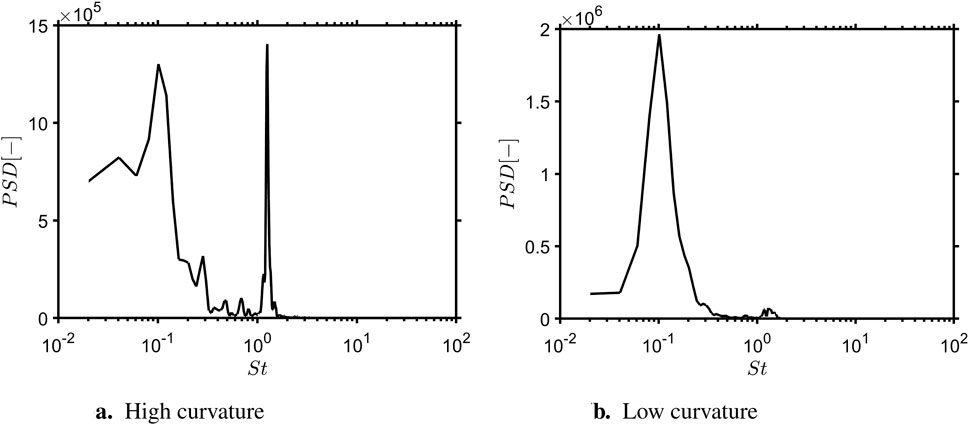
FFT was done for the curved cases after the high-amplitude fluctuations disappeared using a similar time window as for the sharp case discussed earlier (see Figure 6b). Power-spectral densities of the curved cases are shown in Figure 15. In the HC case, the dominant frequencies, characterized by the highest power spectral density (PSD), were identified at Strouhal numbers of $St=0.1017$ and $St=1.2614$. Additionally, superharmonics at $St=0.01017$ were observed, similar to those in the sharp case, albeit with lower PSD values. Notably compared to the sharp case, the PSD at $St=0.1017$ is increased tenfold while the PSD at high-frequency $St=1.2614$ exhibits a fiftyfold amplification; this amplification in high-frequency tone is unique to the HC configuration. For the LC case, a single dominant frequency of $St=0.1017$ was found, which is also the frequency with the highest PSD for the sharp case. The high-frequency signal is attenuated significantly for the LC case.

Figure 15

Figure 15. Dominant frequencies in curved cases. (a) High curvature. (b) Low curvature.

5 Concluding remarks

In this work, Mach 7 flow over a $30^0-55^0$ double-ramp configuration in low-enthalpy conditions was investigated using a high-fidelity compressible CFD solver. The key features of this complex flow, such as leading-edge shock, separation shock, transmitted shock, reattachment shock, separation region and expansion fan, are identified at several instants as the flow progresses. Subsequently, the double ramp configuration is modified to replace the sharp compression corner with curved surfaces while keeping the rest of the domain unaltered. Two different curvatures are simulated, and results are compared against the baseline (sharp) case. Following are the key findings from this study.

1. The average wall heat-flux in the baseline simulation shows a reasonably good match with the experimental data despite uncertainties in initial conditions and the averaging window. This suggests that the thermochemistry effects are not prominent at low enthalpy conditions.

2. During the temporal evolution of flowfield, different Edney interactions are observed. The long-term simulations suggest a quasi-steady state after about 150 flowtimes. Low-frequency unsteadiness $(St\simeq 0.0203)$ was observed in this case.

3. Among the curved cases, the configuration with high curvature ($\kappa =1.01$, $R/L_1=0.99$) does not exhibit a significant change in either overall flow structure or pressure or aerothermal loads compared to the baseline (sharp) case. However, the time needed for the high-amplitude signals to attenuate was much longer. Further, high-frequency signals were also observed.

4. For the low curvature configuration $(\kappa =0.49,R/L_1=2.0408)$, the flow structure changes drastically. The mean separation region almost disappeared, and there were large reductions in the aerothermal loads. The time to reach a quasi-steady state was also reduced. This configuration, therefore, seems beneficial for flow control, although its application depends on the end objective.

These findings underscore the efficacy of curvature modifications in reducing unsteady loads and enhancing flow stability in hypersonic applications, offering valuable insights for the design of aerodynamic surfaces subjected to extreme conditions. Although the current study has been conducted using a $30^0-55^0$ double ramp configuration, it is expected that the use of curved corners may offer similar advantages over sharp corners even at higher aft angles, where flow separation is more pronounced at the junction (Durna et al., 2016; Durna and Celik, 2019; Kumar and De, 2021a). Further, it is important to note that this study was conducted using a two-dimensional setup, which inherently limits the ability to capture three-dimensional structures, such as Görtler vortices, that may arise in realistic geometries (Chen et al., 2024). To gain a deeper understanding of flow structures and stability under more realistic flight conditions, comprehensive three-dimensional simulations and stability analyses are necessary and will be addressed in future work.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AA: Conceptualization, Formal Analysis, Investigation, Validation, Visualization, Writing – original draft, Writing – review and editing. RR: Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Rajesh Ranjan gratefully acknowledges the support of the ISRO-STC (project number STC/AE/2023664J) grant.

Acknowledgments

The authors would like to thank Prof. Abhijit Kushari (IITK) for the technical discussions. The simulations are performed using the resources at CDAC-AIRAWAT and IIT Kanpur Computer Centre.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdolahipour, S., Mani, M., and Taleghani, A. S. (2021). Parametric study of a frequency-modulated pulse jet by measurements of flow characteristics. Phys. Scr. 96, 125012. doi:10.1088/1402-4896/ac2bdf

CrossRef Full Text | Google Scholar

Adityanarayan Ray, A., and De, A. (2023). Leading-edge bluntness effects on the hypersonic flow over the double wedge at multiple aft-wedge angles. Phys. Fluids 35. doi:10.1063/5.0149939

CrossRef Full Text | Google Scholar

[Dataset] Agarwal, R. K. (2024). Grand challenges in aerospace engineering. Front. Aerosp. Eng. 3. doi:10.3389/fpace.2024.1383934

CrossRef Full Text | Google Scholar

Badr, M. A., and Knight, D. D. (2014). “Shock wave laminar boundary layer interaction over a double wedge in a high mach number flow,” in 52nd aerospace sciences meeting, 1136.

Google Scholar

Bhaduri, S., Ray, A., De, A., and Sugarno, M. I. (2024). Flow control in a confined supersonic cavity flow using subcavity. Front. Mech. Eng. 10, 1378433. doi:10.3389/fmech.2024.1378433

CrossRef Full Text | Google Scholar

Cao, S., Hao, J., Guo, P., Wen, C.-Y., and Klioutchnikov, I. (2023). Stability of hypersonic flow over a curved compression ramp. J. Fluid Mech. 957, A8. doi:10.1017/jfm.2023.56

CrossRef Full Text | Google Scholar

Chen, L., Zhang, Y., Wang, J., Xue, H., Xu, Y., Wang, Z., et al. (2024). Görtler vortices in the shock wave/boundary-layer interaction induced by curved swept compression ramp. Aerospace 11, 760. doi:10.3390/aerospace11090760

CrossRef Full Text | Google Scholar

Durna, A., and Celik, B. (2019). Time-periodic shock interaction mechanisms over double wedges at mach 7. Shock Waves 29, 381–399. doi:10.1007/s00193-018-0864-7

CrossRef Full Text | Google Scholar

Durna, A. S., El Hajj Ali Barada, M., and Celik, B. (2016). Shock interaction mechanisms on a double wedge at mach 7. Phys. Fluids 28. doi:10.1063/1.4961571

CrossRef Full Text | Google Scholar

Edney, B. (1968). “Anomalous heat transfer and pressure distributions on blunt bodies at hypersonic speeds in the presence of an impinging shock,”. Flygtekniska Forsoksanstalten, Stockholm Sweden.Tech. Rep. doi:10.2172/4480948

CrossRef Full Text | Google Scholar

Fame, C. M., Correia, J. R., Ghafoori, E., and Wu, C. (2021). Damage tolerance of adhesively bonded pultruded gfrp double-strap joints. Compos. Struct. 263, 113625. doi:10.1016/j.compstruct.2021.113625

CrossRef Full Text | Google Scholar

Fame, C. M., He, L., Tam, L.-h., and Wu, C. (2023). Fatigue damage tolerance of adhesively bonded pultruded gfrp double-strap joints with adhesion defects. J. Compos. Constr. 27, 04022100. doi:10.1061/jccof2.cceng-4015

CrossRef Full Text | Google Scholar

Hashimoto, T. (2009). Experimental investigation of hypersonic flow induced separation over double wedges. J. Therm. Sci. 18, 220–225. doi:10.1007/s11630-009-0220-4

CrossRef Full Text | Google Scholar

Hu, Y.-C., Zhou, W.-F., Wang, G., Yang, Y.-G., and Tang, Z.-G. (2020). Bistable states and separation hysteresis in curved compression ramp flows. Phys. Fluids 32. doi:10.1063/5.0029150

CrossRef Full Text | Google Scholar

Knight, D., Chazot, O., Austin, J., Badr, M. A., Candler, G., Celik, B., et al. (2017). Assessment of predictive capabilities for aerodynamic heating in hypersonic flow. Prog. Aerosp. Sci. 90, 39–53. doi:10.1016/j.paerosci.2017.02.001

CrossRef Full Text | Google Scholar

Komives, J. R., Nompelis, I., and Candler, G. V. (2014). “Numerical investigation of unsteady heat transfer on a double wedge geometry in hypervelocity flows,” in 44th AIAA fluid dynamics conference, 2354.

Google Scholar

Kumar, G., and De, A. (2021a). Modes of unsteadiness in shock wave and separation region interaction in hypersonic flow over a double wedge geometry. Phys. Fluids 33. doi:10.1063/5.0053949

CrossRef Full Text | Google Scholar

Kumar, G., and De, A. (2021b). Role of corner flow separation in unsteady dynamics of hypersonic flow over a double wedge geometry. Phys. Fluids 33. doi:10.1063/5.0040514

CrossRef Full Text | Google Scholar

Mirzaei, M., Taleghani, A. S., and Shadaram, A. (2012). Experimental study of vortex shedding control using plasma actuator. Appl. Mech. Mater. 186, 75–86. doi:10.4028/www.scientific.net/amm.186.75

CrossRef Full Text | Google Scholar

Ninni, D., Bonelli, F., Colonna, G., and Pascazio, G. (2022). Unsteady behavior and thermochemical non equilibrium effects in hypersonic double-wedge flows. Acta Astronaut. 191, 178–192. doi:10.1016/j.actaastro.2021.10.040

CrossRef Full Text | Google Scholar

Phirke, Y., and Ranjan, R. (2024). “Strategies for efficient gpu acceleration of a high-order 3d les solver using openacc,” in 2024 IEEE 31st international conference on high performance computing, data and analytics workshop (HiPCW), 169–170. doi:10.1109/HiPCW63042.2024.00062

CrossRef Full Text | Google Scholar

Ray, A. A., and De, A. (2024). Investigation of turbulent high-speed flow over the double wedge at varying aft-wedge deflections. Eur. J. Mechanics-B/Fluids 111, 20–41. doi:10.1016/j.euromechflu.2024.11.012

CrossRef Full Text | Google Scholar

Reinert, J. D., Gs, S., Candler, G. V., and Komives, J. R. (2017). “Three-dimensional simulations of hypersonic double wedge flow experiments,” in 47th AIAA fluid dynamics conference, 4125.

Google Scholar

Shu, C.-W., and Osher, S. (1988). Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77, 439–471. doi:10.1016/0021-9991(88)90177-5

CrossRef Full Text | Google Scholar

Smith, H. E. (1967). The flow field and heat transfer downstream of a rearward facing step in supersonic flow Aerospace Research Laboratories. United States: Office of Aerospace Research.

Google Scholar

Swantek, A., and Austin, J. (2012). “Heat transfer on a double wedge geometry in hypervelocity air and nitrogen flows,” in 50th AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition, 284. doi:10.2514/6.2012-284

CrossRef Full Text | Google Scholar

Swantek, A., and Austin, J. (2015). Flowfield establishment in hypervelocity shock-wave/boundary-layer interactions. AIAA J. 53, 311–320. doi:10.2514/1.j053104

CrossRef Full Text | Google Scholar

Tang, M.-Z., Wang, G., Xie, Z.-X., Zhou, W.-F., Hu, Y.-C., and Yang, Y.-G. (2021). Aerothermodynamic characteristics of hypersonic curved compression ramp flows with bistable states. Phys. Fluids 33. doi:10.1063/5.0069666

CrossRef Full Text | Google Scholar

Tong, F., Li, X., Duan, Y., and Yu, C. (2017). Direct numerical simulation of supersonic turbulent boundary layer subjected to a curved compression ramp. Phys. Fluids 29. doi:10.1063/1.4996762

CrossRef Full Text | Google Scholar

Unnikrishnan, S., and Gaitonde, D. V. (2020). Linear, nonlinear and transitional regimes of second-mode instability. J. Fluid Mech. 905, A25. doi:10.1017/jfm.2020.781

CrossRef Full Text | Google Scholar

Appendix: Validation of the simulation code

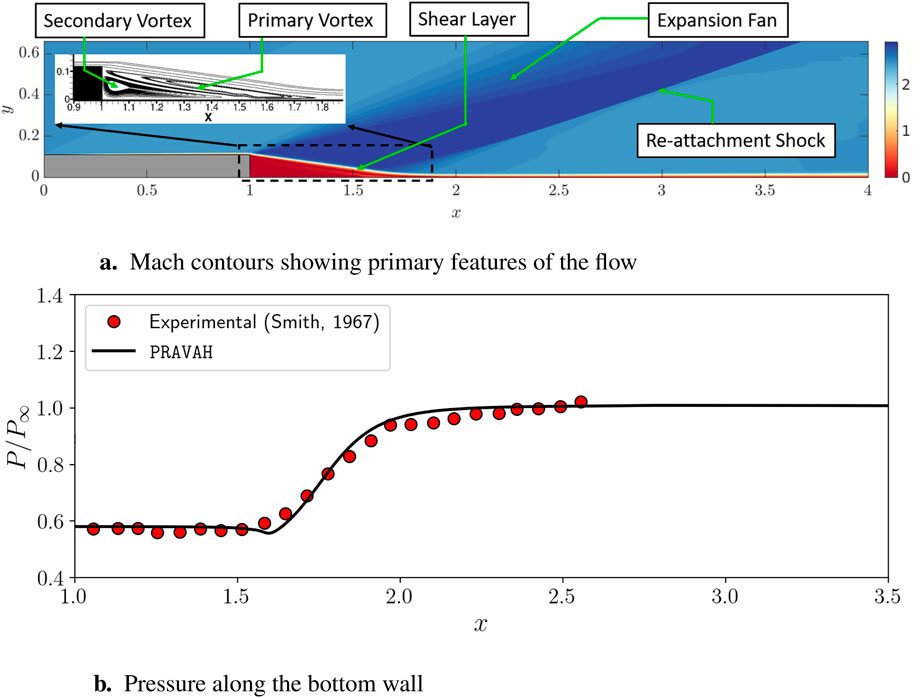
The PRAVAH code used in this study has been extensively validated for various compressible flow cases, including the SOD shock tube, 2D Riemann problems, and shock-boundary layer interactions on a flat plate. The code has shown good accuracy and shock-capturing ability for these problems. Here, we present its validation for flow over a backward-facing step (BFS), based on the experimental study by Smith (1967). The flow conditions for this case are a Reynolds number based on step length, $R{e}_L=2.48\times 10^5$, and a free-stream Mach number, $M_{\infty }=2.5$. The step height to step length ratio is $h/L=0.1107$.

Appendix Figure A1a presents the Mach contours for the BFS flow. The simulation accurately captures key flow features, including the expansion fan near the corner, the reattachment shock, and the recirculation region. The inset provides a closer view of the recirculation region, clearly depicting both primary and secondary vortices. For quantitative validation, Appendix Figure A1b shows the pressure distribution along the bottom wall, normalized by the free-stream pressure. The numerical results are compared with experimental data from Smith (1967), demonstrating a good agreement. PRAVAH effectively captures the pressure plateau associated with the recirculation region, followed by a gradual rise in pressure in the reattachment zone.

FIGURE A1

FIGURE A1. Validation of PRAVAH Code for backward-facing step flow. (a) Mach contours showing primary features of the flow. (b) Pressure along the bottom wall.