Peridynamic simulation of permafrost thawing around an inclined mine working

This study examines unsteady heat transfer in the soil mass surrounding an inclined access mine working. Initially, the soils are considered frozen, but due to contact with warmer air entering the mine during summer, they undergo seasonal thawing. The primary challenge in the calculation of heat transfer is the loosening of soils near the upper boundary of the freezing front, caused by thaw consolidation—an effect particularly common in water-saturated, fine-grained soils. This phenomenon affects both the propagation rate of the pore moisture phase transition front and the stability of frozen soils in this zone. A bond-based peridynamic approach is employed to model heat transfer throughout the frozen and thawing soils surrounding the mine, using a case study of seasonal thawing near an access working in a mine located in the Republic of Yakutia. Numerical simulation was conducted using integral equations describing particle interactions within a finite influence region. The loosening zone is calculated using a simplified solution of the peridynamic motion equation. Model verification was performed to ensure the independence of the solution from numerical method parameters. The temporal evolution of thawing zone depth was analyzed for various thermal properties of the soil. For the first time, it has been demonstrated that thaw consolidation significantly affects the temperature field in soils surrounding a mine working.

1 Introduction

Mining in the Arctic regions presents several challenges, the most significant of which are permafrost and extreme climatic conditions (Solovyov, 2009). The continuous supply of air through access mine workings inevitably leads to the thawing of the surrounding frozen soil mass, significantly reducing its load-bearing capacity as temperatures rise above freezing point (Wu et al., 2006; Wen et al., 2011). Under certain conditions, the thawed zone can expand indefinitely, and once it reaches a critical size, it negatively affects the stability of mine workings. According to estimates (Dyadkin, 1968), when the thawing zone extends 3–4 m, the normal operation of horizontal and inclined mine workings becomes virtually impossible.

The temperature of the air supplied to mines varies daily and seasonally (Novopashin and Kurilko, 2010). Repeated freeze-thaw cycles of soils near ventilated mine workings significantly reduce their strength within the thawed zone. According to (Dyadkin, 1968), one of the key requirements for the thermal regime of mines in permafrost regions is preventing the progressive thawing of frozen soils. Additionally, minimizing the number of freeze-thaw cycles around mine workings is crucial (Novopashin and Kurilko, 2010).

The primary measures for maintaining the stability of workings in frozen soils include passive thermal insulation of their surfaces (Galkin et al., 1992) and the use of anchoring (Wu et al., 2006) or concrete lining (Dyadkin, 1968) to prevent the collapse of thawed soil.

Developing effective methods to ensure the stability of mine workings in permafrost requires predicting the temperature field of the soil mass and determining the thawing zones. Heat transfer in frozen soils with phase transitions is described by the Stefan problem (Solovyov, 2009; Lubini Tshumuka et al., 2022). Key aspects of modeling include phase transitions of moisture, heat exchange at the boundary with the working, nonlinear changes in the thermal properties of soils when crossing the zero isotherm, and moisture migration (Alzoubi et al., 2020). Due to the complexity of these processes, an analytical solution to the Stefan problem is not feasible, so heat transfer calculations in frozen soils are typically performed using numerical methods.

The most well-known numerical approaches for solving the heat transfer equation in frozen soils are:

1. Explicit tracking of the phase transition front (Carslaw and Jaeger, 1964; Meyer, 1978; Nikolaev et al., 2024).

2. The enthalpy method (Crowley, 1978; Levin et al., 2021).

3. The effective heat capacity method (Popov et al., 2018; Samarskii and Moiseenko, 1965; Bonacina et al., 1973).

4. The source term method (Voller and Swaminathan, 1991).

The main differences between these approaches lie in how the time derivative of soil internal energy is computed in the left-hand side of the heat transfer equation, while the term responsible for heat diffusion remains the same and is discretized using finite difference (Levin et al., 2021; Voller and Swaminathan, 1991), finite volume (Alzoubi et al., 2020; Hu and Wang, 2021), or finite element methods (Spiridonov et al., 2023; Zhelnin et al., 2022). All these approaches enable a quantitative description of heat transfer patterns in frozen soils but assume the continuity of the considered medium. However, in the case of thawing frozen soils around an inclined mine working, the situation differs. According to Dyadkin (1968), thawing is inevitably accompanied by soil consolidation (as some of the generated water drains into the working through cracks). Together with lining deformation under load and the sinking of its supports into the ground, this can lead to the formation of a void near the upper boundary of the thawing zone.

Even for small thawing zones, the consolidation and subsidence of thawed soil can lead to soil loosening near the upper boundary of the phase transition front. Accounting for this phenomenon within the framework of continuum mechanics is challenging: when fractures or voids form, the classical concept of spatial derivatives becomes inapplicable (Bobaru and Duangpanya, 2010).

The nonlocal heat transfer models can be used to describe such processes. One of the widely used formulations of continuum mechanics is peridynamics (Nikolaev et al., 2022). Unlike differential spatial operators, peridynamics employs integral equations that describe interactions between particles within a finite influence region (horizon).

In numerical heat transfer simulation using the peridynamic approach, the computational domain is divided into particles, each possessing a finite volume. Interactions occur not only with the nearest neighbors (as in the finite volume method, where heat exchange occurs through adjacent faces) but also with all particles within the interaction horizon, determined by the distance δ from the center of the considered particle. This distance typically exceeds the discretization step (the initial distance between particle centers) by several times (Ladányi and Gonda, 2021). Due to this nonlocal interaction mechanism, which is not tied to specific boundaries between particles, it is possible to accurately model the gradual reduction in heat transfer when material fractures develop.

Studies on heat transfer with phase transitions within the peridynamic framework have been presented in several previous works. There are two main formulations of the peridynamic model: bond-based and state-based (Javili et al., 2019; Anicode and Madenci, 2022). The bond-based approach is more commonly applied in heat transfer problems. The first formulation of an unsteady heat conduction problem using the peridynamic formalism was proposed in Bobaru and Duangpanya (2010). In Chen and Bobaru (2015), the choice of an integral kernel in the heat conduction equation was studied to ensure consistency with the classical heat conduction solution. The peridynamic approach has also been applied to the Stefan problem in studies (Nikolaev et al., 2022). A peridynamic model of the phase transition of water in saturated porous media has been developed, considering nonlocal heat transfer effects and mass redistribution during thawing and freezing. Additionally, the problem of heat transfer in nonlocal formulations has been explored for cases of rotational and spherical symmetry.

However, heat transfer processes in geomaterials with phase transitions of water, in the presence of voids and loosening zones, have not been previously studied within the peridynamic approach. This aspect is of primary importance in our study, as the thawing of frozen soils around an inclined mine working may lead to the formation of a void near the upper boundary of the thawing zone due to the consolidation of thawed soils and the deformation of the lining under load. This introduces additional thermal resistance and reduces heat flow into the frozen soils above the mine working. On the other hand, consolidated soil at the bottom of the thawing zone can facilitate more intensive heat transfer and more rapid thawing during the summer.

To identify heat transfer patterns that account for phase transitions of pore moisture and geomaterial discontinuities in the phase transition zone, this study formulates the heat transfer problem in a nonlocal framework using the bond-based peridynamic formulation. In addition, the peridynamic equation of motion for particles in a gravitational field is solved to determine the intensity of thawed soil compaction. The analysis is carried out using a case study on the design of an access mine working in Yakutia, in the permafrost zone. A numerical solution is obtained, the model is validated, and the results are compared with those from the classical thermodynamic formulation.

2 Methodology

A two-dimensional computational domain is considered in the vertical cross-section of the mine working. The soil mass is represented as a set of particles, each characterized by a position vector $\mathbf{x}$ in a certain coordinate system, with the origin coinciding with the geometric center of the mine working cross-section. Particles are typically defined at the nodes of a regular grid with a given spacing ℎ.

Each particle has a finite volume, specific enthalpy H, and temperature T. A particle with position vector $\mathit{x}$ interacts with other particles with position vectors ${\mathbf{x}}^{\prime }$ within its interaction horizon $\mathrm{\Gamma }$ – an area bounded by a circle of radius δ centered at $\mathit{x}$ (see Figure 1). For simplicity, a particle characterized by position vector $\mathit{x}$ will be referred to as particle $\mathit{x}$.

Figure 1

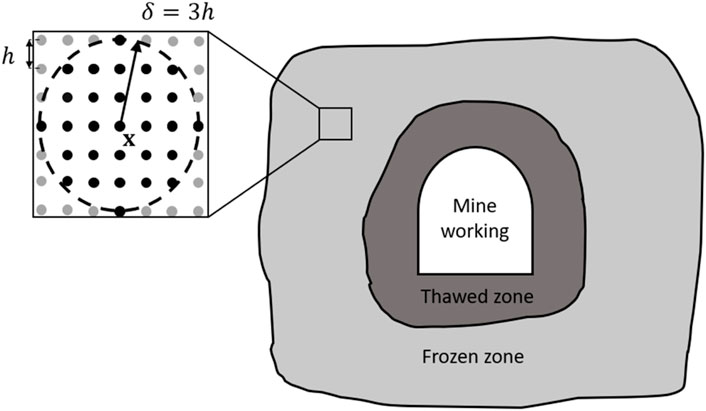
Figure 1. Schematic representation of the computational domain and the neighborhood of particle x within its interaction horizon.

2.1 Heat transfer

The heat transfer dynamics is simulated using the peridynamic heat conduction equation, which accounts for nonlocal interactions between particles. For each particle with position $\mathit{x}$, the change in specific enthalpy H (and temperature T) over time is determined by the equation:

$\frac{dH\left(T\right)}{dt}={\displaystyle \underset{\mathrm{\Gamma }}{\int }}\mathrm{\Lambda }\left(\mathit{x},{\mathit{x}}^{\prime },t\right)\frac{T\left({\mathit{x}}^{\prime },t\right)-T\left(\mathit{x},t\right)}{{‖\mathit{\xi }‖}^2}d{A}_{{\mathit{x}}^{\prime }}(1)$

$\mathit{\xi }={\mathit{x}}^{\prime }-\mathit{x}(2)$

$\mathrm{\Lambda }\left(\mathit{x},{\mathit{x}}^{\prime },t\right)=\frac{4\overline{\lambda }\left(\mathit{x},{\mathit{x}}^{\prime },t\right)}{\pi {\delta }^2}=\frac{2\left[\lambda \left(\mathit{x},t\right)+\lambda \left({\mathit{x}}^{\prime },t\right)\right]}{\pi {\delta }^2}(3)$

where $\mathrm{\Lambda }\left(\mathit{x},{\mathit{x}}^{\prime },t\right)$ is the peridynamic thermal conductivity, W/(m³·°C); $\overline{\lambda }\left(\mathit{x},{\mathit{x}}^{\prime },t\right)$ is the classical (macroscopic) thermal conductivity used in calculating the heat flux between particles $\mathit{x}$ and ${\mathit{x}}^{\prime }$, W/(m·°C); $\lambda \left(\mathit{x},t\right)$ and $\lambda \left({\mathit{x}}^{\prime },t\right)$ are thermal conductivities of particles $\mathit{x}$ and ${\mathit{x}}^{\prime }$, respectively, W/(m·°C); $d{A}_{{\mathit{x}}^{\prime }}$ is the small area (in the 2D case) associated with particle ${\mathit{x}}^{\prime }$, m².

The change in the specific enthalpy of the soil was used to calculate its temperature change. To do this, the equation of state, which relates specific enthalpy to temperature, was applied:

$H\left(T\right)=\left\{\begin{array}{l}{\rho }_l{c}_{l}T+{\rho }_{w}nL,\\ {\rho }_{w}nL\left(T-T_{fr}-\Delta T\right)/\Delta T,\\ {\rho }_s{c}_{s}T,\end{array}\right.\begin{array}{c}{T}_{fr}<T\\ T_{fr}-\Delta T<T\le T_{fr}\\ T\le T_{fr}-\Delta T\end{array}(4)$

where ${\rho }_l$ and ${\rho }_s$ are densities of thawed and frozen soil, kg/m³; $c_l$ and $c_s$ are specific heat capacities of thawed and frozen soil, J/(kg·°C); ${\rho }_w$ is the density of water, kg/m³; $n$ is the porosity of the soil; $L$ is the specific latent heat of ice melting, J/kg; $T_{fr}$ is the water freezing temperature, °C; $\Delta T$ is the temperature range of the water phase transition, °C.

Using condition Equation 4, we assume that the soil is initially fully saturated with ice, prior to the onset of thawing caused by heat exchange with the excavation wall. It is further assumed that the phase transition of moisture occurs over a relatively narrow temperature interval, $\Delta T$, which justifies the use of the piecewise linear function Equation 4. All thermophysical properties in the model are considered to be homogeneously distributed. This is a common assumption in heat transfer modeling in geological media, as it enables reliable predictions of thermal fields, even though, in reality, some degree of property heterogeneity may be present.

Dirichlet boundary conditions within the peridynamic approach are formulated as follows. Several additional layers of particles, $N_B\ge \delta /h$, are added at the boundaries of the computational domain. The additional particles, known as ghost particles, are located outside the computational domain boundaries (Sun et al., 2020; Weißenfels, 2022). When setting the Dirichlet boundary conditions at the outer boundary of the computational domain:

$\mathit{x}\in {\mathrm{\Omega }}_{out}:T=T_0(5)$

a fixed temperature $T_0<T_{fr}$ is assigned to the ghost particles, corresponding to the undisturbed frozen soil mass at the considered depth (see Figure 2).

Figure 2

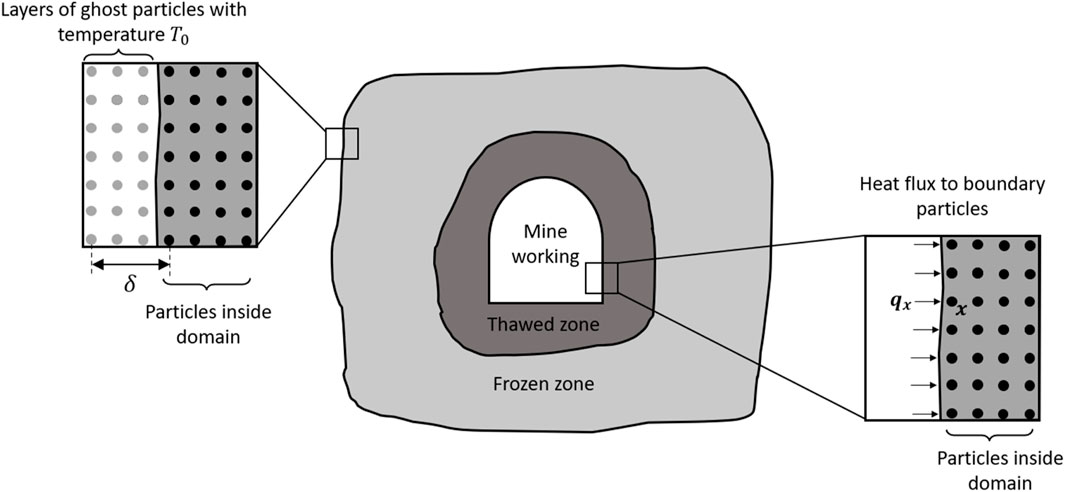
Figure 2. Setting Dirichlet boundary conditions at the outer boundary using ghost particles, and setting Robin boundary conditions on the mine working wall by explicitly defining the heat flux from the air to the boundary particles.

Otherwise, Robin boundary conditions are implemented on the wall of the mine working:

$\mathit{x}\in {\mathrm{\Omega }}_w:\mathit{q}·\mathit{N}=\alpha \left(T_a-T\right)(6)$

where $\mathit{q}$ is the heat flux, W/m²; $\mathit{N}$ is the normal vector to the surface; $\alpha$ is the heat transfer coefficient, W/(m²·°C); $T_a=T_a\left(t\right)$ is the air temperature in the mine working, °C.

In this case, no ghost particle layers are added. Instead, a heat flux ${\mathit{q}}_{\mathit{x}}$ is applied to each boundary particle $\mathit{x}$ on the wall of the mine working:

${\mathit{q}}_{\mathit{x}}=\alpha h^2\mathit{N}\left[T_a-T\left(x,t\right)\right](7)$

In addition to the peridynamic heat conduction Equation 1, we will also use the classical heat conduction equation in the form (Semin et al., 2024; Levin et al., 2023):

$\frac{\partial H\left(T\right)}{\partial t}=\frac{\partial }{\partial x}\left(\lambda \frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(\lambda \frac{\partial T}{\partial y}\right)(8)$

with boundary conditions Equations 5, 6. This is necessary for the verification of the peridynamic model. Its numerical solution will be determined using the finite difference method on a regular grid with a fixed step size h. The absence of mesh refinement at the boundary with the mine working was motivated by the desire to maintain a situation similar to the peridynamic setting, where particles are typically of the same size. Furthermore, a coarse grid at the wall of the working is adequate for sufficiently accurate calculation of weak temperature gradients, with smooth changes in air temperature across seasons.

As an initial condition in both formulations, the assumption of a homogeneous temperature field will be used:

$t=0:T=T_0(9)$

The air temperature $T_a$ in the mine working is considered to be time-dependent. It is given by a sinusoidal curve based on the fluctuations of the average monthly temperature throughout the year:

$T_a=T_{ave}-\frac{\Delta }{2}\mathit{cos}\left(\frac{\pi t}{6}+\phi \right)(10)$

where $t$ is time, months; $T_{ave}$ is the annual average temperature, °C; $\Delta$ is the difference in average monthly temperatures between the warmest and coldest months, °C; $\phi$ is the phase shift of the seasonal temperature fluctuations, rad.

2.2 Settlement of thawed soils

The simulation of thawed soil settlement within the peridynamic approach is performed by solving the integral motion equation (Song et al., 2020; Van Le and Bobaru, 2018):

$\rho \frac{d^2\mathit{u}\left(\mathit{x},t\right)}{d{t}^2}={\displaystyle \underset{\mathrm{\Gamma }}{\int }}\mathit{f}\left(\mathit{x},{\mathit{x}}^{\prime },t\right)d{A}_{{\mathit{x}}^{\prime }}+\rho \mathit{g}(11)$

where $\mathit{u}\left(\mathit{x},t\right)$ is the displacement vector, m; $\mathit{g}$ is the gravitational acceleration vector, m/s²; $\mathit{f}\left(\mathit{x},{\mathit{x}}^{\prime },t\right)$ is the interaction force between particles, N/m⁵. For a linear elastic body, it is determined by the expression (Song et al., 2020):

$\mathit{f}\left(\mathit{x},{\mathit{x}}^{\prime },t\right)=C\frac{‖\mathit{\xi }+\mathit{\eta }‖-‖\mathit{\xi }‖}{‖\mathit{\xi }‖}\frac{\mathit{\xi }+\mathit{\eta }}{‖\mathit{\xi }+\mathit{\eta }‖}(12)$

$\mathit{\eta }=\mathit{u}\left({\mathit{x}}^{\prime },t\right)-\mathit{u}\left(\mathit{x},t\right)(13)$

where $C$ is the peridynamic stiffness coefficient, N/m⁵. It is related to Young’s modulus $E$, which depends on the problem dimension and the horizon radius $\delta$. For two-dimensional problems, it is usually assumed that $C\sim E/{\delta }^3$.

The stiffness coefficient $C$ also depends on the type of deformation (compression or tension) and the temperature of the soil. As the temperature increases and crosses the phase transition point from ice to water, the stiffness coefficient can significantly decrease, even by an order of magnitude. Given that the soils surrounding the mine workings are unstable and prone to delamination, the stiffness coefficient of thawed soils in tension can be considered relatively small. As a result, particles of thawed soil near the upper boundary of the phase transition zone settle almost immediately under the influence of gravity and separate from the frozen soil above the phase transition front.

The settlement of thawed wet soil occurs due to the consolidation, which is characterized by the parameter $P$, describing the relative change in the volume of the soil as it transitions from frozen to thawed state (assuming that the dry skeleton of the soil deforms without a change in volume). The consolidation of thawed soils is associated with the melting of ice, its transformation into water, and the partial outflow of water under the influence of gravity into the underlying layers of thawed soil or into the mine working. The maximum value of the parameter $P$ is determined by the initial porosity of the soil $n$:

$P=n\frac{{\rho }_w-{\rho }_i}{{\rho }_w}(14)$

In practice, the maximum value of the parameter P is unlikely to be achieved, as this would require applying a large compressive force. Moreover, this would necessitate the complete drainage of all thawed moisture from the soil, which is also typically not the case, as a small amount of bound moisture usually remains in the soil. In the situation we are considering, Formula 14 provides an upper estimate for the possible range of values of the coefficient P.

In this study, the most pessimistic scenario is assumed, where all the pore space of the soil is initially filled with ice. The parameter P is introduced into the expression for $\mathbf{f}$ as follows. For the calculation of particle displacements in the frozen zone, Formulas 12–13 are used without changes. In the thawed zone, the equilibrium distance between particles decreases by $P\mathit{\xi }/2$. Thus, the relative displacement of particles in Equation 12 takes the form:

$\mathit{\eta }=\mathit{u}\left({\mathit{x}}^{\prime },t\right)-\mathit{u}\left(\mathit{x},t\right)-P\mathit{\xi }/2(15)$

As a result, particles in the thawed soil zone shift under the influence of gravity (see Figure 3), and near the upper boundary of the thawed zone, a rarefaction zone forms, leading to an increase in the denominator under the integral in Equation 1. Thus, an additional thermal resistance arises in the vicinity of the freezing front.

Figure 3

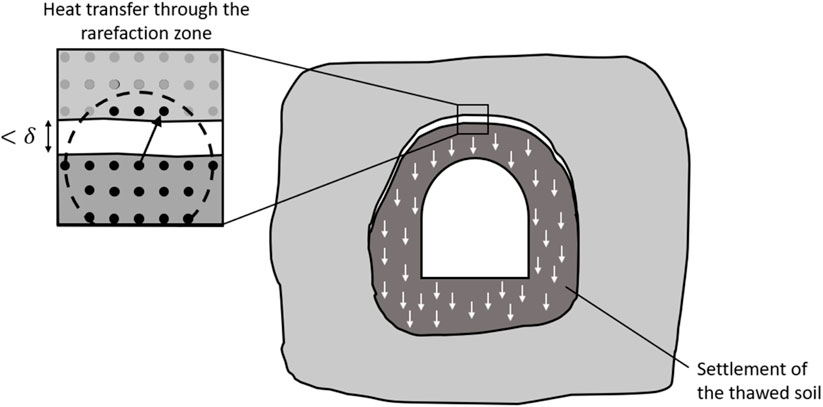
Figure 3. Heat transfer implementation through the discontinuity of the soil mass at the upper boundary of the thawed zone.

In general, approach Equation 15 is rather non-standard, as within its framework, the consolidation deformation of a single soil particle does not depend on the forces acting on it. Most often, consolidation deformation is accounted for using the equation of water filtration in pores proposed by Biot (1973). However, given that the characteristic times for moisture migration are significantly shorter than the characteristic times for the movement of the phase transition front in the problem under consideration, we assume that all gravitational moisture flows out of the pore space of the soil instantaneously. For thawed soils we are considering, hydraulic diffusivity is an order of magnitude higher than thermal diffusivity, which supports this conclusion. However, this may not be the case for other types of soils.

This study investigates the dynamics of the thawed zone over several years, so it is important to understand how the soils will behave after a “thaw-freeze” cycle. Due to the outflow of pore water from the thawed zone in the first year, when this zone re-freezes, a nonzero additional term will remain in the right-hand side of Equation 16. Therefore, when considering the re-freezing of the soil, the new term in Equation 15 should not be excluded. However, in this case, the compaction coefficient may differ slightly from the value of $P$ observed during the warm season, for example, due to the re-freezing and expansion of bound water. For simplicity, we will assume that $P$ remains constant over time after the initial thawing of the soil.

Another important aspect of the geomechanical problem is modeling the collapse of frozen soils above the upper boundary of the thawing front. According to Dyadkin (1968), the width of the thawed zone may exceed the span of the stable frozen soil exposure, leading to periodic collapses and abrupt increases in pressure on the lining of the mine working.

To account for this effect in the calculation of the force $\mathbf{f}$ using Formula 12 for particles in the frozen zone, a maximum value $f_{\mathit{max}}$ is introduced. When this value is exceeded, the bond between particles $\mathit{x}$ and ${\mathit{x}}^{\prime }$ is broken (Isiet et al., 2021). This models the destruction of frozen soil due to shear or tensile stresses. The value of $f_{\mathit{max}}$, proportional to the strength of the frozen soil, is determined based on verification calculations.

The analysis of the strength of the mine working lining and the conditions under which critical stresses develop in the frozen soils above the thawed zone is beyond the scope of this study and will be the subject of future research. In certain situations, the nature of collapses will affect the additional thermal resistance at the upper boundary of the thawed zone. However, for simplicity, it can be assumed that the frozen soils maintain their structural integrity, and Equation 11 in this case will be more useful for calculating the consolidation and settlement of thawed soils.

Dirichlet boundary conditions at the outer boundary of the calculation domain

$\mathit{x}\in {\mathrm{\Omega }}_{out}:\mathit{u}\left(\mathit{x},t\right)=0(16)$

in the mechanical problem are formulated in the same way as in the thermodynamic problem—by assigning several layers of ghost particles and fixing their displacements. In cases where one of the displacements is not fixed (for example, displacement along the vertical axis on the side walls of the calculation domain), the ghost particles move along this axis together with the corresponding boundary particle.

Neumann boundary conditions at the wall boundary of the mine working are naturally set without adding ghost particle layers. Physically, this is equivalent to a condition of zero pressure on the mine working wall. Neumann boundary conditions at the upper boundary of the calculation domain are set by applying a specific force to each boundary particle.

3 Results and discussion

Calculations were carried out for the conditions of an access mine working passing through frozen soils from a quarry berm. The angle of the transport incline is approximately $8-9$°. The temperature of the surrounding soil at the initial time was taken as $-2$°C.

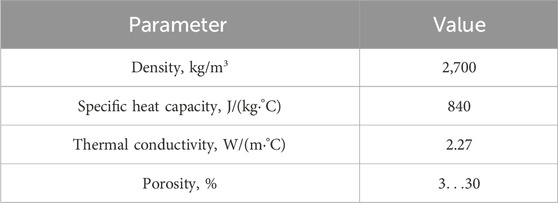
At the entrance to the inclined mine working, the path was cut through aleurites and sandstones. According to geological surveys, the soils are unstable and prone to delamination. The thermophysical properties of the dry soil skeleton are presented in Table 1. The porosity ranged from $3$ to $30$%.

Table 1

Table 1. Thermophysical properties of the soil skeleton.

The thermophysical properties of the soil mass in its thawed and frozen states were recalculated using the following formulas (Semin et al., 2024):

$c={\rho }_s{c}_s\left(1-n\right)+{\rho }_i{c}_{i}n\left(1-\gamma \right)+{\rho }_w{c}_{w}n\gamma (17)$

$\lambda ={\lambda }_s^{1-n}{\lambda }_i^{n\left(1-\gamma \right)}{\lambda }_w^{n\gamma }(18)$

where $\rho$ is the density, kg/m³; $c$ is the specific heat capacity, J/(kg·°C); $\lambda$ is the thermal conductivity, W/(m·°C); and $\gamma$ is the fraction of unfrozen water in the pore space of the soil (zero for ice and one for water). The subscripts s, i, and w refer to the dry skeleton, ice, and water, respectively.

It was assumed that the soil mass was fully ice-saturated at the initial time. The specific latent heat of ice melting was taken as 330 kJ/kg. The following numerical parameters were used when calculating the dependence of air temperature on time Equation 10: $T_{ave}=-5$°C, $\Delta =45$°C, $\phi =0.45$ rad. The heat transfer coefficient α at the boundary with the mine working was assumed to be 5 W/(m²·°C).

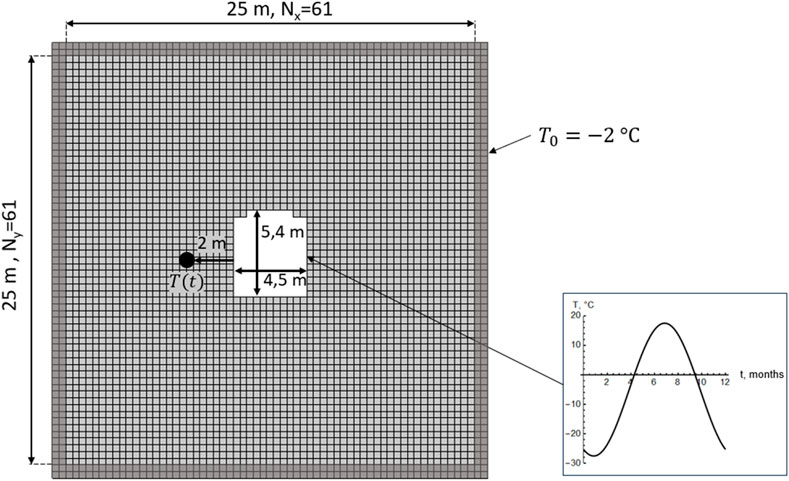
The geometric dimensions of the arched mine working are shown in Figure 4. This figure also illustrates the discretization of the computational domain into particles. Near the external boundary, a different number of layers of ghost particles (from 1 to 3) was assigned; Figure 4, as an example, presents the case with two layers.

Figure 4

Figure 4. Computational grid and boundary conditions of the thermodynamic problem.

The discretized form of Equations 1, 11 is presented below:

$\frac{H\left(\mathit{x},t^{k+1}\right)-H\left(\mathit{x},t^k\right)}{\Delta t}={\displaystyle \sum _{{\mathit{x}}^{\prime }\in \mathrm{\Gamma }}}\mathrm{\Lambda }\left(\mathit{x},{\mathit{x}}^{\prime },t^k\right)\frac{T\left({\mathit{x}}^{\prime },t^k\right)-T\left(\mathit{x},t^k\right)}{{‖\mathit{\xi }+\mathit{\eta }‖}^2}{A}_{{\mathit{x}}^{\prime }}(19)$

$0={\displaystyle \sum _{{\mathit{x}}^{\prime }\in \mathrm{\Gamma }}}C\frac{‖\mathit{\xi }+\mathit{\eta }‖-‖\mathit{\xi }‖}{‖\mathit{\xi }‖}\frac{\mathit{\xi }+\mathit{\eta }}{‖\mathit{\xi }+\mathit{\eta }‖}{A}_{{\mathit{x}}^{\prime }}+\rho \mathit{g}(20)$

$C=\left\{\begin{array}{c}{С}_{compr},\mathit{\xi }·\mathit{\eta }<0\\ {С}_{tens},\mathit{\xi }·\mathit{\eta }>0\end{array}\right.(21)$

where $k$ is the time step number; ${С}_{compr}$ is the peridynamic stiffness coefficient for compression, N/m⁵; ${С}_{tens}$ is the peridynamic stiffness coefficient for tension, N/m⁵; $A_{{\mathit{x}}^{\prime }}$ is the finite area associated with the particle ${\mathit{x}}^{\prime }$, m². The latter was computed as $\beta h^2$, where $h$ is the spacing between adjacent particle and $\beta$ is a calibration parameter (Liu and Hong, 2012).

Equation 19 is linked to Equations 20, 21 through the parameter $\mathit{\eta }$, which appears in the denominator on the right-hand side of Equation 19. Equations 20, 21 are connected to Equation 19 through the parameter ${С}_{tens}$, which is nonzero only at negative temperatures.

The time derivative is omitted on the left-hand side of Equation 20 because Equations 20, 21 are used to study the static equilibrium of the particle system. In this case, the iterative solution of the transient Equation 11 with the inertial term proves to be more computationally expensive than solving the system of linear Equation 21 for the unknown displacements.

For the numerical solution of Equation 19, an explicit integration scheme (first-order Euler method) was used, where the time step $\Delta t$ for Equation 20 in a 2D space is limited by:

$\Delta t=CFL\frac{h^2}{4a_1}(22)$

where $a_1$ is the thermal diffusivity in the ice zone, m²/s; $CFL=0.99$ is the Courant number, empirically selected to ensure the stability of the scheme.

The equations for particle displacement Equations 20, 21 were solved independently of the heat transfer Equation 19 every $M>1$ time iterations. The numerical algorithm for solving the equations was implemented in the Wolfram Mathematica software. This choice of computational software is motivated by the fact that it offers richer functionality for analyzing the suitability of numerical schemes and the independence of the solution from method-specific parameters. At this early stage of the study, where we currently are, computational efficiency was of lesser importance to us.

The elastic modulus of frozen soils was assumed to be 50 GPa. Poisson’s ratio is set equal to 0.2. Based on these values, the peridynamic stiffness coefficient was calculated as $8.6\times {10}^{10}$ N/m⁵.

At the preliminary stage, verification of the heat transfer model was carried out. The verification process included checking the independence of the numerical solution from several parameters:

− The time step size,

− The size of the computational domain,

− The number of particles (spatial discretization step),

− The interaction horizon radius.

The quantitative criterion used to assess solution independence was the time dependence of the temperature of the soil mass at a distance of 2 m from the mine working wall (see Figure 4). Figures 5, 6 present the computed temperature-time dependencies at this point for various time step sizes, computational domain sizes, numbers of particles, and interaction horizon widths.

Figure 5

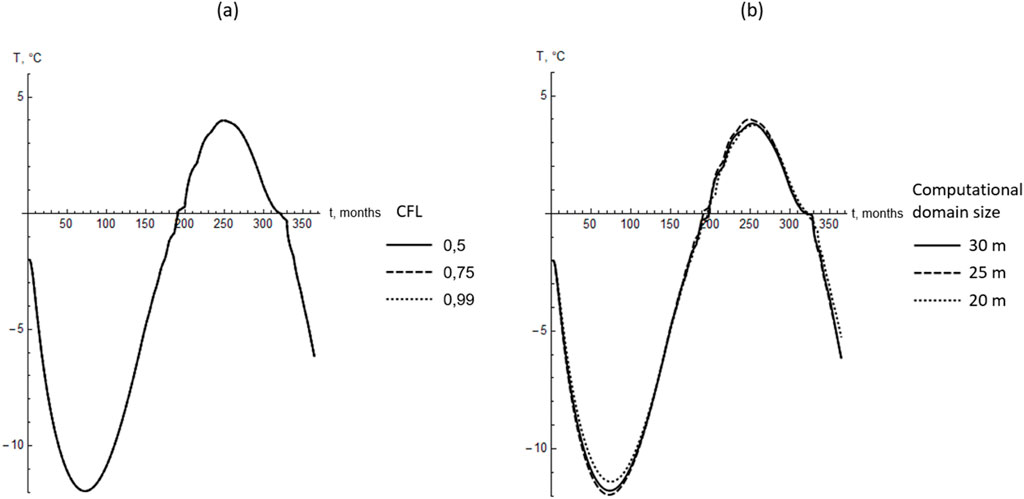
Figure 5. Temporal variations of soil temperature at a distance of 2 m from the mine working wall for different Courant numbers (a) and different computational domain sizes (b).

Figure 6

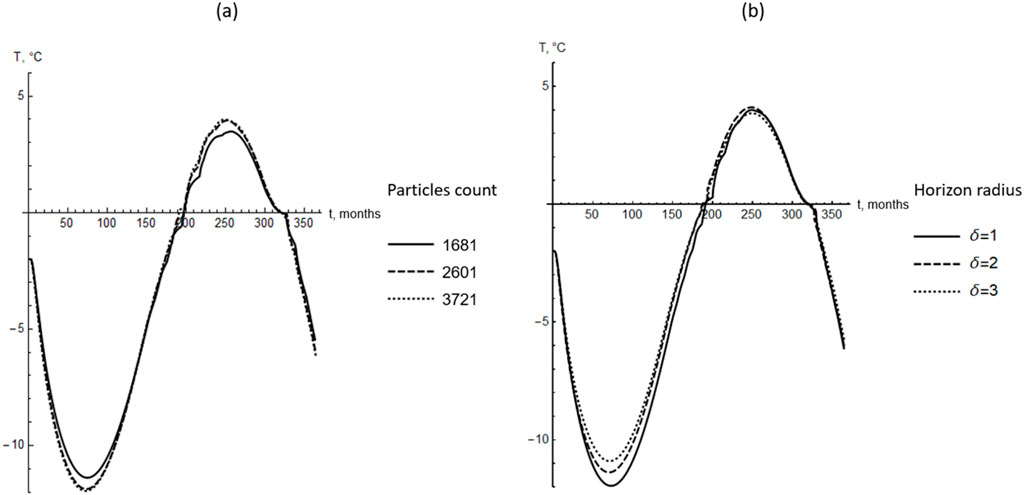
Figure 6. Temporal variations of soil temperature at a distance of 2 m from the mine working wall for different numbers of particles (a) and different horizon radii (b).

Based on a series of heat transfer simulations, the optimal numerical parameters were selected for the subsequent simulation of the thawed zone dynamics around the mine working. The computational domain size was set to 25 m, the Courant number $CFL=0.99$, the number of particles (excluding ghost particles) was $3721$, and the number of ghost particle layers was $2$.

It is important to note that solving the heat transfer problem in the peridynamic formulation depends on the parameter $\delta$ (Bobaru and Duangpanya, 2010). Therefore, to ensure consistency with the classical heat conduction problem formulated in differential form based on Fourier’s law, the coefficient $\beta$ depends on δ. For $\delta =2$, it equals 2.6.

Despite the calibration of the model, achieving full agreement of the time dependencies for different $\delta$ was not possible (see Figure 6b). Therefore, during calibration, we primarily focused on matching the curves in the region of positive temperatures, as this region poses the greatest risk to the stability of the mine working.

Overall, Figures 5, 6 show that the peridynamic approach provides additional smoothing of the time dependencies of temperature due to the “long-range” interactions between particles. In the classical enthalpy formulation of the Stefan problem Equation 8, the dependencies $T\left(t\right)$ near the phase transition front often exhibit a wavelike pattern. This is associated with the finite step of spatial discretization and the characteristics of front propagation at small $\Delta T$ in expression Equation 4. In this context, the use of the peridynamic approach for such problems appears promising.

In the case of $\delta =1$ in Figure 6b, the solution coincides with the numerical solution of the classical parabolic heat equation with a phase transition in the form of Equation 8. This is not surprising, as for $\delta =1$ and a regular computational grid, Equation 19 takes the same form as its finite-difference representation with central differences in space.

If the verification of the thermal model was conducted only for the initial calculation area with a mine working, then the verification of the mechanical model was performed separately by considering the deformation of a vertical soil column H = 10 m high under its own weight. In this case, the solution to the peridynamic problem can be compared with the exact analytical solution, which is obtained by integrating the 1D equilibrium equation. Both scenarios, with and without considering the consolidation of thawed soil, are examined. A comparative analysis of these solutions is presented in Figure 7.

Figure 7

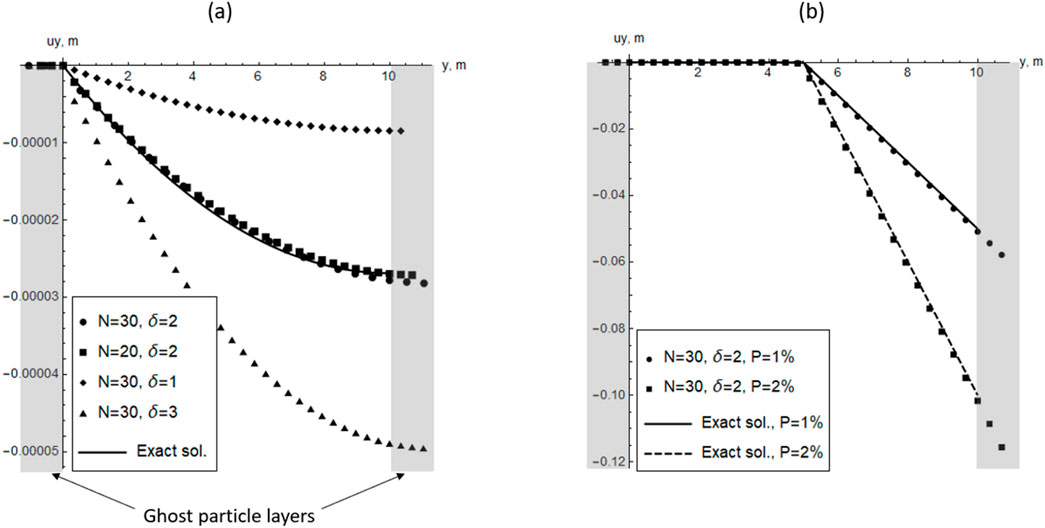
Figure 7. Comparative analysis of numerical and exact analytical solutions for vertical soil column deformation under its own weight: (a) without consolidation of thawed soil and (b) with consolidation of thawed soil.

Figure 7a shows the situation without considering the consolidation of thawed soil. In this case, the vertical displacement $u$ of the soil column is determined by the following quadratic equation:

$u\left(y\right)=-\frac{\rho g}{E}\left(Hy-\frac{y^2}{2}\right)(23)$

It was assumed that the $y$-axis is directed upwards, and at the bottom of the column ($y=0$), the vertical displacements are zero.

The peridynamic model accurately reproduces this power-law quadratic dependence for different parameters, ℎ and δ. However, the peridynamic displacement field in absolute values depends on the choice of δ, which is understandable and has been noted in the literature (Bobaru and Duangpanya, 2010). For further analysis, we selected the model with δ = 2 and calibrated the parameter c specifically to achieve the best fit between the model and the exact analytical solution for δ = 2:

$c=\frac{174E}{\pi {\delta }^3\left(1-2\nu \right)\left(1+\nu \right)}(24)$

The situation considering soil consolidation is shown in Figure 7b. As a result of heating the upper half of the column to a positive temperature, a fixed value of soil consolidation deformation P was applied. In this case, for the upper half of the column ($y>5m$), the key factor influencing displacements was the consolidation of the underlying thawed soil, and the displacement profile became nearly linear.

$u\left(y\right)=-\frac{\rho g}{E}\left(Hy-\frac{y^2}{2}\right)-P\max \left(0,y-\frac{H}{2}\right)(25)$

The figure shows that the peridynamic model accurately reproduces the exact analytical solution without any additional calibrations for different values of consolidation deformation. Thus, the calibrated and verified peridynamic model was subsequently used for further numerical simualtion of soil subsidence due to the thermal influence of air in a mine working.

Figure 8 presents the thawed zone distributions around the mine working for several time points and two different porosity values. For a porosity of 30%, two cases are shown: without considering the consolidation of thawed soils (Figure 8b) and with its consideration (Figure 8c). For a porosity of 3%, the thawed zone is visualized only for the case without consolidation (Figure 8a), as in this case, the factor has a negligible effect.

Figure 8

Figure 8. Propagation of the thawed zone at different soil porosities without considering settlement (a,b) and with considering settlement (c) of the thawed soils.

Calculations considering the consolidation of thawed soils were conducted with a reduced Courant number (CFL = 0.75) due to the local shortening of distances between particles caused by soil compaction. Figure 8c also visualizes the “voids” that appear near the upper boundary of freezing front. Overall, Figure 8 shows that soil mass porosity is a significant factor influencing the formation of the thawed soil zone. Additionally, the consolidation of thawed soils also plays a crucial role.

At the same time, the increase in thermal diffusivity within the thawed consolidated zone has a more pronounced effect on heat transfer than the increase in thermal resistance near the phase transition front, which, on the contrary, should slow down the heat exchange process.

Figure 9a presents temperature profiles along a vertical line extending from the axis of the excavation to the upper boundary of the computational domain. The curves correspond to a time of 200 days. The dashed curve represents the case with thawed soil consolidation, while the solid curve corresponds to the case without it. The figure shows that in the thawed soil zone, the dashed curve lies above the solid one, indicating a more intense heat transfer process when consolidation is considered. Furthermore, the temperature jump near the phase transition front is also greater for the dashed curve, suggesting the presence of thermal resistance in this region.

Figure 9

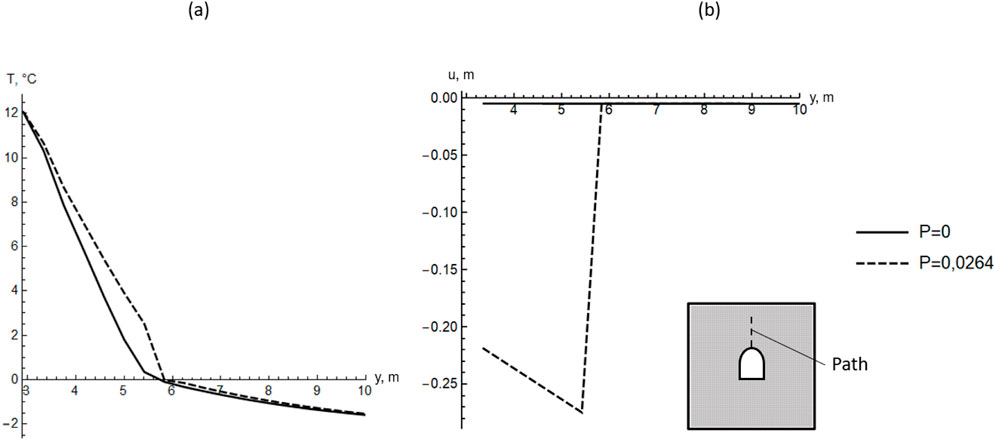
Figure 9. Temperature (a) and vertical displacement (b) profiles of the soil along the vertical path with (P = 0.0264) and without (P = 0) considering the settlement of thawed soils.

Figure 9b shows the vertical displacement profiles along the same line. In the case without considering the consolidation of thawed soils, the displacements do not exceed 5 mm in absolute value. When consolidation is taken into account, the maximum displacements are observed in the thawed zone, reaching 0.26 m (in absolute value) at the upper boundary of the thawed zone. Such large displacements at vertical coordinates y<6 m are primarily caused by the compaction of thawed soils.

The obtained maximum jump in vertical displacements at the transition from the thawed soil zone to the frozen soil zone is smaller than the horizon radius. As a result, a nonzero heat flux through the phase transition front above the thawing zone is maintained.

This raises the question of how physically accurate it is to preserve heat transfer through an air layer or another gas fraction when such wide separation (or void) zones form in the soil. It is likely that beyond a certain threshold $‖\mathit{\eta }‖$ value, it would be more appropriate to break the connections between particles. However, determining such critical values requires additional theoretical analysis and experimental data, which is beyond the scope of this study but remains a subject for future research.

Overall, the behavior of thawing soil above the excavation roof represents just one aspect of a broader set of phenomena that warrant further investigation. A more detailed consideration of various coupled processes—such as support deformation, air migration through pores, and others—is required. These aspects, in turn, demand proper parameterization based on field data or scaled laboratory testing.

4 Conclusion

A peridynamic model of heat transfer in permafrost soil around a mine working, accounting for the consolidation of thawed soil, has been developed, numerically implemented, and verified. This model highlights the significant impact of thawed soil deformations on seasonal temperature variations around the access mine working, driven by changes in the temperature of the atmospheric air supplied through it.

The numerical solution is highly sensitive to parameters such as the initial soil porosity and the degree of consolidation, emphasizing the need for their accurate determination during preliminary engineering surveys. The peridynamic approach has demonstrated its effectiveness in solving the heat transfer equation with moisture phase transitions, even under strong spatiotemporal variability in soil thermophysical properties. By incorporating long-range interactions, the peridynamic approach produces smoother temperature fields, particularly in high-moisture soils where enthalpy-temperature relationships exhibit sharp discontinuities. At the same time, it yields results that are quantitatively comparable to the classical Stefan problem solved with the Laplace diffusion operator.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The study was carried out with the financial support of the Ministry of Science and Higher Education of the Russian Federation within the state assignment (project no. 122030100425–6).

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alzoubi, M. A., Xu, M., Hassani, F. P., Poncet, S., and Sasmito, A. P. (2020). Artificial ground freezing: a review of thermal and hydraulic aspects. Tunn. Undergr. Space Technol. 104, 103534. doi:10.1016/j.tust.2020.103534

CrossRef Full Text | Google Scholar

Anicode, S. V. K., and Madenci, E. (2022). Bond-and state-based peridynamic analysis in a commercial finite element framework with native elements. Comput. Methods Appl. Mech. Eng. 398, 115208. doi:10.1016/j.cma.2022.115208

CrossRef Full Text | Google Scholar

Biot, M. A. (1973). Nonlinear and semilinear rheology of porous solids. J. Geophys. Res. 78 (23), 4924–4937. doi:10.1029/jb078i023p04924

CrossRef Full Text | Google Scholar

Bobaru, F., and Duangpanya, M. (2010). The peridynamic formulation for transient heat conduction. Int. J. Heat. Mass Transf. 53 (19–20), 4047–4059. doi:10.1016/j.ijheatmasstransfer.2010.05.024

CrossRef Full Text | Google Scholar

Bonacina, C., Comini, G., Fasano, A., and Primicerio, M. (1973). Numerical solution of phase-change problems. Int. J. Heat. Mass Transf. 16 (10), 1825–1832. doi:10.1016/0017-9310(73)90202-0

CrossRef Full Text | Google Scholar

Carslaw, G., and Jaeger, D. (1964). Conduction of heat in solids. Moscow: Nauka, 487.

Google Scholar

Chen, Z., and Bobaru, F. (2015). Selecting the kernel in a peridynamic formulation: a study for transient heat diffusion. Comput. Phys. Commun. 197, 51–60. doi:10.1016/j.cpc.2015.08.006

CrossRef Full Text | Google Scholar

Crowley, A. B. (1978). Numerical solution of Stefan problems. Int. J. Heat. Mass Transf. 21 (2), 215–219. doi:10.1016/0017-9310(78)90225-9

CrossRef Full Text | Google Scholar

Dyadkin, Yu. D. (1968). Fundamentals of mining thermophysics for mines of the North. Moscow: Nedra, 255.

Google Scholar

Galkin, A. F., Kiselev, V. V., and Kurilko, A. S. (1992). Sprayed concrete thermal protection support. Yakutsk: YANC SO RAN, 164.

Google Scholar

Hu, T., and Wang, T. (2021). A finite volume-based model for the hydrothermal behavior of soil under freeze–thaw cycles. PLoS One 16 (6), e0252680. doi:10.1371/journal.pone.0252680

PubMed Abstract | CrossRef Full Text | Google Scholar

Isiet, M., Mišković, I., and Mišković, S. (2021). Review of peridynamic modelling of material failure and damage due to impact. Int. J. Impact Eng. 147, 103740. doi:10.1016/j.ijimpeng.2020.103740

CrossRef Full Text | Google Scholar

Javili, A., Morasata, R., Oterkus, E., and Oterkus, S. (2019). Peridynamics review. Math. Mech. Solids 24 (11), 3714–3739. doi:10.1177/1081286518803411

CrossRef Full Text | Google Scholar

Ladányi, G., and Gonda, V. (2021). Review of peridynamics: theory, applications, and future perspectives. J. Mech. Eng. 67 (12), 666–681. doi:10.5545/sv-jme.2021.7289

CrossRef Full Text | Google Scholar

Levin, L., Golovatyi, I., Zaitsev, A., Pugin, A., and Semin, M. (2021). Thermal monitoring of frozen wall thawing after artificial ground freezing: case study of Petrikov Potash Mine. Tunn. Undergr. Space Technol. 107, 103685. doi:10.1016/j.tust.2020.103685

CrossRef Full Text | Google Scholar

Levin, L., Semin, M., and Golovatyi, I. (2023). Analysis of the structural integrity of a frozen wall during a mine shaft excavation using temperature monitoring data. Fract. Struct. Integr. 17 (63), 1–12. doi:10.3221/igf-esis.63.01

CrossRef Full Text | Google Scholar

Liu, W., and Hong, J. W. (2012). Discretized peridynamics for linear elastic solids. Comput. Mech. 50, 579–590. doi:10.1007/s00466-012-0690-1

CrossRef Full Text | Google Scholar

Lubini Tshumuka, A., Krimi, A., and Fuamba, M. (2022). Modeling heat transfer through permafrost soil subjected to seasonal freeze-thaw. Land 11 (10), 1770. doi:10.3390/land11101770

CrossRef Full Text | Google Scholar

Meyer, G. H. (1978). The numerical solution of Stefan problems with front-tracking and smoothing methods. Appl. Math. Comput. 4 (4), 283–306. doi:10.1016/0096-3003(78)90001-2

CrossRef Full Text | Google Scholar

Nikolaev, P., Jivkov, A., Rajabi, H., Yan, H., Zhu, X., and Sedighi, M. (2024). Semi-analytical predictive model for natural and artificial thawing of circular ground-ice walls. Comput. Geotech. 171, 106394. doi:10.1016/j.compgeo.2024.106394

CrossRef Full Text | Google Scholar

Nikolaev, P., Sedighi, M., Jivkov, A. P., and Margetts, L. (2022). Analysis of heat transfer and water flow with phase change in saturated porous media by bond-based peridynamics. Int. J. Heat. Mass Transf. 185, 122327. doi:10.1016/j.ijheatmasstransfer.2021.122327

CrossRef Full Text | Google Scholar

Novopashin, M. D., and Kurilko, A. S. (2010). Properties of geomaterials in permafrost conditions and their impact on mining technology and stability of workings. Min. Inf. Anal. Bull. 4 (12), 21–33.

Google Scholar

Popov, V. I., and Kurilko, A. S. (2018). Approximate method to solve problems of heat and mass transfer under water freezing in permafrost rocks. Min. Inf. Anal. Bull. 12, 57–64. doi:10.25018/0236-1493-2018-12-0-57-64

CrossRef Full Text | Google Scholar

Samarskii, A. A., and Moiseenko, B. D. (1965). Economical through-count scheme for the multidimensional Stefan problem. J. Comput. Math. Math. Phys. 5 (5), 816–827.

Google Scholar

Semin, M., Golovatyi, I., Levin, L., and Pugin, A. (2024). Enhancing efficiency in the control of artificial ground freezing for shaft construction: a case study of the Darasinsky potash mine. Eng. Technol. 18, 100710. doi:10.1016/j.clet.2023.100710

CrossRef Full Text | Google Scholar

Solovyov, D. E. (2009). “Methods for calculating temperature and ventilation regimes of an unsteady mine network in permafrost zones,”. Dissertion (Yakutsk: Cand. Sci. Tech.), 161.

Google Scholar

Song, Y., Liu, R., Li, S., Kang, Z., and Zhang, F. (2020). Peridynamic modeling and simulation of coupled thermomechanical removal of ice from frozen structures. Meccanica 55, 961–976. doi:10.1007/s11012-019-01106-z

CrossRef Full Text | Google Scholar

Spiridonov, D., Stepanov, S., and Vasiliy, V. (2023). An online generalized multiscale finite element method for heat and mass transfer problem with artificial ground freezing. J. Comput. Appl. Math. 417, 114561. doi:10.1016/j.cam.2022.114561

CrossRef Full Text | Google Scholar

Sun, W. K., Zhang, L. W., and Liew, K. M. (2020). A smoothed particle hydrodynamics–peridynamics coupling strategy for modeling fluid–structure interaction problems. Comput. Methods Appl. Mech. Eng. 371, 113298. doi:10.1016/j.cma.2020.113298

CrossRef Full Text | Google Scholar

Van Le, Q., and Bobaru, F. (2018). Objectivity of state-based peridynamic models for elasticity. J. Elast. 131 (1), 1–17. doi:10.1007/s10659-017-9641-6

CrossRef Full Text | Google Scholar

Voller, V. R., and Swaminathan, C. R. (1991). ERAL source-based method for solidification phase change, Numer. Heat Transf. Part B Fundam. 19 (2), 175–189. doi:10.1080/10407799108944962

CrossRef Full Text | Google Scholar

Weißenfels, C. (2022). Peridynamics, simulation of additive manufacturing using meshfree methods: with focus on requirements for an accurate solution, 125–138.

Google Scholar

Wen, Z., Zhang, T., Sheng, Y., Ma, W., Wu, Q., Feng, W., et al. (2011). Managing ice-rich permafrost exposed during cutting excavation along Qinghai–Tibetan railway: experiences and implementation. Eng. Geol. 122 (3–4), 316–327. doi:10.1016/j.enggeo.2011.07.012

CrossRef Full Text | Google Scholar

Wu, H., Bandopadhyay, S., and Izaxon, V. U. (2006). “Optimum insulation for engineering control of mine thermal regime around a mine airway in permafrost,” in 11th US/North American Mine Ventilation Symposium 2006: Proceedings, Pennsylvania, USA, 5–7 June 2006 (Boca Raton, FL: CRC Press), 271.

Google Scholar

Zhelnin, M., Kostina, A., Prokhorov, A., Plekhov, O., Semin, M., and Levin, L. (2022). Coupled thermo-hydro-mechanical modeling of frost heave and water migration during artificial freezing of soils for mineshaft sinking. J. Rock Mech. Geotech. Eng. 14 (2), 537–559. doi:10.1016/j.jrmge.2021.07.015

CrossRef Full Text | Google Scholar