Experimental determination of the ventilation pressure thermal drop effect on the air flows in the inclined mine workings

The increasing use of mechanized facilities in underground mining operations, including conveyor systems, diesel and electric equipment, and rail transport, is driving the expansion into new mineral reserves, often accessed through inclined mine workings. Many of these workings are located in moderately pitched deposits, where mining conditions present particular safety challenges. Among the most critical risks is fire, which can significantly alter airflow patterns and disrupt mine ventilation systems. While fire-induced airflow and temperature distribution have been studied extensively in buildings and road tunnels, similar investigations for underground mine workings remain scarce and are typically limited to simplified one-dimensional models. However, the results from studies on buildings and tunnels cannot be directly applied to mine environments due to significant differences in geometry and ventilation systems. This study investigates the effects of ventilation pressure drops on air velocity and temperature field heterogeneity in inclined mine workings with positive and negative inclination angles. We experimentally determine the relationship between mass airflow rate changes in mine workings with inclination angles ranging from 12° to −15° and a fixed heat source power. For the first time, we examined asymmetrical changes in airflow in inclined mine workings for positive and negative inclination angles. A theoretical justification for the observed experimental phenomenon is provided. Additionally, we identify the critical power range of the heat source at which airflow choking and direction reversal occur in workings with descending ventilation, providing valuable insights for improving mine ventilation safety during fire scenarios.

1 Introduction

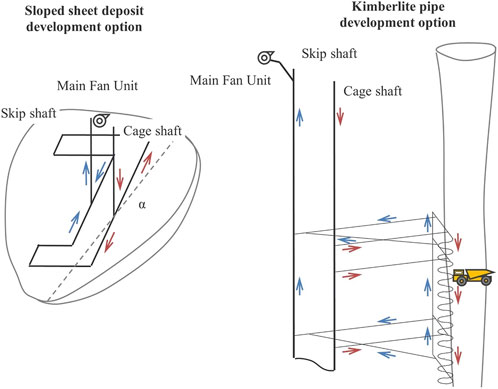
The extraction of minerals from the subsurface is associated with the processes of field development and the construction of mining facilities. The extraction of minerals from the subsurface at their low occurrence is associated with driving the mine working network. Depending on the subsurface conditions of the mineral occurrence, the mine working network may include multiple mining levels, in the case of mining orebodies, as well as a single level, in the case of mining sheet deposits (Figure 1). In case of multiple mining levels at the mines, in most cases they are interconnected through one or more slopes or inclines.

Figure 1

Figure 1. Options of mineral deposit development using the inclined mine workings.

Currently, various mechanization facilities are applied in mining operations to transfer minerals from the mining sites to the places where they are further transported to the surface. For this, self-propelled diesel equipment, conveyor transport, and electric haulage are used. The extensive equipment application is closely related to an increased risk of an emergency caused by this equipment catching fire. Therewith, fires in the inclined mine workings are the most hazardous where, due to the effect of the ventilation pressure thermal drop induced by fire, a change in the ventilation conditions may occur. A change in the ventilation conditions is thought of as any unexpected increase or decrease in the amount of air supplied in this mine working by more than 50%, as well as the change in the air flow direction in accordance Order of the Federal Environmental, Industrial and Nuclear Supervision Service of Russia No504, 2023.

The federal regulations Order of the Federal Environmental, Industrial and Nuclear Supervision Service of Russia No 504, No 520 and No 467 specify the requirements to performing the engineering calculations of emergency condition evolution in the shafts and at the mines when performing mine rescue operations, as well as at the stage of developing the emergency response plans when designing the miner escape routes. However, the regulatory documentation provides no single approach to calculating the effect of the ventilation pressure thermal drop induced by fire on mine ventilation stability. This fact determines the relevance of continued research in this area and the subsequent development of algorithms for calculating the effect of the ventilation pressure thermal drop on mine ventilation stability.

Depending on the direction of air flow along the inclined mine working, the ventilation pressure thermal drop that occurs during a fire has either a positive or a negative effect. The positive and negative effects of the ventilation pressure thermal drop are thought of as the way it affects the residual pressure of the main fan unit in the ventilation system section. With the positive effect of the ventilation pressure thermal drop, the amount of air entering the fire source increases, and in the case of a negative effect of the ventilation pressure thermal drop, three possible effects are identified, depending on the fire source power. In case the power of the fire source is less than the pressure in the sloped part of the mine working with a downdraft, the air flow rate in the inclined mine working decreases. If the ventilation pressure thermal drop induced by fire is equal to the pressure in the inclined mine working, then the air flow thermal choking effect occurs, where the average mass air flow rate in the inclined mine working at a distance from the fire source tends to zero, and the movement of air flows in the inclined mine working is caused by convective vortices in both directions from the fire source. In the latter case, when the ventilation pressure thermal drop induced by fire exceeds the pressure in the ventilation system section, the direction of air flow in the inclined mine working changes.

Many Russian authors have studied the effect of the ventilation pressure thermal drop on the ventilation stability of mine ventilation systems. Some studies of the authors are aimed at determining the stability of mine ventilation under normal operating conditions of the ventilation system (Voropaev, 1950; Mokhirev and Trofimov, 1987; Levin and Grishin, 2013; Levin et al., 2020). The specifics of some shafts and mines is the angle of incidence of the mineral, and therefore the movement of air through the mine workings occurs according to the seam dip or rise. The application of high-performance mining equipment in these shafts and mines, resulting in intensive air heating during normal operation, also affects the stationary air distribution in the ventilation system. Therefore, in some cases, this factor shall be taken into account based on the well-known effects of ventilation pressure thermal drop and the calculation approach.

However, the processes occurring in shaft ventilation systems in emergency ventilation conditions have their own characteristics, as noted in the works of the authors (Medvedev, 1978; Voskoboinikov, 1962; Melnikova et al., 2011; Grigorev, 1968). In general, the approach of previous researchers comes down to a theoretical comparison of the value of the ventilation pressure thermal drop induced by fire and the value of the pressure at this mine working section created by the main fan unit (Grishin, 2013; Terpigoreva, 1959; Grekov and Kaliusskii, 1975; Shalimov, 2014). This approach takes into account the increment of air temperature, determined by various dependencies, and further determines the ventilation pressure thermal drop induced by fire, which does not take into account the actual parameters of the combustible load. However, without calculating the possible fire power, this approach has its own application specifics at the stage of assessing the ventilation stability in the inclined mine workings.

Much less work has been devoted to the study of the positive effects of the ventilation pressure thermal drop induced by fires in the mines, due to the more predictable development of an emergency situation. The authors (Karnaukh et al., 2019; Sobolev, 1988; Ushakov et al., 1987) have proposed an approach for determining the ventilation pressure thermal drop value based on data from changes in air temperature and height differences in the inclined mine working. Against the positive effects of ventilation pressure thermal drop, measures are proposed to artificially limit the air flow rate in the mine working with fire by constructing airway stoppings.

The most hazardous situation is the case of downdraft along an inclined mine working, when the value of the ventilation pressure thermal drop induced by fire exceeds the pressure created by the main fan unit, which in turn results in a change in the air flow direction, and consequentially, in the unpredictable spread of combustion products in the mine ventilation system. Before the numerical modeling methods were developed, the critical ventilation pressure thermal drop in the mine working was determined experimentally and currently, the critical ventilation pressure thermal drop in the mine working may be determined based on the mathematical modeling of the ventilation system parameters (Grishin et al., 2014; Popov and Kormshchikov, 2020; Popov et al., 2020; Brake, 2013; Perestoronin et al., 2023).

The issue of determining the actual fire power has been considered in the most detail by foreign authors with full-scale experimental studies both on the surface, in conditions of road tunnels (Cheong et al., 2013; Ingason et al., 2015), and full-scale experimental studies in mine conditions (Hansen and Ingason, 2013; Hansen, 2010; Hansen, 2015). It should be noted that these studies are aimed directly at determining the actual power of the combustible load, but not its effect on air distribution in inclined mine workings. Also, these studies were performed in the conditions of horizontal mine workings and tunnels. The data obtained in the course of experimental studies are used by the authors to develop and verify the appropriate computational models, including CFD modeling methods (Zhou et al., 2016; Vidmar and Petelin, 2007; Amano et al., 1982) when determining the possible fire source power and calculating the fire risk for people caught in a fire in road tunnels.

Along with full-scale studies, foreign researchers use physical modeling methods, as shown in studies (Zhao S. et al., 2019; Li et al., 2016). These studies explore how thermal depression affects tunnel ventilation during fires. However, the methods for setting the heat source vary widely. The described devices raise concerns about maintaining a stable thermal output, which is crucial for analysis. Additionally, the boundary conditions are more suited to road tunnels, whereas our focus is on underground mines.

No such experimental studies have been conducted in the Russian Federation in mine conditions, and therefore comparing the accuracy of previously used approaches to analyze the effect of the ventilation pressure thermal drop on the mine ventilation system stability, taking into account the actual combustible load power, remains relevant. The criterion of accuracy can be an experiment conducted both in full-scale and in laboratory conditions. Conducting an experiment related to a fire in natural conditions is a major challenge, therefore, in the studies conducted by the team of authors, issues related to the application of physical simulation on a laboratory model that meets the criteria for the similarity (Froude) and the thermal power of the fire source are considered. This provides for parameterizing and validating the heat mass transfer models in the mine systems. The key attention herein is paid to a previously unexplored issue–an experimental study of the air flow thermal choking effect in an inclined mine working at various angles of its inclination, as well as determining the type of dependence of the change in mass air flow rate in an inclined mine working in the case of updraft and downdraft.

2 Materials and methods

To investigate the influence of thermal depression on the stability of airflow in inclined mine workings, this study considers typical inclination angles commonly encountered in potash, ore, and coal mines. The inclination of a working is generally determined either by the mining and geological conditions of a flat-lying deposit or by the need to establish transport connections between two levels at different elevations. In practice, the maximum inclination at which self-propelled mining equipment can operate does not exceed 15°.

The investigation was conducted using a physical scale model, the schematic of which is shown in Figure 2.

Figure 2

Figure 2. Layout diagram of the physical scale model.

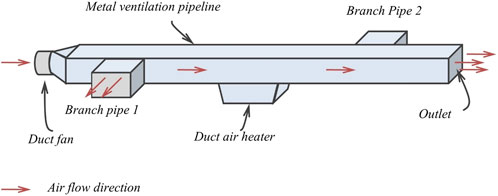
The straight section of the experimental unit between the two pipes, where the heat source is located, represents an inclined mine working. Pipes 1 and 2 simulate the connections between the inclined working and other levels of the mine ventilation network. In this study, a single configuration is considered: Pipe 1 remains open while Pipe 2 is closed. This arrangement enables the simulation of thermal depression effects during both ascending and descending airflow. During ascending movement, air enters the inclined working through Pipe 1, whereas during descending movement, air exits through it.

The use of this physical model is based on the Froude scaling method, which ensures similarity between the model and real mine conditions with respect to key physical processes. Specifically, two similarity criteria are satisfied:

- Dynamic similarity, governed by the Froude number, which ensures correct scaling of inertial and gravitational forces driving natural ventilation; and

- Thermal similarity, which ensures appropriate scaling of buoyancy-driven flow due to temperature differences.

$\frac{{\mathit{V}}_{\mathit{b}}}{{\mathit{V}}_{\mathit{m}}}={\left(\frac{{\mathit{L}}_{\mathit{b}}}{{\mathit{L}}_{\mathit{m}}}\right)}^{\frac{\mathbf{1}}{\mathbf{2}}}$

$\frac{{\mathit{W}}_{\mathit{b}}}{{\mathit{W}}_{\mathit{m}}}={\left(\frac{{\mathit{L}}_{\mathit{b}}}{{\mathit{L}}_{\mathit{m}}}\right)}^{\frac{\mathbf{5}}{\mathbf{2}}}$

where V is the air flow velocity (m/s); W is the HRR from the heat source (W); and L is the characteristic size of the channel (m). The indices “b” and “m” indicate the scale model and mine working, respectively.

These criteria allow the experimental results to be extrapolated meaningfully to full-scale mine conditions, as supported by previous studies (Levin et al., 2024a; 2024b; Atkinson and Wu, 1996).

Geometrically, the scale model is a straight section of a rectangular metal ventilation duct (W = 500 mm, H = 300 mm, L = 10 m). Portions of the side walls are made of glass to allow visual observation of the airflow direction and behavior within the model. Due to the high thermal conductivity and small thickness of the metal, the heat transfer coefficient through the metal is very high and does not significantly affect the studied process. More critical is the heat exchange at the metal–air interface—both inside and outside the setup. However, at this stage of the research, the heat transfer factor was evaluated but not studied in detail. It is important to note that the heat transfer coefficient in the model falls within the range of values typical for real mine workings. The influence of the heat transfer coefficient on heat and mass transfer in the airflow will be addressed in the next stage of the study by applying additional thermal insulation to the outer surface of the experimental unit. A more detailed analysis of the collected data will make it possible to assess the influence of this factor and determine how it should be taken into account.

In the middle of the scale model, an electric duct air heater is installed simulating a heat source with a combined total power of 22 kW with the option of stepwise power control in 2.5 kW increments. In our study, an electric heater is used as the heat source instead of an open-flame source. The electric heater is a safer option compared to open flames such as gas burners or even an actual combustible load. A clear advantage of the electric heater is its consistent heating power, which is not characteristic of open-flame sources.

It is also worth noting that, in general, the development of any fire consists of the ignition/growth stage (increasing heat release rate), a stage of approximately steady burning, and the decay stage (when the combustible load is depleted and the heat release rate decreases). Our study focuses on the scenario in which the fire has reached its fully developed stage, during which the heat release rate remains roughly constant—this represents the most pessimistic scenario.

At the current stage of our research, a scaled physical model is used; therefore, the power of the electric heater is considered as a thermal equivalent of a fire rather than representing an actual fire process. In reality, a fire is a much more complex physical phenomenon, involving changes in the gas-air composition, such as a decrease in oxygen concentration and the formation of toxic gases with densities different from that of normal air, among other factors.

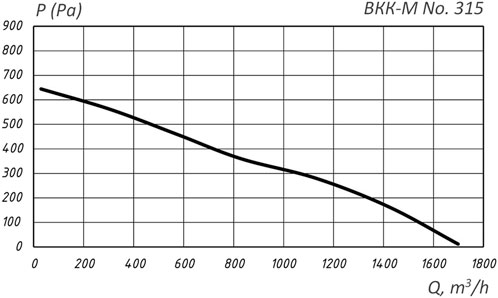
The air is supplied to the scale model by the operation of a duct fan series ВКК-М 315 with the option of smooth delivery change. The aerodynamic performance of ВКК-М 315 fan unit is provided in Figure 3.

Figure 3

Figure 3. Aerodynamic performance of ВКК-М 315 fan unit.

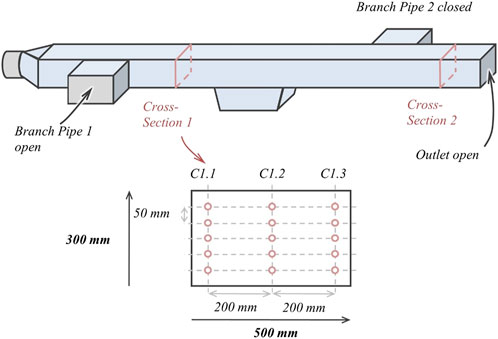
The facility also has three openings (Branch Pipe 1, Branch Pipe 2 and Outlet) through which air can be supplied to and removed from the scale model. Figure 4 shows the overview of the scale model where the experimental studies were conducted.

Figure 4

Figure 4. Overview of the scale model.

A series of experimental studies consisted in determining the field of air velocity and temperature at the cross-section points to the air heater and at the scale model outlet. Each cross-section is divided into 15 measurement points, the diagram of the measurement points is provided in Figure 5.

Figure 5

Figure 5. Air velocity and temperature measurement points.

The measurement procedure included three measurement stages:

• Measuring the air velocity and temperature in the cross-sections under study of the scale model at a heat source constant power of 15 kW at the scale model inclination angles from 0° to −15° with an increment of 3°.

• Measuring the air velocity and temperature in the cross-sections under study of the scale model when the air flow thermal choking effect occurs.

• Measuring the air velocity and temperature in the cross-sections under study of the scale model at a constant heat source power of 15 kW at the scale model inclination angles from 0° to +12° with an increment of 3°.

During measurements, the operating mode of the fan unit corresponds to the minimum delivery. During measurements, Branch Pipe 2 is closed, and Branch Pipe 1 is open. The negative values of the scale model inclination angle mean that the air flows downwards. The steady-state ventilation conditions disturbance shall be assessed by a change in the air flow direction at the outlet of the scale model, which means the ventilation stability is disturbed under the influence of the heat source ventilation pressure thermal drop.

During the measurements, the following instruments and their specifications as shown in Table 1 are used.

Table 1

Table 1. Technical specifications of the measuring instruments used.

3 Results of the experimental studies

3.1 Ventilation pressure thermal drop effect on air distribution in the mine workings with downdraft

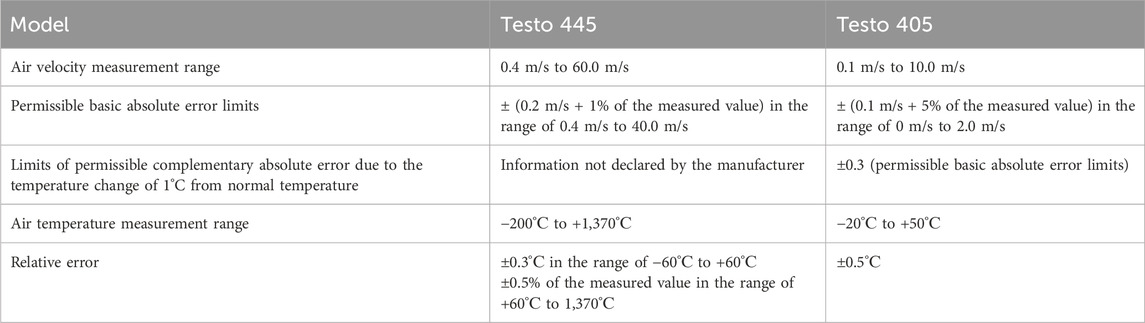
During measurements, the situation of air supply by a duct fan to a scale model is simulated, with Branch Pipe 1 open, simulating an interface with another mine working. To obtain an initial picture of the air flow and temperature distribution field, measurements were performed with a horizontal position of the scale model at a heating power of 15 kW. The results of the air velocity field distribution in Cross-Section 1 and Cross-Section 2, as well as the air temperature distribution at the points of Cross-Section 2 are shown in Figure 6.

Figure 6

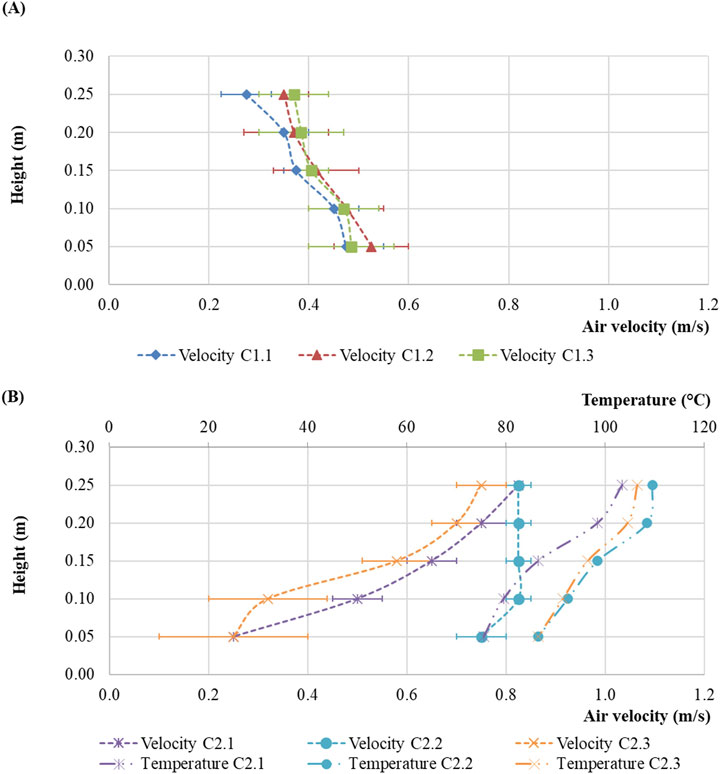
Figure 6. Results of measuring at the points of Cross-Section 1 (A) and Cross-Section 2 (B) with Branch Pipe 1 open and the heating power of 15 kW at a scale model inclination angle of 0°.

The measurements in Cross-Section 1 under study show the heterogeneity of the air velocity field distribution over the height of the cross-section, which is explained by the deepening of the heating elements downstream of Cross-Section 1 under study.

The air temperature at the points of Cross-Section 2 reaches 110°C in the upper part of the scale model and 80°C in its lower part. A major change in air temperature and velocity along vertical Cross-Section 2 is due to a change in air density when it is heated, which causes the bulk of the air to shift to the upper half of the scale model. In the lower part of the scale model, lower air temperatures are caused by heat exchange through the metal body of the scale model with atmospheric air and its faster cooling. Similar measurement results were obtained for the rest of the range of the scale model inclination angles from 0° to −15° with downdraft.

During the measurements, it was registered that for a given heat source power of 15 kW, the initial air flow reversal is achieved at an inclination angle of −6°. However, the effect of the ventilation pressure thermal drop slightly exceeds the pressure from the duct fan, which allows to state the fact of a change in the air flow direction, and the measurement results have a large error and are not provided herein. In more detail, this article will consider the air velocity field distribution at the scale model inclination angle of −15°, where the ventilation pressure thermal drop has the most apparent effect.

The results of measuring the air velocity and temperature in the cross-sections under study at a heat source power of 15 kW and a scale model inclination angle of −15° are shown in Figure 7.

Figure 7

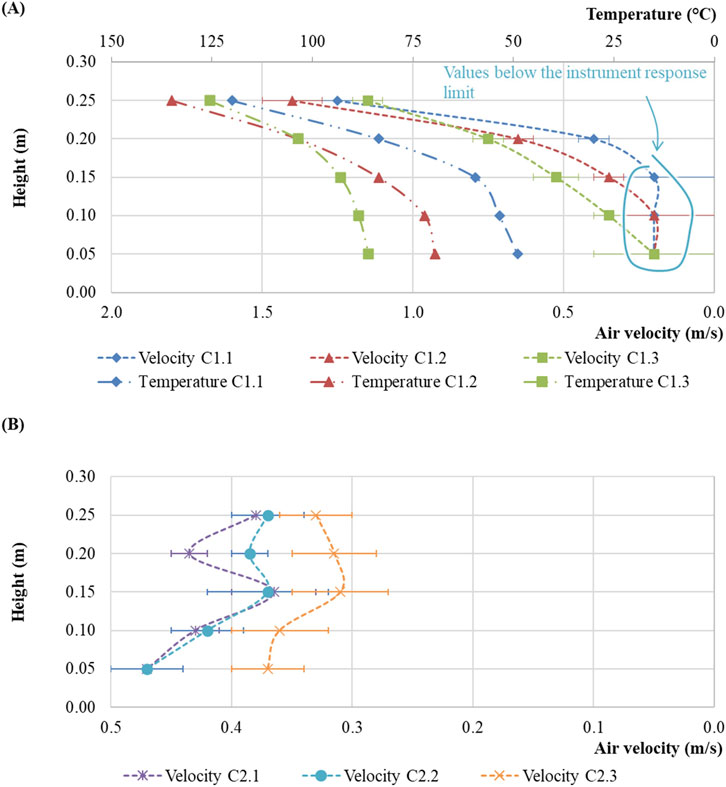
Figure 7. Results of measuring at the points of Cross-Section 1 (A) and Cross-Section 2 (B) with Branch Pipe 1 open, heating power of 15 kW and scale model inclination angle of −15°.

The measurement results are shown in Figure 7 in reverse order of the direction of the air velocity axis to reflect the change in the air flow direction in the cross-sections under study. The analysis of the data in the cross-sections under study shows major changes in the air velocity in the upper part of Cross-Section 1, where they reach 1.1–1.3 m/s, while in the lower part of the scale model the air velocity values are less than the air velocity measuring instrument response range. This air velocity field distribution is explained by the high temperature of the air downstream of the heat source, as a result of which the air tends to rise, as well as by the specifics of the scale model geometry. The highest air temperature is registered at the top point of Cross-Section 1 and reaches 120°C–140°C.

In Cross-Section 2 under study, a change in the air flow direction occurs under the influence of the ventilation pressure thermal drop, as a result of which air enters the scale model. In this case, the air temperature at all points of the cross-section was about 20°C, and the air velocity field has a small range of values, both in height of the scale model and in horizontal cross-sections, which may be caused by the availability of a control damper at the outlet and the proximity of Cross-Section 2 under study to the place of the air flow reversed entry through the scale model outlet. The lowest velocity in this case is also observed from the side of Branch Pipe 2, as in the cases considered previously.

As a result of the measurements, data were obtained on the air velocity distribution at the points of the cross-sections under study at a fixed heat source power of 15 kW, as well as the initial angle of change in the direction of air flow through the scale model outlet, which is −6°.

The average values of the change in mass air flow rate in Cross-Section 1 at a given heat source power of 15 kW are shown in Figure 8.

Figure 8

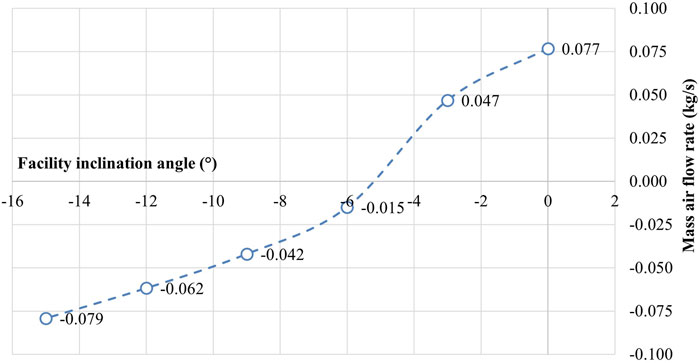
Figure 8. Change in the mass air flow rate in Cross- Section 1 when the scale model inclination angle is changed at a given heating power of 15 kW.

Based on the measurement results, it can be concluded that the ventilation pressure thermal drop has a negative effect in the conditions of downdraft. With a decrease in the mine inclination angle, the effect of the ventilation pressure thermal drop increases, which results in a change in the average mass air flow rate in the inclined mine working by 203% for the conditions of a mine inclination angle of −15°, relative to the case of horizontal position. Therewith, under the influence of the ventilation pressure thermal drop, the direction of air flow through the scale model outlet changes at a scale model inclination angle of −6°, and all the air entering the scale model is removed through Branch Pipe 1.

3.2 Ventilation pressure thermal drop effect on air distribution in an inclined mine working when the air flow thermal choking effect occurs

Additionally, within the experimental studies, the issue of the occurrence of the air flow thermal choking effect, where the average value of the mass air flow rate through the scale model outlet tends to zero, was considered. An example of the results of measuring air velocity and temperature with multidirectional air flow in Cross-Section 1 under study at a scale model inclination angle of −12° is shown in Figure 9.

Figure 9

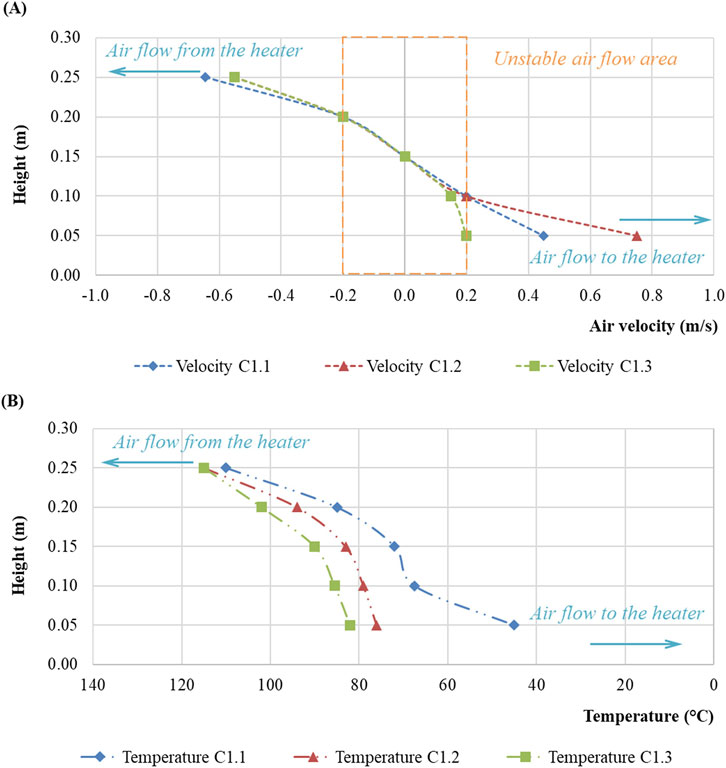
Figure 9. Example of multidirectional air flow (A) and air temperature (B) in Cross-Section 1 under study at a scale model inclination angle of −12° and a heating power of 10 kW.

With multidirectional air flow in the conditions of the scale model, normal and reverse flow generation areas may be identified, which are generated in the lower and upper parts of the scale model, respectively. Therewith, an area of unstable air flow with low velocity is generated in the middle part of the scale model. In these conditions, a major vertical temperature difference occurs, which is about 70°C.

Following the results obtained, it can be concluded that in the event of the air flow thermal choking effect under the influence of the ventilation pressure thermal drop, when the average values of the mass air flow rate through the scale model outlet tend to zero, air movement in the inclined mine working occurs caused by the action of the air flow convection stratification.

The air flow distribution observed in the scale model reflects the characteristic multidirectional patterns in inclined mine workings with downdraft, driven by ventilation pressure and thermal gradients, as reported by previous studies (Kazakov et al., 2014; Gershuni et al., 1994; Kazakov et al., 2014).

3.3 Ventilation pressure thermal drop effect on air distribution in mine workings with updraft

At the third stage of the studies, measurements were performed to determine the effect of the ventilation pressure thermal drop on the updraft in the inclined mine workings at a fixed heat source power of 15 kW. The measurements were taken similarly at 15 points of Cross-Section 1 and Cross-Section 2 under study in the scale model inclination angle range from 0° to +12° in 3° increments.

Figure 10A shows the results of measuring the air velocity at the points of Cross-Section 1 at the scale model inclination angle of 3° and a heating power of 15 kW. Figure 10B shows the results of measuring air velocity and temperature in Cross-Section 2.

Figure 10

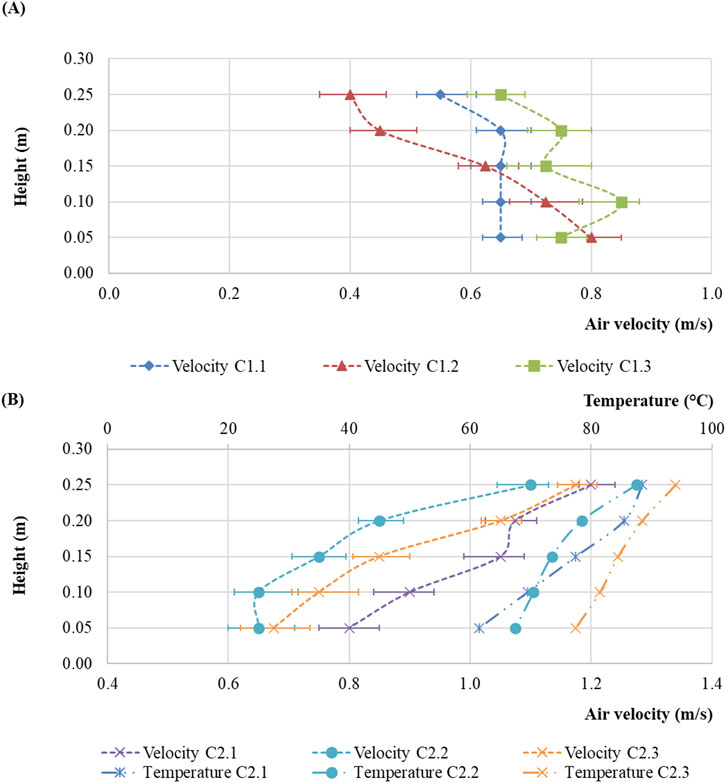
Figure 10. Results of measuring at the points of Cross-Section 1 (A) and Cross-Section 2 (B) with Branch Pipe 1 open and the heating power of 15 kW at a scale model inclination angle of 3°.

When comparing the results of the air flow distribution at the points of Cross-Section 1 and Cross-Section 2 under study, it can be noted that the overall picture is similar to the measurement results at an inclination angle of 0°. In Cross-Section 1, a vertical change in air velocity from the top of the scale model to the bottom is apparent due to the change in the scale model geometry in the area of the heating elements. In Cross-Section 2, due to the operation of the heating elements, the air flow distribution to the upper part of the scale model changes due to the higher air temperature. Therewith, also an uneven air flow distribution occurs between the left and right parts of Cross-Section 2. Similar results were obtained for the scale model inclination angles of 6°, 9° and 12°. The measurement results at a scale model inclination angle of 12° for Cross-Section 1 and Cross-Section 2 are shown in Figure 11.

Figure 11

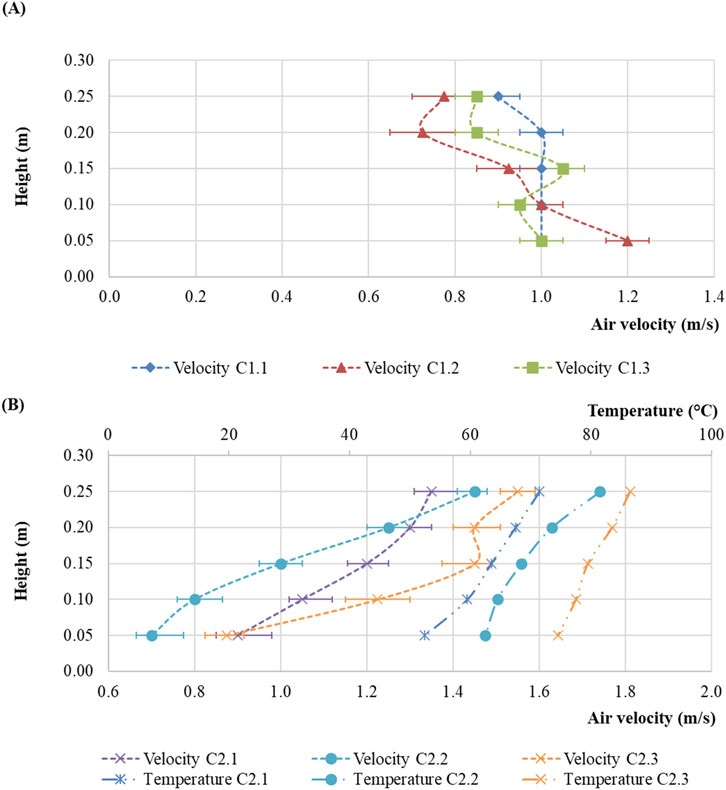
Figure 11. Results of measuring at the points of Cross-Section 1 (A) and Cross-Section 2 (B) with Branch Pipe 1 open and the heating power of 15 kW at a scale model inclination angle of 12°.

The air flow distribution Cross-Section 1, shown in Figure 11A, generally has a similar distribution pattern along vertical lines 1.1–1.3, as in the case shown in Figure 11B. The average values of the mass air flow rate in Cross-Section 1 at the updraft are shown in Figure 12.

Figure 12

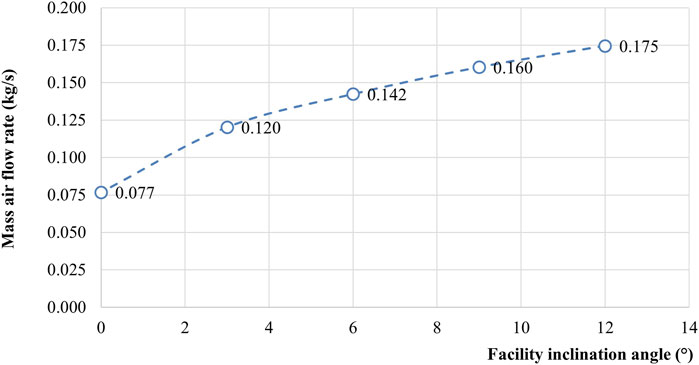
Figure 12. Change in the mass air flow rate in Cross-Section 1 at the updraft and a change in the scale model inclination angle with a given heating power of 15 kW.

The analysis of the results obtained in the case of an updraft in the presence of a 15 kW heat source allows to conclude that the heat source has a positive effect on the total air flow rate in the scale model. Thus, at an inclination angle of 0°, the average air velocity in Cross-Section 1 is about 0.4 m/s, further, with an increase in the scale model inclination angle, the average air velocity increases to 0.95 m/s with the scale model inclination angle of 12°. The resulting increase in air velocity corresponds to a 127% increase in mass air flow rate.

4 Discussion and conclusions

The existing approach to determining the ventilation pressure thermal drop in the event of a fire in a mine is based on calculating the increment of air temperature and, consequently, changes in air density at a known elevation difference, as a result of which the dependence becomes linear. The authors (Oka and Atkinson, 1995; Atkinson and Wu, 1996) conducted studies to determine the critical air velocity on an inclined scale model to determine the effect of the heat source power required to change the air flow direction. As a result, the authors concluded that this dependence is linear. However, the results obtained were investigated on a scale model with no additional branch pipes, as compared to this article.

The aggregate results of the study on determining the minimum power at which the thermal choking effects and changes in the direction of air flow through the scale model outlet occur, depending on the mine working inclination angle, suggest the nonlinear nature of this relationship, due to the absence of air flow reversal through the scale model outlet up to the mine working inclination angle of −6°. Therewith, the power required for the initial air flow reversal is about 15 kW.

To determine the qualitative nature of the dependence, it is proposed to use the following assumptions:

• The greatest effect of the ventilation pressure thermal drop is achieved at the mine working inclination angles of ±90°.

• The application scope of the dependence is in the mine working inclination angles range of 0° to ±90°.

• The dependence is nonlinear.

Based on the Kirchhoff equation for mine ventilation systems, an approximating dependence of the ventilation pressure thermal drop effect on mass air flow rate can be obtained using the equation:

$\mathit{R}{\mathit{Q}}^{\mathbf{2}}=\mathit{H}\pm {\mathit{H}}_{\mathit{T}}$

where Q is the air flow rate (kg/s), R is the system section resistance (Ns²/m⁸), H is the ventilation system section pressure (Pa), H_T is the ventilation pressure thermal drop (Pa).

The ventilation pressure thermal drop from the heat source may be determined as follows:

${\mathit{H}}_{\mathit{T}}=∆\mathit{\rho }\mathit{g}∆\mathit{h}=∆\mathit{\rho }\mathit{g}\mathit{L}\mathit{s}\mathit{i}\mathit{n}\mathit{\alpha }$

where ∆ρ is the air density difference in case of fire with power W and under normal ventilation conditions (kg/m³), g is the free fall acceleration (m/s²), ∆h is the elevation difference between the beginning and the end of the inclined mine working (m), L is the mine working length (m), α is the mine working inclination angle (°).

Based on the assumption that the change in air density is proportional to fire power ∆ρW, the change in air flow rate Q can be determined as:

$∆\mathit{Q}=\sqrt{\frac{\mathit{H}\pm ∆\mathit{\rho }\mathit{g}\mathit{L}\mathit{s}\mathit{i}\mathit{n}\mathit{\alpha }}{\mathit{R}}}\sim \sqrt{\mathit{sin}\mathit{\alpha }}$

Taking into account the initial air distribution (normal ventilation of the mine working) in the inclined mine workings, the dependence will take the following form:

$\mathit{Q}=\mathit{B}\sqrt{{\mathit{Q}}_{\mathbf{0}}^{\mathbf{2}}+\mathit{A}\left(\frac{\mathit{W}}{{\mathit{W}}_{\mathbf{0}}}\right)\mathit{sin}\mathit{\alpha }}$

where Q₀ is the initial air flow rate in the mine working (kg/s), A, B are the function approximation factors, W is the heat source power (kW), W₀ is the reference power (15 kW).

A comparison of the experimental data results and the calculated dependence is shown in Figure 13. Based on the approximation factors obtained for the experimental data obtained, taking into account the heat source power of 15 kW, the expected lines of change in the average mass air flow rate are constructed, taking into account the heat source power of 7.5 kW and 22.5 kW, which are also shown in Figure 13.

Figure 13

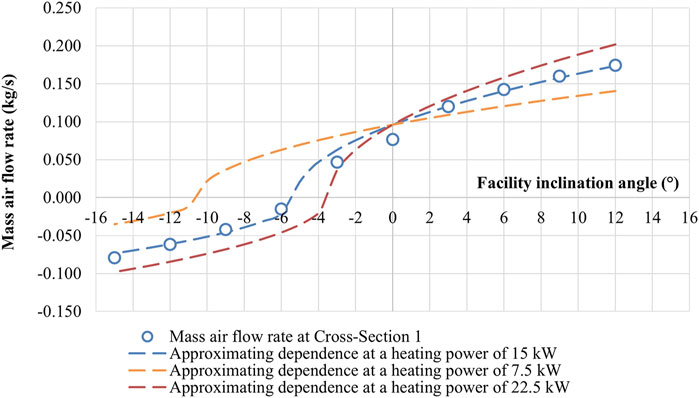
Figure 13. Comparison of experimental data with the proposed approximating dependence of the change in mass air flow rate depending on the mine working inclination angle.

Figure 13 shows that, in general, the proposed dependence in the form of a square root of a sine describes the experimental points properly. However, to describe the experimental data within the proposed model, factor A shall be selected differently for the left (α < −4°) and right (α > −4°) branches of the curve. Therewith, within the 1D approach, factor A is constant, which is due to the unconsidered specifics of the 3D convective air flow in an inclined mine working with a powerful heat source. During the transition from positive to negative angles, the flow structure in the inclined mine working is significantly rearranged, and a circulating convective vortex occurs.

Interestingly, the curve is asymmetric with respect to the ordinate axis. This is because the tilting of the air stream and the significant rearrangement of the flows in the inclined mine working do not occur at zero degrees, but later, in the range from −3° to −6°. For the buoyancy force caused by the heat source to overcome the fan pressure, the mine working must have some nonzero inclination. This is well explained by the theoretical formula for ∆Q presented above.

The smooth S-shaped profile of the curve in the region where return flows emerge, which was obtained experimentally, is also confirmed by theoretical calculations and by studies of other authors on the tilting of air jets in inclined channels simulating transport tunnels (Zhao S. et al., 2019; Li et al., 2016).

Based on the calculated curve, the value of the critical heat power can be obtained, at which the air flow thermal choking effect will occur in the inclined mine working, depending on its inclination angle, as well as the heat source power values, at which a change in the air flow direction in the inclined mine working will occur. The obtained study results can be applied to the conditions of underground mine workings, recalculated according to the Froude scaling method in accordance with the approach described in the study results (Levin et al., 2024a; 2024b; Atkinson and Wu, 1996). The Froude scaling method has been applied to physical modeling of ventilation in road tunnels, subways, and similar structures (Zhao P. et al., 2019; Li et al., 2012). It is generally recognized as the standard and most commonly used approach for simulating heat and mass transfer in long tunnels with intense heat sources, such as fires. Its validity was previously investigated in our study (Levin et al., 2024a), which showed that, for a 1:10 scale model, similarity is achieved with acceptable engineering accuracy. Nevertheless, a more detailed analysis of the applicability of this scaling method to mine workings—where airflow is driven by mine-induced pressure differentials—remains a subject of future research.

As part of further work, additional studies are planned of the unusual behavior of the experimental point at the scale model inclination angle of −3° at different heat source power values. Based on the experimental data obtained, numerical 3D modeling will be performed and a more detailed analysis of changes in the structure of convective air flows under the influence of ventilation pressure thermal drop in the mine workings with descentional ventilation will be conducted.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LL: Conceptualization, Resources, Methodology, Writing – review and editing. EK: Writing – original draft, Data curation, Visualization, Investigation, Writing – review and editing. SZ: Supervision, Writing – review and editing, Project administration, Validation, Formal Analysis.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The study was performed with the financial support of the Ministry of Science and Education of the Russian Federation (Research, Development, and Engineering Work Reg. No.: 124020500030–7).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amano, K., Mizuta, Y., and Hiramatsu, Y. (1982). An improved method of predicting underground climate. Int. J. Rock Mech. Min. Sci.19, 31–38. doi:10.1016/0148-9062(82)90708-2

CrossRef Full Text | Google Scholar

Atkinson, G. T., and Wu, Y. (1996). Smoke control in sloping tunnels. Fire Saf. J. 27, 335–341. doi:10.1016/S0379-7112(96)00061-6

CrossRef Full Text | Google Scholar

Brake, D. (2013). Fire modelling in underground mines using Ventsim Visual VentFIRE software. Aust. Mine Vent. Conf., 1–3.

Google Scholar

Cheong, M. K., Cheong, W. O., Leong, K. W., Lemaire, A. D., Noordijk, L. M., and Tarada, F. (2013). “Heat release rates of heavy goods vehicle fires in tunnels,” in BHR group - 15th international symposium on aerodynamics, ventilation and fire in tunnels 2013 Spain: BHR Group Limited, 779–788.

Google Scholar

Gershuni, G. Z., Shalimov, A. V., and Myznikov, V. M. (1994). Plane-parallel advective binary mixture flow stability in a horizontal layer. Int. J. Heat Mass Transf. 37, 2327–2342. doi:10.1016/0017-9310(94)90374-3

CrossRef Full Text | Google Scholar

Grekov, S., and Kaliusskii, A. (1975). Gas dynamics of inert media and degassing of mine workings in emergencies. Moscow: Nedra.

Google Scholar

Grigorev, Y. V. (1968). Effect of ventilation pressure thermal drop during fire on the ventilation parameters. J. Min. Inst. 55 (1), 100.

Google Scholar

Grishin, E. (2013). Scientific substantiation of ways to increase the underground mine ventilation system reliability. Perm, Russia: Mining Institute of the Ural Branch of the Russian Academy of Sciences.

Google Scholar

Grishin, E., Kormshchikov, D., and Levin, L. (2014). Using the results of thermal and gas dynamic calculations in the analysis of emergencies and the development of an emergency response plan in the aeroset analysis system. Min. Inf. Anal. Bull. Sci. Tech. J. 9, 185–189.

Google Scholar

Hansen, R. (2010). “Overview of fire and smoke spread in underground mines,” in Fourth international symposium on tunnel safety and security, 483–494.

Google Scholar

Hansen, R. (2015). Study of heat release rates of mining vehicles in underground hard rock mines. Dissertations. Västerås, Sweden; Mälardalen University Press.

Google Scholar

Hansen, R., and Ingason, H. (2013). Full-scale fire experiments with mining vehicles in an underground mine.

Google Scholar

Ingason, H., Li, Y. Z., and Lönnermark, A. (2015). Tunnel fire dynamics. New York: Springer.

Google Scholar

Karnaukh, N., Mavrodi, A., Zakhlebin, V., and Agarkov, A. (2019). Computer simulation of mine ventilation emergency conditions. Sci. Bull. Res. Inst. Mine Rescue Work Respir. 2, 37–46.

Google Scholar

Kazakov, B., Shalimov, A., Semin, M., and Grishin, E. (2014). Air flow convection stratification along the section of mine workings, its role in the generation of ventilation pressure thermal drops induced by fire and its effect on the ventilation stability. Gorn. zhurnal 12, 105–109.

Google Scholar

Levin, L., and Grishin, E. (2013). Shaft and mine ventilation system reliability in the occurrence of a ventilation pressure thermal drop in normal ventilation conditions. Min. Inf. Anal. Bull. Sci. Tech. J. 12, 174–178.

Google Scholar

Levin, L., Paleev, D., and Semin, M. (2020). Calculation of the air flow stability in the mine workings in mine ventilation systems by the factor of ventilation pressure thermal drop. Bull. Sci. Cent. Saf. Work Coal Industry 1, 81–85.

Google Scholar

Levin, L., Popov, M., Semin, M., and Zhikharev, S. (2024a). Experimental and numerical study of air flow reversal induced by fire in an inclined mine working. Appl. Sci. 14 (15), 6840. doi:10.3390/app14156840

CrossRef Full Text | Google Scholar

Levin, L., Semin, M., Popov, M., and Zhikharev, S. (2024b). Validating the model of heat mass transfer in the atmosphere of a horizontal mine working in the presence of a powerful heat source. Nedropolzovaniie 24 (3), 169–176. doi:10.15593/2712-8008/2024.3.8

CrossRef Full Text | Google Scholar

Li, Y. Z., Fan, C. G., Ingason, H., Lönnermark, A., and Ji, J. (2016). Effect of cross section and ventilation on heat release rates in tunnel fires. Tunn. Undergr. Space Technol. 51, 414–423. doi:10.1016/j.tust.2015.09.007

CrossRef Full Text | Google Scholar

Li, Y. Z., Lei, B., and Ingason, H. (2012). Scale modeling and numerical simulation of smoke control for rescue stations in long railway tunnels. J. fire Prot. Eng. 22 (2), 101–131. doi:10.1177/1042391512445409

CrossRef Full Text | Google Scholar

Medvedev, B. (1978). Thermal fundamentals of mine ventilation under normal and emergency ventilation conditions. Kyiv – Donetsk Visshaia shkola.

Google Scholar

Melnikova, Ia., Bulgakov, Iu., and Trofimov, V. (2011). Assessing the stability of mining operations in case of fires. Ugol Ukr. 5, 23.

Google Scholar

Mokhirev, N., and Trofimov, N. (1987). Calculation of the natural draught generated in the inclined mine workings in the working areas. Izvestiia vuzov. Min. J. 5, 42–44.

Google Scholar

Oka, Y., and Atkinson, G. T. (1995). Control of smoke flow in tunnel fires. Fire Saf. J. 25, 305–322. doi:10.1016/0379-7112(96)00007-0

CrossRef Full Text | Google Scholar

Perestoronin, M. O., Parshakov, O. S., and Popov, M. D. (2023). Parameterization of a ventilation network model for the analysis of mine working emergency ventilation modes. Min. Sci. Technol. Russ. Fed. 8, 150–161. doi:10.17073/2500-0632-2022-10-13

CrossRef Full Text | Google Scholar

Popov, M., and Kormshchikov, D. (2020). Calculation of the air flow reversal in vertical and inclined mine workings in case of fire by the factor of ventilation pressure thermal drop in the Aeroset analysis system. Gorn. echo 1, 84–89. doi:10.7242/echo.2020.1.18

CrossRef Full Text | Google Scholar

Popov, M., Kormshchikov, D., Semin, M., and Levin, L. (2020). Calculation of air flows stability in the mine workings by the factor of thermal depression in the analytical complex «aeroset». Bezop. Tr. V. promishlennosti 10, 24–32. doi:10.24000/0409-2961-2020-10-24-32

CrossRef Full Text | Google Scholar

Shalimov, A., Kormshchikov, D., Gazizullin, R., and Semin, M. (2014). Modeling alteration of thermal drop of ventilation pressure and its effects on mine working ventilation. Nedropolzovaniie 12, 41–47. doi:10.15593/2224-9923/2014.12.5

CrossRef Full Text | Google Scholar

Sobolev, G. (1988). “Organization and conduct of mine rescue operations,” in Revised and supplemented. Ed. 3. Moscow: Nedra.

Google Scholar

Terpigoreva, A. (1959). “Mine atmosphere and ventilation,” in Fight against dust, gases and fires. Mine rescue work. Moscow: Ugletekhizdat.

Google Scholar

Ushakov, K., Burchakov, A., Puchkov, L., and Medvedev, I. (1987). “Aerology of mining facilities,” in Revised and supplemented. Ed. 3. Moscow: Nedra.

Google Scholar

Vidmar, P., and Petelin, S. (2007). Application of CFD Method for risk assessment in road tunnels. Eng. Appl. Comput. Fluid Mech. 1 (4), 273–287.

CrossRef Full Text | Google Scholar

Voropaev, A. (1950). Mine ventilation pressure thermal drop. Moscow: AN SSSR Publishing House.

Google Scholar

Voskoboinikov, V. (1962). “Investigating the Parameters of the air flow passing through the underground fire seat,” in Proceedings of the seminar on mining heat engineering. Kyiv: AN USSR Publishing House, 42–48.

Google Scholar

Zhao, P., Yuan, Z., Yuan, Y., Yu, N., and Yu, T. (2019b). A study on ceiling temperature distribution and critical exhaust volumetric flow rate in a long-distance subway tunnel fire with a two-point extraction ventilation system. Energies 12 (8), 1411. doi:10.3390/en12081411

CrossRef Full Text | Google Scholar

Zhao, S., Li, Y. Z., Kumm, M., Ingason, H., and Liu, F. (2019a). Re-direction of smoke flow in inclined tunnel fires. Tunn. Undergr. Space Technol. 86, 113–127. doi:10.1016/j.tust.2019.01.006

CrossRef Full Text | Google Scholar

Zhou, L., Smith, A. C., and Yuan, L. (2016). New improvements to MFIRE to enhance fire-modeling capabilities. Min. Eng. 68, 45–50. doi:10.19150/me.6628

PubMed Abstract | CrossRef Full Text | Google Scholar