Study on dynamics and vibration response of shield cutterhead in composite strata based on Hertz contact

The shield cutterhead experiences eccentric loads when excavating through composite strata, leading to potential deviation of the cutterhead. This study examines the static response, modal characteristics, and vibration response of a shield cutterhead in composite strata, utilizing Hertz contact theory. The cutterhead-rock interaction is equivalently modeled as mechanical spring constraints, with contact stiffness derived from elastic contact theory for disc cutter-rock contact. The static and dynamic responses of the cutterhead under maximum thrust and rock-breaking load are analyzed using finite element simulations. Results show that moderately weathered limestone induces larger displacements compared to hard rock. Modal analysis reveals that the natural frequencies increase with rock modulus, with composite strata exhibiting intermediate values compared to the soft and hard rock. Vibration responses under rock-breaking load demonstrate rotational symmetry in uniform strata but asymmetry in composite strata, where the displacement of the upper half exceeds the lower half due to stiffness contrast. This work provides a theoretical framework for optimizing cutterhead design and tunneling parameters in heterogeneous strata.

1 Introduction

Shield machines are widely used in excavation projects such as metro and tunnel construction, featuring safety, high efficiency, strong geological adaptability, and low working noise (Zhu et al., 2008; Yang et al., 2024; Ding et al., 2022; Li et al., 2023). The cutterhead is one of the core components of the shield machine. When tunneling in composite strata, the cutterhead is subjected to eccentric loads due to the inhomogeneous distribution of geological conditions, probably causing the tunneling attitude to shift (Liu et al., 2025; Song et al., 2025).

The structural parameters of the cutterhead and the excavation parameters greatly affect the shield machine’s mechanical characteristics when the cutterhead excavates in composite strata (Göbl, 2010; Kong et al., 2024). Su et al. analyzed the structural characteristics of the panel-type cutterhead and spoke-type cutterhead, and compared the differences in their stiffness, strength, and weight of the two cutterheads (Su et al., 2011). Yang et al. investigated shield tunneling parameters and studied the influences of earth chamber pressure, thrust, and cutterhead rotational speed on tunneling speed and cutterhead torque (Yang et al., 2009). Sun et al. (2016) established a dynamic cutting force model based on the cavity expansion theory and a discretization method (Sun and Gao, 2023). They investigated the effects of geological conditions and operational parameters on the dynamic cutting forces and the vibration characteristics of the cutterhead.

During the tunneling process of the shield machine, due to the unevenness of the loads generated by the composite strata, the working conditions of the cutterhead in the composite strata are significantly different from those in a single stratum (Lin et al., 2021; Sun et al., 2016; Wu et al., 2024). Zhu et al. analyzed the leading causes and laws of the deviation of shield tunneling direction under different geological conditions through the measured deviation data of shield tunneling. They studied the orientation control technology of shield construction (Zhu, 2012). Li et al. conducted a failure analysis on the structural cracking of the cutterhead during construction through numerical simulations. They studied the rate of change of the stress intensity factor of cracks of different shapes (Li et al., 2021). Qian et al. performed a mechanical analysis of the coupling interaction between the cutterhead and the excavation face (Zhang et al., 2013). Zou et al. decoupled and solved the normal and tangential loads acting on the cutterhead, and established analytical expressions of thrust and torque under homogeneous geological conditions (Zou et al., 2024). Zhang et al. studied the dynamic loads received by the cutterhead during the tunneling process, established a thrust and torque prediction model considering the influences of overburden pressure, soil cutting, cabin pressure support, and shield shell friction (Zhang et al., 2014). Shang et al. investigated the free vibration characteristics of the cutterhead of the shield machine and proposed a meshless method based on radial basis functions (Shang et al., 2020). Yang et al. investigated the vibration characteristics of the cutterhead in soft-hard mixed strata through similarity model experiments, demonstrating the influence of the strength differences on the vibration acceleration and frequency distribution (Yang et al., 2020).

When a shield machine is tunneling in composite strata, due to the eccentric loads between the cutterhead and the composite strata, the tunneling posture of the cutterhead is prone to change, causing the tunneling direction to shift. When analyzing the mechanical characteristics of the cutterhead in the composite strata, the existing studies generally equate the interaction between the stratum and the cutterhead to the nonuniform loads acting on the cutterhead surface, ignoring the constraint effects of the rock mass on the cutterhead, which is different from the actual contact. The interaction between the cutterhead and the rock is generated through the disc cutter. Researchers have done investigations on the interaction and contact pressure distribution between the disc cutter and rock. Sun et al. (2016) developed a mechanics model for predicting the cutting forces (normal, rolling, and side forces) of constant cross-section disc cutters by solving the Boussinesq stress field problem (Sun et al., 2023). Zhang et al. employed the discrete element method (DEM) to investigate the contact pressure distribution between the disc cutter and rock surface, revealing that the maximum contact pressure depends solely on rock uniaxial compressive strength (Zhang et al., 2021). The pressure distribution within the rock-disc cutter interface was measured by strain gauges (Rostami, 2013) or digital image correlation experiments (Ashoor et al., 2025). Although studies on contact pressure can help researchers analyze the rock-breaking mechanism, contact pressure cannot be directly embedded into the dynamic model of the cutterhead system. Hertz contact theory translates the complex contact problem into computable spring stiffness via equivalent parameters. While this treatment sacrifices detailed local stress information, it enables the feasibility of dynamic studies for the cutterhead system. This represents the inevitable simplification required when scaling engineering problems down to micro-scale investigations.

In this work, the interaction between the stratum and the cutterhead is equivalent to mechanical spring constraints based on the Hertz contact theory. The static and dynamic characteristics of the cutterhead under different stratum constraints are investigated when the thrust is applied, and the influence of the rock-breaking loads of the disc cutter on the vibration response of the cutterhead is analyzed. The findings are helpful for the design of the cutterhead and the optimization of the tunneling parameters in the composite strata.

2 Elastic contact model of the disc cutter-rock configuration and finite element model establishment

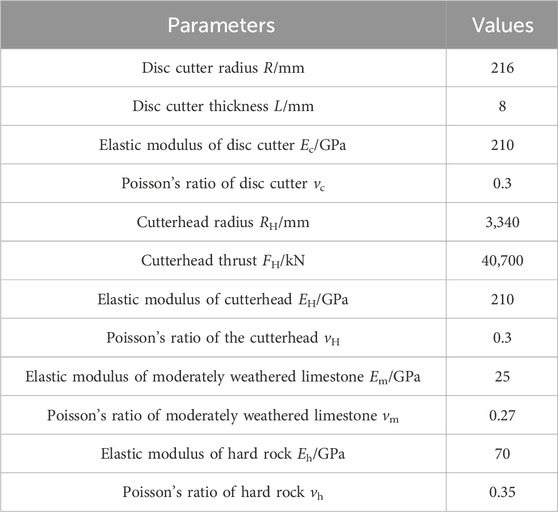
In this work, the Hertz contact model of parallel contact between a plane and a cylinder (axis parallel to the plane) is used to describe the interaction between the disc cutter and rock mass, as shown in Figure 1a. The elastic contact theory calculates the contact stiffness between the disc cutter and the rock mass, and the contact stiffness is equivalent to the spring constraint between the cutterhead and the rock mass. The finite element model of the interaction between the shield cutterhead and the rock mass is further established. The finite element numerical simulation is used to analyze the dynamic characteristics of the cutterhead in different strata, study the static and dynamic responses of the cutterhead under the maximum thrust, and calculate the dynamic response of the shield cutterhead under the rock-breaking load of the disc cutter in different strata, to provide theoretical support for the dynamic control of the cutterhead driving parameters and driving attitude.

Figure 1

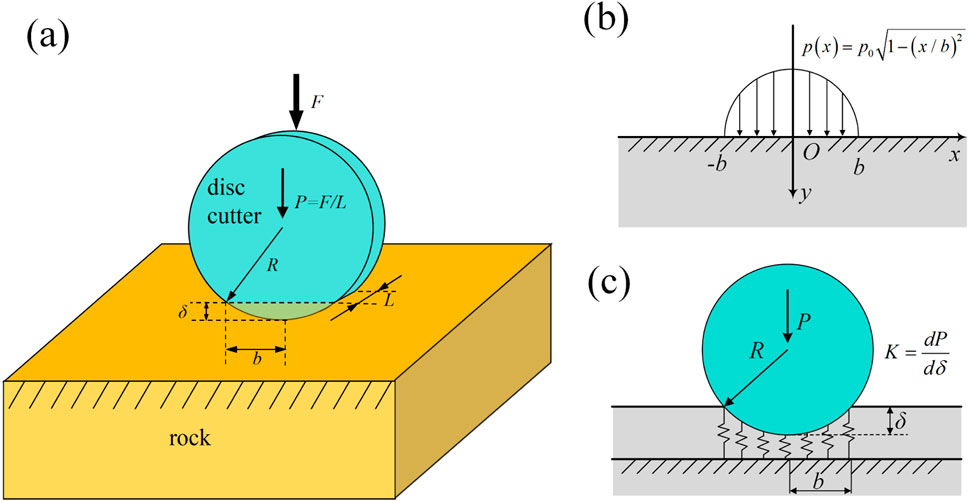
Figure 1. (a) Schematic diagram of the contact between a shield machine disc cutter (modeled as a cylinder) and the rock (modeled as a flat elastic half-space), (b) the pressure distribution between the cylinder and the flat surface, (c) the contact stiffness equivalent for the contact between the cylinder and the flat surface.

Assuming the contact between the cylinder and the elastic half-space is frictionless, and both the deformations of the cylinder and the half-space are small. According to Hertz contact theory, for the line contact between a cylinder and a half-space, the contact region is a rectangle of width 2b, and the contact pressure distribution is semi-elliptical (Figure 1b) and given by Equation 1 (Johnson, 1985; Hills et al., 1993)

$p\left(x\right)=p_0\sqrt{1-{\left(x/b\right)}^2}(1)$

where p₀ is the maximum contact pressure. The load per unit thickness of the disc cutter P=F/L is the integral of the pressure distribution, as shown in Equation 2

$P={\int }_{-b}^{b}p\left(x\right)dx={\int }_{-b}^b{p}_0\sqrt{1-{\left(x/b\right)}^2}dx=\frac{\pi b}{2}{p}_0(2)$

This yields the maximum contact pressure p₀ = 2P/πb. The pressure distribution within the contact zone should meet displacement compatibility, which requires the displacements within the contact zone to match the shape of the cylinder. The Hertz elastic contact solution gives the contact half-width by Equation 3 (Johnson, 1985)

$b=\sqrt{\frac{4\mathit{PR}}{\mathrm{\pi }{E}^{*}}}(3)$

where R is the radius of the cylinder, E^* is the reduced elastic modulus, which is expressed in Equation 4

$\frac{1}{E^{*}}=\frac{\left(1-{\nu }_1^2\right)}{E_1}+\frac{\left(1-{\nu }_2^2\right)}{E_2}(4)$

where E₁ and E₂, ν₁ and ν₂ represent the elastic moduli and Poisson’s ratios of the cylinder and the half-space, respectively.

The indentation depth δ is defined to be the distance of normal approach between the two elastic bodies. For the contact between a cylinder and a half-space under plane-strain conditions, Hertz elastic contact theory gives the indentation depth, as shown in Equation 5 (Johnson, 1985)

$\delta =\frac{P}{\mathrm{\pi }{E}^{*}}\left(\ln \frac{4R}{b}-\frac{1}{2}\right)(5)$

The contact stiffness is defined as the derivative of the load with respect to the indentation depth (Figure 1c) by Equation 6

$K=\frac{dP}{d\delta }=\frac{\mathrm{\pi }{E}^{*}}{\ln \left(4R/b\right)-1}(6)$

Substituting the expression of half-width b into the above equation, the final expression for contact stiffness is obtained, as shown in Equation 7

$K=\frac{dP}{d\delta }=\frac{2\mathrm{\pi }{E}^{*}}{\ln \left(\frac{4\mathrm{\pi }{E}^{*}R}{P}\right)-2}(7)$

The parameters used for the calculation of disc cutter-rock contact stiffness are listed in Table 1. By substituting the parameters into the contact stiffness formula, the reduced elastic modulus for the moderately weathered limestone and the disc cutter is 24.14 GPa, and the contact stiffness is 2.94 × 10⁷ kN/m. The reduced elastic modulus of hard rock and the disc cutter is 59.28 GPa, and the contact stiffness is 6.15 × 10⁷ kN/m.

Table 1

Table 1. The geometric and mechanical parameters of the disc cutter, cutterhead, and rocks.

In the finite element modeling, both the cutterhead and disc cutter employ a linear elastic constitutive model. The material density is 7.85 × 10³ kg/m³, the elastic modulus is 210 GPa, and Poisson’s ratio is 0.3. The cutterhead is meshed using the SOLID187 element type. A fully fixed displacement constraint is applied to the flange end face, while the side surface of the cutterhead is defined with a frictionless support constraint. The maximum thrust applied to the shield machine cutterhead is 40,700 kN. For different ground strata, the constraint between the cutterhead and the rock mass is defined as a normal spring constraint, and a total of 100 spring constraints are applied. The two ends of the spring are connected with the cutterhead and the rock stratum to substitute for the contact stiffness. In the analysis of composite strata, the upper half of the stratum is set as moderately weathered limestone, and the lower half is set as hard rock. The schematic diagram of the contact between the cutterhead and rock stratum and the corresponding equivalent contact model are shown in Figure 2a and Figure 2b, respectively.

Figure 2

Figure 2. (a) Schematic diagram of cutterhead and stratum contact; (b) equivalent contact model between cutterhead and stratum.

3 Results and discussion

3.1 Study on the static response of the cutterhead in composite strata

For shield tunneling in composite strata, the upper half is moderately weathered limestone, and the lower half is hard rock. The total displacement contours of the cutterhead during tunneling in moderately weathered limestone stratum, composite strata, and hard rock stratum are shown in Figure 3.

Figure 3

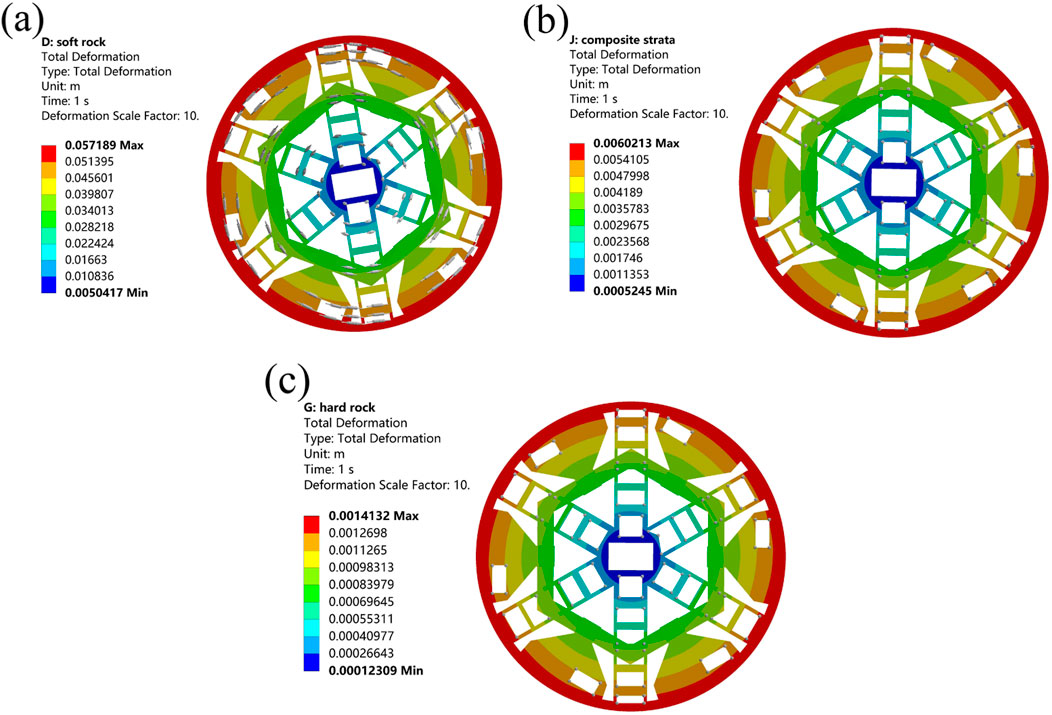
Figure 3. The total displacement contour of (a) moderately weathered limestone stratum, (b) composite strata, and (c) hard rock stratum.

Under the maximum thrust, due to the asymmetry of the installation positions of the disc cutters, the cutterhead demonstrates the phenomenon of rigid body rotation. The cutterhead angles in moderately weathered limestone stratum, composite strata, and hard rock stratum are 0.981^°, 0.103^°, and 0.0242^°, and the corresponding tangential displacements are 57.19 mm, 6.02 mm, and 1.41 mm. The displacement of the cutterhead is larger for a lower modulus of the rock mass, since the equivalent contact stiffness between the disc cutter and rock increases with increasing rock modulus. The equivalent contact stiffness in the composite strata is between the moderately weathered limestone and hard rock; therefore, the maximum displacement is also between the two single-stratum cases.

Figure 4 shows the normal displacement contour of the cutterhead in different strata. The results show that the maximum normal displacement of the cutterhead under the three strata occurs in the connection area between the cutterhead and the flange. The maximum normal displacements of the cutterhead in moderately weathered limestone stratum, composite strata, and hard rock stratum are 1.14 mm, 1.13 mm, and 1.10 mm. The normal displacement trends of the cutterhead in moderately weathered limestone and hard rock strata are similar. However, the displacement distribution of the cutterhead in composite strata is different from that in a uniform stratum. In the composite strata, the displacement of the upper half of the cutterhead is greater than that of the lower half. The maximum displacement is 1.13 mm for the upper half and 0.97 mm for the lower half. These results are expected since the equivalent contact stiffnesses are larger for the lower half of the cutterhead compared to the upper half for overlying soft and underlying hard strata. It is worth noting that due to the idealization of the equivalent model, the cutterhead is connected by multi-node coupling of discrete springs, which leads to significant local stress concentration and makes the stress results meaningless. Therefore, the stress distribution contour of the cutterhead is not displayed.

Figure 4

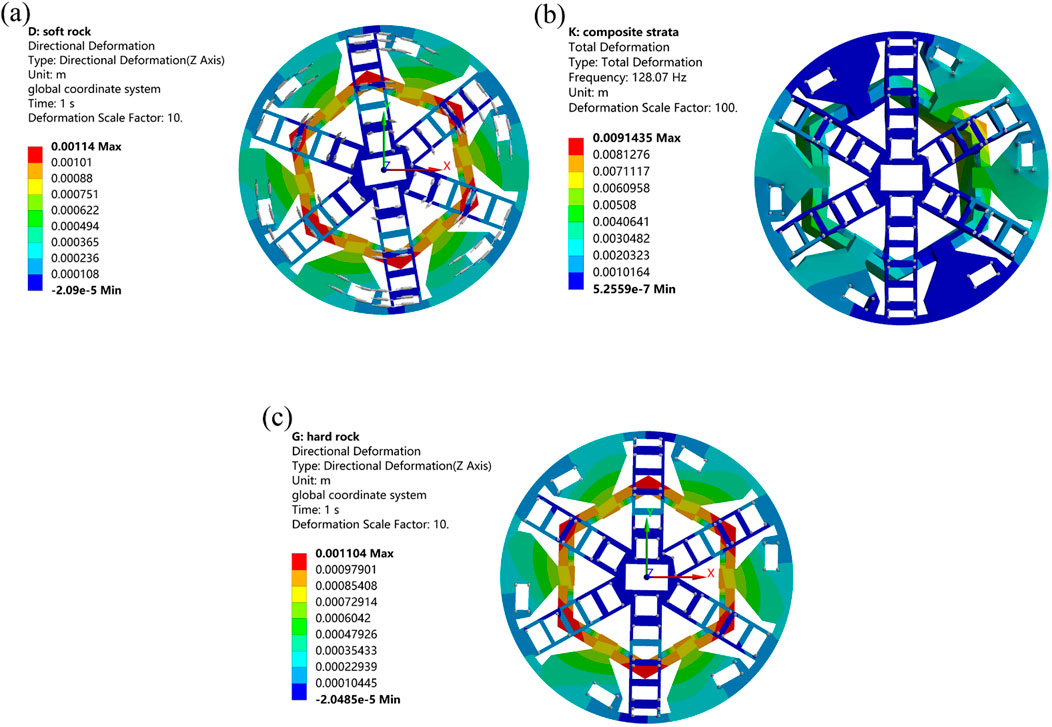
Figure 4. The normal displacement contour of (a) moderately weathered limestone stratum, (b) composite strata, and (c) hard rock stratum.

3.2 Modal analysis of the cutterhead in composite strata

The modal analyses of the cutterhead in moderately weathered limestone stratum, composite stratum, and hard rock stratum are carried out and compared. For the composite strata, the upper half of the cutterhead is in contact with moderately weathered limestone, and the lower half is in contact with hard rock. The flange is subject to rated thrust. The influences of composite strata on the natural frequency and vibration modal shapes of the cutterhead are analyzed. The resonance frequencies of the first five modes of the cutterhead for the unconstrained condition and the three different strata are shown in Figure 5, and the first three vibration modal shapes of the cutterhead are shown in Figure 6.

Figure 5

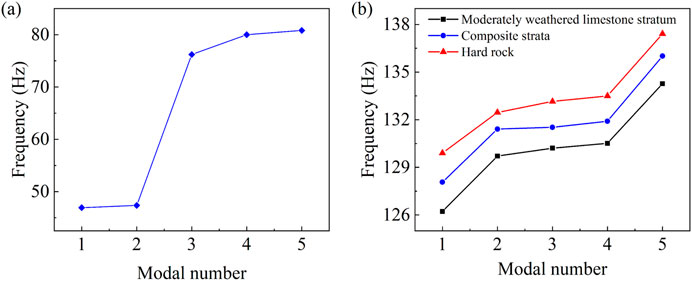
Figure 5. The first five resonance frequencies of the cutterhead for (a) unconstrained condition and (b) the three different strata.

Figure 6

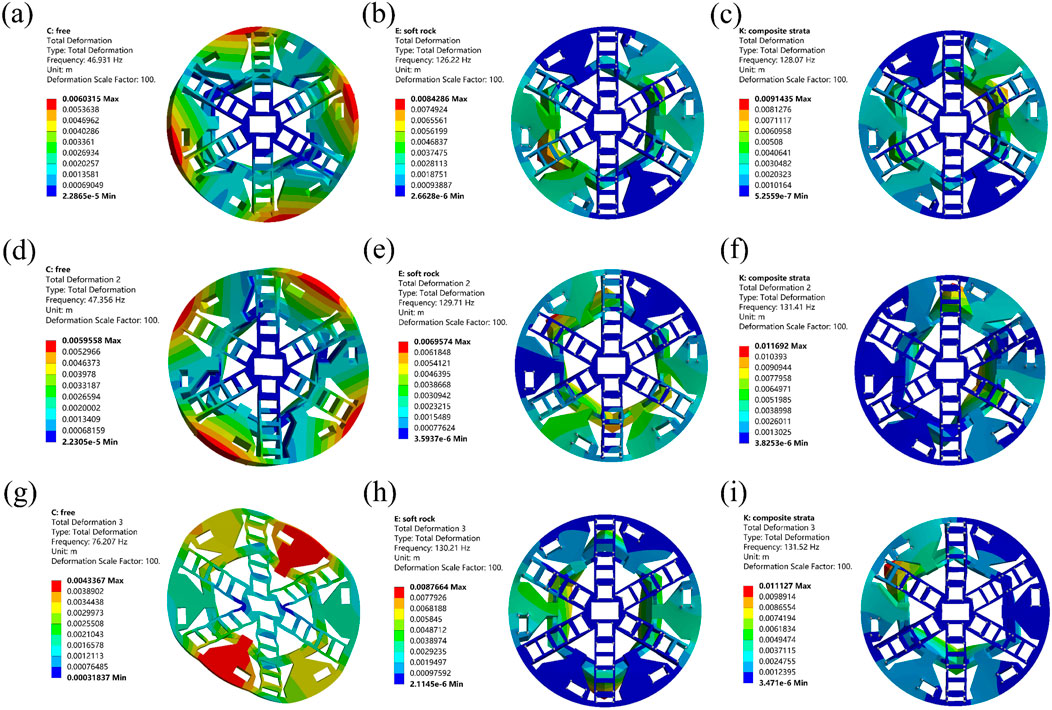
Figure 6. (a–c) The first modal shapes, (d–f) the second modal shapes, and (g–i) the third modal shapes of the cutterhead for unconstrained condition, moderately weathered limestone stratum, and composite strata.

As shown in Figure 5, the first five natural frequencies of the cutterhead for the three different strata are much larger than those for unconstrained conditions. As for the first five natural frequencies of the cutterhead in the three different strata, the natural frequencies are highest in the hard rock stratum, followed by the composite strata, and the lowest in the moderately weathered limestone stratum. With the increase of the rock modulus, the equivalent contact stiffness between the headcutter and rock mass goes up, causing an increase in the modal natural frequencies of the cutterhead. Since the equivalent contact stiffness in composite strata is between the other two uniform strata, the natural frequencies of the cutterhead in composite strata will also correspondingly fall between the two uniform strata.

Figure 6 shows the first three modal shapes of the cutterhead for unconstrained conditions, moderately weathered limestone stratum, and composite strata. The modal shapes for each mode of the cutterhead in hard rock stratum are similar to those in moderately weathered limestone stratum, so they are not shown. For unconstrained conditions, the first modal shape of the cutterhead is the out-of-plane bending vibration of the xoy plane. The first modal shapes of the cutterhead for different strata are the in-plane translational vibration of the xoy plane. For unconstrained conditions, the second modal shape of the cutterhead is similar to the first modal shape, which is out-of-plane bending vibration, perpendicular to the direction of the first modal shape. The second modal shapes for different strata are the bending vibration of the cutterhead and flange in the xoy plane. For unconstrained conditions, the third modal shape of the cutterhead is the in-plane compression vibration of the xoy plane. The difference in the modal shapes of the first mode in different strata is not pronounced. This is primarily attributable to the substantial constraint stiffness imposed by the rock mass, resulting in low variations in the mode shape of the cutterhead among different strata. However, due to the significant increase in modal stiffness of the cutterhead for the second and third modes, the modal shapes in composite strata of these orders exhibit distinct differences compared to those in homogeneous strata or under unconstrained conditions.

In the process of shield tunneling, the vibration response of the cutterhead is detected by an installed vibration sensor. The time-domain dynamic response data and corresponding spectrum results of the cutterhead for the moderately weathered limestone stratum are shown in Figure 7. The monitoring data from the vibration sensor indicate that the primary vibration response of the cutterhead occurs within the frequency range of 0–30 Hz during tunneling, which is far away from the natural frequencies of the cutterhead. Therefore, the external load will not stimulate the resonance of the cutterhead in the tunneling process.

Figure 7

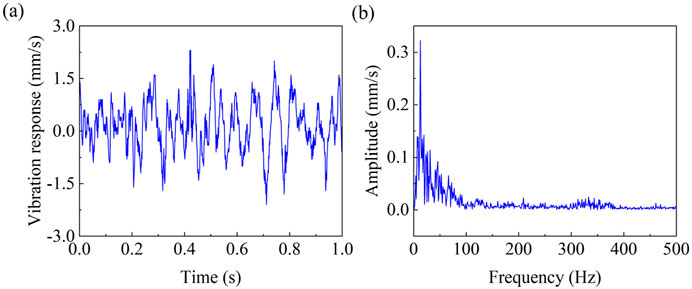
Figure 7. (a) The monitored vibration response curve and (b) the corresponding frequency spectrum of the cutterhead.

3.3 Vibration response analysis of the shield cutterhead under the rock-breaking load of the disc cutter

To further explore the impact of rock-breaking load on the cutterhead, the rock-breaking dynamic load of the disc cutter is applied to the equivalent contact model of the cutterhead. The cutterhead is subject to the equivalent springs constraint and rated thrust, and the dynamic characteristics of the cutterhead under the rock-breaking loads of the disc cutter are analyzed in different strata. The rock-breaking loads in moderately weathered limestone stratum and hard rock stratum are shown in Figure 8, and the vibration responses of the cutterhead under the rock-breaking loads are shown in Figure 9.

Figure 8

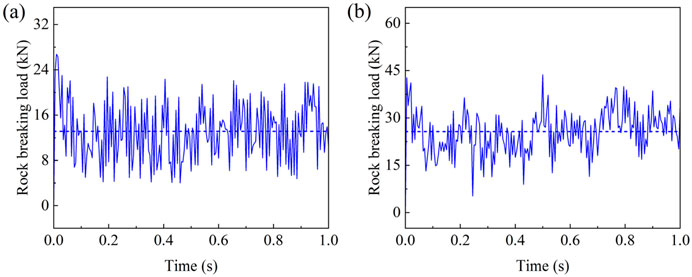
Figure 8. Rock breaking loads imposed on the disc cutters in (a) moderately weathered limestone stratum and (b) hard rock stratum (the dotted line represents the average value of the dynamic load).

Figure 9

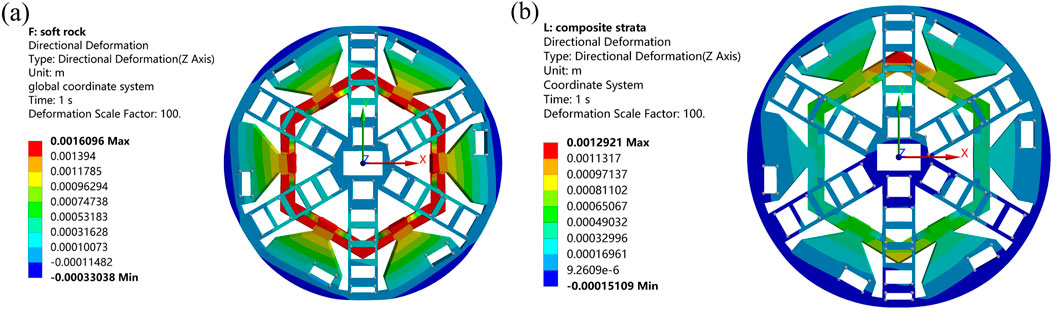
Figure 9. The displacement contour of the cutterhead in (a) moderately weathered limestone stratum and (b) composite strata.

The displacement distribution of the cutterhead is similar in moderately weathered limestone stratum and hard rock stratum. Therefore, only the displacement distributions of the cutterhead in moderately weathered limestone stratum and composite strata are displayed in Figure 9. It can be seen that the displacement of the cutterhead is approximately rotationally symmetric in moderately weathered limestone stratum. The maximum displacement of the cutterhead is located in the contact area between the cutterhead and the flange. The displacement gradually decreases as the distance from the cutterhead-flange contact region increases. The reverse displacement occurred at the edge of the cutterhead. For composite strata, the displacement of the upper half of the cutterhead is greater than that of the lower half. Although the rock-breaking load in the hard rock is higher, the total rock-breaking load of the disc cutter is still far smaller than the rated thrust of the shield. The equivalent contact stiffness between the upper half of the cutterhead and the moderately weathered limestone is lower, while the equivalent contact stiffness between the lower half of the cutterhead and the hard rock is higher. Figure 10 shows the time-domain response curves at the positions where the maximum displacement occurs in three different strata. The response in moderately weathered limestone stratum exhibits low-frequency oscillations with a regular waveform pattern featured by relatively gentle peaks and valleys. In contrast, the responses in composite strata and hard rock stratum display intense oscillations with significant variations in amplitude range. The maximum displacement of the cutterhead in moderately weathered limestone stratum is 1.61 mm. In composite strata, the maximum displacement of the upper half of the cutterhead is 1.29 mm, and the maximum displacement of the lower half is 0.77 mm. The maximum displacement of the cutterhead in hard rock is 1.05 mm, reduced by 34.78% compared to that in moderately weathered limestone. The higher contact stiffness in hard rock inhibits the vibration response amplitude of the cutterhead, but the higher rock-breaking load makes the vibration response of the cutterhead have a larger fluctuation and variation range. The overall displacement magnitude of the cutterhead in composite strata is between the other two strata. The time-domain displacement curve of the cutterhead in the composite stratum demonstrates more complex characteristics compared to the other two rock strata. The simulated vibration response velocities for the three different strata are shown in Figure 11. The averaged responses for the three different strata are also given as the horizontal lines. The average response velocity exhibits the highest values in moderately weathered limestone, followed by composite strata, and the lowest in hard rock stratum.

Figure 10

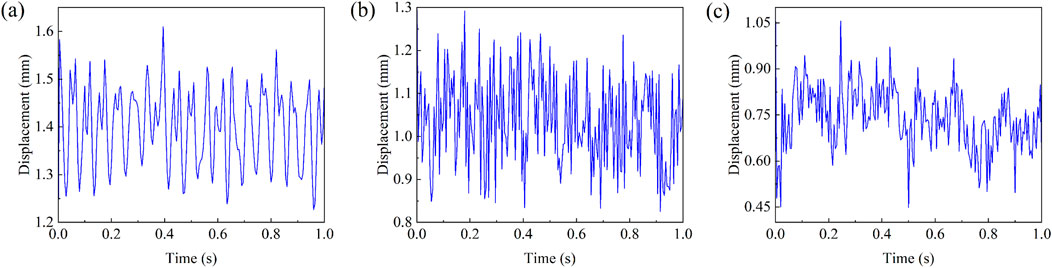
Figure 10. Time-domain displacement curves at the position where the maximum displacement occurs in (a) moderately weathered limestone stratum, (b) composite strata, and (c) hard rock stratum.

Figure 11

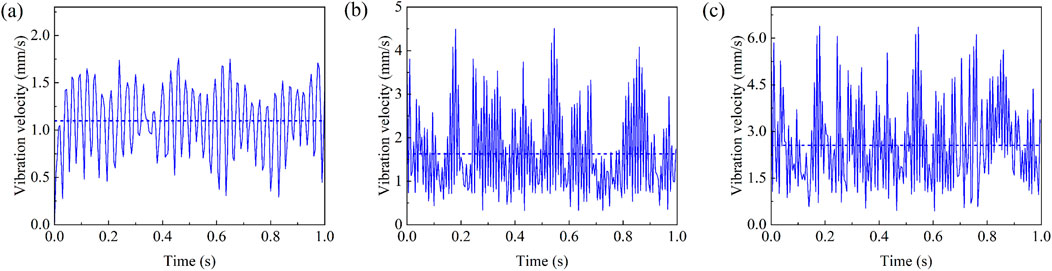
Figure 11. The vibration velocity for the three different strata: (a) moderately weathered limestone stratum, (b) composite strata, and (c) hard rock stratum.

4 Summary and conclusion

In this work, the displacement, modal characteristics, and vibration response of a shield cutterhead operating in composite strata are investigated, utilizing Hertz contact theory to model the cutterhead-rock interaction. The contact between the disc cutter and rock is equivalently represented by mechanical spring constraints, with stiffness derived from elastic contact theory for the cylinder-plane configuration. In composite strata, the displacement distribution of the cutterhead under maximum thrust exhibits significant asymmetry. The displacement of the upper half of the cutterhead is much larger than the lower half due to stiffness contrast. The natural frequencies depend primarily on the equivalent contact stiffness at the cutterhead-stratum interface, increasing progressively from moderately weathered limestone to composite strata, and finally to hard rock. Composite strata induce unique asymmetric modal shapes, resulting from heterogeneous contact stiffness and structural asymmetry. The vibration responses under rock-breaking loads in uniform strata are rotationally symmetric but asymmetric in composite strata. The maximum displacement of the cutterhead in hard rock stratum is reduced by 34.78% compared to moderately weathered limestone stratum. The displacement of the cutterhead in composite strata falls between the other two strata. This work provides a Hertz contact-based framework for analyzing shield cutterhead dynamics in heterogeneous strata.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HX: Conceptualization, Data curation, Investigation, Writing – original draft. JF: Formal analysis, Investigation, Writing – original draft. ZQ: Methodology, Visualization, Writing – original draft. CY: Methodology, Software, Writing – review and editing. XZ: Formal analysis, Supervision, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

Authors HX, JF, and ZQ were employed by Road & Bridge International Co., Ltd.

Authors HX, JF, and ZQ were employed by China Communication North Road & Bridge Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ashoor, F., Abdollahipour, A., and Khosravi, M. H. (2025). Numerical and experimental analysis of contact pressure in rock-disc cutter interaction using displacement discontinuity method and digital image correlation. Transp. Geotech. 52, 101583. doi:10.1016/j.trgeo.2025.101583

CrossRef Full Text | Google Scholar

Ding, X., Li, K., Xie, Y., and Liu, S. (2022). Face stability analysis of large shield-driven tunnel in rock-soil interface composite formations. Undergr. Space 7 (6), 1021–1035. doi:10.1016/j.undsp.2022.01.007

CrossRef Full Text | Google Scholar

Göbl, A. (2010). The interaction of ground, TBM and segment lining with closed shield machines. Geomechanics Tunn. 3 (5), 491–500. doi:10.1002/geot.201000047

CrossRef Full Text | Google Scholar

Hills, D. A., Sackfield, A., and Nowell, D. (1993). Mechanics of elastic contacts. Oxford: Butterworth-Heinemann.

Google Scholar

Johnson, K. L. (1985). Contact mechanics. Cambridge: Cambridge University Press.

Google Scholar

Kong, X., Tang, L., Ling, X., and Li, H. (2024). Development of shield model test system for studying the bias load of shield in soil-rock compound strata. Tunn. Undergr. Space Technol. 143, 105464. doi:10.1016/j.tust.2023.105464

CrossRef Full Text | Google Scholar

Li, J., Zhang, Z., Liu, C., Su, K., and Guo, J. (2021). Numerical failure analysis and fatigue life prediction of shield machine cutterhead. Materials 14 (17), 4822. doi:10.3390/ma14174822

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Liu, A., and Xing, H. (2023). Study on ground settlement patterns and prediction methods in super-large-diameter shield tunnels constructed in composite strata. Appl. Sci. 13 (19), 10820. doi:10.3390/app131910820

CrossRef Full Text | Google Scholar

Lin, Q., Lu, D., Lei, C., Tian, Y., Gong, Q., and Du, X. (2021). Model test study on the stability of cobble strata during shield under-crossing. Tunn. Undergr. Space Technol. 110, 103807. doi:10.1016/j.tust.2020.103807

CrossRef Full Text | Google Scholar

Liu, M. B., Xiao, J. H., Liao, S. M., Liu, Z. Y., He, J. Z., Men, Y. Q., et al. (2025). Model test on the effects of shield machine cutterhead vibration on tunnel face stability in sandy ground. Undergr. Space 22, 39–54. doi:10.1016/j.undsp.2024.04.009

CrossRef Full Text | Google Scholar

Rostami, J. (2013). Study of pressure distribution within the crushed zone in the contact area between rock and disc cutters. Int. J. Rock Mech. Min. Sci. 57, 172–186. doi:10.1016/j.ijrmms.2012.07.031

CrossRef Full Text | Google Scholar

Shang, Y. L., Dang, H. Q., Zhang, Y. X., and Li, Q. (2020). Free vibration analysis of shield cutter head using element-free method. IOP Conf. Ser. Earth Environ. Sci. 510 (5), 052040. doi:10.1088/1755-1315/510/5/052040

CrossRef Full Text | Google Scholar

Song, S., Zhu, S., Wang, J., Xie, C., Lu, W., and Liu, P. (2025). Disturbance analysis of shield tunneling in clay and limestone composite strata using EDEM simulation. Sci. Rep. 15 (1), 12616. doi:10.1038/s41598-025-93424-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, C., Wang, Y., Zhao, H., Su, P., Qu, C., Kang, Y., et al. (2011). Analysis of mechanical properties of two typical kinds of cutterheads of shield machine. Adv. Sci. Lett. 4 (6-7), 2049–2053. doi:10.1166/asl.2011.1545

CrossRef Full Text | Google Scholar

Sun, H. K., and Gao, Y. (2023). Dynamic cutting force model and vibration analysis of the cutterhead in TBM. Rock Mech. Rock Eng. 56 (11), 7883–7903. doi:10.1007/s00603-023-03470-5

CrossRef Full Text | Google Scholar

Sun, W., Zhu, Y., Wang, W., and Zhu, D. (2016). “Evaluation of TBM cutterhead vibration under complicated condition,” in 2016 12th IEEE/ASME international conference on mechatronic and embedded systems and applications (MESA), 1–6.

Google Scholar

Sun, J., Wang, K., Wei, J., Shang, Y., Sun, C., and Ma, F. (2023). A mechanics model of constant cross-section type disc cutter based on dense core forming mechanism. Tunn. Undergr. Space Technol. 140, 105301. doi:10.1016/j.tust.2023.105301

CrossRef Full Text | Google Scholar

Wu, X., Xu, J., Wang, S., Sha, P., Han, Z., Chen, X., et al. (2024). Ground deformation of shield tunneling through composite strata in coastal areas. Buildings 14 (5), 1236. doi:10.3390/buildings14051236

CrossRef Full Text | Google Scholar

Yang, H., Shi, H., Gong, G., and Hu, G. (2009). Earth pressure balance control for EPB shield. Sci. China Ser. E Technol. Sci. 52 (10), 2840–2848. doi:10.1007/s11431-009-0245-7

CrossRef Full Text | Google Scholar

Yang, Z., Pan, D., Zhou, J., Chen, J., Sun, Z., and Liu, H. (2020). Vibration characteristics of cutter-head in soft-hard mixed stratum: an experimental case study on su’ai tunnel. KSCE J. Civ. Eng. 24 (4), 1338–1347. doi:10.1007/s12205-020-0966-5

CrossRef Full Text | Google Scholar

Yang, W., Fang, Z., Wang, J., Chen, D., Zhang, Y., and Ba, X. (2024). Review on vibration monitoring and its application during shield tunnel construction period. Buildings 14 (4), 1066. doi:10.3390/buildings14041066

CrossRef Full Text | Google Scholar

Zhang, Q., Huang, T., Huang, G., Cai, Z., and Kang, Y. (2013). Theoretical model for loads prediction on shield tunneling machine with consideration of soil-rock interbedded ground. Sci. China Technol. Sci. 56 (9), 2259–2267. doi:10.1007/s11431-013-5302-6

CrossRef Full Text | Google Scholar

Zhang, Q., Qu, C., Cai, Z., Kang, Y., and Huang, T. (2014). Modeling of the thrust and torque acting on shield machines during tunneling. Automation Constr. 40, 60–67. doi:10.1016/j.autcon.2013.12.008

CrossRef Full Text | Google Scholar

Zhang, X. P., Ji, P. Q., Zhang, Q., Liu, Q. S., and Wu, S. C. (2021). Study of contact pressure distribution between cutter and rock surface using the discrete element method. Int. J. Rock Mech. Min. Sci. 146, 104875. doi:10.1016/j.ijrmms.2021.104875

CrossRef Full Text | Google Scholar

Zhu, F. B. (2012). Numerical analysis of the influence of shield tunneling to adjacent loaded piles. Adv. Mater. Res. 538, 548–551. doi:10.4028/www.scientific.net/amr.538-541.548

CrossRef Full Text | Google Scholar

Zhu, H., Xu, Q., Zheng, Q., and Liao, S. (2008). Experimental study on working parameters of Earth pressure balance shield machine tunneling in soft ground. Front. Archit. Civ. Eng. China 2 (4), 350–358. doi:10.1007/s11709-008-0051-5

CrossRef Full Text | Google Scholar

Zou, B. P., Yin, J. H., Liu, Z. P., and Long, X. (2024). Transient rock breaking characteristics by successive impact of shield disc cutters under confining pressure conditions. Tunn. Undergr. Space Technol. 150, 105861. doi:10.1016/j.tust.2024.105861

CrossRef Full Text | Google Scholar