Redesigned crinkle washer for piezoelectric energy generation

Structures are used for piezoelectric energy harvesters as a way of redirecting the path of an inputted force so that the piezoelectric element can better convert the mechanical energy to electrical energy. A popular structure used for energy harvesting in compressive force scenarios are the cymbal structure or disc spring due to larger spring rates and the ability to turn compression into radial expansion and thus create surface radial tensile stress on the face plane of a piezoelectric element which has been identified as a beneficial characteristic. The drawbacks of the cymbal washer are found when multiplying the washer in a stack configuration, as the shape of the cymbal is only able to activate a single face and the shape creates increased open space which affects power density of an energy harvesting system. This research is further investigating the wave (crinkle) washer and understanding the benefits of a washer that has a rotational symmetry which a single washer can be used to radially stress two piezoelectric elements simultaneously during compressive loading. Simulations show the iterations of the currently available crinkle washer, adjusting design parameters such as curvatures and waves to create an optimised structure resembling a hyperbolic paraboloid washer. The double piezo compression set up was then simulated to receive an area force of 1000 N/m² vertically onto the top steel backing plate with a diameter of 22 mm and an area of 380 mm² to demonstrate a total compressive load of 0.38 N, and resulted significant performance improvements. The final optimised circular disc washer charged two 10 nF capacitors to 1.13 mV and 0.89 mV, compared to just 0.01 mV and 0.009 mV achieved with the standard crinkle washer, the performance boost was achieved by removing internal stresses found to be localised to the internal diameter wave radii. The optimised novel crinkle hyperbolic paraboloid configuration was further optimised with slits to eliminate inner stress regions between wave peaks, vastly improving both power density and overall energy harvesting performance with final capacitor voltages of 16.03 mV and 19.77 mV.

Introduction

Electrical energy is essential to all aspects of modern civilisation. With advances in battery technology, the proliferation of low-power electronic devices, and the growing reliance on digital information, there is an increasing demand for self-powered devices that minimise dependence on conventional grid power supplies or frequent battery replacements, with smaller personal devices such as pacemakers, insulin pumps & more recent brain-computer interfaces (Gao et al., 2024), but there is also the larger systems – usually arrays - used for powering sensors for traffic signs, and collecting pedestrian footfall kinetic energy (Wang et al., 2018; Liu and Wang, 2019; Cao et al., 2021; Cao et al., 2022). These devices can range in energy requirements based on the amount of information processed or physical action produced and fall in the mW energy band. One promising solution involves integrating energy harvesters directly into devices, enabling the capture and storage of energy from ambient, non-grid sources such as wind, solar radiation, kinetic motion, thermal gradients from the human body or internal combustion engine exhaust, and electromagnetic waves ranging from radio to Wi-Fi signals (Nwalike et al., 2023). The conversion of these diverse energy sources into usable electrical energy requires appropriate electromechanical transduction mechanisms, which depend on the specific environmental conditions, energy source, and power demands of the target electronics. Among various energy conversion approaches, electromagnetic induction is widely employed in linear and rotational applications. However, it has been demonstrated that miniaturising electromagnetic systems leads to a significant reduction in power output, primarily due to the exponential decrease in the coil’s cross-sectional area (Geisler et al., 2016). In contrast, piezoelectric transducers offer more favourable scaling characteristics for miniaturised applications. These materials convert mechanical energy into electrical energy through their intrinsic crystal lattice structures: mechanical deformation induces lattice displacement, resulting in a polarised state that generates a fluctuating electric field. This field produces charge displacement across opposing collector electrodes, which can then store the harvested energy in capacitors for use in electronic loads.

Similar to electromagnetic systems, piezoelectric energy harvesters can be structurally designed to modify voltage output through geometric adjustments, such as altering element thickness or diameter, or stacking multiple elements. Stacked piezoelectric configurations enable higher voltage responses, increased capacitance, and enhanced displacement or deflection for both energy harvesting and actuation applications (Zhu et al., 2010; Alotibi and Khan, 2025). Typically, piezoelectric stacks incorporate alternating electrodes between individual elements, which facilitate voltage matching with storage capacitors, ensuring compatibility with downstream electronic loads that operate within specific voltage ranges. In the context of mechanical activation, compressive forces are often employed to deform the piezoelectric material. To enhance force transmission and deformation, force amplification structures such as flex-tensional and compressive transducers can be integrated into the design (Panda et al., 2015; Wang X. et al., 2016; Wang Y. et al., 2016; Wang et al., 2024; Wu and Xu, 2020; Chen et al., 2024). The use of external spring structures enables pre-loading of piezo stacks, which is especially beneficial as piezo ceramics like lead zirconate titanate (PZT) exhibit superior compressive strength relative to tensile strength; prolonged exposure to tensile stresses can damage the ceramic structure, leading to mechanical failure and reduced energy harvesting performance. Cymbal transducers and bridge structures, which distribute compressive forces across the piezo element faces, have been extensively studied as means to improve the voltage potential. When compressed, these structures expand radially, inducing surface level tensile stress within the piezo material (Zhao et al., 2012; Zhao et al., 2015).

For piezoelectric discs with vertical polarisation between their circular faces, radial shearing or tensile stress with linear compression offers improved charge coefficient than just compression mode (d33), enabling superior mechanical-to-electrical energy conversion under compressive loading (Mo et al., 2013; Long et al., 2021; Zhang et al., 2021; 2024). Consequently, considerable research has focused on optimising cymbal and disc spring structures to maximise radial conversion and power density through structural manipulation (Fernfindez et al., 1998; Yuan et al., 2009; Arnold et al., 2011; Ganilova et al., 2017; Crawley and Luo, 2023; Peng et al., 2023). Although these designs have led to meaningful improvements in increased power density for energy harvesting, cymbal structures inherently activate only one side of the piezo disc, necessitating additional stacked cymbals to achieve multi-layer configurations. This approach increases both the design complexity and dead space within the stack. In contrast, crinkle (or wave) washer structures, which share similarities with cymbals in terms of rotational symmetry and angled arch geometries, have demonstrated the potential for dual-sided radial displacement. Recent studies have shown that crinkle washers can induce force redirection in both on both parallel faces, offering a pathway to more compact and efficient stacking (Crawley and Luo, 2023). However, research on crinkle washers for piezoelectric energy harvesting remains limited.

This work investigates the geometric and mechanical optimisation of crinkle washer structures to improve piezoelectric energy harvesting. Parametric analysis of various design iterations evaluates the electromechanical response of piezoelectric discs under smaller compressive loads, aiming to maximise energy conversion efficiency and power density. The optimised hyperbolic paraboloid washer significantly enhances dual face radial tensile stress and charge output over conventional crinkle washer designs. This dual sided radial-deformation washer mechanism enables more compact, efficient, and simpler energy harvesting systems by reducing dead space, easing fabrication, and improving overall performance. The remaining part of the paper is organised as follows: the Methods section presents the modelling, simulation, and design optimisation; the Results section discusses the performance analysis; and the paper concludes with a summary of the findings and directions for future work.

Methodology

Multiphysics software is used to set up a simulation to study the structural and electro potential characteristics. The crinkle washer is sandwiched between two metal cylindrical metal plates of Ø = 22 mm, each with Ø = 20 mm cylindrical piezo discs at 1 mm thickness (Figure 1A). The metal plates are bounded on the cylindrical face to prevent misalignment, and the crinkle washer is set up with contact faces for simulation deformation into the piezo disc. A 1000 N/m² force is then applied to the top plate using the equation $F=1000\times \sin \left(\pi t\right)$ resulting in a total maximum force of 0.38 N; the bottom plate is a fixed boundary. Simulating with a smaller force was used to decrease simulation time and complexity and to focus the optimisation experiments on the washer design. The 3D crinkle structure can easily be redesigned to analyse the characteristics of each structure under force loading. Stress distribution and electro potential are good indicators of how the structure is interacting with the piezo and using the feedback from the simulations, it provides a starting place to iterate the design. Previous research has shown how the inner radius of the cymbal and the crinkle concentrate force (Red zones); by decreasing this stress build up, the structure is freer to expand radially and thus increasing radial stress and displacement of the piezo face and increase energy transduction. Open circuit voltage can be calculated using the equations below, altering the piezoelectric voltage constant ( $g_{33}$ ) of PZT 5A from 23.2 × 10^-3 Vm/N.

$\mathit{V}=-\left({\mathit{g}}_{\mathbf{33}}\mathit{h}\mathit{T}\right)$

Figure 1

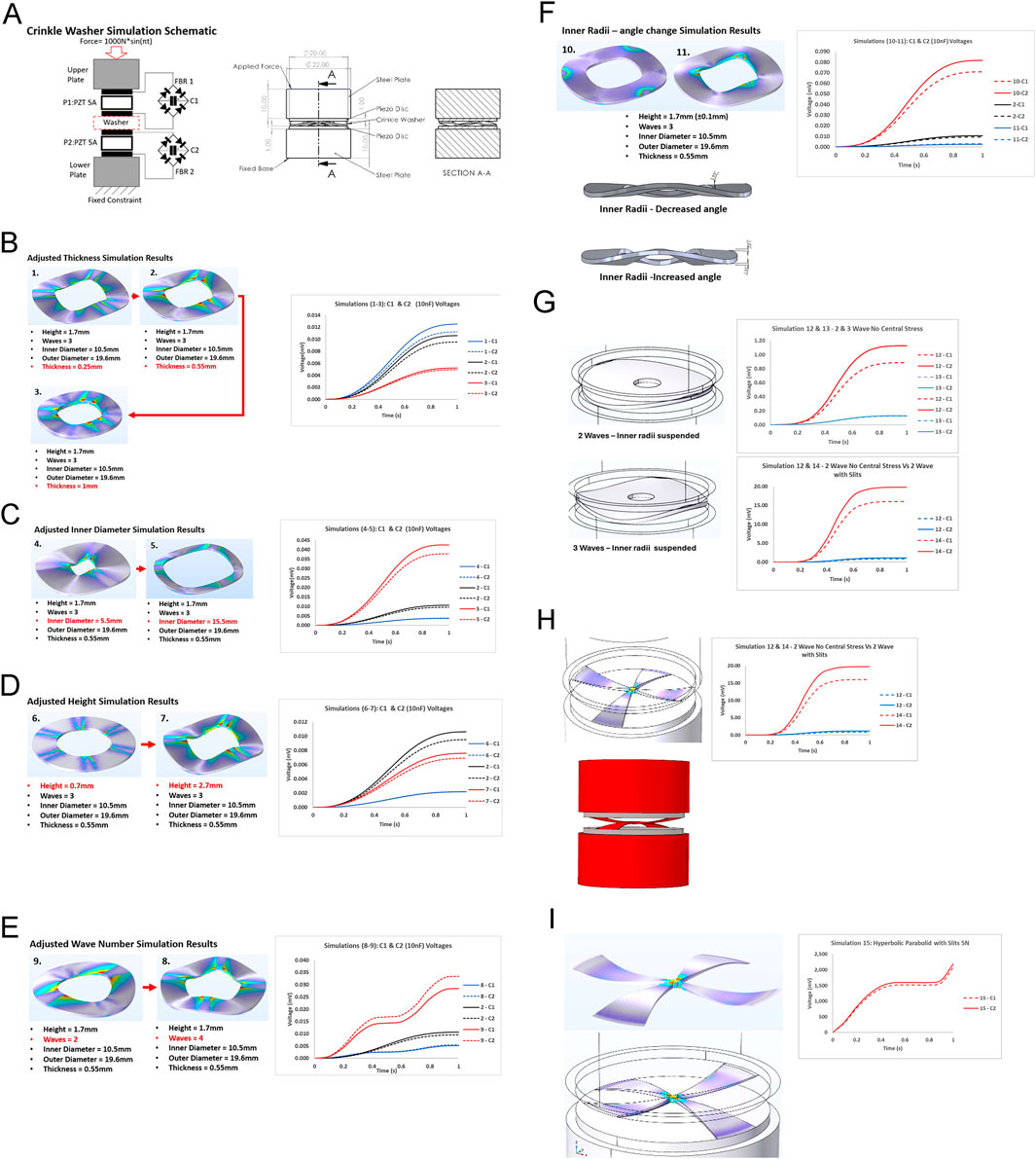
Figure 1. Crinkle Structural Simulations 1-15 and Energy Harvested in Capacitors C1 and C2. (A) Crinkle washer and electronics schematic and technical dimensions. (B) Adjusted thickness: simulated structural stress and voltage stored. (C) Adjusted inner diameter: simulated structural stress and voltage stored. (D) Adjusted height: simulated structural stress and voltage stored. (E) Adjusted wave number: simulated structural stress and voltage stored. (F) Adjusted radii angle: simulated structural stress and voltage stored. (G) Removed interior waves: simulated structural stress and voltage stored. (H) Hyperbolic paraboloid with central stress concentration: simulated structural stress and voltage stored. (I) Hyperbolic paraboloid with central stress concentration at 5N: simulated structural stress and voltage stored.

V = Voltage, $g_{33}$ = Piezoelectric voltage constant (Vm/N), $h$ =Height of the piezo element (m), T = Force over area (m²) or pressure applied on the surface of the piezo (N/m²) (APC International Ltd, 2011).

The crinkle washer also creates tensile radial stress ( $g_{31}$ ) at −11 × 10⁻³ Vm/N, which can be substituted into the equation above. But the real open voltage will be a combination of both constants.

${\mathit{W}}_{\mathit{e}}=\left[\left(\mathbf{1}-{{\mathit{k}}_{\mathbf{33}}}^{\mathbf{2}}\right)\left({\mathit{C}}_{\mathbf{0}}{\mathit{V}}^{\mathbf{2}}\right)\right]/\mathbf{2}$

$W_e$ = Electrical Energy (j), $k_{33}$ = Coupling Factor, $C_0$ = Piezo element capacitance (F), V = Voltage (APC International Ltd, 2011).

To standardise the simulations a 3-wave crinkle was turned into a 3D model to use as a baseline for the simulations (Figure 1B - Simulation 2). From there, characteristic iterations were created logically to test their impact on mechanical to electrical transduction.

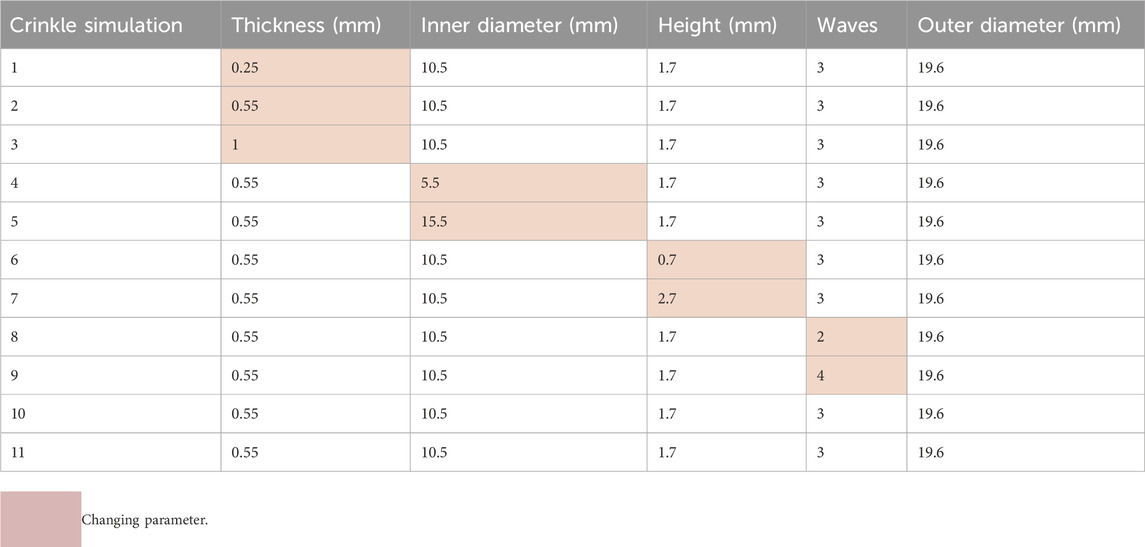
The simulation dimension variables can be found in Table 1. The table shows the dimension steps taken and refer to the crinkle washer dimensions during 3D design.

Table 1

Table 1. Simulation variables.

The simulations are set up to observe the relationship of separate variables with piezo electric energy production. All the simulations use the same configuration as to compare against the commercially available crinkle washer: Simulation 2. The first simulations 1-3 are to examine the effect of thickness change. Simulations 4-5 are varying the inner diameter of the crinkle washer. Simulations 6-7 are to demonstrate the change in height of the washer. Simulations 8-9 are to examine how the number of waves influences energy output. Simulations 10-11 are to changing the slope between the inner and outer radius of the spring. Simulations 12-14 are the result of combining the most beneficial features together.

The theoretical circuit in the COMSOL simulation uses 2 full bridge rectifier diode configurations for each piezo disc with 2 individual capacitors C1 & C2. The simulation structure is set up to use thick metal backing plates to prevent bending deformation and is in a cylindrical boundary to mimic external housing of the energy harvester device (Figure 1A).

Results

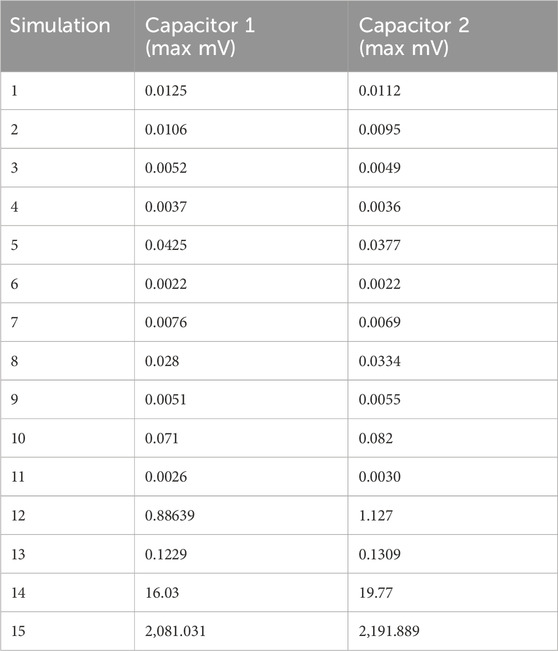
The resultant capacitor (C1 & C2) voltages of the simulations:1-13 can be found in Table 2.

Table 2

Table 2. Simulation results.

Crinkle thickness testing

The results of the simulation (Figure 1B - Simulation 1–3) demonstrated that the thicker the crinkle became the higher the spring constant, and the less it deflected. The less radial deflection resulted in less electrical energy is produced and stored in the capacitors. Noticeably, there is stress concentrations on the inner circumference that was in all 3 thickness tests. Thickness is a simpler design variable during manufacture that can be changed and optimised depending on size of incoming compressive load.

Crinkle inner diameter simulation

Increasing the inner diameter resulted in a noticeable energy increase, (Figure 1C - Simulation 4–5). There were also less high-stress concentration areas on the inner diameter edges of the crinkle waves. Less stress meant better deformation and more radial deformation, which improved electrical energy generation. The loss of material in the centre of the washer would increase open space in the energy harvester which is not ideal for power density and usage of volume, it also creates an area in which the piezo could deform into and increase the chance of disc failure.

Crinkle height simulations

The height simulation results (Figure 1D - Simulation 6–7), show that increasing and decreasing the crinkle washer height causes a negative impact on energy production. The height range 0.7–2.7 mm in which these simulations ran between might have been too large to encompass any peak points at which this washer is at optimal performance; further iterations would be required to get a clearer understanding. Increasing height would increase the length of curvature in the inner and outer diameter bends and this would increase radial expansion length, but it would also decrease curvature radius and lead to a stiffer washer, which would negatively affect the mechanical to electric transduction in the piezoelectric disc.

Crinkle wave simulations

The wave simulations (Figure 1E - Simulation 8–9), show that the less waves in the crinkle circumference, the more energy produced. 2 waves produced a higher electrical yield than 3 & 4 waves, producing 0.03 mV compared to 3 waves 0.01 mV. With increased waves, the wave bend radii decreases and thus the structure get stiffer which prevents radial expansion. In reverse, 2 waves are smaller crinkle washer can be before resembling a disc spring and resembles a bridge structure well known for radial tensile deflection.

Crinkle inner radia simulations

The Inner Radia simulations (Figure 1F - Simulation 10–11) indicate that the removing the inner radius from touching the piezo disc vastly increases electrical generation, as the deformation is shifter outwards. When the angle is tilted in the direction where the inner radius is solely touching the piezo disc, the stress is concentrated decreasing the power produced in the piezo.

Observations

In the simulations various parameters such as thickness, number of waves, height, and inner diameter were adjusted to evaluate their impact on energy production when two piezoelectric discs were coupled on each face of a crinkle washer. Across nearly all crinkle washer simulations, a consistent stress pattern emerged at the inner diameter. However, this stress pattern was less pronounced in one case (Figure 1C - Simulation 5), where the inner diameter was significantly larger, thereby increasing the curvature radius of the inner bends.

When compared to disc spring or cymbal washers, it is evident that the angle toward the centre of these discs is the primary mechanism generating surface level radial tensile stress. In contrast, the crinkle washer, characterized by its radial waves, also relies on this mechanism at a different angle. By introducing an angle between the outer and inner radii, it is possible to merge the geometries of both the crinkle and cymbal washers. This could lead to the development of a novel combined wave-cymbal design, which offers several advantages: double-faced piezoelectric activation, is a single – improving part compactness, and enhanced energy generation and power density.

Optimised crinkle simulation

Based on the simulation results, the most significant energy increases were observed in Simulations 1, 5, and 9. These findings suggest that a crinkle washer design with a thinner profile, increased internal diameter, reduced internal stress, and fewer waves would create a higher performance in energy generation. However, this design also increases the open dead space inside the body by decreasing the number of waves and thus total length of circumference of the crinkled washer.

To address this, decreasing the inner wave edge height on both the upper and lower faces of the crinkle washer could effectively reduce internal contact stress and shift the deformation toward the edges. This adjustment would help optimize the washer’s performance by focusing the mechanical deformation in areas that maximize energy transfer, while also minimizing the impact of dead space.

The redesign (Figure 1G - Simulations 12–13) results indicate that by removing contact of the inner radius of the crinkle washer drastically improves energy generation resulting in a voltage of 0.082 mV compared to 0.011 mV from the standard crinkle washer. This is a near 60 times energy improvement over the standard crinkle washer. Sloping the angle outwards (increased angle) led to energy loss.

The 2-wave version (Figure 1G - Simulation 12 and 13) of this design begins to look like a hyperbolic paraboloid (Pringle crisps being a real-life example) and in the simulation, the result produces a higher voltage with Capacitor 1 (C1) charging to 1.13 mV and Capacitor 2 (C2) to 0.89 mV. Keeping the design close to the original crinkle parameters, the suspended centre has a 0.5 mm difference to the highest points on both sides. The overall height of the washer remains 1.7 mm with a diameter of 19.6 mm. In comparison to the commercial crinkle, the inner bends are no longer in contact with the piezoelectric discs which are responsible for concentrating stress as depicted in Figure 1B – simulation 2. The 2-wave design also allows for the largest curvature between raised points decreasing required bending force of the washer. Further refinements of the washer (Figure 1H) then demonstrate removing material and introducing a taper – thinning towards the edges centralises the stress and allows the outer edges to deform leading to a larger performance boost to voltages to 19.77 mv and 16.03 mV. Increasing the load to a peak of 5N (Figure 1I - Simulation 15) was performed to understand the structural response of the washer as it flattens further, with the electrical performance now having usable voltages stored in the capacitors, Capacitor 1 reaching 2.08 V and Capacitor 2 reaching 2.19 V. Scaling the deformation to exaggerate the washer behaviour shows further flattening of the hyperbolic paraboloid with the curvature in the individual arms still to be flattened and expanded.

The hyperbolic paraboloid design is one that has been used by structural architects and engineers because off the stiffness and ability to absorb force into deformation (Ortega and Robles, 2003; Maeng and Hoon Hyun, 2020). The design can be likened to the disc spring when mirrored as seen in an earlier figure but integrated into a singular spring but uses a double curvature that is intersecting at the centre (Li et al., 2023). The internal radius is removed, and all the force is concentrated into the dead centre of the structure, assuming the washer is perfectly balanced.

In previous experiments using crinkle washers with ceramic piezoelectric discs under very high force loads and rapid accelerations of up to 2000 N for the study in high velocity and shock scenarios (Crawley and Luo, 2023), disc failure was more likely due to several key material and structural factors. Piezo ceramics are inherently brittle material that prefer compressive forces and can be broken by any uneven loads of surface defects. Unlike disc springs or Belleville washers, which distribute force more uniformly and have a smaller inner diameter, crinkle washers allow non uniform material deformation that increases the risk of damage. In earlier tests, the use of a silicone sublayer caused the material to bulge through the central opening during spring flattening, leading to bending and fracture of the piezoelectric disc. Additionally, crinkle washers - depending on size - can undergo significant radial deformation. If this exceeds the maximum lateral tensile stress of the piezoelectric disc, failure occurs; however, this can be mitigated through careful spring design and the use of a radial housing to support the disc.

Conclusion

This study used Multiphysics simulations to optimise the electromechanical performance of a crinkle washer & piezoelectric disc configuration under linear compressive loading. A commercially available crinkle washer served as the baseline, producing a maximum simulated output of 0.1 mV. Parametric optimisation revealed that adjusting geometric and mechanical parameters could significantly enhance performance, with the optimised design achieving a maximum output of 1.13 mV, an order of magnitude improvement over the baseline, and then further to 19.77 mv and 16.03 mV by introducing radial cuts to remove material that would otherwise absorb spring energy.

The optimisation process led to the development of a novel hyperbolic paraboloid structure, which eliminates stress accumulation at the inner radius observed in all crinkle washer simulations. This double-curvature architecture concentrated stress centrally while enhancing radial tensile stress, particularly when configured as a sandwich between two piezoelectric discs.

Initial prototyping attempts via additive manufacturing were unsuccessful due to dimensional inaccuracies, warping, and weak interlayer adhesion, highlighting manufacturing challenges. Current fabrication methods—lithography, etching, stamping, or additive manufacturing—remain cost-prohibitive for small-scale production, though economies of scale may make industrial production viable.

Overall, these findings demonstrate that washer-based structures can generate radial tensile stresses during lower force compression at lower accelerations than previously reported (Crawley and Luo, 2023). The optimised design shows strong potential to increase the power density of piezoelectric energy harvesters, extending beyond conventional cymbal configurations to a compact structure capable of efficient bidirectional operation, but overcoming material structural fragility of ceramics would be required to create higher force capable and more reliable piezoceramic energy harvesters. Other materials could be considered such as single crystal piezoelectric elements that are less brittle. Using piezoelectric arrays per area to decrease the forces concentrated on individual harvesters could allow for the use of more brittle materials.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FC: Writing – original draft, Writing – review and editing. KI: Writing – review and editing. QQ: Writing – review and editing. ZL: Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by Engineering and Physical Science Research Council (EPSRC) funded ICASE project EP/V519509/1.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. Ai was used for grammatical cohesion and spelling.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alotibi, F., and Khan, M. (2025). High foot traffic power harvesting technologies and challenges: a review and possible sustainable solutions for Al-Haram mosque. Appl. Sci. Switz. 15, 4247. doi:10.3390/app15084247

CrossRef Full Text | Google Scholar

APC International Ltd (2011). Piezoelectric ceramics: principles and applications. 11th Edn. Pennsylvania: APC International.

Google Scholar

Arnold, D., Kinsel, W., Clark, W., and Mo, C. (2011). Exploration of new cymbal design in energy harvesting. 7977, 79770T. doi:10.1117/12.880614

CrossRef Full Text | Google Scholar

Cao, Y., Zhang, F., Sha, A., Liu, Z., Hao, Y., and Hao, Y. (2021). Energy conversion models and characteristics under various inner connections of a novel packaged piezoelectric transducer for pavements. Energy Convers. Manag. 245, 114563. doi:10.1016/j.enconman.2021.114563

CrossRef Full Text | Google Scholar

Cao, Y., Li, J., Sha, A., Liu, Z., Zhang, F., and Li, X. (2022). A power-intensive piezoelectric energy harvester with efficient load utilization for road energy collection: design, testing, and application. J. Clean. Prod. 369, 133287. doi:10.1016/j.jclepro.2022.133287

CrossRef Full Text | Google Scholar

Chen, G. T., Zhu, Y., Huang, D. M., and Zhou, S. X. (2024). Self-powered and self-sensing devices based on piezoelectric energy harvesting. Sci. China Technol. Sci. 67, 1631–1667. doi:10.1007/s11431-023-2535-0

CrossRef Full Text | Google Scholar

Crawley, F. J. E., and Luo, Z. (2023). “High force compression mode to shear mode piezoelectric energy harvesting,” in 2023 IEEE 22nd International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS) (IEEE), 130–134. doi:10.1109/PowerMEMS59329.2023.10417175

CrossRef Full Text | Google Scholar

Fernfindez, J. F., Dogan, A., Fielding, J. T., Uchino, K., and Newnham, R. E. (1998). Tailoring the performance of ceramic-metal piezocomposite actuators, “cymbals”. Sensors Actuators A 65, 228–237. doi:10.1016/s0924-4247(97)01668-3

CrossRef Full Text | Google Scholar

Ganilova, O., Awaludin, A., and Dong, R. (2017). Hybrid energy harvesting based on cymbal and wagon wheel inspiration. J. Intell. Mater Syst. Struct. 28, 2872–2884. doi:10.1177/1045389X17704066

CrossRef Full Text | Google Scholar

Gao, Z., Zhou, Y., Zhang, J., Foroughi, J., Peng, S., Baughman, R. H., et al. (2024). Advanced energy harvesters and energy storage for powering wearable and implantable medical devices. Adv. Mater. 36, 2404492. doi:10.1002/adma.202404492

PubMed Abstract | CrossRef Full Text | Google Scholar

Geisler, M., Boisseau, S., Perez, M., Ait-Ali, I., and Perraud, S. (2016). Scaling effects in a non-linear electromagnetic energy harvester for wearable sensors. J. Phys. Conf. Ser. 773, 012044. doi:10.1088/1742-6596/773/1/012044

CrossRef Full Text | Google Scholar

Li, L., Ren, Y., and Jin, Q. (2023). Wave propagation in piezoelectric doubly-curved panels considering thermal effects: piezoelectricity-based synergistic effect analysi. Acta Astronaut. 204, 331–347. doi:10.1016/j.actaastro.2022.12.029

CrossRef Full Text | Google Scholar

Liu, X., and Wang, J. (2019). Performance exploration of A radially layered cymbal piezoelectric energy harvester under road traffic induced low frequency vibration. IOP Conf. Ser. Mater Sci. Eng. 542, 012075. doi:10.1088/1757-899X/542/1/012075

CrossRef Full Text | Google Scholar

Long, S. X., Khoo, S. Y., Ong, Z. C., and Soong, M. F. (2021). Design, modeling and testing of a new compressive amplifier structure for piezoelectric harvester. Smart Mater Struct. 30, 125010. doi:10.1088/1361-665X/ac2e1c

CrossRef Full Text | Google Scholar

Maeng, H., and Hoon Hyun, K. (2020). Optimizing tensile membrane architecture for energy harvesting. 1, 569–578. doi:10.52842/conf.caadria.2020.1.569

CrossRef Full Text | Google Scholar

Mo, C., Arnold, D., Kinsel, W. C., and Clark, W. W. (2013). “Modeling and experimental validation of unimorph piezoelectric cymbal design in energy harvesting,” in Journal of intelligent material systems and structures, 828–836. doi:10.1177/1045389X12463459

CrossRef Full Text | Google Scholar

Nwalike, E. D., Ibrahim, K. A., Crawley, F., Qin, Q., Luk, P., and Luo, Z. (2023). Harnessing energy for wearables: a review of radio frequency energy harvesting technologies. Energies (Basel) 16, 5711. doi:10.3390/en16155711

CrossRef Full Text | Google Scholar

Ortega, N. F., and Robles, S. I. (2003). The design of hyperbolic paraboloids on the basis of their mechanical behaviour. Thin-Walled Struct. 41, 769–784. doi:10.1016/S0263-8231(03)00025-9

CrossRef Full Text | Google Scholar

Panda, P. K., Sahoo, B., Chandraiah, M., Raghavan, S., Manoj, B., Ramakrishna, J., et al. (2015). Piezoelectric energy harvesting using PZT bimorphs and multilayered stacks. J. Electron Mater 44, 4349–4353. doi:10.1007/s11664-015-3959-2

CrossRef Full Text | Google Scholar

Peng, L., Wang, Y., Qi, Y., Ru, X., and Hu, X. (2023). A hybrid piezoelectric-electromagnetic energy harvester used for harvesting and detecting on the road. J. Clean. Prod. 426, 139052. doi:10.1016/j.jclepro.2023.139052

CrossRef Full Text | Google Scholar

Wang, X., Shi, Z., Wang, J., and Xiang, H. (2016). A stack-based flex-compressive piezoelectric energy harvesting cell for large quasi-static loads. Smart Mater Struct. 25, 055005. doi:10.1088/0964-1726/25/5/055005

CrossRef Full Text | Google Scholar

Wang Y., Y., Chen, W., and Guzman, P. (2016). Piezoelectric stack energy harvesting with a force amplification frame: modeling and experiment. J. Intell. Mater Syst. Struct. 27, 2324–2332. doi:10.1177/1045389X16629568

CrossRef Full Text | Google Scholar

Wang, H., Jasim, A., and Chen, X. (2018). Energy harvesting technologies in roadway and bridge for different applications – a comprehensive review. Appl. Energy 212, 1083–1094. doi:10.1016/j.apenergy.2017.12.125

CrossRef Full Text | Google Scholar

Wang, Q., Gu, Y., Gao, H., and Ling, M. (2024). A hybrid summation and multiplication displacement amplification mechanism for piezoelectric actuators. Smart Mater Struct. 33, 125004. doi:10.1088/1361-665X/ad8c06

CrossRef Full Text | Google Scholar

Wu, Z., and Xu, Q. (2020). Design and testing of a new dual-axial underfloor piezoelectric energy harvester. Sens. Actuators A Phys. 303, 111858. doi:10.1016/j.sna.2020.111858

CrossRef Full Text | Google Scholar

Yuan, J., Shan, X., Xie, T., and Chen, W. (2009). Energy harvesting with a slotted-cymbal transducer. J. Zhejiang Univ. Sci. A 10, 1187–1190. doi:10.1631/jzus.A0920183

CrossRef Full Text | Google Scholar

Zhang, J., Yu, X., Zhao, W., and Qu, D. (2021). A piezoelectric vibration energy harvester based on the reverse-rhombus double-bridge force amplification frame. J. Phys. D. Appl. Phys. 54, 365501. doi:10.1088/1361-6463/ac0842

CrossRef Full Text | Google Scholar

Zhang, M., Zhao, Q., Li, Z., Wang, S., He, G., and Zhao, L. (2024). Development of a piezoelectric resonator with in-plane displacement-amplification mechanism. Microsyst. Technol. 31, 231–243. doi:10.1007/s00542-024-05743-7

CrossRef Full Text | Google Scholar

Zhao, H., Ling, J., and Yu, J. (2012). A comparative analysis of piezoelectric transducers for harvesting energy from asphalt pavement. J. Ceram. Soc. Jpn. 120, 317–323. doi:10.2109/jcersj2.120.317

CrossRef Full Text | Google Scholar

Zhao, H., Qin, L., and Ling, J. (2015). Test and analysis of bridge transducers for harvesting energy from asphalt pavement. Int. J. Transp. Sci. Technol. 4, 17–28. doi:10.1260/2046-0430.4.1.17

CrossRef Full Text | Google Scholar

Zhu, D., Almusallam, A., Beeby, S. P., Tudor, J., and Harris, N. R. (2010). A bimorph multi-layer piezoelectric vibration energy harvester. Leuven.

Google Scholar