A novel approach to recoil pad enhancement in rifles via topological design with material extrusion and SLA

Excessive recoil in firearms reduces shooting accuracy, causes user discomfort, and increases mechanical wear over time. This creates a need for effective solutions that can improve recoil management. This study investigates the use of advanced lattice structures made from thermoplastic polyurethane (TPU) and resin to enhance vibration damping and impact absorption in firearm components. Four lattice geometries were used, including Voronoi, Weaire Phelan, Gyroid, and Kelvin Cell. These structures were fabricated using two additive manufacturing methods. Material extrusion was applied for TPU parts to provide flexibility and strength, while Stereolithography (SLA), a light-based resin curing technique, was used to produce intricate resin structures. These approaches highlight the adaptability of additive manufacturing in producing functional parts that offer both vibration control and impact resistance. The performance of each structure was evaluated through vibration damping in two modes, rapid impact testing, and compression strength assessments. TPU samples consistently outperformed resin in both damping and energy absorption. Voronoi TPU exhibited the highest damping ratio, improving by 331 percent in the first mode with a value of 1.25 and by 300 percent in the second mode with a value of 0.20 compared to the original solid part. Weaire Phelan TPU reached the highest impact energy absorption at 6.45 joules, which is an improvement of 18.14 percent. Gyroid TPU absorbed energy the fastest, reaching a peak of 5.4 joules in only 14 milliseconds. This study introduces a new design approach by applying lattice structures to recoil pads, enabling enhanced performance and a high degree of customization.

1 Introduction

Additive manufacturing (AM) has become an increasingly important technology in the defense sector, offering flexibility in producing complex and lightweight components (Cardeal et al., 2021; Attar et al., 2020). Two popular methods are material extrusion using Fused Deposition Modeling (FDM) and Stereolithography (SLA), both of which are gaining traction in the production of defense equipment, including rifle components. Material extrusion is one of the most widely used 3D printing technologies due to its affordability and ease of use. It builds parts layer by layer using thermoplastic materials, which are ideal for non-critical components or prototypes in defense applications (Dudek, 2013). In the context of rifles, material extrusion can be used to manufacture custom grips, stocks, and other non-structural parts that require lightweight properties and ergonomic designs. This technology is favored for its ability to enable rapid prototyping, allowing engineers to quickly iterate on rifle part designs, while also offering cost-effective customization to produce parts tailored to specific operational needs (Chalgham et al., 2021; Froes and Dutta, 2014). Additionally, materials like carbon-fiber-infused thermoplastics used in material extrusion provide enhanced strength and durability. However, due to its layer-by-layer construction, material extrusion parts may not be suitable for high-stress applications where structural integrity is paramount.

Stereolithography, on the other hand, uses a laser to cure resin layer by layer and offers high precision with smooth surface finishes, making it particularly suitable for producing detailed and finely tuned components (Borrello et al., 2018; Hu et al., 2019). In the defense sector, SLA’s accuracy is highly beneficial for parts that require tight tolerances and intricate geometries, such as optics housings, sight components, or custom mounts for rifle accessories. The ability to produce high-fidelity prototypes with SLA makes it ideal for designing and testing new rifle parts. Additionally, when advanced engineering resins are used, SLA can also produce functional components with improved mechanical properties, which can be used for lower-stress structural applications. Both material extrusion and SLA provide significant advantages in rapid prototyping and customization, which are particularly valuable in the defense sector where mission-specific requirements or combat scenarios can quickly evolve. As material technology continues to advance, these additive manufacturing techniques are becoming increasingly viable for producing functional and reliable rifle parts that meet the stringent demands of defense applications (Beaman et al., 2020). Recoil pads play a critical role in firearm design, serving as the primary interface between the shooter and the weapon during firing. Their primary function is to absorb and dissipate the recoil forces generated when a firearm is discharged, thereby reducing the impact felt by the shooter (Hall, 2008). This not only improves shooting comfort but also enhances control, making the firearm more manageable and reducing fatigue over extended use. A well-designed recoil pad can significantly influence shooting accuracy, especially in situations where multiple shots are fired in quick succession (Morelli et al., 2014). Despite their importance, the design of recoil pads has traditionally been straightforward, relying on conventional materials like rubber and foam to provide basic cushioning.

Up until now, recoil pads have rarely, if ever, undergone rigorous optimization to enhance their performance. Most recoil pads are designed based on general principles of cushioning without a deep exploration of how material distribution, geometry, and structural flexibility could be fine-tuned to maximize energy absorption and minimize vibration. This research represents the first significant step toward optimizing recoil pads using advanced design methodologies such as topology optimization. By doing so, it opens up new possibilities for creating highly efficient recoil pads that are precisely engineered to meet the specific needs of different firearms and shooting conditions. A key innovation in this research is the introduction of lattice structures, which are lightweight, highly customizable geometric patterns that can be tailored to offer different levels of stiffness and flexibility (Abou-Ali et al., 2022; Płatek et al., 2020; Yang et al., 2025a). These structures, designed through topology optimization, can significantly improve recoil pad performance by reducing weight and controlling the way the pad deforms under recoil forces (de Ruiter and van Keulen, 2004; Bendsoe et al., 2003; Xu et al., 2024). Lattice structures distribute material only where it's needed most, reducing unnecessary bulk while still providing optimal energy absorption. Additionally, the ability of these structures to absorb and dissipate vibrations further enhances the shooter’s experience by minimizing the aftershocks felt after firing, improving both comfort and control.

This research introduces an innovative approach to improving recoil pads for semi-automatic 9 mm rifles by applying topology optimization through additive manufacturing. Traditional recoil pads are often designed using conventional materials and straightforward engineering methods, which limit their ability to balance performance and material efficiency. The objective of this study is to reduce weight, enhance vibration damping, and improve energy absorption while maintaining structural integrity. Topology optimization was chosen specifically to meet these goals, as it enables the strategic distribution of material within a defined design space, allowing for maximum performance with minimal weight. This method is particularly well suited for recoil pads, which require both flexibility and strength in localized regions to manage recoil forces effectively. By integrating lattice structures generated through topology optimization and fabricated using additive manufacturing, the study addresses a significant gap in existing research. This study extends the principles of mechanical metamaterials to firearm recoil management—a domain where such architected structures have seen little to no prior application. This is the first application of such an approach to recoil pads, offering not only improved comfort and functionality for the shooter but also establishing a new direction for design innovation in firearm components.

2 Materials and methods

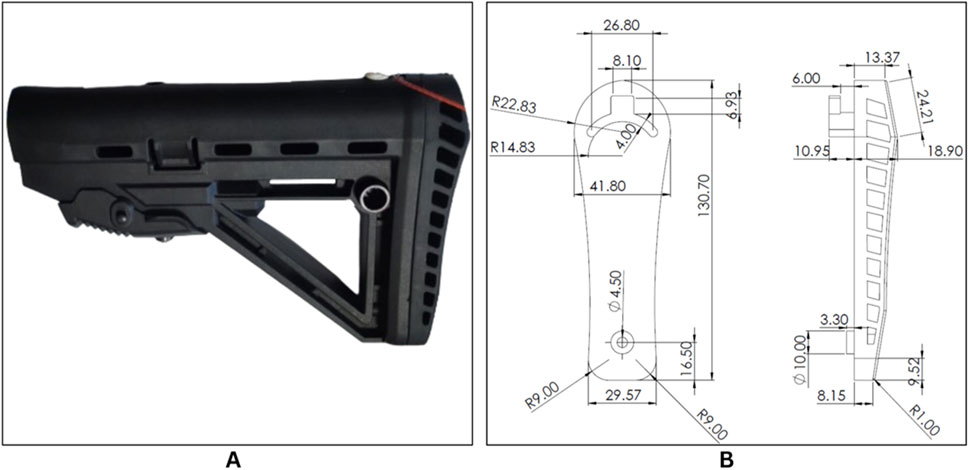
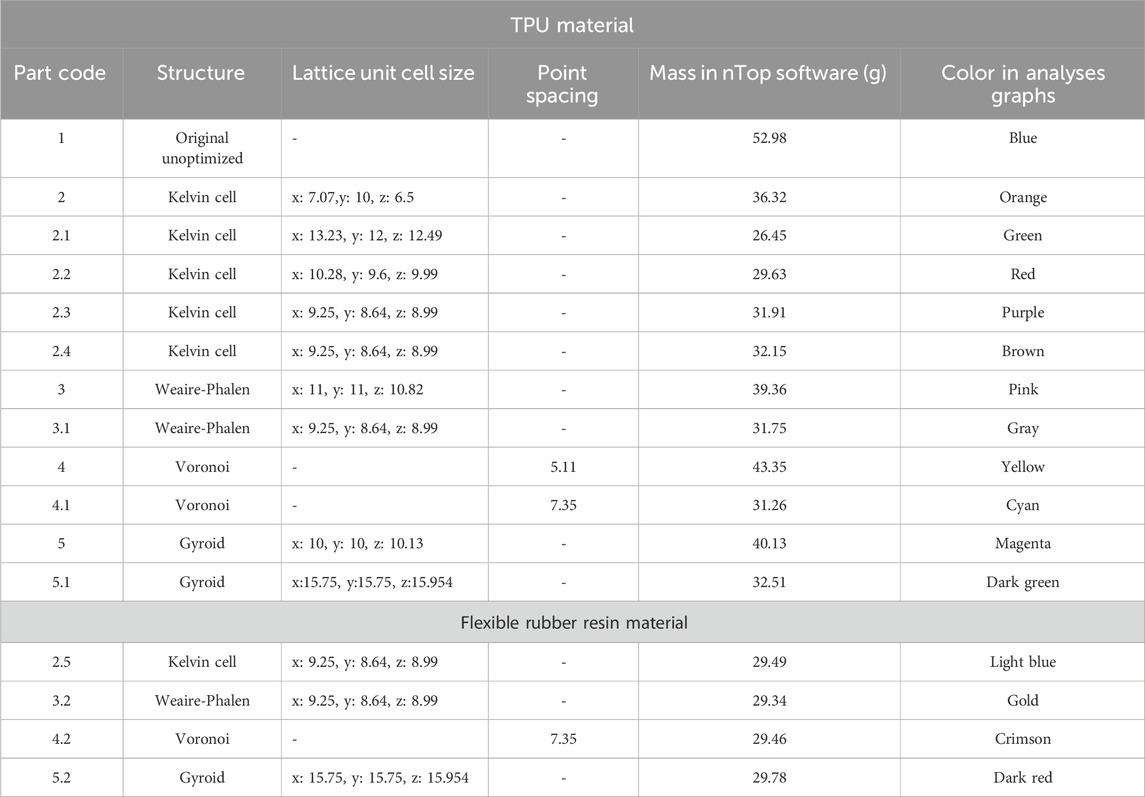
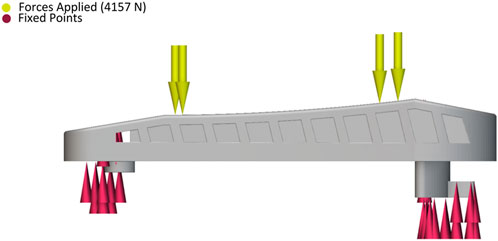
In this research, lattice structures were incorporated into the recoil pad of a semi-automatic 9 mm rifle. Along with achieving substantial weight reduction, the study produced a wide range of results through comprehensive testing that included compression, modal vibration, and rapid impact evaluations. These tests were carried out on four different lattice structures, each modified with varying parameters, resulting in 15 unique parts. The materials used were thermoplastic polyurethane (TPU), fabricated through the material extrusion technique, which accounted for 11 parts, and rubber resin, produced using SLA, which was used for 4 parts. The rubber resin used is the Wanhao rubber flexible resin. A rifle stock part for a semi-automatic 9 mm rifle was sourced from the local defense corporation UTAS, as shown in Figure 1A. The recoil pad of the rifle stock was then accurately modeled in SolidWorks with precise 1:1 dimension based on detailed measurements of the original part. The dimensions of the modelled part can be seen in Figure 1B.

Figure 1

Figure 1. (A) Original 9 mm semi-automatic rifle stock, (B) dimensions of the recoil pad.

2.1 Printing

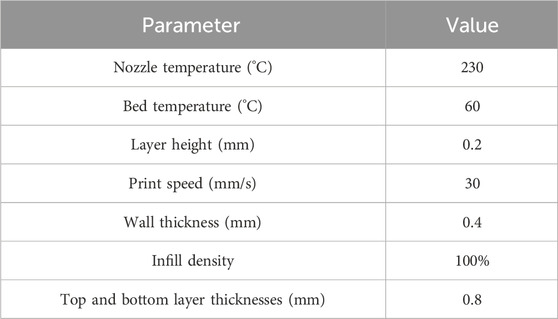
Fused Deposition Modeling (FDM) is a 3D printing method that builds objects layer by layer through the melting and extrusion of thermoplastic filaments. This additive manufacturing technique takes a 3D model and slices it into individual layers, with the printer successively depositing material until the complete object is formed. The performance and quality of material extrusion-printed parts are highly dependent on the parameters used during the process. Key factors such as layer height, print speed, material choice, bed and nozzle temperatures, and post-processing techniques all influence the final product’s properties (Kam et al., 2023; Solomon et al., 2021). Fine-tuning these variables is crucial to achieving the desired strength, dimensional accuracy, and surface finish. 11 distinct parts were manufactured using TPU material through the material extrusion process, and the specific 3D printing parameters applied are listed in Table 1. The parameters were selected based on the default range recommended for Creality TPU.

Table 1

Table 1. Material extrusion manufacturing parameters.

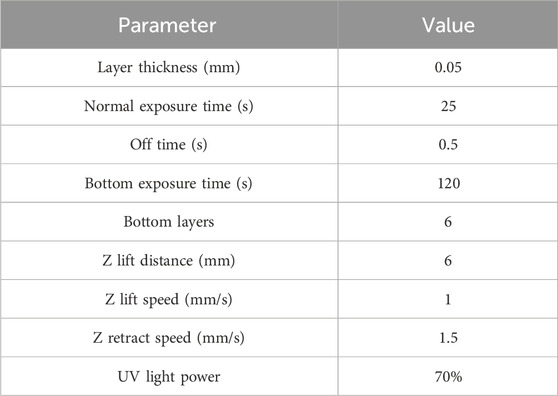
Stereolithography (SLA) is a 3D printing technology that creates objects by curing liquid resin layer by layer using ultraviolet (UV) light. This additive manufacturing process involves a 3D model being sliced into individual layers, with the printer selectively curing the resin to build the object from the bottom up. The quality and accuracy of SLA-printed parts are significantly affected by various process parameters. For parts manufactured using SLA with rubber resin, these parameters include layer thickness, normal exposure time, off time, bottom exposure time, number of bottom layers, Z lift distance, Z lift speed, Z retract speed, and UV light power (Piedra-Cascón et al., 2021; Cosmi and Dal Maso, 2020). Each of these factors plays a crucial role in determining the final part’s strength, precision, and surface quality. In this research, 4 distinct parts were produced using Flexible rubber resin through the SLA process, and the specific printing parameters are detailed in Table 2. The parameters were selected based on the default range recommended for rubber resin.

Table 2

Table 2. SLA manufacturing parameters.

Thermoplastic polyurethane (TPU) is a versatile and durable material widely used in 3D printing due to its flexibility, elasticity, and resilience. Known for its excellent resistance to abrasion, impact, and wear, TPU offers a balance between hard plastics and rubber-like materials (Hu et al., 2021). Its ability to withstand repeated stretching and compression without deformation makes it ideal for applications requiring flexibility and durability, such as cushioning components, gaskets, and wearables. Flexible rubber resin is a specialized material used in SLA 3D printing, offering a combination of flexibility and durability. This resin is designed to produce parts with rubber-like properties, making it ideal for applications that require both flexibility and strength, such as seals, cushioning components, and wearable devices (B et al., 2022). Flexible rubber resin allows for detailed, precise prints with smooth surface finishes, a key advantage of SLA technology. Its ability to withstand repeated bending and compression without cracking or losing shape makes it a preferred choice for creating parts that need to maintain their integrity under dynamic conditions. In Table 3 the mechanical properties of TPU and Wanhao rubber flexible resin materials are listed.

Table 3

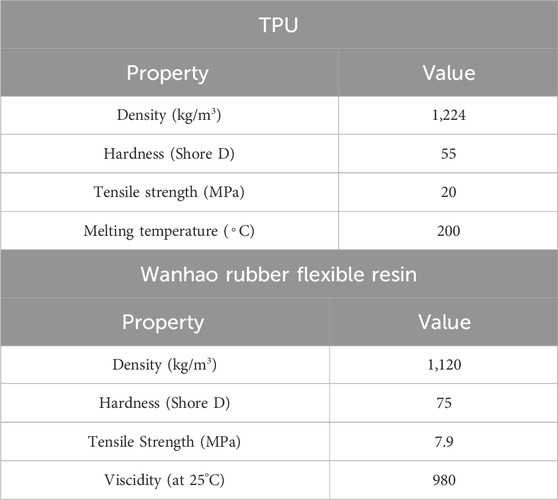
Table 3. Properties of materials (Allami et al., 2021; Wanhao, 2024).

2.2 Optimization

In this research, four different lattice structures were utilized which are the Kelvin cell, Weaire-Phelan, Gyroid, and Voronoi lattice structures. These structures were selected due to their well-documented capabilities in reducing weight, minimizing vibrations, and absorbing forces.

The Kelvin cell, a space-filling tetrakaidecahedron, has shown superior isotropic stiffness and is widely used for lightweight impact-absorbing applications (Płatek et al., 2020). The Weaire-Phelan structure, derived from foam geometry, offers superior packing efficiency and has been reported to reduce peak stresses under compressive loading (Abou-Ali et al., 2022). The Gyroid, a triply periodic minimal surface, is known for its continuous, non-self-intersecting surface and has been proven effective in managing both static and dynamic stresses (Hu et al., 2021). The Voronoi structure provides a stochastic distribution that mimics natural cellular materials such as trabecular bone and has been identified in the literature as effective in dissipating energy through complex deformation paths (B et al., 2022). Compared to more conventional lattices like cubic or octet-truss structures, these geometries provide a broader range of anisotropic and isotropic mechanical behaviors, making them ideal candidates for evaluating recoil absorption and vibration damping in this context.

Some lattice designs, such as the Kelvin cell, were applied to multiple parts, but with variations in parameters and structural configurations. The software nTop was employed to carry out manual topology optimization and to perform stress and strain analysis on each part using finite element analysis (FEA) methods. This approach allowed for precise evaluation of the mechanical behavior of the optimized lattice structures. In Figure 2 the used lattice structures are shown.

Figure 2

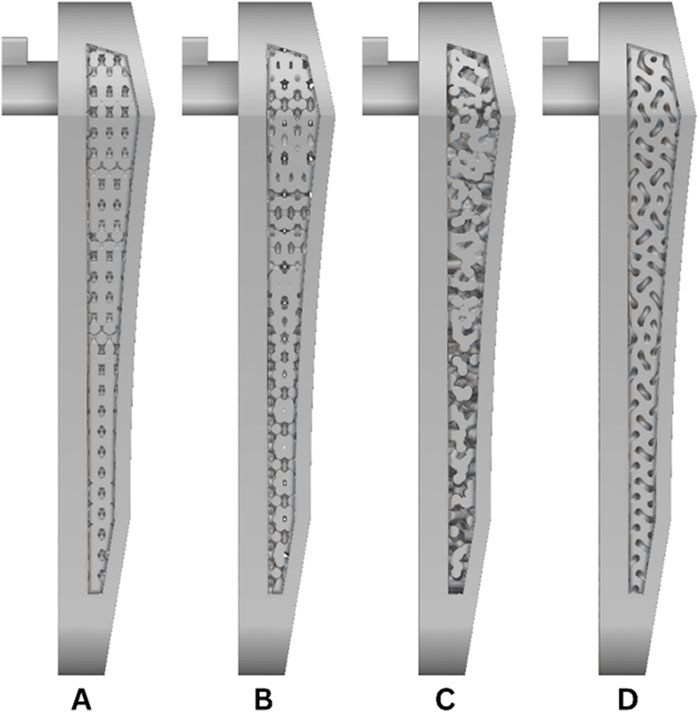
Figure 2. (A) Kelvin cell lattice structure, (B) Weaire-Phelan lattice structure, (C) Voronoi lattice structure, (D) Gyroid lattice structure.

In Table 4, the optimization parameters for each part are presented. These parameters include critical factors such as the size of the lattice unit cell, the point spacing between beams within the structure, and the thickness of the lattice. This study employed a manual topology optimization approach, where each lattice structure was individually applied and adjusted in nTop without automated objectives or convergence criteria. Thickness of lattice was 2 mm for all parts. Each of these factors plays a crucial role in determining the mechanical properties and overall performance of the optimized parts.

Table 4

Table 4. nTop optimization parameters.

Multiple specimens were fabricated and tested for each lattice structure type using varied parameter configurations. This allowed for the identification of consistent behavioral trends within each structure family, providing a solid comparative basis for evaluating the mechanical response of different lattice geometries.

2.3 Simulation analysis setup

A finite element stress and strain analysis was performed on all the designed parts using the nTop software’s static analysis block. In this process, a force was applied to specific areas of each part, primarily on the top surface where the shooter’s force impacts the pad. The recoil force of 4157 N applied in the FEA was selected based on experimental findings reported in (Suchocki and Ewertowski, 2017), which measured peak dynamic shoulder reaction forces ranging from 2.4 to 2.8 kN during rifle firing, along with an additional static preload of 200–350 N, resulting in total peak forces of approximately 2.6–3.15 kN. In this study, the selected value was moderately increased beyond this range to account for possible worst-case recoil events, such as rapid successive firing in semi-automatic rifles, variations in shooter posture, and stiffer recoil pad configurations that may transfer greater force over a shorter duration. This conservative estimate ensures the designed lattice structures remain effective under a wide range of realistic recoil conditions, while still aligning with the upper bound of experimentally supported values. Additionally, displacement restraints were placed in key regions, specifically on the underside of the part and around the screw hole where it attaches to the rifle stock. The boundary conditions for this analysis are illustrated in Figure 3.

Figure 3

Figure 3. Boundary conditions for static loading analyses.

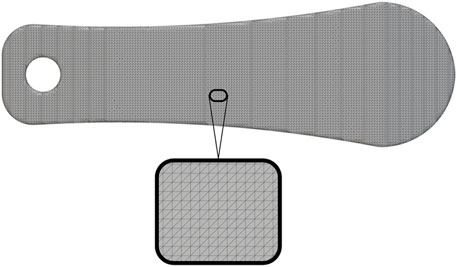
To perform the static analysis, a finite element (FE) model of the normal component was developed, involving several key steps. This process began with generating a volume mesh, using a mesh tolerance of 1 mm and an edge length of 2 mm, as shown in Figure 4. The mesh was created from the implicit bodies of the designed pads and featured a linear geometric order to ensure accurate representation of the component’s structure.

Figure 4

Figure 4. Mesh of the recoil pad.

Using a finite element (FE) analysis program offers a versatile approach to assessing a design’s performance (Yang et al., 2025b). The FE method formulates equations that connect nodal loads and degrees of freedom within the framework of linear static analysis, as illustrated in Equation 1 (de Ruiter and van Keulen, 2004).

$Ku=f(1)$

In this context, $K$ represents the stiffness matrix, $u$ is the vector of degrees of freedom, and $f$ denotes the nodal load vector. The linear elastic stress-strain relationship is expressed in Equation 2 (Rychle and wski, 1984).

$\sigma =E\epsilon (2)$

Here, $E$ denotes Young’s modulus, $\sigma$ represents the stress tensor, and $\epsilon$ is the strain tensor. The primary equation in topology optimization is generally derived from the objective function, which is designed to be minimized while adhering to specific constraints. One frequently used objective function aims to minimize the structural compliance, as detailed in Equation 3 (Bendsoe et al., 2003).

$C=u^{T}K\left(\rho \right)u(3)$

where $C$ is the compliance, $u$ is the displacement vector, and $K\left(\rho \right)$ is the global stiffness matrix as a function of the material density distribution $\rho$. The equation for the element stress tensor, as shown in Equation 4, is a key formula in finite element analysis. It is used to determine the stress within a specific finite element (Alshihabi et al., 2025).

$s=D·e(4)$

This equation relies on the constitutive relationship that links stress and strain in the material, represented by the constitutive matrix $D$. In this context, $s$ denotes the stress tensor, $D$ is the constitutive matrix, and $e$ signifies the strain tensor.

2.4 Vibration and impact test setups

Figure 5 illustrates the equipment and tools necessary for conducting a vibration modal analysis, which includes an accelerometer, a data logger, an impact hammer, and isolation foam. These carefully chosen instruments were integral to the analysis. Accelerometers were positioned at various points on the structure to measure acceleration, while data loggers were essential for capturing and documenting the detailed data. The impact hammer, along with the other equipment, ensured precision in the experiments. SignalCalc software was employed to process and organize the recorded data, using an F span of 1,000 with 400 lines. The final results were derived by averaging the outcomes from three separate tests.

Figure 5

Figure 5. Experimental setup of modal analysis.

The rapid impact test was conducted using the Instron Ceast 9,350, a high-performance impact testing device designed for evaluating the energy absorption and resistance of materials under dynamic loading conditions. This equipment is capable of delivering precise and controlled impacts, making it ideal for testing the durability and performance of components under real-world conditions. In this study, all specimens were subjected to impacts from a height of 96 mm, with an impact velocity of 1.37 m/s, and an impact energy of 5 J. These parameters were carefully chosen to simulate the typical forces the parts would experience during use. The compression test was performed using the Marestek compression testing device, which is designed to measure the mechanical strength and deformation of materials under compressive loads. Each sample in the study was subjected to a controlled compression, with the device applying force until the sample was compressed by 12 mm to enable consistent comparison of compressive performance. This level of displacement was selected to simulate a realistic range of recoil pad compression under high-load conditions. While this deformation may exceed the purely elastic range for some materials, the focus was on evaluating relative structural performance rather than distinguishing elastic and plastic behavior.

3 Results and discussions

The parts were successfully manufactured using two different techniques, resulting in 11 TPU parts produced via material extrusion and 4 flexible rubber resin parts created through SLA. Each part was fabricated according to the design specifications and optimized parameters outlined in the study. In Figure 6, all the manufactured parts are displayed alongside their respective codes.

Figure 6

Figure 6. Manufactured parts.

3.1 Simulation results

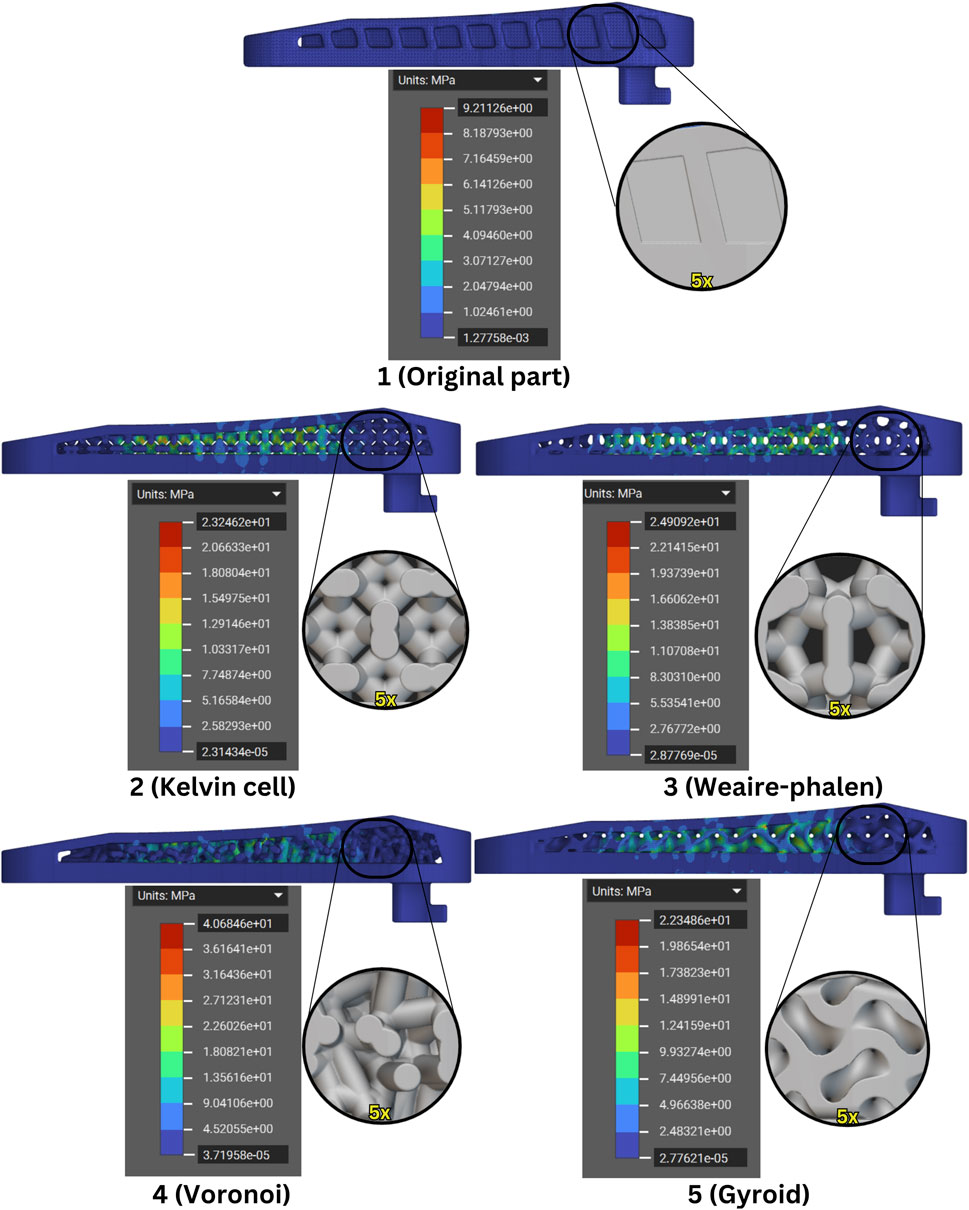
In nTop, the stress and strain analyses were conducted using the static analysis block to evaluate the mechanical performance of the parts. This analysis identified the maximum stress levels, stress distribution, and critical regions within each part. The static analysis was performed once for each lattice structure, resulting in 5 distinct parts being assessed. Figure 7 illustrates the stress distribution patterns derived from the analysis, highlighting the regions where the highest stresses were concentrated.

Figure 7

Figure 7. FEA stress analysis results.

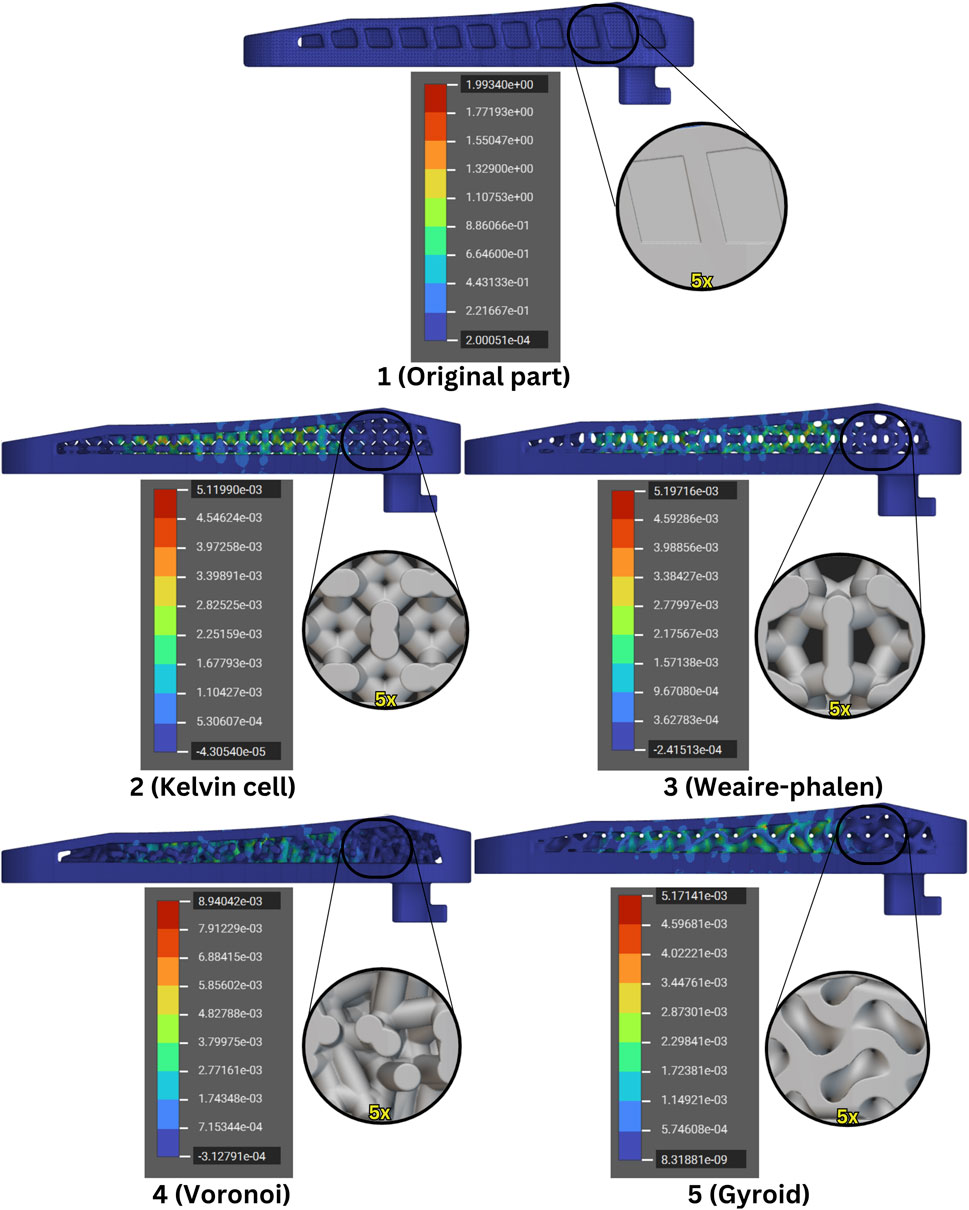
The analysis of maximum stress values for each part reveals significant differences based on the varying lattice structures and mass reductions. The original part, with a mass of 52.98 g, displayed a maximum stress of 9.21 MPa, serving as the baseline for comparison. Among the optimized designs, the Kelvin cell structure, with a mass of 26.45 g, showed a maximum stress of 23.34 MPa, which is significantly higher than the original part. This increase in stress is likely due to the substantial reduction in mass, limiting its ability to distribute the applied forces effectively. The Weaire-Phelan structure, with a mass of 39.36 g, recorded the highest stress at 24.91 MPa, indicating that despite a moderate reduction in mass, this lattice was less effective in handling stress. The Voronoi structure, despite being the heaviest of the optimized parts at 43.35 g, exhibited the highest stress of 40.68 MPa, suggesting it may not be as suitable for this application in terms of stress distribution. Lastly, the Gyroid structure, with a mass of 40.13 g, displayed a maximum stress of 23.48 MPa, a value comparable to the Kelvin cell. This structure seems to achieve a better balance between mass reduction and stress distribution. In Figure 8 the strain analysis results are shown.

Figure 8

Figure 8. FEA strain analysis results.

The original part, with a mass of 52.98 g, exhibits a maximum strain of approximately 0.00199. This value serves as the baseline for comparison against the optimized parts. Among the optimized designs, the Kelvin cell structure, which has a mass of 26.45 g, shows a maximum strain of 0.00511. The increased strain can be attributed to the significant reduction in material, which reduces the structure’s ability to resist deformation under load. The Weaire-Phelan structure, weighing 39.36 g, exhibits a strain of 0.00519, slightly higher than the Kelvin cell, indicating that the material’s ability to handle strain is compromised despite its moderate mass reduction.

The Voronoi structure, with the highest mass among the optimized parts at 43.35 g, shows the highest strain at 0.00894. Despite the larger mass, the Voronoi lattice structure appears to be less effective at controlling deformation, leading to a much higher strain than expected. Lastly, the Gyroid structure, which weighs 40.13 g, has a strain of 0.00517, relatively similar to the Kelvin cell and Weaire-Phelan designs. The Gyroid structure manages to balance mass reduction and strain handling better than the Voronoi structure, but still exhibits a higher strain compared to the original part. The Kelvin cell and Gyroid structures show a more balanced performance, handling strain effectively relative to their reduced mass, while the Voronoi structure struggles with higher strain despite its heavier weight.

3.2 Vibration test results

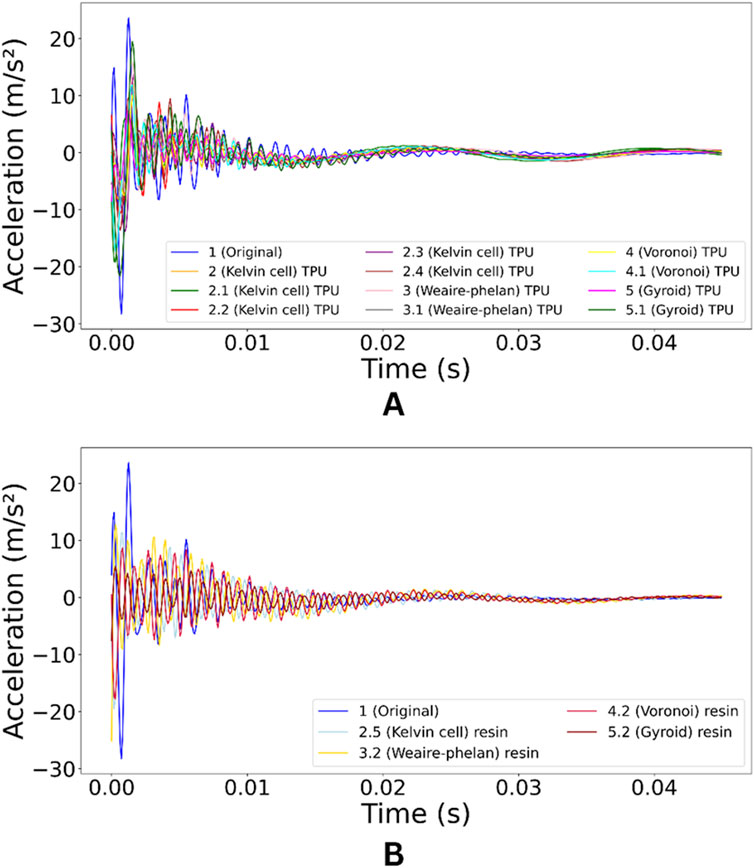
Vibration modal analysis is crucial for investigating recoil pads because it provides detailed insights into how these components behave under dynamic loads. For a recoil pad, understanding its vibration response is essential, as it directly impacts the pad’s ability to absorb and dissipate the forces generated during firearm recoil. By studying the dynamic characteristics, such as natural frequencies and mode shapes, modal analysis helps in optimizing the design of the pad to reduce vibrations and improve shooter comfort. In modal analysis, acceleration data is vital for understanding the dynamic behavior of systems and structures. This analysis also helps identify potential weak points or resonant frequencies that could affect the pad’s performance and durability. Figure 9 shows the acceleration data obtained through a modal analysis conducted on each part, with the analysis performed at a single accelerometer position. By comprehensively understanding the vibration behavior, designers can make informed modifications to enhance energy absorption and minimize the transfer of shock to the user, leading to a more effective and reliable recoil system.

Figure 9

Figure 9. (A) Vibrational acceleration of TPU, (B) vibrational acceleration of resin.

In the left graph (A), the TPU lattice structures (Kelvin cell, Weaire-Phelan, Voronoi, and Gyroid) are compared to the original part. The TPU lattices show a rapid reduction in vibration amplitude within around 0.05 s, indicating effective damping capabilities. Notably, the Kelvin cell and Weaire-Phelan structures stabilize faster than the Voronoi and Gyroid. However, the initial peak acceleration for all TPU lattices is similar to the original part, suggesting that while they dampen vibrations efficiently, they do not significantly reduce the initial shock. Among the TPU structures, the Kelvin cell shows consistent performance, indicating its design can optimize vibration damping. The right graph (B) shows the resin lattice structures’ performance. Resin structures dampen vibrations more slowly, generally reaching a linear state around 0.07 s. However, their vibration amplitudes are closer to the original part, indicating higher resilience to initial shock. While resin structures do not dampen as quickly as TPU, they offer better resistance to initial vibrations, suggesting higher stiffness. The amount of material in each TPU lattice significantly affects damping. Heavier variants, like the Kelvin cell 2 and Voronoi 4, resist initial impact better but take longer to stabilize, while lighter variants, such as the Kelvin cell 2.1, exhibit quicker damping, indicating improved vibration absorption efficiency. This balance highlights that lighter structures dissipate vibrations faster, whereas heavier ones offer better initial shock resistance. For both TPU and resin, the modified lattices dampen vibrations quicker than the original part. Overall, TPU structures stabilize faster, while resin structures resist initial impact better, suggesting TPU is suitable for applications requiring rapid damping, while resin suits those needing initial stiffness.

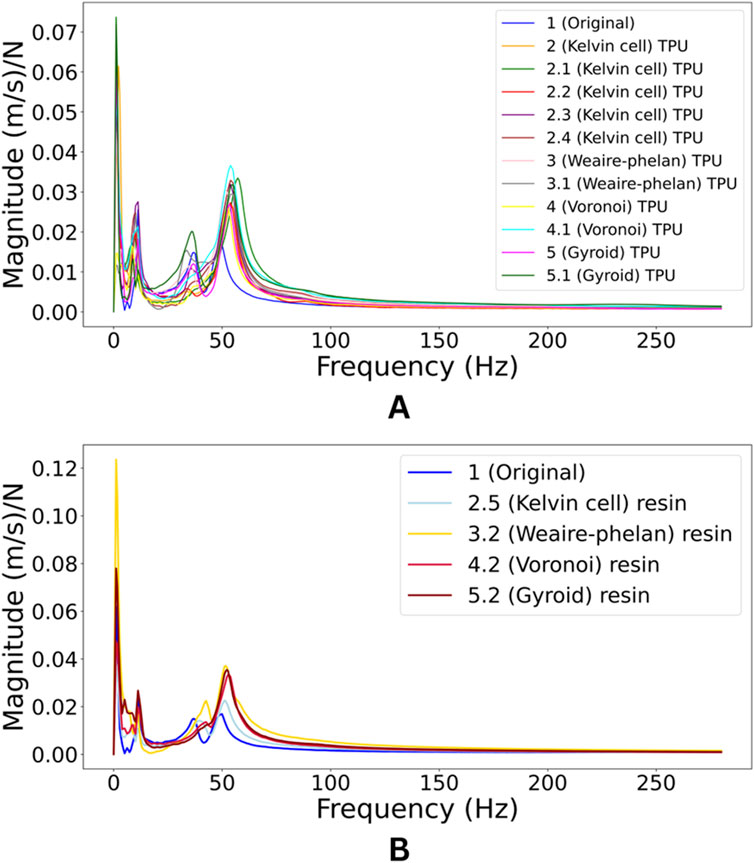
Through the required mathematical computations, velocity data related to the applied Newtonian force as a function of frequency (per unit time) were obtained. Using this data, the mode frequencies and their corresponding magnitudes were identified, resulting in the magnitude-frequency graphs displayed in Figure 10. These graphs provide insights into the intensity of the response at various frequencies, highlighting key modes where the system exhibits significant velocity changes.

Figure 10

Figure 10. (A) TPU’s magnitude of vibration, (B) resin’s magnitude of vibration.

The TPU lattice structures (Kelvin cell, Weaire-Phelan, Voronoi, and Gyroid) exhibit significant peaks around 5 Hz and 50 Hz. While their peak positions are similar to the original part, TPU structures generally have lower peak magnitudes, indicating improved vibration damping capabilities. Among them, lighter variants like the Kelvin cell 2.1 show more distinct reductions in peak magnitudes, while heavier ones (e.g., Voronoi 4) have slightly larger peaks, suggesting a trade-off between stiffness and damping. For resin lattice structures, the primary peaks also occur near 5 Hz and 50 Hz, but they tend to be more pronounced than in TPU, indicating a higher sensitivity to vibrations. However, compared to the original resin part, these lattices still show improvement, as evidenced by slightly reduced peak magnitudes, particularly in the Kelvin cell and Weaire-Phelan variants. While the introduction of lattice structures in resin influences peak magnitudes, the mode frequencies remain relatively constant.

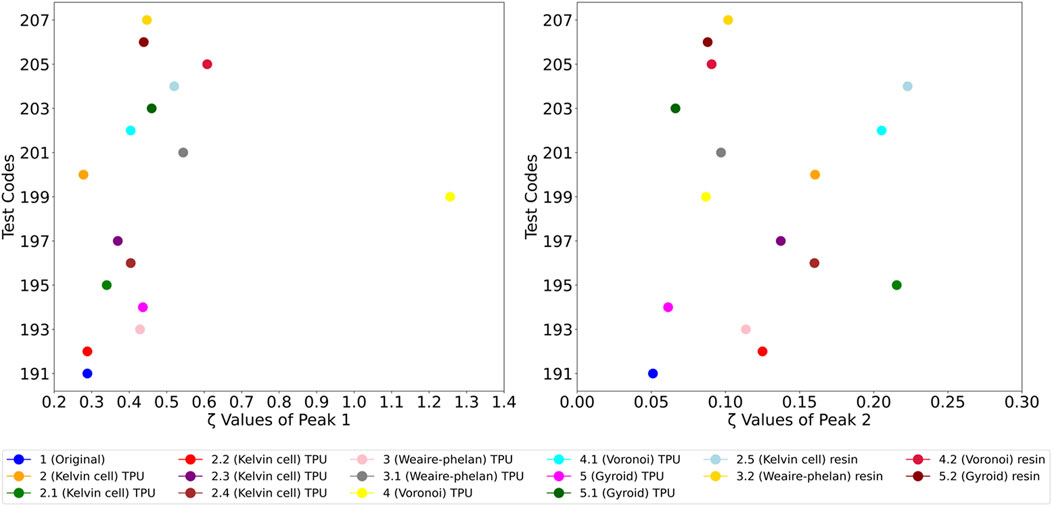
Overall, both TPU and resin lattices enhance vibration control by lowering peak magnitudes compared to the original parts. TPU structures, especially the Kelvin cell and Gyroid, demonstrate more effective damping, whereas resin structures retain higher peak intensities, indicating a balance between stiffness and damping. Thus, TPU is more suited for applications requiring strong vibration damping, while resin offers a more balanced response. Damping ratios “ξ” were calculated considering the first two main vibration modes in the graph and are shown in Figure 11.

Figure 11

Figure 11. Damping ratios “ξ” of all parts.

For Peak 1, the 4 (Voronoi) TPU stands out with the highest damping ratio at 1.25, indicating a significant enhancement in vibration damping compared to all other parts, including the original. This clearly shows that the Voronoi TPU lattice structure is highly effective in managing vibrations in the first mode. Among the resin structures, 2.5 (Kelvin cell) resin shows a relatively high damping ratio of 0.52, followed by 3.2 (Weaire-Phelan) resin at 0.44. These values suggest that certain resin lattice structures also offer improved damping compared to the original part, which has a much lower damping ratio of 0.28. Additionally, other TPU variants like 3.1 (Weaire-Phelan) TPU and 2.3 (Kelvin cell) TPU display enhanced damping capabilities, with ratios of 0.54 and 0.36 respectively, though they do not surpass the 4 (Voronoi) TPU. In a similar study using a thermoplastic material with additive manufacturing to calculate the damping ratio, the best result obtained was 0.014, underscoring the higher and more efficient results achieved in this study (Fau et al., 2008).

For Peak 2, the 2.1 (Kelvin cell) TPU emerges as the top performer, with the highest damping ratio of 0.21, indicating its superior efficiency in reducing vibrations in this mode. Notably, 2.5 (Kelvin cell) resin exhibits a comparable damping ratio of 0.22, suggesting that this resin structure is equally effective in the second mode. The original part, with a damping ratio of 0.05, shows the least effectiveness in vibration damping. Other TPU structures, such as 4.1 (Voronoi) TPU with a ratio of 0.20 and 2 (Kelvin cell) TPU at 0.16, also outperform the original, highlighting the overall benefit of incorporating lattice structures for vibration control. This comparison indicates that, while TPU generally leads in damping efficiency, certain resin variants can be competitive, especially in the second mode. Damping coefficient “C” was calculated considering the first two main vibration modes in the graph in Figure 12.

Figure 12

Figure 12. Damping coefficient “C” values of all parts.

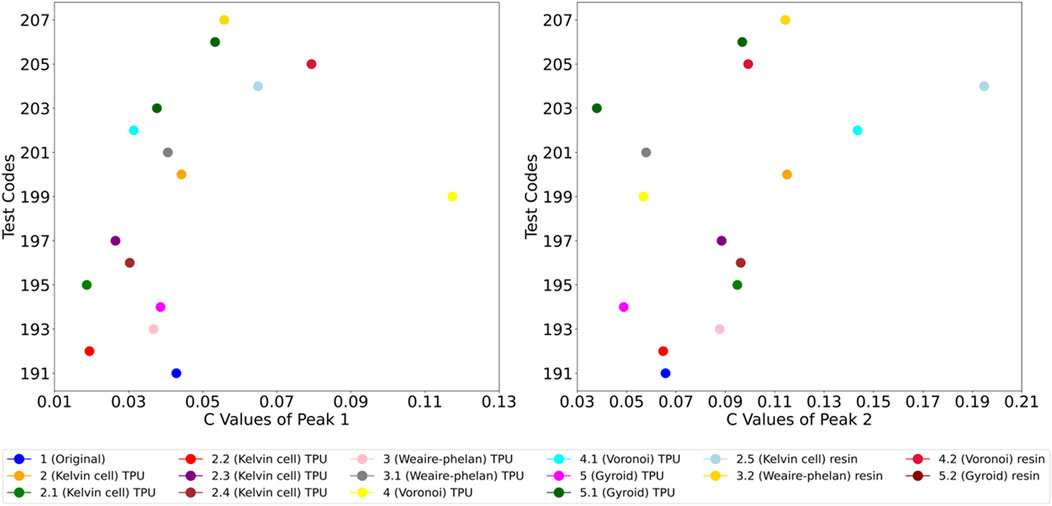
In the first mode, 4 (Voronoi) TPU shows the highest damping coefficient at 0.11, indicating its superior ability to dissipate vibrational energy compared to all other structures. The original part has a lower coefficient of 0.04, confirming the improved performance of most lattice structures, especially the Voronoi TPU. Among the resin parts, 2.5 (Kelvin cell) resin and 3.2 (Weaire-Phelan) resin show noticeable improvements with coefficients of 0.06 and 0.05, though they do not surpass the Voronoi TPU. In the second mode, 4.1 (Voronoi) TPU again exhibits the highest damping coefficient at 0.14, demonstrating the consistent efficiency of the Voronoi design in TPU. For the resin structures, 2.5 (Kelvin cell) resin performs best with a damping coefficient of 0.19, significantly higher than the original part’s 0.06. This highlights the benefit of lattice modifications in both TPU and resin for enhanced vibration control. The damped period values of the all parts are displayed in Figure 13.

Figure 13

Figure 13. Damped period “T_d“ values for all parts.

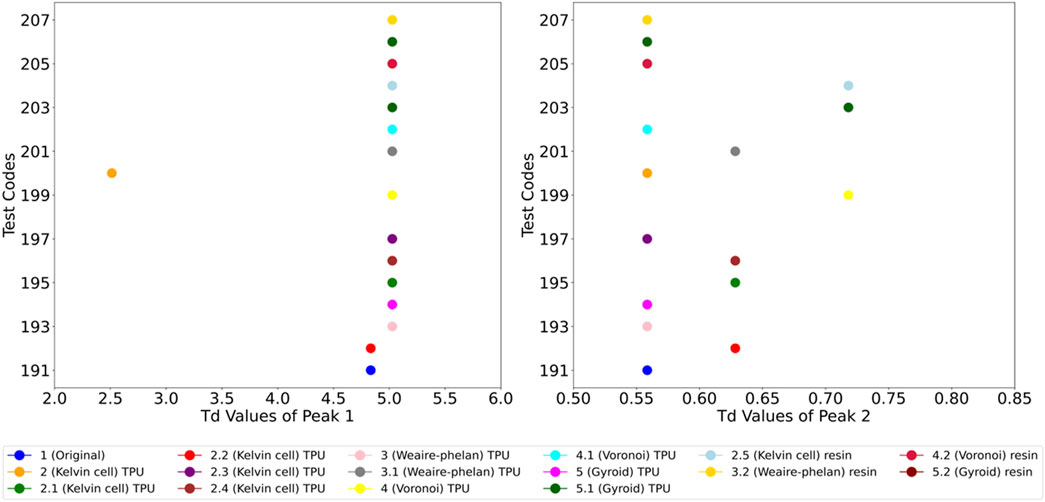
For the first natural frequency, most lattice structures show consistent damped periods around 5.03 s, while the original part has a slightly lower period of 4.83 s, indicating a marginal difference. The 2 (Kelvin cell) TPU stands out with a much shorter damped period of 2.51 s, suggesting faster vibration damping and reduced resonance risk. Among the resin structures, all variants maintain the 5.03 s period, showing no significant change in damping behavior. For the second natural frequency, damped periods range between 0.56 and 0.72 s. The original part and most structures, including TPU and resin variants, exhibit a quick damping response with periods of 0.56 s. However, 2.5 (Kelvin cell) resin, 4 (Voronoi) TPU, 4.2 (Voronoi) resin, and 5 (Gyroid) TPU show slightly longer periods of 0.72 s, indicating a marginally slower damping response. Despite these variations, both TPU and resin structures show effective vibration control in the second mode.

3.3 Compression and impact results

A compression test is a crucial method used to evaluate the strength and mechanical performance of materials and parts. It involves applying a controlled force to compress a specimen, allowing for the measurement of its ability to withstand deformation under load (Dixit and Jain, 2022). Uniaxial compression testing was selected as a practical and controlled method to evaluate the load-bearing capacity and deformation behavior of each lattice structure under peak recoil-like forces. This approach enables consistent comparison across samples and serves as a reliable approximation for the dominant force direction experienced during firing. The results provide valuable insights into a material’s compressive strength, stiffness, and failure behavior, which are essential for determining its suitability in various applications. Compression results are shown in Figure 14.

Figure 14

Figure 14. (A) Compression test results of TPU, (B) compression test results of resin.

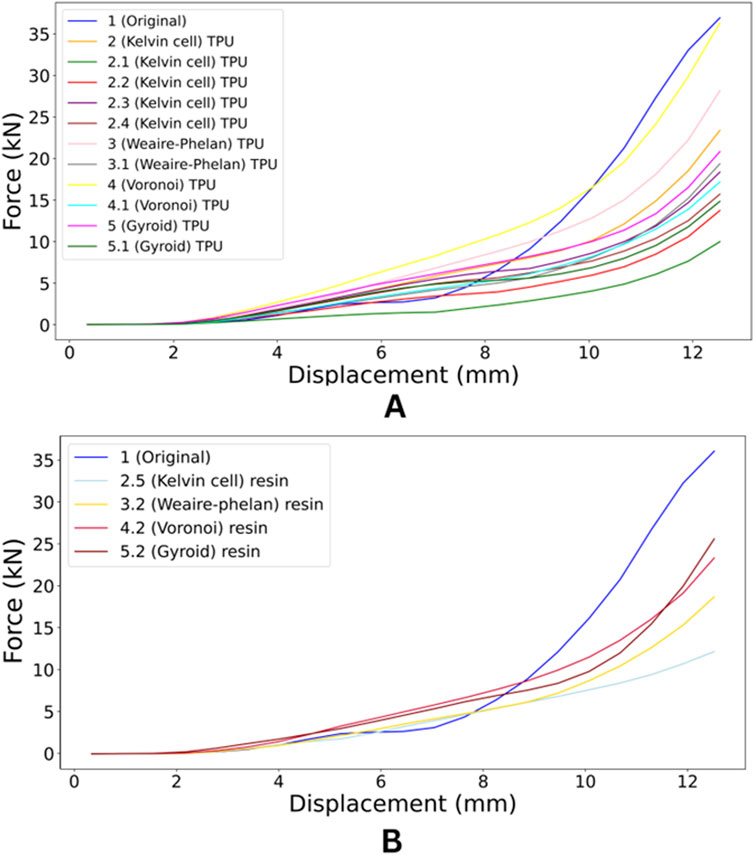
The compression test results reveal that the original part has the highest maximum force, reaching 36.91 kN at a displacement of 12.52 mm, confirming its superior strength compared to all modified structures. Among the TPU variants, the 4 (Voronoi) TPU stands out with a maximum force of 36.31 kN, closely matching the original part and making it the strongest modified TPU design. In contrast, the Kelvin cell TPU variants show significantly lower strength, with 2.1 (Kelvin cell) TPU being the weakest, achieving only 9.96 kN.

The Weaire-Phelan TPU variants perform moderately well, with 3 (Weaire-Phelan) TPU reaching 28.15 kN, but still falling short of the original part’s performance. Among the resin variants, 5.2 (Gyroid) resin is the strongest, with a maximum force of 26.33 kN, making it the best-performing resin design, though it still lags behind the original and the Voronoi TPU. The 4.2 (Voronoi) resin also performs well among resin structures, with 23.9 kN, but it remains weaker than the TPU versions. Overall, the Voronoi TPU variants, particularly 4 (Voronoi) TPU, demonstrate the best compression strength among modified structures, closely rivaling the original part, while resin variants and other TPU designs exhibit lower strength.

In comparing the TPU and resin variants, TPU generally demonstrates superior compression strength. The 4 (Voronoi) TPU achieves a maximum force of 36.31 kN, coming very close to the original part’s performance, while the strongest resin variant, 5.2 (Gyroid) resin, reaches 26.33 kN, which is significantly lower. Overall, TPU structures, particularly the Voronoi design, outperform their resin counterparts in terms of maximum compression strength. Resin variants, such as 4.2 (Voronoi) resin and 5.2 (Gyroid) resin, perform better among resin structures but do not reach the levels of TPU. Thus, TPU is better suited for applications requiring higher compression strength.

A rapid impact test is an essential technique for assessing the dynamic behavior and durability of materials and parts under sudden, high-speed loads. This test simulates real-world impact scenarios, such as collisions or drops, to evaluate how a material responds to shock and strain (Markatos and Pantelakis, 2022). By measuring impact resistance, energy absorption, and deformation, the test provides valuable information on a part’s ability to withstand forces that occur in practical applications. In Figure 15 the absorbed energy results of the impact test are given. Only one sample of each lattice structure was subjected to impact testing in this research.

Figure 15

Figure 15. (A) Impact absorbed energy of TPU, (B) impact absorbed energy of resin.

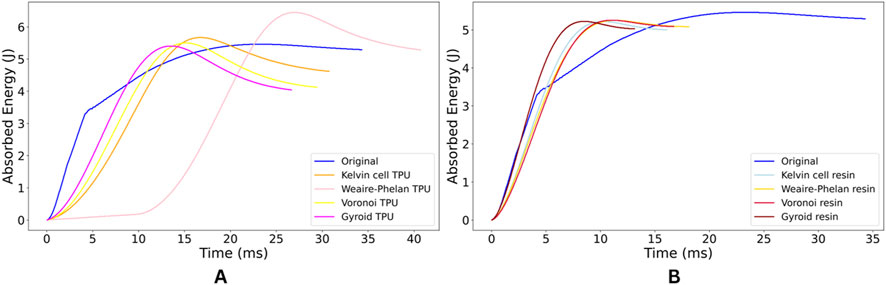
The rapid impact test results highlight the superior energy absorption capabilities of the TPU lattice structures compared to the original part. In graph A, the original part peaks at 5.46 J at 22.5 m, indicating a slower energy absorption rate and a lower peak, which makes it less effective in managing rapid impacts. In contrast, the Kelvin cell TPU reaches 5.67 J at 17 m, absorbing more energy faster than the original, indicating better performance for quicker impacts. The Weaire-Phelan TPU stands out with the highest energy absorption, peaking at 6.45 J at 27 m, making it the most effective design for sustained impacts requiring maximum energy absorption. The Voronoi TPU peaks at 5.5 J at 15 m, absorbing energy quickly, making it ideal for fast impact scenarios. Similarly, the Gyroid TPU, while peaking slightly lower at 5.4 J at 14 m, absorbs energy the fastest, making it highly suitable for handling very rapid impacts. Overall, all TPU lattice designs outperform the original part, with the Weaire-Phelan TPU offering the best overall energy absorption, while the Kelvin cell, Voronoi, and Gyroid TPU variants excel in speed and quick impact response.

In graph B, the rapid impact results for the resin samples showcase their varying abilities to absorb energy and reduce impact forces. The original resin part peaks at 5.46 J at 22.5 m, indicating a relatively slow response in absorbing energy, making it less efficient for rapid impacts compared to the modified lattice structures. The Kelvin cell resin reaches a peak of 5.22 J at 10 m, demonstrating a much faster response than the original part, which makes it better suited for quick impacts despite absorbing slightly less energy. The Weaire-Phelan resin and Voronoi resin both peak at 5.25 J at 11 m, showing nearly identical performance. Both designs absorb energy rapidly, offering better impact protection than the original part by reaching their peaks much earlier. The Gyroid resin stands out for its exceptionally fast response, peaking at 5.22 J at only 8 m, making it the quickest among the resin variants. Although it absorbs slightly less energy compared to some other designs, its rapid energy absorption makes it highly effective for handling very fast impacts. Overall, the resin lattice structures show significantly improved speed in energy absorption compared to the original part, with the Gyroid resin excelling in speed and the Weaire-Phelan and Voronoi resins offering a good balance between energy absorption and response time. These modifications make the resin lattices more suitable for applications requiring quick energy dissipation under impact.

When comparing the TPU and resin samples, the TPU structures generally absorb more energy and take longer to reach their peak, making them better suited for sustained impacts. For instance, the Weaire-Phelan TPU absorbs 6.45 J at 27 m, significantly more energy than its resin counterpart, which peaks at 5.25 J at 11 m. However, the resin structures excel in speed, absorbing energy much faster than TPU. For example, the Gyroid resin peaks at 5.22 J in just 8 m, while the Gyroid TPU takes 14 m to reach 5.4 J.

In summary, TPU is better for applications requiring higher energy absorption and protection over prolonged impacts, while resin is superior for scenarios where fast energy dissipation and quick impact response are critical.

4 Conclusion

In this study, a comprehensive series of tests, including vibration, compression, and rapid impact tests, were conducted on various TPU and resin lattice structures to evaluate their performance in damping vibrations, absorbing impacts, and resisting compression forces. These tests provided valuable insights into the dynamic behavior of both materials under different loading conditions. The results highlight the significant variations in energy absorption, damping efficiency, and structural resilience between the tested lattices. Notably, this study offers a novel application of advanced lattice structures in the context of recoil pads, showcasing their potential to enhance both impact resistance and vibration control. The most significant results:

• Voronoi TPU emerged as the strongest performer, excelling in both vibration damping and compression strength. It achieved a damping ratio of 1.25 in the first mode, reflecting a 331% improvement from the original part (0.29–1.25), and 0.20 in the second mode, showing a 300% increase from the original (0.05–0.20). This highlights its superior ability to dissipate vibrational energy effectively. With a compression strength of 36.32 kN and impact absorption peaking at 5.5 J at 15 m, Voronoi TPU is ideal for applications requiring both vibration control and impact resistance.

• The weaire-Phelan TPU structure excelled in energy absorption, reaching the highest peak in impact tests at 6.45 J at 27 m. While its compression strength (28.15 kN) was slightly lower than other TPU variants, Weaire-Phelan is well-suited for applications focusing on prolonged energy absorption.

• Gyroid TPU showed rapid energy absorption, peaking at 5.4 J at 14 m, and demonstrated mid-range performance in compression at 20.27 kN. Its strength lies in handling short, high-energy impacts efficiently.

• Kelvin Cell TPU delivered balanced performance, with a damping ratio of 0.21 in the second mode and compression strength of 18.63 kN. It absorbed 5.67 J at 17 m, making it a solid choice for moderate applications requiring a balance of vibration control and energy absorption.

• Kelvin Cell Resin is the top performer among the resin structures, particularly in the second mode, where it achieves a high damping coefficient of 0.19. It also shows a relatively high damping ratio in the first mode (0.52), indicating its strong ability to absorb energy and resist vibrations.

• Weaire-Phelan Resin also exhibits competitive performance, with a damping ratio of 0.44 in the first mode and consistent damping coefficients across both modes, making it a reliable choice for applications requiring higher stiffness and vibration control.

TPU outperforms resin in most tests, making it ideal for applications requiring rapid energy absorption and high strength, while resin suits lighter, cost-sensitive uses. The advanced TPU lattice structures, especially Voronoi TPU, greatly improve vibration damping, reducing the harshness of recoil and creating a smoother shooting experience. This minimizes fatigue, allowing for longer shooting sessions. The Weaire-Phelan TPU’s impact absorption distributes recoil forces, reducing shoulder impact and preventing discomfort or injury. These lattice structures enhance recoil management, improving comfort and control. Future studies could explore optimizing lattice designs and hybrid materials for better recoil management and customized shooter preferences, as well as include fatigue testing, firearm-mounted trials, and wearable pressure mapping for real-world validation.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MA: Writing – original draft, Data curation, Methodology, Conceptualization, Writing – review and editing. TB: Methodology, Writing – original draft, Investigation, Writing – review and editing. MK: Writing – review and editing, Investigation, Writing – original draft, Supervision. MF: Writing – review and editing, Methodology, Investigation, Writing – original draft. SA: Investigation, Writing – review and editing, Writing – original draft, Methodology.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was supported by The Scientific and Technological Research Council of Turkey (TUBITAK) under the 2209-A project number 1919B012335426.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. Portions of the written content in this manuscript were generated or edited with the assistance of OpenAI’s ChatGPT (GPT-4 model). The tool was used to improve language clarity and structure. All content was critically reviewed and approved by the authors.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abou-Ali, A. M., Lee, D.-W., and Abu Al-Rub, R. K. (2022). On the effect of lattice topology on mechanical properties of SLS additively manufactured sheet-ligament-and strut-based polymeric metamaterials. Polymers 14, 4583. doi:10.3390/polym14214583

PubMed Abstract | CrossRef Full Text | Google Scholar

Allami, T., Alamiery, A., Nassir, M. H., and Kadhum, A. H. (2021). Investigating physio-thermo-mechanical properties of polyurethane and thermoplastics nanocomposite in various applications. Polymers 13, 2467. doi:10.3390/polym13152467

PubMed Abstract | CrossRef Full Text | Google Scholar

Alshihabi, M., Ozkahraman, M., and Kayacan, M. Y. (2025). Enhancing the reliability of a robotic arm through lightweighting and vibration control with modal analysis and topology optimization. Mech. Based Des. Struct. Mach. 0, 1950–1974. doi:10.1080/15397734.2024.2400207

CrossRef Full Text | Google Scholar

Attar, H., Ehtemam-Haghighi, S., Soro, N., Kent, D., and Dargusch, M. S. (2020). Additive manufacturing of low-cost porous titanium-based composites for biomedical applications: advantages, challenges and opinion for future development. J. Alloys Compd. 827, 154263. doi:10.1016/j.jallcom.2020.154263

CrossRef Full Text | Google Scholar

Bai, D., Liu, F., Xie, D., Lv, F., Shen, L., and Tian, Z. (2022). 3D printing of flexible strain sensor based on MWCNTs/flexible resin composite. Nanotechnology 34, 045701. doi:10.1088/1361-6528/ac9c0b

PubMed Abstract | CrossRef Full Text | Google Scholar

Beaman, J. J., Bourell, D. L., Seepersad, C. C., and Kovar, D. (2020). Additive manufacturing review: early past to current practice. J. Manuf. Sci. Eng. 142, 110812. doi:10.1115/1.4048193

CrossRef Full Text | Google Scholar

Bendsoe, M. P., Martin, P., and Sigmund, O. (2003). Topology optimization: theory, methods and applications/MP bendsoe. Berlin; Heidelberg; New York; Barcelona; Hong Kong.

Google Scholar

Borrello, J., Nasser, P., Iatridis, J. C., and Costa, K. D. (2018). 3D printing a mechanically-tunable acrylate resin on a commercial DLP-SLA printer. Addit. Manuf. 23, 374–380. doi:10.1016/j.addma.2018.08.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Cardeal, G., Sequeira, D., Mendonça, J., Leite, M., and Ribeiro, I. (2021). Additive manufacturing in the process industry: a process-based cost model to study life cycle cost and the viability of additive manufacturing spare parts. Procedia CIRP 98, 211–216. doi:10.1016/j.procir.2021.01.032

CrossRef Full Text | Google Scholar

Chalgham, A., Ehrmann, A., and Wickenkamp, I. (2021). Mechanical properties of FDM printed PLA parts before and after thermal treatment. Polymers 13, 1239. doi:10.3390/polym13081239

PubMed Abstract | CrossRef Full Text | Google Scholar

Cosmi, F., and Dal Maso, A. (2020). A mechanical characterization of SLA 3D-printed specimens for low-budget applications. Mater. Today Proc. 32, 194–201. doi:10.1016/j.matpr.2020.04.602

CrossRef Full Text | Google Scholar

de Ruiter, M. J., and van Keulen, F. (2004). Topology optimization using a topology description function. Struct. Multidiscip. Optim. 26, 406–416. doi:10.1007/s00158-003-0375-7

CrossRef Full Text | Google Scholar

Dixit, N., and Jain, P. K. (2022). Effect of fused filament fabrication process parameters on compressive strength of thermoplastic polyurethane and polylactic acid lattice structures. J Materi Eng Perform 31, 5973–5982. doi:10.1007/s11665-022-06664-0

CrossRef Full Text | Google Scholar

Dudek, P. (2013). FDM 3D printing technology in manufacturing composite elements. Archives metallurgy Mater. 58, 1415–1418. doi:10.2478/amm-2013-0186

CrossRef Full Text | Google Scholar

Faustini, M. C., Neptune, R. R., Crawford, R. H., and Stanhope, S. J. (2008). Manufacture of passive dynamic ankle–foot orthoses using selective laser sintering. IEEE Trans. Biomed. Eng. 55, 784–790. doi:10.1109/TBME.2007.912638

PubMed Abstract | CrossRef Full Text | Google Scholar

Froes, F. H., and Dutta, B. (2014). The additive manufacturing (AM) of titanium alloys. AMR 1019, 19–25. doi:10.4028/www.scientific.net/AMR.1019.19

CrossRef Full Text | Google Scholar

Hall, M. J. (2008). Measuring felt recoil of sporting arms. Int. J. Impact Eng. 35, 540–548. doi:10.1016/j.ijimpeng.2007.03.007

CrossRef Full Text | Google Scholar

Hu, G., Cao, Z., Hopkins, M., Hayes, C., Daly, M., Zhou, H., et al. (2019). Optimizing the hardness of SLA printed objects by using the neural network and genetic algorithm. Procedia Manuf. 38, 117–124. doi:10.1016/j.promfg.2020.01.016

CrossRef Full Text | Google Scholar

Hu, Q., Zhang, R., Zhang, H., Yang, D., Liu, S., Song, Z., et al. (2021). Topological structure design and fabrication of biocompatible PLA/TPU/ADM mesh with appropriate elasticity for hernia repair. Macromol. Biosci. 21, 2000423. doi:10.1002/mabi.202000423

PubMed Abstract | CrossRef Full Text | Google Scholar

Kam, M., İpekçi, A., and Şengül, Ö. (2023). Investigation of the effect of FDM process parameters on mechanical properties of 3D printed PA12 samples using taguchi method. J. Thermoplast. Compos. Mater. 36, 307–325. doi:10.1177/08927057211006459

CrossRef Full Text | Google Scholar

Markatos, D. N., and Pantelakis, S. G. (2022). Assessment of the impact of material selection on aviation sustainability, from a circular economy perspective. Aerospace 9, 52. doi:10.3390/aerospace9020052

CrossRef Full Text | Google Scholar

Morelli, F., Neugebauer, J. M., LaFiandra, M. E., Burcham, P., and Gordon, C. T. (2014). Recoil measurement, mitigation techniques, and effects on small arms weapon design and marksmanship performance. IEEE Trans. human-machine Syst. 44, 422–428. doi:10.1109/thms.2014.2301715

CrossRef Full Text | Google Scholar

Piedra-Cascón, W., Krishnamurthy, V. R., Att, W., and Revilla-León, M. (2021). 3D printing parameters, supporting structures, slicing, and post-processing procedures of vat-polymerization additive manufacturing technologies: a narrative review. J. Dent. 109, 103630. doi:10.1016/j.jdent.2021.103630

PubMed Abstract | CrossRef Full Text | Google Scholar

Płatek, P., Sienkiewicz, J., Janiszewski, J., and Jiang, F. (2020). Investigations on mechanical properties of lattice structures with different values of relative density made from 316L by selective laser melting (SLM). Materials 13, 2204. doi:10.3390/ma13092204

PubMed Abstract | CrossRef Full Text | Google Scholar

Rychlewski, J. (1984). On Hooke’s law. J. Appl. Math. Mech. 48, 303–314. doi:10.1016/0021-8928(84)90137-0

CrossRef Full Text | Google Scholar

Solomon, I. J., Sevvel, P., and Gunasekaran, J. (2021). A review on the various processing parameters in FDM. Mater. Today Proc. 37, 509–514. doi:10.1016/j.matpr.2020.05.484

CrossRef Full Text | Google Scholar

Suchocki, C., and Ewertowski, J. (2017). Experimental and finite element studies on man-rifle reaction force. Problems Mechatronics Armament Aviat. Saf. Eng. 8, 7–22. doi:10.5604/01.3001.0009.8991

CrossRef Full Text | Google Scholar

Wanhao. 3D printing resin rubber resin flexible resin 250ml/500ml/1000ml/bottl (2024). Wanhao. Available online at: https://wanhao.store/products/3d-printing-resin-rubber-resin-1000ml-bottle. Accessed 12 September 2024

Google Scholar

Xu, P., Guo, W., Yang, L., Yang, C., and Zhou, S. (2024). Crashworthiness analysis and multi-objective optimization of a novel metal/CFRP hybrid friction structures. Struct. Multidisc Optim. 67, 97. doi:10.1007/s00158-024-03795-x

CrossRef Full Text | Google Scholar

Yang, C., Nan, Z., Huo, Y., Yang, Y., Xu, P., Xiao, Y., et al. (2025a). Design, characterisation, and crushing performance of hexagonal-quadrilateral lattice-filled steel/CFRP hybrid structures. Compos. Part B Eng. 304, 112631. doi:10.1016/j.compositesb.2025.112631

CrossRef Full Text | Google Scholar

Yang, C., Huo, Y., Meng, K., Zhou, W., Yang, J., and Nan, Z. (2025b). Fatigue failure analysis of platform screen doors under subway aerodynamic loads using finite element modeling. Eng. Fail. Anal. 174, 109502. doi:10.1016/j.engfailanal.2025.109502

CrossRef Full Text | Google Scholar