Load detection of industrial robots in manufacturing environment based on improved FNO network

Introduction: To tackle the insufficient accuracy in load detection of industrial robots, this study proposes a load detection approach based on a Fourier neural network.

Methods: First, a robot dynamics model is constructed, and a Fourier neural operator is introduced to extract spatial physical information. In addition, an attention mechanism is integrated to enhance key load information and mitigate the influence of the external environment.

Results: In the load detection experiment, the proposed model achieved the best prediction accuracy compared with similar models. For example, when the load was 2 kg, 2.5 kg, and 3 kg, the predicted loads were 2.0044 kg, 2.5102 kg, and 3.0190 kg, respectively. Moreover, the model exhibited excellent fusion error compensation performance: the average error in fusion after compensation was 0.82 ms, and the maximum delay time after error correction remained within 3.25%. In terms of single - sample inference time, the proposed model performed best (5.1 ms), which was better than that of similar techniques.

Discussion: The proposed model shows good application effects and will provide technical support for parameter recognition and control optimization of industrial robots.

1 Introduction

With the development of industrial automation, the application of industrial robots in intelligent manufacturing is becoming increasingly widespread. Performance improvement is crucial for production efficiency and product quality (Bo et al., 2022). Accurately identifying robot parameters is a key link in improving robot motion accuracy, dynamic performance, and human-machine cooperation safety. Recently, numerous scholars have conducted research on parameter identification such as load detection and control for industrial robots (Kakinuma et al., 2022). Huang et al. conducted research on the dynamic parameter estimation problem of industrial robots. An iterative hybrid least squares algorithm was proposed. This algorithm estimated the basic parameters and joint friction torque of the robot through an internal and external loop structure, combined with linear matrix inequalities. The experiment showed that this method had high accuracy in parameter recognition and significantly improved the accuracy of mechanical control (Huang et al., 2022). Chen and Zhan explored the insufficient kinematic calibration of industrial robot drilling and riveting. A method based on an improved beetle swarm optimization algorithm was proposed, which adopted a preference random replacement and a dynamic parameter adjustment strategy. The positioning error of the robot’s end-effector was significantly improved compared to the original, which was also significantly superior to similar technologies (Chen and Zhan, 2022). Santhosh R et al. conducted research on operational optimization and product quality improvement in the robot painting industry. The study combined real and virtual research to deeply analyze the motion parameter information of industrial robots, and used dynamic devices and deep learning for morphological parameter evaluation. Taguchi L9 orthogonal experiment and variance analysis were used to determine key factors, while the machine learning was introduced for automatic defect classification and recognition. The test results showed that this technology could accurately identify the parameters of industrial robots and optimize the working effect of robots (Santhosh et al., 2024).

Neural networks, as a powerful nonlinear modeling tool, can handle complex dynamic systems and uncertainty problems. Therefore, it has received widespread attention in the field of industrial robot parameter recognition. Yuan and Sun conducted research on dynamic parameter identification of industrial robots. A method integrated calibration and deep learning identification method was proposed. This method adopted axis configuration space and adjoint error model, simplifying the operation process through static experiments and improving the accuracy of parameter identification. Experimental analysis showed that this technology could improve the recognition accuracy for spatial targets and optimize the control effect (Yuan and Sun, 2023). Ruan et al. explored the target recognition and grasping problems of industrial robots in complex spaces. An autonomous target recognition method based on image feature processing was proposed. A parallel binocular stereo vision system was constructed to achieve high-precision positioning of robot end-effector grasping. The experimental results showed that the technology had good control accuracy, but this method was sensitive to parameter changes, which could affect the control accuracy (Ruan et al., 2023). Yang et al. proposed a calibration model based on extended Kalman filter to address the absolute positioning accuracy in industrial robotic arms. This method significantly improved calibration accuracy by addressing geometric errors and eliminating non-geometric errors. The model performed better than existing techniques on multiple datasets (Yang et al., 2023). Lu et al. conducted research on the load estimation of industrial machines. An optimization method based on a semi-parametric friction model was proposed. This method recognized robot loads by improving the torque observer and optimizing the robot configuration. Experiments showed that this technology had good application effects, but complex scenarios still had low computational efficiency (Lu et al., 2023). Selami et al. conducted research on the positioning accuracy of industrial robots. A calibration method based on an improved Denavit Hartenberg model was built. By calibrating the distance error model, the positioning and distance errors were significantly reduced. This method performed well in improving absolute position accuracy. However, it had a strong dependence on sensor accuracy and calibration equipment, and the calibration process was relatively complex (Selami et al., 2023). Tsapin D explored the application of industrial and logistics robots in civil facility security, and proposed a solution based on big data and computer vision algorithms to address the increasing crime and decreasing identification of criminals in the Russian Federation. By training convolutional neural networks on various architectures and introducing squeeze and excitation blocks, the recognition accuracy of semantic markers of vehicle damage was significantly improved. Under complex video shooting conditions, this method had the same accuracy as traditional methods, but significantly improved speed, providing a more efficient and accurate detection method for parking lot computer vision systems (Tsapin et al., 2024).

In summary, industrial robots currently play a crucial role in the field of industrial manufacturing, and numerous scholars have conducted research on parameter identification issues such as load detection and control of industrial robots. However, current industrial robots still face shortcomings in the field of robot parameter recognition. Traditional dynamic models face three limitations in complex working conditions: (1) Joint friction and temperature drift under low-load conditions significantly increase detection errors; (2) Environmental interference (such as structural flexibility deformation) causes distortion in the solution of the load force matrix; (3) There is an inherent contradiction between real-time requirements and computational complexity. Therefore, the research proposes a core hypothesis: Based on the Fourier Neural Operator (FNO) frequency domain feature extraction mechanism and the attention guided error compensation, it can synchronously solve the low-load sensitivity and environmental interference. There are two innovations in the research. One is to introduce the FNO network to extract spatial physical information and improve the accuracy of load data recognition. The second introduces the Frequency Domain Expansion-Attention Neural Network (FADA) to optimize feature extraction, while using error compensation to improve external environmental impact, further enhancing load detection accuracy. The research content will provide technical reference for high-precision control of industrial robots.

2 Methods and materials

2.1 Load analysis of industrial robots based on dynamics

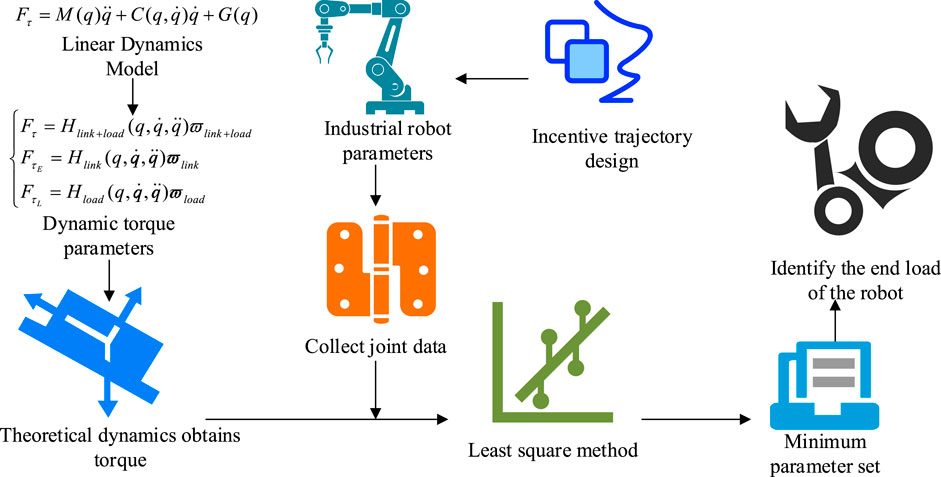
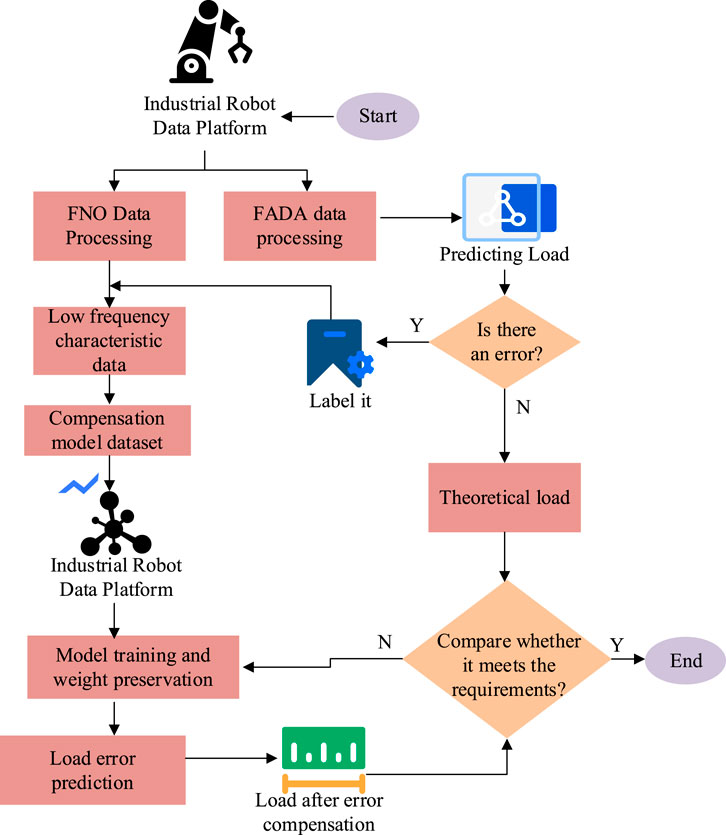
With the advancement of intelligent manufacturing, the demand for intelligence and high-precision control of industrial robots in complex operations is increasing. Robots in different application scenarios require different loads. Therefore, effective industrial robot load detection is the key to ensuring high-precision control. The load detection process of industrial robots is shown in Figure 1.

Figure 1

Figure 1. Industrial robot load detection process.

From Figure 1, industrial robot load detection includes several key processes such as dynamic modeling, excitation trajectory design, data acquisition and processing, and parameter estimation (Papavasileiou et al., 2025). The study focuses on industrial 6-axis robots and uses Fourier series for excitation trajectory design based on the robot dynamics model. The least squares estimation method is used for load solution. The nonlinear dynamic model of the 6-axis industrial robot is shown in Equation 1.

$F_{\tau }=M\left(q\right)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+G\left(q\right)(1)$

In Equation 1, $\dot{q}$ refers to the joint velocity. $q$ refers to the joint position. $\ddot{q}$ refers to the joint acceleration. $F_{\tau }$ refers to the joint torque. $C$ represents the centrifugal force matrix. $G$ refers to the gravity matrix. When industrial robots perform processing tasks, a load is usually applied to their end to perform the corresponding task. The end joint mass is shown in Equation 2 (Luo et al., 2024).

$m=m_V+m_Q(2)$

In Equation 2, $m_Q$ represents the increased load mass. $m_V$ is the self-weight of the end joint. Next, it is necessary to separate the load dynamics related parameters from the industrial robot dynamics parameters to obtain the end joint load parameter model, as shown in Equation 3.

$\left\{\begin{array}{l}{F}_{\tau }=H_{link+load}\left(q,\dot{q},\ddot{q}\right){\varpi }_{link+load}\\ F_{{\tau }_E}=H_{link}\left(q,\dot{q},\ddot{q}\right){\varpi }_{link}\\ F_{{\tau }_L}=H_{load}\left(q,\dot{q},\ddot{q}\right){\varpi }_{load}\end{array}\right.(3)$

In Equation 3, $F_{\tau }$, $F_{{\tau }_E}$ and $F_{{\tau }_L}$ represent three states of torque: loaded, unloaded, and end loaded, respectively. Their corresponding observation matrices are $H_{link+load}$, $H_{link}$, and $H_{load}$, and their corresponding parameter matrices are ${\varpi }_{link+load}$, ${\varpi }_{link}$, and ${\varpi }_{load}$. According to the parameter model, the dynamic parameters under load can be calculated. Next, the study uses Fourier series for excitation trajectory design, representing the original joint parameters in the form of sine and cosine sums to reduce data sampling errors and improve the accuracy of subsequent load parameter detection (Silik et al., 2023). $i$ is defined as the $i$-th joint number of the industrial robot. $j$ is the fundamental frequency index of the excitation trajectory. The updated parameter $q$ is shown in Equation 4.

$q_i\left(t\right)=q_{i0}+{\displaystyle \sum _{k=1}^k}\left[{\left(a_i\right)}_k\sin \left(k{\omega }_{j}t\right)+{\left(b_i\right)}_k\cos \left(k{\omega }_{j}t\right)\right](4)$

In Equation 4, ${\omega }_j$ signifies the fundamental frequency of the trajectory. ${\left(a_i\right)}_k$ and ${\left(b_i\right)}_k$ are both Fourier order correlation coefficients. $k$ is the parameter quantity, set to 5 in the study. $q_{i0}$ represents the joint offset. $t$ represents the sampling time. The updated $\dot{q}$ is shown in Equation 5.

${\dot{q}}_i\left(t\right)={\displaystyle \sum _{k=1}^k}k{\omega }_j\left[{\left(a_i\right)}_k\cos \left(k{\omega }_{j}t\right)+{\left(b_i\right)}_k\sin \left(k{\omega }_{j}t\right)\right](5)$

The joint acceleration $\ddot{q}$ is continuously updated, as shown in Equation 6.

${\ddot{q}}_i\left(t\right)=-{\displaystyle \sum _{k=1}^k}{\left(k{\omega }_j\right)}^2\left[{\left(a_i\right)}_k\sin \left(k{\omega }_{j}t\right)+{\left(b_i\right)}_k\cos \left(k{\omega }_{j}t\right)\right](6)$

To effectively detect the load status of industrial robots, it is necessary to collect raw data from each joint. The research adopts TCP/IP protocol for robot control, and uses Windows Sockets protocol programming to obtain parameter information such as joint current and acceleration of the robot itself (Liu et al., 2023a). Considering the impact of network environment fluctuations on data collection, this study introduces moving average filtering to process data and improve data changes. Next, the study introduces the least squares method to solve the collected end load and obtain robot load information (Nengem, 2023). The objective function is shown in Equation 7.

$J\left({\widehat{\varpi }}_{load}\right)={\displaystyle \sum _{i=1}^n}{\left({\tau }_{ai}-H_{ai}\left(q_i,{\dot{q}}_i,{\ddot{q}}_i\right){\widehat{\varpi }}_{load}\right)}^2(7)$

In Equation 7, ${\tau }_{ai}$ represents the target torque. $H_{ai}$ represents the target observation matrix. ${\widehat{\varpi }}_{load}$ represents the target dynamic parameters. $n$ represents the number of data points collected. Next, the least squares method is used to estimate the dynamic parameters of the target, as shown in Equation 8.

${\widehat{\varpi }}_{load}={\left({\displaystyle \sum _{i=1}^n}{H}_{ai}{\left(q_i,{\dot{q}}_i,{\ddot{q}}_i\right)}^2\right)}^{-1}{\displaystyle \sum _{i=1}^n}{\tau }_{ai}{H}_{ai}\left(q_i,{\dot{q}}_i,{\ddot{q}}_i\right)(8)$

2.2 Modeling of industrial robot load detection based on FNO network

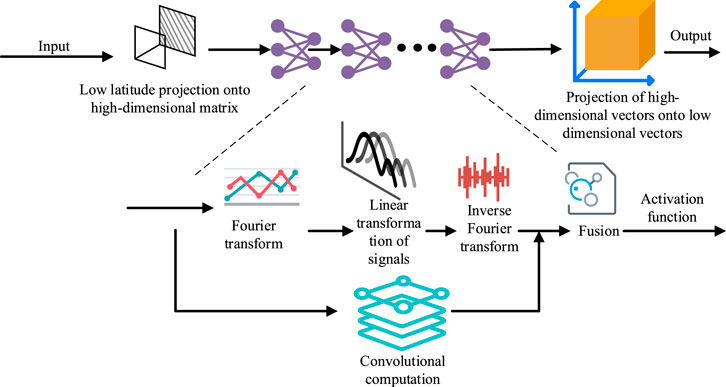
In the previous subsection, a fundamental analysis of robot load is completed based on a dynamic model. Although the load status of the robot is identified from the extracted raw data, the accuracy is low and cannot meet high-precision load detection. Therefore, the study introduces FNO networks to process raw data. The FNO network can perform Fourier transform on the extracted spatial physical information data, and use kernel integration operators to operate on the transformed data to obtain low-frequency feature data in the original data. Accurate load information can be obtained through partial differential solution. The FNO network framework is shown in Figure 2.

Figure 2

Figure 2. FNO network framework.

According to Figure 2, the physical spatial data is Fourier layered into high-latitude space and transformed into the Fourier domain through Fourier transformation. Then, the low-frequency signal is retained through linear transformation, and the data is adjusted to physical space through inverse transformation to preserve more accurate load characteristic information (Basiri et al., 2023). The iterative process of FNO network is shown in Equation (9).

$Y_{r+1}\left(x\right)=\sigma \left(W{Y}_t\left(x\right)+\left(\mathrm{ƛ}\left(a,\varphi \right)Y_t\right)\left(x\right)\right)(9)$

In Equation 9, $\sigma$ represents the activation function. $\mathrm{ƛ}\left(a,\varphi \right)$ represents the integral operator. $W$ represents a local linear transformation. $Y_t\left(x\right)$ represents the input. $x$ represents the spatial physical information. $\left.\left(K\left(a,\varphi \right)v_t\right)\left(x\right)\right)$ is the Fourier kernel integration operator. After Fourier transform, the Fourier kernel integration operator is calculated, as shown in Equation 10.

$\left(\mathrm{ƛ}\left(a,\varphi \right)Y_t\right)\left(x\right)={\mathcal{l}}^{-1}\left(\mathcal{l}\left({\mathrm{ƛ}}_{\varphi }\right)\mathcal{·}\mathcal{l}\left(Y_t\right)\right)\left(x\right),\forall x\in D(10)$

In Equation 10, $\mathcal{l}$ represents the Fourier transform. ${\mathrm{ƛ}}_{\varphi }$ represents the integral operator. The study uses Euclidean norm and mean square error as evaluation functions for FNO networks. The mean square error can effectively distinguish the difference between the label and the predicted value, and improve the convergence effect by reducing the error, as presented in Equation 11 (Cao et al., 2023).

$MSE=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(f\left(x\right)-y\right)}^2(11)$

In Equation 11, $y$ refers to the actual label. $f\left(x\right)$ represents the output value. $n$ is the sample size. In addition, the network utilizes the Euclidean norm to calculate information errors, which provides better feedback on network performance, as displayed in Equation 12.

$T_2=\sqrt{{\displaystyle \sum _{i=1}^d}{\left(y_x-f\left(x_i\right)\right)}^2}(12)$

In Equation 12, $d$ represents the number of summation terms. $y_x$ refers to the label. $x_i$ represents the network output value. In addition, to improve the robustness and convergence of the FNO network and optimize the parameter learning effect, the Adam algorithm is taken as the optimizer for the network. The dynamic parameter after gradient update is shown in Equation 13.

$\Delta \theta =-\alpha \times \widehat{s}/\left(\sqrt{\widehat{r}}+\delta \right)(13)$

In Equation 13, $\alpha$ represents the learning rate. $\widehat{r}$ represents the cumulative variable. $\widehat{s}$ represents the gradient update direction parameter. $\delta$ represents the adjusted parameter. Through the above optimization, the study sets the learning rate of the network to 0.001. The entire load detection process of industrial robots based on FNO network is shown in Figure 3.

Figure 3

Figure 3. Load detection process of industrial robots based on FNO network.

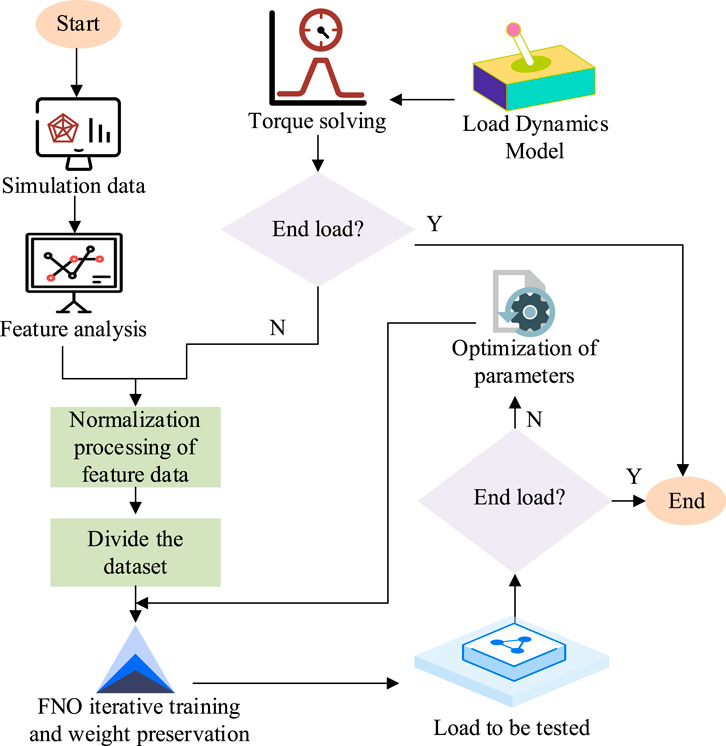
According to the load detection process in Figure 3, the original physical space data and physical end load data are first subjected to feature normalization, and the dataset is divided. Then, the data is input into the FNO network for training, and the Fourier transform is used to filter out low-frequency signals that retain more features. The final industrial robot load detection results are obtained through data feature analysis.

2.3 Modeling of industrial robot load detection based on improved FNO network

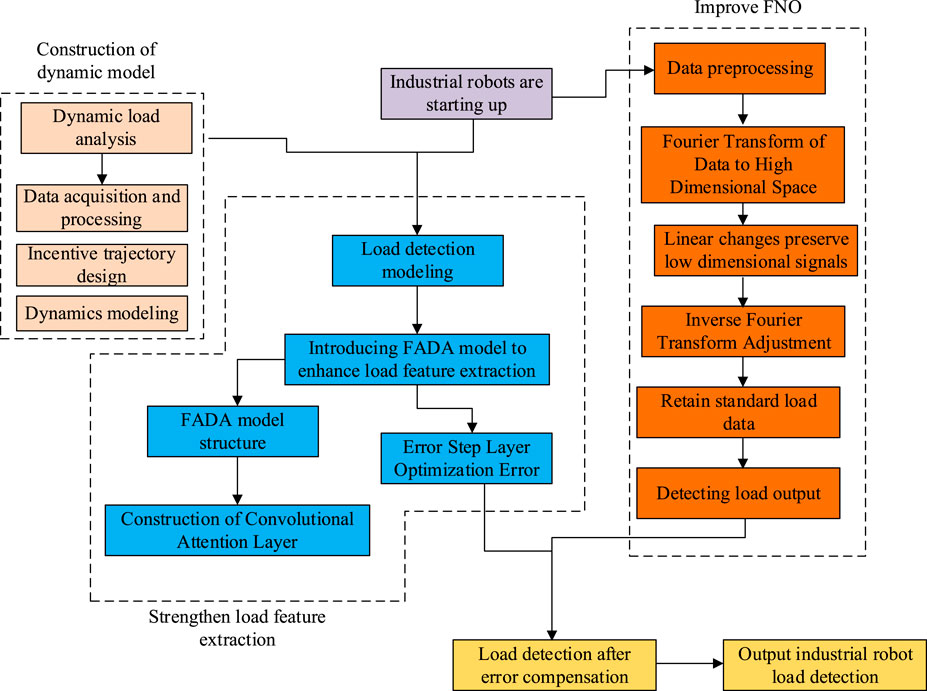
The previous subsection adopts the FNO network for load data analysis and solving to extract more accurate load information and improve the load detection accuracy of industrial robots. However, traditional FON networks also face shortcomings in load feature extraction, including limitations in low-frequency feature extraction. They mainly extract low-frequency feature data through Fourier transform, while load information not only includes low-frequency features, but also has high-frequency detail features. In addition, FNO only relies on the frequency domain features obtained from Fourier transform, which may not fully characterize the complex nonlinear relationship between load and robot dynamic parameters. To address the aforementioned issues, further improvements will be made to the FNO network. The FADA model is introduced to enhance the attention and extraction of important load features of industrial robots by FNO network. Figure 4 presents the structure of the FADA.

Figure 4

Figure 4. Schematic diagram of FADA model structure.

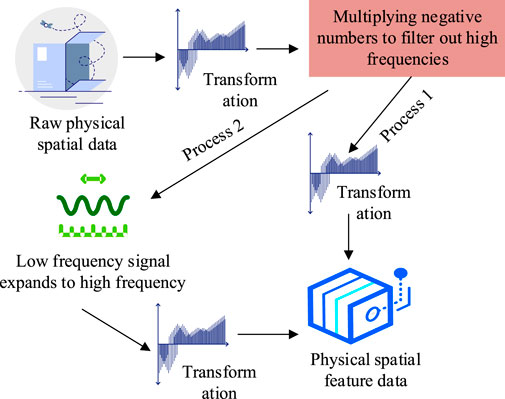
From Figure 4, the Fourier module in the original FNO network can only filter and process specific high-frequency information in the raw data, and then use linear transformation to obtain corresponding feature signals. After introducing FADA, if there is insufficient accuracy in processing low-frequency feature signals (process 2), FADA data processing can continue (process 1). It expands low-frequency information to high-frequency signals, jointly outputting high-frequency and low-frequency features and improving the accuracy of load information extraction. The FADA model includes convolutional attention layers, convolutional layers, input layers, and output layers, where the convolutional attention layer is composed of two parts, spatial attention and channel attention, connected in series (Zhang et al., 2023). The channel attention weighting coefficient is defined as $Gc\left(F\right)$, as shown in Equation 14.

$Gc\left(F\right)=F_c·\sigma \left(W_m\left[c\right]\right)·\sigma \left(W_c\left[c\right]\right)(14)$

In Equation 14, $W_c$ and $W_m$ represent two linear layer weight parameters. $\sigma$ represents the activation function. $c$ represents the convolution calculation. The spatial attention weighting coefficient is shown in Equation 15.

$G_s\left(F^{-}\right)=\sigma \left(c^{7\times 7}\left(M_2;E_2\right)\right)(15)$

In Equation 15, $E_2$ represents the global maximum feature. $M_2$ represents the global average feature. By concatenating the $E_2$ and $M_2$ features, a new feature map with important detailed features can be obtained. Then, FADA is used to extend the feature data from low-frequency to high-frequency, and combined with the original low-frequency data to jointly output (Lokhande and Ganorkar, 2025). In addition, the study also considers that the dynamic model of industrial robots cannot reflect information such as temperature and flexible deformation of linkage motion. Therefore, there are still errors in actual load detection (Liu et al., 2023b; Jia et al., 2024). To compensate for the aforementioned error issues, a compensation layer is added to optimize the error, that is, adding an error compensation layer based on convolutional networks in the FADA output. Its main function is to use the deviation between the benchmark value and the theoretical load as the network training label, and use the deviation compensation layer and FADA to achieve overall data discrimination, thereby optimizing the load detection error caused by external factors (Bastl et al., 2023). The output of the compensation layer is presented in Equation 16.

$F^{n+1}\left(i,j\right)={\displaystyle \sum _{R=1}^{R_i}}{\displaystyle \sum _{x=1}^f}{\displaystyle \sum _{y=1}^f}\left[Y_R^n\left(s_{0}i+x,s_{0}j+y\right){\omega }_R^{n+1}\left(x,y\right)\right]+b(16)$

In Equation 16, $f$ represents the size of the convolution kernel. $b$ represents the bias. $R$ represents the number of network channels. $s_0$ represents the convolution stride. ${\omega }_R$ represents the channel layer weight. $Y_R^n$ represents the input of network $n+1$. In addition, in load detection based on industrial robot dynamics models, the parameter estimation of Equation 8 is affected by current fluctuations, and there are nonlinear errors that have not been considered. These errors are mainly caused by factors such as temperature and deformation (Koshelev, 2024). Therefore, a load detection error compensation process is added, as shown in Figure 5.

Figure 5

Figure 5. Load error compensation process.

According to Figure 5, to improve the accuracy of load detection for industrial robots, based on the raw physical information of robots, dynamic models and FNO networks are used to identify and predict loads. Meanwhile, to improve the detection accuracy of load by FNO, FADA model and convolutional network are introduced to enhance the raw data learning and extract important features. Finally, based on the deviation of the theoretical load and the prediction results of the convolutional network, the error correction is performed by combining the two types of data to obtain the industrial robot load detection results. The whole technical process is shown in Figure 6.

Figure 6

Figure 6. The whole technical process.

According to Figure 6, the whole technology includes three parts: dynamic load analysis, load detection modeling based on FNO network, and load detection modeling of improved FNO network. The technical research is completed through the joint design of the three parts.

3 Results

3.1 Experimental analysis of industrial robot load based on improved FNO network

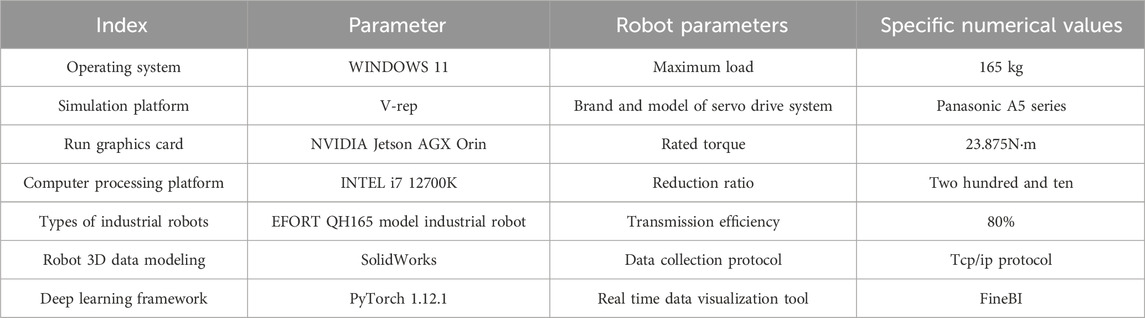
Next, to verify the application effect of the industrial robot load detection technology, corresponding experiments are conducted. The load detection case empirical analysis of EFORT QH165 six axis industrial robot in the automotive manufacturing industry is conducted. The robot has a maximum load of 165 kg and adopts a Panasonic A5 series servo drive system (rated torque 23.875N·m, reduction ratio 210, and transmission efficiency 80%). Experimental process data analysis method explanation: The study uses TCP/IP protocol and Windows Sockets programming to obtain real-time raw data such as joint current and acceleration (sampling frequency 120 Hz, cycle 20 s, and sample size 8,952). The research on data preprocessing process adopts moving average filtering to eliminate network fluctuation noise and extract load change trends. In addition, the improved FNO network module is deployed in the pytorch framework. The low-frequency load characteristics are extracted by Fourier transform, and the key information recognition is strengthened by combining FADA attention mechanism. The real-time data including current and load pressure are visually viewed by finebi tool. The software and hardware parameter information of the experimental environment is shown in Table 1.

Table 1

Table 1. Experimental environment parameter information.

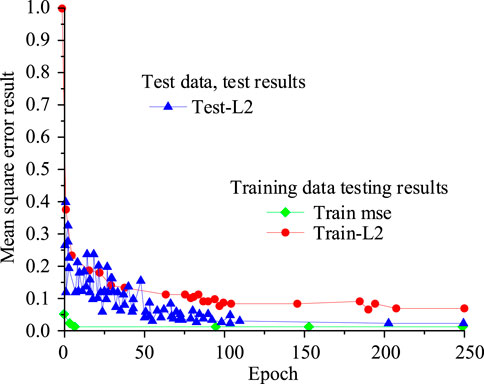
According to Table 1, SolidWorks platform is used for 3D modeling of the motion process of industrial robots, and V-rep is employed for simulation experiment analysis. In addition, the initial model training and parameter optimization are completed on desktop computers equipped with Intel i7-12700K and NVIDIA Jetson AGX Orin. After the final model is determined, it is deployed to the edge IPC (Industrial Personal Computer) located at the factory site for actual load detection verification. Edge IPC uses the same NVIDIA Jetson AGX Orin GPU as the desktop training platform to ensure consistency in computing architecture and avoid inference bias caused by hardware differences. The number of terms K of Fourier series is set to 5 in the experimental process, which is determined by trajectory optimization experiment to balance the data sampling error and computational complexity, and ensure the load parameter detection accuracy. In addition, the learning rate α is set to 0.001, which is set based on the gradient update stability requirement in the Adam optimizer of FNO network. The network batch size is set to 64 to ensure the balance between the processing speed of single batch data and the generalization ability of the model. In the experiment, the current information of the end joint of the industrial robot is collected, and the robot load is detected through torque conversion calculation. The experimental collection period is set to 20 s, the sampling frequency is 120 Hz, and a total of 8,952 samples are collected. The preferred research is to test the training accuracy of neural networks, and the loss function curves of the neural network on test and training sets are shown in Figure 7.

Figure 7

Figure 7. Results of neural network training loss function.

According to Figure 7, the green and red colors represent the training data loss results, the blue color represents the test data loss results, and the evaluation function is the L2 norm. After 250 iterations, the loss function and evaluation function maintained a similar curve. In the test dataset, there were significant fluctuations in the early stage, but gradually stabilized after 100 iterations and maintained a low-loss state, indicating that the neural network has good training performance. Next, the study needs to select the optimal load torque solution method as the computational basis. Common torque solution methods include Global Parameter method (GP), Parameter Difference method (PD), and Torque Solution method (TS). The load detection results are shown in Figure 8 (Amer et al., 2024).

Figure 8

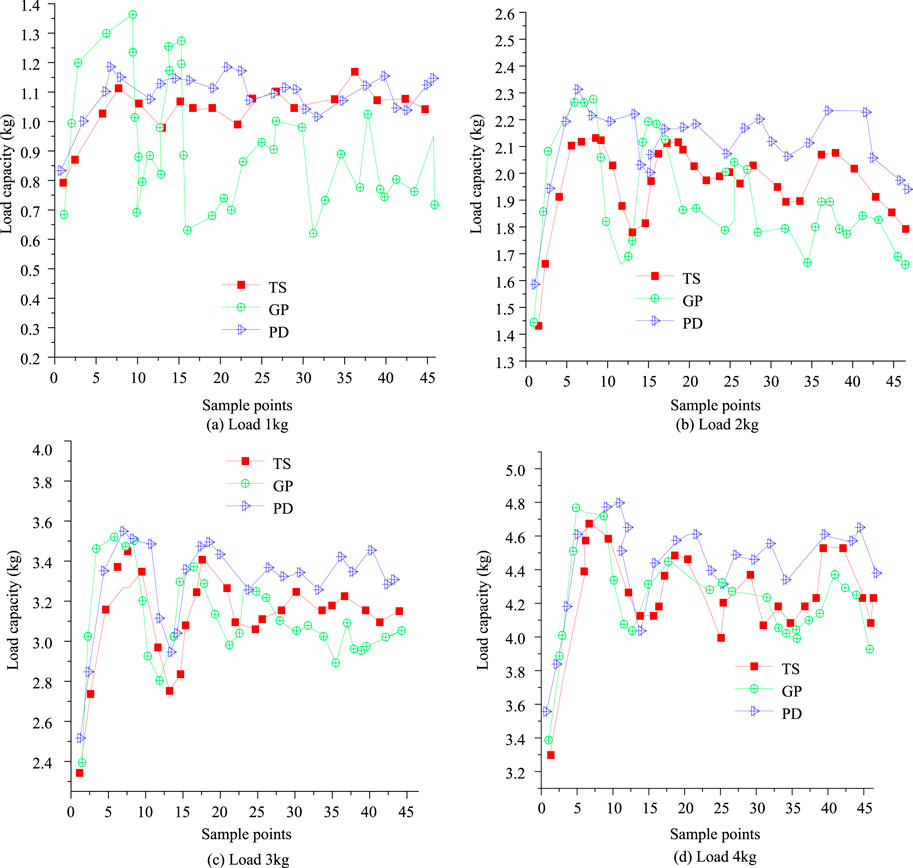
Figure 8. Comparison of the effectiveness of three torque solving methods. (a) Load 1 kg. (b) Load 2 kg. (c) Load 3 kg. (d) Load 4 kg.

Figure 8a shows the test results under a load of 1 kg. GP had significant fluctuations in the solution process, especially in the early sampling where the load fluctuation exceeded the actual load by more than 50%, resulting in poor comprehensive solution performance. The TS and PD solutions were closer, but TS was closer to the actual 1 kg load and had higher accuracy. Figure 8b shows the test results of a 2 kg load scenario. There were significant fluctuations in the three solution methods in the early stage under 2 kg load. In the later stage, the sampling points of TS and PD were closer to the actual 2 kg load solution results, but overall TS still performed better. Figure 8c shows the test results of the 3 kg load scenario. In the early stage, all three solutions had significant deviations from the collected load, but gradually stabilized in the later stage. The GP solution method was closer to the actual value. Figure 8d shows the test results of the 4 kg load scenario. The three methods still have significant fluctuations in the early stages, and the overall accuracy of load solution is poor. Overall, the TS solution method is closer to the actual load of 4 kg and has better comprehensive performance. Next, the relative errors and time consumption of the three solving methods are compared, as presented in Figure 9.

Figure 9

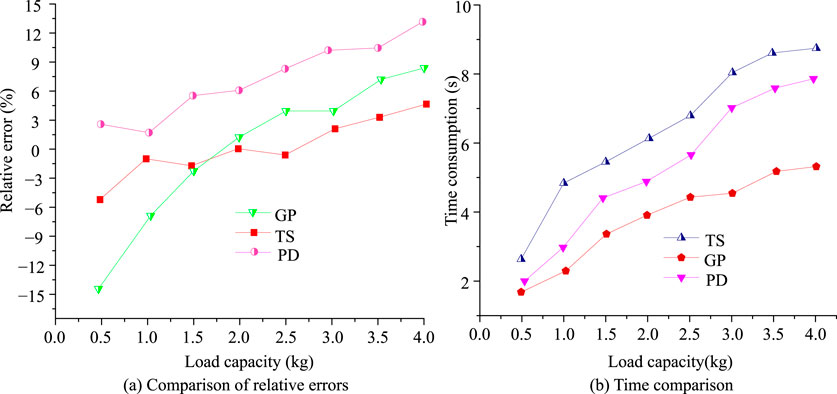
Figure 9. Comparison of relative error and time consumption of three solving methods. (a) Comparison of relative errors. (b) Time comparison.

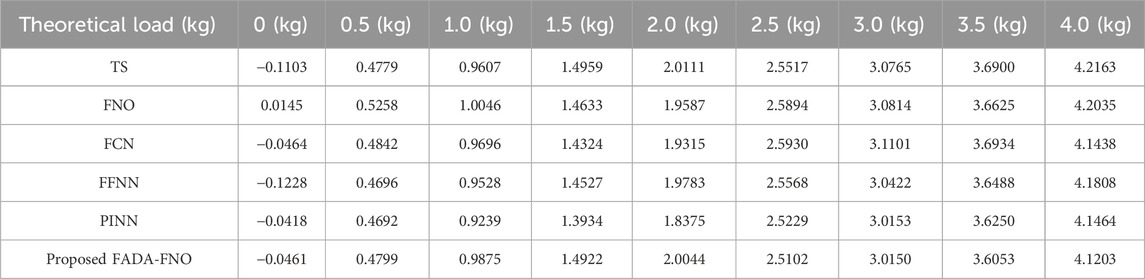
Figure 9a displays the comparison results of relative errors. According to testing, the accuracy of traditional TS solution was lower than that of GP in low-load conditions. For example, when the load was 0.5 kg, the relative error of GP was 2.95%, while that of TS was −5.72%. As the load increased, the accuracy of TS solution was significantly higher. For example, when the load was 4 kg, the relative errors of TS and GP were 3.22% and 8.14%, respectively. Figure 9b compares the time consumption of three solving methods. According to the test results, TS had a longer solving time compared to GP and PD, mainly because it performed two inverse operations, which slowed down the calculation speed. Based on the above results, the study adopts TS as the fundamental method for load solving to ensure the load prediction accuracy. The study introduces FNO network to optimize its low-load detection and solving time problems, and extract key features by introducing FADA model. The learning rate of the proposed FADA-FNO is 0.01, the batch size is 64, and the number of Fourier layers is 4. In the experiment, Fully Convolutional Network (FCN), Feedforward Neural Network (FFNN), and Physics-Informed Neural Network (PINN) are introduced to compare the effect of force matrix solving with the FADA-FNO model. The comparison of load prediction performance among multiple models is presented in Table 2.

Table 2

Table 2. Load prediction accuracy of different models.

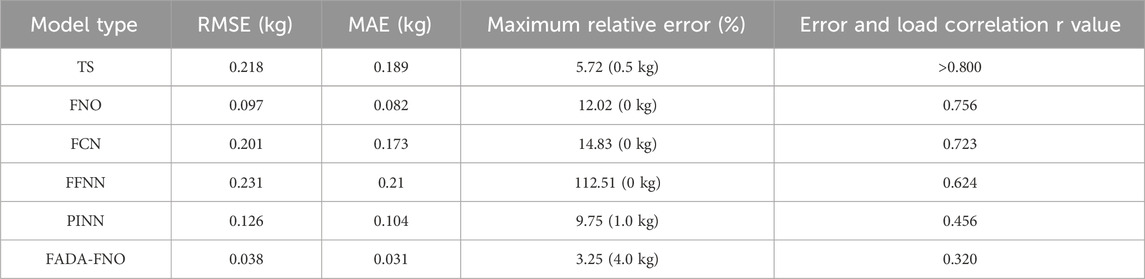
In the multi-model load prediction in Table 2, the overall performance of the proposed model was better, but the performance was relatively average at the low-load. When the load was 0 kg, the predicted value of PINN was closer to the actual load of 0 kg, and the prediction accuracy performed the best, with a predicted load of −0.0418 kg. Next was the proposed model, with a predicted load of −0.0461 kg. When the load was 0.5 kg, the FCN was closer to the actual value at 0.4842 kg, followed by the proposed model at 0.4799 kg. As the load gradually increased, such as when the load was 2 kg, 2.5 kg, and 3 kg, the prediction accuracy of the proposed model was the best, which were 2.0044 kg, 2.5102 kg, and 3.0150 kg, respectively. To further analyze the effectiveness of different technologies in load prediction, the load prediction is quantitatively analyzed, with a load testing range of 0–4.0 kg, and the end joints of industrial robots are loaded to simulate the handling scenario of automotive components (Engine pistons, connecting rods, flywheels, etc.). Quantitative analysis indicators such as Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) are introduced for analysis. The quantitative analysis of load prediction for different technologies is shown in Table 3.

Table 3

Table 3. Quantitative analysis of load prediction for different technologies.

According to the test results in Table 3, the RMSE of the proposed model was 0.038 kg in the typical load range of 2.0–4.0 kg, which was 60.8% lower than that of FNO and 82.6% lower than that of traditional TS method TS. The proposed model uses Fourier transform to effectively extract low-frequency dominant features, while the FADA module enhances the signal-to-noise ratio of low-load signals through frequency domain extension. In addition, in the low-load 0.5 kg test, the absolute error of the proposed model was 3.25 (0.0201 kg), while the TS method was 5.72% (0.5 kg), which was significantly lower than that of the FNO’s 12.02 (0 kg). Finally, in the load sensitivity analysis, the error of the traditional model (TS/FCN) was strongly negatively correlated with the load (r > 0.8), while the correlation of the proposed model was weak, and r = 0.32. The proposed model has good resistance to load disturbances. Next, the relative errors and time consumption of different loads are compared, as shown in Figure 10.

Figure 10

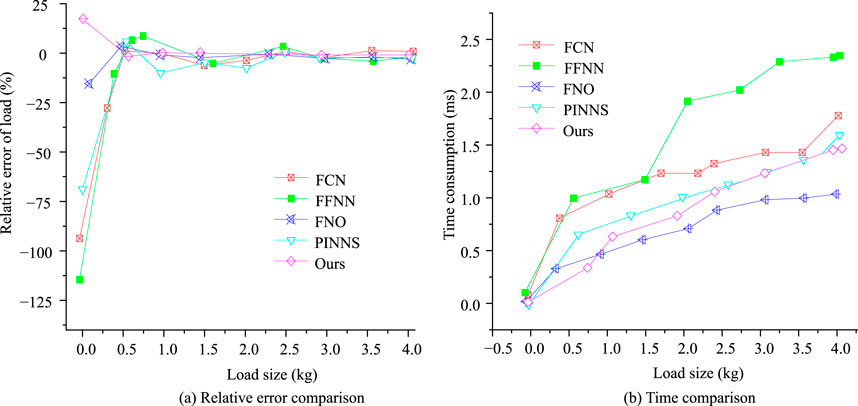
Figure 10. Comparison of relative errors and time consumption among different models. (a) Relative error comparison. (b) Time comparison.

Figure 10a shows the comparison results of relative errors. The results showed that FFNN and FCN had significant errors in the early stage of low-load. For example, when the load size was 0 kg, the detection errors of FFNN and FCN models were −112.51% and −92.25%, respectively, which were larger than those of other models. Further analysis revealed that FNO and the proposed model performed the best on prediction accuracy, with both models being able to control the average error within 6.2% at low-loads. As the load increases, the prediction accuracy of the proposed model is significantly better than that of similar models, and its stability is also stronger. The overall average relative error was 3.25%, indicating the best performance. Meanwhile, a single FNO network also exhibits excellent performance, with an average relative error of 4.58%. Figure 10b compares the time consumption of multiple models. The test results showed that FNO took significantly less time, followed by the proposed model, and FFNN took the longest time. The proposed model took longer time compared to FNO, mainly due to the added FADA module, which enhances load feature extraction and increases model computation time. However, it performs equally well in time-consuming calculations. In addition, at the same 120 Hz sampling rate, FNO took an average of 0.81 ms per sample, while the proposed model took 0.82 ms, showing significantly better performance than similar models.

3.2 Analysis of load detection for industrial robots incorporating error compensation

In the previous subsection, the study tests the performance of the proposed improved FNO network. However, in actual industrial robot load detection, the load is also easily affected by temperature, flexible deformation, and other factors, leading to increased errors. To address this issue, error compensation is introduced to improve the load detection performance. Firstly, the ablation experiment analysis is conducted, including individual FNO, FNO + FADA, and FNO + FADA + CNN. The ablation experiment tests are shown in Table 4.

Table 4

Table 4. Analysis of ablation experiments.

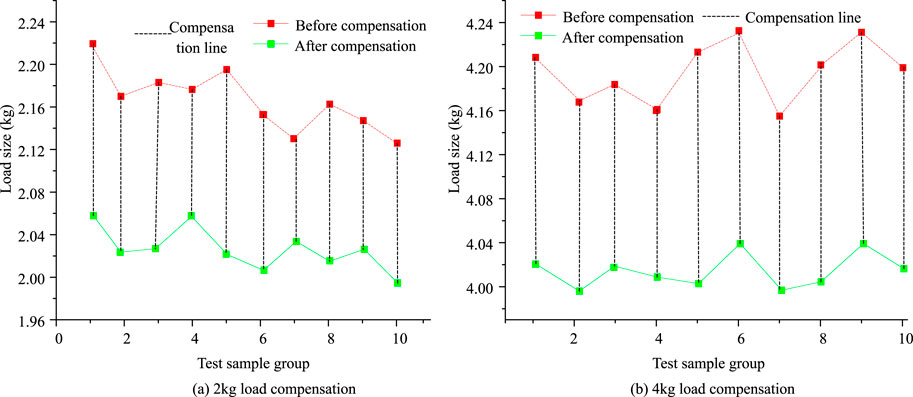
According to the ablation experiment in Table 4, the load detection model integrating FNO + FADA + CNN was significantly better than the single FNO and FADA-FNO models. In the MAE error test, the error values of FNO + FADA + CNN, FADA-FNO, and FNO were 0.082 kg, 3.25 kg, and 2.82 kg, respectively. The overall prediction accuracy of FNO + FADA + CN is better. 2 kg and 4 kg load scenarios are selected to test the error compensation effect, as shown in Figure 11.

Figure 11

Figure 11. Error compensation test. (a) 2 kg load compensation. (b) 4 kg load compensation.

Figures 11a,b show the error compensation results for two load scenarios of 2 kg and 4 kg, respectively. According to the results, the maximum load in a 2 kg load was 2.22 kg. After load compensation, it was 2.06 kg. In the 4 kg load, the maximum load was 4.24 kg. After load compensation, it was 4.05 kg. Load compensation can effectively reduce the interference of external factors on recognition and improve the model detection accuracy. Next, error compensation is introduced in different models for optimization, and the test results are shown in Figure 12.

Figure 12

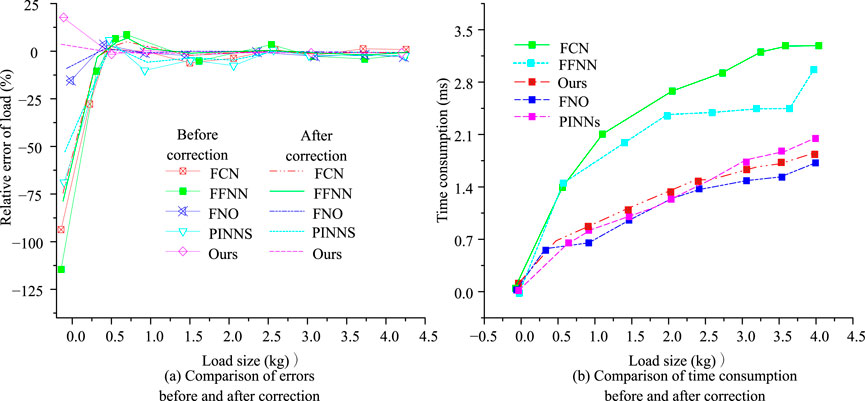
Figure 12. Load detection results after error compensation optimization. (a) Comparison of errors before and after correction. (b) Comparison of time consumption before and after correction.

Figure 12a shows the corrected relative error result. According to the test results, after error compensation, the maximum relative error of the proposed model was controlled within 3.25%, while FNO was controlled within 12.02%. Figure 12b shows the time comparison after correction. The test results show that adding error compensation layers mainly based on convolution to filter irrelevant information improves the prediction accuracy of the model, but the prediction time of all models has increased. FNO had the shortest overall time consumption, with an average time of 0.89 ms, while PINN and the proposed model had similar time consumption, with 0.98 ms and 0.11 ms respectively, both showing good performance in time consumption. In addition, using standard load data to train the model network is difficult to reflect its generalization ability. Therefore, the experiment is conducted with a load interval of 0 kg–4.5 kg, selecting data with 80% load information as the training set for testing, and the remaining as the test set to test the error compensation prediction effect, as shown in Figure 13.

Figure 13

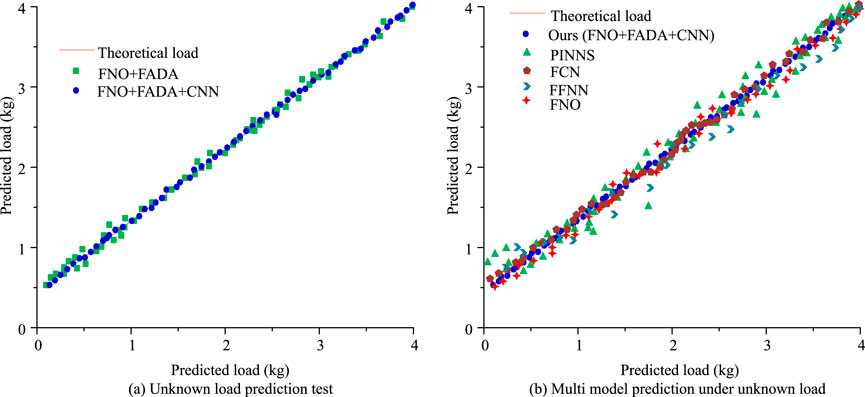
Figure 13. Test results under unknown data. (a) Unknown load prediction test. (b) Multi model prediction under unknown load.

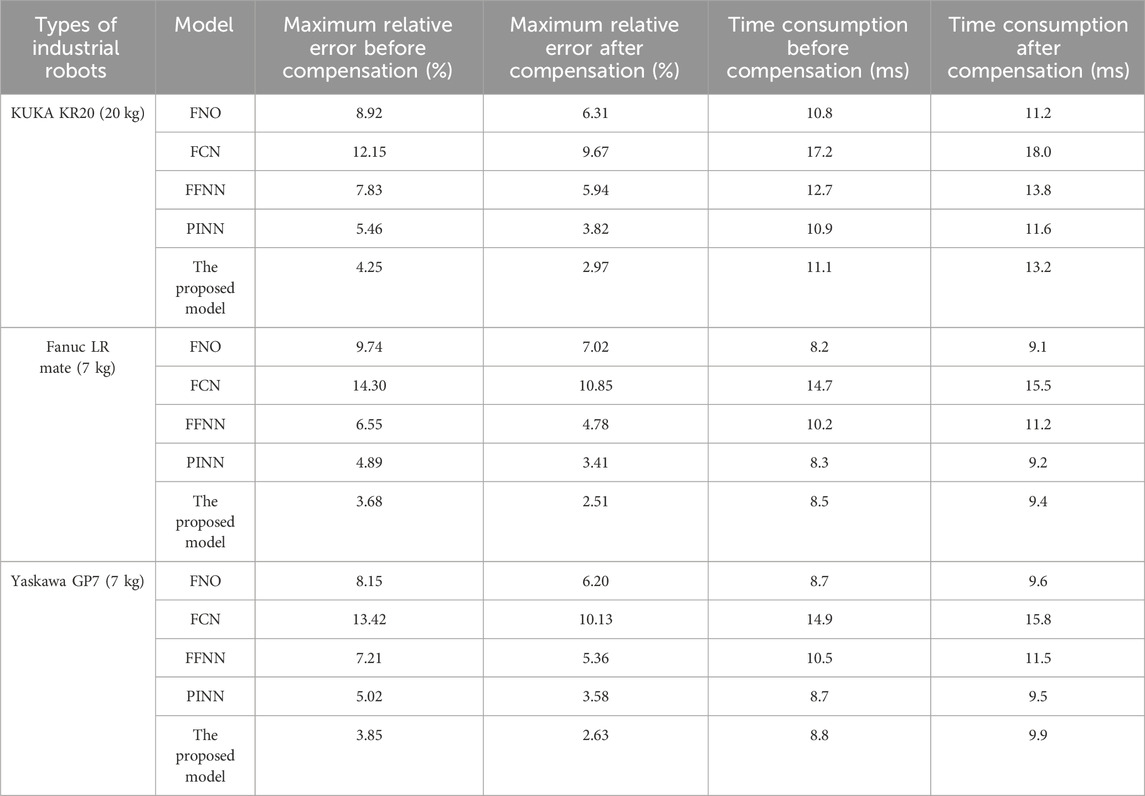
Figure 13a shows the results of the unknown load prediction test. According to testing, the model with added error compensation had excellent theoretical load fitting ability at a low-load below 0.8 kg. Under the high-load, the model with error compensation correction had higher accuracy and was closer to the actual predicted value. Figure 13b shows the multi-model prediction results for unknown data. According to the results, the proposed model adopted error compensation, which was closer to the theoretical value under unknown data, with a relative error control of 4.24%, better than that of FBO (7.25%), and performed the best among similar technologies. In addition, to further explore the generalization and load detection performance of the proposed model, three industrial robots are added: KUKA KR20 (maximum load 20 kg), FANUC LR Mate 200iD (maximum load 7 kg), and Yaskawa GP7 (maximum load 7 kg). The experiment sets an error step size of 0.5 kg and expands the load range to 0–20 kg. All robots are tested under high-load action conditions, and the load detection effects before and after error compensation for each model are shown in Table 5.

Table 5

Table 5. Comparison of load detection effects among multiple models.

According to the test results in Table 5, in the 20 kg high-load (KUKA KR20) scenario, traditional models (such as FFNN) had a maximum relative error of 7.83% due to not considering joint flexibility deformation. The proposed model enhanced low-frequency feature extraction through FADA module, with an error of only 4.25% before compensation and further reduced to 2.97% after compensation, significantly better than similar models. In addition, after compensation, the time consumption of each model has increased, but it is within the lower consumption range. For example, in the KUKA KR20 (20 kg) test, the FNO before compensation was 10.8 ms. After compensation optimization, it was 11.2 ms. Overall, the proposed model, FNO, and PINN perform well on time consumption. In addition, in other industrial robot tests, the proposed model also showed the best overall performance. In the 7 kg load test of Yaskawa GP7, the maximum relative error of the proposed model before compensation was 3.85%, significantly lower than that of other models. Meanwhile, after adjusting the compensation optimization, the relative error of the proposed model was 2.63%, demonstrating excellent overall performance. To verify the effectiveness of the proposed model in real-world scenarios, three types of dynamic task scenarios are set up to test the KUKA KR20 (20 kg), simulating inertial and trajectory related loads in manufacturing to verify the effectiveness of the compensation method. Scenario 1 is workpiece picking (center of mass offset ±30 mm, acceleration 0.5 g). Scenario 2 is welding trajectory (variable acceleration 0.3–0.6 g, curved trajectory). Scenario 3 is polishing operation (reciprocating variable acceleration 0.4 g, load fluctuation ±2 kg). The relative error values of load prediction for the model in different scenarios are shown in Table 6.

Table 6

Table 6. Load detection of industrial robots in real dynamic scenarios.

According to the test results in Table 6, the proposed model performed well in load prediction in real dynamic scenarios, with a maximum relative error controlled at 3.49%, significantly better than that of PINN at 4.85% and FFNN at 6.05%, and overall performed the best. In all scenarios, the proposed model had the highest load prediction accuracy, verifying the effectiveness of the model in real-world scenarios. The research summary of the paper is shown in Table 7.

Table 7

Table 7. Main findings of the research paper.

According to Table 7, in terms of accuracy and efficiency, the improved FNO model extends low-frequency to high-dimensional features and dynamic error compensation through the FADA module, significantly improving load sensitivity and anti-interference ability. Within the typical load range (2–4 kg), the model error is reduced by over 60%. At a low-load (0.5 kg), the error is reduced by over 50% compared to traditional methods. In terms of robustness and generalization, the model has been tested on multiple brands of robots such as KUKA and Yaskawa, with a maximum error stable at 2.51%-2.97%. The weak correlation (r = 0.32) indicates that it is less affected by load fluctuations and solves the error amplification caused by joint friction and temperature drift in traditional models. The error compensation mechanism further controls the impact of external interference (such as structural deformation) within 3.25%.

4 Discussion

Industrial robots need to provide effective control forces based on different loads in complex operating environments, and effective load detection is the key to high-precision control. In recent years, FNO, as a new type of deep learning architecture, has been able to learn mappings of infinite dimensional function spaces, providing a new technological means for load detection in industrial robots. Therefore, this study explores the application effects of related technologies in the field of industrial robot load detection based on improved FNO networks.

In the multi-model load prediction stage, the proposed FADA-FNO predicts the most advanced actual values within the load range of 2.0–4.0 kg, and the results are significantly better than similar models. The main reason is that it enhances the frequency domain features by extending the low-frequency dominant feature to the high-frequency band through the FADA module, solving the insufficient signal-to-noise ratio in traditional FNO for low-load signal extraction. In addition, the FADA-FNO model has improved the attention mechanism, such as the convolutional attention layer suppressing key interference factors such as joint friction and temperature drift. The absolute error is only 0.0201 kg at a low-load of 0.5 kg. Compared with similar advanced technologies, the RMSE of FADA-FNO is 0.038 kg, which is 60.8% lower than that of FNO and 82.6% lower than that of TS. The correlation between error and load (r = 0.32) is significantly lower than that of traditional models (r > 0.8), indicating its stronger ability to resist load disturbances. In addition, various industrial robots with different loads are introduced for load prediction testing, including KUKA, FANUC, and Yaskawa. In the prediction accuracy testing, the error of the optimized research model remains at 2.51%-2.97%, with the best stability and accuracy, verifying that the proposed model has better stability and generalization performance compared to similar technologies. The main reason is that the proposed model adopts FADA module to extract noise signals, which is more conducive to recognize load parameters by the model. In addition, the model can reduce the influence of nonlinear factors such as temperature and deformation through error compensation optimization, and improve the model sensitivity to data. Finally, the study compares the time consumption of the model before and after compensation. After compensation optimization, all models show an improvement in time consumption, but the overall time consumption of the proposed model is at an excellent level. The main reason is that FNO maps data to the frequency domain through Fourier transform, which is more adaptable to strong load characteristics. Moreover, the architecture design of FNO can better process data, ensuring both load recognition accuracy and computational efficiency compared to similar technologies. In addition, the study also compares it with the improved FNO technique proposed in reference (Koshelev, 2024). The research introduces FADA module to enhance low-frequency feature extraction, and introduces CNN error compensation layer to improve the fitting of nonlinear noise data, resulting in better load detection accuracy and stability. This result also indicates that the proposed model has excellent performance in industrial robot load detection.

The improved FNO network in this study has good application effects in industrial robot load detection. High detection accuracy and short detection time meet the high-precision control requirements of robots.

5 Conclusion

The current industrial automation is constantly advancing. Accurately identifying industrial robot parameters, especially load detection accuracy, plays a key role in improving robot motion accuracy and dynamic performance. However, traditional load recognition technology still faces many problems, such as large recognition errors in low-load states and low-solution accuracy. To improve the load recognition performance of industrial robots, a load recognition method based on an improved FNO network was proposed. The study used Fourier series for excitation trajectory design and the least squares estimation method for load solution. Subsequently, FNO was introduced to process the raw data, extracting low-frequency feature data from spatial physical information through Fourier transform, and using kernel integration operator to operate on the transformed data to obtain accurate load information. In addition, FADA was used to enhance the attention and extraction of key load features, thereby improving the accuracy of network recognition. The experimental results showed that the proposed model performed the best overall, such as in the 0–4 kg load range. Compared with traditional TS methods, the RMSE of the model was reduced by 82.6%, and the MAE was significantly reduced. Compared with models such as FNO, the RMSE decreased by 60.8% and the average relative error was only 3.25% in the typical load range of 2–4 kg, while FNO was 4.58% and TS was 5.72%. In the low-load 0.5 kg test, the absolute error of the proposed model was 3.25% (0.0201 kg), significantly lower than that of TS’s 5.72% (0.5 kg) and FNO’s 12.02% (0 kg). The model performed excellently in multi-model testing and had strong generalization ability. For example, in the 20 kg high-load scenario of KUKA KR20, the error before compensation was only 4.25%. After compensation, it further dropped to 2.97%, which was significantly better than that of similar models. However, the proposed model only focuses on detecting the end load of the device and does not take into account the motion impact on the environmental space. In the future, it is necessary to fully consider the impact of factors such as motion inertia and changes in the center of mass on load detection, to improve the effectiveness of technological applications.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FG: Writing – original draft, Supervision, Conceptualization, Methodology. DX: Software, Investigation, Writing – review and editing, Data curation. YX: Software, Investigation, Writing – review and editing, Formal Analysis, Data curation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The research is supported by: 2022 Guangxi University Young and Middle aged Teachers Research Basic Ability Enhancement Project “Research on Analog Integrated Circuit Frequency synthesizer based on EDA technology (Project No. 2022KY1292).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amer, T. S., El-Kafly, H. F., Elneklawy, A. H., and Moosazadeh, S. (2024). Modeling analysis on the influence of the gyrostatic moment on the motion of a charged rigid body subjected to constant axial torque. J. Low Freq. Noise, Vib. Act. Control 43 (4), 1593–1610. doi:10.1177/14613484241276381

CrossRef Full Text | Google Scholar

Basiri, S., Taheri, A., Meghdari, A. F., Boroushaki, M., and Alemi, M. (2023). Dynamic iranian sign language recognition using an optimized deep neural network: an implementation via a robotic-based architecture. Int. J. Soc. Robotics 15 (4), 599–619. doi:10.1007/s12369-021-00819-0

CrossRef Full Text | Google Scholar

Bastl, P., Chakraborti, N., and Valášek, M. (2023). Evolutionary algorithms in robot calibration. Mater. Manuf. Process. 38 (16), 2051–2070. doi:10.1080/10426914.2023.2238368

CrossRef Full Text | Google Scholar

Bo, L. I., Wei, T., Zhang, C., Fangfang, H. U. A., Cui, G., and Li, Y. (2022). Positioning error compensation of an industrial robot using neural networks and experimental study. Chin. J. Aeronautics 35 (2), 346–360. doi:10.1016/j.cja.2021.03.027

CrossRef Full Text | Google Scholar

Cao, H., Wu, Y., Bao, Y., Feng, X., Wan, S., and Qian, C. (2023). UTrans-Net: a model for short-term precipitation prediction. Artif. Intell. Appl. 1 (2), 90–97. doi:10.47852/bonviewaia2202337

CrossRef Full Text | Google Scholar

Chen, X., and Zhan, Q. (2022). The kinematic calibration of an industrial robot with an improved beetle swarm optimization algorithm. IEEE Robotics Automation Lett. 7 (2), 4694–4701. doi:10.1109/lra.2022.3151610

CrossRef Full Text | Google Scholar

Huang, Y., Ke, J., Zhang, X., and Ota, J. (2022). Dynamic parameter identification of serial robots using a hybrid approach. IEEE Trans. Robotics 39 (2), 1607–1621. doi:10.1109/tro.2022.3211194

CrossRef Full Text | Google Scholar

Jia, Z., Wang, M., and Zhao, S. (2024). A review of deep learning-based approaches for defect detection in smart manufacturing. J. Opt. 53 (2), 1345–1351. doi:10.1007/s12596-023-01340-5

CrossRef Full Text | Google Scholar

Kakinuma, Y., Ogawa, S., and Koto, K. (2022). Robot polishing control with an active end effector based on macro-micro mechanism and the extended Preston's law. Cirp Ann. 71 (1), 341–344. doi:10.1016/j.cirp.2022.04.074

CrossRef Full Text | Google Scholar

Koshelev, D. S. (2024). Expert system for Fourier transform infrared spectrum recognition based on a convolutional neural network with multi class classification. Appl. Spectrosc. 78 (4), 387–397. doi:10.1177/00037028241226732

PubMed Abstract | CrossRef Full Text | Google Scholar

Lokhande, H., and Ganorkar, S. R. (2025). Object detection in video surveillance using MobileNetV2 on resource constrained low power edge devices. Bull. Elec. Eng. Inform. 14 (1), 357–365. doi:10.11591/eei.v14i1.8131

CrossRef Full Text | Google Scholar

Liu, Y., Duan, S., Shen, Z., He, Z., and Li, L. (2023a). Grasp and inspection of mechanical parts based on visual image recognition technology. J. Theory Pract. Eng. Sci. 3 (12), 22–28. doi:10.53469/jtpes.2023.03(12).04

CrossRef Full Text | Google Scholar

Liu, Z., Peng, K., Han, L., and Zhang, X. (2023b). Modeling and control of robotic manipulators based on artificial neural networks: a review. Trans. Mech. Eng. 47 (4), 1307–1347. doi:10.1007/s40997-023-00596-3

CrossRef Full Text | Google Scholar

Lu, Y., Shen, Y., and Zhuang, C. (2023). External force estimation for industrial robots using configuration optimization. Automatika: časopis Za Automatiku, Mjerenje, Elektroniku. Računarstvo I Komun. 64 (2), 365–388. doi:10.1080/00051144.2023.2166451

CrossRef Full Text | Google Scholar

Luo, S., Meng, Q., Li, S., and Yu, H. (2024). Research of intent recognition in rehabilitation robots: a systematic review. Assist. Technol. 19 (4), 1307–1318. doi:10.1080/17483107.2023.2170477

PubMed Abstract | CrossRef Full Text | Google Scholar

Nengem, S. M. (2023). Symmetric kernel-based approach for elliptic partial differential equation. J. Data Sci. Intelligent Syst. 1 (2), 99–104. doi:10.47852/bonviewjdsis3202884

CrossRef Full Text | Google Scholar

Papavasileiou, A., Michalos, G., and Makris, S. (2025). Quality control in manufacturing–review and challenges on robotic applications. Int. J. Comput. Integr. Manuf. 38 (1), 79–115. doi:10.1080/0951192x.2024.2314789

CrossRef Full Text | Google Scholar

Ruan, D., Zhang, W., and Qian, D. (2023). Feature-based autonomous target recognition and grasping of industrial robots. Personal Ubiquitous Comput. 27 (3), 1355–1367. doi:10.1007/s00779-021-01589-2

CrossRef Full Text | Google Scholar

Santhosh, R., Sut, D. J., Uma, M., and Sethuramalingam, P. (2024). Optimizing IRB1410 industrial robot painting processes through Taguchi method and fuzzy logic integration with machine learning. Int. J. Intelligent Robotics Appl. 8 (2), 380–400. doi:10.1007/s41315-024-00325-2

CrossRef Full Text | Google Scholar

Selami, Y., Tao, W., Lv, N., and Zhao, H. (2023). Precise robot calibration method-based 3-D positioning and posture sensor. IEEE Sensors J. 23 (7), 7741–7749. doi:10.1109/jsen.2022.3218292

CrossRef Full Text | Google Scholar

Silik, A., Noori, M., Ghiasi, R., Wang, T., Kuok, S. C., Farhan, N. S. D., et al. (2023). Dynamic wavelet neural network model for damage features extraction and patterns recognition. J. Civ. Struct. Health Monit. 13 (4), 925–945. doi:10.1007/s13349-023-00683-8

CrossRef Full Text | Google Scholar

Tsapin, D., Pitelinskiy, K., Suvorov, S., Osipov, A., Pleshakova, E., and Gataullin, S. (2024). Machine learning methods for the industrial robotic systems security. J. Comput. Virology Hacking Tech. 20 (3), 397–414. doi:10.1007/s11416-023-00499-6

CrossRef Full Text | Google Scholar

Yang, W., Li, S., Li, Z., and Luo, X. (2023). Highly accurate manipulator calibration via extended Kalman filter-incorporated residual neural network. IEEE Trans. Industrial Inf. 19 (11), 10831–10841. doi:10.1109/tii.2023.3241614

CrossRef Full Text | Google Scholar

Yuan, Y., and Sun, W. (2023). An integrated kinematic calibration and dynamic identification method with only static measurements for serial robot. IEEE/ASME Trans. Mechatronics 28 (5), 2762–2773. doi:10.1109/tmech.2023.3241302

CrossRef Full Text | Google Scholar

Zhang, H., Zong, Z., Yao, Y., Hu, Q., Aburaia, M., and Lammer, H. (2023). Multi-axis 3D printing defect detecting by machine vision with convolutional neural networks. Exp. Tech. 47 (3), 619–631. doi:10.1007/s40799-022-00577-2

CrossRef Full Text | Google Scholar