A unified perspective on vortical and interfacial instabilities in fluid layers

This work presents a comprehensive and unprecedented synthesis that unifies two fundamental, yet separately studied, paradigms of fluid instability: vortical disturbances in high-speed boundary layers and free-surface instabilities in ultra-thin liquid films. We critically examine the boundary layer instability mechanisms using the Orr-Sommerfeld/Squire (O-S/S) formalism, alongside its necessary extensions for hypersonic and multi-phase flows, with focus on the evolution of Tollmien-Schlichting (TS) waves, Görtler vortices, and streak-breakdown phenomena. In parallel, we explore thin-film dynamics via nonlinear long-wave models incorporating the interplay of gravity, surface tension, and complex rheological effects, capturing the physics of pattern formation, wave amplification, and film rupture. The core of this review is a first-of-its-kind comparative analysis that establishes a structural and mathematical equivalence between the two systems across the classic stages of receptivity, linear growth, and nonlinear saturation, despite their contrasting ultimate fates (transition to turbulence vs. catastrophic film rupture). We emphasize the multiphysics couplings and “shared governing principles, defining a new scope for theoretical modeling, particularly for hybrid instability scenarios” found in modern applications. The review concludes by identifying key open challenges in nonlinear predictive capabilities and advanced diagnostics, positioning this unified perspective as crucial for advancing technologies in aerospace drag reduction, microfluidics, and protective coating stability.

1 Introduction

Fluid instability mechanisms constitute a central theme in modern physical science, fundamentally governing momentum and energy transport, transition to turbulence, and system performance across vast scales. This review directly addresses a critical challenge by unifying the underlying physics of two distinct, yet mathematically analogous, instability types: (a) vortical disturbances that drive transition in sheared boundary layers and (b) interfacial phenomena that control the stability and rupture of thin liquid films. The practical implications of these instabilities are immense. Industrially, they determine the efficacy of multifunctional coatings where uniform film thickness is paramount (Oron et al., 1997; Craster and Matar, 2009) (Figure 1, middle panel), and they limit performance metrics, such as the cooling efficiency of critical components like gas turbine blades (Wang et al., 2022). Environmentally, the generation of wind-driven waves on ocean surfaces (Miles, 1957; Liss and Slater, 1974) (Figure 1, lower panel) is a key process that influences air-sea interactions and global climate modeling. These examples highlight the need for a unified theoretical perspective to bridge the gap between wall-bounded flows and free-surface dynamics, thereby enabling more robust and predictive modeling in both established and emerging fields.

Figure 1

Figure 1. (Upper panel) Schematic of a two-fluid system with a thin liquid film flowing on an inclined substrate and a wavy free interface, overlaid by vortical structures in the upper fluid. Coordinate axes, velocity profiles, and gravity direction are indicated along with real-life examples of a gravity-driven falling film illustrating interfacial instability and wave formation (middle panel) and wind-driven ocean surface waves, representing large-scale natural interfacial instabilities (lower panel).

Instability and transition phenomena control drag, heat transfer, and interfacial transport. In boundary layers, disturbances ranging from Tollmien-Schlichting (TS) waves to Görtler vortices and streak trigger turbulence, especially at high Reynolds numbers and hypersonic flows (Xu et al., 2024; Caillaud et al., 2025). In thin films, long-wave instabilities caused by gravity, inertia, or thermocapillarity can amplify into nonlinear waves, rupture, or patterned states (Gladbach et al., 2023; Selim and Zakaria, 2024). Despite their shared roots in receptivity, modal growth, and nonlinear saturation, these two fields are often studied separately.

Vortical disturbances evolve from freestream turbulence, surface roughness, or localized perturbations, developing into coherent structures such as streaks, hairpin vortices, and Görtler vortices that influence drag, heat transfer, and noise in engineering systems (Saric, 1994; Leib et al., 1999; Nagarajan et al., 2007; Goldstein, 2014). These mechanisms, ranging from shear-sheltering and vortex tilting to lift-up effects, have been clarified by theory, DNS, and experiments (Zaki and Saha, 2009; Saha et al., 2016; Xu et al., 2024; Zhu and Ricco, 2024). Meanwhile, gravity-driven thin films on inclined substrates are inherently unstable, producing interfacial waves, rupture, or droplet formation essential to coating, lubrication, and mixing. Nonlinear models for power-law fluids (Chakraborty, 2012) and later extensions incorporating substrate texture, thermal effects, and viscoelasticity (Yadav et al., 2015; Chakraborty et al., 2019; Selim and Zakaria, 2024; Veremieiev and Wacks, 2019).

This review article bridges the two perspectives and synthesizes the mechanisms, mathematical formulations, and nonlinear pathways, aiming to identify shared frameworks and outline future unified approaches. Section 2 focuses on vortical disturbances in boundary layers, summarizing the governing equations and recent extensions in compressible and hypersonic regimes. Section 3 reviews long-wave instabilities in thin films, highlighting nonlinear saturation, rupture, and the role of substrate and rheological effects. Section 4 provides a comparative synthesis, presenting side-by-side pathways and a research roadmap. Section 5 outlines current challenges and future directions, emphasizing nonlinear prediction, multiphysics coupling, and experimental diagnostics.

2 Vortical disturbances in boundary layers

The receptivity and amplification of vortical disturbances in boundary layers are governed by the mean flow equations and interface conditions presented in Equations 4, 5. These equations define the base velocity and stress fields in $(\zeta ,\eta )$ coordinates, together with the interface location ${\eta }^{*}$. Linearization around the base state yields the coupled Orr-Sommerfeld/Squire system with interfacial jump conditions (Equation 3), which forms the foundation for analyzing both modal and non-modal disturbance growth.

Linear instabilities—Classical linear theory identifies Tollmien-Schlichting (TS) waves and Görtler vortices as key instability modes in incompressible boundary layers. For concave surfaces, the Görtler number $G$ defines the onset of centrifugal instabilities, with critical values of order $0.3-0.5$. Equation 6 incorporates these effects by modifying the Orr-Sommerfeld operator with curvature and interfacial terms. Recent studies have extended these analyses to hypersonic regimes, where high Mach numbers alter both receptivity and amplification characteristics (Xu et al., 2024; Caillaud et al., 2025). Direct numerical simulations and asymptotic analyses now provide critical thresholds and mode selection maps for supersonic and hypersonic boundary layers, complementing earlier incompressible results.

Bypass and streak dynamics—In addition to modal instabilities, non-modal growth associated with streaks plays a major role in bypass transition. Equation 6 naturally accommodates streamwise vortices, which extract energy from the mean shear via lift-up. Weakly nonlinear interactions among streaks, waves, and vortices lead to breakdown, a process investigated in both experiments and DNS (Zhu and Ricco, 2024). The role of receptivity, which involves external acoustic or freestream disturbances coupling into the boundary layer through surface roughness or curvature, has also been clarified through modern numerical simulations. These results confirm that bypass transition can dominate over TS waves in realistic high-disturbance environments.

Two-fluid and interfacial effects—The presence of a liquid film or a density/viscosity contrast at the wall significantly modifies the instability characteristics. In Equation 6, the interfacial conditions introduce additional coupling terms, reflecting the continuity of velocity and stress across $\eta ={\eta }^{*}$. Studies have shown that density ratio ${\rho }_r$ and viscosity ratio ${\mu }_r$ alter the growth rates and preferred modes, while surface tension introduces a stabilizing effect at small scales (Saha, 2011; Saha et al., 2016). Figure 1 illustrates a representative two-fluid boundary-layer configuration, where vortices interact with an underlying film, leading to modified instability pathways. Vortical disturbances in boundary layers progress from receptivity through linear modal growth (TS, Görtler, streaks) and finally to nonlinear amplification and transition. Equations 4–6 capture these mechanisms, while modern DNS and experiments have clarified thresholds, bypass scenarios, and hypersonic extensions. The inclusion of interfacial effects underscores the significance of these instabilities for coupled boundary-layer/film problems, leading to the comparative analysis presented in Section 4.

The stability of laminar boundary layers and their transition to turbulence remain central topics in fluid mechanics, which have been extensively explored through theory, experiments, and simulations (Fedorov, 2011; Ricco et al., 1976). Vortical disturbances, originating from the freestream turbulence, acoustic waves, or surface roughness, can decay or grow into coherent structures, such as streamwise streaks, Görtler vortices, or Tollmien-Schlichting waves, ultimately triggering transition (Schmid and Henningson, 2001). Streamwise vortices, crucial in bypass transition, amplify into streaks through the lift-up effect, redistributing momentum (Brandt, 2014). Saha (2011) analyzed such mechanisms in single- and two-fluid systems, addressing the influence of interfacial dynamics. Görtler vortices arise from centrifugal instability over concave surfaces due to curvature-induced counter-rotating motions (Schrader et al., 2011). Disturbance amplification is governed by interfacial viscosity and density stratification, shear-sheltering effects that filter disturbance scales (Zaki and Saha, 2009), the lift-up process, and curvature-induced centrifugal amplification. Budiman et al. (2015) experimentally visualized these vortices over wavy walls, showing structured formations that can accelerate the transition.

The base equations governing incompressible boundary layer flows are the Navier–Stokes equations under the boundary layer approximation (1) (Nelson et al., 1995):

$F{\partial }_{\eta }^{2}F+\nu {\partial }_{\eta }^{3}f=\zeta \left[{\partial }_{\eta }F\frac{\partial {\partial }_{\eta }F}{\partial \zeta }{\partial }_{\eta }^{2}F\frac{\partial F}{\partial \zeta }\right],(1)$

where the boundary layer coordinates $(\zeta ,\eta )$, $\zeta \equiv \left(\frac{U_{\infty }x}{2{\nu }_2}\right)$, $\eta \equiv y\left(\frac{U_{\infty }}{2{\nu }_{2}x}\right)$, and stream function $(\psi )$ is expressed as $F\equiv \frac{\psi }{\sqrt{2{\nu }_2{U}_{\infty }x}}$ and ${\partial }_{\eta }\equiv \frac{\partial }{\partial \eta }$. The interface height $({\eta }^{*}=\delta \left(\frac{U_{\infty }}{2{\nu }_{2}x}\right))$ is governed by the standard kinematic condition (2)

$\frac{\partial {\eta }^{*}}{\partial \zeta }=\frac{1}{\zeta }\left(\frac{V}{U}-1\right),(2)$

where $U$ and $V$ are the mean streamwise and wall-normal velocities at the interface, respectively. Continuity of velocity and stress are enforced at $\eta ={\eta }^{*}$, according to, $[F]=[{\partial }_{\eta }F]=[\mu {\partial }_{\eta }^{2}F]=0$. Here $[A]$ denotes the jump in the quantity $A$ across the interface. In addition, $F(\zeta ,\eta )$ must satisfy the boundary conditions, $F(\zeta ,0)={\partial }_{\eta }F(\zeta ,0)=0$ at the wall and in the free-stream ${\lim }_{\eta \to \infty }{\partial }_{\eta }F(\zeta ,\eta )=1$.

Superimposing infinitesimal disturbances and linearizing the system leads to the Orr-Sommerfeld (OS), Squire (SQ), and interface equations for stability analysis. We investigate the stability of a base flow $[U_j(y)00]$ with respect to a linear perturbation, $u={[uvw]}^T$, and an infinitesimal perturbation to the interface, $f$, from its mean location ${\eta }^{*}$. The resulting stability equations can be expressed in terms of $v_j$, $f$, and normal vorticity ${\omega }_j={\partial }_{z}u-{\partial }_{x}w$ in the dimensional form:

$\frac{\partial }{\partial t}\left[\begin{array}{c}\hfill {\nabla }^2{v}_j\hfill \\ \hfill f\hfill \\ \hfill {\omega }_j\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill {\mathcal{L}}_{os}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill v\left({\eta }^{*}\right)\hfill & \hfill -U\left({\eta }^{*}\right)\frac{\partial }{\partial x}\hfill & \hfill 0\hfill \\ \hfill d_{y}U{\partial }_z\hfill & \hfill 0\hfill & \hfill {\mathcal{L}}_{sq}\hfill \end{array}\right]\left[\begin{array}{c}\hfill v_j\hfill \\ \hfill f\hfill \\ \hfill {\omega }_j\hfill \end{array}\right](3)$

here operators ${\mathcal{L}}_{os}\equiv d_y^2{U}_j{\partial }_x+{\nu }_i{\nabla }^4-U_j\frac{\partial }{\partial x}{\nabla }^2$, and ${\mathcal{L}}_{sq}\equiv {\nu }_j{\nabla }^2-U_j{\partial }_x$. Here ${\nabla }^2\equiv {\partial }_x^2+{\partial }_y^2+{\partial }_z^2$ and the subscript $j$ indicates the fluid 1 or 2.

The first equation in (3) represents the temporal evolution of normal velocity perturbation, $v_j$, in fluid 1 or 2; while the second equation in (3) represents the evolution of the interface deformation, $f$ that is linearized about the mean interface location, ${\eta }^{*}$, and the last equation represents the temporal evolution of normal vorticity, ${\omega }_j$ in fluid 1 or 2. It is worth noting that the temporal evolution of normal vorticity, ${\omega }_j$, is influenced by the normal velocity, $v_j$, and interface deformation, $f$, but not the converse. Consequently, the normal velocity, $v_j$, and the interface deformation, $f$, evolve in a coupled manner independently of the normal vorticity, ${\omega }_j$ (see Zaki and Saha (2009); Saha (2011); Saha et al. (2016) for an extensive discussion on the applications of Equation 3 to specific scenarios). For curved surface, instability onsets when the Görtler number $G$ exceeds its critical range $O(0.3-0.5)$; in two-fluid layers, the same OS/SQ operator is modified by density/viscosity ratios $({\rho }_r,{\mu }_r)$ and surface tension in the interfacial conditions, shifting preferred modes and growth rates.

3 Interfacial instabilities in thin film flows

Thin liquid films exhibit a wide range of instability mechanisms, often leading to the growth of nonlinear waves, rupture, or the formation of patterned structures. The governing framework is given by the long-wave formulation, in which the local film thickness $h(x,t)$ evolves according to the continuity equation,

$\frac{\partial h}{\partial t}+\frac{\partial q}{\partial x}=0,(4)$

where the constitutive closure defines the volumetric flow rate $q$. For Newtonian fluids, this closure reduces to

$q=\frac{\rho g{h}^3}{3\mu }\sin \theta ,(5)$

while for power-law fluids or more complex rheologies, the exponent and prefactor are modified accordingly. Capillary effects, acting at short wavelengths, provide regularization, and enter through

$q=q\left(h\right)-\frac{\sigma h^3}{3\mu }\frac{{\partial }^{3}h}{\partial x^3},(6)$

ensuring that the system captures both destabilizing and stabilizing contributions.

Linear instabilities—Linear stability analysis of Equations 4–6 identifies long-wave modes as dominant in gravitational films, with growth rates depending on Reynolds number, inclination angle, and material parameters. Capillarity sets a cutoff wavenumber, while substrate heating or cooling can introduce Marangoni instabilities. Recent studies have extended these models to thermocapillary films and viscoelastic liquids, showing significant shifts in the most unstable wavelength (Gladbach et al., 2023; Selim and Zakaria, 2024).

Nonlinear wave dynamics—Nonlinear simulations and experiments demonstrate that linearly unstable modes evolve into large-amplitude traveling waves, solitary humps, or roll waves. Saturation mechanisms include viscous dissipation, surface tension, and nonlinear mode interactions. Figure 2 (upper panel) illustrates representative nonlinear wave profiles that arise from the evolution of Equations 4–6. The transition from small-amplitude periodic waves to steep fronts is crucial to rupture and atomization processes, with direct implications for coating technologies and heat transfer enhancement.

Figure 2

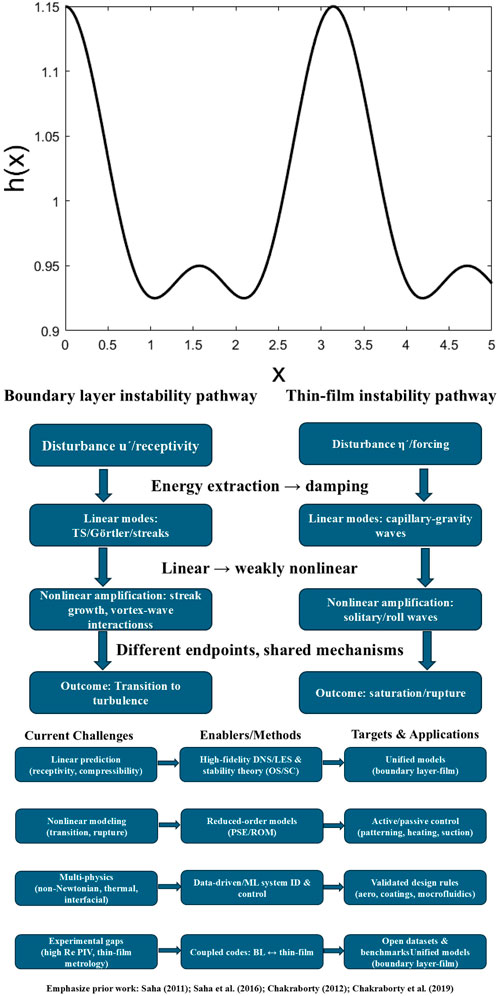
Figure 2. Representative nonlinear wave profiles of thin-film flow illustrating crest-trough evolution and amplitude growth (upper panel). Comparative pathways of boundary-layer (Orr-Sommerfeld/Squire modes) versus thin-film (capillary-gravity modes) instabilities, both progressing from receptivity to linear growth and nonlinear amplification, with outcomes of turbulence or rupture (middle panel). Roadmap of current challenges (nonlinear prediction, multiphysics, experimental limitations), enabling methods (DNS, reduced-order models, machine learning), and application target (unified boundary-layer film models, flow control, validated datasets) (lower panel).

Substrate and multiphase effects—Patterned and flexible substrates modify the base state and the nonlinear outcome. Periodic topography can stabilize or destabilize certain wavenumbers, while compliant substrates couple film motion with substrate deformation. Two-fluid configurations, where an external shear flow drives the film, create additional interfacial terms analogous to those in Equation 3 of the boundary-layer formulation. These effects are of particular importance in aeronautical icing, coating of turbine blades, and environmental flows (Veremieiev and Wacks, 2019). Thin-film instabilities are thus characterized by the interplay of destabilizing gravitational and shear forces, stabilizing capillarity, and nonlinear saturation. The long-wave system Equations 4–6 captures the essential dynamics while allowing extensions to non-Newtonian, thermocapillary, and multi-layer films. Recent studies (2020–2025) complement earlier foundational work, such as non-Newtonian rheology and heating, that shift the instability thresholds (Selim and Zakaria, 2024; Umana and Yang, 2025; Ladjelate et al., 2025), while the authors’ prior contributions have clarified how substrate and rheological effects control wave evolution and rupture (Chakraborty, 2012; Chakraborty et al., 2019). Together with Section 2, this provides a basis for the comparative analysis of boundary-layer and film instabilities in Section 4.

Bypass and non-modal pathways—Although thin-film instabilities are typically framed in terms of modal long-wave growth, recent studies indicate the presence of transient growth and bypass routes analogous to boundary-layer streak dynamics. Perturbations introduced by inlet disturbances or substrate variations can undergo significant transient amplification before nonlinear saturation, providing a non-modal pathway to solitary waves and rupture. This mechanism strengthens the analogy with bypass transition in boundary layers.

Long-wave model and rheology—We retain the lubrication-based evolution for film height $h(x,t)$, i.e., the mass balance (Equation 4), together with the power-law closure for the flow rate $q(h)$ (Equation 5) and capillary regularization in Equation 6. These three equations remain the backbone for our linear and weakly nonlinear interpretations below. Recent advances have emphasized the roles of non-Newtonian rheology, substrate geometry, and interfacial stresses in modulating thin-film instability. Lubrication-based models and linear stability analysis provide critical insight into wave onset and growth, while extended formulations incorporating thermal gradients, elasticity, and substrate design offer new control strategies (Karbalaei et al., 2016; Keogh et al., 2025). Figure 2 (upper panel) illustrates a representative nonlinear wave profile of a thin film, showing finite amplitude crests and troughs arising from the amplification of disturbances. The observed asymmetry and modulation reflect nonlinear interactions and mode coupling, with implications for coating uniformity, film rupture, and interfacial transport.

4 Comparative synthesis of boundary-layer and film instabilities

Although boundary-layer and thin-film instabilities are often studied in separate communities, their governing frameworks reveal striking similarities. Both begin with receptivity, proceed through linear modal growth, and enter nonlinear stages that determine whether the outcome is transition to turbulence or saturation and rupture. In boundary layers, Equation 3 couples the Orr-Sommerfeld/Squire operator with interfacial conditions, admitting TS, Görtler, and streak instabilities. In films, Equations 4–6 capture long-wave amplification driven by gravity or shear, regulated by capillarity. Figure 2 (middle panel) presents a vis-à-vis schematic of these two pathways. Despite the different endpoints, the common structure, receptivity, linear growth, and nonlinear amplification highlight a unified view.

A first point of comparison lies in the receptivity stage. In boundary layers, acoustic and vortical disturbances couple into the near-wall flow through surface roughness and curvature (Xu et al., 2024). In films, receptivity may arise from substrate perturbations, inlet forcing, or external shear (Chakraborty, 2012). In both cases, the disturbance spectrum is filtered by the governing operator (Equations 3, 4), determining amplified modes.

In the linear regime, both systems exhibit preferential amplification of distinct modes. Boundary layers favor TS and centrifugal instabilities, depending on the Reynolds number and curvature, while films exhibit capillary-gravity modes, whose cutoff is determined by surface tension. Recent work on hypersonic layers (Caillaud et al., 2025) and thermocapillary films (Selim and Zakaria, 2024) underscores the importance of multiphysics coupling in altering stability limits.

The nonlinear regime offers the richest ground for comparison. In boundary layers, interactions among streaks, vortices, and waves lead to secondary instabilities and breakdown (Zhu and Ricco, 2024). In films, nonlinear steepening produces solitary waves, fronts, and rupture patterns (Gladbach et al., 2023). In both cases, the balance between nonlinear amplification and dissipative mechanisms determines the eventual state. The similarity of weakly nonlinear expansions in Equations 3, 5, suggest that reduced-order models may be transferable across the two problems.

A second point of synthesis concerns multi-fluid and coupled configurations. When a liquid film underlies a boundary layer, the two systems directly interact: vortical structures in the gas layer penetrate the interface, while film undulations feed back into the shear field (Saha, 2011; Saha et al., 2016). Such two-way coupling modifies both the instability spectrum and the nonlinear evolution, creating hybrid modes that single-phase models cannot capture. Figure 1 already illustrates this mechanism schematically, but its importance is reinforced by recent DNS of coupled boundary-layer/film flows.

Finally, the broader research context can be organized into three main areas: challenges, methods, and applications, as illustrated in Figure 2 (lower panel). Challenges include the accurate prediction of nonlinear stages, the incorporation of multiphysics effects (compressibility, viscoelasticity, and thermocapillarity), and the improvement of experimental diagnostics (high-Reynolds-number PIV and thin-film metrology). Enabling methods range from high-fidelity DNS and stability theory (Orr-Sommerfeld/Squire, parabolized stability equations) to reduced-order models and machine learning. Applications include unified boundary-layer/film models, active and passive flow control (patterned surfaces, heating, suction), and the development of benchmark datasets. Prior contributions (Saha, 2011; Chakraborty, 2012; Saha et al., 2016; Chakraborty et al., 2019) are highlighted within this roadmap, demonstrating how earlier theoretical and experimental insights connect with emerging opportunities. The comparative view clarifies that boundary-layer and film instabilities, while differing in their endpoints, share common mathematical structures and nonlinear mechanisms. By synthesizing these perspectives, Section 4 establishes a framework for unified modeling and motivates the future directions discussed in Section 5.

Figure 2 (middle panel) contrasts “boundary-layer instability” versus “thin-film instability” pathways. Both start from receptivity/forcing, pass through linear modes (OS/SQ versus capillary-gravity), and then enter weakly nonlinear amplification to different endpoints (transition versus saturated waves/rupture). This layout mirrors the governing sets: OS/SQ/interface Equation 3 versus the lubrication system Equations 4–6.

From a practical perspective, both boundary-layer and thin-film systems present distinct challenges. Visualizing boundary-layer vortices remains complex and resource-intensive, requiring techniques like PIV or LDV, whereas thin-film wave patterns are more readily captured through optical interferometry. Computationally, Direct Numerical Simulations (DNS) of boundary-layer transitions are demanding due to the inherent multiscale turbulence Jung and Zaki (2015), while thin film modeling, though more tractable via low-dimensional lubrication theory, is now expanding to include three-dimensional and viscoelastic effects (Gladbach et al., 2023).

Figure 2 (lower panel) summarizes current challenges (predicting nonlinear stages; multi-physics coupling; experimental gaps) mapped to enabling methods (DNS/LES + OS/SQ, PSE/ROM, ML system ID, coupled BL-film solvers) and to application targets (unified BL-film models; control via patterning/heating/suction; open datasets). Understanding these analogies deepens our capability to control flow instabilities in aerospace, coating, and microfluidic applications.

5 Current challenges and future research directions

Predicting and controlling boundary-layer and thin-film instabilities remains a significant scientific challenge, primarily due to three interlocking difficulties. A central difficulty is accurately describing the nonlinear stages that follow linear amplification. In boundary layers, secondary instabilities of streaks and vortex–wave interactions govern the ultimate transition to turbulence. Although Direct Numerical Simulations (DNS) provide valuable insights (Zhu and Ricco, 2024), the prediction of quantitative transitions in realistic hypersonic flows remains elusive (Caillaud et al., 2025). Similarly, in thin films, while current models capture the qualitative features of nonlinear wave steepening, they often fail to predict critical metrics, such as rupture times, with engineering accuracy (Gladbach et al., 2023). A second, critical challenge is multiphysics coupling. The inclusion of compressibility, thermocapillarity, viscoelastic rheology, and multi-layer configurations substantially alters instability characteristics. For example, high Mach numbers significantly modify receptivity in boundary layers (Xu et al., 2024), while thermocapillary stresses can destabilize otherwise stable films (Selim and Zakaria, 2024). Crucially, coupled gas-liquid systems introduce hybrid instability modes (Saha, 2011; Saha et al., 2016), necessitating unified models that systematically account for these interfacial interactions across both fluid domains. Systematic exploration of these couplings is urgently needed. Experimental diagnostics represent a third major bottleneck. While advanced techniques, such as 3D PIV and interferometry, are increasingly revealing detailed flow structures, quantitative measurements of coupled gas–liquid systems remain rare. This scarcity limits the direct validation of unified theories and high-fidelity simulations. Expanding these experimental capabilities is essential for progress. The future is promising: Reduced-order modeling and Machine Learning offer crucial tools for closure and dynamics extraction (Umana and Yang, 2025). Integrating DNS, stability theory, and experiments into unified datasets is key. By extending shear–film coupling efforts with these modern tools, the field will decisively move toward unified, predictive frameworks for controlling multiphysics instabilities in aeronautics, energy, and environmental flows.

6 Conclusion

This review has demonstrated a fundamental structural and mathematical equivalence between two canonical problems in fluid dynamics: vortical disturbances in sheared boundary layers and interfacial instabilities in thin liquid films. Our analysis, based on a systematic comparison of the Orr-Sommerfeld/Squire framework (Equations 1–3) and the long-wave evolution models (Equations 4–6) reveal that these seemingly disparate systems traverse remarkably parallel instability pathways. Both proceed through the essential stages of receptivity, linear modal amplification, and complex nonlinear saturation.

Our central contribution is the formal unified framework of these instability mechanisms. We have shown that, despite the divergence in their ultimate outcomes—transition to wall-bounded turbulence versus catastrophic film rupture—the underlying physics driving the initial growth and nonlinear evolution are governed by analogous mathematical structures (Figure 2, middle panel). By mapping the shared principles, we have not only consolidated existing knowledge but have also provided a unified conceptual roadmap (Figure 2, lower panel) that delineates the most critical and challenging areas for future investigation.

This unified perspective is the groundwork for a new generation of predictive, multi-physics models. Future efforts must prioritize hybrid models for coupled boundary-layer/film scenarios, validated by high-resolution diagnostics and enhanced by data-driven methods (Reduced Order Models and Machine Learning techniques) to tackle complex nonlinear and turbulence challenges.

Author contributions

SS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Software, Supervision, Validation, Visualization, Writing – review and editing, Funding acquisition, Project administration. SC: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Brandt, L. (2014). The lift-up effect: the linear mechanism behind transition and turbulence in shear flows. Eur. J. Mech. - B/Fluids 47, 80–96. doi:10.1016/j.euromechflu.2014.03.005

CrossRef Full Text | Google Scholar

Budiman, A. C., Mitsudharmadi, H., Bouremel, Y., Winoto, S. H., and Low, H. T. (2015). Visualization of pre-set vortices in boundary layer flow over wavy surface in rectangular channel. J. Vis. 18, 669–677. doi:10.1007/s12650-014-0252-z

CrossRef Full Text | Google Scholar

Caillaud, C., Lehnasch, G., Martini, E., and Jordan, P. (2025). Effect of streaks on hypersonic boundary layer linear instability. Phys. Rev. Fluids 10, 043902. doi:10.1103/PhysRevFluids.10.043902

CrossRef Full Text | Google Scholar

Chakraborty, S. (2012). Dynamics and stability of a non-newtonian falling film. Paris: Sorbonne University Pierre and Marie Curie. PhD Thesis.

Google Scholar

Chakraborty, S., Sheu, T. W.-H., and Ghosh, S. (2019). Dynamics and stability of a power-law film flowing down a slippery slope. Phys. Fluids 31, 013102. doi:10.1063/1.5078450

CrossRef Full Text | Google Scholar

Craster, R. V., and Matar, O. K. (2009). Dynamics and stability of thin liquid films. Flow, Turbul. Combust. 81, 1131–1198. doi:10.1103/RevModPhys.81.1131

CrossRef Full Text | Google Scholar

Fedorov, A. (2011). Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95. doi:10.1146/annurev-fluid-122109-160750

CrossRef Full Text | Google Scholar

Gladbach, P., Jansen, J., and Lienstromberg, C. (2023). Non-newtonian thin-film equations: global existence of solutions, gradient-flow structure and guaranteed lift-off. doi:10.48550/arXiv.2301.10300

CrossRef Full Text | Google Scholar

Goldstein, M. E. (2014). Effect of free-stream turbulence on boundary layer transition. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 372, 20130354. doi:10.1098/rsta.2013.0354

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, S. Y., and Zaki, T. A. (2015). The effect of a low-viscosity near-wall film on bypass transition in boundary layers. J. fluid Mech. 772, 330–360. doi:10.1017/jfm.2015.214

CrossRef Full Text | Google Scholar

Karbalaei, A., Kumar, R., and Cho, H. J. (2016). Thermocapillarity in microfluidics - a review. Micromachines 7, 13. doi:10.3390/mi7010013

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] Keogh, M., McTighe, J., Dahl, J., and Bilal, O. R. (2025). Experimental observation of flow instability control by metamaterial subsurfaces. doi:10.48550/arXiv.2504.02053

CrossRef Full Text | Google Scholar

Ladjelate, K., Bouam, N. M., Djema, A., Belhenniche, A., and Chertovskih, R. (2025). The linear stability of a power-law liquid film flowing down an inclined deformable plane. Mathematics 13, 1533. doi:10.3390/math13091533

CrossRef Full Text | Google Scholar

Leib, S. J., Wundrow, D. W., and Goldstein, M. E. (1999). Effect of free-stream turbulence and other vortical disturbances on a laminar boundary layer. J. Fluid Mech. 380, 169–203. doi:10.1017/S0022112098003504

CrossRef Full Text | Google Scholar

Liss, P. S., and Slater, P. G. (1974). Flux of gases across the air-sea interface. Nature 247, 181–184. doi:10.1038/247181a0

CrossRef Full Text | Google Scholar

Miles, J. W. (1957). On the generation of surface waves by shear flows. J. Fluid Mech. 3, 185–204. doi:10.1017/S0022112057000567

CrossRef Full Text | Google Scholar

Nagarajan, S., Lele, S. K., and Ferziger, J. H. (2007). Leading-edge effects in bypass transition. J. Fluid Mech. 572, 471–504. doi:10.1017/S0022112006001893

CrossRef Full Text | Google Scholar

Nelson, J. J., Alving, A. E., and Joseph, D. D. (1995). Boundary layer flow of air over water on a flat plate. J. Fluid Mech. 284, 159–169. doi:10.1017/S0022112095000309

CrossRef Full Text | Google Scholar

Oron, A., Davis, S. H., and Bankoff, S. G. (1997). Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980. doi:10.1103/RevModPhys.69.931

CrossRef Full Text | Google Scholar

Ricco, P., Luo, J., and Wu, X. (1976). Boundary-layer stability and transition. Annu. Rev. Fluid Mech. 8, 311–349. doi:10.1146/annurev.fl.08.010176.001523

CrossRef Full Text | Google Scholar

Saha, S. (2011). On vortical disturbances in single and two-fluid boundary layers. London: Imperial College London. PhD Thesis.

Google Scholar

Saha, S., Page, J., and Zaki, T. A. (2016). Disturbance amplification in boundary layers over thin wall films. Phys. Fluids 28, 024108. doi:10.1063/1.4940221

CrossRef Full Text | Google Scholar

Saric, W. S. (1994). Görtler vortices. Annu. Rev. Fluid Mech. 26, 379–409. doi:10.1146/annurev.fl.26.010194.002115

CrossRef Full Text | Google Scholar

Schmid, P. J., and Henningson, D. S. (2001). Stability and transition in shear flows. New York: Springer.

Google Scholar

Schrader, L.-U., Brandt, L., and Zaki, T. A. (2011). Receptivity, instability and breakdown of Görtler flow. J. Fluid Mech. 682, 362–396. doi:10.1017/jfm.2011.229

CrossRef Full Text | Google Scholar

Selim, R. S., and Zakaria, K. (2024). Gravity-driven film flow of a power-law fluid over a wavy substrate with slip condition. J. Nonlinear Math. Phys. 31, 65–32. doi:10.1007/s44198-024-00223-y

CrossRef Full Text | Google Scholar

Umana, E. M., and Yang, X. (2025). Review of film cooling techniques for aerospace vehicles. Energies 18, 3058. doi:10.3390/en18123058

CrossRef Full Text | Google Scholar

Veremieiev, S., and Wacks, D. H. (2019). Modelling gravity-driven film flow on inclined corrugated substrate using a high fidelity weighted residual integral boundary-layer method. Phys. Fluids 31, 022101. doi:10.1063/1.5063013

CrossRef Full Text | Google Scholar

Wang, W., Yan, Y., Zhou, Y., and Cui, J. (2022). Review of advanced effusive cooling for gas turbine blades. Energies 15, 8568. doi:10.3390/en15228568

CrossRef Full Text | Google Scholar

Xu, D., Ricco, P., and Marensi, E. (2024). Excitation and stability of nonlinear compressible Görtler vortices and streaks induced by free-stream vortical disturbances. J. Fluid Mech. 1000, A93. doi:10.1017/jfm.2024.1064

CrossRef Full Text | Google Scholar

Yadav, A., Chakraborty, S., and Usha, R. (2015). Steady solution of an inverse problem in gravity-driven shear-thinning film flow: reconstruction of an uneven bottom substrate. J. Newt. Fluid Mech. 219, 65–77. doi:10.1016/j.jnnfm.2015.03.003

CrossRef Full Text | Google Scholar

Zaki, T. A., and Saha, S. (2009). On shear sheltering and the structure of vortical modes in single-and two-fluid boundary layers. J. Fluid Mech. 626, 111–147. doi:10.1017/S0022112008005648

CrossRef Full Text | Google Scholar

Zhu, K., and Ricco, P. (2024). Nonlinear evolution of vortical disturbances entrained in the entrance region of a circular pipe. J. Fluid Mech. 998, A19. doi:10.1017/jfm.2024.882

CrossRef Full Text | Google Scholar