Transport in perfluorosulfonic acid (PFSA) membranes: effects of pretreatment, side-chain length, and alkali metal cation

This work investigates the effects of pretreatment, side-chain length, cation type, and the interplay between them on transport properties in the commercial PFSA membranes, Nafion 115 and Aquivion E98-09S. Solutions of 1M LiCl, NaCl, and KCl were used to measure permeability, water uptake, salt partitioning, and conductivity in these membranes. We find that membrane pretreatment can make a one or two order of magnitude difference in permeability and in turn shift the selectivity towards higher-mobility salts. Conversely, in the as-received state, the membranes have lower water contents and cation hydrated radius plays a greater role than ion mobility. This results in as-received membranes exhibiting selectivity for lithium over sodium. These findings challenge the paradigm established by the body of fuel cell literature, indicating that although pretreatment increases water uptake and ionic conductivity in PFSA membrane, it may not be beneficial in applications that require selective ion transport, such as for harvesting minerals from desalination brine or as separators in redox flow batteries. In other words, ion transport through membranes can be made significantly different from that in aqueous solution by minimizing water uptake so that membrane morphology plays a dominant role.

1 Introduction

Ion exchange membrane (IEMs) are an essential component of many separations systems because of their low energy input and chemical versatility for a variety of applications (Geise et al., 2010a; Yu et al., 2020). Perfluorosulfonic acid (PFSA) membranes are high-performing and stable in fuel cell applications, but they may also be used for aqueous separations and electrochemical reactors in which controlled environments are crucial. While it is common practice to pretreat these membranes for high conductivity in fuel cells, there is an inherent tradeoff between conductivity (or permeability) and selectivity, the latter of which is more important for aqueous separations. As membrane technology becomes increasingly important with the rise of more sustainable electrochemical syntheses, choosing the best membrane and environmental conditions can determine process feasibility. IEMs can be broken down into two main classes, cation exchange membranes (CEMs) that have fixed negatively charged functional groups and anion exchange membranes (AEMs) that have fixed positively charged functional groups. A schematic is shown in Figure 1.

Figure 1

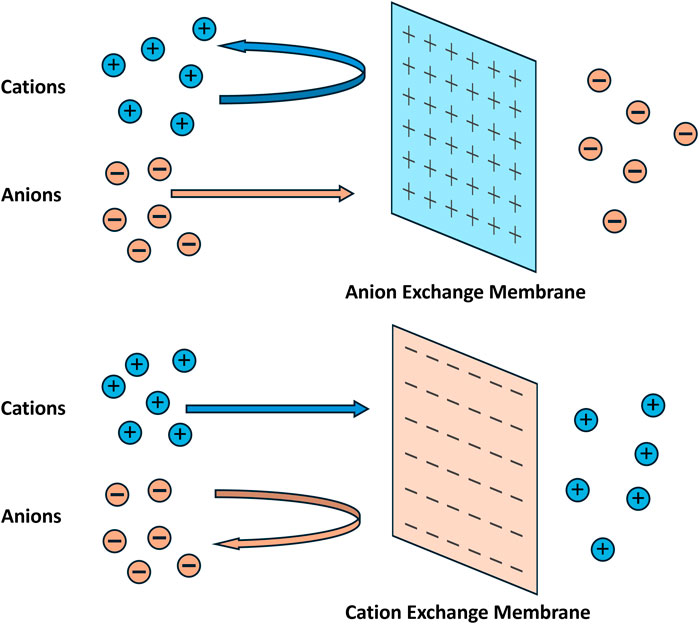
Figure 1. Simplified schematic of an ideal anion exchange membrane and cation exchange membrane. Fixed-charged functional groups in the membranes allow counterions to pass while blocking co-ions.

Under an external electric field, the membranes allow the oppositely charged ions to pass while blocking out the similarly charged ions. Although IEMs have been a topic of interest for industrial applications, there are several factors that must be balanced for optimal performance, including conductivity, ion selectivity, mechanical strength, and thermal resistance (Jiang et al., 2021). Furthermore, the properties of the membrane are affected by external operating conditions, such as salinity, humidity, and temperature (Tekinalp et al., 2023). Because of this, it is not feasible to create one class of membrane that is ideal for all applications. As shown in Figure 2, IEMs have applications in water treatment and in energy generation, utilization, and storage (Jiang et al., 2021; Tekinalp et al., 2023; Petrov et al., 2024).

Figure 2

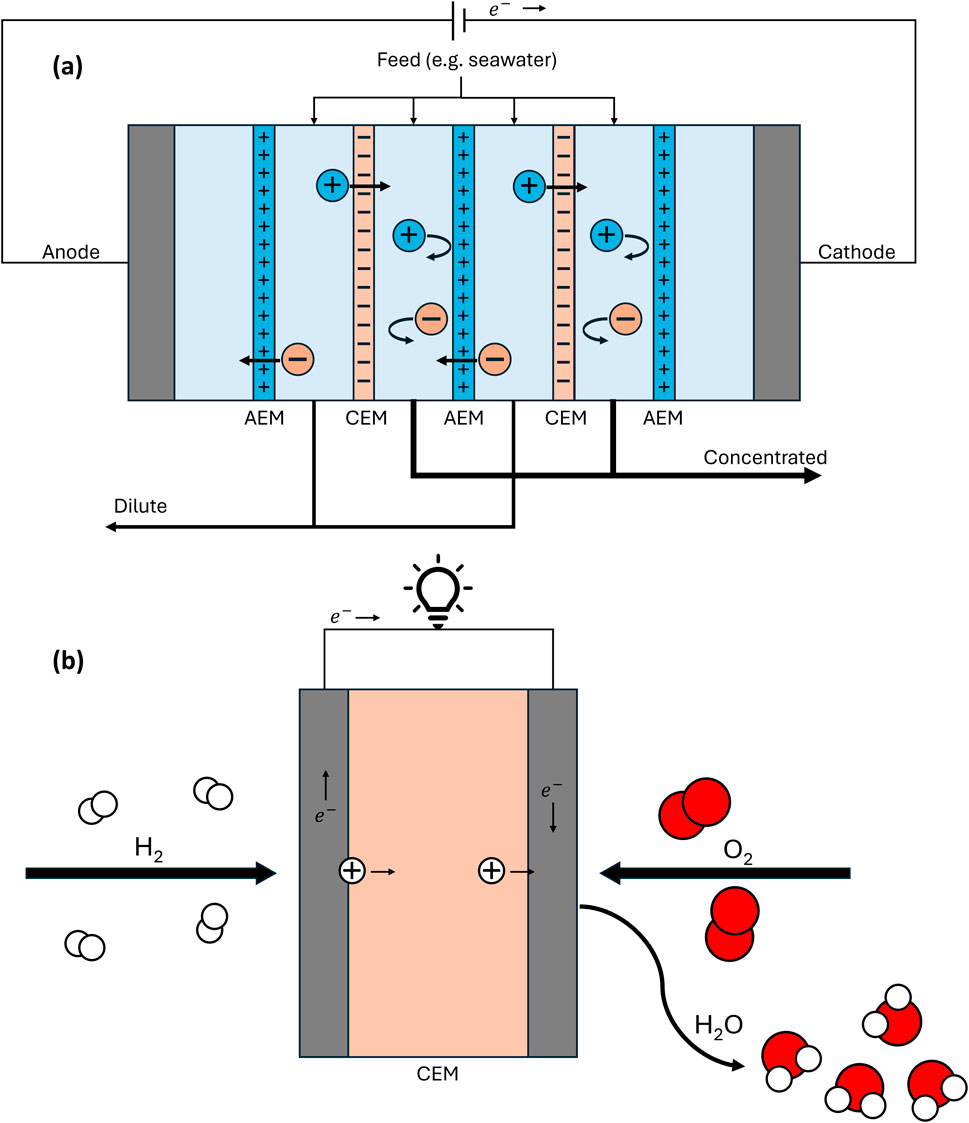
Figure 2. Example applications for IEMs. (a) Electrodialysis stack used for water desalination. (b) Hydrogen fuel cell used for electricity generation.

In most applications, high permeability/conductivity and selectivity are generally desired. However, there is an inherent tradeoff between these properties that is challenging to address (Geise et al., 2010a). While membrane separation systems are primarily dependent on the selectivity of the membrane for a desired species over others, electrochemical cells may emphasize a need for high conductivity, such as for maximizing fuel cell energy output.

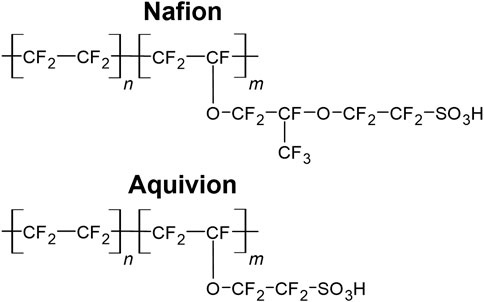
The most widely used IEMs are perfluorosulfonic acid (PFSA) membranes, such as Nafion and Aquivion. They are semi-crystalline polymer CEMs with fixed, negatively charged sulfonate groups (Figure 3) (Safronova and Lysova, 2023; Mauritz and Moore, 2004; Parshina et al., 2023). PFSA membranes have been widely adopted in fuel cells because of their excellent proton conductivity as well as chemical and mechanical stability (Abouricha et al., 2024). Aquivion and Nafion have similar structures, but Aquivion’s short side chains give it different properties, including higher crystallinity, less developed ionic channels, and improved thermal resistance (Primachenko et al., 2021). Pretreatment of these membranes is common, to increase conductivity by expanding hydrophilic channels (Peng et al., 2023; Kusoglu and Weber, 2017).

Figure 3

Figure 3. Chemical structure of Nafion and Aquivion membranes shown in acid form.

From the perspective of separation processes, permeability is dependent on both permeant and membrane properties. It is given by Equation 1, assuming electroneutrality and that the solution-diffusion mechanism dominates:

$P=KD(1)$

Here, P is salt permeability, K is the salt partition coefficient, and D is the salt diffusion coefficient (Geise et al., 2010a). D is assumed to be a constant that is dependent on solute properties as well as the phase of the surrounding environment. K is dependent on thermodynamic interactions of the ions with the membrane. In liquid separations, it is defined as the ratio of the concentration of solute in the membrane, $C_s^m$, to the concentration of solute in the bulk solution, $C_s^s$, as shown in Equation 2.

$K=\frac{C_s^m}{C_s^s}(2)$

One important principle of ion transport in charged membranes is Donnan exclusion, which is the exclusion of co-ions by immobile, charged functional groups of a membrane due to electrical repulsion (Geise et al., 2010a). In theory, this yields low permeability of ions at concentrations lower than that of the functional groups in the membrane. The concentration of functional groups in a membrane can be quantified by the ion exchange capacity (IEC), which has units of meq/g_polymer (Safronova and Lysova, 2023). Without the presence of an applied electrical potential, the transport of cations in PFSA membranes is limited by the exclusion of anions to maintain electroneutrality.

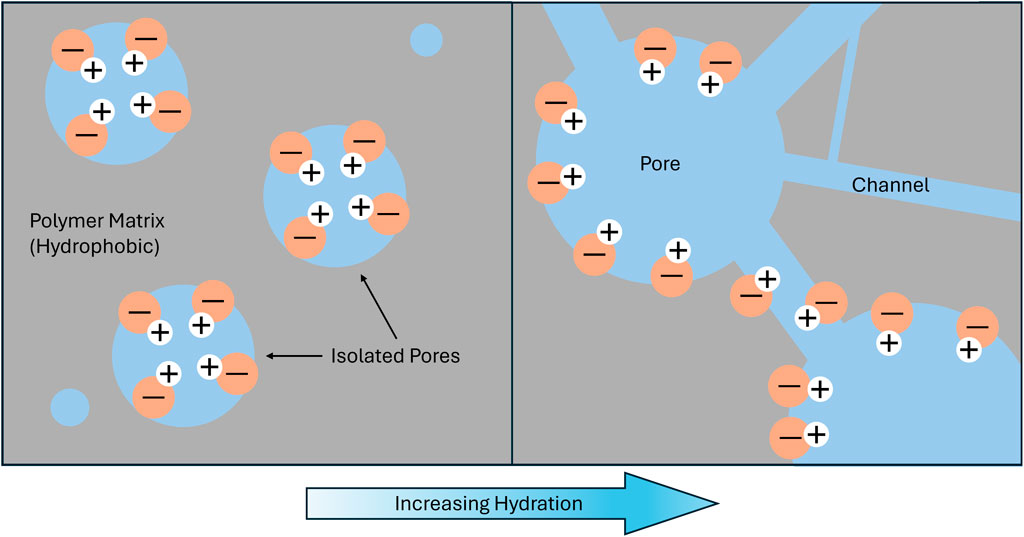
When PFSA membranes are in contact with aqueous solutions, hydrophilic channels and pores form through which water or solute can pass. The size of these regions depends on the degree of water uptake and nature of the ion (Safronova and Lysova, 2023). As charge density of cations increases, the ability to attract water molecules (hydration radius) of alkali metal cations increases, which affects the water uptake and volume fraction of hydrophilic regions of the membranes (Parshina et al., 2023; Izquierdo-Gil et al., 2012; Villaluenga et al., 2006). It has been determined that, for monovalent cations, the diffusion coefficient in highly swollen Nafion membranes increases as cation size increases, due to decreasing hydration shell sizes (Samec et al., 1995; Münchinger and Kreuer, 2019). Protons are the exception to this trend. Although protons have much smaller radii (Nightingale, 1959), their increased rate of diffusion can be attributed to their light mass and difference in mechanism of transport.

As the membrane swells with water, the concentration of fixed charge groups is diluted, which allow negatively charged ions to pass through the center of these channels (Safronova and Lysova, 2023). Figure 4 presents a simplified diagram of how the pores and channels develop as the membrane absorbs water. Short side chain PFSAs, such as Aquivion, have less developed channels due to the limited branching of the chains impeding phase separation (Safronova and Lysova, 2023; Shin et al., 2019). Furthermore, it has been determined that short side chain PFSAs have smaller hydrophilic pores than long side chain PFSAs (Vrána et al., 2018; Safronova et al., 2018). This can lead to reduced mobility and sorption of anions, which leads to increased selectivity at the expense of permeability/conductivity (Vrána et al., 2018).

Figure 4

Figure 4. PFSA membranes with increasing water content.

Research has revealed a positive correlation of membrane permeability with IEC, which is a result of the increased water uptake (Geise et al., 2010b). Higher IECs also yield increased selectivities in electrodialysis (ED) due to the improved ability to exclude anions from the membrane (Parshina et al., 2023). An exception to this can be found when comparing different types of PFSAs. A flow battery study on vanadium and vanadium oxide cation fluxes in various CEMs with constant thickness revealed that Aquivion, with a higher IEC, yielded a lower flux than Nafion (Vrána et al., 2018). This shows that membrane morphology has a significant impact on permeability.

While previous work has been done on commercial short side chain PFSA membranes such as Aquivion (Safronova et al., 2018; Espinoza et al., 2023), there is a lack of research for applications of these membranes in desalination or electrochemical devices for the transport of different ions besides H⁺, and to a lesser extent Na⁺. Additionally, while membrane pretreatment is important for applications in fuel cells in which high power output is important, the study on the effect of PFSA membrane pretreatment on aqueous environments is limited. In order to design more energy efficient desalination processes or electrochemical reactors in which high conductivity and selectivity are important, further research is needed to reveal the effects of membrane structure and composition on the transport of different ions. Having a better understanding of these properties will result in the ability to predict and model systems for performance in a variety of applications.

In this work, we study transport and equilibrium properties of Nafion and Aquivion in both the as-received and pretreated states with 1M LiCl, NaCl, and KCl. Fundamental transport parameters measured include the permeability coefficient, water uptake, salt partition coefficient, and ionic conductivity. Concentration-driven salt permeation was measured by tracking solution conductivity in the receptor compartment of a dead-end permeation cell. Salt partitioning from 1 M aqueous solutions into membranes was measured by desorbing free ions and measuring chloride concentration via ion chromatography. Together, permeation and partitioning were used to calculate salt diffusion coefficient, a key metric for membrane-based separation. Both gravimetric and volumetric swelling were measured so that water volume fraction could be calculated, because it is known to strongly affect ion mobility. In addition to the diffusive ion mobility from permeation, migration-based mobility was measured with electrochemical impedance spectroscopy. Electric field driven mobility is important for applications like dialysis and flow batteries. Pretreatment was found to have a dramatic impact on swelling and transport properties. Alkali metal cation type was also found to have a surprisingly large effect on swelling and transport. In fact, the selectivity of both membranes changed from preferring lithium to preferring sodium upon pretreatment. Data was analyzed using empirical models relating diffusivity and water volume fraction. Similar dependence of conductivity on water volume fraction was observed. These results have been interpreted in the context of known mechanisms reported in the literature.

2 Materials and methods

2.1 Pretreatment

The pretreated membranes used in this study are pretreated following literature protocols (Espinoza et al., 2023). This is done by boiling the membranes in 3 vol% H₂O₂ followed by 0.5 M H₂SO₄ and lastly deionized (DI) H₂O for an hour each with DI H₂O rinses between each step. Some membranes have been studied as received to determine the effects of pretreatment on transport properties.

2.2 Permeation

The permeation experiments measure transient concentration in a dilute cell. At the heart of the apparatus are two 10 mL PermeGear cells, separated by a membrane, shown in Figure 5. Each cell has a 1 cm diameter circular opening, exposing the membrane to the contents of each cell. An initial solution of known salt concentration is inserted into the donor cell, and the receptor cell is filled with deionized water. Both compartments are well-mixed with magnetic stirrers and are sealed to isolate the solutions from the external environment. The receptor cell has an inlet and outlet to allow the dilute solution to be pumped to a Mettler-Toledo InLab 731 conductivity meter. A peristaltic pump is used to generate a volumetric flowrate of 3.0 mL/min. The temperature of the system is maintained at 30 °C by a water bath that circulates water through the exterior jacket of the permeation cells.

Figure 5

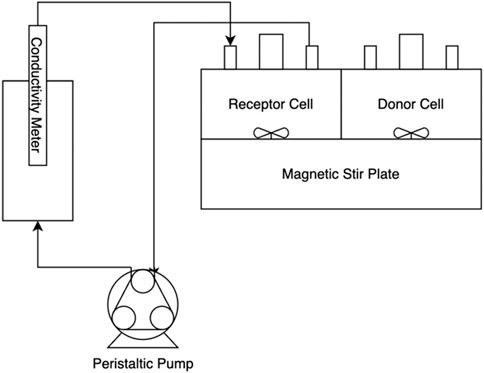
Figure 5. Schematic of the permeation experiment, including the cells separated by a membrane, stir plate used to satisfy well-mixed assumption, and conductivity meter used to determine receptor cell concentration.

The membranes used are Aquivion E98-09S and Nafion 115, purchased from MSE Supplies, which have IEC values of 1.05 meq/g and 0.91 meq/g, respectively (Espinoza et al., 2023). The membranes are soaked in their respective trial solution for at least 24 h to ensure equilibrium. A Mitutoyo micrometer is used to measure the thickness of each membrane, which is taken after each permeation experiment.

Before beginning trials, a calibration was conducted to determine a mathematical relationship between the concentration of each aqueous salt solution and the corresponding conductivity. This is done by making solutions of known concentration, ranging from 0.001 M to 0.01 M, equilibrating them at 30 °C, and measuring the conductivity of each. A quadratic fit provides the necessary equation to relate the two parameters. The calibration equations developed for each salt are:

$\text{LiCl}:C=82.28{\kappa }^2+8.44\kappa (\mathrm{3a})$

$\text{NaCl}:C=80.27{\kappa }^2+7.26\kappa (\mathrm{3b})$

$\text{KCl}:C=44.25{\kappa }^2+7.19\kappa (\mathrm{3c})$

where $C$ is salt concentration in M, and $\kappa$ is solution conductivity in S/cm.

For permeation experiments, the receptor side and temperature of the system are brought to steady state first. Then, the donor cell is filled with the salt solution, and the measurements of receptor side conductivity begin. The permeation experiments are run for 8 h, with measurements recorded every 30 s. Experiments are conducted for initial donor cell concentrations of 1 M for LiCl, NaCl, and KCl. At least three replicates are collected to ensure sufficient repeatability.

The permeability coefficient can be determined experimentally using Equation 4:

$P=-\frac{L{V}_2}{A\left(\frac{V_2}{V_1}+1\right)}\frac{d}{dt}\ln \left[1-\frac{\left(\frac{V_2}{V_1}+1\right)C_2\left(t\right)}{C_{1,0}}\right](4)$

where $P$ is permeability, $L$ is membrane thickness in the hydrated state, $V_1$ is donor cell volume (known to be 10 mL), $V_2$ is receptor cell, tubing, and probe container volume (calibrated to be 22.5 mL), $A$ is area exposed to each solution (0.79 cm²), $C_2\left(t\right)$ is downstream concentration as a function of time, and $C_{1,0}$ is initial donor cell concentration. The equation is derived in a similar manner to Geise et al. (2010b), neglecting water counter-diffusion and recognizing that $C_2\left(0\right)=0$. The function within the derivative is linear within the pseudo-steady state regime. Therefore, the slope of the natural logarithm term plotted versus time is determined between the 3- and 4-h data points.

2.3 Water uptake

Water uptake is measured gravimetrically as has been done in the literature (Espinoza et al., 2023; Kingsbury et al., 2018). The membranes are equilibrated in their respective salt solutions for at least 24 h. Afterwards, they are blotted with a Kimwipe to remove external solution, and the hydrated mass is taken. The membranes are then put on individual petri dishes, covered, and left in a vacuum oven set at 75 °C for at least 24 h to evaporate all the water. One day is sufficient to reach a stable mass. The water uptake, $WU$, is calculated with Equation 5:

$WU=\frac{m_{wet}-m_{dry}}{m_{dry}}(5)$

where $m_{wet}$ is the mass in the hydrated state, and $m_{dry}$ is the mass in the dry state. It is also helpful to attain the water volume fraction, ${\varphi }_w$, as it provides insight into the morphological state of the membrane:

${\varphi }_w=\frac{\left(m_{wet}-m_{dry}\right)/{\rho }_w}{L*\left(\frac{\pi *D^2}{4}\right)}(6)$

where ${\rho }_w$ is the density of water, and $D$ is the diameter of the wet membrane in Equation 6.

2.4 Desorption

Desorption measurements are performed to determine the free salt concentration inside the membranes. After water uptake experiments, the dried membranes are left in vials of 50 mL DI water to allow the free salt to diffuse out. After at least 24 h in a vial, the membranes are carefully extracted and moved to a separate vial of water. One desorption step is sufficient to allow virtually all the free salt to diffuse into the surrounding solution (Kingsbury et al., 2018). The resulting desorption solution is then analyzed using ion chromatography (IC, Dionex Aquion Ion Chromatography System, United States) to detect chloride concentration. The IC is equipped with a Dionex IonPac AS22 analytical column maintained at 30 °C. The eluent consists of 1.1 mM sodium carbonate and 0.4 mM sodium bicarbonate delivered at a flow rate of 1 mL/min. The system operates at a suppressor current of 7 mA. Calibration standards of 0, 1, 5, 10, 30, 60, and 100 mg/L chloride are prepared to establish a calibration curve. The method quantification limit for the chloride is 0.5 mg/L. The free salt concentration in the membranes is then calculated via Equation 7:

$C_s^m=\frac{C_{Cl}{V}_{tot}{\varphi }_w}{\left(m_{wet}-m_{dry}\right)/{\rho }_w}(7)$

where $C_{Cl}$ is chloride concentration from the desorption solution, and $V_{tot}$ is the total volume of the desorption solution. The salt partition coefficient, K, can then be calculated via Equation 2 and the salt diffusion coefficient via Equation 1.

2.5 Conductivity

To characterize electrical performance inside the membranes, conductivity experiments are performed (Luo et al., 2020; Kamcev et al., 2018). The direct contact method developed by Diaz et al. is employed to measure the conductivity of the membranes in various ionic forms (Díaz et al., 2023). A custom cell was designed using stainless steel electrodes that are 2 cm in diameter. The two electrodes are housed in non-conductive plastic, and membranes are placed between them for each measurement. Electrochemical impedance spectroscopy is run at an amplitude of 10 mV from 1 MHz to 1 kHz with 6 points per decade, and the membrane stacking approach (Díaz et al., 2023) is used to decouple the apparatus resistance from the membrane resistance. An example of the measurement is shown in Figure 6.

Figure 6

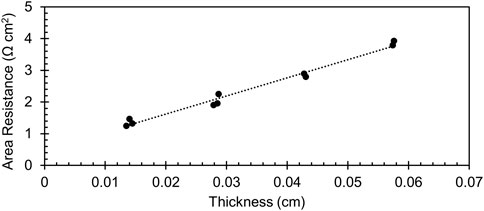
Figure 6. Example of membrane conductivity measurement for pretreated Nafion 115 equilibrated with 1 M NaCl. Clusters represent replicate measurements on stacks of 1–4 membranes.

In short, the resistance of membrane samples equilibrated with different salts is collected at various stack thicknesses, and the area resistance is plotted against thickness. This yields a linear plot, which is extrapolated to zero to get the external resistance. Conductivity is determined using Equation 8, which is the reciprocal of the slope from the linear regression:

$\kappa =\frac{∆L}{∆\left(R*A\right)}(8)$

where $\kappa$ is membrane conductivity, $R$ is measured resistance, and $A$ is the area of the electrodes. A constant force of 3.3 N is applied to press the electrodes to the membrane surfaces, which corresponds to a clamping pressure of 10.5 kPa.

3 Results and discussion

Permeability, water uptake, desorption, and conductivity measurements have been performed for Nafion and Aquivion in 1 M solutions of NaCl, LiCl, and KCl. Tables 1 and 2 show a summary of the data collected.

Table 1

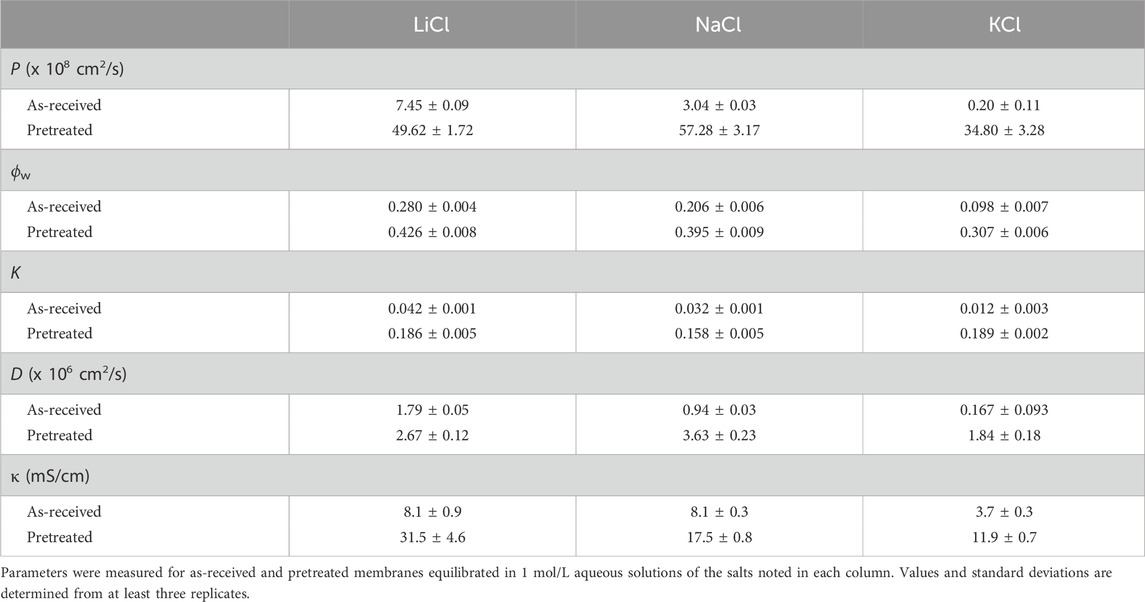
Table 1. Nafion 115 permeability ($P$), water volume fraction (${\varphi }_w$), salt partition coefficient ($K$), salt diffusion coefficient ($D$), and ionic conductivity ($\kappa$).

Table 2

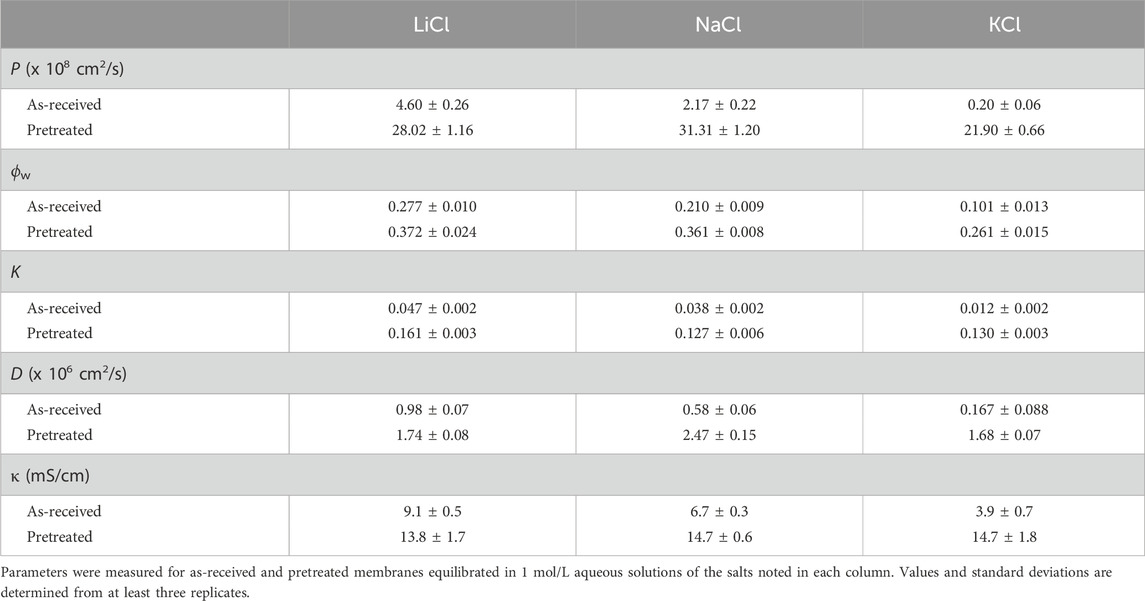
Table 2. Aquivion E98-09S permeability ($P$), water volume fraction (${\varphi }_w$), salt partition coefficient ($K$), salt diffusion coefficient ($D$), and ionic conductivity ($\mathrm{\kappa }$).

Focusing first on permeability, the results in Tables 1 and 2 and Figure 7 show that Nafion has greater permeability than Aquivion for all salts at equivalent conditions (pretreatment and salt type). This can be attributed to the increased $\varphi$_w in Nafion over Aquivion, shown in Figure 8, which falls in line with the understanding that shorter side chains lead to decreased hydrophilic regions in the membranes (Shin et al., 2019). There is a significant effect of pretreatment on salt permeability − an order of magnitude increase for LiCl and NaCl and two orders for KCl.

Figure 7

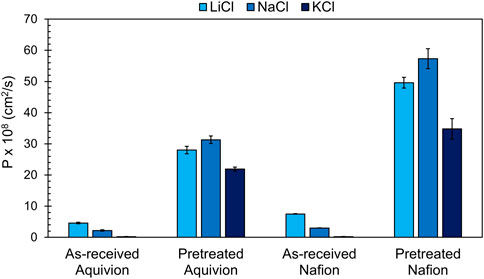
Figure 7. Permeability of Nafion and Aquivion in the pretreated and as-received forms with 1 M LiCl, 1 M NaCl, and 1 M KCl solutions. Error bars represent one standard deviation from the mean value.

Figure 8

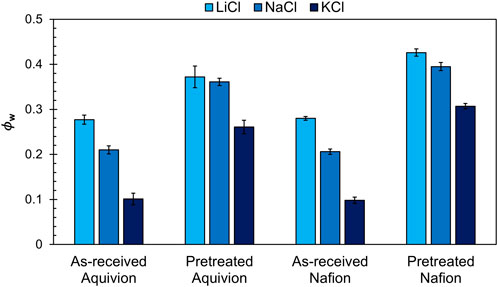
Figure 8. Water volume fraction of Nafion and Aquivion in the pretreated and as-received forms with 1 M LiCl, 1 M NaCl, and 1 M KCl. Error bars represent one standard deviation from the mean value.

Interestingly, pretreatment also causes a change in Li/Na selectivity for both membranes. From literature, we know that as-received (and thermally annealed) membranes exhibit sharper microphase separation between hydrophobic backbone and ionic domains; the ionic domains are less swollen with water and thus smaller and more organized (Shin et al., 2019; Kim et al., 2006). This would mean that, with little free water present, water of hydration will lubricate motion and shield interactions with the fixed sulfonate groups. Thus, ions with larger hydration number will be more mobile and have higher permeability. The data agrees with this analysis, whereby LiCl permeability is greater than that of NaCl in as-received membranes.

On the other hand, in pretreated membranes the ionic domains are more highly swollen with water (as shown in Figure 8) and thus larger but also less well organized. This means that ion transport is more like that in aqueous solution, i.e., the membrane morphology has less effect and an abundance of free water is present to promote ion motion and shield electrostatic (and any specific) interactions with fixed sulfonate groups. In this case, ions with smaller hydrated radius will be more mobile due to the simple fact that smaller species diffuse faster. The data also agrees with this explanation, whereby NaCl permeability is greater than that of LiCl in pretreated membranes.

It is interesting to note that this trend does not extend to K⁺ form. In other words, pretreatment does not induce sufficient swelling for there to be an excess of free water in K⁺ form membranes. Otherwise, KCl permeability would be expected to be greatest in pretreated membranes. When comparing the as-received membranes equilibrated with LiCl versus the pretreated membranes equilibrated with KCl, we see that they have different permeabilities even with similar $\varphi$_w values. This further shows that P is affected by the nature of the salt in addition to the hydration level, but it also suggests that the nature of the pretreatment itself plays a role. Boiling pretreatment of PFSA membranes has been shown to increase normal polymer swelling and the level of continuous hydrophilic channels in these membranes, leading to increased permeability, solute uptake, and conductivity at the expense of selectivity with a reduction in Donnan potential (Peng et al., 2023). While the pretreated KCl membranes have comparable $\varphi$_w to the as-received LiCl membranes, they have more continuous channels that contribute to the transport of ions through the membrane.

As shown in Tables 1 and 2, the membrane water uptake (and proportional water volume fraction in Figure 8) correlates to the hydration radius of the cation—3.82 Å for Li⁺, 3.58 Å for Na⁺, and 3.31 Å for K⁺ (Shin et al., 2019). Sorption, K, follows a similar pattern as water uptake, increasing with increasing cation hydration radius. The low permeability of KCl can be attributed to the low water uptake of the membranes in a KCl environment. The data reinforce the significance of pretreatment and water uptake on ion transport by showing that small changes in water volume fraction can lead to large changes in the permeability of species in a membrane (Kitto and Kamcev, 2022). By comparing our data to traditional membrane transport models that capture water volume fraction dependence, such as the Mackie and Meares model and Yasuda model, we can determine how much our data deviates from the assumptions held in the models. The Mackie and Meares model has been widely used because it is generally accurate and has no adjustable parameters (Kitto and Kamcev, 2022). It is shown in Equation 9 and relates the diffusivity of a species in solution to its diffusivity in a membrane based on the water volume fraction, accounting solely for tortuosity effects:

$D_i^M=D_i^S{\left(\frac{{\varphi }_w}{2-{\varphi }_w}\right)}^2(9)$

Here, $D_i^M$ is the diffusion coefficient of the solute in the membrane, and $D_i^S$ is the diffusion coefficient of the solute in the solution. The Yasuda model, shown in Equation 10, predicts solute diffusivity in a membrane based on its free volume, which is proportional to the water volume fraction (Kitto and Kamcev, 2022):

$D_i^M=D_i^S\exp \left(B\left(1-\frac{1}{{\varphi }_w}\right)\right)(10)$

$B$ is an adjustable parameter which improves model accuracy but requires regression from collected data. Similar to the Mackie and Meares model, the membrane diffusivity in the Yasuda model is dependent on ${\varphi }_w$. Neither model accounts for interactions of ions with fixed charged groups. Specific interactions are known to have a considerable effect on partitioning in IEMs, but immobilization of counter ions due to binding with fixed charge groups appears to largely counteract increased concentration due to specific interactions, such that they have only minor effect on transport, at least in the pretreated state (Münchinger and Kreuer, 2019). Electrostatic (Donnan) interactions are also not explicitly accounted in the models, meaning that systematic deviation from the models is expected. Figure 9 shows a comparison of diffusion coefficients determined from permeation and desorption experiments as well as from both models as a function of water volume fraction from gravimetric sorption. The solute diffusion coefficient at 25 °C in 1 M aqueous solution ($D_{LiCl}=1.30\times {10}^{-7}\mathrm{c}{\mathrm{m}}^2/\mathrm{s}$, $D_{NaCl}=1.48\times {10}^{-7}\mathrm{c}{\mathrm{m}}^2/\mathrm{s}$, and $D_{KCl}=1.89\times {10}^{-7}\mathrm{c}{\mathrm{m}}^2/\mathrm{s}$) (Robinson and Stokes, 1959) was used to normalize the experimental diffusion coefficient data for ease of comparison with both models. These normalized values are shown in Figures 9b,c.

Figure 9

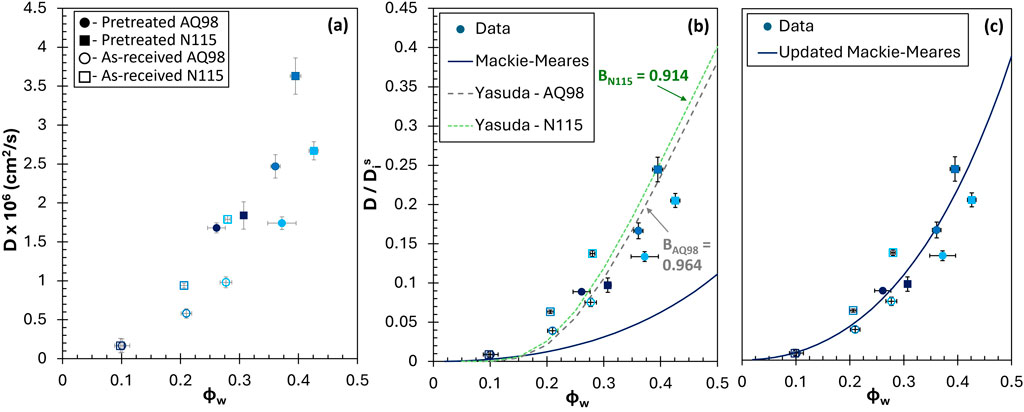
Figure 9. (a) Measured membrane diffusion coefficient of 1 M salts (LiCl, NaCl, and KCl) plotted against water volume fraction. (b) Experimental membrane D normalized to the solution D plotted with the Yasuda and Mackie and Meares models. The Mackie and Meares model consistently underpredicts the true membrane diffusivity. The Yasuda model adjustable parameters are 0.914 and 0.964 for Nafion (N115) and Aquivion (AQ98), respectively. (c) Normalized experimental membrane D plotted with the Mackie and Meares model multiplied by a factor of 3.5. Vertical axis is the same as panel (b).

As shown in Figure 9, there is a clear exponential increase in D for the experimental data and models with increasing ${\varphi }_w$. Performing a least-squares regression for the B parameter in the Yasuda model (Figure 9b) yields values of 0.914 and 0.964 for Nafion and Aquivion membranes, respectively. The similarity of membrane structure explains the similarity in B values, and a singular value fitting all the data can be used to further generalize the model, which was found to be 0.946. Since neither model accounts for Coulombic interactions in the membranes, this B value can be used to account for these effects. The lack of any adjustable parameter in the Mackie and Meares model explains why it consistently underpredicts the diffusion coefficients for all data points. Interestingly, normalizing the experimental D to the Mackie and Meares D reveals that the true salt diffusivity in the membranes is about 3.5 times the value predicted by the model, with no clear trend with pretreatment, salt, or membrane type. This factor significantly improves the predictability of the Mackie and Meares, as shown in Figure 9c, and this finding suggests that the updated model can be used to accurately predict salt diffusion coefficients in PFSA membranes, although more data should be collected to evaluate how universal this empirical value is. A direct comparison between salts is difficult because of the natural change in water uptake that affects the morphology of the membranes. However, once again, for the more hydrated membranes, we see a strong dependence on the mobility of the cation at comparable water content.

Conductivity is also strongly dependent on the hydration level of the membrane. Similar to permeability, there are competing effects between the hydrating ability and the mobility of the cation on the degree of transport in a membrane. In this case, transport occurs under a voltage gradient rather than a concentration gradient. Figure 10 shows that pretreated membranes are more conductive, but the trend with hydrating ability of the cation is not as clear. For pretreated Aquivion, the conductivities for the different cation types are the same within error as is also the case for LiCl and NaCl in as-received Nafion. The pretreated Nafion, however, shows a clear trend in which the membrane equilibrated with LiCl has much higher conductivity. This may be due to conflicting factors including ion mobility, membrane hydration, and ion concentration in the membrane. When plotting conductivity against $\varphi$_w in a similar manner as D, a similar trend is observed in that conductivity increases exponentially (Figure 10b). This further demonstrates the importance of the water uptake in membrane properties.

Figure 10

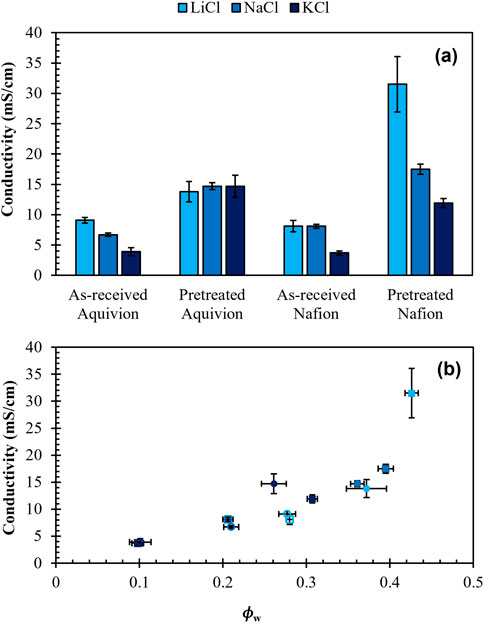
Figure 10. (a) Through-plane conductivity of Nafion 115 and Aquivion E98-09S in the pretreated and as-received form with 1 M NaCl, 1 M LiCl, and 1 M KCl. Error bars represent the standard error of the conductivity. (b) Conductivity plotted against water volume fraction. Squares represent Nafion and circles represent Aquivion. Filled shapes correspond to pretreated membranes and unfilled shapes correspond to as-received membranes. Conductivity increases roughly exponentially with water volume fraction.

From the perspective of harvesting lithium from concentrated desalination brine, we examined the selectivity of these membranes for lithium over sodium as the ratio of lithium to sodium permeability. In the fashion of a Robeson plot, this selectivity is plotted versus lithium permeability in Figure 11a. There is a strong tradeoff between selectivity and permeability in these membranes. Upon pretreatment, both membranes experience a drop in Li⁺ selectivity over Na⁺ because of the reduced dependence on ion type with increasing water content. Concomitantly, the Li⁺ permeability increases significantly with the increasing water content caused by pretreatment. Notably, the pretreated membranes’ selectivity shifts to favor Na⁺ (i.e., drops to a value less than unity) because of the improved mobility in high-water content regions. Qualitatively similar trends are apparent in Figure 11b for Na⁺ over K⁺, but unlike the Li⁺/Na⁺ case, pretreatment does not cause a change in selectivity. In other words, the membranes remain slightly selective for Na⁺ over K⁺ despite the increase in water content with pretreatment. This is likely due to the odd fact that K-form PFSAs take up much less water than they do in the Na and Li forms.

Figure 11

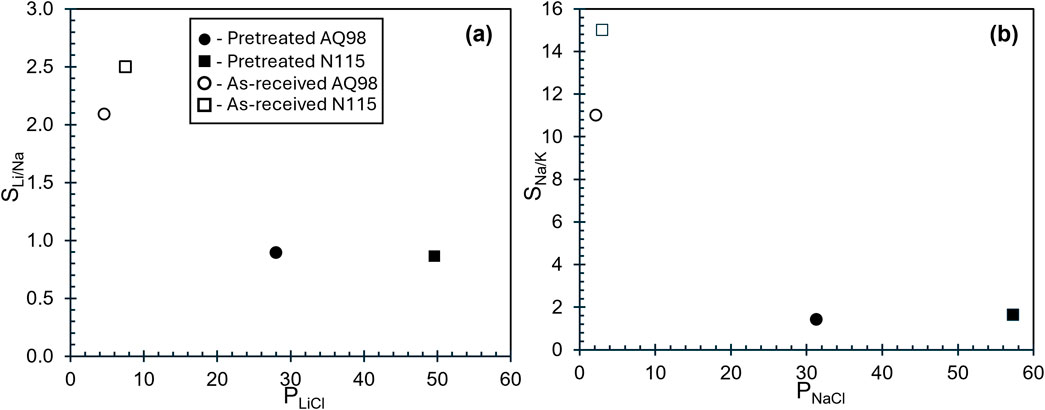
Figure 11. (a) Selectivity of Li⁺ over Na⁺ (P_LiCl/P_NaCl) plotted against P_LiCl. As water content and permeability increase, selectivity decreases and shifts to the more mobile salt. (b) Selectivity of Na⁺ over K⁺ (P_NaCl/P_KCl) plotted against P_NaCl. Selectivity decreases by an order of magnitude with pretreatment (increasing water content), but the membranes remain slightly selective for sodium over potassium, despite the increase in water content.

4 Conclusion

The data show that the external environment and membrane morphology are significant in determining transport properties. Both membranes have comparable water volume fractions in the as-received state, even though Aquivion has a higher IEC than Nafion. Since membranes with higher IEC’s typically yield higher levels of water uptake, this highlights the significance of side chain length on physical properties. The shorter side chains of Aquivion allow the membrane to retain dimensional stability, resisting swelling, and maintaining higher fixed charge concentration in the membrane which results in a stronger Donnan exclusion effect and thus smaller permeability values. The effect of pretreatment further demonstrates the greater hydrophilicity of longer side chains, as the pretreated Nafion shows increased water uptake, permeability, and conductivity over Aquivion. There is a clear tradeoff between conductivity and selectivity for IEMs, which is the main challenge when synthesizing membranes for separations or electrochemical devices. The data show a strong correlation between the water uptake of the membrane and permeability of the salt, but the difference in membrane structure allows Aquivion to selectively block out more co-ions in the as-received state, suggesting that morphology significantly affects transport properties. Based on the data, as-received Aquivion demonstrates potential for improved selectivity.

Pretreatment of the membranes has the largest effect on salt permeability and conductivity. The process, which is standard protocol for these membranes, significantly increases their hydrophilic regions and in turn the rate of ion transport. The water volume fraction of the membranes affects these properties exponentially, which suggests that control of this parameter is perhaps one of the most important considerations when designing systems that use IEMs. This is complicated because $\varphi$_w depends on the external environment (i.e., temperature, salt, concentration), pretreatment, and membrane morphology. To design new IEMs and optimal processes, it is important to have models that aid understanding of how these different factors combine to affect overall transport. A significant challenge is decoupling transport factors, such as salt mobility in the membrane, from thermodynamic factors like equilibrium water uptake. Both play significant roles in the membrane, and we see this tradeoff in high-$\varphi$_w membranes in which ion mobility is the dominating factor in ion transport.

The Mackie and Meares model consistently underestimates the diffusion of the salts in the PFSA membranes, but this is expected because it only accounts for tortuosity effects in the membrane. A consistent factor of about 3.5 was found to relate the true D in the membranes to D predicted by the Mackie and Meares, which is independent of salt, pretreatment, or membrane. This can be used for rough preliminary predictions of diffusivity in these membranes. Future work should verify this with more salts, differing concentrations, and other ion exchange membranes.

The trend with conductivity is more difficult to determine from the data, but it follows a similar exponential trend with water uptake. Although larger cations typically have a higher mobility, the increased water uptake with smaller cations like Li⁺ yields equal or higher conductivity, especially in the as-received state. This is an important consideration for electrolysis reactors in which the cation is a design decision, such as in CO₂ reduction. It is also important for applications like flow batteries and electrodialysis-driven mining of desalination brine, in which ion transport (and selectivity) are important.

As a result of charge dilution, weakened Donnan exclusion leads to reduced membrane selectivity at high $\varphi$_w that results from pretreatment. The larger hydrophilic regions reduce the amount of Coulombic interaction between the solute and the fixed charged groups. For cases in which proton conductivity is more important than ion selectivity, pretreatment is favorable, but for cases of electrochemical separations or reactions where the selective transport of certain species is important, pretreatment may not be favorable. While pretreatment may reduce overpotential in electrochemical cells from the improved conductivity, reduced selectivity will require additional separations downstream in applications such as electrodialysis or electrochemical reactors. In addition, avoiding pretreatment would save time and energy in industrial processes, ultimately leading to reduced costs. This work is generalizable to other membrane types and encourages consideration of side chain length and treatment process, including in the development of more sustainable hydrocarbon membranes.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SC: Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review and editing. DS: Data curation, Investigation, Methodology, Writing – review and editing. YT: Resources, Supervision, Writing – review and editing. DH: Conceptualization, Formal Analysis, Funding acquisition, Project administration, Resources, Supervision, Visualization, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was made possible by funding from the inaugural Florida State University (FSU) President’s Sustainability and Climate Solutions grant program. SC acknowledges the National High Magnetic Field Laboratory’s Research Experiences for Undergraduates (REU) during which part of this work was conducted.

Acknowledgments

The structure provided by the FSU Honors in the Major program as well as the Undergraduate Research Program of the FAMU-FSU Chemical and Biomedical Engineering Department were instrumental in bringing this project to completion.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abouricha, S., Aziam, H., Noukrati, H., Sel, O., Saadoune, I., Lahcini, M., et al. (2024). Biopolymers-based proton exchange membranes for fuel cell applications: a comprehensive review. Chemelectrochem 11 (9), e202300648. doi:10.1002/celc.202300648

CrossRef Full Text | Google Scholar

Díaz, J., Kitto, D., and Kamcev, J. (2023). Accurately measuring the ionic conductivity of membranes via the direct contact method. J. Membr. Sci. 669, 121304. doi:10.1016/j.memsci.2022.121304

CrossRef Full Text | Google Scholar

Espinoza, C., Kitto, D., and Kamcev, J. (2023). Counter-ion conductivity and selectivity trade-off for commercial ion-exchange membranes at high salinities. ACS Appl. Polym. Mater. 5, 10324–10333. doi:10.1021/acsapm.3c02102

CrossRef Full Text | Google Scholar

Geise, G. M., Lee, H. S., Miller, D. J., Freeman, B. D., McGrath, J. E., and Paul, D. R. (2010a). Water purification by membranes: the role of polymer science. J. Polym. Sci. Part B-Polymer Phys. 48 (15), 1685–1718. doi:10.1002/polb.22037

CrossRef Full Text | Google Scholar

Geise, G. M., Freeman, B. D., and Paul, D. R. (2010b). Characterization of a sulfonated pentablock copolymer for desalination applications. Polymer 51 (24), 5815–5822. doi:10.1016/j.polymer.2010.09.072

CrossRef Full Text | Google Scholar

Izquierdo-Gil, M. A., Barragán, V. M., Villaluenga, J. P. G., and Godino, M. P. (2012). Water uptake and salt transport through Nafion cation-exchange membranes with different thicknesses. Chem. Eng. Sci. 72, 1–9. doi:10.1016/j.ces.2011.12.040

CrossRef Full Text | Google Scholar

Jiang, S. X., Sun, H. S., Wang, H. J., Ladewig, B. P., and Yao, Z. L. (2021). A comprehensive review on the synthesis and applications of ion exchange membranes. Chemosphere 282, 130817. doi:10.1016/j.chemosphere.2021.130817

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamcev, J., Paul, D., Manning, G., and Freeman, B. (2018). Ion diffusion coefficients in ion exchange membranes: significance of counterion condensation. Macromolecules 51, 5519–5529. doi:10.1021/acs.macromol.8b00645

CrossRef Full Text | Google Scholar

Kim, M.-H., Glinka, C. J., Grot, S. A., and Grot, W. G. (2006). SANS study of the effects of water vapor sorption on the nanoscale structure of perfluorinated sulfonic acid (NAFION) membranes. Macromolecules 39 (14), 4775–4787. doi:10.1021/ma060576u

CrossRef Full Text | Google Scholar

Kingsbury, R., Zhu, S., Flotron, S., and Coronell, O. (2018). Microstructure determines water and salt permeation in commercial ion-exchange membranes. ACS Appl. Mater. and Interfaces 10, 39745–39756. doi:10.1021/acsami.8b14494

PubMed Abstract | CrossRef Full Text | Google Scholar

Kitto, D., and Kamcev, J. (2022). Manning condensation in ion exchange membranes: a review on ion partitioning and diffusion models. J. Polym. Sci. 60 (21), 2929–2973. doi:10.1002/pol.20210810

CrossRef Full Text | Google Scholar

Kusoglu, A., and Weber, A. (2017). New insights into perfluorinated sulfonic-acid ionomers. Chem. Rev. 117 (3), 987–1104. doi:10.1021/acs.chemrev.6b00159

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, T., Roghmans, F., and Wessling, M. (2020). Ion mobility and partition determine the counter-ion selectivity of ion exchange membranes. J. Membr. Sci. 597, 117645. doi:10.1016/j.memsci.2019.117645

CrossRef Full Text | Google Scholar

Mauritz, K. A., and Moore, R. B. (2004). State of understanding of nafion. Chem. Rev. 104 (10), 4535–4585. doi:10.1021/cr0207123

PubMed Abstract | CrossRef Full Text | Google Scholar

Münchinger, A., and Kreuer, K.-D. (2019). Selective ion transport through hydrated cation and anion exchange membranes I. The effect of specific interactions. J. Membr. Sci. 592, 117372. doi:10.1016/j.memsci.2019.117372

CrossRef Full Text | Google Scholar

Nightingale, E. R. (1959). Phenomenological theory of ion solvation - effective radii of hydrated ions. J. Phys. Chem. 63 (9), 1381–1387. doi:10.1021/j150579a011

CrossRef Full Text | Google Scholar

Parshina, A. V., Safronova, E. Y., Yelnikova, A. S., Stretton, N., and Bobreshova, O. V. (2023). Effect of the nature of counterion on properties of perfluorosulfonic acid membranes with long and short side chains. Membr. Membr. Technol. 5 (5), 323–332. doi:10.1134/s2517751623050062

CrossRef Full Text | Google Scholar

Peng, J., Fan, X., Goenaga, G., Weiss, C., Neal, C., Cantillo, N., et al. (2023). Effect of boiling pretreatment on physicochemical and transport properties of perfluorosulfonic acid membrane. ACS Appl. Polym. Mater. 5, 9940–9951. doi:10.1021/acsapm.3c01772

CrossRef Full Text | Google Scholar

Petrov, K., Koopman, C., Subramanian, S., Koper, M., Burdyny, T., and Vermaas, D. (2024). Bipolar membranes for intrinsically stable and scalable CO2 electrolysis. Nat. Energy 9 (8), 932–938. doi:10.1038/s41560-024-01574-y

CrossRef Full Text | Google Scholar

Primachenko, O., Marinenko, E., Odinokov, A., Kononova, S., Kulvelis, Y., and Lebedev, V. (2021). State of the art and prospects in the development of proton-conducting perfluorinated membranes with short side chains: a review. Polym. Adv. Technol. 32 (4), 1386–1408. doi:10.1002/pat.5191

CrossRef Full Text | Google Scholar

Robinson, R. A., and Stokes, R. H. (1959). Electrolyte solutions. Second Revised ed. United Kingdom: Butterworth and Co.

Google Scholar

Safronova, E. Y., and Lysova, A. A. (2023). Perfluorosulfonic acid polymer membranes: microstructure and basic functional properties. Membr. Membr. Technol. 5 (6), 379–393. doi:10.1134/s2517751623060070

CrossRef Full Text | Google Scholar

Safronova, E. Y., Osipov, A. K., and Yaroslavtsev, A. B. (2018). Short side chain aquivion perfluorinated sulfonated proton-conductive membranes: transport and mechanical properties. Pet. Chem. 58 (2), 130–136. doi:10.1134/s0965544118020044

CrossRef Full Text | Google Scholar

Samec, Z., Trojanek, A., and Samcova, E. (1995). Ion and pore fluid transport properties of a nafion® membrane separating two electrolyte solutions Part I. Kinetics of the proton and alkali metal cation transport. J. Electroanal. Chem. 389 (1-2), 1–11. doi:10.1016/0022-0728(95)03825-2

CrossRef Full Text | Google Scholar

Shin, S.-H., Nur, P. J., Kodir, A., Kwak, D.-H., Lee, H., Shin, D., et al. (2019). Improving the mechanical durability of short-side-chain perfluorinated polymer electrolyte membranes by annealing and physical reinforcement. ACS Omega 4 (21), 19153–19163. doi:10.1021/acsomega.9b02436

PubMed Abstract | CrossRef Full Text | Google Scholar

Tekinalp, O., Zimmermann, P., Holdcroft, S., Burheim, O. S., and Deng, L. Y. (2023). Cation exchange membranes and process optimizations in electrodialysis for selective metal separation: a review. Membranes 13 (6), 566. doi:10.3390/membranes13060566

PubMed Abstract | CrossRef Full Text | Google Scholar

Villaluenga, J. P. G., Barragán, V. M., Seoane, B., and Ruiz-Bauzá, C. (2006). Sorption and permeation of solutions of chloride salts, water and methanol in a Nafion membrane. Electrochimica Acta 51 (28), 6297–6303. doi:10.1016/j.electacta.2006.04.011

CrossRef Full Text | Google Scholar

Vrána, J., Charvát, J., Mazúr, P., Belsky, P., Dundálek, J., Pocedic, J., et al. (2018). Commercial perfluorosulfonic acid membranes for vanadium redox flow battery: effect of ion-exchange capacity and membrane internal structure. J. Membr. Sci. 552, 202–212. doi:10.1016/j.memsci.2018.02.011

CrossRef Full Text | Google Scholar

Yu, J. Z., Fang, D. L., Zhang, H., Leong, Z. Y., Zhang, J. T., Li, X. X., et al. (2020). Ocean mining: a fluidic electrochemical route for lithium extraction from seawater. Acs Mater. Lett. 2 (12), 1662–1668. doi:10.1021/acsmaterialslett.0c00385

CrossRef Full Text | Google Scholar