Stochastic IMT (Insulator-Metal-Transition) Neurons: An Interplay of Thermal and Threshold Noise at Bifurcation

Artificial neural networks can harness stochasticity in multiple ways to enable a vast class of computationally powerful models. Boltzmann machines and other stochastic neural networks have been shown to outperform their deterministic counterparts by allowing dynamical systems to escape local energy minima. Electronic implementation of such stochastic networks is currently limited to addition of algorithmic noise to digital machines which is inherently inefficient; albeit recent efforts to harness physical noise in devices for stochasticity have shown promise. To succeed in fabricating electronic neuromorphic networks we need experimental evidence of devices with measurable and controllable stochasticity which is complemented with the development of reliable statistical models of such observed stochasticity. Current research literature has sparse evidence of the former and a complete lack of the latter. This motivates the current article where we demonstrate a stochastic neuron using an insulator-metal-transition (IMT) device, based on electrically induced phase-transition, in series with a tunable resistance. We show that an IMT neuron has dynamics similar to a piecewise linear FitzHugh-Nagumo (FHN) neuron and incorporates all characteristics of a spiking neuron in the device phenomena. We experimentally demonstrate spontaneous stochastic spiking along with electrically controllable firing probabilities using Vanadium Dioxide (VO₂) based IMT neurons which show a sigmoid-like transfer function. The stochastic spiking is explained by two noise sources - thermal noise and threshold fluctuations, which act as precursors of bifurcation. As such, the IMT neuron is modeled as an Ornstein-Uhlenbeck (OU) process with a fluctuating boundary resulting in transfer curves that closely match experiments. The moments of interspike intervals are calculated analytically by extending the first-passage-time (FPT) models for Ornstein-Uhlenbeck (OU) process to include a fluctuating boundary. We find that the coefficient of variation of interspike intervals depend on the relative proportion of thermal and threshold noise, where threshold noise is the dominant source in the current experimental demonstrations. As one of the first comprehensive studies of a stochastic neuron hardware and its statistical properties, this article would enable efficient implementation of a large class of neuro-mimetic networks and algorithms.

1. Introduction

A growing need for efficient machine-learning in autonomous systems coupled with an interest in solving computationally hard optimization problems has led to active research in stochastic models of computing. Optimization techniques (Haykin, 2009) including Stochastic Sampling Machines (SSM), Simulated Annealing, Stochastic Gradients etc., are examples of such models. All these algorithms are currently implemented using digital hardware which first creates a mathematically accurate platform for computing, and later adds digital noise at the algorithm level. Hence, it is enticing to construct hardware primitives that can harness the already existing physical sources of noise to create a stochastic computing platform. The principal challenge with such efforts is the lack of stable or reproducible distributions, or functions of distributions, of physical noise. One basic stochastic unit which enables a systematic construction of stochastic hardware has long been known—the stochastic neuron (Gerstner and Kistler, 2002)—which is also believed to be the unit of computation in the human brain. Moreover, recent studies (Buesing et al., 2011) have demonstrated practical applications like sampling using networks of such stochastic spiking neurons. There have been some attempts for building neuron hardware (Indiveri et al., 2006; Pickett et al., 2013; Mehonic and Kenyon, 2016; Sengupta et al., 2016; Tuma et al., 2016), but building a neuron with self-sustained spikes, or oscillations, which are stochastic in nature and where the probability of firing is controllable using a signal has been challenging. Here, we demonstrate and analytically study a true stochastic neuron (Jerry et al., 2017a) which is fabricated using oscillators (Shukla et al., 2014a,b; Parihar et al., 2015) based on insulator-metal transition (IMT) materials, e.g., Vanadium Dioxide (VO₂), wherein the inherent physical noise in the dynamics is used to implement stochasticity. The firing probability, and not just the deterministic frequency of oscillations or spikes, is controllable using an electrical signal. We also show that such an IMT neuron has similar dynamics as a piecewise linear FitzHugh-Nagumo (FHN) neuron with thermal noise along with threshold fluctuations as precursors of bifurcation resulting in a sigmoid-like transfer function for the neural firing rates. By analyzing the variance of interspike interval, we determine that for the range of thermal noise present in our experimental demonstrations, threshold fluctuations are responsible for most of the stochasticity compared to thermal noise.

2. Materials and Methods

2.1. IMT Phase Change Neuron Model

A stochastic IMT neuron is fabricated using relaxation oscillators (Shukla et al., 2014b; Parihar et al., 2015) composed of an IMT phase change device, e.g., Vanadium Dioxide (VO₂), in series with a tunable resistance, e.g., transistor (Shukla et al., 2014a) (Figure 1A). An IMT device is a two terminal device with two resistive states—insulating (I) and metallic (M), and the device transitions between the two states based on the applied electric field (which in turn changes the current through the device and the corresponding temperature) across it. The phase transitions are hysteretic in nature, which means that the IMT (insulator-to-metal) transition does not occur at the same voltage as the MIT (metal-to-insulator) transition. For a range of values of the series resistance, the resultant circuit shows spontaneous oscillations due to hysteresis and a lack of stable point (Parihar et al., 2015). Overall, the series resistance acts as a parameter for bifurcation between a spiking (or oscillating) state and a resting state of an IMT neuron.

FIGURE 1

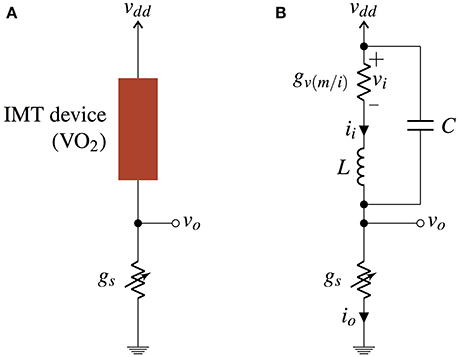
Figure 1. (A) VO₂ based IMT spiking neuron circuit consisting of a VO₂ device in series with a tunable resistance. (B) Equivalent circuit of IMT neuron using a series inductance L and a parallel capacitance C.

The equivalent circuit model for an IMT oscillator is shown in Figure 1B with the hysteretic switching conductance g_v(m/i) (g_vm in metallic and g_vi in insulating state), a series inductance L, and a parallel internal capacitance C. Let the IMT and MIT thresholds of the device be denoted by v_h and v_l, respectively, with v_h > v_l, and the current-voltage relationship of the hysteretic conductance be

$v_i=h(i_i,s)$

where h is linear in i_i and s is the state—metallic (M) or insulating (I).

The system dynamics is then given by:

$\begin{array}{ll}\begin{array}{l}L\frac{d{i}_i}{dt}=(v_{dd}-h(i_i,s))-v_o\\ C\frac{d{v}_o}{dt}=i_i-g_s{v}_o\end{array}& (1)\end{array}$

with i_i and v_o as shown in Figure 1B and s is considered as an independent variable.

2.2. Mechanism of Oscillations and Spikes

In VO₂, IMT, and MIT transitions are orders of magnitude faster than RC time constants for oscillations, as observed in frequency (Kar et al., 2013) and time-domain measurements for voltage driven (Jerry et al., 2016) and photoinduced transitions (Cocker et al., 2012). As such, the change in resistance of the IMT device is assumed to be instantaneous. Figure 2A shows the phase space i_i × (v_dd − v_o). V-I curves for IMT device in the two states metallic (M) and insulating (I) and the load line for series conductance v_o = i_i/g_s for the steady state are shown along with the fixed points of the system S₁ and S₂ in insulating and metallic states respectively. The load line and V-I curves are essentially the nullclines of v_o and i_i, respectively. The capacitance- inductance pair delays the transitions and slowly pulls the system toward the fixed points S₁ and S₂ even when the IMT device transitions instantaneously. For small L/C ratio, the eigenvector (of the coefficient matrix) with large negative eigenvalue becomes parallel to the x-axis, whereas the other eigenvector becomes parallel to AB′ or BA′ depending on the state (M or I). When the system approaches A from below (or B from above) and IMT device is insulating (or metallic) with fixed point S₁ (or S₂), the IMT device transitions into metallic (or insulating) state changing the fixed point to S₂ (or S₁). Two trajectories are shown starting from points A and B each for the system (Equation 1)—one for small L/C value (solid) and the other for large L/C value (dashed). After a transition, the system moves parallel to x-axis almost instantaneously and spends most of the time following the V-I curve toward the fixed point. Before the fixed point is reached the MIT (or IMT) transition threshold is encountered which switches the fixed point, and the cycle continues resulting in sustained oscillations or spike generation.

FIGURE 2

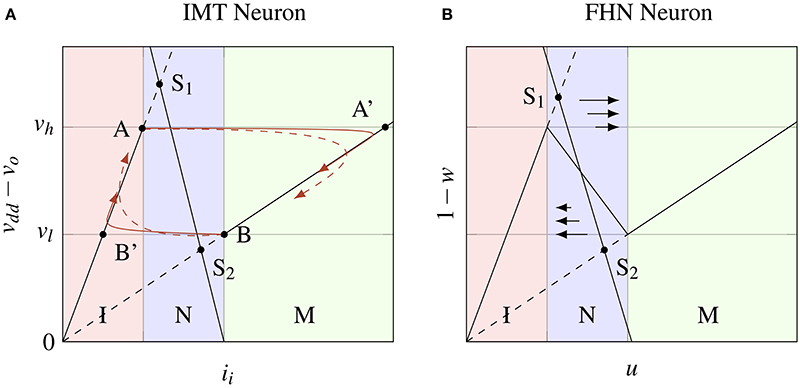
Figure 2. (A) Trajectories (red) of system (1) in the phase space i_i × (v_dd − v_o) for a small L/C value (solid) and a large L/C value (dashed). The i_i-nullclines of system (1) are shown as solid black lines in the metallic (AB') and insulating (BA') states of the IMT device, and S₁S₂ is the v_o-nullcline. Depending on the state, the phase space is divided into three vertical regions - I, M and N. In the region N the i_i-nullclines are dependent on s (B) Nullclines of the FHN model in the phase space u × (1 − w) where f(u) is a piecewise linear function. The dynamics of FHN neuron are equivalent to the IMT neuron in the regions M and I. In the region N, for small L/C, the difference is only in the velocity and not the direction of system trajectories as they are parallel to x-axis.

2.3. Model Approximations and Connections With FHN Neuron

2.3.1. Non-hysteretic Approximation

The model of (Equation 1) is very similar to a piecewise linear caricature of FitzHugh-Nagumo (FHN) neuron model (Gerstner and Kistler, 2002), also called the McKean's caricature (McKean, 1970; Tonnelier, 2003). Mathematically, the FHN model is given by:

$\begin{array}{ll}\begin{array}{l}\frac{du}{dt}=f(u)-w+I_{ext}\\ \tau \frac{dw}{dt}=u-bw+a\end{array}& (2)\end{array}$

where f(u) is a polynomial of third degree, e.g., f(u) = u − u³/3, and I_ext is the parameter for bifurcation, as opposed to g_s in Equation (1). In the FHN model, one variable (u), possessing cubic nonlinearity, allows regenerative self-excitation via a positive feedback, and the second, a recovery variable (w), possessing linear dynamics, provides a slower negative feedback. It was reasoned in McKean (1970) that the essential features of FHN model are retained in a “caricature” where the cubic non-linearity is replaced by a piecewise linear function f(u). Nullclines of (Equation 2) with a piecewise linear f(u) are shown in Figure 2B in the phase space u × (1 − w). A function f(u) is trivially possible such that it is equal to v_dd − h(i_i, s) in the regions M and I, hence making the u-nullcline similar to the i_i-nullcline in those regions. In the region N, the difference between f(u) and v_dd − h(i_i, s) for any state s does not result in a difference in the direction of system trajectories but only in their velocity, because for small L/C the trajectories are almost parallel to x-axis. Bifurcation in VO₂ neuron is achieved by tuning the load line using a tunable resistance (g_s), or a series transistor (Figure 3A). Figure 3B shows two load line curves corresponding to different gate voltages (v_gs), where one gives rise to spikes while the other results in a resting state.

FIGURE 3

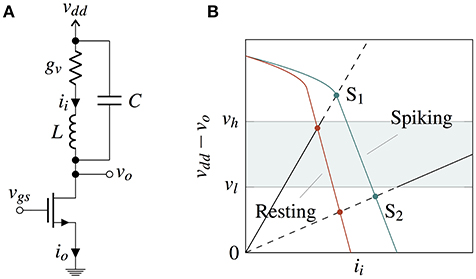
Figure 3. (A) IMT neuron with series transistor used to achieve bifurcation between a spiking and a resting state. (B) Nullclines of the system with series transistor in the phase space i_i × v_dd − v_o for two different v_gs values for spiking and resting states. Bifurcation occurs when a stable points crosses the boundary of region v_dd − v_o ∈ [v_l, v_h].

2.3.2. Single Dimensional Approximation

Moreover, a single dimensional piecewise approximation of the system can be performed using a dimensionality reduction by replacing the movement along the eigenvector parallel to the x-axis with an instantaneous transition from A to A′, or B to B′. This leaves a 1-dimensional subsystem in M and I each along the V-I curves AB′ and BA′. Experiments using VO₂ show that the metallic state conductance g_vm is very high which causes the charging cycle of v_o to be almost instantaneous (Figure 4) and resembles a spike of a biological neuron. As such, the spiking statistics can be studied by modeling just the discharge cycle of v_o. The inductance being negligible can be effectively removed and only the capacitance is needed for modeling the 1D subsystem of insulating state (Figure 6A) making v_i = v_dd − v_o.

FIGURE 4

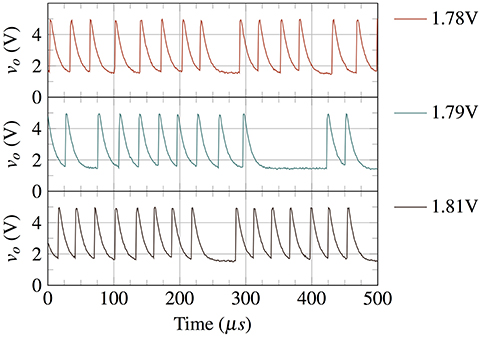
Figure 4. Experimental waveforms of VO₂ based spiking neuron for various v_gs values (1.78, 1.79, and 1.81 V). A VO₂ neuron shows almost instantaneous charging (spike) in metallic state.

2.4. Noise Induced Stochastic Behavior

The two important noise sources which induce stochasticity in an IMT neuron are (a) V_IMT (v_h) fluctuations (Zhang et al., 2016; Jerry et al., 2017b), and (b) thermal noise. Thermal noise η(t) is modeled in the circuit (Figure 6A) as a white noise voltage η(t)dt = σ_tdw_t where w_t is the standard weiner process and ${\sigma }_t^2$ is the infinitesimal thermal noise variance. The threshold v_h is assumed constant during a spike, but varies from one spike to another. The distribution of v_h from spike to spike is assumed to be Gaussian or subGaussian whose parameters are estimated from experimental observations of oscillations. If the series transistor always remains in saturation and show linear voltage-current relationship, as is the case in our VO₂ based experiments, the discharge phase can be described by an Ornstein-Uhlenbeck (OU) process

$\begin{array}{ll}\text{d}x=\frac{1}{\theta }(\mu -x)\text{d}t+\sigma \text{d}{w}_t& (3)\end{array}$

where μ, θ, and σ are functions of circuit parameters of the series transistor, the IMT device and σ_t. The interspike interval is thus the first-passage-time (FPT) of this OU process, but with a fluctuating boundary.

2.4.1. OU Process With Constant Boundary

Analytical expressions for the FPT of OU process (with μ = 0) for a constant boundary were derived using the Laplace transform method in Ricciardi and Sato (1988). Reproducing some of its results, let the first passage time for the system (Equation 3), with μ = 0, which starts at x(0) = x₀ and hits a boundary S, be denoted by the random variable t_f(S, x₀), and its mth moment by τ_m(S, x₀). Also, let $\widetilde{t_f}(S,x_0)$ be the FPT for another OU process with μ = 0, θ = 1, and σ = 2, and $\widetilde{{\tau }_m}(S,x_0)$ be its mth moment. Then time and space scaling for the OU process imply that

$\begin{array}{ll}\begin{array}{l}{t}_f(S,x_0)\stackrel{d}{=}\theta \widetilde{t_f}(\alpha S,\alpha x_0)\\ \therefore {\tau }_m(S,x_0)={\theta }^m\widetilde{{\tau }_m}(\alpha S,\alpha x_0)\end{array}& (4)\end{array}$

where $\alpha =\sqrt{\frac{2}{\theta {\sigma }^2}}$. The first two moments for the base case OU process $\widetilde{{\tau }_1}$ and $\widetilde{{\tau }_2}$ are given by

$\begin{array}{ll}\begin{array}{l}\widetilde{{\tau }_1}(S,x_0)={\varphi }_1(S)-{\varphi }_1(x_0)\\ \widetilde{{\tau }_2}(S,x_0)=2{\varphi }_1{\left(S\right)}^2-{\varphi }_2(S)-2{\varphi }_1(S){\varphi }_1(x_0)+{\varphi }_2(x_0)\end{array}& (5)\end{array}$

where ϕ_k(z) can be written as an infinite sum

$\begin{array}{ll}{\varphi }_k(z)=\frac{1}{2^k}{\displaystyle \sum _{n=1}^{\infty }\frac{{\left(\sqrt{2}z\right)}^n\Gamma \left(\frac{n}{2}\right)\rho (n,k)}{n!}}& (6)\end{array}$

with ρ(n, k) being a function of the digamma function (Ricciardi and Sato, 1988).

2.4.2. OU Process With Fluctuating Boundary

We extend this framework for calculating the FPT statistics with a fluctuating boundary S as follows. Let the IMT threshold be represented by the random variable v_h. For the VO₂ based IMT neuron, the 1D subsystem in the insulating phase can be converted in the form of Equation(3) with μ = 0 by translating the origin to the fixed point. If this transformation is T then x = Tv_i = T(v_dd − v_o), S = Tv_h, and x_o = Tv_l. The start and end points are B′ and A, respectively in Figure 2. v_h is assumed constant during a spike, and across spikes the distribution of v_h is v_h ~ ${D}$, where ${D}$ is either Gaussian, or subGaussian. For subGaussian distributions we use the Exponential Power family EP[κ], κ being the shape factor. Let the interspike interval of IMT neuron be denoted by the marginal random variable $t_{imt}({D},v_l)$. Then t_imt is related to t_f in Equation (4), given common parameters θ and σ, as follows:

$t_{imt}({D},v_l)|(v_h=v)\stackrel{d}{=}{t}_f(Tv,T{v}_l)$

The moments of t_imt can be calculated as:

$\begin{array}{ll}\begin{array}{l}𝔼\left[t_{imt}{\left({D},v_l\right)}^m\right]={𝔼}_{v_h}\left[𝔼\left[t_{imt}{\left({D},\text{T}{v}_l\right)}^m|v_h=v\right]\right]\\ ={𝔼}_{v_h}[{\tau }_m(T{v}_h,T{v}_l)]\\ ={\theta }^m{𝔼}_{v_h}[\widetilde{{\tau }_m}(\alpha T{v}_h,\alpha T{v}_l)]\end{array}& (7)\end{array}$

where $\alpha =\sqrt{\frac{2}{\theta {\sigma }^2}}$. If ${D}$ is Gaussian or EP[κ] distribution and αT is an affine transformation, then αTv_h also has a Gaussian or EP[κ] distribution.

2.5. Experiments

IMT devices are fabricated on a 10nm VO₂ thin film grown by reactive oxide molecular beam epitaxy on (001) TiO₂ substrate using a Veeco Gen10 system (Tashman et al., 2014). Planar two terminal structures are formed by patterning contacts using standard electron beam lithography which defines the device length (L_VO2). Pd (20 nm)/Au (60 nm) contacts are then deposited by electron beam evaporation and liftoff. The devices are then isolated and the widths (W_VO2) are defined using a CF₄ based dry etch.

The IMT neuron is constructed using an externally connected n-channel MOSFET (ALD110802) and the fabricated VO₂ device. A prototypical I-V curve is shown in Figure 5A. Within the experimental data, the current is limited to an arbitrarily chosen 200 μA to prevent a thermal runaway and breakdown of the device while in the low resistance metallic state. It should be noted that as the metallic state corresponds to the abrupt charging cycle of v_o, limiting the current would not have noticeable effect on spiking statistics of the neuron.

FIGURE 5

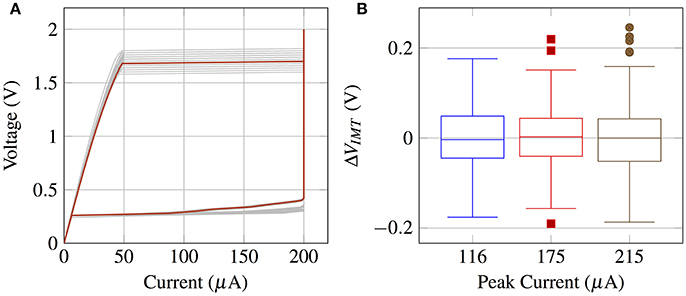
Figure 5. (A) The prototypical DC voltage-current characteristics for a single VO₂ device exhibits abrupt threshold switching at V_IMT and V_MIT. The current in the metallic state has been arbitrarily limited to a 200μA compliance current. (B) V_IMT distribution as a function of the peak current during oscillations (value is set by the MOSFET saturation current). V_IMT is extracted from 300+ cycles.

Threshold voltage fluctuations (cycle to cycle) were observed in all devices which were tested (>10). Threshold voltage distribution was estimated using the varying cycle-to-cycle threshold voltages collected from a single device. Thermal noise is not measured directly, but is estimated approximately by matching the simulation waveforms from the circuit model (Figure 6A) with the observed experimental waveforms. It can be verified that thermal noise of the transistor is not the dominant noise source by measuring the threshold variation as a function of the transistor current (Figure 5B) and observing that the distribution of switching threshold does not change with varying transistor current. Finally, the firing rate and its variation with v_gs (Figure 6B) were measured for a single device.

FIGURE 6

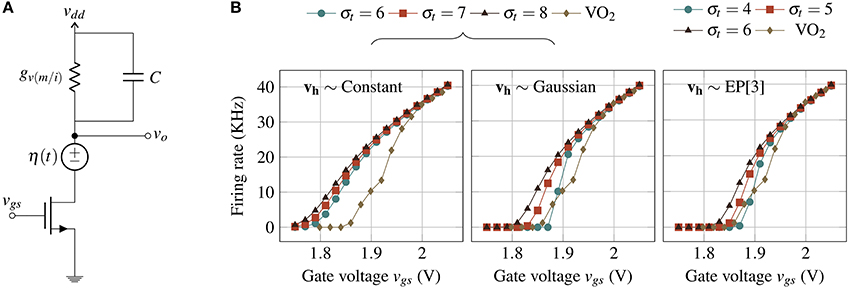
Figure 6. (A) Noise model of IMT neuron where the noise components are the thermal noise voltage source η(t) and the IMT threshold fluctuation. (B) Firing rate plotted against v_gs using the analytical model for different v_h distributions (Constant, Gaussian, and EP[3]) and comparison with experimental observations.

3. Results

3.1. Spiking Statistics

3.1.1. First Moment and the Firing Rate

First moment of t_imt is calculated using Equations (5) and (7) as

$𝔼[t_{imt}(D,v_l)]=\theta ({𝔼}_{v_h}[{\varphi }_1(\alpha T{v}_h)]-{\varphi }_1(\alpha x_0))$

The expansion for ϕ_k(z) in Equation(6) can be used to calculate 𝔼_vh[ϕ_k(αTv_h)] using the moments of αTv_h as follows

${𝔼}_{v_h}[{\varphi }_k(\alpha T{v}_h)]=\frac{1}{2^k}{\displaystyle \sum _{n=1}^{\infty }\frac{{(\sqrt{2})}^n𝔼[{(\alpha T{v}_h)}^n]\Gamma \left(\frac{n}{2}\right)\rho (n,k)}{n!}}$

Figure 6B shows firing rate ($1/𝔼[t_{imt}(D,v_l)]$) as a function of v_gs for various σ_t values and for three distributions of threshold fluctuations. The calculations approximate the experimental observations well for all three v_h distributions, the closest being EP[3] with σ_t = 4.

3.1.2. Higher Moments

For higher moments, higher order terms are encountered. For example, in case of the second moment, using Equations(5) and (7), we obtain

$\begin{array}{l}{𝔼}_{v_h}[\widetilde{{\tau }_2}(\alpha T{v}_h,\alpha T{v}_l)]=2{𝔼}_{v_h}\left[{\varphi }_1{\left(\alpha T{v}_h\right)}^2\right]-{𝔼}_{v_h}\left[{\varphi }_2\left(\alpha T{v}_h\right)\right]\\ -2{𝔼}_{v_h}[{\varphi }_1(\alpha T{v}_h)]{\varphi }_1(\alpha T{v}_l)\\ +{\varphi }_2(\alpha T{v}_l)\end{array}$

with a higher order term ${\varphi }_1{(\alpha T{v}_h)}^2$. In the case of the third moment we obtain ϕ₁(αTv_h)ϕ₂(αTv_h). As each ϕ_k term is an infinite sum, we construct a cauchy product expansion for the higher order term using the infinite sum expansions of the constituent ϕ_ks and then distribute the expectation over addition. For example, if the ϕ_k expansions of ϕ₁(z) and ϕ₂(z) are (∑a_i) and (∑b_i), respectively, then the cauchy product expansion of ϕ₁(z)ϕ₂(z) can be calculated as ∑c_i, where c_i is a function of a_1…i and b_1…i, and the expectation 𝔼[ϕ₁(z)ϕ₂(z)] = ∑𝔼[c_i]. Since c_i is a polynomial in z, 𝔼[c_i] can be calculated using the moments of z.

If μ_imt and σ_imt are the mean and standard deviation of interspike intervals t_imt, the coefficient of variation (σ_imt/μ_imt) varies with the relative proportion of the thermal and the threshold induced noise. Figure 7 shows σ_imt/μ_imt (calculated using parameters matched with our VO₂ experiments) plotted against σ_t for various kinds of v_h distributions fitted to experimental observations. σ_imt/μ_imt as observed in our VO₂ experiments is about an order of magnitude more than what would be calculated with only thermal noise using such a neuron, and hence, threshold noise contributes significant stochasticity to the spiking behavior. As the IMT neuron is setup such that the stable point is close to the IMT transition point (Figure 3B), low σ_t results in high and diverging σ_imt/μ_imt for any distribution of threshold noise, and σ_imt/μ_imt reduces with increasing σ_t for the range shown. For a Normally distributed v_h the variance diverges for σ_t ≲ 8, but for Exponential Power (EP) distributions with lighter tails, the variance converges for smaller values of σ_t. Statistical measurements on experimental data, as indicated in Figure 7, provide measures of σ_imt/μ_imt (dotted line) and σ_t (shaded region). We note that EP distributions provide a better approximation of the stochastic nature of experimentally demonstrated VO₂ neurons as the range of σ_t is estimated to be <5.

FIGURE 7

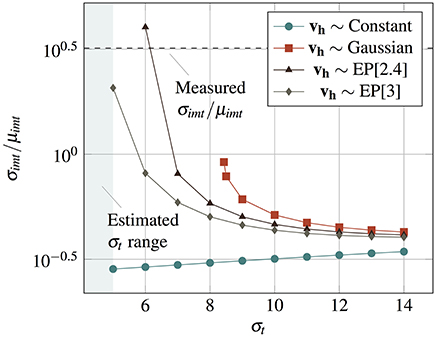
Figure 7. σ_imt/μ_imt for the interspike interval plotted against σ_t for v_gs = 1.8V with Constant, Gaussian, and Exponential Power (EP[κ], where κ is the shape factor) distributions of the threshold noise. The experimentally observed σ_imt/μ_imt for a VO₂ neuron is shown with a dotted line. The shaded region shows the experimentally estimated range of σ_t (σ_t < 5).

4. Discussion

In this paper, we demonstrate and analyse an IMT based stochastic neuron hardware which relies on both threshold fluctuations and thermal noise as precursors to bifurcation. The IMT neuron emulates the functionality of theoretical neuron models completely by incorporating all neuron characteristics into device phenomena. Unlike other similar efforts, it does not need peripheral circuits alongside the core device circuit (an IMT device and a transistor) to emulate any sub-component of the spiking neuron model like thresholding, reset etc. Moreover, the neuron construction not only utilizes inherent physical noise sources for stochasticity, but also enables control of firing probability using an analog electrical signal—the gate voltage of series transistor. This is different from previous works which control only the deterministic aspect of firing rate like the charging rate. A comparison of spiking neuron hardware characteristics in different works is shown in Table 1.

TABLE 1

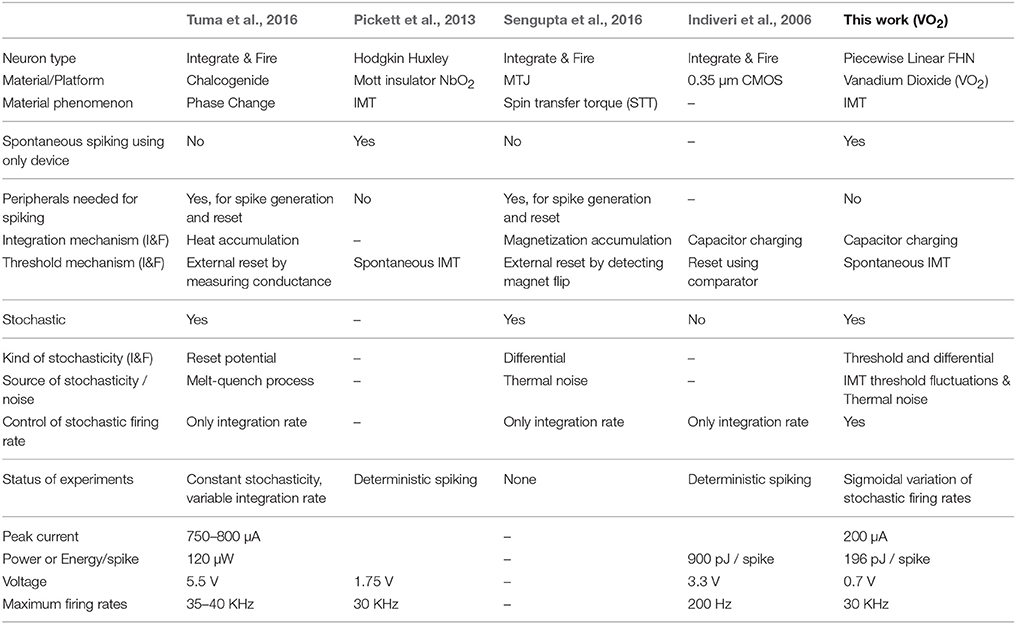
Table 1. Comparison of this work (experimental details from Jerry et al., 2017a) with other spiking neuron hardware works based on different characteristics of spiking neurons.

We also show that the neuron dynamics follow a linear “carricature” of the FitzHugh-Nagumo model with intrinsic stochasticity. The analytical models developed in this paper can also faithfully reproduce the experimentally observed transfer curve which is a stochastic property. Such analytical verification of stochastic neuron experiments is one of the first in this work. It is an important result as it indicates reproducibility of stochastic characteristics and helps in creating the pathway toward perfecting these devices. With a growing concensus that stochasticity will play a key role in solving hard computing tasks, we need efficient ways for controlled amplification and conversion of physical noise into a readable and computable form. In this regard, the IMT based neuron represents a promising solution for a stochastic computational element. Such stochastic neurons have the potential to realize bio-mimetic computational kernels that can be employed to solve a large class of optimization and machine-learning problems.

Author Contributions

AP worked on the development of theory, simulation frameworks, and mathematical models; MJ worked on the experiments; AR advised AP and participated in the problem formulation; SD advised MJ and also participated in the design of experiments and problem formulations.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This project was supported by the National Science Foundation under grants 1640081, Expeditions in Computing Award-1317560 and CCF- 1317373, and the Nanoelectronics Research Corporation (NERC), a wholly-owned subsidiary of the Semiconductor Research Corporation (SRC), through Extremely Energy Efficient Collective Electronics (EXCEL), an SRC-NRI Nanoelectronics Research Initiative under Research Task IDs 2698.001 and 2698.002.

References

Buesing, L., Bill, J., Nessler, B., and Maass, W. (2011). Neural dynamics as sampling: a model for stochastic computation in recurrent networks of spiking neurons. PLoS Comput. Biol. 7:e1002211. doi: 10.1371/journal.pcbi.1002211

PubMed Abstract | CrossRef Full Text | Google Scholar

Cocker, T., Titova, L., Fourmaux, S., Holloway, G., Bandulet, H.-C., Brassard, D., et al. (2012). Phase diagram of the ultrafast photoinduced insulator-metal transition in vanadium dioxide. Phys. Rev. B 85:155120. doi: 10.1103/PhysRevB.85.155120

CrossRef Full Text | Google Scholar

Gerstner, W., and Kistler, W. M. (2002). Spiking Neuron Models: Single Neurons, Populations, Plasticity. Cambridge: Cambridge university press.

Google Scholar

Haykin, S. S. (2009). Neural Networks and Learning Machines. Prentice Hall.

Google Scholar

Indiveri, G., Chicca, E., and Douglas, R. (2006). A VLSI array of low-power spiking neurons and bistable synapses with spike-timing dependent plasticity. IEEE Trans. Neural Netw. 17, 211–221. doi: 10.1109/TNN.2005.860850

PubMed Abstract | CrossRef Full Text | Google Scholar

Jerry, M., Parihar, A., Grisafe, B., Raychowdhury, A., and Datta, S. (2017a). “Ultra-low power probabilistic imt neurons for stochastic sampling machines,” in Proc. Symp. VLSI Technology (Kyoto), T186–T187.

Google Scholar

Jerry, M., Parihar, A., Raychowdhury, A., and Datta, S. (2017b). “A random number generator based on insulator-to-metal electronic phase transitions,” in Device Research Conference (DRC), 2017 75th Annual (South Bend, IN), 1–2.

Google Scholar

Jerry, M., Shukla, N., Paik, H., Schlom, D. G., and Datta, S. (2016). “Dynamics of electrically driven sub-nanosecond switching in vanadium dioxide,” in Silicon Nanoelectronics Workshop (SNW), 2016 IEEE (Honolulu, HI), 26–27.

Google Scholar

Kar, A., Shukla, N., Freeman, E., Paik, H., Liu, H., Engel-Herbert, R., et al. (2013). Intrinsic electronic switching time in ultrathin epitaxial vanadium dioxide thin film. Appl. Phys. Lett. 102:072106. doi: 10.1063/1.4793537

CrossRef Full Text | Google Scholar

McKean, H. P. (1970). Nagumo's equation. Adv. Math. 4, 209–223.

Google Scholar

Mehonic, A., and Kenyon, A. J. (2016). Emulating the electrical activity of the neuron using a silicon oxide rram cell. Front. Neurosci. 10:57. doi: 10.3389/fnins.2016.00057

PubMed Abstract | CrossRef Full Text | Google Scholar

Parihar, A., Shukla, N., Datta, S., and Raychowdhury, A. (2015). Synchronization of pairwise-coupled, identical, relaxation oscillators based on metal-insulator phase transition devices: a model study. J. Appl. Phys. 117:054902. doi: 10.1063/1.4906783

CrossRef Full Text | Google Scholar

Pickett, M. D., Medeiros-Ribeiro, G., and Williams, R. S. (2013). A scalable neuristor built with mott memristors. Nat. Mater. 12, 114–117. doi: 10.1038/nmat3510

PubMed Abstract | CrossRef Full Text | Google Scholar

Ricciardi, L. M., and Sato, S. (1988). First-passage-time density and moments of the ornstein-uhlenbeck process. J. Appl. Probab. 25, 43–57. doi: 10.2307/3214232

CrossRef Full Text | Google Scholar

Sengupta, A., Panda, P., Wijesinghe, P., Kim, Y., and Roy, K. (2016). Magnetic tunnel junction mimics stochastic cortical spiking neurons. Sci. Rep. 6:30039. doi: 10.1038/srep30039

PubMed Abstract | CrossRef Full Text | Google Scholar

Shukla, N., Parihar, A., Cotter, M., Barth, M., Li, X., Chandramoorthy, N., et al. (2014a). “Pairwise coupled hybrid vanadium dioxide-MOSFET (HVFET) oscillators for non-boolean associative computing,” in 2014 IEEE International Electron Devices Meeting (San Francisco, CA), 28.7.1–28.7.4.

Google Scholar

Shukla, N., Parihar, A., Freeman, E., Paik, H., Stone, G., Narayanan, V., et al. (2014b). Synchronized charge oscillations in correlated electron systems. Sci. Rep. 4:4964. doi: 10.1038/srep04964

CrossRef Full Text | Google Scholar

Tashman, J., Lee, J., Paik, H., Moyer, J., Misra, R., Mundy, J., et al. (2014). Epitaxial growth of VO_2 by periodic annealing. Appl. Phys. Lett. 104:063104. doi: 10.1063/1.4864404

CrossRef Full Text | Google Scholar

Tonnelier, A. (2003). The McKean's caricature of the Fitzhugh–Nagumo Model I. The space-clamped system. SIAM J. Appl. Math. 63, 459–484. doi: 10.1137/S0036139901393500

CrossRef Full Text | Google Scholar

Tuma, T., Pantazi, A., Le Gallo, M., Sebastian, A., and Eleftheriou, E. (2016). Stochastic phase-change neurons. Nat. Nanotechnol. 11, 693–699. doi: 10.1038/nnano.2016.70

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, K., Wang, B., Wang, F., Han, Y., Jian, X., Zhang, H., et al. (2016). VO₂-based selection device for passive resistive random access memory application. IEEE Elec. Dev. Lett. 37, 978–981. doi: 10.1109/LED.2016.2582259

CrossRef Full Text | Google Scholar