- 1MOE Key Laboratory for Neuroinformation, The Clinical Hospital of Chengdu Brain Science Institute, University of Electronic Science and Technology of China, Chengdu, China
- 2School of Life Science and Technology, Center for Information in Medicine, University of Electronic Science and Technology of China, Chengdu, China
In the event-related potential (ERP) of scalp electroencephalography (EEG) studies, the vertex reference (Cz), linked mastoids or ears (LM), and average reference (AVG) are popular reference methods, and the reference electrode standardization technique (REST) is increasingly applied. Because scalp EEG recordings are considered as spatially degraded signals, independent component analysis (ICA) is a widely used data-driven method for obtaining ERPs by decomposing EEG data. However, the accurate estimation of the differences in ERP components extracted by ICA with different references remains unclear. In this study, we first provided formal descriptions of the above reference methods (Cz, LM, AVG, and REST) and ICA decomposition in ERP and then investigated the influences of different reference techniques on simulation and real EEG datasets. The results revealed that (1) the reference method did not change the peak amplitudes and latencies of relative ERPs corresponding to some IC time courses; (2) there were non-negligible effects of different reference methods on both temporal ERPs and spatial topographies of some ICs; and (3) compared to Cz, LM, and AR, considering both the performances of temporal ERPs and spatial topographies, the REST reference had overall superiority. These findings provide a recommended choice of REST for ICA analysis at the trial level and contribute to empirical investigations regarding the use of reference methods in ERP domains with ICA analysis.
Introduction
Since the first report in 1929 (Berger, 1929), scalp electroencephalography (EEG) has been a cost-effective and non-invasive technique that directly quantifies the mean electrical activity of the brain at scalp sites with excellent temporal resolution (~milliseconds) (Cohen, 2017). In addition, event-related potentials (ERPs) are one of the most widely used EEG measures to assess brain activity in response to specific sensory, motor or cognitive events, and several ERP components (e.g., N1, P2, and P3) can provide comprehensive information about low or high level cognitive functions of the brain (Luck, 2014). Scalp ERP has remained one of most informative measures in clinical neurophysiology (Johnstone et al., 2013; Li et al., 2019a; Qin et al., 2019) and human cognitive neuroscience (Enriquez-Geppert et al., 2017; Tian et al., 2018; Li et al., 2019b) research for several decades.
In the scalp EEG domain, because of the volume conduction effect, there is no point on the body or head where the reference potential is ideal zero or constant (Dien, 1998; Yao, 2001, 2017). In the cognitive ERP domain, this physical phenomenon is known as the “no-Switzerland principle” (Luck, 2014): there is no electrically neutral site on the body or head, and Switzerland is politically neutral. Obviously, for evaluating the characteristics (e.g., connectivity, latency, and voltage amplitudes) of EEG accurately at the trial level, it is necessary to use an appropriate reference method to minimize the potential effects of the reference on the results. Currently, a number of different reference methods have been proposed, including the vertex reference (Cz) (Lehmann et al., 1998), linked mastoids or ears (LM) (Gevins and Smith, 2000), average reference (AVG) (Offner, 1950) and reference electrode standardization technique (REST) (Yao, 2001; Dong et al., 2017). Under their certain assumptions, reference methods including Cz, LM, and AVG have been commonly used while ignoring that they are not zero references. As a novel method that approximately converts an average or unipolar reference to a zero reference (Yao, 2001; Dong et al., 2017), REST is increasingly acknowledged by EEG research groups around the world and applied in various EEG studies (Mumtaz et al., 2017a,b; Tian et al., 2017; Li et al., 2019a). Moreover, the above different references have been investigated in many comparative EEG studies, including EEG spectrum (Yao et al., 2005; Chella et al., 2014, 2017), EEG coherence (Marzetti et al., 2007), ERPs (Tian and Yao, 2013; Liu et al., 2015; Hu et al., 2017; Mahajan et al., 2017; Qin et al., 2017; Yang et al., 2017; Li et al., 2018) and brain network analyses (Qin et al., 2010; Chella et al., 2016; Lei and Liao, 2017), and the merit of the REST reference has been confirmed. However, at present, the choice of appropriate EEG references in EEG studies across the world remains an open issue, especially in the ERP domain (Luck, 2014).
Due to volume conduction, scalp EEG/ERP recordings can be considered spatially degraded signals, which reflect spatial and temporal mixtures of the electrophysiological signals of multiple independent sources/components that are generated from large-scale synchronous field potentials (Onton and Makeig, 2006; Winter et al., 2007). Because of the EEG mixing problem, blind source separation via independent component analysis (ICA) (Hyvarinen and Oja, 2000) has been one of the most popular methods for decomposing EEG data. On the one hand, ICA can be used to separate artifact components (such as eye blinks, eye movement, facial muscles, and ballistocardiogram) from raw separately or simultaneously recorded EEG data and then reconstruct clean EEG signals (Srivastava et al., 2005; Hoffmann and Falkenstein, 2008). On the other hand, ICA is also utilized to demix EEG data to extract ERP components at the trial level, thereby increasing the signal-to-noise ratio (SNR) of ERPs (Delorme et al., 2012; Dong et al., 2014; Lee et al., 2016). In addition, ICA was also used to derive filter coefficients in re-referencing of intracranial EEG (Michelmann et al., 2018). Furthermore, for overcoming the limitations of ICA at the single subject level (it is not naturally suited to match independent components from each subject to allow group inferences), group level ICA is further proposed to aggregate component information across a group of subjects for decomposition (Eichele et al., 2011) and is commonly used for event-related separate or simultaneous EEG data (Lei et al., 2012; Huster et al., 2015; Huster and Raud, 2018; Labounek et al., 2018). Notably, in the most current EEG/ERP studies (Eichele et al., 2011; Labounek et al., 2018), using average referenced data to perform ICA at the trial level is suggested, while average referencing results in zero total potential for all ICA topographies. However, the potential reason for this issue and the potential effects of reference methods on ICA decomposition remain unclear. In addition, although different reference methods, including Cz, LM, AVG, and REST, have been investigated in many ERP studies (Tian and Yao, 2013; Liu et al., 2015; Hu et al., 2017; Mahajan et al., 2017; Qin et al., 2017; Yang et al., 2017; Li et al., 2018), most of them use EEG data analysis without ICA decomposition, and the accurate estimation of the differences in ERP components extracted by ICA with different references remains unclear.
Given that there are no direct comparisons of the effects of different reference methods on ERPs extracted by ICA, the aim of this study was to directly evaluate the choice influence of Cz, LM, AVG, and REST on ICA components at the trial level. The current study not only provided formal descriptions of potential relations or differences between re-referencing and ICA decomposition but also investigated the effects of different reference techniques on one simulation and one real EEG dataset. We assumed that compared to Cz, LM, and AR, REST would be closer to the true case and provide a superior choice for ICA analysis at the trial level.
Materials and Methods
Theory
Here, we introduce unified matrix representations of ICA decomposition and various reference methods. Considering ideal EEG recordings of ERPs VInf (true infinite reference) with N channels, K sources, M trials, and T time points.
where N is the channel number; K is the number of sources/voxels; K2 is the number of ERPs; M is the number of ERP trials; T is the number of time points for each trial; is a sample at kth channel, ith trial and jth sample point; L is the lead-field matrix; S is true spatial sources; LS is the true spatial topographies; P is true temporal potentials of ERPs; and ε is a noise item.
For a unipolar reference with kth-channel (e.g., Cz) as a reference, the referenced ERP signal can be
where I is a unit matrix with 1 in the diagonal, is a Cz transform matrix, and TCz is the transform matrix from the ideal ERPs to the actual ERP reference.
Similarly, for LM and average references, we have the formulas for referenced ERP signals
where TLM and TAVG are the transform matrix from the ideal recordings VInf to the linked-mastoids/ears and average reference VLM and VAVG, respectively.
As an example, considering the scalp EEG recordings of ERPs with average reference, VAVG, the potential with the REST reference (i.e., estimated infinite reference), VREST, can be obtained as follows:
where is the estimate of reconstructed equivalent sources with temporal potentials, is the Moore-Penrose generalized inverses of lead-field matrix L, VAVG is average referenced ERP signals, and TAVG is the transform matrix from the ideal recordings to the average reference.
Thus, for ICA decompositions of the true infinite, Cz, LM, AVG, and REST references, we have the formulas
where G is the N-by-K1 ICA mixing matrix (corresponding to the spatial topographies), are the K1-by-MT independent component time courses (corresponding to the ERPs), P is true ERPs and ε is ICA error or a recording noise item. Notably, ICA mixing matrix G does not have to equal the final transform matrix from true potentials P to scalp recordings V (e.g., K1 does not have to equal to K2 in some cases). In this work, the potential effects of different EEG reference choices for ERPs extracted by ICA are investigated.
Simulation
To illustrate the previous questions, we employed a disc (one slice) with 2,452 dipoles to generate the simulation EEG data, and “white matter” regions were represented by two holes in the disc. For the basic ERP setup, a concentric three-sphere head model with 129 electrodes was used, and the analytic solution sphere radii were set as [0.87 0.89 1]. The orientations of the ERP sources (dipoles) were fixed as +z axis, and the lead-field matrix was calculated analytically (Yao et al., 2004). The temporal sampling rate of the EEG was typically 1 kHz. As an example, a total of 100 target stimuli (trials) were assumed to be collected from EEG data. The epoch of the ERPs was 1,000 ms, which consisted of 200 time points after downsampling to 200 Hz. Three sources were implemented and drawn with white color on the disc: “anterior cingulate area,” “precuneus area,” and “auditory cortex” (abbreviated as S1–S3). More details regarding the setups can be seen in Figure 1.
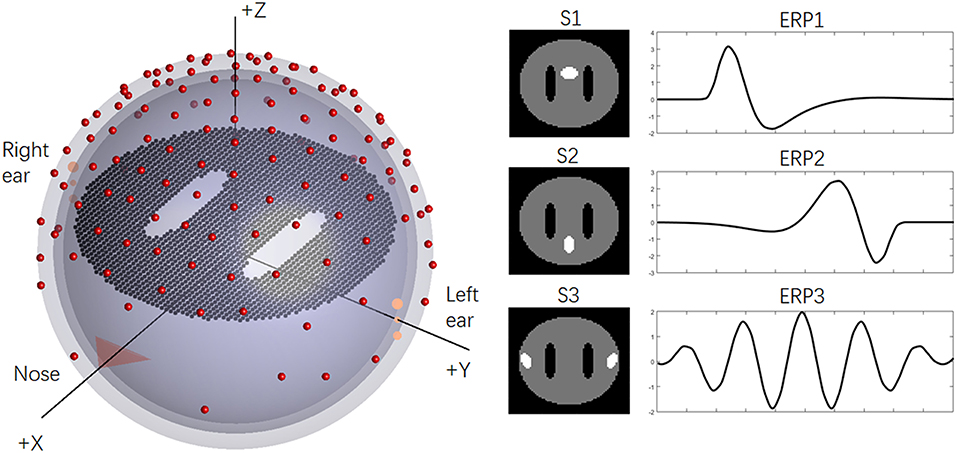
Figure 1. The basic simulation of the head model and sources. On the left, the simplified concentric three-sphere head model; on the right, the source spatial distributions (S1–S3) and corresponding ERPs (ERP1-ERP3).
Different Gaussian noise with independent and identical distributions (IID) was added to EEG data in the abovementioned simulations, and a conservative signal-to-noise ratio was set at 1. Then, the infinite (Inf) EEG data of all trials (129 channels × 20,000 points) were re-referenced to Cz, LM, AVG, and REST references, and Infomax ICA was used to decompose the re-referenced EEG data (the number of ICs was fixed at 3, i.e., K1 = K2 = 3). Next, independent component time courses (i.e., ERPs) were averaged across trials and standard z-scored across time points. These settings and processes were consistent with typical experimental EEG data and analysis (Lei et al., 2010; Dong et al., 2014). Performances of ICA time courses were quantified using root mean square error (RMSE) between the true noiseless ERPs (i.e., P in Equation 1) and ICA-extracted ERPs (i.e., in Equations 6–10) with a reference (Cz, LM, AVG, REST, or Inf). Performances of ICA spatial topographies were quantified using Pearson's correlation between the true topographies (i.e., LS in Equation 1) and ICA-extracted topographies (G in Equations 6–10) with a reference (Cz, LM, AVG, REST, or Inf). The whole simulation process was repeated 100 times to obtain mean results, and the effects of different EEG references for ERPs and topographies extracted by ICA were analyzed using one-way analysis of variance (ANOVA, p < 0.001) and a post-hoc test (Tukey's honest significant difference criterion, p < 0.001). In addition, a range of SNRs from 0.1 to 20 (0.1, 0.2, 0.4, 0.6, 0.8, 1, 1.5, 2, 2.5, 5, 10, and 20) was investigated.
Real Data
Participants and Experiment
In this work, a total of 12 healthy right-handed participants with no history of psychiatric or neurological disorders participated in the experiment after providing written informed consent (10 men and 2 women, mean age: 24.0 years, age range: 20–27 years). An experimental go/no-go task of auditory stimuli was utilized, and sounds were generated by SONAR 6 Producer Edition. The stimulus was presented in 8 blocks (120 trials each) in a random order, and all stimuli were matched for duration and pitch by using Adobe Audition 3.0. All subjects were exposed to a stimulus tone (375 ms in duration, C6/1,046 Hz, 80 ms rise and fall time, American notation) and a loud or soft (58 or 55 dB) timbre piano or violin and were instructed to make a left or right hand (piano or violin) response to a loud violin (go trials, probability 67%) and no response to a soft violin (no-go trials, probability 33%). The higher probability for go trials was chosen to encourage participants to initiate response preparation (Low and Miller, 1999). For each trial, a cross was first presented to instruct the subject to concentrate their attention on the middle of the screen, and a flashing cross was subsequently presented for 500 ms to remind the subject of the upcoming tone (lasting 375 ms). The subject was instructed to respond quickly and accurately in the go trials by pressing a sequence of three keys (the comma, period and slash keys for the right hand, and the C, X, and Z keys for the left hand) with the index, middle and ring fingers. For no-go trials, subjects were instructed to avoid any response. More details of the experimental task can be found in the relevant article (Gong et al., 2012). The study was also approved by the local Ethics Committee of University of Electronic Science and Technology of China (UESTC) in accordance with the standards of the Declaration of Helsinki.
EEG Recording
EEG data were recorded using a 64-channel EEG system (Brain Products GmbH, Gilching, Germany). The sampling rate was set at 500 Hz, the FCz served as the recording reference, and the AFz served as the ground electrode. Sixty-one electrodes according to the 10–20 cap system were used to record EEG data (Figure 2), and two channels were utilized to record vertical and horizontal EOG data. The impedance for all channels was maintained below 5 KΩ, and EEG data were bandpass filtered between 0.01 and 100 Hz. During stimulus presentation and response, subjects were asked to remain relaxed and avoid eye blinking.
EEG Data Processing
In this work, only the go trials with the loud violin are reported. A pipeline tool (WB_EEG_CalcERP) in WeBrain (a cloud computing platform, http://webrain.uestc.edu.cn/) was used to obtain go trials with the loud violin from raw EEG data, and EEGIFT (v2.5, http://trendscenter.org/software/eegift/#) was used to extract ERPs by group ICA. In brief, EEG channels were visually inspected first, and no bad channels were detected for all subjects. Then, EEG data were preprocessed using the WeBrain pipeline, which includes 1–30 Hz bandpass filtering, data segmentation (−200 to 800 ms), baseline correction (−200 to 0 ms), and the exclusion of artifact-containing trials (exceeding amplitude of ±100 μV, exceeding voltage step/sampling point of 50 μV or exceeding absolute difference of 150 μV in the epoch) and wrong-reaction trials. Then, the preprocessed EEG trials were re-referenced to Cz, LM, AVG, and REST references using REST (Yao, 2001; Dong et al., 2017) (EEGLAB Plugin version v1.0, http://www.neuro.uestc.edu.cn/rest/) and NIT (Dong et al., 2018) (v1.3, http://www.neuro.uestc.edu.cn/NIT.html) tools. Next, ERPs according to each reference were obtained by group Infomax ICA (repeated 20 times using ICASSO). The number of ICs was estimated as 4 using the minimum description length criteria, and the ICA time course was standard z-scored across time points.
Considering that true noiseless ERPs in real scalp EEG data were inaccessible and that REST approximately realizes the physical zero reference at infinity (Yao, 2001, 2017; Yao et al., 2019), the performances of ICA time courses were quantified using RMSE between the ERPs with a reference (Cz/LM/AVG) and with the REST reference. Performances of ICA spatial topographies were quantified using Pearson's correlation between the topographies with a reference (Cz/LM/AVG) and with the REST reference. The effects of different EEG references for ERPs and topographies were also investigated using one-way repeated ANOVA (p < 0.05) and post hoc paired t-test (p < 0.05).
Results
Simulation Results
Figure 3 depicts the mean trials, ERPs and topographic maps of ICA components for Inf, REST, AVG, LM, and Cz references separately, while the SNR = 1. ERP1 and ERP2 could be detected by ICA with different choices of references, and the spatial distribution patterns of the spatial components were similar for different references to some degree. ERP3 could be detected by ICA with Inf, REST, and AVG references and could not be well-detected with LM and Cz references. Furthermore, one-way ANOVA and a post-hoc test were performed to quantify the performances of ICA time courses (RMSEs between true noiseless ERPs and ICA-extracted ERPs with a reference) and topographies (spatial correlations between true topographies and ICA-extracted topographies with a reference). There were significant differences [Simu-IC1: F(4, 495) = 1.77 × 105, p < 0.001; Simu-IC2: F(4, 495) = 4.97 × 105, p < 0.001; Simu-IC3: F(4, 495) = 2.19 × 103, p < 0.001] of RMSEs with different references (Figure 4, first row). For RMSEs of Simu-IC1 and Simu-IC2 (corresponding to ERP1 and ERP2), Tukey's tests revealed significant differences (p < 0.001) for almost all pairwise comparisons among these references (except for the comparison between LM and Cz). For Simu-IC3 (corresponding to ERP3), the RMSEs of the LM reference were significantly higher than those of the Inf, REST, AVG, and Cz references, and the RMSEs of the Cz reference were higher than those of the Inf, REST, and AVG references. Significant differences between ICA-extracted topographies [Simu-IC1: F(4, 495) = 8.93 × 104, p < 0.001; Simu-IC2: F(4, 495) = 3.14 × 104, p < 0.001; Simu-IC3: F(4, 495) = 337.38, p < 0.001] with different references were also detected (Figure 4, second row). For the spatial distribution patterns of Simu-IC1 and Simu-IC2 (corresponding to S1 and S2), Tukey's tests revealed significant differences (p < 0.001) for almost all pairwise comparisons among these references (except for the comparison between LM and Cz). For spatial distribution patterns of Simu-IC3 (corresponding to S3, p < 0.001), the spatial correlations of Inf and REST references were significantly higher than those of AVG, LM, and Cz references, and the correlations of the AVG reference were also lower than those of LM and Cz references.
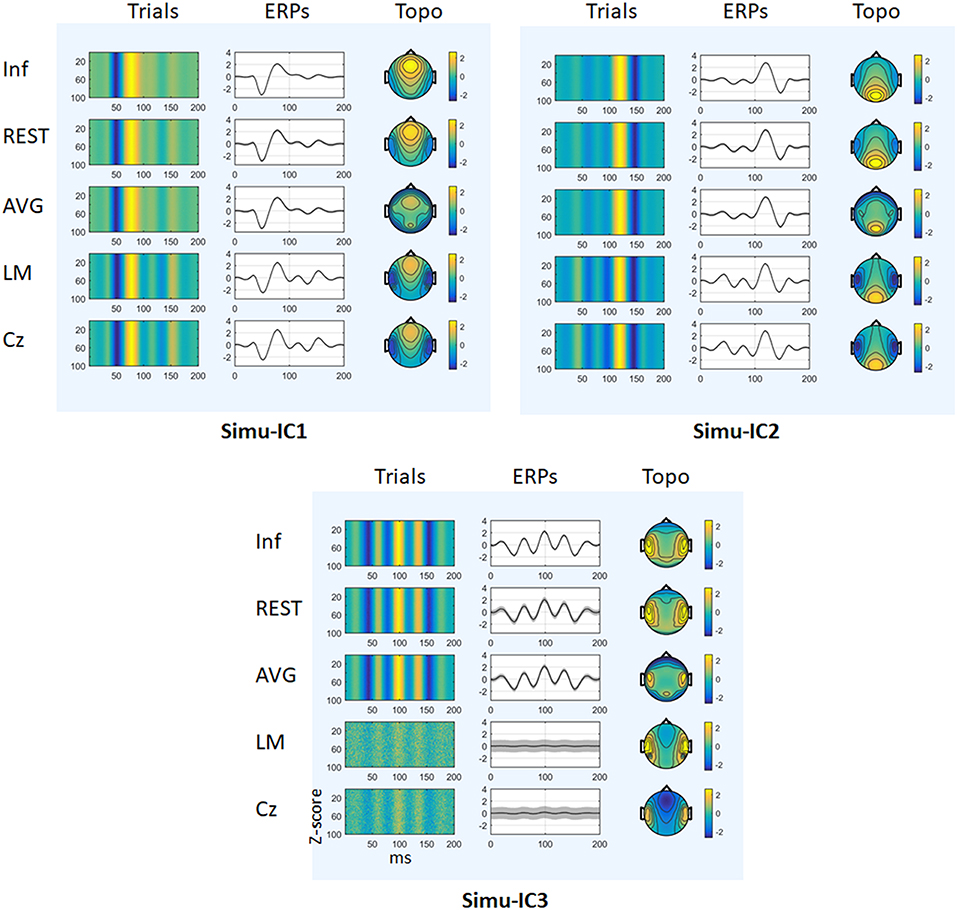
Figure 3. Results of simulation (SNR = 1). The mean trials, ERPs and topographic maps of each ICA component (Simulation IC1–IC3) for the Inf, REST, AVG, LM, and Cz references are shown separately. The gray region in ERPs represents standard deviations across 100 repeats.

Figure 4. Results of one-way ANOVA (p < 0.001) and a post-hoc test (black line means p < 0.001) for simulation of SNR = 1. Vertical axis of the first row is the mean RMSE (with standard deviation) between true noiseless ERPs and ICA-extracted ERPs with a reference, while the vertical axis of the second row is the mean spatial correlation (with standard deviation) between true topographies and ICA-extracted topographies with a reference. Columns from left to right correspond to the ICA components (Simulation IC1–IC3).
In addition, to assess the effects of noise on the performance of the ICA time course and spatial topographies, we considered different SNRs for each reference; the results are shown in Figure 5 (details of ERPs and topographic maps of each ICA component can be seen in Figures S1–S11). For ERPs of Simu-ICs corresponding to ERP1-3, the RMSEs of Inf, REST, and AVG generally decreased as the SNR increased, and the RMSEs of LM and Cz suddenly decreased (cliff-like) with increases in SNR. For the spatial topographies of Simu-IC1, the spatial correlations of REST converged to Inf with increases in SNR, and the correlations of AVG, LM, and Cz decreased. For the spatial topographies of Simu-IC2, the spatial correlations of REST and Inf increased with increases in SNR, and the correlations of LM and Cz increased first and then decreased. For the spatial topographies of Simu-IC3, the correlations of Inf, REST and AVG were constant to some degree, and the correlations of LM and Cz also increased first and then decreased. Considering the amplitudes may be independent across trials, a supplementary simulation of ERP trials with independent amplitudes (uniform distribution from 0.5 to 1.5) were also conducted, and similar results were obtained (Figures S14, S15).
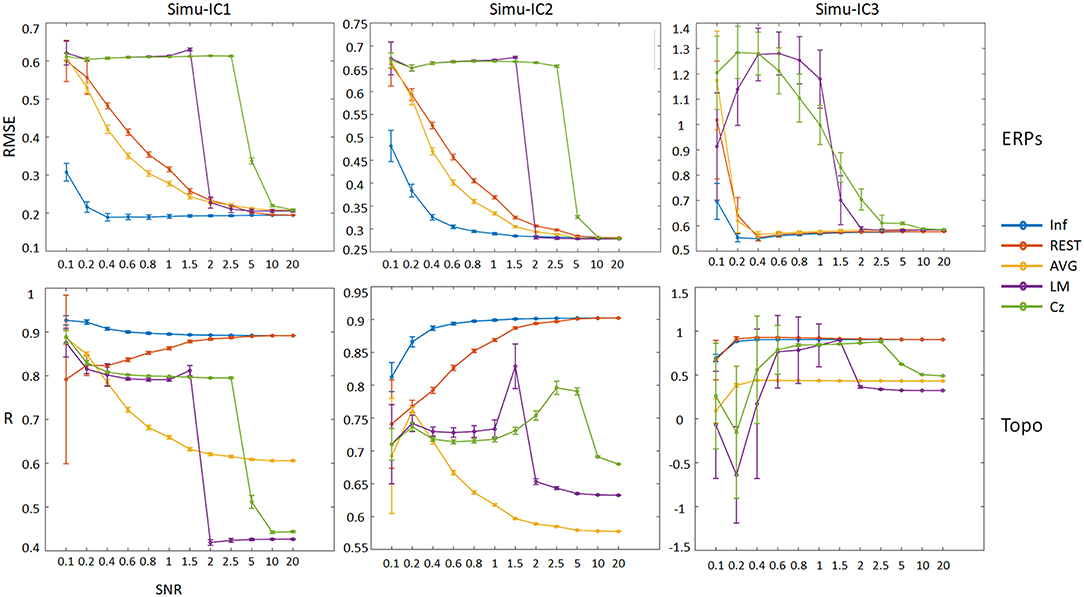
Figure 5. Performances of ICA time courses and topographies with different references (Inf, REST, AVG, LM, and Cz) using a range of SNRs from 0.1 to 20. The vertical axis of the first row is the mean RMSE (with standard deviation) between true noiseless ERPs and ICA-extracted ERPs with a reference, and the vertical axis of the second row is the mean spatial correlation (with standard deviation) between true topographies and ICA-extracted topographies with a reference. Columns from left to right correspond to the ICA components (Simu-IC1, Simu-IC2, and Simu-IC3), and the horizontal axis is the SNR.
Real Data Results
Figure 6 and Table 1 depict the mean ERPs and topographic maps of ICA components of real EEG data for REST, AVG, LM, and Cz references. N1, P2 (indices of sensory processing), and P3 components were detected for all references. Using one-way repeated ANOVA, there were no significant differences among these references for peak and latency values of ICA components (p > 0.05). However, there were significant differences [IC2: F(3, 10) = 117.63, p = 1.11 × 10−16; and IC4: F(3, 10) = 40.07, p = 1.29 × 10−10] for pairwise comparisons of the mean values of topographies (mean values of all channels) among these references. For all topographies of ICs, the mean values of the LM reference were the highest, the mean values of REST were second, the mean values of AVG were approximately 0, and the mean values of Cz were negative. Furthermore, one-way repeated ANOVA and post-hoc paired t-test were performed to quantify the performances of ICA time courses (RMSEs between ICA-extracted ERPs with AVG/LM/Cz and REST references) and topographies (spatial correlations between ICA-extracted topographies with AVG/LM/Cz and REST references). There were significant differences [IC1: F(2, 10) = 9.43, p = 0.0013; IC2: F(2, 10) = 16.36, p = 6.17 × 10−5; IC4: F(2, 10) = 3.90, p = 0.037] of RMSEs with different references (Figure 7, first row). For the ERPs of IC1, IC2 (N1, P3a), and IC4 (P2), the RMSEs of the LM reference were significantly lower than those of the AVG and Cz references. Significant differences [IC1: F(2, 10) = 12.45, p = 3.08 × 10−4; IC2: F(2, 10) = 17.5, p = 4.04 × 10−5] of spatial correlations with different references were also detected (Figure 7, second row). For the spatial distribution patterns of IC1 (p < 0.05), the spatial correlations of AVG and Cz references were significantly lower than those of the LM reference, and the correlations of the AVG reference were lower than those of the Cz reference. For the spatial distribution patterns of IC2 (p < 0.05), the spatial correlations of AVG and Cz references were also significantly lower than those of the LM reference, and the correlations of the AVG reference were higher than those of the Cz reference.
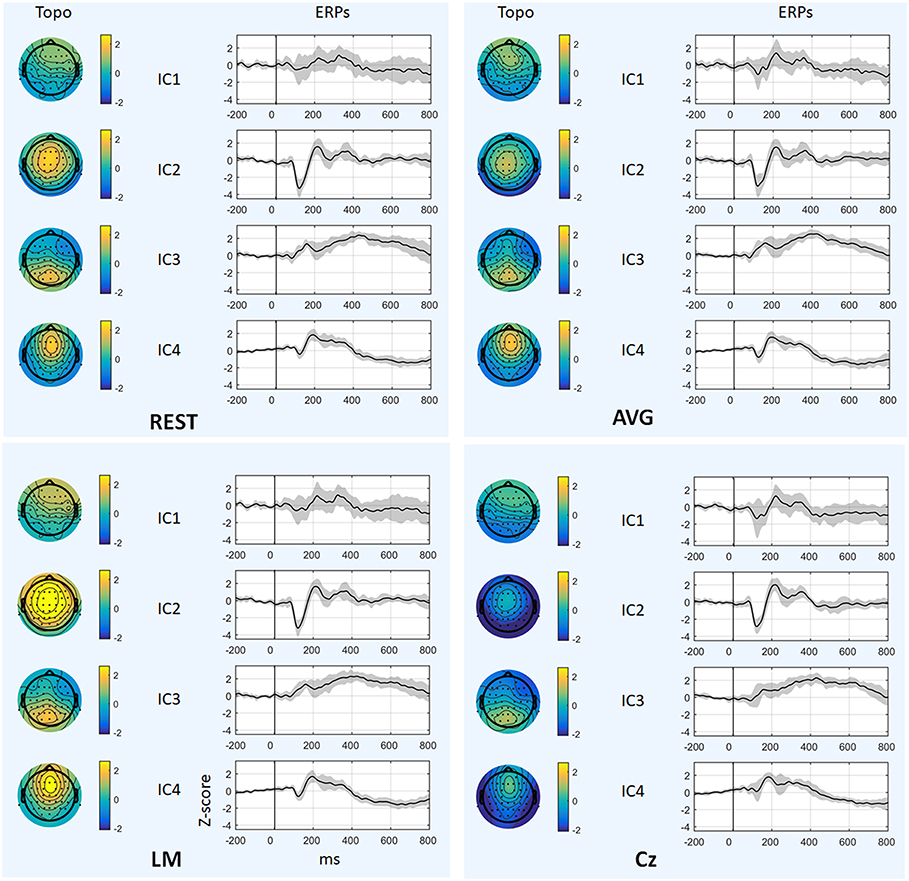
Figure 6. Results of real data. The mean ERPs and topographic maps of each ICA component (IC1–IC4) for REST, AVG, LM, and Cz references are shown separately. The gray region in ERPs represents standard deviation across subjects.
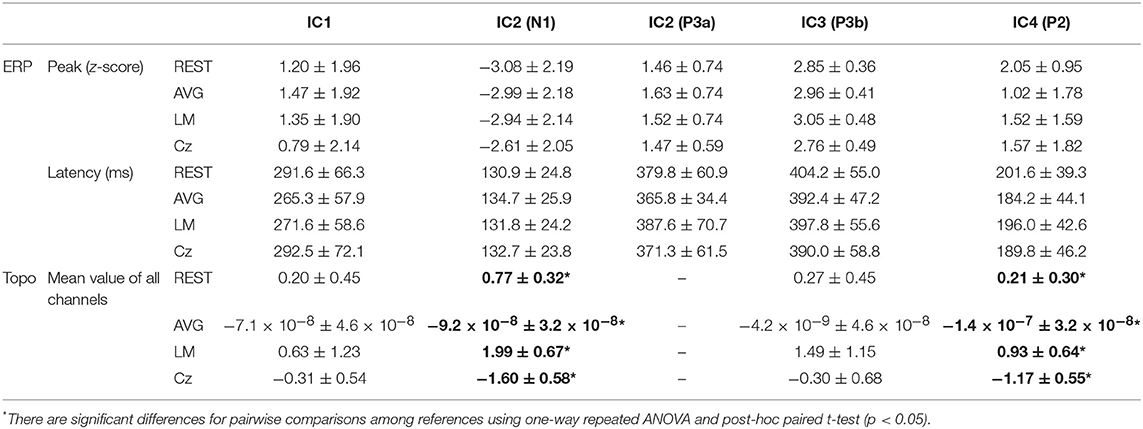
Table 1. Details of ERPs and topographic maps extracted by ICA components of real EEG data for REST, AVG, LM, and Cz references (mean ± standard deviation).
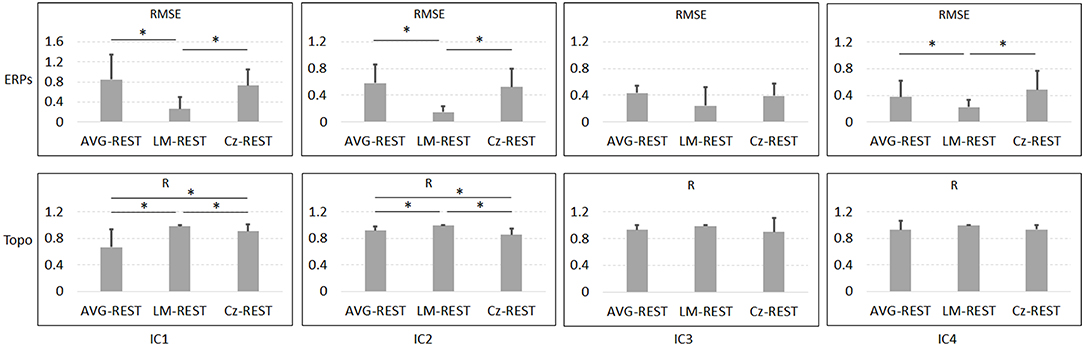
Figure 7. Results of one-way repeated ANOVA (p < 0.05) and post hoc paired t-test (*p < 0.05) for real data. The vertical axis of the first row is the mean RMSE (with standard deviation) between the ICA-extracted ERPs with the AVG/LM/Cz reference and with the REST reference, while the vertical axis of the second row is the mean spatial correlation (with standard deviation) between the ICA-extracted topographies with the AVG/LM/Cz reference and with the REST reference. Columns from left to right correspond to the ICA components (IC1-IC4).
Discussion
In the present study, four commonly used references, Cz, LM, AVG, and REST, were comparatively investigated via the standard ICA analysis of EEG data to reveal the potential effects of different references on ERPs extracted by ICA analysis. The simulation results revealed that the reference approach influenced the IC time courses and corresponding topographic maps, while the SNR = 1. As the SNR increased, the IC time courses of Cz, LM, AVG, and REST converged to Inf; however, only the spatial topographies of REST converged to Inf. Furthermore, we compared the effects of reference methods on the ICs in real EEG data. The results demonstrated that the reference method influenced the most IC time courses but did not change the peak amplitudes and latencies of ERPs corresponding to some IC time courses. In addition, the mean values and distributions of some topographic maps were influenced by reference methods.
Reference Effects on ICA Performance in Simulations
In this work, conventional simulations were utilized to verify the reference effects on ICA analysis. ICA could well reveal simulation ERP1 and ERP2 with all references and simulation ERP3 with Inf, REST and AVG references. Moreover, for the ERPs of Simu-IC1 and Simu-IC2, Inf obviously introduced the smallest error, and AVG and REST introduced intermediate errors, while LM and Cz references had the largest errors. For the ERPs of Simu-IC3, Inf, REST, and AVG introduced similar errors, and their errors were smaller than those of LM and Cz. These results demonstrated that ICA decomposition could obtain similar event-related potentials from scalp EEG with different references to some degree, and REST and AVG exhibited a performance similar to that of Inf (Figures 2, 3, first row). According to Equations (2)–(5), various reference methods, including Cz, LM, AVG, and REST, could theoretically be presented as unified mathematics (Yao et al., 2019). For Cz, LM, and AVG, the transform matrix (TCz, TLM, or TAVG) from the ideal ERPs (i.e., Inf) to the corresponding reference (Cz, LM, or AVG) is just a mathematical operation, with its specific assumption, a vertex point of the scalp (e.g., Cz) (Lehmann et al., 1998), the average of the linked mastoids or ears (e.g., LM) (Gevins and Smith, 2000), and the average of all EEG channels (e.g., AVG) (Offner, 1950), which are all non-physical principle-based hypotheses (Yao, 2017). For REST, which is based on the equivalent sources model, head model and electrode montage, the transform matrix LL+ from the actual ERPs to the REST reference is physically based and reasonable (Yao, 2001, 2017; Yao et al., 2019), and the final transform matrix LL+TAVG from Inf ERPs to REST ERPs also has physical meanings. Therefore, all these reference methods can be expressed as unified transform matrix T** (i.e., T**P = T*LSP) from the ideal temporal potentials of ERPs, P, to the corresponding reference recordings, V, while LS represents the true spatial topographies. As a popular blind source separation method, ICA assumes that signals are Gaussian mixtures containing statistically independent non-Gaussian source time courses (Hyvarinen and Oja, 2000), and the ICA model in ERP decomposition of a single subject can be generally expressed as , where V represents EEG/ERP signal mixtures corresponding to the reference recordings, G is the linearly mixing matrix corresponding to topographies and represents temporal independent components corresponding to ERPs. Noting that ICA decomposition does not have unique solutions, IC time courses are relative changes in ERPs and always are transformed to z-scores (Eichele et al., 2011). Therefore, ideally, for some independent event-related potentials in sources, ICA time courses can be relative changes in ERPs, , and may proportionally converge (or approximate) to true ERPs (i.e., P) in some situations (e.g., for some ERPs with a reference). However, due to the complexity of EEG (e.g., temporal variability across trials, non-stationary, non-linear noise) (Huster et al., 2015; Cohen, 2017) and limitations of ICA (e.g., not suitable for potential non-linear situations, algorithm adaptability, the number of ICs preset may not be appropriate) (Hyvarinen and Oja, 2000; Eichele et al., 2011; Huster et al., 2015), the reference method may have potential influences on the performance of ICA for temporal time courses. Noting that even the number of independent components was set as the true number of ERPs, there were still non-negligible effects of the reference method on ICA time courses.
For spatial topographies of simulation ICs, AVG had the lowest spatial correlations, LM and Cz had intermediate correlations, and Inf had the largest spatial correlations, while REST exhibited a similar performance. These results provide evidence that spatial topographies (i.e., mixing matrix G in the ICA model) could be distinctly influenced by different reference methods, and REST performed similarly to Inf (Figures 2, 3, second row). In the ICA model, the spatial topographies are weights that specify the relative contribution of each channel to IC time courses (Hyvarinen and Oja, 2000), and the standard deviation of topographies are usually fixed at 1 (Eichele et al., 2011). The spatial components (e.g., topographies), G, may reflect the relative contribution of each channel to ERP waves and relate to the transform matrix T** = T*LS corresponding to reference methods in some cases (e.g., Figures S12, S13 show that spatial distributions detected by ICA with REST reference, G, were appropriate to transform matrix T** of REST). Because the REST reference is physically based and reasonable (Yao, 2001, 2017; Yao et al., 2019), topographies could be well-detected by ICA with the REST reference. However, because Cz, LM, and AVG are non-zero reference approaches (Yao, 2017) and their transformations of Cz, LM, and AVG (TCz, TLM, or TAVG) are all seriously singular (Yao et al., 2019), they may influence the mixing matrix of ICA so that the spatial components of ICA have the risk of diverging from the true spatial topographies. Therefore, the effects of reference methods on the topographies of ICs may result in misleading explanations of ERP source generations.
In addition, as the SNR increased, all IC time courses of Cz, LM, AVG, and REST references converged to Inf, and only the spatial topographies of REST converged to Inf (Figure 5 and Figures S1–S11). Meanwhile, considering the amplitudes may be independent across trials, a supplementary simulation of ERP trials with independent amplitudes were conducted, and similar results were obtained (Figures S14, S15). These results provided further evidence that overall, the REST reference had superior performance, which was also consistent with the conclusions of previous simulation studies (Yao, 2001, 2017; Yao et al., 2005; Liu et al., 2015; Chella et al., 2017). Furthermore, for group-level ICA by concatenating subjects (Eichele et al., 2011; Huster and Raud, 2018), REST has a similar unified expression as , while the reference methods can also be expressed as , where Ns is the number of subjects. Therefore, similar effects of the reference method on ICA performance may be obtained in this case.
Reference Effects on ICA in Real Data
To further investigate the potential effects of the reference method on ICA performance, we used real EEG data from an auditory stimulus go/no-go task in this work. A visual inspection of the EEG data showed typical N1, P2, and P3 components corresponding to IC2, IC4, and IC3 in Figure 6 using the Cz, LM, AVG, and REST reference methods, which is also consistent with previous studies (Debener et al., 2005; Eichele et al., 2008; Gong et al., 2012, 2013). Using one-way repeated ANOVA, there were no significant differences among these references for peak and latency values of z-scored ICA components (p > 0.05). Considering that true noiseless ERPs in real scalp EEG data were inaccessible and REST approximately realizes the physical zero reference at infinity (Yao, 2001, 2017; Yao et al., 2019), the ERPs of ICA time courses with Cz/LM/AVG and the REST reference were further compared. Additionally, the RMSEs of the LM (LM vs. REST) reference were lower than those of the AVG and Cz references (Figure 7, first row). These results demonstrated that the reference method influenced some IC time courses to some degree but did not change the peak amplitudes and latencies of relative changes of ERPs corresponding to IC time courses.
Because ICA is a data-driven method of matrix decomposition and the mixing matrix specifies the relative contribution of each spatial dimension to IC time courses (Hyvarinen and Oja, 2000), the spatial distributions of topographies may reflect the contribution of each channel to the ERPs of ICs. Because the LM reference is non-zero and the amplitudes of the linked mastoids or ears are contaminated by brain activity (Yao, 2001; Yao et al., 2019), the amplitudes at the active electrodes with LM reference may be increased or decreased by the recorded potentials at the mastoids or ears. Thus, the topographies of some ICs may be influenced by the LM reference, and the Cz reference may lead to similar impacts. Since the potentials of AVG are the average signal of all EEG channels (Offner, 1950), the AVG reference could make all the ICA topographies have zero total potential. Moreover, REST is an approximate zero reference at infinity, which has been proposed as a standard reference method (Yao, 2001, 2017; Yao et al., 2019). In the current study, we compared the mean values of topographies among these references. We found that for IC2 and IC4, the mean values of the LM reference were highest, the mean values of REST were second, the mean values of AVG were ~0, and the mean values of Cz were negative. In addition, even though the topographical distribution revealed similar patterns with all reference methods for most ICs, the topographies of the LM reference were closer to the REST reference for IC1 and IC2 than to the AVG and Cz references (Figure 7, second row). Overall, these results demonstrated that both time courses and spatial distributions of some ICs could be influenced by different reference methods. These findings are consistent with the results of previous ERP comparative studies highlighting the superiority of the REST reference approach (Tian and Yao, 2013; Hu et al., 2017; Mahajan et al., 2017; Qin et al., 2017; Yang et al., 2017; Li et al., 2018; Tian et al., 2018).
Conclusions
To the best of our knowledge, the present manuscript is the first to investigate the effects of different reference methods on ERPs extracted by ICA analysis over simulation and real EEG datasets. The results of the current study indicated that different EEG reference choices altered both the temporal ERPs and spatial topographies of some ICs. Additionally, compared to Cz, LM, and AR references, the REST reference had overall superiority considering both the performances of temporal ERPs and spatial topographies and could provide a recommended choice for ICA analysis at the trial level. These findings contribute to empirical investigations regarding the use of reference methods in ERP domains with ICA analysis.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by the local Ethics Committee of University of Electronic Science and Technology of China. The patients/participants provided their written informed consent to participate in this study.
Author Contributions
LD, YL, and DY conceived and designed the work. LD, XL, and LZ wrote the code, analyzed the data, and realized the simulation. LD and DG acquired the EEG data. LD, TL, YL, DG, and DY wrote and revised the manuscript. All authors revised the work for important intellectual content and read and approved the manuscript.
Funding
The present study was financially supported by the National Natural Science Foundation of China (Nos. 81701778, 81861128001, 81771925, 81571759), the 111 project (B12027), the Sichuan Science and Technology Program (2018JZ0073), the Young Elite Scientists Sponsorship Program by CAST (2016QNRC001).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnins.2019.01068/full#supplementary-material
References
Berger, H. (1929). Über das elektrenkephalogramm des menschen. Eur. Arch. Psychiatry Clin. Neurosci. 87, 527–570. doi: 10.1007/BF01797193
Chella, F., D'Andrea, A., Basti, A., Pizzella, V., and Marzetti, L. (2017). Non-linear analysis of scalp EEG by using bispectra: the effect of the reference choice. Front. Neurosci. 11:262. doi: 10.3389/fnins.2017.00262
Chella, F., Marzetti, L., Pizzella, V., Zappasodi, F., and Nolte, G. (2014). Third order spectral analysis robust to mixing artifacts for mapping cross-frequency interactions in EEG/MEG. Neuroimage 91, 146–161. doi: 10.1016/j.neuroimage.2013.12.064
Chella, F., Pizzella, V., Zappasodi, F., and Marzetti, L. (2016). Impact of the reference choice on scalp EEG connectivity estimation. J. Neural Eng. 13:036016. doi: 10.1088/1741-2560/13/3/036016
Cohen, M. X. (2017). Where does EEG come from and what does it mean? Trends Neurosci. 40, 208–218. doi: 10.1016/j.tins.2017.02.004
Debener, S., Makeig, S., Delorme, A., and Engel, A. K. (2005). What is novel in the novelty oddball paradigm? Functional significance of the novelty P3 event-related potential as revealed by independent component analysis. Brain Res. Cogn. Brain Res. 22, 309–321. doi: 10.1016/j.cogbrainres.2004.09.006
Delorme, A., Palmer, J., Onton, J., Oostenveld, R., and Makeig, S. (2012). Independent EEG sources are dipolar. PLoS ONE 7:e30135. doi: 10.1371/journal.pone.0030135
Dien, J. (1998). Issues in the application of the average reference: review, critiques, and recommendations. Behav. Res. Methods 30, 34–43. doi: 10.3758/BF03209414
Dong, L., Gong, D., Valdes-Sosa, P. A., Xia, Y., Luo, C., Xu, P., et al. (2014). Simultaneous EEG-fMRI: trial level spatio-temporal fusion for hierarchically reliable information discovery. Neuroimage 99, 28–41. doi: 10.1016/j.neuroimage.2014.05.029
Dong, L., Li, F. L., Liu, Q., Wen, X., Lai, Y. X., Xu, P., et al. (2017). MATLAB toolboxes for reference electrode standardization technique (REST) of scalp EEG. Front. Neurosci. 11:601. doi: 10.3389/fnins.2017.00601
Dong, L., Luo, C., Liu, X. B., Jiang, S. S., Li, F. L., Feng, H. S., et al. (2018). Neuroscience information toolbox: an open source toolbox for EEG-fMRI multimodal fusion analysis. Front. Neuroinform. 12:56. doi: 10.3389/fninf.2018.00056
Eichele, T., Calhoun, V. D., Moosmann, M., Specht, K., Jongsma, M. L., Quiroga, R. Q., et al. (2008). Unmixing concurrent EEG-fMRI with parallel independent component analysis. Int. J. Psychophysiol. 67, 222–234. doi: 10.1016/j.ijpsycho.2007.04.010
Eichele, T., Rachakonda, S., Brakedal, B., Eikeland, R., and Calhoun, V. D. (2011). EEGIFT: group independent component analysis for event-related EEG data. Comput. Intell. Neurosci. 2011:129365. doi: 10.1155/2011/129365
Enriquez-Geppert, S., Huster, R. J., and Herrmann, C. S. (2017). EEG-neurofeedback as a tool to modulate cognition and behavior: a review tutorial. Front. Hum. Neurosci. 11:51. doi: 10.3389/fnhum.2017.00051
Gevins, A., and Smith, M. E. (2000). Neurophysiological measures of working memory and individual differences in cognitive ability and cognitive style. Cereb. Cortex 10, 829–839. doi: 10.1093/cercor/10.9.829
Gong, D. K., Hu, J. H., and Yao, D. Z. (2012). Partial information can be transmitted in an auditory channel: inferences from lateralized readiness potentials. Psychophysiology 49, 499–503. doi: 10.1111/j.1469-8986.2011.01325.x
Gong, D. K., Ma, W. Y., Kendrick, K. M., Hu, Q. Q., and Yao, D. Z. (2013). How cognitive plasticity resolves the brain's information processing dilemma. Sci. Rep. 3:2860. doi: 10.1038/srep02860
Hoffmann, S., and Falkenstein, M. (2008). The correction of eye blink artefacts in the EEG: a comparison of two prominent methods. PLoS ONE 3:e3004. doi: 10.1371/journal.pone.0003004
Hu, Y. X., Zhang, L. P., Chen, M. M., Li, X. Y., and Shi, L. (2017). How electroencephalogram reference influences the movement readiness potential? Front. Neurosci. 11:683. doi: 10.3389/fnins.2017.00683
Huster, R. J., Plis, S. M., and Calhoun, V. D. (2015). Group-level component analyses of EEG: validation and evaluation. Front. Neurosci. 9:254. doi: 10.3389/fnins.2015.00254
Huster, R. J., and Raud, L. (2018). A tutorial review on multi-subject decomposition of EEG. Brain Topogr. 31, 3–16. doi: 10.1007/s10548-017-0603-x
Hyvarinen, A., and Oja, E. (2000). Independent component analysis: algorithms and applications. Neural Netw. 13, 411–430. doi: 10.1016/S0893-6080(00)00026-5
Johnstone, S. J., Barry, R. J., and Clarke, A. R. (2013). Ten years on: a follow-up review of ERP research in attention-deficit/hyperactivity disorder. Clin. Neurophysiol. 124, 644–657. doi: 10.1016/j.clinph.2012.09.006
Labounek, R., Bridwell, D. A., Marecek, R., Lamos, M., Mikl, M., Slavicek, T., et al. (2018). Stable scalp EEG spatiospectral patterns across paradigms estimated by group ICA. Brain Topogr. 31, 76–89. doi: 10.1007/s10548-017-0585-8
Lee, W. L., Tan, T., Falkmer, T., and Leung, Y. H. (2016). Single-trial event-related potential extraction through one-unit ICA-with-reference. J. Neural Eng. 13:066010. doi: 10.1088/1741-2560/13/6/066010
Lehmann, D., Strik, W. K., Henggeler, B., Koenig, T., and Koukkou, M. (1998). Brain electric microstates and momentary conscious mind states as building blocks of spontaneous thinking: I. Visual imagery and abstract thoughts. Int. J. Psychophysiol. 29, 1–11. doi: 10.1016/S0167-8760(97)00098-6
Lei, X., and Liao, K. (2017). Understanding the influences of EEG reference: a large-scale brain network perspective. Front. Neurosci. 11:205. doi: 10.3389/fnins.2017.00205
Lei, X., Qiu, C., Xu, P., and Yao, D. (2010). A parallel framework for simultaneous EEG/fMRI analysis: methodology and simulation. Neuroimage 52, 1123–1134. doi: 10.1016/j.neuroimage.2010.01.024
Lei, X., Valdes-Sosa, P. A., and Yao, D. (2012). EEG/fMRI fusion based on independent component analysis: integration of data-driven and model-driven methods. J. Integr. Neurosci. 11, 313–337. doi: 10.1142/S0219635212500203
Li, F., Wang, J. J., Liao, Y., Yi, C., Jiang, Y., Si, Y., et al. (2019a). Differentiation of schizophrenia by combining the spatial EEG brain network patterns of rest and task P300. IEEE Trans. Neural. Syst. Rehabil. Eng. 27, 594–602. doi: 10.1109/TNSRE.2019.2900725
Li, F., Yi, C., Song, L., Jiang, Y., Peng, W., Si, Y., et al. (2019b). Brain network reconfiguration during motor imagery revealed by a large-scale network analysis of scalp EEG. Brain Topogr. 32, 304–314. doi: 10.1007/s10548-018-0688-x
Li, Y., Wang, Y., Zhang, B., Wang, Y., and Zhou, X. (2018). Electrophysiological responses to expectancy violations in semantic and gambling tasks: a comparison of different EEG reference approaches. Front. Neurosci. 12:169. doi: 10.3389/fnins.2018.00169
Liu, Q., Balsters, J. H., Baechinger, M., van der Groen, O., Wenderoth, N., and Mantini, D. (2015). Estimating a neutral reference for electroencephalographic recordings: the importance of using a high-density montage and a realistic head model. J. Neural Eng. 12:056012. doi: 10.1088/1741-2560/12/5/056012
Low, K. A., and Miller, J. (1999). The usefulness of partial information: effects of go probability in the choice/Nogo task. Psychophysiology 36, 288–297. doi: 10.1017/S0048577299980332
Luck, S. J. (2014). An Introduction to the Event-Related Potential Technique. Cambridge, MA: MIT Press.
Mahajan, Y., Peter, V., and Sharma, M. (2017). Effect of EEG referencing methods on auditory mismatch negativity. Front. Neurosci. 11:560. doi: 10.3389/fnins.2017.00560
Marzetti, L., Nolte, G., Perrucci, M. G., Romani, G. L., and Del Gratta, C. (2007). The use of standardized infinity reference in EEG coherency studies. Neuroimage 36, 48–63. doi: 10.1016/j.neuroimage.2007.02.034
Michelmann, S., Treder, M. S., Griffiths, B., Kerren, C., Roux, F., Wimber, M., et al. (2018). Data-driven re-referencing of intracranial EEG based on independent component analysis (ICA). J. Neurosci. Methods 307, 125–137. doi: 10.1016/j.jneumeth.2018.06.021
Mumtaz, W., Xia, L., Mohd Yasin, M. A., Azhar Ali, S. S., and Malik, A. S. (2017a). A wavelet-based technique to predict treatment outcome for Major Depressive Disorder. PLoS ONE 12:e0171409. doi: 10.1371/journal.pone.0171409
Mumtaz, W., Xia, L. K., Ali, S. S. A., Yasin, M. A. M., Hussain, M., and Malik, A. S. (2017b). Electroencephalogram (EEG)-based computer-aided technique to diagnose major depressive disorder (MDD). Biomed. Signal Process. Control 31, 108–115. doi: 10.1016/j.bspc.2016.07.006
Offner, F. F. (1950). The EEG as potential mapping: the value of the average monopolar reference. Electroencephalogr. Clin. Neurophysiol. 2, 213–214. doi: 10.1016/0013-4694(50)90040-X
Onton, J., and Makeig, S. (2006). Information-based modeling of event-related brain dynamics. Prog. Brain Res. 159, 99–120. doi: 10.1016/S0079-6123(06)59007-7
Qin, Y., Jiang, S., Zhang, Q., Dong, L., Jia, X., He, H., et al. (2019). BOLD-fMRI activity informed by network variation of scalp EEG in juvenile myoclonic epilepsy. Neuroimage Clin 22, 101759. doi: 10.1016/j.nicl.2019.101759
Qin, Y., Xin, X. W., Zhu, H., Li, F. L., Xiong, H. C., Zhang, T., et al. (2017). A Comparative Study on the Dynamic EEG Center of Mass with Different References. Front. Neurosci. 11:509. doi: 10.3389/fnins.2017.00509
Qin, Y., Xu, P., and Yao, D. (2010). A comparative study of different references for EEG default mode network: the use of the infinity reference. Clin. Neurophysiol. 121, 1981–1991. doi: 10.1016/j.clinph.2010.03.056
Srivastava, G., Crottaz-Herbette, S., Lau, K. M., Glover, G. H., and Menon, V. (2005). ICA-based procedures for removing ballistocardiogram artifacts from EEG data acquired in the MRI scanner. Neuroimage 24, 50–60. doi: 10.1016/j.neuroimage.2004.09.041
Tian, Y., Xu, W., Zhang, H., Tam, K. Y., Zhang, H., Yang, L., et al. (2018). The scalp time-varying networks of N170: reference, latency, and information flow. Front. Neurosci. 12:250. doi: 10.3389/fnins.2018.00250
Tian, Y., and Yao, D. Z. (2013). Why do we need to use a zero reference? Reference influences on the ERPs of audiovisual effects. Psychophysiology 50, 1282–1290. doi: 10.1111/psyp.12130
Tian, Y., Zhang, H. L., Xu, W., Zhang, H. Y., Yang, L., Zheng, S. X., et al. (2017). Spectral entropy can predict changes of working memory performance reduced by short-time training in the delayed-match-to-sample task. Front. Hum. Neurosci. 11:437. doi: 10.3389/fnhum.2017.00437
Winter, W. R., Nunez, P. L., Ding, J., and Srinivasan, R. (2007). Comparison of the effect of volume conduction on EEG coherence with the effect of field spread on MEG coherence. Stat. Med. 26, 3946–3957. doi: 10.1002/sim.2978
Yang, P., Fan, C., Wang, M., and Li, L. (2017). A comparative study of average, linked mastoid, and REST references for ERP components acquired during fMRI. Front. Neurosci. 11:247. doi: 10.3389/fnins.2017.00247
Yao, D. (2001). A method to standardize a reference of scalp EEG recordings to a point at infinity. Physiol. Meas. 22, 693–711. doi: 10.1088/0967-3334/22/4/305
Yao, D. (2017). Is the surface potential integral of a dipole in a volume conductor always zero? A cloud over the average reference of EEG and ERP. Brain Topogr. 30, 161–171. doi: 10.1007/s10548-016-0543-x
Yao, D., Qin, Y., Hu, S., Dong, L., Bringas Vega, M. L., and Valdés Sosa, P. A. (2019). Which reference should we use for EEG and ERP practice? Brain Topogr. 32, 530–549. doi: 10.1007/s10548-019-00707-x
Yao, D., Wang, L., Oostenveld, R., Nielsen, K. D., Arendt-Nielsen, L., and Chen, A. C. (2005). A comparative study of different references for EEG spectral mapping: the issue of the neutral reference and the use of the infinity reference. Physiol. Meas. 26, 173–184. doi: 10.1088/0967-3334/26/3/003
Keywords: EEG, event-related potential (ERP), independent component analysis (ICA), reference choices, REST reference
Citation: Dong L, Liu X, Zhao L, Lai Y, Gong D, Liu T and Yao D (2019) A Comparative Study of Different EEG Reference Choices for Event-Related Potentials Extracted by Independent Component Analysis. Front. Neurosci. 13:1068. doi: 10.3389/fnins.2019.01068
Received: 20 June 2019; Accepted: 24 September 2019;
Published: 11 October 2019.
Edited by:
Feng Liu, Tianjin Medical University General Hospital, ChinaReviewed by:
Jing Jin, East China University of Science and Technology, ChinaXu Lei, Southwest University, China
Copyright © 2019 Dong, Liu, Zhao, Lai, Gong, Liu and Yao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dezhong Yao, ZHlhb0B1ZXN0Yy5lZHUuY24=
 Li Dong
Li Dong Xiaobo Liu2
Xiaobo Liu2 Yongxiu Lai
Yongxiu Lai Diankun Gong
Diankun Gong Dezhong Yao
Dezhong Yao